MATEMATICA • SCIENZE e TECNOLO IA 3

Matematica: logica, calcolo mentale, coding Scienze e Tecnologia: esperimenti, educazione civica, ripasso facile studio con la mappa Eserciziario integrato




 salvatore romano
salvatore romano


Matematica: logica, calcolo mentale, coding Scienze e Tecnologia: esperimenti, educazione civica, ripasso facile studio con la mappa Eserciziario integrato




 salvatore romano
salvatore romano




RIPASSIAMO INSIEME
4 Ricominciamo… giocando
6 Costruiamo i… ragionamenti
7 Coloriamo l’autunno
8 I numeri ieri e oggi
NUMERI FINO A 999
10 Il sistema decimale
11 La posizione delle cifre
12 Numeri e cifre
13 Lo zero
14 Scomponi e componi fino a 999
16 Confronta e ordina fino a 999
17 I O C H I A M O ! G Gioco-numero
18 le mie conoscenze
19 le mie competenze
NUMERI FINO A 9999
20 Il migliaio
22 I numeri a quattro cifre
24 Scomponi e componi fino a 9999
25 Confronta e ordina fino a 9999
26 I numeri fino a 9999

27 I O C H I A M O ! G Tipi da spiaggia! 28 le
SOTTRAZIONE
39 La proprietà della sottrazione LOGICA
40 Sottrazioni a mente CALCOLO MENTALE
41 Proprietà e calcolo a mente
42 Sottrazioni in colonna
43 Sottrazioni con il cambio
44 Operazioni inverse
45 Addizione o sottrazione?
46 Addizioni e sottrazioni veloci
47 I O C H I A M O ! G Gioco-conto
48 le mie conoscenze
49 le mie competenze
MOLTIPLICAZIONE
50 La moltiplicazione
51 Ripassiamo le tabelline T OL L IA C
52 Combinazioni
54 Le proprietà della moltiplicazione
56 Moltiplicazioni in colonna
57 Moltiplicatore a due cifre
58 Moltiplicare per 10, 100, 1000
59 Nomi e pixel art CODING
60 le mie conoscenze
DIVISIONE
122 Alla scoperta della geometria
124 Dai solidi ai punti
125 I solidi: tre dimensioni
126 Le figure piane: due dimensioni
127 Le linee: una dimensione
128 Rette, semirette e segmenti
129 Coppie di rette
130 Gli angoli
133 Poligoni e non poligoni
134 Le parti di un poligono
135 La carta d’identità dei poligoni
136 Il perimetro
137 L’area
138 L’area del gatto CODING
139 La simmetria
140 I O C H I A M O ! G Giochiamo con il Tangram
141 I O C H I A M O ! G Logica… mente
142 le mie conoscenze
143 le mie competenze
RELAZIONI, DATI, PREVISIONI

144 Le relazioni
145 Numeri e logica LOGICA
146 La logica del computer CODING
148
È una fredda sera d’inverno: Sophie e Giò decidono di giocare a tombola.
1 I due bambini hanno cominciato a colorare i numeri già estratti. Osserva le cartelle e completa.

• Giò è distratto e non ha segnato un numero, scopri qual è e coloralo di verde.
• Come hai fatto a scoprirlo?
• Quanti numeri mancano a Sophie per fare tombola? ................ E a Giò? ................

Quindi sono in vantaggio, sicuramente vincerò io!
• Secondo te, è vero quello che dice Giò?
Non si può dire
Scrivi brevemente perché: ........................................................

I due amici estraggono un numero a testa, ma hanno uno strano modo di giocare a tombola: invece di dire il numero fanno degli indovinelli…
Gioca anche tu con loro!
2 Indovina il numero estratto e scrivilo. Poi colora la casella corrispondente nelle cartelle di Sophie e Giò.
Il doppio di 4
Il risultato di 60 + 5 .............
Il triplo di 3
Un numero, compreso tra 20 e 30, in cui la cifra delle decine è la metà della cifra delle unità
Il risultato di 7 × 2 .............
Il numero più grande della tombola
Il numero maggiore di 2 e minore di 4
Il numero formato da 3 u e 6 da
Il risultato di 10 × 9 – 1
Il risultato di 7 × 8 .............
3 Rispondi.
• Chi ha vinto la tombola?
• Quanti numeri mancavano a Giò per fare tombola?
Prova a scrivere in modo “strano” i numeri che mancavano a Giò per fare tombola, poi confronta il tuo lavoro con quello delle compagne e dei compagni.
1 Giò ha costruito un castello con dei mattoncini colorati. Osserva, leggi e rispondi.
Ho contato velocemente e so che per il mio castello ho usato 47 mattoncini rossi.
• Quali tra questi calcoli potrebbe aver fatto Giò per contare i mattoncini rossi? Fai attenzione: solo due sono giusti! 9 × 6 – 7 9 × 4 – 11 9 × 7 – 6 9 × 4 + 11

2 Anche Sophie sta giocando con le costruzioni. Leggi, osserva e rispondi.

Voglio costruire tante casette come questa con questi mattoncini.
• Quante casette come quella del modello riuscirà a costruire? ....................
Condividi con le compagne e i compagni i ragionamenti che hai fatto nelle situazioni proposte.
1 In questo disegno puoi scoprire tanti poligoni e tanti non poligoni : colora i non poligoni di grigio e i poligoni con i colori caldi.
Fai attenzione a non usare lo stesso colore per poligoni che hanno una linea di confine in comune!
2 Ora rispondi.
I colori caldi sono tipici dell’autunno, ma anche dell’estate: da quale particolare puoi capire che questo disegno si riferisce all’autunno?


Confronta la tua risposta con quella delle compagne e dei compagni.
3 Adesso prova a fare un disegno simile a questo su metà foglio bianco, ma stavolta per colorare i poligoni usa i colori freddi.
1 Leggete in classe questo brano. Un giorno la maestra ci ha fatto vedere una foto di un osso di renna di quindicimila anni fa, con tante tacche fatte da un uomo preistorico. E perché aveva fatto quelle tacche?
Mettiamo che avesse visto un branco di animali e voleva dirlo a un suo amico, per andare a cacciarli insieme.
Siccome non sapeva contare, perché i numeri non li avevano ancora inventati, lui aveva inciso una tacca per ogni animale e al suo amico
aveva fatto vedere quelle tacche.
Forse quel suo amico, vedendole, gli aveva detto:
Sono proprio tanti animali, da soli non ce la facciamo, dobbiamo portarci anche Thor (un altro loro amico). Insomma, quelle tacche servivano per ricordarsi una quantità.
A quel punto la maestra ha preso dalla sua borsa la chiavetta USB del computer e ha detto:

Vedete questo piccolo oggetto? È il nipote del nipote del nipote… insomma il discendente di quell’osso di renna. Infatti, come lui, serve a memorizzare delle quantità.
Solo che queste quantità sono enormi.
Pensate che può memorizzare 2 miliardi di caratteri, che corrispondono suppergiù a 2 mila libri! Infatti, ha 2 gigabyte di memoria.
Rid. e ad. da A. Cerasoli, Io conto , Feltrinelli Kids
Questo racconto ci fa capire che oggi, più di tanto tempo fa, i numeri sono dappertutto, anche dove non li vediamo.

Gli uomini preistorici, per memorizzare una quantità incidevano delle tacche su ossi, bastoni o sulle pareti delle caverne.

Quest’osso è ancora più antico di quello di cui si parla nel racconto, ha 35 mila anni! Vi sono incise 29 tacche, forse per ricordare la quantità di un branco di animali o per tenere il conto dei giorni che passavano.
In seguito, per rendere più veloce la lettura del numero, gli uomini preistorici cominciarono a raggruppare le quantità per 5 .
2 Osserva i numeri rappresentati dalle tacche e rispondi.
• Qual è il numero inciso sulla parete della caverna? ................

• Qual è il numero inciso sulla lastra di pietra?
• Quale numero hai letto più velocemente?
Spiega a voce perché e confronta la tua risposta con quelle delle compagne e dei compagni.
Secondo te, perché gli uomini preistorici cominciarono a raggruppare proprio per 5?
Discutine in classe.
Il nostro sistema di numerazione è decimale perché raggruppa le quantità di 10 in 10 .
10 unità ( u ) = 1 decina ( da )
Il nostro sistema di numerazione utilizza dieci
1 Osserva, segui l’esempio e completa.
10 decine ( da ) = 1 centinaio ( h )
100 + 40 + 5 = 145
Il nostro sistema di numerazione, oltre a essere decimale, è anche posizionale , perché il valore di una cifra cambia in base alla posizione che occupa all’interno del numero.

da h u
1 u
1 da = 10 u
1 h = 100 u
u
Nel numero 135 il 3 occupa il posto delle decine e vale 30 unità.
da h
h u
3 1
da
5
1 3
Nel 135 la cifra 5 vale 5 unità e la cifra 1 vale 100 unità.
Nel numero 153 il 3 occupa il posto delle unità e vale 3 unità.
1 Osserva come cambia il valore della cifra 3 nei seguenti numeri e stabilisci il valore in unità delle altre cifre. Segui l’esempio. 5
da h u
Nel numero 351 il 3 occupa il posto delle centinaia e vale 300 unità.
Nel 351 la cifra 5 vale ............. unità e la cifra ............. vale ............. unità.
Nel 153 la cifra 1 vale unità e la cifra vale unità. 5 3 1
2 Combina le tre cifre in modo da ottenere sei numeri diversi. Poi rispondi.
• Qual è il numero maggiore che hai ottenuto? E il minore?
Spesso alle parole cifra e numero si dà lo stesso significato. In realtà, non è così: le cifre sono i singoli segni che vengono usati per scrivere un numero.
Il numero 237 è formato da tre cifre : la cifra 2 che indica le centinaia, la cifra 3 che indica le decine e la cifra 7 che indica le unità.
Il numero 37 è formato da due cifre : la cifra 3 che indica le decine e la cifra 7 che indica le unità.
Il numero 7 è formato da una sola cifra : la cifra 7 che indica le unità. In questo caso 7 è sia cifra che numero.
Lo zero è una delle cifre del nostro sistema di numerazione. Lo zero, però, ha due funzioni diverse:
• è segnaposto se si trova in mezzo ad altre cifre per indicare le posizioni “vuote”;
• è operatore se si trova alla fine del numero.
in questo caso occupa il posto delle decine
moltiplica per 10 il 24 e lo fa diventare 240
4 lo zero all’inizio del numero non si scrive mai
1 Combina le tre cifre in modo da ottenere sei numeri diversi. Poi rispondi.
2 • 0 • 1
• In quali numeri lo zero è un segnaposto? ................ e ................
• In quali numeri fa da operatore? e

• Per scrivere quali numeri non è stato necessario usare lo zero? e
è l’ultima cifra a essere stata inventata: prima non era possibile scrivere numeri grandi
ma bisognava inventarne sempre di nuove!
Diego ha comprato una nuova bici e l’ha pagata 249 euro.






Un numero si può scomporre:
• in base al valore delle cifre : 249 = 2 h + 4 da + 9 u .









• come somma di numeri : (2 × 100) + (4 × 10) + (9 × 1).
1 Scomponi i numeri in base al valore delle cifre, poi come somma di numeri.
= ( × 100) + ( × 10) + ( × 1)
( × 100) + ( × 10) + ( × 1)
( ........... × 100) + ( ........... × 10) + ( ........... × 1)
2
valori di ciascun cartellino e componi i numeri corrispondenti.
3 Scomponi i numeri come nell’esempio.
784 = 7 h, 8 da, 4 u = 700 + 80 + 40
462 = =
325 = = 139 =
4
3 h, 4 da, 5 u = 300 + 40 + 5 = 345
7 h, 5 da, 2 u = =
9 h, 3 da, 1 u = =
1 h, 9 da, 9 u = =
5 h, 8 da = =
5 Segui l’esempio e completa.
settecentotrentadue = 732 = 700 + 30 + 2
quattrocentoventitré = =
seicentonovantaquattro = =
1 Leggi bene le regole per confrontare i numeri. Poi completa la classifica scrivendo i nomi e il punteggio di ogni giocatore.
Nel confronto tra due numeri naturali, un numero con più cifre è sempre maggiore di un numero con meno cifre.
Allora possiamo dire che l’ultimo
A parità di numero di cifre, è maggiore il numero che ha
Se le cifre a sinistra sono uguali, si confrontano quelle immediatamente seguenti.
Il secondo classificato è . Il terzo è .
Giulia, Edo, Mohamed e Marta hanno appena finito di giocare a freccette. Giulia ha totalizzato 139 punti, Edo 96, Mohamed 142 e Marta 203. Giocatore
1 Agli incroci scegli la direzione giusta seguendo i numeri dal maggiore al minore . Che cosa troverà Niccolò?
Alla fine del labirinto Niccolò trova
2 Niccolò trova alcune indicazioni sulla combinazione per aprire il baule. Completa.
È un numero minore di 600 e maggiore di 401.
Sarà allora tra il e il .
Nel numero non appare la cifra 4.
Per cui la cifra delle centinaia è sicuramente il .
La cifra delle unità è il doppio di 4. Quindi è .................

La cifra delle decine è dispari. Le possibilità sono: , , , ,
La cifra delle decine non è il 3 ma fa parte della sua tabellina.
Il numero è .
1 Completa.
Nel numero 309: il 3 è la cifra delle , il 9 è la cifra delle , mentre lo 0 occupa il posto delle . Senza lo zero il numero diventa .....................
2 Scomponi i numeri come nell’esempio. 583 5 h + 8 da + 3 u 500 + 80 + 3
3 Metti in ordine e componi come nell’esempio.
5 da + 8 u + 3 h = 300 + 50 + 8 = 358
9 u + 2 h + 5 da =
3 h + 6 u + 4 da =
7 da + 2 h + 1 u =
1 u + 4 da =
5 u + 1 h =
6 da + 7 h = ................................................................................................
4 Ordina i numeri dal minore al maggiore.
5 Ordina i numeri dal maggiore al minore.
Che cosa viene dopo il 999 ? Osserva che cosa succede se al 999 aggiungiamo 1 .
1
9 h + 9 da + 9 u = 999
1 migliaio ( k ) vale
1000 unità
100 decine
Aggiungendo una unità al 999 abbiamo ottenuto 1 migliaio , cioè il numero 1000 ( mille ). da h k u
10 centinaia da h k u .......... .......... .......... ..........
Per rendere più facile la lettura dei numeri a quattro cifre si lascia un piccolo spazio tra la cifra delle migliaia e quella delle centinaia.
Osserva come si leggono i seguenti numeri:
1 345 mille trecentoquarantacinque
1 047 mille quarantasette
1 960 mille novecentosessanta
5 709 cinque mila settecentonove
2 632 due mila seicentotrentadue
9 004 nove mila quattro
Se vuoi, quando scrivi i numeri con le migliaia, puoi anche mettere un puntino in alto per separare la cifra delle migliaia da quella delle centinaia.
3000 + 500 + 90 + 6 = 3596 tremilacinquecentonovantasei
1˙ 345
vale 2000 unità
vale 500 unità
vale 60 unità
vale 8 unità
duemilacinquecentosessantotto
vale unità
vale unità
vale unità
vale ................. unità da h k u
tremiladuecentosettantacinque
vale unità
vale unità
vale ................. unità
vale unità
vale 5000 unità
vale 100 unità
vale 0 unità
vale 2 unità ...........................................................................................................
da
tremilaquattrocentocinquantadue 3452 3000 + 400 + 50 + 2
milleduecentotrentasette
duemilacentoventisei
cinquemilaseicentoquaranta
quattromilatrecentosette
ottomiladiciotto .................... ........................................................................................








1 Scomponi i numeri come nell’esempio.
4723 = 4 k + 7 h + 2 da + 3 u = 4000 + 700 + 20 + 3
1539 = =
3650 = ........................................................................................................... = ..........................................................................................
2024 = =
9 209 = =
2 Metti in ordine e componi come nell’esempio.
7 da + 4 k + 8 u + 3 h = 4000 + 300 + 70 + 8 = 4378
5 u + 2 k + 1 h + 9 da = =
4 k + 2 h + 4 u + 1 da = =
9 k + 4 u + 8 h = =
7 u + 3 k = =
3 Leggi i valori espressi in ciascun cartellino e componi i numeri corrispondenti.
UN PASSO IN PIÙ
Usando una sola volta queste cifre, componi:
• un numero dispari maggiore di 1000
• un numero pari minore di 100
• un numero minore di 1000 e maggiore di 200 ..................................
• un numero maggiore di 100 e minore 200





1 Ogni articolo ha il suo valore: osserva.
2 Ora osserva con attenzione i disegni sotto e scrivi il valore totale degli oggetti di ogni bambino o bambina.


2 Ordina i numeri dell’esercizio
al maggiore.
Clara sta risparmiando per comprare una chitarra nuova, ma non ha ancora i soldi che le servono. Nel salvadanaio ha 123 euro.
Nei giorni scorsi ha aiutato nonno Gustavo a sistemare il giardino.
Il nonno le ha dato questi soldi:
Che bello, adesso ho quasi i 200 euro che mi servono per comprare la chitarra!
• Quanti soldi ha dato il nonno a Clara? euro.




Clara mette i sodi nel salvadanaio; quanto ha adesso di preciso?
Per rispondere alla domanda devi eseguire un’addizione.
1 Prova a eseguirla prima in riga, poi verifica in colonna. Se ci sono errori, correggi.

L’addizione da eseguire
è 123 + 75 =
h da u + = ........ ........ ........



primo addendo secondo addendo somma o totale
Risposta : Clara adesso ha euro.
2 Osserva e inventa un problema di addizione da risolvere sul quaderno.

1 Osserva, leggi e completa.
Ci sono 3 automobiline blu e 5 rosse 3 + 5 = automobiline.
Ci sono automobiline rosse e blu 5 + 3 = automobiline.
• Nelle due addizioni è cambiato l’ordine degli addendi? Sì No
• È cambiato il risultato delle addizioni? Sì No
Hai applicato la proprietà commutativa dell’addizione: cambiando l’ordine degli addendi il risultato non cambia.
Per semplificare alcuni calcoli puoi utilizzare un’altra proprietà dell’addizione. Osserva i due modi in cui può essere eseguita l’addizione 16 + 8 + 4 = .
In entrambi i casi è stata applicata la proprietà associativa dell’addizione: sostituendo a due addendi la loro somma il risultato non cambia.
• Secondo te, è stato più conveniente usarla nel primo o nel secondo modo? Discutine in classe.
Come hai già scoperto, anche le proprietà dell’addizione possono essere utilizzate per rendere più semplici e più veloci alcuni calcoli.
Se, per esempio, devi fare 9 + 37 ti conviene usare la proprietà commutativa : partendo dall’addendo maggiore il calcolo è più facile e ti permette di utilizzare altre strategie di calcolo che hai imparato.
1 Applica la proprietà commutativa e calcola a mente usando le strategie che preferisci.
19
2 Applica la proprietà associativa nel modo più conveniente e calcola a mente.
1 Incolonna correttamente gli addendi ed esegui le addizioni.
+
=
2 Esegui le addizioni in colonna sul quaderno.
3 Incolonna gli addendi ed esegui le addizioni.
4 Esegui le addizioni in colonna sul quaderno.
1 326 + 3 410 =
2 151 + 217 =
4 308 + 531 =
3 032 + 47 =
6 241 + 307 =
3 032 + 5 906 =
Quando esegui un’addizione potresti trovarti di fronte a uno o più cambi ( riporti ) se la somma della colonna supera il 9 . Osserva.
1 Incolonna correttamente gli addendi ed esegui le addizioni. Fai attenzione a eventuali cambi!
2 Applica la proprietà associativa e calcola a mente.

€ 97
€ 75
Luca ha nel salvadanaio 97 euro. Ne spende 75 per comprare un monopattino.
• Quanti euro gli restano?
97 centimetri
75 centimetri
Lin è alta 97 centimetri, il suo fratellino Juan 75 centimetri.
• Qual è la differenza di altezza tra Lin e Juan?
Per rispondere alle domande si esegue la stessa sottrazione, nel primo caso si calcola un resto , nel secondo una differenza .
1 Prova a eseguire la sottrazione prima in riga, poi verifica in colonna. Se ci sono errori, correggi.
97 – 75 = .................
2 Leggi i testi e scrivi se si tratta di una situazione di resto ( R ) o di differenza ( D ).

La collana di Gaia aveva 56 perline, dopo che si è rotta ne ha perse 24.
• Quante perline sono rimaste?
Giuseppe ha 12 anni, sua madre ne ha 46.
• Quanti anni aveva la mamma quando è nato Giuseppe?
3 Inventa sul quaderno due problemi da risolvere con la sottrazione 75 – 14 , uno di resto e uno di differenza. Puoi lavorare anche in coppia.
1 Leggi e completa.
Michela ha 7 euro, Lorenzo ne ha 4.
Michela Lorenzo
Chi ha più euro? Quanti in più? , infatti 7 – 4 =





































Nonno Filippo regala 1 euro a Michela e 1 euro a Lorenzo.
Michela Lorenzo
Quanti euro ha ora Michela? Quanti ne ha Lorenzo?
Chi ne ha di più? Quanti in più? , infatti 8 – 5 =
Michela spende 2 euro per il gelato. Lorenzo spende 2 euro per le figurine.
Michela Lorenzo
Quanti euro restano a Michela? Quanti a Lorenzo?
Chi ne ha di più? .......................................... Quanti in più? .................................., infatti 6 – 3 = ..............
Aggiungendo o sottraendo lo stesso numero al minuendo e al sottraendo è cambiata la differenza? Sì No
Questa è la proprietà invariantiva della sottrazione: se aggiungi o sottrai lo stesso numero al minuendo e al sottraendo, la differenza non cambia.
Prova a raccontare quello che hai capito della proprietà invariantiva della sottrazione, anche facendo degli esempi, e discutine con le compagne, i compagni e l’insegnante.
Se a un numero devi sottrarre 9 o 11 , prova a fare così:
fare – 9 , togli 10 e aggiungi 1 . per fare – 11 , togli 10 poi
2 Fai tappa alla decina più vicina e calcola a mente. Segui l’esempio.
Per
2 Leggi e completa.
Matteo
•
•
correttamente ed esegui le sottrazioni.
2 Esegui le sottrazioni in colonna sul quaderno.
Quando esegui una sottrazione potresti trovarti di fronte a uno o più cambi. Se la cifra del minuendo è minore di quella del sottraendo esegui il cambio ( prestito ).
Sottrai le unità : 1 – 6 non si può fare.
Esegui il cambio:
le unità diventano 11 e le decine 7.
Adesso puoi sottrarre
le unità: 11 – 6 = 5
Sottrai le decine rimaste: 7 – 8 non si può fare.
Esegui il cambio:
le decine diventano 17 e le centinaia 4.
Adesso puoi sottrarre
le decine: 17 – 8 = 9
1 Incolonna correttamente ed esegui le sottrazioni.
Infine, sottrai
le centinaia rimaste: 4 – 2 = 2.
Il risultato della sottrazione
295
1 Leggi, osserva e completa. Nel negozio di giocattoli, nell’angolo dei peluche, sono rimasti solo gufi e ricci.
Sull’espositore ci sono 7 gufi e 5 ricci.
Quanti peluche ci sono?

Sull’espositore ci sono 12 peluche. I gufi sono 7.
Quanti sono i ricci?
Con la sottrazione puoi fare la prova dell’addizione : dopo aver fatto
l’addizione, sottrai dalla somma uno dei due addendi, se il risultato è uguale all’altro addendo, l’addizione è esatta.
Con l’addizione puoi fare la prova della sottrazione : aggiungi il risultato della sottrazione al sottraendo, se ottieni il minuendo, la sottrazione è esatta.
2 Esegui le operazioni sul quaderno e fai la prova.
1 Scrivi il segno corretto: + oppure –.
2 Scrivi il numero che manca.
3 Per ogni problema troverai tre domande: rispondi solo a quelle cui è possibile dare una risposta.
Viola ha 11 anni, suo nonno Beppe ne ha 73.
• Quanti anni aveva il nonno quando è nata Viola?
• Quando è nata Viola, che cosa stava facendo il nonno? ..................
• Quando viola aveva 7 anni, quanti anni aveva il nonno?
Un trattore trasporta 40 conigli e 37 galline.
• Quanti anni ha il conducente del trattore?
• Quanti animali ci sono sul trattore?
• Quanti sono i conigli in più rispetto alle galline?
Teo paga le scarpe che ha comprato con una banconota da 50 euro e due banconote da 20 euro. Il negoziante gli dà 5 euro di resto.
• Quanti soldi ha dato Teo al negoziante?
• Quanto costano le scarpe? ..................
• Quanti soldi ha ora Teo nel portafoglio?
1 Vuoi divertirti a colorare il mondo sottomarino? Esegui le addizioni e le sottrazioni e scrivi i risultati.
azzurro i numeri pari minori di 500; verde i numeri dispari minori di 500; rosso i numeri pari maggiori di 500; giallo i numeri dispari maggiori di 500.
1 Incolonna correttamente e calcola. Fai attenzione a eventuali cambi!
307 + 491 = 136 + 627 = 843 + 96 = 1345 + 724 =
h da u h da u h da u k h da u
342 – 215 = 431 – 190 = 983 – 92 = 6789 – 648 = h da u h da u h da u k h da u
2 Esegui le operazioni e verifica il risultato con l’operazione inversa.
Addizione Prova Prova Sottrazione
h da u h da u
da u h da u 4 3 5 + –
da
k h da u
k h da u k h da u
h da u k h da u




1 Osserva, leggi e completa.
• Quante dita vedi?
Ci sono molti modi per rispondere: – puoi contarle una per una: 1, 2, 3, 4, 5, 6…
– puoi contarle per cinque: 5, 10, 15, 20…
– oppure, più semplicemente, puoi fare una moltiplicazione .
Quante dita in una mano? Quante mani? Quindi × = 40.

2 Completa come nell’esempio.

Qualsiasi numero moltiplicato per 0 dà come risultato
Lo 0 è l’ elemento assorbente della moltiplicazione, perché annulla l’operazione.
Qualsiasi numero moltiplicato per 1 dà come risultato .....................
L’ 1 è l’ elemento neutro della moltiplicazione, perché qualsiasi numero moltiplicato per 1 dà sempre come risultato se stesso.
OL L L IA C
Procuratevi una tavola pitagorica completa, ritagliatela e piegatela lungo la diagonale tratteggiata (come sopra). Con l’aiuto di una persona adulta fate alcuni fori qua e là nel foglio piegato. Riapritelo e confrontatevi in classe su quello che avete scoperto.
UN


Leo va da casa sua a casa della nonna passando per il ponte di pietra. Da casa di Leo al ponte ci sono 3 strade, dal ponte a casa della nonna 2 strade. Quanti sono i possibili itinerari di Leo?

1 Osserva e completa la tabella.
Leo ha 6 possibili itinerari, perché 3 × 2 = 6.
2 Il giorno dopo Via Erbosa è interrotta. Completa la tabella e la frase sotto.
Leo ha possibili itinerari, perché 3 × 1 = .

3 Il terzo giorno anche Via Pietrosa è interrotta. Completa la tabella e la frase sotto.
Leo ha possibili itinerari, perché 3 × 0 = .

La moltiplicazione consente anche di calcolare delle combinazioni.
4 Elena ha a disposizione i seguenti indumenti. Disegna i diversi modi in cui può vestirsi e completa.
Canottiera rossa Camicia blu
Maglia a maniche corte rosa
Maglia a maniche lunghe gialla
Gonna
Pantaloni
1 Osserva, leggi e completa.
• Quanti fichi in tutto? Per rispondere puoi:

– contare i fichi in una cesta e poi moltiplicare per tutti i cesti: 5 × 3 =
– contare i cesti e poi moltiplicare per il numero dei fichi in ogni cesto: 3 × ............. = .............
Cambiando l’ordine dei fattori è cambiato il risultato? Sì No
Hai applicato la proprietà commutativa della moltiplicazione, perché cambiando l’ordine dei fattori il risultato non è cambiato.
2 Applica la proprietà commutativa e completa.
Osserva due diversi modi in cui può essere eseguita la moltiplicazione 2 × 8 × 5 =.
In entrambi i casi è stata applicata la proprietà associativa della moltiplicazione, perché hai sostituito a due fattori il loro prodotto.
• Secondo te, è stato più conveniente applicare la proprietà associativa nel primo o nel secondo modo?
Per semplificare alcune moltiplicazioni con numeri più grandi puoi applicare la proprietà distributiva , cioè scomporre un fattore in addendi e moltiplicare ciascun numero per l’altro fattore. Vediamola insieme.
Osserva come si può eseguire la moltiplicazione 12 × 4 = 48 .
3 Disegna sul quaderno questi schieramenti e calcola usando la proprietà distributiva . 13 × 3 = 17 × 2 = 14 × 5 = 15 × 4 =
4 Applica la proprietà distributiva e calcola a mente. Segui l’esempio.
15 × 6 = 90 13 × 5 = 28 × 2 = 56 × 3 = × 6 10 60
× × ×
5 30 90
5 Applica la proprietà distributiva e calcola a mente. Segui l’esempio.
32 × 3 (30 + 2) × 3 (30 × 3) + (2 × 3) 90 + 6 = 96
17 × 4 ................................................ ................................................ ................................................
23 × 5 35 × 4
237-238
La moltiplicazione in colonna utilizza la proprietà distributiva . Se devi fare 124 × 3 , è come fare 4 × 3 + 20 × 3 + 100 × 3 . Osserva.
Moltiplica 4 unità × 3 = 1 2 unità . Scrivi 2 nella colonna delle unità e riporta 1 decina nella sua colonna.
Ora moltiplica la cifra delle decine: 2 decine × 3 = 6 decine , più 1 di riporto fa 7. Scrivi 7 decine nella sua colonna.
1 Incolonna correttamente ed esegui le moltiplicazioni.
Infine, moltiplica la cifra delle centinaia: 1 centinaio × 3 = 3 .
Scrivi 3 centinaia nella sua colonna.
Quando il moltiplicatore ha due cifre, la proprietà distributiva è ancora più evidente. Se devi fare 25 × 13 , è come fare 25 × 3 + 25 × 10 . Osserva.
25 × 3 unità = 75.
75 è il primo prodotto parziale .
25 × 1 decina = 250.
250 è il secondo prodotto
Ora facciamo la stessa operazione applicando la proprietà distributiva : scomponiamo il 13 in 3 + 10 e calcoliamo.
Infine, somma i due prodotti parziali e ottieni il risultato dell’operazione:
+ 250 = 325 .
13 = 75 10 = 250 25 325 + ×
Secondo te, perché si scrive subito uno 0 nella colonna delle unità del secondo prodotto parziale? Discutine in classe.
Come sai già, uno 0 scritto a destra del numero aumenta il suo valore di 10 volte. Per moltiplicare per 10 , 100 , 1000 basta aggiungere a destra uno , due o tre zeri .
Esegui queste moltiplicazioni e leggi i risultati. Se non riesci, chiedi all’insegnante.

1 Grace e Oscar hanno scritto i propri nomi in modi originali. Grace ha scelto la pixel art e adesso sta cercando di contare in modo veloce i pixel che ha colorato. Ha già cominciato, continua tu.
Per contare i pixel della G ho fatto 5 × 4 e poi ho tolto 6.
5 × 4 – 6 = 14
Somma i pixel di ogni lettera e scopri il totale: .
2 Ora osserva che cosa ha fatto Oscar e completa.
Io, invece, per scrivere il mio nome ho disegnato dei puntini. Mi aiuti a contarli?

3





















Erik ha comprato 3 confezioni di dolcetti.
Ogni confezione contiene 5 dolcetti.
La sua amica Lia gli ha regalato 2 dolcetti. Quanti dolcetti ha ora Erik?
A. 5 + 5 + 5 + 2
B. 3 + 5 + 2
C. 5 × 3 + 2
1 Applica la proprietà associativa nel modo per te più conveniente e calcola a mente.
2 Applica la proprietà distributiva e calcola. Segui l’esempio.
3 Scrivi il moltiplicatore.
5 Esegui in colonna sul quaderno.
6 Leggi i problemi, scrivi l’operazione e calcola a mente.
La scuola di Sonia dista 220 metri da casa. Sonia percorre questa distanza
4 volte al giorno.
Quanti metri percorre in totale?
Operazione:
Adele ha comprato 3 confezioni di uova. Ogni confezione contiene 8
uova. Nel tornare a casa 5 uova si sono rotte. Quante uova sono rimaste?
Operazione:
1 Cecilia, Diego e Zoe si stanno dividendo le fragole in parti uguali. Hanno già cominciato, continua tu e completa.
• Quante fragole? dividendo

• Quanti bambini? divisore
• Quante fragole avrà ogni bambino? quoto




La divisione è l’operazione che distribuisce una quantità in parti uguali.
dividendo divisore quoto : =
2 Distribuisci in parti uguali le papere negli stagni e completa.
• Papere
• Stagni
• Papere in ogni stagno
Operazione : =
Rileggi le divisioni che hai scritto. Che cosa puoi notare?
Parlane con le compagne, i compagni e l’insegnante.
3 Leggi, osserva e completa.
Zia Letizia ha preparato la pizza facendo in modo che su ogni fetta ci sia lo stesso numero di funghi.
• Quanti funghi sulla pizza?
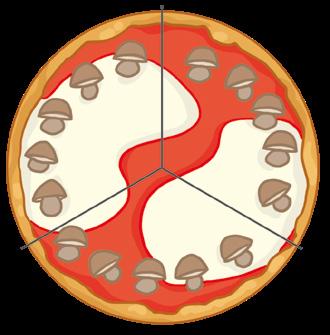

• Quante fette?
• Quanti funghi su ogni fetta?
Operazione : =
4 Dividi i bambini in modo da formare due squadre, ciascuna con lo stesso numero di giocatori. Poi colora i cappellini di ciascuna squadra in modo diverso e completa.
• Quanti bambini? ...........
• Quante squadre?
• Quanti bambini per ogni squadra? ...........

Operazione ................. : ................. = .................
5 Su ogni torta ci sono 12 ciliegine. Tagliale come indicato e in modo che su ogni fetta ci sia lo stesso numero di ciliegine. Poi completa.
1 Al torneo scolastico di mini basket si iscrivono 30 bambini. Quante squadre da 5 bambini si riescono a formare? Osserva, segui l’esempio e completa.
Squadre Bambini

1 5
2 10 ..................... .....................
• Bambini in tutto
• Bambini per squadra
Operazione : =
• Squadre formate
Puoi usare la divisione anche per raggruppare una quantità in parti uguali.
2 Dino il contadino deve disporre 24 pesche in confezioni da 4 . Quante confezioni riuscirà a preparare? Segui l’esempio e completa.
Confezioni preparate Pesche confezionate Pesche da confezionare
1 4 20 ..................... ..................... .....................
• Pesche in tutto

• Pesche per confezione
Operazione : =
• Confezioni preparate
1 Luca deve preparare dei mazzi da 5 fiori ciascuno. Quanti mazzi preparerà con 23 fiori? Avanzeranno dei fiori? Se sì, quanti? Segui l’esempio e completa.



Mazzi preparati Fiori usati Fiori avanzati
1 5 18 ..................... ..................... .....................
• Fiori in tutto ...........
• Fiori per mazzo
• Mazzi preparati
• Fiori avanzati
Operazione
: = resto
dividendo divisore quoziente
Il risultato di una divisione con il resto si chiama quoziente .
2 Eloisa deve realizzare delle cornici per beneficenza. Ciascuna cornice ha 4 bordi. Quante cornici potrà realizzare Eloisa con 14 bordi? Completa.
• Bordi in tutto
• Bordi per cornice
• Cornici preparate ...........
Cornici realizzate Bordi usati Bordi avanzati ..................... ..................... .....................
Operazione ........... ........... ...........
• Bordi avanzati : = resto ..............
Risposta : Eloisa realizzerà cornici e le avanzeranno bordi.
1 Conta con le dita quante volte il divisore è contenuto nel dividendo e scrivi i risultati. Segui gli esempi.
Divisioni esatte
Quante volte il 3 è contenuto nel 12?
12 : 3 = 4
15 : 5 =
18 : 3 = .............
24 : 6 =
35 : 5 =
40 : 8 =
45 : 9 =
Divisioni con il resto
17 : 5 = 3 r 2
16 : 5 = r
17 : 4 = r
20 : 3 = r
34 : 5 = ............. r .............





45 : 6 = r 50 : 9 = r
2 Completa come nell’esempio.

Dividere un numero per 10 , 100 , 1000 significa diminuire il suo valore di 10 , 100 , 1000 volte.
1

Vedo 6 galline in ciascuno dei 3 recinti, quindi 18 galline; perché 6 × 3 = 18 !
Vedo 18 galline suddivise in 3 recinti, quindi ci sono
6 galline in ciascun recinto perché 18 : 3 = 6 !

La divisione è l’ operazione inversa della moltiplicazione.
: 3

18 6 × 3
Con la moltiplicazione puoi fare la prova della divisione .
18 : 3 = 6 , perché 6 × 3 = 18 .
Nella divisione con il resto al risultato della moltiplicazione devi aggiungere il resto:
23 : 4 = 5 resto 3 , perché 5 × 4 = 20 20 + 3 = 23 .
Divisioni con il resto
1 Osserva e rispondi.
Il risultato delle divisioni è cambiato dopo che il dividendo e il divisore sono stati divisi o moltiplicati per lo stesso numero?
Questa è la proprietà invariantiva della divisione: dividendo o moltiplicando per lo stesso numero il dividendo e il divisore il risultato non cambia.
2 La proprietà invariantiva può aiutarti a semplificare alcune divisioni. Segui l’esempio e completa.
3 Applica la proprietà invariantiva nel modo per te più conveniente e calcola a mente.
Racconta quello che hai capito della proprietà invariantiva della divisione facendo degli esempi e discutine con le compagne, i compagni e l’insegnante.
Ilaria ha 369 conchiglie e vuole disporle su 3 mensole in numero uguale. Quante conchiglie dovrà mettere su ogni mensola?
Per eseguire la divisione 369 : 3 Ilaria usa tre cerchi di cartoncino colorato che divide in 3 parti con delle striscioline di cartoncino giallo. Ilaria sa che il numero 369 è composto da 3 h , 6 da e 9 u .


Comincia a dividere le 3 centinaia : 3 h : 3 = 1 h
Poi passa a dividere le 6 decine : 6 da : 3 = 2 da
Infine divide le 9 unità : 9 u : 3 = 3 u
Risposta : Ilaria su ognuna delle 3 mensole dovrà mettere conchiglie.
PER FARE T OL L L IA C
Costruire una raggiera come quelle di Ilaria è facile! Con l’aiuto di una persona adulta ritaglia un cartoncino a forma di cerchio e 9 striscioline per i raggi, poi procurati un fermacampione. Appena le tue raggiere saranno pronte, allenati a fare tante divisioni prima di cominciare con quelle in colonna.
Dividi le centinaia :
3 : 3 = 1 con resto 0 .
Scrivi 1 al risultato e 0 sotto alle centinaia.
Trascrivi le 6 decine accanto al resto delle centinaia e dividile:
6 : 3 = 2 con resto 0 .
Scrivi 2 al risultato e 0 sotto alle decine.
Trascrivi le 9 unità accanto al resto delle decine e dividile:
9 : 3 = 3 con resto 0 .
Scrivi 3 al risultato e 0 sotto alle unità.
osserva come la stessa divisione di Ilaria si può eseguire in colonna.
Le raggiere ti aiutano a capire come funziona il cambio nelle divisioni. Eseguiamo 315 : 2.
Il numero 315 è composto da 3 h , 1 da e 5 u :
3 h : 2 = 1 resto 1
Per dividere il centinaio di resto lo cambiamo in decine.
Le decine diventano 11.
11 da : 2 = 5 resto 1
Per dividere la decina di resto la cambiamo in unità.
Ora osserva come la stessa divisione si esegue in colonna.
Le unità diventano 15.
15 u : 2 = 7 resto 1
Dividi le 3 centinaia per 2. 3 : 2 = 1 con il resto di 1 .
Scrivi 1 al quoziente e 1 (il resto) sotto alle centinaia.
Cambia il centinaio di resto in decine abbassando l’1:
le decine diventano 11.
11 : 2 = 5 col resto di 1 .
Scrivi 5 al quoziente
e 1 sotto alle decine.
Cambia la decina di resto in unità abbassando il 5: le unità diventano 15.
15 : 2 = 7 col resto di 1 .
Scrivi 7 al quoziente e 1 sotto alle unità.
Per eseguire la prova della divisione moltiplica il quoziente per il divisore e aggiungi il resto:
(157 × 2) + 1 = 314 + 1 = 315
1 Esegui le divisioni in colonna e fai la prova. divisioni con il resto
2 Esegui le divisioni in colonna sul quaderno e fai la prova.
Quando la prima cifra del dividendo è minore del divisore , procedi subito al cambio .
Osserva come si esegue la divisione 138 : 3. Il numero 138 è composto da 1 h , 3 da e 8 u :
Per dividere 1 centinaio per 3 cambialo in 10 decine.
Le decine diventano 13.
13 : 3 = 4 resto 1
Per dividere la decina cambiala in 10 unità.
Ora osserva come la stessa divisione si esegue in colonna.
Le unità diventano 18: 18 : 3 = 6
Per dividere 1 centinaio per 3, cambialo in decine: le decine diventano 13.
1 Esegui le divisioni sul quaderno e fai la prova. a.
Per dividere per 3 la decina di resto cambiala in unità abbassando l’8: le unità diventano 18; 18 : 3 = 6 .
1 Collega ciascun problema al segno giusto e risolvi sul quaderno.
Jane legge 6 pagine al giorno del libro preso in biblioteca. Il libro è composto da 192 pagine. Quanti giorni impiegherà per finirlo?
Per allenarsi alla maratona di New York Gianluca percorre 42 chilometri al giorno. Quanti chilometri percorre in 6 giorni?
L’album di Sebastian ha 124 pagine. Su ogni pagina ha incollato 8 figurine. Quante figurine ha incollato Sebastian?
Per addobbare l’albero di Natale Denise ha comprato 14 scatole di palline. Ogni scatola ne contiene
6. Quante palline ha comprato Denise?
Marta ha 135 perline colorate. Ne infila 3 in ogni bracciale intrecciato. Quanti bracciali riesce a confezionare?
Un parcheggio a 4 livelli può contenere in tutto 504 automobili. Quante automobili può contenere ciascun livello?
1 Segui le indicazioni e calcola a mente come negli esempi.
Per eseguire a mente la moltiplicazione 6 × 30 = 180, Angelo ha ragionato così: “Se 6 per 3 fa 18, allora 6 per 3 0 fa 18 0 !”.
7 × 20 = 140
× 5 = 6 × 40 =
× 70 = ...................
× 9 =
× 6 =
× 3 =
Eva, usando la proprietà invariantiva, ha scoperto come eseguire a mente alcune divisioni: toglie dal dividendo e dal divisore lo stesso numero di zeri.
:
2 Risolvi i problemi usando le strategie di calcolo che hai imparato.
• Un pasticciere ha preparato 1200 biscotti. Li suddivide in 100 sacchetti. In ogni sacchetto ci saranno biscotti.
• Per assistere alla partita Milan-Roma, sono partiti da Roma 90 pullman. Su ogni pullman viaggiano 50 tifosi. I tifosi diretti a Milano sono
• 180 confezioni di latte vengono sistemate in 30 scatole. Ogni scatola conterrà confezioni.
1 Esegui le operazioni e scrivi i risultati in lettere, poi leggi quelle evidenziate dall’alto verso il basso e scopri il messaggio.
Nella vita di tutti i giorni ci capita di dover affrontare e risolvere dei problemi. I problemi sono delle situazioni che ci spingono a porci delle domande e a cercare delle soluzioni .
In matematica il testo di un problema contiene delle precise informazioni chiamate dati . Un testo può essere completato anche da immagini , simboli , tabelle …
1 Leggi, osserva attentamente le due situazioni e rispondi.
Maria e Laura sono due sorelle di 10 e 14 anni e oggi hanno deciso con i genitori di andare al Luna Park.
Il biglietto d’ingresso costa 10 euro. I bambini che hanno meno di 12 anni pagano 7 euro.

• Quanto spendono in totale per l’ingresso? .............

• La mamma paga con una banconota da 50 euro, quanto riceve di resto?

Marco e Sonia sono usciti insieme per fare acquisti.
Vorrei comprare le scarpe e la gonna, ma ho solo 70 euro.
Potresti prestarmi il resto?
€ 42 € 35
Volentieri, mi sono rimasti ancora 20 euro.
• Quanti euro Diego dovrà prestare a Sonia?
€ 50
• Quanti euro resteranno a Marco dopo aver fatto il prestito a Sonia?
1 Leggi e osserva la situazione. Un gruppo di amici sta per partire per andare a visitare la città di Siena. Salah acquista i biglietti del treno per tutti.

Ho anticipato io i soldi per i biglietti, ho speso in totale 60 euro.
Alle 9:00 saremo a Siena.
Il nostro treno parte tra mezz’ora.
2 Segna con una ✘ le domande a cui è possibile dare una risposta. Poi rispondi.
Quanti biglietti ha acquistato Salah?
Da quale città stanno per partire?
A che ora si svolge la scena?
Quanto costa un biglietto?
Quanto ha ricevuto di resto Salah?
Quanto tempo durerà il viaggio? ...............................................
A che ora torneranno a casa?
Da quale binario parte il treno per Siena?
In quale stagione dell’anno ci troviamo? ...............................................
1 Leggi e completa.
Lorenzo conta 20 pecore che pascolano nel prato. Scommette con sua sorella Maia di indovinare il numero esatto delle zampe senza contarle.
Qual è il numero di tutte le zampe?
Questo problema contiene un dato nascosto , cioè un numero o un’operazione espressi a parole nel testo.
• Qual è la parte di testo che contiene il dato nascosto? Sottolineala.
• Qual è il numero relativo al dato nascosto?
Scrivi l’operazione e risolvi il problema.
Operazione:

Risposta : ....................................................................................................................................................................................................
2 Collega le parole con il significato numerico.
3 Collega le parole con l’operazione corrispondente. dozzina metà
4 Sottolinea il dato nascosto e risolvi i problemi sul quaderno.
• A dicembre gli alunni della 3ª A andranno a scuola solo 19 giorni.
Quanti giorni staranno a casa?
• Beba ha 27 anni, suo nonno
Leopoldo ne ha il triplo.
Quanti anni ha il nonno?
• Il negoziante ha venduto 8 confezioni di uova. Ogni confezione ne conteneva una dozzina. Quante uova ha venduto?
• Il libro che sta leggendo Giulia ha 168 pagine. Ne ha già lette la terza parte. Quante pagine ha letto Giulia?
1 Leggi, completa le operazioni e rispondi.
Elisabeth ha comprato 12 bustine di figurine. Ogni bustina contiene 5 figurine.
Quante figurine ha comprato Elisabeth?
Regala i 15 doppioni a suo fratello Karim. Quante figurine le sono rimaste?
Per risolvere questo problema si eseguono due operazioni . Il risultato della prima operazione ti fornirà il dato utile per eseguire la seconda.
Quante figurine ha comprato Elisabeth?
Quante figurine le sono rimaste?
Figurine in ogni bustina
Figurine comprate
Bustine comprate Figurine comprate
Doppioni regalati
Figurine rimaste
Risposta : Elisabeth ha comprato figurine.
Dopo aver regalato a Karim i doppioni le sono rimaste figurine.
2 Risolvi i problemi sul quaderno.
• Mariasole deve sistemare 96 libri
nella sua libreria. Ieri ne ha sistemati la metà.
Quanti libri ha sistemato?
Oggi ne ha sistemati solo 13.
Quanti libri le restano da sistemare?

• Un camionista ha caricato 65 confezioni di acqua minerale; ogni confezione contiene 4 bottiglie.
Quante bottiglie ha caricato?
Durante il trasporto si rompono 19 bottiglie.
Quante bottiglie restano intere?
Alcuni problemi hanno una sola domanda, ma per essere risolti hanno bisogno di più operazioni. In questi problemi, in realtà, ci sono delle domande nascoste che bisogna scoprire.
1 Leggi il testo del problema e completa.
Mauro ha una collezione di 60 fossili. Ne regala 15 a Benedetta. Dispone i fossili che gli sono rimasti in numero uguale su 3 mensole.
Quanti fossili mette su ogni mensola?
La domanda ti chiede il numero di fossili che Mauro ha messo su ogni mensola, ma non puoi rispondere senza prima aver scoperto la domanda nascosta.
• Quale potrebbe essere la domanda nascosta?
Operazione per rispondere alla domanda nascosta.
Operazione per rispondere alla domanda del problema.
= .............. .............. .............. : = .............. .............. ..............
Risposta : Mauro ha messo ............. fossili su ogni mensola.
2 Risolvi i problemi sul quaderno indicando la domanda nascosta.
• Per iscrivere la squadra al torneo di beach volley, ciascuno dei 6 giocatori ha versato una quota di 12 euro. Lo sponsor ha contribuito alle spese di iscrizione al torneo con altri 150 euro.
Quanto è costata l’iscrizione al torneo?
• Approfittando dei saldi, Eloisa compra un paio di auricolari a 29 euro, un mouse a 50 euro e una custodia per tablet a 15 euro. Paga con una banconota da 100 euro.
Quanto riceve di resto?
Angela, Arian e Giulio sono usciti insieme per fare acquisti. Si fermano davanti alla vetrina di un negozio.
1 Osserva le immagini, leggi i testi dei problemi e risolvili sul quaderno.
• Angela compra le scarpe rosse e la camicia. Paga con una banconota da 100 euro. Quanto riceve di resto?




• Giulio compra 4 cappelli per la sua squadra di caccia al tesoro. Paga con una banconota da 50 euro. Quanto riceve di resto?
• Arian vorrebbe comprare la felpa giallo e blu e i pantaloni blu, ma ha solo 100 euro. Quanto manca ad Arian?




• Dividetevi in 4 gruppi.
• Ogni gruppo dovrà inventare due problemi con i prezzi degli articoli in alto.
• Infine, ogni gruppo dovrà risolvere i problemi inventati dagli altri 3 gruppi.
Avete collaborato nel gruppo? Sì No Ci abbiamo provato
Quanto ti è piaciuta questa attività? Poco Abbastanza Molto
Al ritorno dalle vacanze, Aurora si accorge di non ricordare più la combinazione per aprire la valigia. Allora decide di telefonare al suo amico Felipe, che gliel’ha gentilmente prestata.
1 Leggi e rispondi.
Ciao Felipe, scusa se ti disturbo ma ho un problema: non ricordo più la combinazione per aprire la valigia. Ricordo solo che è formata dalle cifre 1 – 3 – 6 – 9 ma non la loro posizione!
Ciao Aurora, ben tornata, vorrei tanto aiutarti, ma in questo momento sono al lavoro e la combinazione l’ho segnata su un foglietto che ora è a casa. L’unica cosa che ricordo è che l’ultima cifra è pari

Invece mi hai aiutata tantissimo, grazie: adesso so che le combinazioni possibili sono solo sei!
• Secondo te, perché l’aiuto di Felipe è stato molto prezioso per Aurora?
Confronta la tua risposta con quella delle compagne e dei compagni.
2 A questo punto Aurora decide di provare tutte le combinazioni possibili. Aiutala a scriverle. Poi leggi e completa.
La valigia si apre quando la cifra delle decine è minore della cifra delle unità e maggiore di quella delle centinaia.
• Qual è la combinazione esatta?

1 Leggi e motiva a voce la tua risposta.
• I 160 alunni e i 15 insegnanti di una Scuola Primaria sono stati invitati ad assistere a una partita di beneficenza in una città vicina. La ditta di trasporto ha a disposizione solo pullman da 50 posti. Quanti pullman serviranno per trasportare tutti gli alunni e tutti gli insegnanti?
A. 2 B. 3 C. 5 D. 4

• Alina, Mohamed e Paolo misurano con i passi la lunghezza del corridoio della scuola. Alina conta 14 passi, Mohamed 11 e Paolo 16. Chi ha il passo più lungo?
A. Alina B. Mohamed C. Paolo
• Michele sta controllando lo scontrino del supermercato, ma si accorge che è strappato. Aiutalo a fare i conti.
1 litro di olio costa:
A. 6 euro C. 4 euro
B. 3 euro D. 2,50 euro
5 uova costano:
A. 1 euro C. 2 euro
B. 0,50 euro D. 1,50 euro
I biscotti sono costati:
A. 2 euro C. 4 euro
B. 3 euro D. 3,50 euro
Olio – 3 litri € 12
10 uova € 2
Biscotti €
totale € 17,50
Ricorda: Dopo aver risolto un problema, rifletti sempre sulla risposta che hai dato e chiediti se questa è accettabile oppure no.
1 Quali tra queste risposte, secondo te, non sono accettabili? Segnale con una ✘ e spiega a voce perché.
Antonella per due pacchetti di caramelle ha speso 196 euro.
Il libro che sta leggendo Filippo ha 128 pagine.
Alla prima fermata sono scesi dal pullman 918 passeggeri.
Quando è nato Giulio, sua madre aveva 32 anni.
Il papà di Alexandra ha pagato con una banconota da 20 euro e ha ricevuto 25 euro di resto.
2 Scrivi il motivo per cui il seguente problema non può essere risolto. Per la visita agli scavi di Pompei ciascun alunno della 3ª A deve pagare 15 euro. Quanto costa la gita per tutta la classe? ...................................................................................................................................................................................................
3 Sottolinea il dato nascosto e risolvi i problemi sul quaderno.
• Per l’abbonamento al telefono Gianluca spende 39 euro al mese. Quanto spende in un anno?
• Gino, con il suo go kart percorre 4 giri di pista al minuto. Quanti giri fa in mezz’ora?
4 Scrivi la domanda nascosta e risolvi i problemi sul quaderno. Edo ha speso 89 euro per una macchina fotografica digitale e 39 euro per un gioco della consolle.
Chiara è alta 142 centimetri, Federico è più basso di Chiara di 14 centimetri.
Se aveva nel salvadanaio 156 euro, quanti soldi gli sono rimasti?
Marta è più alta di Federico di 8 centimetri. Quanto è alta Marta?
1 Leggi il problema.
I genitori della classe di Carlotta si sono accordati per organizzare la festa di fine anno. Il papà di Carlotta prende l’incarico di preparare i dolcetti alla marmellata e comprare il succo d’arancia. Dopo aver preparato la lista della spesa qui a lato, il papà e Carlotta si recano al supermercato.
Ora osserva i prezzi dei vari prodotti.
3 litri di latte

1 pacco di farina
8 uova


1 pacco di zucchero
2 vasetti di marmellata

1 panetto di burro

6 litri di succo di arancia



Fai attenzione alle quantità di prodotti da comprare, completa lo scontrino e scrivi il totale della spesa. Poi rispondi.

Il papà paga con queste banconote.
• Quanto riceve di resto? €

1 Osserva e rispondi.
La crostata è intera. La crostata è divisa in parti uguali? Sì No



La crostata è divisa in parti uguali? Sì No
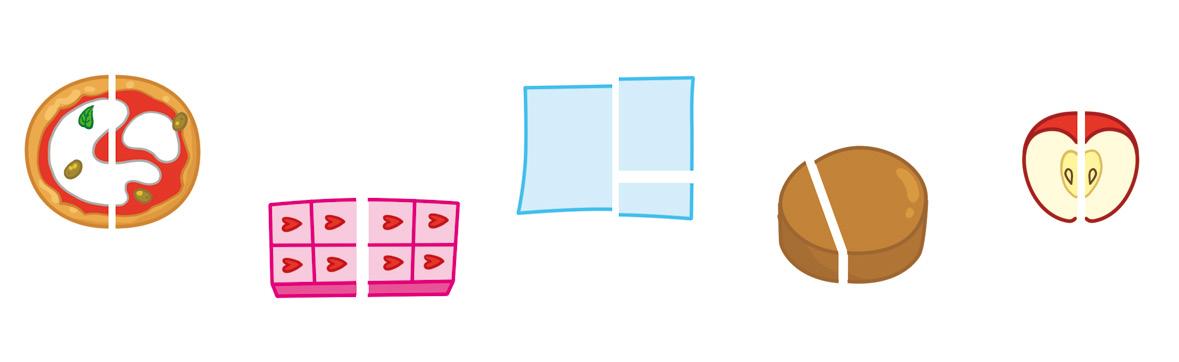
In matematica, quando un intero viene diviso in parti uguali si dice che è stato “ frazionato ”.
2 Segna con una ✘ in quali casi l’ intero è stato frazionato , cioè diviso in parti uguali.
Sì No
Sì No
Sì No
Sì No
3 Segna con una ✘ le figure divise in parti uguali.

Sì No
La nonna di Alex ha preparato una piccola torta. Ha tagliato 4 fette, una per ciascun dei suoi nipoti. Osserva.
Prendete una fetta qualsiasi, sono tutte della stessa quantità!
Proviamo insieme a vedere se quello che dice la nonna è vero.
4 Osserva, leggi e rispondi.
Questa è la torta intera.
Poi ha diviso a metà
la parte a sinistra.
La nonna l’ha divisa prima a metà.
Infine ha diviso a metà anche la parte a destra.
• Secondo te, ciascun bambino mangerà la stessa quantità di torta? Sì No




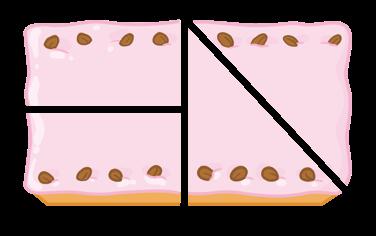
Confronta la tua risposta con quelle delle compagne e dei compagni e discutetene in classe.
Frazionare significa dividere un intero in parti di uguale dimensione , anche se queste hanno forme diverse.
L’intero è stato diviso in 2 parti uguali.
Ogni parte è 1 2 (si legge “ un mezzo ”)
L’intero è stato diviso in 4 parti uguali.
Ogni
è 1 4 (si legge “ un quarto ”) dell’intero.
L’intero è stato diviso in 8 parti uguali.
Ogni parte è 1 8 (si legge “ un ottavo ”)
Osserviamo una frazione da vicino: il cerchio è stato tagliato in 6 parti uguali.
Sono stati tolti 2 pezzi e ne sono rimasti 4, cioè i 4 6 .
4 6
Il numeratore indica le parti considerate.
linea di frazione
Il denominatore indica in quante parti è diviso l’intero.
2 Colora la parte indicata dalla frazione .
Nella vetrina di un negozio di animali ci sono 12 pesci distribuiti in 4 acquari.
I 3 4 dei pesci sono rosa, gli altri gialli.
Quanti pesci devi colorare di rosa e quanti di giallo?
Prima di colorare i pesci ragioniamo insieme.
Gli acquari sono , per cui, ogni acquario contiene



1 4 di tutti i pesci.
A che numero corrisponde 1 4 di 12? ............... Hai trovato l’ unità frazionaria .
• Quanti pesci dovrai colorare di rosa? Quanti di giallo?
• Sapresti dire a che frazione corrispondono i pesci gialli?
2 Piera la pasticciera ha tagliato una torta in 5 fette. Ora vuole dividere 20 stelline di zucchero su tutte le fette per decorarle tutte uguali. Disegnale tu.
• Quante stelline mette su ogni fetta? Infatti 1 5 di 20

• Quante stelline ci sono su 2 fette? Infatti 2 5 di 20
Il cane Argo è un golosone e mentre Piera è distratta mangia 3 fette di torta.
• Quante stelline mangia Argo?


Prova a scriverlo con le frazioni: 5 di 20
PER FARE



A Lara, Filippo e Chiara viene un’idea: osserva e leggi.
Per trovare l’unità frazionaria si fa una divisione, allora possiamo usare la raggiera!
È vero! Se, per esempio, dobbiamo trovare i 2 3 di 18, basta dividere la raggiera in 3 parti e dividere 18 oggetti!
Giusto, poi contiamo gli oggetti che ci sono su 2 parti ed è fatta!
• Ti piace questa idea? Mettila in pratica insieme alle compagne e ai compagni.
1 Osserva, leggi e completa. Segui l’esempio.
L’intero è suddiviso in 10 parti uguali. È stata
colorata 1 parte su 10 , cioè un decimo : 1 10
L’intero è suddiviso in 100 parti uguali. È stata
colorata parte su , cioè un centesimo :
L’intero è suddiviso in 1 000 parti uguali. È stata
colorata parte su , cioè un millesimo :
Le frazioni che al denominatore hanno i numeri 10 , 100 , 1000 si chiamano frazioni decimali .
2 Scrivi le frazioni decimali corrispondenti.
Le frazioni decimali si possono scrivere anche in forma di numeri decimali , cioè quei numeri con la virgola che vedi, per esempio, quando leggi un prezzo o misuri la tua altezza.
Questa figura è stata divisa in 10 parti uguali. Ogni parte rappresenta un decimo. È stata colorata per intero e vale 1 unità .
In questa figura non è stata colorata l’unità intera, ma solo i 4 10 , cioè
0 unità e 4 decimi 0,4
(si legge “ zero virgola quattro ”).
La nonna ha regalato a Ginevra e a Giorgio queste due piccole tavolette di cioccolato.
Ginevra ha mangiato tutta la sua tavoletta più tre pezzettini della tavoletta di Giorgio, cioè ha mangiato 13 pezzettini di cioccolato in tutto.
Rappresentiamo in frazione la quantità di cioccolato mangiata da Ginevra.
1 Completa come nell’esempio.
2 Scrivi i numeri decimali nei riquadri. Segui gli esempi.

Questa figura è stata divisa in 100 parti uguali. Ogni parte rappresenta un centesimo. È stata colorata per intero e vale 1 unità .
1
In questa figura non è stata colorata l’unità intera, ma solo i 5 100 , cioè
0 unità , 0 decimi e 5 centesimi 0,05 (si legge “ zero virgola zero cinque ”).
2
1 Nicola vuole comprare un gelato che costa 2 euro, ma ha solo 1 euro e 60 centesimi. Osserva e completa.



• Quanti centesimi mancano a Nicola?
2 Completa come nell’esempio. Poi cerchia il numero minore e il numero maggiore che hai ottenuto.
3 Ordina i numeri dell’esercizio precedente dal minore al maggiore .


















Quando osservi i cartellini dei prezzi, avrai notato che dopo la virgola ci sono due cifre: questo perché l’ euro è diviso in centesimi.

Questa figura è stata divisa in 1000 parti uguali. Ogni parte rappresenta un millesimo. È stata colorata per intero e vale 1 unità .
In questa figura sono stati colorati gli 8 1000 , cioè 0 unità , 0 decimi , 0 centesimi e 8 millesimi 0,008 (si legge “ zero virgola zero zero otto ”).
1 Scrivi la frazione e il numero decimale corrispondente. Segui l’esempio. =












Misurare è un’azione che facciamo tutti i giorni. Misuriamo quando controlliamo il nostro peso, la nostra altezza o quando versiamo nel misurino una quantità di sciroppo, ma anche quando contiamo i soldi per pagare il gelato o la bibita che vogliamo comprare. Misuriamo anche quando guardiamo l’ora per vedere quanto manca al suono dell’intervallo.


Fin dai tempi più antichi si usavano le unità di misura che facevano quasi sempre riferimento a parti del corpo .
Ogni popolo, però, attribuiva valori diversi alle varie unità di misura e questo causava confusione, soprattutto negli scambi commerciali. Oggi in quasi tutti i Paesi del mondo, tra cui l’Italia, si usa un unico sistema di misura: il Sistema Internazionale . Il primo passo per arrivare a questo Sistema fu fatto verso la fine del 1700, quando alcuni scienziati si riunirono in Francia per dare vita a un sistema di misura che fosse uguale per tutti: nacque così il Sistema Metrico Decimale .


Vediamo insieme come hanno lavorato gli scienziati.
metro
Prima hanno definito l’unità di misura della lunghezza , il metro , e lo hanno realizzato con una barra di platino. Poi lo hanno suddiviso in dieci parti uguali, i decimetri , e hanno costruito un contenitore a forma di cubo con gli spigoli interni di 1 decimetro. Questa sarà l’unità di misura della capacità : il litro .
litro
Infine, hanno stabilito che il peso di un litro di acqua distillata, cioè privata di impurità, fosse l’unità di misura del peso e lo hanno chiamato chilogrammo .
1 Hai scoperto che le unità di misura di lunghezza, capacità e peso sono tutte collegate tra loro. Adesso prova a raccontarlo a voce.
1. Procuratevi o costruite un contenitore come quello degli scienziati e delle scienziate.


2. Riempite di acqua una bottiglia da un litro e versatela nel contenitore. Si è riempito completamente? Sì No


Il metro è l’unità di misura fondamentale delle lunghezze. Il suo simbolo è m .
Osserva la tabella: il Sistema Internazionale è decimale , quindi ogni unità di misura è 10 volte più grande di quella alla sua destra e 10 volte più piccola di quella alla sua sinistra.
Quando si deve misurare l’altezza di un grattacielo, la lunghezza di un ponte o la distanza tra due città, allora puoi usare i multipli del metro .

Con il metro puoi misurare, per esempio, la lunghezza di un corridoio o l’altezza di un mobile. Per misurare dimensioni minori di un metro si usano i sottomultipli del metro .
I simboli che usi per le decine ( da ), centinaia ( h ), migliaia ( k ) o per i decimi ( d ), centesimi ( c ) e millesimi ( m ), nelle misure hanno lo stesso significato:


• chilo ( k ): 1000 volte più grande


• etto ( h ): 100 volte più grande
• deca ( da ): 10 volte più grande

• deci ( d ): 10 volte più piccolo
• centi ( c ): 100 volte più piccolo
• milli ( m ): 1000 volte più piccolo
1 Leggi i fumetti e rispondi.
Giulia è alta 130 centimetri
Sei cresciuta tanto rispetto all’ultima visita adesso sei alta 1 metro e 30 centimetri!
• Secondo te, il dottore e il papà di Giulia hanno espresso la stessa misura? Sì No
Confronta la tua risposta con quelle delle compagne e dei compagni e discutine in classe.
Quando una misura si esprime con una unità di misura diversa, pur conservando lo stesso valore, si dice che si fa una equivalenza . Per esempio, 2 dm = 20 cm .

14 centimetri




1 decimetro 4 centimetri
La matita è lunga 14 cm, cioè 1 decimetro e 4 centimetri 14 cm = 1,4 dm.
La matita è stata temperata più volte, adesso è lunga meno di un decimetro.
7 centimetri
1 decimetro
La matita è lunga 7 cm, cioè 0 decimetri e 7 centimetri 7 cm = 0,7 dm.
1 Misura la lunghezza delle matite e scrivi le misure in centimetri e decimetri .

1 Misura gli oggetti e scrivi le misure in centimetri e millimetri . Segui l’esempio.
2 Inserisci le misure nelle tabelle. Segui l’esempio.

Ricorda, la marca , cioè il simbolo dell’unità di misura, si riferisce sempre alla cifra delle unità.

3 Esegui le equivalenze aiutandoti con la tabella.
Moltiplica se passi da una misura più grande a una più piccola.
Dividi se passi da una misura più piccola a una più grande.
Le misure di capacità si usano per misurare la quantità di liquido che un recipiente può contenere. Il litro è l’unità fondamentale e il suo simbolo è <l .



etto litro deca litro litro deci litro centi litro milli litro
I multipli del litro si usano per misurare la capacità di grandi contenitori come una piscina, un’autobotte o una damigiana.

Con i sottomultipli del litro puoi misurare la capacità di piccoli o piccolissimi contenitori, come una lattina di bibita, una tazzina da caffè o una siringa.

Hai già scoperto che c’è un collegamento tra le misure di lunghezza, di peso e di capacità, infatti, se immergi un decimetro cubo (per esempio, il blocco delle migliaia del BAM) in un contenitore con dell’acqua, il livello dell’acqua salirà esattamente di un litro.
Fai questo esperimento: prendi un misurino, riempilo di acqua fino alla tacca a metà e leggi il numero. Poi prendi delle unità dei BAM o dei regoli bianchi e immergili fino a raggiungere la tacca successiva. Condividi le tue osservazioni con la classe.

Con l’acqua del secchio quanti annaffiatoi puoi riempire?



Con l’acqua della bottiglia quanti bicchieri puoi riempire?
2 Scomponi come nell’esempio.
Ricorda : la marca si riferisce
sempre alla cifra delle unità.
145 <l = 1 h <l , 4 da <l , 5 <l
27 d <l = 123 c <l = ............................................................................
34 da <l = 1 595 m <l =


Con lo sciroppo del flacone quanti misurini puoi riempire?
3 Colora nello stesso modo le coppie di misure equivalenti .

4 Esegui le equivalenze aiutandoti con la tabella.
Moltiplica se passi da una misura più grande a una più piccola.
Dividi se passi da una misura più piccola a una più grande.

L’unità di misura fondamentale del peso è il chilogrammo .
Il suo simbolo è kg .
Il chilogrammo ha un solo multiplo , il Megagrammo . Viene usato per misurare oggetti molto pesanti, per esempio, un camion o una nave.

Se vuoi misurare pesi inferiori a un chilogrammo , come un pezzo di formaggio, una penna o una graffetta, puoi usare i sottomultipli del chilogrammo .

Anche il grammo ha i suoi sottomultipli , che vengono usati per misurare piccolissime quantità di sostanze, per esempio nella preparazione dei farmaci.

Moltiplica se passi da una misura più grande a una più piccola.
Dividi se passi da una misura più piccola a una più grande.
Molti dei prodotti che compriamo sono confezionati in contenitori che hanno un peso.
PESO LORDO
Peso della scatola più il peso dei biscotti
PESO NETTO
Peso dei soli biscotti


TARA

Peso della sola scatola
Se conosci due dei tre elementi, puoi ricavare il terzo.
1 Osserva e completa.
2 Risolvi i problemi sul quaderno.
a. Il peso netto di una vaschetta di fragole è di 445 g, la tara è di 69 g. Qual è il peso lordo?

g 250 g
b. Una nave mercantile, a pieno carico, pesa 943 Mg, la merce che trasporta pesa 78 Mg.
Qual è il peso della sola nave?
c. Un vassoio pieno di pasticcini al pistacchio pesa 2 kg, il vassoio vuoto pesa 3 hg.
Qual è il peso netto in ettogrammi?





1 Osserva gli esempi e completa sotto.
Sono 2 euro e 15 centesimi. Cioè € 2,15









Sono 5 euro e 4 centesimi. Cioè € 5,04
Sono euro e centesimi.
Cioè € .........., ..........
Sono euro e centesimi.
Cioè € ,
Sono 75 centesimi.
Cioè € 0,75



























Sono euro e centesimi.
Cioè € .........., ..........

Sono euro e centesimi.
Cioè € ,
2 Componi i prezzi segnando con una ✘ le banconote e le monete necessarie.
€ 9,50
€ 0,95

Anche per il tempo sono state stabilite unità di misura uguali per tutti. L’unità di misura fondamentale per il tempo
è il secondo ( s ), con i suoi multipli: il minuto ( min ), l’ ora ( h ) e il giorno ( d ).
MULTIPLI UNITÀ
giorno ora minuto secondo
Come già sai dall’anno scorso, lo strumento per misurare il tempo è l’ orologio .
1 Leggi l’ora nei quadranti digitali e disegna le lancette.
2 Completa le equivalenze . 2 min = s
4
. Segui
3 Segna con una ✘ la risposta corretta.
Nahian ha partecipato alla maratona di New York. È partita alle 9:15 ed
è arrivata alle 14:10.
Quanto tempo ha impiegato? 4 h e 5 min
5 h e 45 min 4 h e 55 min
1 Osserva le situazioni e completa.
Il bus parte tra mezz’ora! Farò tardi se non mi sbrigo!
Il bus parte alle ore .
Quale detersivo conviene comprare?




Sono due chili esatti! Ecco i suoi 3 euro!
Conviene comprare quello che costa .
Quanto costa 1 chilo di mele?
Io sono alto 1 metro e 75 centimetri.
L’anno scorso ero più basso di te di 40 centimetri. In un anno sono cresciuto di 10 centimetri.
Qual è l’altezza di Andrea?
1 Osserva il disegno e completa. Il gelataio Totò inizia il suo giro davanti alla scuola e lo termina al parco giochi.

Quanti metri di strada percorre? ...............
Quanti ettometri?
2 Ordina le misure di capacità dei recipienti dalla minore alla maggiore.
4 Leggi i problemi e rispondi.

a. Nonna Irene ha preparato una torta che pesa 2 kg.

La taglia in 10 fette uguali. Quanti grammi pesa ogni fetta? ....................




b. Alessia abita a 4 km da casa di sua nonna.
Per andare a trovarla percorre 500 m a piedi e il resto in autobus.
Quanti metri percorre in autobus? Quanti decametri?
Quanti ettometri?
c. La casa di Nina dista 400 m da scuola.
Tra andata e ritorno quanti ettometri percorre? ....................
d. Nonno Mario compra un litro di olio che costa 7 euro.
Quanto costa una latta da 1 da<l ?
e. Per andare a scuola Enrico esce di casa alle 8:10. Il suo amico
Federico esce 20 minuti prima. A che ora esce Federico?
Per festeggiare il cinquantesimo anniversario di matrimonio, nonno Nicola e nonna Giusy portano tutta la famiglia a pranzo alla “Locanda di zia Isa”. Questo è il menù:
Antipasti
Antipasto di mare € 8,00
Antipasto all’italiana € 8,00
Primi piatti
Spaghetti alle vongole € 10,00
Orecchiette al ragù € 7,00
Secondi piatti
Pesce del golfo 1 kg € 50,00
Carne alla brace 1 kg € 20,00
Dolci
Mousse al cioccolato € 5,00
Tiramisù € 5,00
Bevande
Vino della casa 1 <l € 4,00
Acqua 1 bottiglia € 1,00
Caffè € 1,20
Quando nonno Nicola va a pagare, la signora Isa, proprietaria del ristorante, gli dice di aver fatto uno sconto su alcune portate e su alcune bevande…
1 Sottolinea sulla ricevuta i prezzi scontati, esegui i calcoli necessari e completa.
• Quanto ha risparmiato in totale
nonno Nicola? €
• Quanto avrebbe dovuto pagare se la signora Isa non avesse fatto lo sconto?
€ .................
• Nonno Nicola paga
il conto con queste banconote…
… e riceve di resto .
5 antipasti
2 spaghetti alle vongole
2 orecchiette al ragù
1 kg pesce del golfo
1,5 kg carne alla brace
4 tiramisù
1,5 <l vino della casa
2 bottiglie di acqua
2 caffè
€ 40,00
€ 20,00 € 10,00 € 40,00 € 30,00
€ 10,00


€ 5,00
€ 2,00
€ 2,00
Totale € 159,00

Stai per avventurarti in un viaggio alla scoperta della Geometria, ma prima di incamminarti porta con te un pizzico di fantasia e tanta immaginazione! Sì, perché per capire bene la Geometria dovrai imparare a usare gli “occhi della mente”, che ti permetteranno di veder cose che nella realtà non esistono. Per dimostrartelo cominciamo subito con un gioco.
1 Osserva la figura a destra e rispondi. Non aver paura di sbagliare, perché non esistono risposte sbagliate a questa domanda!
• Secondo te, il triangolo bianco, quello con la punta verso il basso, esiste o non esiste?
In realtà, il triangolo bianco non esiste, nel senso che chi ha realizzato questa figura non ha disegnato un triangolo. Eppure, se riesci a vederlo, vuol dire che c’è! E se lo vedi puoi anche misurare i suoi lati e scoprire, per esempio, se è un triangolo equilatero , cioè con tutti i lati uguali.
2 Allora prova: il lato a sinistra misura 4 cm, come vedi nell’esempio. Ora posiziona il tuo righello e misura gli altri due lati:

• misura del secondo lato: cm.
• misura del terzo lato: cm.
È un triangolo equilatero? Sì No
3 Adesso osserva e rispondi a questa domanda: vola più in alto il palloncino verde o il palloncino blu?

Per rispondere hai tracciato con la mente una linea retta.
Finora hai quindi scoperto che è possibile misurare la lunghezza di una linea che si vede ( Figura 1 ), ma anche di una linea che non si vede ( Figura 2 ). Lo fai tutte le volte che misuri la distanza tra due punti.
4 Infine, rispondi a queste domande, sembrano un po’ strane, ma ti faranno capire un’altra cosa importante della geometria.

• Qual è il tuo nome?

• Il tuo nome cambia quando ti sdrai per dormire? Sì No
Allo stesso modo il nome di una figura geometrica non cambia se la vedi girata in un altro verso. Per esempio, un rettangolo non diventa un rombo se lo fai ruotare!
Queste e tante altre cose scoprirai in questo meraviglioso viaggio che ti aspetta!

Osserva attentamente la LIM e l’immagine che vi è proiettata.
La LIM è un solido , quindi occupa uno spazio. Di un solido possiamo misurare 3 dimensioni: lunghezza , altezza e spessore .
L’immagine proiettata sulla LIM è una figura piana , non occupa uno spazio e possiamo misurarne solo 2 dimensioni: lunghezza e altezza .

Ogni spigolo della LIM o ogni lato dell’immagine è una linea .
Di una linea possiamo misurare solo una dimensione: la lunghezza .
Quando due o più linee si toccano o si incrociano formano un punto .
Di un punto non possiamo misurare nessuna dimensione .



Qualsiasi oggetto che occupa uno spazio, piccolo o grande che sia, è un solido; come per esempio il tuo temperino, il tuo zaino, un aereo…
Il nome delle dimensioni può variare in base alla posizione dell’oggetto.
Ci sono dei solidi che hanno delle caratteristiche specifiche e possono essere classificati: sono i solidi geometrici .
Questi solidi possono essere delimitati solo da superfici piane, come per esempio il cubo , la piramide , il prisma … e si chiamano “ poliedri ”.
Altri, invece, possono essere delimitati da superfici piane e curve , come quelle del cilindro o del cono , o da un’unica superficie curva , come quella della sfera .
Questi solidi si chiamano “ solidi di rotazione ”, perché se li appoggi su un tavolo puoi farli rotolare.

Le foto, i disegni, le immagini che vedi alla TV… sono figure piane, perché hanno solo due dimensioni: lunghezza e altezza ; quindi non occupano spazio, perché non hanno la dimensione dello spessore.
Non è importante distinguere la lunghezza dall’altezza, puoi decidere tu.
Anche tra le figure piane ce ne sono alcune che possono essere classificate, come per esempio, le facce dei poliedri e di alcuni solidi di rotazione.
1 Procurati una scatola di cartone, ritagliala come nell’esempio e distendila.
Hai ottenuto lo sviluppo del solido di partenza, che ti permette di vedere tutte insieme le facce da cui è composto. Fai attenzione, però, concentrati solo sulla forma delle facce .
In questo caso vediamo che ciascuna delle sei facce del parallelepipedo è di forma rettangolare e di ciascun rettangolo possiamo misurare due dimensioni.
2 Cerchia con lo stesso colore ogni solido e il suo sviluppo .
Finora hai imparato che i solidi hanno tre dimensioni (lunghezza, altezza e spessore) e le figure piane hanno due dimensioni (lunghezza e altezza). E le linee ? Vediamolo insieme.
1 Ripassa con un dito il contorno di queste figure piane. Poi completa.
Il contorno di queste figure è formato da una , che può essere spezzata, o mista.
2 Ora osserva e completa.
• Vedi una linea tra il triangolo e il quadrato? Sì No
• Ora prendi il righello, traccia una linea e misura la distanza tra i punti più vicini delle due figure.
La distanza è di cm.
Hai unito due punti e hai misurato una distanza in linea retta .
Le linee hanno una sola dimensione: la lunghezza .
Osserviamo da vicino come si classificano le linee rette .
La retta viene rappresentata con dei trattini alle estremità per far capire che non ha né un inizio né una fine.
È illimitata e non cambia mai direzione. Si indica con la lettera minuscola (r).
Se sulla retta metti un punto (A) ottieni due semirette che hanno un inizio, nel punto A, ma non una fine.
Le due semirette hanno la stessa origine (A), ma verso opposto.
Se sulla retta metti due punti (A, B) ottieni un segmento . Il segmento è una parte di retta che ha un inizio e una fine, delimitato da due punti.
Tra retta, semiretta e segmento c’è solo una linea che può essere misurata, scrivi quale:
“secondo me, l’unica linea che si può misurare è ”.
Ora confronta la tua risposta con quelle delle compagne e dei compagni e discutine in classe.
Due rette che vanno nella stessa direzione, quindi mantengono sempre la stessa distanza tra loro e non si incontrano mai, sono parallele .
1
Due rette che non vanno nella stessa direzione e si incontrano in un punto sono incidenti
Due rette incidenti che formano 4 angoli retti sono perpendicolari .
• Le strade perpendicolari a Corso Donizetti sono .
• Le strade parallele a Via Leoncavallo sono .
• Via Salieri è parallela a Via .
• L’incrocio tra Via Vivaldi e Viale Verdi forma due rette .................................................................
Stamattina, l’insegnante ha portato un gruppo di bambini in cortile, poi ha preso un bastone e lo ha sistemato per terra. Ha chiamato Giulia e le ha detto di posizionarsi vicino a una punta del bastone e di stendere il braccio nella stessa direzione. Infine, ha detto a Giulia di cominciare a ruotare lentamente fino a quando non sente “stop”.
Posizione di Giulia al primo “stop”
Giulia si è spostata ancora e ha descritto un angolo più ampio.
• Quanti bambini sono compresi ora nell’angolo?
C’è anche l’insegnante? Sì No
Giulia, nel muoversi, compie una rotazione e descrive un angolo.
Nell’angolo descritto da Giulia ci sono due bambini e un albero.

Posizione di Giulia al secondo “stop”

Elenca a voce tutti gli elementi compresi nell’angolo.
Giulia ha compiuto un giro completo.
• Puoi dire che Giulia ha compreso nell’angolo tutto ciò che sta intorno a sé? Sì No Spiega a voce perché.
L’ angolo è la parte di piano compresa tra due semirette, che hanno la stessa origine, chiamate lati .

Il punto di origine dell’angolo è il vertice .
Poiché le semirette sono infinite, anche l’ angolo è infinito .
Gli angoli della lavagna, della porta, del banco
o di un libro: sono tutti angoli retti ( ).


Costruire un angolo retto è facilissimo.
Prendi un foglio di carta di qualsiasi forma.
Esegui una prima piegatura in qualsiasi punto. 1 2 3
Esegui una seconda piegatura lungo la prima e il tuo angolo retto è pronto.
Puoi visualizzare gli angoli usando due pezzi di cartoncino uniti con un fermacampione. Tieni fermo uno dei due lati e fai ruotare l’altro. Otterrai diversi tipi di angolo.
Se l’asticella ruota meno di un angolo retto, l’angolo è acuto .
Se l’asticella ruota più di un angolo retto, l’angolo è ottuso .
Se la rotazione è doppia dell’angolo retto, l’angolo è piatto .
Se l’asticella compie un giro completo, l’angolo è giro
Le figure piane delimitate da una linea spezzata chiusa sono poligoni . Le figure piane delimitate da una linea curva o mista sono non poligoni .
1 Disegna un altro poligono .
POLIGONI
2 Disegna un altro non poligono .
NON POLIGONI
3 Con il righello chiudi le linee aperte , poi colora di verde i poligoni e di blu i non poligoni .
Una linea aperta non forma
una figura piana, perché non divide il piano in due regioni: una interna e una esterna .
Enrico vuole scoprire qual è il numero minimo di lati che un poligono può avere. Decide di rappresentare i segmenti con degli stuzzicadenti e comincia a disporli sul tavolo.
1 Osserva e completa.
Enrico scopre che per chiudere una linea spezzata sono necessari almeno 3 segmenti. Quindi non può esistere un poligono con meno di .............. lati. Adesso osserviamo insieme le parti di un poligono.
Ogni segmento della linea spezzata è un lato .
Due lati si incontrano in un punto detto vertice
Due lati che si incontrano in un vertice delimitano un angolo .
2 Completa la scheda di ciascun poligono , poi completa.
Numero lati
Numero vertici
Numero angoli
Numero lati
Numero vertici
Numero angoli
Numero lati
Numero vertici
Numero angoli
Numero lati
Numero vertici
Numero angoli
In un poligono il numero dei lati, dei vertici e degli angoli è sempre .
I poligoni sono tanti e hanno nomi diversi a seconda del numero di lati o di angoli.
1 Insieme alle compagne, ai compagni e all’insegnante prova a scoprire il “segreto” dei nomi di questi poligoni .
Tra i quadrilateri ve ne sono alcuni “speciali” che hanno un nome tutto loro.
In un poligono la misura del suo contorno si chiama perimetro ( P ) ed è la somma della lunghezza dei lati .
1 Leggi, osserva e completa.
Il perimetro del seguente rettangolo è stato rettificato e la sua lunghezza
è stata misurata con il righello.
Il perimetro misura cm, perché + + + = cm
2 Misura il perimetro dei seguenti poligoni usando la lunghezza del quadratino come unità di misura: = 1. P = ..........
3 Misura i lati dei poligoni con il righello e calcola il perimetro .
1 Osserva il disegno, rispondi e completa. Paola ha cucito una coperta di forma rettangolare utilizzando quadratini di lana tutti uguali tra loro.
• Quanti quadratini di lana ha cucito Paola?
Quindi possiamo dire che la coperta di Paola ha una superficie di ............ .
La misura della superficie di un poligono si chiama area ( A ).
Luca, Maya e Sara hanno disegnato un gatto con la pixel art. Adesso stanno cercando un modo veloce per contare i quadratini che hanno colorato, cioè per calcolare l’area del gatto.
Per calcolare l’area della testa ho immaginato di spostare i quadratini del collo in mezzo alle orecchie. Poi ho fatto una moltiplicazione.
1 Scrivi le operazioni che hanno fatto Luca, Maya e Sara e calcola.

Per calcolare l’area del corpo ho moltiplicato 9 × 6, poi ho tolto quelli non colorati.
Io, invece, per contare i pixel della coda ho immaginato di spostare i quadratini più a destra di un posto verso sinistra in modo da avere una coda più dritta. Poi ho aggiunto gli altri.

2 Adesso somma i risultati ottenuti e scopri l’ area del gatto.

1 Traccia, dove possibile, l’ asse di simmetria nei seguenti poligoni. Ricorda, alcune figure possono averne più di uno!

Il Tangram è un antico gioco di origine cinese che si ottiene scomponendo un quadrato in sette parti : un quadrato, un parallelogramma e cinque triangoli, di cui due grandi, uno medio e due piccoli. Lo scopo del gioco è quello di formare delle figure usando tutti i pezzi a disposizione.
Costruire un Tangram è molto semplice, segui queste istruzioni.
1. Disegna un quadrato con il lato di 8 cm, se hai un foglio con i quadratini da 1 centimetro sarà ancora più facile. Poi traccia la diagonale AB.
2. Traccia il segmento CD unendo i due punti a metà dei lati.
3. Traccia il segmento EF facendo attenzione che cada sulla metà del segmento CD.
4. Infine traccia i segmenti FG e CH.
Adesso il tuo Tangram è pronto, coloralo come vuoi, incollalo su un cartoncino e ritaglia i pezzi. Cerca di riprodurre le figure degli esempi e poi inventane altre!
1 Per realizzare le seguenti figure puoi utilizzare dei pennarelli o degli stuzzicadenti. Segui le indicazioni e… buon divertimento!
Spostando un solo bastoncino otterrai l’uguaglianza.
Disegna la soluzione.
La sedia è rivolta verso sinistra, spostando solo due bastoncini puoi girarla verso destra.
Ce l’hai fatta? Disegna la soluzione.
2 Le tre rette dividono il primo cerchio in sei parti. Prova a dividere, sempre con tre rette, il secondo cerchio in sette parti.
Nel disegno, colora di giallo gli angoli acuti, di rosso gli angoli retti e di verde gli angoli ottusi. Se hai dubbi, aiutati con un angolo retto.
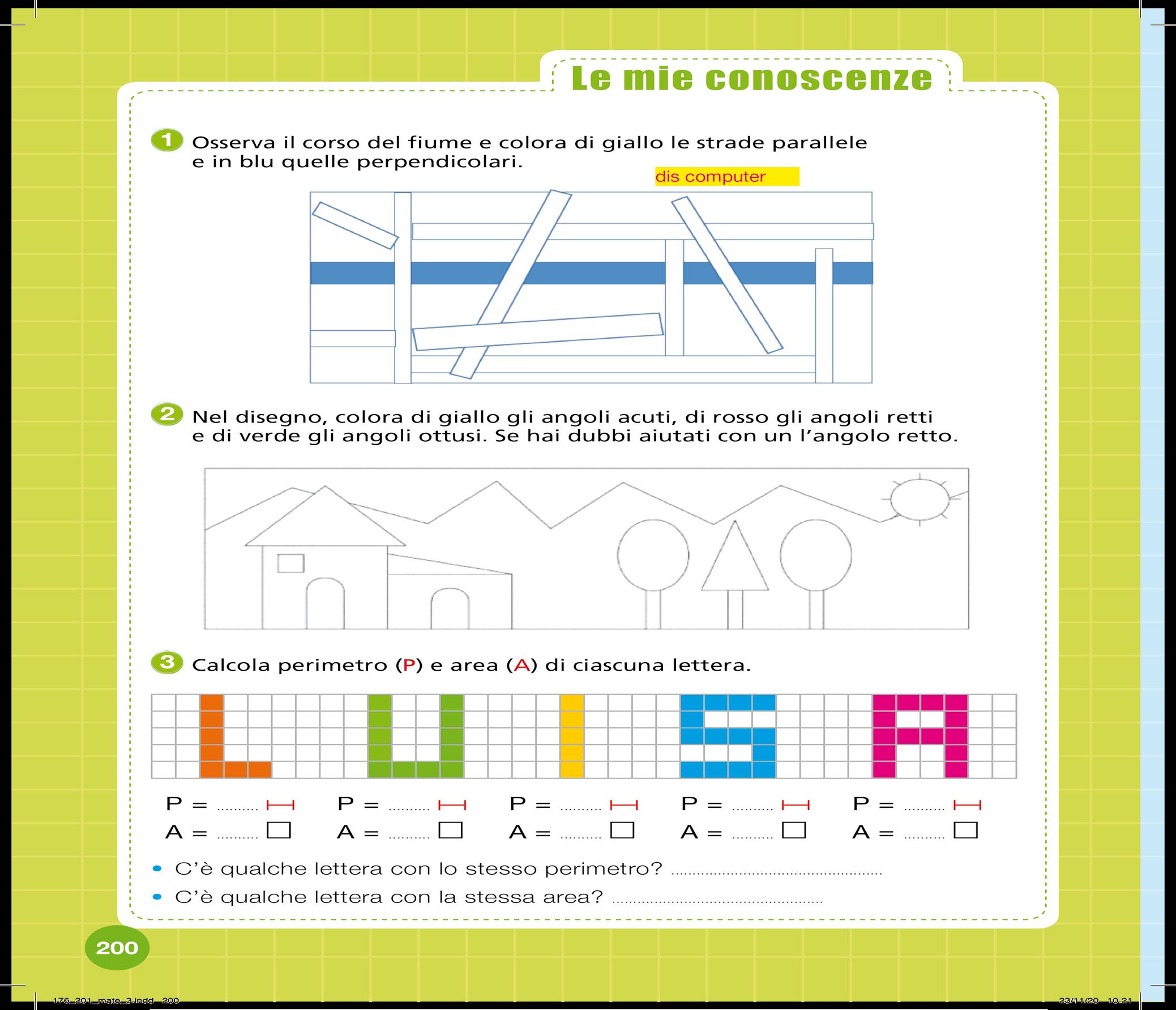
1 Immagina di prolungare i lati degli angoli A e B e colora gli elementi compresi nella loro ampiezza
A B
2 Ora segna con una ✘ la risposta, secondo te, corretta.
È più ampio l’angolo A.
È più ampio l’angolo B.
Motiva la tua risposta:
3 Misura l’area in di queste figure.
1 Leggi i fumetti e completa la tabella. La significa “... ha più anni di...”. Segui l’esempio.
Bea Anton Jozef Eva Jana
Bea ✘ ✘
Anton Jozef
Eva
Jana
Sono Bea e ho 6 anni.
Sono Eva e ho il doppio degli anni di Anton. Sono Anton e ho 9 anni.
Sono Jozef e ho 4 anni.
Sono Jana e ho 1 anno meno di Bea.
2 Cinque ciclisti hanno partecipato a una gara. Osserva la tabella e scrivi l’ordine di arrivo, come nell’esempio.
... è arrivato prima di...
Filippo Ian Stefano Martin Giorgio
Filippo ✘ ✘
Ian ✘ ✘ ✘
Stefano ✘
Martin ✘ ✘ ✘ ✘
Giorgio
3 La significa “... è più alta di...”. Osserva le relazioni e scrivi il nome giusto sotto ciascuna bambina.

Gaia

1
2 La significa “... è il doppio di…”. Segui l’esempio e stabilisci le relazioni.
3 La significa “... è nella tabellina del…”. Segui l’esempio e completa.
Quando comunichiamo con qualcuno, cerchiamo di usare le parole che meglio esprimono ciò che vogliamo dire. Tra queste, ce ne sono alcune che, anche se brevissime, sono molto importanti perché potrebbero cambiare completamente il significato di quello che vogliamo dire. Parliamo dei connettivi logici come “e” e “o”.
1 Leggi.
Anna sta per andare in gita in montagna. La mamma le chiede…
Sì, mamma! Hai preso lo spazzolino e il dentifricio?
Anna ha affermato il vero solo se ha preso sia lo spazzolino sia il dentifricio.
2 Ora osserva bene questa tabella chiamata “Tavola di verità”.
Anna ha preso lo spazzolino
Anna ha preso lo spazzolino
Anna non ha preso lo spazzolino
Anna non ha preso lo spazzolino
Anna ha preso il dentifricio
Anna non ha preso il dentifricio
Anna ha preso il dentifricio
Anna non ha preso il dentifricio
Anna ha detto la verità
Anna non ha detto la verità
Anna non ha detto la verità
Anna non ha detto la verità
Anche i programmatori dei computer usano il connettivo logico “ e ” e il computer risponde “vero” solo in un caso, cioè:
Anna prende spazzolino e dentifricio

Per indicare il connettivo “ e ”, in informatica, si usa la parola inglese AND .

3 Vediamo adesso quest’altra situazione. Leggi. Giovanni e Aurora si stanno scambiando alcune figurine di animali.
Certo! Potresti darmi la figurina di un animale con le macchie o a quattro zampe?
In questo caso Giovanni potrebbe dare a Aurora o un animale con le macchie o un animale a quattro zampe o con entrambe le caratteristiche.


4 Osserva la Tavola di verità.
figurine Animale con le macchie Animale a quattro zampe Risposta del computer
pesce VERO FALSO VERO

leone FALSO VERO VERO
giraffa VERO VERO VERO

uccello FALSO FALSO FALSO
Il programmatore potrebbe dare questo comando al computer:

Figurina Animale a 4 zampe o Animale con le macchie
Per indicare il connettivo “ o ”, in informatica, si usa la parola inglese OR .

La frutta, specialmente di stagione, è un alimento molto sano. Per questo motivo la scuola vuole offrirla come merenda e ha svolto un’indagine sul frutto preferito. Queste sono le preferenze degli alunni della 3ª A.



Mela ✘ ✘ ✘ ✘ ✘
Pera ✘ ✘ ✘
Melagrana ✘ ✘
Uva ✘ ✘ ✘ ✘ ✘ ✘ ✘ ✘
Banana ✘ ✘ ✘ ✘

1 Rappresenta le preferenze nell’ istogramma .

Legenda : = 1 preferenza
• Quanti alunni hanno preso parte all’indagine?
2 Ora osserva i dati riportati nell’ ideogramma e rispondi.
Legenda : = 1 bambino 1 = bambina
Il dato che si
• Qual è la moda?
• Quante bambine preferiscono la mela?
Quanti bambini preferiscono la pera? ..............
Per crescere sani, oltre a una buona alimentazione, è importante fare sport. Il seguente ideogramma rappresenta i dati di un’indagine condotta in una Scuola Primaria sugli sport praticati.
1 Osserva l’ ideogramma e rispondi.
Legenda : = 10 bambini 10 = bambine
Nuoto
Basket
Pallavolo
Calcio
Nessuno sport
• Quante bambine praticano la pallavolo?
• Quanti bambini praticano il basket?
• Quante bambine praticano il calcio?
2 In un’altra scuola hanno condotto la stessa indagine , ma hanno rappresentato i dati in un grafico diverso. Osserva e rispondi.
tennis nuoto rugby calcio
pallavolo
nessuno sport
• Quale sport rappresenta la moda ? ......................................
• Quanti praticano il rugby?
• Quanti non praticano sport? ..............
• Qual è la differenza tra lo sport più praticato e il meno praticato? ...............................................................
In matematica è possibile calcolare la probabilità che un evento si verifichi.
1 Leggi, osserva e rispondi.
A Nico piacerebbe molto vincere un gioco della Pesca della fortuna.
La scatola è divisa in 12 parti, per cui 12 sono gli eventi possibili .
Quanti sono gli eventi in cui Nico non vince nessun gioco?

Quindi la probabilità che Nico non vinca un gioco è 2 su 12 ; in frazione 2 12 .
2 Segui l’esempio e completa.
La probabilità di vincere un vasetto di slime è 4 su 12 ; in frazione 4 12 .



La probabilità di vincere il gioco è su ; in frazione ....... .
La probabilità di vincere una palla è su ; in frazione .
Qual è la probabilità che Nico vinca un gioco? su in frazione




Vuoi imparare a creare grafici con il computer? Segui le indicazioni e scoprirai che sarà facile e divertente. Prima di cominciare devi sapere che le icone che troverai qui potrebbero essere un po’ diverse da quelle che hai sul tuo computer, questo dipende dalla versione installata sul tuo PC.
Clicca sul pulsante start , che in genere si trova in basso a sinistra, scorri fino a trovare il programma excel e clicca.
Comparirà una pagina con tante caselle dette celle . Immetti i dati nelle celle e selezionali tutti.
Clicca sul pulsante inserisci .
L’esempio alla tua destra mostra i dati di un’indagine sugli sport praticati in una classe.
Potrebbe aprirsi questa schermata oppure direttamente il programma. Se si apre una schermata come questa, clicca sul pulsante cartella di lavoro vuota.

Nelle versioni più recenti di excel esiste il pulsante grafici consigliati , che ti presenta i grafici più adeguati al tipo di dati che hai inserito; se non c’è clicca sull’icona del tipo di grafico che ti interessa, per esempio istogramma . Clicca sul tipo di grafico che preferisci, per esempio colonne 3D raggruppate




Ora il tuo grafico è pronto, clicca sulla casella titolo del grafico e scrivi quello relativo alla tua indagine. Se clicchi sul pulsante con il pennello puoi modificare lo stile e il colore .
Infine puoi copiare e incollare il grafico su un altro documento.
Cliccando su uno dei pulsanti dei grafici puoi scegliere di cambiare il tipo di grafico, il computer lo farà in automatico. Ecco alcuni esempi.
Torta 3D
gioca con









Mattia ✘ ✘
Elisa ✘ ✘
Simone ✘ ✘ ✘
David ✘
Mattia Elisa Simone David
2 Stamattina c’è stata un’abbondante nevicata e i bambini vorrebbero uscire in giardino. Leggi il fumetto, osserva e scrivi i nomi al posto giusto nel diagramma.



1 Osserva la tabella e rappresenta le relazioni con le frecce. Segui l’esempio. giubbotto guanti giubbotto e guanti
Può uscire solo chi ha già indossato il giubbotto e i guanti.
•
• case •
• amiche • tavolo • scuola • pesci
singolare plurale singolare plurale
Scrivi in frazione la probabilità di
Ti sei mai chiesto come si fa a organizzare un’uscita scolastica?

Bisogna calcolare le spese di viaggio, quelle d’ingresso a musei, teatri, parchi tematici ecc.
Ora considera questa situazione: tutta la tua scuola parteciperà a una rassegna di cinema per ragazzi .
Innanzitutto si devono fare un po’ di conti :
• ci sarà posto per tutti nella sala o bisognerà fare più gruppi?
• quanti pullman serviranno per il trasporto degli alunni e degli insegnanti?
• quale sarà la spesa per ogni alunno e per ogni insegnante? E la spesa complessiva?
• carta e penna
• in classe, in 2 ore di Matematica
1. Prendete informazioni sul numero preciso delle classi e delle sezioni della scuola e preparate una tabella come questa.
Totale alunni della scuola ............
2. Formate dei gruppi in base al numero di classi che dovete intervistare.
3. Ogni gruppo dovrà raccogliere le informazioni relative al numero di alunni di una o più classi, dopo aver predisposto una scheda così:
• Classe ............
• Sezione ............
• Numero alunni ............
4. Dopo aver raccolto i dati riportateli nella tabella che avete preparato.
5. Quando la tabella sarà completa calcolate il numero complessivo degli alunni della scuola.
A questo punto avete bisogno di altre informazioni :
• ogni classe sarà accompagnata da 2 insegnanti;
• il biglietto del pullman costa 2 euro, sia per gli alunni sia per gli insegnanti;
• il biglietto del cinema costa 3 euro per gli alunni e 5 euro per gli insegnanti;
• i pullman che dovranno accompagnarvi hanno una capienza di 50 passeggeri;
• il cinema ha una capienza di 120 posti.
Adesso che avete tutti i dati, calcolate:
• la spesa complessiva per ogni alunno: € ; per ogni insegnante: €
• la spesa totale per il trasporto: €
• l’incasso del cinema: €
• la spesa complessiva: €
• il numero di pullman che bisognerà prenotare:
• verificate se il cinema riuscirà a ospitare tutta la scuola in un’unica proiezione o ci si dovrà dividere in più gruppi, in quest’ultimo caso calcolate il numero dei gruppi.
Quale parte dell’attività ti è piaciuta di più?
Quale di meno? Perché? ...................................................................................................................................................................................................................................
Avete collaborato nel gruppo? Sì No Ci abbiamo provato
Quanto ti è piaciuta questa attività? Poco Abbastanza Molto
1 Se aggiungi 2 centinaia e 15 unità al numero 40, che numero ottieni?
A. 345
B. 255
C. 615
2 Sono tutte scritture corrette per indicare il numero milletrecentosei tranne una. Indica quella sbagliata.
A. 1 migliaio + 306 unità
B. 1 migliaio + 3 decine + 6 unità
C. 1000 + 300 + 6
D. 1306
3 Osserva la seguente tabella. Poi rispondi.
• Quale numero è scritto nella casella sbagliata?
Cancellalo con una ✘ e riscrivilo nella casella giusta.
4 Usa tre di questi numeri per completare la frase che segue. 12 • 7
19
In una classe ci sono alunni. Le femmine sono ;
i maschi sono la metà delle femmine, cioè
5 Marianna, per il suo compleanno, porta a ognuno dei suoi compagni di classe 5 caramelle. Se ha portato 115 caramelle, quanti sono i suoi amici?
Scegli l’operazione che ti serve per rispondere alla domanda.
A. 115 × 5
B. 115 + 5
C. 115 : 5
D. 115 – 5
6 Sofia, Alessandra e Sebastiano stanno calcolando a mente il triplo di 49.
Io ho fatto 50 + 50 + 50 e poi ho tolto 3.
Io ho fatto 50 × 2 + 49 e poi ho tolto 1.
Io invece ho fatto 50 × 3 – 3.

Sofia Alessandra Sebastiano
Chi di loro ha sbagliato il calcolo?
A. Sofia
B. Alessandra
C. Sebastiano
Motiva la tua risposta.
7 Osserva i segni < , > e scopri i numeri nascosti dalle macchie.
8 Quale numero ottieni se aggiungi 4 unità e 3 decimi al numero 5?
A. 9,3
B. 43,5
C. 7,5
9 L’affitto di una bicicletta costa 2,50 euro l’ora. Francesca prende la bicicletta alle 12:00 e la riconsegna alle 14:00. Attilio prende la bicicletta alle 16:00 e la riconsegna alle 19:00.
Francesca spende € Attilio spende €
10 Letizia, Samuele, Alice e Sofia devono fare a mente la moltiplicazione 15 × 20. Ognuno calcola in modo diverso.
Letizia Samuele 15 × 2 × 10 10 × 20 + 5 × 20
Alice Sofia
15 × 10 × 10 15 × 10 + 15 × 10
Chi di loro ha sbagliato il calcolo?
A. Letizia
B. Samuele
C. Alice
D. Sofia
11 1 ettogrammo di prosciutto costa 3 euro. Angela compra 1 ettogrammo e 1 2 di prosciutto. Quanto spende?
A. € 6,00 B. € 3,50 C. € 4,00 D. € 4,50
12 Il grafico rappresenta il numero di bambini nati in un ospedale nell’ultima settimana.
lunedì martedì mercoledì giovedì venerdì sabato domenica maschi femmine
Segna con una ✘ se le affermazioni sono (V) vere oppure (F) false.
A. Il giorno in cui ci sono state più nascite è sabato. V F
B. Tra i nati di venerdì il numero delle femmine è il doppio di quello dei maschi. V F
C. I nati di martedì sono 24. V F
13 È maggiore la probabilità che esca testa lanciando una moneta o che esca un numero pari lanciando un dado?
A. è maggiore la probabilità che esca testa lanciando una moneta.
B. è maggiore la probabilità che esca un numero pari lanciando un dado.
C. La probabilità è la stessa.
Motiva la tua risposta.
1 Osserva il diagramma.
bambini che possiedono un gatto bambini che possiedono un criceto
Quanti bambini possiedono un criceto?
2 Osserva e rispondi.
Quante mattonelle sono completamente coperte dalla figura?
A. più di 12
B. 12
C. meno di 12
D. non si può sapere perché c’è la figura sopra
3 Osserva la seguente figura e rispondi.

4 m
6 m
Il suo perimetro misura:
A. 20 m
B. meno di 20 m
C. più di 20 m
4 Una matrioska completa pesa 600 grammi. Matilde toglie tre bamboline, poi la pesa di nuovo. Quali bamboline ha tolto Matilde? Cancellale con una ✘ .
5 La scuola ha comprato 300 libri per la biblioteca scolastica scegliendo tra libri di avventura, libri di scienze e fumetti. Con i dati a disposizione è stato costruito questo grafico, ma non è completo. Disegna tu la barra che manca.
6 Osserva la figura e rispondi.
• A quale frazione dell’area della figura corrisponde la parte colorata di rosso?
7 Osserva e rispondi.
: 4 = 10 × 2 =
• Quale numero devi mettere al posto della stella e quale numero al posto del quadrato?
• Al posto della metto il numero A. 60 B. 30 C. 40
• Al posto del metto il numero A. 10 B. 20 C. 40
8 Emma e Maxim misurano lo stesso lato del banco con le loro matite. Emma dice che è lungo 10 matite, Maxim dice che è lungo 7 matite. Chi ha a matita più corta?
A. Emma
B. Maxim
Ne ha spesi la metà per comprare uno zaino.
Poi ha speso 2 euro per un gelato.





• Quanto è costato lo zaino? Quanti soldi sono rimasti a David?
0 1 3
Utilizza tutti i cartellini una sola volta per comporre un numero che sia pari e minore di 200.
Lo scooter sta procedendo a chilometri all’ora.
12 Osserva il poligono e disegnane uno simmetrico rispetto all’asse.
13 Paolo ha due contenitori che contengono palline bianche e palline nere. Osserva, leggi e rispondi.
Paolo dice: “Se metto insieme tutte le palline in un solo sacchetto, la probabilità di estrarre una pallina nera o una pallina bianca sarà la stessa”.
Paolo ha ragione? Sì No
Motiva la tua risposta.







• capisco che cosa sono le Scienze ;
• conosco i diversi tipi di scienziati e scienziate ;
• imparo che per osservare la realtà ci vengono in aiuto vari strumenti ;
• scopro con quale metodo lavorano gli scienziati e le scienziate.

Le Scienze studiano i fenomeni , cioè i fatti che accadono ogni giorno intorno a noi e che possiamo osservare: per esempio gli eventi atmosferici (pioggia, neve, vento, fulmini...), la vita degli animali e delle piante, il movimento degli oggetti...
Gli scienziati e le scienziate vanno alla ricerca del perché accadono i fenomeni ( cause ) e delle loro conseguenze ( effetti ).
I fenomeni sono di varia natura, perciò esistono diversi scienziati.

I BIOLOGI e le BIOLOGHE studiano gli esseri viventi ( animali e vegetali ).
I CHIMICI e le CHIMICHE studiano le sostanze e le loro trasformazioni.
I FISICI e le FISICHE studiano gli elementi non viventi (per esempio la luce , l’ aria e l’ acqua ).
Gli ASTRONOMI e le ASTRONOME studiano i pianeti e gli altri corpi celesti .

I GEOLOGI e le GEOLOGHE studiano com’è fatta la Terra .

Completa: le Scienze studiano .

Sottolinea di rosso i sinonimi di “causa” e di blu i sinonimi di “effetto” : ragione • risultato • motivo • conseguenza • origine
Tu quale scienziato/a preferiresti essere? Perché?




Osservare la realtà significa raccogliere informazioni sul mondo intorno a noi usando i cinque sensi (vista, udito, tatto, olfatto, gusto) ed eventualmente degli strumenti che ci aiutino. Gli scienziati e le scienziate usano diversi strumenti. Conosciamone alcuni.
• La macchina fotografica serve per conservare le immagini di ciò che si osserva.
• Il microscopio ingrandisce ciò che non si vede a occhio nudo.
• Il binocolo permette di osservare elementi lontani.

• Il telescopio permette di osservare elementi lontanissimi, come stelle e pianeti.

• Il computer serve per organizzare e conservare i dati, per realizzare delle ricerche e per confrontarle con quelle di altri scienziati.
Lo scienziato e la scienziata spesso devono anche misurare le caratteristiche della realtà che osservano, per esempio il peso , la capacità , la lunghezza e la temperatura . Per fare questo, utilizzano unità di misura riconosciute da tutti (quelle del Sistema Internazionale delle Misure che studierai in Matematica) e strumenti di massima precisione, come il calibro digitale . Calibro digitale.

Nei loro studi, gli scienziati e le scienziate procedono seguendo un metodo preciso: il metodo sperimentale , che è composto da fasi ordinate.
Lo scienziato e la scienziata, infatti:
1 osservano un fenomeno;
2 si pongono una domanda (Perché accade? Che cosa lo origina?);
3 elaborano un’ ipotesi , cioè provano a immaginare una risposta;
4 realizzano uno o più esperimenti per verificare se la loro ipotesi è giusta;
5 formulano una conclusione , cioè una spiegazione.

1
Perché una moneta leggera affonda e una nave pesante galleggia?
Proviamo a dare una forma diversa a due oggetti dello stesso peso: un pezzo di pongo modellato a forma di pallina affonda, un pezzo uguale modellato a forma di barchetta galleggia.
imparo FACCIO
e
• comprendo che cos’è la materia ;
• distinguo i diversi tipi di materia ;

• scopro le caratteristiche dei materiali e quelle dell’ acqua , dell’ aria e del suolo ;
• capisco perché acqua, aria e suolo sono risorse indispensabili alla vita;
• imparo i comportamenti corretti per non sprecare né rovinare queste preziose risorse.
I banchi, i quaderni, i sassi, i fiumi, i cibi, gli esseri viventi... sono fatti di materia , che possiamo vedere e toccare (legno, ferro, carta, roccia, acqua, farina, carne...). Tutto ciò che ci circonda è fatto di materia e tutta la materia occupa uno spazio .
La materia si dice organica quando fa parte di un essere vivente (pianta o animale) o è prodotta da questo. La materia che non proviene da un essere vivente si chiama invece inorganica .
La materia può presentarsi in tre forme, che si chiamano stati della materia : lo stato solido , lo stato liquido e lo stato gassoso .

• Gli oggetti fatti di materia solida , come il legno, il ferro o la plastica, hanno una loro forma. I solidi, inoltre, occupano uno spazio definito e possiamo afferrarli.
• I liquidi , come l’acqua, il latte o il succo di frutta, non hanno una loro forma, ma prendono quella del recipiente che li contiene. Occupano uno spazio, ma non possiamo afferrarli.

• I gas , come l’aria, non hanno forma, occupano tutto lo spazio che hanno a disposizione e non si possono afferrare.


Solidi, liquidi e gas occupano uno spazio: possiamo far loro occupare uno spazio più piccolo?
Prendi una siringa senza ago, chiudi l’apertura con un dito e premi sullo stantuffo: vedrai che scende un po’ prima di bloccarsi. L’aria, infatti, si può comprimere, cioè schiacciare, per farle occupare meno spazio.
Se metti nella siringa dell’acqua o un gessetto, invece, non puoi comprimerli. I gas si possono comprimere, i solidi e i liquidi no.


Gli oggetti che usiamo ogni giorno sono fatti di materiali diversi: legno, ferro, plastica, marmo, vetro... Ogni materiale ha le sue caratteristiche . Può essere:


• fragile , se si rompe facilmente, come il vetro o la ceramica;
• friabile , se si sbriciola facilmente, come il gesso;
• resistente , se resiste senza rompersi agli urti e alle cadute, come il legno;
• trasparente , se si lascia attraversare dalla luce, come il vetro;
• opaco , se non lascia passare la luce, come il cartone;
• plastico , se si può modellare con le mani o con uno strumento, come la plastilina;

• impermeabile , se non si lascia attraversare dall’acqua, come la plastica;



• permeabile , se lascia passare l’acqua, come la stoffa;
• elastico , se può essere schiacciato o tirato e tornare alla forma iniziale, come la gomma.
L’uomo e la donna hanno imparato a costruire gli oggetti con i materiali che hanno le caratteristiche più adatte ai vari scopi. Le finestre, per esempio, sono fatte di vetro, che è trasparente e lascia passare la luce, e hanno cornici di legno o alluminio, materiali resistenti al vento e alla pioggia.
Elenca i materiali che osservi nell’immagine e indica una caratteristica per ognuno.
I materiali possono essere distinti in:

• naturali esistono in natura;
• artificiali sono prodotti dall’uomo.
L’uomo e la donna ricavano i materiali naturali :
• dalle piante : legno, canapa, lino, cotone…;


• dagli animali : cuoio, lana, seta…;
• dai minerali : marmo, granito, sabbia, ghiaia…
I materiali artificiali vengono prodotti unendo e trasformando i materiali naturali.
Per esempio, la carta si produce dal legno; il vetro si ottiene da un tipo particolare di sabbia; la terracotta e la ceramica derivano dall’argilla; la plastica si ricava dal petrolio.




I metalli , come l’oro, l’argento, il ferro, l’alluminio o il rame, spesso si trovano all’interno delle rocce. Per utilizzarli, devono essere estratti, cioè separati dalla roccia. Come? In forni speciali, ad altissime temperature, i metalli fondono, cioè si sciolgono, e così si separano dalle rocce.
Poi raffreddandosi diventano di nuovo solidi.



Le Scienze studiano i fenomeni, cioè i fatti che accadono intorno a noi e che possiamo osservare. Gli scienziati e le scienziate cercano di spiegare perché i fenomeni accadono (cause) e le loro conseguenze (effetti). Esistono diversi tipi di scienziati e scienziate.
Biologi/biologhe studiano gli esseri viventi.
Fisici/fisiche studiano gli elementi non viventi.
Astronomi/
studiano i pianeti e i corpi celesti.
Per studiare i fenomeni gli scienziati e le scienziate seguono il metodo sperimentale.

Il metodo sperimentale consiste in fasi precise, che partono da un’osservazione, passano attraverso la formulazione di ipotesi e arrivano a una conclusione.
Si osserva un fenomeno.
Ci si pone una domanda.
Si formula un’ipotesi, cioè si immagina una risposta.
Si realizzano esperimenti per verificare se l’ipotesi è giusta.
Si formula una conclusione.
Tutto ciò che ci circonda, che possiamo vedere e toccare e che occupa spazio, è fatto di materia.
La materia si può presentare in tre forme, gli stati della materia: solido, liquido e gassoso (gas).




Materia solida
Ha una sua forma, occupa uno spazio definito e possiamo afferrarla.
Materia liquida

Non ha una sua forma, occupa uno spazio ma non possiamo afferrarla.
Gas
Non ha una sua forma, occupa tutto lo spazio a disposizione e non possiamo afferrarlo.
Completa e osserva le mappe. Poi usale per ripassare.
• Biologi/Biologhe: studiano gli esseri viventi
• Fisici/Fisiche:
gli esperti sono utilizzano
Metodo sperimentale
1. Osservazione
2.
3.
• Astronomi/Astronome:
• Chimici/Chimiche: ...........................................
4.
5. Conclusione
• Geologi/Geologhe: .............................................................................................
• solida
• liquida
• gassosa uno spazio occupa può essere
costituisce
tutti i materiali che sono
• naturali (si trovano in natura)
• artificiali (sono prodotti dall’uomo)
Sulla Terra l’acqua è presente in grande quantità:
• la maggior parte della superficie terrestre
è coperta da mari e oceani ;
• sono fatti di acqua i ghiacciai delle montagne e le distese di neve e ghiaccio delle calotte polari;
• forma le nubi ed è sospesa nell’aria , anche se è invisibile;
• si trova nel suolo .
L’ acqua è una sostanza preziosa : senza di essa, le piante, gli animali e gli esseri umani non potrebbero sopravvivere.
Tutti gli esseri viventi , infatti, sono costituiti in gran parte da acqua e ne hanno un costante bisogno per vivere.
L’acqua dei mari e degli oceani è salata perché è ricca di sali minerali (minuscoli cristalli), come il sale da cucina.
L’acqua dei fiumi, dei laghi, della pioggia, dei ghiacciai e quella nel suolo è dolce .

L’acqua che gli uomini e le donne possono utilizzare per bere, abbeverare gli animali e irrigare le piante è solo quella dolce.
Ma è una minima parte dell’acqua presente sulla Terra: bisogna averne grande cura e rispetto, non dobbiamo né sprecarla né inquinarla.


L’acqua è l’unica sostanza che troviamo in natura nei tre stati:

• l’acqua dei mari, dei fiumi, dei laghi e quella che scorre dal rubinetto è allo stato liquido ;
• la neve, il ghiaccio, la grandine e la brina che copre i prati nelle mattine fredde dell’inverno sono acqua allo stato solido ;


• anche se non lo vediamo, nell’aria è presente vapore acqueo, cioè acqua allo stato gassoso .
Se viene riscaldata o raffreddata, l’acqua passa facilmente da uno stato all’altro. Ogni passaggio ha un nome specifico.
SE RISCALDATA, l’acqua passa dallo…
stato liquido allo stato gassoso
EVAPORAZIONE stato solido allo stato liquido


FUSIONE
SE RAFFREDDATA, l’acqua passa dallo…
stato liquido allo stato solido SOLIDIFICAZIONE

stato gassoso allo stato liquido
CONDENSAZIONE
L’acqua non è l’unica sostanza che può cambiare stato e tu stesso puoi osservare ogni giorno dei cambiamenti di stato che non riguardano questo elemento.
Il burro , per esempio, si scioglie nel pentolino per effetto del calore; se si raffredda torna solido.
La cera della candela si scioglie al calore della fiamma; poi torna solida.


1 Il calore del Sole provoca l’evaporazione dell’ acqua dal mare, dai laghi e dai fiumi.
Essa si trasforma in vapore che sale nel cielo.
2 In cielo l’aria è più fredda e provoca la condensazione del vapore , che si trasforma in minuscole goccioline d’acqua e forma le nuvole .
3 Quando le nuvole incontrano aria più fredda, le goccioline si uniscono, si ingrossano e formano la pioggia .
Se fa molto freddo può avvenire la solidificazione delle gocce d’acqua in neve o grandine .
4 Grazie alle precipitazioni (pioggia, neve, grandine), l’acqua ritorna nel mare, nei fiumi, nei laghi. Una parte penetra nel suolo: qui viene assorbita dalle piante o si deposita in profondità formando le falde acquifere .


Garantire a tutti la disponibilità e la gestione sostenibile dell’acqua e delle strutture igienico-sanitarie.

Quando i rifiuti finiscono in mari, laghi e fiumi inquinano l’acqua, cioè la sporcano e la rendono inutilizzabile: non la si può più bere, né adoperare per dissetare gli animali o per irrigare orti e campi.
A volte la sporcano al punto che le piante e gli animali nell’acqua muoiono.
Quando lasciamo inutilmente i rubinetti aperti , facciamo scorrere l’acqua pulita nello scarico insieme alle acque di rifiuto: è come buttarla via! L’acqua è alla base della vita: è importante comportarsi correttamente nei suoi confronti!
Ci sono piccoli gesti quotidiani che tutti noi possiamo compiere per rispettare l’acqua.

A coppie o a piccoli gruppi riflettete sul vostro modo di utilizzare l’acqua, a casa e a scuola: per esempio avete l’abitudine di lasciare il rubinetto aperto quando vi lavate i denti? Dal bagno della scuola andate via lasciando scorrere l’acqua? Fate la doccia, che consuma poca acqua, o il bagno, per cui ne serve molta di più? Usate l’acqua per giocare? Buttate rifiuti nell’acqua?

Fate un cartellone illustrato da appendere nella vostra aula con elenchi di comportamenti e di suggerimenti. Potete dare due titoli:
• I nostri comportamenti... da correggere / corretti
• Suggerimenti utili a tutti per rispettare
l’acqua
L’aria non ha colore ed è trasparente, quindi non la vediamo , anche se è dappertutto. Possiamo notare però i suoi effetti quando fa muovere le fronde degli alberi, fa sventolare le bandiere, solleva e fa volare le mongolfiere... Quando respiriamo la sentiamo entrare e uscire dal nostro corpo e la sentiamo su di noi quando corriamo.


ESPERIMENTO

L’aria è un insieme di gas diversi . I gas che compongono l’aria sono trasparenti e incolori.


Osserva il diagramma a colonne: esso ti mostra che i gas più abbondanti nell’aria sono l’azoto e l’ossigeno, ma ci sono anche piccole quantità di anidride carbonica, di vapore acqueo e di altri gas.
• L’ ossigeno è il gas che permette di respirare a piante e animali, uomo compreso.
• L’ anidride carbonica è prodotta da tutti gli esseri viventi con la respirazione e dai materiali quando bruciano.
• L’ azoto rende l’ossigeno respirabile, perché puro non potremmo introdurlo nel nostro organismo.
Prendi un bicchiere asciutto e mettilo nel congelatore per circa mezz’ora; poi tiralo fuori.
Vedrai che le sue pareti si riempiono di minuscole goccioline d’acqua.
Infatti, se lo tocchi, le tue dita si bagnano un poco.
La Terra è circondata da uno strato di aria che si chiama atmosfera Oltre a permettere la respirazione dei viventi, l’atmosfera protegge il pianeta dai raggi nocivi del Sole, ma lascia passare quelli utili e impedisce che la Terra si raffreddi.
L’aria contiene particelle invisibili di acqua sotto forma di vapore.
Quando toccano le pareti del bicchiere freddo, si condensano e tornano allo stato liquido.
Che cosa succede all’aria che viene riscaldata?
1 Prendi una bottiglia vuota, un palloncino e un catino pieno di acqua calda.
• Metti il palloncino sul collo della bottiglia. Chiedi a un adulto di immergere per qualche minuto la bottiglia nel catino con acqua molto calda. Vedrai che l’aria dentro la bottiglia, riscaldandosi, gonfia il palloncino.
• Metti la bottiglia con il palloncino sotto l’acqua fredda del rubinetto: il palloncino si sgonfia.
L’aria, se viene riscaldata, si dilata. Lo capiamo perché occupa uno spazio maggiore e gonfia il palloncino.
2 Prendi una bacchetta di legno, della carta velina e della colla. Devi avere a disposizione anche un termosifone acceso.
• Attacca alla bacchetta una decina di striscioline di carta velina.
• Avvicina la bacchetta al termosifone. Vedrai che le striscioline, spinte dall’aria calda, si sollevano.
L’aria calda è più leggera di quella fredda e sale verso l’alto.
Procurati un’asticella di plastica, due palloncini gonfiabili, due graffette, un pezzo di spago lungo 20 cm circa, nastro adesivo.
• Con le graffette fissa alle estremità dell’asticella i due palloncini sgonfi. Fissa l’asticella allo spago con il nastro adesivo e mettila in equilibrio in modo che sia perfettamente orizzontale. Ti basta attaccarla semplicemente a un chiodo.
• Stacca uno dei palloncini e gonfialo, poi appendilo di nuovo nella posizione precedente. Osserva l’asticella e disegna ciò che accade.

L’asticella si abbassa dalla parte del palloncino gonfio.
Gli esperimenti ti hanno permesso di scoprire due caratteristiche importanti dell’aria calda: essa si dilata e diventa leggera, quindi sale verso l’alto.
Ora puoi capire come si forma il vento. Quando il Sole riscalda l’aria , essa diventa più leggera e sale . Lo spazio che lascia vuoto viene immediatamente occupato dall’ aria fredda , che è più pesante.
Vicino alla superficie terrestre gli spostamenti dell’aria danno origine al vento .

e imparo STUDIO
Elenca le caratteristiche dell’aria che hai scoperto in queste pagine.
(ONU) • OBIETTIVO 13.
Promuovere azioni, a tutti i livelli, per combattere il cambiamento climatico.
Gli uomini, le piante e gli animali utilizzano l’ossigeno dell’aria per respirare e quindi per vivere.
Purtroppo, oggi l’aria è minacciata dall’ inquinamento atmosferico . Le industrie, i mezzi di trasporto, gli impianti di riscaldamento delle case producono una grande quantità di anidride carbonica e di altre sostanze , pericolose per i viventi, che modificano la composizione dell’aria, peggiorando la sua qualità.

Non solo: l’aumento dell’anidride carbonica nell’aria fa sì che l’atmosfera trattenga troppo calore. Gli scienziati e le scienziate chiamano questo fenomeno effetto serra , perché l’aria, come i vetri di una serra, “intrappola” il calore del Sole.
Il riscaldamento della Terra ha gravi conseguenze: per esempio, i deserti diventano sempre più grandi e si verificano più spesso fenomeni atmosferici violenti come uragani e alluvioni .
Un’altra causa del peggioramento dell’aria è la deforestazione , cioè la distruzione di boschi e zone verdi: le piante producono ossigeno, perciò meno piante significa meno ossigeno .

Il Sole emette un’enorme quantità di energia sotto forma di luce e calore.
I pannelli solari trasformano quest’energia in energia utile per l’uomo: calore o elettricità.
Questi strumenti permettono di ridurre le emissioni nell’ambiente di anidride carbonica per limitare il surriscaldamento globale.

Discuti insieme alle compagne e ai compagni: che cosa si dovrebbe fare per salvaguardare la qualità dell’aria?

Anche il suolo, come l’acqua e l’aria, è un elemento indispensabile alla vita sulla Terra. Nel suolo le piante affondano le loro radici per assorbire l’acqua e i sali minerali. Nel suolo vivono e scavano la loro tana moltissimi esseri viventi : lombrichi, ricci, talpe, formiche… Il suolo permette all’uomo di coltivare e costruire case e strade.
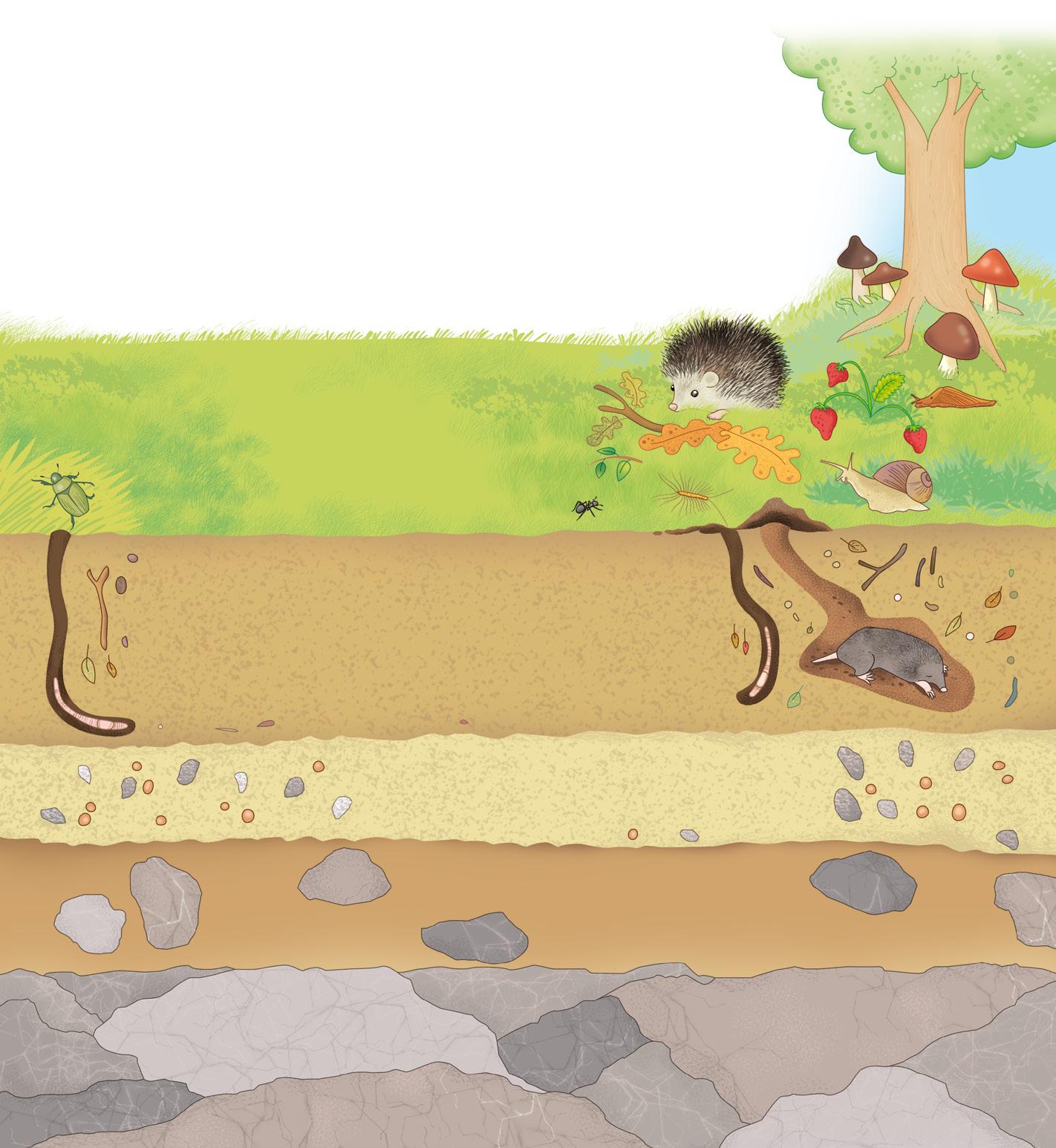
Osserviamolo: il suolo è formato da diversi strati .
1 Lo strato più superficiale è la lettiera . È formata da foglie secche, rametti, frutti caduti, escrementi di animali. È il regno di formiche, millepiedi e centopiedi, lumache e chiocciole.
2 Subito sotto c’è l’ humus , un terriccio scuro e fertile formato dai resti decomposti di piante e animali morti. È qui che le radici delle piante assorbono le sostanze di cui hanno bisogno e che molti animali, come talpe e lombrichi, scavano le loro gallerie.
3 Più sotto troviamo uno strato di argilla , sabbia e ghiaia .
4 Segue il sottosuolo , con grossi pezzi di roccia.
Decomposti significa trasformati in sali minerali; della trasformazione si occupano funghi, muffe, alcuni insetti e altri esseri viventi piccolissimi.
5 Infine c’è uno strato molto compatto di roccia senza terra: la roccia madre
Porre fine alla fame, raggiungere la sicurezza alimentare, migliorare la nutrizione e promuovere un’agricoltura sostenibile. Sulla Terra esistono diversi tipi di suolo , ognuno con una certa composizione. Alcuni sono adatti alla vita delle piante e degli animali, altri no.




• I suoli ricchi di humus e ben aerati (cioè ricchi di aria, soffici) sono fertili : adatti alla vita delle piante e quindi anche alle coltivazioni. Assorbono e trattengono, grazie all’humus, la giusta quantità di acqua.
• Nei suoli ricchi di sabbia o sassi , come quelli delle spiagge e dei deserti, l’acqua penetra in profondità e lascia la parte superficiale asciutta: qui vivono poche piante e pochi animali.
• Alcuni suoli contengono argilla , una terra molto fine, che trattiene l’acqua tra le radici delle piante ed è perciò utile alla loro crescita. Se è troppa, però, forma uno strato impermeabile, così l’acqua non riesce a penetrare nel terreno e rimane in superficie; quando poi l’acqua evapora e l’argilla si asciuga, il terreno si spacca.
È una nuova tecnica di irrigazione che, attraverso un sistema di tubi, distribuisce direttamente alle radici di ogni pianta le quantità sufficienti di acqua e di nutrienti, eliminando sprechi e dispersioni. Sperimentato con successo nel deserto in Israele, questo sistema permette di risparmiare una notevole quantità d’acqua aumentando la resa delle coltivazioni. Per questo l’irrigazione a goccia è già stata esportata con successo in Australia, Cile, Sudafrica e California e si sta diffondendo ora anche in Italia con buoni risultati.

L’acqua è indispensabile per la vita: tutti gli esseri viventi sono formati in gran parte di acqua. Sulla Terra, è presente in grande quantità. Gran parte dell’acqua presente sul nostro pianeta è però costituita da acqua salata.


L’acqua è l’unica sostanza che in natura troviamo nei tre stati: liquido (acqua), solido (ghiaccio) e gassoso (vapore acqueo).

L’acqua passa da uno stato all’altro quando viene riscaldata o raffreddata.
fusione (più calore)
evaporazione (più calore)
ghiaccio acqua vapore acqueo
solidificazione (meno calore)
condensazione (meno calore)
Acqua salata
È ricca di sali minerali, si trova nei mari e negli oceani.
Acqua dolce
È usata per bere e per irrigare i campi, si trova nei ghiacciai, nelle nubi e nell’aria, nei fiumi e nei laghi.
L’acqua sulla Terra passa continuamente da uno stato all’altro: forma così un ciclo. Ecco come funziona.
1 Col calore del Sole, l’acqua si trasforma in vapore acqueo e sale in cielo.
2 Il vapore acqueo si condensa e si formano le nuvole, costituite da piccole goccioline d’acqua.
3 L’aria fredda fa ingrossare le goccioline, che perciò cadono: è la pioggia.
4 La pioggia cade sulla Terra e il ciclo ricomincia.
L’aria non ha colore ed è trasparente, perciò non la vediamo, anche se è dappertutto. La Terra è infatti circondata da uno strato di aria che si chiama atmosfera.
L’aria è formata da un insieme di gas diversi, tra cui i più abbondanti sono:
• l’azoto, che rende l’ossigeno respirabile;
• l’ossigeno, che permette di respirare a piante e animali;

• l’anidride carbonica, prodotta dagli esseri viventi quando respirano e dai materiali che bruciano.
Il suolo è indispensabile alla vita: le piante vi affondano le radici per assorbire acqua e sali minerali; l’uomo lo coltiva e lo utilizza per costruire case e strade; è la “casa” di moltissimi esseri viventi.
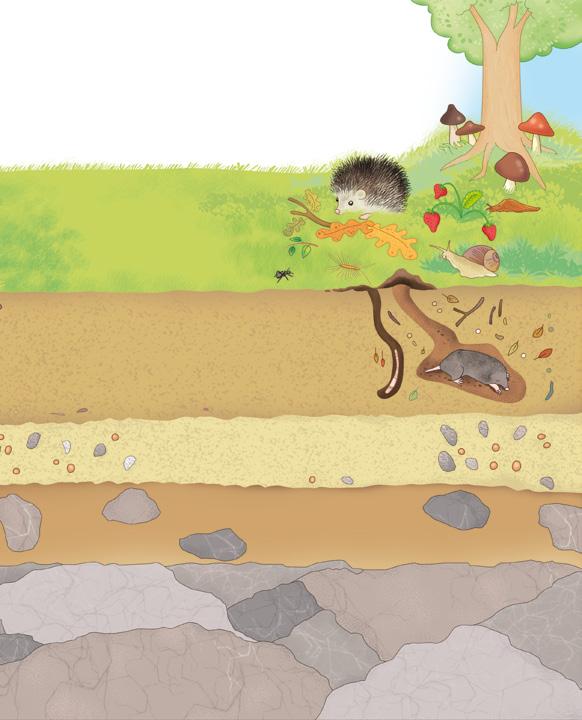
Il suolo è formato da diversi strati:
1 la lettiera, lo strato più superficiale;
2 l’humus, un terriccio scuro e fertile;
3 uno strato di argilla, sabbia e ghiaia;
4 il sottosuolo, con grossi pezzi di roccia;
5 la roccia madre: roccia compatta senza terra.
1 2 3 4 5
Completa la mappa. Scrivi al posto giusto:
condensazione • liquido • esseri viventi • fusione • solido • evaporazione • gassoso • solidificazione
È indispensabile per tutti
gli
I passaggi da uno stato all’altro:
Completa la mappa. Scrivi al posto giusto:
È indispensabile per tutti
gli ............................................................
ACQUA ARIA
Si presenta in tre stati: • • • ...........................................................
ossigeno • esseri viventi • azoto • trasparente • anidride carbonica
È composta da gas: •
È incolore e
Completa la mappa. Scrivi al posto giusto:
lettiera • humus • l’uomo • ghiaia/sabbia/argilla • le piante • roccia madre • gli animali • sottosuolo
È fondamentale per:
È composto da cinque
strati:
1 Segna con una ✘ la risposta corretta.
• Qual è l’ordine corretto delle fasi del metodo sperimentale?
Osservazione, domanda, ipotesi, esperimento e verifica dell’ipotesi, conclusione.
Domanda, esperimento, osservazione, verifica dell’ipotesi, conclusione. Conclusione, osservazione, verifica dell’ipotesi, esperimento, domanda.
• Che cos’è la materia?
È tutto ciò che occupa un edificio.
È tutto ciò che occupa uno spazio.
È tutto ciò che NON occupa uno spazio.
2 Scrivi il nome di:
due materiali naturali di origine animale: due materiali naturali di origine vegetale: due materiali naturali di origine minerale:
due materiali artificiali:
3 Osserva questo pattino. Elenca i materiali che puoi osservare e indica qual è la sua caratteristica principale.

4 Scrivi lo stato dell’acqua nelle tre immagini.

5 Scrivi il nome del passaggio di stato.
• Nel congelatore l’acqua diventa ghiaccio.

• Al Sole la pozzanghera si asciuga.
• I vetri si appannano.
• La neve si scioglie al Sole.


6 Rispondi.
• Che cosa succede all’aria se viene riscaldata?
• Come si forma il vento? ...............................................................................................................................................
7 Scrivi nei cartellini il nome dello strato del suolo.
• imparo a conoscere le piante e comprendo perché sono importanti per tutti i viventi;
• inizio a classificare gli animali e a conoscere le loro strategie di sopravvivenza;
• scopro le relazioni all’interno degli ambienti naturali ( ecosistemi ).

Le piante sono molto diverse tra loro, ma tutte hanno una caratteristica speciale, che le distingue tra i viventi: sono capaci di fabbricarsi il cibo da sole . Sicuramente sai che una pianta vive grazie all’ acqua , ai sali minerali , all’ aria e alla luce del Sole . Osserviamo ora com’è fatta .
Il liquido che circola nella pianta è la linfa: quando è composta da acqua e sali minerali si chiama linfa grezza , quando è già stata trasformata in cibo si chiama linfa elaborata .
Le foglie sono il laboratorio della pianta: trasformano l’acqua e i sali minerali in nutrimento.
Le radici si ramificano sottoterra; tengono la pianta ancorata al terreno e assorbono l’acqua e i sali minerali. Il fusto sostiene la pianta e collega le sue parti. Al suo interno ci sono sottili canali in cui scorre la linfa: quella grezza sale dalle radici alle foglie, quella elaborata raggiunge tutta la pianta.
In base al fusto, i biologi dividono le piante in tre gruppi.
e imparo
Sottolinea di verde la funzione delle foglie , di rosso le funzioni del fusto , di blu le funzioni delle radici .

1 Le erbe hanno un fusto sottile, verde e flessibile, chiamato stelo.
2 Gli arbusti hanno un fusto legnoso che si ramifica da terra.
3 Gli alberi hanno un fusto legnoso (tronco), ricoperto dalla corteccia, che si divide in rami nella parte alta. La corteccia è impermeabile e protegge l’albero dagli urti, dal caldo, dal freddo, dagli insetti.



La foglia è il laboratorio dove la pianta produce il nutrimento di cui ha bisogno. Il processo con cui la pianta produce il nutrimento si chiama fotosintesi clorofilliana e avviene solo di giorno, perché ha bisogno della luce del Sole.


The tree (L’albero) leaves foglie trunk tronco roots radici

Gli zuccheri sono il nutrimento e vengono inviati a tutta la pianta; l’ ossigeno invece è una sostanza di scarto e viene rilasciato nell’aria attraverso gli stomi.

Con la fotosintesi clorofilliana le piante producono una grande quantità di ossigeno. Ne consumano anche una parte, ma ben minore, respirando. Le piante , infatti, respirano .
La fotosintesi avviene solo di giorno; la respirazione, invece, sia di giorno sia di notte.
Come sai già, le piante nascono dai semi . I semi, a loro volta, sono prodotti dai fiori .


2 Quando il polline raggiunge il pistillo dell’altro fiore, scende nell’ ovario Qui il polline incontra l’ ovulo , che comincia a trasformarsi in seme


frutto
3 L’ ovario si ingrossa attorno al seme e diventa un frutto , che ha il compito di proteggere il seme
Per germogliare , cioè per dare origine a una nuova pianta, il seme deve trovare le condizioni adatte: un buon terreno, acqua, la giusta quantità di calore. Deve anche allontanarsi: se le nuove piante crescessero tutte vicino alla pianta madre, dovrebbero dividersi il terreno, l’acqua, la luce.
I semi hanno diversi modi di allontanarsi . Alcuni sono ingeriti dagli animali insieme al frutto e poi espulsi con gli escrementi. Altri invece volano (come i soffioni del tarassaco), galleggiano sull’acqua (come le noci di cocco), si aggrappano con minuscoli uncini al pelo degli animali (come i semi della bardana) o perfino vengono “lanciati” dalla pianta madre.
Cerca le risposte nel testo e sottolineale.
• Che cos’è il polline?
• A che cosa serve il frutto?
• Perché il seme deve germogliare lontano dalla pianta madre?
Le piante, a differenza degli animali, sono capaci di fabbricarsi il cibo da sole. Per vivere, hanno bisogno di acqua, sali minerali, aria e della luce del Sole.


Le piante hanno:

• le radici, che le tengono ancorate al terreno e assorbono l’acqua e i sali minerali;
• il fusto, che le sostiene. Al suo interno ci sono dei sottili canali in cui scorre la linfa;
• le foglie, dove l’acqua e i sali minerali vengono trasformati in nutrimento.
Le piante nascono dai semi, che sono prodotti dai fiori. Ecco come.
1 Sugli stami dei fiori c’è una polverina gialla, il polline. Il vento o gli insetti la trasportano su un altro fiore dello stesso tipo.
2 Quando il polline raggiunge il pistillo, scende nell’ovario. Qui incontra l’ovulo, che così comincia a trasformarsi in seme.
3 L’ovario cresce intorno al seme e diventa un frutto, che ha il compito di proteggere il seme.
Il seme per germogliare, cioè per far nascere una nuova pianta, ha bisogno di un buon terreno, di acqua, di luce e di calore.
Le piante producono il cibo di cui hanno bisogno nelle foglie, mediante un processo che si chiama fotosintesi clorofilliana.
La fotosintesi clorofilliana avviene di giorno perché ha bisogno della luce del Sole. Ecco come avviene:
• alla foglia arrivano l’acqua e i sali minerali del terreno;
• la foglia assorbe dall’aria l’anidride carbonica;

• l’acqua, i sali minerali e l’anidride carbonica vengono trasformati in zuccheri e ossigeno grazie alla clorofilla, una sostanza verde contenuta nelle foglie che cattura la luce solare.

Gli zuccheri sono il nutrimento della pianta; l’ossigeno invece viene rilasciato nell’aria attraverso gli stomi, piccole aperture presenti sulle foglie.
In questo processo perciò le piante producono molto ossigeno.
La fotosintesi clorofilliana avviene solo di giorno; la respirazione, invece, avviene sia di giorno sia di notte.
La linfa è il cibo della pianta. Quella che sale dalle radici alle foglie è formata da acqua e sali minerali e si chiama linfa grezza.
La linfa che è già stata trasformata in nutrimento si chiama linfa elaborata e raggiunge tutte le parti della pianta.
Gli stomi di una foglia Attraverso di essi la pianta assorbe anidride carbonica e rilascia ossigeno.

Completa la mappa e usala per ripassare. sono formate da si dividono in
• trasformano acqua e sali in foglie
• sostengono le rami
tronchi
• sostengono la pianta
• .................................................................................
le sostanze assorbite dal terreno
• ancorate al
radici
• assorbono dal terreno ........................... e
erbe arbusti alberi
funzioni
fotosintesi clorofilliana respirazione traspirazione
avviene in presenza di:
•
• produce il nutrimento
• elimina .....................................
• clorofilla
• luce del sole
• anidride carbonica
• assorbe ossigeno
• elimina ....................................
• elimina l’acqua in eccesso
1 Segna con una ✘ la risposta corretta.
• I biologi e le biologhe dividono le piante in tre gruppi. Quali?
Erbe, arbusti, alberi. Fiori, arbusti, erbe. Alberi, fiori, erbe.


legnoso e ricoperto dalla corteccia
legnoso con rami che partono da terra
...... L’acqua, i sali minerali e l’anidride carbonica vengono trasformati in zuccheri e ossigeno.
La clorofilla cattura la luce solare che fornisce alla foglia l’energia per compierela fotosintesi clorofilliana.
Acqua e sali minerali del terreno (linfa grezza), assorbiti dalle radici, arrivano alla foglia.

La foglia attraverso gli stomi assorbe l’anidride carbonica.
• La pianta quando compie la fotosintesi clorofilliana?
Di giorno. Di notte. Di giorno e di notte.
• La pianta quando respira?
Di giorno. Di notte. Di giorno e di notte.
• Che cosa occorre perché un seme germogli?
Acqua, luce, calore, buon terreno.
Buio, calore, buon terreno.
Acqua, freddo, luce, terreno.
Gli animali sulla Terra sono moltissimi! Per poterli studiare, gli scienziati hanno stabilito una classificazione degli animali in base alle loro caratteristiche. Hanno osservato come funziona e com’è fatto il loro corpo, poi hanno raggruppato gli animali con le stesse caratteristiche.

Il raggruppamento più importante è quello che distingue gli animali che hanno uno scheletro interno , detti vertebrati , da quelli che non ce l’hanno , chiamati invertebrati .

I PESCI vivono nell’ acqua sia salata sia dolce. Hanno un corpo affusolato coperto di scaglie , con coda e pinne

I RETTILI sono quasi tutti terrestri; hanno il corpo allungato che termina con una coda ed è rivestito di squame . Alcuni hanno zampe, altri no.
Vertebrato significa “con le vertebre”. Le vertebre sono le ossa che formano la colonna vertebrale, che sorregge l’intero scheletro.
Animals (Animali)


vertebrates
vertebrati
invertebrates

invertebrati
Gli ANFIBI nascono nell’acqua e da adulti vivono sulla terraferma, ma sempre vicino all’acqua. Hanno la nuda , senza peli né squame.

Gli UCCELLI hanno le ali e il corpo adatto al volo, ricoperto di penne e piume . Hanno il becco e non hanno i denti.
I MAMMIFERI hanno il corpo ricoperto di peli più o meno folti, sono quasi tutti terrestri e hanno quattro arti. Le femmine nutrono i piccoli appena nati con il latte prodotto dalle ghiandole mammarie .

Gli INSETTI hanno
6 zampe e corpo diviso in capo , torace e addome ; possono avere due paia di ali e vivono in tutti gli ambienti.
I CROSTACEI hanno 5 o più paia di arti e 2 paia di antenne . In alcuni gli arti anteriori sono strumenti per afferrare (chele). Sono terrestri e acquatici.






ARACNIDI hanno
8 zampe e corpo diviso in due parti; non hanno ali e sono per lo più terrestri.
Sono animali con corpo molle, a volte protetto da un guscio. Vivono soprattutto nei mari, come le spugne , le meduse , i ricci di mare , le vongole ; alcuni sono terrestri, come i lombrichi .

Fo c u s
Il corpo umano ha una temperatura di 37 gradi circa. Essa rimane uguale sia in estate sia in inverno e aumenta solo se ci si ammala e si ha la febbre. I mammiferi e gli uccelli , infatti, sono animali omeotermi : la temperatura del loro corpo è costante e non dipende da quella dell’ambiente. Tutti gli altri animali , invece, sono eterotermi : la temperatura del loro corpo dipende da quella dell’ambiente esterno. Per questo devono vivere in luoghi dove la temperatura è adatta alla sopravvivenza.

Per sopravvivere, gli animali devono:


• proteggersi dal caldo e dal freddo eccessivi;
• difendersi dai predatori ;
• procurarsi il cibo .
Per far questo, attuano strategie diverse.
Alcuni animali si proteggono dal freddo con folte pellicce o strati di grasso .
Altri, soprattutto gli uccelli, quando arriva l’autunno e le temperature iniziano ad abbassarsi migrano , cioè si trasferiscono in zone più calde, dove possono trovare più cibo. Altri ancora, come le marmotte, si rifugiano nelle loro tane e cadono in letargo. Durante il letargo , che è una specie di sonno, non hanno bisogno di cibo. La lumaca e il rospo possono andare in letargo anche nella stagione più calda.

Una strategia è un sistema, una tattica, a volte un trucco, per ottenere un risultato. Tu, per esempio, usi strategie di calcolo, di gioco e di studio!
Anche tu hai bisogno di difenderti dal freddo e dal caldo eccessivi. Quando fa molto freddo , indossi indumenti di lana o imbottiti : servono a trattenere il calore del corpo. Quando fa molto caldo , il tuo corpo suda, cioè espelle acqua; evaporando, il sudore rinfresca la pelle.

Ricordi? Gli animali possono essere raggruppati secondo le loro abitudini alimentari in erbivori , carnivori e onnivori . Come puoi immaginare, gli erbivori e i carnivori si comportano in modi diversi per procurarsi il cibo e difendersi dai nemici.
Gli erbivori sono le prede dei carnivori, quindi per sopravvivere devono difendersi dagli animali predatori. Molti erbivori si difendono con la fuga Altri si mimetizzano : grazie al colore del loro corpo, si confondono con l’ambiente e così si nascondono alla vista.

Anche la vita di gruppo può essere un sistema di difesa: lo utilizzano alcuni grandi erbivori che abitano la savana e alcuni pesci.
Riconosci l’animale nascosto in questa immagine? Che strategia sta utilizzando?
I carnivori sono sia predatori sia prede , quindi hanno la necessità di attaccare le prede o di scappare dai loro predatori. Per cogliere di sorpresa le prede, alcuni agiscono in velocità, altri si mimetizzano e aspettano. La velocità e il mimetismo sono utili anche per la difesa dai nemici, cioè per scappare o passare inosservati. Alcuni predatori invece cacciano in gruppo per avere più possibilità di catturare la preda, che poi si dividono.
Vero ( V ) oppure falso ( F )? Segna con una ✘.
• Il mimetismo serve solo alle prede. V F
• Tutti i carnivori sono predatori. V F


• Molti erbivori utilizzano la fuga per difendersi. V F
• Gli erbivori sono prede. V F
La farfalla succhia il nettare dei fiori.


Gli animali vivono in tutti i tipi di ambiente : nell’acqua, sopra o sotto il terreno, nell’aria; in luoghi molto freddi e molto caldi.

A differenza delle piante, non sono in grado di fabbricarsi il cibo , quindi dipendono dagli altri esseri viventi per il nutrimento.
Ogni animale, dunque, vive dove riesce a procurarsi il cibo e ha organi adatti a introdurre nel corpo il cibo disponibile.
• Gli insetti sono dotati di pungiglioni (come le zanzare), piccole proboscidi (come le farfalle), mandibole adatte a masticare (come la cavalletta), bocche allungate e con altre forme ancora.
• Gli uccelli hanno becchi di forme diverse. Gli insettivori hanno il becco sottile e appuntito. I carnivori hanno il becco arcuato e tagliente per strappare la carne delle prede. I granivori hanno il becco corto e robusto per beccare chicchi di grano e semi.
Gli altri animali vertebrati sono dotati di denti e mascelle (ossa della bocca).
• I mammiferi erbivori hanno denti taglienti (gli incisivi), per strappare erba e foglie, e altri denti più piatti (i molari), per triturarle.

• I denti dei mammiferi carnivori servono per azzannare la preda e triturarne la carne.

• I denti dei rettili servono solo per trattenere la preda: le loro mascelle si allargano per ingoiare, intere, prede di dimensioni più grandi.
Immagina di dover spiegare da scienziato/a il modo di nutrirsi dell’uomo: descrivi a che cosa servono la bocca e i denti e con quali strumenti l’uomo si aiuta.
L’ ambiente è uno spazio naturale popolato da piante e animali . In ogni ambiente tutti i viventi hanno bisogno uno dell’altro per vivere. Le piante, in particolare, hanno un ruolo fondamentale: producono l’ossigeno necessario alla respirazione, forniscono cibo agli animali e spesso offrono loro ospitalità e riparo.

Negli ecosistemi il Sole ha un’importanza enorme: con la sua luce, infatti, permette la fotosintesi e dunque la vita delle piante.
La vita di animali e piante dipende anche dagli elementi non viventi dell’ambiente, cioè dalla presenza di acqua e luce , dal tipo di suolo , dalla qualità e dalla temperatura dell’aria.


Tutti gli elementi di un ambiente, dunque, sia i viventi sia i non viventi, sono in relazione fra loro e formano un ecosistema , cioè un insieme organizzato .
In ogni ambiente ci sono animali e piante adatti a vivere in quel luogo: i pinguini sono adatti agli ambienti gelidi; i pesci e le alghe a quelli d’acqua salata; il dromedario e alcuni cespugli sopportano il caldo del deserto.

Osserva lo schema: mostra alcuni esseri viventi del bosco; ciascuno è legato a quello successivo e a quello precedente, come gli anelli di una catena, dalla necessità di nutrirsi . Gli scienziati dicono che insieme essi formano una catena alimentare .
Le piante sono il primo anello di tutte le catene alimentari e si chiamano produttori , perché producono da sole il proprio nutrimento e forniscono cibo agli animali.

Contenuti digitali

La freccia significa “è mangiato da”.
Gli animali erbivori si nutrono di vegetali: nella catena alimentare si chiamano consumatori primari .
I funghi , le muffe , i vermi e i batteri si nutrono dei resti di animali e vegetali morti e li trasformano in sali minerali, che servono alle piante. Nella catena alimentare si chiamano decompositori , perché decompongono i resti dei viventi. Sono l’ ultimo anello delle catene alimentari.

Gli animali di un ecosistema si cibano di più piante (o di più animali, se sono carnivori) e vengono a loro volta mangiati da diversi predatori. Appartengono dunque a più catene alimentari e le collegano una all’altra. L’insieme delle catene alimentari di un ecosistema si chiama rete alimentare .
Gli animali carnivori si nutrono di altri animali: nella catena alimentare si chiamano consumatori secondari .


I batteri sono esseri viventi microscopici, invisibili a occhio nudo.
In un ecosistema, viventi e non viventi sono in una condizione di equilibrio naturale.
Tutti i viventi trovano il cibo di cui hanno bisogno:
• le piante bastano per sfamare tutti gli erbivori ;
• gli erbivori bastano per sfamare i carnivori ;
• i decompositori sono in numero sufficiente per decomporre tutti i resti dei viventi.
Anche acqua, aria, luce e suolo contribuiscono all’equilibrio.
Quando un elemento dell’ecosistema viene a mancare o si modifica, tutto l’ecosistema ne risente e l’ equilibrio può rompersi .
Questo può accadere per cause naturali , come alluvioni, terremoti, eruzioni vulcaniche, cambiamenti del clima o malattie di piante e animali. Per esempio, se la siccità fa morire le piante di un ecosistema, gli erbivori muoiono o sono costretti ad andarsene; così anche i carnivori rimangono senza cibo. Anche le attività umane possono minacciare l’equilibrio degli ecosistemi quando per esempio vengono usati troppi pesticidi o vengono disboscate aree verdi per far posto a nuove costruzioni... è importante quindi che l’uomo utilizzi l’ambiente in modo responsabile, cioè con rispetto.
Promuovere azioni, a tutti i livelli, per combattere il cambiamento climatico.

Sottolinea di verde le cause naturali e di rosso le cause umane che possono provocare la rottura dell’equilibrio naturale degli ecosistemi.
L’agricoltura biologica si propone di rispettare l’equilibrio naturale, riducendo ed eliminando l’utilizzo di prodotti chimici come fertilizzanti, pesticidi ecc. Nell’agricoltura biologica vengono usati fertilizzanti naturali come il letame animale e concimi organici come il compost, prodotto con gli scarti vegetali. Invece dei pesticidi, per eliminare i parassiti che danneggiano le piante, si usano preparati di origine vegetale, minerale oppure altri insetti che combattono naturalmente questi organismi nocivi.

Il bosco è un ricchissimo ecosistema organizzato a strati.


Lo strato più alto è formato dalle chiome degli alberi. Tra i rami vivono scoiattoli e uccelli come il picchio. Nelle cortecce si rifugiano ragni e insetti.


Più in basso c’è uno strato di arbusti , come l’agrifoglio, che per vivere si “accontentano” della luce che filtra dall’alto. Qui vivono cervi , caprioli, cinghiali e volano vari insetti.
In penombra, c’è il sottobosco : qui crescono i funghi e le piante che amano l’umidità, come le felci, e vivono chiocciole, lucertole, ricci , volpi.

Lo strato più basso è il suolo , dove abitano talpe, lombrichi, batteri e formiche . Sotto le pietre ci sono millepiedi e porcellini di terra.
e imparo STUDIO
Sottolinea: di verde i produttori , di arancione i consumatori primari , di rosso i consumatori secondari , di blu i decompositori .
Gli scienziati classificano, cioè raggruppano, gli animali in base alle loro caratteristiche. Il raggruppamento più importante distingue tra animali vertebrati e invertebrati






Questi due grandi gruppi a loro volta si dividono in altri sottogruppi.
VERTEBRATI
hanno uno scheletro interno
INVERTEBRATI non hanno uno scheletro interno
Pesci vivono nell’acqua; hanno corpo affusolato, coda, scaglie e pinne.
Anfibi nascono nell’acqua e da adulti vivono sulla terraferma.
Insetti hanno 6 zampe e il corpo diviso in capo, torace e addome.
Aracnidi hanno 8 zampe e non hanno ali.
Rettili hanno corpo allungato e coda; sono ricoperti di squame.
Uccelli hanno le ali e il becco; sono ricoperti di piume e penne.
Mammiferi sono coperti di peli; le femmine nutrono i piccoli con il latte.


Crostacei hanno diverse paia di arti e due paia di antenne.
Animali senza zampe (vermi, spugne, meduse, vongole...) hanno corpo molle, talvolta coperto da un guscio.

L’ambiente è uno spazio naturale popolato da piante e animali, che hanno bisogno l’uno dell’altro per vivere.


La loro vita però dipende anche dagli elementi non viventi, cioè la presenza di acqua, la luce, il tipo di suolo, la qualità e la temperatura dell’aria. Perciò tutti gli elementi di un ambiente, viventi e non viventi, sono in relazione tra loro e formano un ecosistema, cioè un insieme organizzato.
Gli animali e le piante di un ecosistema sono legati tra loro dalla necessità di nutrirsi. Formano quindi una catena alimentare.
Le piante sono produttori: producono da sole il proprio nutrimento e forniscono cibo agli animali.
Gli animali erbivori mangiano le piante; sono consumatori primari

I funghi, le muffe, i vermi e i batteri si nutrono dei resti di animali e vegetali morti e li trasformano in sali minerali necessari alle piante; sono decompositori

Gli animali carnivori mangiano altri animali; sono consumatori secondari.


In un ecosistema, gli erbivori si nutrono di diverse piante e vengono mangiati da diversi predatori. Perciò le catene alimentari di un ecosistema sono collegate le une alle altre e formano le reti alimentari.

Completa la mappa.
con scheletro interno


si dividono in
Invertebrati senza interno







Con le zampe
Senza zampe

sono formati da
relazione fra viventi esseri viventi esseri non in relazione di un
CATENA ALIMENTARE
ambiente
1 Completa la tabella. vertebrato o invertebrato gruppo di appartenenza ambiente in cui vive come si muove come è fatto (corpo)


2 Quali strategie osservi nelle immagini?
3 Scrivi accanto a ogni parola il numero corrispondente alla sua definizione.
1 Sono i funghi, le muffe e i batteri, che si nutrono dei resti di animali e vegetali morti e li trasformano in sali minerali.
2 Sono le piante, che producono da sole il loro nutrimento e forniscono cibo agli animali.
3 Sono gli animali carnivori, che si nutrono di altri animali.



4 Sono gli animali erbivori, che si nutrono di piante.

produttori
consumatori primari
consumatori secondari
decompositori .........
216 La posizione delle cifre
217 Componi e scomponi
218 Confrontare e ordinare numeri
219 Ordina fino al 999
220 Il migliaio
222 A ogni cifra il suo valore
224 Numeri e cifre
225 Confronta e ordina fino al 9999
226 I numeri fino al 9999
227 Le proprietà dell’addizione 228 Addizioni veloci 229 Calcolo mentale 230 L’addizione 231 Addizioni con o senza cambio
232 Ancora addizioni
233 Sottrazione e proprietà invariantiva
234 Sottrazioni con o senza cambio
235 Ancora sottrazioni
236 Addizione o sottrazione?
237 Moltiplicazione e proprietà commutativa
255 Le frazioni
256 La frazione di un numero
257 Dalle frazioni e numeri decimali
258 Decimi, centesimi, millesimi
259 I numeri decimali oltre l’unità
260 Le misure di lunghezza
261 Misure equivalenti
262 Misure di capacità
263 Misure di peso
264 Euro… calcoli
265 Euro… problemi
266 Problemi di misura
267 Da tre a due dimensioni
268 Le line
269 Gli angoli
270 Gli elementi dei poligoni
271 Il perimetro
272 Misurare l’area
273 Giochiamo a hockey!
274 Giochiamo a calcio
275 Al luna park
276 La materia
277 I tre stati della materia
278 L’acqua
279 Dove si trova l’acqua?
280 Di che cosa è fatta l’aria?
281 Il suolo
282 Un laboratorio in una foglia
283 L’albero
284 Vertebrati o invertebrati?
285 Gli animali dormiglioni
286 Comportamenti di difesa/offesa
253 Due domande, due operazioni
254 Una domanda, due operazioni
287 Gli animali si nutrono
288 Una catena alimentare
1 Combina le seguenti cifre in modo da ottenere sei numeri diversi. Poi rispondi.
5 • 7 • 2
• Qual è il numero minore che hai ottenuto? .................. E il maggiore? ..................
2 Per ogni numero scrivi il valore della cifra evidenziata. Segui l’esempio.
1 7 3 = 7 da = 70
7 53 = =
4 = = 2 3 0 = =
3 Completa come nell’esempio.
4 Scrivi il numero minore e il numero maggiore che puoi formare rispettivamente con una, due e tre cifre.
Con una cifra Il minore è .................................................
Con due cifre Il minore è
Con tre cifre Il minore è
5 Completa.
Il nostro sistema di numerazione è:
Il maggiore è .................................................
Il maggiore è
Il maggiore è
• decimale , perché ;
• posizionale , perché .
1 Per ogni treno colora i due vagoni che hanno lo stesso valore della locomotiva.
2 Scomponi come nell’esempio.
138 = 1 h + 3 da + 8 u = 100 + 30 + 8
=
=
=
=
=
4 Completa le scomposizioni.
3 Ordina e componi come nell’esempio.
3 da + 6 h + 2 u = 600 + 30 + 2 = 632
5 u + 1 h + 7 da =
6 u + 8 h =
5 da + 4 u =
3 h + 1 u + 4 da =
7 da + 9 u =
9 h + 4 da = ..................................................................
3 u + 7 h =
352 = 5 da + 2 u + 243 = 40 + 200 +
731 = 7 h + 1 u + 594 = 500 + 4 +
= 8 da +
607 = 7 u + .............................................................
670 = 7 da +
= 9 h +
= 20 +
= 3 + ..................................................................
= 30 +
= 80 +
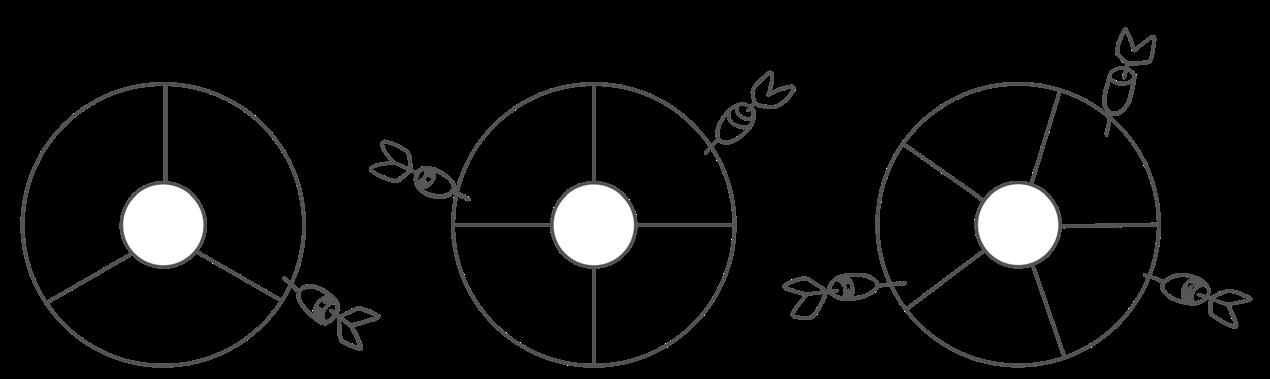
1 Di seguito sono elencati alcuni fiumi italiani. Scrivili in ordine dal più lungo al meno lungo .
Po 652
Volturno 175
Tevere 405
Arno 241
Tagliamento 170
2 Scrivi i numeri nell’ordine richiesto. Poi completa.
• Per ordinare ho guardato prima le cifre delle .
Quando ho trovato numeri con la stessa cifra alle centinaia ho guardato le cifre delle .................................................
• Quando ho trovato numeri con la stessa cifra alle e la stessa cifra alle ho guardato le cifre delle
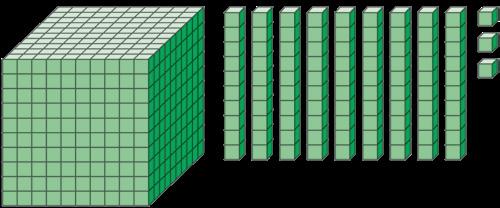
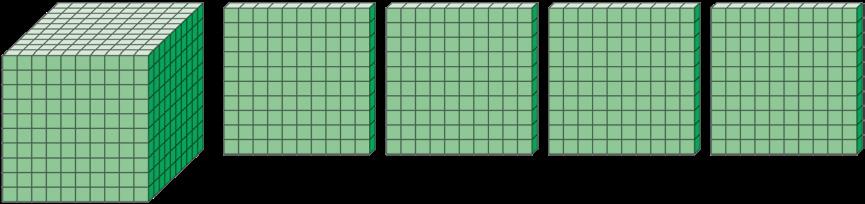
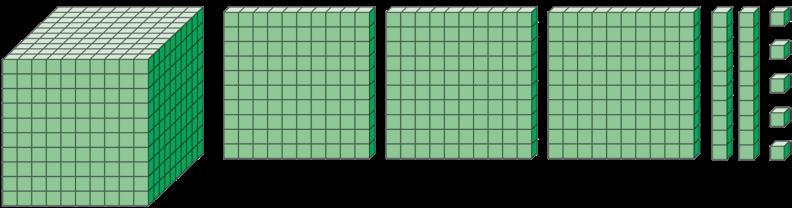
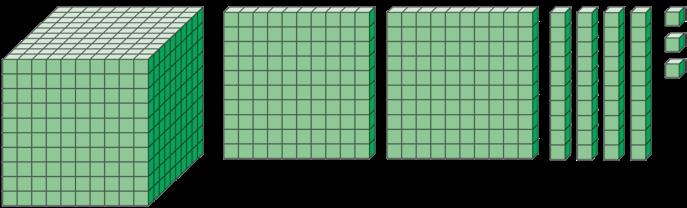
1 Osserva l’esempio e completa.
vale 3 unità
vale 70 unità
vale 400 unità
vale 2000 unità
2 k + 4 h + 7 da + 3 u
2473 = 2000 + 400 + 70 + 3
duemilaquattrocentosettantatré
vale unità
vale unità
vale .............. unità
da h k
= .................................................................................
u 9
7
vale .............. unità
vale unità
vale unità
................................................................................. = MATEMATICA
vale unità
vale .............. unità da h k u 1 1 1 1 222
da h k u 0 0 8 2
vale unità
vale unità
vale .............. unità
vale unità
vale unità
unità
vale .............. unità
vale unità
vale unità
=
vale unità
vale .............. unità
vale unità
................................................................................. =
vale unità da h k u 2 7 5 0 223
1 Scomponi come nell’esempio.
1 967 = 1 k + 9 h + 6 da + 7 u = 1000 + 900 + 60 + 7
5 747 = =
8 523 = ........................................................................................................ = .........................................................................................
3 106 = =
9 035 = =
2 380 = ........................................................................................................ = .........................................................................................
4 723 = =
7 042 = =
2 Metti in ordine e componi come nell’esempio.
4 u + 6 k + 2 da + 9 h = 6 000 + 900 + 20 + 4 = 6 924
1 da + 2 k + 8 h + 6 u = ......................................................................................................................... = ..........................
6 h + 3 da + 2 u + 5 k = =
8 u + 6 h + 9 k + 4 da = =
5 h + 7 k = .............................................................................................................................................................. = ..........................
4 da + 2 k + 8 h = =
9 u + 3 k = =
7 k + 7 u + 3 da = =
3 Per ogni numero scrivi il valore della cifra evidenziata. Segui l’esempio.
1 Disegna sugli abachi le palline del secondo addendo ed esegui le addizioni. Poi rispondi.

• Cambiando l’ordine degli addendi è cambiato il risultato? Sì No
2 Simone e Vanessa stanno raccogliendo i soldi per il regalo del papà. Aiutali a contare i soldi e rispondi.
• Simone e Vanessa hanno la stessa somma? Sì No
• è stato più facile contare i soldi: di Vanessa di Simone?
• Se sostituisci due addendi con la loro somma, il risultato cambia? Sì No








3 Segui l’esempio ed esegui le addizioni.


1 Individua in ogni numero la cifra delle decine (prima tabella), la cifra delle centinaia (seconda tabella), la cifra delle migliaia (terza
2 Fai tappa alla decina più vicina e calcola a
1 Nicolas ha € 31 e Chiara € 24. Decidono di metterli insieme per comporre un puzzle da 1000 pezzi. Per contare più velocemente quanti soldi hanno in tutto, sommano prima le banconote e poi le monete. Osserva e completa.

Gli euro in banconota sono .
Gli euro in moneta sono .

Gli euro in tutto sono






• Per semplificare il calcolo Nicolas e Chiara hanno prima scomposto gli addendi e poi hanno usato la proprietà .

1 Cerchia gli addendi che ti conviene associare e calcola velocemente.
2 Cambia l’ordine degli addendi e verifica che il risultato non cambi.
1 I termini della sottrazione sono: minuendo , sottraendo e resto o differenza . Scrivili al posto giusto.
h da u
5 6 8 –
3 2 5 =
2 4 3 ......................................... o
2 Segna con una ✘ se l’affermazione è vera ( V ) oppure falsa ( F ).
• È possibile eseguire una sottrazione quando il minuendo è minore del sottraendo. V F
• È possibile eseguire una sottrazione quando il sottraendo è uguale al minuendo.
• Quando minuendo e sottraendo sono uguali il risultato è sempre zero.
V F
V F
3
1 Collega ciascun problema al segno giusto e risolvilo sul quaderno.
Lucia ha incollato sul suo album 108 figurine. Per completarlo gliene mancano ancora 69 .
Quante figurine conterrà l’album completo?
Al Palasport ci sono 950 posti a sedere. 732 sono occupati.
Quanti sono i posti liberi?
Lola ha € 96 , ma i suoi jeans preferiti costano € 135 .
Quanti euro mancano a Lola per comprare i jeans?
In un parcheggio su due livelli ci sono 128 auto sul primo livello e 231 sul secondo.
Quante sono le auto in più sul secondo livello?
2 Segna quale operazione devi fare per risolvere i problemi. Poi risolvi sul quaderno.
Su un treno viaggiano 412 passeggeri. Alla prima stazione ne scendono 151 e non sale nessuno. Quanti passeggeri restano sul treno?
Devo fare + –
In un grande albergo sono ospitate 112 persone al primo piano, 107 al secondo e 73 al terzo e ultimo piano. Quante sono le persone ospitate nell’albergo?
Con la nuova auto il papà ha percorso 375 chilometri, la mamma ne ha percorsi 245 . Quanti chilometri sono stati percorsi in totale?
Devo fare + –
Ilenia ha 13 anni. Quando lei è nata sua nonna Mina
ne aveva 64 .
Quanti anni ha ora la nonna di Ilenia?
Devo fare + – Devo fare + –
1 I termini della moltiplicazione sono: moltiplicando , moltiplicatore (detti anche fattori ) e prodotto . Scrivili al posto giusto.
h da u 1 3 4 × 2 = 6 8
moltiplicando
2 Applica la proprietà commutativa e calcola.
7 × 3 = × =
5 × 8 = × =
9 × 2 = ......... × ......... = .............
3 × 6 = × =
Rappresenta il numero 143 per due volte sull’abaco.
6 × 5 = × =
4 × 2 = × =
3 × 8 = ......... × ......... = .............
7 × 10 = × =
da
143 × 2 =
u
237 MATEMATICA

1 Gianni il bibliotecario sta riordinando i libri. Mette 10 libri su ciascuno dei 2 ripiani di ogni scaffale.
A fine giornata ha riordinato 4 scaffali.
Oggi ho riordinato 80 libri, perché 4 × 2 fa 8, 8 × 10 fa 80.
• Per calcolare velocemente, Gianni ha applicato la proprietà associativa . Prova anche tu. Segui l’esempio.
2 Per contare i quadratini di stoffa della coperta, Sara e Luisa hanno calcolato così:
• Per calcolare più facilmente Luisa ha applicato la proprietà distributiva . Ora prova tu.

1 Esegui le moltiplicazioni.
senza cambio h da u h da u h da u h da u h da u h da
2 Esegui le moltiplicazioni in colonna. Fai attenzione a eventuali cambi.
353 × 2 = 225 × 3 = 124 × 5 = 464 × 2 = 147 × 7 = h da u h da u h da u h da u k h da u
1
2
3 Esegui le moltiplicazioni in colonna.
× 3 =
4 Esegui le moltiplicazioni in colonna sul quaderno.
1 Esegui le moltiplicazioni in colonna.
2 Esegui le moltiplicazioni in colonna sul quaderno.
1 Osserva la disposizione dei barattoli nella dispensa. Per contarli velocemente
Eva ha calcolato così:
6 × 3 fa 18
18 + 2 fa 20
cioè: (6 × 3) + 2 = 20
• Forma gli schieramenti e scrivi le espressioni. Segui gli esempi.

2 Imposta le espressioni e risolvi i problemi sul quaderno.
a. Una confezione contiene 24 yogurt. A mensa sono arrivate 9 confezioni più 8 yogurt. Quanti yogurt sono arrivati oggi a mensa?
b. Alice ha collezionato 25 carte da gioco. Compra altre 12 bustine, ciascuna delle quali contiene 5 carte. Quante sono le carte di Alice?
1 Un’industria di elettrodomestici deve spedire 15 lavatrici. Aiuta a distribuire il carico su 3 camion disegnando per ognuno lo stesso numero di lavatrici. Poi completa.
• Lavatrici in tutto
• Camion • Lavatrici su ogni camion
Operazione 15 : 3 = ...............
2 Nonna Lina voleva distribuire 30 bulbi di tulipano nelle sue 5 fioriere. Ma quando i fiori sono spuntati, si è accorta di avere commesso degli errori. Aiutala tu a distribuirli in modo corretto: cancella i fiori dove sono di più e disegnali dove sono di meno.

Ora rispondi alle domande e scrivi la divisione.
• Quanti tulipani ci sono in tutto?
• In quante fioriere sono stati distribuiti?



• Ora ogni fioriera contiene lo stesso numero di tulipani? Sì No
• Quanti tulipani ci sono ora in ogni fioriera?
1 Per le attività di laboratorio l’insegnante ha suddiviso la classe in gruppi uguali. Osserva e completa.
• Da quanti alunni è composta la classe?
• In quanti gruppi è stata divisa?
• Quanti alunni per ogni gruppo? ...............

2 Leggi i problemi e calcola secondo le indicazioni.
Suddividi facendo in modo che ciascuna delle 2 squadre abbia lo stesso numero di giocatori.
Ripartisci le 16 margherite dell’aiuola in 4 gruppi uguali.
Suddividi i 15 muffin in parti uguali su 3 vassoi.

Il negoziante Piero deve disporre in parti uguali 21 barattoli di sottaceti su 3 mensole.
Ha già cominciato; ora continua tu. Quando hai finito, scrivi l’operazione.



Operazione

1 Risolvi il problema con l’aiuto del disegno e della tabella.

Noemi realizza cornici decorate con pietre colorate.
Per ogni cornice usa 8 pietre. Oggi ha comprato una scatola con 48 pietre.
Quante cornici può realizzare? Cerchia 8 pietre per volta e registra in tabella.
Scrivi la divisione : =
Noemi può realizzare cornici.
2 Risolvi i problemi con l’aiuto dei disegni.
Cornici decorate Pietre usate Pietre rimaste ....................... ....................... ....................... ....................... ....................... .......................
Con 30 copertoni a quante biciclette si possono sostituire tutte e 2 le gomme? : =


























































Si possono sostituire le gomme a biciclette.
Con 28 arance quante confezioni da 4 riesci a preparare?
: =
Riesci a preparare confezioni.
1 Giulia ha comprato una scatola di 17 bottoni colorati. Ne vuole applicare 3 a ciascuno dei pupazzi che ha realizzato. Aiutala tu, poi completa.
• È riuscita ad applicare 3 bottoni a ciascuno dei 5 pupazzi? Sì No

• Le sono rimasti dei bottoni? Sì No Se sì, quanti? ...............
Operazione 17 : 3 = resto
3 Risolvi il problema.
Il papà ha dato a Gianni € 30 per comprare delle scatole di caramelle per la sua festa di compleanno. Ogni scatola costa € 7. Quante scatole riuscirà a comprare Gianni? Avanzeranno degli euro? Segui l’esempio e completa.




Operazione : = r









Gianni ha comprato scatole e gli sono rimasti € ...............

1 Esegui le divisioni in colonna e fai la prova.
da u da u da u da u h da u h da u 8 6 2 × 6 9 3 × 4 0 8 4 × da u = da u = h da u =
h da u h da u h da u h da u h da u h da u 6 4 8 2 × 9 6 0 3 × 2 8 0 2 × h da u = h da u = h da u =
1 Collega ciascun problema al segno giusto e risolvilo sul quaderno.
Una fabbrica di spazzolini da denti produce 1350 pezzi al giorno. Quanti ne produce in 6 giorni?
Eva compra un PC a € 890, una stampante a € 199 e un mouse a € 19.

Quanto spende in totale?

In vetrina sono esposti due giubbotti, uno costa € 265, l’altro € 189. Qual è la differenza di prezzo tra i due giubbotti?

4 amici spendono complessivamente € 528 per una gita in montagna. Decidono di dividere la spesa in parti uguali.
Quanto spende ciascuno dei quattro amici?
Antonio ha una collezione di 1248 figurine di calciatori e di 476 figurine di animali.

Quante sono le figurine di Antonio?

Teo colleziona monete antiche e ha completato un album di 62 pagine. Se in ogni pagina ci sono 12 monete, quante sono le monete dell’album?
Il libro che sta leggendo Sabrina è di 235 pagine. Ne ha già lette 74. Quante pagine le restano da leggere? Per il suo compleanno Simone riceve € 90

dai genitori, € 65
dai nonni e € 40
dagli zii. Quanti euro riceve Simone?

1 Leggi attentamente i testi di ogni problema e, in base ai dati, segna con una ✘ solo la domanda o le domande a cui è possibile dare una risposta.
a. Elisa ha 8 anni, suo fratello Filippo ne ha 3 in più.
• Quanti anni ha Filippo?
• Quanti anni aveva Elisa quando è nato Filippo?
• Tra 6 anni, quale sarà l’età di Elisa?
• Quanti anni aveva la mamma quando è nata Elisa?
b. In pizzeria Lucia spende 8 euro per la pizza, 3 euro per la bibita e 2 euro per il coperto.
• Quanto riceve di resto?
• Quanto spende in tutto?
• Con quanti soldi in tasca è uscita di casa?
• Quanto spende per la pizza e la bibita?
c. In un parcheggio ci sono 12 automobili e 7 motociclette.
• Quante ruote puoi contare?
• Quanti sono i veicoli parcheggiati?
• Quanti sono i posti liberi?
• Quante sono le automobili più delle moto?
2 Per ogni operazione inventa un problema sul quaderno. Puoi lavorare anche a coppia o in gruppo.
1 Leggi, osserva e scrivi i dati. Poi risolvi i problemi con l’operazione necessaria e rispondi.
Stefano è un appassionato di musica. Stamattina è andato al negozio di articoli musicali.
Questi sono i soldi che ha a disposizione:
Stefano compra la chitarra e un DVD di video di concerti.

Quanto spende in totale Stefano? Operazione :
Risposta :
Stefano compra la tromba.


Quanti soldi restano a Stefano?
Risposta :
Stefano compra 6 DVD di video di concerti. Quanto spende in tutto?

Dati : Operazione :
Dati : Operazione : .....................................................................
Risposta : ....................................................................................................................................................................................................
2 Inventa un altro possibile problema relativo a questa situazione e risolvilo.
Dati :
Operazione :
Risposta :

1 Leggi i problemi, completa e colora la risposta giusta.
Federico ha 6 paia di scarpe.
Quante sono in tutto le scarpe di Federico?
Il dato nascosto è la parola: .............................
La risposta è:
36 24 12 48
Nel mese di marzo la zia di Johanna ha frequentato un corso di informatica per 18 giorni. Quanti giorni è stata senza frequentare il corso?
Il dato nascosto è la parola: .............................
La risposta è:
9 13 21 8
Il nonno di Luca ha aspettato l’idraulico per 2 ore. Quanti minuti ha aspettato il nonno di Luca?
Il dato nascosto è la parola: .............................
La risposta è: 120 140 60 180
Iacopo ha il quadruplo di carte da collezione del suo amico Giovanni. Se Giovanni ha 13 carte, quante carte ha Iacopo?
Il dato nascosto è la parola: .............................
La risposta è:
36 48 52 71
2 Individua i dati nascosti e risolvi i problemi sul quaderno.
Giulio ha una paghetta di 30 euro al mese.
Quanti euro riceve in un anno?
Diego ha 7 automobiline e 12 motociclette giocattolo. Quante ruote ci sono in tutto?
Nel cortile di nonna Luisa ci sono solo galline e conigli, e sono 7 animali in tutto. Sapendo che le zampe sono 20, sai dire quanti sono i conigli e quante le galline?
Prova a rappresentare la situazione sul quaderno facendo diversi tentativi.
Giulio ha 24 pupazzetti, Emma ne ha la metà, Lucia ha invece il triplo dei pupazzetti di Emma. Quanti pupazzetti ha Lucia?
1 Sottolinea le due domande, osserva lo schema e scrivi le operazioni in riga. Per andare in gita, ciascuno dei 21 alunni della 3ª A ha versato € 15. Quanti soldi hanno versato gli alunni?
La scuola ha contribuito alla spesa con € 180. Quanto è costata la gita?
× =
(soldi versati dagli alunni) ................ + ................ = .....................
(costo della gita, cioè i soldi versati dagli alunni più il contributo della scuola)
Risposta :
2 Risolvi i problemi sul quaderno.
a. Il fiume Brenta è lungo 160 chilometri, l’Adige è più lungo del Brenta di 250 chilometri. Quanto è lungo l’Adige?
L’Arno misura 169 chilometri meno dell’Adige.
Qual è la lunghezza dell’Arno?
b. Al supermercato arrivano 142 confezioni di pomodori. Ogni confezione contiene 6 pomodori. Quanti pomodori in tutto?
Durante il viaggio 98 pomodori si sono rovinati. Quanti pomodori possono essere venduti?
c. Il nonno ha vinto € 405 alla lotteria del Circolo e li distribuisce ai suoi 3 nipoti.
Quanti euro riceve ciascun nipote? Il nipote maggiore spende € 94 della sua parte per comprare la bici. Quanti euro gli restano?
d. Sergio ha comprato 24 bustine di carte da collezione.
Ogni bustina ne contiene 5. Quante carte ha comprato?
Se ne aveva già 354, quante carte ha in tutto?
1 Scrivi nel testo la domanda nascosta e risolvi il problema. Un negoziante ha comprato dal fornitore 9 felpe pagandole € 35 l’una.
Domanda nascosta : ................................................................................................................................................
Se ha pagato con due banconote da € 200, quanto ha ricevuto di resto?
In riga : Risposta :
2 Individua la domanda nascosta e risolvi il problema.
Giorgia ha 20 anni, la mamma ne ha il doppio. Il papà ha 4 anni più della mamma. Quanti anni ha il papà?
Domanda nascosta :
In riga :
Risposta :
3 Risolvi i problemi sul quaderno. Fai attenzione alla domanda nascosta.
a. Il papà ha speso € 75 per il pieno di benzina e € 90 per il cambio dell’olio. Aveva in tasca € 230. Quanti soldi gli sono rimasti?
b. L’anno scorso Anna aveva nel salvadanaio € 60. Oggi ne ha il triplo. Spende la metà per comprare una racchetta da tennis. Qual è il costo della racchetta?
c. Un parcheggio può ospitare 153 auto su ciascuno dei 3 livelli. Stamattina le auto parcheggiate erano 392.
Quanti erano i posti liberi?



 1 Osserva i disegni e scrivi la frazione corrispondente alla parte colorata.
1 Osserva i disegni e scrivi la frazione corrispondente alla parte colorata.
• In quante parti è stata suddivisa la
• Quanti elementi sono stati distribuiti?
• A quale numero corrisponde 1 3 di 15?
• A quale numero corrisponde 2 3 di 15?
1 Osserva e completa. raggiera?1 Completa la tabella delle misure di lunghezza.
MULTIPLI UNITÀ SOTTOMULTIPLI × 10 – : 100
chilometro ettometro decametro metro decimetro centimetro millimetro ...................... ...................... dam m ...................... ...................... ......................
2 Quale unità di misura useresti per queste lunghezze? Segna con una ✘ .
• La lunghezza del tuo temperino: m cm dm
• La distanza tra Roma e Milano: dam m km
• Lo spessore del tuo quaderno: mm dm cm
• La lunghezza di un’automobile: cm m hm
• Il lato lungo della palestra della scuola: hm dm m
3 Inserisci le misure in tabella come nell’esempio. Poi rispondi.
• Qual è la lunghezza maggiore? ..............................................
• E la minore?
1
Usa la tabella a destra per eseguire le equivalenze
più difficili: scrivi la misura da trasformare accanto alla marca indicata, poi raggiungi la misura equivalente moltiplicando o dividendo ogni volta per 10.
2 Ora esegui le equivalenze con l’aiuto della tabella dell’esercizio precedente.
3 Risolvi i seguenti problemi sul quaderno.
a. Il gradino di una scala è alto 20 cm. Una scala di 10 gradini di quanti centimetri ti permette di salire? Di quanti decimetri? Di quanti metri?
b. La pista di un autodromo è lunga 50 hm. Un pilota la percorre 8 volte. Quanti ettometri percorre? Quanti chilometri?
1 Completa la tabella delle misure di capacità. MULTIPLI
2 Inserisci le misure in tabella.

4 Esegui le equivalenze con l’aiuto della tabella a lato.
3 Con la bibita della lattina, quanti bicchieri

1 Completa la tabella delle misure di peso.
MULTIPLI UNITÀ SOTTOMULTIPLI × 100 – : 100

Megagrammo – – chilogrammo ettogrammo decagrammo grammo 100 kg 10 kg kg dag
: 100 grammo decigrammo centigrammo milligrammo
2 Colora nello stesso modo il peso degli oggetti e il gruppo di pesi equivalente.
3 Esegui le equivalenze con l’aiuto della tabella a lato.
74 Mg = kg 25 g = dg
7 g = cg
3 600 mg = dg
9 800 g = hg
500 dag = hg 40 hg = kg


1 700 dg = dag
1 kg = dag 53 hg = g
Mg 100 kg 10 kg kg hg dag g














1 Collega gli euro al valore corrispondente.
€ 135
€ 64
€ 121

€ 59













2 Metti una ✘ in corrispondenza dei soldi necessari a formare il valore richiesto.
€ 500 € 100 € 50 € 20 € 10 € 5 € 2 € 1




€ 127
€ 68 € 573
€ 638
3 Scrivi 3 modi per formare…
1 Calcola e rispondi.
a. Andrea vuole comprare un videogioco e mette insieme i suoi “risparmi”. Andrea ha:
6 banconote da € 5 =


10 monete da € 1 =


2 banconote da € 10 = ..................




• Quanto gli rimane se il videogioco costa € 45?
b. Lo zio ha comprato due DVD di musica classica e ha pagato con le seguenti banconote:
Ha ricevuto il resto di € 2 =
• Quanto sono costati i DVD?
c. Per la gita scolastica i ragazzi dovranno pagare:
– per la prima rata:
– per la seconda rata:
• Quanto costerà in tutto la gita scolastica?
d. Laura vuole comprare 5 pacchetti di figurine per sé e 3 pacchetti per il suo fratellino.
• Se ogni pacchetto di figurine costa 50 centesimi, quanto spenderà in tutto? ..................
1 Leggi i testi e segna con una ✘ se il problema tratta di misure di lunghezza (L), capacità (C), peso/massa (M). Poi risolvi sul quaderno.
a. Stamattina il contachilometri dell’automobile del papà segnava 4932 km, al rientro dal lavoro segnava invece 5018 km.
Quanti chilometri ha percorso il papà? L C M
b. Una damigiana contiene 54 <l di vino. Il vinaio deve travasarlo in bottiglioni da 2 <l .
Quanti bottiglioni gli occorrono? L C M
c. Alice ha il rubinetto della vasca da bagno che perde 4 <l di acqua ogni ora. Quanti litri di acqua si perdono in un giorno? L C M
d. Emilia e Ilenia salgono insieme sulla bilancia pesapersone, totalizzando un peso di 103 kg. Emilia scende e la lancetta della bilancia si ferma sui 59 kg.
Qual è il peso di Emilia? L C M
2 Risolvi i problemi. Fai attenzione alle equivalenze.
a. La signora Eloisa ha comprato 3 hg di prosciutto cotto, 8 hg di pasta fresca e 9 hg di insalata. Quanti chilogrammi pesa la spesa della signora Eloisa?
Operazione : = hg Equivalenza : hg = kg
Risposta :
b. Luca abita a 3 km dalla scuola. Dopo essere sceso dal pulmino, percorre 500 m a piedi. Quanti metri percorre con il pulmino?
Equivalenza : 3 km = ...................... m Operazione : .......................................................................
Risposta :
c. Le mucche di nonno Giuseppe producono 2 h <l di latte in 10 giorni.
Quanti litri di latte producono al giorno?
Equivalenza : Operazione :
Risposta :
1 Osserva le figure e completa le descrizioni inserendo le seguenti parole.
tre • figura piana • lunghezza • solido • altezza • due • spessore

È un ha dimensioni: ,


2 Osserva e completa.
dimensioni:
3 Segna con una ✘ se ciascuna figura piana è delimitata da un confine formato da linee curve (C), spezzate (S) o miste (M).
1 Osserva la retta r e ripassa di rosso tutte le linee del disegno ad essa parallele.
2 Prolunga con il righello le seguenti coppie di rette nella direzione delle frecce e scrivi se sono tra esse incidenti o parallele.
3 Ripassa di rosso il segmento più corto che dal punto A arriva alla retta r e completa la frase.
• Il segmento
è perpendicolare alla ............................................................
1 Classifica in tabella i seguenti angoli. Segui l’esempio.
Angoli
acuto A , retto ottuso piatto giro
2 Collega ogni affermazione al nome dell’angolo a cui si riferisce.
• È ampio come due angoli r etti.
• È più ampio di un angolo retto.
• È ampio come l’angolo di questa pagina.
• È ampio come quattro angoli retti.
• I suoi lati formano una linea retta.
• È ampio la metà dell’angolo piatto.
• È meno ampio di un angolo retto.
• È ampio il doppio dell’angolo piatto.
OTTUSO

1 I poligoni sono figure piane delimitate da una linea spezzata chiusa: con quali dei seguenti elementi riusciresti a costruire un poligono? Completa.
Posso costruire un poligono con gli elementi , non riesco a costruirlo con gli elementi
Per costruire un poligono, una linea spezzata deve avere almeno segmenti.
2 Completa con i termini corretti. lato • vertice • angolo
3 Con il righello unisci i punti A, B, C. Poi ripassa i lati di rosso. Evidenzia gli angoli di giallo e i vertici con un puntino blu.
Ora rispondi.
• Quanti sono i lati? ............................................
• E gli angoli?
• E i vertici?
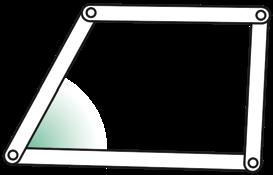
Osserva il perimetro rettificato del poligono e la sua lunghezza misurata prima usando come unità di misura il quadratino, poi il centimetro.
Il perimetro misura 22 , cioè 11 cm .
1 Rettifica i perimetri dei seguenti poligoni e misurali utilizzando il quadratino e il centimetro come unità di misura. Segui l’esempio, poi rispondi.
Il perimetro misura 20 , cioè cm .
Il perimetro misura , cioè cm .
Il perimetro misura , cioè cm
Il perimetro misura , cioè cm .
• Ci sono poligoni che hanno il perimetro della stessa lunghezza? Sì
1 Misurare l’area dei seguenti poligoni utilizzando il come unità di misura.
2 Disegna secondo le indicazioni.
• Un quadrato con l’area di 16 ;
• un rettangolo con l’area di 18 ;
• un poligono che vuoi tu con l’area di 13 .
3 Calcola l’area delle seguenti figure utilizzando come unità di misura.
Al torneo di hockey su ghiaccio possono iscriversi solo i giocatori che hanno, oltre ai pattini, mazza e casco propri.

1 Osserva bene e completa il diagramma. Segui l’esempio. Ha il casco Non ha il casco
2 Ora riproduci la classificazione dell’esercizio precedente in questo diagramma.
mazza casco e Michela Tony Margot1 Classifica i calciatori e le calciatrici nel diagramma ad albero. Segui l’esempio.

CALCIATORI Maglia non a strisce Maglia a strisce
Calzoncini neri Calzoncini neri Calzoncini non neri Calzoncini non neri
2 Classifica i seguenti numeri nel diagramma ad albero.
1 Il grafico rappresenta i dati sui biglietti venduti in un’ora e suddivisi per tutte le attrazioni di un luna park. Osserva e rispondi.
• Quali sono le attrazioni per cui è stato venduto lo stesso numero di biglietti? e .
• Quale attrazione rappresenta la moda ?
• Qual è la differenza di biglietti venduti tra l’autoscontro e la ruota panoramica? .
2 Giovanna è al tiro a segno e ha a disposizione un solo tiro. Osserva e completa.
• Giovanna ha: ............
probabilità su ............ di colpire una casa.
probabilità su di colpire un albero.
probabilità su di colpire un’automobile.

• L’evento più probabile è che Giovanna colpisca .
• L’evento meno probabile è che Giovanna colpisca

1 Cerchia di rosso gli elementi in materia organica e di blu quelli in materia inorganica. Poi completa le frasi.
• Gli elementi costituiti di materia organica provengono da
• Gli elementi costituiti di materia inorganica provengono da ............................................................
1 Qual è lo stato della materia in ogni disegno? Segna con una ✘ .



solido liquido gassoso
solido liquido gassoso
solido liquido gassoso solido liquido gassoso
2 Segna con una ✘ se le seguenti frasi ono vere ( V ) oppure false ( F ).
• I solidi hanno una forma definita. V F
• I liquidi prendono la forma del recipiente che li contiene. V F
• I liquidi possono essere afferrati. V F
• I gas occupano tutto lo spazio a disposizione. V F
• I solidi possono essere compressi. V F
• I gas possono essere compressi. V F
1 Osserva i disegni e completa le frasi con le parole: gassoso • liquido • solido
Il mare è acqua allo stato ................................................
Il ghiaccio è acqua allo stato ................................................
Il vapore acqueo è acqua allo stato .....................................
2 Osserva i disegni e completa le frasi con le parole: condensazione • solidificazione • evaporazione • fusione
La trasformazione dallo stato liquido allo stato gassoso si chiama
La trasformazione dallo stato gassoso allo stato liquido si chiama
La trasformazione dallo stato liquido allo stato solido si chiama ...........................................................................................................................................................................
La trasformazione dallo stato solido allo stato liquido si chiama
1 Leggi il grafico e rispondi alle domande.
Acqua contenuta nel vapore atmosferico.
Acqua contenuta nelle piante e negli animali.
Acqua contenuta nei laghi e nei fiumi.
Acqua contenuta nei ghiacciai.
Acqua sotterranea.
Acqua contenuta negli oceani, nei mari e nei ghiacci polari.
• Dove si trova la maggior parte dell’acqua che c’è sulla Terra?
• L’acqua è presente sulla Terra in tutti i suoi tre stati? ...............................................................................
• In quale stato è maggiormente presente?
• Quali altre informazioni puoi trovare sul grafico?
1 Colora: • 78 quadretti in verde
• 21 quadretti in giallo
• 1 quadretto in rosso
Quanti quadretti hai colorato in tutto?
I quadretti che hai contato indicano, in percentuale, la concentrazione dei vari componenti dell’aria: 78 parti su 100
21 parti su 100

1 parte su 100

1 Individua nel disegno i cinque strati del suolo e scrivi il nome. Scegli tra: roccia madre • humus • sottosuolo • argilla • sabbia e ghiaia • lettiera
.......................................................... .......................................................... ..........................................................
2 Completa le frasi che descrivono la composizione degli strati del suolo.
Lo strato più superficiale del terreno è la lettiera, composta da foglie
Vi è poi uno strato composto di che proviene dagli esseri viventi.
Più sotto c’è uno strato di argilla,
Il sottosuolo è composto da ...........................................
Lo strato più profondo è costituito da
1 Segna con una ✘ .
• La fotosintesi clorofilliana avviene:
solo di giorno. solo di notte.
sia di giorno che di notte.
• La respirazione delle piante avviene: solo di giorno. solo di notte.
sia di giorno che di notte.
• Con la respirazione le piante assorbono dall’aria circostante:
anidride carbonica.
ossigeno.
anidride carbonica e ossigeno.
• Grazie alla respirazione le piante trasformano:
la linfa elaborata in energia.
la linfa grezza in energia.
la linfa grezza in linfa elaborata.




1 Completa le frasi con le parole: foglie • radici • fusto • nervature • rami
L’acqua è assorbita dal suolo attraverso le
L’acqua sale attraverso il e i
L’acqua raggiunge le foglie attraverso le ..................................................................
L’acqua evapora nell’aria attraverso le
Il fusto serve per la riproduzione, perché se è impollinato diventa frutto.
Il seme serve per trasformare i sali minerali in zuccheri e per far respirare e traspirare la pianta.
Il frutto serve per sostenere la pianta e collegare le radici alle foglie.
La foglia serve per assorbire acqua e sali minerali dal terreno.
La radice serve per far nascere una nuova pianta della stessa specie.
Il fiore serve per proteggere il seme.

1 Scrivi i nomi degli animali nell’insieme a cui appartengono. Poi aggiungi tu almeno tre nomi per ogni insieme.
2 Completa le frasi.
• Alcuni animali sono chiamati vertebrati perché
• Alcuni animali sono chiamati invertebrati perché

1 Per trascorrere l’inverno alcuni animali vanno in letargo. Dove? Collega ogni animale al luogo in cui dorme il lungo sonno invernale.
Dorme nel fango vicino allo stagno.
Si rintana in una grotta.
Dorme in un tronco cavo.
Si scava una tana sotto terra.
Si arrotola sotto i sassi.
Si rintana nella fessura di un muro.
1 Osserva gli animali e assegna a ciascuno il numero corrispondente al comportamento di difesa/offesa adeguato. Più animali possono avere lo stesso numero.
1 Si mimetizza.
2 Si appallottola e rizza gli aculei.
3 Rivolge gli aculei verso il nemico.
4 Inietta il suo veleno.
5 Emette un cattivo odore.
6 Colpisce con le corna.
7 Si ritira nella corazza.
8 Usa le chele.
9 Fugge velocemente.
10 Emette un liquido urticante.
11 Emette una “nuvola” di liquido nero e vi si nasconde.
12 Usa i denti.
13 Usa i denti e gli artigli.
14 Usa il becco e gli artigli.
1 Segna con una ✘ .
• Gli erbivori si nutrono di: vegetali.
•
carnivori si nutrono di: vegetali e animali.


•
di:
2 Completa la tabella. Classifica gli animali secondo la nutrizione.
animali.





1 Cerchia di verde i produttori, di blu i consumatori primari (erbivori), di rosso i consumatori secondari (carnivori) e di giallo i decompositori.

2 Disegna una catena alimentare. Ricorda: la freccia significa “è mangiato da”.



Responsabile editoriale: Mafalda Brancaccio
Revisione didattica: Mirna Bernabiti, Alessandra Grandinetti
Coordinamento redazionale: Sarah Farina
Redazione: Valentina Cammilli per Equilibri servizi editoriali, Studio ESSE, Firenze
Responsabile di produzione: Francesco Capitano
Progetto grafico: Monica Marzaioli
Impaginazione: Alberto Sangiorgi
Illustrazioni: Bluedit (Luisa Gaia) - Torino, Mauro Sacco ed Elisa Vallarino
Copertina: Carmen Fragnelli, Elisabetta Giovannini
Ricerca iconografica: Paola Rainaldi
Referenze iconografiche: Shutterstock, Archivio Cetem
Stampa: Tecnostampa – Pigini Group Printing Division
Loreto – Trevi 23.84.018.0
L’editore è a disposizione degli aventi diritto tutelati dalla legge per eventuali e non volute omissioni o errori di attribuzione.
È assolutamente vietata la riproduzione totale o parziale di questa pubblicazione, così come la trasmissione sotto qualsiasi forma o con qualunque mezzo, senza l’autorizzazione della Casa Editrice.
Produrre un testo scolastico comporta diversi e ripetuti controlli a ogni livello, soprattutto relativamente alla correttezza dei contenuti. Ciononostante, a pubblicazione avvenuta, è possibile che errori, refusi, imprecisioni permangano. Ce ne scusiamo fin da ora e vi saremo grati se vorrete segnalarceli al seguente indirizzo: redazione@elionline.com
Tutti i diritti riservati
© 2023 Cetem, Gruppo Editoriale ELi
EquiLibri • Progetto Parità è un percorso intrapreso dal Gruppo Editoriale ELi, in collaborazione con l’Università di Macerata, per promuovere una cultura delle pari opportunità rispettosa delle differenze di genere, della multiculturalità e dell’inclusione.
Si tratta di un progetto complesso e in continuo divenire, per questo ringraziamo anticipatamente il corpo docente e coloro che vorranno contribuire con i loro suggerimenti al fine di rendere i nostri testi liberi da pregiudizi e sempre più adeguati alla realtà.
ISBN per l’adozione: 978-88-473-0715-5



• Letture
• Riflessione Linguistica
• Scrittura e Riassunto Strategie per scrivere e studiare
• Matematica, Scienze e Tecnologia

• Storia,Geografia
ISBN per l’adozione: 978-88-473-0714-8






• Letture
• Riflessione Linguistica e Scrittura
• Matematica
• Storia, Geografia, Scienze, Steam


KIT DOCENTE comprensivo di guida alla programmazione, percorsi semplificati e tutto il necessario per il corso.
LIBRO DIGITALE (scaricalo subito seguendo le istruzioni all’interno della copertina): volumi sfogliabili, esercizi interattivi, audiolibri, tracce audio, canzoni, libro liquido, video tutorial matematica e discipline, percorsi semplificati stampabili.
Benvenute e benvenuti al , un allegro ambiente di apprendimento interattivo che offre tanti oggetti digitali didattici sotto forma di gioco o attività.
Bambine e bambini si divertiranno ad aiutare chef Alfredo: prepareranno insieme a lui tante “ricette” divertenti, organizzeranno feste a tema, allestiranno grandi eventi per tutte le discipline scolastiche, nelle sale o all’aperto! Potranno così rinforzare le abilità e verificare le competenze nelle varie materie attraverso le diverse prove proposte in cucina, facendo ogni volta attenzione al guastafeste Splat, sempre in agguato!

