• Problemi a tappe
• Logica
• Coding
• Operatività
• Sintesi e Mappe per ricordare
Matematica con metodo
Il piacere di apprendere Gruppo Editoriale ELi
3 LIBRO DIGITALE
Big Bang… dal
Con il Big Bang è nata tutta la realtà, ma non sono nati i numeri, le misure, le operazioni.
… alla Matematica
La Matematica è nata quando l’essere umano ha iniziato a contare, calcolare, misurare, classificare… La Matematica è un prezioso strumento per capire la realtà.
SPAZIO
R EL AZIONI, DA E PREVISIONI MISURA
A L TÀ
NUMER I RE
E FIGURE
MATEMATICA
Contenuti digitali del volume
delle cifre 13 Mi esercito 14 Ordinare e confrontare 15 Mi esercito 16 Mi esercito • I numeri fino a 999 18 Il migliaio 19 Mi esercito 20 I numeri oltre il 1000
54 La matematica IN SPIAGGIA
LOGICAmente CON I SAPIENS
Problemi TERZA TAPPA I problemi con più domande 60 Sintesi delle conoscenze I numeri • L’addizione • La sottrazione 62 La moltiplicazione 63 Mi esercito 64 Le tabelline
Le proprietà della moltiplicazione 68 Moltiplicare per 10 • 100 • 1 000 69 Moltiplicazioni in colonna • Moltiplicatore a 1 cifra
Moltiplicazioni in colonna • Moltiplicatore a 2 cifre 71 Mi esercito 72 La matematica IN MONTAGNA 74 La divisione 75 La divisione con il resto 76 Moltiplicazioni e divisioni: operazioni inverse 77 La divisione in colonna 78 La proprietà della divisione 79 Dividere per 10 • 100 • 1 000 80 Mi esercito • Le divisioni 82 La matematica IN PISCINA 84 LOGICAmente CON I SAPIENS 86 Sintesi delle conoscenze La moltiplicazione • La divisione 88 Mi esercito • Le 4 operazioni 90 Problemi QUARTA TAPPA I dati utili, inutili, nascosti 92 Problemi QUINTA TAPPA La domanda nascosta 94 Le frazioni 95 L’unità frazionaria 96 I termini della frazione 97 Mi esercito 98 Uguale o equiesteso? 99 Frazionare una quantità 100 Mi esercito • Le frazioni 4 Il Big Bang e la matematica 6 Un metodo per imparare la matematica 8 UA 1 I numeri e la realtà 10 Il nostro sistema di numerazione 11 Mi esercito 12 Il valore posizionale
24
e i dati 26
TAPPA Il testo e la domanda 28
AL PARCO GIOCHI 30 LOGICAmente CON I SAPIENS 32 L’addizione 33 Mi esercito 34 Le proprietà dell’addizione 36 Strategie di calcolo con l’addizione 37 Addizioni in colonna 38 Addizioni con un cambio o riporto 39 Addizioni con più cambi 40 Mi esercito • Le addizioni 41 Mi esercito • Calcolo rapido 42 La matematica ALLA FESTA DEL LIBRO 44 La sottrazione 45 Mi esercito 46 Operazioni inverse 47 La proprietà della sottrazione 48 Strategie di calcolo con la sottrazione 49 Sottrazioni in colonna 50 Sottrazioni con un cambio o prestito 51 Sottrazioni con più cambi 52 Mi esercito • Le sottrazioni 53 Mi esercito • Calcolo rapido
56
58
66
70
21 Mi esercito 22 Mi esercito • I numeri oltre il 1000
Problemi PRIMA TAPPA Il testo
Problemi SECONDA
La matematica
MATEMATICA
102 La matematica NELLA SERRA 104 Le frazioni decimali 105 Frazioni e numeri decimali 106 Mi esercito • I decimi 107 I numeri decimali 108 I centesimi 109 I millesimi 110 Mi esercito • Frazioni e numeri decimali 112 Mi esercito • I numeri decimali 114 L’euro 115 Mi esercito 116 La matematica AL SUPERMERCATO 118 Problemi SESTA TAPPA So risolvere i problemi! 120 LOGICAmente CON I SAPIENS 122 Sintesi delle conoscenze Le frazioni e i numeri decimali 123 Mappa per ricordare 124 UA 2 La misura e la realtà 126 Le misure di lunghezza 127 I sottomultipli del metro 128 I multipli del metro 129 Le misure di capacità 130 Le misure di peso 131 Peso netto • Peso lordo • Tara 132 Le equivalenze 134 Le misure di tempo 135 Mi esercito • Le misure di lunghezza 136 Mi esercito • Le misure di capacità e di peso 137 Mi esercito • Problemi con le misure 138 La matematica IN AUTOGRILL 140 LOGICAmente CON I SAPIENS 142 Sintesi delle conoscenze • La misura 143 Mappa per ricordare 144 UA 3 La geometria e la realtà 146 Le linee 147 La posizione delle rette 148 Gli angoli 149 Mi esercito 150 I poligoni 151 La classificazione dei poligoni 152 I quadrilateri 153 Mi esercito 154 Mi esercito • Linee e angoli 155 Mi esercito • I poligoni 156 Il perimetro 157 Mi esercito 158 L’area 159 La simmetria 160 I solidi 161 Lo sviluppo dei solidi
Mi esercito • Perimetro e area
Mi esercito • La simmetria • I solidi 164 La matematica NEL CORTILE DELLA SCUOLA 166 LOGICAmente CON I SAPIENS 168 Sintesi delle conoscenze La geometria 169 Mappa per ricordare 170 UA 4 Le relazioni, i dati, le previsioni e la realtà 172 Le classificazioni 173 I diagrammi 174 Indagini statistiche 175 Differenti grafici 176 Le relazioni 177 Certo • Possibile • Impossibile 178 La probabilità 179 Mi esercito 180 Mi esercito • Insiemi e relazioni 182 La matematica PER STRADA 184 LOGICAmente CON I SAPIENS 186 Sintesi delle conoscenze Relazioni • Dati • Previsioni 187 Mappa per ricordare CO D i N G 188 Il coding 189 Comandi precisi 190 I comandi per… 191 La pixel art 192 Compito di realtà Adottiamo uno spazio verde
162
163
Il Matematica Big Bang e la
Il Big Bang è all’origine del tempo, della Terra, della vita… Questo è ciò che studierai quest’anno in Storia, Scienze, Geografia. E la Matematica?
La Matematica è servita agli studiosi e alle studiose per capire e spiegare che cosa è successo anche nel passato così lontano.
Si potrebbe capire la Storia senza la linea del tempo che è fatta di numeri?
Da 4,5 miliardi di anni fa a 600 milioni di anni fa
Da 600 milioni di 250 milioni
senza conoscere i metri e i centimetri?
è alta una montagna e profondo un mare senza la matematica?
4
Da 250 milioni di anni fa a 65 milioni di anni fa
Da 65 milioni di anni fa a 2 milioni di anni fa
Da 2 milioni di anni fa ad ora
E poi…
Nella Preistoria gli uomini e le donne…
… contavano
le amigdale e ne prendevano una parte da portare con sé a caccia. Le prime operazioni.
… con il telaio tessevano quadrati e rettangoli di tessuto.
… cercavano luoghi dove fosse possibile o certo che passasse un branco di animali. Le prime attività di relazione e previsione.
Spiegare ai bambini e alle bambine che con il Big Bang ha avuto origine tutta la realtà che ci circonda, che è poi stata studiata, interpretata attraverso le diverse discipline. La matematica è stata fondamentale per comprendere questa realtà e per risolvere i problemi che via via si presentavano nei diversi studi.
… osservavano il Sole e misuravano il passare dei giorni e il tempo di luce e di buio. L’inizio della misurazione del tempo.
5
la matematica imparare Un metodo
Come imparare?
Per acquisire nuove abilità e competenze in matematica devi imparare a percorrere tutti i passaggi che ti consentono di giungere a una regola, da applicare quando occorre.
Matematica con metodo
Il libro ti spiega come fare
Metacognizione
Per capire attraverso le immagini quanta matematica c’è intorno a te
Cio che gia so
Per recuperare e ricordare ciò che hai già imparato.
Imparo
Tutti i passaggi per comprendere e imparare in modo attivo un procedimento.
La regola
Per sintetizzare e memorizzare quanto hai imparato.
Mi esercito
Pagine per allenarti e consolidare le conoscenze.
6
6
per
CO
PR O B L E M I a tappe
• p proprietà commutativa
matematica... La
LOGICAmente
La sottrazione
La s sottrazione è l’operazione che si fa quando:
• si toglie una quantità e si trova il resto si confrontano due quantità e si trova: la differenza quanto manca
Il s segno è – (meno
I t termini della sottrazione sono: 15 – 4 = 11 minuendo sottraendo resto o differenza
La p proprietà della sottrazione è la proprietà invar antiva
Nella s sottrazione in colonna si sottraggono p prima le unità dal e un tà p poi e decine dal e decine e così via.
A Addizione e sottrazione sono o operazioni inverse
sono:
Nell’aaddizione in colonna si sommano p prima le unità con le unità p poi e decine con le decine, e così via.
Utilizzare queste pagine per spiegare ai bambini e alle bambine come le diverse attività presenti nel volume li/le aiuteranno a seguire il percorso di apprendimento con metodo.
7
61 60 S ntesi de e conoscenze S ntesi del e conoscenze L’addizione I numeri Il nostro s sistema di numerazione è: d decimale perché si raggruppa per 10. 1 k = 1 000 1 h = 1 00 1 d da = 1 0 1 u = 1 0 p posiziona e perché il valore di ogni cifra dipende dalla posizione che occupa nel numero. 231 132 2 1223 L’aaddizione è l’operazione che si fa quando: si a aggiunge una quantità ad un’altra quantità si u uniscono due quantità. Il s segno è + più) I t termini de l add zione sono: 2 + 3 + 1 = 6 addendo somma o totale Le p proprietà dell’addizione
Due simpatici personaggi ti guideranno alla risoluzione di problemi di logica.
10 + 5
1 2 3 p
2 + 2 + 5 = 4 + 5
= 5 + 10 h da u
proprietà associativa
+ 5 15 20 – 5
12 8 = 4 + 2 + 2 14 10 = 4 15 13 = 2 – 2 – 2 13 11 = 2 La
sintesi aiuta a ricordare le regole principali.
Un percorso dedicato alla risoluzione dei problemi matematici diviso in sei tappe. D i N G
Per capire come nella vita di tutti i giorni affrontiamo situazioni problematiche anche senza rendercene conto.
Lo schema riassume gli argomenti trattati e guida a ricordare le conoscenze di base.
Sintesi delle conoscenze
I numeri e la realtà
L’Homo sapiens nella Preistoria non sapeva scrivere i numeri, ma conosceva le quantità e probabilmente contava.
La stessa cosa è successa a te. Anche quando eri molto piccolo/a sapevi quanto valeva 1, quanto valeva 2…
Poi hai cominciato a operare con i numeri.
Classe capovolta: vedo e imparo dalle immagini
Osserva e rispondi.
• Sei a 320. Quale coppa hai vinto?
• Finalmente hai raggiunto quota 599.
Quanto ti manca per conquistare l’oro?
8
UA 1
• Qual è il problema illustrato? .................................
• Come si può risolvere?
• C’è una sola soluzione?
Il bambino è davanti a un negozio di articoli sportivi. Sa se…
• può comperare il pallone?
• avrà un resto?
Per sapere se può comperare l’orsetto a questo bambino manca un dato.
Quale?
Le abilità matematiche possono essere applicate nella realtà e nella vita di tutti i giorni. Per risolvere un problema occorre analizzare la situazione e individuare i dati a disposizione.
La metacognizione aiuta i bambini e le bambine a recuperare le conoscenze pregresse e a utilizzare l’intelligenza numerica innata. Un percorso attraverso la presentazione di situazioni reali aiuta i bambini e le bambine a costruire consapevolmente la propria conoscenza.
9
Ripetiamo insieme
IL NOSTRO SISTEMA DI NUMERAZIONE
Cio che gia so
Per scrivere i numeri si usano le cifre. Le cifre del nostro sistema di misurazione sono:
Quanti numeri posso comporre con 2 cifre? E con 3?
Scrivi un numero… con una sola cifra: con due cifre: con tre cifre:
Imparo
Scrivi il numero.
10 u = 1 da da = 1 h
La regola
Il nostro sistema di numerazione è decimale perché le quantità vengono raggruppate in gruppi da 10. 100 u = 10 da = 1 h
Matematica… 10 con Metodo
numero cifra cifra
0 • 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 4 2
1 u = 1 1 da = ...... 1 h = ......
Ogni decina è formata da unità. Le unità sono in tutto 100. Ho formato decine.
4 Ora raggruppa per 100 usando la matita verde.
Le unità sono in tutto 100. Ho formato centinaio.
Mi esercito 11
1 Colora le unità che mancano e completa.
2 Colora le decine che mancano e completa.
3 Raggruppa per 10 usando la matita rossa. Poi completa.
95
u + u = 100 u = 1 h
88
+
75
7 da + da = 10 da = 1 h
u
u = 100
u = h 5 da + da = da = h
u + u
= u = h 9 da + da = da = h
Poi completa.
I numeri 25 e 52 sono formati dalle stesse cifre, ma il loro valore è diverso.
Scrivi il numero rappresentato su ciascun abaco, poi completa.
Il nostro sistema di numerazione è posizionale. Ogni cifra ha un valore diverso in base alla posizione che occupa nel numero.
Disegna il numero sull’abaco e scrivilo.
con Metodo Matematica… 12
da u 2 5 da u 5 2
Cio che gia so Imparo IL VALORE POSIZIONALE DELLE CI F RE
h da u
da u
da u
u 1 da 6 u 2 h 1 da 4 u 3 da 5 u 1 h 2 da 3 u
h
h
h da
La regola h da u h da u h da u 25 52 3 u 3 3
Mi esercito 13
1 Scrivi il numero.
2 Scomponi il numero, come nell’esempio.
3 Scomponi il numero.
h da u h da u 200 30 4 2 h 3 da 4 u 2 3 4 1 7 8 3 4 2 324 = h da u 2 h 6 da 8 u = 298 = h da u 4 h 2 da 5 u = 170 = 6 h 7 da 2 u = 816 = 4 h 0 da 3 u = 424 = 8 h 1 da 3 u = 502 = 5 h 5 da 5 u =
4 Componi il numero.
Cio che gia so
I numeri devono essere confrontati per stabilire quale sia maggiore e quale sia minore
Ordine crescente vuol dire dal minore al maggiore.
Ordine decrescente vuol dire dal maggiore al minore. > < = maggiore minore uguale
Imparo
Colora il numero maggiore. Poi sottolinea la scelta giusta.
987 98 è maggiore il numero che ha più / meno cifre.
172 291 devo confrontare le centinaia / decine / unità
427 436 devo confrontare le centinaia / decine / unità
501 508 devo confrontare le centinaia / decine / unità.
La regola
Per confrontare i numeri conta le cifre. Se hanno lo stesso numero di cifre, confronta partendo dalla prima cifra a sinistra
con Metodo Matematica… 14
207 27 542 524 305 350 785 875
1 Colora il numero minore e poi inserisci il simbolo > (maggiore), < (minore).
ORDINARE E CONFRONTARE
875 785 758 857 807 909 919 908 930 933 750 753 705 703 735 La
sempre il più piccolo.
2 In ciascuna serie colora in verde il numero maggiore e in rosso quello minore.
punta del simbolo guarda
1 Per ciascun numero scrivi in blu il precedente e in verde il successivo.
2 Scrivi i numeri in ordine crescente.
3 Scrivi i numeri in ordine decrescente.
454 • 545 • 444
445 • 555
4 Inserisci il simbolo > (maggiore), < (minore), = (uguale).
5 Con queste cifre scrivi:
6 Inserisci il simbolo > (maggiore), < (minore), = (uguale).
Mi esercito 15
899 700 659 901
• • • • •
121 • 101 •110 • 111 • 130 • 211
• • • • •
•
• 455
50
7
18
2 h 3 da 1 h 9 da 8 u 7 h 8 h 7 da 5 u 4 h 5 u 4 h 6 h 2 u 2 h 6 u 900
9
450 u 46
78
800
66
2 u
3 h 30 da
da 6 h
h 65 da
h 2 da
u
h
da
da
u
da
100 110 – 10 1 000 500 + 400 30 + 30 60
1 8 9 2 0 4 2 8 5 3 0 9 il numero maggiore possibile 7 9 1 4 2 8 9 1 3 3 2 4 il numero minore possibile i numeri minore e maggiore possibili 5 9 2 2 6 9 1 8 1 3 2 9 10 + 10 + 10 50 – 10 100 – 1 h 100 + 1 h 50 + 70 70 + 50
16 I numeri
1 Componi il numero 100 2 Scrivi il numero. a. 90 + = 100 93 + = 100 99 + = 100 92 + = 100 91 + = 100 97 + = 100 96 + = 100 94 + = 100 95 + = 100 98 + = 100 b. 30 + = 100 20 + = 100 10 + = 100 70 + = 100 80 + = 100 + 0 = 100 + 60 = 100 + 50 = 100 + 40 = 100 + 90 = 100 h da u h da u 3 Scrivi il valore della cifra evidenziata. Osserva l’esempio. 329 2 da 20 476 994 505 ................. ................. 900 849 100 ................. ................. 637 212 h da u h da u h da u h da u
Mi esercito
fino a 999
6 Scomponi e poi scrivi in lettere. Osserva l’esempio.
529 = 500 + 20 + 9 = cinquecento venti nove
855 = + + =
233 = + + =
471 = + + =
7 Componi e poi scrivi in lettere. Osserva l’esempio.
3 h 4 da 8 u = 300 + 40 + 8 = trecento quarant otto
2 h 9 da 4 u = + + =
4 h 2 da 6 u = + + =
1 h 5 da 9 u = + + =
8 Componi il numero.
9 Inserisci ogni cifra nella tabella per comporre i numeri.
Mi esercito
135
1 u
135 + 1 h = 387 + 1 h = 387 + 1 u
387 + 1 da = 578 + 1 da = 146
1 da
146 + 1 u = 578 + 1 u =
Completa. 135 – 1 u = 135 – 1 da = 135 – 1 h = 387 – 1 u = 387 – 1 da = 387 – 1 h = 146 – 1 da = 146 – 1 u = 146 – 1 h =
4 Completa.
+
=
=
+
=
5
4 h 7
1 u 2 h 3 da 5 h 1 u 1 h 9 u 6 h 6 u 7 h 2 da 5 h 3 da 4 u 9 h 1 u 4 h 4 da h
1
6
2
da
da u 5 u 7 da 3 h 2 h 9 u
da
da 8 u
h 4 da 2 h
IL MIGLIAIO
Cio che gia so
Le cifre sono 10. I numeri non si fermano a 999. La nostra numerazione raggruppa per 10.
Imparo
La
Completa. Completa per formare il 1 000.
10 centinaia formano 1 migliaio 10 h = 1 k
1 migliaio è formato da 10 centinaia 1 k = 10 h
1 migliaio è formato da 100 decine 1 k = 100 da
1 migliaio è formato da 1 000 unità 1 k = 1 000 u
con Metodo Matematica… 18
regola
100 + = 1 000 200 + = 1
300 + = 1 000 400 + = 1 000 500 + = 1 000 600 + = 1 000 700 + = 1 000 800 + = 1 000 900 + = 1 000 1
2 h
3
4 h
5 h
6 h
7 h
8 h = 9 h = 10 h = 10 centinaia 1 migliaio cambio
000
h = 100
=
h =
=
=
=
=
1 Completa per formare il 1 000, utilizzando le decine. Osserva l’esempio.
90 da + 10 da = 100 da = 1 000
80 da + da = 100 da = 1 000
10 da + = 100 da = 1 000
50 da + ................ = 100 da = 1 000
70 da + = 100 da = 1 000
2 Completa per formare il 1 000 utilizzando le unità.
998 + = 1 000
992 + = 1 000
994 + = 1 000
996 + = 1 000
3 Completa per formare il 1 000. Osserva l’esempio.
730 + = 1 000
Raggiungi il centinaio successivo
730 + 70 = 800
Ora raggiungi il migliaio
800 + 200 = 1000
730 + 70 + 200 = 1 000
250 + + = 1 000
890 + + = 1 000
640 + + = 1 000
520 + + = 1 000
110 + + = 1 000
360 + + = 1 000
280 + + = 1 000
4 Colora il numero che manca per ottenere 1 000.
5
V (vero) o F (falso).
di 1 k
Mi esercito 19
Scrivi
100 da
400 +
100
12
è maggiore
50 da +
240 + 860 760 800 = 1 000 770 + 23 330 230 = 1 000 995 + 50 5 15 = 1 000 890 + 120 210 110 = 1 000
= 1 k
6 h = 1 000
h = 1 k
h
4 h = 1 000
991 + = 1 000 995 + = 1 000 993 + = 1 000 997 + = 1 000 999 + = 1 000 990 + = 1 000 94 da + = 100 da = 1 000 88 da + = 100 da = 1 000 65 da + = 100 da = 1 000 1 da + ................ = 100 da = 1 000 95 da + = 100 da = 1
000
I NUMERI OLTRE IL 1 000
con Metodo Matematica… Osserva
completa.
il numero rappresentato sull’abaco e
Cio che gia so Imparo Unità, decine, centinaia hanno la loro posizione nel numero.
Scrivi il numero
su ciascun abaco. Osserva e completa. 20 2 000 duemila cento 40 otto k h da u 2 1 4 8 h da u k k h da u k h da u k h da u 2 148
rappresentato
2 k 2000 + duemila
h + quattrocento
da + u =
k + h + da + u =
2 Componi il numero.
3 k 5 h 7 da 5 u = 3 000 + + + =
2 k 1 h 6 da 4 u = ................ + ................ + ................ + ................ = ........................
6 k 8 h 0 da 2 u = + + + =
4 k 7 h 3 da 0 u = + + + =
3 Componi il numero: fai attenzione all’ordine delle cifre.
2 da 4 u 6 k 1 h = 20 + + + =
5 k 6 da 8 u 8 h = + + + =
1da 3 k 0 h 1 u = + + + = 9 k 0 da 2 u 5 h = ................ + ................ + ................ + ................ = ........................
Mi esercito 21
1 Completa.
I numeri oltre il 1 000
Mi esercito 22 quattromila
k h da u duemilatrecentoventisei k h da u cinquemilasettecentodue k h da u novemiladuecento k h da u
4 000
1 Scomponi i numeri inserendoli nella tabella. Poi scrivili in lettere. Osserva l’esempio.
2 Leggi i numeri, scrivili in cifre e poi scomponili.
k h da u 3 4 3 4 3 434 2 720 5 402 6 094 7 500 tremilaquattrocentotrentaquattro
2 500 8 600 6 800 5 200 7 564 7 600 6 700 7 546 8 991 9 990 9 899 8 981 4 897 4 789 9 874 8 974 7 540 7 5 4 0 9 843 3 Scomponi. 6 402 3 021
4 In ciascuna serie colora in verde il numero maggiore e in rosso quello minore.
Mi esercito 23 5 Scrivi il numero successivo. 5 984 7901 4 999 7 020 3 039 2 199 1 900 3 079 6 Scrivi il numero precedente. 7 804 2 756 3 401 6 000 9 100 8 010 1 540 2 001 7 Scrivi il valore della cifra evidenziata. Osserva l’esempio. 7 500 = 5 h = 500 6 340 = = 2 380 = = 4 611 = = 9 000 = = 7 900 = = 8 Con queste cifre scrivi: 4 6 2 1 9 3 5 8 2 1 1 2 7 6 0 9 4 8 0 3 il numero maggiore possibile il numero minore possibile 9 Completa. 5 992 + = 6 000 4 999 + = 5 000 7 998 + = 8 000 4 980 + = 5 000 8 990 + = 9 000 6 970 + = 7 000 3 900 + = 4 000 1 800 + = 2 000 2 700 + = 3 000
Contenuti digitali
Il testo e i dati
Cio che gia so
Il testo di un problema matematico descrive una situazione che deve essere risolta con delle operazioni.
I dati numerici indicano le quantità con cui bisogna operare.
1 Quali sono i dati che puoi ricavare dal disegno? Segna con più X.
Quante penne compera la bambina. Quanto costa una penna. Perché la bambina compera le biro. Quanti soldi ha la bambina. Come si chiama la bambina.
2 Leggi il testo del problema e cerchia i dati.
A Lisa servono 1 penna rossa e 1 penna blu. Va dal cartolaio con 10 euro.
In negozio sceglie 2 penne che costano 2 euro l’una. Quanto spende in tutto per le penne?
3 Leggi il problema, immagina la situazione e completa il disegno e i dati.
Luca ha bisogno di 1 quaderno e di 1 righello
Il quaderno costa 2 euro e il righello costa 3 euro.
Quanto spende Luca?
2 euro = 3 euro =
PR PROBLEMI 24 PRIMA TAPPA
Dati
4 Leggi e completa i dati.
a. Questa mattina il cartolaio Ivan ha venduto 15 quaderni. Quando ha aperto il negozio aveva 35 quaderni. Quanti quaderni ha ora?
Dati
b. Immagina la situazione, poi segna con X quale schema la rappresenta.
= numero dei quaderni che Ivan aveva = numero dei quaderni venduti
5 Leggi e completa i dati. Poi segna con X lo schema che rappresenta la situazione. Mara questa settimana ha in promozione la vendita di biglie. Prende 35 biglie e le espone in vetrina in 5 sacchetti. In ciascun sacchetto vi è lo stesso numero di biglie. Mette poi un bel cartello con scritto: vendita promozionale. Quante biglie ci sono in ogni sacchetto?
Dati
= numero totale delle biglie
= numero dei sacchetti
Per risolvere i PROBLEMI devi prima di tutto:
• capire la situazione
• individuare i dati
Immaginare la situazione e rappresentarla con un semplice disegno ti può aiutare.
Lavorare sulla decodifica del testo e l’individuazione dei dati anche attraverso la drammatizzazione delle situazioni.
CO D i N G
D i N G
CO
25
Contenuti digitali
Il testo e la domanda
Cio che gia so
Nel testo di un problema trovi i dati, ma la parte che ti indica come procedere è la domanda.
Il testo del problema e la domanda sono collegati tra loro.
1 Leggi attentamente i problemi e segna con X la domanda adatta.
a. Oggi nella cartoleria di Ivan è arrivata la nuova raccolta di figurine.
Ivan apre 4 scatole degli album. In ogni scatola ci sono 10 album.
Ivan espone alcuni album.
Quanti album sono arrivati a Ivan?
Quanti album ha esposto Ivan?
b. Alcuni bambini hanno già prenotato i pacchetti di figurine. Viola ne ha chiesti 5, per Rocco sono pronti 4 pacchetti
e per Tamara 8.
Quanti pacchetti rimangono a Ivan?
Quanti pacchetti sono stati prenotati?
2 Leggi attentamente il problema e scrivi tu la domanda.
Ivan controlla le scorte di temperini.
Ha ancora 52 temperini: 15 sono con il serbatoio, gli altri senza.
Domanda
3 Leggi la domanda e indica con X a quale testo si adatta.
Quante scatole riceve Ivan?
Le scatole di tempera ordinate da Ivan contengono 6 tubetti ciascuno;
Ivan ha ordinato 48 tubetti di tempera.
Ivan ha ordinato alcune scatole di tempera perché ne ha vendute
15 al mattino e 6 al pomeriggio.
PR PROBLEMI 26
SECONDA TAPPA
4 Osserva il disegno, leggi la domanda e scrivi un testo adatto.
Testo del problema
Quanto riceve di resto la bambina?
5 Scrivi i dati, l’operazione in riga, l’operazione nel diagramma e la risposta.
a. Ivan ha sugli scaffali 24 libri di fiabe e 42 libri a fumetti.
Quanti libri ha in tutto sugli scaffali?
24 = 42 = Dati
Operazione Risposta
6 Fai attenzione: ora cambia la domanda del problema. Leggi, rispondi e risolvi.
b. Quanti sono in più i libri a fumetti rispetto a quelli di fiabe?
Per risolvere il problema è necessario scrivere di nuovo i dati?
Operazione
7 Collega ciascuna domanda all’operazione necessaria per rispondere.
Usa il colore corrispondente.
Ieri Ivan ha incassato € 250 al mattino e € 320 al pomeriggio.
Quanto ha incassato in tutto ieri?
Quanto ha incassato in più nel pomeriggio?
CO D i N G
Leggi sempre con attenzione:
• sia il testo;
• sia la domanda.
La domanda ti guida alla risoluzione del problema
Sottolineare come la comprensione della domanda aiuti a tracciare il percorso risolutivo.
CO D i N G 27
320 – 250 = 320 + 250 =
Risposta
Nel parco giochi di Poggi Ridenti c’è una festa per l’inizio della scuola. I bambini e le bambine scopriranno di essere molto abili con i numeri.
1 Per i primi giochi occorre scrivere i numeri in cifre o in lettere, rispettando il valore posizionale.
i
Poi disegna una stellina accanto al numero maggiore.
28
k h da u 1 400 1 004 ...... ...... ...... ...... ........................................................ 750 1 070 k h da u milleduecentotrentuno milleduecentotrenta ...... ...... ...... ...... milleduecento milledue
3 Ricomponi
numeri.
= 1 k = 1
=
=
= = = 1 k 2 h 3 da 5 u 7 u 1 k 1 k 4 h 1 da 1 u
2 Scrivi i numeri in cifre.
h
1 da
1 u
4 Collega con una freccia l’operazione al testo del problema.
Alì ha totalizzato 120 punti, 30 in più di Omar. Quanti punti ha totalizzato Omar?
Omar nella gara di raccolta di sassolini ne ha presi 120, cioè 30 meno del vincitore.
Quanti sassolini ha raccolto il vincitore?
120 + 30 =
120 – 30 =
Le parole “in più” suggeriscono sempre un'addizione? E le parole “in meno"?
5 Risolvi i “problemi di foglie”.
Nella gara delle foglie Luana ha raccolto 35 foglie verdi e 57 marroni. Quante foglie ha raccolto Luana?
Camilla aveva 97 foglie. Ne ha perse 15. Quante gliene sono rimaste?
Dopo aver risolto i problemi sai dire chi ha più foglie?
Giochiamo, divertiamoci, ma non buttiamo rifiuti per terra.
6 Osserva il disegno e inventa due problemi: uno si risolverà con un’addizione, l’altro con una sottrazione
Utilizziamo sempre i cestini!
Gli esercizi riepilogano i seguenti argomenti: il sistema di numerazione decimale e posizionale, i numeri oltre il mille, soluzioni di problemi.
29
Educazione Civica
Ramuttina e Ramuttino sono due bambini “sapiens”. Sapiens anche di fatto: amano la logica, risolvono problemi di logica. Ma sono realmente esistiti? No! I bambini e le bambine della Preistoria non scrivevano i numeri, ma è bello immaginare che due bambini siano stati i primi a utilizzare le cifre.
Dunque largo alla fantasia… ma con logica!
Sui sassi scrivi
1 • 2 • 3 • 4 • 5.
Fai attenzione: non devi mai mettere vicini due numeri consecutivi.
Sui sassi
scrivi i numeri
1 • 2 • 3 • 4 • 5.
Le somme in verticale e in orizzontale devono dare lo stesso risultato!
Ora prova con i numeri da 1 a 8 !
Inserisci questi numeri: 1 • 4 • 7 • 10.
La somma di ogni lato deve essere 22.
LOGICA mente 30
CON I SAPIENS
11 8
I numeri crescono di piano in piano. Un aiuto: il numero in ogni mattone è la somma dei due su cui si appoggia.
Urgut ha 20 frecce. Urgat ne ha la metà più 2. Quante frecce ha Urgat?
Ora inserisci tu i numeri:
350 • 550 • 200 • 180 • 20 • 330.
Ho raccolto 18 conchiglie. Ne ho usate la metà meno una per fare una collana. Quante ne ho usate? Disegnale sul filo della collana.
Oggi sono stata proprio fortunata. Ho raccolto le more in 4 cespugli e in ognuno ne ho trovato il doppio del precedente. Nel primo ho raccolto 20 more. Sai dirmi quante ne ho raccolte poi?
Queste pagine di logica sono centrate sulla capacità di utilizzare le cifre, le loro combinazioni (dunque i numeri), non solo in funzione di calcolo, ma per lo sviluppo dell’intelligenza logica e numerica. Le soluzioni delle attività sono in Guida
20 È
tempodiQUIZ
24
12
10 18
10
L’ADDIZIONE
Cio che gia so
Fare un’addizione, cioè addizionare, vuol dire mettere insieme due o più quantità
Imparo
Osserva le due situazioni. Tutti fanno un’addizione.
Io ho 2 euro. Io ho 3 euro. Io ho 1 euro.
• Chi ha unito due o più quantità?
Lia Bea Tea Leo
• Chi ha aggiunto una quantità a un’altra?
Lia Bea Tea Leo
La regola
Si esegue un’addizione quando:
• si uniscono due o più quantità;
• si aggiunge una quantità a un’altra quantità.
2 + 3 + 1 = 6
addendo somma o totale
• Ciascun numero sommato a 0 non cambia. 5 + 0 = 5
• Se a qualsiasi numero si somma 1, si ottiene il numero intero successivo. 5 + 1 = 6
con Metodo Matematica… 32
Colora la risposta giusta.
1 Scrivi l’operazione che risolve il problema. Poi cerchia la parola adatta.
a. Bea e Leo fanno gare di corsa. Bea ha vinto 12 medaglie e Leo ne ha vinte 11. L’allenatore espone tutte le loro medaglie.
• Quante sono le medaglie di Bea e Leo? =
• Con questa operazione l’allenatore ha unito / aggiunto una quantità a un’altra.
b. Tea nel suo medagliere l’anno scorso aveva 8 medaglie.
Quest’anno ne ha vinte altre 4.
• Quante medaglie ci sono ora nel medagliere di Tea? =
• Con questa operazione Tea ha unito / aggiunto una quantità a un’altra.
2 Esegui a mente queste addizioni con due addendi
3 Esegui a mente queste addizioni con tre addendi
4 Risolvi i problemi sul quaderno.
a. Per i bambini e le bambine iscritti alla gara di corsa l’allenatore ha preparato 75 pettorali.
Questa mattina ci sono state 4 nuove iscrizioni.
Quanti sono i partecipanti alla gara?
b. L’anno scorso hanno assistito alla gara 850 persone.
Quest’anno gli spettatori sono 130 in più.
Quanti sono stati gli spettatori quest’anno? Si è raggiunto il migliaio?
Leggi con attenzione i problemi. Solo uno si risolve con un’addizione. Segnalo con X
Alex ha 20 figurine. Sua sorella Emma ne ha 5 più di lui. Quante figurine ha Emma?
Alex ha 20 figurine, 5 più di sua sorella Emma. Quante figurine ha Emma?
Mi esercito 33
10 + 4 = 8 + 5 = ...... 19 + 3 = 100 + 9 = ...... 100 + 30 = 110 + 10 = ...... 70 + 20 = 900 + 50 = ......
7
3
2
9
5
3
10 + 20 + 30 = 15 + 5 + 5 = 100 + 20 + 6 = 100 + 100 + 100 = in salto
+
+
=
+
+
=
LE PROPRIETÀ DELL’ADDIZIONE La proprietà commutativa
Imparo
Osserva. Completa e rispondi.
5 + 3 = 3 + 5 =
• Gli addendi delle due addizioni sono gli stessi?
• Gli addendi hanno la stessa posizione?
• Le addizioni hanno lo stesso risultato?
La regola
In una addizione se si cambia l’ordine degli addendi, il risultato non cambia.
Questa è la proprietà commutativa.
1 Esegui le addizioni contando sulle dita, poi rispondi.
4 + 9 = 9 + 4 =
• In quale delle due addizioni hai contato con più velocità? Colora il
2 Applica la proprietà commutativa e poi esegui le addizioni. 8 + 9 = + =
3 Applica la proprietà commutativa se ti è utile per essere più veloce nel calcolo. Poi esegui le addizioni.
con Metodo Matematica… 34
.......................................................... 26
4
8
42
4
10
..................................................... 150 + 20
............................................................... 290 + 10 = 4 + 1 000 = 2 + 98 = 2 000 + 1 000 = .....................................................
3 + 27 =
+
=
+
=
+ 66 =
+ 134 =
=
10
5 +
2
+ 90 = + =
25 = + =
+ 80 = + =
La proprietà associativa
Cio che gia so
Devi eseguire a mente questa addizione: 2 + 3 + 5 =
Come procedi? Prima, a mente sommi e . Poi aggiungi
La regola
In una addizione se a due o più addendi si sostituisce la loro somma, il risultato non cambia.
Questa è la proprietà associativa.
1 Applica la proprietà associativa ed esegui le addizioni.
2 Rispondi.
• Quale strategia hai usato per scegliere i due numeri da unire per primi?
Li scelgo a caso.
Unisco sempre i primi due addendi.
Unisco due addendi in modo che l’addizione risulti più facile.
in salto 12 + 17 + 3 + 8 =
Teo ha eseguito così 12 + 8 + 17 + 3 = 20 + 20 = 40
Teo ha applicato prima la proprietà , poi la proprietà
35 Matematica
Imparo 2 + 3 + 5 = 5 + 5 = 10 8 + 2 + 15 = + 15 = 24 + 9 + 1 = ........ + ........ = ........ 8 + 2 + 40 = ........ + ........ = ........ 10 + 25 + 5 = ........ + ........ = ........ 50 + 9 + 11 ........ + ........ = ........ 55 + 5 + 40 = + = 7 + 99 + 1 = 7 + = 12 + 30 + 70 = + = 2 + 3 + 5 = 2 + 8 = 10
STRATEGIE DI CALCOLO CON L’ADDIZIONE
Cio che gia so
Per eseguire velocemente un’addizione devi applicare le strategie di calcolo
Tappa al 10
Osserva queste strategie di calcolo.
• Per sommare 11, 21, 31… aggiungi prima 1, poi 10, 20, 30…
• Per sommare 9, 99, 999… aggiungi 10, 100, 1000 e poi togli 1.
• Scomponi gli addendi e poi applica la proprietà associativa.
Questi esercizi sono semplici, se impari le strategie!
con Metodo Matematica… 36 27 + 8 = 27 + 3 + 5 = 30 + 5 = 18 + 7 = 18 + 2 + 5 = + = 45 + 12 = 45 + 5 + 7 = + = 56 + 13 = 56 + + = + = 72 + 16 = 72 + + = + =
Imparo
53
11 = 53 + 1 + 10 = 47 + 21 = 47 + 1 + 20 = 39 + 31 = 39 + 1 + 30 =
+
15 + 9 = 15 + 10 – 1 = 32 + 99 = 32 + 100 – 1 = 28 + 999 = 28 + 1 000 – 1 =
24 + 36 = 20 + 4 + 30 + 6 = 50 + 10 = 32 + 41 = + + + = + = 105 + 43 = + + + = + =
ADDIZIONI IN COLONNA
Cio che gia so
Nell’addizione in colonna si sommano:
• prima le unità con le unità,
• poi le decine con le decine, e così via.
• Le ultime due addizioni hanno gli stessi addendi?
• Gli addendi hanno la stessa posizione?
• Le due addizioni hanno lo stesso risultato?
La regola
Nelle addizioni in colonna le cifre rispettano il valore posizionale. Per eseguire la prova dell’addizione si applica la proprietà commutativa.
37 Matematica
Imparo Incolonna bene i numeri e calcola. 53 + 24 = da u 5 3 + 2 4 = 7 7 1 542 + 224 = k h da u + = 207 + 132 = h da u + = 224 + 1 542 = k h da u + =
171 + 327 = h da u + 3 2 7 = ...... ...... ...... h da u 3 2 7 + = ...... ...... ...... Prova
1 Esegui l’addizione con la prova.
78 + 21 = 53 + 36 = 22 + 70 = 304 + 223 = 156 + 301 = 1 231 + 3 451 = 21 + 33 + 15 = 145 + 210 + 233 = 131 + 403 + 234 = 1 240 + 235 + 22 = 3 040 + 44 + 113 = 204 + 1 324 + 71 = Con due addendi Con tre addendi
2 Esegui le addizioni in colonna sul quaderno con la prova.
ADDIZIONI CON UN CAMBIO O RIPORTO
Cio che gia so Imparo
Il nostro sistema di numerazione è decimale, perciò le quantità si raggruppano in base 10.
Che fare se sommando le cifre si supera il 10?
• Somma le unità
6 + 8 = 14 = 1 da e 4 u
• Scrivi 4 sotto le unità e riporta 1 nella colonna delle da.
• Somma le decine
1 + 3 + 1 = 5
• Scrivi 5 nella colonna delle da
Metti in colonna ed esegui le addizioni con un cambio.
• Somma le centinaia
2 + 4 = 6
Scrivi 6 nella colonna delle h
con Metodo Matematica… 38
245 + 138 = h da u + = 184 + 532
h da u + = 652 + 172 = h da u + = 236 + 418 = h da u 2 3 6 + 4 1 8 = 4 + 1 1 h da u 2 3 6 + 4 1 8 = 5 4 + 1 h da u 2 3 6 + 4 1 8 = 6 5 4 + 1
=
4 561 + 1 229 = k h da u + = 2 034 + 1 372 = k h da u + = 458 + 1 380 = k h da u + = 1 324 + 2 851 = k h da u + = 3 457 + 1 822 = k h da u + =
Che fare se sommando le cifre si supera il 10 più volte?
• Somma le unità 8 + 7 = 15 = 1 da e 5 u
• Scrivi 5 sotto le unità
+ 4 + 6 = 11 = 1 h e 1 da
• Somma le centinaia 1 + 8 + 3 = 12 = 1 k 2 h • Scrivi 2 nella colonna
Metti in colonna ed esegui le addizioni con più cambi.
39 Matematica
ADDIZIONI CON PIÙ CAMBI Imparo
h da u + = 143 + 241 + 127 = h da u + + = 204 + 172 + 135 = h da u + + = 1 208 + 1 294 + 2 406 = k h da u + + = 1 001 + 3 456 + 1 762 = k h da u + + = 2 045 + 1 388 = k h da u + = 149 + 551 = h da u + = 3 573 + 1 542 = k h da u + =
267 + 356 =
e riporta
1 k h da u 8 4 8 + 3 6 7 = 5 + 1 1
1
Scrivi
e riporta 1 nella colonna delle h k h da u 8 4 8 + 3 6 7 = 1 5 + 1 + 1
h e 1 nella colonna
k 1 k h da u 8 4 8 + 3 6 7 = 1 2 1 5 + 1 + 1 1
1 nella colonna delle da 848 + 367 =
• Somma le decine
•
1 sotto le decine
delle
delle
Mi esercito 40 a. a.
b.
c.
1 Esegui le addizioni in colonna Ripassa la tecnica 2 Esegui sul quaderno con la prova Le addizioni 248 + 701 = h da u + = 134 + 525 = h da u + = b. 1 032 + 341 + 425 = k h da u + ...... ...... ...... ...... + = 193 + 234 = h da u + = 2 341 + 1 204 + 1 137 = k h da u + ...... ...... ...... ...... + = 1 427 + 2 324 + 2 536 = k h da u + ...... ...... ...... ...... + = 336 + 185 = h da u + = 84 + 15 = 804 + 155 = 206 + 453 = 1 003 + 784 = 23 + 44 + 32 = 16 + 52 + 21 = 105 + 62 + 321 = 1 005 + 542 + 351 = 56 + 38 = 309 + 157 = 184 + 251 = 1 642 + 1 536 = 53 + 16 + 25 = 24 + 48 + 17 = 167 + 212 + 250 = 1 405 + 1 223 + 2 531 = 135 + 265 = 238 + 384 = 1 708 + 2 506 = 2 815 + 1 326 = 155 + 243 + 274 = 209 + 347 + 162 = 1 806 + 876 + 212 = 459 + 243 + 1 144 = Due addendi SENZA CAMBIO Tre addendi SENZA CAMBIO Due addendi CON UN CAMBIO Tre addendi CON UN CAMBIO Due addendi CON PIÙ CAMBI Tre addendi CON PIÙ CAMBI
d.
e.
f.
1 Applica la proprietà associativa ed esegui le addizioni.
25 + 5 + 50 = + =
3 + 7 + 20 = .......... + .......... = ..........
20 + 8 + 2 = + =
99 + 1
2 Applica la proprietà commutativa e poi la proprietà associativa. Infine esegui le addizioni.
4 + 20 + 6 = 4 + 6 + 20 = + =
90 + 3 + 10 = 90 + 10 + 3 = + =
100 + 15 + 200 = + + = + =
13 + 40 + 7 = + + = + =
1 000 + 4 + 1 000 + 6 = + + + = + =
3 Esegui le addizioni e scrivi il risultato.
4 Calcola velocemente e completa le tabelle.
5 Scomponi gli addendi e poi applica la proprietà associativa.
Mi esercito 41
134
= 13 + 25 = 10 + 3 + 20 + 5 = 30 + 8 = 107 + 202 = 100 + 7 + 200 + 2 = .......... + .......... = .......... 73 + 14 = + + + = + = 210 + 150 = + + + = + = 75 + 2 h = 166 + 2 da = .......... 2 504 + 3 u = 37 + 1 u + 1 da = 235 + 1 u + 1 h = ..........
000 + 4 u + 2 da =
46 + 1 da =
+ 1 h = .......... 1 206 + 1 k
1
=
= + = 96 + 4 + 200 = + =
+ 9 + 99 23 17 56 149 347 + 11 + 101 66 74 158 243 524 + 9 + 11 55 78 354 582 601
4 +
= +
50 + 50 + 16
Calcolo rapido
La matematica
ALLA FESTA DEL LIBRO
La festa del libro è una buona occasione per guardare, sfogliare e sicuramente trovare almeno un libro che ci piace! E quanti numeri possiamo usare!
Un bambino ha trovato un libro divertentissimo, intitolato Caccia all’errore.
1 Ciascuna operazione ha un errore. Scrivi se è di incolonnamento, calcolo, riporto.
2 In queste addizioni è stata applicata la proprietà commutativa. In un caso, però, è stata applicata in modo sbagliato. Segna l’operazione sbagliata.
3 In queste addizioni sono state applicate in modo corretto le proprietà. Segna con X quando è stato sbagliato il nome delle proprietà.
4 Trova il risultato giusto di ciascuna operazione (dovrai eseguire alcune operazioni sul quaderno). Fai una X su quelli sbagliati.
42
25 + 8 + 15 = 25 + 15 + 8 99 + 21 + 1 = 99 + 12 + 1 623 + 48 + 55 = 1 221 728 726 427 + 136 + 1 246 = 1 809 1 509 929 45 + 230 + 1 400 = 1 475 1 675 1 575 9 + 1 507 + 2 407 = 3 933 3563 3 923 450 + 1 h = 550 451 1450 1 k + 3 h + 5 u = 1350 1305 9 8 h + 1 k = 1 008 81 1 800 4 k + 5 u = 4005 4050 4500 h da u 1 3 2 + 1 3 6 + 2 1 = 2 8 8 h da u 2 3 6 + 6 4 + 1 5 = 8 9 1 h da u 4 3 2 + 1 2 9 + 1 2 4 = 6 7 5 25 + 25 + 50 = 50 + 50 proprietà commutativa 75 + 25 + 100 = 100 + 100 proprietà associativa 48 + 50 + 2 = 48 + 2 + 50 proprietà commutativa
5 Esegui le operazioni sul quaderno, poi segna il risultato corretto.
a. Alla festa del libro c'è un incontro con un’autrice. Sono presenti 12 insegnanti, 14 altri adulti e 72 tra bambini e bambine.
Quante persone assistono all’incontro? 99 98 97
b. Sono arrivati 350 libri della casa editrice Alfa, 30 libri in meno di quelli che erano stati ordinati.
Quanti libri erano stati ordinati? 320 380 353
Le parole
“in meno” in questo problema suggeriscono una sottrazione oppure no?
c. La festa è durata due giorni. Il primo giorno della festa sono stati venduti 253 libri, 48 in meno del giorno successivo.
Quanti libri sono stati venduti il secondo giorno? 205 301 325
La casa editrice Beta ha consegnato 58 libri in più della casa editrice Alfa.
Quanti libri ha consegnato la casa editrice Beta? Sai quanti libri ha consegnato la casa editrice Alfa?
Ricava il dato dal problema b
Educazione Civica
La lettura è cibo per la mente e aiuta a viaggiare con la fantasia.
La casa editrice Alfa ha consegnato libri.
La casa editrice Beta ha consegnato .......... libri.
Quanti libri hanno consegnato in tutto?
Le esercitazioni sull’addizione e le sue proprietà sono presentate in contesti e modalità differenti perché i bambini e le bambine possano mettere in atto non solo le abilità, ma anche le competenze.
43
in salto
LA SOTTRAZIONE
Cio che gia so
Fare una sottrazione, cioè sottrarre, vuol dire togliere una quantità da un’altra
Imparo
Osserva le tre situazioni, poi calcola. Tutti fanno una sottrazione.
Devo gettare 4 fiori appassiti. Farò un bel mazzo di 12 rose.
Quanti fiori ho in meno di te?
Quanti fiori ho in più di te?
16
Segna con X la risposta giusta.
• Chi ha trovato quanto resta? Tom Meg Zoe Bob
• Chi ha trovato quanto manca? Tom Meg Zoe Bob
• Chi ha calcolato la differenza? Tom Meg Zoe Bob
La regola
Si esegue una sottrazione quando:
• si toglie una quantità e si trova quanto resta;
• si trova quanto manca per ottenere una quantità;
• si trova la differenza tra due quantità. 15 – 4 = 11
minuendo sottraendo resto o differenza
• Le sottrazioni si possono eseguire solo se il minuendo è maggiore del sottraendo 12 – 15 = 15 – 12 = 3
• Sottraendo 0 da qualsiasi numero si ottiene come risultato il numero stesso. 15 – 0 = 15
• Il numero 1 sottratto a qualsiasi numero dà sempre come risultato il numero precedente. 15 – 1 = 14
con Metodo Matematica… 44
– = 12 – = 11 – =
sottrazioni.
2 Esegui a mente queste sottrazioni.
4 Completa.
Quanto manca a...
12 per arrivare a 19?
27 per arrivare a 32? .........
15 per arrivare a 21?
19 per arrivare a 24?
198 per arrivare a 200? .........
90 per arrivare a 100?
5 Risolvi i problemi sul quaderno.
a. Marta controlla i suoi 25 pennarelli. 8 pennarelli non scrivono più e li getta via. Quanti pennarelli le rimangono?
200 per arrivare a 300?
95 per arrivare a 103? .........
86 per arrivare a 100?
b. Luca controlla la sua scatola di matite colorate. Ne dovrebbe contenere 24, ma ce ne sono solo 18. Quante matite mancano?
Risolvi i problemi sul quaderno.
a. Luca ha 35 anni, 8 anni più di Gemma. Quanti anni ha Gemma?
b. Luca questa settimana ha lavorato 32 ore, 6 ore in meno di Gemma.
Quante ore ha lavorato Gemma?
Mi esercito 45
1 Esegui a mente queste
Cancella con una / le sottrazioni che non si possono eseguire
3 Quanto manca?
10 – 2 = 10 – = 10 – =
in salto
5
7 – 1 = 18 – 0 = 9 – 0 = 31 – 1 = 6 – 8 = 11 – 0 = 100 – 0 = 1 234 – 1 = 102 – 102 = 203 – 1 =
–
= 11 – 3 = 20 – 10 = 75 – 10 = 100 – 40 = 60 – 30 = 80 – 10 = 100 – 2 =
12 – 15 = 3 –
=
12
8
OPERAZIONI INVERSE
Secondo te, si può dire che togliere e aggiungere sono due operazioni proprio contrarie?
Ne regala 4 a Olga. Gliene restano 9 – 4 =
Dario compra altre 4 piantine. Ora ne ha 5 + 4 = Dario ha 9 piantine.
Per eseguire la prova della sottrazione si esegue una addizione. Al risultato aggiungi il sottraendo. Se la somma sarà uguale al minuendo, la sottrazione è giusta!
con Metodo Matematica… 46 Imparo
Completa.
che
Sottrazioni e addizioni sono operazioni inverse La regola – 4 + 4 9 5 20 – 7 = – 7 + 7 20 15 + 9 = + 9 – 9 15 80 – 30 = – 30 + 30 80 25 + 15 = + 15 – 15 25
Cio
gia so
3 4 –1 3 = 2 1 2 1 + 1 3 = 3 4 sottrazione prova sottrazione prova 2 9 8 –1 4 6 = + 1 4 6 =
LA PROPRIETÀ DELLA SOTTRAZIONE La proprietà invariantiva
Imparo
Qual è la differenza tra le due quantità?
8 – 5 =
Sam e Mia aggiungono 2 lecca lecca gialli.
8 + 2 = 5 + 2 =
Qual è la differenza tra le due quantità?
10 – 7 =
Sam e Mia vendono 4 lecca lecca.
10 – 4 = ...... 7 – 4 = ......
Qual è la differenza tra le due quantità?
6 – 3 =
La regola
In una sottrazione se si aggiunge o si toglie lo stesso numero sia al minuendo sia al sottraendo, il risultato non cambia.
Questa è la proprietà invariantiva
Applica la proprietà invariantiva ed esegui le sottrazioni.
47 Matematica
25 – 18 = 27 – 20 = + 2 + 2 57 – 23 = 54 – 20 = – 3 – 3 74 – 29 = 75 – 30 = + 1 + 1 173 – 41 = 172 – 40 = – 1 – 1 103 – 95 = – = + 5 + 5 209 – 102 = – = – 2 – 2 176 – 90 = – = + 10 + 10 68 – 54 = – = – 4 – 4
STRATEGIE DI CALCOLO CON LA SOTTRAZIONE
Imparo
Osserva queste strategie di calcolo.
• Per sottrarre 11, 21, 31… togli prima 1, poi 10, 20, 30…
• Per sottrarre 9, 99, 999… togli 10, 100, 1 000 e poi aggiungi 1.
• Scomponi il sottraendo e poi calcola.
Calcola a mente. Utilizza la strategia più adatta.
235 – 99 = (235 – ) + = + = 273 – 41 = (273 – ) – = – = 74 – 13 = (74 – ) – = – =
– 9 =
– 11 = 718 – 101 =
– 45 =
– 33 =
Anche per la sottrazione le strategie di calcolo ti aiutano a diventare super veloce.
con Metodo Matematica… 48
11
(64
1)
10
63 – 10
85
21
(85 – 1)
20
......... – 20 = ......... 97 – 31
(97 – 1)
30 = ......... – ......... = .........
64 –
=
–
–
=
= .........
–
=
–
=
=
–
(36
26
124
(124
24
1
(1
36 – 9 =
– 10) + 1 =
+ 1 =
– 99 =
– 100) + 1 =
+ 1 =
500 – 999 =
500 – 1 000) + 1 = + 1 =
68
12
(68
10)
58
2
95 – 33 = (95 – 30) – 3 = – = 805 – 104 = (805 – 100) – 4 = – =
–
=
–
– 2 =
–
=
60
109
254
187
254 – 99 =
SOTTRAZIONI IN COLONNA
Cio che gia so
Nella sottrazione in colonna si sottraggono prima le unità dalle unità, poi le decine dalle decine, e così via.
Imparo
Incolonna bene i numeri e calcola.
64 – 23 = da u –
239 – 126 = h da u –
La regola
Incolonna con ordine!
1 768 – 1 528 = k h da u
2 304 – 203 = k h da u
Nelle sottrazioni incolonna bene le cifre Sottrai prima le unità, poi le decine, poi le centinaia e infine le migliaia.
1 Esegui le sottrazioni con la prova
458 – 207 = h da u ...... ...... ......
sottrazione sottrazione prova prova
k h da u ...... ...... ...... ......
4 696 – 2 690 = h da u ...... ...... ...... + =
2 Esegui le sottrazioni in colonna con la prova sul quaderno.
a. 576 – 54 = 87 – 70 = 55 – 43 = 168 – 141 = 342 – 130 = 508 – 407 =
in salto
b. 1 874 – 1 523 =
3 453 – 2 322 =
2 045 – 1 030 =
4 281 – 170 =
5 634 – 603 =
8 904 – 803 =
k h da u ...... ...... ...... ...... +
Valentina ha 23 anni, 5 anni meno di Mia. Quanti anni ha Mia? Per rispondere hai eseguito una sottrazione?
Mirko ha 18 anni, 8 anni più di Ivan.
Quanti anni ha Ivan? Per rispondere hai eseguito un’addizione?
49 Matematica
=
=
–=
–=
–=
–=
=
SOTTRAZIONI CON UN CAMBIO O PRESTITO
Cio che gia so
Il minuendo deve sempre essere maggiore del sottraendo.
Imparo
Che cosa fare se, sottraendo le cifre, la prima è minore della seconda?
546 – 218 =
• Parti dalle unità
6 – 8 = non si può fare
Prendi una decina e aggiungila alle unità.
16 – 8 = 8
Metti in colonna ed esegui le sottrazioni con un cambio.
• Sottrai le centinaia
con Metodo Matematica… 50
h da u
5 4 6 –2 1 8 = 8 3 1
– 1 = 2 h da u 5 4 6 –2 1 8 = 2 8 3 1
• Sottrai le decine 3
4
3 1 174 – 148 = h da u –= 763 – 558 = h da u –= 356 – 183 = h da u –= 809 – 547 = h da u –= 2 456 – 1 275 = k h da u –= 5 432 – 3 361 = k h da u –= 5 642 – 3 326 = k h da u –=
453 – 841 = k h da u –=
non si può fare! 8 – 10 =
5 – 2 = 3 h da u 5
6 –2 1 8 = 3 2 8
7
Questo
SOTTRAZIONI CON PIÙ CAMBI
51 Matematica
Imparo 156 – 88 = h da u –= 542 – 365 = h da u –= 724 – 539 = h da u –= 730 – 458 = h da u –= 2 052 – 1 435 = k h da u –= 3 057 – 1 138 = k h da u –= 3 545 – 1 836 = k h da u –= 5 210 – 3 146 = k h da u –=
1 Metti in colonna ed esegui le sottrazioni con più cambi.
• Parti dalle unità 2 – 9 = non si può fare
aggiungila
. 12
342 – 179 = h da u 3 4 2 –1 7 9 = 3 3 1
Sottrai
Prendi un centinaio e aggiungilo alle decine. 13 – 7 = 6 h da u 3 4 2 –1 7 9 = 6 3 1 • Sottrai le centinaia 2 – 1 = 1 h da u 3 4 2 –1 7 9 = 1 6 3 13 13 2 2 1
a. 137 – 88 = 404 – 95 = 210 – 77 = b. 362 – 187 = 541 – 185 = 624 – 354 = c. 1 243 – 607 = 2 673 – 499 = 3 245 – 166 = d. 2 431 – 1 715 = 4 309 – 1 463 = 2 835 – 1 819 =
• Prendi una decina e
alle unità
– 9 = 3
•
le decine 3 – 7 = non si può fare •
2
Esegui in colonna sul quaderno.
Mi esercito 52
b.
a.
1
Esegui le sottrazioni in colonna. Ripassa la tecnica
2 Esegui le sottrazioni in colonna
468 – 253 = h da u –...... ...... ...... = 766 – 83 = h da u –= 770 – 552 = h da u –...... ...... ...... = 563 – 457 = h da u –= 915 – 568 = h da u –...... ...... ...... = 3 246 – 1 126 = k h da u –= 5 466 – 3 280 = k h da u –= 4 354 – 2 728 = k h da u –= 5 476 – 957 = k h da u –= 9 352 – 5 407 = k h da u –= a. 79 – 56 = 345 – 241 = 682 – 381 = Senza cambio b. 83 – 57 = 312 – 209 = 740 – 338 = Con un cambio c. 1 035 – 920 = 2 453 – 743 = 6 521 – 3 091 = Con un cambio d. 450 – 273 = 2 763 – 1 847 = 3 056 – 2 249 = Con più cambi
3 Esegui sul quaderno con la prova.
Le sottrazioni
Mi esercito 53
4 Calcola velocemente e completa le tabelle.
40 – 20 = 20 – 5 = ......... 18 – 9 = 30 – 7 = 48 – 8 = ......... 35 – 6 = 900 – 500 = 250 – 50 = ......... 480 – 70 = 1200 – 200 = 2 400 – 2 000 = ......... 3 700 – 1 000 =
1 Esegui a mente le sottrazioni.
Calcolo rapido
56 – 12 = (56 – 10) – 2 = 46 – 2 = 97 – 25 = (97 – 20) – 5 = – = 185 – 32 = ( – ) – = – = 48 – 13 = 97 – 61 = 75 – 24 = 66 – 11 = 268 – 51 = ( – ) – = – = a. b.
2 Scomponi il sottraendo.
298 – 28 = – = 204 – 32 = – = 162 – 49 = – = 1 436 – 13 = – = 9 99 999 1 302 3 045 2 651 ............. ............. ............. 8 445 1 780 – 11 21 31 75 182 1 095 ............. ............. ............. 2 537 746 –
3 Applica la proprietà invariantiva ed esegui le sottrazioni.
IN SPIAGGIA La matematica
A Gemma, la bagnina del Lido del Sole, la matematica piace molto. Ha trovato modi originali per permettere ai bambini e alle bambine di dimostrare anche in spiaggia quanto sono capaci in matematica.
1 Scrivi il segno che manca (+ o –).
37 5 = 32
134 12 = 146
15 1 = 16
4 25 = 29
2 h 1 da = 210
1 h 1 da = 90
2 Scrivi sia il segno sia il numero che manca. 100 = 90
= 30 85 = 100
3 Completa.
= 30 –50 – = 30 100 = 140 –90 – = 10 66 = 76 –19 – = 6
4 Osserva il valore delle frecce blu. Esegui su un foglio le sottrazioni e scopri il valore della freccia rossa.
5 Per ciscuna addizione scrivi due sottrazioni.
6 Tea e Teo hanno applicato in modo diverso la proprietà invariantiva Entrambi hanno applicato la regola nel modo corretto, ma ogni volta solo uno ha semplificato il calcolo. Segna con X.
54
–
–
15
100 –
100
60
000 – 999 = 2 001 – 1 000 3 000 – 1 999 98 – 23 = 102 – 27 95 – 20 ......... 70 + 20 + 15 – 30 – 40 150
25 + 15 = 40 40
= 25 40
=
40 + 60 = 100
= 40
– =
2
30
150 = 50 1 h = 30 1 k = 1 200
50
7 Colora l’operazione che devi eseguire. Poi risolvi sul quaderno.
Al bar del Lido del Sole lunedì sono stati venduti 180 gelati confezionati e 95 gelati nel cono.
Quanti gelati sono stati venduti?
addizione sottrazione
Al bar del Lido del Sole martedì sono stati venduti 180 gelati. 95 erano confezionati, gli altri erano nel cono.
Quanti gelati nel cono sono stati venduti?
addizione sottrazione
8 Osserva la situazione e completa il testo dei due problemi.
Gemma osserva il mare. Oggi ci sono atleti con la tavola da surf e con il windsurf.
Quanti
Gemma osserva il mare e vede che in acqua ci sono atleti. atleti stanno usando il windsurf.
Quanti
9 Chi fa un’affermazione impossibile? Segna con X e spiega il perché a voce.
Ho 30 palline. Ne regalerò 25 ai bambini.
Io ne ho 25. Ne regalerò 30.
Ricorda di non lasciare in spiaggia i rifiuti.
55
Educazione Civica
Oggi tocca a Ramuttino proporre esercizi di logica a Ramuttina. Ha preparato lo schema del gioco, poi darà a Ramuttina, di volta in volta, le indicazioni per muoversi.
• Parti dal numero minore di 10, ma maggiore del doppio di 4. Poi dovrai seguire questo ordine e passare nelle caselle dove sono segnati i seguenti numeri.
• Il numero formato da 1 k e 1 u
• Il numero formato da 1 k meno 1 u
• Il triplo di 100
• La metà di 480
• Il doppio di 50 meno una decina
• Il numero maggiore del doppio di 20, ma minore di 42
• Il numero formato da 7 da, 4 u, 1 h
Che cosa ha trovato, Ramuttina, nell’ultima casella? Ti piace?
LOGICA
CON I SAPIENS
mente
741 41 90 147 174 240 1 001 300 8 999 9 1
Che cosa apparirà?
Per saperlo nel primo disegno dovrai partire da 57 e togliere sempre 5 fino a quando puoi. Nel secondo devi partire da 3 e aggiungere sempre 4 fino a quando puoi.
Risolviamo insieme questo quesito? Le caselle colorate indicano la somma della riga o della colonna. Ma quali numeri mancano?
In queste pagine la capacità di utilizzare abilità e competenze è collegata alla capacità di comprendere le consegne espresse non in modo diretto, mettendo in atto un ragionamento.
57
40 20 2 26 8 31 5 53 27 17
LOGICA mente
Contenuti digitali
TERZA TAPPA I problemi con più domande
A volte nel testo ci sono due o più domande, perciò devi cercare i dati necessari per rispondere a ognuna di esse
Domande non collegate
1 Leggi il problema e sottolinea tutti i dati. Poi completa i
Paola è la proprietaria di un’officina meccanica.
Nella sua officina lavorano 6 persone.
In questa settimana ognuna di esse ha revisionato 7 automobili.
Quante automobili sono state revisionate?
Ieri sono state cambiate 42 gomme invernali con gomme estive ad alcuni TIR. Ogni TIR monta 6 gomme.
A quanti TIR sono state cambiate le gomme?
Dati per rispondere alla prima domanda
Dati per rispondere alla seconda domanda
2 Leggi il problema e sottolinea tutti i dati. Poi completa i dati e il diagramma.
Paola ha sponsorizzato la gara di biciclette del quartiere.
Alla gara si sono iscritti 75 partecipanti di cui 42 femmine.
Paola ha regalato 4 luci per la bicicletta a ognuno dei primi 10 classificati.
Quanti maschi si sono iscritti alla gara?
Quante luci ha regalato Paola?
Dati per rispondere alla prima domanda
Dati per rispondere alla seconda domanda
PR PROBLEMI 58
= = = =
= = = =
Domande collegate
A volte nel problema ci sono due domande, ma per rispondere alla seconda occorre utilizzare il dato che hai trovato rispondendo alla prima domanda.
3 Leggi attentamente il problema. Completa i dati e il diagramma.
Paola ha acquistato una scatola di bulloni da 300 e un’altra che ne contiene 250. Utilizza 345 bulloni.
Quanti bulloni ha comperato?
Quanti gliene rimangono?
Puoi rispondere alla domanda: “Quanti gliene rimangono” senza aver risposto alla domanda “Quanti bulloni ha comperato”?
Dato da trovare
Numero dei bulloni comperati.
4 Colora in rosso i dati necessari per rispondere alla prima domanda e in blu quelli necessari per rispondere alla seconda. Poi risolvi sul quaderno.
Nell’officina il lunedì il cambio gomme costa 55 euro, ma al mercoledì c’è uno sconto di 15 euro. Oggi è mercoledì e sono state cambiate le gomme a 46 automobili.
Quanto costa il cambio gomme il mercoledì? Quanto si è incassato oggi per il cambio delle gomme?
CO
D i N G
Se nel testo di un PROBLEMA ci sono più domande, queste possono essere collegate oppure no.
Se le domande sono collegate, è necessario rispondere con un preciso ordine.
I diagrammi possono essere utili per visualizzare il percorso risolutivo dei problemi con più domande.
CO D i N G 59
= = =
Dati conosciuti
I numeri
Il nostro sistema di numerazione è:
• decimale perché si raggruppa per 10
1 k = 1 000 1 h = 1 00 1 da = 1 0 1 u = 1
• posizionale perché il valore di ogni cifra dipende dalla posizione che occupa nel numero
231 123 132
L’addizione
L’addizione è l’operazione che si fa quando:
• si aggiunge una quantità a un’altra quantità
• si uniscono due quantità
Il segno è + (più).
I termini dell’addizione sono:
2 + 3 + 1 = 6
addendo somma o totale
Le proprietà dell’addizione sono:
• proprietà commutativa
10 + 5 = 5 + 10
• proprietà associativa
2 + 2 + 5 = 4 + 5
h da u 1 2 3
Nell’addizione in colonna si sommano prima le unità con le unità, poi le decine con le decine, e così via.
60
Sintesi delle conoscenze
La sottrazione
La sottrazione è l’operazione che si fa quando:
• si toglie una quantità e si trova il resto
• si confrontano due quantità e si trova:
• la differenza
• quanto manca
Il segno è – (meno).
I termini della sottrazione sono: 15 – 4 = 11
minuendo sottraendo resto o differenza
La proprietà della sottrazione è la proprietà invariantiva.
12 – 8 = 4
Nella sottrazione in colonna si sottraggono prima le unità dalle unità, poi le decine dalle decine, e così via.
Addizione e sottrazione sono operazioni inverse.
Il minuendo deve sempre essere maggiore del sottraendo.
+ 5 15 20 – 5
La sintesi aiuta a ricordare le regole principali.
61 Sintesi delle conoscenze
14
12 = 2 – 2 – 2 12
10 =
+ 2 + 2 14 – 10 = 4
–
–
2
LA MOLTIPLICAZIONE
La moltiplicazione è un modo più breve per scrivere un’addizione con addendi tutti uguali
Cio che gia so Imparo
Osserva le due situazioni. Poi rispondi.
Quante caramelle in un sacchetto?
Quanti sacchetti?
Quante caramelle in tutto?
5 + 5 + 5 = 15 5 × 3 = 15
Quanti cioccolatini in ogni riga?
Quante sono le righe?
Quanti cioccolatini in tutto?
6 + 6 + 6 + 6 = 24 6 × 4 = 24
Si esegue una moltiplicazione quando:
• si ripete più volte la stessa quantità
6 × 4 = 24
moltiplicando moltiplicatore prodotto
fattori
• Se nella moltiplicazione uno dei fattori è 0, il risultato è sempre 0.
3 × 0 = 0
• Ciascun numero moltiplicato per 1 dà come risultato il numero stesso.
3 × 1 = 3
con Metodo Matematica… 62
La regola
a. Il pasticciere prepara 4 vassoi di pasticcini. In ciascun vassoio mette 8 pasticcini. Quanti pasticcini servono al pasticciere?
b. Il pasticciere prepara alcuni vassoi di pasticcini. In ciascun vassoio mette 8 cannoncini e 5 bignè. Quanti pasticcini mette in ciascun vassoio?
Quale dei due problemi si risolve con una moltiplicazione?
a. b.
Mi esercito 63 9 + 9 + 9 = × = 5 + 5 + 5 + 5 + 5 = × =
1 Osserva gli schieramenti e scrivi le moltiplicazioni.
7 × 3 = 3 × = 5 × = × = × = × = × = × = 10 + 10 + 10 = × = 2 + 2 + 2 + 2 + 2 + 2 = × =
3 Trasforma le addizioni in moltiplicazioni.
4 × 3 = 3 × 4 = × = × = × = × =
2 Segna gli incroci e completa. Osserva l’esempio.
4 Scrivi l’operazione che risolve ciascun problema.
Cio che gia so
Lo scorso anno hai studiato le tabelline. Ora ripassale.
1 Completa le tabelline.
2 Completa la numerazione del 3.
3 Completa la numerazione del 4
con Metodo Matematica… 64
LE TABELLINE
2
2
2
2
2
2
2
2
2
2
3
3
1
3
2
3
3 = 3
4 = 3
5 = 3
6 = 3
3
= 3
= 3
4 × 0 = 4 × 1 = 4 × 2 = 4 × 3 = 4 × 4 = 4 × 5 = 4 × 6 = 4 × 7 = 4 × 8 = 4 × 9 = 4 × 10 = 5 × 0 = 5 × 1 = 5 × 2 = 5 × 3 = 5 × 4 = 5 × 5 = 5 × 6 = 5 × 7 = 5 × 8 = 5 × 9 = 5 × 10 = 0 0 6 24 15 12 28 30 a. 4 × 9 = 5 × 7 = 2 × 9 = 4 × 8 = 3 × 6 = 2 × 10 = 3 × 8 = 5 × 9 = 4 × 7 = 5 × 5 = b. × 5 = 20 4 × = 24 3 × = 21 × 5 = 15 3 × = 30 2 × = 18 5 × = 50 × 4 = 16 × 4 = 36 2 × = 10
4 Completa. 2 × 0 =
× 1 =
× 2 =
× 3 =
× 4 =
× 5 =
× 6 =
× 7 =
× 8 =
× 9 =
× 10 =
× 0 =
×
=
×
=
×
×
×
×
× 7 =
× 8
× 9
× 10 =
65 Matematica
Completa le tabelline. 6 Completa la numerazione del 6. 7 Completa la numerazione del
9 Completa. 6 × 0 = 6 × 1 = 6 × 2 = 6 × 3 = 6 × 4 = 6 × 5 = 6 × 6 = 6 × 7 = 6 × 8 = 6 × 9 = 6 × 10 = ....... 7 × 0 = 7 × 1 = 7 × 2 = 7 × 3 = 7 × 4 = 7 × 5 = 7 × 6 = 7 × 7 = 7 × 8 = 7 × 9 = 7 × 10 = ....... 8 × 0 = 8 × 1 = 8 × 2 = 8 × 3 = 8 × 4 = 8 × 5 = 8 × 6 = 8 × 7 = 8 × 8 = 8 × 9 = 8 × 10 = ....... 9 × 0 = 9 × 1 = 9 × 2 = 9 × 3 = 9 × 4 = 9 × 5 = 9 × 6 = 9 × 7 = 9 × 8 = 9 × 9 = 9 × 10 = ....... 6 24 35 7 8 Completa la numerazione dell’8. 0 40 80 60 63 a. 6 × 6 = 7 × 8 = 9 × 10 = 8 × 8 = 8 × 5 = 7 × 10 = 6 × 7 = 6 × 9 = 9 × 9 = 6 × 10 = b. × 6 = 30 6 × = 18 7 × = 63 × 8 = 24 9 × = 0 9 × = 9 8 × = 32 × 8 = 16 × 7 = 21 6 × = 48
5
7.
LE PROPRIETÀ DELLA MOLTIPLICAZIONE
La proprietà commutativa
Imparo
Quante candeline?
4 × 3 oppure 3 × 4?
4 × 3 = 3 × 4 =
Il risultato delle due moltiplicazioni
La regola
In una moltiplicazione se si cambia l’ordine dei fattori, il prodotto non cambia.
Questa è la proprietà commutativa.
La proprietà associativa
Imparo
Quante candeline?
4 × 3 × 2 = 12 × 2 = 24
La regola
In una moltiplicazione se a due fattori sostituisci il loro prodotto, il risultato finale non cambia.
Questa è la proprietà associativa
2 × 4 × 5 = 8 × 5 = 40
4 × 3 = 12
3 × 4 = 12
con Metodo Matematica… 66
è
La proprietà distributiva
Imparo
Osserva e completa.
5 × 12 =
5 × 10 = 50 +
La regola
• Scompongo 12 (10 + 2).
• Moltiplico 5 x 10 e 5 x 2.
• Poi sommo i risultati
5 × 12 =
5 × (10 + 2) =
5 × 10 + 5 x 2 =
50 + 10 = 60
5 × 2 = 10 = 60
In una moltiplicazione posso scomporre uno dei due fattori. Poi moltiplico il fattore per entrambi gli addendi e sommo i risultati. Questa è la proprietà distributiva
3 × 16 =
(3 × 10) + (3 × 6) =
30 + 18 = 48
1 Applica la proprietà associativa.
5 × 4 × 3 = (5 × 4) × 3 = × =
6 × 10 × 10 = 6 × (10 x 10) = × =
3 × 5 × 2 = × ( × ) = × =
4 × 4 × 2 = × ( × ) = × =
2 Applica la proprietà distributiva.
Le proprietà della moltiplicazione sono utilissime per essere veloci nel calcolo mentale.
8 × 15 = 8 × (10 + 5) = 8 × 10 + 8 × 5 = + = 13 × 7 = (10 + 3) × 7 = 10 × 7 + 3 × 7 = + = 9 × 14 = 9 × ( + ) = × + × = + =
67 Matematica
MOLTIPLICARE PER 10 • 100 • 1 000
Cio che gia so
Moltiplicare un numero per 10, 100, 1 000 significa aumentare il suo valore di 10, 100, 1 000 volte.
Imparo
Osserva e completa.
• Quando moltiplichi un numero per 10 ciascuna cifra aumenta il suo valore di 10 volte e perciò si sposta verso sinistra di 1 posto.
• Quando moltiplichi un numero per 100 ciascuna cifra aumenta il suo valore di volte e perciò si sposta verso sinistra di posti.
• Quando moltiplichi un numero per 1 000 ciascuna cifra aumenta il suo valore di volte e perciò si sposta verso sinistra di posti.
La regola
Per moltiplicare un numero per 10, 100, 1 000, si aggiungono a destra del numero 1, 2, 3 zeri.
con Metodo Matematica… 68
1 Completa le tabelle. 2 Completa. × 10 57 435 31 6 802 70 × 100 62 24 8 93 40 99 × 1 000 6 5 9 8 1 4 a. 65 × 10 = 23 × 100 = 6 × 100 = 2 × 1 000 = c. × 8 = 800 × 8 = 8 000 × 73 = 730 ........ × 73 = 7 300 b. 32 × = 320 10 × = 1 000 2 × = 2 000 88 × = 880 d. 1 × = 1 000 7 × 1 000 = × 21= 210 × 6 = 600 k h da u 5 4 2 5 4 2 0 542 × 10 = k h da u 6 4 6 4 0 0 64 × 100 = k h da u 3 3 0 0 0 3 × 1 000 =
MOLTIPLICAZIONI IN COLONNA Moltiplicatore a 1 cifra
Cio che gia so 34 × 2 = da u × =
bene i numeri e calcola. 132 × 3 = h da u × =
1 221 × 4 = k h da u × =
Scrivi 1 riporta 2 alle decine
• Moltiplica per le decine 3 × 2 = 6
• Aggiungi il riporto 6 + 2 = 8
645 × 4 = k h da u 6 4 5 × 4 = 2 5 8 0 2 1 PIÙ CAMBI
• Moltiplica le unità 4 × 5 = 20
Scrivi 0 e riporta 2 alle decine.
Aggiungi il riporto 16 + 2 = 18
Scrivi 8 e riporta 1 alle centinaia.
• Moltiplica le centinaia 4 × 6 = 24
Aggiungi il riporto 24 + 1 = 25
Scrivi
Esegui in colonna sul quaderno.
27 × 3 = da u 2 7 × 3 = 8 1 2 UN SOLO CAMBIO Senza cambio a. 33 × 3 = 1 022 × 4 = Con un cambio b. 36 × 2 = 114 × 5 = 116 × 6 = 1 008 × 9 = Con più cambi c. 243 × 9 = 153 × 7 = 1 064 × 3 = 2 048 × 4 =
69 Matematica
Imparo Incolonna
Nella moltiplicazione in colonna si moltiplica il moltiplicatore prima per le unità, poi per le decine, e così via. Senza cambio Con il cambio o riporto
• Moltiplica le decine 4 × 4 = 16
25
• Moltiplica le unità 3 × 7 = 21
La
MOLTIPLICAZIONI IN COLONNA
Moltiplicatore a 2 cifre
Che cosa occorre fare se il moltiplicatore ha 2 cifre?
Fai due moltiplicazioni! Osserva.
• Ora moltiplica
× 2 decine
uno 0
alle unità.
Quando il moltiplicatore ha due cifre applichi la proprietà distributiva. Esegui cioè due moltiplicazioni:
• le unità del moltiplicatore per il moltiplicando;
• le decine del moltiplicatore per il moltiplicando.
Infine esegui l’addizione dei due prodotti parziali.
Nel moltiplicare una o entrambe le cifre e nel sommare i prodotti parziali potresti avere dei riporti.
Per fare la prova invece applichi la proprietà commutativa
La moltiplicazione è giusta se il risultato finale è uguale.
con Metodo Matematica… 70
regola
Imparo
h da u 4 2 × 3 = 1 2 6 + = h da u 2 3 × 4 2 = 4 6 + 9 2 0 = 9 6 6
42
h da u 4 2 × 2 3 = 1 2 6 + 8 4 0 =
• Prima esegui
× 3
Metti
segnaposto
h da u 4 2 × 2 3 = 1 2 6 + 8 4 0 = 9 6 6
risultati. Esegui in
a. 13 × 12 = 14 × 21 = 22 × 42 = 11 × 12 = 34 × 12 = 30 × 13 = b. 12 × 12 = 25 × 11 = 33 × 22 = 21 × 44 = 24 × 21 = 40 × 20 = c. 121 × 13 = 203 × 32 = 322 × 31 = 204 × 42 = 513 × 13 = 822 × 11 = 42 × 23 = PROVA
42
• Infine somma i
colonna sul quaderno le moltiplicazioni senza cambio
1 Esegui in colonna sul quaderno. Fai la prova applicando la proprietà commutativa.
Con un cambio
b. 23 × 43 = 93 × 17 = 16 × 15 = 24 × 23 =
c. 44 × 27 =
e. 53 × 34 = 29 × 45 = 18 × 36 = 37 × 49 =
10
= 2 × 5 × 4 = ( × ) × = × = 7 × 10 × 10 = × ( × ) = × = 5 × 4 × 6 = ( × ) × = × =
× =
83 × 10
000 = 75 × = 750 104 × = 1 040 9 × ........ = 900
= 10 × 97 = 100 × 28 = 1 000 × 7 = ........
5 Risolvi i problemi sul quaderno.
Mi esercito 71
Con più cambi
39
78
95
63 = d. 42
56 = 46
a. 12 × 36 = 35 × 12 = 15 × 18 = 12 × 17 = 34 = 52 × 65 = 39 × 72 =
× 24 =
× 52 =
×
×
×
2 Applica la proprietà associativa
× 4 × 3 = × ( × ) = ×
+ = 10
× + × = + = 8
+
= × + × = + = 5
+
= × + × = + =
3 Applica la proprietà distributiva. 6 × 12 = 6 × ( + ) = × +
× 17 = 10 × ( + ) =
× 14 = × (
)
× 25 = × (
)
a. Nella scuola ci sono 32 aule. Sulla porta di ciascuna aula c’è una ghirlanda formata da 14 fiori confezionati dai bambini e dalle bambine. Quanti fiori sono stati preparati?
66 × 100 = 4 × 1
b. Nel corridoio di una scuola, davanti alle aule, ci sono 9 gruppi di appendiabiti. In ogni gruppo ci sono 15 ganci. Quanti ganci ci sono in tutto? Oggi sono occupati 128 ganci. Quanti sono i ganci liberi? ........
4 Completa. 31 × 10 = 483 × 10 = 40 × 100 = ........
IN MONTAGNA
Anche in montagna nella fattoria di Rosa si incontra la matematica e si può lavorare con i numeri.
1 Calcola a mente e scrivi il risultato.
In fattoria, oltre alle mucche al pascolo, ci sono 4 recinti di pecore.
In ognuno ci sono 25 pecore.
Quante pecore ci sono in tutto?
Quante zampe si possono contare?
2 Esegui le moltiplicazioni in colonna sul quaderno. Poi colora nello stesso modo il rettangolino della moltiplicazione e il suo risultato.
3 In queste moltiplicazioni sono state applicate in modo corretto le proprietà. Segna con X quando è stato sbagliato il nome delle proprietà.
72
37 × 14 = 25 × 16 = 41 × 22 = 51 × 21 = 64 × 33 = 80 × 16 =
400 518 1 071 2 112 1 280 902 3 × 2 × 10 = 10 × 3 × 2 = 60 proprietà commutativa 9 × 11 = 9 × 10 + 9 × 1 = 90 + 9 = 99 proprietà distributiva 2 × 2 × 2 × 5 = 4 × 10 = 40 proprietà distributiva 15 × 7 = 7 × 15 = 105 proprietà associativa
È arrivato un gruppo di 16 turisti. Ciascun turista ha comperato un formaggella di pecora e un vasetto di miele.
Quanto ha speso ciascun turista?
Quanto hanno speso in tutto?
Formaggella di capra € 18
Formaggella di pecora € 15
Yogurt (vasetto piccolo) € 2
Miele (vasetto grande) € 13
5 Completa il testo del problema scrivendo una domanda possibile
Le ricottine vengono conservate in una cassa che ha 15 file da 12 ricottine ciascuna.
Le esercitazioni proposte permettono di mettere in atto le competenze anche attraverso la richiesta di ricavare dati e informazioni dalle immagini.
Rosa ha organizzato una gita a cavallo. Ogni partecipante pagherà 25 euro per il cavallo e 14 euro per il pranzo al sacco.
Quanto costa partecipare alla gita?
Si sono iscritte 18 persone. Rosa incasserà più o meno di 700 euro?
Nel bosco vicino alla fattoria di Rosa erano stati tagliati tanti alberi. Rosa ha promosso nella scuola della valle la “Giornata dell’Albero”. Tutte le classi hanno piantato nuovi alberi per salvaguardare l’ambiente e la biodiversità. Educazione
73
Civica
4 Ricava dal disegno i dati che mancano.
LA DIVISIONE
Cio che gia so
Fare una divisione, cioè dividere, vuol dire distribuire una quantità in parti uguali oppure formare gruppi che hanno la stessa quantità di elementi.
Imparo
Osserva le due situazioni. Tutti fanno una divisione.
In
Colora la risposta giusta.
• Chi ha distribuito in parti uguali? Carlo Julia
• Chi ha raggruppato in parti uguali? Carlo Julia
La regola
Si esegue una divisione quando:
• si distribuisce in parti uguali;
• si raggruppa in parti uguali.
12 : 4 = 3
dividendo divisore quoziente
1
2
con Metodo Matematica… 74
ogni piatto metto
Distribuisci usando le frecce. Poi completa la divisione.
Raggruppa per 4. Poi completa la divisione.
20 : 4 = ........ 6 : 2 = ........
LA DIVISIONE CON IL RESTO
A volte, quando si distribuisce o raggruppa in parti uguali, c’è un resto
Cio che gia so Imparo
Julia prepara gli spiedini di pomodorini.
Mette 5 pomodorini per stecchino.
Ha 17 pomodorini.
Raggruppa per 5.
Quanti spiedini può preparare Julia?
Quanti pomodorini avanzano?
17 : 5 = resto
1 Raggruppa e scrivi il risultato della divisione.
18 : 4 = r 21 : 6 = r
2 Esegui le divisioni. Ricorda che il resto (r) può essere 0.
a.
3 Leggi e segna con X. Poi risolvi sul quaderno.
a. Julia ha comperato 24 bicchieri e li dispone in parti uguali su 3 mensole. Quanti bicchieri ci sono su ciascuna mensola?
Julia
distribuisce in parti uguali. raggruppa in parti uguali.
b. Carlo prepara i cestini del pane. Ha 35 panini. In ogni cestino mette 5 panini.
Quanti cestini riesce a riempire?
Carlo…
distribuisce in parti uguali. raggruppa in parti uguali.
75 Matematica
19 : 2 = r 25 : 3 = r 57 : 8 = r
50 : 7 = r 35 : 5 = r 72 : 9 = r 55 : 6 = r
48 : 8 = r 35 : 6 = r 88 : 9 = r 21 : 5 = r
33 : 7 = r 11 : 2 = r 38 : 9 = r 20 : 3 = r
24 : 6 = r
b.
c.
d.
MOLTIPLICAZIONI E DIVISIONI: OPERAZIONI INVERSE
Imparo 5 × 3 = 15
Divisioni e moltiplicazioni sono operazioni inverse.
Per eseguire la prova della divisione si esegue una moltiplicazione
Se la divisione non ha resto 0, esegui la moltiplicazione e poi aggiungi il resto.
con Metodo Matematica… 76
La regola
È
No! 15 : 3 = 5 È una divisione! : 3 × 3 15 5
una moltiplicazione!
20 : 5 = 4 resto 0 divisione 5 × 4 = 20 prova 23 : 5 = 4 resto 3 divisione 5 × 4 = 20 + 3 = 23 prova Completa. 45 : 5 = × 5 = 10 × 8 = : 8 = 72 : 9 = × 9 = 11 × 7 = : = : 5 × 5 45 × 8 10 : 9 72 × 7 11
LA DIVISIONE IN COLONNA
Imparo
Anche la divisione, come le altre operazioni, si può eseguire in colonna. La divisione è l’unica operazione in cui si comincia a dividere dalla prima cifra a sinistra.
Primo caso: il resto è sempre zero
64 : 2 = h da u
• 6 : 2 = 3 con il resto 0
Scrivi 3 al risultato e 0 sotto le decine
• Abbassa il 4 4 : 2 = 2 resto 0.
Scrivi 2 al risultato e 0 sotto le unità.
Il risultato della divisione è 32 con il resto di 0.
64 : 2 = 32 (r 0)
Secondo caso: il resto è diverso zero
97 : 5 = h da u
• 9 : 5 = 1 con il resto 4.
Scrivi 1 al risultato e 4 sotto le decine
• Abbassa il 7 47 : 5 = 9 resto 2.
Scrivi 9 al risultato e 2 sotto le unità.
Il risultato della divisione è 19 con il resto di 2.
97 : 5 = 19 (r 2)
Terzo caso: la prima cifra del dividendo è minore del divisore
Se la prima cifra del dividendo è minore del divisore, all’inizio si prendono in considerazione le prime 2 cifre del dividendo.
• 25: 6 = 4 con il resto1.
Scrivi 4 al risultato e 1 sotto le decine
• Abbassa il 5 15 : 6 = 2 resto 3.
Scrivi 2 al risultato e 3 sotto le unità.
Il risultato della divisione è 42 con il resto di 3.
255 : 6 = 42 (r 3)
Queste stesse regole vanno applicate anche se il divisore è di tre o più cifre
77 Matematica
6 4 2 0 4 3 2 0
9
4
7 5
7 1 9 2
2 5 5 6 1 5 4 2 3
255 : 6 = h da u
LA PROPRIETÀ DELLA DIVISIONE La proprietà invariantiva
Ho 24 gigli e voglio dividerli in 4 mazzi.
• Quant
• Quanti gigli ha Meg?
• Quanti mazzi vuole fare Meg?
• Quanti gigli ci saranno nei mazzi fatti da Meg?
In una divisione, se si moltiplica o si divide per lo stesso numero sia il dividendo sia il divisore, il risultato non cambia. Questa è la proprietà invariantiva
Applica la proprietà invariantiva ed esegui le divisioni.
con Metodo Matematica… 78
regola Imparo
La
15 : 5 = 30 : 10 = × 2 × 2 63 : 21 = : = : 3 : 3 80 : 16 = 10 : 2 = : 8 : 8 48 : 12 = : = : 2 : 2 45 : 15 = : = : 5 : 5 32 : 16 = : = : 4 : 4 25 : 5 = : = × 2 × 2 90 : 45 = : = : 9 : 9 24 : 4 = 12 : 2 = 6 : 2 : 2
Osserva e completa.
Cio che gia so
Dividere un numero per 10, 100, 1 000 significa diminuire il suo valore di 10, 100, 1 000 volte
• Quando dividi un numero per 10 ciascuna cifra diminuisce il suo valore di 10 volte e perciò si sposta verso destra di 1 posto.
• Quando dividi un numero per 100 ciascuna cifra diminuisce il suo valore di volte e perciò si sposta verso destra di posti.
• Quando dividi un numero per 1000 ciascuna cifra diminuisce il suo valore di ........... volte e perciò si sposta verso destra di ........ posti.
La regola
Per dividere per 10, 100, 1000 un numero che termina con gli zeri, si tolgono a destra del numero 1, 2, 3 zeri.
79 Matematica
DIVIDERE PER 10 • 100 • 1 000
Imparo Osserva e completa. : 10 590 300 970 6 800 200 90 : 100 800 2 400 900 9 000 3 300 1 000 : 1 000 1 000 4 000 6 000 5 000 2 000 3 000 k h da u 2 5 7 0 2 5 7 2 570 : 10 = k h da u 2 5 0 0 2 5 2 500 : 100 = k h da u 2 0 0 0 2 2 000 : 1 000 =
1 Completa le tabelle.
150 : 10 = 4 300 : 100 = 8 000 : 1 000 = 970 : = 97 700 : = 7 5 000 : = 5 : 10 = 19 : 100 = 5 : 1 000 = 7
2 Completa.
1 Esegui
2 Esegui le divisioni in riga con la prova, come nell’esempio.
3
le divisioni in colonna ed eseguile.
Mi esercito 80 72 : 8 = r 81 : 9 = r 56 : 7 = ........ r ........ 80 : 8 = 36 : = 9 : 5 = 8 47 : 6 = 7 r 5 perciò (6 × 7) + 5 = 42 + 5 = 47 38 : 7 = r perciò ( × ) + = + = 38 43 : 3 = r perciò ( × ) + = + = 57 : 9 = r perciò ( × ) + = + = 64 : 8 = r 42 : 6 = r 36 : 4 = ........ r ........ : 7 = 6 45 : = 5 81 : 9 = 45 : 5 = r 49 : 7 = r 36 : 9 = ........ r ........ : 2 = 10 : 4 = 3 54 : = 6 54 : 6 = r 27 : 3 = r 56 : 8 = ........ r ........ 63 : = 7 36: = 4 : 5 = 7
le
mente
divisioni a
Scrivi
745 : 6 = h da u 7 4 5 6 279 : 9 = h da u 349 : 8 = h da u 2 258 : 7 = k h da u 6 732 : 5 = k h da u 225 : 7 = h da u
4 Completa le divisioni con i numeri mancanti.
Le divisioni
a. Con 72 matite quante confezioni da 6 si possono preparare?
Quante confezioni da 8?
E quante confezioni da 9?
b. Con 48 muffin quanti vassoi da 6 si possono preparare?
Quanti vassoi da 4 muffin?
Quanti vassoi da 8 muffin?
Quanti vassoi da 3 muffin?
a. In un ristorante ci sono 112 posti. I tavoli sono tutti uguali e ogni tavolo ha 8 posti. Quanti tavoli ci sono nella sala del ristorante?
b. Viola ha comperato 10 lecca lecca alla fragola, 10 al lampone e 10 all’arancia. Li vuole regalare ai suoi 6 amici che festeggiano con lei il compleanno.
Quanti lecca lecca ha comperato in tutto? Quanti lecca lecca regala a ciascun bambino?
Mi esercito 81 a. 170 : 10 = 400 : 100 = 8 000 : 1 000 = 600 : 100 = 1 250 : 10 = 9 000 : 1 000 = b. 4 500 : = 450 5 000 : = 50 9 900 : = 99 7 800 : = 78 780 : = 78 7 800 : = 780 c. : 100 = 42 : 100 = 15 : 10 = 94 : 1 000 = 1 : 1 000 = 5 : 10 = 830
5 Completa.
8 Rispondi alle domande. 9 Risolvi i problemi sul quaderno. 99 : 18 = : = : 3 : 3 150 : 30 = : = : 10 : 10 850 : 50 = : = : : a. 58 : 7 = 75 : 8 = 38 : 4 = 23 : 5 = 40 : 9 = b. 226 : 2 = 690 : 3 = 606 : 6 = 507 : 5 = 887 : 4 = c. 672 : 6 = 542 : 3 = 894 : 8 = 785 : 7 = 997 : 9 = d. 356 : 4 = 309 : 5 = 218 : 4 = 102 : 3 = 591 : 8 = e. 248 : 5 = 500 : 7 = 409 : 8 = 553 : 6 = 247 : 4 =
6 Applica la proprietà invariantiva per facilitare il calcolo ed esegui le divisioni. 7 Esegui sul quaderno con la prova.
14 000 : 7 000 = : = : :
IN PISCINA
A Poggi Ridenti hanno costruito una nuova piscina. In questo ambiente si può fare sport, ci si diverte e, perché no, ci si esercita con i numeri.
1 Per ciascuna moltiplicazione scrivi due divisioni.
6 × 7 = 42 42 : 6 = 42 : 7 =
3 × 9 = 27 27 : =
2 Completa. Il risultato finale ti permette di controllare se hai compiuto errori.
3 Manca il segno dell’operazione (× o :). Scrivilo tu.
C’è una situazione in cui il segno possibile non è uno solo. Colorala!
4 In queste divisioni è stata applicata la proprietà . Completa ed esegui le divisioni.
5 Inserisci > (maggiore), < (minore), = (uguale).
82
40 : 10 2 × 2 25 : 5 50 : 10 24 : 6 24 : 4 9 × 0 8 × 0 20 : 4 3 × 2 30 : 3 2 × 4 8 × 2 16 : 2 7 × 2 14 : 2
8 × 4 = 32 32 : = 32 : = 5 × 7 = ........ : = : = 9 90 × 100 : 10 : 10 × 1 000 : 10 : 10 × 10 : 10 15 2 = 30 30 1 = 30 30 3 = 10 30 3 = 90 8 0 = impossibile 7 7 = 1 50 : 5 = 10 : 1 = : .... : .... 130 : 5 = : = 200 : 50 = : =
27 : =
Pino sul bordo della piscina ha messo i tubi per galleggiare in cesti. In ogni cesto ci sono tubi.
Quanti ?
a. Nel ripostiglio della piscina ci sono 8 confezioni da 24 braccioli ciascuna. Quanti braccioli sono a disposizione dei bambini?
moltiplicazione divisione
b. Il bagnino Pino ha ritirato 24 braccioli e li ha ordinati in scatole da 8 braccioli ciascuna. Quante scatole ha riempito?
moltiplicazione divisione
Pino sul bordo della piscina ha messo tubi ordinati in parti uguali in cesti.
Quanti ?
In piscina sono state organizzate gare di nuoto. Per lo stile libero si sono iscritti 72 concorrenti. Si svolgeranno gare da 8 concorrenti ciascuna.
Quante gare si svolgeranno?
Se le gare fossero da 6 concorrenti, quante gare si svolgerebbero?
Il focus centrale di queste esercitazioni è il confronto tra moltiplicazioni e divisioni come operazioni inverse.
Praticare uno sport fa bene al corpo, alla salute e alla mente.
Insegna a rispettare gli avversari e a essere leali.
83
6 Colora l’operazione che devi eseguire. Poi risolvi sul quaderno.
7 Osserva il disegno e completa il testo dei due problemi.
8 Risolvi sul quaderno.
Educazione Civica
Ramuttina accompagna Ramuttino nei pressi della palude. Per prendere le uova di anatra, cibo per il loro pranzo, devono attraversare la palude.
Alla fine del percorso quale numero ha trovato Ramuttino?
Sai spiegare perché?
Quante coppie di operazioni inverse ha fatto Ramuttino?
Quali?
Ho visto altre uova. Risolvi i quesiti e ti dirò dove sono!
Qual è la relazione tra i due divisori che hai utilizzato in alto e il divisore che hai scritto in basso?
100 80 90 70 : 2 : 5 + 12 : 2 × 2 : 3 ....... – 12 96 84 60 54 72 48 : 3 : 2 : :
È tempodiQUIZ
Ora risolvi i quiz. Ho pensato un numero. Ho aggiunto 40 e ho tolto 10. Ho ottenuto 100. Che numero ho pensato?
50 70
Ho pensato un numero. Ho diviso per due e poi ho aggiunto 10. Ho ottenuto 20.
Che numero ho pensato?
10 20
Per tornare a casa Ramuttino e Ramuttina dovranno passare sulle grandi foglie delle ninfea “victoria regia”.
Queste pagine di logica sono centrate sulla capacità di individuare la relazione tra differenti operazioni numeriche e di operare attraverso algoritmi.
85
+ 15 + 25 × 1 : 4 + 10 : ..... : ..... × 3 20 ......... ......... 5 ......... .........
× 3
La moltiplicazione
La moltiplicazione è l’operazione che si fa quando si ripete più volte la stessa quantità.
È un’addizione con gli addendi tutti uguali.
5 + 5 + 5 = 5 × 3
Il segno è × (per).
I termini della moltiplicazione sono:
6 × 4 = 24
moltiplicando moltiplicatore prodotto
fattori
Le proprietà della moltiplicazione sono:
• proprietà commutativa
2 × 5 = 5 × 2
• proprietà associativa
× 4 =
• proprietà distributiva 5 × 12 = 5 × (10 + 2) =
5 × 10 + 5 × 2 =
50 + 10 = 60
Nelle moltiplicazioni in colonna si comincia l’operazione sempre dalle unità.
Per moltiplicare un numero per 10, 100, 1 000, si aggiungono a destra del numero 1, 2, 3 zeri.
86 Sintesi delle conoscenze
10
2 × 5 × 4 =
La divisione
La divisione è l’operazione che si fa quando:
• si distribuisce una quantità in parti uguali
• si raggruppa in parti uguali
Il segno è : (diviso).
I termini della divisione sono: 12 : 4 = 3 dividendo divisore quoziente
La proprietà della divisione è la:
• proprietà invariantiva
Nella divisione in colonna si comincia a dividere dalla prima cifra a sinistra.
Per dividere per 10, 100, 1 000 un numero che termina con gli zeri, si tolgono a destra del numero 1, 2, 3 zeri.
Moltiplicazione e divisione sono operazioni inverse.
× 2 10 20 : 2
Per eseguire velocemente moltiplicazioni e divisioni occorre conoscere a memoria le tabelline.
87 Sintesi delle conoscenze
15 : 5 = 3 30 : 10 = 3 × 2 × 2 15 : 5 = 3 3 : 1 = 3 : 5 : 5
Le 4 operazioni
3
Confrontati con i compagni e le compagne. Avete completato tutti nello stesso modo? Spiegate le vostre scelte.
5 Esegui le operazioni sul quaderno con la prova.
Mi esercito 88 a. 919 + 27 = 168 + 49 = 549 – 407 = 15 × 7 = 99 : 8 = b. 186 + 246 + 750 = 1 567 – 1 359 = 2 457 – 748 = 36 × 22 = 346 : 5 = c. 9 754 + 11 + 524 = 8 745 – 3 807 = 25 × 52 = 239 : 7 = 409 : 6 = d. 6 057 – 3 038 = 33 × 27 = 41 × 61 = 309 : 4 = 620 : 7 = a. 35 + 24 + 191 = 240 150 250 752 + 254 + 176 = 1 182 1 172 1 082 1 526 + 600 + 1 420 = 2 546 8 946 3 546 b. 854 – 603 = 151 251 351 439 – 185 = 253 254 353 3 240 – 1 826 = 1 414 1 416 1 406 c. 18 × 42 = 756 98 766 51 × 73 = 4723 3723 510 64 × 24 = 384 1436 1536 d. 126 : 6 = 21 r 0 20 r 0 22 r 0 459 : 5 = 81 r 4 114 r 4 91 r 4 287 : 6 = 8 r 1 47 r 5 47 r 0
giusto
Inserisci il segno mancante
1 Esegui le operazioni sul quaderno con la prova, poi colora il risultato
2
Inserisci
numero
Colora tutte le operazioni
8 + 4 = 15 – 3 = 12 : 1 = 22 – 1 da 12 × 0 = 6 × 2 = 2 + 1 da =
il segno e il
mancanti. 4
che danno come risultato 12.
150 4 = 154 150 10 = 140 150 10 = 15 150 10 = 1 500 10 = 20 10 = 50 30 = 10 45 = 9
6 Colora il segno dell’operazione necessaria. Poi risolvi i problemi sul quaderno.
a. In un prato pascolano 125 mucche e 75 buoi. Quante mucche ci sono in più dei buoi?
b. La mucca Rosina ha dato 14 litri di latte, 5 litri meno della mucca Bianchina. Quanti litri di latte ha prodotto la mucca Bianchina?
c. Sono state raccolte 86 uova. Vengono vendute in confezioni da 6 uova. Quante confezioni vengono preparate? Avanzano delle uova?
d. Oggi sono stati riempiti 15 bidoni di latte da 24 litri ciascuno. Quanti litri di latte sono pronti per essere trasportati alla Centrale del latte?
7 Risolvi i problemi sul quaderno.
a. Nel suo orto Mia ha interrato piantine di pomodoro in 5 file. In ogni fila ci sono 12 piantine. Quante sono le piantine di pomodoro?
Nell’orto ci sono anche 8 piantine di zucchine e 12 piantine di melanzane.
Quante piantine ci sono in tutto nell’orto di Mia?
b. Mia ha raccolto 87 fiori di zucchina. Ne tiene per sé 15 e regala gli altri ai suoi 4 amici.
Quanti fiori di zucchina regala in tutto ai suoi amici?
Quanti fiori di zucchina riceverà ciascuno di loro?
c. Oggi Mia ha comperato 3 confezioni da 12 vasetti di vetro.
Mia ha riempito di marmellata 28 vasetti.
Quanti vasetti ha comperato?
Quanti gliene sono rimasti vuoti?
d. Mia al vivaio compera 9 confezioni da 8 vasetti di primule ciascuna. A casa trasferisce i vasetti di primule in 6 grandi vasi. In ogni vaso mette lo stesso numero di piantine. Quante piantine di primule ha comperato?
Quante ne mette in ciascun vaso?
Mi esercito 89
+ – × : + – × : + – × : + – ×
Contenuti digitali
I dati utili, inutili, nascosti QUARTA TAPPA
In un problema ci sono sempre i dati A volte alcuni sono “inutili”, cioè non servono per trovare la soluzione. A volte sono “nascosti”, ma si possono trovare.
I dati nascosti
1 Leggi il problema e cerchia in blu le informazioni numeriche. Poi rispondi.
Il centro commerciale rimane aperto 12 ore al giorno tutti i giorni, compresa la domenica. Quante ore rimane aperto in una settimana?
3 Osserva l’immagine e completa il problema inserendo le informazioni numeriche. Poi rispondi.
Le T-shirt vengono vendute in confezioni da magliette, al prezzo complessivo di euro.
Quanto costa una sola T-shirt?
PR PROBLEMI 90
Dati utili o inutili
4 Leggi il problema e cerchia in blu tutte le informazioni numeriche. Poi rispondi.
Il centro commerciale apre alle ore 9 tutte le mattine e chiude alle ore 21.
Al primo piano ci sono 7 negozi di abbigliamento, 2 negozi di telefonia, 1 gioielleria e 3 negozi di scarpe. Se passeggi al primo piano, in quanti negozi potresti entrare?
• Quali dati NON ti occorrono per rispondere alla domanda?
• Quali dati ti occorrono per rispondere alla domanda?
• Qual è l’operazione che risolve il problema?
5 Leggi con attenzione il problema. Poi cerchia in rosso le informazioni utili, in blu quelle inutili. Quindi rispondi.
In uno dei negozi di scarpe oggi sono state vendute
12 paia di scarpe da tennis del numero 36 a 28 euro al paio. Sono state vendute anche 8 paia di sandali del numero 35 e 6 paia di scarponcini del numero 37.
Quanto si è incassato oggi dalla vendita delle scarpe da tennis?
Quante paia di calzature sono state vendute oggi?
• Quali dati ti occorrono per rispondere alla prima domanda? e .
• Quali dati ti occorrono per rispondere alla seconda domanda? , e
• Quali dati sono inutili? , e
CO
Il testo di un PROBLEMA deve rappresentare una situazione.
I dati nascosti si possono dedurre:
• dall’immagine;
• da parole che indicano numerosità.
I dati inutili NON vanno presi in considerazione.
Centrare l’attenzione sulla comprensione del testo per individuare i dati nascosti e inutili. Questo tipo di lavoro deve essere accompagnato dalla capacità di argomentare perché alcuni dati sono inutili e come si possono trovare i dati nascosti.
CO D i N G 91
D i N G
La domanda nascosta
Nei problemi non sempre è possibile rispondere direttamente alla domanda con i dati a disposizione. A volte è necessario prima ricavare un dato rispondendo a una “domanda nascosta”.
Nella sala giochi del centro commerciale, Léon organizza la festa del suo compleanno.
L’animatore ha preparato 9 bustine di palloncini di differenti colori. In ogni bustina ci sono 10 palloncini. Mentre li gonfia 8 scoppiano. Quanti palloncini rimangono?
Puoi rispondere subito alla domanda del problema?
Quale dato manca per poter rispondere alla domanda?
Il numero totale dei palloncini comperati.
Il colore dei palloncini che l’animatore vuole appendere.
Qual è la domanda nascosta? Scrivila.
Sono state preparate 22 pizzette con la mozzarella, 24 con i würstel, 30 con le olive.
Le pizzette vengono disposte in parti uguali in 4 vassoi.
Quante pizzette ci saranno in un solo vassoio?
PR PROBLEMI 92
1 Leggi con attenzione il problema. Poi rispondi.
2 Scrivi la domanda nascosta. Poi risolvi sul quaderno.
QUINTA TAPPA
Domanda nascosta
Contenuti
Domanda nascosta
digitali
a. Per la festa di compleanno, sul tavolo delle bibite sono state messe 4 confezioni da 12 succhi di frutta l’una.
Domanda nascosta
Al termine della festa sono rimasti 9 succhi di frutta.
Quanti succhi di frutta sono stati bevuti?
b. Il direttore della sala della festa, per pubblicizzare una nuova raccolta di figurine, ha regalato 4 pacchetti a ciascuno dei 22 partecipanti.
Domanda nascosta
A Léon, che è il festeggiato, ne ha dati 12. Quanti pacchetti di figurine sono stati regalati?
a. In ognuno dei 12 pacchetti di figurine ci sono 8 figurine. Léon trova 8 figurine doppie.
Quante figurine non doppie ha trovato?
• Per poter rispondere alla domanda devo trovare
b. Al termine della festa si mette tutto in ordine!
Sul tavolo erano stati preparati 25 piatti blu, 22 piatti rossi e 20 piatti gialli. Ne sono stati utilizzati 45.
Quanti piatti potranno essere utilizzati per la prossima festa?
• Per poter rispondere alla domanda devo trovare
Per risolvere un PROBLEMA devi farti queste domande:
• Ho a disposizione tutti i dati che mi servono per la risoluzione?
• Devo trovare un dato?
• Quale domanda mi devo porre per trovare il dato che manca?
La drammatizzazione della situazione può essere un valido strumento per aiutare i bambini e le bambine a trovare le domande nascoste.
CO D i N G 93
i N G
CO D
3 Scrivi la domanda nascosta. Poi risolvi sul quaderno.
4 Scrivi che cosa ti manca per poter rispondere alla domanda. Poi risolvi sul quaderno.
Cio che gia so
Tutti i giorni usiamo le frazioni.
Mezzo litro di latte!
LE FRAZIONI
Arrivo tra un quarto d’ora.
Oggi è assente un terzo dei bambini.
Contenuti digitali
Ecco 25 centesimi di resto.
Imparo
Uno dei bambini sbaglia. Chi? Colora in rosso il suo quadratino.
Io ho frazionato la torta.
Anche io ho frazionato la torta.
La regola
In matematica frazionare significa dividere in parti uguali.
Colora in verde il quadratino vicino agli elementi che sono stati frazionati.
con Metodo Matematica… 94
L’UNITÀ FRAZIONARIA
Imparo
Osserva che cosa hanno fatto questi due bambini. Poi fallo anche tu.
Ho diviso in 2 parti uguali.
Ho diviso in 4 parti uguali.
Ciascuna parte corrisponde a un mezzo.
Si scrive 1 2 . Significa 1 parte su 2
Ciascuna parte corrisponde a un quarto.
Si scrive 1 4 . Significa 1 parte su 4
Ciascuna parte uguale in cui viene diviso l’intero si chiama unità frazionaria La
95 Matematica
regola
1 3 un terzo 1 10 un decimo 1 2 un mezzo 1 4 un quarto 1 6 un sesto 1 8 un ottavo Collega l’unità frazionaria
disegno corrispondente, colorando il quadratino. 1 4
al
I TERMINI DELLA FRAZIONE
Imparo
Ho colorato 2 4 .
Ho colorato 3 4 .
Bea e Teo hanno frazionato l’intero (il loro foglio) in 4 parti uguali. Ogni parte è 1 4 .
Bea ha colorato parti, cioè 2 4 (si legge due quarti).
Invece Teo ha colorato parti, cioè 3 4 (si legge tre quarti).
La regola
I termini della frazione:
3 numeratore indica quante parti sono state considerate linea di frazione indica che l’intero è stato frazionato
4 denominatore indica in quante parti è stato diviso l’intero
1 Osserva e completa.
L’intero è stato diviso in parti uguali. Sono state colorate parti.
La parte colorata corrisponde alla frazione 2 5 (si legge due quinti).
2 Scrivi in cifre e in parole le frazioni corrispondenti alla parte colorata. Osserva l’esempio.
3 5 tre quinti
con Metodo Matematica… 96
Mi esercito 97
1 Scrivi l’unità frazionaria e colorala.
2 Dividi ciascun intero come indica il denominatore e colora l’unità frazionaria.
3 Scrivi la frazione rappresentata dalla parte colorata.
1 ...... 1 ...... 1 ...... 1 ...... 1 2 1 3 1 4 5 8 2 5 3 3 4 6 2 7 3 11 1 5 ...... ...... ...... ...... ......
4 Rappresenta la frazione, colorando.
UGUALE O EQUIESTESO?
Imparo
• Tutti gli interi sono uguali?
• Tutti gli interi sono stati suddivisi in 4 parti?
• Nell’ultimo intero le parti sono uguali, cioè hanno la stessa forma e la stessa grandezza?
• Nell’ultimo intero le parti sono equiestese, cioè occupano lo stesso spazio, anche se hanno forme diverse?
La regola
Quando si fraziona un intero le parti devono essere uguali tra di loro o equiestese, cioè occupare lo stesso spazio (avere la stessa superficie).
1 Dividi il rettangolo usando 4 unità frazionarie come questa:
2 Dividi il rettangolo usando 4 unità frazionarie come questa:
3 Dividi il rettangolo usando 2 unità frazionarie come questa: e 2 come questa:
4 Osserva e rispondi.
In quante parti è stato diviso ciascun rettangolo? Le parti sono equiestese (conta i quadretti)?
Ogni parte è 1 .
Nel primo rettangolo colora l’unità frazionaria, nel secondo colora 3 8 , nel terzo colora 7
con Metodo Matematica…
98
8 a c b 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4
Conta i quadratini!
FRAZIONARE UNA QUANTITÀ
Cio che gia so
Sai frazionare figure geometriche. Sai anche che “mezzo litro di latte”, “un terzo degli alunni” sono frasi che indicano una frazione.
Imparo
Mia ha 9 lamponi.
Ne usa 1 3 per decorare un pasticcino.
Mia divide la quantità di lamponi in 3 parti uguali e ne prende una sola parte.
1 3 di 9 = 3
La regola
Anche le quantità possono essere frazionate. Si divide la quantità per il numero di parti indicate dal denominatore e si prende il numero di parti indicate dal numeratore
Osserva e completa.
a. Marina ha 6 piantine di primule. Nel vuole mettere
• Dividi le 6 piantine in 3 parti uguali, circondando i gruppi.
Utilizza la matita.
Ripassa in rosso 2 gruppi di piantine.
Marina mette sul balcone piantine.
b. Alex ha 10 pennarelli. Ne scarta 2 5 perché non funzionano più.
• Dividi i 10 pennarelli in 5 parti, circondando i gruppi. Utilizza la matita.
Ripassa in rosso 2 gruppi di pennarelli. Alex scarta pennarelli.
99 Matematica
1 Osserva la frazione e rispondi.
5 8
Le frazioni
• Qual è il denominatore? Qual è il numeratore?
• In quante parti è stato diviso l’intero?
• Quante parti sono state prese in considerazione? ........
2 Colora l’unità frazionaria, quando è possibile.
• In tutte le figure hai potuto colorare l’unità frazionaria? Perché
3 Segna con X la frazione che indica la parte colorata.
4 Colora la parte indicata dalla frazione, poi scrivi le frazioni in ordine crescente.
Mi esercito 100
• Quale frazione corrisponde all’intero? 2 9 1 9 3 9 6 15 5 15 5 9 4 6 6 6 2 6 1 6 5 6 3 6
6 Dividi l’intero e colora la frazione.
7 Colora ed esegui come indicato.
• In 1 3 delle palline.
Dividi in 3 gruppi uguali e colora 1 solo gruppo.
• In 2 5 delle palline.
Dividi in gruppi uguali e colora gruppi.
• In 3 4 delle palline.
Dividi in gruppi uguali e colora gruppi.
in salto
Mi esercito 101
5 Per ciascuna figura scrivi una frazione e poi colora la parte corrispondente.
Completa, frazionando l’intero in 6 parti equiestese, ma non tutte uguali. 2 3 3 8 4 10
1 Colora l’unità frazionaria, usando i colori indicati dai quadratini.
2 Rappresenta la frazione, colorando.
3 Scrivi la frazione corrispondente alla parte colorata.
6 8 7 13 2 9 4 7 3 12 5 16 1 3 1 4 1 5 102
Nel vivaio “Foglie e radici” si vedono tanti colori, si odorono tanti profumi e... fioriscono situazioni matematiche.
NELLA SERRA
• Quanti sono i fiori esposti? ........
• In quanti gruppi sono stati frazionati?
• A quale frazione corrisponde ciascun gruppo?
• Quanti fiori ci sono in ogni gruppo?
Perciò 1 4 di 12 =
• Quanti sono i fiori esposti?
• In quanti gruppi sono stati frazionati?
• A quale frazione corrisponde ciascun gruppo?
• Quanti fiori ci sono in ogni gruppo?
• Quanti gruppi di fiori rossi ci sono?
• Quanti sono i fiori rossi?
Perciò 2 3 di 18 =
Le esercitazioni proposte in queste pagine sono incentrate sull’utilizzo del disegno, fondamentale per la comprensione del concetto di frazione e per riportare nella realtà il saper operare con le frazioni.
Le piante e i fiori non solo abbelliscono l’ambiente, ma sono indispensabili per la nostra vita. Prova a prenderti cura di una piccola pianta di salvia o
103
rosmarino.
4 Con gli annaffiatoi sono state bagnate alcune piante. Scrivi la frazione corrispondente all’acqua rimasta nell’annaffiatoio.
5 Un gruppo di fiori è stato diviso in piccoli mazzi. Osserva e rispondi.
...... ...... ...... ......
6 Ecco un altro gruppo di fiori. Osserva e rispondi.
Educazione Civica
LE FRAZIONI DECIMALI
Cio che gia so
La nostra numerazione è in base 10. Le frazioni che hanno come denominatore 10, 100, 1000 saranno particolari?
Imparo
Frazioni speciali!
• L’intero è stato diviso in parti uguali.
• Ogni parte corrisponde a 1 10
• Si legge “un decimo”.
• L’intero è stato diviso in parti uguali.
• Ogni parte corrisponde a 1 100 . Si legge “un centesimo”.
• L’intero è stato diviso in ............ parti uguali.
• Ogni parte corrisponde a 1 1 000
• Si legge “un millesimo”.
La regola
Le frazioni che hanno come denominatore 10, 100, 1000 si chiamano frazioni decimali.
Colora secondo le indicazioni e poi rispondi.
• Hai colorato una parte maggiore di 0?
• Hai colorato una parte maggiore o minore dell’intero, cioè di 1?
con Metodo Matematica… 104
1 10
FRAZIONI E NUMERI DECIMALI
Osserva le quantità e collegale alla linea dei numeri.
Con le frazioni hai imparato che esistono quantità che valgono meno di un intero, cioè meno di 1. La torta intera è rappresentata dal numero 1. Con quale numero posso rappresentare le 5 fette?
La regola
• Le frazioni decimali possono essere trasformate in numeri decimali.
• Nei numeri decimali la virgola separa la parte intera dalla parte decimale.
• Il simbolo del decimo è d
105 Matematica
Imparo 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 Completa. un decimo 0,1 frazione decimale in lettere numero decimale 1 10 PARTE INTERA unità u decimi d 0 5 , PARTE DECIMALE =
0,5 5 10
I decimi
esercito 106
Mi
1 Colora le frazioni indicate e completa la tabella.
2 Completa la linea dei numeri da 0 a 1.
0 ....... ....... ....... ....... ....... ....... ....... 0,2 0,5 1
0,1 + = 1 0,2 + = 1 0,3 + = 1 0,4 + = 1 0,5 + = 1 0,6 + = 1 0,7 + = 1 0,8 + = 1 0,9 + = 1 un decimo 0,1 ........................ decimi decimi decimi decimi decimi decimi decimi decimi decimi frazione decimale numero decimale 1 10 2 10 3 10 4 10 5 10 6 10 7 10 8 10 9 10 10 10
3 Completa per formare il numero 1.
Completa la linea dei numeri da 1 a 2.
PARTE
PARTE
PARTE
107 Matematica
1 ....... ....... ....... ....... ....... ....... ....... 1,2 1,7 2
I NUMERI DECIMALI
Imparo
decimi
1
, PARTE DECIMALE
INTERA unità u
d
2
1
PARTE DECIMALE
INTERA unità u decimi d
8 ,
decimi
2 , PARTE DECIMALE
INTERA unità u
d
u decimi
, PARTE DECIMALE 1 intero + 2 decimi = 1 + 0,2 = 1,2 1 intero + 8 decimi = 1 + 0,8 = 1,8 2 interi + 7 decimi = 2 + 0,7 = 2,7
interi + 5 decimi = 3 + =
PARTE INTERA unità
d
3
I CENTESIMI
L’unità è stata divisa in 100 parti uguali.
Ciascuna parte corrisponde a 1 100 (un centesimo).
Quanti centesimi hai colorato?
Quanti decimi?
Corrisponde il numero decimale
Quanti centesimi hai colorato?
Quanti decimi?
Corrisponde il numero decimale
con Metodo Matematica… 108
La regola Imparo
PARTE INTERA unità u decimi d centesimi c 0 0 1 , PARTE DECIMALE
1
decimale corrispondente. 1 100 = 0,01 4 100 = 9 100 = 90 100 10 100 10 c = 1 d 100 c = 1 u Il simbolo
c 10
100
2 Colora la frazione indicata e rispondi.
Colora la frazione indicata e scrivi il numero
del centesimo è
centesimi corrispondono a 1 decimo.
centesimi corrispondono a 1 unità.
1 100 = 0,01
1
1 000 = 0,001
Il simbolo del millesimo è m
10 millesimi corrispondono a 1 centesimo.
100 millesimi corrispondono a 1 decimo
1 000 millesimi corrispondono a 1 unità
L’unità è stata divisa in 1 000 parti uguali.
Ogni parte corrisponde a 1 1 000 (un millesimo).
10 m = 1 c
100 m = 1 d
1000 m = 1 u
Il millesimo è 10 volte più piccolo del centesimo.
4,365 4 unità 3 decimi 6 centesimi 5 millesimi
3,76
1,256
5,155
61,27 7 centesimi
109 Matematica
I MILLESIMI
1 Colora la frazione indicata e scrivi il numero decimale corrispondente.
2 Scomponi il numero. Osserva l’esempio.
6 1 000 = Imparo La regola PARTE INTERA unità u decimi d centesimi c millesimi m 0 0 0 1 ,
DECIMALE
24
39 0,45 2,502
3 Indica il valore della cifra colorata. Osserva l’esempio.
PARTE
5,7
1,
Frazioni e numeri decimali
Mi esercito 110 0,18 18 centesimi 0,9 0,04 0,006 0,25 0,136
2
1 Colora la frazione indicata. Poi scrivi il numero decimale
Completa. Osserva gli esempi.
3 Inserisci > (maggiore), < (minore), = (uguale).
300 1 000 = 6 100 = 48 100 = 8 10 = 0,8 1 d 10 c 4 u 50 d 20 d 2 u 150 c 1 u 1000 m 4 u 100 c 10 d 500 c 3 u 4 u 400 m ......... 2 centesimi 0,02 2 100 5 100 4 10 12 100 224 1 000 7 1 000 numero decimale in lettere frazione 18 100 numero decimale in lettere frazione
Mi esercito 111
4 Colora la parte decimale indicata.
5 Inserisci i numeri decimali in tabella.
0,7 0,07 0,23 0,008 0,3 0,350 0,19 0,9 parte
3,48 14,5 5,8 2,906 1,27 36,01 da u d c m , , , , , , , 2,2 = 2 4 0,64 = 0 6 4 1,36 = 1 3 6 1,748 = 1 7 4 8 38,5 = 3 8 5 27,94 = 2 7 9 4 81,364 = 8 1 3 6 4 0,01 = 0 0 1 0,001 = 0 0 0 1 12,908 = 1 2 9 0 8
6 Scomponi i numeri.
intera parte decimale
esercito 112
Mi
1 Colora nello stesso modo la frazione decimale e il numero decimale corrispondente.
2 Con frecce colorate collega ogni numero al suo posto sulla linea dei numeri.
3 Componi i numeri scrivendo ogni cifra in tabella al posto giusto.
0,6 0,05 0,8 0,5 0,001 0,01 2,5 1,9 2,9 3,3 3,8 0,5 0,2 0,8 1,1 1,5 1,8 3,9 0,008 0,06 5 10 8 10 6 10 1 100 6 100 5 100 8 1 000 1 1 000 0 1 2 0 1 2 3 4 parte intera
2 u 4 d 5 c 8 da 3 u 1 d 6 c 3 da 6 u 2 c 7 u 9 m 6 da 4 d 1 u 5 c da u d c m .......... .......... , .......... .......... .......... , , , , , ,
I numeri decimali
parte decimale numero
4 Completa per formare il numero 1.
0,1 + = 1 0,01 + = 1
5 Cerchia in viola i decimi.
6 Cerchia in rosa i centesimi.
7 Cerchia in verde i millesimi.
8 Inserisci i numeri in tabella. Poi scrivi i numeri in ordine dal minore al maggiore.
con facilità, aggiungi gli zeri
Mi esercito 113
Per
ai millesimi.
In ciascun gruppo circonda in rosso il numero minore e in blu il numero maggiore. 10 Completa le tabelle. u d c m 0 , 2 0 0 , , , , , 0,5 + = 1 0,93 + = 1 0,8 + = 1 0,85 + = 1 0,2 + = 1 0,55 + = 1 2,456 3,56 15,6 93,39 105,1 1004,33 0,4 • 0,45 • 0,3 0,56 • 0,58 • 0,48 0,175 • 0,75 • 0,5 156,09 0,256 104,79 1865,207 21,05 7,934 31,821 0,702 5987,465 0,005 105,998 1,954 • • • • • – 1 d + 1 d 6,1 .......... 0,24 .......... 0,37 1,48 2,86 – 1 c + 1 c 4,15 .......... 0,46 .......... 0,76 1,32 5,268 – 1 m + 1 m 1,598 .......... 1,005 .......... 0,024 0,152 4,003 0,2 • 0,156 • 0,32 • 0,1 • 0,23
confrontarli
fino
9
Quando paghi qualcosa con l’euro utilizzi le unità (un euro), le decine (10 euro), i numeri decimali (i centesimi di euro).
Imparo
Ricorda il valore delle banconote e delle monete. Scrivilo.
Circonda in rosso le banconote e le monete che valgono più dell’unità.
Circonda in blu le monete che valgono meno dell’unità.
L’euro è la moneta che si usa in Italia e in altri Paesi europei.
1 euro è un intero, un’unità
L’euro è diviso in 100 centesimi.
con Metodo Matematica… 114
La regola
Cio che gia so Completa le tabelle. centesimi di euro 0,10 centesimi di euro centesimi di euro 100 100 100 1 centesimo di euro 0,01 centesimi di euro centesimi di euro 1 100 ...... 100 100 € € € € € € € € € centesimi centesimi centesimi centesimi centesimi centesimi
L’EURO
15 centesimi + centesimi = € 1
80 centesimi + centesimi = € 1
45 centesimi + centesimi = € 1
centesimi + 10 centesimi = € 1
centesimi + 5 centesimi = € 1
centesimi + 50 centesimi = € 1
7 euro e 55 centesimi = € 7,55
euro e centesimi = €
Mi esercito 115
1 Scrivi quanto manca per formare un euro.
2 Scrivi a quanto corrispondono.
Rosa ha comperato: da u , d c 1 , 6 0 + 1 3 , 4 0 + 3 , 8 0 = ,
in salto da u , d c 2 0 , 0 0 –...... ...... , ...... ...... = ,
Ha pagato con 20 euro.
Esegui le operazioni per sapere quanto ha speso e quanto ha ricevuto di resto.
euro e centesimi = € euro e centesimi = €
La matematica
AL SUPERMERCATO
Il supermercato è una vera palestra per diventare super matematici e super matematiche: si aggiunge, si toglie, si mette in relazione, si distribuisce...
1 Claudia, la direttrice del supermercato, porta le monete alle cassiere e ai cassieri che ne hanno bisogno.
Completa le uguaglianze.
Cassa 1
€ 50 = da € 2
€ 200 = da € 5
€ 200 = da € 10
€ 10 = da € 5
€ 10 = da € 1
€ 10 = da € 2
Cassa 2
€ 1 = da 10 centesimi
€ 1 = da 20 centesimi
€ 1 = da 50 centesimi
€ 2 = da 50 centesimi
€ 2 = da 10 centesimi
€ 2 = da 20 centesimi
2 Nel supermercato hanno installato un nuovo apparecchio. Legge le cifre dei prezzi e dei pesi e li dice in parola, ma a volte sbaglia. Trova gli errori, segnali con X e poi correggili.
13,09 tredici virgola zero-nove
24,06 ventiquattro virgola sei
140,3 centoquaranta virgola tre
40,25 quaranta virgola venticinque
7,50 sette virgola zero-cinque
Quando si leggono
i numeri decimali si deve sempre leggere la virgola.
116
3 Leggi e completa la tabella.
Davanti al supermercato c’è un parcheggio. È gratuito per chi effettua acquisti, a pagamento per chi non li fa. Il costo per un’ora di parcheggio è di 90 centesimi.
4 Stefano deve parcheggiare a pagamento per 3 ore e ha queste monete. Segna con X quelle che dovrà utilizzare, poi rispondi.
tempo costo
1 ora 90 centesimi
2 ore euro e centesimi
3 ore euro e centesimi
4 ore euro e centesimi
5 ore euro e centesimi
Quanto rimarrà a Stefano?
5 Serena compera un maglione che costa 75 euro. Non riceve resto. Con quali banconote paga? Cerchiale.
6 Giulia vuole comperare un pallone che costa € 9. Però le manca € 1,50. Cerchia quanto ha Giulia.
7 Al parcheggio ci sono due colonnine per la ricarica delle auto elettriche. Per utilizzarle bisogna abbonarsi. L’abbonamento mensile costa € 25. 6 dipendenti del supermercato hanno l’auto elettrica. In un mese, tutti insieme spendono più o meno di 200 euro? + –
I bambini e le bambine conoscono e utilizzano l’euro. L’ambientazione realistica delle esercitazioni li aiuta a compiere il processo di astrazione.
I gas di scarico delle auto inquinano l’aria. Se possibile, meglio muoversi a piedi o con i mezzi pubblici.
Educazione Civica
117
So risolvere i problemi!
È arrivato il momento di dimostrare che sei in grado di risolvere qualsiasi problema.
1 Riporta i dati sul quaderno e risolvi i problemi.
a. In lavanderia oggi sono state lavate 15 giacche e 32 paia di pantaloni. Il lavaggio per ogni giacca costa € 6. Quanto è stato incassato per il lavaggio delle giacche?
• Qual è il dato inutile? Sottolinealo.
b. In lavanderia sono state lavate 144 lenzuola di un albergo. Vengono riconsegnate in pacchi da 8. Quanti pacchi si confezionano?
c. Greta nel negozio di vestiti ha comperato alcuni capi di abbigliamento. La giacca a vento è il capo più caro, la camicetta è il meno caro. Ha comprato anche una gonna. Il prezzo dei tre indumenti è di € 124, € 55, € 27.
Quanto ha speso in tutto?
d. Gaetano ha comperato 5 camicie e un maglione. Le camicie costano € 27 ciascuna.
Gaetano ha pagato in tutto € 170.
Quanto costano in tutto le camicie? Quanto costa il maglione?
e. In occasione dei saldi viene rinnovata la vetrina. Si dispongono 56 pantaloni di velluto, ordinati in modo uguale per 7 colori. In vetrina ci sono anche 12 jeans.
Quanti pantaloni di velluto ci sono per ciascun colore?
Quanti pantaloni sono esposti in vetrina?
PR PROBLEMI 118
facile
SESTA TAPPA facile facile
un po’ piu impegnativo
Gino e Lara oggi hanno questo orario di lavoro.
Gino dalle 8 alle 13, Lara dalle 12 alle 20.
Quante ore ha lavorato Gino?
Quante ore ha lavorato Lara?
Quante ore ha lavorato Lara questa settimana?
Chi ha un orario settimanale di lavoro più lungo?
a. Lara deve sistemare le confezioni di biscotti sugli scaffali. Sul carrello ci sono 8 scatoloni da 32 confezioni ciascuno.
Sugli scaffali ci sono già 54 confezioni di biscotti.
Quante confezioni di biscotti ci saranno quando Lara avrà terminato il suo lavoro?
b. Nel reparto panetteria sono stati sfornati 320 panini. 140 panini vengono venduti a peso e i rimanenti vengono confezionati in sacchetti da 6 panini ciascuno. Quanti sacchetti vengono confezionati?
c. Nel reparto pescheria questa mattina sono stati venduti 7 kg di orate, 12 kg di branzini e 14 kg di calamari. Oggi tutto il pesce era venduto a 9 euro al chilogrammo. Quanto si è incassato dalla vendita del pesce questa mattina?
I bambini e le bambine hanno completato il percorso per tappe e ora potranno constatare di essere in grado di risolvere i problemi senza particolari difficoltà.
CO D i N G 119
2 Segna con X le domande a cui puoi rispondere.
3 Risolvi i problemi sul quaderno.
4 Risolvi il problema osservando l’immagine.
’
La torta costa
Risposta
Ramuttina pone diversi problemi aritmetici e Ramuttino li deve risolvere. Aiutalo tu.
Collega ciascun problema alla frase che spiega la sua risoluzione.
Otzi e la sua amica Etzi giocano con i sassolini. Etzi ha vinto tante volte.
Quanti punti ha totalizzato?
Otzi aveva 40 sassolini. Giocando con Etzi ne ha prima persi 8 e poi ne ha vinti 2.
Quanti sassolini ha ora Otzi?
Etzi ha 15 sassolini bianchi e altrettanti sassolini neri.
Quanti sassolini neri ha Etzi?
Il problema si può risolvere.
Non si può risolvere: mancano i dati necessari.
Il problema si può risolvere: ma non servono i numeri, occorre un’azione!
Non è proprio un problema: la risposta è già nel testo.
Otzi e Etzi vogliono fare una pittura rupestre. Si accorgono di non avere il carboncino per disegnare. Che cosa fanno?
CON I SAPIENS LOGICA mente 120
Il vasaio ha preparato dei doni per i bambini e le bambine del villaggio: alcuni vasi con le conchiglie. Ciascun vaso è contrassegnato da un simbolo.
4 vasi con 2 conchiglie 3 vasi con 3 conchiglie 1 vaso con 1 conchiglia
È tempo QUIZ
Scrivo il numero 0,25. Se inverto l’ordine delle cifre 2 e 5, ottengo un numero maggiore o minore di 0,25?
Ora scrivo un altro numero: 1,65.
Cambia tu l’ordine delle cifre per ottenere un numero maggiore: un numero minore:
Le sfide di logica non sono finite.
Ecco i quiz!
Queste pagine di logica presentano situazioni problematiche che, esposte in modo particolare, richiedono al bambino e alla bambina attenzione, ragionamento, immedesimazione.
LOGICA mente 121
Le frazioni e i numeri decimali
Frazionare significa dividere in parti uguali. Ciascuna parte uguale in cui viene diviso l’intero si chiama unità frazionaria.
I termini della frazione sono: 5 8
Si può frazionare un intero, ma anche una quantità.
Le frazioni che hanno come denominatore 10, 100, 1 000 si chiamano frazioni decimali.
Le frazioni decimali possono essere trasformate in numeri decimali.
Nei numeri decimali la virgola separa la parte intera dalla parte decimale.
122
Sintesi delle conoscenze
denominatore
numeratore linea di frazione
Parte intera unità u decimi d centesimi c millesimi m 1 2 5 7 , Parte decimale 1 10
Insegnare ai bambini e alle bambine a utilizzare la mappa per focalizzare quanto imparato. Le icone e le parole sui bracci aiutano a ricordare i concetti più importanti.
123
SISTEMA DECI M A L E PROBLEMI OPERAZIONI addizione sot t r a zione divisi on e moltiplicazione FRAZIONI ndecimali umeri deci m al i NUMERI k h da u 6 + 2 6 – 2 6 × 2 6 : 2 0,3 3 10 1 3 Mappa per ricordare
La misura e la realtà
Contenuti digitali
Metacognizione: ciò che già so Conosci la misura della tua altezza? Sai quanto pesi?
Quanta acqua bevi in un giorno? Quanti minuti impieghi per arrivare a scuola? Per rispondere a queste domande devi utilizzare le unità di misura: il metro, il chilogrammo, il litro…
Fin dall’antichità le persone hanno sentito la necessità di misurare: il tempo, la quantità delle merci, la grandezza dei campi… Le unità di misura però non erano uguali dappertutto. Con il tempo si è giunti a utilizzare il Sistema Internazionale di unità di misura , adottato in quasi tutto il mondo.
Classe capovolta: vedo e imparo dalle immagini
Nel rettangolino giallo scrivi che cosa si sta misurando.
Scegli tra: lunghezza • peso • capacità • tempo • valore
Nel rettangolino rosso scrivi l’unità di misura.
Scegli tra: metro • chilogrammo • litro • minuto • euro.
124
UA 2
Attraverso la metacognizione la classe si renderà conto che già nella vita quotidiana utilizza le misurazioni e particolari strumenti di misura. Con l’attività di classe capovolta i bambini e le bambine constatano che per ciascuna differente grandezza da misurare occorre una particolare unità di misura.
Si possono misurare lunghezze, pesi, capacità, superfici, tempo, valori. Occorrono, però, strumenti particolari. Misurare significa confrontare una grandezza con l’unità di misura scelta.
125
Ripetiamo insieme
LE MISURE DI LUNGHEZZA
Il metro, il chilometro… sono unità di misura di lunghezza.
Servono per misurare piccole o grandi lunghezze.
Cio che gia so Imparo
Ma il piede di un adulto è lungo come quello di un bambino?
Osserva le unità di misura di lunghezza che si usavano tanto tempo fa.
Scrivi: pollice • piede • spanna • passo
Secondo te, quanto misura? Colora il pallino: se misura circa 1 m se misura più di 1 m se misura meno di 1 m
Con le misure di lunghezza si possono misurare l’altezza, la lunghezza, la larghezza, lo spessore di un oggetto, la distanza tra due punti.
Oggi usiamo unità di misura convenzionali, cioè uguali per tutti.
L’unità fondamentale delle misure di lunghezza è il metro (m).
126
La regola
multipli unità di misura sottomultipli chilometro ettometro decametro metro decimetro centimetro millimetro km hm dam m dm cm mm 1 000 m 100 m 10 m 1 m 0,1 m 0,01 m 0,001 m
con Metodo Matematica…
I SOTTOMULTIPLI DEL METRO
Cio che gia so
Sai che decimo, centesimo, millesimo sono grandezze dieci, cento, mille volte più piccole dell’unità. I loro simboli sono: d • c • m
Imparo 1 cm 1 mm
Osserva il righello e completa.
1 dm
• Un decimetro è formato da cm 1 dm = cm
• Un centimetro è formato da mm 1 cm = mm
• Un decimetro è formato da mm 1 dm = mm
La regola
I sottomultipli del metro sono: il decimetro, il centimetro, il millimetro
1 m = 10 dm Il decimetro è la decima parte del metro.
1 m = 100 cm Il centimetro è la centesima parte del metro.
1 m = 1 000 mm Il millimetro è la millesima parte del metro.
Se esprimi una misura con unità di misura diverse, esegui una equivalenza:
1 m = 10 dm = 100 cm = 1 000 mm
Misura questi oggetti con il righello.
127 Matematica
mm dm cm
I MULTIPLI DEL METRO
Cio che gia so
Sai che decine, centinaia, migliaia sono grandezze dieci, cento, mille volte più grandi dell’unità. I loro simboli sono: da • h • k
Imparo
Per misurare grandi distanze, grandi lunghezze, si usano i multipli del metro.
I multipli del metro sono: il chilometro, l’ettometro, il decametro
1 km = 1 000 m Il chilometro è mille volte più grande del metro.
1 hm = 100 m L’ettometro è cento volte più grande del metro.
1 dam = 10 m Il decametro è dieci volte più grande del metro.
1
Un ponte su un torrente
La lunghezza di un corridoio della scuola
hm 1 dam 1 km
dam 3 hm 3 km
La larghezza di un posto auto 2 m 2 dam 2 hm
1 dam = m 1 hm = m 1 km = m
128
Distanza Roma-Milano 600 m 600 km 600 dam
1
3
La regola
Segna con X qual è la misura possibile.
2 Completa.
1 km 1 500 m 120 m 2 hm 35 m 3 dam 5 hm 70 m 1
1
1
con Metodo Matematica…
3 Segna con X la misura più corta.
km = 1 000 m
hm = 100 m
dam = 10 m
La regola
LE MISURE DI CAPACITÀ
multipli unità di misura sottomultipli ettolitro decalitro litro decilitro centilitro millilitro
1 Segna con X qual è la misura possibile
2 Rispondi.
• Per riempiere una caraffa da 1 ℓ, quanti bicchieri da 1 dℓ occorrono? .........
• Quanti centilitri ci sono in un litro? Quanti millilitri?
• Quanti centilitri ci sono in un decilitro?
3 Completa.
• Un decalitro è formato da ℓ 1 daℓ = ℓ
• Un ettolitro è formato da ℓ 1 hℓ = ℓ
4 Segna con X la capacità maggiore.
129 Matematica
200 mℓ 200 daℓ 200 ℓ 33 dℓ 33 cℓ 33 ℓ
1 ℓ 200 cℓ 1500 mℓ 1 ℓ 3 hℓ 200 ℓ 5 dℓ 2 ℓ
100 cℓ 100 ℓ 100 hℓ
Con le misure di capacità puoi misurare la quantità di liquidi contenuti in recipienti diversi. L’unità fondamentale delle misure di capacità è il litro (ℓ). hℓ daℓ ℓ dℓ cℓ mℓ 100 ℓ 10 ℓ 1 ℓ 0,1 ℓ 0,01 ℓ 0,001 ℓ
LE MISURE DI PESO
La regola
L’unità fondamentale delle misure di peso è il chilogrammo (kg).
multipli
unità di misura sottomultipli
Megagrammo (tonnellata) centinaio di kg (quintale) decina di kg chilogrammo ettogrammo decagrammo grammo Mg (t) q – kg hg dag g
000 kg 100 kg
Il quintale e la tonnellata sono unità di misura in uso, soprattutto in agricoltura, anche se non sono inserite nel Sistema Internazionale di unità di misura.
Per i pesi molto piccoli si usano i sottomultipli del grammo.
Sono unità di misura generalmente utilizzate per i farmaci o per i gioielli.
unità di misura sottomultipli grammo decigrammo centigrammo milligrammo g dg cg mg
g
1 Segna con X qual è la misura possibile.
150 g
150 kg
150 mg
g 0,01 g 0,001 g
hg
2 Completa.
• Un chilogrammo è formato da hg 1 kg = hg
• Un chilogrammo è formato da g 1 kg = g
• Un ettogrammo è formato da g 1 hg = g
g
130
1
0,1
35
35
35
30
kg
Mg 30 kg 30 hg
10
1 kg 0,1
0,01
0,001
con Metodo Matematica…
1
kg
kg
kg
kg
PESO NETTO • PESO LORDO • TARA
Cio che gia so Imparo
Molti prodotti sono venduti già preconfezionati. La confezione e il contenuto hanno pesi differenti.
Il peso lordo è il peso del contenitore e della merce contenuta in esso.
Il peso netto è il peso del contenuto.
La tara è il peso del contenitore.
La regola
peso netto + tara = peso lordo peso lordo – peso netto = tara peso lordo – tara = peso netto
Completa scrivendo peso lordo, peso netto, tara e i pesi mancanti.
131 Matematica
...........................
g 500 125 g 250 g 525 g g g 30 g g 70 g 15 g 450 g
........................... ...........................
LE EQUIVALENZE
Sai già che una lunghezza può essere espressa con unità di misura differenti.
Chi ha ragione?
Tutti e due i bambini! Quando si scrive la stessa lunghezza utilizzando unità di misura diverse si fa una equivalenza
Per fare un’ equivalenza devi:
• capire il valore di ciascuna cifra;
• inserire ciascuna cifra al posto giusto nella tabella;
• scrivere il nuovo numero, ricordando che la marca indica sempre la cifra delle unità (se necessario, aggiungi gli zeri).
132 La
marca corrisponde alla cifra delle unità
La
Cio che gia so Imparo
regola
km hm dam m dm cm mm 350 dm 3 5 0 35 m 4 cm 4 0 40 mm 5 000 m km 870 dam m 18 m dm 9 m cm dm cm 5 5 0
CO
D i N G
1 Circonda la cifra che corrisponde alla marca. Osserva gli esempi.
157 cm 32,6 cm 53 mm 84 km 8 hm 7 090 m 623 dam 0,65 m 11,6 km 4,9 dam 53,2dm 8,44 hm
con Metodo Matematica…
2 Inserisci le misure nella tabella ed esegui le equivalenze. Osserva gli esempi.
La sedia è larga 5 dm.
No,
è larga 50 cm. 52 cm
Quando fai un’equivalenza passi:
• da un’unità di misura di valore maggiore a una di valore minore oppure
• da un‘unità di valore minore a una di valore maggiore
Se passi da un’unità di valore maggiore a una di valore minore, moltiplichi:
• per 10 se ti sposti di una sola marca
• per 100 se ti sposti di due marche
• per 1 000 se ti sposti di tre marche
3 Completa le tabelle.
Se passi da un’unità di valore minore a una di valore maggiore, dividi:
• per 10 se ti sposti di una sola marca
• per 100 se ti sposti di due marche
• per 1 000 se ti sposti di tre marche
4 Esegui le equivalenze. a.
133 Matematica
dam m 1 8 20 12 150 daℓ hℓ 10 80 200 320 1 500 ℓ cℓ 1 4 60 75 36 cm m 100 800 1 000 1 600 9 700 kg g 1 5 9 3 10 mg g 1 000 8 000 7 000 3 000 4 000 × 10 : 10 × 100 : 100 × 1 000 : 1 000 km chilometro hm ettometro dam decametro m metro dm decimetro cm centimetro mm millimetro × 10 × 10 × 10 × 10 × 10 × 10 : 10 : 10 : 10 : 10 : 10 : 10
300 cm = m 5 000 m = km 1 km = m 4 dam = m 10 m = dam b. 1 ℓ = .............. dℓ 4 hℓ = ℓ 20 dℓ = ℓ 400 cℓ = ℓ 300 dℓ = ℓ
1 kg = hg 8 hg = g 200 g = hg 10 dg = g 5 000 g = hg Imparo
c.
Gli anni, i mesi, i giorni, le ore… servono per misurare il tempo
Cio che gia so Imparo
• Se la lancetta corta (che segna le ) si è spostata da 12 a 1, è trascorsa un’
• Se la lancetta lunga (che segna i ) si è spostata da 12 a 1, sono trascorsi minuti.
• Se la lancetta lunga fa un giro completo dell’orologio sono passati minuti, cioè un’
• Se la lancetta più sottile (che segna i ) si è spostata da 12 a 1, sono trascorsi secondi.
• Se la lancetta più sottile fa un giro completo dell’orologio significa che sono passati ........... secondi, cioè un ..........................
L’unità fondamentale delle misure di tempo è il secondo (s).
• A quanti minuti corrisponde un quarto d’ora?
• A quanti mezz’ora?
• A quanti un’ora e un quarto?
• A quanti tre quarti d’ora?
134
LE MISURE DI TEMPO
La regola 1 Completa le uguaglianze. 2 Rispondi alle domande. × 365 × 30 × 7 1 secondo (s) 1 minuto (m) 1 ora (h) 1 settimana 1 mese 1 anno × 60 × 60 × 24 1 giorno (d)
48 h = d 3 d = h 2 min = s 180 s = min 4 h = min 120 min = h 4 quarti d'ora formano un'ora! con Metodo Matematica…
3
Le misure di lunghezza
4
5
6 Quanto manca per formare un metro?
Mi esercito 135
1 Inserisci le misure nella tabella ed esegui le equivalenze
2 Scomponi ciascuna misura. Osserva l’esempio.
Esegui le equivalenze.
Esegui le equivalenze.
Colora la misura equivalente a quella data.
a. 153 m = 1 hm 5 dam 3 m 951 mm = 9 5 1 6 892 m = 6 8 9 2 703 dam = 7 0 3 b. 850 m = 8 5 0 210 cm = 2 1 0 326 dm = 582 m = a. 50 m = dm 6 km = m 500 cm = dm 2 000 m = dm 80 dm = m 3 hm = dam b. 1 km = 100 3 km = 3 000 4 m = dam 70 dm = 7 800 cm = 80 30 dam = 3 50 cm + cm = 1 m 2 cm + cm = 1 m 7 dm + dm = 1 m 9 dm + dm = 1 m 950 mm + mm = 1 m 190 mm + mm = 1 m
km hm dam m dm cm mm 150 cm dm 7 000 m km 900 dm m 6 hm m dm cm mm 4 m dm m mm 500 cm dm m mm 1 000 cm 5000 m 5 km 50 km 500 dam 9 km 9 000 m 900 m 90 hm
1 Inserisci le misure nella tabella ed esegui le equivalenze.
Le misure di capacità
hℓ
6 hℓ ℓ
14 ℓ cℓ
3 000 mℓ ℓ
40 ℓ daℓ
2 Scomponi ciascuna misura. Osserva l’esempio.
a. 350 cℓ = 3 ℓ 5 dℓ 0 cℓ
162 ℓ = 1 6 2
7 500 dℓ = 7 5 0 0
3 Esegui le equivalenze.
a. 25 dℓ = cℓ
2 hℓ = ℓ
80 ℓ = daℓ
1 Inserisci le misure nella tabella ed esegui le equivalenze.
4 000 mℓ = ℓ
3 daℓ = ℓ
500 cℓ = ℓ
b. 921 cℓ = 9 2 1
500 ℓ = 5 0 0
2 430 mℓ =
b. 2 ℓ = 200
5 daℓ = 50
300 cℓ = 3
Le misure di peso
40 dℓ = 4
1 000 mℓ = 1
6 hℓ = 60
kg hg dag g dg cg mg
600 g hg
100 g dag
7 hg g
4 kg g
2 Scomponi ciascuna misura. Osserva l’esempio.
a. 590 dag = 5 kg 9 hg 0 dag
456 cg = 4 5 6
8 900 g = 8 9 0 0
3 Esegui le equivalenze.
a. 2 Mg = kg
12 kg = hg
700 cg = .......... dg
10 dag = hg
80 g = dag
1 hg = .......... dag
b. 1 100 g = 1 1 0 0 840 mg = 8 4 0
750 g =
b. 4 000 kg = 4
200 g = 2
7 hg = 700 ..........
1 500 g = 15
400 cg = 4
2 000 mg = 2 ..........
Mi esercito 136
daℓ ℓ dℓ cℓ mℓ
Problemi con le misure
1 Risolvi i problemi con le misure di lunghezza indicando l’operazione e l’equivalenza.
a. Gioia, per allenarsi, ogni giorno fa 20 giri di una pista lunga 4 hm. Quanti chilometri percorre ogni giorno?
Operazione Equivalenza
b. Il contachilometri della bicicletta di Ismail segnava 156 km. Ismail ha percorso poi 7 000 m. Quanti chilometri segna ora il contachilometri?
Equivalenza Operazione
2 Risolvi i problemi con le misure di capacità sul quaderno.
a. Raja ha una bottiglia di succo di mela da 2 ℓ. Riempie 5 bicchieri da 20 cℓ
Quanti litri di succo di mela ha versato nei bicchieri? Quanto succo rimane?
b. Per innaffiare le sue piante Simone usa l’acqua contenuta nella cisterna. Oggi ha usato 204 ℓ per innaffiare l’orto e 33 ℓ per bagnare le piante della serra.
Ora nella cisterna sono rimasti 63 ℓ di acqua.
Quanti litri di acqua ha consumato? Quanti litri c’erano nella cisterna prima che innaffiasse le piante della serra e dell’orto? Quanti ettolitri?
3 Risolvi i problemi con le misure di peso sul quaderno.
Dal fornaio Beatrice compera 6 panini del peso di 50 g l’uno.
Quanto pesano tutti i panini? Compra anche una pagnotta da 5 hg.
Quanti ettogrammi di pane ha comperato in tutto?
4 Prima di risolvere il problema scrivi: peso lordo, peso netto, tara. Giacomo ha comperato una cassetta di uva che pesa in tutto 12 kg ( ).
La cassetta vuota pesa 2 kg ( ).
Quanto chilogrammi di uva ha comperato ( )?
L’uva costa 2 euro al chilogrammo. Quanto ha speso Giacomo?
5 Risolvi il problema con le misure di tempo sul quaderno.
Jacopo per andare al lavoro impiega 3 quarti d’ora con l’autobus oppure 1 ora e un quarto con la sua auto. Quanti minuti risparmia quando utilizza l'autobus?
Mi esercito 137
2 m + 30 cm = 230 1 km + 5 m = 1 005 5 cm + 8 mm = 5,8
6 ℓ + 5 dℓ = 6,5 1 hℓ + 9 ℓ = 109 3 daℓ + 2 ℓ = 32
1 kg + 5 hg = 1,5 1 Mg + 4 kg = 1 004 2 g + 6 dg = 2,6
2 In ciascun gruppo c’è una uguaglianza sbagliata. Segnala con X.
3 Cerchia la cifra che corrisponde…
700 cℓ + 300 cℓ = 1 ℓ 100 m + 900 m = 1 km 90 g + 10 g = 1 dag 8 hg + 2 hg = 1 kg al litro 156 dℓ 0,75 ℓ 3,4 daℓ 1,25 hℓ al metro 5,78 m 700 cm 1,74 hm 8,45 dam al kg 1 500 g 12 hg 3,76 kg 1,009 Mg
4 Completa le tabelle.
IN AUTOGRILL kg hg dag 50 25 100
Anche in un autogrill ci si può esercitare con la matematica! Quando si compera un panino, un gelato, una bibita…. ℓ dℓ cℓ 500 6 40
5 Colora il quadratino…
… di tutte le bottiglie da 0,5 litri che servono per riempire una bottiglia da 2 litri.
… di tutte le scatole di biscotti da 200 g che servono per ottenere 1 kg di biscotti.
138
1 Scrivi la marca. m dm cm 3 90 800
a. Ginevra sta tornando a casa. Ecco il contachilometri della sua automobile. Quale numero segnerà il contachilometri quando Ginevra arriverà a Venezia?
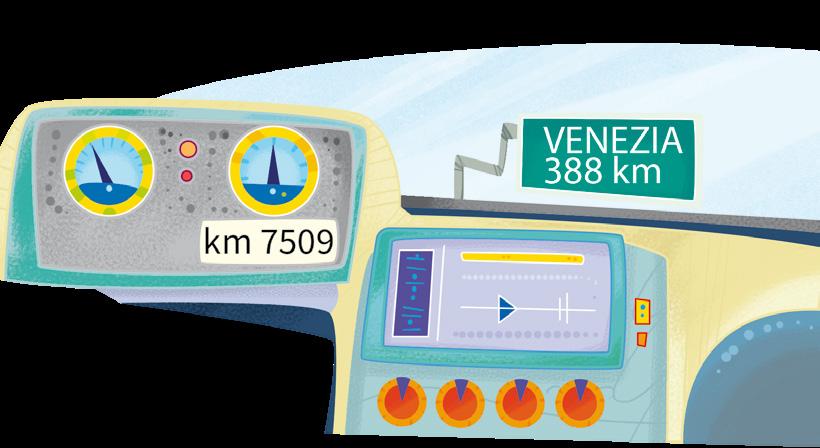
b. Un vassoio per il pranzo preconfezionato contiene 250 g di verdure, 150 g di pasta con il sugo, 80 g di formaggio e una mela da 182 g. Quanto grammi pesa tutto il cibo contenuto nel vassoio? Quanti ettogrammi?
c. Al bar dell’autogrill c’è una botticella per la distribuzione del succo d’arancia. La botticella ora contiene 6 ℓ di succo d’arancia. Ogni bicchiere di succo d’arancia contiene 3 dℓ. Quanti bicchieri si potranno riempire?
All’autogrill è arrivato un pullmino con 7 persone.
Tutti riempiono d’acqua la loro borraccia.
6 persone hanno borracce da 75 cℓ e una da 50 cℓ.
Quanta acqua mettono nelle borracce?
Le esercitazioni aiutano i bambini e le bambine a comprendere l’importanza delle equivalenze nell’operare con quantità espresse con marche diverse. I problemi aiutano a capire la necessità di eseguire equivalenze nella realtà.
Per una sana alimentazione non devono mai mancare cibi freschi come frutta e
139
6 Risolvi i problemi sul quaderno.
7 Scrivi la domanda intermedia e poi risolvi il problema.
verdura.
Educazione Civica
Ramuttina e zia Argut hanno misurato la lunghezza della caverna. Ramuttina e Argut hanno ottenuto risultati differenti.
Argut 15 passi, Ramuttina 24 passi.
Quale potrebbe essere il motivo della diversa misurazione. Segna con X.
Argut fa passi più lunghi di Ramuttina.
Ramuttina ha sbagliato.
Ramuttina ha fatto il percorso due volte.
L’anno scorso il mio risultato era di 30 passi.
Ciascun bambino misura la larghezza dell’ingresso della caverna con un bastone diverso.
Sai capire quale bastone ha usato?
Disegna il simbolo.
Lo avete fatto anche l’anno scorso?!
Perché l’anno precedente il risultato di Ramuttina era diverso? Quale potrebbe essere il motivo? Segna con X.
Ramuttina era più bassa. Lo scorso anno Ramuttina non sapeva contare.
Ramuttina aveva contato più lentamente.
LOGICA
140
CON I SAPIENS
mente
Misura circa 20 volte il bastone
Ramuttina
Misura circa 30 volte il bastone
Ramuttino
Misura circa 10 volte il bastone
Nurut
Misura circa 16 volte il bastone
Narut
Ramuttina ha costruito una bilancia. Si accorge che ogni vaso pesa come 4 ciotole.
Aiuta Ramuttino a disegnare le ciotole e i vasi necessari perché ogni bilancia sia in equilibrio.
Anche Narut e Nurut hanno portato l’acqua al villaggio. Ma in un contenitore hanno messa una quantità di acqua doppia rispetto alle altre. Colora l’acqua che c’è in ciascun contenitore.
Ramuttina travasa l’acqua in parti uguali in 5 contenitori più piccoli.
Tu ora disegna l’acqua nei contenitori più piccoli.
Attraverso questi quesiti di logica i bambini e le bambine comprendono la necessità di utilizzare un’unità di misura, anche arbitraria, per confrontare le grandezze.
141 LOGICA mente
La misura
Misurare significa confrontare una grandezza con l’unità di misura scelta.
L’unità fondamentale delle misure di tempo è il secondo (s).
Quando si scrive la stessa misura utilizzando unità di misure diverse si fa un’equivalenza.
Per fare un’equivalenza si cerca il valore di ciascuna cifra oppure si moltiplica/divide per 10, 100, 1 000.
Il denaro si usa per misurare il costo di una merce.
L’euro è la moneta che si usa in Italia e in altri Paesi europei.
Il suo simbolo è €.
Un euro è diviso in 100 centesimi.
142 Sintesi delle conoscenze
multipli unità di misura sottomultipli hℓ daℓ ℓ dℓ cℓ mℓ 100 ℓ 10 ℓ 1 ℓ 0,1 ℓ 0,01 ℓ 0,001 ℓ Misure di capacità multipli unità di misura sottomultipli Mg (t) (q) – kg hg dag g 1 000 kg 100 kg 10 kg 1 kg 0,1 kg 0,01 kg 0,001 kg unità di misura sottomultipli g dg cg mg 1 g 0,1 g 0,01 g 0,001 g Misure di peso
di tempo
di valore Misure di lunghezza multipli unità di misura sottomultipli km hm dam m dm cm mm 1 000 m 100 m 10 m 1 m 0,1 m 0,01 m 0,001 m
Equivalenze Misure
Misure
Insegnare ai bambini e alle bambine a utilizzare la mappa per focalizzare quanto imparato. Le icone e le parole sui bracci aiutano a ricordare i concetti più importanti.
143
PESO (chilogram m o) M I S U R E DI TEMPO (s) CAPACITÀ(litro) VALORE(denaro• euro) E QUIVALENZE v alore delle cifre × : 10 , 100 , 1 0 0 0 MISURA € m kg ℓ
LUNGHEZZA (metro)
Mappa per ricordare
La geometria e la realtà
Metacognizione: ciò che già so
Lunghezza, larghezza e altezza sono parole che senti abitualmente nella vita di tutti i giorni e sai a che cosa si possono riferire.
Classe capovolta: vedo e imparo dalle immagini
Il palazzo, la fontana e l’aiuola sono solidi. Hanno tre dimensioni.
Scrivi:
1 lunghezza
2 larghezza
3 altezza
La geometria è una scienza molto antica. Quando nella Preistoria l’uomo e la donna iniziarono a costruire case in muratura, a recintare i rifugi per gli animali, a realizzare lunghe corde con le fibre vegetali, utilizzavano la geometria.
Il posto auto è una figura piana. Ha due dimensioni.
Scrivi:
4 lunghezza
5 larghezza
144
UA 3
.....
Osserva queste linee. Hanno una sola dimensione. Quale?
Completa scrivendo: area • angolo • perimetro.
Il punto in cui si batte il calcio d’
I solidi sono figure che hanno tre dimensioni.
Le figure piane hanno due dimensioni. Le linee hanno una sola dimensione. Area, perimetro, angolo sono “parole della geometria”.
Attraverso la metacognizione i bambini e le bambine imparano a vedere nella realtà le figure geometriche e a rilevarne le dimensioni che permettono di classificarle in solidi, figure piane, linee.
145
Il del campo.
Ripetiamo insieme
L’ di rigore.
Cio che gia so
Le linee non sono tutte uguali. Una linea può essere retta, curva, spezzata, mista
Una linea può essere aperta o chiusa. Una linea può essere semplice o intrecciata.
Imparo
La retta
Questa linea mantiene sempre la stessa direzione?
I puntini ti indicano che non ha né un inizio né una .
La regola
La semiretta
Questa linea mantiene sempre la stessa direzione ?
Ha un inizio?
Ha una fine?
Le linee hanno un sola dimensione: la lunghezza
La linea retta è una linea che mantiene sempre la stessa direzione. Non ha un inizio né una fine.
La semiretta ha un inizio ma non ha una fine.
Il segmento ha un inizio e ha una fine.
Il segmento
A B
Questa linea mantiene sempre la stessa direzione ?
Ha un inizio?
Ha una fine?
1 Disegna: segui le indicazioni.
Una retta Una semiretta
Un segmento
2 Per ciascuna linea segna le sue tre caratteristiche (una per ogni gruppo).
Ricordi? Le hai studiate lo scorso anno!
aperta chiusa semplice intrecciata retta curva spezzata mista
con Metodo Matematica… 146
LE LINEE
r
O
LA POSIZIONE DELLE RETTE
• Rispetto alla sua posizione sul piano una retta può essere:
parallele
Due rette sono parallele quando mantengono sempre la stessa distanza e non si incontrano mai.
incidenti
Due rette sono incidenti quando si incontrano in un punto. Dividono il piano in 4 parti.
perpendicolari
Imparo verticale orizzontale obliqua e f
Due rette sono perpendicolari se, quando si incontrano in un punto, dividono il piano in 4 parti uguali.
147 Matematica
1 Traccia una retta perpendicolare.
4 Ripassa in rosso le rette incidenti, in verde quelle parallele, in blu quelle perpendicolari.
2 Traccia una retta incidente.
r r r
3 Traccia una retta parallela.
• Due rette sul piano possono essere: a b c d
Imparo
GLI ANGOLI
L’angolo retto è quello che si usa per classificare gli altri angoli.
La porta aprendosi ha delineato sul terreno angoli di diversa ampiezza.
• L’angolo minore di un angolo retto si chiama angolo acuto
• L’angolo maggiore di un angolo retto si chiama angolo ottuso
• L’angolo formato da due angoli retti si chiama angolo piatto
• L’angolo formato da quattro angoli retti si chiama angolo giro
La regola
• L’angolo è la parte di spazio compresa tra due semirette che hanno la stessa origine.
• Le semirette sono i lati dell’angolo, il punto di origine è il vertice, lo spazio compreso tra i due lati è l’ampiezza
• L’ampiezza di un angolo non dipende dalla lunghezza dei suoi lati!
• In base alla sua ampiezza un angolo può essere: retto, ottuso, acuto, piatto, giro
con Metodo Matematica… 148
O O O O ampiezza lato vertice O
1 Utilizza un angolo retto come campione (l’angolo della squadra, l’angolo del quaderno) e scrivi se questi angoli sono retti, acuti, ottusi.
Un angolo rimane ottuso, acuto, retto… qualsiasi sia la sua posizione sul piano. È vero?
2 Disegna l’altro lato dell’angolo.
angolo acuto angolo retto angolo ottuso
3 Segna con X la scelta giusta.
• Un angolo piatto è formato da
• Un angolo giro è formato da
• Un angolo giro è formato da
Disegna l’altro lato di un angolo retto. Non sarà nella “solita” posizione, ma tu sarai capace di disegnarlo.
Mi esercito 149
in salto ..............................
I POLIGONI
Cio che gia so
Esistono figure piane diverse tra di loro perché hanno un differente numero di lati e angoli.
Imparo
Colora il quadratino come indicato per collegare alla definizione.
È un poligono perché è chiuso da una linea spezzata
Non è un poligono perché non è una figura chiusa
Non è un poligono perché è chiuso da una linea mista.
Scrivi al posto giusto angolo, vertice, lato
La regola
I poligoni sono figure piane chiuse da una linea spezzata
I lati sono i segmenti che chiudono il poligono.
L’angolo è la parte di piano delimitata tra due lati.
Il vertice è il punto in cui si incontrano due lati.
Colora il quadratino in: accanto ai poligoni accanto ai non poligoni.
con Metodo Matematica… 150
LA CLASSIFICAZIONE DEI POLIGONI
• Che cosa ti fa pensare il prefisso tri (trifoglio, triciclo…)?
• Che cosa ti fa pensare il prefisso quadri (quadrifoglio, quadrimestre…)?
Cio che gia so Imparo
Circonda in rosso il triangolo e in verde i quadrilateri.
E gli altri poligoni come si classificano?
Completa la tabella.
La regola
I poligoni prendono il nome dal numero di lati e di angoli che hanno. Ogni poligono ha lo stesso numero di lati, di angoli e vertici
151 Matematica
triangolo 3 3 3 quadrilatero pentagono esagono numero vertici numero angoli numero lati forma nome
I QUADRILATERI
Cio che gia so
Scrivi il nome di questi quadrilateri che già conosci.
Imparo
Spiegazione
Osserva questi particolari quadrilateri e completa le loro caratteristiche.
Trapezio
Ha lati paralleli.
Parallelogramma o romboide
Ha coppie di lati paralleli e uguali.
Rombo
Ha 2 coppie di lati paralleli.
Ha tutti i lati
Rettangolo
Ha coppie di lati paralleli e uguali.
Ha tutti gli angoli uguali e
Quadrato
Ha 2 coppie di lati paralleli.
Ha tutti i lati .
Ha tutti gli angoli uguali e
La regola
I quadrilateri sono poligoni con 4 lati, 4 angoli, 4 vertici
Alcuni quadrilateri hanno caratteristiche particolari e nomi diversi:
trapezio, parallelogramma (romboide), rettangolo, rombo, quadrato.
con Metodo Matematica… 152
.
1 Completa, poi colora i poligoni secondo le indicazioni.
triangolo ( lati, angoli, vertici)
quadrilatero ( lati, angoli, vertici)
pentagono ( lati, angoli, vertici)
esagono ( lati, angoli, vertici)
2 Indica se le affermazioni sono vere (V) o false (F).
• I poligoni sono figure geometriche piane. V F
• I poligoni sono figure aperte. V F
• Il punto di incontro di due lati si chiama vertice. V F
• Lo spazio compreso tra due vertici si chiama angolo. V F
3 Colora gli angoli di queste figure secondo le indicazioni. angoli retti angoli acuti angoli ottusi. Poi completa scrivendo il nome della figura e quanti angoli hai colorato.
È un angoli retti:
angoli acuti:
angoli ottusi:
È un angoli retti:
angoli acuti:
angoli ottusi:
È un angoli retti:
angoli acuti:
angoli ottusi:
È un
angoli retti:
angoli acuti:
angoli ottusi:
Mi esercito 153
Linee e angoli
1 Leggi le caratteristiche che possono avere le linee e scrivile al posto giusto. Le linee possono essere:
aperte o chiuse semplici o intrecciate
rette, curve, spezzate, o miste
2 Colora in rosso la retta, in verde la semiretta, in viola il segmento. Indica la posizione colorando il quadratino come indicato: verticale • orizzontale • obliqua
3 I tre angoli si sono spostati in differenti posizioni. Cercali e colorali nello stesso modo.
Mi esercito 154
I poligoni
1 Collega le definizioni colorando nello stesso modo. Poligono
Non poligono
Figura piana delimitata da una linea spezzata chiusa.
Figura piana delimitata da una linea curva o mista.
4
il nome del quadrilatero che ha queste caratteristiche.
Poi scrivi la lettera accanto alla figura corrispondente.
A. Ha 4 angoli retti e i lati uguali a 2 a 2.
B. Ha una sola coppia di lati paralleli.
C. Ha 4 angoli retti e i lati tutti uguali.
D. Ha 4 lati tutti uguali, e gli angoli uguali a 2 a 2. .....................................................
Mi esercito 155
Scrivi
2 Cerca i poligoni e colora il quadratino.
3 Colora il poligono che ha 2 angoli retti e 2 lati uguali.
IL PERIMETRO
Passa il dito lungo il contorno di queste figure piane Poi colora il contorno.
Ho disegnato i 4 lati del trapezio tutti in fila. Voglio calcolare il perimetro.
Con il righello misura ciascun lato sulla figura e sulla linea disegnata da Tea.
Imparo La regola
Il perimetro è la misura del contorno di un figura piana. Si calcola sommando le lunghezze di tutti i lati. Si indica con la lettera P.
Misura ciascuno dei 4 lati dei rettangoli e riportali sulla linea colorandola. Poi calcola il perimetro.
156
cm cm cm cm cm cm cm cm cm + cm + cm + cm = cm cm + cm + cm + cm = cm + cm cm + cm + cm = cm
con Metodo Matematica…
1 Calcola il perimetro (P) di ciascuna figura. Utilizza il lato del quadretto (1 cm).
2 Misura i lati di ciascuna figura, poi calcola il perimetro (P).
3 Risolvi i problemi sul quaderno.
a. Il quaderno ha la forma di rettangolo.
Il lato lungo misura 30 cm, quello corto 21 cm.
Quanto misura il perimetro?
b. Un giardino ha forma di quadrato. Il lato misura 18 m.
Quanto misura il perimetro?
c. Un triangolo ha i lati che misurano rispettivamente 15 m, 18 m, 24 m.
Quanto misura il perimetro?
Mi esercito 157
cm cm cm cm cm cm cm cm cm cm cm cm cm cm + + + = P = cm + + + = P = cm + + = P = cm + + = P = cm P = cm P = cm P = cm
Imparo
Passa il dito sopra tutto lo spazio occupato da queste figure piane. Poi colorale.
Ho ricoperto la superficie di un rettangolo con foglietti tutti uguali. Voglio calcolare l’area.
La regola
L’area è la misura della superficie di un poligono. Per calcolare l’area occorre:
• scegliere un’unità di misura adatta;
• ricoprire con il campione la superficie;
• contare quante volte il campione è contenuto nella superficie da misurare.
Per calcolare l’area, l’unità di misura più adatta è un campione di forma quadrata. Due figure che hanno la stessa area sono equiestese.
Calcola l’area di ciascuna figura, poi completa.
A B
• La figura A e la figura sono equiestese.
• La figura ......... e la figura ......... sono equiestese.
con Metodo Matematica… 158
L’AREA
C D area = area = area = area = area =
LA SIMMETRIA
Imparo
Riproduci su un foglio un disegno uguale a questo.
Piega il foglio lungo la linea rossa e osserva: la figura viene divisa in due parti che si sovrappongono perfettamente.
La linea rossa è l’asse di simmetria ed è interno alla figura.
Riproduci questo disegno.
L’asse di simmetria è esterno alla figura.
La regola
L’asse di simmetria può essere interno o esterno alla figura.
Può essere in posizione verticale, orizzontale, obliqua.
1 Disegna la parte simmetrica.
159 Matematica
2 Disegna la figura simmetrica.
Cio che gia so Imparo
Scrivi il numero corrispondente.
1 solido • 2 figura piana • 3 linea
Scrivi al posto giusto: lunghezza • larghezza • altezza
I SOLIDI
La regola
Osserva:
• Le figure piane che chiudono il solido sono le facce.
• Il lato comune a due facce è lo spigolo
• Il punto in cui si incontrano tre spigoli è il vertice.
I solidi sono figure che hanno tre dimensioni: lunghezza, larghezza, altezza. Sono chiusi da figure piane.
1 In questi solidi colora in: un vertice uno spigolo una faccia
2 Osserva e scrivi il numero di facce, spigoli, vertici.
160
n. facce ......... n. spigoli n. vertici n. facce ......... n. spigoli n. vertici n. facce ......... n. spigoli n. vertici Contenuti digitali con Metodo Matematica…
LO SVILUPPO DEI SOLIDI
Imparo
I solidi sono delimitati da figure piane. Se si “apre” un solido, si ha il suo sviluppo, cioè si appoggiano sul piano le figure piane che lo formano.
Osserva lo sviluppo dei solidi e completa. Poi colora nello stesso modo le facce uguali.
Lo sviluppo del cubo
è formato da 6 .
Lo sviluppo del cilindro è formato da e da .
Lo sviluppo del parallelepipedo
è formato da 6
Lo sviluppo della piramide
è formato da e da .
161 Matematica
In Guida altri sviluppi per costruire differenti solidi.
Perimetro e area
1 Colora in azzurro la superficie e in rosso il contorno. Poi completa.
• La misura del contorno di una figura piana è il .
• La misura della superficie di una figura piana è l’ .
2 Sulla linea sono stati riportati i 4 lati del quadrilatero. Misurali e calcola il perimetro
3 Con le tue parole spiega come si calcola la misura del perimetro di un poligono.
4 Collega ciascun poligono alla sua area colorando il quadratino. Poi completa.
22 33 17 31
• Due figure sono equiestese quando hanno la stessa .
Mi esercito 162
+ cm cm + cm + cm = cm
La simmetria • I solidi
1 In ciascuna lettera traccia l’asse di simmetria interno e scrivi V se è verticale, O se è orizzontale. Poi rispondi.
• In quale lettera non hai potuto tracciare l’asse di simmetria?
2 In ciascuna lettera traccia due assi di simmetria: uno verticale e uno orizzontale.
3 Completa i cartellini e collegali alla definizione numerando.
1. Le facce sono le figure piane che chiudono il solido.
2. Lo spigolo è il lato comune a due facce.
3. Il vertice è il punto di incontro di 3 spigoli.
Mi esercito 163
..... ..............................
La matematica
NEL CORTILE DELLA SCUOLA
Spesso i giochi che fai con i compagni e le compagne nel cortile della scuola sono “giochi geometrici”.
1 Aiuta i bambini e le bambine a completare le figure geometriche.
rettangolo
trapezio
2 Una bambina sta giocando a “campana”.
quadrato triangolo
Quali figure geometriche riconosci?
Scrivi il nome e scegli un colore diverso per la superficie di ciascuna forma.
................................................................................
3 Mirko sta osservando un cubo. Aiutalo segnando la risposta giusta.
La faccia del solido è: una figura piana. una linea. un punto.
Il vertice del solido è: una figura piana. una linea. un punto.
Lo spigolo del solido è: una figura piana. una linea. un punto.
164
4 Un gruppo di bambini e bambine sta facendo una gara. Devono completare i disegni dati dall’insegnante con la parte o il disegno simmetrico.
in salto
Nel cortile della scuola di Andrea ci sono una griglia e un tombino per lo scolo dell’acqua. Osserva le misure dei lati. Scrivi quelle mancanti.
Ora calcola i perimetri (P).
P griglia = cm + cm + cm + cm = cm
P tombino = cm + cm + cm + cm = cm
C’è un altro modo per calcolare il perimetro del tombino. Completa.
cm × = cm
Le esercitazioni proposte in queste pagine permettono di consolidare il concetto di poligono, perimetro del poligono, solido, simmetria.
165 80 cm ... cm ... cm 40 cm 50 cm ... cm ... cm ... cm
Ramuttino ha preparato alcuni quiz di logica “geometrica”. Riuscirà Ramuttina a risolverli tutti?
Nelle due pitture di Ramuttino ci sono 5 elementi che non sono simmetrici. Cercali e segnali con una X. Uno è già stato trovato.
Guarda le mie pitture. È tutto simmetrico?
La mamma di Ramuttino ha preparato questi due tessuti cucendo insieme figure geometriche.
Aiuta Ramuttina a rispondere alle domande di Ramuttino.
• Per realizzare il primo tessuto mia mamma ha utilizzato più tessuto verde o più tessuto giallo?
• E per realizzare il secondo?
166
CON I SAPIENS LOGICA mente
X
La mamma di Ramuttino ha fatto tanti quadrati di tessuto, tutti uguali a questo
Li userà per confezionare 4 stuoie di forme diverse per le sue amiche: Argat, Irgut, Ergut, Orgut. Dovrà però tagliare alcuni quadrati.
• Quanti quadrati serviranno per la stuoia di Argat?
• Quanti per quella di Irgut? E per Ergut?
• E Orgut?
Il vasaio del villaggio ha ideato dei vasi dalle forme originali. Ramuttino disegna sulla sabbia le impronte dei vasi. Poi accompagna Ramuttina dal vasaio. Le chiede di abbinare ai vasi il simbolo dell’impronta.
• Quale impronta non corrisponde a nessun vaso? Cerchiala.
Operare sulle figure geometriche attraverso la logica permette di avvicinarsi al concetto di area in modo intuitivo. Il bambino e la bambina scopriranno che una figura piana occupa sempre uno spazio sul piano.
167 LOGICA mente
Argat
Irgut Ergut Orgut
Sintesi delle conoscenze
La geometria
La geometria studia le forme geometriche: linee, angoli, figure piane, solidi.
Le linee
Le linee hanno una sola dimensione: la lunghezza.
linea retta semiretta segmento
Gli angoli
angolo
Le figure piane hanno 2 dimensioni: larghezza, lunghezza.
I poligoni sono figure piane chiuse da una linea spezzata (senza parti curve).
Di un poligono si può calcolare la misura:
• del contorno (perimetro)
• dello spazio occupato (area)
I solidi
faccia spigolo vertice vertice lato angolo
168
ottuso angolo
L’angolo è la parte di spazio compresa tra due semirette che iniziano nello stesso punto. angolo acuto
retto
Le figure piane
I solidi hanno 3 dimensioni: altezza, larghezza, lunghezza.
GEOMETRIA
Insegnare ai bambini e alle bambine a utilizzare la mappa per focalizzare quanto imparato. Le icone e le parole sui bracci aiutano a ricordare i concetti più importanti.
169 Mappa per ricordare
ANGOLI LINEE retto acuto ottuso SOLIDI rettasemiretta s e g m ento non p ol i g o n i poligoni
Le relazioni, i dati, le previsioni e la realtà
Metacognizione: ciò che già so
Nella tua casa i giocattoli, i vestiti, i piatti sono conservati nello stesso posto o sono raggruppati in base al loro utilizzo?
A volte guardi le previsioni del tempo? Perché?
Quando compri le figurine pensi alla probabilità di trovare figurine doppie?
Tutti i giorni, anche senza accorgertene, fai delle classificazioni, ad esempio quando getti la carta nel contenitore giusto. Ti poni alcune domande per capire le relazioni, ad esempio quando ti chiedi chi è il fratello della tua compagna di banco. Fai delle previsioni, ad esempio quando ti chiedi se la tua squadra vincerà la gara.
Classe capovolta: vedo e imparo dalle immagini
Osserva e rispondi.
Quale criterio è stato utilizzato per classificare gli oggetti esposti nelle tre teche?
170
UA 4
pietra
metallo
terracotta
ATTIVITÀ NEL NEOLITICO
Grafico A
Classificare, mettere in relazione, calcolare la probabilità sono attività che i bambini e le bambine, inconsapevolmente, compiono tutti i giorni. Soffermarsi a riflettere su questo fatto è un modo per vedere la matematica veramente applicata nella realtà.
Grafico B
cacciatori
1% legumi
1% frutta
1% altre piante
97% cereali
Questi grafici riportano teorie elaborate da differenti studiosi e studiose.
A colpo d’occhio quali informazioni ti fornisce il grafico A?
E il grafico B?
Non esistono documenti scritti del periodo del Neolitico. Perciò questi dati, secondo te, sono certi, possibili, impossibili?
Per poter classificare occorre riconoscere le caratteristiche comuni. Gli avvenimenti possono essere certi, possibili o impossibili. I grafici permettono di visualizzare con facilità una situazione.
171
Ripetiamo insieme
agricoltori pastori pescatori
L’agricoltura in Italia nel 5000 a.C.
LE CLASSIFICAZIONI
Sai disegnare un insieme di animali erbivori e un insieme di animali carnivori. Quindi sai già che cosa significa classificare.
Cio che gia so Imparo
All’ingresso del supermercato ci sono questi carrelli. Classificali riportando la lettera nell’insieme.
con il fiocchetto con 4 ruote e con fiocchetto
La regola
Classificare significa raggruppare insieme tutti gli elementi di un gruppo che hanno delle caratteristiche comuni.
CO D i N G
Per classificare gli ELEMENTI occorre:
• definire il gruppo a cui ci stiamo riferendo;
• definire quali sono le caratteristiche prese in considerazione;
• utilizzare uno schema o un diagramma.
Fai riferimento ai carrelli che hai osservato e rispondi.
• Quali NON hanno 4 ruote? , , ,
• Quali NON hanno il fiocchetto? , , , .
• Quali NON hanno 4 ruote e NON hanno il fiocchetto? , .
• Quali hanno 4 ruote E il fiocchetto? , .
con Metodo Matematica… 172
I DIAGRAMMI
Imparo
Per classificare si possono utilizzare schemi o diagrammi differenti
Classifica riportando le lettere negli schemi.
Diagramma di Eulero-Venn
Homo sapiens di una tribù
con lancia
con clava con lancia e clava
Diagramma di Carroll
con lancia senza lancia con clava
senza clava
Diagramma ad albero
Homo sapiens di una tribù
con clava senza clava
con lancia con clava senza clava
senza lancia
173 Matematica
INDAGINI STATISTICHE
Cio che gia so Imparo
Le indagini statistiche servono per conoscere i gusti, le abitudini delle persone grandi e piccole. Nella biblioteca del comune di Poggi Ridenti hanno fatto un’indagine con i bambini e le bambine di una classe terza per conoscere i loro gusti e acquistare poi nuovi libri. Ai bambini e alle bambine è stata fatta questa domanda. Ogni bambino/a ha dato una sola risposta.
Come deve essere un libro?
• A fumetti
• Con tante fotografie.
• Con tanti disegni.
• Con tante pagine.
• Con poche pagine.
Ecco i risultati dell’indagine.
3aA (20 bambini/e)
caratteristica preferenze
a fumetti X X X
con tante foto X X X X X
con tanti disegni X X X X X X X
con tante pagine X X X X
con poche pagine X
CO
In un’ INDAGINE occorre:
• definire quale informazione si vuole avere;
I bambini e le bambine hanno riportato i dati in un grafico.
= 1bambino/a
• scegliere qual è il gruppo campione su cui si svolge l’indagine;
• raccogliere i dati;
Fai la stessa indagine nella tua classe e riporta i dati in un grafico.
con Metodo Matematica… 174
• rappresentarli con un grafico. D i N G
Istogramma
DIFFERENTI GRAFICI
I dati raccolti nelle indagini possono essere rappresentati attraverso grafici differenti. In questo istogramma puoi vedere quali e quanti libri ci sono nella biblioteca delle classi terze di Poggi Ridenti.
1 Osserva l’istogramma e segna V (vero) o F (falso).
• I libri di avventura sono quelli in maggior numero. V F
• I libri di fiabe e quelli di favole sono in ugual numero. V F
• I libri di fantasy sono meno dei libri a fumetti. V F
• I libri di miti sono tanti quanti quelli delle favole. V F
Ideogramma
In questo ideogramma è rappresentato il numero di libri presi in prestito nella biblioteca della scuola.
2 Osserva l’ideogramma, la legenda, poi rispondi alle domande.
• In quale mese è stato preso in prestito il maggior numero di libri?
• In quale mese è stato preso in prestito il minor numero di libri?
• Quanti libri sono stati presi in prestito a maggio?
Legenda = 10 libri
175 Matematica
ottobre novembre dicembre gennaio febbraio marzo aprile maggio
5 10 15 20 25 30
avventure fiabe favole miti fumetti fantasy
LE RELAZIONI
Imparo
La freccia rossa significa “è più pesante di”.
La freccia verde significa “è meno pesante di”.
Colora le frecce nel giusto modo. Poi completa.
• Dall’elefante partono due frecce di colore perché è il pesante di tutti.
• Dallo scorpione partono due frecce di colore perché è il pesante di tutti.
• La scimmia è più pesante dello , ma meno pesante dell’ .
Indica la relazione segnando le X al posto giusto.
è più pesante di... elefante scimmia
scorpione
è meno pesante di... elefante scimmia
scorpione
Una relazione è un legame tra due o più elementi secondo una regola
Le relazioni si possono rappresentare utilizzando frecce o tabelle.
con Metodo Matematica… 176
La regola
Cio che gia so
È certo che tu sei in terza? È possibile che l’anno prossimo tu vada in seconda? È possibile che tu cambi aula?
Imparo
Osserva e completa inserendo certo, possibile, impossibile.
• È che questa pittura sia stata dipinta su una parete di roccia.
È che abbiano utilizzato tubetti di colore a tempera.
È che sia stata dipinta da più persone.
La regola
• Un evento è certo se si è verificato o si verificherà sicuramente.
• Un evento è possibile se può verificarsi oppure no.
• Un evento è impossibile se non può verificarsi.
1 Accanto a ciascuna affermazione scrivi certo, possibile, impossibile.
• 145 è un numero di 3 cifre.
• 1 h è maggiore di 1 da.
• Si può disegnare un triangolo con 2 lati.
• 10 è un numero dispari.
• Giorgio conosce molto bene le tabelline.
• Il problema assegnato a Lara si risolve con due operazioni.
2 Giulia prenderà una di queste rose. Disegna e colora i fiori in modo che tutte le frasi siano vere.
• È possibile che Giulia prenda una rosa gialla.
• È certo che Giulia prenderà una rosa con le spine.
• È impossibile che Giulia prenda una rosa rossa.
• È possibile che Giulia prenda una rosa blu.
Matematica CERTO • POSSIBILE • IMPOSSIBILE
LA PROBABILITÀ
Cio che gia so
Se lanci un dado, sai che i numeri che possono uscire sono 6. Hai solo una probabilità che esca il numero più alto.
Imparo
Questi 5 bambini giocheranno a nascondino. Stanno scegliendo, con una conta, chi “starà sotto”.
• Quante possibilità ci sono che capiti a Isa? su 5.
• È più probabile che capiti a una bambina o a un bambino?
La regola
Tra gli eventi possibili alcuni hanno più probabilità di altri di verificarsi.
1 Osserva, rispondi o completa. Maria prende a occhi chiusi una caramella dal sacchetto.
• Quante sono le caramelle?
• Maria ha 1 su 7 probabilità di pescare una caramella alla .
• Maria ha su 7 probabilità di pescare una caramella alla menta.
• Maria ha su 7 probabilità di pescare una caramella al .
• Quale tipo di caramella ha più probabilità di essere pescata?
2 Completa e colora le caramelle in modo che ci siano:
5 probabilità su 10 di pescare una caramella alla menta
3 probabilità su di pescare una caramella al limone
2 probabilità su di pescare una caramella alla fragola
con Metodo Matematica… 178
• Con la ruota della fortuna si vince sempre! Ma il regalo dipende dal colore su cui si ferma la freccia.
• Quanti spicchi sono viola? Quanti sono gli spicchi in tutto?
Ci sono casi favorevoli su che la freccia si fermi sul viola.
• Quanti spicchi sono gialli? Quanti sono gli spicchi in tutto?
Ci sono casi favorevoli su che la freccia si fermi sul giallo.
• Quanti spicchi sono azzurri? Quanti sono gli spicchi in tutto?
Ci sono casi favorevoli su che la freccia si fermi sull’azzurro.
• Quanti spicchi sono arancioni? Quanti sono gli spicchi in tutto?
Ci sono casi favorevoli su che la freccia si fermi sull’arancione.
• Qual è il colore che ha più probabilità di uscire?
• Qual è il colore che ha meno probabilità di uscire?
• Le possibilità che esca una carta blu sono su 24.
• Le possibilità che esca un 4 sono su .
• Le possibilità che esca una carta con numero pari sono su
• Le possibilità che esca una carta non verde sono su
Mi esercito 179
1 Colora un quadratino per ciascuna probabilità che esca quel colore. Poi rispondi e completa.
2 Alcuni bambini e alcune bambine giocano con queste carte. Completa.
Insiemi e relazioni
1 Scrivi la caratteristica che contraddistingue ciascun insieme.
2 Completa il diagramma di Carroll e quello ad albero riportando le caratteristiche e le lettere che contraddistinguono le tazze.
rossa dice: è il doppio. Disegna.
Mi esercito 180
20 40 100 50 600 300 1 000 2 000
b. La freccia
3 a. La freccia blu dice: è la metà. Completa.
Tazze senza il con il con i con i senza i senza i con i senza i con il senza il 10 ......... 8 ......... ......... 4 ......... 12 A B C D E F G H
Nuoto 10
Calcio 3
Pallavolo 3
Basket 4
1 ortaggio 5 kg
più probabile estrarre una macchina rossa che una macchina gialla. È impossibile estrarre una macchinina
Mi esercito 181
4 Segna con X il grafico che rappresenta gli sport praticati dai bambini e dalle bambine della 3a C.
6 Colora in modo che le frasi siano vere.
2 4 6 8 10 12 0 2 4 6 8 10 12 0 20 kg
È
rossa.
5 Questi dati riportano le vendite di ortaggi nel negozio di Sara la scorsa settimana.
• Colora l’ideogramma in base alla quantità di ortaggi venduta.
5 10 15 20 25 30 35 0
• Disegna l’istogramma.
La matematica
Quando cammini per strada osservi i numeri civici delle abitazioni, vedi forme geometriche, osservi vetrine che espongono prezzi… vedi la matematica intorno a te.
Non conosciamo il numero di posti disponibili nel grande parcheggio sotterraneo a più piani. Sappiamo solo che è composto da queste tre cifre.
1 2 3
1 Quali numeri si possono ottenere?
Per ciascun numero usa una sola volta ciascuna cifra.
2 Scrivi certo, possibile, impossibile.
• Combinando le tre cifre si ottiene un numero: maggiore di 100 minore di 100 pari
3 Questo grafico rappresenta il numero di automobili parcheggiate durante la settimana nel grande parcheggio. Osserva e rispondi.
Legenda = 30 automobili
lunedì
martedì
mercoledì
giovedì
venerdì
sabato
domenica
• In quale giorno è stato parcheggiato il maggior numero di automobili?
• Quando sono state parcheggiate 180 automobili?
• Quante automobili sono state parcheggiate mercoledì?
• Quante domenica? .........
• In quali giorni è stato parcheggiato lo stesso numero di automobili?
182
PER STRADA
4 Leggi e segui le indicazioni.
Il bar “Di tutti i colori” ha le sedie colorate. Il barista per pulirle le ha messe tutte in fila rispettando una sequenza di colori.
• Colora tu le sedie che hanno perso il colore.
• Le sedie non sono solo 12. Sai dire di che colore sarà la tredicesima?
5
Le esercitazioni su classificazioni, relazioni, dati e previsioni sono estremamente pratiche e possono essere un ottimo spunto per invitare la classe a individuare situazioni analoghe nella vita di tutti i giorni. I bambini e le bambine possono utilizzarle per proporre indagini, raccogliere e rappresentare dati e relazionare.
Tutti devono rispettare le regole della strada, anche i bambini e le bambine. Scrivi che cosa rappresentano le immagini.
183
Oggi in strada ci sarà una festa del quartiere. I vigili sono pronti ad aiutare i cittadini. Scrivi il criterio con cui sono stati classificati.
Educazione Civica
A ogni bivio ti darò indicazioni.
Ramuttina e Ramuttino si sono allontanati dal villaggio per esplorare il territorio. Ora è tempo di tornare a casa.
Ramuttina propone a Ramuttino un quiz di logica per decidere la strada da percorrere.
Bivio A Andiamo dove è probabile che ci sia un cacciatore.
Bivio B Andiamo dove è impossibile raccogliere fiori.
Bivio C Andiamo dove è impossibile prendere dell’acqua.
Bivio D Andiamo dove è certo che potremo mangiare un frutto.
Bivio E Andiamo dove è probabile incontrare le raccoglitrici di miele.
184
Ramuttina vuole salutare quattro bambine e bambini del villaggio confinante. Chiede a Ramuttino di scoprire i loro nomi.
con lancia con fiaccola con copricapo con capelli lunghi
Il gruppo di amici è arrivato al villaggio. Tutto è pronto per il pranzo.
Tutti avranno una coscia di pollo e poi ciascuno sceglierà che cosa aggiungere. Scrivi tutte le combinazioni possibili.
Questi quesiti di logica sviluppano le competenze nel mettere in relazione i fatti.
185 LOGICA mente
Simut Semut Samut Sumut X X X X X X X X X
Relazioni, dati e previsioni
Classificare significa raggruppare insieme tutti gli elementi di un gruppo che hanno delle caratteristiche comuni. Per classificare si possono utilizzare schemi o diagrammi differenti.
con baffi senza baffi con cappello senza cappello
quadrati
rossi non rossi
Indagini e grafici
Le indagini statistiche servono per conoscere i gusti, le abitudini delle persone grandi e piccole. I dati raccolti nelle indagini possono essere rappresentati attraverso grafici differenti:
Legenda = 10 automobili lunedì martedì mercoledì giovedì
Le relazioni
Le relazioni indicano legami tra due o più elementi secondo una regola.
La probabilità
Un evento è certo se si è verificato o si verificherà sicuramente.
Un evento è possibile se può verificarsi oppure no.
Un evento è impossibile se non può verificarsi.
Tra gli eventi possibili alcuni hanno più probabilità di altri di verificarsi.
186 Sintesi delle conoscenze
Diagramma di Eulero-Venn
Diagramma di Carroll
Diagramma ad albero
2 4 6 0 • istogramma
ideogramma
•
4 ruote con il fiocchetto con 4 ruote e con fiocchetto
Insegnare ai bambini e alle bambine a utilizzare la mappa per focalizzare quanto imparato. Le icone e le parole sui bracci aiutano a ricordare i concetti più importanti.
187 INDAGINI , GR A F I C I
CLASSIFICAZIONI,
istogram m a ideogramma RELAZIONI,
E
di Eulero -V e n n d iaCarroll d albero possibili pr ob a b ilità impossibili certi con
carrelli 2 4 6 8 10 12 0
EVENTI
DIAGRAMMI
DATI
PREVISIONI
Mappa per ricordare
Il coding è l’“arte” di programmare.
IL CODING
Che cosa fa una persona che programma?
1 Per risolvere un problema occorre fantasia. Bisogna immaginare varie possibilità di soluzione.
Studia la soluzione dei problemi.
Anche noi nella vita di tutti i giorni risolviamo problemi!
2 Per risolvere un problema occorre scomporlo in parti più piccole e facili da risolvere.
Ora ho capito!
3 Per risolvere un problema, dopo aver individuato il percorso, occorre seguire delle tappe ben precise.
Fare coding, anche senza computer, aiuta ad acquisire la capacità di “vedere” i problemi, saperli scomporre, trovare una o più strategie di risoluzione.
Pensiero computazionale CO D i N G 188
Comandi precisi
Lea Explorer vuole raggiungere il masso delle pitture rupestri. Ma lungo il cammino ci sono molti ostacoli e pericoli. Se seguirà i comandi in modo preciso, non avrà difficoltà.
1 Segui i comandi e disegna il percorso. La freccia indica la direzione, il numero indica di quanti quadretti ci si deve spostare.
in basso a destra a sinistra in alto obliquo verso sinistra obliquo verso destra
2 Mia e Teo dovevano eseguire un disegno. Dovevano partire dal punto rosso e seguire i comandi. Ma in un disegno c’è un bug (un errore). Segnalo.
Il coding favorisce l’acquisizione del pensiero computazionale indispensabile per le attività di matematica, l’acquisizione di un metodo di studio, la capacità di progettare testi e riassumere. Il coding unplugged permette attività propedeutiche al pensiero computazionale senza l’uso di dispositivi elettronici. Sono sufficienti fogli a quadretti, matite, attenzione e fantasia.
Pensiero computazionale CO D i N G 189
1 2 2 2 2 2 1 1 2 2 4 2 2 2 2 2 3 y
I COMANDI PER…
… disegnare
Quando disegni una cornicetta o una sequenza di forme o oggetti applichi le regole del coding. Ecco alcune proposte per aiutarti a prestare attenzione, orientarti nello spazio, seguire comandi precisi e... divertirti.
1 Segui i comandi: che cosa apparirà? La partenza è .
… tracciare un percorso
2 Scrivi i comandi per questo percorso. La partenza è .
3 Adesso disegna tu un percorso diverso e scrivi i comandi. Non conosciamo la strada che traccerai.
Utilizza solo i riquadri che ti occorrono.
190
Pensiero computazionale CO D i N G
2 5 5 3 6 2 4 4 6 2 3 3 3 3 1 5 9 6 2 3 1 1 3 1
Conosci già la pixel art Anche la pixel art ha bisogno di comandi precisi per produrre capolavori. I comandi possono essere dati in modo diverso. 1 Colora
2
191
Pensiero computazionale CO D i N G A B C D E F G H I L 11 10 9 8 7 6 5 4 3 2 1 A B C D E F G H I L M N O P Q
LA PIXEL ART
indicazioni A = 1 2 1 2 B = 1 2 1 2 1 C = 3 1 3 2 3 2 D = 2 4 2 2 1 2 E = 1 6 2 3 F = 1 2 1 4 2 1 G = 1 10 H = 1 2 7 I = 2 7 L = 3 5 A,5 • C,6 C,4 • D,4 • E,4 • F,4 • G,4 • H,4 • I,4 • L,4 • B,5 • C,5 • D,5 • E,5 • F,5 • G,5 • B,6 • D,6 • E,6 • F,6 C,7 • D,7 • E,7 D,3 • E,3 • I,3 • L,3 M,4 • N,4 • O,4 • H,5 • I,5 • L,5 • M,5 • N,5 • O,5 • P,5 • G,6 • H,6 • I,6 • L,6 • M,6 • N,6 • O,6 • P,6 • Q,6 • F, 7 • G, 7 • H,7 • I,7 • L,7 • M,7 • N,7 • O,7 • P,7 • Q,7 • C,8 • D,8 • E,8 • F,8 • G,8 • H,8 • I,8 • L,8 • M,8 • N,8 • O,8 • P,8 • Q,8 • D,9 • E,9 • F,9 • G,9 • H,9 • I,9 • L,9 • M,9 • N,9 • O,9 • P,9 • E,10 • F,10 • G,10 • H,10 • I,10 • L,10 • M,10 • N,10 • P,10 • F,11 • H,11 • L,11 • N,11
seguendo le
Colora seguendo le indicazioni delle coordinate.
Adottiamo uno spazio verde
Quest’anno hai imparato come i numeri ti aiutino a conoscere e interpretare la realtà. La matematica renderà ancora più interessante il progetto “Adottiamo uno spazio verde”.
Scegliere uno spazio e decidere le modifiche
Le modifiche da apportare allo spazio verde dovranno essere scelte seguendo i desideri condivisi da insegnanti, bambini e bambine della vostra classe.
Rispondete insieme alla domanda dell’indagine, poi completate l’ideogramma, così sarà più semplice capire che cosa fare. Ricordate di disegnare un simbolo per la legenda.
Indagine
Che cosa vorresti nello spazio verde?
• giochi disegnati sui viali • mangiatoie per uccelli • più fiori • casetta per lo scambio di libri
giochi disegnati sui viali mangiatoie per uccelli più fiori casetta per lo scambio di libri
Documentare il lavoro
Io vorrei una casetta per lo scambio di libri!
Legenda = 4 bambini/e
Sai già che è importante documentare il lavoro. Fotografate il luogo prima e dopo gli interventi fatti. È anche importante conoscere l’opinione delle persone che frequentano lo spazio verde. Pensate insieme alle domande da porre a un campione di bambini e bambine che lo frequentano, poi raccogliete i dati ed esponeteli con un istogramma. Non dimenticate di mostrare il grafico nella mostra che preparerete a scuola!
Diario di bordo
• Ti è piaciuto lavorare con i tuoi compagni e le tue compagne?
• Qual è stata la cosa più facile da fare?
• Quale la più difficile?
• E la più divertente?
192
Compito di realtà
Responsabile editoriale: Mafalda Brancaccio
Coordinamento e redazione: Chiara Tricella
Revisione didattica: Annalisa Pomilio
Responsabile di produzione: Francesco Capitano
Progetto grafico e impaginazione: Rosanna Oronesu
Illustrazioni: Mauro Sacco ed Elisa Vallarino
Copertina: Elisabetta Giovannini
Ricerca iconografica: Chiara Tricella
Referenze iconografiche: Shutterstock, Archivio Spiga
Stampa: Tecnostampa – Pigini Group Printing Division
Loreto – Trevi 23.83.184.0
È assolutamente vietata la riproduzione totale o parziale di questa pubblicazione, così come la trasmissione sotto qualsiasi forma o con qualunque mezzo, senza l’autorizzazione della Casa Editrice.
Produrre un testo scolastico comporta diversi e ripetuti controlli a ogni livello, soprattutto relativamente alla correttezza dei contenuti. Ciononostante, a pubblicazione avvenuta, è possibile che errori, refusi, imprecisioni permangano. Ce ne scusiamo fin da ora e vi saremo grati se vorrete segnalarceli al seguente indirizzo: redazione@elionline.com
Tutti i diritti riservati
© 2023 La Spiga, Gruppo Editoriale ELi info@gruppoeli.it
EquiLibri • Progetto Parità è un percorso intrapreso dal Gruppo Editoriale ELi, in collaborazione con l’Università di Macerata, per promuovere una cultura delle pari opportunità rispettosa delle differenze di genere, della multiculturalità e dell’inclusione.
Si tratta di un progetto complesso e in continuo divenire, per questo ringraziamo anticipatamente il corpo docente e coloro che vorranno contribuire con i loro suggerimenti al fine di rendere i nostri testi liberi da pregiudizi e sempre più adeguati alla realtà.
2 Classe
• Lettura e scrittura
• Riflessione linguistica
• Matematica
• Scienze, Geografia, Storia, STEAM
ISBN per l’adozione:
978-88-468-4354-8
3 Classe
• Lettura e scrittura
• Riflessione linguistica
• Matematica
• Storia, Geografia, Scienze, STEAM
ISBN per l’adozione:
978-88-468-4355-5
#altuofianco
KIT DOCENTE comprensivo di guida alla programmazione, percorsi semplificati e tutto il necessario per il corso
LIBRO DIGITALE (scaricalo subito seguendo le istruzioni all’interno della copertina): volumi sfogliabili, esercizi interattivi, audiolibri, tracce audio, canzoni, libro liquido, video tutorial matematica e discipline, percorsi semplificati stampabili
Benvenute e benvenuti al , un allegro ambiente di apprendimento interattivo che offre tanti oggetti digitali didattici sotto forma di gioco o attività.
Bambine e bambini si divertiranno ad aiutare chef Alfredo: prepareranno insieme a lui tante “ricette” divertenti, organizzeranno feste a tema, allestiranno grandi eventi per tutte le discipline scolastiche, nelle sale o all’aperto! Potranno così rinforzare le abilità e verificare le competenze nelle varie materie attraverso le diverse prove proposte in cucina, facendo ogni volta attenzione al guastafeste Splat, sempre in agguato!
www.gruppoeli.it Allegato a SOTTOSOPRA 3 Non vendibile separatamente
