Vector 15 - oktober 2022

MET ZONNIGE

ONZICHTBAAR,

BEGRIPPEN: CUSPIDEN

BOUWEN

FIBONACCI-DAG

15-PUZZEL

EEN UURTJE TIJD: BELONING VAN

TANDEN

NEERGESCHOTEN DRAAK VAN

HET VOLUME VAN EEN BOL

ALGEBRA

VECTOR

STOEIEN MET ZONNIGE GETALLEN

OP 11 MAART DEDEN MEER DAN 700 LEERLINGEN MEE AAN DE TWEEDE RONDE VAN DE NEDERLANDSE WISKUNDE OLYMPIADE. DIE WEDSTRIJD KON — NA TWEE CORONA-EDITIES — GELUKKIG WEER OP DE TWAALF UNIVERSITEITEN IN HET LAND PLAATSVINDEN. DE TWEEDE RONDE BESTAAT UIT VIJF B-OPGAVEN, WAARBIJ NET ALS BIJ DE EERSTE RONDE EEN EXACT GETAL ALS ANTWOORD MOET WORDEN GEGEVEN, EN DAARNAAST TWEE C-OPGAVEN WAARBIJ OOK DE ONDERBOUWING VAN BELANG IS. IN DIT ARTIKEL WERPEN WE EEN BLIK OP OPGAVE C2, WAARVOOR DE DEELNEMERS GEMIDDELD ONGEVEER 3 VAN DE 10 PUNTEN WISTEN TE BEHALEN. DOOR QUINTIJN PUITE,

Voor de tweede ronde worden de winnaars van de eerste ronde uitgenodigd, die eind januari op alle deelnemende scholen plaatsvindt. Uiteraard zijn de opgaven bij de tweede ronde weer van een niveau hoger dan bij de eerste ronde. De deelnemers hebben bijvoorbeeld hun hoofd gebroken over het zo efficiënt mogelijk vullen van een 3 x 2-rechthoek met de getallen 1 tot en met 6, in de zin dat de zeven onderlinge verschillen tussen buurgetallen in totaal zo klein mogelijk moeten zijn. Ook was er een vraag over een vierkant waarop steeds kleinere vierkantjes groeien zodat er een fractalachtige figuur ontstaat; probeer daar maar eens de omtrek van te berekenen… Deze en alle andere opgaves zijn terug te vinden op www.wiskundeolympiade.nl in het Wedstrijdarchief. De tweede C-opgave ging over getallen die voor de gelegenheid zonnige getal len waren gedoopt.

OPGAVE C2, TWEEDE RONDE 2022

We noemen een positief geheel getal zonnig als het uit vier cijfers bestaat en als bovendien elk van de twee buitenste cijfers precies 1 groter is dan het cijfer ernaast. De getallen 8723 en 1001 zijn bijvoorbeeld zonnig, maar 1234 en 87245 zijn dat niet.

(a) Hoeveel zonnige getallen zijn er waarvan het dubbele ook weer een zonnig getal is?

(b) Bewijs dat elk zonnig getal groter dan 2000 deelbaar is door een getal van drie cijfers dat een 9 in het midden heeft.

Om een beetje vertrouwd te raken met zo’n nieuw begrip kan het geen kwaad eens te bedenken hoeveel zonnige getallen er überhaupt zijn. Een manier om dit te zien, is als volgt: de middelste twee cijfers kun je vrij kiezen, bijvoor beeld (van links naar rechts) a en b; dan liggen het eerste (meest linkse) en laatste cijfer automatisch vast (namelijk a 1 respectievelijk b 1). Elk zonnig getal is dus van de volgende vorm:

a 1 a b b 1

Voor a (en ook voor b) zijn er in eerste instantie tien moge lijkheden (0 tot en met 9), maar omdat a 1 ook een cijfer moet zijn, valt a 9 af. We concluderen dat er voor a dus negen opties zijn (0 tot en met 8) en idem voor b, wat ons in totaal 9 9 = 81 zonnige getallen geeft. Wat we hierbij even onder het tapijt hebben geschoven, is dat een getal natuur lijk nooit met het cijfer 0 mag beginnen. Maar dat gaat hier automatisch goed omdat a 1 sowieso minstens 1 is.

EEN TABEL MET 81 ZONNIGE GETALLEN?

DAT KAN SLIMMER!

We zouden nu onderdeel (a) kunnen oplossen door daadwerkelijk een tabel met alle 81 zonnige getallen op te schrijven (hieronder is een overzichtelijk beginnetje gemaakt), van elk van die getallen het dubbele uit te rekenen, en dan telkens te kijken of dat weer een zonnig

getal is. Dat zou zeker tellen als een volledige oplossing; erg elegant is het alleen niet en bovendien zou het best wel veel tijd kosten. Vandaar deze variant op het bekende spreekwoord: wie geen tijd heeft, moet slim zijn! Om daarbij de goede ideeën te krijgen, gaan we een paar voorbeelden bekijken. Een van de manieren om je in een probleem te verdiepen is immers: durf te proberen!

Neem een willekeurig zonnig getal, bijvoorbeeld 2134. Het dubbele daarvan is 4268; dat is verre van een zonnig getal. En we krijgen meteen ons eerste goede idee: eigenlijk is het ook wel logisch dat het hier ‘misgaat’, want de cijfers worden verdubbeld en dus wordt het verschil tussen de laatste twee cijfers nu 2 (en het verschil tussen de eerste twee cijfers trouwens ook in dit voorbeeld). Dit argument gaat op voor alle zonnige getallen die eindigen op ..01, ..12, ..23 of ..34, want dan eindigt het dubbele hiervan op ..02, ..24, ..46 of ..68 zodat de uitkomst hoe dan ook geen zonnig getal is. Kortom, als 0 b 3, dan krijgen we zeker niet een zonnig getal na verdubbeling. Daarmee hebben we dus direct al 9 4 = 36 van de 81 getallen afgestreept; de hele linkerkant van onderstaande tabel.

We bekijken een volgend voorbeeld: 2145. Het dubbele hiervan is 4290 en dat is zeker niet zonnig. We realiseren ons dat elk zonnig getal dat op ..45 eindigt, na verdubbeling op ..90 eindigt en dus zeker niet zonnig is. De hele kolom b 4

uit de tabel valt dus ook weg, waarmee er nog eens 9 getallen zijn afgestreept.

We bedenken een nieuw voorbeeldje waarbij de laatste twee cijfers allebei groter dan 4 zijn, zodat er minstens twee keer een 1 gaat overspringen bij het verdubbelen. Hoe zit het bijvoorbeeld met het zonnige getal 2178? Daarvan is het dubbele 4356, en dat is wel zonnig! Yes, we hebben een zonnig getal gevonden dat ‘het doet’. We hebben hier blijkbaar te maken met twee gunstige overspring-enen: het dubbele van 8 is 16, waarvan de 1 samen met 14 (het dubbele van 7) leidt tot een 5 op de plek van de tientallen zodat het resultaat eindigt op ..56. En die 1 van 14 leidt samen met het dubbele van 21 tot 43.. aan het begin van het getal. Zowel aan het begin als aan het eind is het buitenste cijfer dus 1 hoger dan het binnenste cijfer. In welke gevallen doet dit fenomeen zich nog meer voor? Dat is als het zonnige getal eindigt op ..56, ..67, ..78 of ..89; dan is het dubbele namelijk 112, 134, 156 respectievelijk 178, zodat het wat de laatste twee cijfers betreft wel goed zit. En bovendien komt de 1 er bij de honderdtallen bij, zodat voor zonnige getallen die beginnen met 10.., 21.., 32.. of 43.. het resultaat na verdubbeling begint met 21.., 43.., 65.. of 87.., en het dus wat de eerste twee cijfers betreft ook goed gaat. We hebben hiermee 4 ˘ 4 = 16 zonnige getallen gevonden waarvoor de gevraagde eigenschap wel geldt; om precies te zijn als 0 a 3 en 5 b 8, de rechterbovenhoek van bovenstaande tabel.

We hebben alleen de rechteronderhoek nog over en bekijken dus maar eens een zonnig getal dat met een 5 of hoger begint, zoals 5478. Daarvan is het dubbele 10956, een getal van vijf cijfers in plaats van vier, dus dat gaat sowieso mis (hoe leuk die 56 op het eind ook is). Kortom, de zonnige getallen met 4 a 8 (zodat het eerste cijfer a 1 5) kunnen we ook afschieten, want dan bestaat het resultaat na verdubbeling uit te veel cijfers. Daarmee vervalt ook het hele onderste deel van de tabel op pagina 4 (waarvan we de eerste vijf kolommen natuurlijk al eerder hadden afgestreept).

We concluderen dat er precies 16 zonnige getallen bestaan waarvan het dubbele ook weer zonnig is. Zoals bij elk wiskundig probleem waar je alle oplossingen moet vinden, moesten we hier twee dingen laten zien: dat er 16 zonnige getallen zijn waarvoor dit zo is, en bovendien dat de overige 81 − 16 = 65 zonnige getallen deze eigenschap juist niet hebben.

ALTIJD DEELBAAR DOOR *9*

Onderdeel (b) gaat over de 8 9 = 72 zonnige getallen die groter dan 2000 zijn, dus de getallen met 1 a 8 en 0 b 8. Meteen moet er een alarmbelletje bij je afgaan, of — beter gezegd — juist een labeltje bij je aangaan: waarom zou deze extra voorwaarde hier eigenlijk staan? Ongetwijfeld heb je die later ergens nodig! Hoe dan ook, als deze uitspraak waar is, dan zou het ons moeten lukken om het in ieder geval in afzonderlijke voorbeelden te laten zien. Dus laten we weer eens een voorbeeldje bekijken. Kunnen we het getal 2134 schrijven als een product van twee getallen waarvan eentje tussen de 100 en de 999 ligt met een 9 als middelste cijfer? Omdat dat driecijferige getal minstens 100 is, moet de andere deler hooguit 100 2134 = 21,34 en dus zelfs hooguit 21 zijn. Laten we dus proberen om 2134 door een kleine deler te delen en dan hopen dat we *9* als quotiënt over houden. Het getal is even, dus deelbaar door 2: 2134 = 2 ˘ 1067, maar hier is het quotiënt niet van de gewenste vorm. Door 3 is het niet deelbaar, en door 5 of 7 evenmin. Het volgende priemgetal dat we proberen is 11, en dat geeft een hit: 2134 = 11 ˘ 194; ons zonnige getal is deelbaar door 11 en het quotiënt is een driecijferig getal met een 9 in het midden! Hoe zit dat met 2178? Dat is niet alleen deelbaar door 2 en 3 (met als quotiënten 1089 en 726, dus niet van de gewenste vorm), maar ook weer door 11, waarbij we vinden dat 2178 = 11 198. Volgend voorbeeld: 5478. Ja hoor, ook dat kunnen we door 11 delen: 5478 = 11 498. Het lijkt wel of elk zonnig getal door 11 deelbaar is. Zelfs zonnige getallen kleiner dan 2000, bijvoorbeeld 1012 = 11 92. We zetten de eerste drie voorbeelden even op een rij:

Wiskunde is soms ook: patronen herkennen. In deze drie gevallen zien we dat de honderdtallen van ons zonnige getal en het gevraagde quotiënt overeenkomen, evenals het laatste cijfer (de eenheden). Dus als ons zonnige getal uit de cijfers a 1, a, b en b 1 bestaat zoals we eerder invoerden, dan bestaat in deze drie voorbeelden het quotiënt bij deling door 11 uit a, 9 en b 1. Maar dat dat in deze drie voorbeelden zo is, wil nog niet zeggen dat het voor alle 72 zonnige getallen groter dan 2000 geldt. Ook hier zouden we weer een lijst met al die getallen kunnen maken en telkens het quotiënt kunnen uitrekenen. Maar ook nu weer kunnen we slimmer te werk gaan. We gaan bewijzen dat

a 1 a b b 1 = 11 x a 9 b 1

In plaats van de deling door 11 uit te voeren, berekenen we juist het product van de twee getallen aan de rechterkant en bewijzen we dat dit het linkergetal als uitkomst heeft. Het getal bestaande uit de cijfers a, 9 en b 1 is, wegens de rol van deze cijfers als honderdtallen, tientallen en eenheden, niets anders dan de uitkomst van de berekening a ˘ 100 9 ˘ 10 (b 1) ˘ 1, oftewel 100a 91 b. Doen we dat keer 11, dan krijg je 11 ˘ (100a 91 b), oftewel 1100a 11 ˘ 91 11b = 1100a 11b 1001. Nu is 1100a + 11b precies het getal bestaande uit de cijfers a, a, b en b, en tellen we daar nog 1001 bij op, dan krijgen we precies ons zonnige getal bestaande uit de cijfers a 1, a, b en b 1. Dus kunnen we omgekeerd elk zonnig getal bestaande uit de cijfers a 1, a, b en b 1 ontbinden als 11 maal het getal bestaande uit de cijfers a, 9 en b 1 Hiermee hebben we het gevonden patroon bewezen!

En waarom stond die voorwaarde er nou bij? Als a gelijk is aan 0, dan zou dat quotiënt beginnen met het cijfer 0. Maar dan is het natuurlijk geen getal van drie cijfers meer! Toch geldt de bewezen ontbinding natuurlijk nog steeds; zo is 1001 = 11 (0)91 en 1067 = 11 (0)97.

Die laatste twee voorbeeldjes kunnen, hoewel ze dus eigenlijk niet meedoen, overigens ook goede ideeën ople

veren om te zien dat de ontbinding altijd opgaat.

Want van 1001 naar 1067 is een toename van 66, en dat is 6 ˘ 11, dus als de een deelbaar is door 11, is de ander dat zeker ook. En van 1001 naar bijvoorbeeld 2134 is een toename van 1133, en dat is 11 103 dus ook weer een 11-voud. Tellen we 103 op bij 91 (het quotiënt van 1001 bij deling door 11), dan komen we uit op 194 (het quotiënt van 2134 bij deling door 11). Omdat deelbaarheid door 11 in ieder geval voor één zonnig getal geldt (1001) en er steeds een 11-voud bijkomt (dat moet je dan natuurlijk nog wel even netjes bewijzen), weet je nu zeker dat elk zonnig getal deelbaar is door 11. En met nog wat meer argumenten kun je ook wat zeggen over hoe dat quotiënt er dan uitziet.

EEN GETAL IS ZELFS SUPERZONNIG

In onderdeel (a) hadden we gezien dat voor precies 16 zonnige getallen geldt dat het dubbele weer zonnig is. Laten we dit de 16 bijzonder zonnige getallen noemen; die zitten in de rechterbovenhoek van eerdergenoemde tabel. Behoort dat dubbele zonnige getal nou zelf ook weer tot die 16 bijzonder zonnige getallen, dan is zelfs het viervoud van het oorspronkelijke zonnige getal weer zonnig. Dat geldt voor de vier zonnige getallen 1078, 1089, 2178 en 2189. En als het viervoud ook weer bijzonder zonnig is, is zelfs het achtvoud van het oorspronkelijke zonnige getal weer zonnig. Er is precies één getal waarvoor dit geldt, namelijk 1089. Dat wil dus zeggen dat 1089, het dubbele 2178, het dubbele daarvan 4356 en het dubbele daar weer van 8712 allemaal zonnig zijn! Als dat geen superzonnig getal is…

En alsof dat nog niet spectaculair genoeg is: zelfs de andere (viercijferige) veelvouden van 1089 zijn allemaal zonnig! Zo is 7 1089 bijvoorbeeld gelijk aan 7623. Hoe kan dat nou weer? We kunnen de resterende veelvouden natuurlijk gemakkelijk even uitrekenen: 3 1089 = 3267, 5 1089 = 5445, 6 1089 = 6534 en 9 1089 = 9801. We zien dat we inderdaad telkens een zonnig getal als uitkomst krijgen; sterker nog, dat dit pre cies de zonnige getallen op de diagonaal van rechtsboven naar linksonder van onze tabel zijn. Maar het is nóg leuker om ook een reden te vinden waarom dit werkt.

Je kan 1089 schrijven als 1100 − 11. Ga nu uit van een getal op die diagonaal, bijvoorbeeld 3267. Tel je hier 1100 bij op, dan krijg je 4367, en trek je er ook nog 11 van af, dan krijg je 4356; het volgende getal op de diagonaal!

Door die twee acties blijft inderdaad de zon nigheid behouden zolang de cijfers nog netjes tussen de 0 en de 9 zitten, want als de eerste twee cijfers in eerste instantie 1 verschillen, doen ze dat natuurlijk nog steeds nadat we ze beide eentje hoger maken, en als de laatste twee cijfers in eerste instantie 1 verschillen, doen ze dat natuurlijk nog steeds nadat we ze beide eentje lager maken. Zo kun je van het getal rechtsboven (1089) naar het getal linksonder (9801) lopen waarbij je telkens het volgende zonnige getal op deze diagonaal tegenkomt. En omdat je dan in feite met 1089 begint en er telkens 1089 bij optelt, doorloop je dus eigenlijk gewoon de tafel van 1089.

0 10..

1089

1067 1078 1089

1 21.. 2112 2134 2156 2167 2178 2189

2 32.. 3256 3267 3278 3289

3 43.. 4312 4334 4356 4367 4378 4389

4 54..

5 65.. 6512

In een computerspel Nortfite zijn er twee soorten strijders: Norts, die elk bewapend zijn met drie speren en één zwaard, en Fites, die elk één speer en twee zwaarden hebben. Om het volgende level te bereiken, moet je een groep strijders langs twee magische hindernissen sturen. Ze kunnen enkel voorbij de eerste hindernis als ze samen hoogstens 11 speren hebben en enkel voorbij de tweede als ze samen hoogstens 17 zwaarden hebben. De strijders mogen onderweg geen wapens achterlaten. Wat is het grootst mogelijke aantal strijders waaruit jouw groep kan bestaan om het volgende level te halen?

6578

WISKUNDE: VAAK ONZICHTBAAR, MAAR ZONDER GAAT HET NIET

SAMEN MET ALLE UNIVERSITEITEN IN VLAANDEREN EN NEDERLAND BRENGEN PLATFORM WISKUNDE VLAANDEREN EN PLATFORM WISKUNDE NEDERLAND DE VITALE ROL VAN WISKUNDE IN ONZE WERELD ONDER DE AANDACHT. “IMAGINARY: PRACHT EN KRACHT VAN WISKUNDE”, ZO HEET DE TENTOONSTELLING DIE DE KOMENDE MAANDEN 14 STEDEN IN DE LAGE LANDEN AANDOET. NIET ALLEEN KIJKEN, MAAR OOK PROBEREN EN BEWONDEREN, DAAR WORDT DE BEZOEKER TOE AANGEZET. EN WIE HET AANDACHTIG DOET, KAN ER NOG EEN PRIJS MEE WINNEN!

PAUL IGODT, AN SPEELMAN, MARNIX VAN DAELE WWW.IMAGINARYMATHS.BE

“IMAGINARY” is een naam met internationale bekendheid als het op wiskunde-outreach aankomt. Open wiskunde, aansprekend voor het grote publiek en interactief voor wie graag probeert, daarover gaat het bij het inmiddels tot non-profitorgani satie gegroeide project dat startte in 2008. “Imaginary: through the eyes of mathematics”, zo heette de eerste tentoonstelling samengesteld door het onderzoeksinstituut voor wis kunde in Oberwolfach (MFO). 2008 was in Duitsland uitgeroepen tot ‘Jahr der Mathematik’. Onder leiding van Gert-Martin Greuel (Univ. Kaiserslau tern), toenmalig directeur van het instituut, en dankzij reeds bekende beelden gemaakt door zijn collega

algebraïsch meetkundige Herwig Hauser (Univ. Wenen en Innsbruck), ontstond die allereerste tentoonstel ling. Ze bleek zodanig succesvol dat het Imaginary-concept inmiddels wereldwijd in meer dan 160 steden talrijke bezoekers aantrok. Hauser en Greuel, samen met Andreas Daniel Matt (momenteel directeur van de Imaginary-organisatie), slaagden toen ook in het maken van het soft warepakket SURFER, dat eenieder toelaat “te spelen” met algebraïsche oppervlakken. Wiskundevoorkennis onnodig, plezier en verwondering gegarandeerd. SURFER is nog steeds een grote publiekstrekker. Al in 2015-2016 reisde de eerste Imaginary-tentoonstelling langs alle

Vlaamse universiteitssteden, het jaar nadien gevolgd door een analoge trip in Nederland.

Van september 2022 tot en met juli 2023 doet dit initiatief in totaal 14 universiteitssteden van de Lage Landen aan. Dynamisch onderzoek, zowel curiosity-driven als toepas singsgericht, zorgt ervoor dat iedere burger in onze maatschappij dage lijks gebruikmaakt van realisaties waarbij wiskunde (meestal goed verborgen) onder de motorkap zit. Zowel wiskunde die decennia geleden ontstond, zonder ook maar aan één toepassing te denken, als wiskunde die sterk gericht is op het oplossen van concrete problemen

(aangereikt uit een zeer grote variatie van disciplines) komt in de tentoon stelling aan bod.

Op de tentoonstelling kan de bezoe ker ook zelf aan de slag met een collectie apps, via grote touchscreens. Enkele denk- en puzzelopstellingen, en een voor deze keer bijzondere aanwezigheid van origamistukken, naast specifieke 3D-prints, maken het concept van de tentoonstelling compleet. Gratis rondleidingen voor groepen leerlingen en rondleidingen voor allerlei specifieke groepen belangstellenden zijn mogelijk op alle locaties. We plukken een paar voor beelden uit de pracht en de kracht.

1 ORDE EN CHAOS: DE KAT VAN ARNOLD

Een kleine wijziging in de begintoe stand kan soms, zelfs na korte tijd al,

leiden tot een zeer grote verandering van een groot systeem. Dat is wat wiskundigen “chaotisch gedrag”, kort weg chaos, noemen. Denk aan het stoten van een biljartbal: de kleinste aanpassing bij de start kan ervoor zorgen dat de bal ergens helemaal anders terechtkomt.

Maar soms is er toch een vorm van orde in de chaos. Dit illustreren we aan de hand van een eenvoudige transformatie van het vlak, die wereldwijd bekendstaat als “Arnolds katafbeelding”. Op https://www.jasondavies.com/ catmap/ probeer je het uit op een foto die je zelf oplaadt. De pixels worden herschikt en al na enkele stappen wordt je foto onherken baar: chaos treedt op. Dergelijke transformaties zijn interessant voor cryptosystemen, je kan er snel

een goed gestructureerd geheel (“foto”) mee versleutelen en dus onherkenbaar maken. Maar wie veel geduld uitoefent en de originele foto voldoende vaak laat vervormen, ziet het oorspronkelijke beeld toch terugkeren. Wat is hier aan de hand?

Laten we kijken naar de transformatie met matrix

Die matrix werkt als een transforma tie van het vlak . Een punt wordt afgebeeld op

. Je kan narekenen dat, als en , terwijl waarbij en

Figuur 1 De “mascottes” van de vorige en de aankomende tentoonstelling. Met dank aan Herwig Hauser, Robert de Keijzer en Oliver Tse.

Figuur 2 In de richting van v1 (rode vector) gebeurt een expansie, terwijl in de richting van v 2 (blauwe vector) een inkrimping plaatsvindt.

In figuur 3 hierboven bekijken we in eerste instantie wat de transfor matie doet met de punten van het eenheidsvierkant ([0, 1] × [0, 1]), en in tweede instantie wat dit betekent indien we “modulo ” rekenen. Als we de figuur meer in detail bekij ken, dan zien we dat vier gekleurde delen van het originele vierkant op vier plaatsen in het parallellogram terechtkomen. De hoekpunten van het vierkant worden hierbij opnieuw op roosterpunten (punten met coördinaten in ) afgebeeld. Dit is

Figuur 3 In de eerste stap wordt het eenheidsvierkant omgevormd tot een parallellogram. In de tweede stap kijken we enkel naar het decimale gedeelte van de coördinaten; we rekenen “modulo” het gehele gedeelte.

geen toeval, maar blijkt voor alle roosterpunten zo te zijn. Alhoewel de individuele punten bewegen, wordt het rooster als geheel behouden.

Om de afbeelding duidelijker te visualiseren, brengen we nu de delen van het parallellogram als puzzelstukken terug naar het eenheidsvierkant, zoals in de tweede stap op de tekening. We onthouden met andere woorden niet langer in welk vak van het rooster een punt

terechtkomt, maar enkel zijn positie in het vak.

Elke vierkante foto kun je bekijken als een verzameling pixels die punten zijn uit het eenheidsvierkant. Punten die bovendien rationale getallen als coördinaten hebben. Transformatie A kun je dus ook uitvoeren op de pixels van een vier kante foto, en vele keren herhalen.

Dit is wat er gebeurt met de foto van een watervliegtuig.

Figuur 4 Er zijn meer dan 300 iteraties nodig om deze foto terug in originele toestand te krijgen.

1

Het blijkt dat ieder rooster waarvan de punten rationale coördinaten hebben na verloop van tijd weer op zichzelf terugkeert. Dit is bij uitstek het geval met de pixels van eender welke foto. Het is best mogelijk dat je wat geduld moet hebben. Het aantal keer dat je de transformatie na elkaar moet uitvoeren, kan hoog oplopen. Maar geduld zal beloond worden, dat kunnen wiskundigen aantonen.

Echter, alle gekheid op een stokje, alhoewel er dus periodiciteit is op de punten met rationale coördinaten, is dat niet het geval op de punten met irrationale coördinaten. En die punten zijn bijzonder talrijk in het eenheidsvierkant. Wiskunde kent zo weer één van die bijzondere eigenaardigheden.

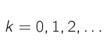
Meer over orde en chaos vind je op de tentoonstelling.

2 NULPUNTEN BEREKENEN EN FRACTALEN

Het algoritme van Newton-Raphson is een klassieker uit de numerieke wiskunde in het hoger onderwijs. De opdracht bestaat erin een nulpunt1 te vinden voor een gegeven functie , en zeker meer in het bijzonder als er geen algebraïsche oplossing voor is. Er wordt verondersteld dat de functie “voldoende braaf” is, en een mooie “gladde” grafiek heeft. De functie is m.a.w. overal afleidbaar.

Het intuïtieve idee van de NewtonRaphson-methode is eenvoudig, en beslist uit te leggen in het secundair onderwijs. Je vertrekt van een eerste schatting voor het nulpunt die we de startwaarde noemen en noteren. Je bepaalt de vergelijking van de raaklijn aan de grafiek van in het punt ; dit is een eerstegraadsfunctie. Omdat je veronderstelt dat die raaklijn een interessante benadering voor de functie is, neem je vervolgens het nulpunt van die eerstegraadsfunctie als een volgende benadering, , voor het nulpunt van . Al in de derde graad kunnen leerlingen berekenen dat

Herhalen we dit proces vertrek kend van , dan volgt een tweede benadering, , en meer algemeen geldt dus dat

waarbij

Indien het startpunt voldoende dicht bij het gezochte nulpunt ligt, dan wordt dit nulpunt heel snel voldoende goed benaderd. Wis kundigen spreken van kwadratische convergentie: ietwat ruw gesproken zal het aantal correcte cijfers bij elke iteratiestap verdubbelen.

Nemen we als voorbeeld even de functie met voorschrift We kennen de twee nulpunten (−1 en 1). Hier wordt de iteratiestap nu gegeven door

We maken het even wat meer visueel.

Figuur 5 De basisstap in het algoritme van Newton-Raphson.

Om een of andere, voor ons eerder duistere reden spreekt men in het secundair onderwijs over nulwaarden van een functie. Naar ons gevoel is een nulwaarde gelijk aan . . . 0.

Vertrekken we bijvoorbeeld met startwaarde , dan vinden we en dit vervolgt met

Om de nauwkeurigheid te bepalen, definiëren we het verschil tussen en het gezochte nulpunt , met andere woorden de fout (error) bij stap als . Bekijken we nu in dit voorbeeld de opeenvolgende fouten:

Een moeilijk punt bij deze aanpak is dat de startwaarde het best “voldoende dicht bij ” ligt. Dat is ietwat heikel, omdat het afhangt van de functie die men onderzoekt. Indien zich te ver van bevindt, is het mogelijk dat er geen nulpunt gevonden zal worden (in wiskundige termen, dat er geen convergentie zal optreden), of zelfs dat er convergentie is naar een ander nulpunt dan het verwachte.

Als voorbeeld nemen we nu even de functie met voorschrift . De nulpunten zijn duidelijk eenvoudig, , en , en we zien een grafische voorstelling hieronder (zie figuur 6).

als startwaarde zouden kiezen voor deze methode, dan zal het fout lopen. Zie jij ook waarom? Ook als we een startwaarde kiezen zodanig dat, bij een zekere of wordt, is er een probleem. Over het algemeen echter zal een startwaarde met het algoritme van Newton-Raphson leiden naar een van de 3 bekende nulpunten. Voor zal er convergentie optreden naar het nulpunt 0. Voor zal er convergentie optreden naar het nulpunt 3. Voor tussen en is de uitkomst van het algoritme heel wat moeilijker te voorspellen, en ook het aantal iteraties dat zal nodig zijn om een gewenste nauwkeurigheid te bereiken kan hier al eens tegenvallen.

Na 5 iteratiestappen wordt het nulpunt – in dit geval – reeds gevonden met een nauwkeurigheid van

De grafiek laat duidelijk twee extre men zien: een maximum voor en een minimum voor De concrete waarden van en zijn niet zeer belangrijk hier. Indien we één van die twee -waarden

Op de tentoonstelling kun je zien wat er gebeurt bij het zoeken naar de nulpunten voor de vergelijking , waarbij x ook een complex getal mag zijn. Afhankelijk van de startwaarde die men kiest (in ) wordt een ander nulpunt gevonden, en met een andere convergentiesnelheid. Maakt men die verschillen ook visueel duidelijk door kleurtjes te gebruiken, dan zie je dat een fractaal beeld ontstaat: een Newtonfractaal! Een wonder!

3 TIEN THEMA’S EN OOK WAT GESCHIEDENIS

De organisatoren hebben de 50 Gallery-Prints gerangschikt in 10 topics. Orde en Chaos enerzijds, en Fractalen anderzijds zijn slechts twee van deze tien. Er zijn ook bij zonder mooie beelden en verhalen, in de catalogus bovendien rijkelijk aangevuld met extraatjes, in de

Figuur 7 Met dank aan Toon Baeyens. Newton-Raphson genereert een opmerkelijke figuur als het op de vijfde wortels van 1 aankomt.

volgende thema’s:

• Algebraïsche oppervlakken

• Composities

• Wereldrecord oppervlakken

• Vlakvullingen en polytopen

• Kosmologie

• Netwerken

• Wiskunde en origami

• Wiskunde verrassend

Je kan niet over belangrijke wiskunderealisaties spreken zonder het te hebben over enkele historische figuren. Waar relevant komen deze ook duidelijk aan bod in de cata logus van de tentoonstelling. Het gaat om wetenschappers die zich vaak toelegden op reeds bestaande historische problemen of net, bijna visionair, een totaal nieuwe kijk op een gebied van de wiskunde of natuurwetenschappen aanreikten.

Vladimir Arnold (1937 - 2010) is één van de grote wiskundigen van de twintigste eeuw. Zijn wiskundewerk situeert zich in een veelheid van disciplines. Op 19-jarige leeftijd vond hij een oplossing voor het dertiende probleem van Hilbert. In 1974 werd hij genomineerd voor de Fieldsmedaille, de hoogste wetenschappelijke onderscheiding voor een wiskundige. Een hoogst merkwaardig optreden van of namens de Sovjet-Unie zorgde er echter voor dat die bekroning hem niet toegekend werd.

Isaac Newton (1642-1726) is zonder enige twijfel één van de grootste wetenschappers (wiskundige, fysicus, sterrenkundige,…) uit de geschiedenis. Hij legde de grondbeginselen van de klassieke mechanica vast en ontwikkelde ook belangrijke technieken voor de wiskundige analyse. Als één van de grootste Britten werd hij begraven in Westminster Abbey.

Onlinewedstrijd voor bezoekers aan de tentoonstelling: bezoekers aan de tentoonstelling kunnen op elke locatie deelnemen aan een onlinewedstrijd. Aandachtig de tentoonstelling bezoeken zal beslist helpen. Per locatie zijn er enkele mooie prijzen te winnen.

Paul Igodt en An Speelman zijn allebei verbonden aan het departement Wiskunde van de KU Leuven. Marnix Van Daele is verbonden aan de Vakgroep Toegepaste Wiskunde, Informatica en Statistiek van de Universiteit Gent. Zij zijn de 3 Vlaamse collega’s in de kerngroep voor de Imaginary-tentoonstelling.

VERGETEN BEGRIPPEN: CUSPIDEN

Bij het bestuderen van functies komen we soms knikken tegen: als er wortels voorkomen in het functie voorschrift of absolutewaardetekens. Maar de ene knik is de andere niet.

Zo heeft de functie een knik met slechts één raaklijn in het knikpunt (de volle grafiek in figuur 1). Zo'n knik noemen we officieel een cuspide. In oude geschriften las ik wel eens de toepasselijke naam doornpunt. Maar zelf zou ik het liever een speerpunt noemen. Cuspis is immers de Latijnse benaming voor de punt van een lans, een pijl, de drietand van Neptunus en de angel van een schorpioen.

Er zijn ook knikpunten waarbij er twee verschillende raaklijnen voorkomen in het knikpunt: een linkerraaklijn en een rechterraaklijn. Een typisch voorbeeld is de functie (de gestreepte grafiek in figuur 1). Zo'n knikpunt wordt ook wel eens een snavelpunt genoemd. Vooral wanneer de grafiek in dit punt overgaat van hol naar bol heeft dit stukje van de grafiek wel iets weg van de snavel van een ara of een kaketoe.

Figuur 1 Twee grafieken met een knik

Cuspiden komen meestal ter sprake in de theorie van de algebraïsche krommen. Algebraïsche krommen zijn grafieken met als voorschrift waarbij een veel term is in de variabelen en . Als deze veelterm van de tweede graad is, zijn deze algebraïsche krommen parabolen, hyperbolen en ellipsen (en eventueel ontaardingen). Maar als de graad hoger mag zijn, kun je tot de verbeelding sprekende krommen verkrijgen die eruitzien als vlinders, peren, halters en gestileerde botanische curiosa.

Algebraïsche krommen bezitten soms merkwaardige punten, singulariteiten genoemd. Een van deze singulariteiten is de cuspide of het keerpunt. De grafiek keert daar op zijn stappen terug. Dit fenomeen zie je bij spirograaftekeningen. Je laat een radertje binnen of buiten een cirkelrad rollen en zet een volgstift op de rand van het kleine radertje. Zo kun je een hartkromme tekenen met één keerpunt of een nierkromme met twee keerpunten.

Een andere singulariteit is het zelfdoorsnijdingspunt of de node Die zie je bijvoorbeeld centraal in de lemniscaat van Bernoulli. Omdat het kruispunt twee keer voorkomt in de grafiek noemen we dit punt ook een dubbelpunt

Een heel merkwaardig verschijnsel bij sommige algebraïsche krom men is het geïsoleerde punt of de acnode. Mocht je de grafiek van de kromme met computersofware tekenen, dan zou het losse punt in de oorsprong wel eens ’vergeten’ kunnen worden. Toch behoort het tot de grafiek. Een mooie Nederlands benaming voor dit punt is er bij mijn weten niet. Daarom stel ik het hermietpunt voor, geleend uit de Engelse vakliteratuur.

Ik eindig met het begrip tacnode, dat ik zou kunnen vertalen als een zelf aanrakingpunt. Sommige krommen hebben twee takken die beide in een bepaald punt aan een bepaalde rechte raken, zoals de kromme (twee parabolen met de buiken tegen elkaar). Maar er zijn ook mooiere voorbeelden van deze soort dubbelpunten, bijvoorbeeld bij de keratoïde uit figuur 2. De naam van deze kromme komt van het Griekse keratose, dat hoorn betekent. "Er is nog werk aan de winkel voor wiskundige vertalers", zou Simon Stevin bij deze aflevering van 'vergeten begrippen' opmerken.

Dit artikel verscheen in Uitwiskeling 36/4 in het kader van een reeks artikelen over vergeten begrippen in de wiskunde. Op www.uitwiskeling.be vind je alle info.

Seppe heeft een strook papier met daarop de getallen 1, 2, 3, 4 en 5 zoals in de figuur. Hij vouwt de strook volgens de stippellijnen zodat vijf lagen ontstaan. In welke volgorde kunnen de getallen in de opeenvolgende lagen niet voorkomen?

3, 5, 4,

3, 4, 5,

2,

EEN OTHD VOUWEN

Maak in een vel A4 of A5 eerst vouwlijnen langs de rode streep jeslijnen en daarna langs de groene streepjeslijnen (figuur 1). Vouw de lijnstukken AH en HD om de groene streepjeslijnen HE en HG tegen elkaar aan zodat ze samenvallen. Plak ze bij ontbreken van plakstroken met tape aan elkaar vast. Laat evenzo door vouwen om de groene streepjeslijnen EF en GF de lijnstuk ken BF en FC samenvallen en plak ze ook met tape aan elkaar vast. Vouw vervolgens om EG de punten A, B, C en D naar elkaar toe zodat ze in een punt samenkomen. Plak dat zo goed mogelijk met tape aan elkaar. De lijnstukken AE en BE komen dan tegen elkaar aan en vallen samen. Hetzelfde geldt voor de lijnstukken DG en CG. Het resultaat is een obte trahedrille, af te korten tot OTHD

MET PLAKRANDEN

Om een wat mooier model zonder tape te krijgen kan het ook met plakranden. Neem dan nog een tweede vel A4 of deel het doormidden tot twee vellen A5. Maak in beide vellen

de aangegeven vouwen. Knip van het tweede vel de randen af, zodat er een ruit overblijft die over de flap pen van het eerste vel geplakt kan worden (figuur 2).

A-REEKS PAPIERFORMATEN

Er bestaan verschillende reeksen van papierformaten. De bekendste is de A-reeks. Een vel A4 uit die serie is in het dagelijks leven het gangbaarste formaat. De A-reeks bestaat uit een serie gelijkvormige rechthoekige vellen die opeenvolgend steeds een tweemaal zo kleine oppervlakte hebben. Bovendien is de verhouding tussen de lange en de korte zijde in die opeenvolgende rechthoekige vellen steeds hetzelfde. Wanneer een vel in oppervlakte wordt gehal veerd door het in de breedte in twee gelijke stukken te snijden, ontstaan twee even grote rechthoekige vellen waarvan de zijden dezelfde verhouding hebben als die van het oorspronkelijke rechthoekige vel. Uitgaande van de gegeven omschrij ving kan die verhouding worden berekend. Neem bijvoorbeeld een rechthoekig vel met lengte L en

breedte B. Snij dat in de breedte in twee gelijke delen, dan hebben die delen een lengte B en een breedte L/2. In de oorspronkelijke rechthoek is de verhouding van de zijden L/B en in de twee delen is die B/(L/2). En die verhoudingen moeten gelijk zijn, dus ofwel

Daaruit is de verhouding tussen L en B te berekenen als of .

De serie begint met een A0-vel dat bij afspraak een oppervlakte van 1 m2 heeft. Daarmee kunnen dan met de gegeven lengte-breedte verhouding de afmetingen van het A0-vel en alle andere vellen worden berekend (figuur 3). Bij A0 zijn de maten L= 1189 mm en B = 841 mm, enzovoort.

VERHOUDINGEN

De vier zijvlakken van een OTHD zijn congruente gelijkbenige driehoeken. Uitgaande van de lengte-breedte verhouding in de A-reeks papier formaten kunnen de verhoudingen van de zijden van die gelijkbenige driehoeken en dus van de ribben

Figuur 3

of randen van een OTHD worden berekend. De basis verhoudt zich tot de beide gelijkbenige zijden als

Uit de verhouding van de zijden zijn vervolgens de tophoek en de beide basishoeken te berekenen. De tophoek is 70,53° en de beide basishoeken zijn 54,74°.

OTHD IN KUBUS

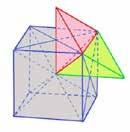
Normaal gesproken wordt een OTHD verkregen door uit te gaan van een kubus en die bijvoorbeeld op te delen in acht kleinere kubusjes. Vier van die op elkaar gestapelde kleinere kubusjes zoals geel aangegeven in figuur 4, sluiten dan een OTHD in. Neem voor de ribben van de grote kubus 2, dan worden de ribben van de acht kleine kubusjes 1.

Eenvoudig is dan na te gaan dat de zijden van de rode OTHD in figuur 4 zich verhouden als . En daar mee kunnen ook weer de hoeken van de zijvlakken van de rode OTHD worden berekend.

Figuur 4 toont ook dat een OTHD vier zijden met lengte heeft en twee met lengte 2. Die laatste twee krui sen elkaar onderling loodrecht. Het zal duidelijk zijn dat het vouwen van een velletje papier uit de A-formaat reeks tot een OTHD een constatering achteraf is, zoals William Gibb in 1990 liet zien.

SCHUIVEN

De hoeken tussen de zijvlakken van een OTHD zijn met behulp van figuur 4 te bepalen. Eenvoudig blijkt al door goed kijken dat de

Figuur 4

hoek tussen de zijvlakken aan weerszijden van de langste zijde 90° is. Dat wordt nog eens bevestigd door de figuren 5 en 6. Figuur 5 zal geen toelichting behoeven. En in figuur 6 zijn twee OTHD’s zo tegen elkaar aangeschoven dat zonder meer duidelijk is dat de hoek tussen genoemde vlakken 90° is. De hoeken tussen de vlakken aan weerszijden van de andere randen zijn lastiger te berekenen. Maar gebruikmakend van die hoeken, kunnen drie OTHD´s zo tegen elkaar worden geschoven dat duidelijk wordt dat die hoeken 60° zijn (figuur 7).

Uit de figuren 6 en 7 blijkt dat OTHD´s handig tegen elkaar gescho ven kunnen worden. Zo levert figuur 6 een piramide met als grondvlak

een ruit met zijden waarin de loodrecht op elkaar staande diago nalen zich verhouden als of beter

STAPELEN

In figuur 4 is met acht eenheids kubussen een grotere gemaakt. Daarin zijn alle afmetingen tweemaal zo groot. Evenzo kan met acht OTHD´s een grotere OTHD worden gemaakt waarin ook alle afmetingen tweemaal zo groot zijn (figuur 8). In figuur 8B is de grote groene OTHD gemaakt met vellen papier van het formaat A5 en de acht kleinere met

A7 velletjes. Merk nog op dat de afmetingen van de piramide in figuur 8B tweemaal zo groot zijn als die van figuur 6.

NOG EEN PIRAMIDE

Maak in een vel A4 of A5 de in figuur 9A aangegeven vouwlijnen. Daarin worden de drie doorgetrokken groene lijnen dal-vouwen en de gestippelde lijnen berg-vouwen (figuur 9B). Plak de driehoeken aan weerszijden van de doorgetrokken groene lijnen tegen elkaar en het resultaat is een piramide met een vierkant grondvlak (figuur 9C). De

opstaande vier zijvlakken zijn gelijk benige driehoeken met dezelfde verhoudingen als de zijvlakken van een OTHD. Ga na dat deze piramide bestaat uit vier halve OTHD’s. Dat wordt helemaal duidelijk als in figuur 10 de driehoeken aan weerszijden van de korte horizontale groene lijnen tegen elkaar worden geplakt en de punten A naar elkaar toe worden gevouwen om de lange verticale groene lijn die nu berglijn is en dus gestippeld. Op die manier ontstaan twee tegen elkaar gescho ven hele OTHD’s zoals in figuur 6, dus vier halve.

NOG EEN MANIER

Snij uit liefst eenzijdig gekleurd passe-partout karton vier rechthoe ken met zijden die zich verhouden als (figuur 11, links). Pas op elk van die rechthoeken de aangegeven driehoek af. Snij tot halfweg de zijden van die driehoek inkepingen, iets breder dan de dikte van het karton. Schuif de vier rechthoeken middels die inkepingen rekening houdend met de kleur in elkaar (figuur 11, rechts). De vier rechthoeken sluiten dan een OTHD in die net als in figuur 4 op één hoekpunt staat. De acht uitstekende hoekpunten van de recht hoeken spannen de vier kubusjes op waarin de OTHD is in te sluiten. Vergelijk figuur 12 met figuur 4. Overigens is op deze manier naast een OTHD ook het regelmatig vier vlak en elk ander gewenst viervlak te maken.

BOUWEN

Uit de figuren 6, 7 en 8 blijkt al dat OTHD’s gemakkelijk in- en tegen elkaar aan te schuiven zijn. In de grote kubus van figuur 4 passen nog drie rechtopstaande OTHD’s. Samen met de al aanwezige rode hebben ze dan de rechtop

staande grote rand gemeenschap pelijk en twee aan twee hebben ze een gemeenschappelijk zijvlak. Die vier OTHD’s vormen een achtvlak waarvan de zijvlakken congruent zijn aan die van een OTHD. Dit is ook aan te tonen door de holle piramide van figuur 9C als een soort schaaltje te gebruiken om er vier OTHD’s in te zetten (figuur 13).

Twee piramides van figuur 9C met de grondvlakken tegen elkaar geplakt levert hetzelfde achtvlak. Zes van de piramides uit figuur 9C kunnen steeds met een zijvlak tegen elkaar worden geplakt. Dat levert een kubus (figuur 14). In die kubus zitten dus precies 6X4 = 24 halve OTHD’s, dus eigenlijk 12 hele. Met die consta tering is het volume van een OTHD gemakkelijk te bepalen: namelijk een twaalfde deel van dat van de kubus. Anders gezegd: het volume van een OTHD is (a3)/12 met a de lengte van een van de twee lange randen van de OTHD, die ook de ribben van de kubus vormen.

RUITENTWAALFVLAK

Op elk van de zes zijvlakken van de kubus van figuur 14 kan weer een piramide van figuur 9C worden

gezet. Dat zijn dan 24 hele OTHD’s samengepakt tot een ruitentwaalf vlak (figuur 15). Uit figuur 16 blijkt dat de zijvlakken van dat ruitentwaalfvlak worden gevormd door het ruitvormige grondvlak van de piramide uit figuur 6. De zijden en de twee diagonalen van zo’n ruit verhouden zich als

Zo wordt onder andere ook duidelijk dat het volume van een ruitentwaalf vlak tweemaal dat van de ingesloten kubus is. De twaalf ribben van deze kubus zijn de twaalf korte diagonalen van de twaalf zijvlakken van het ruitentwaalfvlak. Kortom, het volume van een ruitentwaalfvlak is 2r3 met r de lengte van de korte diagonaal van een ruitvormig zijvlak.

TOTAAL OBJECT

In zijn Cube-Rhombic Dodecahedron heeft de Nederlandse kunstenaar Rinus Roelofs de vlakken van een ruitentwaalfvlak met die van de inge sloten kubus tot één totaal object weten te verenigen (figuur 17). Ook hier wordt weer duidelijk hoe door piramides of daken op een kubus te plaatsen een ruitentwaalfvlak zoals in figuur 15 ontstaat.

UNIEK

Door kubussen op elkaar te stapelen kan de ruimte volledig worden opgevuld. Zonder kieren of gaten tussen de kubussen. Ze kunnen volledig op elkaar aansluiten. Door een kubus opgedeeld te denken zoals in figuur 14, zal duidelijk worden dat OTHD’s ook zo op elkaar kunnen worden gestapeld dat de ruimte vol ledig wordt opgevuld. Zonder kieren of gaten tussen de verschillende OTHD’s. Met een blokkendoos vol met OTHD’s zijn dus allerlei objecten te maken. De figuren 6, 7, 8 en 13 zijn daar enige eenvoudige voorbeelden van. Daarvan afgeleid zal het duide lijk zijn dat met het achtvlak uit figuur 13 en het ruitentwaalfvlak hetzelfde kan: door stapelen kunnen ze de ruimte volledig opvullen. Anders gezegd ze zijn ruimtevullend. Die ruimtevullende eigenschap maakt de OTHD tot een uniek viervlak. Het is namelijk het enige viervlak waarmee dat kan! Zelfs met het overbekende regelmatige viervlak kan het niet.

FIBONACCI-DAG

MET DE AMERIKAANSE DATUMNOTATIE 11/23 VERWIJST MEN NAAR 23 NOVEMBER. OMDAT 1, 1, 2 EN 3 DE EERSTE VIER GETALLEN ZIJN IN DE RIJ VAN FIBONACCI, WERD DEZE DAG UITGEROEPEN TOT FIBONACCI-DAG. WIE VOOR DIE GELEGENHEID OP ZOEK IS NAAR EEN ZINVOLLE EN VAKOVERSCHRIJDENDE ACTIVITEIT IN DE WISKUNDELES KRIJGT HIER EEN SUGGESTIE: SCHRIJF EENS EEN PHIBONO.

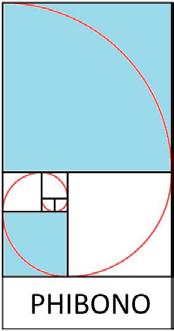
Ter gelegenheid van de poëzieweek (27 januari2 februari 2022) heb ik een nieuwe versvorm gelan ceerd: de PHIBONO. Het woord PHIBONO telt zeven letters omdat er zeven regels zijn in het gedicht en het aantal lettergrepen per regel is een getal uit de rij van Fibonacci. PHI is het getal van de gulden snede en de twee letters O wijzen erop dat de vijfde en de zevende regel moeten rijmen. BONO wijst er dan weer op dat er in het versje een positieve gedachte moet steken.

Op de website https://phibono.jouwweb.be/ vind je mijn collectie van meer dan 100 phibono’s, waarvan ruim de helft wiskundig getint is. Uiteraard kan ook in diverse andere lessen (Nederlands, Frans, Engels, … esthetica, fysica, wetenschappen …) een phibono een plaatsje krijgen.

Hieronder vind je vier voorbeelden, die hopelijk een aantal collega’s zullen inspireren op de Fibonacci-dag.

Op het PHIBONO-logo staan vierkanten met zijde 1, 1, 2, 3, 5, 8 en 13. De gekleurde vakjes verwijzen naar de twee versregels die moeten rijmen en de spiraal van Fibonacci is dan weer een verwijzing naar de positieve gedachte in het gedicht.

DR. LUC GHEYSENS, ERE-PEDAGOGISCH ADVISEUR VAN HET KATHOLIEK ONDERWIJS VLAANDEREN.

Priemtweelingen kleiner dan 200

PRIEMGETALLEN

1 Ik 1 vind 2 het paar 3 drie en vijf 5 toch wat zonderling 8 want ondanks een verschil van twee 13 vormen ze in de getallenleer een priemtweeling.

Afbeelding: mammothmemory.net

GELIJKVORMIG

1 Met 1 een 2 stelling

3 deed Thales 5 ons uit de doeken 8 hoe hoog de piramides zijn; 13 dat is het nut van gelijkvormige driehoeken.

MIJN ALLEREERSTE PHIBONO

1 Een 1 klein 2 versje 3 speciaal 5 voor jou geschreven 8 opdat wiskunde elke dag 13 een portie werkvreugde mag brengen in jouw leven.

PINK FLOYD

1 Wat 1 had 2 Pink Floyd, 3 de rockband, 5 met Newton van doen?

8 Een prisma met lichtbreking 13 stond op de platenhoes van The Dark Side of the Moon.

Op mijn website is er ook een eregalerij, waarin ingezonden phibono’s van vrienden en collega’s een plaatsje kunnen krijgen. Ook jouw PHIBONO is welkom op lucgheysens@yahoo.com.

Ontplooi je met wiskunde!

DE 15-PUZZEL

EEN KLASSIEKER ONDER DE WISKUNDIGE PUZZELS IS DE 15-PUZZEL, DIE IN 1880 UITGEVONDEN EN GEPATENTEERD WERD DOOR NOYES CHAPMAN. DE UITVINDING WERD LATER ONTERECHT GECLAIMD DOOR DE PUZZELBEDENKER SAM LOYD.

In een 4 × 4-schuifbord zitten 15 verschuifbare tegeltjes in een geordend patroon. Vaak zijn het de getallen van 1 tot 15 die op de tegeltjes zijn afgebeeld maar soms zijn het afbeeldingen die in 15 fragmenten zijn onderverdeeld.

Een 15-puzzel met getallen

Figuur

met een afbeelding

Zoals je op deze figuren ziet, ontbreekt er één tegeltje in het schuifbord. Elke tegel die naast de ontbrekende tegel ligt, kan horizontaal of verticaal in de opening geschoven worden. Zo kun je het hele schuifbord door elkaar hus selen. Dat doe je bij het begin van de puzzel. De opdracht bestaat er dan in om zo snel mogelijk de beginconfiguratie terug te vinden.

Het is aangetoond (zie Brungger e.a., 1999) dat hiervoor ten hoogste 80 tegeltjes moeten worden verschoven. Maar liefst 17 configuraties vereisen deze 80 zetten (zie Korf, e.a., 2005).

EEN OPLOSSINGSSTRATEGIE

Als de tegeltjes van de 15-puzzel op een reglementaire manier door elkaar gehusseld zijn, kan de puzzel altijd opgelost worden door de tegeltjes in omgekeerde zin terug te schuiven. Dat is niet altijd de snelste methode. We beschrijven hier een andere oplossingsstrategie.

Schuif eerst het getal 1 naar de linkerbovenhoek. Het getal 2 kan hier zonder problemen naast geschoven worden. Deze twee tegels blijven nu gedurende de hele oplossing roerloos liggen. Om de 3 en de 4 op hun plaats te krijgen, is er een truc nodig. De hoekjes met hoekstenen vullen is immers niet zo eenvoudig. Schuif eerst de 4 naar de derde plaats van de bovenste rij en zorg ervoor dat de 3 hieronder kan. Manoeuvreer het lege vakje naar de rechterboven hoek. Schuif tot slot de 4 naar rechts en de 3 omhoog en de eerste rij is OK.

Voor de tweede rij met de 5, 6, 7 en 8 kun je analoog te werk gaan. Maar voor de derde rij is er niet genoeg plaats om deze strategie vol te houden. Daarom ordenen we de tegels nu van links naar rechts. Eerst zetten we de 9 en de 13 op hun plaats. Hiervoor gebruiken we dezelfde truc als hierboven. Schuif de 13 naar de eerste plaats van de derde rij en zorg ervoor dat de 9 hier rechts naast kan. Laat het lege vakje opschuiven tot het linksonder zit. Duw daarna de 13 naar onder en de 9 naar links. Zo zitten deze vakjes op hun plaats. Op dezelfde manier ordenen we de 10 en de 14.

Alleen de rechterbenedenhoek met de getallen 11, 12 en 15 moet nu nog geordend worden. Als je de 11 en het lege vakje naar de correcte positie schuift dan staan de 12 en de 15 automatisch op hun juiste plaats. Dat bewijzen we hieronder. Immers, een configuratie waarbij alleen de 15 en de 12 verwisseld zijn, kan nooit bereikt worden door tegeltjes op een normale manier te verschuiven.

Merk op dat deze strategie ook geldt voor gelijkaardige schuifborden van een groter formaat.

DE 15-14-PUZZEL KAN NIET OPGELOST WORDEN: EEN BEWIJS DOOR INVARIANTIE

Als twee tegeltjes met een koevoet uit het schuifbord gebroken worden en ze er verwisseld weer in worden gemonteerd, dan kan het bord nooit meer in de oorspron kelijke configuratie geschoven worden. Meestal wordt dat geïllustreerd door de 15-14-puzzel waarbij de 14 en 15 van plaats gewisseld zijn. We bewijzen hieronder dat het niet mogelijk is om deze puzzel terug te schuiven naar de oorspronkelijke configuratie met oplopende getallen.

We bewijzen dit door een getal te construeren dat invariant blijft tijdens het schuiven. De invariant ontstaat uit de som van drie getallen:

• het aantal verwisselingen van twee tegeltjes of van een tegeltje en een leeg hokje (1)

• het aantal rijen dat het lege vakje uiteindelijk verwijderd is van rechtsonder (2)

• het aantal kolommen dat het lege vakje uiteindelijk verwijderd is van rechtsonder (3)

tijdens het schuiven. Dat is het geval bij een horizontale verschuiving, want (1) neemt bij elke horizontale verschui ving met 1 toe en (3) neemt met 1 toe of af. De som van (1), (2) en (3) behoudt dus de pariteit. Als ze even was, blijft ze even. Als ze oneven was, blijft ze oneven. Bij een verticale verschuiving neemt (1) met 1 toe en neemt (2) met 1 toe of neemt (2) met 1 af. Ook hier blijft de pariteit van de som van (1), (2) en (3) behouden.

De beginconfiguratie met 14 en 15 in opklimmende volg orde heeft invariant 1. Er zijn immers geen verwisselingen gebeurd en het lege vakje is 0 rijen en 0 kolommen verwijderd van rechtsonder. Als we alleen de 14 en de 15 verwisselen, wordt de invariant −1. Er is immers 1 verwisse ling gebeurd en het lege vakje is 0 rijen en 0 kolommen verwijderd van rechtsonder. Een invariant 1 kan nooit in de invariant −1 overgaan enkel door tegeltjes te verschuiven. Vandaar dat de 14-15-configuratie niet volgens de spelre gels kan overgaan in de 15-14-configuratie. Omgekeerd is het uiteraard ook niet mogelijk.

Als we de tegeltjes uit het schuifraam mogen halen, zijn er in totaal 16! manieren om ze terug te zetten. Precies de helft van dit aantal heeft invariant 1, de andere helft heeft invariant −1. Alleen de configuraties met invariant 1 kunnen door te schuiven uit de oorspronkelijke 15-puzzel verkre gen worden. Dat zijn er in totaal 10 461 394 944 000.

BRONNEN

Korf, R., Schultze, P. (2005). Large-scale parallel breadth-first search. Proceedings of the 20th National Conference on Artificial Intelligence (AAAI-05), 1380-1385. Brungger, A., Marzetta, A., Fukuda, K., Nievergelt, J. (1999). The parallel search bench ZRAM and its applications. Annals of Operations Research 90. 45-63. Wm. Woolsey Johnson, & Story, W. (1879). Notes on the “15” Puzzle. American Journal of Mathematics, 2(4). 397-404. doi:10.2307/2369492, ISSN 0002-9327, JSTOR 2369492.

Dit artikel verscheen in Uitwiskeling 36/2. Op www.uitwiskeling.be vind je alle info.

POST-QUANTUM CRYPTOGRAFIE GEBROKEN OP EEN UURTJE

Cybersecurity en databeveiliging zijn meer dan ooit een hot topic. Het is een samenspel van veel factoren zoals protocollen, hardware, implementaties, wetgevingen, en dit alles op een basis van wiskunde. Fundamenteel aan het uitwisselen van geheime sleutels over mogelijks onveilige kanalen is een cryptogra fische eenwegsfunctie. Dit is een wiskundige functie die efficiënt te evalueren valt maar heel moeilijk te inverteren is.

Het stereotype voorbeeld van een eenwegsfunctie is het factorizeren van getallen. Als je aan leerlingen vraagt om met de hand alle delers van 1.421.851 te vinden, dan zal je zelfs na een klassikale inspanning hoogst waarschijnlijk bot vangen. Als je daarentegen zou vragen om de priemgetallen 941 en 1.511 te vermenigvuldigen, dan zou iedereen die de lagere school succesvol

heeft afgewerkt 1.421.851 moeten kunnen vinden als antwoord. Ook voor computers is dit een eenwegsfunctie, maar in plaats van getallen van zeven cijfers spreken we dan over getallen van honderden tot duizenden cijfers. Tot op de dag van vandaag is dit één van de meest gebruikte eenwegsfuncties in dataversleuteling in het RivestShamir-Adleman (RSA) protocol. Het populairste alternatief is gebaseerd op elliptische krommen en heet Elliptic-Curve Diffie-Hellman (ECDH). ECDH is een pak efficiënter en heeft in de voorbije tien jaar dan ook RSA voorbijgestoken in populariteit en gebruik.

QUANTUMCOMPUTERS

Helaas dreigt er een einde te komen aan alle eenwegsfuncties die tegen woordig gebruikt worden in dataver sleuteling. In 1994 publiceerde Peter Shor reeds een algoritme dat met

gemak RSA en ECDH kan breken. Het enige “detail” is dat Shor een quantumcomputer nodig heeft om het algoritme te implementeren. De eerste minimale quantumcomputer kwam er in 1998, maar die was veel te zwak om ook maar iets mee te doen. Tegenwoordig spenderen bedrijven zoals Google en IBM miljoenen aan research om betere quantumcomputers te maken. Hoewel er al grote stappen vooruit zijn gezet richting grootschalige quantumcomputers moeten we voorlopig nog niks vrezen voor onze dataversleuteling. Er is ook geen consensus in wetenschappelijke kringen over voorspellingen wan neer quantumcomputers wel groot genoeg zouden zijn. Sommigen spreken over 10 jaar, anderen over 30 jaar, en nog anderen denken dat er fysische beperkingen zijn die quantumcomputers nooit groot genoeg zullen kunnen laten worden.

THOMAS DECRU, POSTDOCTORAAL ONDERZOEKER BIJ COSIC-IMEC, KU LEUVEN SEPTEMBER

Door deze mogelijke toekomstige aanval heeft het National Institute of Standards and Technology (NIST) in 2016 al een post-quantum standaardisatieproces in gang gezet. Het onderliggende idee is dat we op zoek gaan naar nieuwe eenwegsfuncties die ook voor quan tumcomputers moeilijk te inverteren zijn. Dit lijkt misschien voorbarig, maar de beveiligingsanalyse en de implementatie van hard- en software van dergelijke protocollen duurt vele jaren. Bovendien zijn er geheimen die vandaag versleuteld moeten worden waarvan we liever hebben dat ze binnen pakweg 15 jaar nog altijd veilig versleuteld zijn.

Het NIST post-quantum stan daardisatieproces heeft begin juli 2022 zijn derde ronde afgesloten. Hieruit kwam één protocol uit de bus waarin NIST het meest vertrouwen had met betrekking tot veiligheid en efficiëntie. Het schema heet CRYSTALS-Kyber en is gebaseerd op een eenwegsfunctie met betrekking tot roosters. Om niet alle eieren in één mand te leggen stelde NIST wel een vierde ronde voor waarin nog vier kandidaat protocollen onderzocht moesten worden als alternatieve schema’s. Deze vier protocollen hadden ook alle voorgaande rondes overleefd, maar schoten net iets tekort op bepaalde aspecten ten opzichte van CRYSTALS-Kyber. Drie ervan waren gebaseerd op foutenverbeterende codes (Classical McEliece, BIKE, HQC), en één op isogenieën tussen elliptische krommen (SIKE). Ondanks

naar de Indiase wiskundige Srinivasa

Laat staan het kortste pad.

het feit dat SIKE een wiskundig inge wikkelder buitenbeentje was, kreeg het toch het vertrouwen van een groot deel van de cryptografische gemeenschap. Zo waren er ook onderzoekers bij Microsoft die mee hadden gewerkt aan het protocol en werd er door hen een beloning van $50.000 beloofd aan mensen die het wisten te breken.

AANVAL OP SIKE VANUIT HOGERE DIMENSIE

SIKE is gebaseerd op isogenieën tussen elliptische krommen. Een elliptische kromme is een verza meling punten ( , ) die allemaal vol doen aan een bepaalde vergelijking zoals bijvoorbeeld ,

waar en parameters zijn. Een isogenie : is een afbeelding tussen twee elliptische krommen die zijn oorsprong vindt in de algebraïsche meetkunde. Gegeven een bepaalde elliptische kromme is het gemakkelijk om isogenieën te bepalen en berekenen met domein . Als je daarentegen enkel twee elliptische krommen en gegeven krijgt, is het moeilijk om een isogenie er tussen te bepalen. Isogenieën worden daarom reeds sinds de jaren ’90 onderzocht als eenwegsfuncties in het teken van cryptografie.

SIKE is een isogenie-gebaseerd cryptografisch protocol en maakt gebruik van het onderliggende Supersingular Isogeny Diffie-

Hellman (SIDH) dat in 2011 ontdekt werd. In dit kader kan men gemak kelijk en correct gebruik maken van grafentheorie om de eenwegsfunc tie grafisch te verduidelijken. We kunnen een graaf definiëren waarvan de knopen elliptische krommen zijn en de bogen de isogenieën tussen deze elliptische krommen. In de context van het SIDH-protocol beko men we dan een Ramanujangraaf.1 Een Ramanujangraaf is een graaf met niet al te veel bogen, maar waar alle knopen wel verbonden zijn door een relatief kort pad.

Een illustratie van een Ramanujangraaf met 23 knopen is gegeven in figuur 1. Iedere knoop heeft slechts drie uitgaande bogen, maar ieder paar knopen is wel verbonden door een pad van maximum zes bogen. Gegeven een paar knopen in deze al bij al kleine graaf is het echter niet eens altijd evident om een pad te vinden tussen de knopen.2 Ook voor klassieke en quantumcomputers is dit een moeilijk probleem, maar dan moet de graaf wel minstens 2430 knopen hebben in plaats van 23. In het SIDH-protocol wordt echter niet enkel de begin- en startknoop gebruikt, maar ook extra informatie. Deze extra informatie is nodig om het protocol correct en snel te laten verlopen, maar werd uiteindelijk wel zijn ondergang.

Twee elliptische krommen kunnen immers aan elkaar gelijmd worden via een isogenie naar een hogere dimensie. Het bekomen object van dit lijmen is dan gebaseerd op een

Figuur 1 Grafische voorstelling van een Ramanujangraaf met 23 knopen: alle knopen zijn verbonden met elkaar met een relatief kort pad, maar gegeven twee knopen is het vinden van een pad niet altijd triviaal.

hyperelliptische kromme, wat een verzameling punten is gegeven door een vergelijking van de vorm

, Hyperelliptische krommen zijn een natuurlijke veralgemening van elliptische krommen, net zoals kwadratische vergelijkingen een verderzetting zijn van eerstegraads vergelijkingen.

Dit lijmen kan echter ook soms falen, waardoor we simpelweg weer overblijven met een paar elliptische krommen. Een stelling van Ernst Kani uit 1997 karakteriseert precies wanneer dit lijmen faalt. De extra informatie die in het SIDH-protocol

gebruikt wordt, bepaalt echter precies zo een falen, en de stelling van Kani kan bovendien ook gebruikt worden om het volledige pad in de Ramanujangraaf bloot te leggen. Het probleem om een isogenie tussen twee elliptische krommen in het SIDH-protocol te vinden kan via Kani’s stelling dus relatief snel opgelost worden. In ongeveer een uur tijd kon iedere sleutel in het laagste beveiligingsniveau van SIKE reeds gebroken worden. De $50.000 beloning van Microsoft was gebaseerd op iets kleinere parame ters dan dit beveiligingsniveau en werd gebroken op zes minuten op een tien jaar oude computer met één processor.

CONCLUSIE

Hoewel er nog geen officieel bericht werd meegedeeld door NIST zal SIKE ongetwijfeld ronde 4 van het post-quantum standaardisatieproces niet overleven. Het alternatieve sleuteluitwisselingsprotocol zal dus op foutenverbeterende codes gebaseerd zijn, tenzij daar ook baanbrekende ontdekkingen gedaan worden.

Merk op dat vlak voor het einde van ronde 3 nog een veelbelovend protocol gebroken werd: Ward Beullens (onderzoeker bij IBM Zürich, gedoctoreerd aan de KU Leuven) haalde begin 2022 Rainbow onderuit, een schema gebaseerd op multivariate veeltermvergelijkingen. Sceptici stellen de vraag of NIST niet te hard van stapel loopt en we niet wat meer tijd moeten geven aan de wetenschappelijke gemeenschap om de eigenschappen van deze pro tocollen beter te begrijpen. Anderen beweren dan weer dat het net dóór NIST is dat deze protocollen veel aandacht genieten en gebroken worden.

Over het algemeen zijn er slechts een handvol praktische eenwegsfuncties waarvan gedacht wordt dat een quantumcomputer ze niet kan inverteren. Het is een delicate balans om extra structuur toe te voegen aan deze functies om ze in de praktijk efficiënt genoeg te maken, en niet te veel structuur zodat die niet gebruikt kan worden om ze aan te vallen. Voor SIKE was het doorspelen van extra informatie cruciaal om het schema correct en snel te doen

verlopen, maar die informatie maakte het inverteren van de eenwegsfunctie gemakkelijk.

Dankzij de ERC-beurs ISOCRYPT, toegekend aan de KU Leuven, vonden Wouter Castryck en ik deze fatale fout in SIKE, gelukkig nog voor het protocol in de praktijk gebruikt werd. De algemenere eenwegsfunctie met betrekking tot het vinden van een isogenie tussen twee elliptische krommen zonder extra informatie staat echter nog altijd sterk overeind. Er bestaan andere isogeniegebaseerde protocollen die dan ook helemaal niet onderhevig zijn aan onze aanval. Ons doel is om deze protocollen verder te onder zoeken op gebied van veilig heid, efficiëntie, etc, en wie weet, misschien versleutelen we binnen pakweg tien jaar onze data deels aan de hand van isogenieën. Dan belandt de grafentheorie ongetwijfeld opnieuw in de nieuwe nieuwe nieuwe eindtermen.

OEFENING 3

Colette meet de lengtes van de zijden van een vijfhoek en schrijft ze op van klein naar groot. Welk van de onderstaande antwoorden kan ze niet opgeschreven hebben?

A 5, 5, 5, 5, 5

B 5, 6, 7, 8, 9

C 5, 7, 9, 11, 13

D 5, 10, 15, 20, 25

E 5, 25, 125, 625, 3125

Welk van de onderstaande getallen is het kleinste?

EFFICIËNT

TANDEN POETSEN

IN PYTHAGORAS KUN JE DE DAGELIJKSE BESLOMMERINGEN VAN DE FAMILIE VAN DER TORUS VOLGEN. DE FAMILIE VAN DER TORUS IS EEN HEEL NORMALE, GEMIDDELDE FAMILIE. VOOR ZOVER EEN FAMILIE VAN WISKUNDIGEN NORMAAL KAN ZIJN. ZE KOMEN ALLERLEI ALLEDAAGSE PROBLEMEN TEGEN. KOM JE ZELF UIT EEN WISKUNDIG GEZIN OF BEN JE EEN (MOGELIJK TOEKOMSTIGE) WISKUNDIGE, DAN KUN JE JE ERVARINGEN, VRAGEN EN IDEEËN DELEN MET DE FAMILIE VAN DER TORUS VIA EMAIL NAAR FAM.V.D.TORUS@PYTH.EU.

DOOR IRIS EN TOM VERHOEFF

PHI

Micro staat te treuzelen in de badkamer. Draait een rondje, doet een dansje, leest alle etiketten van de flessen die al duizend keer gelezen zijn. Micro wil geen tanden poetsen. Niet dat tanden poetsen vreselijk is, maar het is zo onhandig. Het lukt Micro nooit om het efficiënt te doen, zonder een tand dubbel te poetsen of de tandenborstel rare sprongen te laten maken. Micro zou zo graag net als Milli en Phi en Pi tanden willen poetsen. In een vloeiende beweging met de tandenborstel, zonder rare sprongen en dubbele plekjes, maar toch alles poetsen.

‘Micro, schiet eens op!’ dringt Phi aan van buiten de badkamer. Het is bedtijd. ‘Ja, ja’, mompelt Micro, een arm naar de tandenborstel bewegend en eentje naar de tandpasta. De elektrische tandenborstel gaat aan met een klein klikje en begint dan te zoemen. Micro probeert het zo hard, maar het lukt niet. De tandenborstel komt op een doodlopende plek terecht en er is maar een optie mogelijk: het perfecte pad verpesten. De tandenborstel kan opgetild worden of tanden dubbel poetsen. Dat maakt nu niet meer uit. Verdrietig, borstelt Micro verder. Zelfs het liedje aan het einde van de twee minuten vrolijkt Micro niet op.

Met een lang gezicht komt Micro de badkamer uit.

‘Wat is er aan de hand?’ vraagt Phi bezorgd.

‘Ik wil ook zo netjes kunnen poetsen als jullie! In een keer.’ Micro stormt voorbij en gaat boos in bed zitten.

‘Oooh!’ Phi snapt eindelijk wat er elke avond aan de hand is de afgelopen weken bij het naar bed gaan. ‘Vind je het fijn als ik je help om het te leren?’

‘Nee’, zegt Micro meteen. Maar een paar seconden later komt er toch een verlegen, ‘Ja’.

‘Weet je nog hoeveel vlakken een snijtand of hoektand heeft?’ vraagt Phi, om Micro een beetje te helpen. ‘Een voor- en een achterkant’, antwoordt Micro.

‘Inderdaad. En een kies?’

‘Die heeft ook nog een kauwvlak. Dus drie’, zegt Micro, iets meer opgebeurd nu er vragen komen die Micro wel kan beantwoorden.

‘Dat klopt. Kan je ook bedenken hoe je kan wisselen tussen boven en onder zonder de tandenborstel van je tanden af te laten komen?’ Phi maakt de vragen langzaam iets lastiger.

‘Ja’, Micro heeft dit al heel veel geoefend om het hele trucje te leren. ‘Als ik mijn tanden op elkaar zet!’

‘Heel goed! Je bent er al heel dichtbij. Denk er vanavond en morgenochtend maar even goed over na’, stelt Phi voor. ‘En als je het dan nog niet snapt, dan kunnen we het samen uittekenen.’

HINT

De volgende dag heeft Micro toch nog wat hulp nodig.

‘Pak jij een papier en potlood?’ instrueert Phi en samen gaan ze aan tafel zitten om te kijken of ze er met een tekening uit kunnen komen.

Micro pakt het potlood vast en Phi vertelt wat er gete kend moet worden.

‘We gaan een graaf tekenen’, begint Phi. Gelukkig weet Micro al wat een graaf is, want in dit wiskundige gezin gebruiken ze die wel vaker. ‘Alle vlakken zijn knopen en je mag ze met elkaar verbinden als je van dat vlak naar het andere vlak kan gaan met je tandenborstel zonder ‘m op te tillen.’

IJverig begint Micro te tekenen. Het helpt enorm, want als de tekening af is, denken ze samen nog even goed na en snapt Micro het!

Opeens is het een stuk makkelijker voor Pi en Phi om Micro ‘s avonds in bed te krijgen. Micro wil niets liever dan tanden poetsen en het nieuwe trucje testen.

OPLOSSING

Micro wilde graag leren poetsen zoals Phi en Pi dat zo handig doen met hun elektrische tandenborstel. Maar Phi gaf het recept niet zo maar prijs. Het werd een ontdekkingsreis. Eerst eens een plaatje tekenen van het bovengebit met alle vlakken van tanden en kiezen die gepoetst moeten worden (het onder gebit is hetzelfde). Elk vlak is met een vette punt weergegeven in het bovenste diagram. Een lijntje tussen twee punten betekent dat je met de borstel zonder optillen van dat ene vlak naar het andere kan doorpoetsen. Dit is een gebit met verstandskiezen. Als je die niet hebt moet je het diagram aan beide uiteinden inkorten. Je ziet dat de kiezen ook een kauwvlak hebben naast het voor- en achtervlak. En op de uiteinden zijn er zijvlakken, die je natuurlijk ook moet poetsen.

De kunst is om in dat diagram een pad langs de lijntjes te vinden dat precies één keer langs elk punt (vlak) komt. Dit wordt wel een Hamiltonpad genoemd. Hamilton was een Iers wiskundige uit de 19e eeuw die zich met zulke problemen bezig hield. In het tweede diagram zie je hoe je alle vlakken precies één keer kan poetsen. Er zijn nog wel andere perfecte oplossingen, maar er moet ergens gezig zagd worden. Snap je waarom? Het derde diagram toont een oplossing met het minste aantal zigzags. Met wat meer zigzags lukt het zelfs om terug te komen waar je was begonnen (vierde diagram). Dat is een zogenaamde Hamiltoncykel. Als je zelf ook een mooie oplossing hebt gevonden dan wil de familie Van der Torus die graag horen.

Voor het ondergebit werkt hetzelfde diagram (even tueel gespiegeld). Aan de uiteindes zijn de paden langs het boven- en ondergebit aan elkaar te maken door via een voorvlak over te stappen.

Pi vindt dat zigzaggen toch niet zo handig en volgt het onderste diagram, waarbij de achterkant van de tanden dubbel worden gepoetst (wat niet eens zo'n slecht idee is omdat daar, zeker bij het ondergebit, makkelijker tandsteen ontstaat). Heb je gezien dat Pi ook smokkelt door van een kauwvlak van een kies naar het achtervlak van een hoektand te springen en omgekeerd (de twee rode lijntjes)?

5

Vier van de vijf onderstaande vierhoeken hebben dezelfde oppervlakte. Welke vierhoek heeft een afwijkende oppervlakte?

OEFENING

Stambreuken zijn breuken waarvan de teller 1 is en de noemer een natuurlijk getal verschillend van nul. Mats wil het getal 2 kunnen schrijven als som van een aantal verschillende stambreuken. Hoeveel stambreuken heeft hij daarvoor minstens nodig?

In elk bolletje van de figuur hieronder moet het getal 1, 2, 3, 4 of 5 geplaatst worden zodat in elke rij, in elke kolom en in elke ketting van vijf verbonden bolletjes vijf verschillende getallen staan. Welk getal komt op de plaats van het vraagteken?

OEFENING

ARCHIMEDES, DE NEERGESCHOTEN

DRAAK VAN DAENERYS EN HET VOLUME VAN EEN BOL

RUDI PENNE, FACULTEIT TOEGEPASTE

De Schorpioen is een uit de kluiten gewassen kruisboog, die door een schutter kan opgespannen worden dankzij een mechanische krachtver menigvuldiger. Met dit tuig wordt in het laatste seizoen van Game of Thrones een draak van Daenerys Targaryen uit de lucht geschoten tijdens de belegering van King’s Landing. Dit fantasiefeit greep plaats in 304 n. Chr.

Weinig liefhebbers van deze fantasyreeks weten dat de Scorpio al rond het begin van onze jaartelling door de Romeinen gebruikt werd, en

UANTWERPEN.

waarschijnlijk zelfs al door het leger van koning Uzzia van Juda in de 8ste eeuw v. Chr.

Maar mij deed dit mechanisch ver nuft vooral denken aan de befaamde Griekse wiskundige Archimedes, geboren in Syracuse (287 v.Chr.), waar hij in 212 v.Chr. vermoord werd tijdens de tweede Punische oorlog door een Romeinse soldaat. Volgens de geschiedschrijver Livius gebeurde dit na de irritatie van Archimedes omdat de lompe Romein op een meetkundige figuur stapte die in het zand op de vloer getekend was. Vol

gens diezelfde Livius waren “Verstoor mijn cirkels niet” de laatste woorden van Archimedes. Soms is wiskunde onverantwoord interessant.

Nochtans had de Romeinse bevel hebber Marcus Marcellus expliciet opgedragen om Archimedes levend gevangen te nemen. In zijn tijd was Archimedes immers een levende legende wegens zijn uitvindingen van werktuigen (zoals de schroefpomp) en militaire toestellen (variaties van de katapult en de schorpioen, de klauw, de zonnespiegels,…). Dankzij deze

krijgstuigen kon Syracuse twee jaar standhouden tegen de Romeinse belegering. In de oudheid was hij ook beroemd wegens zijn ontdek kingen van natuurkundige principes in de statica (hefboomregel) en de hydrostatica (opwaartse stuwkracht), terwijl zijn wiskundige inzichten pas eeuwen later en druppelsgewijs tot de wetenschap doordrong. Zijn tijdsgenoten bewonderden Archimedes omdat deze de kroon van de koning van Syracuse in water onderdompelde en hierdoor bewees dat de edelsmid geen zuiver goud gebruikt had.

Maar bijna niemand wist dat hij (als eerste) het getal nauwkeurig kon benaderen, en dat hij de oppervlakte van parabolische gebieden exact kon berekenen, a propos m.b.v. limiet- en integraaltechnieken die pas 2000 jaar nadien werden uitgevonden. Zelfs nu nog zal een gemiddelde leerling uit zijn schoollessen zich Archimedes vooral herinneren als de naakte man die uit zijn bad sprong terwijl hij Eureka riep, en niet zozeer als wiskundige. Twee eeuwen na zijn dood bezocht Cicero de stad Syracuse en ging hij op zoek naar het graf van Archimedes. Behalve de soldaat die zijn voeten veegde aan de bewuste cirkeltekening was ongeveer iedere Romein fan van Archimedes. Naar eigen zeggen heeft Cicero dat graf effectief gevonden. De Romeinse redenaar beschrijft een grafsteen met een reliëftekening van een bol in een cilinder. Dit kan kloppen want van al zijn ontdekkingen was Archimedes het meest trots op zijn formule om

het volume van een bol te bereke nen. Eigenlijk was hij vooral trots op de methode waarmee hij de volumes van de bol, de kegel en de cilinder wist te vergelijken met elkaar. En deze fierheid was meer dan terecht! Zie foto hieronder.

Natuurlijk was mijn associatie tussen de Schorpioen van Game of Thrones en de uitvindingen van Archimedes sterk beïnvloed door een recente vakantietrip naar Syracuse, waar ik iedereen een bezoek aan TechnoParco kan aanbevelen, een soort Archimedes-pretpark: zie foto volgende pagina.

Wie in dit klein gezellig openlucht museum moest aanspoelen, mag zeker niet nalaten om de eigenaar te laten uitpakken met zijn kennis over de Archimedes-puzzel Stomachion. Maar tijdens mijn bezoek had ik minder geluk dan Cicero, want het echte graf van Archimedes heb ik

niet gevonden, enkel een replica om toeristen te plezieren. De bewuste methode van Archimedes is een combinatie van het versnijden van een object in dunne schijfjes (de uitputtingsmethode), gecombineerd met zijn hefboomprincipe. Eigenlijk weten we dit nog maar sinds het begin van vorige eeuw, toen de Deen Johan Ludvig Heiberg in Constanti nopel een perkament bestudeerde dat hergebruikt was en dat onder de bovenste lagen een originele brief van Archimedes aan zijn vriend Eratosthenes van Cyrene bevatte. Laten we eerst het hefboomprincipe in beeld brengen, waarvan Archi medes inderdaad de auteur is. De olifant in de figuur op de volgende pagina weegt 100 000 keer meer dan de muis, maar toch is de wip in evenwicht omdat de muis 100 000 keer verder van het steunpunt F staat dan de olifant. Het product van gewicht en afstand is aan beide kanten van het steunpunt gelijk.

Belangrijk hierbij is dat de afstand tot het steunpunt steeds gemeten wordt vanaf de positie van het zwaartepunt van het voorwerp (muis, olifant of wat dan ook). In zijn bewijsvoering gebruikte Archimedes meestal homogene voorwerpen waarvan hij veronderstelde dat ze alle uit hetzelfde materiaal gemaakt waren (zelfde dichtheid), zodat de verhouding van de gewichten van twee voorwerpen gelijk is aan de verhouding van hun volumes. Dus de evenwichtsvergelijking voor een balans kan geformuleerd worden

als , voor lichamen met volumes en , en met respectieve afstanden en tot het steunpunt.

Dan zijn we nu beland aan de uitputtingsmethode, die met recht mag beschouwd worden als de allereerste integraalcalculus, niettegenstaande de uitvinding van de integraal in de handboeken Analyse meestal toegekend wordt aan Newton of Leibniz (naargelang de auteur de taal van Shakespeare of Goethe spreekt). In de brief die

Heiberg aan de oppervlakte bracht, schreef Archimedes de eer voor deze methode geheel toe aan Democritus (460 – 370 v.Chr.). Deze laatste was ook redelijk geniaal te noemen, zodanig zelfs dat een jaloerse Plato ooit voorstelde om al diens geschriften te verbranden. Maar eigenlijk was Archimedes de eerste die nieuwe resultaten behaalde met de uitputtingsmethode.

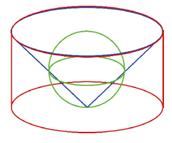
Bereid jullie dan nu voor op een con frontatie met de duizelingwekkende genialiteit waarmee Archimedes de volumes van de bol, de cilinder en de kegel met elkaar wist te vergelij ken. Neem een cilinder, een kegel en een bol zoals in onderstaande figuur. We bestuderen de situatie waarbij de straal en de hoogte van de cilinder gelijk zijn aan de diameter van de bol, en waarbij de kegel juist in de cilinder past. Als we noteren voor de straal van de bol, dan is de straal van de cirkelvormige basis van zowel de kegel als de cilinder gelijk aan Bovendien is de hoogte van de kegel gelijk aan die van de cilinder en ook gelijk aan de diameter van de bol.

In dit gedachte-experiment wordt de cilinder op zijn kant op een (horizon tale) wip gelegd met steunpunt in (zie figuur). Deze wip kan een as zijn waar de cilinder brochette-gewijs over geschoven is, of gewoon een plank waar de cilinder op ligt, dat doet niets ter zake (zie figuur boven aan).

Belangrijk is dat de cirkelvormige doorsneden van de cilinder loodrecht op de wip staan, met het grondvlak op het steunpunt . Het

bovenvlak bevindt zich in positie van de wip op een afstand van , omdat de hoogte van de cilinder gelijk is aan de diameter van de bol. In gedachte plaatsen we de kegel in deze cilinder (wat juist lukt, en op slechts 1 manier), en ook de bol verbeelden we in de cilinder, zodanig dat de cilinder-as (= kegelas) samenvalt met een diameter van de bol. Gelukkig is dit een gedachteexperiment want praktisch gezien is het onmogelijk om kegel en bol tegelijkertijd in de cilinder te wringen.

Nu treedt de uitputtingsmethode in werking, waarbij Archimedes deze drie objecten in dunne schijfjes versnijdt, loodrecht op de cilinder-as, van links naar rechts (van naar dus). Op ieder moment snijden we simultaan 3 schijfjes uit onze objec ten: een cilinderschijf, een bolschijf en een kegelschijf. Deze schijfjes moeten we ons visualiseren als de stenen van een sjoelbak (zie figuur), en zijn dus zelf cilindervormig, weliswaar erg plat, met een kleine hoogte (= dikte van de schijf). Strikt genomen heeft enkel de cilinderschijf een rand loodrecht op het snijvlak, terwijl de rand van een kegelschijf schuin is en die van een bolschijf gebogen, maar als we onze schijfjes voldoende dun snijden zijn deze afwijkingen te verwaarlozen.

De moderne mens heeft noties van het limietbegrip en van infinitesima len, maar in die tijd was het een hele krachttoer om met schijfjes te werken waarvan de dikte oneindig klein is maar toch niet nul. Ze hebben dus een volume, zoals de sjoelschijven, namelijk de oppervlakte van het cir kelvormige snijvlak vermenigvuldigd met de (infinitesimale) dikte . De formule voor de oppervlakte van een cirkel was trouwens gekend door Archimedes (en bewezen!), zijnde maal het kwadraat van de straal.

Stel dat onze snijmachine zich in positie bevindt, op afstand van het steunpunt (zie figuur). De 3 schijfjes die we simultaan uitsnijden hebben uiteraard verschillende stralen:

1 De cilinderschijf is in iedere snijpositie even groot, met een

H C

P AK R

N S

schijfstraal gelijk aan (de straal van de grote cilinder).

2 De straal van de kegelschijf neemt toe volgens een constante helling van 100% omdat de hoogte van de kegel ( ) juist gelijk is aan de straal van zijn grondvlak. Dus in snijpositie met is de straal van de kegelschijf ook gelijk aan .

3 Om de straal van de bolschijf te bepalen, gebruiken we de stelling van Pythagoras in het vlak door het middelpunt van de bol en loodrecht op het snijvlak. Hier zien we een rechthoekige driehoek (zie figuur). In snijpositie x is het kwadraat van de bolschijfstraal dus gelijk aan

De plaats varieert weliswaar van tot , terwijl het punt vastligt, maar de kegel- en bolschijf worden natuurlijk alsmaar groter. Misschien heeft de lezer problemen met het plaatsen van twee schijven in 1 minuscuul punt, maar we bedoelen dat het zwaartepunt van beide schijven zich ter hoogte van moet bevinden. Het evenwicht volgt uit de berekening van de verhouding van beide volumes (rechts op links):

evenwichten per schijfje. Met andere woorden: de cilinder, helemaal versneden (uitgeput) zoals hij daar ligt tussen en , wordt t.o.v. het steunpunt in evenwicht gehou den door de kegel en de bol zoals links gereconstrueerd in het punt .

Nu had Archimedes het inzicht dat de cilinderschijf in om het even welke snijpositie in evenwicht gehouden wordt als we de twee andere schijven (zoals uitgesneden op plaats ) in het punt H plaatsen, waarbij dit punt H op een afstand 2r ligt van het steunpunt

Omdat deze 3 schijven dezelfde (infinitesimale) dikte hebben, kan de verhouding beschouwd worden als de verhouding van de oppervlaktes van de cirkelvormige doorsneden. Omdat een gemeen schappelijke factor is, kunnen we ons zelfs beperken tot de kwadraten van de stralen in de berekening van deze verhouding:

Het speelt geen rol hoe de kegel en de bol juist geplaatst zijn, zolang hun gezamenlijk zwaartepunt zich ter hoogte van het punt bevindt. Anderzijds, wegens symmetrie, bevindt het zwaartepunt van de cilinder zich juist in het midden van de cilinder, wat overeenkomt met positie op de wip. Dit globaal evenwicht betekent dus dat

welke identiek is aan de verhouding van de afstanden zwaartepuntsteunpunt (links op rechts):

zodat we in iedere snijpositie een evenwicht hebben volgens het hefboomprincipe. De conclusie van de uitputtingsmethode is dat een globaal evenwicht volgt uit de lokale

of Nu wist Archimedes dat het volume van een kegel juist een derde is van het volume van de cilinder met dezelfde hoogte en grondvlak als de kegel. Dit staat bijvoorbeeld als Pro positie 10 in boek XII van het boek van Euclides. Uit ons kegel-bol-cilinder evenwicht volgt dus dat het volume van een bol 1/6 is van het volume van de cilinder met hoogte en straal gelijk aan de diameter van de bol. Het volume van dergelijke cilinder (hoogte = straal = ) is gelijk aan , en dus dat van de bol .

In een rechthoekige driehoek ontstaat een rechthoek door een punt op de schuine zijde te verbinden met twee punten op de rechthoekszijden zoals in de figuur. Waaraan is de oppervlakte van die rechthoek gelijk?

Na de bekerfinale spreekt een trainer zijn elf spelers toe: “Jullie gaven gemiddeld 50 passes per speler, maar helaas gaf iedereen behalve Kevin een aantal passes dat onder dat gemiddelde ligt.” Hoeveel passes gaf Kevin minstens?

LOGICA IN ALGEBRA

MICHEL ROELENS, REDACTIE UITWISSELING

BEGIN LESACTIVITEIT

FORMULE UITSPREKEN

Hoe spreek je uit? Als je zegt ‘het kwadraat van plus ’, dan kan dit ook als begrepen worden. Als je zegt ‘ plus in het kwadraat’, dan kan dit ook als begrepen worden.

1. Bedenk een manier om het uit te spreken zodat elke verwarring uitgesloten is.

2. Voor welke koppels maakt het allemaal niets uit?

formules is ook belangrijk bij het berekenen van afgeleiden in de derde graad.

Voor de tweede vraag moeten we alle zoeken waarvoor . Dit is een stelsel van twee vergelijkingen.

Het laatste stelsel is een klassiek stelsel van twee eerstegraadsvergelijkingen in twee onbekenden. Met de substitutie- of combinatie methode vind je als oplossing . De drie andere stelsels los je op het zicht op. Er zijn dus vier gevallen waarbij het niet uitmaakt hoe je uitspreekt

WAT MAAKT DEZE OEFENING MOOI?

Ik kwam op het idee van deze oefening bij het lezen van een kort fragmentje uit een artikel in Euclides (Kindt, 2020). Deze opgave had niet misstaan in het artikel over ‘gewoon mooie oefeningen’ dat je vindt in Uitwiskeling 35/1. Bovendien kun je bij het oplossen gebruik maken van logica. Met de nieuwe eindtermen wordt logica binnenkort leerstof in onze tweede graad.

OPLOSSING

Een goede manier om uit te spreken is: ‘het kwadraat van de som van en ’. Zoals bij het pellen van een ajuin, ga je best van buiten naar binnen. Wat is het? Een kwadraat. Een kwadraat waarvan? Van een som. Een som waarvan? ... Het van buiten naar binnen analyseren van

Hier komt wat logica bij kijken. Het stelsel is, logisch bekeken, van de vorm

Dit kun je ‘uitwerken’ als

Wiskundig is dit de distributiviteit van ten opzichte van . Maar het gaat ook met ‘gezond verstand’: is waar wanneer zowel als waar zijn. Dat betekent dat van en minstens eentje waar moet zijn en van en ook.

We krijgen dus:

De combinatie van een merkwaardig product, een stelsel en een portie logica.

BRONNEN

Kindt, M. (2020). Haakjes, hokjes, hekjes. Euclides 95/7, 10-13. Vanlommel, e.a. (2019). Gewoon mooie oefeningen. Uitwiskeling 35/1, 18-47.

Dit artikel verscheen in Uitwiskeling 36/4. Op www.uitwiskeling.be vind je alle info.

EINDE

A-stroom

en

DÉ REFERENTIE VOOR WISKUNDEONDERWIJS

Basis

wiskundeonderwijs

Nando

WISKUNDE MET PIT

betekent

A-stroom

en D&Afinaliteit

B-stroom en A-finaliteit

vreugde’.

methode biedt vernieuwend en motiverend

een sterke focus op differentiatie. Nando staat voor wiskunde met

Eigentijdse wiskundemethode

wiskundetaal

eindtermen

de leerplannen

HAAL HET MAXIMUM UIT WISKUNDE

Max-wiskunde brengt begrippen, concepten, eigenschappen en methodes aan in betekenisvolle contexten. Zo ontdekken de leerlingen de samenhang en wisselwerking tussen wiskunde en de maatschappij waarin ze leven.

Eenvoud en eenduidigheid centraal

Transferopdrachten om de leerstof in een nieuwe context toe te passen

Aandacht voor probleemoplossend denken