WISKUNDE: VAAK ONZICHTBAAR MAAR ZONDER GAAT HET NIET

SAMEN MET ALLE UNIVERSITEITEN IN VLAANDEREN EN NEDERLAND BRENGEN PLATFORM WISKUNDE VLAANDEREN EN PLATFORM WISKUNDE NEDERLAND DE VITALE ROL VAN WISKUNDE IN ONZE WERELD ONDER DE AANDACHT. “IMAGINARY: PRACHT EN KRACHT VAN WISKUNDE”, ZO HEET DE TENTOONSTELLING DIE DE KOMENDE MAANDEN 14 STEDEN IN DE LAGE LANDEN AANDOET. NIET ALLEEN KIJKEN, MAAR OOK PROBEREN EN BEWONDEREN, DAAR WORDT DE BEZOEKER TOE AANGEZET. EN WIE HET AANDACHTIG DOET, KAN ER NOG EEN PRIJS MEE WINNEN!

PAUL IGODT, AN SPEELMAN, MARNIX VAN DAELE

WWW.IMAGINARYMATHS.BE

“IMAGINARY” is een naam met internationale bekendheid als het op wiskunde-outreach aankomt. Open wiskunde, aansprekend voor het grote publiek en interactief voor wie graag probeert, daarover gaat het bij het inmiddels tot non-profitorganisatie gegroeide project dat startte in 2008. “Imaginary: through the eyes of mathematics”, zo heette de eerste tentoonstelling samengesteld door het onderzoeksinstituut voor wiskunde in Oberwolfach (MFO). 2008 was in Duitsland uitgeroepen tot ‘Jahr der Mathematik’. Onder leiding van Gert-Martin Greuel (Univ. Kaiserslautern), toenmalig directeur van het instituut, en dankzij reeds bekende beelden gemaakt door zijn collega algebraïsch meetkundige Herwig Hauser (Univ. Wenen en Innsbruck), ontstond die allereerste tentoonstelling. Ze bleek zodanig succesvol dat het Imaginary-concept inmiddels wereldwijd in meer dan 160 steden talrijke bezoekers aantrok. Hauser en Greuel, samen met Andreas Daniel Matt (momenteel directeur van de Imaginary-organisatie), slaagden toen ook in het maken van het softwarepakket SURFER, dat eenieder toelaat “te spelen” met algebraïsche oppervlakken. Wiskundevoorkennis onnodig, plezier en verwondering gegarandeerd. SURFER is nog steeds een grote publiekstrekker. Al in 2015-2016 reisde de eerste Imaginary-tentoonstelling langs alle Vlaamse universiteitssteden, het jaar nadien gevolgd door een analoge trip in Nederland.

Van september 2022 tot en met juli 2023 doet dit initiatief in totaal 14 universiteitssteden van de Lage Landen aan. Dynamisch onderzoek, zowel curiosity-driven als toepassingsgericht, zorgt ervoor dat iedere burger in onze maatschappij dagelijks gebruikmaakt van realisaties waarbij wiskunde (meestal goed verborgen) onder de motorkap zit. Zowel wiskunde die decennia geleden ontstond, zonder ook maar aan één toepassing te denken, als wiskunde die sterk gericht is op het oplossen van concrete problemen

Figuur 1 De “mascottes” van de vorige en de aankomende tentoonstelling. Met dank aan Herwig Hauser, Robert de Keijzer en Oliver Tse.

(aangereikt uit een zeer grote variatie van disciplines) komt in de tentoonstelling aan bod.

Op de tentoonstelling kan de bezoeker ook zelf aan de slag met een collectie apps, via grote touchscreens. Enkele denk- en puzzelopstellingen, en een voor deze keer bijzondere aanwezigheid van origamistukken, naast specifieke 3D-prints, maken het concept van de tentoonstelling compleet. Gratis rondleidingen voor groepen leerlingen en rondleidingen voor allerlei specifieke groepen belangstellenden zijn mogelijk op alle locaties. We plukken een paar voorbeelden uit de pracht en de kracht.

1 ORDE EN CHAOS: DE KAT

VAN ARNOLD Een kleine wijziging in de begintoestand kan soms, zelfs na korte tijd al, leiden tot een zeer grote verandering van een groot systeem. Dat is wat wiskundigen “chaotisch gedrag”, kortweg chaos, noemen. Denk aan het stoten van een biljartbal: de kleinste aanpassing bij de start kan ervoor zorgen dat de bal ergens helemaal anders terechtkomt.

Maar soms is er toch een vorm van orde in de chaos. Dit illustreren we aan de hand van een eenvoudige transformatie van het vlak, die wereldwijd bekendstaat als “Arnolds katafbeelding”. Op https://www.jasondavies.com/ catmap/ probeer je het uit op een foto die je zelf oplaadt. De pixels worden herschikt en al na enkele stappen wordt je foto onherkenbaar: chaos treedt op. Dergelijke transformaties zijn interessant voor cryptosystemen, je kan er snel een goed gestructureerd geheel (“foto”) mee versleutelen en dus onherkenbaar maken. Maar wie veel geduld uitoefent en de originele foto voldoende vaak laat vervormen, ziet het oorspronkelijke beeld toch terugkeren. Wat is hier aan de hand?

Laten we kijken naar de transformatie met matrix .

Die matrix werkt als een transformatie van het vlak . Een punt wordt afgebeeld op

. Je kan narekenen dat,

als en

terwijl

waarbij en

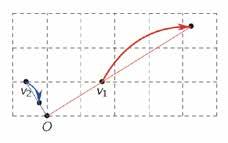
Figuur 2 In de richting van v1 (rode vector) gebeurt een expansie, terwijl in de richting van v 2 (blauwe vector) een inkrimping plaatsvindt. Figuur 3 In de eerste stap wordt het eenheidsvierkant omgevormd tot een parallellogram. In de tweede stap kijken we enkel naar het decimale gedeelte van de coördinaten; we rekenen “modulo” het gehele gedeelte.

Figuur 4 Er zijn meer dan 300 iteraties nodig om deze foto terug in originele toestand te krijgen.

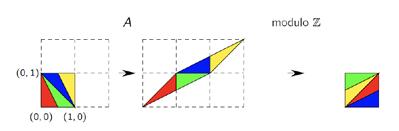
In figuur 3 hierboven bekijken we in eerste instantie wat de transformatie doet met de punten van het eenheidsvierkant ([0, 1] × [0, 1]), en in tweede instantie wat dit betekent indien we “modulo ” rekenen. Als we de figuur meer in detail bekijken, dan zien we dat vier gekleurde delen van het originele vierkant op vier plaatsen in het parallellogram terechtkomen. De hoekpunten van het vierkant worden hierbij opnieuw op roosterpunten (punten met coördinaten in ) afgebeeld. Dit is geen toeval, maar blijkt voor alle roosterpunten zo te zijn. Alhoewel de individuele punten bewegen, wordt het rooster als geheel behouden.

Om de afbeelding duidelijker te visualiseren, brengen we nu de delen van het parallellogram als puzzelstukken terug naar het eenheidsvierkant, zoals in de tweede stap op de tekening. We onthouden met andere woorden niet langer in welk vak van het rooster een punt terechtkomt, maar enkel zijn positie in het vak.

Elke vierkante foto kun je bekijken als een verzameling pixels die punten zijn uit het eenheidsvierkant. Punten die bovendien rationale getallen als coördinaten hebben. Transformatie A kun je dus ook uitvoeren op de pixels van een vierkante foto, en vele keren herhalen. Dit is wat er gebeurt met de foto van een watervliegtuig.

Het blijkt dat ieder rooster waarvan de punten rationale coördinaten hebben na verloop van tijd weer op zichzelf terugkeert. Dit is bij uitstek het geval met de pixels van eender welke foto. Het is best mogelijk dat je wat geduld moet hebben. Het aantal keer dat je de transformatie na elkaar moet uitvoeren, kan hoog oplopen. Maar geduld zal beloond worden, dat kunnen wiskundigen aantonen.

Echter, alle gekheid op een stokje, alhoewel er dus periodiciteit is op de punten met rationale coördinaten, is dat niet het geval op de punten met irrationale coördinaten. En die punten zijn bijzonder talrijk in het eenheidsvierkant. Wiskunde kent zo weer één van die bijzondere eigenaardigheden.

Meer over orde en chaos vind je op de tentoonstelling.

2 NULPUNTEN BEREKENEN

EN FRACTALEN Het algoritme van Newton-Raphson is een klassieker uit de numerieke wiskunde in het hoger onderwijs. De opdracht bestaat erin een nulpunt1 te vinden voor een gegeven functie , en zeker meer in het bijzonder als er geen algebraïsche oplossing voor is. Er wordt verondersteld dat de functie “voldoende braaf” is, en een mooie “gladde” grafiek heeft. De functie is m.a.w. overal afleidbaar. Het intuïtieve idee van de NewtonRaphson-methode is eenvoudig, en beslist uit te leggen in het secundair onderwijs. Je vertrekt van een eerste schatting voor het nulpunt die we de startwaarde noemen en noteren. Je bepaalt de vergelijking van de raaklijn aan de grafiek van in het punt ; dit is een eerstegraadsfunctie. Omdat je veronderstelt dat die raaklijn een interessante benadering voor de functie is, neem je vervolgens het nulpunt van die eerstegraadsfunctie als een volgende benadering, , voor het nulpunt van . Al in de derde graad kunnen leerlingen berekenen dat

We maken het even wat meer visueel. Herhalen we dit proces vertrekkend van , dan volgt een tweede benadering, , en meer algemeen geldt dus dat

waarbij

Indien het startpunt voldoende dicht bij het gezochte nulpunt ligt, dan wordt dit nulpunt heel snel voldoende goed benaderd. Wiskundigen spreken van kwadratische convergentie: ietwat ruw gesproken zal het aantal correcte cijfers bij elke iteratiestap verdubbelen.

Nemen we als voorbeeld even de functie met voorschrift . We kennen de twee nulpunten (−1 en 1). Hier wordt de iteratiestap nu gegeven door

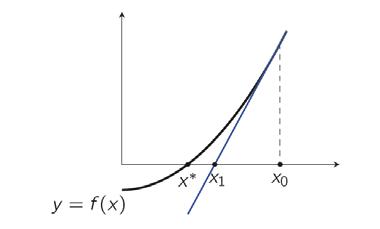
Figuur 5 De basisstap in het algoritme van Newton-Raphson.

1 Om een of andere, voor ons eerder duistere reden spreekt men in het secundair onderwijs over nulwaarden van een functie. Naar ons gevoel is een nulwaarde gelijk aan . . . 0.

Vertrekken we bijvoorbeeld met startwaarde , dan vinden we en dit

vervolgt met

Om de nauwkeurigheid te bepalen, definiëren we het verschil tussen en het gezochte nulpunt , met andere woorden de fout (error) bij stap als . Bekijken we nu in dit voorbeeld de opeenvolgende fouten:

Na 5 iteratiestappen wordt het nulpunt – in dit geval – reeds gevonden met een nauwkeurigheid van . Een moeilijk punt bij deze aanpak is dat de startwaarde het best “voldoende dicht bij ” ligt. Dat is ietwat heikel, omdat het afhangt van de functie die men onderzoekt. Indien zich te ver van bevindt, is het mogelijk dat er geen nulpunt gevonden zal worden (in wiskundige termen, dat er geen convergentie zal optreden), of zelfs dat er convergentie is naar een ander nulpunt dan het verwachte.

Als voorbeeld nemen we nu even de functie met voorschrift . De nulpunten zijn duidelijk eenvoudig, , en , en we zien een grafische voorstelling hieronder (zie figuur 6).

De grafiek laat duidelijk twee extremen zien: een maximum voor en een minimum voor . De concrete waarden van en zijn niet zeer belangrijk hier. Indien we één van die twee -waarden als startwaarde zouden kiezen voor deze methode, dan zal het fout lopen. Zie jij ook waarom? Ook als we een startwaarde kiezen zodanig dat, bij een zekere of wordt, is er een probleem. Over het algemeen echter zal een startwaarde met het algoritme van Newton-Raphson leiden naar een van de 3 bekende nulpunten. Voor zal er convergentie optreden naar het nulpunt 0. Voor zal er convergentie optreden naar het nulpunt 3. Voor tussen en is de uitkomst van het algoritme heel wat moeilijker te voorspellen, en ook het aantal iteraties dat zal nodig zijn om een gewenste nauwkeurigheid te bereiken kan hier al eens tegenvallen.

Op de tentoonstelling kun je zien wat er gebeurt bij het zoeken naar de nulpunten voor de vergelijking , waarbij x ook een complex getal mag zijn. Afhankelijk van de startwaarde die men kiest (in ) wordt een ander nulpunt gevonden, en met een andere convergentiesnelheid. Maakt men die verschillen ook visueel duidelijk door kleurtjes te gebruiken, dan zie je dat een fractaal beeld ontstaat: een Newtonfractaal! Een wonder!

3 TIEN THEMA’S EN OOK

WAT GESCHIEDENIS De organisatoren hebben de 50 Gallery-Prints gerangschikt in 10 topics. Orde en Chaos enerzijds, en Fractalen anderzijds zijn slechts twee van deze tien. Er zijn ook bijzonder mooie beelden en verhalen, in de catalogus bovendien rijkelijk aangevuld met extraatjes, in de

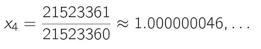
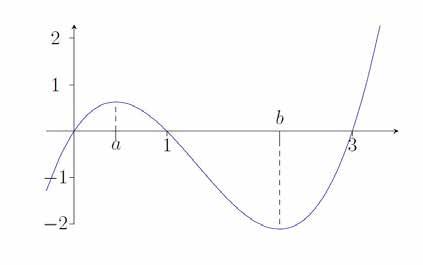
Figuur 6 Grafiek van de functie met voorschrift f (x) = x (x − 1)(x − 3).

Figuur 7 Met dank aan Toon Baeyens. Newton-Raphson genereert een opmerkelijke figuur als het op de vijfde wortels van 1 aankomt.

volgende thema’s: • Algebraïsche oppervlakken • Composities • Wereldrecord oppervlakken • Vlakvullingen en polytopen • Kosmologie • Netwerken • Wiskunde en origami • Wiskunde verrassend Je kan niet over belangrijke wiskunderealisaties spreken zonder het te hebben over enkele historische figuren. Waar relevant komen deze ook duidelijk aan bod in de catalogus van de tentoonstelling. Het gaat om wetenschappers die zich vaak toelegden op reeds bestaande historische problemen of net, bijna visionair, een totaal nieuwe kijk op een gebied van de wiskunde of natuurwetenschappen aanreikten. Vladimir Arnold (1937 - 2010) is één van de grote wiskundigen van de twintigste eeuw. Zijn wiskundewerk situeert zich in een veelheid van disciplines. Op 19-jarige leeftijd vond hij een oplossing voor het dertiende probleem van Hilbert. In 1974 werd hij genomineerd voor de Fieldsmedaille, de hoogste wetenschappelijke onderscheiding voor een wiskundige. Een hoogst merkwaardig optreden van of namens de Sovjet-Unie zorgde er echter voor dat die bekroning hem niet toegekend werd.

Isaac Newton (1642-1726) is zonder enige twijfel één van de grootste wetenschappers (wiskundige, fysicus, sterrenkundige,…) uit de geschiedenis. Hij legde de grondbeginselen van de klassieke mechanica vast en ontwikkelde ook belangrijke technieken voor de wiskundige analyse. Als één van de grootste Britten werd hij begraven in Westminster Abbey.

Onlinewedstrijd voor bezoekers

aan de tentoonstelling: bezoekers aan de tentoonstelling kunnen op elke locatie deelnemen aan een onlinewedstrijd. Aandachtig de tentoonstelling bezoeken zal beslist helpen. Per locatie zijn er enkele mooie prijzen te winnen.

Paul Igodt en An Speelman zijn allebei verbonden aan het departement Wiskunde van de KU Leuven. Marnix Van Daele is verbonden aan de Vakgroep Toegepaste Wiskunde, Informatica en Statistiek van de Universiteit Gent. Zij zijn de 3 Vlaamse collega’s in de kerngroep voor de Imaginary-tentoonstelling.