LEERWERKBOEK
Meetkunde
Björn Carreyn
Filip Geeurickx
Roger Van Nieuwenhuyze
CARTOONS
Dave Vanroye
Hoe gebruik je VBTL ?
INKIJKEXEMPLAARDIEKEURE
Dit boek bevat zes hoofdstukken vol meetkunde. Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.
Bij de inhoudstafel van elk hoofdstuk kun je ook een QR-code vinden. Via die codes kun je extra filmpjes met uitleg bekijken.
Achteraan in dit boek vind je een DIY-poster met de wiskundige symbolen uit dit boek.
Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.
Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt.
Wiskunde kent veel links met andere vakken We tonen zo’n link in een paarsgekleurd kadertje.
1 2 *
Na de samenvatting vind je een reeks oefeningen
Bij oefeningen die extra uitdagend zijn, zie je een sterretje naast het nummer.
Bij sommige oefeningen moet je verder denken dan de net geziene leerstof. Je maakt dan gebruik van heuristieken. Deze oefeningen herken je aan de wiskunderugzak
ICT is een ideaal hulpmiddel.
Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets. Die vind je terug via www.polpo.be.
Vaardigheden
Na elk hoofdstuk wordt een wiskundige vaardigheid in de kijker gezet. Ook in het portfolioschriftje kun je vaardigheden inoefenen.
Wat moet je kennen en kunnen ?
Na de vaardigheden zie je een handig overzicht van wat je moet kennen en kunnen na het geziene hoofdstuk. Kleur de eerste kolom smileys als je de leerstof herhaalde voor een grote toets. Kleur de laatste kolom als je de leerstof beheerst voor je examen.
Herhalingsoefeningen
Wanneer je wiskunde studeert, maak je uiteraard heel wat oefeningen opnieuw en maak je oefeningen die je in de klas niet maakte. Elk hoofdstuk sluit af met drie pagina’s herhalingsoefeningen
Een ideale test voor jezelf om te zien of je de leerstof beheerst.
INKIJKEXEMPLAARDIEKEURE
Wiskunde is veel meer dan alleen maar optellen en vermenigvuldigen. Ook meetkunde en ruimtemeetkunde moeten tot je wiskundige bagage behoren.
We vullen onze wiskunderugzak en trekken bijvoorbeeld naar Zwitserland, waar deze Bernina Express een cirkelvormige baan moet afleggen voordat hij in de Alpen verdwijnt om er nadien in Italië weer uit te rijden.
Hou je potlood, gom, passer en geodriehoek in de aanslag voor een realistische portie meetkunde
Meetkunde
1
De wereld van 3D naar 2D
1.1 Ruimtefiguren en vlakke figuren herkennen 9
1.2 Begrippen in de vlakke meetkunde 33 Extra’s 44
4
Ruimtefiguren
4.1 Aanzichten en perspectieven van ruimtefiguren 161 4.2 Opbouw van ruimtefiguren 176
2
Eigenschappen van rechten en hoeken
2.1 Rechten 53
2.2 Hoeken 69
3
Vlakke figuren
3.1 Vlakke figuren rondom ons herkennen
3.2 Driehoeken
3.3 Vierhoeken
3.4 Cirkels
Omtrek en oppervlakte van vlakke figuren
5.1 Omtrek van vlakke figuren
5.2 Oppervlakte van vlakke figuren
6
Oppervlakte en volume van ruimtefiguren
6.1 Oppervlakte van ruimtefiguren
Volume van ruimtefiguren
De wereld van 3D naar 2D 1
Een oude keizer in China liet per ongeluk een vierkante tegel op de grond vallen. Toen hij probeerde om de zeven stukken weer in elkaar te passen, ontdekte hij dat hij veel meer mooie figuren kon maken dan enkel de vierkante tegel. De tangram, een Chinese legpuzzel, was geboren.
Hiernaast zie je de zeven standaardstukken (mooie vlakke figuren) waarmee je heel wat nieuwe figuren kunt vormen. Van vissen tot vogels, van huizen tot helikopters : alles is mogelijk.
INKIJKEXEMPLAARDIEKEURE
De wereld van 3D naar 2D
1.1 Ruimtefiguren en vlakke figuren herkennen
1 Ruimtefiguren herkennen 9
2 Kubus, balk, prisma en cilinder 11
3 Vlakke figuren herkennen 13
4 Aanzichten 16
5 Schaal 17
6 Schaalproblemen oplossen 18
7 Samenvatting
8 Oefeningen
1.2 Begrippen in de vlakke meetkunde
1 Punt, vlak en rechte 33
2 Halfrechte en lijnstuk 34
3 Meten van lijnstukken
4 Midden van een lijnstuk
5 Samenvatting
6 Oefeningen
Bekijk de instructievideo’s
1.1 Ruimtefiguren en vlakke figuren
herkennen
1 Ruimtefiguren herkennen
Overal ter wereld vind je allerhande ruimtefiguren (of ruimtelichamen) terug. In oude en moderne gebouwen, kunstwerken … overal zie je ruimtelichamen waar je een speciale naam op kunt kleven.
Pont du Gard in Frankrijk
Herken je hier bepaalde patronen die terugkeren ? Weet je waarvoor dit bouwwerk werd gebruikt ?
INKIJKEXEMPLAARDIEKEURE
Taj-Mahal in India
Sinds 2007 officieel een ‘wereldwonder’. Dit gigantische 17e-eeuwse bouwwerk werd gebouwd als grafmonument en zit vol marmer en symmetrie.
Planetarium Sir Thomas in Brisbane, Australië
Binnenin worden de sterren geprojecteerd op een halve bol. Die rust dan weer op een grote cilinder.
Het koninklijk paleis in Brussel
Vaak komt er ook symmetrie voor in een gebouw. Beeld je in dat we in het midden een verticale rechte zouden tekenen. Links en rechts van die lijn zie je dan hetzelfde.
Kubushuizen in Nederland
In Rotterdam treffen we deze zeer unieke kubushuizen. Ze werden in 1982 gebouwd en het lijkt alsof ze op een van hun hoekpunten rusten.
De Sphere in Las Vegas
Eind 2023 opende dit bolvormig entertainmentgebouw : The Sphere. Het is 112 m hoog en wordt bedekt door 54 000 m2 led-schermen.
Kakslauttanen in Finland
’s Ochtends wakker worden in een iglohotel met boven jou het noorderlicht ? Of in de zomermaanden de middernachtzon ? Dan moet je naar Saariselkä in Finland.
Futuroscope
Dit is een van de vele knappe bouwwerken in het Franse pretpark Futuroscope. Buiten ziet het eruit als een groot ijskristal, binnen zie je o.a. IMAX-films.
INKIJKEXEMPLAARDIEKEURE
Egyptische piramides
Meer dan 4000 jaar oud en gebouwd als graftombe voor de farao.
Sommige ruimtefiguren hebben een regelmatige vorm. Andere ruimtefiguren (zoals een kei of het ijskristal van Futuroscope) hebben een willekeurige vorm.
Ze hebben dit gemeen : allemaal nemen ze ruimte in en worden ze begrensd door grensvlakken. Deze grensvlakken zijn vlakke of gebogen opper vlakken.
Niet alle ruimtelichamen hebben een bovenvlak en een grondvlak. Zo hebben een kegel en een piramide geen bovenvlak en heeft een bol geen van beide. Die ruimtefiguren bestuderen we in het tweede jaar.
ruimtefiguren
Een kubus, een balk, een recht prisma, een cilinder, een kegel, een piramide en een bol zijn ruimtefiguren.
2 Kubus, balk, prisma en cilinder
a De kubus
hoekpunt
ribbe zijvlak
Een kubus wordt begrensd door 6 grensvlakken of zijvlakken. Dat zijn even grote vierkanten. De vlakken snijden elkaar in de ribben. We tellen 12 ribben. In een hoekpunt van de kubus komen telkens 3 ribben samen. We tellen 8 hoekpunten.
De kubus heeft één grondvlak en één bovenvlak. De vier opstaande zijvlakken vormen samen de mantel.
Opmerking :
Onzichtbare ribben worden in streepjeslijnen getekend.
b De balk
zijvlak
ribbe
hoekpunt
Een balk wordt begrensd door 6 grensvlakken. Elk grensvlak is een rechthoek. We tellen 12 ribben en 8 hoekpunten. Er zijn 3 maal 4 even lange ribben.
Opmerking :
Een balk heeft één grondvlak en één bovenvlak, die steeds even groot zijn.
c Het rechte prisma
INKIJKEXEMPLAARDIEKEURE
hoekpunt
ribbe zijvlak
Een recht prisma is een lichaam dat wordt begrensd door twee evenwijdige en even grote veelhoeken (driehoek, vierhoek, vijfhoek …) als grond- en bovenvlak. De opstaande zijvlakken zijn rechthoeken, die samen de mantel vormen. Er zijn zoveel opstaande zijvlakken als er zijden aan de veelhoek van het grond- of bovenvlak zijn.
De opstaande ribben zijn allemaal evenwijdig en even lang.
Opmerkingen :
De opstaande ribben staan loodrecht op grondvlak en bovenvlak. – Een kubus en een balk zijn speciale gevallen van prisma’s.
Een cilinder is een lichaam dat begrensd wordt door twee even grote cirkelschijven en een gebogen zijvlak. De cirkelschijven worden grond- en bovenvlak genoemd. Het gebogen zijvlak is de mantel
Kubus, prisma en cilinder
De woorden ‘kubus’, ‘prisma’ en ‘cilinder’ komen uit Griekenland. Zo is ‘cubos’ een soort dobbelsteen met zes vlakken. ‘Cilinder’ betekende eigenlijk ‘rol’ en prisma betekent letterlijk ‘het afgezaagde”.
G B
d De cilinder
B G
3 Vlakke figuren herkennen
Voorbeeld 1 : door te kijken naar ruimtefiguren Bespreek welke figuren het mannetje ziet.
RUIMTEFIGUUR MANNETJE DAT
ERVOOR STAAT
KUBUS
BALK
PRISMA
CILINDER
PIRAMIDE
KEGEL
BOL
MANNETJE DAT
ER LINKS VAN STAAT
MANNETJE DAT
ERBOVEN HANGT
Voorbeeld 2 : in bouwplaten
Een kubus, een balk, een prisma en een cilinder zijn allemaal ruimtefiguren die we kunnen ontwikkelen.
We hebben dan als het ware een bouwplaat die (met wat knip- en plakwerk) de originele ruimtefiguur oplevert.
Dankzij die ontwikkeling kunnen we gemakkelijk zien wat de grensvlakken zijn van de ruimtefiguur.
Zo zijn alle zijvlakken bij een kubus vierkanten. Een vierkant heeft vier even lange zijden en vier rechte hoeken.
INKIJKEXEMPLAARDIEKEURE
De zijvlakken bij een balk zijn rechthoeken, die per twee even groot zijn. Een rechthoek heeft vier rechte hoeken.
De zijvlakken bij een recht prisma zijn rechthoeken, die niet noodzakelijk even groot zijn.
Het grond- en bovenvlak van een cilinder zijn cirkels. Bij een cirkel liggen alle punten even ver van het middelpunt.
Voorbeeld 3 : in patronen Vlakke figuren kom je overal tegen. – de tegels in de badkamer ; – de stenen op de speelplaats ; – figuren op het behangpapier; – de r uitjes op het hemd van de leraar of de jurk van de juf ; – het zebrapad ; – de lijnen op het spor tveld.
De speelplaats kan gewoon een aaneenschakeling zijn van vierkante tegels. We noemen dat een vlakvulling met vierkanten. De zijgevel van je huis is misschien een vlakvulling van rechthoeken ?
Vlakke figuren zijn delen van het vlak. Je vindt ze in allerlei vormen terug.
INKIJKEXEMPLAARDIEKEURE
vlakke figuren
Een vierkant, een rechthoek, een driehoek, een ruit, een parallellogram, een trapezium en een cirkel zijn voorbeelden van vlakke figuren
4 Aanzichten
Maak kennis met Max, onze bordercollie, die even blijft stilstaan zodat de tekenaar drie aanzichten kan weergeven.
Max in vooraanzicht
INKIJKEXEMPLAARDIEKEURE
Max in linkerzijaanzicht
Max in bovenaanzicht
Max heeft ook een eigen hondenhok. Ook daar lukt het om de drie aanzichten weer te geven.
hondenhok in vooraanzichthondenhok in linkerzijaanzichthondenhok in bovenaanzicht
bovenaanzicht
Niet alleen honden en hun hokjes kunnen we vanuit verschillende posities bekijken. Het lukt ook met ruimtefiguren, zoals deze blokkencombinatie.
linkerzijaanzicht
rechterzijaanzicht
vooraanzicht
linkerzijaanzicht rechterzijaanzicht vooraanzicht
bovenaanzicht
5 Schaal
Schepen, auto’s en monumenten zoals de Eiffeltoren zijn in werkelijkheid heel groot. In de modelbouw wordt het allemaal op schaal nagemaakt. Dat gebeurt heel precies en de afmetingen worden steeds met eenzelfde factor verkleind.
Voor de Eiffeltoren hiernaast is de schaal 1 75
Voor heel wat speelgoedautootjes is de schaal 1 : 64.
We noemen dit allebei een breukschaal
In een atlas, op een wegenkaart of bij een luchtfoto vind je ook een schaal terug. Die noemen we een lijnschaal. 0
INKIJKEXEMPLAARDIEKEURE
Soms is het nodig de werkelijkheid te vergroten. Een watervlo is in het echt een heel klein diertje. Als we het willen bekijken, leggen we de vlo het best onder een microscoop. Op het oculair vinden we de breukschaal terug. de water vlo in het echt de watervlo uitvergroot
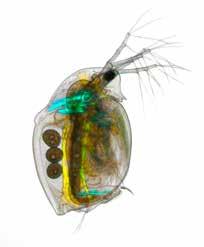
De gebruikte schaal is hier 24 : 1. We hebben te maken met een vergroting van de werkelijkheid.
6 Schaalproblemen oplossen
Voorbeeld 1 : de druivenfietsroute
De druivenroute is een fietsroute in Vlaams-Brabant. Hieronder zie je een stukje van de kaart met onderaan een lijnschaal. Op de kaart is de afstand tussen knooppunt 60 en knooppunt 57 (een knooppunt is aangeduid met een cirkel) in vogelvlucht precies 5 cm. Wat is de werkelijke afstand in vogelvlucht ?
Oplossing:
– Maak een schatting.
– Zet de lijnschaal eerst om naar een breukschaal.
– Maak een tabel.
– Noteer bovenaan de gegevens van de tekening, onderaan de gegevens in werkelijkheid. – Bereken met hoeveel 5 cm op de tekening in werkelijkheid overeenkomt.
Om te schatten kun je je duim tegen de lijnschaal leggen. Je duim komt ongeveer overeen met 1000 m. Schat nu hoeveel keer je duim in de gevraagde afstand past.
Uit de lijnschaal leer je dat 1 cm overeenkomt met 500 m. Als we dezelfde eenheden hanteren, komt 1 cm overeen met 50 000 cm. De schaal is dus 1 : 50 000.
AANTAL CM OP TEKENING 15
AANTAL CM IN WERKELIJKHEID 50 000250 000 5 5
INKIJKEXEMPLAARDIEKEURE
Antwoord : In werkelijkheid bedraagt de afstand in vogelvlucht 250 000 cm of 2,5 km.
KASTEEL ROCKENBORCH
Voorbeeld 2 : Gloster Gladiator
Oplossing :
Maak een tabel.
– Noteer bovenaan de gegevens van het model, onderaan de gegevens in werkelijkheid.
Vul de gegevens in.
Laura’s vader is fan van modelbouw en stak al heel wat vliegtuigjes in elkaar. Op een rommelmarkt tikt hij een ongeopende doos van de Gloster Gladiator op de kop, een Engelse dubbeldekker. De schaal die op de doos vermeld staat, is 1 : 72. Als zijn vliegtuigje helemaal af is (zie foto hiernaast), meet hij de totale lengte : 11,6 cm. Om de lengte van het echte vliegtuig te kennen, kun je werken met een tabel.
– Bereken met hoeveel 11,6 cm op het model in werkelijkheid overeenkomt.
Antwoord :
In werkelijkheid is de Gloster Gladiator 835,2 cm of 8,352 m lang.
Voorbeeld 3 : de Lærdalstunnel
De langste autotunnel van de wereld bevindt zich in Noorwegen en is bijna 25 km lang. Om de 6 km krijg je door de extra verlichte uitbouw de indruk dat je door een ijsberg rijdt.
Op het kaartje vind je de tunnel terug, hij is aangegeven met een oranje lijn.
Op welke schaal is de kaart weergegeven?
Oplossing :
– Maak een tabel.
– Noteer bovenaan de gegevens van de tekening, onderaan de gegevens in werkelijkheid.
Vul de gegevens in.
– Bereken met hoeveel 1 cm op de tekening in werkelijkheid overeenkomt.
AANTAL CM OP TEKENING 51
AANTAL CM IN WERKELIJKHEID 2 500 000500 000 : 5 : 5
Antwoord : De kaart is getekend op schaal 1 : 500 000.
AANTAL CM OP SCHAAL 1
7 Samenvatting
• Je kunt vlakke figuren herkennen in de zijvlakken van een ruimtefiguur.
• Je kunt van een kubus (of een figuur die opgebouwd is door enkele kubusjes) en een balk aanzichten herkennen en aanzichten tekenen.
• Je herkent de volgende ruimtefiguren : kubus balk recht prisma cilinder kegel
• Je herkent de volgende vlakke figuren : vierkantrechthoekdriehoekruitparallellogramtrapeziumcirkel
• Je kunt vlakke figuren en ruimtefiguren herkennen in voorbeelden uit je eigen leefomgeving, wetenschappen, techniek en kunst.
• Je kunt voorbeelden geven van vlakke figuren en ruimtefiguren uit je eigen leefomgeving, wetenschappen, techniek en kunst.
• Je kunt de schaal bij een gegeven figuur aflezen en op een figuur gemeten lengtes omzetten naar ware grootte. Je kunt gegevens in ware grootte omrekenen naar een voorstelling op schaal.
• Je kent de verschillende notatievormen van een schaal en kunt de ene in de andere omzetten.
8 Oefeningen
Welke meetkundige lichamen herken je in de volgende voorwerpen ?
Noteer de namen van twee voorwerpen uit het dagelijkse leven die de vorm hebben van
a een kubus
b een balk
c een cilinder
INKIJKEXEMPLAARDIEKEURE
d een pr isma
Vul het gepaste getal in.
a Een kubus heeft in totaal ribben en hoekpunten.
Het heeft opstaande ribben.
Het heeft grensvlakken. De mantel bestaat uit grensvlakken.
b Een balk heeft in totaal ribben en hoekpunten.
Het heeft opstaande ribben.
Het heeft grensvlakken. De mantel bestaat uit grensvlakken.
c Een prisma met een vijfhoek als grondvlak heeft opstaande ribben.
Het heeft grensvlakken. De mantel bestaat uit grensvlakken.
d Een prisma met een zeshoek als grondvlak heeft in totaal ribben.
Waar of vals ?
Omcirkel het juiste antwoord.
a Alle r ibben van een balk zijn even lang.
b Alle r ibben van een kubus zijn even lang.
c De ribben van een balk kunnen even lang zijn.
d De lengte van de mantel van een cilinder is de omtrek
WAAR VALS
WAAR VALS
WAAR VALS
WAAR VALS van het grond- of bovenvlak.
a Zijn de volgende ontwikkelingen de ontwikkelingen van een kubus ? Indien niet, verklaar de fout. 1 2 3 4
b Zijn de volgende ontwikkelingen de ontwikkelingen van een balk ? Indien niet, verklaar de fout.
2 3 4
Aïcha neemt een familiefoto. Welke foto zal op het scherm van haar toestel te zien zijn ?
Thomas maakte een peperkoekenhuis, beplakt met snoep. Noteer telkens welk aanzicht werd afgebeeld.
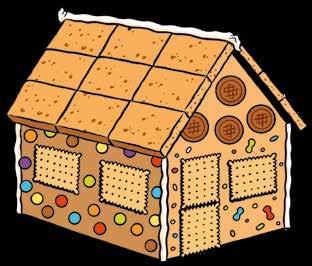
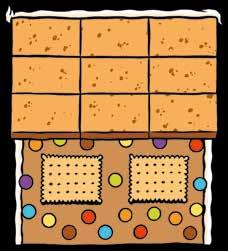
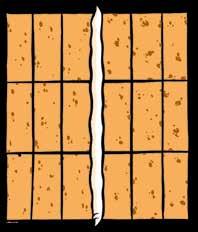
Noteer de juiste naam van het aanzicht.
Onderstaande lichamen zijn getekend in perspectief. Kleur het vooraanzicht BLAUW, het linkerzijaanzicht R OOD en het bovenaanzicht GEEL. a b c
Zet een kruisje als het aanzicht zichtbaar is op de voorstelling.
VOORSTELLING
Kleur de even lange ribben van volgende lichamen in eenzelfde kleur.
Noteer de juiste naam van elk lichaam en kleur het bovenvlak geel en het ondervlak paars.
a b c d e
Bij welk(e) aanzicht(en) zien we het rode blokje ? Plaats telkens een kruis in de tabel.
figuur 4
figuur 5
figuur 6
figuur 7
figuur 1
figuur 2
figuur 3
Kleur het gevraagde vlak in de tekeningen.
a Kleur het voorvlak blauw.
c Kleur het achter vlak paars.
b Kleur het rechterzijvlak groen. d Kleur het linker zijvlak rood.
In de volgende tekeningen zijn al vier zichtbare ribben gegeven. Teken de andere ribben in volle lijn als ze zichtbaar zijn en in streepjeslijn als ze onzichtbaar zijn.
a c e
b d f
De ruimtefiguur hiernaast heeft twee groen ingekleurde vlakken. Hieronder zie je vier aanzichten van de ruimtefiguur.
Kleur dezelfde vlakken groen als ze bij het aanzicht zichtbaar zijn. a b c d
Ruimtefiguren en regelmaat.
Schets steeds de volgende ruimtefiguur en vul nadien de tabel aan.
a Een leuk kristal.
figuur 1 figuur 2
figuur 3
figuur 1 figuur 2
figuur 1 figuur 2
figuur 1 figuur 2
b Blikjes stapelen.
figuur 1 figuur 2
figuur 1 figuur 2
figuur 1 figuur 2
c Bollen stapelen.
figuur 1 figuur 2
figuur 3
figuur 3
figuur 3
figuur 3
figuur 3 figuur 3
figuur 3
Bepaal bij iedere getekende lijnschaal de bijbehorende breukschaal.
a 0 km
b 0 m 50 m 100 m
Vul de tabellen aan.
a België op één A4.
Gebruikte schaal 1 : 1 000 000
b Plattegrond van een woning.
Gebruikte schaal 1 : 50
c Microscoop.
Gebruikte schaal is afhankelijk van het gebr uikte oculair.
Vul de tabel aan.
Teken in deze rechthoek ABCD een nieuwe rechthoek :
a op schaal 1 : 2
b op schaal 1 : 4
c Vul de tabel aan.
OPGAVE
SCHAAL 1 : 2
SCHAAL 1 : 4
d Noteer.
Bij schaal 1 : 2 zal de opper vlakte
Bij schaal 1 : 4 zal de opper vlakte
Bij schaal 1 : x zal de opper vlakte
Vraagstukken i.v.m. schaal.
a Een auto rijdt gemiddeld 100 km per uur. Om 20 cm op kaart af te leggen, reed de wagen twee uur. Op welke schaal is de kaart getekend ?
b Deze houten bouwset nodigt je uit om een sportwagen uit 1910 te bouwen op schaal 1 : 16. Na het nodige knutselwerk blijkt de lengte van de wagen 22,8 cm te zijn. Hoe lang was de werkelijke racewagen waarop dit model is gebaseerd ?
c Nadat hij deze spin gebouwd heeft, meet Lucas als lengte 28 cm.
De werkelijke lengte van de spin is slechts 4 cm.
Op welke schaal is deze spin nagebouwd ?
d Een vlinder (met lengte 3,5 cm) werd op een foto uitvergroot en heeft zo als lengte 14 cm. Op welke schaal werd de vlinder uitvergroot ?
Kleur het vakje in van START. Kleur vervolgens het vak in met de juiste oplossing en maak dan de opdracht in het vak waar deze oplossing naar leidt. Kleur ook dit vak weer in, alsook de oplossing. Vind op die manier de weg naar de finish (en achterhaal wat er bijzonder is aan de niet ingekleurde vakjes).
Je gemeente wordt weergegeven op kaart A (schaal 1 : 20 000) en kaart B (schaal 1 : 40 000). Welke kaart is de grootste?
Je hebt een postkaart (met lengte 12 cm) vergroot naar een posterformaat van 72 cm op 48 cm. Wat is de breedte van de oorspronkelijke postkaart?
Jack maakt een modelwagen die 12 cm lang is.
Op de doos stond als schaal 1 : 40. Wat is de lengte van de echte wagen?
Op het plan van je huis is de lengte van het dak 28 cm.
In werkelijkheid is die lengte 14 m.
Welke schaal wordt gebruikt?
Een mier met lengte 5 mm wordt onder een microscoop gelegd waardoor de lengte 2 cm wordt.
Wat is de gebruikte schaal?
Volgens welke schaal is een A2-blad een schaalmodel van een A4-blad?
Een kubus wordt vergroot weergegeven op schaal 3 : 1. Hoeveel keer kan de eerste kubus in de vergroting?
Figuur A wordt weergegeven op schaal 2 : 1. Zo bekom je figuur B. Daarna wordt figuur B vergroot op schaal 4 : 1 zodat je figuur C bekomt. Als je van figuur A onmiddellijk naar figuur C wil, welke schaal gebruik je dan?
Wat is de gebruikte schaal?
Dit fietsje van 3,6 cm lang is in werkelijkheid 1,8 m lang. Wat is de gebruikte schaal?
De LEGO-versie van de Notre-Dame in Parijs is 33 cm hoog.
De gebruikte schaal is 1 : 291.
Wat is de echte hoogte van de Notre-Dame?
Willy stapelt een aantal identieke kubussen recht boven elkaar op een vlakke vloer en verkrijgt het bouwwerk uit de figuur. Bepaal het kleinste aantal kubussen dat volstaat om dit bouwwerk te realiseren.
(A) 17(B) 18(C) 19(D) 20(E) 21
JWO 2025 eerste ronde, probleem 19 © Vlaamse Wiskunde Olympiade vzw
Rubi vouwt de figuur hiernaast tot een kubus. Ze telt de getallen van overstaande vlakken juist op. Welke 3 sommen krijgt Rubi ?
(A) 4, 6, 11(B) 4, 5, 12(C) 5, 6, 10(D) 5, 7, 9 (E) 5, 8, 8
WALLABIE 2015 probleem 9 © Vlaamse Wiskunde Olympiade vzw
Schilder Cas verft de 6 vlakken van een kubus zwart, grijs of wit. Van zijn baas mogen tegenover elkaar liggende vlakken niet dezelfde kleur hebben. Als hij de kubus uitvouwt, kan hij 1 bouwplaat niet krijgen.
Welke bouwplaat is dat ?
WIZSMART 2018 probleem 14 © Stichting Wiskunde Kangoeroe
Johan heeft een groot aantal gelijke kubussen.
Hij maakt een bouwwerk door op elk zijvlak van een kubus een andere kubus te plakken.
Hij wil zijn bouwwerk uitbreiden, door op elk zijvlak van zijn bouwwerk een andere kubus te plakken. Hoeveel extra kubussen heeft hij daarvoor nodig ?
(A) 10 (B) 12 (C) 14 (D) 16 (E) 18
WALLABIE 2024 probleem 14 © Vlaamse Wiskunde Olympiade vzw
(A) (B) (C) (D) (E)
1.2 Begrippen in de vlakke meetkunde
1 Punt, vlak en rechte
Meetkunde kun je perfect vergelijken met een spelletje dammen, stratego of schaken. Er zijn verschillende begr ippen die meespelen (speelstukken), er moeten afspraken gemaakt worden (spelregels) en er is het vlak waarin alles gebeurt (het spelbord).
STRATEGO
SCHAKEN MEETKUNDE spelbord schaakbord het vlak maarschalk, kapitein, spion … pion, loper, toren …punt, lijnstuk, rechte
een verkenner mag meer dan één vakje vooruit of opzij
een toren mag zich alleen horizontaal of verticaal verplaatsen door twee verschillende punten kun je precies één rechte tekenen
De vlakke meetkunde speelt zich af in het vlak p (lees : pi).
Het vlak p (het vlak van het bord, van je blad of van je werktafel) is een oneindige verzameling van punten. Het is onbegrensd en beperkt zich niet tot datgene wat je bijvoorbeeld van het bord kunt zien. Het loopt oneindig door naar boven, onder, links en rechts.
In de ruimte kun je werken met meerdere vlakken.
Een punt stellen we voor door een stip en benoemen we met een hoofdletter.
Een rechte is een verzameling van punten. Een rechte is onbegrensd.
We duiden een rechte aan met een kleine letter of met twee punten die op die rechte liggen.
Voorbeeld : rechte AB of rechte BA of rechte a
het punt A ligt op de rechte a het punt C ligt niet op de rechte a de rechte a is een deelverzameling van het vlak p
Onderzoeksopdrachten :
– Teken een punt A.
Hoeveel rechten kun je tekenen door dit punt ?
– Formuleer je besluit in een zin.
– Teken twee verschillende punten A en B.
Hoeveel rechten kun je tekenen die door A en B gaan ?
– Formuleer je besluit in een zin.
eigenschappen
Door een punt A gaan oneindig veel rechten.
Door twee verschillende punten A en B gaat juist één rechte.
collineaire punten
Collineaire punten zijn punten die op eenzelfde rechte liggen.
Voorbeeld :
A, B en D zijn collineair.
A, B en C zijn niet collineair.
2 Halfrechte en lijnstuk
Als we een schaar zetten in een rechte, dan hebben we plots twee halfrechten. Een halfrechte is langs één kant begrensd. Een lijnstuk is langs twee kanten begrensd. Bij het lijnstuk [ AB] noemen we A en B de grenspunten van het lijnstuk.
De rechte waar de halfrechte of het lijnstuk op ligt, noemen we de drager Zo is a de drager van [ AB] en ook de drager van [ AC]
Notatie : rechte a of AB
halfrechte [ AB
halfrechte [ AC
lijnstuk [ AB]
Collineair
Het woord collineair is afgeleid van het Latijnse ‘collineare’. Dat betekent ‘in rechte lijn sturen’. Het voorzetsel ‘co’ (of col/con/com/cor) duidt erop dat wat volgt gemeenschappelijk is. Denk maar aan collega, collage, collectie, compagnie … Het woord ‘lineair’ vinden we ook terug in liniaal (ligne is Frans voor lijn), wat synoniem is voor je meetlat.
3 Meten van lijnstukken
Doordat een lijnstuk begrensd is, kunnen we dat lijnstuk meten.
Meten is eigenlijk bepalen hoe dikwijls een eenheid in een gegeven grootheid gaat.
GROOTHEID
lengte
temperatuur oppervlakte l t A meter graad Celsius vierkante meter m
Meten is in het dagelijkse leven een belangrijke activiteit. Als we willen behangen, moeten we meten hoe hoog en hoe breed de muren zijn.
Als we een nieuw pak willen kopen, neemt de verkoopster de maten.
Daarvoor gebruikt ze een lintmeter.
INKIJKEXEMPLAARDIEKEURE
Als we een nieuwe eetkamer willen kopen, moeten we eerst de woonkamer goed opmeten om te weten hoe lang, hoe hoog en hoe breed de meubels mogen zijn. Hiervoor gebruiken we een plooimeter of een rolmeter.
In de meetkunde (= de kunde van het meten) gebruiken we een meetlat.
Nauwkeurig meten is belangrijk.
Ook de keuze van de meeteenheid is belangrijk.
In Europa wordt meestal gemeten in meter (m).
Van deze eenheid zijn volgende eenheden afgeleid : 1000 m100 m10
De decameter (dam) en hectometer (hm) worden in het dagelijkse leven niet veel meer gebruikt. We zullen eerder spreken van 10 m en van 100 m.
Herkomst van de meter
De ‘meter’ werd gedefinieerd ten tijde van Napoleon. Hij liet een metalen staaf aanmaken, zei dat dit vanaf nu één meter was en liet zo’n metalen staaf brengen naar alle steden van zijn rijk. Hij liet ook de meter in 10 verdelen en daarna nog eens in 10. Hij had een naam voor tien meter en tien keer tien meter. Nu nog kun je de eerste ‘meter’ gaan bezichtigen in een museum in Parijs, onder glas. Want Napoleon was één ding vergeten : metaal zet uit met de warmte, en daardoor was de meter iets langer in de zomer
In landen waar Napoleon niets te zeggen had, zoals Engeland, Amerika en Australië, werden andere lengtematen gebruikt. Daar werd en wordt gerekend in o.a. mijlen, duimen en voeten. Een mijl komt overeen met ongeveer 1,85 kilometer, een voet is ongeveer 30,47 cm lang en een duim 2,54 cm.
De lengte van dit lijnstuk [ AB] is 4 cm.
De afstand tussen A en B is 4 cm.
Notatie :
| AB | = 4 cm
Hierbij noemen we
• | AB | de lengte van het lijnstuk [ AB]
• 4 is het maatgetal
• cm is de eenheid
Om aan te duiden dat lijnstukken even lang zijn, gebruiken we eenzelfde merkteken :
| XY | = | CD |
| VW | = | AB |
In een cirkel zijn alle stralen even lang.
| MA | = | MB | = r
Opmerking :
Om lijnstukken te tekenen met eenzelfde lengte, zal de nauwkeurigheid bepaald worden door je meetinstr ument. Gebruik je een geodriehoek, dan werk je tot op 1 millimeter nauwkeurig.
– Meet de lengte van het gegeven lijnstuk.
Teken daarna een lijnstuk met eenzelfde lengte.
4 Midden van een lijnstuk
Onderzoek :
Is M het midden van het lijnstuk ? Verklaar waarom (niet).
Voorbeeld : Tegenvoorbeeld 1 : Tegenvoorbeeld 2 :
midden van een lijnstuk in woorden :
M is het midden van het lijnstuk [ AB] als en slechts als M op het lijnstuk [ AB] ligt en het lijnstuk in twee even lange stukken verdeelt.
in symbolen : M = mi [ AB] ⟺ M ∈ [ AB] en | AM | = | BM |
5 Samenvatting
• Je weet dat de meetkunde is opgebouwd uit een aantal basisbegrippen zoals vlak, punt en rechte.
Het vlak is een oneindige verzameling van punten.
Door twee verschillende punten gaat precies één rechte.
Door één punt gaan oneindig veel rechten.
INKIJKEXEMPLAARDIEKEURE
hoofdletters of één kleine letter
lengte van een lijnstuk
• Je kunt bij afstanden een geschikte eenheid kiezen.
• Je weet dat elk lijnstuk precies één midden heeft. M is het midden van het lijnstuk [AB] als en slechts als M op het lijnstuk [ AB] ligt en het lijnstuk in twee even lange stukken verdeelt.
in symbolen : M = mi [ AB] ⟺ M ∈ [ AB] en | AM | = | BM |
• Je weet wat collineaire punten zijn. Collineaire punten zijn punten die op eenzelfde rechte liggen.
• Je kunt een lijnstuk tekenen dat even lang is als een gegeven lijnstuk tot op 1 mm nauwkeurig.
6 Oefeningen
Gebruik van symbolen.
Wat stelt elk van deze notaties voor ?
Kies uit rechte, lijnstuk, halfrechte, punt, vlak, lengte van het lijnstuk.
a [ AB] e p
b [ AB f | BA |
c | AB | g AB
d a h A
INKIJKEXEMPLAARDIEKEURE
Maak met de gegeven punten (in de gevraagde kleur) een voorstelling van :
a [ AB] in blauw
b [ CD in blauw
c [ ED in groen
d AC in groen
Enkele tekenopdrachten.
a Teken een lijnstuk [ AB] van 6 cm lang. Teken daarna [ KL] zodat | KL | = | AB |
b Teken een lijnstuk [ CD] van 8,5 cm lang. Teken daarna [ MN] zodat | MN | = | CD |
Gevraagd : Wat kan je besluiten over | BC | ? 4
Onderzoek op de tekening of onderstaande gelijkheden juist zijn.
a Is [ AB] = [ BA]?
b Is [ AC = [ AB ?
c Is [ BA = [ BC ?
d Is [ CB = [ AC ?
Gegeven : De punten A, B en C zijn collineair.
| AB | = 2 cm en | AC | = 8 cm
Gevraagd : Hoe groot is | BC | ?
Geef alle oplossingen en maak telkens een duidelijke tekening.
Gegeven : De punten A, B en C zijn niet collineair.
| AB | = 2 cm en | AC | = 8 cm
8
Vul in met ∈, ∉, ⊂ of =
a Q a
b Q p a S R Q P
c a p g R [ SQ k P a
d P QP h R [ QS l RS a
e RS p i S [ RQ] m [ QS [ QR
f Q [ PR j SQ RS n PS p
Meet volgende lijnstukken tot op 1 mm nauwkeurig.
a [ AB] e [ BS]
[ BC]
Meet de lengte van onderstaande schroef en spijkers tot op 1 mm nauwkeurig. a b c
In welke eenheid zou jij de volgende afstanden of lengtes uitdrukken ? Zet een kruisje in de juiste kolom.
a De afgelegde afstand in de Tour de France.
b Je eigen lichaamslengte.
c De afstand van bij mij thuis tot in Parijs.
d De hoogte van een literfles water.
e De dikte van een muntstuk van twee euro.
f De lengte van een voetbalveld.
g De lengte van een bordlat.
h De hoogte van een deur.
i De afstand van de aarde tot de maan.
Ziehier een bovenaanzicht van een museum van de prehistorie. In elke hoek hangt er een beveiligingscamera.
Welk beeld komt van welke camera ?
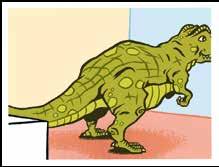
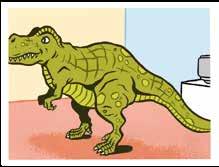
Moeder plaatst op haar keukentafel een pak melk (balkvormig), een leeg glas (cilindervormig) en een bol kaas.
Anouk kijkt gehurkt naar de ronde tafel.
a Waar moet Anouk gaan staan om niets van de kaas te zien ?
b Waar moet Anouk gaan staan om niets meer van het glas te zien ?
c Waar moet Anouk gaan staan om niets meer van de melk te zien ?
d Waar moet Anouk gaan staan om het glas mooi tussen de melk en de kaas te zien ?
Een stuntman beklimt een appartementsgebouw. Vijf personen observeren die stuntman en nemen een foto van het gebouw. Eén persoon, Bert, bevindt zich in een luchtballon die het gebouw overvliegt. Tine staat op het kruispunt dat vanuit dit standpunt niet zichtbaar is. Wie nam welke foto ?
De Zweedse kunstenaar Reutersvärd was de eerste die het tekende, maar de figuur wordt vernoemd naar de Britse wiskundige Roger Penrose die het samen met zijn vader publiceerde : de (onmogelijke) Penrose-driehoek.
a Neem een donkere markeerstift en ga over deze lijnstukken. Ze zijn steeds per vier onderling evenwijdig.
[ AB] [ JK] [ CL] [ DE] [ AF] [ EG] [ HL] [ CD] [ BC] [ AJ] [ GI] [ EF]
b Breng wat kleur aan in de drie zichtbare zijvlakken van je 3D-figuur.
Annelies
WISKUNDE & AARDRIJKSKUNDE
Een maansverduistering doet zich voor wanneer de maan in de schaduwkegel van de aarde komt. Zon, aarde en maan bevinden zich dan ongeveer op één lijn. We spreken van een volledige maansverduistering als de maan zich in de kernschaduw van de aarde bevindt. Er valt dan geen enkel zonlicht meer op de maan.
Duid op de tekening aan vanop welke plaats op aarde je die volledige maansverduistering kunt waarnemen.
zon aardemaan
zon aardemaan
Een zonsverduistering komt veel minder vaak voor, maar is wel sensationeel : het wordt op dat plekje van de aarde donker, iets kouder en de vogels worden stil omdat ze denken dat het nacht is … De eerstvolgende volledige zonsverduistering in ons land vindt plaats in 2090. Een gedeeltelijke zonsverduistering komt vaker voor. Wel opletten voor het nog zichtbare deel van de zon. Gebruik zeker een eclipsbrilletje.
zon aarde maan
Duid op de tekening aan op welke plaats op aarde je een volledige zonsverduistering waarneemt.
zon
aarde maan
Vaardigheden | Schetsen en tekenen
Schetsen
Vaak is het niet nodig om met een geodriehoek en een lat een tekening te maken. Om bepaalde eigenschappen te achterhalen, heb je soms al voldoende met een schets. Schetsen kan ook nuttig zijn om een eerste idee te vormen of een vlugge redenering op te bouwen. We spreken van een schets als we met de vrije hand een tekening maken.
Bij een schets kun je ook afmetingen, merktekens of waarden noteren. Dat kan handig zijn om bepaalde problemen op te lossen.
Tekenen
Om te tekenen, gebruik je een geodriehoek. Dat is een zeer handig latje met heel wat extra’s zoals een dubbele gradenboog, evenwijdige lijnen en een meetlat.
Ook een gradenboog en een meetlat kunnen bruikbaar zijn.
Zo gebruik je een geodriehoek om evenwijdige rechten te tekenen :
Opgave : teken door A een rechte die evenwijdig is met a
1 :
Vaardigheden | Titel van de vaardigheden
Zo gebruik je een geodriehoek om loodlijnen te tekenen :
Opgave : teken door A een loodlijn op a .
Construeren
We spreken van construeren als we constructies uitvoeren met passer en liniaal.
Bij construeren mag je de maatverdeling van je geodriehoek of liniaal niet gebruiken.
Op bladzijde 153 zie je hiervan een eerste voorbeeld.
Oefeningen
Schets volgende figuren.
a parallellogram d rechthoek g cirkel b balk e kubus h cilinder c trapezium f vierkant i rechthoekige driehoek 1
Schets volgende ruimtefiguren.
a Schets een kubus waarbij het onder vlak en
c Schets een cilinder waarbij het onder vlak het linkerzijvlak zichtbaar zijn en arceer die vlakken. zichtbaar is en arceer dat vlak.
b Schets een balk waarbij het bovenvlak en
d Schets een balk waarbij het linker zijvlak en het rechterzijvlak zichtbaar zijn en arceer die vlakken. het bovenvlak zichtbaar zijn en arceer die vlakken.
Teken in een parallellogram ABCD het lijnstuk [ AC].
Teken daarna in de punten B en D de loodlijnen op [ AC]
De wereld van 3D naar 2D 1 INKIJKEXEMPLAARDIEKEURE
dit
moet ik leren
❒ Ik herken volgende ruimtefiguren : kubus, balk, recht prisma, cilinder, kegel, piramide en bol.
❒ Ik weet wat bedoeld wordt met grond- en bovenvlak, grensvlakken en mantel.
❒ Ik herken volgende vlakke figuren : vierkant, rechthoek, driehoek, ruit, parallellogram, trapezium en cirkel.
❒ Ik kan aanzichten herkennen en tekenen.
❒ Ik kan de schaal bij een gegeven figuur aflezen.
❒ Ik kan problemen i.v.m. schaal oplossen.
❒ Ik weet dat het vlak (voorgesteld door een Griekse letter zoals p) is opgebouwd uit oneindig veel punten.
33
❒ Ik weet dat door één punt oneindig veel rechten gaan. 34
❒ Ik weet dat door twee verschillende punten juist één rechte gaat.
❒ Ik weet wat collineaire punten zijn.
❒ Ik weet hoe een rechte, punt, vlak, halfrechte en lijnstuk worden voorgesteld.
❒ Ik kan de lengte van een lijnstuk bepalen en weet hoe dit genoteerd wordt.
❒ Ik ken de definitie van het midden van een lijnstuk in woorden.
❒ Ik ken de definitie van het midden van een lijnstuk in symbolen.
❒ Ik ken het verschil tussen schetsen en tekenen.
❒ Ik kan met een geodriehoek een evenwijdige aan een gegeven rechte tekenen.
❒ Ik kan met een geodriehoek een loodlijn op een gegeven rechte tekenen.
34
34
34
36
36
36
44
44
45
De wereld van 3D naar 2D
Van welke ruimtefiguren zijn de volgende ontwikkelingen ?
Bij welke aanzichten zie je het gekleurde blokje ?
FIGUUR
FIGUUR
FIGUUR
Punt, vlak, rechte, lijnstuk, halfrechte, lengte van het lijnstuk
3 /3
Noteer onder elke symbolische voorstelling het correcte woord.
[ AB ] [ AB | BA | a p AB
INKIJKEXEMPLAARDIEKEURE
4 / 2
Vul in met = of ≠
a AB BA c [ AB [ BA
b [ AB] [ BA] d | AB | | BA |
5 / 5
Het parallellogram ABCD.
a Meet volgende lijnstukken tot op 1 mm nauwkeurig.
b Vul de tekening aan en teken DC, [ CA en [ BD.
c Teken alle punten die op 3 cm liggen van C.
6 / 3
Hieronder is een rechthoekig bloemperk getekend op schaal 1 : 100. Vul aan.
a De werkelijke omtrek van dit bloemperk is
b Hoeveel boordstenen van 0,5 m lengte heb je nodig om dit perk af te bakenen?
c De werkelijke oppervlakte van dit bloemperk is
Vul de tabel aan.
7 / 4
1 : 30 000
1 : 100 000
25 : 1 5 cm
150 : 1
cm
8 / 4
In een autogarage kun je een schaalmodel van het nieuwste model van een auto zien. Het model is gemaakt op schaal 1 : 50. In de reclamefolder vind je deze informatie. Bepaal de afmetingen van het schaalmodel van deze auto.
AFMETINGEN EN GEWICHT
Aantal deuren 5
Aantal zitplaatsen 5
Lengte (mm) 4330
Breedte (mm) 1760
Hoogte (mm) 1475
Gewicht (kg) 1310
9 / 4
a Teken drie punten A, B en C die niet collineair zijn zodat geldt :
• | AB | = 8 cm en | BC | = 4 cm.
• Het punt K is het midden van [ AB].
• Het punt L is het midden van [ BC].
b Bepaal de onderlinge ligging van AC en KL.