8 minute read
POST-QUANTUM CRYPTOGRAFIE GEBROKEN OP EEN UURTJE TIJD: BELONING VAN $50.000 VOOR WISKUNDIGE DOORBRAAK
POST-QUANTUM CRYPTOGRAFIE GEBROKEN OP EEN UURTJE TIJD:
BELONING VAN $50.000 VOOR WISKUNDIGE DOORBRAAK
THOMAS DECRU, POSTDOCTORAAL ONDERZOEKER BIJ COSIC-IMEC, KU LEUVEN SEPTEMBER 2022
Cybersecurity en databeveiliging zijn meer dan ooit een hot topic. Het is een samenspel van veel fac- toren zoals protocollen, hardware, implementaties, wetgevingen, en dit alles op een basis van wiskunde. Fundamenteel aan het uitwisselen van geheime sleutels over mogelijks onveilige kanalen is een cryptografische eenwegsfunctie. Dit is een wiskundige functie die efficiënt te evalueren valt maar heel moeilijk te inverteren is.
Het stereotype voorbeeld van een eenwegsfunctie is het factorizeren van getallen. Als je aan leerlingen vraagt om met de hand alle delers van 1.421.851 te vinden, dan zal je zelfs na een klassikale inspanning hoogst waarschijnlijk bot vangen. Als je daarentegen zou vragen om de priemgetallen 941 en 1.511 te vermenigvuldigen, dan zou iedereen die de lagere school succesvol heeft afgewerkt 1.421.851 moeten kunnen vinden als antwoord. Ook voor computers is dit een eenwegsfunctie, maar in plaats van getallen van zeven cijfers spreken we dan over getallen van honderden tot duizenden cijfers. Tot op de dag van vandaag is dit één van de meest gebruikte eenwegsfuncties in dataversleuteling in het RivestShamir-Adleman (RSA) protocol. Het populairste alternatief is gebaseerd op elliptische krommen en heet Elliptic-Curve Diffie-Hellman (ECDH). ECDH is een pak efficiënter en heeft in de voorbije tien jaar dan ook RSA voorbijgestoken in populariteit en gebruik.
QUANTUMCOMPUTERS Helaas dreigt er een einde te komen aan alle eenwegsfuncties die tegenwoordig gebruikt worden in dataversleuteling. In 1994 publiceerde Peter Shor reeds een algoritme dat met gemak RSA en ECDH kan breken. Het enige “detail” is dat Shor een quantumcomputer nodig heeft om het algoritme te implementeren. De eerste minimale quantumcomputer kwam er in 1998, maar die was veel te zwak om ook maar iets mee te doen. Tegenwoordig spenderen bedrijven zoals Google en IBM miljoenen aan research om betere quantumcomputers te maken. Hoewel er al grote stappen vooruit zijn gezet richting grootschalige quantumcomputers moeten we voorlopig nog niks vrezen voor onze dataversleuteling. Er is ook geen consensus in wetenschappelijke kringen over voorspellingen wanneer quantumcomputers wel groot genoeg zouden zijn. Sommigen spreken over 10 jaar, anderen over 30 jaar, en nog anderen denken dat er fysische beperkingen zijn die quantumcomputers nooit groot genoeg zullen kunnen laten worden.
Door deze mogelijke toekomstige aanval heeft het National Institute of Standards and Technology (NIST) in 2016 al een post-quantum standaardisatieproces in gang gezet. Het onderliggende idee is dat we op zoek gaan naar nieuwe eenwegsfuncties die ook voor quantumcomputers moeilijk te inverteren zijn. Dit lijkt misschien voorbarig, maar de beveiligingsanalyse en de implementatie van hard- en software van dergelijke protocollen duurt vele jaren. Bovendien zijn er geheimen die vandaag versleuteld moeten worden waarvan we liever hebben dat ze binnen pakweg 15 jaar nog altijd veilig versleuteld zijn.
Het NIST post-quantum standaardisatieproces heeft begin juli 2022 zijn derde ronde afgesloten. Hieruit kwam één protocol uit de bus waarin NIST het meest vertrouwen had met betrekking tot veiligheid en efficiëntie. Het schema heet CRYSTALS-Kyber en is gebaseerd op een eenwegsfunctie met betrekking tot roosters. Om niet alle eieren in één mand te leggen stelde NIST wel een vierde ronde voor waarin nog vier kandidaatprotocollen onderzocht moesten worden als alternatieve schema’s. Deze vier protocollen hadden ook alle voorgaande rondes overleefd, maar schoten net iets tekort op bepaalde aspecten ten opzichte van CRYSTALS-Kyber. Drie ervan waren gebaseerd op foutenverbeterende codes (Classical McEliece, BIKE, HQC), en één op isogenieën tussen elliptische krommen (SIKE). Ondanks het feit dat SIKE een wiskundig ingewikkelder buitenbeentje was, kreeg het toch het vertrouwen van een groot deel van de cryptografische gemeenschap. Zo waren er ook onderzoekers bij Microsoft die mee hadden gewerkt aan het protocol en werd er door hen een beloning van $50.000 beloofd aan mensen die het wisten te breken.
AANVAL OP SIKE VANUIT HOGERE DIMENSIE SIKE is gebaseerd op isogenieën tussen elliptische krommen. Een elliptische kromme is een verzameling punten ( , ) die allemaal voldoen aan een bepaalde vergelijking zoals bijvoorbeeld
waar en parameters zijn. Een isogenie : is een afbeelding tussen twee elliptische krommen die zijn oorsprong vindt in de algebraïsche meetkunde. Gegeven een bepaalde elliptische kromme is het gemakkelijk om isogenieën te bepalen en berekenen met domein . Als je daarentegen enkel twee elliptische krommen en gegeven krijgt, is het moeilijk om een isogenie er tussen te bepalen. Isogenieën worden daarom reeds sinds de jaren ’90 onderzocht als eenwegsfuncties in het teken van cryptografie.
SIKE is een isogenie-gebaseerd cryptografisch protocol en maakt gebruik van het onderliggende Supersingular Isogeny DiffieHellman (SIDH) dat in 2011 ontdekt werd. In dit kader kan men gemakkelijk en correct gebruik maken van grafentheorie om de eenwegsfunctie grafisch te verduidelijken. We kunnen een graaf definiëren waarvan de knopen elliptische krommen zijn en de bogen de isogenieën tussen deze elliptische krommen. In de context van het SIDH-protocol bekomen we dan een Ramanujangraaf. 1 Een Ramanujangraaf is een graaf met niet al te veel bogen, maar waar alle knopen wel verbonden zijn door een relatief kort pad.
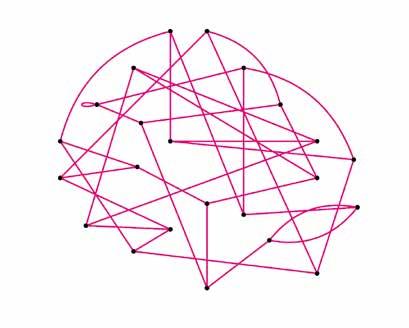
Een illustratie van een Ramanujangraaf met 23 knopen is gegeven in figuur 1. Iedere knoop heeft slechts drie uitgaande bogen, maar ieder paar knopen is wel verbonden door een pad van maximum zes bogen. Gegeven een paar knopen in deze al bij al kleine graaf is het echter niet eens altijd evident om een pad te vinden tussen de knopen.2 Ook voor klassieke en quantumcomputers is dit een moeilijk probleem, maar dan moet de graaf wel minstens 2430 knopen hebben in plaats van 23. In het SIDH-protocol wordt echter niet enkel de begin- en startknoop gebruikt, maar ook extra informatie. Deze extra informatie is nodig om het protocol correct en snel te laten verlopen, maar werd uiteindelijk wel zijn ondergang.
Twee elliptische krommen kunnen immers aan elkaar gelijmd worden via een isogenie naar een hogere dimensie. Het bekomen object van dit lijmen is dan gebaseerd op een
1 Genoemd naar de Indiase wiskundige Srinivasa Aaiyangar Ramanujan. 2 Laat staan het kortste pad.
Figuur 1 Grafische voorstelling van een Ramanujangraaf met 23 knopen: alle knopen zijn verbonden met elkaar met een relatief kort pad, maar gegeven twee knopen is het vinden van een pad niet altijd triviaal.
hyperelliptische kromme, wat een verzameling punten is gegeven door een vergelijking van de vorm
Hyperelliptische krommen zijn een natuurlijke veralgemening van elliptische krommen, net zoals kwadratische vergelijkingen een verderzetting zijn van eerstegraadsvergelijkingen.
Dit lijmen kan echter ook soms falen, waardoor we simpelweg weer overblijven met een paar elliptische krommen. Een stelling van Ernst Kani uit 1997 karakteriseert precies wanneer dit lijmen faalt. De extra informatie die in het SIDH-protocol gebruikt wordt, bepaalt echter precies zo een falen, en de stelling van Kani kan bovendien ook gebruikt worden om het volledige pad in de Ramanujangraaf bloot te leggen. Het probleem om een isogenie tussen twee elliptische krommen in het SIDH-protocol te vinden kan via Kani’s stelling dus relatief snel opgelost worden. In ongeveer een uur tijd kon iedere sleutel in het laagste beveiligingsniveau van SIKE reeds gebroken worden. De $50.000 beloning van Microsoft was gebaseerd op iets kleinere parameters dan dit beveiligingsniveau en werd gebroken op zes minuten op een tien jaar oude computer met één processor. CONCLUSIE Hoewel er nog geen officieel bericht werd meegedeeld door NIST zal SIKE ongetwijfeld ronde 4 van het post-quantum standaardisatieproces niet overleven. Het alternatieve sleuteluitwisselingsprotocol zal dus op foutenverbeterende codes gebaseerd zijn, tenzij daar ook baanbrekende ontdekkingen gedaan worden.
Merk op dat vlak voor het einde van ronde 3 nog een veelbelovend protocol gebroken werd: Ward Beullens (onderzoeker bij IBM Zürich, gedoctoreerd aan de KU Leuven) haalde begin 2022 Rainbow onderuit, een schema gebaseerd op multivariate veeltermvergelijkingen. Sceptici stellen de vraag of NIST niet te hard van stapel loopt en we niet wat meer tijd moeten geven aan de wetenschappelijke gemeenschap om de eigenschappen van deze protocollen beter te begrijpen. Anderen beweren dan weer dat het net dóór NIST is dat deze protocollen veel aandacht genieten en gebroken worden.
Over het algemeen zijn er slechts een handvol praktische eenwegsfuncties waarvan gedacht wordt dat een quantumcomputer ze niet kan inverteren. Het is een delicate balans om extra structuur toe te voegen aan deze functies om ze in de praktijk efficiënt genoeg te maken, en niet te veel structuur zodat die niet gebruikt kan worden om ze aan te vallen. Voor SIKE was het doorspelen van extra informatie cruciaal om het schema correct en snel te doen
verlopen, maar die informatie maakte het inverteren van de eenwegsfunctie gemakkelijk.
Dankzij de ERC-beurs ISOCRYPT, toegekend aan de KU Leuven, vonden Wouter Castryck en ik deze fatale fout in SIKE, gelukkig nog voor het protocol in de praktijk gebruikt werd. De algemenere eenwegsfunctie met betrekking tot het vinden van een isogenie tussen twee elliptische krommen zonder extra informatie staat echter nog altijd sterk overeind. Er bestaan andere isogeniegebaseerde protocollen die dan ook helemaal niet onderhevig zijn aan onze aanval. Ons doel is om deze protocollen verder te onderzoeken op gebied van veiligheid, efficiëntie, etc, en wie weet, misschien versleutelen we binnen pakweg tien jaar onze data deels aan de hand van isogenieën. Dan belandt de grafentheorie ongetwijfeld opnieuw in de nieuwe nieuwe nieuwe eindtermen.
OEFENING 3
Colette meet de lengtes van de zijden van een vijfhoek en schrijft ze op van klein naar groot. Welk van de onderstaande antwoorden kan ze niet opgeschreven hebben?
A 5, 5, 5, 5, 5
B 5, 6, 7, 8, 9
C 5, 7, 9, 11, 13
D 5, 10, 15, 20, 25
E 5, 25, 125, 625, 3125









