SEÇÕES CÔNICAS13

` Reconhecer as superfícies cônicas.

` Identificar as cônicas: elipse, hipérbole, parábola e circunferência.

` Obter as equações das cônicas.

13.1 INTRODUÇÃO

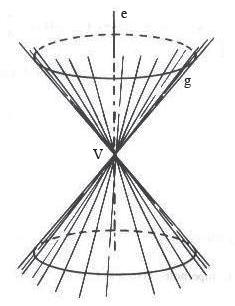
Consideremos duas retas distintas e e g, concorrentes num ponto V e não perpendiculares. Se girarmos g em torno de e, teremos uma superfície de forma cônica com duas partes, que se estendem infinitamente em ambas as direções de e a partir de V. Chamaremos a superfície formada de cone de duas folhas.

Figura 13.1

O ponto V é chamado de vértice, a reta e de eixo de simetria e a reta g de geratriz do cone. Entendemos que toda reta do cone contém o ponto V e pode ser considerada uma geratriz.

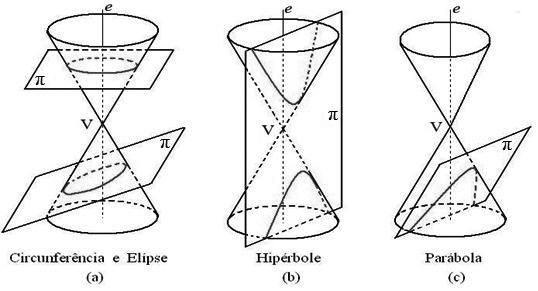
Uma secção cônica ou, simplesmente, cônica é uma curva obtida pela interseção de um plano com o cone de duas folhas.

Se o plano π que intercepta o cone não contém V, então teremos:

• Elipse, se π não for paralelo a qualquer das geratrizes e interceptar apenas uma das folhas do cone (Figura 13.2(a)). Caso π seja perpendicular a e, teremos uma circunferência.

• Hipérbole, se π for paralelo a duas geratrizes e, neste caso, interceptar as duas folhas do cone, conforme ilustra a Figura 13.2(b).

• Parábola, se π for paralelo a uma só das geratrizes (Figura 13.2(c)).

A hipérbole, tal como o cone de duas folhas, possui dois ramos e deve ser entendida como uma só curva.

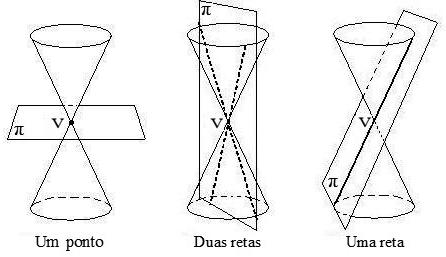
Se o plano π que intercepta o cone contém V, teremos, correspondentemente aos casos a), b) e c) da Figura 13.2, cônicas degeneradas: um ponto, duas retas concorrentes em V e uma só reta contendo V, conforme ilustra a Figura 13.3.

As secções cônicas estão presentes em estudos de astronomia, arquitetura, indústrias, balística etc.

Podemos citar, como exemplo de cônicas, as órbitas elípticas dos planetas do nosso Sistema Solar, arcos de forma parabólica em alguns portais e viadutos, o modelo hiperbólico do sistema LORAN que, utilizando pulsos sincronizados transmitidos por estações suficientemente distantes, orientam a navegação aérea, marítima, etc.

Definiremos as cônicas como sendo o lugar geométrico dos pontos de um plano satisfazendo propriedades geométricas as quais são caracterizadas por:

13.2 PARÁBOLA

Sejam dados um ponto F e uma reta d num plano, de modo que F não pertença à reta d. Chama-se parábola o conjunto dos pontos do plano que são equidistantes de d e F. O ponto F chama-se foco e d a diretriz da parábola.

Dizemos que um ponto P está na parábola se, e somente se, a distância de P a F é a mesma de P a d. Notação: d(P, F) = d(P, d).

A Figura 13.4 nos faz entender que os pontos do gráfico da parábola são simétricos em relação à reta e que é perpendicular a diretriz d contendo o foco F. A reta e é denominada de eixo de simetria da parábola e o ponto V, intersecção da parábola com e é o vértice da parábola.

É natural que, neste instante, façamos a seguinte pergunta: conhecidos a reta d e o ponto F, não pertencente a ela, como poderemos obter um ponto P da parábola?

Vamos responder a essa pergunta fazendo a seguinte construção:1

• escolher, arbitrariamente, um ponto D em d;

A matemática é considerada a ciência do raciocínio e abstrato, base de todas as ciências. É usada como ferramenta essencial em praticamente todas as áreas do conhecimento, como engenharia, medicina, física, química, biologia e sociais.

Resultados e teorias milenares se mantém válidos e úteis e, ainda assim, a matemática continua a se desenvolver permanentemente.

Apresentaremos a coleção Matemática com aplicações tecnológicas, que foi concebida e organizada por experientes professores da Faculdade de Tecnologia de São Paulo (FATEC-SP) em cinco volumes, respectivamente: Matemática Básica, Calculo I, Cálculo II, Matemática Financeira e Geometria Analítica.

Este livro, quinto volume da coleção, apresenta a Geometria analítica de forma simples e objetiva com textos, ilustrações, exemplos resolvidos e propostos com os respectivos resultados. A proposta do livro visa conduzir o aprendizado de modo prático e objetivo e, também, o desenvolvimento do raciocínio lógico.

Destina-se a alunos e professores de cursos superiores de Tecnologia, Engenharia, bacharelado em Matemática e em Física, Ciência da computação e áreas a ns.