COMBINAÇÃO E DEPENDÊNCIA LINEAR 5

` Conceituar dependência linear de vetores.

` Exemplificar conjuntos de vetores linearmente dependentes e independentes.

Vimos que o espaço vetorial (V, +, . ) dos segmentos orientados dispõe de duas operações, a interna, de adição e, a externa, de multiplicação por escalar. Pretendemos estudar as condições para que um vetor de V possa ser escrito a partir de outros vetores de V, relacionando-os, de modo conveniente, utilizando as operações definidas de adição e multiplicação por escalar.

5.1 COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES

Acreditamos que os conceitos de combinação linear (CL) e de dependência linear serão melhor entendidos se forem apresentados a partir de dois vetores e, depois, generalizados para uma quantidade qualquer finita de vetores.

5.1.1 COMBINAÇÃO LINEAR DE VETORES

Sejam u  e v  dois vetores não nulos e não paralelos de V. Considerando dois números reais 1α e 2α quaisquer, teremos os vetores 1 u α  e 2 v α  que deverão ser, respectivamente, paralelos a u  e v 

O vetor 12uvαα +  representa todas as somas obtidas com base em u  e v 

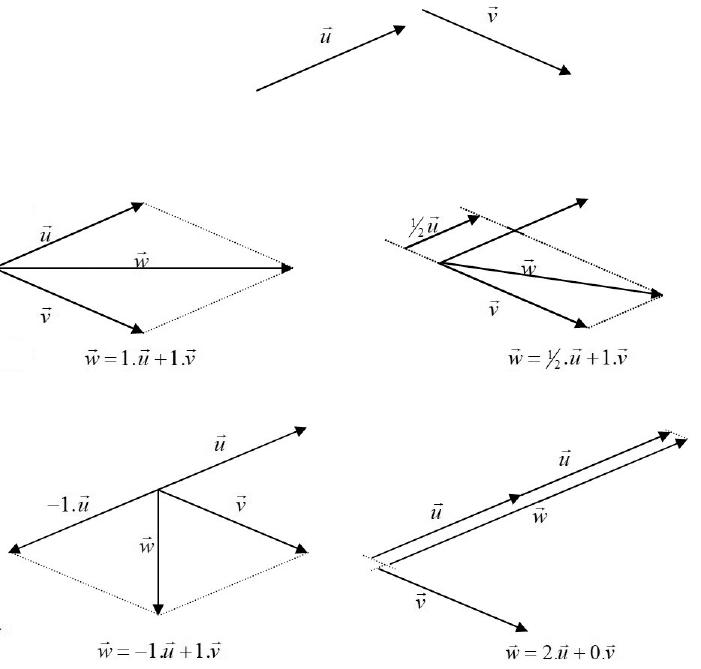
Chamamos a cada vetor 12 wuv =+αα   de uma combinação linear (CL) dos vetores u  e v 

Matemática com aplicações tecnológicas – Geometria analítica – Volume 5

Exemplo 5.1:

Dados os vetores:

Tem-se:

Portanto, a cada par de números reais 1α e 2α estará associado um vetor w  . Nessas condições, imagina-se uma infinidade de vetores  que são gerados por u  e v  .

Definição 5.1. Generalizando:

, (n ≥ 1), vetores distintos de um conjunto V e escalares (números reais) 1234 ,,,,..., nααααα , (n ≥ 1). O vetor w  tal que:

Sejam 1234 ,,,,..., nvvvvv

5.1.2 DEPENDÊNCIA LINEAR

Queremos discutir 0 w =   como combinação linear de um conjunto finito com n vetores de V, isto é, a) Seja o conjunto { u  , v  } de vetores de V, com u  e v  paralelos e não nulos. b) Seja o conjunto { u  , v  }, com u  e v  não nulos e não paralelos.

A pergunta que se faz é: a única maneira de se obter o vetor 0  é tornando todos os coeficientes da soma de vetores iguais a zero?

Afirmamos que existe a possibilidade em certos casos de obtermos o resultado 0  sem que todos os coeficientes dos vetores sejam zero. Exemplificaremos as situações utilizando dois vetores.

Se u  é paralelo a v  , então existe um número real (escalar) k ≠ 0 tal que v  = k . u  . Nesse caso, o módulo de v  é | k | vezes o módulo de u  . Vê-se que 0  = -1. v  + k. u  .

Note, no exemplo, que os coeficientes dos vetores u  e v  não são todos zeros.

A outra possibilidade de se escrever o vetor nulo é o caso óbvio 0  = 0. v  + 0. u  .

Neste caso, a única maneira de escrever o vetor nulo é com os coeficientes de u  e de v  ambos iguais a zero: 0  = 0. v + 0. u  . Vejamos:

Imaginem a possibilidade de se obter 0..rusv=+   , sendo:

1º) apenas um dos coeficientes r ou s igual a zero. Se, por exemplo, r = 0, então teríamos 0  = 0. u  + s. v  e, daí, 0  = s . v  e, assim, v  = 0  . Esse fato contradiz a hipótese de que os vetores não seriam nulos. Isso ocorreu por termos admitido que apenas um dos coeficientes fosse igual a zero.

2º) os coeficientes r e s não são iguais a zero. Assim, de 0  = r. u  + s. v  , temos que . sv  = - r u  e, daí, (/). vrsu =−  , evidenciando que u  e v  sejam paralelos, mas isso é uma contradição, pois supomos que u  não seria paralelo a . v  A contradição ocorreu porque admitimos que r e s eram diferentes de zero.

Logo, r e s são ambos iguais a zero.