PRODUTO VETORIAL8

` Definir produto vetorial e apresentar propriedades.

` Obter a direção e sentido do produto vetorial de dois vetores.

` Calcular altura e áreas de triângulos e quadriláteros.

8.1 INTRODUÇÃO

A operação produto vetorial será definida para vetores de V3 em relação à base ortonormal positiva E = ( i  , j  , k  ).

8.2 PRODUTO VETORIAL

Sejam os vetores 123 (,,)uuuu =  e 123 (,,)vvvv =  . O produto vetorial dos vetores u  e v  é o vetor

Exemplo 8.1:

Dados os vetores u  = (2,0,1) e

= (3,1,2), pede

Observação 8.1 imaginá-lo “como se fosse” a expansão do determinante

Uma forma mais fácil de obter o produto vetorial pela regra de Laplace, aplicada a sua primeira linha.

Veja a coincidência do resultado desse procedimento quando comparado com o do Exemplo 8.1 acima, no qual a definição foi aplicada:

Note que a ordem dos vetores no interior do determinante simbólico para obter uv segue a ordem da indicação do produto vetorial, primeiro depois

Observe também que a mudança de ordem dos vetores no interior do determinante implica resultados distintos:

O exemplo mostra que os vetores uv ∧ e vu são opostos. Esse fato ocorre porque a segunda e terceira linhas dos “determinantes” estão permutadas!

Veja que os módulos dos vetores são iguais:

Entendemos que a igualdade do produto vetorial com a obtida pela expansão do determinante é apenas formal!

8.2.1 PROPRIEDADES DO PRODUTO VETORIAL

A correspondência estabelecida entre o produto vetorial e a expansão do determinante por Laplace, aplicado a sua primeira linha, nos permitirá memorizar as propriedades do produto vetorial, simplesmente considerando as propriedades dos determinantes, estudadas no Capítulo 2.

V3 em relação à base ortonormal positiva

1.

O determinante troca o sinal quando se permutam duas de suas linhas (ver item 2.2.3).

2. Produto de um real por produto vetorial:

Se multiplicarmos uma linha do determinante por um número α real, o determinante fica multiplicado por α. Isto é, o produto vetorial será multiplicado por α se apenas um dos vetores que participa da operação for multiplicado por α. A

Se os elementos de uma linha do determinante são somas de n parcelas (cada elemento da terceira linha possui duas parcelas), o determinante pode ser decomposto numa soma de n determinantes (no caso, dois determinantes), sendo que cada um deles tem os elementos da linha correspondente formada com uma das parcelas das somas inicialmente indicadas, isto é, vale a propriedade distributiva do produto vetorial à esquerda (ou à direita) em relação à soma de vetores. Cuidado: lembre-se de que o produto vetorial não é comutativo!

O fato de que ()()()

` Conceituar produto misto e apresentar suas propriedades.

` Calcular altura e volume de paralelepípedos, prismas e tetraedros.

9.1 INTRODUÇÃO

A operação produto misto será definida para vetores de V3 em relação à base ortonormal positiva E = ( i  , j  , k  ).

9.2 PRODUTO MISTO

Sejam os vetores 123 (,,)uuuu =  , 123 (,,)vvvv =  e 123 (,,)wwww =  . O produto misto dos vetores u  , v  e w  é o número real

Notações: uv w ∧ rr r • ou [ ] ,, uvw

Exemplo 9.1:

(lê-se: produto misto de u  , v  e w  ).

Dados os vetores u  = (2,0,1), v  = (3,1,2) e (2,3,0) w =  , pede-se uv w ∧

Solução:

.

Matemática com aplicações tecnológicas – Geometria analítica – Volume 5

Observação 9.1 a) O produto misto, indicado por uv w ∧

) e w se

, sugere que seja obtido pelo produto escalar dos vetores ( uv b) Não é necessário utilizar parênteses para indicar o produto vetorial quando se apresenta c) A expressão ()uv w r • não representa produto misto de vetores, pois () vw não é vetor e, nesse caso, não é possível realizar o produto indicado.

, pois ele (produto vetorial) é realizado em primeiro lugar.

O produto misto é um determinante, e o seu valor se mantém inalterado quando as suas linhas são permutadas em número par de vezes.

Observe que o segundo produto misto, indicado acima, tem em sua terceira linha as coordenadas do vetor u  e o seu valor é igual ao do primeiro produto misto que tem as coordenadas de u  na primeira linha. O terceiro produto misto tem em sua primeira linha as coordenadas de w  e essas (coordenadas) aparecem na terceira linha do primeiro produto misto. Houve, nos dois casos, dupla permutação das linhas em relação ao primeiro determinante e, por isso, todos são iguais.

O determinante troca o sinal quando se permutam suas linhas em número ímpar de vezes. Assim, [ ] ,, uvw

,, vuw

. Houve permutação da primeira linha com a segunda, portanto, uma só mudança de posição. As coordenadas de u  passaram para a segunda linha do determinante.

O exposto acima nos permite entender que:

Observação 9.2

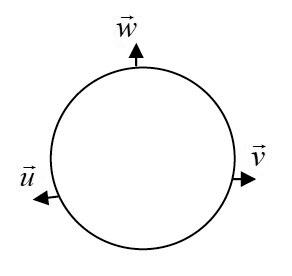
O ciclo nos ajuda a memorizar os produtos mistos de mesmo valor. Basta considerar os produtos que têm os seus vetores seguindo a ordem horária ou a anti-horária. Os produtos mistos de vetores em ordem horária têm sinais contrários aos produtos mistos dos mesmos vetores em ordem anti-horária.

Uma consequência dessa propriedade é que: () que o produto vetorial é realizado em primeiro lugar e, depois, o produto escalar que é comutativo. Temos, também, que

A propriedade é provada utilizando-se o fato:

“Um determinante fica multiplicado por α real se apenas uma de suas linhas for multiplicada por α .”