PRODUTO ESCALAR 7

` Conceituar produto escalar e apresentar propriedades.

` Obter ângulos entre vetores e projeção de um vetor na direção de outro vetor.

` Calcular altura e área de triângulos.

7.1 INTRODUÇÃO

A operação produto escalar será definida para vetores de V3 em relação à base ortonormal E = ( i  , j  , k  ).

7.2 PRODUTO ESCALAR

Sejam os vetores 123 (,,)uuuu =  e 123 (,,)vvvv =  . O produto escalar dos vetores u  e v  é o número real

Matemática com aplicações tecnológicas – Geometria analítica – Volume 5 d) Se (0,1,0) j =  e (0,1,0) j =  , então 0.0 1.1 0.0 j j rr = 1 e) Se (1,0,0) i =  e (0,1,0) j =  , então 1.0 0.1 0.0 ij rr = 0 (observe: ij ⊥  ).

7.2.1 PROPRIEDADES DO PRODUTO ESCALAR

Sejam 123 (,,)uuuu =  , 123 (,,)vvvv =  e 123 (,,)wwww =  vetores de V3 em relação à base ortonormal E = ( i  , j  , k  ) e ℝ.

1. Comutativa: uv r r = vu r r r r = = 112233 ... uvuvuv ++ = 112233 ... vuvuvu ++ = vu r r

2. Produto de um real por produto escalar ()uv r r = ()uv rr = () uv rr

Comparando (a) e (b), temos que

Observação 7.1

Vê-se

Aplicando as propriedades 7.2.1(4), e ao primeiro membro de (1), segue:

Comparando (1) e (2), teremos:

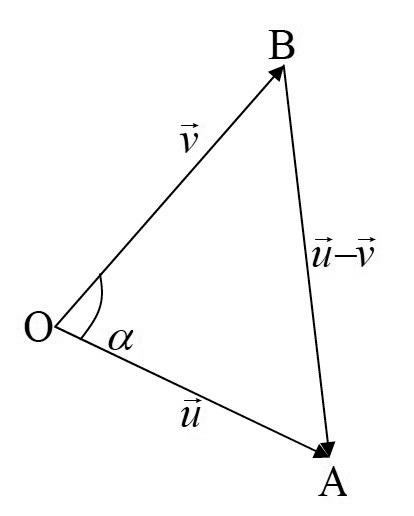
Portanto, se desejarmos obter o valor α , em radianos ou graus, do ângulo interno do triângulo OAB em O, basta interpretar o resultado da relação: