BASE E SISTEMA DE REFERÊNCIA 6

` Conceituar base e sistema de referência de um espaço vetorial.

` Conhecer bases ortogonais.

` Exemplificar mudança de base.

6.1 INTRODUÇÃO

Vamos entender as condições para que um número mínimo de vetores de um dado espaço vetorial nos permita escrever todos os vetores desse espaço como combinação linear desses vetores e, assim, constituir um sistema de referência.

6.2 BASE E SISTEMA DE REFERÊNCIA DE UM ESPAÇO VETORIAL

Consideremos um conjunto de vetores linearmente independentes de um espaço vetorial V. Diz-se que esse conjunto de vetores constitui uma base E de V se todo vetor de V for uma combinação linear dos vetores de E.

O fato de E ser uma base de V equivale a dizer que E gera V e que a dimensão de V, indicada por dimV, é igual ao número de vetores de E.

Os conceitos acima motivam o que segue.

6.2.1 ESPAÇO VETORIAL DE DIMENSÃO 1

Suponha que V1 seja o espaço vetorial sobre ℝ, cujos vetores são classes de equivalência de segmentos equipolentes considerados numa reta.

Os vetores de V1 têm a direção da reta r, portanto, são paralelos.

• Sistema de referência - V1

Se O é um ponto fixo de r e 0 v ≠   um vetor que tem a direção de r, torna-se possível imaginar uma correspondência biunívoca (de um para um) entre os vetores de V1 com origem em O e os pontos de r, pois a extremidade de cada representante dos vetores de V1 estará associado a um ponto P de r.

O conjunto { v  } formará uma base E de V1, isto é, a cada vetor w  de V1 existirá λ real tal que wv λ =  . O valor λ será a abscissa de P em r em relação à origem O.

A base E será denotada por E = ( v  ). Toda base de V1 deverá possuir exatamente um vetor não nulo com direção de r e, por isso, dizemos que V1 tem dimensão 1 (notação: dimV1= 1). Entendemos que (O, v  ), em que O é ponto fixo de r e v  não nulo formando uma base E, constitui um referencial em V1.

6.2.2 ESPAÇO VETORIAL DE DIMENSÃO 2

Suponha que V2 seja o espaço vetorial sobre ℝ, cujos vetores são classes de equivalência de segmentos equipolentes consideradas num plano.

Imaginemos os vetores de V2 representados num plano π

Vimos, no Exemplo (b) do item 5.1.2, que dois vetores não nulos e não paralelos formam um conjunto LI e, no caso 1 do Exemplo 5.2, que três vetores não nulos e coplanares formam um conjunto LD. Assim, se considerarmos os vetores u  e v  não nulos e não paralelos, então qualquer outro vetor w  de V2 é escrito como combinação linear de u  e v  . Isto é, existem 1α , 2α e 3α reais não todos iguais a zero, tais que:

Supondo 30α ≠ , tem-se

Entende-se que os vetores u  e v  formam um conjunto LI e constituem uma base E para V2, e que os demais vetores de V2 são escritos como combinação linear de u  e v  .

A base E é denotada por E = ( u  , v  ).

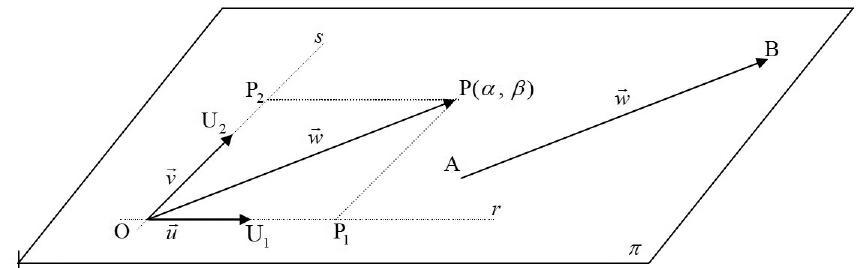
• Sistema de referência – V2

Observe a construção no plano π :