SISTEMAS DE EQUAÇÕES LINEARES 3

` Apresentar sistemas lineares ilustrados por situações-problema.

` Reconhecer e classificar sistemas lineares.

` Resolver sistemas lineares pela regra de Cramer, inversão de matrizes e método de escalonamento.

3.1 INTRODUÇÃO

Chama-se equação linear a toda sentença da forma:

112233 nnxxxx aaaab +++ += , sendo reais as incógnitas 123,,,..., xxxxn , os coeficientes das incógnitas 123,,,..., aaaan e o termo b independente de variável.

Caso 0 b = , a equação é denominada de equação linear homogênea.

Exemplo 3.1:

São equações lineares: 2527,34e530... xyzxyzxy +=+= +−=− , pois os expoentes das incógitas são iguais a 1.

Não são lineares: 43210,30eln(2)sen0... x xxxexxx −−+=−−=+=

Dizemos que um conjunto de equações lineares forma um sistema linear. Portanto, um sistema linear de m equações e de n incógnitas tem a forma:

A solução de um sistema linear é uma n-upla de reais ordenados 123 () ,,,..., sn sss que, simultaneamente, é solução de todas as equações do sistema.

Se 123,,,..., bm bbb forem todos zeros, o sistema é denominado de homogêneo Queremos resolver sistemas de n equações lineares com n incógnitas e, para isto, vamos iniciar com exemplos de sistemas lineares de 2 equações e 2 incógnitas.

Considere o seguinte problema:

Pedro e Ana Beatriz foram a uma padaria tomar o café da manhã. Pedro pediu 1 xícara de café e 2 pães de queijo e Ana pediu 2 cafés e 3 pães de queijo. Pedro pagou R$ 8,00, e Ana Beatriz, R$ 13,00 pelos produtos consumidos. Qual é o preço do café e do pão de queijo cobrados pela padaria?

Solução:

Sejam as matrizes A do consumo dos produtos e X dos preços dos produtos, sendo que x é o preço do café, y do pão de queijo e B a matriz dos gastos efetuados por Pedro e Ana Beatriz:

Consideremos a equação matricial x AX=B , isto é, o produto da matriz consumo pela matriz dos preços praticados, resultando na matriz dos gastos:

Efetuando o produto indicado e comparando os elementos da matriz obtida com os correspondentes valores da matriz B, obtemos o sistema de equações lineares:

Sistemas de equações lineares e, daí, =2 x e =3 y é a solução do sistema.

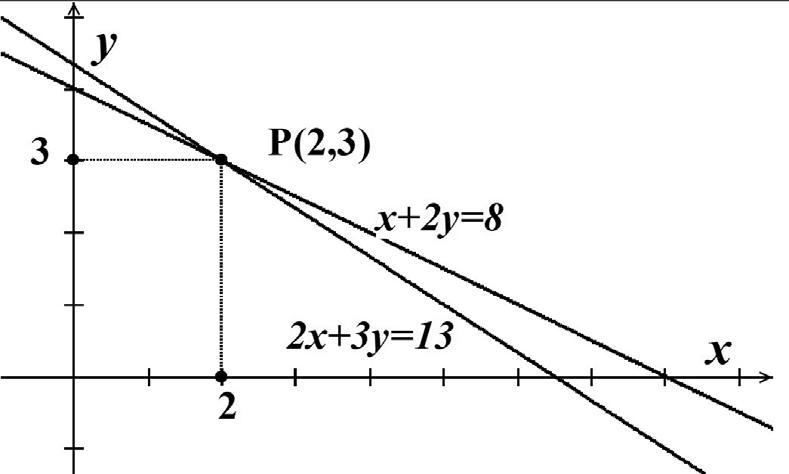
O gráfico cartesiano (Figura 3.1) apresenta as retas obtidas a partir das equações do sistema:

Vemos que as retas se interceptam num só ponto e, por isso, o sistema é denominado de possível e determinado. Se as duas retas fossem coincidentes, o sistema possuiria infinitas soluções e seria denominado de sistema possível e indeterminado. Se as retas fossem paralelas, não teriam ponto comum e, nesse caso, o sistema seria denominado de sistema impossível.

3.2 SISTEMAS DE EQUAÇÕES LINEARES

Apresentaremos procedimentos para resolver sistemas com duas equações e duas incógnitas e, também, de n equações e n incógnitas.

3.2.1 SISTEMAS LINEARES DE DUAS EQUAÇÕES E DUAS INCÓGNITAS

Considere uma equação matricial semelhante ao problema de Pedro e Ana Beatriz: