BACHILLERATO DE INVESTIGACIÓN: CONTRIBUCIÓN DEL AJEDREZ AL AUMENTO DE LA CAPACIDAD DE COMPRENSIÓN MA

2.3

AGRADECIMIENTOS

Quiero expresar mi más sincero agradecimiento a todas las personas y organizaciones que han contribuido a la realización de este trabajo de investigación.

En primer lugar, agradezco profundamente a mi tutora de proyecto, la profesora Alicia García Castro, por su invaluable orientación, paciencia y apoyo constante a lo largo de este proceso, por sus valiosas sugerencias y comentarios que han enriquecido significativamente este trabajo.

Agradezco también al profesor Vicente González-Horcajo Serrano, por promover esta iniciativa en el IES Juan Gris y guiarnos en la experiencia de realizar un proyecto de investigación.

Mi gratitud se extiende a las escuelas de ajedrez de la agrupación deportiva de ajedrez de Móstoles, al club diagonal Alcorcón y al CEIP Vicente Aleixandre de Móstoles, que con la ayuda de sus profesores y monitores me han brindado la oportunidad de poner en práctica el trabajo de investigación en las aulas.

Amifamiliayamigos,graciasporsuamor,comprensiónyapoyoincondicionaldurante todo este tiempo. Su aliento y confianza en mí han sido esenciales para superar los desafíos de este camino.

Finalmente, agradezco a todos los alumnos que, de una manera u otra, han contribuido a la realización de este trabajo.

1. OBJETIVOS Y JUSTIFICACIÓN DEL PROYECTO DE INVESTIGACIÓN

1.1 INTRODUCCIÓN

Cualquier jugador de ajedrez competitivo debe preparar un repertorio de aperturas, entrenar la táctica y conocer los finales. Estas son las tres fases principales de una partida de ajedrez. Para prepararse en estas áreas, los jugadores federados suelen utilizar programas informáticosquelesayudana evaluarlaventajaodesventajadeunaposiciónmediantecálculos matemáticos. El uso de estas herramientas basadas en cálculos para evaluar las posibilidades de cada jugador en una partida implica una relación estrecha entre las matemáticas y el ajedrez.

El uso de las matemáticas como herramienta para diseñar aperturas, resolver finales o calcular quién tiene más posibilidades de ganar en una posición determinada, es sin duda un tema interesante. Sin embargo, hay otro aspecto que llama la atención y que en este proyecto se va a analizar en profundidad: se observa en los jugadores participantes en torneos de ajedrez que la mayoría de los jugadores tienen muy buenos resultados académicos en matemáticas.

Esto invita a pensar que el ajedrez puede ser una herramienta muy efectiva para mejorar en las capacidades matemáticas y, en concreto, muy útil para mejorar la argumentación matemática ya que fomenta los siguientes aspectos:

✓ Desarrollo del pensamiento lógico: El ajedrez requiere que los jugadores piensen de manera lógica y estructurada, anticipando las posibles respuestas del oponente y planificando sus movimientos en consecuencia. Este tipo de pensamiento es esencial para la argumentación matemática, donde se deben seguir pasos lógicos para llegar a una solución.

✓ Identificación de patrones: Los jugadores de ajedrez aprenden a reconocer patrones en el tablero, lo cual es similar a identificar patrones en problemas matemáticos. Esta habilidad ayuda a los estudiantes a formular argumentos basados en la observación y el análisis de datos.

✓ Resolución de problemas complejos: El ajedrez enseña a los jugadores a descomponer problemas complejos en partes más manejables, una habilidad crucial en matemáticas. Al resolver problemas de ajedrez, los estudiantes practican la formulación de argumentos claros y coherentes para justificar sus movimientos.

✓ Fomento de la creatividad: Aunque el ajedrez tiene reglas estrictas, también permite la creatividad en la forma de resolver problemas. Esta creatividad es útil en matemáticas, donde a menudo se necesitan enfoques innovadores para resolver problemas difíciles.

✓ Mejora de la concentración y la memoria: La capacidad de concentrarse y recordar movimientos y estrategias es vital en el ajedrez y también en la argumentación matemática. Una buena memoria ayuda a los estudiantes a recordar teoremas, fórmulas y procedimientos necesarios para construir argumentos sólidos.

Como jugador de ajedrez y alumno que le gustan las matemáticas, estas conexiones han llamado mi atención y ha impulsado este trabajo.

1.2 OBJETIVOS DEL PROYECTO DE INVESTIGACIÓN

El objetivo principal de esta investigación es diseñar un conjunto de sesiones de ejercicios de ajedrez que permitan:

➢ Introducir conceptos matemáticos: Se va a utilizar el ajedrez como herramienta lúdica para introducir conceptos matemáticos fundamentales como patrones, paridad, coordenadas y simetría. A través de la resolución de ejercicios de ajedrez, los alumnos podrán familiarizarse con estos conceptos de una manera divertida y práctica.

➢ Mejorarlaargumentación yexplicación:Sevaa trabajarlacapacidaddelosalumnos para explicar de manera clara y coherente la resolución de los ejercicios de ajedrez pidiendo que redacten sus razonamientos. Esta habilidad es transferible a la argumentación de problemas matemáticos, mejorando así su capacidad para razonar y justificar sus respuestas en matemáticas. Como consecuencia del objetivo principal, se pretende conseguir dos objetivos más:

➢ Evidenciar el impacto del ajedrez en la resolución de problemas: Demostrar que el entrenamiento en ajedrez desarrolla significativamente la capacidad de resolver y argumentar problemas en comparación con aquellos que se enfrentan por primera vez a estos ejercicios. Se espera que los alumnos con entrenamiento en ajedrez muestren mejores resultados en la argumentación de problemas matemáticos.

➢ Mejorar el diseño de las sesiones: Obtener conclusiones metodológicas que ayuden a mejorar la forma de impartir futuras sesiones utilizando este material o adaptaciones de este. Esto permitirá optimizar el proceso de enseñanza y asegurar que los conceptos se transmitan de manera efectiva.

Para llevar a cabo esta investigación, se diseñarán sesiones de ejercicios de ajedrez que incorporen los conceptos matemáticos mencionados. Los alumnos participarán en estas sesiones y se evaluará su capacidad para resolver y argumentar los ejercicios.

Los alumnos que van a participar están estudiando los últimos cursos de primaria, donde la argumentación y resolución de problemas son habilidades clave dentro de la asignatura de matemáticas. Se realizarán las sesiones con alumnos de diferentes niveles ajedrecísticos para poder comparar resultados y extraer conclusiones significativas.

2. BASE TEÓRICA

2.1 INTRODUCCIÓN

Este apartado se centrará en explorar la relación entre el ajedrez y las matemáticas. En él se tratarán los siguientes temas:

➢ La relación de las matemáticas y el ajedrez: donde se explicarán las ideas geométricas que se aplican en el ajedrez, la resolución de problemas ajedrecísticos y los programas matemáticos que pueden jugar al ajedrez: los primeros, incapaces de ganar a un ajedrecista experimentado, hasta los actuales capaces de vencer al mejor ajedrecista del mundo.

➢ Los patrones y razonamientos que se utilizan en las partidas.

➢ El ajedrez como juego y recurso educativo. El ajedrez es un juego que requiere pensamiento crítico y habilidades analíticas, y se ha demostrado que su práctica regular puede tener numerosos beneficios académicos, especialmente en el desarrollo de habilidades matemáticas

Algunos de los principales beneficios del ajedrez estudiados por autores como Frank (1974), Ferguson (1995), Liptrap (1977), Dauvergne (2000), Thompson (2003), Stefurak (2003), Drenda(2003), Ferreira y Palharse (2008) citados por Farhad Kazemi, Mozafar Yektayar yAli Mohammadi Bolban Abad (2011) son los siguientes:

➢ Desarrollo del pensamiento estratégico: El ajedrez obliga a los jugadores a pensar varios pasos adelante, anticipando los movimientos del oponente y planificando sus propias estrategias. Esta habilidad es crucial no solo en el ajedrez, sino también en la resolución de problemas matemáticos complejos, donde es necesario prever las consecuencias de diferentes enfoques y elegir el más adecuado.

➢ Fomento de la concentración y la paciencia: Cada movimiento en el ajedrez requiere una concentración y un análisis cuidadoso, lo que ayuda a desarrollar la capacidad de enfoque y la paciencia. Estas habilidades son esenciales en matemáticas, donde a menudo se necesita un enfoque meticuloso y persistente para resolver problemas difíciles.

✓ Mejora de la memoria y la capacidad de observación: Los jugadores de ajedrez deben recordar los movimientos realizados y observar la posición de las piezas en el tablero, mejorando así la memoria y las habilidades de observación. En matemáticas, la capacidad de recordar fórmulas, teoremas y métodos de resolución es fundamental, al igual que la habilidad para observar patrones y detalles en los problemas.

✓ Desarrollo de la capacidad de resolución de problemas: El ajedrez presenta desafíos que requieren análisis, planificación y la búsqueda de soluciones creativas, mejorando la capacidad de resolución de problemas. Esta habilidad es directamente aplicable a las matemáticas, donde los problemas a menudo requieren un enfoque creativo y bien planificado para ser resueltos.

Además de estos beneficios generales, el ajedrez puede ayudar a entender y aplicar diferentes conceptos matemáticos específicos:

➢ Geometría: El tablero de ajedrez, una cuadrícula de 8x8, facilita la comprensión de conceptos geométricos como las coordenadas, las líneas y los ángulos. Por ejemplo, la

regla del cuadrado en los finales de peones es una aplicación directa de la geometría en el ajedrez.

➢ Álgebra: Las estrategias del ajedrez pueden representarse mediante ecuaciones y fórmulas algebraicas, lo que ayuda a desarrollar el pensamiento algebraico. Por ejemplo, la valoración de las posiciones y la planificación de las jugadas pueden ser vistas como problemas algebraicos donde se buscan soluciones óptimas.

➢ Probabilidad y estadística: El ajedrez permite analizar las probabilidades de éxito de diferentes movimientos y la estadística de las posiciones. Los jugadores pueden evaluar las probabilidades de diferentes resultados basándose en la posición actual y en las jugadas posibles, lo que es una aplicación práctica de la probabilidad y la estadística.

En resumen, el ajedrez no solo es un juego fascinante y desafiante, sino también una herramienta educativa poderosa que puede mejorar significativamente las habilidades matemáticas y cognitivas de quienes lo practican. A lo largo de esta sección, se explorarán en detalle las diversas formas en que el ajedrez y las matemáticas están interrelacionados, proporcionando una base teórica sólida para entender cómo la práctica del ajedrez puede contribuir al desarrollo académico y personal.

2.2 RELACIÓN DE LAS MATEMÁTICAS CON EL AJEDREZ

En esta sección se explorará en profundidad la relación entre las matemáticas y el ajedrez, destacando cómo los conceptos matemáticos pueden aplicarse para mejorar la comprensión y el desempeño en el juego. El ajedrez, con su estructura y reglas bien definidas, ofrece un campo fértil para la aplicación de diversas ramas de las matemáticas, desde la geometría hasta la teoría de probabilidades.

Primero, analizaremos las ideas geométricas aplicables al ajedrez, especialmente en las fases de apertura y final del juego. La geometría nos permite entender y prever el desarrollo de las partidas mediante reglas y teorías específicas, como la regla del cuadrado, la regla de Bähr, y la teoría de las casillas conjugadas. Estas reglas geométricas proporcionan una base metódica para evaluar posiciones y planificar movimientos, facilitando la toma de decisiones estratégicas.

A continuación, abordaremos la resolución matemática de problemas ajedrecísticos. Veremos cómo las matemáticas han sido fundamentales para resolver problemas clásicos del ajedrez, como el problema de las 8 damas y el problema del salto del caballo de Euler. Estos problemas no solo ilustran la aplicación de algoritmos matemáticos en el ajedrez, sino que también demuestran cómo estos algoritmos pueden ser extrapolados a situaciones más complejas dentro del juego.

Finalmente, se discutirán los programas matemáticos que pueden jugar al ajedrez Desde los primeros intentos de crear máquinas capaces de jugar al ajedrez hasta los avanzados programas actuales, se verá cómo los algoritmos matemáticos han evolucionado para superar incluso a los mejores jugadores humanos. Se explorarán los primeros programas, como el autómata de Leonardo Torres Quevedo y el programa Turochamp de Alan Turing, así como los desarrollos más recientes que han llevado a la creación de programas con una fuerza de juego superior a la de cualquier ajedrecista humano.

Este capítulo demostrará cómo las matemáticas no solo enriquecen nuestra comprensión del ajedrez, sino que también potencian nuestras habilidades para resolver problemas y tomar decisiones estratégicas, tanto en el tablero como en otros ámbitos de la vida.

2.2.1 Ideas Geométricas aplicables al ajedrez

El análisis del ajedrez en dos de sus tres fases (apertura y final) puede realizarse a partir de un estudio metódico propio de las ciencias.

En el caso de los finales, el desarrollo de la teoría relacionada se alimenta de la geometría. Al haber un número menor de piezas es posible comprender los finales a partir de estructuras geométricas, de manera que echando un vistazo a la posición de las piezas puedas valorar el resultado final. Existen varias reglas geométricas aplicables en los finales, se van a exponer cuatro por su especial relevancia

2.2.1.1 La regla del cuadrado:

Trata de decidir si un peón va a coronar (alcanzar la octava fila, primera fila del oponente, que permite poder cambiar el peón por una pieza de mayor valor, generalmente una dama), o, por lo contrario, no coronará y llegará a pararlo el rey del bando opuesto. Un peón llega a coronar si el número de filas entre el peón y la casilla de coronación es menor que el número de columnas entre el peón y el rey enemigo. El peón corona. El peón no corona.

Figura 1: Regla del cuadrado

2.2.1.2 La regla de Bähr:

Otra sencilla regla para decidir a simple vista el resultado de un final de peones muy elemental pero frecuente en las partidas prácticas, es aquella conocida como “regla de Bhär” Representa una manera muy visual de conocer de antemano el resultado de un final de reyes y peones como los de la figura 2.

Si el peón y el rey blanco logran que el rey negro no pueda mover sin estar en jaque habrán ganado la partida.

Esta regla se apoya en los conceptos geométricos de oposición y triangulación.

✓ Oposición: La oposición se produce cuando los reyes de ambos jugadores ocupan casillas de la misma línea (vertical, horizontal o diagonal) y hay una distancia impar de casillas entre ellos. En otras palabras, los reyes están "en oposición" si nopueden capturarse entre sí.

✓ Triangulación: La triangulación es una maniobra geométrica en la que un jugador mueve su rey en forma de triángulo para ocupar casillas clave en el tablero y forzar al rey contrario a ocupar una casilla determinada. La triangulación es útil para ganar la oposición y para ganar espacio en el tablero.

Estos conceptos geométricos son esenciales en el ajedrez y su dominio puede suponer la diferencia entre la victoria y la derrota en una partida.

Figura 2: Regla de Bähr

2.2.1.3 La teoría de las casillas conjugadas

Esta teoría se apoya en el concepto matemático de la oposición, generalizando la regla de Bähr. La casilla conjugada sería aquella que debe ocupar el rey defensor en la defensa de la posición una vez que el rey atacante ha ocupado una determinada casilla. Por lo tanto, a cada casilla que ocupa un rey le corresponde otra casilla o varias casillas que debe ocupar el rey oponente para defenderse Se dice que las casillas están conjugadas o emparejadas.

Laideamatemáticadetrásdelascasillasconjugadases asociaralascasillasimportantes del tablero un número, en función de su posición. El rey defensor debe evitar perder la oposición y en todo caso evitar que el oponente alcance las casillas claves.

Veamos la siguiente posición, donde mueven blancas con un peón de ventaja:

Figura 3: Teoría de las casillas conjugadas

Como vemos en la imagen de la izquierda los reyes están en situación de oposición distante. Pero ¿cuál sería el sistema de casillas conjugadas que se establece en esta situación de oposición?

Lo primero es situar las casillas claves que debe defender el bando negro. En este caso son c5, d5, y e5 porque es la fila 5 aquella que si el rey blanco consigue ocupar conseguirá invadir la posición.

En la imagen de la derecha aparece el mapa de casillas conjugadas marcadas con números de colores y X para las casillas críticas.

A cada movimiento a una determinada casilla numerada del rey blanco le debe responder el rey negro a una numerada con el mismo número.

Si el rey negro consigue estar en la casilla conjugada a la casilla en la que se encuentra el rey blanco conseguirá defenderse y estará en posición de tablas.

2.2.1.4 Regla de Romanovsky

Peter Romanovsky estableció en 1950 una regla geométrica muy sencilla para predecir el resultado: si el rey blanco se halla fuera del cuadrado que tiene como dos vértices la esquina del tablero que se encuentra en la misma columna que el peón blanco y la posición final de la torre después del primer movimiento natural para “cortar” el paso al rey blanco, entonces el resultado es tablas. Si, por el contrario, el rey blanco se encuentra en el interior de dicho cuadrado, entonces las blancas ganan la partida.

Figura 4: Regla de Romanovsky

2.2.2 Resolución matemática de problemas ajedrecísticos

Lasmatemáticashanayudadoaresolverproblemaspropiosdel ajedrezclásico (partidas de ajedrez en las que cada jugador tiene un tiempo mayor o igual a una hora para jugar toda la partida), proponiendo algoritmos que son extrapolables a cualquier número de piezas que queramos incluir. Dos problemas ajedrecísticos muy famosos pendientes de resolver si los extrapolamos a cualquier tamaño de tablero (número de casillas) son:

El problema de las 8 damas: Este problema consiste en colocar 8 damas en el tablero sin que se amenacen entre ellas.

Es decir, dos damas no pueden compartir ni filas, ni columnas ni diagonales.

Este problema fue planteado por primera vez por el ajedrecista Max Bezzel en 1848, en la revista ‘Berliner Schachzeitung’.

No es demasiado difícil encontrar una de las 92 soluciones posibles, pero es un verdadero desafío dar con todas ellas. Para ello hay que ser sistemáticos y rigurosos a la hora de buscar estrategias lo mismo que en la resolución de problemas en matemáticas.

En 2022, más de 150 años después, el matemático Michael Simkin tras 5 años de duro trabajo, ha sido capaz de calcular el número de soluciones posibles extrapolando a cualquier tamaño del tablero. Aunque aún no se ha conseguido obtener el algoritmo que permite obtener todas las soluciones para cualquier número de casillas, sí se ha conseguido ir mejorando el mismo con la creciente potencia de computación de los ordenadores. Apoyándose en algoritmos de backtracking (algoritmos que exploran una solución y retroceden al estado anterior cuando la solución no es correcta).

Figura 5: Problema de las 8 damas

El problema del salto del caballo (Euler): Este problema del caballo es un problema matemático inventado por Euler en el que se pide que, un caballo de ajedrez colocado en una posición cualquiera pase por todas las casillas y una sola vez.

Actualmente no hay consenso acerca de todas las posibles soluciones que puede haber a este problema, con la ayuda de ordenadores se han obtenido resultados de billones de soluciones. Probarlas todas requiere una gran capacidad de computación.

2.2.3 Programas matemáticos que pueden jugar al ajedrez

Hoy en día se puede considerar que los avances en el desarrollo de programas han sido más que exitosos. Vamos a ver cómo han evolucionado ya que actualmente, los mejores programas creados por algoritmos matemáticos tienen una fuerza de juego mayor que la de cualquier humano, incluido el campeón mundial Magnus Carlsen.

2.2.3.1 Primeros programas (SXIX-S.XX)

La primera máquina o el primer algoritmo creado para jugar al ajedrez fue inventado por el famoso matemático e inventor Leonardo Torres Quevedo (1852-1936-España). Este autómata era capaz de jugar posiciones muy sencillas de ajedrez y se considera de gran importancia para el avance y el perfeccionamiento de posteriores máquinas.

Claude Shannon, matemático e ingeniero (1916-2001 Estados Unidos), propone dos estrategias de búsqueda utilizadas por los programas: la primera, de tipo A, emplea el cálculo de todas las jugadas posibles a partir de una posición (algoritmo fuerza bruta) lo cual es imposible para los ordenadores de los años 50. La segunda, de tipo B, sólo calcula las jugadas que, por así decirlo, “tienen sentido o son correctas” (simulando el comportamiento humano) Para ello se utiliza una función que pueda dar un valor numérico a cada posición. Teniendo en cuenta que el valor relativo de las piezas es el siguiente:

● Peón: 1 punto

● Alfil=Caballo=3 puntos

● Torre=5 puntos

● Dama=9 puntos

Figura 6: Problema del salto del caballo

2.2.3.1.1 Programa Turochamp (1948)

El programa Turochamp fue creado por Alan Turing, un famoso matemático, científico e ingeniero considerado padre de la informática moderna.

Turochamp es un programa de ajedrez que fue desarrollado de forma teórica, ya que en ese tiempo no había una máquina de cálculo capaz de ejecutar las instrucciones de Turochamp.

Las mayores contribuciones de Alan Turing en este campo no fueron los resultados y la fuerza de juego del programa, sino las nuevas ideas de mejora del algoritmo que se proporcionaron para avances posteriores. La función de evaluación del programa consistía en cuatro factores:

- El valor numérico de las piezas.

- Lamovilidadqueteníanlaspiezas endeterminadasposiciones,estolocalculaba con la raíz cuadrada del número de jugadas posibles.

- Seguridad de las piezas, sumaba puntos o los restaba en función de la seguridad del rey.

- Posición de los peones, sumaba 0,2 si el peón estaba avanzado y 0,3 si estaba protegido.

Esto hoy en día no es nada realista, pero se considera un gran avance para la época ya que el programa de Alan Turing introdujo unas rutinas que realizaban nuevas operaciones hoy en día muy habituales y esenciales que no habían sido desarrolladas antes.

2.2.3.1.2 Programa Kotok-McCarth (1962)

A partir de la segunda mitad del siglo XX hubo gran desarrollo de programas porque los investigadores en inteligencia artificial de aquel tiempo usaban el ajedrez y los avances en su programación como forma de comprobar sus ideas.

Los avances anteriormente presentados a nivel de ideas por Alan Turing encontraron su aplicación práctica en la creación del programa Kotok-McCarthy, desarrollado a partir de 1959, cuya implementación realizaron varios alumnos de McCarthy.

Se considera que este programa, realizado en el MIT, ha sido el primer programa informático implementado de forma práctica que pudo jugar ajedrez a un nivel aceptable.

Se llegó a considerar que el programa Kotok-McCarthy tenía la fuerza de un principiante con la experiencia de 100 partidas jugadas.

2.2.3.2 Nuevas ideas para programas

Gracias al programa de ajedrez creado por McCarthy se pudieron elaborar máquinas y ordenadores más complejos y con mucha mayor fuerza ajedrecística.

Varios ejemplos son el programa Mac Hack (1969) por Richard Greenblatt (Inglaterra 1943-) o el programa Kaissa (1974) creado por Mikhail Donskoy (Unión Soviética) y Georgy Adelsonvelsky Unión Soviética) cuya base partió del programa Kotok.

Estos programas se usaron hasta finales del siglo XX.

2.2.3.3 Programas actuales (S.XXI)

Los programas empiezan a tener una fuerza de juego tan grande que ya son capaces de ganar torneos a grandes maestros y desafiar a los campeones mundiales del momento. Se considera que a partir de los años 2006-2007 los mejores programas de ordenador llegan a superar a los mejores jugadores humanos. La estimación de su capacidad de juego hoy en día supera los 3000 puntos Elo (ranking que mide la fuerza de juego en el ajedrez, actualmente el mejor jugador de ajedrez Magnus Carlsen tiene un Elo de 2800).

Esta explosión en la fuerza de los programas de ajedrez se debe a varios factores, por un lado la gran mejora de la potencia computacional de los ordenadores actuales, la implementación de técnicas para seleccionar jugadas y la mejora y creación de algoritmos. Por otro, siguen una estrategia muy parecida a la de tipo A, empleando el cálculo de todas las jugadas posibles a partir de una posición, pero con técnicas avanzadas de selectividad para mejorar el rendimiento computacional.

Algunas de las técnicas características de la nueva generación de programas son las siguientes:

➢ Uso de las tablas de transposición. Esto consiste en grandes tablas con estructuras de datos que guardan cada posición previamente investigada junto con algunas de sus características de su análisis.

➢ Heurística de la “jugada asesina” . Se refiere a una estrategia en la que un jugador busca realizar un movimiento decisivo que cambie drásticamente la situación del tablero a su favor. Este tipo de jugada suele ser inesperada y puede llevar a una ventaja significativa o incluso a la victoria inmediata. La idea es encontrar un movimiento que "mate" las posibilidades del oponente de recuperarse en la partida.

De todas las máquinas inventadas en la última década, destacan por su mayoritario uso por parte de ajedrecistas las siguientes:

➢ Fritz o Deep Fritz con su versión multiprocesador y está promocionado por Mathias Feist.

➢ Komodo que fue desarrollado en 2010 y tiene una fuerza de juego superior a 3200 de Elo, imposible de igualar por ningún ser humano.

➢ Stockfish la máquina/módulo más importante y potente de la historia. Utiliza sistemas de análisis de datos y de jugadas muy complejos y se necesitaron más de 20 personas para crearlo.

2.3 PATRONES: RAZONAMIENTO, ARGUMENTACIÓN Y ESTRATEGIAS

El estudio de patrones, razonamiento y estrategias en ajedrez es un campo fascinante que combina habilidades matemáticas y de pensamiento crítico.

Los patrones en Ajedrez son secuencias recurrentes de movimientos o posiciones que los jugadores pueden reconocer y utilizar para planificar sus estrategias. Identificar estos patrones ayuda a anticipar las jugadas del oponente y a tomar decisiones más informadas.

El ajedrez fomenta el razonamiento lógico yla argumentación, ya que los jugadores deben justificar sus movimientos y prever las consecuencias de sus decisiones. Esto se traduce en una mejora de las habilidades de resolución de problemas y pensamiento crítico.

Las estrategias incluyen tácticas como el control del centro del tablero, fundamental para dominar el juego, el centro del tablero está compuesto por las casillas e4, e5, d4 y d5. La protección del rey, un rey seguro es menos vulnerable a ataques y tácticas del oponente, y la coordinación de piezas para establecer una posición sólida y preparar ataques efectivos. Estas estrategias se desarrollan a través del estudio de partidas anteriores y la práctica constante.

2.3.1 Patrones

Diversos currículos de matemáticas en todo el mundo dan una gran importancia al trabajo con patrones. En concreto, en la Comunidad de Madrid, en el DECRETO 65/2022 de 20 de julio, en los contenidos de la asignatura de Matemáticas de 1º de la ESO viene lo siguiente:

“Técnicas de resolución de problemas: descomposición de problemas complejos en otros más pequeños, identificación de patrones repetitivos y secuenciación de operaciones.”

El trabajo con patrones implica la búsqueda de una regla general que permita obtener de manera eficaz los elementos de una sucesión. Se pueden agrupar los patrones atendiendo a la siguiente clasificación (Morales et al., 2017):

➢ Patrones visuales o espaciales: la regularidad se percibe mediante la vista, por lo que pertenecen al campo de la geometría.

➢ Patrones lineales o de repetición: se repite de forma cíclica una unidad ala que se conoce como núcleo.

➢ Patrones numéricos: son aquellos que se construyen con números, en estos es interesante conocer el valor numérico de los elementos en cada posición.

➢ Patrones lógicos: el razonamiento está basado en la igualdad y la diferencia de ciertos atributos entre los objetos.

Los patrones en ajedrez son secuencias recurrentes de movimientos o posiciones que los jugadores pueden reconocer y utilizar para planificar sus estrategias. Identificar estos patrones ayuda a anticipar las jugadas del oponente y a tomar decisiones más informadas. A lo largo de la historia del ajedrez se han identificado gran cantidad de patrones, a continuación, se enumeran algunos de los patrones más conocidos en el mundo del ajedrez según las fases del juego (apertura, medio juego, final). A continuación se exponen algunas de las más conocidas:

Patrones de Apertura:

➢ Apertura Española (Ruy López): Una de las aperturas más antiguas y populares, que comienza con 3 movimientos:

1.e4 e5

Las blancas mueven su peón a la casilla e4 y las negras responden moviendo su peón a e5. Este es uno de los movimientos más comunes para controlar el centro del tablero.

2.Nf3 Nc6

Las blancas desarrollan su caballo a la casilla f3, atacando el peón negro en e5. Las negras responden desarrollando su caballo a c6, defendiendo el peón en e5 y controlando el centro.

3.Bb5

Las blancas mueven su alfil a la casilla b5, atacando el caballo negro en c6. Este movimiento pone presión sobre las negras y puede llevar a una ventaja en el desarrollo de las piezas.

El objetivo de esta apertura es la siguiente:

Controlar el centro: Al mover el peón a e4 y el caballo a f3, las blancas buscan controlar las casillas centrales del tablero.

Desarrollar piezas: El movimiento del alfil a b5 presiona al caballo negro en c6, lo que puede llevar a una ventaja en el desarrollo de las piezas.

Preparar el enroque: Al desarrollar rápidamente las piezas, las blancas pueden enrocarse pronto, asegurando la seguridad del rey.

➢ Defensa Siciliana: Comienza con.e4 c5.

Las blancas mueven su peón a e4, controlando el centro del tablero. Las negras responden moviendo su peón a c5, atacando el centro desde un ángulo lateral. La idea principal de la defensa Siciliana es la siguiente:

Desbalancear el juego: En lugar de seguir el camino más tradicional y simétrico (como 1... e5), las negras buscan crear un juego asimétrico y dinámico.

Controlar el centro: Aunque no ocupan el centro directamente con peones, las negras ejercen presión sobre las casillas centrales y preparan el desarrollo de sus piezas.

Oportunidades de contraataque: La estructura de peones en la Siciliana a menudo permite a las negras lanzar contraataques efectivos y buscar oportunidades tácticas.

Patrones de Medio Juego:

➢ Ataque de Minorías: Una estrategia donde un jugador ataca con menos peones en un flanco para crear debilidades en la estructura de peones del oponente, como que tenga peones doblados (dos peones en la misma casilla) o aislados (sin poder ser defendidos por otros peones)

➢ Sacrificio de Calidad: Entregar una torre por una pieza menor (caballo o alfil) para obtener una ventaja posicional o táctica. Por ejemplo, dominar el centro o crear debilidades, como en el anterior patrón creando peones doblados o aislados.

Patrones de Finales:

➢ Final de Peones: Conocer patrones como el cuadrado del peón y la oposición es crucial para convertir una ventaja mínima en una victoria.

➢ Final de Torres: Patrones como la posición de Lucena y la posición de Philidor son esenciales para dominar los finales de torres (torre peón contra torre)

En el caso de la posición de Lucena la técnica clave es mover la torre a una posición que permita al rey avanzar y proteger al peón. Esto se logra moviendo la torre a la cuarta fila (o quinta, dependiendo del lado) para crear un escudo contra los jaques. El objetivo del jugador con el peón es promoverlo a dama. Para lograrlo, debe crear un "puente" con su torre para proteger al rey de los jaques continuos de la torre contraria.

En el caso de la posición de Philidor, si el peón atacante avanza, la torre defensora se mueve a la primera fila (o la octava si eres negras) para dar jaques al rey contrario desde atrás, evitando que el peón pueda avanzar sin ser capturado. El objetivo del defensor es mantener la torre en la tercera fila para evitar que el rey atacante avance y apoye el peón.

2.3.2 Razonamiento y argumentación

El ajedrez es un juego que va más allá de mover piezas en un tablero, es una batalla de mentes donde el razonamiento lógico y la argumentación juegan un papel crucial. Los jugadores deben analizar constantemente la posición, prever las posibles respuestas del oponente y justificar cada movimiento que realizan. Este proceso de toma de decisiones no solo mejora las habilidades cognitivas, sino que también fomenta un pensamiento crítico y estructurado. En este apartado, se explorará cómo el razonamiento deductivo e inductivo, junto con la capacidad de argumentar y justificar movimientos, son esenciales para desarrollar estrategias efectivas y alcanzar el éxito en el ajedrez.

El razonamiento deductivo es un proceso lógico en el que se llega a una conclusión específica a partir de premisas generales. Es una forma de razonamiento en la que, si las premisas son verdaderas, la conclusión también debe ser verdadera. En ajedrez hay razonamientos de este tipo:

➢ Análisis de Variantes: Evaluar diferentes secuencias de movimientos posibles y sus consecuencias.Por ejemplo, calcularunaserie dejugadas forzadas que llevanaunmate o a una ganancia de material.

➢ Reconocimiento de Tácticas: Identificar tácticas como horquillas, clavadas y descubiertas. Estas tácticas se basan en patrones recurrentes que los jugadores aprenden a reconocer y explotar.

El razonamiento inductivo es un proceso lógico en el que se hacen generalizaciones a partir de observaciones específicas. En otras palabras, se observa un patrón en casos particulares y se infiere una regla general, en el caso del ajedrez existen ejemplos de este tipo de razonamiento en los siguientes casos:

➢ Aprendizaje de Partidas Anteriores: Estudiar partidas de grandes maestros para identificar patrones y estrategias que se pueden aplicar en futuras partidas.

➢ Desarrollo de Planes: Basado en la estructura de peones y la posición de las piezas, los jugadores desarrollan planes alargoplazo.Por ejemplo, decidirsi atacar enel flanco de rey o de dama.

La argumentación es el proceso de presentar razones o pruebas para apoyar o refutar una afirmación o punto de vista, en ajedrez este tipo de razonamiento se presenta en las siguientes actividades:

➢ Justificación de Movimientos: Cada movimiento debe tener una justificación lógica, por ejemplo, mover una pieza para controlar una casilla clave o para preparar una combinación táctica.

➢ Evaluación de Posiciones: Argumentar por qué una posición es favorable o desfavorable. Esto incluye evaluar factores como la seguridad del rey, la actividad de las piezas y la estructura de peones.

2.3.3 Estrategias

Para terminar, el ajedrez es un juego de estrategia por excelencia, donde cada movimiento debe ser cuidadosamente planificado y ejecutado. Las estrategias en ajedrez no solo se centran en el control del tablero y la coordinación de las piezas, sino también en la anticipación de las jugadas del oponente y la adaptación a las cambiantes dinámicas del juego. Desde las aperturas hasta los finales, las estrategias abarcan una amplia gama de tácticas y planes que buscan maximizar las fortalezas propias y explotar las debilidades del adversario. En este apartado, se explorarán las principales estrategias que los jugadores utilizan para dominar el juego, incluyendo el control del centro, el desarrollo de piezas, la seguridad del rey y las técnicas de ataque y defensa.

El control del centro proporciona varias ventajas estratégicas:

✓ Mayor movilidad: Las piezas ubicadas en el centro tienen más opciones de movimiento y pueden influir en más áreas del tablero.

✓ Desarrollo de piezas: Colocar peones en el centro (por ejemplo, e4 y d4 para las blancas) abre líneas para el desarrollo de otras piezas, como caballos y alfiles

✓ Control de espacio: Tener el centro bajo control limita las opciones del oponente y facilita la ejecución de planes tácticos y estratégicos.

Tenemos varios conceptos ajedrecísticos que implementan esta estrategia como son:

➢ Aperturas Clásicas: Movimientos como 1.e4 y 1.d4 buscan controlar el centro del tablero desde el principio. El control del centro permite una mayor movilidad de las piezas y facilita el desarrollo.

➢ Defensas Hipermodernas: Estrategias como la Defensa India de Rey, donde se permite al oponente ocupar el centro con peones para luego atacarlo con piezas.

La estrategia de desarrollo de piezas en ajedrez es fundamental. Acciones ajedrecísticas para implementar esta estrategia son:

➢ Desarrollo Rápido: Sacar las piezas menores (caballos y alfiles) rápidamente para controlar el centro y preparar el enroque.

➢ Coordinación de Piezas: Asegurarse de que las piezas trabajen juntas. Por ejemplo, colocar las torres en columnas abiertas o semiabiertas para maximizar su efectividad.

Algunas estrategias clave para proteger al rey son:

➢ Enroque: Enrocar temprano para proteger al rey y conectar las torres.

➢ Creación de Refugios: En el medio juego, crear refugios para el rey moviendo peones para evitar amenazas de mate.

Las técnicas de ataque y defensa en ajedrez son esenciales para desequilibrar la partida a tu favor y protegerte de las amenazas del oponente. Técnicas de ataque y defensa en ajedrez son:

Técnicas de ataque:

➢ Doble ataque: Consiste en atacar dos piezas o casillas al mismo tiempo con una sola jugada. Esto puede forzar al oponente a perder material

➢ Clavada: Una pieza está clavada cuando no puede moverse sin exponer una pieza más valiosa detrás de ella. Las clavadas pueden ser absolutas (cuando la pieza detrás es el rey) o relativas (cuando la pieza detrás es otra pieza valiosa)

➢ Sacrificio: Entregar material (como un peón o una pieza) para obtener una ventaja posicional o táctica, como abrir líneas de ataque o debilitar la posición del rey enemigo.

➢ Ataque descubierto: Mover una pieza para revelar un ataque de otra pieza que estaba oculta. Si el movimiento de la pieza que se mueve también crea una amenaza, se llama doble ataque descubierto.

➢ Ataque a la descubierta: Similar al ataque descubierto, pero la pieza que se mueve también da jaque al rey.

Técnicas de defensa:

➢ Defensaactiva:Contrarrestarlasamenazasdeloponenteconmovimientos quetambién crean amenazas propias. Esto puede desviar la atención del oponente y darle menos tiempo para atacar.

➢ Interposición: Colocar una pieza entre una pieza atacante y su objetivo para bloquear el ataque

➢ Simplificación: Cambiar piezas para reducir la presión del ataque del oponente. Esto es especialmente útil cuando se está bajo ataque y se busca aliviar la tensión

➢ Fortaleza: Crear una posición defensiva que sea difícil de penetrar para el oponente. Esto puede incluir una estructura de peones sólida y piezas bien coordinadas.

➢ Contraataque: Responder a un ataque con un ataque propio, obligando al oponente a defenderse en lugar de continuar su ofensiva

Los finales en ajedrez son una fase decisiva del juego donde quedan pocas piezas en el tablero y se decide el resultado de la partida.

➢ Activación del Rey: En los finales, el rey se convierte en una pieza activa. Llevar el rey al centro del tablero es una estrategia común.

➢ Creación de Peones Pasados: Avanzar peones para crear peones pasados que puedan convertirse en damas.

Todas estas estrategias se ponen en juego a lo largo de una partida, el jugador debe tenerlas en cuenta a la hora de su toma de decisiones. A continuación, se muestra un ejemplo de estrategia en una partida de ajedrez.

➢ Cuando le toca jugar A MI RIVAL: Debo analizar y valorar la posición en el tablero y calcular variantes y posibles jugadas según las debilidades del rival.

➢ Cuando me toca jugar A MÍ: Elijo jugadas posibles o candidatas y valoro y comparo las posibles posiciones que pueden surgir.

o Cuando me toca a mí mover me debo hacer 3 preguntas.

o ¿Qué jugada ha realizado mi rival y qué amenaza?

o ¿Qué jaques y capturas amenaza?

o ¿Qué jugadas puedo hacer yo?

Existe un decálogo de evaluación de una posición, que es el siguiente:

➢ Seguridad de los reyes: Los reyes deben estar enrocados y seguros para que no se les pueda dar mate.

➢ Material: Si un bando tiene más material que otro, es decir, tenga más piezas o más peones.

➢ Desarrollo: Las piezas deben estar ocupando muchas casillas y en el centro, si están en sus casillas iniciales no están desarrolladas.

➢ Centro: Los peones y las piezas deben estar en el centro para controlar muchas casillas.

➢ Espacio: Cuantas más piezas desarrolladas y fuera de sus casillas iniciales tenga un bando, más espacio tendrán en el tablero.

➢ Actividad y armonía de piezas: Las piezas deben entenderse entre sí, por ejemplo, que una dama y un alfil apunten al rey para dar mate.

➢ Estructura de peones: Los peones deben estar juntos para que se puedan proteger.

➢ Dominio de columnas o filas abiertas: Si hay columnas o filas abiertas significa que no hay ninguna pieza con lo cual debes colocar una torre ahí.

➢ Dominio de diagonales: Coloca tus alfiles en diagonales largas para que actúen de manera activa.

➢ Puestos avanzados: Delante de un peón puedes colocar una pieza y así estará bien protegida.

A la hora de jugar, es importante también tener en cuenta las debilidades en una posición, lo que perjudica ….

➢ Rey expuesto: Un rey sin enrocar y sin defensa.

➢ Contactos múltiples: Varias piezas amenazan a una.

➢ Pieza colgada: Una pieza que está siendo atacada y no está siendo defendida.

➢ Piezas mal alineadas: Piezas que van cada una por su lado y no van todas en la misma dirección.

➢ Coronaciones: Se amenaza la coronación cuando tienes un peón en séptima fila y lo puedes convertir o coronar en dama.

2.4 AJEDREZ COMO JUEGO Y RECURSO EDUCATIVO

El juego tiene un gran valor como recurso didáctico, hace más fácil la enseñanza de las matemáticas ya que a través del juego se pueden desarrollar conceptos como razonamiento espacial, abstracción matemática y resolución de problemas de acuerdo con Ernest (1986) y Bragg (2012). Además, el uso de juegos en las clases, ayuda a desarrollar en los alumnos una determinada actitud hacia las matemáticas haciendo del aprendizaje de estas un proceso activo y lúdico.

En esta simbiosis que se da entre las matemáticas y el juego, hay veces que se vuelve complejo discernir cuál de los dos aporta el beneficio y cuál lo aprovecha. De entre todos los juegos podemos resaltar el ajedrez, ya que contribuye a la mejora del rendimiento escolar, la concentración, la memoria y la creatividad (Gliga y Flesner, 2014). El carácter competitivo y divertido del ajedrez motiva a los estudiantes a participar activamente, lo que puede aumentar su interés y compromiso con las matemáticas. A través del juego, los estudiantes aprenden de manera activa y práctica, lo que facilita la comprensión y retención de conceptos matemáticos.

La relación entre un juego y un problema matemático radica en que ambos comparten un proceso heurístico similar, las acciones o decisiones a realizar tienen gran coincidencia. En la figura 7 se muestra la relación entre las fases de resolución de un problema y la de un juego (Edo, 2002).

Figura 7: Fases de resolución en juegos y problemas

Además, también es útil para desarrollar habilidades de cálculo numérico y razonamiento lógico, así como conceptos matemáticos primarios los cuales ya hemos numerado anteriormente

3. ESTADO DEL ARTE

Enestasecciónsellevaráacabounarevisiónexhaustivadeestudiosprácticosyteóricos respecto al ajedrez como herramienta educativa para ayudar a mejorar el rendimiento académico en general y la capacidad matemática en particular, incluyendo la mejora en la argumentación de problemas matemáticos.

En el estudio de Berkman RM (2004), La conexión entre ajedrez y matemáticas: más queunsimplejuego. seconcluyeque el ajedrez promuevehabilidades depensamiento deorden superior y que el análisis de las posiciones del ajedrez tiene mucho en común con la resolución de problemas en matemáticas.

Otro estudio de Gobet F., & Campitelli G. (2006). Educational benefits of chess instruction: A critical review concluye, por lo contrario, que todavía es una cuestión abierta si la enseñanza del ajedrez mejora el aprendizaje en otras áreas además del ajedrez.

Por último, Bart WM (2014). Sobre los efectos del entrenamiento en ajedrez sobre el rendimiento escolar. resume un conjunto de estudios más recientes en el que se concluye que existe una relación entre la enseñanza del ajedrez y el rendimiento en matemáticas y la capacidad cognitiva no verbal, la inteligencia y la capacidad de resolución de problemas. Sin embargo, la muestra utilizada no es suficientemente representativa.

Por otro lado, dentro de los estudios realizados sobre esta relación, hay dos de ellos que por las conclusiones obtenidas merece la pena detallar, pues, además las conclusiones de ambos, han motivado el objetivo principal de este trabajo de investigación.

El primero es Rosholm M, Mikkelsen MB, Gumede K (2017) Tu jugada: El efecto del ajedrez en las puntuaciones de los exámenes de matemáticas

Los investigadores analizaron el efecto de sustituir una lección semanal de matemáticas por una lección de matemáticas basándose en el ajedrez como herramienta de ayuda en una clase de Primaria en un colegio de la ciudad de Aarhus en Dinamarca.

La conclusión de este estudio basado en el resultado de pruebas matemáticas realizadas a alumnos que había y no habían usado el ajedrez en el colegio evidenció que el conocimiento adquirido a través del ajedrez se podía transferir al juego de las matemáticas.

Pero analizando el efecto a nivel de subgrupo reveló un hecho aún más sorprendente, el efecto positivo se limitaba al grupo de niños que estaban aburridos e infelices. Este hecho sugiere que el ajedrez puede causar un efecto indirecto en el incremento de las capacidades matemáticas a través del aburrimiento reducido y el aumento de la felicidad.

El otro estudio es Trinchero R., & Sala G. (2016). Entrenamiento de ajedrez y resolución de problemas matemáticos: el papel de la enseñanza de la heurística en la transferencia del aprendizaje

Llevaronacabo un estudiocon931alumnos detercer,cuartoyquinto cursodeprimaria de 20 escuelas diferentes. Los estudiantes fueron asignados aleatoriamente a un entrenamiento de ajedrez realizado por instructores de ajedrez, a un entrenamiento de ajedrez realizado por profesores de escuela o a un grupo de control. Los instructores de ajedrez recibieron

instruccionesespecíficas sobrecómo enseñarheurísticas deresolución deproblemas deajedrez a los niños, mientras que los maestros de escuela no.

Las pruebas de capacidad de resolución de problemas matemáticos antes y después de la intervención de 6 meses indicaron que las instrucciones de ajedrez sólo mejoran la capacidad de resolución de problemas si transmiten heurísticas de resolución de problemas a los alumnos. Es decir, esto implica que no basta con mostrarle aalguien las reglas del juego: para que mejore en la resolución de problemas, también debe aprender sobre las estrategias y tácticas involucradas en el juego. Los autores sugieren que los instructores de ajedrez pueden haber facilitado habilidades más amplias para la resolución de problemas y un pensamiento flexible durante las instrucciones, mientras que los maestros de escuela pueden haberse centrado más en transmitir reglas básicas.

Estos estudios muestran una variedad de enfoques y resultados, pero en general, sugieren que el ajedrez puede tener un impacto positivo en el rendimiento académico, especialmente en matemáticas, cuando se enseña de manera efectiva.

El ajedrez puede ayudar a desarrollar habilidades analíticas y de razonamiento lógico que son útiles en matemáticas, puede mejorar la inteligencia y la capacidad de resolución de problemas, aunque las muestras utilizadas no siempre son representativas, lo que limita la generalización de los resultados.

En definitiva, el ajedrez puede mejorar el rendimiento académico, especialmente en matemáticas, los resultados varían según cómo se enseñe el ajedrez y las características de las muestras estudiadas.

Como conclusión a estos estudios se puede decir que el ajedrez puede tener un efecto indirecto en el rendimiento matemático al reducir el aburrimiento y aumentar el estado de ánimo, lo que podría mejorar la disposición de los estudiantes para aprender.

4. DISEÑO SESIONES AJEDREZ

Una vez introducido el marco teórico, se va a proceder a describir cómo se han creado las sesiones, qué ejercicios que se han incluido y objetivos que se persiguen con cada una de ellas.

Cada uno de los ejercicios tiene como objetivo introducir conceptos matemáticos simples en las que los alumnos tienen que elegir las estrategias adecuadas para conseguir resolverlos, argumentando convenientemente la solución adoptada.

Losejerciciosseleccionadosnoincluyenlas64casillasdeltableroysólo el movimiento de alguna de sus piezas (principalmente la torre y el alfil) son los utilizados para explicar los contenidos matemáticos

Los contenidos han sido cuidadosamente seleccionados teniendo en cuenta que se van a aplicar a alumnos de diferentes niveles. Algunos saben jugar al ajedrez y otros casi no conocen los movimientos de las piezas.

Cada sesión está diseñada del siguiente modo:

✓ El profesor resolverá los ejercicios de la anterior sesión dando las directrices necesarias que deben utilizarse para una buena argumentación.

✓ Cada alumno resolverá las actividades planificadas en la sesión del siguiente modo:

✓ Planteará la solución de la actividad.

✓ Argumentará la solución indicada, explicando las estrategias o razonamientos que ha seguido basados en los conocimientos que posee del ajedrez (los conocimientos previos básicos que debe tener el alumno es conocer el movimiento de las piezas que forman parte del ajedrez)

✓ Anotará el tiempo invertido en cada problema.

Las actividades queconformancadaunadelassesionesimpartidas estándiseñadas para cubrir uno o más de los siguientes objetivos:

➢ Conocer el juego del ajedrez y el tablero que lo compone.

➢ Conocer el movimiento de alguna de sus piezas

➢ Identificar figuras planas

➢ Introducción de conceptos geométricos (diagonales, verticales, horizontales…)

➢ Compresión de enunciados

➢ Practicar estrategias (experimentación, exploración, organización, codificación)

➢ Procesos de razonamiento siguiendo un orden de ejecución, revisión de operaciones, comprobación de resultados coherentes.

➢ Darherramientas,comolaintroduccióndeusodecoordenadasdelascasillasdeltablero para ayudar a argumentar los problemas que propone resolver cada una de las actividades.

➢ Diseñar problemas a partir de unas condiciones determinadas

Los ejercicios se han clasificado en cinco tipos:

En el primero, los alumnos ya tienen todas las piezas de ajedrez dibujadas en el tablero, tienen que responder razonando si dichas piezas se comen o no.

En el segundo, los alumnos tienen en el mini tablero algunas piezas ya colocadas y el enunciado exige colocar más piezas de ajedrez que cumplan unas determinadas condiciones como pueden ser: que se coman dichas piezas, que no se coman dichas piezas…Los alumnos deben dar una argumentación.

En el tercero, los alumnos tienen los mini tableros sin piezas colocadas y tienen que dibujar las piezas que se indiquen siguiendo las instrucciones del enunciado. Las respuestas terminan dependiendo del jugador y deben de dar una argumentación.

En el cuarto, los alumnos tienen que crear un enunciado, resolverlo y argumentar.

En último grupo, los alumnos tienen que identificar los patrones propuestos, explicar la estrategia de búsqueda seguida y explicarla.

Se va a proceder a describir cada uno de los ejercicios que forman parte del proyecto, con los objetivos que se persigue, así como la solución al problema planteado en cada uno de ellos. Para aquellos que requiera de una argumentación, se comenta en detalle una correcta explicación para que el monitor pueda comparar la respuesta dada por el alumno y pueda valorar si la argumentación es completa o no.

En las argumentaciones es muy importante explicar cuáles son los datos en los que se basa para dar la respuesta, por ejemplo, describir cuál es el movimiento de cada una de las piezas incluidas en el ejercicio, o describir mediante notación ajedrecística un movimiento podrá explicar con mayor precisión cuál es el razonamiento que se ha seguido para resolver el problema.

EJERCICIO1

Coloca un alfil para que las piezas no se puedan comer entre ellas. Dibújalo. Explica brevemente tu solución

8: Tablero gráfico Ejercicio 1

Objetivos matemáticos

Concepto geométrico de diagonal, horizontalidad y verticalidad Argumentación en resolución de problemas.

Solución c2 (casilla central).

Argumentación correcta No se pueden comer si el alfil se coloca en c2 porque el alfil se desplaza en diagonal y las torres en horizontal y vertical.

EJERCICIO2

¿Se comen unas piezas a otras? Si no, por qué. Nota: No tener en cuenta los colores

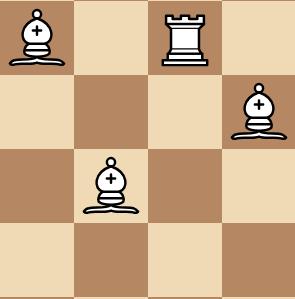
Figura 9: Tablero gráfico ejercicio 2

Objetivos matemáticos

Concepto geométrico de diagonal, horizontalidad y verticalidad Argumentación en resolución de problemas.

Solución El alfil come a la torre o bien que la torre come al alfil.

Argumentación correcta Enumerar los alfiles e indicar que el alfil X como se mueve en diagonal se come a la torre y la torre como se mueve en horizontal y vertical se come al alfil Y.

Figura

EJERCICIO3

Coloca 1 torre y 3 alfiles de manera que no se puedan comer entre ellos. Explica por qué no se comen.

Objetivos matemáticos

Solución

Concepto geométrico de diagonal, horizontalidad y verticalidad. Creación de problemas que cumplan unas condiciones según el enunciado.

Argumentación en resolución de problemas

Cualquier solución que cumpla con que no se puedan comer

Argumentación correcta No se pueden comer en esa posición porque la torre se mueve en horizontal y vertical y el alfil en diagonal, por lo tanto, de esa manera nunca se van a encontrar.

Figura 10: Tablero gráfico ejercicio 3

EJERCICIO4

Coloca dos alfiles sin que las piezas se coman. Explica por qué deben colocarse ahí.

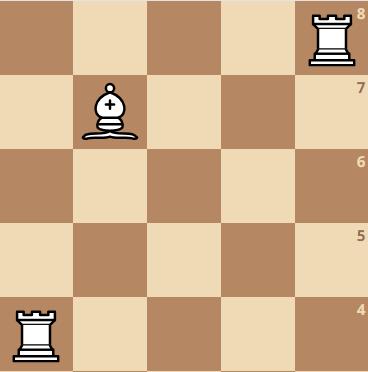
Figura 11: Tablero gráfico ejercicio 4

Objetivos matemáticos Concepto geométrico de diagonal, horizontalidad y verticalidad. Argumentación en resolución de problemas

Solución

Cualquier solución que cumpla con que no se puedan comer

Argumentación correcta Las piezas no se comen debido a que las torres se mueven en horizontal y vertical por el tablero y los alfiles en diagonal, de esta manera dichas piezas nunca se encontrarán.

EJERCICIO5

Este rey quiere alejarse todo lo posible. Ayúdale a escapar. Si realiza un movimiento tiene 8 casillas para elegir.

Figura 12.1: Tablero gráfico ejercicio 5

Si realiza 2 movimientos tiene 16 casillas para elegir

Figura 13: Tablero gráfico ejercicio 5

Si realiza 3 movimientos, ¿cuántas casillas tiene para elegir?

Figura 14: Tablero gráfico ejercicio 5

Objetivos matemáticos Reconocimiento de patrones. Argumentación en resolución de problemas Revisión de Estrategias

Solución 24 casillas.

Argumentación correcta Se puede utilizar razonamiento de conteo con ayuda visual o aplicar patrones, sabiendo que para un movimiento fueron 8, para dos movimientos 16, para 3 movimientos 24, para 4 movimientos 32…

EJERCICIO6

Coloca a un alfil para que pueda comer a las dos torres y no sea comido por ellos. Explica por qué lo has colocado ahí.

Objetivos matemáticos

Solución

Conceptos geométricos: Horizontalidad, Verticalidad yDiagonal. Argumentación en resolución de problemas

Alfil en b4

Argumentación correcta Como el alfil mueve en Diagonal y las torres en horizontal y vertical, el alfil puede comerse a ambas torres, mientras que las torres no pueden comer al alfil.

EJERCICIO7

Coloca un caballo para que coma a la torre del centro y no sea comido. Busca todas las soluciones posibles.

Objetivos matemáticos

Conceptos geométricos: Horizontalidad, Verticalidad y Movimiento en L

Argumentación en resolución de problemas.

Solución Es correcto si se es capaz de colocar los 4 caballos en las posiciones en las que pueden comer la torre del centro

Argumentación correcta Como el caballosemueveen Lenlasposicionesindicadas comen a la torre del centro.

Figura 15: Tablero gráfico ejercicio 6

Figura 16: Tablero gráfico ejercicio 7

EJERCICIO8

Meter dos caballos sin que las piezas se coman. Explica por qué.

17: Tablero gráfico ejercicio 8

Objetivos matemáticos

Conceptos geométricos: Horizontalidad, Verticalidad, Diagonales y Movimiento en L Argumentación en resolución de problemas.

Solución Es correcto si se es capaz de colocar los 2 caballos sin que las piezas se coman.

Argumentación correcta Se considera correcta la argumentación si es capaz de dar una explicación de por qué las piezas no se comen debido a los movimientos de ellas. Por ejemplo, las piezas no se comen porque como el alfil se mueve en diagonal, los caballos en L y la torre en horizontal o vertical, no podrán comerse”.

EJERCICIO9

Este alfil se ha desplazado de la casilla marcada con una equis (x) a la casilla d5. Siempre se mueve de la misma manera. Encuentra la siguiente casilla a la que llegará.

18: Tablero gráfico ejercicio 9

Objetivos matemáticos

Concepto geométrico de diagonal. Reconocimiento de patrones. Argumentación en resolución de problemas

Solución Es correcto si se coloca el alfil en g4.

Argumentación correcta Se considera correcta la argumentación si el alumno es capaz de indicar la posición correcta explicando que el alfil realiza dos movimientos a6-c4-d5 y repites el mismo patrón d5-f3-g4.

Figura

Figura

EJERCICIO10

En este tablero se muestran algunas casillas a las que puede acudir el caballo realizando un movimiento (círculos) o dos movimientos (cuadrados). Completa las casillas que faltan.

19: Tablero gráfico ejercicio 10

Encuentralascasillasalasquepuedeirconsutercermovimiento.Márcalasconuntriángulo. Dibuja los ejes de simetría que encuentres en el tablero. El caballo todavía no ha ido a algunas casillas. ¿Cuántos movimientos tiene que hacer para ir a ellas? Explica cómo lo has averiguado.

Objetivos matemáticos

Concepto geométrico de movimiento del caballo.

Patrones visuales

Ejes de simetría.

Argumentación en resolución de problemas Estrategias aplicadas para la resolución

Solución Son 4 movimientos, se puede sacar por diferentes tipos de razonamiento. Por conteo, por movimiento anterior, por prueba y error.

Argumentación correcta Los ejes de simetría son aquellas líneas que dividen al tablero en dos partes exactamente iguales

Figura 20: Tablero gráfico ejercicio 10

Para llegar a las esquinas es necesario realizar 4 movimientos. Se averigua a partir de si desde las casillas marcadas con triángulo puedo llegar a las esquinas.

Figura

EJERCICIO11

Aquí puedes ver el número de casillas a las que amenazan estas piezas desde distintas posiciones. Completa los tableros:

Figura 21: Tablero gráfico ejercicio 11

Compara los tableros que acabas de rellenar ¿Qué relación observas entre ellos? ¿Por qué crees que pasa esto?

Objetivos matemáticos Concepto geométrico de diagonal, verticalidad, horizontalidad Reconocimiento de patrones Argumentación en resolución de problemas.

Solución

Figura 22: Solución ejercicio 11

Argumentación correcta El alumno explica que la relación que une los tableros es que el movimiento de la dama es el resultado de la suma de los movimientos de la torre y el alfil

EJERCICIO12

Estando la torre en a1, la torre debe visitar todas las casillas y volver a a1. Dibújalo en el menor número de movimientos.

Figura 19: Tablero gráfico ejercicio 12

Objetivos matemáticos Concepto geométrico de verticalidad, horizontalidad.

Solución

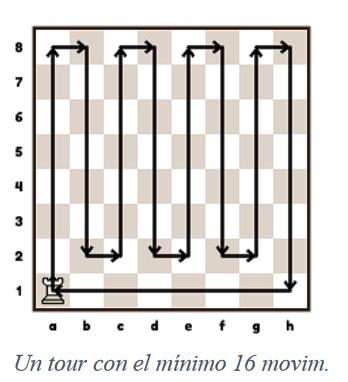
Figura 23: Solución ejercicio 12

Argumentación correcta Aquí tienes algunas razones por las que este camino es óptimo: Cobertura Completa: La torre visita cada fila y columna del tablero una vez.

Movimientos Lineales: La torre se mueve en líneas rectas, lo que minimiza el número de cambios de dirección. Regreso a la Casilla Inicial: El recorrido está diseñado para que la torre regrese a la casilla a1 después de cubrir todas las demás casillas.

EJERCICIO13

Coloca un caballo, un alfil y una torre de manera que: la torre sea capturada por el caballo, el alfil sea capturado por la torre y el alfil capture al caballo.

Figura 24: Tablero gráfico ejercicio 13

Objetivos matemáticos

Concepto geométrico de diagonal, verticalidad, horizontalidad Argumentación y resolución de problemas. Creación de problemas a partir de unas condiciones iniciales.

Solución La solución es correcta si son capaces de colocar las piezas cumpliendo las especificaciones.

Argumentación correcta

El alumno es capaz de explicar por qué ha colocado así las piezas atendiendo a los movimientos de las mismas y a las indicaciones del enunciado. Respuesta del tipo “como el alfil mueve en diagonal, las torres en horizontal y vertical y el caballo en L, evitamos que se coman entre sí”.

EJERCICIO14

Coloca dos caballos, dos alfiles y una torre de manera que no se coman entre ellos.

Figura 25: Tablero gráfico ejercicio 14

Objetivos matemáticos

Concepto geométrico de diagonal, verticalidad, horizontalidad. Argumentación y resolución de problemas. Creación de problemas a partir de unas condiciones iniciales.

Solución La solución es correcta si son capaces de colocar las piezas cumpliendo las especificaciones.

Argumentación correcta El alumno es capaz de explicar por qué ha colocado así las piezas atendiendo a los movimientos de las mismas y a las indicaciones del enunciado. Respuesta del tipo “como el alfil mueve en diagonal, las torres en horizontal y vertical y el caballo en L, evitamos que se coman entre sí”.

EJERCICIO15

Coloca una torre, un alfil y dos caballos, de manera que no se coman las piezas entre ellas. Justifica la respuesta.

Figura 26: Tablero gráfico ejercicio 15

Objetivos matemáticos

Concepto geométrico de diagonal, verticalidad, horizontalidad Argumentación y resolución de problemas. Creación de problemas a partir de unas condiciones iniciales.

Solución La solución es correcta si son capaces de colocar las piezas cumpliendo las especificaciones.

Argumentación correcta El alumno es capaz de explicar por qué ha colocado así las piezas atendiendo a los movimientos de las mismas y a las indicaciones del enunciado. Respuesta del tipo “como el alfil mueve en diagonal, las torres en horizontal y vertical y el caballo en L, evitamos que se coman entre sí”.

EJERCICIO16

¿Se comerán los caballos? Dibuja su movimiento y explica por qué sí o porqué no.

Figura 27: Tablero gráfico ejercicio 16

Objetivos matemáticos

Concepto geométrico de movimiento del caballo. Argumentación y resolución de problemas

Solución La solución es correcta si contestan que los caballos no se comerán.

Argumentación correcta El alumno es capaz de explicar por qué ha colocado así las piezas atendiendo a los movimientos de estas y a las indicaciones del enunciado.

Respuesta del tipo “como los caballos mueven en L, no hay ningún movimiento pueda comer al otro caballo”.

EJERCICIO17

¿Se comen entre ellas las siguientes piezas? Si, no porque… Coloca otro caballo más que sea comido por el alfil y que coma a la torre y justifica cómo has encontrado esa casilla.

Objetivos matemáticos

Concepto geométrico de diagonal, verticalidad, horizontalidad y movimiento del caballo. Argumentación y resolución de problemas.

Solución La solución es correcta si contestan que las piezas sí se comerán y de colocar y dibujar otro caballo cumpliendo las características que indica el ejercicio.

Argumentación correcta Consideramos correcto la argumentación del ejercicio si dan una respuesta del tipo: “Sí, el caballo come al alfil porque su movimiento es en L. El caballo mueve en L y se come a la torre y el alfil mueve en diagonal y se come al caballo”.

EJERCICIO18

Posiciona 4 torres negras de manera que entre ellas amenacen a todas las casillas blancas. Justifica respuesta

Objetivos matemáticos

Concepto geométrico de horizontalidad y verticalidad. Argumentación y resolución de problemas.

Solución a1-c3-e5-g7.

Argumentación correcta Es correcta si argumentan que han colocado las torres ahí porque su movimiento es horizontal y vertical, y debían cubrir las filas y columnas que no estaban cubiertas por las torres que originalmente estaban ubicadas en el tablero.

Figura 28: Tablero gráfico ejercicio 17

Figura 29: Tablero gráfico ejercicio 18

EJERCICIO19

Crea un ejercicio con al menos un caballo, un alfil y una torre. Inventa y escribe el enunciado y resuélvelo justificando.

Figura 30: Tablero gráfico ejercicio 19

Objetivos matemáticos

Concepto geométrico de horizontalidad, verticalidad, diagonal y movimiento del caballo.

Argumentación y resolución de problemas. Creación de problemas a partir de condiciones iniciales indicadas en el enunciado

Solución Es correcto si plantean bien el ejercicio.

Argumentación correcta Es correcta si argumentan basándose en los movimientos de cada una de las piezas, que se ha conseguido el objetivo planteado.

EJERCICIO20

Crea tu propio enunciado con dos alfiles, una torre y un caballo. Justifica las respuestas.

Figura 31: Tablero gráfico ejercicio 20

Objetivos matemáticos

Concepto geométrico de horizontalidad, verticalidad, diagonal y movimiento del caballo.

Argumentación y resolución de problemas Creación de problemas a partir de condiciones iniciales indicadas en el enunciado.

Solución Es correcto si plantean bien el ejercicio

Argumentación correcta Es correcta si argumentan basándose en los movimientos de cada una de las piezas, que se ha conseguido el objetivo planteado.

5. EXPERIMENTACIÓN

La experimentación ha constado de dos fases. La primera ha sido el pilotaje, etapa en la que se selecciona a un alumno que realice las actividades para comprobar lo siguiente:

➢ Si los ejercicios diseñados eran comprensibles

➢ Si el nivel de dificultad era adecuado

➢ Si las respuestas eran las esperadas o podían dar lugar a diferentes interpretaciones, en ese caso, habría que completar el enunciado para evitar varias soluciones.

➢ El tiempo medio que lleva la resolución de cada ejercicio

El criterio seguido para elegir al candidato adecuado fue que tuviera un nivel ajedrecístico medio y una edad que permitiera sacar conclusiones de sus argumentaciones.

Se han usado los datos del pilotaje para crear las sesiones y los ejercicios a incluir en cada sesión de la segunda fase: el trabajo en el aula. Esta fase se impartió en grupos de alumnos de ajedrez y de colegios, compuestos por alumnos de niveles de ajedrez heterogéneos

5.1 Pilotaje

La fase de pilotaje fue celebrada durante el mes de febrero de 2024 con una alumna de 5º de primaria, hermana de un monitor de ajedrez con conocimiento medio del juego. Conoce los movimientos de las piezas, pero no es jugadora asidua ni asiste a clases particulares de este deporte.

Durante el pilotaje se ha medido el tiempo que se necesita para realizar cada ejercicio. Esto ha permitido valorar la dificultad de cada uno de ellos, pudiendo así configurar sesiones que incluya ejercicios de una dificultad homogénea, para que las sesiones duren un tiempo similar y puedan encajar más fácilmente como parte de las clases que se imparten en un curso general de ajedrez. Es decir, hay que tener en cuenta que la idea de estas sesiones es que sea una parte más de una clase de enseñanza de ajedrez que aporte dinamismo y así el profesor pueda distribuir esta experimentación dentro de su plan de clase, asumiendo una duración media de las sesiones.

La experiencia conseguida ha contribuido a mejorar aspectos importantes en la explicación de las respuestas y ejercicios para conseguir que, con cada sesión, el alumno comprenda el ejercicio y en las respuestas mejore en sus capacidades de argumentación aplicablesposteriormente duranteeltrabajoenel aula.Además,verificóqueelpúblicoobjetivo al que deben estar orientado los ejercicios era el adecuado. Por último, ha ayudado a encontrar los parámetros que se van a medir para la comparativa de resultados entre aulas de diferentes niveles, tiempo, resoluciones acertadas y argumentaciones correctas, y a la comprobación de la eficacia de las sesiones a medida que se iban desarrollando.

A continuación, se muestras las respuestas del alumno y comentarios de cada una de las respuestas que sirvieron para aplicar en el trabajo del aula.

EJERCICIO1

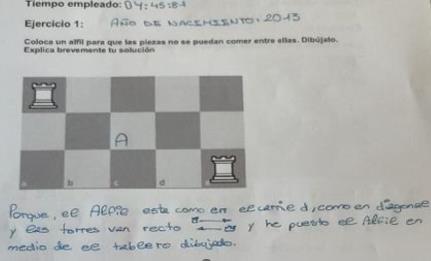
32: Pilotaje Ejercicio 1

Comentarios La solución es correcta y el tiempo invertido en realizarlo está dentro de lo que se esperaba por lo que el ejercicio es válido para el trabajo en el aula. Sin embargo, se observa que en la argumentación se tiene que ayudar de dibujos y deun vocabulario no apropiado que le genera dificultad para explicar la respuesta dada. Se detecta la necesidad de explicar la notación ajedrecística que ayude a argumentar su respuesta fácilmente.

Figura

Comentarios

EJERCICIO2

33: Pilotaje Ejercicio 2

La solución es correcta sin embargo la argumentación no. Es importante explicar cuál es el movimiento de cada pieza para que el lector comprenda por qué una pieza puede comer a otra. No podemos dar por supuesto que una torre comerá un alfil, sin antes explicar que una torre puede mover en horizontal o vertical. Se explica a la alumna cómo debe hacerlo en siguientes ejercicios. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

Figura

EJERCICIO3

Comentarios La solución es correcta. La argumentación ha mejorado, puesto que ha explicado que los alfiles se mueven en diagonal, sin embargo en su respuesta ha olvidado explicar el movimiento de la torre dando por sentado que en ciertas casillas la torre puede atacar el alfil. Se explica a la alumna cómo debe hacerlo en siguientes ejercicios. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

Figura 34: Pilotaje Ejercicio 3

Comentarios

EJERCICIO4

35: Pilotaje Ejercicio 4

La solución es correcta. Para llegar a la solución se empleó estrategia de prueba y error. Se ha ayudado de dibujos (flechas indicando movimiento de cada pieza). En la argumentación escrita se ha mejorado, aunque sigue sin utilizar un vocabulario que le permita explicar con exactitud su respuesta. Utiliza para describir el movimiento de la torre “recto” cuando es más exacto indicar movimiento horizontal o vertical. También se advierte la necesidad de explicarme como es la notación de ajedrez para que sea más fácil explicar su respuesta. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

Figura

Comentarios

EJERCICIO5

Figura 36: Pilotaje Ejercicio 5

La solución es correcta. Para explicarlo se ha ayudado de un dibujo donde a través de conteo ha podido llegar a la solución. Otras maneras de llegar a esta solución serían aplicando distintos patrones que eviten tener que realizar el dibujo para obtener el número de casillas correcto. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

Comentarios

EJERCICIO

La solución es correcta. En la argumentación sigue olvidando explicar el movimiento de la torre y el alfil, se insiste en la necesidad de explicar esas premisas para que el lector entienda la argumentación dada. Comienza a introducir la notación de coordenadas para describir la posición de las piezas en el tablero, que facilitará la explicación y la comprensión del lector. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

Figura 37: Pilotaje Ejercicio 6

Comentarios

EJERCICIO

Figura 38: Pilotaje Ejercicio 7

La solución es correcta se ha ayudado de dibujos y flechas para explicar los movimientos. La argumentación escrita ha mejorado mucho ya que explica inicialmente los movimientos que pueden hacer las piezas y después añade notación ajedrecística para explicar la ubicación correcta del caballo. Se nota que ha interiorizado las indicaciones dadas en los ejercicios anteriores. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

EJERCICIO8

Figura 39: Pilotaje Ejercicio 8

Comentarios La solución es correcta se ha ayudado de dibujos y flechas para explicar los movimientos. La argumentación escrita ha mejorado mucho ya que explica inicialmente los movimientos que pueden hacer las piezas y después añade notación ajedrecística para explicar la ubicación correcta del caballo. Se nota que ha interiorizado las indicaciones dadas en los ejercicios anteriores. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

Comentarios

Figura 40: Pilotaje Ejercicio 9

La solución es correcta se ha ayudado de dibujos y flechas para explicar el patrón seguido. La argumentación escrita explica inicialmente los movimientos que pueden hacer las piezas y después añade notación ajedrecística para explicar la ubicación final del alfil, sin embargo, para explicar el patrón le ha faltado seguir usando la notación ajedrecística. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

Comentarios

EJERCICIO

Figura 41: Pilotaje Ejercicio 10

La solución no es del todo correcta. Los ejes de simetría están incompletos. Sin embargo, la solución a las casillas cubiertas en el tercer movimiento del caballo y la solución a las casillas de la esquina se resolvió completamente y de una manera especialmente elegante la última pregunta al ayudarse del dibujo de una estrella para explicar el número de movimientos. Respecto a la argumentación escrita se echa de menos el explicar inicialmente que el caballo mueve en L y que partiendo de las ubicaciones del tercer movimiento se cubren las esquinas. El ejercicio por el tiempo empleado y haberse podido resolver casi completamente se considera apto para el trabajo en el aula.

Comentarios

La solución es correcta. La argumentación escrita ha mejorado mucho ya que explica inicialmente los movimientos que pueden hacer las piezas para después explicar la solución. Se nota que ha interiorizado las indicaciones dadas en los ejercicios anteriores. Respecto a la identificación de patrones se ha dado cuenta de que el movimiento de la dama es la suma de los movimientos del alfil y la torre por lo que el tablero de la dama es la suma de los de la torre y el alfil. El ejercicio por el tiempo empleado y haberse podido resolver se considera apto para el trabajo en el aula.

Figura 42: Pilotaje Ejercicio 11

EJERCICIO12

43: Pilotaje Ejercicio 12

Comentarios

La solución es correcta se ha ayudado de dibujos y flechas para explicar los movimientos. La argumentación escrita ha utilizado notación ajedrecística de coordenadas para ayudar a explicar la solución, aunque olvidó comentar el movimiento de una torre. Tampoco se ha dado explicación de por qué piensa que esta es la combinación con el menor número de movimientos. Aunque la argumentaciónnoes completasehadecididoincluiresteejercicio en el trabajo en el aula, al trabajar patrones y ser un ejercicio bastante visual y divertido.

Figura

Comentarios

EJERCICIO

La solución es correcta se ha ayudado de dibujos y flechas para explicar los movimientos. La argumentación escrita ha vuelto a olvidar que se deben explicar inicialmente los movimientos de las piezas, y no ha empleado notación ajedrecística para explicar la solución. Aunquelaargumentación noes completasehadecidido incluir este ejercicio en el trabajo en el aula porque el tiempo empleado no fue demasiado y la solución es correcta.

Figura 44: Pilotaje Ejercicio 13

EJERCICIO

Comentarios La solución es correcta se ha ayudado de dibujos y flechas para explicar los movimientos. La argumentación escrita ha vuelto a olvidar que se deben explicar inicialmente los movimientos de las piezas, y no ha empleado notación ajedrecística para explicar la solución. Aunquelaargumentación noes completasehadecidido incluir este ejercicio en el trabajo en el aula porque el tiempo empleado no fue demasiado y la solución es correcta.

Figura 45: Pilotaje Ejercicio 14

46: Pilotaje Ejercicio 15

Comentarios La solución es correcta se ha ayudado de dibujos y flechas para explicar los movimientos. Al hacer hincapié en los ejercicios anteriores de la necesidad de explicar inicialmente los movimientos de cada pieza, de ayudarse en la notación ajedrecística para una correcta argumentación, la solución al ejercicio se ha argumentado correctamente. Por el tiempo empleado y la solución dada el ejercicio se considera adecuado para el trabajo en el aula.

Figura

EJERCICIO16

47: Pilotaje Ejercicio 16

Comentarios La solución es correcta, la argumentación es correcta explicando inicialmente como es el movimiento del caballo, aunque se echa de menos haber usado notación ajedrecística para explicar en detalle el argumento de la solución. Por otro lado, el uso de dibujos permite seguir estrategias de ensayo y error para dar con la solución. Por el tiempo empleado y la solución correcta. El ejercicio es apto para el trabajo en el aula.

Figura

Comentarios

EJERCICIO

Figura 48: Pilotaje Ejercicio 17

La solución es correcta, la argumentación es correcta explicando inicialmente como es el movimiento de cada una de las piezas, aunque se echa de menos haber usado notación ajedrecística para explicar en detalle el argumento de la solución. Por otro lado, el uso de dibujos permite seguir estrategias de ensayo y error para dar con la solución. Por el tiempo empleado y la solución correcta. El ejercicio es apto para el trabajo en el aula.

EJERCICIO

Comentarios

La solución es correcta, sin embargo, la argumentación es incompleta, se olvida de usar notación ajedrecística y de explicar los movimientos de la torre para un mejor entendimiento de la solución por parte de un lector. Por el tiempo empleado y la solución correcta, el ejercicio es apto para el trabajo en el aula.

Figura 49: Pilotaje Ejercicio 18

EJERCICIO

Figura 50: Pilotaje Ejercicio 19

Comentarios

La solución es correcta, y la argumentación es completa, usa notación ajedrecística y explica los movimientos de cada pieza para un mejor entendimiento de la solución por parte de un lector. En la resolución del ejercicio se ayuda de dibujos que le permiten seguir una estrategia de ensayo y error para conseguir la solución. Por el tiempo empleado y la solución correcta, el ejercicio es apto para el trabajo en el aula.

EJERCICIO20

Figura 51: Pilotaje Ejercicio 20

Comentarios La solución es correcta, y la argumentación es completa, usa notación ajedrecística y explica los movimientos de cada pieza para un mejor entendimiento de la solución por parte de un lector. En la resolución del ejercicio se ayuda de dibujos que le permiten seguir una estrategia de ensayo y error para conseguir la solución. Por el tiempo empleado y la solución correcta, el ejercicio es apto para el trabajo en el aula.

Las conclusiones obtenidas tras el pilotaje para aplicar en el trabajo en el aula fueron las siguientes:

➢ La argumentación que se busca en las respuestas requiere madurez en el alumno que lo va a realizar, por lo que el rango de edades ideal para poderlo hacer es de 10 a 12 años. Si bien, según la madurez del participante podría oscilar en un año más o menos.

➢ Con estos ejercicios se busca que el alumno mejore en la capacidad de entendimiento del problema y en la capacidad de argumentación de la respuesta, Se observa que es importante insistir en la respuesta correcta en cada ejercicio que finalizan para que, en elsiguiente,utilicenlaspautasdadasparallegarmásrápido alarespuestaylaexpliquen pensando en que el lector entienda qué razonamiento le ha llevado a dar la respuesta. De esta manera se decide incorporar como actividad en cada sesión, corregir los ejercicios de la sesión anterior para que los alumnos interioricen cuales son las claves que debían seguir para poder argumentar las respuestas de la mejor manera en los siguientes ejercicios.

➢ Identificar puntos que requerían una explicación más completa del enunciado. En los ejercicios 13 y 14 no se indicó en el enunciado explícitamente que se justificase la respuesta. Para el trabajo en el aula se ha indicado al monitor en qué puntos debía prestar mayor atención en sus explicaciones.

✓ Explicar al alumno que puede ayudarse de coordenadas o de dibujos para facilitar sus argumentaciones

✓ Recordar al alumno justificar siempre su respuesta explicando su estrategia basándose en sus conocimientos previos que deben explicarse explícitamente.

➢ Cada sesión se compondrá de dos actividades, una que pertenezca a la mitad de los ejercicios para los que se haya empleado más tiempo y otra que se encontrará en la mitad de los ejercicios para los que se haya empleado menos tiempo. Las sesiones tendrán así una dificultad similar y su tiempo empleado en resolverlo será homogéneo, de modo que después pueda encajar fácilmente en un plan de clases que conformen un curso de ajedrez.

➢ Las sesiones incluirán generalmente ejercicios de diferentes tipos para que el alumno encuentre variedad en los ejercicios planteados de modo que la realización de estos sea para el alumno lo más entretenida posible. La dificultad con el paso de las sesiones no se incrementará, el objetivo final es lograr que sus capacidades de argumentación aumenten a través de la práctica.

➢ El tiempo medio que cada sesión requerirá, será de 20-25 minutos, esto incluye corrección de ejercicios de la anterior sesión, explicación de los nuevos y ejecución de estos últimos

5.2 Trabajo en el aula

El trabajo en el aula se realizó durante los meses de abril y junio de 2024. Los ejercicios seleccionados, junto con la solución correcta y un modelo de referencia en la argumentación serepartieronalos distintos monitores, así comolasindicacionesoportunas delasconclusiones del pilotaje.

5.2.1

Descripción de la experimentación

Se seleccionaron cuatro grupos diferentes de alumnos para realizar el trabajo, cada uno de ellos tienen características diferentes en cuanto a nivel ajedrecístico del alumnado y de formación de los monitores. El experimento se llevó a cabo en situaciones similares, es decir, como información previa, los monitores contaban únicamente con la experiencia del pilotaje junto con las respuestas y argumentaciones propuestas en los ejercicios diseñados.

Las características de los grupos fueron los siguientes:

El grupo de la Escuela Ajedrez Nivel Inicial estaba formado por 9 alumnos de 5º y 6º de primaria fundamentalmente, con un nivel de ajedrez inicial con 1-2 años de clases. No estaban iniciados en competición y el instructor posee el título de monitor de la Federación Madrileña de ajedrez. Las clases impartidas semanalmente con 1 hora de duración.

El grupo de la Escuela de Ajedrez Nivel Medio estaba formado por 10 alumnos de 4º 5º y 6º de primaria, con un nivel de ajedrez medio con 2-3 años de clases como bagaje Estaban iniciados en competición y el instructor posee el título de monitor de la Federación Madrileña de ajedrez. Las clases son impartidas semanalmente con 1 hora de duración.

El grupo de la Escuela Ajedrez Nivel Alto estaba formado por 2 alumnos de 5º y 6º de primaria, con un nivel de ajedrez alto con 4 o más años de cursos realizados Estaban acostumbrados a competir en competiciones oficiales habitualmente. Las clases a las que asisten están enfocadas a competición impartidas por un monitor de la Federación Madrileña de ajedrez.

El grupo del Colegio Primaria Nivel Inicial estaba formado por 18 alumnos de 5º y 6º de primaria, con un nivel de ajedrez inicial sin clases previas. La realización de estos ejercicios fue dirigida por una profesora de primaria con nociones de ajedrez.

Los ejercicios fueron divididos en diez sesiones, de una duración de entre 20-25 minutos, en las que se incluían dos ejercicios siguiendo el orden indicado en el diseño final de las sesiones que se muestra en el anexo 1 de este documento. En el caso de las escuelas, estos ejercicios se realizaron al final de cada clase, dejando el tiempo necesario tomando como referencia el tiempo tomado de cada ejercicio en el pilotaje. En el caso del grupo de primaria, los ejercicios se realizaron fundamentalmente, coincidiendo con los recreos o con las actividades culturales realizadas a final de curso asegurando el tiempo suficiente para poder realizar cada sesión.

El proceso de presentación y realización de estos ejercicios ha sido el mismo para todos los grupos, puesto que el objetivo era poder establecer una comparativa de resultados entre los grupos, teniendo en cuenta la diversidad de estos, tanto a nivel de alumnado como de profesorado.

En cuanto a la metodología, inicialmente en cada sesión el profesor corrige los dos ejercicios anteriores, explicando a los alumnos las soluciones correctas y el razonamiento seguido para llegar hasta ellas, en el apartado de argumentación hacer hincapié en que este apartado debe enfocarse a que el lector entienda muy bien cómo ha llegado a la solución. Es fundamental que los alumnos expliquen en sus argumentaciones cuáles son los movimientos de cada pieza correctamente y describan las posiciones utilizando notación ajedrecística de coordenadas. El objetivo en esta primera etapa de la sesión es que los alumnos adquieran herramientas para mejorar sus capacidades de argumentación. Estas explicaciones previas les sirve para tener mayor consciencia de lo que se les pide y mejorar en los siguientes ejercicios, emplear menos tiempo en realizarlos y explicar mejor la solución adoptada.

A continuación, en la segunda parte de la sesión el monitor lee a los alumnos el enunciado de los ejercicios de la sesión y resuelve las posibles dudas que puedan surgir sobre el vocabulario utilizado. Los alumnos resuelven los dos ejercicios planteados anotando el tiempo empleado para realizarlo.

Las sesiones se han realizado de forma semanal para las escuelas, pero, en el caso del colegio, al no estar enmarcada en unas clases semanales se han adecuado a los huecos que las actividades del colegio marcaban, aprovechando actividades culturales y horas de recreo donde los niños estaban más relajados.

5.2.2 Análisis de las sesiones

En este apartado se exponen algunos ejercicios resueltos por los alumnos y que tienen una especial relevancia para ayudar al lector a entender el transcurso de las mismas:

EJERCICIO1

Evidencias

52: Evidencia Ejercicio 1

Figura 53: Evidencia Ejercicio 1

Comentarios En general, este ejercicio se ha resuelto correctamente, sin embargo, en algunos casos, como en la figura 52 se ha resuelto muy rápido por el nivel ajedrecístico del alumno, pero en la argumentación ha supuesto que el lector conocía el movimiento de las piezas En la figura 53 se ha limitado a explicar que otros movimientos no podían realizarse

Figura

Evidencias

EJERCICIO2

Figura 54: Evidencia Ejercicio 2

Figura 55: Evidencia Ejercicio 2

Comentarios En general, este ejercicio se ha resuelto correctamente, en la figura 54 se ha resuelto con una argumentación completa. En la figura 55 el razonamiento es erróneo, suponemos que no leer bien el enunciado puede dar lugar a esta interpretación.

Evidencias

EJERCICIO3

56: Evidencia Ejercicio 3

57: Evidencia Ejercicio 3

Comentarios Como evidencias en este ejercicio, se ha seleccionado un primer ejercicio figura 56 resuelto de manera elegante y sencillo, y un segundo ejercicio Figura 57 resuelto correctamente también, pero además se muestra la estrategia de ensayo y error seguida por el alumno.

Figura

Figura

Evidencias

EJERCICIO4

Figura 58: Evidencia Ejercicio 4

Figura 59: Evidencia Ejercicio 4

Comentarios Se han seleccionado un primer ejercicio figura 58 donde se ha argumentado erróneamente invirtiendo mucho más tiempo que en la figura 59 cuya argumentación se basa en explicar los movimientos de las piezas, siendo mucho más fácil de leer con una menor inversión de tiempo empleado.

Evidencias

EJERCICIO5

Figura 60: Evidencia Ejercicio 5

Figura 61: Evidencia Ejercicio 5

Comentarios. Se han seleccionado dos ejercicios con dos soluciones correctas, pero con diferentes razonamientos, el primero basado en las matemáticas

Figura 60 y el segundo basado en el conteo apoyándose en el dibujo Figura 61.

Evidencias

EJERCICIO6

Figura 62: Evidencia Ejercicio 6

Figura 63: Evidencia Ejercicio 6

Comentarios El primero de los ejercicios seleccionados Figura 62 es argumentado y solucionado correctamente, sin embargo, el segundo Figura 63 aunque es solucionado correctamente no está bien argumentado para explicar al lector por qué se ha llegado a esa solución.

Evidencias

EJERCICIO7

64: Evidencia Ejercicio 7

Comentarios. El primero de los ejercicios seleccionados Figura 64 es argumentado correctamente, pero mal solucionado a lo mejor porque no leyó correctamente el enunciado.

Figura

Evidencias

EJERCICIO8

65: Evidencia Ejercicio 8

Figura 66: Evidencia Ejercicio 8

Figura 67: Evidencia Ejercicio 8

Comentarios. Los tres ejercicios dan soluciones correctas al ejercicio, sin embargo, en la figura 65 no explica correctamente cómo ha llegado a ella, las otras dos sí explica de manera teórica como llegaron a la solución.

Figura

Evidencias

EJERCICIO9

68: Evidencia Ejercicio 9

Comentarios. Este ejercicio ha sido resuelto correctamente en la mayoría de los casos. El patrón es identificado rápida y correctamente, sin embargo, no se explica la respuesta. Parece más un problema de enunciado del ejercicio, porque se olvidó indicar la frase, justifica la respuesta.

Figura

Evidencias

EJERCICIO10

69: Evidencia Ejercicio 10

Figura 70: Evidencia Ejercicio 10

Comentarios El primero de los ejercicios seleccionados Figura 69 es argumentado y solucionado correctamente, sin embargo, el segundo, aunque es solucionado correctamente no está bien argumentado para explicar al lector por qué se ha llegado a esa solución.

Figura

Evidencias

EJERCICIO11

71: Evidencia Ejercicio 11

72: Evidencia Ejercicio 11

Comentarios El primero de los ejercicios seleccionados Figura 71 es argumentado y solucionado correctamente, sin embargo, el segundo no se ha entendido absolutamente el ejercicio, hubiera sido importante por parte del alumno que, si un enunciado no se entiende, se asegure entenderlo preguntando.

Figura

Figura

Evidencias

EJERCICIO12

73: Evidencia Ejercicio 12

74: Evidencia Ejercicio 12

Comentarios. En los ejercicios seleccionados se observa como ambos alumnos utilizan distintas estrategias de razonamiento. En la figura 73 correctamente resuelto y en la figura 74 no porque, aunque se visitan todas las casillas no se ha contabilizado correctamente el número de movimientos.

Figura

Figura

Evidencias

EJERCICIO13

Figura 75: Evidencia Ejercicio 13

Comentarios. Este ejercicio ha sido resuelto correctamente en la mayoría de los casos. Sin embargo, no se explica la respuesta, parece más un problema de enunciado del ejercicio, porque se omitió indicar la frase, justifica la respuesta. En estos casos, se avisó al profesor para que completase en la explicación el enunciado. Algunos alumnos no lo tuvieron en cuenta.

Evidencias

EJERCICIO14

Figura 76: Evidencia Ejercicio 14

Comentarios. Este ejercicio ha sido resuelto correctamente en la mayoría de los casos. Sin embargo, no se explica la respuesta, parece más un problema de enunciado del ejercicio, porque se omitió indicar la frase, justifica la respuesta. En estos casos, se avisó al profesor para que completase en la explicación el enunciado. Algunos alumnos no lo tuvieron en cuenta.

Evidencias

EJERCICIO

15

15

15

Comentarios. En los ejercicios seleccionados se observa como la solución en ambos casos es correcta, pero en la argumentación la primera es completa y sencilla, pero en la segunda no termina de ser completa y además ha invertido mayor tiempo. Se ha resuelto de manera más eficaz el primero atendiendo a las instrucciones dadas por el profesor.

Figura 77: Evidencia Ejercicio

Figura 78: Evidencia Ejercicio

Evidencias

EJERCICIO16

Figura 79: Evidencia Ejercicio 16

Figura 80: Evidencia Ejercicio 16

Figura 81: Evidencia Ejercicio 16

Comentarios En los ejercicios seleccionados se observa como en el primer caso la argumentación sigue los principios dados por el instructor y además de forma rápida. En el segundo, aprovecha un enunciado incompleto para dar una respuesta asociada al color de las piezas, y en el tercer no fue capaz de dar una solución correcta ni tampoco una argumentación válida.

Evidencias

EJERCICIO17

82: Evidencia Ejercicio 17

83: Evidencia Ejercicio 16

Comentarios Ejemplos de soluciones correctas y malas argumentaciones.

Figura

Figura

Evidencias

EJERCICIO18

Figura 84: Evidencia Ejercicio 18

Comentarios El ejercicio seleccionado es un ejemplo de no realizar un análisis de lo que el ejercicio pedía, sin reflexión alguna, 11 segundos el tiempo de respuesta.

Evidencias

EJERCICIO19

85: Evidencia Ejercicio 19

Figura 86: Evidencia Ejercicio 19

Figura 87: Evidencia Ejercicio 19

Comentarios. Ejercicio de creatividad, algunos ejemplos realizados por los alumnos.

Figura

Evidencias

EJERCICIO20

88: Evidencia Ejercicio 20

Figura 89: Evidencia Ejercicio 20

Figura 90: Evidencia Ejercicio 20

Comentarios. Ejercicio de creatividad, algunos ejemplos realizados por los alumnos.

Figura

5.2.3

Captura de resultados

Para el análisis de resultados se han separado los ejercicios en cuatro bloques de cinco ejercicios cada uno Cada bloque incluye ejercicios de distintos tipos, generalmente todos los tipos de ejercicios planteados (mini tablero con todas las piezas, con alguna pieza a añadir, vacíos, uso de patrones y planteamiento de problemas). Además, esta agrupación permite ver más fácilmente el avance de la habilidades estratégicas y argumentativas del individuo y del grupo. Uno de los objetivos es sin duda, valorar si es eficaz la realización de estas sesiones de modo iterativo para mejorar las capacidades anteriormente indicadas del alumno.

Los datos que se van a analizar son los siguientes:

✓ El tiempo medio que ha tardado en realizar cada ejercicio en cada uno de los bloques. Se medirán en minutos.

✓ La resolución del problema: Si está bien resuelto 1 punto y si no lo está 0. Como máximo podrán tener 5 puntos por bloque.

✓ Laargumentación del alumno,si su argumentación es completaseleasignará un punto y si no lo es 0 Como máximo podrán obtener 5 puntos por bloque.

La captura de resultados se ha realizado primero de manera individual, pero para el análisis de datos y para sacar conclusiones se han agrupado los resultados por cada una de las escuelas y colegios participantes.

5.2.3.1 Individual

Los resultados individuales de cada alumno se presentan en la siguiente tabla cuya leyenda es la siguiente:

✓ T= Tiempo.

✓ R= Resolución del ejercicio.

✓ A= Argumentación del alumno.

✓ Bloque 1: Resultados para los ejercicios del 1 al 5

✓ Bloque 2: Resultados para los ejercicios del 6 al 10

✓ Bloque 3: Resultados para los ejercicios del 11 al 15.

✓ Bloque 4: Resultados para los ejercicios del 16 al 20

Figura 91: Resultados ejercicios en aula

5.2.3.2 Agrupación de resultados

Para poder realizar un análisis de resultados se han agrupado los datos los grupos de alumnos que han participado en el experimento.

La siguiente tabla se ha realizado calculando la media de los datos obtenidos de los integrantes del grupo. La leyenda es la misma que en la tabla anterior.

Figura 92: Resultados agrupados ejercicios en aula

Grupo Alumnos Nivel

6. ANÁLISIS DE RESULTADOS

Después de haber realizado las pruebas y de haber sintetizado los resultados en este capítulo se va a analizar en detalle los datos a partir de los parámetros medidos teniendo en cuenta las circunstancias que han rodeado la ejecución de las sesiones en cada uno de los grupos Analizar estas circunstancias, generalmente son claves para ayudar a mejorar resultados en futuras experimentaciones en el mismo campo de investigación.

Para que el lector tenga un entendimiento completo del análisis realizado a continuación, es importante recordar que la dificultad de los ejercicios en el transcurso de las sesiones no se incrementa. Se trata de ejercicios de similar dificultad, en la que se valora la evolución del alumno a partir de la repetición de procesos de estrategia o razonamiento y argumentación.

6.1 Tiempo

El tiempo de realización de la prueba se resume en la siguiente tabla y gráfica.

Tiempo Bloque 1 Bloque 2 Bloque 3 Bloque 4

Escuela Ajedrez Inicial

Figura 93: Zoom Resultados Tiempo

TiempoResoluciónEjercicios(min)

Bloque1

Bloque2

Bloque3

EscuelaAjedrezInicial EscuelaAjedrezMedio

EscuelaAjedrezAlto Colegio

Figura 94: Gráfica Resultados Tiempo

Bloque4

Se puede observar a la luz de los resultados que, en el caso de cualquiera de los grupos, el tiempo en resolver los ejercicios va disminuyendo a medida que las sesiones se imparten

También se puede observar que la media de resolución de tiempos de cada bloque en el caso de alumnos de nivel medio-alto es bastante inferior a los alumnos que están en proceso de iniciación.

Paraterminar,se observa quelos alumnos con menornivelexperimentanunaevolución mayor en el tiempo usado a medida que transcurren las sesiones.

Por tanto, se puede constatar en la gráfica de tiempos que podemos decir que a medida que el alumno avanza en la resolución de los distintos problemas va mejorando la velocidad de resolución, aunque se aprecia levemente en un número de ejercicios limitados, con un número mayor de ejercicios se llegaría a notar con mayor claridad.

6.2 Resolución

Lapuntuación obtenidaparalaresolucióndeejerciciosserefleja enlassiguientestablas y gráficas.

Resoluciones correctas Bloque 1 Bloque 2 Bloque 3 Bloque 4

Escuela Ajedrez Inicial 3,5 3,5 4 4

Escuela Ajedrez Medio 4 4 4,5 4,5

Escuela Ajedrez Alto

Figura 95: Zoom Resultados Resolución

Resolucionescorrectas

Colegio

EscuelaAjedrezAlto

EscuelaAjedrezMedio

EscuelaAjedrezInicial

Bloque4 Bloque3 Bloque2 Bloque1

Figura 96: Gráfica Resultados Resolución

Se advierte que los niveles medio-alto tienen una tasa de acierto mayor que los niveles más bajos. Todos los grupos con el paso de las sesiones van mejorando en su tasa de aciertos. El proceso iterativo de repasar la resolución de los ejercicios realizados en la sesión anterior, junto con la experiencia de haber acumulado la realización de ejercicios similares en anteriores sesiones ayuda a tener mejores resultados en sesiones posteriores.

6.3 Argumentación

La puntuación obtenida para argumentación se refleja en las siguientes tablas y gráfica.

Resoluciones correctas Bloque 1 Bloque 2 Bloque 3 Bloque 4

Escuela Ajedrez Inicial 3,5 3,5 4 4

Escuela Ajedrez Medio 4 4 4,5 4,5

Escuela Ajedrez Alto

EscuelaAjedrezAlto Colegio

Figura 97: Zoom Resultados Argumentación

Argumentacionescorrectas

EscuelaAjedrezMedio

EscuelaAjedrezInicial

Bloque4 Bloque3 Bloque2 Bloque1

Figura 98: Zoom Resultados Argumentación

Nuevamente, se muestra que los niveles medio-alto tienen ligeramente una tasa más alta. Todos los grupos con el paso de las sesiones van mejorando en argumentar sus respuestas. El proceso iterativo de repasar la resolución de los ejercicios realizados en la sesión anterior, junto con la experiencia de haber acumulado la realización de ejercicios similares en anteriores sesiones, ayuda a tener mejores resultados en sesiones posteriores. Insistir en cómo explicar los razonamientos apoyándose en un procedimiento que comienza por la explicación de los movimientos de cada pieza y el uso de una notación de coordenadas que ayude a explicar los resultados sin duda mejora los resultados.

7. CONCLUSIONES

El trabajo tenía como objetivo crear un material educativo compuesto de actividades relacionadas con el ajedrez que permitiera mejorar las capacidades matemáticas del alumno.

Mediante la introducción de nuevos conceptos matemáticos y la práctica por parte de los alumnos de la argumentación de las soluciones al resolver los ejercicios, el alumno tenía que adquirir una mejora en sus capacidades matemáticas. Se pretendía apreciar también una evolución en sus capacidades conceptuales, de razonamiento y argumentación de soluciones ante problemas (en la práctica ajedrecísticos, pero perfectamente extrapolables a las matemáticas).

Para conseguir tener un material que cubra los objetivos mencionados se ha realizado un pilotaje que ha servido para identificar posibles mejoras al ponerlos en práctica en las aulas. Estas mejoras estuvieron enfocadas principalmente a conseguir un mejor entendimiento de los enunciados por parte del lector, tanto en la descripción del problema como de lo que se solicita al alumno asegurando que en todos ellos se les pide la justificación de sus respuestas. Además, el pilotaje ha proporcionado información para que los monitores pudieran utilizar en sus explicaciones a los alumnos, tanto de los problemas que iban a resolver, como de los resueltos en las sesiones anteriores.

Ambos objetivos creo que se han cumplido, en el primer caso, los ejercicios incluyen conceptosgeométricos(verticales,diagonales,horizontales,ejesdesimetría)yusodepatrones, en el segundo, los alumnos han justificado sus respuestas, que han ido mejorando con el ensayo y las correcciones que los monitores han realizado en cada sesión.

También se pretendía evidenciar el impacto del ajedrez en la resolución de problemas. En este aspecto creo que el análisis de los resultados obtenidos explicados en el capítulo anterior, evidencia que, con el paso de las sesiones, los alumnos disminuían los tiempos de respuesta, mejorando además en la calidad de sus soluciones (mayores aciertos), y en el razonamiento explicado en la justificación, sin embargo, no es suficiente como para crear una relación directa que permita afirmar con rotundidad que el ajedrez mejora la capacidad de un alumno en la resolución de problemas matemáticos

Finalmente, el objetivo de mejorar el diseño de las sesiones, implícitamente en el proceso de pilotaje la propuesta evolucionó, después del trabajo en el aula, con las opiniones de los monitores y de los alumnos, se ha diseñado una propuesta mejorada expuesta en el siguiente capítulo con el fin de que sea la base para otras futuras experimentaciones.

Si profundizamos en los parámetros medidos en el capítulo de análisis de resultados, respecto al parámetro tiempo, podemos concluir que cuanto más conocimiento ajedrecístico hay por parte de los alumnos, menor es el tiempo empleado en la realización correcta del ejercicio, esto puede deberse a que el entrenamiento de un jugador de ajedrez está enfocado en la resolución de problemas similares, por lo que tienen mayor habilidad adquirida con la práctica. Por contra, la realización de estas sesiones en niveles altos tiene una menor evolución con el paso de estas, que en alumnos con menores conocimientos de ajedrez. La evolución observada a medida que se avanzan en los bloques de ejercicios en los cuatro grupos, lo confirman.

En cuanto a la resolución de actividades, se puede decir que según se van haciendo los ejercicios aumenta la capacidad de resolverlas, argumentarlos y pensar de una manera más lógica y ordenada. Esto puede deberse a que los alumnos se van familiarizando con la resolución de los ejercicios y además van interiorizando el procedimiento que deben seguir en laargumentación delasrespuestas.Primero,explicarmovimientos delaspiezas correctamente, después ayudarse de la notación de coordenadas y explicarlo siempre pensando en que sea entendible para un tercero Sin duda, el feedback que se realiza al comienzo de cada sesión, explicando cómo se resolvieron los ejercicios de la anterior, ayudan a que el alumno interiorice el proceso y lo realice más rápido en los siguientes ejercicios Obviamente el nivel influye y por tanto el porcentaje de problemas resueltos correctos aumenta con el nivel, precisamente por la misma razón que el anterior, la práctica adquirida en la escuela.

Por lo general, suele ser más complicado explicar la solución de manera coherente y detallada que dar una solución sin decir un por qué. Esto se ha ido viendo a lo largo del programa de ejercicios y se nota más en niveles iniciales y medios. Sin embargo, en los niveles altos tienen adquirido por su entrenamiento la necesidad de tener que explicar por qué cada movimiento es realizado. De hecho, en ajedrez se utiliza una notación especial que ayuda a explicar más ágilmente la argumentación.

A la vista de estos resultados, podemos concluir que la eficacia de estos ejercicios a medida que se van realizando, tiene mucho que ver con quien imparta las sesiones. La forma en que el monitor o profesor es capaz de explicar las pautas a seguir, en cuanto a razonamiento y a argumentación que se plantea, junto con la capacidad de hacerlo atractivo para los alumnos aumenta la eficiencia.

Por otro lado, la evolución en la argumentación o razonamiento es más alto en alumnos que no tienen conocimientos ajedrecísticos, por lo tanto, se recomienda realizar estos ejercicios con alumnos que conozcan el movimiento de las piezas, pero no es necesario más conocimiento. En consecuencia, es más práctico y útil usar este material en los colegios para introducir el ajedrez y el razonamiento como ayuda en la asignatura de matemáticas.

Respecto a la edad de los alumnos, sí se requiere un nivel de madurez suficiente, por lo que una edad de entre 10 y 13 años es la edad ideal para poder mejorar las capacidades argumentativas del individuo

Por otro lado, se ha observado que han sido demasiado pocas sesiones para la implantación de la secuencia y la muestra del estudio ha sido baja como para poder sacar conclusiones o ver una mejora clara en las aptitudes de argumentación de problemas.

Por último, para poder ver resultados más concretos, lo ideal sería que el desarrollo de la propuesta se hiciera a lo largo de un trimestre y poder, con exámenes de matemáticas, antes, durante y después, ver si hay una evolución en los razonamientos.

Como reflexión final, en líneas generales, la experimentación ha conseguido los objetivos buscados, con algunos puntos de mejora identificados para mejorar los resultados en aplicaciones futuras ya que los monitores que usaron el material consiguieron mejorar las capacidades matemáticas (aprendieron nuevos conceptos) y de argumentación de sus alumnos. Sin embargo, esa comprobación que parece obvia es muy difícil de demostrar con datos. Como se indicaba en las conclusiones de los estudios presentados en la sección del estado del arte, para llegar a demostrarlo se requeriría un enorme número de muestras y años

Para lograr aumentar la eficacia de las sesiones en el incremento de la capacidad de razonamiento del alumno se han identificado algunas premisas y acciones a aplicar en sesiones futuras que son propuestas en el siguiente capítulo.

8. PROPUESTA MEJORADA

Tras la experimentación y con los resultados obtenidos se ha modificado la propuesta de enseñanza. Sigue contando con diez sesiones con las mismas actividades, aunque cambian algunos aspectos como el papel del profesor, redacción de algunos enunciados y un nuevo orden de sesiones y de composición de los ejercicios que se incluyen en cada una.

En referencia al orden y composición de actividades de las sesiones, por el resultado no tan bueno de alguno de los ejercicios en el trabajo en el aula, se ha preferido incluirlos en sesiones más tardías con el fin de que el alumno con el transcurso de los ejercicios adquiera las habilidades necesarias para poder realizarlos mejor. Se ha observado que un enunciado más largo o con movimiento de una determinada pieza, como el movimiento vertical u horizontal de un alfil o una torre sea más fácil para empezar a interiorizar consejos en el proceso de argumentación, que el movimiento en “L” del caballo, que, en este caso, puede requerir algo más de experiencia en haber realizado ejercicios previos. En la siguiente tabla se pueden observar las sesiones afectadas y la nueva propuesta se adjunta en el anexo 2.

SESIONES

Sesión 2

Sesión 3

Sesión 5

Sesión 6

Sesión 7

Sesión 10

EJERCICIOS INCLUIDOS

Ejercicio 5 y 6

Ejercicio 3 y 4

Ejercicio 9 y13

Ejercicio 19 y 12

Ejercicio 10 y 14

Ejercicio 11 y 20

Figura 99: Tabla modificaciones incluidas en propuesta

En cuanto al papel del instructor, antes de comenzar las sesiones debería dedicar un tiempo para conocer lo que ya saben o no los alumnos sobre el ajedrez y los movimientos de las piezas. También trabajar con anterioridad el vocabulario para usar en la resolución de los ejercicios. Es importante que el profesor insista en la argumentación y recuerde el proceso de razonamiento antes de empezar a realizar los ejercicios.

Por ese motivo es quizá preferible que el instructor tenga muy interiorizado como objetivo el incremento de capacidades matemáticas (adquisición de conceptos y resolución de problemas matemáticos). Por eso hubiera sido interesante que fuese el mismo monitor que indicara las mismas pautas para todos los grupos, así podríamos ver si esta variable afecta o no en los resultados.

Otros puntos para mejorar en esta experimentación para lograr mayor eficacia, sería añadir en cada sesión la posibilidad de que las respuestas fueran explicadas por los alumnos que dieron una respuesta correcta al ejercicio. De modo que mientras explica se pudieran corregir los puntos que no estuvieran completos en su argumentación. Además de llamar la atención del resto de alumnos además se trabajaría el aprendizaje entre iguales. Otra sugerencia interesante,sería realizar lascorreccionescon el tablerodelante,viendotodas lasposibilidades, explorando diferentesmodos derazonamiento conellos, endefinitiva,mostrarlodeunamanera más lúdica.

En cuanto a la redacción de los enunciados, como se puede observar en el anexo 2 se han modificado los ejercicios 2,5,7,9,12 y 14 añadiendo en el enunciado que se necesita justificación a la respuesta.

Respecto al tiempo, se aumenta a 30 minutos la duración de las sesiones para dar más espacio a las explicaciones del profesor y a la corrección de los ejercicios anteriores que ahora son realizados por los alumnos. Finalmente, en caso de tener más sesiones en el futuro para experimentar, resultaría interesante incluir más piezas del juego como la reina o los peones.

El presente proyecto de ajedrez propone no solo fomentar el desarrollo de habilidades cognitivasyestratégicas enlos participantes, sino tambiéncontribuiral cumplimiento devarios Objetivos de Desarrollo Sostenible (ODS) de la agenda 2030. A través de la práctica del ajedrez, se busca promover la educación de calidad (ODS 4) al ofrecer un espacio de aprendizaje inclusivo y accesible para todos. Además, el ajedrez puede ser una herramienta eficaz para fomentar la paz, la justicia y la construcción de instituciones sólidas (ODS 16), enseñando a los jóvenes la importancia del respeto, la tolerancia y la resolución pacífica de conflictos.

Este proyecto también se alinea con la igualdad de género (ODS 5), ya que puede ser realizado en igualdad de condiciones por chicos y chicas, y con la reducción de desigualdades (ODS 10), promoviendo la participación de todos los estudiantes, independientemente de su contexto socioeconómico. Asimismo, los programas de ajedrez pueden ser efectivos para alejar a los alumnos de conductas de riesgo, como el consumo de drogas y la delincuencia. De este modo, el proyecto no solo se centra en el desarrollo personal de los individuos, sino que también avanza hacia un futuro más sostenible y equitativo.

9. VALORACIÓN PERSONAL

Este proyecto me ha dado la oportunidad de poder investigar en profundidad la relación entrelasmatemáticasyel ajedrez, curiosidadquesemedespertóconlalecturadellibroRazvan Iagar (2017): Matemáticas y ajedrez, CSIC Madrid, y cómo el ajedrez puede ser un recurso valioso para la enseñanza de conceptos matemáticos y hacerlo de una manera lúdica para el alumno.

Aunque es difícil probar la eficacia de los ejercicios propuestos, sí que se percibe una mejora a la hora de argumentar la respuesta por parte del alumno con el paso de las sesiones. Aunque eso no es suficiente como para que el experimento sea concluyente, sí creo que puede servir como herramienta de ayuda para la asignatura de matemáticas incluyendo los puntos de mejora mencionados en el capítulo anterior.

Por otro lado, creo que se ha conseguido llevarlo a cabo de manera lúdica, hecho muy importante para motivar a los alumnos durante la enseñanza. Durante el proyecto se pidió a los alumnos del colegio que dieran su opinión acerca de los ejercicios que acababan de realizar y si lo veían útil para el aprendizaje de las matemáticas. Sus respuestas no dejan lugar a dudas de que el recurso del ajedrez puede ayudar a poner en práctica muchos conceptos y razonamientos matemáticos de una manera realmente divertida.

Figura 100: Opinión Alumnos Ejercicios

Figura 101: Opinión Alumnos Ejercicios

Lo que sí que han destacado ha sido la dificultad de justificar la respuesta Me atrevería a decir, que en la asignatura de Lengua podría ser también una herramienta muy útil para mejorar la expresión escrita.

Figura 102: Opinión Alumnos Ejercicios

Figura 103: Opinión Alumnos Ejercicios

Figura 104: Opinión Alumnos Ejercicios

Figura 105: Opinión Alumnos Ejercicios

Finalmente, querría intentar dar respuesta a la pregunta que motivaba mi deseo de realizar este proyecto ¿podemos explicar por qué a una gran mayoría de ajedrecistas se les dan bien las matemáticas? La respuesta no es sencilla, pero sí podemos asegurar que entre las matemáticas y el ajedrez hay una estrecha relación en ambos sentidos y que, el gusto por explicar por qué se realiza cada uno de los movimientos en una partida, lo tiene un ajedrecista y eso es un punto a favor para mejorar las capacidades argumentativas ante un problema, ya sea de ajedrez, vital o matemático.

Figura 106: Opinión Alumnos Ejercicios

10.REFERENCIAS BIBLIOGRÁFICAS

• Bart WM (2014). Sobre los efectos del entrenamiento en ajedrez sobre el rendimiento escolar. Fronteras en psicología, vol. 5, artículo 762.

• Bragg(2012) Testing the effectiveness of mathematical games as a pedagogical tool for children's learning

<https://www.researchgate.net/publication/257570815_Testing_the_effectiveness_of_ mathematical_games_as_a_pedagogical_tool_for_children's_learning>

• Berkman RM (2004), La conexión entre ajedrez y matemáticas: más que un simple juego. Enseñanza de las Matemáticas en la Escuela Secundaria, vol. 9, 246–250.

• Chess and mathematics in Primary School Erasmus + 50 ejercicios de Ajedrez y matemáticas para las escuelas.

<https://ec.europa.eu/programmes/erasmus-plus/project-result-content/9109730f8d25-41f3-90ad-

32f1b3e77fe8/CHAMPS_Teacher_Training_for_Chess_and_Mathematics_Final_110 319.pdf>.

• Chess and mathematics in Primary School Erasmus + Teacher Training for Chess and Mathematics

<https://ec.europa.eu/programmes/erasmus-plus/project-result-content/9109730f8d25-41f3-90ad-

32f1b3e77fe8/CHAMPS_Teacher_Training_for_Chess_and_Mathematics_Final_110 319.pdf>

• Dámaso Miguel Vera Sáez-Benito, Alberto Arnal Bailera (2022)

Trabajo con patrones a través de actividades basadas en el ajedrez. Un estudio sobre estrategias y niveles de razonamiento de los estudiantes de Educación Primaria. <https://ajedrezalaescuela.eu/wp-content/uploads/2022/06/Articulo-IJISMETFSM.pdf>

• Ernest (1986)

La matemáticanunca deja deser un juego: investigaciones sobrelos efectos del uso de juegos en la enseñanza de las matemáticas< https://somidem.com.mx/descargas/Vol26-3-4.pdf>

• Fernández Santiago (1991) Revista Suma 7/1991 El ajedrez, un recurso en el aula de las matemáticas

<https://revistasuma.fespm.es/sites/revistasuma.fespm.es/IMG/pdf/7/053-060.pdf>

• Gobet F., & Campitelli G. (2006). Educational benefits of chess instruction: A critical review. InRedmanT.(ed),ChessandEducation:SelectedEssaysfromtheKoltanowski Conference, Dallas TX: Chess program at the University of Texas at Dallas, 124–143

• González Peralta, Juan Gabriel Molina, Mario Sánchez Aguilar (2013) Investigaciones sobre los efectos del uso de juegos en la enseñanza de las matemáticas<https://www.redalyc.org/articulo.oa?id=40540689005>

• Maz-Machado (2012) Épsilon - Revista de Educación Matemática 2012, Vol. 29(2), nº 81, 105-111, ISSN: 1131-9321 Ajedrez para trabajar patrones en matemáticas en Educación Primaria. <https://core.ac.uk/download/pdf/60888611.pdf>

• Razvan Iagar (2017): Matemáticas y ajedrez, CSIC Madrid Obra en la que se reflexiona sobre la relación entre las matemáticas y el ajedrez. Parte de la base teórica del proyecto se basa en este libro.

• Rosholm M, Mikkelsen MB, Gumede K (2017) Tu jugada: El efecto del ajedrez en las puntuaciones de los exámenes de matemáticas.

• Trinchero R., & Sala G. (2016). Entrenamiento de ajedrez y resolución de problemas matemáticos: el papel de la enseñanza de la heurística en la transferencia del aprendizaje. Eurasia Journal of Mathematics , Science & Technology Education , 12 ( 3 ), 655–668.

11.ANEXO1:SESIONESDE TRABAJO EN ELAULA

11.1 SESION 1

Identificador del alumno:

Tiempo empleado:

Ejercicio 1:

Coloca un alfil para que las piezas no se puedan comer entre ellas. Dibújalo.

Explica brevemente tu solución.

Identificador del alumno:

Tiempo empleado:

Ejercicio 2:

¿Se comen unas piezas a otras? Si no, por qué. No tener en cuenta los colores

11.2 SESION 2

Identificador del alumno:

Tiempo empleado:

Ejercicio 3:

Coloca 1 torre y 3 alfiles de manera que no se puedan comer entre ellos. Explica por qué no se comen.

Identificador del alumno:

Tiempo empleado:

Ejercicio 4:

Coloca dos alfiles sin que las piezas se coman. Explica por qué deben colocarse ahí.

11.3 SESION 3

Identificador del alumno:

Tiempo empleado:

Ejercicio 5

Este rey quiere alejarse todo lo posible. Ayúdale a escapar. Si realiza un movimiento tiene 8 casillas para elegir.

Si realiza 2 movimientos tiene 16 casillas para elegir

Si realiza 3 movimientos, ¿cuántas casillas tiene para elegir?

Identificador del alumno:

Tiempo empleado:

Ejercicio 6:

Coloca a un alfil para que pueda comer a las dos torres y no sea comido por ellos. Explica por qué lo has colocado ahí.

11.4 SESION 4

Identificador del alumno:

Tiempo empleado:

Ejercicio 7:

Coloca un caballoparaquecomaala torredel centroynoseacomido.Buscatodas las soluciones posibles.

Identificador del alumno:

Tiempo empleado:

Ejercicio 8:

Meter dos caballos sin que las piezas se coman. Explica por qué.

11.5 SESION 5

Identificador del alumno:

Tiempo empleado:

Ejercicio 9:

Este alfil se ha desplazado de la casilla marcada con una equis (x) a la casilla d5. Siempre se mueve de la misma manera. Encuentra la siguiente casilla a la que llegará.

Identificador del alumno:

Tiempo empleado:

Ejercicio 10

En este tablero se muestran algunas casillas a las que puede acudir el caballo realizando un movimiento (círculos) o dos movimientos (cuadrados). Completa las casillas que faltan.

Encuentra las casillas a las que puede ir con su tercer movimiento. Márcalas con un triángulo.

Dibuja los ejes de simetría que encuentres en el tablero.

El caballo todavía no ha ido a algunas casillas. ¿Cuántos movimientos tiene que hacer para ir a ellas? Explica cómo lo has averiguado.

11.6 SESION 6

Identificador del alumno:

Tiempo empleado:

Ejercicio 11

Aquí puedes ver el número de casillas a las que amenazan estas piezas desde distintas posiciones. Completa los tableros

Compara los tableros que acabas de rellenar ¿Qué relación observas entre ellos? ¿Por qué crees que pasa esto?

Identificador del alumno:

Tiempo empleado:

Ejercicio 12

Estandola torreen a1,latorredebevisitartodas las casillas yvolveraa1.Dibújalo en el menor número de movimientos.

11.7 SESION 7

Identificador del alumno:

Tiempo empleado:

Ejercicio 13

Coloca un caballo, un alfil y una torre de manera que: la torre sea capturada por el caballo, el alfil sea capturado por la torre y el alfil capture al caballo.

Identificador del alumno:

Tiempo empleado:

Ejercicio 14:

Coloca dos caballos, dos alfiles y una torre de manera que no se coman entre ellos.

11.8 SESION 8

Identificador del alumno:

Tiempo empleado:

Ejercicio 15:

Coloca una torre, un alfil y dos caballos, de manera que no se coman las piezas entre ellas.

Justifica la respuesta

Identificador del alumno:

Tiempo empleado:

Ejercicio 16

¿Se comerán los caballos? Dibuja su movimiento y explica por qué sí o porqué no.

11.9 SESION 9

Identificador del alumno:

Tiempo empleado:

Ejercicio 17

¿Se comen entre ellas las siguientes piezas? Si, no porque…

Coloca otro caballo más que sea comidopor el alfil y que coma ala torre y justifica cómo has encontrado esa casilla.

Identificador del alumno:

Tiempo empleado:

Ejercicio 18

Posiciona 4 torres negras de manera que entre ellas amenacen a todas las casillas blancas. Justifica respuesta

11.10 SESION 10

Identificador del alumno:

Tiempo empleado:

Ejercicio 19

Crea un ejercicio con al menos un caballo, un alfil y una torre.

Inventa y escribe el enunciado y resuélvelo justificando.

Identificador del alumno:

Tiempo empleado:

Ejercicio 20

Crea tu propio enunciado con dos alfiles, una torre y un caballo. Justifica las respuestas

12.ANEXO2:SESIONES PROPUESTA MEJORADA

12.1 SESION 1

Identificador del alumno:

Tiempo empleado:

Ejercicio 1:

Coloca un alfil para que las piezas no se puedan comer entre ellas. Dibújalo.

Explica brevemente tu solución.

Identificador del alumno:

Tiempo empleado:

Ejercicio 2:

¿Se comen unas piezas a otras? Justifica tu respuesta. No tener en cuenta los colores

12.3 SESION 2

Identificador del alumno:

Tiempo empleado:

Ejercicio 5

Este rey quiere alejarse todo lo posible. Ayúdale a escapar. Si realiza un movimiento tiene 8 casillas para elegir.

Si realiza 2 movimientos tiene 16 casillas para elegir

Si realiza 3 movimientos, ¿cuántas casillas tiene para elegir? Explica tu respuesta. Ayúdate de dibujos si es necesario

Identificador del alumno:

Tiempo empleado:

Ejercicio 6:

Coloca a un alfil para que pueda comer a las dos torres y no sea comido por ellos. Explica por qué lo has colocado ahí.

12.2 SESION 3

Identificador del alumno:

Tiempo empleado:

Ejercicio 3:

Coloca 1 torre y 3 alfiles de manera que no se puedan comer entre ellos. Explica por qué no se comen.

Identificador del alumno:

Tiempo empleado:

Ejercicio 4:

Coloca dos alfiles sin que las piezas se coman. Explica por qué deben colocarse ahí.

12.4 SESION 4

Identificador del alumno:

Tiempo empleado:

Ejercicio 7:

Coloca un caballoparaquecomaala torredel centroynoseacomido.Buscatodas las soluciones posibles. Razona tu respuesta.

Identificador del alumno:

Tiempo empleado:

Ejercicio 8:

Meter dos caballos sin que las piezas se coman. Explica por qué.

12.5 SESION 5

Identificador del alumno:

Tiempo empleado:

Ejercicio 9:

Este alfil se ha desplazado de la casilla marcada con una equis (x) a la casilla d5. Siempre se mueve de la misma manera. Encuentra la siguiente casilla a la que llegará. Justifica tu respuesta.

Identificador del alumno:

Tiempo empleado:

Ejercicio 13

Coloca un caballo, un alfil y una torre de manera que: la torre sea capturada por el caballo, el alfil sea capturado por la torre y el alfil capture al caballo.

12.6 SESION 6

Identificador del alumno:

Tiempo empleado:

Ejercicio 19

Crea un ejercicio con al menos un caballo, un alfil y una torre.

Inventa y escribe el enunciado y resuélvelo justificando.

Identificador del alumno:

Tiempo empleado:

Ejercicio 12

Estandola torreen a1,latorredebevisitartodas las casillas yvolveraa1.Dibújalo en el menor número de movimientos. Justifica tu respuesta

12.7 SESION 7

Identificador del alumno:

Tiempo empleado:

Ejercicio 10

En este tablero se muestran algunas casillas a las que puede acudir el caballo realizando un movimiento (círculos) o dos movimientos (cuadrados). Completa las casillas que faltan.

Encuentra las casillas a las que puede ir con su tercer movimiento. Márcalas con un triángulo.

Dibuja los ejes de simetría que encuentres en el tablero.

El caballo todavía no ha ido a algunas casillas. ¿Cuántos movimientos tiene que hacer para ir a ellas? Explica cómo lo has averiguado.

Identificador del alumno:

Tiempo empleado:

Ejercicio 14:

Coloca dos caballos, dos alfiles y una torre de manera que no se coman entre ellos. Justifica tu respuesta

12.8 SESION 8

Identificador del alumno:

Tiempo empleado:

Ejercicio 15:

Coloca una torre, un alfil y dos caballos, de manera que no se coman las piezas entre ellas.

Justifica la respuesta

Identificador del alumno:

Tiempo empleado:

Ejercicio 16

¿Se comerán los caballos? Dibuja su movimiento y explica por qué sí o porqué no.

12.9 SESION 9

Identificador del alumno:

Tiempo empleado:

Ejercicio 17

¿Se comen entre ellas las siguientes piezas? Si, no porque…

Coloca otro caballo más que sea comidopor el alfil y que coma ala torre y justifica cómo has encontrado esa casilla.

Identificador del alumno:

Tiempo empleado:

Ejercicio 18

Posiciona 4 torres negras de manera que entre ellas amenacen a todas las casillas blancas. Justifica respuesta

12.10 SESION 10

Identificador del alumno:

Tiempo empleado:

Ejercicio 11

Aquí puedes ver el número de casillas a las que amenazan estas piezas desde distintas posiciones. Completa los tableros

Compara los tableros que acabas de rellenar ¿Qué relación observas entre ellos? ¿Por qué crees que pasa esto?

Identificador del alumno:

Tiempo empleado:

Ejercicio 20

Crea tu propio enunciado con dos alfiles, una torre y un caballo. Justifica las respuestas