a a c rt c T cANT AN 3




Voce, testi e musiche di DAVID CONATI


 R. Maggi
A. Calcabrini
P. Cantarini
E. Battiston
R. Maggi
A. Calcabrini
P. Cantarini
E. Battiston





Voce, testi e musiche di DAVID CONATI



 R. Maggi
A. Calcabrini
P. Cantarini
E. Battiston
R. Maggi
A. Calcabrini
P. Cantarini
E. Battiston

•
•
•
45 La proprietà della divisione
46 Sono bravo - calcolo a mente
48 Divisioni in colonna
49 Ancora divisioni
50 Operazioni inverse




51 Moltiplicazione e divisione
52 Operazioni a confronto
53 Alleniamoci con le operazioni
54 Strategie di calcolo e di soluzione
56 Più facile
57 Sono competente?
I PROBLEMI
58 Problemi matematici
59 Dentro le parole
60 Problemi e rappresentazioni
61 La domanda nei problemi
62 I dati utili e inutili
63 I dati mancanti e nascosti
64 Con due domande
65 Una domanda è nascosta
66 Operazioni e problemi
67 Problemi, immagini e tabelle
68 Problemi logici
69 Sono competente?
70 Insieme nella realtà
72 Frazionare 73 Le frazioni 74 L’unità
130 Succederà?
131 Quanto è probabile?
132 Più facile
133 Sono competente?
134 Insieme nella realtà
Cerca e ascolta le canzoni di David

Sai perché è importante studiare la matematica?




La matematica insegna a ragionare, apre la mente e contribuisce a sviluppare la capacità di comunicare e discutere in modo corretto, di comprendere meglio la realtà e gli altri.
La nostra vita è regolata dalla matematica. Usiamo i numeri per contare, per misurare il tempo e spesso facciamo semplici operazioni a mente, senza neanche accorgercene.
1 Cerchia i numeri formati da cifre tutte uguali.
2 Completa la tabella con i numeri mancanti, poi colora di azzurro tutti i numeri che hanno 2 u, di giallo i numeri da 51 a 59 e infine rispondi.
• Come sono disposti i numeri che terminano con 2 u? ..........................................................................................
• Nella tabella, muovendoti dall’alto al basso, i numeri aumentano di una decina. 12 22 ........... ...
• Che cosa cambia nella serie dei numeri da 51 a 59 che incontri muovendoti da sinistra a destra?
3 Ora che hai scoperto le "regole", completa queste reti con i numeri mancanti.


 4 Scrivi i numeri in lettere.
6 Riscrivi i numeri in ordine crescente.
7 Riscrivi i numeri in ordine decrescente.
8 Colora della stessa tinta i cartellini che contengono le stesse quantità.
4 Scrivi i numeri in lettere.
6 Riscrivi i numeri in ordine crescente.
7 Riscrivi i numeri in ordine decrescente.
8 Colora della stessa tinta i cartellini che contengono le stesse quantità.
Il nostro sistema di numerazione è decimale perché si raggruppano le quantità per dieci.
1 Osserva e completa.
Il nostro sistema di numerazione è posizionale: in ogni numero il valore delle cifre dipende dalla loro posizione.

2 Completa gli abachi e rispondi.
È possibile leggere la cifra 2 sempre con la stessa parola? Perché?
3 Osserva, cerchia la cifra 2 e scrivi i numeri in parola.
4 Osserva l’esempio e completa.
1 Scrivi i numeri rappresentati con i diversi metodi e completa come nell’esempio.

2 Completa le tabelle: fai attenzione alla posizione delle cifre e al significato delle frecce.
3 Colora il numero maggiore in ogni bandiera.
4 Completa con i numeri mancanti.
1 Leggi e rifletti.
Lo zero è inutile: se lo tolgo, 3 u restano 3 u. 30 03
Lo zero è necessario: se lo tolgo, 3 da diventano 3 u.
2 Osserva, poi cancella con una X gli zeri inutili dai numeri nelle tabelle.
Lo zero è una cifra "segnaposto" importante: serve a indicare che, nella posizione dove si trova, ci sono zero unità, oppure zero decine e così via...

3 Componi i numeri come nell’esempio. Fai attenzione agli zeri "segnaposto".
4 Completa la tabella come nell’esempio.
Insieme con i compagni scopri quali strategie si possono usare per confrontare i numeri. Quali cifre confronti per prime?

1 Osserva, leggi e completa.
ECCO IL 1 000 1 migliaio 1 k 1 centinaio 1 h 1 decina 1 da
× 100 × 1 000
Una decina è formata da unità.
Dieci decine formano un ................................................, che vale .................... unità.
Un migliaio è formato da .................... centinaia, ossia .................... decine oppure .................... unità.
1 k = 10 h = 100 da = 1 000 u
1 k si legge mille e si scrive 1 000.
h
Trova quelli di 1 000, segui l’esempio. 100 e 900
400 e 600 e 200 e 300 e 500 e ...........
MEGA ESERCIZI PAG. 5 10 MATEMATICA da
u h k
Insieme ai compagni prova a spiegare che cosa cambia tra gli amici di 10, 100 e 1 000.
3 e 7 30 e 70 300 e 700
1 Osserva come si legge ciascun numero.
2 Scrivi il numero in lettere.

3 Scrivi quanto vale la cifra 8 in ogni numero.
4 Osserva, completa e scrivi il numero ottenuto in lettere.
uno si legge
5 Componi i numeri: fai attenzione agli zeri segnaposto e all’ordine delle cifre.
1 Componi i numeri e scrivili in lettere. Segui l’esempio.
2 k 5 h 3 da 8 u = = =
4 k 3 h 0 da 2 u =
2 Completa le uguaglianze come nell’esempio.
3 Riordina le scomposizioni e scrivi il numero. Attenzione agli zeri segnaposto utili!

9 da 3 u 2 h = ...................................................................
h 4 k =
Insieme con i compagni divertiti a fare indovinelli all’insegnante come nell’esempio.
 1 Completa la tabella.
3 Scrivi i numeri nel riquadro adatto sulla linea.
4 Completa la tabella come nell’esempio.
1 Completa la tabella.
3 Scrivi i numeri nel riquadro adatto sulla linea.
4 Completa la tabella come nell’esempio.
1 decina (da) 10 unità (u)
Il nostro sistema di numerazione è detto decimale perché raggruppa le quantità per dieci.
10 decine (da)
1 centinaio (h)
POSIZIONALE
10 centinaia (h)
1 000 + 300 + 40 + 2
1 migliaio (k)
Posizionale perché il valore delle cifre dipende dalla posizione che esse occupano nel numero.
Quando c’è solo 1 k si legge “mille”
Quando ci sono più k si legge “mila”
1. Osserva il numero indicato dalla bambina, completa e rispondi.
• In parola si scrive ..............................................................................................................
• È formato da cifre; le k sono ; le h sono , non ci sono e le u sono
• Cerchia la cifra che vale di più: è quella delle .......................................
• Il numero 1 305 precede il ............................... e segue il ...............................

• La cifra zero nel numero dato è un segnaposto utile? SÌ NO Perché? .........................................................................................................................................
2. Colora le nuvole in cui la cifra 7 corrisponde alle centinaia.
4. Completa con il precedente e il successivo.






I termini dell’addizione MATEMATICA
L’addizione è l’operazione che permette di mettere insieme, cioè unire le quantità, e di aggiungere una quantità a un’altra.
1 Leggi e completa.
7 + 5 + 6 = 18
addendi somma o totale
a. Aggiungere b. Mettere insieme
Andrea ha risparmiato € 35; in occasione del suo compleanno riceve altri € 50. Quanti euro possiede ora Andrea?

50 ? 35
Operazione + =
Nel maneggio Lucia ha contato 8 cavalli e 4 pony. Quanti animali vi sono complessivamente?

4 ? 8
Risposta Risposta
2 Osserva l’operazione e completa il testo dei problemi.
64 + 14 = 78
a. Serena ha letto 64 pagine di un libro. ................................................................................................. .................................................................................................
25 + 23 = 48
b. Kim ha 25 automobiline blu. ................................................................................................. .................................................................................................
Per eseguire più velocemente le addizioni, puoi utilizzare le seguenti strategie.

1 Leggi, osserva e completa.
2 10
+ +
10 = 2 = ...................
Se si cambia l’ordine degli addendi, la somma non cambia: è la proprietà commutativa dell’addizione.
40 100
+ + 60 +
30 = 30 =
Se si sostituisce a due o più addendi la loro somma, il risultato non cambia: è la proprietà associativa dell’addizione.
2 Associa gli addendi “amici” di 10, 100, 1 000 e calcola velocemente.
Continua qui Continua sul quaderno

141 + 32 + 9 =
26 + 15 + 85 =
150 + 32 = 26 + 100 =
La proprietà commutativa ti serve per controllare l’esattezza del risultato, cioè per fare la prova.
140 + 75 + 60 =
148 + 23 + 7 =
200 + 800 + 126 =
600 + 18 + 400 =
3 Osserva e completa.
Calcola in riga: somma prima le unità, poi le decine, quindi le centinaia e così via... Segui l’esempio.
146 + 322 = 468
151 + 246 = ..................................
302 + 574 = 1 692 + 3 203 = ........................
Osserva l’esempio, rifletti e calcola rapidamente.
8 + 6 = 14
8 0 + 6 0 = 14 0
8 00 + 6 00 = ........ 00
Completa le addizioni e raggiungi...
... la decina successiva
... il centinaio successivo ... il migliaio successivo
425 + 132 = .................................
864 + 125 =
2 316 + 4 251 = ..........................
Calcola le addizioni e cerchia quelle in cui conviene usare la proprietà commutativa.
Applica le proprietà dell’addizione e calcola.
In alcuni casi, per eseguire più velocemente un’addizione, conviene scomporre gli addendi. Osserva l’esempio e continua tu.
Completa: raggiungi prima la decina, poi il centinaio e infine il migliaio successivi.

Attenzione!
Il cambio può trovarsi anche solo nelle decine.

Incolonna le unità sotto le unità, le decine sotto le decine e così via.
Addiziona sempre prima le unità.
Sono più di 9?
Continua e addiziona le decine e poi le centinaia. no
Scrivi le unità nella colonna delle unità e riporta le decine nella colonna delle decine.
Addiziona le decine e poi le centinaia.
2 Calcola in colonna facendo attenzione al cambio.Fai
La sottrazione è l’operazione che permette di calcolare il resto, la differenza fra due quantità, quanto manca per raggiungere una quantità e quanti elementi non appartengono a un gruppo.
1 Leggi e completa.
a. Resto
Un muratore deve sistemare 120 piastrelle. Se ne ha già posizionate 40, quante gliene restano da sistemare?

120 ? 40
Operazione – =
I termini della sottrazione
36 – = 4 32
minuendo sottraendo resto o differenza
b. Differenza
Nel campionato di basket le due squadre hanno totalizzato 18 e 13 punti. Qual è la differenza?

18 ? 13
Operazione – =
Risposta
c. Quanto manca
Alessia vuole acquistare un libro che costa € 14, ma possiede solo € 6. Quanti euro le mancano?


d. Quanti sono gli altri
Sullo scaffale di una libreria ci sono 65 libri, di cui 23 sono fumetti e gli altri sono fiabe. Quanti sono i libri di fiabe?
65 ? 23
Operazione ................. – ................. = .................
Risposta Risposta
Operazione ................. – ................. = .................
1 Leggi, osserva e completa.
In una pasticceria c’è un vassoio con 5 bignè al cioccolato e 3 alla crema.


Vengono tolti 2 bignè per tipo.
Qual è la differenza? 5 – 3
Qual è la differenza?
Vengono aggiunti 3 bignè per tipo.
Se si aggiunge o si toglie una stessa quantità al minuendo e al sottraendo il risultato non cambia: è la proprietà invariantiva della sottrazione.
2 Applica la proprietà invariantiva per eseguire questi calcoli nella maniera più conveniente.
3 Risolvi il seguente problema.
Il nonno ha 62 anni e la nonna ne ha 58. Qual è la loro differenza di età? Tra 10 anni quale sarà la loro differenza?
Ora imparerai a calcolare le sottrazioni velocemente!

Calcola in riga: sottrai prima le unità, poi le decine, quindi le centinaia e così via...
Correggi dove è stata usata male la proprietà invariantiva. Poi esegui i calcoli.
Scopri il numero che manca per ottenere quello scritto nella striscia colorata.
In alcuni casi, per eseguire più velocemente una sottrazione, conviene scomporre il sottraendo. Osserva l’esempio e continua tu.
Gioca con gli amici del 100 nelle seguenti sottrazioni.
Completa aiutandoti con i suggerimenti.
2?
Se ci sono più cambi, segui ogni volta le stesse istruzioni.

Incolonna le unità sotto le unità, le decine sotto le decine e così via.
Sottrai sempre prima dalle unità del minuendo quelle del sottraendo.
La cifra del minuendo è maggiore di quella del sottraendo?
Sottrai le unità.
Sottrai le decine e poi le centinaia.
Prendi una decina e cambiala con 10 unità.
Aggiungi le 10 unità alle unità.
1 Leggi con attenzione e osserva. 2 Calcola in colonna facendo attenzione ai cambi.1 Leggi attentamente e osserva. Poi calcola tu.
Fai attenzione quando il minuendo ha gli zeri. Il centinaio si cambia con 10 decine e una decina passa alle unità.
Per controllare se la sottrazione è esatta, fai la prova con l’addizione.
– 60 = 40
40 + 60 = 100
Se
 1 Osserva e rifletti.
2 Completa i diagrammi.
1 Osserva e rifletti.
2 Completa i diagrammi.
1 Osserva le frecce e completa i calcoli nelle tabelle. Quando non puoi eseguire un calcolo, colora di rosso la casella corrispondente.
–0
3
Osserva i risultati della prima tabella: hai potuto eseguire tutti i calcoli?
SÌ NO
1 2 3 4 LE OPERAZIONI
2 Rifletti e completa.
L’addizione è un’operazione sempre possibile
Osserva i risultati della seconda tabella: hai potuto eseguire tutti i calcoli?
SÌ NO
La sottrazione non è sempre possibile; può essere calcolata solo quando il minuendo è maggiore o uguale al sottraendo.
• Che cosa accade quando aggiungi 1 a un numero?
0 + 1 = ................. 3 + 1 = .................. Il risultato è sempre ..............................................................
• Che cosa accade quando un addendo è 0?
2 + 0 = ................ 10 + 0 = ............. Il risultato è sempre ..............................................................
• Che cosa accade se sottrai 1 a un numero?
1 – 1 = 13 – 1 = Il risultato è sempre
• Che cosa accade se sottrai 0 a un numero?
• Che cosa noti se minuendo e sottraendo sono uguali?
3 – 3 = ................. 10 – 10 = ............ Il risultato è sempre ..............................................................
0 + 29


1 Chi conta più velocemente? Leggi e rispondi a voce.

Per calcolare + 9, conviene andare avanti un numero alla volta.
Per calcolare + 9, conviene aggiungere 1 da e poi sottrarre 1 u.
2 Completa le tabelle aiutandoti con le regole.
3 Osserva le regole e calcola.
Che strategia useresti se dovessi aggiungere 190? Trova la soluzione con i

Quanto paghi in tutto?
€ ? LE OPERAZIONI
Quanto costa la corda?
8
Quale articolo costa di più?



19
 4 Osserva, calcola in riga e risolvi.
4 Osserva, calcola in riga e risolvi.
3 10
1. Indica se le affermazioni sono vere (V) o false (F).
Gli addendi sono presenti nell’addizione.
Nella sottrazione calcoli sempre il resto. Addizione e sottrazione sono l’una il contrario dell’altra.
50 è la somma degli addendi 30 e 20. La differenza tra 60 e 20 non è 40.
COME L’INVALSI
Ogni macchia copre un numero. Indica con una X quello corretto.
La moltiplicazione è l’operazione che permette di ripetere più volte la stessa quantità, oppure di calcolare le combinazioni possibili.
1 Leggi e completa.
a. Ripetere una quantità
Se per fare una torta occorrono 6 mele, quante mele servono per 3 torte?
moltiplicando
I termini della moltiplicazione moltiplicatore
8 x = 9 72 prodotto
b. Calcolare le combinazioni
Quanti pacchetti diversi si possono confezionare con 2 tipi di scatole e 3 nastri di colori diversi?

6 + 6 + 6 = o 6 × = Operazione × =
2 Leggi e risolvi sul quaderno.
a. Il nonno percorre 4 chilometri al giorno per accompagnare Karim a scuola. Quanti chilometri percorre in sei giorni?
b. Anna ha 2 gonne e 4 magliette. In quanti modi diversi potrà vestirsi per andare a scuola?
3 Con un tuo compagno inventa il testo di un problema adatto a questo disegno.


MATEMATICA
1 Leggi, osserva e completa.
Se si cambia l’ordine dei fattori, il prodotto non cambia: è la proprietà commutativa della moltiplicazione. La proprietà commutativa serve anche per fare la prova della moltiplicazione.
2 × 4 = .............. 4 × 2 = ..............
2 Su ogni ripiano ci sono 2 vasi con 4 fiori ciascuno. Quanti fiori ci sono in tutto?

Puoi risolvere in due modi: osserva e rispondi.
4 × 2 × 3 = 8 × 3 = 24
fiori in tutto
fiori in tutto
fiori in ogni vaso
Il prodotto di tre o più fattori non cambia se sostituisci a due di essi il loro prodotto. Questa è la proprietà associativa della moltiplicazione.
3 Applica la proprietà commutativa e calcola.
b. 7 × 4 = 4 × = 9 × 6 = × = 8 × 7 = × = 4 × 8 = × =
















4 Associa i fattori scritti in rosso e calcola. 4 × 5 × 8 = ............ × ............ = ............
2 × 9 × 3 = ............ × ............ = ............ MEGA ESERCIZI PAG. 18 36
5 Leggi, osserva e completa.
15 x 3 = 45 Puoi rappresentare questa moltiplicazione con uno schieramento e “tagliarlo” al 10 così:

In una moltiplicazione si può scomporre un fattore in addendi, moltiplicare separatamente ciascun addendo per l’altro fattore e sommare i prodotti ottenuti: è la proprietà distributiva della moltiplicazione.
6 Ora prova tu con questa operazione: 17 × 4 = 68. Osserva e completa.
7 Applica la proprietà distributiva come nell’esempio.
8 Ora applica la proprietà distributiva in tabella come nell’esempio.

Quando moltiplichi un numero per 10, 100, 1 000 basta scrivere alla sua destra uno, due o tre zeri.

Quando si moltiplica un numero per 10, 100, 1 000, il valore di ogni cifra diventa 10, 100, 1 000 volte maggiore Completa

Calcola velocemente scomponendo come nell’esempio.
Calcola velocemente moltiplicando prima le cifre evidenziate e poi
uno zero a destra.
1 Leggi con attenzione le istruzioni e osserva.
Puoi trovare anche più cambi. Segui ogni volta le stesse istruzioni.

Moltiplica le unità del secondo fattore per le unità del primo.
Le unità sono più di 9?
Scrivi le unità nella colonna delle unità e riporta 1 decina.
Moltiplica le unità del secondo fattore per le decine del primo.
Scrivi il risultato nella colonna delle unità. Moltiplica le unità del secondo fattore per le decine del primo.
Aggiungi al risultato il riporto.
Scrivi il risultato nella colonna delle decine.
2 Calcola in colonna sul quaderno.
1 Leggi le istruzioni e calcola.
Moltiplica le unità del secondo fattore per il primo fattore.
Ottieni il 1° prodotto parziale.
Metti lo zero segnaposto nella colonna delle unità.
Moltiplica le decine del secondo fattore per il primo fattore.
Ottieni il 2° prodotto parziale.
Insieme ai compagni osserva che per queste moltiplicazioni si applica la proprietà distributiva.
43 × 12
Somma i due prodotti parziali e ottieni il prodotto totale.
43 × (2 + 10)
(43 × 2) + (43 × 10)
86 + 430 = 516
2 Calcola ed esegui la prova. Fai attenzione ai riporti.
1. Colora gli spazi con le coppie di numeri il cui prodotto è quello indicato. Con i numeri restanti scrivi la moltiplicazione e calcola.
2. Calcola e colora il nome della proprietà utilizzata.
7 × 8 = 8 × 7 = .........................................................
3 × 8 × 10 = 10 × 8 × 3 =
25 × 4 = (20 × 4) + (5 × 4) =
4 × 3 × 5 = 12 × 5 =
3. Calcola in colonna.
COME L’INVALSI
Leggi e indica con una X la soluzione corretta.
Il commesso del supermercato dispone di 6 scatole con 5 buste di caramelle ciascuna. Ogni busta contiene 10 caramelle. Quante sono tutte le caramelle?
La divisione serve per distribuire in parti uguali e per raggruppare
È l’operazione che permette di calcolare quante volte una quantità è contenuta in un’altra.
1 Leggi e completa.
Mario ha 8 fragole da distribuire in parti uguali in 2 torte. Quante fragole conterrà ogni torta?

8
? ?
20 : = 4 5
dividendo
I termini della divisione divisore (quoziente se c’è resto)
a. Distribuire b. Raggruppare
Ada ha 8 fragole e ne vuole disporre 4 in ogni torta. Quante torte le occorrono?
8
4 4 Quanti gruppi? Quante in ognuna?
Operazione : 2 =
Operazione : 4 =
Risposta Risposta
Quando distribuisci vuoi conoscere quanti elementi puoi mettere in ogni gruppo.
Quando raggruppi vuoi conoscere quanti gruppi puoi formare.
2 Leggi e ripassa la cornice in blu se la divisione distribuisce, in rosso se raggruppa. Infine risolvi sul quaderno.
a. Con 28 pile quanti telecomandi puoi far funzionare se ne servono 4 per ogni telecomando?
b. 15 amici formano 3 squadre per giocare. Da quanti amici è formata ogni squadra?
1 Osserva e completa. Poi segui le frecce e calcola.
risultato è sempre lo stesso?

Moltiplicando o dividendo i due termini della divisione per uno stesso numero diverso da zero il risultato non cambia: è la proprietà invariantiva della divisione.
2 Applica la proprietà invariantiva e calcola. Poi segui l’esempio.
3 Calcola le divisioni applicando la proprietà invariantiva.



Vero
1 Leggi le istruzioni con attenzione e calcola.
INIZIO

Considera la prima cifra a sinistra, indicala con un e calcola.
Il 3 è contenuto
2 volte nel 6 perché
3 x 2 = 6
Considera la seconda cifra, indicala con un , trascrivila a destra del resto parziale e calcola.
FINE
Il 3 è contenuto
3 volte nel 9 perché
3 x 3 = 9
Osserva che cosa succede quando le divisioni non hanno resto 0. Con il resto
Il 2 è contenuto
4 volte nel 9 perché
2 x 4 = 8 9 – 8 = 1
Il 2 nel 17 è contenuto
8 volte perché
8 x 2 = 16 17 – 16 = 1
RAGIONIAMO
2 Dividi in colonna sul quaderno.
a.
Rispondi insieme ai compagni.
• Da dove hai iniziato il calcolo delle divisioni?
• Nelle altre operazioni, da dove si inizia a calcolare?
Se

Il 5 nel 12 è contenuto 2 volte perché
2 x 5 = 10 Per trovare il resto sottrai: 12 – 10 = 2
Il 5 nel 25 è contenuto 5 volte perché 5 x 5 = 25 Per



 1 Osserva e rifletti.
1 Osserva e rifletti.
Per la prova moltiplica il quoziente per il divisore e poi aggiungi il resto finale se è presente.
1 Osserva la freccia e completa la tabella. Poi rispondi.
Hai ottenuto sempre un risultato? SÌ NO
La moltiplicazione è un’operazione sempre possibile.
• Che cosa accade quando uno dei fattori è 1? Il risultato è
• Che cosa accade quando uno dei fattori è 0? Il risultato è sempre
2 Osserva la freccia e completa la tabella solo con le divisioni che danno resto 0. Poi rispondi.
Hai ottenuto sempre un risultato? SÌ NO
La divisione con resto 0 non è sempre possibile.
• Che cosa accade se dividendo e divisore sono uguali?
• Che cosa accade quando il divisore è 1?
• Che cosa accade se dividi 0 per qualsiasi numero diverso da 0?
Il risultato è
È impossibile dividere un numero per 0.
1 : 0 = impossibile
2 : 0 = impossibile
1 Per eseguire più facilmente le divisioni applica la proprietà invariantiva: ottieni il divisore a una cifra!
2 Completa con i fattori mancanti.
3 Quanto manca per arrivare a 1 000? Raggiungi prima il centinaio successivo e poi 1 000, come

1 Chi conta più velocemente? Leggi e rispondi a voce.

Per moltiplicare una quantità × 9 conviene mettere in colonna.
2 Calcola seguendo la strategia di Silvia.
Per moltiplicare x 11, calcola prima x 10 e poi aggiungi il numero del 1° fattore.
15 = 150 + 15 = ..................... Continua qui
4 Calcola e rifletti. Poi esegui sul quaderno.
Per moltiplicare x 5, moltiplica prima x 10 e poi dividi per 2.
5 Osserva, calcola e risolvi.
Quanto costano tutti i palloncini?


Quanto costa ogni cono?
Quanto costano 1 tazzina di caffé e 3 bicchieri di succo?





Quanto costa un cornetto?


1. Cerchia il divisore e correggi le divisioni errate scrivendo il risultato esatto.
2. Completa usando la proprietà invariantiva.
3. Calcola in colonna.
4. Scrivi i numeri che mancano.
COME
Cerchia il risultato corretto. Indica la risposta corretta.
La metà della metà di 128 è: Alex regala una scatola con 4 automobiline a ogni amico. Se ha 24 automobiline, quanti amici accontenta?
1 Leggi la procedura per risolvere i problemi matematici e applicala al problema dato.
Leggi il testo attentamente.
Il fruttivendolo prepara 4 cestini mettendo 3 ananas dentro ciascuno. Quanti ananas utilizza?
Immagina la situazione. Puoi aiutarti con un disegno o uno schema.
Individua la domanda e analizza i dati necessari.
3 3 3 3
Legenda =
Rifletti, scegli l’operazione adatta e calcola.
Hai controllato la correttezza della soluzione e dei calcoli?
sì
Formula la risposta
no
Domanda ..................................................................................................................
Dati ....................................................................................................... .......................................................................................................
Operazione ..................................................................................
Risposta ..................................................................................................................
2 Cerchia i dati, sottolinea la domanda e risolvi.
Aisha e le due sorelle vanno al cinema. Ciascun biglietto costa € 8, quanto spendono in tutto?
Operazione ..................................................................................
Risposta
Leggi con attenzione, colora le parole adatte al testo del problema e poi risolvilo sul quaderno.
Emma ha 4 pacchetti buste di biscotti; in ciascuno pochi ce ne sono 20.

Quanti sono i biscotti in tutto in ciascuno ?
Leggi attentamente e completa il testo dei problemi con le parole ogni e tutto. Poi collega il testo all’operazione corretta e calcola.
a. Un fioraio prepara 30 mazzi di rose. In .............................. mazzo mette
6 rose. Quante rose gli servono in ?
b. Yasir ha incollato in 30 figurine in un album di 6 pagine. Quante figurine ha messo in pagina?
RAGIONIAMO
Insieme ai compagni rifletti e rispondi.
• Hai messo sempre la parola "ogni" nella domanda?
• Quando "ogni" sta nella domanda, quale operazione si usa di solito?
Completa il testo con le parti adatte e poi risolvi.
Il cinema ha ....................................... posti.

Allo ....................................... delle ore ....................................... sono presenti
adulti e 90
Quante sono rimaste libere?
1 Leggi il testo, indica con una X la rappresentazione adatta e risolvi.
In spiaggia ci sono 3 file di ombrelloni. In ogni fila ci sono 10 ombrelloni: quanti ombrelloni vi sono in tutto?
2 Osserva il disegno e cancella con una X il testo non adatto.
Irene compra dei quaderni che costano € 3 ciascuno. Se ha speso € 12, quanti quaderni acquista?
Irene spende € 3 per ogni quaderno. I quaderni sono 12. Quanti euro le servono?
















Irene ha comprato 4 quaderni. Ognuno costa € 3. Quanto spende in tutto?
3 Leggi, osserva le rappresentazioni, poi rispondi alle domande e risolvi.
a. Lea ha vinto 15 figurine e le aggiunge alle 10 che già possedeva. Quante figurine ha in tutto ora?
b. Raya sta preparando 5 dolcetti e mette 3 confetti sopra a ognuno. Di quanti confetti ha bisogno? 15 10 ? 3 3 3 3 3 ?
• Conosci il numero totale di figurine? ...................................................................................................
• Devi trovare il numero totale di figurine o solo una parte di esse?
• Quale operazione ti serve per aggiungere? ..................................................................
• Conosci il numero di confetti per ogni dolcetto? ...........................................................................
• Conosci il numero dei confetti in tutto?
• Che operazione devi fare per trovarlo? ...................................................................................................
1 Indica con una X la domanda adatta al testo del problema e risolvi.
In biblioteca sono arrivati 5 pacchi di libri. Ogni pacco contiene 40 libri.
Quanti sono i pacchi?
Quanti libri ci sono in ogni pacco?
Quanti libri sono arrivati in tutto?
3 Inventa una domanda collegata al problema.
La mamma ha preparato 25 panini per una festa; ne deve preparare altri 35.

2 Indica con una X il testo più adatto alla domanda e risolvi.
Quanti piatti servono?
La nonna ha preparato 36 panini e ne mette 9 in ogni piatto.
La nonna ha preparato 5 piatti con 10 panini in ognuno.
RAGIONIAMO I PROBLEMI
Marco ha speso € 35 e Sara € 40. .......................................................................................... ..........................................................................................
Per risolvere un problema puoi usare il diagramma, uno strumento utile per rappresentare il percorso fino alla soluzione.
4 Inventa sul quaderno un problema adatto a ogni diagramma e risolvi.
I dati nei problemi possono essere
utili: servono per trovare la soluzione inutili: non servono per trovare la soluzione
1 Leggi i problemi, completa le tabelle e risolvi.

a. Il papà si reca al supermercato che dista 200 m da casa e spende € 15 per il gelato, € 28 per la carne e € 2 per il latte. Quanto spende in tutto?
Dati utili Dati inutili ,
b. L’anno scorso gli alunni della scuola “Prato fiorito” erano 138 e le maestre erano 12. Quest’anno si sono iscritti altri 50 bambini. Quanti sono ora gli alunni?

Dati utili Dati inutili ................................................. .................................................
................................................. .................................................
2 Inserisci i dati utili nei problemi e risolvi.
2
Operazione ...........................................................................
Risposta .................................................................................
750 48 200
Per Carnevale la maestra prepara mascherine e ogni alunno ne ritaglia ............. Da quanti alunni è formata la classe?
Fabio acquista un computer che costa
€ ....................... Paga subito € .......................
Quanto gli resta da pagare?
Operazione Operazione
Risposta ................................................................................. Risposta .................................................................................
1 Leggi il testo e completa.
Mohamed ha comprato 6 scatole di pennarelli. Quanti pennarelli ha in tutto?
• Puoi risolvere il problema? SÌ NO
• Quale dato manca? .............................................................................
• Inventa tu il dato, poi risolvi sul quaderno.
2 Inventa i dati mancanti e risolvi sul quaderno.
a. Sam sta leggendo un libro di avventura. Ha letto 24 pagine. Quante pagine gli mancano per finire il libro?
Se nei problemi mancano i dati utili, non è possibile trovare la soluzione.
b. In biblioteca l’anno scorso c’erano 138 libri. I bambini quest’anno ne hanno portati di nuovi. Quanti libri ci sono adesso in biblioteca?
In alcuni problemi i dati possono essere nascosti, cioè indicati con delle parole che hanno un valore numerico.
3 Collega ogni dato nascosto al valore numerico o all’operazione corrispondente.
4 In questi due problemi ci sono dei dati nascosti. Individuali e risolvi sul quaderno.

a. Adele ha messo in lavatrice 18 paia di calzini. Quanti calzini dovrà stendere?
b. Marcello ieri ha raccolto 16 pomodori e oggi ne ha raccolto il triplo. Quanti pomodori ha raccolto oggi?
Nei problemi si può trovare più di una domanda e, per rispondere a ciascuna, occorrono dati e operazioni adeguate. A volte il risultato della prima operazione diventa un dato utile per rispondere alla seconda domanda.
1 Leggi attentamente e completa le operazioni e il diagramma.
Il giornalaio Mario questa mattina aveva 150 copie di quotidiani. Alla chiusura ne sono rimasti 20.
Quanti giornali ha venduto?
Se ha venduto ogni copia a € 2, quanto ha incassato?
1a domanda
Per rispondere alla 1a domanda occorre calcolare – = giornali venduti
.............
2
giornali iniziali giornali rimasti costo di una copia giornali venduti incasso totale
? ?
2 Osserva il diagramma, completalo e scrivi un problema adatto con due domande. Lavora con un compagno.
mele rosse mele verdi cassette
10
+ :
Per rispondere alla 2a domanda occorre usare il risultato della 1a operazione .............. × .............. = .............. 154 146 ............. .............
............. ............. –MEGA ESERCIZI PAGG. 33-34 64 MATEMATICA
Alcuni problemi presentano una sola domanda, ma per risolverli occorrono due operazioni perché una domanda è nascosta.
1 Leggi con attenzione e risolvi utilizzando il diagramma.
Un treno è formato da 10 vagoni; in ogni vagone ci sono 60 posti a sedere.
Quanti posti restano liberi se i passeggeri sono 485?
Per risolvere questo problema devi prima rispondere a un’altra domanda.
Quanti posti ci sono in tutto?
Questa è la domanda nascosta.
............. ............. ......
.............
posti in ogni vagone numero vagoni passeggeri .................... ? ?
2 Scrivi la domanda nascosta e risolvi sul quaderno.
Stefania ha acquistato 5 confezioni di succhi con 6 succhi ciascuna. ?
In una settimana la famiglia ne ha bevuti 18. Quanti succhi sono rimasti?
? Domanda nascosta ..............................................................................................................................
3 Leggi, scrivi le domande nascoste e risolvi sul quaderno.
Tre amici giocano con le figurine.
Amici Figurine
Luca 40
Carlo il doppio di Luca
Gabriele la metà di Luca
Domande nascoste ........................................................................................................
Quante figurine hanno in totale? ........................................................................................................................................
1 Colora le caselle con il segno adatto a ogni situazione.
La cuoca prepara 10 torte e su ciascuna mette 7 fragole. + : x –
Francesco ha 12 anni e sua sorella Gaia ne ha 4 di meno. + : x –
Carlo ha sistemato 50 libri su 5 mensole. + : x –
Il papà di Fatim ha acquistato 13 quaderni a righe e 9 a quadretti. + : x –
2 Collega ogni problema all’operazione che lo risolve.
• Nel porto di Ancona arrivano ogni giorno 48 imbarcazioni. La terza parte di esse riparte dopo 6 ore. Quante imbarcazioni partono?
48 × 3 = 144 MATEMATICA
• Nel porto di Ancona sono arrivate 48 imbarcazioni; in quello di Genova il triplo. Quante imbarcazioni arrivano a Genova?
– 3 = 45 48 : 3 = 16 48 + 3 = 51
• Nel porto di Ancona ieri fino alle ore 20 c’erano 48 imbarcazioni, più tardi ne sono arrivate altre 3. Quante imbarcazioni ci sono ora in tutto?
48

1 Colora la rappresentazione adatta (a o b), poi indica con una X se le affermazioni sono vere (V) o false (F) e risolvi.
Omar ha acquistato tre coppette di gelato e una confezione di 4 coni da € 12. Ogni coppetta costa € 2. Quanto spende in tutto Omar?
a.

• Ogni cono gelato costa € 12. V F
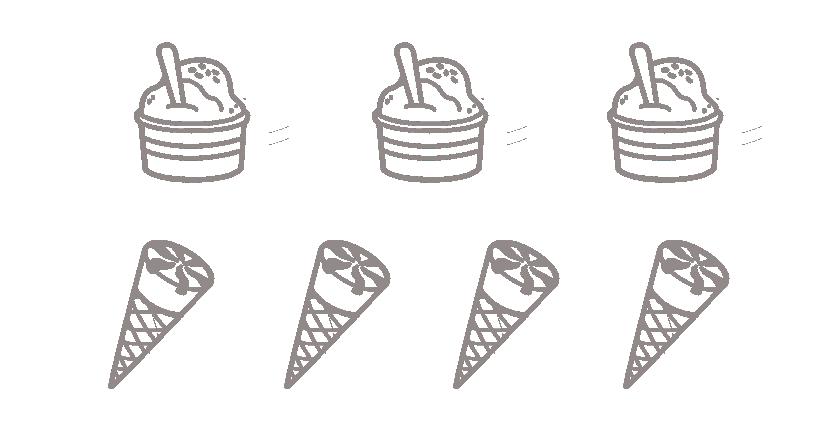
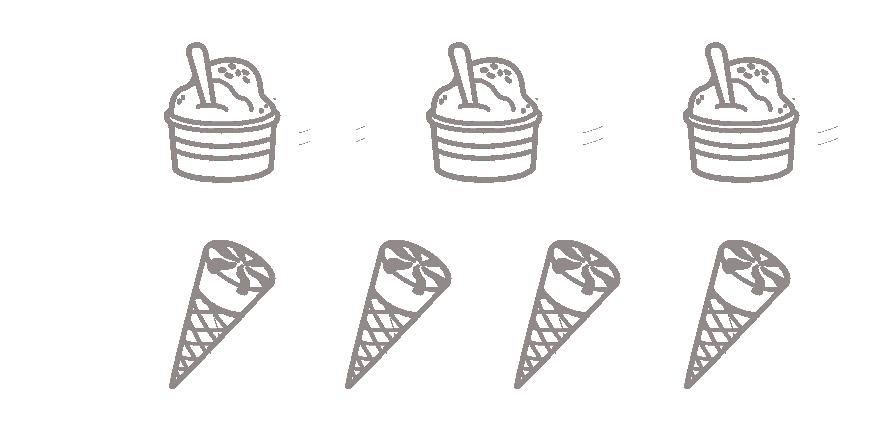
• Una confezione di coni costa € 12. V F
• Le coppette costano € 2 l’una. V F
• Omar spende in tutto € 12. V F
Operazioni
€ 2
2 Completa la tabella, poi indica con una X se le affermazioni sono vere (V) o false (F).
Tre amici giocano a lanciare delle palline colorate in un cestino. Ciascuno di loro registra i lanci sulla tabella. Scopri chi ha vinto.
Paolo
• Paolo fa solo tiri da 20 punti. V F
• Alcuni tiri di Kevin valgono 10 punti. V F
• Ogni tiro di Ling vale 5 punti. V F
• Tutti hanno fatto 5 tiri. V F
Alcuni problemi per essere risolti non richiedono numeri e operazioni, ma solo un ragionamento che invita a fare molta attenzione al testo.
1 Leggi e colora.
Tra le immagini che vedi c’è la sorella di Enrico. Colorala sapendo che:
• ha la borsa; • ha la gonna; • ha il cappello; • ha gli orecchini.
In altri casi un problema ammette più soluzioni e tutte possono essere corrette purché rispettino quanto riportato nel testo.
2 Leggi, osserva e completa.
Se in un parcheggio conti 14 ruote tra auto e moto, quante possono essere le auto? E le moto?
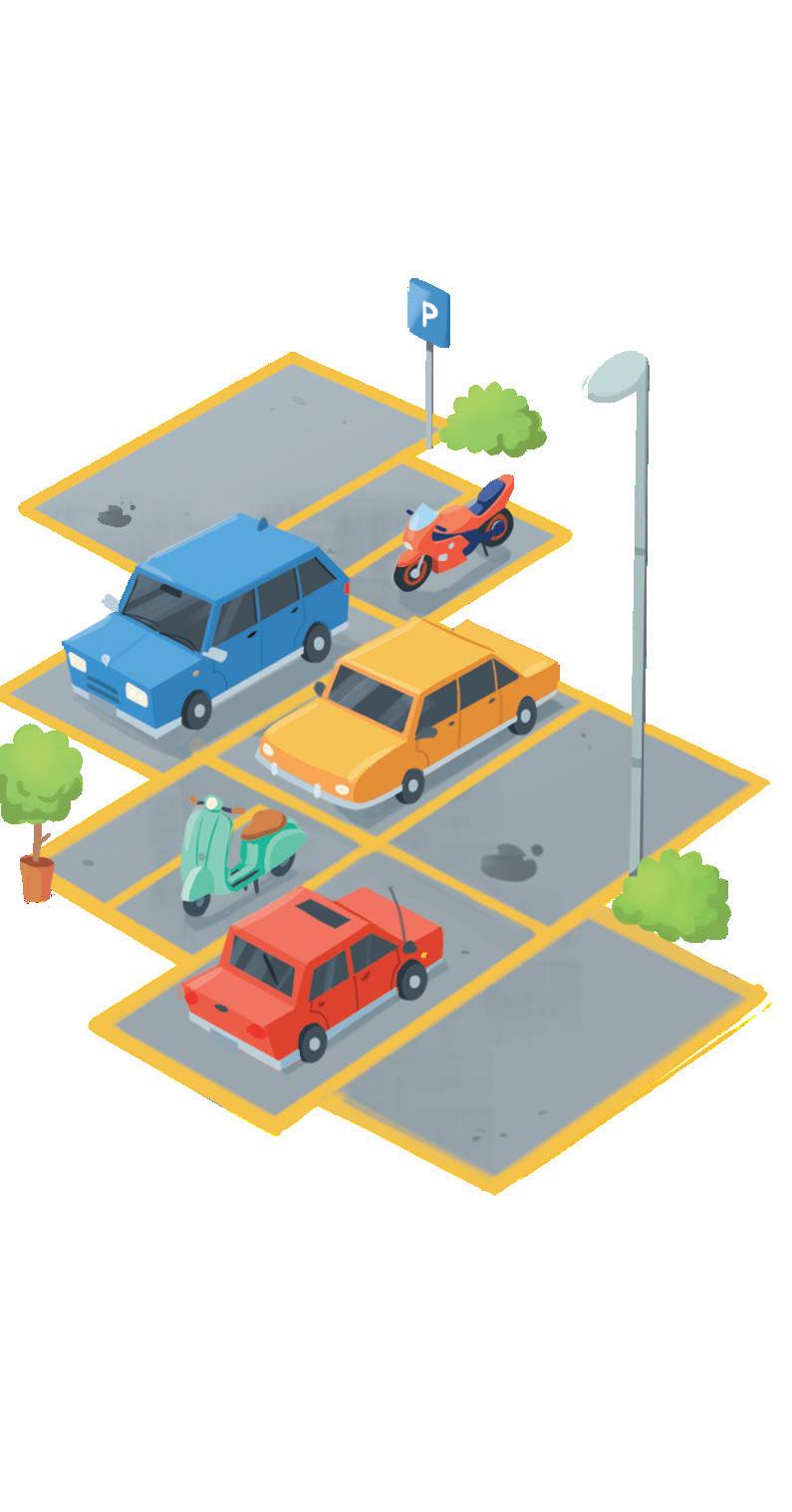

1 auto 4 ruote 1 moto
14 – 4 = 10 10 : 2 = ............ moto
1. Osserva, scrivi la domanda adatta e risolvi.

Il nonno ordina 3 panini e 3 succhi per i suoi 3 nipoti e un caffè per sé.
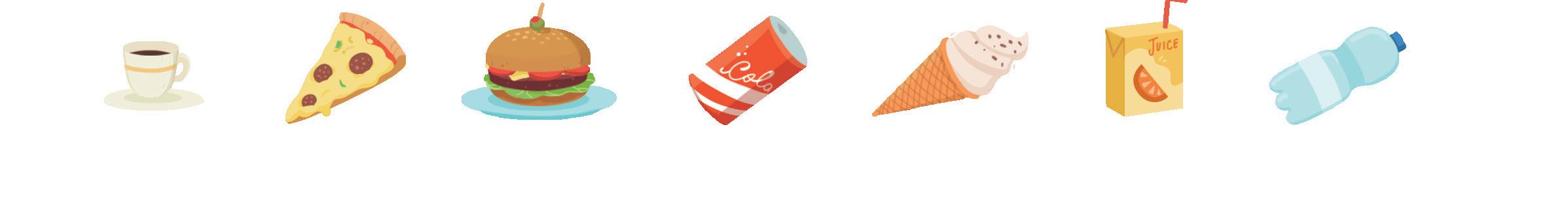
Domanda .......................................................................................................................................................................................................
Operazioni ...................................................................................................................................................................................................
2. Leggi il problema, cerchia solo le informazioni utili per la soluzione e risolvi.
Allo stabilimento “Mareblu” ci sono 258 ombrelloni. Il bagnino ha organizzato un torneo di beach-volley con inizio alle ore 17. Gli iscritti sono 82, ma si ritirano 10 ragazzi e 9 ragazze. Quanti partecipanti gareggiano?

Operazione
Risposta
3. Scopri il dato mancante, aggiungilo e risolvi.
a. Yuri ha pagato lo zaino con una banconota da € 100. Quanto ha speso per lo zaino?
b. Un parcheggio può ospitare 120 auto su ogni piano. Quanti mezzi entrano in tutto?
Dato mancante ................................................................. Dato mancante .................................................................
Operazione Operazione
Risposta ................................................................................. Risposta .................................................................................
Quanto costano 3 succhi?


Per la Festa della Matematica vi viene chiesto di risolvere dei problemi matematici. Lavorate in gruppi da tre: vincerà la squadra che farà meno errori.
Leggete il testo dei problemi e cercate di capire la soluzione corretta seguendo il diagramma di flusso. Ragionate ad alta voce. Per seguire più agevolmente le indicazioni del diagramma, procuratevi un segnaposto simile a quello del “Gioco dell’oca”.
Le quantità si devono mettere insieme?
Si uniscono quantità tutte uguali?


Uso la moltiplicazione.
Si separano quantità tutte uguali?
no no no
Uso l’addizione.
Uso la sottrazione.
Io leggo più volte ad alta voce, poi ragioniamo insieme seguendo il diagramma.
INIZIO 1 2 3
Uso la divisione.
Dopo aver riflettuto tutti insieme, io scrivo la soluzione.
a. Mirco ha 130 figurine di animali, ma alcune sono doppie, perciò decide di darle a Luca. Ora gliene rimangono 83. Quante figurine ha regalato?
b. Maya riordina i 162 libri che tiene in soffitta e ne mette 9 in ogni scatolone. Quanti scatoloni utilizza?
c. La cuoca ha cucinato le polpette e ne ha messe 12 in ciascuno dei 9 vassoi che ha preparato. Quante polpette ha cucinato?
d. Livia paga una bici con i suoi risparmi. Possiede € 198 e € 120 che le sono stati regalati dai nonni. Se li usa tutti, quanto paga la bici?
A turno, ogni gruppo spiega le soluzioni che ha trovato.
L’attività svolta è stata:
Hai lavorato bene con il tuo compagno?
Ti sei divertito?
1 Osserva e leggi.
Questi sono esempi di interi



Questi invece non sono interi.
È un intero È un intero spezzato È un intero frazionato
L’intero diviso in parti uguali è frazionato
2 Indica con una X gli interi frazionati.
3 Fraziona in modo diverso questi interi uguali.

1 Osserva, leggi e completa.
2
2 3
Il rettangolo è frazionato in parti uguali.
I gettoni colorati corrispondono a 2 parti su 3, cioè 2 3 (due terzi). Colorane 4. Hai colorato 4 parti su 6, cioè 4 6 (quattro sesti).
4 6 e 2 3 sono frazioni. Una frazione indica in quante parti è stato diviso l’intero e quante parti vengono considerate.
numeratore: indica il numero delle parti considerate.
linea di frazione: indica che l’intero è stato diviso.
denominatore: indica in quante parti è stato diviso l’intero e dà il nome alle parti.
Nel leggere una frazione si nomina prima il numeratore e poi il denominatore. Il numeratore è un numero cardinale (due, quattro...) mentre il denominatore è un numero ordinale (quarto, sesto...). Il denominatore 2 si legge mezzo.
3 Collega ciascuna frazione al disegno corrispondente.
1 4 quarto
 Cerchia di verde il denominatore e scrivilo a parole. Segui l’esempio.
Cerchia di verde il denominatore e scrivilo a parole. Segui l’esempio.
Ogni parte in cui viene diviso un intero si dice unità frazionaria. Il numeratore è sempre 1
1 Osserva e completa.L’intero è stato frazionato in 10 parti uguali
Ogni parte è 1 10 (un decimo).
L’intero è stato frazionato in 100 parti uguali
Ogni parte è 1 .......... (un centesimo).
L’intero è stato frazionato in 1 000 parti uguali.
Ogni parte è 1 (un millesimo).
Le frazioni che al denominatore hanno 10, 100, 1 000 si chiamano frazioni decimali.
2 Scrivi la frazione decimale corrispondente alla parte colorata o colora quella indicata. Segui l’esempio.
1 Osserva e completa.Le frazioni decimali possono diventare numeri decimali, cioè numeri in cui la parte intera, l’unità (u), si scrive separata dai decimi (d) per mezzo della virgola. I decimi occupano il 1° posto a destra della virgola.
intera parte decimale
I millesimi (m) nei numeri decimali occupano il 3° posto a destra
1 I numeri decimali si possono rappresentare in tabella. Osserva l’esempio e poi continua tu.
0
2 Cerchia in verde la parte intera e in giallo quella decimale.
k h da u , d c m
3 2 5 , 9 6 7 , , , , ,

0
4 Ora colora i palloncini che contengono numeri con zeri inutili.
5 Indica V (vero) o F (falso).
16,88 8 da V F
5,909 9 m V F
8,736 3 h V F
= RAGIONIAMO MEGA ESERCIZI PAGG. 44-45 79 I DECIMALI
Anche i numeri decimali si possono rappresentare sulla linea dei numeri.
1 Il tratto tra 0 e 1 è stato diviso in 10 parti uguali, i decimi. Osserva e completa.
2 Inserisci i numeri mancanti.
3 Il tratto tra 0 e 0,1 è stato ancora diviso in dieci parti: ognuna è 1 centesimo. Osserva e completa.
4 Collega i numeri alla posizione adatta.
Per confrontare i numeri decimali, segui queste semplici regole.
1. Confronta la parte intera
2. Se la parte intera è uguale, confronta i decimi.
3. Se la parte intera e i decimi sono uguali, confronta i centesimi.
4. Fai lo stesso con i millesimi
15,62 > 14,29 perché 15 > 14
7,32 < 7,86 perché 3 < 8
12,54 > 12,51 perché 4 > 1
< 3,457 perché 2 < 7
1 Aiutandoti con la linea dei numeri, trova la relazione tra queste coppie di numeri inserendo <1 Leggi, osserva e completa. Segui l’esempio.
1 euro è un intero.







= 1 100 di € 1 = 0,01
= 2 100 di € 1 =
= 5 di € 1 =
= 10 .......... di € 1 =
= 20 di € 1 = .............
= 50 .......... di € 1 =
L’euro è la moneta unica dell’Unione Europea, presente in Italia dal 2002.































1 Quanto possiedi? Osserva e scrivi il numero decimale corretto. Segui l’esempio.
2
comprare la pizza perché
 Chi può comprare la pizza? Osserva, calcola e rispondi.
Chi può comprare la pizza? Osserva, calcola e rispondi.
































 1 Scrivi la stessa lettera per indicare euro, frazioni e numeri decimali corrispondenti.
2 Scrivi sotto forma di frazione e di numero decimale quanti centesimi mancano per avere € 1. Segui l’esempio.
3 Cancella con una X le monete in eccesso rispetto al valore indicato.
1 Scrivi la stessa lettera per indicare euro, frazioni e numeri decimali corrispondenti.
2 Scrivi sotto forma di frazione e di numero decimale quanti centesimi mancano per avere € 1. Segui l’esempio.
3 Cancella con una X le monete in eccesso rispetto al valore indicato.
1 Quanto resta dopo ogni acquisto? Osserva l’esempio e completa.
2 Scrivi altri due modi di pagare il lecca lecca.
3 Leggi lo scontrino della spesa di Noemi, calcola il totale e rispondi.
SPENDI BENE
Shampoo € 2 +
Dentifricio € 1,10 +
















Gel da barba € 3,70 +
Bagnoschiuma € 2,30 +

Fazzoletti € 0,75 =





Totale €
• Qual è il prodotto con il prezzo minore?
• Qual è il prodotto con il prezzo maggiore?
• Noemi spende più o meno di € 10?
• Per saperlo devi eseguire un’
Frazionare significa dividere un intero in parti uguali:
numeratore denominatore linea di frazione
1. Riconosci le figure frazionate mettendo una X.
2. Colora come indicato dalla frazione e scrivi la frazione corrispondente alla parte non colorata.



3. Cerchia di blu le frazioni decimali.
4. Scrivi accanto a ogni immagine la frazione e il numero decimale corretti.
Qual è la somma data dalle monete?
1 Misura la lunghezza del lato più lungo del tuo quaderno come indicato di seguito e registra le misure in tabella.
Unità di misura Quanti pollice spanna gomma
........... pollici ........... spanne gomme

• Confronta le misure che hai indicato con quelle dei compagni.
• Hai ottenuto gli stessi valori? SÌ NO
• Perché? .....................................................................................................................................................................................................

• Se usassi il centimetro del righello, uguale per tutti, tu e i tuoi compagni potreste ottenere le stesse misure? SÌ NO perché
Misurare significa contare quante volte l’unità di misura scelta è contenuta nella grandezza che si sta misurando.
Per misurare occorre usare unità di misura fondamentali uguali per tutti. Per questo motivo, si è creato il Sistema Internazionale di unità di misura (SI), un sistema di riferimento diffuso in tutto il mondo in cui ogni grandezza ha la sua unità di misura fondamentale.

Grandezza Unità di misura Marca
lunghezza metro m
peso chilogrammo kg capacità litro tempo secondo s
La marca è il simbolo che rappresenta l’unità di misura.
2 Leggi e rifletti.
1 Osserva, leggi e rispondi.
Per riempire la caraffa ho usato 8 bicchieri d’acqua.

Io per riempire la caraffa ho usato 12 tazzine di acqua.

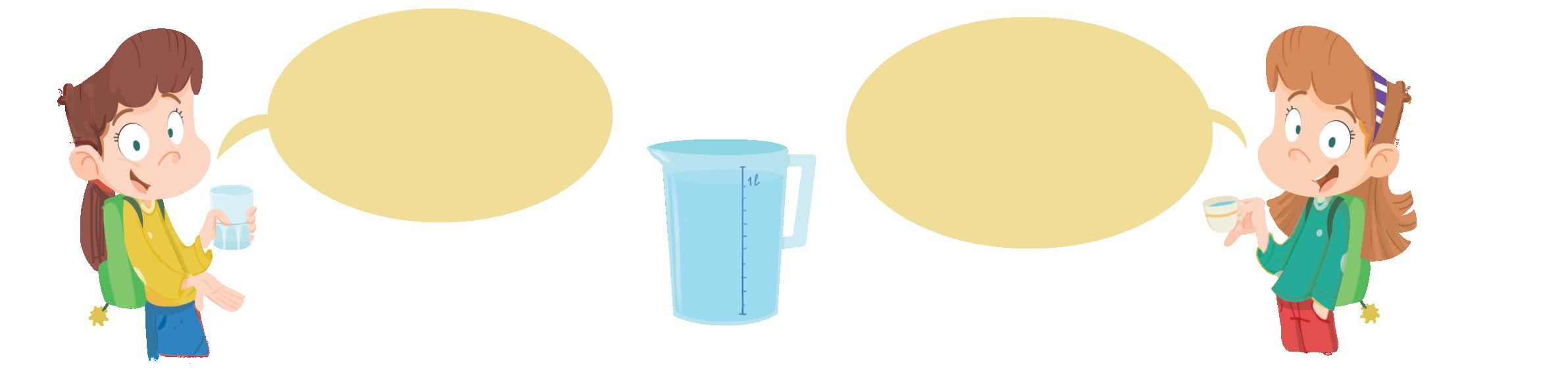
• Quale recipiente può contenere più acqua?



• Sai dire quanta acqua può contenere la caraffa? SÌ NO
Per saperlo occorre la caraffa graduata: ha la capacità di 1 litro ( ) e indica anche unità di misura più piccole.

2 Per misurare con precisione, occorrono degli strumenti adatti ai diversi tipi di grandezza. Cancella con una X quelli non adatti alla situazione.



Il peso della frutta

La lunghezza della piscina
1 litro 1 decilitro
Il tempo di una corsa

La capacità di un fiasco di vino
Il costo di un divano
La temperatura del tuo corpo



La lunghezza è una grandezza che permette di scoprire quanto è lunga una strada o un ago o quanto è profondo il mare o alta una torre.
L’unità di misura fondamentale della lunghezza è il metro (m) e ha multipli e sottomultipli.
multipli sottomultipli unità

chilometro ettometro decametro metro decimetro centimetro millimetro km hm dam m dm cm mm
1 000 m 100 m 10 m 1 m 0,1 m 0,01 m 0,001 m
Il nostro sistema di misura è decimale: ogni misura è 10 volte maggiore di quella immediatamente più piccola e 10 volte minore di quella immediatamente più grande.
x 10 : 10
Esempio: km hm
dam m
x 10 : 10
cm mm
x 10 : 10
1 Con l’aiuto della tabella colora il completamento corretto.
Il decametro contiene 10 100 1 000 metri.
L’ettometro contiene 10 100 1 000 metri.
Il chilometro contiene 10 100 1 000 metri.
2 Scrivi se la misura di lunghezza corrisponde a un multiplo o a un sottomultiplo del metro.
Mi servono 80 cm di nastro. .................................................................
La distanza tra Roma e Firenze è di 288 km. .................................................................
Il corridoio della scuola è lungo 3 dam. .................................................................
1 Osserva il
Il decimetro (dm) è 1 10 del metro: occorrono ........... dm per formare un metro.
1 dm = 0 m 1 dm = 0,1 m
Il centimetro (cm) è 1 100 del metro: occorrono ........... cm per formare un metro.
1 cm = 0 m 0 dm 1 cm = 0,01 m
RAGIONIAMO

Insieme ai compagni rifletti sulla parola DECIMETRO
Il millimetro (mm) è 1 1 000 del metro: occorrono .............. mm per formare un metro.
1 mm = 0 m 0 dm 0 cm 1 mm = 0,001 m

decima parte del metro
Analizza anche cm e mm!
Il dm, il cm, il mm sono sottomultipli del metro. 1 m = 10 dm 1 m = 100 cm 1 m = 1 000 mm
mm 10 dm 0,05 m 0,4 m

2 000 mm
40 mm
righello, leggi e completa con attenzione. 2 Misura con il tuo righello. 3 Collega le misure equivalenti.1 Completa la tabella con le misure mancanti.

si riferisce sempre
2 Scrivi le misure in tabella.
3 Scomponi e scrivi il valore di ogni cifra.

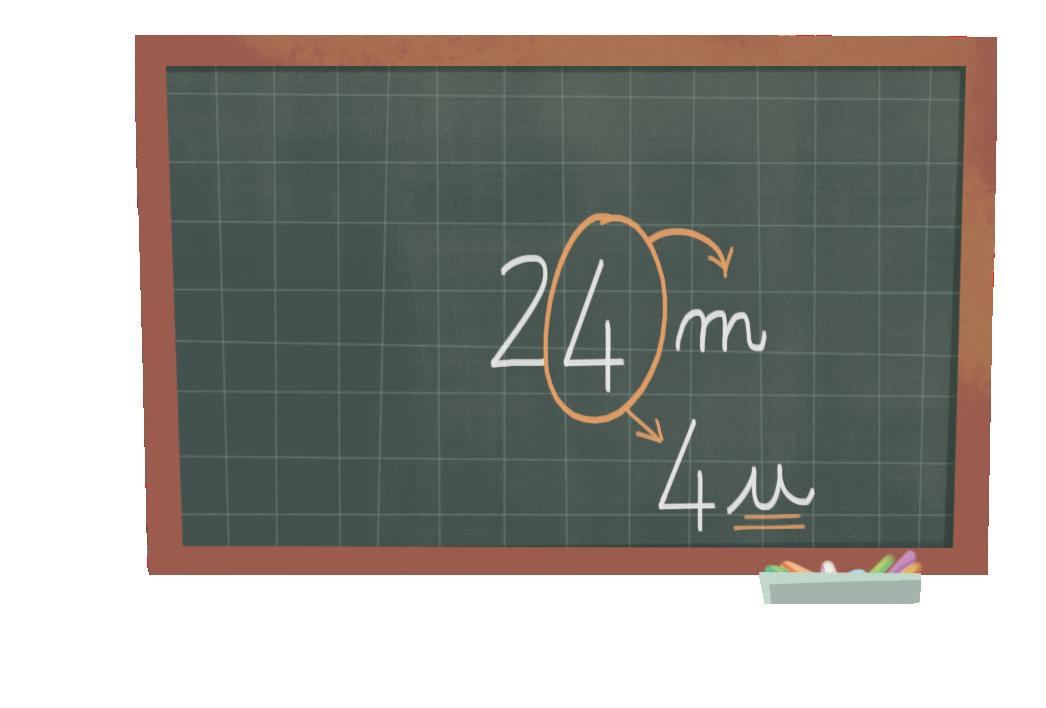
4 È esatta l’affermazione di Carmen? Verificalo in tabella e colora la risposta corretta.
Mia sorella
Caterina è alta 168 cm, cioè 1,68 m!
L’affermazione di Carmen è scorretta corretta perché 1,68 m = 168 cm.
Questa è una equivalenza!
1 Leggi, osserva con attenzione e completa.
km dm dam mm hm cm m
Per passare da un’unità di misura di valore maggiore a una di valore minore, si moltiplica:
• × 10 se ti sposti di una marca;
• × 100 se ti sposti di due marche;
• × 1 000 se ti sposti di tre marche.
4 dm = mm
Per passare da un’unità di misura di valore minore a una di valore maggiore, si divide:
• : 10 se ti sposti di marca;
• : 100 se ti sposti di ...........................marche;
• : 1 000 se ti sposti di 7 000 cm = dam × 100 : 1 000
2 Completa le tabelle.
3 Completa le equivalenze.
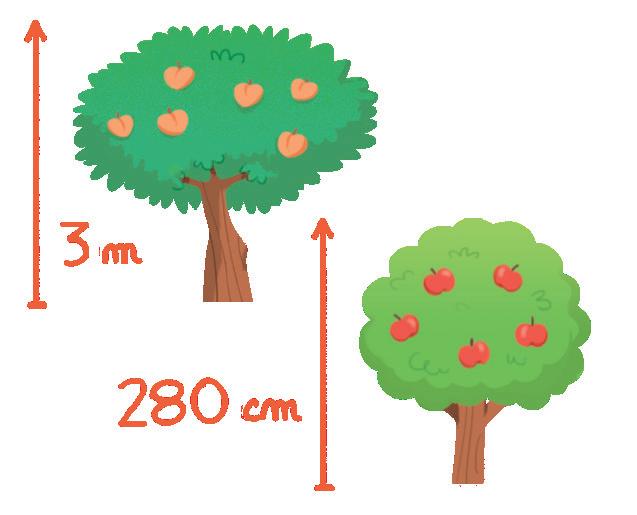
RAGIONIAMO
Insieme ai compagni discuti e spiega come occorre ragionare per scegliere l’albero più alto.
La capacità è una grandezza che permette di scoprire la quantità di liquido che può essere contenuta in qualsiasi recipiente.
L’unità di misura fondamentale è il litro ( ) e ha multipli e sottomultipli.
ettolitro decalitro litro decilitro centilitro millilitro


2 Colora l’unità che useresti per misurare il liquido che possono contenere questi oggetti.




3 Osserva e completa.
Quanto tè c’è nella tazza?
Quanta acqua serve per un lavaggio?

• Quanti c ? ............... • Quanti m ? .............
• Quanti ? ..................
4 Scomponi. La marca si riferisce alla cifra delle unità.
• Quanti d ? ...............
1 Leggi e ricorda.




1 Completa la tabella con le misure mancanti.


2 Colora solo i cartellini delle misure equivalenti alla capacità del contenitore.
3 Indica con una X i contenitori con la capacità minore di un litro.




4 Completa le tabelle.
5 Numera in ordine crescente le seguenti misure. Aiutati con le equivalenze.


Per misurare il peso di un oggetto si usa come unità di misura fondamentale il chilogrammo (kg). Anche il chilogrammo ha multipli e sottomultipli.

2 Osserva gli strumenti per misurare il peso: ne esistono di diversi tipi a seconda dell’oggetto da pesare.
Ora indica il numero della bilancia che utilizzeresti per pesare:



• una mela
• un grande pacco
• una collanina
1 Leggi e ricorda. 1. Bilancia per alimenti 3. Bilancia da pavimento 2. Bilancia pesapersone
1 Segna con una X l’unità di misura adatta per indicare il peso di ogni oggetto.
g mg g mg hg dag hg kg kg Mg Mg 100 kg10 kg kg hgdaggdg cg mg




2 Scrivi le misure in tabella: ricordati di partire dalla cifra delle unità che corrisponde alla marca.
3 Osserva i numeri in tabella e componili. Segui l’esempio.
Alcune misure non più previste nel SI sono ancora usate:
- tonnellata: 1 000 kg
- quintale: 100 kg

4 La freccia dice è meno pesante di... . Disegna le frecce, poi rispondi.

Qual è l’animale più pesante?


1 Completa le tabelle.
1 Osserva le immagini e completa.
Peso netto: è il peso del solo prodotto.
Tara: è il .................................. del vuoto.
Peso lordo: è il peso del insieme al
2 Osserva e completa.
PESO LORDO PESO NETTO TARA
3 Leggi, analizza i dati e risolvi dopo aver scritto la domanda.
Un camioncino caricato con 4 000 kg di sabbia, pesa 9 750 kg. ......................................................................................................... ......................................................................................................... P.N. T. .................................................................................................... P.L. .............................................................................................
4 Completa la tabella.
Pacco di merendine 364 g 30 g

Pacco di caffè ................
250 g 10 g
Cassetta di frutta




15 kg

13 kg ................


1 Leggi e completa.
Anche il tempo è una grandezza che possiamo misurare. L’unità di misura fondamentale è il secondo
× 60 : 60
minuto min ............ s
2 Completa le equivalenze.
3 h = min
2 d = .............................................. h
4 min = s
4 h = min
1 h e mezzo = ................. min
× 60 : 60
ora h ............ min
× 24 : 24
Fai attenzione: le misure di tempo non seguono il sistema decimale! secondo s 1 s
giorno d ............ h
120 s = min
1 h e 1 quarto = ............. min
1 d = h
240 s = min
240 min = ................................. h
mezz’ora = min
3 d = .............................................. h
5 min = s
3 h e mezzo = min
5 h = ........................................ min
3 Collega le durate uguali, poi rappresentale con le lancette negli orologi disegnati di seguito e colora l’angolo corrispondente.



1 Leggi e osserva.
Quando si parla di misure di valore, dobbiamo pensare al denaro che si misura con gli euro, alle sue banconote e alle sue monete. Anche l’euro (€) presenta multipli e sottomultipli multipli sottomultipli unità


1 eurocent C 0,01

2 eurocent C 0,02






€ 12 e 50 cent

5 eurocent C 0,05

10 eurocent C 0,10









€ 6 e 80 cent



















20 eurocent C 0,20
50 eurocent C 0,50

 2 Cerchia gli euro necessari per comprare i fiori senza ricevere il resto.
3 Indica come puoi cambiare i soldi usando una sola moneta o una sola banconota.
C 2
C 5 C 10 C 20
2 Cerchia gli euro necessari per comprare i fiori senza ricevere il resto.
3 Indica come puoi cambiare i soldi usando una sola moneta o una sola banconota.
C 2
C 5 C 10 C 20
1 Leggi, osserva attentamente e completa.
Quanto costano 3 blocchetti per appunti?
Valore Unitario × Quantità = Valore Totale
Quanto costa ogni penna?
Valore Totale : Quantità = V U
Per trovare la quantità, ragioniamo e operiamo così.
Valore Totale : V U = Quantità
2 Leggi e completa i diagrammi.

Mario ha 4 damigiane da 5 di olio ciascuna. Quanti litri di olio ha in tutto?
30 biscotti pesano 600 g. Quanto pesa un biscotto?
Samia usa 200 cm di nastro. Per un pacco servono 40 cm. Quanti pacchi prepara?
3 Completa con l’operazione adatta.
Ogni cono pesa 120 g. Quanto pesano 5 coni in tutto?
2 bicchieri contengono 8 d Quanti d contiene ogni bicchiere?

1 Osserva, leggi e risolvi.
a. Quanti chilogrammi pesano tutti i biscotti?
Se nel problema le marche sono uguali, puoi fare subito l’operazione.
3 hg
4 hg
3 hg
Operazione .................................. = ................. hg
b. Cecilia e le sue amiche prendono 200 g di biscotti da una scatola da 1 kg. Quanti grammi ne restano?
Equivalenza 1 kg = ................. g

2 Leggi e risolvi.
a. Quanti litri sono stati bevuti?
1 da
Equivalenza ................. hg = ................. kg in tutto
Se le misure sono espresse in marche diverse, esegui un’equivalenza prima dell’operazione.
Operazione ................................. = ................. g rimasti
6

Equivalenza
Operazione .........................................................................
3 Leggi e risolvi sul quaderno.
b. Quanti metri di rete occorrono per la recinzione?
35m 35m
5 dam
Equivalenza
Operazione .........................................................................
a. Una scatola piena di caramelle pesa 490 g. Tutti i 420 g di caramelle vengono mangiati. Quanti decagrammi pesa la scatola vuota?
b. Una famiglia consuma 140 d di latte alla settimana. Quanti litri consuma al giorno?
Il Sistema Internazionale di misura.
multipli unità sottomultipli
multipli unità sottomultipli
multipli unità sottomultipli
La marca si riferisce sempre alla cifra dell’unità.
Ricordalo quando completi le equivalenze.
LORDO
1. Colora solo i multipli del litro.
2. Cerchia i nastri che insieme formano 1 metro.
3. Completa con peso lordo, peso netto e tara. Poi calcola e fai l’equivalenza.






4. Completa la tabella con i dati corretti. Rispondi.

a. Avevi 2 euro. Ora ti restano: Quanto hai speso?


b. Una lavatrice impiega 25 min per il lavaggio, 1 4 d’ora per il risciaquo e 5 minuti per la centrifuga. Se parte alle ore 9:05, il lavaggio finirà alle ore:


1 Collega ogni solido al suo nome scrivendo la lettera corretta.
Poliedri Solidi di rotazione
a b c d e f g
parallelepipedo
cubo cono piramide
cilindro prisma sfera
Le figure solide occupano uno spazio detto volume e hanno tre dimensioni: lunghezza, larghezza e altezza. Si classificano in poliedri e solidi di rotazione
Osserva gli elementi di un poliedro:
faccia: figura piana
vertice: punto d’incontro di tre spigoli
spigolo: linea d’incontro di due facce
lunghezza
altezza
larghezza
Non ha vertici
Ha 5 facce
Ha 6 facce quadrate
Ha 6 facce
2 Leggi le caratteristiche e collegale al solido adatto.Osserva che cosa accade se “apri” un solido. Ottieni delle figure piane che rappresentano il suo sviluppo
Le figure piane hanno due dimensioni: la lunghezza e la larghezza. Occupano una parte di piano detta superficie. Sono limitate da linee chiuse.
lunghezza
superficie larghezza
1 Ogni solido può lasciare varie impronte, che cambiano a seconda di come il solido viene appoggiato. Collega le facce del solido alla corrispettiva impronta lasciata.
2 Collega ogni solido a una sua possibile impronta scrivendo la lettera corretta.
a b c d e
Linea chiusa
Percorrendola nello stesso verso, ritorni al punto di partenza.
Linea intrecciata
Passa più volte per uno stesso punto, chiamato nodo
Linea retta
Non ha origine né fine: è illimitata. Non contiene cambi di direzione.
Linea spezzata
Contiene improvvisi cambi di direzione.
La linea ha una sola dimensione: la lunghezza.
Linea aperta
Percorrendola nello stesso verso, non ritorni al punto di partenza.
Linea semplice
Non ci sono nodi.
Linea curva
Contiene continui cambi di direzione.
Linea mista

È formata da tratti di linea curva e spezzata.
1 Inserisci nella casella corretta le lettere che indicano le linee disegnate di seguito.
Linee aperteLinee non aperte
Linee semplici
Linee non semplici
confine di una figura piana è una linea. linea
Questa è una retta, il tratteggio ti fa capire che non ha origine né fine. Si indica con una lettera minuscola dell’alfabeto (in questo caso a).
Fissa un punto (O) sulla retta, otterrai due semirette; esse hanno origine (O), ma non hanno fine.
Fissa i punti R e S sulla retta, otterrai due semirette e il segmento RS. Il segmento ha origine e fine; si indica con due lettere maiuscole chiamate estremi e con un trattino sopra di esse.
1 In relazione al livello della terra, la posizione di una retta può essere:


2 In ogni riquadro, disegna quanto ti viene richiesto.


1 Ripassa il tratteggio che indica il percorso degli atleti.
Le rette parallele non si incontrano mai e mantengono la stessa distanza.
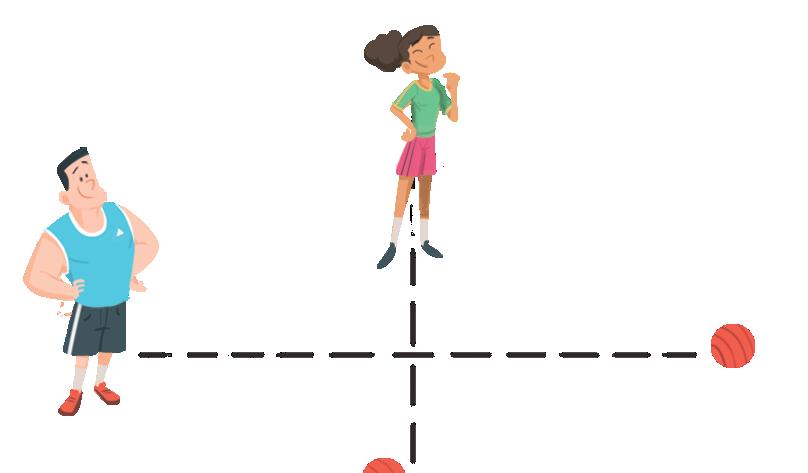
Le rette incidenti si incontrano in un punto.
Le rette incidenti perpendicolari si incontrano in un punto e dividono il piano in 4 parti uguali.
2 Riconosci il tipo di rette disegnate. Colora il cerchietto come richiesto.
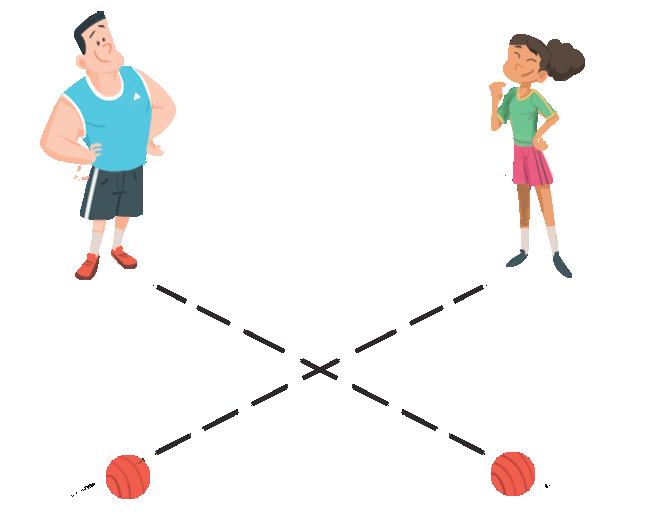
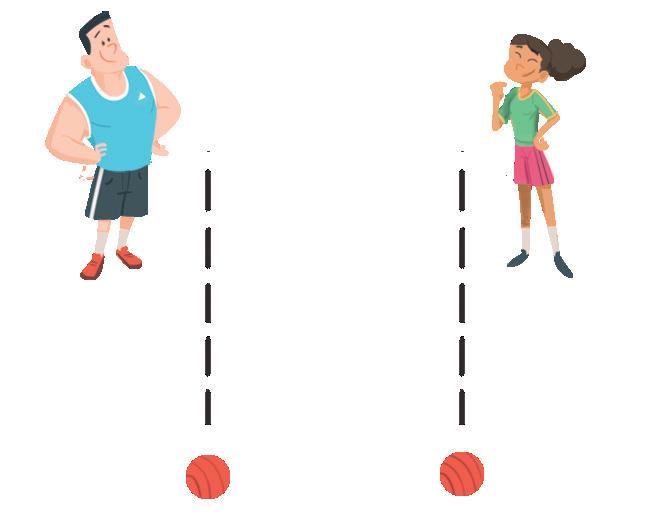
rette incidenti rette parallele rette perpendicolari
3 Osserva questo quadro di Piet Mondrian. Suddividi lo spazio bianco a tua disposizione come preferisci, utilizzando solo linee incidenti, e poi colora.



1 Osserva i due percorsi che Arianna fa in palestra utilizzando del nastro adesivo.
Arianna procede sempre dritta, non cambia direzione e non cambia verso
Ora Arianna non cambia verso, ma cambia continuamente direzione.
Ogni cambio di direzione forma un angolo.
2 In ogni percorso indica con una freccia i cambiamenti di direzione e scrivi il numero degli angoli.

N° angoli ................
N° angoli ................
3 Amina deve andare dalla nonna. Costruisci il suo percorso in modo che contenga 4 angoli.
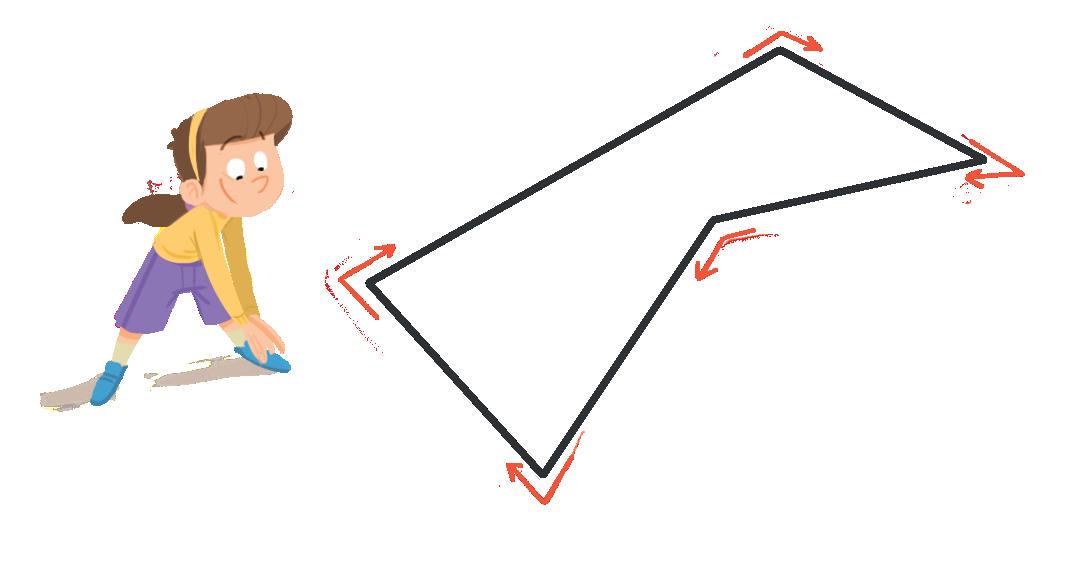
Un angolo è una parte di piano compresa tra 2 semirette che hanno l’origine (O) in comune.
O vertice: punto di origine
lato: semiretta ampiezza: spazio compreso tra i due lati dell’angolo. Può avere diverse misure.
1 Colora di rosso il vertice degli angoli che trovi in questi oggetti.
2 Colora gli angoli interni e scrivi quanti ne contiene ogni figura. Segui l’esempio.
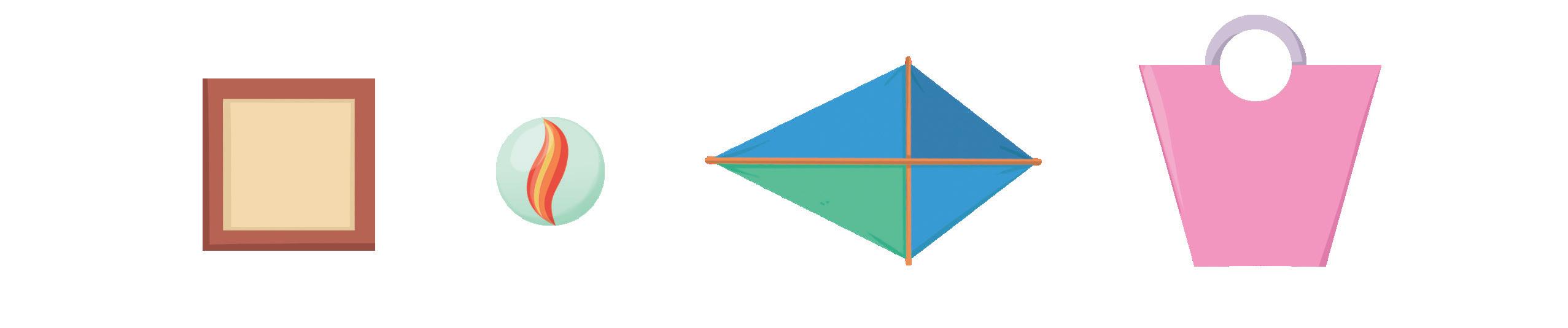
Insieme ai compagni rifletti sulla differenza tra i due tipi di angoli. Se necessario, fatti aiutare dall’insegnante.
angolo concavo angolo convesso
Costruisci uno strumento per giocare con gli angoli, utilizzando due striscette di cartoncino unite da un fermacampione su un’estremità.
È un angolo giro: una striscia compie un giro completo.
È un angolo piatto: una striscia ruota di mezzo giro.
È un angolo acuto: l’ampiezza è minore di quella dell’angolo retto.
1 Scrivi accanto a ogni angolo il suo nome.
È un angolo retto: una striscia ruota di 1 4 di giro.
È un angolo ottuso: l’ampiezza è maggiore di quella dell’angolo retto.
................................. ................................. SPAZIO E FIGURE
2 Riconosci gli angoli formati da queste coppie di rette e colorali come indicato.
Un poligono è una figura geometrica piana delimitata da una linea spezzata, chiusa, semplice. Un poligono ha più angoli.

1 Riconosci e colora solo i poligoni.
Quelli che non hai colorato sono non poligoni.
2 Disegna, aiutandoti con il righello, i segmenti che mancano per ottenere dei poligoni. Fai attenzione! Ci sono anche dei non poligoni.
3 Disegna due poligoni e due non poligoni.
Poligoni
Non poligoni
L’angolo interno è la parte di piano compresa tra due lati consecutivi.
La diagonale è il segmento che unisce due vertici non consecutivi.
E C B F A
È un lato ogni segmento che forma il confine.
Il vertice è il punto d’incontro di due lati.
1 Riconosci gli elementi di ogni poligono colorando come indicato.
lati vertici angoli interni
2 Completa la tabella e rispondi.
poligono n° vertici n° lati n° angoli A ................. ................. ................. B
Che cosa noti? ........................................................................................................................................................................................
Poligono con:
3 lati triangolo
4 lati quadrilatero
5 lati pentagono
6 lati esagono
RAGIONIAMO SPAZIO E FIGURE
Insieme ai compagni prova a rispondere: perché tre è il numero
1 Questi poligoni sono stati costruiti usando delle strisce di cartoncino e dei fermacampioni. Conta i listelli utilizzati per ogni poligono e scrivi il loro numero.
Hai calcolato il perimetro.
.......... ..........
Il perimetro (P) di un poligono è la misura della lunghezza del suo contorno. Si ottiene sommando la misura della lunghezza di tutti i lati.
2 Calcola il perimetro di questi poligoni, partendo dal vertice indicato e utilizzando come unità di misura il lato del quadretto . Poi completa e rispondi.
Quale poligono ha il perimetro più lungo? Il numero

Quale poligono ha il perimetro più corto?
Ci sono poligoni con lo stesso perimetro? SÌ NO Quali? ........................................................................
Due figure che, pur avendo forme diverse, hanno lo stesso perimetro si chiamano isoperimetriche.
1 Misura con il righello la lunghezza di ogni lato di questi poligoni, poi calcola il loro perimetro.
2 Utilizza le misure date e calcola il perimetro dei poligoni.
1 Luigi sta riempiendo con tessere quadrate la figura che vedi. Quante tessere gli servono? Contale e completa.

Hai calcolato l’area.
L’area (A) è la misura della superficie di un poligono. Per calcolarla, si sceglie una figura piana come unità di misura e si contano quante di queste figure occorrono per ricoprire tutta la superficie del poligono.
2 Calcola la misura dell’area di questi poligoni. Utilizza come unità di misura il , completa e infine rispondi.
Ci sono poligoni con lo stessa area? SÌ NO Quali? ......................................................................................
Due figure che, pur avendo forme diverse, hanno la stessa area si chiamano equiestese o equivalenti.
3 Calcola l’area di questo poligono utilizzando le seguenti unità di misura. Registra i risultati.
1. Piega un foglio a metà e su una metà fai due macchie colorate.
2. Sovrapponi le due metà e premi leggermente.
3. Riapri il foglio.
Sull’altra metà del foglio sono apparse macchie dello stesso colore ma disposte diversamente, come se ci fosse uno specchio al posto della piega. Le macchie sono simmetriche.
La piega del foglio è l’asse di simmetria. L’asse di simmetria può essere esterno o interno e può avere posizione orizzontale, verticale o obliqua.

1 Disegna e poi colora la parte simmetrica di ogni figura.

2 Individua e traccia i possibili assi di simmetria.

retta
rette parallele
rette incidenti
rette incidenti perpendicolari segmento
L’area è la misura della superficie. lato vertice angolo
Il perimetro è la misura del confine.
1. Collega il solido al cartellino con il suo nome. Quale rimane senza? Cerchialo.
parallelepipedo piramide cilindro prisma sfera
2. Quale solido è stato sviluppato? Indicalo con una X.
3. Calcola il perimetro della figura.
D C
A B
AD = 1 cm
AB = 3 cm
COME L’INVALSI
Indica con una X la risposta corretta.
a.
A. angolo acuto
B. angolo piatto
C. angolo ottuso
D. angolo giro
b.
A. rette perpendicolari
B. rette incidenti
C. rette parallele


Filippo osserva lo schermo di un videogioco e decide di spostare il gettone nero di 2 caselle a destra, poi di 3 in alto e infine di 5 a sinistra. Esegui il percorso e rispondi.
• Quale cassaforte raggiunge? ......................... ......................................................................................................
• Per aprire la cassaforte gialla, quale altro comando deve dare? ................................ ......................................................................................................
Filippo cambia gioco. Aiutalo e indica con una X il percorso che deve effettuare il pirata per aprire prima lo scrigno blu e poi quello rosso.
Inventa un percorso per permettere al robot di raggiungere il computer. Puoi dargli questi comandi:
vai avanti gira a destra su te stesso gira a sinistra su te stesso
Ora descrivi il percorso con le frecce utilizzate: ...............................................................................................................................................................................................................................

Rispetta le istruzioni e traccia il percorso compiuto dal robot. Poi rispondi.
Quale computer raggiunge il robot? ......................................................................................

Colora secondo le istruzioni date e scoprirai una lettera dell’alfabeto.

G. 1 1 4
H. 6
Le immagini del computer sono formate da tanti piccoli quadrati colorati chiamati PIXEL. Per disegnarle occorre un codice elaborato da un programmatore.
Diventa tu il programmatore e scrivi le istruzioni relative a questa lettera.

Osserva le lettere nella tabella e scrivi il messaggio in base ai codici indicati.
4 A B C D E
Ora osserva l’esempio. Scopri la chiave del codice e decifra il nome che si nasconde.
1 Collega i numeri tra loro in base a ciò che indica la freccia e completa.
376 è maggiore di , il quale a sua volta è maggiore di ..................
Quindi: > >

Insieme con i compagni spiega perché questa freccia è a doppia punta e scopri il suo significato.
2 Osserva la tabella con attenzione e rispondi alle domande.
• Quali strumenti suona Elia? ................................................................................................
Amadou
• E Amadou?
• Chi suona un solo strumento?




• Qual è lo strumento più scelto? ................................................................................................
3 Completa le relazioni dell’esercizio 2 e collega con le frecce.
Frutti










Quando classifichi, metti insieme degli elementi in base ad almeno una caratteristica.
Numeri da 1 a 20 11
Nello spazio comune, chiamato intersezione, ci sono gli elementi che possiedono entrambe le caratteristiche.
A una cifra NON a una
RAGIONIAMO
Insieme ai compagni prova a descrivere gli elementi delle classificazioni proposte usando le parole E e NON
 1 Osserva gli elementi di ciascun gruppo e scrivi le caratteristiche che li accomunano. Infine cerchia la parola adatta.
2 Completa la classificazione dei numeri da 1 a 20 nel diagramma di Eulero-Venn in base alle caratteristiche evidenziate.
3 Ora scrivi i numeri della classificazione precedente nel diagramma di Carroll.
1 Osserva gli elementi di ciascun gruppo e scrivi le caratteristiche che li accomunano. Infine cerchia la parola adatta.
2 Completa la classificazione dei numeri da 1 a 20 nel diagramma di Eulero-Venn in base alle caratteristiche evidenziate.
3 Ora scrivi i numeri della classificazione precedente nel diagramma di Carroll.
MATEMATICA
1 Completa il diagramma ad albero disegnando tutte le possibili combinazioni, infine rispondi.
a. Quante sono le bandierine possibili?
b. Quante sono le forme?
c. Quanti i colori a disposizione?
d. Se i colori a disposizione fossero stati 6, quante sarebbero le possibili combinazioni totali? .................. × .................. =
× = tutte le possibili combinazioni Yuri MEGA ESERCIZI PAG. 69 128
2 In palestra si può scegliere di giocare con la palla, la corda e il cerchio. Ogni bambino pensa alle possibilità di scelta che ha. Quante possibilità vi sono in totale? Collega usando le frecce e lo saprai.

Sara, palla

1 Leggi, osserva e rispondi.
L’insegnante ha svolto un’indagine e ha registrato i dati raccolti nella seguente tabella di frequenza. Ogni alunno intervistato ha indicato una sola preferenza.
sport frequenza
nuoto 8
calcio 5
basket 6
pallavolo 4

• Quale domanda avrà fatto l’insegnante?
• Quanti alunni sono stati intervistati? ....................................
• Qual è lo sport con più preferenze?
. Questo rappresenta la moda
La moda è il dato più frequente, cioè quello che ha più preferenze.
2 Completa i grafici in base ai dati raccolti. Fai attenzione alla legenda e rispondi.
Istogramma
Legenda = 1 preferenza
tennis 7 nuoto ............................ ............................
Ideogramma
Legenda = 2 preferenze = 1 preferenza
• Quali informazioni non puoi ricavare dai dati raccolti?
La frequenza dello sci
Il numero degli intervistati
Lo sport che ha avuto minore frequenza
1 Leggi e osserva.
Se per merenda scegliessi a occhi chiusi tra i prodotti rappresentati, sarebbe...







... possibile scegliere una mela: l’evento può verificarsi, ma non c’è certezza.
... impossibile scegliere un gelato: è un evento che non può verificarsi di sicuro.
... certo scegliere un frutto: è un evento che si verificherà sicuramente!
2 Osserva il borsellino e scrivi se le affermazioni sono vere (V) o false (F).
• È possibile pescare una moneta da € 2. V F
• È impossibile pescare una banconota. V F
• È certo pescare una moneta. V F
• È possibile pescare una moneta da 5 cent. V F








• È certo pescare una moneta da 50 cent. V F
• È certo pescare una banconota. V F
3 Giada si diverte a lanciare un dado. Aiutala a completare le frasi.
• È possibile che ...........................................................................................
Chissà quale numero uscirà?

• È certo che ..................................................................................................... .....................................................................................................................................
• È impossibile che .....................................................................................................................................
1 Immagina di prendere una pallina a occhi bendati.
• Quale pallina è più probabile prendere? .............................
• Quale è meno probabile che ti capiti?
Se un evento è possibile può essere più o meno probabile. Puoi usare le frazioni per indicare la maggiore o la minore probabilità di un evento.


2 Ora imparerai a calcolare la probabilità degli eventi. Osserva e completa.
Le palline nel sacchetto in tutto sono , quindi i casi possibili sono 10.
• La probabilità che tu prenda una pallina blu è di 1 su 10
• La probabilità che tu prenda una pallina gialla è di .............. su ...............
• La probabilità che tu prenda una pallina rossa è di .............. su ...............
3 Osserva le lettere della parola.
1 su 10 ................ su ................ ................ su ................
1 10 1 pallina blu 10 palline totali ...... palline gialle ...... palline totali ...... palline rosse ...... palline totali
• Quante probabilità ci sono di estrarre una...
B I A S M R S V I I I ? ...... una vocale? ...... una consonante? ......
• Quale consonante è più probabile estrarre? .......................................................................................................
Perché? ......................................................................................................................................................................................................
più FACILE 132







I grafici servono per rappresentare e interpretare più facilmente i dati di un’indagine.
I più usati sono:

• l’ISTOGRAMMA o grafico a colonne;
• l’IDEOGRAMMA, dove i dati sono indicati da figure che ricordano l’argomento dell’indagine.
Rossi
Non

1. Considera le seguenti figure e completa le rappresentazioni con le lettere.
2. È stata svolta un’indagine tra 60 bambini sulle loro maggiori paure. Completa il grafico e rispondi.
Legenda = 5 preferenze
• Quale dato rappresenta la moda?
Osserva i gelati e scegli la risposta corretta.








Leggi e mettiti in azione.
Per la festa della scuola si devono creare dei giochi matematici da proporre ai bambini delle altri classi. Occorre lavorare in coppie e preparare un crucinumero.



Inserite nello schema sottostante dei numeri a vostro piacere.
Io preparo le definizioni verticali.
Leggi le possibili definizioni che si possono scrivere per il numero 81.
Possiamo descrivere i numeri in tanti modi diversi!
• È il numero composto da 8 da e 1 u
• È il prodotto di 9 × 9.
• Segue il numero 80.
• Se aggiungi 9 a questo numero arrivi a 90.
• È la somma di 40 + 39 + 2.
• È il risultato di 100 – 19.
Io preparo quelle orizzontali.
Completa le definizioni.
Una volta terminato, scambiatevi tra di voi le definizioni e divertitevi a risolvere i crucinumeri ideati dai vostri compagni.

MI VALUTO
L’attività svolta è stata:
Hai lavorato bene con il tuo compagno?
Ti sei divertito?







Scienza vuol dire “conoscenza” e studia tutto ciò che è intorno a noi, viventi e non viventi, sulla Terra e nell’Universo. Ogni cosa che accade in natura è un fenomeno naturale. La Scienza si basa proprio sull’osservazione dei fenomeni naturali e sulla capacità di porsi delle domande di fronte a essi. Capire il perché di tanti fenomeni e quindi fornire delle risposte e delle spiegazioni è alla base del lavoro degli scienziati. Lo scienziato è un ricercatore che spiega le cause e le possibili conseguenze di un fenomeno. Per farlo, spesso ha bisogno di compiere degli esperimenti, cioè di “fare per capire”. In questo modo, lo scienziato riesce a dare il suo contributo alla conoscenza scientifica e permette il progresso tecnologico dell’umanità. Fin dall’antichità, le persone sono sempre state curiose di sapere come era fatto il mondo e perché avvenivano i fenomeni. I primi studiosi che hanno cercato di dare delle risposte sono stati i filosofi. Nell’antica Grecia i filosofi pensavano che gli elementi principali fossero aria, acqua, terra e fuoco: da questi aveva origine la materia che formava tutte le cose.

Il biologo studia gli esseri viventi.



Oggi, chi studia ciò che accade intorno a noi, si chiama scienziato Gli scienziati, attraverso il metodo scientifico, hanno raggiunto molte più conoscenze dei filosofi dell’antichità. Dal momento che i fenomeni da studiare sono tanti, gli scienziati si sono specializzati e, a seconda dell’argomento che studiano, hanno nomi diversi.


Lo zoologo studia il mondo degli animali.

L’astronomo studia le stelle, la Terra e i pianeti.

Il chimico studia la composizione della materia.
Il botanico studia il mondo delle piante.


Completa il testo con il nome corretto degli scienziati.
Luca da grande vorrebbe studiare le stelle: vuole diventare un
Il geologo studia il suolo e le rocce.


Ginevra ama gli animali e sogna di diventare una ...............................................................................................
Philip è appassionato della composizione delle sostanze, da grande vorrebbe essere un
Tu vorresti diventare uno di questi scienziati? Quale?



Ciascuno di noi può essere un piccolo scienziato utilizzando prima di tutto i cinque sensi, che ci permettono di raccogliere molte informazioni sul mondo intorno a noi.
Gli scienziati, però, per poter svolgere al meglio il loro lavoro devono utilizzare degli strumenti, che rendono le loro ricerche molto più precise. Eccone alcuni.

Completa scrivendo il numero corrispondente all’immagine.

Per osservare da vicino un animale o una pianta si usa...
Per misurare e analizzare le sostanze si usa...
Lo scienziato che deve osservare le stelle usa...

Per osservare qualcosa di molto piccolo in laboratorio si usa...
Se uno scienziato deve ricordare tutti i particolari di ciò che sta osservando usa...
2 La macchina fotografica 5 La provetta graduata 3 Il microscopio 4 Il telescopio CON METODORita Levi Montalcini è stata una delle più grandi scienziate italiane. Ha vinto un prestigioso premio per la medicina, il premio Nobel, e ha dedicato la sua vita alla ricerca e alla sperimentazione. È morta nel 2012 all’età di 103 anni.
Rita Levi Montalcini, come tutti gli altri scienziati, per compiere le sue ricerche ha utilizzato il metodo scientifico sperimentale


Questo metodo si compone di diverse fasi.
1
OSSERVAZIONE
Lo scienziato osserva ciò che accade, ovvero un fenomeno.
2
DOMANDA
Si pone alcune domande.
3
IPOTESI
Formula una o più ipotesi, ovvero delle possibili risposte per spiegarlo.
4
ESPERIMENTO
Fa degli esperimenti per verificare se le ipotesi sono corrette.
5
RACCOLTA DEI DATI
Registra i dati durante lo svolgimento degli esperimenti.
6
CONCLUSIONE
Se gli esperimenti dimostrano che le ipotesi sono vere, formula una legge.
7
PUBBLICAZIONE
Pubblica i risultati, in modo che la conclusione possa essere convalidata, cioè confermata o meno da altri scienziati.

Ripeti l’esperimento in tutti i suoi passaggi, completa e verifica se puoi confermare ciò che è stato scritto.
Di solito, i vestiti vengono stesi ad asciugare all’aperto.
Un oggetto bagnato si asciuga meglio all’aperto? Perché?
L’acqua evapora e si disperde nell’aria, lasciando il vestito asciutto.

ESPERIMENTO
Metto due fazzoletti bagnati in due bicchieri: uno scoperto A , l’altro coperto con la pellicola trasparente B , come se il fazzoletto fosse in una stanza chiusa.
RACCOLTA DEI DATI
Osservo la situazione nei giorni seguenti.
Dopo giorni il fazzoletto nel bicchiere A
è bagnato asciutto
Dopo giorni il fazzoletto nel bicchiere B
è bagnato asciutto
L’acqua nel bicchiere è evaporata.


Nel bicchiere l’acqua non è evaporata ed è rimasta nel fazzoletto e sulle pareti del bicchiere.
Mi confronto con i compagni per convalidare o meno la mia conclusione.
Spesso gli scienziati consultano le ricerche di altri scienziati
La materia è tutto ciò che ci circonda e che occupa uno spazio. Ha molti aspetti e si trova in tutte le cose che puoi percepire con i sensi: la vedi anche se è lontana come le stelle; la tocchi se è vicina come questo libro; la gusti se si tratta di cibo; la annusi se ha un odore; la senti se cade come l’acqua che esce dal rubinetto. Fai attenzione: a volte la materia è trasparente e ti può ingannare! Se una porta a vetri è pulita puoi non vederla e sbatterci contro; oppure puoi pensare che dentro una stanza vuota non ci sia materia, ma se muovi velocemente le mani davanti al viso percepisci il movimento dell’aria: anch’essa è materia.

Comprendo IL TESTO
Completa utilizzando le seguenti parole: sensi • aspetti • spazio • circonda.
La materia è tutto ciò che ci e occupa uno

Ha molti ..................................................................... e si può percepire con i .....................................................................
Indica con una X se le affermazioni sono vere (V) o false (F).
La materia si vede sempre. V F
La materia a volte si può gustare. V F
L’aria è materia. V F
L’acqua non è materia. V F

Tutta la materia è formata da particelle piccolissime chiamate molecole, che si legano le une alle altre. A seconda del tipo di legame, la materia si presenta in tre stati differenti.


Il legame è forte. La materia mantiene la propria forma.
Comprendo CON IL CORPO
Il legame è debole. La materia non mantiene la propria forma ma prende quella del recipiente che la contiene.
Raggruppiamoci come le molecole. Dividetevi in gruppi e rappresentate i tre stati della materia:

• Stato solido: prendetevi per mano. Potete decidere di tenere le braccia rigide, tese o piegate, purché restino sempre nella stessa posizione.
• Stato liquido: prendetevi per mano, tenete le braccia rilassate e muovetevi all’interno dell’aula senza lasciarvi le mani.



• Stato gassoso: non prendetevi per mano e muovetevi all’interno dell’aula, occupando tutto lo spazio a vostra disposizione.
Decidete un capo-gioco che darà gli ordini: quando dirà “solido” o “liquido” o “gassoso”, i gruppi eseguiranno il movimento corrispondente.
Il legame è debolissimo.
Le molecole possono muoversi liberamente occupando tutto lo spazio disponibile.
STATO SOLIDO STATO LIQUIDO STATO GASSOSO Stato solido Stato liquidoL’acqua è una materia liquida, inodore, incolore e insapore che utilizziamo ogni giorno in casa per bere, lavarci, cucinare, pulire... Anche gli animali e le piante hanno bisogno dell’acqua; i pesci addirittura ci vivono dentro! In natura puoi trovare l’acqua allo stato solido, liquido e gassoso perché con il caldo e con il freddo l’acqua può cambiare il suo stato. L’acqua allo stato solido si chiama ghiaccio; allo stato gassoso, invece, si chiama vapore acqueo
I passaggi da uno stato all’altro assumono nomi diversi.
1. Se riscaldi tra le mani un pezzetto di ghiaccio, vedrai che inizierà a sciogliersi diventando acqua. Questo passaggio si chiama fusione
3. Se metti un coperchio sopra a una pentola d’acqua bollente, il vapore si raffredda. Vedrai formarsi delle goccioline di acqua: è la condensazione.









Comprendo IL TESTO
2. Se metti l’acqua in un pentolino sul fornello essa inizierà a bollire, cioè si trasformerà in vapore acqueo. Questo passaggio si chiama evaporazione
4. Se metti l’acqua nel congelatore, diventerà ghiaccio. Questa trasformazione si chiama solidificazione.
Completa con: fusione • evaporazione • condensazione • solidificazione.
GASSOSO LIQUIDO SOLIDO vapore acqua ghiaccio
I passaggi di stato che hai visto usando il fornello e il congelatore avvengono continuamente anche in natura, grazie al calore del Sole. Osserva.
Con il calore del Sole l’acqua si trasforma in vapore acqueo.
Quando le goccioline delle nubi incontrano aria ancora più fredda, diventano grosse e pesanti. Cadono quindi sotto forma di precipitazioni: pioggia oppure grandine e neve se la temperatura è molto bassa.
2
Il vapore acqueo incontra l’aria fredda e condensa in minuscole goccioline di acqua, formando le nuvole
Seguendo i numeri, leggi, osserva le immagini e ripeti a voce alta il ciclo dell’acqua.
L’acqua cade nei fiumi, nei laghi o nel mare, oppure si infiltra nel terreno formando le falde acquifere, cioè serbatoi o fiumi sotterranei che scorrono verso il mare. Poi il ciclo ricomincia.

In natura, l’acqua riesce a modificare il paesaggio: trascina la terra e i detriti, crea dei fossi o dei rilievi e, con il tempo, riesce anche a levigare la roccia. Le piogge molto abbondanti, inoltre, possono provocare frane, ingrossare il corso dei fiumi e farli straripare, causando danni alle costruzioni e ai campi vicini. Le persone, da sempre, cercano di limitare i danni studiando le caratteristiche del terreno per edificare abitazioni sicure, costruendo argini ai fiumi, canali di emergenza e dighe. La vegetazione, grazie alle radici, può impedire al terreno di cedere durante precipitazioni forti.


Collega ogni causa all’effetto corretto.
Cadono piogge molto abbondanti.
Le persone costruiscono argini.
L’acqua del fiume aumenta.
Detriti: frammenti di roccia e altri materiali.
Straripare: fuoriuscita dell’acqua dagli argini.
Il fiume straripa.

Possono esserci frane.
Le case sono più sicure.
L’acqua manifesta la sua forza anche quando è allo stato gassoso. Infatti, in natura, l’acqua esce con forza sotto forma di vapore acqueo dai vulcani e dai geyser. Puoi vedere la forza del vapore anche nella tua cucina quando l’acqua bolle nella pentola e riesce a spostare il coperchio. Le persone, in passato, hanno utilizzato la forza del vapore per far funzionare alcuni macchinari, come i primi treni e i battelli a vapore, e lo fa ancora oggi nelle centrali che producono energia elettrica.

La forza dell’acqua si manifesta anche quando è sotto forma di ghiaccio. Quando l’acqua si solidifica occupa uno spazio maggiore, per questo il ghiaccio è in grado di causare fratture alle rocce o di spostarle.
Ricerca alcuni video dei mezzi di trasporto del passato.

Realizza l’esperimento e completa la conclusione.
Prendi una bottiglietta di plastica e riempila di acqua fino all’orlo.
Invece del tappo, mettici sopra un pezzo di alluminio fissato con un elastico.
Metti la bottiglietta nel congelatore. Dopo un giorno, che cosa succede?
Quando l’acqua diventa ghiaccio lo spazio che occupa aumenta diminuisce Se il contenitore fosse stato di vetro e chiuso con un tappo, che cosa sarebbe successo? Chiedi a un adulto.

 Locomotiva a vapore
Locomotiva a vapore


Le persone hanno capito che potevano sfruttare la forza dell’acqua a loro vantaggio. Per questo, fin dai tempi antichi, hanno costruito dei macchinari che, servendosi di questa forza, le aiutavano nei lavori faticosi, come il taglio del legname o la macinatura dei cereali nei mulini Osserva il disegno di un’antica segheria: la ruota mossa dall’acqua fa girare un perno che, a sua volta, muove dei congegni meccanici al cui termine c’è una grande sega.
L’acqua fa girare la RUOTA
ruota
perno
Il PERNO trasmette il movimento agli ingranaggi.
sega
Gli ingranaggi fanno funzionare la SEGA che taglia il legno.
Costruisci tu una sega circolare mossa da un mulino ad acqua.

- 4 stecche di legno (puoi usare quelle del gelato)
- 1 tappo di sughero
- 1 stecchino da spiedino
- 1 cannuccia
- 1 vassoio di alluminio
- colla a caldo
- forbici
1 Facendoti aiutare da un adulto, infilza e fissa le stecche al tappo di sughero con la colla a caldo. Poi infilza lo stecchino al centro del tappo.

2
Taglia un pezzo di cannuccia e infilala nello stecchino, in modo da tenerlo tra le dita senza bloccarlo.
Ritaglia dal vassoio di alluminio un disco con il bordo seghettato simile a quello del disegno e fissalo all’estremità libera dello stecchino, senza bloccare la cannuccia.
4
Ora metti le “pale” sotto l’acqua del rubinetto: vedrai che il tuo mulino girerà e farà girare il cerchio seghettato.

È tutto ciò che ci circonda.
È formata da molecole unite da legami forti: stato solido.
unite da legami deboli: stato liquido.
Occupa uno spazio.
unite da legami debolissimi: stato gassoso.
È incolore, inodore, insapore.
Compie
È presente in natura allo stato solido, liquido, gassoso.
Evaporazione: dallo stato liquido a quello gassoso.



Condensazione: dallo stato gassoso a quello liquido.
Solidificazione: dallo stato liquido a quello solido.
Fusione: dallo stato solido a quello liquido.
fusione
condensazione
1. Completa le fasi del metodo sperimentale.
2. Completa la tabella sugli stati della materia.
- Non hanno una loro forma.
– Occupano uno spazio.
- Le molecole hanno legami deboli.
- Hanno una forma ben precisa.
- Occupano uno spazio.
- Le molecole hanno legami debolissimi.
Solidi Liquidi Gas
Prendono la forma del recipiente che li contiene.
Occupano tutto lo spazio a loro disposizione.
Le molecole hanno legami forti.
3. Completa il testo sui passaggi di stato.
L’acqua in natura si trova allo stato ................................................................. nel mare, nei fiumi e nei laghi, allo stato solido sotto forma di nei ghiacciai e, allo stato gassoso, sotto forma di nelle nuvole.
4. Collega in modo corretto.
Evaporazione
Condensazione
Dallo stato solido allo stato liquido.
Dallo stato liquido allo stato solido.
Dallo stato gassoso allo stato liquido.
Dallo stato liquido allo stato gassoso.

L’aria è la materia gassosa che ti permette di respirare. Spesso, pur essendone circondato, non ti accorgi della invisibile e incolore
Non ne senti neanche il peso, ma ti accorgi della sua
Eppure anch’essa è fondamentale alla vita di tutti gli esseri viventi: oltre alla respirazione permette il volo degli uccelli, il movimento delle nuvole e ti fa sentire
L’aria avvolge la Terra formando un involucro, chiamato , che lascia passare i raggi solari utili e ci
miscuglio di gas che sono
è il gas necessario per rendere respirabile l’ossigeno, poiché non riusciremmo a introdurlo allo stato puro all’interno dell’organismo;
è il gas che permette ai viventi di respirare; è il gas prodotto dagli esseri viventi durante la respirazione.

colori diversi.

• Che cos’è l’aria?
• Come si chiama lo strato di aria che circonda la Terra?
• Che cosa lascia passare?
• Che cosa non lascia passare?
• Da quali gas è formata l’aria?

1 L’aria è invisibile ma occupa uno spazio
L’aria è presente in tutti gli spazi anche se non la vediamo, infatti un contenitore o una bottiglia che a noi sembrano vuoti in realtà contengono aria.

Se immergi una cannuccia in un bicchiere con dell’acqua e soffi, l’acqua si sposta per fare spazio all’aria. Se invece aspiri, riesci a far salire l’acqua lungo la cannuccia.
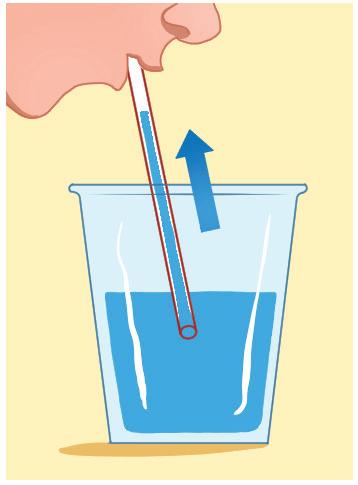

2 L’aria è comprimibile ed elastica
Se fai entrare aria in una siringa senza ago e tappi il foro con il dito, spingendo lo stantuffo con forza riuscirai a schiacciare l’aria: per questo si dice che è comprimibile. Se lasci lo stantuffo, esso tornerà indietro da solo come una molla: per questo si dice che l’aria è elastica.
3 L’aria è materia, quindi ha un peso
Se con una bilancia di precisione pesi un palloncino prima e dopo averlo gonfiato con l’aria, noterai che, anche se di poco, aumenta di peso. Questo avviene perché, anche se non ce ne rendiamo conto, l’aria ha un peso



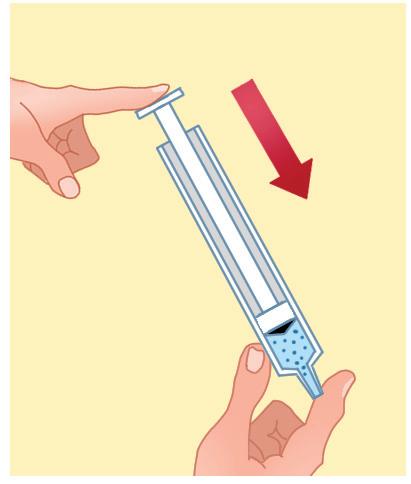
4 L’aria calda si dilata, cioè occupa più spazio; è più leggera di quella fredda e sale verso l’alto.
SPERIMENTA
Prendi delle strisce di carta velina e attaccale con del nastro adesivo sopra un termosifone acceso.
Che cosa noti? ............................................................................................
Ho sperimentato che l’aria calda ..............................................
In natura, quando una massa di aria calda si sposta verso l’alto, l’aria fredda prende il suo posto: questo movimento è il vento



Il vento può essere leggero o soffiare con grande forza. A volte riesce a modificare il paesaggio: solleva polvere, sabbia e piccoli detriti e, quando li deposita, forma distese sabbiose o deserti. Quando questi granelli incontrano delle rocce le incidono e, nel corso di milioni di anni, le erodono creando delle forme particolarissime. Il vento forte è pericoloso per le persone e causa molti danni: abbatte gli alberi, i cartelli stradali, distrugge le coltivazioni, scoperchia i tetti. Se forma un violento vortice, detto tromba d’aria, è in grado di distruggere anche le abitazioni. Incanalata nel modo giusto, però, la forza del vento può essere sfruttata: i mulini a vento, come quelli ad acqua, trasformano il movimento delle pale in un lavoro utile. Oggi si costruiscono le pale eoliche (da Eolo, nome del dio greco dei venti), che trasformano la forza del vento in energia elettrica.
Completa lo schema con le parole corrette. Poi ripeti a voce alta.
vento • calda • causa • paesaggio • scende • utile

Per gli individui primitivi, la scoperta del fuoco è stata fondamentale per la sopravvivenza e il progresso dell’umanità.
Il calore viene percepito in modo soggettivo, ovvero in modo diverso, da persona a persona: lo puoi sperimentare quando in uno stesso ambiente le persone indossano vestiti più o meno pesanti, nonostante ci sia la stessa
temperatura

Per misurare la temperatura occorre uno strumento preciso: il termometro La maggior parte dei termometri moderni sono digitali e funzionano con un sensore che rileva la temperatura e la visualizza in un display, mentre fino a pochi anni fa si utilizzavano i termometri tradizionali. Un termometro che sicuramente conoscerai è quello medico, che usi per misurare la temperatura del corpo quando sei malato. Il termometro ambientale permette, invece, di misurare la temperatura di un ambiente.

TECNOLOGIA Il termometro tradizionale
SPERIMENTA
Termometro medico
Utilizza i termometri e completa.
Che temperatura c’è oggi?
Qual è la temperatura del tuo corpo oggi?
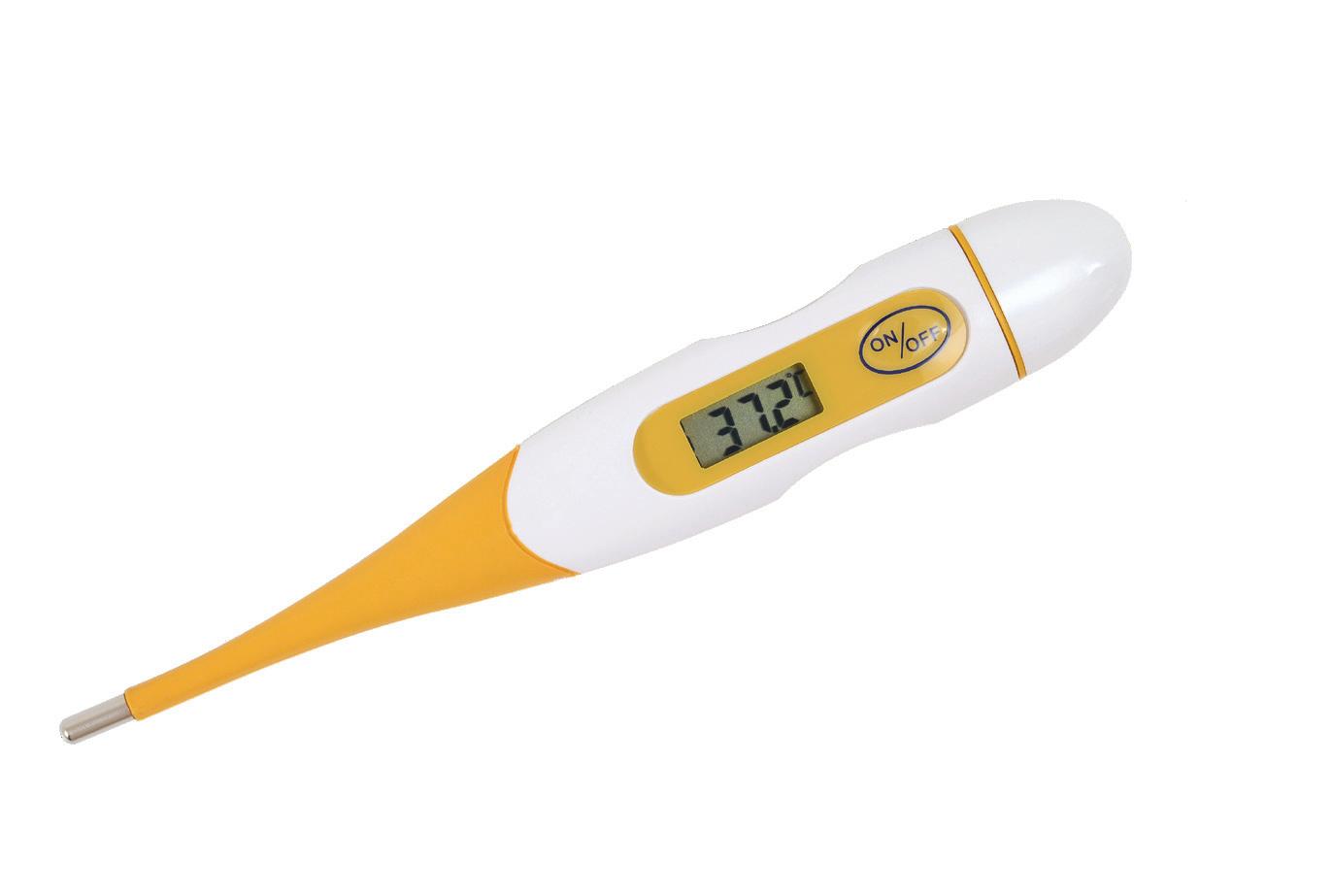
Cannello: tubicino nel quale sale o scende il liquido a seconda della temperatura esterna.
Scala graduata: 0 corrisponde alla temperatura di fusione del ghiaccio e 100 corrisponde a quella di ebollizione dell’acqua. Lo spazio tra 0 e 100 è diviso in 100 parti uguali, i gradi Celsius, che si indicano con °C
Bulbo: contiene il liquido che sale nel cannello.
Se hai la mano fredda e stringi la mano calda di un compagno, il suo calore passerà alla tua: questo avviene perché il calore si trasmette da un corpo all’altro e sempre dal più caldo al più freddo. Anche i materiali riescono a passare il calore da uno all’altro: questa caratteristica si chiama conducibilità. Materiali diversi hanno però comportamenti diversi: alcuni sono dei buoni conduttori, perché conducono il calore velocemente; altri, invece, sono cattivi conduttori, perché conducono il calore molto lentamente o per niente. Questi ultimi sono detti isolanti.

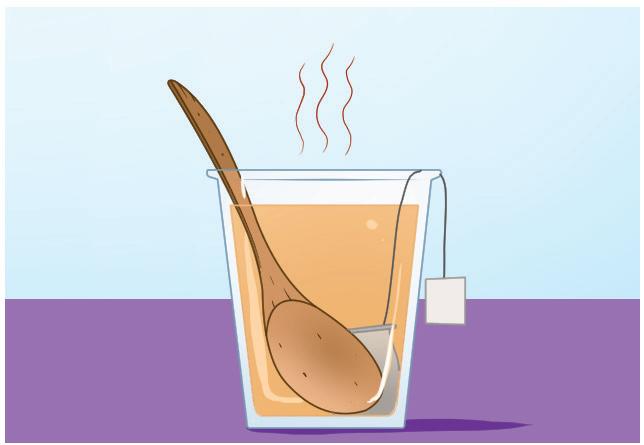


Fai l’esperimento e completa la conclusione.
Prendi tre tazze di tè caldo.
In una immergi un cucchiaino di metallo, nell’altra un cucchiaino di plastica, nell’ultima uno di legno.
Dopo qualche minuto, tocca i manici dei cucchiaini e registra ciò che senti.
Il metallo è un buon cattivo conduttore perché conduce il calore velocemente.
Infatti, le pentole sono di metallo perché trasmettono il calore ai cibi.
La plastica e il legno sono buoni cattivi conduttori perché conducono il calore molto lentamente, infatti vengono usati per i manici delle pentole per non scottarci.
 Il cucchiaino di plastica Il cucchiaino di legno
Il cucchiaino di metallo
Il cucchiaino di plastica Il cucchiaino di legno
Il cucchiaino di metallo
Per stare bene è importante avere una giusta temperatura nell’ambiente in cui si vive. Per questo, durante l’inverno, gli edifici vengono riscaldati con impianti di vario tipo.

Un esempio: L’IMPIANTO AD ACQUA
1 L’acqua contenuta in un serbatoio, chiamato caldaia, viene scaldata con il gas metano o altri combustibili (come il legno o il pellet) oppure attraverso i pannelli solari.
2 Una pompa spinge l’acqua calda nei tubi che arrivano fino ai termosifoni delle stanze, riempiendoli di acqua calda.
3 L’acqua scalda il metallo di cui è fatto il termosifone e, di conseguenza, scalda l’aria della stanza.
4 Raffreddandosi, l’acqua scende dai termosifoni ai tubi e torna alla caldaia, dove viene nuovamente scaldata e spinta in un ciclo continuo.
La temperatura in casa deve essere di circa 20 gradi Celsius. Se hai ancora freddo, non aumentare la temperatura della caldaia… metti un maglione!
Leggi la spiegazione e segui con il dito il percorso dell’acqua. Poi, osservando l’immagine, ripeti a voce alta il funzionamento dell’impianto.



Gli oggetti che utilizziamo tutti i giorni sono fatti di materiali diversi, che vengono scelti in base alle loro caratteristiche. Alcuni materiali sono naturali, quindi presenti in natura, altri sono artificiali, cioè prodotti dalle persone, combinando insieme più materiali e trasformandoli. I materiali possono avere origini diverse.

Dalla pianta del cotone si realizzano tessuti resistenti, permeabili e traspiranti, cioè che lasciano passare l’aria e proteggono dal caldo.
Prodotta dal baco da seta, è un tessuto molto pregiato e utilizzato per abiti leggeri ma resistenti.

Vengono estratte nelle cave, come il marmo e il granito. Sono materiali duri e resistenti, utilizzati nella costruzione di edifici e monumenti.
Ricavata dal manto delle pecore, è utilizzata per realizzare tessuti per abiti invernali.


Deriva dagli alberi, è rigido e resistente ma facile da lavorare. Brucia a basse temperature ed è un buon isolante.
Prodotto dalla pelle degli animali, è resistente e impermeabile.

Vengono estratti nelle miniere, come l’oro, il rame e il ferro.
Sono lucenti, modellabili con il calore e buoni conduttori.
Cotone Seta Rocce Lana MetalliSi ricava dal legno e da fibre vegetali. Può essere riciclata, brucia facilmente e assorbe l’acqua.
Carta Ceramica


Deriva dalla cottura dell’argilla. È impermeabile, rigida e resistente al calore,
Plastica

Si ricava dalla lavorazione del petrolio e può essere riciclata. È impermeabile e facilmente modellabile con il calore.
Proviene dalla fusione di sabbia e altre sostanze. È trasparente, impermeabile e rigido, ma fragile.
Gomma

Deriva da alcune piante tropicali. È impermeabile, isolante ed elastica.
È composto da ferro e altre sostanze. È rigido, resistente ed è un buon conduttore di calore.
Scegli i materiali con cui costruiresti questi oggetti, poi confrontati con i compagni.

- piatto
Fibre sintetiche

Sono composte da tessuti misti, in parte derivati dal petrolio. Sono generalmente resistenti e traspiranti.

- bicchiere
- forchetta
- pentola
- sottopentola
- manici della padella
- coltello
- quaderno
- mestolo
Le persone si sono accorte che la quantità dei materiali che trovano in natura ha un limite, per cui hanno imparato a riciclarli.

I vari tipi di carta vengono smistati manualmente e con dei macchinari.

La carta e il cartone vengono prelevati dai cassonetti e portati negli impianti di selezione.


Le balle di carta vengono affinate, depurate e unite alla cellulosa che si ricava dal legno degli alberi.
Il materiale raccolto viene suddiviso in base al tipo di prodotto.


Le balle di carta vengono trasferite alle industrie cartiere che le lavorano.
Si ottiene così la carta riciclata, con cui vengono fatti giornali, libri, quaderni e scatole di cartone.

La carta, una volta selezionata, viene schiacciata con una pressa e imballata.
Voi riciclate la carta e il cartone che utilizzate a scuola?
Ci sono contentori appositi per la raccolta differenziata? E a casa vostra?


Prova anche tu a fare un foglio di carta riciclata. Fatti aiutare da un adulto.


OCCORRENTE
- carta di giornale

- secchio
- bacinella larga
- acqua
1
4

Immergi il setaccio e raccogli la parte più solida della poltiglia, poi stendila sopra un panno in maniera uniforme.
- panno
- setaccio
- frullatore
- mattarello
5
Passa
Prendi il giornale e strappa la carta in piccoli pezzi. 2 Mettili a bagno in un secchio con dell’acqua e lasciali in ammollo per almeno un giorno. 3 Frullali fino a ottenere una poltiglia, poi versala in una bacinella più larga. sopra con il mattarello, in modo da appiattire bene il composto fino a farlo diventare sottile come un foglio. 6 Lascia asciugare.L’aria diventa inquinata quando viene “sporcata” da sostanze nocive, quasi sempre prodotte da attività umane.
1. “Filtra l’aria” eliminando gli agenti inquinanti. Cancella le parole indicate e riscrivi le lettere rimaste in modo da formare una frase.
smog • gas di scarico • fabbriche • auto • fumo • incendi • riscaldamento • polveri

2. Per diminuire l’inquinamento dell’aria si possono usare mezzi di trasporto ecologici. Guarda le immagini e completa il cruciverba.







L’uomo ha scoperto come produrre il calore e lo utilizza per riscaldare le proprie abitazioni. Occorre però utilizzarlo nel modo corretto, perché il riscaldamento domestico è una delle principali fonti di inquinamento e di spreco di energia.
1
Le tende coprono il calore dei termosifoni.


1. Procurati un dado e gioca con i tuoi compagni. Scoprirai in maniera divertente alcuni suggerimenti per ridurre l’inquinamento. 2 3 Partenza
Il tuo impianto di riscaldamento funziona bene.
Stai fermo un giro.
Fai una doccia lunga con acqua molto calda.
Vai indietro di due caselle.
Hai controllato porte e finestre e non ci sono spifferi di aria.
Avanza di una casella.
Di notte metti una coperta in più e abbassi il riscaldamento.
Avanza di due caselle.
4 5 6 7 8 9 10 11 12 14 13 15 16 17 18 20 19
Senti freddo: ti metti un maglione e non alzi la temperatura.
Avanza di tre caselle.
È inverno ma tieni la temperatura dei termosifoni troppo alta.

Avanza di due caselle. Il tuo impianto di riscaldamento non viene controllato da troppo tempo.
Stai fermo un giro.
Hai i termosifoni accesi, ma le finestre non si chiudono bene.
Vai indietro di una casella.
È materia trasparente, non ha forma ma occupa uno spazio e ha un peso.
NATURALI




È un miscuglio di gas: azoto, ossigeno, anidride carbonica e altri gas. Forma l’atmosfera che avvolge la Terra.
L’aria
La materia costituisce tutti i materiali, che possono essere

quando sono presenti in natura e vengono lavorati dalle persone.


quando sono prodotti dalle persone mescolando e trasformando diverse sostanze.

1. Completa con le caratteristiche dell’aria.
• Se soffio con una cannuccia dentro un bicchiere d’acqua, l’aria fa spostare l’acqua perché ..........................................................
• Se pesi un palloncino dopo averlo gonfiato con l’aria peserà di più perché ......................

• Se fai entrare aria in una siringa senza ago e tappi il foro con il dito, l’aria si schiaccia perché l’aria è Se lasci lo stantuffo, l’aria torna indietro perché è
• Se attacchi delle strisce di carta velina sopra un termosifone acceso, queste si muoveranno perché l’aria
calda ...............................................................................
2. Collega i materiali alla loro caratteristica.
legno plastica metallo
buon conduttore cattivo conduttore
3. Scrivi almeno un materiale e un oggetto per ogni caratteristica.

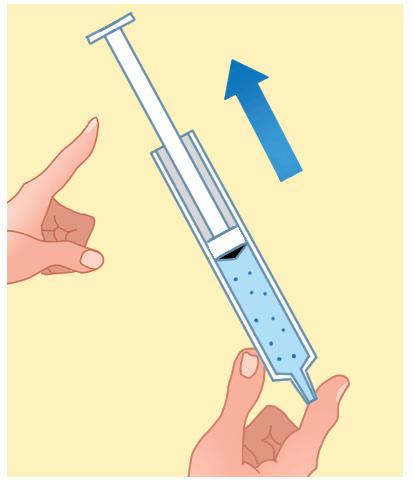

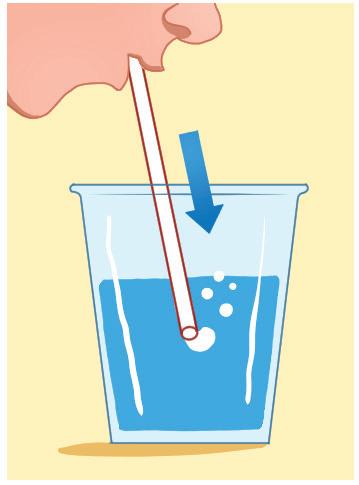
Caratteristica
Materiale Oggetto fragile impermeabile rigido resistente elastico
La Terra, il pianeta in cui viviamo, si è formata circa 5 miliardi di anni fa e ha cambiato aspetto molte volte.
L’essere umano, negli ultimi secoli, grazie all’intelligenza e all’uso delle mani, ha imparato a vivere in quasi tutti gli ambienti della Terra costruendo edifici e utilizzando tecnologie sempre più moderne. La tecnologia, inoltre, ha permesso ad alcune persone, gli astronauti, di viaggiare nello spazio, dove hanno fotografato la Terra e fatto esperimenti.
Come tutti i pianeti anche la Terra si muove. Sebbene ti sembra il contrario, la Terra gira su se stessa mentre il Sole resta fermo. Non te ne accorgi perché anche noi ci muoviamo insieme a lei, dentro l’atmosfera.



Comprendo CON IL CORPO
Completa il testo.
La Terra è un che si è formato di anni fa.
Le persone hanno imparato a vivere in quasi tutta
la Terra grazie al progresso della ...........................................
La Terra si girando su se stessa dentro l’ e noi insieme a lei.
Sperimenta il movimento della Terra.
In piedi, fissa una lampada immaginando che sia il Sole. Comincia a girare su te stesso senza girare la testa. Inizierai a vedere la lampada solo con la coda dell’occhio (tramonto), dopo, quando sarai di spalle, a non vederla affatto (notte), e poi a vederla nuovamente (alba).
Il primo sbarco sulla Luna. L’astronauta Samantha Cristoforetti nello spazio.La parola terra con la “t” minuscola indica il composto marrone che vedi al parco o nei vasi delle piante. Molti esseri viventi compiono qui il loro ciclo vitale. Tanti animali vivono sopra e sotto la terra e le piante vi affondano le loro radici. L’aria e l’acqua, infatti, penetrano nella terra permettendo la sopravvivenza degli organismi che ci vivono.
Il luogo su cui camminiamo e costruiamo edifici e strade viene chiamato suolo: è la parte più esterna della crosta terrestre ed è composto da diversi strati.
LETTIERA : parte più esterna del suolo formata da materiali organici come foglie, rametti, frutti, semi ed escrementi di animali.
HUMUS : strato di terriccio molto fertile formato da resti di animali e piante.
SOTTOSUOLO : strato formato da argilla, sabbia e ghiaia, ovvero rocce frantumate.
ROCCIA MADRE : strato di roccia molto dura dove non sono presenti esseri viventi.
Completa la mappa sul SUOLO con le parole adatte, poi ripeti a voce alta.
È la parte più ......................................... della crosta terrestre.
SUOLO
Contiene ......................................... e acqua.
È composto da vari strati: , , sottosuolo e madre.


Sulla Terra esistono tante forme di vita diverse. Tutte compiono lo stesso ciclo vitale: nascono, crescono, si riproducono e muoiono. In tutto l’arco della vita, inoltre, si svolgono alcune funzioni fondamentali: la respirazione, la nutrizione e il movimento. Gli scienziati hanno classificato gli esseri viventi in diversi gruppi, in base alle loro caratteristiche
ANIMALI


Vivono e si muovono sulla terra o nell’acqua. Se hanno uno scheletro interno che li sostiene e permette loro il movimento, si dicono vertebrati. Se non hanno uno scheletro interno oppure hanno una corazza o un guscio che li protegge, si dicono invertebrati


VEGETALI
Vivono sulla terra (alberi, arbusti, piante erbacee) o immersi nell’acqua (alghe e piante acquatiche). Fanno solo piccoli movimenti e molti hanno in comune la stessa struttura: rami, foglie, tronco e radici.
FUNGHI

Assorbono le sostanze di cui hanno bisogno dal terreno o direttamente da altri organismi. Anche le muffe sono funghi.


Le monere, i protisti e i batteri sono visibili solo al microscopio.

Tu conosci alcuni batteri “buoni”, che non vedi ma mangi nello yogurt, e alcuni batteri cattivi, che ti causano, per esempio, mal di gola.
Studio CON METODO
Memorizza i gruppi di esseri viventi e trova un altro esempio per ognuno.

All’interno dei due grandi gruppi di animali vertebrati e invertebrati, gli zoologi hanno individuato dei sottogruppi.








I mammiferi allattano i propri cuccioli.
I pesci vivono nell’acqua, hanno le pinne e la coda per nuotare.
Gli insetti hanno sei zampe e il corpo diviso i tre parti: capo, torace, addome.
I crostacei hanno una corazza esterna.
I rettili sono ricoperti di squame.
Gli uccelli hanno il becco e le ali e sono ricoperti di piume e penne. Non tutti volano.
Gli anfibi possono vivere sia nell’acqua sia sulla terraferma.
I vermi hanno il corpo lungo e molle, formato da anelli.
molluschi hanno un corpo molle, a volte protetto da un guscio.

Gli aracnidi hanno otto zampe e il corpo diviso in due parti: torace e addome.
Per ogni animale, scrivi sul quaderno se è vertebrato o invertebrato e a quale sottogruppo appartiene.
orso
farfalla
Gli esseri viventi, per crescere, hanno bisogno di nutrirsi. Gli animali trovano in natura il loro cibo perché, in generale, si nutrono di altri esseri viventi.
Gli animali che si cibano di piante e vegetali sono detti erbivori, come per esempio il cavallo, il coniglio, la giraffa, la pecora o l’ippopotamo. Hanno i denti molari piatti e larghi, adatti a triturare il cibo.

Sono carnivori gli animali che si nutrono di carne, ovvero di altri animali, vivi o morti, compresi insetti, vermi e larve. Hanno i denti canini lunghi e appuntiti, adatti a tagliare la carne. Sono carnivori il gatto e tutti i felini, lo squalo, la rana, l’aquila e molti altri.

Gli onnivori sono animali che si nutrono sia di piante sia di altri animali. La loro dentatura è formata da grossi molari e canini meno appuntiti rispetto ai carnivori. Tra questi troviamo l’orso, il cane, la scimmia e alcune specie di tartarughe. Anche l’essere umano è onnivoro.


Molari: denti posteriori adatti alla masticazione.

Ricerca con i tuoi compagni almeno cinque esempi di animali erbivori, carnivori e onnivori e raggruppali in una tabella sul quaderno.

La respirazione è un procedimento attraverso cui gli animali assorbono ossigeno ( ) e liberano anidride carbonica ( ). Gli animali di specie diverse utilizzano organi differenti per respirare.
I mammiferi terrestri e gli uccelli respirano attraverso i polmoni, degli organi spugnosi che si dilatano quando si riempiono d’aria. Anche alcuni animali marini, come i delfini e le balene, respirano con i polmoni, ma per prendere aria devono risalire in superficie e utilizzare un’apertura sul dorso: lo sfiatatoio



I rettili, i vermi e alcuni anfibi respirano attraverso dei piccoli fori sulla pelle: i pori.
I pesci usano le branchie, delle fessure poste dietro la bocca, attraverso le quali assorbono l’ossigeno dall’acqua.
Gli insetti usano le trachee, dei piccoli tubicini che dall’interno del corpo sbucano su alcuni fori chiamati stigmi.

Completa la descrizione della rana prendendo le informazioni dal testo. Come respira la rana?
Quando le rane nascono vengono dette girini, vivono nell’acqua e, come i pesci, respirano con le ................................................ Durante la crescita le branchie spariscono e vengono sostituite dai ........................................................, come nei mammiferi. Da adulte, le rane riescono a vivere sia in acqua sia sulla terraferma, come tutti gli anfibi. Esse, però, assorbono l’ossigeno attraverso la , come i rettili.
La riproduzione negli animali avviene in modi diversi.
Nei vivipari i cuccioli crescono all’interno del corpo della madre fino a che non sono completamente formati. Una volta partorito, il cucciolo viene allattato e accudito dalla madre fino a che non diventa autonomo.
Gli animali ovipari depongono le uova, che contengono animali non ancora sviluppati. Dopo un periodo di incubazione, le uova si schiudono, cioè si aprono, e nascono i piccoli.




Incubazione: periodo di sviluppo delle uova.

Gli animali ovovivipari trattengono le uova all’interno del proprio corpo, fino a che i piccoli non sono completamente formati e pronti a nascere. A quel punto, vengono deposte le uova che si schiudono subito. Sono ovovivipari la vipera, lo squalo, gli scorpioni e alcuni insetti.


Collega nel modo giusto ed esponi a voce alta.
depone le uova, quindi
Il pettirosso è ovoviviparo.
partorisce cuccioli già formati, quindi
Lo scorpione è oviparo.
trattiene le uova nel proprio corpo, quindi
Il coniglio è viviparo.
Studio A VOCE ALTA Dentro LE PAROLELe piante producono da sole il proprio nutrimento attraverso un procedimento chiamato fotosintesi clorofilliana. Questo processo avviene grazie alla luce del Sole (perciò solo di giorno) e alla clorofilla, una sostanza presente nelle parti verdi della pianta.
1 Le radici assorbono acqua e sali minerali dal terreno: la linfa grezza.
2 La linfa grezza, attraverso il fusto, arriva alle foglie.
3 Le foglie assorbono l’anidride carbonica, un gas dell’aria.

4 A questo punto avviene la fotosintesi: la clorofilla, attivata dalla luce del Sole, trasforma la linfa grezza e l’anidride carbonica in linfa elaborata, ricca di zuccheri: è il nutrimento della pianta.

5 Durante questo processo, le foglie liberano nell’aria l’ossigeno
Fai l’esperimento e rispondi. Procurati un gambo di sedano e osserva con la lente di ingrandimento i tubicini che ci sono all’interno.
Completa il testo.
La fotosintesi clorofilliana è un processo per cui, grazie alla .............................................. nelle foglie e alla ................................... del Sole, le piante usano la linfa e l’
carbonica per produrre linfa elaborata, ricca di ..................................................... Durante la fotosintesi le piante liberano ............................................... nell’aria.
Versa dell’acqua in un bicchiere, fino a metà, e metti nell’acqua alcune gocce di colorante alimentare. Immergi il gambo di sedano nell’acqua colorata. Che cosa
è successo alle foglie dopo un giorno?


anidride carbonica
ossigeno ossigeno ossigeno
Come gli animali, anche le piante respirano per mantenersi in vita: assorbono ossigeno e liberano anidride carbonica. La respirazione avviene sia di giorno sia di notte ma, durante il giorno, grazie alla fotosintesi, la pianta libera molto più ossigeno che anidride carbonica. L’anidride carbonica esce attraverso gli stomi, piccoli fori presenti sulle foglie.
anidride carbonica
anidride carbonica
Sempre attraverso gli stomi le piante “sudano” come gli animali. Questo processo si chiama traspirazione e serve per eliminare l’acqua sotto forma di vapore acqueo.
Sperimentiamo la traspirazione.
Appoggia una busta trasparente sopra una pianta.
Che cosa noti dopo qualche ora?
La pianta ha liberato ossigeno e che si è condensato sulla busta trasformandosi in goccioline d’acqua.
Indica con una X se le affermazioni sono vere (V) o false (F).
La respirazione delle piante avviene solo di notte. V F
La respirazione delle piante produce ossigeno. V F
La traspirazione delle piante è simile alla sudorazione. V F
Gli stomi sono delle sostanze che vengono eliminate dalle piante. V F
Le fasi della riproduzione delle piante sono:
IMPOLLINAZIONE

I fiori delle piante contengono il nettare, una sostanza nutritiva per alcuni insetti, piccoli uccelli e pipistrelli Quando questi animali si posano sui fiori, il polline si attacca al loro corpo e viene trasportato verso altri fiori. Alcune piante, invece, rilasciano il polline nell’aria e il vento o l’acqua lo trasportano lontano.
FECONDAZIONE
Il polline, attaccato ai piccoli animali o trasportato dal vento, cade nel pistillo dei fiori e poi nell’ovario, dove incontra gli ovuli e forma il seme. Il fiore perde i petali, l’ovario si ingrossa e si trasforma in frutto

DISSEMINAZIONE
I frutti cadono sul terreno o vengono mangiati dagli animali che trattengono i semi nella pancia, li trasportano e li depositano nella terra, insieme agli escrementi. Il vento trasporta lontano i semi piccoli e leggeri di alcune piante.
GERMINAZIONE

Dai semi caduti su un terreno adatto nasceranno nuove piante
Studio CON METODO
Procurati diversi frutti (mela, arancia, kiwi, limone…) poi tagliali a metà e osservali da vicino. Disegna ciò che vedi. Quale frutto ha più semi all’interno?

Colora con colori diversi le fasi della riproduzione e memorizzale.

Piante e animali si difendono dai nemici o dalle condizioni ambientali difficili con diverse strategie



Le piante grasse sono in grado di difendersi dal caldo grazie alle loro foglie che, rigonfiandosi, riescono a immagazzinare acqua.
Alcune piante sono ricoperte di spine per difendersi dall’attacco degli animali erbivori.

Il calamaro, per sfuggire agli attacchi dei nemici, emette una sostanza scura in modo da confondere i predatori e coprire la propria fuga.
Mimetismo: animali o piante che, per difendersi, assumono colori e forme dell’ambiente in cui vivono.


L’orso polare riesce a sopravvivere in un ambiente molto freddo poiché è capace di respirare l’aria gelida, riscaldandola attraverso una serie di passaggi prima di farla arrivare ai polmoni. Un folto mantello bianco lo protegge dal freddo e lo mimetizza con l’ambiente circostante.


Osserva le immagini e cerchia gli animali che si stanno mimetizzando nell’ambiente.
Ogni essere vivente è costantemente alla ricerca di cibo per garantire la sua sopravvivenza nell’ambiente. Per esempio, l’erba cresce solo se trova la luce del Sole, l’aria, l’acqua e un terreno ricco di sali minerali. L’erba 1 diventa cibo per altri esseri viventi, come la cavalletta 2 , che può essere mangiata dalla lucertola 3 oppure può morire naturalmente.
In questo caso, i suoi resti rimarranno sulla terra e diventeranno cibo per i funghi e i microrganismi 4 ; questi li trasformeranno in sali minerali che, disciolti nell’acqua e nella terra, verranno assorbiti dalle piante. Il ciclo ricomincia come una catena circolare, chiamata catena alimentare.
Nei diversi ambienti, le relazioni tra gli esseri viventi e quelli non viventi, come terreno, acqua, aria e luce, formano un ecosistema, ovvero un insieme organizzato in perfetto equilibrio. Se una sola componente cambia, l’ecosistema deve riadattarsi e trovare un nuovo equilibrio per continuare a funzionare.

Racconta a voce tutti i passaggi della catena alimentare usando le parole chiave:
• produttore;
• consumatore primario;
• consumatore secondario;
• consumatore terziario;
• decompositore.


Il bosco è un ecosistema terrestre caratterizzato da una fitta vegetazione, in cui si possono individuare diversi strati
In questo ambiente ci sono molte specie animali che qui trovano cibo e riparo, garantendo l’equilibrio naturale del bosco. Gli uccelli rapaci, per esempio, si nutrono di topi e impediscono che questi aumentino troppo di numero. Troppi topi, infatti, sarebbero dannosi per gli alberi perché rosicchiano le loro radici.
Strato erbaceo o sottobosco: formato da piante erbacee e numerose specie di funghi.

Strato arbustivo: composto da arbusti e siepi.
Strato arboreo: formato dalle chiome degli alberi ad alto fusto.
Immagina quale potrebbe essere un esempio di catena alimentare del bosco, poi ripeti a voce alta.

È nutrimento per
Consumatori primari
Produttori
Decompositori
Consumatori secondari

si dividono in:

- vertebrati, come pesci, uccelli, rettili, anfibi e mammiferi;
- invertebrati, come vermi, molluschi, crostacei, aracnidi e insetti.

si nutrono: producono da sole il cibo per nutrirsi attraverso la fotosintesi. Durante questo processo assorbono anidride carbonica e rilasciano ossigeno.
si nutrono: possono essere erbivori, carnivori, onnivori.
si riproducono: dal seme si sviluppa la pianta; dalla pianta si sviluppano i fiori, poi i frutti e, infine, di nuovo i semi.

si riproducono: possono essere ovipari, vivipari, ovovivipari.
respirano: attraverso le foglie, assorbono ossigeno e liberano anidride carbonica.
respirano: attraverso polmoni, branchie, pelle e trachee.
traspirano: rilasciano vapore acqueo attraverso le foglie.
1. Completa la tabella sulla composizione degli strati del suolo.
Formato da:
lettiera
humus ...................................................................................................................................................................................
sottosuolo ...................................................................................................................................................................................
roccia madre ...................................................................................................................................................................................
2. Cancella in ogni frase l’opzione errata.
La clorofilla è presente nel fusto nelle foglie
La fotosintesi avviene di giorno di notte .
Il nutrimento della pianta è la linfa grezza elaborata
Nel processo di fotosintesi la pianta libera ossigeno anidride carbonica
Attraverso la respirazione la pianta libera ossigeno anidride carbonica
3. Completa con le parole adatte.
germinazione • fecondazione • seme • pistillo • impollinazione disseminazione • animali
Durante la fase di , il polline prodotto dalle piante viene trasportato da piccoli animali o dall’aria. Il polline cade nel dei fiori e poi nell’ovario, dove incontra gli ovuli e forma il
Questo processo si chiama ....................................................... La ...................................................... è il processo per cui i semi vengono portati lontano dal vento o dagli
Attraverso la dai semi nasceranno nuove piante.
4. Leggi le frasi e scrivi V (vero) o F (falso).
I vermi respirano attraverso la pelle.
I serpenti respirano con i polmoni.
I pesci respirano attraverso le branchie.
I mammiferi respirano con i polmoni.
Le balene respirano con le branchie.
I rettili respirano con le branchie.
5. Cerchia il completamento corretto.
• Gli animali che partoriscono piccoli già formati sono ovovivipari / vivipari

• I mammiferi allattano / non allattano i loro piccoli.
• Gli animali ovovivipari / vivipari trattengono le uova all’interno del proprio corpo fino a che i piccoli non sono completamente formati e pronti a nascere.
6. Leggi le frasi e scrivi V (vero) o F (falso).
Le piante grasse riescono a immagazzinare poca acqua per resistere al caldo. Alcune piante sono ricoperte di spine per difendersi dall’attacco degli animali.
Il calamaro, per sfuggire agli attacchi dei nemici, emette una sostanza scura.
Il corpo dell’orso polare è coperto da un folto pelo scuro che lo protegge dal freddo e lo mimetizza con l’ambiente circostante.
7. Completa la mappa mettendo le parole al posto giusto.
esseri • animali • acqua • equilibrio • insieme • terreno non viventi • piante • aria • luce
Nella vostra classe organizzate una “Fiera della Scienza”. Dividetevi in gruppi da tre e ogni gruppo preparerà un esperimento. A turno, due bambini useranno i materiali mentre il terzo spiegherà il procedimento e la conclusione.




Prendete una cannuccia e immergetela nell’acqua; chiudete con il dito l’estremità libera e sollevate la cannuccia.
Potete utilizzare anche le attività suggerite a pagg. 149 e 153.
Questo esperimento dimostra il funzionamento del contagocce. Come potete vedere, l’acqua non cade. Se si apre e si chiude velocemente l’estremità della cannuccia, cadrà poca acqua: uscirà esattamente tanta acqua quanta aria sarà entrata.
Come potete vedere, la pallina non cade neanche se il phon viene inclinato. L’aria, che esce con forza, forma un vortice, cioè una specie di “tubo” da cui la pallina non riesce a uscire.
1 Collega ogni parola al suo significato.
Metodo scientifico
Fenomeno
Scienza
Zoologo
Telescopio
Sperimentare
Biologo
Ipotesi
Microscopio
Chimico
Prima osserva, poi formula l’ipotesi, la verifica con gli esperimenti e trova la conclusione.
Conoscenza dei fenomeni attraverso la sperimentazione.
Strumento che permette di ingrandire gli oggetti migliaia di volte.
Possibile risposta per spiegare un fenomeno.
Procedura usata dagli scienziati per studiare i fenomeni.
Scienziato che studia gli esseri viventi e l’ambiente in cui vivono.
Tutto ciò che accade in natura e che possiamo osservare e studiare.
Strumento per osservare oggetti lontanissimi, come stelle e pianeti.
Scienziato che studia gli animali.
Eseguire uno o più esperimenti per verificare un’ipotesi.
Scienziato che studia la composizione della materia.
Prima osserva, poi formula l’ipotesi e infine trae la conclusione.
1 Leggi e completa il testo inserendo le parole mancanti. Scegli tra quelle proposte.
sensi • solido • gassoso • molecole • liquido • particelle • precisa spazio • contenitore • propria
La materia occupa uno . Noi possiamo percepirla grazie ai nostri ......................................... È formata da piccolissime ........................................, che si chiamano .
Quando le molecole sono lontane tra loro e sono libere di muoversi la materia è allo stato , se le molecole sono vicine, ma possono muoversi, la materia è allo stato , se le molecole sono vicinissime e non possono muoversi la materia è allo stato . I solidi hanno una forma , i liquidi possono assumere la forma del in cui si trovano, i gas non hanno forma e possono espandersi in tutto lo spazio che hanno a disposizione.
2 Per ogni stato della materia scrivi due esempi.
Solido
Liquido
Gassoso
3 Indica in ogni passaggio di stato se viene aggiunto (+) o tolto (-) calore.
Materia Variazione di calore Passaggio di stato Materia modificata
Fusione Formaggio fuso
Condensazione Pioggia
Solidificazione Ghiacciolo ...................................................
Evaporazione Vapore
1 In ogni gruppo indica l’affermazione sbagliata.
La fiamma è acqua luce calore
Osserva la foto e rispondi.
Con il calore puoi scaldarti condensare cuocere

Il calore fonde il legno il cioccolato il metallo
Di quale strumento si tratta?
A che cosa serve?
Sai se ne esistono altri tipi?
A che cosa servono?
3 Completa i passaggi che descrivono il ciclo dell’acqua.
Con l’aria il vapore diventa . Con aria ancora più fredda si formano le .
Grazie al l’acqua si scalda, evapora e sale verso il
Al suolo forma laghi e fiumi e torna al . Oppure va sottoterra, nelle
1 Colora i cartellini: in rosso i minerali, in verde i vegetali e in viola gli animali. Poi rispondi.
• Quali cartellini non hai colorato?
• Perché?
• Ne conosci altri? Fai qualche esempio:
2 Indica da che cosa si ricavano questi materiali naturali e artificiali.







• Vetro .......................................................
• Plastica

• Ceramica .......................................................
• Legno .......................................................

• Lana
• Seta .......................................................
Orizzontali
1. Gli animali non sono produttori, ma sono...
2. Lo sono i mammiferi poiché allattano i piccoli che nascono completamente sviluppati.
3. Animali con corpo molle o corazza esterna.
4. Le balene sono mammiferi...
5. Vertebrati che possono essere o terrestri o acquatici.
6. Le depongono gli animali ovipari.
Verticali
1. Animali che mangiano un po’ di tutto.
2. Animali con uno scheletro interno.
3. Gli insetti respirano grazie alle...
4. Organi con cui respirano i pesci.
5. Lo sono i ragni.
1 Rispondi alle domande.
• Perché le piante sono dette produttori? .
• Da che cos’è composta la linfa grezza?
• Quale parte della pianta assorbe la linfa grezza? .
• In quale parte della pianta la linfa diventa elaborata?
• A che cosa serve la linfa elaborata? .
• Che cosa sfrutta la clorofilla per fare la fotosintesi?
• Quali sono i prodotti della fotosintesi? .
2 Collega con una freccia ogni termine alla definizione corretta.
Stomi Respirazione Traspirazione
Processo che permette alle piante di rilasciare acqua, come se sudassero.
Piccoli fori che si trovano sulle foglie.
Processo che permette alle piante di scambiare con l’ambiente ossigeno e anidride carbonica.
3 Completa la riproduzione del melo scrivendo le fasi mancanti.
1 Scrivi gli elementi della catena al posto giusto.
volpe insalata riccio chiocciola lombrico
Produttore
Consumatore primario
Consumatore secondario
Consumatore terziario
Decompositore
2 Descrivi le caratteristiche principali di queste categorie di viventi.
Produttori:
Consumatori primari:
Consumatori secondari:
Consumatori terziari:
Decompositori:
3 Se nella catena alimentare dell’esercizio 1 mancassero i decompositori che cosa succederebbe? Perché ogni anello è importante?
1 Indica con una X il completamento corretto.
Un ecosistema è formato da animali.
vegetali.
elementi non viventi come il suolo, l’aria e l’acqua. tutti i precedenti.
2 Scrivi i nomi degli ecosistemi al posto giusto.
• Lago
• Foresta
• Palude
• Deserto
• Prato
• Oceano
Ecosistemi terrestri Ecosistemi acquatici
3 Scrivi al posto giusto gli elementi non viventi e i viventi animali e vegetali dell’ecosistema del prato qui rappresentato.
ELEMENTI VIVENTI animali
ELEMENTI VIVENTI vegetali
ELEMENTI NON VIVENTI


Strumenti per la didattica personalizzata, individualizzata, inclusiva, per la lezione in classe con la LIM e il ripasso a casa.
Il tuo libro si arricchisce di video di approfondimento, video lezioni, video tutorial, laboratori di ascolto, lettura dei testi, canzoni, mappe ed esercizi interattivi, audio CLIL in lingua inglese e tanto altro ancora. Puoi ascoltare l'audiolibro completo, letto da speaker professionisti, modificare il carattere dei testi, utilizzare il dizionario interattivo e la traduzione multilingue.
Per accedere ai contenuti e agli strumenti digitali, entra in Raffaello Player (rp.raffaellodigitale.it) o scarica l’applicazione Raffaello Player dal portale www.raffaellodigitale.it, da Google Play o dall’App Store e inserisci il codice di attivazione. Non è richiesta alcuna registrazione.
Personalizza i tuoi contenuti, allega file, crea nuovi documenti e condividili con gli altri. Connessione internet necessaria.
Inquadra e visualizza i contenuti presenti nel libro digitale. Connessione internet necessaria.
Installa l'app Raffaello Player e inquadra la pagina.
QR CODE
Inquadra i QR Code direttamente con la fotocamera oppure con un’app a tua scelta.

Collegati al portale www.raffaellodigitale.it per scaricare il materiale digitale extra e richiedere assistenza. Registrati per ricevere gli aggiornamenti del testo digitale.
Coordinamento: Emilia Agostini
Redazione: Corrado Cartuccia, Federica Paparelli, SEI servizi editoriali
Grafica e impaginazione: Mauda Cantarini, Dania Fava, Marco Mancini, SEI servizi editoriali
Illustrazioni: Archivio Raffaello, Manuel Berselli, Andrea Rossetto
Copertina: Mauro Aquilanti, Valentina Mazzarini
Referenze fotografiche: Archivio fotografico Raffaello, iStock, Shutterstock, AdobeStock, Alamy
Coordinamento multimedia: Paolo Giuliani
Redazione multimedia: Sara Ortenzi, Giulio Pieraccini
Ufficio multimedia: Enrico Campodonico, Claudio Marchegiani, Luca Pirani
Stampa: Gruppo Editoriale Raffaello
Per esigenze didattiche alcuni testi sono stati ridotti e/o adattati. L’Editore è a disposizione per eventuali omissioni o inesattezze nella citazione delle fonti. Tutti i diritti sono riservati. È vietata la riproduzione dell’opera o di parti di essa con qualsiasi mezzo, compresa stampa, fotocopia, microfilm e memorizzazione elettronica, se non espressamente autorizzata.
Questo testo tiene conto del codice di autoregolamentazione Polite (Pari Opportunità Libri di Testo), per la formazione di una cultura delle pari opportunità e del rispetto delle differenze.
2020
Raffaello Libri S.p.A. Via dell’Industria, 21 60037 - Monte San Vito (AN) www.grupporaffaello.it - info@grupporaffaello.it
Ristampa:

Pack A
Codice adozionale 978-88-472-3507-6
CLASSE 1a
Pack B - METODO con i QUATTRO CARATTERI








Codice adozionale 978-88-472-3508-3
CLASSE 2a Pack
Codice adozionale 978-88-472-3516-8
• Letture
• Discipline
• MEGA esercizi Ortografia
• MEGA esercizi Matematica
• Scrittura e Grammatica
In allegato a MEGA esercizi i fascicoli di logica
A richiesta i volumi con i percorsi semplificati di 1a, 2a e 3a, anche in versione audiolibro
PER L’INSEGNANTE E LA CLASSE
CLASSE 3a Pack
Codice adozionale 978-88-472-3522-9
• Letture
• Discipline (Storia e Geografia) con Eserciziario
• Discipline (Matematica, Scienze e Tecnologia) con Eserciziario


• MEGA esercizi Grammatica con verifiche a livelli
• MEGA esercizi Matematica con verifiche a livelli








• Scrittura e Grammatica
Risorse digitali
Il testo è ricco di contenuti per la lezione in classe e a casa

In allegato a MEGA esercizi i fascicoli di logica
In allegato al Sussidiario StudioMap per prepararsi alla classe 4a
• Guida al testo con programmazione, suggerimenti per coding, STEAM e classe capovolta, schede operative, soluzioni delle verifiche a livelli

• Cartelloni: Tabelle forma-sillabe; Accoglienza; I compleanni della classe; Le tabelline; L’evoluzione dell’umanità; Le cinque Ere
• L’alfabetiere murale
il libro digitale e contenuti extra visualizzabili anche in assenza di connessione internet audiolibro


Alta leggibilità
Alta leggibilità (formato ePub) con testo modificabile

Audiobook


Audiolibro integrale a cura di speaker professionisti
Attivazione delle risorse digitali tramite smartphone o tablet