International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072
Enhancing Machine Learning via Quantum Computing: An Integrated Approach for Enhanced Data Processing and Optimization
Thamizh Selvam D1, Keerthana R2 and Santhakumar R3
1Department of Computer Science, Rajiv Gandhi Arts & Science College, Thavalakuppam, Puducherry, India
2Tata Consultancy Services, Chennai, India
3Department of Computer Science, Pondicherry University, Puducherry, India
Abstract - Machine learning (ML) and quantum computing (QC) together form a new area in computational science that improves data processing and optimization beyond traditional computing. Quantum Machine Learning (QML) uses quantum mechanics, like superposition and entanglement, to create faster algorithms. Key aspects of QML include quantum-augmented support vector machines, quantum neural networks, and vibrational quantum algorithms that blend classical and quantum techniques. Quantum computing enhances ML with better solutions for gradient descent and generative model training. Libraries like PennyLane, TensorFlow Quantum, Qiskit Machine Learning, and Cirq aid in QML development. QML shows promise in sectors like finance, healthcare, and materials science, suggesting a Combined Strategy for Superior Data Processing and Optimization.
Key Words: Quantum Neural Networks, Quantum Machine Learning, Quantum Computing, Machine Learning, PennyLane, TensorFlow, Noisy IntermediateScaleQuantum
1. INTRODUCTION
The swift advancement of Machine Learning (ML) has resulted in transformative innovations across multiple domains, such as healthcare, finance, autonomous systems, and natural language processing [1, 2, 3]. Notwithstanding its significant advancements, traditional ML faces limitations due to computational constraints as models increase in complexity and the data volume rises exponentially [4, 5]. Training deep learning models and addressing high-dimensional optimization issues demand substantial computational resources, resulting in slow convergencespeedsandprocessinginefficiencies[6].This requires the investigation of different computational paradigms that can surpass these restrictions, one of whichisQuantumComputing(QC)[7].
Quantum Computing signifies a revolutionary advancement in computer science, employing principles from quantum mechanics to handle and alter data in fundamentally different ways than conventional computing [8]. In contrast to conventional binary computing that uses bits as either 0 or 1, quantum
computingutilizesqubitsthatcanbeinasuperpositionof both states at the same time [9]. This distinctive feature allows quantum computers to carry out numerous calculations simultaneously, greatly enhancing computational efficiency [10]. Quantum phenomena like superposition, entanglement, and quantum interference enable quantum computing to exceed the capabilities of classical computing, particularly in data handling and optimizationactivities,offeringsubstantialadvantagesfor improvingmachinelearningmethods[11,12,13]
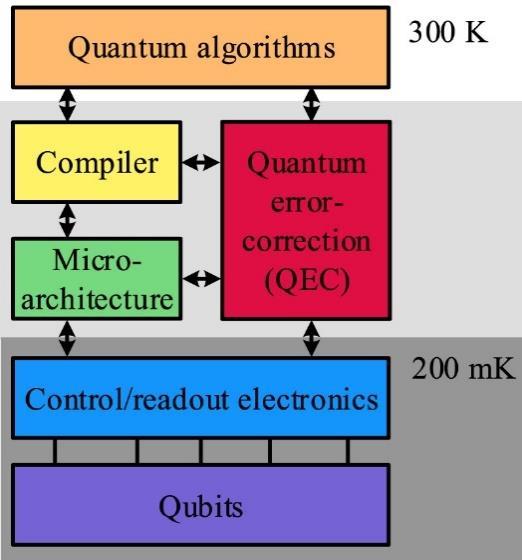
The integration of Quantum Computing and Machine Learning, referred to as Quantum Machine Learning (QML), is a burgeoning interdisciplinary field aimed at harnessing quantum concepts to refine ML models [14]. QML utilizes quantum algorithms for various applications such as classification, clustering, regression, and generative modeling, possibly offering greater speed and efficiencythanstandardmethods[15].
Various quantum computing frameworks and libraries have been created to aid the incorporation of quantum computing into machine learning workflows. PennyLane, TensorFlow Quantum, Qiskit Machine Learning, and Cirq offer reliable resources for creating and implementing QMLalgorithmsonquantumsimulatorsandrealquantum hardware[16,17].Theseplatformsallowresearchersand developers to test quantum circuits, create quantumboostedMLmodels,andconnecttheoreticalprogresswith practicalapplication[18,19].
Fig.1. Quantum Architecture
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072
Inspite of persistent obstacles,the collaboration between quantum technology and ML offers significant chances to transform data-driven areas, resulting in remarkable scientific discoveries and innovative advancements. This study investigates the collaboration between Quantum Computing and Machine Learning, offering a cohesive approachtoimprovedatahandlingandefficiency.
2. RELATED WORKS
Quantum Machine Learning (QML) has emerged as an interdisciplinary area dedicated to combining the strengths of quantum computing with the versatility of machine learning approaches [1, 5]. Foundational theoretical work, such as Shor’s algorithm for integer factorization [6] and Grover’s algorithm for database searching [7], illustrated that quantum computing could exceed traditional methods in particular computational challenges. These innovations fueled excitement for the applicationofquantumprinciplesinmachinelearning[8].
Early QML studies, particularly by Lloyd, Mohseni, and Rebentrost, concentrated on quantum-augmented versions of conventional algorithms such as Quantum Support Vector Machines (QSVM), suggesting possible quantum speedup in the inversion of kernel matrices, an essentialphaseinSVMtraining[9].Asaresult,theideaof QuantumNeuralNetworks(QNN)wasdeveloped,utilizing quantum circuits to create neural network structures capableofmanagingintricatedatatransformations[10]
Research by Farhi et al. highlighted quantum circuits as essential instruments for enhancing neural network calculations and explored the capability of quantum parallelism to boost learning efficiency [11]. Additionally, quantumclusteringtechniques,suchasquantumk-means, have been developed to enhance conventional clustering methods using quantum speedup, as demonstrated in researchbyKerenidisetal.[12].Thesestudiesemphasize thediverseapplicationsofquantumcomputinginmachine learning, focusing on optimization, classification, regression,andclusteringtasks[13].
Despite these advancements, challenges persist, such as the limitations of Noisy Intermediate-Scale Quantum (NISQ) systems and the necessity for efficient quantum data representation [1, 14]. Instruments and frameworks such as PennyLane, TensorFlow Quantum, and Qiskit MachineLearninghaveplayeda crucial roleinfacilitating thepracticalapplicationofquantumalgorithms[15,16].
With advancements in quantum technology, QML's ability toaddressintricateissuesinfieldslikehealthcare,finance, and materials science enhances significantly. These advancements offer exciting possibilities for innovative
applications of machine learning, particularly in dataintensivedomains[17,18]
3. CHALLENGES IN CONVENTIONAL MACHINE LEARNING
Conventionalmachinelearning(ML)hasmadesubstantial progress in recent years, facilitating innovations across various domains, such as healthcare, finance, natural language processing, and autonomous systems. Nonetheless,inspiteoftheseaccomplishments,traditional ML encounters various ongoing obstacles that affect its effectiveness,precision,scalability,andinterpretability.
3.1. Data Quality and Accessibility
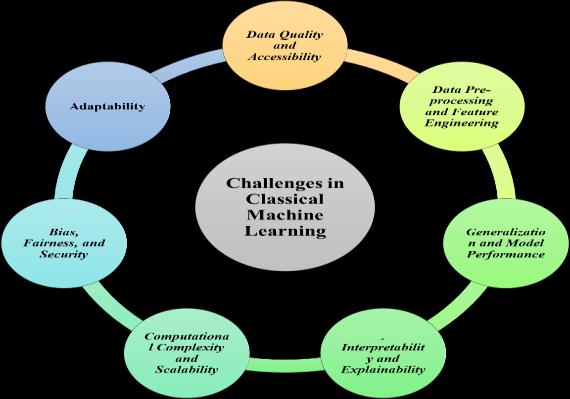
The effectiveness of machine learning models is largely contingentupontheavailabilityofsubstantialhigh-quality data for both training and evaluation; nevertheless, the acquisition of such data is frequently problematic in various real-world applications. Data collection is often hindered by privacy issues, ethical dilemmas, and technical constraints, especially in sensitive sectors like healthcare, where it is essential to anonymize patient information, or in finance, where access to private datasetsisrestricted[1],[2].
Moreover, even when data is available, it may suffer from class imbalance, leading to the underrepresentation of certain categories or labels. In fraud detection systems, fraudulenttransactionsaresignificantlylesscommonthan legitimate ones, which impedes machine learning models from recognizing important patterns within the minority class. Class imbalance can lead to biased models that performwellonthemajorityclassbuthavedifficultywith theminorityclass,thusreducingtheoverallrobustnessof themodel.Thisissuenecessitatestargetedstrategiessuch as oversampling, undersampling, and synthetic data generation techniques like SMOTE (Synthetic Minority Over-sampling Technique) to ensure that the model is
Fig.2. Challenges inClassical Machine Learning
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072
trained on a balanced representation of diverse data classes[3],[4].
3.2. Data Pre-processing and Feature Engineering
Datasets from the real world frequently have absent values, redundant entries, and noisy or unimportant attributes that can interfere with the model's training process. Dealing with missing data necessitates approaches like imputation or elimination, yet incorrect treatmentcanresultinbiasedordeceptiveoutcomes[5].
Choosingthemostimportantvariablesformodeltraining, knownasfeatureselection, isanessential butchallenging task, as adding too many irrelevant features can raise computational complexity and diminish model performance, whereas having too few could result in underfitting[6],[7].
3.3. Generalization and Model Performance
Animportantconcerninconventionalmachinelearningis model generalization, which pertains to an ML model's capacity to maintain strong performance on unfamiliar data. Generalization is influenced by two primary conflictingfactors:overfittingandunderfitting.
Overfitting arises when a model captures both the critical patterns in the training data and the noise or random variations, which results in excellent performance on the training data but inadequate performanceonthetestdata[8].
Underfitting occurs when a model is excessively simplistic, failing to discern the fundamental pattern in the data, leading to insufficient performance on bothtrainingandtestingdatasets
3.4. Interpretability and Explainability
Another significant challenge in classical ML is model interpretability and explainability, particularly as models grow increasingly complex. Simple models such as decision trees, logistic regression, and linear regression are relatively easy to interpret, as their decision-making processes can be visualized or mathematically explained [11]. However, more sophisticated models, such as deep neural networks, support vector machines, and ensemble models, operate as “black boxes,” making it difficult to understandwhyaparticulardecisionwasmade[12].
3.5. Computational Complexity and Scalability
Training large-scale ML models requires significant computational resources, often necessitating high-
performance GPUs, TPUs, or distributed computing frameworks.Thischallengeisparticularlyevidentindeep learning, where training state-of-the-art models can take days or weeks and require large amounts of memory and processingpower[13].
3.6. Bias, Fairness, and Security
ML models are prone to reflecting and amplifying biases presentintrainingdata.Biasescanleadtodiscriminatory or unfair outcomes, raising serious ethical concerns. Additionally, adversarial attacks where small, carefully crafted input perturbations mislead ML models pose security risks in areas like cybersecurity, autonomous driving,andfacialrecognition[14].
3.7. Adaptability
Many ML models rely on static datasets and struggle to adapt to dynamic environments. Real-time adaptability is essential in applications such as fraud detection and recommendation systems, yet remains challenging [15], [16]
4. QUANTUM COMPUTING’S ROLE IN MACHINE LEARNING
Quantum computing (QC) is a swiftly progressing area that has the capacity to transform machine learning (ML) by providing computational advantages that outstrip classical computing abilities. By harnessing the principles of quantum mechanics such as superposition, entanglement, and quantum interference quantum computing can carry out complicated computations more effectively than traditional systems. Machine learning, which is fundamentallyreliant on optimization,data processing, and pattern recognition, stands to gain considerably from the parallelism and speed enhancements offered by quantum computing. Quantum Machine Learning (QML), the integration of quantum computing and ML, aims to create quantum-enhanced algorithms capable of processing large datasets more efficiently, addressing complex problems more rapidly, and improving generalization in predictive modeling. This section investigates how quantum computing aids ML, focusing on significant algorithms, applications,andchallengesinthisdevelopingfield. In classical ML, training involves optimization tasks such as gradient descent, where model parameters are iteratively updatedusingEquation(1): ����+1 =���� ������(����) (1) Quantum computing offers an alternative approach by leveraging quantum parallelism and interference effects to accelerate optimization tasks. A quantum equivalent of gradient-based optimization can be represented using unitarytransformations,asshowninEquation(2):
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072
|θ��+1⟩=��(η,∇��̂)|θ��⟩ (2)
Quantum optimization algorithms such as the Quantum Approximate Optimization Algorithm (QAOA) provide solutions for complex optimization problems using the followingcostfunctionrepresentation(Equation3):
��(��,��) = ⟨��,��|�� ��|��,��⟩ (3)
where HC is the problem Hamiltonian encoding the cost function, and parameters �� and �� are iteratively optimized. Another widely used approach in quantum machine learning is the Variational Quantum Eigensolver (VQE), whichaimstominimizeanexpectationvaluewithrespectto parameterizedquantumstates,asgivenbyEquation(4):
������*��+⟨��(��)|��|��(��)⟩ (4)
��ℎ������(��) is the Hamiltonian representing the problem, and (|��(��)⟩) is the variational quantum state. In addition, quantumkernelmethodstransformclassicaldataintohighdimensional quantumfeaturespaces using kernel functions oftheformpresentedinEquation(5):
��,����)=⟨��(����)|��(����)⟩ (5) where (ϕ(��)) represents a quantum feature mapping that leverages entanglement and superposition to capture complexrelationshipswithinthedata.
4.1. Quantum Algorithms and Techniques
One of the most promising contributions of quantum computing to machine learning (ML) is its ability to speed up classical algorithms. Classical ML models, such as support vector machines (SVMs), neural networks, and clustering techniques, require substantial computational resources when handling high-dimensional data. Quantum computing offers acceleration in various ML tasks via quantum kernels, which facilitate quantum-enhanced feature mapping. Quantum kernel methods transform classical data into quantum states, allowing quantum computers to detect patterns in complex datasets more efficiently than classical approaches. For instance, quantum SVMs take advantage of quantum kernels to enhance classification tasks, providing exponential speedup in some instances.
In classical machine learning, optimization tasks often utilize stochastic gradient descent (SGD), where parameter updates are based on mini-batches of data, as described in Equation(6):
The classical approach to solving machine learning problems often involves calculating cost functions such as mean squared error (MSE) for regression tasks, shown in Equation(7):
4.2. Optimization and Quantum Neural Networks
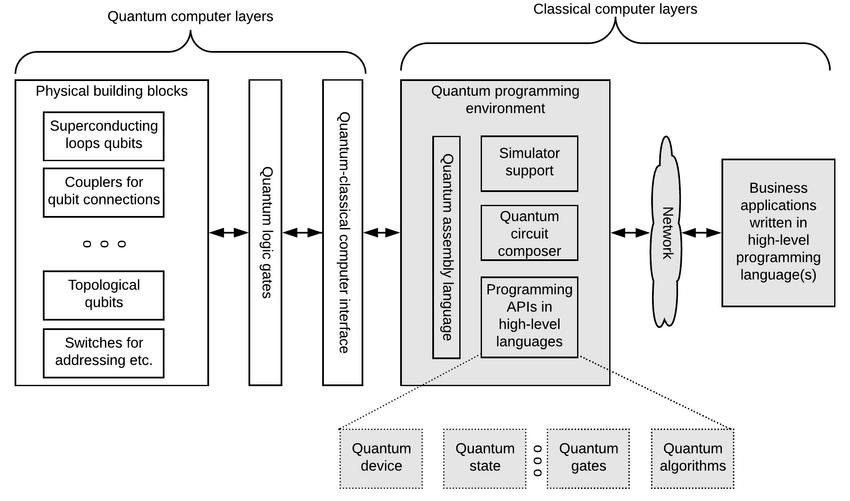
Another area where quantum computing enhances ML is optimization, which is a core component of many learning algorithms. Traditional optimization techniques, such as gradient descent, often struggle with high-dimensional and non-convex optimization problems. In classical machine learning, gradient descent updates model parameters iterativelyusingthefollowingequation: θ��+1 =θ�� η∇��(θ��) (8)
Quantumcomputingoffersimprovedoptimizationmethods, including Quantum Approximate Optimization Algorithm (QAOA) and Variational Quantum Eigensolver (VQE), which provide more efficient solutions to combinatorial optimization problems [8]. The QAOA approach aims to minimizetheexpectationvalueofacostfunctionencodedin aHamiltonianHCH_CHCusingtheformula:
��(γ,β) = ⟨γ,β|�� ��|γ,β⟩ (9) where γ and β are variational parameters optimized to findtheminimumenergystate.
Another widely used quantum optimization approach is VQE, which seeks to minimize the expectation value of the systemHamiltonianH:
min *θ+⟨ψ(θ)|��|ψ(θ)⟩ (10)
These quantum optimization methods are particularly useful in training deep learning models, where optimizing large numbers of parameters is a time-consuming process. Byleveragingquantum-enhancedoptimization(Equations2 and3),MLmodelscanpotentiallyconvergefasterandavoid local minima more effectively than classical approaches (Equation1)[9].
In addition to optimization, quantum neural networks (QNNs) are a promising avenue in QML. Unlike classical neuralnetworksthatrelyonclassicallogicgatesandmatrix multiplications, QNNs utilize quantum circuits to represent and process information. These networks exploit quantum entanglement and superposition to represent complex relationships within data, potentially leading to more efficient learning processes [10]. The evolution of a
Fig. 3. Layers of Classical Computer vs Quantum Computer
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072
quantum state in a QNN is governed by unitary transformations,commonlyrepresentedas:
⟩ (11) where U(θt) represents a parameterized quantum gate actingonthequantumstate∣ψt⟩ . Early research suggests that QNNs could outperform classical deep learning modelsin specific applications, such as reinforcement learning and generative modeling (Equation4).
EarlyresearchsuggeststhatQNNs could outperform classical deep learning models in specific applications, such asreinforcementlearningandgenerativemodeling[11].
4.3. Clustering, Dimensionality Reduction, and PCA
Quantum computing also contributes to clustering and principal component analysis (PCA), which are essential techniques in ML for dimensionality reduction and data segmentation. Classical k-means clustering aims to minimize the within-cluster variance using the cost function:
(12)
Quantum k-means clustering algorithms have been proposed to enhance classical clustering methods by reducing the computational complexity of distance calculationsbetweendatapoints[12].
(13)
Similarly, Quantum PCA (QPCA) provides a quantumenhanced approach to extracting the most significant features from high-dimensional datasets. The quantum analogof PCA is based on estimating the eigenvalues of the covariancematrixΣ[13].
(14)
These quantum techniques enable faster and more efficient analysisoflargedatasets,makingthemvaluabletoolsinbig dataapplications[14].
5. CHALLENGES & ADVANCEMENTS
In spite of these advancements, QML encounters numerous challenges and limitations that need to be resolved prior to achieving widespread adoption. One of the primary challenges is hardware constraints, as existing quantum computers especially Noisy Intermediate-Scale Quantum (NISQ)devices experienceissueswith noise,limitedqubit coherence, and elevated error rates [15]. These constraints hinderthescalabilityofquantumMLmodelsandcomplicate the reliable execution of complex computations. Another significant challenge is the encoding of quantum data, as classical data must be transformed into quantum states before it can be processed by a quantum computer [16].
This encoding procedure is frequently computationally intensiveandaddsfurthercomplexitytoMLworkflows[17].
Notwithstanding these challenges, research in QML is advancing,withtheemergenceofframeworkssuchasQiskit Machine Learning, PennyLane, TensorFlow Quantum, and Cirq, which offer tools for simulating and implementing quantum ML algorithms. These frameworks allow researchers to explore hybrid quantum-classical models, mergingquantumspeedadvantageswithclassicalreliability. Asquantumhardwarecontinuestoimprove,thesetoolswill aid in the integration of QML into practical applications, potentially leading to significant breakthroughs in areas such as drug discovery, financial modeling, materials science,andartificialintelligence[18],[19].
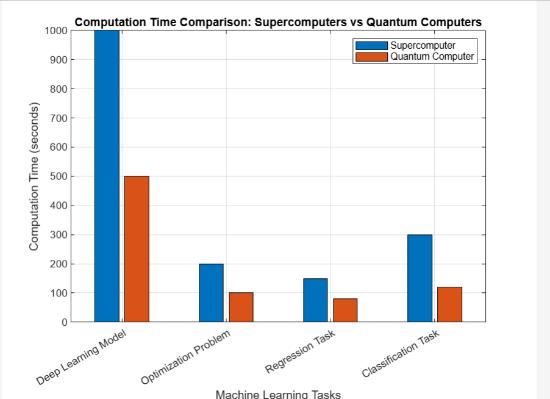
Ultimately, quantum computing has the capability to markedly boost machine learning by expediting computations, enhancing optimization, and introducing ground breaking algorithms that excel beyondconventional methods
Fig. 4. Computation Time
Fig.5. Energy Consumption
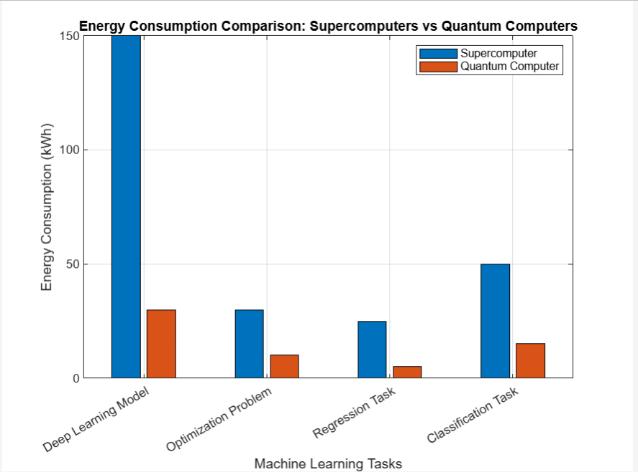
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072
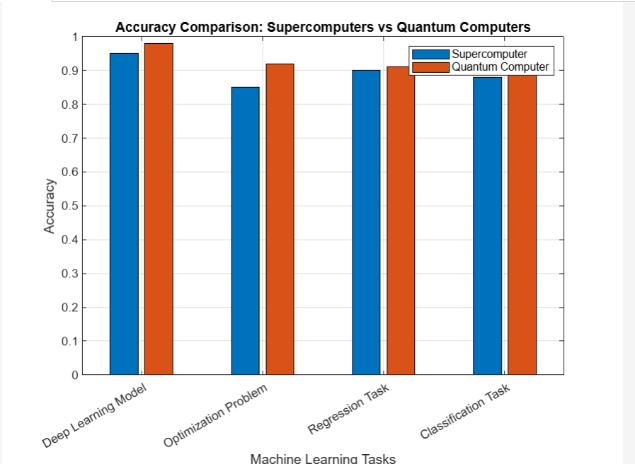
Fig.6. Accuracy
Although the practical application remains difficult due to hardwarerestrictionsandalgorithmicchallenges,persistent research and advancements in quantum hardware and software are consistently broadening thescope of what can be achieved. As quantum technology develops, its integrationwithmachinelearningisprojectedtounveilnew avenues for tackling complex issues that were previously unattainable with classical computing methods. Quantum Machine Learning exists at the junction of two ground breaking fields, promising a future where computational intelligence attains extraordinary levels of efficiency and capability.
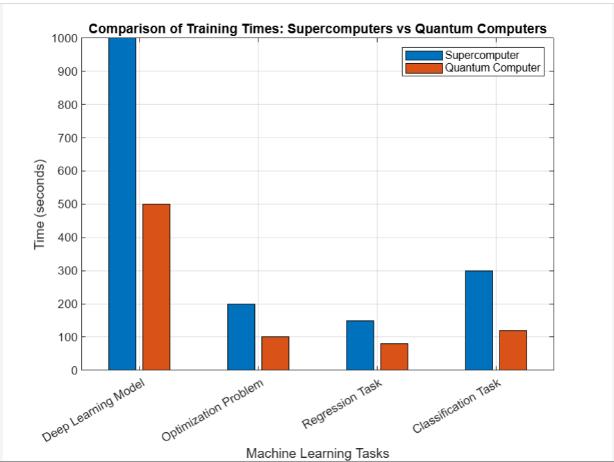
Fig.7.TrainingTime Feature Classical Computing Quantum Computing
Computational Model Deterministic and sequential Probabilistic and parallel processing
Processing Unit CPU/GPU/TPU Qubits
Optimization Speed Slower for highdimensionaldata Potentialexponentialspeedup
Parallelism
Limitedtoafixed number of processors Exploits superposition for massiveparallelism
Algorithm Efficiency Polynomialscaling Exponential scaling (for specificproblems)
Memory Handling Requires large memory for highdimensionaldata Can encode large states compactlyusingentanglement
Energy Consumption Highenergyusage for complex computations
Potentially lower due to parallelism
Noise Sensitivity Robust against minorerrors Highly sensitive to decoherenceandnoise
Scalability Scales well with available hardware Limitedbycurrentqubitcount andcoherencetime
Maturity Well-established with extensive libraries Emerging with ongoing hardwareimprovements
Table 1. Feature comparison of Classical Computing vs Quantum Computing.
6. CONCLUSION
Quantum Machine Learning (QML) merges quantum computing with standard machine learning to enhance data processing and modeling. By employing quantum properties such as superposition and entanglement, QML aims to surpass the limitations of traditional machine learning, resultinginfaster andmore efficientalgorithms. Traditional machine learning struggles with issues like data quality, high computational requirements, and difficulties in scaling and interpreting models. These challenges complicate the handling of large data sets and the resolution of complex problems. Quantum computing may provide solutions to these challenges by managing multiple states simultaneously, leading to improvements inareaslikeneuralnetworksandclustering.
Nevertheless, QML is still in its developmental phase, encountering challenges such as hardware constraints from existing quantum devices, especially Noisy Intermediate-Scale Quantum systems, which suffer from errors and limited complexity. The process of converting classical data into quantum formats is also intricate. In spite of these hurdles, platforms like Qiskit and TensorFlow Quantum are being created to facilitate the application of QML. Hybrid approaches that combine quantum and classical techniques exhibit potential across various domains, yet further research and collaboration areessentialtofullyrealizeQML'scapabilities.
REFERENCES
[1] S.Sharma,A.Gupta,andR.Singh,"QuantumMachine Learning:Acomprehensivereviewonoptimizationof machine learning algorithms," in Proceedings of the
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072
IEEE International Conference on Computing, Communication,andAutomation(ICCCA),(2021)
[2] M. A. Khan and S. A. Khan, "An Introduction to Quantum Machine Learning Techniques," in Proceedings of the IEEE International Conference on EmergingTechnologies(ICET),(2021)
[3] Sharma and P. K. Mishra, "Machine Learning: QuantumvsClassical,"IEEEAccess,vol.8,(2020)
[4] S. Das, A. Ghosh, and S. Chakrabarti, "Quantum Machine Learning and Recent Advancements," in Proceedings of the IEEE International Conference on ComputerScienceandEngineering(ICSEC),(2022)
[5] M. Schuld and F. Petruccione, "Quantum Machine Learning: Recent Advances and Outlook," IEEE TransactionsonComputers,vol.70,no.10,(2021)
[6] Y.Li,X.Liu,andJ.Du,"QuantumMachineLearning:A Comprehensive Overview and Analysis," in Proceedings of the IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA),(2022)
[7] Kumar and S. Sharma, "Implementation of Quantum Machine Learning Algorithms: A Review," in Proceedings of the IEEE International Conference on Electronics, Computing and Communication Technologies(CONECCT),(2022)
[8] P. Rebentrost, M. Mohseni, and S. Lloyd, "Quantum Support Vector Machine for Big Data Classification," in Proceedings of the IEEE International Conference onSystems,Man,andCybernetics(SMC),(2014)
[9] N.Wiebe,D.Braun,andS.Lloyd,"QuantumAlgorithm for Data Fitting," IEEE Transactions on Information Theory,vol.56,no.1,(2015)
[10] M. Schuld, I. Sinayskiy, and F. Petruccione, "Prediction by Linear Regression on a Quantum Computer," IEEE Transactions on Neural Networks andLearningSystems,vol.26,no.1,(2015)
[11] W. Harrow, A. Hassidim, and S. Lloyd, "Quantum Algorithm for Solving Linear Systems of Equations," in Proceedings of the IEEE Annual Symposium on FoundationsofComputerScience(FOCS),(2009)
[12] D. W. Berry, A. M. Childs, and R. Kothari, "Hamiltonian Simulation with Nearly Optimal DependenceonAllParameters,"inProceedingsofthe IEEE Annual Symposium on Foundations of ComputerScience(FOCS),(2015)
[13] S.Lloyd,M.Mohseni,andP.Rebentrost,"Quantum PrincipalComponentAnalysis,"IEEETransactionson QuantumEngineering,vol.1(2014)
[14] Z. Zhao, J. K. Fitzsimons, and J. F. Fitzsimons, "Quantum Assisted Gaussian Process Regression," IEEETransactions on Neural Networks andLearning Systems,vol.29,no.5,(2018)
[15] N. Soklakov and R. Schack, "Efficient State Preparation for a Register of Quantum Bits," IEEE TransactionsonQuantumEngineering,vol.2,(2005)
[16] V.Giovannetti,S.Lloyd,andL.Maccone,"Quantum Random Access Memory," IEEE Transactions on InformationTheory,vol.51,no.6.(2005)
[17] S. Aaronson, "Read the Fine Print," IEEE Transactions on Information Theory, vol. 52, no. 10, (2006)
[18] J. Bang, A. Dutta, S.-W. Lee, and J. Kim, "Optimal Usage of Quantum Random Access Memory in Quantum Machine Learning," IEEE Transactions on NeuralNetworksandLearningSystems,vol.30,no.1, (2019)
[19] D.Peddireddy,V.Bansal,Z.Jacob,andV.Aggarwal, "Tensor Ring Parametrized Variational Quantum Circuitsfor Large Scale Quantum MachineLearning," in Proceedings of the IEEE International Conference on Quantum Computing and Engineering (QCE), (2022)
[20] Griol-Barres, S. Milla, A. Cebrian, Y. Mansoori, and J. Millet, "Variational Quantum Circuits for Machine Learning: An Application for the Detection of Weak Signals,"IEEEAccess,vol.9,(2021)