Fig. 2.0.1 Axonometriea punctului
2. Reprezentarea proiecțiilor punctului
Din punctele găsite pe axele de referință se duc linii ne ordine în planele de proiecție. Fiecărui punct de pe axă îi corespunde două linii de ordine trasate în plane de proiecție diferite, exceptând situația când una dintre coordonate este nulă.
La intersecția liniilor de ordine situate în același plan se găsește proiecția punctului din spațiu pe planul respectiv, astfel :
a – proiecția orizontală a punctului A (se află la intersecția liniilor de ordine trasate din ax și ay)
a’ - proiecția frontală (verticală) a punctului A (se află la intersecția liniilor de ordine trasate din ax și az)
a” - proiecția laterală a punctului A (se află la intersecția liniilor de ordine trasate din ax și az)
3. Reprezentarea punctului în spațiu
În fiecare proiecție a punctului, se desenează linii de ordine perpendiculare pe planul respectiv. La intersecția celor trei linii de ordine, aferente celor trei proiecții, se găsește punctul real din spațiu.
Toate cele trei linii de ordine trebuie să se întîlnească în același punct.
Reprezentarea unui punct în epură presupune parcurgerea doar a primilor doi pași pe care i-am prezentat anterior. Punctul fizic din spațiu nu poate fi reprezentat deoarece se află într-un sistem cu un număr de dimensiuni superior epurei.
24
Punctul poate ocupa în spațiu o infinitate de poziții, însă raportat la sistemul de referință, acesta se poate situa într-unu din cele 8 triedre, în funcție de valorile coordonatelor care sunt prezentate în tabelul 1.2 În continuare vom vedea cum se reprezintă punctul în epură, parcurgând toate cele opt triedre posibile. Pentru a distinge ma bine elementele geometrice, vom recurge la următoarea convenție cromatică: planul orizontal de proiecție este reprezentat cu roșu, planul vertical cu albastru și planul lateral cu galben. Toate elementele geometrice ce aparțin planelor de referință vor fi reprezentate în culoarea planului respectiv. Pentru a facilita parcurgerea desenelor, planele de referință vor fi colorate doar în triedrul I, unde toate valorile sunt pozitive fiind asociat spațiului real în care se află și observatorul.
Triedrul 1 (T1)
Fie punctul “A” de coordonate A (30,40,50)
Fig. 2.0.2 Epura punctului
2.2 ALFABETUL PUNCTULUI.
25
Reprezentare axonometrică
Reprezentare
Triedrul 2 (T2)
Fie punctul “B” de coordonate B (30, -20, 30)
Reprezentare
Reprezentare
Triedrul 3 (T3)
Fie punctul “C” de coordonate C (20, -60, -20)
Fig.2.1 Punctul „A”
Fig.2.2 Punctul „A”
în epură
Fig.2.3 Punctul „B”
Fig.2.4 Punctul „B”
axonometrică
în epură
26
Triedrul 4 (T4)
Fie punctul “D” de coordonate D (40, 10, -30)
Triedrul 5 (T5)
Fie punctul “E” de coordonate E (-40, 30, 50)
Fig 2.5 Punctul „C”
Fig.2.6 Punctul „C” Reprezentare axonometrică Reprezentare în epură
Fig 2.7 Punctul „D”
Fig.2.8 Punctul „D” Reprezentare axonometrică Reprezentare în epură
27
Triedrul 6 (T6)
Fie punctul “F” de coordonate F (-40, 30, 50)
Triedrul 7 (T7)
Fie punctul “G” de coordonate G (-40,-30,-60)
Fig.2.9 Punctul „E”
Fig.2.10 Punctul „E” Reprezentare axonometrică Reprezentare în epură
Fig.2.11 Punctul „F”
Fig.2.12 Punctul „F” Reprezentare axonometrică Reprezentare în epură
28
Reprezentare
Triedrul 8 (T8)
Fie punctul “H” de coordonate
Reprezentare
Fig.2.13 Punctul „G”
Fig.2.14 Punctul „G”
axonometrică Reprezentare în epură
Fig.2.15 Punctul „H”
Fig.2.16 Punctul „H”
29
axonometrică Reprezentare în epură
CAPITOLUL 3 DREAPTA
Definiție: Dreapta este element fundamental unidimensional, determinat de două puncte, un punct și o direcție sau intersecția a două plane.
3.1 REPREZENTAREA DREPTEI
Dreapta este locul geometric al punctelor situate pe traseul cel mai scurt dintre două puncte aflate pe dreaptă (fig. 3.1). Suma tuturor proiecțiilor punctelor de pe o dreaptă generează proiecțiile de aceași natură ale dreptei.
Fie dreapta E, de poziție oarecare, determinată de punctele A(30,40,55) și B(60,25,20). Se construiesc proiecțiile celor două puncte pe planele de referință. Proiecțiile de aceași natură se unesc între ele, obținându-se astfel proiecțiile dreptei aferente fiecărui plan ortogonal (fig. 3.2).
30
Fig.3.2 Epura dreptei E
3.2 URMELE DREPTEI
Poziția unei drepte în spațiul definit de sistemul de referință triortogonal, poate fi stabilită cu ajutorul urmelor dreptei. Punctele de intersecție dintre dreaptă și planele de proiecție se numesc urmele dreptei. O dreaptă de poziție oarecare are trei urme, fiecare aferentă intersecției dreptei cu unul dintre planele de proiecție. În funcție de pozițiile particulare ale dreptei, aceasta poate avea cel puțin o urmă.
Urmele sunt puncte importante pe dreaptă, ele marcând trecerea acesteia de la un triedru la altul de-a lungul parcurgerii spațiului.
În continuare vom analiza modul în care se construiesc urmele unei drepte și care sunt pașii pentru aflarea lor în epura dreptei.
Fig.3.1 Axonometria izometrică a dreptei E
31
Fig.3.3 Urmele dreptei E, în reprezentare axonometrică izometrică
Urmele dreptei se află în același timp situate pe dreapta din spațiu și planul de proiecție pe care dreapta îl înțeapă (fig. 3.3).
Se prelungește dreapta E până când intersectează planele de referință în cele trei urme :
E ∩ (H) = H - Urma orizontală a dreptei
E ∩ (V) = V - Urma verticală a dreptei
E ∩ (L) = L - Urma laterală a dreptei
H , V , L ∈ E
Construcția urmelor în epură (fig. 3.4) necesită parcurgerea logică a unor
etape:
1. În planul frontal de proiecție se prelungește e ' (proiecția
frontală a dreptei) până intersectează axa OX ,(respectiv planul
Fig.3.4 Urmele dreptei E în epură
32
orizontal de proiecție) în punctul h’ (proiecția frontală a urmei orizontale a dreptei).
2. Din punctul h’ aflat, se duce linie de ordine în planul orizontal de proiecție până când aceasta intersectează dreapta e (proiecția orizontală a dreptei E) sau prelungirea acesteia. La intersecția celor două drepte se află punctul H (urma orizontală a dreptei E). Urma orizontală coincide cu proiecția ei pe planul (H), astfel H ≡ h’ .
3. În planul orizontal de proiecție se prelungește e (proiecția orizontală a dreptei) până intersectează axa OX ,(respectiv planul frontal de proiecție) în punctul v (proiecția orizontală a urmei frontale a dreptei).
4. Din punctul v aflat, se duce linie de ordine în planul frontal de proiecție până când aceasta intersectează dreapta e ' (proiecția frontală a dreptei E) sau prelungirea acesteia. La intersecția celor două drepte se află punctul V (urma frontală a dreptei E). Urma frontală coincide cu proiecția ei pe planul (V), astfel V ≡ v’ .
5. În planul frontal de proiecție se prelungește e ' (proiecția frontală a dreptei) până intersectează axa OZ ,(respectiv planul lateral de proiecție) în punctul w’ (proiecția frontală a urmei laterale a dreptei).
6. Din punctul w’ aflat, se duce linie de ordine în planul lateral de proiecție până când aceasta intersectează dreapta e ¿ (proiecția laterală a dreptei E) sau prelungirea acesteia. La intersecția celor două drepte se află punctul W (urma laterală a dreptei E). Urma laterală coincide cu proiecția ei pe planul (L), astfel W ≡ w’ .
7. După aflarea celor trei urme, corectitudinaea desenului se verifică prin corelarea grafică a valorilor obținute:
a. În planul orizontal de proiecție se prelungește e până intersectează axa OY ,(respectiv planul lateral de proiecție) în punctul “w” (proiecția orizontală a urmei laterale a dreptei).
b. Punctul w coincide cu wy (depărtarea urmei laterale), w≡ wy . Depărtarea se rabate pe planul frontal de proiecție împreună cu planul lateral din care face parte, astfel wy devine wy1 măsurat pe axa OY 1.
c. Din punctul wy1 aflat, se duce linie de ordine în planul lateral de proiecție până când aceasta intersectează dreapta e ¿ exact în punctul W.
33
d. În planul lateral de proiecție se prelungește e ¿ până intersectează axa OY 1 ,(respectiv planul orizontal de proiecție) în punctul h” (proiecția laterală a urmei orizontale a dreptei).
e. Punctul h” coincide cu hy1 (depărtarea urmei orizontale rabătută pe planul frontal de proiecție), h”≡ . Depărtarea se aduce pe planul frontal în poziția sa inițială , împreună cu planul lateral din care face parte, astfel hy1 devine hy măsurat pe axa OY
f. Din punctul hy aflat, se duce linie de ordine în planul orizontal de proiecție până când aceasta intersectează dreapta e exact în punctul H.
g. În planul lateral de proiecție se prelungește e ¿ până intersectează axa OZ ,(respectiv planul frontal de proiecție) în punctul v” (proiecția laterală a urmei frontale a dreptei).
h. Din punctul v” aflat, se duce linie de ordine în planul frontal de proiecție până când aceasta intersectează dreapta e ' exact în punctul V.
Corelarea grafică dintre urmele unei drepte, reprezentate în epură, este rezultatul direct al relațiilor spațiale tridimensionale ce se stabilesc între dreaptă și sistemul de referință și sunt simultane.
Etapele prezentate mai sus într-o susccesiune logică, a demersului grafic, sunt cu aspect general putând fi aplicate la toate tipurile de drepte indiferent de poziția lor față de sistemul de referință.
3.3 CLASIFICAREA DREPTELOR ÎN FUNCȚIE DE POZIȚIA FAȚĂ DE PLANELE DE PROIECȚIE
În funcție de poziția dreptelor față de planele ortogonale de proiecție, acestea se pot clasifica după cum urmează:
A. Drepte de poziție generală (Oarecare)
B. Drepte paralele cu planele de proiecție
a. Drepte paralele cu planul orizontal de proiecție (Orizontale)
b. Drepte paralele cu planul frontal de proiecție (Frontale)
c. Drepte paralele cu planul lateral de proiecție (De profil)
C. Drepte perpendiculare pe planele de proiecție
a. Drepte perpendiculare pe planul orizontal de proiecție (Verticale)
34
b. Drepte perpendiculare pe planul frontal de proiecție (De capăt)
c. Drepte perpendiculare pe planul lateral de proiecție (Frontoorizontale)
D. Drepte conținute de planele de proiecție
E. Drepte conținute de planele bisectoare
F. Drepte conținute de axele sistemului ortogonal de proiecție În funcție de felul cum se proiectează pe planele de referință ale sistemului ortogonal, dreptele pot fi : - în mărime reală, deformate, total deformate
3.3.1 DREAPTA PARALELĂ CU PLANELE DE PROIECȚIE
a. Drepte paralele cu planul orizontal de proiecție (Orizontale)
-Fie dreapta determinată de punctele A (100,15,20) și B (50,40,20)
-Cotele punctelor situate pe o dreaptă orizontală, sunt egale
-Dreapta E se proiectează în mărime reală pe planul orizontal de proiecție, e= mărimea reală.
-Unghiul dintre e și axa OY este unghiul real dintre dreapta E și planul lateral de proiecție. Unghiul dintre e și axa OX este unghiul real dintre dreapta E și planul frontal de proiecție.
-În epură, proiecția frontală se suprapune peste proiecția laterală a dreptei.
-Urma orizontală a dreptei se află la infinit
35
Fig. 3.5 Dreapta de orizontală
b. Drepte paralele cu planul frontal de proiecție (Frontale)
-Fie dreapta determinată de punctele A (120,40,80) și B (50,40,20)
-Depărtările punctelor situate pe o dreaptă frontală, sunt egale
-Dreapta E se proiectează în mărime reală pe planul frontal de proiecție, e ' = mărimea reală.
-Unghiul dintre e ' și axa OX este unghiul real dintre dreapta E și planul orizontal de proiecție. Unghiul dintre e ' și axa OZ este unghiul real dintre dreapta E și planul lateral de proiecție.
-În epură, proiecția orizontală și proiecția laterală a dreptei sunt perpendiculare pe axele OY respectiv OY 1 .
- Urma frontală a dreptei se află la infinit
36
Fig. 3.6 Dreapta frontală
c. Dreapta paralelă cu planul lateral de proiecție (de profil)
-Fie dreapta determinată de punctele A (50,120,80) și B (50,40,20)
-Abscisele punctelor situate pe o dreaptă de profil, sunt egale
-Dreapta E se proiectează în mărime reală pe planul lateral de proiecție, e ¿ = mărimea reală.
-Unghiul dintre e ¿ și axa OY 1 este unghiul real dintre dreapta E și planul orizontal de proiecție. Unghiul dintre e ¿ și axa OZ este unghiul real dintre dreapta E și planul frontal de proiecție
-În epură, proiecția frontală se suprapune peste proiecția orizontală a dreptei.
-Urma laterală a dreptei se află la infinit.
37
Fig. 3.7 Dreapta de profil
CAPITOLUL 4 PLANUL
4.1 REPREZANTAREA PLANULUI
Definiție: Planul este element fundamental bidimensional, determinat de două drepte paralele sau intersectate, un punct și o dreaptă sau trei puncte necolineare.
Planul se reprezintă, atât în axonometrie cât și în epură, cu ajutorul urmelor (Fig.4.1).
Urmele unui plan sunt dreptele de intersecție dintre planele de proiecție ale sistemului de referință și planul respectiv. Putem distinge următoarele proprietăți generale ale urmelor:
Un plan poate avea cel puțin două urme și cel mult trei.
Urmele sunt drepte conținute de plan, dar în același timp sunt drepte situate pe plane de proiecție.
Toate dreptele conținute de un plan, au urmele situate pe urmele de aceași natură ale planului.
Toate dreptele orizontale dintr-un plan sunt paralele cu urma orizontală. Toate dreptele frontale conținute de un plan sunt paralele cu urma frontală. Toate dreptele de profil conținute de plan sunt paralele cu urma laterală a planului.
Urmele unui plan sunt concurente două câte două, iar punctul de intersecție se află pe axele de refeință.
Dacă o dreaptă este paralelă cu una dintre urmele planului, atunci dreapta este paralelă cu planul respectiv.
Prin convenție, urmele planului se notează astfel:
o Urma orizontală – “Ph” – unde “P” este denumirea planului iar “h” este indicele planului de proiecție din care face parte (orizontal)
o Urma verticală – “Pv” – unde “P” este denumirea planului iar “v” este indicele planului de proiecție din care face parte (vertical).
49
o Urma verticală – “Pw” – unde “P” este denumirea planului iar
“w” este indicele planului de proiecție din care face parte (lateral).
4.2 DEFINIREA PLANULUI
4.2.1 PLAN DETERMINAT DE DOUĂ DREPTE CONCURENTE
Fie dreptele D 1, D 2, concurente în punctul “I” (Fig. 4.2). Planul (P) determinat de cele două drepte are urmele definite de dreapta ce leagă urmele de aceași natură ale dreptelor. Astfel pentru a afla urmele unui plan determinat de două drepte, este suficient să aflăm urmele celor două drepte și să le unim (Fig. 4.3.). Se observă că punctul de intersecție dintre drepte se află pe aceleași linii de ordine în toate proiecțiile, aceasta fiind o condiție a concurenței lor.
Fig. 4.1
50
51
(Fig. 4.2)
(Fig. 4.3)
4.2.2 PLAN DETERMINAT DE DOUĂ DREPTE PARALELE
Fie dreptele D 1, D 2, două drepte paralele (Fig. 4.4). Planul (P) determinat de cele două drepte are urmele definite de dreapta ce leagă urmele de aceași natură ale dreptelor. Astfel pentru a afla urmele unui plan determinat de două drepte, este suficient să aflăm urmele celor două drepte și să le unim (Fig. 4.5.), la fel ca în cazul dreptelor concurente. Se observă că proiecțiile de aceași natură ale dreptelor , sunt paralele între ele.
4.2.3 PLAN DETERMINAT DE O DREAPTĂ ȘI UN PUNCT
Pentru a construi un plan cu ajutorul unei drepte și un punct exterior acesteia, vom avea nevoie de o construcție auxiliară:
De pe dreaptă se alege în mod aleatoriu un punct care se va uni cu punctul exterior dreptei, obținându-se astfel o dreaptă auxiliară ce are un punct comun cu dreapta dată. Se ajunge astfel la situația precedentă (fig. 4.3), în care am avut de determinat un plan cu ajutorul a două drepte concurente.
Prin punctul exterior dreptei se duce o dreaptă auxiliară paralelă cu dreapta dată. Se obține astfel situația prezentată în fig.4.5.
4.2.4 PLAN DETERMINAT DE TREI PUNCTE
Pentru a construi un plan cu ajutorul a trei puncte, vom avea nevoie de o construcție auxiliară ce ne aduce în situația precedentă. Astfel din cele trei puncte se unesc două și se obține o dreaptă, iar prin al treilea punct se duce o dreaptă concurentă sau paralelă cu cea precedentă. Aflarea urmelor celor două drepte construite ne determină urmele planului determinat de cele trei puncte.
Pentru a reprezenta grafic urmele unui plan va trebui să căutăm construcțiile auxiliare cele mai ușoare astfel încât să ne aflăm în situația determinării planului cu ajutorul a două drepte concurente sau paralele.
52
53
(Fig. 4.4)
(Fig. 4.5)
4.3 CLASIFICAREA PLANULUI ÎN FUNCȚIE DE POZIȚIA FAȚĂ DE PLANELE DE PROIECȚIE
În funcție de poziția față de sistemul de referință se pot distinge mai multe tipuri de plan:
1. Plan de poziție oarecare – Poziția față de sistemul de referință este aleatorie. Planul are trei urme, iar proiecțiile elementelor conținute de plan sunt diferite în epură față de acestea.
2. Plan de poziție particulară:
a. Plane paralele cu planele de proiecție:
i. Plan orizontal (de nivel)
ii. Plan frontal
iii. Plan de profil
b. Plane perpendiculare pe planele de proiecție (plane proiectante):
i. Plan vertical
ii. Plan de capăt
iii. Plan perpendicular pe planul lateral de proiecție (paralel cu axa OX )
iv. Plan concurent cu axa OX
În continuare vom analiza caracteristicile planelor de poziție particulară
4.3.1
PLANUL PARALEL CU PLANELE DE PROIECȚIE
Plan orizontal (de nivel)
- Este locul geometric al punctelor de aceași cotă.
- Planul are urmă verticală paralelă cu axa OX (Pv ∥ OX ) și urmă laterală paralelă cu axa OY (Pw ∥OY ).
- Toate elementele conținute de plan se proiectează în mărime reală pe planul orizontal de proiecție.
54
- Proiecțiile frontale și laterale ale elementelor conținute de plan, se proiectează pe urma frontală respectiv urma laterală a acestuia. (Fig. 4.6)
(Fig. 4.6)
Plan frontal (de front)
- Este locul geometric al punctelor egal dep[rtate de planul frontal de proiecție
- Planul are urmă orizontală paralelă cu axa OX (Ph∥OX ) și urmă laterală paralelă cu axa OZ (Pw ∥OZ).
- Toate elementele conținute de plan se proiectează în mărime reală pe planul frontal de proiecție.
- Proiecțiile orizontale și laterale ale elementelor conținute de plan, se proiectează pe urma orizontală respectiv urma laterală a acestuia. (Fig. 4.7)
(Fig. 4.7)
55
Plan de profil
- Este locul geometric al punctelor de aceași abscisă.
- Planul are urmă verticală paralelă cu axa OZ (Pv ∥OZ) și urmă orizontală paralelă cu axa OY (Ph∥ OY ).
- Toate elementele conținute de plan se proiectează în mărime reală pe planul lateral de proiecție.
- Proiecțiile frontale și orizontale ale elementelor conținute de plan, se proiectează pe urma frontală respectiv urma orizontală a acestuia. (Fig. 4.8)
(Fig. 4.8)
4.3.2 PLANUL PERPENDICULAR PE PLANELE DE PROIECȚIE
Plan vertical (Fig. 4.9)
- Urma frontală și laterală a planului sunt drepte perpendiculare pe axele OX respectiv OY (Pv ⊥ OX ∧ Pw ⊥ OY ).
56
- Elementele conținute de plan se proiectează deformat pe planul orizontal de proiecție, suprapunându-se pe urma orizontală a planului Ph.
- Unghiul format de urma orizontală cu axa OX și axa OY sunt mărimile reale ale unghiului dintre plan și planele frontal respectiv lateral de proiecție:
∢ ¿) = ∢ ((V ) , ( P ))
∢ ¿) = ∢ (( L ) ,( P ) )
(Fig.
Plan de capăt (Fig. 4.10)
- Urma orizontală și laterală a planului sunt drepte perpendiculare pe axele OX respectiv OZ ( Ph⊥ OX ∧ Pw ⊥ OZ).
- Elementele conținute de plan se proiectează deformat pe planul frontal de proiecție, suprapunându-se pe urma frontală a planului Pv.
4.9)
57
- Unghiul format de urma frontal cu axa OX și axa OZ sunt
mărimile reale ale unghiului dintre plan și planele orizontal respectiv lateral de proiecție:
∢ ¿) = ∢ (( H ) , ( P ))
∢ ¿) = ∢ (( L ) ,( P ) )
Plan perpendicular pe (L) (Fig. 4.11)
- Urma frontală și orizontală a planului sunt drepte perpendiculare pe axele OZ respectiv OY (Pv ⊥ OZ ∧ Ph ⊥OY ).
- Elementele conținute de plan se proiectează deformat pe planul lateral de proiecție, suprapunându-se pe urma lateral a planului Pw.
- Unghiul format de urma laterală cu axa OZ și axa OY sunt
mărimile reale ale unghiului dintre plan și planele frontal respectiv orizontal de proiecție:
∢ ¿) = ∢ ((V ) , ( P ))
∢ ¿) = ∢ (( H ) , ( P ))
(Fig. 4.10)
58
(Fig. 4.11)
Plan concurent cu axa OX (Fig. 4.12)
- Este un plan perpendicular pe planul lateral de proiecție, deci va avea proprietățile mai sus menționate.
- Urma vertical (frontal) coincide cu urma orizontală și în același timp cu axa OX : OX ≡ Pv ≡ Ph
(Fig. 4.12)
4.3.3 PLANUL CONȚINUT DE PLANELE DE PROIECȚIE (AXIALE)
Dacă un plan coincide cu unul dintre cele trei plane de proiecție, atunci punctele conținute de plan au una dintre coordonate egală cu zero.
Urmele planului inclus într-un plan de proiecție sunt în număr de două și coincid cu axele sistemului de referință. (Fig.4.13).
(Fig. 4.13)
59
4.4 POZIȚIA RELATIVĂ A DOUĂ PLANE
Două plane, (P) și (Q) pot ocupa următoarele poziții unul în funcție de altul :
- Plane paralele
- Plane concurente
-Plane confundate
-Plane perpendiculare.
4.4.1 PLANE CONCURENTE
Dacă două plane au cel puțin un punct comun atunci ele sunt concurente (Fig. 4.14). Palanele secante, denumite în figură (P) și (Q), se intersectează după o dreaptă comună, identificată prin urma sa verticală V și urma orizontală H.
Dreapta de intersecție dintre două plane are întotdeauna urmele situate la intersecția urmelor de același nume ale planurilor (Fig.4.15) .
60
(Fig. 4.14) Intersecția a două plane.
Pentru determinarea dreptei de intersecție a două plane în epură, se urmăresc următorii pași:
1. Se află intersecția urmelor de aceași natură a celor două plane. Urmele planurilor sunt considerate știute.
2. În proiecție frontală se coboară linie de ordine din punctul V (urma frontală a dreptei de intersecție) pe planul orizontal de proiecție. La intersecția cu axa OX se află punctul v, proiecția orizontală a urmei verticale.
3. Trecem în planul orizontal de proiecție unde vom uni punctul v găsit, cu urma orizontala a dreptei de intersecție, punctul H . Dreapta rezultată reprezintă proiecția orizontală a dreptei de intersecție. Din punctul H se duce linie de ordine pe planul vertical de proiecție. La intersecția cu axa OX se află punctul h’, proiecția verticală a urmei orizontale.
4. Revenim în planul frontal de proiecție unde vom uni punctul V cu punctul h’ găsit, rezultând astfel proiecția frontală a dreptei de intersecție a celor două plane.
5. Proiecția laterală a dreptei de intersecție se obține prin unirea proiecțiilor laterale a celor două urme găsite, v” și h” .
6. Pentru a vedea dacă am lucrat corect, se prelungește proiecția laterală a dreptei de intersecție. Dacă aceasta trece exact prin punctul W, (urma laterală a dreptei de intersecție) ce se află la concureța urmelor laterale a celor două plane, înseamnă că am obținut un desen corect.
Desenul din fig. 4.15 este realizat pentru următoarele valori:
Planul (P) definit de PX (218,0,0); PY(0,108,0); Pz( 0,0,125)
61
Planul (Q) definit de QX (130,0,0); QY(0,210,0); Qz(0,0,157)
Intersecția
și
Axonometrie 62
(Fig. 4.15)
planelor (P)
(Q)
Epură
În cazul în care nu avem acces în desen, la punctul de intersecție dintre urmele de aceași natură ale planelor, se va utiliza următoarea construcție grafică, pe care o vom numi “metoda paralelorgramului” pentru aflarea dreptei comune.
Se respectă următorii pași :
1. Se trasează un plan paralel cu planul (P), respectiv planul (P1), definit de urma verticalăPv 1 ( Pv 1 ∥ Pv ) și urma orizontală Ph 1 ( Ph 1 ∥ Ph ).
2. Se trasează dreapta de intersecție dintre (P1) și (Q), reprezentată în desen prin proiecția verticală x ' 1 și proiecția orizontală x 1. (P1) ∩ (Q) = X 1.
3. Se alege ca plan de lucru planul frontal unde se efectuază următoarele construcții grafice:
i. În punctele Px1 și h’1 se duc paralele la urma verticală a planului (Q), dreptele a respectiv b.
ii. La intersecția a cu urma verticală Pv a planului (P), rezultă punctul
1. Din punctul 1 se duce o paralelă la dreapta OX până intersectează dreapta b în punctul 2.
iii. Prin punctul 2 se duce paralelă la dreapta x ' 1 rezultând asfel drepta x ' - proiecția frontală a dreptei de intersecție dintre (P) și (Q).
4. Se alege ca plan de lucru planul orizontal unde se efectuează aceleași construcții grafice ca în cazul planului frontal. În urma acestor
operațiuni va rezulta drepta x ' - proiecția orizontală a dreptei de intersecție dintre (P) și (Q).
63
4.4.2 PLANE PARALELE
Fig. 4.16)
Intersecția planelor (P) și (Q), în dublă proiecție ortogonală
Două plane sunt paralele atunci când urmele de aceași natură ale planelor sunt paralele între ele. (Fig. 4.17).
4.5 DREPTE IMPORTANTE ALE PLANULUI
(
(P) ∥ (Q) ⇒ Pv ∥ Qv ∧ Ph ∥Qh ∧ Pv ∥ Qv (Fig. 4.17)
64
Într-un plan pot fi situate o infinitate de drepte. Dintre acestea anumite drepte, cu o poziție particulară față de sistemul de refeință, sunt utilizate în rezolvarea unor probleme și evidențierea anumitor caracteristici ale planului din care fac parte.
Astfel, în plan putem gasi următoarele drepte de poziție particulară:
- Orizontala planului
- Frontala planului
- Dreapta de profil a planului
- Linia de cea mai mare pantă a planului (l.d.c.m.m.p)
4.5.1 DREAPTA ORIZONTALĂ CONȚINUTĂ DE UN PLAN
Definiție:
Locul geometric al punctelor situate în planul (P), ce au valoarea cotei egală.
Caracteristici:
- Este o dreaptă situată în planul (P) și paralelă cu planul orizontal de proiecție: D1⊂(P) ∧ D1∥(H); D2 ⊂ (P) ∧ D1 ∥ (H); D1∥ D2 (Fig. 4.18)
- Prezință toate caracteristicile unei drepte orizontale enunțate la capitolul 3.3.1
- Urmele frontală și laterală a dreptei se găsesc pe urmele de aceași natură a planului (P).
- Este utilizată de cele mai multe ori, în rezolvarea problemelor, ca linie de construcție.
65
(Fig. 4.18)
4.5.2 DREAPTA FRONTALĂ CONȚINUTĂ DE UN PLAN
Definiție:
Locul geometric al punctelor situate în planul (P), ce au valoarea depărtării, constantă.
Caracteristici:
- Este o dreaptă situată în planul (P) și paralelă cu planul frontal de proiecție: D ⊂ (P) ∧ D ∥ (V) (Fig. 4.19)
- Prezință toate caracteristicile unei drepte frontale enunțate la capitolul 3.3.1
- Urmele orizontală și laterală a dreptei se găsesc pe urmele de aceași natură a planului (P).
66
(Fig. 4.19)
4.5.3 DREAPTA DE PROFIL A PLANULUI
Definiție:
Locul geometric al punctelor situate în planul (P), ce au valoarea abscisei, constantă.
Caracteristici:
- Este o dreaptă situată în planul (P) și paralelă cu planul lateral de proiecție: D ⊂ (P) ∧ D ∥ (L) (Fig. 4.20)
- Prezință toate caracteristicile unei drepte de profil enunțate la capitolul 3.3.1
- Urmele orizontală și frontală a dreptei se găsesc pe urmele de aceași natură a planului (P).
67
(Fig. 4.20)
4.5.4 LINIA DE CEA MAI MARE PANTĂ A PLANULUI
Definiție:
Dreapta conținută de un plan (P) perpendiculară pe una dintre urmele planului.
Caracteristici:
- Este o dreaptă situată în planul (P), perpendiculară pe una dintre cele trei urme ale planului: D ⊂ (P) ∧ D ⊥ Qh (Fig. 4.21)
- Fiind o dreaptă ce aparține planului (P), atunci urmele acesteia se găsesc pe urmele de aceași natură ale planului:
D ⊂ (P) ⇒ H ∈ Qh ∧ V ∈ Qv ∧ W ∈ Qw .
- Se poate face referire la „linia de cea mai mare pantă” a unui plan (sau prescurtat l.d.c.m.m.p.), doar în raport față de unul dintre cele trei plane de referință, astfel un plane poate avea l.d.c.m.m.p față de planul orizontal, planul vertical sau lateral de proiecție.
- În funcție de planul de proiecție la care ne raportăm, l.d.c.m.m.p a planului (P) are anumite proprietați: Spre exemplu în figura 4.21 este reprezentată l.d.c.m.m.p a planului (P) față de planul orizontal de proiecție și este denumită cu D. Se observă că aceasta este conținută de (P) și perpendiculară pe urma orizontală Qh . Putem observa următoarele proprietăți ale acesteia:
o Proiecția orizontală a dreptei D este la rândul ei perpendiculară pe urma orizontală a planului: d ⊥ Qh.
o În aplicațiile practice l.d.c.m.m.p, se utilizează pentru a pune în evidență unghiul ce îl formează planul (P) cu unul dintre cele trei plane de referință: ∢ [(P),(H)] = ∢ ¿,d ]=∢ α .
68
o L.d.c.m.m.p reprezintă direcția pe care o poate avea o dreaptă conținută de planul (P) astfel încât aceasta să formeze unghiul maxim posibil dintre dreaptă și planul orizontal de proiecție:
∢ ¿,(H)]= ∢ ¿,d ] = ∢ α = maxim ; D ⊂ (P).
o Un plan poate avea o infinitate de l.d.c.m.m.p, toate perpendiculare pe urma orizontală.
o L.d.c.m.m.p este perpendiculară pe toate orizontalele conținute de planul (P).
- Caracteristicile prezentate în exemplul de mai sus și reprezentate în figura 4.21, pot fi extrapolate și la l.d.c.m.m.p față de planul frontal și cel lateral de proiecție.
- Linia de cea mai mare pantă poate să existe și între două plane de poziție oarecare (caz în care l.d.c.m.m.p este perpendiculară pe dreapta de intersecție a celor două plane) însă în practică, utilizând metodele geometriei descriptive, unul dintre cele două plane se aduce în poziție de coincidență cu unul dintre planele de proiecție, ajungându-se astfel la situația precedentă.
69
(Fig. 4.21 – Linia de cea mai mare pantă a planului (P) față de planul orizontal (H) de proiecție.)
4.6 POZIȚIA UNEI DREPTE FAȚĂ DE UN PLAN
Dreapta poate avea două poziții față de un plan :
1. Dreapta concurentă cu planul. În această categorie putem distinge și situația particulară când dreapta are o poziție de perpendiculară pe planul (P) (fig. 4.22).
2. Dreapta paralelă cu planul (fig. 4.23)
4.6.1 DREAPTA PERPENDICULARĂ PE UN PLAN
O dreaptă este perpendiculară pe un plan (P) atunci când, proiecțiile dreptei sunt perpendiculare pe urmele de aceași natură ale planului.
D ⊥ (P) ⇒ d ⊥ Qh ∧ d ' ⊥ Qv ∧ d ¿ ⊥ Qw
70
4.6.2 DREAPTA PARALELĂ CU UN PLAN
O dreaptă este paralelă cu un plan atunci când aceasta este paralelă cu cel puțin una din dreptele cuprinse în planul (P). În aplicații, o dreaptă oarecare se verifică dacă este paralelă cu un plan urmănd următorii pași:
o Se duce paralelă la dreaptă printr-un punct ce aparține planului (P).
o Se verifică cu ajutorul dreptelor orizontale auxiliare dacă un alt punct de pe dreapta trasată aparține planului (P). Dacă această condiție este îndeplinită înseamnă că pe dreapta trasată vom avea două puncte ce aparțin planului (P), deci dreapta este inclusă în planul (P).
o Dacă situația prezentată mai sus, este îndeplinită atunci dreapta din spațiu este paralelă cu planul (P).
Fig. 4.22 – Dreapta perpendiculară pe plan
71
CAPITOLUL 5
METODELE GEOMETRIEI DESCRIPTIVE
Studierea modului în care un element se proiectează pe unul dintre cele trei plane de proiecție în epură, nu este suficient pentru a extrage informații complete ale unui obiect geometric. De cele mai multe ori elementele geometrice (dreapta, planul) au reprezentări deformate în epură, iar mărimile reale ale acestora nu pot fi aflate decât dacă aceste sunt aduse în poziții particulare față de sistemul de referință. Astfel s-au dezvoltat o serie de metode specifice geometriei descriptive, prin care obiectul geometric se poate aduce într-o poziție particulară, operând doar în epură.
Informațiile grafice ce pot fi extrase, aplicând metodele geometriei descriptive, relevă în totalitate caracteristicile geometrice ale unui obiect oferind astfel științelor exacte un istrument complet prin care își pot materializa fizic rezultatele cercetărilor în diferite domenii.
Plecând de la idea de a poziționa obiectul cât mai favorabil față de planele de proiecție, metodele geometriei descriptive s-au realizat plecând de la două principii fundamentale :
1. Obiectul geometric își păstrează poziția în spațiu, iar observatorul se repoziționează astfel încât obiectul și observatorul ajung în poziții favorabile extragerii unor informații grafice reale. În momentul deplasării observatorului, întreg sistemul de referință (origine, axe de referință, plane de proiecție) se repoziționează față de obiectul fix. Se preferă acest mod de lucru pentru obiecte geometrice cu o complexitate ridicată și în general se aplică local pentru relevarea unor
72
caracteristici ale elementelor sau subansamblurilor ce intră în alcătuirea obiectului.
2. Observatorul, implicit sistemul de proiecție, este fix, obiectul geometric fiind repoziționat astfel încât acesta să se proiecteze în mod favorabil pe planele de proiecție. Această metodă este utilizată în general pentru obiecte cu o alcătuire geometrică mai simplă, și la fel ca în situația precedentă, se poate aplica local doar pentru unele elemente componente sau subansamble. Indiferent de modul de lucru și metoda aplicată, informațiile grafice extrase sunt complete și coincid ca rezultat final.
Aceste două puncte de vedere au dus la apariția a două metode :
A. Metoda schimbării planelor de proiecție – corespondentă primului principiu enunțat.
B. Metoda rotației – corespunde celui de-al doilea principiu.
5.1 METODA SCHIMBĂRII PLANULUI DE PROIECȚIE
Metoda schimbării planului de proiecție constă în repoziționarea sistemului de referință față de obiectul proiectat, ce are o poziție fixă în spațiu. În general aplicațiile practice operează doar cu schimbarea planului orizontal de proiecție (H) și cel frontal (V).
Metoda este aplicată cu scopul de a releva informații importante despre obiectul geometric analizat prin proiectarea acestuia în poziții particulare pe plane de proiecție special alese.
Schimbarea de plan de proiecție presupune alegerea unei noi axe de referință 0 X ce va determina noi plane de proiecție. Atât axa de referință nou aleasă cât și planele de proiecție rezultate, se vor nota cu aceleași litere, însă vor primi câte un indice ce va marca ordinea în care s-au efectuat schimbările. (fig. 5.1)
5.1.1 SCHIMBAREA PLANULUI FRONTAL DE PROIECȚIE
73
Vom analiza aplicarea metodei, succesiv pentru elementele geometrice elementare: punctul, dreapta, planul. Având în vedere faptul că proiecția orizontală nu se modifică, vom începe rezolvarea grafică plecând de la planul orizontal de proiecție, axa noului sistem de referință propus fiind amplasată pe planul orizontal al sistemului inițial de referință. În epură, sensul de rabatere a planului V1 pe planul frontal de proiecție (V), determină sensul axei X1O1.
Fie punctul A (a,a’,a”) situat în spațiu într-o poziție oarecare. Ne propunem aplicarea schimbării planului frontal de proiecție și vom parcurge următorii pași:
1. Se trasează noua axă de proiecție pe care o vom nota cu X1O1. Noua axă de referință marchează intersecția noului plan vertical de proiecție (V1) cu planul orizontal de proiecție (H) (fig. 5.1). Originea O1 poate fi poziționată oriunde pe noua axă de referință, neinfluențând rezultatul final.
2. Avand în vedere că se operează doar cu planul frontal de proiecție înseamnă ca proiecția orizontală a punctului nu se modifică.
Din punctul A din spațiu, se duce linie de ordine, perpendiculară pe noul plan frontal de proiecție ales, astfel se formează o nouă proiecție a punctului A pe care o vom nota cu a1’.
3. Deoarece prin schimbarea planului frontal de proiecție, cota punctului A nu se modifică, aceasta poartă denumirea de “paramentru constant” și este o caracteristică a schimbării planului frontal de proiecție.
4. Depărtarea precum și abscisa punctului A se modifică prin trecerea la noul sistem de proiecție.
PUNCTUL
74
Se cunoaște poziția în spațiu a dreptei AB determinată ce cele două puncte. Vom opera o schimbare de plan frontal de proiecție, pentru această dreaptă, urmând următorii pași:
1. Se alege axa noului sistem de proiecție X1O1. În cazul de față (fig.5.2), axa are o direcție aleatorie, însă în practică ea se poziționează în funcție de proiecția orizontală a dreptei, astfel încât dreapta să aibă o poziție particulară în noul sistem de proiecție ales, fie perpendiculară pe planul frontal de proiecție (dreaptă de capăt) sau paralelă cu acesta (dreaptă frontală).
2. După trasarea axei noului sistem, se duc linii de ordine din punctele A și B, determinându-se coordonatele ax1 respectiv bx1. Din cele două puncte de pe axă, se duc linii de ordine, perpendiculare pe axa de referință, egale ca valoare cu înălțimile (cotele) punctelor A și B din sistemul inițial. Astfel : ax a ' ≡ ax 1 a 1 ' ∧ bx b ' ≡ bx 1 b 1 ' .
3. După aflarea proiecțiilor frontale a punctelor A și B în noul sistem de referință, acestea se unesc rezultând proiecția frontală a dreptei după schimbarea de plan frontal de proiecție.
Fig. 5.1 – Schimbarea de plan frontal de proiecție pentru punct.
DREAPTA
75
76
Fig. 5.2 – Epura schimbării planului frontal de proiecție pentru o dreaptă
Fig. 5.3 – Axonometria izometrică a schimbării planului frontal de proiecție pentru o dreaptă PLANUL
Fie planul (Q) situat în spațiu într-o poziție oarecare. Ne propunem aplicarea schimbării planului frontal de proiecție și se parcurg următorii pași:
1. Se trasează noua axă de referință a sistemului propus de noi. Axa X1O1 intersectează urma orizontală a planului (Q), sau prelungirea acesteia în punctul QX1, ce reprezintă totodată și intersecția urmei orizontale a planului cu urma frontală, în noul sistem de referință.
2. După cum aminteam anterior, proiecția orizontală nu se modifică deci și urma orizontala a planului (Q) din sistemul inițial, își păstrează poziția și aspectul în noul sistem de referință ales. Dificultatea constă în trasarea urmei verticale în noul sistem de referință, iar pentru asta vom avea nevoie de o construcție ajutătoare.Deja se cunoaște un punct situat pe urma verticală a planului (Q) în noul sistem de referință, respectiv punctul Q X1. Cel de-al doilea punct de pe urma verticală se află prin intersectarea celor trei plane: planul frontal din sistemul inițial (V), planul frontal din sistemul propus de noi (V1) și planul (Q) – (fig 5.4). Cele trei plane se intersectează în punctul V, ce are proprietatea de a se afla în același timp în cele trei plane și mai mult, chiar pe urmele frontale ale acestora. Pentru aflarea punctului V în primul sistem de referință, se intersectează urma frontală Q v a planului (Q) cu urma frontală Vv1 a planului (V1). Planul (V1) este un plan vertical, de unde rezultă că urma acestuia este o dreaptă perpendiculară pe 0 X în punctul v (intersecția urmei orizontale X1O1 cu axa 0 X ).
3. Se transmite punctul V găsit, în cel de-al doilea sistem de referință având grijă ca valoarea cotei să rămână constantă. Punctul devine V1, ca notație în epură, deși în realitate este unul și același punct.
77
4. Se unește Qx1 cu V1 (ambele aflându-se pe urma frontală a planului (Q) în cel de=al doilea sistem de referință) și se obține Q v1 – urma frontală a planului (Q).
78
Fig. 5.4 – Schimbarea planului frontal de proiecție pentru un plan (Axonometrie izometrică și reprezentare în epură)
5.1.2 SCHIMBAREA PLANULUI ORIZONTAL DE PROIECȚIE
La fel ca în cazul precedent, vom studia în continuare metoda schimbării planului orizontal de proiecție pentru elementele geometrice primare: punctul, dreapta, planul. Având în vedere faptul că proiecția frontală nu se modifică, vom începe rezolvarea grafică în epură, plecând de la planul frontal de proiecție, axa noului sistem de referință propus fiind amplasată pe planul frontal al sistemului inițial de referință. În epură, sensul de rabatere a planului H2 pe planul frontal de proiecție (V), determină sensul axei X2O2.
Fie punctul A (a,a’,a”) situat în spațiu într-o poziție oarecare. Ne propunem aplicarea schimbării planului frontal de proiecție și vom parcurge următorii pași:
1. Se trasează noua axă de proiecție pe care o vom nota cu X2O2. Noua axă de referință marchează intersecția noului plan orizontal de proiecție (H2) cu planul vertical de proiecție (V) (fig. 5.1). Originea O2 poate fi poziționată oriunde pe noua axă de referință, neinfluențând rezultatul final. Planul pe care îl propunem să fie plan orizontal de proiecție în noul sistem de referință, este de fapt un plan de capăt în sistemul inițial.
2. Avand în vedere că se operează doar cu planul orizontal de proiecție înseamnă că proiecția frontală a punctului nu se modifică.
Din punctul A din spațiu, se duce linie de ordine, perpendiculară pe noul plan frontal de proiecție ales, astfel se formează o nouă
PUNCTUL
79
proiecție orizontală a punctului A pe planul (H2), pe care o vom nota cu a2.
3. Deoarece prin schimbarea planului orizontal de proiecție, depărtarea punctului A nu se modifică, aceasta poartă denumirea de “paramentru constant” și este o caracteristică a schimbării planului orizontal de proiecție.
4. Cota precum și abscisa punctului A se modifică prin trecerea la noul sistem de proiecție.
Se cunoaște poziția în spațiu a dreptei AB determinată de cele două puncte. Vom opera o schimbare de plan frontal de proiecție, pentru acest segment, urmând următorii pași:
1. Se alege axa noului sistem de proiecție X2O2. În cazul de față (fig.5.6), axa are o direcție aleatorie, însă în practică ea se poziționează în funcție de proiecția orizontală a dreptei, astfel încât dreapta să aibă o poziție particulară în noul sistem de proiecție ales, fie perpendiculară pe planul orizontal de proiecție (dreaptă verticală) sau paralelă cu acesta (dreaptă orizontală).
Fig. 5.5 – Schimbarea de plan frontal de proiecție pentru punct.
DREAPTA
80
2. După trasarea axei noului sistem, se duc linii de ordine din punctele A și B, determinându-se coordonatele ax1 respectiv bx1. Din cele două puncte de pe axă, se duc linii de ordine, perpendiculare pe noua axă de referință, egale ca valoare cu depărtările punctelor A și B din sistemul inițial. Astfel : ax a ≡ ax 2 a 2 ∧ bx b ≡ bx 2 b 2.
3. După aflarea proiecțiilor orizontale a punctelor A și B în noul sistem de referință, acestea se unesc rezultând proiecția orizontală a dreptei după schimbarea de plan orizontal de proiecție.
81
Fig. 5.6 – Epura schimbării planului orizontal de proiecție pentru o dreaptă.
Fie planul (Q) situat în spațiu într-o poziție oarecare. Ne propunem aplicarea schimbării planului orizontal de proiecție și se parcurg următorii pași:
1. Se trasează noua axă de referință a sistemului propus de noi. Axa X2O2 intersectează urma orizontală a planului (Q), sau prelungirea acesteia în punctul QX1, ce reprezintă totodată și intersecția urmei orizontale a planului cu urma frontală, în noul sistem de referință.
2. După cum aminteam anterior, proiecția orizontală nu se modifică deci și urma orizontala a planului (Q) din sistemul inițial, își păstrează poziția și aspectul în noul sistem de referință ales. Dificultatea constă în trasarea urmei verticale în noul sistem de referință, iar pentru asta vom avea nevoie de o construcție ajutătoare.
3. Deja se cunoaște un punct situat pe urma verticală a planului (Q) în noul sistem de referință, respectiv punctul QX2. Cel de-al doilea punct de pe urma verticală se află prin intersectarea celor trei plane: planul orizontal (H) din sistemul inițial, planul orizontal din sistemul propus de noi (H2) și planul (Q) – (fig 5.8). Cele trei plane se intersectează în punctul H, ce are proprietatea de a se afla în același timp în cele trei plane și mai mult, chiar pe urmele orizontale ale acestora. Pentru aflarea punctului H în primul sistem de referință, se intersectează urma orizontală Qh a planului (Q) cu urma orizontală
Hh2 a planului (H2). Planul (H2) este un plan de capăt, de unde rezultă că urma acestuia este o dreaptă perpendiculară pe 0 X în punctul h (intersecția urmei orizontale X2O2 cu axa 0 X ).
Fig. 5.7 – Axonometria izometrică a schimbării planului orizontal de proiecție pentru o dreaptă.
PLANUL
82
4. Se transmite punctul H găsit, în cel de-al doilea sistem de referință având grijă ca valoarea depărtării să rămână constantă. Punctul devine H2, ca notație în epură, deși în realitate este unul și același punct.
5. Se unește Qx2 cu H2 (ambele aflându-se pe urma orizontală a planului (Q) în cel de=al doilea sistem de referință) și se obține Q h2 – urma orizontală a planului (Q).
83
5.2 METODA ROTAȚIEI
Metoda rotației constă în modificarea poziției în spațiu a obiectului geometric reprezentat, fără a modifica sistemul de referință
Metoda este aplicată cu scopul de a releva informații importante despre obiectul geometric analizat prin proiectarea acestuia în poziții particulare pe plane de proiecție ale sistemului de referință.
Rotația prresupune utilizarea unor elemente caracteristice metodei :
- Axa de rotație, care se alege în general perpendiculară pe planul frontal (V) sau pe planul orizontal (H). Axa de rotație poate avea însă și o poziție oarecare în spațiu.
- Centrul de rotație reprezintă punctul situat pe axa de rotație, ce determină poziția planului de rotație aflat întotdeauna într-o poziție perpendiculară pe axă
- Raza de rotație este distanța de la centrul de rotație la elementul pe care vrem să-l rotim. Raza se află întotdeauna în planul de rotație.
- Unghiul de rotație
- Sensul de rotație se alege în funcție de particularitățile desenului și de informația pe care vrem să o extragem din desen.
Vom studia în continuare două tipuri de rotații utilizate frecvent în geometria descriptivă :
1. Rotația de nivel – Când axa de rotație este perpendiculară pe planul orizontal de proiecție (dreaptă verticală), iar planele de rotație sunt plane orizontale.
Fig. 5.8 – Schimbarea planului orizontal de proiecție pentru un plan (Axonometrie izometrică și reprezentare în epură)
84
2. Rotația de front – Când axa de rotație este perpendiculară pe planul frontal de proiecție (dreaptă de capăt), iar planele de rotație ale elementelor sunt plane frontale.
5.2.1 ROTAȚIA DE NIVEL
Axa, în cazul rotației de nivel , este o dreaptă verticală. Poziționarea axei de rotație, față de obiectul pe care vrem să-l rotim, este aleatorie. Toate punctele operate prin această metodă descriu în spațiu, prin deplasarea lor, arce de cerc situate în plane orizontale de proiecție. Centrul acestor arce de cerc sunt puncte situate pe axa de rotație, la cote identice cu înălțimile punctelor rotite.
În timpul deplasării pe traiectoriile circulare, punctele își păstrează constante înălțimile, deci putem spune că parametrul constant, specific rotației de nivel, este cota.
Se utilizează acest tip de rotație atunci când vrem să extragem informații despre obiectul geometric analizat, din proiecția lui frontală.
Fie punctul A(ax, ay, az ), de coordonate știute, vrem să-l rotim în plan orizontal cu un unghi ∢ α (Fig. 5.9). Se vor parcurge următoarele etape:
PUNCTUL
85
Fig. 5.9 – Rotația de nivel pentru un punct.
1. Se poziționează axa verticală de rotație D: D ⊥ (H).
2. Din punctul A(ax, ay, az ) se duce perpendiculară pe axa de rotație. În epură, se unește urma orizontală a axei de rotație cu punctul A: AM ⊥ D. Punctul M din spațiu se numește centrul de rotație al punctului A, aflându-se la aceași cotă cu acesta.
3. Se rotește punctul A în jurul centrului de rotație cu un unghi ∢ α pe care îl alegem în funcție de cerințele problemei. Unghiul de rotație se proiectează în mărime reală pe planul orizontal de proiecție. În epură, după obținerea proiecției orizontale a punctului rotit a 1, se duce linie de ordine în planul frontal de proiecție, și la înălțimea a z, se găsește proiecția frontală a punctului A1, respectiv punctul a1’.
DREAPTA
Se cunoaște poziția în spațiu a dreptei AB determinată de cele două puncte, A(ax,ay,az) și B(bx,by,bz). Vom opera o rotație de nivel, pentru acest segment, urmând următorii pași:
1. Se alege axa de rotație în funcție de informația pe care vrem să o obținem în urma efectuării rotației. În general axa se alege a.î. să treacă printr-un punct al dreptei. În figura 5.10 , axa de rotație s-a poziționat aleatoriu față de dreaptă. Axa de rotație, în cazul rotației de nivel, este o dreaptă verticală, astfel D ⊥ (H) , unde D este axa de rotație a dreptei AB .
2. După trasarea axei de rotație, în proiecție orizontală, vom folosi o dreaptă auxiliară m, ce trece prin proiecția orizontală a axei de
86
rotație d , și este perpendiculară pe ab, proiecția orizontală a dreptei AB: d ∈ m; m ⊥ ab.
3. Se rotește, în proiecție orizontală, dreapta ab , împreună cu dreapta m , în jurul punctului d, cu un unghi ∢ α oarecare. În general unghiul de rotație se alege astfel încât dreapta ab să ajungă într-o poziție particulară, fie dreaptă de capăt sau frontală.
4. După rotația de nivel, dreapta ab devine a 1 b1 . Se proiecteză pe planul frontal punctele a1 și b1, cu ajutorul liinilor de ordine având grijă să păstrăm neschimbate cotele celor două puncte. Rezultă astfel, în proiecție frontală, punctele a1’ și b1’ , care prin unire determină proiecția frontală a dreptei rotite, a 1 b1 . În continuare se construiește proiecția laterală a dreptei A1 B 1, cu ajutorul liniilor de ordine.
5. Observații :
a. Cotele punctelor nu se modifică în timpul rotației de nivel, ele deplasându-se pe traiectorii circulare în plane orizontale.
b. În proiecție orizontală, axa de rotație este total deformată, fiind reprezentată printr-un punct, respectiv “d”.
c. Centrele de rotație ale punctelor se află situate pe axa de rotație, la aceași cotă cu punctul ce se rotește.
d. Se operează rotația dreptei AB, doar în proiecție orizontală și frontală, proiecția laterală având rol pasiv sau de control.
87
Se cunoaște poziția în spațiu a planului (Q) determinat de urma orizontală Qh, urma verticală Qv și urma laterală Qw. Se operază o rotație de nivel, pentru acest plan, urmând următorii pași:
1. Se alege axa de rotație în funcție de informația pe care vrem să o obținem în urma efectuării rotației. În figura 5.11 , axa de rotație s-a poziționat aleatoriu față de plan. Axa de rotație este o dreaptă verticală, astfel R ⊥ (H) , unde R este axa de rotație a planului (Q).
2. După stabilirea poziției dreptei R, în proiecție orizontală, vom folosi o dreaptă auxiliară m, ce trece prin proiecția orizontală a axei de rotație r , și este perpendiculară pe urma orizontală Qh.
r ∈ m; m ⊥ Qh
3. Se rotește, în proiecție orizontală, dreapta Qh , împreună cu dreapta f , în jurul punctului r, cu un unghi ∢ α oarecare. În general unghiul de rotație se alege astfel încât urma orizontală Qh ajunge într-o poziție particulară, fie dreaptă de capăt sau frontală, planul (Q) devenind astfel plan de capăt respectiv, frontal .
4. După efectuarea rotației, dreapta Qh devine Qh 1, iar m devine m 1 Intersecția urmei orizontale Qh 1 a planului rotit, cu axa OX este punctul Qx1, comun atât Qh 1 cât și urmei frontale a planului rotit Qv 1. Dificultatea efectuării rotației de nivel pentru un plan, constă în aflarea urmei verticale după rotire. Pentru aceasta avem nevoie de o construcție auxiliară, astfel se va trasa o dreaptă orizontală ce aparține planului (Q), și trece prin axa R, (Fig. 5.12):
F ∈ (Q); F ∥ (H);
PLANUL
Fig. 5.10 – Rotația de nivel pentru o dreaptă. Reprezentare în epură.
88
F ∩ R = C , C este centrul de rotație a dreptei F
f ∥ Qh , f este proiecția orizontală a dreptei F
5. Dreapta orizontală F are urma verticală V situată pe Qv -urma frontală a planului (Q) - deoarece aparține (Q). După rotirea de nivel în jurul centrului de roatație C, punctul V devine V 1 și se va afla pe urma frontală rotită Qv 1 a planului (Q). Unind punctele V1 și Qx1, ambele situate pe urma frontală rotită Qv 1 a planului (Q), se determină Qv 1.
6. Observații :
a. Cotele punctelor nu se modifică în timpul rotației de nivel, ele deplasându-se pe traiectorii circulare în plane orizontale.
b. În proiecție orizontală, axa de rotație este total deformată, fiind reprezentată printr-un punct, respectiv “r”.
c. Centrele de rotație ale punctelor se află situate pe axa de rotație, la aceași cotă cu punctul ce se rotește.
d. Se operează rotația planului (Q), doar în proiecție orizontală și frontală, proiecția laterală având rol pasiv sau de control.
89
Axa, în cazul rotației de front , este o dreaptă de capăt. Poziționarea axei de rotație, față de obiectul pe care vrem să-l rotim, este aleatorie. Toate punctele operate prin această metodă descriu în spațiu, prin deplasarea lor, arce de cerc situate în plane verticale. Centrul acestor
Fig. 5.11 – Rotația de nivel pentru un plan. Reprezentare în epură.
Fig. 5.12 – Rotația de nivel pentru un plan. Reprezentare în axonometrie izometrică.
5.2.2 ROTAȚIA DE FRONT
90
arce de cerc sunt puncte situate pe axa de rotație, la depărtări identice cu depărtările punctelor rotite.
În timpul deplasării pe traiectoriile circulare, punctele își păstrează constant distanța față de planul frontal de proiecție, deci putem spune că parametrul constant, specific rotației de nivel, este depărtarea.
Se utilizează acest tip de rotație atunci când vrem să extragem informații despre obiectul geometric analizat, din proiecția lui orizontală.
PUNCTUL
Fie punctul A(ax, ay, az ), de coordonate știute, vrem să-l rotim în plan frontal cu un unghi ∢ α (Fig. 5.13). Se vor parcurge următoarele etape:
1. Se poziționează axa de rotație D(dreaptă de capăt): D ⊥ (V).
2. Din punctul A(ax, ay, az ) se duce perpendiculară pe axa de rotație. În epură, se unește urma frontală a axei de rotație cu punctul A: AM ⊥ D. Punctul M din spațiu se numește centrul de rotație al punctului A, aflându-se la aceași depărtare cu acesta.
3. Se rotește punctul A în jurul centrului de rotație cu un unghi ∢ α pe care îl alegem în funcție de cerințele problemei. Unghiul de rotație se proiectează în mărime reală pe planul frontal de proiecție. În epură, după obținerea proiecției frontale a punctului rotit a1’, se duce linie de ordine în planul orizontal de proiecție, și la depărtarea ay, se găsește proiecția orizontală a punctului A1, respectiv punctul a1.
91
Fig. 5.13 – Rotația de front pentru un punct.
DREAPTA
Se cunoaște poziția în spațiu a dreptei AB determinată de cele două puncte, A(ax,ay,az) și B(bx,by,bz). Vom opera o rotație de front, pentru acest segment, urmând următorii pași:
1. Se alege axa de rotație în funcție de informația pe care vrem să o obținem în urma efectuării rotației. În general axa se alege a.î. să treacă printr-un punct al dreptei. În figura 5.14 , axa de rotație s-a poziționat aleatoriu față de dreaptă. Axa de rotație, în cazul rotației de front, este o dreaptă de capăt, astfel D ⊥ (V) , unde D este axa de rotație a dreptei AB .
2. După trasarea axei de rotație, în proiecție frontală, vom folosi o dreaptă auxiliară m, ce trece prin proiecția orizontală a axei de rotație d ' , și este perpendiculară pe a ' b ', proiecția frontală a dreptei AB: d ' ∈ m; m ⊥ a ' b '
3. Se rotește, în proiecție frontală, dreapta a ' b ' , împreună cu dreapta m , în jurul punctului d’, cu un unghi ∢ α oarecare. În general unghiul de rotație se alege astfel încât dreapta ab să ajungă într-o poziție particulară, fie dreaptă orizontală sau verticală.
4. După rotația de front, dreapta a ' b ' devine a 1 ' b1 ' . Se proiecteză pe planul orizontal punctele A1 și B1, cu ajutorul liinilor de ordine având grijă să păstrăm neschimbate depărtările celor două puncte. Rezultă astfel, în proiecție orizontală, punctele a1 și b1, care prin unire determină proiecția orizontală a dreptei rotite, A1 B 1. În continuare se construiește proiecția laterală a dreptei A1 B 1, cu ajutorul liniilor de ordine.
5. Observații :
92
a. Depărtările punctelor nu se modifică în timpul rotației de front, ele deplasându-se pe traiectorii circulare în plane frontale.
b. În proiecție frontală, axa de rotație este total deformată, fiind reprezentată printr-un punct, respectiv d’.
c. Centrele de rotație ale punctelor se află situate pe axa de rotație, la aceași depărtare cu punctul ce se rotește.
d. Se operează rotația dreptei AB, doar în proiecție frontală și orizontală, proiecția laterală având rol pasiv sau de control.
93
Fig. 5.14 – Rotația de front pentru o dreaptă. Reprezentare în epură. PLANUL
Se cunoaște poziția în spațiu a planului (Q) determinat de urma orizontală Qh, urma verticală Qv și urma laterală Qw. Se operază o rotație de front, pentru acest plan, urmând următorii pași:
1. Se alege axa de rotație în funcție de informația pe care vrem să o obținem în urma efectuării rotației. În figura 5.16 , axa de rotație s-a poziționat aleatoriu față de plan. Axa de rotație este o dreaptă de capăt, astfel R ⊥ (V) , unde R este axa de rotație a planului (Q).
2. După stabilirea poziției dreptei R, în proiecție frontală, vom folosi o dreaptă auxiliară m, ce trece prin proiecția orizontală a axei de rotație r ' , și este perpendiculară pe urma orizontală Qv . r ' ∈ m; m ⊥ Qv .
3. Se rotește, în proiecție frontală, dreapta Qv , împreună cu dreapta m , în jurul punctului r, cu un unghi ∢ α oarecare. În general unghiul de rotație se alege astfel încât urma orizontală Qv ajunge într-o poziție particulară, fie dreaptă verticală sau orizontală, planul (Q) devenind astfel plan de capăt respectiv, orizontal .
4. După efectuarea rotației, dreapta Qv devine Qv 1, iar m devine m1 .
Intersecția urmei frontale Qv 1 a planului rotit, cu axa OX este punctul Qx1, comun atât Qh 1 cât și urmei frontale a planului rotit Qv 1.
Dificultatea efectuării rotației de front pentru un plan, constă în aflarea urmei orizontale după rotire. Pentru aceasta avem nevoie de o construcție auxiliară, astfel se va trasa o dreaptă frontală ce aparține planului (Q), și trece prin axa R, (Fig. 5.15):
F ∈ (Q); F ∥ (V);
F ∩ R = C , C este centrul de rotație a dreptei F
f ' ∥ Qv , f ' este proiecția frontală a dreptei F
5. Dreapta frontală F are urma orizontală H situată pe Qh -urma orizontală a planului (Q) - deoarece aparține (Q). După rotirea de nivel în jurul centrului de roatație C, punctul H devine H1 și se va afla pe urma orizontală rotită Qh 1 a planului (Q). Unind punctele H1 și Qx1, ambele situate pe urma orizontală rotită Qh 1 a planului (Q), se determină Qh 1.
6. Observații :
94
a. Depărtările punctelor nu se modifică în timpul rotației de front, ele deplasându-se pe traiectorii circulare în plane frontale.
b. În proiecție frontală, axa de rotație este total deformată, fiind reprezentată printr-un punct, respectiv r’.
c. Centrele de rotație ale punctelor se află situate pe axa de rotație, la aceași depărtare cu punctul ce se rotește.
d. Se operează rotația planului (Q), doar în proiecție frontală și orizontală, proiecția laterală având rol pasiv sau de control.
95
Fig. 5.15 – Rotația de front pentru un plan. Reprezentare în axonometrie.
Fig. 5.16 – Rotația de front pentru un plan. Reprezentare în epură.
5.3 METODA RABATERII
Metoda rabaterii constă în rotirea planului ce conține elementul pe care vrem să-l analizăm, în jurul axei de rabatere. Această metodă este asemănătoare cu metoda rotației dar este folosită în special când avem de evidențiat informații despre elemente plane. Spre deosebire de rotație, rabaterea operează cu întregul plan ce conține elementul și nu cu elementul în sine. Rabaterea se realizează, în mod curent, pe unul dintre cele trei plane de proiecție sau pe un plan oarecare din spațiu. Axa de rabatere este dreapta de intersecție dintre planul pe care vrem să-l rotim și planul pe care vrem să rabatem.
Caracteristici generale ale rabaterii:
- Axa de rabatere este dreapta de intersecție dintre planul ce se rabate și planul pe care se realizează rabaterea.
- Rabaterea este utilizată pentru:
o relevarea mărimii reale a elementelor incluse în planul ce se rabate, iar în acest caz, planul pe care se rabate este chiar unul dintre cele trei plane de proiecție sau paralel cu acestea.
o Rezolvarea unor probleme de tangență a suprafețelor poliedrelor sau corpurilor de rotație.
- Punctele de pe planul ce se rabate realizează deplasări circulare în planuri perpendiculare pe axa de rotație.
- Centrele de rabatere (sau de rotație) a punctelor se află pe axa de rabatere.
- Punctele aflate pe axa de rabatere sunt propriile lor rabătute
- Raza de rabatere este ipotenuza triunghiului de poziție a punctului pe care vrem să-l rabatem, fiind situată întotdeauna pe dreapta de intersecție dintre planul ce se rabate și planul determinat de mișcarea circulară a punctului rabătut.
96
Toate punctele din planul ce se rabate se rotesc cu același unghi în jurul axei. Unghiul rabaterii este unghiul format de planul rabătut și planul pe care se rabate.
Rabaterea pe unul dintre planele de proiecție se poate realiza prin două metode:
A. Cu ajutorul triunghiului de poziție. Această metodă de rabatere este una generală ce se utilizează indiferent de poziția planului pe care realizăm rabaterea.
B. Cu ajutorul dreptelor paralele cu planul pe care vrem să rabatem. În genereal această metodă este utilizată atunci când planul pe care se realizează rabaterea este un plan de proiecție, sau paralel cu un plan de proiecție.
În continuare vom vedea cum se realizează rabaterea unui plan oarecare pe planul orizontal și vertical de proiecție prin ambele metode enumerate mai sus.
5.3.2
Rabaterea pe planul orizontal de proiecție este metoda cea mai des utilizată pentru aflarea mărimii reale a unui element plan, sau care poate fi inclus într-un plan. Metoda constă în rotirea planului, împreună cu elementele conținute de acesta, în jurul urmei orizontale până se suprapune peste planul orizontal de proiecție.
În figura 5.17 se cunoaște poziția punctului A(ax,ay,az) și a planului (Q) ce include punctul A. Pentru a rabate punctul A și planul (Q) cu ajutorul triunghiului de poziție se parcurg, în ordine logică, următorii pași :
1. Prin punctul A se trasează linia de cea mai mare pantă a planului (Q) față de planul orizontal de proiecție, respectiv dreapta AH 1 , ce are urma orizontală în punctul H1, situat pe urma orizontală Qh a planului (Q), astfel:
i. A ∈ AH 1 ; A ∈ (Q)
-
5.3.1 RABATEREA UNUI PLAN OARECARE PE PLANELE DE PROIECȚIE
RABATEREA UNUI PLAN OARECARE PE PLANUL ORIZONTAL
97
ii. AH 1 ⊥Q h ⟹ aH 1 ⊥Qh ; AH 1 – l.d.c.m.m.p. (Q) față de (H)
iii. H1 ∈ Qh ; H1 ¿ centrul de rabatere a punctului A.
2. În spațiu se formează triunghiul ⊿ AaH1 ,dreptunghic în ⊾a . Acest triunghi se rabate pe planul orizontal de proiecție, purtând denumirea de triunghiul de poziție a punctului A(ax,ay,az). Triunghiul ⊿ A1aH1 este mărimea reală, în epură, a triunghiului ⊿ AaH1 din spațiu, de unde rezultă că AH 1 ≡ A1 H 1 :
i. ⊿ AaH1 ≡ ⊿ A1aH1 ⟹ AH 1 ≡ A1 H 1
ii. ∢ α = ∢( AH 1 , aH 1 )=∢ [(Q),(H)]=∢( A1 H 1 , aH 1 )
3. Prin rotirea (rabaterea ) punctului A în jurul Qh , acesta descrie un arc de cerc situat într-un plan vertical, perpendicular pe axa de rotație, ce are urma orizontală dreapta aH 1. Raza arcului de cerc descris de A este egală cu A H 1, iar AH 1 = A1 H 1 . În epură (fig. 5.18), se trece valoarea razei de rabatere pe urma orizontală aH 1, reprezentând momentul când punctul A ajunge , prin rabatere pe planul orizontal. Astfel se determină punctul A0 ce reprezintă rabătutul punctului A pe planul orizontal :
i. AH 1 = A1 H 1= A0 H
A0(a0x, a0y,a0z
0
1 98
1 ⟹
); A
∈ aH
4. Pentru rabaterea Planului (Q) se trasează l.d.c.m.m.p. (Q) față de (H) poziționată a.î, în epură să avem acces la urma frontală V și urma orizontală H. Se parcurge același raționament logic ca în cazul rabaterii punctului A, însă punctul pe care îl rabatem este chiar urma verticală a dreptei, situat pe urma verticală Qv a planului (Q), respectiv punctul V. Se construiește triunghiul de poziție al punctului V și se află V0 , rabătutul punctului V pe planul orizontal (H). Având în vedere că V și Qx se află pe urma frontală a planului (Q) iar Q x se află pe axa de rabatere fiind propriul rabătut pe planul orizontal, unind V0 cu Qx se obține urma frontală Qv 0 rabătută pe planul orizontal de proiecție. Urma orizontală Qh a planului (Q) nu se modifică în urma rabaterii fiind chiar axa de rabatere. Urma Qv 0 ,determinată anterior, împreună cu Qh ,inițială, definesc în epură planul (Q0), rabătutul planului (Q) pe planul orizontal de proiecție. Planul (Q0) se suprapune peste planul orizontal (H), iar toate elementele conținute de acesta se proiectează în mărime reală în proiecția orizontală.
Fig. 5.17 – Rabaterea pe planul Orizontal de proiecție (Axonometrie)
99
În figura 5.19 se cunoaște poziția punctului A(ax,ay,az) și a planului (Q) ce include punctul A. Pentru a rabate punctul A și planul (Q) cu ajutorul dreptelor orizontale se parcurg, următorii pași :
1. Prin A se duce o dreaptă orizontală ce aparține planului (Q). Punctul V este urma frontală a dreptei orizontale și se află pe Qv , urma frontală a planului (Q).
i. AV ∥ (H) ∥ Qh ; AV ⊂ (Q).
ii. A ∈ AV
iii. V ∈ Qv
2. Se rabate punctul V, împreună cu urma frontală a planului (Q), pe planul orizontal de proiecție. Pentru a realiza această operație se va
Fig. 5.18 – Rabaterea pe planul Orizontal de proiecție (Epură)
Fig. 5.19 – Rabaterea pe planul Orizontal de proiecție (Axonometrie)
100
trasa prin V linia de cea mai mare pantă a planului (Q) față de planul orizontal (H), respectiv dreapta HV , formându-se astfel triunghiul
⊿ QXHV dreptunghic în ⊾H. Triunghiul format se rabate în jurul axei Qh, pe planul orizontal de proiecție, devenind ⊿ QXHV0. În proiecția orizontală (Fig. 5.20), punctul v (proiecția orizontală a punctului V) se deplasează pe o dreaptă perpendiculară pe Qh . Se poziționează vârful compasului în Qx și se trasează un arc de cerc cu raza egală cu VQx , iar la intersecția dreptei pe care se deplasează punctul v, cu arcul de cerc astfel trasat, rezultă punctul V0. Prin unirea punctelor QX și V0 se obține urma frontală rabătută a planului (Q), pe planul orizontal (H).
i. HV ⊂ (Q) ; HV ⊥ Qh ; V ∈ HV
ii. ⊿ QXHV ≡ ⊿ QXHV0 ; ⊾H = 90°
iii. HV 0 ⊥ Qh
iv. Q X V 0 ≡ VQ X
101
3. Din V0 aflat anterior se trasează o dreaptă paralelă cu Qh , respectiv dreapta V 0 A 0 , care este defapt dreapta VA rabătută pe planul orizontal de proiecție. Prin rabatere punctu A se deplasează, în proiecție orizontală, pe o dreaptă perpendiculară pe Qh. La intersecția dreptei V 0 A 0 cu direcția de deplasare a punctului A, se află punctul A0 (rabătutul punctului A pe planul orizontal de proiecție).
i.
Observații:
Elementele geometrice adimensionale sau cu o singură dimensiune (puncte, drepte) pot avea mai multe imagini rabătute pe planul de proiecție orizontal sau vertical, în funcție de planul în care este inclus elementul respectiv.
Rabaterea pe planul orizontal de proiecție este utilizată în special pentru relevarea mărimii reale a elementelor plane.
Triunghiurile de poziție a punctelor situate într-un plan, sunt triunghiuri asemenea.
În exemplul din figurile 5.21, 5.22 este prezentată rabaterea △ABC pe planul orizontal de proiecție. În general este preferată în rezolvarea problemelor, metoda dreptelor paralele cu planele de proiecție.
Spre deosebire de metoda rotației, axa de rabatere nu este la alegere, fiind determinată de intersecția dintre planul ce se rabate și planul pe care se rabate.
Fig. 5.20 – Rabaterea pe planul Orizontal de proiecție (Epură)
V 0 A 0 ∥ Qh
0
h
ii. H 1 A
⊥ Q
1 A 0 ∩ V 0 A 0 = A0
iii. H
102
Fig. 5.21 – Rabaterea △ABC pe planul Orizontal de proiecție (Axonometrie)
103
Fig. 5.22 – Rabaterea △ABC pe planul Orizontal de proiecție (Epură)
Rabaterea unei forme plane, în cazul nostru triunghiul △ABC, se realizează prin rabaterea fiecărui punct pe planul orizontal de proiecție. Metoda de rabatere poate fi una dintre cele două prezentate mai sus. În cazul exemplului nostru, s-a ales rabaterea cu ajutorul dreptelor orizontale duse prin fiecare vârf al triunghiului.
5.3.3 RABATEREA UNUI PLAN OARECARE PE PLANUL VERTICAL
Metoda rabaterii pe planul vertical de proiecție constă în rotirea planului, împreună cu elementele conținute de acesta, în jurul urmei frontale până se suprapune peste planul vertical de proiecție.
În figura 5.23 se cunoaște poziția punctului A(ax,ay,az) și a planului (Q) ce include punctul A. Pentru a rabate punctul A și planul (Q) cu ajutorul triunghiului de poziție se parcurg, în ordine logică, următorii pași :
1. Prin punctul A se trasează linia de cea mai mare pantă a planului (Q) față de planul vertical de proiecție, respectiv dreapta AV 1, ce are urma verticală în punctul V1, situat pe urma frontală Qv a planului (Q), astfel:
i. A ∈ AV 1 ; A ∈ (Q)
ii. AV 1 ⊥ QV ⟹ a ' V 1 ⊥QV ; AV 1 – l.d.c.m.m.p. (Q) față de (V)
iii. V1 ∈ QV ; V1 ¿ centrul de rabatere a punctului A.
2. În spațiu se formează triunghiul ⊿ Aa’V1 ,dreptunghic în ⊾a’ . Acest triunghi se rabate pe planul frontal de proiecție, purtând denumirea de triunghiul de poziție a punctului A(ax,ay,az). Triunghiul ⊿ A1a’V1 este mărimea reală, în epură, a triunghiului ⊿ Aa’V1 din spațiu, de unde rezultă că AV 1 ≡ A1 V 1 :
i. ⊿ Aa’V1 ≡ ⊿ A1a’V1 ⟹ AV 1 ≡ A1 V 1
ii. ∢ α = ∢( AV 1 , a ' V 1)=∢ [(Q),(V)]=∢( A1 V 1 , a ' V 1)
3. Prin rotirea (rabaterea ) punctului A în jurul QV , acesta descrie un arc de cerc situat într-un plan de capăt, perpendicular pe axa de rotație, ce are urma orizontală dreapta a ' V 1. Raza arcului de cerc
104
descris de A este egală cu AV 1, iar AV 1 ≡ A 1 V 1 . În epură (fig. 5.24), se trece valoarea razei de rabatere pe urma orizontală a ' V 1, reprezentând momentul când punctul A ajunge , prin rabatere pe planul frontal. Astfel se determină punctul A0 ce reprezintă rabătutul punctului A pe planul frontal:
4. Pentru rabaterea Planului (Q) se trasează l.d.c.m.m.p. (Q) față de (V) poziționată a.î, în epură să avem acces la urma frontală V și urma orizontală H. Se parcurge același raționament logic ca în cazul rabaterii punctului A, însă punctul pe care îl rabatem este chiar urma orizontală a dreptei, situat pe urma orizontală Qh a planului (Q), respectiv punctul H. Se construiește triunghiul de poziție al punctului H și se află H0 , rabătutul punctului H pe planul frontal (V). Având în vedere că H și Qx se află pe urma frontală a planului (Q) iar Q x se află
i. AV 1 ≡ A1 V 1 ≡ A0 V 1 ⟹ A0(a0x, a0y,a0z); A0 ∈ a ' V 1
Fig. 5.23 – Rabaterea pe planul Frontal de proiecție (Axonometrie)
105
pe axa de rabatere fiind propriul rabătut pe planul frontal, unind H 0 cu Qx se obține urma orizontală Qh 0 rabătută pe planul frontal de proiecție. Urma frontală Qv a planului (Q) nu se modifică în urma rabaterii fiind chiar axa de rabatere. Urma Qh 0 ,determinată anterior, împreună cu Qv ,inițială, definesc în epură planul (Q0), rabătutul planului (Q) pe planul frontal de proiecție. Planul (Q0) se suprapune peste planul frontal (V), iar toate elementele conținute de acesta se proiectează în mărime reală în proiecția frontală.
Frontal de proiecție (Epură) În figura 5.25 se
cunoaște poziția punctului A(ax,ay,az) și a planului (Q) ce include punctul A. Pentru a rabate punctul A și planul (Q) cu ajutorul dreptelor frontale se parcurg, următorii pași :
Fig. 5.24 – Rabaterea pe planul
106
1. Prin A se duce o dreaptă frontală ce aparține planului (Q). Punctul H este urma orizontală a dreptei frontale și se află pe Qh, urma orizontală a planului (Q).
i. AH ∥ (V) ∥ QV ; AH ⊂ (Q).
ii. A ∈ AH
iii. H ∈ Qh
Fig. 5.25 – Rabaterea pe planul Frontal de proiecție (Axonometrie)
2. Se rabate punctul H, împreună cu urma orizontală a planului (Q), pe planul frontal de proiecție. Pentru a realiza această operație se va trasa prin H linia de cea mai mare pantă a planului (Q) față de planul frontal (V), respectiv dreapta HV , formându-se astfel triunghiul ⊿ QXHV dreptunghic în ⊾V. Triunghiul format se rabate în jurul axei QV , pe planul frontal de proiecție, devenind ⊿ QXVH0. În proiecția frontală (Fig. 5.26), punctul h’ (proiecția frontală a punctului H) se deplasează pe o dreaptă perpendiculară pe QV . Se poziționează vârful compasului în Qx și se trasează un arc de cerc cu raza egală cu HQ x, iar la intersecția dreptei pe care se deplasează punctul h’, cu
107
arcul de cerc astfel trasat, rezultă punctul H0. Prin unirea punctelor QX și H0 se obține urma orizontală rabătută a planului (Q), pe planul frontal (V).
i. HV ⊂ (Q) ; HV ⊥ Qv ; H ∈ HV
ii. ⊿ QXHV ≡ ⊿ QXVH0 ; ⊾V = 90°
iii. VH 0 ⊥ Qv
iv. Q X H 0 ≡ HQ X
3. Din H0 aflat anterior se trasează o dreaptă paralelă cu QV , respectiv dreapta H 0 A 0 , care este defapt dreapta HA rabătută pe planul frontal de proiecție. Prin rabatere, punctul A se deplasează, în proiecție orizontală, pe o dreaptă perpendiculară pe Qv . La intersecția dreptei H 0 A 0 cu direcția de deplasare a punctului A, se află punctul A0 (rabătutul punctului A pe planul frontal de proiecție).
i. H 0 A 0 ∥ Qv
ii. V 1 A 0 ⊥ Qv
Fig. 5.26 – Rabaterea pe planul Frontal de proiecție (Epură)
108
iii. V 1 A 0 ∩ H 0 A 0 = A0 BIBLIOGRAFIE Autor Denumire Editura An 1 Prună Liviu Geometrie descriptivă Societății Academice “Matei-Teiu Botez”; Iași 2006 Slonovschi Andrei Antonescu Ion 2 Aneta Stănilă Geometrie descriptivă Tehnică, Științifică și Didactică “CERMI”; Iași 2002 Toma AnaMaria 3 Dănăilă Wanda Descriptive Geometry TEHNOPRESS; Iași 2006 Anghel Alina Angelica 4 Botez Mihail Ștefan Geometrie descriptivă Tipografia Alexandru A. Țerek, Iași 1946 5 Botez Mihail Ștefan Geometrie descriptivă Didactică și Pedagogică; București 1965 6 Fucke Rudolf Darstellende Geometrie VEB FachBuchVerlag; Leipzig 1980 Kirch Konrad Nickel Heinz 7 Moncea Jean Geometrie descriptivă și desen tehnic Didactică și Pedagogică; București 1982 8 Chelcea Mirela Geometrie descriptivă Matrixrom 2007 Gheorghiu Monica Iliescu Madalin 9 Anghel Alina Geometrie descriptivă Performantica 2004 Dănăilă Wanda 10 Popa Constantin Geometrie descriptivă Rotaprint; Iași 1991 Onofrei Ligia Popa Iordache 11 Prună Liviu Geometrie Tehnică, Științifică și 2002 109
descriptivă Didactică “CERMI”; Iași Slonovschi Andrei Antonescu Ion 12 Tănăsescu Aurelian Geometrie descriptivă Didactică și Pedagogică; București 1965 13 Vasilescu Ecaterina Geometrie descriptivă. Curs și Aplicații I.P.B; București 1995 Zgură Alexandru Marin Dumitriu 14 Velicu Doru Geometrie descriptivă. Curs și Aplicații Universitatea Transilvania, Brașov 1991 Dogariu Mariana Ivan Maria Corelia Brana Mircea Gageaonea Elena Olteanu Felicia Sava Rodica Renel Roxana 15 Rehbock Fritz Darstellende Geometrie Springer-Verlag; Berlin Heidelberg; New York 1969 16 Ruse Gheorghe Geometrie descriptivă. Probleme Printech; București 1997 17 Popa Constantin Geometrie descriptivă. Venus; Iași 1998 Hâncu Grațiela Popa Iordache Onofrei Ligia 18 Precupețu Paul Probleme de geometrie Descriptivă cu Aplicații în Tehnică Editura Tehnică; București 1987 Dale Constantin 19 Hâncu Grațiela Desen Tehnic în Construcții Venus; Iași 1998 Stănilă Aneta 20 Tănăsescu Aurelian Geometrie descriptivă. Perspectivă. Axonometrie. Didactică și Pedagogică; București 1975 21 Vraca Ileana Desen Tehnic Didactică și Pedagogică; București 1979 110
Fig. 1.1 Proiecție paralelă oblică
Fig. 1.5
Fig. 1.10 Sensul numerotării triedrelor.
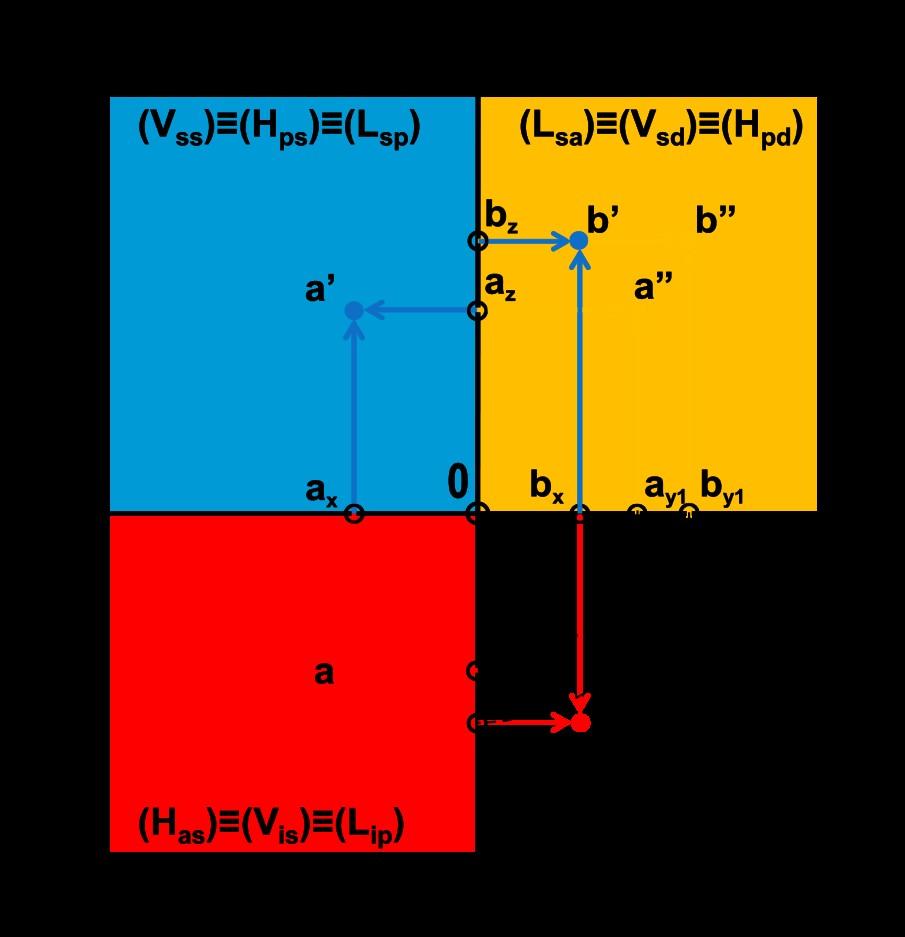
Fig. 1.12 Alcătuirea sistemului axonometric ortogonal.
Fig. 3.13
