Number of Rising Sequences of the Riffle and Overhand Card Shuffles

Number of Rising Sequences of the Riffle and Overhand Card Shuffles

Leonardo Bruzze – Cherrybrook Technology High School

Abstract

This experimental study examined the number of rising sequences of the riffle and overhand card shuffles, intending to compare the two card shuffling strategies for use in casinos and social settings. By starting with two decks of 52 playing cards in their natural order, 40 riffle and 40 overhand shuffles were completed using separate decks, before recording the positions of the cards following each shuffle. The number of rising sequences was then determined by manually counting the number of sets of 3 or more cards that follow their natural order within the deck. While the mean value of the riffle shuffle was higher than the overhand shuffle, after performing a t-Test: Paired Two Sample for Means it was concluded that there was no statistically significant difference between the rising sequences of both card strategies. Thus, the null hypothesis was accepted, and the alternative hypothesis was rejected.

Literature Review

The process of randomising a deck of cards is essential to reduce predictability in the arrangement of the cards, with this issue being recognised by mathematicians, scientists and the general public alike. By ensuring the positions of the cards vary following each shuffle, the deck of cards can be dealt with fairly, minimising the chance of capitalisation by casinos. Furthermore, card cheats have taken advantage of predictable patterns in the arrangement of cards after being shuffled, calling attention to the need of mixing cards to a satisfactory extent (Aldous and Diaconis 1986, p. 345).

Randomisation of a deck of cards can be regarded as inducing a non-predictable permutation on the cards following a shuffle (Pemantle 1989, p. 38). This requires a shuffle technique and a shuffle count to be identified which contribute to achieving the greatest variations in the card positions. This issue has been widely recognised by literature, including the study by Diaconis et al. (2013, p. 1693) whereby the variations of cards as a result of self-shuffling machines are analysed to draw practical application for games including poker and blackjack in casinos. Such paper identified the number of valleys in the permutation produced by the self-shuffler to be an indicator of the randomness of the cards, with no valleys being a uniform distribution (Diaconis et al. 2013, p. 1698). Their result of using a 10-shelf shuffler was found to be insufficiently random, recommending a 200-shelf machine to achieve total variation (Diaconis et al. 2013, p. 1717).

As demonstrated by the results of Diaconis et al., the problem of determining the number of shuffles to achieve total variation concerning automatic shufflers or computer modelling is comprehensively examined. The randomisation of cards from manual shuffling methods, however, has been minimally investigated. Since shuffling relies on the skill of the shuffler, the distribution of cards via the same shuffle will differ between different shufflers, pointing toward the importance of examining the effect of human shuffle practices on the arrangement of cards (Aldous and Diaconis 1986, p. 343). This is apparent due to the flaws involved with manual shuffling since single cards are dropped 50% of the time and pairs of cards are dropped 25% of the time while shuffling (Aldous and Diaconis 1986, p. 345). Thereby, the study conducted by Diaconis et al. was limited in its scope and application by disregarding the inconsistent and imperfect shuffle practices of humans despite the continued use of manual shuffling in casinos and other card-playing settings.

Pivotal research surpasses this method by comparing mechanical shuffling with the manual riffle shuffle, whereby 19 riffle shuffles were conducted to an initially ordered deck of cards (Silverman 2019, pp. 272-273). This study involved 5 randomness tests for both the manual and mechanical shuffles including rank correlation and the theory of rising sequences to determine the number of shuffles required to produce a random deck of cards. Whilst 12 automatic shuffles were required to mix a deck of cards to a satisfactory extent, only 8 hand shuffles were required for satisfactory mixing when comparing the statistical results of rising sequences (Silverman 2019, p. 295). Thereby, this study points towards the need to investigate the randomness of human shuffling practices, whilst is conversely limited in scope by directly focusing on just the riffle shuffle, despite both the overhand and riffle shuffles being widely practised in society as the most popular shuffling methods (Pemantle 1989, p. 37).

This leads to the central question of whether card players should use the riffle or overhand shuffle when shuffling a deck of cards. The riffle shuffle involves separating the deck into two roughly equal parts and interlacing the cards as per the Gilbert-Shannon-Reeds model of shuffling, which can be mathematically defined as a permutation with 1 or 2 rising sequences (Aldous and Diaconis 1986, pp. 342-343). The overhand shuffle, on the other hand, requires the shuffler to slide small packets of cards out of the deck before successively depositing them back onto the top of the deck. A visual representation detailing how both the riffle and overhand card strategies can be performed is displayed below (Griffiths 2015).

Figure 1 Visual Representation of Riffle and Overhand Card Shuffles

Pemantle (1989, p. 49) suggested that between 1000 to 3000 overhand shuffles are required to randomise an ordered deck of cards as opposed to 7 riffle shuffles, thus highlighting that the riffle shuffle leads to the greater variation of the cards in a reduced number of shuffles as opposed to the overhand shuffle. The broad bounds of the recommended overhand shuffle count highlight the poor internal reliability of this study since the exact shuffle count to achieve randomness was not determined. This 2000 shuffle range reduces the statistical significance of the study and thus causes it to stand as an unsatisfactory representation of the imperfect nature of human shuffling. Further, the results from Silverman’s (2019, p. 295) investigation reported imprecise results for a riffle shuffle after conducting various tests of randomness. He concluded that while 6 shuffles were required to achieve randomness when utilising the statistical test of rank-ordering, 10 shuffles were needed to achieve randomness when using the measure of runs relative to the mean (Silverman 2019, p. 295).

Thus, both Pemantle’s and Silverman’s studies are unreliable due to their inconsistent results when being compared. This possibly arises from the adopted measure of variation affecting the number of shuffles in achieving randomness, causing disparities to exist when identifying the precise shuffle count to achieve a random arrangement of cards. The key implication drawn from this research is the requirement to find a measure of randomness which best corresponds to unpredictability in the arrangement of cards. This may include the theory of rising sequences, which involves the identification of subsets of cards that are consecutively increasing following a shuffle. The number of such sequences between the two shuffle strategies can be compared to determine which strategy produces a more predictable arrangement of cards, hence holding critical importance in the card randomisation problem within society (Silverman 2019, p. 280).

Existing literature largely focuses on the randomisation of cards from the riffle shuffle or as a result of automatic shuffling devices. The investigation into both the manual riffle and overhand shuffles, however, is critical due to their continued use in casinos and cardplaying settings. Literature also utilises different methods of determining randomness contributing to overall unreliable results, further pointing towards the necessity of completing further experimentation to gain an improved understanding of card randomisation. Consequently, by completing a designated shuffle count of both the riffle and overhand shuffles and utilising rising sequences as a measure of their variation, the randomisation of the initially ordered deck of 52 cards can be compared to determine the best strategy of card shuffling.

Scientific Research Question

Does the riffle shuffle or overhand shuffle produce the greater number of rising sequences of a deck of cards following the same shuffle count?

Scientific Hypothesis

Null Hypothesis: There is no statistically significant difference in the number of rising sequences produced by the riffle shuffle and overhand shuffle following the same shuffle count.

Alternative Hypothesis: There is a statistically significant difference in the number of rising sequences produced by the riffle shuffle and overhand shuffle following the same shuffle count.

Methodology

The independent variable for this experiment was the shuffle number while the dependent variable was the number of rising sequences for each shuffling method.

There were no significant risks involved with the experiment, but regular breaks between shuffling and recording card positions were taken to reduce fatigue and eye strain.

Two identical decks of 52 playing cards in their natural order were used, starting with the Ace of clubs, Ace of spades, Ace of diamonds and Ace of hearts, and finishing with the King of clubs, King of spades, King of diamonds and King of hearts. The jokers or any instructional cards present were removed from the deck, as these cards are generally not used in casinos and many card games. These two decks were both new and of the same brand to ensure this variable was controlled, as different decks of cards would be made from different materials and of a different quality which could affect the shuffling of the cards.

The card shuffler started with one deck of cards, with a list from Ace of clubs to King of hearts from 1-52, forming a table with the numbers 1-40 as column headings to indicate the shuffle number. A single riffle shuffle was performed, before the positions of each card were recorded in the table (i.e. If the first card was a three of diamonds, a number ‘1’ would be recorded in the row corresponding to the card's initial position of ‘11’). This was completed for all 52 cards of the deck. Using the same deck of cards and the current rearranged order, the shuffler completed another riffle shuffle before recording the positions in the table. For this shuffle and all subsequent shuffles, the halves of the deck were split into the same hands to ensure consistency in the shuffling. The same card shuffler completed this another 38 times, for a total of 40 card shuffles in the same environment.

After 40 riffle shuffles were completed, the card shuffler progressed to completing the overhand shuffle. The second deck of cards (new deck) was used, ensuring this variable was controlled as the previous deck underwent 40 shuffles which affect the quality of the deck of cards and could influence the results. The card shuffler constructed another table identical to the first to record the positions of the cards after each overhand shuffle. After a single overhand shuffle was performed, the positions of the 52 cards were recorded in the table.

Using the same deck of cards, the current rearranged order and starting with the deck of cards in the same hand, the same card shuffler completed another 39 overhand shuffles, for a total of 40 times in the same environment.

Once a total of 80 shuffles were completed (40 overhand shuffles and 40 riffle shuffles), and the positions of the cards after each shuffle were recorded, the number of rising sequences was determined. This estimator of randomness was chosen as it has decreased variability when compared to other randomness tests such as Kendall’s tau, enabling a statistical difference to be more aptly determined if one existed (Caudle 2018, p. 103). This required the shuffler to manually count the number of times in which a minimum of 3 cards are ascending within each shuffle.

This is shown in Table 1, whereby the positions of cards are displayed after the 0th and 19th shuffle with each highlighted colour indicating a separate rising sequence. For example, the number ‘2’ under the heading ‘0th shuffle’ is indicative of the Ace of spades, and thus after the 19th shuffle, the Ace of spades has moved to position 6 in the deck.

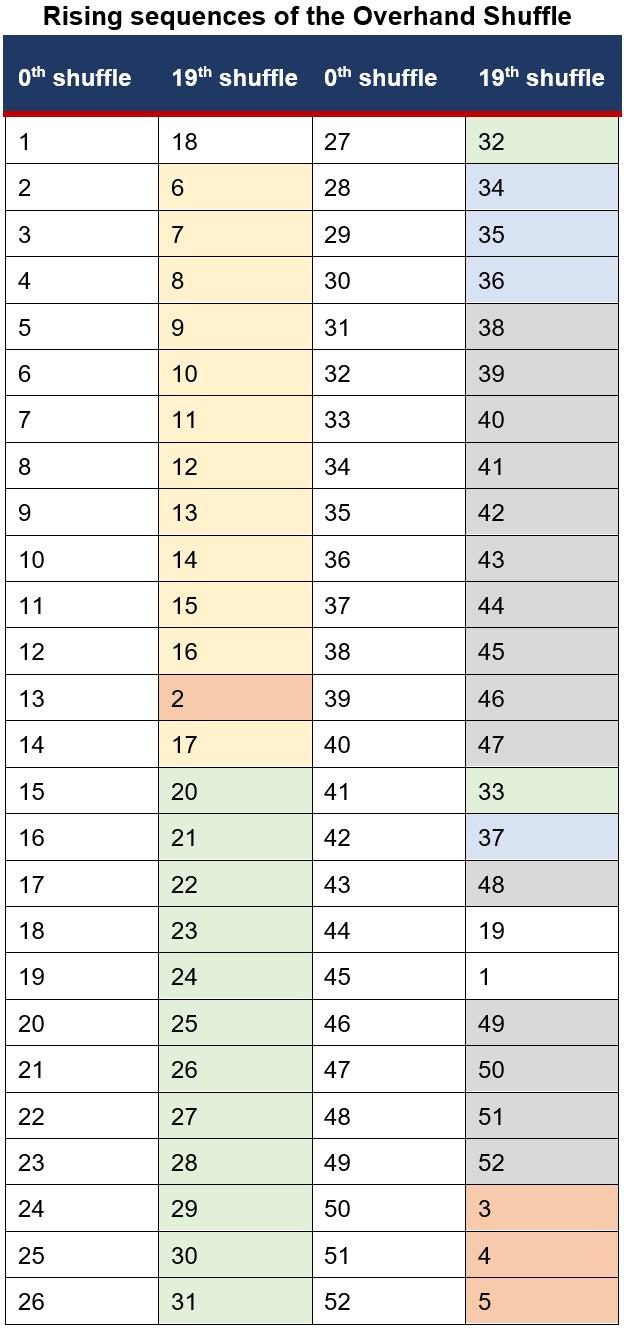
Table 1 Visual Representation of Rising Sequences of the Overhand Shuffle

Thereby the 5 sets of rising sequences are:

1. 2-5 in orange

2. 6-17 in yellow

3. 20-33 in green

4. 34-37 in blue

5. 38-52 in grey

While the position numbers must be in ascending order, they do not need to be successive in the deck, so elements of a rising sequence can be separated by other elements (Silverman 2019, p. 280).

The mean number of rising sequences for both the riffle and overhand shuffles was calculated, before measures of variability such as variance and standard deviation were calculated, followed by a t-Test: Paired Two Sample for Means with significance determined at an alpha value of 0.05.

Results

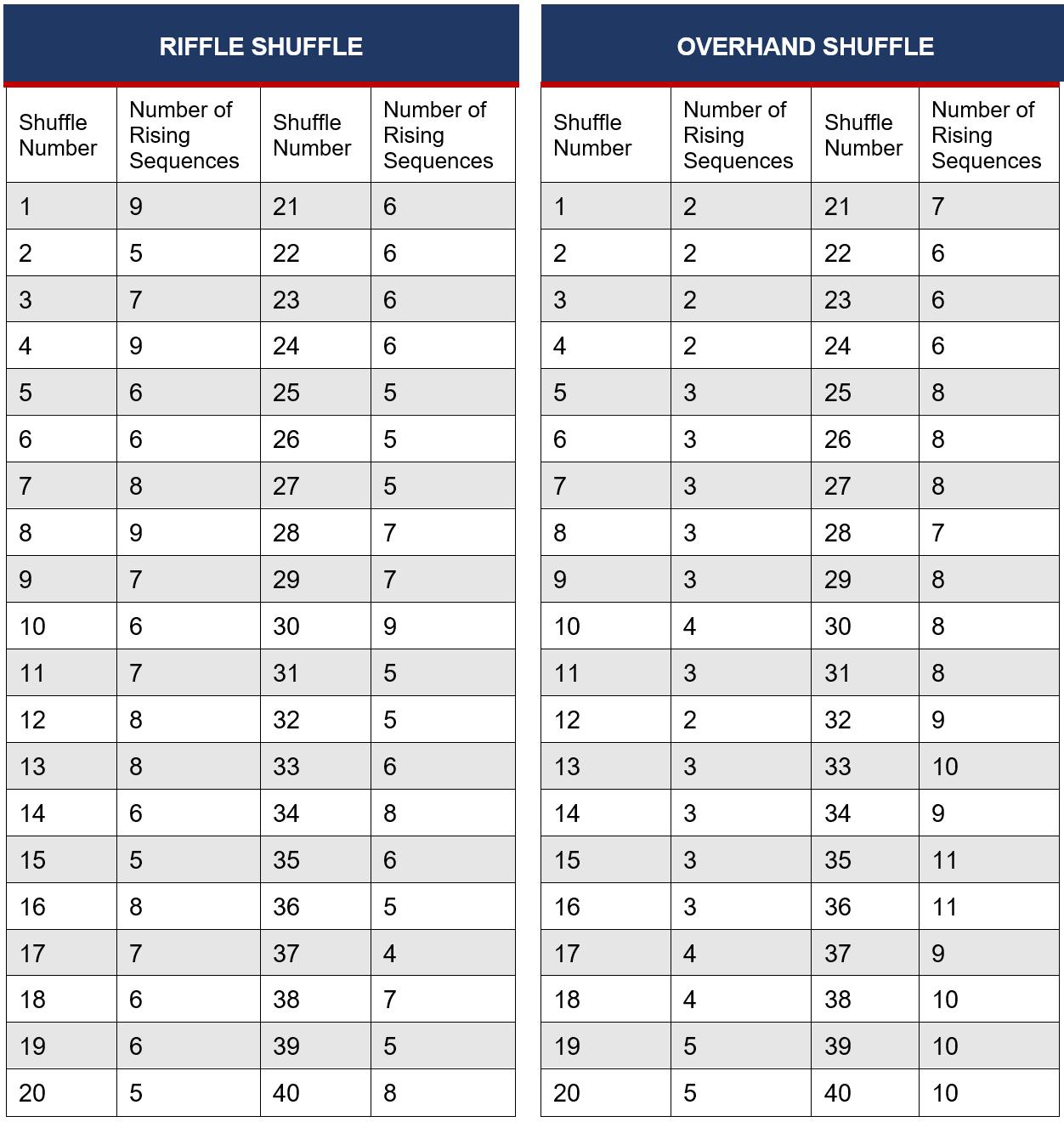
Table 2 Rising Sequences of the Riffle Shuffle Table 3 Rising Sequences of the Overhand Shuffle

Table 4 Statistical Analysis of the Rising Sequences of Riffle and Overhand Shuffles

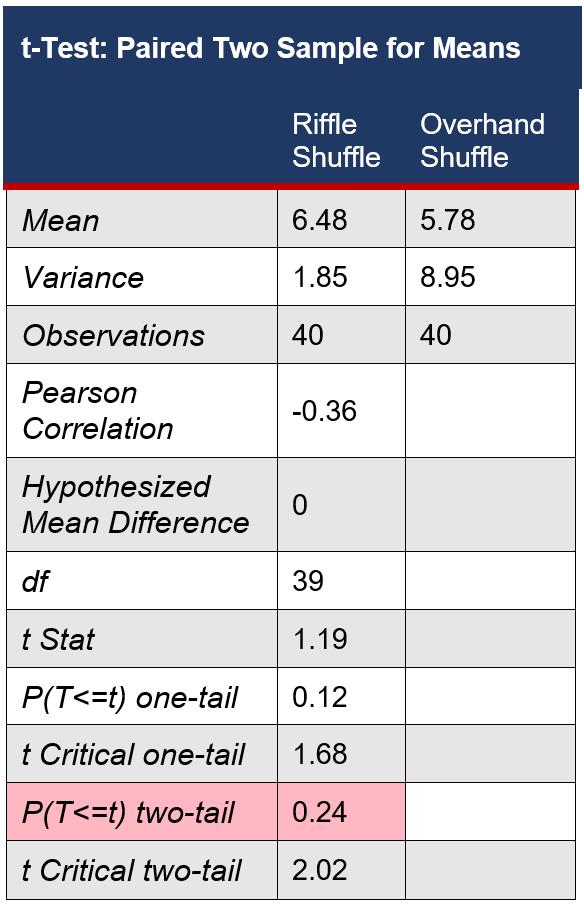
Table 5 t-Test: Paired Two Sample for Means

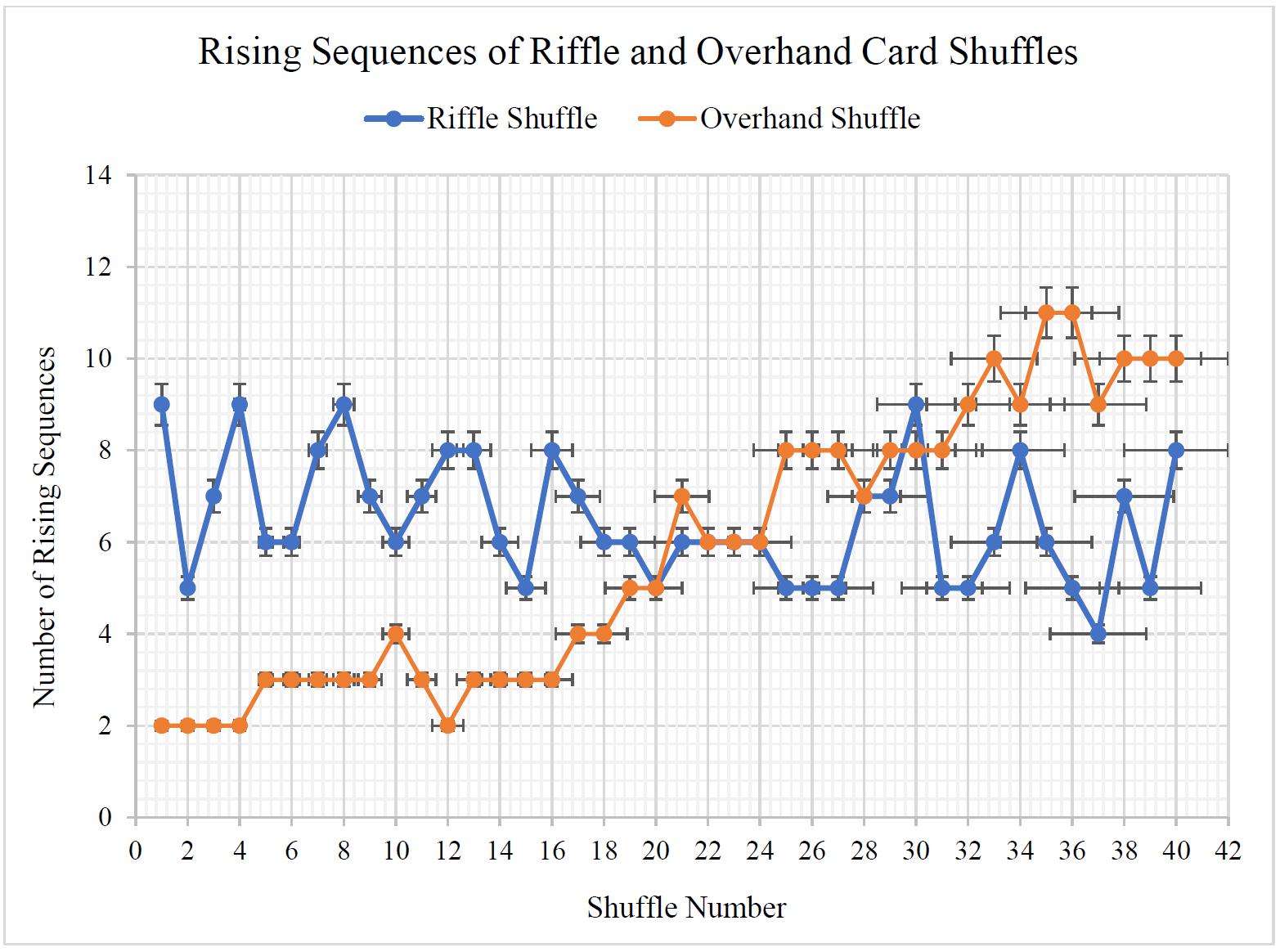
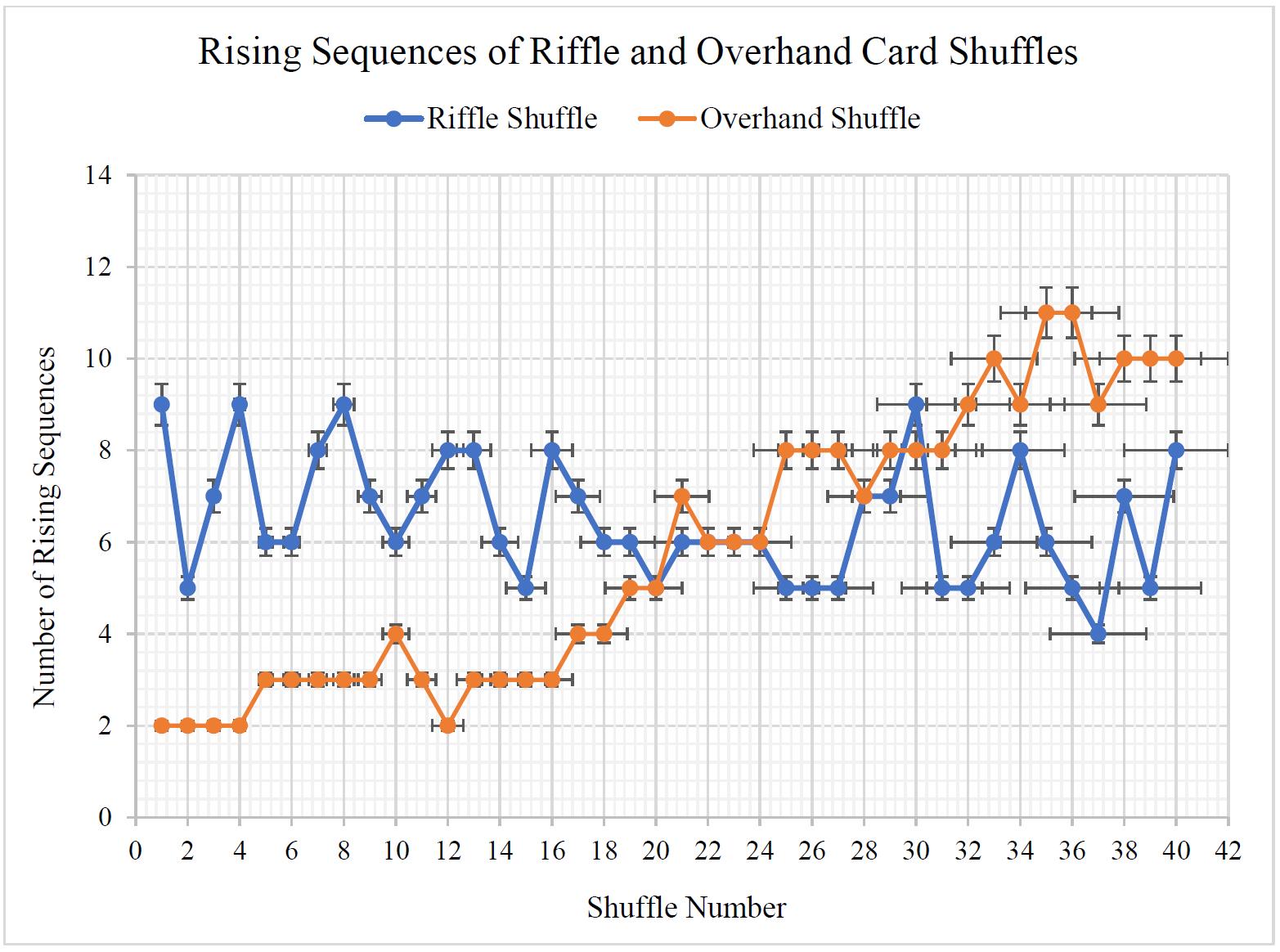
Figure 2 Line Graph of the Rising Sequences of the Riffle and Overhand Shuffle

As demonstrated in Table 4, the mean value of rising sequences for the riffle shuffle (6.48) was higher than the mean value for the overhand shuffle (5.78) suggesting that the riffle shuffle produced a greater number of rising sequences than the overhand shuffle. Further, the overhand shuffle had a significantly higher variance (8.95) and sample standard deviation (2.99) as opposed to the riffle shuffle (variance of 1.85 and sample standard deviation of 1.36), demonstrating that the rising sequences of the overhand shuffle had a greater spread.

As displayed in Table 5, a ‘t-Test Paired Two Sample for Means’ was performed with a set alpha value of 0.05, thus it had a confidence interval of 95%. Since the P(T<=t) two-tail value of 0.24 was significantly higher than the alpha value of 0.05, it was concluded that the result was statistically insignificant. This had a confidence interval of only 76%, which was too low to be generally accepted within the scientific community as an accurate result.

Further, since the t Stat of 1.19 was less than the t Critical two-tail of 2.02, the null hypothesis was accepted, and the alternative hypothesis was rejected Therefore, there was no statistically significant difference in the number of rising sequences produced by the riffle shuffle and overhand shuffle following the same shuffle count.

Discussion

There are no credible studies that compare the rising sequences of the manual riffle and overhand card shuffles. While the study conducted by Silverman (2019, p. 295) suggested that 8 hand shuffles using the riffle strategy are required for satisfactory mixing, this result was only compared to automatic shuffling rather than another manual shuffling strategy.

Neither this paper nor other credible sources which investigate shuffling practices draw comparisons between these manual shuffling methods. Thereby, the lack of scientific papers available causes this study to have poor reliability, and as such the statistically insignificant result drawn in this experiment is unreliable, requiring further similar studies to be conducted for it to be deemed a reliable result. This provides a route for future studies to explore, allowing contemporary scientific research to delve further into this card shuffling issue which has vast relevance to society.

In addition, previous studies such as the experiment conducted by Bayer and Diaconis (1992, p. 297) suggest that successive riffle shuffles should double the number of rising sequences, and as such after a third shuffle a deck should have 8 rising sequences. This experiment, however, demonstrates that after the first shuffle there were 9 rising sequences, followed by 5 after the second shuffle and 7 after the third shuffle, which is inconsistent with previous studies hence further reiterating the unreliable nature of this study.

Further, rising sequences are just one measure of randomness, and even if it was found that one shuffling method had more rising sequences based on a statistically significant result, one could not conclude that the strategy with more rising sequences leads to greater randomness in the arrangement of cards. This is because while the cards may not ascend in large portions, they may remain in a similar or unchanged position from the previous shuffle. As such, a variety of methods to determine the randomness should be used to achieve a more accurate result that aligns with the true value, yet the time constraints involved with this experiment limited the study’s ability to test multiple randomness indicators. As such, this study is limited in its practical application as it doesn’t suggest which shuffling method should be used in casinos and social settings.

Human shuffling practices wield a variety of random errors which affect the results achieved and reduce the accuracy of the experiment. This is because of the imperfect nature of human shuffling whereby each shuffle isn’t identical in nature even if it is performed by the same shuffler. This includes errors from dropping cards or mistakenly rearranging a part or whole of the deck, with inexperienced card shufflers dropping cards about 60% of the time while shuffling (Aldous and Diaconis 1986, p. 345). Further, the riffle shuffle requires the shuffler to divide the deck into roughly two equal parts before interleaving them, and this division would differ between shuffles resulting in different card placements. In addition, with each successive shuffle, the shuffler’s ability to perform the shuffling technique will become more fluent and efficient, which would skew the results and may cause a greater number of rising sequences.

Further, a larger sample size would also cause the result to have a greater level of internal reliability. Since only 40 riffle shuffles and 40 overhand shuffles were completed due to time restraints, bias exists as the results are not truly representative of the number of rising sequences produced for each shuffling method. Thereby, to increase the reliability of this study a greater number of shuffles must be performed.

This is demonstrated in Figure 2. The line graph of the rising sequences of both the riffle and overhand shuffles shows inconsistencies in the result with many fluctuations across both shuffling methods. While the overhand shuffle demonstrates a positive relationship, the riffle shuffle fluctuates across a similar number of rising sequences as the shuffle number increases. The length of the error bars also increased as the shuffle number increased which demonstrates the increasing number of errors in the results with a greater number of shuffles.

Conclusion

It is difficult to draw a definitive conclusion as many factors beyond the control of the shuffler, such as unintentionally dropping cards while shuffling, can cause the results to be inaccurate due to random errors. Furthermore, the time constraints associated with this study have resulted in a small sample size of data, requiring further experimentation under similar conditions which compares the riffle and overhand shuffles to achieve a more reliable result.

The mean value of the number of rising sequences of the riffle shuffle (6.48) is higher than that of the overhand shuffle (5.78), however, the result of the difference in the number of rising sequences between the two shuffling practices has proved to be statistically insignificant. This is because the P(T<=t) two-tail of 0.24 is higher than the defined alpha value of 0.05, causing the null hypothesis to be accepted and the alternative hypothesis to be rejected.

Future research can be influenced by this experiment, however, as it demonstrates the need to compare the rising sequences and other measures of randomness of the riffle and overhand shuffles. Further, technological advancements have resulted in the increased use of mechanical shuffling devices in casinos, pointing towards further direction for experimentation to compare the randomness between the riffle and overhand manual shuffling practices with a mechanical shuffle. This would allow for reduced predictability in card arrangements in casinos and social settings, thus being imperative in both the scientific community and amongst the general public.

References

Aldous, D. and Diaconis, P. 1986, ‘Shuffling Cards and Stopping Times’, The American Mathematical Monthly, vol. 93, no. 5, pp. 333-348, accessed 30 January 2022 from Taylor and Francis Online, ISSN; 0002-9890, <https://doi.org/10.1080/00029890.1986. 11971821>.

Bayer, D. and Diaconis, P. 1992, ‘Trailing the Dovetail Shuffle to its Lair’, The Annals of Applied Probability, vol. 2, no. 2, pp. 294-313, accessed 4 April 2022 from Institute of Mathematical Statistics, <http://www.jstor.org/stable/2959752>.

Caudle, K.A. 2018, ‘You betcha it’s random: riffle shuffling in card games –when is enough, enough?’, Teaching Statistics, vol. 40, no. 3, pp. 98-107, accessed 29 May 2022 from Wiley Online Library, <https://doi.org/10.1111/test.12163>.

Diaconis, P., Fulman, J. and Holmes, S. 2013, ‘Analysis of Casino Shelf Shuffling Machines’, The Annals of Applied Probability, vol. 23, no. 4, pp. 1692-1720, accessed 23 January 2022 from Institute of Mathematical Statistics, <https://doi.org/10.1214/12- AAP884>.

Griffiths, S. 2015, ‘How to shuffle cards like a pro: Mathematician shows why the ‘riffle’ technique is more effective than the flashy ‘overhand’’, Daily Mail Australia, accessed 25 May 2022, <https://www.dailymail.co.uk/sciencetech/ article-3011046/How-shuffle-cards- likepro-Mathematician-shows-riffletechnique-effective-flashyoverhand.html>.

Pemantle, R. 1989, ‘Randomisation Time for the Overhand Shuffle’, Journal of Theoretical Probability, vol. 2, no. 1, pp. 37-49, accessed 5 February 2022 from SpringerLink, <https://doi.org/10.1007/BF01048267>.

Silverman, M.P. 2019, ‘Progressive Randomisation of a Deck of Playing Cards: Experimental Tests and Statistical Analysis of the Riffle Shuffle’, Open Journal of Statistics, vol. 9, no. 2, pp. 268-298, accessed 22 January 2022 from Scientific Research Publishing, ISSN; 2161-7198, <https://doi.org/10.4236/ojs.2019.92020>.

Appendices

Table 1 Positions of cards after 40 successive riffle shuffles

Table 2 Positions of cards after 40 successive overhand shuffles