Disproving the misconception that microscopic black holes can expand

Disproving the misconception that microscopic black holes can expand

Surabhi Hebbar – Blacktown Girls High School

This report disproves the common misconception that microscopic black holes produced in supercolliders would expand and absorb matter until it grew to the size of a cosmic black hole. This is done by deriving Hawking’s equations from his 1975 paper using dimensional analysis and observing the relationship between the variables of mass and time to evaporation. It showed that as mass increases the time to evaporation also greatly increases (t_evap = 10^16 × M^3 ). This shows that microscopic black holes cannot expand as it releases energy too quickly and evaporates to be able to absorb energy. Therefore, there is no time for microscopic black holes to start accreting matter to the size of a cosmic black hole. The impact of this area of research can lead to new discoveries and development of technologies that will advance our knowledge and understanding of the universe.

Literature review

The nature of microscopic black holes is still under ongoing research, however, basic knowledge about their lifetime and mass-energy properties can be understood. Contrary to common belief, a microscopic black hole cannot expand like a cosmic black hole would, due to its very small mass or energy.

Misunderstandings of the production of a microscopic black hole in the Large Hadron Collider (LHC) caused a legal battle between CERN and critics.

According to Lisa Zyga (2010), in May of 2008 a lawsuit was filed against the operation of the LHC based on the concern that the LHC would produce a black hole that could expand and destroy the Earth. Although this lawsuit concluded that there are no potential adverse effects of the operation of the LHC, many people are concerned with the experiments conducted in the LHC (Johnson, 2009).

Thus, it is required to examine the nature of black holes, cosmic and microscopic to better understand the relationship between their mass and lifetime to disprove that microscopic black holes can expand.

Particle accelerator/collider

A particle accelerator or collider is a machine that uses electromagnetic fields to direct and accelerate charged particles to speeds close to the speed of light (CERN, 2022). The particles are accelerated into beams that travel in opposite directions in the ring, then they collide with one another, and the effect is observed and analysed. A microscopic black hole forms when two particles travelling the same plane as they do in the LHC have almost reached each other. However, observing these phenomena is very difficult due to their volatile nature and the difficulty in producing and containing one (Cavaglià, 2010).

Microscopic black hole

A microscopic black hole is a very small black hole that can be produced by highenergy collisions of protons in protonproton (p-p) collision. The black hole produced would be smaller than the size of an atom (Khachatryan, 2011). A Schwarzschild black hole is the simplest form of a black hole, as they are only defined by their mass i.e., they have no electric charge or spin (Xiao, 2020). The main issue with trying to observe the nature of microscopic black holes is that they have very small lifetimes, making it difficult to observe any of their properties (CERN, 2022).

The common misconception

The common misconception about the microscopic black hole is that it will continue to expand and consume matter similar to cosmic-sized black holes. However, this is not the case, as once a microscopic black hole is produced it would decay thermally via Hawking radiation (Hawking, 1975). The time taken for black holes to evaporate can be calculated through dimensional analysis and used to understand the relationship between mass and time to evaporation.

Cosmic Black Holes

Cosmic Black holes are categorised based on size. Stellar Black holes are the smallest weighing a few solar masses, these black holes were large stars that collapsed onto themselves. Intermediate black holes were large stars or smaller primordial black holes. Supermassive black holes are primordial black holes that have huge masses (Gebhardt, 2013). Cosmic black holes are used to investigate the relationship between mass and time to evaporation as they can be better observed and studied as they have a greater lifetime. They are also used to prove using real data that microscopic black holes have a very short lifetime.

Deficiencies in the evidence

Research into the nature of cosmic black holes has been extensively advanced by the work of Stephen Hawking in his 1975 paper Particle Creation by Black Holes, and later extended to the general public in more simple terms in his novel A Brief History of Time. Despite this, there is little published to the public to examine the nature of microscopic black holes. The experiments conducted by CERN (2022) and other research into quantum mechanics and black holes (Xiao, 2020) are still ongoing and uncertain as to the nature and properties of the micro black hole. There is also a lack of observable proof that microscopic black holes cannot expand, this paper attempts to find proof in cosmic black holes to explain the nature of microscopic black holes.

There are many speculations about what we could achieve by harnessing a microscopic black hole, among which are time travel into the past and proving existing theories like string theory. The impact of understanding its nature opens many pathways for study and technological progress in the future. This report also helps improve the understanding of microscopic black holes to the reader by disproving their misconceptions, allowing them to be assured there is no danger in experimenting with microscopic black holes.

Hawking radiation and temperature

Hawking radiation is thermal radiation that is theorised to be emitted from black holes. It is emitted from the region of space surrounding the event horizon. Although it hasn’t been observed it has been widely accepted in the scientific community (Kováčik, 2021)

Hawking temperature is the temperature of the thermal radiation emitted from a black hole. Since, mass and energy are seen as equivalent according to Einstein’s famous equation, E=mc^2. By that logic when a black hole radiates energy, it also loses mass and should eventually evaporate (Johnson, 2009).

Dimensional analysis of Hawking equations

Dimensional analysis is a problem-solving method that uses the fact that any number or value can be multiplied by one without changing its value. It is used to analyse the relationship between different quantities. This method is used to derive a more simplified version of Hawking’s equations that display the relationship between the variables associated with a black hole, in this case, will be its mass and time to evaporation (LoPresto, 2003). It is not able to derive its product constants, however, this is unnecessary to understand the relationship between mass and time to evaporation.

Scientific research question

To what extent is there a relationship between mass and time to evaporation of black holes?

Aim

The aim of the research is to disprove the misconception that a microscopic black hole of small mass produced in a supercollider can expand its event horizon and gain mass until its gravitational force is enough to grow into a cosmic black hole.

Scientific Hypothesis

There is a significant correlation between the mass and time to evaporation of black holes, such that as the mass of a black hole increases so will the time to evaporation. Therefore, a microscopic black hole will have a very small lifetime as it will evaporate in a very short time due to its extremely small mass/energy. It cannot absorb mass/energy and grow, as it will in fact emit energy in the form of Hawking radiation.

Methodology

The method of dimensional analysis was used to derive an equation with variables of mass and time to evaporation. To simplify the calculations a Schwarzschild black hole is considered. In the case of particle accelerators forming black holes, it cannot produce a Schwarzschild black hole as the collision between two charged particles will inevitably cause the black hole to become electrically charged (a particle accelerator cannot accelerate neutral particles, as it uses the electric and magnetic fields). However, for the purpose of analysing only the mass of black holes and their correlation to evaporating time its charge can be disregarded for simplicity. This would have no effect on the analysis between variables, but rather the accuracy of the physical values, as they are not being calculated they can be consciously discarded. A regression/correlation test is then conducted between black hole mass and time to evaporation using a secondary source of cosmic black hole masses (Gebhardt, 2013) to observe if there is a significant correlation between the mass and time to evaporation of black holes. This secondary data was taken from the University of McDonald Texas Observatory.

Materials

The materials required to carry out this experiment are a scientific calculator, secondary data source from the University of McDonald Texas Observatory and Excel spreadsheets.

Design

The experimental design is a regression correlation study to measure the statistical correlation between mass and time to evaporation of black holes. Then the paired t-statistic was used to calculate the p-value, with a confidence level of 95% to determine its significance.

Procedure

Deriving Hawking Equation(s) using Dimensional Analysis.

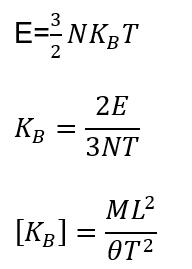
Discard 2/3 in dimentional analysis (just a constant),

N is no of atoms (constant, also discard)

Area of Event Horizon:

Black holes are massive, involve speed of light (M,G,C)

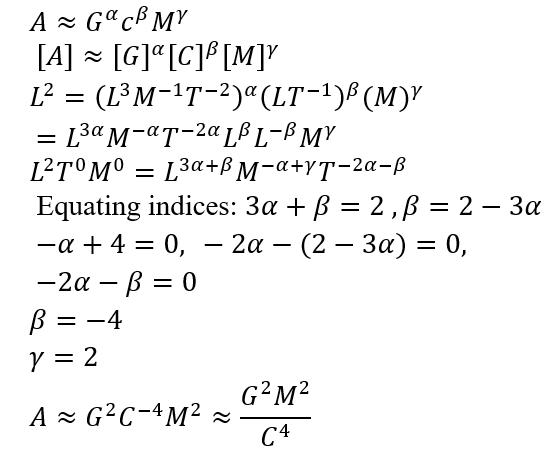
The area of Event Horizon increases with mass A∝M^2

The actual Formula for Area of Event Horizon (constant of 16π):

According to classical physics nothing can escape from the event horizon, as a velocity greater than C is needed. Thus, the area of a black hole can only increase (2nd law of thermodynamics).

Black Hole Entropy:

Entropy of an isolated system must increase with time (cannot decrease)

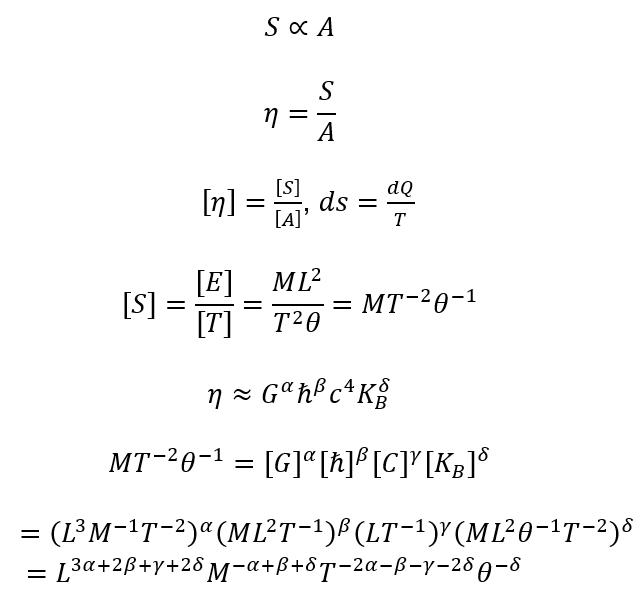
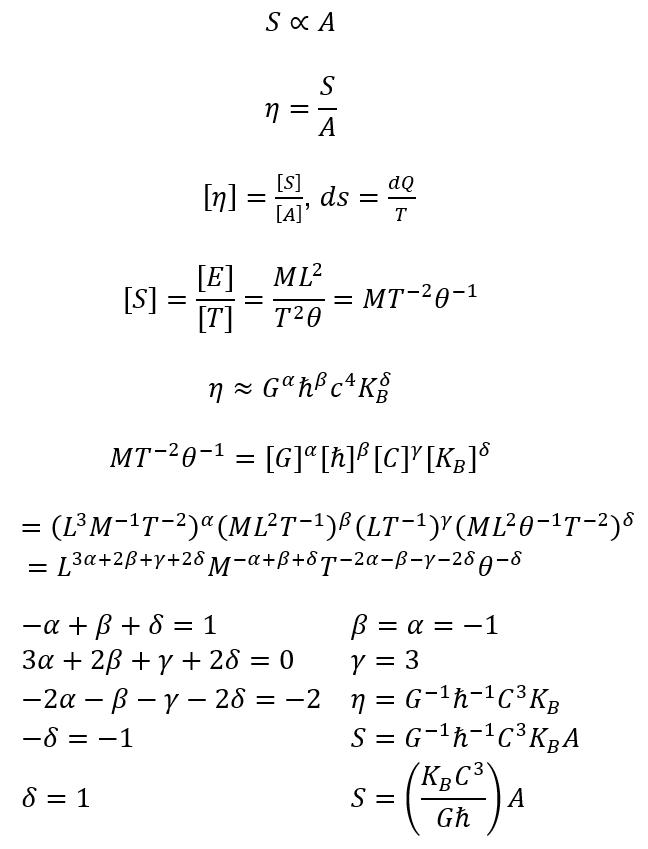
Exact equation for entropy (with constant 1/4)

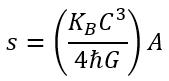
S is very large as C^3 is in numerator and ℏ and G in denominator.

1 st Law of thermodynamics

dE = dQ + dw

2 nd Law of thermodynamics

ds = dQ/T

Assuming black hole does no work on its surroundings, dw =0

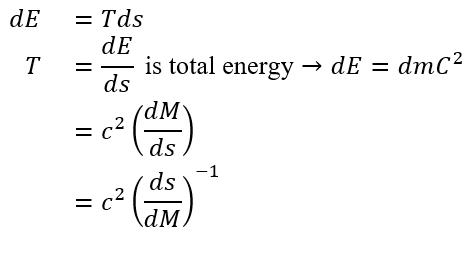
Differentiate black hole entropy with respect to mass.

Time taken for a Black Hole to Evaporate:

t is time

P is power

E is energy

A is area

P=E/t

t=E/P

Power emitted per unit area from object of temperature

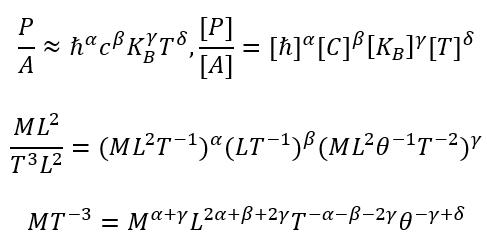
Equate powers

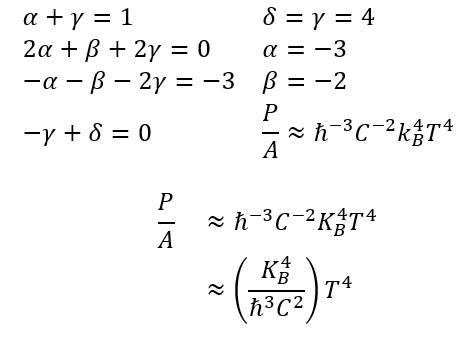
Real equation (with constant π^2/60)

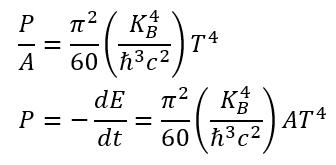
Sub A = 16πG^2M^2/c^4, and entropy equation for temperature T=ℏc^2/8πK_BGM (derived using entropy of black hole)

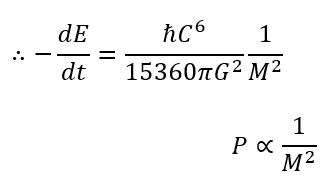
The smaller the mass the greater the Power output or energy released

where t = t_evap → Moment in time where mass of black hole is reduced to 0,

∴ smaller the mass, smaller the evaporation time.

Consider a microscopic black hole of mass of 2 protons ≈ 3.346 × 10^-27

t_evap = 10^-16 × (3.346 × 10^-27 )^3 =3.746 × 10^-96 s.

The equation for time to evaporation (t_evap = 10^-16 × M^3 ) was then used to calculate the time to evaporation for various cosmic black holes (stellar, intermediate, and supermassive). The masses of these black holes were then substituted into the derived equation to obtain a value for the time taken for the black hole to evaporate. These values were recorded in a table and a regression/correlation test was run to determine the r-value, t-score, and pvalue between the dependent variables of mass and time to evaporation.

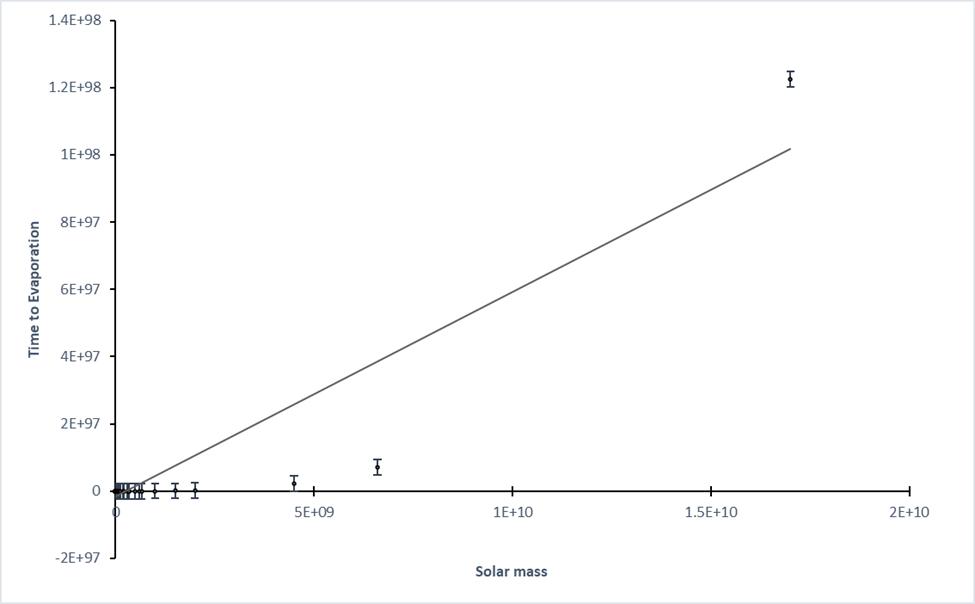
Figure 1: Graph of the relationship between mass and time to evaporation of black holes.

Note: This figure demonstrates the relationship between the variables of mass and time to evaporation of black holes using 54 data points.

The trend line is linear with R^2 value of 0.847 and correlation coefficient (r) is 0.9205. The error bars show standard error of data. T-statistic of 16.99 was calculated and P-value of 0.0174 (less than 0.05) was obtained. Therefore, data is statistically significant.

Discussion

The data shown in figure one shows an exponential relationship where, as the mass of black holes increases, the time to evaporation also increases exponentially. This trend is confirmed through dimensional analysis, it is shown that the time to evaporation is proportional to the mass cubed, which explains that as the mass increases slightly the time to evaporation increases much greatly. The correlation coefficient (r) is 0.9205 which shows that the graph has a strong and positive correlation between variables.

Thus, there is a clear correlation between the mass of black holes and their time to evaporation. There is also a causation between them, as proved through dimensional analysis, the relationship between mass and temperature showed that the smaller the black hole the greater the temperature. In addition, the time to evaporation is related to the temperature of the black hole, where the higher the temperature the shorter the time to evaporation. The results from the experiment confirmed the hypothesis, as there was a relationship between black hole mass and time to evaporation that was statistically significant as the p-value is less than 0.05.

Since energy and mass are essentially equivalent as Einstein showed in his famous equation E = mc^2 , then a black hole emitting Hawking radiation is a black hole that is losing mass. Black holes have a temperature that varies inversely with their mass and so large black holes would be extremely cold and would radiate energy extremely slowly. Conversely, the smaller the black hole, the greater the temperature and the faster it would radiate energy. The faster that energy is radiated the faster its evaporation rate becomes. Thus, microscopic black holes of a mass of approximately two protons (3.346×10 27 kg), will have an evaporation time proportional to its mass cubed, which is extremely fast (3.746× 10 96 s) shown through dimensional analysis. Therefore, a microscopic black hole would be unable to absorb mass, as its evaporation time is too fast. Therefore, microscopic black holes cannot be compared to a cosmic black hole and will evaporate very quickly. These findings are verified by various literature published by CERN 2022 on their website and previous research conducted on microscopic black holes (LoPresto, 2003). In addition, Stephen Hawking’s published work in 1975 confirms equations derived through dimensional analysis. This further verifies the validity and accuracy of the experiment conducted and the results obtained from the investigation.

Figure 1 mainly shows that larger supermassive black holes, and the smaller mass black holes have very close data points at the bottom. This shows the large range of the time to evaporation of these black holes, indicating that a change in mass had a great effect on the time to evaporation of black holes. However, due to the large range of values the graph cannot display all the values accurately and is forced to increase with larger increments on the y-axis. This reduced the accuracy of the graph when viewed and made it more difficult to observe the linear relationship without referring to the correlation coefficient. Despite this, the systematic errors are minimised as results received from investigation are confirmed with existing data from a Hawking radiation calculator (Toth, 2016). Validity and accuracy were maintained as there was a sufficient number of data points (n=54), the systematic errors were minimised, statistical tests used were appropriate and results were confirmed. Random errors have been accounted for in error bars on the graph, however, the experimental procedure conducted would have minimised the extent of the errors, as the calculations were conducted through Excel Spreadsheets and data taken from a reputable secondary source (Gebhardt, 2013), improving the precision of the data. The experiment was reliable as a correlation was found between the variables over multiple data points and this relationship was consistent across the data points.

This research report was able to successfully accept the hypothesis and conclude that microscopic black holes cannot expand by deriving and providing both theoretical and experimental proof to support the hypothesis. However, the limitation of the experiment was the method of derivation used. Dimensional analysis is not completely accurate and requires the constants derived using quantum physics to complete the process, however, it was reasonably close. The report was able to disprove the misconception that microscopic black holes can expand to the public audience and combined areas of research in quantum theory, particle physics, and astronomy by comparing the nature of cosmic black holes with microscopic black holes. This comparison provided a unique understanding of why microscopic black holes do not expand but cosmic black holes do, disproving the danger of creating microscopic black holes. The future directions of this research are analysing microscopic black hole signatures to uncover further qualities of microscopic black holes. Methods such as mathematical simulations and energy readings from the LHC can further build upon the research into microscopic black holes. Research into this area is beneficial for the technological advancement and study of black holes in space.

Conclusion

In summation, this report disproved the common misconception that microscopic black holes produced in supercolliders would expand and absorb matter until it grew to the size of a cosmic black hole. This was done by deriving Hawking’s equations from his 1975 paper using dimensional analysis and observing the relationship between the variables of mass and time to evaporation. Furthermore, the mass of cosmic black holes was used to demonstrate the relationship between mass and time to evaporation and showed that as mass increases that time to evaporation also greatly increases. This unique comparison between cosmic black holes to microscopic black holes showed the differences in their properties, as microscopic black holes have a very short lifetime compared to cosmic black holes to cause any macroscopic effects. The limitation of the report is the accuracy of dimensional analysis, as without the knowledge of quantum physics the derived equations do not have accurate constants. The future of research into black holes can be built upon our understanding of microscopic black holes and their properties can be used in technologies that could revolutionise our society.

References

Cavaglià, M. (2010). Particle accelerators as black hole factories? « EinsteinOnline. Einstein-online.info. Retrieved 24 August 2022, from https://www.einsteinonline.info/en/spotlight/accelerators_bh/

Gebhardt, K. (2013). Supermassive black holes directory - StarDate's Black Hole Encyclopedia. Blackholes.stardate.org. Retrieved 24 August 2022, from http://blackholes.stardate.org/objects/type -supermassive.html

Hawking, S. (1975). Particle creation by black holes. Communications In Mathematical Physics, 43(3), 199-220. https://doi.org/10.1007/bf02345020

Johnson, Eric.E. (2009). The Black Hole Case: The Injunction Against the End of the World. Vol. 67, Pg. 820-849. https://doi.org/10.48550/arXiv.0912.5480.

Khachatryan, Vardan & Sirunyan, Albert & Tumasyan, Armen & Adam, Wolfgang & Bergauer, Thomas & Dragicevic, Marko & Erö, Janos & Fabjan, Christian & Friedl, Markus & Frühwirth, Rudolf & Ghete, Vasile & Hammer, Josef & Haensel, Stephan & Hartl, Christian & Hoch, Michael & Hörmann, Natascha & Hrubec, Josef & Jeitler, Manfred & Kasieczka, Gregor & Weinberg, Marc. (2011). Search for Microscopic Black Hole Signatures at the Large Hadron Collider. Physics Letters B. 697. 434. 10.1016/j.physletb.2011.02.032.

Kováčik, S. (2021). Hawking-radiation recoil of microscopic black holes. Vol 34, Pg. 1. https://doi.org/10.1016/j.dark.2021.10090

LoPresto, M. (2003). Some Simple Black Hole Thermodynamics. The Physics Teacher, 41(5), 299-301. https://doi.org/10.1119/1.1571268.

The Safety of the LHC | CERN. Home.cern. (2022). Retrieved 24 August 2022, from https://home.cern/science/accelerators/lar ge-hadron-collider/safety-lhc

Toth, V. (2016). Viktor T. Toth - Hawking radiation calculator. Vttoth.com. Retrieved 24 August 2022, from https://www.vttoth.com/CMS/physicsnotes/311-Hawking-radiation-calculator.

Xiao, Y. (2020). Microscopic derivation of the Bekenstein-Hawking entropy for Schwarzschild black holes. Physical Review D, 101(4). 46 020.

Zyga, L. (2010). LHC lawsuit case dismissed by US court. Phys.org. Retrieved 24 August 2022, from https://phys.org/news/2010-09-lhclawsuit-case-dismissed-court.html