Matematika-ucebnica-8.2.-rocnik-ZS

Soňa Čeretková, Ondrej Šedivý, Ivan Teplička

matematika

pre 8. ročník základnej školy a 3. ročník gymnázia s osemročným štúdiom

Slovenské pedagogické nakladateľstvo

Milí ôsmaci,

v druhej časti učebnice matematiky sa oboznámite s ďalšími zaujímavými a dôležitými matematickými poznatkami. Podarí sa vám získať zručnosti, z ktorých väčšinu využijete aj v každodennom reálnom živote. V témach o kružniciach, kruhoch a hranoloch pochopíte, že súčasťou veľkého množstva matematických úloh je kreslenie výstižného obrázka. Tým si môžete riešenie úlohy výrazne priblížiť, alebo aj úlohu takmer vyriešiť. Dôležitými témami sú i štatistika a pravdepodobnosť. Pri úlohách z pravdepodobnosti sa trochu pohráte „so šťastím“ a úlohy zo štatistiky môžete formulovať i vy sami. Denná tlač, časopisy, digitálne médiá neustále prinášajú rôzne prehľady o výsledkoch ankiet, prieskumov a výskumných experimentov. Tieto sa vyhodnocujú a zobrazujú pomocou rôznych štatistických grafov či diagramov. Pozorným štúdiom riešení problémov a príkladov, úspešným riešením úloh a cvičení, ako aj vypracovaním testov na konci každej kapitoly sa opäť presvedčíte o dôležitosti matematickej gramotnosti i o ďalších súvislostiach a prepojeniach matematických vedomostí.

Želáme vám veľa správnych a pekných riešení úloh, veľa pozitívnych zážitkov pri štúdiu matematiky.

Pri orientácii v učebnici vám budú pomáhať tieto symboly:

– príklad s riešením

– problém s riešením

– zapamätať si

– zhrnutie alebo vysvetlenie

– úloha

– poznámka

Autori © doc. PaedDr. Soňa Čeretková, PhD., prof. RNDr. Ondrej Šedivý, CSc., Ivan Teplička

Recenzenti: prof. RNDr. Jozef Doboš, CSc., Ing. Mgr. Martin Hriňák, Mgr. Marcela Švirlochová

Ilustrovali: akademická maliarka Táňa Žitňanová, obálku navrhol Ing. Zsolt Urbán

Grafický dizajn © SPN – Mladé letá, s. r. o.

Ministerstvo školstva, vedy, výskumu a športu Slovenskej republiky schválilo pod č. 2023/11302:7-C2901 súbor edukačných publikácií Matematika pre 8. ročník ZŠ a 3. ročník GOŠ – 1. a 2. časť.

Doložka nadobúda účinnosť 27. septembra 2023 a má platnosť do 31. augusta 2026.

Druhé vydanie, 2024

Všetky práva vyhradené. Toto dielo ani žiadnu jeho časť nemožno reprodukovať bez súhlasu majiteľa práv.

Zodpovedná redaktorka RNDr. Judita Hollá

Odborná redaktorka RNDr. Jana Belasová Technická redaktorka Ivana Bronišová

Vyšlo vo vydavateľstve Slovenské pedagogické nakladateľstvo – Mladé letá, s. r. o., Sasinkova 5, 811 08 Bratislava

Vytlačili TBB, a. s., Banská Bystrica

ISBN 978-80-10-04332-3

Autori

4.1 Kružnica a kruh 4

ZOPAKUJME SI

Kružnica

Kruh

(S, r) ... kružnica k so stredom S K (S, r) ... kruh K so stredom S a polomerom r a polomerom r

SC = r polomer kružnice

AB = d priemer kružnice

POZNÁMKA

Slovo polomer používame v dvoch významoch:

SC = r polomer kruhu

AB = d priemer kruhu

a) polomer kružnice (kruhu) so stredom S je úsečka SC, kde C je ľubovoľný bod kružnice (hraničnej kružnice kruhu),

b) polomer kružnice (kruhu) je dĺžka tejto úsečky, teda r = SC, ale tiež r = SC 

Slovo priemer používame v dvoch významoch:

a) priemer kružnice (kruhu) je úsečka AB, kde A, B sú body kružnice (hraničnej kružnice kruhu), pričom úsečka AB prechádza stredom S kružnice (kruhu),

b) priemer kružnice (kruhu) je dĺžka tejto úsečky, teda d = AB, ale tiež d = AB .

Pre polomer r a priemer d kružnice (kruhu) platí: d = 2r

Kružnicu k so stredom S a polomerom r  0 tvoria všetky body X v rovine, pre ktoré platí SX = r.

Kruh K so stredom S a polomerom r  0 tvoria všetky body X v rovine, pre ktoré platí SX r.

ÚLOHA

Na obrázku je kružnica k(S, 2 cm) a niekoľko bodov.

a) Zapíšte vzťahy, ktoré platia medzi vzdialenosťou týchto bodov od stredu S kružnice a polomerom kružnice.

b) Ktoré z bodov ležia na kružnici k?

c) Ktoré z bodov ležia vo vnútornej oblasti kružnice k?

d) Ktoré z bodov ležia vo vonkajšej oblasti kružnice k?

ÚLOHA

Na obrázku je kruh K (S, 2 cm) a niekoľko bodov.

a) Ktoré z týchto bodov ležia v kruhu K ?

b) Ktoré z týchto bodov neležia v kruhu K ?

PRÍKLAD

Zvoľme si bod S a body A, B tak, že SA = 1,5 cm, SB = 2 cm.

Narysujte kružnice k(S, r1 = SA ), l(S, r2 = SB ).

RIEŠENIE

Rozbor

Konštrukcia

1. S

2. A; SA = 1,5 cm

3. k; k(S, r1 = SA = 1,5 cm)

4. B; SB = 2 cm

5. l; l(S, r2 = SB = 2 cm)

Zvolíme si bod S. Vyznačíme ľubovoľný bod A, ktorý má od bodu S vzdialenosť 1,5 cm, to bude polomer kružnice k Kružidlom zostrojíme kružnicu k. Potom vyznačíme bod B, ktorý má od bodu S vzdialenosť 2 cm, to bude polomer kružnice l. Kružidlom zostrojíme kružnicu l

Kružnice, ktoré majú spoločný stred, sa nazývajú sústredné kružnice.

ÚLOHA

Narysujte priamku p a na nej bod M. Zostrojte tri rôzne kružnice, ktorých stredy ležia na priamke p a každá z kružníc prechádza bodom M

ÚLOHA

Narysujte do zošita obrázky:

Narysujte kružnicu k(S, 3 cm). Narysujte dva navzájom kolmé priemery AB a CD kružnice k.

2. Narysujte kružnicu k(S, 4 cm). Na kružnici zvoľte bod A. Na úsečke SA zvoľte dva body M, N Zostrojte sústredné kružnice m, n s kružnicou k, pričom kružnica m prechádza bodom M a kružnica n prechádza bodom N.

3. Narysujte úsečku MN, ktorej dĺžka je 3 cm. Narysujte kružnicu m, ktorá má stred N a prechádza bodom M. Narysujte kružnicu n, ktorá má stred M a prechádza bodom N. Vyznačte spoločné body kružníc m a n. Akú zaujímavú vlastnosť majú tieto spoločné body?

4. Narysujte úsečku MN, ktorej dĺžka je 5 cm. Nájdite všetky body v rovine, ktoré majú od bodu M vzdialenosť 3 cm a od bodu N vzdialenosť 4 cm. Koľko takých bodov existuje?

1.

5. Na obrázku je priamka p a na nej tri rôzne body A, B, C. Zostrojte kružnicu k, ktorá má stred na priamke p a prechádza bodmi A a B. Zostrojte kružnicu l, ktorá má stred na priamke p a prechádza bodmi B a C

B AC p

6. Narysujte štvorec ABCD so stranou a = 4 cm. Zostrojte kružnicu k, ktorá prechádza všetkými vrcholmi štvorca ABCD.

7. Narysujte kruh K(S; 2,5 cm). Vyznačte body A, B, C, pre ktoré platí: 0  SA   2,5 cm; 2,5 cm  SB  4 cm; SC  = 2,5 cm.

8. Narysujte tento obrázok do zošita.

4.2 Tetiva kružnice

ZOPAKUJME SI

Os úsečky AB je priamka, ktorá prechádza stredom úsečky AB a je na ňu kolmá.

PROBLÉM 1

Zvoľme na osi o úsečky AB tri rôzne body C, D, E.

Zistite, čo platí o vzdialenostiach bodov C, D, E od bodov A, B.

RIEŠENIE

Pre trojuholníky ASC a BSC platí: AS  BS, ASC  BSC, SC  SC

Teda trojuholníky ASC a BSC sú zhodné podľa vety sus, preto AC BC. To znamená, že AC = BC 

Podobne odôvodníme, že AD = BD  a AE = BE .

3 cm2 cm

Každý bod osi úsečky AB má rovnakú vzdialenosť od bodu A aj od bodu B Žiadny iný bod roviny túto vlastnosť nemá.

Na obrázku je kružnica k a úsečky AB, CD, EF, ktorých krajné body ležia na kružnici. Takéto úsečky sa nazývajú tetivy kružnice.

Tetiva kružnice je úsečka, ktorej krajné body ležia na kružnici.

PRÍKLAD

Narysujte kružnicu k(S, 2 cm) a bod A, ktorý leží na kružnici k. Zostrojte tetivu kružnice k, ktorej jeden krajný bod je A a jej dĺžka je: a) 3 cm, b) 4 cm, c) 5 cm.

RIEŠENIE

Rozbor

A S B

l

Konštrukcia

1. k; k(S, 2 cm)

2. A; A  k

Druhý krajný bod B tetivy je od bodu A vzdialený 3 cm, preto leží na kružnici l ( A, 3 cm). Keďže má ležať aj na kružnici k, bude to ich priesečník.

3. l; l1(A, 3 cm); l2(A, 4 cm); l3(A, 5 cm)

4. B; B1  k  l1; B2  k  l2; B3  k  l3

5. AB

Skúška

Z konštrukcie vyplýva, že úsečky AB1, AB2, AB3 sú tetivy kružnice k a majú požadované dĺžky.

Diskusia

Ak je dĺžka tetivy menšia ako priemer kružnice, tak kružnica l pretne kružnicu k v dvoch bodoch, teda úloha má dve riešenia.

Ak sa dĺžka tetivy rovná priemeru kružnice, tak kružnica l má s kružnicou k spoločný jeden bod, teda úloha má jedno riešenie.

Ak je dĺžka tetivy väčšia ako priemer kružnice, tak kružnica l nemá s kružnicou k spoločný bod, preto úloha nemá riešenie.

Priemer kružnice je najdlhšia tetiva kružnice.

ÚLOHA

Narysujte kružnicu k(S; 3,5 cm). Narysujte tetivu kružnice k, ktorá má dĺžku: a) 3 cm, b) 4 cm, c) 5 cm, d) 7 cm. k

PROBLÉM 2

Na obrázku je kružnica k(S; 1,5 cm).

Úsečka AB je jej tetivou.

Odôvodnite, že os tetivy AB prechádza stredom S kružnice k.

RIEŠENIE

Stred S kružnice k má od krajných bodov

A, B tetivy AB rovnakú vzdialenosť rovnajúcu sa polomeru kružnice, preto leží na osi tetivy AB.

AB S o k

AB S o r k r

Os každej tetivy kružnice prechádza stredom kružnice.

PRÍKLAD

Vo vnútornej oblasti kružnice k (S, 3 cm) leží bod P  S. Zostrojte tetivu AB kružnice k tak, aby bod P bol stredom tejto tetivy. o1 o2 o3

RIEŠENIE

Rozbor

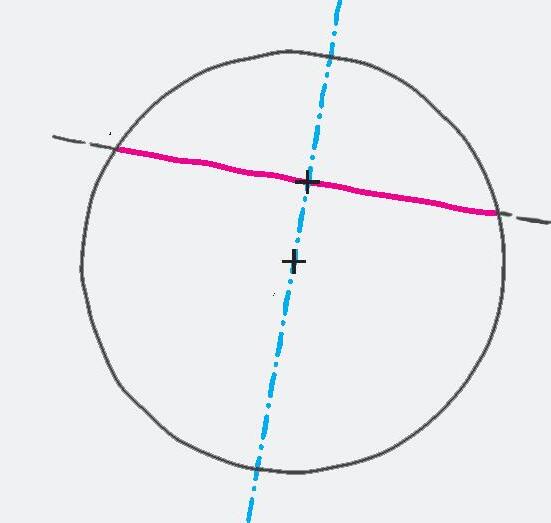
Konštrukcia

1. o; o = PS

2. s; s  o; P  s

3. A, B; A, B  s  k

4. AB

Skúška

Bod P je stred tetivy AB, ktorej os prechádza stredom kružnice k. Preto priamka PS je osou tetivy AB. Teda tetiva AB bude ležať na kolmici na priamku PS cez bod P.

Z konštrukcie vyplýva, že úsečka AB je tetivou kružnice k Úloha má jedno riešenie.

ÚLOHA

Daná je úsečka AB s dĺžkou 4 cm. Zostrojte kružnicu s polomerom 3 cm tak, aby úsečka AB bola jej tetivou.

ÚLOHA

Daná je kružnica k(S, 3 cm). Narysujte jej tetivy s dĺžkami 2 cm, 4 cm, 5 cm a 6 cm. Odmerajte vzdialenosť každej z tetív od stredu kružnice. Ako súvisí dĺžka tetivy s jej vzdialenosťou od stredu kružnice?

ÚLOHA

Dané sú úsečky AB a BC podľa obrázka. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami.

1. Daná je kružnica k(S, 3 cm) a bod P, ktorý leží na kružnici k. Narysujte tetivu kružnice k, ktorej jeden krajný bod je P a jej dĺžka je: a) 2 cm, b) 3 cm, c) 4 cm, d) 6 cm.

2. Narysujte kružnicu k(S, 4 cm). Narysujte tetivu kružnice k, ktorá má dĺžku: a) 2 cm, b) 4 cm, c) 6 cm, d) 8 cm.

3. Narysujte kružnicu k(S, 4 cm). Narysujte niekoľko tetív s dĺžkou 5 cm. Na akom útvare budú ležať stredy týchto tetív?

4. Daná je úsečka AB s dĺžkou 6 cm. Zostrojte kružnicu s polomerom 4 cm tak, aby úsečka AB bola jej tetivou.

5. Daná je úsečka AB s dĺžkou 4 cm. Zostrojte kružnicu s polomerom 5 cm tak, aby úsečka AB bola jej tetivou.

6. Vo vnútornej oblasti kružnice k(S, 4 cm) leží bod R  S. Zostrojte tetivu AB kružnice k tak, aby bod R bol stredom tetivy. Koľko riešení má úloha?

7. Dané sú úsečky AB a BC podľa obrázka tak, že uhol ABC je pravý. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami.

8. Dané sú úsečky AB a CD podľa obrázka. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami.

9. Na obrázku je kružnica k. Nájdite jej stred.

10. Na obrázku je časť kružnice. Nájdite stred tejto kružnice a narysujte ju celú.

4.3 Vzájomná poloha kružnice a priamky

PROBLÉM 3

Daná je priamka p a bod A, ktorý na nej neleží. Ktorá z úsečiek AX, kde X je bod ležiaci na priamke p, je najkratšia?

RIEŠENIE

Zvoľme na priamke p body X1 až X5. Odmeraním dĺžok úsečiek AX1 až AX5 zistíme, že úsečka AX3, ktorá je kolmá na priamku p, má najmenšiu dĺžku. To ale neznamená, že medzi úsečkami, ktoré nie sú narysované, a teda sme ich nemerali, nie je úsečka s menšou dĺžkou. My to zatiaľ nevieme odôvodniť, ale v matematike je známe, že úsečka AX3, ktorá je kolmá na priamku p, má zo všetkých úsečiek spájajúcich bod A s niektorým bodom priamky p najmenšiu dĺžku. Táto dĺžka sa nazýva vzdialenosť bodu A od priamky p a označuje sa Ap.

ÚLOHA

Narysujte priamku p a tri body A, B, C neležiace na priamke p. Zistite vzdialenosť každého z bodov A, B, C od priamky p

ÚLOHA

Daná je priamka p. Narysujte tri body, ktorých vzdialenosť od priamky p je 2 cm. Koľko takých bodov v rovine existuje? Aký útvar vytvoria?

PRÍKLAD

Máme kružnicu k(S, r). Narysujte priamku p tak, aby s kružnicou k: a) nemala žiadny spoločný bod, c) mala práve dva spoločné body, b) mala práve jeden spoločný bod, d) mala viac ako dva spoločné body.

RIEŠENIE

a) Narysujme priamku p tak, aby vzdialenosť stredu S kružnice od priamky p bola väčšia ako polomer kružnice. Potom každý bod priamky p má od stredu S vzdialenosť väčšiu ako polomer kružnice, preto priamka p nemá s kružnicou k žiadny spoločný bod.

Priamka, ktorá nemá s kružnicou žiadny spoločný bod, sa nazýva nesečnica kružnice. Nesečnica má od stredu kružnice vzdialenosť v  r

b) Narysujme priamku p tak, aby sa jej vzdialenosť od stredu S kružnice rovnala polomeru kružnice. Potom každý bod X priamky, rôzny od bodu T, má od stredu kružnice vzdialenosť XS   r, preto priamka má s kružnicou jediný spoločný bod T.

Priamka, ktorá má s kružnicou jediný spoločný bod, sa nazýva dotyčnica kružnice. Jediný spoločný bod T priamky a kružnice sa nazýva bod dotyku

Dotyčnica kružnice má od stredu kružnice vzdialenosť v = r.

Dotyčnica kružnice je vždy kolmá na polomer v bode dotyku.

c) Narysujme priamku p tak, aby jej vzdialenosť od stredu S kružnice bola menšia ako polomer kružnice. Potom priamka p má s kružnicou k práve dva spoločné body.

S r p k T v B A

Priamka, ktorá má s kružnicou spoločné práve dva rôzne body, sa nazýva sečnica kružnice.

Sečnica má od stredu kružnice vzdialenosť v < r

d) Každá priamka má od stredu kružnice vzdialenosť väčšiu, rovnú alebo menšiu ako polomer kružnice. Preto každá narysovaná priamka je buď nesečnicou, dotyčnicou, alebo sečnicou kružnice, teda má s kružnicou najviac dva spoločné body.

ÚLOHA

Daná je kružnica k(S, 3 cm). Narysujte sečnicu, dotyčnicu a nesečnicu kružnice k. Odmerajte vzdialenosť každej z nich od stredu S kružnice k a porovnajte ju s polomerom kružnice.

PRÍKLAD

Narysujte kružnicu k(S, 3 cm), na kružnici zvoľte bod T . Zostrojte dotyčnicu t , ktorá má s kružnicou k bod dotyku T .

RIEŠENIE

Rozbor

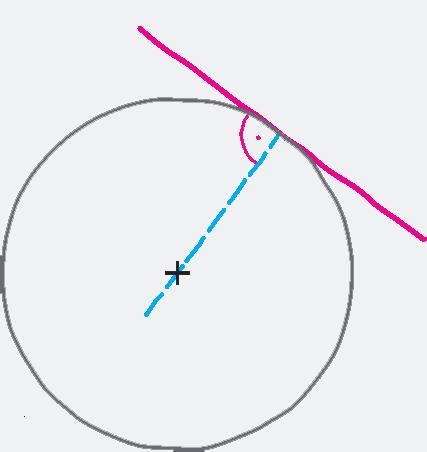
Konštrukcia

1. k; k(S, 3 cm)

2. T; T  k

3. ST

4. t; T  t; t  ST

Skúška

Priamka t má s kružnicou k spoločný bod T a je kolmá na polomer ST, preto je dotyčnicou kružnice k v bode T Úloha má jedno riešenie. k t T S S T k t 

Dotyčnica ku kružnici k v bode T je kolmá na polomer ST, preto keď narysujeme úsečku ST, stačí narysovať kolmicu na ňu v bode T

PRÍKLAD

Daná je kružnica k(S, 3 cm) a priamka p, ktorej vzdialenosť od stredu S kružnice k je 5 cm. Zostrojte dotyčnicu t kružnice k, ktorá je rovnobežná s priamkou p.

RIEŠENIE

Rozbor

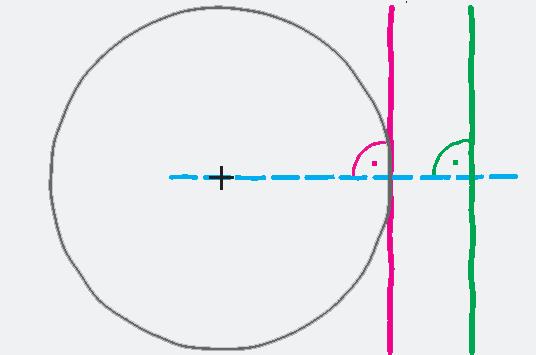
Konštrukcia

1. k; k(S, 3 cm)

2. m; m p; S  m

3. T1, T2; T1, T2  k  m

4. t1; T1  t1; t1  m

5. t2; T2  t2; t2  m

Skúška

Priamky t1, t2 sú rovnobežné s priamkou p, majú s kružnicou k spoločný bod T1, resp. T2 a sú kolmé na polomer ST1, resp. ST2, preto sú dotyčnicami kružnice k. Úloha má dve riešenia.

ÚLOHA

Pri konštrukcii dotyčnice najprv nájdeme bod dotyku. Pretože dotyčnica t má byť rovnobežná s priamkou p, bude bod dotyku ležať na kolmici na priamku p, ktorá prechádza stredom S kružnice k

Narysujte kružnicu k(S; 3,5 cm), na kružnici zvoľte bod T. Zostrojte dotyčnicu t, ktorá má s kružnicou k bod dotyku T. Potom zostrojte ďalšiu dotyčnicu kružnice k, ktorá je: a) rovnobežná s dotyčnicou t, b) kolmá na dotyčnicu t.

CVI Č ENIA

1. Narysujte priamku p a body A, B ležiace v rôznych polrovinách určených priamkou p. Zistite vzdialenosť každého z bodov A, B od priamky p.

2. Daná je priamka p. Nájdite: a) bod A, ktorého vzdialenosť od priamky p je 3 cm, b) bod B, ktorého vzdialenosť od priamky p je 4 cm, c) bod C, ktorého vzdialenosť od priamky p je 5 cm.

3. Daná je priamka p. Nájdite všetky body v rovine, ktorých vzdialenosť od priamky p je 3 cm. Aký útvar vytvoria tieto body?

4. Daná je kružnica k(S, 4 cm) a na nej bod T. Zostrojte dotyčnicu kružnice k v bode T

5. Zvoľte v rovine bod A. Zostrojte priamku p tak, aby na nej neležal bod A. Potom zostrojte kružnicu k tak, že bod A je jej stred a priamka p je jej dotyčnica.

6. Narysujte kružnicu k(S, 3 cm) a jej ľubovoľnú tetivu AB, ktorá nie je jej priemerom.

a) Zostrojte dotyčnice kružnice k s bodmi dotyku A, B.

b) Aká je vzájomná poloha týchto dotyčníc?

c) Aká bude vzájomná poloha dotyčníc, ak tetiva AB bude priemerom kružnice k?

7. Zostrojte tetivu AB z predchádzajúceho cvičenia tak, aby dotyčnice v bodoch dotyku A, B boli na seba kolmé.

8. Daná je kružnica k ( S ; 2,7 cm) a priamka p vo vzdialenosti 5,2 cm od bodu S . Zostrojte dotyčnicu kružnice k , ktorá je kolmá na priamku p . Koľko takých dotyčníc existuje?

9. Narysujte priamku t a na nej bod T. Zostrojte všetky kružnice s polomerom 3 cm, ktoré sa dotýkajú priamky t v bode T. Koľko ich je?

10. Na obrázku je daná priamka t, na nej bod T a bod A, ktorý neleží na priamke t. Ďalej je zostrojená kružnica k, ktorá sa dotýka priamky t v bode T a prechádza bodom A. Napíšte postup konštrukcie kružnice k S T A k o m

PROBLÉM 4

Narysujte kružnicu k ( S , r ) a jej priemer AB

Na kružnici k zvoľte niekoľko bodov X 1, X 2, X 3, ... rôznych od bodov A , B . Zostrojte uhly

AX 1B , AX 2B , AX 3B , ... a uhlomerom odmerajte ich veľkosť. Ak ste dobre merali, dostali ste vždy hodnotu veľmi blízku 90. Aká je presná veľkosť narysovaných uhlov? Prečo to je tak? Platí to pre každú kružnicu s priemerom AB?

RIEŠENIE

Narysujme kružnicu k(S, r) a jej priemer AB

Na kružnici k zvoľme bod X rôzny od bodov A, B. Úsečka SX rozdelí trojuholník ABX na dva rovnoramenné trojuholníky AXS a BXS, ktorých ramená sú polomermi kružnice k, preto majú dĺžku r. Trojuholník AXS má pri základni AX zhodné uhly s veľkosťou α. Trojuholník BXS má pri základni BX zhodné uhly s veľkosťou β. Potom v trojuholníku ABX platí:

α + β + (α + β) = 180

2α + 2β = 180

α + β = 90

Uhol AXB má veľkosť 90, teda je pravý.

ÚLOHA

Narysujte kružnicu k(S, 3 cm) a jej priemer AB. Zvoľte body X1, X2, X3, ktoré ležia vo vonkajšej oblasti kružnice k a body X4, X5, X6, ktoré ležia vo vnútornej oblasti kružnice k. Uhlomerom odmerajte veľkosť uhlov AX1B až AX6B. Čo platí o veľkostiach týchto uhlov?

4.4 Tálesova kružnica

Tálesova veta

Každý bod X kružnice k s priemerom AB, okrem bodov A, B, je vrcholom pravého uhla AXB

Tálesova kružnica

Vrcholy pravých uhlov všetkých pravouhlých trojuholníkov s preponou AB v rovine tvoria kružnicu s priemerom AB, okrem bodov A, B Táto kružnica sa nazýva Tálesova kružnica.

ÚLOHA

Daná je úsečka AB, ktorej dĺžka je 5 cm. Zostrojte Tálesovu kružnicu s priemerom AB

ÚLOHA

Daný je trojuholník ABC, kde AB = 6 cm, BC = 5 cm, AC = 4 cm. Zostrojte Tálesovu kružnicu s priemerom AB. Viete z narysovaného obrázka rozhodnúť, či je uhol ACB ostrý, pravý alebo tupý? (Pomôžte si úlohou 13.)

ÚLOHA

Daný je štvorec ABCD so stranou dĺžky 5 cm. Zostrojte Tálesovu kružnicu s priemerom BD Aká je poloha vrcholov A a C vzhľadom na Tálesovu kružnicu?

ÚLOHA

Narysujte pravouhlý lichobežník ABCD so základňami AB, CD, pričom AB  CD

a pravým uhlom BAD. Zostrojte Tálesovu kružnicu s priemerom BD. Aká je poloha vrcholov A a C vzhľadom na Tálesovu kružnicu?

PRÍKLAD

Daná je kružnica k (S, 2 cm) a bod M, pre ktorý platí SM = 5 cm.

Zostrojte dotyčnicu t kružnice k z bodu M

RIEŠENIE

Rozbor

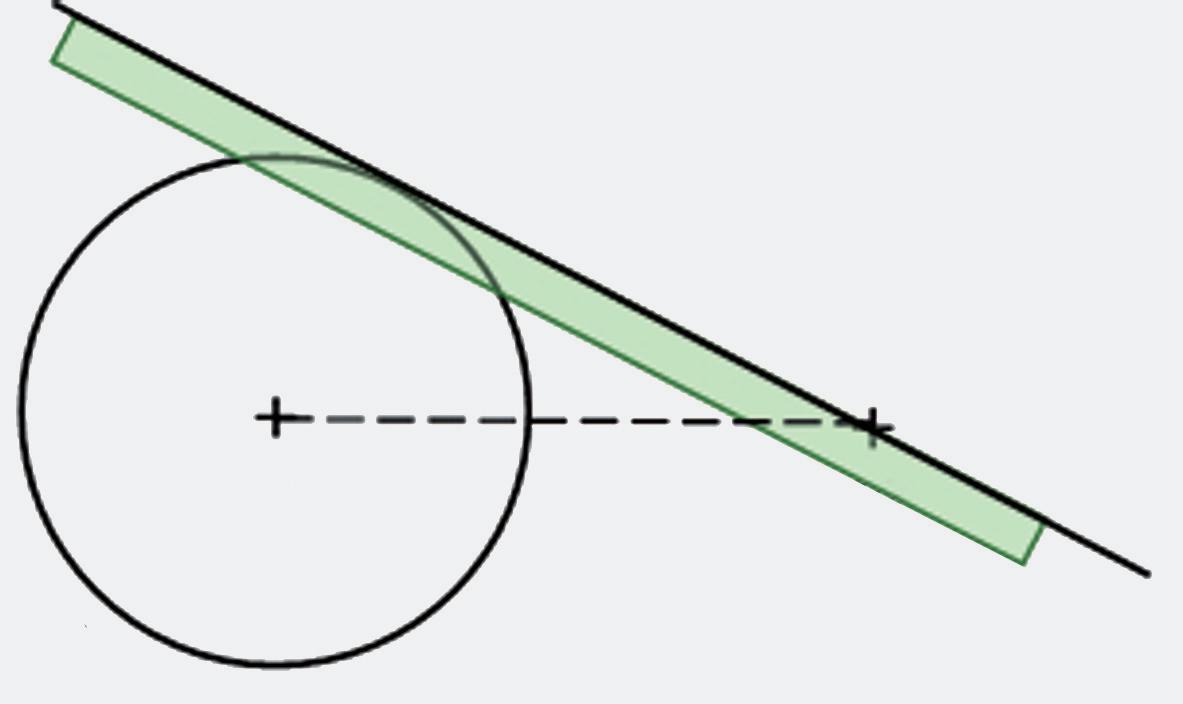
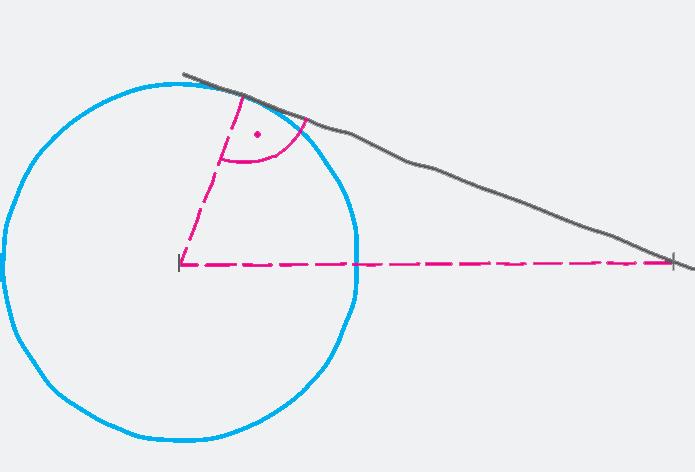
Prvá myšlienka by mohla byť taká, že priložíme pravítko tak, aby prechádzalo bodom M, zároveň dotýkalo sa kružnice k a narysujeme dotyčnicu t. Táto konštrukcia je nepresná, preto ju nepovažujeme za správnu.

Na presné narysovanie priamky potrebujeme poznať jej dva rôzne body. Preto pri zostrojovaní dotyčnice z bodu M najprv nájdeme bod dotyku T. Pretože dotyčnica ku kružnici je kolmá na polomer v bode dotyku, je ST  t, teda bod T je vrcholom pravého uhla pravouhlého trojuholníka SMT s preponou SM. Preto bod T leží na Tálesovej kružnici s priemerom SM.

Konštrukcia

1. k; k(S, 2 cm)

2. M; SM= 5 cm

3. O; O je stred SM

4. l; l(O, SO)

5. T1, T2; T1, T2  k  l, T1  T2

6. t1; t1 = MT1

7. t2; t2 = MT2

Skúška

l

Priamky t1, t2 sú kolmé na polomery v bodoch dotyku s kružnicou k, majú s kružnicou k spoločné body T 1, resp. T 2 a prechádzajú bodom M , teda sú dotyčnicami kružnice k z bodu M Úloha má dve riešenia.

ÚLOHA

Daná je kružnica k(S, 3 cm) a bod A, pre ktorý platí SA= 4 cm.

Zostrojte dotyčnicu kružnice k z bodu A

PRÍKLAD

Zostrojte pravouhlý trojuholník ABC s pravým uhlom pri vrchole C, ak AB = 7 cm a AC = 4 cm.

RIEŠENIE

Budeme riešiť dvomi spôsobmi: bez Tálesovej kružnice a pomocou Tálesovej kružnice. Rozbor bez Tálesovej kružnice Rozbor pomocou Tálesovej kružnice

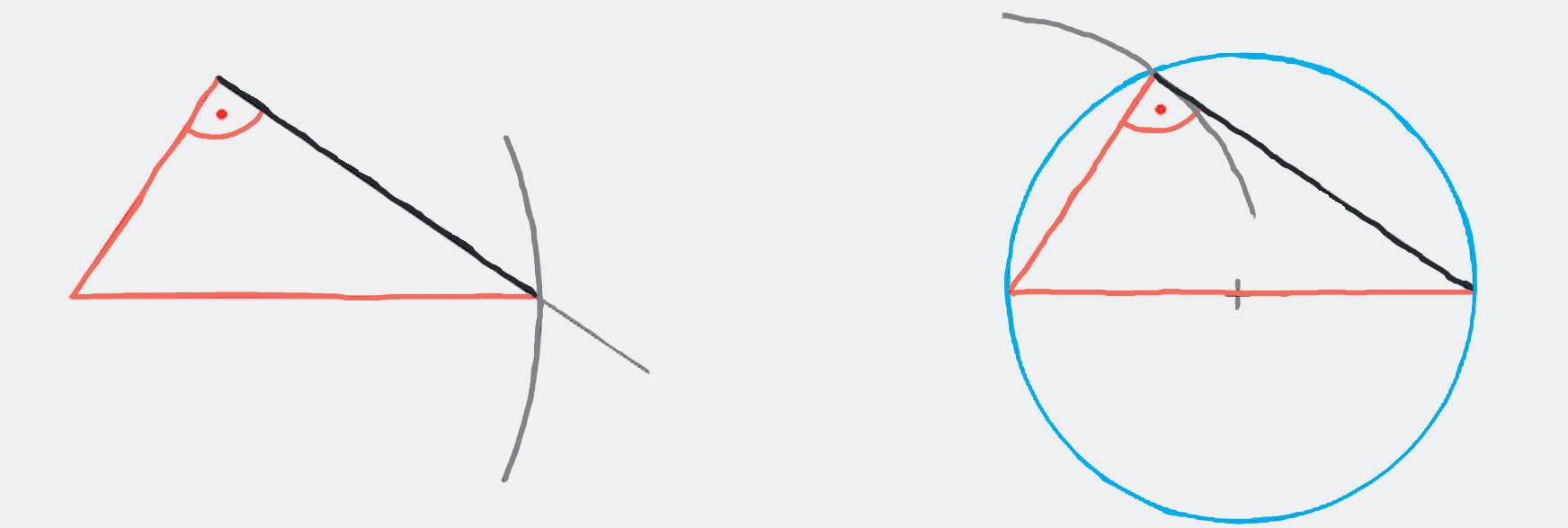
Úsečku AC vieme zostrojiť.

Neznámy bod je B. Bod B leží na kolmici p na priamku AC v bode C a na kružnici k(A, 7 cm).

Teda bod B je priesečníkom priamky p a kružnice k.

Úsečku AB vieme zostrojiť.

Neznámy bod je C, ktorý je vrcholom pravého uhla pravouhlého trojuholníka ABC s preponou AB, preto leží na Tálesovej kružnici k s priemerom AB

Bod C má od bodu A vzdialenosť 4 cm, preto tiež leží na kružnici l (A, 4 cm).

Bod C teda je priesečníkom kružníc k a l

Konštrukcia bez Tálesovej kružnice

1. AC; AC = 4 cm

2. p; p  AC; C  p

3. k; k(A, 7 cm)

4. B; B  p  k

5. ABC

Skúška

Konštrukcia pomocou Tálesovej kružnice

1. AB; AB = 7 cm

2. S; S je stred AB

3. k; k(S; 3,5 cm)

4. l; l (A, 4 cm)

5. C; C  k  l

6. ABC

Zostrojený trojuholník vyhovuje zadaniu.

Uhol pri vrchole C je pravý, AB = 7 cm

a AC= 4 cm. Úloha má jedno riešenie. k

PRÍKLAD

Zostrojte trojuholník ABC, ak je dané: c = 8 cm, va = 6,5 cm, vb = 6 cm. j j j

RIEŠENIE

EŠENIE

Rozbor

zbor

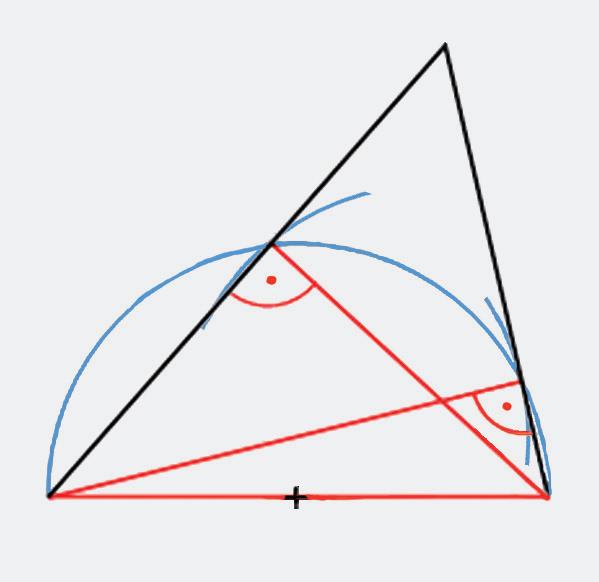
Konštrukcia

1. AB; AB = 8 cm

2. S; S je stred AB

3. k; k (S, 4 cm)

4. l; l (A; 6,5 cm)

5. A1; A1  k  l

6. m; m(B, 6 cm)

7. B1; B1  k  m

8. BA1

9. AB1

10. C; C  BA1  AB1

11. ABC

Trojuholníky ABA1 a BAB1 sú pravouhlé s pravými uhlami pri vrchole A1, resp. B1. Preto body A1 a B1 budú ležať na Tálesovej kružnici s priemerom AB

Skúška Zostrojený trojuholník vyhovuje zadaniu úlohy. Úloha má jedno riešenie.