Matematika-ucebnica-8.1.-rocnik-ZS

Soňa Čeretková, Ondrej Šedivý, Ivan Teplička

matematika

pre 8. ročník základnej školy a 3. ročník gymnázia s osemročným štúdiom

Slovenské pedagogické nakladateľstvo

Milí ôsmaci,

vitajte po prázdninách opäť v škole. Čaká vás nový školský rok plný zaujímavých informácií a dôležitých vedomostí. Ste už skúsení žiaci druhého stupňa základnej školy a istotne ste postrehli, že vedomosti z tematických celkov predmetu matematika sa v jednotlivých ročníkoch rozširujú a dopĺňajú o nové poznatky. Viete už, že znalosti z rôznych predmetov sa navzájom prelínajú a daný problém či úlohu riešite z viacerých uhlov pohľadu. Najbližšie k využitiu matematických poznatkov a k metódam riešení úloh má fyzika a informatika, či ďalšie prírodovedné predmety ako chémia, biológia, geografia. Ale i história má s matematikou veľa spoločného. Nie sú to iba dátumy dôležitých udalostí či obdobia vládnutia panovníkov a existencie štátov. Súčasný archeologický výskum je založený na fyzikálno-matematických metódach, na formulovaní, vyhodnocovaní, overovaní a dokazovaní vedeckých hypotéz o vlastnostiach rôznych odhalených objektov a nájdených predmetov. V prvej časti učebnice už tradične uvádzame riešené problémy, príklady i neriešené úlohy a cvičenia. Zopakujete si poznatky o číslach, rozšírite si svoje vedomosti o celých a racionálnych číslach i aritmetických operáciách s nimi. Osvojíte si zručnosti v práci s premennými, ktoré sú dôležité pri stručnom a všeobecnom vyjadrovaní matematických vzťahov a vzorcov, naučíte sa riešiť jednoduché rovnice. Súčasťou vedomostí o premenných je aj porozumenie významu ich hodnoty v pravouhlej sústave súradníc v rovine. Riešené príklady vám znovu potvrdia, ako v matematike pojmy a ich vlastnosti navzájom súvisia. Napríklad tak, že jednotlivým bodom na priamkach, na úsečkách či vrcholom geometrických útvarov v rovine môžeme priradiť čísla, ktoré nazývame súradnice. Učebnica obsahuje aj kapitolu ďalších vhodných funkcií v práci s dynamickým geometrickým softvérom.

Neoddeliteľnou súčasťou obsahu predmetu matematika sú poznatky z geometrie. V tejto časti učebnice sa bližšie oboznámite s ďalším významným štvoruholníkom, ktorý nazývame lichobežník. Naučíte sa riešiť konštrukčné i výpočtové úlohy o lichobežníku a s novými znalosťami prepojíte tie, ktoré už máte osvojené.

Množstvo úloh a cvičení, ktoré sú v učebnici uvedené, vás iste znova presvedčí o dôležitosti matematických vedomostí pre každodenný život. Vypracovaním testov na konci každej kapitoly si overíte nadobudnuté zručnosti. Želáme vám veľa pekných chvíľ s matematikou v ôsmom ročníku.

Pri orientácii v učebnici vám budú pomáhať tieto symboly:

Autori

– príklad s riešením

– problém s riešením

– zapamätať si – zhrnutie alebo vysvetlenie

– úloha

– poznámka ––––––

Autori © doc. PaedDr. Soňa Čeretková, PhD., prof. RNDr. Ondrej Šedivý, CSc., Ivan Teplička

Recenzenti: prof. RNDr. Jozef Doboš, CSc., Ing. Mgr. Martin Hriňák, Mgr. Marcela Švirlochová

Ilustrovali: akademická maliarka Táňa Žitňanová, obálku navrhol Ing. Zsolt Urbán

Grafický dizajn © SPN – Mladé letá, s. r. o.

Ministerstvo školstva, vedy, výskumu a športu Slovenskej republiky schválilo pod č. 2023/11302:7-C2901 súbor edukačných publikácií Matematika pre 8. ročník ZŠ a 3. ročník GOŠ – 1. a 2. časť.

Doložka nadobúda účinnosť 27. septembra 2023 a má platnosť do 31. augusta 2026.

Druhé vydanie, 2024

Všetky práva vyhradené. Toto dielo ani žiadnu jeho časť nemožno reprodukovať bez súhlasu majiteľa práv.

Zodpovedná redaktorka RNDr. Judita Hollá

Odborná redaktorka RNDr. Jana Belasová Technická redaktorka Ivana Bronišová

Vyšlo vo vydavateľstve Slovenské pedagogické nakladateľstvo – Mladé letá, s. r. o., Sasinkova 5, 811 08 Bratislava

Vytlačili TBB, a. s., Banská Bystrica

ISBN 978-80-10-04331-6

3.7

3.13

1 KLADNÉ A ZÁPORNÉ ČÍSLA, POČTOVÉ VÝKONY

S CELÝMI A DESATINNÝMI ČÍSLAMI, RACIONÁLNE ČÍSLA

1.1 Kladné a záporné čísla

PROBLÉM 1

Skúste prečítať aj napísať teploty vzduchu v uvedených európskych mestách v decembri.

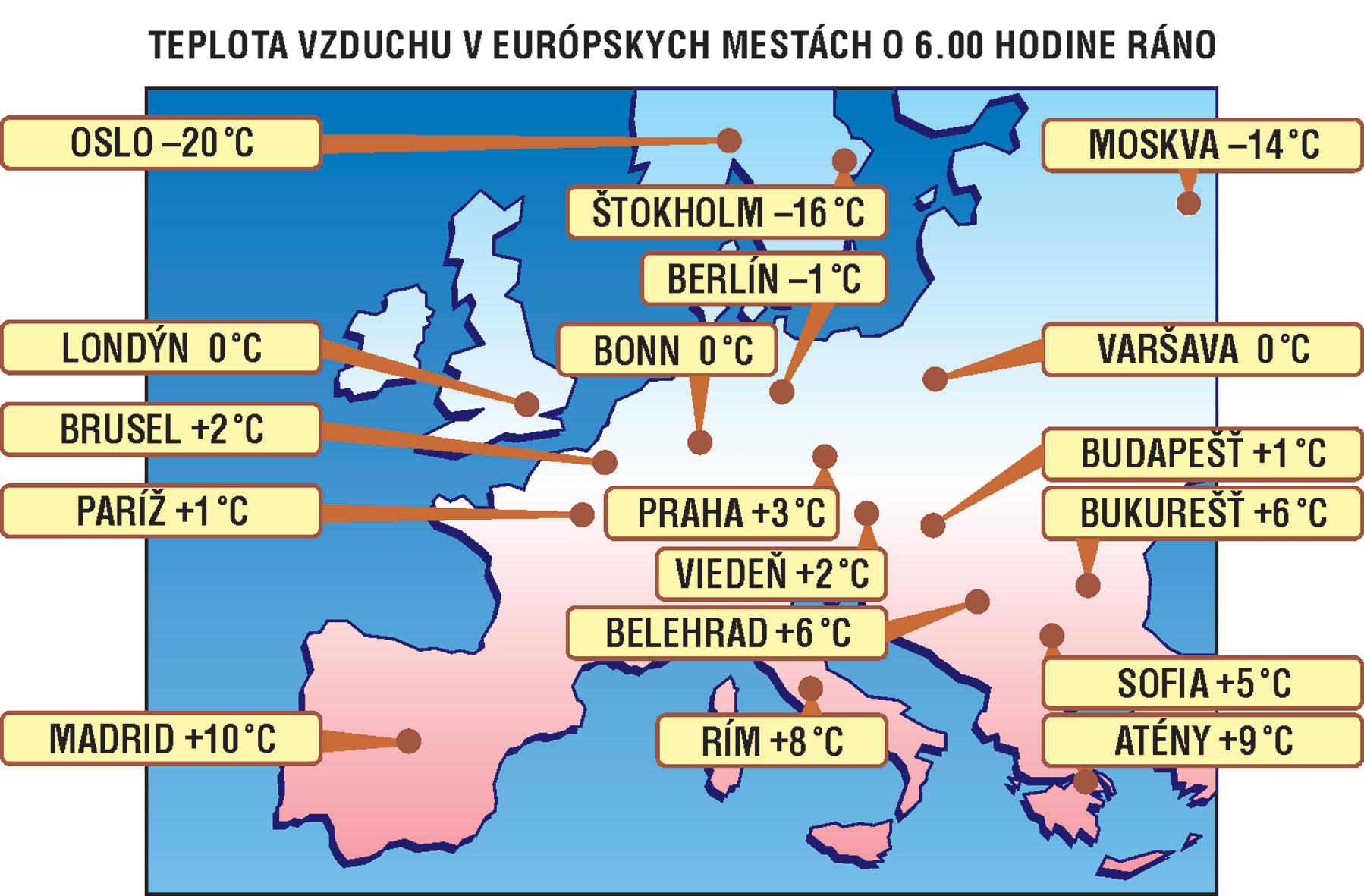
RIEŠENIE

Čítame:

Oslo mínus dvadsať stupňov Celzia

Štokholm mínus šestnásť stupňov Celzia

Moskva mínus štrnásť stupňov Celzia

Berlín mínus jeden stupeň Celzia

Varšava nula stupňov Celzia

Londýn nula stupňov Celzia

Bonn nula stupňov Celzia

Praha plus tri stupne Celzia

Brusel plus dva stupne Celzia

Paríž plus jeden stupeň Celzia

Zapisujeme:

Oslo –20 C

Štokholm –16 C

Moskva –14 C

Berlín –1 C

Varšava 0 C

Londýn 0 C

Bonn 0 C

Praha +3 C

Brusel +2 C

Paríž +1 C . Pokračujte ďalej, čítajte a zapisujte teploty vzduchu.

PRÍKLAD

Vyznačte teploty v mestách: Atény, Praha, Varšava, Moskva a Oslo podľa obrázka z predchádzajúceho problému na modeli okenného teplomera.

RIEŠENIE

Podľa okenného teplomera narysujeme zvislú číselnú os, na ktorú potom vyznačíme namerané teploty v určených mestách a správne ich prečítame:

ÚLOHA

40 30 20 10

+9

Atény +3 Praha 0 Varšava –14 Moskva –20 Oslo 0 –10 –20

Mesto Teplota VyznačímeČítame

Atény +9 C 9 stupňov nad nulouplus 9 C

Praha +3 C 3 stupne nad nulou plus 3 C

Varšava 0 C nula stupňov 0 C

Moskva –14 C 14 stupňov pod nulou mínus 14 C

Oslo –20 C 20 stupňov pod nulou mínus 20 C

Vyznačte na zvislej číselnej osi teploty v ostatných mestách Európy podľa obrázka z problému 1.

Čísla ..., –3, –2, –1, 0, 1, 2, 3, nazývame celé čísla

Čísla +1, +2, +3, ... sú kladné celé čísla. Znamienko + (plus) sa zvyčajne nepíše. Čísla –1, –2, –3, ... sú záporné celé čísla. Píšeme ich so znamienkom – (mínus). Číslo 0 nie je ani kladné ani záporné.

PROBLÉM 2

RIEŠENIE

Číselná os je priamka. Môžeme ju predlžovať doprava a znázorňovať stále väčšie čísla, ale aj doľava, až za číslo 0, ako keby sme zvislú os z príkladu 1 otočili vodorovne.

Nakreslíme a vyznačujeme:

Ako a kde vyznačíte na vodorovnej číselnej osi záporné celé čísla: –1, –3, –5, –13? záporné celé čísla nula kladné celé čísla prirodzené čísla

ÚLOHA

Na číselnej osi s jednotkovou úsečkou 1 cm vyznačte obrazy čísel 3, 5, –2, –6, 4, –5.

ÚLOHA

Doplňte na číselnej osi chýbajúce čísla:

PRÍKLAD

Výška hladiny rieky sa meria od zvoleného pevného bodu, ktorému prislúcha hodnota 0, teda nie od dna rieky. Počas šiestich mesiacov výška hladiny vody v rieke takto kolísala (údaje sú v metroch): +0,20; –0,10; –0,05; +0,15; –0,18; –0,13.

Vyjadrite údaje v decimetroch a vyznačte ich na vodorovnej číselnej osi.

RIEŠENIE

Číselné údaje vyjadríme v decimetroch: premieňame m  dm ... násobíme číslom 10 +0,20 m = +2,0 dm +0,15 m = +1,5 dm –0,10 m = –1,0 dm –0,18 m = –1,8 dm –0,05 m = –0,5 dm –0,13 m = –1,3 dm

Vyznačíme tieto údaje ako obrazy jednotlivých čísel na číselnej osi.

Jednotkovú úsečku si zvolíme takto: 3 cm na osi = 1 dm v skutočnosti.

0 –1 –2 –1,8–1,3–0,5 1,5 12

záporné desatinné čísla nula kladné desatinné čísla – majú pred sebou znamienko + 0 –0,2 – 0,5 –0,4–0,3–0,10,10,20,30,40,5

POZNÁMKA

Pri zápise celých kladných čísel a kladných desatinných čísel môžeme znamienko + vynechať. Napríklad: +9 = 9; +1,25 = 1,25

ÚLOHA

Na číselnej osi s jednotkovou úsečkou 1 cm vyznačte obrazy týchto čísel: a) 0; 2; –5; 5; –4; 6; –1 b) 0,8; 0; –0,5; 1; –1; 5,5; –3,5

1 cm

a) 2, –4, 6, 0, –1, 10, 1

b) –0,7; 0; 4,6; –6,3; 1,0; –2,5; 2,5

1. Narysujte si číselnú os podľa obrázka a vyznačte na nej obrazy daných čísel:

c) 0,9; 0; –5,8; –0,9; 5,8; 4; –4

d) 1,5; –0,5; 0; –1,5; 3,5; –3,5; 0,5

2. Zapíšte, obrazy ktorých čísel sú vyznačené na číselnej osi bodmi A, B, C, D, E. (Napríklad A = –4.) a)

b)

3. Doplňte na číselnej osi chýbajúce čísla: a)

1.2 Opačné čísla

Narysujeme si číselnú os a na nej vyznačíme dve čísla:

Čím je táto dvojica čísel zaujímavá?

Čísla 6 a –6 sa odlišujú iba znamienkom, preto ich obrazy ležia na číselnej osi na opačných stranách od obrazu čísla 0. Vzdialenosť ich obrazov na číselnej osi od obrazu čísla 0 je rovnaká. Takéto čísla nazývame navzájom opačné čísla.

Platí: číslo –6 je opačné k číslu 6.

Platí to aj obrátene: číslo 6 je opačné k číslu –6.

ÚLOHA

Nájdite na číselnej osi obrazy opačných celých čísel k daným číslam. Zapíšte nájdené dvojice opačných čísel. Zistite, aká je vzdialenosť obrazov opačných čísel od obrazu čísla 0 na číselnej osi.

Čísla, ktorých obrazy na číselnej osi majú rovnakú vzdialenosť od obrazu čísla 0, sa nazývajú navzájom opačné čísla.

Opačné číslo ku kladnému číslu je záporné číslo.

Opačné číslo k zápornému číslu je kladné číslo.

Opačné číslo k číslu 0 je číslo 0.

ÚLOHA

K daným celým číslam nájdite opačné čísla: 12, –5, –45, 6, –100, 102, –56, 8, –18.

ÚLOHA

Na číselnej osi sú vyznačené obrazy kladných a záporných desatinných čísel. Zistite, či sú medzi nimi dvojice opačných čísel.

ÚLOHA

Narysujte číselnú os podľa obrázka, vyznačte na nej obrazy daných čísel a nájdite obrazy čísel k nim opačných.

a) 3,5; 5,3; 7,0

b) –2,4; –1,5; –6,2

c) 0,2; –0,5; 1,25; –1,75

CVI Č ENIA

1. K daným celým číslam napíšte opačné čísla: a) 25, 60, 14, 587, 1 025, 5, 75, 12

b) –15, –96, –4, –78, –102, –8 759, –35

c) 4, –8, 2, –58, –16, 16, 48, –84, –234, 324

2. Prekreslite si do zošita číselnú os a nájdite k vyznačeným číslam obrazy čísel k nim opačných:

3. Vypíšte z tabuľky všetky dvojice opačných čísel: a) b)

5. Prekreslite do zošita číselnú os a nájdite k vyznačeným číslam obrazy čísel k nim opačných: a) b) 8 –2 2 6 410 –10 –8 12

4. K daným desatinným číslam napíšte opačné čísla: a) 0,6; 1,23; 6,5; 1,44; 3,965; 0,001 b) –1,56; –21,36; –0,547; –87,002; –90,5 c) 0,4; –6,2; 4,8; –12,3; 9,55; 15,01; –10,75

Vzdialenosť obrazu čísla a na číselnej osi od obrazu čísla 0 nazývame absolútna hodnota čísla a Absolútnu hodnotu čísla a označujeme  a

Na obrázku je číselná os.

Vzdialenosť obrazu čísla 5 od obrazu čísla 0 je 5 jednotkových dielikov, preto  5  = 5.

Vzdialenosť obrazu čísla –3 od obrazu čísla 0 je 3 jednotkové dieliky, preto  –3  = 3.

Obrazy navzájom opačných čísel majú rovnakú vzdialenosť od obrazu čísla 0, preto absolútna hodnota navzájom opačných čísel je rovnaká, teda:

Absolútna hodnota čísla a  0 je kladné číslo.

0

= 0

ÚLOHA

Určte a zapíšte absolútne hodnoty čísel vyznačených na číselnej osi: a) b) c)

ÚLOHA

Určte a zapíšte absolútne hodnoty daných čísel a čísel k nim opačných: a) 9, 5, –4, 2, 6, –11, 50, –87 b) 0,22; –0,49; 12,1; –14,5; 148,3; 456,5; –54,8

PRÍKLAD

Nájdite všetky čísla a , b , pre ktoré platí: a)  a  = 2 b)  b  = 5,3

Nájdite ich obrazy na číselnej osi s jednotkovou úsečkou 1 cm.

RIEŠENIE

Narysujeme číselnú os a vyznačíme na nej jednotkovú úsečku:

1 cm

a)  a  = 2 znamená, že obraz čísla a je od obrazu čísla

0 vzdialený 2 jednotkové úsečky.

Vo vzdialenosti 2 od bodu 0 ležia obrazy práve dvoch

navzájom opačných celých čísel: 2 a –2.

Platí: ak a = 2, tak a = 2 alebo a = –2.

b) b = 5,3 znamená, že obraz čísla b je od obrazu čísla

0 vzdialený 5,3 jednotkovej úsečky.

Vo vzdialenosti 5,3 od bodu 0 ležia obrazy práve dvoch

navzájom opačných desatinných čísel: 5,3 a –5,3.

Platí: ak b = 5,3, tak b = 5,3 alebo b = –5,3.

ÚLOHA

Na číselnej osi s jednotkovou úsečkou 1 cm nájdite obrazy všetkých čísel x, y, z, v, pre ktoré platí:

y

= 3

= 7

= 1,5

= 4,8

–5

= 5

2. Vypočítajte:

1. Prečítajte nasledujúce zápisy a skontrolujte, či sú absolútne hodnoty čísel správne určené:

3. Určte a zapíšte absolútne hodnoty čísel vyznačených na číselnej osi: a) b) c)

4. Dané sú čísla: 6; –18; 12,5; –47,8; 7,11; –9,36; –3,66; 54; –8,45. Napíšte k nim opačné čísla a zapíšte ich absolútne hodnoty.

5. Na číselnej osi s jednotkovou úsečkou 1 cm nájdite obrazy všetkých čísel p, q, s, t, pre ktoré platí:  p  = 1;  q = 5;  s  = 2,5;  t  = 6,3

6. Nájdite všetky celé čísla x, pre ktoré platí:

3

1.4 Porovnávanie a usporadúvanie celých a desatinných čísel

Vyznačme na číselnej osi celé čísla 3, 4 a 5. Číslo 4 je väčšie ako číslo 3 a obraz čísla 4 leží napravo od obrazu čísla 3. Číslo 5 je väčšie ako číslo 4 a obraz čísla 5 leží napravo od obrazu čísla 4.

Z dvoch celých čísel je väčšie to, ktorého obraz na číselnej osi leží napravo od obrazu druhého čísla.

Vyznačme na číselnej osi celé čísla –3 a –4. Obraz čísla –3 leží napravo od obrazu čísla –4, preto číslo –3 je väčšie ako číslo –4.

PROBLÉM 3

Ako porovnávame celé záporné čísla?

Doplňte znaky nerovnosti: a) –1 0 c) –5 0 e) –7 –3 b) –2 1 d) –6 3 f) –12 –10

RIEŠENIE

Pomôžeme si číselnou osou.

Platí: a) –1 < 0 c) –5 < 0 e) –7 < –3 b) –2 < 1 d) – 6 < 3 f) –12 < –10 0 13 –7–6–5–3–2–1 –12–10

Každé záporné celé číslo je menšie ako 0.

ÚLOHA

Porovnajte podľa veľkosti čísla: a) 6 a 0 c) –8 a 6 e) 0 a –9 b) –6 a 0 d) 8 a –6 f) 10 a –15

ÚLOHA

Porovnajte podľa veľkosti čísla: a) –6 a –4 c) –12 a –5 e) –13 a –23 b) –4 a –6 d) –1 a –7 f) –5 a –12

PROBLÉM 4

Pre prirodzené čísla 5 a 7 platí nerovnosť 5 < 7.

Aký vzťah platí pre čísla k nim opačné?

RIEŠENIE

Vyznačíme obrazy čísel na číselnej osi: 5 < 7 –7 < –5

Platí: 7 > 5 a –7 < –5 5 < 7 a –5 > –7

Každé záporné celé číslo je menšie ako každé kladné celé číslo. 0 57 –7–5 Ak pre ľubovoľné celé čísla a, b platí a  b, tak pre čísla k nim opačné platí – a  – b

ÚLOHA

Porovnajte podľa veľkosti čísla: a) –7 a 7 c) 17 a –17

e) 1 a –2 b) –28 a –29 d) –100 a –99 f) –8 a –9

ÚLOHA

Usporiadajte vzostupne čísla: –3; 6; 5; –5; –8; 9; 0; –1; 7; –2.

Desatinné čísla porovnávame rovnako ako celé čísla.

ÚLOHA

Porovnajte dvojice čísel: a) 3,1 a 4,2 c) –4,1 a –4,09

e) 0,01 a 0,001 g) –3,52 a –3,54 b) –2,8 a –2,85 d) 5,8 a 5,08 f) –0,02 a –0,002 h) –1,12 a –1,02

ÚLOHA

Porovnajte dvojice čísel: a) 0 a –1 c) –6,4 a 4,6

e) –10,24 a –0,86 g) –5,35 a –3,35 b) –0,1 a 0 d) –4,6 a 6,4 f) –0,4 a –0,5 h) –2,40 a –2,04

PRÍKLAD

Určte, medzi ktorými dvomi po sebe idúcimi číslami leží každé z čísel 6,2 a –6,2. Výsledky zapíšte pomocou nerovností.

RIEŠENIE

Pomôžeme si číselnou osou:

Číslo 6,2 leží medzi celými kladnými číslami 6 a 7.

Zapíšeme: 6 < 6,2 < 7

Prečítame: Číslo 6,2 je väčšie ako číslo 6 a zároveň menšie ako číslo 7.

Číslo –6,2 leží medzi celými zápornými číslami –7 a –6.

Zapíšeme: –7 < –6,2 < –6

Prečítame: Číslo –6,2 je väčšie ako číslo –7 a zároveň menšie ako číslo –6.

ÚLOHA

Určte a zapíšte pomocou nerovností, medzi ktorými dvoma po sebe idúcimi celými číslami leží každé z čísel: a) 9,5 a –9,5 b) 24,8 a –24,8 c) –215,6 a 215,6

CVI Č ENIA

1. Usporiadajte čísla vzostupne: a) –5, 8, –14, –10, 0, 2, –3, –20, 5, –4 b) 2,8; –1,2; 5,4; –4,3; –1,8; 6,5; –5,4 c) 10; –5,5; 9,4; –12,5; –1; 1,1; –8,4

2. Doplňte znaky <, >, = tak, aby ste dostali správne zápisy: a) 4 7 c) 12 –12 e) –12 12 g) –8 –9 b) –4 –7 d) 0 –32 f) –8 –8 h) –8 –4

3. Dané je číslo 10. Napíšte päť celých kladných čísel, ktoré: a) nasledujú bezprostredne za číslom 10, b) číslu 10 bezprostredne predchádzajú. c) Napíšte to isté postupne pre čísla –10, –5, –2.

4. Porovnajte podľa veľkosti čísla a zapíšte pomocou znakov nerovnosti: a) 15,7 a 17,5 c) 15,7 a –17,5 e) 0,5 a 0,3 g) 0,5 a –0,3 b) –15,7 a 17,5 d) –15,7 a –17,5 f) –0,5 a 0,3 h) –0,5 a –0,3

5. Nájdite chybné zápisy:

a) 0 > –5 c) –8 < 8 e) –18 < –20 g) 18,6 > –2,5 b) –6 > 0 d) –12 > –18 f) 10,5 < –10,5 h) –3,4 < –4,3

6. Z čísel –5,6; –5; –5,9; –5,4; –6; –6,1 vyberte tie, ktoré sú: a) menšie ako –5,5 b) väčšie ako –5,7

7. Zapíšte pomocou znakov nerovnosti, medzi ktorými dvoma po sebe idúcimi celými číslami ležia čísla: a) 4,1 b) –2,95 c) –0,1 d) 7,001

8. Nájdite všetky celé čísla, ktoré sú: a) väčšie ako 2 a menšie ako 7

c) väčšie ako –2,97 a menšie ako 2,02 b) väčšie ako –5,9 a menšie ako –4,99 d) väčšie ako –4,95 a menšie ako –2,001

1.5 Sčitovanie a odčitovanie celých a desatinných čísel

ZOPAKUJME SI

Doteraz sme sa učili sčitovať prirodzené čísla a kladné desatinné čísla.

Súčet dvoch kladných celých alebo desatinných čísel je kladné číslo.

5 + 3 = 8

0,5 + 0,3 = 0,8

PROBLÉM 5

Porozmýšľajte: Ak je ráno teplota +5 C a počas dňa sa oteplí o 3 C, aká je výsledná teplota? Ak je večer teplota –5 C a v noci sa ochladí o 3 C, aká je výsledná teplota?

RIEŠENIE

Nakreslíme teplomer a porovnávame výpočtom:

Odpoveď: Cez deň je výsledná teplota +8 C, v noci je výsledná teplota –8 C.

C

C

oteplí sa teplota stúpa 5 + 3 = 8

ochladí sa teplota klesá (–5) + (–3) = –8

Záporné celé alebo záporné desatinné čísla sčítame tak, že si odmyslíme znamienka, sčítame ich ako kladné a k výsledku pridáme znamienko mínus. (–8) + (–5) = –13 (–4,7) + (–3,6) = –8,3

POZNÁMKA

a) Súčet (+5) + (+3) môžeme napísať aj v tvare +5 + 3 alebo 5 + 3. Znamienko + v zátvorke pred číslom označuje kladné číslo, obyčajne ho vynechávame. b) Súčet (–5) + (–3) môžeme písať aj v tvare –5 + (–3). Ak je prvý sčítanec záporné číslo, prvú zátvorku môžeme vynechať. Znamienko – na začiatku príkladu alebo v zátvorke pred číslom nevynechávame, pretože označuje záporné číslo.

ÚLOHA

Napíšte súčty jednoduchšie a sčítajte:

a) (+5) + (+11) c) (+12) + (+13) e) (+5,2) + (+3,5) g) 11,2 + (+5,9) b) (+7) + 6 d) (+19) + (+20) f) +1,7 + (+2,8) h) (+4,6) + 9,9

ÚLOHA

Sčítajte: a) (–11) + (–7) c) (–5) + (–13) e) –5,5 + (–3,9) g) –5,3 + (–3,5) b) (–26) + (–13) d) (–6) + (–8) f) –0,8 + (–0,5) h) –18,2 + (–2,7)

PROBLÉM 6

Žiaci zapisovali vonkajšiu teplotu vzduchu počas troch dní. Ráno bola teplota vždy –5 C.

Prvý deň bola najvyššia teplota o 8 C vyššia, druhý deň o 5 C vyššia, tretí deň o 3 C vyššia ako ráno. Aká bola najvyššia teplota každý deň?

RIEŠENIE

Žiaci nakreslili teplomer na každý deň: 1. deň 2. deň 3. deň –5 + 8 = 3 –5 + 5 = 0 –5 + 3 = –2 Zapísali výsledky podľa teploty na teplomeroch.

Odpoveď: Prvý deň bola najvyššia teplota +3 C, druhý deň 0 C a tretí deň –2 C.

Celé alebo desatinné čísla s opačnými znamienkami sčítame tak, že si odmyslíme znamienka, od väčšieho čísla odčítame menšie číslo a k výsledku pridáme znamienko väčšieho čísla.

PRÍKLAD

Sčítajte: a) –4 + 9 b) 5 + (–13) c) –3,8 + 8,6 d) 7,2 + (–12,7)

RIEŠENIE

a) –4 + 9 ... 9 > 4 ... 9 – 4 = 5 ... –4 + 9 = +5

b) –13 + 5 ... 13 > 5 ... 13 – 5 = 8 ... –13 + 5 = –8

c) –3,8 + 8,6 ... 8,6 > 3,8 ... 8,6 – 3,8 = 4,8 ... –3,8 + 8,6 = 4,8 d) 7,2 + (–12,7) 12,7 > 7,2 12,7 – 7,2 = 5,5 7,2 + (–12,7) = –5,5

ÚLOHA

Sčítajte:

a) 11 + (–7) c) –15 + 13 e) 5,5 + (–3,9) g) –5,3 + 3,5 b) 26 + (–13) d) –6 + 8 f) 0,8 + (–0,5) h) –18,2 + 2,7

ÚLOHA

Sčítajte:

a) 19 + (–11) c) –22 + 15

6,4 + (–3,2) g) –15,8 + 13,2 b) 16 + (–25) d) –11 + 18

ÚLOHA

8,8 + (–10,5) h) –24,2 + 16,1

Pokúste sa spamäti určiť nasledujúce súčty: 6 + (–6) 0,2 + (–0,2) 100 + (–100) 32,5 + (–32,5) –4 + 4 –5,8 + 5,8 –155 + 155 –116,4 + 116,4

Pre každé celé alebo desatinné číslo a platí: a + (–a) = 0

Súčet dvoch navzájom opačných čísel sa rovná nule.

PROBLÉM 7

Meteorológovia merajú teplotu vzduchu o 7.00, 14.00 a 21.00 hodine. V tabuľke sú teploty vzduchu namerané v štyroch dňoch o 7.00 a o 14.00 hodine. Vypočítajte zmenu teploty od 7.00 do 14.00 hodiny v každom dni.

RIEŠENIE

Zmena teploty od 7.00 do 14.00 hodiny je rozdiel teploty o 14.00 hodine a o 7.00 hodine.

Zvýšenie teploty vyjadríme kladným číslom, pokles teploty záporným číslom.

1. deň: teplota stúpla o 3 C, teda

5 – 2 = 3 ... 5 – 2 = 5 + (–2) = 3

2. deň: teplota stúpla o 6 C, teda

3 – (–3) = 6 ... 3 – (–3) = 3 + 3 = 6

3. deň: teplota stúpla o 4 C, teda

–1 – (–5) = 4 ... –1 – (–5) = –1 + 5 = 4

4. deň: teplota klesla o 5 C, teda –2 – 3 = –5 ... –2 – 3 = –2 + (–3) = –5

7.00 hodina14.00 hodina 1. deň 2 C 5 C 2. deň –3 C 3 C

3. deň –5 C –1 C 4. deň 3 C –2 C

1. deň2. deň3. deň4. deň

Odčítať číslo od iného čísla znamená pripočítať k nemu opačné číslo. a – b = a + (–b) a – (–b) = a + b

PRÍKLAD

Vypočítajte:

a) 5 – 2 c) – 9 – 5 e) 3 – (–7) b) 4 – 9 d) 5 – (–2) f) –7 – (–13)

RIEŠENIE

a) 5 – 2 = 3

b) 4 – 9 = 4 + (–9) ... 9 > 4 ... 9 – 4 = 5 ... 4 – 9 = –5

c) – 9 – 5 = –9 + (–5) = –14

d) 5 – (–2) = 5 + 2 = 7

e) 3 – (–7) = 3 + 7 = 10 f) –7 – (–13) = –7 + 13 ... 13 > 7 ... 13 – 7 = 6 ... –7 – (–13) = 6

ÚLOHA

Vypočítajte: a) 15 – 7 c) –4 – 11 e) – 12 – 8 g) 25 – (–50) i) –140 – 100 b) 2 – 9 d) –8 – 3 f) –10 – (–7) h) 66 – 96 j) –130 – (–128)

ÚLOHA

Vypočítajte:

a) 15 – 8 c) –6 – 13 e) – 15 – 11 g) 12 – (–28) i) –26 – 40 b) 9 – 14 d) –18 – 13 f) –9 – (–4) h) 32 – 54 j) –51 – (–63)

ÚLOHA

Vypočítajte: a) 6,8 – 3,2 c) –8,7 – (–2,3) e) 0,4 – 1,4 g) –2,5 – (–1,5) i) 6,8 – (–3,2) b) 5,7 – 9,3 d) –4,6 – 7,3 f) 2,5 – (–5,2) h) –6,8 – 3,2 j) 5 – (–1,2)

ÚLOHA

Vypočítajte: a) 15 – 9, 9 – 15, –15 – 9, –9 – 15 b) 105 – 20, 20 – 105, –20 – 105, –105 – 20 c) 0,6 – 0,3; –0,6 – 0,3; 0,3 – 0,6; –0,3 – 0,6

PROBLÉM 8

Počítajte príklady s nulou: 12 + 0 = 12 12 – 0 = 12 (–12) + 0 = –12 (–12) – 0 = –12 0 + 12 = 12 0 – 12 = 0 + (–12) = –12 0 + (–12) = –12 0 – (–12) = 0 + (+12) = 12

Čo zaujímavé ste si všimli?

Počítanie s nulou

Pre každé celé a pre každé desatinné číslo a platí: a + 0 = a 0 + a = a a – 0 = a 0 – a = – a