Matematika-ucebnica-7.2.-rocnik-ZS

Soňa Čeretková, Ondrej Šedivý, Ivan Teplička

matematika

pre 7. ročník základnej školy a 2. ročník gymnázia s osemročným štúdiom

Slovenské pedagogické nakladateľstvo

Milí siedmaci,

máte v rukách druhú časť učebnice matematiky pre 7. ročník základnej školy a pre 2. ročník gymnázia s osemročným štúdiom. Nájdete v nej veľa jednoduchých i náročnejších úloh a tiež veľa zaujímavostí.

Pri práci s učebnicou venujte pozornosť riešeným príkladom a problémom. Pozorne si prečítajte, premyslite a osvojte postupy riešení, ktoré vám pomôžu pri úspešnom riešení úloh a cvičení. Pomocou učebnice zvládnete nové pojmy nielen z matematiky, ale aj z reálneho života. Naučíte sa riešiť zaujímavé úlohy o kvádri a kocke. Dôležitou kapitolou je kapitola o percentách. Prehĺbite si tiež svoje vedomosti z riešenia kombinatorických úloh.

Učebnica obsahuje aj prvky náročnejšieho, rozširujúceho učiva. Postrehnete, že v matematike jednotlivé vedomosti nie sú izolované, ale navzájom spolu súvisia. V časti o diagramoch nájdete inšpiráciu k vlastným matematickým projektom o zbere a zobrazovaní konkrétnych údajov o vás a vašom okolí. Vypracovaním testov na konci každej kapitoly si overíte nadobudnuté vedomosti. Na konci učebnice nájdete súhrnné cvičenia na opakovanie a nezabudnite na Rozum do hrsti. Veľa úspechov a chuti do učenia.

Pri orientácii v učebnici vám budú pomáhať tieto symboly:

– príklad s riešením

– problém s riešením

– zapamätať si

– zhrnutie alebo poučka

– úloha

– poznámka

Autori © doc. PaedDr. Soňa Čeretková, PhD., prof. RNDr. Ondrej Šedivý, CSc., Ivan Teplička

Recenzenti: prof. RNDr. Jozef Doboš, CSc., Ing. Mgr. Martin Hriňák, PaedDr. Monika Bučíková

Ilustrovali: akademická maliarka Táňa Žitňanová, obálku navrhol Ing. Zsolt Urbán

Grafický dizajn © SPN – Mladé letá, s. r. o.

Ministerstvo školstva, vedy, výskumu a športu Slovenskej republiky schválilo pod č. 2022/17394:8-A2201 súbor edukačných publikácií Matematika pre 7. ročník základnej školy a 2. ročník gymnázia s osemročným štúdiom – 1. a 2. časť. Doložka nadobúda účinnosť 30. septembra 2022 a má platnosť do 31. augusta 2026.

Tretie vydanie, 2024

Všetky práva vyhradené. Toto dielo ani žiadnu jeho časť nemožno reprodukovať bez súhlasu majiteľa práv.

Zodpovedná redaktorka RNDr. Judita Hollá

Odborná redaktorka RNDr. Jana Belasová

Technická redaktorka Ivana Bronišová

Vyšlo vo vydavateľstve Slovenské pedagogické nakladateľstvo – Mladé letá, s. r. o., Sasinkova 5, 811 08 Bratislava

Vytlačili TBB, a. s., Banská Bystrica

ISBN 978-80-10-04330-9

Autori

4 Kváder a kocka, ich objem a povrch

4.1 Kváder, kocka

Na obrázku sú zobrazené rôzne telesá. Telesá sú geometrické útvary v priestore. Poznáme veľa druhov telies. Pri pohľade okolo seba vidíme, aké rôzne tvary majú predmety, ktoré nás obklopujú. Telesá na obrázku sa nazývajú hranaté telesá

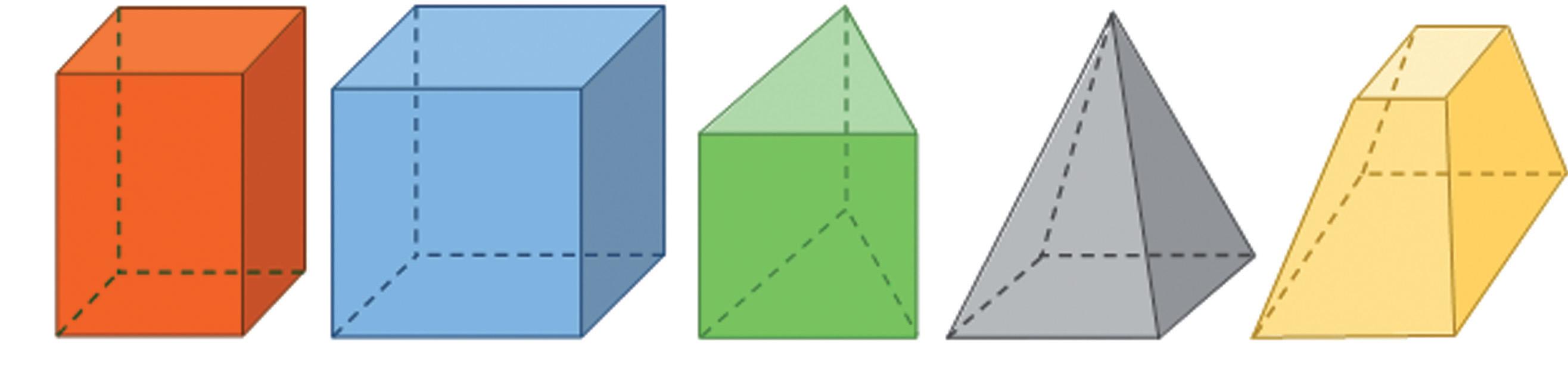
kváder kocka hranol ihlan zrezaný ihlan

Hranaté telesá sú ohraničené mnohouholníkmi, ktoré sa nazývajú steny telesa. Strany týchto mnohouholníkov sa nazývajú hrany telesa. Hrany sa pretínajú v bodoch, ktoré sa nazývajú vrcholy telesa.

ÚLOHA

Vyplňte tabuľku pre telesá znázornené na úvodnom obrázku.

TelesoPočet vrcholov Počet hrán Počet stien kváder kocka hranol

ihlan

zrezaný ihlan

Porovnajte pre každé teleso súčet počtu vrcholov a počtu stien s počtom hrán. Čo zaujímavé ste spozorovali?

V tejto učebnici sa budeme venovať hlavne dvom druhom hranatých telies – kvádrom a kockám.

KOCKAKVÁDER

má 8 vrcholov

má 12 hrán, ktoré sú zhodné úsečky

má 6 stien, ktoré sú zhodné štvorce

má 8 vrcholov

má 12 hrán, ktoré možno rozdeliť do troch skupín tak, že v každej skupine sú 4 hrany, ktoré sú rovnobežné a zhodné

má 6 stien, ktoré sú po dvoch zhodné obdĺžniky alebo štvorce

PROBLÉM 1

Adam si všimol, že všetky steny kocky sú štvorce a steny kvádra sú obdĺžniky alebo štvorce.

Rozmýšľa, či kváder môže mať aj všetky steny štvorce.

RIEŠENIE

Pani učiteľka vysvetľuje: Kváder môže mať aj všetky steny štvorce, potom to bude kocka. Kocku považujeme za špeciálny prípad kvádra.

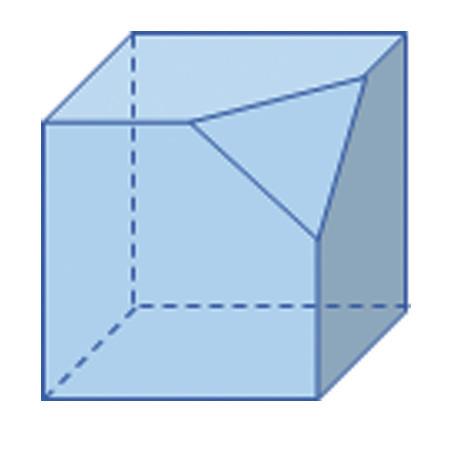
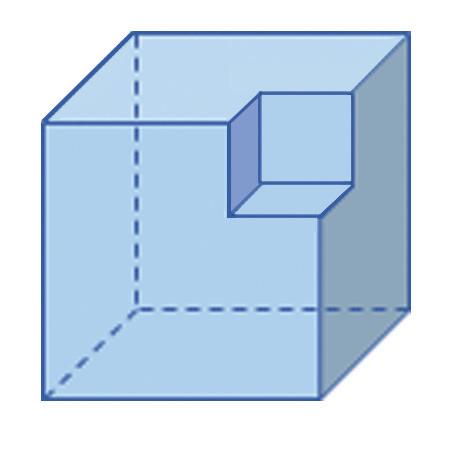
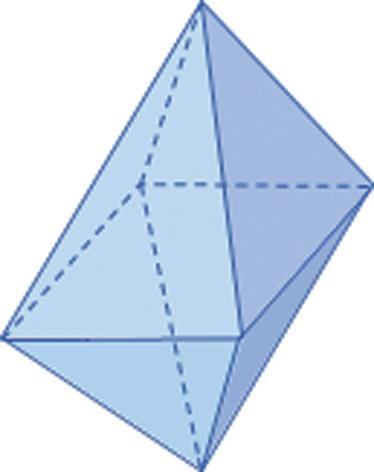
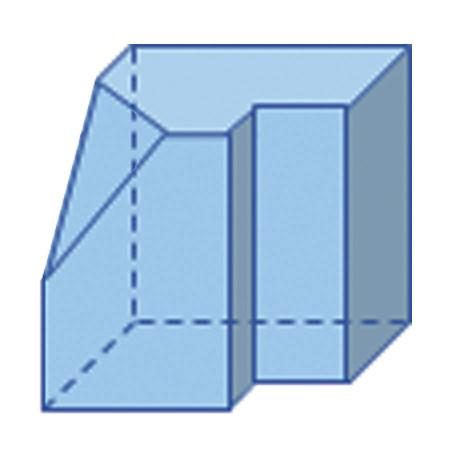
1. Zistite, koľko vrcholov, hrán a stien má teleso na obrázku.

2. Zistite, koľko vrcholov, hrán a stien má teleso na obrázku.

3. Zistite, koľko vrcholov, hrán a stien má teleso na obrázku.

4. Zistite, koľko vrcholov, hrán a stien má teleso na obrázku.

5. Overte, či pre telesá v cvičeniach 1, 2, 3 a 4 platí: súčet počtu vrcholov a počtu stien je o 2 väčší ako počet hrán.

CVI Č ENIA

4.2 Zobrazovanie kvádra a kocky

V škole, ale aj v rôznych povolaniach, potrebujeme zobraziť priestorové útvary do roviny – na výkres, do zošita, na tabuľu, na maliarske plátno atď. Vzniklo niekoľko spôsobov, ako to uskutočniť. V matematike sa na zobrazovanie telies do roviny – nákresne – používa zobrazovacia metóda, ktorá sa nazýva voľné rovnobežné premietanie. Ide o spôsob zobrazovania, pri ktorom dodržiavame tieto pravidlá:

1. Obrazce, ktoré ležia v nákresni alebo v rovine rovnobežnej s nákresňou, sa zobrazujú v skutočnej veľkosti.

2. Úsečky kolmé na nákresňu sa zobrazujú obyčajne pod uhlom 45a v polovičnej dĺžke.

3. Rovnobežné a zhodné úsečky sa zobrazujú ako rovnobežné a zhodné úsečky.

PRÍKLAD

Narysujte vo voľnom rovnobežnom premietaní kocku ABCDEFGH , ktorej hrana má dĺžku 3 cm.

RIEŠENIE

Príklad rieši Julka, najskôr spraví rozbor, náčrt a až potom rysuje.

Rozbor

1. Stenu ABFE narysujeme ako štvorec so stranou dlhou 3 cm.

2. Úsečky AD, BC, EH a FG sú rovnobežné a kolmé na nákresňu. Narysujeme ich tak, že BAD  = 45 a budú rovnobežné s úsečkou AD. Ich dĺžka je 1,5 cm.

3. Stena DCGH leží v nákresni, preto ju rysujeme ako štvorec so stranou dlhou 3 cm.

4. Hrany, ktoré vidíme, narysujeme plnými čiarami. Hrany, ktoré nevidíme, narysujeme čiarkovanými čiarami.

Náčrt

Náčrt

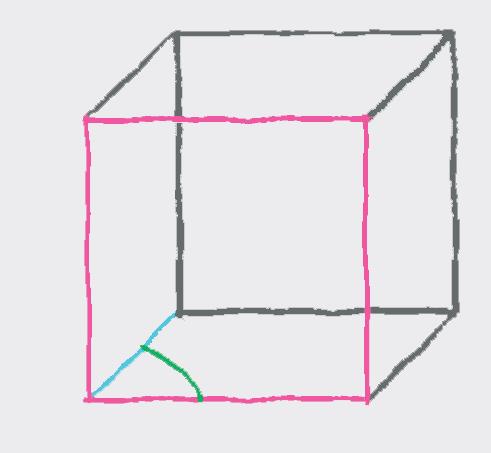
Takýto spôsob zobrazenia kocky sa nazýva nadhľad sprava , lebo kocku zobrazujeme tak, že sa na ňu pozeráme zhora a sprava. Je to najčastejší spôsob zobrazovania kocky. Podľa toho, či sa na kocku, kváder alebo iné zobrazované teleso pozeráme zhora alebo zdola, sprava alebo zľava, rozoznávame štyri spôsoby zobrazenia: nadhľad sprava, nadhľad zľava, podhľad sprava, podhľad zľava.

nadhľad sprava

nadhľad zľava

podhľad sprava

PROBLÉM 2

podhľad zľava

Peter nevie, prečo hrany kolmé na nákresňu rysujeme v polovičnej dĺžke.

RIEŠENIE

ÚLOHA

Tomáš mu vysvetľuje, že on narysoval kocku tak, aby hrany kolmé na nákresňu mali skutočnú dĺžku. Obrázok, ktorý dostal, sa však podobal skôr na kváder ako na kocku. Preto treba hrany kolmé na nákresňu rysovať približne v polovičnej dĺžke.

Narysujte vo voľnom rovnobežnom premietaní kocku KLMNOPQR, ktorej hrana má dĺžku 4 cm. Narysujte nadhľad sprava. Z narysovanej a označenej kocky KLMNOPQR vypíšte všetky: a) vrcholy, b) hrany, c) steny.

ÚLOHA

Narysujte vo voľnom rovnobežnom premietaní kocku ABCDA

, ktorej hrana má dĺžku 6 cm. Narysujte nadhľad zľava.

PRÍKLAD

Narysujte vo voľnom rovnobežnom premietaní kváder ABCDEFGH ak AB = 3 cm, AD = 4 cm, AE = 5 cm. Narysujte nadhľad sprava.

RIEŠENIE

Juraj konštatuje, že pri rysovaní kvádra vo voľnom rovnobežnom premietaní postupujeme rovnako, ako pri rysovaní kocky.

Rozbor Náčrt

1. Stenu ABFE narysujeme ako obdĺžnik so stranami dlhými 3 cm a 5 cm.

2. Úsečky AD, BC, EH a FG sú rovnobežné a kolmé na nákresňu. Narysujeme AD = 2 cm tak, že BAD = 45  ostatné budú rovnobežné a zhodné s úsečkou AD

3. Stena DCGH leží v nákresni, preto ju rysujeme ako obdĺžnik so stranami dlhými 3 cm a 5 cm.

4. Hrany, ktoré vidíme, narysujeme plnými čiarami. Hrany, ktoré nevidíme, narysujeme čiarkovanými čiarami.

ÚLOHA

ÚLOHA

Narysujte vo voľnom rovnobežnom premietaní kváder KLMNOPQR , ak KL  = 6 cm, KN = 4 cm, KO = 3 cm. Narysujte nadhľad sprava.

Narysujte vo voľnom rovnobežnom premietaní kváder ABCDABC

D

, ak

AB

= 3 cm, AD = 8 cm, AA = 2 cm. Narysujte nadhľad sprava.

ÚLOHA

Dokončite obraz kvádra vo voľnom rovnobežnom premietaní: a) b) c)

PROBLÉM 3

Samo bol s rodičmi v galérii. Pri prezeraní obrazov si všimol, že predmety nie sú na obrazoch zobrazené tak, ako sa učili v škole. Napríklad hrany predmetu tvaru kocky alebo kvádra, ktoré sú v skutočnosti rovnobežné, neboli na obraze rovnobežné.

RIEŠENIE

Pani učiteľka vysvetľuje: Voľné rovnobežné premietanie je spôsob zobrazovania, ktorý sa používa hlavne v matematike. V maliarstve sa už od 15. storočia používa iný spôsob zobrazovania, ktorý sa nazýva lineárna perspektíva. ežné.

Lineárna perspektíva je spôsob zobrazovania priestoru do roviny, ktorý sa snaží zobraziť realitu tak, ako ju vidí ľudské oko, alebo ako ju zobrazí fotoaparát. Základným princípom lineárnej perspektívy je, že čím sú predmety vzdialenejšie, tým sa pozorovateľovi javia menšie. Napríklad kváder, ktorý je vo voľnom rovnobežnom premietaní znázornený na ľavom obrázku, sa v lineárnej perspektíve znázorní takto:

CVI Č ENIA

lineárna perspektíva

1. Narysujte vo voľnom rovnobežnom premietaní kocku ABCDEFGH, ktorej hrana má dĺžku 4,5 cm. Narysujte nadhľad sprava aj nadhľad zľava.

2. V kocke ABCDEFGH z cvičenia 1 vypíšte všetky: a) vrcholy, b) hrany, c) steny.

3. Narysujte vo voľnom rovnobežnom premietaní kváder KLMNK  L  M  N , ak KL  = 8 cm, KN = 6 cm, KK = 2 cm. Narysujte kváder tak, že predná stena má rozmery: a) 8 cm a 2 cm, b) 8 cm a 6 cm. Narysujte nadhľad sprava.

4. V kvádri KLMNK LM N  z cvičenia 3 vypíšte všetky: a) vrcholy, b) hrany, c) steny.

5. Dokončite obraz kocky vo voľnom rovnobežnom premietaní: a) b) c)

6. Dokončite obraz kvádra vo voľnom rovnobežnom premietaní: a) b) c)

4.3 Nárys, pôdorys, bokorys

Ukázali sme si dve zobrazovacie metódy, ktoré sa používajú na zobrazovanie priestorových útvarov do roviny – voľné rovnobežné premietanie a lineárnu perspektívu. V niektorých technických odboroch, napríklad v strojárstve či v stavebníctve, sa na zobrazovanie priestorových útvarov používa iná metóda. Jej podstata je v tom, že zobrazovaný útvar nakreslíme v troch pohľadoch. Pohľad spredu sa nazýva nárys, pohľad zhora je pôdorys a pohľad zboku je bokorys. Bokorys môže byť pravý alebo ľavý podľa toho, či na zobrazovaný útvar pozeráme sprava alebo zľava.

PRÍKLAD

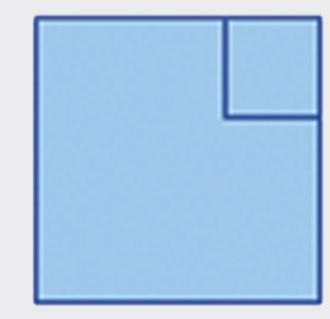
Nakreslite nárys, pôdorys, ľavý bokorys a pravý bokorys telies na obrázku. a) b)

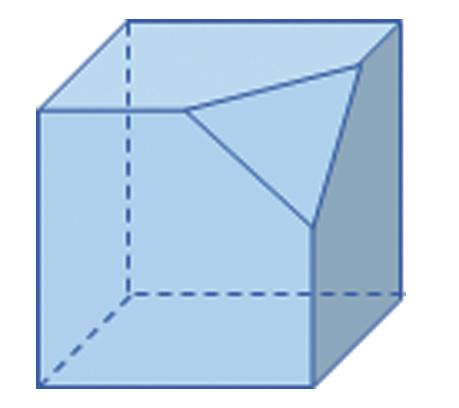
RIEŠENIE

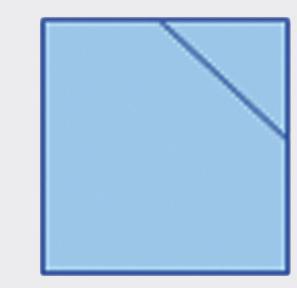
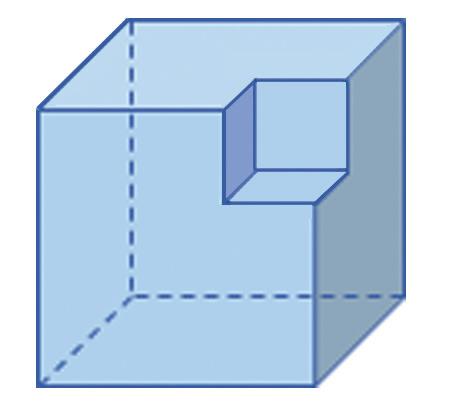
Ema poprosila brata, aby z drevených kociek stavebnice vyrobil telesá na obrázku. Prezrela si ich zľava, sprava, spredu, zhora a nakreslila štyri pohľady: a) ľavý bokorys nárys pravý bokorys pôdorys b) ľavý bokorys nárys pravý bokorys pôdorys

PRÍKLAD

Nakreslite nárys, pôdorys, ľavý bokorys a pravý bokorys telesa na obrázku zloženého z kociek.

RIEŠENIE

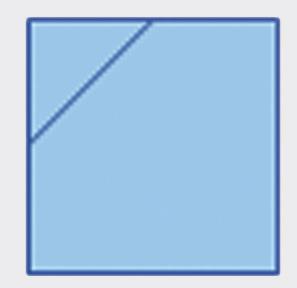
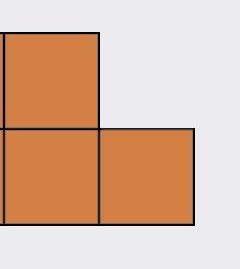
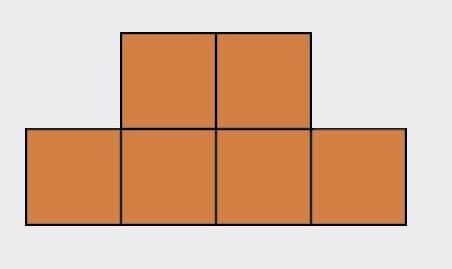
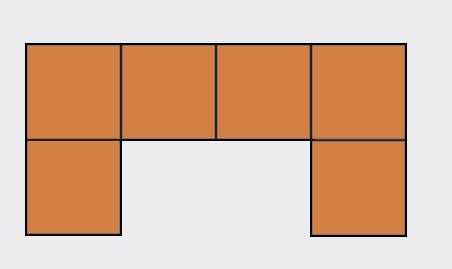
ľavý bokorys nárys pravý bokorys pôdorys p y

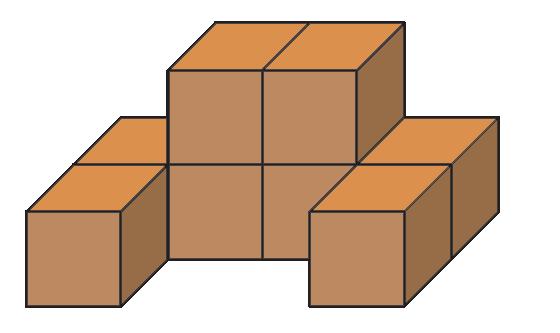
Ema si z kociek postavila teleso na obrázku. Prezrela si ho zľava, sprava, spredu, zhora a nakreslila štyri pohľady:

ÚLOHA

Nakreslite nárys, pôdorys a pravý bokorys telesa na obrázku zloženého z kociek.

ÚLOHA

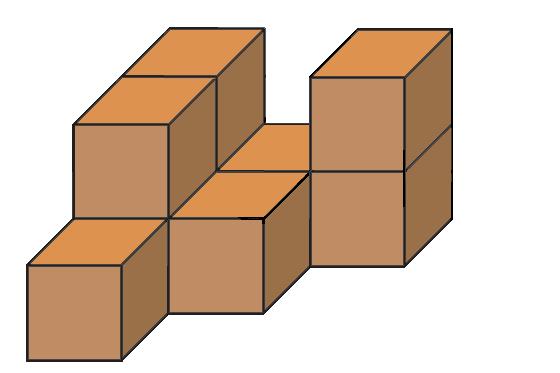
Nakreslite nárys, pôdorys a pravý bokorys telies na obrázku zložených z kociek. a) b) c) d)

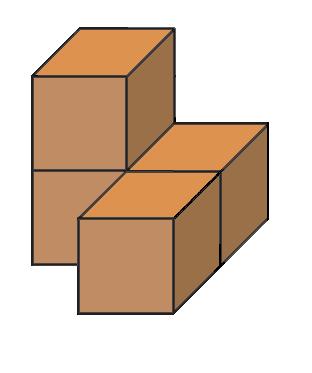
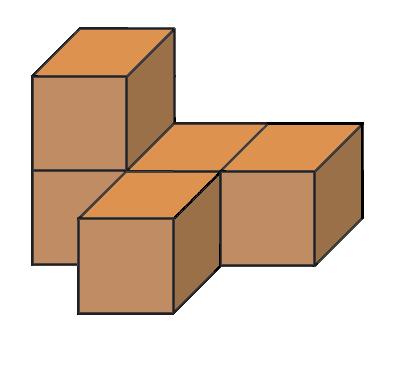
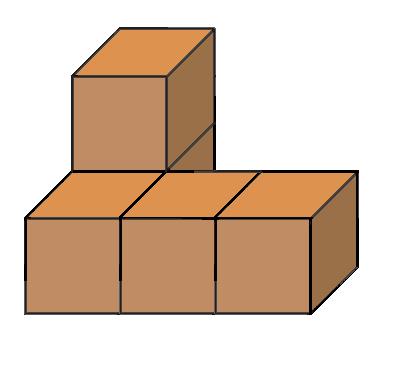
ÚLOHA

Nakreslite nárys, pôdorys a pravý bokorys telies na obrázku zložených z kociek. a) b)

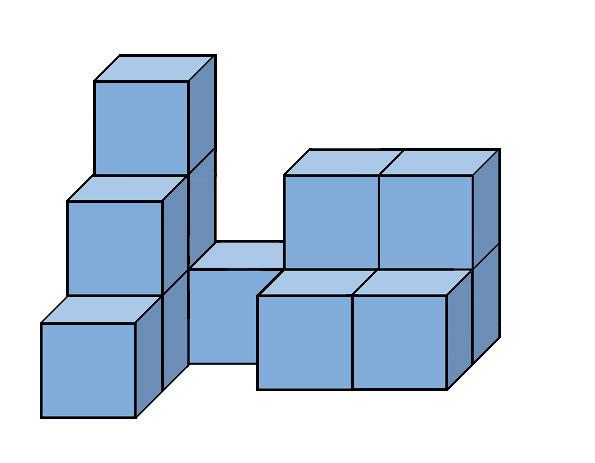
ÚLOHA

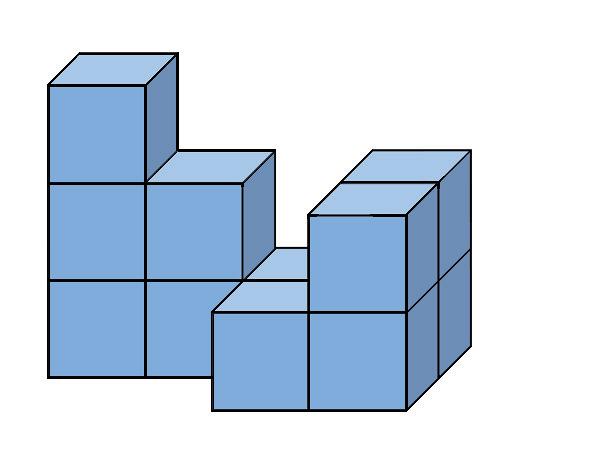
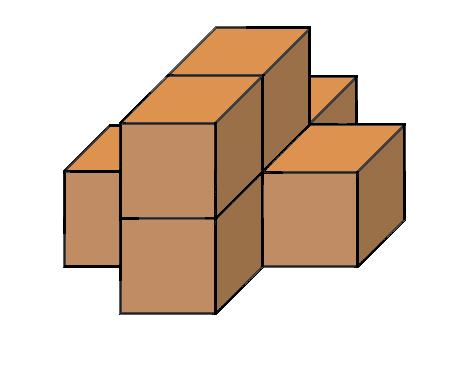
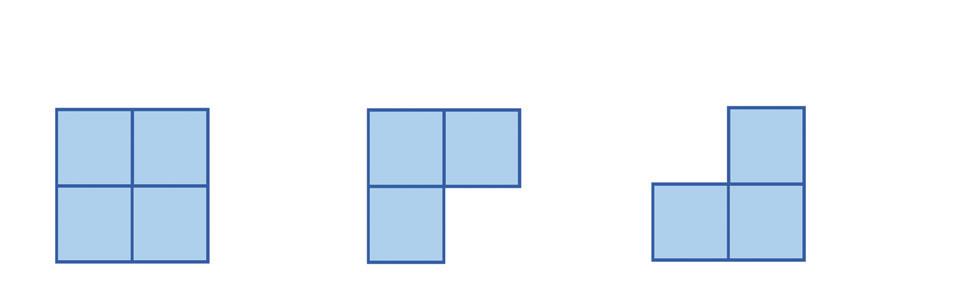
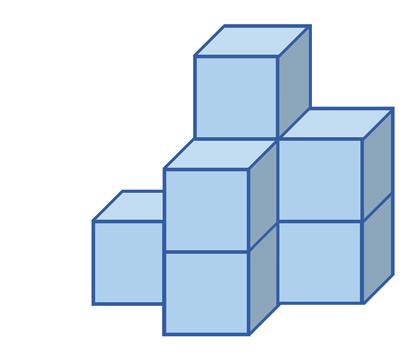
Priraďte k pohľadom A, B, C správne telesá 1, 2 alebo 3. POHĽADY

nárys pôdorys pravý bokorys

pôdorys pravý bokorys

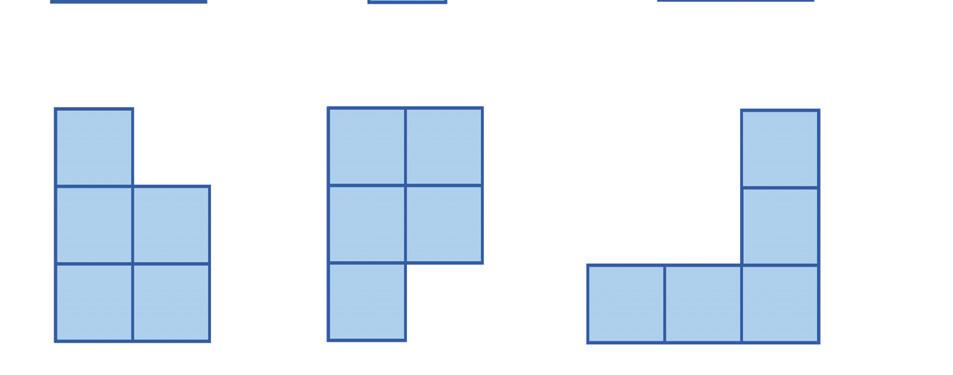
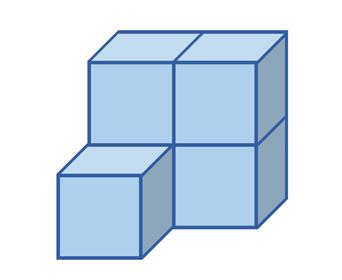
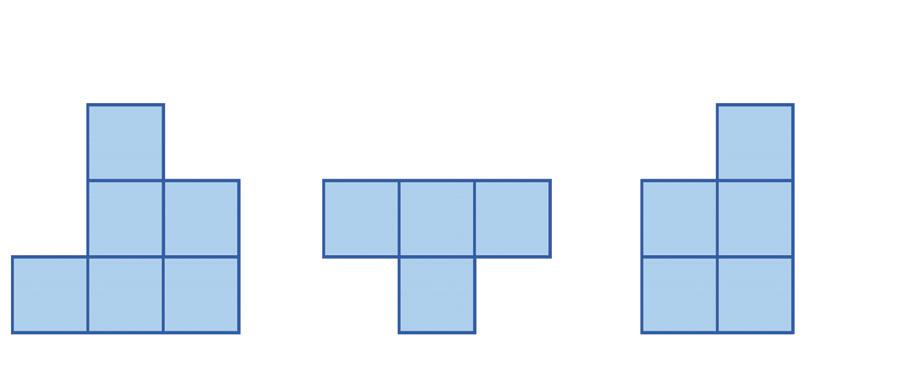
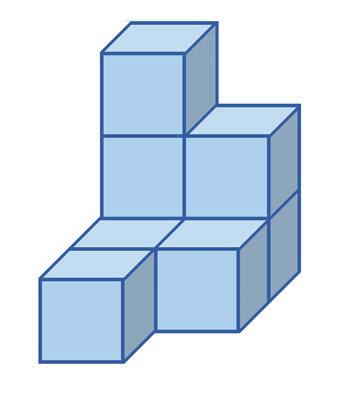
ÚLOHA

Z kociek postavte telesá, ktorých nárys, pôdorys a pravý bokorys je na obrázkoch.

nárys pôdorys pravý bokorys

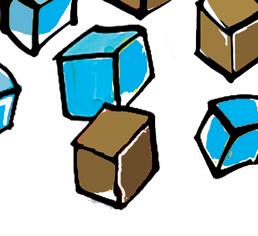
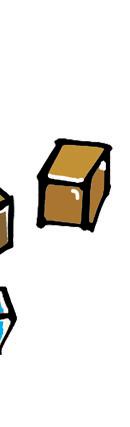
CVI Č ENIA

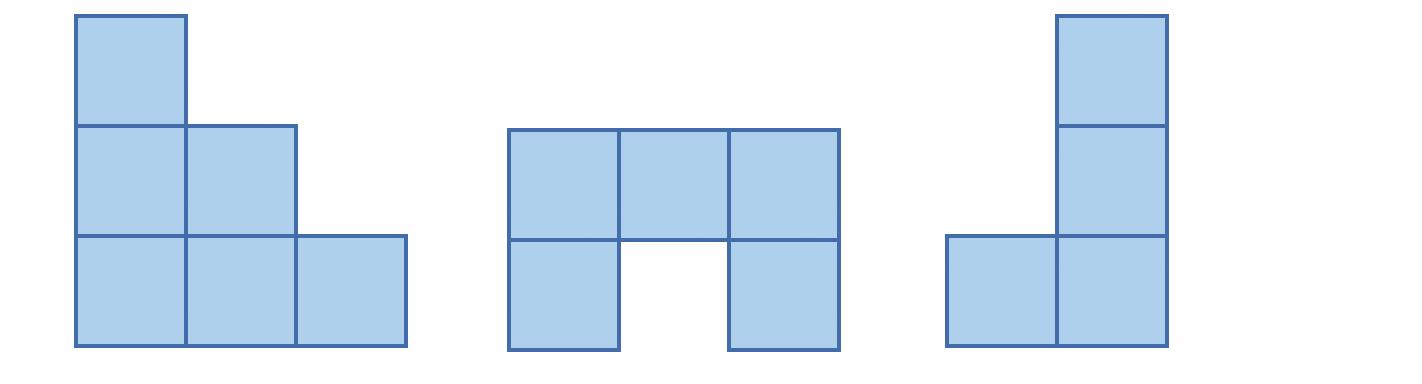
nárys pôdorys pravý bokorys

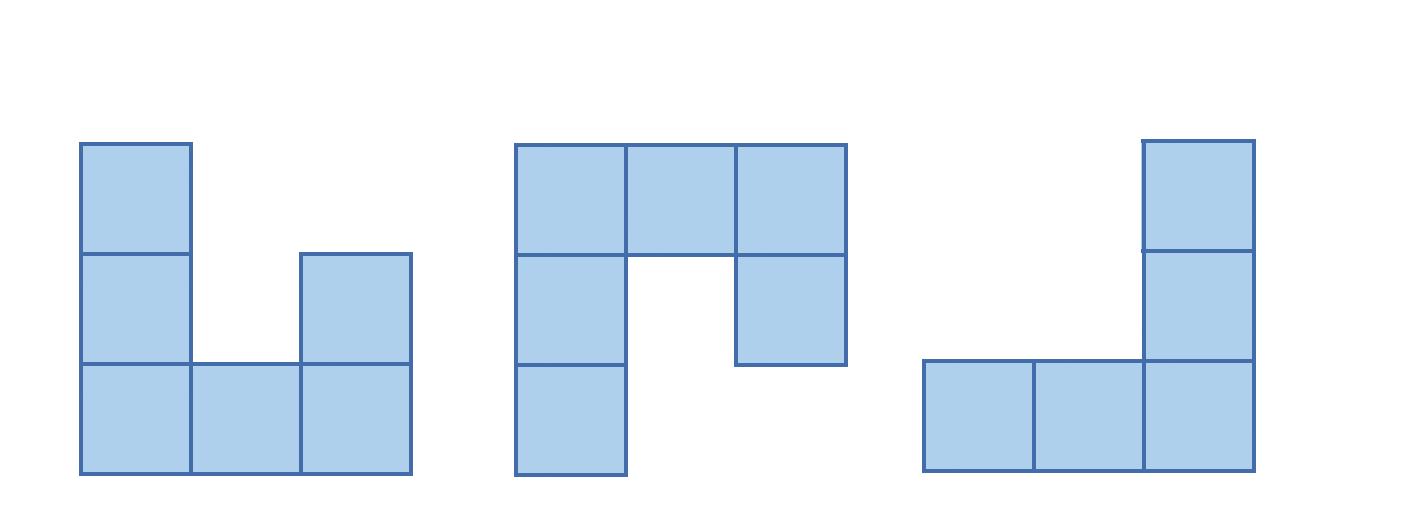
nárys pôdorys pravý bokorys

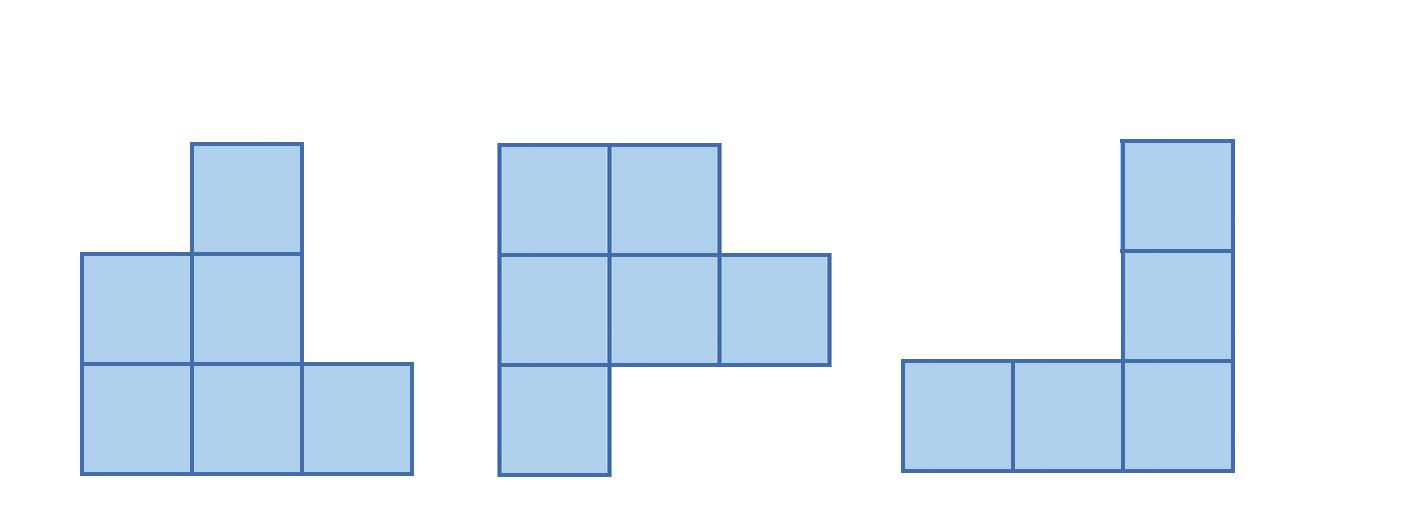
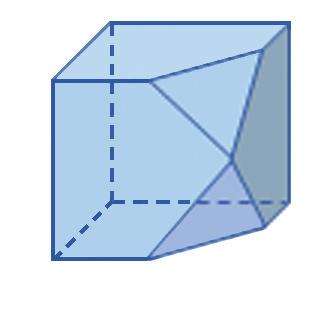
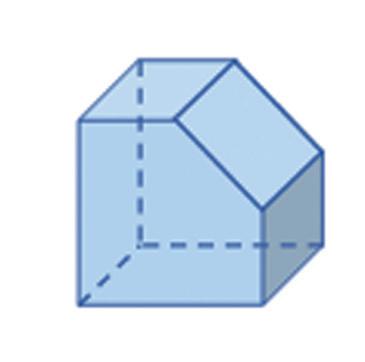
1. Nakreslite nárys, pôdorys, ľavý bokorys a pravý bokorys telesa na obrázku.

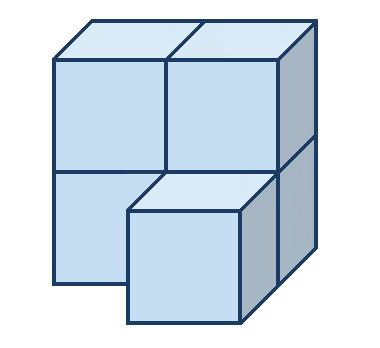
2. Nakreslite nárys, pôdorys, ľavý bokorys a pravý bokorys telesa na obrázku.

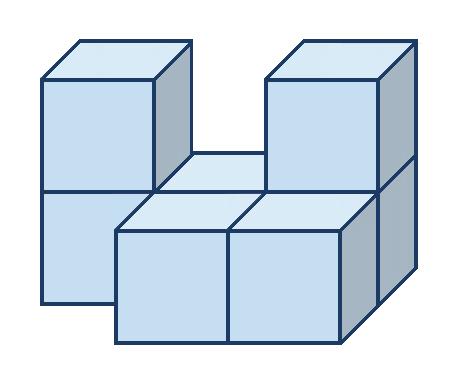
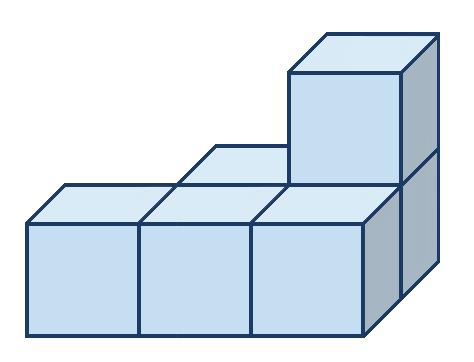
3. Nakreslite nárys, pôdorys a pravý bokorys telies na obrázku zložených z kociek. a) b) c)

4. Nakreslite nárys, pôdorys a pravý bokorys telies na obrázku zložených z kociek. a) b)

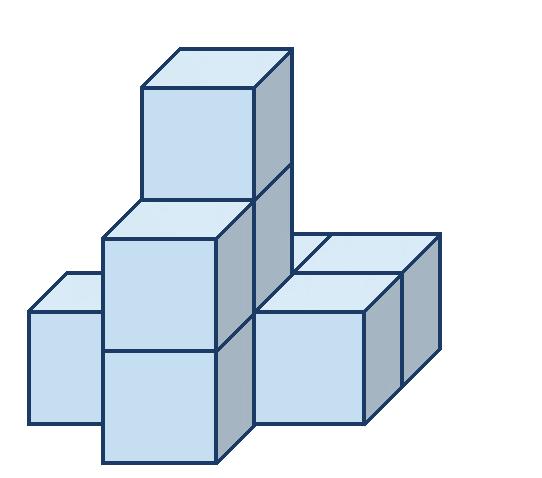
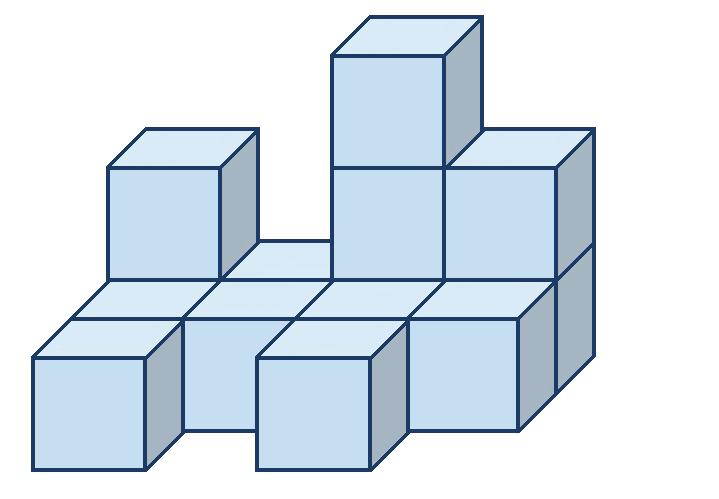
5. Priraďte k pohľadom A, B správne telesá 1 alebo 2

POHĽADY

nárys pôdorys pravý bokorys

TELESO

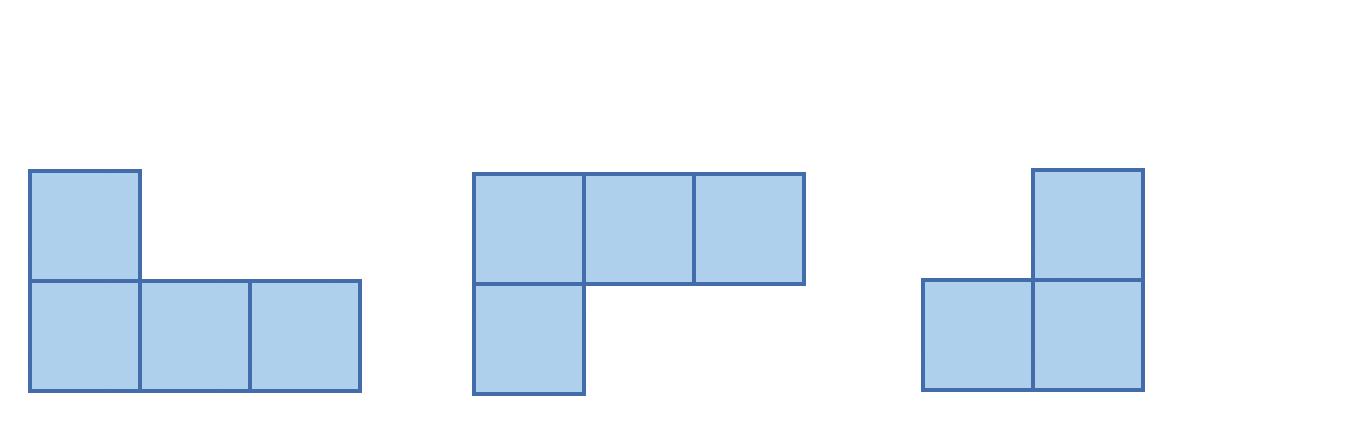
nárys pôdorys pravý bokorys

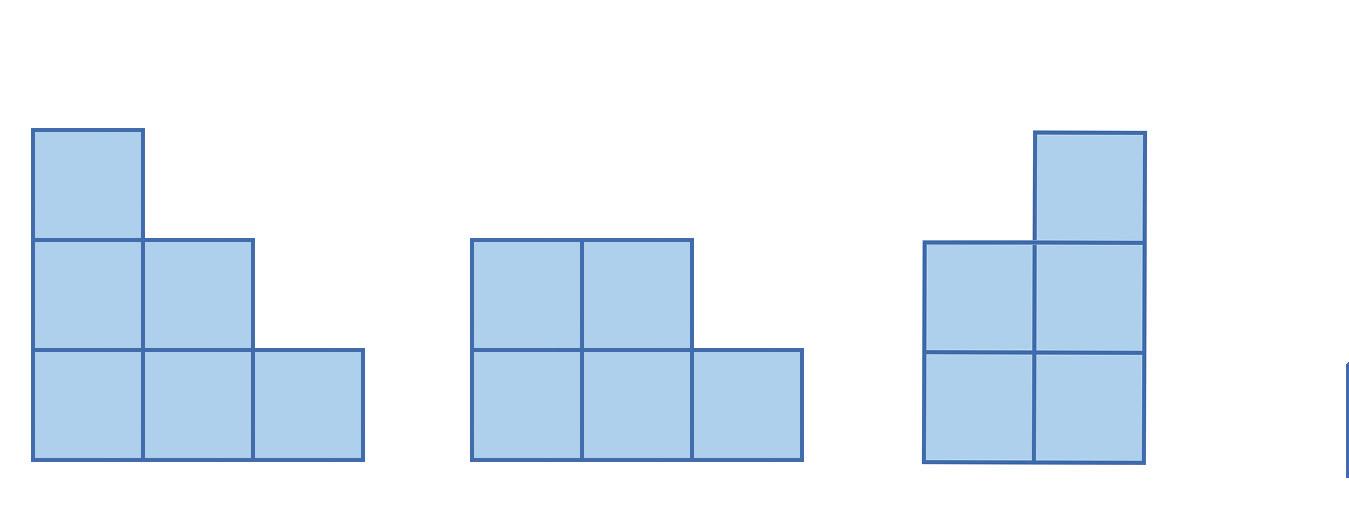
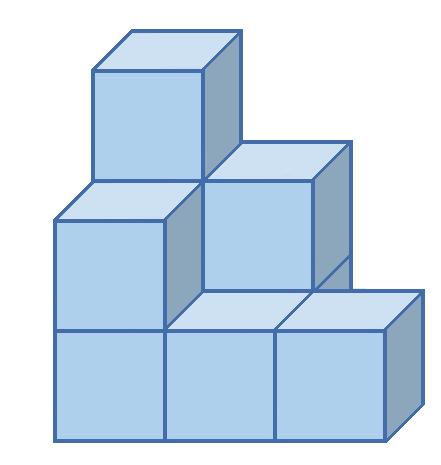
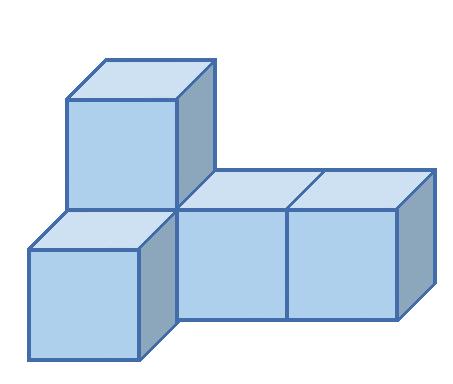
6. Z kociek postavte telesá, ktorých nárys, pôdorys a pravý bokorys je na obrázkoch.

nárys pôdorys pravý bokorys

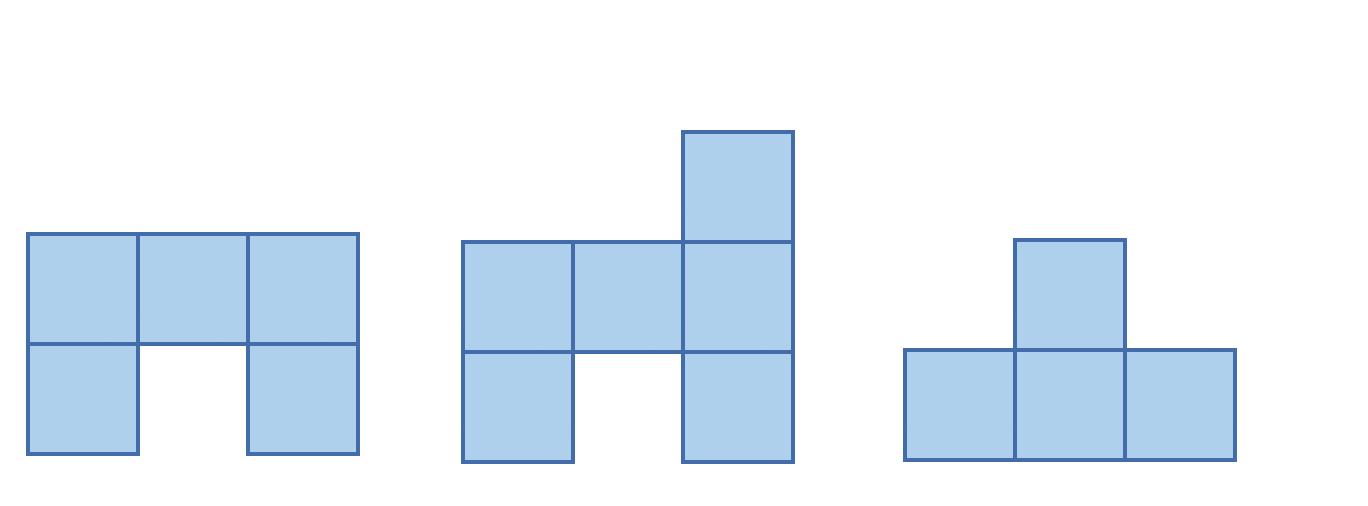
nárys pôdorys pravý bokorys

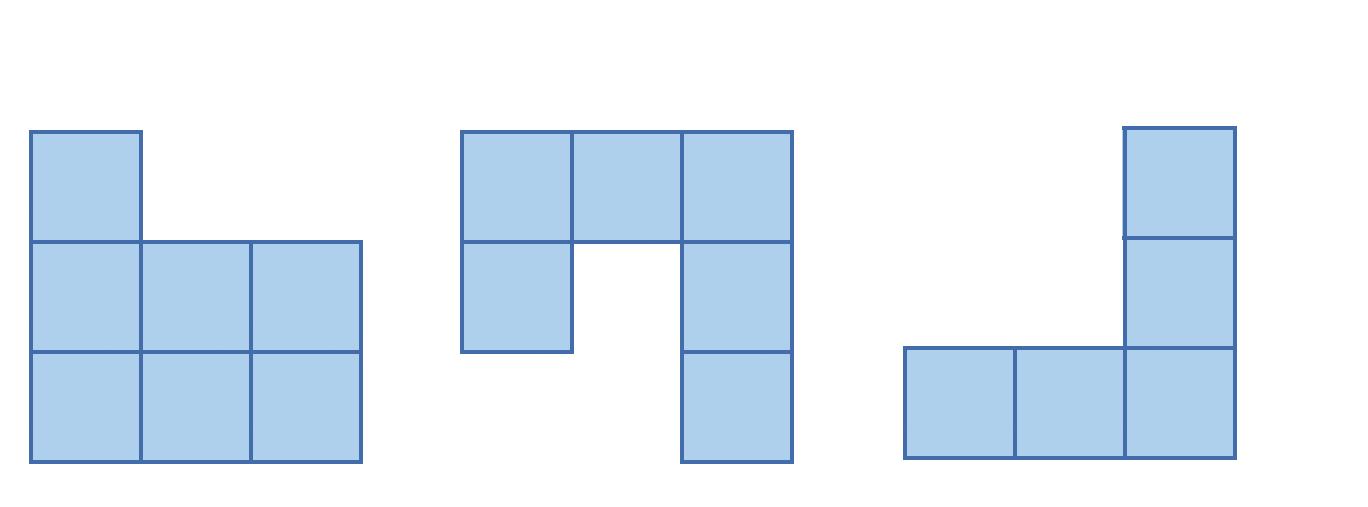
nárys pôdorys pravý bokorys

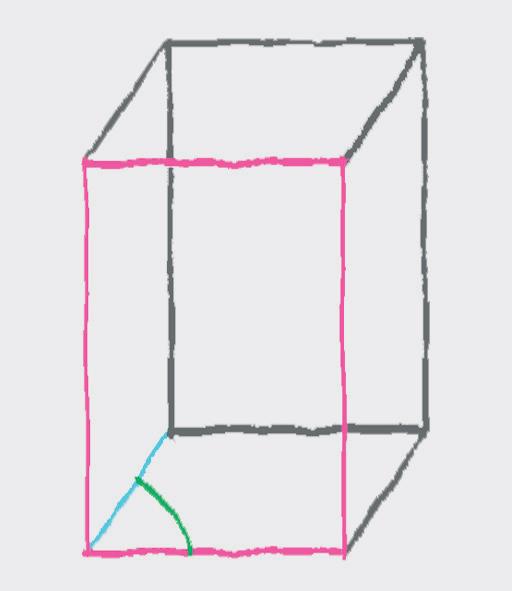
7. Na priehľadnej kocke je navinutý drôt podľa obrázka. Nakreslite nárys, pôdorys a pravý bokorys tejto kocky.

8. Na obrázku je nárys, pôdorys a pravý bokorys priehľadnej kocky, na ktorej je navinutý drôt.

Nakreslite kocku s navinutým drôtom vo voľnom rovnobežnom premietaní.

nárys pôdorys bokorys

4.4 Sieť kvádra a kocky

PROBLÉM 4

Jakub má lepenkovú škatuľu tvaru kocky a chce si z lepenky vyrobiť rovnakú škatuľu. Rozmýšľa, ako sa to dá urobiť.

RIEŠENIE

Spolužiačka Danka mu radí, aby škatuľu rozstrihol po niektorých hranách, rozložil ju, a tak získal tvar lepenky, z ktorej sa dá zložiť škatuľa. Rozmýšľa, po ktorých hranách má škatuľu strihať. Jakub najprv rozstrihol hrany označené červenými krížikmi a škatuľu otvoril.

Potom rozstrihol ďalšie hrany označené červenými krížikmi a steny škatule rozložil do roviny.

Dostal rovinný útvar, ktorý sa nazýva sieť kocky.

Dostal útvar, sa sieť k

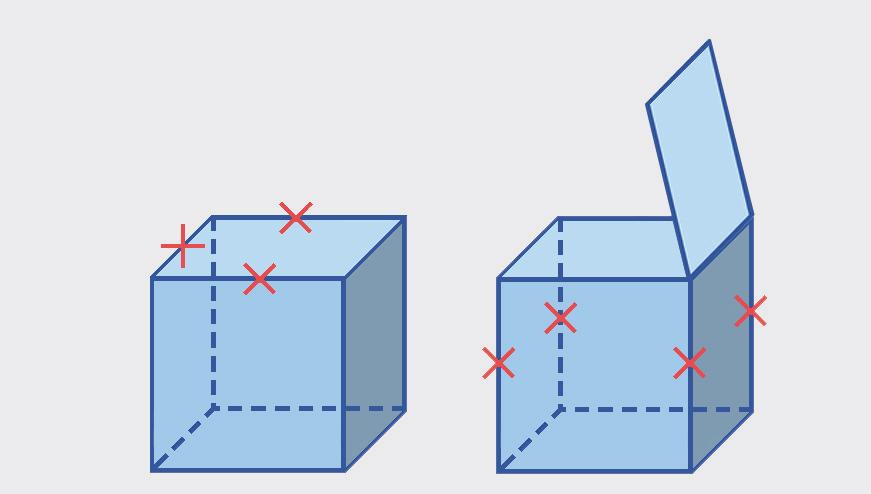
Keď si Jakub rovnaký útvar vystrihol z lepenky, zistil, že z neho vie zložiť rovnakú škatuľu, ako bola pôvodná škatuľa.

Sieť kocky vznikne, ak steny kocky rozložíme do roviny tak, aby po ich opätovnom zložení vznikla kocka.

Keďže kocka má šesť sien tvaru zhodných štvorcov, sieť kocky tvorí šesť zhodných štvorcov. a a a a a a

Povzbudený úspechom sa Jakub rozhodol, že si podobným spôsobom vyrobí rovnakú škatuľu tvaru kvádra, ktorú našiel doma.

Postupoval rovnako ako v prípade kocky. Po rozstrihnutí hrán označených červenými krížikmi a rozložení stien kvádra do roviny dostal sieť kvádra.

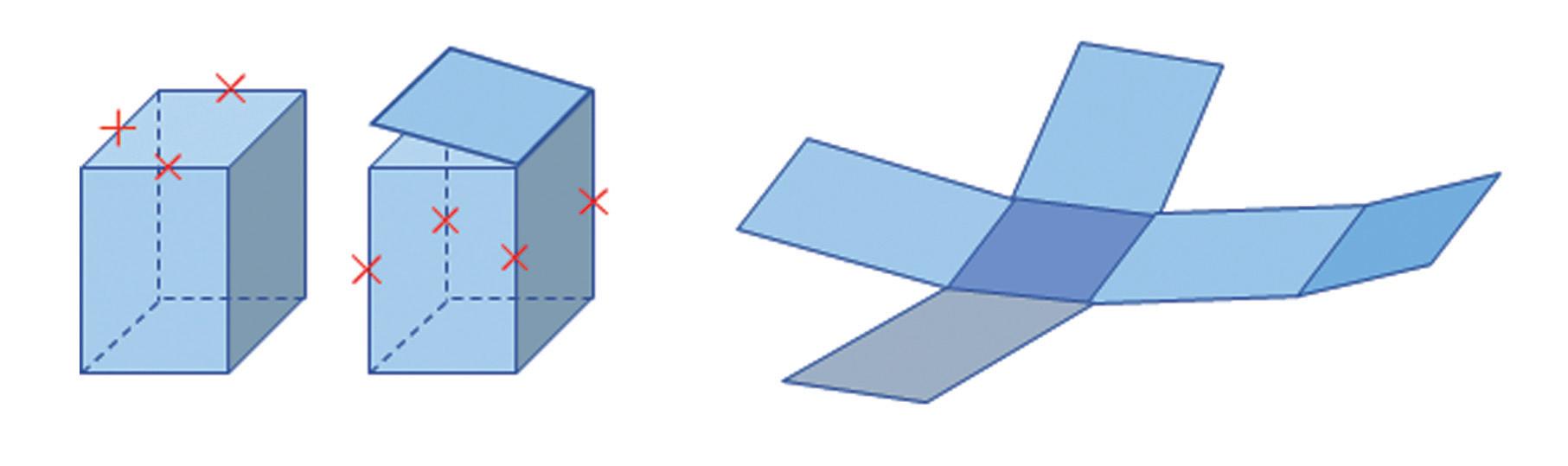
Keď si Jakub rovnaký útvar vystrihol z lepenky, zistil, že z neho vie zložiť rovnakú škatuľu, ako bola pôvodná škatuľa.

Sieť kvádra vznikne, ak steny kvádra rozložíme do roviny tak, aby po ich opätovnom zložení vznikol kváder.

Keďže kváder má šesť sien, ktoré sú po dvoch zhodné obdĺžniky alebo štvorce, sieť kvádra tvorí šesť po dvoch zhodných obdĺžnikov alebo štvorcov.

Dĺžky troch hrán kvádra, ktoré vychádzajú z toho istého vrcholu, nazývame rozmery kvádra.

PROBLÉM 5

Jakub a Danka rozmýšľajú, či by bolo možné škatuľu tvaru kocky alebo kvádra rozstrihať po hranách aj iným spôsobom, ako to urobil Jakub a ako by vyzerala sieť, ktorá by tak vznikla.

RIEŠENIE

do dostal sieť, ktorá je na obrázku.

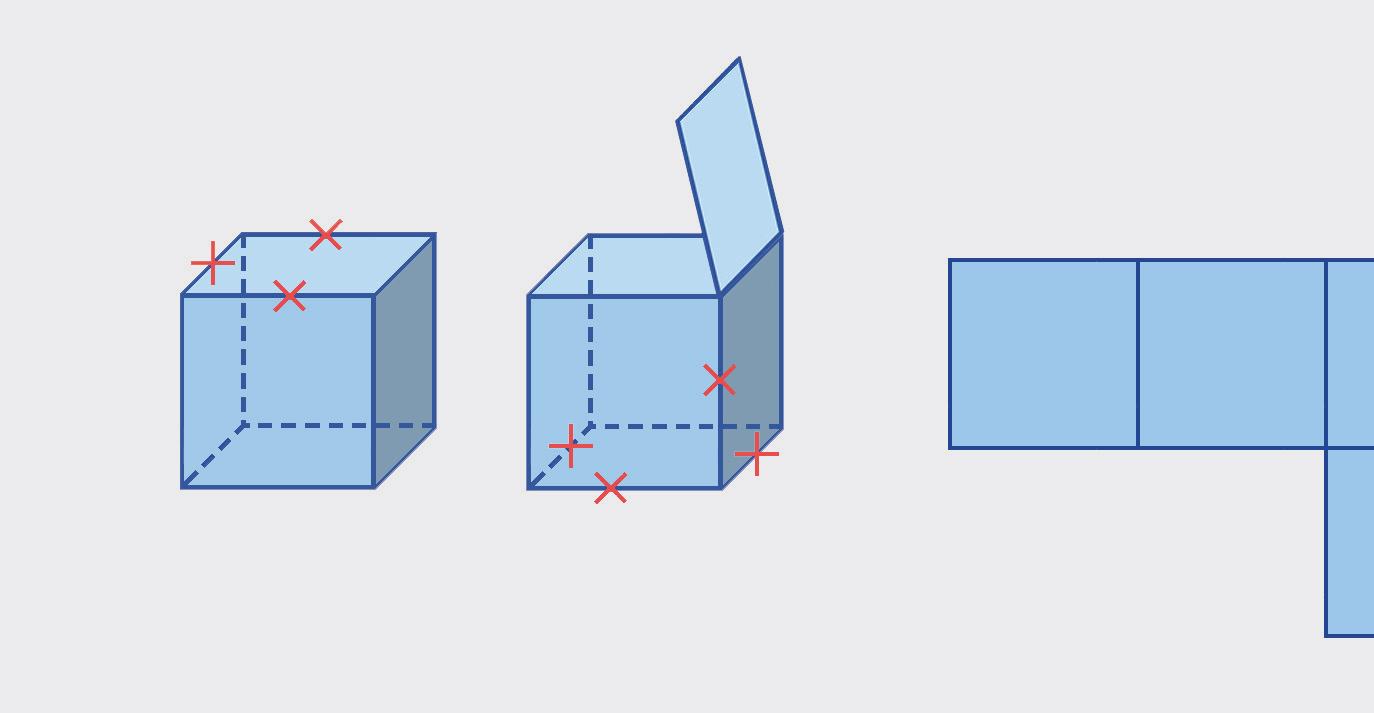
Jakub rozstrihal kocku spôsobom, ktorý je naznačený červenými krížikmi. Po rozložení stien do roviny dostal sieť, ktorá je na obrázku.

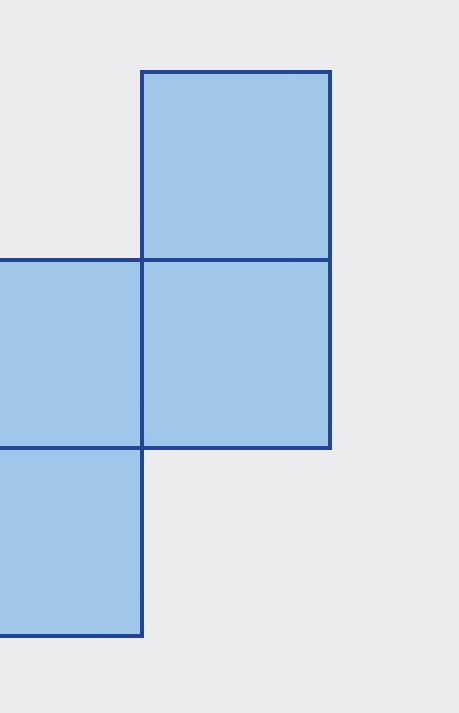
Jakuba Danku zaujímalo možno kocku rozstrihať vznikl

Jakuba aj Danku zaujímalo, koľkými rôznymi spôsobmi možno kocku rozstrihať, aby vznikla vždy iná sieť. Pátrali na internete a zistili, že kocka môže mať 11 rôznych sietí.

ÚLOHA

Narysujte sieť kocky, ktorej hrana má dĺžku 3 cm.

ÚLOHA

Narysujte sieť kvádra, ktorého rozmery sú 2 cm, 3 cm a 5 cm.

ÚLOHA

Narysujte sieť kvádra, ktorého rozmery sú 3 cm, 3 cm a 4 cm.

ÚLOHA

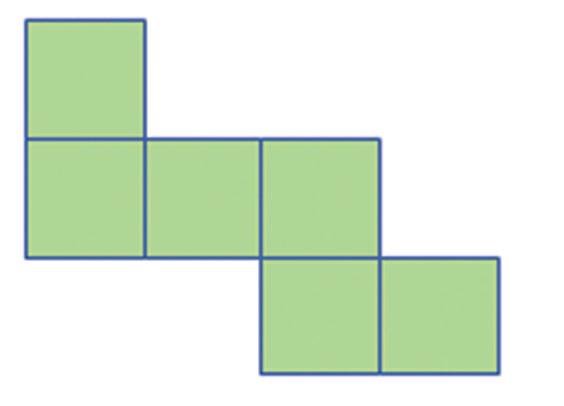
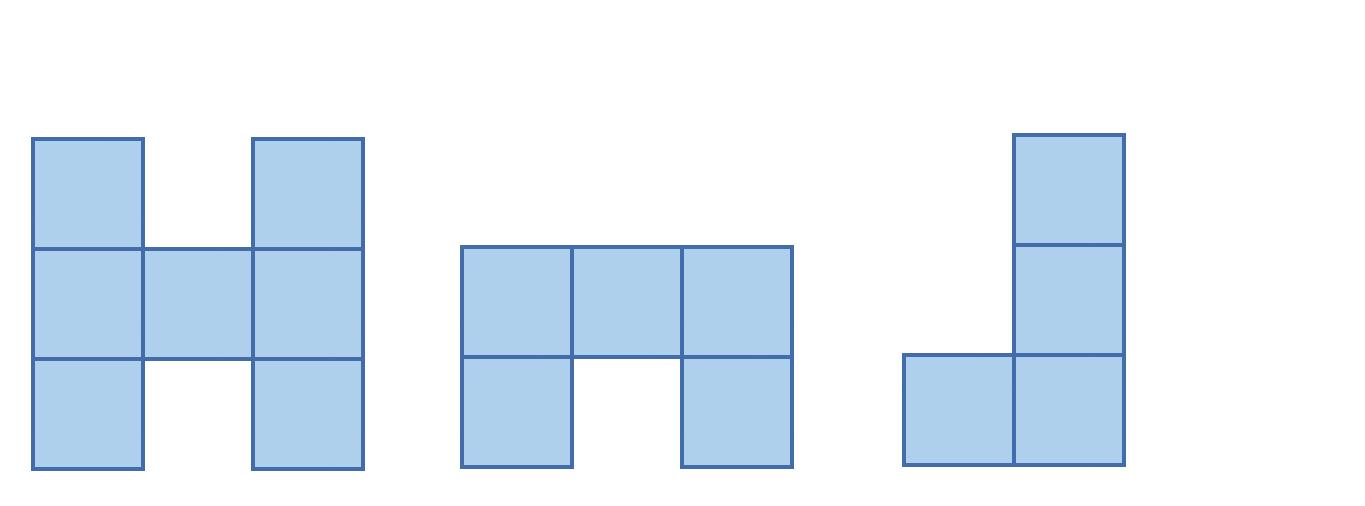
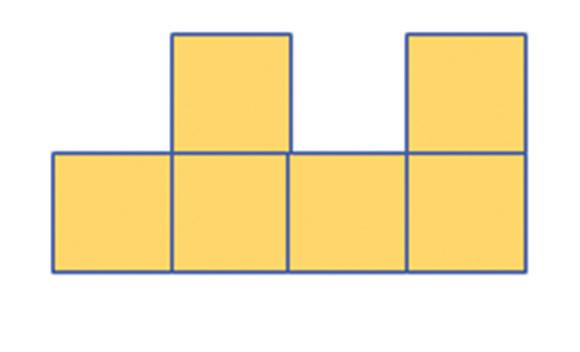
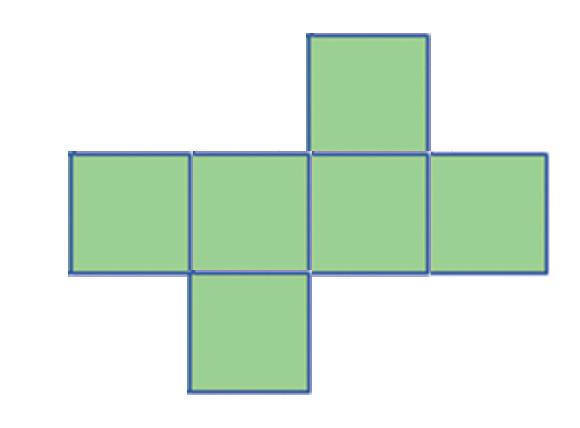
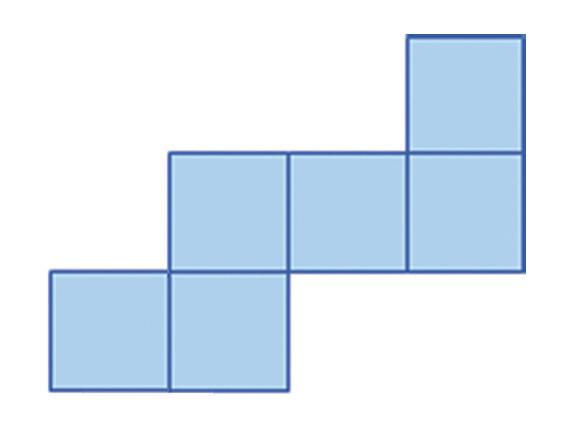
Na ktorých obrázkoch je sieť kocky? a) b) c) aa b bc c b

ÚLOHA

Na obrázku je sieť kocky.

a) Aké číslo bude na stene protiľahlej k stene číslo 5?

b) Aké číslo bude na stene protiľahlej k stene číslo 3?

ÚLOHA

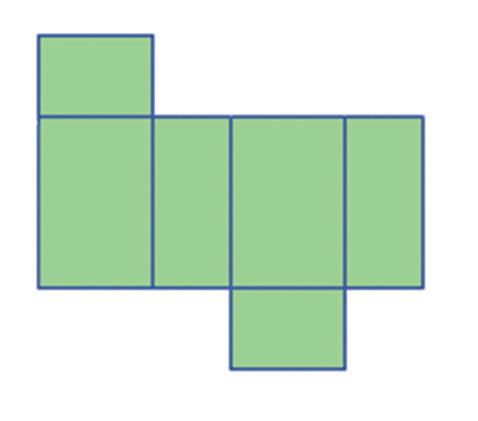
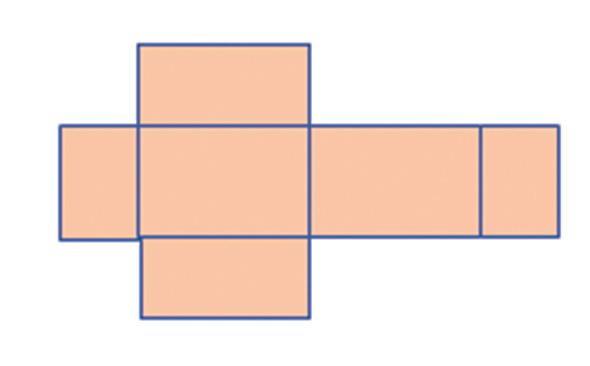
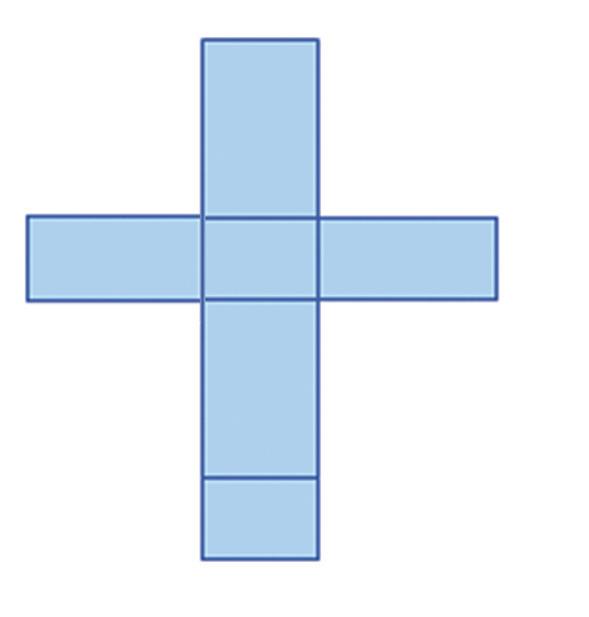
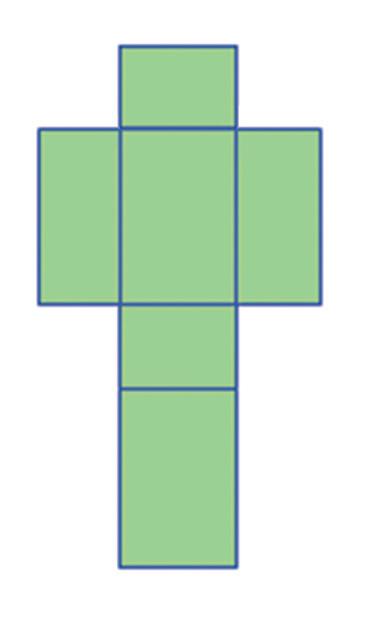
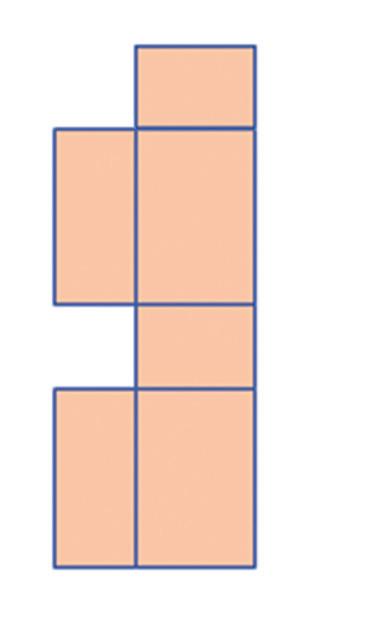
Na ktorých obrázkoch je sieť kvádra? a) b)

5. Na obrázku sú siete dvoch kociek. a) Aké písmeno bude na stene protiľahlej k stene B? b) Aké písmeno bude na stene protiľahlej k stene F? c) Aké číslo bude na stene protiľahlej k stene V? CVI

1. Narysujte sieť kocky, ktorej hrana má dĺžku 2,5 cm.

2. Narysujte sieť kvádra, ktorého rozmery sú 3 cm, 3 cm a 4 cm.

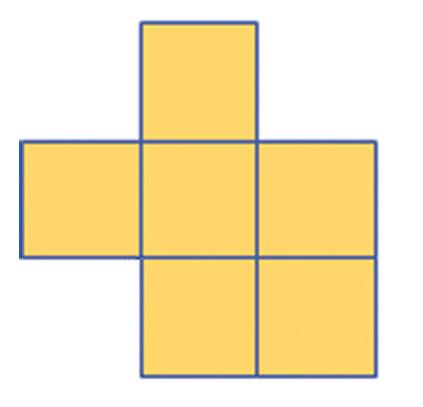
3. Na ktorých obrázkoch je sieť kocky? a) b)

4. Na ktorých obrázkoch je sieť kvádra?