matematika
pre 6. ročník základnej školy a 1. ročník gymnázia s osemročným štúdiom
6
Slovenské pedagogické nakladateľstvo
2. č as ť
Milí šiestaci,
táto učebnica vás bude sprevádzať v druhom polroku školského roka na hodinách matematiky a tiež pri riešení domácich úloh. Čo vás v matematike čaká? Ako vždy, veľa užitočných vedomostí, ktoré neskôr využijete v štúdiu ale i v bežnom živote. Pripravili sme pre vás riešené problémy a príklady na oboznámenie sa so základnými poznatkami z daného tematického celku a tiež neriešené úlohy a cvičenia, ktoré sú určené na samostatnú prácu alebo na prácu v skupinách, kde budete môcť zdieľať svoje názory a postupy riešenia.
V tomto polroku sa budeme venovať najmä geometrii. Riešením úloh a cvičení v štvrtej kapitole sa naučíte správne analyzovať rôzne obrázky i nákresy z praxe, v ktorých sa vyskytujú rozmery štvorcov a obdĺžnikov. Osvojíte si tiež výpočet obvodu a obsahu týchto rovinných útvarov. Správna znalosť jednotiek dĺžky a obsahu, pomocou ktorých vyjadrujeme obvod a obsah a ich premena, je neodmysliteľnou súčasťou vzdelania každého človeka. Vyriešite i niekoľko úloh o obvode a obsahu pravouhlého trojuholníka a uvedomíte si vzťahy medzi štvorcom, obdĺžnikom a pravouhlým trojuholníkom. Tieto vedomosti vám pomôžu riešiť veľa praktických úloh. Dôležitá je piata kapitola o uhloch a trojuholníkoch. Možno viete, že naša krajina i celý povrch Zeme je presne vymeraný pomocou rozdelenia na trojuholníky. Tento systém sa nazýva triangulácia. Na mnohých miestach Slovenska, na budovách miest i v horách, nájdete tzv. triangulačné body – vrcholy týchto trojuholníkov. Vedieť rozhodnúť o zhodnosti trojuholníkov a trojuholník správne narysovať, patrí k základom dobrých matematických vedomostí. V konštrukciách trojuholníkov, ale i ďalších rovinných útvarov, ktoré sa z trojuholníkov skladajú, vám pomôže aj dynamický geometrický softvér. V šiestej kapitole sa pohráte s kartičkami, farbami, kockami a inými pomôckami a prvkami. Pomôžu vám riešiť zaujímavé úlohy o usporiadaniach prvkov. Svoje vedomosti z učiva celého šiesteho ročníka si môžete overiť vyriešením testov na konci každej kapitoly a súhrnných cvičení v závere učebnice. Dúfame, že s učebnicou budete radi pracovať a vyriešenie úlohy či cvičenia vám prinesie radosť z nových vedomostí z matematiky. Niektoré úlohy a cvičenia vás vyzvú k vlastnému skúmaniu, či k vytvoreniu zaujímavých matematických projektov. Možno aj vy sami vymyslíte pre svojich spolužiakov originálne matematické úlohy. Želáme vám veľa chuti do práce a dobré výsledky pri štúdiu matematiky.
Autori
Pri orientácii v učebnici vám budú pomáhať tieto symboly:
Recenzenti: prof. RNDr. Jozef Doboš, CSc.; Ing. Mgr. Martin Hriňák
Grafický dizajn © SPN – Mladé letá, s. r. o.
– príklad s riešením
– problém s riešením
– zapamätať si
– zhrnutie alebo vysvetlenie
– úloha
– poznámka
Autori © doc. PaedDr. Soňa Čeretková, PhD., prof. RNDr. Ondrej Šedivý, CSc., Ivan Teplička
Ilustrovali: akademická maliarka Táňa Žitňanová, obálku navrhol Ing. Zsolt Urbán
Ministerstvo školstva, vedy, výskumu a športu Slovenskej republiky odporučilo pod. č. 2021/16529:5-A2201 didaktický prostriedok Matematika pre 6. ročník základnej školy a 1. ročník gymnázia s osemročným štúdiom – 2. časť. Odporúčacia doložka nadobúda účinnosť 13. septembra 2021 a má platnosť do 31. augusta 2026.
Tretie vydanie, 2023
Všetky práva vyhradené. Toto dielo ani žiadnu jeho časť nemožno reprodukovať bez súhlasu majiteľa práv.
Zodpovedná redaktorka RNDr. Judita Hollá
Odborná redaktorka RNDr. Jana Belasová Technická redaktorka Ivana Bronišová
Vyšlo vo vydavateľstve Slovenské pedagogické nakladateľstvo – Mladé letá, s. r. o., Sasinkova 5, 811 08 Bratislava
Vytlačili TBB, a. s., Banská Bystrica
ISBN 978-80-10-04300-2
7.3
Obsah 4 OBSAH OBDĹŽNIKA A ŠTVORCA ............................................................................................ 4 4.1 Jednotky dĺžky, obvod mnohouholníka ................................................................................ 4 4.2 Obsah mnohouholníka v štvorčekovej sieti .......................................................................... 6 4.3 Jednotky obsahu, premeny jednotiek obsahu ......................................................................... 9 4.4 Obsah obdĺžnika a štvorca ................................................................................................... 13 4.5 Úlohy na výpočty obsahov a obvodov obrazcov zložených z obdĺžnikov a štvorcov ............. 18 4.6 Obsah pravouhlého trojuholníka .......................................................................................... 20
Stavby z kociek, objem ....................................................................................................... 22 TEST 4 ......................................................................................................................................... 24 5 TROJUHOLNÍK, ZHODNOSŤ TROJUHOLNÍKOV ................................................................. 26 5.1 Základné prvky trojuholníka, trojuholníková nerovnosť ...................................................... 26 5.2 Vnútorné uhly trojuholníka ................................................................................................. 29 5.3 Vonkajšie uhly trojuholníka ................................................................................................ 32 5.4 Výšky trojuholníka ............................................................................................................... 35 5.5 Zhodnosť trojuholníkov ........................................................................................................ 37 5.6 Vety o zhodnosti trojuholníkov ........................................................................................... 39 5.7 Konštrukcia trojuholníkov .................................................................................................. 44
Rovnoramenný trojuholník ................................................................................................. 51 5.9 Rovnostranný trojuholník .................................................................................................... 56 5.10 Konštrukcia trojuholníkov pomocou dynamického geometrického softvéru ...................... 59 TEST 5 ......................................................................................................................................... 68 6 KOMBINATORIKA .................................................................................................................... 70 6.1 Všetky možné usporiadania daného počtu prvkov ............................................................... 71 6.2 Výber a usporiadanie prvkov ............................................................................................... 76 TEST 6 ......................................................................................................................................... 84 7 SÚHRNNÉ CVIČENIA ............................................................................................................... 86 7.1 Počtové výkony s prirodzenými číslami. Deliteľnosť ........................................................... 86
Uhol a jeho veľkosť. Operácie s uhlami ............................................................................... 86
4.7
5.8
7.2
Desatinné čísla, počtové výkony s desatinnými číslami ...................................................... 87 7.4 Obsah obdĺžnika a štvorca ................................................................................................... 88 7.5 Trojuholník, zhodnosť trojuholníkov .................................................................................... 88 7.6 Kombinatorika ..................................................................................................................... 89 ROZUM DO HRSTI ......................................................................................................................... 90 VÝSLEDKY ................................................................................................................................... 92
4.1 Jednotky dĺžky, obvod mnohouholníka
ZOPAKUJMESI
Dĺžku predmetov ľudia vyjadrovali spočiatku v rôznych jednotkách, ktoré odvodili z rozmerov ľudského tela. Tak vznikli jednotky ako lakeť, stopa, palec. Pretože takéto jednotky dĺžky mohli byť v každom meste iné, dohodli sa na používaní jednotiek, ktoré sú vo veľkej časti sveta rovnaké.
Základnou jednotkou dĺžky je meter (m).
Menšie jednotky dĺžky sú decimeter (dm), centimeter (cm), milimeter (mm).
Väčšou jednotkou dĺžky je kilometer (km). Platí:
1 km = 1 000 m = 10 000 dm = 100 000 cm = 1 000 000 mm 1 m = 0,001 km
1 m = 10 dm = 100 cm = 1 000 mm 1 dm = 0,1 m = 0,000 1 km
1 dm = 10 cm = 100 mm 1 cm = 0,1 dm = 0,01 m = 0,000 01 km
1 cm = 10 mm 1 mm = 0,1 cm = 0,01 dm = 0,001 m = 0,000 001 km
PRÍKLAD
Premeňte dané dĺžky na jednotky uvedené v zátvorke:
a) 58 cm (mm) c) 76 dm (m)
b) 7,82 dm (mm) d) 852,6 mm (dm)
RIEŠENIE
Príklad rieši Mariana.
a) 58 cm = 58 . 10 mm = 580 mm;
b) 7,82 dm = 7,82 10 cm = 78,2 cm = 78,2 10 mm = 782 mm; c) 76 dm = 76 . 0,1 m = 7,6 m;
d) 852,6 mm = 852,6 . 0,1 cm = 85,26 cm = 85,26 . 0,1 dm = 8,526 dm.
ÚLOHA
Premeňte na jednotky uvedené v zátvorke: a) 35 km (m) d) 4 250 dm (mm) g) 27,35 km (m) j) 4 627 m (km) b) 723 m (cm) e) 5 736 cm (m) h) 32,45 m (dm) k) 936 dm (m) c) 253 dm (cm) f) 8 276 cm (dm) i) 42,532 dm (cm) l) 5 275 cm (m)
ÚLOHA
Premeňte na jednotky uvedené v zátvorke: a) 31 m 5 dm (cm) d) 48 dm 320 cm (m) g) 532 cm 5 200 mm (dm) b) 27 dm 350 mm (cm) e) 13 m 253 cm (dm) h) 24 dm 28 652 mm (cm) c) 0,03 km 52 cm (dm) f) 64,2 dm 86 cm (mm) i) 42 532 dm 5 m (m)
4
obdĺžnika a štvorca
Obsah
4
Obvod ľubovoľného mnohouholníka je súčet dĺžok všetkých jeho strán. Obvod mnohouholníka budeme označovať o Štvorec má všetky strany rovnako dlhé, preto pre obvod štvorca
s dĺžkou strany a platí: o = 4 a.
Pretože obdĺžnik má dve dvojice rovnako dlhých strán, pre obvod obdĺžnika s dĺžkami strán a, b platí: o = 2 . (a + b).
ÚLOHA
Vypočítajte obvod štvorca, ktorého strana má dĺžku:
a) a = 5 cm
c) a = 9 mm e) a = 7,6 dm
b) a = 7 dm d) a = 3,72 cm f) a = 11,4 mm
Každý výsledok vyjadrite postupne v mm, cm, dm, m.
ÚLOHA
Vypočítajte obvod obdĺžnika, ktorého strany majú dĺžky:
a) a = 5 cm, b = 7 cm c) a = 4 mm, b = 11 dm e) a = 8,3 cm, b = 7,2 dm
b) a = 3 cm, b = 8 dm d) a = 5,3 cm, b = 7,42 cm f) a = 48 mm, b = 11,42 dm
Každý výsledok vyjadrite postupne v mm, cm, dm, m.
ÚLOHA
Vypočítajte v centimetroch dĺžku strany štvorca, ktorého obvod je:
a) o = 5,6 cm b) o = 8,36 dm c) o = 9,24 m
CVI Č ENIA
1. Premeňte na jednotky uvedené v zátvorke:
a) 5 300 m (km) d) 43,2 dm (m) g) 9 750 mm (dm) b) 854 cm (dm) e) 739 cm (dm) h) 8,26 m (cm) c) 53 850 mm (m) f) 5 851 cm (mm) i) 728 dm (m)
2. Premeňte na jednotky uvedené v zátvorke: a) 3,2 dm 5,8 cm (mm) c) 0,5 km 48 dm (m) e) 27 m 483 cm (dm) b) 35 dm 86 mm (cm) d) 73 cm 380 mm (dm) f) 527 cm 95 mm (dm)
3. Vypočítajte obvod obdĺžnika, ktorého strany majú dĺžky: a) a = 3,8 cm, b = 4,2 cm b) a = 9,3 dm, b = 6 cm c) a = 13,5 cm, b = 125 mm Každý výsledok vyjadrite postupne v mm, cm, dm, m.
4. Vypočítajte v centimetroch dĺžku strany štvorca, ktorého obvod je: a) o = 69 cm b) o = 486,6 mm
5. Obvod záhrady tvaru obdĺžnika je 56 m, jedna jeho strana má dĺžku 8 m. Vypočítajte dĺžku druhej strany záhrady.
6. Obdĺžnik má rozmery 42 cm a 8,3 dm. Akú dlhú stranu má štvorec, ktorý má rovnaký obvod ako obdĺžnik? Vypočítajte v centimetroch.
7. Obdĺžnik má rozmery 28,6 cm a 4,52 dm. Akú dlhú stranu má štvorec, ktorý má rovnaký obvod ako obdĺžnik? Vypočítajte v centimetroch.
8. Štvorec má stranu dlhú 4,8 cm. Obdĺžnik má jednu stranu dvakrát dlhšiu ako štvorec a druhú stranu trikrát kratšiu ako štvorec. Ktorý útvar má väčší obvod a o koľko?
5
ZOPAKUJMESI
Obsah útvaru v štvorčekovej sieti budeme určovať počtom štvorčekov, ktoré obsahuje. Ak strana štvorčeka má dĺžku 1 cm, tak obsah jedného štvorčeka je 1 cm2 (jeden štvorcový centimeter). Obsah útvaru budeme označovať písmenom S.
POZNÁMKA
Na obrázku je štvorčeková sieť tvorená štvorčekmi so stranou 1 cm – centimetrová štvorčeková sieť. V centimetrovej štvorčekovej sieti sú znázornené mnohouholníky s obsahom 1 cm2, 2 cm2, 3 cm2 a 4 cm2.
ÚLOHA
Určte obsahy mnohouholníkov v centimetrovej štvorčekovej sieti.
6
4.2 Obsah mnohouholníka v štvorčekovej sieti
A BC DE 1 cm2 2 cm2 3 cm2 4 cm2 4 cm2
PRÍKLAD
Určte obsah (červeného) šesťuholníka v centimetrovej štvorčekovej sieti.
RIEŠENIE
ÚLOHA
Príklad rieši Tomáš. Červený šesťuholník obsahuje 12 štvorčekov so stranou 1 cm (na vedľajšom obrázku žlté) a tri trojuholníky, ktoré sú polovicami takýchto štvorčekov (jeden z nich je zelený). Dvanásť žltých štvorčekov má obsah 12 cm2. Jeden trojuholník je polovica štvorčeka, preto jeho obsah je 0,5 cm2. Potom pre obsah šesťuholníka na obrázku platí:
S = 12 . 1 cm2 + 3 . 0,5 cm2 = 13,5 cm2
Určte obsahy mnohouholníkov v centimetrovej štvorčekovej sieti.
ÚLOHA
V centimetrovej štvorčekovej sieti nakreslite tri rôzne obdĺžniky, ktorých obsah je 12 cm2.
ÚLOHA
V centimetrovej štvorčekovej sieti nakreslite dva rôzne šesťuholníky, ktorých obsah je 14 cm2
7
A C B D
Určte obsahy mnohouholníkov v centimetrovej štvorčekovej sieti.
2. Rozdeľte útvary na obrázku na tri časti, ktoré majú rovnaký tvar aj obsah.
3. Rozdeľte útvary na obrázku na štyri časti, ktoré majú rovnaký tvar aj obsah.
4. V centimetrovej štvorčekovej sieti je obdĺžnik a trojuholník. Určte, o koľko cm2 je obsah obdĺžnika väčší ako obsah trojuholníka. Akú časť obsahu obdĺžnika tvorí obsah trojuholníka?
5. Záhrada má tvar štvorca. V strede jednej jeho strany je studňa S. Janko, Anka a Mirka si rozdelili polievanie záhrady tak, že Janko má poliať polovicu záhrady, Anka a Mirka po jednej štvrtine. Ako si rozdelia záhradu tak, aby každý chodil po vodu iba po svojej časti záhrady?
6. V centimetrovej štvorčekovej sieti je štvorec a mnohouholník. Určte, o koľko cm2 je obsah štvorca väčší ako obsah mnohouholníka: a) b) S
A B C D
8 CVI Č ENIA C
1.
7. Určte v m2 obsah jednotlivých miestností v nasledujúcom pláne bytu znázorneného v štvorčekovej sieti, ktorej štvorčeky v skutočnosti majú strany s dĺžkou 1 m.
1 – Hala
2 – Kuchyňa
3 – Obývacia izba
4 – Detská izba
5 – Spálňa
6 – Kúpeľňa
7 – Špajza
8 – WC
Vypočítajte celkovú výmeru bytu.
4.3 Jednotky obsahu, premeny jednotiek obsahu
V predchádzajúcich úlohách sme obsah vyjadrovali v jednotkách cm2 (štvorcový centimeter).
Jednotku štvorcový centimeter môžeme používať napríklad na vyjadrenie obsahu útvarov, ktoré máme nakreslené v učebnici alebo v zošite, ale nie je vhodná napríklad na vyjadrenie výmery záhrady alebo rozlohy futbalového ihriska. Preto používame rôzne jednotky obsahu, napr.:
1. štvorcový milimeter – mm2 – je obsah štvorca so stranou 1 mm:
2. štvorcový centimeter – cm2 – je obsah štvorca so stranou 1 cm:
3. štvorcový decimeter –dm2 – je obsah štvorca so stranou 1 dm:
4. štvorcový meter –m2 – je obsah štvorca so stranou 1 m.
9
1 dm2 ÚLOHA Narysujte na tabuľu štvorec s obsahom 1 m2 7 2 1 4 6 5 8 3
PROBLÉM 1
Ako sa premieňajú jednotky obsahu 1 mm2, 1 cm2, 1 dm2 a 1 m2?
RIEŠENIE
1. 1 cm2 obsahuje 10 mm . 10 mm = 100 mm2, teda 1 cm2 = 100 mm2.
2. Na obrázku na s. 9 vidieť, že 1 dm2 obsahuje 10 cm . 10 cm = 100 cm2, teda 1 dm2 = 100 cm2.
3. Ak si na tabuľu narysujeme štvorec so stranou 1 m, ktorého obsah je 1 m2, zistíme, že obsahuje 10 dm 10 dm = 100 dm2, teda 1 m2 = 100 dm2.
PRÍKLAD
1 cm2 = 100 mm2
1 dm2 = 100 cm2
1 m2 = 100 dm2
Premeňte na jednotky uvedené v zátvorke:
a) 7 cm2 (mm2) c) 76 dm2 (m2)
b) 5,4 dm2 (mm2) d) 852,6 cm2 (m2)
RIEŠENIE
Príklad rieši Jurko.
a) 7 cm2 = 7 100 mm2 = 700 mm2;
1 mm2 = 0,01 cm2
1 cm2 = 0,01 dm2
1 dm2 = 0,01 m2
b) 5,4 dm2 = 5,4 . 100 cm2 = 540 cm2 = 540 . 100 mm2 = 54 000 mm2; c) 76 dm2 = 76 0,01 m2 = 0,76 m2; d) 852,6 cm2 = 852,6 0,01 dm2 = 8,526 dm2 = 8,526 0, 01 m2 = 0,085 26 m2.
ÚLOHA
Premeňte na jednotky uvedené v zátvorke:
a) 52 dm2 (cm2) e) 52,3 dm2 (mm2) i) 5 863 dm2 (m2) m) 358,8 cm2 (dm2) b) 24 m2 (dm2) f) 12,6 m2 (dm2) j) 4 635 mm2 (cm2) n) 785,6 cm2 (m2) c) 483 dm2 (mm2) g) 58,7 dm2 (cm2) k) 75 cm2 (dm2) o) 358,25 mm2 (dm2) d) 526 cm2 (mm2) h) 8,57 cm2 (mm2) l) 1 482 cm2 (m2) p) 826,4 mm2 (dm2)
ÚLOHA
Premeňte na jednotky uvedené v zátvorke: a) 7 dm2 5 cm2 (mm2) c) 0,8 dm2 85 mm2 (cm2) e) 5,3 dm2 495 mm2 (cm2) b) 6 m2 73 cm2 (dm2) d) 2,4 m2 452 cm2 (dm2) f) 0,75 dm2 0,2 cm2 (mm2)
ÚLOHA
Doplňte tabuľku: m2 dm2 cm2 mm2
000
10
200
135 0,72 1,02
PROBLÉM 2
RIEŠENIE
Problém vysvetlila pani učiteľka.
Jeden ár je obsah štvorca so stranou 10 m, teda 1 a = 100 m2.
Jeden hektár je obsah štvorca so stranou 100 m, teda 1 ha = 10 000 m2 = 100 a.
Pani učiteľka ešte dodala, že poznáme aj väčšiu jednotku obsahu – jeden štvorcový kilometer (1 km2), ktorá sa používa na vyjadrenie rozlohy krajín a ich častí.
Števko má starých rodičov, ktorí bývajú na dedine. Dozvedel sa, že poľnohospodárska pôda v okolí dediny má výmeru 2 500 hektárov. Miško zasa pripomenul, že oni majú záhradu s výmerou 10 árov. Obaja chceli vedieť, čo je hektár a čo je ár. m, ted e a
1a=100m2
Jeden štvorcový kilometer je obsah štvorca so stranou 1 km, teda 1 km2 = 100 ha = 10 000 a = 1 000 000 m2.
1 a = 100 m2
1 ha = 100 a
ÚLOHA
Premeňte na jednotky uvedené v zátvorke:
1 m2 = 0,01 a
1 a = 0,01 ha 1 km2 = 100 ha
1 ha = 0,01 km2
a) 5,35 km2 (ha) e) 27,3 ha (a) i) 42 536 a (km2)
b) 0,785 km2 (a) f) 2,68 ha (m2) j) 42 760 m2 (km2)
c) 0,852 km2 (m2) g) 28,3 a (m2) k) 3 625 m2 (ha) d) 427 ha (km2) h) 352 a (ha) l) 276 m2 (a)
ÚLOHA
V tabuľke je uvedená rozloha niektorých štátov zaokrúhlená na stovky km2.
Napíšte poradie štátov podľa rozlohy od najmenšej po najväčšiu.
Štát SlovenskoČeskoPoľskoMaďarskoRakúskoŠvajčiarsko
Rozloha [km2]49 00078 900312 70093 00083 90041 300
CVI Č ENIA
1. Premeňte na jednotky uvedené v zátvorke:
a) 3 720 cm2 (dm2)
b) 173 dm2 (m2)
c) 35 700 mm2 (dm2)
d) 9 830 cm2 (dm2)
e) 635 000 mm2 (dm2)
f) 126 000 cm2 (m2)
g) 5,85 m2 (dm2)
h) 32,57 cm2 (mm2)
2. Premeňte na jednotky uvedené v zátvorke:
a) 5,3 dm2 3,7 cm2 (mm2) c) 352 cm2 6 300 mm2 (dm2)
b) 7,5 m2 274 dm2 (cm2) d) 520 dm2 360 cm2 (m2)
i) 17,53 dm2 (cm2)
j) 127,5 dm2 (mm2)
k) 75 m2 (cm2)
l) 24,92 m2 (mm2)
e) 3,5 dm2 620 mm2 (cm2)
f) 0,68 m2 530 cm2 (dm2)
11
3. Doplňte tabuľku: a) b)
4. Premeňte na jednotky uvedené v zátvorke:
a) 3,74 km2 (ha) d) 4,53 ha (m2) g) 28 300 a (km2)
b) 0,452 km2 (a) e) 72,3 a (m2) h) 3 520 a (ha)
c) 85,5 ha (a) f) 6 335 ha (km2) i) 138 ha (a)
5. Premeňte na jednotky uvedené v zátvorke:
a) 7 ha 3 750 m2 (a) c) 0,53 ha 27 a (m2) e) 2,7 ha 352 a (m2)
b) 0,85 km2 5 200 m2 (ha) d) 0,56 km2 4 820 a (ha) f) 268 ha 4 256 a (km2)
6. Najväčšia rekreačná vodná plocha na Slovensku je Zemplínska šírava.
Jej rozloha je 3 290 ha.
Koľko je to km2?
7. Najväčšie jazero na Zemi je Kaspické more. Jeho rozloha je asi 371 000 km2 Vyjadrite rozlohu jazera v hektároch a v ároch.
8. Rozloha lesov na Slovensku je 2 006 939 ha. Vyjadrite ju v km2.
9. Rozloha Bratislavy je 367,6 km2. Koľko je to hektárov?
10. Pohorie Alpy sa nachádza na území siedmich štátov: Francúzska, Talianska, Švajčiarska, Nemecka, Lichtenštajnska, Rakúska a Slovinska. Alpy sú klimatické a vodné rozhranie medzi strednou a južnou Európou. Rozloha Álp je 192 753 km2. Vyjadrite rozlohu Álp v hektároch.
11. V tabuľke je uvedená rozloha krajov Slovenska v km2
Napíšte poradie krajov podľa rozlohy od najmenšieho po najväčší.
Koľko hektárov má najmenší kraj a koľko hektárov má najväčší kraj?
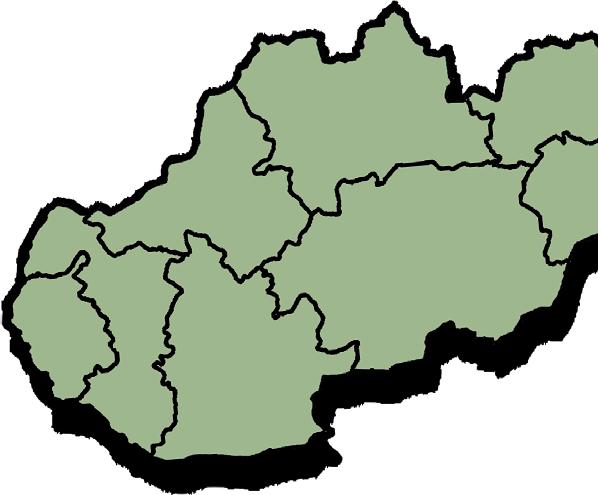
KrajRozloha [km2]
Bratislavský (BA) 2 053
Trnavský (TT)4 147
Trenčiansky (TN)4 502
Nitriansky (NR) 6 344
Žilinský (ZA)6 809
Banskobystrický (BB)9 454
Prešovský (PO)8 974
Košický (KE)6 755
12
m2 dm2 cm2 mm2 2,48 457 65 300 8 450 000 km2 haam2 5,27
384 27 250
6 830 000
PROBLÉM 3
Vypočítajte obsah obdĺžnika, ak poznáte dĺžky jeho
susedných strán a , b
RIEŠENIE
Problém riešia Matúš a Natália.
Matúš uvažuje, že ak chce určiť obsah obdĺžnika, napríklad v cm2, potrebuje určiť, koľko štvorčekov centimetrovej štvorčekovej siete obdĺžnik obsahuje.
Obdĺžnik A na obrázku obsahuje 12 štvorčekov centimetrovej štvorčekovej siete, preto jeho obsah je S = 12 cm2, teda S = ab
Obdĺžnik B na obrázku obsahuje 15 štvorčekov centimetrovej štvorčekovej siete, preto jeho obsah je S = 15 cm2, teda opäť S = a . b.
bAB = 4 cm b = 3 cm
a = 3 cm
a = 5 cm
Natália mierni jeho nadšenie. Obdĺžniky A aj B majú dĺžky strán prirodzené čísla, teda obsahujú celé štvorce centimetrovej štvorčekovej siete. Ako vypočítame obsah obdĺžnika, ak dĺžky jeho strán budú desatinné čísla?
bCD = 4 cm
a = 3,5 cm a = 4,5 cm
0,25 cm2
b = 2,5 cm
Natália vidí, že obdĺžnik C obsahuje 12 celých štvorčekov centimetrovej štvorčekovej siete a 4 polovice štvorčekov. Keď celý štvorček má obsah 1 cm2, tak polovica štvorčeka bude mať obsah 0,5 cm2, potom štyri polovice štvorčekov budú mať obsah 4 0,5 cm2 = 2 cm2. Obsah obdĺžnika C bude: S = (12 + 2) cm2 = 14 cm2
Matúš počíta inak: S = 3,5 cm 4 cm = 14 cm2. Výsledky sa rovnajú, teda overil, že aj pre obsah obdĺžníka C platí S = a . b
Podľa Natálie obdĺžnik D obsahuje 8 celých štvorčekov centimetrovej štvorčekovej siete, 6 polovíc štvorčekov a 1 štvrtinu štvorčeka, ktorej obsah je 0,25 cm2. Potom obsah obdĺžnika D bude: S = 8 cm2 + 6 . 0,5 cm2 + 0,25 cm2 = (8 + 3 + 0,25) cm2 = 11,25 cm2.
Matúš použije vzorec S = a . b = 4,5 cm . 2,5 cm = 11,25 cm2. Výsledky sa rovnajú.
13
štvorca
4.4 Obsah obdĺžnika a
Matúš rozmýšľa, ako by vypočítal obsah obdĺžnika E, ktorého strany sú a = 4,7 cm, b = 3 cm. Obdĺžnik E obsahuje 12 celých štvorčekov centimetrovej štvorčekovej siete a 3 časti štvorčekov. Aký obsah má jedna z nich? Štvorček rozdelil zvislými úsečkami na 10 rovnakých „pásikov“, preto jeden „pásik“ má obsah 0,1 cm2, 7 „pásikov“ má obsah 0,7 cm2
Potom obsah obdĺžnika E bude:
b = 3 cm
E a = 4,7 cm
S = 12 cm2 + 3 0,7 cm2 = (12 + 2,1) cm2 = 14,1 cm2. Ak použije vzorec S = a . b , tak S = 4,7 cm . 3 cm = 14,1 cm2. Výsledok je rovnaký.
Natáliu ešte zaujíma, ako sa dá vypočítať obsah štvorca, ktorého strana má dĺžku a. Uvažuje, že ak chce určiť obsah štvorca napríklad v cm2, potrebuje určiť, koľko štvorčekov centimetrovej štvorčekovej siete štvorec obsahuje. Rovnakými úvahami ako pre obdĺžnik príde k záveru, že obsah štvorca so stranou a sa vypočíta podľa vzorca:
S = aa.
Obsah obdĺžnika vypočítame tak, že vynásobíme dĺžky jeho dvoch susedných strán:
S = ab
Obsah štvorca vypočítame tak, že vynásobíme dĺžky jeho ľubovoľných dvoch strán:
S = aa
Dĺžky strán musia byť vždy vyjadrené v rovnakých jednotkách.
POZNÁMKA
Ak chceme obsah obdĺžnika alebo štvorca vypočítať v mm2 (cm2, dm2, m2), vyjadríme dĺžky jeho strán v mm (cm, dm, m).
ÚLOHA
Spamäti vypočítajte obsah obdĺžnikov s rozmermi: a) 4 m a 6 m c) 5 dm a 7 dm e) 4 m a 0,5 m b) 10 cm a 20 cm d) 6 dm a 20 cm f) 0,6 m a 8 dm
PRÍKLAD
Vypočítajte obsah obdĺžnika ABCD , ktorého susedné strany majú dĺžky a = 5,8 cm a b = 4,5 cm.
RIEŠENIE
Zapíšeme známe údaje: a = 5,8 cm b = 4,5 cm
Zapíšeme, v akých jednotkách vypočítame obsah obdĺžnika: S = ... cm2
Zapíšeme vzorec pre obsah obdĺžnika: S = a . b
Do vzorca dosadíme: S = 5,8 cm . 4,5 cm
Vypočítame: S = 26,1 cm2
Napíšeme odpoveď: Obsah obdĺžnika ABCD je 26,1 cm2.
14
D Aa b C B
PRÍKLAD
Vypočítajte v m2 obsah dosky stola tvaru obdĺžnika, ak jej rozmery sú 135 cm a 0,8 m.
RIEŠENIE
PRÍKLAD
a = 135 cm = 1,35 m S = ab
b = 0,8 m
S = ... m2
S = 1,35 m . 0,8 m
S =1,08 m2
Obsah dosky stola je 1,08 m2. a b
Obsah obdĺžnika ABCD je 46,98 m2. Dĺžka strany AB je 8,7 m. Vypočítajte dĺžku susednej strany a obvod obdĺžnika.
RIEŠENIE
1. Vypočítame dĺžku susednej strany: S = 46,98 m2
S = a . b
a = 8,7 m 46,98 m2 = 8,7 m . b
b = ... m
b = (46,98 : 8,7) m
b = 5,4 m
2. Vypočítame obvod obdĺžnika:
ÚLOHA
Dĺžka jednej strany obdĺžnika je 6 dm.
Dĺžka susednej strany obdĺžnika je 5,4 m.
a = 8,7 m
o = 2 (a + b)
b = 5,4 m o = 2 . (8,7 m + 5,4 m)
o = ... m o = 2 . 14,1 m
o = 28,2 m
Obvod obdĺžnika je 28,2 m.
Spamäti vypočítajte dĺžku susednej strany, ak obsah obdĺžnika je:
a) 12 dm2
b) 24 dm2
ÚLOHA
Doplňte do tabuľky chýbajúce
c) 42 dm2
d) 54 dm2
údaje pre obdĺžnik so susednými stranami a, b
ÚLOHA
Strana a Strana b Obvod o Obsah S 4,7 cm 5,2 cm 2,6 dm 14,82 dm2 0,8 m 44 dm
4,6 dm 166 cm
Nájdite rozmery aspoň troch obdĺžnikov, ktorých obsah je 27 cm2.
15
D Aa b C B S b
D Aa b C B o=
o =
=?
?
PRÍKLAD
Vypočítajte obsah a obvod štvorca so stranou dĺžky 6,5 cm.
RIEŠENIE
AB DC a
a = 6,5 cm S = a . ao = 4 . a
S = ... cm2 S = 6,5 cm 6,5 cm o = 4 6,5 cm
o = ... cm S = 42,25 cm2 o = 26 cm
Obsah štvorca je 42,25 cm2 a obvod štvorca je 26 cm.
ÚLOHA
Spamäti vypočítajte obsah štvorca so stranou dĺžky: a) a = 6 cm c) a = 5 mm b) a = 4 dm d) a = 10 m
ÚLOHA
a) Aký je obvod štvorca, ktorého obsah je 16 cm2?
b) Aký je obsah štvorca, ktorého obvod je 24 cm?
PRÍKLAD
Vypočítajte obvod a obsah obrazca na obrázku. Rozmery sú v centimetroch.
RIEŠENIE
Príklad riešia Natália a Samo. Natália rozdelí obrazec na dve časti – obdĺžnik so stranami 25 cm a 35 cm a štvorec so stranou 15 cm. Navrhne vypočítať obsah každej časti. Obsah celého obrazca potom bude súčtom obsahov obidvoch častí. Samo začne počítať:
1. a = 35 cm 2. c = 15 cm
b = 25 cm
S1 = ... cm2 S2 = ... cm2
S1 = a . bS2 = c . c
S1 = 35 cm . 25 cm S2 = 15 cm . 15 cm
S1 = 875 cm2 S2 = 225 cm2
3. Obsah obrazca je: S = S1 + S2
S = 875 cm2 + 225 cm2
S = 1 100 cm2
4. Obvod obrazca je: o = ... cm o = 25 cm + 50 cm + 15 cm + 15 cm +10 cm + 35 cm o = 150 cm
Obsah obrazca je 1 100 cm2 a obvod obrazca je 150 cm.
ÚLOHA
Samo rozdelí obrazec z príkladu 8 takto: Vypočítajte obsah obrazca v tomto prípade.
16
25 15 15 50 35 3 4 O 25 50 35 15