MATEMATIK

Hej elev!
Vi som har skrivit Scala Matematik 9 heter Daniel och Stina och är lärare i matematik. Vi hoppas att du ska tycka att det är roligt att arbeta i Scala och att du kommer lära dig riktigt mycket.
Boken är indelad i fyra kapitel som alla är uppbygda på samma sätt.
Inledning
Varje kapitel har ett Mål. Det talar om vad du ska kunna när du har arbetat klart med kapitlet.
I texten Visste du att… tar vi upp intressanta fakta med koppling till innehållet i kapitlet, sådant som är både användbart och kul att veta.
Aktivitet är en förberedelse inför kapitlet. Problemet i aktiviteten har många lösningar och du får en möjlighet att påminnas om allt du redan kan.
Teori
och uppgifter
I teoritexterna presenterar vi de begrepp som du behöver lära dig. Till texterna hör Begreppsfrågor som hjälper dig att förstå vad du har läst.
Exempel visar hur du använder viktiga metoder. Lösning visar vad du behöver redovisa skriftligt och Tankegång hur du kan tänka och ibland redovisa muntligt.
Uppgifterna är indelade i tre nivåer. Du kan börja på nivå 1 eller 2 och det är bra att göra minst två nivåer – nivå 1 och 2 eller nivå 2 och 3.
I Mixat får du repetera, träna på att välja metod och väva ihop nya kunskaper med gamla.
Avslutning
I Sammanfattning har vi samlat det viktigaste i kapitlet på ett uppslag.
Med hjälp av Kapiteltest kan du testa dina nya kunskaper. Efter testet kan du välja repetitionsuppgifter på den nivå som passar dig.
Om du vill utmana dig själv och försöka lösa riktigt svåra uppgifter är
Fördjupning något för dig.
Efter kapitel 4 hittar du Sammanfattning och Repetition av allt innehåll i Scala 7–9.
Sist i boken finns ett kapitel om Programmering i Python.
Lycka till!
Daniel och Stina
Innehåll
3.2 Förändring
3.3 Jämförelser och förhållanden
4.1 Skala 184
Bestämma längdskalan 186
Beräkningar med längdskala 188 Kartor 190 Areaskala 192
Volymskala 194 Mixat 1.1–4.1 196
4.2 Likformighet och kongruens 198
Likformiga och kongruenta figurer 200
Likformiga och kongruenta trianglar 202
Räkna med likformighet 204
Problemlösning med likformighet 206
Topptrianglar och likformighet 208
Area och volym i likformiga figurer 210 Mixat 1.1–4.2 212
4.3 Pythagoras sats 214
triangeln rätvinklig? 216
1.2 Potenser, enheter och prefix
En summa med flera likadana termer kan vi kortare skriva som en produkt
En produkt med flera likadana faktorer kan vi kortare skriva som en potens.
Potensen 25 uttalas ”två upphöjt till fem”.
2:an kallas för potensens bas och talar om att det är faktorn 2 som ska multipliceras. 5:an kallas för potensens exponent och talar om hur många gånger faktorn 2 ska multipliceras med sig själv.
Ett tal kan skrivas i potensform. Det innebär att man skriver talet som en potens med en bas och en exponent. Till exempel kan talet 125 skrivas som en potens med basen 5 och exponenten 3.
125 = 5 ∙ 5 ∙ 5 = 53
En potens med basen 10 kallas för en tiopotens
Tabellen visar hur man skriver talen 10, 100 och 1 000 med tiopotenser. Dessa tiopotenser kan vi använda för att skriva tal i decimalform på olika sätt, till exempel
125 = 1,25 ∙ 100 = 1,25 ∙ 102
125 = 12,5 ∙ 10 = 12,5 ∙ 101
125 = 0,125 ∙ 1 000 = 0,125 ∙ 103
Skrivsättet 1,25 ∙ 102 kallas för grundpotensform
grundpotensform 1,25 ∙ 102 tiopotens tal mellan 1 och 10 grundpotensform
Ett tal i grundpotensform är skrivet som produkten av ett tal mellan 1 och 10 och en tiopotens.
Grundpotensform gör det enklare att uttrycka, jämföra och räkna med stora och små tal, till exempel jordens massa
5 972 000 000 000 000 000 000 000 kg = 5,972 ∙ 1024 kg
Begreppsfrågor
1 Vilket alternativ visar ett annat sätt att skriva 3 ∙ 3
3?
2 Hur uttalas 75?
A ”sju gånger fem” B ”fem upphöjt till sju”
C ”sju upphöjt till fem”
3 Vilket alternativ visar ett annat sätt att skriva 103?
A 10 ∙ 3 B 10 + 3 C 10
4 Vilket alternativ är lika med 23?
5 Vilket alternativ visar talet 800 skrivet i grundpotensform?
6 Vilka alternativ visar tal som är skrivna i grundpotensform?
3
105
3,5 ∙ 105
7 Vilka alternativ visar samma tal? A
Problemlösning
Tom har en stor flagga av tyg som är 1 mm tjockt. Han viker flaggan på mitten så att den blir dubbelt så tjock. Tänk dig att han sedan fortsätter att vika den på mitten.
• Hur tjock skulle den vikta flaggan vara efter – två vikningar – tre vikningar – fem vikningar?
• Hur många gånger skulle Tom behöva vika flaggan för att den ska bli mer än 1 m tjock?
Läs teorin och svara på frågorna.
Exempel
Skriva och beräkna värdet av potenser
Skriv potensen som en produkt och beräkna.
a) 62 b) 34
Lösning
a) 6 2 = 6 ∙ 6 = 36 b) 3 4 = 3 ∙ 3 ∙ 3 ∙ 3 = 9 ∙ 9 = 81
Tankegång
6 multiplicerat med sig självt 2 gånger.
3 multiplicerat med sig självt 4 gånger.
8 Skriv potensen som en produkt och beräkna. a) 52 b) 33 c) 24 d) 15
9 Skriv produkten som en potens.
5
10 Vad ska stå i stället för A–F i tabellen.
11 Skriv tiopotensen i decimalform. a) 102 b) 105 c) 101 d) 103
12 Skriv talet som en tiopotens. a) 100 b) 1 000 c) 1 000 000 d) 10
13 Vilken av punkterna på tallinjen visar talet a) 33 b) 26 c) 62?
14 Skriv potensen som en produkt och beräkna. a) 72 b) 702 c) 0,72 d) 0,22 e) 2002 f) 0,23
15 Vilket tecken ska stå i rutan? Välj mellan <, > eller = a) 0,22 0,4 b) 8 000 402 c) 32 23
16 Vilket tal ska stå i stället för x? a) 64 = 8x b) 27 = 3x c)
17 Skriv som en potens med basen 2.
a) 4 b) 2 c) 8 d) 32
18 Prioriteringsreglerna talar om att potenser beräknas efter parenteser, men före multiplikation och division.
Använd prioriteringsreglerna och beräkna.
a) (3 · 2)2 b) 3 · 22 c) 4 + 32 d) (4 + 3)2
e) 20 – 52 f) 102 + 103 g) 104 – 302 h) 3 · 103
19 En aktie är värd 100 kr.
Prioriteringsregler
1. Parenteser
2. Potenser
3. Multiplikation och division
4. Addition och subtraktion
Hur mycket skulle aktien vara värd efter 5 år om värdet fördubblas varje år?
Skriv som en produkt och beräkna.
a) (–3)2 b) –32
a) (-3) 2 = (-3) ∙ (-3) = 9
b) -3 2 = -3 ∙ 3 = -9
Basen är negativ, alltså (–3) multiplicerat med sig självt 2 gånger.
Potensen är negativ, alltså 3 multiplicerat med sig självt 2 gånger.
20 Skriv potensen som en produkt och beräkna.
a) (–8)2 b) –82 c) (–2)3 d) –23
21 Beräkna
a) (0,2 + 0,6)2 b) 2 ∙ (0,9 – 1)2 c) (1 – 0,5)2 (105 – 95)2 d) (8 – 10)4 – 2
22 I rumstemperatur fördubblas en viss sorts bakterier var 10:e minut.
Hur många bakterier finns det efter 1 h om det från början fanns a) 1 bakterie b) 2 000 bakterier?
23 Skriv talet 16 och talet –16 som potenser med basen a) 4 b) 2 c) (–2) d) (–4)
24 Beräkna och svara i enklaste bråkform.
a) ( 1 4 )2 b) ( 3 7 )2 c) 5 ∙ ( 2 3 )2 d) ( 4 3 )2 – 8 ∙ ( 1 2 )2
25 Beräkna a) ( 1 2 )8 om du vet att ( 1 2 )7 = 1 128 b) (–2)11 om du vet att (–2)10 = 1 024
Exempel
Multiplikation och division av potenser med samma bas
En produkt av potenser med samma bas kan förenklas till en potens.
102 ∙ 103 = 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 = 105
Vi får samma resultat om vi adderar exponenterna.
102 ∙ 103 = 102 + 3 = 105
En kvot av potenser med samma bas kan också förenklas till en potens.
54 52 = 5 · 5 · 5 · 5 5 · 5 = 5 ∙ 5 = 52
Vi får samma resultat om vi subtraherar exponenterna.
54 52 = 54 – 2 = 52
Skriv uttrycket som en potens.
Tankegång
En potens med exponenten 0 har alltid värdet 1. Till exempel är 100 = 1:
Multiplikation och potenserna har samma bas. Adderar exponenterna. 6 = 61
Multiplikation och potenserna har samma bas. Adderar exponenterna.
Division och potenserna har samma bas. Subtraherar exponenterna.
26 Skriv uttrycket som en potens.
27 Skriv uttrycket som en potens.
28 Vilket tal ska stå i stället för x?
29 Skriv först som en potens och beräkna sedan värdet.
Nivå 3
30 Vilket eller vilka av uttrycken i rutan har värdet 16?
31 Bill och Bull gör på olika sätt när de förenklar uttrycket (42)3 till en potens.
Skriv som en potens på Bills eller Bulls sätt. a) (43)2 b) (32)4 c) (104)2
32 Vilket tal ska stå i stället för x?
a) (53)x = 518 b) 1010 10x = 100 c) 25 2x = 1
Vilket tal i potensform är en femtedel av talet 54?
54 5 = 54 51 = 5 4 - 1 = 5 3
Bills lösning: (42)3 = 42 ∙ 42 ∙ 42 = 42 + 2 + 2 = 46
Bulls lösning: (42)3 = 42 ∙ 3 = 46
Dividerar med 5 för att få en femtedel av talet. Förenklar till en potens.
33 Vilket tal i potensform är
a) en tredjedel av talet 38 b) dubbelt så stort som talet 213?
34 Pelle skriver uttrycket 310 + 310 + 310 som en potens.
Skriv som en potens på samma sätt som Pelle. a) 28 + 28 b) 43 + 43 + 43 + 43
Pelles lösning: 310 + 310 + 310 = 3 ∙ 310 = 311
35 Skriv först som en potens och beräkna sedan värdet. a) (45)2 (42)4 b) 104 · 102 (102)3 c) 35 + 35 + 35 32 · 32 d) 24 + 24 8
Skriv a) 84 som en potens med basen 2 b) 2200 som en potens med exponenten 100. a) 8 4 = (2 3) 4 = 2 3 ∙ 4 = 2 12 b) 2 200 = 2 2 ∙ 100 = (2 2) 100 = 4 100
Skriver basen 8 som 23 och förenklar.
Skriver exponenten 2 som 2 ∙ 100 och förenklar.
36 Skriv a) 94 som en potens med basen 3 b) 410 som en potens med basen 2 c) 29 som en potens med exponenten 3 d) 108 som en potens med exponenten 4.
37 Vilket tal ska stå i stället för x? a) 2x = 16 b) 2x = 83 c) 10x = 1003 d) 27x = 915
Stora tal i grundpotensform
Skriv talet i grundpotensform.
a) 300 b) 61 000
Lösning
a) 300 = 3 ∙ 100 = 3 ∙ 10 2
b) 61 000 = 6¸1 ∙ 10 000 = 6¸1 ∙ 10 4
Tankegång
Siffran 3 står på hundratalsplatsen, så 300 = 3 ∙ 100
Sätter in 102 i stället för 100.
Siffran 6 står på tiotusentalsplatsen, så 61 000 = 6,1 ∙ 10 000
Sätter in 104 i stället för 10 000.
38 Skriv talet i grundpotensform.
a) 400 b) 40 000 c) 45 000
d) 4 500 000 e) 600 000 f) 6 800
39 Vilket tal ska stå i rutan?
a) 8 000 = 8 ∙ 10 b) 70 = 7 ∙ 10 c) 78 000 = 7,8 ∙ 10 Skriv talet i decimalform.
a) 9 ∙ 103 b) 1,37 ∙ 106
a) 9 ∙ 10 3 = 9 ∙ 1 000 = 9 000
b) 1‚37 ∙ 10 6 = 1‚37 ∙ 1 000 000 = 1 370 000
40 Skriv talet i decimalform.
a) 4 ∙ 103 b) 4 ∙ 105 c) 4,2 ∙ 105 d) 1,42 ∙ 103 e) 9 ∙ 107 f) 8,9 ∙ 104
Sätter in 1 000 i stället för 103
Skriver siffran 9 på tusentalsplatsen.
Sätter in 1 000 000 i stället för 106.
Skriver siffran 1 på miljontalsplatsen
41 Vilken enhet ska stå efter mätetalet? Välj i rutan.
a) höjden av Kebnekaise: 2,1∙ 103 b) djupet i en pool: 1,35 ∙ 102
c) jordens omkrets: 4 ∙ 104 d) tjockleken av en bok: 1,5 ∙ 101
cm km mm m
42 Skriv avståndet mellan jorden och månen i grundpotensform.

3
43 Skriv talet i grundpotensform.
a) 9 800 b) 251 000 c) 50 700 d) 6 003 000 000
44 Skriv talet i decimalform.
a) 3,9 ∙ 104 b) 8,2 ∙ 106 c) 70,1 ∙ 102 d) 0,467 ∙ 107
45 En buss väger 16 250 kg och en lastbil väger 4,1 ∙ 104 kg.
Vilket fordon väger mest, bussen eller lastbilen?
46 Skriv i decimalform och beräkna. Svara i grundpotensform.
a) 5 ∙ 104 + 3 ∙ 103 b) 5 ∙ 104 + 3 ∙ 102 c) 5 ∙ 102 + 3 ∙ 102 d) 9 ∙ 105 – 7 ∙ 104 e) 9 ∙ 105 – 7 ∙ 103 f) 9 ∙ 103 – 7
47 1 mm3 blod innehåller ungefär 5 ∙ 106 röda blodkroppar och 7 ∙ 103 vita blodkroppar.
a) Hur många röda och vita blodkroppar innehåller 1 mm3 blod sammanlagt?
Svara i grundpotensform.
b) Hur många fler röda än vita blodkroppar innehåller 1 mm3 blod?
Svara i grundpotensform.
Skriv talet 95 ∙ 103 i grundpotensform. 95 ∙ 10 3 = 9‚5 ∙ 10 1 ∙ 10 3 = 9‚5 ∙ 10 4
Skriver 95 i grundpotensform och multiplicerar tiopotenserna 101 ∙ 103 = 101+3 = 104

48 Skriv talet i grundpotensform.
49 Skriv talet i grundpotensform.
a) 6,5 miljoner b) 65 miljarder
c) 0,65 miljoner d) sexhundrafemtio tusen
50 Skriv talen i rutan i storleksordning. Börja med det minsta. 7 ∙ 103 0,1 miljoner 6,99 ∙ 103
51 Beräkna och svara i grundpotensform. a) 2,25
52 Vilket tal ska stå i stället för x? a) 58 ∙ 1010 = 5,8 ∙ 10x b) 10,2 ∙ 105 = x ∙ 104 c) 0,94 ∙ 1014 = 94 ∙ 10x
1
Små tal i grundpotensform
När vi ska förenkla 102 103 kan vi tänka på två olika sätt:
• 102 103 = 10 · 10 10 · 10 · 10 = 1 10 = 0,1
• 102 103 = 102 – 3= 10–1
Det betyder att 0,1 = 10–1
På samma sätt är 0,01 = 10–2 och 0,001 = 10–3 och så vidare. Det innebär att vi även kan skriva tal mellan 0 och 1 i grundpotensform.
Skriv talet i grundpotensform.
a) 0,5 b) 0,0061
Lösning
a) 0¸5 = 5 ∙ 0¸1 = 5 ∙ 10 -1
b) 0¸0061 = 6¸1 ∙ 0¸001 = 6¸1 ∙ 10 -3
Tankegång
Siffran 5 står på tiondelsplatsen, så 0,5 = 5 ∙ 0,1
Sätter in 10–1 i stället för 0,1.
Siffran 6 står på tusendelsplatsen, så 0,0061 = 6,1 ∙ 0,001
Sätter in 10–3 i stället för 0,001.
53 Skriv som en tiopotens.
a) 0,01 b) 0,001 c) 0,1 d) 0,0001
54 Skriv talet i grundpotensform.
a) 0,08 b) 0,008 c) 0,0083 d) 0,083 e) 0,6 f) 0,00069
Skriv talet i decimalform.
a) 9 ∙ 10–3 b) 1,3 ∙ 10–2 a) 9 ∙ 10 -3 = 9 ∙ 0‚001 = 0‚009 b) 1‚3 ∙ 10 -2 = 1‚3 ∙ 0‚01= 0‚013
Sätter in 0,001 i stället för 10–3. Skriver 9 på tusendelsplatsen.
Sätter in 0,01 i stället för 10–2. Skriver siffran 1 på hundradelsplatsen
55 Skriv tiopotensen i decimalform.
a) 10–2 b) 10–3 c) 10–1 d) 10–4
–5
3
56 Skriv talet i decimalform.
a) 2 ∙ 10–3 b) 2 ∙ 10–4 c) 2,7 ∙ 10–4 d) 2,7 ∙ 10–3 e) 9 ∙ 10–1 f) 9,9 ∙ 10–2
57 Vilket alternativ visar fiskelinans tjocklek i decimalform. A 0,003 m B 0,3 m C 0,0003 m D 0,03 m
58 Skriv talet i grundpotensform. a) 0,0067 b) 0,0607 c) 0,374 d) 0,0003091
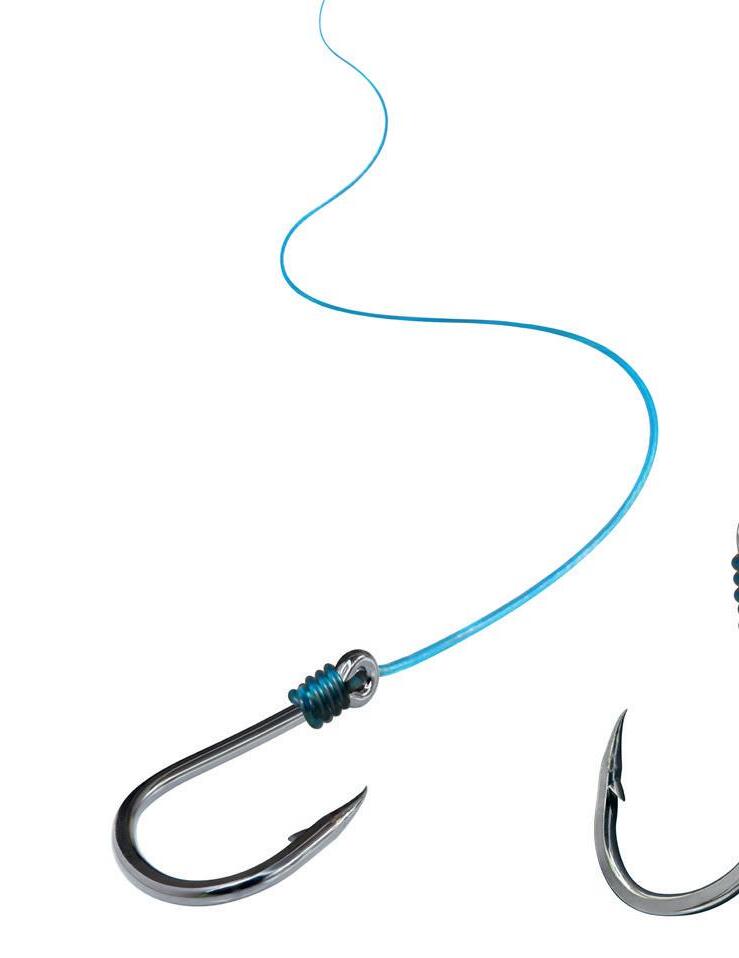
59 Skriv talet i decimalform. a) 1,3 ∙ 10–3 b) 1,66 ∙ 10–1 c) 10,7 ∙ 10–4 d) 0,18 ∙ 10–6
60 Skriv i decimalform och beräkna. Svara i grundpotensform. a) 2 ∙ 10–1 + 6
61 Kvalster är mycket små spindeldjur. Den minsta sorten är ungefär 8 ∙ 10–5 m lång och den största sorten är ungefär 2 ∙ 10–4 m lång.
Beräkna längdskillnaden mellan största och minsta kvalstersorten.
Skriv talet 0,37 ∙ 10–4 i grundpotensform.
Skriver 0,37 i grundpotensform och multiplicerar sedan tiopotenserna 10–1
62 Skriv talet i grundpotensform.
63 Vilket eller vilka tal i rutan är större än 6,4 ∙ 10–4 och mindre än 2,3 ∙ 10–3?
64 Skriv talet i bråkform.
65 Vilket tal ska stå i stället för x?
Exempel
Multiplikation och division av tal i grundpotensform
När vi ska multiplicera och dividera tal i grundpotensform kan vi börja med att skriva talen i decimalform och sedan utföra beräkningen.
3
=
Men vi kan lika gärna beräkna 3 ∙ 2 för sig och 102 ∙ 105 för sig.
3
Beräkna och svara i grundpotensform.
Lösning
Tankegång
1
66 Beräkna och svara i grundpotensform.
2
67 Beräkna och svara i grundpotensform.
68 En bit guld som väger 1 g består av 3 ∙ 1021 guldatomer.
Hur många guldatomer består en guldtacka av om den väger 1
Skriv som en tiopotens.
10

69 Skriv som en tiopotens.
a) 102 ∙ 10–6
10–2 ∙ 106
d) 10–1 10–2 e) 101 10–2
70 Beräkna och svara i grundpotensform.
d) 5 ∙ 10–2 1
10–3
71 Ett glas blåbärssoppa innehåller 6 ∙ 10–2 g C-vitamin.
Hur många gram C-vitamin innehåller a) 3 glas blåbärssoppa b) 10 glas blåbärssoppa?
72 Tabellen visar tre länders befolkning och storlek.
Beräkna befolkningstätheten (invånare/km2) i de tre länderna.
73 Vilket tal i grundpotensform är
a) dubbelt så stort som 2,4 ∙ 107 b) tio gånger så stort som 3,9 ∙ 10–5
c) hälften av 2,4 ∙ 107 d) en tiondel av 3,9 ∙ 10–5?
74 Beräkna och svara i grundpotensform. a) 1,4 · 10–7 · 2 · 105 7 · 10–4 b) (3 ∙
75 De röda blodkropparna i blodet och har till uppgift att transportera syre från lungorna till cellerna. En röd blodkropp innehåller ungefär 300 miljoner hemoglobinmolekyler, som var och en kan transportera fyra syremolekyler.
Hur många syremolekyler kan en röd blodkropp transportera? Svara i grundpotensform.
76 Avståndet mellan jorden och solen är 1,5 ∙ 108 km.
Ljusets hastighet är 3,0 ∙ 105 km/s.
Hur många minuter tar det för ljuset att färdas från solen till jorden?

prefix
Enheter och prefix
Enheten kilometer (km) består av två delar, prefixet kilo (k) och enheten meter (m).
Prefixet kilo betyder tusen. Vi använder det för att göra enheten större så att mätetalet blir mindre.
3 000 m = 3 ∙ 103 m = 3 km
Prefixet kilo kan användas ihop med andra enheter, till exempel
32 000 g = 32 ∙ 103 g = 32 kg
850 W = 0,85 ∙ 103 W = 0,85 kW
Tabellen visar de vanligaste prefixen och vad de betyder.
Skriv i decimalform utan prefix.
a) 4 hg b) 15 ms
Lösning
a) 4 hg = 4 ∙ 10 2 g = 400 g
b) 15 ms = 15 ∙ 10 -3 s = 0‚015 s
Nivå 1
Namn Beteckning Tiopotens Decimalform
tera T 1012 1 000 000 000 000 giga G 109 1 000 000 000 mega M 106 1 000 000 kilo k 103 1000 hekto h 102 100 deci d 10–1 0,1 centi c 10–2 0,01
milli m 10–3 0,001 mikro μ 10–6 0,000001 nano n 10–9 0,000000001 piko p 10–12 0,000000000001
Tankegång
Sätter in 102 i stället för prefixet hekto. Skriver siffran 4 på hundratalsplatsen.
Sätter in 10–3 i stället för prefixet milli. Skriver siffran 5 på tusendelsplatsen.
77 Vilken tiopotens ska stå i rutan?
a) 4 dl = 4 ∙ l b) 19 µs = 19 ∙ s c) 0,3 GW = 0,3 ∙ W
78 Skriv i decimalform utan prefix.
a) 5 hg
d) 2 ml
b) 5,8 hg
e) 2,6 ml
79 Vilket prefix ska stå i rutan?
a) Eva har 3 l mjöl i smeten.
c) En banan väger 1,3 g.
80 Vilket prefix ska stå i rutan?
a) 1,7 ∙ 10–1 m = 1,7 m
c) 0,5 ∙ 10–6 s = 0,5 s
Watt (W) är en enhet för effekt.
c) 58 hg
f) 26 ml
b) Till skolan är det 7,2 m.
d) Ett hårstrå är 80 m tjockt.
b) 98 ∙ 109 B = 98 B
d) 11,2 · 106 W = 11,2 W
Byte (B) är en enhet för digital information.
81 Skriv i decimalform utan prefix.
a) 8 km b) 9,4 ml c) 118 µg d) 0,52 MB
82 Tabellen visar innehållet i en dagsdos kosttillskott.
Skriv mängden av ingrediensen i decimalform utan prefix.
a) mangan b) kalium c) folsyra
83 Vilket tal i rutan är lika med
a) 5 dm b) 5 mm c) 50 mm d) 500 µm? e) 0,5 cm f) 0,00005 km?
INNEHÅLL PER DAGSDOS
Ingrediens Mängd
B1-vitamin 8 mg
B2-vitamin 12 mg
folsyra 200 µg
B12-vitamin 20 µg
kalium 240 mg
magnesium 240 mg mangan 4 mg
Skriv med prefixet giga (G).
a) 5 700 000 000 B b) 650 000 000 W
a) 5 700 000 000 B = 5‚7 ∙ 10 9 B = 5‚7 GB
b) 650 000 000 W = 0‚65 ∙ 10 9 W = 0‚65 GW
84 Skriv med prefixet mega (M).
Skriver talet med tiopotensen 109 och sedan prefixet giga i stället för tiopotensen.
Skriver talet med tiopotensen 109 och sedan prefixet giga i stället för tiopotensen.
a) 4 500 000 B b) 61 100 000 m c) 900 000 W d) 230 000 V
85 Skriv med prefixet mikro (µ).
a) 0,000003 m b) 0,000062 N c) 0,00708 s d) 0,00000092 g
86 Ugnsfolie är 15 µm tjockt.
Skriv tjockleken i grundpotensform utan prefix.
87 Ett sandkorn är 6,3 ∙ 10–5 m i diameter.
Hur stor är diametern uttryckt i a) millimeter b) mikrometer?
Volt (V) är en enhet för elektrisk spänning.
Newton (N) är en enhet för kraft.

88 Avståndet mellan jorden och solen är 150 miljoner km.
Skriv avståndet i grundpotensform utan prefix.
89 Vilket prefix ska stå i rutan?
a) 1,7
10–2
Nivå 1
1 Skriv potensen som en produkt och beräkna.
a) 32 b) 23 c) 34
2 Skriv produkten som en potens.
a) 6 ∙ 6 ∙ 6 b) 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3
3 Skriv uttrycket som en potens.
a) 105 ∙ 103 b) 27 ∙ 2
c) 105 103 d) 27 2
4 Vilket tal ska stå i stället för x?
a) 42 ∙ 4x = 48 b) 7x ∙ 73 = 75
c) 58 5x = 52 d) 2x 2 = 27
5 Skriv talet som en tiopotens.
a) 100 b) 1 000 c) 10 000
d) 0,1 e) 0,01 f) 0,0001
6 Skriv talet i grundpotensform.
a) 3 000 b) 3 500
c) 0,003 d) 0,0035
7 Ett hårstrå är ungefär 0,00008 m tjockt.
Skriv 0,00008 m i grundpotensform.
8 Skriv talet i decimalform.
a) 2 ∙ 104 b) 2,5 ∙ 104
c) 2 ∙ 10–4 d) 2,5 ∙ 10–4
9 Ljusets hastighet i en laserpekare
är 3,0 ∙ 108 m/s.
Skriv hastigheten i decimalform.
10 Beräkna och svara i grundpotensform.
a) 3 ∙ 106 ∙ 2 ∙ 104 b) 3 · 106 2 · 104
c) 4,4 ∙ 105 ∙ 2 ∙ 103 d) 4,4 · 105 2 · 103
11 Skriv i decimalform utan prefix.
a) 43 km b) 2 hg
c) 5 dl d) 15 cm
Nivå 2
12 Skriv som en potens med basen 3. a) 9 b) 27 c) 3
13 Skriv som en produkt och beräkna.
a) (–3)2 b) –32 c) –0,32
14 Vilket tal ska stå i stället för x?
a) 100 = x b) 5x = 1 c) 2,5x = 1
15 Skriv uttrycket som en potens.
a) 23 ∙ 22 ∙ 2 b) 103 · 104 102
16 Vilket tal i potensform är
a) dubbelt så stort som 29 b) hälften så stort som 29?
17 Skriv uttrycket som en potens.
a) (53)2 b) (52)3 c) (23)5
18 Vilket tal ska stå i stället för x?
a) (62)x = 68 b) (2x)2 = 212
c) 37 · 32 3x = 35 d) 45 · 4x 42 = 47

19 Skriv talet i grundpotensform.
a) 982 000 b) 60 200
c) 0,000982 d) 0,0206
20 Avståndet från jorden till solen är ungefär 149 600 000 000 m.
Skriv avståndet i grundpotensform.
21 Skriv talet i decimalform.
a) 3,75 ∙ 106 b) 2,04 ∙ 105
c) 1,25 ∙ 10–5 d) 5,09 ∙ 10–6
22 En mätning visar att en av jordens kontinentalplattor rör sig med hastigheten 2,5 ∙ 10–8 m/s.
Skriv hastigheten i decimalform.
23 Beräkna och svara i grundpotensform.
a) 3 · 102 + 5 · 10–1 b) 8 · 10–1 – 6 · 10–2
24 Beräkna och svara i grundpotensform.
a) 4 ∙ 108 ∙ 2 ∙ 10–2 b) 4 · 108 2 · 10–2
c) 8 ∙ 108 ∙ 4 ∙ 10–2 d) 2 · 108 4 · 10–2
25 Skriv i decimalform utan prefix.
a) 3,5 µg b) 30 ms
c) 300 Mm d) 350 µg
26 Skriv med prefixet inom parentes.
a) 12 000 m (k ) b) 1 500 000 W (M)
c) 0,00005 g (µ ) d) 0,0003 l (m )
Nivå 3
27 Skriv som en potens.
a) (– 1) ∙ (– 1) ∙ (– 1) b) x ∙ x ∙ x ∙ x
28 Skriv som en produkt.
a) y5 b) (–x)3 c) –53
29 Vilket tal ska stå i stället för x?
a) 2x = 32 b) 410 = 2x
c) 3x = 96 d) 812 = 16x
30 Vilket tal ska stå i stället för x?
a) 825 ∙ 106 = 8,25 ∙ 10x
b) 528 ∙ 10–6 = 5,28 ∙ 10x
31 Skriv ett tal i grundpotensform som är
a) dubbelt så stort som 8 ∙ 1050
b) hälften så stort som 1050
c) en femtedel av 1050
32 Skriv med prefixet inom parentes.
a) 2,7 ∙ 105 m (k ) b) 4,3 ∙ 10–4 m (µ )
c) 6,2 ∙ 107 W (G) d) 5,0 ∙ 10–13 g (p )
33 Blodet hos en vuxen person innehåller
2,5 ∙ 1013 röda blodkroppar. En röd blodkropp väger 1 pg.
Hur många kilogram väger de röda blodkropparna sammanlagt?
34 Vilket tal i grundpotensform ligger mitt emellan 6 ∙ 10–7 och 7 ∙ 10–6?
35 Vilket tal är störst?
a) 47 eller 85 b) 640 eller 380
c) 3150 eller 9100 d) 2300 eller 3200
1.1
De hela talens egenskaper
Heltal som är större än 1 och som endast är delbara med 1 och sig självt kallas för primtal. Alla andra heltal större än 1 är sammansatta tal.
2 3 5 7 11 ... primtal
4 6 8 9 10 ... sammansatta tal
Delbarhet
Sammansatta tal kan skrivas som en produkt av andra heltal.
6 = 6 ∙ 1 6 = 3 ∙ 2
Det betyder att heltalet 6 är delbart med faktorerna 1, 2, 3 och 6.
Mer om delbarhet
Ett heltal är delbart med
• 2 om talet är jämnt
• 3 om siffersumman är delbar med 3
• 5 om sista siffran är 0 eller 5
• 10 om sista siffran är 0.
Faktorisering
Sammansatta tal kan faktoriseras på olika sätt.
24 = 2 ∙ 12 24 = 3 ∙ 8 24 = 3 ∙ 2 ∙ 4
Om alla faktorer är primtal är talet primtalsfaktoriserat.
24 = 2 ∙ 2 ∙ 2 ∙ 3
Faktorisera och förkorta
När man förkortar 6 15 med 3 kan man visa det på två olika sätt.
Dividera täljaren och nämnaren med 3:
6 15 = 6 / 3 15 / 3 = 2 5
Skriva täljaren och nämnaren som produkter med en faktor 3 och stryka faktorn 3:
6 15 = 2 · 3 5 · 3 = 2 5
1.2
Potenser, enheter och prefix
En produkt med flera likadana faktorer kan skrivas som en potens.
2 · 2 · 2 · 2 · 2 = 25 potens
Skriva och beräkna värdet av potenser
Basen talar om vilken faktor 25 exponent bas som ska multipliceras.
Exponenten talar om hur många gånger faktorn ska multipliceras med sig själv.
En potens med exponenten 0 har värdet 1.
20 = 1 100 = 1 0,50 = 1
Multiplikation och division av potenser med samma bas
102 ∙ 103 = 102 + 3 = 105
54 52 = 54 – 2 = 52
Stora tal i grundpotensform
Ett tal i grundpotensform är skrivet som produkten av ett tal mellan 1 och 10 och en tiopotens.
61 000 = 6,1 ∙ 10 000 = 6,1 ∙ 104
tal mellan 1 och 10 tiopotens
Små tal i grundpotensform
0,0061 = 6,1 ∙ 0,001 = 6,1 ∙ 10–3
tal mellan 1 och 10 tiopotens med negativ exponent
Multiplikation och division av tal i grundpotensform
3 ∙ 105 ∙ 2 ∙ 102 = 6 ∙ 105 + 2 = 6 ∙ 107
3 · 105
2 ∙ 102 = 1,5 ∙ 105 – 2 = 1,5 ∙ 103
Enheter och prefix
Enheten kilometer (km) består av två delar, prefixet kilo (k) och enheten meter (m).
Prefixet kilo betyder tusen.
3 000 m = 3 ∙ 103 m = 3 km
1.3
Uttryck, ekvationer och formler
3x + x + 3x + x och 3x ∙ x är två exempel på algebraiska uttryck med variabeln x
Förenkla uttryck
4x ∙ 5x = 4 ∙ x ∙ 5 ∙ x = 20 ∙ x2 = 20x2
14x2 2x = 2 ∙ 7 ∙ x ∙ x 2 · x = 7 ∙ x = 7x
Förenkla uttryck med parenteser
Plustecken framför en parentes
x + (x + 4) = x + x + 4 = 2x + 4
Minustecken framför en parentes
x – (x + 4) = x – x – 4 = –4
En faktor multiplicerat med en parentes
x · (x + 4) = x ∙ x + x ∙ 4 = x2 + 4x
Bryta ut en faktor
2x + 8 = 2 ∙ x + 2 ∙ 4 = 2 ∙ (x + 4) = 2(x + 4)
Multiplicera parenteser
Multiplikation av två parenteser
(x + 5)(x + 2) = x2 + 2x + 5x + 10
Ekvationer med nämnare x 0,3 = 8 x 0,3 ∙ 0,3 = 8 ∙ 0,3 x = 2,4
Att lösa ut ur formler
A = b · h 2 h = 2A b b = 2A h b A h
1.4
Kvadrater, kvadratrötter och andragradsekvationer
Talet 32 utläses ”3 upphöjt i 2”, ”3 i kvadrat” eller ”kvadraten på 3”.
Talet √ 9 utläses ”kvadratroten ur 9”.
Beräkna kvadrater och kvadratrötter
42 = 4 ∙ 4 = 16
√16 = 4 eftersom 42 = 4 ∙ 4 = 16
Mer om kvadratrötter
2√ 9 = 2 · 3 = 6
√2 + 9 = √11 ≈ 3,3
√100 4 = √25 = 5
Andragradsekvationer
Ekvationen x2 = 25 har två lösningar:
x = √25 = 5 eftersom 52 = 5 ∙ 5 = 25 och
x = –√25 = –5 eftersom (–5)2 = (–5) ∙ (–5) = 25
Endast svar till uppgifterna 1–8
1 Vilka av talen i rutan är primtal?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2 Skriv talet som en produkt av primtal.
a) 6 b) 30 c) 72
3 Vilken av de markerade punkterna på tallinjen visar talet
a) √16 b) 24 c) 80 ?
A B C D E
0 15 10 5
4 Vilket tal ska stå i stället för x?
Utvärdera hur det gick när du är klar med testet.
a) 96 ∙ 9x = 911 b) 49 4x = 43 c) (5x)3 = 56
5 Ett saltkorn med formen av ett klot har radien 6 ∙ 10–4 m.
a) Beräkna saltkornets diameter.
Svara i grundpotensform med enheten meter.
b) Skriv saltkornets diameter i millimeter.
6 Förenkla uttrycket
a) 4(x – 3) b) x(5x + 3) – x(x – 3) c) 10x + 5x 10x – 5x
7 Vilka uttryck är lika med 8 + 4x?
A 2(4 + 2x) B 4(2 + x) C 4(x + 2) D 4(2 + 2x)
8 Vilken eller vilka ekvationer har a) en lösning b) två lösningar c) ingen lösning?
A x2 – 2 = 5 B x2 + 2 = 5 C 2 – 5x = 5x – 2 D 2 + 5x = 5x – 2
Lösningar och svar till uppgift 9–14
9 Formeln v = s t visar att medelhastigheten v beräknas genom att dividera sträckan s med tiden t
a) Lös ut t ur formeln.
b) Beräkna t när s = 12 m och v = 0,75 m/s.
c) Hur många minuter tar det att åka 24 km med medelhastigheten 30 km/h?
10 Beräkna längden av x med en ekvation. Avrunda svaret till närmaste tiondel. a)
11 Ett pollenkorn från en björk väger ungefär 7,9 ng. En fullvuxen björk kan producera 10 miljarder pollenkorn under en säsong.
a) Skriv 7,9 ng i grundpotensform utan prefix.
b) Skriv 10 miljarder i grundpotensform.
c) Hur många gram väger 10 miljarder björkpollenkorn?
12 Multiplicera och förenkla.
a) (x + 5)(x + 7) b) (5x – 7)(5x + 7) c) (x + 5)(x – 5)(x – 7)
13 Om ett antal ägg packas i kartonger med 6, 8 eller 10 ägg i varje kartong blir det alltid ett ägg över.
Vilket är det minsta möjliga antalet ägg?
14 Det finns ett positivt tal som när det multipliceras med sig självt blir dubbelt så stort som när det multipliceras med sig självt tre gånger.
Vilket är talet?
Hur gick det?
Kunde inte Arbeta vidare på s. 66–67
Osäker Arbeta vidare på s. 68–69
Kunde Arbeta vidare på s. 70–71
REPETITION Nivå 1
Uppgifterna till vänster är samma som kapitlets exempel.
Numret på uppgiften visar på vilken sida du hittar exemplet.
Det gör att du enkelt kan ta hjälp av lösningen om du behöver.
Uppgifterna till höger är mer träning på samma sak.
Kapitlets exempel
Vilka tal är
a) 16 delbart med
b) 17 delbart med?
Är talet 256 delbart med
a) 2 b) 5?
Talet 18 är ett sammansatt tal.
a) Dela upp talet 18 i primtal med hjälp av ett faktorträd.
b) Skriv talet 18 som en produkt av primtal.
Förkorta bråket med 4 genom att skriva täljaren och nämnaren som produkter med en faktor 4.
a) 8 20 b) 4 28
Skriv potensen som en produkt och beräkna.
a) 62 b) 34
Skriv uttrycket som en potens.
a) 102 · 104 b) 63 · 6 c) 76 75
Skriv talet i grundpotensform.
a) 300 b) 61 000
Skriv talet i grundpotensform. a) 0,5 b) 0,0061
1 2 3
Gör uppgifterna till höger om du behövde titta på lösningen.
Liknande uppgift
Vilka tal är
a) 20 delbart med
b) 19 delbart med?
Är talet 375 delbart med a) 2 b) 5?
Talet 24 är ett sammansatt tal.
a) Dela upp talet 24 i primtal med hjälp av ett faktorträd.
b) Skriv talet 24 som en produkt av primtal.
Förkorta bråket med 5 genom att skriva täljaren och nämnaren som produkter med en faktor 5.
a) 15 20 b) 5 35
Skriv potensen som en produkt och beräkna.
a) 72 b) 25
Skriv uttrycket som en potens.
a) 4 · 46 b) 53 · 52 c) 107 105
Skriv talet i grundpotensform.
a) 1 800 b) 700
Skriv talet i grundpotensform.
a) 0,002 b) 0,027
30
Beräkna och svara i grundpotensform.
a) 2 · 103 · 4 · 102 b) 4 · 106 2 · 103
32
Skriv i decimalform utan prefix.
a) 4 hg b) 15ms
38
Förenkla uttrycket
a) 3x · 2x b) 3x · x
40
Skriv uttrycket utan parentes.
a) x(x + 5) b) 4x(5 – x )
42
Bryt ut
a) faktorn 2 ur uttrycket 2x + 8
b) faktorn 5 ur uttrycket 10x – 5
44
Multiplicera parenteserna och förenkla.
(x + 4)(x + 3)
46
Lös ekvationen
a) x 0,5 = 6 b) x 10 = 6 15
Lös ut x ur formeln a = x b
Beräkna
a) 42 b) √16
Beräkna och avrunda till närmaste tiondel.
a) 2√10 b) √2 + 10
c) 100 π
Lös ekvationen
a) x2 = 16 b) 2x2 = 10
Beräkna och svara i grundpotensform.
a) 3 · 104 · 2 · 102 b) 8 · 107 4 · 104
Skriv i decimalform utan prefix.
a) 5 kg b) 68 ns
Förenkla uttrycket
a) 4y · 3y b) 5y · y
Skriv uttrycket utan parentes.
a) 2y(y + 8) b) y(6 – 2y)
Bryt ut
a) faktorn 8 ur uttrycket 16x + 8
b) faktorn 3 ur uttrycket 3x – 24
Multiplicera parenteserna och förenkla.
(6 + x)(2 + x)
Lös ekvationen
a) x 0,4 = 7 b) x 8 = 4 10
Lös ut b ur formeln a = x b
Beräkna
a) 62 b) √36
Beräkna och avrunda till närmaste tiondel.
a) 4√ 8 b) √3 + 8
c) 50 3
Lös ekvationen
a) x2 = 81 b) 5x2 = 15
1 Vilka tal är
a) 18 delbart med b) 42 delbart med?
2 Vilket är det minsta talet som är delbart med både
a) 6 och 8 b) 9 och 12?
3 Barnen på ett kollo ska ställa sig i rader med lika många barn i varje rad.
Vilket är det minsta antalet barn som kan finnas på kollot om de kan ställa sig i 6 eller 10 rader?
4 Vilka av talen i rutan är delbara med 3?
102 429 712 1098 28 282
5 Vilket eller vilka tal mellan 70 och 80 är delbara med både 2 och 3?
6 Skriv talet som en produkt av primtal.
a) 48 b) 80 c) 90
7 Beräkna och svara i enklaste bråkform.
a) 7 9 ∙ 9 8 b) 4 9 ∙ 7 8
c) 3 5 6 7 d) 3 8 5 8
8 Skriv som en produkt och beräkna.
a) 82 b) 802 c) 0,82
9 Skriv uttrycket som en potens.
a) 52 ∙ 53 ∙ 5 b) 103 ∙ 105 104
c) 36 · 34 3 · 36 d) 102 102 · 102
10 Vilket tal i potensform är
a) dubbelt så stort som 210
b) hälften så stort som 210?
11 Skriv som en potens med basen 3.
a) 9 b) 27 c) 1
12 Skriv uttrycket som en potens.
a) (74)2 b) (72)4 c) (1010)10
13 Vilket tal ska stå i stället för x?
a) (53)x = 59 b) (4x)3 = 412
c) 105 ∙ 103 10x = 104 d) 57 ∙ 5x 52 = 57
14 Skriv talet i grundpotensform.
a) 760 000 b) 45 200 000
c) 0,00760 d) 0,0000425
15 Ett hårstrå från en katt är
0,000015 m tjockt.
Skriv tjockleken i a) grundpotensform
b) med prefixet mikro (μ).
16 Skriv talet i decimalform.

a) 2,25 ∙ 107 b) 1,02 ∙ 1010
c) 9,75 ∙ 10–6 d) 8,05 ∙ 10–8
17 I april 2025 var jordens befolkning
8,218 ∙ 109 personer.
Skriv antalet personer i decimalform.
18 Beräkna och svara i grundpotensform.
a) 3 ∙ 105 ∙ 2 ∙ 10–5 b) 3 ∙ 105 2 ∙ 10–5
c) 3 ∙ 106 ∙ 6 ∙ 10–3 d) 3 ∙ 106 6 ∙ 10–3
19 Skriv sträckorna i storleksordning med den kortaste först.
620 nm 2 cm 0,5µm 0,0004 dm
20 Förenkla uttrycket
a) 5x + 4x x b) 5x · 4x 2
c) 5x · 4x 2x d) x – 5x 4
21 Förenkla uttrycket
a) 4(3x + 5) + 2(6 + 2x)
b) x(8x – 3) – x(x – 6)
22 Förenkla uttrycket
a) 10x + 6 2 b) x2 – 6x x
c) 5x2 + 5x 5x d) 5x – 5 5
23 Bryt ut största möjliga faktor.
a) 8x + 12 b) 16 – 24x
c) 8x2 + 12x d) 16x2 – 24x
24 Multiplicera och förenkla.
a) (x + 5)(x + 2) b) (x + 5)(x – 2)
c) (x – 5)(x – 2) d) (x – 5)(x + 2)
25 Vilket tal ska stå i rutan?
a) 6(x – 3) = (2x – 6)
b) (x + 3)(x + ) = x2 + 6x + 9
c) (x + 6)(x + 2) = x2 + x + 12
26 Vilken av de markerade punkterna på tallinjen visar talet
a) √10 b) √35 c) √18
23 47 89 10 56 A B C D E
27 Beräkna
a) √ 4 ∙ √25 b) √4 · 25 c) √ 8 ∙ √ 2 d) √0,9 ∙ √10
28 Beräkna a) √100 √25 b) 100 25 c) √ 8 √ 2
29 Lös ekvationen
a) x2 – 16 = 0 b) 3x2 = 27 c) 3x2 4 = 3 d) 4x2 + 16 = 20
30 Klas ska sätta upp ett staket runt hästhagen. Hagen är formad som en rektangel med arean 1 800 m2. Den ena sidan är dubbelt så lång som den andra sidan. Hur långt kommer staketet runt hästhagen att bli?

31 De fyra första kvadrattalen är 1, 4, 9 och 16.
a) Vilket är nästa kvadrattal?
b) Skriv alla kvadrattal som är mindre än 100.
32 Talet a är ett kvadrattal och talet b är ett primtal.
Vilka tal är a och b om a + b = 48?
1 I det femsiffriga talet 8 14 är tusentalet och entalet samma siffra.
Vilken siffra ska stå i rutorna om talet ska vara delbart med 2 och 3?
2 Skriv som en produkt av primtal.
a) 504 b) 1 650 c) 6 750
3 På ett företag arbetar 120 kvinnor och 144 män. De anställda ska delas in i grupper med lika många kvinnor och män i varje grupp.
Hur många grupper kan man göra som mest?
4 Skriv i enklaste bråkform.
a) 48 88 b) 234 288 c) 195 780
5 Vilket tal ska stå i stället för x?
a) 2x = 45 b) 9x = 274
c) 1010 = x5 d) 2400 = x100
6 Skriv ett tal i grundpotensform som är
a) dubbelt så stort som 5 ∙ 1020
b) hälften så stort som 1020.
7 Vilket tal i grundpotensform ligger mitt emellan 6 ∙ 109 och 4 ∙ 108?
8 En regndroppe väger 5 µg.
Hur många regndroppar behövs för att fylla en tunna med 200 kg vatten?

9 Förenkla så långt som möjligt.
a) 8x2 + 12x 4x b) 4xy + 6y2 2y
c) 18x + 9 6x d) 18x + 24 12x + 18
e) 18x – 24 12x – 16 f) 12x + 18x2 15x + 10
10 Multiplicera och förenkla.
a) (x + 1)(x – 1) b) (x + 2)(x – 2)
c) (x + 3)(x – 3) d) (a + b)(a – b )
11 Så här beräknar Edgar multiplikationen 22 ∙ 18:
22 18 = (20 + 2)(20 - 2) = = 202 - 22 = 400 - 4 = 396
Beräkna på samma sätt som Edgar.
a) 32 ∙ 28 b) 23 ∙ 17
c) 51 ∙ 49 d) 105 ∙ 95
12 Vilket tal ska stå i rutan?
a) (x + 2)(x + ) = x2 + x + 6
b) (x + )(x + ) = x2 + 5x + 6
c) (x + )(x + ) = x2 + 7x + 12
d) (x + )(x – ) = x2 + 4x – 12
e) (x – )(x – ) = x2 – 11x + 24
f) (x + )(x – ) = x2 – 49
13 Lös ekvationen
a) √ x + 8 = 12 b) √ x = √ 5 ∙ √ 5
c) √ 2 ∙ x = √50 d) √0,2 ∙ √ x = 2
14 Lös ekvationen
a) 4x2 = 1 b) (x + 4)(x – 4) = 0 c) 4x2 – 9 = 0 d) 5 – 7x2 = 9x2 – 4
FÖRDJUPNING Scala upp!
1 För ett positivt heltal gäller att
• varje siffra i talet är en etta, två eller trea
• talet har minst två ettor, två tvåor och två treor
• talet är inte delbart med 2 eller 3.
Vilket är det minsta talet som uppfyller dessa villkor?
2 Vilken siffra är entalet om potensen skrivs i decimalform? a) 210 b) 221 c) 32011
3 Donald vill skriva positiva heltal i de skuggade rutorna i pyramiden. Varje ruta måste innehålla produkten av talen i de två rutorna under den. Talet i den översta rutan ska vara 720.
Hur många olika värden kan heltalet n ha?
1 4 5 6 8
(Kängurutävlingen Cadet 2024)
4 Hur många siffror har produkten av de två heltalen
3 456 712 345 876 989 och 16 567 456 510 302 456 745?
(Högstadiets matematiktävling 1988)
5 Beräkna x + y om 2x ∙ 5y = 1 000
6 Matilda har ett antal kvadratiska pappersbitar med sidan 1 cm.
Hon har tänkt bygga en större kvadrat med sidan n centimeter.
Det visar sig att Matilda då får 157 bitar över.
Om Matilda i stället hade byggt en kvadrat med 3 centimeter längre sidor hade hon haft 110 bitar för lite.
Hur många små kvadratiska bitar har Matilda?
(Högstadiets matematiktävling 2006)
7 Sara beräknar 34 ∙ 45 ∙ 56 och skriver produkten i decimalform.
Hur många nollor kommer att finnas i slutet av produkten?
Scala 9
MATEMATIK
Ordet scala har vi lånat från latin. Det betyder trappa eller stege. Kunskaper och färdigheter i matematik är något som du utvecklar stegvis.
Scala Matematik är ett helt nytt läromedel i matematik för högstadiet, skrivet för kursplan 2022. Läromedlet är lätt att använda, betonar matematiska begrepp och metoder och ger stöttning till alla elever oavsett nivå.
I Scala Matematik hittar du
• mängder av övningsuppgifter – från grundläggande nivå till verkliga utmaningar
• återkommande repetition – innehåll från tidigare kapitel saxas in och vävs ihop med ny kunskap
• rikligt med exempel och lösta uppgifter – visar också tankegången bakom lösningen
• digitalt extramaterial med övningar, diagnoser och lektionsaktiviteter
Läromedelsserien Scala Matematik
• elevböcker till årskurs 7, 8 och 9
• digitalböcker
• webbaserad lärarguide
• digitalt träningsmaterial med möjlighet att följa upp elevernas arbete och skapa diagnoser
Läs mer om Scala Matematik på www.nok.se/scala
