VBTL 3/4 D - Leerwerkboek Statistiek - inkijk methode

LEERWERKBOEK

Statistiek

D-finaliteit

Philip Bogaert

Filip Geeurickx

Marc Muylaert

Roger Van Nieuwenhuyze

Erik Willockx

CARTOONS

Dave Vanroye

Hoe gebruik je VBTL ?

Dit boek bevat zes hoofdstukken vol statistiek. Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.

6 Samenvatting Je kent de betekenis van populatie, populatieomvang, steekproef, steekproefomvang, waarnemingsgetallen en uitkomstenverzameling. – populatie is de verzameling van alle elementen waarvan een bepaalde eigenschap wordt De populatieomvang is het aantal elementen van de populatie. – steekproef is een deel van de populatie waarvoor er waarnemingen worden verricht om een bepaalde eigenschap te bestuderen. De steekproefomvang is het aantal elementen van de steekproef. – Waarnemingsgetallen zijn resultaten van een steekproef, uitgevoerd op een deel van een bepaalde populatie. Je weet dat statistiek de wetenschap is die gegevens over bepaalde verschijnselen via een steekproef verzamelt, ordent, samenvat en analyseert om zo tot betrouwbare conclusies te komen voor de hele populatie. Je weet wanneer een steekproef representatief is. Je kent verschillende mogelijkheden om data voor te stellen lijndiagram, staafdiagram, cirkeldiagram, dotplot en stengelbladdiagram. cirkeldiagram lijndiagram Verdeling schoolbevolking secundair onderwijs Leeftijdsgroep 0- tot 19-jarigen staafdiagram

Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.

1 2 *

De nummers van de oefeningen hebben een gele kleur. Een sterretje duidt op een extra uitdaging. Achteraan in het boek vind je de oplossingen

76

Ongelijke

4,79 4,95 5,30 4,25 5,37 3,77 5,49 4,93 5,21 4,59 5,80 4,09 5,39 4,05 5,99 5,50 4,50 5,45 4,76 5,12 4,73 5,09 6,24 5,05 4,69 5,13 5,84 4,74 5,71 5,45 4,29 4,58 5,61 4,99 5,42 5,00 5,58 5,90 5,30 5,20 5,37 4,73 5,55 4,76 5,41 4,52

Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt.

opstellen.

– De gegevens van de steekproef verzamelen, rangschikken en samenvatten. de beschrijvende statistiek – Op basis van die steekproef besluiten

Engeland het Domesday Book opstellen. In dat boek werd de verdeling van de bevolking maar ook de verdeling van de veestapel en van de landbouwgronden werd er keurig in genoteerd. Historici halen daar vandaag nog waardevolle inlichtingen uit. Ook nu komen er nog tellingen voor. Zo vindt er bij ons in België om de tien jaar een volkstelling plaats Statbel, het Belgische statistiekbureau (statbel.fgov.be).

Je kunt voor het eerst spreken van statistiek wanneer landen gegevens begonnen te verzamelen over allerlei zaken de samenstelling van de bevolking, eigendommen en inkomsten, het bedrag van geïnde belastingen, het aantal weerbare mannen (geschikt om oorlog te voeren), het aantal vaklui en werktuigen, eenvoudigweg te tellen, wat al in de tijd van de Romeinen gebruikelijk was. Bekend is de volkstelling die ten tijde van Christus door keizer Augustus werd bevolen.

Wat moet je kennen en kunnen ?

ICT is een onmisbaar hulpmiddel in de wereld van statistiek.

Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets.

Daarnaast bieden we bijna alle oplossingen van het boek aan in ICT-vorm. Je vindt dat alles terug op www.polpo.be, zowel bij het lesmateriaal als in het bordboek.

150

Histogram en enkelvoudige frequentiepolygoon Om dit histogram te van de A.F. (merk op dat we een hebben toegevoegd zowel in het begin als op het einde). dan voor Aanbevolen grafieken Daar nemen we het passende type. de rechtermuisknop op

Vervolgens klikken we met de rechtermuisknop in het tekengebied en kiezen we voor Gegevens selecteren We klikken op het icoontje uiterst rechts vanWe klikken nadien opnieuw in het tekengebied en kiezen opnieuw voor Gegevens selecteren We klikken onder het witte kader op de en vervolgens klikken we bij op het icoontje uiterst rechts. We selecteren dan opnieuw de kolom voor A.F., geven die door met het icoontje uiterst rechts en We klikken met de rechtermuisknop op de laatst getekende staven, kiezen voor Grafiektype wijzigen kiezen bij Lijn voor het eerste type.

Sompolygoon gebaseerd op de C.A.F. Om dit te tekenen selecteren we de kolom van de C.A.F. We klikken op en kiezen bij het eerste type uit de tweede rij. Bij de C.A.F. hebben we als eerste element een genomen. Dat zorgt ervoor dat We klikken dan met de rechtermuisknop op de getekende lijn en kiezen nog voor Gegevenslabels toevoegen

Vaardigheden

Na elk hoofdstuk wordt een wiskundige vaardigheid in de kijker gezet.

Na de vaardigheden zie je een handig overzicht van wat je moet kennen en kunnen na het geziene hoofdstuk. Kleur de eerste kolom smileys als je de leerstof herhaalde voor een grote toets. Kleur de laatste kolom als je de leerstof beheerst voor je examen.

Herhalingsoefeningen

Wanneer je wiskunde studeert, maak je uiteraard heel wat oefeningen opnieuw en maak je oefeningen die je in de klas niet maakte. Elk hoofdstuk sluit af met twee pagina’s herhalingsoefeningen Een ideale test voor jezelf om te zien of je de leerstof beheerst.

WAT MOET JE KENNEN EN KUNNEN

Centrummaten

Vaardigheden | Histogram en frequentiepolygoon tekenen met de TI-84 en met GeoGebra Histogram en frequentiepolygoon tekenen met de TI-84 Kogelstoten (continu geval) In een school werd op een sportdag aan kogelstoten gedaan. De volgende resultaten (in m) werden opgetekend van 8,11 8,35 8,75 8,62 7,25 7,50 9,45 9,78 6,55 6,40 8,64 9,15 6,22 6,00 8,67 8,11 7,55 7,62 8,14 8,99 5,89 6,20 6,36 7,66 7,59 8,24 8,36 9,02 8,32 7,68 7,00 9,01 8,56 7,12 6,88 7,45 8,56 7,85 8,36 9,55 7,45 6,12 8,11 7,49 8,02 9,10 5,95 7,42 6,89 7,15

We werken deze opgave uit met de TI-84.

Eerst brengen we de gegevens in een lijst L1 in.

We drukken op en vullen volgend scherm in

4 80

dit moet leren pagina ken het oké voor ❒   ❒ Ik kan het gemiddelde berekenen met ICT.   ❒ Ik ken de eigenschappen in verband met het rekenkundig gemiddelde.   ❒ Ik kan de eigenschappen in verband met het rekenkundig gemiddelde bewijzen.   ❒ Ik ken de betekenis, notatie en definitie van de modus. 94   ❒   ❒ Ik ken de betekenis, notatie en definitie van de mediaan.   ❒ Ik kan de mediaan berekenen met ICT. 95   ❒   ❒ Ik weet wat bedoeld wordt met kwartielen en kan ze berekenen (met ICT). 97  

Gegevens verwerken 3 110

1 6 /

131 152 121 114 147 127 109 138 125 131 155 148 142 131 122 124 148 117 112 125 135 131 141 116

b Maak een stengelbladdiagram. Teken het histogram en de enkelvoudige frequentiekromme. d Teken een ogief. Hoeveel leerlingen sprongen minstens 120 cm hoog Hoeveel % van de leerlingen sprong 132 cm of meer maar minder dan 144 cm hoog Hoeveel leerlingen sprongen 138 cm of hoger

Op de werkvloer, in dagbladen, tijdschriften of boeken, op het internet … overal zie je cijfertabellen, diagrammen en grafieken met gegevens uit de politiek, het onderwijs, de sport en de dagelijkse werkelijkheid.

In de omgangstaal noemen we die gegevens statistieken. Ze geven een mooi beeld weer van wat bepaalde mensen aanbelangt.

In dit boek maken we kennis met de beschrijvende statistiek. Daarmee leer je in hoofdzaak waargenomen gegevens verzamelen en verwerken. Je zult statistische gegevens overzichtelijk weergeven aan de hand van tabellen en grafieken, maar je gebruikt ook bijzondere getallen. Het gemiddelde, de mediaan en de modus ken je al, maar nu maak je ook kennis met kwartielen, de standaardafwijking en spreidingsdiagrammen. Met behulp van statistiek zul je leren om gegevens te verzamelen, die kritisch te bekijken en conclusies op hun betrouwbaarheid te toetsen.

Inhoud

Inhoud

Geschiedenis van de statistiek 8

1Methodes om gegevens voor te stellen

1 Inleiding  12 2 Statistische terminologie  16 3 Representativiteit van een steekproef  18 4 Mogelijke voorstellingen van gegevens  19 5 Diagrammen tekenen met ICT  21 6 Samenvatting  24 7 Oefeningen  25

Extra’s :

Vaardigheden : datasets vergelijken met behulp van ICT 32 Wat moet je kennen en kunnen ? 34 Herhalingsoefeningen 35 2

Soorten gegevens en opstellen van frequentietabellen

1 Soorten gegevens  37 2 Sommatieteken  38 3 Frequentietabellen  40 4 Absolute frequentie  41 5 Relatieve frequentie  42 6 Cumulatieve frequentie  43 7 Samenvatting  46 8 Oefeningen  47

Extra’s :

Vaardigheden : een eigen onderzoek uitvoeren 54 Wat moet je kennen en kunnen ? 55 Herhalingsoefeningen 56

3

Gegevens verwerken

1

Numerieke gegevens verwerken  58 2 Categorische gegevens verwerken  59 3 Histogram en enkelvoudige frequentiepolygoon  62 4 Sompolygoon, ogief of cumulatieve frequentiepolygoon  64 5 Kijken naar verdelingen  66 6 Misleiding  69 7 Samenvatting  72 8 Oefeningen  73

Extra’s

Vaardigheden : histogram en frequentiepolygoon tekenen met de TI-84 en met GeoGebra 80 Wat moet je kennen en kunnen? 84 Herhalingsoefeningen 85

Centrummaten

1 Het rekenkundig gemiddelde  87

2 Berekening van het gemiddelde vanuit een frequentietabel  89

3 Het gemiddelde als evenwichtspunt  93

4 De modus  94 5 De mediaan  95 6 Berekening van de mediaan vanuit een frequentietabel  96 7 Voor- en nadelen van centrummaten  96 8 De kwartielen  97 9 Samenvatting  100 10 Oefeningen  101

Extra’s :

Vaardigheden : taalvaardigheid: een bingo van statistiekwoordenschat 109 Wat moet je kennen en kunnen? 110 Herhalingsoefeningen 111

5

Spreiding en spreidingsmaten

1 Inleiding  113 2 De variatiebreedte  114 3 De interkwartielafstand  114 4 De boxplot  115 5 Constructie van de boxplot   117 6 Uitschieters  120 7 Variantie en standaardafwijking  121 8 Betekenis van de standaardafwijking  123 9 Welke spreidingsmaat kies je ?  124 10 De z-score  124 11 Samenvatting  126 12 Oefeningen  127

Extra’s :

Vaardigheden : wiskundetaal 134 Wat moet je kennen en kunnen ? 135 Herhalingsoefeningen 136

6

Spreidingsdiagrammen

1 Verbanden  138 2 Afhankelijke en onafhankelijke variabele  140 3 Spreidingsdiagram  141 4 Trendlijnen  143 5 Valkuilen  144 6 Samenvatting  144 7 Oefeningen  145

Extra’s

Vaardigheden : ICT-herhalingsoefening 149 Wat moet je kennen en kunnen? 157 Herhalingsoefeningen 158

Oplossingen 160

Trefwoordenregister 168

Geschiedenis van de statistiek

Wat is statistiek ?

Statistiek omvat de wetenschap, de methodiek en de techniek van het verzamelen, bewerken en interpreteren van gegevens in verband met massaverschijnselen. Het statistisch onderzoek bestaat uit drie fasen.

– Een steekproef opstellen.

– De gegevens van de steekproef verzamelen, rangschikken en samenvatten. Dat onderdeel noemen we de beschrijvende statistiek

– Op basis van die steekproef besluiten trekken omtrent de hele populatie. Dat noemen we de verklarende statistiek

J aar 1

In de 11e eeuw liet Willem de Veroveraar in Engeland het Domesday Book opstellen.

In dat boek werd de verdeling van de bevolking over de verschillende standen weergegeven, maar ook de verdeling van de veestapel en van de landbouwgronden werd er keurig in genoteerd.

Historici halen daar vandaag nog waardevolle inlichtingen uit.

Ook nu komen er nog tellingen voor. Zo vindt er bij ons in België om de tien jaar een volkstelling plaats ; de allereerste was er al in 1846.

Je kunt voor het eerst spreken van statistiek wanneer landen gegevens begonnen te verzamelen over allerlei zaken : de samenstelling van de bevolking, eigendommen en inkomsten, het bedrag van geïnde belastingen, het aantal weerbare mannen (geschikt om oorlog te voeren), het aantal vaklui en werktuigen, het aantal stuks vee ...

Dergelijke informatie kon je verkrijgen door eenvoudigweg te tellen, wat al in de tijd van de Romeinen gebruikelijk was. Bekend is de volkstelling die ten tijde van Christus door keizer Augustus werd bevolen.

In ons land is dat de taak van Statbel, het Belgische statistiekbureau (statbel.fgov.be).

KEIZER AUGUSTUS

Het eerste, zeg maar echt statistische materiaal vinden we terug in Engeland. Dat hebben we te danken aan zakenman John Graunt (1620-1674) en aan Thomas Robert Malthus (1766-1834), die bekendstaat om zijn pessimistische visie over de bevolkingsgroei. De Londense lakenkoopman John Graunt publiceerde in 1662 zijn boek Natural and Political Observations, waarin een statistische analyse stond van de wekelijkse lijst van sterftegevallen in en rond Londen, de zogenaamde Bills of mortality.

1662

JOHN GRAUNT

EDMOND HALLEY

In 1693 maakte de sterrenkundige Edmond Halley (1656-1742), ook al een Brit, een Ievensverwachtingstabel gebaseerd op de sterftecijfers van de Poolse stad Breslau (nu gekend als Wrocław). Op die manier begon de wetenschap met het verzamelen en beschrijven van feiten. Zo kwamen bijvoorbeeld ook de eerste statistieken bij de firma's die levensverzekeringen afsloten. De gegevens die verzameld werden, konden ook gebruikt worden om lijfrenten te berekenen. Het woord statistiek werd trouwens voor het eerst gebruikt in 1672 en is afgeleid van het Latijnse woord status (staat).

Maar het bleef niet bij tellen. Vanaf de 17e eeuw werd kansrekening of waarschijnlijkheidsrekening gebruikt om statistische gegevens te ontleden en statistische hypothesen te formuleren. De Zwitserse wiskundige Jakob Bernoulli (1654-1705) en zijn Franse collega Pierre-Simon Laplace (1749-1827) hebben de beschrijvende statistiek via de waarschijnlijkheidsrekening in de wiskunde opgenomen. Zo ontstond de wiskundige of verklarende statistiek.

PIERRE-SIMON LAPLACE

De eerste zinvolle, systematische en doelgerichte bewerking van statistisch materiaal vinden we in een werk uit 1835 met een lange titel : Sur l’homme et le développement de ses facultés ; essai d’une physique sociale. Dat werk is van de hand van onze landgenoot Adolphe Quetelet (1796-1874). Daarin publiceerde hij talrijke statistische gegevens over de fysieke eigenschappen van de mens. Hij legde het verband tussen misdadigheid en leeftijd, geslacht, opvoeding, seizoen enz. Hij riep ook het eerste internationale statistische congres bij elkaar in 1855 in Brussel. Quetelet wordt onder andere daardoor de stichter van de moderne statistiek genoemd.

QUETELET

ADOLPHE

Jakob Bernoulli

We vermelden ook graag de bijdrage die Florence Nightingale (1820-1910) leverde aan de statistiek. Zij staat bekend als the lady with the lamp, een bijnaam die ze kreeg toen ze als verpleegster gewonde Engelse soldaten verzorgde tijdens de Krimoorlog. Maar ze was ook een wiskundige, die sterk beïnvloed was door het werk van Quetelet. Op wiskundig gebied werd ze vooral bekend door haar diagram waarmee ze de sterftegevallen in de Britse militaire hospitalen in beeld bracht (zie hierboven). De oppervlakten van de cirkelsegmenten geven de verhoudingen weer van het aantal doden. Met dit diagram wilde ze de Engelse politici duidelijk maken dat de sterfte onder de soldaten eerder een gevolg was van slechte hygiënische omstandigheden dan van oorlogsgeweld. Zo kon ze de autoriteiten overtuigen om te investeren in hygiënische hervormingen in de militaire hospitalen.

Na 1940 werd het mogelijk om met een moderne computer zeer grote hoeveelheden gegevens te verwerken en op die gegevens statistische methodes toe te passen. De statistiek is daarmee de meest toegepaste tak van de wiskunde geworden. Economie, sociologie, psychologie, biologie, het verzekeringswezen, meteorologie en de verkeerspolitiek zijn enkele van de talrijke disciplines waarvoor statistiek onmisbaar is geworden.

FLORENCE NIGHTINGALE

Methodes om gegevens voor te stellen

1 Inleiding

In dagbladen, tijdschriften, boeken en op het internet vind je geregeld heel wat info die weergegeven wordt in tabellen, diagrammen of grafieken.

Corona in

België 12 000 10 000 8 000 6 000 4 000 2 000 0

Actuele bezetting ziekenhuizen Doden Waarvan op intensieve Ziekenhuis mogen verlaten 12 309 7844 3056 674 15/03 22/03 29/03 05/04 12/04 19/04 26/04 03/05 Bron: Sciensano, 5 mei 2020

a Hoeveel doden waren er tot 3/5/2020 te betreuren door de coronacrisis in België ?

b Hoeveel personen hebben tot 3/5/2020 al het ziekenhuis mogen verlaten ?

c Waarom is de bezetting in de ziekenhuizen een belangrijke factor om de evolutie van de pandemie op te volgen ?

d Wat betekent pandemie ?

Huishoudens zonder internetverbinding

Percentage huishoudens zonder internetverbinding

Totaal 10%

België

Inkomen < € 1500 27% Inkomen ⩾ € 1500 5% Totaal 8%

Vlaanderen Inkomen < € 1500 26% Inkomen ⩾ € 1500 5%

Totaal 13%

Wallonië Inkomen < € 1500 31% Inkomen ⩾ € 1500 7%

Brussel

Totaal 11%

Inkomen < € 1500 21% Inkomen ⩾ € 1500 6%

a 27% van de gezinnen in België heeft een inkomen dat kleiner is dan 1500 euro. Hoeveel % van hen geeft in Vlaanderen aan dat ze geen internetverbinding hebben ?

b Scoort Brussel beter dan Vlaanderen ?

c Wat betekent de 6% onderaan in de tabel rechts ?

Drukste luchthavens ter wereld

Top 10 grootste/drukste vliegvelden, 2018

Bron : Statbel, 30 april 2020

Positie Vliegveld

Totaal passagiers 1

Hartsfield-Jackson Atlanta Airport (Verenigde Staten) 107 394 029 2 Beijing Capital Airport (China) 100 983 290 3 Dubai International Airport (Verenigde Arabische Emiraten) 89 1 49 387 4 Los Angeles Airport (Verenigde Staten) 87 534 384 5 Tokyo Haneda Airport (Japan) 87 098 683 6 Chicago O’Hare Airport (Verenigde Staten) 83 245 472 7 London Heathrow Airport (Verenigd Koninkrijk) 80 1 02 01 7 8 Hong Kong Airport (China) 74 51 7 402 9 Shanghai Pudong Airport (China) 74 006 331 10 Parijs Charles de Gaulle Airport (Frankrijk) 72 229 723

a Hoeveel passagiers worden (gemiddeld) dagelijks verwacht in de luchthaven van Atlanta ?

Bron : vliegveldinfo.nl, 26 juni 2020

b Als je aan de luchthaven van Atlanta de waarde 100 toekent, welke waarde zou je dan aan de luchthaven van Charles de Gaulle toekennen ?

c In Zaventem was er in 2018 een totaal van 25 675 939 passagiers. Welke waarde ken je dan aan Zaventem toe ?

d Zoek op hoeveel passagiers de luchthaven van Charleroi telde in 2018.

e Zoek de huidige cijfers op. Bespreek de (eventuele) verschillen.

a Hoe wordt zo’n voorstelling genoemd ?

b Hoeveel leerlingen hebben thuis een gezinswagen van het merk Ford ?

c Hoeveel leerlingen zitten er in de klas van leerkracht Herman ?

d Waarom heeft het hier geen zin om van de mediaan te spreken ?

e Vraag aan elke klasgenoot met welk merk van auto thuis gereden wordt en teken zelf een passend diagram.

Voldoende openbaar vervoer in de buurt Aandeel (%) van de inwoners dat vindt dat er voldoende openbaar vervoer is in de buurt

a Hoeveel % van de inwoners van Gent vindt dat er voldoende openbaar vervoer in de buurt is ?

b Is dat percentage lager of hoger in het Vlaamse Gewest ? Formuleer een verklaring.

c Bij de eerste groep staven is de oranje staaf het hoogst. Is dat goed of minder goed ?

Met welk merk van auto rijden de ouders van de leerlingen van leerkracht Herman ?

Audi Citroën Ford Mercedes Opel Renault merk

Lengte van 20 vrouwen

Van 20 vrouwen werd de lengte opgetekend in cm : 15 2 7 8 8 9 9 16 0 2 3 3 4 4 6 8 8 9

a Hoe wordt zo’n voorstelling genoemd ?

b Hoeveel vrouwen hebben een lengte die groter is dan 170 cm ?

c Wat is de mediaan en de gemiddelde lengte ?

Aantal fraudes met phishing

In 2019 werden 12 432 gevallen van phishing vastgesteld (bijna vier keer zoveel als twee jaar daarvoor). Phishingcriminelen stelen steeds vaker kleinere bedragen, maar maken veel buit aan het einde van de rit. In totaal gingen de fraudeurs aan de haal met meer dan 7,5 miljoen euro.

a Wat is phishing ?

b Met hoeveel % is het aantal fraudegevallen gestegen van 2017 naar 2018 ? c Worden er de laatste tijd grote of kleine bedragen via fraude gestolen ?

a Hoeveel % van de leerkrachten was in 2019 in het basisonderwijs van het mannelijk geslacht ?

b Hoeveel % van de leerkrachten was in 2019 in het secundair onderwijs van het vrouwelijk geslacht ?

c Bereken het percentage mannelijke leerkrachten die bij jou op school lesgeven.

2 Statistische terminologie

Als je een gerichte kwaliteitscontrole op bepaalde zuivelproducten zoals melk wilt uitvoeren, zal je niet alle verpakkingen onderzoeken, maar lukraak dozen melk uitkiezen en ze aan het nodige onderzoek onderwerpen. Je voert dus steekproeven uit.

Anders zou zo’n controle enorm tijdrovend zijn, alle producten beschadigen en dus enorm veel geld kosten.

Arne zit in het voorlaatste jaar van het secundair onderwijs en wil weten hoe zijn medeleerlingen naar school komen.

Omdat de school ongeveer 1200 leerlingen telt, besluit hij om enkel de gegevens van een paar klassen te onderzoeken.

Arne is dus van plan om een bepaald onderzoek of experiment te verrichten.

Het onderwerp van het onderzoek, namelijk de wijze waarop een leerling naar school komt, noemen we de variabele

Hoe komen de leerlingen naar school ?

Dit onderzoek is gericht op een groep waarvan we een bepaalde eigenschap willen bestuderen : de populatie. Populatie : alle leerlingen van de desbetreffende school

Het aantal elementen van een populatie noemen we de populatieomvang. Populatieomvang : aantal leerlingen van de school van Arne

Omdat de school te groot is, concentreert Arne zijn onderzoek op een deel van de populatie, een steekproef. Steekproef : de onderzochte gegevens

Het aantal elementen van een steekproef noemen we de steekproefomvang. Steekproefomvang : aantal ondervraagde leerlingen van de school

De ondervraagde leerlingen geven natuurlijk een antwoord aan Arne. De resultaten (waarnemingen) van een onderzoek of experiment noemen we uitkomsten of waarnemingsgetallen. De verzameling van alle elementen die als mogelijke uitkomsten kunnen optreden, noemen we de uitkomstenverzameling.

Hier is dat bijvoorbeeld : te voet met de fiets met de bromfiets met de wagen met de bus/tram met de trein

Notaties : P : populatie

N : (aantal elementen van P) populatieomvang S : steekproef

n : (aantal elementen van S) steekproefomvang

V : uitkomstenverzameling

We omschrijven enkele belangrijke begrippen.

populatie en populatieomvang

De populatie is de verzameling van alle elementen waarvan een bepaalde eigenschap wordt bestudeerd. Het aantal elementen van de populatie noemen we de populatieomvang

Opmerking :

In onze taal wordt met populatie bevolking bedoeld. In de statistiek kan populatie echter een verzameling schoenen zijn, een verzameling medicijnen, de lengte van een aantal personen, een verzameling fietsen …

steekproef en steekproefomvang

Een steekproef is een deel van de populatie waarvoor er waarnemingen worden verricht om een bepaalde eigenschap te bestuderen.

De steekproefomvang is het aantal elementen van de steekproef.

waarnemingsgetallen en uitkomstenverzameling

Waarnemingsgetallen of uitkomsten zijn de resultaten van een steekproef, uitgevoerd op een deel van een bepaalde populatie.

De uitkomstenverzameling is de verzameling van alle mogelijke waarnemingsgetallen.

statistiek

Statistiek is de wetenschap die gegevens over bepaalde verschijnselen via een steekproef verzamelt, ordent, samenvat en analyseert aan de hand van tabellen, getallen (gemiddelde, mediaan, standaardafwijking ...) en grafieken (lijndiagram, staafdiagram, cirkeldiagram, stengelbladdiagram, boxplot, histogram, ogief ...) om zo tot betrouwbare conclusies te komen voor de hele populatie.

Met behulp van statistiek kun je gegevens, die een antwoord geven op belangrijke vragen, kritisch leren bekijken en verzamelen. Bovendien leert statistiek je beoordelen hoe betrouwbaar bepaalde conclusies zijn.

3

Representativiteit van een steekproef

Arne wil nagaan hoe de leerlingen naar school komen. Om zichzelf werk te besparen besluit hij slechts één klas te ondervragen, en dan wel die met het minst aantal leerlingen.

De kleinste klas telt 9 leerlingen.

Wat denk je ? Is dat een goed idee ? Waarom (niet) ?

Wil een steekproef min of meer een getrouwe weerspiegeling zijn van de volledige populatie, dan moet het aantal waarnemingen voldoende groot zijn.

Arne zag zijn fout gelukkig tijdig in. Hij besluit nu om meer klassen te ondervragen.

Hij besluit om er één jaar uit te nemen, bijvoorbeeld de eerstejaars. Is dat een goed idee ?

Hoeveel van de eerstejaars komen volgens jou met de bromfiets naar school ? Wat is er dus fout ?

Elk element van de populatie moet dezelfde kans hebben om geselecteerd te worden. Het is dus nodig dat de objecten of personen die in de steekproef opgenomen worden willekeurig of aselect gekozen worden.

representatief

Een steekproef is representatief als :

1 het aantal waarnemingen voldoende groot is ;

2 de elementen ervan willekeurig of aselect gekozen worden.

Als je zou willen weten wat de favoriete vakantiebestemming is van de Vlamingen, dan moet je zowel jongeren, volwassenen als ouderen ondervragen.

Ook moet je ervoor zorgen dat alle lagen van de Vlaamse bevolking vertegenwoordigd zijn : arbeiders, bedienden, ambtenaren, werklozen …

De steekproef moet ook voldoende groot zijn. Pas dan zal je een betrouwbaar antwoord krijgen op de gestelde vraag en zal de steekproef dus representatief zijn.

Een goed opgestelde steekproef vormt de basis van elk statistisch onderzoek.

statistisch onderzoek verloopt in een aantal stappen

1 Voorbereiden van het onderzoek.

2 Verzamelen van de gegevens door het uitvoeren van een (representatieve) steekproef.

3 Verwerken van de gegevens in diagrammen, tabellen, grafieken.

gegevens

Staafdiagram

Aantal fietsen per land

Nederland telt meer fietsen dan inwoners. Hoe bijzonder is dat eigenlijk ? Pas als je meerdere landen op een rijtje zet, zie je hoe fietsgek Nederland is.

5 Diagrammen tekenen met ICT

Lijn-, staaf- en cirkeldiagrammen tekenen we het best met Excel. Dotplots en stengelbladdiagrammen tekenen we met GeoGebra.

a Een lijndiagram tekenen

Cocaïnevangst in de haven van Antwerpen (in ton) : 2014 2015 2016 2017 2018 2019 8,1 14,4 29,8 41,2 50,1 62,0

• Breng de tabel in een rekenblad in.

• Selecteer de 2 rijen en klik op invoegen. Kies nadien voor lijn en neem dan op de eerste lijn de vierde mogelijkheid.

• Klik met de rechtermuisknop op de getekende lijn en kies voor gegevenslabels toevoegen.

• Klik opnieuw op de getekende lijn en kies voor gegevenslabels opmaken. Vink bij labelpositie de optie onder aan.

• Vul een passende titel in.

• Klik met de rechtermuisknop op de horizontale as en voeg secundaire rasterlijnen toe.

Je krijgt dan :

Bron : Radio 2, 8 januari 2020

b Een staafdiagram tekenen Diefstallen en afpersing in België (2019), aantal inbreuken volgens het geslacht : MANNEN

Bron : federale politie, 2019

Breng de tabel in een rekenblad in.

• Selecteer de 2 kolommen en klik op invoegen. Kies nadien voor aanbevolen grafieken en vervolgens voor staafdiagram.

• Klik met de rechtermuisknop op een staaf en kies voor gegevenslabels toevoegen

• Vul een passende titel in.

• Zorg er wel voor dat de verticale as op 0 begint (klik met de rechtermuisknop op die as, kies voor as opmaken en zet het minimum op 0) en voeg ook secundaire rasterlijnen toe.

c Een cirkeldiagram tekenen :

• Stel een tabel op en breng die tabel in een rekenblad in.

• Selecteer de gegevens en klik op invoegen. Kies nadien voor aanbevolen grafieken en vervolgens voor een cirkeldiagram.

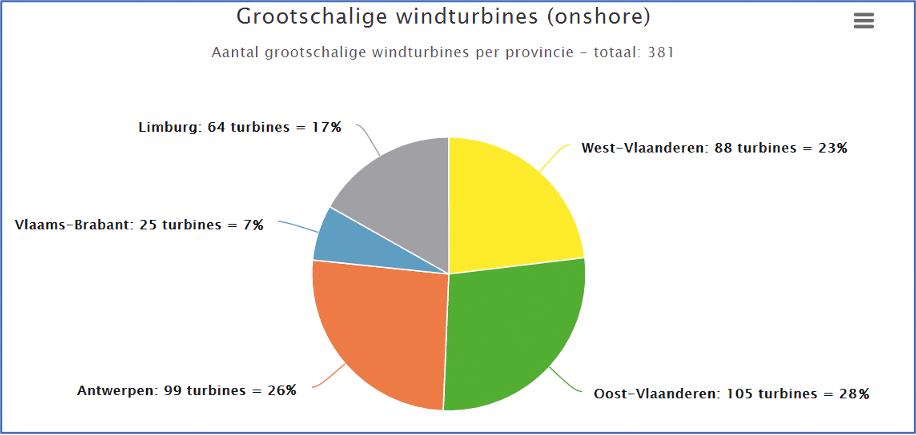
• Klik met de rechtermuisknop op de getekende grafiek en kies voor gegevenslabels toevoegen

• Klik met de rechtermuisknop op de legenda. Kies voor legenda opmaken en vink de optie rechts aan.

d Een dotplot tekenen :

Aan 30 leerlingen werd gevraagd hoeveel dagen ze per week sporten.

2 7 3 2 3 5 3 5 1 0 0 4 5 2 3 7 6 4 5 2 2 4 3 5 5 2 4 3 4 5

• Breng de gegevens in het rekenblad van GeoGebra in.

• Selecteer de gegevens en maak er een lijst l1 van.

• Geef in het algebravenster het commando puntenplot ( l1) in.

• Pas de labels op de assen aan. Daarvoor druk je eerst op de selecteerknop en klik je vervolgens met de rechtermuisknop in het tekenvenster. Kies daarna onderaan voor tekenvenster en pas dan zowel op de x -as als de y -as de labels aan.

e Een stengelbladdiagram tekenen :

Van 25 vrouwen werd de leeftijd opgetekend als hun eerste baby geboren werd.

• Breng de gegevens in het rekenblad van GeoGebra in.

• Selecteer de gegevens en maak er een lijst l1 van.

• Geef in het algebravenster het commando stengelbladdiagram( l1) in.

Samenvatting

• Je kent de betekenis van populatie, populatieomvang, steekproef, steekproefomvang, waarnemingsgetallen en uitkomstenverzameling.

– De populatie is de verzameling van alle elementen waarvan een bepaalde eigenschap wordt bestudeerd.

De populatieomvang is het aantal elementen van de populatie.

– Een steekproef is een deel van de populatie waarvoor er waarnemingen worden verricht om een bepaalde eigenschap te bestuderen.

De steekproefomvang is het aantal elementen van de steekproef.

– Waarnemingsgetallen zijn resultaten van een steekproef, uitgevoerd op een deel van een bepaalde populatie.

De uitkomstenverzameling is de verzameling van alle mogelijke waarnemingsgetallen.

• Je weet dat statistiek de wetenschap is die gegevens over bepaalde verschijnselen via een steekproef verzamelt, ordent, samenvat en analyseert om zo tot betrouwbare conclusies te komen voor de hele populatie.

• Je weet wanneer een steekproef representatief is.

• Je kent verschillende mogelijkheden om data voor te stellen : lijndiagram, staafdiagram, cirkeldiagram, dotplot en stengelbladdiagram.

cirkeldiagram lijndiagram

7 Oefeningen

Geef bij elke opgave de gevraagde begrippen.

GEGEVEN GEVRAAGD OPLOSSING

a Een gemeente met meer dan 25 000 inwoners wil een idee krijgen over de houding van haar inwoners tegenover de aanleg van een windmolenpark in haar gemeente. Daarom houdt ze een enquête bij 3000 inwoners.

– populatie – variabele – steekproef

b Iemand wil een onderzoek doen naar het aantal kinderen in een doorsnee Vlaams gezin.

– populatie – een zinvolle steekproef – de mogelijke uitkomstenverzameling

c Een waspoederproducent wil een enquête houden onder zijn klanten over de tevredenheid van zijn producten.

– populatie – een mogelijke uitkomstenverzameling – een zinvolle steekproef

d Een firma die stalen ringen maakt als onderdeel van een bepaalde machine neemt 100 ringen uit het productieproces en meet ze na.

– populatie – variabele – steekproef – steekproefomvang

– populatie – variabele – steekproef

Jelle van de leerlingenraad wil iets doen aan de overvolle boekentassen die de leerlingen van de tweede graad elke dag moeten sjouwen. Hij wil daarom de massa van de boekentassen van een representatief aantal leerlingen van de tweede graad bepalen om de directie en de leerkrachten te overtuigen dat dit probleem ernstig genomen moet worden. Het aantal leerlingen in de tweede graad bedraagt 320. Hij besluit om 60 boekentassen te wegen. Omschrijf het onderzoek van Jelle.

a Wat is de variabele ?

b Wat is de populatie ?

Wat is de populatieomvang ?

c Wat is de steekproefomvang ?

d Wat zijn de mogelijke uitkomsten die Jelle kan verkrijgen ?

e Omdat hij dan de resultaten in de namiddag kan verwerken, besluit Jelle het onderzoek op een woensdag te doen. Is dat een goed idee ? Verklaar.

f Jelle besluit om in een aantal klassen de massa van de boekentassen te bepalen. Is dat een goed idee ? Bekijk je eigen lessenrooster. Is de massa van je boekentas elke dag even groot ?

g Geef een voorbeeld van een slechte en een goede steekproef.

Een onderzoeksbureau wil de mening weten van de Vlamingen over het al dan niet bepalen van taks op de autowegen. Waarom zijn volgende steekproeven niet representatief ?

a Op een zaterdagmiddag wordt op een druk kruispunt in Gent een groot aantal voorbijgangers bevraagd.

b In de ochtendspits wordt in een file in de Brusselse binnenstad een aantal automobilisten bevraagd.

c In Blankenberge wordt een groot aantal toeristen op de zeedijk naar hun mening gevraagd.

Wat denk je van volgende situaties ?

a Als er zich een ernstig ongeval met een vrachtwagen voordoet op onze Vlaamse wegen, blijkt de chauffeur meestal een man te zijn van Europese afkomst. Wanneer ik nu een eigen transportfirma zou beginnen met enkel Afrikaanse vrouwen aan het stuur, maken mijn chauffeurs dan minder kans op een ongeluk ?

b De vuilnisdienst van een stad wil nagaan hoeveel huisvuil een gezin uit die stad wekelijks buitenzet. Daarom besluiten ze om in een bepaalde week de massa van de huisvuilzakken van alle inwoners van vijf grote winkelstraten op te tekenen. Krijgen ze zo een goed beeld ?

c Voor het onderzoek ‘Wat is jouw favoriete supermarkt ?’ worden aan de ingang van de plaatselijke Colruyt 150 personen bevraagd. Krijgt de onderzoeker zo een goed beeld ?

d Een krant wenst de mening van de Vlamingen te kennen over het onderwijsbeleid van de minister van Onderwijs. Daarom schrijft ze al haar abonnees aan (meer dan 5000). Als ze die antwoorden verwerken, krijgen ze dan een goed beeld van wat de Vlaming denkt ?

e De laatste jaren zijn er erg veel overstromingen in het Dendergebied. Daarom wil een bureau, dat statistische gegevens verwerkt, een aantal vragen stellen aan 500 inwoners van Geraardsbergen. Krijgen ze zo een goed beeld van wat de Vlamingen in het Dendergebied denken ?

Joris moet een kleine maar delicate chirurgische ingreep ondergaan. In de stad zijn er twee gespecialiseerde ziekenhuizen : Alfa en Bèta. Hij besluit om bij beide eens te gaan informeren. In ziekenhuis Alfa krijgt hij het volgende te horen : Ons ziekenhuis doet minder van deze soort behandelingen dan onze concurrent, maar we zijn beter. Wij behandelden de afgelopen 5 jaar zo’n 1200 patiënten en slechts bij 24 onder hen mislukte de operatie. In het andere ziekenhuis daarentegen deed men 3000 operaties waarvan er 85 mislukten.

a Zet dit in een tabel.

aantal operaties aantal mislukte aantal gelukte

% aantal mislukte

% aantal gelukte

ZIEKENHUIS ALFA

ZIEKENHUIS BÈTA

b Joris zou graag nog een aantal jaren blijven leven. Aan welk ziekenhuis geeft hij volgens jou het best de voorkeur ?

c Om zichzelf te overtuigen dat dit de juiste keuze is, gaat Joris nog eens langs bij ziekenhuis Bèta en hij confronteert hen met bovenstaande tabel. Dit is hun reactie :

Die cijfers zijn correct, maar een kleine opmerking is hier wel op zijn plaats. Er zijn twee soorten patiënten : patiënten met een goede conditie en patiënten met een minder goede, zeg maar slechte conditie. Ons ziekenhuis had 900 patiënten met een goede conditie. Bij 9 van hen mislukte de operatie. Ook ziekenhuis Alfa had 900 patiënten met een goede conditie en bij 12 patiënten mislukte de operatie. Wat jouw conditie is, weet ik niet. Daarvoor moet je eerst onderzocht worden. Maar in beide gevallen … reken maar na!

Zet ook dat in een tabel. GOEDE CONDITIE

aantal operaties aantal mislukte aantal gelukte % aantal mislukte % aantal gelukte

d Als Joris de cijfers bekijkt, aan welk ziekenhuis zal hij dan de voorkeur geven ?

Je kunt hieruit besluiten dat cijfers en grafieken soms misleidend kunnen zijn. Let dus goed op en wees kritisch.

Een jongerenwebsite vroeg aan zijn bezoekers wat ze doen als ze ruzie hebben met hun ouders. 1218 lezers gaven een antwoord. Dit is het resultaat.

a Teken een cirkeldiagram dat de gegevens weergeeft.

Als ik ruzie met mijn ouders heb, dan … ga ik schreeuwen 38% loop ik weg 37% probeer ik het meteen uit te praten 15% ik heb nooit ruzie met mijn ouders 10% 1218 lezers hebben gestemd.

b Hoeveel jongeren die op de vraag geantwoord hebben, hebben nooit ruzie met hun ouders ?

Wat doe jij het liefst als je een beetje down bent? muziek luisteren 49 % chocolade eten 24 % naar mijn vriendje gaan 12 % met mijn moeder shoppen 9 % 1084 lezers hebben gestemd

Kristel heeft een mooie verzameling strips. In de volgende tabel vind je een overzicht. Zet de gegevens om in een staafdiagram. Suske en Wiske 60 De Kiekeboes 30 Jommeke 24 De Kampioenen 16 Andere 50

vriendinnen opbellen 6 %

Van een voetbalclub die speelt in een lagere afdeling werd gedurende een aantal jaren het gemiddelde aantal toeschouwers genoteerd.

gemiddeld aantal toeschouwers

a Teken een lijndiagram dat dit alles weergeeft.

b In welk jaar speelde die ploeg (wellicht) aan de top van de rangschikking ?

c Bereken het gemiddelde aantal toeschouwers over die jaren heen.

Aantal vluchten – vertrek en aankomst

2018 bij vertrek bij aankomst

Aantal vluchten 162 186 161 447 Zaventem (Brussels Airport) 111 357 111 154 Oostende (Ostend-Bruges) 4033 3982 Charleroi (Brussels South) 24 285 24 275 Antwerpen (Antwerp Airport) 7653 7529 Luik (Liege Airport) 14 858 14 507

Bron : Statbel

a Geef het aantal vluchten bij aankomst van de 5 vermelde luchthavens weer in een staafdiagram.

b Hoeveel % van het totale aantal vluchten (bij vertrek) neemt elke luchthaven in beslag ?

c Stel de resultaten voor in een cirkeldiagram.

UNICEF is het kinderfonds van de Verenigde Naties en werd in 1946 opgericht met als doel alle kinderen te helpen die slachtoffer zijn van oorlog, natuurrampen en mishandeling. Ook gezondheid en onderwijs zijn twee pijlers van UNICEF. Geld wordt opgehaald bij donateurs, overheden en bedrijven. In de voorstelling hieronder zie je waar het ingezamelde geld in België voor diende in 2019.

d Zoek twee voorbeelden van ontwikkelingsprogramma’s van UNICEF die specifiek gaan over het onderwijs.

Aan 20 leerlingen van een muziekschool werd gevraagd wat hun lievelingsinstrument is : piano viool trompet dwarsfluit viool viool harp blokfluit piano klarinet saxofoon trompet viool viool piano harp viool trompet saxofoon harp

Teken een dotplot van de data.

Van 2 klassen van telkens 20 leerlingen werden de scores (op 100 punten) bijgehouden op een toets wiskunde.

KLAS A 45 63 61 72 38 72 74 76 69 60 52 78 82 54 66 65 90 81 72 39 KLAS B 59 76 86 88 92 78 74 49 57 72 92 89 85 67 62 72 84 91 67 89

a Teken een stengelbladdiagram van klas A. b Teken een stengelbladdiagram van klas B.

c Welke klas scoorde het best op de toets ? Verklaar aan de hand van de twee getekende diagrammen.

In een klas zitten 50% meer jongens dan meisjes. Van de jongens is 62% geslaagd en van de hele klas is 68% geslaagd. Hoeveel procent van de meisjes is geslaagd ?

(A) 68% (B) 71% (C) 74% (D) 77% (E) 80%

JWO 2017 tweede ronde, vraag 13 © Vlaamse Wiskunde Olympiade vzw

In het staafdiagram zien we hoe de bezoekers van de vijf meest bezochte Europese pretparken over de pretparken verdeeld zijn. Die parken hebben samen 56 miljoen bezoekers per jaar. Hoeveel bezoekers heeft Disneyland Parijs elk jaar meer dan de Efteling ?

JWO 2018 eerste ronde, vraag 5 © Vlaamse Wiskunde Olympiade vzw

Vaardigheden | Datasets vergelijken met behulp van ICT

Voorbeeld 1 :

Noor noteerde in een bepaalde week op een dinsdag en een donderdag van 17.00 u. tot 18.00 u. het aantal fietsers, voetgangers en ander verkeer in haar straat. DINSDAG

aantal voetgangers 12 28 aantal fietsers 3 11 andere 45 23

We geven deze situatie in een dubbel staafdiagram weer.

• Breng deze tabel zo in Excel in.

• Selecteer alle gegevens. Klik op Invoegen en kies bij Aanbevolen grafieken voor het passende type.

We zien dat er in die week op donderdag meer voetgangers en fietsers door Noors straat kwamen dan op dinsdag, maar veel minder ander verkeer.

Aantal voetgangers, fietsers en ander verkeer

20 % 30 % 40 % 50 %

10 % 0 %

Aantal voetgangers Aantal fietsers Ander verkeer

Dinsdag Donderdag

Voorbeeld 2 :

Van 30 vrouwen en 30 mannen van dezelfde leeftijdscategorie werd het gewicht (in kg) genoteerd.

Mannen 68 82 77 70 95 64 78 77 84 87 96 69 76 80 81 104 91 83 76 70 69 68 77 79 73 68 93 78 67 82

Vrouwen 58 63 57 67 69 64 74 82 59 63 66 70 56 82 60 64 92 68 70 72 64 69 62 84 75 69 62 65 71 67

We tekenen een parallelle dotplot van de gegevens.

– Breng de gegevens in het rekenblad in.

– Selecteer de gegevens en maak er lijsten l1 en l2 van.

– Geef de commando’s puntenplot ( l1) en puntenplot( l2) in.

– Verander de stijl van de getekende punten van de mannen door voor een blauw kruisje te kiezen (klik op een puntje met de rechtermuisknop en ga naar instellingen ; klik dan op stijl en kies een passende puntstijl).

– Verplaats de y -as door met de rechtermuisknop in het tekenvenster te klikken en te gaan naar tekenvenster. Klik dan op y As en plaats snijpunt assen op 54.

• We zien dat er bij de opgetekende data heel wat mannen zijn die een gewicht hebben van 80 kg en meer. 5 hebben een gewicht van meer dan 90 kg.

• Er zijn ook maar 7 mannen die minder dan 70 kg wegen tegenover 20 vrouwen.

We tekenen nu ook een stengelbladdiagram dat het gewicht van de mannen weergeeft en een stengelbladdiagram voor het gewicht van de vrouwen :

Aan die stengelbladdiagrammen herkennen we ook snel de hiervoor gemaakte opmerkingen. We tekenen nu op papier een dubbel stengelbladdiagram. We plaatsen rechts het gewicht van de mannen en links het gewicht van de vrouwen.

Hierbij herkennen we ook volgende zaken :

• 5 mannen hebben een gewicht van meer dan 90 kg.

• Veel mannen hebben een gewicht van meer dan 80 kg tegenover 4 vrouwen.

• 20 vrouwen maar slechts 7 mannen hebben een gewicht van minder dan 70 kg.

• Iemand van de mannen weegt 104 kg.

• Geen enkele man weegt minder dan 60 kg.

• De gewichten van de mannen liggen veel meer naar onderen toe (als je de stengel bekijkt).

Methodes om gegevens voor te stellen

JE KENNEN EN

WAT MOET

dit moet ik leren pagina ik ken het ! oké voor examen

❒

❒

❒

❒

❒

❒

Ik weet wat bedoeld wordt met populatie(omvang), steekproef(omvang), waarnemingsgetallen en uitkomstenverzameling. 16  

Ik weet wanneer een steekproef representatief is. 18  

Ik ken de drie stappen van een statistisch onderzoek. 18  

Ik kan een grootheid onderzoeken die in een dataset voorgesteld is als een staafdiagram, dotplot, cirkeldiagram, lijndiagram en stengelbladdiagram. 19  

Ik kan grafische voorstellingen maken met ICT : staafdiagram, dotplot, cirkeldiagram, lijndiagram en stengelbladdiagram. 21  

Ik kan datasets vergelijken. 32  

Methodes om gegevens voor te stellen

/ Stiptheid

b 5 0 0 1 3 2 4 6 6 9 0 1 3 5 1 2 4 3 2

Datum Nummer Hoe noem je deze voorstellingswijzen van data ? a 5 0 0 1 3 2 4 6 6 9 0 1 3 5 1 2 4 3 2

c 5 0 0 1 3 2 4 6 6 9 0 1 3 5 1 2 4 3 2

d 5 0 0 1 3 2 4 6 6 9 0 1 3 5 1 2 4 3 2

e 5 0 0 1 3 2 4 6 6 9 0 1 3 5 1 2 4 3 2

a b c d e

Tewerkstelling in de toeristische sector in Vlaanderen Diensten voor sport en recreatie 9% Accommodatie 11% Diensten voor cultuur 12% Personenvervoer 17% Voedings- en drankverstrekkers 46% Overige 5% Bron : RSZ, statistiek Vlaanderen, januari 2020

a Zet de gegevens om in een cirkeldiagram. b Lore werkt aan de programmering van een cultureel centrum. Tuur werkt in de cafetaria van een cultureel centrum. Areeb bestuurt de toeristische stoomtrein in Dendermonde. Waar horen ze thuis in die data ? Lore : Tuur : Areeb :

Naam Totaal Orde

Waarvoor dienen de belastingen en sociale bijdragen (€ 239,6 miljard) ?

Pensioenen Gezondheidszorg Onderwijs Economisch beleid Overheidsbestuur

Invaliditeit en ziekte Vervoer

Werkloosheid en sociale uitsluiting Staatsschuld Andere

Bron : financien.belgium.be

€ 50,1 mld. (……………%)

€ 34,9 mld. (14,6%)

€ 28,6 mld. (11,9%)

€ 17,5 mld. (7,3%)

€ 16,7 mld. (7%)

€ 15,4 mld. (6,4%)

€ 12,7 mld. (5,3%) € 11,7 mld. (4,9%) € 10,6 mld. (4,4%)

€ 41,4 mld. (17,3%)

In België betalen we veel belastingen en sociale bijdragen. Belastingen betaal je onder andere op alle goederen en diensten die je aankoopt (btw). Iedereen die een inkomen krijgt, geeft een bijdrage aan de RSZ. Die Rijksdienst voor Sociale Zekerheid haalt ook geld op bij de werkgevers en zal dat geld uitgeven aan bijvoorbeeld pensioenen, ziektevergoedingen, groeipakketten en werkloosheidsuitkeringen.

a Hoe noemen we die voorstellingswijze van data ?

b Vul bovenaan het percentage aan dat de overheid uitgeeft aan Pensioenen.

c Geef twee voorbeelden van wat bij Andere genoteerd zou kunnen worden.

Spendeert de jeugd veel tijd aan sociale media ? Je wilt onderzoeken hoeveel minuten jongeren per dag aan sociale media besteden. Je zal hiervoor aan al je klasgenoten de vraag stellen.

a Wat is de variabele ?

b Wat is de populatie ?

Wat is de populatieomvang ?

c Wat is de steekproefomvang ?

d Geef enkele mogelijke uitkomsten die je kunt verkrijgen.

e Wat zou je veranderen aan je onderzoek om het meer representatief te maken ?