LEERWERKBOEK
Analyse D&A-finaliteit
Philip Bogaert
Filip Geeurickx
Marc Muylaert
Roger Van Nieuwenhuyze
Erik Willockx
CARTOONS
Dave Vanroye
Hoe gebruik je VBTL?
uit verschillende paragrafen met aan het einde een handige samenvatting.
Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.
Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt. Wiskunde kent veel links met andere vakken We tonen zo’n link in een paarsgekleurd kadertje.



1 Kenmerken van een functie 1.1 Verschillende representaties van een functie Begrippen Input-outputmodel van een functie De grafiek van een functie construeren De grafiek van een functie construeren Domein, bereik en nulwaarden bepalen op de grafiek 1.7 Verloop van reële functies 22 Toepassing: inhoud van een doosje zonder deksel 25 2 Machten 2.1 Machten met een natuurlijk getal als exponent 2.2 Machten met een geheel getal 2.3 Vierkantswortels in 72 Derdemachtswortel van een reëel getal 2.5 -demachtswortels in 90 Machten met een rationaal getal als exponent 3 Exponentiële groei Inleiding: soorten groei 3.2 Lineair versus exponentieel 116 Groeifactor en procentuele toename of afname 119 Exponentiële functies 3.5 Grafieken van functies met voorschrift 3.6 Grafieken van functies met voorschrift 3.7 Exponentiële vergelijkingen 130 Toepassingen op exponentiële functies 131 4 Logaritmen 4.1 Instap 155 Definitie Briggse en neperiaanse logaritmen Eigenschappen voor logaritmen Rekenregels voor logaritmen Verband tussen logaritmen met een verschillend grondtal Toepassingen Benaderen, afronden en schatten 4.9 Logaritmische schaal en logaritmisch papier 5 Gemiddelde verandering en differentiequotiënt Gemiddelde verandering 5.2 Differentiequotiënt van een functie 5.3 Gemiddelde helling en gemiddelde hellingshoek 5.4 Ogenblikkelijke verandering 192 Ogenblikkelijke snelheid Oplossingen Trefwoordenregister 223 Analyse
Bij functies met een graad hoger dan twee doen we een beroep op ICT. Plot de grafiek van de functie met wiskunDemathematiseren De inhoud van het doosje is maximaal bij: een lengte van:66,46 cm Functies Het woord ‘functie’ werd voor het eerst gebruikt door de Duitse wiskundige Leibniz (1646–1716), die het begrip koppelde aan gelijk welke grootheid verbonden met een kromme. In 1718 definieerde de Zwitserse wiskundige Johann Bernoulli (1667–1748) een functie als een willekeurige constanten. Zijn landgenoot Euler (1707–1783) voerde de notatie f(x) in. Het is de Duitser Dirichlet (1805–1859) die de uiteindelijke definitie vastlegde en ook begrippen zoals ‘definitiegebied’ en ‘bereik’ omschreef. Het ‘definitiegebied’ noemen we nu ‘domein’.
Dit boek bevat vijf hoofdstukken. Elk hoofdstuk is opgebouwd
2 De breuk wordt omgedraaid. De exponent verandert van teken. 1 1 5 2 5 2 Er geldt dus ook: 2 5 4 125 64 macht met een negatieve exponent 2Eigenschappen We vragen ons af of de rekenregels die gelden voor gelijksoortige machten met een natuurlijke exponent geldig blijven als de exponent een geheel getal is. aProduct van gelijksoortige machten 10 10 10 10 ✚ ✚ ✚✚ 10 ✚✚ 10 10 ✚ ✚ Besluit: Rekenregel 1: product van gelijksoortige machten R Z VBTL5_Lwb_Analyse_D&A_H2.indd 59
De nummers van de oefeningen hebben een gele kleur. Een sterretje duidt op een extra uitdaging. Achteraan in dit boek vind je de oplossingen
ICT is een ideaal hulpmiddel. Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets. Die vind je terug via www.polpo.be.


Wat moet je kennen en kunnen?
Op het einde van elk hoofdstuk zie je een handig overzicht van wat je moet kennen en kunnen Kleur de eerste kolom smileys als je de leerstof herhaalde voor een grote toets. Kleur de laatste kolom als je de leerstof beheerst voor je examen.
WAT MOET JE KENNEN EN KUNNEN dit moet leren pagina ken het oké voor ❒ Ik ken de verschillende representaties van een functie: verwoording, tabel, voorschrift en grafiek. ❒ Ik ken de betekenis van een functie. 13 ❒ ❒ Ik kan het domein van een functie bepalen. ❒ Ik kan het bereik van een functie bepalen. ❒ Ik weet wat bedoeld wordt met het input-outputmodel van een functie. ❒ Ik kan de grafiek van een functie construeren. 17 ❒ ❒ ❒ Ik kan het domein, het bereik en de nulwaarden bepalen op de grafiek. ❒ Ik weet wanneer een functie stijgend, dalend of constant is. ❒ Ik ken de betekenis van de extreme waarden minimum en maximum. 23 ❒ Kenmerken van een functie 1
Bij voorbeeld op blz. 11 wordt het functievoorschrift van de functie √ of )= √ ( √ –dom R ber R Elk reëel getal heeft juist één tweevoud, dus dit verband is een functie – –Beschouw de functie – 1 – – – 1 –28 – –VBTL5_Lwb_Analyse_D&A_H1.indd 14
Oplossingen 1 Kenmerken van een functie 1a tijd 1246 afgelegde weg100200400600 tijd; afgelegde weg 100 recht evenredig 2a 1245 101620 –h ja b 6 )= 0,30 d15000km p )= cja c4maalkleiner fkwadratisch gja 7a1m d 2,4 ,kwadratisch 9b8maalkleiner dja 10afunctie;dom =[ 3,7 ;ber =[ 4,4 nulwaarden:2 bfunctie;dom =] ,4 ;ber =[ 4, + cfunctie;dom R\{ };ber R nulwaarden:geen dfunctie;dom =] ;ber =] nulwaarden:2 =] nulwaarden:geen fgeenfunctie ber =] 4, 1,0 ;nulwaarden:geen { nulwaarden:geen ifunctie;dom ;ber =[ 4, jgeenfunctie 1
2 *
In dit boek snijden we een thema aan dat je zeker nog herkent van vorig jaar: functies. We breiden nu de eerstegraadsfuncties uit naar de reële functies. Een functie die we bijvoorbeeld zullen onderzoeken, is de exponentiële functie, die we in talloze alledaagse situaties tegenkomen, van de intrest op een spaarboekje tot de schimmel op etenswaren. Een (bos)brand is er ook een voorbeeld van: die gaat steeds sneller uitbreiden als de brandweerlui of blusvliegtuigen niet tussenbeide komen.
Ook machten en n-demachtswortels komen in dit boek aan bod: we frissen je kennis op en breiden die uit. Tot slot maak je kennis met enkele nieuwe begrippen, zoals logaritmen, gemiddelde verandering en het differentiequotiënt.

Inhoud

Exponentiële
5
Gemiddelde verandering en differentiequotiënt
Kenmerken van een functie 1.1 Verschillende representaties van een functie 9 1.2 Begrippen 13 1.3 Input-outputmodel van een functie 16 1.4 De grafiek van een functie construeren 17 1.5 De grafiek van een functie construeren met ICT 18 1.6 Domein, bereik en nulwaarden bepalen op de grafiek 19 1.7 Verloop van reële functies 22 1.8 Toepassing: inhoud van een doosje zonder deksel 25
Machten 2.1 Machten met een natuurlijk getal als exponent 53 2.2 Machten met een geheel getal als exponent 58 2.3 Vierkantswortels in � 72 2.4 Derdemachtswortel van een reëel getal 83 2.5 n-demachtswortels in � 90 2.6 Machten met een rationaal getal als exponent 100
1
2
3
groei 3.1 Inleiding: soorten groei 115 3.2 Lineair versus exponentieel 116 3.3 Groeifactor en procentuele toename of afname 119 3.4 Exponentiële functies 123 3.5 Grafieken van functies met voorschrift f(x) = a x 124 3.6 Grafieken van functies met voorschrift f(x) = b · a x 126 3.7 Exponentiële vergelijkingen 130 3.8 Toepassingen op exponentiële functies 131
4.1 Instap 155 4.2 Definitie 155 4.3 Briggse en neperiaanse logaritmen 156 4.4 Eigenschappen voor logaritmen 157 4.5 Rekenregels voor logaritmen 158 4.6 Verband tussen logaritmen met een verschillend grondtal 161 4.7 Toepassingen 162 4.8 Benaderen, afronden en schatten 165 4.9 Logaritmische schaal en logaritmisch papier 166
4 Logaritmen
5.1 Gemiddelde verandering 183 5.2 Differentiequotiënt van een functie over een interval 186 5.3 Gemiddelde helling en gemiddelde hellingshoek 189 5.4 Ogenblikkelijke verandering 192 5.5 Ogenblikkelijke snelheid 194 Oplossingen 215 Trefwoordenregister 223
Analyse
Machten 2

Machten en wortels zijn begrippen die al lang gebruikt worden. Het waren de Babyloniërs die voor het eerst √2en √3 √2en √3 benaderden. Jij maakte er kennis mee in je eerste jaar middelbaar onderwijs.


Minder gebruikte synoniemen voor vierkantswortel zijn tweedemachtswortel en kwadraatswortel. Voor een derdemachtswortel werd vroeger dan weer wel eens kubiekwortel of teerlingwortel gebruikt. Vind je de link naar de betekenis van die woorden? Een blokje kaas als aperitief helpt je wellicht op weg …

Machten
52
2.1 Machten met een natuurlijk getal als exponent 1 Het begrip macht 53 2 Gelijksoortige machten 53 3 Eigenschappen 54 2.2 Machten met een geheel getal als exponent 1 Inleiding 58 2 Eigenschappen 59 3 Samenvatting 62 4 Oefeningen 63 2.3 Vierkantswortels in � 1 Begrippen 72 2 Grafische interpretatie 73 3 Eigenschappen van vierkantswortels 74 4 Vierkantswortels vereenvoudigen 75 5 Bewerkingen met vierkantswortels 75 6 Samenvatting 77 7 Oefeningen 78 2.4 Derdemachtswortel van een reëel getal 1 Inleiding 83 2 Grafische interpretatie 84 3 Toepassingen 85 4 Oefeningen 86 2.5 n-demachtswortels in � 1 Inleiding 90 2 Definitie 92 3 Eigenschappen 92 4 Benaderen, afronden en schatten 93 5 Samenvatting 94 6 Oefeningen 95 2.6 Machten met een rationaal getal als exponent 1 Definitie 100 2 Eigenschappen van machten met rationale exponenten 101 3 Samenvatting 101 4 Oefeningen 102 Wat moet je kennen en kunnen ? 112 2
2.1 Machten met een
getal als exponent
1Het begrip macht
natuurlijk
35 is een macht waarbij we 3 het grondtal noemen en 5 de exponent
2Gelijksoortige machten
42 en 43 zijn gelijksoortige machten omdat ze hetzelfde grondtal hebben.
(
3)2 en (
3)3 zijn ook gelijksoortige machten.
Maar 23 en 53 zijn geen gelijksoortige machten omdat hun grondtallen niet gelijk zijn: 2 ≠ 5.
Machten
De term ‘macht’ vindt zijn oorsprong in de Latijnse taal (potentia), maar zou eigenlijk fout vertaald geweest zijn uit het Grieks. Daar werd de Griekse term ‘vermenigvuldiging’ gebruikt, niet onlogisch. Machten werden in het prille begin van de wiskunde sowieso vooral gebruikt om oppervlaktes te berekenen (tweede macht) en volumes (derde machten).
In de loop van de geschiedenis zijn er al verschillende manieren geweest om een macht te noteren en al evenveel manieren om pakweg een tweede of derde macht te omschrijven. De schrijfwijze an, zoals we die nu kennen, werd door de Fransman Descartes in 1637 systematisch gebruikt met natuurlijke getallen als exponenten; de Engelsman Thomas Harriot zou dit wel kort daarvoor voor het eerst gebruikt hebben. De negatieve gehele exponenten en rationale exponenten werden in 1656 ingevoerd door John Wallis via zijn belangrijkste werk Arithmetica Infinitorum en ze werden verder bestudeerd door Isaac Newton. Net als enkele andere wiskundigen vond Newton het trouwens niet nodig om een exponent te gebruiken bij een tweede macht, ax² noteerde hij dus liever als axx.
53 2 Machten
35 = 3 · 3 · 3 ·
·
42 = 4 · 4 5factoren 2factoren machten a n = a a ... a met a ∈ R en n ∈ N0 n factoren a 1 = a met a ∈ R a 0 = 1 met a ∈ R 0 Voorbeelden: ( 3)2 =( 3) ( 3)= 9 25 = 2 2 2 2 2 = 32 π3 = π · π · π ≈ 31,006 1 2 2 = 1 2 1 2 = 1 4 a 3 b 4 = a · a · a · b · b · b · b ( 3)2 =( 3) ( 3)= 9 25 = 2 · 2 · 2 · 2 · 2 = 32 π3 = π π π ≈ 31,006 1 2 2 = 1 2 1 2 = 1 4 a 3 b 4 = a · a · a · b · b · b · b
3
3
–
–
3Eigenschappen
aProduct van gelijksoortige machten
Volg onderstaande redeneringen. We leiden hier een eerste rekenregel af.
Rekenregel 1: product van gelijksoortige machten
Om machten met hetzelfde grondtal te vermenigvuldigen:
– behoud je het grondtal;
– tel je de exponenten op.
54
24 · 23 = (2 · 2 · 2 · 2) · (2 · 2 · 2) 4factoren3factoren = 2 2 2 2 2 2 2 7factoren = 27 = 2 4+3 ( 3)2 ( 3) = (( 3) ( 3)) ( 3) 2factoren1factor = ( 3) · ( 3) · ( 3) 3factoren =( 3)3 =( 3)2+1 a 3 · a 4 = (a · a · a ) · (a · a · a · a ) 3factoren4factoren = a · a · a · a · a · a · a 7factoren = a 7 = a 3+4 Zovindenweook: b 2 b = b 2 b 1 = b 2+1 = b 3 a 2 · b 3 · a · b 2 = a 2 · a 1 · b 3 · b 2 = a 3 · b 5
In symbolen: a n · a p = a n+p met a ∈ R0 en n, p ∈ N
bQuotiënt van gelijksoortige machten
Volg onderstaande redeneringen. We leiden hier de tweede rekenregel af.
Rekenregel 2: quotiënt van gelijksoortige machten
Om machten met hetzelfde grondtal door elkaar te delen:
– behoud je het grondtal; – trek je de exponenten van elkaar af.
In symbolen:
55 2 Machten
25 :22 = 25 22 = 2 2 2 2 2 2 · 2 = 2 2 2 = 23 = 25 2 √2 3 : √2 2 = √2 √2 √2 √2 √2 = √2 = √2 3 2 a 4 : a 2 = a · a · a · a a a = a 2 = a 4 2 Zovindenweook: 74 73 = 74 3 = 7 a 2 b 5 a b 2 = a 2 1 · b 5 2 = a · b 3
a n : a p = a n–p met a ∈ R0 en n, p ∈ N
cMacht van een macht
Volg onderstaande redeneringen. We leiden hier de derde rekenregel af.
Rekenregel
3: macht van een macht
Om een macht tot een macht te verheffen:
– behoud je het grondtal;
– vermenigvuldig je de exponenten.
In symbolen:
56
23 2 = 23 · 23 = 23+3 = 26 = 23 2 ( 2)2 4 =( 2)2 ( 2)2 ( 2)2 ( 2)2 =( 2)2+2+2+2 =( 2)8 = ( 2)2 4 a 3 3 = a 3 a 3 a 3 = a 9 = a 3 3 b 2 5 = b 2 5 = b 10 b 0 3 = b 0 3 = b 0 = 1
(a n )p = a n p met a ∈ R0 en n, p ∈ N
dMacht van een product
Volg onderstaande redeneringen. We leiden hier een volgende rekenregel af.
eMacht van een quotiënt
Rekenregel 5: macht van een quotiënt Om
te verheffen, verhef je deeltal en deler tot die macht.
57 2 Machten
(2 10)2 =(2 10) (2 10) = 2 · 10 · 2 · 10 = 22 · 102 (a b )3 =(a b ) (a b ) (a b ) = a · b · a · b · a · b = a 3 · b 3 Zovindenweook: a 2 bc 3 2 = a 2 2 · b 2 · c 3 2 = a 4 b 2 c 6 2 bc 2 2 =( 2)2 · b 2 · c 2 2 = 4 b 2 c 4
een product tot een macht
In symbolen: ( a · b)n = a n b n met a, b ∈ R0 en n ∈ N
Rekenregel 4: macht van een product Om
te verheffen, verhef je elke factor tot die macht.
(8:3)3 = 8 3 3 = 8 3 8 3 8 3 = 8 8 8 3 · 3 · 3 = 83 33 a 2 b 2 = a 2 b a 2 b = a 2 · a 2 b b = a 4 b 2 Zovindenweook: ab 3 c 3 ab 2 2 = ✚✚ a 2 b 6 c 6 ✚✚ a 2 b 4 = b 2 c 6 ofeenvoudiger ab 3 c 3 ab 2 2 = bc 3 2 = b 2 c 6
een quotiënt
In symbolen: ( a : b)n = a n : b n a b n = a n b n met a, b ∈ R0 en n ∈ N
tot een macht
2.2 Machten met een geheel getal als exponent 1Inleiding
58
willen een betekenis geven aan 2–5 : 2 : 2 :2 : 2 : 2 : 2 : 2 :2 : 2 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1 2−1 = 1 2 = 1 21 2−2 = 1 4 = 1 22 2−3 = 1 8 = 1 23 2−4 = 1 16 = 1 24 2−5 = 1 32 = 1 25 Er geldt dus ook: 3 3 = 1 33 = 1 27 ( 2) 4 = 1 ( 2)4 = 1 16 a 3 = 1 a 3 10 1 = 1 10 macht met een negatieve exponent a n = 1 a n met a ∈ R0 en n ∈ N
We
3 = 1 2 5
Gevolg: De breuk wordt omgedraaid. De exponent verandert van teken.
Er geldt dus ook:
1 2 2 = 22 = 4
4 5 3 = 5 4 3 = 53 43 = 125 64
a b c
2 = c ab 2 = c 2 a 2 b 2
macht met een negatieve exponent
a b n = b a
3 = 1 23 53 3
= 53 23 = 5 2
n met a, b ∈ R0 en n ∈ N
2Eigenschappen
aProduct
van gelijksoortige machten 10 3 · 102 = 1 103 · 102 = 102 103 = ✚✚ 10 ✚✚ 10 ✚✚ 10 · ✚✚ 10 · 10 = 1 101 = 10 1 = 10 3+2 a 3 a 2 = a 3 1 a 2 = a 3 a 2 = ✚ a ✚ a a ✚ a · ✚ a = a 1 = a 3+( 2)
Rekenregel 1: product van gelijksoortige machten a n ·
a p
59 2 Machten
2 5
We vragen ons af of de rekenregels die gelden voor gelijksoortige machten met een natuurlijke exponent geldig blijven als de exponent een geheel getal is.
Besluit:
= a n+p met a ∈ R0 en n, p ∈ Z
bQuotiënt van
machten
60
gelijksoortige
103 :10 2 = 103 : 1 102 = 103 102 = 103+2 = 105 = 103 ( 2) a 3 : a 6 = a 3 : 1 a 6 = a 3 · a 6 = a 3+6 = a 3 = a 3 ( 6) Besluit: Rekenregel 2: quotiënt van gelijksoortige machten a n : a p = a n–p met a ∈ R0 en n, p ∈ Z cMacht van een macht 10 2 3 = 10 2 10 2 10 2 = 10 6 = 10 2 3 a 2 2 = 1 a 2 2 = 1 a 4 = a 4 = a 2 ( 2) a 2 3 = 1 a 2 3 = a 2 3 = a 2 3 = a 6 = a 2 ( 3) Besluit: Rekenregel 3: macht van een macht (a n )p = a n p met a ∈ R0 en n, p ∈ Z
dMacht van een product
3a 4 2 = 1 3a 4 2 = 1 32 a 8 = 3 2 · a 8
Besluit:
Rekenregel 4: macht van een product
( a b)n = a n b n met a, b ∈ R0 en n, p ∈ Z
eMacht van een quotiënt
6a 2 b 3
3 = b 3 6a 2
3 = b 9 63 a 6 = 6 3 a 6 b 9
Let steeds goed op waarop de exponent zal inwerken. evenmacht
3 4
2 =+ 32 42 = 9 16 resultaatispositief
Deexponent2moetinwerkenopalleswattussenhaakjesstaat.
1 2 2 = 12 22 = 1 4 resultaatisnegatief
Deexponent2werktinopalleswattussenhaakjesstaat,dusnietophetmintekenvoordehaakjes.
2 3 3 = 23 33 = 8 27
Onevenmacht.Hetresultaatisnegatief.
( 3)2 = 9 9
Besluit:
Rekenregel 5: macht van een quotiënt ( a : b)n = a n : b n a b n = a n b n met a, b ∈ R0 en n, p ∈ Z
61 2 Machten
↓
↓
↓
3Samenvatting
• Je kent de definitie van machten.
a n = a a ... a met a ∈ R en n ∈
a 1 = a met a ∈ R
a 0 = 1 met a ∈ R 0
• Je weet dat gelijksoortige machten machten zijn met hetzelfde grondtal.
• Je kent de rekenregels voor het rekenen met machten (in woorden en symbolen).
product van gelijksoortige machten
quotiënt van gelijksoortige machten
Om machten met hetzelfde grondtal te vermenigvuldigen:
behoud je het grondtal;
tel je de exponenten op.
Om machten met hetzelfde grondtal door elkaar te delen:
behoud je het grondtal;
trek je de exponenten van elkaar af.
Om een macht tot een macht te verheffen:
behoud je het grondtal;
vermenigvuldig je de exponenten.
62
N0 n factoren
REKENREGEL IN SYMBOLEN
REKENREGEL IN WOORDEN
–
–
a n a p = a n+p met a ∈ R0 en n, p ∈ Z
–
–
a n : a p = a n–p met a ∈ R0 en n, p ∈ Z
macht van een macht
–
–
(a n )p = a n p met a ∈ R0 en n, p ∈ Z
een product Verhef
( a · b)n = a n · b n met a, b ∈ R0 en n ∈ Z
quotiënt Verhef
( a : b)n = a n : b n met a, b ∈ R0 en n ∈ Z a b n = a n b n
macht van
elke factor tot de macht.
macht van een
deler en deeltal tot de macht.
4Oefeningen
2 63 Machten
Schrijf als een macht. a a a a = e ( 1) ( 1) ( 1)= b ( c ) · ( c ) · ( c ) · ( c )= f 1 2 · 1 2 · 1 2 · 1 2 = c7 7 5 5 7 = g ( 3) ( 5) ( 3) ( 5)= d x y x y = h abcabc = Bereken. a52 = b ( 5)2 = c 52 = d 1 2 3 = e 15 = f90 = g 3 2 2 = h 3 2 3 = i ( 4)2 = j ( 5)3 = k ( 2)3 = l0,13 = m 18 = n ( 1)8 = o 6 7 2 = p 62 7 = 1 2
64
a22 23 g 1 2 3 1 2 2 b 1 2 2 · 1 2 h x 4 · x c a 2 a 3 i a a 2 a 3 d ( b ) b 2 j ( b )2 b 3 e c 2 · c 4 k a 2 · b 3 · a · b f ( c )3 c 2 l c 2 c 2 b b 3 3
Werk uit door een rekenregel toe te passen.
Werk uit met behulp van de rekenregels.
2 65 Machten
a23 :22 g a 2 c 3 ac b104 :103 h ( y )4 : ( y )2 c a 4 a 2 i a 2 b 2 c abc d53 :50 j x 4 y 2 x 3 y e a 2 b 4 ab 2 k ( x )3 : x 2 f ( 2)5 ( 2)3 l 4 x 2 y 3 2 xy 4
66
uit
a 22 2 g b 2 0 b ( 3)2 2 h a 2 4 c a 2 3 i a 2 2 a 4 d ( b )2 3 j c 3 2 · c 2 e ( 4)0 2 k x 2 y 2 2 f b 3 3 l x 2 3 x 3 2 5
Werk
met behulp van de rekenregels.
Werk uit met behulp van de rekenregels.
2 67 Machten
a (2a )2 g 1 2 cd 2 b 2ab 2 2 h ( 3ab )3 c 4 xy 2 3 i 2 xy 2 2 d ( abc )2 j a 2 b 2 c 2 e 3ab 2 2 k 4 xy 2 3 f 1 2 c 2 d 2 l ( 2a )4 6
68 Werk uit. a2 3 g 3 4 2 b3 1 h ( 0,1) 3 c ( 2) 2 i 2 3 2 d4 2 j 1 4 2 e 1 3 1 k0,2 3 f 2 5 2 l ( 5) 1 Welke exponent ontbreekt in de opgave? a 2ab 2 c 3 = 16a 4 b 8 c 12 d 2ab 2 c 3 = 1 8a 3 b 6 c 9 b a 4 · a = a 6 e a 4 : a = a 6 c ab 2 a 4 = a 4 b 8 f ab 2 a 2 = a 4 b 4 7 8
Werk uit. Zorg ervoor dat in je antwoord enkel positieve exponenten staan.
2 69 Machten
a3 2 34 g 0,1 1 2 b a 3 · a h ( 2)2 1 c5 2 5 2 i a 2 1 b 3 d0,12 0,1 3 j 2 3 1 2 e a 2 · a 2 k a 2 b 3 a 2 a 2 1 f ( a )3 ( a ) 5 l a 4 b 8 b 3 2 9
Werk uit. Zorg ervoor dat in je antwoord enkel positieve exponenten staan.
70
a ( ab ) 1 g 3 1 3 2 b a 1 b 2 c a 2 b 2 h 50 52 5 3 72 · 7 3 c 2a 2 b 2 i abc a 2 b 2 1 d 2a 2 b 2 j a 4 b 2 a 3 b 4 e x 2 y 4 z 3 xy 2 2 k ( 2a ) 2 a 2 b 2 f a a 2 a 3 2 a 3 a 3 a 4 1 l a a 6 a 2 3 a a 1 2 10
Op expeditie naar het noorden van Scandinavië ?
Alvast geen slecht idee. Als je echt bijna in het meest noordelijke punt van Noorwegen, Zweden of Finland (je mag zelf kiezen) bent, passeer je de poolcirkel. Boven die magische grens gaat de zon in de zomer gedurende zestig dagen niet onder! Je ziet dan ’snachts de middernachtzon (zie foto). De plaatselijke bevolking moet in de winter wel een even lange poolnacht doormaken! Ter plaatse kun je kennismaken met een ijskathedraal, een ijshotel, het noorderlichtmuseum, prehistorische rotstekeningen (zelfs tot 8000 jaar oud) en in één dorpje vind je nog een attractie: de enige echte …

Om te weten te komen over wie of wat we het hier hebben, los je elke oefening op.
Zoek de letter die bij het antwoord staat en vorm hiermee het antwoord. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.
2 71 Machten
a 2 c 2 b 4 a 4 b 2 7 b 3 9 1 9 0 9 4 1 4 b 4 a 2 c 2 157 53 a 2 b 3 c 2 b 2 a 4 1 4 52 1 O Z T K S B S D F A R L M E N U A C ( 9)2 ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1) 3 52 5 1 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1) 3 52 5 1 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 · ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1) 3 52 · 5 1 · 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 · ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 · ( 1) 2 ( 1) 3 52 5 1 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 · ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 · ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1) 3 52 · 5 1 · 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 · ( 1) 2 ( 1) 3 52 5 1 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 · ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1) 3 52 · 5 1 · 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1) 3 52 · 5 1 · 54 5 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 · ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1) 3 52 · 5 1 · 54 2 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 · ( 9)3 ( 9)4 5 2 1 2 b 1 2 7 b 1 2 a bc ab 3 2 1 ( 1) 3 52 · 5 1 · 54 5 2 a 1 b 2 2 c ac 3 4 4 ( 4) 4 ( 9) 11
2.3 Vierkantswortels in 1Begrippen
vierkantswortel
in woorden:
Een vierkantswortel van een reëel getal is elk reëel getal waarvan het kwadraat gelijk is aan het gegeven getal.
in symbolen:
b iseenvierkantswortelvan a ⇐⇒ b 2 = a met a , b ∈ R
Omdat a = b 2, is a ⩾ 0. Enkel positieve getallen kunnen dus een vierkantswortel hebben.
Nul heeft juist één vierkantswortel, namelijk 0.
De definitie kunnen we dus als volgt herschrijven :
b = √a ⇐⇒ b 2 = a met a , b ∈ R +
Opmerkingen:
• √16 = 4 is de positieve vierkantswortel van 16, het resultaat is dus positief.
• √ 16bestaatniet, √ 16 / ∈ R .
Er bestaat geen enkel reëel getal waarvan het kwadraat –16 is.
• Met behulp van ICT kunnen we vierkantswortels benaderen.
√7 = 2,64575...
√123 = 11,09053...
• √2en √7 zijn irrationale getallen.
Dergelijke getallen kunnen niet in breukvorm genoteerd worden.
• Ook de lengten van lijnstukken kunnen irrationaal zijn:
72
GETAL VIERKANTSWORTELS NOTATIE 25 5 en –5 want 52 = 25 en ( –5)2 = 25 √25 = 5 √25 = 5 √144 = 12 √144 = 12 144 12 en –12 want 122 = 144 en ( –12)2 = 144 √25 = 5 √25 = 5 √144 = 12 √144 = 12
A = 10 cm2 z = √10cm A B C 1 1 |AC| = √2 (stellingvanPythagorasin ∆ ABC) R Q … √2 √7 p 3 4 17 –28
2Grafische interpretatie
Hier zie je duidelijk dat 4 twee vierkantswortels heeft, nl. 2 en –2, want: 22 = 4 = (

2)2
Merk ook op dat een negatief getal geen vierkantswortel heeft.
Vierkantswortels
Vierkantswortels werden al heel lang geleden onder de ene of de andere vorm gebruikt. De Babylonische wiskunde kende benaderende waarden voor getallen die we nu schrijven als √2 en √3
Aan Aristoteles (384 – 322 v.Chr.) wordt toegeschreven dat hij als eerste aangetoond zou hebben dat √2 geen rationaal getal is. Euclides (365 – 300 v.Chr.) komt bij de behandeling van de stelling van Pythagoras en van de regelmatige veelhoeken en veelvlakken op een aantal irrationale uitdrukkingen terecht. Archimedes (287– 212 v.Chr.) kon langs meetkundige weg vierkantswortels van niet-volkomen kwadraten benaderen. De oorsprong van het woord wortel, dat zowel voor een met wortelteken geschreven getal als voor de oplossing van een algebraïsche vergelijking met één onbekende gebruikt wordt, dient gezocht te worden bij de Arabieren. Al-Chwarizmi (780 – 850) gebruikt hiervoor in 830 voor het eerst een woord dat wortel (van een plant) betekent. Hij vermeldt ook de formules a√b = √a 2 b en √a √b = √a b
Ons wortelteken, een vervorming van de letter r (van radix), vinden we in 1525 bij Christoff Rudolff. Hij gebruikte de volgende symbolen: V voor 2 √2 , VV voor 3 √2 enz.

73 2 Machten
KWADRATEREN x y ±√... y x
–
Aristoteles
3Eigenschappen van vierkantswortels
Volg
De
Het kwadraat van de positieve vierkantswortel van een positief reëel getal is steeds dat getal zelf.
De positieve vierkantswortel van een product van positieve reële getallen is gelijk aan het product van de positieve vierkantswortels van de factoren.
De positieve vierkantswortel van een quotiënt van positieve reële getallen waarvan de deler niet nul is, is gelijk aan het quotiënt van de positieve vierkantswortels van deeltal en deler.

onderstaande redeneringen,
eigenschappen. 52 = √25 = 5 √49 2 = 72 = 49 √4 9 = √36 = 6 √4 √9 = 2 3 = 6 81 100 = 9 10 want 9 10 2 = 81 100 √81 √100 = 9 10 besluit: 52 = 5 besluit: √49 2 = 49 52 = √25 = 5 √49 2 = 72 = 49 √4 9 = √36 = 6 √4 · √9 = 2 · 3 = 6 81 100 = 9 10 want 9 10 2 = 81 100 √81 √100 = 9 10 worteltrekken en kwadrateren zijn bewerkingen die elkaar opheffen 52 = √25 = 5 √49 2 = 72 = 49 √4 · 9 = √36 = 6 √4 √9 = 2 3 = 6 81 100 = 9 10 want 9 10 2 = 81 100 √81 √100 = 9 10 besluit: √4 · 9 = √4 · √9 52 = √25 = 5 √49 2 72 49 4 9 = √36 = 6 √4 · √9 2 · 3 6 81 100 = 9 10 want 9 10 2 = 81 100 √81 √100 = 9 10 besluit: 81 100 = √81 √100 Veralgemening: a 2 = a √a 2 = a √a b = √a √ b a b = √a √ b met a ∈ R+
die zullen leiden naar enkele handige
positieve vierkantswortel van
kwadraat van een positief reëel
is dat getal zelf. a 2 = a √a 2 = a √a b = √a √ b a b = √a √ b met
het
getal
a ∈ R+
a 2 = a √a 2 = a √a b = √a √ b a b = √a √ b met a, b ∈ R+
a 2 = a √a 2 = a √a · b = √a · √ b a b = √a √ b met a ∈ R+ en b ∈ R0 +
4Vierkantswortels vereenvoudigen
Met het vereenvoudigen van vierkantswortels bedoelen we dat we het grondtal zo eenvoudig mogelijk zullen schrijven.
√
Probeer om onder het wortelteken zo veel mogelijk even machten te verkrijgen.
5Bewerkingen met vierkantswortels
We merken vooraf op dat in het resultaat de vierkantswortel steeds zo ver mogelijk wordt vereenvoudigd.
aVierkantswortels optellen en aftrekken
Vierkantswortels met hetzelfde grondtal noemen we gelijksoortige vierkantswortels.
√3en2√3zijngelijksoortigevierkantswortels.
3√2en5√3zijnnietgelijksoortigomdat2 = 3.
– Om gelijksoortige vierkantswortels op te tellen of af te trekken, passen we de distributieve eigenschap toe van het vermenigvuldigen ten opzichte van het optellen in R.
– Niet-gelijksoortige vierkantswortels kunnen we soms vereenvoudigen tot gelijksoortige vierkantswortels zodat we die vierkantswortels kunnen optellen en aftrekken.
75 2 Machten
Webrengen9buitenhetwortelteken.
135 = √9 · 15 = 3√15 a 3 = a 2 a = a √a (a 0) a 4 b 6 = a 2 b 3 16a 5 b 3 = 42 · a 4 · a · b 2 · b = 4a 2 b √ab (a , b 0)
18 = √9 2 = 3√2
√
Methode:
( 4) · ( 9) = √ 4 · √ 9 bestaatniet bestaatniet ( 4) ( 9)= √36 = 6
Opmerking:
3√5 + 4√5 =(3 + 4) √5 = 7√5 3√2 4√2 + 2√2 =(3 4 + 2)√2 = 1 · √2 = √2
Voorbeelden : √8 + √18 = √23 + √32 2 = √22 2 + 3√2 = 2√2 + 3√2 = 5√2 4a 3 9a 4 + 16a 3 a 4 = 4a 2 a 3a 2 + 16a 2 a a 2 a 0 = 2a √a 3a 2 + 4a √a a 2 = 6a √a 4a 2 2 + 3 2√3 + 3√3 = 5√3
bVierkantswortels vermenigvuldigen
Om vierkantswortels te vermenigvuldigen passen we eerst de commutatieve en de associatieve eigenschappen van de vermenigvuldiging toe en daarna de rekenregels in R
cVierkantswortels delen
76
Voorbeelden : 3√2 · 4√3 = 3 · 4 · √2 · √3 = (3 · 4) · √2 · √3 = 12 √6 = 12√6 √2 2 √6 = 2√2 √12 = 2√2 2√3 √3 1 · √6 + 2 = √18 + 2√3 √6 2 = 3√2 + 2√3 √6 2 5√2 b · 2a √2ab = 10a · 4ab 2 a 0en b 0 = 10a 4 b 2 a = 10a 2 b √a = 20ab √a
√20: √5 = 20 5 √400: √48 = 400 48 = √4 = 100 12 = 2 = 10 √12 = 10 √4 · 3 = 10 2√3 Opgelet! 20 5 = √ 20 √ 5 → bestaatniet → bestaatniet Ergeldtwel: 20 5 = √4 = 2 3 2 3√2 2√5 = 6√10 2 5
dVierkantswortels tot een macht verheffen
Om een vierkantswortel tot een macht te verheffen, passen we eerst de rekenregel voor de macht van een product toe en daarna de rekenregel voor de macht van een vierkantswortel.
Voorbeelden :
5√3 3 = 53 √3 3 = 125 · 33 = 125 · 32 · 3 = 125 · 3√3
= 375√3
3 b √2 b 3 = 27 b 3 8 b 3 b 0
= 27 b 3 √4 b 2 · 2 b
= 27 b 3 2 b √2 b
= 54 b 4 √2 b
6Samenvatting
• Je kent de definitie van een vierkantswortel van een reëel getal en kent de grafische interpretatie.
Een vierkantswortel van een reëel getal is elk reëel getal waarvan het kwadraat gelijk is aan het gegeven getal.
∀a , b ∈ R : b iseenvierkantswortelvan a ⇐⇒ b 2 = a
Elk positief reëel getal a heeft in R+ precies één vierkantswortel b
∀a , b ∈ R + : b = √a ⇐⇒ b 2 = a
• Je kent de eigenschappen van vierkantswortels.
met a ∈ R+ De positieve vierkantswortel van het kwadraat van een positief reëel getal is dat getal zelf.
a 2 = a
a 2 = a
√a 2 = a
a 2 = a √a 2 = a √a · b = √a · √ b
√a 2 = a
√a b = √a √ b
met a ∈ R+ Het kwadraat van de positieve vierkantswortel van een positief reëel getal is steeds dat getal zelf.
a 2 = a √a 2 = a √a · b = √a · √ b
√a · b = √a · √ b
met a, b ∈ R+
De positieve vierkantswortel van een product van positieve reële getallen is gelijk aan het product van de positieve vierkantswortels van de factoren.
a b = √a √ b
a
b = √a √ b
b = √a √ b
a
a b = √a √ b met a ∈ R+ en b ∈ R0
De positieve vierkantswortel van een quotiënt van positieve reële getallen waarvan de deler niet nul is, is gelijk aan het quotiënt van de positieve vierkantswortels van deeltal en deler.
• Je weet hoe je een vierkantswortel vereenvoudigt.
• Je kunt volgende bewerkingen uitvoeren met vierkantswortels:
(gelijksoortige vierkantswortels) optellen en aftrekken;
vermenigvuldigen;
delen;
tot een macht verheffen.
77 2 Machten
3√5 4 = 34 · √5 4 = 34 54 = 34 52 =
2025
–
–
–
–
62 (6√3)2 = 36 3 = 108 (√3)2
7Oefeningen
Vereenvoudig volgende vierkantswortels.
Vereenvoudig volgende vierkantswortels. Alle letters stellen positieve reële getallen voor.
Bereken met ICT en rond af tot op 4 decimalen nauwkeurig.
78
a √25
g √40 = b √100
h √200 = c √72
i √48 = d √121
j √98 = e √18 = k √10000 = f √20
l √128 =
=
=
=
=
=
a a 3 = g a 4 4 = b 9a 4 b 2 = h a 6 b 8 = c b 2 c 5 = i 16 x 2 y 2 = d 48a 5 b 4 = j x 2 y 4 = e 90a 3 b = k √a 3 = f a 3 b 3 = l √ab 4 =
a √19 ≈ e π√π ≈ b √2π ≈ f2√2 ≈ c √20,49 ≈ g √17 5 √11 8 ≈ d √365 ≈ h 5√3 3√2 √11 ≈ 1 2 3
2 79 Machten Bereken. a2√5 + 7√5 e2√3 5√12 + 9√75 b2√7 9√7 + 2√7f √8 √80 + 3√2 + 7√5 c √48 + √75 g2 + √50 √72 √8 d √18 + √72 h3√2 2 5√2 √8 4
Noteer in elke bouwsteen de som van de twee onderliggende bouwstenen.
80
a b Werk uit. a √5 · √15 e √48: √3 b √8 · √9f √125: 1 2 √5 c3√15 · √20 g √0,06 · √0,8 d2√3 √12 h 3√2 2√8 5 √5 √20 √45 √80 √3 √12 √27 √108 6
2 81 Machten Werk uit. a √3 √6 + √8 e √3 2 √2 3 √6 b 2√2 √3 · √12 f √2 √3 √2 + 1 c 3√5 √20 + √80 √5 g3√2 √2 √6 d 2√2 1 3 √2 h √3 1 √6 1 7
82 Werk uit ( a , b ∈ R+) a √a + √9a d √a √a √a 2 b √64a 3 + 2√a 5 e2√a 2 b 3√a 4 b 3 c2√2a √4a √8a 2 f √9a 5 : √4a 2 8
2.4
Derdemachtswortel van een reëel getal
1Inleiding
We bepalen het volume van deze kubussen.
4 cm
2 cm
z kubus = 4cm
Vkubus = z z z = 43 cm3 = 64cm3
z kubus = 2cm
Vkubus = z · z · z = 23 cm3 = 8cm3
z kubus = 4cm
Vkubus = z z z = 43 cm3 = 64cm3
z kubus = 2cm
Vkubus = z · z · z = 23 cm3 = 8cm3
83 2 Machten
GETAL DE DERDEMACHTSWORTEL IS NOTATIE 64 4 want 43 = 64 3 √64 = 4 3 √8 = 2 3 √125 = 5 3 √ 8 = 2 3 27 64 = 3 4 8 2 want 23 = 8 3 √64 = 4 3 √8 = 2 3 √125 = 5 3 √ 8 = 2 3 27 64 = 3 4 125 5 want 53 = 125 3 √64 = 4 3 √8 = 2 3 √125 = 5 3 √ 8 = 2 3 27 64 = 3 4 –8 –2 want ( 2)3 = 8 3 √64 = 4 3 √8 = 2 3 √125 = 5 3 √ 8 = 2 3 27 64 = 3 4 27 64 3 4 want 3 4 3 = 27 64 3 √64 = 4 3 √8 = 2 3 √125 = 5 3 √ 8 = 2 3 27 64 = 3 4
derdemachtswortel in woorden:

De derdemachtswortel van een reëel getal is het reëel getal waarvan de derde macht gelijk is aan het gegeven getal.
in symbolen:
2Grafische interpretatie
Hier zie je duidelijk dat elk positief getal juist één derdemachtswortel heeft.
Je ziet ook dat elk negatief getal juist één derdemachtswortel heeft.
84
3 √a = b ⇔ b 3
a
a, b ∈ R
=
met
√
2,5713
√
≈
√
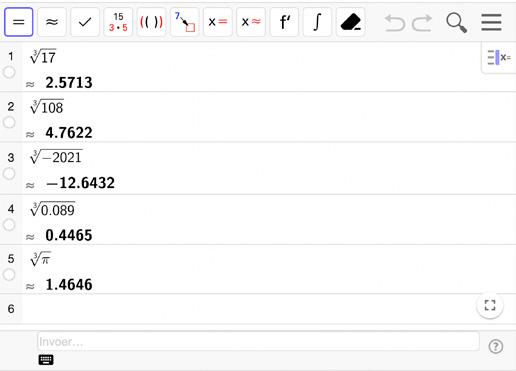
MetICTkunnenwenagaandat: 3
17 ≈
3
108
4,7622 3
2021 ≈−12,6432
DERDE MACHT x y 3 √ y x
3 Toepassingen
Toepassing 1:
Gegeven:Eenbalkheeftalsafmetingen: l = 32cm b = 8cm h = 2cm
Gevraagd:Berekendezijdevaneenkubuszodathetvolumevandekubusgelijkisaanhetvolumevande gegevenbalk.Werkop2decimalennauwkeurig.
Oplossing: Vbalk = l b h wordt: V = 32 8 2cm3 = 512cm3 Vkubus = z 3 wordt: z 3 = 512cm3

Antwoord:Dekubusheeftzijdendie8cmlangzijn.
Toepassing 2:
Gegeven:Eenbolheefteenvolumevan1m3 .
Gevraagd:Berekendestraalvandebol.Werkop0,01mnauwkeurig.
Antwoord:Destraalvandebolisongeveer0,62m.
85 2 Machten
⇕ z =
⇕ z
3 √512cm
= 8cm
Oplossing: Vbol = 4 3 π r 3 wordt: 4 3 π r 3 = 1 ⇕ r 3 = 1 4 3 π ⇕ r 3 = 3 4π ⇕ r 3 = 0,23873... ⇕ r = 3 √0,23873... ⇕ r ≈ 0,62
Vbol = 4 3 π r 3
4Oefeningen
a Bereken de lengte van de zijde van een kubus met volume 2744 cm3
b Bereken het volume van een bol met straal 10 cm. Werk tot op 0,001 cm3 nauwkeurig.
c De diameter van een voetbal is 23 cm. Bereken zijn volume. Werk tot op 0,001 cm3 nauwkeurig.
d Een bol heeft een volume van 10 cm3. Wat is zijn straal? Werk tot op 0,001 cm nauwkeurig.
86
1
e Siebe heeft van de Sint 2500 kubusvormige houten speelblokken gekregen. Hoeveel blokken bevat de grootste volledig gevulde kubus die je met die blokken kunt maken door ze op elkaar te stapelen ?
f In de leraarskamer staat een kubusvormige diepvrieskast met een volume van 512 liter. Ze willen er kubusvormige doosjes in plaatsen met een ribbe van 12 cm. Hoeveel van die doosjes kunnen in de diepvrieskast ?
g Hoeveel kubusjes met een volume van 1cm3 krijg je maximaal in een balkvormige doos met binnenafmetingen 10cm, 2cm en 2cm ?
h Een balk heeft een volume van 166,375cm3
Welke zijde heeft een kubus met hetzelfde volume ?
2 87 Machten
*
Een kubus heeft een volume van 274,625cm3. De ribben worden 1cm verlengd. Wat is het volume van de nieuwe kubus ?
De eerste sneeuw dit jaar was de aanleiding voor Koen en Wouter om een grote sneeuwman te maken. Verklaar telkens je antwoord en bereken op 1 mm nauwkeurig.
a Als een sneeuwbal een volume heeft van 1 m3, kunnen we dan met de bal door een tuinpoortje met een breedte van 1 m ?
b Het hoofd van de sneeuwman heeft een diameter van 35 cm. Koen wil op het hoofd van de sneeuwman een kubusvormige doos zetten met een volume van 50 dm3. Kan hij de doos als hoed gebruiken of is ze te groot ?

88
2 3
Het speelblad van een snookertafel heeft als afmetingen 3,57 m bij 1,78 m. De ballen hebben een volume van 75,77 cm3
Hoeveel ballen kun je maximaal op het speelblad leggen als ze op de aangegeven manier liggen?
2 89 Machten
4
2.5 n-demachtswortels in


1Inleiding
Elk positief getal heeft twee vierkantswortels. Een negatief getal heeft geen vierkantswortels.
Elk reëel getal heeft één derdemachtswortel.
90
NOTATIE
22 = 4 √4 = 2 √4 = 2 –2
( –2)2 = 4 √4 = 2 √4 = 2
2 is de positieve vierkantswortel van 4 want
is de negatieve vierkantswortel van 4want
NOTATIE
23 = 8 3 √8 = 2 3 √ 8 = 2 –2
derdemachtswortel
–
( –2)3 = –8 3 √8 = 2 3 √ 8 = 2
2 is de derdemachtswortel van 8want
is de
van
8 want
Elk positief getal heeft twee vierdemachtswortels. Een negatief getal heeft geen vierdemachtswortels.
Voorbeelden:
4 √81 = 3want34 = 81

5
100000 = 10want ( 10)5 = 100000 4
64 isnietgedefinieerd 3
0 = 0 want03 = 0
91 2 Machten NOTATIE
de positieve vierdemachtswortel
16want 24 = 16 4 √16 = 2 4 √16 = 2 –2
de negatieve vierdemachtswortel van 16want ( –2)4 = 16 4 √16 = 2 4 √16 = 2
2 is
van
is
NOTATIE 2 is de vijfdemachtswortel van 32want 25 = 32 5 √32 = 2 5 √ 32 = 2 –2 is de vijfdemachtswortel van –32want ( –2)5 = –32 5 √32 = 2 5 √ 32 = 2
Elk reëel getal heeft één vijfdemachtswortel.
√
√
√
√
5
17 ≈ ICT 1,7623
2Definitie
n -demachtswortel
in woorden: Voor een van nul verschillend natuurlijk getal n is de n -demachtswortel van een reëel getal elk reëel getal waarvan de n -de macht gelijk is aan het gegeven getal.
in symbolen:
b is een n -demachtswortel van a ⟺ b n = a met a , b ∈ R en n ∈ N0
Voorbeelden :
4 √81 = 3want34 = 81
5 √ 32 = 2want ( 2)5 = 32
6 106 want (10)6 = 106
6 √ 64isnietgedefinieerdin R (verklaar)
3 √0 = 0want03 = 0
Bij het werken met lettervormen stellen we dat de letters positieve getallen voorstellen. De nieuwe definitie kunnen we dan beperken tot :
n -demachtswortel
Elk positief reëel getal a heeft in R+ precies één n -demachtswortel b .
n √a = b ⇐⇒ b n = a met n ∈ N0 en a , b
3Eigenschappen
92
R +
∈
• 3 √a 3 = a • 4 √a 4 = a wantmachtsverheffingenworteltrekkingheffenelkaarop • 4 √48 ≈ 2,6321 4 √16 4 √3 = 2 4 √3 ≈ 2,6321dus: 4 √48 = 4 √16 3 = 4 √16 4 √3 • 4 16 81 = 4 2 3 4 = 2 3 4 √16 4 √81 = 4 24 4 34 = 2 3 dus: 4 16 81 = 4 √16 4 √81 • 3 26 = 22 = 2 6 26 = 2 dus: 3 26 = 6 26
Algemeen: eigenschappen van n -demachtsworteltrekking
De eerste vier eigenschappen zijn een veralgemening van de eigenschappen die gelden bij de vierkantswortel van een reëel getal.
4Benaderen, afronden en schatten
Voorbeeld 1:
Tussen welke twee opeenvolgende natuurlijke getallen ligt √130 ?
Oplossing: √121 < √130 < √144
11 < √130 < 12
√130 ∈ ]11,12[
Voorbeeld 2:
Tussen welke twee opeenvolgende natuurlijke getallen ligt 3 √185 ?
Oplossing: 3 √125 < 3 √185 < 3 √216
5 < 3 √185 < 6
3 √185 ∈ ]5,6[
93 2 Machten
n √a n = a n √a n = n √a n = a n √a b = n √a n √ b n a b = n √a n √ b m n √a = mn√a met a , b ∈ R + 0 en m , n ∈ N0
Voorbeelden: • 4 √32 = 4 √16 2 = 4 √16 4 √2 = 2 4 √2 • 5 √0,1 10 = 5 0,15 2 = 0,12 = 0,01 • 4 256 625 = 4 4 5 4 = 4 5 • 6 38 = 3 2 34 2 = 3 34 = 3 33 · 3 = 3 33 3 √3 = 3 3 √3 • 3 √8 = 6 √8 = 6 23 = 3 23 = √2
Voorbeeld 3:
Aan welke afgeronde waarde is de gegeven wortelvorm gelijk?
3 √120 ≈ 5,21 A 4,93 B 6,05 C
Taak:
Zoek een getal waarvan de derde macht in de buurt ligt van 120.
3 √64 = 4en 3 √125 = 5
Het antwoord ligt dus tussen 4 en 5. Omcirkel de voorlaatste mogelijkheid.
Zoek nu zelf het antwoord op de vraag: aan welke afgeronde waarde is de gegeven wortelvorm gelijk?
5Samenvatting
• Je kent de definitie van de n-demachtswortel van een reëel getal. in woorden:
Voor een van nul verschillend natuurlijk getal n is de n -demachtswortel van een reëel getal elk reëel getal waarvan de n -de macht gelijk is aan het gegeven getal. in symbolen:
b is een n -demachtswortel van a ⟺ b n = a met a , b ∈ R en n ∈ N0
Elk positief reëel getal a heeft in R+ precies één n -demachtswortel b .
n √a = b ⇐⇒ b n = a met n ∈ N0 en a , b ∈ R +
• Je kent de eigenschappen van de worteltrekking.
met a , b ∈ R + 0 en m , n ∈ N0
• Je kunt de waarde van een n-demachtswortel benaderen door een schatting uit te voeren.
94
√100 ≈ 4,25 A 5,00 B 3,16 C 5 √60 ≈ 2,27 A 6,20 B 12,00 C
4
√a n = a n √a n = n √a n = a n √a · b = n √a · n √ b n a b = n √a n √ b m n √a = mn√
n
a
2 95 Machten
zonder ICT (indien zinvol). a 3 √ 27 = i 3 69 = b 5 √ 1 = j 3 √ 1 = c 5 1 32 = k 5 √0 = d √64 = l √121 = e 6 √1 = m 3 √ 8 = f 4 ( 2)4 = n 4 √10000 = g 4 24 = o 4 √ 10000 = h 5 310 = p 6 √64 =
met ICT en rond af tot op 10–5 a 3 √456 f 3 4,272 5,05 b 3 3 10 g 5 √ 2007,45 c 5 √5 h 4 17 39 d 7 √ 210 i √6,4 e 80 123 j 3 √100 1 2
6Oefeningen Bereken
Bereken
Tussen welke twee natuurlijke getallen liggen volgende uitdrukkingen?
96 Bereken x a x 4 = 256 d x 3 5 = 13 b2 x 5 = 100 e 3 x 4 + 1 = 2 c x 7 + 2 = 9f x 3 = 1 27
a √93 d 4 √456 b 3 √50 e 4 √9999 c 3 √124 f 5 √100 3 4
2 97 Machten
eenvoudiger door eigenschappen van n-demachtswortels toe te passen. a √5 √3e 4 102 b 3 √4 3 √2f √10 c √10: √2g 103 2 d 3 √3 3 √27 h 3 a 6 5
Noteer
Voor het getal a zijn drie benaderende waarden gegeven. Schat de best mogelijke uitkomst.
Tussen twee variabelen x en y is volgende waardetabel gegeven:
aAlsgegevenisdathetverbandtussen x en y uitgedruktkanwordenmetdeformule y = ax 4 , bepaaldandeevenredigheidsfactor a .
bTekenmetICTdebijbehorendegrafiek.
cBereken y als x = 6.
dBereken x als y = 1250.
98
a a = √372 19,3 25,3 12,6 b a = 3 √100 10 4,6 5,2 c a = 4 √50 5 2,6 3,1 d a = 3 √900 30 9,65 3
x –3 –
–1 01234 y 16232 202 32162512
2
6 7
In de tabel hiernaast staan voor enkele planeten in ons zonnestelsel de gemiddelde afstanden tot de zon in miljoenen km en de omlooptijd in jaren.
Volgens de derde wet van Kepler is het kwadraat van de omlooptijd van een planeet rond de zon ( t ) recht evenredig met de derde macht van de gemiddelde afstand tot de zon ( s ).
a Schrijf s in functie van t
b Bereken de afstand (in miljoenen km) van de planeet Jupiter tot de zon als je weet dat de omlooptijd 11,862 jaar is.
c Hoeveel bedraagt de afstand van Jupiter tot de zon in astronomische eenheden als je weet dat 1 A.E. = gemiddelde afstand aarde-zon = 149600000 km.

2 99 Machten
8 planeetafstandomlooptijd Mercurius580,241 Saturnus142729,46 Uranus287084 Mars2281,881 aarde149,6 1
2.6 Machten met een rationaal getal als exponent
De nieuwe exponent is een rationaal getal geschreven als een breuk met als teller de exponent die bij het getal onder de wortelvorm hoort en met als noemer een natuurlijk getal verschillend van nul.

100
1Definitie 5 √a 10 = a 2 = a 10 5 √78 = 72 4 = 74 = 7 8 2 3 √56 = 3 53 2 = 52 = 5 6 3 4 √a 4 = 4 1 a 4 = 1 a = a 1 = a 4 4 macht met rationale exponent a m n = n √a m met a ∈ R + 0 , m ∈ Z en n ∈ N0 Voorbeelden : 32 1 5 = 5 √32 = 5 25 = 2 81 3 4 = 4 √81 3 = 33 = 27 125 2 3 = 1 125 2 3 = 1 3 √125 2 = 1 52 = 1 25
5 a 8 = a 8 5
2Eigenschappen van machten met rationale exponenten
We nemen aan dat de eigenschappen voor machten met gehele exponenten blijven gelden voor machten met strikt positieve reële grondtallen en met rationale getallen als exponenten.
3Samenvatting
101 2 Machten
eigenschappen a p a q = a p +q (a b )p = a p b p a p a q = a p q a b p = a p b p (a p )q = a p q met a , b ∈ R + 0 en p , q ∈ Q Voorbeelden : 5 1 2 · 5 2 3 = 5 1 2 + 2 3 = 5 7 6 = 6 57 = 6 56 · 5 = 5 6 √5 10 1 2 10 1 4 = 10 1 2 1 4 = 10 1 4 = 4 √10 8 1 2 4 = 8 1 2 4 = 82 = 64 (64 125) 1 3 = 64 1 3 125 1 3 = 3 √64 3 √125 = 4 5 = 20 4 9 1 2 = 4 1 2 9 1 2 = √4 √9 = 2 3 Toepassingen : (4a 2 b 4 ) 1 2 b 2 = 4 1 2 a 1 b 2 b 2 = √4 a = 2 a √a 5 · 3 √a 2 3 √a = a 5 2 · a 2 3 6 √a = a 11 6 a 1 6 = a 12 6 = a 2 = 1 a 2 Opgelet! a 11 12 = 12 a 11 a 1 4 = 4 √a a 1 10 b 3 8 = 10 √a · 8 b 3
Je kent de betekenis van een macht met een rationale exponent. a m n = n √a m met a ∈ R + 0 , m ∈ Z en n ∈ N0 • Je kent de eigenschappen van machten met rationale exponenten. a p · a q = a p +q (a · b )p = a p · b p a p a q = a p q a b p = a p b p (a p )q = a p q met a , b ∈ R + 0 en p , q ∈ Q
•
4Oefeningen
Schrijf met een rationale exponent.
a 5 a 2 =
b 6 a 5 =
c 3 √17 =
d √39 =
e 3 a 4 =
f 5 √2 =
g 3 x 5 =
h 4 2a 3 =
i 5 48 x 4 =
Schrijf als een n-demachtswortel. a5
102
4
1 2
8
2 3
3 5 1 3
3
3
2 3
2
3 5
h 3 7 3 7
3
= b7
= c (
)
= d
= e a 1
= f (
)
= g (
)
=
= 1 2
2 103 Machten Werk uit. a 3 103 b 3 √125000 c 4 √7 d √5 6 e 4 √16 5 f 5 √3 15 g2 1 6 2 1 3 h3 1 2 3 1 4 i 5 1 10 2 j 33 26 1 3 k25 3 2 l4 5 2 m1000 2 3 n16 3 4 o 3 √5000 3
Voor het getal a zijn vier mogelijke benaderende waarden gegeven. Schat de best mogelijke uitkomst.
104 Bereken zonder ICT. a4 1 2 f64 1 6 + 5 √32 b8 2 3 g16 1 4 c ( 32) 1 5 h 3 82 d8 1 3 i27 2 3 121 1 2 e 3 43 j1 4 7
a a = 4 √45 11,2 4,5 2,6 22,3 b a = 30 1 3 10 3,1 15,3 2,6 c a = 4 √40 12,3 8 2,5 4,5 d a = 20 3 4 15,2 3,4 19,2 9,5 4 5
2 105 Machten Bereken zonder gebruik te maken van ICT. a √169 g3 · 28 b 3 √125 h4 · 3 8 1 c2 · 4 √81 i 5 2434 d3 · 5 √32 j 4 25 2 e 3 10002 k 7 77 f 6 43 l 3 230 6
106
b ∈ R + 0 a 3 a 9 g 4 16 b 4 625 b 4 a 8 b 12 h 3 ab 2 6 c 5 32a 15 i a 4 a 4 d 3 √a 6 j 3 a 6 a 2 e a 3 4 k 3 a 6 · b 12 f 3 a 6 2 l ab 3 a 9 b 15 7
Bereken zonder gebruik te maken van ICT a ,
2 107 Machten Bereken zonder gebruik te maken van ICT. a32 2 5 g81 3 4 b216 2 3 h10000 1 4 c100000 2 5 i16 1 4 d 1 4 1 2 j 1 8 5 3 e (0,001) 1 3 k 1003 5 6 f 8 125 4 3 l 0,012 3 4 8
Werk uit en schrijf zonder rationale exponenten. Alle letters stellen positieve getallen voor, verschillend van 0.
108
a a 1 2 a 1 3 e x 2 y 3 x 2 x 1 2 y 2 b x 1 2 x 2 f √a a 1 2 c a 1 a 2 3 a 5 3 g a 1 2 2 b 2 3 6 a 1 2 · b 2 d b 2 b 3 b 5 4 b 1 4 h x 2 3 · x 2 9 * *
Bereken met ICT.
De Zuid-Chinese zee bevat veel prachtige vissoorten. Blijkbaar is er een verband tussen de oppervlakte van een zeegebied en het aantal verschillende vissoorten dat je er tegenkomt. In formulevorm is dat :
s ( x ) = 60 x 0,4
met s ( x ): het aantal vissoorten

x : de oppervlakte van het leefgebied in vierkante kilometer
a Teken de grafiek met ICT.
b Bereken het aantal vissoorten in gebieden met een oppervlakte van 100 vierkante kilometer.
c In een gebied komen zo’n 709 vissoorten voor. Bereken de oppervlakte van dat gebied met ICT.
2 109 Machten
a 10 √1000 e 5 √3 + 3 √5 b2 7 √2023 f √3 3 √12 + 4 √6 c 3 · 3 √3 g0,10,1 + 0,20,2 + 0,30,3 d 4 7 5 5 3 2 6 4 3 h √3 √2 + √5
10 11 *
De pH meet de zuurtegraad van een vloeistof. Bij een neutrale oplossing ligt de pH rond 7, bij zure oplossingen ligt dat onder 7 en bij basische oplossingen erboven. Belangrijk detail: een pH van 2 is tienmaal zuurder dan een pH van 3 (de schaal is dan ook logaritmisch, zie volgend hoofdstuk). Los elke opgave op, verzamel de letters en je krijgt een voorbeeld waar de zuurtegraad vaak gecontroleerd moet worden.
110
a a 4 a 4 = R M Z S –1 0 a 8 a –8 b 3 √a = A W E T a 1 5 a 1 6 a 6 a 5 6 c Als 1 3n 1 2 = 5 2 , dan is n gelijk aan G C E A 1 1 10 –1 1 3 d Als a 2 a 1 3 a 2 a n = a 5 , dan is n gelijk aan O L E M 14 3 19 3 19 3 14 3 e Als a 1 2 a 3 a n = a , dan is n gelijk aan Y B F P 0 5 2 3 2 2 3 f 7√7 = A M E L 7 3 4 72 7 1 4 7 1 2 g Als a 0,24 = 5, dan is a 1,2 = E I D V 25 6 3125 125 h Als 184 1,8 = 9n , dan is n gelijk aan ON AN IN EN 0,2 20 200 6480 12
Oplossing:

2 111 Machten Reken alles hieronder uit.
112 WAT MOET JE KENNEN EN KUNNEN ? dit moet ik leren pagina ik ken het ! oké voor examen ❒ Ik ken de definitie van machten. 53 ❒ Ik weet dat gelijksoortige machten hetzelfde grondtal hebben. 53 ❒ Ik ken de rekenregels van machten. 54 ❒ Ik ken de betekenis van een macht met een negatieve exponent. 59 ❒ Ik ken de definitie van de vierkantswortel van een reëel getal. 72 ❒ Ik ken de eigenschappen van vierkantswortels. 74 ❒ Ik kan een vierkantswortel vereenvoudigen. 75 ❒ Ik kan rekenen met vierkantswortels. 75 ❒ Ik ken de definitie van een derdemachtswortel van een reëel getal. 84 ❒ Ik kan de theorie rond machten toepassen in een gegeven voorbeeld. 85 ❒ Ik ken de definitie van een n-demachtswortel van een reëel getal. 92 ❒ Ik ken de eigenschappen van n-demachtswortels. 93 ❒ Ik ken de definitie van een macht met een rationale exponent. 100 ❒ Ik ken de eigenschappen van machten met rationale exponenten. 101
Machten 2

























