Sistema Pi conjugados y aromáticos. Metodo de Huckel by carlos.hernandez-umce

SistemasPiConjugadosyAromáticos

1MétododeHuckel

Lossistemaspidelasmoléculasorgánicashansidoampliamenteestudiadosenlateoríadelenlacequímico. Lareactividadquímicadelossistemasconjugadosyaromáticossedebealadistribucióndeladensidad electrónica(nubepideslocalizada)entrelosátomospresenteenestetipodemoléculas.Encontrarioaestos tiposdemoléculaseslaescasaonulareactividaddecompuestosquenopresentansistemapi(paraﬁnas).

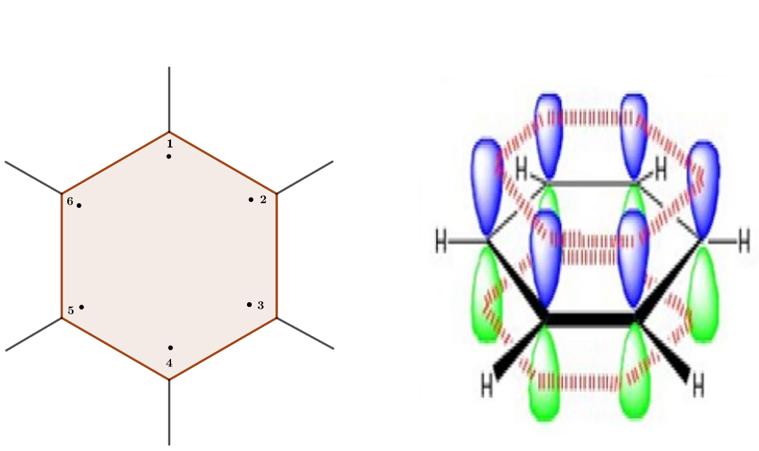
Uncasotipicodemoléculasconsistemapiconjugadoseslamoléculadebenceno.Susistemasigma (esqueletomolecular)sepuederepresentarcomoorbitalesmoleculareslocalizados,constituídosporhibridos sp2 decadacarbonoyorbitalesatómicos 1S deloshidrógenos.Elsistemapiquedaconstituídoporlosorbitales atómico pπ decadacarbonoquenoparticiparonenlahibridaciónsigma.Enlaﬁgurasiguientesepresentala representaciónsigmaypidelamoléculadebenceno.

Ladeslocalizacióndelanubepillevaadescribiracadaelectrónconunafunciónvariacionaldeltipo:

1MÉTODODEHUCKEL

Lasenergíasasociadasalafuncióndescrita,enquelas xj sonfuncionesorbitalesatómicos 2pπ decada unodelosseisátomosdecarbonodelbenceno,sonlasraícesdeldeterminantedesecularde 6x6 (Teorema variacional):

Losorbitalesatómicos xj sonfuncionesnormalizadas,porloque

55 = S66 =1.

Conelpropósitodesimpliﬁcareldeterminantesecular:Huckelsugierelassiguientesaproximaciones:

1.-Considerarquelasintegralesderecubrimiento Sij =0. Estosuponequelosorbitalesatómicos xj son ortogonales.Estaesunasimpliﬁcaciónmatemáticaynorespondeauncriteriofísicopuestoque,estaaproximación,signiﬁcaquenoexistiríaelsistemapi.Entodocaso,laaproximacióntieneelmayorefectoentre orbitalesatómicospertenecientesaátomosvecinosparaloscualeslaintegral Sij esaproximadamenteiguala 0, 25 Enelcasodeorbitalesatómicosparaátomosnovecinoslaintegral Sij esaproximadamentenula.

2.-Lasintegrales Hij = χi Hχj dv, seconsiderannulassilosorbitalesatómicos χi yχj nosonátomos vecinosinmediatos.Sisetratadelmismoorbitalatómico.entonceslasintegrales Hii sesuponenigualesyse

1MÉTODODEHUCKEL Φi = ci1 x1 + ci2 x2 + ci3 x3 + ci4 x4 + ci5 x5 + ci6 x6 (i =1, 2,... 6) (1)

H11 ES11 H12 ES12 H13 ES13 H14 ES14 H15 ES15 H16 ES16 H21 ES21 H22 ES22 H23 ES23 H24 ES24 H25 ES25 H26 ES26 H31 ES31 H32 ES32 H33 ES33 H34 ES34 H35 ES35 H36 ES36 H41 ES41 H42 ES42 H43 ES43 H44 ES44 H45 ES45 H46 ES46 H51 ES51 H52 ES52 H53 ES53 H54 ES54 H55 ES55 H56 ES56 H61 ES61 H62 ES62 H63 ES63 H64 ES64 H65 ES65 H66 ES66 =0 (2)

S11 = S22 = S33 = S

44 =

designangenéricamentepor α. Laigualdadentretodaslas Hii sólosecumpleensistemascomoelbenceno dondetodoslosátomosdecarbonosonequivalentesentresí(tienenelmismoentorno).Enelcasodequede unsistemapideunhidrocarburoquepresenteátomosdecarbononoequivalentes,comosemuestraenla ﬁgura:

Lasintegrales H11 = H22 = H33 ysolo H33 = H44 Laaproximaciónconsisteennoconsideraresasdiferencias eigualarlastodaslasintegralesconelvalor α. Conelmismocriterio,todaslasintegrales c paralascuales iyj sonátomosvecinosestasintegralesseconsideranigualesyseevalúaniguala β.

Cadahidrocarburotienesupropia α ysupropia β. Estosparámetrosnosontransferiblesdeunsistema molecularaotroporloque,noconfundirse,puestodassedenotancomo αoβ

Enconsecuencia,yatendiendoalasaproximacionessugeridasporHuckel,eldeterminantesecular (2) se reescribedelasiguienteforma:

1MÉTODODEHUCKEL

Hij                  = α (i = j) = β (i = j,vecinos) =0(i = j,novecinos)

Laexpansióndeestedeterminantesimplicaunpolinomiocaracterísticodegrado6,y,portanto,una ecuacióndegrado6paralaenergía.Esdecir,quedelaresoluciónseencuentranseisvaloresparalaenergía. Paraelcasodelbenceno,dichaecuaciónnoresultadifícilresolvermedianteresoluciónalgebraicadirectao conapoyodesoftware.Noobstante,siseintentalaresoluciónporálgebradirectalatareapuedellegaraser arduayengorrosa.Laresoluciónconapoyodesoftwarealivianayfacilitalatarea.Acontinuaciónsemuestra laresoluciónparaelcasodelbencenoempleandoMaple.

Porresolucióndelpolinomiocaracterístico,queseobtienedeldeterminante,seencuentranseisvalorespara laenergía,correspondientesalosrespectivoorbitalesmolecularesqueconformanelsistemapidelbenceno. Comoseobserva,haydosparesdeorbitalesmolecularesdegenerados(igualenergía).Unpardeorbitales

molecularesconenergía α + β yotroparconenergía α β

1MÉTODODEHUCKEL α Eβ 000 β βα Eβ 000 0 βα Eβ 00 00 βα Eβ 0 000 βα Eβ β 000 βα E =0

Dadoque β< 0, eldiagramadediagramaenergíaparalosorbitalesmolecularesdelsistemapidelbenceno es:

Encasocontrario,unamaneraeﬁcazdereducirladimensióndelproblemaconsisteenreformularlabase mediantelaconstruccióndeorbitalesmolecularesdesimetría ΦΓ = k ck xk

Método de Huckel con uso de Teoría de Grupos

i.-ElprimerpasoconsisteenclasificarlamoléculaenunGupopuntualdesimetría.Aplicandoelprocedimiento presentadoenelcapítuloprevio,seclasificalamoléculadebencenoenelgrupoputualdesimetría D6h. Estees ungrupoquecontieneunaltonúmerodeoperacionesdesimetría,demaneraquedificultaeltratamiento,porello seoptaportrabajarconelGrupo D6 queesunsubgrupodelGrupo D6h.

ii.-Obtenerlarepresentaciónreducible,esdecir,contabilizar(*)elcompartamientoparacadaunodelosorbitales atómicosquecontribuyenalaconformacióndelsistemapiantelasoperacionesdesimetríadelgrupoosubgrupo desimetríaalcualpertenecelamolécula,asignandolasiguientepuntuación:

1MÉTODODEHUCKEL

(*)lamoléculaestáenelplano xy

Larepresentaciónreducible (Γπr ) sehadescomponerparaencontrarlasumadirectadelasrepresentaciones irreducible (Γπi )quelaconstituyen.Enelloseconsideraelcarácterdelarepresentaciónreducibleparauna operacióndesimetría,elcarácterdelarepresentaciónparalamismaoperacióndesimetriacomponentedela representaciónqueseexaminayelordendelgrupo,queeslasumadelasoperacionesdesimetríadelGrupo.

Paraelcasodelgrupo D6 elordendelgrupoes h =1+2+2+1+3+3=12. Acontinuacióneldesarrollo deestaoperaciónparalamoléculadebenceno:

1MÉTODODEHUCKEL 1sielorbitalatómicopermaneceenlamismaposiciónydirección -1sielorbitalatómicopermaneceenlamismaposiciónycambiadirección

E 2C6 (z) 2C3 (z) C2 (z) 3C′ 2 3C′′ 2 Γπr 6 0 0 0 -2 0

0cambiadeposición

a) Para A1 1 12 [6 · 1 · 1+0 · 1 · 2+0 · 1 · 2+0 · 1 · 1+( 2) · 1 · 3+0 · 1 · 3]=0 b) Para A2 1 12 [6 · 1 · 1+0 · 1 · 2+0 · 1 · 2+0 · 1 · 1+( 2) · ( 1) · 3+0 · ( 1) · 3]=1 c) Para B1 1 12 [6 · 1 · 1+0 · ( 1) · 2+0 · 1 · 2+0 · ( 1) · 1+2 · ( 1) · 3+0 · ( 1) · 3]=0 6

Larepresentaciónreducible (Γπr ) seexpresaenlasumadirectadelassiguientesrepresentacionesirreductiblesdelGrupo D6 :

Larepresentaciones A2 yB2 sonrepresentacionesmonodimensionales. Encambiolasrepresentaciones E1 yE2 sonrepresentacionesbidimensionales,suman,entonces,seisorbitalesmolecularesdesimetríaque transformancomolasrepresentaciónesirreduciblesquesonpartedelarepresentaciónirreducibledelsistema

π. Apartirdeloanterior,latareaesencontrarlacombinaciónlinealdelosorbitalesatómicosparacada unodelosseisorbitalesmolecularesdelsistema π delbenceno,quetransformencomolasrepresentaciones irreductiblesquecomponenelsistemapidelsistemamolecular.

iii.-Paracadaunadelasrepresentacionesquesonpartedelarepresentaciónirreducibledelsistema π aplicaroperadoresdeproyecciónacadaorbitalatómicoaportado.Dadoqueseránseislosorbitalesmolecularesdesimetría,serequierenseisoperacionesdesimetría.Desagregandolasoperacionesdesimetríaderotaciónpropia 2C6 (z) y 2C3 (z) a favoryencontradelospunterosdelreloj,máslaoperaciónidentidad EyC2 (z) setienenlasseisrequeridas.

1MÉTODODEHUCKEL d) Para B2 1 12 [6 · 1 · 1+0 · ( 1) · 2+0 · 1 · 2+0 · ( 1) · 1+( 2) · ( 1) · 3+0 · 1 · 3]=1 e) Para E1 1 12 [6 · 2 · 1+0 · 1 · 2+0 · ( 1) · 2+0 · ( 2) · 1+( 2) · 0 · 3+0 · 0 · 3]=1 e) Para E2 1 12 [6 · 2 · 1+0 · ( 1) · 2+0 · ( 1) · 2+0 · 2 · 1+( 2) · 0 · 3+0 · 0 · 3]=1

Γπi = A2 + B2 + E1 + E2

B2 iguala:

1MÉTODODEHUCKEL E ←− C6 (z) −→ C6 (z) ←− C3 (z) −→ C3 (z) C2 (z) A2 1 1 1 1 1 1 ϕ1 ϕ1 ϕ6 ϕ2 ϕ5 ϕ3 ϕ4 ϕ2 ϕ2 ϕ1 ϕ3 ϕ4 ϕ6 ϕ5 ϕ3 ϕ3 ϕ2 ϕ4 ϕ1 ϕ5 ϕ6 ϕ4 ϕ4 ϕ5 ϕ3 ϕ6 ϕ2 ϕ1 ϕ5 ϕ5 ϕ6 ϕ4 ϕ1 ϕ3 ϕ2 ϕ6 ϕ6 ϕ5 ϕ1 ϕ4 ϕ2 ϕ3 Aplicandolaoperación j,i χj (Rj ) Rj ϕi, enque χj (Rj ) eselcarácterdelarepresentaciónirreducible delaoperacióndesimetría Rj ; resultalafuncióndeondaorbitalmoleculardesimetríaquetransforman comolarepresentación A2 iguala: 1 √6 [ϕ1 + ϕ2 + ϕ3 + ϕ4 + ϕ5 + ϕ6] Ahoralamismaaccióndescritaenelpárrafoanteriorparalarepresentaciónirreducible

E ←− C6 (z) −→ C6 (z) ←− C3 (z) −→ C3 (z) C2 (z) B2 1 -1 -1 1 1 -1 ϕ1 ϕ1 ϕ6 ϕ2 ϕ5 ϕ3 ϕ4 ϕ2 ϕ2 ϕ1 ϕ3 ϕ4 ϕ6 ϕ5 ϕ3 ϕ3 ϕ2 ϕ4 ϕ1 ϕ5 ϕ6 ϕ4 ϕ4 ϕ5 ϕ3 ϕ6 ϕ2 ϕ1 ϕ5 ϕ5 ϕ6 ϕ4 ϕ1 ϕ3 ϕ2 ϕ6 ϕ6 ϕ5 ϕ1 ϕ4 ϕ2 ϕ3

1 √6 [ϕ1 ϕ2 + ϕ3 ϕ4 + ϕ5 ϕ6] Ahoralarepresentaciónirreducible E

lafuncióndeondaorbitalmoleculardesimetríaquetransformancomolarepresentación

Larepresentación E1 esbidimensional,portantodeberíaencontrarsedoscombinacioneslinealesdiferentes ynoseis.Observeseque:

diferentes.Observeseque:

1MÉTODODEHUCKEL E ←− C6 (z) −→ C6 (z) ←− C3 (z) −→ C3 (z) C2 (z) E1 2 1 1 -1 -1 -2 ϕ1 ϕ1 ϕ6 ϕ2 ϕ5 ϕ3 ϕ4 ϕ2 ϕ2 ϕ1 ϕ3 ϕ4 ϕ6 ϕ5 ϕ3 ϕ3 ϕ2 ϕ4 ϕ1 ϕ5 ϕ6 ϕ4 ϕ4 ϕ5 ϕ3 ϕ6 ϕ2 ϕ1 ϕ5 ϕ5 ϕ6 ϕ4 ϕ1 ϕ3 ϕ2 ϕ6 ϕ6 ϕ5 ϕ1 ϕ4 ϕ2 ϕ3 Alaplicarlaoperación(operadordeproyección) j,i χj (Rj ) Rj ϕi, paralarepresentaciónirreducible E1 resulta: (a)2ϕ1 + ϕ2 ϕ3 2ϕ4 ϕ5 + ϕ6 (b) ϕ1 +2ϕ2 + ϕ3 ϕ4 2ϕ5 ϕ6 (c) ϕ1 + ϕ2 +2ϕ3 + ϕ4 ϕ5 2ϕ6 (d) 2ϕ1 ϕ2 + ϕ3 +2ϕ4 + ϕ5 ϕ6 (e) ϕ1 2ϕ2 ϕ3 + ϕ4 +2ϕ5 + ϕ6 (f ) ϕ1 ϕ2 2ϕ3 ϕ4 + ϕ5 +2ϕ6

(a) = -(d) (b) = (e) (f ) = (c)

(b)+(f )=2ϕ1 + ϕ2 ϕ3 2ϕ4 ϕ5 + ϕ6 =(a) (b)-(f )=3ϕ2 +3ϕ3 3ϕ5 3ϕ6 enestecasolarelaciónentreloscomponentesdelacombinación linealesdeunoesauno,porlotantoseexpresacomo ϕ2 + ϕ3 ϕ5 ϕ6. 9

Ahoralasituaciónsereduceatrescombinacioneslinealesdeentrelascualeshayqueencontrardos

Endeﬁnitivalasdosfuncionesdeondaorbitalmoleculardesimetríaquetransformancomolarepresentación

Larepresentación E2 esbidimensional,portantodeberíaencontrarsedoscombinacioneslinealesdiferentes ynoseis.Observeseque:

1MÉTODODEHUCKEL

E1 son: 1 √12 [2ϕ1 + ϕ2 ϕ3 2ϕ4 ϕ5 + ϕ6] 1 2 [ϕ2 + ϕ3 ϕ5 ϕ6] Paralarepresentaciónirreducible E2 E ←− C6 (z) −→ C6 (z) ←− C3 (z) −→ C3 (z) C2 (z) E1 2 -1 -1 -1 -1 2 ϕ1 ϕ1 ϕ6 ϕ2 ϕ5 ϕ3 ϕ4 ϕ2 ϕ2 ϕ1 ϕ3 ϕ4 ϕ6 ϕ5 ϕ3 ϕ3 ϕ2 ϕ4 ϕ1 ϕ5 ϕ6 ϕ4 ϕ4 ϕ5 ϕ3 ϕ6 ϕ2 ϕ1 ϕ5 ϕ5 ϕ6 ϕ4 ϕ1 ϕ3 ϕ2 ϕ6 ϕ6 ϕ5 ϕ1 ϕ4 ϕ2 ϕ3 Alaplicarlaoperación j,i χj (Rj ) Rj ϕi, paralarepresentaciónirreducible

2 resulta: (a)2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6 (b) ϕ1 +2ϕ2 ϕ3 ϕ4 +2ϕ5 ϕ6 (c) ϕ1 ϕ2 +2ϕ3 ϕ4 ϕ5 +2ϕ6 (d)2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6 (e) ϕ1 +2ϕ2 ϕ3 ϕ4 +2ϕ5 ϕ6 (f ) ϕ1 ϕ2 +2ϕ3 ϕ4 ϕ5 +2ϕ6

(a) = (d) (b) = (e) (c) = (f ) 10

Ahoralasituaciónsereduceatrescombinacioneslinealesdeentrelascualeshayqueencontrardos diferentes.Observeseque:

Endeﬁnitivalasdosfuncionesdeondaorbitalmoleculardesimetríaquetransformancomolarepresentación

iv.-Yaseconocenlascombinacioneslinealesdeorbitalesatómicosquedanformaalasfuncionesdeondas orbitalmoleculardesimetría.Elsiguientepasoesencontrarlasenergíascorrespondientesacadacombinación lineal.Estoimplica,deacuerdoconelteoremavariacional,resolvereldeterminantesecularentrefunciones conigualsimetría.Dadoquelascombinacioneslinealesdeorbitalesatómicos,queconformanlosrespectivo orbitalesmolecularesdesimetria,transformancomolasrepresentacionesirreductibles A2,B2,,E1,E2, eldeterminantesecularsereduceporconsideracionesdesimetría,entreaquelloelementosconigualsimetría, puestoqueaquelloselementosdeldeterminantequeseseandedistintasimetríaresultaránigualacero.

Reescribiendolafunciónvariacional(1)entérminosdelosorbitalesmolecularesdesimetría,sóloquedaránpor

1MÉTODODEHUCKEL

(b)+(f )=2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6 =(a) (b)-(f )=3ϕ2 3ϕ3 +3ϕ5 3ϕ6 enestecasolarelaciónentreloscomponentesesdeuno esauno,porlotantoseexpresacomo ϕ2 ϕ3 + ϕ5 ϕ6

E2 son: 1 √12 [2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6] 1 2 [ϕ2 ϕ3 + ϕ5 ϕ6] Resumiendo: Simetría Funcióndeondaorbitalmoleculardesimetría A2 Φ1 = 1 √6 [ϕ1 + ϕ2 + ϕ3 + ϕ4 + ϕ5 + ϕ6] B2 Φ2 = 1 √6 [ϕ1 ϕ2 + ϕ3 ϕ4 + ϕ5 ϕ6] E1 Φ3 = 1 √12 [2ϕ1 + ϕ2 ϕ3 2ϕ4 ϕ5 + ϕ6] E1 Φ4 = 1 2 [ϕ2 + ϕ3 ϕ5 ϕ6] E2 Φ5 = 1 √12 [2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6] E2 Φ6 = 1 2 [ϕ2 ϕ3 + ϕ5 ϕ6]

resolverlasintegrales Hij deigualsimetría,demaneraqueeldeterminantesecularsefactorizaendeterminantes máspequeños,generandobloques,contérminosdeigualsimetría.

Enconsecuenciahaycuatrodeterminantesporresolver:

1.-Determinantesdedimensión1x1;consimetría A2

2.-Determinantededimensión1x1consimetría B2

3.-Determinantededimensión2x2consimetría E1

4.-Determinantededimensión2x2consimetría E2

1MÉTODODEHUCKEL

H11 = Φ1 H Φ1 dτ = 1 √6 [ϕ1 + ϕ2 + ϕ3 + ϕ4 + ϕ5 + ϕ6] H 1 √6 [ϕ1 + ϕ2 + ϕ3 + ϕ4 + ϕ5 + ϕ6] H11 = Φ1 H Φ1 dτ = 1 6 ϕ1 Hϕ1 dτ + ϕ1 Hϕ2 dτ + ϕ1 Hϕ3 dτ + ϕ1 Hϕ4 dτ + ... ... ϕ2 Hϕ4 dτ + ϕ1 Hϕ5 dτ + ϕ1 Hϕ6 dτ + ϕ2 Hϕ1 dτ... + ϕ2 Hϕ2 dτ + ϕ2 Hϕ3 dτ + ϕ2 Hϕ5 dτ + ϕ2 Hϕ6 dτ... ... + ϕ3 Hϕ1 dτ + ϕ3 Hϕ2 dτ + ϕ3 Hϕ3 dτ + ϕ3 Hϕ4 dτ + ... + ϕ3 Hϕ5 dτ + ϕ3 Hϕ6 dτ + ϕ4 Hϕ1 dτ + ϕ4 Hϕ2 dτ... ... ϕ4 Hϕ3 dτ + ϕ4 Hϕ4 dτ + ϕ4 Hϕ5 dτ + ϕ4 Hϕ6 dτ + ... ϕ5 Hϕ1 dτ + ϕ5 Hϕ2 dτ + ϕ5 Hϕ3 dτ + ϕ5 Hϕ4 dτ + ... + ϕ5 Hϕ5 dτ + ϕ5 Hϕ6 dτ + ϕ6 Hϕ1 dτ + ϕ6 Hϕ2 dτ + ... ... + ϕ6 Hϕ3 dτ + ϕ6 Hϕ4 dτ + ϕ6 Hϕ5 dτ + ϕ6 Hϕ6 dτ H11 = Φ1 H Φ1 dτ = 1 6 [α + β + β + β + α + β + β + α + ...] ... [β + β + α + β + β + α + β + β + β + α + ...]= 1 6 [6α +12β] H11 = Φ1 H Φ1 dτ = 1 6 [6α +12β]= α +2β 12

1.-Determinantesdedimensión1x1;consimetría A2

Luego:

2.-Determinantesdedimensión1x1;consimetría B2

1MÉTODODEHUCKEL

α +2β

H11 E = α +2β E1 =0=⇒

1 =

H22 = Φ2 H Φ2 dτ = 1 √6 [ϕ1 ϕ2 + ϕ3 ϕ4 + ϕ5 ϕ6] H 1 √6 [ϕ1 ϕ2 + ϕ3 ϕ4 + ϕ5 ϕ6] H22 = Φ1 H Φ1 dτ = 1 6 ϕ1 Hϕ1 dτ ϕ1 Hϕ2 dτ + ϕ1 Hϕ3 dτ ϕ1 Hϕ4 dτ + ... + ϕ1 Hϕ5 dτ ϕ1 Hϕ6 dτ ϕ2 Hϕ1 dτ + ϕ2 Hϕ2 dτ... ... ϕ2 Hϕ3 dτ + ϕ2 Hϕ4 dτ ϕ2 Hϕ5 dτ + ϕ2 Hϕ6 dτ.... ... + ϕ3 Hϕ1 dτ ϕ3 Hϕ2 dτ + ϕ3 Hϕ3 dτ ϕ3 Hϕ4 dτ... ... + ϕ3 Hϕ5 dτ ϕ3 Hϕ6 dτ ϕ4 Hϕ1 dτ + ϕ4 Hϕ2 dτ... ϕ4 Hϕ3 dτ + ϕ4 Hϕ4 dτ ϕ4 Hϕ5 dτ + ϕ4 Hϕ6 dτ... ... ϕ5 Hϕ1 dτ ϕ5 Hϕ2 dτ + ϕ5 Hϕ3 dτ ϕ5 Hϕ4 dτ + ... ... ϕ5 Hϕ5 dτ ϕ5 Hϕ6 dτ ϕ6 Hϕ1 dτ + ϕ6 Hϕ2 dτ... ... ϕ6 Hϕ3 dτ + ϕ6 Hϕ4 dτ ϕ6 Hϕ5 dτ + ϕ6 Hϕ6 dτ H22 = Φ2 H Φ2 dτ = 1 6 [α β β β + α β β + α β...] [ β + α β β + α β β β + α]= 1 6 [6α 12β] H22 = Φ2 H Φ2 dτ = 1 6 [6α 12β]= α 2β Luego: H22 E = α 2β E2 =0=⇒ E2 = α 2β 3.-Determinantesdedimensión2x2;consimetría E1 H33 = Φ3 H Φ3 dτ H33 = 1 √12 [2ϕ1 + ϕ2 ϕ3 2ϕ4 ϕ5 + ϕ6] H 1 √12 [2ϕ1 + ϕ2 ϕ3 2ϕ4 ϕ5 + ϕ6] dτ H33 = Φ3 H Φ3 dτ = 1 12 4 ϕ1 Hϕ1 dτ 2 ϕ1 Hϕ2 dτ 2 ϕ1 Hϕ3 dτ... ... 4 ϕ1 Hϕ4 dτ 2 ϕ1 Hϕ5 dτ +2 ϕ1 Hϕ6 dτ + ... 13

1MÉTODODEHUCKEL +2 ϕ2 Hϕ1 dτ + ϕ2 Hϕ2 dτ ϕ2 Hϕ3 dτ 2 ϕ2 Hϕ4 dτ... ... ϕ2 Hϕ5 dτ + ϕ2 Hϕ6 dτ 2 ϕ3 Hϕ1 dτ ϕ3 Hϕ2 dτ + ... ... + ϕ3 Hϕ3 dτ +2 ϕ3 Hϕ4 dτ + ϕ3 Hϕ5 dτ ϕ3 Hϕ6 dτ... ... 4 ϕ4 Hϕ1 dτ 2 ϕ4 Hϕ2 dτ +2 ϕ4 Hϕ3 dτ +4 ϕ4 Hϕ4 dτ + ... ... +2 ϕ4 Hϕ5 dτ 2 ϕ4 Hϕ6 dτ ϕ5 Hϕ1 dτ ϕ5 Hϕ2 dτ + ... ... + ϕ5 Hϕ3 dτ +2 ϕ5 Hϕ4 dτ + ϕ5 Hϕ5 dτ ϕ5 Hϕ6 dτ... ... +2 ϕ6 Hϕ1 dτ + ϕ6 Hϕ2 dτ ϕ6 Hϕ3 dτ... ... 2 ϕ6 Hϕ4 dτ ϕ6 Hϕ5 dτ + ϕ6 Hϕ6 dτ H33 = Φ3 H Φ3 dτ = 1 12 [4α +2β +2β +2β + α β β + α +2β + ] ... [+2β +4α +2β +2β + α β +2β β + α]= 1 12 [12α +12β] H33 = Φ3 H Φ3 dτ = 1 12 [12α +12β]= α + β H34 = H43 = Φ3 H Φ4 dτ = Φ4 H Φ3 dτ H34 = H43 1 √12 [2ϕ1 + ϕ2 ϕ3 2ϕ4 ϕ5 + ϕ6] H 1 2 [ϕ2 + ϕ3 ϕ5 ϕ6] H34 = Φ3 H Φ4 dτ = 1 2√12 2 ϕ1 Hϕ2 dτ +2 ϕ2 Hϕ3 dτ 2 ϕ1 Hϕ5 dτ 2 ϕ1 Hϕ6 ϕ2 Hϕ2 dτ + ϕ2 Hϕ3 dτ ϕ2 Hϕ5 dτ ϕ2 Hϕ6 dτ... ... ϕ3 Hϕ2 dτ ϕ3 Hϕ3 dτ ϕ3 Hϕ5 dτ ϕ3 Hϕ6 dτ... ... 2 ϕ4 Hϕ2 dτ 2 ϕ4 Hϕ3 dτ +2 ϕ4 Hϕ5 dτ +2 ϕ4 Hϕ6 dτ + ... ... ϕ5 Hϕ2 dτ ϕ5 Hϕ3 dτ + ϕ5 Hϕ5 dτ + ϕ5 Hϕ6 dτ... ... + ϕ6 Hϕ2 dτ + ϕ6 Hϕ3 dτ ϕ6 Hϕ5 dτ ϕ6 Hϕ6 dτ H34 = Φ3 H Φ4 dτ = 1 2√12 [2β 2β + α + β α β +2β 2β + α + β α β]=0 H34 = Φ3 H Φ4 dτ =0 H44 = Φ4 H Φ4 dτ = 1 2 [ϕ2 + ϕ3 ϕ5 ϕ6] H 1 2 [ϕ2 + ϕ3 ϕ5 ϕ6]= 14

1MÉTODODEHUCKEL H44 = Φ4 H Φ4 dτ = 1 4 ϕ2 Hϕ2 dτ + ϕ2 Hϕ3 dτ ϕ2 Hϕ5 dτ ϕ2 Hϕ6 dτ + ... ϕ3 Hϕ2 dτ + ϕ3 Hϕ3 dτ ϕ3 Hϕ5 dτ ϕ3 Hϕ6 dτ... ... ϕ5 Hϕ2 dτ ϕ5 Hϕ3 dτ + ϕ5 Hϕ5 dτ + ϕ5 Hϕ6 dτ +... ... ϕ6 Hϕ2 dτ ϕ6 Hϕ3 dτ + ϕ6 Hϕ5 dτ + ϕ6 Hϕ6 dτ... H44 = Φ3 H Φ4 dτ = 1 4 [α + β + β + α + α + β + β + α]= 1 4 [4α +4β] H44 = Φ3 H Φ4 dτ = α + β Determinanteseculararesolver: α + β E 0 0 α + β E =0=⇒ E2 2E (α + β)+(α + β)2 =0        Energ´ ıa1 = α + β Energ´ ıa2 = α + β 4.-Determinantesdedimensión2x2;consimetría E2 H55 = Φ5 H Φ5 dτ H55 = 1 √12 [2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6] H 1 √12 [2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6] dτ H55 = Φ5 H Φ5 dτ = 1 12 4 ϕ1 Hϕ1 dτ 2 ϕ1 Hϕ2 dτ 2 ϕ1 Hϕ3 dτ... ... +4 ϕ1 Hϕ4 dτ 2 ϕ1 Hϕ5 dτ 2 ϕ1 Hϕ6 dτ + ... 2 ϕ2 Hϕ1 dτ + ϕ2 Hϕ2 dτ + ϕ2 Hϕ3 dτ 2 ϕ2 Hϕ4 dτ... ... + ϕ2 Hϕ5 dτ + ϕ2 Hϕ6 dτ 2 ϕ3 Hϕ1 dτ + ϕ3 Hϕ2 dτ + ... ... ϕ3 Hϕ3 dτ 2 ϕ3 Hϕ4 dτ + ϕ3 Hϕ5 dτ + ϕ3 Hϕ6 dτ ... 4 ϕ4 Hϕ1 dτ 2 ϕ4 Hϕ2 dτ 2 ϕ4 Hϕ3 dτ +4 ϕ4 Hϕ4 dτ... ... 2 ϕ4 Hϕ5 dτ 2 ϕ4 Hϕ6 dτ ϕ5 Hϕ1 dτ + ϕ5 Hϕ2 dτ + ... ... ϕ5 Hϕ3 dτ 2 ϕ5 Hϕ4 dτ + ϕ5 Hϕ5 dτ + ϕ5 Hϕ6 dτ... ... 2 ϕ6 Hϕ1 dτ + ϕ6 Hϕ2 dτ + ϕ6 Hϕ3 dτ 2 ϕ6 Hϕ4 dτ + ... 15

1MÉTODODEHUCKEL ϕ6 Hϕ5 dτ + ϕ6 Hϕ6 dτ H55 = Φ5 H Φ5 dτ = 1 12 [4α 2β 2β 2β + α + β + β + α 2β...] ... [ 2β +4α 2β 2β + α + β 2β + β + α]= 1 12 [12α 12β] H55 = Φ5 H Φ5 dτ = 1 12 [12α +12β]= α β H56 = H65 = Φ5 H Φ6 dτ = 1 √12 [2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6] H 1 2 [ϕ2 ϕ3 + ϕ5 ϕ6]= H56 = Φ5 H Φ6 dτ = 1 2√12 2 ϕ1 Hϕ2 dτ 2 ϕ1 Hϕ3 dτ 2 ϕ1 Hϕ5 dτ 2 ϕ1 Hϕ6 ... ϕ2 Hϕ2 dτ + ϕ2 Hϕ3 dτ ϕ2 Hϕ5 dτ + ϕ2 Hϕ6 dτ... ϕ3 Hϕ2 dτ ϕ3 Hϕ3 dτ ϕ3 Hϕ5 dτ + ϕ3 Hϕ6 dτ +2 ϕ4 Hϕ2 dτ 2 ϕ4 Hϕ3 dτ +2 ϕ4 Hϕ5 dτ +2 ϕ4 Hϕ6 dτ + ... ... ϕ5 Hϕ2 dτ + ϕ5 Hϕ3 dτ ϕ5 Hϕ5 dτ + ϕ5 Hϕ6 dτ... ϕ6 Hϕ2 dτ + ϕ6 Hϕ3 dτ ϕ6 Hϕ5 dτ + ϕ6 Hϕ6 dτ H56 = Φ5 H Φ6 dτ = 1 2√12 [2β 2β + α + β β α 2β +2β α + β β + α]=0 H56 = Φ5 H Φ6 dτ =0 H66 = Φ6 H Φ6 dτ = 1 2 [ϕ2 ϕ3 + ϕ5 ϕ6] H 1 2 [ϕ2 ϕ3 + ϕ5 ϕ6]= H66 = Φ4 H Φ4 dτ = 1 4 ϕ2 Hϕ2 dτ ϕ2 Hϕ3 dτ + ϕ2 Hϕ5 dτ ϕ2 Hϕ6 dτ + ... ... ϕ3 Hϕ2 dτ + ϕ3 Hϕ3 dτ ϕ3 Hϕ5 dτ + ϕ3 Hϕ6 dτ... ... + ϕ5 Hϕ2 dτ ϕ5 Hϕ3 dτ + ϕ5 Hϕ5 dτ ϕ5 Hϕ6 dτ + ... ϕ6 Hϕ2 dτ + ϕ6 Hϕ3 dτ ϕ6 Hϕ5 dτ + ϕ6 Hϕ6 dτ H66 = Φ3 H Φ4 dτ = 1 4 [α β β + α + α β β + α]= 1 4 [4α 4β] H66 = Φ3 H Φ4 dτ = α β Determinanteseculararesolver: 16

Resumiendo:

Simetría Funcióndeondaorbitalmoleculardesimetría

Dadoque β< 0, eldiagramadediagramaenergíaparalosorbitalesmolecularesdelsistemapidelbenceno es:

1MÉTODODEHUCKEL α β E 0 0 α β E =0=⇒ E2 2E (β α)+(α β)2 =0        Energ´ ıa1 = α β Energ´ ıa2 = α β

Energía A2 Φ1 = 1 √6 [ϕ1 + ϕ2 + ϕ3 + ϕ4 + ϕ5 + ϕ6] α +2β B2 Φ2 = 1 √6 [ϕ1 ϕ2 + ϕ3 ϕ4 + ϕ5 ϕ6] α 2β E1 Φ3 = 1 √12 [2ϕ1 + ϕ2 ϕ3 2ϕ4 ϕ5 + ϕ6] α + β E1 Φ4 = 1 2 [ϕ2 + ϕ3 ϕ5 ϕ6] α + β E2 Φ5 = 1 √12 [2ϕ1 ϕ2 ϕ3 +2ϕ4 ϕ5 ϕ6] α β E2 Φ6 = 1 2 [ϕ2 ϕ3 + ϕ5 ϕ6] α β

0 17

Método de Huckel para el trimetilenmetano. Enlaﬁgurasemuestralaestructuradeestamolécula.

Cadacarbonoaportaunelectrónalsistemapi.Eldesarrolloseexpondráenformatoresumido.

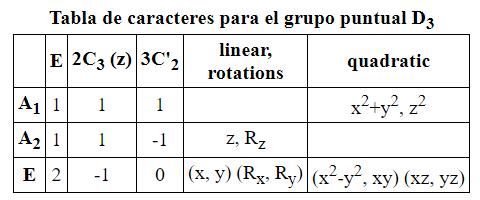
Lamoléculaclasiﬁcaenelgrupopuntual D3h . Porsimplicidadseoptaporelsubgrupo D3.

Larepresentaciónreduciblees:

Larepresentaciónirreduciblesdelsistemapiparaeltrimetilenmetanoes: Γ

=2A1 + E. Aplicandoel

paracadaunadelascomponentesdelarepresentaciónirreducible

1MÉTODODEHUCKEL

E 2C3 (z) 3C ′ 2 Γπr 4 1 2

πi

operadordeproyección j,i χj (Rj ) Rj ϕi,

Γπi 18

sional,asíquesedebenencontrardoscombinacioneslinealesdiferentes.Examinandolasexpresiones:

Eldeterminantearesolveresdeltipo:

1MÉTODODEHUCKEL D3 E ←− C3 (z) −→ C3 (z) C2 (1,4) C2 (1,2) C2 (1,3) A1 1 1 1 1 1 1 E 2 -1 -1 0 0 0 ϕ1 ϕ1 ϕ1 ϕ1 ϕ1 ϕ1 ϕ1 ϕ2 ϕ2 ϕ4 ϕ3 ϕ3 ϕ2 ϕ4 ϕ3 ϕ3 ϕ2 ϕ4 ϕ2 ϕ4 ϕ3 ϕ4 ϕ4 ϕ3 ϕ2 ϕ4 ϕ3 ϕ2 Transformancomolarepresentación A1 : ϕ1 y 1 √3 [ϕ2 + ϕ3 + ϕ4] Lasituaciónsereduceados combinacioneslinealesdiferentesquetransformancomolarepresentación A1: Φ1 = ϕ1 y Φ2 = 1 √3 (ϕ2 + ϕ3 + ϕ4) Transformancomolarepresentación E : 1 √3 [2ϕ2 ϕ3 ϕ4](a) 1 √3 [2ϕ3 ϕ2 ϕ4](b) 1 √3 [2ϕ4 ϕ3 ϕ2](c) larepresentación E esbidimen-

(b + c) = (2ϕ2 ϕ3 ϕ4) = a (b c) = 3ϕ3 3ϕ4 Ahoralasituaciónsereduceadoscombinacioneslinealesdiferentesquetransformancomolarepresentación E: Φ3 = 1 √6 (2ϕ2 ϕ3 ϕ4) y Φ4 = 1 √2 (ϕ3 ϕ4)

Porsimetríaeldeterminatede4x4sereduceados,unoentrelascombinaciones (Φ1 y Φ2) quetransforman como A1, yunsegundodeterminanteentrelascombinacioneslineales (Φ3 y Φ4) quetransformancomola representación

1 y

2) quetransformancomo

Conocemoslasenergíasdelosorbitalesmolecularesdesimetríaquetransformancomo A1.Faltaconocerla combinaciónlinealdelosorbitalesatómicosquedanformaaesosorbitalesmoleculares.Paraelloserequiere resolverelsiguientesistemadeecuaciones:

Porloanterior,lacombinaciónlinealdeorbitalesatómicosquecontribuyenalorbitalmolecularque transformacomolarepresentaciónirreducible A1 con Energ´ ıa1 = α +

3 es:

1MÉTODODEHUCKEL H11 EH12 H13 H14 H21 H22 EH23 H24 H31 H32 H33 EH34 H41 H42 H43 H44 E =0 (3)

E Combinaciones (Φ

A1, H11 EH12 H21 H22 E =0=⇒ α E 3 β √3 3 β √3 α E =0        Energ´ ıa1 = α + β√3 Energ´ ıa2 = α β√3

Con Energ´ ıa1 = α + β√3 α α β√3 · c1 + 3 β √3 · c2 =0 c2 1 + c2 2 =1 ⇐⇒ c1 = c2 = 1 √2

β√

Φ1 = 1 √2 ϕ1 + 1 √6 (ϕ2 + ϕ3 + ϕ4) Con Energ´ ıa2 = α β√3 α α + β√3 · c1 + 3 β √3 · c2 =0 c2 1 + c2 2 =1 ⇐⇒ c1 = 1 √2 yc2 = 1 √2 20

Porloanterior,lacombinaciónlinealdeorbitalesatómicosquecontribuyenalorbitalmolecularque transformacomolarepresentaciónirreducible

2Índicesdereactividadestáticos

Luegodeconocidaslasfunciónesorbitalesmolecularesdelaentidadmolecularqueseestudia,sedisponede unavaliosainformaciónquedacuentadeladistribucióndeladensidaddeprobabilidadentornoaloscentros

2ÍNDICESDEREACTIVIDADESTÁTICOS

A1 con Energ´ ıa2 = α β√3 es: Φ2 = 1 √2 ϕ1 1 √6 (ϕ2 + ϕ3 + ϕ4) Combinaciones (Φ3 y Φ4) quetransformancomo E, H33 EH34 H43 H44 E =0=⇒ α E 0 0 α E =0        Energ´ ıa3 = α Energ´ ıa4 = α estadosdegenerados Simetría Funcióndeondaorbitalmoleculardesimetría Energía A1 Φ1 = 1 √2 ϕ1 + 1 √6 (ϕ2 + ϕ3 + ϕ4) α + β√3 A1 Φ2 = 1 √2 ϕ1 1 √6 (ϕ2 + ϕ3 + ϕ4) α β√3 E Φ3 = 1 √6 (2ϕ2 ϕ3 ϕ4) α E Φ4 = 1 √2 (ϕ3 ϕ4) α

2.1Densidadelectrónica 2ÍNDICESDEREACTIVIDADESTÁTICOS

atómicosqueconformanelsistemapi.Delacontribucióndecadaorbitalatómicoalsistemapi(coeficientes departicipacióndelosrespectivosorbitalesatómicosenlosorbitalesmoleculares),yconbaseenelteorema Vdelamecánicacuántica,sedefinenlossiguientesíndices:ladensidadelectrónica,ladensidaddecarga, elordendeenlaceylavalencialibre.Conellossedisponedeunconjuntodeparámetrosquedancuenta delapotencialactividadelectrofílicaonucleofílicadecadaunodeloscentrosatómicosqueconformanel sistemapi,delafactibilidadderomperunenlace,ydelapotencialcapacidaddeenlazamientodealgunos deloscentrosatómicosdelsistemamolecularenestudio.Todoelloconstituyenbaseparasuponereventual reactividadquímica.Esteconjuntodeparámetrossonconocidosconelnombredeíndicesdereactividad.A continuaciónseahondaráensudefiniciónymecanismodecálculo.

2.1Densidadelectrónica

Enunorbitalmolecularcadaelectrónserepresentapor Φi = p c2 ipxp

cumpliendoconlacondicióndenormalización p c2 ip =1.Loanteriorrepresentalaprobabilidaddepresencia delelectrónentodoelespaciodescritopor Φi, lascantidades c2 ip correspondenalaprobabilidaddepresencia delelectrónenlaregióncorrespondientealorbitalatómico xp dentrodelorbitalmolecular Φi Esladensidad electrónicaasociadaalátomopenelorbitalmolecular Φi. Ladensidadelectrónicatotalenunátomop (qp) es lasumadelasdensidadeselectrónicasaportadasporcadaelectrónenelorbitalmolecular.

c2 ip eselcoeﬁcientedelorbitalatómico xp eneli-ésimoorbitalmolecularcon ni electrones.Lasumadebeconsiderarseparatodoslosorbitalesmolecularesocupadosdelsistemapi.Lasumadelasdensidadeselectrónicas correspondenalnúmerodeelectronesqueaportantodoslosátomosqueconformanelsistemapi.

Deloanteriorsederivaladensidaddecarga (δp) asociadaacadaátomo.Ladensidaddecargaseobtiene restandoladensidadelectrónica qp alnúmerodeelectronesaportadosporelátomo p alsistemapi.Esun

índiceinteresante,yaquepuederesultarpositivo,negativooigualaceroy,portanto,eventualmenteserun

       i = Orbitalmolecular p = orbitalat´ omicoenelorbitalmoleculari

qp = i ni c2 ip

2.2Ordendeenlace pj rs

centroreactivopotencialmenteatractordenucleóﬁlosoelectróﬁlos.Lasumadelasdensidadesdecargade todoslosátomosqueformanelsistemapidebeserigualalacargadelamolécula.

2.2Ordendeenlace

Esteíndicerepresentaladensidadelectrónicaasociadaalaregióncomprendidaentrelosátomos rys, enel orbitalmolecular Φj . Elordendeenlaceseevalúapor prs = j pj rs = j nj cjr cjs. Donde nj eselnúmerode electronesenelorbitalmolecular Φj ,aportadosporlosátomosdecarbono rys. Esteíndicerepresentaelgrado deinteracciónentrelosátomosinteractuantesvariandoentrelocalizadaagradosdedeslocalización.Cálculo

Cálculodelosordenesdeenlaceeneltrimetilenmetano

Conocidoelordendeenlacesepuedeestimarlalongituddeenlace.Paraelloseconsideraque,ladistancia deunsimpleenlacesigma,conceroordendeenlace

yordendeenlace π esiguala1es 1, 33 ˚ A

Enelcasodelamoléculadetrimetilenmetanolalongituddeenlace

2ÍNDICESDEREACTIVIDADESTÁTICOS

(pj rs)

deladensidadelectrónicaydensidaddecargaeneltrimetilenmetano átomo qp δp 1 2· 1 √2 2 =1 1 1=0 2 2· 1 √6 2 +1· 2 √6 2 =1 1 1=0 3 2· 1 √6 2 +1· 1 √6 2 +1· 1 √2 2 =1 1 1=0 4 2· 1 √6 2 +1· 1 √6 2 +1· 1 √2 2 =1 1 1=0

átomo prs p1,2 2· 1 √2 · 1 √6 = 1 √3 p1,3 2· 1 √2 · 1 √6 = 1 √3 p1,4 2· 1 √2 · 1 √6 = 1 √3

Ayundobleenlace,conunsimpleenlacesigma

C1 C2 = C1 C3 = C1 C4 23

2.3Valencialibre (Fr) 2ÍNDICESDEREACTIVIDADESTÁTICOS

Enestecasoel C1 estáenlazadocontodoslosotrosátomosdelamoléculay,portanto,suordende enlace π totales: N1 =3· 1 √3 = √3. Esteeselvalormásaltoquepuedetenerunátomodecarbonoen cualquiertipodecompuesto.Siseincluyeelsistemasigmaresultaría 3+√3=4, 73 enlaces,queeslamáxima saturaciónalcanzable.Paracualquiercarbono,enotrosistema π, elordendeenlacetotalserásiempremenor que

2.3Valencialibre (Fr)

Ladeﬁnicióndeesteíndicesehaceenreferenciaauncarbonoconmáximasaturación(carbono1dela moléculadetrimetilenmetano).Eselresultadodesumar,paraunátomoenparticular,losordenesde enlacesendondedichoátomoparticipa (Nr) . Ladiferenciaaestevalor,paraelordendeenlacetotalde cualquierátomo r, esunamedidadelaposibilidadadicionaldesaturación. Fr = √3 Nr

Cálculodeladensidadelectrónicaydensidaddecargaenelbenceno

orden π longituddeenlace 0 1, 54 ˚ A 1 √3 x 1 1, 33 ˚ A =⇒ (0 1) 1 √3 1 = (1,54 1,33) (x 1,33) =⇒ x = 1, 42 ˚ A ˚ A ∼ 1, 40 ˚ Aexperimental

√

2.3Valencialibre (Fr) 2ÍNDICESDEREACTIVIDADESTÁTICOS átomo qp δp 1 2· 1 √6 2 +2· 2 √12 2 =1 1 1=0 2 2 1 √6 2 +2 1 √12 2 +2 1 2 2 =1 1 1=0 3 2· 1 √6 2 +2· 1 √12 2 +2· 1 2 2 =1 1 1=0 4 2· 1 √6 2 +2· 2 √12 2 =1 1 1=0 5 2· 1 √6 2 +2· 1 √12 2 +2· 1 2 2 =1 1 1=0 6 2· 1 √6 2 +2· 1 √12 2 +2· 1 2 2 =1 1 1=0 Cálculodelosordenesdeenlaceenelbenceno átomo prs p1,2 2· 1 √6 · 1 √6 +2· 2 √12 · 1 √12 = 2 3 p1,6 2· 1 √6 · 1 √6 +2· 2 √12 · 1 √12 = 2 3 p2,3 2· 1 √6 · 1 √6 +2· 1 √12 · 1 √12 +2· 1 2 · 1 2 = 2 3 p3,4 2· 1 √6 · 1 √6 +2· 1 √12 · 2 √12 = 2 3 p4,5 2· 1 √6 · 1 √6 +2· 2 √12 · 1 √12 = 2 3 p5,6 2· 1 √6 · 1 √6 +2· 1 √12 · 1 √12 +2· 1 2 · 1 2 = 2 3 Enelcasodelamoléculadebencenolalongituddeenlace C1 C2 = C2 C3 = C3 C4 = C4 C5 = C5 C6 = C6 C1 orden π longituddeenlace 0 1, 54 ˚ A 2 3 x 1 1, 33 ˚ A =⇒ (0 1) ( 2 3 1) = (1,54 1,33) (x 1,33) =⇒ x = 1, 40 ˚ A 1, 39 ˚ Aexperimental 25

Cálculodelavalencialibreenelbenceno

Método de Huckel en moléculas con heteroátomos y uso de Teoría de Grupos Estecasonomodiﬁca

lasetapasdelmétodo,sílavalorizacióndelasintegrales Hii,Hij , demodoqueestassecorrigen,pues implicanlainteracciónentreheteroátomos(átomodistintoalcarbono)oentreunátomodecarbonoyun heteroátomo.Engenerallacorreccióntienelasiguienteforma:

Losparámetros hx ykC x dependedelheteroátomoquesetratey,paraunmismoheteroátomo,puedevarirasegúnelnúmerodeelectronesqueaportealsistemapi.Algunosde estosvaloressepresentanenlasiguientetabla:

2.3Valencialibre (Fr) 2ÍNDICESDEREACTIVIDADESTÁTICOS

átomo Nr Fr 1 2 3 + 2 3 √3 4 3 =0, 399 2 2 3 + 2 3 √3 4 3 =0, 399 3 2 3 + 2 3 √3 4 3 =0, 399 4 2 3 + 2 3 √3 4 3 =0, 399 5 2 3 + 2 3 √3 4 3 =0, 399 6 2 3 + 2 3 √3 4 3 =0, 399

αx = α + hxβ βx = kC xβ

EjemploparalamoléculadeAcetilenimina C3H3N.Estamoléculaclasiﬁcaenelgrupopuntualdesimetría C2v

Cadaunodelosátomosdecarbonoaportaunelectrónalsistemapiytambiénunelectrónelátomode nitrógeno.Aplicandolosoperadoresdeproyecciónacadaorbitalatómicoseencuentrantresfuncionesdeonda desimetría A1, yunafunciónquetransformacomolarepresentaciónirreducible B1; lascualescontribuirán aconformarloselementosdedosdeterminantesseculares.Unode 3x3 entrelasfuncionesconsimetría A1, yunode 1x1 paralafunciónconsimetría B1. Paraelcasodelelectrónqueaportaelátomodenitrógenoal sistemapiserepresentarápor Ψ1 y χi paraelcasodecadaunodeloselectronesaportadosporlosátomosde carbono.

2.3Valencialibre (Fr) 2ÍNDICESDEREACTIVIDADESTÁTICOS Nitr´ ogenohx kC x ˙ N 0, 5 ¨ N 1, 5 2, 0 Ox´ ıgeno

Sonintegralentreorbitalesatómicosdenitrógenoycarbonoquesonvecinos.Elátomodenitrógenoaporta

2.3Valencialibre (Fr) 2ÍNDICESDEREACTIVIDADESTÁTICOS Transformancomolarepresentación A1 : ϕA1 (1)= Ψ1 (a) ϕA1 (2)= 1 √2 [χ2 + χ3](b) ϕA1 (3)= Ψ1χ4 (c)

.-Determinantesdedimensión3x3;consimetría A1 H11 EH12 H13 H21 H22 EH23 H31 H32 H33 E H11 = ϕA1 (1) HϕA1 (1) dτ = Ψ1 HΨ1 dτ = α +0, 5β. Esunaintegralentreorbitales atómicosdenitrógenoqueaportaunelectrónalsistemapi H12 = ϕA1 (1) HϕA1 (2) dτ = Ψ1 H 1 √2 [χ2 + χ3] dτ = 1 √2 Ψ1 Hχ2 dτ + 1 √2 Ψ1 Hχ3 dτ.

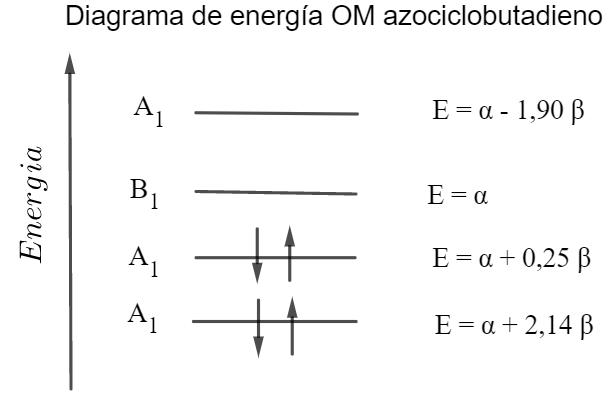
unelectrónalsistemapi.Porlotanto H12 =√2β H13 = ϕA1 (1) HϕA1 (3) dτ = Ψ1 Hχ4 dτ =0 H22 = ϕA1 (2) HϕA1 (2) dτ = 1 √2 [χ2 + χ3] H 1 √2 [χ2 + χ3] dτ = 1 2 χ2 Hχ2 dτ +2 χ2 H22 = αH23 = ϕA1 (2) HϕA1 (3) dτ = 1 √2 [χ2 + χ3] Hχ4 dτ = 1 √2 χ2 Hχ4 dτ + χ3 Hχ √2β. H33 = ϕA1 (3) HϕA1 (3) dτ = χ4 Hχ4 dτ = α. α +0, 5β E √2β 0 √2βα E √2β 0 √2βα E =0              Energ´ ıa1 = α +2, 14β Energ´ ıa2 = α +0, 25β Energ´ ıa3 = α 1,90β 28

Porloanterior,lacombinaciónlinealdeorbitalesatómicosquecontribuyenalorbitalmolecularque transformacomolarepresentaciónirreducible

2.3Valencialibre (Fr) 2ÍNDICESDEREACTIVIDADESTÁTICOS Con Energ´ ıa1 = α +2, 14β (α +0, 5β E α 2, 14β) · c1 + √2β· c2 +0· c3 =0 √2β· c1 +(α α 2, 14β) · c2 + √2β· c3 =0 c2 1 + c2 2 + c2 3 =1                C1 =0, 54 C2 =0, 63 C3 =0, 56

Energ´ ıa1 = α +2, 14β es: ΦA1 (a)=0, 54Ψ1 +0, 45(χ2 + χ3)+0, 56χ4 Con Energ´ ıa2 = α +0, 25β (α +0, 5β E α 0, 25β) · c1 + √2β· c2 +0· c3 =0 √2β· c1 +(α α 0, 25β) · c2 + √2β· c3 =0 c2 1 + c2 2 + c2 3 =1                C1 =0, 73 C2 = 0, 12 C3 = 0, 66

con

A1 con Energ´ ıa2 = α +0, 25β es: ΦA1 (b)=0, 73Ψ1 0, 08(χ2 + χ3) 0, 66χ4 Con Energ´ ıa3 = α 1, 90β (α +0, 5β E α +1,90β) · c1 + √2β· c2 +0· c3 =0 √2β· c1 +(α α +1, 90β) · c2 + √2β· c3 =0 c2 1 + c2 2 + c2 3 =1                C1 =0, 43 C2 = 0, 73 C3 =0, 54

Energ´ ıa1 = α 1 09β es: ΦA1 (c)=0, 43Ψ1 0, 52(χ2 + χ3)+0, 54χ4 29

con

Lafunciónconsimetría B1 esúnica ΦB1 = 1 √2 (χ2 χ3)

Simetría Funcióndeondaorbitalmoleculardesimetría Energía

Cálculodeladensidadelectrónicaydensidaddecargaenelazociclobutadieno

2ÍNDICESDEREACTIVIDADESTÁTICOS

2.3Valencialibre (Fr)

A1 ΦA1 (a)=0, 54Ψ1 +0, 45(χ2 + χ3)+0, 56χ4 α +2, 14 β A1 ΦA1 (b)=0, 73Ψ1 0, 08(χ2 + χ3) 0, 66χ4 α +0, 25β A1 ΦA1 (c)=0, 43Ψ1 0, 52(χ2 + χ3)+0, 54χ4 α 1, 90 β B1 Φ4 = 1 √2 (ϕ2 ϕ3) α

átomo qp δp 1 2· (0, 54)2 +2· (0, 73)2 =1, 65 1 1, 65= 0, 65 2 2· (0, 45)2 +2· ( 0, 08)2 =0, 42 1 0, 42=0, 58 3 2· (0, 45)2 +2· ( 0, 08)2 =0, 42 1 0, 42=0, 58 4 2· (0, 56)2 +2· ( 0, 66)2 =1, 50 1 1, 50= 0, 50

Cálculodelosordenesdeenlaceenelazociclobutadieno

Estimacionesdelalongituddeenlaceenelazociclobutadienio:

2.3Valencialibre

2ÍNDICESDEREACTIVIDADESTÁTICOS átomo prs p1,2 2· (0, 54) · (0, 45)+2· (0, 73) · ( 0, 08)=0, 37 p1,3 2· (0, 54) · (0, 45)+2· (0, 73) · ( 0, 08)=0, 37 p2,4 2· (0, 45) · (0, 56)+2· ( 0, 08) · ( 0, 66)=0, 61 p3,4 2· (0, 45) · (0, 56)+2· ( 0, 08) · ( 0, 66)=0, 61

(Fr)

a) Caso N1 C2 = N1 C3 orden π longituddeenlace 0 1, 465 ˚ A 0,37 x 1 1, 279A =⇒ (0 1) (0,37 1) = (1,465 1,279) (x 1,279) =⇒ x =1, 40 ˚ A b) Caso C2 C4 = C3 C4 orden π longituddeenlace 0 1, 54 ˚ A 0,61 x 1 1, 33A =⇒ (0 1) (0,61 1) = (1,54 1,33) (x 1,33) =⇒ x =1, 41 ˚ A

átomo Nr Fr 1 0, 37+0, 37 √3 0, 74=0, 99 2 0, 37+0, 61 √3 0, 98=0, 75 3 0, 37+0, 61 √3 0, 98=0, 75 4 0, 61+0, 61 √3 1, 22=0, 51 31

Cálculodelavalencialibreenelazociclobutadieno

2.3Valencialibre (Fr) 2ÍNDICESDEREACTIVIDADESTÁTICOS 32