Partícula en una esfera by carlos.hernandez-umce

Partículaenlaesfera

Ψ(x,y,z) y ∇2 = ∂2 ∂x2 + ∂2 ∂y2 + ∂2 ∂z2 [ h2 8π2m ∇2 + Ep] Ψ= ET Ψ h2 8π2m [∂2Ψ(x,y,z) ∂x2 + ∂2Ψ(x,y,z) ∂y2 + ∂2Ψ(x,y,z) ∂z2 ] + EpΨ(x,y,z)= ET Ψ(x,y,z) 1

1 r2 ∂2 Ψ (θ,ϕ) ∂θ2 + cos θ r2 sin θ ∂Ψ (θ,ϕ) ∂θ + cos θ r2 sin2 θ ∂2 Ψ (θ,ϕ) ∂ϕ2 + 8 π2 masaE h2 Ψ (θ,ϕ)=0 (1) Sea Ψ (θ,ϕ)= Θ (θ)Φ(ϕ) reemplazandoen(1)ymultiplicandopor r2 sen2 θ Θ(θ)Φ(ϕ) queda: sen2 θ Θ(θ) d2 Θ(θ) dθ2 + cos θsenθ Θ(θ) d Θ(θ) dθ + 8 π2 masar2 sen2θ h2 E = 1 Φ(ϕ) d2Φ(ϕ) dϕ2 sen2 θ Θ(θ) d2 Θ(θ) dθ2 + cos θsenθ Θ(θ) dΘ(θ) dθ + 8 π2 masar2 sen2θ h2 E = m2 , multiplicandopor 1 sen2 θ d2 Θ(θ) dθ2 + cos θ senθ d Θ(θ) dθ + (8 πmasar2 E h2 m2 sen2θ ) Θ(θ)=0 1 Φ(ϕ) d2Φ(ϕ) dϕ2 = m2 =⇒ ecuaciónanálogaalapartículaenunanillo,luego: Φ(ϕ)= 1 √2π eimϕ =⇒ conm =0, ±1, ±2 ... Sedeﬁnelasiguientevariableauxiliar: x =cos θ con 1 ≤ x ≤ 1. Ademássea 2

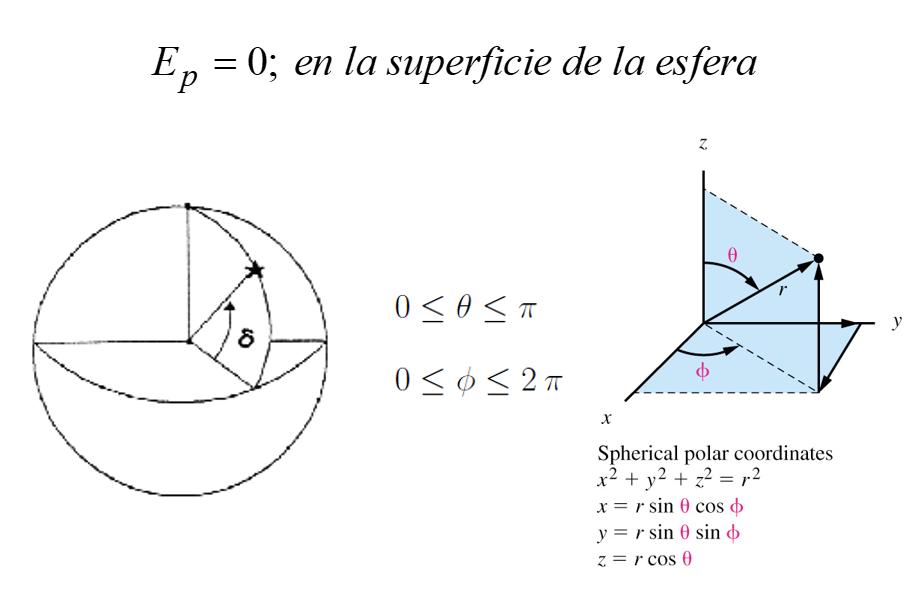
Reemplazandoenlaecuaciónquedadelasiguiente

Laecuación (1) seidentiﬁcaconlaecuaciónasociadadeLagrangequetienecomosoluciónlospolinomios asociadosdeLegendredegrado l yorden m

) eslafunciónsoluciónparaeltratamientomecanocuánticodeunapartículaenunaesfera. Estafunciónesconocidacomoarmónicoesféricoyserepresentapor Yl,m (θ,ϕ) .Losarmónicosesféricos constituyenunconjuntoortonormalenelrango:

ApartirdelasrelacionesdeEuler,losarmónicosesféricospuedenexpresarsecomofuncionestrigonométricasrealesde ϕ.

l (l +1)= 8 π2 masar2 E h2 , con l =0, 1, 2,....

(1 x 2) d2 Θ(θ) dx2 2 x d Θ(θ) dx + [l (l +1) m2 (1 x2)] Θ(θ)=0 (2)

manera:

Θl,m (θ)= Nl,m P m l (cosθ) donde Nl,m = √ (2 l+1) 2 (l−|m|!) (l+|m|!) como Ψl,m (θ,ϕ)=Θl,m (θ)Φm (ϕ) entonces,reemplazando Φm (ϕ) y Θl,m (θ) queda: Ψl,m (θ,ϕ)= Nl,m P m l (cosθ) 1 √2 π eimϕ porloque,alincorporar Nl,m resulta: Ψl,m (θ,ϕ)= √(2 l +1) 4 π (l −|m|!) (l + |m|!) P m l (cosθ) eimϕ (3) Ψl,m

θ,ϕ

0 ≤ θ ≤ π y 0 ≤ ϕ ≤ 2 π

(

Lapartículademueveconenergíapotencialigualaceroenlasuperﬁciedelaesfera.Porlotanto,toda laenergíaesenergíacinética.Luego,considerandoque p

yque L = pr entonces

(1) eikx =cos kx + i sin kx (1) (2) ⇒ sin kx = i 2 (eikx e ikx) (2)e ikx =cos kx i sin kx (1)+(2) ⇒ cos kx = 1 2 (eikx + e ikx) Como l (l +1)= 8 π2 masar2 E h2 entonces E = l(l+1)h2 8 π2 masar2 . Dadoque l correspondealgrado delpolinomioasociadodeLegrandey m elordendederivacióndeeste,entoncessedebecumplirque | m |≤ l =⇒ m =0, ±1, ±2,... ± l Losarmónicosesféricossepuedenexpresarentérminosreales (R) atravésdelasecuacionesdeEuler l M x = r sin θ · cos ϕy = r sin θ · sin ϕz =cos θ 0 0 Y0,0(θ,ϕ)= 1 2 √ 1 π = 1 √4π 1 0 Y1,0(θ,φ)= 1 2 √ 3 π · cos θ = Yz 1 √2 (Y1,1(θ,φ)+ Y1, 1(θ,φ))= √ 3 4π sin θ cos ϕ = Yx 1 √2 (Y1,1(θ,φ) Y1, 1(θ,φ))= √ 3 4π · sin θ · sin ϕ = Yy 2 0 Y2,0(θ,φ)= 1 4 √ 5 π · (3cos2 θ 1)= Yz2 1 √2 (Y2,1(θ,φ)+ Y2, 1(θ,φ))= √ 15 4π sin θ cos θ cos ϕ = Yxz i √2 (Y2,1(θ,φ) Y2, 1(θ,φ))= √ 15 4π · sin θ · cos θ · sin ϕ = Yyz 1 √2 (Y2,2(θ,φ)+ Y2, 2(θ,φ))= √ 15 16π · sin2 θ · cos2ϕ = Yx2 y2 i √2 (Y2,2(θ,φ) Y2, 2(θ,φ))= √ 15 4π sin2 θ sin2ϕ = Yxy

masaE

L2 = p2 r2 , porloque L2 =2 masaEr2

E = l(l+1)h2 8 π2 masar2 , queda: L2 = l (l +1) h2 4 π2 = l (l +1) ℏ2 =⇒ L = √l (l +1) ℏ paral =1=⇒ L = √2 ℏ y Lz = ℏ 4

2 =2

,reemplazando

L2 = l (l +1)= L2 x + L2 y + L2 z, veamoscualeselefectoenlascomponentesdelmomentun angularsiseconoce LyLz :

(a) l =1 y m =0 ylosvaloresparacadacomponentessona,bymrespectivamente:

2= a2 + b2 +0, quesesatisfacesi a =1 y b =1

(b) l =1 y m =1 ylosvaloresparacadacomponentessona,bymrespectivamente:

2= a2 + b2 +12 ,quesesatisfacesi a =1 yb =0, o a =0 yb =1

Noesposibleconocersimúltaneamentelastrescomponentesdelmomentunangular.Estoconstituyeun aspectobásicodelaMecánicaCuántica.Comolacomponente z delmomentunangularestácuantizadapor

, estacomponentepuedeserconocible,aligualqueelmomentun

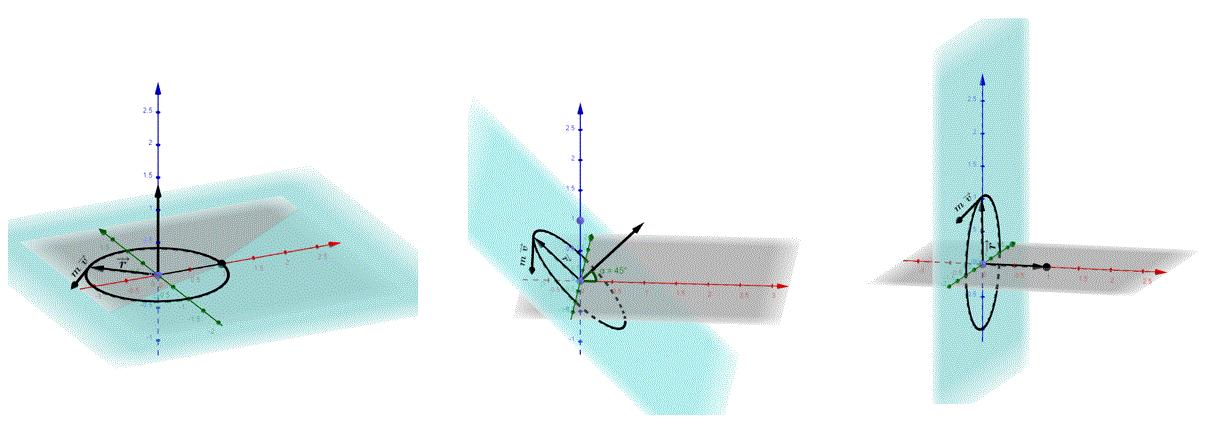
angulartotal,resultandoentoncesindeterminadaslascomponentes Lx yLy Demaneradecontribuirconmásargumentaciónconsidéreseque,desdelaperspectivaclásica,elmomentun angularesunvectorquecorrespondealproducto −→ L = −→ rx −→ p. Así,porejemplo,unapartículaquegiraen movimientocircularuniformeentornoalorigen,ladireccióndelmomentunangulardependedeladirección delmovimientodelapartículaydelainclinacióndelaorbitaconrespecto,porejemploalejez(seelijeel ejezporlasimplicidaddelaexpresiónparaelmomentunangular Lz = m ℏ.

m,Lz = m h 2 π ⇒ L2 z = m2 h2 4 π2

Segúnlainclinacióndelplanoorbital,lacomponente Lz puedevariardesde Lz =1 a Lz =0. Mientras giralapartícula,sielvectormomentunangular L presentaunángulorespectodeleje z,seproduceun movimientodeprecesiónde −→ L entornoaleje z,porloquelaproyeccióndesuscomponentesenelplano x,y (Lx yLy) varíanconstantemente. Activarenlace.

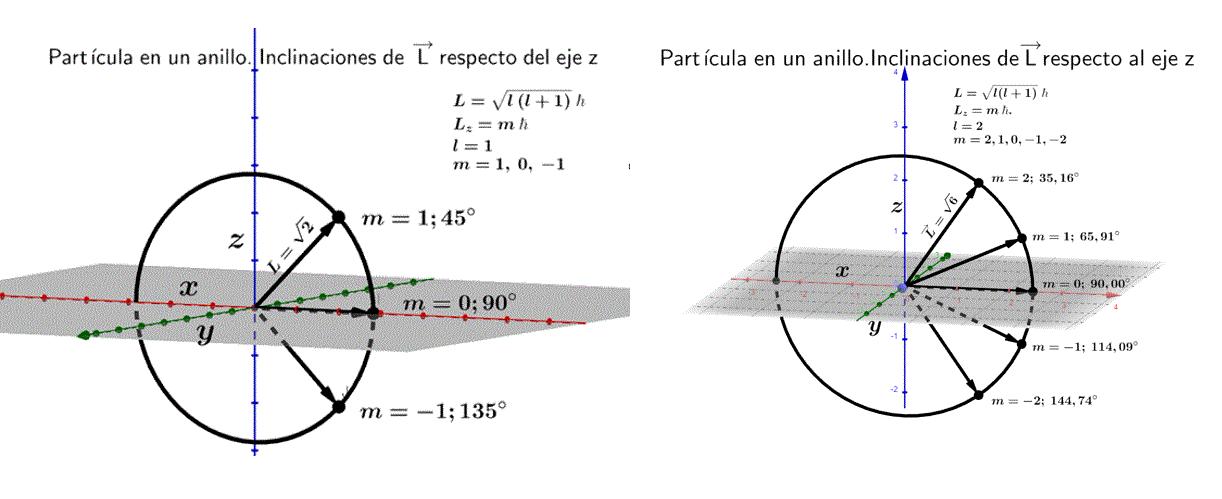
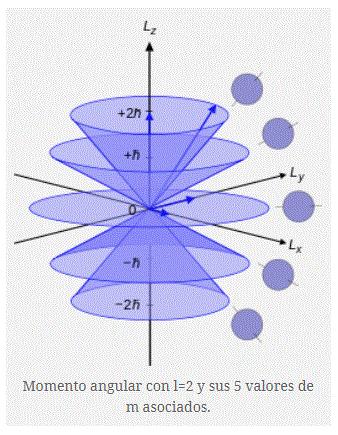
Lacuantizaciónde Lz limitalasposiblesinclinacionesde −→ L conrespecto z.Enlaﬁgurasquesepresentan segraﬁcanlasposiblesinclinacionesdepara l =1 y l =2.

Paraevaluarlaprobabilidadangularenunaciertorango,sedeberesolverlasiguienteintegral

Lasgráﬁcasparalasfuncionesdeprobabilidadangular,para l =0, 1, 2, sepresentanacontinuación:

´ ϕ2 ϕ1 ´ θ2 θ1 |Ψl,m (θ,ϕ)|2 sin θdθdϕ

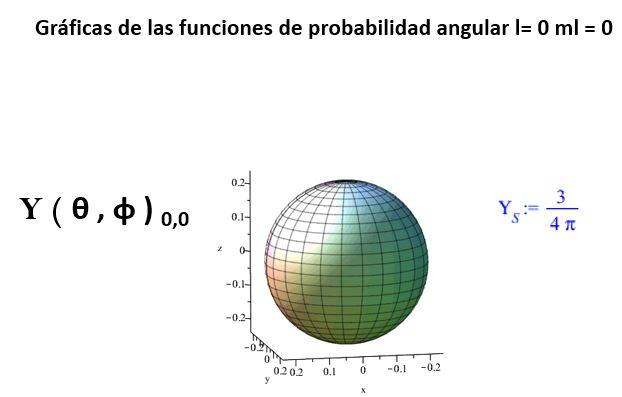
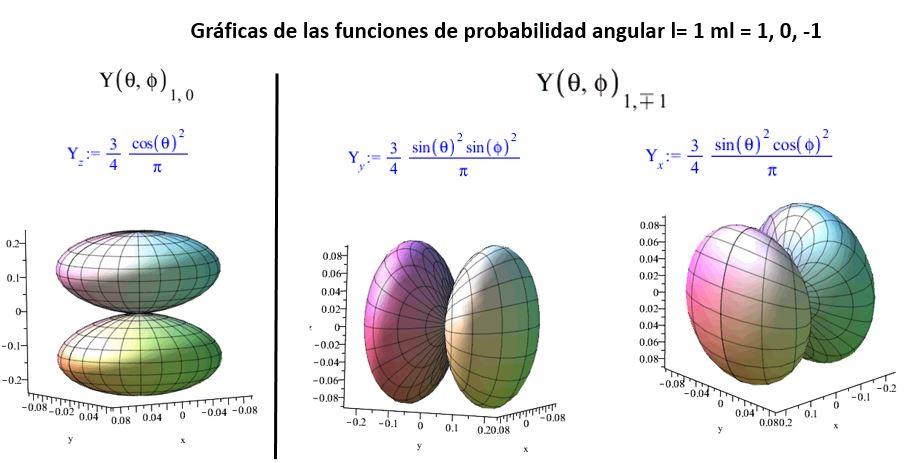
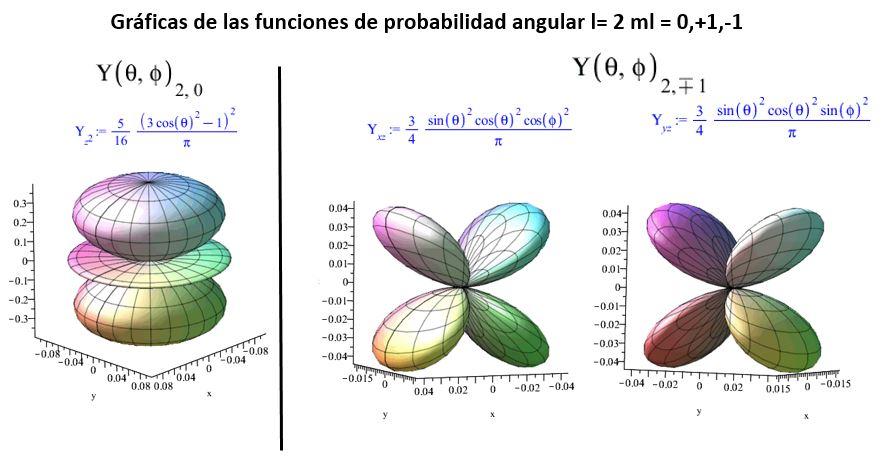
Delaobservacióndelagráficasdedistribucióndelasprobabilidadangularseinfiereque,lacantidadde planosnodalesesiguala l. Tambiénseinfierequeamayor |m| , másalejadadelejezsehallalazonade mayorprobabilidaddepresencia.Para Ψz elplanoecuatorialnodaldelaesferaesunaregiónnodal,donde laprobabilidaddepresenciadelapartículaesnula.Porotraparte, Ψx, lalíneanodalesaquellaquelimitael plano yx. Paralasfuncionescon l =2, laslíneasnodalessondos,mutuamenteperpendicularespara |M| =1 o 2, yenángulode 70, 54◦ para |M| =0.