Estructuras para edificios 2025
Septiembre 9 de 2025
Equilibrios en vigas isostáticas e hiperestáticas
Trabajo en MD SOLIDS y LINPRO
El caso de una luz
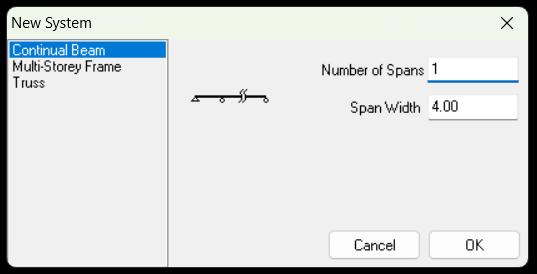
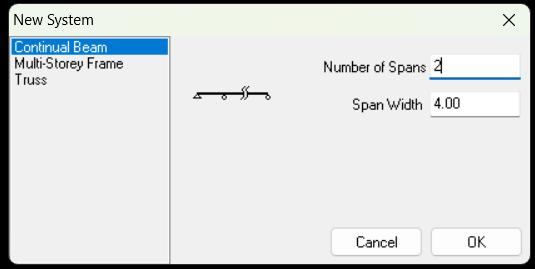
Viga isostática: Es aquella viga en la que las reacciones de apoyo pueden calcularse únicamente con las ecuaciones básicas de equilibrio (ƩF = 0 y ƩM = 0), sin necesidad de fórmulas adicionales.
En otras palabras, no tiene más apoyos de los necesarios y por eso sus esfuerzos internos (cortante y momento) se pueden obtener de manera directa.
Deflexión
Viga simplemente apoyada
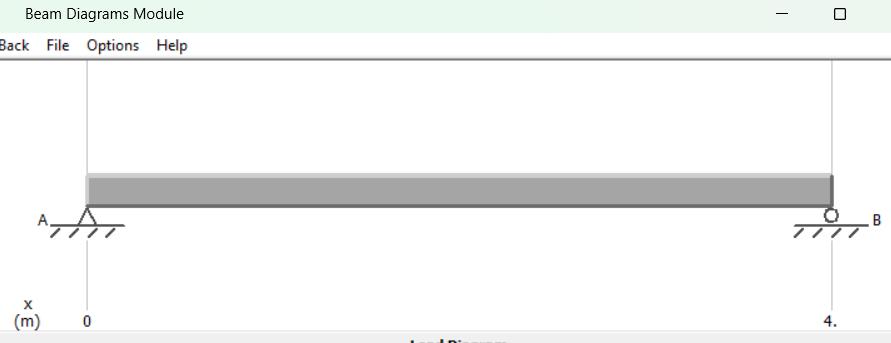
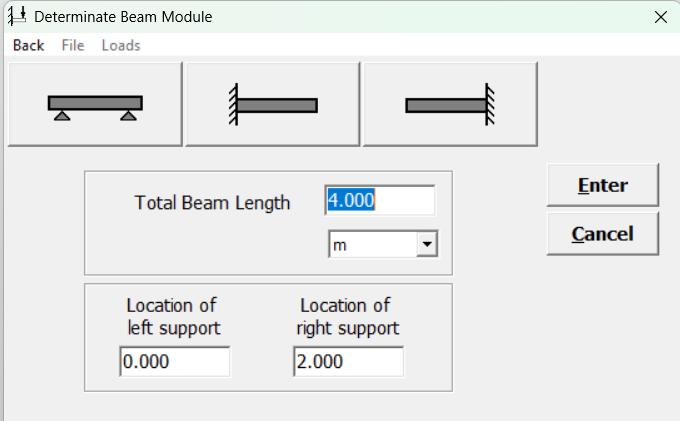
3000 / 4 = 1200 / x
X=1.60m (en donde el cortante se hace cero en el primer tramo)
Voladizo
Resuelva para una viga continua de 4 tramos:
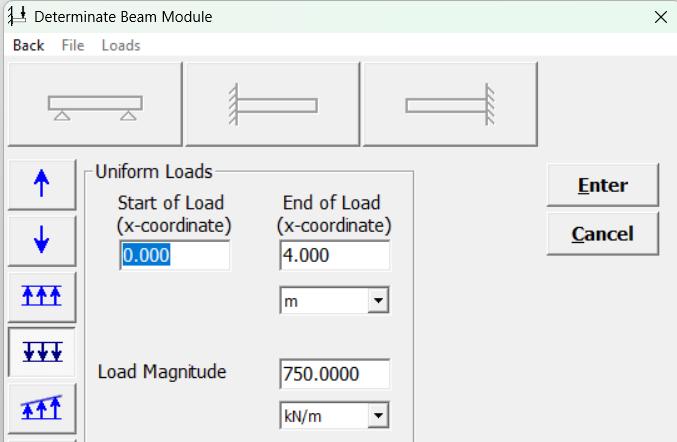
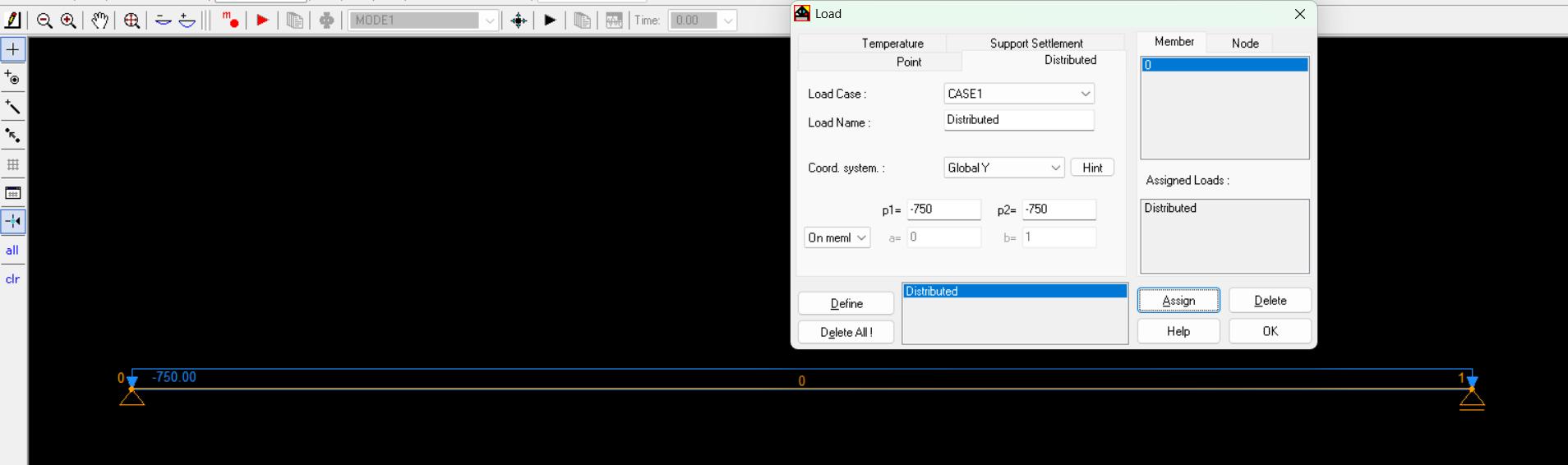
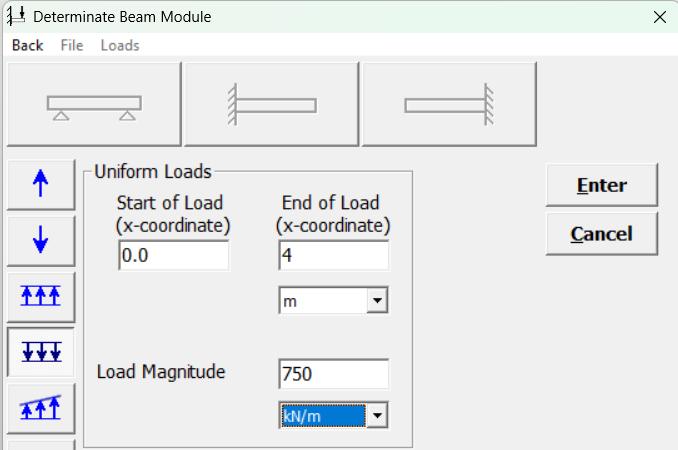
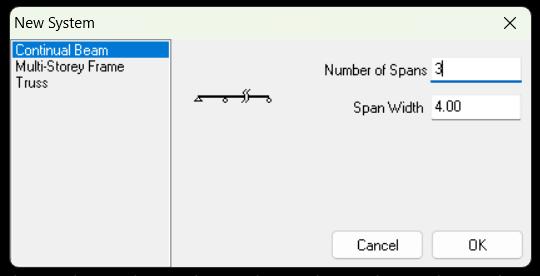
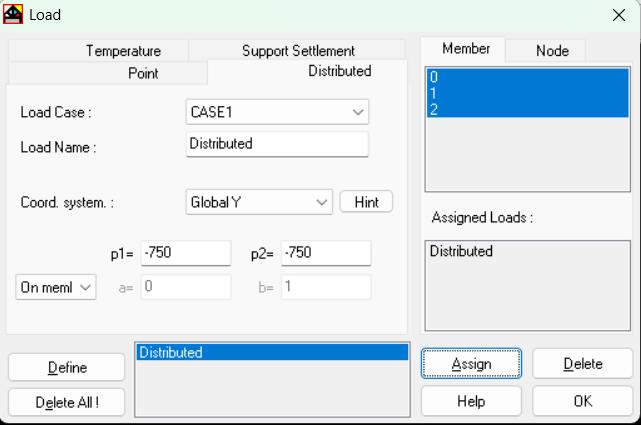
Carga P = -750 (on member)
Todos los tramos (Todos los miembros)
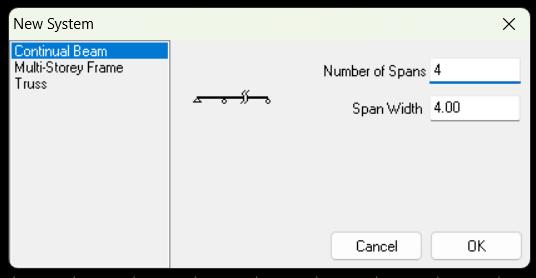
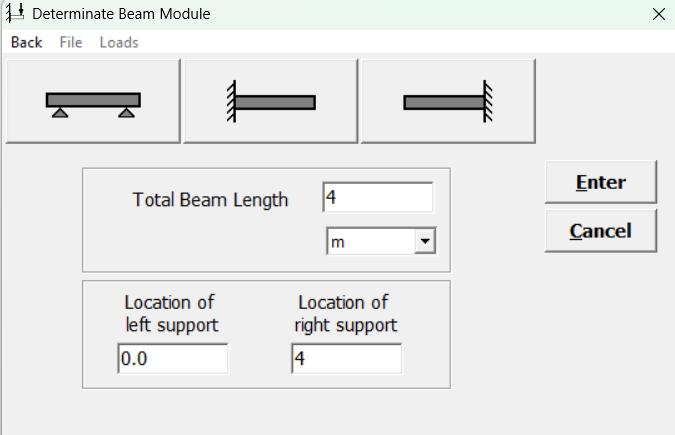
Analizar apoyos por defecto: No cambiarlos
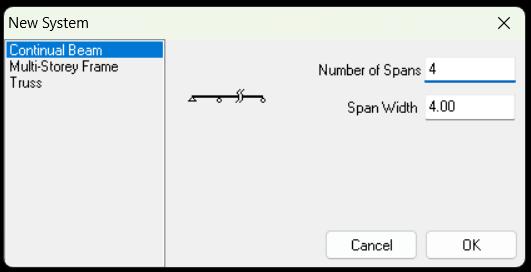
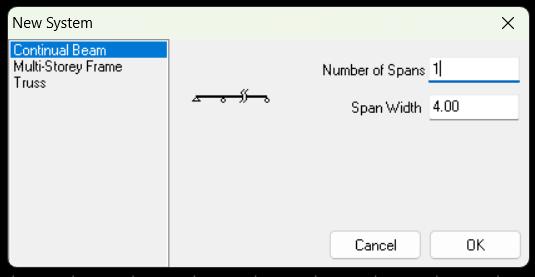
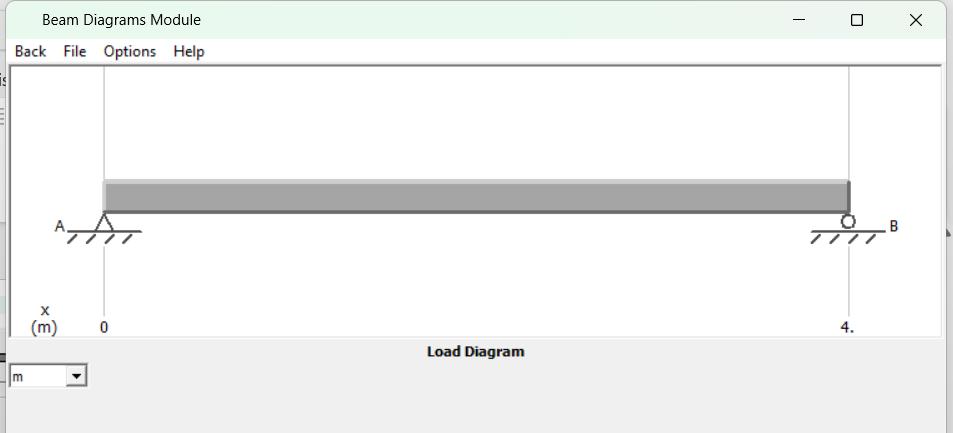
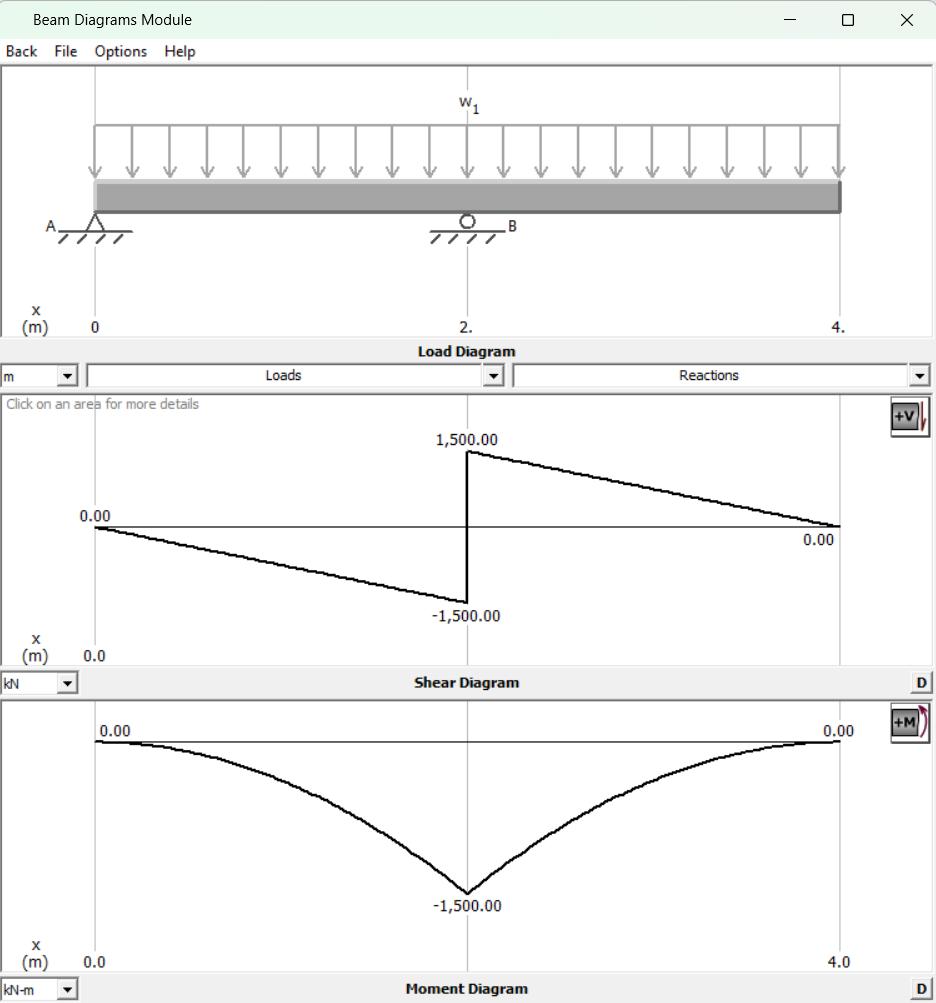
1) Analice el comportamiento de la viga de 4 tramos a través de su comportamiento externo: Cargas y reacciones
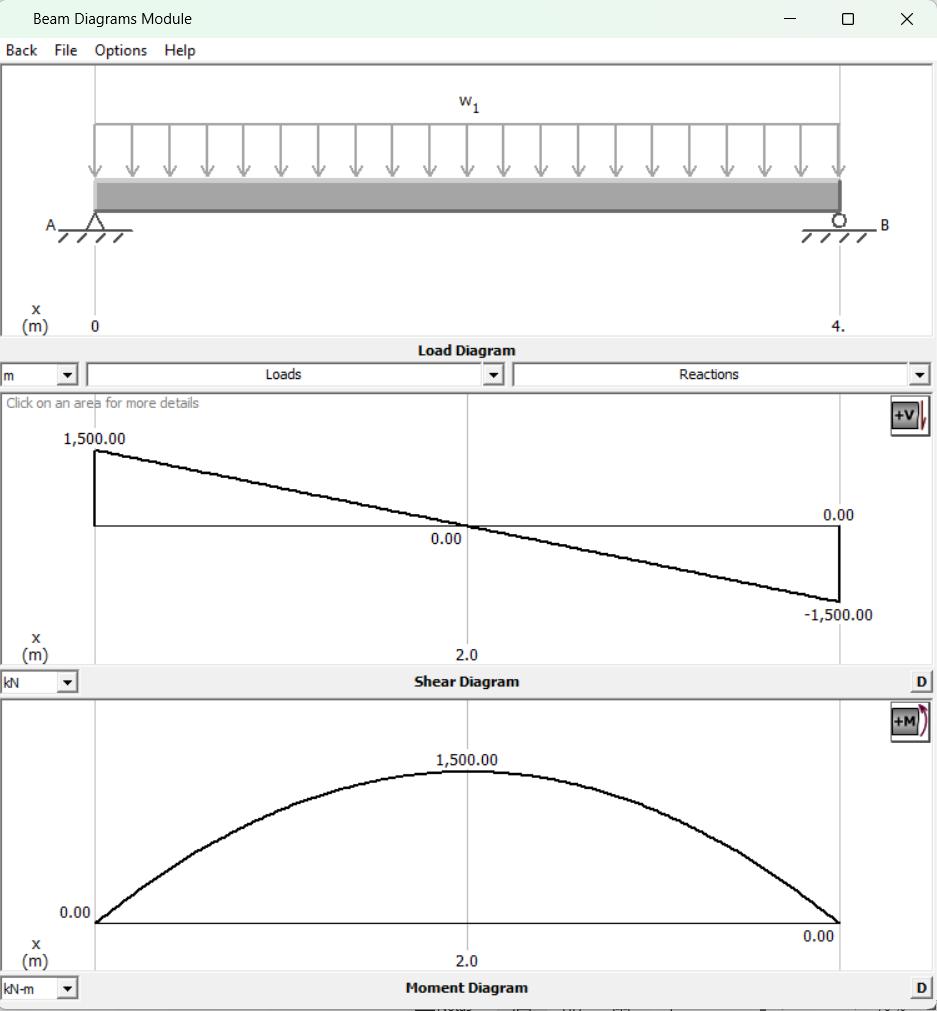
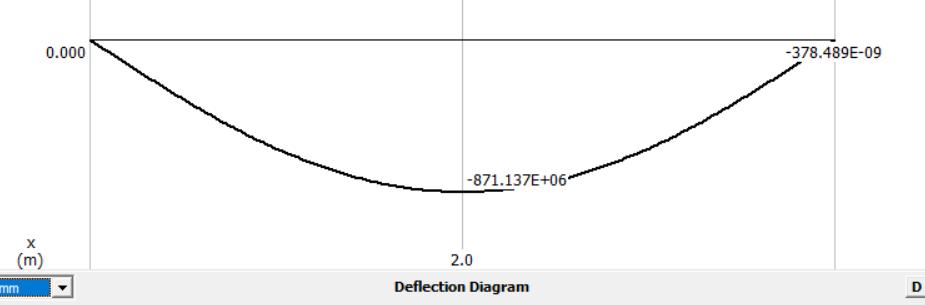
2) Analice el comportamiento de la viga de 4 tramos a través de su comportamiento interno:
Fuerzas cortantes máximas (En dónde)
Momentos flexionantes máximos (En dónde)
Nota: Utilice un método geométrico para calcular posición del lugar en donde la fuerza cortante se hace cero.