Sébastien Bleus
Livre de l’enseignant(e) B
Sébastien Bleus
ÉditionsVANIN
Livre de l’enseignant(e) B
Carrément MATH
Composition de Carrément math 6
Pour l’élève : 2 livres-cahiers A et B
Pour l’enseignant(e) :
Deux livres de l’enseignant(e) (comprenant le corrigé des livres-cahiers)
Leurs versions numériques sur Wazzou
Les annexes, des exercices supplémentaires et des évaluations disponibles sur Wazzou
Les manuels numériques (A et B) téléchargeables sur Wazzou
Carrément math 6 – Livre de l’enseignant(e) B
Auteur : Sébastien Bleus
Illustrations : M-A IZU (Marie-Anne Gueguen) et K’Naye (Karine Nayé-Roy)
Conception graphique : Octopus Creative Communication
Mise en page : NORDCOMPO
Couverture : Kiv’là
Voici le code qui vous donnera accès aux documents reproductibles en ligne liés au présent ouvrage.
Pour activer ce matériel complémentaire, rendez-vous sur www.monactivation.be et suivez-y la procédure d’inscription.
• Une fois votre accès activé, vous pourrez consulter le matériel complémentaire aussi souvent que vous le désirez et aussi longtemps que la version imprimée du présent ouvrage ne sera pas remplacée par une nouvelle édition.
• L’accès au matériel complémentaire ne peut être utilisé que par une seule personne.
• L’accès au matériel complémentaire vous est fourni gratuitement à l’achat de l’ouvrage Carrément Math 5 A Livre de l’enseignant(e). Aucune indemnité ne sera exigible en cas de non-fonctionnement ou d’indisponibilité du site hébergeant le matériel complémentaire ou du matériel complémentaire en lui-même, pour quelque raison que ce soit.
En cas de non-fonctionnement et/ou de question, nous sommes à votre disposition par courriel à l’adresse support@vanin.be.
L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si malgré cela quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur.
L’orthographe telle que rectifiée le 6 décembre 1990 par le Conseil Supérieur de la langue française est d’application dans la collection. Toutefois, afin de respecter les écrits des auteurs, l’orthographe d’origine y est respectée.
Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent. La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages. En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes. Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due. C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.
ÉditionsVANIN
En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.
1re édition : 2025
© Éditions VAN IN, Mont-Saint-Guibert – Wommelgem, 2025. Tous droits réservés. L’exploration de textes et de données (TDM) n’est pas autorisée.
ISBN 978-94-641-7811-1
D/2025/0078/37
Art. 602859/01
SO LO
Table des pictos
Travail individuel
D U O
PETIT G ROUPE
Travail en duo
ÉditionsVANIN
COLL ECTIF
Travail en petits groupes
Travail en groupe-classe
Nombres et opérations
Documents à télécharger sur Wazzou : exercices supplémentaires, évaluations et annexes
Savoir(s)
Chapitre 8
Bienvenue au Royaume des briques !
ATTENDUS PAR MATIÈRE
LES SOLIDES ET FIGURES
(Se) repérer et communiquer des positionnements ou des déplacements
Attendus
Utiliser le vocabulaire exprimant des positions absolues : à côté de, contre, à l’intérieur, à l’extérieur, entre, sous, sur, dans, hors, autour de, face à face, dos à dos.
Les visions de l’espace.
Savoir-faire
Situer, placer un objet ou soimême.
Utiliser le vocabulaire exprimant des positions relatives (liées au regard) : devant, derrière, à droite, à gauche, en haut, en bas, au-dessus, en dessous, en face de, de face, de dos, de profil.
Utiliser le vocabulaire exprimant des positions ordinales : – premier, deuxième, troisième... dernier ; – au début, à la fin, avant, après.
Attendus
Situer (exprimer la position absolue, relative ou ordinale) un objet ou soi-même avec le vocabulaire adéquat : – dans l’espace 2D (photo, plan) ; – selon le point de vue de l’élève ou d’une autre personne.
Placer un ensemble d’objets ou soi-même selon des consignes données ou un modèle observé dans l’espace 2D (photo, plan).
Déplacer un objet ou soi-même.
Situer, placer un objet dans un quadrillage.
Expliquer, oralement ou par écrit, un déplacement à l’aide du vocabulaire adéquat en identifiant des points de repère. Tracer un déplacement sur un plan en suivant un enchainement de consignes orales ou écrites.
Situer (exprimer la position) un objet dans un quadrillage codé.
Placer des objets dans un quadrillage en utilisant le codage.
Compétence(s) Attendus
Lire, interpréter des représentations de l’espace et les confronter au réel.
N-O
Savoir-faire
ÉditionsVANIN
Verbaliser, avec précision, un itinéraire à partir des points de départ et d’arrivée définis, en respectant au moins quatre points de repère pertinents identifiés.
Se déplacer dans l’espace 3D en suivant un trajet donné sur un plan.
LES NOMBRES
Opérer sur des nombres et sur des expressions algébriques
Attendus
Utiliser une calculatrice.
Estimer et vérifier.
Utiliser, en fonction de l’opération et des nombres, la calculatrice pour effectuer des opérations.
Estimer l’ordre de grandeur du résultat d’une opération (addition, soustraction, multiplication et division), avant de calculer précisément.
Vérifier la plausibilité d’un résultat.
Utiliser la calculatrice pour vérifier le résultat d’une opération.
Utiliser les opérations réciproques (+, –) et (×, :) pour vérifier le résultat d’une opération.
Compétence(s) Attendus
Résoudre des problèmes en mobilisant des nombres et des opérations.
Résoudre un problème faisant intervenir des opérations sur les nombres : – en traduisant une situation contextualisée par un dessin, une verbalisation, puis l’écriture d’opérations mathématiques (+, –, ×, :) ; – en estimant le résultat ; – en effectuant les calculs ; – en communiquant le résultat avec précision ; – en vérifiant la plausibilité de la réponse en verbalisant sa démarche. Rédiger un énoncé en partant : – de la communication du résultat. Ex. : Mes parents ont commandé pour 480 € de fournitures ; – de maximum trois calculs consécutifs et des résultats. Ex : 15 l : 1,5 l = 10 ; 10 × 0,25 € = 2,5 € ; 10 € – 2,5 € = 7,5 €.
LE TRAITEMENT DE DONNÉES
Collecter, organiser, représenter et interpréter des données
Savoir(s) Attendus
Utiliser les mots : – trier : « a ou n’a pas… » selon le critère défini. Ex. : la couleur ; – classer selon des caractéristiques définies au sein d’un critère. Ex. : rouge, jaune, bleu…
L’organisation d’objets, de données.
Reconnaitre une représentation de données en : – tableau ; – ensembles ; – arbre (multichotomique) ; – diagramme à bandes.
Savoir-faire Attendus
Recueillir des informations.
Trier, classer des objets ou des données.
Présenter des données.
Formuler une question : – exigeant une réponse par oui ou par non ; – permettant un classement des données récoltées.
Organiser des données : – par tri selon des critères considérés successivement ; – par classement selon des caractéristiques déterminées au sein d’un critère.
Représenter, à l’aide du support déterminé et en fonction de la situation, un tri ou un classement par : – trois ensembles incluant une intersection ; – un arbre multichotomique ; – un tableau à double entrée ; – un diagramme à bandes horizontales ou verticales.
Compétence(s) Attendu
Lire et interpréter des données pour en extraire de l’information.
ÉditionsVANIN
Prélever des informations issues d’une représentation : – d’ensembles incluant des intersections ; – d’un arbre ; – d’un tableau ; – d’un diagramme (à bandes, en bâtonnets et circulaire).
MATIÈRES ABORDÉES
Utilisation de la calculatrice
Les nombres
Les partages inégaux
Les solides et figures Situer, placer, déplacer un objet ou soi-même Traitement de données Organisation d’objets, de données
Exercices supplémentaires et évaluations disponibles pour ce chapitre en téléchargement.
Activité 1 – Situer, placer, déplacer un objet ou soi-même
Objectifs pédagogiques
• Utiliser des repères spatiaux précis (à gauche, à droite, à côté, en face, points cardinaux).
• Lire et interpréter un plan simple.
• Décrire clairement un itinéraire.
Exercice 1
Mise en situation :
Présenter aux élèves le plan interactif du parc « Le Royaume des briques ». Demander aux élèves d’imaginer qu’ils (elles) entrent dans ce parc et qu’ils (elles) choisissent une attraction à visiter en premier. Introduire ainsi naturellement la notion de repérage spatial et l’utilisation pratique d’un plan.
ÉditionsVANIN
COLL ECTIF
Chapitre
Bienvenue au Royaume des briques !
1. Situer, placer, déplacer un objet ou soi-même
Observe ce plan du parc « Le Royaume des briques ». 1.
ÉditionsVANIN
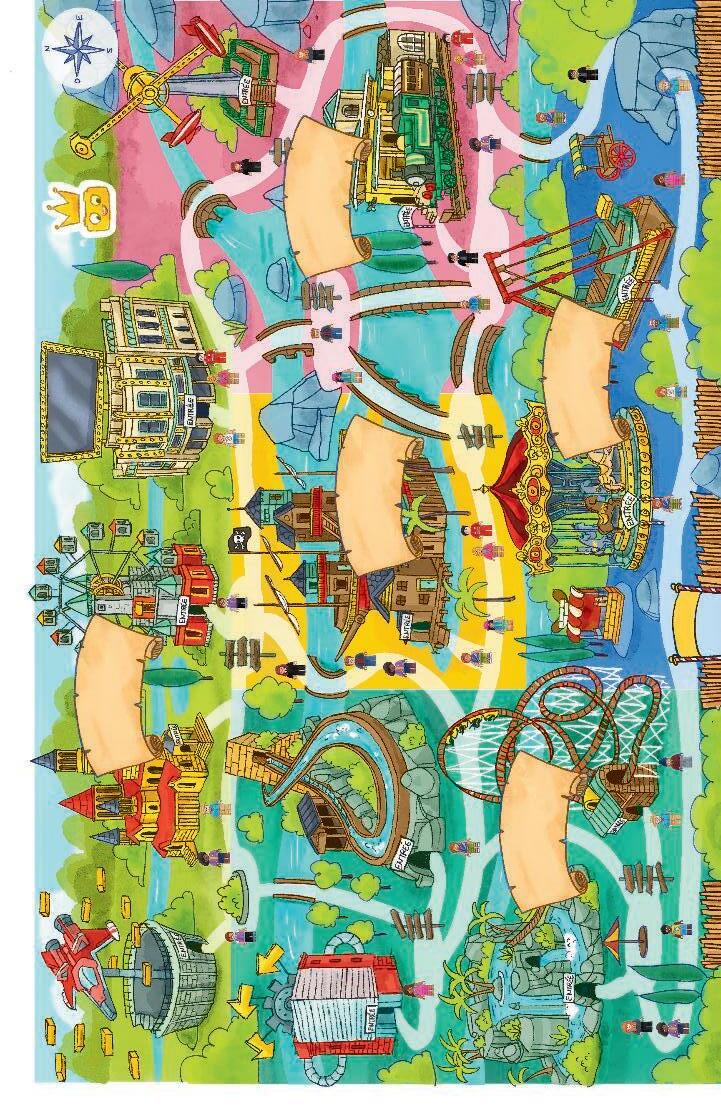
À partir du plan, localise l’attraction La Machine à briques en utilisant les termes de position (à l’ouest, à l’est, à droite, à gauche, à côté de, en face de).
La Machine à briques se situe dans l’Archipel des briques aventureuses, dans la zone ouest du parc, à gauche de La Glissage en bloc.
Dessine les symboles suivants sur le plan.
Un personnage devant le Cinéma.
Une étoile sur La Grande roue infernale.
Un cercle autour de La Glissade en bloc.
Une flèche pointant vers l’entrée principale.
Décris oralement à ton (ta) voisin(e) un itinéraire dans le parc en démarrant de l’entrée. Il (elle) devra comprendre à quelle attraction tu t’es arrêté(e).
Explique par écrit comment aller de La Croisière des briques volantes aux Chutes infernales en utilisant les points de repère visibles sur le plan.
Exemple de réponse attendue :
En quittant La Croisière des briques volantes, dirige-toi vers l’ouest du parc. Passe devant le Manège enchanté, puis devant le Looping de l’éclair. Après un virage serré, tu arriveras devant l’entrée des Chutes infernales.
Suis les indications et trace sur le plan un itinéraire en surlignant le chemin. Choisis le chemin le plus rapide.
Départ : Démarre de l’entrée principale et dirige-toi vers l’ouest.
Étape 1 : Va jusqu’au carrefour de La Machine à briques et de La Glissade en bloc.
Étape 2 : Rends-toi jusqu’au Palais des briques sans passer dans La Baie des corsaires de briques.
ÉditionsVANIN
Étape 3 : Termine ta route au Cinéma.
Dans quel monde se trouve-t-on lorsqu’on est dans la case F3 du plan ?
La Baie des corsaires de briques
Exercice 2
SO LO
Demander aux élèves de repérer visuellement, puis d’utiliser des termes précis comme « à l’ouest » ou « à gauche » pour indiquer la localisation. Insister sur l’importance de préciser la position relative par rapport à d’autres attractions.
Exercice 3
SO LO
Inviter les élèves à identifier clairement les lieux (Cinéma, Grande roue infernale, Glissade en bloc, entrée principale) avant de dessiner les symboles. Leur conseiller de vérifier avec un(e) voisin(e) pour assurer la précision du placement.
Exercice 4
D U O
En binômes, encourager une description claire et progressive, en utilisant systématiquement les repères spatiaux donnés sur le plan. Guider les élèves vers des descriptions structurées pour éviter toute confusion.
Exercice 5
SO LO
D U O
Travail individuel où les élèves rédigent un itinéraire précis en utilisant des points de repère tels que « Le Manège enchanté » ou « Le Looping éclair ».
Relire par binômes pour assurer la compréhension avant la correction collective.
Exercice 6
SO LO
ÉditionsVANIN
Demander aux élèves d’utiliser différentes couleurs pour les différentes étapes de l’itinéraire (ex. : l’entrée principale → la Machine à briques → le Palais des briques → le Cinéma). Vérifier ensemble les chemins les plus rapides en les projetant au tableau.
Exercice 7
SO LO
Faire un rappel rapide sur la lecture de coordonnées sur un quadrillage avant la réponse individuelle rapide, suivie d’une correction collective.
Exercice 8
SO LO
Reproduire un chemin visible sur une image de ville. L’élève observe attentivement le trajet, puis le redessine. Inviter à comparer avec un(e) camarade avant la correction projetée.
Exercice 9
SO LO
Placer des symboles (voiture de police, personnages à casquette rouge, bateau) en se basant sur l’observation. Encourager à bien justifier le choix de l’emplacement lors de la correction.
ÉditionsVANIN
Rayane s’amuse avec sa ville en petites briques. Il veut que son personnage se rende à la plage. Le chemin qu’il va lui faire parcourir est représenté par un trait bleu sur le plan. Peux-tu retracer ce même chemin sur l’image de la ville en petites briques ? 8.
En te basant sur la ville en petites briques, place sur le plan : – une croix bleue pour indiquer la voiture de police ; – une croix rouge pour indiquer les personnages avec une casquette rouge ; – une croix verte pour indiquer le bateau. 9.
Dans sa ville, Rayane a reproduit le musée d’histoire naturelle de New York. Voici une image représentant ce qu’il a construit. En observant celle-ci, réponds aux questions en entourant la bonne réponse.
a) Le laveur de vitres est en train de laver une vitre du : 1er étage – 2e étage – 3e étage
b) On peut voir le personnage présent sur la nacelle de face – profil – dos
c) Où se situe la boite aux lettres par rapport au personnage assis sur le banc ? à gauche – à droite – devant
d) Il y a un personnage qui tient un balai. Dans quelle main le tient-il ? droite – gauche
Zone de travail
ÉditionsVANIN
Exercice 10
Les élèves répondent à des questions comme : « À quel étage est le laveur de vitres ? ». L’enseignant(e) demande des justifications orales. L’élève peut être appelé(e) au tableau face à l’image projetée pour venir montrer directement ses réponses.
Anticipation des difficultés
• Confusion fréquente entre droite et gauche ou nord et sud.
• Difficulté à transposer une information visuelle en indication spatiale verbale ou écrite.
• Méconnaissance de l’utilisation d’un quadrillage avec coordonnées.
Pistes de remédiation
• Exercices concrets dans la cour ou en classe pour manipuler les directions.
• Réutilisation du plan sur le tableau avec déplacement de personnages aimantés.
• Reprise, en petits groupes, des notions de quadrillage avec exercices de coloriage guidé.
Propositions de dépassement
• Demander à l’élève de créer le plan d’un mini-parc avec repères et une série de questions à poser à un(e) camarade.
• Rédiger une consigne d’itinéraire « piégée » à faire tester par les autres.
Conseils pédagogiques complémentaires
• Toujours introduire ou rappeler les repères spatiaux avant les activités (boussole murale, droite et gauche).
• Utiliser les déplacements corporels pour ancrer les directions (faire un jeu « boussole vivante » en classe).
• Proposer une carte plastifiée que l’élève peut annoter ou colorier avant de passer à une consigne écrite définitive.
ÉditionsVANIN
Activité 2 – Qui est-ce ? Organisation d’objets, de données
Le jeu « Qui est-ce ? » se trouve à la fin du livre-cahier B. Il est nécessaire que les élèves le découpent avant de commencer les activités. Veillez à prévoir cette étape en début de séance.
Objectifs pédagogiques
• Classer des informations selon plusieurs critères.
• Manipuler des données dans des tableaux à double entrée.
Exercice 1
COLL ECTIF
D U O
Commencer par une explication collective des règles du jeu « Qui est-ce ? » Un(e) élève pense à un personnage du jeu, les autres doivent poser des questions fermées (donc la réponse est toujours « oui » ou « non ») pour éliminer progressivement les possibilités. Expliquer l’intérêt de poser des questions liées à des critères visibles (couleur de cheveux, lunettes, chapeau, etc.).
Exercice 2
SO LO
COLL ECTIF
Une fois les règles bien comprises, organiser une ou deux parties rapides en binômes avec les cartes découpées du livre-cahier. Cette mise en action permettra d’initier les élèves à l’observation précise et à la classification par critères.
Identifier les personnages portant du rouge sur leur tenue. Demander une observation très attentive. Les élèves peuvent d’abord répondre individuellement, puis vérifier en binômes.
Lors de la correction collective, projeter les personnages pour faciliter la discussion.
ÉditionsVANIN
2. Qui est-ce ? Organisation d’objets, de données
Découpe les cartes du jeu « Qui est-ce ? » qui se trouvent à la fin de ton livre. Joue une partie avec un(e) de tes camarades de classe.
Parmi les personnages, cite ceux qui ont du rouge sur leur tenue.
Ce sont les personnages 1, 4 et 8.
4. 5. 6.
Parmi les personnages, cite ceux qui ont des cheveux roux.
Trie les personnages dans ce tableau à double entrée. Utilise leur numéro pour les classer.
Longueur des cheveux
Ce sont les personnages 3, 6, 13 et 15. 14 7, 10, 11, 15 13 2, 3, 5, 6, 9 4, 8, 12, 16
Chapeau Oui non longs mi-longs courts chauve impossible à définir
Donne un nom à chacun de ces ensembles.
Ensemble A :
Figurines portant un chapeau.
Figurines ayant des lunettes.
Ensemble B : Voici 3 ensembles. Définis des critères pour chacun, puis classe correctement les personnages.
Nombreuses réponses possibles.
ÉditionsVANIN
Ensemble A :
Ensemble B :
titre du critère selon le choix de l’élève
Ensemble C : ............................................................................................................................................................
Exercice 3
SO LO
Insister sur l’importance de différencier les nuances de couleur (par ex. : roux vs blond).
D U O
Comparaison en binômes.
COLL ECTIF
Correction collective avec justification orale.
Exercice 4
SO LO
COLL ECTIF
Compléter un tableau à double entrée avec les critères suivants : « longueur de cheveux » et « chapeau ». Expliquer clairement aux élèves qu’il s’agit de placer les personnages en fonction de leur numéro de carte. Proposer de manipuler les cartes découpées pour trier physiquement les personnages avant de remplir le tableau.
Exercice 5
SO LO
D U O
Une correction collective est indispensable : projeter le tableau vide et le compléter ensemble, en discutant chaque croisement.
Identifier des ensembles et trouver les critères : « chapeau » et « lunettes ».
Demander aux élèves de justifier chaque choix auprès d’un(e) camarade. Correction en binômes, puis affichage projeté pour vérification.
ÉditionsVANIN
Exercice 6
SO LO
Compléter le diagramme de Venn à partir de 3 critères choisis librement. Les élèves écrivent leur consigne ; activité libre qui permet une différenciation. L’enseignant(e) peut demander une présentation orale à ceux qui le souhaitent.
Anticipation des difficultés
• Confusion entre certains critères (cheveux attachés vs courts, lunettes de soleil vs lunettes de vue).
• Difficulté à comprendre l’organisation d’un diagramme de Venn.
• Erreur d’interprétation des images (détail mal vu ou négligé).
Pistes de remédiation
• Faire des tris physiques avec les cartes avant de remplir les tableaux ou diagrammes.
• Utiliser des fiches de critères illustrées pour guider la sélection.
• Travailler en petits groupes pour permettre une verbalisation plus approfondie.
Propositions de dépassement
• Créer un nouveau tableau ou diagramme croisant des critères inventés.
• Imaginer et dessiner un nouveau personnage correspondant à des critères choisis par un(e) camarade.
• Inverser l’exercice : proposer un groupe de personnages et demander de retrouver les critères.
Conseils pédagogiques complémentaires
• Encourager systématiquement les justifications orales pour chaque réponse.
• Proposer un affichage mural des tableaux complétés pour favoriser la comparaison.
• Prévoir une fiche de vocabulaire liée aux critères visuels (longs vs courts, accessoires, etc.) pour soutenir les élèves moins à l’aise.
Activité 3 – Utiliser la calculatrice
Objectifs pédagogiques
• Découvrir les principales touches et fonctions de la calculatrice.
• Savoir effectuer des opérations de base, des pourcentages et des arrondis.
• Vérifier des calculs à l’aide de la calculatrice.
Exercice 1
COLL ECTIF
Les élèves découvrent une image représentant un enfant en train de regarder l’écran de sa calculatrice. On voit qu’il y inscrit un nombre et qu’en retournant l’appareil, un mot lisible apparait. Demander aux élèves d’observer attentivement l’image et de noter ce qu’ils (elles) constatent. Un échange oral collectif permet de formuler l’hypothèse qu’on peut lire des mots en inversant certains chiffres. Cela crée une entrée ludique dans le thème.
Après cette discussion, proposer aux élèves d’observer la calculatrice. L’élève examine la disposition des touches de sa calculatrice (notamment les touches numériques et les opérations de base). Il s’agit ici d’un repérage simple, qui peut être fait en duos pour verbaliser les découvertes. Correction rapide sous forme d’échange collectif où l’enseignant(e) liste les principales touches utiles pour la suite.
ÉditionsVANIN
3. Utiliser la calculatrice
Observe ces calculatrices, puis explique avec tes mots ce que tu constates.
Maintenant, c’est à toi de jouer ! Avec ton (ta) voisin(e), remettez ces nombres dans le bon ordre et essayez-les sur ta calculatrice afin de retrouver le mot caché ! Indiquez le mot qui apparait, ainsi que la bonne suite de chiffres sur la calculatrice.
D U O
En duos, inviter les élèves à faire de même et à essayer de trouver les noms qui « se cachent » derrière les nombres inscrits sur les différentes calculatrices.
ÉditionsVANIN
ÉditionsVANIN
Choisis la méthode que tu utiliseras face à ces calculs.
232 × 10 =
157 + 1 348 + 34 =
8 283,2 × 23,237 =
2 320 1 539 192 476,718 2 000
1 250 + 750 =
91 747 : 6 =
720 : 9 =
762 × 14 =
668
Note la réponse à chacun des calculs dans le tableau ci-dessus.
Exercice 3
Les élèves doivent choisir, pour chaque opération proposée, la méthode qu’ils (elles) jugent la plus appropriée : réflexion mentale (représentée par un garçon pensif), calcul posé (fille qui écrit) ou utilisation de la calculatrice (main qui tape sur les touches). Par exemple, un calcul simple comme 1 250 + 750 peut être réalisé mentalement, tandis qu’un produit avec des décimaux comme 8 283,2 × 23,237 justifie l’usage de la calculatrice. Ils (elles) cochent d’abord l’image correspondant à la méthode choisie. L’enseignant(e) pourra demander aux élèves de justifier leurs choix à l’oral, afin de faire émerger les stratégies de résolution. L’objectif ici est d’apprendre à estimer la complexité d’un calcul et à adopter une démarche autonome et réfléchie.
ÉditionsVANIN
L’enseignant(e) peut inviter les élèves à réaliser les différents calculs en fonction du choix posé précédemment.
Exercice 4
SO LO
Les élèves doivent estimer mentalement la réponse d’un calcul, puis la vérifier avec la calculatrice. Noter l’estimation entre parenthèses, puis le résultat réel. Cela aide à développer le sens du nombre. L’enseignant(e) accompagne en projetant certains calculs et en discutant des écarts.
Exercice 5
SO LO
Utilisation de la touche %. Les élèves réalisent différents calculs en lien avec des pourcentages. Il faut veiller à bien faire comprendre que la calculatrice permet ici un gain de temps, à condition d’utiliser la bonne syntaxe (valeur × pourcentage %).
retiens
ÉditionsVANIN
Pour expliquer comment effectuer un pourcentage avec la calculatrice, une vignette montre que pour calculer 25 % de 820, on entre « 820 × 25 % ». L’enseignant(e) doit expliciter cette méthode et rappeler que taper directement le pourcentage (et non 0,25) facilite le calcul et rend l’usage plus intuitif. Cette synthèse permet de stabiliser les acquis sur la touche %.
COLL ECTIF
Note ton estimation de la réponse entre les parenthèses, puis vérifi e avec ta calculatrice.
)
332 + 16 038 = ( )
6 =
) 815,13 : 9 = ( )
× 50 =
) 213,6 × 11 =
)
)
Comme tu l’as surement constaté, ta calculatrice a une touche %. À l’aide de cette touche, effectue ces calculs.
)
)
Pour effectuer le calcul suivant à la calculatrice : 25 % de 820, je tape sur ma calculatrice : 820 × 25 % = 25 % de 820 est donc égal à 205.
)
Effectue ces calculs à l’aide de ta calculatrice, mais arrondis au centième près.
9 203 : 17 =
8 812,23 × 12,97 =
983,012 × 128,927 =
212,10 029 – 0,00 281 =
8,00 821 + 174,1 981 =
4 520 : 33 =
823,092 × 6,67 =
12 329 : 11 =
1 099 × 81,12 × 1,99 =
912 : 7 =
98 723 : 128 = 4,41 x 19,43 x 2,06 =
Affiche le nombre de départ sur ta calculatrice et tente d’arriver au nombre demandé.
Pour cela, tu peux utiliser les symboles
Attention, tu as droit à 3 opérations et tu ne peux pas utiliser un même symbole plusieurs fois. Seuls des nombres entiers sont autorisés.
ÉditionsVANIN
Nombreuses solutions possibles
Exercice 6
SO LO
Réaliser un calcul complexe, puis arrondir. L’élève effectue le calcul, puis applique la règle d’arrondi. Correction collective possible en affichant les réponses et en expliquant les arrondis.
Exercice 7
SO LO ou D U O
Problème multi-étapes avec la calculatrice. L’élève suit les instructions, effectue les calculs successifs, puis rédige les résultats. Encourager le travail en binômes pour comparer les démarches. Préciser aux élèves qu’il existe plusieurs réponses possibles.
Anticipation des difficultés
• Mauvaise utilisation des touches (en particulier celle des %).
• Problèmes pour lire les chiffres retournés.
• Erreurs dans la gestion des étapes d’un calcul complexe.
Pistes de remédiation
• Donner une fiche-guide avec les correspondances chiffre/lettre pour les mots à l’envers.
• Proposer des exercices dirigés avec étapes explicites pour les pourcentages.
• Faire reformuler oralement chaque étape avant de valider par la calculatrice.
Propositions de dépassement
• Proposer d’écrire des messages codés avec des nombres à faire découvrir à un(e) camarade.
• Résoudre des problèmes où il faut choisir entre plusieurs méthodes de calcul.
• Utiliser la calculatrice pour vérifier des estimations faites sans elle.
Conseils pédagogiques complémentaires
• Veiller à ce que tous les élèves aient une calculatrice fonctionnelle et identique si possible.
• Prévoir un affichage des touches-clés sur un poster.
• Encourager l’alternance entre travail en autonomie, binômes et phases collectives pour dynamiser la séance.
ÉditionsVANIN
Activité 4 – Les partages inégaux
Objectifs pédagogiques
• Comprendre et résoudre des problèmes de partage inégal.
• Représenter la situation à l’aide de schémas.
• Calculer une valeur de part, puis la part de chaque élément en jeu.
• Rédiger une phrase réponse correcte à partir des calculs.
Mise en situation :
Énoncer oralement une situation similaire : « Tom et Zoé reçoivent ensemble 600 €. Zoé reçoit le double de ce que reçoit Tom. Combien chacun reçoit-il ? » Laisser les élèves proposer des stratégies. Introduire ensuite la notion de partage inégal : une même somme partagée selon des rapports inégaux.
Exercice 1
L’élève suit une démarche guidée : représentation graphique des parts (1 pour Enzo, 2 pour Laurie), calcul du total des parts, valeur d’une part, puis répartition. Insister sur le fait que c’est la relation entre les parts (× 2) qui détermine le schéma. L’élève termine par une phrase réponse. Il est essentiel que la phrase réponse reprenne clairement les données du problème et réponde précisément à la question posée (ex. : « Enzo a 240 € tandis que Laurie a 480 €. »). Cela permet de valider la compréhension de l’élève et de l’amener à formuler une réponse complète et justifiée.
Je retiens
COLL ECTIF
ÉditionsVANIN
Il est recommandé de travailler cette partie collectivement avec les élèves pour formaliser les étapes de résolution d’un partage inégal et les ancrer dans une procédure claire et reproductible. Cette synthèse peut être affichée en classe ou résumée dans une fiche-mémo.
1.
4. Les partages inégaux
Enzo et Laurie ont ensemble 720 €. On sait aussi que Laurie a deux fois plus d’argent qu’Enzo. Combien ont-ils chacun ?
Réponds à la question en passant par plusieurs étapes.
a) Entoure la bonne représentation des parts de chacun.
Enzo
Enzo
Enzo
Laurie Laurie Laurie
b) Combien y a-t-il de parts au total ?
c) Calcule la valeur d’une part :
d) Calcule la part d’Enzo et de Laurie.
Enzo : Laurie :
e) Réponds à la question par une phrase.
Enzo a 240 € tandis que Laurie a, elle, 480 €.
Je retiens
Les partages inégaux sont, comme l’indique le titre, des partages en parts inégales.
Comment les résoudre ?
a) Je traduis d’abord ce que je sais par un dessin.
Enzo
Laurie
b) Je divise le nombre total par le nombre de parts afin d’obtenir la valeur d’une seule part.
c) Je multiplie cette valeur par le nombre de parts de chacun.
Laurie a
Ex. : 720 € : 3 = 240 € 2 × 240 € = 480 €
Enzo a 3 720 € : 3 = 240 € 1 × 240 € = 240 € 2 × 240 € = 480 €
× 240 € = 240 €
Linda et Céline ont une collection de cartes Pokemon. Au total, elles en comptabilisent 672. Sachant que Céline en a le triple de Linda, combien chacune en a-t-elle ?
Réponds à la question par une phrase et utilise les différentes étapes.
Schéma Calculs
Zone de recherche
672 : 4 = 168 cartes
C = 168 × 3 = 504 cartes
L = 168 × 1 = 168 cartes
Phrase
Céline a 504 cartes tandis que Linda en a 168.
Kévin et Dorian ont effectué des randonnées à vélo durant leurs vacances. Ils ont parcouru à eux deux 2 450 km. Sur ce total, Kévin a parcouru 4 fois plus de km que Dorian. Combien de km Kévin a-t-il parcouru ?
Schéma Calculs
Zone de recherche
2 450 km : 5 = 490 km
K : 4 × 490 km = 1 960 km
D : 490 km
ÉditionsVANIN
Kévin a parcouru 1 960 km.
Phrase
Exercice 2
SO LO
Même démarche avec Linda et Céline. Céline possède 3 fois plus de cartes que Linda. La représentation se fait à l’aide de 1 part pour Linda, 3 parts pour Céline. Total des parts : 4. Division, puis multiplication pour déterminer les quantités respectives. Terminer par une phrase complète. L’enseignant(e) insiste ici sur la méthode et la cohérence du raisonnement. Afficher cette démarche comme référence pour d’autres cas similaires.
Exercice 3
SO LO
ÉditionsVANIN
Même logique avec Kevin et Dorian. Kevin a parcouru 4 fois plus de kilomètres. Représentation : 1 part pour Dorian, 4 pour Kevin → 5 parts au total. Diviser, puis multiplier. Insister sur l’interprétation correcte du rapport (× 4).
Exercice 4
SO LO
Cas d’un écart fixe : Sofiane a reçu 150 € de plus que Maxime. Cette fois, on soustrait 150 € du total pour obtenir deux parts égales (800 – 150), puis on redistribue les 150 € à l’un. Introduire la notion de compensation ou d’ajustement. Revoir la logique du schéma qui change.
Je retiens
COLL ECTIF
Les synthèses rappellent que pour résoudre un partage inégal :
1. On schématise les parts ou on utilise une différence.
2. On calcule la valeur d’une part (si le total est connu).
3. On attribue ensuite la bonne part à chaque personne selon le schéma. Ces rappels doivent être affichés en classe comme étapes-clés de résolution.
Exercice 5
ÉditionsVANIN
Même cas d’un écart fixe. Shannon a 278 chansons de plus que Camille. On enlève d’abord la différence du total, puis on divise par deux et ajoute l’écart à la plus grande part. Travailler ce type de situation avec des objets concrets si besoin.
e) Réponds à la question par une phrase. 4.
Maxime et Sofiane reçoivent 800 € à eux deux. Combien Sofiane a-t-il reçu sachant qu’il a eu 150 € de plus que Maxime ?
a) Entoure la bonne représentation des parts de chacun.
Maxime Maxime Maxime + 150 €
Sofiane + 150 € Sofiane + 150 € Sofiane
b) Combien y a-t-il de parts au total ?
c) Calcule la valeur d’une part :
(800 € – 150 €) : 2 = 325 €
d) Calcule la part de Maxime et de Sofiane.
Maxime : Sofiane :
325 € 325 € + 150 € = 475 €
So ane a reçu 475 €.
Je retiens
Dans cette situation, le développement général est le même. Il faut juste être attentif à ce que le style de schéma soit différent.
Phrase 5.
ÉditionsVANIN
Camille et Shannon ont ensemble 1 456 chansons sur leur Cloud. Sachant que Camille en a 278 de moins que Shannon, combien Shannon en a-t-elle ?
Schéma Calculs
Zone de recherche
(1 456 – 278) : 2 = 589
C = 589
S = 589 + 278 = 867
Shannon a 867 chansons sur son Cloud.
Résous ces problèmes. N’hésite pas à utiliser une feuille de brouillon pour y placer tes schémas si tu en as besoin.
a) Sandra, Loïc et Steve ont ensemble 12 617 Pingping sur Wazzou. Sachant que Sandra en a 4 fois plus que Steve et Loïc 2 fois moins que Steve, combien de Pingping ont-ils chacun ?
1 part = 12 617 : 11 = 1 147 pp
Loïc : 1 147 pp
Steve : 1 147 × 2 = 2 294 pp
Sandra : 1 147 × 8 = 9 176 pp
b) Trois camions ont livré 55,3 tonnes de pierres devant notre école. Le premier camion a transporté le double du second et le dernier camion en a livré la moitié du second. Combien de tonnes a livré chaque camion ?
1 part = 55,3 : 7 = 7,9 t
Camion 1 = 4 × 7,9 t = 31,6 t
Camion 2 = 2 × 7,9 t = 15,8 t
Camion 3 = 1 × 7,9 t = 7,9 t
ÉditionsVANIN
c) Cette année, nos 3 poules ont pondu 578 œufs. Cocote en a pondu le triple de Chicken. Kip, elle, en a pondu 48 de plus que Chicken. Combien d’œufs chaque poule a-t-elle pondu ?
1 part = (578 – 48) : 5 = 106 œufs
Cocote = 106 × 3 = 318 œufs
Kip = 106 + 48 = 154 œufs
Chicken = 1 × 106 = 106 oeufs
Un concessionnaire a vendu 4 marques de voitures différentes cette année. Il a vendu 6 fois plus de Fiat que de Mercedes et 4 fois plus de Peugeot que de Hyundai. Mais on sait qu’il a vendu 2 fois moins de Fiat que de Peugeot et 3 fois plus de Hyundai que de Mercedes. Sachant qu’il a vendu 418 voitures cette année, combien de Peugeot a-t-il vendues ?
1 part = 418 : 22 = 19 voitures
Peugeot = 19 × 12 = 228 voitures
Il a vendu 228 Peugeot cette année.
Exercice 6
Résolution de problèmes plus complexes :
a) Trois personnes avec des rapports variés : Steve a 2 fois plus que Loïc, Sandra 4 fois plus que Steve → 11 parts en tout.
b) Trois camions avec un jeu d’équivalences : 1er = 2 × 2e, 3e = 0,5 × 2e → représentation en parts à établir (4 + 2 + 1 = 7 parts).
c) Trois poules : Cocote = 3 × Chicken, Kip = Chicken + 48. D’abord retirer 48, puis répartir 5 parts.
d) Voitures vendues selon des rapports multiples avec une base commune → utiliser le total des parts : Peugeot (× 4), Fiat (× 2), Mercedes (× 1), Hyundai (× 3) → total : 22 parts.
Anticipation des difficultés
• Confusion entre « plus de » (écart) et « fois plus » (rapport).
• Difficulté à représenter les parts.
• Mauvais ordre dans les étapes de résolution (multiplier avant de diviser).
Pistes de remédiation
• Manipuler des jetons ou des cubes pour visualiser les rapports ou les écarts.
• Reprendre chaque étape avec un exemple concret.
• Proposer une fiche-outil synthétique à coller dans le cahier.
Propositions de dépassement
• Créer soi-même un problème de partage inégal.
• Représenter un problème en schéma, puis le faire résoudre par un pair.
• Résoudre un problème avec 3 ou 4 éléments à comparer.
Conseils pédagogiques complémentaires
• Toujours faire verbaliser les rapports ou différences avant de poser les calculs.
• Alterner entre représentation graphique et résolution numérique.
• Proposer des problèmes oraux à résoudre en petits groupes pour ancrer les stratégies.