Carrément Math 6A - Guide - Extrait

Livre de l’enseignant(e) A Sébastien Bleus

Sébastien Bleus

ÉditionsVANIN

Livre de l’enseignant(e) A

Carrément MATH

Composition de Carrément math 6

Pour l’élève : 2 livres-cahiers A et B

Pour l’enseignant(e) :

Deux livres de l’enseignant(e) (comprenant le corrigé des livres-cahiers)

Leurs versions numériques sur Wazzou

Les annexes, des exercices supplémentaires et des évaluations disponibles sur Wazzou

Les manuels numériques (A et B) téléchargeables sur Wazzou

Carrément math 6 – Livre de l’enseignant(e) A

Auteur : Sébastien Bleus

Illustrations : M-A IZU (Marie-Anne Gueguen) et K’Naye (Karine Nayé-Roy)

Conception graphique : Octopus Creative Communication

Mise en page : NORDCOMPO

Couverture : Kiv’là

Voici le code qui vous donnera accès aux documents reproductibles en ligne liés au présent ouvrage.

Pour activer ce matériel complémentaire, rendez-vous sur www.monactivation.be et suivez-y la procédure d’inscription.

• Une fois votre accès activé, vous pourrez consulter le matériel complémentaire aussi souvent que vous le désirez et aussi longtemps que la version imprimée du présent ouvrage ne sera pas remplacée par une nouvelle édition.

• L’accès au matériel complémentaire ne peut être utilisé que par une seule personne.

• L’accès au matériel complémentaire vous est fourni gratuitement à l’achat de l’ouvrage Carrément Math 5 A Livre de l’enseignant(e). Aucune indemnité ne sera exigible en cas de non-fonctionnement ou d’indisponibilité du site hébergeant le matériel complémentaire ou du matériel complémentaire en lui-même, pour quelque raison que ce soit.

En cas de non-fonctionnement et/ou de question, nous sommes à votre disposition par courriel à l’adresse support@vanin.be.

L’éditeur s’est efforcé d’identifier tous les détenteurs de droits. Si malgré cela quelqu’un estime entrer en ligne de compte en tant qu’ayant droit, il est invité à s’adresser à l’éditeur.

L’orthographe telle que rectifiée le 6 décembre 1990 par le Conseil Supérieur de la langue française est d’application dans la collection. Toutefois, afin de respecter les écrits des auteurs, l’orthographe d’origine y est respectée.

Les photocopieuses sont d’un usage très répandu et beaucoup y recourent de façon constante et machinale. Mais la production de livres ne se réalise pas aussi facilement qu’une simple photocopie. Elle demande bien plus d’énergie, de temps et d’argent. La rémunération des auteurs, et de toutes les personnes impliquées dans le processus de création et de distribution des livres, provient exclusivement de la vente de ces ouvrages. En Belgique, la loi sur le droit d’auteur protège l’activité de ces différentes personnes. Lorsqu’il copie des livres, en entier ou en partie, en dehors des exceptions définies par la loi, l’usager prive ces différentes personnes d’une part de la rémunération qui leur est due. C’est pourquoi les auteurs et les éditeurs demandent qu’aucun texte protégé ne soit copié sans une autorisation écrite préalable, en dehors des exceptions définies par la loi.

ÉditionsVANIN

Tous droits réservés. En dehors des exceptions définies par la loi, cet ouvrage ne peut être reproduit, enregistré dans un fichier informatisé ou rendu public, même partiellement, par quelque moyen que ce soit, sans l’autorisation écrite de l’éditeur.

1re édition : 2025

© Éditions VAN IN, Mont-Saint-Guibert – Wommelgem, 2025

ISBN 978-94-641-7810-4

D/2025/0078/36

Art. 602858/01

Chapitre 1

Les vacances de Manon et Raphaël

ATTENDUS PAR MATIÈRE

LES SOLIDES ET FIGURES

(Se) repérer et communiquer des positionnements ou des déplacements

Savoir-faire

Situer, placer un objet dans un quadrillage.

Savoir(s)

L’identification et la comparaison de grandeurs d’objets.

Savoir-faire

Comparer des objets selon une de leurs grandeurs.

Comparer les durées d’évènements, d’actions.

Savoir(s)

L’usage des unités conventionnelles.

Savoir-faire

Construire le système des unités conventionnelles.

Attendus

Situer un objet dans un quadrillage codé (exprimer sa position). Placer des objets dans un quadrillage en utilisant le codage.

LES GRANDEURS

Concevoir des grandeurs

Attendus

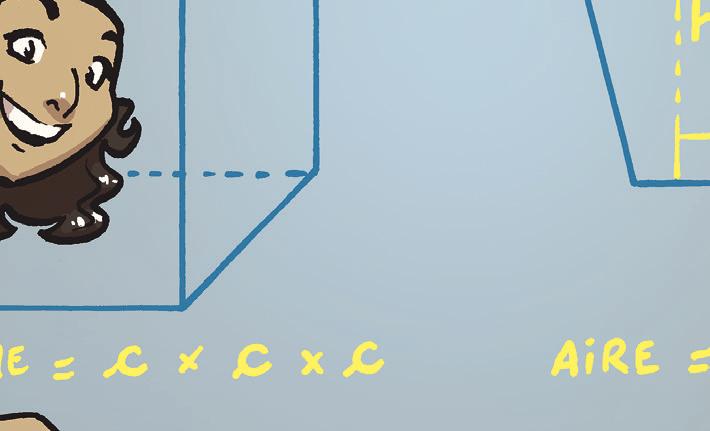
Utiliser de manière adéquate les termes relatifs aux grandeurs : la longueur, la masse, la capacité, le cout, l’aire, le volume.

Utiliser de manière adéquate les termes longueur, largeur, épaisseur, profondeur, hauteur, périmètre, aire et volume.

Attendus

Classer des objets donnés selon une de leurs grandeurs.

Trier des énoncés donnés désignant le temps instantané (ordinal) ou des durées (cardinal).

Agir sur des grandeurs

Attendus

Utiliser et symboliser : –les unités de longueur ; –les unités de capacité ; –les unités de masse ; – les unités d’aire y compris les mesures agraires : l’are (a), l’hectare (ha), le centiare (ca) ; – les unités de volume : le mètre cube (m3), le décimètre cube (dm3), le centimètre cube (cm3), le millimètre cube (mm3).

Attendus

Donner du sens aux préfixes : déci, centi, milli, kilo, hecto, déca dans les unités conventionnelles travaillées.

Réaliser des conversions significatives (longueur, masse, capacité, aire, volume) en lien avec les unités conventionnelles travaillées, avec ou sans abaques (construits préalablement).

Associer à l’écriture d’une grandeur prélevée dans le quotidien (longueur, capacité, masse, aire, volume), d’autres écritures donnant du sens aux nombres décimaux.

Ex. : 20 kg d’engrais pour 400 m2, c’est 0,05 kg ou 50 g d’engrais par m2

Donner du sens à des unités usuelles de durées.

Associer des unités de temps à des durées de situations variées.

Compétence(s)

Résoudre des problèmes dans des situations contextualisées.

Savoir(s)

La relation de la proportionnalité directe.

Savoir-faire

Exploiter des situations de proportionnalité directe entre grandeurs.

Attendus

Résoudre des problèmes d’achats mobilisant : – des prix exprimés en euros et centimes ; – les expressions comme « 1 + 1 gratuit », « le deuxième à moitié prix », « prix à partir de… » et « jusqu’à 70 % de remise » ; – la notion de bénéfice et de perte.

Mettre en relation des grandeurs

Attendus

Reconnaitre des grandeurs directement proportionnelles parmi un ensemble : – de représentations en graphe fléché ; – de tableaux de nombres ; – de situations libellées en français.

Énoncer un lien entre deux grandeurs proportionnelles.

Attendus

Déterminer une quantité dans une situation contextualisée de proportionnalité directe (nombre de… pour…).

Compétence(s)

Résoudre des situations de proportionnalité directe.

N-O

Savoir(s)

Représenter une situation contextualisée de proportionnalité directe par un graphe fléché ou un tableau de proportionnalité.

Identifier un lien (multiplicatif ou additif) entre deux grandeurs dans un tableau de proportionnalité.

Compléter un graphe fléché, un tableau de proportionnalité en lien avec une situation de proportionnalité directe.

Attendu

Écrire le résultat et sa démarche de résolution d’une situation de proportionnalité.

LES NOMBRES

Appréhender le nombre puis la lettre dans tous leurs aspects

Attendus

Utiliser des nombres pour communiquer : – une quantité ; – une position ; – un numéro ; – etc.

Des nombres naturels aux nombres réels.

ÉditionsVANIN

De la comparaison de collections puis de nombres à la relation d’ordre.

Savoir-faire

Dire, lire, écrire et représenter les nombres dans la numération décimale.

Utiliser de manière adéquate le nom des rangs (unité, dizaine, centaine) et le nom des classes (des millions, des mille, des unités simples, des millièmes).

Associer le nom d’un nombre naturel jusqu’aux milliards.

Associer le nom d’un nombre composé d’une partie entière limitée aux unités de mille et d’une partie non entière limitée aux millièmes, à son écriture en chiffres.

Utiliser de manière adéquate les termes liés à la comparaison de nombres (cardinalité).

Associer les symboles d’ordre (<, >, =) aux expressions « est plus petit que », « est plus grand que », « est égal à ».

Attendus

Dire, lire des nombres jusqu’aux milliards et les écrire en chiffres. Dire, lire des nombres composés d’une partie entière limitée aux unités de mille et d’une partie non entière limitée aux millièmes et les écrire en chiffres.

Expliquer la présence du zéro dans l’écriture des nombres jusqu’aux milliards et dans un nombre décimal.

Savoir-faire

Décomposer et recomposer les nombres.

Comparer, ordonner, situer des nombres.

Attendus

Décomposer et recomposer des nombres de trois à six chiffres en lien avec la numération décimale.

Décomposer un nombre en sa partie entière et sa partie non entière.

Comparer deux nombres en utilisant le symbole adéquat (<, >, =). Encadrer un nombre écrit sous sa forme décimale au centième, au millième près.

Ordonner des nombres de trois à six chiffres, avec ou sans virgule, de façon croissante ou décroissante.

Exprimer la position d’un nombre, avec ou sans virgule, limité au millième (par encadrement, par approximation selon un degré de précision donné) sur une portion de droite numérique.

Créer des familles de nombres, relever des régularités.

Savoir-faire

Appliquer un algorithme de calcul écrit pour en comprendre le mécanisme.

Estimer et vérifier.

Les nombres

Compléter les portions d’un tableau numérique où sont donnés des nombres écrits sous leur forme décimale limitée au millième.

Déterminer la régularité présente dans une suite de nombres donnée.

Compléter une suite de nombres donnée par des éléments qui en ont été extraits.

Opérer sur des nombres et sur des expressions algébriques

Attendus

Effectuer des additions de maximum trois termes (limités au millième).

Effectuer des soustractions limitées au millième (technique de compensation et/ou d’emprunt).

Estimer l’ordre de grandeur du résultat d’une opération (addition, soustraction et multiplication, division), avant de calculer précisément.

Vérifier la plausibilité d’un résultat.

MATIÈRES ABORDÉES

Des millièmes aux milliards –lire –écrire –décomposer –classer

Calculs écrits : –additions –soustractions

Les solides et figures Se repérer dans un quadrillage

ÉditionsVANIN

Les grandeurs

Les instruments de mesures et leurs unités : –longueur –capacité –masse –durée –euros Situation-problème La proportionnalité

Exercices supplémentaires et évaluations disponibles pour ce chapitre en téléchargement.

Activité 1 – Bataille navale

Exercice 1

Objectifs pédagogiques

• Se familiariser avec le repérage spatial sur un quadrillage.

• Introduire le vocabulaire mathématique spécifique (coordonnées, lignes, colonnes).

Déroulement

SO LO

Chaque élève lit individuellement la BD.

COLL ECTIF

SO LO

Observation guidée de la BD. Des questions générales sont posées (« Qui sont les personnages ? », « Quel jeu pratiquent-ils ? », etc.).

Anticipation des difficultés

• Difficulté possible à distinguer lignes et colonnes.

• Risque de confusion dans l’ordre des coordonnées.

Pistes de remédiation

• Représentation collective au tableau d’une grille simplifiée.

• Exercices rapides pour nommer et localiser des coordonnées oralement et en groupe.

ÉditionsVANIN

Chaque élève examine seul(e) la grille, repère les coordonnées et se familiarise avec le système de repérage (couleur + chiffre).

Chapitre

Les vacances de Manon et Raphaël

1. Bataille navale

Lis cette BD. 1.

As-tu déjà joué à la bataille navale ? Réponds aux questions.

Si tu as déjà joué, explique les règles du jeu à la classe.

Après avoir observé le plateau de jeu de Raphaël, quelle case aurait-il dû choisir pour remporter la partie ?

Mauve 3

Avec ton (ta) voisin(e), effectue une bataille navale.

Dessine 5 bateaux de manière verticale ou horizontale :

– 2 bateaux de 3 cases ;

– 2 bateaux de 2 cases ;

– 1 bateau de 1 case.

Attention, les bateaux ne peuvent pas se toucher ! Place tes bateaux dans la grille de gauche et note ceux de ton (ta) voisin(e) dans la grille de droite.

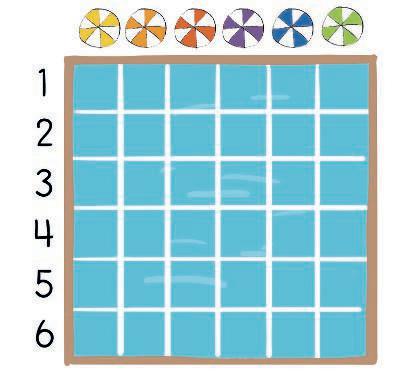
En observant le plateau de jeu, note à côté de chaque bateau sa position.

ÉditionsVANIN

(E,4) (F,4) (B,5) (B,9)

(F,6) (F,7)

(A,2) (B,2) (C,2)

Exercice 2

Objectifs pédagogiques

• Développer les capacités d’observation et d’analyse.

• Favoriser l’expression orale.

Déroulement

COLL ECTIF

Rappel oral des règles du jeu (participation active des élèves).

SO LO

Les élèves répondent seul(e)s, par écrit, aux questions posées sur la fiche (identification de la case gagnante).

Anticipation des difficultés

• Difficulté potentielle à identifier rapidement la case correcte (« Mauve 3 »).

• Difficulté à argumenter et justifier leur choix.

Pistes de remédiation

• Débat collectif rapide sur les choix possibles pour faciliter la justification.

• Exercice complémentaire de repérage simplifié pour les élèves en difficulté.

Exercice 3

Objectifs pédagogiques

• Mobiliser les compétences de repérage spatial en situation ludique.

• Développer la communication orale, la coopération et la logique par déduction.

Déroulement

SO LO

Chaque élève place individuellement ses 5 bateaux sur la grille de gauche en les dessinant.

D U O

Jeu interactif avec notation précise (croix pour « touché », rond pour « dans l’eau »).

Notation des résultats

ÉditionsVANIN

• Croix « X » dans une case lorsqu’un bateau adverse est touché.

• Si l’adversaire dit « touché-coulé », il faut entourer toutes les croix concernées.

• Placer des ronds « O » autour du bateau coulé par déduction.

• Si l’adversaire dit « coulé » pour indiquer qu’aucun bateau n’est touché, noter un rond « O » dans cette case.

Anticipation des difficultés

• Bateaux mal positionnés.

• Erreurs dans la notation ou difficulté de raisonnement déductif après un bateau coulé.

Pistes de remédiation

• Présentation collective d’une grille-modèle à l’aide du livre numérique.

• Mini-exercice de logique en collectif avant de démarrer le jeu.

• Accompagnement individualisé si besoin.

• Demander à un(e) voisin(e) de classe qui ne sera pas l’adversaire de vérifier si les bateaux sont bien placés (aucun bateau ne peut se toucher).

Exercice 4

Objectifs pédagogiques

• Renforcer la maitrise du repérage spatial précis sur une grille à double entrée.

• Développer la précision, la rigueur et l’attention aux détails.

Déroulement

SO LO

COLL ECTIF

Chaque élève identifie et note précisément les coordonnées des bateaux représentés sur la grille proposée.

Correction collective. Validation et échanges autour des réponses proposées.

Anticipation des difficultés

• Inversion possible entre lettre et chiffre.

• Oubli potentiel de certaines cases occupées par les grands bateaux.

Pistes de remédiation

• Courte révision collective préalable sur la manière de lire les coordonnées.

• Vérification croisée des réponses par binômes avant la correction collective.

• Exercices simplifiés en atelier pour les élèves en difficulté persistante.

ÉditionsVANIN

Exercice 5

Objectifs pédagogiques

• Consolider la compétence de repérage précis sur un quadrillage à double entrée (lignes et colonnes).

• Développer la rigueur et l’attention dans la notation des coordonnées.

• Favoriser l’autonomie des élèves dans l’observation et la transcription d’informations.

Déroulement

SO LO

Les élèves réalisent individuellement l’exercice en identifiant et notant précisément les coordonnées des différents objets placés sur la grille proposée.

COLL ECTIF

Correction collective. Elle permet aux élèves de valider leurs réponses et de verbaliser leur stratégie pour repérer les objets rapidement (partir des colonnes, puis des lignes ou inversement).

Anticipation des difficultés

• Certains élèves pourraient inverser les coordonnées (colonne-ligne).

• Difficulté pour repérer rapidement l’intersection des lignes et des colonnes sur un quadrillage relativement grand.

Pistes de remédiation

• Proposer, en phase collective, un rappel rapide à l’aide du tableau sur la méthodologie de lecture des coordonnées (exemple concret : « lunettes en C1 »).

• Fournir une grille plus simple ou plus petite pour les élèves ayant besoin d’une étape intermédiaire.

• Utiliser des supports matériels tels que des pions placés sur un quadrillage au tableau pour une visualisation concrète.

Propositions de dépassement

• Demander aux élèves plus rapides de placer oralement d’autres objets imaginaires en indiquant précisément leurs coordonnées devant la classe.

• Leur proposer de rédiger des énigmes en utilisant des coordonnées à trouver par leurs camarades (ex. : « Quel objet se trouve en G6 ? »).

ÉditionsVANIN

Exercice 6

Objectifs pédagogiques

• Approfondir la compétence de repérage spatial en passant cette fois des coordonnées à la localisation sur une grille.

• Encourager la précision dans le dessin et la localisation spatiale d’éléments.

• Favoriser l’autonomie dans la réalisation d’une tâche précise et claire.

Déroulement

SO LO

D U O

COLL ECTIF

Chaque élève dessine individuellement les objets demandés sur le quadrillage selon les coordonnées imposées.

Ensuite, les élèves s’associent brièvement en binômes pour comparer leurs réponses, identifier d’éventuelles erreurs et se corriger mutuellement.

Anticipation des difficultés

Une correction collective finale permet de vérifier définitivement les dessins effectués sur la grille projetée au tableau.

• Risque de confusion par rapport aux coordonnées, notamment pour les élèves ayant encore du mal à se repérer précisément.

• Difficulté possible à dessiner clairement les objets dans les cases correspondantes.

Pistes de remédiation

• Encourager les élèves en difficulté à d’abord marquer la case d’un point avant de dessiner l’objet afin de s’assurer du bon emplacement.

• Distribuer temporairement des petites grilles individuelles plastifiées sur lesquelles les élèves pourraient s’entrainer à placer et déplacer des jetons avant de dessiner.

• Travailler en atelier de remédiation avec des grilles simplifiées ou plus grandes si nécessaire.

Propositions de dépassement

• Inviter les élèves rapides à créer une petite scène supplémentaire en utilisant d’autres coordonnées qu’ils (elles) auront eux-mêmes (elles-mêmes) choisies, tout en restant précis dans leur repérage.

• Leur demander d’imaginer, puis de rédiger de courtes consignes de placement d’objets pour leurs camarades, en vue d’un échange rapide en classe.

ÉditionsVANIN

En t’aidant du quadrillage ci-dessous, donne les coordonnées des objets.

Dans le quadrillage ci-dessus, dessine ces éléments.

− Une casquette en (B,7)

− Un tube de crème solaire en (D,6)

− Un avion en (E,9)

− Un palmier en (I,3)

(B,3)

Palmier

Crème solaire

Avion

Casquette

Observe ce quadrillage.

Quelle différence observes-tu par rapport aux quadrillages rencontrés précédemment ?

Dans ce dernier quadrillage, nous avons un repère sur un croisement, alors que dans les quadrillages précédents, le repère était dans une case.

Repérer une case

Dans un quadrillage, on peut avoir besoin de repérer

Repérer un croisement

Dans un quadrillage, on peut avoir besoin de repérer

La case bleue a pour coordonnées ( , ).

On donne d’abord la lettre de la colonne, puis le nombre de la rangée.

Le croisement bleu a pour coordonnées ( , ).

On donne d’abord la lettre de la ligne verticale, puis le nombre de la ligne horizontale.

Exercices 7 et 8

Objectifs pédagogiques

• Amener les élèves à comparer différents types de quadrillages et à expliciter clairement les différences observées.

• Consolider les notions de repérage spatial sur un quadrillage, en passant du repérage « dans une case » au repérage « sur une intersection de lignes ».

• Développer chez les élèves une capacité d’observation fine et de verbalisation des différences entre des supports graphiques proches.

Déroulement

COLL ECTIF

Dans un premier temps, la grille proposée est projetée au tableau interactif afin de faciliter l’observation collective. Les élèves observent attentivement la grille et localisent mentalement les différents objets placés cette fois-ci sur des intersections de lignes et non plus à l’intérieur des cases comme précédemment.

Une réflexion collective orale rapide permet de s’assurer que chaque élève comprend bien ce nouveau type de repérage : les coordonnées ne désignent plus une case, mais un croisement précis entre une colonne (lettre) et une ligne (chiffre).

SO LO

Ensuite, les élèves répondent par écrit à la question de l’exercice 8. Ils (elles) expliquent en une ou deux phrases la différence observée entre ce nouveau quadrillage (où le repère se trouve sur une intersection de lignes) et les quadrillages précédents (où le repère était situé à l’intérieur d’une case).

Anticipation des difficultés

• Risque que les élèves ne perçoivent pas spontanément la différence entre les deux systèmes de repérage (intersection versus intérieur d’une case).

• Risque de confusion entre la lettre de la colonne et le chiffre de la ligne lors du repérage sur intersection.

Pistes de remédiation

• Proposer une démonstration claire et visuelle en utilisant le tableau interactif : pointer distinctement une intersection (pour le quadrillage actuel), puis pointer l’intérieur d’une case (quadrillage précédent), en verbalisant clairement cette différence.

• Réaliser une courte activité intermédiaire : demander aux élèves de nommer à voix haute quelques coordonnées simples sur chacun des types de quadrillage afin de renforcer leur compréhension de manière concrète.

Conseils pédagogiques complémentaires

• Encourager les élèves à exprimer précisément leurs observations par des phrases complètes afin de favoriser la maitrise du vocabulaire mathématique lié au repérage spatial (lignes, colonnes, intersections).

• Pour les élèves plus rapides, leur demander d’inventer quelques énigmes à destination des camarades, nécessitant l’utilisation du repérage sur intersection pour être résolues. Cela stimule leur créativité tout en consolidant les compétences visées.

Je retiens

Objectifs pédagogiques

• Synthétiser clairement les deux méthodes distinctes de repérage spatial sur un quadrillage à double entrée (case et intersection).

• Construire une trace écrite claire et précise à destination des élèves pour favoriser une référence méthodologique ultérieure.

Déroulement

COLL ECTIF

Projection du manuel numérique sur le tableau interactif pour visualiser simultanément les deux types de quadrillages :

– Le repérage à l’intérieur d’une case : chaque case est définie par une colonne (lettre) et une ligne (chiffre). Exemple : la case bleue a pour coordonnées (B,2).

– Le repérage à l’intersection de lignes : le repère est placé précisément à la croisée d’une ligne verticale (lettre) et d’une ligne horizontale (chiffre). Exemple : l’intersection se trouve précisément au croisement de la colonne B et de la ligne 2.

Formuler clairement avec les élèves :

« Dans un quadrillage, on peut repérer une position :

– soit à l’intérieur d’une case (en donnant d’abord la colonne puis la ligne) ;

– soit précisément sur l’intersection de deux lignes (en donnant également la colonne puis la ligne). »

Souligner explicitement avec les élèves l’importance de respecter l’ordre : lettre d’abord, puis chiffre, pour éviter toute confusion.

Anticipation des difficultés

• Confusion possible persistante entre les deux systèmes de repérage (case ou intersection).

• Difficulté pour certains élèves à généraliser la démarche de repérage spatial.

Pistes de remédiation

• Proposer des exercices rapides au tableau interactif en demandant aux élèves d’identifier oralement des repères précis selon les deux systèmes.

• Afficher clairement en classe un rappel visuel permanent illustrant les deux méthodes côte à côte (quadrillage à cases et quadrillage sur intersections).

Conseils pédagogiques complémentaires

• Utiliser régulièrement le manuel numérique interactif pour visualiser concrètement et simultanément les deux types de repérage et favoriser l’ancrage visuel.

• Encourager systématiquement les élèves à préciser oralement quel type de repérage ils (elles) utilisent (« je suis dans une case » ou « je suis sur une intersection »).

ÉditionsVANIN

Activité 2 – On mesure !

Exercice 1

Objectifs pédagogiques

• Identifier et associer correctement des grandeurs physiques, leurs unités de mesure et les instruments appropriés.

• Développer la compréhension du vocabulaire spécifique lié aux grandeurs, unités et instruments.

• Stimuler la réflexion logique, la catégorisation et le raisonnement par association.

Déroulement

COLL ECTIF

Phase 1 : Mise en situation collective (au choix de l’enseignant(e)) Proposer, en collectif, une des deux mises en situation suivantes afin d’introduire de manière concrète et motivante la notion d’association des grandeurs, d’unités et d’instruments.

• Situation 1 : Organisation d’une fête d’anniversaire surprise (échange oral, puis recherche en ateliers)

« Imaginons que nous devions préparer une fête d’anniversaire surprise en classe. Pour l’organiser correctement, nous devrions prévoir certaines quantités précises (boissons, nourriture), mesurer des grandeurs comme la température de la classe, disposer d’une certaine somme d’argent, ou encore connaitre la taille des tables à prévoir selon le nombre d’invités. Quelles grandeurs devrions-nous mesurer précisément ? Quels instruments de mesure utiliserions-nous et quelles unités de mesure seraient adaptées à chaque cas ? »

Organisation

COLL ECTIF

Lancer un rapide échange oral collectif.

PETIT G ROUPE

COLL ECTIF

Répartir ensuite les élèves en petits ateliers de recherche (environ 4 élèves par groupe) : chaque groupe réfléchit et note ses propositions.

Un rapide retour collectif permet de confronter les réponses avant de passer à l’exercice individuel dans le cahier.

ÉditionsVANIN

• Situation 2 : Jouer à un jeu Memory préparé par l’enseignant(e) (jeu en petits groupes puis synthèse collective)

« Imaginons que nous devions jouer à un jeu Memory en classe où il faudrait retrouver, par paires, des grandeurs (longueur, température, capacité, etc.), leurs instruments de mesure (thermomètre, balance, etc.) et leurs unités correspondantes (gramme, litre, degré, etc.). Quelles cartes associerions-nous pour réussir à former des paires logiques ? »

Organisation :

PETIT G ROUPE

Proposer directement aux élèves, répartis en petits groupes de 4 élèves environ, le jeu Memory préalablement préparé par l’enseignant(e) (jeu téléchargeable sur Wazzou en complément à cet exercice, reprenant exactement les mêmes étiquettes que celles proposées dans le cahier).

COLL ECTIF

Après quelques minutes de jeu, une synthèse rapide en collectif permet d’expliciter les associations trouvées, avant de débuter l’exercice individuel.

Phase 2 : Travail individuel écrit dans le cahier

SO LO

Chaque élève effectue individuellement l’exercice en coloriant d’une même couleur les éléments qui doivent être associés (ex. : masse – gramme – balance de cuisine).

Phase 3 : Validation collective interactive

COLL ECTIF

La correction est effectuée en collectif grâce à la projection du livre numérique sur le tableau interactif (ou à partir d’une version papier agrandie sur le tableau noir). Les élèves viennent relier ou associer les éléments directement sur le support projeté, expliquant oralement et justifiant leurs choix.

Anticipation des difficultés

• Difficultés possibles à différencier certaines grandeurs physiques proches (masse/capacité, température/thermomètre, etc.).

• Risque d’erreurs de vocabulaire spécifique ou de méconnaissance des instruments de mesure.

Pistes de remédiation

• Effectuer un rappel rapide et explicite en collectif des différentes grandeurs, des unités correspondantes et des instruments appropriés avant ou pendant la correction interactive.

ÉditionsVANIN

• Proposer, pour les élèves ayant des difficultés, un affichage simplifié reprenant clairement les grandeurs, unités et instruments associés.

Proposition de dépassement

• Permettre aux élèves rapides de créer leur propre version simplifiée d’un Memory reprenant d’autres associations de grandeurs, unités et instruments, afin de prolonger leur apprentissage de manière créative.

2. On mesure !

Colorie d’une même couleur ce qui doit être associé.

compteur d’une voiture

balance de cuisine

gramme

degré

contenu d’un petit jus

longueur

ÉditionsVANIN

vitesse

cout

kilomètre/heure

caisse enregistreuse

Retrouve la grandeur adéquate et colorie la bonne case.

kmkm/hglkgheures€

Le prix pour acheter du pain

La quantité d’eau dans une baignoire

La distance entre Namur et Portiragnes

La masse d’une grosse pomme

La vitesse maximale d’une petite voiture

Le temps de notre trajet en avion

La masse de ton (ta) voisin(e) de classe

La somme de ton compte en banque

La durée d’une journée à l’école

La capacité d’une piscine

Avec ton (ta) voisin(e), reconstruis ci-dessous tes différents abaques (longueurs, capacités et masses).

ÉditionsVANIN

Exercice 2

Objectifs pédagogiques

• Consolider la capacité à associer correctement des situations concrètes aux grandeurs et aux unités de mesure adaptées.

• Développer la réflexion logique, l’analyse et la précision dans l’utilisation des unités de mesure.

• Favoriser l’autonomie et l’autocorrection.

Déroulement

COLL ECTIF

SO LO

Avant de réaliser l’exercice individuellement, projeter le tableau des mesures au tableau interactif (ou en version papier agrandie sur tableau noir) pour rappeler brièvement aux élèves les différentes unités proposées (km, km/h, g, l, kg, heures, €) ainsi que les types de grandeurs qu’elles peuvent mesurer (distance, vitesse, masse, capacité, temps, cout).

Inviter les élèves à réaliser ensuite l’exercice individuellement, en coloriant clairement la case correspondant à chaque situation décrite, selon la grandeur qui convient le mieux.

Anticipation des difficultés

• Difficultés éventuelles à distinguer clairement certaines grandeurs proches (par exemple masse/capacité, vitesse/temps).

• Risque de confusion entre unités semblables (ex. : kg et g).

Pistes de remédiation

• Proposer aux élèves en difficulté un affichage visuel clair en classe, reprenant les unités, les grandeurs associées et quelques exemples concrets.

• Organiser un atelier d’aide où les élèves manipuleraient des objets concrets (balance, bouteille d’eau graduée, mètre, chronomètre, etc.) afin de bien comprendre, par l’expérience directe, la nature des grandeurs concernées et leurs unités.

Exercice 3

Objectifs pédagogiques

• Reconstruire et maitriser la structure des abaques de mesure de longueur, de capacité et de masse.

• Renforcer la mémorisation et la compréhension des liens entre les différentes unités de mesure.

• Développer l’esprit collaboratif par un travail en duo.

Déroulement

COLL ECTIF

ÉditionsVANIN

Débuter par un bref rappel collectif oral des trois types d’abaques (longueur, capacité, masse). Ce rappel peut être réalisé en utilisant la projection du manuel numérique au tableau interactif (ou de la version papier agrandie au tableau noir).

D U O

En duo, les élèves réalisent ensuite l’exercice proposé. Ils (elles) reconstruisent correctement les abaques en plaçant les unités données dans le bon ordre.

COLL ECTIF

Après le travail en duo, organiser une correction collective interactive sur le tableau interactif (ou sur version papier agrandie), en invitant des binômes à venir placer directement les unités au tableau.

Anticipation des difficultés

• Risque de confusion entre les unités proches (ex. : dg et dag ou dl et cl).

• Risque de mélange entre les ordres de grandeur (passage incorrect d’une unité à une autre).

Pistes de remédiation

• Proposer aux élèves en difficulté un support visuel clair (tableau mural ou fiches récapitulatives personnelles) reprenant précisément les trois abaque-types de mesure.

• Effectuer des exercices simples en manipulation directe (étiquettes à replacer) en atelier pour consolider leur maitrise des abaques.

Conseil pédagogique complémentaire

• Pour rendre l’activité plus dynamique et plus ludique, l’enseignant(e) pourrait proposer une petite activité préparatoire complémentaire sous forme de jeu.

Activité : Jeu de reconstruction d’abaques en équipes

PETIT G ROUPE

– Proposer aux élèves, en petits groupes de 3 ou 4, un ensemble d’étiquettes détachées représentant les unités de mesure.

– Chaque équipe reçoit les étiquettes mélangées correspondant aux trois types d’abaques (longueur, capacité, masse).

– Les élèves tentent, par recherche et essais-erreurs, de reconstruire les abaques correctement en les plaçant dans le bon ordre sur leur banc ou sur une affiche prévue à cet effet.

– Ce jeu de classement rapide faciliterait ainsi la compréhension pratique des élèves avant le travail à réaliser en duo sur le cahier.

ÉditionsVANIN

Exercices 4, 5 et 6

Cette page est essentiellement une phase d’exercisation individuelle permettant aux élèves de consolider et de mobiliser leurs connaissances relatives aux grandeurs, unités, instruments de mesure et aux transformations d’unités.

Objectifs pédagogiques

• Consolider la compréhension pratique des unités de mesure.

• Associer correctement ces unités avec un instrument de mesure adapté et une situation concrète.

• Renforcer les compétences des élèves à réaliser des transformations plus complexes d’unités.

• Développer la précision et la rigueur dans l’utilisation des abaques de mesure.

Exercice 4

Présentation et déroulement

SO LO

D U O

L’exercice est réalisé individuellement afin de favoriser une réflexion autonome sur des exemples concrets et personnels.

Ensuite, une validation rapide en duos permet aux élèves d’échanger, de confronter leurs réponses et de justifier leurs choix.

Anticipation des difficultés

• Difficultés à trouver spontanément des exemples concrets pour certaines unités.

• Difficultés à formuler clairement les justifications.

Pistes de remédiation

• Encourager les élèves à trouver des situations simples et personnelles tirées directement de leur quotidien immédiat.

• Permettre, si besoin, un court échange oral collectif pour aider certains élèves à identifier plus facilement des exemples concrets.

Conseil pédagogique complémentaire

• L’exercice étant ouvert à plusieurs réponses possibles, ne pas prévoir une correction collective exhaustive. Se limiter à quelques échanges oraux pour enrichir les propositions des élèves.

Exercice 5

ÉditionsVANIN

Présentation et déroulement

SO LO

Réalisation individuelle pour entrainer les élèves aux conversions simples.

COLL ECTIF

Correction collective rapide projetée au tableau interactif (ou en version papier agrandie) afin de permettre une autocorrection immédiate et visuelle.

Anticipation des difficultés

• Erreurs possibles dans les facteurs de conversion (× 10, × 100, × 1 000).

• Difficulté à comprendre la notion de changement d’échelle (passage aux unités plus grandes ou plus petites).

Piste de remédiation

• Prévoir si nécessaire un rappel collectif rapide des règles de conversion en projetant clairement les abaques au tableau interactif ou sur papier.

Exercice 6

Présentation et déroulement

SO LO

Travail individuel approfondi : chaque élève réalise les transformations proposées.

COLL ECTIF

Correction collective interactive détaillée, en utilisant la projection du manuel numérique au tableau interactif (ou version papier agrandie) pour expliciter clairement chaque conversion.

Anticipation des difficultés

• Risque élevé d’erreurs liées au déplacement de la virgule dans les nombres décimaux.

• Confusion fréquente entre unités proches ou rarement utilisées.

Adaptations spécifiques (remédiation et dépassement)

• Pour les élèves en difficulté

– Mettre à leur disposition un abaque personnel plastifié sur lequel ils (elles) peuvent écrire avec un marqueur effaçable. Cet outil concret et réutilisable permettra aux élèves de mieux visualiser les conversions, de les expérimenter activement et pourra être conservé par les élèves comme support personnel.

– Fournir un aide-mémoire simplifié (version papier ou affichage en classe), reprenant clairement les déplacements nécessaires pour chaque type de conversion.

– Sélectionner et indiquer précisément quelques exercices plus simples afin de limiter les difficultés rencontrées.

• Pour les élèves en avance

– Proposer d’inventer d’autres conversions plus complexes, impliquant des unités moins courantes ou des nombres décimaux complexes, afin d’approfondir leur compréhension.

– Inviter ces élèves à rédiger une courte fiche méthodologique expliquant comment réaliser ces conversions complexes, fiche qu’ils pourront présenter à la classe.

Conseils pédagogiques complémentaires

ÉditionsVANIN

• Pendant la correction collective, illustrer concrètement les déplacements de la virgule à l’aide du tableau interactif afin de permettre à l’ensemble des élèves une meilleure compréhension visuelle et dynamique.

• Encourager régulièrement l’utilisation personnelle de l’abaque plastifié chez les élèves en difficulté, favorisant ainsi leur autonomie et leur confiance en eux lors des phases de conversion.

Pour chaque unité de mesure proposée, trouve un instrument et une situation de la vie réelle. Justifie tes choix avec ton (ta) voisin(e) lorsque vous avez terminé.

Unité de mesure

masse d’un sac de pommes

Plusieursréponsespossibles

Complète.

Exemple : 1 m × 100 = 1 hm

1 km : = 1 m

1

1

1 cl × = 1 dal × 100 = 1 kg

1 dag

Transforme

1 g × = 1 hg 1 l : = 1 ml 1 kg × 1 000 = 1

200 ml =  l23 cm =  m

40 g =  mg5,3 dm =  mm

2 500 m =  km8 000 kg =  T

3,75 kg =  g32,5 dag =  kg

5 hl =  l5 000 mg = hg

28 cl =  ml23 dam =  cm

0,3 m =  mm34 cm =  m

5,3 l = ml 6 T =  kg

Résous ces problèmes.

a) Lorsqu’ils sont allés au marché, Manon et Raphaël ont acheté quelques ingrédients pour préparer un apéritif. Voici ce qu’ils ont acheté : 250 g de fromage, 1/5 kg d’olives, 5 400 mg de chips, 45 dag de saucisson. Quelle quantité totale de nourriture ont-ils achetée ?

1/5 kg d’olives = 200 g 5 400 mg de chips = 5,4 g 45 dag de saucisson = 450 g

250 g de fromage + 200 g d’olives + 5,4 g de chips + 450 g de saucisson = 905,4 g

Ils ont acheté une quantité totale de 905,4 g de nourriture.

b) Pour ce même apéritif, ils ont décidé de proposer à leurs amis un petit cocktail fruité. Voici les jus qu’ils ont achetés : 1,5 l de jus d’orange, 100 cl de jus de cerise, 0,2 dal de jus de mangue et 500 ml de jus de citron. Auront-ils assez pour eux et leurs 8 amis, sachant qu’ils prendront au moins 2 verres de 25 cl chacun ? Justifie ta réponse.

Quantité dont on a besoin pour 10 personnes (les 8 amis plus Manon et Raphaël) :

(2 × 25 cl) × 10 = 500 cl = 5 l

Total des boissons achetées : 1,5 l + 0,1 l + 2 l + 0,5 l = 4,1 l

Ils n’auront donc pas assez pour offrir au moins 2 verres à chacun. Il manque 0,9 l.

c) Léa et Nathan jouent chacun sur leur tablette lorsqu’un message d’alerte apparait : les batteries sont presque vides !

Ils doivent attendre que les tablettes se rechargent pour pouvoir continuer à jouer.

La batterie de Léa est à 15 % et met 2 minutes pour recharger 1 %.

Celle de Nathan est à 20 % et met 1 minute 30 secondes pour recharger 1 %.

Ils ne pourront reprendre leur jeu que lorsque les batteries auront atteint 80 %.

Combien de temps Léa devra-t-elle attendre avant d’atteindre 80 % de charge ?

Il faut gagner : 80 % – 15 % = 65 %

Léa devra attendre 65 × 2 min = 130 min ou 2 h 10 min.

Combien de temps Nathan devra-t-il attendre avant d’atteindre 80 % de charge ?

Il faut gagner : 80 % – 20 % = 60 %

Nathan devra attendre 60 × 90 s = 5 400 s ou 90 min ou 1 h 30 min

ÉditionsVANIN

Lequel pourra recommencer à jouer en premier et avec combien de minutes d’avance sur l’autre ?

Nathan pourra recommencer à jouer le premier, 40 minutes avant Léa.

Exercice 7

Objectifs pédagogiques

• Mobiliser les connaissances relatives aux grandeurs et aux conversions d’unités dans des contextes concrets.

• Développer les compétences en résolution de problèmes : compréhension, analyse, calcul, conversion et justification claire de la démarche.

• Favoriser l’autonomie dans l’analyse et la résolution de problèmes complexes.

Déroulement

COLL ECTIF

SO LO

COLL ECTIF

Avant de commencer, projeter clairement les énoncés au tableau interactif. Réaliser une lecture collective rapide pour clarifier la compréhension de chaque situation (vocabulaire, unités concernées, données essentielles).

Chaque élève résout seul(e) les trois problèmes proposés (a, b et c). Le travail consiste à bien comprendre la situation, effectuer les conversions nécessaires et réaliser les calculs.

Après un travail individuel, une correction interactive au tableau permet aux élèves volontaires d’expliquer clairement les démarches utilisées. Cette correction est particulièrement pertinente pour les deux premiers problèmes, qui sont accessibles à la plupart des élèves. Pour le problème c, plus complexe en termes de calculs et de conversions, la correction collective sera expliquée clairement étape par étape par l’enseignant(e) au tableau interactif, en insistant sur les différentes démarches possibles (minutes ou heures-minutes, etc.).

Anticipation des difficultés

• Risque important d’erreurs liées aux conversions entre les unités (grammes/kg, litres/ml, temps en secondes/minutes/heures).

• Difficultés possibles dans l’identification claire des données utiles au problème.

• Difficulté potentielle à justifier précisément une démarche écrite.

Pistes de remédiation

• Fournir aux élèves en difficulté un rappel sous forme d’un aide-mémoire simplifié des abaques et conversions utilisés fréquemment.

• Pour les élèves ayant besoin d’un accompagnement supplémentaire, organiser ponctuellement un atelier dirigé où les problèmes seront simplifiés ou fragmentés en étapes plus accessibles.

ÉditionsVANIN

• Pour le problème c, particulièrement complexe, prévoir un accompagnement pas-à-pas (guidage explicite par étapes) avec l’enseignant(e) pour les élèves en difficulté importante.

• Mise en place du tutorat : organiser, dès que certains élèves ont terminé les problèmes, un tutorat au sein de la classe. Ces élèves volontaires pourront ainsi venir en aide à leurs camarades en difficulté en expliquant leurs démarches, en répondant à leurs questions et en vérifiant avec eux les conversions ou les calculs.

Propositions de dépassement

• Les élèves qui terminent rapidement pourront inventer un problème supplémentaire en lien avec leur quotidien, reprenant clairement différentes unités et nécessitant plusieurs conversions, à présenter ensuite à leurs camarades.

• Proposer également à ces élèves une réflexion sur différentes stratégies possibles pour résoudre le problème c, notamment sur la manière d’optimiser la démarche (calcul direct en heures-minutes plutôt qu’en minutes seules, par exemple). Ils (elles) pourraient ensuite comparer leur stratégie à celles des autres élèves lors d’une discussion collective.

Conseils pédagogiques complémentaires

• Pour rendre la correction interactive plus efficace et dynamique, projeter clairement les énoncés sur le tableau interactif (ou version papier agrandie au tableau noir) pour faciliter la visualisation collective de chaque étape du raisonnement.

• Encourager fortement la verbalisation des démarches de résolution par les élèves eux-mêmes (ellesmêmes), afin de renforcer la compréhension et l’ancrage méthodologique.

• Valoriser fortement le rôle du tuteur en classe afin de favoriser un climat d’entraide et de coopération entre élèves.

ÉditionsVANIN

Activité 3 – Des millièmes aux milliards

Exercice 1

Objectifs pédagogiques

• Découvrir et manipuler des nombres variés en les reliant à leur écriture en lettres.

• Développer la maitrise des nombres entiers et décimaux ainsi que la lecture des grands nombres.

• Favoriser une approche multidisciplinaire en intégrant l’utilisation des outils numériques.

COLL ECTIF

Mises en situation introductives possibles (au choix de l’enseignant(e))

Ces mises en situation seront introduites collectivement en projetant le détail informatif de la ville de Portiragnes (tableau interactif ou version papier agrandie sur tableau noir).

Situation

1 : Un voyage scolaire à Portiragnes

« Imaginons que nous partions en voyage scolaire à Portiragnes. Pour préparer ce voyage, nous souhaiterions obtenir quelques informations sur cette ville : combien d’habitants y vivent ? Quelle est sa superficie exacte ? À quelle altitude se trouve-t-elle ? Toutes ces informations sont représentées par des nombres précis, parfois très grands. Serions-nous capables de bien lire et comprendre ces nombres ?

Arriverions-nous facilement à les associer à leur écriture en lettres ? »

Organisation pédagogique

COLL ECTIF

SO LO

– D’abord une observation collective rapide en projetant au tableau interactif la fiche présentant Portiragnes (ou papier agrandi sur tableau noir).

– Recueil oral rapide de quelques hypothèses sur la lecture des grands nombres (20 160 000, 161…).

– Passage ensuite à l’exercice individuel du cahier.

Situation alternative : Jeu « Enquête numérique à Portiragnes »

« Imaginons que nous soyons chargés d’une petite enquête sur la ville de Portiragnes. Nous devrions noter dans un carnet d’enquête toutes les informations importantes sur cette commune pour les communiquer à nos camarades : son nombre d’habitants, sa densité, sa superficie, etc. Mais pour présenter ces informations clairement, il faut être capable de lire et d’écrire correctement ces nombres en lettres et en chiffres. »

Organisation proposée

ÉditionsVANIN

• Projeter les informations de la ville (via tableau interactif ou affichage papier) et demander aux élèves, en petits groupes de recherche (3 ou 4 élèves) de choisir quelques nombres et de s’entrainer à les écrire en toutes lettres avant la phase individuelle.

Déroulement

SO LO

Les élèves effectuent individuellement l’exercice proposé dans leur cahier, en reliant chaque nombre à son écriture en lettres.

COLL ECTIF

Une validation interactive collective rapide pourra suivre en utilisant la projection numérique (ou affichage agrandi en papier sur tableau noir si nécessaire) où chaque élève viendra relier clairement les associations.

Anticipation des difficultés

• Difficulté possible à lire correctement les grands nombres (millions, milliers, centaines) et à respecter l’orthographe des nombres écrits en toutes lettres.

• Risque de confusion entre des écritures.

Pistes de remédiation

• Proposer un rappel collectif rapide sur le tableau interactif avec une méthode claire de la lecture des grands nombres par tranches de 3 chiffres (classe des unités, milliers, millions).

• Prévoir une fiche simplifiée d’aide méthodologique pour les élèves ayant du mal à retenir l’ordre précis de lecture ou d’écriture des nombres (fiches individuelles d’aide disponibles sur leur banc).

Propositions de dépassement

• Inviter les élèves les plus rapides à rédiger quelques phrases personnelles contenant d’autres nombres importants issus de leur quotidien (population de leur commune, distance entre leur domicile et un lieu connu, etc.) en chiffres, puis en lettres.

• Leur proposer de présenter oralement ces nombres à la classe en expliquant la stratégie utilisée pour les écrire ou les lire correctement.

Conseils pédagogiques complémentaires

• Insister clairement sur la lecture à haute voix lors de la correction collective pour vérifier et renforcer la bonne prononciation et compréhension des nombres complexes ou très grands.

• Éventuellement, les élèves rapides pourront être sollicités pour aider leurs camarades en difficulté (tutorat ponctuel) en réexpliquant eux-mêmes (elles-mêmes) la démarche à suivre pour lire et écrire ces grands nombres.

• Proposition ludique et numérique pour renforcer la multidisciplinarité et ajouter une dimension concrète et motivante à l’activité : proposer aux élèves d’utiliser une carte interactive (type Google Maps) pour localiser précisément la ville de Portiragnes. Ensuite, proposer aux élèves équipés (tablette ou ordinateur) d’utiliser Google Street View pour visualiser en direct l’hôtel de ville de Portiragnes et vérifier ensemble si l’illustration proposée dans l’exercice correspond à la réalité du lieu. Cette activité pourrait être réalisée soit en collectif via la projection au tableau interactif, soit en ateliers numériques en petits groupes pour développer la compétence numérique et le plaisir de la découverte concrète.

ÉditionsVANIN

3. Des millièmes aux

milliards

Durant leurs vacances à Portiragnes, Manon et Raphaël se rendent à la municipalité locale afin d’obtenir quelques informations sur la ville où ils séjournent. Voici ce qu’ils ont reçu : Paris

PORTIRAGNES

Nice Portiragnes

Relie chaque nombre à son écriture en lettres.

Blason

ÉditionsVANIN

Pays France

Région Occitanie

Département Hérault Arrondissement Béziers

Administration Démographie

Gentilité Portiragnais

Population 3 247 hab. (2021 ) municipale Densité 161 hab./km²

Géographie

Coordonnées 43° 18’ 19” nord 3° 20’ 11” est Altitude 0 m – 41 m – 15 m (min. – max. – moy.)

Superficie 20,16 km² ou 20 160 000 m²

trois-mille-deux-cent-quarante-sept

cent-soixante-et-un

vingt-mille-cent-soixante

zéro

quarante-et-un

quinze

vingt et seize centièmes

cinquante-et-un vingt-millions-cent-soixante-mille

Toulouse

2. 3. 4. 5. 6.

Complète les noms des colonnes et, ensuite, place ces nombres correctement dans l’abaque.

1 238,91

1 239 129 021 384 348,382 67 601 129,003

Pour savoir comment compléter ton abaque, discutes-en avec ton (ta) voisin(e).

Classe des  Classe des  Classe des  Classe des unités Classe des

Relie chaque nombre à son écriture.

210 199

5 280 199

1 000 192 199

203 300 000

Dictée de nombres

deux-cent-trois-millions-trois-cent-mille

deux-cent-dix-mille-cent-nonante-neuf

cinq-millions-deux-cent-quatre-vingtmille-cent-nonante-neuf

un-milliard-cent-nonante-deux-mille-centnonante-neuf

Entoure le chiffre des UM en bleu, des D en rouge et des m en vert. Retrouve le nombre.

Exercices 2 et 3

Objectifs pédagogiques

• Structurer clairement la représentation des grands nombres en utilisant un abaque.

• Identifier les différentes classes numériques (milliards, millions, mille, unités, millièmes).

• Renforcer la compréhension du système décimal à travers des nombres entiers et décimaux.

COLL ECTIF

Avant de réaliser ces exercices, projeter clairement l’abaque vierge sur le tableau interactif (ou papier agrandi au tableau noir).

Introduire brièvement la notion de classes numériques en prenant pour exemple un des nombres proposés dans l’exercice (ex. : 1 239 129 021). Inviter les élèves à observer et à réfléchir collectivement à la manière dont ce nombre est structuré par tranches de trois chiffres.

D U O

COLL ECTIF

Les élèves commencent, en duos, par compléter le nom des colonnes des différentes classes numériques et à placer correctement les nombres proposés dans l’abaque. Cette démarche favorise la coopération et le dialogue mathématique entre élèves.

Durant cette phase, les élèves échangent et discutent de leur raisonnement afin de placer chaque nombre précisément dans l’abaque proposé à l’exercice 3.

Une correction collective interactive suivra ensuite, réalisée grâce à la projection de l’abaque au tableau interactif (ou sur papier agrandi au tableau noir si nécessaire), où chaque duo pourra venir placer ou corriger les nombres et les noms des colonnes.

Anticipation des difficultés

• Difficultés possibles à identifier clairement les classes numériques et à positionner correctement les nombres décimaux.

• Risque de confusion dans l’ordre et le nombre de chiffres par classe numérique (millions, milliards, etc.).

Pistes de remédiation

• Proposer une explication collective supplémentaire en début d’activité pour rappeler visuellement le découpage des grands nombres (projection d’un abaque complet au tableau interactif).

• Pour les élèves ayant plus de difficultés, mettre à disposition des fiches individuelles simplifiées rappelant clairement la structure des abaques (classes et sous-classes numériques), afin qu’ils (elles) puissent s’y référer tout au long de l’exercice.

Conseils pédagogiques complémentaires

ÉditionsVANIN

• Utiliser le tableau interactif pour afficher clairement les nombres en grand format afin de faciliter leur manipulation lors de la correction collective.

• Encourager systématiquement la verbalisation des choix effectués : les élèves expliqueront pourquoi ils (elles) placent chaque chiffre dans telle ou telle colonne, renforçant ainsi leur compréhension profonde du système décimal.

Exercice 4

Objectifs pédagogiques

• Vérifier la compréhension et la maitrise de l’écriture littérale des nombres complexes (mille, million, milliard).

• Consolider l’association rapide entre les nombres écrits en chiffres et leur écriture en lettres.

Déroulement

SO LO

Les élèves réalisent cet exercice individuellement et de manière autonome, en reliant les nombres aux écritures correspondantes.

COLL ECTIF

Une correction collective rapide et interactive peut être effectuée en projetant clairement les associations au tableau interactif (ou sur papier agrandi).

Anticipation des difficultés

• Confusion potentielle entre les grands nombres ou les nombres proches dans leur écriture (ex. : millions et milliards).

Piste pédagogique

• Rappeler brièvement la stratégie de lecture en tranches de trois chiffres (milliards, millions, mille, unités) pour faciliter l’identification rapide.

Conseil pédagogique complémentaire

• L’exercice étant relativement simple et court, prévoir un temps rapide d’autocorrection entre pairs avant la validation collective afin d’encourager les échanges entre élèves.

Exercice 5

Objectifs pédagogiques

• Vérifier la compréhension auditive et visuelle des grands nombres.

• Identifier clairement la valeur de position des chiffres (Unités de Mille, Dizaines, millièmes).

Déroulement

SO LO

ÉditionsVANIN

L’enseignant(e) dicte clairement les nombres suivants aux élèves, qui les notent ensuite individuellement dans leur cahier :

• Cent-vingt-trois-mille-nonante-trois (123 093)

• Un-million-deux-cent-trente-neuf-mille-nonante-et-un (1 239 091)

• Vingt-et-un-mille-quatre-cent-dix-sept (21 417)

• Deux-cent-mille-nonante-et-un (200 091)

Après avoir noté les nombres, les élèves entourent individuellement et précisément :

• Le chiffre des Unités de Mille (UM) en bleu.

• Le chiffre des Dizaines (D) en rouge.

• Le chiffre des millièmes (m) en vert (si présents).

COLL ECTIF

Une validation interactive et rapide est effectuée par projection numérique sur le tableau interactif. Les élèves viennent à tour de rôle entourer ou vérifier les chiffres directement au tableau.

Anticipation des difficultés

• Difficulté potentielle à distinguer clairement la position précise des chiffres (en particulier UM et D).

• Confusion possible dans l’écriture de certains nombres complexes.

Piste de remédiation

• Avant la dictée, rappeler brièvement et visuellement au tableau interactif la place des chiffres (UM, D, m…) dans un nombre à l’aide d’un exemple simple.

Conseils pédagogiques complémentaires

• Dicter lentement chaque nombre et le répéter au besoin afin de permettre à tous les élèves de réussir l’exercice.

• Valoriser la correction interactive en invitant quelques élèves à reformuler oralement comment ils (elles) identifient clairement chaque nombre demandé.

ÉditionsVANIN

Exercices 6 à 14

Objectifs pédagogiques globaux

• Renforcer la maitrise de la structure des nombres (classe des millièmes, unités, mille, millions, milliards).

• Consolider les compétences en lecture, écriture et comparaison des grands nombres et des nombres décimaux.

• Développer l’autonomie et la rigueur dans les exercices individuels variés.

Déroulement

SO LO

COLL ECTIF

L’ensemble des exercices (de 6 à 14) est à réaliser individuellement par chaque élève afin de mobiliser, exercer et consolider son acquis sur les nombres, leurs représentations (abaques, décomposition) et leur classement (croissant/décroissant).

L’enseignant(e) organisera une correction collective approfondie uniquement pour les exercices jugés essentiels et complexes (notamment les exercices 7, 9, 10, 13 et 14), en projetant clairement les réponses sur le tableau interactif. Une correction rapide pourra être réalisée pour les exercices plus simples comme les exercices 6 et 11.

Anticipation des difficulté globales

• Difficultés dans la lecture correcte des nombres complexes (millions, milliards, décimaux).

• Risque important de confusion dans la décomposition en classes numériques (unités, mille, millions, milliards, millièmes).

• Difficultés dans l’organisation logique pour classer les nombres décimaux ou très grands.

Pistes de remédiation pour les exercices les plus complexes

• Fournir une fiche méthodologique rappelant explicitement le rôle de chaque classe numérique (milliards, millions, mille, unités, millièmes) pour appuyer les exercices 6, 7, 9 et 10, qui sont souvent plus problématiques.

• Mettre à disposition un abaque individuel plastifié sur lequel les élèves pourront placer visuellement les chiffres pour faciliter la décomposition et les conversions nécessaires. Cet outil, réutilisable régulièrement, leur offrira une visualisation concrète de la structure numérique.

• Organiser ponctuellement un atelier de résolution assistée où les élèves peuvent, en petits groupes, refaire certains exercices avec accompagnement direct de l’enseignant(e), notamment les exercices 7, 10, 13 et 14.

Adaptations spécifiques (remédiation et dépassement)

• Pour les élèves en difficulté

ÉditionsVANIN

– Proposer systématiquement l’utilisation d’un abaque plastifié individuel afin de les aider à visualiser précisément chaque classe numérique.

– Simplifier certains exercices en réduisant le nombre ou la complexité des nombres à décomposer (par exemple, ne garder que 2 ou 3 nombres les plus simples des exercices concernés).

– Organiser ponctuellement un tutorat entre élèves, où les élèves ayant terminé rapidement et maitrisant bien les notions viendront en aide à ceux (celles) rencontrant plus de difficultés.

• Pour les élèves en dépassement

– Leur demander de créer de nouvelles décompositions plus complexes avec des nombres décimaux variés ou des nombres comportant plusieurs classes numériques (millièmes, milliards, etc.).

– Proposer un petit atelier de recherche où ils (elles) réaliseraient eux-mêmes (elles-mêmes) des classements croissants ou décroissants avec des nombres qu’ils auront inventés, en justifiant précisément leurs critères de classement aux autres élèves lors de la correction collective.

Effectue cette fois le contraire et décompose les nombres en « classes ».

2 298 002 =

2UM 2CM 9DM 8UM 2U

4 000 000 256 =

87 823 000,2 =

67 000,723 =

37,238 =

4UM 2C 5D 6U

8DM 7U 8CM 2DM 3UM 2d

6DM 7UM 7d 2c 3m

3D 7U 2d 3c 8m

Que représente le 3 dans chaque nombre ci-dessous ? Complète

2 348 092

472 128 302

1 000 000,23

Zone de travail

3 029 201 984

920 123,129

78 120,306

Complète par classe.

236 126 123 =   millions + mille + unités

2 183 931 012 =   milliards +  millions + mille + unités

128 031, 382 =  mille + unités + millièmes

93 128 001, 981 =   millions + mille + unité + millièmes

Décompose comme dans l’exemple.

239 234 = 200 000 + 30 000 + 9 000 + 200 + 30 + 4

12 120 =

13 100 409 =

310,32 =

239 006, 007 =

610 021, 209 =

<, > ou = .

2 039 923 3UM 2DM 4C 9d 9C

8 291,327 1DM 5d

720 192 102 7UM 2DM 3CM 8DM 192,428 1CM 9DM 2UM 4d 2c 8m

12. 13. 14. Zone de travail

<, > ou = .

7DM 8CM 5C 3D 6UM 989 928,923

1UM 3DM 8CM 1d 9 283 283,29 9m 6U 8,009 9CM 6DM 7UM 6CM 4DM 1 021 122 002

Classe ces nombres dans l’ordre croissant.

Dans les nombres ci-dessus, entoure le chiffre des U en bleu, des UM en vert et des d en rouge.

Classe ces nombres dans l’ordre décroissant.

Conseils pédagogiques complémentaires

• Favoriser la verbalisation des élèves durant la correction collective pour expliquer clairement chaque démarche de résolution des exercices complexes (comme les exercices 7, 9, 10, 13 et 14).

• Lors de la correction, utiliser activement la projection au tableau interactif (ou la version papier agrandie si tableau interactif indisponible) afin de faciliter la visualisation des réponses correctes, notamment pour les exercices nécessitant un repérage précis (classement croissant et décroissant, décomposition précise).

• En complément ludique et numérique, les élèves pourraient, pour le côté concret, vérifier à partir d’une carte interactive (Google Maps) la superficie réelle d’une ville voisine ou d’un lieu de leur choix, puis comparer et classer ces nombres obtenus en groupe afin de consolider leurs acquis de manière motivante. Cette activité serait pertinente particulièrement pour compléter et enrichir les exercices 13 et 14 (classement croissant et décroissant).

ÉditionsVANIN

Activité 4 – Les proportionnalités

Exercice 1

Objectifs pédagogiques

• Introduire concrètement la notion de proportionnalité à travers une activité pratique.

• Favoriser la compréhension intuitive des quantités proportionnelles.

• Développer des compétences de mesure, de calcul et de collaboration entre élèves.

Matériel nécessaire (à préparer avant la leçon)

• Mettre en place, dans la classe, un comptoir ou un étalage contenant différents ingrédients nécessaires pour la recette des cookies (farine, sucre, beurre, chocolat noir, œufs, sucre vanillé, sel et levure chimique).

• Prévoir plusieurs paquets ou boites de chaque ingrédient en unités entières (par exemple 1 kg de farine, des paquets de sucre, des plaquettes de beurre entières, des tablettes de chocolat, etc.) afin que les élèves soient obligés d’effectuer des mesures précises pour prélever les quantités nécessaires.

• Mettre à disposition divers instruments de mesure clairement identifiables et utilisables par les élèves (balances, cuillères graduées, verres doseurs, etc.).

Déroulement

PETIT G ROUPE

• Former des groupes d’élèves en classe, idéalement des groupes de 4 (pas besoin de calculer au départ pour les élèves rencontrant des difficultés et attirer l’attention sur le côté ludique) ou 6 élèves pour simplifier les calculs initiaux et accompagner ceux rencontrant plus de difficultés.

• Expliquer clairement la consigne : « Chaque groupe va devoir préparer virtuellement la recette des cookies affichée au tableau (ou projetée sur tableau interactif). Mais attention, vous allez devoir adapter précisément les quantités d’ingrédients indiquées en fonction du nombre exact d’élèves dans votre groupe. Si la recette est prévue pour 4 personnes et que votre groupe est composé de 6 élèves, à vous de calculer précisément les quantités d’ingrédients nécessaires. Une fois votre calcul terminé, allez faire votre « shopping » au comptoir installé en classe. Prélevez uniquement les quantités nécessaires à votre groupe en utilisant les outils de mesure mis à votre disposition (balance, verre doseur, cuillères graduées, etc.). »

• Durant cette activité, l’enseignant(e) reste idéalement proche du comptoir afin d’observer et de valider les prises de mesure effectuées par les élèves, leur fournir des conseils pratiques et vérifier la pertinence de leurs calculs et proportions.

Anticipation des difficultés

• Difficultés éventuelles pour calculer les proportions (passage d’un groupe de 4 élèves à un groupe plus ou moins nombreux).

• Risque d’erreurs lors des mesures concrètes (lecture de balances, dosage précis).

Pistes de remédiation immédiate

ÉditionsVANIN

• Prévoir au départ un tableau affiché clairement en classe, facilitant les calculs de proportions les plus courantes (ex : multiplier ou diviser par 2, puis éventuellement par 1,5 pour les groupes de 6 élèves).

• Laisser à disposition des élèves en difficulté un petit guide simplifié avec quelques exemples de calculs proportionnels déjà réalisés.

Propositions de dépassement

• Demander aux élèves rapides ou avancés d’adapter les quantités pour un nombre plus complexe d’élèves (par exemple 5 ou 7 élèves), en leur proposant de justifier clairement et oralement leur méthode devant la classe.

• Proposer éventuellement aux élèves en dépassement d’imaginer une variante de recette en modifiant certains ingrédients, tout en respectant strictement le principe de proportionnalité, et leur demander de justifier oralement ces changements aux autres groupes.

1.

4. Les proportionnalités

Observe cette recette de cuisine.

Cookies maison

Dessert Temps de préparation : 15 min

Difficulté de la recette : ❀❀❀ Temps de cuisson : 10 min

Ingrédients (pour 4 personnes)

– 80 g de beur�e – 1 œuf

– 80 g de sucre

– 1 sachet de sucre vanillé

– 160 g de farine

– 100 g de chocolat noir

– 1 cuillère à café de sel

– 1 cuillère à café de levure chimique

Préparation de la recette

Préparer le four à 180° (thermostat 6).

Faire ramollir le beurre à température ambiante. Dans un saladier, mettre 80 g de beurre, incorporer le sucre, l’œuf entier, la vanille et mélanger le tout.

Ajouter petit à petit la farine mélangée à la levure, le sel et le chocolat coupé en petits morceaux.

Beurrer une plaque allant au four et former les cookies sur la plaque. Pour former les cookies, utiliser 2 cuillères à soupe et faire des petits tas espacés les uns des autres ; ils grandiront à la cuisson.

Recopie la liste des ingrédients nécessaires afin de pouvoir la réaliser en classe. Sois attentif(-ive) au nombre de personnes.

Oralement, explique ta réponse.

Cela dépend du nombre d’élèves en classe.

Nous organisons une fancyfair à l’école. Nous avons décidé de cuisiner des cookies pour 200 personnes afin de gagner de l’argent pour notre voyage de fin d’année. Dresse ci-dessous la liste des ingrédients nécessaires.

Il faut multiplier le tout par 50.

4 kg de beurre

50 œufs

50 sachets de sucre vanillé

8 kg de farine

5 kg de chocolat noir

50 cuillères à café de sel

4 kg de sucre

50 cuillères à café de levure

Réponds par vrai ou faux en fonction de la recette des cookies.

– Avec 1 kg de farine, j’aurai assez pour 80 personnes.

– Pour réaliser cette recette, j’ai besoin de 200 g de chocolat blanc pour 8 personnes.

– Avec 1 kg de chocolat noir, je peux en faire pour 20 personnes.

Complète ces étiquettes.

Conseils pédagogiques complémentaires

• Cette activité concrète et ludique facilite grandement l’entrée en matière de la notion mathématique de proportionnalité, tout en mobilisant des compétences transversales (mesure, travail en équipe, calcul mental et écrit).

• Il est conseillé de valoriser explicitement auprès des élèves la précision, la méthode et la coopération au sein des groupes durant cette activité pratique.

• Cette activité peut également être prolongée concrètement à la maison par la réalisation réelle de la recette en famille, favorisant ainsi le transfert des apprentissages mathématiques dans le quotidien des élèves.

Exercice 2

Objectifs pédagogiques

• Transférer concrètement la notion de proportionnalité travaillée en groupe vers une situation élargie à toute la classe.

• Renforcer les capacités à calculer précisément des quantités proportionnelles en fonction d’un nombre réel de personnes.

Déroulement

Après avoir réalisé la mise en situation précédente par groupes, attirer l’attention des élèves sur le fait qu’on aurait également pu envisager la réalisation de cette recette non plus par petits groupes, mais pour l’ensemble de la classe (enseignant(e) compris(e)).

Proposer clairement la consigne suivante : « Nous allons maintenant imaginer que nous réalisions les cookies pour toute la classe, sans oublier d’y inclure l’enseignant(e). Recopie donc dans ton cahier une nouvelle liste précise des ingrédients nécessaires à la réalisation de cette recette pour le nombre exact de personnes présentes aujourd’hui en classe. Sois attentif(-ive) à bien respecter les proportions ! Tu devras également expliquer oralement comment tu as obtenu ces nouvelles quantités. »

Organisation pédagogique

SO LO

Chaque élève réalise d’abord seul(e) le calcul précis des ingrédients nécessaires.

COLL ECTIF

Un temps de partage oral collectif suivra, durant lequel plusieurs élèves présenteront leurs calculs et expliqueront leur démarche clairement à la classe.

Anticipation des difficultés

• Risque de difficultés dans la réalisation précise des calculs proportionnels, notamment en passant d’un groupe restreint (4 ou 6 personnes) à un groupe plus important (classe entière).

Pistes de remédiation

ÉditionsVANIN

• Laisser à la disposition des élèves en difficulté une fiche simplifiée comportant les exemples de calculs précédents pour qu’ils (elles) puissent s’y référer facilement.

• Permettre à ces élèves d’effectuer cet exercice avec l’aide d’un(e) camarade (tutorat).

Proposition de dépassement

• Pour les élèves avancé(e)s, leur demander de réfléchir à une quantité supplémentaire en cas d’imprévu (par exemple, si une autre personne arrivait soudainement dans la classe), en explicitant clairement comment ils (elles) calculeraient rapidement les nouvelles quantités.

Conseils pédagogiques complémentaires

• Valoriser la diversité des stratégies utilisées par les élèves lors des explications orales afin de montrer clairement qu’il existe plusieurs façons d’obtenir une réponse juste dans ce type de calcul proportionnel.

• Utiliser cette activité pour sensibiliser les élèves à l’importance du calcul proportionnel précis dans des contextes réels et concrets du quotidien.

Exercices 3 à 5

Objectifs pédagogiques

• Vérifier la capacité des élèves à mobiliser leurs connaissances sur la proportionnalité dans des contextes différents (recette, affirmations vraies/fausses, prix).

• Renforcer l’autonomie et la confiance des élèves dans la manipulation des quantités proportionnelles.

Déroulement

SO LO

Ces trois exercices sont réalisés individuellement par chaque élève afin d’évaluer précisément sa maitrise de la proportionnalité à travers des contextes variés (recette multipliée, vrai/faux sur quantités, calcul de prix).

Exercice 3 :

COLL ECTIF

Les élèves adaptent une recette pour un grand nombre de personnes (200), exigeant des calculs proportionnels précis.

Exercice 4 :

Les élèves répondent par vrai ou faux à des affirmations en utilisant leur raisonnement proportionnel.

Exercice 5 :

Les élèves calculent des prix proportionnels ( 1 2 kg, 1 4 kg, etc.) à partir d’un prix au kg indiqué.

Une correction collective rapide et interactive est menée après la réalisation individuelle pour permettre à chacun(e) de vérifier ses réponses et de clarifier les éventuelles incompréhensions.

Anticipation des difficultés

• Risque d’erreurs fréquentes lors des calculs de proportions (notamment dans l’exercice 3).

• Difficultés possibles à comprendre rapidement les situations proposées dans l’exercice vrai/faux (exercice 4).

Pistes de remédiation

• Fournir un tableau récapitulatif simplifié avec quelques exemples clairs de calculs proportionnels courants.

• Permettre à certains élèves d’utiliser temporairement une calculatrice, si nécessaire, afin de vérifier rapidement leurs calculs.

Proposition de dépassement

• Pour les élèves rapides, proposer de créer eux-mêmes (elles-mêmes) quelques énoncés supplémentaires (vrai/faux ou prix proportionnels) pour enrichir l’activité et les présenter à leurs camarades en fin de séance.

ÉditionsVANIN

Conseils pédagogiques complémentaires

• Durant la correction collective, privilégier la participation orale des élèves pour expliquer et justifier clairement leurs démarches afin de renforcer la compréhension collective des stratégies utilisées.

• Encourager l’entraide et les échanges de stratégies entre pairs lors de la validation des réponses afin de favoriser l’autonomie et la confiance en eux.

Exercices 6 à 9

Objectifs pédagogiques

• Identifier clairement ce qu’est une proportionnalité directe et ce qui ne l’est pas.

• Analyser différentes situations concrètes (graphiques, tableaux, situations écrites) pour vérifier la présence ou non de proportionnalité directe.

• Expliquer oralement et justifier clairement son raisonnement à partir de critères mathématiques précis.

Processus clair à expliquer aux élèves (méthodologie)

COLL ECTIF

Présenter cette démarche collective sur le tableau interactif (ou affichage papier agrandi au tableau noir) avant que les élèves commencent leurs exercices individuellement.

Comment savoir si une situation est directement proportionnelle ?

Étape 1 : Observer attentivement la situation proposée.

Étape 2 : Identifier les deux grandeurs à comparer.

Étape 3 : Vérifier si les rapports entre ces grandeurs sont constants.

Pour cela, choisir plusieurs exemples différents dans la situation : – si les rapports entre ces grandeurs restent toujours identiques, alors la situation présente une proportionnalité directe ; – si les rapports varient, la situation n’est pas proportionnelle.

SO LO

COLL ECTIF

Les élèves réalisent individuellement les exercices, appliquant le processus expliqué ci-dessus. Ils (elles) analysent précisément chaque situation proposée (graphiques des pommes/oranges, énergie dépensée, tableaux de consommation, etc.) et concluent sur la présence ou non d’une proportionnalité directe en justifiant leur réponse clairement dans leur cahier.

À l’aide de la projection numérique ou du papier agrandi, réaliser collectivement une validation interactive pour chaque situation afin d’expliciter le raisonnement utilisé (rapport constant ou non entre les grandeurs concernées).

Anticipation des difficultés

• Difficultés potentielles à calculer ou vérifier les rapports entre grandeurs (erreurs de calcul fréquentes).

• Risque de confusion entre régularité et proportionnalité directe (ne pas confondre une augmentation constante avec une augmentation proportionnelle).

ÉditionsVANIN

Pistes de remédiation

• Proposer aux élèves en difficulté une fiche méthodologique plastifiée claire résumant le processus étape par étape.

• Permettre un travail assisté en petits groupes pour recalculer ensemble les rapports et visualiser plus clairement les liens proportionnels ou non.

Voici deux graphes fléchés représentant chacun une situation. Indique si la situation montre une relation de proportionnalité directe. Justifie ta réponse.

Situation A

Dans un verger, un agriculteur récolte des pommes. Le graphe fléché montre la relation entre le nombre de pommes récoltées et le temps passé à travailler dans le verger.

Récolte de pommes

Kg de pommes récoltées

Situation B

– 2 heures → 10 kg de pommes

– 4 heures → 20 kg de pommes

– 6 heures → 30 kg de pommes

Nombres d’heures passées dans le verger (en h)

Une machine emballe des oranges en sacs. Le graphe fléché montre la relation entre le nombre de sacs emballés et le nombre d’oranges utilisées.

Emballage d’oranges

Nombre d’oranges

– 1 sac → 8 oranges

– 2 sacs → 14 oranges

– 3 sacs → 23 oranges

Nombre de sacs

La situation A montre une proportionnalité directe. Chaque fois que le temps de travail double, le nombre de pommes récoltées double également. La relation entre le temps et la quantité est constante (rapport constant de 5 kg par heure). Tandis que la situation B ne montre pas une proportionnalité directe. Le nombre d’oranges n’augmente pas de façon proportionnelle par rapport au nombre de sacs (les écarts ne sont pas constants).

ÉditionsVANIN

Voici deux situations. Indique si la situation montre une relation de proportionnalité directe. Justifie ta réponse.

Situation A

Un sportif mesure la relation entre le nombre de répétitions d’exercices et l’énergie dépensée.

– 5 répétitions → 90 kcal

– 10 répétitions → 185 kcal

– 15 répétitions → 290 kcal

Situation B

Un second sportif effectue des répétitions d’exercices et la dépense d’énergie est mesurée.

– 5 répétitions → 150 kcal

– 10 répétitions → 300 kcal

– 15 répétitions → 400 kcal

La situation B, car la dépense d’énergie est constante, tandis que dans la situation A, la dépense d’énergie n’augmente pas de manière proportionnelle par rapport au nombre de répétitions. Les écarts ne sont pas constants.

Lesquels de ces tableaux représentent une proportionnalité directe ? Justifie ta réponse en vérifiant les rapports entre les grandeurs.

1. Consommation d’eau (en litres) en fonction du nombre de jours

Nombre de jours Consommation d’eau (en litres)

2. Distance parcourue (en km) en fonction du nombre d’heures

d’heures

3. Quantité de pommes achetées (en kg) en fonction du prix payé (en €)

Les tableaux 1 et 3 montrent des grandeurs proportionnelles, car le rapport entre les grandeurs reste constant. Le tableau 2, en revanche, ne montre pas de proportionnalité directe, car le rapport entre le temps et la distance n’est pas constant.

Pour chaque situation, identifie s’il s’agit d’une relation de proportionnalité directe. Colorie la bonne réponse.

Situation 1 : Paniers de légumes

– Analyse : Chaque panier coute 22 € et le prix total est proportionnel au nombre de paniers vendus. Pour chaque panier supplémentaire, le prix augmente de 22 €, ce qui est un rapport constant.

ÉditionsVANIN

Proportionnalité directe

Pas de proportionnalité directe

Situation 2 : Randonneurs

– Analyse : Au fil de la marche, le rythme diminue, ce qui rend les écarts de distance irréguliers (4 km, puis + 3 km, puis + 2 km, puis + 1 km).

Proportionnalité directe

Pas de proportionnalité directe

Proposition de dépassement

• Inviter les élèves avancés à créer eux-mêmes (elles-mêmes) une situation de proportionnalité directe et une autre sans proportionnalité directe, à présenter oralement à leurs camarades. Ils (elles) justifieront clairement la différence à travers des exemples de leur choix.

Conseils pédagogiques complémentaires

• Encourager fortement la verbalisation des élèves pendant la correction collective afin de s’assurer qu’ils (elles) maitrisent clairement le concept mathématique de proportionnalité directe.

• Renforcer l’analyse visuelle et orale des graphiques en utilisant la projection au tableau interactif (ou sur papier agrandi) pour faciliter la compréhension et encourager l’explication orale des choix effectués.

• Le tutorat ponctuel peut être organisé entre élèves rapides et élèves rencontrant des difficultés sur ces exercices, ce qui favorise une dynamique d’entraide efficace au sein de la classe.

ÉditionsVANIN

Activité 5 – Un peu d’entrainement : l’addition écrite

Objectifs pédagogiques

• Rappeler et consolider les stratégies de l’addition écrite posée (alignement des chiffres par classe : unités, dizaines, centaines, etc.).

• Introduire ou rappeler clairement le concept mathématique d’estimation.

• Comprendre l’utilité pratique de l’estimation avant de réaliser une opération précise.

Déroulement

COLL ECTIF

1. Rappel sur l’addition écrite

• L’enseignant(e) projette sur le tableau interactif (ou sur papier agrandi au tableau noir) une addition écrite simple en colonne (par exemple : 12 345 + 6 789 + 23).

• Rappeler explicitement les étapes importantes :

– Aligner soigneusement les nombres (unités sous unités, dizaines sous dizaines, etc.).

– Commencer l’addition par les unités, puis les dizaines, puis les centaines, etc.

– Faire attention aux retenues éventuelles.

2. Présentation du concept d’estimation

• Expliquer clairement que l’estimation consiste à simplifier les nombres en les arrondissant afin de pouvoir calculer mentalement et rapidement une approximation du résultat.

• Souligner l’utilité concrète de l’estimation :

– Permettre de vérifier rapidement la cohérence d’un résultat obtenu.

– Éviter des erreurs grossières et vérifier la pertinence des résultats finaux.

Exemple d’estimation présenté au tableau

Si je dois calculer précisément 345 + 289, je peux d’abord estimer en arrondissant : 350 + 290 ≈ 640. Ainsi, après le calcul précis (634), je vérifie que mon résultat est cohérent avec mon estimation.

SO LO

Les élèves réalisent seuls les additions proposées. Avant chaque opération précise, ils (elles) notent une estimation approximative du résultat, en arrondissant mentalement les nombres proposés. Une fois l’estimation notée, ils (elles) réalisent l’addition écrite précisément dans les cases prévues.

COLL ECTIF

Après la phase individuelle, procéder à une correction collective dynamique en envoyant plusieurs élèves au tableau interactif.

Chaque élève volontaire (ou désigné) réalisera au tableau une des additions proposées et expliquera brièvement devant la classe sa stratégie d’estimation ainsi que sa méthode pour poser correctement l’addition écrite.

L’enseignant(e) veillera à valoriser explicitement les stratégies efficaces utilisées par les élèves au tableau, ainsi que leur capacité à vérifier la cohérence entre les estimations initiales et les résultats exacts obtenus.

Anticipation des difficultés

• Difficultés possibles à aligner correctement les chiffres par colonne pour l’addition écrite.

• Difficulté à estimer efficacement (arrondis non maitrisés ou hésitations sur les nombres à arrondir).

Pistes de remédiation

• Distribuer aux élèves en difficulté une fiche-rappel plastifiée sur l’alignement des chiffres en colonnes.

• Proposer également une fiche méthodologique simplifiée rappelant clairement les étapes d’une bonne estimation par arrondi.

5. Un peu d’entrainement : l’addition écrite

Estime avant d’opérer.

8 239 128 + 140 751 =

Estimation : 2 200 281 + 101 + 24 239 114 = Estimation :

672 001,24 + 265 + 12 101,008 =

Estimation :

Estimation : 1 923 + 243 038 + 82 362 =

Estimation :

+ 450 312 =

+ 2 099,003 + 183 939 =

Proposition de dépassement

• Pour les élèves avancés, proposer d’effectuer d’autres additions écrites plus complexes ou de créer leurs propres opérations en intégrant des nombres décimaux, en réalisant également les estimations préalables.

Conseils pédagogiques complémentaires

• Valoriser explicitement la cohérence entre estimation et résultat exact durant la correction collective afin que les élèves perçoivent l’intérêt concret du processus d’estimation dans la vérification de leurs résultats.

• Encourager les élèves à verbaliser leurs stratégies arrondi et leurs méthodes de calcul afin d’enrichir les échanges méthodologiques entre pairs.

• Favoriser une ambiance constructive et bienveillante où les élèves se sentent confiants pour partager leurs méthodes et stratégies devant la classe.

ÉditionsVANIN

6. Un peu d’entrainement : la soustraction écrite

Estime avant d’opérer.

– 145 262 = Estimation :

– 23 839 =

Activité 6 – Un peu d’entrainement : la soustraction écrite

Objectifs pédagogiques

• Rappeler et renforcer les stratégies liées à la soustraction écrite posée (alignement des chiffres, gestion des retenues).

• Réinvestir explicitement le concept d’estimation déjà utilisé dans l’addition écrite.

• Montrer l’utilité pratique de l’estimation pour anticiper et vérifier les résultats d’une soustraction.

COLL ECTIF

1. Rappel sur la soustraction écrite

• Projeter au tableau interactif (ou sur papier agrandi si tableau interactif indisponible) une soustraction écrite simple (par exemple : 7 452 – 3 678).

• Rappeler oralement les étapes essentielles :

– Alignement précis des nombres (unités, dizaines, centaines, etc.).

SO LO

COLL ECTIF

– Soustraire toujours en commençant par les unités, puis les dizaines, puis les centaines, etc.

– Rappel du concept d’emprunt : comment l’utiliser correctement.

2. Faire un lien avec l’estimation revue précédemment (addition)

• Réactiver oralement le principe déjà vu : « Comme pour l’addition, avant de calculer précisément, nous pouvons d’abord estimer en arrondissant les nombres afin d’avoir une idée rapide et approximative du résultat attendu. Cela nous permet ensuite de vérifier que notre résultat précis semble cohérent. »

• Illustrer par un exemple rapide projeté : Si je dois calculer précisément 452 – 198, je peux d’abord estimer : 450 – 200 ≈ 250.

Après le calcul précis (254), je vérifie rapidement que mon résultat exact est proche de mon estimation.

Chaque élève réalise individuellement les soustractions écrites proposées.

Avant de procéder à chaque opération précise, les élèves notent une estimation approximative du résultat, basée sur un arrondi mental simple.

Ils (elles) procèdent ensuite à la soustraction précise dans les cases prévues à cet effet.

Après la réalisation individuelle, organiser une correction collective dynamique en envoyant plusieurs élèves au tableau interactif.

Chaque élève sélectionné(e) présente et explique brièvement, devant la classe, sa stratégie d’estimation ainsi que la manière dont il a posé et résolu sa soustraction écrite précisément.

L’enseignant(e) valorise clairement la cohérence entre les estimations initiales et les résultats précis obtenus en encourageant explicitement les élèves à justifier leurs stratégies.

Anticipation des difficultés

ÉditionsVANIN

• Risque de difficultés dans l’utilisation correcte des emprunts lors des soustractions.

• Possibilité d’erreurs d’alignement des chiffres.

• Difficulté éventuelle à effectuer une estimation rapide et juste.

Pistes de remédiation

• Fournir aux élèves en difficulté une fiche-rappel plastifiée sur la gestion des emprunts dans les soustractions.

• Proposer un rappel méthodologique clair sur la technique d’estimation par arrondi, similaire à celle déjà utilisée pour l’addition.

Propositions de dépassement

• Pour les élèves avancés, proposer des soustractions plus complexes impliquant davantage de nombres décimaux ou à grands nombres.

• Les inviter à créer eux-mêmes de nouveaux exercices avec des estimations préalables, à proposer ensuite à la classe.

Conseils pédagogiques complémentaires

• Favoriser la verbalisation des méthodes de calcul et d’estimation afin de rendre visibles les différentes stratégies utilisées par les élèves.

• Encourager fortement l’entraide entre pairs durant la correction interactive afin de valoriser les réussites individuelles tout en soutenant collectivement les élèves en difficulté.

• Maintenir un climat de confiance et de respect durant les présentations au tableau pour renforcer positivement l’estime de soi des élèves lorsqu’ils (elles) expliquent leur raisonnement devant leurs camarades.

ÉditionsVANIN