LIVRE-CAHIER
MATH PERSPECTIVE
Versionprovisoire
Versionprovisoire
TABLE DES MATIÈRES
Perspective Math ‒ 1re année (version provisoire)
Chapitre 1 : Différents types de nombres
Partie 1 – Nombres positifs
A.Nombres positifs
B.Plusieurs écritures pour un même nombre
C.Transformation de l’écriture d’un nombre
D.Fractions équivalentes
E.Droite graduée
F.Comparaison
G.Encadrement et valeurs approchées
H.Arrondis
Partie 2 – Nombres négatifs
A.Nombres entiers
B.D’autres nombres négatifs
C.Comparaison
D.Encadrement et valeurs approchées
E.Arrondis
Partie 3 – Ensembles de nombres
Chapitre 2 : Objets de base en géométrie
Défi
A.Notations, codages et mesures
B.Positions relatives de droites
C.Médiatrice d’un segment et bissectrice d’un angle
D.Paires d’angles
Retour au défi
Chapitre 3 : Opérations sur des nombres
Partie 1 – Nombres positifs
A.Opérations et estimation
B.Propriétés des opérations
C.Techniques de calcul de produits et de quotients
D.Puissances d’un nombre
E.Puissances de 10 et préfixes
F.Priorités des opérations
Partie 2 – Nombres négatifs
A.Somme de deux nombres
B.Différence entre deux nombres
C.Somme et différence de deux nombres
D.Somme et différence de plus de deux nombres
E.Produit et quotient de deux nombres
Versionprovisoire
F.Produit de plusieurs nombres
G.Opérations
H.Priorités des opérations
Chapitre 4 : Repérage dans le plan
Défi
A.Coordonnées d’un point dans un repère orthonormé
B.Ensemble de points
Chapitre 5 : Fractions et pourcentages
Question de réflexion
A. Pourcentage d’une quantité
B. Pourcentage ajouté ou déduit
C. Pourcentages successifs
D. Rapport en pourcents
Retour au défi
Chapitre 6 : Figures planes
Partie 1 – Les triangles
A. Constructions de base
B. Amplitude des angles
C. Droites remarquables
D. Triangle et cercles
Partie 2 – Les quadrilatères
A. Types de quadrilatères
B. Amplitude des angles d’un quadrilatère
C. Droites remarquables d’un quadrilatère
Partie 3 – Figures complexes
A. Programme de construction
B. Amplitude des angles
C. Polygones réguliers
D. Défi artistique
Chapitre 7 : Traitement de données
A. Première analyse de données
B. Population et variable statistique
C. Modalité, effectif, fréquence et étendue
D. Moyenne
Chapitre 8 : Isométries
A. Des mouvements vers les isométries
B. La translation
C. Symétrie orthogonale
D. Axe(s) de symétrie
E. La rotation
F. La symétrie centrale
G. Centre de symétrie
Chapitre 9 : Périmètre et aire de figures
Défi
A. Périmètre de polygones
B. Périmètre du cercle
C. Aires de figures simples
D. Aire du disque
E. Aire et périmètre de figures complexes
Retour au défi
Versionprovisoire
Chapitre 10 : Expressions algébriques
Chapitre 11 : Proportionnalité directe
Versionprovisoire
CHAPITRE 2
O bjets de base en gé O métrie
Versionprovisoire
s ouviens-toi
1. Associe l’objet géométrique à son nom et à sa notation mathématique.
Objet Nom
Notation
Un point [ AB ]
Une droite A Un segment a
2. Associe la représentation géométrique de chaque objet à sa description et à sa notation mathématique.
Représentation
Deux droites perpendiculaires
Deux droites parallèles a // b
Un point sur une droite a ⊥ b
3. Indique le numéro des angles qui sont…
aigus : droits : obtus :
4. Convertis les cm en mm et inversement. 13 cm = mm 47 mm = cm 5 mm = cm 3,5 cm = mm
5. Mesure chaque segment et indique sa longueur.
6. Observe le dessin et coche, dans chaque cas, la proposition correcte.
(1) La droite perpendiculaire à la droite d et passant par le point C est… f g h
(2) Le point d’intersection des droites h et f est…
(3) Les droites g et f sont… parallèles perpendiculaires
7. Trace une droite… (1) perpendiculaire à la droite d. (2) parallèle à la droite f.
d éfi
Versionprovisoire
Tu as peut-être déjà vu une lumière s’allumer sur le rétroviseur d’une voiture. Il s’agit d’un détecteur d’angle mort.
Dans cette situation, les détecteurs d’angle mort de la voiture rouge se sont allumés.
Quel(s) usager(s) de la route l’a (les ont) déclenché(s) ?
À la fin de ce chapitre, tu seras capable de répondre à cette question.
n otations, codages et mesures
1. Un jeu consiste à assembler des lattes en bois au moyen de vis. De cette manière, il est possible de former des angles d’amplitudes variables. Observe les différentes photos, qualifie chaque angle marqué et indique toutes les amplitudes possibles de ce type d’angle. N° Type d’angle
Amplitude(s) possible(s)
2. Observe l’image et réponds aux questions.
(1) Catégorise les trois angles distincts formés par les deux lattes.
(2) Que représente la vis de fixation par rapport à ces angles ?
(3) À quel objet géométrique te fait penser la latte horizontale ?
(4) Quelle différence y a-t-il entre la latte horizontale et la latte oblique ?
3. Observe le dessin simplifié des lattes en bois sur lequel plusieurs points ont été ajoutés.
(1) Décris les objets géométriques cités.
[AX :
MY :
(2) Indique toutes les notations mathématiques possibles de l’objet géométrique MY.
(3) Marque les trois angles sur le dessin et, en t’aidant de l’indice, donne une notation mathématique pour chacun d’eux.
Pour différencier les angles, on nomme chacun d’eux en utilisant trois points : un provenant de chaque côté de l’angle et un pour le sommet, toujours noté au milieu.
Pour un angle de sommet B et dont les côtés passent par les points A et C, on note ABC ou CBA
(4) Il aurait également été possible de numéroter tous les angles sur le dessin. De cette manière, modifie les notations de la question précédente en t’inspirant de l’exemple.
4. Complète le tableau avec le descriptif ou la notation mathématique.
Descriptif
Le segment dont les extrémités sont les points M et N.
La droite passant par les points X et Y.
L’angle de sommet A dont les côtés sont les demi - droites [ AB et [ AC.
Notation mathématique
5. (1) Construis les objets géométriques
[ AC ] , [ XV, MF et XOM
(2) Complète par ∈ ou ∉ .
P MF P OX
6. Entoure les objets qui peuvent être mesurés.
PointSegmentDemi-droiteAngleDroite
Pour noter la mesure d’un objet, on indique son nom entre deux barres verticales
L’ amplitude de l’angle A se note .
La longueur du segment [ AB ] se note | AB |
7. Dans chaque cas, traduis en langage mathématique l’information indiquée sur le dessin.
8. Sur la base des notations mathématiques fournies, annote le dessin au moyen de codes, de lettres ou de mesures.
(1) | CA | = 3 cm (4) | AC | = | CD |
(2) DE ⊥ BC (5)
(3) ACB = 80° (6) F ∈ [ AB ] et | AF | = | FB |
9. Complète chaque étiquette en qualifiant l’angle marqué. Ensuite, mesure son amplitude en prolongeant, si nécessaire, un de ses côtés.
10. Dans un premier temps, mesure et indique les longueurs des côtés et l’amplitude des angles intérieurs de la figure. Ensuite, sur le dessin, indique le codage qui te permet de repérer les angles de même amplitude et les côtés de même longueur.
11. Construis les angles si tu sais que DAC = 84°, MEL = 130°, TUV = 210° et O = 105°.
Je rédige mon procédé pour utiliser correctement le rapporteur
Positions relatives de droites
1. Pour embellir un mur, on utilise parfois une frise géométrique formée de figures qui se répètent. Dans ce cas, il s’agit d’un assemblage de triangles rectangles isocèles.
(1) Sans mesurer et en ne traçant que des parallèles et des perpendiculaires, poursuis la frise proposée.
(2) Repère deux droites parallèles et nomme-les a et b.
Exprime leur position relative en langage mathématique :
(3) Repère deux autres droites qui sont perpendiculaires et nomme-les c et d.
Code le dessin et exprime leur position relative en langage mathématique :
(4) Repère deux autres droites qui possèdent un point d’intersection et qui ne se coupent pas en formant quatre angles droits. Nomme-les e et f.
Exprime leur position relative en français et en langage mathématique.
2. Poursuis la construction en suivant les étapes.
– Trace la droite AB.
– Construis la droite d parallèle à la droite AB passant par C.
– Construis la droite f perpendiculaire à la droite AB passant par C.
– Nomme E le point d’intersection de AB et de la droite f.
3. Réalise la construction en suivant les étapes.
– Construis un segment [ XY ] de 28 mm.
– Construis un segment [ MX ] de 20 mm perpendiculaire au segment [ XY ] . – Trace la droite MY.
– Construis la droite b parallèle à la droite MY passant par le point X.
4. Poursuis la construction en suivant les étapes.
– Trace AB.
– Construis d ⊥ AB telle que B ∈ d. – Place C ∈ d tel que | BC | = 20 mm. – Construis b // AB telle que C ∈ b.
– Construis AD // BC telle que D ∈ b.
5. Reproduis ces figures en vraie grandeur en tenant compte de toutes les informations présentes.
médiatrice d’un segment et bissectrice d’un angle
1. Le tir à l’arc classique est un sport qui consiste à viser une cible de 122 cm de diamètre placée à une distance variant de 20 à 70 m selon la catégorie du tireur. Les archers fixent l’encoche de la flèche à la corde avant de la mettre sous tension pour viser et tirer.
(1) Décris la position de la flèche par rapport à la corde et code chaque dessin.
Encocher la flèche Viser pour tirer
(2) Dans chaque situation, trace avec précision la droite sur laquelle positionner la flèche. Ensuite, complète les phrases.
La droite tracée est du segment [ BC ]
La droite tracée est de l’angle BAC .
Je rédige ma définition de la médiatrice d’un segment et de la bissectrice d’un angle
2. Complète le tableau en indiquant une croix lorsque la droite citée est la médiatrice du s egment [ AB ] et/ou la bissectrice de l’angle BCA
Médiatrice de [ AB ]
Bissectrice de BCA
d 1 d 2 d 3 d 4 d 5 d 6 d 7
3. Construis la médiatrice des segments et la bissectrice des angles.
4. Construis…
(1) le segment [ BF ] dont la droite m est la médiatrice.
(2) l’angle IHG dont la droite b est la bissectrice.
5. (1) Réalise la construction en respectant les indications.
| AB | = 40 mm
d ⊥ [ AB ] et B ∈ d
C ∈ d et | BC | = 4 cm
P ∈ [ AB ] et
(2) Caractérise la droite PC.
(3) Complète par = ou ≠.
| AC | | BC | | AB | | BC | | AP | | PB |
Paires d’angles
1. (1) Procède par étape pour identifier les figures à éliminer.
Étape 1 : Barre les figures dont les angles marqués n’ont pas le même sommet.
Étape 2 : Parmi les figures restantes, barre celles dont les angles marqués n’ont pas de côté commun.
Étape 3 : Parmi les figures restantes, barre celles dont les angles marqués ne sont pas situés de part et d’autre de leur côté commun.
Les paires d’angles qui n’ont pas été barrés portent les numéros et Ces angles sont appelés angles adjacents
(2) Complète.
Deux angles adjacents ont le même , un commun et sont situés de ce côté commun.
2. Observe les angles formés par la grande aiguille, la petite aiguille et la trotteuse de ces deux horloges. Réponds aux questions.
(1) Dans chaque cas, les angles marqués sont-ils adjacents ?
(2) Complète.
Sur la première horloge, les deux angles forment un angle
Ils sont appelés angles
A 1 + = A 2 | || |
Sur la seconde horloge, les deux angles forment un angle
Ils sont appelés angles B 1 +B 2 = ||||
3. Pour chaque figure, indique une croix dans la (les) case(s) adéquate(s). Si les angles sont complémentaires ou supplémentaires, écris la relation entre leurs amplitudes.
N°AdjacentsComplémentairesSupplémentaires Relation entre les amplitudes
4. On a marqué et nommé deux angles formés par les aiguilles d’une horloge.
(1) Réponds par vrai ou faux.
Les angles ont le même sommet.
Les angles sont adjacents.
Les angles sont complémentaires.
Les angles sont supplémentaires.
Les angles ont la même amplitude.
Ces angles sont appelés angles opposés par le sommet
(2) Complète.
Deux angles opposés par le sommet ont le même et les côtés de l’un sont des côtés de l’autre.
(3) Complète la propriété des amplitudes de cette paire d’angles.
Des angles opposés par le sommet ont Traduis cette propriété en langage mathématique.
5. Dans chaque cas, indique par oui ou non si les angles marqués sont opposés par le sommet.
6. Dans chaque cas, détermine l’amplitude de l’angle BAC . Justifie.
D, A et B sont alignés.
E E, A et D sont alignés.
Je rédige mon procédé pour déterminer l’amplitude d’un angle
D, A et B ainsi que E, A et C sont alignés.
r etour au défi
Les angles morts sont les zones que le conducteur ne peut pas, ou très difficilement, voir lorsqu’il conduit.
Le système de détection des angles de la voiture utilise des capteurs pour détecter les véhicules situés dans ces angles. Dans ce cas, le système alerte le chauffeur grâce à un témoin lumineux discret intégré aux deux rétroviseurs extérieurs.
Reprenons la situation décrite en début de chapitre.
(2) Sans mesurer, qualifie les angles décrits.
L’ensemble des angles verts forment un angle
(1) Quel(s) usager(s) de la route a (ont) déclenché les détecteurs d’angle mort ?
L’ensemble des angles couverts par les rétroviseurs forment un angle
(3) Mesure l’amplitude de chaque angle mort.
(4) Quelle portion de la vision à 360°, exprimée par une fraction irréductible, est réellement couverte par le chauffeur ?
Détermine, au pour cent près, le pourcentage de visibilité du chauffeur.
Vision nette
Mouvement des yeux
Mouvement des yeux
Angle mort droit
Rétro intérieur
Rétro extérieur droit
Rétro extérieur gauche
Angle mort gauche
Mouvement de la tête et des yeux
Mouvement de la tête et des yeux
Versionprovisoire
CÔ té P rati QU e e X er C i C es CO m PL émentaires
1. Traduis chaque phrase par une notation mathématique.
La droite passant par les points M et N.
L’amplitude de l’angle de sommet O vaut 70°.
Le segment dont les extrémités sont les points A et B.
2. Traduis chaque notation mathématique par une phrase.
[ XY | KL | = 7 cm | AP | T RS
3. Mesure l’amplitude des angles marqués et qualifie-les.
4. Construis les angles mesurant respectivement…
(1) 45°, 60°, 120° et 270°. (2) 35°, 95°, 162° et 214°.
5. Des caméras munies de capteurs de mouvement (C 1 , C 2 …) ont été placées à certains points stratégiques d’un mur d’enceinte d’une propriété privée.
(1) Mesure l’amplitude des angles de vue de chacune des caméras.
(2) Un capteur détecte un mouvement autour de lui jusqu’à 20 m. En tenant compte que, sur le plan, 1 cm représente 10 m, colorie la zone qui n’est pas couverte par les capteurs de mouvement.
(3) Le propriétaire pourrait-il faire le gain de quelques caméras, car leur action est déjà couverte par une autre ? Si oui, cite leur numéro.
6. Traduis par une phrase.
AB // CD [ AB ] // [ CD ] A ∈ b a ⊥ d [ AB // d B ∉ AC /
C5
C4
C3
C2
C1
C6
7. L is les informations et indique, sur le dessin, le nom de chacune des droites.
8. (1) Construis les droites a et b parallèles à la droite d passant respectivement par les points A et B.
Exprime la position relative des droites a et b à l’aide de la notation mathématique adéquate.
(2) Construis les droites AX et BY perpendiculaires à la droite d sachant que les points X et Y lui appartiennent.
Exprime la position relative des droites AX et BY à l’aide de la notation mathématique adéquate.
9. (1) Trace une droite d perpendiculaire à la droite c.
Décris la position relative des droites d et b.
Quelle conclusion peux-tu tirer de cet exercice ?
(2) Complète par //, // ou ⊥ .
10. Dans chaque cas, réalise la construction en respectant les étapes. Réponds ensuite à la question qui t’est posée.
(1)
– Construis un segment [ AB ] de 4 cm.
– Par A, construis la droite d perpendiculaire au segment [ AB ]
– Place un point C sur la droite d.
– Trace la droite t passant par B et par C.
– Par A, construis la droite p parallèle à la droite t.
Quelle est la position relative des droites d et p ?
(2)
– Construis ARB || = 100° avec | RA | = 3 cm et | RB | = 4 cm.
– Construis CB // RA avec | BC | = 3 cm.
Envisage toutes les possibilités. Quelle est, dans chaque cas, la position relative des droites AC et RB ?
11. Reproduis les figures, réalisées à main levée, en vraie grandeur et code tes constructions.
(1) A, E et D sont alignés et C ∈ BD.
12. (1) Code la figure avec toutes les informations.
| CP | = | PB | d ⊥ CB
| PE | = 4 cm
CBA || = 130° | PB | = | BA | | DE | = 2 cm DEP= PEA ||||
(2) De quel segment et de quel angle la droite d est-elle respectivement la médiatrice et la bissectrice ? Justifie à l’aide des notations mathématiques.
La droite d est la … du segment [ BC ] , car …
La droite d est la … de l’angle DEA , car …
13. En prenant soin de coder tes constructions, construis…
(1) la médiatrice du segment.(2) la bissectrice de chaque angle.
14. Dans la figure, repère les droites AF, CE et DE. Pour chacune d’entre elles, reconnais s’il s’agit d’une médiatrice et/ou d’une bissectrice. Précise de quel segment et/ou de quel angle.
15. En te basant sur l’amplitude de l’angle marqué sur le dessin, détermine l’amplitude de l’angle A 2 et celle de l’angle A 3 . Justifie.
16. Parmi les angles marqués, trouve une paire d’angles…
(1) complémentaires adjacents.
(2) supplémentaires adjacents.
(3) complémentaires non adjacents.
(4) opposés par le sommet.
(5) supplémentaires non adjacents.
17. Construis…
(1) deux angles supplémentaires non adjacents dont l’un des deux mesure 132°.
(2) deux angles complémentaires adjacents dont l’un des deux mesure 30°.
(3) deux angles opposés par le sommet de 50°.
18. Sur la figure, la droite EY est la médiatrice du segment [AB] et la bissectrice de l’angle XEZ
Détermine l’amplitude des angles XEY , AEY et E AX . Justifie.
CÔTÉ PRATIQUE
Représentation et notation
Le point A A
Segment
Point
Représentation, notations et mesure
Le segment [AB] ou le segment [BA] A B
3,5cm3,5cm
La longueur du segment [AB] est de 3,5 cm.
On note : |AB| = 3,5 cm.
Représentation et notation
La demi-droite [AB A B A B d
Demi-droite
Représentation et notations A
La droite d, la droite AB ou la droite BA
Représentation, notations et mesure
Droite Angle
40° B O
L’angle O, l’angle AOB ou l’angle BOA
L’amplitude de l’angle O est de 40°.
On note : |O| = 40° ou |AOB| = 40°.
Particularités des angles
Types d’angles
Rentrant
Paires d’angles particuliers
Adjacents
Complémentaires
Supplémentaires Opposés par le sommet
= 180° = 90°
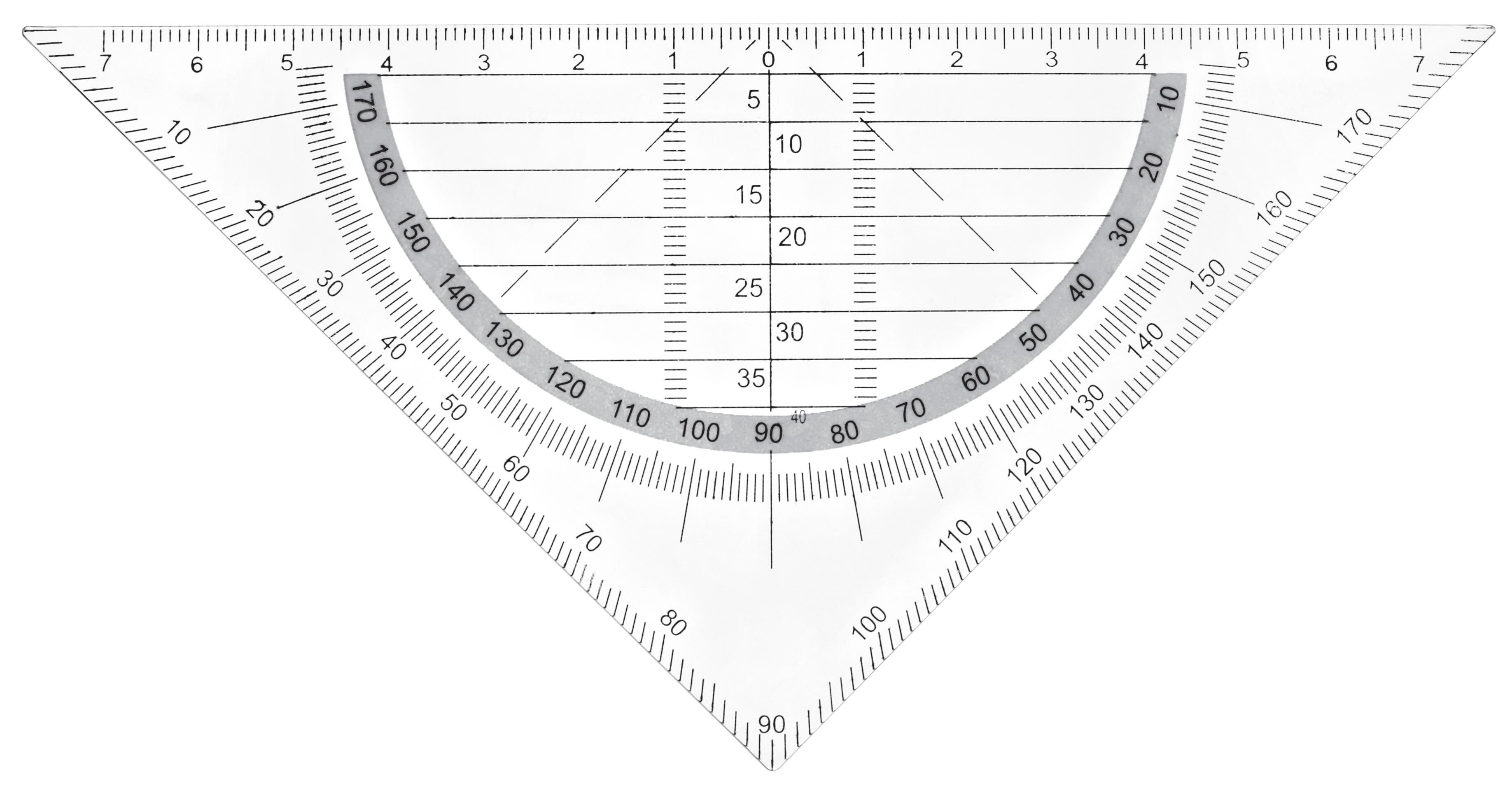
Mesure de l’amplitude d’un angle
1. Place le « zéro de l’équerre » sur le sommet de l’angle et aligne sa base avec un des côtés de l’angle.
2. Des deux rapporteurs présents sur l’équerre, choisis celui dont 0° se situe sur ce côté.
3. Repère l’amplitude de l’angle indiquée par le deuxième côté (après l’avoir prolongé si c’est nécessaire).
4. Note cette amplitude sur le dessin ou en notation mathématique.
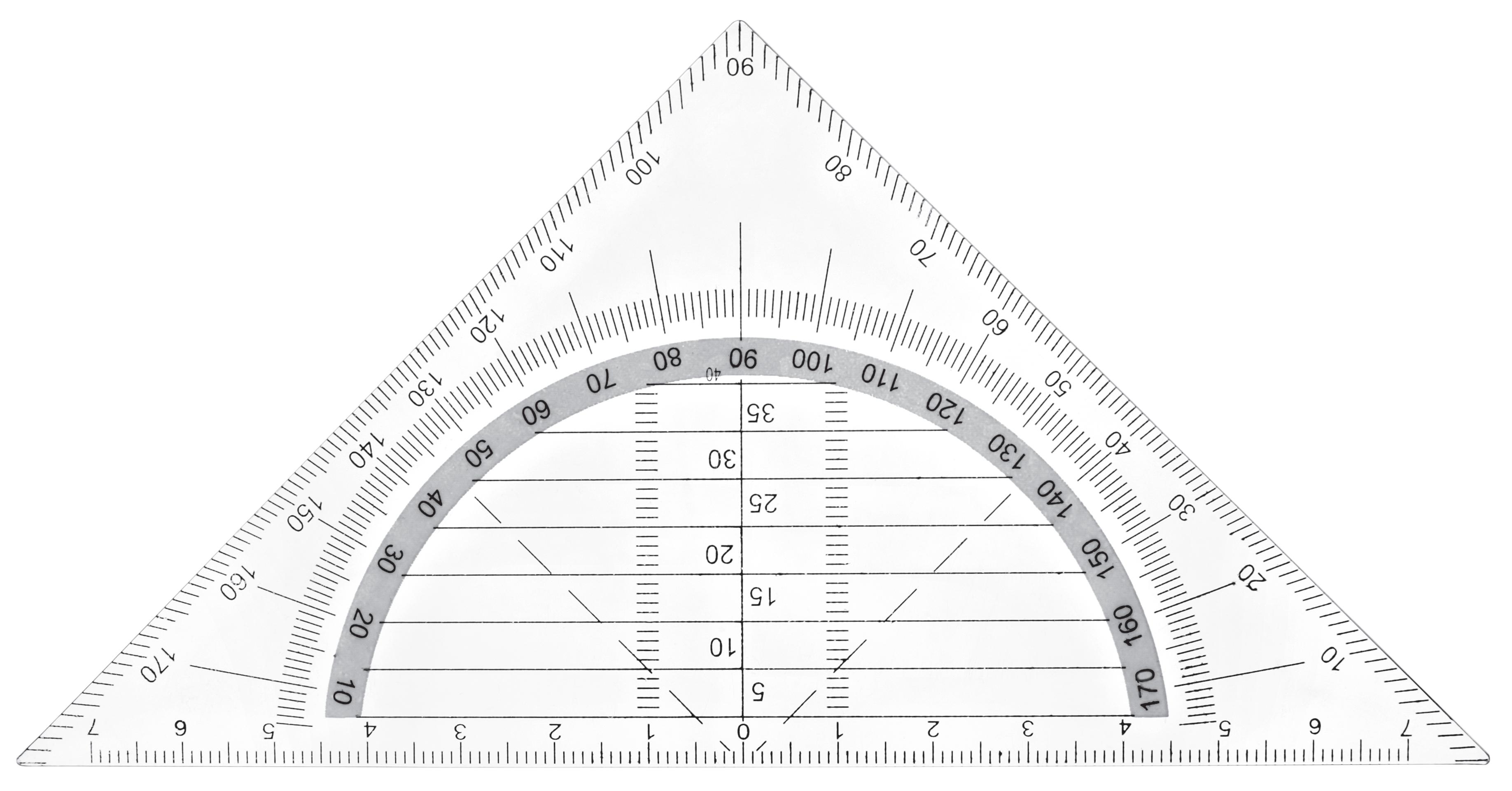
|A| = 40°
Construction d’un angle dont l’amplitude est donnée
1. Place le « zéro de l’équerre » sur le sommet de l’angle et aligne sa base avec le côté de l’angle déjà construit.
2. Des deux rapporteurs présents sur l’équerre, choisis celui dont 0° se situe sur ce côté.
3. Marque un trait au niveau de l’amplitude demandée.
4. Trace le deuxième côté de l’angle en reliant le trait au sommet de l’angle.
|A| = 120°
Positions relatives de deux droites b a b a ⊥ // /
Parallèles Sécantes Perpendiculaires b b // b b a a a a
Particularités des droites
Construction de la médiatrice d’un segment
1. Mesure le segment.
|YX| = 2,8 cm
2. Marque un point au milieu du segment.
Z ∈ [YX]
|YZ| = |ZX| = 1,4 cm
3. Trace la droite perpendiculaire au segment passant par ce milieu.
Z ∈ m et m ⊥ [YX]
Cette droite est la médiatrice du segment.
La droite m est la média⊥rice du segment [YX]
m Z
Construction de la bissectrice d’un angle
1. Mesure l’amplitude de l’angle.
== 28° = 56°
2. Marque un trait à la moitié de l’amplitude mesurée.
3. Trace la droite passant par ce trait et le sommet de l’angle. BE
Cette droite est la bissectrice de l’angle.
La droite BE est la bissectrice de l’angle CEL.
CÔTÉ THÉORIQUE
n otion d éfinition
Angle nul
Angle aigu
Angle droit
Angle obtus
Angle plat
Angle rentrant
Angle plein
Angle dont l’amplitude vaut 0°.
Angle dont l’amplitude est comprise entre 0° et 90°.
Angle dont l’amplitude vaut 90°.
Angle dont l’amplitude est comprise entre 90° et 180°.
Angle dont l’amplitude vaut 180°.
Angle dont l’amplitude est comprise entre 180° et 360°.
Angle dont l’amplitude vaut 360°.
Droites parallèlesDroites qui n’ont aucun point d’intersection.
Droites sécantesDroites qui ont un point d’intersection.
Droites perpendiculairesDroites sécantes qui forment des angles droits.
Médiatrice d’un segmentDroite perpendiculaire au segment et passant par son milieu.
Bissectrice d’un angleDroite coupant l’angle en deux angles de même amplitude.
Angles adjacents
Deux angles qui ont le même sommet, un côté commun et qui sont situés de part et d’autre de ce côté commun.
Angles complémentairesDeux angles dont la somme des amplitudes vaut 90°.
Angles supplémentairesDeux angles dont la somme des amplitudes vaut 180°.
Angles opposés par le sommet
Deux angles qui ont le même sommet et dont les côtés de l’un sont dans le prolongement des côtés de l’autre.
n otation mathématique
A Point nommé A
A 1 Point nommé A portant le numéro 1
d Droite nommée d
d 1 Droite nommée d portant le numéro 1
AB Droite passant par les points A et B
[ AB Demi-droite dont l’origine est le point A et passant par le point B
[ AB ] Segment dont les extrémités sont les points A et B
| AB | Longueur du segment [ AB ]
A Angle dont le sommet est le point A
BAC Angle de sommet A dont les côtés sont les demi-droites [ AB et [ AC
A 1 Angle dont le sommet est le point A et portant le numéro 1
A || Amplitude de l’angle A
//Parallèle
//Sécant
/
⊥ Perpendiculaire
Versionprovisoire
Vous avez une question pédagogique ? Vous souhaitez une présentation ou une formation numérique dans votre école ?
Contactez le (la) délégué(e) pédagogique de votre région : www.vanin.be/contact-delegues
Découvrez nos autres collections Pacte :
Versionprovisoire
collections
