Blocos retangulares
Geometria
IDENTIFICANDO
Tema: Blocos retangulares.
Nível Canguru: Student (S).
Anos escolares: 3a série do EM.
Eixo Canguru: Geometria.
Tempo total: 2 aulas.
Objetivo:
Analisar a estrutura e os elementos dos blocos retangulares e calcular seus volumes.
Habilidades:
Esta aula permeia a seguinte habilidade da Base Nacional Comum Curricular: (EM13MAT309) Resolver e elaborar problemas que envolvem o cálculo de áreas totais e de volumes de prismas, pirâmides e corpos redondos em situações reais (como o cálculo do gasto de material para revestimento ou pinturas de objetos cujos formatos sejam composições dos sólidos estudados), com ou sem apoio de tecnologias digitais.
Materiais e recursos:
• Professor: giz/canetão colorido, lousa e modelos reais de blocos retangulares.
• Aluno: caderno, lápis grafite, lápis de cor, tesoura, régua (30 cm), caixinhas de pasta de dente, sabonete ou similares e algumas caixas maiores (como as de sapatos e de papelão).
Organização da turma: toda a turma.
Materiais de apoio:
• Concursos Canguru

• Revistas Canguru
AQUECENDO
Professor(a), você pode iniciar a aula pedindo a atenção dos alunos para as figuras tridimensionais (3D) que aparecem na imagem ao lado.
• Diga a eles que essas figuras representam alguns dos chamados sólidos geométricos.
 Nível S – Student
Nível S – Student
retangulares

• Peça a seus alunos que observem a imagem com atenção e que identifiquem nela os dois principais tipos de sólidos geométricos: os poliedros (poli=várias, edros=faces) e os chamados corpos redondos.
• Pergunte qual a principal diferença entre esses dois tipos de sólidos geométricos.
• Peça que marquem X nas cores dos corpos redondos da figura.
Amarelo Verde Lilás Laranja Azul Vermelho
• Agora peça que marquem X nas cores dos poliedros da figura.
Amarelo Verde Lilás Laranja Azul Vermelho
• Poliedros
Professor, a atividade a seguir propõe diferenciar os poliedros dos outros sólidos geométricos a partir da observação da quantidade, formato e disposição de suas faces. Para isso, peça a seus alunos que observem a imagem e que marquem X na cor do poliedro que possui:
• 4 faces formadas por triângulos equiláteros.
Amarelo Verde Lilás Laranja Azul Vermelho
• 6 faces formadas por quadrados:
Amarelo Verde Lilás Laranja Azul Vermelho
• 6 faces formadas por 2 tipos de retângulos.
(Neste caso, poderá ser necessário lembrar que os quadrados também são retângulos).
Amarelo Verde Lilás Laranja Azul Vermelho
• 2 faces formadas por triângulos equiláteros e 3 faces formadas por retângulos
Amarelo Verde Lilás Laranja Azul Vermelho
• 2 faces formadas por pentágonos e 5 faces formadas por retângulos
Amarelo Verde Lilás Laranja Azul Vermelho
• 2 faces formadas por hexágonos e 6 faces formadas por retângulos
Amarelo Verde Lilás Laranja Azul Vermelho
• 1 face formada por um quadrado e 4 faces formadas por triângulos
Amarelo Verde Lilás Laranja Azul Vermelho
• 1 face formada por um hexágono e 6 faces formadas por triângulos.
Amarelo Verde Lilás Laranja Azul Vermelho
retangulares
• Blocos retangulares
Professor, apresente os blocos retangulares a seus alunos como poliedros formados por 6 faces retangulares.
Avalie, mais uma vez, se será necessário lembrar que o quadrado é um caso especial de retângulo e que, portanto, o cubo (poliedro formado por 6 faces quadradas) é um caso especial de bloco retangular
Alguns blocos retangulares
No cotidiano, chamamos os blocos retangulares de “caixas” que, de diferentes formas, tamanhos e materiais (madeira, papelão, isopor etc.), são muito utilizadas em embalagens.
• Para reforçar o conceito de bloco retangular, peça aos alunos exemplos de produtos que são vendidos em embalagens com a forma de blocos retangulares.
• Pergunte onde mais eles veem blocos retangulares no dia a dia.
• Se quiser, peça também exemplos de embalagens que não são blocos retangulares.
• Incentive, receba e valorize a participação dos alunos.
DESENVOLVENDO
• Peça aos alunos que utilizem a imagem do bloco retangular para descobrir e escrever os elementos que faltam em cada linha:
• Vértices: A, B,

• Arestas: AB, AD, AE, .
• Faces: ABCD, .
• Diagonais das faces:
DB, .
• Diagonais internas do bloco retangular:

DF,

Blocos retangulares
• Ainda com relação à imagem do bloco retangular da atividade anterior, solicite aos alunos que completem a tabela com as quantidades:
Elementos Quantidades

Vértices

Arestas
Faces
Diagonais das faces
Diagonais internas do bloco retangular
Professor, proponha o desafio de descobrir se essas quantidades são as mesmas para todos os blocos retangulares e peça que justifiquem suas respostas.
• Arestas do bloco retangular
Professor, esta atividade fica mais interessante se for realizada a partir de blocos retangulares reais que podem ser caixas quaisquer.
• No exemplo, peça aos alunos que façam os cálculos para descobrir a soma das medidas das arestas nos três tamanhos de caixas de pasta de dentes na tabela. Tamanho
VISUALIZANDO
A seguir, sugerimos trabalhar uma questão do Concurso Canguru de Matemática Brasil, nível S, edição de 2020.

Uma formiga andava cinco metros todos os dias para ir do ponto A ao ponto B em linha reta. Um dia, João colocou nesse caminho duas caixas de um metro de altura. Agora a formiga anda na mesma reta ou acima dela, tendo que subir ou descer pelos obstáculos, conforme figura abaixo. Quanto ela precisa andar agora para ir de A até B?
1 m
Peça aos alunos que façam uma leitura cuidadosa da questão e que observem a imagem com atenção especial ao percurso realizado pela formiga entre A e B. Pergunte a eles:
• Como pode ser o caminho percorrido pela formiga (em vermelho) quando visto de cima?
• Quando vistos de cima, existe diferença entre os caminhos percorridos pela formiga antes e depois de João colocar as caixas?
• O que podem dizer sobre as distâncias percorridas na subida e na descida da formiga?
• A distância que a formiga percorre nas bases superiores dos blocos interfere no trajeto?
A expectativa é que os alunos percebam que a única diferença é a distância percorrida na vertical, que antes não fazia parte do caminho da formiga.

Possibilidade de resolução:
A única mudança no percurso é a caminhada vertical. Com o obstáculo, a formiga tem que subir dois metros e descer dois metros. Na horizontal, ela caminha a mesma distância que antes. Portanto, agora ela precisa andar 5 + 4 = 9 metros.
As alternativas apresentadas são:
Alternativa correta: B.
• Áreas da superfície do bloco retangular.
Professor, retome com os alunos a informação de que o bloco retangular possui 6 faces, divididas em 3 pares de faces paralelas, das quais cada par é formado por retângulos iguais.
Lembre-os de que a planificação do bloco, ou seja, sua representação no plano, tem o aspecto da figura a seguir e facilita a compreensão de como é essa superfície e de como podemos determinar sua área a partir das medidas das arestas das faces.
Peça aos alunos que observem o bloco retangular e sua planificação.
A área de cada face é obtida pelo produto das medidas de suas dimensões e a área da superfície do bloco retangular é a soma das áreas das 6 faces.

Professor, uma sugestão é envolver os alunos na escolha de partes da planificação (ou de toda ela) e – utilizando as dimensões a, b e c – pedir a eles que representem algebricamente as áreas das partes escolhidas.
• Por exemplo, solicite que façam os cálculos para descobrir a área total da superfície nos três tamanhos de caixas dados na tabela.
Antes de dar início aos cálculos, discuta com eles as estratégias que podem ser utilizadas na resolução como, por exemplo, as vantagens de utilizar a planificação.
Tamanho da caixa a b c Soma das medidas das arestas
INVESTIGANDO

• Para mostrar como o assunto Área aparece associado aos blocos retangulares (as populares “caixas”), selecionamos uma questão do nível S, da edição de 2020 – 1a aplicação do Concurso Canguru de Matemática Brasil.
Quatro caixas iguais sem pintura são coladas para formar a estrutura a seguir.
Um litro de tinta é necessário para pintar o exterior de cada uma dessas caixas. Quantos litros de tinta são necessários para pintar o exterior da estrutura?
• Peça aos alunos que façam uma leitura cuidadosa e que observem com atenção a disposição das quatro caixas coladas como na figura.
É importante que eles percebam que as quatro caixas coladas formam um novo sólido geométrico. Um poliedro que, neste caso, não é um bloco retangular.

• Questione:
Lembre os alunos de que: A leitura cuidadosa do problema é muito importante para desenvolver uma estratégia de resolução e assim chegar à solução.
• O que podemos dizer sobre a quantidade de faces do poliedro formado?
• Há faces iguais no poliedro? Quantas?
retangulares
• Quantas são as faces diferentes?
• Quantas faces do mesmo tipo temos?
• Quantas faces de cada tipo pinta 1 litro de tinta?
Considerando a estrutura, para calcular a quantidade de tinta necessária, precisamos considerar as faces coladas?
• Se necessário, chame atenção para o fato de que:
Para pintar o exterior de uma caixa, ou seja, as 6 faces de uma caixa, é necessário 1 litro de tinta.
Na estrutura obtida após a colagem, somente as faces do poliedro obtido serão pintadas.
Possibilidade de resolução:
Cada uma das caixas tem duas faces com área A, duas com área B e duas com área C.
Ao colar as caixas, de acordo com a figura, desaparecem duas faces A, duas faces B e duas faces C, ou seja, o correspondente às faces de uma caixa. Portanto, a quantidade de tinta necessária para pintar o exterior da estrutura é 4 - 1 = 3 litros, alternativa B.
Se possível, você pode levar 4 blocos retangulares (quatro caixas de pasta de dente) para representar a estrutura, e assim torná-la real e manipulável, o que vai ajudar muito na visualização e no entendimento.
Apresente as seguintes alternativas e peça para que marquem a correta.
(A) 2,5 (B) 3
SOCIALIZANDO
(C) 3,25
(D) 3,5 (E) 4
• Para retomar o conceito do volume do bloco retangular, questione:
• O que vocês entendem por volume?
• Como é feito o cálculo do volume do bloco retangular?
Se necessário, complemente as respostas dos alunos com as informações:

• Muitos sólidos geométricos podem ser imaginados como uma sobreposição de figuras iguais: um prisma de base triangular como uma sobreposição de triângulos iguais, um cilindro como uma sobreposição de círculos iguais, um bloco retangular como uma sobreposição de retângulos (ou quadrados) iguais.

retangulares
• O volume desses sólidos (inclusive do prisma), é produto da área da base do sólido por sua sua altura.
Considere que a área de um retângulo (base do bloco retangular) é a b, em que a e b são as medidas dos lados desse retângulo. Sendo c a altura do bloco retangular que tem esse retângulo como base, seu volume é V = a b c
Essa relação mostra que o volume do bloco retangular é o produto das medidas de suas três dimensões: altura, largura e comprimento
• Para que os alunos trabalhem juntos, permitindo interação e trocas, vamos utilizar a questão trabalhada no Concurso Canguru de Matemática Brasil, nível S, edição de 2018.
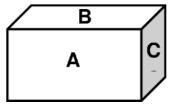
As áreas das faces de um bloco retangular são A, B e C, conforme figura. Qual é o volume do bloco?
Peça aos alunos que observem a figura.
• Questione:
• O que podemos dizer sobre as faces?
• O que precisamos saber para calcular o volume?
• Como podemos usar o que temos?
• Se necessário, complemente os questionamentos com:
O que precisamos saber para calcular a área de cada face?
Lembre seus alunos que devem compartilhar, escutar ativamente e valorizar as contribuições dos colegas.
Facilita a resolução se nomearmos as arestas? (Exemplo: usar x, y e z).
Agora, como podemos usar as arestas para descobrir a área? E o volume?
Apresente as seguintes alternativas e peça para que escolham a desejada.
(A) ABC
(B) 2 ( A+ B+ C )
(C) AB + AC + BC
(D) ABC 3
(E) ABC

Possibilidade de resolução:
Sejam x, y, z as dimensões do bloco, tais que A = xy, B = yz, C = xz . O volume do bloco é xyz . Temos:
Alternativa E AMPLIANDO
• Para aprofundar, você pode usar uma questão do Concurso Canguru de Matemática Brasil, nível S, edição de 2014.
As dimensões de um bloco retangular são a, b, c, tais que a < b < c . Aumentando qualquer uma dessas medidas de um mesmo valor positivo, o volume do bloco aumenta. Em qual dos casos o volume do bloco é o maior?
(A) Quando aumentamos a
(B) Quando aumentamos b.
(C) Quando aumentamos c
(D) É igual para as três dimensões.
(E) Depende dos valores iniciais de a, b e c
Dê um tempo para que os alunos leiam a questão e analisem as informações. Permita que eles tentem desenvolver a questão por eles mesmos.
• Se necessário, questione:
Dar valores numéricos a a, b, e c pode ajudar na resolução da questão?
Possibilidade de resolução:
O volume do bloco original é igual a a
b

c . Se x é o aumento (positivo) de uma das medidas, temos:
Logo, o volume do bloco é o maior quando aumentamos a dimensão a.
Alternativa A .
