Hexágonos – Área e Perímetro
Geometria
IDENTIFICANDO
Tema: Decompondo hexágonos.
Nível Canguru: Junior (J).
Anos escolares: 1a e 2a séries do EM.
Eixo Canguru: Geometria.
Tempo total: 2 aulas.
Objetivo:
Nível J – Junior
Explorar algumas das propriedades geométricas do hexágono regular em problemas que trabalham cálculos de áreas e perímetros.
Habilidades:
Esta aula permeia as seguintes habilidades da Base Nacional Comum Curricular:
(EM13MAT201) Propor ou participar de ações adequadas às demandas da região, preferencialmente para sua comunidade, envolvendo medições e cálculos de perímetro, de área, de volume, de capacidade ou de massa.
(EM13MAT307) Empregar diferentes métodos para a obtenção da medida da área de uma superfície (reconfigurações, aproximação por cortes etc.) e deduzir expressões de cálculo para aplicá-las em situações reais (como o remanejamento e a distribuição de plantações, entre outros), com ou sem apoio de tecnologias digitais.
Materiais e recursos:
• Professor: giz/canetão colorido, cartolina , lousa e projetor (opcional).
• Aluno: caderno, lápis grafite, lápis de cor, tesoura e sulfites.
Organização da turma: em dupla e toda a turma.
Materiais de apoio:
• Acervo do Concurso Canguru
• Revistas Canguru

AQUECENDO
Para começar, mostre a figura para os alunos e pergunte o que eles veem.
• Quais as características dessa figura?
Explore aspectos como: quantidade de lados, comprimentos dos lados, ângulos internos e externos etc.
Depois, mostre essa outra figura e pergunte:
• O que estão vendo?
• Quais as características dessa figura?
Explore aspectos como: quantidade de lados, comprimentos dos lados, ângulos internos e externos etc.
• Quais as características em comum entre as duas figuras?
Explore semelhanças e diferenças entre elas.
Algumas conclusões dessas comparações podem ser:

• A primeira figura é um hexágono não regular, ou seja, possui 6 lados e ângulos não congruentes.
• A segunda figura é uma hexágono regular, ou seja, um polígono de 6 lados e 6 ângulos de mesma medida, ou seja, congruentes.

Você também pode perguntar:
• Onde vemos hexágonos regulares no nosso cotidiano?
Para exemplificar, você pode mostrar a figura de uma colmeia, abrigo construído por abelhas. Curiosamente, mas não à toa, a colmeia é composta por diversos hexágonos regulares iguais, unidos pelos seus lados.




Colmeia com células hexagonais
Além dos hexágonos nas colmeias, encontramos essas figuras geométricas em outros lugares:


É importante destacar as propriedades geométricas do hexágono regular, dentre as quais, o fato de poder ser dividido em 6 triângulos equiláteros iguais.


Isso pode ser feito traçando algumas de suas diagonais como na figura:
Também é possível dividir um hexágono regular a partir de outras diagonais, de modo a obter triângulos não equiláteros, como nos exemplos:

Observe nos exemplos que dividir o hexágono em triângulos pode ser uma boa estratégia em problemas que envolvem cálculos de áreas e perímetros.
Finalizando, você pode questionar se os alunos conseguem visualizar outras divisões desta figura.
DESENVOLVENDO

Na atividade a seguir, convide os alunos a apontar todas as diagonais possíveis no hexágono.

É importante que você encoraje todos a participar e reconheça cada contribuição. Para isso, você pode fazer novas perguntas, complementar as falas dos alunos e elogiar o trabalho deles, esforço e persistência.
Ao final, peça que identifiquem quantos comprimentos diferentes de diagonais eles encontraram.
CONTEXTUALIZANDO
Para trabalhar com a decomposição de hexágonos, vamos nos basear em questões do Concurso Canguru
• Para iniciar, apresente a questão do Concurso Canguru de Matemática Brasil, nível J, edição de 2018.
Chamamos de X, Y e Z as áreas em cinza nos hexágonos regulares iguais A, B e C, respectivamente, na figura abaixo. Qual das afirmações a seguir é verdadeira?
(A) X = Y = Z
(B) X = Z Y
(C) X = Y Z
(D) Y = Z X
(E) As três áreas são diferentes.
Você pode iniciar a resolução dando um contexto ao problema. Por exemplo, dizer que Ana e Júlia estavam mexendo com peças brancas e cinzas e que, com essas peças, elas formaram três hexágonos do mesmo tamanho.
A seguir coloque uma questão importante: Será que existe uma relação entre as áreas cinza?
Peça aos alunos que observem os 3 hexágonos A, B e C, e que respondam:
• Eles são regulares?
• Eles são congruentes?
• Eles foram divididos da mesma maneira?
• A divisão se deu a partir das suas diagonais?
• As diagonais possuem todas o mesmo comprimento?
Possibilidade de resolução:
Traçando as diagonais dos hexágonos, vemos em A que há 12 triângulos congruentes, metade brancos, metade cinza. Em B há seis triângulos congruentes, metade brancos, metade cinza. Em C, ocorre o mesmo que em A. Logo, X = Y = Z, alternativa A .


VISUALIZANDO
• Sugerimos, agora, a seguinte questão do Concurso Canguru de Matemática Brasil, nível J, edição de 2014.
Na figura, o lado do hexágono maior é o dobro do lado do hexágono menor, que tem 4 cm2 de área. Qual é a área do hexágono maior, em cm2 ?
Apresente as seguintes alternativas:
8

10
Para auxiliar os alunos na resolução, você poderá comentar que:
• A figura apresenta dois hexágonos regulares, um grande e um pequeno.
16
• O menor dos hexágonos está inscrito no maior e dois de seus lados estão contidos nos lados do maior.
• Há uma relação entre as medidas dos lados, o que certamente ajudará na resolução.
• A partir de relações de proporcionalidade de áreas ou da decomposição de figuras (por meio das diagonais, por exemplo), é possível descobrir a área do maior.
Possibilidade de resolução:
Os dois hexágonos são figuras semelhantes por serem regulares. Se o lado do hexágono maior é o dobro do lado do menor, a sua área é quatro vezes maior, ou seja, é igual a 4 4 = 16 cm2 . Logo, a alternativa correta é a E
Outra possibilidade de resolução:
Se traçarmos segmentos de reta paralelos aos lados passando pelo ponto médio dos lados adjacentes e as diagonais, o hexágono maior fica com 24 triângulos equiláteros congruentes e o menor com 6 desses mesmos triângulos. Logo, fica uma razão de 24 6 = 4.


INVESTIGANDO

• Para que os alunos sejam desafiados a explorar mais a fundo, sugerimos a questão trabalhada do Concurso Canguru de Matemática Brasil, nível B, edição de 2011.
A figura é composta por um hexágono regular de lado 1, seis triângulos e seis quadrados. Qual é o perímetro da figura?
(A) 6 ( 1 + 2 )
(B) 6 1 + 3 2
(C) 9
(D) 6 + 3 2
(E) 12
No início, sugerimos pedir aos alunos que observem com atenção os tipos e quantidades de cada figura que formam a composição. É importante que reconheçam e identifiquem cada uma das figuras presentes.
Lembre os alunos que a leitura cuidadosa do problema é muito importante para desenvolver uma estratégia de resolução e assim chegar à solução.
Para encaminhar a resolução da questão, você pode pedir aos seus alunos que:
• Identifiquem cada uma das figuras geométricas presentes na composição;
• Descrevam as características que possuem em comum – principalmente com relação às medidas dos lados.
E ainda vale lembrar:
• O que é perímetro? Como calcular?
Possibilidade de resolução:
Os triângulos têm lados de mesma medida que os quadrados. Como há seis triângulos ao redor do hexágono, o perímetro da figura é 6 + 6 = 12. Logo, a alternativa E é a correta.
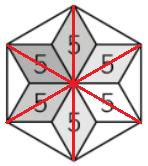

SOCIALIZANDO
• Para que os alunos trabalhem juntos no desenvolvimento da resolução, sugerimos uma questão do Concurso Canguru de Matemática Brasil, nível B, edição de 2021 adaptada.
Ana montou a estrela da figura formada por 6 losangos congruentes de área 5 cm2 cada um. As pontas desses losangos, quando ligadas, formam um hexágono regular. Então, Ana desafiou Clara a descobrir qual a área desse hexágono.

Na estrela, formada por 6 losangos congruentes de área 5 cm2 cada um, as pontas, quando ligadas, formam um hexágono regular. Qual é a área desse hexágono?
(A) 36 cm2 (B) 40 cm2 (C) 45 cm2
(D) 48 cm2 (E) 60 cm2
Uma sugestão é iniciar perguntando aos seus alunos o que é um losango e identificando esse quadrilátero na figura.
Losango: é um polígono que possui 4 lados, todos congruentes, e ângulos internos opostos congruentes.
Se necessário, você pode sugerir aos seus alunos que decompor o hexágono é uma boa estratégia para resolver o problema em questão.
Possibilidade de resolução:
Cada losango da figura é formado por dois triângulos isósceles (cuja base é a diagonal maior do losango) de área 5 2 cada um. Os triângulos brancos têm a mesma área que cada um desses triângulos isósceles. Portanto, a área da figura toda, o hexágono, é igual a 6 5 2 + 6 5 = 15 + 30 = 45 cm2 . Logo, a alternativa C é a correta.





AMPLIANDO
• Para aprofundar, você pode propor o seguinte desafio aos alunos:
• Peça para desenharem ou entregue impressa a figura ao lado em tamanho grande. Se possível, utilize cartolina.
• Peça para recortarem a figura por todos os segmentos de reta.
• Depois, desafie os alunos a montar três hexágonos de mesmo tamanho, área e lados, usando essas peças.
• Verifique se realizaram a seguinte montagem:

RETOMANDO
Aproveite para destacar como a decomposição de figuras é uma habilidade muito útil para solucionar problemas em diferentes áreas, como a mecânica, a marcenaria, a confecção de vestuário etc.
