Meten, meetkunde en verbanden - inkijkexemplaar - 9789006432688

Meten, meetkunde en verbanden

Reken-wiskundedidactiek

Marc van Zanten

Petra van den Brom-Snijders

Geeke Bruin-Muurling

Meten, meetkunde en verbanden

Reken-wiskundedidactiek

Petra van den Brom-Snijders

Geeke Bruin-Muurling

Marc van Zanten

COLOFON

auteurs

Marc van Zanten

Petra van den Brom- Snijders

Geeke Bruin-Muurling

redactie

Singeling Tekstproducties, Amersfoort

opmaak binnenwerk

Imago Mediabuilders, Amersfoort

ontwerp binnenwerk

Studio Fraaj, Rotterdam

ontwerp omslag

Studio Vlak, Utrecht

beeld omslag

Studio Vlak, Utrecht

technisch tekenwerk

Imago Mediabuilders, Amersfoort

Over ThiemeMeulenhoff

ThiemeMeulenhoff ontwikkelt zich van educatieve uitgeverij tot een learning design company. We brengen content, leerontwerp en technologie samen. Met onze groeiende expertise, ervaring en leeroplossingen zijn we een partner voor scholen bij het vernieuwen en verbeteren van onderwijs. Zo kunnen we samen beter recht doen aan de verschillen tussen lerenden en scholen en ervoor zorgen dat leren steeds persoonlijker, effectiever en efficiënter wordt.

Samen leren vernieuwen.

www.thiememeulenhoff.nl

ISBN 978 90 06 43268 8

Derde druk, eerste oplage, 2022

© ThiemeMeulenhoff, Amersfoort, 2022

Alle rechten voorbehouden. Niets uit deze uitgave mag worden verveelvoudigd, opgeslagen in een geautomatiseerd gegevensbestand, of openbaar gemaakt, in enige vorm of op enige wijze, hetzij elektronisch, mechanisch, door fotokopieën, opnamen, of enig andere manier, zonder voorafgaande schriftelijke toestemming van de uitgever.

Voor zover het maken van kopieën uit deze uitgave is toegestaan op grond van artikel 16B Auteurswet 1912 j° het Besluit van 23 augustus 1985, Stbl. 471 en artikel 17 Auteurswet 1912, dient men de daarvoor wettelijk verschuldigde vergoedingen te voldoen aan Stichting Publicatie- en Reproductierechten Organisatie (PRO), Postbus 3060, 2130 KB Hoofddorp (www.stichting-pro.nl). Voor het overnemen van gedeelte(n) uit deze uitgave in bloemlezingen, readers en andere compilatiewerken (artikel 16 Auteurswet) dient men zich tot de uitgever te wenden. Voor meer informatie over het gebruik van muziek, film en het maken van kopieën in het onderwijs zie www.auteursrechtenonderwijs.nl.

De uitgever heeft ernaar gestreefd de auteursrechten te regelen volgens de wettelijke bepalingen. Degenen die desondanks menen zekere rechten te kunnen doen gelden, kunnen zich alsnog tot de uitgever wenden.

Deze uitgave is volledig CO2-neutraal geproduceerd. Het voor deze uitgave gebruikte papier is voorzien van het FSC®-keurmerk. Dit betekent dat de bosbouw op een verantwoorde wijze heeft plaatsgevonden.

Inhoud

1 Samenhang meten en meetkunde 9

1.1 Meten en meetkunde: onderscheid en verwevenheid 9

1.1.1 Ruimtelijk redeneren met lengte, oppervlakte en inhoud 10

1.1.2 Uit de geschiedenis van meten en meetkunde 15

1.2 Meten en meetkunde op de basisschool 18

2 Meten 27

2.1 Meten en meetgetallen zijn overal 27

2.1.1 Internationale standaarden voor maateenheden 29

2.1.2 Meetinstrumenten 31

2.1.3 Wat er mis kan gaan bij meten 33

2.1.4 Uit de geschiedenis van meten 35

2.1.5 Wiskundetaal bij meten 41

2.2 Grootheden en maten 45

2.2.1 Lengte 45

2.2.2 Oppervlakte 49

2.2.3 Inhoud 55

2.2.4 Gewicht 62

2.2.5 Temperatuur 63

2.2.6 Tijd 65

2.2.7 Snelheid 69

2.2.8 Geldelijke waarde 71

2.2.9 Dichtheid 72

2.2.10 Hoek 72

2.2.11 Digitaal vastgelegde informatie 74

3 Meten op de basisschool 77

3.1 Schets van de leerlijn meten 78

3.2 Wiskundetaal bij meten op de basisschool 79

3.3 Ontluikend maatbesef 83

3.3.1 Groeiend inzicht in grootheden 83

3.3.2 Vergelijken 87

3.3.3 Afpassen met een maateenheid 89

3.4 Inzicht in meten en maten 93

3.4.1 Introductie van standaardmaten 93

3.4.2 Meetinstrumenten hanteren 97

3.4.3 Maatverfijning 102

3.5 Formeel redeneren en rekenen met maten en grootheden 104

3.5.1 Inzicht in het metriek stelsel 104

3.5.2 Grootheden 108

3.5.3 Samengestelde grootheden 113

3.5.4 Rekenen en redeneren met meetgetallen 116

3.6 Samenhang meten met andere domeinen 119

3.6.1 Samenhang met getallen 119

3.6.2 Samenhang met verhoudingen 122

4 Verbanden 125

4.1 Verbanden zijn overal 126

4.1.1 Variabelen 127

4.1.2 Grafische representaties 129

4.1.3 Centrummaten en spreiding 141

4.2 Zoeken naar verbanden 146

4.2.1 Trends in een grafiek 146

4.2.2 Formules en verbanden 151

4.3 Wat er mis kan gaan 155

4.3.1 Misleidende weergaven 156

4.3.2 Andere fouten 159

4.4 Wiskundetaal bij verbanden 161

5 Verbanden op de basisschool 165

5.1 Schets van de leerlijn verbanden 165

5.2 Wiskundetaal bij verbanden op de basisschool 167

5.3 Grafieken en diagrammen 167

5.3.1 Staafdiagrammen 168

5.3.2 Lijngrafieken en andere diagrammen 169

5.4 Tabellen 177

5.5 Het gemiddelde 180

6 Meetkunde 183

6.1 Meetkunde is overal 183

6.1.1 Uit de geschiedenis van de meetkunde 184

6.2 Deelgebieden van meetkunde 185

6.2.1 Oriëntatie in de ruimte 186

6.2.2 Viseren en projecteren 188

6.2.3 Transformeren 195

6.2.4 Construeren 215

6.2.5 Visualiseren en representeren 217

6.3 Wiskundetaal bij meetkunde 221

7 Meetkunde op de basisschool 223

7.1 Schets van de leerlijn meetkunde 225

7.2 Wiskundetaal bij meetkunde op de basisschool 231

7.3 Oriënteren in de ruimte 233

7.3.1 Lokaliseren en navigeren 233

7.3.2 Innemen van een standpunt 240

7.4 Construeren 244

7.5 Opereren met vormen en figuren 253

7.5.1 Spiegelen en symmetrie 254

7.5.2 Vergroten en verkleinen 258

7.5.3 Licht en schaduw 260

7.6 Samenhang met andere domeinen 263

7.6.1 Samenhang met verhoudingen 263

8 Gelegenheid om te leren: meten, meetkunde en verbanden 265

8.1 Leerinhouden en prestatieverwachtingen 265

8.1.1 Functies en waardes van rekenen-wiskunde 266

8.1.2 Gecijferdheid 267

8.1.3 Doelen 268

8.1.4 Differentiatie in doelen 273

8.2 Faciliteren van leren 275

8.2.1 Concreet handelen 276

8.2.2 Instructie 278

8.2.3 Het denken bevorderen 281

8.2.4 Differentiatie in het faciliteren van leren 285

8.3 Uit de geschiedenis van onderwijs in meten, meetkunde en verbanden 286

Over de auteurs 289

Geraadpleegde bronnen 290

Register 295

A B C

Voorwoord bij de 3e editie

Rekenen-wiskunde is een kernvak. Het komt op de basisschool elke dag aan bod en is belangrijk voor de voorbereiding op het vervolgonderwijs en het functioneren in de maatschappij. De realiteit is doordrenkt met rekenen-wiskunde: bij het boodschappen doen, in de gaten houden van de tijd, plannen van een vakantiereis, lezen van de krant, of als je iemand de weg wijst. Al van jongs af aan komen kinderen rekenen-wiskunde overal tegen: bij het inschatten van afstanden, vergelijken wie het grootste is, onthouden van de weg naar huis en op welk nummer je woont, of het sparen van zakgeld. Op de basisschool leren kinderen met al deze reken-wiskundige zaken omgaan en leren ze ook in meer formele zin rekenen-wiskunde. Daarbij komen de volgende domeinen aan bod: getallen, verhoudingen, meten, meetkunde en verbanden. In dit boek worden meten, meetkunde en de meetkundige en statistische onderwerpen van het domein verbanden behandeld.

Volgens de Kennisbasis wiskunde Lerarenopleiding basisonderwijs moeten basisschoolleraren professioneel gecijferd zijn. Dat houdt in dat zij:

■ zelf beschikken over voldoende rekenvaardigheid en gecijferdheid;

■ rekenen-wiskunde betekenis kunnen geven voor kinderen;

■ oplossingsprocessen en niveauverhoging bij kinderen kunnen realiseren;

■ wiskundig denken van kinderen kunnen bevorderen.

De geactualiseerde boekenserie Reken-wiskundedidactiek helpt (aanstaande) leraren om deze kennis, vaardigheden en attitude te verwerven. Naast het voorliggende boek omvat de serie de boeken Hele getallen en Verhoudingen, procenten, breuken en kommagetallen en een ondersteunende website eDition. De serie is volledig dekkend voor de herziene Kennisbasis wiskunde lerarenopleiding basisonderwijs

De boeken kennen drie invalshoeken voor het leren van (aanstaande) basisschoolleraren:

Activiteiten – ideeën om in de praktijk mee aan de slag te gaan en opdrachten om de leerstof nader te verwerken;

Bronnen – informatie over rekenen-wiskunde in realiteit en theorie, wiskundetaal, leerlijnen, en leren en onderwijzen van rekenen-wiskunde, inclusief differentiatie;

GeCijferdheid – opgaven om te werken aan de eigen professionele gecijferdheid.

opportunity to learn (gelegenheid om te leren), en de nieuwste tussendoelen en reken-wiskundemethodes. Verder is er nadrukkelijker aandacht voor verschillende instructievormen en de betekenis daarvan voor het leren en onderwijzen van rekenen-wiskunde.

De auteurs

1

Samenhang meten en meetkunde

grootheid

maateenheid

meetgetal

Vijfhonderd vel A4-papier zijn ingepakt in een groter vel papier. Wat zijn ongeveer de afmetingen van het grotere vel?

1.1 Meten en meetkunde: onderscheid en verwevenheid

BDe domeinen meten en meetkunde hebben veel raakvlakken, maar verschillen in hun essentie. Bij meten gaat het om het kwantitatief greep krijgen op eigenschappen van dingen als lengte, oppervlakte, inhoud, gewicht en tijdsduur. Zo’n eigenschap heet een grootheid. De essentie van meten is dat je een handeling uitvoert om te bepalen hoeveel er van een grootheid is, door het afpassen of aflezen van een maateenheid. Voor het meten van de grootheid lengte gebruik je bijvoorbeeld de maateenheid meter. Een meting levert een meetgetal op, bijvoorbeeld 2 meter. Dat meetgetal geeft aan hoe vaak de maateenheid afgepast kan worden op datgene dat gemeten is. Voor het meten kunnen allerlei meetinstrumenten worden ingezet, zoals een liniaal, meetapp, weegschaal of maatbeker.

B C

Bij meetkunde draait het om ruimtelijk redeneren: het beschrijven en verklaren van de ons omringende ruimte. Het gaat daarbij bijvoorbeeld om plattegronden, routes, richtingen en eigenschappen van vormen en figuren. Verder gaat het om projecties, schaduwen, symmetrieën, patronen en om twee- en driedimensionale weergaven van de werkelijkheid. Meetkunde is in essentie op te vatten als ruimtelijke oriëntatie in wiskundige zin. Bij sommige vraagstukken lopen meten en meetkunde door elkaar, zoals bij de vraag naar het pak A4-papier. Als je in gedachten het grote vel om het pak heen vouwt om te bepalen hoeveel groter het is dan een A4, dan is dat ruimtelijk redeneren. Je kunt de afmetingen van een A4’tje ook opmeten, of misschien heb je paraat dat dat ongeveer 20 bij 30 centimeter is. De hoogte van het pak kun je ook meten (5 centimeter) of weten (500 vel van 0,1 millimeter dik). Vervolgens kun je een (schattende) berekening maken van de afmetingen van het grote vel papier.

1.1.1 Ruimtelijk redeneren met lengte, oppervlakte en inhoud

Je kunt grootheden bepalen door te meten, maar soms speelt ruimtelijk redeneren daarbij ook een rol. Bijvoorbeeld bij het bepalen van de oppervlakte van meetkundige figuren. Bij een rechthoek is dat nog heel eenvoudig: neem het aantal rijen van een bepaalde maateenheid (hier: een hokje) en vermenigvuldig dat met het aantal kolommen van die maateenheid. Deze redenering ligt ten grondslag aan de bekende formule oppervlakte rechthoek = lengte × breedte.

Een driehoek kun je in gedachten insluiten in een rechthoek. De oppervlakte van die driehoek is dan de helft van die omsluitende rechthoek. Vandaar de formule oppervlakte driehoek = 1 2 x basis x hoogte.

Een vreemde rechthoek

Knip uit ruitjespapier een vierkant van 8 bij 8 hokjes, dus met een oppervlakte van 64 hokjes. Knip het in vier stukken, zoals getekend in figuur a hierna. Leg de stukken weer aan elkaar zoals in figuur b hierna. Deze rechthoek is 5 bij 13, dus 65 hokjes. Hoe kan dat?

1

C C

De kortste route

a Een slimme mier zit op de zijkant van een schoenendoos en ontdekt wat voedsel op de bodem van die doos. Vind de kortste weg naar het voedsel. Doe dit zo dat de mier geen millimeter te veel aflegt.

b Zet op een leeg A4’tje een stip (A) op een willekeurige plaats. Keer het blad om en zet op de achterkant een stip (B), ook op een willekeurige plek. Stel je nu voor dat de slimme mier over je A4’tje van A naar B wandelt. Vind de kortste route die de mier kan lopen.

A

B

Omtrek en oppervlakte

ab c

a Stel je verschillende rechthoeken voor met een oppervlakte van 48 vierkante, ondeelbare tegels. Hoe ziet de rechthoek met de kleinst mogelijke omtrek eruit? En met de grootst mogelijke omtrek?

b Stel je verschillende rechthoeken voor van vierkante, ondeelbare tegels met een omtrek van 48 tegelzijkanten. Wat is de kleinst mogelijke oppervlakte? En wat de grootste?

Kokers van A4

CNeem twee A4-blaadjes. Vouw het ene in de lengte in vieren en het andere in de breedte, zoals in de afbeelding. Maak er twee rechthoekige kokers van. Stel je voor dat je deze kokers vult met rijst. Is de inhoud van de kokers gelijk? Of is de inhoud van een van de twee kokers meer dan die van de andere?

Twee kokers gevouwen van een A4’tje

Geef eerst een antwoord door alleen te redeneren, nog zonder daarbij te rekenen. Helpt het bij het redeneren als je beide kokers (in gedachten) neerlegt?

Geef daarna een antwoord door een berekening uit te voeren. Komt dat antwoord overeen met je eerste antwoord? Zo nee, zoek uit hoe het zit: klopte je beredenering niet of klopte je berekening niet?

Melkverpakkingen

Veel dranken kun je in verschillende verpakkingen kopen. Zo zie je hier vijf verschillende melkverpakkingen. In de tabel hieronder staan de inhouden en de belangrijkste afmetingen tot op een halve centimeter nauwkeurig (de plastic dopjes, de plakranden en de inkepingen bovenaan zijn weggelaten).

Welke verpakking is het beste voor het milieu? Welke informatie uit de tabel gebruik je om deze vraag te beantwoorden?

Bonbonverpakkingen

a Welke verpakking bevat de meeste bonbons?

b Kun je beredeneren welke verpakking de grootste oppervlakte heeft, zonder dat je de precieze afmetingen weet?

B C C

Vlakvulling

Het werken met vlakvullingen ligt op het snijvlak van meten en meetkunde. Als een bepaalde oppervlakte wordt volgelegd met meetkundige vormen, kan die oppervlakte worden uitgedrukt in het aantal vormen. In de tekening hieronder, bijvoorbeeld, kan de oppervlakte worden uitgedrukt in het aantal ruiten, of in het aantal zeshoeken dat je in de vlakvulling kunt herkennen.

Vlakvulling met vierkanten

Een tegelvloertje leggen met even grote vierkante tegels is niet ingewikkeld. Het wordt lastiger als de vierkante tegels verschillende afmetingen hebben. Bijvoorbeeld met drie formaten tegels, van respectievelijk 1 × 1, 2 × 2 en 3 × 3. Kun je met deze drie formaten tegels een rechthoekige vloer vol leggen als je van elk formaat tegels dezelfde hoeveelheid gebruikt?

Vlakvulling met driehoeken

Stel dat je verantwoordelijk bent voor de productie van mozaïekdozen bij een speelgoedfabriek. Er worden driehoekjes van deze vorm gemaakt:

rechthoekige driehoek

1.1.2 Uit de geschiedenis van meten en meetkunde

De stelling van Pythagoras

BOok in de beroemde stelling van Pythagoras uit de klassieke oudheid komen meten en meetkunde samen. Het is een mooi voorbeeld hoe mensen al lang geleden de ruimte om zich heen zowel getalsmatig als ruimtelijk beschreven.

Deze stelling beschrijft de vaste relatie tussen de lengtes van de drie zijden van een rechthoekige driehoek: a2 + b2 = c2. Daarbij zijn a en b de twee zijden die haaks, met een rechte hoek, op elkaar staan, en is c de langste, schuine zijde.

pythagorese drietallen

Op deze Griekse postzegel is de stelling van Pythagoras in beeld gebracht. De kwadraten van de lengtes van de zijden van de driehoek zijn getekend als vierkanten. Volgens de stelling van Pythagoras is de oppervlakte van de twee kleine vierkanten samen (9 + 16) even groot als de oppervlakte van het grote vierkant (25). Bij willekeurige driehoeken komt het niet zo mooi uit met gehele getallen zoals hier bij a = 3, b = 4 en c = 5. Als het wel zo is dat a, b en c gehele getallen zijn, worden dat pythagoreïsche of pythagorese drietallen genoemd. De stelling van Pythagoras werkt ook andersom. Dat wil zeggen: als voor de lengtes a, b en c van een driehoek geldt dat a2 + b2 = c2, dan is het een rechthoekige driehoek. Met deze kennis konden bouwmeesters in de oudheid al met rechte hoeken werken.

De stelling van Pythagoras bewijzen

CEr zijn heel veel verschillende bewijzen van de stelling van Pythagoras. Met de volgende tekeningen is het mogelijk om een aanschouwelijk, oftewel visueel, bewijs te leveren van deze beroemde stelling. Lukt dat jou ook?

C C

Pythagorese drietallen

Hier zie je een paar voorbeelden van pythagorese drietallen: 3, 4 en 5 32 + 42 = 9 + 16 = 25 = 52 5, 12 en 13 52 + 122 = 25+ 144 = 169 = 132

a De getallen 3, 4 en 5 vormen een pythagorees drietal. Verdubbel je elk van deze drie getallen, dan vormt zich weer een pythagorees drietal: 6, 8 en 10. Dat is ook zo bij 5, 12 en 13: 10, 24 en 26 zijn ook een pythagorees drietal. Algemeen: als je elk van de getallen van een pythagorees drietal met dezelfde factor vergroot, vind je een ander pythagorees drietal. Kun je uitleggen waarom dat zo is?

b Kun je nog andere pythagorese drietallen vinden, die níet een veelvoud zijn van 3, 4 en 5 of van 5, 12 en 13?

De stelling van Pythagoras toepassen: zendantenne

Zendantennes zijn hoge masten die met draden getuid oftewel vastgezet worden, zoals te zien op de afbeelding links. Een mast wordt op 24 meter hoogte op drie plaatsen van tuidraden voorzien, zoals in de tekening rechts. Bereken de lengte van elk van de tuidraden.

De stelling van Pythagoras toepassen: beeldschermdiagonaal In de specificaties van een laptop staat dat het beeldscherm van 17 inch een resolutie heeft van 1 920 × 1 080 pixels. De 17 inch is de lengte van de diagonaal van het beeldscherm.

a Hoeveel cm is 17 inch? (1 inch = 2,54 cm)

b Welke lengte-breedteverhouding heeft het beeldscherm?

c Als je de lengte van het beeldscherm heel nauwkeurig opmeet, dan is deze 38,30 cm. Wat is de hoogte van het beeldscherm?

B verhouding

Bron: Praktisch rekenen voor jongens (1944)

CIn deze oude opgave lijkt het alleen te gaan om het uitrekenen. Toch laat de opgave ook aan de leerlingen van toen zien dat a2 + b2 = c2 niet de enige manier is om de stelling van Pythagoras te noteren. Dat misverstand komt weleens voor, net zoals het idee dat a altijd zou moeten staan voor de kortste zijde van de rechthoekige driehoek.

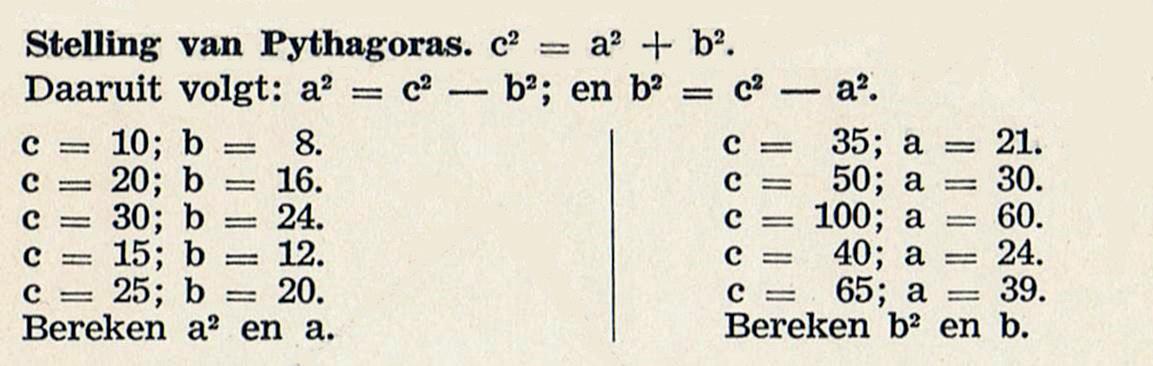
a Om welk(e) pythagorese drietal(len) gaat het in deze opgave?

b Wat is het verschil tussen het linker rijtje en het rechter rijtje?

De gulden snede

De gulden snede is een verhouding die sinds de zeventiende eeuw staat voor een schoonheidsideaal: de mooiste verhouding die bestaat. Als je een lijnstuk zo in tweeën verdeelt dat de verhouding van het kleinste deel ten opzichte van het grootste deel dezelfde is als de verhouding van het grootste deel tot het hele lijnstuk, dan heb je de gulden snede te pakken. Hieronder zie je dat voor een lijnstuk van 1 meter. De verhouding 38,2 staat tot 61,8 is dezelfde verhouding als 61,8 centimeter staat tot 1 meter. Ongeveer, want dit zijn afgeronde getallen.

φ (phi)

Een veelgebruikte benadering van de gulden snede is 0,618. De gulden snede is dus een verhoudingsgetal. Het precieze verhoudingsgetal heeft een oneindig aantal decimalen en wordt aangeduid met φ (phi)

De gulden snede in een lijnstuk

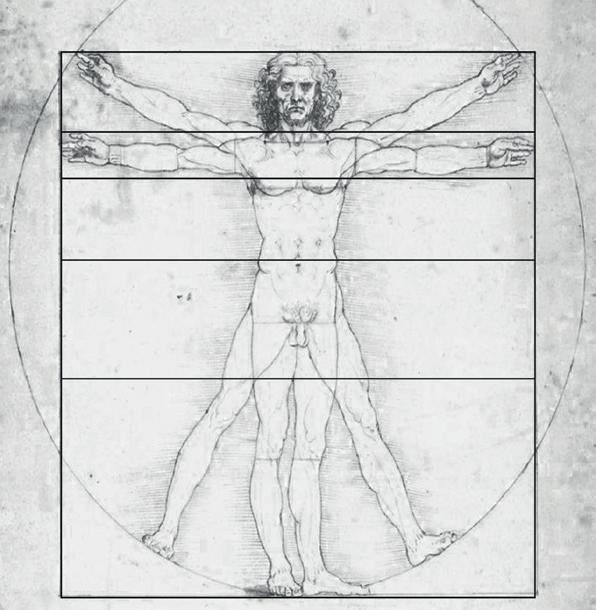
Een rechthoek waarvan de korte en de lange zijde zich verhouden als de gulden snede, zou de mooist denkbare rechthoek opleveren. Men zocht en vond de gulden snede terug op allerlei plekken, bijvoorbeeld in de architectuur en de kunst. Denk aan de tekening De Vetruvische man van Leonardo da Vinci, uit de vijftiende eeuw. In de natuur kan de gulden snede ook herkend worden bij sommige bloemen en planten. Dat de gulden snede op zoveel plekken voorkwam, werd gezien als teken dat alles was geschapen met een vooropgezet plan. Daarom werd de gulden snede wel de goddelijke verhouding

A B

genoemd. Er is nog geen wetenschappelijke verklaring waarom bij sommige planten de gulden snede kan worden herkend in de manier waarop ze groeien. Misschien is het wel toeval, want er zijn ook veel planten en bloemen die op andere manieren groeien. Meer over verhoudingen lees je in het boek Absoluut en relatief uit deze serie.

Een rechthoek waarvan de zijden de verhouding van de gulden snede hebben

De Vetruvische man van Leonardo da Vinci, met daarop de gulden snede geprojecteerd

Samenhang met andere domeinen en vakgebieden Meten en meetkunde hebben onderling raakvlakken, maar zijn ook verweven met andere reken-wiskundige domeinen. De gulden snede is een voorbeeld van samenhang met het domein verhoudingen. Meten en meetkunde worden verder, zoals zoveel in de wiskunde, ook toegepast in andere vakgebieden. Maak een mindmap van de samenhang tussen meten en meetkunde onderling, met andere reken-wiskundige domeinen en met andere vakgebieden. Illustreer met concrete voorbeelden. Wissel zo mogelijk uit met medestudenten, om te kijken of er nog meer raakvlakken zijn dan je zelf al bedacht.

1.2 Meten en meetkunde op de basisschool

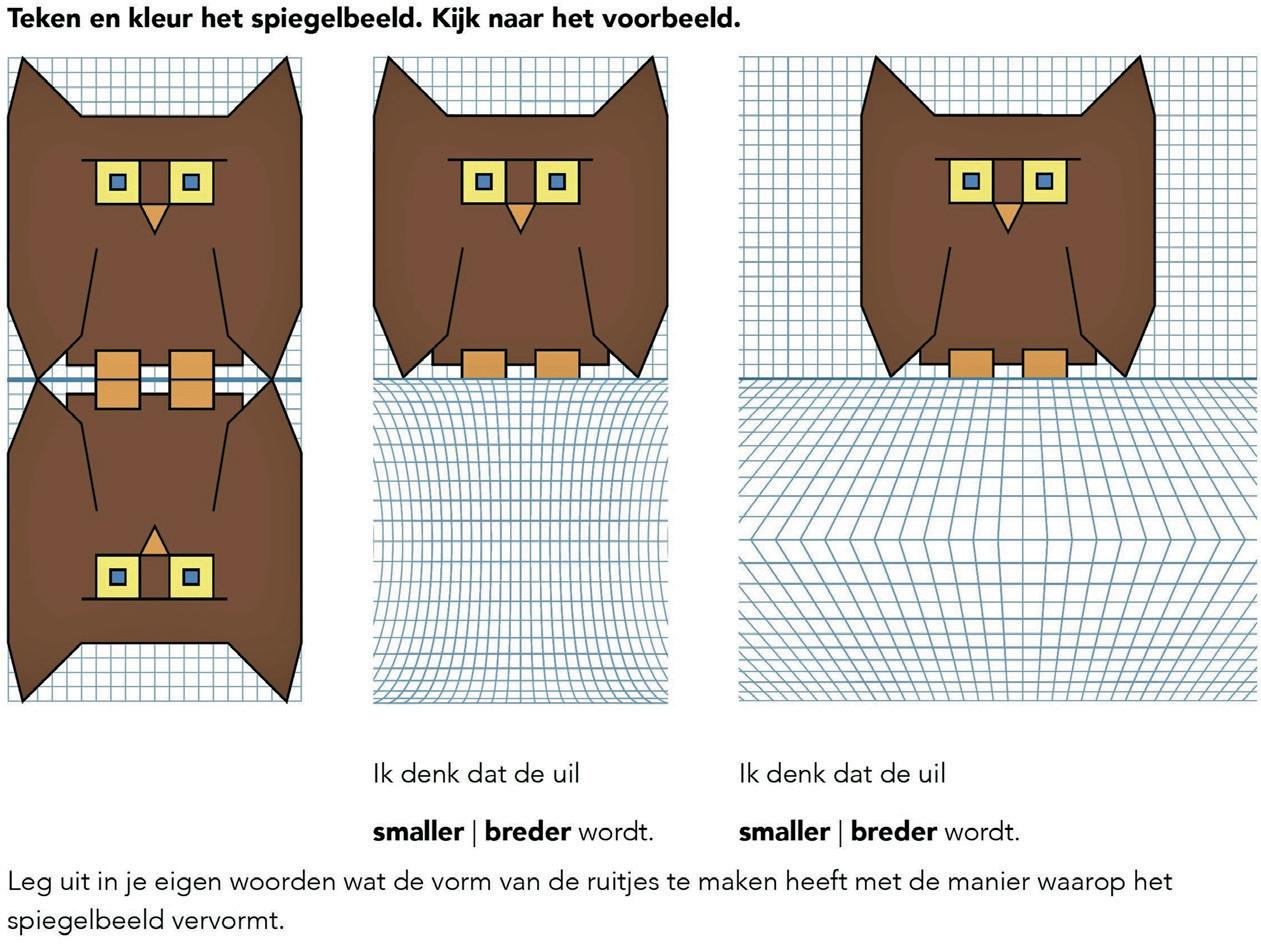
Deze activiteiten kenmerken zich door waarnemen, ervaren, beschrijven, beschouwen en verklaren. Hieronder staat daarvan een voorbeeld waarbij het gaat om spiegelen

Verschillende onderwerpen binnen meten en meetkunde komen op de basisschool afzonderlijk van elkaar aan de orde. Maar aan meten en meetkunde kan ook goed in samenhang worden gewerkt. Bijvoorbeeld door activiteiten als de inrichting van een winkelhoek (in de onderbouw) of het ontwerpen van een nieuw schoolgebouw of een dierenverblijf (in de bovenbouw). Daarbij komen tellen, rekenen, meten en meetkunde als vanzelf in samenhang aan de orde, waardoor betekenisvolle leeractiviteiten kunnen worden opgedaan.

De schoenenwinkel

Een rijke activiteit voor groep 1 tot en met 4 is het inrichten van een schoenenwinkel. Stel de leerlingen veel vragen, gericht op het opdoen van leerervaringen. Laat leerlingen, afhankelijk van de groep, bijvoorbeeld nadenken en overleggen over:

• het verzamelen van schoenen in verschillende maten en soorten, voor verschillende gelegenheden en weersomstandigheden;

• het verzamelen van schoenendozen waar de verschillende schoenen goed in passen;

• wat er nog meer wordt verkocht in een schoenenwinkel;

• hoe de winkel overzichtelijk moet worden ingericht, zodat klanten kunnen zien waar de schoenen in hun maat staan;

• hoe het personeel het beste overzicht heeft over de hele winkel;

• hoe de spiegels op zo’n manier neergezet moeten worden dat de klanten

Bron: Pluspunt, groep 6

Samenhang meten en meetkunde

goed kunnen zien hoe de schoenen hen staan;

• de prijzen voor de schoenen en andere artikelen en over het maken van de prijskaartjes;

• een reclamefolder met een kortingsactie, bijvoorbeeld tweede paar voor de helft, en ga na wat dat betekent voor de verschillende prijzen;

• hoe je je schoenmaat kunt bepalen als je die niet weet;

• een poster waarop de klanten kunnen zien wanneer de winkel open is.

Wat leren leerlingen van deze activiteit op het gebied van meten en meetkunde? Welke vragen van jou als leerkracht helpen daarbij? Wissel je ervaringen uit met je medestudenten.

Een goed dierenverblijf

AVoor groep 5 en hoger is het ontwerpen van een verantwoord en diervriendelijk verblijf voor (wilde) dieren een rijke opdracht. Laat de leerlingen eerst kiezen voor welke diersoort(en) ze een verblijf willen ontwerpen. Welke diersoorten kunnen bij elkaar in één verblijfsruimte? Laat leerlingen vervolgens nadenken welke informatie ze nodig hebben om een goed verblijf te kunnen ontwerpen. Laat ten slotte een maquette maken van het ontwerp. Ook bij deze activiteit wordt het leren bevorderd door de leerlingen te voorzien van veel input en vragen. Denk bijvoorbeeld aan:

• Zijn het solitaire dieren of leven ze in een groep? Met hoeveel?

• Hoeveel oppervlakte is er nodig? Is er ook een binnenverblijf nodig en zo ja, van welke afmetingen?

• Hoe schaduwrijk of zonnig moet het verblijf zijn?

• Moeten de dieren kunnen spelen, klimmen, zwemmen en zich verstoppen? Wat is daarvoor nodig?

• Wat is er nodig om de dieren van voedsel te voorzien in het verblijf? Om welk voedsel gaat het? Hoeveel is er dagelijks nodig en wat zijn daarvan de kosten? Wat is er nodig om de ontlasting af te voeren? Hoe kunnen de verzorgers veilig voor dit alles zorgen?

• Wat voor afscheiding is er nodig tussen de dieren en de bezoekers? Hoe hoog, breed, diep?

• Wat zijn de kosten om het verblijf te realiseren?

• Hoe zorg je ervoor dat bezoekers de dieren zo goed mogelijk kunnen zien? Is er een brug over het verblijf mogelijk en hoe hoog en lang moet deze dan zijn?

• Welke schaal moet de maquette hebben om niet te groot of te klein te worden?

Wat leren leerlingen van deze activiteit op het gebied van meten en meetkunde? Welke vragen van jou als leerkracht helpen daarbij? Wissel je ervaringen uit met je medestudenten.

Samenhang in methodes

BDe samenhang tussen meten, meetkunde en andere reken-wiskundige domeinen herken je ook in methodes. Naast opgaven over afzonderlijke onderwerpen kom je ook veel opdrachten tegen waarbij verschillende domeinen door elkaar heen spelen. Bij de opgave hieronder bijvoorbeeld gaat het om meten (bepalen van oppervlakte en omtrek) en bewerkingen (rekenen met geld en rekenen met de rekenmachine). Het gaat hier niet alleen om het uitrekenen van het antwoord, maar ook om het zelf bedenken hoe dat antwoord kan worden bepaald (welke ‘sommen’ daarvoor nodig zijn).

Raakvlakken met wereldoriëntatie, zoals je die zag bij De schoenenwinkel en Een goed dierenverblijf, kom je ook tegen in de methodes. Denk aan activiteiten met plattegronden, landkaarten en routes, coördinaten en windrichtingen. Bij schaal is er ook samenhang met het domein verhoudingen. Schaal is immers de verhouding tussen afmetingen in de werkelijkheid en afmetingen op een afbeelding.

Bron: De Wereld in Getallen, groep 7

Bron: Alles Telt Q, groep 5

schaal

Samenhang meten en meetkunde

wiskundetaal C

Hierboven zie je een voorbeeldopgave met meten en schaal. Merk op dat het in deze opgave voor groep 5 nog niet gaat om rekenen met schaal, maar alléén nog om schaalbegrip: het idee dat de afstanden op de afbeelding staan voor grotere afstanden in de werkelijkheid.

Wiskundig gereedschap en wiskundige attitude

BMet meten en meetkunde verwerven leerlingen wiskundig gereedschap om de wereld te kunnen beschrijven, begrijpen en verklaren. Dat gereedschap kun je letterlijk opvatten: met behulp van bijvoorbeeld een liniaal of maatbeker krijgen kinderen greep op de grootheden lengte en inhoud. Maar in bredere zin kun je het ook opvatten als het beheersen van de wiskundetaal die van pas komt in het dagelijks leven. Denk bijvoorbeeld aan begrippen als hoog en smal, richtingen als links, noord en westelijk, en het begrip dode hoek in het verkeer.

Bron: Alles Telt Q, groep 7

Meten en kijklijnen

a Welke maateenheid hoort bij de vermelde meetgetallen?

b Kun jij over de auto heen kijken?

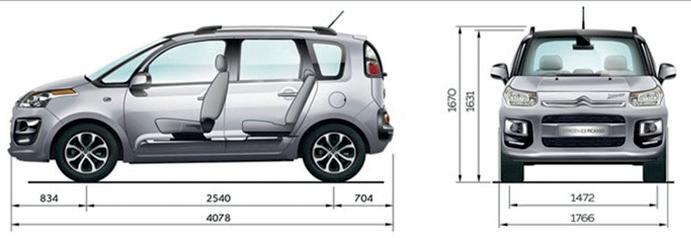
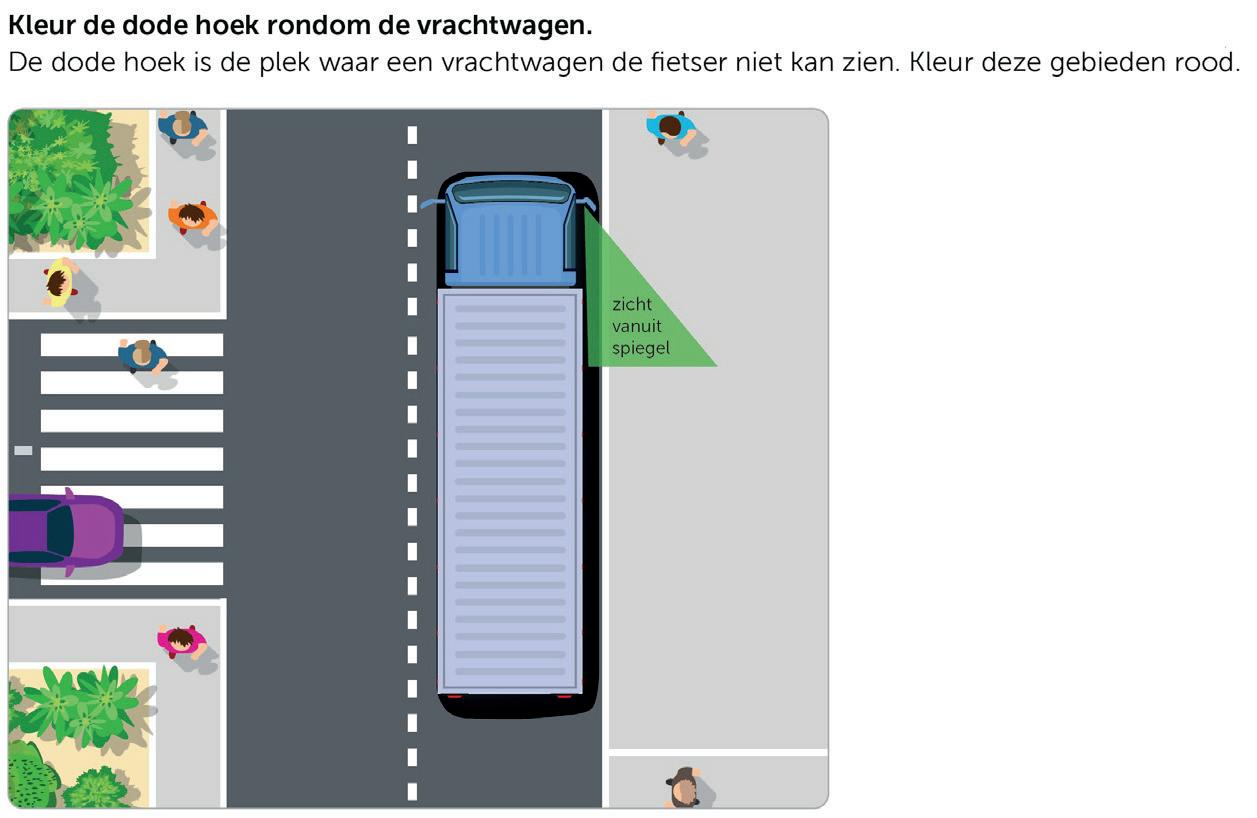
wiskundige attitude

c Stel je voor dat jij op de bestuurdersstoel zit. Welke gedeelte van het wegdek voor de auto kun je dan niet zien doordat de motorkap ervoor zit?

Teken deze dode hoek. Maakt het veel uit hoe lang jij bent?

d Vanaf hoeveel meter voor de auto kun je het wegdek wel zien vanaf de bestuurdersplek?

gecijferdheid

BHet onderwijs in meten en meetkunde kan bijdragen aan de ontwikkeling van een wiskundige attitude. Dat is een positieve houding ten opzichte van wiskundige activiteiten op school en daarbuiten. Met een wiskundige attitude herken je wiskunde in dagelijkse en minder alledaagse situaties, en gebruik je wiskunde om zaken te beschrijven, te verklaren en aan te pakken. Denk bijvoorbeeld aan de vragen over de dode hoek hierboven. Een wiskundige attitude kenmerkt zich door een onderzoekende, reflectieve, communicatieve en doelgerichte houding, en door een zekere mate van gecijferdheid. Wie gecijferd is, beschikt onder andere over een groot aantal referenties in het dagelijks leven. Veel van die referenties zijn meetgetallen. Denk bijvoorbeeld aan de afstand die je loopt of fietst in een uur. Om de ontwikkeling van een wiskundige attitude te bevorderen, is veel gelegenheid nodig voor leerlingen om zelf te redeneren, te ervaren en te onderzoeken. Daarvoor moeten er veel vragen aan leerlingen worden gesteld, met name denkvragen en waaromvragen, oftewel vragen naar verklaringen voor meetkundige verschijnselen en observaties, zoals in de voorbeeldopgave hierna.

Bron: Getal en Ruimte Junior, groep 6

C A B

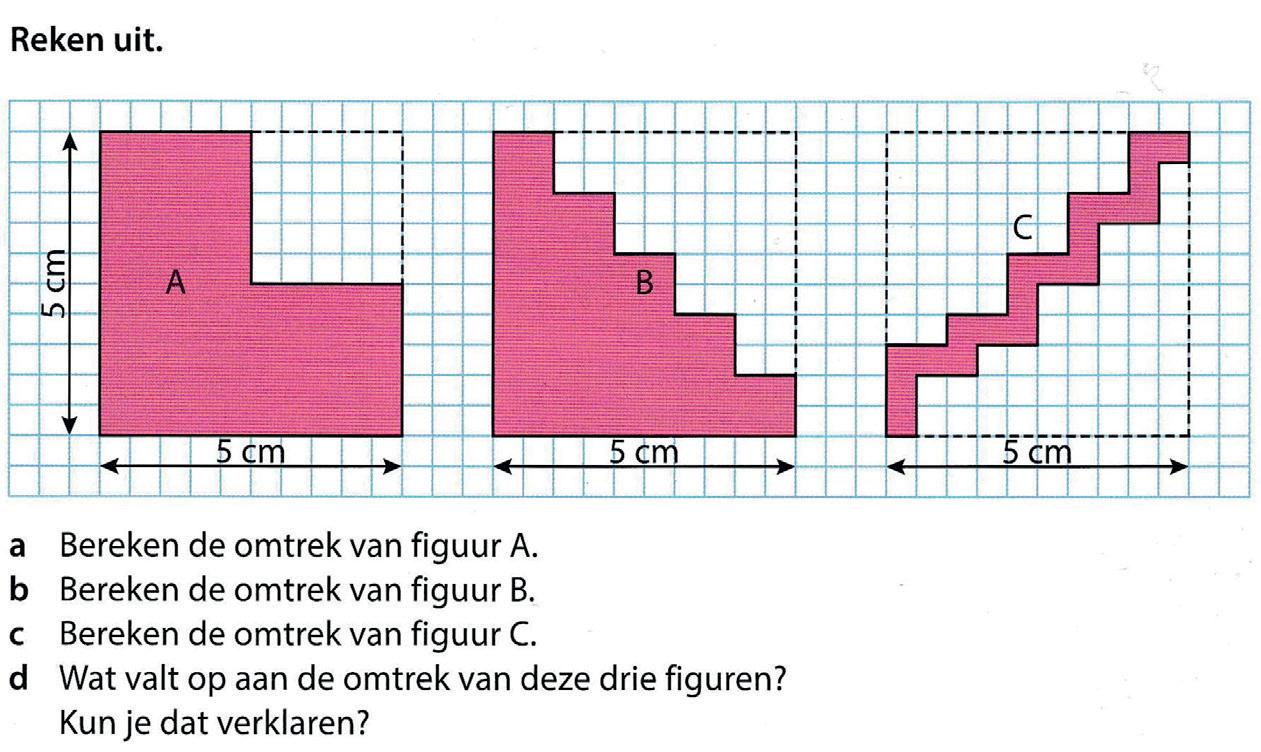
Gecijferdheid – meten, meetkunde, getallen en bewerkingen in samenhang

Gecijferd zijn houdt ook in dat je de samenhang tussen verschillende reken-wiskundedomeinen weet te benutten. Zoals bij de volgende vragen, waarbij je verschillende redeneerstappen moet zetten, zowel getalsmatig als ruimtelijk.

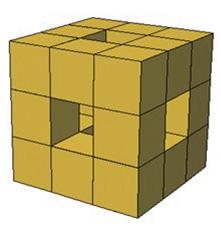
Een betonnen bouwsel is opgebouwd uit kubussen van 1 m3.

a Hoeveel liter beton is in het bouwsel verwerkt?

b Het bouwsel wordt aan alle zijden geverfd, behalve natuurlijk de onderkant. Een blik betonverf is goed voor 11 m2. Hoeveel blikken verf zijn nodig?

Meetkunde en breuken – Plezier met A4

a Vraag leerlingen uit groep 3, 4 of 5 hoe ze een vel A4-papier eerlijk over vier kinderen kunnen verdelen. Hoe zouden ze dat kunnen doen? Geef ze ieder een vel papier, een pen en een schaar. Je kunt het moeilijker maken door ze het vel te laten verdelen over acht kinderen, of over een nog lastiger aantal als zes.

b Vraag in je nabespreking waarom ze vinden dat het eerlijk is verdeeld. Gaat dat over een gelijke oppervlakte? Kan het ook zo zijn dat omtrek of vorm meespeelt? Welke wiskundetaal gebruiken ze bij hun uitleg?

c Wat vinden de kinderen van de volgende oplossingen?

Anton Britt Carola Dwayne

Vierkuberhuisjes

Zoals elk blokkenbouwsel kunnen vierkuberhuisjes worden beschreven door middel van aanzichten, zoals je hieronder ziet. De tekening rechts van het bovenaanzicht heet een bouwplattegrond met hoogtegetallen. De getallen in de vakjes geven aan hoe hoog de blokken op die plek gestapeld zijn.

Kabouterhuisjes in de onderbouw

AIn de onderbouw tot en met groep 4 kan het gaan om kabouterhuisjes. Een reus heeft per ongeluk het hele kabouterdorp omvergelopen. De leerlingen worden uitgedaagd het dorp opnieuw te bouwen met allemaal verschillende huisjes. Hoeveel kunnen dat er zijn? Afhankelijk van de groep kun je nog allerlei andere vragen aan de leerlingen voorleggen. Welke hoogtes hebben de huisjes? Welke plattegronden horen erbij en hoeveel grondoppervlak nemen ze in beslag? Is de omtrek van elk huisje even lang? Ook zijn vragen mogelijk die meer meetkundig redeneren uitlokken, zoals: wanneer zijn huisjes echt verschillend? Zijn bijvoorbeeld de huisjes uit de afbeelding hieronder verschillend of toch hetzelfde?

Een vierkubervilla

CHieronder zie je een futuristische vierkubervilla. Het ontwerpcriterium voor zo’n villa is weer dat ze bestaan uit vier kubussen die met minstens één zijvlak aan een andere kubus vastzitten, alleen nu mogen kubusjes ook overhangen zonder verdere ondersteuning.

a Hoeveel verschillende ontwerpen zijn er mogelijk?

b Welke ontwerpen hebben hetzelfde vooraanzicht of zijaanzicht? Kun je erachter komen hoe vaak dat voorkomt?

c Hoe zou je een bouwplattegrond met hoogtegetallen kunnen tekenen van ontwerpen met overhangende kubusjes?

ABlokkenbouwsels in de bovenbouw Bedenk een variant op de ontwerpopdracht vierkuberhuisjes voor groep 5 of hoger. Welke vragen kun je in jouw groep aan de orde stellen? Hoe kun je de opdracht verder variëren? Denk bijvoorbeeld aan aantallen kubussen en het berekenen van kosten als grondprijs, kosten van schilderwerk per zijvlak, en kosten voor een hangende constructie per blok. Ook kun je bijvoorbeeld meetkundige begrippen als draaien en spiegelen meer nadrukkelijk in de activiteit betrekken.

De lijst met alle begrippen uit dit hoofdstuk vind je op eDition.