Got it rekenen 2F mbo

Nella Keemink

Ferry Luijbe

Rekenen naar 2F

Ferry Luijbe

Nella Keemink

Voorwoord

Je goed voorbereiden op de Rekentoets 2F kon al met het online adaptieve leerplatform Got it Rekenen. Nu is op verzoek van veel Got-it-gebruikers het Handboek Rekenen naar 2F erbij ontwikkeld.

Het Handboek Rekenen naar 2F en het leerplatform Got it sluiten naadloos op elkaar aan: de elf onderwerpen in Got it zijn ook terug te vinden in dit handboek.

In hoofdstuk 1 staat de basis van het rekenen: de bewerkingen optellen, aftrekken, vermenigvuldigen en delen voor hele getallen en kommagetallen. Ook de basis van het rekenen met breuken komt aan bod. In de rekentoets worden deze bewerkingen vooral getoetst in de sectie met de contextloze opgaven. In hoofdstuk 2 tot en met 5 staan de vier rekendomeinen centraal: getallen, verhoudingen, meten en meetkunde en verbanden. Met in hoofdstuk 2 een slim stappenplan om de contextrijke opgaven in de rekentoets goed te kunnen maken.

In de paragrafen bouwen we de kennis per domein op, tot het eindniveau 2F, geactualiseerd naar de laatste Syllabus voor het VO en MBO.

Rekenen is vooral doen: daarom volgt na elke paragraaf een set oefenopgaven om het geleerde gelijk toe te passen. De antwoorden staan achterin het boek. Zo kan de leerling of student zelf snel zien of hij de rekenvaardigheid ook echt onder de knie heeft.

Aan het eind van elk hoofdstuk staat ‘Waar let je op?’, met tips om veel gemaakte fouten in de rekentoets voor te zijn. Samen met het adaptieve leerplatform Got it en de opgaven met hints bij ‘Zo wordt het gevraagd’ zorgt dit voor een optimale voorbereiding op de rekentoets.

In Got it kan de leerling of student zelf kiezen met welk onderwerp hij aan de slag gaat: dat kan hij ook in het handboek. Het is dus niet nodig om de hoofdstukken in volgorde door te nemen.

Het handboek en het online adaptieve leerplatform Got it zijn flexibel in te zetten:

• U kunt met de klas starten met een domein in het handboek, waarna iedereen individueel kan oefenen in Got it.

• U kunt de leerlingen of studenten ook laten beginnen met de instaptoets in Got it en ze op hun eigen niveau online laten oefenen. Daar waar extra uitleg nodig is, pakt de leerling of student het handboek erbij.

• Of u wisselt het handboek en het oefenen in Got it af, voor variatie in werkvormen en in klassikaal en individueel onderwijs.

Hoe u het handboek en het online adaptieve leerplatform Got it ook inzet, uw leerlingen of studenten zijn daarna optimaal voorbereid op de Rekentoets.

Het handboek is met de grootste zorg ontwikkeld. Wij hopen dat u met plezier werkt met het handboek en Got it. Meer informatie vindt u op onze website www.got-it.nl. Wanneer u vragen of suggesties heeft, dan kunt u contact met ons opnemen.

De auteurs en de uitgever

Reeksinformatie

Online adaptieve Leeromgeving op got-it.nl voor 1F, 2F en 3F

Handboek Rekenen naar 2F

Handboek Rekenen naar 3F

1 De basis

Dit hoofdstuk legt de basis voor het rekenen in de volgende hoofdstukken. Je krijgt een overzicht van de basisbewerkingen bij rekenen met hele getallen. Je gaat aan het werk met een aantal manieren om zonder rekenmachine hele getallen op te tellen, af te trekken, te vermenigvuldigen en te delen. Kies zelf de manier die jij het handigst vindt of die het best bij de opgave past. Het tweede deel van het hoofdstuk gaat over de basis van rekenen met breuken en kommagetallen.

1.1 Getallen

Rekenen doe je met getallen. Een getal bestaat uit (een combinatie van) de cijfers 0 tot en met 9. De plaats van een cijfer in een getal geeft de waarde van dat cijfer aan. Dus de plaats van het cijfer geeft aan of de waarde een tiental is of een honderdtal. Dit wordt ook wel de positiewaarde genoemd.

Positiewaarde

VOORBEELD In het getal 34515 heeft 1 de waarde 10 en 4 de waarde 4000.

Getallen kunnen verschillende betekenissen hebben. Denk aan:

• een hoeveelheid: 6 vrienden, 6 glazen limonade;

• nummering: huisnummer 21, rugnummer 8;

• een maat: 1,75 meter lang, 1 liter melk, 750 gram kaas;

• de volgorde: de 3e plaats.

Er zijn vier soorten getallen:

• positieve gehele getallen zoals 5, 7, 100;

• negatieve gehele getallen zoals −25, −8, −2;

• kommagetallen zoals 0,10 en 3,25;

• gebroken getallen (breuken) zoals 1 2 .

Rekenen zonder rekenmachine

Tips bij het rekenen zonder rekenmachine.

1 Je mag altijd kladpapier gebruiken. Rekenen uit het hoofd betekent dus niet dat je niks mag opschrijven. Gebruik bij voorkeur ruitjespapier.

2 Soms is het handig om getallen in een DHTE-schema te zetten. DHTE staat voor Duizendtal, Honderdtal, Tiental, Eenheid. Op die manier zie je goed wat de positiewaarde is van de cijfers in het getal.

VOORBEELD Plaats 4135 in het DHTE-schema.

Uitleg:

4 heeft de waarde 4000, dus 4 staat onder de D(uizend).

1 heeft de waarde 100, dus 1 staat onder de H(onderd).

3 heeft de waarde 30, dus 3 staat onder de T(ien).

5 heeft de waarde 5, dus 5 staat onder de E(enheid).

3 Soms kan een getallenlijn helpen. Je zet dan de getallen op een lijn op de goede positie naast elkaar.

4 Soms werkt het om getallen een betekenis te geven. Denk bijvoorbeeld aan geld.

VOORBEELD 80 : 0,2 = 400

Uitleg:

Je kunt hierbij de volgende betekenis bedenken: 0,2 is 0,20 euro, dus 20 eurocent. Hoeveel munten van 20 eurocent passen er in 80 euro?

1 euro = 5 munten van 20 eurocent, dus 8 euro = (5 × 8 =) 40 munten van 20 eurocent, dus 80 euro = 400 munten van 20 eurocent.

Oefenen 1.1 Getallen

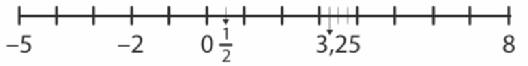
Positiewaarde

1 Wat is de waarde van de verschillende cijfers in 48319?

4 heeft de waarde

8 heeft de waarde

3 heeft de waarde

1 heeft de waarde

9 heeft de waarde

Rekenen zonder rekenmachine

2 Zet de getallen 68, 4581, 305 en 9 in het DHTE-schema.

3 Zet de vier getallen −1, 3, 6,3 en 7

2 op de juiste plaats.

1.2 Hele getallen optellen

In deze paragraaf zie je meerdere manieren om getallen op te tellen. Je mag zelf de manier kiezen die het best bij jou past.

Kijk wel goed naar de getallen in de opgave. Soms is door de getallen één manier het handigst.

Hier volgen vier manieren:

• cijferen;

• rijgen;

• splitsen;

• handig rekenen.

1e manier: cijferen

Cijferen gaat zo:

1 Zet van de getallen het duizendtal (D), het honderdtal (H), het tiental (T) en de eenheid (E) recht onder elkaar in een DHTE-schema.

2 Tel daarna eerst de eenheden, dan de tientallen, dan de honderdtallen als de getallen zo groot zijn, en dan de duizendtallen bij elkaar op.

3 Kom je in een kolom boven de 9, dan schuift de 1 naar de kolom ernaast. Neem boven in het schema een extra rij op om te onthouden Je zet dan de 1 boven de kolom in de rij om te onthouden.

4 In de onderste rij vind je dan het antwoord.

VOORBEELD 176 + 247 = 423

H T E

1 1 * rij om te onthouden

1 7 6 2 4 7 +

4 2 3 Eerst 6 + 7 = 13; 3 opschrijven en 1 bij de kolom tiental onthouden*

Dan 1 + 7 + 4 = 12; 2 opschrijven en 1 bij de kolom honderdtal onthouden*

Dan 1 + 1 + 2 = 4

Je kunt dit ook doen als je meerdere getallen bij elkaar op moet tellen. Je maakt dan meer rijen in het DHTE-schema.

VOORBEELD 23 + 156 + 545 = 724

H T E

1 1 * rij om te onthouden 2 3

1 5 6

5 4 5 +

7 2 4 Eerst 3 + 6 + 5 = 14; 4 opschrijven en 1 onthouden*

Dan 1 + 2 + 5 + 4 = 12; 2 opschrijven en 1 onthouden*

Dan 1 + 1 + 5 = 7

2e manier: rijgen

Rijgen gaat zo:

1 Hak het tweede getal in stukken.

2 Tel die stukken een voor een bij het eerste getal op. De getallenlijn helpt daarbij. Je kiest zelf welke stukken je neemt.

VOORBEELD 176 + 217 = 176 + 200 + 10 + 7 = 376 + 10 + 7 = 386 + 7 = 393

3e manier: splitsen

Splitsen gaat zo:

1 Zet de getallen onder elkaar.

2 Splits de getallen eerst in duizendtallen, honderdtallen, tientallen en eenheden.

3 Die tel je apart op.

4 Daarna tel je de uitkomsten bij elkaar op.

VOORBEELD 176 + 247 = 423

Uitleg:

1 7 6 (zet de getallen onder elkaar) 2

7 + 3 0 0 = 100 + 200 (honderdtallen noteren en bij elkaar optellen: 100 + 200 = 300) 1 1 0 = 70 + 40 (tientallen noteren en bij elkaar optellen: 70 + 40 = 110)

= 6 + 7 (eenheden noteren en bij elkaar optellen: 6 + 7 = 13)

4 2 3 (uitkomsten bij elkaar optellen: 300 + 110 + 13 = 423)

4e manier: handig rekenen

Soms kun je een handigere manier gebruiken om op te tellen. Dat hangt af van de getallen in de opgave. Zo kun je een getal handig opsplitsen door te kijken naar een mooi getal in de buurt.

VOORBEELD

• 111 + 99 = 210

Uitleg:

Beide getallen liggen in de buurt van een mooi getal. Bijvoorbeeld: Splits het eerste getal in 110 en 1. 110 + 1 + 99 = 110 + 100 = 210

of:

111 + 100 − 1

211 − 1 = 210

• 235 + 1215 = 1450

Uitleg:

Bij deze getallen zijn 35 en 15 samen 50. Dan is het handig om de getallen zo op te splitsen dat je ze goed bij elkaar kunt optellen.

235 + 1215 = 200 + 35 + 1200 + 15 = 200 + 1200 + 35 + 15 = 1400 + 50 = 1450

Bij een optelling van drie of meer getallen mag je kiezen welke getallen je eerst bij elkaar optelt.

VOORBEELD 2325 + 10 + 15 = 2350

Uitleg:

Tel eerst 10 en 15 bij elkaar op en tel de uitkomst daarna op bij 2325: 2325 + 10 + 15 = 2325 + 25 = 2350

Oefenen 1.2 Hele getallen optellen

1e manier

Reken uit met cijferen.

4 386 + 548 =

*rij om te onthouden

5 67+ 851 + 248 =

*rij om te onthouden

2e manier

Reken uit met rijgen.

6 275 + 164 =

3e manier: splitsen Reken uit met splitsen.

7 425 + 107 =

4e manier

Reken uit met handig rekenen. Noteer hoe je tot je antwoord komt.

8 101 + 745 =

9 394 + 106 =

Kies zelf een manier

Reken uit. Noteer de tussenstappen.

10 416 + 75 =

11 199 + 753 =

12 638 + 219 =

13 2345 + 312 + 28 =

1.3 Hele getallen aftrekken

In deze paragraaf zie je meerdere manieren om getallen af te trekken. Je mag zelf de manier kiezen die het best bij jou past.

Kijk wel goed naar de getallen in de opgave. Soms is door de getallen één manier het handigst.

Hier volgen vier manieren:

• cijferen;

• rijgen;

• splitsen;

• handig rekenen.

1e manier: cijferen

Cijferen gaat zo:

1 Zet van de getallen het duizendtal (D), het honderdtal (H), het tiental (T) en de eenheid (E) recht onder elkaar in een DHTE-schema.

2 Trek eerst de eenheden, dan de tientallen, dan de honderdtallen en dan de duizendtallen van elkaar af.

3 Kom je in een kolom tekort, dan leen je van de kolom ervoor. Je zet het nieuwe getal in de kolom erboven, in de rij om te onthouden. Dan kun je het cijfer er wel van aftrekken.

4 In de onderste rij vind je dan het antwoord.

VOORBEELD

353 − 34 = 319

Het antwoord staat in de onderste rij. H

4 13 *rij om te onthouden

3 5 3 13 − 4 = 9 (je leent 10 van de 50)

3 4

3 1 9

2e manier: rijgen

Rijgen gaat zo:

1 Hak het tweede getal in stukken.

2 Trek die stukken een voor een van het eerste getal af. De getallenlijn helpt daarbij. Je kiest zelf welke stukken je neemt.

3e manier: splitsen

Splitsen gaat zo:

1 Zet de getallen onder elkaar.

2 Splits de getallen eerst in duizendtallen, honderdtallen, tientallen en eenheden.

3 Die trek je apart van elkaar af.

4 Daarna tel je de uitkomsten bij elkaar op. Als je een tekort hebt, trek je dat ervan af.

VOORBEELD 247 – 176 = 71

Uitleg:

2 4 7 (zet de getallen onder elkaar)

1 7 6 –

1 0 0 = 200 – 100 (honderdtallen noteren en van elkaar aftrekken: 200 – 100 = 100)

3 0 tekort = 40 – 70 (tientallen noteren en van elkaar aftrekken: 40 – 70 = 30 tekort)

1 + = 7 – 6 (eenheden noteren en van elkaar aftrekken: 7 – 6 = 1)

7 1 (uitkomsten bij elkaar optellen, tekorten ervan aftrekken: 100 – 30 + 1 = 71)

Let op: de uitkomsten van de eerdere stappen tel je bij elkaar op, behalve als de uitkomst een tekort is.

4e manier: handig rekenen

Soms kun je een handigere manier gebruiken om af te trekken. Dat hangt af van de getallen in de opgave. Zo kun je een getal handig opsplitsen door te kijken naar een mooi getal in de buurt.

VOORBEELD 356 − 101 = 255

Uitleg:

Het tweede getal ligt vlak bij een mooi getal. Splits het tweede getal in 100 en 1 en trek deze daarna van het eerste getal af.

356 − 101 = 356 − 100 − 1 = 256 − 1 = 255

Je kunt ook bij beide getallen een getal optellen om mooie getallen te krijgen, die je daarna gemakkelijk van elkaar aftrekt.

VOORBEELD 111 − 99 = 12

Uitleg:

Het tweede getal ligt vlak bij een mooi getal. Tel bij beide getallen hetzelfde getal op. Daarna trek je ze van elkaar af.

111 − 99 = (111 + 1) − (99 + 1) = 112 − 100 = 12

Oefenen 1.3 Hele getallen aftrekken

1e manier Reken uit met cijferen.

14 265 − 38 = H T E

*rij om te onthouden

2e manier

Reken uit met rijgen.

15 275 − 164 =

3e manier

Reken uit met splitsen.

16 425 − 107 =

4e manier

Reken uit met handig rekenen.

17 437 − 98 =

18 156 − 147 =

Kies zelf een manier

Reken uit. Noteer de tussenstappen.

19 76 − 45 =

20 217 − 199 =

21 654 − 376 =

22 402 − 175 =

1.4 Hele getallen vermenigvuldigen

In deze paragraaf zie je meerdere manieren om getallen te vermenigvuldigen. Je mag zelf de manier kiezen die het best bij jou past.

Kijk wel goed naar de getallen in de opgave. Soms is door de getallen één manier het handigst.

Hier volgen drie manieren:

• cijferen;

• splitsen;

• handig rekenen.

1e manier: cijferen

Cijferen gaat zo:

1 Zet duizendtal (D), honderdtal (H), tiental (T) en eenheid (E) recht onder elkaar.

2 Maak boven in het schema een extra rij om te onthouden.

3 Vermenigvuldig de cijfers in de bovenste rij één voor één met het cijfer in de onderste rij.

4 In de onderste rij vind je dan het antwoord.

VOORBEELD 82 × 6 = 492

Uitleg:

6 × 2 = 12 (schrijf de 2 op en onthoud de 1 in de rij om te onthouden)

6 × 8 = 48 en 48 + 1 (die je hebt onthouden) = 49

Het antwoord staat in de onderste rij.

2e manier: splitsen

Splitsen doe je zo:

1 Zet de getallen onder elkaar.

2 Splits een van de getallen in tientallen en eenheden. Je mag zelf kiezen of je het eerste getal of het tweede getal neemt.

3 Vermenigvuldig deze met het andere getal.

4 Tel daarna de uitkomsten bij elkaar op.

VOORBEELD • 6 × 82 = 492

Uitleg: 8 2 (zet de getallen onder elkaar) 6 × 4 8 0 = 80 × 6 (tientallen met onderste getal vermenigvuldigen: 80 × 6 = 480)

1 2 + = 2 × 6 (eenheden met onderste getal vermenigvuldigen: 2 × 6 = 12)

4 9 2 (uitkomsten bij elkaar optellen 480 + 12 = 492)

• 63 × 82 = 5166

Uitleg:

6 3 (zet de getallen onder elkaar) 8 2 × 4 8 0 0 = 60 × 80 (tiental bovenste getal met tiental onderste getal vermenigvuldigen: 60 × 80 = 240)

1 2 0 = 60 × 2 (tiental bovenste getal met eenheid onderste getal vermenigvuldigen: 60 × 2 = 120)

2 4 0 = 3 × 80 (eenheid bovenste getal met tiental onderste getal vermenigvuldigen: 3 × 80 = 240)

6 +

= 3 × 2 (eenheid bovenste getal met eenheid onderste getal vermenigvuldigen: 3 × 2 = 6)

5 1 6 6 (uitkomsten bij elkaar optellen 4800 + 120 + 240 + 6 = 5166)

3e manier: handig rekenen

Soms kun je een handigere manier gebruiken om te vermenigvuldigen. Dat hangt af van de getallen in de opgave.

Zo kun je zoeken naar een mooi getal in de buurt.

VOORBEELD 5 × 299 = 1495

Uitleg: 299 ligt vlak bij 300. 300 is 1 meer dan 299.

Reken eerst 5 × 300 uit. Daarna trek je er nog 5 × 1 van af.

5 × 299 = 5 × 300 − 5 × 1 = 1500 − 5 = 1495

VOORBEELD

Je mag cijfers in een vermenigvuldiging halveren en verdubbelen. Dit doe je om mooie getallen te krijgen waarmee je makkelijker rekent.

• 5 × 28 = 140

Uitleg:

Het dubbele van 5 is een mooi getal, namelijk 10.

Verdubbel de 5 en halveer de 28, dit geeft hetzelfde antwoord.

10 × 14 = 140

• 200 × 15 = 3000

Uitleg:

De helft van 200 is een mooi getal, namelijk 100.

Halveer de 200 en verdubbel de 15, dit geeft hetzelfde antwoord.

100 × 30 = 3000

Oefenen 1.4 Hele getallen vermenigvuldigen

1e manier

Reken uit met cijferen.

23 36 × 7 =

*rij om te onthouden

2e manier Reken uit met splitsen.

24 53 × 7 =

3e manier Reken uit met handig rekenen.

25 99 × 4 =

26 8 × 102 =

27 5 × 36 =

28 25 × 2 × 14 =

Kies zelf een manier Reken uit. Noteer de tussenstappen.

29 7 × 175 =

30 357 × 12 =

31 199 × 301 =

32 301 × 702 =

1.5 Hele getallen delen

In deze paragraaf zie je meerdere manieren om getallen te delen. Je mag zelf de manier kiezen die het best bij jou past.

Kijk wel goed naar de getallen in de opgave. Soms is door de getallen één manier het handigst.

Hier volgen drie manieren:

• veelvoud weghalen;

• staartdeling;

• handig rekenen.

1e manier: veelvoud weghalen

Veelvoud weghalen gaat zo:

1 Haal telkens een veelvoud weg uit het getal dat je moet delen. Je mag zelf kiezen hoe groot de veelvouden zijn.

2 Trek de uitkomst van die veelvouden van het getal af, totdat het niet meer kan.

3 Tel de aantallen veelvouden bij elkaar op.

VOORBEELD 434 : 7 = 62

van 7 weg uit het getal

Het kan voorkomen dat je aan het eind nog een getal overhoudt. Bij hele getallen schrijf je dat op als ‘rest’.

VOORBEELD 437 : 7 = 62 rest 3

2e manier: staartdeling

Bij een staartdeling werk je van links naar rechts. In het voorbeeld kijk je eerst hoeveel honderdtallen er in het getal passen, daarna hoeveel tientallen en tot slot hoeveel eenheden. Je trekt de uitkomst elke keer van het getal af en zo kom je tot het antwoord.

VOORBEELD 516 : 3 = 172

Uitleg:

3 / 5 1 6 \ 172

3 0 0 (= *100 × 3, schrijf de 1 op)

2 1 6

2 1 0 (= **70 × 3, schrijf de 7 op) 0 6

6 (= ***2 × 3, schrijf de 2 op) 0

* 100 × 3 = 300 is het grootst mogelijke honderdvoud van 3 dat past in 516

** 70 × 3 = 210 is het grootst mogelijke tienvoud van 3 dat past in 216

*** 2 × 3 = 6 is het grootst mogelijke veelvoud van 3 dat past in 6

3e manier: handig rekenen

Soms kun je de opgave handiger uitrekenen. Dat hangt af van de getallen in de opgave. Zo kun je beide getallen delen door hetzelfde getal om een makkelijkere som te krijgen. Deel dan wel beide getallen door hetzelfde getal.

VOORBEELD 25 000 : 500 = 50

Uitleg:

Je kunt beide getallen door 100 delen (streep in beide gevallen twee nullen weg).

Dan is 25 000 : 500 hetzelfde als 250 : 5 = 50

Of je vermenigvuldigt eerst beide getallen met hetzelfde getal om mooie getallen te krijgen waarmee je makkelijker rekent. Je moet dan wel beide getallen met hetzelfde getal vermenigvuldigen.

VOORBEELD 75 : 5 = 15

Uitleg:

Je krijgt mooie getallen als je beide getallen met 2 vermenigvuldigt.

Dan is 75 : 5 hetzelfde als 150 : 10 = 15

Oefenen 1.5 Hele getallen delen

1e manier

Reken uit door een veelvoud van 6 weg te halen.

33 762 : 6 =

2e manier

Reken uit met een staartdeling.

34 875 : 5 =

3e manier

Reken uit met handig rekenen.

35 48 000 : 200 =

36 260 : 5 =

Kies zelf een manier

Reken uit. Noteer de tussenstappen.

37 414 : 6 =

38 425 : 5 =

39 1010 : 10 =

40 28 000 : 70 =

1.6 Kommagetallen

Tot nu toe heb je gerekend met hele getallen. Als een getal cijfers achter de komma heeft, is het een kommagetal.

Het aardige van kommagetallen is dat ze erg lijken op de hele getallen, alleen met een komma. Dat komt door de decimale structuur. Daardoor kun je de basisbewerkingen voor hele getallen ook gebruiken voor kommagetallen. Let op de plaats van de komma! Kijk ook goed wat de positiewaarde is van de cijfers achter de komma:

• het eerste cijfer na de komma is een tiende;

• het tweede cijfer na de komma is een honderdste;

• het derde cijfer na de komma is een duizendste.

VOORBEELD Geef de waarde van de cijfers in 0,781.

Uitleg:

7 heeft de waarde 7 tiende.

8 heeft de waarde 8 honderdste.

1 heeft de waarde 1 duizendste.

Je kunt dit goed zien in een DHTE-schema. Je breidt dit uit met een kolom voor de komma en kolommen voor t (tienden), h (honderdsten) en d (duizendsten). Let op: de positiewaarden na de komma schrijf je met kleine letters, de waarden voor de komma met hoofdletters.

VOORBEELD Plaats 54,781 in het DHTE,thd-schema.

Uitleg:

5 heeft de waarde 50, dus 5 staat onder de T(ien).

4 heeft de waarde 4, dus 4 staat onder de E(enheid).

7 heeft de waarde 7 tiende (0,7), dus 7 staat onder de t(iende).

8 heeft de waarde 8 honderdste (0,08), dus 8 staat onder de h(onderste).

1 heeft de waarde 1 duizendste (0,001), dus 1 staat onder de d(uizendste).

Dit geeft het volgend schema:

Tip: Het kan helpen om bij kommagetallen te denken aan geld. In het geldsysteem werk je veel met twee cijfers achter de komma. Bijvoorbeeld: 20 eurocent is 0,20 euro.

1.7 Kommagetallen optellen

De basisbewerkingen voor hele getallen kun je ook gebruiken voor kommagetallen. Hierna volgen vier manieren voor optellen, nu met kommagetallen:

• cijferen;

• rijgen;

• splitsen;

• handig rekenen.

1e manier: cijferen

Cijferen met kommagetallen gaat zo:

1 Maak eventueel eerst het aantal decimalen gelijk door nullen erachter toe te voegen.

2 Zet de komma’s recht onder elkaar.

3 Zet duizendtal (D), honderdtal (H), tiental (T), eenheid (E), tiende (t) en honderdste (h) recht onder elkaar.

4 Tel daarna de cijfers bij elkaar op. Begin aan de rechterkant van het schema.

VOORBEELD 350,21 + 35,2 = 385,41

Uitleg: Verander de opgave eerst in 350,21 + 35,20 (dus beide getallen evenveel decimalen). Het antwoord staat in de onderste rij.

5 Kom je in een kolom boven de 9, dan schuift de 1 naar de kolom ernaast. Neem boven in het schema een extra rij op om te onthouden Je zet dan de 1 boven de kolom in de rij om te onthouden.

6 In de onderste rij vind je het antwoord.

VOORBEELD

158,7 + 63,8 = 222,5

Uitleg:

Beide getallen hebben evenveel decimalen, dus dit hoef je niet aan te passen. Het antwoord staat in de onderste rij. H T E , t

*rij om te onthouden

eerst 7 + 8 = 15; 5 opschrijven 1 onthouden

,

Met Got it ben je volledig voorbereid op je rekentoets.

Het Handboek Rekenen naar 2F is een uitstekende aanvulling op het adaptieve online leerplatform Got it en helpt jou om snel en gemakkelijk alle rekenvaardigheden uit de vier rekendomeinen te overzien en te oefenen.

Wat vind je in het Handboek Rekenen naar 2F?

- Beknopte en heldere uitleg.

- Oefenopgaven en oefenexamens.

- Hints en trucs.

- Voorbereiding op de rekentoets.

Naast het Handboek Rekenen naar 2F is ook het Handboek Rekenen naar 3F beschikbaar.

Kijk voor meer informatie over het online leerplatform en de boeken op www.got-it.nl.