9789127467835

L ÄRARHANDLEDNING

MED LÄRARWEBB

Sofie Bellman

Janna Malmgren

Kurt Rosenlund

Karin Nygårds

Introduktion

INNEHÅLL

OLA HELENIUS Få eleverna att redovisa skriftligt 12

KENNY SKAGERLUND

Välkommen till Flex!

VI SOM ÄR FÖRFATTARE till Flex matematik lärde känna varandra på Södermalmsskolan i Stockholm.

Idén till Flex matematik föddes av Kurt Rosenlund, som tidigare skrivit läromedel i matematik. Kurt ville skapa ett klimat där alla elever var delaktiga och när datorerna gjorde intåg i klassrummen började han experimentera. Med hjälp av genomgångar som stöddes av bildspel blev fler elever engagerade. Men det var först när de fick var sin liten skrivtavla för att snabbt kunna anteckna lösningar och funderingar, som alla blev riktigt delaktiga.

Mycket av vår undervisning går ut på att vi gör saker gemensamt. Det är inte läraren som avgör om en lösning är rätt, utan det resonerar vi om tillsammans och i stället för att avfärda något som ”fel” säger eleverna ”jag har tänkt annorlunda” eller ”jag håller inte med”. Det skapar ett öppet klassrumsklimat.

Vi svarar sällan på frågan ”Är det rätt?” , i stället bollar vi tillbaka med ”Hur kan vi ta

reda på det?” Och vid korrekta lösningar utmanar vi med frågor som ”Hur kan du säkert veta att det stämmer?” Allt för att främja meningsfulla samtal om matematik.

En annan viktig aspekt av läromedlet är att det är anpassat efter den enskilde elevens behov. Ingen behöver göra 15 uppgifter om sådant de redan kan och heller inte möta något som är alldeles för svårt.

Det vi uppskattar mest med Flex matematik är att det tydligt skapar engagemang hos eleverna. Alla deltar i genomgångarna, funderar, skriver på sina skrivtavlor, samtalar och argumenterar. Eventuella missuppfattningar blir då lätta att upptäcka och skapar bra utgångspunkter för matematiska resonemang, i en miljö där man vågar ha fel.

Det känns också tryggt att undervisningen vilar på en stabil grund och att den blir likvärdig i alla klasser på skolan. Mycket goda resultat på de nationella proven talar också sitt tydliga språk.

Vi hoppas att du ska uppskatta Flex matematik lika mycket som vi gör!

KURT ROSENLUND

SOFIE BELLMaN JaNNa MaLMGREN

Undervisa med Flex matematik

1. BILDSPEL

Med Flex matematik undervisar du i 3 steg:

Varje lektion inleds med ett bildspel. Du leder genomgången med hjälp av frågorna som finns i handledningen. Eleverna funderar först enskilt och skriver ned sina svar. Sedan kan de parvis eller i grupp komma överens om ett svar och på så sätt få träning i att argumentera. Låt eleverna visa svaren. Du får snabbt en överblick över klassens kunskaper och kan använda elevernas skrivtavlor för att visa exempel på olika lösningsstrategier. Genom att undvika handuppräckning och själv fördela ordet får du eleverna aktiva under lektionen. Ställ frågor som:

– Vilka olika svar hade ni från början?

– Vilka argument använde ni när ni enades om det ena svaret och inte det andra?

– Håller ni andra med om deras argument?

Lektionen avslutas alltid med en minicheck (exit ticket) som visar hur eleverna har förstått lektionens innehåll.

2. LEKTIONSBOK

Efter bildspelet är det dags för eleverna att lösa liknande uppgifter på egen hand i lektionsboken. Den första uppgiften är kopplad till bildspelet medan efterföljande uppgifter är kopplade till arbetsområdet i stort.

Lektionsboken redovisas gemensamt genom att du tar fram uppgifterna på helskärm (finns i bildspelen) och elever kommer fram till tavlan där de skriver och berättar om sina lösningar. Använd handuppräckning eller annat sätt att fördela turen på, så att många elever får möjlighet att redovisa sina svar. Blyga elever kan gå fram i par. Tänk på att i detta skede inte låta någon kommentera det som skrivs. När alla uppgifter är besvarade kan du fråga vilka elever som har tänkt annorlunda och vilka som håller med. Passa gärna på att ställa frågor som lyfter vanliga missuppfattningar.

När eleverna är färdiga med lektionsboken loggar de in på elevwebben. Här finns blandade övningar på flera olika nivåer. Med hjälp av ledtrådar blir ingen uppgift för svår och medaljerna triggar eleverna att räkna vidare. Uppgifterna är adaptiva, de anpassas efter elevernas svar och utmanar eleverna på den nivå de befinner sig.

3. FLEX WEBB

Grovplanering

Flex matematik årskurs 5 är fördelat på sju kapitel. Det finns möjlighet att förlänga eller förkorta undervisningen utifrån dina elevers behov. Förslag på läsårsfördelning:

Problemlösning

Kluringarna är problemlösningsuppgifter som finns i lektionsboken och på lärarwebben. I Flex finns det en kluring per vecka. Du kan inleda med att visa kluringen på helskärm och samtidigt låta eleverna ha motsvarande kluring i lektionsboken framför sig. Gå tillsammans igenom svåra ord och be eleverna att stryka under viktig information i kluringen. Ni kan med fördel arbeta enligt metoden EPA (Ensam, Par, Alla). Välj ut två till tre lösningar där olika metoder och strategier har använts och låt eleverna gå fram och redovisa på tavlan. Efter varje redovisning får övriga elever ställa frågor om sådant de inte förstått eller ge tips om andra metoder. Låt inte eleverna kommentera lösningarna genom att bara säga ”det är fel” utan uppmuntra formuleringar som ”jag håller inte med” , ”jag har gjort annorlunda” , ”jag har en annan lösning”. Det skapar ett tryggare klassrumsklimat. Diskuera inte rätt svar förrän alla som redovisat på tavlan är klara. Om redovisningarna leder till olika svar, så samtala gemensamt om hur ni kan bevisa vilket svar som är korrekt. Avsluta genomgången med att lyfta vanliga missuppfattningar och effektiva strategier.

KAP 1 Tal 6 v.

KAP 2 Bråk och procent 5 v. KAP 3 Statistik 4 v.

Talföljder B

14 Fortsätt talföljderna.

KAP 4 Geometri 5 v.

KAP 5 Räknesätt och algebra 6 v. KAP 6 Enheter 5 v.

KAP 7 Programmering 2 v. TRÄNA MER 0 – 3 v.

Talsorter B

15 Upptäck mönstret.

35 Fortsätt talföljderna.

ut

? KLURING 3

36 Skriv som decimaltal och räkna ut svaret.

I ledningarna på bilden rinner 300 liter vatten. Vid varje förgrening delas vattnet i två lika stora delar. Hur många liter vatten kommer att hamna i behållare A?

Svar:

a) 1 tiondel + 1 hundradel = 0¸1 + 0¸01 = b) 1 tiondel – 1 hundradel = – = c) 1 tiondel + 10 hundradelar = + = d) 10 tiondelar – 1 hundradel = – = ? KLURING 6

En bagare har just lagt 98 bullar på jäsning när hans fru kommer in i bageriet. Hon tycker att 14 bullar är för stora. Därför delar hon dem på mitten, så att de blir dubbelt så många. Hon tycker även att 14 andra bullar är för små, så dem slår hon ihop två och två. Hur många bullar ligger det sedan på plåten?

Svar:

Formativ bedömning

I Flex matematik finns flera olika stöd för att synliggöra elevers lärande genom formativ bedömning. Förutom att du på lärarwebben kan följa elevernas individuella arbete på elevwebben finns följande stöd för formativ bedömning:

Check in är det första bildspelet i varje kapitel och motsvarande uppgifter ligger även först i varje kapitel i elevboken. Tanken är att eleverna ska få pröva och reflektera över olika uppgifter som de kommer att möta i kapitlet. Samtidigt som du klickar fram en uppgift i taget i bildspelet, så testar eleverna att svara i lektionsboken. De gör även individuella skattningar av uppgifterna på en skala från ”aldrig sett” till ”löser lätt” .

CHECK IN MINICHECK

Till varje lektion finns en avslutande uppgift i form av en Minicheck, som testar hur väl eleverna hängt med. Denna uppgift har ofta fyra svarsalternativ och är tänkt att kunna lösas förhållandevis snabbt, som en ”exit ticket” på att eleven förstått. Eleverna kan använda sina skrivtavlor eller något digitalt alternativ med mentometerfunktion för att svara. Uppgiften Minicheck ligger sist i varje bildspel.

CHECK OUT

När ett kapitel är klart gör eleverna en Check out (prov) med uppgifter som testar det som tränats i det aktuella kapitlet. Efter att uppgifterna är rättade får eleverna reflektera över sitt lärande genom att jämföra sin Check in med sin Check out. Du hittar Check out i pdf:format på lärarwebben.

Flex matematik och kursplanens centrala innehåll

Taluppfattning och tals användning

Rationella tal, däribland negativa tal, och deras egenskaper samt hur talen kan delas upp och användas.

Positionssystemet och hur det används för att beskriva hela tal och tal i decimalform.

Olika talsystem och några talsystem som använts i olika kulturer genom historien.

Tal i procentform och deras samband med tal i bråk- och decimalform.

Hur tal i bråk- och decimalform kan användas i vardagliga situationer.

De fyra räknesätten och regler för deras användning vid beräkningar med naturliga tal.

Metoder för beräkningar med naturliga tal och enkla tal i bråk- och decimalform vid överslagsräkning, huvudräkning och skriftlig beräkning.

Användning av digitala verktyg vid beräkningar.

Bråk och procent

Bråk och procent ? Kluringar

Räknesätt och algebra

Tal Räknesätt och algebra

Flex matematik stämmer överens med läroplanen Lgr22. För att ge en överblick visas här vilka delar av det centrala innehållet i matematik som behandlas i respektive kapitel och årskurs.

Bråk och procent

Bråk och procent Enheter ? Kluringar

Räknesätt och algebra

Tal Räknesätt och algebra

Bråk och procent

Bråk och procent Enheter ? Kluringar

Räknesätt och algebra

Tal Räknesätt och algebra

Tal ? Kluringar ? Kluringar ? Kluringar

Rimlighetsbedömning vid uppskattningar och beräkningar. Tal

Algebra

Matematiska likheter och hur likhetstecknet används för att teckna enkla ekvationer.

Variabler och deras användning i enkla algebraiska uttryck och ekvationer.

Metoder, däribland algebraiska, för att lösa enkla ekvationer.

Mönster i talföljder och geometriska mönster samt hur de konstrueras, beskrivs och uttrycks.

Programmering i visuella programmeringsmiljöer. Hur algoritmer skapas och används vid programmering.

4

Tal

Tal Räknesätt och algebra

Räknesätt och algebra

Tal Geometri

Tal

5

Tal Räknesätt och algebra

Tal Räknesätt och algebra

Tal Räknesätt och algebra

Tal Räknesätt och algebra

Tal Räknesätt och algebra

Räknesätt och algebra Räknesätt och algebra

Tal Räknesätt och algebra

Tal Räknesätt och algebra

Programmering Programmering

Grundläggande geometriska två- och tredimensionella objekt samt deras egenskaper och inbördes relationer. Konstruktion av geometriska objekt, såväl med som utan digitala verktyg.

Jämförelse, uppskattning och mätning av längd, area, massa, volym, tid och vinkel med standardiserade måttenheter samt enhetsbyten i samband med detta.

Metoder för hur omkrets och area hos olika tvådimensionella geometriska figurer kan bestämmas och uppskattas.

Skala vid förminskning och förstoring samt användning av skala i elevnära situationer.

Symmetri i planet och hur symmetri kan konstrueras.

Enheter

Enheter

Slumpmässiga händelser, chans och risk med utgångspunkt i observationer, simuleringar och statistiskt material. Jämförelse av sannolikhet vid olika slumpmässiga försök.

Enkel kombinatorik i konkreta situationer.

Tabeller och diagram för att beskriva resultat från undersökningar, såväl med som utan digitala verktyg. Tolkning av data i tabeller och diagram.

Lägesmåtten medelvärde, typvärde och median samt hur de används i statistiska undersökningar.

Samband och förändring

Proportionalitet samt hur proportionella samband uttrycks i bråk-, decimal- och procentform.

Koordinatsystem och gradering av koordinataxlar.

Bråk och procent ? Kluringar

Bråk och procent ? Kluringar

Bråk och procent ? Kluringar

Statistik

Grafer för att uttrycka proportionella samband. Statistik

Problemlösning

Strategier för att lösa matematiska problem i elevnära situationer.

Formulering av matematiska frågeställningar utifrån vardagliga situationer.

Kluringar

Kluringar

Kluringar ? Kluringar

Geometri

KaPITEL 4 Geometri

Mål för kapitlet

• Beskriva, mäta och rita geometriska figurer.

• Förminska och förstora i olika skalor.

• Mäta och rita vinklar.

• Känna igen spegelsymmetri och rotationssymmetri.

• Bestämma omkrets och area.

• Lösa problem.

Kapitel 4

GEOMETRI

Centralt innehåll Lgr22

Geometri

• Grundläggande geometriska två- och tredimensionella objekt samt deras egenskaper och inbördes relationer. Konstruktion av geometriska objekt, såväl med som utan digitala verktyg.

• Jämförelse, uppskattning och mätning av längd, area, massa, volym, tid och vinkel med standardiserade måttenheter samt enhetsbyten i samband med detta.

Innehåll i kapitel Geometri

Det här kapitlet kretsar kring geometriska objekt och eleverna möter nya figurer, undersöker och beskriver deras egenskaper, samt lär sig deras namn. De tränar på att mäta figurernas sidor i olika längdenheter, att mäta och rita vinklar och att räkna ut omkrets och area.

• Metoder för hur omkrets och area hos olika tvådimensionella geometriska figurer kan bestämmas och uppskattas.

• Skala vid förminskning och förstoring samt användning av skala i elevnära situationer.

Eleverna lär sig även att förstora och förminska figurer i olika skalor, att upptäcka spegelsymmetri och rotationssymmetri, samt att lösa problem där geometri är i fokus.

Problemlösning

• Symmetri i planet och hur symmetri kan konstrueras.

• Strategier för att lösa matematiska problem i elevnära situationer.

Förväntade förkunskaper

Vi utgår från att eleverna har förkunskaper (enligt Lgr22) om de vanligaste geometriska objekten och att de på ett enkelt sätt kan beskriva deras egenskaper.

De bör även kunna göra enklare mätningar, jämförelser, uppskattningar och vara bekanta med skala vid enkel förminskning och förstoring, samt uppfatta symmetri i vardagen och känna till vad en vinkel är.

liksidig triangel likbent triangel rätvinklig triangel spegelsymmetri rotationssymmetri rät vinkel trubbig vinkel spetsig vinkel vinkelben parallelltrapets parallellogram area romb

Begrepp

VECKa 1

Översikt veckoplanering

LEKTION 1

Bildspel

Lektionsbok s. 81–82 CHECK

LEKTION 2

Bildspel

Lektionsbok s. 83

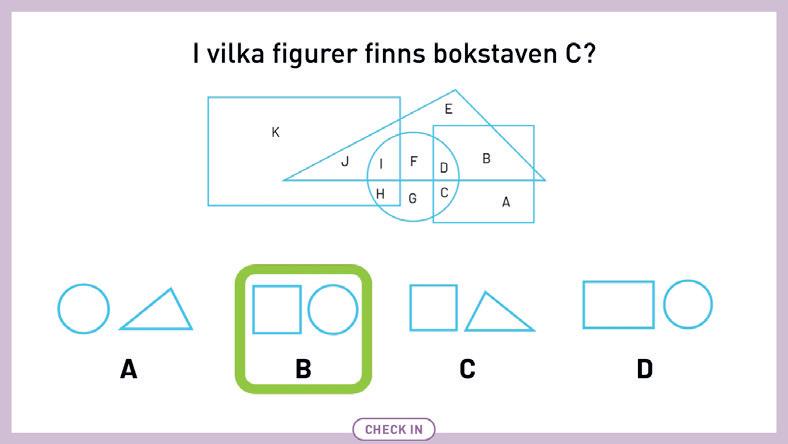
Geometriska figurer A 1 Skriv rätt bokstäver i figurerna.

A rektangel B cirkel C likbent triangel D liksidig triangel

E kvadrat F ellips G rätvinklig triangel

2 I vilken eller vilka av de geometriska figurerna står varje bokstav?

Skriv rätt bokstav i var och en av de vita rutorna.

Minicheck Bildspel

VECKa 1

Översikt veckoplanering

LEKTION 3

VECKANS KLURING

3

Längs

Svar: Bildspel

Lektionsbok s. 84

? KLURING 1

gatlampan?Minicheck Bildspel

? KLURING 1

Längs

LEKTION 1

DU BEHÖVER:

• Bildspel – CHECK IN Geometri

• Lektionsboken s. 81–82

• Skrivtavlor

Bildspel CHECK IN Geometri

SÅ HÄR KAN DU GÖRA

1

Öppna bildspelet och ta fram det på helskärm. Se till att alla elever är beredda med sina skrivtavlor.

Berätta att arbetsområdet är Geometri och skriv ordet geometri på tavlan. Låt var och en fundera på egen hand kring begreppet under någon minut och göra noteringar på sin skrivtavla. Ställ sedan frågor:

– Vad tänker ni på när ni hör begreppet geometri?

– Kan ni ge exempel på vad geometri kan vara?

– Vilka geometriska figurer hittar ni i klassrummet?

– När har ni användning av att kunna förminska och förstora figurer?

Sammanfatta elevernas tankar, till exempel i en tankekarta på din whiteboard.

2

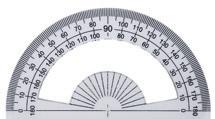
Visa kapitlets introduktionsbild i bildspelet och samtala om vilken matematik som eleverna ser i bilden. Det kan vara till exempel att mätverktygen har olika geometriska former och olika vinklar som går att mäta med gradskivan.

3

Visa Check in i bildspelet och berätta att uppgifterna här ger en översikt av vad eleverna kommer att möta i kapitlet Geometri. Betona att det inte är ett test, utan är till för att eleverna ska få chans att bekanta sig med innehållet.

Klicka fram en uppgift i taget i bildspelet och låt eleverna svara i lektionsboken.

Flex webb

Efter genomgången av Check in påbörjar eleverna arbetet med kapitel Geometri på Flex webb.

LEKTION 2

DU BEHÖVER:

• Bildspel – Geometriska figurer A

• Lektionsboken s. 83

• Skrivtavlor

Bildspel Geometriska figurer A

Träna på att namnge och beskriva geometriska figurer.

SÅ HÄR KAN DU

GÖRA

1

Öppna bildspelet och ta fram det på helskärm. Se till att alla elever är beredda med sina skrivtavlor.

2

Bilden visar en vinkel och en triangel. Samtala om vad som skiljer figurerna åt. Konstatera att om vi sätter samman två räta linjer så bildas en vinkel och att om vi sätter samman tre räta linjer bildas en geometrisk figur. Peka och visa att varje linje motsvarar en sida i figuren.

Fråga eleverna vad den punkt där två sidor möts kallas. Peka på punkten som är inringad. Låt dem fundera enskilt först och skriva ned sina svar. Sedan samtalar de parvis och enas om ett förslag som de redovisar. Enas om att den punkten kallas hörn och klicka vidare i bildspelet och visa svaret.

3

Bilden visar en triangel. Fråga eleverna vad vi kallar en figur med tre sidor och tre hörn. Låt dem fundera enskilt först och skriva ned sina svar. Sedan samtalar de parvis och enas om ett förslag som de redovisar. Konstatera att svaret är triangel.

Klicka vidare för att visa eleverna tre olika trianglar. Fråga vad de olika typerna av trianglar kallas. Låt dem fundera enskilt först och skriva ned sina svar. Sedan samtalar de parvis och enas om ett förslag som de redovisar. Ställ frågor, exempelvis:

–

Finns det något annat som är lika i den liksidiga triangeln än sidorna? Vinklarna är lika stora även om det inte hörs på namnet.

– Det heter likbent eftersom vi kallar linjerna som går ut från en vinkel för vinkelben och här är två av vinkelbenen lika långa. Vilken vinkel i var och en av de här trianglarna har två lika långa vinkelben? Peka på de likbenta trianglarna. Berätta att en likbent triangel inte behöver ha de lika benen ”ståendes upp” utan att triangeln kan vara vriden på olika sätt.

– Är alla vinklarna i de likbenta trianglarna också lika stora? Nej, men två av vinklarna är alltid lika stora.

–

Vilken vinkel är rät i den rätvinkliga triangeln?

– Kan en triangel ha två räta vinklar? Nej, eftersom det bara finns tre vinklar, så skulle de två räta behöva vara bredvid varandra. Sidorna skulle då bli parallella, det vill säga de kan inte utgöra sidor i en triangel.

4

Innan du klickar fram bilden så fråga eleverna om de kan rita fyra linjer, som sitter samman, på sin skrivtavla och som inte bildar en fyrhörning. Be dem att samtala parvis och hitta argument för att det inte är en fyrhörning. Gå sedan igenom de olika argumenten i klassen. Enas om att det inte går att sätta samman fyra räta linjer till en figur utan att det bildas en fyrhörning. Kom fram till villkor för hur det blir en fyrhörning och klicka nu fram bilderna på fyrhörningarna. Lyft följande villkor:

• Varje linje måste börja där en annan slutar och sluta där en annan börjar. Den sista linjen måste sluta där den första börjar.

• Man måste kunna ”gå” längs linjerna och komma hela vägen runt figuren.

• Figuren måste vara sluten och linjerna måste innesluta en sammanhängande yta.

• Linjerna får inte korsa varandra.

Visa eleverna att en fyrhörning kan se ut på olika sätt och berätta att hörnen som går inåt på två av figurerna också räknas som hörn. Fråga eleverna vad de tror att den nedersta figuren kallas. Låt dem fundera enskilt först och skriva ned sina svar, sedan samtala parvis och enas om ett förslag som de redovisar. Konstatera gemensamt att det är en sjuhörning och klicka vidare i bildspelet för att visa svaret.

5

Bilden visar parallella linjer. Fråga eleverna vad den här typen av linjer kallas. Låt dem fundera enskilt först och skriva ned sina svar. Sedan samtalar de parvis och enas om ett förslag som de redovisar.

Konstatera att svaret är parallella linjer. Samtala om att parallella linjer aldrig korsas och att avståndet mellan linjerna alltid är lika stort.

6

Bilden visar en rektangel och en kvadrat.

Fråga vad en rektangel med lika långa sidor kallas och enas om att den kallas kvadrat. Berätta att en kvadrat räknas som en speciell typ av rektangel, en liksidig rektangel (jämför med en liksidig triangel).

Be eleverna att parvis diskutera och skriva ned vilka egenskaper en rektangel har. Samtala om att de vanligaste fyrhörningarna är uppbyggda av parallella linjer och repetera vad parallella linjer innebär. Klicka vidare och visa vilka kriterier som ska vara uppfyllda för att en fyrhörning ska få kallas rektangel.

7

Bilden visar en cirkel. Förklara att avståndet från medelpunkten till en punkt på cirkelbågen alltid är lika stort, oavsett var cirkelbågens punkt ligger. Berätta att om du sätter en pinne i marken och tar ett rep av en viss längd och sedan går ett varv runt pinnen med ett spänt rep, så kommer du att gå längs en cirkel. Spåret du gör bildar en cirkel på marken. Klicka vidare i bildspelet och samtala om begreppen medelpunkt och cirkelbåge.

Klicka fram bilden av ellipsen och hur den delas upp av linjerna a, b, c och d. Samtala om att om vi delar ellipsen på mitten två gånger, så gäller följande, a + b = c + d. Det innebär att alla fyra delarna av ellipsen är lika stora och har samma form och area. Ellipsen kan vikas på mitten och det kommer inte att ”sticka ut” något.

8

ELEVUPPGIFT: Eleverna ritar en geometrisk figur och låter sedan en klasskamrat beskriva figuren med hjälp av matematiska begrepp.

Lektionsboken s. 83

Geometriska figurer A 1 Skriv rätt bokstäver i figurerna.

Flex webb

Eleverna arbetar vidare med uppgifter på Flex webb fram till redovisning. Efter redovisning av lektionsboken arbetar samtliga elever med Flex webb.

I vilken eller vilka av

geometriska figurerna står varje bokstav? Skriv rätt bokstav i var och en av de vita rutorna.

Redovisning av lektionsboken

Ta fram lektionsboken på helskärm. När eleverna har redovisat sina lösningar går ni gemensamt igenom och diskuterar dem. Uppmärksamma till exempel vanliga missförstånd. Repetera gärna figurernas egenskaper när ni går igenom uppgift 1. Fråga också eleverna om de vet namnen på de figurer som de inte skrivit bokstäver i. Kanske känner de även till de grekiska namnen för femhörning (pentagon) och sexhörning (hexagon).

Minicheck

UPPGIFT 1: Eleverna skriver rätt bokstav i var och en av figurerna. Berätta att det blir några figurer över. Utmana eleverna genom att uppmuntra dem att skriva ut namnen på de figurer som blir över, om de kan.

TIPS:

Påminn eleverna om kriterierna som presenterades i bildspelet.

UPPGIFT 2: Eleverna placerar ut bokstäverna i de vita rutorna utifrån vilken/vilka figurer de står i. Bokstaven M står exempelvis bara i rektangeln och cirkeln och ska därför skrivas i rutan längst till höger på den översta raden.

TIPS:

Uppmuntra eleverna att arbeta strukturerat genom att titta på en bokstav i taget och fundera över i vilken figur/vilka figurer just den bokstaven står.

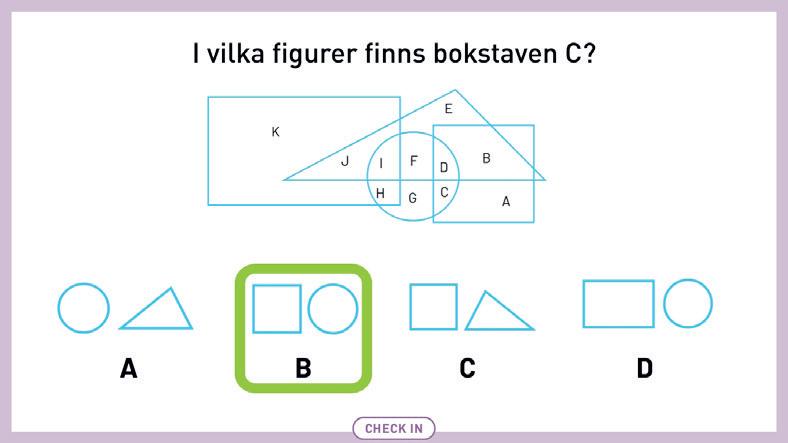
GEOMETRISKa FIGURER: Eleverna tar reda på i vilka figurer bokstaven C finns. Samtala även om vilka bokstäver som motsvarar figurerna från alternativen A (F), C (B) och D (H).

LEKTION 3

DU BEHÖVER:

• Bildspel – Sträckor

• Lektionsboken s. 84

• Skrivtavlor

Bildspel Sträckor

Träna på rumsuppfattning genom att beräkna sträckor på en kub.

SÅ HÄR KAN DU GÖRA

1

Öppna bildspelet och ta fram det på helskärm. Se till att alla elever är beredda med sina skrivtavlor.

2

Bilden visar en kub. Berätta för eleverna att en kub är en tredimensionell figur där alla kanter är lika långa. Det vi kallar sida i en tvådimensionell figur kallas för kant i en tredimensionell figur. Sidor i en tredimensionell figur är själva ”väggarna” som den är uppbyggd av och kallas också för sidoytor.

Ställ frågor, exempelvis:

– Hur många sidor har en kub? 6 sidor.

– Hur ser sidorna ut? Alla är kvadrater och har lika långa kanter.

– Hur många kanter har en kub? 12 kanter.

– Hur ser kanterna ut? De är lika långa, parvis parallella och parallella i 4­grupper.

Klicka fram myrans väg och att kubens kant är 6 cm. Fråga eleverna hur långt myran går. Låt dem fundera enskilt först och skriva ned sina svar,

sedan samtala parvis och enas om ett förslag som de redovisar. Enas om att myran går 30 cm och klicka vidare i bildspelet för att visa svaret.

3

Bilden visar en myra som går längs kanten på en kub. Klicka fram myrans väg och att kubens kant är 7 cm. Fråga eleverna hur långt myran går. Låt dem fundera enskilt först och skriva ned sina svar, sedan samtala parvis och enas om ett förslag som de redovisar. Ställ frågor, exempelvis: – Har ni något tips på hur vi kan räkna ut myrans väg?

Samtala om att ett sätt är att ”göra den delade vägen hel” och räkna ”hela kanter”. Vi kan också multiplicera alla ”hela kanter” med kantens längd.

Uppmärksamma att delsträckor tillsammans kan motsvara längden av en hel kant. Exempelvis är den övre delade sträckan ihop med den undre sammanlagt 7 cm lång. Det vet vi dels eftersom alla sidor är lika långa, dels eftersom den tredje sträckan från myran räknat är vertikal. Det vill säga den är parallell med en av kubernas vertikala sidor och därför lika lång som en sådan.

Enas om att myran går 28 cm och klicka vidare i bildspelet för att visa svaret.

4

ELEVUPPGIFT: Eleverna ritar en myras väg på en kub, byter sedan med en kompis och beräknar längden av vägen.

Lektionsboken s. 84

Sträckor

3

Längs en parkväg står det tio gatlampor.

Det är samma avstånd mellan alla gatlampor.

Från den första till den fjärde gatlampan är det 60 m.

Hur långt är det från den första till den sista gatlampan?

Flex webb

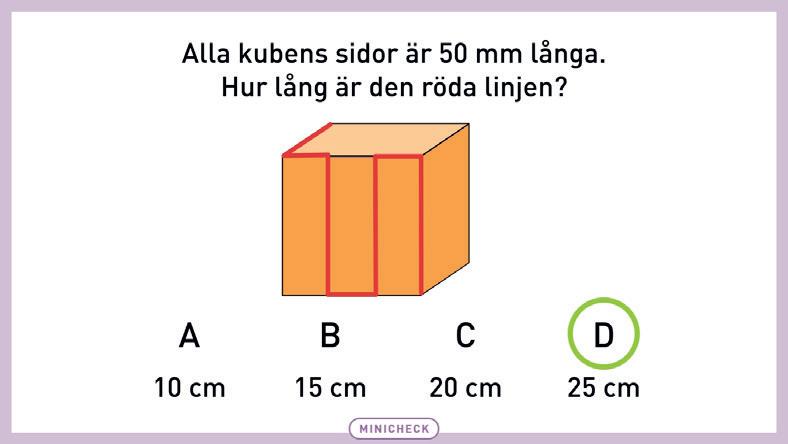
UPPGIFT 3: Eleverna räknar ut myrans väg längs kanten på kuben. Myran går längs den röda linjen och det står angivet hur lång kanten i varje kub är. Eleverna svarar i centimeter

Svar:

TIPS:

• Uppmuntra eleverna att räkna ut hur många ”hela kanter” myran går och multiplicera det antalet med kantens längd. Uppmärksamma att delsträckor tillsammans kan motsvara längden av en hel kant.

• Påminn eleverna om att skriva ut enheten.

Eleverna arbetar vidare med uppgifter på Flex webb fram till redovisning. Efter redovisning av lektionsboken arbetar samtliga elever med Flex webb.

Redovisning av lektionsboken

Ta fram lektionsboken på helskärm. När eleverna har redovisat sina lösningar går ni gemensamt igenom och diskuterar dem. Uppmärksamma till exempel vanliga missförstånd.

Låt eleverna som redovisar visa vilka delsträckor som tillsammans utgör en hel kant på respektive kub, för att förtydliga för resten av klassen hur många kanter myran går.

Minicheck

STRÄCKOR: Eleverna tar reda på hur lång den röda linjen är. Alla sidor är 50 mm långa. Fråga hur många ”hela 50 mm-sträckor” det är. Samtala om enhetsomvandlingen från millimeter till centimeter.

Sträckor

3 Skriv myrans väg i centimeter under varje kub.

VECKANS KLURING

Kom

DU BEHÖVER:

• Bildspel – Kluring 1

• Lektionsboken s. 84

ELEVLÖSNING 2 L L L L L L L L L L

60 3 = 180

Svar: 180 m.

• Skrivtavlor

Kluring 1 s. 84

Träna problemlösning.

? KLURING 1

Längs en parkväg står det tio gatlampor.

Det är samma avstånd mellan alla gatlampor. Från den första till den fjärde gatlampan är det 60 m. Hur långt är det från den första till den sista gatlampan?

Svar: Det är 180 m.

SÅ HÄR KAN DU GÖRA

• Visa kluringen på helskärm.

• Läs problemet högt för eleverna.

Den här eleven har sett att avståndet från den första till den fjärde lampan är lika långt som från den fjärde till den sjunde och från den sjunde till den tionde. Sedan har hen multiplicerat 60 med 3.

ELEVLÖSNING 3 = 15 m

• Fråga vilken viktig information som finns i texten.

Eleverna arbetar med problemet enligt metoden EPA (Ensam, Par, Alla).

TIPS:

Uppmuntra eleverna att rita en bild som visar hur lamporna är placerade.

ELEVLÖSNING 1

L L L L L L L L L L = 20 m

Det är 20 meter mellan varje stolpe.

Det är 9 mellanrum.

9 20 = 180 m

Svar: 180 meter.

Eleven har ritat upp stolparna och sedan utgått från mellanrummen för att räkna ut avståndet.

15 10 = 150

Svar: 150 meter.

Den här eleven har inte ritat lamporna. Eleven har felaktigt tänkt 60 meter uppdelat på 4 lampor och beräknat

Det ska dock vara tre mellanrum mellan första och fjärde lampan och således 20 meters mellanrum mellan varje lampa.

Flex webb

När arbetet med kluringen är avslutat loggar eleverna in på Flex webb och arbetar på egen hand med uppgifter. 60 4 60 4

Programmering

• Känna till att en dator bara kan läsa av ett eller noll och vad det innebär för programmering.

Mål för kapitlet

• Förstå att det finns många olika slags kod som gör att datorn fungerar, till exempel maskinkod och programmeringskod.

• Förstå vikten av sekvens vid programmering.

• Känna till att loopar och villkor är grundläggande funktioner i programmering.

• Förstå att mönster är viktiga vid programmering.

• Veta vad begreppet algoritm betyder i programmering.

• Kunna följa principer för programmering genom att skriva låtsaskod.

Om författaren

JAG SOM HAR SKRIVIT det här kapitlet heter Karin Nygårds och är legitimerad lågoch mellanstadielärare. Någon gång runt 2011 började jag tycka att det kändes konstigt att jag kunde undervisa om atomer och molekyler, men inte svara på hur en mobil fungerar.

Jag bestämde mig för att lära mig mer om programmering och internet. För mig är det självklart att vi som lever i en värld där det digitala har en stor roll, också måste förstå hur det fungerar.

När den digitala tekniken fungerar som den ska, är den osynlig för oss. Vi svajpar och swishar till höger och vänster och det är så det ska vara. Vi ska inte behöva kämpa för att ta oss in i datorer eller program. Men vad händer med förståelsen för det digitala när tekniken blir osynlig? Vissa av oss lärare kan fortfarande minnas ljudet av modemet som kopplade upp oss till internet, men för våra elever är internet lika naturligt som luft. Att vi lär våra elever vad luft består av är självklart sedan många årtionden, men det är fortfarande inte givet att vi lär eleverna hur vår digitala värld är uppbyggd.

Det digitala har vissa grundprinciper som påverkar hur det fungerar och som i sin tur påverkar oss som lever med tekniken.

För det första är allt digitalt skapat av människor. Även om det finns AI som kan skriva kod, så är den upplärd på kod som är skriven av människor. Att teknik är skapat av människor innebär att det någonstans finns upphovspersoner som kan ställas till svars för hur tekniken fungerar. Precis som att vi kan kräva att fabriker inte släpper ut gifter, kan vi kräva att teknikbolag inte skapar skadliga bieffekter.

För det andra är den digitala världen binär. Även om det går att skriva program som är raffinerande lika verkligheten, så är det binära fortfarande en viktig princip som styr. Människan och naturen är långt mer komplex än bara ett eller noll. De flesta program som vi möter i dag är fortfarande rätt stolpiga när det gäller hur vi måste passa in ett ja eller ett nej, när vi egentligen skulle behöva flera alternativ där emellan.

Vi har valt att inleda kapitlet om programmering med det binära talsystemet. Det är det svåraste momentet i hela kapitlet, men eftersom det är grunden för hur den digitala tekniken fungerar så har vi valt att lägga det först. När eleverna väl har tagit sig igenom ettorna och nollornas matematik, kommer det sedan bara att bli lättare och förhoppningsvis roligare. Att lära sig programmera är som att lära sig läsa. Det kan vara svårt i början, men den som väl lärt sig grunderna kan gå vidare och skapa nya spel, appar och program som vi inte ens kan föreställa oss i dag.

KaRIN NYGåRDS

PROGRaMMERING Kapitel 7

Centralt innehåll Lgr22

Taluppfattning och tals användning

• Olika talsystem och några talsystem som använts i olika kulturer genom historien.

och följs som grund för programmering, samt hur symboler används vid stegvisa instruktioner.

algebra

• Mönster i talföljder och geometriska mönster samt hur de konstrueras, beskrivs och uttrycks.

Vi utgår från att eleverna åtminstone har kommit i kontakt med detta, men det är också sannolikt att det behövs repetition. Därför börjar vi väldigt grundläggande i kapitlet.

Om det visar sig att den generella nivån i gruppen ligger över bokens, föreslår vi en snabbare genomgång och repetition av begreppen.

• Programmering i visuella programmeringsmiljöer. Hur algoritmer skapas och används vid programmering.

Programspråk och begrepp

Innehåll i kapitel Programmering

Det här kapitlet är en introduktion till programmering. Eftersom innehållet fortfarande är relativt nytt i läroplanen, så kan de kunskaper som eleverna har med sig variera. Därför skiljer sig kapitlet något från övriga kapitel i boken. Tanken är att du som lärare ska ha en stabil grund att utgå från när det gäller att lära ut viktiga byggstenar som behövs för att förstå hur programmering fungerar.

Matematiken har vuxit fram under årtusenden. Begrepp har slipats och fastställts. Så ser det inte ut inom programmering. Det finns tusentals programspråk, där vissa har en egen logik och terminologi. Det gör att samma funktion kan heta olika saker, beroende på vilket programspråk som används.

Det går att närma sig programmering från olika håll. Den utforskande leken och det kreativa problemlösandet är två vanliga angreppssätt. Här har vi valt att fokusera på att befästa några grundläggande begrepp.

Förväntade kunskaper

De vanligaste programspråken, världen över, bygger på engelska. Vissa inom den svenska datavetenskapen anser att begrepp ska översättas till svenska, medan många anser att de ska användas på engelska eftersom det är det internationella språket.

Enligt kursplanen i matematik för årskurs 1–3 ska eleverna ha lärt sig entydiga stegvisa instruktioner och hur de konstrueras, beskrivs

Begreppet loop heter till exempel repetition eller slinga på svenska. Vi kan säga att vi skapar en slinga eller vi kan säga att vi skapar en loop. Bägge orden innebär att vi gör ett program som repeterar sig. Vi använder begreppet loop i den här boken. Eleverna kommer också att möta engelska i den låtsaskod som vi har hittat på för bokens övningar.

Grundläggande begrepp

PROGRaMMERING

Precis som i matematiken så finns det i programmering vissa grundstenar som alltid är lika. Oavsett vilket av tusentals programmeringsspråk som används, är det ändå samma funktioner som återkommer.

• MaSKINKOD kan också kallas binärkod och är den enda kod som datorn kan läsa av. Att en dator är binär är en viktig egenskap, som påverkar tekniken. En dator måste programmeras till antingen ett eller noll, medan vi människor kan vara både ett, noll och en halv samtidigt.

• PROGRaMKOD är den kod som skrivs i ett programspråk. Det går bra att säga programmeringskod och programmeringsspråk också, det är samma sak. Programkod översätts till maskinkod.

• LOOPaR är kod som gör att datorn upprepar något. Det kan också kallas för slinga eller repetition på svenska.

• VILLKOR är bland det vanligaste som vi jobbar med i programmering. Vi skriver instruktioner för vad datorn ska göra i olika situationer, hur länge och på vilket sätt. OM vi klickar på en knapp – DÅ ska detta hända. Vi kallar det för att vi skriver en if-sats.

• SEKVENS handlar om att förstå innebörden av att kod skrivs i rätt ordning. I programmering för nybörjare är det sällan ett problem att just sekvens blir fel, men i mer avancerade strukturer är det avgörande för hur program fungerar.

• aLGORITM är ett begrepp som vi ofta hör när det talas om hur sociala medier fungerar, att algoritmerna styr våra sökresultat eller hur ett flöde ser ut. En algoritm är en del i ett program, som löser ett visst problem eller styr en viss funktion. Om vi exempelvis ser programkod för ett spel, så kan vi se att det finns flera olika algoritmer i spelet. Begreppet algoritm översätts ofta med ”recept” och det är en ganska bra liknelse.

Begrepp

decimala talsystemet binära talsystemet maskinkod programkod sekvens algoritm villkor loop

VECKa 1

Översikt veckoplanering

LEKTION 1

Bildspel

Lektionsbok s. 155

Räkna som en dator

1 Tabellen visar tal skrivna det binära talsystemet. Skriv motsvarande tal i det decimala talsystemet.

2 De här talen är skrivna i det decimala talsystemet.

Skriv talen i det binära talsystemet. 11 15 20 50 69

3 De här talen är skrivna i det binära talsystemet. Skriv talen i det decimala talsystemet.

Minicheck Bildspel

LEKTION 2

Bildspel

Lektionsbok s. 156 –157

Minicheck Bildspel

VECKa 1

Översikt veckoplanering

LEKTION 3

Bildspel

Lektionsbok s. 158 –159

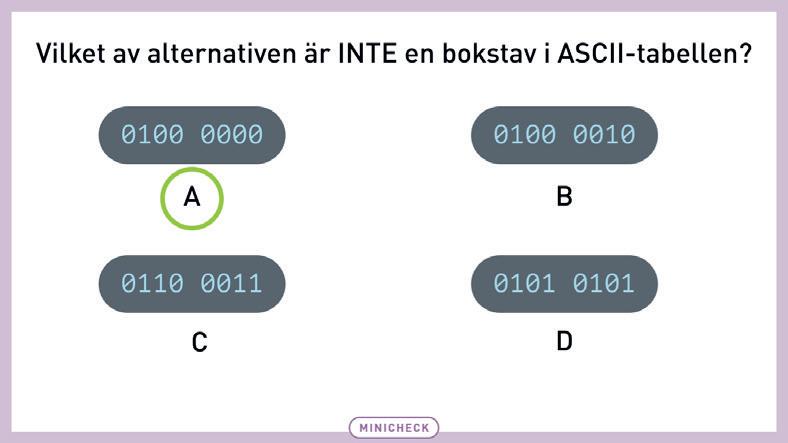
Sekvens

8 Skriv instruktioner i rätt sekvens till hur barnen kan göra sina glassar:

a Vera vill ha fyra smaker. Hon gillar inte frukt- eller bärsmaker. Hon vill ha saltlakrits överst. Hon vill inte ha choklad botten. 1. 2. 3. 4. 5. b) Majed vill ha fem kulor, men bara tre smaker. Han vill ha viol botten. Han tycker inte om choklad eller lakrits. 1. 2. 3. 4. 5.

9 a Vilken instruktion ger samma mönster som på vanten? Ringa in.

A Rosa rand, gula prickar, lila sicksack, rosa rand, gul sicksack och lila prickar.

B Lila prickar, gul sicksack, rosa rand, gula prickar, lila sicksack, rosa rand och rosa rand.

vanilj jordgubb stracciatella blåbär päron viol saltlakrits

C Rosa rand, rosa rand, gula prickar, lila sicksack, rosa rand, gul sicksack och lila prickar. D Lila prickar, rosa rand, rosa rand, lila prickar, gul sicksack, rosa rand, lila sicksack och lila prickar.

b Skriv en instruktion till ett eget mönster. Rita sedan mönstret på vanten.

PROGRAMMERING 158 Vecka 1 Lektion 3

Kopiering av detta engångsmaterial är förbjuden enligt lag och gällande avtal.

Det saknas tal de här lösenorden. Lista ut mönstret och fyll i de tal som saknas. 27

b) 64 49 36 16

c) 0 75 100

11 Flex har gjort ett lösenord som följer en känd talföljd som heter Fibonaccis talföljd. a) Vilka tal saknas lösenordet?

0 1 1 2 3 5 8 13 21 34 55

b) Förklara hur Fibonaccis talföljd är uppbyggd.

Lösenord måste alltid komma rätt sekvens.

Minicheck Bildspel

LEKTION 1

DU BEHÖVER:

• Bildspel – Räkna som en dator

• Lektionsboken s. 155

• Skrivtavlor

Bildspel Räkna som en dator

Träna på att använda det binära talsystemet.

SÅ HÄR

KAN DU GÖRA

1

Öppna bildspelet och ta fram det på helskärm. Se till att alla elever är beredda med sina skrivtavlor. Berätta att arbetsområdet är Programmering och att ni ska arbeta med grunderna till programmering under två veckor. Låt var och en fundera på egen hand kring begreppet under någon minut och göra noteringar på sin skrivtavla. Ställ sedan frågor, exempelvis:

– Vad tänker ni på när ni hör begreppet programmering?

– Kan ni ge exempel på programmering?

– Vad har vi här i klassrummet som är programmerat?

Sammanfatta elevernas tankar, till exempel i en tankekarta på din whiteboard.

2

Bilden visar ett par som leker en gissningslek och en person som programmerar ett gissningsspel. Fråga eleverna vad som skiljer människors språk från språket vi använder i datorer. Låt dem fundera enskilt först och skriva ned sina förslag, för att

sedan samtala parvis och tillsammans komma på fler skillnader. Exempel på skillnader:

• Barnen som leker gissningsleken kan lista ut saker genom att se på den andras kroppsspråk.

• Ett barn kan svara ”både och” om svaret på en fråga inte är ett självklart ja eller nej.

• Ett barn förstår felsägningar som ”Är det ett puiano ?”

• Ett barn förstår ofullständiga instruktioner som: ”Piano!”

• En dator behöver mycket detaljerade instruktioner.

• En dator förstår inte felstavningar.

• En dator måste programmeras för att veta vad den ska göra.

• En dator kan inte förstå om instruktionerna kommer i fel ordning.

Kom gemensamt fram till att en dator måste ha tydliga instruktioner som är mer detaljerade än instruktioner till en människa. Instruktionerna måste dessutom vara rättstavade och skrivna i rätt ordning. Fråga eleverna varför det är så och låt dem på nytt börja med att fundera enskilt och sedan samtala parvis. Exempel på orsaker:

• Ett barn kommunicerar med tonfall, kroppsspråk och miner som ger mer information än själva orden.

• Ett barn förstår utifrån situationen om exempelvis ordet ”banan” betyder en frukt eller en skridskobana.

• En dator tänker inte själv. Den läser av signaler som kommer i en viss ordning. (Vi brukar kalla signalerna för ettor och nollor.) Om ordningen är fel, så förstår inte datorn vad de betyder. Ett endaste litet fel gör att allt blir fel.

3

Bilden visar en av de allra första datorerna, Eniac. Den programmerades genom att 6 000 strömbrytare skulle vara på eller av. När vi säger att en dator bara förstår ett eller noll, betyder det att den bara förstår på eller av. Om strömmen är på, skriver vi en etta. Om strömmen är av skriver vi en nolla.

På bilden ser vi hur programmerarna sätter in kablar på rätt ställen, så att strömmen ska vara av eller på, beroende på vad datorn ska göra.

ENIAC

Electronic Numerical Integrator And Computer, började byggas i USA år 1943 för att användas under andra världskriget. Eniac skulle beräkna hur missiler skulle skjutas för att träffa rätt. Den blev klar först efter kriget år 1946.

Eniac vägde 33 ton och tog upp en golvyta på 167 m2. Tung som tio bussar och stor som två klassrum.

På den här datorn kunde man inte spela spel eller kolla på film. Den kunde bara räkna.

4 –5

Bilden visar åtta glödlampor och åtta ettor och nollor. Ettorna och nollorna kallas för maskinkod och är den kod som datorn läser. Fråga eleverna hur lamporna ska tändas enligt maskinkoden. Låt dem rita på sina skrivtavlor innan ni klickar fram nästa bild som visar resultatet.

6

Bilden illustrerar vad som händer när vi trycker på startknappen på en dator. Berätta för eleverna att vi här ser en startknapp, en programkod för att starta när någon trycker på startknappen, maskinkod och en cpu (Computer Process Unit), som är datorns hjärna.

Samtala om att år 2024 var storleken på världens minsta cpu 0,3 mm. Jämför det med storleken på Eniac, som var stor som två klassrum.

Förklara att när vi trycker på startknappen så säger programkoden åt datorn att starta. Programkoden översätts då till maskinkod, vilken i sin tur gör att cpu startar.

7

Bilden visar att en etta eller nolla kallas för en bit och att 8 bitar tillsammans blir en byte. Fråga eleverna hur många bitar, alltså ettor eller nollor,

10 byte består av. Konstatera tillsammans att 10 byte måste bestå av 80 bitar.

8

Bilden förklarar att en bild i mobilen kan vara på 10 megabyte (MB) och att den består av 83 886 080 bitar. Ställ frågor, exempelvis:

– Hur läser ni talet 83 886 080?

– Vilka värden har de olika åttorna?

Påminn om positionssystemet i vårt decimala talsystem. Enas om att åttan längst till höger står på positionen tiotal och därför är värd 80 och så vidare. Samtala om att samma siffra får olika värde beroende på i vilken kolumn i positionstabellen den står, att det är positionen som avgör värdet.

9

Bilden visar en tabell över talsorterna i det decimala talsystemet. Samtala om hur ettorna och nollorna i de här talen har olika värde beroende på i vilken kolumn (på vilken position) de står.

10

Bilden visar en tabell över det binära talsystemet, där bara talet 1 står utplacerat. Berätta för eleverna att i det binära talsystemet finns också kolumner (positioner), men att de inte står för samma värden som i det decimala talsystemet. Klicka stegvis vidare i bildspelet och samtala utifrån frågor om tabellens uppbyggnad, exempelvis:

– Hur skulle ni skriva talet 2 om ni bara får använda ettor och nollor? 10

– Vilka rubriker ska stå i de två kolumnerna längst till höger? Tvåtal och ental.

– Hur skulle ni skriva talet 3 om ni bara får använda ettor och nollor? 11

– Hur skulle ni skriva talet 4 om ni bara får använda ettor och nollor? 100

– Vilken rubrik ska stå i den tredje kolumnen från höger räknat? Fyrtal.

– Går det att förenkla tabellrubrikerna? Låt eleverna samtala parvis och enas om ett svar som de presenterar.

11

Bilden visar hur vi kan förenkla tabellrubrikerna genom att ersätta dem med decimala siffror i stället för ental, tvåtal, fyrtal och så vidare. Klicka vidare och ställ frågor, exempelvis:

– Vilket tal i det decimala talsystemet motsvaras av det binära talet 101? Talet 5, eftersom det är ett fyrtal (4), noll tvåtal och ett ental (1), 4 + 1 = 5.

– Vilket tal i det decimala talsystemet motsvaras av det binära talet 111? Talet 7, eftersom det är ett fyrtal (4), ett tvåtal (2) och ett ental (1), 4 + 2 + 1 = 7.

12

Bilden visar samma tabell som tidigare. Fråga om någon kan lista ut vilka rubriker som ska stå i de sista kolumnerna. Klicka sedan vidare för att visa att det är 8, 16 och 32. Ställ frågor, exempelvis:

– Vilket mönster kan ni se? Talen dubblas, 2, 4, 8, 16 och 32.

– Om vi fyller på med två kolumner till, vilka rubriker ska de ha? Låt eleverna samtala parvis och enas om ett svar som de presenterar.

13

Bilden visar att vi har lagt till två kolumner med rubrikerna 64 och 128. Ställ frågor, exempelvis:

– Stämmer mönstret? Ja, eftersom 32 2 = 64 och 64 · 2 = 128.

– Om vi fyller på med ytterligare tre kolumner, vilka rubriker ska de ha? Låt eleverna samtala parvis och enas om ett svar som de presenterar.

14

Bilden visar att vi har lagt till tre kolumner med rubrikerna 256, 512 och 1 024. Samtala om att talen i tabellrubrikerna följer samma mönster som i minneskort, mobiler och datorer.

Titta på de sex binära talen som är uppställda i tabellen och fråga vilka decimala tal de motsvarar. Gå igenom de första tillsammans och visa

på din whiteboard hur det går att tänka kolumn för kolumn, exempelvis:

–

På den första raden finns bara en etta och den står i kolumnen för 1 024. Vad betyder det? Att det binära talet motsvarar det decimala talet 1 024.

– Talet på rad två har en etta på 1 024, en på 512 och en på 2, vilket decimalt tal motsvarar det?

Talet 1 538, eftersom 1 024 + 512 + 2 = 1 538.

Låt eleverna arbeta parvis för att ta reda på vilka decimala tal de fyra sista motsvarar. Uppmuntra dem att skriva ned additionerna för att vara säkra på att de räknar rätt.

Lektionsboken s. 155

Räkna som en dator

1 Tabellen visar tal skrivna i det binära talsystemet. Skriv motsvarande tal i det decimala talsystemet.

BINÄRA TALSYSTEMET DECIMALA TALSYSTEMET

2 De här talen är skrivna i det decimala talsystemet. Skriv talen i det binära talsystemet.

3 De här talen är skrivna i det binära talsystemet. Skriv talen i det decimala talsystemet.

UPPGIFT 1: Eleverna skriver de decimala talen som motsvarar de binära som visas i tabellen.

UPPGIFT 2–3: Eleverna skrivet talen som visas i det binära respektive decimala talsystemet.

TIPS :

• Uppmärksamma eleverna på att de kan använda tabellen i uppgift 1 även för att lösa uppgift 2 och 3.

• Påminn eleverna om att de kan addera summorna för kolumnerna på varje rad för att få fram det decimala talet.

Redovisning av lektionsboken

Ta fram lektionsboken på helskärm. När eleverna har redovisat sina lösningar går ni gemensamt igenom och diskuterar dem. Uppmärksamma till exempel vanliga missförstånd.

Minicheck

BINÄR a Ta L: Eleverna tar reda på vilket tal i det decimala talsystemet som motsvarar det binära talet 101010.

LEKTION 2

DU BEHÖVER:

• Bildspel – Skriva med maskinkod

• Lektionsboken s. 156 –157

• Skrivtavlor

Bildspel Skriva med maskinkod

Träna på att skriva maskinkod med hjälp av ASCII-tabellen.

SÅ HÄR KAN DU GÖRA

Öppna bildspelet och ta fram det på helskärm. Se till att alla elever är beredda med sina skrivtavlor.

2

Bilden visar tre bokstäver skrivna med maskinkod. Påminn eleverna om att de under förra lektionen lärde sig att räkna som en dator. I dag ska de lära sig att läsa och skriva som en dator, med hjälp av maskinkod.

Fråga eleverna om de kommer ihåg vad de olika kolumnerna är värda i det binära talsystemet. Låt dem fundera enskilt och skriva ned sina svar. Samtala om vad eleverna kommit fram till och klicka sedan fram värdena i tabellrubriken.

Beräkna nu tillsammans vilka tal i det decimala talsystemet som varje rad representerar och klicka sedan vidare för att visa svaren 72, 69 respektive 74. Berätta att bitarna för 72 betyder bokstaven H, bitarna för 69 betyder bokstaven E och bitarna för 74 betyder bokstaven J och klicka fram bokstäverna.

L ÄRARHANDLEDNING

Flex matematik är ett läromedel för dig som vill ha ett elevaktivt klassrum. Med hjälp av färdiga veckoplaneringar och bildspel blir undervisningen både rolig och varierad. Eleverna är delaktiga genom att diskutera strategier och lösningar som de visar på sina skrivtavlor. Färdighetsträningen sker först i lektionsboken och sedan på elevwebben, där var och en arbetar vidare på sin nivå.

Lärarhandledningen vägleder dig under genomgångarna med bildspelen och veckoöversikten underlättar din planering. På lärarwebben finns alla bildspel och här kan du följa dina elevers utveckling.

Läs mer på nok.se/flexmatematik

består av lärarhandledning med lärarwebb samt lektionsbok med elevwebb.