La Parábola y Trigonometría

La Parábola

1.Concepto:

Una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo (llamado foco) y de una recta fija (denominada directriz). Por tanto, cualquier punto de una parábola, está a la misma distancia de su foco y de su directriz.

Normalmente las parábolas que utilizaremos tendrán el eje horizontal o vertical y para obtener su ecuación basta hacer una traslación de ejes, como se puede ver en la figura siguiente.

2. Elementos de una Parábola:

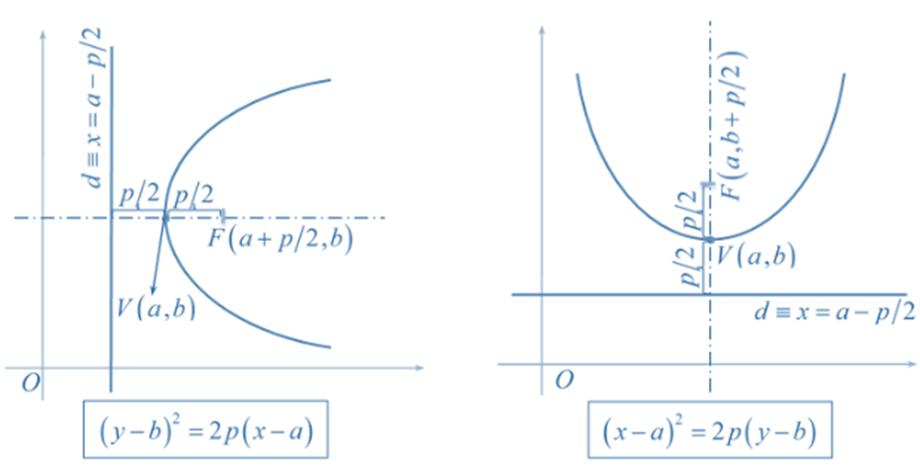
• Foco (F): es un punto fijo del interior de la parábola. La distancia de cualquier punto de la parábola al foco es igual a la distancia de ese mismo punto a la directriz de la parábola.

• Directriz (D): es una recta fija externa a la parábola. Un punto de la parábola tiene la misma distancia a la directriz que al foco de la parábola.

• Parámetro (p): es la distancia desde el foco hasta la directriz.

• Radio vector (R): es el segmento que une un punto de la parábola con el foco. Su valor coincide con la distancia del punto hasta la directriz.

• Eje (E): es la recta perpendicular a la directriz que pasa por el foco y es el eje de simetría de la parábola, en la gráfica de abajo corresponde al eje de las ordenadas (eje Y). También se dice eje focal.

• Vértice (V): es el punto de intersección entre la parábola y su eje.

• Distancia focal: es la distancia entre el foco y el vértice, o entre la directriz y el vértice. Su valor siempre es igual a P/2

3. Lado Recto:

El lado recto de una parábola es la cuerda comprendida dentro de la parábola que pasa por el foco y es paralela a la directriz.

4. Ecuaciones de la Parábola:

La ecuación de una parábola es un tipo de función cuadrática porque siempre debe de tener como mínimo un término elevado al cuadrado. Además, la ecuación de una parábola depende de si esta está orientada horizontalmente o verticalmente.

Así pues, en geometría analítica existen varias maneras de expresar matemáticamente una parábola: la ecuación canónica o reducida, la ecuación ordinaria y la ecuación general de la parábola.

a)Ecuación Canónica o Reducida de la Parábola:

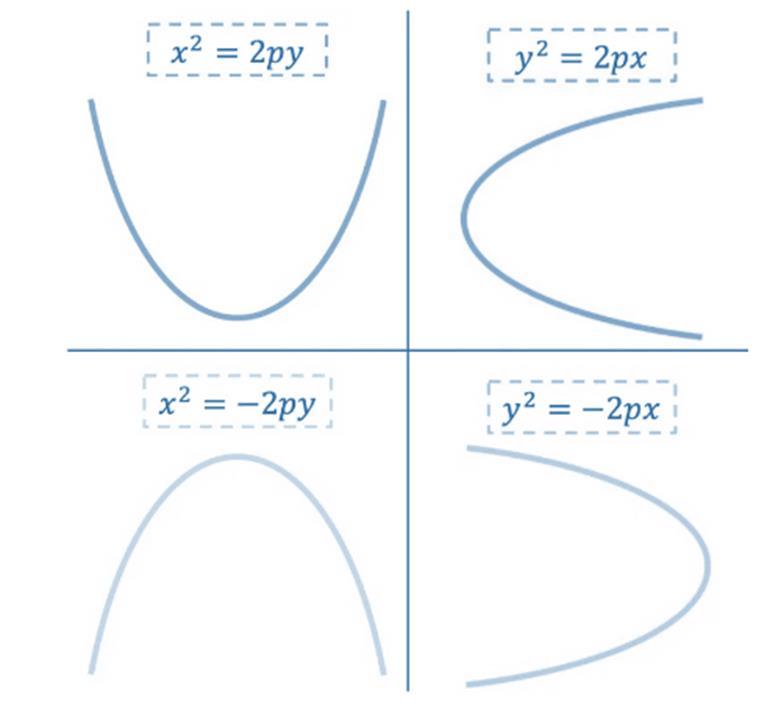
En la ecuación reducida o canónica de las otras ecuaciones parabólicas, es que el vértice de la parábola es el origen de coordenadas, es decir, el punto (0,0). La forma de la ecuación reducida de la parábola depende de si esta es horizontal o vertical. Fíjate en la siguiente representación gráfica donde se muestran las 4 posibles variantes:

Donde p es el parámetro característico de la parábola. Como se puede ver en la imagen anterior, cuando la variable x está elevada al cuadrado la parábola es vertical, en cambio, cuando la variable y está elevada al cuadrado la parábola es horizontal. Por otra parte, el sentido de las ramas de la parábola depende del signo de la ecuación.

b)Ecuación Ordinaria de la Parábola:

Acabamos de ver cómo es la ecuación de la parábola cuando su vértice o centro corresponde al origen de coordenadas (la ecuación reducida o

canónica), pero ¿cuál es la ecuación de la parábola si el vértice está fuera del origen?

Cuando el vértice de la parábola es un punto cualquiera utilizamos la ecuación ordinaria de la parábola, cuya expresión es:

Donde el centro o vértice de la parábola es el punto V (x0, y0). La ecuación anterior corresponde a la parábola que está orientada de manera vertical, o, dicho con otras palabras, el eje focal de la parábola es paralelo al eje Y.

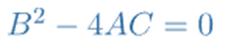
Análogamente, para definir una parábola orientada de manera horizontal (su eje focal es paralelo al eje X), debemos usar la siguiente variante de la ecuación ordinaria de la parábola:

Al igual que antes, el centro o vértice de la parábola es el punto V (x0, y0).

c)Ecuación general de la Parábola:

Hasta ahora todas las ecuaciones de las parábolas que hemos analizado sirven para expresar parábolas horizontales o verticales. Pero, evidentemente, una parábola también puede ser oblicua o inclinada.

Pues para expresar este tipo de parábolas se usa la ecuación general de la Parábola, cuya fórmula es la siguiente:

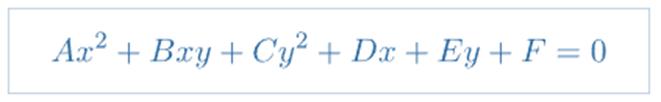
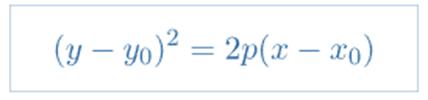
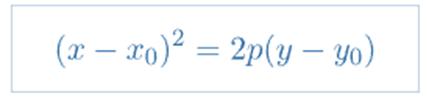
La ecuación anterior se trata de una parábola si, y solo si, los coeficientes A y C no son simultáneamente nulos y, además, se cumple la siguiente condición:

Situación:

Cómo hallar el vértice, el foco y la directriz de una parábola a partir de su ecuación En muchos ejercicios y problemas de parábolas se pide calcular el vértice, el foco y la directriz de una determinada parábola. Por tanto, vamos a ver cómo se hace mediante un ejemplo:

Halla el vértice, el foco y la directriz de la siguiente parábola:

Lo fundamental para resolver este tipo de problemas de parábolas es determinar el parámetro p de la parábola. En este caso, la ecuación de la parábola corresponde a la ecuación reducida o canónica (parábola vertical):

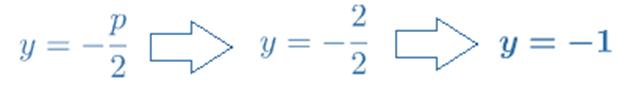
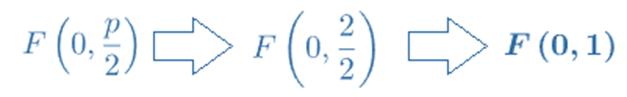
Por lo tanto, el parámetro p es:

Por otro lado, como la parábola sigue la ecuación reducida o canónica, significa que su vértice o centro está en el origen de coordenadas:

Una vez sabemos el vértice y el valor del parámetro de la parábola, podemos hallar su foco y directriz fácilmente.

El término cuadrático de la ecuación es la variable x de manera que el eje de la parábola será paralelo al eje OY y, de hecho, como su vértice es el punto (0,0), el eje de la parábola será el propio eje OY. Entonces, el foco de una parábola siempre está situado en el eje de la parábola y a una distancia de p/2 del vértice de la parábola, por lo que sus coordenadas son:

Del mismo modo, la recta directriz será la recta horizontal que está a una distancia p/2 del vértice de la parábola, que es el origen de coordenadas. Por tanto, la ecuación de la recta directriz será:

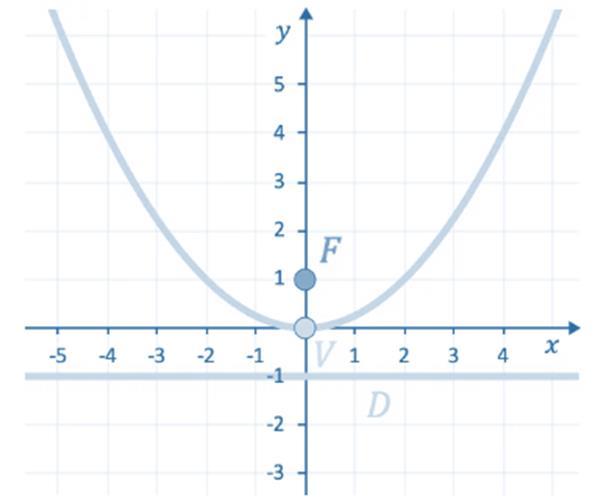
A continuación, se ha representado gráficamente la parábola para que puedas comprobar los resultados:

Trabajo Domiciliario

1. ¿Qué ecuaciones de las expuestas a continuación determinan una parábola, una recta horizontal, una recta vertical, dos rectas horizontales, rectas verticales, el conjunto vacío? de ser una parábola determinar p y el vértice.

A) x² 4x + 8y + 28=0

B) y² 8y + 7=0

C) x² 2x + 5 = 0

D) x² + 4x 21=0

E) y² + 8y + 16 =0

F) x² – 6x + 9=0

G) y² + 6y – 2x +11=0

2. Hallar la ecuación de la parábola:

i) Con vértice (2; 5) y foco (2; 3)

ii) Con vértice en (5; 2) y foco (7; 2)

Ii) Con recta directriz ℒ: y = 5 y foco (7; 2)

iv) Con recta directriz ℒ: x = 2 y vértice en (5; 1)

v) Con vértice (2; 6) y extremos del lado recto: (6; 8) y ( 2; 8)

3. En base a la ecuación de las siguientes parábolas determina las coordenadas de sus focos, ecuaciones de sus directrices, distancia de sus lados rectos y la gráfica.

4.Determina las ecuaciones de las parábolas que tienen::

De directriz x = 3, de foco (3, 0)

De directriz y = -5, de foco (0, 5).

De directriz x = 2, de foco (-2, 0).

De directriz y = 4, de vértice (0, 0).

Trigonometría

1. Funciones trigonométricas:

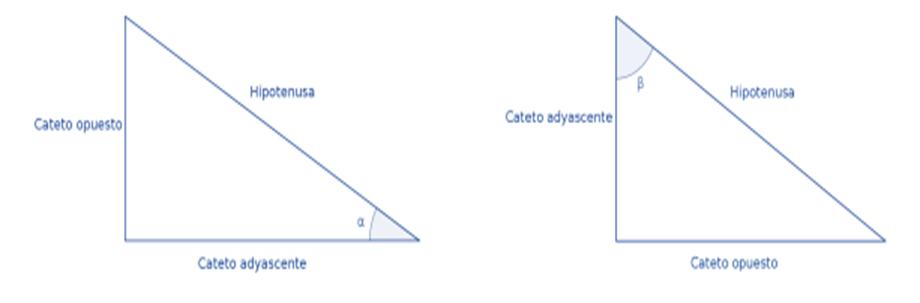
Una primera manera de definir las funciones trigonométricas es a partir de un triángulo rectángulo. Un triángulo rectángulo es aquél que tiene un ángulo recto como uno de sus ángulos interiores. En este caso, los lados que forman el ángulo recto se llaman catetos, y el tercer lado es la hipotenusa. Si uno toma un ángulo interior, que no sea el ángulo recto, entonces el cateto que forma dicho ángulo será el cateto adyacente, mientras que el otro será el cateto opuesto.

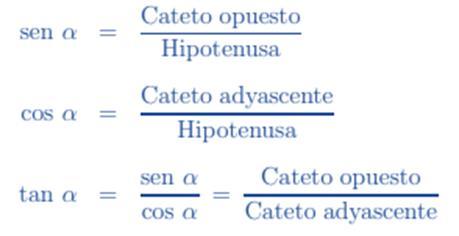
Las funciones trigonométricas son el seno, sen; el coseno, cos, y la tangente, tan y se definen como:

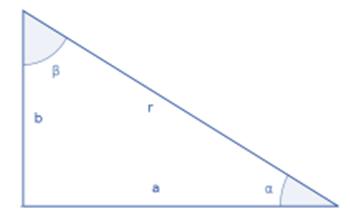
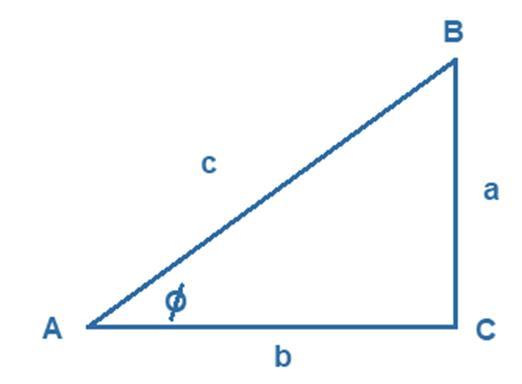
Entonces en el triángulo, de la figura siguiente, formado por los lados r, a y b, las funciones trigonométricas serán:

El teorema de Pitágoras (que demostraremos más a delante) dice que: r 2 = a 2 + b 2

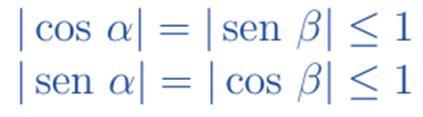
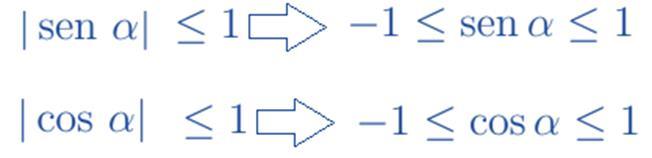
De aquí se tiene que r 2 ≥ a 2 y r 2 ≥ b 2. Aplicando raíz cuadrada en ambos miembros obtenemos que r ≥ a y r ≥ b. Luego 1 ≥ | a / r | y 1 ≥ | b / r |. Finalmente, teniendo en cuenta que cos α = sen β = a /r y sen α = cos β = b / r resulta que:

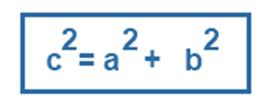
2. Identidades Trigonométricas:

Las identidades trigonométricas son igualdades que involucran funciones trigonométricas y se verifican para cualquier valor permitido de la variable o variables que se consideren, es decir, para cualquier valor que pudieran tomar los ángulos sobre los cuales se aplican las funciones. Si la gráfica de dos funciones coincide, entonces es una identidad. En cambio, si solamente se cortan en uno o algunos puntos, entonces se trata de una ecuación trigonométrica cuyas soluciones son las abscisas de los puntos de corte.

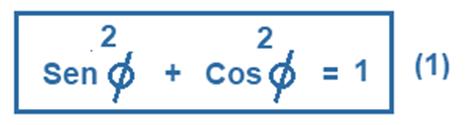
A) Identidades Trigonométricas Pitagóricas:

Las identidades trigonométricas pitagóricas se obtienen al aplicar el Teorema de Pitágoras a las definiciones de las funciones trigonométricas. Son tres identidades y se cumplen para cualquier valor del ángulo x. A continuación, te mencionamos cuáles son y cómo se obtienen.

Trabajo Domiciliario

1. Si el sen α = -2/3 y α es un ángulo del tercer cuadrante hallar el resto de razones trigonométricas.

2. Calcular sen α, sabiendo que tag α = 3/2 y que α es un ángulo del tercer cuadrante.

3. Calcular α sabiendo que sen α = 1/2 y 90º < α < 270º

4. Si cos x = 1/3 y π < x < 2π. Halla el resto de sus razones trigonométricas

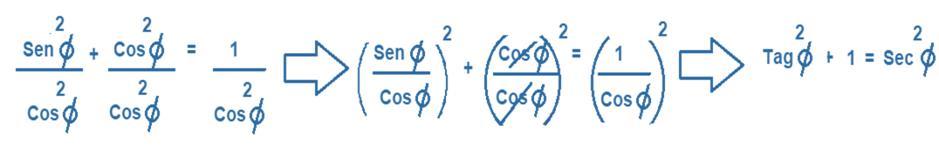
5. Si Sec α = 2 y 3π/2 < α < 2π, calcular las restantes razones trigonométricas.

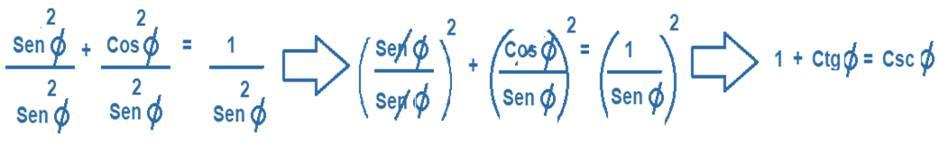
6. Sabiendo que cotg α = -1/2 y que 0< α < π, calcular las razones trigonométricas de α.

7. Sabiendo que cosec α = -5 y que π < α < 3π/2, calcular las razones trigonométricas de α.

8. Sabiendo que cos (π/2 + α) = 2/3 y que π < α < 3π/2, calcular las razones trigonométricas de α.

9. Sabiendo que sen (π + α) = ¾ y que 3π/2 < α < 2π, calcular las razones trigonométricas de α.

10.Simplificar las siguientes expresiones trigonométricas: