


CARLOS JAVIER RINCÓN




CARLOS JAVIER RINCÓN
CON EJEMPLOS EN R
Introducción a la estadística no paramétrica con ejemplos en R
CARLOS JAVIER RINCÓN
Reservadostodoslosderechos
©PontificiaUniversidadJaveriana
©CarlosJavierRincón
Primeraedición:febrerode2025
ISBN:(impreso)978-958-781-943-4
ISBN:(digital)978-958-781-944-1
DOI:https://doi.org/10.11144/ Javeriana.9789587819441
Númerodeejemplares:300
ImpresoyhechoenColombia
PrintedandmadeinColombia
EditorialPontificiaUniversidadJaveriana Carrera7.ªn.º37-25,oficina1301 Bogotá,EdificioLutaima
Teléfono:(601)3208320,ext.4205 www.javeriana.edu.co/editorial editorialpuj@javeriana.edu.co
Correccióndeestilo: SamuelCurrea
DiseñodepautaConTEXtydiagramación: AndrésConradoMontoyaAcosta
Diseñodecubierta: AndrésConradoMontoyaAcosta
Impresión:
DGPEditoresSAS
PontificiaUniversidadJaveriana|Vigilada Mineducación.Reconocimientocomo Universidad:Decreto1270del30demayo de1964.Reconocimientocomopersonería jurídica:Resolución73del12dediciembrede 1933delMinisteriodeGobierno.
PontificiaUniversidadJaveriana.BibliotecaAlfonsoBorreroCabal,S.J. Catalogaciónenlapublicación
Rincón,CarlosJavier,autor IntroducciónalaestadísticanoparamétricaconejemplosenR/CarlosJavierRincón.–Primeraedición.–Bogotá:EditorialPontificiaUniversidadJaveriana,2024.
210páginas;17×24cm.
Incluyereferenciasbibliográficas
ISBN:978-958-781-943-4(impreso)
ISBN:978-958-781-944-1(electrónico)
1.Estadística no paramétrica 2.Estadística 3.Estadística matemática 4.Probabilidades 5.Variables (Matemáticas)6.FuncionesI.PontificiaUniversidadJaveriana.Bogotá.
CDD519.5edición23
CO-BoPUJ
23/08/2024
A los profesores Daniel Camilo AguirreAcevedo, estadístico, informático y doctor en Epidemiología, y Julián SantaellaTenorio, doctor en Salud Pública en Epidemiología, por realizar la revisión de este libro y hacer importantes recomendaciones para su publicación. Especialmente, quiero agradecerles por su generosidad al dedicar parte de su valioso tiempo a apoyar este tipo de iniciativas.
A los estudiantes de la asignatura de Estadística no Paramétrica del programa de Maestría en Bioestadística de la Pontificia Universidad Javeriana, por su dedicación y aportes durante el estudio de este material.
Amifamilia,quesonlabasedetodo.Amispadres,quesonelejemplopara un maestro.
La estadística clásica se divide en dos categorías:
1. Estadística descriptiva.
2. Estadística inferencial o inductiva.
La estadística descriptiva muestra, de manera global, el comportamiento de las características (variables) de una población, a partir de medidas de resumen (de tendencia central, dispersión y forma), tablas de frecuencias absolutas y relativas y gráficos. La estadística inferencial busca, a partir de la selección aleatoria de una muestra, realizar la estimación (intervalos de confianza) o evaluar una afirmación (pruebas de hipótesis) sobre un parámetro; este último se entiende como una cantidad obtenida a partir de los valores observados en toda la población.
Enlaestadísticainferencial,paraquelosresultadosobtenidosrepresenten a la población, se deben cumplir los supuestos definidos sobre la distribución de los valores en esta población; en este escenario, la estadística inferencial se denomina estadística paramétrica. Cuando los supuestos nose cumplen o las afirmaciones que se van a evaluar no son sobre un parámetro, serequieren otras alternativas entre las que se encuentra la estadística no paramétrica. Esta se compone de métodos que evalúan afirmaciones más generales, no necesariamente sobre un parámetro, y métodos en los cuales su aplicación no depende de la distribución de la variable de interés en la población de estudio (estos últimos se denominan pruebas de libre distribución).
Los métodos paramétricos y no paramétricos se pueden ver como un conjuntodeherramientasqueseseleccionanacordeconlapropuestadeinvestigación detallada en su protocolo. En esta selección se deben considerar los supuestos de cada método, la naturaleza de las variables que se analizan
En la estadística no paramétrica se han identificado, con relación a los métodos paramétricos, las siguientes características:
1. Son más rápidos y fáciles de aplicar (cálculos aritméticos simples: menor recurso computacional).
2. Con frecuencia son más fáciles de entender.
3. Son relativamente insensibles a datos atípicos.
4. En general, los supuestos requeridos son más fáciles de cumplir.
5. Se pueden aplicar en muestras pequeñas en las que no se pueden verificar los supuestos de la estadística paramétrica.
6. Resuelven preguntas en nuevos escenarios, por ejemplo, cuando se utilizan variables categóricas.
Este libro presenta diferentes métodos no paramétricos junto con su aplicación en el programa R [1] a través de RStudio [2]. Esta revisión se basa principalmente en los libros clásicos de la estadística no paramétrica de Jean Dickinson Gibbons y Subhabrata Chakraborti, Nonparametric Statistical Inference [3], y W. J. Conover, Practical Nonparametric Statistics [4]. También se incluyó en esta revisión el libro de Wayne W. Daniel, Bioestadística.Base para el análisis de las ciencias de la salud [5] y, en temas relativamente más recientes, el libro de J. Kloke y J.W. McKean, Nonparametric Statistical Methods Using R [6].
En este libro, aunque se hace hincapié en la práctica más que en la teoría, se incluyen las expresiones matemáticas que componen los distintos métodos y que soportan los resultados obtenidos por las funciones implementadas en R; no se incluyen demostraciones de teoremas en cuyos resultados se basan estas aplicaciones. Se presentan algunas consideraciones de cada prueba, a fin de aportar al momento de aplicarlas en situaciones reales. Se utilizará un nivel de significancia típico de ��=0.05 en todas las aplicaciones, a menos que se especifique lo contrario.
IntroducciónalaestadísticanoparamétricaconejemplosenR ylostamañosdemuestrarequeridosenelestudio.Ensituacionesenlascuales se pueden aplicar ambos métodos, en general, las pruebas paramétricas tienen un mayor poder siempre y cuando se cumplan sus supuestos.
Los temas que se incluyen en este libro se resumen en la siguiente tabla:
Tabla1.1 Métodospresentadosencadacapítulo
Temas
Capítulo2.Pruebasdebondadyajustey normalidad
Capítulo3.Evaluacionesenunaodos poblacionesindependientesopareadas
Capítulo4.Construccióndeintervalosde confianzaparalamediana
Capítulo5.Aleatoriedadymuestras pareadascondesenlacedicotómico
Capítulo6.Comparacióndetresomás muestrasindependientesodependientes
Capítulo7.Independencia,homogeneidad ybondaddeajuste
Métodos
Gráficos,KolmogórovSmirnov,Lilliefors, ShapiroWilk,ShapiroFranciayprueba D'Agostino.
Signo,sumaderangosdesignosde WilcoxonyUdeMannWhitneyWilcoxon.
Técnicasderemuestreo(bootstrapping).
RachasWaldWolfowitzypruebade McNemar.
Lamediana,KruskalWallis,Friedmany �� deCochran.
Prueba��2dePearson.
Capítulo8.Medidasdeasociación �� deKendallycoeficientedecorrelaciónde rangosdeSpearman (��).
Capítulo9.Medidasdeasociaciónpara variablesordinales
Capítulo10.Relaciónentredosvariablesa partirdemétodosdesuavizamientos
Capítulo11.Regresióncuantílica
Coeficientes: ��,��− Yule,����,���� y ��− Somers
Friedman,ClevelandyNadarayaWatson.
Repasoregresiónlinealeintroducciónala regresióncuantílica.
Fuente:elaboraciónpropia.
Para abordar los temas descritos en este libro, el lector requiere de conocimientos básicos en estadística clásica en los temas de variables, probabilidad,funcionesdedistribucióndeprobabilidades,estimaciónporintervalos de confianza y prueba de hipótesis. Adicionalmente, se requiere de un conocimiento básico en el uso de los programas R y RStudio en temas como: instalación de los programas, tipos de objetos, uso de paquetes y funciones e importación de datos. Para las personas que no han utilizado estos programas, a continuación, se incluye una breve introducción que permite revisar los requerimientos anteriores dando ejemplos e indicaciones de cómo utilizarlos. Se recomienda al lector que, a medida que se van mostrando los ejemplos, los vaya tratando de reproducir por cuenta propia siguiendo las
indicaciones. Con esta sección, no se buscó presentar una revisión detallada del uso de los dos programas, pero sí dar al lector las bases que le permitan desarrollar las prácticas incluidas en este libro. El lector que ya ha utilizado estos dos programas puede saltarse esta sección.
Finalmente, este libro se encuentra dirigido a jóvenes investigadores en temasrelacionadosconeláreadelasalud,comoestudiantesdeposgradoen epidemiología, bioestadística, salud pública o economía de la salud, que requieran del uso de métodos no paramétricos clásicos en sus proyectos de investigación y estén interesados en aprender el uso de herramientas para el análisis de sus datos.
Instalación
En esta sección encontrará una breve descripción de algunos aspectos básicos del programa R y RStudio que le permitirán comenzar a utilizar estas herramientas. RStudio se define como un entorno de desarrollo integrado (integrated development environment) que, a partir de un ambiente que incluye múltiples herramientas, facilita el manejo de R. Es decir que utilizaremos R a través de RStudio. Primero, debe instalar los dos programas. En los siguientes enlaces se descargan los instaladores según el sistema operativo que utilice:
• R (Windows): https://cran.r-project.org/bin/windows/base/
• R (macOS): https://cran.r-project.org/
• RStudio (Windows y macOS): https://www.rstudio.com/products/rstudio/download/#download
Después de instalar los dos programas, abra RStudio donde encontrará cuatro paneles (figura1.1).
IntroducciónalaestadísticanoparamétricaconejemplosenR
En el panel 1 se escriben las instrucciones o comandos requeridos para el análisis de un conjunto de datos; en el panel 2 se encontrarán, principalmente, los datos que están por analizar, organizados en distintos “objetos” (que revisaremos más adelante); en el panel 3 se ubican los resultados obtenidos al ejecutar una instrucción y en el panel 4 se presentan, entre otras cosas, los gráficos que se generen y la ayuda o documentación de los comandos que se utilicen en el programa.
Cuando comienza la etapa de análisis de un proyecto que utiliza R, se acostumbra (recomienda) especificar una carpeta en su equipo/estación local, donde se guarden todos los archivos relacionados con el proyecto como:basesdedatosoriginales,basesdedatospreparadasparaelanálisis, archivos con el código, salidas de resultados, imágenes y gráficos. Para definir la ubicación de esta carpeta, que se denominará directorio de trabajo, se escribe la siguiente instrucción en el panel 1:
setwd("C:/ruta")
En"C:/ruta"sedebeincluirladirecciónolocalizaciónenlacualseencuentra ubicada la carpeta correspondiente. Después de escribir la instrucción anterior, se coloca el cursor en cualquier parte de este código y se teclea Ctrl+Enter (si usaWindows) o Command+Enter (si usa macOS).
La acción anterior es la forma de ejecutar/“correr” una instrucción en RStudio.
Después de que el directorio de trabajo esté definido, para conocer su ruta o ubicación se ejecuta la siguiente instrucción nuevamente en el panel 1: getwd()
Enelpanel3aparecerálarutacorrespondiente.Paraconocerquéarchivos se encuentran en el directorio de trabajo, se utiliza el siguiente código: dir()
El directorio de trabajo también se puede definir por ventanas de una forma tal vez más intuitiva como se presenta en la figura1.2.

Figura1.2 Definireldirectoriodetrabajo Fuente:elaboraciónpropia.
IntroducciónalaestadísticanoparamétricaconejemplosenR
Definido el directorio de trabajo, siempre que se quiera importar o exportar una base de datos, o guardar salidas del análisis como tablas o gráficos, no será necesario especificar una ruta, ya que todo estará enlazado a esta carpeta. En esta carpeta se encontrarán, entonces, todos los archivos relacionados con el proyecto.
Paquetes y funciones en R
Algunasinstruccionescomolasanteriores(setwd,getwd,dir)yaseencuentran instaladas en R y se pueden utilizar directamente. En general, las instrucciones se denominan funciones y un conjunto de funciones se puede organizaroalmacenardentrodeun paquete.Paraverunejemplodecómo utilizar otras funciones ya instaladas, primero tabulemos 10 edades en el panel 1 de la siguiente forma (cada línea de código es una instrucción diferente en R):
edad<-c(12,14,15,14,16,13,18,17,19,15) edad
## [1] 12 14 15 14 16 13 18 17 19 15
Notequelaformadeasignaroguardarunconjuntodevaloresconunnombreespecífico se realiza con el símbolo: <-. Adicionalmente, en el panel 2 apareció el objeto edad acorde al nombre que le asignamos. Cada vez que se necesiten utilizar estos valores,bastaconescribiredadenelpanel1.
Ahora, por ejemplo, para calcular la media de estas edades, utilizaremos la función mean del paquete {base} ejecutando la siguiente instrucción:
mean(edad,trim = 0.1,na.rm=TRUE)
## [1] 15.25
Veremos que en el panel 3 aparece el resultado solicitado. Algunos ejemplosdeotrasfuncionesyapreinstaladasqueutilizanlos10datosdelaedad son los siguientes:
hist(edad,main = "Histograma de la edad",xlab = "edad",col = "grey")
Figura1.3. Histogramadelaedad
Fuente:elaboraciónpropia.
boxplot(edad,main="Cajas y bigotes",ylab="edad", col="lightblue")
Figura1.4 Cajasybigotes
Fuente:elaboraciónpropia.
Notará que cada función tiene un nombre específico y que dentro de los paréntesis se deben colocar los “parámetros” que se requieren para su ejecución. Para conocer la definición de los parámetros de una función específica junto con su documentación, se puede solicitar la ayuda del programa tecleando —por ejemplo, para la función mean— lo siguiente:
?mean
IntroducciónalaestadísticanoparamétricaconejemplosenR
La documentación de la función aparece en el panel 4. A continuación, se presenta un listado de funciones comúnmente utilizadas para obtener estadísticas descriptivas e inferenciales paramétricas:
Tabla1.2. Algunasfuncionesde Rparaestadísticadescriptivaeinferenciaparamétrica
Funciones
Descripción:permiteobtener table()
Frecuenciasabsolutasdeunavariablecategórica. prop.table() Frecuenciasrelativasdeunavariablecategórica.
max() Elmáximodeunavariablenumérica. min() Elmínimodeunavariablenumérica. mean() Lamediadeunavariablenumérica. var() Lavarianzamuestraldeunavariablenumérica.
sd() Ladesviaciónestándarmuestraldeunavariablenumérica.
median() Lamedianadeunavariablenumérica. quantile()
barplot()
Percentilesdeunavariablenumérica.
Gráficodebarrasdeunavariablecategórica. hist() Histogramadeunavariablenumérica. boxplot()
Gráficodecajasybigotesdeunavariablenumérica. plot()
pie()
Gráficodedispersiónparadosvariablesnuméricas.
Gráficodetortaopiedeunavariablecategórica. pnorm()
qnorm()
pt()
qt()
pchisq()
qchisq()
pf()
qf()
t.test()
prop.test()
varTest()
var.test()
Probabilidadacumuladabajounadistribuciónnormal.
Percentilesdeunadistribuciónnormal.
Probabilidadesacumuladasparaladistribución ��.
Percentildeladistribución ��
Probabilidadacumuladaparaladistribución ��2
Percentilesdeladistribución ��2.
Probabilidadacumuladadeladistribución ��
Percentildeladistribución ��.
Pruebadehipótesiseintervalodeconfianzaparalamediade unaydospoblaciones.
Pruebadehipótesiseintervalodeconfianzaparaproporcionesdeunaodospoblaciones.
Pruebadehipótesiseintervalodeconfianzaparalavarianza unapoblación(requiereinstalarelpaquete “EnvStats”).
Pruebadehipótesiseintervalodeconfianzaparalavarianza dospoblaciones.
Fuente:elaboraciónpropia.
Como ya se mencionó, las funciones se encuentran organizadas en paquetes y los paquetes que ya se encuentran instalados en el programa se pueden consultar con el siguiente código: library()
o se pueden ver en el panel 4 en la pestaña “Packages”.
También se pueden instalar nuevos paquetes con funciones adicionales. Para instalar un nuevo paquete, se debe conocer su nombre y colocarlo dentro de la siguiente instrucción:
install.packages("nombre del paquete")
Por ejemplo, para instalar el paquete cowsay [7] se corre el siguiente código: install.packages("cowsay")
Ahora, después de haber finalizado la instalación del paquete, debemos “llamarlo” con la instrucción library() para poderlo utilizar, así: library(cowsay)
ahora sí, podemos utilizar la función say de este paquete corriendo el siguiente código:
say("Hola mundo!", by="cow") # otras opciones para "by" son: chicken, clippy, bigcat, ant ...
##
## -----------
## Hola mundo!
## -----------
## \ ^__^
## \ (oo)\ ________
## (__)\ )\ /\
## ||------w|
## || ||
El texto que se escribe después del signo # corresponde a documentación que el usuariopuedeincluirsinafectarelcódigo.
También se pueden instalar nuevos paquetes a través de ventanas siguiendo la ruta: Tools > Install Packages, como se presenta en la figura1.5.
IntroducciónalaestadísticanoparamétricaconejemplosenR
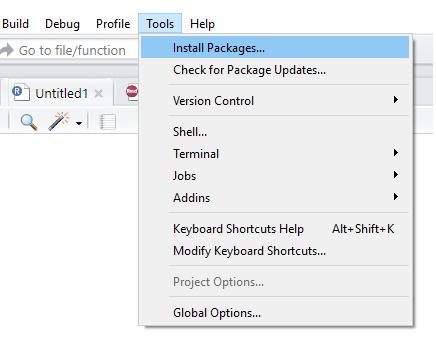
1.5 Rutaparainstalarpaquetes Fuente:elaboraciónpropia.
Uno de los paquetes más utilizados para gráficos y preparación de datos para el análisis es tidyverse [8], el cual se utilizará en las aplicaciones de este libro, por lo cual se recomienda desde ya realizar su instalación.
Existen distintos tipos de arreglos de datos, que llamaremos objetos, que se pueden crear y utilizar en el programa. A continuación, se describen.
Un vector corresponde a un conjunto de valores con la misma estructura. Por ejemplo, creemos 4 vectores corriendo el siguiente código:
peso<-c(60,54,55,62,75,64,58,69,71,52)
talla<-c(1.74,1.68,1.59,1.6,1.78,1.65,1.75,1.69,1.71,1.59)
sexo<-c("H","M","M","H","H","M","M","H","M","M") educacion<-c("secundaria","universitario","posgrado","universitario", "universitario","primaria","secundaria","universitario","secundaria", "posgrado")
Los dos primeros tienen una estructura de valores numéricos y los dos últimos de caracteres (texto).
La estructura de un vector se puede consultar así:
str(peso)
## num [1:10] 60 54 55 62 75 64 58 69 71 52
Aunque esta información ya se presenta en el panel 2.
También se pueden crear vectores utilizando la función rep: id<-rep(1:10);id
## [1] 1 2 3 4 5 6 7 8 9 10 pais<-rep("COL",time=10);pais
## [1] "COL" "COL" "COL" "COL" "COL" "COL" "COL" "COL" "COL" "COL" depto<-rep(c("BOG","ATL"),each=5);depto
## [1] "BOG" "BOG" "BOG" "BOG" "BOG" "ATL" "ATL" "ATL" "ATL" "ATL"
El “ ; ” incluido en el código anterior permite colocar dos instrucciones en la misma línea.
Podemos consultar la longitud (cantidad de valores) y los distintos valores de un vector así:
length(educacion)
## [1] 10 unique(educacion)
## [1] "secundaria" "universitario" "posgrado" "primaria"
Si queremos cambiar la estructura de un vector y guardarlo con otro nombre, tenemos:
educacion_ord<-factor(educacion,levels = c("primaria","secundaria", "universitario","posgrado"))
str(educacion_ord)
20
IntroducciónalaestadísticanoparamétricaconejemplosenR
## Factor w/ 4 levels "primaria","secundaria",..: 2 3 4 3 3 1 2 3 2 4
En el ejemplo anterior, la estructura factor corresponde a una variable categórica ordinal donde la jerarquía de su respuesta se determina en el parámetro levels. Para cambiar a una estructura de números o de texto, tenemos las siguientes funciones:
educacion_num<-as.numeric(educacion_ord) str(educacion_num)
## num [1:10] 2 3 4 3 3 1 2 3 2 4
educacion_carac<-as.character(educacion_num) str(educacion_carac)
## chr [1:10] "2" "3" "4" "3" "3" "1" "2" "3" "2" "4"
Continuemos, pero antes borremos los tres vectores creados anteriormente, ya que no los necesitamos más, así:
rm(educacion_ord,educacion_num,educacion_carac)
Ahora, para reportar valores ubicados en una posición específica dentro de un vector o cambiar este valor, tenemos:
sexo[4] # mostrar el valor ubicado en la 4ta posición.
## [1] "H"
edad[9]<-21; edad # cambiar el valor en la posición 9 por 21:
## [1] 12 14 15 14 16 13 18 17 21 15
Por último, veamos algunas operaciones básicas entre vectores:
edad+peso-talla # sumas y restas
## [1] 70.26 66.32 68.41 74.40 89.22 75.35 74.25 84.31 90.29 65.41
edad*talla # multiplicación
## [1] 20.88 23.52 23.85 22.40 28.48 21.45 31.50 28.73 35.91 23.85
sqrt(talla) # raíz cuadrada
## [1] 1.319091 1.296148 1.260952 1.264911 1.334166 1.284523 1.322876 1.300000
## [9] 1.307670 1.260952
peso/talla^2 # cociente y potencia
## [1] 19.81768 19.13265 21.75547 24.21875 23.67125 23.50781 18.93878 24.15882
## [9] 24.28098 20.56881
MATRICES
Corresponde a un objeto que tiene dos dimensiones, donde la primera determinaelnúmerodefilasylasegundaelnúmerodecolumnas.Sepueden crear matrices a partir de los vectores anteriores, así:
datos<-matrix(c(edad,peso,talla),nrow = 10,ncol = 3, dimnames = list(1:10,c("edad","peso","talla")));datos
## edad peso talla
## 1 12 60 1.74
## 2 14 54 1.68
## 3 15 55 1.59
## 4 14 62 1.60
## 5 16 75 1.78
## 6 13 64 1.65
## 7 18 58 1.75
## 8 17 69 1.69
## 9 21 71 1.71
## 10 15 52 1.59
Para consultar valores específicos dentro de una matriz, entre paréntesis cuadrados (“[ , ]”) se colocan las coordenadas de número de fila y número de columnas requerido, como se presenta a continuación:
datos[4,2]
## [1] 62
IntroducciónalaestadísticanoparamétricaconejemplosenR
# Al dejar vacío un espacio obtiene toda la columna o toda la fila: datos[6,]
## edad peso talla
## 13.00 64.00 1.65
datos[,3]
## 1 2 3 4 5 6 7 8 9 10
Así se puede transponer una matriz:
datos2<-t(datos);datos2
## 1 2 3 4 5 6 7 8 9 10
Ahora, construimos una matriz adicionando el vector sexo y reportamos su estructura:
datos3<-matrix(c(edad,peso,talla,sexo),nrow = 10,ncol = 4, dimnames = list(1:10,c("edad","peso","talla","sexo")))
datos3
## edad peso talla sexo
## 1 "12" "60" "1.74" "H"
## 2 "14" "54" "1.68" "M"
## 3 "15" "55" "1.59" "M"
## 4 "14" "62" "1.6" "H"
## 5 "16" "75" "1.78" "H"
## 6 "13" "64" "1.65" "M"
## 7 "18" "58" "1.75" "M"
## 8 "17" "69" "1.69" "H"
## 9 "21" "71" "1.71" "M"
## 10 "15" "52" "1.59" "M"
str(datos3)
## chr [1:10, 1:4] "12" "14" "15" "14" "16" "13" "18" "17" "21" "15" "60" ...
## - attr(*, "dimnames")=List of 2
## ..$ : chr [1:10] "1" "2" "3" "4" ...
## ..$ : chr [1:4] "edad" "peso" "talla" "sexo"
Lo anterior muestra que todos los valores dentro de una matriz tienen la misma estructura. En el ejemplo anterior, todos los elementos quedaron como caracteres al incluir la variable sexo.
Este objeto permite reunir vectores con diferentes estructuras. Creemos un data.frame a partir de los vectores iniciales y veamos su estructura, así:
bd<-data.frame(edad,peso,talla,sexo);bd
## edad peso talla sexo
## 1 12 60 1.74 H
## 2 14 54 1.68 M ## 3 15 55 1.59 M ## 4 14 62 1.60 H
## 5 16 75 1.78 H
## 6 13 64 1.65 M
## 7 18 58 1.75 M
## 8 17 69 1.69 H
## 9 21 71 1.71 M
## 10 15 52 1.59 M
str(bd)
## 'data.frame': 10 obs. of 4 variables:
## $ edad : num 12 14 15 14 16 13 18 17 21 15
## $ peso : num 60 54 55 62 75 64 58 69 71 52
## $ talla: num 1.74 1.68 1.59 1.6 1.78 1.65 1.75 1.69 1.71 1.59
## $ sexo : chr "H" "M" "M" "H" ...
Para identificar información específica dentro de un data.frame, se utiliza el símbolo $ para obtener los valores de una columna y los paréntesis cuadrados para valores específicos, como se presenta a continuación:
bd$edad
IntroducciónalaestadísticanoparamétricaconejemplosenR
## [1] 12 14 15 14 16 13 18 17 21 15
bd$sexo[1]
## [1] "H"
bd[1,4]
## [1] "H"
bd[5,]
## edad peso talla sexo
## 5 16 75 1.78 H
Guardemos en “talla_sexo” todos los valores distintos que toma la talla clasificada por sexo utilizando las funciones by y unique:
talla_sexo<-by(bd,bd$sexo,function(bd)unique(bd$talla));
talla_sexo$H
## [1] 1.74 1.60 1.78 1.69
talla_sexo$M
## [1] 1.68 1.59 1.65 1.75 1.71
Finalmente, podemos obtener la cantidad de valores distintos de la talla por sexo de esta forma:
length(talla_sexo$H)
## [1] 4
length(talla_sexo$M)
## [1] 5
Dentro de una lista podemos colocar todos los objetos descritos. Guardemos en “varios” un vector, una matriz y un data.frame: varios<-list(peso,datos,bd)
Así se ubica información específica dentro de un objeto tipo lista: varios[[1]]
## [1] 60 54 55 62 75 64 58 69 71 52 varios[[1]][5]
## [1] 75 varios[[2]]
## edad peso talla
## 1 12 60 1.74
## 2 14 54 1.68
## 3 15 55 1.59
## 4 14 62 1.60
## 5 16 75 1.78
## 6 13 64 1.65
## 7 18 58 1.75
## 8 17 69 1.69
## 9 21 71 1.71
## 10 15 52 1.59 varios[[2]][2,3]
## [1] 1.68 varios[[3]]
## edad peso talla sexo
## 1 12 60 1.74 H
## 2 14 54 1.68 M
## 3 15 55 1.59 M
## 4 14 62 1.60 H
IntroducciónalaestadísticanoparamétricaconejemplosenR
## 5 16 75 1.78 H
## 6 13 64 1.65 M
## 7 18 58 1.75 M
## 8 17 69 1.69 H
## 9 21 71 1.71 M
## 10 15 52 1.59 M
varios[[3]]$peso
## [1] 60 54 55 62 75 64 58 69 71 52
varios[[3]]$peso[5]
## [1] 75
En RStudio se tienen ventanas (figura1.1, panel 2) para realizar la importación de datos, al igual que otros programas como Excel, SPSS, SAS o Stata.
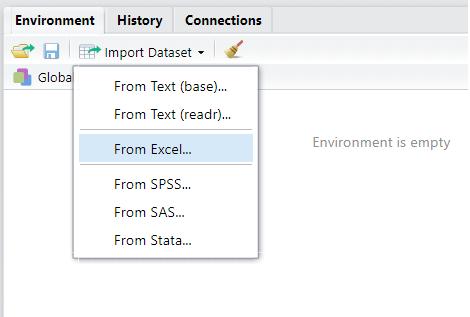
Figura1.6. Importardatos Fuente:elaboraciónpropia.
Tambiénexistenpaquetesquesepuedeninstalarquecumplenestepropósito de importación y exportación. Uno de los más utilizados es el paquete rio [9] con su función import y export.
Práctica
Para finalizar esta sección, a continuación, se sugiere una actividad que permite repasar lo visto previamente. Al final, se presenta el código de solución del ejercicio.
Responda a los siguientes requerimientos:
1. Cree 2 vectores con 16 números cada uno.
2. Cree 2 vectores con 16 caracteres cada uno.
3. Utilizando la función rep, cree un vector que contenga los siguientes valores: – “A” “A” “B” “B” “A” “A” “B” “B” “A” “A” “B” “B” “A” “A” “B” “B”
Apóyese en la ayuda de la función.
4. ¿Cuántos valores diferentes tiene cada uno de los vectores tipo carácter que creó?
5. A uno de los vectores con estructura número cámbielo a una estructura carácter.
6. A uno de los vectores con estructura carácter, cámbielo a una estructura tipo factor.
7. Coloque el valor “casa” en la posición 10 de uno de los vectores tipo carácter.
8. Creeunamatrizconlosdosvectoresnuméricosylosdosvectorestipo carácter.
9. ¿Qué valor hay en la fila 2 y en la columna 3?, ¿qué valores hay en la fila 6?
10. Cree un data.frame con los 4 vectores creados al inicio de la actividad.
11. ¿Qué valor hay en el tercer vector en la posición 13?
12. Instale el paquete gmodels.
13. ¿Qué hace la función CrossTable de este paquete?
14. UselafunciónCrossTableconlasdosvariablestipocarácterincluidas en el data.frame.
15. Cree una lista con dos vectores, una matriz y un data.frame.
IntroducciónalaestadísticanoparamétricaconejemplosenR
16. Reporte la posición 8 del segundo vector incluido en la lista.
17. Reporte el valor en la fila 3 y la columna 2 de la matriz guardada en la lista.
18. Reporte la segunda columna del data.frame incluido en la lista.
Código de respuesta:
# pregunta 1
v1<-c(2,5,6,8,1,3,4,6,9,5,1,2,3,6,5,6)
v2<-c(6,8,4,9,7,2,6,5,8,3,1,6,8,5,4,6)
# pregunta 2
v3<-c("A","B","F","G","T","H","J","R","D","G","E","F","U","P","Y","Z")
v4<-c("D","T","H","R","D","B","I","P","Q","S","Y","B","A","L","F","I")
# pregunta 3 rep(c("A","B"),each=2,time=4)
#pregunta 4 length(unique(v3)) length(unique(v4))
# pregunta 5
v1.chr<-as.character(v1)
# pregunta 6
v3.fac<-factor(v2,levels = c("A","B","F","G","T","H","J","R","D","E","U", "P","Y","Z"))
# pregunta 7
v3[10]<-"casa"
# pregunta 8
m1<-matrix(c(v1,v2,v3,v4),nrow = 16,ncol = 4, dimnames = list(1:16,c("v1","v2","v3","v4")))
# pregunta 9
m1[2,3] m1[6,]
# pregunta 10
df<-data.frame(v1,v2,v3,v4)
# pregunta 11
df$v3[13]
# pregunta 12 install.packages("gmodels")
# pregunta 13 library(gmodels)
?CrossTable # Crea tabla de contingencia reportando # frecuencias absolutas y relativas y prueba chi2.
# pregunta 14
CrossTable(df$v3,df$v4)
# pregunta 15
lista<-list(v1,v2,m1,df)
# pregunta 16 lista[[2]][8]
# pregunta 17 lista[[3]][3,2]
# pregunta 18 lista[[4]]$v2
Tabla1.3. Resumendefuncionesde R
Función
Descripción(paquete)
setwd() Defineeldirectoriodetrabajoespecificandosuubicación. getwd() Reportalarutadeldirectoriodetrabajodefinido. dir() Reportalosarchivosguardadoseneldirectoriodetrabajo. install.packages() Instalaunnuevopaquete. library() Cargaunnuevopaquetequesehainstaladopreviamente. say() Representaunaimagenjuntoconuntexto. c() Combinavaloresdentrodeunvector. matrix() Creaunamatrizapartirdeungrupodevaloresdeterminados. t() Transponeunamatriz. data.frame() Creaunobjetotipodata.frame. list() Creaunobjetotipolista. str() Reportalaestructuradelosdatosregistradosenelobjeto. rep() Repiteunconjuntodevaloresdeterminados.
Continúa
IntroducciónalaestadísticanoparamétricaconejemplosenR
Función
length()
Tabla1.3(continuación). Resumendefuncionesde R
Descripción(paquete)
Reportalacantidaddevaloresregistradaenunobjeto. unique() Reportalosvaloresúnicosqueseencuentranenunobjeto. factor()
as.numeric
Convierteunobjetoaunaestructuratipofactor.
Convierteunobjetoaunaestructuratiponumérico. as.character
Convierteunobjetoaunaestructuratipocarácter.
rm() Remueve/borraunobjeto.
by() Ejecutaunafunciónensubgruposdefinidosporunacaracterística.
Fuente:elaboraciónpropia.
[1] TeamRC.R:Alanguageandenvironmentforstatisticalcomputing.En:R FoundationforStatisticalComputing[Internet].Vienna,Austria;2022.Disponible en:https://www.R-project.org/
[2] TeamRs.RStudio:integrateddevelopmentenvironmentforr.RStudio[Internet]. Boston,MA:PBC;2020.Disponibleen: http://www.rstudio.com/
[3] GibbonsJD,ChakrabortiS.Nonparametricstatisticalinference.BocaRaton: Chapman&Hall/CRC;2010.
[4] ConoverWJ.Practicalnonparametricstatistics.3.aed.NewYork:JohnWiley&Sons; 1999.
[5] DanielWW.Bioestadística:baseparaelanálisisdelascienciasdelasalud.4.aed. Limusa;2002.
[6] KlokeJ,McKeanJ.Nonparametricstatisticalmethodsusingr.BocaRaton;2014.
[7] ChamberlainS,DobbynA,RinkerT.Cowsay:messages,warnings,stringswithascii animals[Internet].2020.Disponibleen:https://CRAN.R-project.org/package=cowsay
[8] WickhamH.Tidyverse:easilyinstallandloadthe ‘tidyverse’[Internet].2021. Disponibleen: https://CRAN.R-project.org/package=tidyverse
[9] BeckerJ,ChanC,ChanGC.Rio:aswissarmyknifefordatai/o[Internet].2021. Disponibleen: https://CRAN.R-project.org/package=rio
[10] GibbonsJD,ChakrabortiS.Testsofgoodnesoffit.TheKolmogorovSmirnovonesamplestatistic.En:Nonparametricstatisticalinference.4.aed.NewYork:CRC Press;2003.p.111-30.
[11] GrossJ,LiggesU.Nortest:Testsfornormality.2015.
[12] ConoverWJ.Statisticsofthekolmogorovsmirnovtype.En:Practicalnonparametric statistics.3.aed.NewYork:JohnWiley&Sons;1999.p.450-4.
[13] NCSSL.Chapter194normalitytest[Internet].2016.Disponibleen: https://pdf4pro.com/view/chapter-194-normality-tests-5d794a.html
[14] KomstaL,NovomestkyF.Moments:Moments,cumulants, skewness,kurtosisandrelatedtests[Internet].2022.Disponibleen: https://cran.r-project.org/web/packages/moments/moments.pdf
[15] ArnoldJB,DarocziG,WerthB,WeitznerB,KunstJ,AuguieB,etal.ggthemes:extra themes,scalesandgeomsfor«ggplot2».LondonJ[Internet].2021.Disponibleen: https://CRAN.R-project.org/package=ggthemes
[16] TraplettiA,HornikK,LeBaronB.Tseries:Timeseriesanalysisandcomputational finance[Internet].2022.Disponibleen:https://CRAN.R-project.org/package=tseries
[17] GibbonsJD,ChakrabortiS.Onesampleandpairedsampleprocedures.5.7The wilcoxonsignedranktestandconfidenceinterval.En:Nonparametricstatistical inference.4.aed.NewYork:CRCPress;2003.p.204.
[18] ArnholtAT,EvansB.BSDA:Basicstatisticsanddataanalysis[Internet].2021. Disponibleen: https://CRAN.R-project.org/package=BSDA
[19] GibbonsJD,ChakrabortiS.Onesampleandpairedsampleprocedures.5.4Thesign testandconfidenceintervalforthemedian.En:Nonparametricstatisticalinference. 4.aed.NewYork:CRCPress;2003.p.170-1.
[20] NoetherGE.Samplesizedeterminationforsomecommonnonparametrictests.J AmStatAssoc.1987;82(398):645-7.
[21] RipleyB,VenablesB,BatesDM,HornikK,GebhardtA,FirthD.MASS:Support functionsanddatasetsforvenablesandripley'sMASS[Internet].2022.Disponible en:https://cran.r-project.org/web/packages/MASS/MASS.pdf
[22] HothornT,HornikK.exactRankTests:exactdistributionsforrankandpermutation tests.2022.
[23] CanavosGC.Métodosnoparamétricos:pruebasnoparamétricaspara observacionesporpares.En:Probabilidadyestadistica:aplicacionesymetodos. México:McGrawHill;1990.p.581.
[24] CantyA,RipleyB.Boot:BootstrapFunctions[Internet].2021.Disponibleen: https://CRAN.R-project.org/package=boot
[25] CarpenterJ,BithellJ.Bootstrapconfidenceintervals:when,which,what?A practicalguideformedicalstatisticians.StatMed.2000;19:1141-64.
[26] GibbonsJD,ChakrabortiS.Testsofrandomness.En:Nonparametricstatistical inference.4.aed.NewYork:CRCPress;2003.p.83.
[27] CareiroF,MateusA.Randtests:testingrandomnessinr[Internet].2014.Disponible en:https://cran.r-project.org/web/packages/randtests/index.html
[28] ConnorRJ.Samplesizefortestingdifferencesinproportionsforthepairedsample design.Biometrics.1987;43(1):207-11.
[29] FayMP,HunsbergerSA,NasonM,GabrielE,LumbardK.exact2x2:Exact testsandconfidenceintervalsfor2x2tables[Internet].2021.Disponibleen: https://CRAN.R-project.org/package=exact2x2
[30] HervéM.RVAideMemoire:Testingandplottingproceduresforbiostatistics [Internet].2022.Disponibleen: https://cran.r-project.org/web/packages/ RVAideMemoire/index.html
IntroducciónalaestadísticanoparamétricaconejemplosenR
[31] PohlertT.PMCMRplus:Calculatepairwisemultiplecomparisons ofmeanranksumsextended[Internet].2022.Disponibleen: https://cran.r-project.org/web/packages/PMCMRplus/index.html
[32] SweetDL.Nonpar:Acollectionofnonparametrichypothesistests[Internet].2020. Disponibleen: https://CRAN.R-project.org/package=nonpar
[33] MangiaficoS.Rcompanion:Functionstosupportextension educationprogramevaluation[Internet].2022.Disponibleen: https://cran.r-project.org/web/packages/rcompanion/index.html
[34] NavarroD.Lsr:Companionto«learningstatisticswithr»[Internet].2021. Disponibleen: https://cran.r-project.org/web/packages/lsr/index.html
[35] MeyerD,ZeileisA,HornikK,GerberF,FriendlyM.Vcd:Visualizingcategoricaldata [Internet].2022.Disponibleen:https://cran.r-project.org/web/packages/vcd/index.html
[36] WarnesGR,BolkerB,LumleyT.SAICFrederickandRCJCfromRCJareC(2005), ProgramIFbytheIR,NIHofthe,InstituteNC,NO1-CO-12400CforCRunderNC [Internet].2022.Disponibleen: https://CRAN.R-project.org/package=gmodels
[37] GibbonsJD,ChakrabortiS.Measuresofassociationforbivariatesamples.En: Nonparametricstatisticalinference.4.aed.NewYork:CRCPress;2003.p.399-445.
[38] McLeodAI.Kendall:KendallrankcorrelationandMannKendalltrendtest [Internet].2022.Disponibleen: https://cran.r-project.org/web/packages/Kendall/ Kendall.pdf
[39] EslavaSchmalbachJH,BuitragoGutiérrezG,RincónRodríguezCJ.Inequidadde lamortalidadevitable.En:Conceptos,desarrollosymedición.Bogotá:Universidad NacionaldeColombia;2013.
[40] WeiT,SimkoV,LevyM,XieY,JinY,ZemlaJ,etal.Corrplot:visualizationofa correlationmatrix[Internet].2021.Disponibleen: https://CRAN.R-project.org/ package=corrplot
[41] SignorellA,AhoK,AlfonsA.DescTools:toolsfordescriptivestatistics[Internet]. 2022.Disponibleen:https://cran.r-project.org/web/packages/DescTools/index.html
[42] SchloerkeB,CookD,LarmarangeJ.GGally:Extensionto«ggplot2»[Internet].2021. Disponibleen: https://cran.r-project.org/web/packages/GGally/index.html
[43] SavickyP.Pspearman:Spearman'srankcorrelationtest[Internet].2022.Disponible en:https://cran.r-project.org/web/packages/pspearman/pspearman.pdf
[44] SomersRH.Anewasymmetricmeasureofassociationforordinalvariables.Am SociolRev.1962;27(6):799-811.
[45] GöktaşA,İşçiÖ.Comparisonofthemostcommonlyusedmeasuresofassociation fordoublyorderedsquarecontingencytablesviasimulation.AdvMethStat. 2011;8(1):17-37.
[46] FriendlyM,TurnerH,ZeileisA,MurdochD,FirthD,KumarM,etal.vcdExtra: ‘Vcd’ extensionsandadditions.2022.
[47] EkstrømCT.MESS:Miscellaneousesotericstatisticalscripts[Internet].2022. Disponibleen: https://CRAN.R-project.org/package=MESS
[48] HyndmanR,AthanasopoulosG,BergmeirC,CaceresG,ChhayL,KuroptevK, etal.Forecast:Forecastingfunctionsfortimeseriesandlinearmodels[Internet]. 2022.Disponibleen:https://cloud.r-project.org/web/packages/forecast/index.html
[49] FriedmanJH.Avariablespansmoother.JAmStatAssoc.1984.
[50] ClevelandWS.Robustlocallyweightedregressionandsmoothingscatterplots.JAm StatAssoc.1979;74(368):829-36.
[51] AltmanNS.AnintroductiontoKernelandnearestneighbornonparametric regression.TheAmericanStatistician.1deagostode1992;46(3):175-85.
[52] WangX,JiX.fANCOVA:nonparametricanalysisofcovariance[Internet].2020. Disponibleen: https://CRAN.R-project.org/package=fANCOVA
[53] RacineJS,HayfieldT.Np:nonparametrickernelsmoothing methodsformixeddatatypes[Internet].2021.Disponibleen: https://cran.r-project.org/web/packages/np/np.pdf
[54] KoenkerRW,D'OreyV.AlgorithmAS229:Computingregressionquantiles.ApplStat. 1987;36(383).
[55] KleinbaumDG,KupperLL,NizamA,RosenbergES.Appliedregressionanalysisand othermultivariablemethods.5.aed.Boston,MA:CengageLearning;2013.
[56] KoenkerR,code.Quantreg:Quantileregression[Internet].2022.Disponibleen: https://CRAN.R-project.org/package=quantreg
[57] PortnoyS,KoenkerR.Thegaussianhareandthelaplaciantortoise:Computability ofsquarederrorversusabsoluteerrorestimators.StatSci.1997;12(4):279-96.
IntroducciónalaestadísticanoparamétricaconejemplosenR
Este libro se compuso usando tipos Erewhon, con el sistema de composición tipográfica ConTEXt. Se terminó de imprimir en los talleres de DGP Editores SAS en febrerode2025.
Este libro explica diferentes métodos de la estadística no paramétrica con un ejemplo de aplicación que utiliza los programas R y RStudio, además de las expresiones matemáticas que fundamentan los resultados. Este texto presenta material de consulta para que el estudiante comprenda de manera autónoma los métodos y los aplique en sus proyectos. El libro está dirigido principalmente a jóvenes investigadores del área de la salud, como estudiantes de pregrado de medicina y de posgrado en epidemiología clínica, bioestadística, salud pública o economía de la salud, que requieran del uso de métodos no paramétricos clásicos y estén interesados en aprender a usar herramientas para el análisis de los datos. Es deseable que el lector tenga conocimientos básicos de estadística clásica —en temas como variables, probabilidad, funciones de distribución de probabilidades, estimación por intervalos de confianza y prueba de hipótesis— y en los programas R y RStudio, aunque se incluye una introducción a su uso en el primer capítulo.