Spis treści
Wprowadzenie
Co nowego w tym wydaniu
Ksi ki elektroniczne
Podzi kowania
Rozdział 1 Wczesne liczby i symbole
1.1. Prymitywne liczenie
Sens liczby.
Naci cia jako znaki w liczeniu
Peruwia skie kipu: w z y jako liczby
1.2. Zapisywanie liczb u Egipcjan i Greków.
Historia Herodota
liczenie hieratyczne
liczbowy
Rozdział 2 Matematyka we wczesnych cywilizacjach.
papirusy
Klucz do odszyfrowania: kamie z Rosetty
Egipska arytmetyka.
Wczesne egipskie mno enie
Reprezentacja liczb wymiernych
2.3. Cztery problemy z papirusu Rhinda
Metoda fa szywej linii prostej.
Ciekawy problem.
Matematyka egipska jako matematyka stosowana
2.4. Egipska geometria.
Aproksymacja powierzchni okr gu
Obj to ostros upa ci tego
Spekulacje na temat Wielkiej Piramidy
2.5. Matematyka babilo ska.
Tablica odwrotno ci
Babilo skie podej cie do równa kwadratowych
Dwa charakterystyczne problemy babilo skie
2.6. Plimpton 322
Tabliczka dotycz ca trójek liczbowych
Babilo skie wykorzystanie twierdzenia Pitagorasa
Matematyczny papirus z Kairu
Rozdział 3 Początki matematyki greckiej
3.1. Geometryczne odkrycia Talesa
Grecja i obszar Morza Egejskiego
Pocz tek geometrii pogl dowej: Tales z Miletu
Pomiary z u yciem geometrii
3.2. Matematyka pitagorejska
Pitagoras i jego nast pcy.
Introductio Arithmeticae Nikomachosa
Teoria liczb wielok tnych
Paradoks Zenona
3.3. Problem Pitagorasa
Geometryczne dowody twierdzenia Pitagorasa
Wczesne rozwi zania równania Pitagorasa
Kryzys wielko ci niewspó miernych
Teona liczby boku i przek tnej
Eudoksos z Knidos
3.4. Trzy problemy konstrukcyjne staro ytno ci
Hipokrates i kwadratura ko a
Podwojenie sze cianu
Trysekcja k ta
3.5. Kwadratrysa Hippiasza
Powstanie so stów
Hippiasz z Elidy
Gaj Akademosa: Akademia Plato ska
Rozdział 4 Szkoła aleksandryjska: Euklides
Euklides i jego Elementy
Centrum nauki: Muzeum
ycie i twórczo Euklidesa
4.2. Geometria Euklidesa
Podstawy geometrii wed ug Euklidesa
Postulaty
Poj cia pospolite
Ksi ga I Elementów
Dowód Euklidesa twierdzenia Pitagorasa
Ksi ga II o algebrze geometrycznej
Konstrukcja pi ciok ta foremnego
4.3. Teoria liczb Euklidesa
Cechy podzielno ci wed ug Euklidesa
Algorytm Euklidesa
Podstawowe twierdzenie arytmetyki
Niesko czono liczb pierwszych
4.4. Eratostenes, m drzec z Aleksandrii
Sito Eratostenesa
Pomiary Ziemi
Almagest Klaudiusza Ptolemeusza
S ownik geogra czny Ptolemeusza
4.5. Archimedes
Geniusz staro ytnego wiata
Szacowanie warto ci
O liczeniu piasku
Kwadratura odcinka parabolicznego
Apoloniusz z Pergi: Sto kowe
Rozdział 5 Zmierzch greckiej matematyki: Diofantos
5.1. Schy ek matematyki aleksandryjskiej
Kres z otego wieku
Rozprzestrzenianie si chrze cija stwa
Konstantynopol – schronienie dla greckiej nauki
5.2. Arithmetica
Teoria liczb Diofantosa
Zadania z Arithmetica
5.3. Równania diofantyczne w Grecji, Indiach i Chinach
Problem liczebno ci stad byd a w uj ciu Archimedesa
Wczesna matematyka w Indiach
Chi ski problem stu kur
5.4. Pó niejsi komentatorzy
Zbiór matematyczny Pappusa
Hypatia, pierwsza kobieta matematyk
Matematyka rzymska: Boecjusz i Kasjodor
5.5. Matematyka Bliskiego i Dalekiego Wschodu
Algebra al-Chuwarizmiego
Abu Kamil i Thabit ibn Qurra
Omar Chajjam
Astronomowie al-Tusî i al-Kashî
Staro ytne chi skie Dziewi rozdzia ów
Pó niejsze chi skie dzie a matematyczne
Rozdział 6 Pierwsze przebudzenie: Fibonacc
6.1. Upadek i odrodzenie nauki
Prerenesans karoli ski.
Przeniesienie nauki arabskiej na Zachód
Pionierscy t umacze: Gerard i Adelard
6.2. Liber Abaci i Liber Quadratorum
Liczby hindusko-arabskie
Liber Quadratorum Fibonacciego
Prace Jordanusa de Nemore
6.3. Ci g Fibonacciego
Problem z królikami z Liber Abaci
Niektóre w asno ci liczb Fibonacciego
6.4. Fibonacci i problem Pitagorasa
Trójki liczb Pitagorasa
Problem turniejowy Fibonacciego
Rozdział 7 Renesans matematyki: Cardano i Tartaglia
7.1. Europa w XIV i XV wieku
W oski renesans
Sztuczne pismo: wynalazek druku
Powstanie wielkich uniwersytetów.
G ód nauki klasycznej
7.2. Bitwa uczonych.
Przywracanie tradycji algebraicznej: Robert Recorde
W oscy algebraicy: Pacioli, del Ferro i Tartaglia
Cardano, matematyk hulaka
7.3. Ars Magna Cardana
Rozwi zanie Cardana równania sze ciennego
Bombelli i pierwiastki urojone równania sze ciennego
7.4. Rozwi zanie równania czwartego stopnia wg Ferrariego
Rozwi zuj ce równanie sze cienne
Historia równania pi tego stopnia: Ru ni, Abel i Galois
Rozdział 8 Świat mechaniki: Kartezjusz i Newton
8.1. wit nowo ytnej matematyki
Rozprzestrzenianie si wiedzy w XVII wieku
Obserwacje teleskopowe Galileusza.
Pocz tki wspó czesnej notacji: François Viète
U amki dziesi tne Simona Stevina
Wynalezienie logarytmów przez Napiera
Odkrycia astronomiczne Brahego i Keplera
8.2. Kartezjusz: Rozprawa o metodzie
Pisma Kartezjusza
Wynalezienie geometrii kartezja skiej
Algebraiczny aspekt Geometrii
Zasady lozo i Kartezjusza
Geometria rzutowa: Desargues i Poncelet
8.3. Newton: Principia Mathematica
Podr czniki Oughtreda i Harriota
Arithmetica In nitorum Wallisa
Katedra Lucasa: Barrow i Newton
Z ote lata Newtona
Prawa dynamiki.
Pó niejsze lata: powo anie do mennicy
8.4. Gottfried Leibniz: kontrowersje wokó rachunku ró niczkowego i ca kowego
Wczesne prace Leibniza
Stworzenie rachunku ró niczkowego i ca kowego przez Leibniza
Rachunek ró niczkowy ( uksje) Newtona
Spór o pierwsze stwo
Maria Agnesi i Emilie du Châtelet
Rozdział 9 Powstanie teorii prawdopodobieństwa: Pascal, Bernoulli i Laplace
9.1. Geneza teorii prawdopodobie stwa.
Tabele miertelno ci Graunta (Bills of Mortality)
Gry losowe: ko ci i karty
Precyzyja m odego Pascala.
Pascal i cykloida
Paradoks kawalera de Méré
9.2. Trójk t arytmetyczny Pascala
Traité du Triangle Arithmétique
Indukcja matematyczna
Zastosowanie indukcji przez Francesco Maurolico
9.3. Bracia Bernoulli i Laplace
Pam et na temat prawdopodobie stwa Christiaana Huygensa
Bracia Bernoulli: Johann i Jakob
Dokryna szans de Moivre’a
Matematyka zjawisk niebieskich: Laplace
Mary Fairfax Somerville
Badania Laplace’a w teorii prawdopodobie stwa
Daniel Bernoulli, Poisson i Czebyszew
X Spis treści
Rozdział 10 Odrodzenie teorii liczb: Fermat, Euler i Gauss
10.1. Marin Mersenne i poszukiwanie liczb doskona ych
Towarzystwa naukowe
Matematyczne spotkania Marina Mersenne’a
Liczby, doskona e i nie tak doskona e
10.2. Od Fermata do Eulera
Arithmetica Fermata
S ynne wielkie twierdzenie Fermata
Osiemnastowieczne o wiecenie
Treatise on Fluxions Maclaurina
ycie i wk ad Eulera
10.3. Ksi matematyków: Carl Friedrich Gauss
Okres rewolucji francuskiej: Lagrange, Monge i Carnot
Disquisitiones Arithmeticae Gaussa
Spu cizna Gaussa: teoria przystawania
Dirichlet i Jacobi
Rozdział 11 Osiągnięcia XIX wieku: od Łobaczewskiego do Hilberta
11.1. Próby udowodnienia postulatu równoleg o ci
Wysi ki Proklosa, Playfaira i Wallisa
ty Saccheriego
Legendre’a
Eléments de géométrie Legendre’a
11.2. Twórcy geometrii nieeuklidesowej
Próby Gaussa dotycz ce nowej geometrii
Walka Jánosa Bolyaia
Stworzenie geometrii nieeuklidesowej: obaczewski
Modele nowej geometrii: Riemann, Beltrami i Klein
Grace Chisholm Young
11.3. Epoka cis o ci
D’Alembert i Cauchy o granicach
Szeregi Fouriera
Ojciec wspó czesnej analizy, Weierstrass
Sofja Kowalewska
Ruch aksjomatyczny: Pasch i Hilbert
11.4. Arytmetyka uogólniona
Babbage i maszyna analityczna
Treatise on Algebra Peacocka
Przedstawianie liczb zespolonych
Odkrycie kwaternionów przez Hamiltona
Algebra macierzy: Cayley i Sylvester
Algebra logiki Boole’a
Rozdział 12 Przejście do XX wieku: Cantor i Kronecker
12.1. Pojawienie si ameryka skiej matematyki
Przewaga niemieckich uniwersytetów
Ameryka ska matematyka zapuszcza korzenie: 1800–1900
Konsolidacja w XX wieku
12.2. Obliczanie niesko czono ci
Ostatni uniwersalista: Poincaré
Teoria zbiorów niesko czonych Cantora
Teoria zbiorów w uj ciu Kroneckera
Zbiory przeliczalne i nieprzeliczalne
Liczby transcendentalne
Hipoteza ci g o ci
12.3. Paradoksy teorii zbiorów
Wczesne paradoksy
Zermelo i aksjomat wyboru
Szko a logistyki: Frege, Peano i Russell
Formalistyczne podej cie Hilberta
Intuicjonizm Brouwera
Rozdział 13 Rozszerzenia i uogólnienia: Hardy, Hausdorff i Noether
13.1. Hardy i Ramanujan
Egzamin Tripos
Wyj tkowa wspó praca: Hardy i Littlewood
Indyjski marnotrawca, Ramanujan
13.2. Pocz tki topologii zbiorów punktowych
Przestrzenie metryczne Frecheta
Przestrzenie s siedztwa Hausdor a
Przestrzenie liniowe Banacha i normalizowane
13.3. Rozwój sytuacji w XX wieku
Teoria pier cieni Emmy Noether
Von Neumann i komputer
Kobiety we wspó czesnej matematyce
Kilka najnowszych osi gni
Bibliografia ogólna
Lektury dodatkowe
Alfabet grecki
Rozwiązania wybranych zadań
Skorowidz
Niektóre ważne nazwiska, daty i wydarzenia historyczne
ROZDZIAŁ 1. Wczesne liczby i symbole
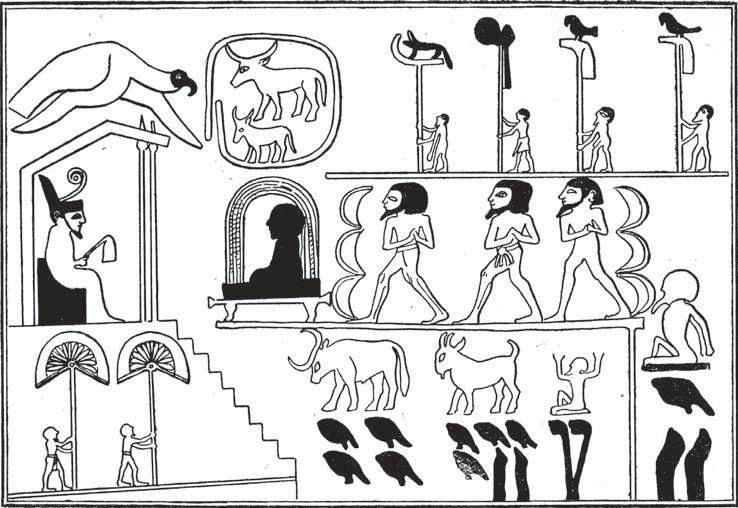
Scena pochodzi z wielkiego kamienia reliefu Narmera, który odkrył w Nechen J.E. Quibell w 1898 roku. Jest to posumowanie łupów, które zdobył Narmer podczas swoich wojen, a konkretnie „krów 400000, , kóz 1422000, oraz pojmanych 120000, ” (Odrys sceny: Ernest Alfred Wallis/Wikimedia Commons)
Spektakularne pojawienie si pod rz dami faraonów pierwszych dwóch dynastii egipskiego rz du i administracji nie mog oby si wydarzy bez metody pisania i metod tak znajdujemy i w wypracowanych „ wi tych znakach”, czyli hieroglifach, i w szybkiej odr cznej kursywie pisma rachunkowego. System piania hieroglifami to pismo obrazkowe, w którym ka dy znak reprezentuje konkretny obiekt, a jego znaczenie nadal w wielu przypadkach mo na rozpozna . W jednym z grobowców w pobli u piramidy w Gizie znaleziono hierogli czne symbole liczbowe, w których liczba jeden by a reprezentowana przez pojedyncz pionow kresk lub obraz s u cego, a rodzaj podkowy lub znak ko ci pi towej jest u ywany jako zbiorczy symbol zast puj cy dziesi pojedynczych kresek. Innymi s owy, system egipski by systemem dziesi tnym (od aci skiego decem oznaczaj cego „dziesi ”), który wykorzystywa przy liczeniu pot gi 10, Liczba 10 jest tak cz sto znajdowana u staro ytnych ludów jako podstawa ich systemu liczenia, e bez w tpienia wynika to z dziesi ciu palców cz owieka i zwyczaju liczenia na nich. Z tego samego powodu symbol jak nasza cyfra 1 jest niemal wsz dzie u ywany do wyra enia jedynki.
U ywano specjalnych piktogramów dla ka dej pot gi 10 a do 10 000 000: 100 jako zakr cony sznur, 1000 jako kwiat lotosu, 10 000 jako zagi ty palec, 100 000 jako kijanka, 1 000 000 jako osoba trzymaj ca dwie r ce w górze, jakby bardzo zdziwiona i 10 000 000 jako symbol czasami traktowany jako wschodz ce s o ce.
ROZDZIAŁ
2. Matematyka we wczesnych cywilizacjach
Obliczenia s przeprowadzone wed ug wzoru
A = ½(b + b )h
Czy autor papirusu uwa a , e pole trapezoidu by o po ow sumy d ugo ci boków równoleg ych razy nachylona wysoko , czy te jeden uko ny bok mia by prostopad y do boków równoleg ych? W tym ostatnim przypadku mia by racj . Nie jest wcale wykluczone, e ten diagram, który jest do zgrubnym szkicem, jest le narysowany i jeden z na pozór równych boków jest w rzeczywisto ci prostopad y do boków równoleg ych.
Objętość ostrosłupa ściętego
W papirusie moskiewskim jest tylko 25 problemów, ale jeden z nich dotyczy arcydzie a staro ytnej geometrii. Problem 14 pokazuje, e oko o roku 1850 p.n.e. Egipcjanie znali poprawny wzór na obj to ostros upa ci tego o kwadratowej podstawie (czyli bry y ci tej). W naszej notacji ma to posta : , gdzie h jest wysoko ci , za a i b to d ugo ci boków kwadratu podstawy i kwadratu wierzcho kowego.
Rysunek powi zany z problemem 14 wygl da jak trapezoid równoramienny,
ale obliczenia wskazuj , e chodzi o ostros up ci ty o podstawie kwadratu. Dok adny tekst opisuj cy ten problem podano tak:
Przyk ad obliczania ostros upa ci tego. Je li zosta o powiedziane: dany jest ostros up ci ty o wysoko ci 6, podstawie 4 na dole i 2 na górze. Masz podnie do kwadratu to 4, a wynik 16. Masz podwoi 4, a wynik 8. Masz podnie do kwadratu to 2, a wynik 4. Masz doda 16 i 8 i 4, a wynik 28. Masz wzi z 6, a wynik 2. Masz podwoi 28, a wynik 56. Masz oto 56. A wynik jest poprawny.
Wprawdzie to rozwi zanie dotyczy konkretnego problemu, a nie ogólnej teorii, i tak zapiera dech. Niektórzy historycy matematyki chwalili to osi gni cie jak najwi ksze z egipskich piramid.
2.4. Egipska geometria
Ogólnie przyjmuje si , e Egipcjanie znali wzór na obj to ostros upa o kwadratowej podstawie i zapewne by on poprawny:
Przez analogi do wzoru na powierzchni trójk ta, Egipcjanie zapewne odgadli, e obj to ostros upa to sta a razy ha2. Mo emy nawet przypuszcza , e odgadli oni t sta jako . Ale wzór
nie za bardzo móg by odgadni ty. Móg zosta otrzymany tylko na podstawie pewnej analizy geometrycznej lub algebraicznie z V = (h/3)a2. Rekonstrukcja metody, dzi ki której mogli wydedukowa wzór na ostros up ci ty na podstawie materia ów, jakimi dysponowali, nie jest jednak atwym zadaniem.
Spekulacje na temat Wielkiej Piramidy
Ka da analiza matematyki Egipcjan powinna obejmowa krótkie odwo anie do Wielkiej Piramidy z Gizy, wzniesionej oko o roku 2600 p.n.e. przez Chufu, którego Grecy zwali Cheopsem. Daje ona monumentalny dowód doceniania formy geometrycznej i do dobrze rozwini tej in ynierii konstrukcyjnej, nie mówi c ju o niezwyk ej spo ecznej i rz dowej organizacji. Wed ug Herodota przy jej budowie pracowa o 400 tys. robotników rocznie przez 30 lat – cztery oddzielne grupy po 100 tys., a ka da grupa zatrudniona przez trzy miesi ce. (Obliczenia wskazuj , e nie wi cej ni 36000 ludzi mog o pracowa jednocze nie przy piramidzie bez przeszkadzania sobie wzajemnie w ruchach.)

Fragment ze skórzanego zwoju zawierającego proste zależności między ułamkami takimi jak (Za zgodą British Museum)
3.5. Kwadratrysa Hippiasza
Gaj Akademosa: Akademia Platońska
Dialogach