Nou Biaix, 36

Revista de la FEEMCAT i de la SCM

biaix

banouiix

número 36

sumari

Consell de Redacció:

Manel Sol / Josep Lluís Solé (coords.)

Marianna Bosch

Joan Carles Ferrer

Joan Miralles

Josep Pla

Romà Pujol

Manuel Udina

Juanjo Cárdenas (responsable pàgina web)

© dels autors dels articles

Coediten:

Federació d’Entitats per a l’Ensenyament de les Matemàtiques (FEEMCAT) Campus de Montilivi, edi ci P-IV 17071 Girona feemcat.org

Societat Catalana de Matemàtiques (SCM) lial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat noubiaix@gmail.com sites.google.com/site/noubiaix

Periodicitat: semestral Preu d‘exemplar ordinari: 12 € Nombre d‘exemplars: 1.700

Fotogra a de la coberta: Margarida i ordre

Josep Rey Museu de Matemàtiques de Catalunya (MMACA)

ISSN: 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Grá cas Rey

Publicacions i Edicions de la Universitat de Barcelona

Adolf Florensa, s/n 08028 Barcelona

Tel.: 934 035 430

Fax: 934 035 531 comercial.edicions@ub.edu www.publicacions.ub.edu

Bótes i barrils

Armengol Gasull

Resoldre no és aprendre. De la resolució a la competència matemàtica i de la vivenciació a l’abstracció i la generalització matemàtica

Josep Callís i Franco

El raonament probabilístic en alumnes d’educació infantil i de cicle mitjà d’educació primària

Paula López, Sílvia Serra i Laia Torres

Descobertes matemàtiques

Núria Cardet

Editorial 8 29 48 55 66 80 100 3

Matemàtiques i entorn a l’educació infantil

Fàtima Dalmau i Àngel Alsina

Construir, conjecturar, comprovar i demostrar amb el GeoGebra

Pep Bujosa

Concurs de resolució grà ca de «sangakus» amb el GeoGebra

Carlos Giménez Esteban articles

Per pensar d’un minut a una hora

Jordi Deulofeu

Construint matemàtiques

Anton Aubanell

El racó del MMACA

Josep Rey i Manuel Udina

El racó del Cesire-Creamat

AquestmesdejuliolesfaràladissetenaediciódelesJAEM,organitzadaperlaSEMRM alaciutatdeCartagena.Éslamillormostradelavitalitatilail·lusióquetéelprofessorat dematemàtiquesdetotl’Estatespanyolperlafeinaquefem.Malgratlesdificultats delstempsactuals,alvoltantd’unmilerdeprofessorsiprofessoresdediquenuns diesacompartiriaprendrenovesideespermillorarelnostretreballalesaules.Els organitzadorshanpreparatunprogramabeninteressantquepodeuveureambdetall alasevapàginaweb:http://17jaem.semrm.com

D’altrabanda,uncursméss’acabaijahemdemirarelsegüent,que,coméshabitual, espresentaambunsquantscanvis.Aprimàriaescompletaràlaimplementaciódela LOMCEatotal’etapa.Pelquefaasecundària,escomençaràlaLOMCEaprimeritercer d’ESOiaprimerdebatxillerat.Enelmomentd’escriureaquesteslínies,elDepartament d’EducaciódelaGeneralitatencaranohafetpúblicselscurrículums,peròsíquees podenveureelsquehapublicatelMinisteriodeEducaciónalBOEdel3degener d’aquestany.

L’abastquetindrantotsaquestscanvisdependràenbonamesuradequinasiguil’evolució detoteslesqüestionspolítiquesobertesal’Estatespanyol.Siguicomsigui,l’aprenentatge percompetènciescontinuaestantalabasedelcurrículumdematemàtiques.Pertant, atenint-nosalquediuensobreelpaper,nos’hihauriendeproduirgransmodificacions.Diem aixòperfernotarquetotselsesforçosques’hanfetdesdel’any 2007peranarintroduint eltreballpercompetènciesalesaulesnohauranestatestèrils,jaqueinterpretemque aras’hauràdecontinuartreballantenlamateixalínia.Animemtotelprofessorataseguir innovant,formant-seicompartintlesbonesexperiències,comhafetfinsara.

Enaquestnúmero36usproposemarticlesdetotselsnivellseducatius.Recordeuqueun delsobjectiusdelanostrarevistaésquepuguiinteressaralsprofessorsdematemàtiques desd’infantilfinsalauniversitat.Creiem,comdiemalcomençament,queelsquiensenyem matemàtiquessomuncol lectiuambbonesidees,bonespràctiquesimoltail lusióperla nostrafeinaalesaules.

Enprimerlloc,trobemunarticledel’ArmengolGasullsobrelesmatemàtiquesassociades aunaqüestiópràcticacoméselcàlculdelvolumd’unabótaobarril.L’Armengolens explicaqueaquestproblemainteressàaKepler,queel 1615publicàsobreeltemaunllibre titulat Novastereometriadoliorumvinariorum.Aquestllibre,previaldesenvolupamentdel càlculdiferencialiintegral,esconsideral’avançmésseriós,juntamentambelsresultatsde BonaventuraCavalieri,delcàlculd’àreesivolums,desdelstempsd’Arquimedes.Ambaquest problemacomafilconductor,al’articlehiapareixenmatemàticsoastrònomscomOughtred, JohnNewton,Simpson,CavalieriiGauss.

A«Resoldrenoésaprendre»,enJosepCallísposademanifestlasevapreocupaciópelpas d’unaprenentatgebasatenlamemòriaaunaprenentatgecompetencial.L’articleexplica unaexperiènciaquehafetambelsseusalumnesdemagisteriiambmestresenactiu.Són interessantslesreflexionssobrecomelmestreprenlesdecisions,reflexionsquepoden tambéserútilsaaltresnivellseducatius.

L’articledePaulaLópez,SílviaSerraiLaiaTorrespresentaunestudiquehanportata termesobrelesdificultatsquetenenelsnensinenesd’infantiliprimàriaperacomprendre l’atzar.Lesautoresmostrenque,malgratserconceptesnoimmediats,podemintroduir-losi treballar-losal’aulad’unamaneraapropiada.

Unabonapràcticadeladescobertamatemàticasobrelaformageomètricadelsnombresens lapresentaNúriaCardet.Estractad’unaexperiènciafetaambalumnesdequartdeprimària. Duesqüestionscaracteritzenelseutreball:laintegraciódetotl’alumnatieldesenvolupament delescompetències.AquesttreballvaserexposatalesjornadesdeLleimat«Enriquiment competencial».

EnPepBujosaensmostral’úsdelGeoGebraperatreballarprocessosmatemàticscomara construir,conjecturar,comprovaridemostrar.Amésamés,tambéposademanifestcom l’einainformàticapermetdonarmésprotagonismeal’alumnatalaclassedematemàtiques, almateixtempsqueliprovocauntreballreflexiu.Hitrobareubonespropostesperaportara lesaulesdesecundària.

A«Matemàtiquesientornaeducacióinfantil»,laFàtimaDalmauil’ÀngelAlsinaexpliquen unaexperiènciad’aulaambunplantejamentteòricdeltreballcompetencialdematemàtiquesainfantil,concretamentunexempled’aprenentatgedematemàtiquesapartirdels coneixementintuïtiusqueelsnensadquireixenenlessevesexperiències.Aquesttreballés unresumdelquevaguanyarelpremiMariaAntòniaCanalsalainnovacióeneducació matemàticaenl’edicióde 2014,enlacategoriad’educacióinfantil.

CarlosGiménezenspresentaunaltreexempledel’úsdelGeoGebraalaclassedematemàtiques.Enaquestcasestractaderesoldreproblemesgeomètricsal’estildels sangakus japonesos.Aquesttreballtambéésunresumdelquevaguanyarunaccèssitenelpremid’innovaciómatemàticaMariaAntòniaCanalsal’edicióde 2014,enlacategoriad’ensenyament secundari.

JordiDeulofeuensrecordaqueel 2014s’hacelebratelcentenaridelnaixementdeMartin Gardner,motiupelqualarreudelmóns’hancelebratactescommemoratius.Acontinuació,i fidelaltítoldelasevasecció,ensproposaunabonacol lecciódeproblemesperpensaruna mica,demaneragradual:alcomençamentunsdeméssenzillsidesprésunsaltresquenoho sóntant.

L’AntonAubanell,alasevasecció«Construintmatemàtiques»,enspresentaunabonatasca enlaquall’experimentacióambmaterialsescomplementaambl’abstracció.Estractad’un problemaquePuigAdamjapresentavaa Didácticamatemáticaheurística,enelqualcombina l’aritmèticaamblageometriaapartirdel’experimentacióambtrianglesirombesis’amplia desprésal’estudidemosaics.

Al«RacódelMuseu»,enJosepReyienManelUdinadescriuenunsmòdulsdelesexposicions delMuseuquemostrenalgunesdelesclàssiquespropietatsdelnombred’orilasevarelació amblasuccessiódeFibonacci.

DesdelCesire-Creamatenspresentenlescampanyesquehandissenyatperafavorirels canvisalesaulesentrestemescomsónlageometria,l’estadísticailesinvestigacions.Amb bonaidealesanomenen«impulsem»,amblavoluntatd’animarelprofessorataportar-ho endavant.Lespropostesquefanvandesd’infantilfinsabatxillerat.Mireu-vos-ho,quesegur quehitrobareubonesidees.

Finalment,encoratgemtotselslectorsaexplicar,permitjàdel NouBiaix,lespropostes,experiènciesoideesqueconsiderind’interèsperalacomunitatd’ensenyantsdematemàtiques delnostrepaís.Esperemelsvostresarticles!

articles articles

Bótesibarrils

ArmengolGasull

DepartamentdeMatemàtiques,EdificiC, UniversitatAutònomadeBarcelona, 08193Bellaterra(Barcelona) gasull@mat.uab.cat

Resum Abstract

Enaquesttreballensinteressemperla validesadedistintesfórmulesusadesa lapràcticaperacalcularlacapacitatdeles bótesdeviodesidra.Hitrobareu,per exemple,lafórmuladeSimpsonpera calcularintegralsdefinides,unllibreescrit pelmateixKeplersobreeltemaiel mètodedelsmínimsquadrats,introduït perGaussiLegendreperatrobarlamillor solucióperasistemessobredeterminatsi incompatibles.

Inthispaperweconsiderthevalidityof severalpracticalformulasusedtocalculate thevolumeofwineorciderbarrels.Inour studywewillfind,forinstance,Simpson’s formulaforcalculatingdefiniteintegrals;a bookwrittenbyKepleronthesubject;and themethodofleastsquaresestablishedby GaussandLegendre,forcalculatingthebest solutionforoverdeterminedand incompatiblesystems.

Rellegintl’enciclopèdia1 amblaqualvaigestudiarquanerapetit,aixícomaltresenciclopèdies illibresanticsquehihaviapercasa(vegeuperexemple[3, 11]),vaigtrobarunparellde fórmulesquepermetiencalcularelvolumd’unabótadeviambseccionscirculars.Si anomenen D i d elsdiàmetresdelapartmésamplaidelesbasesdelabóta,respectivament, h lasevaalturai ℓ ladistànciaentreelforatperomplirlabótail’extremmésallunyatd’aquest forat(vegeulafigura 1),lesfórmuleseren:

1.Alsanyscinquantaiseixanta,comalgunsdevosaltressegurquerecordareu,amoltesescolesde Catalunyas’estudiavaambunllibre(enciclopèdia)queconteniatoteslesmatèriesiserviapermoltsd’anys.Defet, enalgunstemeshihaviafinsitotduesmidesdelletra,demaneraquequaneresméspetitnomésllegieslalletra mésgranienunasegonapassada,demésgran,hohaviesd’estudiartot.

BuscantperInternettambévaigveurequeenunapàginawebdedicadaalasidra([16])es donavalafórmulaalternativa

Peraunmatemàticésunproblemaforçasuggerenttrobarexplicacionssobrelavalidesade lestresfórmules.Ambunamicadereflexió,benaviathoms’adonaquelaformula V2 ha depressuposaralgunainformacióaddicional.Nopotserquenomésambunamida ℓ ja puguemsaberelvolumdelabóta.Detotesmaneres,aquestafórmulajafamoltdetemps ques’usaaaltresllocsdelmón,comperexempleaÀustria(consulteulasecció 2)oales Canàries(vegeu[7]ilessevesreferències,otambé[1]).Pertant,hadeser«bona»,almenys enalguncontext.Lafórmula V3 tambésemblapocnatural.

L’objectiuprincipald’aquesttreballseràdonarjustificacionsmatemàtiquesdelestres fórmules.Buscantenlaliteraturatrobemaltrestreballsquehantingutunamotivaciósimilar (vegeu,perexemple,[6, 10, 15]).Lafórmula V1 esbasaenelcàlculd’unvolumderevolució iaaproximar π perlafracció 22/ 7 Defet,enelcamíd’aquestafórmulaid’altresdeben semblants,enstrobaremKepler,queesvainteressarprecisamentperaquestproblema,cosa queelvamotivarperserelcontinuadord’Arquimedesenelcàlculdevolums,abansdela creaciódelcàlculintegral(vegeu[8]).Pelquesabem,lesexplicacionsquedonaremdeles altresduesfórmulessónoriginals.

Éscuriossaberque,segonseldiccionaridel’Institutd’EstudisCatalans,unbarrilésuna bótapetita.Mésconcretamentesdiuqueunabótaés«unrecipientdefustamésllargque ample,desecciótransversalaproximadamentcircular,majorenelcentrequeenelsextrems, lesbasesdelqualsónduespecesdefustailasuperfícielateralestàformadaperdogues encorbadesiacobladesmantingudesunidesambcèrcolsdefustaoferro,queserveixpera guardaritransportarviialtreslíquids,especialmentdecapacitatsuperioraquatrecargues». D’altrabanda,seguintlamateixafont,unacargadeviequivala 128porrons,ésadir,a 121.60 litres.Pertant,ladiferènciaentrebótaibarrilésd’uns500 litres.Enaquesttreballhemdecidit parlarnomésdebótes,peròtotselsresultatsqueesdonensóntambéaplicablesalsbarrils.

Figura1.Mesuresenunabótadevi.

1.Volumsderevolució:fórmulesexactaiaproximada ab y x y = f (x )

Figura2.Unvolumderevolució.

Donadaunafiguraderevolució,respecteal’eix OX iambperfil y = f (x ),comladelafigura 2, elseuvolumésdonatperlafórmula

Quanlaintegralde(f (x ))2 ésmoltcomplicadadecalcular,obélafuncióenqüestióno téprimitivaexpressableentermesdelesfuncionselementals,potserútilusarlafórmula d’integraciódeSimpsonperacalcularunaaproximacióde Vr . Aquestafórmulas’escriucom

on s ésunpuntdesconegutdel’interval(a,b)i g(IV ) denotaladerivadaquartade g.Sino tenimencompteeldarrerterme(anomenattermedel’error),obtenimunaaproximacióde laintegralbuscada.

Siapliquemaquestafórmulaaproximadaalcàlculdelaintegral(3)arribema

o,enaltresparaules,

on Ai , Am i As sónrespectivamentlesàreesdelesseccionsinferior,mitjanaisuperiord’un volumderevolució,ambaltura h. Aquestafórmulaapareixa[10,p. 24]ambelnomde fórmulauniversal.Elmotiud’aquestnomésquesis’aplicaperacalcularelvolumd’unprisma,

uncilindre,unapiràmide,uncon,unapiràmidetruncada,uncontruncat(totsrectes)ouna esfera,entotselscasosdónaelresultatexacte.Defet,peralesfiguresderevolucióanteriors, que(6)ensdonielvolumexacteésunaconseqüènciadel’expressiódel’erroralafórmulade Simpson(4).Observeuqueenaquestafórmulal’errorészerosil’apliquemaunpolinomi g degraumenorque4,jaque g(IV ) = 0. Pertantsifemgirarperfils y = f (x )demaneraque(f (x ))2 siguiunpolinomidegraumenoroigualque3,elresultatobtingutusant(6)seràexacte.

Aquestéselcasdelcilindre,enquèelgraude(f (x ))2 és 0,idelcon,elcontrucatil’esfera,tots ambgraude(f (x ))2 iguala 2.Així,perexemple,elvolumd’unaesferaderadi r serà

1.1.Aplicaciódelesbótesdevi.Unaexplicaciódelafórmula

V 1

Pertald’aplicarlesfórmules(3)i(5)posaremcoordenadesadientsacertspuntsdelabóta. Així,elspuntssuperiorsdelesduesbasesielpuntdemésalturaseran b

=( ± h/ 2,d/ 2)i c =(0,D/ 2), respectivament(vegeulafigura3).

Figura3.Coordenadesenunabóta.

Arateniml’opciód’aplicardirectamentlafórmulauniversal(6),obébuscarcorbessenzilles quetinguinunperfilsimilarald’unabótadeviiaplicarlafórmula(3).Enelprimercas, obtenim

Peralasegonaopciópodemconsiderardiversespossibilitats:

(a)Perfilformatperdossegments,elsqueuneixenelspunts b i c ielspunts c amb b+ L’equacióés: y = (D d )x/h + D/ 2 per h/ 2 ≤ x ≤ 0, (d D)x/h + D/ 2 per 0 ≤ x ≤ h/ 2, ienaquestcaslafiguraderevolucióeslauniódedosconstruncats.

(b)Perfilformatperuntrosd’el lipse.Lasevaequacióés: y = d 2 D2 h2 x 2 + D2 4 .

(c)Perfilformatperuntrosdeparàbola.Lasevaequaciócorresponentés: y = 2(d D) h2 x 2 + D 2 .

(d)Perfildonatperuntrosdelafunciócosinus.Enaquestcasl’equacióés: y = D 2 cos 2 arccos(d/D) h x .

Tambéespodenprendrealtresperfils.Perexemple,a[17]esconsideraelcasenquèelperfil ésuntrosdecircumferència.

Aplicantencadasituaciólafórmula(3),arribemadiferentsexpressionsperaobtenirelvolum delanostrabóta.Perexemple,enelcas(c)tenim:

= 2π (d D)2 40 + (d D)D

Fentunscàlculssimilars,enelsaltrestrescasosanteriorsobtenimlesfórmulessegüents:

(a) V5 = π 12 D2 + Dd + d 2 h.

(b) V6 = π 12 2D2 + d 2 h.

(c) V

(d) V8 =

D2 8 1 + d D √1 (d/D)2 arccos(d/D) h.

Defet,nocaldriahavercalculat V6 fentservir(3),jaquehauríempogutaplicardirectament lafórmuladeSimpson V4 ,perquèenaquestcas(f (x ))2 ésunpolinomidegrau 2.Ésclar quelafórmula V5 éslapitjordetotes,jaqueaproximalabótaperdosconstruncats,queclara-

menttenenunvolummenorqueelquebusquem.Amés,perexemple, V6 éssempremés granque V7 ,jaquepera D>d ,

Sisubstituïmenlesformulesqueensdonen V4 = V6 elnombre π perlasevaaproximació racional 22/ 7,degudaaArquimedes,obtenimque

iarribemenconseqüènciaaunajustificaciómatemàticadel’expressió V1 ,talcomdesitjàvem.

Volemremarcaraquíqueal’èpocadelesenciclopèdies,enquènoesdisposavaencara decalculadores,erahabitualtreballarenelscàlculsconcretsambaproximacionsde π com a3.14,3.1416oelmateix 22/ 7=3.1428...;d’aquívequealafórmula V1 esprescindeixi de π iesposidirectamentunaaproximaciósevaquedónallocaunaexpressióamb nombressenzills.Nopodemdeixardemencionaraquílafantàsticaaproximacióracional de π,355/ 113,jaconegudadesdelsegle V pelmatemàticxinèsTsuCh’ung-Chih.Defet, |π 355/ 113| < 3 × 10 7 . Aquestesaproximacionsracionalssónprecisamentdosdels convergentsdeldesenvolupamentde π enfracciócontínua:

(vegeu[4,p.68]).Acabaremaquestaseccióambalgunscomentarishistòricssobreles fórmules V4 = V6 i V5 iambmencionsaaltresfórmulessimilars.Lafórmula V5 vaserdonada perJohannesKepler(1571-1630).Comqueesbasaaaproximarlabótaperlauniódedos construncats,jaespotconsiderarconegudadesdel’èpocadelsegipcisielsbabilonis([15]). L’expressió V6 (ienconseqüèncialade V1 )ésdegudaalmatemàticanglèsWilliamOughtred (1574-1660),inventor,entred’altrescoses,delregledecàlcul.

Defet,lestresfórmules V5 , V6 i V7 admetenunformatcomú: Vi,j,k = π 4 iD2 + jDd + kd 2 i + j + k h, (8)

amb(i,j,k ),nombresnaturals.Ésadir,queentoteselvolumés πh/ 4vegadesunamitjana ponderadade D2 , Dd i d 2 .Aquestaestructuraésmoltraonable,jaqueenelcasparticular d’unabótacilíndrica(D = d = 2r ),on r éselradidelabase,lafórmulaanteriorenshade proporcionarsempreelvolumdelcilindre:

Lafórmula(8)ensdóna,perexemple,lasenzillafórmuladonadaa[6],queusalamitjanade D i d ,

lesfórmulesproposadesl’any 1692 perJohnNewton,astrònomaCambridge([15]),

lafórmuladonadaenunaordreMinisteridel’Interiorfrancèsdel’any2 1799,

olafórmulaproposadaperM.Dez,professoral’EscolaReialMilitarfrancesal’any 1773([5]), usadaperexempleenunreglamentdeduanesal’illadeCubal’any 1847:

Peraaquestadarrerafórmulaesproposavatambéreemplaçarelvalor5/ 8= 0.625per 2/ 3 ≈ 0.667silabótaeramoltbombada(precisamentlafórmulaanterior),oper 0.55,o 0.6en cascontrari([6]),donantllocalesfórmules V121, 198, 81 i V9, 12, 4 ,respectivament.Altresfórmules d’aquesttipus,aixícomunmanualsobrel’úsdereglesdecàlculperacalcularvolumsde bótesespottrobara[9].Ésfàcilveurequetoteslesfórmulesdelaforma V

tambédonenllocafórmulesdeltipus(8)amb(i,j,k )=(p2 , 2(q p)p, (q p)2 ).

L’expressióde V8 éstotalmentdiferentisemblaquenoméstéinterèsmatemàtic,vegeu[17].

2.A[17]ésparladePluviósdel’anyVII,sensecapmésexplicació.Defet,elsanysdelcalendarirevolucionari francèss’acostumavenaescriureambxifresromanes,iescomptavenapartirdel’inicidel’EraRepublicana,que començàeldia 22 desetembrede 1792.Així,perexemple,elnumeralromàVIIindicaelsetèany oany7 dela Repúblicafrancesa.Elsmesosteniennomsrelacionatsamblanatura.Així,elsmesosd’hivernerenNivós,Pluviósi Ventós.

2.LabodadeKepler

L’any 1613,Keplervadecidircomprarunesquantesbótesdeviperalescelebracionsdela sevasegonaboda.Quanvaveurelamaneracomelvenedormesuravalaquantitatdevi quecontenienlesbótesvaquedarastorat.L’homeusavalafórmula V2 = 0 625 ℓ3 donada alaintroducció.ImmediatamentKeplervacomençarapensarquinahaviadeserlaforma delabótaquelisortiamésacomptetriar,jaqueésevidentqueentrebótesamblamateixa distància ℓ elvolumrealnosempreéselmateix.Peraclarirbéelproblemavatractarelcas «ideal»debótescilíndriques D = d ambuna ℓ fixada.

Enaquestcas,ésclarqueelvolumésdonatper

onhemusatque d 2 +(h/ 2)2 = ℓ2 , iqueenaquestcas D = d (vegeulafigura3).Pertald’obtenir elmàximde V (h)perauna ℓ donada,resolem

iobtenim h = 2ℓ/ √3,oequivalentment ℓ = √3h/ 2 o d = h/ √2.Ésfàcilveurequeaquest valorde h ésunmàximabsolutquan 0 <h< 2 ℓ,queésquanelproblematésentit.Recordeu queenelseutempselcàlculdiferencialnoesconeixiai,pertant,vahaverderesoldrela qüestióambaltresmitjans.Lasevaaproximacióalproblemavasergeomètrica(vegeuel teorema V delasegonapartde[8]).

Alafigura5podemveureungravatiunafotografiaons’il.lustraelmètoded’aplicarla fórmula V2 peracalcularvolumsdebótes.Encastellà,aquestprocedimenttéelnomd’«aforo diagonal».Nohesabuttrobarelnomcatalàd’aquestmètode,peròpotserespodriaanomenar «cabudadiagonal».

Figura5.Mètodedecàlculdevolumsbasatenl’úsdelafórmula V 2 .

Pertant,hemvistquesiescompleixque h ≈ 2ℓ/ √3,aleshoreselmètodedonatperala fórmula V2 ,suposantquelafórmulaensdonirealmentelvolum,ésjust,enelsentitqueno hihauràbótesamblamateixa ℓ ambessencialmentmenyscapacitat.

Figura6.PortadaiunapàginadelllibredeKepler, Novastereometriadoliorumvinariorum.

Semblaqueperalesbótesd’Àustria,queésonescasava,síqueescompleixaproximadament aquestaproporció,iaixòvatranquil.litzarrelativamentKepler(consulteu[2,8]).Peròaquest fetnoexplicadecapmaneralavalidesadelafórmula V2 .Pertant,seguramentmotivatper lasevainsatisfacció,vaseguirbuscantfórmulesmillorsperacalcularelvolumd’unsòlidde revolució,iunparelld’anysméstardescrivíeltractat Novastereometriadoliorumvinariorum, [8].Aquestllibrehaestat,desprésdelacontribuciód’Arquimedes(287-212 aC),l’avançament mésseriósjuntamentambelsdeBonaventuraCavalieri(1598-1647),enelscàlculsd’àrees ivolumsfinsaldesenvolupamentdelcàlculdiferencialiintegralperpartdeGottfriedW. Leibnitz(1646-1716)iIsaacNewton(1642-1727).

Observeufinalmentquealadiscussiódelprimerparàgrafd’aquestasecció,basadaenl’estudi deKepler,nos’hanconsideratencapcasbótesnocilíndriques.Acontinuaciófaremunestudid’optimitzaciósimilarperadiversesdelesfórmulesquehemobtingutenlaseccióanterior. Aquestaqüestió,usantnoméslafórmula V5 ,estractajaa[13].

Percomençar,seràútilintroduirunnouparàmetre, ρ = D/d ≥ 1,queensmesuraelbombamentdelabóta,jaque ρ = 1 corresponalcascilíndric.Amés,observemquepelteorema dePitàgores,4ℓ2 =(D + d )2 + h2 =(ρ + 1)2 d 2 + h2 , onelcatetverticalés D/ 2 + d/ 2 (vegeula figura3).Pertant,

Aleshoreslesformules Vj per j =5, 6i7,estransformenen

Ara,siconsideremfixoselvalors ℓ i ρ ,tenim Vj = Vj (h)i,comenelcasdelcilindreenquè g(ρ ) ≡ 3/ 4,lacondiciód’extremés

Pertant,enelstrescasosobtenimquetambé ℓ = √3h/ 2.Ara,sisubstituïmaquestvalord’ℓ alestresfuncions,obtenimelsvalorsmàximssegüentsperalscorresponentsvolums

Finalment,siimposemquelafórmula V2 siguicertaperaaquestesbótesambcapacitat màxima(uncop ℓ i ρ hanestatfixades),arribemalestresequacions:

Aquestesequacionssónequivalentsaequacionsquadràtiquesdefàcilsolució.Perexemple, pera j =6tenim

ambsolucionsaproximades 1.0992... i 0.16690.... Defet,nomésensinteressalasoluciómés granque 1,ésadir, ρ6 ≈ 1 1.Demanerasimilarobtenim ρ5 ≈ 1 9 i ρ7 ≈ 1 1 Elfetquela formadelabótas’aconsegueixiforçantlafustaacorbar-seensfadecidirperescollirnomés

Figura7.Construcciódebótes.

lafórmula V7 ,obtingudausantelperfilparabòlic3 ,obélafórmula V6 , queésunadelesmés usadesiquerecordemqueprovédel’anomenadafórmulauniversal.Volemremarcaraquí quelaconstruccióefectivadebótesnoésgensfàcil.Alafigura7podemveureunpasdel procésdeconstruccióenunafactoriamoderna,aixícomunafotografiaantigadeboters treballantaTarragona.

Finsara,hemvistquetésentitaplicarlafórmula V2 peralesbótesenquè D/d ≈ 1.1.Ala taula 1 donemunsquantsexemplesdedadesdebótesibarrils,orelacionsentre D, d i h que hemrecollit,juntamentamblasevesrespectivesfonts.

Referència D d h cas [6] 18h/ 21 16h/ 21 h I

[17] 7.01 dm 6.06dm 8.05dm II

[14] 10.5pol. 9 pol. 12.25pol. III

Taula1.Diversesrelacionsentre D, d i h.

ObserveuqueenelscasosI,IIiIIItenimqueelsvalorsde D/d són 18 16 = 1.125, 701 606 ≈ 1.157i

respectivament;pertant,aprimeravistal’úsdelafórmulasemblaraonableperaaquests casos.Del’estudianteriors’obtenenlesproporcionscompletesperalesbótesquedonen volummàximperaunes ρ i ℓ fixades.Aquestessón:

(D,d,h)= ρ d,d, ρ + 1 √2 d o,equivalentment,(D,d,h)= √2 ρ ρ + 1 h, √2 ρ + 1 h,h , amb ρ ≈ 1.1. Pertant,peraaquestesbótess’hadecomplirtambé

Malauradament,aquestesdadesnos’ajustentanbé,jaqueaquestcopenelscasosI,IIiIII tenimqueelsvalorsde d/h són

respectivament.Ésadir,toteslesbótesdelataulasónunamicamésbaixesquelesbótes ambcapacitatmàxima.

Detotesmaneres,alasecciósegüentveuremqueperaunagranvarietatdemidesdebótes lafórmula V2 espotaplicarsensecometreerrorsgairegrans.

3.Igualquepassaambelsreglesflexiblesdedibuixtècnicenquèlaformaqueagafaelregleéslad’un «spline»,queestàformatpertrossosdepolinomiscúbics.Elpolinomicúbicquepassapelspunts b± i c delafigura3 és,defet,quadràtic.

3.Lesfórmules V 2 i V 3

Dedicaremaquestaseccióabuscarjustificacionsperalesfórmules V2 i V3 . Ésclarquees podenprendrevalors D, d i h demaneraquecapdelesduesdonillocaunaaproximació raonablealvolumrealdelabóta.Pertant,elquefaremseràconsiderarnomésdadesde bótesibarrilsreals.Enparticular,usaremelsvalorsintroduïtsalataula 1 delaseccióanterior. Comjahemvistenaquellasecció,uncopconeguts D,d i h,ésclarpelteoremadePitàgores que ℓ = 1 2 (D + d )2 + h2 , (9) (vegeudenoulafigura3).Pertant,podemusarqualsevoldelesfórmulesquehemdonata lasecció 1 peratrobarunaestimaciódelvolumdelabótacorresponent.

ElscasosIIiIIIcorresponenabótesconcretes,peròpensaremqueaquestsvalorsdeterminenlesproporcionsentrelesdades.Així,perexemple,enelcasIItindrem(D,d,h)= k (701, 606, 805), perauncert k> 0.Observeuquequalsevolfórmularaonableperacalcular volumshadecomplir

V (kD,kd,kh)= k 3 V (D,d,h)peratot k> 0 (10)

Defet,toteslesquesurtenenaquesttreballhocompleixen.

Així,aplicantalcasIlafórmula V6 ,tenim:

onhemusatque h =42 ℓ/ √1597, talcomesdedueixde(9).Demanerasimilar,aplicantla fórmula V7 ,obtenim:

Aquestresultatésforçasimilaral’anterior,iunamicamenor,comjasabíemaprioriper(7).

Fentelscàlculscorresponents,peralcasIIobtenim:

Demanerasimilar,peralcasIIIarribema

6 ≈ 0.633 ℓ3 i V7 ≈ 0.631 ℓ3 .

Pertant,hemtrobatunaprimeraexplicacióbasadaendadesrealsdelmisteriós 0.625que apareixalafórmulade V2 ,jaqueentotselscasoselvolums’hapogutexpressarcoma cℓ3 , perauna c moltproperaaaquestvalor.

3.1.Unajustificacióexperimentaldelafórmula V 2

Hihaunpuntdevistatotalmentexperimentalperintentarvalidarunafórmuladeltipus

= cℓ3 .

Considerem m bótes,peralesqualsmesuremelsvalors ℓj idelesqualssabemlesrespectives capacitats Vj , j = 1, 2,...,m.Aleshoress’hauriadecomplir:

Clarament,encaraquenoméssiguipelserrorsdemesura,elsistemaanterior,amb m equacionsiunasolaincògnita, c,seràincompatible,peròpodembuscarla«millor»solució. Defet,semblaraonableprendrecomavalorcandidatamillorsolucióunamitjanaapropiada delessolucionsdecadascunadeles m equacions.Tenimdoscandidatsclars,lamitjana aritmèticailageomètrica,ésadir:

L’aproximacióquehemfetésnaturalitècnicamentsenzilla;amés,nousaperaresl’anomenat mètodedelsmínimsquadratsperatrobarlamillorsoluciódesistemessobredeterminatsi incompatibles.Defet,aquestmètodevaserdesenvolupatperGauss(1777-1855)iLegendre (1752-1833)demaneraindependent(avuiendiaencaraespolemitzasobrequindelsdos matemàticsvaserelprimerafer-loservir),molttempsdesprésdel’apariciódelafórmula

V2 .Pertant,ésmésqueplausiblequeels«descobridors»d’aquestafórmulafessinunaanàlisi similaral’exposadaalsparàgrafsanteriorsperatrobarelvalor 0.625.

Detotesmaneres,aprofitaremaquílesideesdeGaussiLegendreilapotènciadelcàlcul diferencialperbuscarelvalormésraonablede c usantlesideesdelmètodedemínims quadrats.Lamaneraestàndarddebuscarelmillor c éslinealitzarprimerelproblemaibuscar despréselcorresponentvalorde c.Així,enllocdelesequacions(11),consideraremles equacionsequivalents

ln(Vj )= C +3ln(ℓj ), per j = 1, 2,...,m, (13)

on C =ln(c).Diremquelamilloraproximacióéselvalorde C quefamínimalasumadels errorsalquadratcomesosencadascunadeles m equacions(13).Mésconcretament,definim lafunció

E1 (C )= m j=1 C +3ln(ℓj ) ln(Vj ) 2 ,

ibusquemelseumínim.Aquestespotobtenirimposantque E1 (C )= 0. Elscàlculsdonen

E1 (C )= 2 m j=1 C +3ln(ℓj ) ln(Vj ) = 2 mC + m j=1 3ln(ℓj ) ln(Vj ) = 0,

ipertantelmínims’obtési C = C = 1 m m j=1 ln(Vj ) 3ln(ℓj ) .

Traslladantaquestresultatalavariable c,arribemadeterminarquelamillorsolucióés c = c = eC =exp 1 m m j=1 ln(Vj ) 3ln(ℓj ) = m m j=1 Vj ℓ3 j ,

ésadir,lamitjanageomètricaproposadaa(12).

D’altrabanda,peralcassenzill V = cℓ3 ,espotintentarbuscardirectamentl’aproximacióde mínimsquadrats,sensenecessitatdelinealitzarlesequacions(11).Així,desd’aquestpunt devista,elquevolemésminimitzarlafunció E2 (c)= m j=1 cℓ3 j Vj 2 .

Imposantaraque E2 (c)= 0,tenim: E2 (c)= 2 m j=1 cℓ3 j Vj ℓ3 j = 2 c m j=1 ℓ6 j m j=1 Vj ℓ3 j = 0.

Així,usantaquestavia,lamilloraproximaciópera c és:

Tenim,doncs,tresfórmulesraonablesperaobtenirel c queajustimillorunafórmuladel tipus V = cℓ3 ,uncopdisposemdelesdades V i ℓ pera m bótes.Aquestesfórmulessón:

Avuiendiaéscadacopméshabitualsubstituireltreballpesatdecamp queconsistiria aanarperdiversoscellersmesurantdadesdebótesdirectament perunasimulació.Així, prenentcomabaselesproporcionsd’unabótaidealdonadesa[6],ésadir, D = 18h/ 21 i d = 16h/ 21, elquefaremseràsuposar

on U(a,b)denotaunavariablealeatòriauniformeal’interval[a,b].Amés,agafaremlesdues variablesaleatòriesindependents.Enaltresparaules,éscomsisuposéssimquecadabótaque agafemtémesures D, d , h on h ésunvalorarbitrari, D = Kh i d = kh on 17/ 21 <K< 19/ 21, i 15/ 21 <k< 17/ 21, itotselsvalors K i k tenenlamateixaprobabilitat.Observeuquenoés restrictiusuposar h = 1,jaque,comhemdit,qualsevolfórmulaperacalcularvolumshade complir(10).

Volemremarcaraquíque,ambaquestnoupuntdevista,incloemtambélesbótesquetenen lesproporcionsdonadesa[10],quenohemconsideratalataula 1.Peraveure-ho,notem quea[10]esdiuqueunabótaesconstrueixusualmentdemaneraqueelradidelabase majorsuperaelradidelabasemenorenunacinquenapartd’ellmateix,ésadir, R = r + R/ 5. Entermesdediàmetrestenimque4 D =5 d ipertant D/d =5/ 4= 1.25.Precisamentpera lesvariables(14)queconsideremescompleixperlaproporciómàximaentre D i d és 19/ 15, ésadir

ipertant,elcasqueensocupaquedaràtambécobertenaquestestudi.

Alestaules 2 i3donemelsdiferentsvalors cj obtingutsquansimulem m bótes,peradiferents valorsde m,amblescondicionsesmentadesadaltiencalculemelscorresponentsvolums amblesfórmules V6 o V7 .

Taula2.Valors cj obtingutsusantlafórmula V 6 peracalcularelsvolums.

Taula3.Valors cj obtingutsusantlafórmula V 7 peracalcularelsvolums.

Alafigura 9 considerem m =500.Hipodemveure500 punts(ℓj , (V6 )j ),aixícomlacorba V = c1 ℓ3 ,ondenotempera(V6 )j elsvalorscalculatsamblafórmula V6 .

Figura9.Lacorba V = c1 ℓ3 i500punts(ℓj ,(V 6 )j )calculatsusant V 6 .

Comaconseqüènciad’aquestessimulacionspodemconcloureque c = 0.625ésunbon candidatperaproximarelvolumsiestempropdelabóta«ideal»,jaquequalsevoldeles nostressisfamíliesd’aproximacionsdónaunvalormoltsemblantaaquest.Defet,sembla que c hauriadeserunamicaméspetit,peròpotseresvatriar 0 625perquèésiguala5/ 8,que ésunafraccióambnumeradoridenominadormoltpetitsi,amés,ésmoltfàcild’operar-hi. Observeuquemultiplicarper5/ 8espotferdemaneramoltsenzilla,iquasidecap,jaque s’hademultiplicarprimerper 10 iferlameitat,delameitat,delameitat,delameitat,ésadir, 5/ 8= 10/ 24 .

Noteutambéquehemtriatvariablesaleatòriesuniformes,enllocdeferl’opciópotsermés usuald’agafarvariablesaleatòriesgaussianes,perquènoconsideremqueesconstrueixin lesbótesambl’objectiufinal(D,d,h)=(18 h/ 21, 16 h/ 21,h)iqueesprodueixinerrorsen aquestesdades.Elquepensemésquelesbótesesconstrueixenambaquestaideaalament, peròteninttambéencomptediferentsideesestètiques,costumslocals,ofinsitotlamida delesfustesadisposició,peròentotcassenseallunyar-segaired’unestàndardtradicional.

Enspotquedarencaraeldubtedesilafórmula V2 ésvàlidaperalesbótesques’allunyin mésdelaproporció(D,d,h)=(18/ 21, 16/ 21, 1).Peraaixòvegemquèpassasiconsiderem

peralsvalorsde D i d variablesaleatòriesuniformesindependentsqueprenguinvalorsmés allunyatsd’aquestsvalorsideals.Considerem,pera n ∈ N,

h = 1,D = Un =

Ambaquestesnotacionsenlessimulacionsanteriorshavíemconsiderat U1 i W1 .Alataula4 esmostrenelsvalors c1 obtingutsusant m = 1000 ilafórmula V6 peradiferents n.Observeu tambéquesi n> 1 esgenerentambébótesamb D<d .Delsresultatsd’aquestataula esdedueixque 0.625segueixsentelmillorcandidatperabótesmésallunyadesdeles proporcionsbase.Detotesmaneres,serelmillorcandidatnoésgarantiadeserunbonvalor peralcàlculdelsvolums,comveuremacontinuació.

Taula4.Valors c1 usantlafórmula V 7 per1000puntsiperadiferentsvariablesaleatòries Un i W n .

Ambaquestafinalitat,vegemaraquinerrorrelatiurepresental’úsde V2 enfrontdel’úsde V6 . Peraaixò,comencemdefinintelsquadrats

onviuenleslleisdelsvectorsaleatoris(Un ,Vn ).D’altrabanda,considereml’aplicacióde R2 en ellmateix,

Figura10.Conjunts F (Qn )per n =1i n =3icorba V =0.625 ℓ3 .

Observeuqueprecisament F (D,d )=(ℓ,V6 )peraunabótaambmides D,d i h = 1. Pertant, F (Qn )dónaleslongitudsielsvolumssegons V6 detoteslesbótesamb(D,d ) ∈Qn . Ala figura 10 podemveure F (Qn ),pera n = 1 i n =3, juntamentamblacorba V = 0.625 ℓ3 . A més,ésclarqueelsvalors(ℓk , (V6 )k )corresponentsalspunts(Dk ,dk ),quehemgeneratamb lesvariablesaleatòries Un i Wn ,acabenomplint,quan m creix,elsrectangles F (Qn ).Aixòes potapreciarperexemplecomparantlafigura 9 ambelgràficdel’esquerradelalafigura 10.

Apartirdelesfronteresdelsconjuntdelafigura 10,podemcalcularfàcilmentperacada ℓ quinéselvalormàximdel’errorrelatiuquanaproximem V6 per V2 , ésadir,de

Er(ℓ)= V6 (D,d,1) V2 (ℓ) V6 (D,d,1) quan ℓ = 1 2 (D + d )2 + 1.

Elsvalorsd’aquestserrorsrelatiuspelspuntsdelafronterade F (Q3 ),donatsalgràficdela dretadelafigura 10,sónelsqueesrepresentenalafigura 11.Pertant,l’errorrelatiumàxim peraaquestcasésd’un 14%.Sifemelmateixestudiperaaltresvalorsde n,obtenimel resultatsdelataula5.

Figura11.Errorsrelatiusmàximsenfuncióde ℓ quanaproximem V 6 per V 2 pelsvalors(D, d ) alafronterade Q3 .

Taula5.Errorsrelatiusmàximsquanaproximem V 6 per V 2 per(D, d ) ∈Qn .

Així,enresum,lafórmula V2 nomésdónavalorsraonables(errorrelatiumenordel 9%)quan lesbótescompleixenlesproporcions(D,d,h)=(Kh,kh,h)amb(K,k ) ∈Q2 ,ésadir,quan

iaixòéscertfinsitotsi D<d.

3.2.Lafórmula V 3

Lafórmula V3 obeeixaunesrestriccionssimilarsalafórmula V2 .Defet,silesduessóncertes, s’hauriadecomplirque V2 = V3 ,ipertant,que 0.625 ℓ3 = 0.82 Ddh.Usant(9)obtenimque aquestaigualtatésequivalenta

Calculantunamica,tenimquel’anteriorigualtatéscertasi

Vegemaraquantvalaquestquocientencadascundelscasosdelataula 1.Perexemple,per alcasIobtenim:

PeralscasosIIiIIIobtenimque V2 /V3 valaproximadament 1.008i 1.005,respectivament.En resum,peralesbótesamblesproporcions«adients»(peralesqualslafórmula V2 proporciona unabonaaproximaciódelvolum),lafórmula V3 tambéésvàlida.

Peracabar,noméscomentaremque,perexemple,alMidifrancèstambésesolutilitzarla fórmula

V9 =3.2 Rrh,

on R i r sónelsradisrespectiusdelesbasesilapartmésampladelabóta,ésdir, D = 2 R i d = 2 r .Ésclarquedelafórmula V3 tenim

= V9 , fetquejustificaaquestadarreramaneradecalcularvolums.

Defet,a[12]esdónaunaexplicacióheurísticade V9 ,apartirdelafórmula V5 ,amblaqual acabaremaquesttreball.

Expressant V5 entermesdelsradis R i r ,tenim:

Observeuquealapenúltimaexpressióhemeliminatelterme π R r 2 / 3,queperabótes nogairebombadeshadeserunnúmerobastantpetit.Pertant,sielquefemescompensar aquestapèrduaincrementantunamica π iposantalseulloc3.2, obtenim

5 = πRrh + π 3 R r 2 h ≈ 3.2 Rrh, comvolíemveure.

Agraïments

L’autorvolagrairalseucol.legaiamicGoriGuaspelsseuscomentaris,aixícomlasevaajuda enlapreparaciódelesfigures.

L’autortèelsuportdelsprojectesMINECOMTM2013-40998-PidelaGeneralitatdeCatalunya, projecte 2014SGR568.

Referències

[1]L.BalbuenaCastellano(2001).Elvinoylasmatemáticas, Vinalletras3.Accessibleawww. tacovin.com/dota/espanol/publicaciones.html

[2]R.Cardil(2014). Kepler:Elvolumendeunbarrildevino i Kepler:Lasproporcionesóptimas deunbarrildevino,awww.matematicasvisuales.com/html/historia/kepler/keplerbarril.html. VegeutambélaversióanglesapublicadaperlaMathematicalAssociationofAmerica: Kepler: TheVolumeofaWineBarrel,awww.maa.org/publications/periodicals/convergence/keplerthe-volume-of-a-wine-barrel

[3]J.DalmauCarles(1926). Leccionesdearitmética.Girona:CarlesDalmauPla.

[4]J.-P.Delahaye(1997). Lefascinantnombre π.PourlaScience,DiffusionParís:Belin.

[5]M.Dez(1773). Mémoiresurlathéoriedujaugeage,p.383-389 a«Mémoiresdemathématiqueetdephysique»,París.

[6]J.M.GonzálezRodríguez(1992).Tecnologíapopulartradicional:medicióndelacapacidad debarrilesytonelespormétodosempíricos. Suma, 11-12,p. 118-127.

[7]J.M.GonzálezRodríguez(2004). Lamatemáticaylasabiduríapopulardeloscanarios. DinsM.I.MarreroRodrígueziR.TrujilloGonzález(coord.), Sociedad,ciencia,tecnologíay matemáticas (p.67-80).SanCristóbaldeLaLaguna:UniversidaddeLaLaguna.

[8]J.Kepler(1615). Novastereometriadoliorumvinariorum.Accessiblepercortesiade«the PosnerMemorialCollectionoftheCarnegieMellonUniversityLibraries»aposner.library. cmu.edu/Posner/books/book.cgi?call=520_K38PN

[9]G.Martin(2014). ReglasdecáculoparalasbebidasalcohólicasutilizadasporlaAduanaen GranBretaña.Accessiblea:www.photocalcul.com/Calcul/Regles/Notices-regles/notices.html.

[10]Y.Perelman(2003). Geometríarecreativa.Moscou:EditorialMIR.Disponiblealaweb:www. librosmaravillosos.com

[11]J.PlaCargoliJ.M.PlaDalmau(1942). Enciclopediaautodidáctica.Girona:CarlesDalmau Pla.

[12]E.RouchéiCh.deComberousse(1898). Élémentsdegéometrie.París:Gauthier-Villars.

[13]B.-S.Shechter(2002). Kepler’swinebarrelprobleminadynamicgeometryenvironement. Proceedingsofthe 2ndInternationalConferenceontheTeachingofMathematics,at Hersonissos,CreteGreece.

[14]G.U.A.Vieth(1835). Courspopulairedessciencesmathématiques.Hesse.

[15]W.Wieslaw(2004). Exemplamensuraecapacitatiscuparum.Dins Mathematicsthroughout theages,vol. II.Praga(p. 23-40).

[16]Procesoyelaboracióntradicionaldelasidraasturiana,Accessiblea:http://www.sidravillaviciosa.es/4.html.[Consulta:desembrede 2014]

[17]Tonneau(formules).Wiquipèdia:fr.wikipedia.org/wiki/Tonneau_(formules).[Consulta: desembrede 2014]

Resoldrenoésaprendre.

Delaresolucióalacompetència

matemàticaidelavivenciacióa l’abstraccióilageneralització

matemàtica

JosepCallísiFranco

Mestre.ProfessordeDidàcticadelesMatemàtiques(UdG) CoordinadordelsgrupsdetreballdeRosaSensat d’innovaciómatemàticaainfantil,primàriaiEE josep.callis@udg.edu

Resum Abstract

Atravésdelatranscripciód’unessessions declasse,l’articleplantejalanecessitatde transformarelprocedimentde transferènciaeducativaenelquales tinguinencomptelagraduaciódeles diferentsfasesoetapesdidàctiquesque possibilitinl’abstraccióilageneralització matemàtica.Enaquestprocésesposauna atencióespecialenlesfasesdevivenciació imanipulacióienaquellaenquèla vivenciacióprenunaposicióclauen aquestcamídidàcticique,sovint, malauradamentnoestéencomptea causa,fonamentalment,d’unafaltade capacitacióenaquestatècnicaeducativa. Alhora,portaalareflexiósobrela necessitatdeplantejarsituacions problemàtiquesseqüencialspertal d’arribaraprocessosdeductiusoinductius quepermetinlageneralitzacióde fenòmensilleis,demaneraquel’objectiu essencialenl’activitatmatemàticanoés resoldre,sinóaprendre.

Usinganumberofclasstranscripts,this articlesetsouttheneedfortransformationof theeducationaltransferprocess,takinginto accountthegraduationofthevarious learningphasesthatenablemathematical abstractionandgeneralization.Special emphasisisplacedupontheexperientialand manipulativestages,andthekeyrolethat experientialismplaysinthislearningprocess, whichisunfortunatelynotalways recognizedduetoalackofteachertraining inthisarea.Italsoaimstoraiseawarenessof theneedtosetsequencesofproblems,in ordertostimulatethedeductiveand inductivereasoningprocessesthatallowfor thegeneralizationofmathematical phenomenaandlaws.Thus,theessential goalofmathematicalactivityisnottosolve problemsbuttolearn.

ElsresultatsdelesavaluacionsexternesefectuadestantdesdelaGeneralitatcomenàmbits internacionalsitambécomhodemostrenelsdiversosestudisefectuatsperanalitzarel graudefuncionalitatsocialdelesmatemàtiques(InformeCockcroft, 1982;COPIRELEM, 1982;NationalScienceBoard, 1983;RecommendationsforSchoolMatehaticsofthe 1980s (NCTM);informesICMI;Eurydice, 2011;provesPISA...)evidencienlapocaincidènciadels aprenentatgesmatemàticsperdonarrespostaalessituacionsdevidaialesdemandes socialsdelmónactual.Aquestadesconnexióentreelcurrículumimpartitilesnecessitatsdel currículumaprèsqueesmanifestatantaprimàriacomasecundària,aprenentatgessovint descontextualitzatsdelarealitatidelasevafuncionalitatpràctica,és,entred’altres,unade lescausesfonamentalsdelsbaixosresultatsavaluatiusidelabaixacomprensiómatemàtica entrel’alumnat.

Perintentardonarrespostaaaquestrepteitransformarelsaprenentatgesmemorísticsen competencials,alesaulesdelesnostresescolestrobemexperiènciesdiversesqueintenten repararenelquepodenaquestsdèficitsestructuralsimetodològicsintroduintiaplicant metodologiesdiversescentradesenlaresoluciódeproblemes,l’aprenentatgecooperatiu, l’aprenentatgeservei,elmètodedeprojectesid’altres,enquèlarecercailainvestigació compartidaambinterrelacionsinterdisciplinàriesfonamentenlesbasesdeltreball.

Resultaobvique,totilagrandiversitatexistentenrelacióambelconceptedecompetència, existeixunacordtàcitenladirecciódeconsiderar-la«unaaccióconscientefectuadaamb l’objectiudesolucionarunaproblemàticacontextualitzada,aplicantiposantenjocels condicionantsnecessarisiadequats(coneixements,procediments,actituds,estratègies, habilitats...)aaquellcontext,ambcapacitatperaanalitzarcríticamentelprocésielresultat ifer-hi,sical,lesmodificacionspertinents.Undominicompetencialrepresenta,doncs,un complexprocésintegradord’estructuresmentalsihabilitatsnomentals»(CallísiCallís, 2007, p. 9).És,pertant,unaestructuracomplexaque«hadepermetresaberanalitzarigestionar (identificar,interpretar,transcriure,transfeririavaluar)elscontextsisituacionsrealsiels processosmentalsqueesnecessitenis’apliquen[...].Totacompetència,enelfons,ésalhora multicompetencial,jaquecadacompetèncianecessitasubcompetènciesquepossibilitin organitzarigestionartantlainformaciócomelpropicontrolpersonalielssabersconceptuals iprocedimentalsambcapacitatpersaberresoldresituacionsiproblemestotadequant-losa l’especificitatialscanvisdecadacontextifer-hosotaunavisiócríticaquecercalaqualitat ilainnovació»(Callís, 2006).Resultaevident,pertant,quel’avaluaciód’unacompetència difícilmentespotferperunadeterminadaresoluciód’unmomentod’unaactivitatpuntual, jaquelacompetènciaésunprocésevolutiui,pertant,l’avaluacióenundeterminatmoment noméspossibilitadetectarl’estadievolutiud’aquestaadquisicióenaquellmomentconcret, sensequeaixòsignifiquielpledominicompetencial.Elscontrolsavaluatiusnoméssón factiblesapartirdelsproductesoaccionsqueesgenerenenaplicar-losencontextsdominats i,especialment,enelsnoconeguts.

Desdelmarcdelaresoluciódeproblemes(Polya, 1957;Mason,BurtoniStancey, 1989; Schoenfeld, 1981 i 1992;Lakatos, 1977;Gascon, 1992;Vila, 1998),ladiferènciaentreactivitats d’aplicacióiproblemasónconcepcionsepistemològicamentdeltotdiferenciades.Mentre queenlesactivitatsd’aplicacióesposal’alumnatsotaelsupòsitquepotresoldrel’activitat proposada,jaqueespressuposaqueconeixoquehadeconèixerelscontingutsimplicats perquèhanestatpresentatsitreballatsal’aula,lessituacionsproblemàtiques,alcontrari,

plantegenpropostesenquèl’alumnat,d’entrada,notéelsconeixementsielsdominispera lasevaresolució.

Enelprimercas,lapropostaté,essencialment,l’objectiud’aplicaripracticaraquellscontinguts determinatspelcurrículumqueesvalorencomabàsicsique,consegüentment,caldominar persuperarpositivamentl’avaluació,dominiques’adquireixapartirdeprocedimentsméso menysconductistesfonamentatsenlarepetició,atravésdelaquals’assoleixenis’interioritzen aquellsconeixementsprocedimentalsoconceptualsqueesconsideraquehandesaberi entendre;i,enlessituacionsproblemàtiques,secercaquemitjançantelprocésresolutori delproblemasiguil’alumnatmateixquiconstrueixielseupropiconeixementiadquireixi estratègiesresolutòriessignificativesicompetencials.

Enlesactivitatsd’aplicacióqueespresentenoesfanferal’alumnatenfinalitzaroalllargd’un determinatcontinguttemàtic,comsolenserlagranmajoriad’activitatsqueesproposen enelsllibresdetext,elqueespreténésquel’alumnatresolguicorrectamentoquetrobi unresultat,normalmentaritmètic,aunsexercicis,generalmentsemblantselsunsambles altrespertald’agafarunaalgorismitzaciódelprocedimentresolutori.Aquestprocediment detreballpersimateixnosignificanicomporta,d’entrada,lacomprensióol’aprenentatge delcontingutconceptualoprocedimentalqueportaimplícitlaindicadaactivitat.

Resultaobvi,pertant,que,alcontrari,enelprocésd’aprenentatgedelessituacionsproblemàtiquescaltenirencomptetantelprocedimentdetreballol’aplicaciód’unametodologiaque tinguienconsideraciólesdiferentsfasesevolutivesnecessàriesperconquerirlacapacitatde raonamentiabstracciómatemàticacom,alhora,elprocésperaconseguirquel’aprenentatge siguicompetencialinosimplementresolutori.

Exemplificaciópràctica

Analitzaremaquestadobleincidènciaatravésdelatranscripciódetalladadelaseqüència didàcticafilmadaicentradaenunaactivitatpràcticapresentadacomunjocplantejatcom uncampionatd’encistellarunobjecte.Lapropostaestreballadesd’unaperspectivade metodologiaactivaid’aprenentatgebasatenproblemes(ABS)iportadaatermeamb alumnatdemagisteriitambéambgrupsdemestresdeprimàriaenactiu.

Periniciarl’activitatielprocésdidàctic,esdemanalaparticipaciódetrespersonesdelesquals unaaguantaràl’objectequefaràdecistella(paperera,cubell,capsadecartró...)iduesseran elsjugadorsquecompetiraniquehaurand’encistellarunobjecte(pilota,guix,retolador, esborrador...).L’activitatresultamésefectivasiesfaenunespaiampliquetinguipossibilitats demobilitat(patí,gimnàs...),sibéenaquestcasésfetaal’aula.Sesituaràelsdosjugadors (llançadors)enunsdeterminatspuntsdel’aulaodelpatidelsqualsnoespodenmourei esdisposaràunacordaqueelsuneixi.Totseguits’indicaràqueelquiportalacistellahade situar-seenellloconvulgui,peròdemaneraqueaquestaposiciósiguiacceptadapelsdos competidorstenintencomptequeelpuntescollitnopotbeneficiarcapdelsdosjugadors,o siguiquecadascúvegiqueaquellaposiciónobeneficiaeljugadorcontrariperòtampocaell. Enelcasquealgundelsjugadorsnoestiguid’acordambelpuntons’hasituatelcistellador, caldràqueenjustifiquielmotiu(noméssónvàlidesraonsdediferènciadedistàncies),isité raó,elcistelladorhademodificarlaposicióperarribaral’acordambelsdosllançadors.

Foto1.Posicióentredosjugadors.

Uncopexplicadeslesnormatives,s’aniràdesenvolupantunprocésdialògicentremestrei alumnatientrel’alumnatmateixqueportialareflexió,l’anàlisiilarecercapertinentsia lesconclusionsfinals.Elprocésdetreballperanarresolentelsinterrogantsqueesvagin generant,lesconjecturesileshipòtesisquesorgeixin,esfaatravésd’unaevolucióenla tipologiadetreballquevadeltreballpersonalaldecontrastperparelles,contrastentredues otresparellesidebaticonclusionsgeneralsperretornarauntreballdesíntesipersonal.

Lessiglesutilitzadesperadescriureelprocésieldiàlegestablertqueesdetallaacontinuació són:M(mestre),C(portadordelacistellaocistellador),AA(algunalumneoalumna)iAAs (conclusionsdelaparticipaciócol·lectivadel’alumnat).

M(dirigint-sealaclasse):Abansd’iniciarelcampionat,ésimportantquealllargde l’activitatobserveuipareumoltaatencióenquèéselquemiraicomhofalapersona quetélacistellapersituar-se.Comencem!

M(desprésqueelcistelladors’hasituatenunindretquetél’acorddelsdosjugadors): Heuvistcomhohafetpertrobarelllocons’hasituat?

AAs:Anavaprovantperveuresitrobavaelpuntexacte.Miravacadaundelsqui juguenisen’anavaacostantoallunyantperveuresitrobavaelpuntquecreiaqueera equidistantperatotsdos.

AA:Hofeiaperassaigierror.

M(dirigint-sealcistellador):Hofeiesaixícomdiuen?

C:Sí.Anavaprovantperveuresimésomenysemsemblavaqueeraalamateixa distànciadecadascun.

M:Comhopodríemferpersabersis’hasituatcorrectament?

AA:Mesurant-hoambpasses.

M:Creieuqueaquestprocedimentseràseguriexacte?

AAs:No.Espodenferpassesmésllarguesoméscurtessenseadonar-se’n.

M:Quèpodríemfer?

AA:Fer-hoambpeus.

AAs:Podríemagafaralgunacosacomunacintamètrica,unacorda,elpaldel’escombra, llibres...imesurar-ho.

M:Iara,delquetenimamàaquíalaclasse(prèviaments’haurandeixatrecursos diversosquepuguinestaralavista:corda,llistons...),quèéselqueenspodriaanar millor?

AA:Unacorda.

M:Doncs,comprovem-ho.Comhofaràs?

AA:Faréqueelcistelladoragafiunextremdelacordaijoperl’altrabanda,tensantla corda,laposaréjustonhihaunjugador;llavors,mantenint-latensada,emmouréper arribaralsegonjugadoriveurésihihalamateixadistància.

M(desprésdelescomprovacionspertinentsiconstatadalaigualtatdeposiciódel cistelladorrespectealsaltresdosjugadors):Aixòeraunproblema?

AAs(enalgunscasosesmanifestendubtesclarsdavantlapregunta):Sí.

M:Perquè?

AAs:Perquèestractaderesoldreunasituació.

M:Aixídoncs,siésunproblema,l’hemresolt?

AAs:Sí,perquèhemsolucionatihemdonatrespostaalqueesdemanava.

M:Defet,lapreguntamésimportantnoéssil’hemresolt,sinó:hemaprès?

AAs:Sí.

M:Iquèhemaprès?

AAs:Doncs...hemaprèsautilitzardiferentsrecursospermesurarunadistància.Afer estimaciódelongitud...

M:Segurquehemaprès?Comprovem-ho.

Ara,elmestresituaelsdosjugadorsenunsaltrespuntsdiferentsdelsinicialsidemanaal cistelladorque,comabans,sesituïenunpuntambelqualelsdosjugadorsestiguind’acord, icontinuademanantques’observicomhofapertrobarlasituacióiquèéselquemira. Desprésques’hagitrobatelpunticomprovadalaigualtatdedistàncies,esdemanaque expliquinquèhafetelcistelladorpertrobarelpunt.

AAs:Hohafetcomabans,perassaigierror.

Totseguitesposamésdificultatalproblemaindicantqueaquellpunttrobatcomasolució noespotutilitzarjustificantqualsevolmotiu,iaixísesegueixambtresoquatrecasosmés fentque,entrobarelpunt,cadavegadaesvagimarcantaquellpuntodeixant-hiunobjecte cadacopesvademanantquinhaestatelprocedimentresolutori.

M:Segonsdieu,encadacashohemfetsempreigual,perassaigierror.Pertant,sibé cadavegadahemresoltelqueesdemanava,laresolucióadoptadaoelprocediment utilitzatpermetensolucionaraltrescasososituacionsdiferentsd’unamaneraexactai precisa?

AAs:No.Cadacasésdiferenticadacops’handefercomprovacionsiestimacions diferents.

M:Pertant,resolíemelproblema,però,apreníem?Éselmateixresoldrequeaprendre?

AAs:No,perquèsolucionemuncasihofempertempteigisemprehofemigual,iel quefeméscomcomençarsempredezero.

M:Veieualgunacosacuriosaenmirarelspuntsdelessolucionsquehemanattrobant encadacas?

AAs:Semblaqueestanenlíniarecta.

M:Comhopodemsaber?

AAs:Posantunacordaquepassiperaquestspunts.

M(desprésdesituarlacorda):Araquesíqueveiemqueaquestspuntsestanenlínia recta,podríeuindicaralgunescuriositatsopropietatsquehiveieu?

AAs:Passapelcentredelalíniaqueuneixelsdosjugadors.

AAs:Cadapuntésalamateixadistànciadelsjugadors.

AAs:Tallaperpendicularmentlalíniaqueuneixelsdosjugadors.

Foto2.Disposiciómediatriu.

M:Quèvoldirperpendicularmenticomhopodemsaber,queésperpendicular?

AAs:Quansiguienanglerecte.Podemposar,perexemple,unllibre,ounacarpeta, demaneraqueuncostatestiguisobrelalíniadelsjugadorsiveuresil’altrecostat coincideixamblarectaqueuneixelspuntsdelessolucionsdecadacas.

M:Aixídoncs,podríeuresumirtotaixòqueacabeudedir?

AAs:Larectapassapelcentredeformaperpendicularielspuntsestanalamateixa distànciadelsdosextrems.

M:Enmatemàtiquesexisteixunaparaulaquedefineixtotaixòi,utilitzant-la,janocal descriureaquestespropietatsqueheudescobert.Laparaulaés«mediatriu».Percert, hemresoltelproblema?

AAs:Sí.

M:Hemaprès?

AAs:Sí.

M:Quèhemaprès?

AAs:Quelasolucióéslamediatriuinounúnicpunt.

M:Pertant?

AAs:Queelproblematéinfinitessolucions.

M:Sihihadospunts,sempreespodràtrobarunpuntqueensiguiequidistant?

AAs:Sí.Sempre,perquèsemprehipodremtraçarlamediatriu.

M:Semblaquehemaprèsforçacoses,peròdeveritathemaprès?Comprovem-ho.

Enaquestaocasióesplantejalasituacióproblemàticaapartirdelfetquearasóntresels jugadorsinodos.S’uneixenlessevesposicionsambunacordaposadaaterrademaneraque esformauntriangle.Desprésdedistribuir-los,demanemalcistelladorquesesituïalamateixa distànciadelstresi,uncoptrobadalaposicióaproximada,denouresoltapertempteig,es continuaambelmateixprocedimentd’interpel lacióperferreflexionariconstatarelresultat.

M:Coms’hatrobatelpunticomhofarempersaberquesónalamateixadistància?

AAs:Comabans.Hohafetpertempteigoperassaigierror,abasedeprovar.Iper comprovar-ho,tambéhofaremcomabans,osigui,amblacordatensadadesdellloc onestrobaelcistellador,lafaremarribaraunaposicióidesprés,mantenint-lasempre tensada,veuremsicoincideixamblaposiciódelsaltresjugadors.

M:Agafemunpalounguixiellliguemal’extremdelacordaenladistànciadel jugadorprimeri,aixítensada,dibuixemelrecorregut.Quèobtenim?

AA:Unacircumferència.

M:Pertant,onéselcistellador?

AA:Alcentredelacircumferència.

M:Iquinapropietattéaquestpunt?

AAs:Quepassapelstrespuntsonhihaelsjugadors.

M:Doncs,enmatemàtiques,tambéhihaunnomperaaixò:circumcentre.

Desprésderepetir-hoendiversoscasosenquèescontinuatreballantambelprocediment detempteigienquèesconstata,encadacas,queelpuntésuncentredecircumferència,es portaalaconsideraciódeveureelstrespuntscomatrianglesquetenenuncircumcentre.

M:Hemresoltelproblema?

AAs:Sí.

M:Hemaprès?

AAs:Sí.Sabemquèésuncircumcentreiquetotselstrianglespodentenir-neun, circumcentrequeavegadesésal’interioriavegadesal’exterior.

M:Abansm’heuditquehavíeuaprèselqueeraunamediatriu,iaraelqueésun circumcentre;peròencadacascontinueufentsempreelmateix.Saberquèésla mediatriuoelcircumcentreenshaajudatasolucionarelproblema?

AAs:No.

M:Aixídoncs,aprendreconceptesésaprendre?

AAs:Sí,perònomésvoldiraprendreconceptes;noésaprendreaaprendre,osigui,que empermetiresoldresituacionsnovesrealsosolucionaraltrescoses,jaqueseguim cadavegadacomalprincipi,sensesaberquèfer.

M:Aveure,araplantejaremunnoucasiusajudaréunamica(secercaunanovaposició detrespersones).

M(alcistellador):Imagina’tque,encaraquesóntres,nomésenjuguendues,lesque vulguis.Quinaéslasolució?

C:Lamediatriu.

M:Doncs,araambunacorda,situa-laicomprovaquecompleixilestrespropietats quehavíeuditquetenialamediatriu.Lesrecordeu?

Foto3.Posiciótresjugadors.Circumcentre.

M(desprésderecordarlespropietatsdelamediatriuisituarunacordacomamediatriu entredosdelsjugadors):Ara,imagina’tquejuguenduesaltrespersones.Quinaésla sevasolució?

C:Igualqueabans,lasevamediatriu.

M:Construeix-laiobservemquèpassa.

AA:Estallenenunpunt.

M:Iquèésaquestpunt?

AAs:Elcircumcentre.

M:Perquè?

AAs:Perquèésequidistantdelstresjugadors,jaqueéssobrelaprimeramediatriui aixòvoldirquel’1 iel 2 estrobenalamateixadistància,icomquetambééssobrela segonamediatriuvoldirquetambéestrobaalamateixadistànciadel3.

M:Aixídoncs,entrespuntssempreseràpossiblesituarunpunt,uncircumcentre,que equidistidetotstres?

AAs(desprésdereflexionar):No,noseràpossiblesielstrespuntsestanalineats,jaque llavorslesmediatriusseranparal·lelesentreelles.Enqualsevoltriangle,sí.

M:Aracontinuarem,ifixeu-vosbéquèfaràicomhofaràlapersonaqueagafilacistella, ésadir,sihofacomsempre,perassaigierrorimirantsempreelsjugadors.(Enaquest momentesposaunanovasituacióapartirdetrespersonesiesresolelproblema.)

AAs:Arahacanviatdeprocediment.Abansdesituar-se,elquemiravaerenelscentres delsespaisqueseparencadajugadoriambl’ajudadelamàodelbraçtraçava lamediatriuimaginàriadecadaparelladejugadorsisesituavaenunpuntsense demanaralsjugadorssihiestavenonod’acord.

M:Just,arahemaprès.Iquèenshafetaprendre?

AAs:Lamaneradefer-ho,osigui,l’aplicaciód’unprocediment.

Acontinuació,canviemelprocedimentdetreball.Sifinsaquíelproblemarequeiadirectament sobreelpropialumnatieraunasituaciódevida(vivencial),arase’lsproporcionamaterial (suros,xinxetes,gomeselàstiquesifilsdedoscolors,unperunirelspuntsiunaltrede diferentperconstruirlesmediatrius)pertalque,manipulant-lo,practiquinsituacionsenquè calguiposarlestresxinxetesonvulguinitrobinlaposiciódelcircumcentre.Lamanipulació, pertant,enshaobertelsullsperveure-himésenllàdelproblemaespecíficienspermet aplicariconsolidarlapràcticadelsprocedimentsresolutorisalhoraquedesvetllamultitud d’interrogantsqueestimularanlarecercailainvestigacióposteriors.Enaquestmoment

Foto4.Manipulantsobresuro.

s’entraràenunafasedenoucanvid’enfocamentdidàcticis’iniciaràeltreballsimbòlicen quèlarealitatviscudaomanipuladaseràrepresentadaosubstituïdaperparaules,dibuixoso esquemes,obéperllenguatgematemàtic.

M:Enquinscasoselstrianglestindranelcircumcentreenposicióinteriorienquins exterior?Dequinamanerapodemtreballarmésràpidpertrobarlasolució?

A.A:Fent-hodirectamentapartirdedibuixos.

AAs:Elstrianglesacutanglestenensempreelcircumcentreinterior,elsobtusanglesel tenenexteriori,enelcasdelsrectangles,sempreinteriorienalguncassobrelameitat delahipotenusa.Fer-hosobrelabasedelaclassificaciódecostatsnotésentit,jaque, perexemple,elsescalenspodenserdetotstrestipussegonsl’angle,ielsisòsceles podenser,també,detotstrestipus.

AAs:Enelcasdelstrianglesrectangles,elcircumcentresesituaràsobrelameitatdela hipotenusaquansiguiisòsceles.

M:Ienaquestcas,quinespropietatsocuriositatsespodenconstatar?

AAs:Quelamediatriusobrelahipotenusapassapelvèrtexdel’anglerectei,pertant, eldivideixendosanglesde45graus...Que,enconseqüència,elvèrtexonhihal’angle recteésalamateixadistànciaquedesdelcircumcentrealsaltresdosvèrtexs...Quela distànciadesdelcentredelahipotenusafinsal’anglerecteésigualquelameitatde lahipotenusa...Queesformendostrianglesrectanglestambéisòsceles...

M:Bé,araquejadominemelsprocedimentsresolutoris,investigaremsipodemtrobar elcircumcentreenunasituaciódequatrepunts,cosaquepodremfertreballant sobrepaperperanarmésràpids,jaquecaldràresoldrecasosdiferentsposantels quatrepuntsenformesdiverses.(Esfaeltreballdemaneraindividualidespréses revisaoescontrastaperpetitsgrups.)Recordemlesdiferentstipologiesovarietats dequadrilàters?(S’obreundebatenquèesrecordeniesvisualitzenelsdiferents quadrilàterscercantformesdel’entorn,retallant-lesodibuixant-les,projectantombres apartird’unquadratounrectangle,cercantpuntsoreferentsal’aulapertaldecercar-hi ovisualitzar-hialgunquadrilàterifer-neunafotografia.Totseguitestreballapergrups lasevaclassificacióaportantelscriterisclassificatorisqueesconsiderenadequats:tenir costatsigualsono,teniranglesigualsono,tenircostatsparal lelsono...isintetitzant, alfinal,elsseuscriterisenunataulaclassificatòria.)

M:Enelsquadrilàtersqueheufet,heutrobatsempreelcircumcentre?

Eldebatgenerat,acausadelsresultatsdiferentsobtinguts,portaaplantejar-seinterrogantsi aferconjecturesdiverses,jaquealgunsgrupsmanifestenquenohihacircumcentreid’altres quesíquehantrobatcasosambcircumcentre.

AAs:Noméselsquadrats,elsrectangles,elstrapezisisòsceles,ialgunstipusde trapezoidespodenteniruncircumcentre.Enlamajoriadecasosdequadrilàters irregularsresultaimpossible.

M:Podríemtrobaralgunprocedimentperinvestigarelsquadrilàtersquepodentenir uncircumcentre?

AAs:Éslògicquesitenencircumcentre,lacircumferènciahadepassarpelsseus vèrtexs;pertant,podemferelprocésalainversa,osigui,tenimunacircumferènciai miremquinsquadrilàtershipodemconstruirdemaneraqueelsseusvèrtexssempre estiguindinslacircumferència.

Foto5.Treballindividual.

Foto6.Treballpergrups.

AAs:Enresultenelsmateixosquehavíemditqueteniencircumcentre.Nopodem fer-hicaprombe,nicapromboide,nicaptrapezirectangle;sí,encanvi,unquadrat, unrectangle,untrapeziisòscelesiuntrapezoide.Elquesemblaobviésquetotsels polígonsregularspodranteniruncircumcentre.

M:Aixídoncs,dequèdependràl’existènciadelcircumcentre?Delsangles,delscostats, d’algunaaltracosa?I,enaquestscasosquetenencircumcentre,onestroba:dinsde lafigura,afora...?

AAs:Tenintencomptequeelsregularstenensemprecircumcentreiquetenencostats ianglesiguals,talvegadaelsdosfactorshiinflueixend’unamaneraconjunta.

AAs:Laigualtatdecostatscomaclauexplicativadetenircircumcentreésevidentque noésvàlida,jaqueelrombeelstéigualsinotécircumcentreielrectangle,queelsté diferents,síqueenté.Tampocnohoindicaelfetdetenirelsanglesiguals,perquèel trapeziisòscelesnoelstéigualsitécircumcentreialgunstrapezoidesharesultatque tambéenpodentenir.

AAs:Elcircumcentreenelquadratielrectangle,sempreésinterioricentrat;encanvi enelstrapezisisòscelesienelstrapezoides,avegadesquedaadintreiavegadesa fora.Anosaltres,eneltrapeziisòscelesensquedaadintre,iend’altresgrupselsqueda afora;enalguns,sobrelabasegran...

M:Pertant,podeuanalitzaricercarquinessónlescondicionsdeltrapeziisòscelesque generenaquestestrespossibilitats.

AAs:Seguramentdeuvenirdeterminatpersiladistànciaentrelesbasesoalturaés menor,igualosuperiorquelameitatdelabasepetita.

M:Podeuformularunahipòtesi?

AAs:Entottrapeziisòsceles,silasevaalturaésinferior,igualosuperioralameitat delalongituddelasevabasemenor,elcircumcentreseràexterior,sobrelabase,o exterioralapròpiafigura.

M:Comproveusiaquestahipòtesiescompleixisilapodemdonarpervàlida.Com sempre,treballpersonalprimer;totseguit,compartiu-hoambalguncompanyo companya,idesprés,contrasteu-hoambaltresgrups.

AAs(desprésdelstreballspersonalsidegrups):Certament,hihapartderaó,jaquesí quesemblaqueenelsd’alturamenorquelameitatdelabasemenorelcircumcentre elveiemaforaienelsdemésalturaésinterior,peròenelsd’igualtattambéenssurten aforatotiquehihagrupsenquèsíquecoincideixalabase.

M:Enconseqüència,creieuquedeudependred’algunaaltracosa...

AAs:Ésevidentquelamediatriuensfaanglesde 90◦ sobreelscostats;pertant,si lamediatriuarribaalcentredelcostatdelabasemajorambunangle,perexemple,

Foto7.Fulldetrapezis.

de45◦ jaqueentreaquestamediatriu,mitjabasegranimigcostatinclinatfanun trianglei,pertant,lasumadelsseusangleshadeserde 180◦ ,llavorsl’angleentre laintersecciódelcostatinclinatilabasemajorhadetenirtambé45◦ .Enaquestcas, segurquevaalcentredelabasegran.Llavors,segurament,lescondicionsdel’altura idelabasepetitadependrandelamesuradelabasegranidel’angleentreelcostat delabasegranielcostatinclinat.

M:Pertant,aixònoporpassattambéquanl’alturasiguimésgranquemitjabase petita?Ipodriaserpossiblequanl’alturasiguimenorquemitjabase?Penseu-hi, investigueu-hoienparlemenlaproperasessió.

Apartird’aquí,novesaccionsdetreballmanipulatiuodetreballsimbòlicpermetrandonar respostaalsinterrogantsilesconjecturesplantejades,fentpossibleaprofundir-hiicrear coneixementespecíficsobreaquestcontingutmatemàtic.

Aquestdominiconceptualiprocedimentalaconseguitiambcreaciódeconeixement personalpermetrà,finalment,donarrespostaasituacionsnovesentroncadesamblarealitat iaixíresoldresituacionscomara:

• Situarunquadredemaneraquerebilamateixaintensitatdellumrespecteatrespunts dellumofocus.

• Ubicaralpatiundeterminatobjecte(paperera,font...)pertalquesiguialamateixa distànciadelaportadesortidadeP3,P4iP5.

• Donatunplànolcomarcal,situaroncaldriainstal larunabocadorounaltreserveipúblic quesiguialamateixadistànciadetrespoblacions.

• Plantejariresoldresituacionsqueespuguingenerarenlavidarealenquècalguiubicar algunpuntquehagideseralamateixadistànciad’altres.

• Inventaroreconèixersituacionsdelavidarealqueespuguinresoldresobrelabasedels coneixementsadquirits.

Lesetapesieldesenvolupamentdelacomprensiómatemàtica

Laseqüènciad’aprenentatgedescritahapassatperdiferentsmomentsdidàcticsquepodem sintetitzaren:

1. Evoluciódelesfasesdidàctiques necessàriesiimprescindiblesperaunbonaprenentatge matemàtic,lesquals,atenint-nosalsestudisdepsicologiagenèticaiconstructivista(Piaget, Kamii,Vigotski,Brunner,Diennes...),perlanostrapartconcretemiestructuremsobrela basedelesfasessegüents:

ABSTRACCI Ó

SIMBOLIT Z ACI Ó

MANIPULACI Ó

VIVENCIACI Ó

a) Vivenciació. Faseenquèl’alumnatéselprotagonistadirecte,sobreelqualrecauel problema.Portaalacomprensiódelproblemaamblescorresponentsreflexionssobre lesdificultatsilessevesestratègiesresolutòries.

b) Manipulació.Contextenquèlasituacióviscudaestraslladaarealitatsd’objectes materials.Enaquesttreballs’aconsegueixaprofundirenlesdificultatsresolutòriesdel problemaienl’oberturad’interrogantsihipòtesis.

c) Simbolització.Faseenquèestreballasubstituintlarealitatperelementsquelarepresentencompodenserlesexplicacionsorals,gràfiquesoambllenguatgematemàtic.

d)Abstracció.Estadiresolutoriambl’úsdelasimbolitzaciódelllenguatgematemàticiles tècniquesalgorísmiquesadients.

GENERALIT Z ACI Ó

e) Generalització.Apartirdel’anàlisidediversoscasosparticularsidelarecollidadels seusresultatss’abstreuenconclusionsgeneralsquepermetencrearconeixementsi generaroformularlleis.

Ensíntesi,lavivenciacióenshapermèsentendreicomprendreelproblemailasevasolució. Lamanipulacióenshafetpossibleaprofundirenlacomprensiódelaproblemàticaicrear nousdubtesinousinterrogantstotgenerantiplantejantconjecturesihipòtesisque,a travésdeltreballsimbòlic,enshapermèsinvestigarsobreelsinterrogantsplantejatsd’una maneramésràpidaipoderrespondrealesconjecturesialeshipòtesisformuladestot donantvialliureal’abstraccióamblaconsegüentcreaciódeconeixementilaformulació degeneralitzacions.

2. Evolucióperal’adquisiciódelconeixementil’aprenentatgecompetencial .Enaquest procéss’hadiferenciatelfetdelaresoluciódeld’aprenentatgei,enaquestcas,de l’aprenentatgeconceptualiprocedimentalidelsignificatiuicompetencial.

Unaresoluciód’unaactivitatd’aplicacióperellamateixadifícilmentportaaunaprenentatgecompetencial,sinósimplementaunaresoluciódesconnexionada.L’aprenentatge esprodueixapartirdelcontrastdelsconeixementsadquiritsiseqüenciatsdemanera queelproblemaesvaampliantivanecessitantlessolucionsprèviesperpoderseguir endavantperconstruirelpropiconeixement.Laresolucióconnectivaéslaqueesdóna enaquellessituacionsenquèesvaestirantelfiliampliantlasituacióinicial.Resoldreel problema,pertant,nocomportanecessàriamentaprenentatge.Delamateixamanera, l’aprenentatgedeconceptesqueespotconvertirenlabasedelsaprenentatgescurricularssovintresultainsuficientperpoderdonarrespostesasituacionsrealsdelavida iesconverteixexclusivamentenaprenentatgeresolutoridesituacionspuntualssense capacitatdeservirperanovessituacions.

L’aprenentatgesignificatiufaimprescindibleeldominidelsprocedimentsadequats,que hauriendeconvertir-seenelnuclidelsdissenyscurricularssielqueespreténésaconseguir unainnovacióeducativaqueserveixiperaprepararciutadansambcapacitatsperdonar respostesalavida.Noméslaconfluènciadelsaprenentatgesconceptualsambels procedimentalspossibilitaunsaprenentatgessignificatiusqueconfigurenl’aprenentatge competencial.

Amaneradeconclusió

Latranscripciódel’activitatdesenvolupadaensportaaconclourequeelmésimportant enelmomentdetreballaral’aulamatemàtiquesoqualsevolaltramatèrianoésque l’alumnatensresolguielseguitd’activitatsqueliposemaldavant,sinóquetinguemcura queaquestesactivitatssiguinunfactorquepossibilitil’aprenentatge,quenoesfaefectiu senseunprocésdecontrast.Osigui,queaixònomésseràpossiblecomelfruitd’unes seqüènciesd’aprenentatgequecalplanificar,enlesqualsesvagiampliantgradualmentel contextreflexiuienquèelsdominisinicialsvaginsentnecessarisperseguirendavantiels nouscontingutsassolitshosiguin,alhora,percontinuarresolentnousinterrogantsinoves situacions,fetqueenshadeposarenalertadavantelrendimentol’aprenentatgequeespot generarenactivitatsindependentsodesconnexionadesquedemanennomésunresultat d’unsdeterminatsvalorsqueesdonen.

RESOLUCI Ó

DESCONNE X IONADA

CONCEPTUAL

CONNECTIVA

APRENENTATGE

PROCEDIMENTAL

APRENENTATGE

SIGNIFICATIU

RESOLUTORI

COMPETENCIAL

L’adquisiciódelpoderd’abstraccióigeneralitzaciómatemàticahadeseriéselvertaderimés importantobjectiudel’aprenentatgematemàtic,demaneraque,senseaquestaadquisició, allòqueesfacomaacciómatemàtica,sinos’haplanificatperarribaraaquestafitad’abstracció igeneralització,noespotdirqueelqueestreballasiguideveritatfermatemàtiques.

Ésobviqueconqueriraquestpodermatemàticnoresultaniésgensfàcil,comtampocno hoéspujaral’Everest.Totescaladorsapmoltbéqueperemprendreaquestaconquestael quenopotferéssituar-sedecopivoltaalcamp6sensehaverfetelprocésd’adaptacióal campbaseiposteriormentanar-lorepetintenaltresbasesprèviesalcamp6.Situar-sede copivoltaalcamp6illançar-seaconquerirlesalturesésgarantiadefracàsiprobablement delapròpiamort.Tambéenl’àmbitmatemàticnopodemposarelsnostresescaladorsala conquestadelcimdel’abstraccióilageneralitzaciósituant-losencampsquenecessitenuna adequacióprèvia.Sovint,idemaneranormal,enelnostreprocésdidàcticsitueml’alumnat perquèiniciïlasevaescaladad’aprenentatgedesdelcamp6,queenelsestadisdidàctics significapartirdelstreballsdesimbolitzaciónumèricao,elqueéselmateix,eltreballde llapisipaper.Situarl’alumnatdecopivoltaenaquestestadisimbòlicpotcomportargreus problemàtiques,compotserlade«cremarmotors»perforçar-nelessevesrevolucions.Com méspetitssónelsnostresalumnesmésimportantésdedicartempsalcampbasedela vivenciació,fased’adaptaciócomprensivaimprescindibleisenselaqualal’alumnatliresulta complicatentendreelquerepresentaaquellconcepte,aquellproblemaoaquellasituacióa laquall’enfrontem.

Treballarambconsciènciaidominidelesmetodologiesdidàctiquescomportaplantejarles seqüènciesdidàctiquesdemaneraqueevolucionindelavivenciacióalamanipulaciói, d’aquesta,alasimbolitzacióperarribaralafitaúltimadel’abstracció.Seguiraquestcamí resultaunfactorclauperalacomprensiómatemàticai,pertant,delposteriordesvetllament delraonamentcompetencialmatemàtic.

Resultaobvi,pertant,queperpotenciarlainnovaciódidàcticaalesnostresaulessotal’objectiu generaldemillorarlacomprensiódelsaprenentatgesiconvertir-losencompetencials,siguin matemàticsodequalsevolaltratipologia,calcanviarievolucionardesdelaresolucióala competènciaidelavivenciacióal’abstraccióenelnostreferdiari.Nomésaixíaconseguirem queelnostrealumnatcomprenguiigaudeixidelesmatemàtiquesiqueesconverteixien

competencialalserveidelavidai,atravésd’ella,controliidominil’espaiieltempsqueli corresponviure.

6.Bibliografia

AATT(1998).Resoluciódeproblemes. Biaix, 13.Girona.

(1996).Laresolucióndeproblemas. UNO,8.Barcelona:Graó.

Callís,J.(2006).Saberanalitzarigestionar(identificar,interpretar,transcriure,transferir iavaluar)lessituacionsielscontextseducatius.DinsA.Geli, Aproximacióalesnoves competènciesenelsnoustítolsdemestres (p. 123-127).Girona:UdG.

(2008).Elquè,com,quaniperquèdelamanipulació. Manipularperaprendre:Perspectiva Escolar,329,8-21.Barcelona:AssociaciódeMestresRosaSensat.

(2010).Delavivenciacióal’abstraccióoelcamíverslacompetènciamatemàtica.

PerspectivaEscolar,341, 2-16.

Callís,J.,Callís,C.(2007).Competènciesmatemàtiques:necessitatsiperspectives. Escola Catalana,445, 9-13.

Callís,J.,Mallart,A.(2011).Adquisicióidesenvolupamentdelacompetènciamatemàtica. RevistaCatalanadePedagogia,7, 113-136.

Cockcroft,W.H.(1985). Lasmatemáticassícuentan.InformeCockcroft.Madrid.MEC.

Freire,P.(1972). Culturalactionforfreedom.Harmondsworth.Londres:PenguinEducation.

Gardner,H.(2003). Lainteligenciareformulada.Lasinteligenciasmúltiplesenelsigloxxi Barcelona:Paidós.

Gascon,J.(1992).Quès’enténperresoluciódeproblemesdematemàtiques?. Biaix, 2, 10-17. Reus.

Habermas,J.(1974). TheoryandPractice.Londres:Heinemann.

Lakatos,I.(1977). ProofsandRefutations:TheLogicofMathematicalDiscovery.Cambridge: CambridgeUniversityPress.[Trad.castellà: Pruebasyrefutaciones.Madrid:AlianzaEditorial, 1981]

Lieblich,A.,Tuval-Mashiach,R., Zilber,T.(1998). NarrativeResearch.Reading,Analysisand Interpretation.NewburyPark,CA:Sage.

Mason,J.,Burton,L.,Stancey,K.(1989). Pensarmatemáticamente.Barcelona:Labor,MEC.

Polya,G.(1957). HowtoSolveIt.Princeton:OxfordUniversityPress.

Schoenfeld,A.H.(1981).EpisodesandexecutiveDecisionsinMathematicalProblemSolving. Dins ConventionAnnualoftheAERE.LosAngeles.ResearchinMathematicsTeachingand Learning (p.334-389).NovaYork:MacMillan.

(1992).Learningtothinkmathematically:ProblemSolving,MetacognitionandSenseMakinginMathematics.DinsD.A.Grouws(ed.). HandbookforResearchonMathematics TeachingandLearning (p.334-370).NovaYork:Macmillan.

VanHiele,P.M.(1986). Structureandinsigth.NovaYork:AcademiaPress.

Vila,A.(1998).Laideadeproblemaentrel’alumnat:reflexionsperalacreaciód’unambient deresoluciódeproblemesal’aula. Biaix, 11, 16-22.Reus.

Vygotsky,L.S.(1996). Eldesarrollodelosprocesospsicológicossuperiores.Barcelona:Crítica.

Elraonamentprobabilístic enalumnesd’educació infantilideciclemitjà d’educacióprimària

PaulaLópez,SílviaSerraiLaiaTorres

UniversitatdeGirona

Resum Abstract

Espresentaunestudirealitzatamb alumnesd’educacióinfantilid’educació primàriaperdetectarelsconeixementsi elsraonamentsprevisquetenensobre probabilitatiatzar.Apartird’unaactivitat senzilla,s’hananalitzatelsseus raonamentsprobabilísticsis’hafetuna comparativaentreelsalumnesd’educació infantilielsd’educacióprimària.Els resultatsnomostrendiferències significativesentrelesduespoblacionsde l’estudi,jaquelamajoriadelsalumnesté unaòpticatotalmentdeterministaino enténl’atzar.Aquestsresultats coincideixenambelsd’altresautorscom InhelderiPiaget(1955),queafirmenque aquestraonamentnos’obtéfinsafinalsde l’educacióprimària.

Introducció

Thisarticlepresentsastudyofkindergarten andprimaryschoolstudentsdesignedto detectpre-existingknowledgeandreasoning withrespecttoprobabilityandchance.A simpleactivitywasusedtoanalyse probabilisticreasoningandacomparison betweenkindergartenandprimaryschool studentsmade.Theresultsshowno significantdifferencesbetweenthetwo groups,asmostchildrendonotunderstand chanceduetotheircompletelydeterministic perspective.Theseresultsalignwithother authors,suchasPiagetandInhelder(1951), whoarguethatthistypeofreasoningisnot obtaineduntiltheendof primaryeducation.

Sóndiversoselsestudisqueremarquenlaimportànciad’incloureelscontingutsmatemàtics relacionatsambelblocd’estadísticaiprobabilitatdinslesorientacionscurriculars,pertres motius:laimportànciadel’estadísticacomaobjecteinstrumentalperacomprendreianalitzar larealitatqueensenvolta,lanecessitatd’unsconeixementsmínimsenalgunesprofessionsila transcendènciadel’úsdelraonamentprobabilísticenlapresad’algunesdecisions.

Igualment,enelscurrículumsactualsdeCatalunyaqueregulenlesdiferentsetapeseducatives (Decrets 181/2008i 192/2007),tambéapareixencontingutsd’estadísticaiprobabilitattanta EIicomaEP.Perexemple,enelsegoncicled’EI,esparlade«representaciógràficadelprocés seguitenl’experimentacióidelainterpretaciódelsresultats»od’«elaboracióiinterpretació derepresentacionsgràfiquessenzillessobredadesdelavidaquotidiana».Centrant-nos enEP,enelciclemitjàs’exposaquecaltreballarla«Comprensióiaplicaciódeconceptes bàsicsd’atzar»,la«descripciódesuccessosidiscussiódelseugraudeprobabilitatutilitzant expressionscomsegur,possible,impossible»o«l’inicialaquantificaciódelaprobabilitatque unsuccéssiguisegur,possible,impossible».

Comqueel 2013vaserl’AnyInternacionaldel’Estadística,l’organitzacióinternacionalThe WorldofStatisticsesvaproposartresgransobjectius:augmentarlaconsciènciapública sobreelpoderil’impactedelesestadístiques,fomentarl’estadísticacomunaprofessió, especialmententreelsjoves,ivetllarperlacreativitatieldesenvolupamentdelesciències delaprobabilitatil’estadística.

Dinsdelaformacióinicialdelsmestres,enshemplantejatduratermeunainvestigacióque enspermetitreballarperl’assolimentdelatercerafita,ésadir,estudiareldesenvolupament del’estadísticailaprobabilitatalesprimeresedats.Perfer-ho,enshemcentratenelsegon cicled’educacióinfantil(EI)ienelciclemitjàd’educacióprimària(EP).Elssubjectesdela nostrainvestigació,alumnesdeP5ideterceriquartdeprimària,hanportatatermelamateixa activitatmitjançantlaqualpodremcompararl’úsdelraonamentprobabilísticdelsinfantsmés petitsambeldelsmésgrans.Desprésdeferunaanàlisidelcurrículumdel’educacióinfantil idel’educacióprimària,veiemqueenelprimerapareixenmenyscontingutsmatemàtics relacionatsambl’estadísticailaprobabilitatqueenelsegon.Peraquestaraó,inicialment suposemqueelsinfantsdeP5,enpresentar-losunasituacióquerequereixuncertnivellde raonamentprobabilístic,noserancapaçosd’entendre-laidedonar-hiunarespostacorrecta, ique,encanvi,elsdeeducacióprimària,sí.

Marcteòric

Elsorganismesdereferènciaaescalainternacionalendidàcticadelesmatemàtiques,el NationalCouncilofTeachersofMathematics(NCTM)ilaCommonCoreStateStandard Initiative(CCSSI),evidencienenlessevesorientacionscurricularslanecessitatdetreballar al’escolaelblocd’estadísticaiprobabilitatjadesdel’educacióinfantil(Alsina, 2012).Enel campdelaprobabilitat,esremarcalaimportànciadeferservirtermesespecíficscomara «probable»,«segur»i«impossible».

D’acordambAlsina(2012),creiemqueelscontingutsprobabilísticsiestadísticstenenpoca presènciadinslesorientacionscurricularsnacionalsiquehihapocatradiciódetreballar-los durantlesprimeresetapeseducatives.Aixòpotsercausatperdosmotius:lainvestigacióen didàcticadel’estadísticailaprobabilitatésmoltrecentaEspanya(fanomésduesdècades quehacomençataagafarforça)ilaformacióinicialdelsmestresrespecteaaquesttemaés moltdeficitària,iéspràcticamentinexistentenalgunesfacultatsdeformaciódemestres.

Coneixentaquestesduescauses,autorscomPierceiChick(2011)indiquenquehihamestres dematemàtiquesqueesmostreninsegursal’horad’ensenyaraquestamatèria.Bataneroi

Sánchez(2013)exposenqueelprimerquecalésqueelsmestressàpiguendequinamanera elsalumnesutilitzenelraonamentprobabilístic.

ElsprincipalsautorsquecomencenaparlarsobreaquesttemasónInhelderiPiaget(1955). Elprimerqueespreguntenésaquinaedatl’infantcomençaadiferenciareldeterminisme del’atzar.Piagetprencomareferènciaelsestadisqueellmateixestableixquanparladel desenvolupamentcognitiuisocialdelnen.Exposaqueenl’etapapreoperacional(4a7anys) elsnensrefusenlaidead’atzar,olaconsiderendesd’unaòpticatotalmentdeterminista; tenendificultatsperdiferenciarcertesaiincertesa,ielsmanquenestratègiescombinatòries. Nomésutilitzenelscasosfavorablespercompararprobabilitats.Encanvi,segonsFischbein (1975),abansdels7anyselsinfantsjapodenteniralgunaintuïciód’atzarisóncapaçosde diferenciarentrefenòmensaleatorisideterministes.

Durantl’etapad’operacionsconcretes(7a 11 anys),elsinfantsadquireixenprogressivament unacomprensiódel’atzar.Comencenasercapaçosd’anomenarsituacionscombinatòries senzilles,totique,senselaguiaadequada,l’estratègiausadanoéssemprelacorrecta. Lessevesestratègiesdecomparaciódeprobabilitatss’amplienifanservirtantelscasos favorablescomelsdesfavorables.Finalment,enl’etapad’operacionsformals,elsnens comencenaconcebrel’atzarcoml’absènciadepatronsilaimprevisibilitatifanservirpatrons, estratègiessistematitzades,percompararprobabilitats.Pertant,segonsl’autor,laidead’atzar noescomprènfinsals 11 o 12 anys,queésquanesdesenvolupaelraonamentcombinatori.

Metodologia

Perpoderdetectarelraonamentielvocabulariprobabilísticdelsnensd’EIiEP,esvadura termeunaactivitatquedetallemacontinuació.

Mostra i participants

Lainvestigacióvatenirunamostratotalde43nensinenes.D’aquests, 27cursavenciclemitjà (9 alumnesdetercerdeprimàriai 18dequart)ilaresta, 16infants,erendeP5,totsd’una escolapúblicadeGirona.

Material de l’activitat

Pertaldeduratermel’activitatproposadaenlarealitzaciódel’estudi,vasernecessariel disseny,laconstruccióilautilitzaciód’unasèriedematerials.

Enprimerlloc,esvanpreparartresbossetestransparentsambpedresdevidreadins.Cada unadelesbossescontenia8pedres.Alanúmero 1,hihaviaunabarrejade4pedresverdesi 4deblaves.Alanúmero 2,hihavia8pedresverdesialanúmero3les8pedreserenblaves.

Amés,esvadissenyarunaplantillaamblesfotografiesdecadaunadelesbosses.Aquesta làminaserviaperapoderpreguntard’unamaneravisualalsinfantslesdiversesqüestions entorndelespedresextretessensenecessitatd’ensenyar-loslesbossestransparentsalllarg del’activitat.

Desenvolupament de l’activitat

Engrupsreduïtsdequatreocincalumnes,se’lsensenyavenlestresbossesielseucontingut. Desprésdemanipularelmaterial,s’amagavenlesbossesid’unas’extreienduespedresque esmostravenalsalumnes.Posteriorment,elsalumneshaviend’encerclarenlasevafitxade quinaoquinesbossespodienhaversigutextreteslesduespedressegonselseucolor.

Primerse’lsvapresentarunexemple,demaneraqueellsveiessinentotmomentd’on s’extreienlespedres.Posteriorment,esvarepetirl’activitatamblestressituacionspossibles:

1.Extracciód’unapedraverdaiunadeblava.

2.Extracciódeduespedresblaves.

3.Extracciódeduespedresverdes.

Posteriorment,esrecollienlessevesfitxesiescomentavenelsresultatsenveualtaperpoder entendreelraonamentdelsnensal’horadeprendrelessevesdecisions,ifinalmentse’ls explicavalarespostacorrecta:

1.Lespedresnoméspodensortirdelabossa 1

2.Lespedrespodensortirdelabossa 1 odelabossa 2.

3.Lespedrespodensortirdelabossa 1 odelabossa3.

Resultats

Desprésdeduratermel’experiència«Pedresdecolors»ambelsalumnesdeP5idecicle mitjàdeprimàriaifentelbuidatgedelesdadesobtingudesapartirdelarealitzaciódeles fitxesproposades,elsresultatssónelssegüents:

Situació1:Extracciód’unapedraverdaiunapedrablava

Respostacorrecta

Curs

Respostesincorrectes

Barreja(núm.1) Blavaiverda(núm.2inúm.3) Altresrespostes

81,3%(13) 6,3%(1) 12,5%(2)

88,9 %(24) 3,7%(1) 17,4%(2)

Taula1.Respostesdelsalumnesenextreureunapedraverdaiunapedrablava.

Lesdadespresentadesenlataulaanteriormostrencommajoritàriamentelsalumnes participantshanarribatalarespostacorrectadesdelcomençamentquanse’lsensenya d’entradaunapedraverdaiunadeblava.El88,9 %delsalumnesd’EP,quanse’lsmostrava unapedraverdaiunadeblava,anotavenqueaquestesduestansolsespodienhaverextret delabossanúmero 1 (pedresverdesiblavesbarrejades).AEIvanserunamicamenys,però sílagranmajoria(81,3%).Larestad’alumnesesdivideixentreelsquenovancontestarde maneraadequadaalapreguntaiunalumned’EIiund’EPquevarespondrequelaparella depedrespodiasortirtantdelabossa 2 (pedresblaves)comdela3(pedresverdes).Els altresvandonaraltresrespostes,com,perexemple,marcarduesbossesdiferents,peròen l’explicacióposteriordeienqueunapedraerad’unabossail’altrapedraerad’unabossa diferent(senseentendrequelesdueshaviendeserdelamateixabossa).

Situació2:Extracciódeduespedresverdes Respostacorrecta Respostesincorrectes

Curs Barrejaiverda (núm.1inúm.3)

Barreja(núm.1)

Verda(núm.3) Altresrespostes

Taula2.Respostesdelsalumnesenextreureduespedresverdes.

Alataula 2 espotobservarquenomésunalumned’EParribaalasoluciócorrectaquanse’ls mostrend’entradaduespedresverdes,ésadir,quetantpodenserdelabossaverdacomde labossadebarreja.Lamajoria(mésd’un80 %),tantd’EIcomd’EP,coincideixenquelesdues pedreshandeserdelabossanúmero3(pedrestotesverdes),senseadonar-sequetambé podrienserdelabossanúmero 1 (bossaambpedresverdesiblaves).

Situació3:Extracciódeduespedresblaves

Respostacorrecta

Respostesincorrectes

Curs Barrejaiblava (núm.1inúm.2) Barreja(núm.1) Blava(núm.2) Altresrespostes

Taula3.Respostesdelsalumnesenextreureduespedresblaves.

Alataula3,esmostrenelsresultatsquanalsalumnesse’lsensenyavend’entradaduespedres blavesprocedentsd’unaúnicabossa.Aquestasituació,totisermoltsemblantal’anterior, s’hapresentatposteriormental’explicacióperpartdelamestradelasituació 2;pertant, algunsalumnespodenhaverentèsqueestractadelamateixasituacióiaplicar-hoenaquesta novaproposta.Adiferènciadelcasanterior,arasíqueenstrobemambunalumned’EIitres d’EPqueses’adonenquepodenserdeduesbosses(labossaambpedresdelsdoscolorsi labossaambpedresdecolorblau).Larestad’alumnescontinuamajoritàriamentcontestant quenoméspodenserdelabossanúmero 2 (enlaqualtoteslespedressónblaves).

Discussió

Desprésdeduratermelanostraactivitatid’analitzarlesdadesobtingudes,enshemadonat que,totiqueinicialmentpodíempensarqueelsalumnesd’EPrespondrienmillorqueels alumnesd’EI,elsresultatsmostrenquenohasigutaixí.Lagranmajoriadelsnensinenesd’EI vanrespondreerròniamentenlestressituacions,talcomesperàvem,inovansercapaços d’entendre’nelraonament.Noobstantaixò,adiferènciadelquepensàvem,elsdeCMtampoc novansaberrespondrecorrectamentalessituacionsplantejades,inoméstresalumnesvan raonarcorrectamentenlasituació3desprésd’haverexplicatambclaredatelfuncionament delasituació 2.

AquestsresultatsestanenlalíniadelqueapuntavenautorscomInhelderiPiaget(1955), quedefensenqueelsnensinenes,persisols,nosóncapaçosd’entendrel’atzarfinsals 11

o 12 anys.Elsdosgrupsparticipantsenl’estudiestrobariendinsl’etapapreoperacional (EI)idinsl’etapad’operacionsconcretes(EP).Enl’etapapreoperacional,elsnensrefusenla idead’atzar,olaconsiderendesd’unaòpticatotalmentdeterminista;tenendificultatsper diferenciarcertesaiincertesa,ielsmanquenestratègiescombinatòries.Nomésutilitzenels casosfavorablespercompararprobabilitats.Enelnostreestudi,tansolsundelssubjectes varaonarcorrectamentdavantlasituació3plantejada.Larestavacomportar-sed’acord ambl’estadienquèsesuposaqueestrobensegonslasevaedatitenintencompteque anteriormentnohavientreballataquestsconceptes.Ambelseupensamentdeterministai lespoquesestratègiescombinatòries,novansercapaçosd’entendrequelespedresblaves podiensortirtambédelabossaambpedresbarrejades.Pelquefaalgrupd’EP,éspossible queelsinfantstinguessinunacertacomprensiódel’atzar(totiquenohohavientreballaten cursosanteriors),peròcreienqueelpodiencontrolar,encertantdequinabossa(nomésuna) s’havienextretlespedres.Peraixòtotsellsresponienunasoladelesopcions:onomésdela bossadepedresblavesodelabarreja,peròencapcasdequalsevoldelesdues.

Fischbein(1975)afirmavaqueabansdels7anyselsinfantsjapodenteniralgunaintuïció d’atzarisóncapaçosdediferenciarentrefenòmensaleatorisideterministes.Malgratqueels resultatshanmostratqueelsalumnesnofeienelraonamentcorrecteenlaproposta,síqueés certque,enelcasd’EP,quanse’lsdemanavaqueraonessin,lesrespostesdonadesutilitzaven paraulescom«mésprobable»o«hihamésquantitat».Enaquestsentitveiemque,encara quenoutilitzencorrectamentaquestsconceptes,tenenunacertaintuïcióprobabilística.

Creiemqueunaltrefactorclauquehainfluenciatenelsresultatséslapocapresènciaenel currículumdelaprobabilitatil’estadística.TalcomdiuenCorbalániSanz(2012),l’estadística ilaprobabilitatsónelsparentspobresdel’educaciómatemàtica;enelsprogramesestroben alfinalienelscentresestreballen(quans’hiarriba)alfinaldelcurs,ambpressesipoc temps,totiquesónpartdelaculturaenlasocietatdelainformaciód’avuiendia,aixícom unaeinafonamentalenlapolíticail’administracióienlainvestigaciódetoteslesàreesde coneixement.

Amésamés,talcomindicaAlsina(2012),elsmestresdisposendepocsconeixementsentorn delaprobabilitat(idelasevadidàctica),demaneraqueelgraud’abstraccióenl’estadísticaila probabilitatésméselevatqueenaltresblocsdecontingutsmatemàtics.Aquestfetprovoca quesovintelsprofessorsprefereixintreballarmatemàtiquesmésdecaireestàtic,queporten moltamenysproblemàticaidavantlesqualssesentenméssegurs.Ésmésfàciltreballarels altresblocsperquèsónprocessosreversibles,queparteixendelamanipulaciód’objectesde larealitat.Quansumem,podemafegirduesboles,isidespréslestraiem,tornaremal’estat inicial.Aixònopotpassaramblaprobabilitat,jaqueésimprevisibleirequereixunacapacitat d’abstracciómésaltaqueelsaltresblocsdecontingutsmatemàtics.Creiemqueaixòfaque noestreballinprouleshabilitatspròpiesdelaprobabilitatil’estadísticaique,pertant,noes mostricapmenad’evolucióentreelsresultatsobtingutsdelsalumnesd’EIid’EP.

Davantd’aquestasituacióientenentqueunadelescausesmésimportantsdelapoca presènciad’aquestblocalesaulesd’infantiliprimàriaéslapocaformaciódelprofessorat, ensplantegemsinocaldriaincidir-himés,tantenlaformaciócontínua,conscienciantels equipsdeformaciópermanent,comenlaformacióinicialdelmestred’educacióinfantili primària,revisantelsplansd’estudidelesfacultatsdeformaciódeprofessorat,pertalque

elprofessoratpuguipartird’unsbonsconeixementsiadonar-sedelaimportànciad’aquest blocperassolirlacompetènciamatemàticanecessàriaperlarealitatd’avuidia.

Referènciesbibliogràfiques

Alsina,A.(2012).Laestadísticaylaprobabilidadeneducacióninfantil:conocimientos disciplinares,didácticosyexperienciales. RevistadeDidácticasEspecíficas,7,4-22

Batanero,C.,Díaz,C.(2012).Trainingschoolteacherstoteachprobability. Reflectionsand challenges:ChileanJournalofStatistics,3(1),3-13.

Batanero,C.,Sánchez,E.(2013).Atzariprobabilitatal’EscolaPrimària. PerspectivaEscolar, 370,37-41.

Corbalán,F.,Sanz,G.(2012).Laestadística. RevistadeDidácticadelasMatemáticas,59,5-8.

Decret 142/2007,del 26dejuny,d’ordenaciódelsensenyamentsdel’educacióprimària. DOGC,núm.4915 --21824.

Decret 181/2008,del 9 desetembre,d’ordenaciódelsensenyamentsdesegoncicled’educació infantil.DOGC,núm.5216 68265.

Fischbein,E.(1975). Theintuitivesourcesofprobabilisticthinkinginchildren.Dordrecht:Reidel.

Inhelder,B.,Piaget,J.(1955). Delalogiquedel’enfantàlalogiquedel’adolescent. París:Presses UniversitairesdeFrance.

Pierce,R.,Chick,H.(2011).Teachers’beliefsaboutstatisticseducation.DinsC.Batanero,G. Burrill,iC.Reading(ed.), Teachingstatisticsinschoolmathematics. Challengesforteachingand teachereducation (p. 151-162).NovaYork:Springer.

Descobertes matemàtiques

NúriaCardet

MestraespecialistaenCiènciesiEducacióInfantil EscolaJoanMaragall,Lleida nuriacardet@gmail.com

Resum Abstract

L’activitatqueespresentaésunacurta investigaciósobrelaformageomètrica delsnombresdutaatermeambl’alumnat dequartdel’escolaPaïsosCatalansde Lleida.Esféucomunadescoberta matemàticaenhorarid’unasessió setmanal. Ésunatascaquevapartird’unapregunta fetaperl’alumnat:Quinaforma geomètricatenenelsnombres?Esva treballarenpetitsgrupsiesvaanar regulant:vaconnectarpartsdecurrículum amblarealitat,vapermetrediferentstipus derepresentacionsivaprovocarla necessitatd’explicaralsaltresles descobertesqueesfeien. L’atencióaladiversitatésgarantida,jaque apartirdelsmaterialsidelespròpies representacionss’arribaalarespostaque reculltoteslesaportacionsdelaclasse. Ajudaapotenciarlamiradamatemàtica. Esvapresentarenla X JornadaLleimat, «Enriquimentcompetencial»,fetaaLleida elfebrerde 2014.

Introducció.Organitzacióalcentre

Thefollowingisabriefresearchproject onthegeometricalshapeofnumberscarried outbyfourth-yearprimarystudentsatthe PaïsosCatalansschoolinLleida.Itwas completedasanactivityofmathematical discoveryoverascheduleofoneclassper week.Thetaskbeganasanattemptto answeraparticularquestionaskedbythe pupilsthemselves:Whatisthegeometrical shapeofnumbers?Itwasdevelopedinsmall, regulatedgroups,andlinkedelementsofthe curriculumtoreallife.Italsoallowedfor differentkindsofrepresentation,and encouragedtheneedamongstudentsto explaintotheothersanynewfindings. Awarenessofdiversitywasinevitable,sinceit wasbyusingvariousmaterialsandthrough thedifferentrepresentationsthemselvesthat asolutionincorporatingalltheknowledgeof thewholegroupwasfinallyarrivedat. Ultimately,thisencouragesmathematical thinking.TheprojectwasincludedintheX LleimatConventionforCompetence Enrichmentthattookplaceinthecityof LleidainFebruary2014.

Faunsquantsanys,al’escolam’encomanaven,dinsdelmeuhorari,algunaclassede matemàtiquesencursosdelsqualsnoeratutora.M’agradenlesmatemàtiquesihoagraïa. ImpartiaunasessiósetmanaldeDescobertesMatemàtiquesalscursosenquèl’horariho

permetia.Amés,erenhoresdeSEPintern,éremdosmestresal’aulaiespodiencompartir maneresdeferiatendremillorladiversitatdel’alumnat.

Caldirtambéquedurantelcurspassatesvaferunassessoramentinterndecentreper aprimària,enelqualvaparticipargairebétotelclaustre,tambéd’educacióinfantil,ique preteniarecollirlesdescobertesmatemàtiques,lesbonespràctiquessobrel’àreaqueesferen pertaldefixar-nealgunesperacursosisobretotperadebatresobremetodologiaigaudien l’ensenyamentdel’àrea.

Encomençarelcurs,esvaferunareunióambelstutorspertraçarunalíniadecontinguts enquèelsproblemes,lespreguntesielsmaterialss’anarenentortolligantperferdescobrir relacions,curiositats,regularitatsiperconnectarelssabersdelsdiferentsblocsdel’àreaamb larealitat.

L’activitatqueespresentaaquífoudutaatermeambl’alumnatdequartdel’escolaPaïsos Catalans,deLleida,ifouexposadaenla X JornadaLleimat 2014,«Enriquimentcompetencial», celebradaalfebrer.

Nasquéd’aportacions,preguntesiintervencionsdel’alumnat,ienveure-hipotencialmatemàticvaigprocurarestirar-laitreballar-lafinsalpuntd’exposar-laiararedactar-la.Sincerament, hededirqueencomençarnosabiafinsonpodriaarribarisipotserresultariaprouadequada perala ZDPdel’alumnat,peròalfinal,desprésdetreballar-la,qualificol’activitatdepotenti susceptiblederepetir-laencursosposteriors.

«Laformageomètricadelsnombres»éseltítolqueesvatriar,jaqueevidenciaconnexions entrelageometriailanumeració.

D’onvasorgirlapregunta/problema?

Lesfontsd’aquestaactivitatsóntres:

• Elquadratdel’Anna.

• Lestaulesdemultiplicar(elmuraldetercerilallibretadesegon).

• L’aportaciódel’Albert.

El quadrat

de l’Anna

Elcurspassat,atercer,l’Annavaportaraquesttreballmanualfetacasa,jaquehiveiaquadrats ivapensarquealamestraliagradaria.Hovaencertar!

AlaclassedeDescobertesvaigpreguntaraterceriaquartquinesmatemàtiquesveienen aquestamanualitatija«se’nvatreuresuc»(maneradefer,metodològicamentparlant,que provocapreguntesidescobertes).Atercervancomptarquantespeceshihaviadecada color,vanconstruirtaules,vanadonar-sedecomcreixienelsquadrats(parells),vancomptar angles,costats,diagonals...Aquart,amés,vancomptarlespecestotals: 196(14 × 14),les pecesdedinselquadratgroc(12 × 12)...També,alfinal,enféremrepresentacionsenuna quadrícula.

Imatge1.Elquadratdel’Anna.

Imatge2.Representaciódelquadrat del’Anna.

Aquestaaportaciódematerialdel’Annavaprovocarquealtresalumnesportessinmosaics fetsambpecessimilarsiambaltrescolorsiformes.

Imatge3.Noumodelaportatperl’alumnat,deformesrectangulars.

Les taules de multiplicar

Tambéatercer,elcurspassaticomarecordatoriaquart,buscantregularitatsenlestaulesde multiplicaresvarecordarelmuraldelestaulesfetentretotalaclasseambpaperquadriculat. Hiapareixienformesrectangularsiquadrades(diagonaldelmural).Tambés’havienfet representacionsdelesdiferentstaulesdemultiplicarenfullsquadriculats,segonsesveuen lafotografiaquevaservirderecordatori.

Imatge4.Representaciódelatauladel8.

L’aportació de l’Albert

DesprésdelesvacancesdeNadal,l’Albertvaarribaralaclasseivadirqueellsabiaqueels nombreserenquadratsicubsperquèlihohaviaexplicatlasevamare.

Lapreguntaestavaservida:Elsnombrestenenformesgeomètriques?

Quèensabíem,deltema?Caliarepensarquèhavíemfetirecordaraltresmoments.

Som-hi!Comesvatreballar?

Percomençar,esvainiciarundiàlegsobrelesformesgeomètriques:quinessabíemiquines volíeminvestigar.Vaquedarclarquelaformafeiareferènciaalarepresetaciódelsnombres

Imatge5.Comunicaciód’ungrupdetreball.

inoalaformadelasevagrafia(elzeroielvuittenenformescirculars,peròelcercleno l’estudiaríem).Vaserunbonmomentperrecordarlesfontsabansesmentadesiparlarde nombresquadrats,rectangularsquehaviensortitabans,idelscúbicsquehaviaditl’Albert.

ComqueenlessessionsdeDescobertesestreballasovintenparellesoenpetitsgrupsia laclassehihaviasetgrups,esvandistribuirlesquatreformesgeomètriquesperiniciarel treball:quadrat,rectangle,triangleicub.Toteslesformesestavenestudiadesperdosgrups excepteelcub,quenomésteniaungrupd’estudi(alesacaballesdeltreballtambévansortir altresformes,comaraprismes,piràmides,pentàgons...).

Lespreguntesinicialserenlesmateixesperatotselsgrups:

• Quinssónelsnombresquadratsfinsa 100?Quantsn’hiha?

• Quinssónelsnombresrectangularsfinsa 100?Quantsn’hiha?

• Quinssónelsnombrestriangularsfinsa 100?Quantsn’hiha?

• Quinssónelsnombrescúbicsfinsa 100?Quantsn’hiha?

Elmaterialdonatacadagrupvaser:

• Fullsquadriculatsalsgrupsdequadratsirectangles.

• Xapesalsgrupsdetriangles.

• Multicubsalgrupdecubs.

Cadadia,enfinalitzarlasessió,elsgrupssortienacomunicaroralment(elportaveu)elsseus avençosenlesdescobertes,demaneraquel’altregrupqueestudiavalamateixaformapodia

Imatge6.Muralfinal.

Imatge7.Modeldenombreprismàtic: 12=3 × × × 2 × × × 2.

Imatge8.Modeldenombrecúbic: 4 × × × 4 × × × 4=16.

incorporarelsaprenentagescomapuntdepartidaperalasessióposteriorilarestadela classepodiapreguntarodonaridees.

Paral·lelament,esvaferunmuralqueesvaanarcompletantdurantlessessionsdetreball.

Tambéesvaninventarunnom,eldelsnombresprismàtics,jaqueenconstruirelscubsvan veurequen’hihaviapocsiqueelssortienmoltsprismes,jaquetotselsnombreshopodrien ser,iaixíelsvanbatejarambelnomdeprismàtics.

Elserrorserenunafontvaluosad’aprenentatge,demaneraqueafirmacionsqueundia podiensemblarcertes,unaltrediaesveiaqueerenerrònies,iaixís’avançava.

Imatge9.Plàsticaambnombresquadrats.

Imatge10.Plàsticaambnombrestriangulars.

Desdel’àreadePlàsticaesvanrepresentarelsdiferentstipusdenombres.

Finalment,esvaelaboraruninformeindividualpercomunicarperescritelprocésseguiten eltreballdedescoberta(avaluació).

Lessessions,pasapas

Elgrupquehivaparticiparhivadedicarcincsessionsdetreball,amésdelesdepreparació peral’exposiciófinal.

Enlaprimerasessió,esvaplantejarlasituació,esvanferelsgrups,esvarepartirelmateriali elsalumnesvanescriurealapissarralapreguntainicialperiniciareltreball:

Quinssónelsnombres.......finsa 100?Quantsn’hiha?

Esvananotaralguneshipòtesis.

Enlasegonasessió,cadagrupinvestigava,dibuixava,escriviaelsnombresfinsa 100,els ordenavaianotavalesideesodescobertesqueanavensorgint.Enelsdarrersminuts,el portaveuexplicavaquinsnombreshavientrobat.L’altregrupquehaviatreballatlamateixa classedenombrescomplementavaocorregialainformacióaportada.

Vansorgirnovespreguntes,ques’anotavenafiderespondre-lesquanespogués.

• Hihanúmerosquepodentenirduesformes?

• N’hihaalgunquelespottenirtotes?

• Comcreixen?

Enlatercerasessió,esvanescriureelsnombresordenatsiesvadescobrircomcreixien.Calia buscarregularitats!Perexemple:

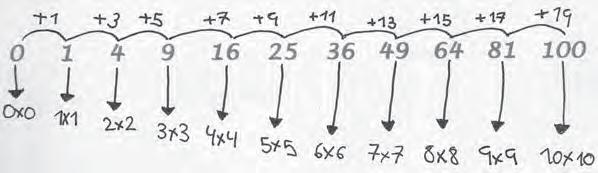
Imatge11.Sèriedenombresquadrats.

Elsgrupsquetreballavenelmateixtipusdenombresvancompartirdescobertesitotsvan arribaralasèriedemanada.

Ungrupdelsquitreballavenelsnombrestriangularsvaposarlesxapesformantpiràmidesi després,ambunnoumaterial(Geomag),vaconstruirpiràmidesambelsnombrestriangulars.

Imatge12.Nombrepiramidalamb sumadetriangles.

Imatge13.Nombrestriangularsi piramidalsambGeomag.

Enlaquartasessió,esvaescriurealapissarralainformaciódetotselsgrups,esvadiscutirquè passavaambl’1 iambel 0,vamacordarqueel 0 noelposaríemperquènotérepresentació, encaraquehaguésanatbépercomençarlasèrie,quel’1 eraunpuntcoml’origen...iaixíes vanpodercontestarpreguntesques’havienplantejati,comerad’esperar,envansorgirde noves.

Vandescobrirque:

• unnombrepodiatenirduesformesgeomètriquesalhora;

• el36eraespecial(recordançadels360◦ idels3.600 segonsd’unahora);

• elsquadratssónuntipusderectangle,igualqueelcubésuncasespecialdeprisma;

• elsquadratsestrobenenladiagonaldelestaulesdemultiplicar;

• ambelsnombrestriangularssurtenpiràmides.

Vansorgirnovespreguntescom:

• Quinarelaciótenenelsnombresquadratsielsrectangulars?

• Quinarelaciótenenelsnombrescúbicsielsprismàtics?

Imatge14.Seriacionsdelsnombresalapisarra.

• Quantsrectanglesespodenferambelnúmero 12?Iambel 13?Iambl’11?...

• Quinéselnombreméspetitquepotserquadratitriangularalhora?

• Quinsnombrestenenrelacióamblestaulesdemultiplicar?

• Totselsnombrestenenduesotresdimensions;hihanombresambunadimensió?

• Sielsprismesoelscubsesrepresentenmultiplicanttresnombres,comesrepresentael 2 × 2 × 2 × 2?

• Perquèl’1 noéstriangular?

Enlacinquenasessió,s’iniciàelredactatdel’informeindividual.Esdonàunapautaies treballàl’expressióescrita.Quèhaviadeconteniruninforme?

Títol

Introduccióbreu(pregunta,problema)

Cos(passos,dibuixos,errors,hipòtesis)

Conclusions(descobertes,aplicacions,novespreguntes)

Annexos(fotos,fullsd’esborrany)

Imatge15.Elementsd’uninforme. Tambéesvanmostrarinformesfetsperaltrescompanysid’altrescursos.Elsvanacabara casacomadeures.

Comunicació

Lacomunicacióésunapartclauenl’assolimentdecompetències,iamésésunabonaeina d’avaluació.

Esvanfermurals,esvanexplicaralfinaldecadasessióelsavençosfets,esvanescriureels informesindividuals,esvaprepararl’exposicióalajornadaLleimat,onparticiparencatorze alumnes,iesvaferunaexposicióoralamestresicompanysdecinquè.

Enlapresentaciód’informeshihaguémoltadiversitat;alguns,però,destacarenenrigorositat ienpresentació.Forensorprenents!

Imatge16.Fulldel’informe del’alumnat.

Conclusions

Enlavaloraciódeltreballperpartdel’alumnatitambédelprofessoratliposenl’etiquetade bonapràctica.Treballarengrupéslaclaudel’èxit,ienaquesttreballl’alumnathoevidencià. Connectarblocsdelamatemàticaiconnectaramblarealitat,ferveurematemàtiquesen propagandes,encartells,enlapresentaciódeproductesalmercat,comperexempleels bombons,ajudaacomprendrel’àreaiaestimar-la.

Eltreballvaprepararelterrenyalsconceptesmatemàticsdemúltiplesidivisors,alsnombres primersicompostos,alespotències,alesordenacions,alarecercaderegularitats,al’arrel quadradaicúbica,alcàlculd’àreesivolums...

Comamestraemvaobrirelcampdelsnombrespoligonalsisobretotemvaensenyarcom l’alumnatpotarribarmésenllàdelquejohaviapensat(delstriangularsalspiramidals)icomde bépodenfereltreballsiestanmotivats,sisabenambclaredatelquese’lsdemanaitroben quetésentitelquefan.Ensenyants’aprèn!

Bibliografia

GonzálezUrbaneja,PedroMiguel(2014). Losnúmerospoligonales.DivulgaMAT. http://virtual.uptc.edu.co/ova/estadistica/docs/autores/pag/mat/Pitagoras11.asp.htm. [Consulta: 21 desetembrede 2014]

Planas,Núria(coord.)(2010). Pensaricomunicarmatemàtiques.Barcelona:FundacióPropedagògic.

Matemàtiquesientorna l’educacióinfantil

FàtimaDalmau∗ iÀngelAlsina∗∗

EscolaCamins(Banyoles)

UniversitatdeGirona

Resum Abstract

Enlaprimerapartd’aquestarticlees defensalanecessitatdepassard’un currículumorientatal’adquisicióde contingutsauncurrículumorientata l’adquisiciódelacompetènciamatemàtica desdel’educacióinfantil,is’argumenta queelsprocessosmatemàticssónlaclau peraconseguir-ho.Enlasegonapartes presental’experiència«larotondaque veiemdesdelpati»,enlaqualesmostra unamaneradetreballarlesmatemàtiques alesprimeresedatsenlaquals’usen situacionsdelavidaquotidianai problemescontextualitzatscomapuntde partida.Mitjançantunaplanificacióiuna gestióquetenenencompteeltreballdels contingutsatravésdelsprocessos matemàtics,esfomentaqueelsnens interpretinlesmatemàtiquesambl’ajuda d’unadult,encomptesd’intentar transmetre’lsunamatemàtica preconstruïda.

Introducció

Thefirstpartofthisarticledefendstheneed forashiftfromacurriculumbasedonthe acquisitionofcontenttooneoriented towardtheacquisitionofmathematical competencefromEarlyChildhoodEducation onward,andarguesthatmathematical processesarekeytoachievingthis. Thesecondpartofthearticlepresentsthe experience«theroundaboutwecanseefrom theplayground»,whichillustratesawayof workingonmathematicsatanyearlyage usingdailylifesituationsandcontextualised problemsasastartingpoint.Thisformof educationalplanningandmanagement worksoncontentthroughmathematical processes,thusencouragingstudentsto interpretmathematicswiththehelpofan adult,ratherthantryingtoteachthem pre-constructedmathematics.

L’educaciómatemàticaésunadisciplinadinàmica,atentaalsreptessocials,alsqualsprocura donarresposta.Enaquestsentit,unadelespreocupacionsactualséslanecessitatdeformar personescapacesd’usard’unamaneracomprensivaieficaçelsconeixementsmatemàtics queaprenenal’escolaenlessituacionsdelavidaquotidianaenquèaquestsconeixements sónnecessaris.

Dinsd’aquestmarc,enelsdarrerstempsl’educaciómatemàticahaprocuratdonarresposta aaquestreptesocialdesdeperspectivesdiverses:l’elaboraciódemodelsteòricsque intentenexplicarcoms’aprenenlesmatemàtiquesicoms’hauriend’ensenyar,l’anàlisi delsconeixementsdidàcticsidisciplinarisdelsmestresperdetectar-nelesfortalesesiles debilitats,obél’estudidelssistemesdecreencesquedonenllocaunadeterminadaidentitat professionaldelsmestresdematemàtiques,entrealtresaspectes.

Demicaenmica,elsresultatsd’aqueststreballss’hananatincorporantenelscurrículumsde matemàtiquesdelamajoriadepaïsos.Enaquestsentit,unadelesinnovacionscurriculars quehatingutmésressòúltimamentéslaincorporaciódelaideaquecaldeixardeformar personesacadèmicamentcompetents(onomésacadèmicamentcompetents)perpassara formarpersonessocialmentcompetents.Enaltresparaules,elscurrículumshanincorporat ambmoltaforçalaideadecompetència.

Perafavorirquelasocietattinguilacapacitatdepensariraonarmatemàticament,elConsell NacionaldeProfessorsdeMatemàtiquesdelsEstatsUnitsplantejadeuestàndardsque constitueixenunconjuntcoherentdeconeixementsicompetènciesmatemàtiques(NCTM, 2000):elsestàndardsdecontinguts(nombresioperacions,àlgebra,geometria,mesuraianàlisi dedadesiprobabilitats),quedescriuenexplícitamentelscontingutsques’hand’aprendre, ielsestàndardsdeprocessos(resoluciódeproblemes,raonamentiprova,comunicació, connexionsirepresentació),queposenenrelleulesformesd’adquisicióiúsdelscontinguts.

Diversosautors(Guzmán, 2001;Niss, 2002;Alsina, 2011, 2012,entred’altres)indiquenqueels processosmatemàticssónunadelesclausperaconseguiraquestpropòsit.Així,perexemple, elmalauratGuzmán(2001,p. 9)javaposardemanifestque:«Enlasituaciódetransformació vertiginosadelacivilitzacióenquèenstrobem,ésclarqueelsprocessosveritablement eficaçosdepensament,quenoestornenobsoletsambtantarapidesa,éselmésvaluósque podemensenyaralsnostresjoves.Enelnostremóncientíficiintel·lectualtanràpidament mutantvalmoltmésproveir-sedeprocessosdepensamentútilsquedecontingutsque ràpidamentesconverteixenenideesinertes».

Peraaquestautor,lamatemàticaés,sobretot,saberfer,ésunaciènciaenlaqualelmètode predominaclaramentsobreelcontingut.Peraquestmotiuconsideraqueelsprocessossón elcentredel’educaciómatemàtica.Enunalíniasimilar,Niss(2002)assenyalalanecessitat desubstituirelscurrículumsdematemàtiquesorientatsal’adquisiciódecontinguts,jaque secentrenexclusivamentenl’adquisiciódesímbolsidetècniquesmitjançantcurrículums orientatsal’ússignificatiud’aquestscontingutsenunavarietatdesituacionsenquè lesmatemàtiquespodenexercirunpaper.Alsina(2011, 2012)ofereixalguneseinesal professoratdelesprimeresedatsperduratermeaquestatransformaciódelapràctica docent.Argumentalaimportànciadetreballarelscontingutsmatemàticsatravésdels processos,iplantejaeltreballdelesmatemàtiquesapartirdecontextosdelavidaquotidiana perafavorireldesenvolupamentdelacompetènciamatemàticadesdel’educacióinfantil.

Desd’aquestmarcdereferència,l’experiència«larotondaqueveiemdesdelpati»,implementadaal’EscolaBalandraudeGironadurantelcurs 2012-2013ambungrupd’alumnes decincanys,preténmostrarunamaneradetreballarlesmatemàtiquesalesprimeresedats enquès’usensituacionsdelavidaquotidianaiproblemescontextualitzatscomapuntde partida.Apartird’unaplanificacióquetéencompteeltreballdelscontingutsatravésdels

processos,aquestessituacionsesmatematitzenperformarprogressivamentrelacionsmés formalsiestructuresabstractes.Imitjançantunagestióqueafavoreixlainteraccióal’aula entrealumnesientremestraialumnes,esfomentaqueelsnensinenesinterpretin lesmatemàtiquesamblamediaciód’unadult,encomptesd’intentartransmetre’lsuna matemàticapreconstruïda.Desd’aquestaperspectiva,elsinfantsesdevenenelsprotagonistes delseuprocésd’aprenentatge.

Descripciódel’experiència«larotondaqueveiemdesdelpati»

L’EscolaBalandrauestàsituadaenunazonadelaciutatdeGironaonconflueixendiverses carreteresqueconnectenendiferentsdireccionscapalcentreicapaforadelaciutat.Sempre queentremosortimdel’escolahemdepassarperlarotondaqueregulalesviesdetrànsit,i desdelpativeiemcircularelsvehiclesquegirenalseuvoltant.Queaquestfetse’nsfacitan visibleiproperal’escolafaque,enalgunmoment,elsnensinenesesfixinenelsvehiclesque elscridenmésl’atencióquanpassenogirenperlarotondaihoexpressinverbalment:«mira quincamiómésgranquepassa»,«arahapassatunautobús»,«mira,unagruamoltgrossa», «aquestamotoquehapassatfamoltsoroll...».Finsitotalgundia,al’horadelpati,ambun grupetpetitd’infantsenshemdedicatacomptarquantscamionsobéquantscotxespassen durantunaestoneta.Itambéésgratificantobservarquealgunavegadahofandeformamés espontània.

Apartird’aquí,lesmestresensadonemqueaquestcontextconcretensofereixunabona oportunitatdeposarintencionalitatmatemàticaaunasituacióquotidianaquesorgeix al’escolaiqueestàrelacionadaambl’entornmésproper.Peraixò,d’unamaneramés planificada,aprofitemperproposaralsinfantselrepted’indagarsobreelstipusdevehicles quepassenperlarotonda;unaexperiènciaque,ensersignificativaicontextualitzada, despertal’interèsperresoldreinterrogantsireptesiensofereixl’oportunitatd’expressar lesideesprèviesquetécadascúsobreaquestaqüestió posantenmarxaestratègiesper resoldreelsdubtes ,decontrastardadesquantitativesidedialogarapartird’uncontext real.Ialavegada,resultaunabonamaneradepropiciarqueelsinfantsobservinambatenció elseuentorn,afinantlamiradaipensantenallòqueveuencadadia.

Abandad’aquestafinalitatinicial,l’experiènciavamoltmésenllà:elsnensmateixos,apartir delatransformacióestèticaquepateixlarotondaambmotiudelapreparaciódelTempsde FlorsaGirona,suggereixenunanovalíniadetreballengrescadoraques’aprofita,idelaqual s’obtenenresultatssorprenents.Peraquestmotiu,ladescripciódel’experièncias’estructura enduesfases: 1)quinsvehiclespassenperlarotonda?,i 2)quèestàpassantalarotonda?

Quins

vehicles passen per la rotonda?

Aquestaprimerafasedel’experiència,enlaqualelsnensindaguensobreelsdiferentstipusde vehiclesquepassenperlarotonda,preveutresmoments:elplantejamentdelrepte,lainvestigacióielreculldedades,ifinalmentlarepresentaciódelesdadesambdiversosmaterials.

Enrelacióambelplantejamentdelrepte,al’aulaformuleml’interrogant:«quinéseltipusde vehiclequepenseuquepassamésperlarotonda?»,iapartird’aquíencetemunaconversa

Alarotondahipassenméscotxes,semprepassenmoltscotxes. Avegadestambéhihaautobusos.

Peròelsautobusosnoméspassenavegades,perquèhipujalagentd’aquíalaparada.Undia vaigveurequepassavaunagruamoltgran.

Passenmoltesfurgonetesquevanatreballar,itambécamions.

Ilesbicicletes,moltesbicicletes,vanpassar.Perònomésundia..../...

Taula1.Diàlegapartirdel’interrogantplantejat.

quegiraal’entorndelessevesestimacionsihipòtesis,delessevesideesprèvies,intuïcions, observacions...Posteriorment,percomprovarsiaquesteshipòtesishanestatencertades, utilitzaremdiversosprocedimentsiprocessosmatemàtics.

Perrecollirlesdades,ensorganitzemengrupsdesisosetnens,icadagrupescullelmitjà detransportquevolcomptabilitzard’unallistaquehemelaboraticonsensuatentretots.La sevatascaseràcomptabilitzardirectamentsobreelterrenyelnombredevegadesquepassa untipusdemitjàdetransportconcretdurantuntempsdeterminat.Uncopcadagruptingui elseuresultat,posaremencomúlesdadesicompararemlesquantitats.

Pertaldecontrolarlavariabledeltempsdeduradaal’horadecomptarcadascundels vehicles,necessitemuninstrumentqueensmesuriaquesttempsiquealavegadaens permetigarantirquelaunitatdemesurasiguiigualperatotselsgrups,percompararaixíels resultatsitreure’nconclusions.Decidimqueelrellotgedesorrapotserunboninstrument, elpresentemiplantegemqüestionssobreaquestinstrumentdemesura:quèés,comipera quès’utilitza,etc.Apartird’aquíesgeneraunanovaconversaal’aula.

Éssorra,aixòquehihaadins.Ésunrellotgedesorra.

Ésunrellotgedesorraambsalperquèésblanc.

Éscomsiunacosaestiguésplenaiarasen’omplísunaaltra.

Éssorrablanca!

Tambéhiharellotgesdesolquefuncionenamblallumdelsol.

Potsfer-loservirperquanestiguemalsgronxadors...Llavors,quans’acabaeltemps,etcanvies. Éscomelmeurellotge,peròdesorra.

Uaaah,quaneltombess’ompledesorrafinsques’emplena. Hoprovem:

Sí,sí,estàcaient. Jaestàpleabaix.

Prou!,janotenimméstemps.

Joacasamevaentinctresallavaboperrentar-melesdentsmésestona.Tincelgroc,queés d’unminut;elvermell,dedosminuts,ielblau,detresminuts.

Joacasamevatambétincunrellotgedesorraeneljocdelfantasma,ésperquèsitardamolta estonal’ataquem.

(mestra):Sianemalarotondaacomptarquantscotxespassen,podríemportarelrellotgede sorra,aixítotselsgrupsestaremlamateixaestonacomptant,no?,perquèquèpassasiungrup s’estàmoltaestonaiunaltremoltpoca...

Sihiestàsmoltaimoltaestonapassenmoltscotxes,sihiestàsnomésunminutpotserno passaniuncotxe,ésclar.

Jaséquèpodemfer.Aniremalarotonda,giraremelrellotgeiveuremquantscotxesi furgonetespassen.

Quantotalasorrasiguiaquíbaixjaparem.

Taula2.Diàlegapartirdelapresentaciódelrellotgedesorra.

Uncopelgrupsesituadavantdelarotondaitéclarquintipusdevehiclehadecomptar, uncompanyésl’encarregatdecontrolarelrellotgedesorra;pertant,seràquianunciaràel momentapartirdelqualelgruppotcomençaracomptarielmomentenquèhadeparar. Elfetd’organitzar-nosengrupspetitsfaqueesgenerinsituacionsdecomunicacióidiàleg, d’intercanvid’ideesipuntsdevistaquetenenaveureamblesinterpretacionsquefacadascú delarealitat,ajudantaixíacompartiriintercanviarelconeixement.Alestaules3i4esmostra ladocumentaciódelesaccionsdelsnens(visual,atravésdefotografies;iverbal,atravésde transcripcions)iunapossibleinterpretaciódelsconeixementsmatemàticsqueapreneniusen.

Hanpassatsisfurgonetes.

No.Aquestaquehapassatnoeraunafurgoneta,erauncamió,perquèésmésgros.Han passatcincfurgonetes.

Sicomptéssimtractorsinopassacaptractorposaremunzero,otambépodemposar ratllat,unacreu.

Sipassenmoltesfurgonetesnopodremcomptartandepressa.

No,defurgonetesenpassenpoques,elgrupquecomptacotxesnosésipodràcomptar tanttotal’estona.

Sipassenmoltesfurgonetespodemcomptarcamions,perquèuncamiótambés’hi assembla.

No,nopodemperquèelscamions,elscomptenelsaltres.

Ó Contingutsmatemàtics:

Nombresioperacions:quantificadors(molts,pocs,etc.);elsnombresfinsal6;enumeració (comptarambcomprensió).

Mesura:percepciódeltemps;quantificacióimesuraatravésd’uninstrument(rellotgede sorra).

Estadísticaiprobabilitat :recollidadedadesquantitatives.

Processosmatemàtics:

Resoluciódeproblemes:aplicaciód’unaestratègiapercomptarlaquantitatdevehicles durantuntemps(úsdelrellotgedesorra)iúsd’unatècnica(l’enumeració).

Raonamentiprova:argumentacióenrelacióamblaquantitatdevehiclesieltemps disponiblepercomptar-los.

Comunicació:úsdellenguatgematemàticadequat(elnomdelsnombres,etc.).

Connexions:entrelesmatemàtiquesil’entorn.

Taula3.Documentacióiinterpretaciódelscontingutsielsprocessosmatemàticsqueusenelsnensque comptenlesfurgonetes.

Ambelresultatqueaportacadagrup,recollimlesdadesperpoder-lesidentificariinterpretar d’unamaneramésclaraivisible.Apartirdelespreguntesquefalamestra:«Dequinsvehicles

enpassenmés?»;«dequinsmenys?»;«quèpassenmés,camionsofurgonetes?»,elsinfants verbalitzenicomparteixenconjuntamentallòquepenseniinterpreten.

Elsquepassenméssónelscotxes.Sí,sí,jahopensàvem,això.

Elsquepassenmenyssónlesmotos.

No,elstractors.

No,perquèsinopassacaptractorenpassenzero,llavorselstractorsnocompten. Passenmésfurgonetesquecamions,peròquasiigual.

Ó Contingutsmatemàtics:

INTERPRETACI

Nombresioperacions:elsnombresfinsal 14;comparaciódequantitats(més...que; menys...que;igual...que).

Estadísticaiprobabilitat :organitzaciódedadesenunataula.

Processosmatemàtics:

Resoluciódeproblemes:expressióoraliescritadelsresultatscorresponentsalarecollida dedades.

Raonamentiprova:argumentaciódelvalor 0. Comunicació:úsdellenguatgematemàticadequat(elnomdelsnombres,etc.).

Connexions:entrelesmatemàtiquesil’entorn.

Taula4.Documentacióiinterpretaciódelscontingutsiprocessosmatemàticsqueusenelsnensdurantla recollida,verbalitzacióiquantificaciódelesdades.

Desprésdelarecercaielreculldedades,cadagruprepresentaelsresultatsambdiferents materialsiambformatsdiversos.Aixòpermetràidentificarelsresultats,fernovesinterpretacions,establirrelacionsquantitatives,exposaricompartirlesrepresentacionsambels companysdelsaltresgrups,treureconclusions,isobretot,ajudarelsinfantsacrearunabase sòlidaal’horad’anarelaborantlesprimeresrepresentacionsmentalsdelsnombres.

Perduratermelarepresentació,facilitemfustesenformaderectangle,totesiguals,icadafusta representaunaunitat.Algunsgrupsrepresentenlesquantitatsdevehicleshoritzontalment, aterra,oncadabarrasignificauntipusdevehicle:podenpassar-hipersobrecomptantcada unitat,id’aquestamaneracomprovendeformaperceptivaquelalongituddecadabarraés proporcionalalaquantitat.

Unaltregrupdecideixrepresentarlesquantitatsdevehiclesverticalment,ifantorresamb lesfustesenformadeprismadelamateixamida:cadapeçadefustarepresentaunaunitati cadatorreocolumna,untipusdevehicle.

Abandadelesfustesenformaderectangle,elsnensinenestambépodenaccediraaltres materialsperferlasevarepresentació:quadratsdecolors,pals,etc.Ungrup,perexemple, utilitzafustetesdefustadecolorsdeformaquadrada,peròse’lspresentaunadificultat:van col locantelsquadratsdecolorssegonslaquantitatcorresponentacadatipusdevehicle seguintunafilerasobrelataula,peròquanhanderepresentarlafileramésllarga,que correspon,aladelscotxes,s’adonenquenotenenprouespaiinohicapalataula...

Representacióhoritzontalambfustesrectangulars:

Representacióverticalambfustesrectangulars:

Aquestaéslatorredecotxesperquèésmésalta,iaquestaéslademotosperquèn’hiha nomésdues.

Representacióhoritzontalambfustesquadradesdecolors:

Lafileradelscotxesnoenshicap.

Traiemlafileradecotxes,noposemelscotxes. Posemelsquadratsaterra,quehihamésespai. Posemlesfilerescapallà,enaquestcostat(referint-sealcostatverticalqueocupal’espai delestaules).

Lafiladelscotxesarribaatrestaulesiladecamionsilademotosnomésaunataula. (Prencomareferèncialalíniaqueseparacadascunadelestaules.)

(mestra):Quantespecesnecessitemperocuparunataula?

Johocompto...sis!(vanfentfileresambelsquadratsocupantnomésunataulaper comprovarqueefectivamentsemprenecessitemsisquadratsperocuparunataula).

Representacionshoritzontalsiverticalsambaltresmaterials:

Representacióenelpaper:

Ó Contingutsmatemàtics:

Nombresioperacions:elsnombresfinsal 14;enumeració(comptarambcomprensió); comparaciódequantitats(més...que;menys...que;igual...que).

Mesura:longitud(curtillarg).

Estadísticaiprobabilitat :representaciódedadesenundiagramadebarrres(usant materialsdiversos);interpretaciódedadesenundiagramadebarres.

Processosmatemàtics:

Resoluciódeproblemes:aplicaciód’estratègiesdiversesperrepresentardadesapartirde materials;expressióoraldelesestratègiesusades.

Raonamentiprova:argumentaciódelesestratàgiesusades.

Comunicació:úsdellenguatgematemàticadequat(elnomdelsnombres,etc.).

Connexions:entrelesmatemàtiquesil’entorn.

Representació:visual(ambmaterials)iescrita(enelpaper).

Taula5.Documentacióiinterpretaciódelscontingutsiprocessosmatemàticsqueusenelsnensdurantla representaciódelesquantitatsdevehicles.

Què està passant a la rotonda?

Faunsdiesqueveiemquealmigdelarotondahihaunsnoisquetreballen:porteneines,fan forats,excaven,piqueniclavenunspalsdecolors.Expliquemelqueveiem;enspreguntem quèdeuenestarfent,parlem.L’Albert,elbidelldel’escola,quetreballaal’Ajuntament,ens explicaqueambmotiudel’ExposiciódeFlorsdeGironavolendecorarlarotondacol·locant unspalsquesegueixenunadegradaciódecolorsformantunacircumferència.

Plantegemalsnensinenessinosaltrestambépodríemferunaconstrucciócomlaquehan fetalarotonda,iapartird’aquísuggereixendiversesideesipossibilitatsis’iniciaundiàleg peralaplanificaciódelprocésdeconstrucciódelanostra«escultura».

Podemferunarotondaambpalsdeterradelpati. Podemferunamuntanyadesorraielsclavem.

Deixaremunespaiperquèentrinelsnensisurtin.Enspodemestiraradinsitambéquanplogui podemposarunarobaasobreinoensmullem. No,perquèalasorreraelsnenshodestrossaran. (mestra):Hopodemferielsdemanemquenohodestrossin.

Taula7.Diàlegperalaplanificaciódelaconstruccióalpati.

Algunsnensprimertracenidibuixencircumferènciesamblapalapermarcaroncol·locaran elspals,d’altresfanmuntanyesdesorraiclavenelspals,d’altresfanforatspertaldefixar-los, etc.Esgaranteixl’espaiieltempsnecessariperquècadascúfacielseuprocésiutilitziles pròpiesestratègies,ifinalmentexpressenelquehanfet.

Vamrecollirpalsivamferunarotondaivamexcavaramblapala. Amblapalavamferunavoltaivamferunarodona. Perquègires,gires,isurtunarodona. Ambelpalsvamconstruirunarotonda. Elspalselsposàvemtotsrectes,comunafila,perònoerarecta,eh!,erarodona. Semblaunsol!

DOCUMENTACI

Ó Contingutsmatemàtics:

INTERPRETACI

Geometria:construcciódelíniescorbes(obertesitancades);transformacionsgeomètriques(girs).

Processosmatemàtics:

Resoluciódeproblemes:aplicaciód’estratègiesdiversesperconstruirunaescultura; expressióoraldelesestratègiesusades.

Raonamentiprova:argumentacióintuïtivadelaformadeconstruirunacircumferència. Representació:visual(ambmaterials)d’unacircumferència.

Taula8.Documentacióiinterpretaciódelscontingutsielsprocessosmatemàticsqueusenelsnensenla construcciódel’escultura.

Unaltrediadecidimrepresentarlarotondadepalsdecolorsambretoladors.Al’horade fer-ho,se’nspresentaelreptedereproduir-laseguintelmateixordredecolorsqueel modeloriginal;peraixòenscalrecordariidentificarentretotsquinésaquestordre.Després d’observardirectamentlaconstrucció,al’aulaintentemverbalitzarquinésaquestordre,per taldereproduir-loseguintelmateixmodel.Primerutilitzemunspalsdecolorsquetenima l’aula,idesprésampollesdecolors.Finalment,femlareproducciógràficaambelsretoladors.

Representaciógràfica:

Ó Contingutsmatemàtics:

Lògica:classificaciópercolors.

Geometria:líniesrectesicorbes;transformacionsgeomètriques(girs).

Processosmatemàtics:

Resoluciódeproblemes:aplicaciód’estratègiesdiversesperrepresentardadesapartirde materials.

Representació:visual(ambmaterials)igràfica(enelpaper).

Taula9.Documentacióiinterpretaciódelscontingutsielsprocessosmatemàticsqueusenelsnensenla representaciódel’escultura.

Conclusions

Enprimerlloc,calassenyalarqueenl’experiènciadescritaesdónalaconnexiómésimportant enelsprimersaprenentatgesmatemàtics,queésl’existententrelesmatemàtiquesintuïtives queelsnensaprenenatravésdelessevesexperiències,enelcontextdepràctiquesinformals, ilesmatemàtiquesmésformalsques’aprenenal’escola.Aquestesmatemàtiquesintuïtivesi informalssón,d’acordambelsplantejamentsdelNCTM(2000),unabasefonamentalper anardesenvolupantelpensamentmatemàticdurantlesprimeresedatsd’escolarització.

Atravésdeladocumentaciódelesaccionsqueelsnenshanportatatermeidelainterpretació posteriordelscontingutsielsprocessosmatemàticsques’hanposatenjocdurantaquestes accions,s’haevidenciatqueelsinfantsapreneniusencontingutsreferentsalsdiferentsblocs decontingutmatemàtic:

• Lògica:elscolorsilasevaclassificació.

• Nombresioperacions:elsquantificadorsilesquantitatselementals,l’enumeració,la comparaciódequantitats,etc.

• Geometria:lespropietatsgeomètriquesdeformesdiverses(lalíniarecta,lalíniacorba, lesfiguresplanes,etc.).

• Mesura:lalongitud(curtillarg),l’úsd’unitatsperalamesuradeltemps(elrellotgede sorra),etc.

• Estadísticaiprobabilitat:elreculldedadessignificatives,l’organitzacióentaules,la representacióilainterpretacióendiagramesdebarres(atravésdematerialsdiversosi enelpaper)ilaposteriorinterpretació.

Comjas’haindicatenlaintroducció,l’aspecteprobablementmésinnovadordel’experiència descritaésque,d’unamaneraprèviamentplanificadaperlamestra,elsnensaprenenaquests diversoscontingutsatravésdelsprocessosmatemàtics.Així,lagestiódelamestrahaafavorit:

• Laresoluciódeproblemes:atravésdelplantejamentdereptes,delarecercad’estratègies itècniquesderesolució,obémitjançantl’expressiódelprocésderesolucióidelresultat, entrealtresaspectes.

• Elraonamentilaprova:laformulaciódebonespregunteshaafavoritqueelsnens argumentinijustifiquinlessevesaccions,iquealgunesvegadeslescomprovin.

• Lacomunicació:s’hanpromogutdosaspectesfonamentalsdelacomunicacióal’aula dematemàtiques l’úsdellenguatgematemàticcadavegadamésajustatiaprendre aescoltarelsaltres atravésdelainteraccióentreelsnens,ientreelsnensilamestra.

• Lesconnexions:elsnenshanpogutconnectarlessevesexperiènciesinformalsambles matemàtiquesmésformals.Aixímateix,s’hanimpulsatlesconnexionsentrediferents tipusdecontinguts,entreelscontingutsielsprocessosi,naturalment,entreles matemàtiquesil’entornimmediat.

• Larepresentació:atèsqueunadelesfinalitatsdelesmatemàtiquesésprecisamentla modelitzaciódelarealitat,s’hanimpulsatdiversostipusderepresentacionsajustades alsnensdelesprimeresedats(atravésdematerialsmanipulablesdiversos,dibuixos, etc.).

Aquestesconclusionsreferentsalsaprenentatgesquehanadquiritelsinfantssónfruitde l’observaciósistemàtica,ladocumentaciódelesaccionsatravésdetranscripcionsifotografies

ilaposteriorinterpretaciódelscontingutsielsprocessosmatemàticsques’hanposaten jocdurantl’experiènciadescrita.Enaquestsentit,caltenirpresentqueenelsprocessos d’interpretaciódelesaccionsdelsnenspotproduir-seunefectequeBrousseau(2007)va anomenar«l’efecteJourdain»,quetéllocquans’intel lectualitzenisesacralitzenlesrespostes ielscomportamentsdelsnensperconèixerindicisdeconeixementmatemàtic,encaraque aquestesrespostesicomportamentstinguincauses,motivacionsisignificatstrivials.Enaltres paraules,potpassarquequiinterpretavegimatemàtiquespertotarreu,mentrequeels nenssimplementestiguinjugantinopercebinenllocelselementsmatemàticsqueobserva l’adult.Perevitaraquestefecte,ésimprescindiblequeenlesproposteseducativeshihagiuna planificacióprèviaiunagestióadequadaperpartdelprofessoratqueconsiderielscontinguts atreballarielsprocessosatravésdelsqualstreballar-los.Encombinar-seelscontingutsiels processos,esgenerennovesmiradesqueposenl’accentnosolamentenelcontingutiel procés,sinó,iespecialment,enlesrelacionsques’estableixenentreells.

Endefinitiva,aquestnouplantejamentcurricularimplicapartird’unenfocamentmoltmés globalitzatquenoeslimitialscontingutsd’unaúnicaàrea,sinóquecomportitreballard’una maneraintegrada,explorantcomespotencieniusant-lossenseprejudicis.Amés,exigeix treballarperafavorirl’autonomiamentaldel’alumnat,potenciantl’elaboraciód’hipòtesi, lesestratègiescreativesderesoluciódeproblemes,ladiscussió,elcontrast,lanegociació designificats,laconstruccióconjuntadesolucionsilarecercadeformespercomunicar plantejamentsiresultats.Endefinitiva,estractad’ajudaragestionarelconeixement,les habilitatsilesemocionsperaconseguirunobjectiusovintmésproperasituacionsfuncionals iencontextosdevidaquotidianaquenopasalseuúsacadèmic,facilitantaixíl’adquisició progressivadel’alfabetismeilacompetènciamatemàtica.

Bibliografia

Alsina,À.(2011). Aprendreausarlesmatemàtiques.Elsprocessosmatemàtics:propostes didàctiquesperal’EducacióInfantil. Vic:Eumo.

(2012).Másalládeloscontenidos:LosprocesosmatemáticosenEducaciónInfantil. Edma 0-6:EducaciónMatemáticaenlaInfancia, 1 (1), 1-14.

Brousseau,G.(2007). Iniciaciónalestudiodelateoríadelassituacionesdidácticas. BuenosAires: Librosdel Zorzal.

Guzmán,M.de(2001).Tendenciasactualesdelaeducaciónmatemática. Sigma, 19,5-25.

NCTM:NationalCouncilofTeachersofMathematics(2000). Principlesandstandardsforschool mathematics.Reston,Va.:TheNationalCouncilofTeachersofMathematics.

Niss,M.(2002). Mathematicalcompetenciesandthelearningofmathematics:TheDanishKOM Project. Roskilde:RoskildeUniversity.

Construir,conjecturar, comprovaridemostrar ambelGeoGebra

PepBujosa

Professordematemàtiques.

Presidentdel’AssociacióCatalanadeGeoGebra. FormadordeGeoGebra.Autordematerialsdeformació jbujosa@xtec.cat

Resum Abstract

Construir,conjecturar,comprovari demostrarsónquatreprocedimentsque sovinthauremdeferservirperaresoldre problemesdegeometriaoperaestudiar algunapropietat.ElGeoGebrapermet resoldreaquestessituacionsd’unamanera moltcreativa.Enelpresentarticlerepasso elsnivellsdeVanHieleperalaconstrucció delpensamentgeomètricimostro exemplesd’activitatsdissenyadesambel GeoGebraquepodenajudarenelcamí capalamilloradelseuaprenentatge. Tambéfaigunarevisiódelconceptede demostracióperajustar-loalcontextdeles nostresaules,donantmoltvaloratotel procésquel’alumnehadeseguirfinsa arribaralesportesdeles demostracionsfinals.

Construct,propose,verifyandprovearefour actionsweoftenperforminsolvingproblems ofgeometryorstudyingparticular properties.GeoGebraallowsustoresolve thesesituationsinaverycreativeway.Inthis articleIreviewtheVanHielelevelsforthe constructionofgeometricthinkingand presentsomeexamplesofactivitiesdesigned withGeoGebrathatcanhelpusonthepath towardimprovedlearning.Ialsoreviewthe conceptofdemonstrationandhowtoadapt ittothecontextoftheclassroom, emphasizingthevalueofthewholeprocess studentsmustfollowinordertoarriveatthe pointofafinalproof.

Introducció

Quanensdisposemaresoldrequalsevolreptegeomètric,segurquehauremde comprovar algunapropietat, construir algunafigurao demostrar algunahipòtesi.Aqueststresprocedimentssónbàsicsperaavançarenelconeixementdelageometriai,pertant,sóntambémolt necessarisenl’aprenentatged’aquestamatèriapelnostrealumnat.

UnprogramacomelGeoGebraésunaeinamoltútilperaaquestsprocediments.El dinamismedelprogramapermetquel’alumnatpugui explorar i,sobretot, conjecturar.Aquests

dosprocedimentsfaranquelametodologiaperaposarenpràcticaelsaltrestressiguimolt diferentdequanhohavíemfetabansdel’apariciódellageometriadinàmica,ésadir,només ambllapisipaper.EnaquestarticlepassarérevistaalespossibilitatsdelGeoGebraal’hora deconstruir,conjecturar,comprovaridemostrar,ilesil lustraréambalgunsexemples.

Construcciódelpensamentgeomètric.ElsnivellsdeVanHiele

Abansd’entrarenelsexemplesconcrets,deixeu-mequerepassilateoriadeVanHielesobre elsnivellsdeconstrucciódelpensamentgeomètric.

Aquestateoria,lacomencenadesenvoluparafinalsdelsanysvuitantaDinaiPierreVan Hiele.Totiquehanpassatmoltsanys,encaraaraesconsideravàlidaiésunareferènciapera moltsautors.Finsitot,l’apariciódelageometriadinàmicahaactualitzatlesactivitatsquees considerenimportantsperavançarenlaconstrucciódelconeixementgeomètric.

Laideabàsicadelateoriaésquel’aprenentatgedelageometrias’aconsegueixpassant perdiversosnivellsdepensamenticoneixement,demaneraseqüencial iquenoestan directamentassociatsal’edat .Nomésquans’haassolitunnivelldeterminatespotpassar alsegüent.Elsautorsafirmenquehihadoselementsimportantsenelprocés:elllenguatge utilitzatilasignificaciódelsseuscontinguts.Eldissenydelesactivitatsd’aprenentatgeseran fonamentalsperpassard’unnivellaunaltre.

Aquestsnivellsesclassifiquendelamanerasegüent:

Nivell Nom

0 Visualització

1 Anàlisi

2 Classificació

Descripció

Lesfiguresgeomètriqueses percebenenelseuconjuntsense posaresmentnienlesseves propietatsnienlessevesparts.

Podenreconèixerlespartsiles propietatsdecadafigura,peròno podenclassificarobjectesni figuresapartirdelesseves propietats.

Podenassenyalarlespropietats necessàriesisuficientsquetenen lesfigures.Japodenclassificarles figuresperlessevespropietats.

Exemple

Podenidentificarunquadrat, perònoidentifiquenelscostats igualsnielsanglesrectes.

Davantd’unparal lelogram podenreconèixerelscostats paral·lels,perònopoden classificartotselsparal lelograms.

Entenenladefinicióde paral·lelogramapartirdeles sevespropietats.

3 Deduccióformal

4 Rigor

Japodenferdemostracions, deduccionslògiquesiformals. Veuenlanecessitatd’aquestes demostracionsperajustificar hipòtesis.

Coneixendiferentssistemes axiomàticsicomparenianalitzen situacionsendiversesgeometries.

Podendemostrarteoremesi resoldreformalmentproblemes geomètrics.

Relacionenpostulatsiaxiomes d’unamaneratotalment abstracta.

Ésevidentqueenl’ensenyamentnouniversitarinoméss’arribaalnivell3.

Elprofessorathad’aconseguirque,ambunesactivitatsbentriades,elnostrealumnatpugui anarpassantd’unnivellaunaltre.Tambéhemdeserconscientsdelnivelldecadaalumne: notothompodràarribaraunademostracióformal(nivell3)sinohasuperatcorrectamentel nivell 2.

ElteoremadePitàgoresendibuixosanimats

Sensdubte,aquestésundelsteoremesbàsicsenl’aprenentatgedelageometriaasecundària. AmbelGeoGebraespodenferdiferentscomprovacionsdelteoremaitambéespodenveure animacionsqueeljustifiquen.Emreferiréaraaalgunad’aquestesanimacions.

Segurament,moltsdevosaltresconeixeualgunesdelesdemostracionsvisualsdelteorema. Aran’esmentaréduesenconcret:ladePappusiladePerigal.

AlamagníficawebdeManuelSada(http://docentes.educacion.navarra.es/msadaall/geogebra/), hitrobemmoltíssimesimoltbonesaplicacionsdelGeoGebraadiversespartsdelesmatemàtiques.TéunaseccióespecialdedicadaalesdemostracionsvisualsdelteoremadePitàgores.SiensfixemenladePappus,trobaremunaanimacióquereprodueixoacontinuació:

Figura1

Figura2

Figura3

Figura4

L’usuari,desplaçantelpuntlliscantdelapartsuperior,faqueesmoguinlesfiguresicomprova visualmentquelasumadelesàreesdelsquadratsquetenenpercostatselscatetsésiguala l’àreadelquadratquetépercostatlahipotenusa.

D’unamaneramoltsimilar,espotveurel’animaciódelademostracióvisualdePerigal:

TothomquedabenconvençutdelaveracitatdelteoremadePitàgores.

Però,siproposemques’observiaquestaanimació:

Figura5

Figura6

Figura7

Figura8

Figura9

Figura10

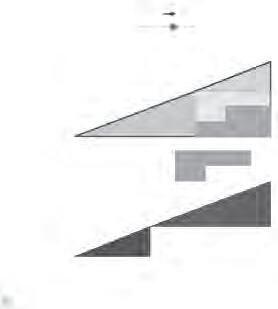
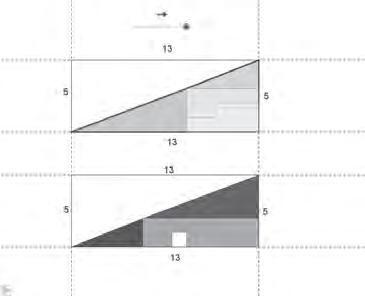
Quèpodencreure?Isiveuenaquesta?

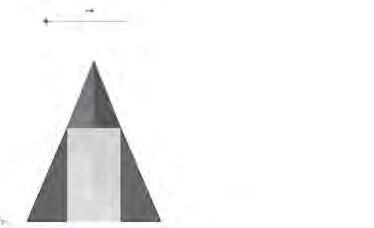
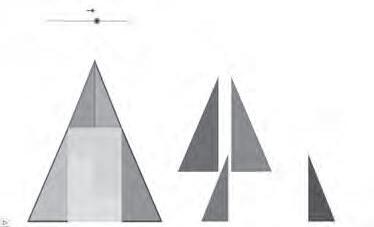
Aixídoncs,non’hihaproudeveure,passivament,unesanimacionsmoltbenfetesperestar convençutdelaveracitatd’unteoremaod’unapropietat.Calqueelnostrealumnatsigui méscríticipuguiactuar,ésadir, construir, conjecturar, comprovar i demostrar.

AnàlisidelademostraciódePappus

Unavegadavistal’animaciódelademostraciódePapus,proposoquel’analitzem,demanera quel’alumnatlapuguiseguirambtotselsdetallsilavagiconstruint.Ésdifícilreproduirenpa-

Figura11

Figura12

Figura13

Figura14

Figura15

Figura16

pertotselpassosquehand’anarfentambelGeoGebra.Precisamentaquestaéslagrandiferència!Podeuseguirtotalaconstruccióa:http://geogebra.pepbujosa.info/geometriaplana/ Pitag.htm.

L’aplicacióespresentaambunadoblefinestra.Aladel’esquerraespotseguirlademostració visualdePappus,peròambmésdetallsiestructuradaentresparts,quecrecquesónles pecesclau.Siseguiulaconstruccióal’enllaçanterior,veureuquecadaparttéunpuntlliscant diferent.Lafinestradeladretaésl’espaionl’alumnathadeferlasevaconstruccióper reproduirlademostració.Perònotansolshad’imitarlaconstrucciódel’altrafinestra,sinó quehadecontestarunasèriedepreguntes,quehauràd’anotaralasevallibretadeclasse,per entendrerealmenttotelprocés.Reprodueixoacontinuacióalgunesd’aquestespreguntes:

Figura17

Figura18

AnàlisidelademostraciódePerigal

D’unamanerasimilar,espotanalitzarlademostraciódePerigal.Aquestaanàlisiespottrobar alamateixaadreçaabanscitada.Reprodueixo,acontinuació,duesdelespreguntesquees proposenal’alumnatenduesdelesetapesdelademostració:

Figura19

Figura20

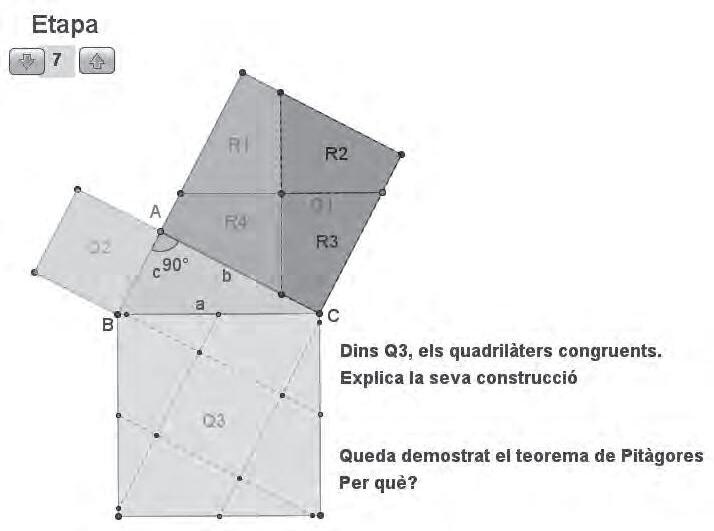
Perrespondrealespreguntesplantejadesenambduesdemostracions,calferservirunes determinadespropietatsgeomètriques.Caldràquel’alumnatqueleshagidecontestarjahi estiguifamiliaritzat.

Enaquestprocés,l’alumnathaurà:

• analitzatlespartsdelademostració;

• construïtlesfiguresnecessàries;

• comprovatlessevespropietatsfonamentals;

• demostratelteorema,fentserviraquestespropietats.

Figura21

Figura22

Tot i que aquest procés ha estat dirigit, i per tant hi ha poques conjectures, l’alumnat no ha estat passiu mirant l’animació i ha hagut d’intervenir per a la comprensió de la demostració.

Activitats directes i recíproques

En tota construcció de coneixement s’ha d’insistir que els enllaços conceptuals s’hagin relacionat en més d’un sentit. Les activitats anteriors estan pensades per analitzar una demostració que ja estava feta i acabada. L’objectiu era la seva comprensió fent servir les propietats geomètriques necessàries. Ara plantejo un pas més: comprovar i, en alguns casos, demostrar propietats amb activitats directes i recíproques.

La seqüència d’activitats que proposo està basada en una recerca feta per Víctor Larios Osorio a Mèxic el 2006 i que jo he adaptat per al nostre alumnat. Es tracta d’estudiar la relació que hi ha entre un polígon (aquí només ho presento per a triangles i quadrilàters, però es podria fer també amb polígons amb més costats) i el que es construeix amb els punts mitjans dels costats. En el cas dels quadrilàters, estarem estudiant el teorema de Varignon. Però la part més especial d’aquestes activitats és que n’hi haurà de directes i de recíproques. Així doncs, l’alumnat haurà de fer servir el GeoGebra per:

Construir els polígons, obser var i comprovar* propietats geomètriques de paral·lelisme

Construir la gura original a par tir de les propietats obser vades I després

∗ Segons el nivell de l’alumnat es podrà arribar a les demostracions o no.

Propietat del triangle

Comencem per una propietat senzilla:

• Construeix un triangle qualsevol.

• Troba els punts mitjans dels seus costats.

• Construeix el triangle que tingui per vèrtexs aquests punts mitjans.

En aquesta primera part, l’alumnat ha construït la figura.

• Desplaça els vèrtexs del triangle gran i observa com varia el triangle interior.

• Escriu totes les propietats que observis que relacionin els costats del triangle interior amb els de l’exterior.

• Comprova-les.

Fent servir els arrossegaments dels vèrtexs es poden començar a fer conjectures. Ens interessa que es fixin en la propietat del paral lelisme dels costats. Podem fer preguntes que els condueixin cap a l’observació.

• Observesalgunparal·lelismeentreelscostatsdeltriangleinteriorielsdel’exterior?

• Descriuambdetallelqueobserves.

• Creusqueescompliràsempre?Perquè?

Comhocomproven?Hihadiferentspossibilitats,peròunaqueésprouconvincentésdefinir unaparal·lelaquepassiper F icomprovarquepassasempreper D,facinelmovimentque facin.

Espotrepetirelprocedimentambelsaltresdoscostatsinteriors.

Aquícalques’escriguimoltclaramentquinapropietats’haaprès,perquèlafaranservirde seguida.

Úsdelapropietatapresa

Acontinuació,laconstrucciórecíproca.

• Construeixuntrianglequalsevol.

• Construeixunaltretriangledemaneraqueelsvèrtexsdelprimersiguinelspunts mitjansdelsegon.

Enaquestaactivitathaurand’utilitzarlapropietatapresaenl’activitatanteriorcomahipòtesi peralaconstrucció.

Figura23

Figura24

• Comprovaqueefectivamentelvèrtexsdeltriangleinicialsónelspuntsmitjansdels costatsdelnoutriangle.

• Arrossegaelsvèrtexsiobserva.Escompliràsempre?Perquè?

AquestacomprovacióespotferdibuixantunacircumferènciadecentreA,perexemple,que passipelsvèrtexscorresponentsdeltrianglegran.

Propietatdelsquadrilàters

Acontinuacióplantegemunasituaciósimilarperalsquadrilàters.Arribarem,doncs,al teoremadeVarignon.

• Construeixunquadrilàterqualsevol.

• Trobaelspuntsmitjansdelsseuscostats.

• Construeixelquadrilàterquetinguipervèrtexsaquestspuntsmitjans.

• Arrossegaelsvèrtexsdelquadrilàterexterniobservacomesmodificalaformadel quadrilàterintern.

• Explicaenquès’assemblentotselsquadrilàtersinterns.

• Escompliràsempre?

• Comprovaaquestapropietat.

Enaquestcas,peralacomprovaciódelapropietatquetotselsquadrilàtersinternssempre sónparal lelogramss’hauriad’aconseguirqueapliquessinlapropietatapresadel’activitat delstriangles.Japodemparlarde demostració.

• Demostraqueelscostatsoposatsdelquadrilàteranteriorsempresónparal·lels.

Indicació: dibuixalesdiagonalsdelquadrilàterexterioriaplicalapropietatdel’activitat anterior.

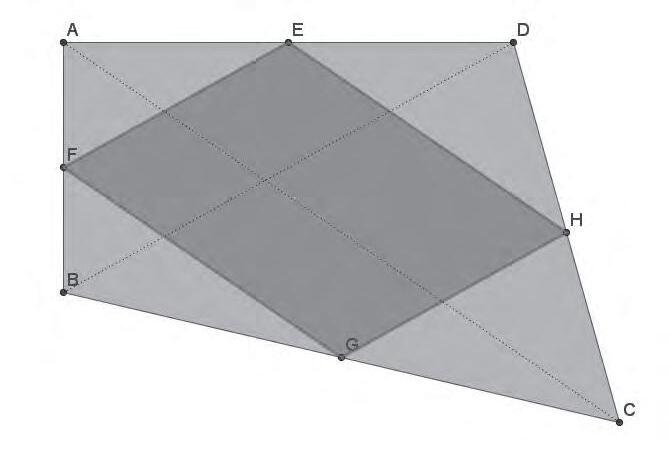
• AquestapropietatesconeixcomateoremadeVarignon.

Aquestaseràunavertaderademostració,perquès’aplicaràunapropietatanterior.Encanvi, lademostraciórigorosadelapropietatdeltriangledependràdelnivelldel’alumnat.

Figura25

ConstrucciórecíprocaapartirdelteoremadeVarignon

Comenelcasanterior,aquíinteressaquefacinlaconstrucciórecíproca.

• Construeixunparal lelogramqualsevol.

• Construeixunaltrequadrilàterdemaneraqueelsvèrtexsdelprimersiguinelspunts mitjansdelsegon.

Segurament,aquestaéslaconstrucciómésdifícildetotalaseqüència.Segonselnivellila realitatdel’aula,s’hauriendedonaralgunesindicacionsquejoaranofixoideixoalavoluntat delsusuaris.

Aquestpodriaseruncamíperarribaralaconstrucció:

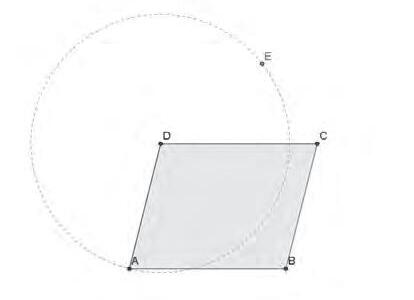
Figura26.Dibuixeuunacircumferènciadecentre D iradi DA.Dibuixeuunpuntqualsevol E asobredela circumferència.

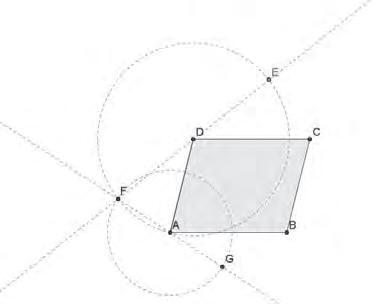
Figura28.Repetiuelprocésanteriorambunacircumferènciadecentre A iradi AF.

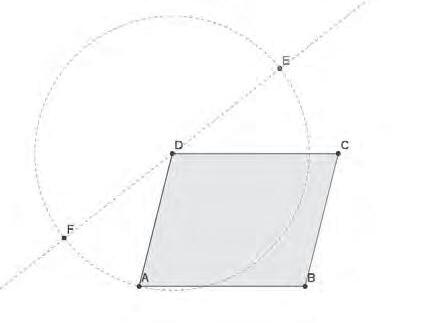
Figura27.Dibuixeularectaquepassaper D i E. Dibuixeuelpuntd’intersecció F.

Figura29.Seguiuelprocésfinsaarribaracompletar elquadrilàter.

Figura30.’Esimportantveurequehihainfinitessolucionsquedepenendellloconestàsituatelpunt E.

Figura31.Simodifiqueuelparal lelograminicialhi apareixenquadrilàterscòncausquetambécompleixenelteoremadeVarignon.

Relacióentreeltipusdequadrilàtersinterioriexterior

Acontinuació,plantegempreguntescomaquesta:

• Comhadeserelpolígonexteriorperquèl’interiorsiguiunquadrat?Iperquèsiguiun rombe?

Enaquestcas,tambéesfaràúsdelGeoGebraperarrossegarelsvèrtexsdelspolígonsinicials, tantenlaconstrucciódirectacomenlarecíproca.Acontinuacióespecificaréelsdiferentstipus d’arrossegamentsquel’alumnatfaràservir,utilitzantlanomenclaturadel’articled’Arzarello etal. (2002).Siensfixemenlaprimerapregunta,lesfasesdelprocéssón:

• Exploració.Faranprimerarrossegamentsimprovisats(Wanderingdragging),peradonarsequehihasoluciói,després,arrossegamentsmésguiatsambl’objectiudeformar,en algunmoment,elquadratoelrombeinterior(Guideddragging).

• Elaboraciód’unaconjectura.Unavegadahanaconseguitqueelpolígoninteriorsigui unquadrat,elsarrossegamentsvoldranmanteniraquestafiguraal’interior(Dommy locusdragging).Éscomsiesdesplacessinsobreunllocgeomètricinvisible.

• Comprovació.Faranservir,amésdelsarrossegamentsdetest(Draggigtest ),altreseines delGeoGebra,comlamesurad’anglesidecostatspercomprovarquelaconjecturaes compleix.

Propietatsdelscentresd’untriangle

UnaltretemaenquèespottreballarambelGeoGebraperestudiarpropietatsgeomètriques éseldelaconstrucciódelsquatreprimerscentresd’untriangle.Emrefereixoalcircumcentre, l’incentre,l’ortocentreielbaricentre.

Noentroenelsdetallsdelasevaconstruccióambelprograma,perquèésbenconeguda.Una vegadaconstruïtsésbenimportantquel’alumnatendedueixilespropietatsiconstrueixila rectad’Euleriquecomproviperquinscentrespassasempre.

Comentaréaraunad’aquestespropietatsqueemsemblamoltinteressant,perquèperala sevajustificacióespotferservirunadelescaracterístiquesmésimportantsdelGeoGebra: lainterconnexióentrelesdiferentspartsdelesmatemàtiquesi,enparticular,entrelageometriail’anàlisi.

Presentemal’alumnatunaconstruccióenlaqualapareixenelsquatrepuntsnotablesqueja hantreballatanteriorment,demaneraqueundelsvèrtexs(A)deltriangleestàsituatasobre d’unarectaparal·lelaalcostatcontrari.

• Arrossegaelvèrtex A sobrelarectaiidentificacadascundelsquatrecentresques’aniran movent.Sivols,potsactivaridesactivareltraçdelspunts.

Enaquestaprimeraactivitat,l’alumnathauràdeposarenpràcticalespropietatsapresesque caracteritzencadacentre.Ambeltraçactivatfaranunaseqüènciacomaquesta:

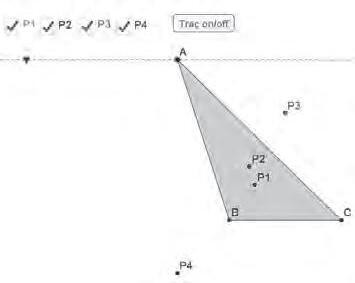
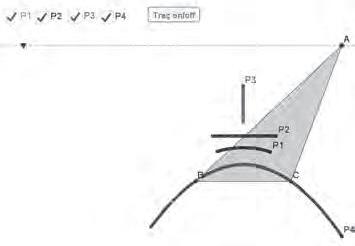
Lestrajectòriesdelafigura32 representenelsllocsgeomètricsgeneratspercadacentrequan desplacemelvèrtexApersobrelarecta.

Unavegadal’alumnathaidentificatelsquatrecentres,dibuixantfinsitotlarectad’Eulerper assegurar-se’n,ensfixaremenl’ortocentre(P4)ilasevatrajectòria.

• Fixa’tenlacorbaquedibuixal’ortocentre.Lareconeixes?Coms’anomenenaquests tipusdecorbes?

• Modificalesmidesdeltriangleitornaadesplaçarelvèrtex A persobrelarecta.Quina corbaapareix?Enquèesdiferènciadel’anterior?

• Continuafentprovesiexplicasihihaalgunarelacióentreaquestacorbailesmidesdel triangle.

Aquestessónunesactivitatsenquèl’alumnatpodràelaboraralgunaconjecturasobrela relacióentrel’alturadeltriangle,queesmantéconstantenarrossegarA,ilaformadelaparàbola.Aquestesconjecturespodriencomençaraentrarenelcampdel’anàlisidefuncions.

Espresentaaquest applet (figura33)onespodenmodificarlesmidesdeltriangleiespot dibuixarlaparàbolaquedescriul’ortocentreperacadatriangle.Ambelpuntlliscant A,

Figura32

Figura33

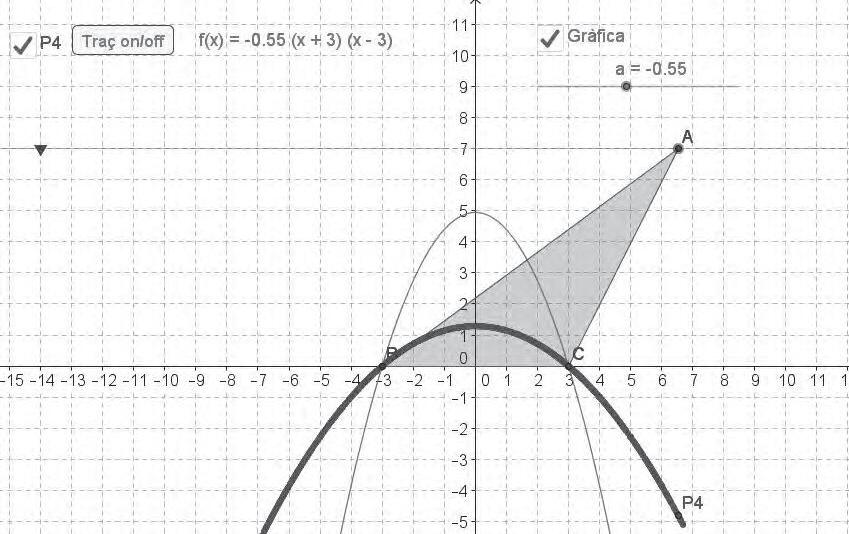
l’alumnatpotajustarlagràficadelaparàbolaalacorbadel’ortocentreiconjecturardequè depènl’expressiódelafunció.

Enaquestcas,lademostraciódelapropietatespotdeduird’unageneralitzaciódelteorema del’altura.Ambaquest applet espotveurequelasegonacoordenadadel’ortocentreD depèndel’alturadeltriangle.

Figura34

Figura35

Ilesdemostracions,quan?

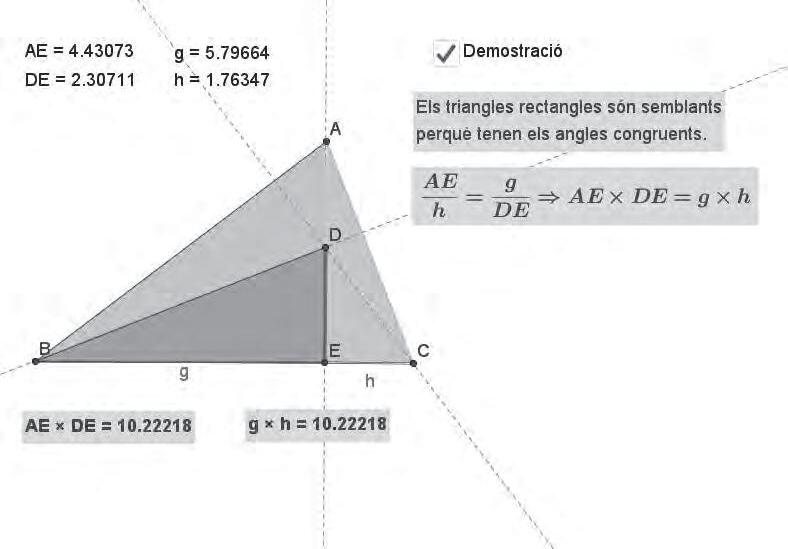
Entoteslesactivitatsproposadesidescritesfinsara,l’alumnat,sobretot,hadeconstruir, conjecturaricomprovar.Lesdemostracionsquehepresentat,obésónguiades(teorema dePitàgores),obésónparcials(delapropietatdelstriangles,nodemostrada,s’arribaa lademostraciódelteoremadeVarignon).Lapartdelesdemostracionséslaméselevada, peralnostrealumnat,enelsentitdelsnivellsdeVanHielequeheexposatalprincipi. L’alumnathad’estarpreparatihaverassolitelsaltresnivellsanteriors,que,sensdubte,amb lesconstruccions,conjecturesicomprovacionsquelipermetelGeoGebrapotassolir.

Amés,elconceptededemostraciónoéselmateixentotselsambientsenquèelcitem.Em referiréaraal’articledeGodinoiRecio(2001)enelquals’analitzenelssignificatsdelaidea dedemostracióendiversoscontextosinstitucionalsqueresumeixoacontinuació.

• Lògicaifonamentsdelamatemàtica.Enaquestentornesparteixd’unsistemaaxiomàtic ambafirmacionssensedemostrarquesónlabasedetotselsaltresenunciatsquees dedueixenmitjançantunconjuntdereglesdetransformació.

• Matemàticaprofessionalactual.Unapartdelesdemostracionsmatemàtiquesprofessionalsenl’actualitatjahansuperatelsimplismedelalògicadeductivaclàssicais’han convertitendeduccionsnosempreformals,reforçadesambl’úsd’ordinadors.Alguns autors(Lakatosentred’altres)veuenqueelconceptededemostraciótécaracterístiques diferentsdelesclàssiquesiarribenaafirmarquelaveracitatd’algunesproposicions matemàtiquesavançadesnoquedaplenamentgarantida.

• Ciènciesexperimentals.Enaquestcontext,lademostracióesbasaprincipalmenten pràctiquesempiricodeductivesianalògiques.Aquíl’experimentacióésfonamentalper deduirunateoria.

• Vidaquotidiana.Lesargumentacionsquefemservirperaconvènceralgúd’una afirmaciósóninformals.Enaquesttipusderaonament,l’analogiaocupaunpapermolt important.Aquestraonamentinformalesfaservirentotselsdominisdelconeixement, finsitotenlesmatemàtiques.

• Classesdematemàtiques.Enlesclassesdematemàtiquesdeprimàriaidesecundària podenpredominarlespràctiquesaugmentativesnoanalítiques,extrapoladesd’altres contextoscomlavidaquotidianailesciènciesexperimentals.

Ambtot,aquellsautorsconclouenquecaltenirencomptequenohihaunsolconcepte dedemostracióiquel’alumnat,queestàpresentendiversoscontextos,inicialmentfarà serviresquemesargumentatiusdiferents.Afirmenquel’argumentacióanalíticahadequedar integradacomunafasemésdelprocésmatemàtic,perònol’única.Elconceptededemostració had’anarevolucionantenelcursdel’escolaritatiaquestprocésnecessitatempsicontextos adients.

ÉsenaquestsentitquelageometriadinàmicaielGeoGebraenparticularpodenjugarun paperfonamental.Lesconstruccions,conjecturesicomprovacionspodenserunbonpunt departidaperaraonamentsmésformals,jaquel’alumnatestaràsegurquevaperboncamí iqueprobablementnointentademostrarunapropietatfalsa.L’autoconvencimentésbàsic perconvèncerelsaltres.

LesdemostracionsenlesúltimesversionsdelGeoGebra

UnadeleseinesquehatingutsempreelGeoGebra,desdelaprimeraversióquevasortir durantelcurs 2001-2002,vaserl’anomenada«Relacióentreobjectes»( ).

Alafigura36,enquèesreprodueixlaversió 1.0,podeuveurequeensindicaquelesrectes s i q,ques’hanconstruïtaplicantelteoremadeVarignon,sónparal·leles.Pertant,ambaquesta eina,determinadespropietatsquedaven«demostrades»perl’autoritatdelprograma,que lescomprovavademaneranumèricaAquestnopodiaserunargumentdefinitiuperauna demostració,peròdecaraal’alumnatsíqueserviaperaconfirmar,enelcontextquehe comentatabans,algunesconjectures.Totiaixò,esproduïendiversos«falsospositius»,a causadelserrorsdeprecisiódelscàlculsefectuats.

Figura37

Enelcurs 2014-2015hasortitlaversió5.0 delprograma,enlaqual,entremoltesaltres incorporacionsimportants,comeltreballen3D,s’hamilloratforçaaquestaeina.Això començaaserelfruïtd’unprojecteanomenatAutomatedTheoremProving,quepreténla demostracióautomàticadeteoremesdegeometria.Enaquestprojectehitreballencientífics tanimportantscomFranciscoBotana(UniversitatdeVigo),MarkusHohenwarter(Universitat JohannesKeplerdeLinzicreadordelGeoGebra),PredragJanicic(UniversitatdeBelgrad),

Figura36

ZoltánKovács(UniversitatJohannesKeplerdeLinz),IvanPetrovic(UniversitatdeBelgrad), TomásRecio(UniversitatdeCantàbria)iSimonWeitzhofer(UniversitatJohannesKeplerde Linz).Alaversió5.0 jas’hanincorporatalgunsdelsalgoritmesquefanquelademostració dedeterminadespropietatsiteoremesjasiguiproufiable.

Enaquestaversió,perexemple,sidibuixemunquadrilàterambelparal·lelograminterior complintelteoremadeVarignon,trieml’eina«Relacióentredosobjectes»iseleccionemdos costatsoposatsdelafigurainterior,ensapareixeninicialmentaquestsmissatges:

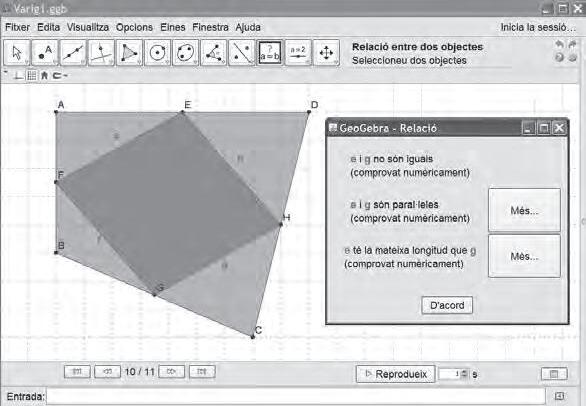
Compodeuobservar,lesafirmacionsestancomprovadesdemaneranumèrica,segurament amblametodologiatradicional.Encanvi,siprememelsbotonsde«Més...»,apareixenels missatgessegüents:

Figura38

Figura39

Lesafirmacionsquelapropietatcitada éssempreveritat jacorresponenal’aplicaciódelnou mètodededemostracióautomàtica.Aixòsignificaquepodemmourelafiguraiquesempre escompliràlapropietatques’estàcomprovant.

Quanaquestmètodeestiguitotalmentimplementatenproperesversions,crecqueseràtot unrepteveurecoml’apliquemalesnostresclassessivolemmantenirel«suspens»dela necessitatdelademostracióformalperaaquellalumnatquepuguiarribar-hi.Jopensoque, decaraal’alumnatmitjà,nosuposaràcapcanvideparadigma,peròqueelsquivulguin arribarmésenllàdelacomprovacióautomàticaestaranmotivatsperesbrinarperquè és semprecerta unadeterminadapropietat.

Consideracionsfinals

Ésprouevidentquel’apariciódeprogramescomelGeoGebrafaquel’ensenyament il’aprenentatgedelageometriahagincanviatmolt.Lapossibilitatdel’arrossegament d’elementsperobservarquinespropietatssónestablesiquinesnohafetquedelscasos particularsdeldibuixdefiguresenllapisipapers’hagipassatalageneralitzaciódetipusde figures.Aquí,doncs,l’assolimentdelaclassificaciódefiguresenelsentitdelnivell 2 deVan Hieleespotveuremoltbeneficiat.

Noobstantaixò,caltenirpresentquenopodemcremaretapesatotavelocitat,perquèel nostrealumnatnecessitatempsperreflexionariactuar.Enaquestsentit,noéssuficient lapresentaciód’unesanimacionsmoltconvincentsperalaresoluciódedeterminades situacions.L’alumnathadeconstruir,conjecturaricomprovarlessevesconjectures,cosa queeldinamismedelGeoGebralipermet,ajustant-seaunesbonesactivitatstriadespel professorat.

Elcasdelesdemostracionsmereixunaatencióespecial.Hemvistqueelconceptevaria segonselcontext;elquepotserunabonademostració,enelsentitdecertesaenuncontext, potnoser-hoenunaltre.Elquesemblaclarésquenopodemdecapmanerareduircappart delesmatemàtiquesaunconjuntdeproposicions,teoremesidemostracions.Aixòdesvirtua elsentitrealdelesdiferentspartsitiraenreremoltalumnat.

LageometriatractadaambelGeoGebrapottenirunaspectelúdicderecercaquecal potenciar.Lafeinademestresiprofessorsésfonamentalperaconseguirlesactivitatsiel climaqueafavoreixiaquestarecercaconstant.Endefinitiva,deixemquel’alumnatgaudeixi delageometriaiqueenl’entorndelaclassequediconvençutdelacertesadelesseves comprovacions.Iquetotelcamíqueelportaràalesportesdelesdemostracionsfinalssigui ricdeconeixementidecreativitat.

Referències

Arzarello,F.,Olivero,F.,Paola,D.,Robutti,O.(2002).Acognitiveanalysisofdraggingpractices inCabrienvironments.ZDM,34(3),66-72.

Bujosa,P.(2014).http://geogebra.pepbujosa.info/geometriaplana/Pitag.htm

Fouz,F.(2006).TestgeométricoaplicandoelmodelodeVanHiele.Sigma, 28,33-56.

Godino,J.D.,Recio,A.M.(2001).Significadosinstitucionalesdelademostración.Implicaciones paralaeducaciónmatemática.EnseñanzadelasCiencias, 19 (3),405-414.

LariosOsorio,V.(2006).Larigidezgeométricaylapreferenciadepropiedadesgeométricas enunambientedegeometríadinámicaenelnivelmedio.Relime, 9 (3),361-382.

Rynhart,P.(2012).http://proactiveplay.com/the-van-hieles-model-of-geometric-thinking

Sada,M.(2009).http://docentes.educacion.navarra.es/msadaall/geogebra/pitagoras.htm

Zoltán,K.(2014).TheportafolioproverinGeoGebra5.ADG2014, 191-206.

Zoltán,K.,Recio,T.,Weitzhofer,S.(2012).ImplementingtheoremprovinginGeoGebraby exactcheckofastatementinaboundednumberoftestcases.DinsJ.RafaelSendraPons iC.VillarinoCabellos(ed.). LibrodeResúmenesdelXIIIEncuentrodeÁlgebraComputacionaly Aplicaciones (EACA 2012)(p. 123-126).AlcaládeHenares:UniversidaddeAlcalá.

Concursderesoluciógràfica de«sangakus» ambelGeoGebra

CarlosGiménezEsteban

Col legiSantGabrieldeViladecans.AssociacióCatalanadeGeoGebra carlos.gimenez@gmail.com

Resum Abstract

Enaquestarticleespresentauna experiènciad’aulaconsistenten l’organitzaciód’unconcursderesolució gràfica,mitjançantel GeoGebra,de problemesgeomètricspresentatsal’estil delsclàssics sangakus japonesos,pera alumnesdematemàtiquesdebatxillerat. Lasituaciódepartidadelsalumnesinclou untreballprevihabitualambel GeoGebra endiversesmodalitats,tantd’unamanera dirigidacomenformadesuportdeles explicacionsdelprofessor,comunús autònomdelsalumnesapartirdepetites propostesdedescoberta.Elsobjectius didàcticsd’aquestaexperiènciasón despertarlacuriositatdelsalumnesperla bellesadelespropietatsgeomètriquesi reforçarlasevaconfiançailasevadestresa enl’úsdel GeoGebra.

Objectiusicontext

Thispaperdescribestheorganizationofa GeoGebra-basedgraphicalproblem-solving competitionasaclassroomexperiencefor secondaryschoolmathematicsstudents, specificallycomprisingtheresolutionof geometricproblemspresentedintheform ofclassicJapaneseSangaku.

Priortothecompetitionstudentswouldhave carriedoutdifferentactivitiesusing GeoGebra onaregularbasis,bothina supervisedclassroomcontextasasupportto lessonsandindependentlywhileworkingon shortdiscoveryassignments.

Theeducationalobjectivesofthisexperience aresetoninspiringstudents’curiosityforthe beautyofgeometricpropertiesand expandingtheirtrustandskillinusing GeoGebra.

Ésevidentquecaltenirclarsdeboncomençamentquinssónelsobjectiusdidàcticsque s’intentenassolirambqualsevolnovaactivitatqueportemal’aula.

Elcontextdepartidadel’experiènciaquepresentoéselsegüent:

• L’activitatesvaplantejarperalsalumnesdelamatèriadeMatemàtiquesdeprimerde batxilleratdelamodalitatcientificotecnològica.

• Laideaerapodertreballarambellsaspectesdegeometriaplanaméscomplexosque elsqueabordemhabitualment.

D’altrabanda,aquestsalumnesestanhabituatsal’úsdelGeoGebraendiferentsmodalitats, tanapartirdeconstruccionsqueesprojectenal’aulacomd’unamaneraindividual,per aresoldresituacionssenzillesendiferentsàmbits(anàlisi,probabilitat,àlgebra,geometria, etc.).

Hi ha vida més enllà de la recta d’Euler?

Espodriadirqueaquestareflexióvaser,probablement,elmeupuntdepartida.Alapràctica, quantreballemlageometriaplanaaprimerdebatxilleratnoacostumemaanarmésenllàde ladeterminaciódelarectad’Euler,bàsicamentperleslimitacionsqueensimposenelsreduïts coneixementsalgebraicsdelsnostresalumnes,queelsimpedeixenresoldresituacionsgaire méscomplexes.

Aleshores,lapreguntaésòbvia:«Atèsqueelslimitatsconeixementsd’àlgebradelsnostres alumnessónelprincipalobstacleperpoderaprofundirunamicamésenconceptesde geometria,sidisposemd’unaeinacomelGeoGebra,queenspermetesquivarladificultat algebraica,potservallapenasacrificarelrigord’unademostracióformalacanvid’analitzar idescobrirnovessituacionsdelesqualspodemobteniruncertgraudecertesaambuna comprovacióinformàtica?».

Larespostaquedonoaaquestapreguntaésafirmativa.Crecque,enaquestnivelleducatiu, limitareltipusdesituacionsgeomètriquesalesqualsexposemelsnostresalumnesaaquelles quesiguincapaçosdemanipularalgebraicamentamblasoltesasuficientimplicaunadoble renúncia.

Perunabanda,elsalumnesambmillorsaptitudssónprivatsdelapossibilitatdeplantejar-se altressituacionsquesensdubteelsestimularienintel·lectualmentielspermetriendescobrir lavarietatilabellesadelespropietatsiregularitatsgeomètriques.

Perunaaltrabanda,peralsalumnesquepresentenmésdificultatsenlaresolucióde problemesalgebraics,lapossibilitatdeparticiparactivamentenladescobertadepropietats interessantsfentúsdelasevaintuïcióidelGeoGebracomaassistentqueresollesdificultats elspermetrecuperarpartdelamotivacióperduda.

Demostrar. comprovar i representarconstruir vs vs.

SiacceptemqueelGeoGebraésunrecursexcepcionalperaladidàcticadelesmatemàtiques, elfetqueelsnostresalumnesesdevinguincompetentsenelseuúspassaaserun objectiupedagògicensimateix,pelsavantatgesqueelsreportaràenelseutreballambles matemàtiquesengeneral.

Undelsprimersaprenentatgesqueensproporcionaeltreballhabitualambeinesde geometriadinàmicacomelGeoGebraéscomprendreladiferènciaentre representar unasitua-

ciógeomètricai construir-la (definintcadanouobjecteapartirdelessevesrelacionsamb elsobjectesanteriors).Poquessituacionsresultenmésinstructivesperaalgunsalumnesque veureelsefectestandiferentsqueprovocaeldesplaçamentd’unpuntsobreunarepresentació (lespropietatsobservadesdesapareixen)osobreunaconstrucció(lespropietatsobservades esmanteneninvariants).

Laqüestióésbensenzilla:sienslimitematreballarenaquestcampallòqueelsnostres alumnespodendemostrar,reduïmtantlessituacionsqueelspresentemquelaideadela geometriaqueesformenésforçapobra.

Pertant,demostremtotelquepodemicomprovemmoltesméscoses;deixemquees veginobligatsaaplicarlasevaintuïcióperaplantejariresoldresituacionsnovesiatractives almargedelesequacionsquelesdescriuen.Queconjecturin,descobreixiniprovinsense sentir-seencotillatsperlesobligacionsqueimposal’àlgebra.

Adopta,adapta,creaicomparteix

Qualsevolprofessionaldel’ensenyamentalseglexxiqueestimideveritatlasevafeinahauria d’actuarseguintalgunaideasimilaraaquesta,pelbédelsseusalumnes,delseucentre educatiu,delacomunitatdedocentsipelseupropidesenvolupamentprofessional.

Adoptar

Òbviament,enunmónhiperconnectatcomelnostre,laprimeratascaquequalsevoldocent hadeduratermequanesplantejaintroduiralgunanovetatalasevaaulaéscercar,investigar, consultar,indagar;ensuma,observarexemplesproduïtsperaltresprofessionals.

Elsmitjanssónobvis:perunabanda,hemdetenirpresènciaenlesxarxessocials(especialment aTwitter),iperunaaltrabanda,hemdeparticiparentoteslestrobadesdeprofessoratque enssiguipossible(afortunadament,sen’organitzenmoltesalnostreentorn).

Enelcasd’aquestaexperiència,perpoderdur-laatermevaigadoptarrecursosprovinents d’aquestsdosàmbitsjaindicatsmésamunt:

• AtravésdeTwitter(@gogeometry),vaigconèixerl’existènciadelwebGoGeometry, mantingutdesdelPerúpelSr.AntonioGutiérrez,enelqualespottrobarunacol·lecció deproblemesgeomètricsenormeicreixentdiareredia(enelmomentdetancaraquest escritconté 1.067problemes),algunsdeclàssicsialtresdegeneratsperellmateix.

• Vaigsentirparlarperprimeravegadadels sangakus aenRamonNollaenla XIIIJornada dedidàcticad’ABEAM(Barcelona, 13denovembrede 2010).Aleshoresemvansemblar unacuriositat,ambpotencialevident,peròambunproblemad’aplicació:jonoem sentiacapaçdeplantejarproblemesprouricsinovolialimitar-meatreballarnomésels problemesclàssicsrecuperats.Enaquestmomentvaigrecordarelwebabansesmentat.

Adaptar

Apartird’aquí,laideaesvaformarautomàticament,quasisensevoler:elquehaviadefer eracombinarlaideajaponesadels sangakus,lafontpràcticamentinesgotabledeproblemes quesuposavaelwebGoGeometryil’einaessencialenlamevaactivitatal’aula,elGeoGebra.

Adaptarnovoldirapropiar-sedelesideesd’altresifer-lespassarperpròpies.

Peraquestmotiu,lamevaprimerapreocupacióvasercontactarambl’autordelsproblemes, elSr.AntonioGutiérrez,iexposar-lilamevaideapertaldedemanar-liautoritzaciópera utilitzarelseumaterialamblareferènciacorresponent.TambéemvaigadreçaraenRamon Nollaperfer-lopartícipdelamevainiciativa.

Caldirqueentotsdoscasosvaigrebreunarespostapositivaiencoratjadora,iemvan autoritzarautilitzarelsseusmaterialsamblacitaciócorresponent.

Crear

Arribatsaaquestpunt,empreocupavalamaneradedonaratotplegatunaformaque aconseguís:

• Donarunsentital’activitatquepartísdelsobjectiusdidàcticsplantejats.

• Aprofitardelamillormanerapossibleelpotencialdelstresrecursosdisponibles: sangakus,GoGeometryielGeoGebra.

• Resultarengrescadoriatractiuperalsalumnes.

Lasolucióquevaigtrobar,iqueaquípresento,vaconsistirenl’organitzaciód’unconcurs deresoluciódeproblemesgeomètricsmitjançantl’úsdelGeoGebrapresentatsal’estildels sangakus.

Compartir

LaprimeramesuraquecalprendreésladepublicarelsmaterialsaInternetsotaunallicència deltipusCreativeCommons,que,sotaunesrestriccionsmínimes,permetaqualsevolusuari defer-neús.

Elpassegüenthadeserlapresentacióenalgunatrobadadeprofessorat.Enaquestsentit, aquestaexperiènciad’aulaesvapresentarperprimercopenformatdecomunicacióalesV Jornadesdel’AssociacióCatalanadeGeoGebra(Barcelona, 16defebrerde 2013).

Posteriorment,amblaparticipaciód’enPepBujosa,presidentdel’AssociacióCatalanade GeoGebra,aquestaideavadonarllocalarealitzaciód’untallerales XVIJAEM(Jornadespera l’Aprenentatgeil’EnsenyamentdelesMatemàtiques,PalmadeMallorca,4dejuliolde 2013).

AquestaexperiènciahaestatreconegudaambunaccèssitalpremiMariaAntòniaCanals 2014convocatperlaFeemcat,conjuntamentamblaSBM-Xeix,laSEMCVAl-Khwaritzmiila SCMenlacategoriad’ensenyamentsecundari,atorgatel4d’octubrede 2014.

Enaquestsmoments,apeticiód’enSergiMuria,estàpendentl’adaptaciód’aquestmaterial peralasevaincorporacióal’AplicaciódeRecursosalCurrículum(ARC)gestionatpel CESIRE-CREAMAT.

Descripciódel’experiència

Lamevaideavaserlasegüent:«Intentaréqueelsmeusalumnestreballinambalgunes propietatsgeomètriquesrelativamentcomplexes,aprofitantlespossibilitatsqueensdóna elGeoGebrapersuperarlesdificultatsalgebraiquesiutilitzantunacol·lecciódeproblemes produïtsalPerú,presentant-losdemaneraoriginalal’estildels sangakus japonesos,ihofaré enunformatmotivadorcomésunconcurs».

Què son els? sangakus

Els sangakus sóntauletesdefustaquecontenienproblemesmatemàtics,generalmentbasats enlageometria,queespenjavenalssostresdelstemplesbudistesidelssantuarissintoistes alJapódel’èpocaEdo(1603-1867).

Construcció de les tauletes: una mica de bricolatge

Uncopvaigtenirclaralaideaihaviatriatelsproblemesd’acordambelscriterispedagògics queexposarémésendavant,elquecaliaeraintentargenerarunmaterialatractiuioriginal presentatd’unamaneradiferentiquepermetésjustificarelreferentdels sangakus.

Perfer-ho,emvancaldreunsquantsmaterialssenzills,queespodentrobarambfacilitat,i unamicadebricolatge(alqualnosócespecialmentaficionat).

Figura1.Unexemplede sangaku clàssic.

Elresultatvanserunestauletesprouconvincentsique,uncoppenjadesalsostredelpassadís del’escola,vancontribuirforçaaengrescarelsalumnes.

Posada en escena

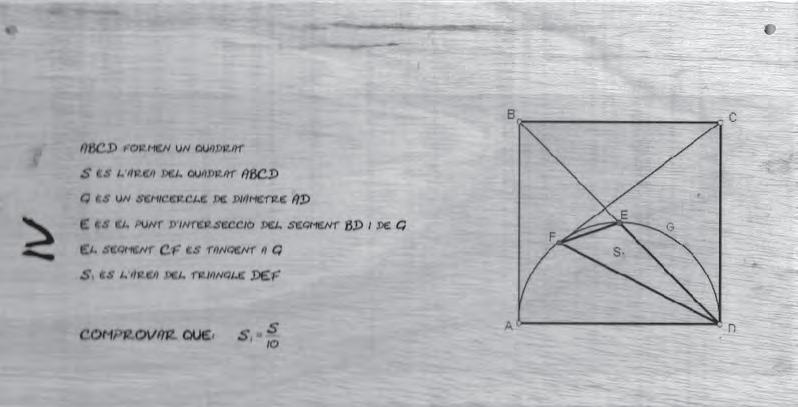
Vaigpenjardelsostrelestauletesdefustaambels sangakus,alpassadísdebatxillerat,d’una maneravolgudamentirregular,pertalquedonessinunaambientacióquepoguésferpensar encomesdevienveureelsoriginalsenunsantuarisintoista.

Unfetmoltimportantpercontribuiracrearexpectacióvasereldemuntarlainstal lacióun divendresalatarda,quanelsalumnesjahavienmarxat.D’aquestamanera,quanvanarribar dillunsesvantrobarelpassadíscanviat,comperartdemàgia.

Noemvaigidentificarcoml’autordelmuntatgenivaigexplicar-neelmotiufinsaúltimahora delmatí.D’aquestamanera,elsalumnes imoltsprofessors vanpassar-seelmatíintrigats ifenthipòtesis(sospitantdemi,peròsenseentendreaquètreiacaptotplegat).Crecqueés difícilaconseguirméspredisposicióireceptivitatperpartdelsalumnesambunaestratègia mésconvencional.

Enelmomentd’explicarelsignificatdelmuntatge,vaigferpúbliqueslesbasesdelconcurs tantencartellscomenformatweb,onelsalumnespodienconsultarambméscomoditatels enunciatsdelsproblemes,ivaigresoldrepersonalmentaclassealgunsexemplesextrade sangakus perdonarorientacions.

Lestauletesesvanestarbenbédosmesospenjadesdelsostre.Durantaquesttemps,els alumnesquevolienjaestavenmirantderesoldreelsproblemesplantejatsi,pertant,hihavia detantentantconversesentreellssobreeltema.

Figura2.Unexempledels sangakus utilitzatsalconcurs.

Bases del concurs

• Alllargdelcurs 2012-2013esportaràatermeunconcursderesolucióde sangakus amb elGeoGebraentrel’alumnatdematemàtiquesdeprimerdebatxilleratdelcentrequehi vulguinparticipar.

• Resoldrecorrectamentun sangaku proposats’enténcomconstruirambelGeoGebraun applet dinàmicquedonirespostaalapreguntaplantejadaique,enmoureelsseusdiversos elements,mantinguiconstantlapropietatcomprovada.

• Elconcursconstaràdeduesfases.

Enlaprimerafaseesplantejarancinc sangakus. Persuperaraquestaprimerafase,caldràlliuraralmenysquatre sangakus resoltscorrectamentenelterminid’unmes.

Qualsevolalumnequecompleixielsrequisitsanteriorsesclassificaràautomàticamentper alasegonafaseirebràundiplomadefinalista.

Lasegonafasedelconcurstindràllocenunasessiópresencial.Enaquellmomentes plantejarandos sangakus.

Elsilesprimeresalumnesquelliurincorrectamentresoltcadascundelsdos sangakus proposatsrebranrespectivament 10,5i3punts.Esproclamaràguanyadoroguanyadora delconcursl’alumneoalumnaamblapuntuaciótotalmésalta.Encasd’empat,es proposaràuntercer sangaku iesproclamaràguanyadoroguanyadoraelprimerola primeraalumnaqueellliuricorrectamentresolt.

Exemples utilitzats

Unelementfonamentalpertalqueaquestainiciativanotansolstinguièxit,sinóque simplementtinguisentit,resideixenunacorrectaselecciódelsproblemesaplantejar, aplicantuncriteribàsic:«Elsproblemesplantejatshandeconsistirenlacomprovacióde propietatsgeomètriques,relativamentcomplexes,queespuguindeduird’unamanera unívocaapartirdepocsobjectesinicialsiderelacionselementalsentreellsiqueespuguin posardemanifestutilitzanteinesdelGeoGebraqueelsalumnesconeguin».

Acontinuacióesmostrenalguns sangakus utilitzatsenelconcurs,amblanumeració corresponentalacol·lecciódelaqualprovenen,delwebGoGeometry.

Problema#112

ABCD formenunquadrat

S ésl’àreadelquadrat ABCD

G ésunsemicercledediàmetre AD

E éselpuntd’intersecciódelsegment BD ide G

Elsegment CF éstangenta G

S1 ésl’àreadeltriangle DEF

Comproveuque: S1 = S 10

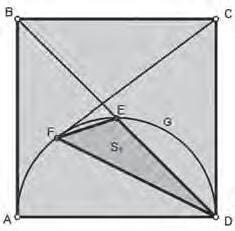
Problema#164

ABCD formenunparal·lelogram

E ésunpuntqualsevoldelsegment BC

S ésl’àreadeltriangle AFD

S1 ésl’àreadeltriangle BFE

S2 ésl’àreadeltriangle CDE

Comproveuque: S = S1 + S2

Resultat del concurs

D’unapoblaciótotalde 26alumnes, 14(un54%)vanparticiparalconcursitotsvanpresentar lesrespostescorrectesalscinc sangakus plantejatsalaprimerafasedinsdelterminiestablert.

Totiquelarestad’alumnesnoesvaanimaraparticipardirectamentenelconcurs,síque vanviureaquellsdiesl’activitat,vanveureelsexemplesquevaigresoldreaclasseienalguns casosvandiscutirambelsseuscompanyslesestratègiesderesolució.

Conclusions

Lesconclusionsqueheextretd’aquestaexperiènciaparlenespecialmentdel’aspecteclau:la motivació,tantladelsmeusalumnesengrescatsmirantderesoldreproblemescomlameva sentintlessevesdiscussionscomparantlesdiferentsestratègiesperresoldre’ls.

• Elquehanobtingutelsmeusalumnes:

Enprimerlloc,iprobablementelmésimportant,s’hohanpassatbétreballantproblemes dematemàtiques.

Peralagranmajoriad’alumnesharesultatunasorpresadescobrirl’enormequantitat depropietatsgeomètriquesqueespodenobtenirapartird’elementssenzills.

Elsalumnesmésbrillantss’hansentittemptatsademostraralgunesdelespropietats queanavencomprovant,cosaqueambmajoromenorèxithanaconseguitenalguns casos.

Algunsalumnesgeneralmentpochàbilsambl’àlgebras’hansentitmotivatsaparticipar ienalgunscasoshanestatcapaçosderesoldreelsreptesplantejats,laqualcosaelsha suposatunreforçpositiud’autoestimamatemàticaquegeneralmentnotenen.

Elsalumneshanmilloratsensdubtelasevahabilitatiseguretatenl’úsdelGeoGebra ihandemanatofinsitothaninvestigatpelseucomptealtreseinesipossibilitatsdel programa.

Larevisióperpartdelsalumnesd’alguneserradescomeses,aixícomlacercadela millorestratègiaperresoldrecadaconstrucció,elshaajudataserautocríticsambles sevesproduccions.

• Elqueheobtingutjo:

Enprimerlloc,iprobablementelmésimportant,m’hohepassatbéplantejantproblemes dematemàtiques.

Heaconseguitfervisibleslesmatemàtiquesiprovocarcuriositatenalumnesicompanys declaustrepocpredisposats,superantelrebuiginicialqueaquestadisciplinaprovoca enmoltespersones.

Hepogutintroduiralgunsreferentsd’històriadelesmatemàtiquesquehanobert debatsiquehanportatatreballarenaltresmomentsapartirdematerialsaudiovisuals diversos.

Hepogutdonarunvalorforadel’àmbitestrictamentacadèmicalraonament,elrigori l’autocríticacomaeinesfonamentalseneltreballmatemàtic.

Hepogutpresentarpropietatsgeomètriquescomplexesd’unamaneraquehagenerat receptivitatperpartdelsalumnesiqueelshaportataimplicar-sepersonalmentenla sevaresolucióiasuperarl’habitualactitudpassivaquemostrenenmolscasos.

Sensecapdubte,undelsmillorsindicadorsdel’èxitd’unainiciativacomaquestas’obtéquan elsalumnes,comenaquestcas,etdemanen:«L’anyqueveenfaremunaltre?».

Bibliografia

Bujosa,J.,Giménez,C.(2013).ResolucióngráficadesangakusconGeoGebracomorecursoparatrabajarlageometríaplana. XVIJAEM.Llocweb:http://prezi.com/n6wspao8cnpj [Consulta: 20 dejuliolde 2014]

Giménez,C.(2012).PrimerCampionatderesoluciódesangakusambelGeoGebra.Col legi SantGabrieldeViladecans.Llocweb:http://carlosgimenez.info/sangakus[Consulta: 14de juliolde 2014]

(2013).ConcursderesoluciógràficadesangakusambelGeoGebra.VJornadesdel’AssociacióCatalanadeGeoGebra.Llocweb:http://prezi.com/jealiy24dwki[Consulta: 21 dejuliolde 2014]

Gutiérrez,A.(2008).Fromthelandoftheincas.LlocwebGoGeometry:http://www. gogeometry.com[Consulta: 12 dejuliolde 2014]

Hohenwarter,M.(2005).LlocweboficialdeGeoGebra:http://www.geogebra.org/[Consulta: 14dejuliolde 2014]

Nolla,R.(2009).Sangakus.Contemplacióiraó.Llocwebde.XTEC:http://www.xtec.cat/~rnolla/ Sangaku/Sangakus3b.pdf[Consulta: 23dejuliolde 2014]

seccions seccions rcions

JordiDeulofeu

DepartamentdeDidàcticadelesMatemàtiques idelesCiènciesExperimentals UniversitatAutònomadeBarcelona jordi.deulofeu@uab.cat

EncaraquefauntempsvaigdedicarunarticleaMartinGardner,nopucevitardefer-hi referèncianovament,atèsquementreescricaquesteslíniess’estàcelebrantelcentenari delseunaixement(Tulsa,Oklahoma, 21 d’octubrede 1914)itantarreudelmóncomenel nostreentorns’hanprogramatnombrososactes,entreelsqualslamatinalcelebradaalaseu permanentdeCornellàdeLlobregatdelMuseudeMatemàtiquesdeCatalunya,eldissabte 25d’octubre,laxerradaquejomateixvaigtenirelgoigdeferenla XVIITrobadad’ABEAM, el8denovembre,olaqueféuaVilanovailaGeltrú,enunadataproucuriosa: 14-11-14,el professorPedroGonzálezUrbaneja,dinselmarcdelsberenarsmatemàticsqueorganitzen elsamicsdelGarraf.

Tanmateix,nousproposaréproblemesextretsdelaimmensaobradelquifouelmésgran divulgadordelesmatemàtiquesdelseglexx.Tansolsusrecomano,tantaaquellsquija coneixeuMartinGardnercomalsquivoleuapropar-vos-hiperprimeravegada,l’excel lent monogràficdelarevista InvestigaciónyCiencia,edicióespanyolade ScientificAmerican,la revistaenlaqualGardnerpublicàd’unamaneraininterrompudadurantvint-i-cincanys (1956-1981),iqueportapertítol: EluniversomatemágicodeMartinGardner.Juegos,acertijos, paradojasyotrasmaravillasrecreativas.Hitrobareuelprimerarticlequevaescriureperala revista(desembrede 1956),aixícomalgunsdelstextosmésrellevantsquehivapublicar. L’editord’aquestamonografiaigranconeixedordeGardner,FernandoBlasco,titulaelseu articleintroductoriambunafrasequedefineixperfectamentelqueaquestgrandivulgador vaaconseguir:«MartinGardner,elhombrequeconvirtióamilesdeniñosenmatemáticosy amilesdematemáticosenniños».

SeguintlaideadeGardner,queconsisteixaanardelsimplealcomplex,començaremla propostadeproblemesambalgunesqüestionssenzilles,peròquefan«pensar»unamica,ja quenosempre,niperatothom,sónderesolucióimmediata.Sónpetitsproblemesadequats peraalumnesdesecundària.Elsdosprimersesvanproposaralsberenarsmatemàtics celebratsaVilanovailaGeltrúelmesdenovembredel 2014.

Problema1. Quinéselnombreenterpositiuméspetittalquelasumadelessevesxifres és 2014?Éssorprenentcomunasenzilladivisióenteraensdónatotalainformaciópera obteniraquestnombre.Tésentitfer-selamateixapreguntasiconsideremelconjuntdels nombresenters?Ipreguntar-sepelnombremésgran?

Problema2. Unabótaesplenadevi.Omplimunagerraambvidelabótaisubstituïmla quantitatextretaperunaquantitatiguald’aigua.Repetimelprocéscincvegadesdemanera quealfinallaquantitatd’aiguaalabótaéslameitatqueladevi.Siarabuidemlabóta, quantesgerresnecessitaremperomplir-la?

Seguiremambunsaltresdosproblemes,senzillscomelsanteriors,peròlaresoluciódels qualsrequereixunamicamésd’atenció.Elprimerésdepercentatges,untemaquesempre generaproblemescuriosos,interessantsdeplantejaralsalumnesiambelsqualscalanaramb compteal’horaderesoldre’ls.Tantaquestproblemacomelsegüent,uncuriósplantejament sobrelespuntuacionsd’untorneig,me’lshaproposatl’amicJoanMiralles,delaUniversitat PompeuFabra.

Problema3. Unasíndriade6kgcontéun 94%d’aigua.Desprésdedeixar-launeshoresal sol,téun 90%d’aigua.Quantpesaaralasíndria?

Avegadeshihaproblemesque,desprésdellegir-los,semblaqueensfaltiinformacióper poderrespondreelqueensdemanen,obéquelamaneradetrobarlasolucióésmolt complicada.Aixòéselquesemblaquepassaambelproblemasegüent,peròsipenseuuna micaveureuquetoteraunmiratgeiqueespotresoldred’unamanerasimpleielegant.

Problema4. Elcentrehaorganitzatuntorneigd’escacsambunbonèxitdeconvocatòria, ienLluíss’hihaapuntat.Cadajugadordisputaràunapartidacontracadascundelsinscrits, excepte,òbviament,contraellmateix.Elguanyadordelapartidas’anotaunpunt.Sienuna partidaesfantaules,cadajugadors’anotamigpunt.Alfinaldeltorneigresultaque,sense comptarenLluís,larestadejugadorss’hananotatuntotalde 99 punts.Quantsjugadors s’havieninscritaltorneig?QuantspuntshaaconseguitenLluís?

Elmesdejuliolde 2014esvacelebraraBarcelonal’edicióvint-i-cinquenadel’Olimpíada matemàticaperalspetits,organitzadaperlaFEMCAT,ienlaqualvaigtenirl’oportunitatde participar,primerproposantproblemesperalaprovaindividualielsdiesdelconcursjaamb elsparticipants,unsseixantaestudiantsprovinentsdetotl’Estatespanyol,enunasessióque vamferunanitd’estiu,desprésdesopar,al’albergMaredeDéudeMontserratdelbarride VallcarcadeBarcelona,ons’hostatjaven,analitzantidiscutintlesresolucionsdelsdiferents problemesdelaprova.Unavegadamés,vaigquedarmeravellatdelesdiversesienginyoses solucionsqueaquestconjuntd’alumnesambtalentmatemàticvansaberdescobrir,ide comesfeiarealitatlacitaciódePólya:«[peraaprendrematemàtiques]ésmillorresoldreun problemadecincmaneresdiferentsqueresoldre’ncinc».

Enrecordd’aquestavetlladatanespecialusproposoundelsproblemesdelaprova.Estracta d’uncasdegeometriaqueheud’intentarresoldrepermètodesgeomètricselementals,ien totcas,sensenecessitatdeplantejarcapsistemad’equacions.L’enunciatéselsegüent:

Problema5. Enunrectangledecostats a i b dibuixemunadiagonaliunsegmentque uneixunvèrtex,quenoésenladiagonal,ambelpuntmitjàd’uncostatoposat(vegeula figura).Elrectangleinicialquedadividitenquatrefigures,trestrianglesiunquadrilàter.Quina ésl’àreadecadascunadelesquatrefigures?Podeuexpressarcadaàreacomunafraccióde l’àreadelrectangleinicial.

Elproperproblema,queemvaproposaren XavierValls,téuncairegeomètriccoml’anterior, encaraqueenlasevaresolucióelsnombresilessevespropietatsjuguenunpaperrellevant. Compassasovint,lesrelacionsentrearitmèticaigeometriaensajudaranatrobar-nela solució.

Problema6. Posemunabolaalcentred’unatauladebillarquemesuradosmetresde llargperund’ample.Llancemlabolademaneraquevagirebotantpelscostatsdelataula.Si labolatornaaseralcentredelataula,perprimeravegada,desprésdeferunrecorregutde 25metres,sabríeudeterminarquantesvegadesharebotatlabolaenelscostatsdelataula debillardurantaquestrecorregut?

Elproblemasegüent,tambédegeometria,me’lvaproposar,enuntreballdeproblemesi recreacionsmatemàtiquessobreLewisCarroll,laSaraCambrón,unaestudiantdemagisteri delamevaassignaturasobrejocsiactivitatsmatemàtiques.Talcomellaexplica,elproblema estrobaenelllibredelreverendCharlesLutwidgeDogson Problemasdealmohada.

Problema7. a)Donatuntrianglequalsevol ABC ,estractadetrobarperonhauremde traçarunaparal·lela(DE )aundelscostatsdeltriangle(BC ),detalmaneraquelasumadeles longitudsdelsdossegmentsdeterminatssobreeltriangleentrelaparal lelaielcostat BC siguiigualalalongituddelcostat BC .Ésadir,volemqueescompleixique BD + CE = BC .

b)Isivolemquelasumadelsdossegmentsanteriorssiguiigualalsegment DE ?

Siensfixemenlasituacióqueenshapermèsplantejarelproblemaanterior,aviatens adonaremqueapartird’unamateixaidea,aparentmentsimple,éspossibleplantejar diversosproblemesdedificultatvariable.Lasituació,podríempensar-laaixí:Tallemun triangleambunarecta(paral·lelaonoaundelscostats).Enelcasdeconsiderarlarecta paral lela,amésdelproblemaanterior,podemplantejarunproblemaclàssic:perontraçarem laparal·lelasivolemquelesàreesdelesduesfiguresdeterminadessiguiniguals?Isivolem queestiguinenunaraódonada?

Apartirdelamateixasituació,podemplantejarunproblema,proposatperPólyaenlaseva obra MathematicalDiscovery,d’unadificultatmoltsuperior,almeuentendre,atotsalsante-

riorsiquebensegurusfaràpensarunamicamésquetotselsaltresjunts.L’enunciatésel següent:Donatuntriangle ABC ,traceuunarecta(quedeterminaelspunts D,sobre AB,i E , sobre AC )detalmaneraqueelssegments BD, DE i EC tinguinlamateixalongitud

Peracabaraquestamiscel làniadeproblemespetitsinotanpetits,nopodiafaltar-neun d’estratègia,prousenzillderesoldre,iquetambévaigproposaralsalumnesdel’Olimpíada. Eljocdiuaixí:

Problema8. a)Jocperadosjugadors.S’escriuendosnombresmenorsque 100 enun fulldepaper:perexemple,35i 24.Elprimerjugadorrestaelsdosnombres(sempreelgran menyselpetit)ianotaelresultatenelpaper.Araelsegonjugadortriadosdelstresnombres escrits,elsrestaianotaelresultatenelmateixpaper.Eljocsegueixdemaneraque,encada jugada,esrestendosnombresprèviamentescritsis’anotaunnounombre.Sempreesfala restademaneraqueelresultatsiguiunnombrepositiu.Noéspossiblerestardosnombres sielresultatésunnombrequejaestàescrit.Eljugadorquenopotescriurecapnounombre perdlapartida.Quinjugador,elprimeroelsegonajugar,téavantatge?Coms’hadejugar perguanyar?

b)Generalitzeueljoc,ésadir,determineu,peradosnombresqualssevol,quiguanyaicom s’hadejugarperafer-ho.

Acabarél’articleamblabonicadedicatòriaqueMartinGardnerfaal’inicidelseullibre Gardner’sWorkout.TrainingtheMindandEntertainingtheSpirit.Diuaixí:«Toalltheunderpaid teachersofmathematics,everywhere,wholovetheirsubjectandareabletocommunicate thatlovetotheirstudents».Bensegurqueelslectorsdel NouBiaix ustrobeuentreels dedicataris.Quesiguiaixípermoltsanys.

Bibliografia

Carroll,L.(2005). Problemasdealmohada.Madrid:Nivola.

Gardner,M.(2001). Gardner’sWorkout.TrainingtheMindandEntertainingtheSpirit.Natick, Mass.:A.K.Peters.

(2014).EluniversomatemágicodeMartinGardner.Juegos,acertijos,paradojasyotras maravillasrecreativas.Selecciód’articlesipresentaciódeFernandoBlasco.Investigacióny Ciencia.Temas,77,tercertrimestrede 2014.

Pólya,G.(1981). MathematicalDiscovery.NovaYork:J.Wiley&Sons.

construint construint

AntonAubanell claudio.alsina@upc.edu

Avegadessemblaquelesactivitatsd’experimentacióielsmaterialsmanipulablessón especialmentadequatsperal’educacióinfantiliprimària,peròquejanohosóntantpera l’ESOoelbatxillerat,comsilaprogressivanecessitatdecultivarl’abstracciós’adiguéspoc ambl’úsdematerialsenl’aprenentatge,comsil’abstraccióielsmaterialss’excloguessin mútuament.

Probablementpodríemdiscutirsilesmatemàtiquessónonounaciènciaexperimental,però l’educaciómatemàtica,elprocésdeconstrucciódelconeixementmatemàtic,síquehauria detenirunimportantcomponentexperimentalenqualsevoldelesetapeseducatives,desde l’educacióinfantilfinsalaformacióuniversitària.Ésinnegableelbeneficidel’úsdematerials manipulablesenlesprimeresetapeseducatives(MariaMontessorideiaque«elnentéla intel ligènciaalesmans»),peròtambésemblaclarquelesactivitatsd’experimentació(sigui ambmaterialsmanipulables,siguiambeinestecnològiquescomelGeoGebra)podenfer excel lentscontribucionsencursosmésavançatstantperalaintroducciód’ideescomper alasevaaplicacióconcreta.Ensónexemplesalgunesexperiènciesclauenelcampdeles còniques(construccióambreglesifils,doblegantpaperiambeinesdegeometriadinàmica, estudidelespropietatsfocalsambelsrebotsd’unlàser...),l’experimentacióidescobertade determinadesrelacionsengeometriaplana,eltreballsobreladistribucióbinomialmitjançant lamàquinadeGalton,lesactivitatsdeprobabilitatgeomètricabasadesenelllançamentde monedessobretramats(lesmonedesdeBuffonilessevesvariants)oelsmodelsmaterials peral’estudidelaregressiólineal.Entotsaquestscasos(ienmoltsd’altresqueespodrien citar),elsmaterialsnotansolsserveixenperamotivariintroduirconceptes,sinóqueobren portesiconvidenal’aprofundiment.

L’essencialcomponentabstracteiformaldelconeixementmatemàticnoexcloulapotència delsuportexperimentalniescontraposaalaintuïcióial’experiènciadelconcret.Ben alcontrari,elsmaterialsmanipulablesil’abstracciópodensergransaliats,especialment

ensituaciód’aprenentatge.Lesactivitatsexperimentalsambmaterialsenspodenajudara construirideesabstractesiadonar-hiunmajorsignificat.Lesideesabstractespodenobrir novesperspectivesenlamiradaquefemsobreunobjecte,unaexperiènciaounasituació concreta.GeorgePólya1 citalafrasedeKant«Totconeixementhumàcomençaambintuïcions, continuaambconcepcionsifinalitzaambidees»(I.Kant: Críticadelaraópura)ienfalalectura didàcticasegüent:«L’aprenentatgecomençaambaccióipercepció,continuaambparaules iconceptes,ihadefinalitzarambhàbitsmentalsdesitjables.[...]‘‘Accióipercepció»ushan desuggerirmanipulariveurecosesconcretescompedres,opomes,oregletsCuisenaire;o regleicompàs;oinstrumentsenunlaboratori’’.Avegades,eneducaciómatemàtica,alguns temess’hanplantejatentermesd’exclusió(experimentació versus abstracció,intuïció versus formalisme,materials versus TIC,calculadora versus càlculmental...)enllocdeplantejar-seen termesd’integració,decomplementarietat,dereforçamentmutu.Potserel versus anglosaxó, ambunsentitdecontraposició,s’hauriadesubstituirpel versus originalllatíambunsentitde moviment,d’avenç vers algunacosa.Encadascundelsexemplesques’hanapuntat,undels dostermespotcontribuiraavançarcapal’altre,areforçar-lo,aconsolidar-lo.

Unexempled’aquestacomplementarietatenl’educaciómatemàticaentrel’experimentació ambmaterialsil’abstraccióésl’activitatoriginaldePerePuigAdamqueesdescriutotseguit iquevaigconèixergràciesaJosepRey,quel’estavatreballantambelpropòsitdeconvertir-la enunmòdulperalMuseudeMatemàtiquesdeCatalunya(MMACA).Estractad’unaproposta quejaapareixenelllibre Didácticamatemáticaheurística dePerePuigAdam(1956)coma based’unalliçóqueelltitula«Iniciaciónalcálculoconirracionalescuadráticos».Tambélava publicarelmateixanyalarevistabelga Mathematica&Pedagogica (núm. 10).

Repartimentreelsalumnesunbonnombredepecestriangularscomladelafigurablava (trianglesrectanglesisòsceleselcatetdelqualsmesuraunaunitat)ipecesròmbiquescomla delafigurataronja(rombesdecostatunitatialtura √2 2 ):

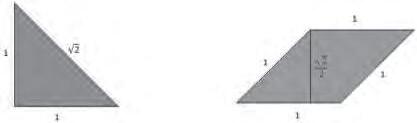
D’entrada,convémanipularlespeces,moure-les,comparar-les.Despréspodempreguntar alsalumneselsvalorsdelsperímetresd’aquestesfigures,delsseusanglesinteriors,deles sevesàrees...Veuremquel’àreadeltriangleval 1 2 iladelrombeval √2 2 unitatsquadrades. Aixòseràimportantmésendavantenl’activitat!

Convidaremelsalumnesaconstruir,ambaquestespeces,figuresdiversesi,uncopens hauremfamiliaritzatambelmaterialihauremconstruïtpetitsmosaics,espotplantejarla preguntasegüent:«Seriapossibleconstruirunafiguraformadatansolspertrianglesque tinguéslamateixaàreaqueunafiguraformadatansolsperrombes?».Ladescobertaqueaixò ésimpossibleesderivadelaincommensurabilitatde √2.Unabonicarelacióentrearitmètica

1.G.Pólya,OnLearning,TeachingandLearningTeaching. AmericanMathematicalMonthly,70, 1963, 605-619

igeometria!IencarapodemavançarunpasmésfentdescobrirelquediuPuigAdam:«L’àrea detotafiguracompostadetrianglesiderombestindràunapartracionalprocedenttansols delstrianglesiunapartirracionalprocedenttansolsdelsrombes».

Acontinuació,mostremalsalumnesunquadratformatperunacombinaciódetrianglesi rombescomeldelafigurasegüent,extretadelmateixllibredePuigAdam.

Tapemimmediatamentaquestmosaicquadratdeixanttansolsaldescobertunapetitafranja enundelscostats,comenlafigurasegüent.

Ipreguntem:«Observanttansolsaquestapetitabandadelmosaic,podríemdeduirquants trianglesiquantsrombeselcomponen?».Semblaunapreguntaagosaradaamblapetita informaciódequèdisposem!

Observantlaimatge,deduiremquelamesuradelcostatdelquadratés4+ 2√2.Elcàlculde l’àreaésunexerciciaritmètic:

Apartird’aquí,elraonament,emprantlesdeduccionsfetesenlesexploracionsinicials,és moltelegant:

• Lapartracionaldel’expressiódel’àreaesdeuràalstrianglesquetenenàrea 1 2 ,de maneraquenecessàriamenthihauràd’haver48triangles.

• Lapartirracionalprovindràdelsrombesquetenenàrea √2 2 ;pertant,hihaurà32 rombes.

Éssorprenentque,gràciesalaindependènciadelapartracionalidelapartirracionalde l’expressiódel’àrea,coneixenttansolsunapetitafranjaenundelscostatsdelquadratn’hem pogutdeduirtotalacomposició.

Raonamentssemblantsespodenrepetirambdiversosmosaicsquadratsqueconstrueixin elsalumnesitambéambmosaicsrectangulars(enaquestcas,peresbrinarelnombrede pecesdecadatipus,caldràconèixertantlabasecoml’altura).Semprepodremdeduir(sense veure-ho!)elnombredetrianglesielnombrederombesquehihaencadacomposició.Es tractad’unainesperadaaplicació,enelcampdelageometria,delaseparacióentrelapart racionalilapartirracionald’unaexpressióaritmètica.

Sobrel’origend’aquestaactivitat,PerePuigAdamafirma:«Laincommensurabilitatdeles àreesd’aquestespecesemsuggeríunalliçóactivasobreirracionalsquadràticsielseu càlcul».Estractad’unexempleperfecteperil·lustrarelfetquecomentàvemalprincipi: malgratserunaactivitatd’experimentacióambmaterials,niéselementalenelnivellenquè ésadequadaniestàallunyadadel’abstracció.Benalcontrari,permetapropar-nos,d’una manerapràcticaiambunpuntdesorpresa,aaspectestanprofundscomlairracionalitat de √2 ilaincommensurabilitatd’unamagnitudrespected’unaunitat.Lageometriaiels nombrestenenaquíunesplèndidatrobada!

Precisamenttrobemaquestespecesenunmosaicdel’ermitadeSantCristinadeLloretde Mar,comhomostralafotografiasegüent.2

Enaquestmosaics’hipodenobservarquadratsdecostat4+ 2√2 que,amés,tenenuna configuracióbendiferentdeladelquadratquemostraPuigAdam...perònopodriaserd’altra manera,jaquetenenelmateixnombredepecesdecadatipus!Unmagníficenllaçcontextual peral’activitatdescrita!

Ambcompanysmatemàticscomentàvemaquestaactivitattotdinantenunrestaurantde Barcelonaquanvam«descobrir»queelmosaicquetrepitjàvemtambéoferiaunaoportunitat excel·lentpertreballarideesmatemàtiques(vegeulaimatge).

2.FotografiafetaperSílviaMargelí.

ConstruiraquestmosaicambGeoGebra(vegeulafigurasegüent)ésunabonamanera decomprendrelasevaestructura.Prenentelcostatdelquadratblaucomaunitat,amb raonamentsgeomètricsfàcilsibonicspodremdeduirelscostatsilesàreesdelescincfigures queformenelmosaic:quadratspetits(comeldecolorblau),decostat 1 unitatid’àrea 1 unitatquadrada;rectangles(comeldecolorgris),decostats 1 i 2 unitatsid’àrea 2 unitatsquadrades;trapezis(comeldecolorvermell),decostats 2, 1, 1 i √2 unitatsid’àrea 1,5unitatsquadrades;quadratsgrans(comeldecolortaronja),decostat √2 unitatsid’àrea 2 unitats quadrades,iromboides(comeldecolorverd),decostats 1 i √2 unitatsid’àrea 1 unitatquadrada.

Aquestarelacióentrelaunitati √2 quehemobservattantenelmosaicdePuigAdamcomen eldelterradelrestaurant,tambélatrobemd’unamaneraevidentenlesrajolesdecartabó: lestradicionalsrajolesquadradesdivididesperladiagonalenuntrianglegrociundeverd. Fapoc,laSílviaMargelíemvaferarribarunmagníficrecursdidàctic:unaabundantcol lecció derajolesdecartabódeceràmicaenminiaturaperpoderemprarcòmodamentaclasse(5cm decostat).Apartird’unmotiumoltsimple,ambaquestesrajolesespotcrearungrannombre demosaicsenelsqualsésfàcilidentificarlestransformacionsgeomètriquesimplicades (isometries:translacions,simetriesigirs)oferintunmuntd’oportunitatsdetreballaclasse inventant,reproduintianalitzantmosaics.Sorprènl’abundànciadepossiblescomposicions queofereixenaquestesrajoles.Enlesquatrefiguressegüentsse’npresentenalgunes.

L’elementdel’ARC«Femunterraderajoles(ambGeoGebra)»,deBernatAncocheaiIsabel Sorigué,faunamagníficapropostapertreballarambunaversiódigitald’aquestesrajolesa l’educacióinfantil(http://apliense.xtec.cat/arc/node/1319).

ElMMACAtéunmòdulambquatrerajolesdecartabóformantunquadratsituatentredos mirallsparal lels,commostralafotografia.Observantlaimatgequeesprodueixsobreun d’aquestsmiralls,fruitdesuccessivescomposicionsdesimetries,descobriremunasanefa infinital’estructuradelaqualdepèndecomposemlesquatrerajoles«reals».Siposemquatre miralls,unacadacostatdelquadrat,obtindremunmosaicques’estendràcapal’infinit.No ésdifícilreproduiraquestaexperiènciaal’escola.

Ésfreqüentobservarlesrajolesdecartabóenladecoraciód’espaispúblicsoprivats.Així,per exemple,lestrobemenelmagníficmosaicdelperímetredelpatídelaCasadeConvalescència (partdel’anticHospitaldelaSantaCreuaBarcelona,seglexvii),seudel’Institutd’Estudis Catalans,oenelsbancsdelPasseigMarítimdeSitges,sobreelsqualshihaunainteressant propostad’activitatalblocPuntMat(http://puntmat.blogspot.com.es/2012/04/bancs-delpasseig-maritim-de-sitges.html).

Malgratquenoésintenciód’aquestescritferunadescripciógeneraldel’úsdelsmosaics enl’ensenyamentdelesmatemàtiquesiobrintlaperspectivaatotamenademosaics,és imprescindibleesmentarlesideesdetreballsobresanefesimosaicsqueapareixenenelllibre PasseigmatemàticperCatalunya deTeresaTicó,lesproposesdeJoséAntonioMorasobre mosaicsemprantGeoGebra(http://jmora7.com)ilesqueesdescriuenendiversoselements del’ARC.

Lesactivitatsques’hancomentatmostrenquel’experimentacióambrecursosmaterialspot fer-seenqualsevoletapaeducativaique,atravésseu,podenposar-seenjocaspectes profundsdelamatemàtica.ElprofessorisraeliàAbrahamArcavi,enuncicledeconferències organitzatpelCREAMAT,vaafirmar:«Lavisualitzaciónoésunguarniment,sinóunamanera depensar».Potserpodríemferunaafirmaciósemblantambreferènciaal’experimentació ambmaterialsmanipulables.Elsrecursosmaterialsnosónfrivolitatsnitrivialitzacions,són instrumentspotentspercomunicariperconstruirqueconvidenalareflexióiquepermeten treballarideesdefons!Peraixòencapçalàvemaquestescritambeltítol«Materialsper construirmosaics...imatemàtiques!».

mmaca el racó del mmaca

VariacionssobreFibonacciielnombred’or

JosepRey,ManuelUdina

Enaquestarticlevolemreferir-nosaalgunsdelsmòdulsdelesexposicionsdelMuseude MatemàtiquesdeCatalunya(MMACA)relacionatsambFibonacciielnombred’or.Enalguns casosestractademòdulsinteractius,iend’altres,d’informacióqueespresentaenelspòsters del’exposició.Pensemqueelsunsielsaltrespodenaportarideesperalpossibletreballa classed’aquestatemàtica.

LasuccessiódeFibonacci

LasuccessiódeFibonaccitél’origeneneltractat Liberabaci deLeonardodePisa(1170-1250), conegutcom Fibonacci.

Enaquestllibreplantejalasuccessióques’obtéapartirdel«problemadelsconills»:«Unhome vaposarunaparelladeconillsenvoltatspertotselsllocsperunaparet.Quantesparelles deconillsespodenproduirapartird’aquestaparelladurantunanysisesuposaquetots

elsmesoscadaparellaengendraunanovaparellaiquenomésespodenreproduirdesdel segonmes?».

Aquestproblemaespotil·lustrarambl’esquemasegüentenquècadacerclesignificauna parelladeconills,enblancperalaparellajoveiennegreperaquanjaespotreproduir. 1213581321

Cadacolumnarepresentaunmes.Elnombredeparellesquetenimcadameséslasuccessió deFibonacci,enlaqualespotobtenircadatermedemanerarecursivafentlasumadelsdos anteriors:

Siperveurelaproporciódecreixementdelnombredeparellesdeconillsmesames, dividimlesd’unmesperlesdelmesanterior,obtenimresultatsdiferents,peròcadavegada s’assemblenmésitendeixenalnombre

anomenatnombred’oroproporcióàuria:

Sivolemcalcularaquestlímit,veiemque an+1 an = an + an 1 an = 1 + an 1 an = 1 + 1 an an 1

Araobservemquetantéslímitd’aquestasuccessióellímitde an+1 an comellímitde an an 1 (untermedividitpelseuanterior).Així,

(considerantnoméslasoluciópositiva).

RectanglesdeFibonacci

SiconstruïmrectanglesambcostatsdenombresconsecutiusdelasuccessiódeFibonacci,la proporciódelsseucostatss’aproximacadavegadamésalaproporcióàuria Φ.

Aixòhopodemexperimentarenunmòdulfísicdel’exposició.

Partimdelfetquesisobreposemdosrectanglessemblantsfentcoincidir,perexemple,dos costatsielvèrtexinferioresquerre,lesdiagonalscoincideixen.Justamentsihomiremcomen unsistemadecoordenadesamborigenenaquestvèrtexcoincident,elpendentdelarecta corresponentaladiagonaldelsrectanglesésaquestaproporció(defet,segonssihemposat aquestsrectanglesenposicióverticalohoritzontal,elpendentseràaquestaproporció Φ ola fracciórecíproca 1/Φ).

Elmòduldisposad’untaulerambdoseixosdecoordenadesenelquals’handibuixatles rectesy= Φx i y =(1/ Φ)x ,id’unsquantsrectanglesquetenenpercostatselsdelasuccessió deFibonacci.Espotanarcomprovantcom,amesuraqueavancemenlasuccessió,cada vegadaméselvèrtexlliuredelrectangles’ajustaaunadelesduesrectes(segonsqueposem elcostatllarghoritzontalovertical).

L’espiraldeFibonacci

UnarepresentacióambrectanglesdelasuccessiódeFibonacciensvadonant,encréixer, unaaproximaciócadacopmésajustadadelrectangleauri.Presentemunmòdulenquèels successiusquadratssónpecesdefusta,i,apartirdelsdosquadratsinicials,espodenanar afegintquadratsfinsaobtenirunrectanglemoltpròximalrectangleauri.Amés,encadaun d’aquestsquadratshihagravatunquartdecercleque,enferlaconstrucciódelsrectangles, vaconstruintunaespiral,l’espiraldeFibonacci.

Aquestaespiralésunaaproximacióal’espiralàuria,unaespirallogarítmica(lesquedonen unmodeldelcreixementd’algunscaragols)quenoescorrespon,comdevegadesesdiu,a ladel nautilus,ques’aproximaaunadelogarítmicaperònoal’àuria.

Tambéesdisposad’un«compàsauri»(instrumentarticulatquetétrespuntesquesempre estanenproporcióàuria)ambelqualpodemveurecomenelsrectanglesmésgransles midesdelscostatss’ajustenmésimésalaproporcióàuria.

Ambelmateixcompàspodemcomprovarcommoltesmesuresdelcoshumàtambésegueixenaquestaproporció.

Pantògrafauri

Unpantògrafésuninstrumentdedibuixqueserveixperacopiardibuixosaescala.AlMMACA hemoptatperferpantògrafsonelsdosdibuixosjasónfets,l’originalilacòpia,ielvisitant potexperimentarambelseufuncionament.

Enelcasdelpantògrafauri(d’escala 1:Φ),hemoptatperposar-hieldibuixdel’espiralàuria,i amésdeposar-hiaquelldelqualéscòpia,hihemposattambél’anteriordelqualseriacòpia aquest,il’anterior,il’anterior...(mireulaimatge).Elpantògrafserveixperatots.

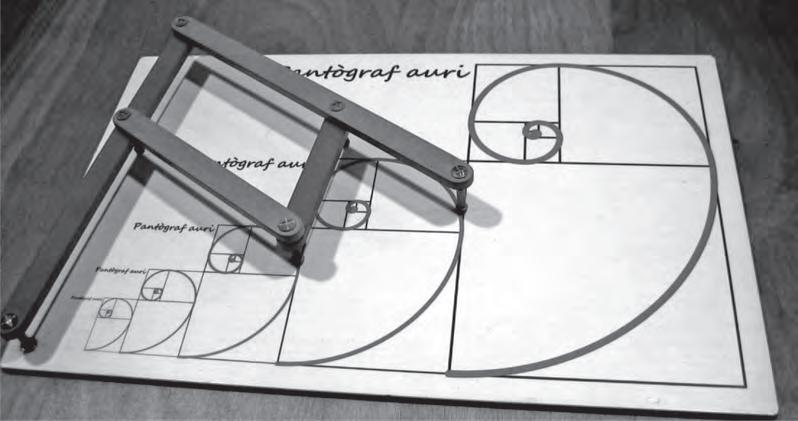
Enrealitat,ésunaprogressiógeomètricadedibuixos,deraó Φ.Comquelesprogressions geomètriquesques’acostumenaestudiarsónnumèriques,podemdirqueelqueespresenta enaquestmòdulésunaprogressiógeomètrica-geomètrica.

Seccióàuria

Estractadedividirunsegmentenduesparts

italcomhemvistabans,

Construcciódelrectangleauriambregleicompàs

Construcciódelrectangleauriplegantpaper

Delrectangleaurialaseccióàuria

Delaseccióàuriaal’angleauri

Lamargarida

Éssabutqueelnombred’oréspresentalanaturalesa.AlMMACAhemvolgutferunmòdul perexperimentar-ho.Hemescollitunamargarida.

Lesflorsacostumenatenirelsseuspètalsbendistribuïtsencercleienmoltscasosels pètalsapareixenensimetriesd’ordre3,4,5...etc.Seguramentaquestasimetriaésundels componentsdelasevabellesa.

Aquestnoéselcasdelamargarida.Defet,noésunaflor.Ésunaflorcompostaielque serienelspètalsenrealitatsónflorsexteriorsquefandepètalsis’anomenenlígules.Amés, aquesteslígulesnoestanrepartidessimètricamentifinsitotesveuendesordenades.Pot semblarqueestanrepartidescaòticament.

Defet,enbotànicas’anomenaanglededivergènciaaquellqueformaunalígulaambla següent(tambés’utilitzaelnomperadesignarl’angleentrebranquessuccessivesd’un arbreoladisposiciódefullesalllargd’unatija).Segonsaquestangle,espodenobtenir diferentsconfiguracions.Perquèladistribuciósiguiòptima,«l’anglededivergènciahauria deserunmúltipleirracionalde360◦ :commésirracionalméseficient.Enteoriadenombres esconsideraqueelnombreauriéselmésirracionaldetotselsnombres»(IanStewart, Deshojandolamargarita, InvestigaciónyCiencia, 222).

Almòduls’hipotveurelafotografiad’unamargaridaambleslígulesnumeradesdemanera quelanúmero 1 éslamésallunyadaila 13éslamésproperaorecent.Hihaunarcquefa 137,5◦ iqueésaproximadamentl’angleauri.Elvisitantexperimentafentlliscaraquestarcal voltantdelamargaridaicomprovantcomapartird’unalígulasempres’arribaalasegüent.

Encasqueesvulguiportaratermeaquestacomprovacióaclasseambl’alumnat,espot ferapartirdefotosfetespelsmateixosalumnesaalgunamargaridaoflorsimilar.Enuna reproducciódemidadinA4ihaventretallatunanglede 137,5◦ enunatransparènciai punxantelvèrtexenelcentredelamargaridaespodenferlesmateixescomprovacions.De fet,ésdivertitdescobrirquinaéslaprimeraiquinaladarrera,jaqueavegadesnoésbenclar. Noméscalanarseguintelprocésfinsquefalli.Aleshores,voldirquelalígulaanteriorerala darreraqueanavabé.Fentelprocésalainversa,s’arriba,arasí,finsalaprimera.

Latargetadecrèdit

Lestargetesdecrèdittenenunesproporcionssimilarsal’àuria.Sibélaintenciódeviaserque fosàuria,esvafixarlanormaambmesuresanglosaxonesambunaaproximacióraonable.

/ 8

Elnombred’orcomafracciócontínua

Comhemvistabans, Φ2 = Φ + 1,dividintper Φ tenim Φ = 1 + 1 Φ ,d’onesdedueixqueel desenvolupamentdelnombreaurienfracciócontínuaserà

Podemcomprovarqueagafantl’aproximaciódonadaperunnombrefinitdefraccions obtenimunadelesfraccionsdeFibonacci.

Impuls:acciód’impel

Estaremtotsd’acordque,detantentant,convéremourelescosesiintroduirnovetatsa l’aula.Sacsejar,niquesiguiunamica,lanostramaneradeferhabitual.Hemvistsovint,il’ús delesnovestecnologiesn’ésunexempleclar,quedevegadeshihacanvismésaparents querealsquefancertaaquellafamosafrasequepronunciavaelpríncepdeSalinaa Il Gattopardo («Sevogliamochetuttorimangacomeè,bisognachetuttocambi»).Elscanvis realspodenvenir,perexemple,demodificaractivitatsquejafemtotreorientantlaforma degestionar-les:canviantexplicacionsperpreguntesodiscussions,noconformant-nosamb la«bondat»delsresultats,mirantsiaqueststenensentitono,fentargumentarcoms’hiha arribat,incloentalguntipusdemanipulaciórealovirtualqueajudiaarribaralesresposteso donantl’oportunitatafer-senovespreguntes.

Peròaquestspetitsogranscanvisnotenenrelaciónomésamblagestiódelesactivitats, sinóquetambéhand’afectarelscontinguts,lasevatipologiaielseuequilibri.Noseriagaire exageratafirmarque,encaraavui,alamajoriadelesnostresaulesesdedicalamajorpartdel tempsal’adquisicióil’entrenamentderutines.Itampocnoseriaexageratdirqueaprimària aquestesrutinesesrefereixenalcàlculnumèriciasecundària,alcàlculalgebraic.Sovint,dela geometria,l’estadísticailaprobabilitatse’nfauntractamenttangenciali,enmoltsaspectes, ambpocaevolucióconceptual.Aixòpernoparlardelainvisibilitatgeneraldelbloccurricular de«Relacionsicanvi»alaprimària.

Somconscientsquehihaunagranquantitatdeprofessoratquesent(iutilitzemaquestverba plenaconsciència)quecalfercanvisenlesdireccionsapuntades:tipologiad’activitats,canvis degestióal’aulaireequilibridecontinguts.Peròtambé,devegades,sentque«nosapcom fer-ho»,ilainseguretatllastalapossibilitatdecanvi.Unadelesopcionspercomençarafer canvisésdisposard’unsprimersmodelsd’activitatsquepodemincorporaralesnostresaules, totadaptant-lesalpropicontext.Lanostraaspiracióésqueaquestespropostesserveixinde llavorperfer-necréixerdenoves.

Totpensantqueperposarenmovimentalgunacosasovintnoméscalunapetitaempenta, desdelCesire-Creamatenshemplantejatendiferentscursosunespetitescampanyesque, enl’àmbitintern,anomenem«Impulsem».Demoment,n’hemfetdues,dedicadesala geometriaial’estadística,ienguanyn’heminiciatunadeterceraorientadaapromoureles petitesinvestigacionsmatemàtiques.

Unadelescaracterístiquescomunesalestrescampanyesésqueintentencobrirtotl’espectre educatiu:desdel’educacióinfantilfinsalbatxillerat.Devegadesgraduantunamateixa proposta,devegadesdiversificant-les,peròacollidessotaunmateixtretquelesrelacioni. Unaaltracaracterísticacomunaésquepredominenlespropostesqueespodenportar directamental’aula,jaqueundelsobjectiusqueenshemmarcatésfacilitarlatransferibilitat ràpida.

PodeutrobaraquestescampanyesenelmenúlateraldelwebdelCesire-Creamat.

Impulsemlageometria!

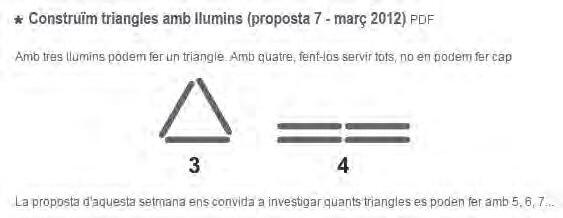
Aquestaprimeracampanyaesvaferdurantelcurs 2012-2013ienelseuorigenhihavia l’observacióqueelsresultatsmésbaixosenlesprovesexternesdecompetènciesbàsiqueses donavenenaquestcamp.Esvanelaborardosdocuments(unperaeducacióprimàriaiunaltre perasecundària)ambpropostesdel’ARC(http://apliense.xtec.cat/arc/)relacionadesambla geometria.Amés,esvananarpublicantalwebperiòdicamentfinsadinoupropostesamb diferentsgrausdecomplexitat.Esvaintentarquetractessinaspectesdiversosrelacionats amblamanipulaciódematerials,treballamb applets,petitesinvestigacions,representació 3Den 2D,estudidetransformacions,aspectesdetopologia,oactivitatsqueconnectessinla geometriaambaltresblocsdelcurrículumcomelde«Numeracióicàlcul»oelde«Relacions icanvi»,percitaralgunesdelessevescaracterístiques.

Femestadística!

Lacampanyad’estadísticaesvafercoincidirambl’AnyInternacionaldel’Estadísticaiesvanfer tretzepropostesalllargdelsdosprimerstrimestresdel 2013.L’enfocamentdelespropostes vaserdiferentdeldelageometria,senseperdredevista,però,laintencióderepresentar unajutperalasevaaplicaciódirectaal’aula.Així,hitrobaremactivitatsconcretes(relatives alamesura,alacriptografia,alaprobabilitatexperimental...),novamentambadaptacions peradiferentsetapeseducatives.Tambérecullsdewebsambbibliografiairecursos,idees generals(coml’aprofitamentdelserrorsestadísticsdelsmitjansdecomunicació),petites pautessobrecomefectuarinvestigacionsestadístiquescompletessegonselnivelleducatiu, mostresdediferentsformesdefergràficsestadístics(en3D,amb applets...),vídeosfetsper alumnat,etc.

Investiguem

Aquestaésladarreracampanyaquehemengegat.Laideabàsicaconsisteixaproposarpetites (omitjanes,ograns,que«totestàperferitotéspossible»)investigacionsmatemàtiquespera lesdiversesedats.Hemcomençatperunpetitreculldeproblemesdel Femmatemàtiques idel +Mates amblaintenciódepromouretambéaquestsconcursos.Lespropostessegüentsaniran abordantinvestigacionsnumèriques,geomètriques,sobrejocs,recreacionsmatemàtiques... itotesaquellesideesqueenssuggereixinelsvostrescomentaris.