Nou Biaix, 32

biaix

editorialeditorial

Arafadosanys,larevista Biaix iniciàunnouperíodeambelnomde NouBiaix. Fouelresultat d’unacol laboraciórigorosaiseriosaentrelaFEEMCATilaSCM,societatfilialel’IEC.

L’objectiuaassolireramúltiple.Espreteniad’ampliarelventalldecontingutsque Nou Biax podriaoferiralslectors,cobrinttoteselsetapesdocentsidiscentsi,commostrenels númerosquejahansortitd’aleshoresençà—30i31—,aquestprimerobjectius’haassolit ambungranèxit,atesalaqualitatdelsarticlespublicats,cadaunenelseuàmbit.

Alhoras’estenienelssubscriptorsilectorsi,enconseqüència,elsàmbitsd’influènciadelsseuscontingutsaventallsmésamplisdecol·lectiusdedicatsaladocènciadelamatemàtica:dematernala universitari.

Enllaçantambaquestobjectiu,esvolimpulsarunlligamestretambelMàsterdeformaciódelprofessorat,convertint NouBiaix enunreferentatenirpresentenaquestensenyamentiincorporant,quan tinguinlaqualitatnecessària,algunsdelstreballsdefidemàster,cosaqueheminiciatenaquest número.

Unaltreobjetiuprogramàticdelacol·laboracióeraaconseguirl’ediciódedosnúmerosanuals,un propòsitqueenelsdosanysprecedentsnos’haassolit,peròqueenguanyseràjaunarealitat.

TotaaquestatascanohauriaarribatabonportsenselafeinadelaMequèEdo,codirectorafinsarai que,apartird’aquestnúmeroseràsusbtituïda,comarepresentantdelaFEEMCAT,perManelSol.

L’equipderedaccióvolagrairalaMequèlaseriositat,laprofessionalitatil’entusiasmequehadedicat,primera Biaix,idesprésa NouBiaix,il’esperitdediàlegquehapermèseltrànsit,queenalguns momentsnohaestatfàcil,de Biaix a NouBiaix;i,alManel,livolretreunacollimentafectuósiuna col laboraciósincera.

articl artices les rticles

Scratch:unrecursdidàctic peralesclasses dematemàtiques

MireiaLópezBeltran INSMilàiFontanalsdeBarcelona mireia.lopez@gmail.com

Resum Abstract

Enaquestarticles’exposendiferents experiènciesdidàctiquesques’han desenvolupatfentservirl’Scratch,pertalde crearcrearcrearprojectesambaquestllenguatge deprogramacióadreçatalsalumnesdeprimària isecundària,elaboratpelMIT(Massachusetts InstituteofTechnology)idedistribuciógratuïta.

1. Siguem creatius amb l’ordinador

Thisarticlereportseducationalexperiencesthat havebeendevelopedusingtheScratch,while creatingprojectswiththisprogramminglanguage forprimaryandsecondarystudentsthathasbeen developedbyMIT(MassachusettsInstituteof Technology)andthatisoffreedistribution.

Actualment,lamajorpartdelapoblaciótéaccésaunagranvarietatdeprogramesinformàtics:jocs, animacionsialtresprogramesinteractius,peròlamajoriad’aquestselementssónun«carrerdesentit únic»:nomésespotveureiclicarallòquealtreshancreat,ésadir,homnopotdissenyaricrearelseu propiprograma.

Resnick(2002)ensproposaveureelsordinadorscomunmitjàper«creariexpressar-se»inoposar gairel’accentnomésenl’accésalainformació.Ambl’Scratch,elsalumnes,enllocde«veure,clicar ixatejar»,poden«crearicontrolarcosesenelmón on-line»,ésadir,passendeserconsumidorsa serproductorsicreenlessevespròpieshistòriesinteractives,elsseuspropisjocsilessevespròpies animacionsielscomparteixenalweb(Resnick2007,pàg.20).

Amblaintencióderecuperarperalaprimàriailasecundàrial’aprenentatgeapartirdelamanipulació,Resnick,atravésdelMITMediaLab,vacrearels manipulatiusdigitals perexpandir«elrangde conceptesqueelsnens(ielsadults)podenexploraratravésdelamanipulaciódirectad’objectes físics»(Resnick1998,pàg.44).

Apartird’aquestsmaterials,Resnickvaestablirtresconceptescomaguiadelasevarecerca.Respectealfetde fomentareldissenydeprojectes,l’autorensapuntalesraonsperlesqualseldissenyde projectespotproduiroportunitatsriquesperaprendre:

• Elsnenssón«participantsactius»,fetqueelsdónauncontrol«mésgranounamésgranimplicació enelprocésd’aprenentatge».

• Esfomenta«elpensamentplural»,jaqueevitemla«dicotomiacert/fals»,boisuggerintquehiha «múltiplesestratègies»imésd’unasoluciópossible.

• Esproveeixd’uncontextperala«reflexió»iaixís’aconsegueixqueelnen«reflexioni,revisiifinsi totestengui»elsseusmodelssobreelmónquel’envolta.

• Esfomentalacapacitatempàticadelnen,jaquenecessitapensarcomelsaltresentendranles sevesconstruccions(Resnick1998,pàg.44).

Aquestèmfasieneldissenyd’activitatsformapartd’unafilosofiadel’educaciómésàmpliaconeguda coma construccionisme (Papert1993).Basant-seenlesteoriesconstructivistesdeJeanPiaget,argumentaquel’aprenentatgeésunprocésactiuenquèhomconstrueixactivamentelconeixementa partirdelessevesexperiènciesenelmón.Lagentnoreplesidees;lagentleselabora.Ésadir,el construccionismeafegeixlaideaquelespersonesconstrueixennouconeixementambunaeficàcia particularquanestancompromesesenlaconstrucciódeproductesambsignificatpersonal.Aixòes potproduirfentcastellsdesorra,màquinesambpecesdeLegooprogramesinformàtics,peròelque ésimportantésquelespersonesestiguincompromesesenlacreaciód’algunacosasignificativa.

Enelsanyssetantadelsegle XX,PapertielsseusestudiantsdelMITArtificialIntelligenceLabvan començaraferrecercasobremètodesperintroduirelsnensenelmóndelaprogramació(McNerney 2004,pàgs.326-327)ivancrearunllenguatgedeprogramacióperanens:elLogo.

Amblaproliferaciódelsordinadorspersonalsafinalsdelssetanta,la tortugadeterra,queal’iniciera unrobotdelamidailaformademitjapilotadebàsquet,esvacanviarperla tortugadepantalla, que algunsdenosaltres(ja)recordem.Enunestadisegüent,larecercasobreels manipulatiusdigitals es vafocalitzarenelLego/Logo,enquèesrelacionavaelpopularjocdeconstruccióambelllenguatge deprogramació(Resnick1998).

2. Arribem a l’Scratch

ElprojecteScratchneixperdotard’unaeinaelsnoisquevulguininvolucrar-seenuna«culturade laprogramació»foradel’ambientestrictamentescolar.Foradelesaules,elsautorsvandetectaruna «culturadelPhotoshop»,enquèelsnoismanipulavengràfics,animacionsifinsitotvídeosimúsica, perònoobservarenelmateixcomportamentenverslaprogramació.Apartird’observarquèfeienels alumnesquefreqüentavenelsclubssocialscreatsenleszonesmésdesafavoridesdelsEstatsUnits, elgrupdetreballdelMITMediaLabvaconclourequelesnoveseinesde software triomfaven,entre d’altres,si:

• Elsjovesveuenelvalorielpotencialdel’einaimmediatamentquancoincideixambelsseusinteressosilessevespassions.

• Elsjovespodencrearproductesfinalsquepodenmostraralsaltres.

• L’einasuportaunamplirangdediversostipusd’activitatsqueatrauenjovesdediferentsedats, gènere,orígensicultura.

• Elsjovespodenaprendre’nlescaracterístiquesaddicionalsdemaneragradual.(Maloney,J. etal. 2004,pàg.3).

Ambaquestesidees,l’equipdeLifelongKindergartendelMITMediaLab,dirigitperMitchelResnick, vadissenyarelllenguatgedeprogramacióperanens,quevananomenarScratchiquepresentales següentscaracterístiquesprincipals:

• Programacióapartirdeblocsdeconstrucció:ambl’Scratch,lescomandesielsdiferentstipusde dadesestanrepresentatsperblocsdediferentsformes;lespecesnomésencaixensilasintaxiés correcta.Ambl’Scratch,l’usuariarrossegablocsd’ordresd’unapaletapercrearelsprocediments. Amésamés,espodenexecutardiferentsprocessosenparal lel.

• Unaprogramacióricadediferentsmitjansdecomunicació:apartdelstradicionalsnombres,cadenes igràfics,ambl’Scratchtambéespermetmanipularimatges,animacions,pel lículesisoperpoder programaractivitatsqueestiguinambméssintoniaambelsinteressosdelsjoves.

• Unprofundcompartiment :l’Scratchpermetexportarobjectesatotselsnivells:desdecompartir noméselspersonatgesanimatsfinsatotelprojecteiintercanviar-losambelsamics.

• Integracióambelmónfísic:l’Scratchtambépotserusatpercontrolarlessevescreacionsapartir desensorsfísics(continuaciódelprojecteLego/Logo).

• Suportamúltiplesllengües (Maloney,J. etal.2004,pàg.4).

ElllenguatgedeprogramacióScratchvaserpresentatel2007juntambl’espaiwebpercompartir elsprojectes,unelementquehaesdevingutclau:enelstresprimersmesoss’hivanpujarmésde 20.000projectes.Peròl’Scratchnoésnomésunllenguatgequepermetmanipularimatgesisons, sinóqueundelsseusobjectiusés:«fomentarelpensamentcreatiu»(Resnick2007,pàg.21),i,segons l’autor:«enelprocésdeprogramarlessevescreacionsambScratch,elsalumnesaprenenimportants conceptesmatemàticsenuncontextmotivadorisignificatiu».Iposacomaexempleunalumnede 8ècurs(13-14anys)quelivademanarcompodiaguardarlapuntuacióenunjocqueestavacreant; Resnicklivaensenyarcomcrearunavariableambl’Scratchil’alumnelivadonarlesgràciesmolt efusivament.

Enaquestarticleespresententresexperiènciesdutesatermeambl’Scratch: Jocsnumèricsamb l’Scratch, IntroduccióalaprogramacióambScratch i Creemunproblemaambl’Scratch.Lesduesprimeresespresentarandemanerabreuilaterceraambunamicamésdedetall.

3. L’Scratch a l’aula de matemàtiques (I): l’alumne és usuari

Enlaprimeraexperiència,l’alumnenomésésusuaridel’activitatcreadaambl’Scratch,i,pertant,pot serunabonamanerad’introduir-loalsalumnesimotivar-losapartirdelfetdemostrarallòquees potferenaquestentorndeprogramació.Els Jocsnumèricsambl’Scratch espodentrobarcomun elementdel’ARC.AquestsjocsnumèricssónlaversióelectrònicadetrentajocsrecollitsperIgnasi delBlancocomaactualitzaciódediferentsjocsnumèricsclàssicsooriginalsseusiestanadreçats principalmentalciclesuperiordeprimàriaia1ri2nd’ESO.Laversióelectrònicapermetpodertreballar ambelmateixjocambtotselsalumnesdel’aulasensenecessitatdetenir25-30còpiesfísiquesdel mateixjoc.Alessessionsobertesdeformaciódelprofessorat:elsrecursosinformàticsalesclasses dematemàtiquesdel14i15degenerde2011alaUniversitatPompeuFabra,esvapresentaruna experiènciadidàcticadutaatermeapartirdeljocnumèricnúmero7ambungrupd’alumnesde diversitatde2nd’ESOdel’INSMilàiFontanalsalRavaldeBarcelona.L’activitatconsistianotansols abuscarunasoluciódelasituaciópresentada,sinótambéaraonarquineserentoteslessolucions d’aquestjocnumèric.Enelmaterialdelajornadaespottrobarunresumdel’activitatdutaaterme.

4. L’Scratch a l’aula de matemàtiques (II): l’alumne programa

Lasegonaexperiència, IntroduccióalaprogramacióambScratch, s’hadutatermeenunasessiódel projecteESTALMAT(EStímuldelTALentMATemàtic).Aquestprojectereuneixencadapromoció25 noisinoiesd’entre12i15anysdetotCatalunyaquedurantelsdissabtesdedoscursosrealitzenactivitatsmatemàtiquesensessionsdetreshores.Elcurs2010-2011,vaserelsegonanyque,juntament ambelprofessorAntoniGomà,vamimpartirunasessiódeprimercursperintroduir-losal’Scratch. Unaadaptacióenversiówebdelmaterialqueempremelpodeutrobartambécomunelementde l’ARC.Alllargdelesdueshoresimitjadetreballefectiudelasessió,elsalumnesesvanintroduinta lescaracterístiquesdelllenguatgeidel’entorndeprogramacióapartirdelapropostadediferents programesdedificultatcreixent.Undelsprimersprogramesquese’lsplantejaéseldibuixd’untriangleequilàter;totseguitse’lsplantejaquemodifiquinelprogramaperdibuixarunquadratidesprés quepintinelpolígonregulardetantscostatscomintrodueixil’usuari.D’aquestamanerasorgeix,en unentornsignificatiuperal’alumne,lanecessitatdecrearvariables.TalcomindicaResnick,apartir delasituacióproposada,ésl’alumnequivolferunamodificaciódelprogramaperalaqualnecessita elconceptedevariableiaixípoderampliar-nelesfuncionalitats.Acontinuaciótrobemelcodidel programarealitzatperundelsalumnesd’ESTALMATielresultatdelasevaexecucióperaunpolígon desetcostats.

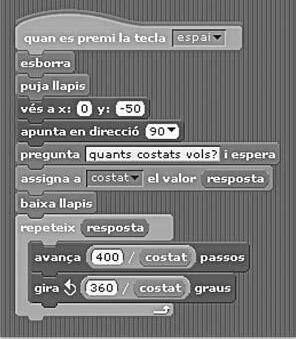
Figura 1. Codi del programa Polígon_regular.sb realizat per un alumne de 1r d’ESTALMAT del curs 2010-2011.

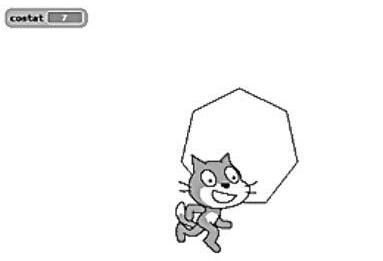
Figura 2. Execució del programa Polígon_regular.sb realizat per un alumne de 1r d’ESTALMAT del curs 2010-2011 per a 7 costats.

crea l’entorn d’un problema

Laterceraactivitat, Creemunproblemaambl’Scratch,esvaduratermeambelmateixgrupd’alumnes d’atencióaladiversitatambquèesvatreballarlaprimeraactivitat,i,pertant,jahavientreballatamb l’Scratch,totiquenomésanivelld’usuari.Elgrupd’aquestsalumnesestàdinsdelprojecte1x1i,per tant,disposàvemd’unordinadorperpersonaaixícomdepissarradigitalal’aula.Aquestaactivitat esvaemmarcarenlesdarreressessionsdelaunitatdidàcticadeproporcionalitatipercentatges.En primerllocesvadedicarunasessióalareflexiósobreelsllenguatgesdeprogramació,alaintroducció delesprincipalscaracterístiquesdel’Scratchidel’entorndeprogramació.Lasituacióintroductòria

5. L’Scratch a l'aula de matemàtiques (III): l’alumne

delaunitatdidàcticahaviaestatlarelaciódeproporcionalitatdirectaqueenstrobemquananem acomprarentreelsquilogramsdefruitaielseupreu/kg.Apartird’aquestasituaciójatreballadaa l’aula,esvaplantejaralsalumnesqueelaboressinunprograma(denommercat)queescenifiqués lasituaciópresentadaenanaracomprar.Aquestaprimeraactivitatesvapresentardemaneraforça pautadaienprimerllocse’lsvademanarquecreessinl’escenari;perfacilitarlatascaencomanada, se’lsvanpenjarelparelld’imatgesnecessàriesenel moodle delcursi,amésamés,se’lsvamostrar unmodeldel’escenariquehavienderealitzar(figura3):

Desprésse’lsvaproposarquecreessinelcodiquecalculéselpreuencasdecomprardosquilograms depréssecs.Totaquestprocéselvamanarfentengrupclasseilapissarradigitalvaserdegranajuda, jaqueperprogramarambl’Scratchcal,essencialment,«arrossegarideixaranar»(drag&drop).Elfet quelescomandesestiguinagrupadespercolorstambéfacilitaengranmesuralasevalocalització perpartdelsalumnes.Apartird’aquestprogramainicialse’lsvaplantejarqueelmodifiquessinperquèdemanésal’usuariquantsquilogramsdefruitavoliaiqueapartirdelarespostadelcomprador aleshorescalculésidiguéselpreuques’haviadepagar.Aprofitantlafunciódepantallacompletaes vapodermostraralsalumnesquèhaviadeferelprogramasensenecessitatdemostrar-loselcodi.

Així,tambéenaquestcas,apartirdelasituacióplantejadavasorgirlanecessitatdelconceptede variable(ambaquestsalumnesencaranos’haviaintroduïtelllenguatgealgebraic)ise’lsvamostrar comcrearvariablesambl’Scratch.

Lamajoriadelsalumnesvanacabarcreantunprogramacomelsegüent:

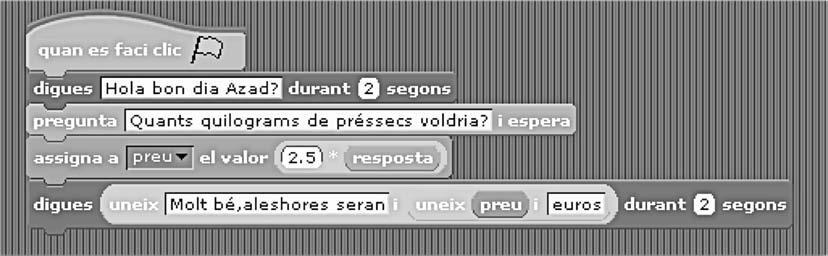
Figura 3. Escenari del programa mercat.

Figura 4. Codi mercat.sb realitzat per un alumne.

Apartird’aquestprogramase’lsvanproposarduesactivitats:

• Activitat1:modificarelprogramadelmercatpertalquehihaguésdosproductes:pomesipréssecs. Elcompradorhaviadedonarelsquilogramsdecadascundelsdosproductesialeshorescalcular idonarelpreufinal.

• Activitat2:comaactivitatdesíntesi,pensarunproblemaqueinvolucrésalgunsdelsconceptes treballatsalllargdelaunitat(proporcionalitatdirectaopercentatges)iqueelprogramessinamb l’Scratch.

Elsresultatsdelesactivitatsproposadeshanestatirregulars.Laprimeraactivitatvaserrelativament assequibleperalsalumnes,malgratlesdificultatsmostradespergestionarladescàrregadelesimatges,lacreaciódenovesvariables,laintroducciódelesvariacionsenelprogramaifinalmentelprocés depenjarlanovaversiódelprogramaalacorresponenttascadel moodle.Esvanobservarforçadificultatsambelmaneigdel’ordinadorientasquesquesuposadamenthaviendedominar,comtrobar elsfitxersquehavienestatprèviamentdescarregatsiguardatsperells.Llunydetrobarunesdestreses àmpliesigeneralitzades,talcomespregonasotal’etiquetade nadiusdigitals dePrensky,larealitatva sermésenlalíniadeBennett,MartoniKervin(2008).Segonsaquestsautors,sotal’expressió nadius digitals esreculll’assumpcióque«elsjovesdelageneraciódenadiusdigitalsposseeixenunsconeixementsiuneshabilitatssofisticadessobrelestecnologiesdelainformació»(pàg.777),i,encanvi,els pocsestudisempíricsquehihanomostrenresultatsqueenglobintotaunageneraciódelamateixa manerasotaelcomúdenominadordetenirmoltadestresaenelmaneigdelesnovestecnologies, sinóquemésaviatelsresultatssuggereixenquelafreqüènciailanaturaenl’úsd’internet«difereix entreelsgrupsd’edatil’entornsocioeconòmic»(pàg.778).

Lasegonaactivitatproposadaeralaqueteniamésinterès,sobretotdesdelpuntdevistacompetencial,perquèsuposavalarealitzaciód’unacreaciópròpiaquenotansolsinvolucravaposarencontext contingutsmatemàtics,sinótambéeltreballdelacompetèncialingüísticaperescenificarlasituació quevolguessinplantejar(enaquestgrupdediversitathihaalumnesdesegonanyd’aulad’acollida dellengüesnoromàniquesiperaixòésungrupreduïtde15-20alumnes).Malauradament,aquesta segonaactivitatnoméslavancompletardosdelsquinzealumnesdelgrup,totiquelamajoriadels alumnesvantreballarenlaproposta.

Figura 5. Execució del programa mercat.sb realitzat per un alumne per a 3 quilograms de préssecs.

6. Conclusions

ApartirdelesdiferentsexperiènciesenlaintroducciódelllenguatgedeprogramacióScratchal’aula dematemàtiquesambdiferentsgrupsd’alumnesde1ri2nd’ESO,esfanlesobservacionssegüents:

NoespotdonarpersuposatquetotselsalumnestenengransdestreseseneldominidelesTICpel seuanydenaixement,comenspodensuggerirexpressionscom nadiusdigitals,sinóque,seguint Bennett,MartoniKervin(2008),lasituacióésforçaméscomplexai,totihaver-hipocsestudisempírics, aquestsmostrenunarealitatambalumnesambdiferentsnivellsdedestresasegonsmúltiplesfactors.

Aquestespossiblesdificultatshandeserprevistesitingudesencompteal’horadedissenyarl’activitat,perquènosuposinunescullinsalvablequeimpedeixiresoldrelatascaencomanadaal’alumne.

Enlesdiferentsexperiènciesdutesaterme,elsalumnesde1ri2nd’ESOs’hanadaptatambrapidesaal maneigdel’Scratchcomaeinaperprogramargràciesaestratègiescoml’agrupaciódelescomandes percolorsquefacilitaengranmesuralasevalocalització.

Plantejarlaprogramaciódeproblemesmatemàticsambl’Scratchpotserunbonaoportunitatper introduirl’úsdelesvariablesa1ro2nd’ESOenuncontextsignificatiuiambunaeinaconcebuda especialmentperaalumnesd’aquestesedats,talcomensexposaResnick(2007).

Apartirdelesactivitatsproposades,hihaencaramoltdepotencialdel’einaexplorar,comperexempletreballarl’escenificacióambl’Scratchdesituacionsdelavidarealqueimpliquinmatemàtiques tantal’auladematemàtiquescomaaltresaules(aulesdellengües,incloent-hil’aulad’acollida).

Agraïments

Agraeixolainestimablecol·laboraciód’AntoniGomàtantenlarealitzaciódelesdiferentsexperiènciesexposadescomenlessevesaportacionsielsseuscomentarisaaquestarticle.

Bibliografia

Bennett,S.,Maton,K.iKervin,L.(2008).The«digitalnatives»debate:Acriticalreviewoftheevidence. BritishJournalofEducationalTechnology,39(5),775-786.

[URL:http://onlinelibrary.wiley.com/doi/10.1111/j.1467-8535.2007.00793.x/pdf] (consultat27/06/2011)

Maloney,J. etal.(2004).Scratch:ASneakPreview.SecondInternational.Dins ConferenceonCreating, Connecting,andCollaboratingthroughComputing. Kyoto,Japan,104-109.

McNerney,T.S.(2004).FromturtlestoTangibleProgrammingBricks:explorationsinphysicallanguagedesign. PersonalandUbiquitousComputing, 8(5),326-337.

Papert,S.(1993). TheChildren’sMachine:RethinkingSchoolintheAgeoftheComputer.NewYork:Basic Books.

Resnick,M.(2007).Sowingtheseedsforamorecreativesociety. LearningandLeadingwithTechnology, 35(4),18-22.

[URL:http://web.media.mit.edu/∼mres/papers/Learning-Leading-final.pdf](consultat27/06/2011)

Resnick,M.(2002).RethinkingLearningintheDigitalAge.InTheGlobalInformationTechnology.Dins G.Kirkman(ed.). Report:ReadinessfortheNetworkedWorld.Oxford:OxfordUniversityPress.

Resnick,M.(1998).TechnologiesforLifelongKindergarten. EducationalTechnologyResearchandDevelopment,46(4).

Recursosweb

Arc.AplicaciódeRecobrimentCurricular:

http://apliense.xtec.cat/arc/(consultat27/06/2011)

LifelongKindergarten:relaciód’articlesdelgrup.

http://llk.media.mit.edu/papers.php(consultat27/06/2011)

Elconceptedelímitde NewtonaCauchy: entrelageometriail’àlgebra ielpaperdelssignes [Primerapart]

GertSchubring

Resum Abstract

Elconceptedelímitésconstitutiuperalcàlcul diferencialiintegral.Aixònoobstant,lasevaaparició històricanos’haestudiatprouacuradament.Newton fouelprimerquel’introduícomunaalternativaales aproximacionsinfinitesimals,peròsensereflexions conceptualsisensecaptècnicaoperacionales mantinguévinculatalscontextosgeometricocinètics. Aquestarticleestudiaeldesenvolupamentlentdel conceptedurantelsegledivuit,ienparticularles primeresdefinicionsielseuspassosgradualsvers l’algebraïtzació.Gràciesal’apropamentaunarecerca delesaportacionsalsidelescomunitats matemàtiquesengeneral,ensrevelaqueautors aparentmentmarginalshanfetavenços considerablescapaunateoriaoperacional algebraïtzadadelslímits.Tanmateix,aquestprocés mostraquenoés,enabsolut,continuiquedepèn d’epistemologiesquedifereixend’unpaís—id’una comunitat—aunaltre.L’anàlisifinalitzacontrastant duesaproximacionsdel1820querevelenaquestes visionsdiferents:CauchyaFrançaiDirksena Alemanya. Aquestaprimerapartdel’articlepresentaelmarc conceptualdelqueesconeixcomaprocés d’algebraïtzacióis’hianalitzadequinamanera Newtonpresentaelprocésenelconceptedelímit —coml’usaMaclaurincomarespostaaBerkeleyi d’Alembertal’Encyclopédie —perendinsar-se desprésenellímitcomaaproximacióiestancaamb elsinicisdel’algebraïtzaciód’aquestnouconcepte:el límit.Obrelaportaalasegonapartquepublicarem enelpropernúmero.

Theconceptoflimitisconstitutiveforthedifferentialand integralcalculus.Yet,itshistoricalemergencehasnot beencloselystudied.Asanalternativetoinfinitesimal approaches,ithadfirstbeenintroducedbyNewton,but withoutconceptualreflectionsandwithoutan operationaltechnique;itremainedtiedto geometrical-kinematicalcontexts.Thepaperstudiesthe slowdevelopmentoftheconceptduringtheeighteenth century,andinparticularthefirstdefinitionsandtheir gradualstepstowardsalgebraization.Thankstothe approachtoinvestigatethecontributionswithinthe contemporaneousmathematicalcommunitiesatlarge, apparentlymarginalauthorsrevealtoachieve considerablestepstowardsanalgebraizedoperational theoryoflimits.Yet,thisprocessprovesnottobea continuousoneanddependingonepistemologies differingovervariouscountriesandcommunities.The analysisfinalizesincontrastingtwoapproachesofthe 1820srevealingsuchdifferingvisions:CauchyinFrance andDirkseninGermany.

Thisfirstpartofthepaperpresentstheconceptualframe ofthatknownasthealgebraizationprocessand analizeswichwayNewtonpresentsthisprocessinthe conceptoflimit howtousesMaclaurininresponseto Berkeleyandd’AlembertintheEnciclopèdie toenter afterinthelimitasapproach.Itcloseswiththestartof thealgebraizationofthisnewconcept:thelimit.It opensthedoortothesecondpartwhichwillpublish theminthenextissue.

Enlahistoriografiadelamatemàticahivahaverunperíodeenelqualtotselsdescobrimentsmatemàticsessencialss’atribuïenalsgrecsdelaGrèciaclàssica.Evidentment,elcàlculdiferencialiintegral plantejavaunproblemaaaquestaaproximacióahistòrica,produïdaperl’admiracióal’antiguitatclàssica.S’intentavadepresentarelmètoded’exhaustiócomquelcomequivalent.

Defet,aquestmètodenomésésunprocedimentdedemostracióinoproporcionacapmarcconceptualperestudiarelprocésdepasallímit,cosaqueinvolucral’infinit.Unadelesformulacions clàssiquesladónaEuclidesenlaproposició X,1:

Donadesduesmagnitudsdesiguals,sidelamajortraiemmésdelameitat,idelqueenquedamés delameitat,isiaquestprocéselrepetimcontínuament,assoliremunamagnitudméspetitaque lamenordelesduesmagnitudsdonades(citataEdwards1979,pàg.16).

Aquestsmètodespercalcularlímitserenrigorosos,peròelsmatemàticsqueelsusaven,comara Euclides,Arquimedesialtresmatemàticsgrecs,evitaven,engeneral,processosinfinits,iencapcas noimaginavenelpasallímitcomunacosaques’acomplísactualment.Aleshores,pertald’evitar l’úsil’acceptaciódel’infinit,tendienadesenvoluparelementscrucialsd’unacertaàlgebradeles desigualtats.

AvuiestemconvençutsquelaprimeraconceptualitzaciórigorosaiextensadellímithaestatelaboradaperCauchy.Encaraques’admetiquematemàticsdiversosdelsegle XVIII vanefectuaralgunes reflexionsiaplicacionsalanociódelímit,elsresultatsexitososassolitsperCauchys’hanpresentat comunainnovaciófonamentalicomunacontribuciópersonal(Grabiner1981,pàg.9).Homconsideraquelaclaucaracterísticad’aquestaconceptualitzaciórigorosaésl’algebraïtzaciódelsconceptes subjacents,fetqueesdetecta,enparticular,perl’úsd’unacertaàlgebradelesdesigualtats.

Tanmateix,defet,mainos’explicaquèsignifica,enaquestcampconceptual,elterme algebraïtzació Desitjaria,doncs,reflexionarsobrel’algebraïtzaciócomaprocésianalitzarlescontribucionsfetes pelsmatemàticsdelsegle XVIII d’acordambaquestacategoria.Elpaperdelssímbols,delssignes,se’ns mostraràcomelpivotdetotelprocésdeldesenvolupamentd’algebraïtzació.Amés,se’nsfaràpalès, ambtotaclaredat,queeldesenvolupamentconceptualnos’esdevinguénid’unamaneracontínua nitampocunidireccional.

Pertald’analitzarmillorelprocésd’algebraïtzaciódelnaixementdel’àlgebra,recordarébreument elstresestadis-modeldeNesselmannrelatiusal’evoluciódel’algebraïtzació.Ambtotaseguretat, aquestmodel,proposatl’any1842,noésunmodelgeneralmentvàlid,peròésunaeinatanútilcom heurística:

• L’estadiprimeriinferiors’anomenaàlgebra retòrica:elprocésmatemàticsencer,ambtoteslessevesoperacions,s’expressaambparaules.Ésadir,nis’hanintroduïtnitampocnos’emprensímbols. Sónlesparaulesdelllenguatgepropilesqueserveixenperexpressarelsignificatmatemàtic.

• Enelsegonestadi,hihal’àlgebra sincopada:lapresentaciódelsresultatsmatemàticséstambé bàsicamentretòrica,però,ara,s’introdueix,peralsconceptesilesoperacionsques’usenamb freqüència,semprelamateixaabreviació—enllocdelesparaulessenceres.Tanmateix,s’hauria deserprouhàbilperretornar,enqualsevolmoment,del’abreviacióaltermecompletoriginal.

• Eltercerestadi,eldel’àlgebra simbòlica,representatoteslesformesiexpressionsambunllenguatgedesímbols,constituïtindependentmentdelllenguatgenormal.Pràcticamentnohiharetorn delesoperacionsfetesambsímbolsaltextretòric(Nesselmann1842,pàg.302).

1. Newton

Elprimerúsdelconceptedelímitperalcàlculestrobaenl’obradeNewton.Defet,comésben conegut,Newtonempràdiversosmètodescomafonamentsdelcàlculnou.Lanociódelímitapareix enlasevaaproximacióviaelques’haanomenatraonsprimeraidarrera.

L’avantatgeil’atractiud’aquestmètodeera,conaccentuàNewton,queusavanomésquantitatsfinites,iaixíaconseguiaunacordamblametodologiageomètricadelsgrecs,laqualcosaelsalvavade lacrítica.

Ambquantitatsfinites[...]instituirl’anàlisid’aquestamaneraiinvestigarlesraonsprimeresidarreres delesquantitatsfinitesixentsievanescentsestàenharmoniaamblageometriadelsantics,ivolia mostrar,amés,que,enelmètodedelesfluxions,nohihacapmenadenecessitatd’introduir,al sidelageometria,figuresinfinitamentpetites(Newton1969,1929).

Newton,enelseu PrincipiaMathematica (1687),reflectiaexplícitamentlaideacontingudaenelconceptedeles raonsprimeresidarreres perdeterminar,enelcasdelesvariablesdepenentsdeltemps, ellímitalquallesvariabless’aproximenenuncertinstant—ique,desdelseupuntdevista,aconsegueixend’assolir—comunestudidelslímits,i,peraixò,introduïaeltermede limes

Newtonintroduïaaquestmètodecomunaalternativaalsmètodesgeomètricsgrecs,ambelpropòsitd’evitarlesllarguesdemostracions adabsurdum,icomunaalternativaalmètodedelsindivisibles: lahipòtesidelsindivisiblessemblavamassaofensiva(«durior »),deia,ielmètodelisemblavaqueno erasuficientmentgeomètric.L’alternativaeradeterminarlessumesúltimes,respectivamentraons, dequantitatsevanescents,respectivamentdelesprimeresquantitatsgenerades,iaixòconsistiaprecisamentadeterminarelslímitsdelessumesrespectivamentdelesraons:

Aixòés,[reduir]elslímitsaaquellessumesiraons(Newton1969,pàg.38;org.1972,pàg.87).

Iemfasitzàelseupropiconceptedecontinuïtatafirmantquenocompreniaelsindivisibles,sinóque concebiaquantitatsesvanescentsdivisibles;cosaquenosignificapasl’existènciadelespartsúltimes, sinó:

[no]indivisibles,sinóquantitatsdivisiblesevanescents;nolessumesilesraonsdedeterminades parts,sinósempreelslímitsdelessumesilesraons(Ibid.).

AquíNewtonposàcuraaemfasitzarquelasevapròpiaexpressió raonsúltimes significavaefectivament límits,elsqualserenaproximatsmésimésperlesraons:

Aquestesraonsúltimesalesqualslesquantitatss’esvaeixennosónpas,defet,lesraonsdeles quantitatsúltimes,sinóelslímitsalsqualslesraonsdelesquantitatss’apropenmésquequalsevol diferènciadonada(Ibid.,pàg.39;orig.pàg.88).

Simultàniament,Newtondeclara,doncs,queelslímitsexisteixen,iqueexaminaraquestsvalorsconstitueixunatascagenuïnamentgeomètricaperquèelslímitsestanfixatsideterminats:

Icomqueaquestslímitssóncertsidefinits,determinar-losésunproblemaestrictamentgeomètric (Ibid.,pàg.39;orig.pàg.87f.).

Finalment,Newtondónajaunapistadelconceptedelprocésdematematitzaciódellímitquemés endavantvaserformalitzatdientquelesquantitatsinfinitamentpetitessónvariablesespecials;ésa

dir,successionsnul·les.Arreuonesrefereix,enlespartssegüentsdelseutext,aquantitatspetites, oesvanescents,oaquantitatsúltimes,mainoleshemd’entendrecomaquantitatsfixesquetenen unadeterminatvalor,sinócomaquantitatsquedisminueixeninfinitament:

Així,entotelquesegueix,pertaldesercomprèsambmésfacilitat,allàons’esdevinguiquemencioniquantitatsfinals,oevanescents,odarreres,noheudesuposarencapcasqueestractade quantitatsd’unadeterminadamagnitud,sinóqueestanconcebudescomquelcomquedisminueixsempresensefi(Ibid.,pàg.39;orig.pàg.88).

MalgratqueNewtonnodesenvolupaunalgorismeocàlculperaladeterminaciódelslímits,estableix unprincipiperfer-ho,quevaserelaboratextensamentpelsautorsposteriors:elprincipiqueellímit podriainferir-sedelcomportamentquepresentenlesvariables enelfinit:

Lesquantitats,ilesraonsdequantitats,queentempsfinittendeixendeformaconstantalaigualtat,iqueabansdelafideltempss’apropenunaal’altramésquequalsevoldiferènciadonada, finalmentesdeveniguals(Newton1969,pàg.29;orig.1972,pàg.73).

Aquestprincipiconstitueixlabaseperdecidirlaidentitatd’expressionsenelcàlculnou.

Guicciardinianomenaaquestaconcepcióuna teoriaintuïtivadelslímits (Guicciardini1989,pàg.5).En qualsevolcas,podemafirmarqueNewtonnovaelaborarunateoriaalgebraïtzadadellímit.Nopresentacaptractamentoperatiudelslímits,capdesignacióperalesvariablesielsíndexslímitsdel procés,icapsigneparticularperallímit.Commostrenlescitacionsanteriors,lesdescripcionsiles argumentacionssóncompletamentverbals.

2. Els límits com a resposta de Maclaurin a Berkeley

LaGranBretanya—onesvancrearels infinitèsims —fouelpaísquemésràpidamentelsvaabandonar.Forenreemplaçatspelsmètodesdellímit,basatssempre,però,enprocessosgeometricocinètics.DesprésdelsprimersintentsdeThomasBayes(1702-1761)ideBenjaminRobins(1707-1751) peraconseguird’establirunmètodedellímit(cf ibid.,pàg.46i45),elvoluminós ATreatiseofFluxions (1742)del’eminentmatemàticescocèsColin Maclaurin formulavaelrefúsmatemàticdels infinitesimals ielaboravacomabasedel càlcul unmètodegeomètricdellímit.

Elpuntinicialdel’amplíssimaaproximacióalajustificaciódel càlcul deNewtoneraquerefusava —comNewton(cf.secció5)—suposar(l’existènciade)quantitatsinfinitamentpetitesiadmetianomésquantitatsfinites:

Sempreherepresentatlesfluxionsdetotselsordresambquantitatsfinites,essentlasuposició demagnitudsinfinitamentpetitesun postulat massaatrevitperaunaciènciacomlageometria (Maclaurin1742,pàg. IV).

Maclaurinnomésadmetiaquantitatsquetinguessinuna«existènciareal»(ibid.pàg.3).Lesquantitats infinitamentpetitesnoerenquantitatsadmissibles;unadivisióinfinitanoeraexecutable.Elterme clauenladiscussiódeMaclaurinéselterme assignable.Ladivisióenunnombreassignabledeparts ésadmissible:

Però[unamagnituddonada]nopotser,consegüentment,divididaenunnombredepartsmés granqueunad’assignable(ibid.,pàg.43).

Encontrast,perexemple,ambl’argumentaciódeVarignoncontraRolle,Maclaurinesbasavaenels geòmetresantics pertaldejustificarlano-admissiódequantitatsquepodienesdevenirinfinitament gransoinfinitamentpetites(ibid.,pàg.40).IgualmentestavacompleamentconvençutqueelsAntics mainosubstituiriencorbesperpolígons(ibid.,pàg.3i33).D’aquestamanera,Maclaurintreiaundels pilarsessencialsdelconceptedelcàlculdiferencialelaboratperLeibnizipelsautorsfrancesos,tot substituint-loperunaltreconcepteque,segonsell,haviaestatlabasedelageometriadel’antiguitat, osimésnodelageometriad’Arquimedes:elconceptedelímit.Arquimedes,deia,nosubstitueixmai corbesperpolígons,sinóque,mésaviat,haviarefinatelspolígonscircumscritsiinscritsfinsalpunt quelipermetessind’aconseguirproposicionsrelativesalescorbesinscritesentesescoma«límits».

ElqueresultarealmentsorprenentdeltextméssubstancialdeMaclaurinésqueusava,comunautènticprincipi(ibid.,pàg.10),elconceptede límit comquelcomtanevidentquenoprecisavaser introduïtdemaneraexplícitaoreflexiva.Enelsuplementposteriordelprimervolum,hihanomésun paràgrafbreu,«Delslímitsdelesraons»(pàg.420-424),perònocontécapfonamentaciódelmètode delslímits,sinómésaviatindicacionspràctiquespertaldecalcularelslímitsderaons.

Elqueésnotable,però,enl’úspràcticdelmètodedelslímitsdeMaclaurinéselfetquesempreinclou reflexionssobresiellímitbuscat existeix (cf.,perexemple: ibid.,pàg.217is.),quelcomquemoltsdels seussuccessorsjanofaran.Laqüestióconstantenaquestaferéssihihaun límitassignable o,si«no télímit»,éslaconseqüènciadelaposiciófundacionald’admetresolamentelfinit,ésadir,quantitats assignables

Sempres’hafetnotarqueel Treatise deMaclaurinésdelecturadifícil(cf.Guicciardini1989,pàg.50).

Aquestaconsideració,tanmateix,noésnoméselresultatdel’úsquefadedemostracionsgeomètriquesindirectes.Eltretcaracterísticdelseuestilésmésaviatqueformulaenlaméspuratradició,de manerapuramentverbal—senseequacions,isensel’úsdesignesalgèbricsiesconfinaaixíasimateix exclusivamental’estudidelsllocsgeomètrics.ComdeclaravaMaclaurin,aquestestileraintencionat afid’eliminarqualsevolmenadecríticatotapel lantalsmètodestradicionals.

És,doncs,comprensiblequeMaclaurin,acausadelseupropiconceptegeomètricdelímit,contrari al’algebraïtzació,nofacicapintentpertald’algebraïtzar-neelconcepte:nienlaprimerapart,una partexclusivamentgeomètrica,nitampocalasegona,enlaqualadmetperexemplemètodesinfinitesimalscomabreviacionsessencialmentexactesiheurístiques.Maclaurinnointrodueixcapsigne propiperal límit,nitampocnoestableixlleisperoperar-hi.Pertald’entendrelaposiciódeMaclaurin pelquefaalafonamentació,ésdeltotessencialadonar-sequesuposacomunapremissainqüestionablequetoteslesvariables(«fluents»)esbasenenprocessosgeometricocinemàtics—basats enoperacionalitzacionsdelmoviment,l’espai,ilavelocitat(cf. ibid.,pàg.52is.).Lapremissa,actuantencaramésacusadamentqueenNewton,produeixquelacontinuïtatiladiferenciabilitatsiguin pressupostosfonamentalsautoevidentssensecapnecessitatdereflexióulterior.

Enciclopédie

3. Recepció a l’ i l’expansió ulterior

Tanmateix,però,l’adopciómésintensadelrefúsdelesquantitatsméspetitesilasubstituciópel mètodedellímitnos’esdevinguéacausadel’obradeMaclaurin,sinótanmateixacausad’unautor francès,elqualhaviallegitelllibredeMaclauriniaportàideesulteriorspròpies.Aquestautorera D’Alembert,iteniacomaobjectiulaclaredatielrigorconceptuals.Enaquestcontext,D’Alembert afavoríunaposicióquesostenial’algebraïtzaciódelsconceptesfonamentalsdel’àlgebra.

L’objectiuprimaridel’Encyclopédie consistiaaclarificarelsconceptesbàsicsdel’anàlisioaclarificar «lamétaphysiqueducalculdifférentiel »(D’Alembert, Différentiel,1751,pàg.985).La métaphysique més precisaiexactadelcàlculdiferencialhaviaestataplicadaperNewton,sibédeiaquenos’haviapreocupatd’aprofundir-la:

Podemdirquelametafísicad’aquestgrangeòmetra[Newton]sobreelcàlculdefluxionsésmés exactaimésil luminadora,enlamesuraqueenspermetdeveure’l. Mainoconsideràelcàlculdiferencialcomuncàlculdequantitatsinfinitamentpetites,sinó comelmètodedelesraonsprimeresidarreres,queéselmètodedecercadelímitsderaons[...]. Ladiferenciaciódelesequacionsconsistianomésenlarecercadelímitsdelesraonsentreles diferènciesdelesduesvariablesdel’equació(ibid,pàg.985is.).

L’entrada,pròpiamentdita,de límit al’Encyclopédie ésmoltbreu.D’unabanda,esrefermaenlaposició deprincipiqueestableixqueelcàlculdiferencialestablertdemaneracorrectanoméspoterigir-se sobreels límits:

Lateoriadels límitséslabasedelavertaderaMetafísicadelcàlculdiferencial (D’Alembert, Límit,1765, pàg.542).

I,alhora,enaquestpunt,éselprimeraintroduiraproximacionsperaunareflexióconceptualdel conceptedelímit,totdeclarantque,sibélaquantitatpodriaaproximar-seallímitarbitràriament,mai noelpodriaatrapar:

El límit mainocoincideix[amblaquantitat],omainoesdevéigualalaquantitatdelaqualn’és el límit :però,elprimers’hiapropacadavegadamésimés,idifereixd’elltanpoccomesdesitgi (ibid.).

Aquestadeterminaciódelconcepteimplicaalhoralaposicióexcepcionaldelzero.Amés,ladeterminacióaclareixqueaquí,debellnou,elconceptefonamentaltractad’una quantitatgeomètrica —inopasencaradelconceptedefunció.Enl’entrada Différentiel hompottrobarunaaproximació queintentaposarderelleul’aspectedel’algebraïtzació.Enaquestaentrada,D’Alembertdistingeixentreel límitgeomètric dequantitatscomladeterminaciód’unacertalíniadelafigura,iel límitalgèbric comeltermealgèbricexpressatamblletresquefanreferènciaaquantitats(D’Alembert, Différentiel, 1751,pàg.986).Elseuinterèsprimordial,tanmateix,eraelproblemageomètric.Elcàlculdiferencial consistiaatrobarl’expressióalgèbricadelaraódelíniesjaconegudes:

Aquestcàlculconsisteixnomésadeterminaralgèbricamentellímitd’unaraóquanjahaestat expressadaamblíniesiaigualaraquestsdoslímits,peralaqualcosapotdeteminar-seunadeles líniesdesitjades(ibid.).

D’acord,doncs,ambaquestdominidelconceptegeomètricdequantitat,al’obradeD’Alembertno trobemcapintentdereflexionar,oestablir,operacionsamblímits.

ElpredominigeomètricdeD’Alembertesdevéencaramésnotablepelfetquel’entradade límit de l’Encyclopédie téunaentradaparal lela,encompetència,del’abat DelaChapelle!L’entradaparal lela del’abat,encaraquenoadvocaperunaposicióessencialmentdiferent,tendeixclaramentauna comprensiómésfortamentalgebricooperativadelconceptedelímit.

D’entrada,DelaChapellepresentalasevanociódelímitenelseumanual InstitutionesdeGéométrie, 1746,i,probablement,éselprimeraaplicardemaneraexplícitalímitsengeometriaelementalino

pasenanàlisi,comeraelcostum.Laseccióquefareferènciaala Solidesadelscossos s’iniciaambuna polèmicaagudaencontradelpuntdevistatradicional—moltmésadreçadaencontradelmètode delsindivisiblesquenopasencontradelesquantitatsinfinitamentpetites.DelaChapelleanomena elsquehisónfavorables Indivisibilistes,ienparlacomsifossinmembresd’unasecta:«Sectarisde Cavalieri»(DelaChapelle,t. II,1765,pàg.338).

ComjahaviafetMaclaurinabansqueell,DelaChapellenogosatampocpresentarelmètodedels límitscomunacosanovella.S’esforçatambéa allitar-se enl’autoritatdelAnticsidesignaelmètode delslímitscomsifoselmètoded’exhaustió(ibid.,pàg.343).Tanmateixestableixunapuntualització endeclararquel’aspectenouqueacabavad’introduirconsistiaaafegir,almètode,dues proposicions novesquelipermetienpresentar-locomquelcom«indubtable».

• Laprimeraeralaproposicióqueestablia:Siduesquantitats A i B sónelslímitsdelamateixaquantitat C ,lesduesquantitats, A i B,sóniguals.Elpropòsitd’aquesta proposició erapermetrelainserció d’unlímitjadeterminatnumèricament(ibid.,pàg.363).

• Lasegonaproposicióconsistiaatransferirlapropietatdelímitalproducte.Si C ésellímitd’una quantitat A,i D ellímitd’unaquantitat B,aleshores C × D ésellímitde A × B (ibid.,pàg.360is.). Mésendavant,aquestaproposiciólieranecessàriaperpoderdeterminarelvolumdelssòlidsles superfíciesdelsqualsestavenlimitadesperlíniescorbes.

DelaChapelledónauna definició delímit,nomésenaquestindret—isolamentenunanotaapeu depàgina:

Homdiuqueunamagnitud[grandeur ]ésellímitd’unaaltramagnitud[grandeur ]quanlasegona espotaproximaralaprimeramésqueunacertaquantitatdonada,tanpetitacomhompugui arribaraimaginar.D’aixòenresultaqueladiferènciaentreunaquatitat[quantité]ielseulímités absolutamentindeterminable(ibid.,pàg.360).

Enaquestadefinició,elfetremarcableéslaindeterminaciódelesexpressions: grandeur i quantité,ja ques’usenl’unaalcostatdel’altrasensecapdiferènciadesignificat.Potsermésreveladorencaraés elfetquenos’usaelterme variable iquetampocnoapareixenllocelterme constant

Al’entrada límit del’Encyclopédie,enparal lelalacontribuciódeD’Alembert,DelaChapellerepeteix aquestadefinicióalpeudelalletraihiafegeix,desprésdedonaralgunsexemples,lessevesdues proposicions (DelaChapelle, Límit,1765,pàg.542).Malgratlaindeterminaciód’aquestadefinicióde límit—D’Alembert,ennodonar-necap,haviaseguitMaclaurin—,lasegona proposició,enparticular,ofereixunaaproximacióal’operativitatamblímits,is’adreçacapaunaalgebraïtzaciód’aquest concepteque,desdelprincipi,haviaestatusatd’unamanerapuramentgeomètrica.

4. Les primeres explicacions decom a aproximació límit

Comhemvist,elmètodedels límits finsaras’haviaproclamatmésaviatcomunaaproximacióteòrica, peròencapcascomquelcomrealmentperal’úspràctic,nitampocelscàlculsdiferencialiintegral nos’havienpresentatpas,comuntot,sobreaquestabase.

Lesprimereselaboracionsdelcàlculdiferencialiintegralqueanessinmésenllàdesimplesmencions eclèctiquesenmanualsuniversitarisvanserpresentadesendosllibresdetextadreçatsaunpúblic amplinonecessàriamentconnectatambelcontextescolar.Unproblemacomúenaquestsdostextos

de1777i1781,deJ.A.L.CousiniR.Martin,eraqueinterpretavenelmètodedels límits,basant-seenles indicacionsdeNewtoniMaclaurin,comunaconcepcióelaboradajapelsAnticsi,pertant,intentaven d’establir-nelaprecisiótreballantsobreconceptesdegeometriaelemental.

Elprimertextqueafirmaqueesfonamentaexclusivamentenels límits ésl’obra Leçonsdecalcul différentieletdecalculintégral (1777)deCousin.SibéJacques-Antoine-Joseph Cousin (1739-1800) —membredel’AcadémiedesSciencesdeParís—haviaestatprofessordematemàtiquesal’École RoyaleMilitairedeParísdesde1770finsquelainstitució,fundadal’any1755peral’educaciódels jovesnobles,fouclausuradaen1776,lasevaocupacióprimordialeraladeprofessordematemàtiquesifísicaexperimentaldelCollègeRoyal,laqualocupàdesquehiaccedíel1769finsalamort. LeslliçonsdelCollègeRoyal,unainstitucióquenofeiaexàmensniconcediatítols,anavenadreçades alpúblicengeneral.EltextdeCousinmostraquenohaviaestatestructuratambpropòsitsdocents, sinócomunamenadecompendiquerecolliaelconeixementcontemporani.Elseuvolum—tenia mésde800pàgines—confirmaquenos’haviapensatperaladocència.

Enunllarg Discourspréliminaire,Cousindesenvolupala métaphysique delcàlcul.Perfer-ho,critica totselsmètodesempratsfinsaleshores:rebutjaladoctrinadels infinimentpetits,dientqueningúés capaçdeformar-seuna«idéenetteetprécise»d’aquestesquantitats.LasoluciódeLeibnizdesubstituir quantitatsinfinitamentpetitesperquantitatsincomparablementepetitesdestrueix,afirma,l’exactituddelmètode(Cousin,1777,pàg. V f.).ElmètodedelesfluxionsdeNewton,sibénocontradiuel rigormatemàtic,hadeconfiarenelsconceptesdemovimentivelocitat.Això,afirma,introdueixuna ideaqueéscompletamentalienaalamatemàticaique,encapcas,noéssimple.Lajustificacióde Maclaurin—queestableixqueelmètodedelesfluxionsésalmenystanrigoróscomelmètodedels Antics—reposasobrelateoriadelmoviment(ibid.,pàg. VI f.).

Encanvi,CousinatribueixaD’Alembertelmèritd’haverestatelprimeraprovarquelabaserealdel càlculdiferencialiintegralesderivavadelmètodedelsAnciens,elqualhomconeixiaambelnomde Méthodedeslimites.AbansdelapublicaciódeD’Alembert,al’Encyclopédie,aquestmètode,«lavraie métaphysique»,eracompletamentdesconegut(ibid., VII).Ell(Cousin)intentavadepresentar-lodela maneramésclarapossible.

Cousinenteniaellímitcomunaquantitatarbitrària,aproximadaindefinidamentperunavariable sensearribarmaiaidentificar-s’hi—comenl’exempledelcercleinscritocircumscritperpolígons (ibid.,pàg. X).

Fentqueunavariabledisminueixiprodríemaproximararbitràriamentelzero,senseassolir-lomai:«La ideaquetenimdelzeroésqueésunlímitalqualraonsdecreixentss’hiaproximendemaneracontínua,senseatrapar-lomai»(ibid.,pàg. IX).Mésendavant,Cousindeclaraexplícitamentque«Nil’infinit nielzeronosónquantitats».Iaclareix:«Ambdóssónlímitsalsqualscertesquantitatss’aproximen contínuament,senseassolir-lesmai»(ibid.,pàg. IX).

Peroperaramblímits,Cousin,comDelaChapelle,ambquiòbviamentestavavinculat,estableix dos principis.ElseuprimerprincipioperacionalésidènticalprimerdeDelaChapelle(duesquantitatsque sónellímitdelamateixaquantitatsónidèntiques).Tanmateix,Cousinsubstitueixelsegonprincipi relatiualproductedequantitatsperunprincipiqueconcerneixalesrelacionsentreduesvariables:

Siduesmagnituds,quecreixenodecreixencontínuament,mantenenentresiunaraóinvariant, aquestaraóseràladellímitdelesduesmagnituds(ibid.,pàg. X).

Cousinnodóna,però,capjustificaciód’aquestsdosprincipis,quedeclaraquesónlabasedetotel mètodedels límits.Mésendavant,noobstantaixò,dónaunexempledecoms’apliquen.Aproxima unacircumferènciaiunael·lipse—ambduescorbesambelmateixeix,ipelquefaal’el·lipse,el llarg—ihiinscriuambdóspolígons,quetenenlaraódel’eixllargdel’el·lipsealcurt.Aquestaraó, diu,éssemprelamateixa.Pertant,elslímitstambé,essentaquestslímitslacircumferènciail’el lipse (ibid.,pàg. XIII).

Aquestesprimereselaboracionsdelmètodedelslímitsnoerenespecífiquesperal’anàlisi,sinóque reflectienmésaviatconceptesdegeometriaelemental.Enconseqüència,aquestestadiéscomparableambeldelsindivisibles,enelqualobjectesestàticsdegeometriaerentambétractatssense disposarencaradelsconceptesdevariableodefunció.Aquestcaràcterparal·lelesfatambéevident enla definició generaldelconceptedels límits delseutextprincipal:

Homdiuqueunamagnitudentéunaaltracoma límit,quanhomimaginaquel’aproximademaneraquenomésdifereixend’unaquantitattanpetitacomesvulgui,sensearribarperòacoincidir mai(ibid.,pàg.17).

AquíCousinadoptaelconceptevaguedeltextdegeometriadeDelaChapelle,idel’entradaposterior del’Encyclopédie,senseintroduireltermede variable,isensefercapdiferenciacióentrequantitats variablesiconstants.D’altrabanda,podemobservarunanovetatsubstancial.

S’adonaòbviamentdelfetqueelmètodedellímitrequereixqueellímittinguielseupropisigne.1 Aleshoreshodeclarausantun signe distingitperdesignarellímit.Nointrodueix,noobstantaixò,un signegeneral,sinóúnicamentunsigneperalslímitsdelsquocientsdediferències:2

Usaremunsigneperdesignarlaraódelesdiferènciesdeduesquantitatsvariables.Silesdues quantitatssón x,y i Δ x : Δ y laraódelesdiferències,enlarestadeltextusarem dx : dy perdesignar elseulímit(ibid.,pàg.32).

ElsegonautorquehemdediscutircominfluïtperGarçãoStocklerésRoger Martin,ielseutext ÉlémentsdeMathématiques (1781).EltextdeMartin,d’acordambelsubtítol«àl’usagedesécolesde philosophieduCollègeRoyaledeToulouse»,estavaclaramentdestinatalcontextuniversitari.I,atèsque, d’altrabanda,vaelaborarunapresentaciómésdetalladadelseupuntdevistasobrel’infinit,idelcàlcul diferencial,endostractatsadreçatsaunaacadèmia,podemconsiderarqueelsseustractatsestaven pensatstambéperaunpúblicmésampli.Lesduespublicacionstinguerenunacertainfluènciaa l’estranger.

ComCousin,MartinestavaconvençutqueD’Alembert,amblasevaideade límit,presentadacomuna adaptaciódelmètoded’exhaustiógrec,haviaestatelprimeraformularunajustificacióexactadelcàlculdiferencial(Martin1781,pàg. LVI).Difereix,tanmateix,deCousinenlasevadefinició independent delímit:

Perlímitd’unaquantitatvariableentendremelvaloroestatalqualtendeixsemprequanvaria, sensemaiatrapar-la;peròalqual,noobstantaixò,s’apropatantquearribaadiferir-himenysque qualsevolquantitatdonada(ibid.,pàg.317).

Nosolamenttrobemformuladaaquílapetitesadeladiferènciagairebéambtantaprecisiócomla queaconseguiràlaformaestàndard,sinóque,d’unabanda,relacionaclaramentelprocésdellímit

1.«Recordemque,eneltextdeSchubring, signe significa‘símbol’».(N.delt.)

2.«Elquecorresponaladerivada,entermesactuals».(N.delt.)

aunavariable,i,d’unaaltra,el valor (constant)delavariablecomalímit,laqualcosasignificauna conquestad’innovaciógenuïna.Martinhaviaintroduïtelconceptede valor enlasevasecciódedicada al’anàlisi,explicantl’anàlisi «comelmitjàpertrobarunaexpressióalgèbrica,elvalorespecíficdeles quantitatsquanestrobencombinadesambd’altres».Sensehaverdefinitdemaneraformal valor, eltextdeMartinnodeixamaiclarque,perquantitats,enténquantitatsconstantsquesatisfanles condicionsalgèbriquesrespectives—perexemple,lesarrelsdelesequacions(ibid.,pàg.132).Martin nointrodueix,tanmateix,capsigneperalseulímit.

Enelsfonamentsdelmètodedellímit,MartinesrelacionadirectamentambCousin,itambé,pertant, amblesconcepcionsdel’objectequepertanyenalageometriaelemental.I,sibénoadoptaelprimer principideDelaChapelleideCousin,adoptaelsegondeCousinielconverteixenun«teorema» sensedemostració.Elqueinteressa,tanmateix,ésqueMartin,generalitzantaquestprincipi/teorema, estableixelprimerprincipid’intercanvidelímits.Comateorema III,estableixlaproposiciósegüent:

Siduessuccessionsdevariables—creixentsodecreixents—,delesqualslasuccessióquetéels elements a,c,e,g, ... portaalaquantitat u,ilasegona,queconstadelselements b,d,f,h, ... ,ala quantitat x ,aleshoreslasuccessiódelesraonsdelstermesrespectius—i.e.: a : b,c : d,e : f, portaalaraódelsdoslímits.3

Explícitamentafegeixunaformulaciódelprincipid’intercanvidelímits—queusarepetidament— iqueéslasegüent:

Osigui,queellímitdelesraonsseràlaraódelslímits.

Potsers’haobservatqueMartin,enelseu«teorema»,designaellímitcomuna«quantitat»inopas comun«valor».Peraellaixòtéunsignificatsistèmic,jaquetotseguitafirmaqueelteoremanose satisfàenelcasenquèelslímitssiguinnuls.Elzero,diu,noésuna quantitat i,pertant,nohipothaver capraóentredoslímitsd’aquestafaiçó.

Podemconsiderarqueaixòeraunacreençabàsicademoltsdelsmatemàticsd’aquestperíode.Elzeroeraconsiderat,coml’infinit,unaexcepció,iencapcasseliconcedial’estatusdenombre.Aquesta opinióhaviapresentat,desdefeiamoltdetemps,conseqüènciespunyentsenl’elaboraciódelconceptedelímit.

Unfetremarcablerelatiualsdosautorsesmentatsenaquestasecció,CousiniMartin,ésqueambdós vaneditarelsseustextos,ensegonaedició,uncopacabadalaRevolucióFrancesa,iaixòsignifica quehoforendurantl’estadieufòricd’algebraïtzaciódel’anàlisi.Ésreveladorconsultarelscanvisque esprodueixenenaquestessegonesedicions.L’ediciódeltextdeMartinapareguéel1802,vintanys desprésdelaprimera.Comhemvist(cf.Schubring,2005,cap. II.2.10.1,pàg.116),Martinestrobava involucratenlatascaparlamentàriaposterioralaRevolució.Pelquefaalsconceptes,lasegonaedició ésidènticaalaprimera,iàdhucenelstermesielssignesinvolucrats.Nomésapareixenpetitscanvis enelsmots.

Cousinvapublicarlasegonaedicióen1796.Ésparticularmentremarcableunainnovaciórelativaals signes.Alasegonaedició,Cousin,perprimeravegada,aplicaelsigne lím il’insereixoperativament, perexempleenl’equació:

3.«Ésclarqueencaranoeraunapràcticamatemàticausarlanotaciódelssubíndexosperadesignarelstermesde lessuccessions».(N.del’a.)

lím. Δ(E · CK )

=

(Cousin1976,pàg.135). 4

Enl’úsdelsseussignes,Cousinnoera,però,consistent.Elsconfinàaunúniccapítol,eldelamecànica. Enelcapítolprecedent,usavasempreunaformaverbalitzada,comara

5. Expansió de l’aproximació amb límits i inici de la seva algebraïtzació

Seguintaquestsprimersintentsd’elaborarelconceptedelímit,veiemunconsiderablecreixement enlareflexiód’aquestconcepte.Unadelescausesestrobaenelbenconegutreptedel’Acadèmia deBerlínde1784,unacompeticióquedonàunreconeixementcientíficdelmésaltnivellalrebuig dels infinitamentpetits

Eltractatqueguanyàelpremiaquiresolguéslatascaqueproposaval’AcadèmiadeBerlínfou Exposititionélémentairedesprincipesdescalculssupérieurs deSimonde L’Huilier,del1786,iprovocà,a més,unimpacteconsiderable.L’Huilier(1750-1840),nascutieducataGinebra,fouenprimerllocun mestreprivatdelaresidènciad’unprínceppolonès,idesprésdel1795professordematemàtiquesde l’AcadémiedeGinebra,unestablimentd’educaciósuperior.Elsseustreballsmatemàticsestavenfocalitzatsentòpicsdegeometriaelemental,enparticular,políedres,poligometria,ienladeterminació dellocsgeomètrics.L’Huiliernoeraunexpertenanàlisi.

Enl’assaigpremiat,quehaviapublicatperprimeravegadaen1796,objectavafortamentl’úsdeles quantitatsinfinitamentpetites,resp.infinitamentgrans,ihaviaelaboratunamicamésencaraelconceptedelímit.Amés,enteniaaquestconceptecomquelcomqueestavad’acordambelmètode delsAnciens,encaraquedemaneraapropiada:

Elmètodedelsantics,conegutambelnomdeMètoded’Exhaustió,entèsdemaneraapropiada, éssuficientperestablir,d’unacertamanera,elsprincipisdelcàlculnou.(L’Huilier1786,pàg.6).

UnmomentcaracterísticdelpuntdevistadeL’Huilieréslasevaconcepciódelzero—iaixòmostra unavegadamésl’íntimarelacióentreelsconceptesdequantitatsinfinitamentpetitesielconcepte denombre,enparticularl’estatusdelsnombresnegatius,itambédelzero.PeraL’Huilier,nomésel «zeroabsolut»ésméspetitquequalsevolquantitatassignable(«asignable»)(ibid.,pàg.137).Elzero és,tanmateix,l’expressiód’una«privationdetouteexistence»—decancel laciódetotaexistència(ibid., pàg.126).Elsnombresestanjustificatsnoméspelcaràcterontològicdel’existènciadelesquantitats. Elzeronoésadmissiblecomaconcepterelacional.Ésnoméslapersonificaciómetafísicadelno-res.

EncaraqueL’Huiliernoproporcionacapfontperalseuconceptedelímit,ésforçaevidentqueestava influïtperCousiniperMartin.LadefiniciódelímitdeL’HuilierésforçamésespecíficaqueladeCousin. Empracomaconceptebàsicelde quantitatvariable.

Hihaunaquantitatvariable,sempreinferiorosuperioraunaquantitatquehomsuposaconstant; peròquepotdiferird’ellamenysquequalsevolquantitatques’hagidonatméspetitaqueella

4.Cousinsempreescriuunpuntdesprésdelsigne«lím»,probablementpersuggerirl’abreviaciódelsigne.(N.del’a.)

mateixa:aquesta quantitat s’anomenael límit enexcésoendefectedelaquantitatvariable(ibid., pàg.7).

SibéL’HuilierusaladefiniciómésespecíficadelímitdeMartin,introdueixlanovetatdediferenciar entre limiteengrandeur i limiteenpetiteusse

Enintroduiraquestadiferència,L’Huilierexpressalaideaqueelsconceptesdelímitques’havienestablertabansd’ellnofeienatencióalfetquel’aproximacióallímitpotsertantl’efectedevariables devalorscreixentscomdevariablesdevalorsdecreixents.Comqueencaranoesdisposavadelconceptedevalorabsolut,ellseparavalesdefinicionsen:

• límit«perl’esquerra»—limiteengrandeur ien

• límit«perladreta»—limiteenpetiteusse

Tanmateix,nofouhàbilperafegir-hivariablesquemostressinalhoracomportamentsalternatsd’aquestafaisó.

D’acordambelseupropicampdetreballmatemàtic,tantelconceptedevariablecomelconcepte delímitestavenmotivatsis’aplicavengeomètricament.Elseucontextprimarieraeldeles corbes geomètriques,inopaselsdelesfuncions(cf ibid.,pàg.8is).MalgratqueL’Huilierdiscuteixlesfuncionsi elsseuslímitsenlapartintroductòria,entenentlesfuncions,d’acordambelteoremadeTaylorenla sevaexpressióformalalgèbrica,comsèriesdepotències(ibid.,pàg.21is.),aquestespartsalgèbriques sóncol·locadeseclècticamentalcostatdelpuntdominantdelescorbes.

Enmoltesdelesproposicionsdelapartintroductòria,L’Huilierestableixcomunsupòsitexplícitl’obtenciódelslímitsinopasllurexistència.Unadelesformulacionstípiquesés:«Soientdeuxquantités variablessusceptiblesdelimites»(ibid.,pàg.11).Tanmateix,enlesaplicacions,noesfacapmencióde ladistincióentre susceptible i nosusceptible

L’úsdellímitdeL’Huilierenrelacióambelssigneséstambérevelador.Enlapartintroductòria,no usacapsímbolpropiperallímitiexpressatoteslessevesproposicionssobrelímitsverbalment —e.g.per«lelimitede».Desprésd’unavintenadepàgines,apareixelsigne«lim.»,usattambéper Cousin—tambédesignatamblamateixafunciócom«Lim»—,peròsolamentcomunindicadorimmotivatsensecapexplicaciónijustificació(ibid.,pàg.24).Eneltextsubsegüent,L’Huilierusaelsigne noméscomunaabreviacióocasional,sensecapreflexiósobrel’úsdelsigne,ocapaplicacióoperativa independent.L’únicindretonmencionademaneraexplícitaelsigneésquancalreemplaçar-lopel quocientdiferencial:

Unanotacióconvenientescurçaelscàlculsielsfamésfàcils.Així,doncs,perindicarlaraódels canvissimultanisde P i x ésconvenientusar dP dx enllocdelím ΔP Δx .Pertant,lím ΔP Δx i dP dx fan referènciaalmateixobjecte(ibid.,pàg.31).

Peròl’éxitmésexcel·lentdeL’Huilierfouunaexpansióconsiderabledel’aplicabilitatdelconceptede límit.Mentrequeelsseuspredecessorsambproufeinesvanestablirdueslleisbàsiques,ellféuuna elaboraciósistemàtica.Unaaproximaciódenouencunyenaquestalíniaésl’intentd’inferirlalleide laderivadaproductededuesfuncions P i Q de x delímitsrespectius A i A .Obtél’expressió

lím. ΔPQ Δx = PA + QA (ibid.,pàg.31)

Pelquefaalprogrésgeneraldelconceptedelímit,ésimportantd’observarqueL’Huiliercomença adoptantlaproposiciód’intercanviabilitatrelativaalprocésdelslímits(comundelsseus«théorèmes»: «Laraólímitdelaraódeduesquantitatsvariablesqueacceptenlímitsésigualalaraódellurslímits» (ibid.,pàg.24),icontinuaambunageneralitzacióenelsentitdelsegondelssignificatsmetafísicsde lalleidecontinuïtatdeLeibniz:

Siunequantitévariable,susceptibledelimite,jouitconstanmentd’unecertainepropriété,salimite jouitdelamêmepropriété(ibid,pàg.167).

L’Huilierdeclaravaqueaquestaproposiciósobrelavalidesapercontinuïtatdelespropietatsdeles variableseratanbonaqueconsideravaquehaviadeserel principi guiadelseutractat,elqual,alhora, n’eraelseucordecisiu(ibid.).

Eneltractatquevaguanyarelpremi,L’Huiliernoanomenacapmatemàticcomasuportconvenient delessevessolucions.Enunanotadepeudepàginaulteriordestinadaalapublicacióproporciona unallistad’autorsrellevantsperl’encertd’evitarlesquantitatsinfinitamentpetites:D’AlembertiCousinitambéelsalemanysKästner,KarsteniTempelhoff.OmetmencionarMartin,peròenlareedicióde 1795(L’Huilier,1795,pàg.1)del’obrapremiada,isolamentenaquestaocasió,inclouunareferència aRobert Simson (1687-1768)—delqualhaviacopiatgairebéalpeudelalletralesdefinicionsfonamentals.Simsonfouelprimerquededicàuntextseparatalconceptedelímit.Aquesttractat,que solamentesconservademaneraparcial,foupublicatpòstumamentenlarecopilaciódelesobresde Simsonde1776ireeditatperMaseresen1807ambeltítol, DelimitibusQuantitatumetRationum

L’obradeSimsoneslimitasolamentadesenvolupar,iaplicar,elconceptedelímitaquantitatsgeomètriqueselementals.Aixòexplicatambélasevafocalitzaciósobreaplicacionsaraonsgeomètriques («rationes»).Desprésdelesdefinicionsintroductòries—delesquantitatsconstantsivariables—,Simsonhaviadonatduesdefinicionsdelímitinferior,resp.superior,d’unavariable,definicionsqueL’Huiliers’haviaapropiatdirectamentcomabasepròpia(vegeulapàg.17):

III.Siquantitasmutabilissemperminorfueritquantitatedata,seditaaugeripoterit,utmajorfiat quacunquequantitatedataquaeminorestprimaquantitatedata;velsiquantitasmutabilissempermajorfueritquantitatedata,seditaminuipoterit,utminorfiatquacunquequantitatedata quaemajorestprimaquantitatedata;inutroquecasuquantitasprimadatadicaturLimesquantitatismutabilis.

IV.Siratiomutabilissemperminorfueritquamratiodata,seditaaugeripoterit,utmajorfiatratione quacunquedataquaeminorestrationeprimadata;velsiratiomutabilissempermajorfueritquam ratiodata,seditaminuipoteritutminorfiatrationequacunquedataquaemajorestrationeprima data;inutroquecasudicaturratioprimadataLimesrationismutabilis,inprimosciliectcasudicatur Limescrescentisrationis,inaltero,Limesdecrescentisrationis (Simson1776,pàg.3f.).

AmbaquesttextveiemqueL’Huiliermanllevàladiferenciacióentrelímitsuperior,resp.inferior,del deSimson.NomésutilitzàMartinenlaclaraclassificaciódellímitcomaconstant.

Simsonnodisposavadesigneperal límit,iescriviaeltextdemaneratotalmentverbal,sensecap menad’algebraïtzació,iusantexclusivamentraons.Enaquestalínia,tambédiscutí—circumscrivintsealcàlculdiferencial—laraód’increments,perexempleenelcasdelessecants,delaformació derectangles,etc.Nomésalesacaballesdeltext,Simsonusa ˙ x i dx perdesignarelslímitsdelsincrements,palesantaleshoresquelasevaintencióésclarificarelsproblemesfundacionalsdel’anàlisi(ibid., pàg.26).

Bibliografia

D’Alembert,J.leRond(1754).Differentiel.DinsD.DiderotiJ.d’Alembert, Encyclopédie,ouDictionnaire RaisonnédesSciences,ArtsetdesMétiers.París:Briasson etalii,tom IV,pàg.985-989.

—(1765).Limite.DinsD.DiderotiJ.d’Alembert, Encyclopédie,ouDictionnaireRaisonnédesSciences, ArtsetdesMétiers. París:Briasson etalii,tom IX,pàg.542.

DelaChapelle,J.B.(1746). Institutionsdegéométrie,enrichiesdesnotescritiquessurlanatureetlesdeveloppmentsdel’esprithumain.París:Debure,dosvols.,quartaedició:1765.

—(1765).Limite(Mathémat.).DinsD.DiderotiJ.d’Alembert, Encyclopédie,ouDictionnaireRaisonné desSciences,ArtsetdesMétiers.París:Briasson etalii,tom IX,pàg.542.

Cousin,J.-A.-J.(1777). Leçonsdecalculdifférentieletdecalcultntégral.París:Cl.A.Jombert,segonaedició:1796.

Edwards,C.H.,Jr.(1979). TheHistoricalDevelopmentoftheCalculus.NovaYork:Heidelberg.

Guicciardini,N.(1989). TheDevelopmentofNewtonianCalculusinBritain1700-1800.Cambridge:CambridgeUniversityPress.

Grabiner,J.V.(1981). TheOriginsofCauchy’sRigorousCalculus.Cambridge,Mass.:TheMITPress.

L’Huilier,S.(1786). Expositionélémentairedesprincipesdescalculssupérieurs,quiaremport’eleprixproposépatl’AcadémieRoyaledesSciencesetBelles-Lettrespourl’anné1786.Berlín:G.J.Decker.

Maclaurin,C.(1742). ATreatiseofFluxions.InTwoBooks.Edimburg:Ruddimans.

Martin,R.(1781). Élemensdemathématiques,peral’úsdelesescolesdefilosofiadelCollègeRoyalde Tolosa.Tolosa:Robert.

Nesselmann,G.H.F.(1842). VersucheinerkritischenGeschichtederAlgebra.ErsterTheil.DieAlgebrader Greichen.Berlín.Reimpressió:Frankfurt:Minerva,1969.

Newton,I.(1729). MathematicalPrinciplesofNaturalPhilosophyandhisSystemoftheWorld.Traducció anglesad’AndrewMottede1729.Latraducciórevisadaiacompanyadad’unaparellexplanatorii històricésdeFlorianCajori.NovaYork:Greenwood,1969.

Newton,I.(1726). PhilosphiNaturalisPrincipia.Terceraedició,amblecturesdiverses.Reunitieditatper AlexandreKoyréiI.BernardCohen.Volm I.Cambridge:CambridgeUniversityPress,1972. Schubring,G(2005). KonfliktezwischenGeneralisierung.StrengeundAnschaulichkeit:zurEntwicklungder GrundbegriffederAnalysisim18,un19JahrhundertinDeutschlandunFrankreich.Springer:NovaYork. Simson,R.(1776).DeLimitibusQuantitatumetRationum.Fragmentum.DinsR.Simson,M.D.,MatheseosNuperinAcademiaGlasguensiProfessoris, OperaQuaedamReliqua.Stanhope:Glasgow, IV,pàg. 1-33.

Unapartidadefutbolí

CatalinaM.PizàMut

CPMestreColom.Bunyola,Mallorca

Resum Abstract

Estractadelaconstrucciód’unfutbolíperpart d’ungrupde4tdeprimàriadelCPMestre ColomdeBunyola,Mallorca.Apartird’una peticiódelgrup(jugarafutbolí)s’hafabricatun futbolídefustaipotetsdeplàstic.Enlaseva realitzaciós’hanhagutdeplantejarqüestions matemàtiques,especialmentde mesurai càlcul (lesmidesdelcamp,delesporteries,de lesàrees,l’estaturadelsjugadors,ladistribució delsjugadorsdamuntlesbarres),tambéde geometria (una-duesdimensions,superfície, radiidiàmetre,concepted’àreai,perdamunt, algunesnocionsd’espai:dissenyplànol, dreta-esquerra,capauncostat,capal’altre)i algunade tractamentdelainformació (gràfic estatures).S’haaprofitatpertreballardiferents textosrelacionatsambelfutbolí(instruccionsde joc,notíciaesportiva,retransmissió«radiofònica» d’unapartd’unpartitiexposicióoraldel projectealesfamílies).Resolententrebancs hemaprès,hemgaudit,enshememocionat.

Theaimwastobuildatablefootballfollowinga requestfromthechildreninthe4thyearofprimary intheCPMestreColominBunyola,Mallorca.We builtatablefootballusingwoodandsomeplastic containers.Inordertobeabletodothiswehadto answersomequestionsrelatedtomaths, particularlymeasurementandcalculus (dimensionsforthepitch,area,goal,player’s height,thespaceinbetweeneachplayeronthe bars),alsogeometry(one-twodimensions,radius, diameter,theconceptofareaandsomesimple conceptsrelatedtospacesuchasplans,right-left, tooneside,toanother).Therehavealsobeensome issuesrelatedtodataanalysis(charts).Wehave alsoworkedwithdifferentfootballrelated documents(gameinstructions,articlesabout football,radiobroadcastingandanoral presentationtotheparents).Wehavelearntand enjoyedourselvessolvingdifferentproblems.

1. Introducció

Elprojectequeesdescriuacontinuaciól’handesenvolupatdurantelcurs2011-2012els20alumnes dequartdeprimàriadelCPMestreColomdeBunyola,unpobledeMallorca.

Al’inicidecurs,perferparticiparl’alumnatdelprocésd’aprenentatge,esplantejalaqüestiósegüent: «Quèvoleuferenguany?»

Entrelesrespostes,moltesd’ellesdirigidesaincrementarlesactivitatslúdiques,duesninesproposaren«jugarafutbolí»,lapropostavaserampliadaperuncompany,«home...jugar...almancoconstruirlo,no?Isienfeimun?»

Vaseraixícomvacomençaraquestprojecte.Ambellespreteniatreballargeometria,peròenrealitat nosen’hafetgaire,almancoladelspolígons,comespensava,encaraquesílageometriadeles nocionsd’espai,itambémesura,moltdecàlcul,unpocdetractamentdelainformacióibastant d’elaboraciódetextos.

EnlafabricaciómaterialdelfutbolíenshaajudatmoltenVicenç,elconserge:perògairebétotsels càlculsilaresoluciódelamajoriadelsproblemesquehansorgit,haestatdelsinfants.

2. El procés

1.Laprimerafeinavaserferundissenyindividualdelfutbolí.N’hivahaverdetottipus,deplastilina, deferro,defang,ambcapsesdesabates,ambjugadorsdecartró,dexapes...finalmentesvadecidir fer-lodefusta,aproximadamentcomelsdelmercat.

2.Lasegüentqüestióaresoldrevaserlagrandària.Ellsiellesproposavende2x3rajolesdelaclasse, peròcomquequedavamésallargatdelquesolenserelscamps,decidíremconsultarcomerenels campdeveresi,entreelspares,entrenadorsiinternet,comprovàremqueelscampsperapartits internacionalsfan70 × 110m.

Sensemassaentrebancshopassàremacm,pertant,escala1:100(fàcildecomprendrepera ells:1centímetredelsnostressón100alarealitat),ihomesuràrementerra,al’aula.

Elsvaagradar,eraaproximadamentde2 × 3rajoles,perònotanallargat,arajaera proporcional alarealitat.(Unconceptedifícilperalamoltsdelsalumnes:igual,deformaexacta,perònode grandària.Unrectanglede2 × 3rajolesdelaclasseounde70 × 110cmnosóntandiferents icostamoltdeveureladiferènciaentreigual,proporcional,diferentnomésenunadimensió... Aquesttemavaquedar,pertant,nomésencetat,parlatdeformaintuïtiva.)

3.Lasegüentqüestióvasercomanarlafustaperalabase.De70 × 110?No,perquèhavíemdeposar les«paretsdelsfutbolí»,peraixòhavíemd’afegir1cmperbanda.Hivahaverdiversessolucions; 71 × 111(n’afegiennomésauncostat),74 × 114(n’afegienels4detoteslesbandes)...finsque vàremarribara72 × 112.L’endemà,enVicençensteniapreparadaunafustadeconglomeratde 72 × 112cmalaportadelaclasse!

4.Lapintàremdeverd,jasemblavauncampdefutbol.Elsvaigplantejarunapreguntaperquèla resolguessenindividualment:Onposaremlameitatdelcamp?

Totd’unasorgirenpreguntescom: Lameitatdequè? Lameitatdelllargodel’ample?

Anarenfenti,comqueaclassesovinthemfetelqueanomenam«Problemessensecomptes» (figura1)qualcunscalcularenmentalmentlameitatde100ilameitatde12;altresdoblegaren

Figura 1

lacintamètricaperlameitatiafegirenlameitatde12;unsaltreshoferenatanteig,altresamb l’algoritmeescritimolts,amés,hodibuixaren...Hivahavercamps«quadriculats»,perquèalguns haviencalculatlameitatdelallargària,pertantde112,peròtambélameitatdel’ampladadel camp,pertantde72,quenaturalmentelshaviasortit36.

Vàremveurequenomésensfeiafaltalameitatde112,peròquepossiblementenunaltre momentensservirialadadaquehavientrobat(36cm).

Ambelregledepissarramarcàrem56alsdoscostatsielsunirem.Noéstanobvipelsalumnes de4tdeprimàriaquepermarcarunalíniaenunsentithasdecol·locarelregleperpendicularment aladireccióenqueestaràdibuixadalalínia,nitampocquefanfaltaalmancoduesmarquesper talquelalíniasurtibendreta.Totesaquestespetitesqüestionss’anavenresolent,amesuraque sorgien,engrangrup,amblesideesd’unsialtres...Japodíemposarlacintaadhesivablancaper damunt!

5.Lasegüentqüestióqueelsvaigplantejarperescritvaser:Onposaremlesporteries,aquinadistànciadelesvoreres?Itambévasuscitarunanovapreguntaperpartseva: Comsóndegrosses?

Unninvadirquefeien7m.Decidíremmesurar7cmdamuntlanostrabase,onaproximadamenthihauriad’haverlesporteries,iensvarensemblarmoltpetites,tant,queresultariaimpossible ficarcapgol,peraixòproposarenfer-lesmésgrosses.Icomdegrosses?Doncs,...coml’àreapetita, de20cm.Tothomd’acord.

Lesmaneresderesoldre-hovarenserdues.Laprimera:cercarlameitatde72(arasíques’utilitzavaaquestadada!)imarcar10cmcapauncostati10cmcapal’altre.Lasegonamanera:a 72cmrestar-n’hi20idesprésdividir52entre2,26(novamentlamajoriaferenmeitatde50imeitat de2).Així,jasabienquemarcaríemlesporteriesa26cmdelesvoreres.

6.Ambelmateixsistema(preguntaambrespostaescritaindividual,desenvolupamentsdiversosi discussióengrup)marcàremlesàreespetitaigrossa(onvatornarasortirelplantejamentde una/duesdimensions)itambél’àreacentral.Aquívasorgiruntemainteressant.Quantenguérem elrotlledel’àreacentralmarcatambcompàsadamuntlafusta,unpetitgrupd’alumness’havia d’encarregardemarcarelrotlledamuntelpaperadhesiublanciunalumnes’acostaidiu:«S’han equivocatperquèhemditquel’àreacentralseriade10inosaltresl’acabamdemesurariésde 20».Esvaaturarunmomentlaclasseperexposarelquedeiaelpetitgrupielsvaigdirqueelsdos grupets—elquehaviamarcatalafustaielquehoestavafentalpaperblanc—totsdos,tenien raó,elrotlleerade10ierade20.Desprésd’unpocdediscussió,«quesiunestàencmil’altreno, quenopodentenirraóelsdos»,etc.s’adonarenqueuneral’oberturadelcompàs(elradi)il’altra mesuraeradebandaabanda(eldiàmetre).Decidíremquesemprehavíemd’especificaraquèes referialamesura,iqueaixòjaenshaviapassatalcasdel’ampladailallargàriadelcamp.Aixíl’àrea centralfeia10cmderadio20cm.dediàmetre,eraigual. Jateníemelcampmarcat!

7.Novapregunta:Quantsdejugadorshadetenirelnostrefutbolí?20,jaquenosaltressom20a classeiaixí,enpodremferunperhom.Quedarien2equipsde10.Enrealitatsón2equipsd’11 jugadors,jaqueafegíremelporter.

8.Comelscol·locarem?Almercathihamoltespossibilitats,duguerenfotos,catàlegs,mirareneldel bardelpoble,eld’uncentrecomercial...Lasolucióquemésvaagradarvaser:4davanters,3mitjos, 3defensesi...elporter.

9.Lasegüentproposta:Quantesbarreshihauràperequip?Comseran?Aquílarecercadesolucions novaserindividual,sinóperpetitsgrupsde4(massaemociópertreballarsols,massadificultats

perresoldre-lessols).Novespreguntesperpartseva:jahanexperimentatmoltdepicsquela faltadedadesnopermetresoldresatisfactòriamentelsproblemesqueesplantegen;peraixòtots voliensaberlalongituddelesbarresdefustaquecompraríem.

Faran102,5cm.Elsdiferentsgrupsarribena:

• Barresd’unsoljugador,lesdelsporters(2)...fàcil,alameitat...però«descomptamelmànec ielstopes,no?»...Lamajoriadegrupsassignen10cmpelsmànecs,desprésdecomprovar elquemesuraelseupunytancat,i2,5cmpelstopes,perdeixarunnúmerorodó:90.Així,el porterelsituarana45cm.

• Barresde3jugadors,lesdelsmitjosidefenses(4)...fàcil,eljugadorcentralcomelporteriels altresdoselscol·loquenalameitatdelquequedaaunnúmeroconcretdecm.Aquíel queéscuriósésquehihaprincipalmentduesformesderepresentar-ho:obémarcant elcentímetreconcretonaniràeljugadoripertantseriacomunarectanumèrica,obémarcantelscentímetresdelsespaisapartird’unpuntconcret,capauncostaticapaunaltre sensemiraraquinnúmerodelacintamètricacorrespon(figura2).

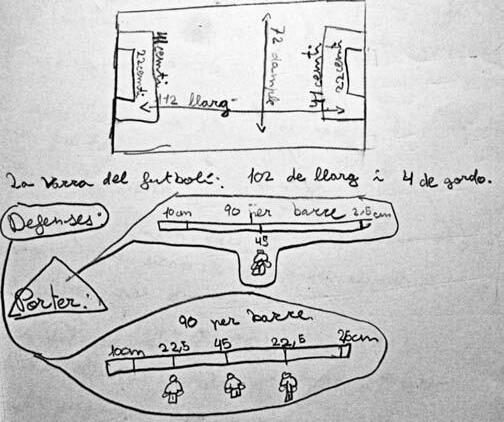
• Barresde4jugadors,lesdelsdavanters(2)...notanfàcil...janohihajugadoralameitatperò totshiparteixenimarquenelsintervalsquedeixaranentrejugadors...massapossibilitats...

Aquívaighaverd’interveniramblesmesures.Nopodiasernomésuncàlculdemeitats,sinó ques’haviadetenirencomptequeelsjugadorsarribassinpertoti,quel’espaiexterioralcamp fossuficientperpoderdesplaçarelsjugadorssensequelabarrapassàsperull...Massacomplicat peraells...Elsvaigdirqueutilitzariaelsseuscàlculsienfariaunqueensservísatots.Elsvaigfer representarambelmovimentdelseucosquesiunjugadoresmoviacapaladreta,haviad’arribar finsalameitatdelcamíiqueeljugadordeladretasiesmoviacapal’esquerra,recorrerial’altre meitat.Vasermoltdivertitmoure’scomelsjugadorsd’unfutbolí,totsquatre,ototstresalauna... Aixíhopoguerenentendreunamica.

10.Jaacabàvem,peraixòse’lsvaproposarquedibuixassinelfutbolítalcomsel’imaginavenaaquell moment.

Figura 2

Varenaparèixermoltsdemodels,ques’aprofitarenperaferunaprimeraavaluació.

Se’lsvarendonar5delsmodelstipusielsvarenhaverd’analitzarindividualmentperextreure lescaracterístiquescomunespelnostreprojecte.

Vaserinteressantposar-hoencomú.

• Vàremveurequelesbarresdelsjugadorshand’anarmesclades,sinoésmassadifícilfergol... elsjugadorsnoespodenmourecapendavant!(figura3).

Figura 3

• Quelespersonesquejuguens’handecol·locarabandaibandadelfutbolí,enfrontades:no hipothavertotselsmànecsalmateixcostat!

• Queelnombredejugadorsdecadaequiphadeserelmateix:sinounequipsempretendria avantatge!

• Quedavantlabarradelporter,hihad’haverladelsdefensesdelseumateixequip:sino estariensempreenforadejociseriamassafàcilfergol!...

Imaginarelcamp...ésmoltmésdifícildelquesembla.Elfetderepresentar-hodamuntun paperajudaielfetdeparlar-neiescriurelesconclusionsajudaencaraunpocmés.Així,ananti venentdelcapalpaperidelpaperalesparaules,poguéremarribaraundissenydefutbolímolt precís.

11.Desprésféremeldissenydelarobadecadaequipientriàremdosperconsens,pintàremels jugadorsfetsambpotetsdeiogurtlíquidplensdeguixfins2/3parts,perquèpesassinilaresta d’espumadepoliuretàexpandida,perpoderarrodoniruncapiaferrar-hillana.Elspintàremsegons larobadel’equipielsdibuixàremlacaraambretoladorspermanents.Esvadecidirquefossin equipsmixtos.

12.Mentrestant,féremelmarcador(entenguérem7models:ambcordaixapes,ambtargetesgiratòries,fixes,pissarretesadhesives...),elnomdecadaequip(CràtersiFerotges)ilasevamascota

(unatigressaiunmarcià),lafotodel’equip,elcromo individualperacadajugador(figura4)ambdeterminadescaracterístiques(nom,nacionalitat,edat,estatura,equipsonhajugatanteriorment,posicióqueocupa actualment.Totesaquestesdadespodienserinventadesoreals.)

Peral’estaturaesvaaprofitarque,acomençament delcursanterior,s’havienmesuratenrelacióaunconte«Nicoelpirata»...iteníemlesdadespenjadesdesdel mesdesetembrede2010alaportadelaclasse.Donavajoc,perquèteniencertatendènciaamesurarsi haviencrescutono,moltopoc...Peraixò,aljunyde 2012,estornarenamesurarsuperposantlanovaestaturaambunpaperd’acetatdamuntlesmesuresanteriorsi,ambelprogramaOppenOffice.orgCalc,vàrem emplenarlesdadescorresponentsiobtinguéremun gràficcomparatiu.

Observàremaixíelseucreixement(figura5).

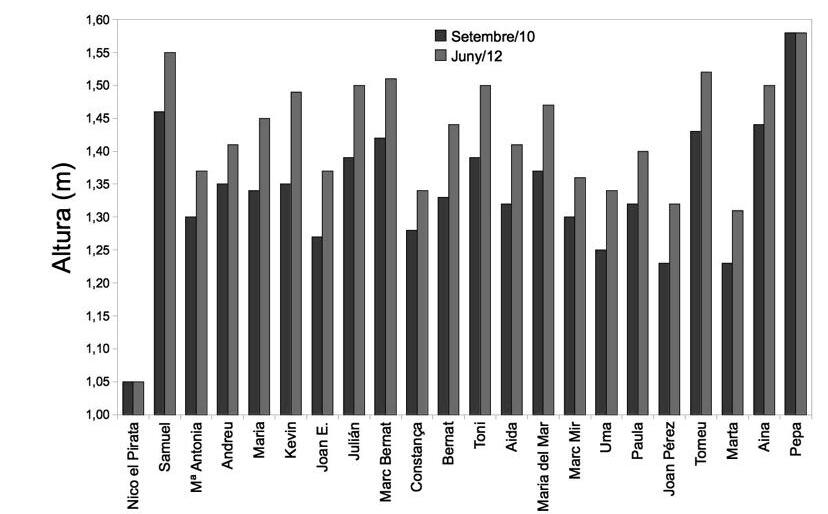
I...japodíemcomanardeformaprecisaaenVicenç,l’elaboraciódelesbarresdeljugadorsila sevadistribucióalcamp.

13.Unaaltrapartdel’avaluacióvaconsistirenunproblemaclàssic. Lapreguntaera:Imaginaquelatevataulaésuncampdefutbol.Onposarieslalíniademig campsilesmidesdelataulasón64 × 45cm? Diversesrespostes.

• Lamajoria:a32cmdelallargària.

• Qualcuns,afegirenencaralameitatdel’amplada...Tornàremaveurequenofeiafalta,que quedariauncampquadriculat.

Figura 4

Figura 5

• Ungrupetmésd’alumnesmultiplicaren64 × 45...Elseuresultatera2880.Davantlameva pregunta...onposaries,pertant,lalíniademigcamp?...Varenveurequeaquellresultatno elsserviaperaixò,però,elsvaigdirquesíserviaperqualquecosa.Unbongrupd’alumnes recordarenquel’anyanteriorhavíemtreballatelspolígonsper«omplirotesselar»iquela multiplicacióenaquestscasoseramoltútil,serviatambéperaixò,justament.Aixíel2880 eratotelcampple.Parlàremdelanociódesuperfícieid’àrea,ivéremqueel2880erencm2 Unaltrepic,comjahemvist,apartirdelserrors,apareixenconceptesnous.

14.Peraltrabandatreballàremdiferentstextosambunaseqüènciadidàcticacompleta(esborrany, extracciódecaracterístiquesielaboraciódelguióbase,aprofundimentdelsaspecteslingüístics oportunsimilloradelsaspectesnecessarisconcrets,segonaelaboració,correccióortogràfica,text definitiuanet,avaluacióiautoavaluaciósegonspautainicialfixada).Vaserelcasdelesinstruccions dejocidelanotíciaesportiva,amblesqualsféremuna«revista».Altrestextosvarensertreballats notanintensament,comlaretransmissiód’unpartit(peralaqualconsultàremunarticleamb vocabulariespecíficdefutbolencatalàicercàremsinònimsdegol,dexutar);tambépetitscartells convidantenVicençialtrescursosdel’escolaajugaritambépreparàreml’exposicióoralales famíliesambpetitsdiàlegsintroductorisdelesdiapositivesd’unapresentacióprojectadaamb ordinador.

15.Féremunainauguracióal’aula,ambelconsergeimoltescoques!Itambéféremunapresentació amblesfamílies,onpoguéremjugarmares,pares,fillsifillesimestresambunapilotadepingpongpintadaambelshexàgonsnegrestípicsdelespilotesdefutbol.

16.Féremuntorneig.Cadadiaperacabarelmatíjugàvemunpartitelsdarrers5minuts(unpartit acabaals10golsd’unequipoals5minutsdetemps,segonsdiuenlesinstruccions).Elssistema perferelsequipsielscontrincantstambévasertemadediscussió.Detrespropostestriàremla següent:elprimerieldarrerdelallistacontraelsegonielpenúltim,...Moltdivertit.

17.Ladarrerapartdel’avaluacióvaserescriuretotelprocés,perveureelquehavienentèsdetot elquehavíemanatfent...Jasabem,quealesconversesdegrangrupsempreapareixelnivell màxim,iquenoescorrespon,pertant,ambcadauniunadelsalumnes;peraixòl’avaluaciódel procésvaserindividualivarenaparèixertantlesidees,comelscàlculs,lesemocionsifinsitotla metodologiaolesdinàmiquesrealitzades.

Aquestaavaluacióvaserbensatisfactòria.Totshavienseguitgairebécronològicamentelque havíemanatfent,moltsespecificavenelsentrebancsmésgrossos,lamajoriatornavenarepetir elscàlculsifeien,amés,comentaristanvariatsiespontaniscom:

• «Primerhovàrempensar,despréshovàremfer»(importànciadelareflexióinicial,delsplantejaments)

• Hemnecessitat:fustes,pals,potsdeiogurt,unapilota,porteries,pinturaverda,elcampde fusta...cintablancaiaenVicenç»(materialfísici...humà)

• «Toteltempshemutilitzatcintamètrica»(einesmatemàtiques)

• «Vàrem‘‘discutir’’comferlesporteries»(importànciadeldiàleg)

• «Tothohemfetenequip»(importànciadelacooperació)

• Aquestesmidesserveixenperexplicaralagent,persienvolenferun»(utilitat-extrapolació)

18.Naturalment,tépossibilitatsd’aprofundiment,mainos’acabaelqueespotaprendre:anàlisiestadísticadelsresultats,càlculdelesàreesparcials,finsitotladelcercle...Nosésitotaixòesfarà,

...peròelqueésbensegurésqueelgrupets’hainteressatpersaberonestaràubicatelfutbolí elpropercurs,perquèellsiellescanviend’aulaidecicle.Demanar«onseranelsproblemesiles feinesquehanresoltdurantelcurs»ésunbonindicadordelaimplicacióqueaquesttipusde feinasuposa...encaraquesiguisobretot,perl’emociódejugar!

3. Anàlisi de la tasca realitzada

Enlarealitzaciód’unprojecte,comaquest,ésdifícilestabliraprioriobjectiusicontingutsconcrets, peròelqueespotferésprecisarelsobjectiusgeneralsquevertebrenaquesttipusdefeina,ianar assenyalantelsobjectius,contingutsicriterisd’avaluacióqueesvanposantenmarxaalllargdel treball.

Ésmoltimportantquel’alumnatsiguipartactivadelseuaprenentatge,ques’enfrontiareptesque hagidesolucionar,quepuguirelacionarelquesapambelquenecessitaenunasituacióqualsevol, queutilitzidiferentsestratègiesderesolució,entrelesqualscompartiridiscutirpossibilitats,ique, endefinitiva,avancienelseuconeixement,queaprenguid’unaformavitaliquesempretenguila curollad’aprendreicomprendreelmónqueensenvolta,perpoder-hiintervenir.

Ésadir,aaquesttipusdetasca,l’objectiuprincipalésquel’alumnataprenguideformadivertidai contextualitzada,continguts«difícils»iqueliserveixenenlavidaquotidiana.

Comhemvists’hantreballatdiversescompetències,com:

• Competèncialingüísticacomunicativaiaudiovisual,perexempleal’exposicióoral.

• Competènciamatemàtica,perexemplealsproblemesdelesbarresdelsjugadors.

• Aprendreaaprendre,perexempleamblaseqüènciadidàcticadelstextosescrits.

• Autonomiaiiniciativapersonal,perexemplealarealitzaciódelspropisdissenys.

• Tractamentdelainformacióicompetènciadigital,perexemplealcasdelesestatures.

• Artística,comenlarealitzaciódelsjugadors.

Figura 6

3.1. Objectius treballats especialment

Amblarealitzaciódelfutbolí,dels14objectiusgeneralsd’etapaal’àreadematemàtiquespublicats pelGoverndelesIllesBalearsiqueapareixenalWeibdelesIllesBalears,sen’hanposatenmarxa12 (totsexcepteelsnúmeros7i8),peròmoltespecialmentelsquatresegüents:

12.Proposar,resoldreiplantejarproblemesmatemàticsutilitzantelsprocedimentsadequatsdecàlcul,mesura,estimacióicomprovacióderesultats,valorantlaperseverança ilesdiferentsestratègiesenlarecercadelresultatiemprantdemaneralògicaicreativa lacomunicacióoraliescrita.

1.Utilitzarelconeixementmatemàticpercomprendre,valorariproduirinformacionsi missatgesoralsiescritssobrefetsisituacionsdelavidaquotidianaireconèixer-neel caràcterinstrumentalperaaltresàmbitsdeconeixement.

5.Conèixer,valorariadquirirseguretatenlespròpieshabilitatsmatemàtiques(acceptant l’errorcomaestímuld’aprenentatge)perafrontarsituacionsdiversesquepermetin gaudirdelsaspectescreatius,estèticsoutilitarisiconfiarenlessevespossibilitatsd’ús.

14.Posarenpràcticahàbitsiestratègiesquepermetintantl’activitatindividualcomla col·laboracióactivailaresponsabilitatenl’aprenentatgecooperatiu.

’

3.2. Criteris davaluació aplicats

Quantalscriterisd’avaluació,dels13queapareixenalcurrículum,n’hemtengutencompte6,però elsques’hanprioritzatis’hanseguitperavaluarsónelstressegüents:

4.Utilitzarestratègiespersonalsdecàlculmentalencàlculsrelatiusalasuma,resta,multiplicacióidivisiósimples.

5.Resoldreproblemesrelacionatsambl’entornqueexigeixincertaplanificació,aplicant duesoperacionsambnombresnaturalscomamàxim,aixícomelscontingutsbàsicsde geometriaotractamentdelainformacióiutilitzantestratègiespersonalsderesolució.

10.Obtenirinformaciópuntualidescriureunarepresentacióespacial(croquisd’unitinerari,plànold’unapista,etc.)prenentcomareferènciaobjectesfamiliarsiutilitzarles nocionsbàsiquesdemovimentsgeomètrics,perdescriureicomprendresituacionsde lavidaquotidianaipervalorarexpressionsartístiques.

3.3. Continguts treballats especialment

Quantalscontinguts,sen’hantreballatdecadaundelsquatreblocsdeconeixement(nombresioperacions,mesura,geometriaitractamentdelainformació,atzariprobabilitat)extretsdeldocument delCurrículumesmentat.Lestaulessegüentsrelacionenlesactivitatsrealitzadesambelscontinguts treballatsdelcurrículumdematemàtiques.

Nombres i operacions

Disposició perdesenvolupar aprenentatges autònoms enrelació ambelsnombres, les sevesrelacions i operacions

constructiva… Interès perla presentació neta, ordenadaiclara dels càlculs i dels resultats

Utilitzaciód’estratègiespersonalsde càlculmental. Confiançaen les pròpiespossibilitats, afrontantl’error de manera

resolució de problemes:suma,resta, multiplicaciói divisióperun nombre d’unaxifra

Realització d’operacionsamb nombresnaturals,utilitzantels algoritmes estàndard en contextos de

Utilitzaciód’estratègiespersonalsde càlculmental

els resultats o btinguts

Interès per l’ús dels nombres idel càlcul numèric per resoldreproblemes en situacions reals, explicant oralment i per escritelsprocessosderesoluciói

Utilitzacióen contextosreals de la divisióper repartir iper agrupar

Utilització en situacionsfamiliarsde lamultiplicaciócom a suma abreujada perefectuar recomptes,en disposicions r ectangulars

Ordenacióiestablimentderelacions entre els nombres

Propostesi activitats realitzades on s’han treballatnombres i operacions

2. Mesures

Valorar la importància de la realització acuradade les mesures

Interèsper utilitzarlamesura iexpressarels resultatsamb unitats

Estimacióde mesures d’objectesdela vidaquotidiana

Elaboraciói utilització d’estratègies personalsper mesurar

Comparaciói ordenacióde quantitatsd’una mateixamagnitud

Utilització en situacionsreals de les unitat del sistema mètric decimal

Realitzacióde mesuramentsamb unitatsdemesura convencionals o no

Propostes i activitats realitzades

Dissenys futbolí

Dissenyd’equipatges

Nomde l’equip Mascotes Elaboració dejugadors Nou dissenyconsensuat

Estatura personal

Marcador Torneig Instruccions Notíciaesportiva Retransmissió esportiva Exposició a les famílies Cartells per c onvidar

Confiança en les possibilitats per resoldre relacions espacials

Resoluciódeproblemes geomètricsexplicant,la situació,procési solucions les pr opietat s i dels Lacircumferènciaiel cercle:descripcióde elements bàsics

Interpretació de croquis i plànols senzills

Representació elemental de plànolsi maquetes. Descripció deposicionsen un contexttopogràfic

Localització precisa d’elements en l’espai

Bloc 3. Geometria Propostesi activitats realitzades

Dissenys futbolí

Grandària

Líniamigcamp

Porteries

Àrees petita igran

Àrea central

Nombre dejugadors

Distribució dejugadors

Dissenyd’equipatges Nomde l’equip Mascotes Elaboració dejugadors Nou dissenyconsensuat

Cromo Estatura personal Marcador Torneig Instruccions

Notíciaesportiva Retransmissió esportiva Exposició a lesfamílies Cartells per convidar

4.Tractament de la informació, atzar i probabilitat

Bloc

Disposició perala presentació de gràfics i taulesde manera ordenada i clara

Realització de gràfiques senzilles: elecció deltipus de gràfic més convenient

Interpretaciói descripcióverbal d’elements significatiusde gràficssenzills

Lectura, interpretaciói elaboraciódetaules dedobleentrada

Recollidai registramentde dadesutilitzant tècniqueselementals

Iniciacióal’ús d’estratègies eficacesde recomptededades

Propostesi activitats realitzades

Dissenys futbolí Grandària Línia migcamp Porteries Àrees petita igran Àrea central Nombre dejugadors

Distribució dejugadors

Dissenyd’equipatges

Nomde l’equip

Mascotes

Elaboració dejugadors Nou dissenyconsensuat

Cromo

Estatura personal

Marcador Torneig

Instruccions

Notíciaesportiva

Retransmissió esportiva

Exposició a lesfamílies x Cartellsper convidar

Continguts comuns a tots els blocs

Col·laboració activa i responsableenel treballenequip

Gustper compartirels processos deresolució i els resultats obtinguts

Confiança en les pròpies possibilitatsi curiositat, interèsi constància en la resolució d’interrogants…

Disposició per desenvolupar aprenentatges autònoms

Interès perla presentació neta, ordenadaiclara dels treballs

Propostesi activitats realitzades

futbolí

dejugadors

4. Conclusions

Aquesttipusdefeinaésmoltric,esposenenmarxamoltdelsconeixementsquejaestenen,però tambésen’handedescobriraltres.Ésadir,peraunalumnedequartdividir112entre2notécap dificultat,nitansolscalcularqualsevolmeitat,peròseleccionarelquehadeferiposaraquestcontingutenreferènciaauntauler,janoéstanfàcil.Esdonenmoltesinterrelacions,elconeixementno estàjatancompartimentat,peraixòesconnectamésfàcilmentamblarealitati,probablementala llargaespuguinfermésinferènciesiextrapolacions.Ladinàmicaqueescreaquanelgrups’enfronta aunreptecomúésmoltaglutinadoraiaixòpotencial’intercanvitandesitjateneducació.

Lanostratascacomamestresconsistiràenacompanyaracomprendredeformacientíficaelque esviu:estructurar,representar,ferabstraccions,precisarvocabulari...Pelmestreolamestrasuposa ungraud’implicaciómajorambelseualumnatiaixòfaquel’aprenentatgesiguicompartit...iles emocionstambé.Endefinitiva,totallòviscutperduraràmésfàcilment.

Bibliografia consultada pels infants

1. Cómohacerunaminicanchadefútbol http://www.hagaloustedmismo.cl/data/pdf/fichas/ma-is12_hacer%20cancha%20de%20ftbol.pdf

2. Mesuresd’uncampdefutbol http://www.enciclopedia.cat/fitxa_v2.jsp?NDCHEC=0110817

3. Petitdiccionarifootball/català http://www.milloringlix.org/2010/06/petit-diccionari-football-catala.html

4. Tecnolectefutbolísticcatalà.DavidIglesiasMasò. http://www.udg.edu/LinkClick.aspx?fileticket=pPspmZxfN0s%3D&tabid=13225&language=ca-ES

Bibliografia utilitzada per a aquest treball

1. CurrículumdelesIllesBalears http://weib.caib.es/Normativa/Curriculum_IB/educacio_primaria_.htm

Referents

Enaquestapartatnopucdeixard’esmentaralgunespersonesquem’haninspiratenaspectesconcretsd’aquesttreball.

1.Eneldissenydels«Problemessensecomptes»ilaimportànciadetrobarlespròpiesestratègiesde càlcul,enCarlosGallego.

2.Enelfetdeconsiderarlesnocionsespacialscomapartdelageometria,imoltespecialmentenla granimportànciademanipularmaterials,naMariaAntòniaCanals.

3.Enlaimportànciadeltrianglepensar-fer-comunicar,naTeresaPigrau.

4.Enelcostumd’incorporareltractamentdelainformació,amblessevesrepresentacions,ales paretsdel’aula,enDaniMartínez.

5.Enelvalordeladiscussió,elscompanysdelcentreilamevaparella.

Gràciesatotsellsiellesperajudar-meagaudirencaramésdelesmatemàtiques.

L’harmoniadelmón

CarlesPerelló

DepartamentdeMatemàtiques

Nohohevistescritnihohesentitadirqueels Elements (Stoiheia)d’Euclidesnosónnomésunmanual degeometrianiundesenvolupamentdelmètoderigorósdedemostraciómatemàtica.Certament hosón,peròaixònoméséselmètode,quecertamentcontéunmissatge,peròelmissatgepregon, l’objectiudetotplegat,ésmostrarl’harmoniadelselementsqueconstitueixenelnostremónfísic.

Plató,enlasevaobrapòstuma,el Timeu,vaestablirqueelmónqueobservemestàformatpercinc elements—foc,aire,aigua,terraicosmos—,elsqualsestanconstituïtsrespectivamentpertetraedres,octaedres,icosaedres,cubsidodecaedres,elsúnicscincpoliedresregulars.Vafernotarque, sis’escalfaproul’aigua,elsicosaedresquelaformenesdisgreguen,iquelessevescares,triangles equilàters,estornenaajuntarformantoctaedres,aire.Isis’escalfaproul’aire,lescaresdelsseusoctaedressesepareniestornenaajuntarperformartetraedres:foc.Laterraielcosmosnocanvientan fàcilment.

Elstretzellibresdels Elements mostrencomespodenconstruirracionalmentelscincpoliedres,imostralesrelacions,diguem-neharmonioses,entreelsseuselementsgeomètrics.Resulta,doncs,queels Elements ésunaobradematemàticaaplicadaamostrarl’harmoniadelmón.

Lairresolubilitatdels problemesclàssicsgrecs.

Recursdidàcticpera l’ensenyamentil’aprenentatge

AnaManzanaresMoreno

Enginyeradecamins,canalsiports amm@integras.es

Resum Abstract

Actualment,aCatalunya,l’ordenaciócurricularintegrael conceptedecompetènciabàsicaperestablircomhande desenvolupar-sel’accióeducativaielprocés d’ensenyament-aprenentatge,cosaquecomportala necessitatd’actualitzarelscontingutsielsrecursosque s’estanemprantdiàriamentalesaules. Elsnousrecursoshand’estardefinitsiplanificatsenfunció d’unasèriedepautescomsón:laconcreciódelscriteris metodològics,organitzatiusid’avaluació,laduraciódecada activitat,lacontextualitzacióperreforçarelsaprenentatges, lesmesuresadequadesd’atencióaladiversitatialabona gestiódel’aula...Endefinitiva,laplanificacióprèviadels recursosilamàximaconcreciópossibleenladefinicióseran condicionsnecessàries,quenosuficients,peral’èxitde l’accióeducativa. Entrealtrestipusdecontingutsmésteòricsiconceptuals (nombres,mesures,símbols,elementsgeomètrics,etc.),el currículumdel’assignaturadematemàtiquesconsiderala històriadelesmatemàtiquescomuncontingutmés.Ino aaatansolscontemplalahistòriacomuncontingut,sinó que,amés,suggereixaproximacionsdecaràcterhistòrica determinatscontingutsteòricsmatemàticsamblesqualses preténmostrareldesenvolupamenthistòricdeles matemàtiquescomaciènciaenevolucióievidenciar contextosonelscontingutsadquirirensignificat. Lautilitzaciódelahistòriadelesmatemàtiquesper dissenyaractivitatstémúltiplesopcions:potservircoma introducciód’untemaod’unconceptenou,potsituarun conceptematemàticeneltemps,contribueixafer l’aprenentatgeméssignificatiu,ajudaafinalitzaruna seqüènciad’activitats,potservirtambéperaprofundirenun temaconcretitélacapacitatd’interrelacionar transversalmentlesdiferentsàreesdelesmatemàtiques. Veientlanecessitatdecrearnousrecursosdidàcticsi aprofitanttotesaquestesopcionsquelahistòriadeles matemàtiquesensproporciona,esvancrearlestres activitatsproposadesapartirdela«falsa»irresolubilitatdels problemesclàssicsgrecs.

CurrentlyinCatalunya,the«ordenaciócurricular»integratesthe conceptof«competènciabàsica»toestablishhowtheyshould developeducationalactivitiesandteaching-learningprocess, whichimpliestheneedtoupdatethecontentandresourceswe areusingeverydayintheclassroom.

Thenewresourcesmustbedefinedandplannedaccordingtoa seriesofguidelinesas:specificationofmethodological, organizationalandassessmentcriteria,thedurationofeach activity,thecontexttoreinforcethelearning,appropriate measurestoattentiontodiversityandgoodclassroom management...Inshort,thepre-planningofresourcesandthe highestpossibleprecisioninthedefinitionbenecessary,butnot sufficient,forthesuccessofaneducationalactivity. Amongothermoretheoreticalandconceptualcontent (numbers,measurements,symbols,geometricelements,etc.), themathematicscurriculumconsidersthehistoryof mathematicsasacontent.Andnotonlycoversthehistoryasa content,butalsosuggestsahistoricalapproachtocertain theoreticalmathematicsasanattempttoshowthehistorical developmentofmathematicsasascienceinevolutionand demonstratecontextswherecontentsachievemeaningful. Usingthehistoryofmathematicshasmanyoptionsfordesign activities:itcanserveasanintroductiontoatopicoranew concept,amathematicalconceptcanbelocatedintime,help tomakelearningmoremeaningful,helptofinishasequenceof activities,canalsobeusedtofurtheraparticulartopicandhas theabilitytointeractacrossdifferentareasofmathematics. Seeingtheneedtocreateneweducationalresourcesandtaking advantageofalltheoptionsthatthehistoryofmathematics provides,threeactivitieswerecreatedandproposedfromthe «dummy»insolvabilityofclassicalGreekproblems.

1. La història de les matemàtiques com a recurs didàctic

Seguintladefiniciódecompetènciaques’estableixalcurrículum,marclegalvigentavuidia,lesmatemàtiquessónuninstrumentdeconeixementid’anàlisidelmónqueensenvoltaialmateixtemps constitueixenunconjuntdesabersdegranvalorcultural,queajudenaraonar,demaneracrítica, sobrelesdiferentsrealitatsielsdiferentsproblemesactuals.

L’assolimentdelacompetènciamatemàticarequereixundeterminattipusdetasquesal’aula,amb objectiusdiversos:introduirtermesmatemàtics,facilitarcontextosontrobaridees,aplicarconceptes desenvolupatsanteriorment,revisaroconsolidarconceptesperpromourelareflexióilaintegració... (Guevara,citantMasoniJohnston-Wilder,1 2009).Laintroduccióal’aulad’uncontexthistòricmatemàticpotajudarenlaconsecuciód’aquestsobjectius.

Lahistòriadelesmatemàtiquesmostraeldesenvolupamentdelconeixementmatemàticiexplica elsprocessosquehancalgutperarribaralmomentactual.Així,elllegatquedeixalahistòriapera lesgeneracionssegüentspermetanalitzarunsfetsdesdediferentsperspectives,totreinterpretantel passatambelsullsdelpresent(Guevara,citantGrattan-Guiness,2 2009).Aquestllegatespotrelacionar ambl’ensenyamentdelesmatemàtiquesactualsdesdedosvessants:l’úsdelahistòriacomacontext d’aprenentatgeil’aportaciódelahistòriaalesmatemàtiques(Guevara,2009).

Diversosautors3 hanplantejatqueunfactorimportantenl’úsdelahistòriaperal’ensenyamentde lesmatemàtiqueséslarelacióentreeldesenvolupamentdelpensamentdelsalumnesieldesenvolupamentdelapròpiahistòria.Atravésdelesdificultatsielsencertsques’hanproduïtdurantel desenvolupamenthistòricdelesmatemàtiques,elsalumnespodenarribaraidentificarelperquède lessevesdificultatsdavantl’aprenentatge,demaneraques’estàtreballantimplícitamentenl’àmbit deldesenvolupamentemocionalisocialdel’alumne,millorantlasevaautoestimaiajustantelseu autoconcepte.

D’altrabanda,l’aportaciódelahistòriaalprofessoratpotserimplícita:perdecidirseqüènciesimaneresd’introduirelsconceptesiperquèdónaelementsperentendrelesreproduccionsdel’alumnat;i tambépotserexplícita:comaelementdereferènciaperdissenyaractivitatsambsituacionshistòriques(Guevara,2009).

Lesteoriesdel’aprenentatgeparlendelanecessitatqueelsalumnescomencinambexperiències concretesi,apartird’aquestesexperiències,generalitzin.Experimentarambaplicacionsmúltiples delsnombresidelsobjectesmatemàtics,amblesdiferentsmaneresderepresentar-losidedescriure’ls,comespottrobarenlahistòria,ajudaràenelprocésdegeneralització(Guevara2009).

Lahistòriamostraquelesmatemàtiquess’handesenvolupatapartirdelaresoluciódeproblemesi queaquestaésunadelesraonsperferquelaresoluciódeproblemessiguielnuclidelesactivitats d’aprenentatgeal’aula(Guevara,citantBarbin,4 2009).Peròespotprendrecomaestratègiadidàctica,amés,lainclusiódelahistòriademaneraexplícitaperdissenyarlesactivitats,explicantelcontext

1.Mason,John;Johnston-Wilder,Sue(2006). DesigningandUsingMathematicalTasks. St.Albans/MiltonKeynes,UK: TarquinPublications&OpenUniversity.

2.Grattan-Guiness,Ivor(2004). HistoryoftheMathematicalSciences.India:HindustanBookAgency.

3.Guevara,citantFuringhetti,FulviaiRadford,Luis(2008)«Contrastsandobliqueconnectionsbetweenhistorical conceptualdevelopmentsandclassroomlearninginmathematics».Dins:English,LynD., etal. (eds.), HanbookofInternational researchinmathematicseducation.NovaYork:Taylor&Francis,626-655;JonhFauvel,JanvanMaanen,2000.

4.Barbin,Evelyn(2000).Integratinghistory:researchperspectives.DinsJohnFauvelIJanvanMaanen(eds.)(2000), HistoryinMathematicsEducation.TheICMIStudy.Dordrecht/Boston/Londres:KluwerAcademicPublishers,63-90.

culturalenelqualesdesenvolupen,localitzantelconeixementsdinslahistòriadelahumanitatide lesidees.Tenintencompte,però,queencapcaslesmatemàtiquesespodensubstituirperl’ensenyamentdelasevahistòria.

Lautilitzaciódelahistòriaperensenyarmatemàtiquesésunrecursreconegutinternacionalment.En elsdarrersanys,diversospaïsos(RegneUnit,Grècia...)hanintroduïtexplícitamentlahistòriadeles matemàtiquesenelseucurrículum,comhaestatelcasdeCatalunya.DesdelRegneUnit(2009),per exemple,esdefensaquelahistòriapermetestablirconnexionsentrelesdiferentsàreesdelcurrículum itambéentrediferentspartsdelesmatemàtiquesquetradicionalmentnos’havienrelacionat.Desde Grècia(2007)esjustificaquelahistòriaestimulal’interèsdel’alumnatilifatenirunaactitudpositiva, revelaireforçalanaturalesahumanadelesmatemàtiquesicontribueixaentendreelsconceptesi elsproblemes,perquèdónaaconèixerelcontextilescircumstànciesqueelsvanoriginar,aixícom lescondicionsdelseudesenvolupament.

Pertant,lahistòriadelesmatemàtiquesésunrecursperduratermelesmatemàtiquesforadel’àmbit estretdeladisciplina,perbuscarconnexionsivinclesambaltrescontextosdisciplinaris,perdeterminarelseucanvid’imatgeambelsestudiants,perressaltarlafontdelcontextsociocultural(Demattè, 2006).Unrecursquepermetcontextualitzarmillorelcontingutmatemàticiqueproporcionados componentsdetreball:elmateixdesenvolupamenthistòricielsaspectesdelacompetènciamatemàticaqueesvolenfomentar.

Queenelsnouscurrículumsesreconeguiquelahistòriadelesmatemàtiquesésunrecursaconsiderarenlaplanificaciódelaprogramacióidelesactivitatsésunelementmotivadorperdissenyar nousexercicisenaquestcontext.

Detotesmaneres,s’hadetenirpresentquemostrarl’evolucióhistòricadelsconceptesoraonaments ésunprocésllargienuncursacadèmicnoespodràfermésdetresoquatrecops.

Espreténelaborarnoveseinesirecursosquepermetinaldocentpresentaractivitatsqueelsalumnes puguinrebreambunabonadisposicióperal’aprenentatgeiqueelsfaciaconseguirmésimillors nivellsdeconeixement;assolir,pertant,lescompetènciesbàsiques.Tambéespreténcol·laborarper aunamilloreficiènciaieficàciadeltreballdelprofessorat.

Lesactivitatsqueespresentens’handissenyatapartirdelmarcqueproporcionenelsactualscurrículumsdel’ESOidelBatxillerat,quedonenunagranimportànciaal’aportaciódidàcticaicompetencial iqueconsiderenlahistòriadelesmatemàtiquescomunrecursmés.Dinsdelscurrículums,alfinal delscontingutsdecadacurs,sesuggereixen,atalld’exemple,aproximacionsdecaràcterhistòrica contingutsdeterminats,amblesqualsespretén,d’unabanda,mostrareldesenvolupamenthistòric delesmatemàtiquescomaciènciaenevolucióisotmesaacanvis,i,del’altra,evidenciarcontextos onaquestscontingutsvanadquirirelseusignificat.

Noobstantaixò,tambéestanplantejadesapartirdelesnecessitatsquehageneratl’úsdelesTICa lesaules,querequereixenpropostesdidàctiquespertreballarambl’ordinador.

D’altrabanda,espreténaportarrecursosinnovadors,ambnovesestratègiesdetreballdinsdel’aula, d’atencióaladiversitat,peralamilloradelagestiódel’aula,permillorarlamotivaciódel’alumnat,

2. La necessitat de crear nous recursos didàctics

ambcriterisd’avaluaciósumativa...intentantintegrartotelqueimplical’ensenyamentpercompetències.

Amés,esvapodercomprovarqueaquestapartatdelahistòriadelesmatemàtiquesnos’haviacontemplatencaraencapdelesactivitatsdisponiblesenelprojecteARC5 delCreamat.6

Latemàticaproposadaconsisteixaconsiderarelstresproblemesclàssicsgrecssensesolucióamb reglaicompàs:latrisecciódel’angle,laquadraturadelcercleiladuplicaciódelcub,perplantejar diversesactivitatsperrealitzaral’aula.Aquestespropostesdidàctiquespodranserutilitzadespera lapràcticaprofessionalis’hipodrantreballarmoltsconceptesmatemàticspertald’abastardiferents nivellsdeconeixements,mitjançantrecursosieinestradicionalsialtresd’innovadors,aixícomaprofitantl’estudidelahistòriadelesmatemàtiques.

3. Plantejament dels recursos

Hihanombrosostreballspublicatssobreaqueststresproblemes.Perexemple,l’article«Trisecció, quadraturaiduplicació:tresproblemesdelamatemàticaclàssicagrega»deFrancescXavierBarca Salom(2009),enquèesfaunadetalladadescripciódel’evoluciód’aqueststresproblemesalllarg delahistòria,desdelseuorigenfinsalesdiferentssolucionsplantejades.Amés,s’explicaperquè aqueststresproblemessónirresolublesamblageometriaeuclidiana.

Apartdeladocumentacióteòrica,tambéesdisposadeconstruccionsinteractives,comperexemple lespràctiquesqueproposaelprofessorPepBujosaalweb:http://www.xtec.es/∼jbujosa/GeoGebra/ problemesclassics/classics.htm,onespottreballarunasolucióperacadaundelstresproblemesamb elprogramaGeogebra.

Malgratlanombrosaquantitatdedocumentaciótrobadaenrelacióambelstresproblemesclàssics grecs,finalmentduesdelestresactivitatsplantejadesenaquesttreballesbasenenlessolucions proposadesenelllibre Vitaminasmatemáticas deClaudiAlsina(2008).Enaquestllibrededivulgació matemàtica,esplantegencentqüestionsquepretenenincitarlacuriositatdellector,ambunllenguatgesenzillicomprensible.Entreaquestescentqüestionshihatrespossiblessolucionsperalstres problemesqueensocupen.

Apartird’aquestessolucions,s’hanplantejatlesactivitatscorresponentsalaquadraturadelcercle ialaduplicaciódelcub.Encanvi,l’activitatcorresponentalatrisecciódel’angleestàbasadaen aportacionspròpies.

Activitat 1.Trisecció d’angles amb regle i compàs

Comqueaquestaactivitatestàprevistaperalprimercursdel’ESO,elcontinguthadeseradientper aalumnesambedatscompresesentreelsdotzeielscatorzeanys,queacabend’arribaral’educació secundàriaprovinentsdel’educacióprimàriaambdiferentsnivellsdeconeixementsprevis.

5.ARC: AplicaciódeRecobrimentCurricular.Reculld’activitats,seqüènciesdidàctiquesirecursosqueenllacendirectamentambelcurrículumdelesàreesdematemàtiques.S’hacreatiesmantédesdelsCESIRES,CentresdeSuportalaInnovació ialaRecercaEducativadelDepartamentd’Educació.(http://arc-educacio.cat)

6.CREAMAT:CentredeRecursosperEnsenyariAprendreMatemàtiquesdelDepartamentd’EducaciódelaGeneralitat deCatalunya.(http://phobos.xtec.cat/creamat/joomla)

Enaquestcass’haoptatperunaactivitatmanipulativasenzilla,basadaenuncontexthistòric,però ambeinestradicionalsdelageometria(escaire,cartabóicompàs).L’objectiuprincipalésfixarconceptesbàsicsdelageometriacoml’anglerecte,labisectriu,elstrianglesisòscelesiescalè...apartde plantejarunasessiónomagistralisímanipulativa,ambunaintroduccióhistòricaperalgrupclasse.

Planificació

Estàprevistferlesexplicacionsielraonament,enconjunt,peralgrupclasseiposteriormentpassaral treballmanipulatiu,perparelles.Cadaparellad’alumneshauràdetenirunreglegraduat,unescaire, uncartabó,untransportadord’anglesiuncompàs,amésdepaperblanc(nollibretes).Peralatotalitat delgrupclasse,elprofessorprepararàunesdiapositivesperalesexplicacionssobrelahistòriadels problemesclàssicsgrecssensesolució,amésdecompàs,escaireicartabópertreballaralapissarrai elfulldel’alumneambladescripciódel’activitat.Laduraciódelasessióésd’unahora.

Avaluació

S’hauràd’avaluarl’expressióverbalderaonamentsiinformacionsqueincorporinelementsmatemàticsivalorarlautilitatdelllenguatgematemàtic.Caldràanalitzariavaluarlesestratègiesielpensament matemàticdelsaltres,atravésdeltreballperparellesienlaposadaencomúambtotalaclasse.Es valoraranelsfetsd’utilitzarnombresenters,fraccions,decimalsipercentatges;aplicarelconeixement geomètricperdescriureelmónfísic;estimar,mesurariresoldreproblemesdelongitudsiamplituds.

Tambéesfaràunavaloraciódeltreballaclasse,delesaportacionsielscomentarisdurantelraonamentidelapresentaciódel’activitatacabada.

Actuació docent

1.Introduccióhistòricasobreelsproblemesclàssicsgrecs(15min).

2.Definiciódebisecció(bisectriu)itrisecció(15min).

3.Identificaciódelsanglesconegutsdel’escaireielcartabó(10min).

4.Treballmanipulatiupertrisecarelsanglesqueespodentrisecar(20min).

Atenció a la diversitat

Aquestaactivitat,ensimateixa,esconsideracomunaopcióperatendrealumnesambgreusmancancesenconceptesbàsicsgeomètrics,quenopodranavançarenmatemàtiquessenseconsolidar-los prèviament.

Noobstantaixò,tambépotseradaptadaperaalumnesambaltresnecessitats:

• AquestaactivitattambéespottreballarambelprogramaGeogebraoambelsoftwareR.a.C.(alternativaalGeogebraespecíficperadibuixosambregleicompàs)http://zirkel.sourceforge.net

• Peralsalumnesambméscapacitatespodriaexplicarbreumentlacorbad’Hípiesol’inventde ladestralíndia.

• Unaaltraopciópotsertreballarelprocésd’Arquimedes,quenecessitanomésunregle,un compàs,unatransparènciaiunrotulador.7

7.Alsina,C.(2008). Vitaminasmatemáticas (1aed.).Barcelona:Ariel,pàg.86-88.

DOCUMENTDEL’ALUMNE

LATRISECCIÓDEL’ANGLE

Apartirdel’escaireielcartabó,identifiqueuanglesqueespuguintrisecar:

Introducció històrica

Desdelsseusorígens,l’homehaintentatrepresentarelmóniesconsideraqueaquestesrepresentacionssónl’origendelageometria.L’homeprimitiu,enintentarrepresentarelmedionvivia,reflectia enformadefiguresesquemàtiqueslarealitatqueobservava.Pertant,lespinturesrupestrespoden serconsideradesl’origendelageometria.

Lageometriaperalsegipcis,elsbabilonisialtrespoblesanticsorientals,comelsindisoelsxinesos, consistiaenunconjuntdereglesiconeixementspràcticsobtingutsexperimentalment,perònoera unaciènciaestructurada.Novaserfinselsegle VII aC,queesvaintroduirlageometriaaGrèciades d’Egipte.

Lageometriagregaparteixdelsconeixementspràcticsdelescivilitzacionsanteriorsifaunpascap al’abstracció.Així,vanarribaralesformesgeomètriquesperfectesatravésdel’observaciódelanaturalesa.Euclideséselmàximrepresentantiésconsideratelparedelageometria.Enlasevaobra, Elements,agrupatotelconeixementiformalitzalageometriacomunaciènciadeductiva.Aleshores necessitencrearinstrumentsperpoderrepresentarlesfiguresques’imaginavenivancrear,entre d’altres,elregleielcompàs.

Elsgrecsnopodienfercàlculsaritmètics,perquèelseusistemadenumeraciónomésrepresentava elsnombresnaturals,noteniaelzero,elsnegatius,nielsdecimals.Esvanbasarenelregleielcompàs perfertoteslesconstruccions.Unreglesensemarquesperquè,sinotenienaritmètica,noelsservien deres.Elsgrecssolucionavenelsproblemesgràficament,fentconstruccionsambregleicompàs, comasubstituciódel’aritmètica.

Escaire

Cartabó

Durantlasegonameitatdelsegle V aC,esvaproduirungrandesenvolupamentdelageometria:els pensadorsgrecsesvandedicaral’estudideqüestionspuramentteòriquesinotanpràctiquescom finsalmoment.Ésenaquestperíodequanesplantegenelstresproblemesclàssics:laquadraturadel cercle,laduplicaciódelcubilatrisecciód’unangle.Donatunanglearbitrari,consisteixaconstruir ambregleicompàsunanglequetinguiunterçdel’oberturadel’angleoriginal.

D’aquestproblemanose’nconeixl’origen,noméssesapquetambédatadel’antigaGrècia.Més de2.200anysdesprésesvademostrarqueaquestproblemaésirresolubleutilitzantnomésreglei compàs.Totiaixò,l’estudid’aquestproblema,entred’altres,hacontribuïtdemaneramoltimportant alllargdelahistòriaaldesenvolupamentdelesmatemàtiquesgràciesalsesforçosfetsperresoldre’l. LaimpossibilitatdetrisecarunanglevaserdemostradaperPierreWantzel(1814-1848)l’any1837.

Activitat 2. La quadratura del cercle

L’activitatestàprevistaperaltercercursdel’ESO,enquèelsalumnestenenedatscompresesentre elscatorzeielssetzeanysiquejahansuperatelprimercicle.

Enaquestcass’haoptatperlasolucióproposadapelcatedràticClaudiAlsina,8 perquès’hapogut plantejarunaactivitatquecombinaelementsmanipulatiusambl’úsdeprogramesinformàticsper resoldreunproblemageomètricamentperòques’hadecomprovarapartirdecàlculsalgebraics.A més,s’aprofitaelcontextdel’activitatperanalitzarelconcepted’exactitud.Totplegat,partintd’una introduccióhistòricaqueplantejaelproblemaquecalresoldre,conduïtpelprofessoratiincidintmés enlautilitzaciódeleseinesmatemàtiques(geometria,àlgebra...),enl’aplicaciódeconeixementsja apresosienlacontextualitzacióhistòrica,quenopasenlamateixaresolució.

Planificació

Estàprevistdonarexplicacionsiferraonamentsperalgrupclasseiposteriormentuntreballmanipulatiuindividualilaresolucióescritadelproblema,aixícoml’úsd’einesinformàtiques.Cadaalumne disposaràd’uncilindre,d’unreglegraduatid’unordinador.Peralgrupclasse,elprofessorprepararà elmaterialsegüent:diapositivesperalesexplicacionssobrelahistòriadelsproblemesclàssicsgrecs sensesolució,pissarradigitaliordinadorifulldel’alumneambladescripciódel’activitat.Laduració delasessióésd’unahora.

Avaluació

S’avaluaràelfetderesoldreproblemesutilitzantsímbolsimètodesalgebraicsialtresmètodesderesoluciópossibles,perexemple,larepresentaciógeomètrica;elfetd’expressarverbalmentambprecisió,raonaments,relacionsquantitativesiinformacionsqueincorporinelementsmatemàtics,lautilitat ilasimplicitatdelllenguatgematemàticilasevaevolucióalllargdelahistòria.S’analitzaranis’avaluaranlesestratègiesielpensamentmatemàticdelsaltres,atravésdelaposadaencomúambtota laclasse.Estindràencomptelacomunicaciódelpensamentmatemàticpropiielfetdecontrastar-lo ambelsdelscompanys.

8. Op.cit.,pàg.83-87.

Actuació docent

1.Introduccióhistòricasobreelsproblemesclàssicsgrecs(10min).

2.Plantejamentdelproblemaambeldocumentdel’activitat(5min).

3.Treballmanipulatiuperpoderresoldreelproblema(5min).

4.Treballindividualperrealitzarl’activitat(30min).

5.Posadaencomúdelsresultats(10min).

Atenció a la diversitat

Aquestaactivitattambéespottreballarambel software R.a.C.,alternativaalGeogebraespecíficper adibuixosambregleicompàsiméssenzill.Peralsalumesambméscapacitat,espotplantejaruna últimaqüestióperresoldreacasa:perquèelnombre √π noespotdibuixarambregleicompàs.

DOCUMENTDEL’ALUMNE

LAQUADRATURADELCERCLE

Donatuncerclederadi r,elproblemaqueensplantegemésdeterminarelcostat, a =?, d’unquadratquetinguilamateixaàreaqueelcercleinicial.

a)Determineulesàreesd’ambduesfigures

Àreadelcercleinicial: AO =

Àreadelnouquadrat: AC =

b)Resoleuaquestproblemaalgebraicament.Trobeuelvalorde a = ? Enaquestmomenttenimresoltelproblema,peròelquebusquemésunasoluciógràficainotan solsalgebraica.Hofaremapartirdelcilindre.

c)Marqueuunpuntalavoradelcilindreifeu-lorodarpelpaperfinsquefaciunavoltasencera.Què mesuraaquestsegment?

d )TraslladeuaquestsegmentalGeogebraiseguiuelprocésdeconstrucciógeomètricadetallata continuaciómitjançantelGeogebra:

• Denomineu A i B alsextremsdelsegment.

• Traceulamediatriudelsegmentimarqueuelpuntmig Q.

• Acontinuaciódel’extrem B,afegiuunaltresegmentdelongitud r ,elradidelabasedelcilindre, idenomineu C elnouextrem.

• Feuunacircumferènciaentreelspunts Q i C ,extremsdeldiàmetrehoritzontal,idibuixeula rectaperpendicularaaquestdiàmetrequepassipelpunt B.Denomineu R elpuntdetallde laperpendicularamblacircumferència.

Hemtrobatelsegment BR apartird’unconstrucciógeomètrica.Demostraremqueaquestsegmentmesuraexactament a,costatdelquadratquebusquem.

e)Calculeuelvalorde BR apartirdeplantejarelteoremadePitàgoresenelstrestrianglesresultants delafigura:Triangle1: QBR,Triangle2: BCR iTriangle3: QCR

f )Quinamesuratindràelcostatdelquadrat?Considereuquetémoltaopocaexactitud?

Introducció històrica

Desdelsseusorígens,l’homehaintentatrepresentarelmóniesconsideraqueaquestesrepresentacionssónl’origendelageometria.Peralsegipcis,elsbabilonisialtrespoblesanticsorientals,comels indisoelsxinesos,consistiaenunconjuntdereglesiconeixementspràcticsobtingutsexperimentalment,perònoeraunaciènciaestructurada.Novaserfinsalsegle VII aC,quanesvaintroduirla geometriaaGrèciadesd’Egipte.

Lageometriagregaparteixdelsconeixementspràcticsdelescivilitzacionsanteriorsifaunpascap al’abstracció.Noobstantaixò,elsgrecsnopodienfercàlculsaritmètics,perquèelseusistemade numeraciónomésrepresentavaelsnombresnaturals,noteniaelzero,nielsnegatius,nielsdecimals. Esvanbasarenelregleielcompàsperfertoteslesconstruccions.Elreglenoteniamarquesperquè, sinotenienaritmètica,noelsserviaderes.Elsgrecssolucionavenelsproblemesgràficament,fent construccionsambregleicompàs,comasubstituciódel’aritmètica.

LaquadraturadelcercleésunproblemageomètricproposatpermatemàticsdelaGrèciaclàssica.És elreptedeferlaconstrucció,ambregleicompàs,d’unquadratamblamateixaàreaqueuncercle donatutilitzantunnombrefinitdepassos.Laprimerareferènciahistòricaqueestérespecteaquest problemaésd’Anàxàgores,undelsmatemàticsdel’èpocaheroica,delsvoltantsdel450aC,però novaserfinsel1882queesvademostrarqueelproblemaerairresoluble,comaconseqüènciadel teoremadeLindemann-Weierstrass,quedemostraque π ésunnombretranscendent,enllocdeser unnombrealgebraic.Ésadir, π noésl’arreldecappolinomiambcoeficientsracionals.

Aquestproblema,juntamentambladuplicaciódelcubilatrisecciódel’angle,vaservird’incentiu alsmatemàticsgrecsperalarecercadenovescorbes.Aixívanaparèixerlescòniquesialtrescorbes cúbiquesotranscendentals.Ésperaixòquel’estudid’aqueststresproblemesconstitueixunmaterial privilegiatperconèixereldesenvolupamentdelestècniquesgeomètriques.

Lasorpresaésqueaquestproblemaimpossibleambregleicompàsténombrosessolucionsamb altresinstruments,comcomprovaremenaquestaactivitat.

Activitat 3. La duplicació del cub

L’activitatestàprevistaperalprimercursdebatxillerat,enquèelsalumnestenenedatssuperiorsals setzeanys,jahansuperattotal’educacióobligatòriais’estanpreparantperal’ensenyamentuniversitari.

Enaquestcass’haoptatperlasolucióproposadapelcatedràticClaudiAlsina,7 perquès’hapogut plantejarunaactivitatqueproposaunrepteal’alumne,quehaderesoldreapartirdeprogramesinformàticsideconeixementsjaestudiatsambanterioritatdediferentsbranquesdelesmatemàtiques (funcions,còniques,polinomis...).Partintd’unaintroduccióhistòrica,esplantejal’activitat,peròno conduïdapelprofessor,quehad’actuarméscomaobservadoriintervenirnomésencasdenecessitat,iesbasaenl’aplicaciódeconeixementsprevisperresoldreunproblemaenuncontexthistòric.

Planificació

Estàprevistferexplicacionsiraonamentperalgrupclasseiposteriormenttreballindividualiresolució escritadelproblema,aixícoml’úsindividuald’einesinformàtiques.Cadaalumnehauràdedisposar

d’unordinador.Peralatotalitatdelgrupclasse,elprofessordisposaràdelmaterialsegüent:diapositivesperalesexplicacionssobrelahistòriadelsproblemesclàssicsgrecssensesolució,pissarradigital iordinador,ifulldel’alumneambladescripciódel’activitat.Laduraciódelasessióésd’unahora.

Avaluació

S’avaluaranelsfetsdedistingirelsnombresrealsdelessevesaproximacions;relacionarentredescomposiciódepolinomisilaresoluciód’equacionspolinòmiques;relacionarzerosd’unpolinomi amblessolucionsdel’equaciópolinòmica;operaralgebraicament;treballaramblesequacionsde lescòniques;conèixerlescaracterístiquesdelafunciódeproporcionalitatinversa;utilitzarambsoltesalacalculadorail’ordinadorperfacilitarcàlculs,ferrepresentacionsgràfiques,iexplorarisimular situacions.Esvaloraràferservirintel ligentmentlesTICiinterpretarelsresultatsd’unaoperacióautomàticaenelcontextdelproblemaresolt.Tambéestindràencomptelacomunicaciódelpensament matemàticpropi.

Actuació docent

1.Introduccióhistòricasobreelsproblemesclàssicsgrecs(10min).

2.Plantejamentdelproblemaatravésdeldocumentdel’activitatperal’alumne(10min).

3.Treballindividualperpoderresoldreelproblema(40min).

Atenció a la diversitat

Utilitzaciódeprogramesinformàtics(Wiris)perresoldreelsistemad’equacionsinohaverd’aturarel procedimentderesoluciódelproblema.Amés,serviràpercompararresultats.

Participaciómésactivadelprofessorsicomprovaqueelsalumnesnosegueixenelraonamentinduït delespreguntesproposades.Enprincipi,elprofessornohaviadecol·laborarperquèesbuscala deduccióperpartdel’alumne,però,evidentment,hopotfer.

Peralsalumesambméscapacitat,espotplantejarunaúltimaqüestióperresoldreacasa:perquèel numero 3 √2noespotdibuixarambregleicompàs.

DOCUMENTDEL’ALUMNE

LADUPLICACIÓDELCUB

Donatuncubquetécomacostatlaunitat, c =1,elproblemaqueensplantegemés determinarelcostat, L =?,d’unnoucubquetinguieldobledevolumqueelcubinicial.

g)Determineuelsvolumsd’ambdóscubs

Volumdelcubinicial: VO =

Volumdelnoucub: Vl =

h)Resoleuaquestproblemaalgebraicament.Trobeuelvalorde L = ?

Enaquestmomenttenimresoltelproblema,peròelquebusquemésunasoluciógràficainotan solsalgebraica.

i)DibuixeuambGeogebralafunció f (x ) = 2 x

j )DibuixeuambGeogebralacircumferènciadecentre A(1, 0.5)iquepassipelpunt P(2, 1)

k )Determineul’equaciódelacircumferència.

l )Busqueuelspuntsquetenenencomúambduesfiguresiresoleuelsistemad’equacions,apartir delafactoritzaciópolinòmica.

m)VerifiqueulasoluciótrobadaamblacalculadoraWiris.

n)Identifiqueugràficamentelvalorde 3 √2

Introducció històrica

Aquestproblematéunorigenmístic.Alvoltantdel’any428aC,unaepidèmiadepestavaarrasar Atenesi,persolucionar-ho,esvaenviarunmissatgeraconsultarl’oracled’Apol·loaDelfos.Laresposta del’oraclevaserqueperacabarambl’epidèmiacaliaconstruirunnoualtarcúbicperaldéuApol·lo quedupliquésl’altarcúbicquehihaviaaltemple.Comqueelproblemanotésolució,l’epidèmia continuàelseuprocésnatural,enelsupòsitdelainfal libilitatdel’oracle.

Lageometriagreganopodiafercàlculsaritmètics,perquèelseusistemadenumeraciónomésrepresentavaelsnombresnaturals,noteniaelzero,nielsnegatius,nielsdecimals.Pertant,maiesdefiniala longitudd’unsegment,nil’àread’unafiguraplana,sinóqueestreballavaambfiguresgeomètriques establintcriterisd’igualtaticomparacióentreelles.Així,vanentendreque,perferelquedeial’oracle, haviendeconstruiruncubqueesdividísenduesfiguresigualsquel’altarquetenien.Elshabitants d’Atenesvanconstruiruncubqueteniaeldobledecostatieravuitvegadesmésgran.Il’epidèmia noesvaacabar.

Siguinonocertesaquesteshistòries,elfetésquealgunsmembresdel’AcadèmiaPlatònicavanestudiarelproblemadeladuplicacióivanproposarsolucions.Aquestproblema,juntamentamblaquadraturadelcercleilatrisecciódel’angle,vaservird’incentiualsmatemàticsgrecsperalarecercade novescorbes.Aixívanaparèixerlescòniquesilescorbescúbiques.Ésperaixòquel’estudid’aquests tresproblemesconstitueixunmaterialprivilegiatperconèixereldesenvolupamentdelestècniques geomètriques.

UnadelessolucionsvaserplantejadaperMenecm(aprox.350aC)apartirdelainterseccióentreuna paràbolaiunahipèrbolaequilàtera.Apartird’aquestasoluciós’atribueixaMenecmeldescobriment ielsestudisdelesprimerespropietatsdelescòniques(el·lipse,hipèrbolaiparàbola)comaseccions d’unconrectedebasecircumferència.

SesapqueMenecmvasermestred’AlexandreelGraniunallegendaliatribueixque,aunapreguntadelrei,sobresihihaviaalgunadreceraperadquirirelsconeixementsgeomètrics,Menecm

vacontestar:«Oh,rei!Perviatjarpelpaíshihacaminsrealsicaminsperaciutadanscomuns,peròen Geometriahihaunúniccamíperatots».

Novaserfinsl’any1837queP.Wantzelvademostrarlaimpossibilitatderesoldreaquestproblema ambregleicompàs.

Conclusions

Comaresum,espotconclourequeelnouenfocamentdel’ordenaciócurricularfanecessarisl’aportaciódenousrecursos,l’elaboraciód’activitats,laprogramaciód’unitatsdidàctiques,elplantejament denousproblemes...queestiguindissenyatsdesd’unpuntdevistacompetenciali,enparticular,es potferatravésd’uncontexthistòricperaprofitartoteslesaportacionsquese’npodenextreure.

Queda,pertant,moltafeinaaferperpartdelsmembresdelacomunitateducativa,perpoderaugmentarlaquantitatderecursosdisponiblesambunbondissenycompetencialperpresentaral’aula iqueestiguindesenvolupatssegonsrequereixl’aplicaciódelcurrículumvigentactualment,jasiguin contextualitzatsenlahistòriadelesmatemàtiquesoenaltrescontextossignificatius.Aquís’hiha volgutposarunpetitgradesorra,peròlamuntanyas’hadefermésgran.Ànimsibonafeina.

Bibliografia

Alsina,C.(2008). Vitaminasmatemáticas (1aed.).Barcelona:Ariel,pàg.83-87.

Barca,F.X.(2010). Trisecció,quadraturaiduplicació:tresproblemesdelamatemàticaclàssicagrega. Barcelona:UniversitatPolitècnicadeCatalunya.<http://hdl.handle.net/2117/10355>[Consulta:abril 2011]

Barrow,J.D.(2009). Elsaltodeltigre:Lasmatemáticasdelavidacotidiana (1aed.).Barcelona:Crítica.

Demattè,A.(2006). Farematematicaconidocumentistorici.Unaraccoltaperlascuolasecondariadi primoesecondogrado.Trento:EditoreProvinciaAutonomadiTrento-IPRASEdelTrentino.

Guevara,I.(2009). Lahistòriadelesmatemàtiquesdinsdelsnouscurrículumsdesecundària:Laintroducció decontextoshistòricsal’aula,unrecurspermillorarlacompetènciamatemàtica.<http://phobos.xtec.es/ sgfprp/resum.php?codi=1864>[Consulta:maig2011]

Guzman,M.de(2003). Cómohablar,demostraryresolverenMatemáticas (1aed.).Barcelona:Anaya.

Margalef,J.iOuterelo,E.(2007). Matemàticasalalcancedetodos (1aed.).Madrid:PearsonEducación, pàg.201-206.

Currículumsicompetències

http://phobos.xtec.cat/edubib/intranet/file.php?file=docs/ESO/curriculum_eso.pdf

CurrículumEducacióSecundàriaObligatòria.Departamentd’EducaciódelaGeneralitatdeCatalunya. [Consulta:9demaigde2011]

http://phobos.xtec.cat/edubib/intranet/index.php?module=Pages&func=display&pageid=22 CurrículumBatxillerat.Departamentd’EducaciódelaGeneralitatdeCatalunya. [Consulta:9demaigde2011]

http://phobos.xtec.cat/creamat/joomla CREAMAT,CentredeRecursosperEnsenyariAprendreMatemàtiques.Departamentd’Educacióde laGeneralitatdeCatalunya.

Pàginesweb

http://www.cidse.itcr.ac.cr/revistamate/MundoMatematicas/Triseccion/node5.html ElMundodelasMatemáticas.Imposibilidaddealgunasconstrucciones. [Consulta:abril2011]

http://www.xtec.es/∼jbujosa/GeoGebra/problemesclassics/classics.htm PràctiquespertreballarambelprogramaGeogebra [Consulta:abril2011]

http://zirkel.sourceforge.net SoftwareR.a.C.,programaespecíficperadibuixosambregleicompàs [Consulta:abril2011]

http://portales.educared.net/wikiEducared/index.php?title=Ángulos#.C3.81ngulos_de_la_escuadra_ y_el_cartab.C3.B3n Educared.Fundacióntelefónica [Consulta:maig2011]

Unaaproximació etimològica4: elementsde geometriaplana

Enaquestnúmerodelarevista NouBiaix donarél’etimologiad’algunstermesquefemservirengeometriaplana.Intentaréquelesimatgesadjuntessecentrinmésenl’etimologiadelstermes,queen elconceptematemàticpròpiamentdit.

AbansdecontinuarvullagrairalaprofessoraMartaBeriniLópezialsresponsablesdel’equipde redacciódelarevistaquehaginconfiatenmipertaldecontinuarambaquestasecció.Tambévull agrairalaprofessoradegrecBegoñaUsobiagaArtaloitiaialprofessordellatíAntonioDachsLecina pelseuassessoramentlingüístic.

Geometria: Provédelsubstantiugrec γεωμετρία ,iestàcompostdelssubstantius γη ~ ,‘terra’,i μέτρον ,‘mesura’.Literalmentsignifica‘mesuradelaterra’.Eltermeequivalentllatíés agrimensura.L’origend’aquesttermevedelsegipcis,elsquals,desprésdelainundacióanualdelessevesterres acausadelescrescudesdelriuNil,esveienobligatsadonaracadaagricultorunaporciódeterra equivalentalaqueteniaabansperquèelslímitsdelsterrenysdesapareixien.

JaumeSolsonaVillaplana

Punt: Delllatí punctum,‘punxada,picadura’. Punctus éselparticipidelverb pungere (‘punxar,picar’).

Recta: Del’adjectiullatí rectus,derivatde regere,‘dirigir’.

Semirecta: Delllatí, semi,‘mig,meitat’i rectus,‘recte’,derivatde regere,‘dirigir’.

Segment: Delllatí segmentum, derivatde secare,‘tallar’.

Angle: Delllatí angulus,‘angle,racó’,iaquest,del’adjectiugrec άγκύλος (ángulos),‘encorbat,tort’.

Paral·lel: Delapreposiciógrega παρά ,‘alcostat’,idelpronomrecíproc άλληλος ,‘elsunsalsaltres, l’unal’altre’.

Perpendicular: Del’adjectiullatí perpendicularis,‘perpendicular’,delsubstantiullatí perpendiculum, ‘plomada’,delverbllatí perpendo,perpendere,‘pesarcurosament’,idelverbllatí pendo,‘pesar’.

Pla: Delllatí planum,‘pla,planura’.Laparaulallatina, planus,vedel’arrelindoeuropea pelә-, pl-ā que significa‘plaoextensió’;underivatde pelә-, pl-ā éslaparaulagrega πλανήτης ,‘planeta’,quesignifica ‘errant’.

seccions seccions rcions

pensar per pensar d’un minut a una hora

JordiDeulofeu

DepartamentdeDidàcticadelaMatemàtica idelesCiènciesExperimentals UniversitatAutònomadeBarcelona jordi.deulofeu@uab.cat

Lesvacancesd’estiusónunbonmomentperdedicarestonesaresoldreproblemes,especialmentper aaquellsquebusquemllocstranquils,jasiguialmaroalamuntanya,perpassarunsquantsdiessense resespecialperfer,mésenllàdellegir,passejarotrobar-seambelsamicsenunàpatestiuenc.Els problemesqueconstitueixenlamevacol·laboraciód’avuitenenaquestaireiperaixòsóndecamps inivellsforçadiferents,peròtenenencomúlaideaderepte,avegadesd’endevinalla,pròpiadeles situacionslúdiquesiplaents.Així,trobareuunproblemadedemostraciósobreunacuriosasuccessió numèrica,elcàlculdel’àread’unquadrilàterespecial,ladeterminaciód’unraonamentlògicenun problemadebarrets,ladeducciód’unafórmulaquerelacionalaquantitatd’elementsd’unaxarxa,i encara,alfinal,unproblemademovimentqueespotresoldreraonantmatemàticamentisensefer capmenadecàlcul.

D’acordamblaintroduccióanterior,vullcomençarl’articlecelebrantlainiciativadelaSocietatCatalanadeMatemàtiques,persegonanyconsecutiusinom’equivoco,d’inclourecadadiadelmes d’agostunproblemaorepteelemental,extretdelacol·lecciódeproblemesdelCangur,enlasecció queportapertítol«Elcervellmatemàtic»deldiari LaVanguardia

Vaigtrobarinteressantelreptedeldia21d’agost,percertunadatacapicua(21-8-12),queempermetproposarelprimerproblemad’avui.Elproblemapublicata LaVanguardia començaexplicant quès’enténperunaxarxa,unafigurarectangularformadaperquadrats—queenspotremetre,entrealtrescoses,auntauler—,iquinssónelsseuselements(vegeueldibuix):malles(regions—o quadrats—delaxarxa),nusos(vèrtexsinteriors)iboles(vèrtexsdelafrontera).Concretament,elproblemademanaqueesdeterminiquantesmallescontéunaxarxaquetéexactament32nusosi28 boles.Encaraqueelrepteésforçatancat(desolucióúnica)iprousenzill,lasituaciópermetgenerar altresproblemesinteressants,atravésdel’estudidelarelacióentreelnombredemalles,denusosi deboles.

Dibuix 1. Xarxa amb 28 malles (regions), 18 nusos (vèrtexs interiors) i 22 boles (vèrtexs exteriors)

Problema1. Mésqueunproblemaconcretusproposoqueprengueulasituacióanterioritracteude trobarrelacionsnumèriquesentreelnombred’elements.Considereuprimerelnombredevèrtexs, regionsicostats:estractadelaconegudafórmulad’Eulerperòenelpla,senzilladeconjecturarperò unamicamésdifícildedemostrar.Després,deixeudebandaelscostatsicentreu-vosenregionsi vèrtexs,boidistingint-hinusosiboles.Donatelnombredenusos(oeldeboles),quantesxarxes diferentsespodenformar?Siconeixemlaquantitatdedosdelstreselements(malles,nusosiboles), laxarxaquedadeterminada?Engeneral,quinaformatindràl’expressióquepermetrelacionarles quantitatsd’aquestselementsenunaxarxa?

Siheuarribatfinsaquí,bensegurquevosaltresmateixosuspodreuplantejar,sinohoheufetja,altres preguntesinteressantsalvoltantd’aquestasituació.

Tambélestrobadesestiuenquessónpropíciesperproposarendevinalles,entretenimentsojocslògicsalvoltantd’unataula.Afinalsd’agostd’aquestany,enunsoparfamiliaraBegur,lamevaneboda Caro,estudiantdesociologiaiaficionadaalesrecreacionsmatemàtiques,emvaproposarunproblemaquejonoconeixiaiquepertanyalgrupdeproblemesrecreatiusquepodríemtitular: endevinael colordelbarretqueportes.L’enunciatéselsegüent.

Problema2. Ungrupde30presonershandepassarunaprova:endevinarelcolordelbarret(blanco negre)queportenposatiquenopodenveure.Sil’endevinenseranalliberats;sino,seranexecutats. Abansdedirelcolordelbarret,esposarantotsenfilaicadascúveuràelsbarretsdetotselsqueté aldavantalafila,perònoelseunielsdedarrere.Començaràadirelnomdelcolordelseubarretel queocupaeldarrerllocalafila,desprésel29èiaixísuccessivamentfinsalprimer.Elsbarrets,blancs onegres,esposaranal’atzaridurantlaprovacappresonernopodràdirresmésqueelnomdelcolor delbarret(nomquepodransentirtotselsaltres),quansiguielseutorn.

Lanitabansdelaprova,quantotselspresonersenconeixenlescondicions,esreuneixtotelgrupper intentarcercarunaestratègiaqueelspermetiminimitzarelnombred’execucions;desprésdepensarhiunaestona,entrobenunaqueelspermetràsalvar-setotsmenysun,quetindràunaprobabilitat del50%desalvar-se.

Sabríeutrobaraquestaestratègia?Sivariaelnombredepresonersespotaplicarigualment,ocalfer algunamodificació?

ElsegüentproblemaésunabonicasituaciógeomètricaqueemvaproposarlaLauraMorera,companyadeldepartament,iqueusproposoperquèvaiggaudirresolent-lo.Comsempreenaquests tipusdeproblemes,estractadetrobarunasolucióapartirdemètodesgeomètricselementals.Un copl’hagueuresolt,nouscostaràgairefer-neunageneralitzacióinteressant.

Problema3. Consideremunquadrantdecircumferència,osihopreferiuunsectorcirculard’amplitud90◦ ,formatperdosradisil’arcdecircumferènciacorresponent.PrenemunpuntPsobrel’arcde circumferènciaitracemelsdossegmentsqueuneixenPambelspuntsonelsdosradisintersecten lacircumferència.Silamesurad’aquestsdossegmentsés2i3cmrespectivament,quinaésl’àreadel quadrilàterformatpelsdosradisiaquestsdossegments?

Siambundibuix(cosaimprescindibleperabordarelproblema)noenteniuprou,preneuelGeogebra ibenaviatcomençareuaferconjecturesinteressantssobrelesrelacionsentreelselementsd’aquest curiósquadrilàter.Potserfinsitotobservareuque,enunadelespossiblesmaneresderesoldreel problema,s’hiamagaunconegutteoremarelacionatambelteoremadePitàgores.

Acabarél’articleambunparelldeproblemessorgitsdelarelectura,quetambéhefetaquestestiu,del llibre OneHundredProblemsinElementaryMathematics (Steinhaus,1979),uninteressantivariatrecull deproblemesdediferentstemes,queHugoDynoizySteinhaus(1887-1972)vapublicarinicialmentel 1964,isobreelsqualsMartinGardnerdestacalasevaoriginalitat.L’autord’origenjueuésunreputat matemàticpolonèsformatalaUniversitatdeGöttingen,onvallegirlatesidoctoral(1911)sobreel principideDirichletsotaladirecciódeDavidHilbert;acabadalaSegonaGuerraMundial,desdela UniversitatdeWroclaw,vaserundelsprincipalsartífexsdelrenaixementdelamatemàticapolonesa,delaqualenvansorgirmatemàticscomBanach,quevaserestudiantdeSteinhausiambquiva col·laborar.Amésd’unmoltbonmatemàticquevafercontribucionsrellevantsencampsmoltdiversos,esvapreocuparpertemesrelacionatsambelseuensenyament,atravésdellibresdeproblemes decaràcterdivulgatiuirecreatiu.

Enlaintroducciódelaprimeraediciódelllibreesmentat,diu:«Ambaquestacol·lecciódeproblemes vullapel·laraallòquehihad’infantenuncientíficiaallòquehihadecientíficenuninfant,encara quepotsernoméshereeixitenpassar-m’hobéjomateix».

Problema4. Construïmunasuccessiód’entersd’unasolaxifradelasegüentmanera:comencem ambelsnombres2i3.Elsmultipliquemitenim6(3rterme).Multipliquem3per6iobtenim18.El4t termeserà1iel5èserà8.Lasuccessióésfinsaquí:2,3,6,1,8,ielsúltimsdígitsquehemmultiplicat sónel3iel6.Pertant,arahemdemultiplicar6 1 = 6(6èterme);seguim:1 8 = 8(7èterme),iaixí successivament.Seguintlasuccessiótindrem:

Pernoequivocar-seelmillorésanarconstruintlasuccessióiassenyalantelsdarrersnombresquehem multiplicat,tenintencomptequecadascund’ells,llevatdel1r,formapartdeduesmultiplicacions consecutives.

Podeuobservarqueenelsvintprimerstermesjahanaparegutelsnombres1,2,3,4,6i8.Laconjecturasemblaclara:elsaltresnombresd’unaxifranoapareixeranenlasuccessió,peròtambépot haver-hialtresconjecturesinteressants.Sabríeudemostrarquenopothaver-hidosnombressenars consecutius?Proveutambéqueelsdígitsquefalten(5,7i9,isivoleutambéel0)noapareixeranmai enaquestasuccessió.

Elproblema,prousenzilldesprésdepensar-hiunaestona,portaaunainteressantreflexiósobreels resultatsques’obtenenenlestaulesdemultiplicar,enparticularsobrelesxifresqueformenelsnombresresultants.

Acabaréambunaltreproblemadel’esmentatllibredeSteinhausqueapareixeneldarrercapítoli quecorresponaunasèriedeproblemesdel’anomenatDr.Abracadabrus.

Problema5. Imagineuunàbacformatperdeuvaretesparal·lelesd’iguallongitud,quesuposarem situadeshoritzontalment,iacadavaretahihaunabola.Laposicióinicialdelesbolesésdesconeguda ilesbolesesmouenambunavelocitatconstantiigualperatotes.Suposemuneixdesimetria, perpendicularalesvaretes,quedivideixl’àbacenduesparts,queanomenaremdretaiesquerra. Suposemqueelmovimentesprodueixdetalmaneraquealabandadretadel’àbacnohihamai mésdesetboles.Enaquestescondicions,elDr.Abracadabrusasseguraquealabandadretadel’àbac tampocnohihauràmaimenysdetresboles.Éscertaaquestaafirmació?Sabríeudemostrar-la?

Aixòéstotperaquestavegada.Nomésdesitjo,seguintSteinhaus,l’autorrememoratavui,queusho passeutanbéresolentaquestsproblemescomm’hohepassatjopreparant-los.

Bibliografia

Steinhaus,H.(1979). OneHundredProblemsinElementaryMathematics.NovaYork:Dover.

Sapsquèhihasimbolitzatal

campanardeSantBernabé delaSagradaFamília?

ClaudiAlsina claudio.alsina@upc.edu

L’úniccampanarque,justabansdelasevamortel1926,vapoderenllestirGaudífoueldeSant Bernabé.Tantlacuriosaconcreciódelesformescomlasevaconstruccióidecoracióforenmotiu d’unllargperíodedeconcepcióiexecució,jaqueeldeSantBernabéhaviadeserelcampanarde «referència»,perferelsaltres.

Els dotze pinacles dels Apòstols

Gaudífixadebellantuvique:«Elscampanars,acabatsambelsatributsepiscopalsilalloança Hosanna Excelsis,serandedicatsalsapòstols».

Coms’hadit(Bonet2000a,b)sobreelspinaclesdelscampanars:«Lasiluetadelseutroncsuperiorsimulaelbàculdelsbisbes,elnussimbolitzal’anell,ielfinaldelcampanarésundoble,essentsemblant aunamitra,quecontéunacreudauradaamblesinicialsdelsapòstolsaquiesdediquen».

Aquestsimbolisme,comveurem,s’acabaconcretantenunspinaclesdegrancomplexitat.

Sobre els símbols bisbals tradicionals

Alllargdelssegless’hananatconcretantunasèried’elementsdistintiusisimbòlicsdel’altajerarquia eclesiàstica. Mitres,anells,creus,bastóipal·li sónpartdistingidadelacol·lecciód’objecteslitúrgics propisdelPapa,elscardenals,elsbisbes,elsabats,etc.Lesreglesdelseuúsiatorgamentilesvariantsartístiquesqueapareixenenlasevaproduccióartesanalhanaportatunagranvariacióhistòrica d’aquestscomplements.Observemlasevadescripciógeneral:

• Lamitra:aquestcapellplegabledeformatancaracterísticapresenta,segonsel CaerimonialeRomannum,tresvariantsornamentals(mitrapretiosa, auriphrygiata i simplex )ques’utilitzensegons elsactesquetenenlloc.Sibés’haespeculatmoltsobrel’origendelamitraenreligionsiculturesanteriorsalcristianisme,elquesemblamésplausibleésafirmarqueenlabiografiadelpapa ConstantíI(708-815)jaesparlad’unacoberturadecapdistintivadelPapa(mitra,engrec,voldir una«cintadecapodiadema»).

• Lacreupectoral :elbisbehadeportarunacreupenjadad’unacadenaalvoltantdelcollisituada al’alturadelcor(cruxpectorialis).Lacreupottenirformesdiverses(creugrega,creullatina...),pot sermoltbarrocaosenzillaipotconteniralgunapetitarelíquia.Elsimbolismedelacreuéslaforça delSenyorenfrontdeldiableielsenemicsielrecorddelaPassiódeCrist.

• Elbàculpastoral :elbàculdelbisbe(baculuspastoralis)simbolitzaelseupapercomapastorguia delpoble(Joan10:1-21)pertransitarambordreiprotecciópelcamídelasalvació,ésadir,guiar elpoble.Elbàculéscilíndricimoltaltisovintacabaenunaformacircularoespiral.

• Elpal·li:estractad’unacintablancadellanacol·locadaentorndelcoll,quedónallocaduestiressobrecadascunadelesqualshihatrescreusnegresbrodades.Aquestelementsimbolitzala fidelitataCrist.

• L’anelldebisbe:quanenlacerimòniad’esdevenirbisbes’imposal’anell,elsimbolismeassociatésel delcasamentdelbisbeamblasevadiòcesi,ésadir,símboldefeifidelitat.Aquellanellpotserbesat ensenyalderespecte,peròavuinotéusoslitúrgics.Antigamentl’anellserviadesegellpersonal perautentificardocumentssobreelsqualsesposavalacrecalentperferlamarcacorresponent. Sovint,doncs,laformadel’anellera,iés,enformadesegellquadratiformacilíndricaenlapart querodejaeldit(elquartdelamàdreta).Tambéhanexistitversionsd’anellsde formatquadrat ambunapedrapreciosa (ametista,normalment).

El pinacle de Sant Bernabé a la Façana del Naixement

CommaterialitzaGaudílarepresentaciódelssímbolsbisbalsquehemdescritalspinaclesdelscampanars?

• Lesmitresdelscampanars. PeralaculminaciódelsdotzecampanarsdelsApòstols,lesimatges (idèntiques)delesmitress’hanconcretaten dosquadratsvermellsinclinats entresiambun paraboloidehiperbòlic entreells.

• Lacreupectoralalscampanars. Lacreupectoralbisbals’incorporasuperposadaalapròpiarepresentaciódelamitraenformadecreugregaambarrodoniments.Elseuacabatplatejatdestaca sobreelfonsvermellósmitral.

• Elbàculpastoralalscampanars. Larepresentaciódel baculuspastoralis estàmoltbenconcretada amblapresènciadelfinalespiralhabitualdelbàculbisbalquesurtdeldarreredecadacampanar isesituajustdavant,asotadelarepresentaciómitral.

• ElSantRosariilesesferes. Espodriaconjecturarquelesesferesblanquescomperlesqueenvolten elspinaclessimbolitzenelsrosaristradicionalscomenelParkGüellhofanlesesferesdepedraal llargdelpasseigsobrelaplaçacentral.Perònohihaevidènciesquehidoninsuport.

• Elpal lidelscampanars. Tambéenelslateralsdelspinaclesdelscampanarss’aprecialarepresentaciódelacintapal liquecauperdoscostats,decoradaambrombesdecolors.

TotselselementsesmentatsfinsaquívanserfetsambcuraalcampanardeSantBernabé,jaque s’havienderepetirenelsaltresonzecampanars.Eraprecisamentlaconcreciódel’anellbisballa quediferenciarialestresfaçanes.

• L’anellbisbalalcampanardeSantBernabé.

Incrustatsenelsuportdelpinacledestaquenelspolíedresrepresentatiusdelapedradel’anellbisbal. Elsforatsenaquestspolíedresdestinatsaconteniril·luminacióexterioracabarandefacilitarl’asso-

ciacióentreaquestselementsarquitectònicsilasevaevocaciódepedrapreciosa,jaqueamblallum quedaclaralaideadebrillantor:lallumquesurtd’unapedrapreciosail·luminada.Tambéelsraigs solarsil·luminaraniesreflectiranenelsacabatsceràmicsdelscossospolièdrics.

EnelpinacledeSantBernabé,lapedradel’anellbisbals’obtéd’una intersecció(maclatge)d’uncub ambunoctàedreregular. Evidentment,elpolíedreresultantnoésregular,peròté siscaresquadrades i vuitcareshexagonals.Aquestafiguras’intersecaambunaesferaquedeterminaentoteslessevescatorzecaresuncasquetesfèricdelqualse’nbuidasemprelazonacilíndrica(determinadaperdoscasquetsparal lelssituatsencareshexagonals)perquèpuguicontenirelementselèctricsd’il luminació.

Enelvellsimbolismeplatònic,elcubrepresentalaterrail’octàedrel’airei,pertant,enclaumitològica, elpolíedred’aquestcampanarseriaunasíntesientrelaTerraielCel,«elcelinteracciona/apareixa laterra»...elNaixementdeCrist.Caldirquelapartrepresentantelcèrcoldel’anellbisbalestrobaen aquestcampanardiscretamentcol locadaalazonadeldarreredelpinacle,ialvoltantdel’anellapareixunforatel·lipsoïdalonespotcol·locarunfocusdellumperil·luminarelsaltrespinaclescentrals delTemple.

Endiversosllocsheminsistitqueel númerosecret delaSagradaFamíliaésel12.Recordantqueel sistemadeproporcionsalaSagradaFamíliaesbasaenelsdivisorsde12(1:1,1:4,1:2,3:4,1:3,2:3),no ésestranyqueperals12campanarsGaudífixésl’atencióenalgunselementspolièdricsonel12 hiéspresent.Enefecte,elcubielseudual,l’octàedre,tenen12arestes.Gaudíconeixiaperfectament queenjoierias’usavensempreformesoctaèdriquespertallarelsbrillantsolespedrespreciosesdels anells.

Sihommiralageneraciód’aquestcampanarobservaqueésunatorredeperfilparabòlicqueté unquadratenlasevabasequevagirantlleugeramentalllargdelcampanarfinsaenllaçarambun quadratdelpolíedredescrit.Enelbellmigdel’interiorestrobaunaescalahelicoïdalambcentrebuit percontenirl’allargadacampanatubular(enforma d’hiperboloided’unfull ).Unameravellageomètrica culminant.

Referències

Alsina,C.(2002). Macladegeometries. DinsGaudí, LarecercadelaForma.Barcelona:ICB,Ajuntament deBarcelona,LunwergEditores,pàg.118-125.

Alsina,C.(2005-2008). ProjectedeRecercaHum-ArtHum2055-03043/ARTEdelMinisterid’EducacióiCiència

Alsina,C.iGómez,J.(2002).Gaudí,geométricamente. LaGacetadelaRSME,5(3),pàg.523-558.

Bonet,J.(2000). L’últimGaudí. Barcelona:Pòrtic.

Bonet,J.(2000). TempleSagradaFamília.Barcelona:EscudodeOro.

La FEEMCAT(Federaciód’Entitats per a l’Ensenyament de les Matemàtiques a Catalunya), la SCM (Societat CatalanadeMatemàtiques), i la RealAcademiadeCiencias anuncienla convocatòria per a l’admissióenel seu

projecteESTALMATaCatalunya (DeteccióiestímuldeltalentprecoçenMatemàtiques)

Onzenapromoció2013-2015

Objectiudelprojecte:fomentarl’aficióihabilitatespecialenmatemàtiquesdenoisinoiesque l’ viuenaCatalunyaiamb datadenaixementl’any2000oany2001. l’

Activitats:Totselsdissabtesdelperíodelectiudelscursos2013-2014i2014-2015,de10ha13ha laFacultatdeMatemàtiquesiEstadística(FME)delaUPC,aBarcelona.

Aquestesactivitatsserangratuïtes peralsnoisinoiesseleccionats,elsparesotutorsdelsquals s’haurandecomprometreaportar-losirecollir-losaleshoresesmentades.

Procésdeselecció:

La selecciódel grupde 24nois i noies queparticiparanenelprojectetéduesfases:

1. Testd’aptitud: eldissabte8dejunyde2013ales10halesciutatsdeBarcelona,Girona, LleidaiReus.

2. Entrevistapersonal ambelsparesotutorsielsnois/espreseleccionats/des.

Inscripció:

formulari

Lamare,elpareotutorlegalhaurand’omplirunquetrobaranalapàginawebdel’organització,www.estalmat.org.Veuranquehihaunenllaçespecialperalsdetallsd’aquestaconvocatòria,iunaltreenllaçonpodranllegirinformaciódelprojecteaCatalunya.

Termini: del15dabrilfinsal31demaigde2013. ’

Dadesqueesdemanen: nomidatadenaixementdel’alumne/ainteressat/daaparticiparenel projecteESTALMAT,adreça,correuelectrònic,númerodetelèfondecontacteicentreescolaron estudiadurantelcurs2012-2013.

aquinapoblaciódesitjarienferlaprova (Barcelona,Reus,Gironao Caldràqueindiquin

Lleida).

Lallistad’inscritsielsdetallsdelarealitzaciódelaprovadeseleccióespodranconsultaralweb www.estalmat.org,onzenapromoció2013-2015.Tambéespotdemanarinformaciósobreelprocés d’inscripcióalaNúriaFuster,SocietatCatalanadeMatemàtiques(telèfon:933248583;correu electrònic:scm@iec.cat).

creamat el racó del creamat

Ponts entre divulgació i educació matemàtica. Què fem des del Creamat?

Podemdefinirladivulgaciócientíficaimatemàticacomaquellconjuntd’activitatsques’ocupend’interpretarelconeixementcientíficambl’objectiudefer-loaccessiblealpúblicgeneral.Siacceptem aquestadefinició,encaraquenoméssiguiperuninstant,seguramentestaremd’acordquelessinergiesentreladivulgacióil’educacióresultenmésomenysevidents.Enaquestarticleusproposem passejarpelspontsqueuneixenladivulgacióil’educaciómatemàtica.Unpasseigd’unadirecciói dedossentits.D’anada,exemplifiquemambuncasconcretcomladivulgaciópotserunallavorque donillocariquesactivitatsd’aula.Detornada,presentemunapetitamostradelesmagnífiquesactivitatsdedivulgacióqueesfaniespodenferdesdel’escola.Enl’últimapartdel’articlerepassemles accionsquehemfetiestemfentdesdelCreamatenaquestsdossentits.

Com podem connectar la divulgació matemàtica amb l’activitat a l’aula?

Siagafemelfulld’undiariqualsevol,quantscopscreieuqueelpodremdoblegar?(Unplecsobre l’altreisempreperlameitat.)Usconvidemqueanticipeuunarespostaabansdeseguirllegint.Quin nombredeplecsussemblariaraonable?

Enunprimermomentpodempensarquemolts,però,sienshiposem,enarribaralsisèplecveurem quenoéspossibleanargairemésenllà.Defet,moltprobablement,noméspodremferunplecmés acausaqueelgruixilamidadelfulldoblegatenshoimpedeixen.Ésunabonicavariantdelaclàssica llegendasobrelainvenciódelsescacs,queenspermetintroduiral’aulaelcreixementexponencialde maneraintuïtivaiexperimental.Elproblemaespotcontinuartotestudiantelgruixdepaperobtingut, enquèintervenenlespotènciesde2.Efectivament,alsetèplectindremunblocde27 = 128capes depaper,quehauremdemultiplicarpelgruixdelfull.Cosaqueenssuggereixunaaltrapregunta: quinéselgruixdelfulldepaper?

Lesactivitatsd’aulaqueesgenerenapartirdeladivulgaciósónfàcilsd’enriquirperquèsovintes podentrobarabundantsfontsmaterials,referènciesbibliogràfiques,presentacionsivídeos.Enaquest casconcretpodemtrobarinformaciódiversa,comaquestmagníficvídeodeTED-Ed.Usanimeua investigar-hoambelsvostresalumnes?Sereucapaçosdesuperaraquestlímitde7plecs?Comacuriositat,inomésapteperavalentsivalentes,elrècordmundialestàen13plecsutilitzant16kmde paperdevàter(http://goo.gl/WU9z6).

Encaraenspodemferméspreguntes:quinalongitudtindràelfullplegatsihihavia16kmdepaper desprésdel13èplec?Perquèlaimatgefinaldelfullplegatnoescorresponamblamidaobtinguda?

Quinsucdidàcticpodemextreured’unapreguntaaparentmenttannaïf!

Url imatge: http://goo.gl/9V9Yc

Podem fer divulgació des de les escoles?

Siladivulgaciócientíficas’ocupadeferaccessibleslesmatemàtiquesatothom,desdelscentres educatiuspodemcomplementarlanostratascaformadoraimpulsantaccionsambempremtadivulgadora.Estaremd’acordqueenlamajoriadelscasosnoestractaràdedivulgacióensentitestricte:hi hamagníficsprofessionalsquesen’ocupen,peròsíd’unabonaoportunitatpertreballarcontinguts curricularsmentrevivimenprimerapersonaunaexperiènciadivulgadora.

Usproposemunapetitallistadetipusd’accionsqueespodenferdesdel’escola,acompanyadad’una mostradelesmagnífiquesexperiènciesques’handutatermeendiferentscentres:

• Publicacionsmatemàtiquesdelcentre,elaboradesperl’alumnat,comrevistesenpaper(Revista DousPiErre:http://goo.gl/A56Y5)oenformatdigitaliblocsonespresentinactivitatsfetesales aules(BlocdeP3del’EscolaDiputació:http://goo.gl/9fpJ8).

• Exposicions:temàtiques,detreballs,deconcursosfotogràfics...

• Elaboraciódevídeos(Estudidelesombresdelsol ;INSManuelRaspall:http://goo.gl/uLIjH).

• Participacióenconcursosdeproblemes,jasiguininternsdelcentreoexterns(Cangur,Femmatemàtiques,Problemesal’esprint,defotografiamatemàtica...).

• Realitzacióde«muntatges»comcrearanamorfismes(EscolaMariàCubí:http://goo.gl/ofdIx),construirfractalscomeltrianglesdeSierpinski(INSLlavaneres:http://goo.gl/hIxXc),teatres,ballsokaraokesmatemàtics...(INSCendrassos:http://goo.gl/5OQ67).

• Muntarclubsmatemàticsque,amés,podendonarsuportamoltesdelespropostesanteriors(INS LluísDomènechiMontaner:http://goo.gl/1NxvD).

• Organitzarfiresogimcanesalpropicentreoencol·laboracióambaltrescentres,comlesque s’hanfetaBerga,Manresa,Lloret,Igualada,SantBoi...

• Ferentrarl’actualitatal’aula,jasiguiapartirdenotíciesoaprofitantefemèrides,comperexemple laqueesfaenguany,l’anydedicataAlanTuring(http://goo.gl/P4Xiu).

• Ompliriferviurelabibliotecadelcentreincorporant-hicontes,novel les,recullsderecreacions, textosdivulgatius...relacionatsamblesmatemàtiques.

Què fem des del Creamat?

Enaquestaúltimapart,ensagradariaconvidar-vosapassejarpelquefemdesdelCreamat.Buscant enllaços,nosaltresdiemmigenbromaquevolemserun hub queajudiaposarencontacteaspectesmatemàticsqueapareixenenlasocietatambl’educaciómatemàticaal’escola.Lagranmajoria d’accionsquecomentemlespodemtrobaralnostreweb.

Mirantd’acostarelmóndivulgatiual’educatiutrobarem:

• Vídeosdeconferències,delesqualsunamitjadotzenatenenuncairenetamentdivulgador,com lesdeMàriusSerra,RafelPérez,FernadoBlasco,PereGrima,DavidJuher...

• Alasecció Hemvist trobareupropostesrecollidesdesdelaxarxa,desdelsmitjans...odesdeles pròpiesaules.

• Alasecció Llibres ensfemressòdemúltiplespublicacionsifempropostesespecífiquesperSant Jordi,Nadalol’estiu.

• Informemd’exposicions,conferències,tallers...queesfanarreudelpaís.

• Puntualmentoferimmiradesmatemàtiquesaexposicionspuntualsnoestrictamentmatemàtiques(d’història,depintura...).

Peròtambécol·laboremsovintambmitjansdecomunicació(premsa,televisióoràdio)perajudara descobrirelsaspectesmatemàticsdelnostrevoltant.Procuremqueelsproductesd‘aquestescol·laboracionsquedinrecollitsalwebpertalquepuguinserutilitzatsposteriormentpelprofessorat.Així elCreamathaparticipatenproduccionscomlasèrie Àlia,alguneshistòriesd’Unamàdecontes,en programesderàdiocoml’Extraradi deCOMRàdio...delsqualstrobareualwebelsvídeosielsenregistramentssonors.

Estàdintredelsnostresobjectiusajudaramillorarlaimatgesocialdelesmatemàtiques.Compartim, doncs,elspropòsitsdeladivulgaciómatemàtica.Peròelnostreobjectiuprincipaléselsuportal professoratielfetdeproporcionar-loseinesqueajudinalamilloraeducativaalesaules.Entenent queeducacióidivulgaciótenenconnexionsquecalindagariexplotar,intentemconstruirpontsentre aquestsdosmons.

Desitgemqueaquestarticleserveixiperposarderelleuqueladivulgaciómatemàticaenspotajudar aenriquirlanostrapràcticadiària,aixícomperencendrel’esperitdecomunicaridifondreallòque ensapassiona.DesdelCreamatensagradariaanimar-vosaaprofitaraquestessinergiesiquecadascú desdelseuàmbitcontribueixiamillorarlaimatgequelasocietattédelesmatemàtiques.

Notafinal: aquestarticleésunresumdelaintervenciódelCreamatalaIXJornadad’Ensenyament delesMatemàtiques(IEC,29-9-12).Lapresentacióespottrobarahttp://goo.gl/syzl8

L’equipdel creamat

Màster Oficial de Recerca en Didàctica deles Matemàtiques i de les Ciències

DepartamentdeDidàctica delaMatemàticailes CiènciesExperimentals–UAB

Lafinalitatdel

éscapacitarl’estudiantperidentificarunproblemaderecercaenl’àmbitdel’educació matemàticaocientífica,tantformalcomnoformal,persituar-loenelseucontextsocialiteòric, donant-hirespostaatravésdelesmetodologiesadientsicomunicar-neelsresultatsiles conclusionsalacomunitatcientíficaieducativaialesadministracionscorresponents.

MàsterOficialdeRecercaenDidàcticadelesMatemàtiquesidelesCiències Elsestudiantsaquivadirigitaquestmàstersónaquellsllicenciats,diplomatsograduatsque,a mésdecomplirelsrequisitsilescondicionsestablertesperlanormativaoficial,teneninterèsen:

Aprofundiricontribuiralscampsdeconeixementpropisdelesàreesdedidàcticadeles matemàtiquesidelesciènciesid’àreesafins,atravésdeprocessosderecercadecaràcterfonamental.

Incidirenlainnovacióeducativa,atravésdeprocessosderecercadecaràcteraplicaten elsdiferentscontextosdaprenentatgematemàticicientífic.

Conèixerelsmecanismesperalamilloradelaformaciódelsagentsresponsables d’educarenmatemàtiquesienciènciesalapoblació,tantenàmbitsformalmentinstitucionalitzatscomforad’ells.

Analitzarelsaspectessocials,culturalsipolíticsimplicatsenl’educaciódelapoblacióen matemàtiquesienciències,ambl’objectiudefer-hiincidència,tantanivelld’institucions comdepolítiqueseducatives.

Avaluar,entenentl’avaluaciócomaprocésderegulaciótantinterncomextern,lapràctica docent,lainnovacióilaformacióqueespromouen.

Haversuperatambèxitaquestmàsterpermet,entrealtrescoses,al’estudiantiniciareldoctorat enl’àmbitdeladidàcticadelesmatemàtiquesidelesciències.

Pla d’estudis:60 crèditsECTS.

Enfunciódelaformacióprèviadel’estudiant,lacoordinaciódelmàsterpodràdemanarquees cursincomplementsdeformació.

Preu:elcurs2012-2013,elpreudelsmàstersoficialsdelaUABsesituacapals40percrèdit peralsestudiantsdepaïsoscomunitarisiperalsestrangersambresidència.

Informaciói inscripció:

http://www.uab.cat/servlet/Satellite/estudiar/masters-oficials/informacio-general/recerca-en-didacticade-les-matematiques-i-de-les-ciencies-1096480139517.html?param1=1096482842172

Peramésinformació:conxita.marquez@uab.cat