Nou Biaix, 31

biaix

Revista de la FEEMCAT i de la SCM

Juny

2012

noubaiix

número 31

Consell de Redacció:

Mequè Edo / Josep Pla i Carrera (coordinadors)

Marianna Bosch

Juanjo Cárdenas

Joan Carles Ferrer

Romà Pujol

Manuel Udina

Josep Lluís Solé Manel Sol

© dels autors dels articles

Coediten:

Federació dEntitats per a lEnsenyament de les Matemàtiques (FEEMCAT )

Pau Gargallo, 5 08028 Barcelona feemcat.org

Societat Catalana de Matemàtiques (SCM) filial de l’Institut d’Estudis Catalans Carme, 47 08001 Barcelona scm.iec.cat ’’

noubiaix@gmail.com sites.google.com/site/noubiaix

Periodicitat: semestral Preu d‘exemplar ordinari: 12 €

Hexàgons de mel

Fotografia de la portada: , de Teresa Gutiérrez

ISSN: 2014-2021

Dipòsit legal: B-22.314-2012

Impressió: Gráficas Rey

Publicacions i Edicions de la Universitat de Barcelona

Adolf Florensa, s/n

08028 Barcelona

Tel.: 934 035 530

Fax: 934 035 531 comercial.edicions@ub.edu www.publicacions.ub.edu

sumari

El M àster de Formació del Professorat de Secundària: especialitat Matemàtiques

Joan Miralles de Imperial Llobet i PelegríViader Canals

Reflexions ober tes d’un neòfit en Didàctica de la Matemàtica

Josep Pla i Carrera

Més sobre conjectures i demostracions

George Pólya

Lluís Antoni Santaló i Sors (1911-2011)

Claudi Alsina

L’adquisició de competències matemàtiques d’alumnes de primària en contex tos de jocs de taula i resolució de problemes

Edelmira Badillo, Mequè Edo i Jordi Deulofeu

La construcció del pentàgon regular de l’ . Un primer pas en la ruta cap a les estrelles

Carles Ignasi Gómez Ruiz

Intuïcions dels alumnes de secundària sobre la probabilitat. Una recerca sobre la influència del treball empíric en el cas d’un esdeveniment compost

Fermí Rojo Cort i Jordi Deulofeu Piquet

Jocs de car tes i matemàtiques

Lluís Sabater Anticó Almagest

Per pensar un minut

Sabies que...

Sistemes de referència

Mar ta Berini

Cròniques

El racó del creamat

articl artices les rticles

ElMàsterdeFormació delProfessorat deSecundària:especialitat Matemàtiques

JoanMirallesdeImperialLlobet

UniversitatPompeuFabra

PelegríViaderCanals

UniversitatPompeuFabra

1. Els precedents

Moltsdelslectorsdel NouBiaix sónprofessorsdesecundària.Peramoltsd’ells,l’accésalaprofessióes deviaferperunad’aquestesduesvies:atravésdelCAPoatravésdetenirunmínimdedotzemesos d’experiènciaprofessionalenalguncentredesecundàriareconegut.

LaviadelCAPeralaméshabitual.Moltsestudiantsd’últimcursdellicenciaturacursavenelCAPdurant unsquantscapsdesetmanaifeienlespràctiquespreceptivesenalguninstitutpúblicdesecundària. ElCAPl’organitzaval’ICEdelesuniversitats.Eraunaactivitateducativarendibleatèsquerequeriauna estructurasimple:lagranmajoriadelesclassesteòriqueserenmagistralsilespràctiquesencentres educatiuserencurtesi,enalgunscasos,sotmesesapocscontrols.Lapartteòricaconsistia,enmoltes ocasions,enxerradessobrelapsicologiadel’aprenentatge,algunespinzelladessobrelaproblemàticadel’adolescènciaisobrel’organitzaciódecentreseducatius,elcurrículumilanormativalegal aplicablealasecundària.Sobrematemàtiques,l’ensenyamentdelesmatemàtiquesilestècniques quecaldominarperpoderexercirdeprofessordematemàtiques,se’nparlavamésaviatpoc.

Laconseqüènciadetotplegaterauncursforçateòric,ambunacàrregaimportantderutinaiuna sensacióde«tràmit»quecaliasuperarpertaldepoderapuntar-sealesllistesd’interinatgeipresentarseaoposicions.Lasensaciódominanteraqueladidàcticadelesmatemàtiqueseraunadisciplina ambpocaentitatpròpiaiqueperferclassen’hihaviaprouamblesques’aprenienalafacultat.La restajavindriaambl’experiència.

Defet,permoltsdelsprofessionalsqueavuidiaestanreconegutscomagransprofessorsdelasecundàriadelnostrepaís,aquestvaserelseuparadigmaperiniciar-seenlaprofessió.Moltsexpliquen anècdotesdecomelsprimersanyslessevesclassesalBUPoméstardl’ESOielbatxilleratvanser

un«desastre»desdelpuntdevistadelsresultatsd’aprenentatgedelsseusestudiants.Aquests,però, almenysvansaberreconèixerquelarèplicadelquehavienvistalesfacultatsdematemàtiquesconstituïaunerroriestraduïaenunsresultatsforçadecebedorsperpartdelgruixdelsestudiantsque rebienlessevesclasses.Comquel’assignaturaeramatemàtiquesijasesapquesóndifícils,ningú noprotestavaiquidiapassa,anyempeny...Nosabemquantsd’aquellsprofessorscontinuen,molt tempsdesprés,ensenyantdelamateixamanerasensehavercopsatelfetquelesgeneracionsd’estudiantsquepassenperlessevesaulesensurtensenseobtenircapbeneficipelquefal’aprenentatge delesmatemàtiques.

Larealitatdelsúltimsanys,amblaincorporaciómassivadelaimmigracióilaconsciènciaquel’educacióobligatòriahad’aconseguiralgunsresultatsobjectivamentútilsperalasocietat,hafetcanviar moltescoses.

2. El nou Màster

Feiatempsquemoltssectorsdel’ensenyamentreclamavenuncanviradicalenlamanerad’accedira laprofessió.Caliaunamanerad’iniciar-sealaprofessióquetinguésencomptelarealitatdelscentres educatiusiquedotéselsfutursprofessorsdeproueinesperafrontarlacomplexitatd’unaaulaactual. Alnostreentendre,caliaqueaquestainiciaciólaconduïssinengranmesuraelsmateixosprofessors desecundària,ielseuèxithaviad’estarlligatdirectamentaaquestaparticipació.L’objectiudeclaratde lasubstituciódelCAPpelMàsterdeFormaciódelProfessoratdeSecundàriahaestatdonarresposta alsnousialsvellsreptesquecalafrontarperdonarunserveieducatiudequalitat.

ElsalumnesdelMàstertenenprocedènciesmoltvariades.Enlesduesedicions,nomésunpetitpercentatgeprovéd’estudisdematemàtiquesofísica.Lamajoriadelsestudiantssónenginyers,debranquesmoltdiverses;algunssónarquitectes,iunnombreimportantprovédelsestudisd’economiai empresa.Nodisposemdedadesconcretesperò,defet,alasecundàriaactualladistribuciódelprofessoratdematemàtiquesdeusersemblantalaqueacabemd’esmentar.Elcontextdecrisieconòmica contribueixenormementalfetquemoltsenginyers,arquitectesoeconomistessensefeinaenelsseus campsveginl’ensenyamentasecundàriacomunasortidalaboral.Aixòincrementaladificultatdela tascadelMàster:lamancademotivaciódebonapartdelsestudiantsquehiaccedeixen.ElMàster had’aconseguirtambéqueaquestsestudiantsambunabaixamotivaciómatemàtica,futursprofessors,veginlesmatemàtiquesdesd’unaaltraperspectivaiaprenguinaestimar-lesiatransmetre-les demaneraprofitosa.Noenspodemenganyar:elMàsternopotensenyarmatemàtiquesaquinoen sap,peròpotferveureagentintel·ligentiambformaciócomespotprepararperasaberquèsóni coms’hand’ensenyar.Iunelementcentralperdonarrespostaaaquestsrepteséselpràcticumdel Màster.

3. El paper del pràcticum

Enpoquesparaules:unabonapartdel’alumnatques’inscriualMàsterdeFormaciódelProfessoraten l’especialitatdematemàtiqueslimitaelsseusconeixementsdelamatèriaaallòquelivanensenyar asecundàriaméslespinzelladesdeconeixementsmatemàticsquepothaveradquiritencarreresen quèlesmatemàtiquessóninstrumentals.Amés,enlamajoriadelscasosaquestsalumnesnohan tingutcapcontacteambl’oficideprofessormésenllàdelpuntdevistacomaalumnes.Undelspilars delaformacióques’ofereix,pertant,consisteixaposar-losencontacteamblarealitatdel’oficide professormitjançantelpràcticumque,d’aquestamanera,esconverteixenl’eixcentraldelMàster.

Elpràcticum,juntamentambeltreballfinaldemàsterquehiestàíntimamentrelacionat,téunpes d’aproximadament(depèndecadauniversitat)vintcrèditsECTSsobreeltotaldeseixantadequè constaelMàster.Pertant,elseupesconceptualesreflecteixenelpesdededicacióques’hidemana.Consideremelpràcticumcomellloconescontrastenelsconeixementsques’hanrebutenles matèriesmésteòriques,alhoraques’aprènl’oficideprofessoriescontrastaamblavisióprèviaque l’alumnepodiatenirsobreelquesignificaaquestofici.Ambaquestafinalitat,l’organitzaciódelMàster assignaal’alumneuncentredesecundàriaonrealitzaràelseupràcticum.

ÉsdesdelMàsterques’escullenelscentresqueseranformadorsdelsnostresalumnes,laformació pràcticadelsqualstéduesfigurescentrals:ladelcoordinadordecentre,queésquiorganitzal’alumnatenpràctiques,ielmentor,queéselprofessorresponsabledecadaalumneconcretin’hadefer elseguiment.Ambaquestscentresestreballenprèviament,demaneraconjunta,elsobjectiusiles competènciesquecalqueelsseusfutursalumnesassoleixin.Estractad’untreballestructuratiaprofundit,enquècaladaptarelsobjectiusquecalquel’alumneassoleixialarealitatconcretadecada centre.Sobreaquestabaseisegonselperfildecadaalumne,lacoordinaciódelMàsterassigna cadaalumneauncentre.

Pertald’aconseguiraquestsobjectius,elpràcticums’estructuraentresfases.Enlaprimera,la fased’observació,espreténquel’alumneconeguil’estructurad’uncentredesecundària,icomencia participardelavidaacadèmica.Amés,encontacteambelseumentor,començaaparticiparenla preparaciódelesclassesconcretesienlasevarealització.Enlasegonafase,d’intervencióacompanyada,l’alumnecontrastatotallòquevaaprenentenelscursosteòricsamblarealitatconcretadeles aules,oncol·laboraambelseumentorenlapreparacióil’execuciódelasevadocència.Alllargde darrerafase,d’intervencióautònoma,l’alumnepreparaiportaalapràcticaunaunitatdidàctica,sota lasupervisiódelseumentor.

Hemconcebutelpràcticumcomuna plujafina:començapocdesprésdel’inicidelmàsteri,quanacaba,l’alumnejaestàenplenafased’elaboraciódelseutreballfinal,queésunaconseqüènciadirecta delafeinafetadurantl’estadaalcentre;quel’adquisiciódelsfonamentsteòricsescontrastinsimultàniamentamblapràcticaésunelementclauperalaformaciódelfuturprofessordesecundària.

4. Dificultats i reptes de futur

Totiquefeiamoltsanysquese’nparlava,elMàsteresvaengegardemaneraprecipitadaisensehaverdefinittotselsparàmetresnecessarisperalseufuncionament.Algunss’hanpogutcorregiralllarg delprimerany,peròencaraarrosseguemalgunesimprovisacions.Atalld’exemple:lamancad’acord entreelsdepartamentsdelaGeneralitatdeCatalunyaresponsablesd’Universitatsid’Educació,sumadaal’errord’identificarlespràctiquesdelaFormaciódeMestresambelpràcticumdelMàster,va tenircomaconseqüèncialadecisiódenoretribuirlafeinadelprofessoratdesecundàriaqueparticipaenlaformaciódelfuturprofessorat.Sihiafegimelfetquealtrescomunitatsautònomessíquela retribueixen,elresultatvaserquemoltsprofessorsvandecidirnoparticipar-hi,ambelconsegüent empobrimentdel’oferta.Desdelauniversitatencaranohemperdutl’esperançaqueescorregeixi aquestaanomaliadifícilmentjustificable.

L’especialitatdematemàtiquesté,amés,comjas’haindicatmésamunt,unproblemaestructuralafegit:laimmensamajoriadelsaspirantsaprofessorsdematemàtiquesdesecundàriaprocedeixende titulacionsenquèlesmatemàtiquessónestrictamentinstrumentals.Enginyers,arquitectes,informàticsillicenciatsenadministracióidirecciód’empresessónmajoriaalesnostresaules,laqualcosaté

comacorol·larilanecessitatd’impartirtambéconeixementsdematemàtiquessimultàniamentamb lasevadidàctica.Simiremlesincorporacionsdeprofessoratdematemàtiquesalscentresdocents durantaquestsdarrersanys,podeminferirqueestractad’unatendènciacreixentaquèhauremde ferfront.

Decaraalfuturimmediat,se’nsplantegentresreptes.Elprimeréslacoordinacióentreelsmàsters deformaciódelprofessoratdematemàtiquesdeCatalunya.Percaminarenaquestadirecció,aquest curshihauràunasetmanaenquèl’alumnatdetoteslesuniversitatsassistiràcadadiaaunadediferent,ons’impartiranconferènciesiesrealitzarantallerssobretemesespecífics.Esperemqueaquesta intercomunicacióentrel’alumnatsuposaràunenriquimentperalasevaformació.

ElprofessoratdelMàsterés,demaneraàmpliamentmajoritària,professoratdesecundària.Aixògaranteixlaformaciódelsnostresalumnesenl’oficideprofessorque,senseoblidarlateoriadidàctica, éselnostreobjectiucentral.Tanmateixtenimelreptedemillorarlaimplicaciódelprofessoratmentor,quejacol·laboraenelpràcticum,enl’elaboracióperpartdel’alumnatdeltreballfinaldemàster. Aquesttreballnohadeserunatesina,sinóeldesenvolupamentd’aspectesdidàcticsconcretsque posindemanifestallòques’haaprèsalllargdelcurs.

Eltercerrepteésmésdifícild’assolir,peròd’aixòdependràenbonapartlapossiblemilloraquehade suposarelmàsterenlaformaciódelprofessorat.Enelfuturimmediatelprofessoratdematemàtiques desecundàriaestaràformatperpersonesquehauranrebut,majoritàriament,unaformaciómatemàticauniversitàriaaltamentdeficient.Amésd’ensenyar-losl’oficideprofessor,elnostrerepteconsistirà atransmetre’lsl’amorperlesmatemàtiquesilasevabellesa.Noméssuperantaquestreptepodrem afirmarqueformempersonesquecompleixeneldobleobjectiudeserprofessorsdesecundàriaide transmetreunesmatemàtiquesútilsiinteressantsalsseusalumnes.

Reflexionsobertes d’unneòfitenDidàctica delaMatemàtica

JosepPlaiCarrera

DepartamentdeProbabilitat,LògicaiEstadística FacultatdeMatemàtiques,UniversitatdeBarcelona

Resum Abstract

Laideaprincipald’aquesteslíniesésreflexionar sobrelaimportànciadela històriadela matemàtica enlaformaciódelsdocents d’ensenyamentpreuniversitariienl’adquisió d’unaculturatotalmentirrenunciableen aquestaformació.

Themainideaoftheselinesistoreflectonthe importanceofthe historyofmathematics in teachertrainingofpre-universityeducationand alsointheculture’sacquisitionculturecompletely essentialinthistraining.

Enaquestcomplicatedificiconstruïtpelsmestresdelaciènciamatemàtica,non’hihaprouamb afirmarlasolidesadecadapartdel’edificiiadmirarlafeinadelconstructor;hemdecomprendre’n tambéelplaarquitectònic.

Arabé,percomprendreelplas’handeveuredecoptoteslesparts,inoméslaintuïcióens proporcionaelsmitjanspercopsar,decop,latotalitat.

HENRI POINCARÉ1

Enaquestanovaetapadelarevista NouBiaix —abans Biaix —m’hasemblatoportúferunareflexiópersonaldel valordocentdelahistòriadelamatemàtica que,almeuentendre,ésindiscutiblei indefugible.Ihovullferdefensantalhoraelgran valorcultural d’aquestconeixemententèscoma formació.

Entencper«valorcultural»el pòsit quequedaquand’algunamaneraelfocmésvius’haapavaigat.RecordemlesparaulesdeJohannHeinrichPestalozzi: 01.VegeuPoincaré(1900,p.125).

Laculturatéelpoderd’unirelshomescomaindividus,independentsilliures,atravésdelalleii del’art.Lescivilitzacions,desproveïdesdecultura,elsuneixen,amblacoerció,enunamassasense capconsideracióperlaindependència,lallibertat,lalleiil’art.2

Aquestvalorcultural—complementaridelvalorprofessional—ésundelsgransoblidatsacasanostraienlanostrallengua—elcatalà—quanestractadelaciènciaidelatecnologia.Amés,enla matemàtica,adiferènciadelesciènciespositives,elsresultatsestablertsenelpassatgairebémaino esdevenenobsolets.Benalcontrari,sónunterrenyadobatperaladocènciaiperal’aprenentatge perquèaportenidees,problemes,conjectures,demostracions,suggeriments,possibilitatsdegeneralitzacions,etc.,denouencuny.Lamatemàticaés,d’algunamanera,unadisciplinahistòrica—una disciplinaambhistòria—vivaenelsentitquemainoesdevécaduca.Aquestavivesa,juntamentamb elprocéshistòric,proporcionamolteseinesd’unenormevalordidàctici—comveurem—sónuna fontindiscutibleperenriquir-nos.

Peròaquestsfetss’hanoblidat,massasovint,tantenelbagatgeculturalcatalàcomenelscurrículums iprogramesdocentsdetotselgrausicategories.Sortosament,moltsdocents—i,enparticular,els que«saben»matemàticaperquèl’hanapresaambseriositat—hanaconseguitpal·liarl’efectede lespolítiquesformativesieducativesdelamatemàticatanerràtiquesierrònies.3

1. Dels docents matemàtics

Enaquestcontext,doncs,vullposarenrelleu,ambconsideracionsadients,la necessitat queels docentsdematemàtica detotselsnivells—peròd’unamaneramoltparticularenelsnivellsd’ESOi Batxilleratqueprecedeixenelsestudisuniversitaris— tenen ohauriendetenirdel coneixementdela històriadelamatemàtica id’algunsdelseustextosmésparadigmàtics.

Elfetcentralinuclearperserunbondocentd’unamatèria—siguilaquesigui—és estarbenformat enallòques’had’ensenyar,ésadir,conèixer-neunapartimportantideformasòlida.Éscompletamentimpossible—permésesforçosaddicionalsdeformacióenlalíniametodològicaipedagògica quedesprésesfacin—ensenyarallòquehomnosapiquenoestima,perquèhoensenyarà sense passió,queéseltretmésimportantdelsingredientsquefanqueundocentesdevinguiunmestre, enelsentitmésnobledelterme.4 Elsesforçosqueesfacinpersuplirlamancançadeconeixements resultarantansolspal·liatius—i,enmoltscasos,inútilsopocfructuososi,enconseqüència,molt cars.5 Sónesforçosperapuntalarquelcomques’haconstruïtenunterrenybenpantanósigenssegur.Sinos’acceptaaquestapremissa—comjahedit,totalmentpersonal—,l’anàlisiquefaigen

02.CitatperJung(1945,volum16,paràgraf227,n.10).

03.Ésrealmentincomprensibledesd’unpuntdevistaacadèmic—novamentlesqüestionspolítiquess’imposenper damuntdelesqüestionsacadèmiques—queelsquecursenelsmàstersespecífics—delesàreesdebiologia,filosofia,física, geologia,història,històriadel’art,llengua,matemàtica,química,etc.—notinguincappossibilitatd’accediraladocènciapúblicadel’ESO idelBatxillerat.Elscalferelmateix«màsterformatiu»quequalsevolaltregraduatelgraudebasedelqualnosigui l’específicdelamatèriaquehad’ensenyar.Ihihaquidespréssesorprènd’uncert«fracàsescolar».Elsdosingredientsbàsics deldocentsónelconeixementdelamatèriaqueexplica—essencialperserdocent—ilapassióqueaquestconeixement lidesperta—essencialperserprofessoro magister —.Parlodelapassióque,dejove,l’hadutprecisamentatriaraquellgrau específicafid’aconseguir-neelsconeixementsnecessaris.

04.Consulteu-nel’accepció2.1del Diccionaridelallenguacatalana (ediciódel2007,pàg.1102):«Personaque,d’una ciència,d’unart,etc.,ensapperaensenyar-ne,peraésserprescomamodel».

05.Elpolíticshauriendetenirsempremoltclaralaqüestiórelativaaladualitatcost/benefici.I,enparticular,encara quesembliparadoxal,enlesèpoquesdebonança,perquèlesdecisionsespodenprendreambmoltaméstranquil litatsense elsxantatgesprovinentsdelasituaciódeprecarietatquees dónaenelsmomentsdecrisieconòmica.Curiosamentaquesta ésunalliçóqueelsnostrespolítics,enparticular,ilasocietat,engeneral,nohaaprèsimoltemsemblaquenovolaprendre.

aquestarticlepotserdiscutiblei,finsitot,arbitrària.Aixònoobstantpotservir,almenys,perrepensarlavalidesa,ono,delapremissa.Faré,doncs,unaanàlisidelaimportànciaidelaconveniència deconèixer—juntamentambelscontingutsméstècnics—lahistòriadelamatemàticai,pertant, implícitamentdefensarélanecessitatd’incloure-laenelscurrículumsformatiusdelsnostresdocents dematemàtica.

2.Anàlisi d’aspectes metodològics i conceptuals lligats a la història de la matemàtica: una reflexió general

Caltenirpresent,iésunaraósobrelaqualcalreflexionariaprofundir,queenlacivilitzacióoccidental,l’antiguitatdelesreflexionssobrelamatemàtica—queesremuntaal’èpocadel’Acadèmiade Plató—ielfetquematemàticsd’unagranvàlua—JulesHenriPoincaré,DavidHilbert,JacquesSalomonHadamard,GeorgePólya,PaulErdös,PaulRichardHalmos,etc.— 6 hagindedicatunapartno gensmenyspreabledelseutempsalapresentació,l’anàlisiil’aprofundimentepistemològiciheurístic d’aquestadisciplina.

L’existènciad’excel·lentstextosd’històriadelamatemàticaielsesforçosrealitzatsperlessocietatsiles institucionsdedocentsquehiestanrelacionadesd’arreuenladifusiódelahistòriadelamatemàtica comunafontderiquesaformativaiconceptualésunaltreaspectequenopodemobviar.

Ifinalment,l’interèsperdisposarderecullsdetextosoriginals«rellevants»d’històriadelamatemàtica perpoder-losllegir,comprendre,interpretarisituarenelcontextillenguatgedelmomentenquè forenproduïtsn’ésencaraunatercera.

Sóntresraons,doncs,quesuggereixeniexigeixenunaanàlisimésdetalladaipregonadelaqüestió.

Lanecessitatdel’anàlisil’efectuarem,doncs,totdesenvolupantmitjadotzenad’ítemsquecalexemplificarambcasosconcrets—elsexemplesconcrets,qüestionsdelogísticanumèrica,vinculades al’escripturaialsalgoritmesdecàlculd’altrescivilitzacions;degeometria,vinculadesal’Elements; d’àlgebra,amblamatemàticamesopotàmica,xinesa,àrabirenaixentista;detrigonometria,lligadaa qüestionsd’astronomiagregaiíndia;decàlcul,vinculadesaproblemessenzillsdefísicadelssegles XVI i XVII;degeometriacartesina,vinculadesal’obradeRenéDescartesiPierredeFermat,etc.,s’hand’adequaralsinteressosicontingutsdelmomentdelprocésformatiuenelqualespresenten.Elfet d’esmentaraquestsítems—quepodenserunsaltres—télaintenciód’explicitardeformamésclara ientenedoralesideesqueproposoidefenso.Moltesdelesqüestionshanestatexposadesidefensadesambmoltahabilitatperestudiososdelahistòriadelamatemàticaquen’hananalitzatamb rigorelslligamsambl’ensenyamentiamblacomprensióglobaldelamatemàtica,comaraAvital (1995),Calinger(1996),Katz(2000),Grattan-Guinness(2004)iGrattan-Guinness(2009),peresmentarautorsbenactuals.Elprofessornohohauriad’oblidarmai—quelcomquesucceixambmassa freqüència—ileshauriadetenirsemprebenpresentspertaldepoderprendre,quanhocregués convenient,ladecisiód’aproximar-hil’alumne.7

06.I,malgratdelquen’opinava,Hardy.VegeuHardy(1940,ediciócatalana,pàg.13-72).

07.Unariquesamoltimportantd’aquestaaproximacióésquenocalqueestiguinitotalmentreguladanireglada.L’eleccióquedaal’arbitridelmestre.Defet,adequarelprogramaalescapacitatsiespecificitatsconcretesdelsalumnesiales situacionsrealesdel’aula,enl’úsdela«llibertatdocent»—quelcomqueactualmenttambétendimalimitarexcessivament—, ésprecisament una —sinolamésimportant— delesfuncions del’autènticmestratge.

2.1. La història com a referent del grau de dificultat intel·lectual

Nohihadubtequeelprocésd’evoluciódelamatemàtica—engloboenaquestnom,comesfa avui,toteslesbranques—haestatforçainteressanti,malgratlaunitatderesultats,avoltes,en culturesdiverses,espresentatambédeformadiversaenlametodologia.

L’evolucióconceptualésunaevolucióquevadelsconceptesmés elementals —enelsentitdemés intuïtius—capaconceptesmésabstractesievolucionatsintel·lectualment.Unbonconeixement delahistòriadelamatemàticapermet,doncs,aldocent—quanésunbonprofessor—8 feruna presentaciódecertesqüestionsd’unamanerametodològica—i,pertant,mésentenedora—força mésapropadaalnivelldel’alumnequeeldocenttéaldavant.9 Pensemqueunmateixresultatespot —i s’hade—reveureenestadisformatiusforçaallunyatseneltemps.Defet,enl’actedocentdels nostresdiesaquestespresentacionsesfanenelsid’uncontextquenosempreéselmésnaturaldes delpuntdevistaintuïtiu,nid’aquellonvanaparèixerinicialmentdeformanatural.

2.2. La presentació dels conceptes matemàtics a partir d’un problema concret

S’haparlatmoltíssim,enelscerclesespecialitzatsen didàcticadelamatemàtica,delmètodedel«solvingproblems»deGeorgePólya.Tanmateix,però,nom’esticpasreferintaaquestaspectedepresentaciódelfetmatemàtic—defet,prouconegutidivulgat[vegeulasecció§2.4]—encaraque naturalmentambduessituacionsestanmolttravades.Emrefereixoalanecessitatderecórrer,detant entantperòtansovintcomcalgui,aalgunproblemaconcretidoniqueajudiasuggerirelsconceptes,lesmetodologies,lestècniques,elsalgorismesiàdhuclesteoriesmatemàtiquesquetenimentre mansiquevolemtransmetre.

Aixòformapartdeltreballpersonaldepreparaciódel’acteformatiuqueéslaclasseentesa,nocom unaunitatdiària,sinòcomun projecte d’ensenyamentid’aprenentatgeglobalestèseneltemps formatiu.10

M’atreviriaadirqueundocentesdevéun«mestre»—enelsentitmésdignedelterme,explicitatala nota4—quanaconsegueixquelapresentaciód’allòqueensenyaestiguibenfalcadaen problemes concrets,interessantsientenedors,suggeridorsicapaçosd’obrirlaportaalsresultatsgenerals.

2.3. Globalment l’aprenentatge de la matemàtica és un conte

Independentmentdeltrosquetoquiacadadocent,acadafranjad’edat,acadaetapadelprocés educatiu,alfinaldelprocésformatiul’alumnehauriadesercapaçdereferpartsimportantsdela matemàticacomunconteenelqualhihaunodiversospersonatgesprotagonistesquetenenunes aventuresque,perauns,seranapssionantsi,perad’altres,notindrancapmenad’interès—com

08.Usoelterme«professor»comasinònimde«mestre».

09.D’aquílanecessitatdedeixaralessevesmans—comdeiaabans—latriaconcretadelsexemplesquecalemprar encadasituacióconcretadelprocésdocent.

10.Vullemfasitzarelfetqueelprocésdocentnocomençaavuiiacabaavui—imoltmenysencaraalamevaaulai amblamevalliçóconcretaoambelmeucurs—sinóqueésquelcomques’esdevéeneltempsi,enelcasdelamatemàtica,es produeixpermitjàd’undesenvolupamentenespiral.HohedefensatabastamentaPlaiCarrera(2006).

passatambéamblesnovel·les,lespel·lícules,elscòmics,etc.Aixòtanmateixnofapasqueelconte noexisteixiitinguielseuargument.11

Arabé,perpoderexplicar-neuncapítolounadelesaventures,caltenirunconeixementdelconte enlasevatotalitat.12 Aquí—abandad’unaformaciósòlidaenmatemàtica,quelcomque,comjahe ditabans,donoperdescomptatentotdocentdelamatemàticatantsijaestàformatiestrobaen actiucomsiencaraestàenprocésdeformació—hiajudamoltíssimunabonaformacióenlahistòria delamatemàtica,entensacoml’evolucióconceptualensimateixa.13

Valadirque,entesad’aquestamanera,esdevétambéoficidematemàtic—idematemàticglobal,encaraquelaglobalitatsiguinomésd’unapartdel’universmatemàtic.Senseunaformacióiconeixementsmatemàticsprofundsiarrelatsésimpossibleoferir-neunavisióhistòricacoherent,evolutiva igeneralitzadoraenelsentitquevadelparticularalqueésmésgenerali,siconvé,crítica.Caltenirles ideesmoltbenassentadesperpoderentendrecomvannéixerelsproblemesielsconceptesmatemàtics,quèelsvamotivar,perquèvanevolucionard’aquestamaneraenunmomentdelprocésde desenvolupament,id’aquestaaltra,enunaltre,etc.

2.4. Els problemes, la plausibilitat i la conjectura

Alasecció§2.2,parlavadelaconveniènciad’usarproblemespertald’introduirunconcepte.Ara,en canvi,m’agradariaparlar—enlalíniadePólya—delanecessitatd’usarelsproblemesafid’aconseguirunconeixementrealipersonalitzatdelamatemàtica.Lamatemàtica,comlesarts,noenté prouamblateoria;precisadelapràctica,unapràcticapersonal,individual,íntima;cal«ferdits»,«esborranys»,«copiardelsmestres»,etc.Iaixòs’aconsegueixresolentproblemeso,enqualsevolcas, plantejant-seproblemesimirantderesoldre’ls.

Aquestapràctica—quehequalificatde necessària—téunaderivaimportantíssimaimetodològicamentvital.Permetdistingirl’anàlisi dela síntesi,entesesenelsentitclàssicgrecdeltermeireformuladesafinalsdelsegle XVI iconsolidadesal XVII.14 I,dinsl’anàlisi,laconstataciódelaplausibilitat.

M’atreviriaadirqueunaanàlisimatemàticanoésunaanàlisiautènticasideixadebandalaqüestió delaplausibilitat.15

11.VegeuPlaiCarrera(2009).

12.Recordo—recordfugisser—l’experiènciadelanovel·lapolicíacaindividual-col·lectiva, Thefloatingamiral (1931),delsautorsG.K.Chesterton,CanonVictorL.Whitechurch,G.D.H.,M.Cole,HenryWade,AgathaChristie,JohnRhode,MilwardKennedy,DorothyL.Sayers,RonaldA.Knox,FreemanWillsCrofts,EdgarJepson,ClemenceDaneiAnthonyBerkeley.Esdonavenperendavantdoscapítolsincialsd’unatramapolicíaca.Llavorsuntercerautorescriviauntercercapítoliseguia lanovel lafinsalfinal.Elstresprimerscapítolspassavenaunquartautorqueprocediadeformaanàloga.Elquefacuriosal’experiènciaésquecadaautor,apartirdelquerepcomaprevi,confegeixunanovel ladiferent.Aixònotindriasentit—opotser sí?—enelfeteducatiudelaformaciómatemàtica.

13.Enaquestsentitvallapenaconsultar,perexemple,Schubring2005.PeròelstextosqueresultenrealmentparadigmàticssónelsdeMarcusdeSautoy(Sautoy,2004,2008).

14.Unqüestióqueensremetalageometriagrega,enparticular,aPappos,ialhoraal’àlgebradeVièteiDescartes.

15.Unamaneradecomençaracomprendreunresultatmatemàticésconvèncer-sequeésplausiblequesiguiprecisamentaquellinounaltre.Ésplausibleque«lestresalçadesd’untriangle arbitrari estallensempreenunpunt»;que«elsnombres 22k + 1siguinprimersquan k prenelsvalors0,1,2,3, ... »;que«lesarrels x1 ,x2 del’equaciódesegongrau X 2 bX + c = 0, satisfacin x1 + x2 = b, x1 x2 = c»?,etc.Novamentnecessitemunautènticmestreid’unconeixementmoltacuratdels conceptesidelsproblemes.

Peròelplantejamentil’anàlisidelaplausibilitatpermetenencaraunaltraqüestió—tannaturalen lahistòriadelamatemàticaitanoblidadaenladocència:la conjectura.Pensarunpossibleresultat—propioaliè—iconjecturar-nelaposssiblevalidesa.Comensomdemalsmestresenaquest aspecte!Qui,denosaltres,plantejalanecessitatdeferconjecturesiderespondre-les?

Lahistòriadelamatemàticaésunafontinesgotabled’aquestestreseinesitècniques.Totdocent s’hihauriad’haverapropatdurantelprocésd’aprenentatgefinsaarribaraconsiderar-lesquelcom naturalenlessevespresentacionsal’aula.16

2.5. Conèixer les crisis epistemològiques

Arabé,avoltes,hihahagut trencamentsdelaplausibilitat :elsexemplessónincomptables(geometries noeuclidianes,existènciadel’infinitactual,existènciamatemàticacontracalculabilitat,trencament aparentdelconceptededimensió,aproximacióalconceptedefunció,determinismeicaos,etc.).17

Entendrelanaturalesaiprofunditatd’aquestamenadetrencamentsésl’objectiudelques’anomena,deformagenèrica,la fonamentaciódelamatemàtica,queésunalecturafilosòfica—defet,ontològica,epistemològicaiheurística,fonamentalment—delapròpiahistòriadelamatemàtica. EnconstitueixunexempleparadigmàticelcontrovertittextdeKline(1980)i,méstècnic,l’esmentatde Schubring(2005).

16.Avuidiaenquèelvalorintel lectualintrínsecdelprocésformatiudelamatemàticasesubstitueixcadacopmés pelsvalorslúdicid’aplicabilitat,ésboderecordarqueelprocéshistòricdecreaciódelamatemàticaproporcionatotestres vessants:laintel lectual,lalúdicailamodelitzadoraihofalligant-lesentresiambtotanaturalitat.VegeuPlaiCarrera(2007).No n’hauríemd’oblidarcap!

17.Caltenirpresentquelataxonomiaoclassificacióentotamenad’exposicióargumentativaésquelcomqueve obligatperunintentdeprecisióiclaredat.Però,enlamajoriadelscasos—i,enparticular,pelquefareferènciaalesqüestions metodològiquesdelamatemàtica—ésunartificiexpositiu.Totestàbarrejatperquèsóncaresd’unmateixdiamant,oreflexos d’unamateixacarai,defet,sónindestriables.S’escau,potser,recordarel contebudista —unaadaptaciólliured’unconteque vaigllegirunavegadaenund’aquestsllibressobreelconeixementdelamentalitatbudistaidelqualnoenrecordolesdades bibliogràfiques:

Undeixeblelipreguntaalmestre:

—Mestre,quèésuncigró?

Elmestre,decidit,lirespon:

—Uncigróésunagramínia...

Peròelvaileteltallaincisivamental’inicimateixdelarespostailidiu:

—Mestre!,novullsaberlaclassificacióocaracteritzacióbotànicaquen’hanfetelsnaturalistes.Simplementvullsaberquè ésuncigró.

—Bé—diuelmestre—,uncigróésuncompostorgànic...

Peròelnoi,tossut,sensedeixar-loacabar,lidiudebellnou:

—Novullpassaber-nelacomposicióquímica.Vullsaberquèésuncigró.

Elmestre,cansatderespondred’acordambelsseusmúltiplesconeixementsparcialssenseaconseguir,però,desatisferla curiositatfebriliprofundadeldeixeble,agafauncigrói,totmostrant-li-ho,lidiu: —Aixòésuncigró.

Aleshoreselmarrecdiuambestranyesa:

—Si,defet,nosapsquèésuncigró,comsapsqueaquestobjectequem’estàsensenyantésuncigró?

Elmestre,enunintentdesesperatpersalvaguardarlasevaautoritat,lidiu:

—Séquehihaacordentreelsignevocàlic‘cigró’il’objectequet’esticmostrantaramateix. Elvailetnose’nsapaveniripreguntadebellnou:

—Bé,mestre,peròelquejoetdemanoésprecisament:«Quèésaquestobjectealqualapliquemelsignevocàlicde ‘cigró’?»

Iaixí,desprésd’intentarderespondreunapreguntagenèricaambtantesrespostes concretes,resultaquemestreideixeblees trobenaltrecopalcomençamentdelaqüestiósensehaveravançatgaireenelconeixementintrínsec.

2.6. Els algorismes i la introducció a la informàtica

Lahistòriadelamatemàticaéstambélahistòriadeldesenvolupamentd’algorismesdecàlculde totamenai,enparticular,d’algorismesrecurrents.Moltsd’aquestsalgorismeselsaprenemdeben menuts,quelcomque,almeuentendre,caldriamantenirencaraqueavuiesdisposideginysde càlculimmediat.18

Elconeixementhistòricd’aquestsalgorismesensproporcionenmodelsperpoderrealitzar programes —i,deretruc, models—iaixícomençaraaprendrel’úsdelescalculadorestotfabricantestratègiesi programesqueelsexecutin.

Aquestéstambéuncampdetrobada—peròmoltmésrecent—entrel’ensenyamentdelamatemàticail’aprenentatgedelsalgorismes:lasevaclassificacióievolució,quelcomquenohapassat desapercebutcompalesen,perexemple,eltextcoraldeChabert(1994)iKao(2008).

2.7.

Ningúnodiscuteixqueésformatiullegirfragmentsdeliteraturadelsautorsinorecórrersempre aaquellsqueelsexpliquenoelscritiquen—sensequeaixòsignifiquiquenopuguinajudarauna millorcomprensió.19 Peròprèviamentcalhaverestatprotagonistaenl’acted’apropamentaltext.

Tambéapropemelsestudiantsal’artatravésdelesobresconcretes,quelcomquecaldriaestendre ambmoltamésconvicció,decisióifermesaalamúsica,parentapobradelprocésculturalbàsic.

Arabé,quanestractadeciènciai,enparticular,dematemàtica,semblatalmentqueaquestaactivitat perdtotelseubagatgeformatiu.Estendeixacreurequelalecturad’untextclàssicpotarribara dificultarlacomprensiód’allòquecalaprendre,comsil’autorclàssicnofoscapaçdetransmetre l’acteiniciàticdecreacióod’exposarl’evolucióconceptual.20

Ésunadiscussiód’ungranabastques’escapadel’àmbitd’aquestesnotesdereflexiómetodològica.Arabé,elquenos’escapa,enabsolut,aaquestareflexiócol lectivaésqueelsdocentsenciència,en general,ienmatemàtica,enparticular,hauriend’haver-seapropatalstextosmésrellevantsdelsprohomsdelasevadisciplina.Aixòformapartconsubstancialdelaformacióques’hadetransmetreenun cursd’històriadelamatemàticabenconfegit.Apropar-sealsmestres—alsclàssics—i,després,amb l’ajudailacol·laboraciódelprofessord’històriaidelsprofessorsdelesdisciplinesespecífiques,analitzartextosconcrets,adequatsacadamomentformatiu,perquèaquestactecultural—quanesdevé unacteformatiu—ajudaacomprendre’nelcontext,elllenguatge,lamotivació,lanovetat,lesdificultats,l’evolucióconceptual,l’evolució...enresum,elprocéscreatiu.

18.Caldriaunarevisióacuradadeldiàlegques’hauriad’establir—imantenir—entre«algorismemanual»i«úsdeles einesdecàlculinformàtiques».

19.Semprerecordaréambmoltd’afecteelcurssobreliteraturacatalanadeMariaAurèliaCapmanyalqualvaigtenir l’encertd’assitir,alaUniversitatCatalanad’EstiudePrada, alConflent,onjomateixfeiadeprofessor,unagostd’arafaja quarantaanys.

20.Enmoltesocasionsherepetitqueunadiferènciaentreelqueanomenem«leshumanitats»i«lesciències»ésla maneracom,lesunesilesaltres,tractenelsclàssicsrespectius.Ésclarque,avui,enlaciènciapositiva,l’avençésmoltràpid —gairebévertiginós—il’únicamanerademantenir-sealdiaéslalecturaicomprensiódelsresultatsmésrecents.Peròaixò nohad’impedirconèixerelsclàssics,autènticafontdecultura.

La lectura dels textos clàssics

2.8. La matemàtica és un llenguatge

Amés,comjadeiaabansdepassada,apropar-nosalsclàssicsenspermetapropar-nosalllengutage matemàtic.Potservallapenarecordar,uncopmés,eltextparadigmàticdeGalileoGalilei:

Lafilosofiaestàescritaenaquestllibretangranquetenimobertdavantdelsulls,l’univers.No éspossibled’entendre’lsiabansnos’aprènaentendreelllenguatge,aconèixer-neelscaràcters ambquès’haescrit.Estàescritenllenguatgematemàticielsseuscaràcterssóntriangles,cerclesi d’altresfiguresgeomètriques.Senseellsésdeltotimpossibleentendre’nunasolaparaula.Sense ellsenstrobaríemvoltantvanamentenunlaberintfosc.21

IelprofessorMichaelAtiyah,eneldiscursquepronunciàeldia25d’abrilde2008enl’acteenelqual fouinvestitdoctorhonoriscausadela FME dela UPC,digué:

Quèsónlesmatemàtiques?

[...]Lamevarespostaésquelesmatemàtiquessónunllenguatge,unmitjàespecíficdecomunicacióqueespotcompararprofitosamentambelsllenguatgesnaturals,comaral’anglèsoel català.Són constructesculturals quehanevolucionatdurantmilersd’anysiqueforneixenelmarc delacivilització.

[...]Amésdecompararl’evolucióhistòricadelesmatemàtiquesidelllenguatgenatural,tambépodemcomparar-nelesfuncions,descrivint-neelsdiversosusos.

[...]Així,elllenguatgetéunúspràcticperalsafersdiaris,unúsliteraripertransmetreidees mésabstractesiunúspoèticperexpressarlesemocions.Hihaunadivisiósimilarenlamatemàticaentreutilitat,quemenaalamatemàticaaplicada,ilamatemàticapura,mésenfocadaaidees abstractes.22

Aquestapartessencialdelamatemàtica—undelsllenguatgeselaboratspelpensamenthumà— tambéhadeformarpartessencialdel’autènticaprenentatge—enl’específicienelcultural—i,per tant,del’ensenyament.23

Iencarahihaunaaltraqüestiómoltinteressant—comhiésentoteslesexpressionshumanes:pintura,escultura,música,literatura,etc.—,iésquecadacultura—i,dinsdecadascuna,cadaautor—téun estilpropipersonal,comvaposardemanifestenunllibreexcel·lent—lalecturadelqualrecomano— jafaunsquantsanyselmatemàticifilòsofcastellàJavierdeLorenzo.24

3. De l’interès suscitat per la història de la matemàtica

Aratractarédereflexionarmésacuradamentsobreelsítemsqueheassenyalatamblaconfiançaque siguind’utilitatperaunabonacomprensiódelesideesmatemàtiquesilasevaevolució.Espero quesintetitzindeformaclaraipositiva—aquestésl’esperitambelqualheescritaquesttext—els conceptesepistemològicsquehauríemdetrobarenelscurrículumsdel’ensenyamentdelamatemàticaienelsdeformaciódelsdocentsdematemàtica.Endefinitiva,estractadeformarprofessors

21.VegeuGalilei(1623,ediciócastellana,p.61).

22.Vegeuhttp://www.upc.edu/saladepremsa/al-dia/mes-noticies/el-matematic-michael-atiyahinvestit-doctor/441. Enrecomanolalectura.L’èmfasiésmeu.

23.Heintentatrecollirelllenguatgematemàtic,lasevaevolució,aPlaiCarrera(2006).

24.VegeuLorenzo(1971).

modernsdematemàtica.Itotaixòambl’esperançadecoincidiramblesideesexpressadesambmolt d’encertperunnombreimportantdepensadorsquem’hanpreceditenaquestamenadereflexions.

3.1. A la recerca d’esperits crítics

Endefinitiva,eltext—ambtoteslesreflexionsqueconté—volserútiliadequatperalcurrículum formatiudelsdocentsdelamatemàtica:ricenidees,conceptes,teories,mètodes,etc.,desd’una perspectivaglobal—quevagidelpassatalpresent,delaintuïcióalaformalitzacióigeneralització mésrigoroses,delsalgorismesalacomputació,etc.—,peròmantenintsempreuncertpuntd’esperit crítico,siesprefereix,noexcessivamentdogmàtic.

Esticconvençutque,enunatascacomladocentenlaquals’imposaal’alumneallòquelicalaprendreipertantallòquelihemd’ensenyarique,enconseqüència,espresentaalsullsdelquiaprèn comquelcominamovible,ésindispensablequeelquiensenyaconeguilescrisisqueelconcepte hasofert,lesdificultatsquehatingutperimposar-se,lesraonsperlesqualshaassolitl’èxit,etc.Siel professorlesconeix,lasevaactituddocentseràméslúcida,méscríticai,deretruc,mésformativai educativaenunsentitamplidelaparaula.

Ésadir,ensíntesi,calqueeldocenttinguiunesperitobert,comelqueproporcionaelconeixement històricdelsprocessosdecreació,d’assentament,deconsolidació,decrisiid’evolució.

3.2. De l’interès històric per la història de la matemàtica

PotsorprendrequeEudemdeRodes,deixebled’Aristòtil,elaboréstextosd’històriadelamatemàtica delesèpoquesquel’havienprecedit.Sipensemquelamatemàticagreganeixalsegle VI aCamb lesfiguresparadigmàtiquesdeTalesdeMiletiPitàgoresdeSamos,ésmoltsuggeridorqueunsdoscentsanysméstarddelnaixementdelqueavuis’anomenala matemàticagrega,undeixebledel Liceu aristotèlicdediquielsseusesforçosaescriureuna històriadel’aritmètica,una històriadelageometria i una històriadel’astronomia,itotesen,almenys,dosllibres.Perdesgràciaaqueststextosd’històriade lamatemàticadelperíodegrecs’hanperdutenlapolsil’oblitdeltempspassat.

Lapreocupacióperlesqüestionshistòriquesdelamatemàticaés,doncs,quelcomquetrobemjaala Grèciaclàssica.Forçaseglesméstard,Papposd’Alexandriaelaborala Sinagogé (Σιναγογέ μαθηματιχή) o Col lecciómatemàtica (∼340)(Μαθηματικ ˆ ωνσυναγωγ ˆ ων),untextlainformaciódel qualnosolamentapropaellectoral’evolucióconceptualdelamatemàticagrega,sinóqueproporcionaunaenormeinformaciósobrellibresperduts,delsqualsenfaunaressenyasuccinta.

TambéProcleenel ComentarialllibreprimerdelsElementsd’Euclides (ΕιζτοπρωοντωνΕύχλείδου Στοιχείωνβιβλίον),abandadeferunaanàlisimoltdetalladadelselementscentralsdelateoria euclidiana,proporcionaunagranquantitatdedetallsd’índolehistòrica.

Aquestdarrertextfouindispensable,apartirdelsegle XVI,quanl’ordedelsjesuïtesi,enparticular,ChristophoreClavius,vaintentarrepensarla geometriaeuclidiana alsideladiscussiófilosòfica entrearistotèlicsiplatònicsambrelacióacomcaliaentendre—interpretar—laciènciaalallumde la SagradesEscriptures idelsensenyamentsdel’EsglésiadeRoma.D’algunamaneraaquestareflexió portaria,ambelpasdeltempsigràciesalesdificultatsquel’anàlisicomportavaialesideesque suggeria,lanecessitatdel’existènciad’altresgeometriesi,enparticular,dela geometriahiperbòlica.

ElllibredePapposesdevingué,tambéalsegle XVI,untextd’ungranvalor metodològic i docent.Permetéamatemàticsnotablesdelssegles XVI i XVII,comaraMarinoGhetaldi,FrançoisVièteiPierrede Fermat,aprendrematemàticatotmirantdereferelsllibresperduts,esmentatsperPappos.

3.3. Prohoms de la matemàtica interessats per la història de la matemàtica

Ésremarcablel’interèsquelahistòriadelamatemàticahadesvetllatenmatemàticsmoltrellevants. Algunsnomssón:

1.MichelChasles. Aperçuhistoriquesurl’origineetledéveloppementdesméthodesengéométrie (1837), unautènticclàssicenlaqüestió.

2.GuglielmoLibri,que,entre1838i1841,publicàquatrevolumsd’HistoiredessciencesmathématiquesenItalie,depuislarénaissanacedeslettresjusqu’àlafindudix-septièmesiècle

3.EricTempleBell. MenofMathematics (1937), TheDevelopmentofMathematics (1940).Sóndues obresentredivulgativesiformativesi,enqualsevolcas,forçaamenes.

4.BartelLeendertvanderWaerden. GeometryandAlgebrainAncientCivilizations (1983)i AHistoryof Algebra (1985).Lapreocupacióperlahistòriadelamatemàticanofoupasunaaficiódelesdarreries delasevavida.Jal’any1947,haviaescrituntreballrealmentnotablesobrel’escolapitagòrica, Die ArithmetikderPythagoreer.

5.AndréWeil. NumberTheory:anapproachthroughhistory:fromHammurapitoLegendre (1984).Als setzeanysvallegirensànscrit,lallenguaoriginal,eltextmatemàticindi BhagavadGita

6.JulioReyPastor,que,ambJoséBabini,vaescriure HistoriadelaMatemática (1951).

7.Finsitot,NicolasBourbaki—quelcomquerealmentpotsorprendre—vaconsiderarquecalia elaborar,amblasevavisiópeculiardelamatemàtica,unahistòria: Élémentsd’histoiredesmathématiques.

3.4. Alguns textos d’història de la matemàtica

Peracabaraquestesreflexionsvoldriaindicarquelahistòriadelamatemàticahatingutsempretextos notables,d’entreelsqualspodríemesmentar:

1.JeanÉtienneMontucla. Histoiredesrecherchessurlaquadratureducercle,publicataParísperJombertl’any1754.

Histoiredesmathématiques,unapetitaobramestra.París,1754.ReeditatperBlanchard,París, 1968.

2.M.MaximilienMarie. Histoiredessciencesmathématiquesetphysiques.Gauthier-Villars.París,18831888.

3.MoritzCantor. VorlesungenüberGeschichtederMathematik.Teubner.Berlín,1913-1922,unaobra dereferència.

4.DirkJanStruik. AConciseHistoryofMathematics.DoverPublications,Inc.NovaYork,1948.Unasíntesibreuperòexcel·lent.

5.CarlBenjaminBoyer. AHistoryofMathematics.Wiley.NovaYork,1968.

6.MorrisKline. MathematicalthoughtfromancienttomodernTimes.OxfordUniversityPress.Nova York,1972.

7.HowardWhitleyEves. AnIntroductiontothehistoryofmathematics.SaundersCollegePublishing. Filadèlfia,1953.Reeditatel1964iel1983,iel1990ambconnexionsculturalsdeJamieH.Eves.

8.IvorGrattan-Guinness. TheFontanaHistoryoftheMathematicalSciences:theRainbowofMathematics.FontanaPress.Hammersmith,1997.

9.RogerCooke. TheHistoryofMathematics.ABriefCourse.JohnWiley&Sons,Inc.NovaYork,1997.

10.DavidM.Burton. TheHistoryofMathematics:anIntroduction.Primeraedició,1989.Cinquenaedició.McGraw-Hill.Boston(Massachusetts),2003.

11.VictorJ.Katz. AHistoryofMathematics:anIntroduction.Primeraedició,1993.Segonaedició,corregida.Addison-Wesley.Reading(Massachusetts),1998.

12.RonaldCalinger. AContextualHistoryofMathematics:anIntroduction.PrenticeHall.NovaJersey, 1999.

13.JeffSuzuki. AHistoryofMathematics.PrenticeHall.NovaJersey,2002.

Ometovoluntàriamenttotareferènciaahistòriesparticularsdelamatemàtica,jasiguinpertemeso percivilitzacions.Sóncopiosesin’hihadeveritablementexcel·lents.

Peròelquenovoldriaferésacabaraquestareflexiósenseposardemanifestencaraalgunsaltres fetsgenerals.Nohihagairebécapllenguadesenvolupadaquenodisposid’unaomésrevistesdedicadesalahistòriadelamatemàtica.Hihagranquantitatderevistesdedicadesal’artd’ensenyar matemàticailamajoriadediquenunapartimportantalesqüestionshistòriques.Penso,entred’altres,en MathematicsTeachers delNationalCouncilofTeachersofMathematics—unainstitucióque l’any1969publicàl’actualmentclàssic(Col lectiu,1969)—,25 en MathematicsMagazine ien TheCollegeMathematicsJournal delaMAA.Aquestainstituciódedicaungranesforçpertalqueelsllibresde lacol lecció NewMathematicalLibrary siguinformatiusiquelaformaciórepositantcompuguien l’anàlisihistòrica.Tampocpodemoblidarelsesforçosque,enaquestcamp,fanelsIREMfrancesosi eldegotalldetextos El·lipses,elstextosdel’APMEPielsllibresdeleseditorialsBeliniPole,ambles col·leccions Pourlascience i Tangente,respectivament.

Mésalavoranostra,hemd’esmentarla Gaceta delaRSEM,quecontéunasecciódedicadaprecisamentalahistòriadelamatemàticaiunaaltraaqüestionsmetodològiquesididàctiquesdelamatemàticaambarticlesexcel·lents,iel ButlletídelaSocietatCatalanadeMatemàtiques,encatalà,que técurademantenirobertesaquesteslíniesdelpensamentmatemàtic.D’altresrevistesdedicadesa qüestionsdemetodologiaididàcticadelamatemàticaquenopodemoblidarsón: L’Escaire,dissortadamentdesapareguda, Suma i Biaix,araenlanovaetapade NouBiaix,amblavoluntatd’aplegar esforçosiserútilamestresillicenciatsqueesdediquenaladocènciadelamatemàtica.

Tanmateix,elsintentsdeproporcionarcol leccionsdellibreshanestatmúltiplesperònosemprehan tingutl’èxitqueencaliaesperar.Pensem,perexemple,enl’intentdelacol lecció LatortugadeAquiles,quenoassolíladotzenadetítols,malgratlaqualitatdeltextostriats,nitampocelsdel’editorial Labor.Aixònoobstant,nopodemoblidaralgunesdelespàginesmagnífiquesiinoblidablesdeMigueldeGuzmán,d’entrelesqualsvoldriaposarenrelleulesdeGuzmán(1995),nitampocl’esforç del’EditorialNivola,quehaaconseguitmantenirvival’edicióde Lamatemáticaensuspersonajes que compta,horesd’ara,ambmésdetrentatítols,quelcomrealmentlloablemalgratlagranirregularitat enlaqualitatdelscontingutsdelstextos.

Calindicartambél’esforçrealitzatperespecialistesd’històriadelamatemàticaanglesaperdisposar de SourceBooks deMatemàtiques:Smith(1959),Midonick(1964),Struik(1969),Calinger(1995)iKatz (2007).Il’OpenUniversity ofereixunaassignaturad’històriadelamatemàticaquedisposadevídeosi d’untext(FauvelandGray,1987)enlalíniadels SourceBooks

25.Aquestatascaexcel lenthaestatrepresaperVictorJ.KatziKarenDeeMichalowicz,enqualitatd’editorsde HistoricalModulesfortheTeachingandLearningofMathematics

4. Conclusió succinta

Tincelconvencimentferm—haanatcreixentambelsanysil’experiència—quenos’aconsegueix unaautènticaformació—l’objectiudelprocésformatiu—sinos’aconsegueixqueelsalumnesassoleixinunautènticbagatgecultural.Ésperaquestaraóqueemsemblaadequatacabaraquesttext ambunafrasedeCarlGustavJakobJacobi,queestimomolt.

Unfilòsofcomell[comJosephFourier]hauriahagutdesaberquel’únicobjectiudelaciènciaés l’honordel’esperithumà,iqueaquestnomaixoplugatantunaqüestiósobreelsnombrescom unaqüestiósobreelsistemadelmón.26

IamblesreflexionssintètiquesdeJorgeWagensberg:

[148]Lavidaésunestatrardelamatèriainert. [149]Laintel ligènciaésunestatrardelamatèriaviva. [150]Laculturaésunestatrardelamatèriaintel·ligent. [151]Lacivilitzacióésunestatrardelamatèriaculta.27

Referències

Avital,M.(1995).HistoryofMathematicsCanHelpImproveInstructionandLearning.InF.Swetz(Ed.), LearnfromtheMasters!,p.3-12.Washington,D.C.:MAA.

Bell,E.T.(1937). MenofMathematics.NovaYork:Simon&Schuster.Traducciófrancesad’AmiGandillon, LesGrandsMathématiciens.París:Payot,1950.

—(1940). TheDevelopmentofMathematics.NovaYork:McGraw-HillCo.TraducciócastellanadeR. Ortiz, Historiadelasmatemáticas.Mèxic:FondodeCulturaEconómica,1949.

Bourbaki,N.(1960). Élémentsd’histoiredesmathématiques.Paris:Hermann.Traducciócastellanade JesúsHernández, Elementosdehistoriadelasmatemáticas.Madrid:AlianzaEditorial,1976.

Boyer,C.B.(1968). AHistoryofMathematics.NewYork:JohnWiley&Sons.RevisatperUtaC.Merzbach en1989.TraducciócastellanadelaprimeraediciódeMarioMartínezPérez, Historiadelamatemática Madrid:AlianzaEditorial,1986.

Burton,D.M.(1989). TheHistoryofMathematics.AnIntroduction.NovaYork:TheMcGraw-HillCompanies,Inc.Reeditatprofusament:el1991,1995,1997,2003i2007.

Calinger,R.(1995). ClassicsofMathematics.NovaJersey:PrenticeHall.RonaldCalingern’ésl’editor.

—(1996). VitaMathematica:HistoricalResearchandIntegrationwithTeaching.Washington,D.C.:MAA. RonaldCalingern’ésl’editor.

—(1999). AContextualHistoryofMathematics:AnIntroduction.NovaJersey:PrenticeHall. Cantor,M.(1880-1907). VorlesungenüberGeschichtederMathematik.Berlín:Teubner.

26.Vegeuhttp://turnbull.mcs.st-and.ac.uk/history/Quotations/Jacobi.htm 27.VegeuWagensberg(2002,p.52).

Chabert,J.L.(1994). Histoired’Algorithmes,duCaillouàlapuce.París:Belin.Elsautorssón:Chabert, JeanLuc;Barbin,Evelyne;Guillemot,Michel;Michel-Pajus,Anne;Borowczyk,Jacques;Djebar,Ahmed; iMartzloff,Claude.N’existeixunatraduccióanglesadeChrisWeeks, AHistoryofAlgorithms,Fromthe PebbletotheMicrochip.Berlín:Springer-Verlag,1999.

Chasles,M.(1837). Aperçuhistoriquesurl’origineetledéveloppementdesméthodesengéométrie.Brussel les:M.Hayez.

Col lectiu(1969). HistoricalTopicsfortheMathematicsClassroom.NovaYork:NationalCouncilof TeachersofMathematics.

Cooke,R.(1997). TheHistoryofMathematics.ABriefCourse.NovaYork:JohnWiley&Sons,Inc.

Drake,S.(1957). DiscoveriesandopinionsofGalileo.NovaYork:DoubledayAnchorBooks.Traducció anglesaambunaintroduccióinotesdeStillmanDrake.

Eves,H.(1953). AnIntroductiontotheHistoryofMathematics.Filadèlfia:SaundersCollegePublishing. Reeditatel1964iel1983.L’ediciódel1990contéconnexionsculturalsdegudesaJamieH.Eves.

Fauvel,J.andJ.Gray(1987). TheHistoryofMathematics.Areader.Londres:MacMillanandOpenUniversity.

Galilei,G.(1623). IlSaggiatore (1623).Roma:AccademiadeiLincei.Traducciócastellana,pròleg,comentariinotesdeJoséManuelRevuelta, Elensayador.BuenosAires:Aguilar,1981;anglesa(Drake 1957).

Grattann-Guinnes,s.I.(1997). TheFontanaHistoryoftheMathematicalSciences:theRainbowofMathematics.Hammersmith:FontanaPress.

—(2004). HistoryoftheMathematicalSciences.NovaDelhi:Hindustan,BookAgency.

—(2009). Routesoflearning:highways,pathways,andbywaysinthehistoryofmathematic.Baltimore, Md.:JohnsHopkinsUniversityPress.

Guzmán,M.d.(1995). Aventurasmatemáticas.Madrid:Pirámide.

Hardy,G.H.(1940). AMathematician’sApology.Cambridge:CambridgeUniversityPress.Traducció castellanadeJesúsFernández, Apologíadeunmatemático,Nivola:Madrid,1999;icatalanadeMònica MeríniSales, Apologiad’unmatemàtic,ambunaintroducciódeJosepPlaiCarrera.SantaColomade Queralt:ObradorEdèndum,2008.

Jung(1945).«Psycotherapytoday».InG.Adler(ed.), CollectedWorks,20volums.Princeton:Princeton UniversityPress.

Kao,M.Y.(2008). EnciclopediaofAlgorithms.Illinois:NorthwesternUniversityPress.Ming-YangKao n’ésl’editor.

Katz,V.J.(1993). AHistoryofMathematics.AnIntroduction.NovaYork:Harper-CollinsCollegePublishers.Reimprèsenunasegonaedició,corregida.Reading.Massachusetts:AddisonWesleyLogmanInc., 1998.

—(2000). UsingHistorytoTeachingMathematics:AnInternationalPerspective.Washington,D.C.:MAA. VictorJ.Katzn’ésl’editor.

—(2007). TheMathematicsofEgypt,Mesopotamia,China,India,andIslam.ASourceBook.Princeton, NovaJersey:PrincetonUniversityPress.Elsautorssón:AnnetteImhausen,EleanorRobson,JosephW. Dauben,KimPlofker,J.LennartBerggren.

Kline,M.(1972). MathematicalThoughtfromAncienttoModernTimes.Oxford:OxfordUniversityPress. TraducciócastellanadeCarlosFernándeziAlejandroGarciadiego,sotalacoordinaciódeJesúsHernández, ElpensamientomatemáticodelaAntigüedadanuestrosdias,entresvolums.Madrid:Alianza Editorial,1992.

—(1980). Mathematics.ALossofCertainty.Oxford:OxfordUniversityPress.Traducciócastellana,d’AndrésRuizMerino, Matemáticas.Lapérdidadelacertidumbre.Madrid:SigloXXI,1985.

Libri,G.(1838/1841). HistoiredessciencesmathématiquesenItalie,depuislarénaissanacedeslettresjusqu’àlafindudix-septièmesiècle,4volums.París:J.Renouart.

Lorenzo,J.D.(1971). Introducciónalestilomatemático.Madrid:Tecnos.

Marie,M.M.(1883-1888). Histoiredessciencesmathématiquesetphysiques.París:Gauthier-Villars. Midonick,H.(1964). TheTreasuryofMathematics.Harmondsworth,Middlesex:PenguinBooks.

Montucla,J.E.(1754a). Histoiredesmathématiques.París:Jombert.ReeditataParís:Blanchard:1968. —(1754b). Histoiredesrecherchessurlaquadratureducercle.París:Jombert.

PlaiCarrera,J.(2006). Introduccióalametodologiadelamatemàtica.Barcelona:UBe. —(2007).«DelsproblemesdeHilbertalsproblemesdelmil·leni».InJ.Quer(ed.), Elssetproblemesdel mil·leni,p.127-168.Sabadell:CaixadeSabadell.

—(2009). Paraulesd’agraïmentperlaconcessiódeladistincióMagístercumlaudedelaFacultatdeMatemàtiquesiEstadísticadelaUPC.Barcelona:PublicacionsdelaUPC.

Poincaré,H.(1900).Duroledel’intuitionetdelalogiqueenmathématiques.In ComptesRendusII CongresInternationaldesMathématiciens,p.115-130,París:Gauthier-Villars.

ReyPastor,J.iJ.Babini(1951). HistoriadelaMatemática.Argentina:Espasa-Calpe.ReeditataBarcelona: Gedisa(1984).

Schubring,G.(2005). Conflictbetweengeneralization,rigor,andintuition:numberconceptsunderlying thedevelopmentofanalysisin17-19thcenturyFranceandGermany.NovaYork:Springer.

Smith,D.E.(1959). ASourceBookinMathematics.NovaYork:DoverPublications,Inc.

Struik,D.J.(1967). AConciseHistoryofMathematics.NovaYork:DoverPublications,Inc.ReeditataNova York:DoverPublications,Inc.,1967.

—(1969). ASourceBookinMathematics,1200-1800.Cambridge.Massachusetts:HarvardUniversity Press.

Suzuki,J.(2002). AHistoryofMathematics.NovaYork:Prentice-Hall.

Waerden,B.L.v.d.(1983). GeometryandAlgebrainAncientCivilizations.Berlín:Springer-Verlag.

—(1985). AHistoryofAlgebra.Berlín:Springer-Verlag.

Wagensberg,J.(2002). Silanaturalezaeslarespuesta,¿cuáleralapregunta? Barcelona:Tusquets, Col.Metatemas.

—(2003). Silanaturalesaéslaresposta,quinaeralapregunta? TraducciócatalanadeMàriusSerra. Barcelona:Tusquets.

Weil,A.(1984). NumberTheory.Anapproachthroughhistory.FromHammurapitoLegendre.Boston: Brikhäuser.

Méssobreconjectures idemostracions1

GeorgePólya DepartamentdeMatemàtiques

ElprofessorGeorgePólya,professoremèritdematemàtiquesalaUniversitatdeStanford,ésun reconegutmatemàticderecerca,autord’aproximadamentdos-centscinquantaarticlesenmatemàtiquesieneducaciómatemàtica,aixícomd’unsquantsllibresàmpliamentllegits.Entred’altres: Complantejariresoldreproblemes, Matemàtiquesiraonamentplausible i Eldescobrimentenmatemàtiques,entred’altres.Lessevesconferències,vídeosiescritshanestimulatextraordinàriament l’interèsenlaresoluciódeproblemesihaninfluïtenensenyantsdetoteslesetapeseducatives.

More on Guessing and Proving

Sócunprofessordemates.Tambésócmoltvelli,pertant,tothomesperaquesiguiantiquat.Encanvi, defet,sócperfectamentconscientqueelsjovesd’avuidianoaprecienespecialmentelsconsellsola filosofiadelsvells,ifinsitotpucentendreperquènohofan.Perquè,sabeu,jotambévaigserjovei recordoalgunsacuditssobre«elsconsells»ila«filosofia».

—Quinéselmillorconsell?—Nodonar-necap. —Quèésunfilòsof?—Unfilòsofhosap tot,perònosapresmés.

Arapodeucomprendrequemen’estigui,dedonar-voscapconsell,iquetambémen’estigui,de deixaranargeneralitatsdetipusfilosòfic.Parlarésobrealgunsproblemesdelmeuofici.Potserhi trobareualgunarelacióambelsvostresestudisielsvostresproblemes.

Eltítoldelmeuarticleparlade«conjecturaridemostrar».Sócconscientquepotserteniureserves sobreaquesttítol,perquèpotserestàmoltbéqueunmatemàticparlisobre demostrar,peròquèhi pintaunmatemàticparlantsobre endevinar ?2

1.Aquestarticleésunaversió,lleugeramenteditada,d’una xerradaimpartidaalclaustredelaUniversitatdeWaterloo, el22d’octubrede1971,publicadaa TheTwo-YearCollegeMathematicsJournal,10,4(setembredel1979),p.255-258.Traducció alcatalàdePelegríViaderCanals.

2.Aquíhihaunadificultatdetraducciódifícilmentsalvable.Pólyautilitza«guess»,queestradueixper‘suposar’,‘conjecturar’otambé‘endevinar’,ihiaprofitaunamicaaquestdoblesentit.

Elsquehiteniurecels,al’institutpotservàreuseralumnesd’algunprofessordematespassatdemoda. Alessevesclasses,conjecturareratabú,iquanlidonàveuunarespostatitubejant,usescridassava: «Nofacissuposicions!Hohasdesaber!».

Jo,però,m’oposoaaquestamenadeprofessorso,mésbendit,intentoconvertir-los.Crecqueles conjectureshandeformarpartdetoteslesclasses,iespecialmentdeladematemàtiques.

Perquè?Desdelmeupuntdevista,perduesraons.Enprimerlloc,perquèésimportantquetothom tinguiunaactitudcorrectarespecteaconjecturar.Iensegonlloc,perquèaprendrematemàtiquesés mésdivertit,idónamésbonsresultats,sielprofessorengrescaaferconjectures.

Començaremcentrant-nosenlaimportànciadeconjecturar.Nocalqueusrecordiquevivimenmig d’unacrisimundial,3 enunmónaltamentcomplex,pledeperillsidementidesEnsbombardegen ambtotamenad’afirmacionspertotesbandes:delsvellsidelsjoves;deladreta,elcentreil’esquerra; perlapremsa,laràdioilatelevisió;endiscursospúblicsienconversesprivades...Pertaldefiltrarel quesentiuielqueveieuuscal.

Criteri

Però,quèéscriteri?Essencialment,ésl’habilitatdesaberdistingir:entrefetsifantasia,entrefetsiimpressions,entrefetsisospites,fetsiteoria,fetsiconjectures,demostracionsiconjectures.Peròpotser elmésimportantéssaberdistingirentreunesconjecturesiunesaltres.Lesconjecturespodenser

mésraonablesomenys, mésdefiaromenys, mésbenargumentadesomenys, mésrespectablesomenys.

Enqualsevolprofessió,laclauconsisteixadistingirentreunesconjecturesd’unamenailesdel’altra. Laprovacircumstancialdel’advocat,laprovadocumentaldel’historiador,laprovaestadísticade l’economistaolaprovainductivadelnaturalistasónexhibidesperreforçarconjectures.Icaltotala subtilitatdel’expertpertaldevalorarfinsaquinpuntlaprovaaportadasustentalaconjecturaen qüestió.

Iésqueusfaràfaltatotelcriteridelmónperdistingirentreunesconjecturesilesaltresenunmón pled’enganysiafirmacionscontradictòries.Inocalqueusdiguiqueelnostremónésentabanador. Oésqueuscreieuelquediuenelsanuncis?,oelquellegiualsdiaris?

Novullentrarendetallssobreelqueenpenso,peròusexplicaréunaanècdota.Fasetantaanys,el diariméspopulardeBerlínerael BerlinerZeitung.Lagentelconeixiaperlessevesinicials,BZ.Ideien: «El BerlinerZeitung éselmillordiari».Sabeuperquè?«PerquèelsaltresdiarismenteixendelaAalaZ iel BerlinerZeitung noméshofadelaBalaZ.»

Queuscreieuelquediuenelspolítics?Òndia!,nohohauriad’haverdit,això.Enspodriaportara barallar-nosijasócmassavellperbarallar-me.Deixeu-mequehoplantegid’unaaltramanera:Us creieuelqueusdiuenelsdiplomàtics?(Totpolíticnecessitaunamicadediplomàcia.)Altrecopno vullentrarendetallssobreelqueenpenso,peròusexplicaréunaanècdota.

3.Pólyadeiaaixòl’any1976.Éscuriósquelasituaciódecrisiencarasiguivigent!

Enuncertanydeladècadadelscinquanta,vaigferclasseaGinebradurantunesquantessetmanes. Almateixtemps,però,hiteniallocunesdevenimentmoltmésimportantquelesmevesclasses:la conferènciainternacionalenlaqualFrançaabandonavaIndoxina.Novullrecordarquirepresentava elsEstatsUnitsperquèlasevanegativaasignarelprotocolvaserelprincipidel’espantósembolicde Vietnam.LaGranBretanyaestavarepresentadaperEden,RússiaperMolotoviXinaperChouEn-lai. Alaciutat,encorriaaquestacudit:EdenvaferungransoparivaconvidarMolotoviChouEn-lai.Chou En-laivaanaraveureMolotovilivademanarconsell:«Mira,elcasésquemaiheestatconvidata capsoparoficiald’undiplomàticoccidentalinosécomm’hihedecomportar.Comquetuhasestatensoparsd’aquests,empodriesdirquèhedefer?»«Ésfàcil»,vacontestarMolotov,«youchew andlie».4

Aratornemalamevapreguntaprincipal:quèpotferelprofessordematemàtiques?Primerdetot,pot introduirelsseusalumnesalesdemostracionsmatemàtiques.Iaixò,perquèésrellevant?Nohiha demostracionsrealmentestrictesforadelesmatemàtiques:ladiferènciaentreunaconjecturaiuna altrapotsermoltgran,inconfusible;peròladiferènciaentreunademostraciómatemàticaiqualsevol conjecturaésmésacusada.Téelcaràcterd’absoluta,siésquetalcosaexisteixalmón.

Pertant,sócdelparerquefinsitotl’estudiantquenofaràservirmailesmatemàtiqueshauriade tenirl’oportunitatdeveureunademostraciómatemàtica.Nos’hadepreocuparperlesdemostracionsdecosesqueesdedueixendemaneraintuïtiva;nosel’had’obligaraaprendredemostracions dememòria—aquestescosessimplementeldesmotivarien—,peròunbonllibredetextiunbon professorquefacinservirbonsexempleslihauriendeferentendreel paper il’interès quetenenles demostracionsrigoroses.Peraalgunsestudiantspotrepresentarunagranexperiènciaihihamoltes probabilitatsqueatotselsenriqueixiessencialmentenlasevaculturageneralielsajudiaferunpas endavantcapalamaduresa.Quansapsquèésunademostraciórigorosailapotsdistingirinequívocamentd’unaconjectura,llavorsrealmentestàsbenpreparatperdistingirentreunesconjecturesde lesaltres.

Arausdiréunaaltracosaquehauriadeferunprofessordematemàtiques:

Ensenyar a conjecturar

Enlarecercamatemàticahotenimgairebécomunaregla:«Primerconjecturaidesprésdemostra». Laconjecturapotserincompleta;lasevademostraciópottrigarhoresodiesofinsitotmesosoanys —normalmentaquestsdetallsnoesfanpúblics,encaraquealgunscopssí—.ElgranEulerpublicavaproposicionsimportantsquenoméserenconjecturesi,desprésd’anysd’esforços,entrobavala demostracióilapublicava.

Crecquedelapropostad’ensenyaraconjecturarme’npucatribuirelsmèrits(oacceptar-neles culpes).Enqualsevolcas,hoheprovat(ialgunsprofessorsquehanseguitlesmevesclassestambéhohanprovat)ielsresultatssónmoltbons.Caltenirencompte,també,peraquiesfalaclasse.

Asecundària,quanelprofessorproposaunproblemaques’hadediscutir,hauriadecomençarper deixaralsestudiantsl’oportunitatdeconjecturar-neelresultat.D’aquestamanera,elsqueestanimpacientspersabersilasevaconjecturaéscorrectaonotreballaranambmoltmésd’interès.

4.Labromaperdtotagràciaamblatraducció:«chewandlie»voldir‘mastegarimentir’,isonaexactamentcom ChouEn-lai.

Enunaclasseperafutursenginyers,lesdemostracionsllarguesienrevessadesnosóngairepopulars. Encomptesd’unademostraciórigorosa,ésmoltmésprofitósqueelprofessorpresentiuna«demostracióheurística»—que,estrictamentparlant,noéscapdemostració:contéforatsques’omplenamb suposicionsplausibles.

Enunaclasseperafutursmatemàticsespotferalgunacosaméssofisticada:espotpresentaren primerllocunademostracióheurísticai,després,larigorosa,demaneraquelesideesprincipalsdela demostraciórigorosavaginprecedidesiinsinuadesperlademostracióheurística.Iambaixòestareu fentunacosamoltimportantperalsvostresalumnes:elsensenyeuaensenyar.5

Enqualsevolestadi,elsestudiantsmésintel·ligentsdelaclasseusestaranespecialmentagraïtsper haver-losmostratcompotsorgirunaconjecturaicoms’hauriadesospesar.

L’estudidelesmatemàtiquespotenriquirdemoltesmanereslavostraculturageneralidesenvolupar lavostrapersonalitat.Hefetèmfasienallòqueéspocconegutipocpracticatalesescoles:entendrelanaturalesadelesdemostracions,distingir-lesdelesconjecturesidistingirentreunamenade conjecturesiunesaltres.Aforçad’anarfentèmfasienaquestescoses,laclassedematemàtiquespot desenvoluparelvostrecriteri.Ienelsnostrestempsdecrisimundial,elcriteripotserelqueusfarà mésfaltadavantlescomplexitatsielsenganysdelavidamoderna.

5.Peraunexempleexplícitimportant,vegeuGeorgePólyaiGordonLatta, ComplexVariables [JohnWiley&Sons Inc.,1974.N’hihaunatraduccióal’espanyoldel’EditorialLimusa,Mèxic,1976],enquèlafrasequeencetaladarreralíniadela pàgina157[primeralíniadelapàgina174enl’edicióespanyola]diu:«Ellectors’hauriad’adonarquelademostracióprecedent, mésformal,defetfamésexplícitalademostracióintuïtivadelaSecció5.2il’explicaambmésprofunditat».

LluísAntoniSantalóiSors (1911-2001)

ClaudiAlsina DepartamentdeMatemàtiques

El6d’octubrede2011s’hacommemorataGironaelcentenaridelnaixementdeLluísAntoniSantaló iSors(Girona,9deoctubrede1911-BuenosAires,23denovembrede2001).LaSocietatCatalana deMatemàtiqueshareeditatambencertlabiografiadeXavierDuransobreaquestil·lustregironíi laCàtedraSantalódelaUniversitatdeGirona,ambCarlesBarcelóalcapdavant,nosolshaorganitzat elsactesdelcentenarisinóquediaadiarememoraelseunomifapossiblequelabibliotecadela universitatgironinadisposidelseullegatescritcomplet;aixídoncs,totsteniml’oportunitatdesabermoltescosessobreelmésil·lustredelsmatemàticscatalansdelsegle XX.Enaquestbreuescrit d’homenatge,m’agradariacompartirambelslectorsdel NouBiaix algunesconsideracionssobre aquestgranpersonatge,fetesdesdelamevaadmiracióperlasevavidailasevaobrairecordant lamevaamistatpersonalambellalllargdequasivint-i-cincanys.

Elprimerquem’agradariasubratllarésqueSantalópertanyalageneraciócatalanadel’exiliforçat, d’aquellsmestresque,comPerePiCallejaoErnestCorominas,trobarenal’Argentinaunaterrad’acollidaondesenvoluparenlasevaobraielseumestratge,gràciesalagenerosaacollidaqueelsprocurà JulioReyPastor.Vaserunageneraciódematemàticseminentsquenovàrempodertenirentrenosaltres.SienelcasdePiCallejacaldirquegràciesaoposicionsitrasllatsvapoderacabartenintuna càtedraal’ETSd’ArquitecturadeBarcelona,Santalónovaretornari,quanhauriaestatpossible,ja eramassatard.Afortunadament,apartirdeldoctorathonoriscausadelaUniversitatPolitècnicade CatalunyaqueimpulsàEnricTrillas,LluísSantalóvaanarrebentaCatalunyaiaEspanyanombrosos reconeixementsalllargdelasevajubilació.

ElsegonpuntremarcableéslaingenttascaderecercadeSantalóliderantelcampdelaGeometria Integral,peròsempreambunaactitudpositivaiactivaversl’educaciómatemàticaicommillorar-la.Ell vaserl’avaladordelaOlimpíadaMatemáticaArgentinaperal’estímuldeltalentmatemàticatravésde laresoluciódeproblemes;vaescriurellibresdetextuniversitarisquevarenformarmoltesgeneracions d’estudiantsiberoamericans,ifinsitotalgunsllibresdetextdesecundàriaqueincidienespecialment enlacreativitatmatemàtica;vacol·laborarsempreenlesrenovacionscurricularsaportantsenyibons criteris,i,jaenlasevaetapademaduresa,vaferformaciódeprofessorsargentinspermotivaruna millordocència.Totiquehihanombrosesdiferències,hompodriaestabliruncertparal·lelismeen quantatasquesiactitudsentreelquevaferSantalóielqueferenPerePuigAdamoMiguelde Guzmán.

Eltercerpuntquem’agradariadestacar-necrecquesónelsseusvalorshumans,comaparedefamília, comaamicicomapersonahumiligenerosa.Moltagentvarebreelsseusconsells,responiaatotes

lescartes,dirigiatreballs,ajudavaelsquel’hidemanaven...LavidadeSantalónovaserfàcil:vapatir guerra,exili,campdeconcentració,emigracióaunnoupaís,canvispolíticsargentinsquevarenportar asituacionsmoltdifícils...Ientretotaquestbrogit,Santalópujavaunafamília,escriviaamblaseva arcaicamàquinad’escriurearticlesdegranqualitat,feiacursos,traduccionspercompletarelsou,etc.

DarrerelafiguradeSantaló,doncs,hihaunhomebo,unmatemàticreferencialiunprofessorinnovador.

AlmeudespatxuniversitaritincemmarcadaunafotografiadeSantalóiunafrased’ell:«Vaigaprendre aaprendreperapoderensenyarivaigaprendreaensenyarperapoderaprendre».Totaunadeclaració deprincipisqueensmostrauncamíperseguir.

Perdesigseu,lescendresdeSantalóvarenserrepartides.Unapartvarenanarapararaljardídela FacultatdeMatemàtiquesdelaUniversitatdeBuenosAires,quefoulasevacasaintel lectualdurant tantsanys.LesaltresvarenserenterradesaGirona,alcostatdelesrestesdelasevaestimadamare.

Al’ArgentinaoaCatalunya,totsteniml’oportunitatdepreservar-neelllegatirememorar-ne l’exemple.

L’adquisiciódecompetències

matemàtiquesd’alumnes deprimàriaencontextos dejocsdetaulairesolució deproblemes

EdelmiraBadillo,MequèEdoiJordiDeulofeu

DepartamentdeDidàcticadelaMatemàticaidelesCiènciesExperimentals UniversitatAutònomadeBarcelona edelmira.badillo@uab.cat,meque.edo@uab.cat,jordi.deulofeu@uab.cat

Resum

Enaquestarticleespresentaunareflexióteòrica imetodològicasobreunamanerad’entendre l’aprenentatgeil’ensenyamentdeles matemàtiques,basatenunenfocament competencial.Desd’aquestaperspectiva,hem anatdissenyantiimplementantseqüències didàctiques,validadesendiferentsaulesde primàriad’EuropaiLlatinoamèrica,quebusquen tanteldesenvolupamentdelacompetència matemàtica—elconeixementmatemàtic,els processosassociatsal’activitatmatemàticaiel contextd’aprenentatge—iel desenvolupamentd’altrescompetències,com l’argumentativail’autonomiapersonal.La propostaquepresentempreténserunapetita aportacióaaquestgrandesafiament,mostrant queéspossibledesenvoluparcompetències matemàtiquesenuncontextd’úsdidàcticde jocsdetaula.Enparticular,enscentremenel desenvolupamentd’estratègiesderesolucióde problemesitècniquesdecàlculmentali,en general,eneldesenvolupamentdelsentit numèricfraccionari.

Abstract

Thispaperpresentsatheoreticaland methodologicalreflectionaboutonewayto understandlearningandteachingmathematics, basedonacompetenceapproach.Fromthis perspective,wehavebeendesigningand implementingdidacticsequences,validatedin primaryclassroomsinEuropeandLatinAmerica, seekingboththedevelopmentofmathematical competence mathematicalknowledge,the processesassociatedwithmathematicalactivity, andthelearningcontext andthedevelopment ofotherskills,suchastheargumentativeability andpersonalautonomy.Ourproposalaimstobea smallcontributiontothisgreatchallenge,showing thatitispossibletodevelopmathematicalskillsin acontextwithaneducationalgame.Inparticular, wefocusonthedevelopmentofstrategiesfor problemsolvingandmentalcalculation techniquesand,ingeneral,thedevelopmentof fractionalnumbersense.

1. Introducció

Qualsevoljocgeneraunasituacióregidaperunesnormesireglesespecials,singularsipròpiesde cadajoc.EnaquestsentitVigotski(1988)afirmaque«eljoccreaunaZonadeDesenvolupamentProximalenl’infant.Mentreduraeljoc,l’infantsempreestàperdamuntdel’edatmitjana,perdamunt delaconductadiària;eneljocéscomsifosuncapmésaltdelqueésenrealitat»(pàgs.125-126).Per aquestautoreljocésunaactivitatessencialeneldesenvolupamenthumàperquèproporcionabeneficiscognitius,socialsimoralsquenonomésnos’handereprimirencapetapadeldesenvolupament infantil,niposteriormentd’adult,sinóques’handepotenciar.

Diversosautorsafirmenquel’úsdeljocal’aula,especialmenteljoccol lectiu,ésunaactivitatque permeteldesenvolupamentdediversesàrees:social,política(normesiregles),moral,delllenguatge, emocionalicognitiva(KamiiiDeVries,1980;Cockcroft,1982).Elsresultatsd’estudisquevinculenl’ús delsjocscol·lectiusal’auladematemàtiquesrevelenqueeltempsdestinatajugaralaclassedematemàtiquespotserunainversiódegranvalorsisabemescollirelsjocsadequatsiaconseguiminvolucraractivamentelsalumnesenaquestaactivitat(Edo,1998;CorbalániDeulofeu,1996).Delamateixa manera,mostrenquelaconnexiódelsjocsamblesmatemàtiquesésmúltipleiesrefereixentanta l’aprenentatgedeconceptesidetècniquescomd’estratègies.Enaquestpunthihaunarelaciódirectaamblaresoluciódeproblemes(Edo,DeulofeuiBadillo,2007;Edo,Baeza,DeulofeuiBadillo,2008).

Elpunt227del’informeCockcroft(1982)recomana,endiferentsedatsienqualsevolnivelldeconeixementdelsalumnes,lautilitzacióbenplanificadadetrencaclosquesijocsmatemàticsperintroduir contingutscurricularsiperaldesenvolupamentdelpensamentlogicomatemàtic.D’altrabanda,Edo (2002)vaanalitzardiferentscurrículumsdematemàtiquesdelesdiferentscomunitatsautònomes del’Estatespanyolivaconclourequeentotshihareferènciesconcretesirecomanacionsperquè s’utilitzinjocsirecreacionsperal’ensenyamentil’aprenentatgedelesmatemàtiquesaprimària,ien destacaqueespromoul’úsdelsjocsal’auladematemàtiquesperalaresoluciódeproblemes.

Desdelainvestigacióendidàcticadelamatemàticatambéhihaunapreocupacióperanalitzarla relacióquehihaentrelesfasesderesoluciód’unproblemamatemàticielprocésderecercadel’estratègiaguanyadorad’unjocdeterminat(Edo,Baeza,DeulofeuiBadillo,2008).Desd’aquestcontext, ensinteressademostrarlaimportànciaquetélaintroducciódejocsmatemàticseneldesenvolupamentdecompetènciestantdecaràctergeneralcommatemàtiques.

Aquestarticles’estructuraencincapartats.Enelsegon,situemlanostrapropostadinsdelatendència actualdelcurrículumdeCatalunya.Enl’apartatsegüent,descrivimelsreferentsteòricsquesustenten laproposta.Posteriorment,presentemunapropostadidàctica,ques’il lustraambunjocd’exemplei amblesdiferentsactivitatsdissenyadesquerelacionenelsjocsd’estratègiaamblaresoluciódeproblemes,centrant-nosenelconceptedefracció.Finalment,presentemalgunesconclusionssobrela potencialitatqueofereixelcontextdejocsdetaulailaresoluciódeproblemesperaldesenvolupamentdecompetènciesmatemàtiquesinomatemàtiques.

2. Enfocament competencial de l’aprenentatge de les matemàtiques

Adúriz-Bravo(2011)postulaqueenladidàcticadelesciènciesidelesmatemàtiques,aixícomen lainvestigacióeducativaengeneral,lanociódecompetènciaésconsideradaalhoraproblemàticai potent.Talcomafirmal’autor

elsproblemesprovenen,entrealtrescoses,delsorígensextraeducatiusdelconcepte(principalment,desdelscampsdel’economia,eldesenvolupamentieltreball)idelsseusnombrosos

—idelicats—matisospoliticoideològics;lapotència,perlasevabanda,esderivadelasevacapacitatdeferqueesreestructurinafonselscurrículums,l’avaluació(formadoraoacreditativa,interna oexterna)ilaformaciódelprofessorat.

Enaquestarticles’assumeixeltermedecompetència,demaneraglobaldesdelaperspectivade l’àmbitdel’EspaiEuropeud’EducacióSuperior:

Lacapacitatgeneralbasadaenelsconeixements,experiències,valorsidisposicionsqueunapersonahadesenvolupatmitjançantelseucompromísamblespràctiqueseducatives.(Eurydice,2002:13)

Noobstantaixò,matisemelterme,demaneraparticular,talcomelplantejaAdúriz-Bravo(2011),el qualproposaunadefinicióoperativadecompetència,quedenomina«modeldelestresces(3C)»que potajudarelsprofessorsdeciènciesidematemàtiquesaveuredemanerapotentialhorasenzilla larelacióquehihad’haverentreelsdiferentscontingutsdematemàtiques,enlesseqüènciesque dissenyem,pertalqueelsalumnesconstrueixinconeixementcientífical’aula:

[...]unacompetènciacientíficaescolarésqualsevol capacitat (cognitiva,discursiva,material,afectiva)d’ordresuperiorespecíficadeferalgunacosasobreun contingut (científic)determinat,dins d’un context delimitatrecognoscible(escolarsignificatiui,pertant,transferiblealavidaciutadana).

Desd’aquestavisió,Sanmartí(2009)afirmaqueuntreballcompetencialal’aulaimplicatenirencomptecincvariables:

1.Complexitat,queimplicaxarxadeconeixements,incertesa,emergència,etc.

2.Integraciódeconeixementsenlaresoluciódeproblemes

3.Funcionalitatitransferibilitatdelconeixementenl’aplicacióasituacionsrellevantssocialmenti imprevisibles

4.Autonomia,peraprendreiactuareficaçment,gestionarelconeixementsiperregular-se

5.Avaluabilitat,perpoderautoregularelpensament,elsvalors,lesemocionsil’actuació.

Així,elsnousplanscurricularsensplantegenatotselsprofessorsundesafiamentimportant:passar d’unaformaciócentradaenl’assolimentd’objectiusespecíficsdefinitsdesdelscontingutsdel’àrea, aunensenyamentcentrateneldesenvolupamentdecompetènciesorientadaapotenciarelpensamentmatemàticdelsestudiants.Assumiraquestenfocamentimplicareconèixerlaimportànciatant del’acciócomdelacomprensióipertantreconèixerqueenlanociódecompetèncias’involucreni esrelacionendiversosconeixements:saberquè,saberquèferisabercom,quaniperquèfer-ho.En aquestsentit,hemdetenirencomptequequanparlemdelacompetènciamatemàtica,ésnecessari tenirencomptetresaspectesqueesrelacionenpermanentment:elconeixementmatemàtic(tantel conceptualcomelprocedimental),elsprocessosassociatsal’activitatmatemàtica(formulariresoldreproblemes,modelarprocessosifenòmensdelarealitat;comunicar;raonariformularcomparari exercitarprocediments)ielcontextd’aprenentatge(Badillo,JiméneziVanegas,2011).

Enelcurrículumactual,basatenunenfocamentcompetencial,iconcretamenteneldesplegament curricularproposatperlaGeneralitatdeCatalunya,esremarcaelsegüent:

Lescompetènciesbàsiquessónl’eixdelprocéseducatiu.Elcurrículumorientatal’adquisicióde competènciesestableixquelafinalitatdel’educacióobligatòriaésaconseguirqueelsalumnesi lesalumnesadquireixinleseinesnecessàriesperentendreelmónisiguinpersonescapacesd’interveniractivamenticríticaenlasocietatplural,diversaiencanvicontinuqueenshatocatviure. Uncurrículumpercompetènciessignificaensenyarperaprendreiseguiraprenentalllargdetota lavida(Gencat,2009,pàg.6)

COMPETÈNCIES BÀSIQUES

1. Comunicativa lingüística i audiovisual

2. Artística i cultural comunicatives

3.Tractament de la informació i competència digital

metodològiques personals

conviure i habitar el món

4. Matemàtica

5. Aprendre a aprendre

6. Autonomia i iniciativa personal

7. Coneixement i interacció amb el món físic

8. Social i ciutadana

PER APRENDRE A

Ser i actuar de manera autònoma

Pensar i comunicar

Descobrir i tenir iniciativa

Conviure i habitar el món

Figura 1. Esquema sobre competències bàsiques del web de la Generalitat de Catalunya.

Així,s’identifiquendosgrupsdecompetènciesbàsiques.D’unabanda,lescompetènciestransversals, quesónlabasedeldesenvolupamentpersonalidelaconstrucciódelconeixement,entrelesqualses consideren:(1)lescomunicatives,percomprendreiexpressarlarealitat;(2)lesmetodològiques,que activenl’aprenentatge,entrelesqualshihalacompetènciamatemàtica;i(3)lespersonals.D’altra banda,lescompetènciesespecífiquesperconviureihabitarelmónrelacionadesamblaculturaila visiódelarealitat.Ensíntesi,lescompetènciesbàsiquessónlesvuitquepresentemenlafigura1.

3. Una perspectiva teòrica sobre l’ús dels jocs d’estratègia a l’aula de matemàtiques de primària

Enelcampdeladidàcticadelesmatemàtiquesexisteix,desdefaanys,uninterèsespecialperla investigacióenl’ensenyamentil’aprenentatgedelaresoluciódeproblemes,queenocasionsesvinculaambelfetd’utilitzarjocsal’aula.Aquestinterèsradicaenl’èmfasiqueelsactualscurrículumsde matemàtiquescompetencialsposenalaresoluciódeproblemes,comundelsprocessosques’ha depotenciarperquèelsalumnesadquireixinlacompetènciamatemàtica.Aquestfethaportataconsiderarelsjocsmatemàticscomaelementsclauenelprocésd’aprenentatgedelesmatemàtiquesi ausar-losnonomésperintroduircontinguts,sinótambé,imoltespecialment,perafavorireldesenvolupamentdeprocessosmatemàticsvinculatsalaresoluciódeproblemes(Gómez-Chacón,1992).

Entenemperjocmatemàticl’activitatcol lectivabasadaenreglesfixes,senzilles,comprensiblesi assumidespertotselsparticipants(Edo,DeulofeuiBadillo,2007).Lesreglesestablirannonomésels objectiusperalconjuntdejugadors,sinótambéelsobjectiusespecíficsdecadascundelsparticipants quehaurandebuscarlesestratègiesperbloquejari/oguanyarlarestadelsparticipants.

Depenentdel’objectiueljocpresentadiversespotencialitatsal’auladematemàtiquesipottenir diferentsfinalitats.CorbalániDeulofeu(1996)distingeixenentreduesgranscategoriesdejocsque espodenutilitzarenelmarcescolar:

a)Elsjocsdeconeixement,quepersegueixenlacomprensiódeconceptesolamilloradetècniquesmatemàtiques.

b)Elsjocsd’estratègia,quesecentrenenl’adquisiciódemètodesoheurístiquesderesolucióde problemes.

Peraquestsautors,elsjocsd’estratègiasónaquellsenelsqualshihaunaestratègia,entesacom unadeterminadamaneradejugar,quepermetguanyarsempreundelsdosjugadors(oalmenysno perdre,quanlestaulessónpossibles).Enaquesttipusdejocstoteslesdecisionsestanenmansdels jugadors,jaqueentotmomentlainformaciódequèdisposenéstotainohiintervél’atzar.Pertant, mésenllàdepracticareljoc,estractaqueelsjugadorsdescobreixinl’estratègiaguanyadora,ésadir, quetrobinunamaneradejugarquepermetiaundelsjugadorsguanyarsempre,oevitarquel’altre jugadorguanyi,depenentdeltorndelajugada(Edo,DeulofeuiBadillo,2007).

Corbalán(1994)afirmaqueelsjocsenelcontextescolartambénecessitenl’úsdematerialquepermetiregistrarelsprocessosderesoluciódelproblemamatemàticimplicatseneljoc,talscomtaulers ifitxesosimplementllapisipaper.Sianalitzemelsjocsdetaula(ambcartes,taulers,fitxes,daus, etc.)unamaneradeclassificar-losésenfunciódelgraud’atzarquecontenen.Espodendistingirtres categories(Edo,DeulofeuiBadillo,2007):

a)Jocsd’atzarpur.Perexemple,l’ocaol’escala.Sónjocsenelsqualselsjugadorseslimitena executarlesordresdictadespeldau.Nonecessiten,nipoden,decidirresipertantlasevaactuaciónomésconsisteixamourelapeçaassociantlaquantitatquemarcaeldauambelvalor posicionaldelapeçaaltauler.Enaquestgruppodemsituarelbingo.

b)Jocsambalgunaestratègiaafavoridora.Perexemple,elparxís.Sónjocsambpresènciadel’atzar, peròenelqualelsjugadorshandeprendredecisionsquepodeninfluirenelresultatdelaseva partida:ambquinadelesmevespecesavanço?ésmillorposarforadeperillaquestapeça? simocaquestapucmataruncontrincant?,etc.Encaraquelespartidescontinuendepenent engranpartdel’atzarperquèelsdaussegueixenmanant,elresultatfinaltambédepènde l’estratègiaafavoridoraqueadoptinelsjugadors.Enaquestgruppodemsituartambéeldòmino imoltsjocsdecartescomlabotifarraoelbridge.

c)Jocsd’estratègia.Perexemple,elmarro.Enaquestsjocstoteslesdecisionsestanenmansdels jugadors,quepodenarribaradescobrirunaestratègiaguanyadora.Ésadir,peraunadeterminadacondició(comaraserelprimeratirar)éspossibledescobrirquinssónelspassosper guanyarsempreoperquèl’altrejugadornoguanyimai.Enaquestgruptambépodemsituar elsgransjocsd’estratègiacomelsescacs,elgoielsmancala,ielspetitsjocsd’estratègiacom elnim

Elsjocscategoritzatsen b)i c)comportenuntipusderaonamentestretamentvinculatalpensament matemàticdesitjableenelsprocessosderesoluciódeproblemes,talscomreconeixementiidentificaciódedadesrellevants,planificació,aplicaciód’estratègies,anticipació,etc.(Edo,DeulofeuiBadillo, 2007).Peraixò,recomanemqueesdestinitemps,al’auladematemàtiques,perensenyarlesregles d’algunsjocs(especialmentdecurtadurada),perjugar-hienpetitsgrupsiperanalitzaridiscutiren grangrupelsdescobrimentsrealitzats.

Delamateixamanera,consideremquetotsaquestsjocspodenajudaraldesenvolupamentilacomprensiódecontingutsmatemàticsespecífics,comelsrelacionatsambelssistemesdenumeració,el valordeposició,ladescomposiciódequantitats,elcàlculmentalexacteiaproximati,engeneral, eldesenvolupamentdelsentitnumèric,peròtambéelgeomètricenjocsdeposició.

Unterceraspectequecaldestacardel’úsd’aqueststipusdejocsal’auladematemàtiques,inoper aixòmenysimportant,éselvalordeldesenvolupamentdelacompetènciadel’autonomiapersonal isocialquepotcomportaraquestaactivitat,semprequeelprofessortinguiencompte,d’unabanda, laimportànciaqueelsalumnesenpetitsgrupsrealitzinunatascaquenomésespotduraterme amblaimplicacióielseguimentdelesnormesperpartdetotsells,senselaparticipaciódecapadult, i,del’altra,lacondiciódejugarenparellesqueformenunsolequip(contraaltresequips)iquehande pactarlesjugadesabansderealitzar-les,laqualcosaafavoreixlacomunicacióentrecompanysperquè intentenexplicar-seraonamentscomplexos(ambientderesoluciódeproblemes)almateixtemps ques’afavoreixl’empatiailadiversiópròpiad’unjoc(ambientlúdicvinculatalesmatemàtiques).

Finalment,unaspecteclauquehemdetenirencompteenl’úsdelsjocsd’estratègiarelacionats amblaresoluciódeproblemesésquetotsdoscomparteixenelmateixprocésheurístic.Pertant, al’horaderelacionarlesfasesdel’heurísticadelaresoluciód’unjocd’estratègiaid’unproblema matemàtic,talcomafirmaPólya(1965),ésimportantl’anàlisidelesheurístiquesderesoluciód’un problemamatemàticdeterminat,perquèimplicacomprendreelmètodequecondueixaresoldre’l. Enparticular,lesoperacionsmentalstípicamentútilsenaquestprocés.Aquestesoperacionsmentals impliquen,entred’altres,laindagació,l’exploracióieldescobriment,quetenenunaestretarelació ambeldesenvolupamentdeleshabilitatsqueactivaunalumnequanbuscal’estratègiaguanyadora d’unjocmatemàtic(Edo,Baeza,DeulofeuiBadillo,2008).

Perestudiarelpossibleparal lelismeentreelprocésderesoluciód’unproblemamatemàticielprocés dedescobrimentdel’estratègiaguanyadorad’unjocmatemàtic,consideremelparal·lelismeproposatperEdo,Baeza,DeulofeuiBadillo(2008),quealseutornesvanbasarenl’estudid’Edo(2002)sobre l’anàlisientrelesfasesdelaresoluciód’unproblemamatemàticenl’àmbitdel’educacióprimàriailes fasesderesoluciód’unjoc(quadre1).

Fasesderesoluciódeproblemes (Pólya,1979)

I.Comprensiódelproblema.

II.Dissenyiexecuciód’unplageneralode plansparcialssuccessius

III.Verificaciódelasolucióobtinguda

Fasesderesoluciód’unjoc (Edo,2002)

• Comprensiódelsobjectiusdeljocideles normesquecalseguir.

• Desenvolupamentdelapartida: experimentació,realitzaciódeconjectures, dissenydeplansparcials,planificació d’unaestratègia

• Validacióorebuigdel’estratègiaianàlisi delquehapassat

Quadre 1. Relació entre les fases de resolució d’un problema i les fases de resolució d’un joc (Edo, Baeza, Deulofeu i Badillo, 2008).

4.Unsjocsd’estratègiapertreballarelsentitnumèricdelesfraccions a primària: recobrir els hexàgons

Comjahemesmentatenl’apartatanterior,elsjocsengeneral,ielsdetaulaenparticular,tenen unaestretarelacióamblesmatemàtiques.Enprimerlloc,moltsjocsutilitzenlesmatemàtiquesen elseudesenvolupament,jasiguiperlesrelacionsnumèriques(perexemple,eldòmino)operles

geomètriques(perexemple,elmarro),peròsobretot,peltipusd’estratègiesquecaldescobrirquan s’intentaguanyarlapartida.Aquestesestratègiesoheurístiquesqueutilitzenelsalumnespodenser moltvariadesd’acordamblescaracterístiquesdeljociimpliqueneldesenvolupamentdeprocessos matemàticsquetenenunagransimilitudamblesestratègiesutilitzadesenlaresoluciódeproblemesmatemàtics(Shoenfeld,1985).

Ensegonlloc,lanaturalesadelesmatemàtiquesfaquesovints’assemblinaunjoc.Nopodemafirmar quelesmatemàtiquessiguinunjoc,perquèlafinalitatilessevesaplicacionssónmoltméscomplexesitranscendeixenelcaràcterdediversiódelsjocs.Noobstantaixò,quanfemmatemàtiquesi, concretament,quanresolemproblemes,síquetrobemobjectiuscomunsalprocésdedeterminar l’estratègiaguanyadorad’unjoc.Enaquestsentit,elscurrículumscompetencialsactualsemfatitzen lanecessitatquefermatemàtiquesesconverteixienunaactivitatlúdicaisobretotintel·lectualestimulant.Així,elcaràcterlúdicdelsjocsdetaulaielreptequeensplantejajugar-his’assemblenmolta fermatemàtiques.D’aquestamanera,consideremqueimplementar-losal’aulacreaunentornideal perreflexionarsobreconceptesmatemàticsisobrelesheurístiquesderesolucióaplicadesdurantla recercadel’estratègiaguanyadora.

Peralaimplementaciód’untallerdejocsdetaulaquepromoguieldesenvolupamentd’estratègies decàlculmentalenunentornsignificatiuilúdic,elsjocssónescollitsatenentelnivelld’escolaritat,els contingutsmatemàticsiladificultatdelesestratègiesimplícitesperguanyar.Pelquefaalametodologia,proposemescollirdosjocsdetaulapernivell(curs).Cadajococupaunaunitatdeprogramació i,generalment,suggerimimplementar-laenl’últimtrimestredelcursambunadedicaciódequatre sessionsd’unahorapercadajoc(ambuntotaldevuitsessionsdeclassed’unahora).Pertant,enel tercertrimestreesfanduesunitatsdeprogramacióquecorresponenadosjocs(figura2).

S1S2S3S4

Unitat de programació 1

S1S2S3S4

Unitat de programació 2

Cadasessiódeltaller—siguilaS1,laS2,laS3olaS4(figura2)—téunaseqüènciad’activitatspròpia, itotselsalumnesjuguenalhoraaunjocescollitprèviamentpelmestre.Lessessionsestanestructuradesdelamanerasegüent:

• Primerasessió:s’expliquenlesreglesonormesdeljocmentreesrealitzaunaprimerapartidaen laqualjuguenelmestreielsalumnes.Enacabarlapartidainicials’aturaeljocis’encetaundiàleg preguntantalsalumnesquèconsiderenqueaprendranjugantenaquestjoc.L’objectiudeldiàlegésqueelsalumnesfacinunarepresentació,tanajustadacomsiguipossible,delquefaran,com hofarani,sobretot,perquèhofaran.Elmestre,mitjançantpreguntes,suggerimentsireflexions alvoltantdeljocqueacabendeconèixer,ajudaelsalumnesaferconjectures,plantejarhipòtesis idescobririverbalitzarelconeixementielsprocessosmatemàticsques’esperaqueaprenguin jugant.Totseguit,elsalumnesescol loquenpergrups(unmaterialpertaulade4alumnes)i comencenajugarsols.Elmestreobservaifaanotacions(enlataulad’observaciópreparadaper acadajoc),iquanhotrobiconvenientintervéjugantiactuantconjuntamentambelsgrupsi alumnesqueconsiderinecessari.

Figura 2. Organització de les sessions del taller de jocs de taula a primària.

• Segonaitercerasessió:s’inicienambunaconversacol·lectivaambdiferentsfocusd’atenció.Es podenrecordarlesreglesdeljoc,elsalumnespodenexplicaralmestredescobrimentsoaprenentatgesrelacionatsoespodencomentarincidènciespositivesonegativessobreconductesentre elscompanysdegrupenlessessionsanteriors.Seguidament,elsalumnesjuguenenpetitsgrups ielmestreelsobserva,enfaanotacionsihiintervénomésquansiguinecessari.

• Quartasessió:elmestrerecordaqueaquestaseràl’últimasessiódeljocicomentaalsalumnesque jugarannomésentreells,peròquedespréshaurand’exposarengrupl’estratègiaolesestratègies guanyadoresielscontingutsmatemàticsutilitzats.Sihoconsideraimportant,demanaalsalumnes queredactinlessevesimpressions,queexpliquinl’estratègia(olesestratègies)iquejustifiquinels contingutsmatemàticsimplícitsenlesestratègiesguanyadores.

Amanerad’exemple,presentemunjocquepotajudaradesenvolupardiversosdelscontingutspresentats,queformapartd’unacol·lecciódejocsdeprimàriaelaborada,ienfased’experimentació, pelsautorsd’aquestarticleidocentsdelgrupderecercaPREMATdelaUAB.Elsjocsd’estratègies permetenexploraridesenvoluparelsentitnumèricfraccionariquetenenalumnesde10a12anys quecursencinquèdeprimària.

Entenempersentitnumèriclacomprensiógeneralquetéunalumnesobreelsnombresilesoperacionsjuntamentamblacapacitatperusar-losdemaneraflexibleperemetrejudicismatemàtics idesenvoluparestratègiesútilsperresoldreproblemescomplexos(Godino,Font,KoniciWilhelmi, 2009);enelnostrecastrobariargumentarlavalidesadel’estratègiaguanyadorad’unjoc.ElNational CouncilofTeachersofMathematics(1989)vaidentificarcinccomponentsquecaracteritzenelsentit numèric:elsignificatdelnombre,lesrelacionsnumèriques,lagrandàriadelsnombres,lesoperacions ambelsnombresielsreferentsperalsnombresiquantitats.

Eldesenvolupamentd’unsentitnumèricòptimimplical’adquisiciódedestresesrelacionadesambel càlculmental,l’estimaciódelagrandàriarelativadelsnombresidelresultatd’operacions,elreconeixementdelesrelacionspart-tot,aixícomelconceptedevalorposicionalilaresoluciódeproblemes (Godino,Font,KoniciWilhelmi,2009).TalcomassenyalenGodinoetal.(2009),«alavidaquotidianaapareixendiversostipusdesituacionsenquès’utilitzenexpressionsquerelacionendosnombres demaneramultiplicativa;talsnombrespodenserdivisiblesentresiono.Aquestesrelacionsesdescriuenmitjançantfraccions,raons,decimalsipercentatges,iengeneralestanlligadesaquantitats demagnitudsiapràctiquesespecífiquessegonselstipusdesituacionsenquèparticipin».Aquests autorsfanunarevisiósobreestudisques’hancentratenl’anàlisisemànticadelesfraccionsinocions relacionades,ihanassenyalatquesóndiverseslesinterpretacionsques’atribueixen,tantalsracionals comalesfraccions.Tambédestaquencomaconceptescentralselquocient,laraó,l’operadoriuna versiódelarelaciópart-tot.

4.1. Un joc d’estratègia: recobrir els hexàgons

Enelquadre2espresentalafitxadidàcticadeljoc,quefareferènciaalsaspectessegüents:

a)nivelld’escolaritat;

b)materialsnecessarisqueespodenfabricarambcartolinaiplastificar-los;

c)nombredejugadors;

d )lesnormesdeljoc;

e)algunesvariantsdelesnormesinicials,peròqueelmestrehadetenirclarqueimpliquenl’apariciód’altrestipusd’estratègiesil’aplicaciód’altresconceptesmatemàtics,i

Nivell: 5èi6èdeprimària(10-12anys)

Taulerformatporcinchexàgonsregularsiguals.

Material: Trestipusdepecesdediferentscolors:10trapezisisòsceles(1/2hexàgon),15rombes(1/3dehexàgon)i30trianglesequilàters(1/6dehexàgon).

Nombrede jugadors: Jocperadosjugadors,enelqualenjuguenquatre(enparelles).

Normes: Enuntaulerformatpercinchexàgonsregularsiguals,dosjugadors,pertorns, col·loquenunapeçaencadajugadaperrecobrirelshexàgons.Eljugadorque col·local’últimapeçaideixatotselshexàgonsplens,guanyalapartida.

Hihatrestipusdepecesquepermetenrecobrirtoteltauler:10trapezisisòsceles, 15rombesi30trianglesequilàters.

S’hijugalliurement(posantcadapeçaonvol),peròhihaduescondicions:

a)Cadapeçahauràdequedarcompletamentcol·locadaadinsd’unhexàgon(una peçanopotcobrirpartsdedoshexàgonsalhora).

b)Escomençaajugaromplinthexàgonahexàgon,ésadirnoespodencol locar pecesaunaltrehexàgonfinsquenoestiguideltotplel’anterior.

Variants:

Situació

problema:

1.Lesmateixesnormesanteriors,peròamblavariantqueespotanarcol·locant pecesaqualsevolhexàgonencaraquenoestiguicomplet(s’hipodendeixar forats).

2.Sienposarunapeçajan’hihaunaaltraenaquellhexàgon,s’hadeposarde maneraquetinguinuncostatcomú.Pertant,nopodenquedardosforatsenun mateixhexàgon.

• ¿Quinaésl’estratègiaguanyadora?

• ¿Quèpassasivariemelnombredehexàgonsdeltauler?

Quadre 2. Fitxa didàctica del joc de recobrir els hexàgons.

f )algunessituacionsproblemesqueespodenplantejardesdelaprimerasessióperquèelsalumnespuguinintentarrespondreamesuraqueconeixeniintententrobarl’estratègiaguanyadora. Aquestessituacionsseranelcentredediscussióenlaquartaiúltimasessiódejocdelaunitat deprogramació.

Enlaprimerasessió,enpresentarlesnormesdeljocienelprocésdefamiliaritzaciódelsalumnes ambelsmaterialsdeljoc,elmestrepotaprofitarperplantejarunsprimersreptesalsalumnes:

1.Identificarlesfiguresgeomètriquespresentseneljociclassificar-les:

Polígons

Regulars

Irregulars Triangle Equilàteracutangle

Hexàgon

Quadrilàter paral lelogram Rombe

Quadrilàter Trapeziisòsceles

2.Identificarfiguresenposicionsnoprototípiques,aspectefonamentalperdisminuirl’emergència d’errorsiobstaclesenl’aprenentatgedelsalumnes(importànciadepresentarlarepresentació gràficadelesfiguresendiferentsrotacions):

3.Buscarlarelaciónumèricaentrelesfiguresqueformenlespecesdeljocprenentcomaunitatun delshexàgonsdeltauler: Unitat Unasisenapart Duessisenesparts Tressisenesparts

4.Introduirl’equivalènciadefraccions:

5.Introduir(oampliar)operacionsambfraccionshomogèniesiheterogèniesapartirdelaforçade latraducciódelavisualitzaciógràficacapal’algorismenumèric.Amanerad’exemple,perqüestió d’espai,n’il·lustremnoméslasumailarestaambalgunadelespossiblesoperacions:

Sumairestadefraccionshomogènies

Sumairestadefraccionsheterogènies

6.Introduir(oampliar)diferentsexpressionsd’unnombreracional:diferentsrepresentacionsdela relaciópart-tot(a/b),decimal,percentatge,etc.

Representació gràfica

7.Introduirl’expressiódefraccionsmajorsquelaunitatenformadenombremixt.

Unaunitatiunsisèdelaunitat

Quatreunitatsidosterçosdelaunitat

Elgraud’aprofundimentqueelsmestresposinenelsaspectesanteriorsafavoriràelgraudedesenvolupamentdelsentitnumèricfraccionaridelsalumnes.

4.2. Cap a la determinació d’estratègies guanyadores

Quanelsalumnespractiquenianalitzenaquestjoc,amblafinalitatdetrobarunaestratègiaguanyadora,utilitzendosenfocamentsdiferents.Elprimerdecaràcteraritmètic,secentraenelsespais ocupatsielbuitsquedeixendesprésdelessevesjugadesenunmateixhexàgon,tenintencompte quecadahexàgonequivala6triangles,3rombeso2trapezis.Elsegon,decaràctergeomètricglobal, secentraenlasimetria.L’aplicaciódequalsevoldelesduesestratègiespermetassegurarquesempreguanyaràelsegonjugadorsilesaplicacorrectamentencadascunadelesjugadesdelapartida.El jugadorquedominalesduesestratègiesarribaaserconscientqueelqueompleelprimerhexàgon deltaulers’asseguraguanyarlapartida

• Estratègianumèrica:enlafigura3s’il·lustrenlesdiferentsopcionsdeguanyaraplicantl’estratègia numèrica.

Primerajugadaguanyadora:quanunjugadoriniciaposantlapeçadeltrapezi,perdperquèel segonjugadortéduesopcionsperguanyar:(a)col·locaruntrapezii,(b)col·locaruntriangle peròdeixant2/6separats;ésadir,1/6acadacostat.

Segonajugadaguanyadora:quanunjugadoriniciaamblapeçadeltriangle,l’opciónumèrica guanyadoraésla(b),ésadir,col·locaruntrapezideixant1/6acadacostat.

Tercerajugadaguanyadora:quanunjugadoriniciaamblapeçadelrombe,l’opciónumèrica guanyadoraésla(c),queconsisteixacol·locarunrombeperòdeixant2/6separats;ésadir, 1/6acadacostat.

a)

b)(c)

Figura 3. Estratègia numèrica: operacions amb fraccions (deixar 2/6 separats).

• Estratègiageomètrica:enlafigura4,s’il·lustrenlesdiferentsopcionsdeguanyaraplicantl’estratègiageomètrica,queconsisteixacol·locarlapeçasimètricaalaquecol·locaelprimerjugador queinicialapartida(simetriaaxial).

Primerajugadaguanyadora:semprequeelprimerjugadorcol·localapeçadeltrapezi,automàticamentperdperquèelsegonjugador(queseràelguanyador)col·localafigurasimètrica queéseltrapezi(a).

Segonajugadaguanyadora:semprequeelprimerjugadorcol localapeçadeltriangle,l’opció geomètricaguanyadoraésla(b),queconsisteixaanarcol locantlafigurasimètricaalapeça col locadaenaquestcasunaltretriangle.Aquestajugadaesrepeteixfinsatresocasionsque ésquanesguanyaelprimerhexàgoni,enconseqüència,lapartida.

Tercerajugadaguanyadora:semprequeelprimerjugadorcol·localapeçadelrombe,l’opció geomètricaguanyadoraésla(c),queconsisteixaanarcol·locantlafigurasimètricaalapeça col·locadaqueseràunaltrerombe,inomésdeixaalprimerjugadorl’opciódecol·locarun triangle.Esguanyaelprimerhexàgonencol locareltrianglesimètrici,enconseqüència,la partida.

Figura 4. Estratègia geomètrica: simetria axial de polígons regulars.

5. A manera de conclusió

Undelsaspectesclau,desprésd’haverimplementatdiversesseqüènciesdidàctiquesutilitzantcontextosdejocsmatemàticsperaldesenvolupamentdelsentitnumèricaprimària,éslamotivaciódels alumnesduranttoteldesenvolupamentdel’activitatqueesgeneraal’aula.Unaltreaspectequecal destacarésqueelcontextdejocsd’estratègiapermetlaconstrucciódesignificatscol·lectiusenrelacióambelsconceptesnumèricsigeomètricsimplicatsenlarecercadelesestratègiesguanyadores ienelsproblemesmatemàticsimplícitsencadajoc.

Delamateixamanera,lesrespostesdelsmestresquehanparticipatenelsdiferentsprogrames deformaciósobrecommillorarl’aprenentatgeil’ensenyamentdelesfraccionsenelciclesuperiorde primàriahanvaloratpositivamentlesexperiènciesproposadesenunmarccompetencial,perquè considerenqueelcontextdejocmatemàticpermet:

1.Establirconnexionsdemanerapermanententreelsconeixementsmatemàticsimplícitsenladeterminaciódelesestratègiesguanyadores,distingint-neaspectesconceptualsiprocedimentals.

2.Desenvolupardemaneraprogressivaelsentitnumèric,iconcretamentelsentitnumèricfraccionariperquèfacilita:laconstrucciódelsignificatdelnombreracionalcomaquocient,raó,operador irelaciópart-tot;l’establimentderelacionsnumèriques;lacomparaciódelagrandàriadelsnombres;lacomprensiódelesoperacionsambelsnombresutilitzantdiferentsregistressemiòticsila construcciódereferentsperalsnombresilesquantitatsqueapareixen.

3.Centrarl’atencióenelsprocessosassociatsal’activitatmatemàtica,jaqueescreaunambientde formulacióiresoluciódeproblemes,modelitzaciódeprocessosifenòmensdelarealitatapartir del’estudiil’argumentaciómatemàticadurantl’anàlisidelesestratègiesqueutilitzenelsalumnes perguanyarunapartida.

4.Generarcontextosd’aprenentatgefuncionalisignificatiu,perquèestreballaambigualtatd’importànciaelsaspectesmatemàticsielsaspectesemocionalsiafectiusassociatsaladinàmicad’interacciódelsalumnesenlarecercadelesestratègiesguanyadores.

6. Bibliografia

Adúriz-Bravo,A.(2011).Competenciasmetacientíficasescolaresdentrodelaformacióndelprofesoradodeciencias.A:E.Badillo,L.García,A.MarbàiM.Briceño(ed.) Eldesarrollodecompetenciasenlas clasesdecienciasymatemáticas.Mérida:FondoEditorialMarioBriceñoIragorry.Universidaddelos Andes.

Badillo,E.,Giménez,J.iVanegas,Y.(2011).Desarrollodecompetenciasenuncontextoartístico:construyendosignificadossobrelaforma.A:E.Badillo,L.García,A.MarbàiM.Briceño(ed.) Eldesarrollode competenciasenlasclasesdecienciasymatemáticas.Mérida:FondoEditorialMarioBriceñoIragorry. UniversidaddelosAndes.

Corbalán,F.(1994). Juegosmatemáticosparasecundariaybachillerato.Madrid:Síntesis.

Corbalán,F.iDeulofeu,J.(1996).Juegosmanipulativosenlaenseñanzadelasmatemáticas. Uno, RevistadeDidácticadelasMatemáticas,7,71-80.

Edo,M.(1998).Juegosymatemáticas.Unaexperienciaenelcicloinicialdeprimaria. Uno,Revistade DidácticadelasMatemáticas,18,21-37.

—(2002). Jocs,interaccióiconstrucciódeconeixementsmatemàtics.Tesidoctoral.Bellaterra:Universitat AutònomadeBarcelona.

Edo,M.,Deulofeu,J.iBadillo,E.(2007).Juegoymatemáticas:Untallerparaeldesarrollodeestrategias enlaescuela. ActasXIIIJAEM,JornadasparaelAprendizajeylaEnseñanzadelasMatemáticas,Granada.

Edo,M.,Baeza,M.,Deulofeu,J.iBadillo,E.(2008).Estudiodelparalelismoentrelasfasesderesolución deunjuegoylasfasesderesolucióndeunproblema. Unión,RevistaIberoamericanadeEducación Matemática 14,61-75.

Eurydice(RedEuropeadeInformaciónenEducación)(2002). Lascompetenciasclave:Unconceptoen expansióndentrodelaeducacióngeneralobligatoria. Madrid:Ministerid’Educació,CulturaiEsport.

Gencat(2009). CurrículumEducacióPrimària.Barcelona:ServeideComunicació,DifusióiPublicacions. GeneralitatdeCatalunya.Departamentd’Educació.

Godino,J.,Font,V.,Konic,P.iWilhelmi,M.(2009).Elsentidonuméricocomoarticulaciónflexiblede lossignificadosparcialesdelosnúmeros.A:J.M.CardeñosoiM.Peñas. Investigaciónenelaula deMatemáticas.SentidoNumérico (p.117-184).Granada:SAEMThalesyDepartamentodeDidácticadelaMatemáticadelaUniversidaddeGranada.[enlínia]http://thales.cica.es/granada

Gómez-Chacón,I.(1992).Losjuegosdeestrategiaenelcurrículumdematemáticas. ApuntesIEPS,55. Madrid:Narcea.

Kamii,C.iDeVries,R.(1980). Juegoscolectivosenlaprimeraenseñanza:implicacionesdelateoríade Piaget. Madrid:Visor.

NationalCouncilofTeachersofMathematics(1989). CurriculumandEvaluationStandardsforSchool Mathematics. Reston,VA:NCTM.

Pólya,G.(1965). Cómoplantearyresolverproblemas. Mèxic:Trillas.

Sanmartí,N.(2009).¿Quécambiosimplicalaintroduccióndelconceptodecompetenciaenlaeducacióncientífica?Conferenciadictadaenel VIIICongresoInternacional.Barcelona.[Disponibleenlínia]

Shoenfeld,A.H.(1985). MathematicalProblemSolving.Orlando:AcademicPress,Inc.

Vigotski,L.S.(1988). LievSemiònovitxVygotski:Pensamentillenguatge. [ed.acàrrecd’IgnasiVilaiRosa Colomina].Vic:EUMO/Barcelona:DiputaciódeBarcelona.

Laconstrucciódelpentàgon regulardel’Almagest. Unprimerpasenlaruta capalesestrelles

CarlesIgnasiGómezRuiz

Resum Abstract

Explicaciód’unamanerasenzilladeconstruir ambregleicompàsunpentàgonregularinscrit enunacircumferència,descritaidemostrada perClaudiPtolemeuenelseutractatsobre astronomiaimatemàtiquesanomenat Almagest, ibasadaendiversesproposicionsdels Elements d’Euclides.

Estudi,també,d’altresaspectesrelacionatsque formenpartdelcontexthistòricicientíficdel problema,ambimplicacionsdidàctiques.

1. Introducció

Explanationofasimplewaytobuildwithrulerand compassaregularpenthagoninscribedina circumferencedescribedanddemostratedby ClaudiusPtolomeusinhisessayaboutastronomy andmathsnamed Almagest,andbasedon severalproposicionsofthe Elements ofEuclides. Thisessayisalsoaboutotherrelatedaspectsthat belongtothehistoricandscientificknowledgeof theproblem,withdidacticimplications.

Eltemacentrald’aquestarticleéslaconstrucciódelpentàgonregular.Comienquinscursosresolem habitualmentaquestproblema?

Seguramentpodemtrobarrespostesdiverses.Totespodensersímptomesdecomensenyemhabitualmentlageometria.

Elmètodequeproposoesfaalamaneradelsgeòmetresgrecs,ambreglaicompàs(estrisavuien diaemulablesambprogramescomelGeogebra)iésaplicablealsprimerscursosdel’ESO.

Éselméssenzillquehetrobatdesprésd’experimentardiversessolucions.Aixònovoldirquesigui banal,ésadir,quenotinguicaporiginalitatointerès.Sobretotsiensdemanemd’onprocedeixiper quèfunciona.

L’originalitats’hadecercar,ésclar,enl’obraprimitiva,iaixòm’hadutaferunviatgealpassat,ales arrels,queusinvitoacompartir.

Totjustacabavadecomençarelcurs,iensvamtrobardavantdelprimerrepte:elprofessorJosep Pla1 ensvademanarlarecercad’unabonamaneradeconstruirelpentàgonregular.Ambaquesta propostaensconvidavaavisitarterritorismatemàticsquenoperquèsónconegutssempresónprou explorats.

Quantessorpresesenspotoferirunestudiacuratdelahistòriadelesmatemàtiques?Personalment n’hetrobatunesquantesenaquestpetitviatgealarecercadelaconstrucció,ambregleicompàs,i d’unamanerasenzilla,d’unpentàgonregular.

Perresoldreunproblemad’aquestamena,noésdifíciltrobar-hireferènciesdetottipusenlesabundantsfontsd’informacióqueactualmenttenimal’abast.Peròsivolemaprofundir-hi,resmillorquerecórreralsclàssics.ElpuntdepartidavaserEuclides,ideseguidavamcomprovarqueelsseus Elements contenengairebétoteslesrespostesalespreguntesqueensplantejalaresoluciód’aquestproblema.

Continuantlarecerca,méstardvaigdescobrirunaaltraconstruccióqueemvacridarl’atencióperla sevasenzillesaieficàcia.Lavaigveurefullejantl’Almagest,deClaudiPtolemeu(Ptolemeu,1984).No emvacostargairetrobar-la.Quanaquestgranastrònomvainiciarelseuviatgecientíficcapal’estudi delfirmamentielscossosquel’habiten,enprimerllocvaelaborarambgranprecisióunataulade cordes.2 Comapasprevi,vaestudiarlaconstrucciód’algunspolígonsregularsielprimerdetotsva serelpentàgon(conjuntamentambeldecàgonil’hexàgon),mitjançantelmètodequeésobjecte d’aquestestudi.

Noeslimitaafer-nelaconstrucció,sinóquedemostraqueésexacta,comtambéveurem.LajustificacióesbasaenteoremesjademostratsperEuclides,quetenenencomptelescaracterístiques peculiarsd’aquestpolígon:

D‘entretotselspolígonsregulars,elpentàgon(iperextensióeldecàgon,elpentadecàgon...)éselque gaudeixmésclaramentd'unaestretarelacióamblaraóàuria,tambéanomenadadivinaproporció (LucaPacioli)osecciódivina(JohannesKepler).

Noésobjected’aquestarticleincrementarelsinnombrablesestudisquejas’hanfetsobreelnombre d’or,peròlarecercasobreelpentàgonregular(ilesformesdeconstruir-lo)nopotpassar-nel’existènciaperalt,jaque Φ estrobaindissolublementunitalanaturalesad’aquestencisadorimàgicpolígon, demúltiplesisorprenentsmaneres.

Tampocnoestrobaràaquíuntractatexhaustiudelahistòriadelesmatemàtiques,peròsíquese’n recullenalgunsaspectesque,amésd’il·lustratius,tambépodenserunafontdepropostesdidàctiquesaplicablesal’aula.Quanesvolabordarafonsl’estudid’unproblemad’aquestamenanoconvé aïllar-lodelseucontexthistòric,nideixardeconsiderarlesconnexionsambaltresproblemesialtresciències.Sideixéssimlahistòriaoblidadaenvoluminososllibrespolsososamagatsenracons recònditsdecertesbiblioteques,seriaunahistòriamortaquenoserviriaperres,isienslimitéssima digitalitzar-laiaconvertir-laencadenesdebitstancatsengransmagatzemsdediscsdursoaltres

01.EnelcursdepostgraudedidàcticadelesmatemàtiquesdelaUPF.

02.Elconceptede corda ésmoltsimilaralde sinus,talcomquedaexplicatenl’apartat3.2.2.

dispositiusdememòriatambéseriaunconeixementinert.Enlesnostresclassesdiàrieshemdeser capaçosdedonar-hiunanovavida,revifarelfocdelconeixement,recuperarlesideesileslliçonsque sónl’herènciad’unallargaifecundatradició.

2. Els antecedents: un breu viatge a través de la història

Ésunatascaàrduaintentarresseguirlesempremtesqueportenal’origendelesideesmatemàtiques. Elseurastreesperdmésenllàdelesboiresqueensimpedeixenmirarenrere.

Quivadibuixarelprimertriangleequilàterolaprimeracircumferènciaperfecta?Idequinamanera?, sobrelasorraoalaparetd’unacova?,ambquinamenad’estris?Nohosabem.Probablementnoho sabremmai.

Peròenelsvestigisconservatsdelesculturesprehistòriquesjapodemobservarladèriadelshumans perrepresentarlarealitatqueelsenvoltaambgràficsestilitzats,moltsovintdecairegeomètric,iel gustperladecoracióambformessimètriques.

Seguramentlageometrianeixtantdel’observaciódelesformessobrelaterracomdeldesigde desxifrarelsmisterisdelfirmamentestudiantlaposicióielmovimentdelSol,laLluna,elsplanetes... HihaunacertatradicióqueatribueixaEgiptelainvenciódelageometria,necessàriapermesurarels camps,inundatsdemanerarecurrentperlesaigüesdelNil.TalcomrelataHeròdotenelsnoullibres d’Històries:

Elssacerdotsdeienqueaquellrei[Sesostris]distribuílesterresd’Egipteentreelsseushabitants,i donàacadascúuntrosigual,enformadequadrat[...].Sielrius’emportavaunapartdellotd’algun,[...]elreienviavagentperexaminarimesurarlareducciódelterreny[...].Crecqueaquíesva inventarlageometria,quedespréspassàaGrècia.

Aquestaopiniólapodemveurerepetidaenmoltstextosposteriors,iperexempleProcles’hirefereix enelscomentarisalllibre I dels Elements d’Euclides.S’haanattransmetentdegeneracióengeneració.

Evidentmentésunavisióetnocèntrica.Nohemd’oblidarelsconeixementsassolitsperaltrescultures demanerasimultània(idevegadescoincident)comaralababilònicailahindú,otambélaxinesa (Pla,2009)ilamaia—peresmentarlesmésconegudesavuidia—,peròcertamentEgiptevaser,ja famoltssegles,undelsllocsdelmónonlageometriavaassolirfitesméselevades.

Pelquefaalsconeixementsmatemàticsd’aquestaantigacultura,ambproufeinesensn’hanarribat documentsescrits(unnombrereduïtdepapirscomelRhindoeldeMoscou),peròsíinteressants rastresquepodemtrobarenlessevesobresarquitectòniques.Perexemple,coneixeml’existència dels«tensadorsdecordes»gràciesaalgungravatques’haconservatalfonsdelaberínticspassadissos protegitspercarreusdepedresiquecorroborenelqueexplicavaHeròdot,entred’altres.

Sabemqueelsconstructorsdelespiràmideserenconeixedorsdel«secret»delstrianglesrectangles (elposteriorteoremadePitàgores),iquesabienfertotselscomplexoscàlculsnecessarisperrealitzar admirablesisorprenentsconstruccions(Buhigas,2008).

D’altrabanda,l’observaciódelcel,origendel’astronomia,haestatsempre(iencarahoés)unestímul importantenlagènesidemoltesifecundesideesmatemàtiques.L’origend’aquestesobservacions

esperdenlanitdelstemps,peròpersortencarase’nconserventaulesicàlculsd’èpoquesmolt antigues.

L’escolad’Alexandria,comveuremmésendavant,vatenirunpapermoltimportantenelsbalbucientsorígensdel’astronomiaialtresconeixementsrelacionats,comlatrigonometria.Aquestaciutat properaaldeltadelNilvaserl’escenaridelahistòriadelaconstrucciódelpentàgonregular,tema centrald’aquestarticle,peròabanshemdeviatjarcapal’altraribadelMediterrani,fenttambéunsalt cronològic.

ElpentagramapitagòricvaserunsímbolemblemàticdelsseguidorsdePitàgores.Elsintegrantsd’aquestaescolavanserdevotsdelesformesperfectesilesproporcionsexactes,ilesconsideravenun reflexdelanaturalesadivinadelacreació.Aixídoncs,vanquedarespecialmentcorpresosperl’anomenatpentagramamísticpitagòric,símboldevidaisalut,emblemadelasevacomunitat.

Diversoshistoriadorsconsiderenqueeldescobrimentdelsincommensurablesprobablementesva produirapartird’aquestafigura3 (Fritz,1945);ambelllenguatgeactual,sabemqueelnombred’or, omnipresentenelpentàgon,ésunirracional.Plató,enel Timeu,tambéfareferènciaaaquestaproporciócomadivina,iconsideraquequantresnúmeroslaverifiquenformenunaunitatperfecta.

Ésunaopiniópreponderantconsiderarquel’origendelesmatemàtiquescomaciènciaestrobaenla culturagrega,iprobablementlesmatemàtiquesactualsserienbendiferentssensel’alèdelseupensamentilasevafilosofia.PerònopodemoblidarquePitàgoresvabeuredelafontdelsconeixements babilònicsiegipcis,mitjançantelsviatgesquevaferperconselldelseumestreTales,delqualsabem quehaviatrobatl’alturadelespiràmidesaplicantelseuconegutteoremaimesurantombres.També éscertquequasisenseexcepciólamatemàticaegípciaibabilònicaanterioraTaleséseminentment empírica,desenvolupadaenformade«receptes»iquetractaderesoldreproblemespràcticscomels relacionatsambl’agrimensura,ladeterminaciódevolums,elcàlculd’impostos...Defet,espotafirmar queelconceptededemostracióésproductedelaculturagrega.

L’obrad’Euclidesvanéixeral’escolad’Alexandria,sobrel’ègidadelaculturahel lènica.Ptolemeu,4 successord’AlexandreelGran,haviaestablertenaquestaciutatlacapitaldel’imperihel·lènicis’iniciavaaixíunllargifecundperíode.Alexandriavabrillarambllumpròpia,inonomésacausadelseu famósfar.

HerevadetotalasaviesaantigadesdelasevafundacióperAlexandreelGran,vatenirunaricai fascinantbiblioteca,queformavapartdelMuseu.

Desprésd’Euclides,Eratòstenesvaexercircomadirectordelabiblioteca,quevaacolliril·lustresestudiososcomArquimedes.Aristarctambéhivaestudiar,gaudintdelasaviesaacumuladaalsseus nombrososvolums,fruitdelesmentsmésprivilegiadesdetotselsconfinsdelmónconegut.Iposteriorment,alamateixaciutat,Diofantvaelaborarlasevainteressant Aritmètica.Aquestavitalitat culturalesvamantenirdurantmoltsanys,finsalamalauradadesapariciódelavalentaisàviaHipàtia.

Jahavienpassatquatre-centsanysdesdelamortd’EuclidesquanPtolemeuhivadesenvoluparla sevaobrai,entrealtrescoses,vadeixarconstànciadelprocedimentperconstruirelpentàgonregular quehetriatcomapreferitiqueexposarémésendavant.Elnaixementieldesenvolupamentdeles matemàtiquesésproducted’unaingentobracol lectiva,enlaqualalgunsgenisbrillenambllum

03.Unaaltrapossibilitatesderivadelamesuradeladiagonaldelquadrat. 04.Nos’hadeconfondreaquestgeneral(PtolemeuISoter,segle IV aC)ambelcreadordel’Almagest

pròpia,claramentdistingible,comunfarenlafoscor,peròquesemprehandesenvolupatelseu treballfentcomaprimerpasunestudidelesobresdelsseuspredecessors.Enaquestsentit,ésben conegudaunafrasedeNewton:«Siheaconseguitveure-himésllunyqueelsaltres,ésperquèhe pujatal’esquenadegegants».

Totesaquestesreflexionshansorgitquanhevolgutseguirlapistad’unabonaconstrucciódelpentàgonregular.NopodemdiscutiraEuclideselmèritdeserelprimerquehoresoldemanerasistemàtica. Omésbendit,elprimerqueenfaunaexposicióclaraicompleta,jaquemoltshistoriadorsconsiderenquelasevaobraésunarecopilacióordenada,sintèticaibastantcompletaderesultatsanteriors, unafeinadecompilacióambindiscutiblesmèritsquenolipodemnegar.Aixídoncs,ladivisiód’un segmentenmitjanaiextremaraó(EuclidesVI,definició3)n’éslaportad’entrada:

Esdiuqueunarectahaestattalladaenextremaimitjanaraóquanlarectasenceraésalsegment majortalcomelsegmentmajorésalsegmentmenor.

Laproposició11delllibre II (Euclides1991)resolelproblemadetrobarlaseccióàuriad’unsegment. Lesproposicions10i11delllibre IV expliquenlaconstrucciódelpentàgonregular,mètodequealguns autorsatribueixenal’escolapitagòrica.

Nohetriataquestprocedimentcomelpreferit,perquè,sensediscutir-neelvalorteòric,crecqueens portaaunaconstruccióbastantcomplexa.Enprimerllocs’hadeconstruiruntriangleisòscelesde maneraquecadascundelsanglesdelabasesiguieldoblequel’anglerestant,ésadir,untriangle ambanglesde72◦ ,72◦ i36◦ .Perarribaraaquestaconstrucció,abanss’hadetrobarlaseccióàuria d’unsegment—noéscasualitat,comhemcomentatmésamunt,acausadelasevarelacióambel pentàgon—,ilarestadepassosespodenconsultarenlesduesproposicionsesmentades.

Unaaltraproposicióinteressantéslavuitenadelllibre XIII:

Enunpentàgonequilàteriequiangular,unesrectesoposadesadosanglessuccessiusestallen entresienextremaimitjanaraóielsseussegmentsmajorssónigualsalcostatdelpentàgon.

Enaquestaproposicióesdemostra,entrealtrescoses,laconegudarelacióentreladiagonalielcostat d’unpentàgonregular,queésiguala Φ,perònoofereixunmètodedirectedeconstrucció.

Trobaremunmètodeméssenzillenl’Almagest dePtolemeu,queéselqueexplicoacontinuació.

Mésendavant,tambévaserutilitzatperAlbertDürer,consideratelmillorgeòmetradelsartistesdel Renaixementitalià.Avuiendia,ésfàciltrobar-hoperinternet,perònomésenformaderecepta,sense capjustificació.Ptolomeu,totiquelautilitzaambmotiuspràctics,noenpassaperaltlademostració, requisitimprescindibledelpensamentmatemàtic.

3.1. Context històric

L’obradeClaudiPtolemeuesdesenvolupaíntegramentdintrel’escolad’Alexandria,alsegle II dela nostraera.Noesconeixengairesaspectesdelasevavida,peròtotsemblaindicarquevaviuremolts anys,almenyselsnecessarisperpoderduratermeunafructíferaobracientífica.

3. La construcció de Claudi Ptolemeu

Elsseusestudisastronòmicssónelsmésconegutsielsquevantenirmésinfluènciaalllargdemolts segles.Sibéelseumodeldel’univers(geocèntric,comelquevaproposarAristòtil)esconsidera superatapartirdelarevoluciócopernicana,noenpodemignorarelsmèrits.Totiserfonamentalment erroni,vapredirlaposicióielmovimentdetotselsplanetesambmésprecisióquequalsevolmodel anterior,inclòselsistemaheliocèntricd’Aristarc.

Enl’Almagest 5 vadesenvoluparelprimerintentseriósdemodelitzarelmovimentdelscossoscelestes. Intentantdonarversemblançaalasevateoria,vaconstruirunenginyóssistemageomètricbasaten cicles,epicicles,òrbitesexcèntriquesiequants.Lessevesobservacionsastronòmiquesvansermolt importants;envautilitzardepròpiesialtresdemésantigues,fetesperAristarc,Hiparc,Teód’Esmirna, itambéalgunsregistresbabilònicsanteriors,queconeixemgràciesalasevaobra,jaques’hanperdut lesdadesoriginals.

Espotconsiderarundelsprecursorsdelatrigonometria.Elsestudisd’Hiparcsónanteriors,peròPtolemeuensvadeixarelregistredelesprimerestaulestrigonomètriquesqueesconserven,iambuna precisiógensmenyspreable,moltsovintamberrorsabsolutsmenorsqueundeumil·lèsim.Estracta delessevestaulesdecordes,conceptemoltproperal’actualdelsinus.

Tambévaproposarlaprojeccióestereogràfica,utilitzadamésendavantenlaconstrucciódel’astrolabiienlaconfecciódemapes,disciplinaquetambévaconrearelaborantlasevaconeguda Geografia. Diversosestudisd’òpticaimecànicaformenpartdelasevaobraconeguda,senseoblidarel Tetràbiblos,untractatd’astrologiademoltainfluènciaentotal’edatmitjana.Ptolomeunovaconsiderar incoherentnisensefonamentsrelacionarelmovimentdelsastresambcertsesdevenimentsdelmón sublunar,ésadir,delaTerraielsseushabitants.

Aquestadiversitatd’interessosintel lectualsnon’eclipsenlaimportànciaencertsaspectesdeles matemàtiques.L’Almagest éssobretotunaobrad’astronomia,peròambunasòlidabasematemàtica.

Noésestrany,doncs,que—perposar-nenomésunexemple(Vernet,2004)—elsavijueudelsegle XII AbrahamBarHiyya,nascutaBarcelona,recomanésalsqueesvolieniniciarenelconeixementdeles matemàtiquesquellegissinenprimerllocels Elements d’Euclidesiacontinuacióunsquantsllibres intermedisabansd’abordarl’Almagest dePtolemeu:les Esfèriques deTeodosiideMenelau,l’Esferaen moviment d’Autòlic,les Còniques d’Apol·loni,i L’esferaielcilindre d’Arquimedes,entred’altres.

Lainfluènciad’Euclidesenl’Almagest ésindiscutible:seguramentels Elements esconservavenalamateixabibliotecad’Alexandriaquatreseglesdesprés,potserl’originaloentotcasalgunacòpia,jaquehi facontínuesreferències.PeròPtolemeuteniaunobjectiuclar:desxifrarelmisteridelmovimentdels cossoscelestes.Vaconrearlesmatemàtiquessobretotcomunaeinaquelipermetiaassoliraquest objectiu,unaeinafiableiexacta,ésclar,peròambunautilitatpràctica,notancadaenellamateixa. Aquestaéslaimpressióquefalalecturadel’Almagest

3.2. Construcció del pentàgon regular

Elmètodequehetriatésprecisamentelprimerresultatmatemàticdetotelllibre,queestrobaen elcapítol I,apartat10,desprésd’unaintroduccióenquèdesenvolupalasevaconcepciósobrela

05.Eltítoloriginald’aquestllibrevaser Hèmegalèsintaxis [Elgrantractat ].Generacionsposteriorsvanafegir-hiel superlatiu«megiste»,quevoldir‘elmésgran’.Quanelsàrabsvantraduiraquestaobraalasevallengua,hivanafegirl’article el («al»enàrab).

filosofiadelaCiència.Noometcapaspectedelademostració,peròelseuinterèsenlaconstrucció delcostatdelpentàgonregular(quefademanerasimultàniaambladelcostatdeldecàgon)téun clarobjectiu:elcàlculdelescordesdediferentsangles,començantper72◦ ,36◦ i60◦ (apartirdel pentàgon,decàgonihexàgon);acontinuaciótambétrobalesde90◦ i120◦ (apartirdelquadrati deltriangleequilàter).Després,mitjançantaltresteoremes,enparticularelconegutpelseunom,6 trobalacordadelasuma,ladiferència,l’angledoble...ambfórmulessimilarsalesdelatrigonometria actual,finsaarribaratrobarlescordesdelarestad’anglesenintervalsdemiggrau.

CalobservarquePtolemeueslimitavaaconstruirelcostatdelpentàgon,conjuntamentambelcostat deldecàgon,queéselquerealmentnecessitava,talcomapareixenlafigura5.Apartird’aquestpunt, completarelpentàgonnoofereixcapdificultat.

Lesfigures1,2,3i4,queil lustrenelprocediment,estanfetesambprogramaGeogebra,inoamb regleicompàs,encaraqueemulenelprocedimentmanual.Aprofitoalgunsavantatges,comelfet queelprogramapermettrobarelpuntmitjà E delsegment DG directament.Sinomésfemservirel regleielcompàs, E espottrobarconstruintlamediatriudelsegment DG

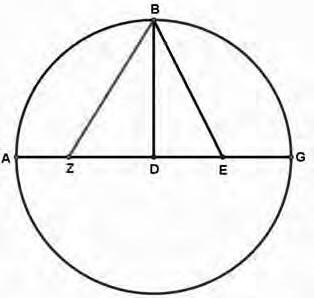
2 i 3. Passos següents.

06.Aquestteoremaafirmaque«elproductedelesdiagonalsd’unquadrilàterinscritenuncercleésigualalasuma delsproductesdelscostatsoposats».

Figura 1. Inici del procés.

Figures

3.2.1.

Passos a seguir per construir el pentàgon

• Construïmlacircumferència,eldiàmetre AG ielradi DB,perpendicularaaquestdiàmetre.

• Construïmacontinuaciól’arcdecircumferènciaambcentre E iradi EB finsatrobarelpunt Z ,punt detalld’aquestacircumferènciaambeldiàmetredelacircumferènciainicial.Aleshores,

El costat del pentàgon és igual a. BZ

• Trasllademaquestcostatalaposició BC ambunsimplemovimentdecompàs(dibuixantunarc ambcentre B iradi BC finsquetallilacircumferènciainicial).Pertant BC tambééselcostatdel pentàgon.

• Prenentlamida BC (costatdelpentàgon)quatrevegadesmés,completemlafigura.

’

3.2.2.

Justificació daquest procediment

PROPOSICIÓ:Consideremunsemicercle ABG ambcentre D idiàmetre ADG.Dibuixem DB perpendicular a AG per D.Biseccionemelsegment DG ientrobemelseupuntmitjà E .Unim E amb B (construïm EB).Fem EZ iguala EB,iunim Z amb B.Aleshores,

• ZD éselcostatdeldecàgonregular.

• BZ éselcostatdelpentàgonregular.

Figura 5. Reproducció de la imatge de l’sobre la qual es basa la demostració. Almagest

Figura 4. Final del procés. El pentàgon ja construït.

TotelraonamentquefaPtolemeuiqueexplicoacontinuacióespotconsultaral’Almagest (Ptolemeu, 1984).Comjaheditmésamunt,estrobaalprincipi,concretamentenelcapítol I,apartat10,titulat «Lamesuradelescordes».

Nosempreésfàcildesxifrar-lo.Sivolemcomprendrebétotselspassosésimprescindibleteniramàun exemplarcompletdels Elements d’Euclides(Euclides,1991),jaquePtolemeuconsideravaquemolts delsresultatsquen’utilitzasónprouconeguts,iqueintentaréclarificar.

DEMOSTRACIÓ:

• Enprimerlloc,Ptolemeudemostraelsegüent:

PROPIETAT: ZG quedadividitenextremaimitjanaraópelpunt D.Utilitzantunaexpressiómésactual, elpuntDdeterminaunaseccióàuriasobreelsegment ZG.

Mésconcretament,Ptolemeudemostraqueesverifica GZ ZD = DG2 .[1]

Enprimerlloc,assegura,sensemésexplicacions,que GZ · ZD + ED2 = EZ 2 .[2]

Éscertaaquestaigualtat?D’entrada,calpensar-hiunamicaabansdedonar-lapervàlida.Desd’un puntdevistaalgèbricactual,noméscalaplicarlafórmula(2a + b) · b + a2 = (a + b)2 .[3]

Fent a = ED i b = ZD,aleshores GZ = 2a + b,jaque2DE = DG.Pertant,larelació[2]ésclara.

Ptolemeuladónapervàlidadirectament.Potserhitéencomptelaproposició II,6d’Euclides,que afirmaelmateixque[3]peròdesd’unpuntdevistageomètric,noalgèbric,ésclar.

Larestadepassossónmésevidents:comque EZ = EB → EZ 2 = EB2 .D’altrabanda, EB2 = ED2 + DB2 (perPitàgores,teorematambéinclòsals Elements). Pertant,apartirde[2]: GZ ZD + ED2 = ED2 + DB2 → GZ ZD = DB2 (restant ED2 acadamembre). Comque DB = DG,larelació[1]quedademostrada: GZ ZD = DG2 ,elsegment ZG quedadividit enmitjanaiextremaraó.7

• Perdemostrarlarestadelaproposició,raonadelamanerasegüent:

ZD éselcostatdeldecàgonregular

Justificaaquestaafirmacióaplicantclaramentlaproposició XIII,9d’Euclides,totiquelasuposa coneguda:«Sis’uneixenelcostatd’unhexàgonield’undecàgoninscritsenelmateixcercle, larectasenceraquedatalladaenextremaimitjanaraó,ielseusegmentmajoréselcostatde l’hexàgon».

Quedaclarquetambétéencomptequeelcostatdel’hexàgonregularésigualalradide l’hexàgon.8 Defet,quanPtolemeuaplicaaquestaproposició,estàraonantdemanerainversa, mésomenysaixí:«Silarectasencera ZG (talcomhaestatconstruïda)quedatalladaenextrema

07.Aplicantladefinició3delllibre VI d’Euclides:«Esdiuqueunarectahaestattalladaenextremaimitjanaraóquan larectasenceraésalsegmentmajortalcomelsegmentmajorésalsegmentmenor».

08.AquestapropietattambéésbenconegudaperEuclides,quelautilitzaenlaproposició15delllibre IV:«Inscriure unhexàgonequilàteriequiangleenuncercledonat».

imitjanaraóper D,ielseusegmentmajor DG éselcostatdel’hexàgon,aleshores ZD éselcostat deldecàgonregular».

D’aquestamanera,estàconsiderantquelacondicióesmentadaéssuficient,nonomésnecessària.Sitenimencompteque,donadaunacircumferència,lesmidesdelscostatsdel’hexàgon, ieldecàgonsónúniques,podemdonarpervàlidelseuraonament.

BZ éselcostatdelpentàgonregular

Araaplicalaproposició XIII,10d’Euclides,querelacionaelscostatsdelpentàgon,l’hexàgoni eldecàgonregularsinscritsenunacircumferència:«Sis’inscriuunpentàgonequilàterenun cercle,elquadratdelcostatdelpentàgonésigualalsquadratsdelscostatsdel’hexàgoniel decàgoninscritsenelmateixcercle».

Eneltriangle BDZ,esverificalarelació: BZ 2 = BD2 + DZ 2 .Jasabemque BD éselcostatde l’hexàgon, DZ eldeldecàgon,ipertant BZ éselcostatdelpentàgon.Ilaproposicióqueda demostrada.Semprequeconsideremcorrectes,ésclar,lesdemostracionsprèviesd’Euclides.

Desprésd’unallargapresènciadeseglesenels curricula del’estudidelesmatemàtiques,els Elements hancaigutenmoltscasosenlaindiferènciail’oblit.Elstempsevolucionen,inoestractaavuiendia defonamentarl’ensenyamentdelageometriaenunseguimentdogmàticdels Elements d’Euclides, peròsilacuriositatensmouaobrir-nealgundelsvolumsifullejar-lo,ensadonaremquemoltescoses queexpliquemenlesnostresclasseshitenenl’origenielsfonament.

Id’altrabanda,tambéhipodemtrobarunafontd’inspiracióiestímulperresoldrenousreptesmatemàtics.Senseanarméslluny,podemcercarianalitzarlesduesdarreresproposicionsesmentades, queesrefereixenadosteoremesinteressantsinogaireconeguts:Ptolemeuaprofitaaquestarelació entreelscostatsdelpentàgon,deldecàgonielradidelacircumferència(queéselcostatdel’hexàgon)percomençaraelaborarlasevatauladecordes.Aquíraulaimportànciad’aquestdarrerresultat.

4. Aspectes

complementaris

4.1. El número d’or. Una demostració alternativa a la donada per l’A lmagest

4.1.1. Èxits i limitac ions de les matemàtiques en el període hel·lènic

Lesmatemàtiqueselaboradesperlaculturagregavanassolirfiteselevadesalllargdegairebéun mil lenni,peròaixònoensfaoblidar-neleslimitacions;parlemmésaviatdegeometria,moltalmarge del’aritmèticail’àlgebra,quasiinexistents.

Aixídoncs,elsgrecsvanviureladescobertadelsincommensurablescomunaexperiènciatraumàtica, ielsvacondicionarmoltlavisiódel’universmatemàtic.Lafaltadeconfiançaenlanaturalesadeles magnitudsrelacionadesd’algunamaneraambl’infinitilainexistènciadelzero,mésunanotacióno gaireeficientqueassignavaacadanúmerounalletra,vanserlescausesprincipalsd’unalimitació operacionalimportant.

Durantmolttempsnovanassignaralesfiguresgeomètriquesnombresquepoguessinmesurar-ne leslongituds,lesàreesielsvolums,iestrobaafaltarlapresènciad’unaàlgebraensentitalgorísmic

isimbòlic.Aixòcomplicalacomprensiódelsseustextosmatemàtics,malgratreconèixereldomini quevantenirdesofisticadestècniquesgeomètriques.

D’altrabanda,lafilosofiaplatònicaimperantvaimposarenlamatemàticagregaunrigordominant persobredequalsevolaltrevalor(creativitat,intuïció...)quevacristal·litzarenobrescomels Elements d’Euclides,paradigmadelamaneradeferidepensard’aquellaèpoca.Durantmolttemps,lacultura hel·lenísticavadesenvoluparunaciènciamésaviatteòricaiabstracta,feliçambelsseusmètodes iprocedimentsallunyatsdelesaplicacionspràctiquesrelacionadesamblarealitatsensible,corpòria.Donavapreponderànciaaunavisiódelamatemàticapura,considerantqueelveritablecientífic basavaelseuprestigienunsaberteòric,l’únicquelipodiaproporcionarunaposiciósocialeminent.

Peròtambéformenpartdelaculturahel lenística(delasegonapartd’aquestperíode)saviscom ArquimedesiPtolemeu,entremoltsd’altres.Ellsvancontribuirdemaneraimportantaldesenvolupamentdelamecànica,lafísica,l’astronomia... malgrat larelaciód’aquestesciènciesambelmón sensible.

Ptolemeudesenvolupatècniquesdecomputacióquelipermetenfercàlculsposicionalsambuna precisiómoltacurada,inoeslimitaalconreud’unamatemàticaabstracta,jaqueelseuobjectiu éspràctic,sibéconsideral’astronomiaunadelesciènciesfísiquesdemésrang,inopassaperaltel compromísambelrigormatemàtic.Al’escolad’Alexandria,quatreseglesméstard,l’ombrad’Euclides encaraeraallargada.

4.1.2. El número d’or i la secció àuria

Euclidesconeixelsincommensurables;totesles115proposicionsdelllibre X hifanreferència.Caltenir encomptequeesconsideraqueelsllibres V i VI sónbàsicamentd’unaltrematemàtic.Estractad’Èudox deCnidos,que,amblasevateoriadelaproporció,resollacrisiprovocadaenelsfonamentsdela matemàticagregapeldescobrimentdelesmagnitudsirracionals(designadespelmotgrec alogon), peròquenovangaudird’unaidentitatpròpiacomanombres.Elslímitsimposatsperlaracionalitati l’ordrehel·lènicsquenoméspodientenirencompteunmónregitpelsnombres«racionals»novan permetreanarmésenllà.

Euclidessapquelaseccióàuria(anomenadamitjanaiextremaraó)produeixsegmentsincommensurables:

Siunarectacommensurableestallaenextremaimitjanaraó,cadascundelssegmentséslarecta senseraóexpressableanomenadaapòtoma.(Euclides,XIII,6)

Peròsempreesparlaentermesdeproporció,inodenombre.

Actualment,tambépodemparlardeproporcióoraó,peròelresultatd’aquestaproporciótéentitat pròpia,éselnúmerod’or,

Figura 6. Divisió àuria d’un segment.

Observemlafigura6:Si B determinaunaseccióàuriasobreelsegment AC ,aleshores

AC AB = AB BC .

Siconsiderem AB comaunitat,ianomenen AC = x ,obtenimlarelacióequivalent:

Aquestaequaciónoméstéunasoluciópositiva,queés Φ

4.1.3. Una demostració alternativa de la que es dóna en l’Almagest

Lautilitzacióde Φ enspermetunademostracióalternativaalapropietatdel’apartat2.3,diferentde laquefaPtolemeu.EstractadeprovarqueelpuntDdeterminaunaseccióàuriasobre ZG

Tornemalafigura5.Siagafemcomaunitatelradidelacircumferència, DG = BD = 1,noméscal demostrarque ZG = Φ

SiapliquemelteoremadePitàgoreseneltriangle BDE,

Pertant,

4.2. La trigonometria de Ptolemeu. Les cordes

4.2.1. Origen de la trigonometria

SegonselGènesi,l’origendeltempsidelesclausqueenspermetendesxifrar-loésanterioralacreació del’home(ideladona).ElquartdiaDéuvadir:«Quehihagillumeneresalfirmamentdelcel,que separineldia,lanit,ifacindesenyalperalesfestes,ielsdiesielsnits».VacrearelSol,laLlunailes estrellesper«regulareldiailanitisepararlallumdelestenebres».Laseparaciónovaserradical, persortperatotselsque,desprésd’aquestacreació(jasiguirealovirtual),hanvolgutdesentranyar elsmisterisinherentsalpasdeltemps,lesestacions,elsdiesileshores.Noéstotallafoscordela nit,atenuadaperlallumdelaLlunailesestrelles,iduranteldiaelSolescampaombressobretota lasuperfícieil·luminadadelaTerra.Iaixíl’estudidecertesombreshadonatlallumnecessàriaper entendremoltsesdeveniments.Segonsunaforismed’unanticllibrexinès,«elconeixementsurtde l’ombra,il’ombrasurtdelgnòmon».9

Sabemque,utilitzantelmètodedelesombres,Talesvamesurarl’alturadelespiràmidesiEratòstenes elradidelaterra.L’estudidelaproporcionalitatpermesurardistànciesespotconsiderarunpas importantenlagestaciódelatrigonometria.Hiparc,quevaviurealsegle II aC,iésconsideratun delsastrònomsmésimportantsdel’antiguitat,hivaferavençosimportants,peròenconeixeml’obra nomésperreferències.10 Sabemquevaconstruirunataulamoltcompletadecordes,quevadonar laposiciód’unmilerd’estrelles,vadescobrirlaprecessiódelsequinoccisitambévadesenvoluparel mètodedeprojeccióestereogràficaquepermetelaborarmapesdelcelidelaTerra.

TotsaquestsresultatsvanserrecollitsperPtolemeuenl’Almagest.Aquestllibretambéconstadetretzecapítols(comels Elements d’Euclides),itambéespotconsiderarunarecopilaciódemoltsconeixementsanteriors,amésdelesaportacionspròpiesdel’autor.I,sobretot,lesduesobress’hanconservat completes,ipertantsónunstestimonisimportantsdelsconeixementscientíficsdelasevaèpoca.

4.2.2. Les cordes

Cadacorda AB determinaunarcsobrelacircumferènciaiunanglecentral α corresponent:

LatauladecordesqueelaboraPtolemeudónalalongituddecadacordaenfunciódel’anglecentral corresponentde0◦ a180◦ enintervalsdemiggrau.Aquestatabulacióésnecessària,jaquel’amplitud del’angleilalongituddelacordanosónvalorsdirectamentproporcionals.

Elconceptedecordaésmoltproperalconceptedelsinusipotsermésnatural.Sianomenem d ala longituddelacordai r alradidelcercle,aleshores d = corda (α) = 2r sin (α/2).

Ptolemeuagafacomaradidelcercleelvalor r = 60,jaquetreballaenelsistemasexagesimalbabilònic.Siconsiderem r = 1,aleshores

sin (α/2)= d /2.

Talcomjaheexplicatabans,desprésdedonarperjustificadalaconstrucciódelcostatdelpentàgon regular,Ptolemeuutilitzaaquestaconstruccióialtresresultatsmatemàticspercalcularunataulade

10.Perexemple,gràciesalcomentarisdeTeód’Alexandriaal’Almagest dePtolemeu.

Figura 7

cordesmoltcompleta.Concretamentenunciaidemostral’anomenatteoremadePtolemeu(vegeu nota6)iapartird’aquestteoremacalculalacordadeladiferènciadedosanglesiladel’anglemeitat, ambfórmulessimilarsaladelsinusdeladiferènciaielsinusdel’anglemeitatdelatrigonometria actual.D’aquestamanera,calculalescordesd’anglesseparatspermiggrau.Jaheobservatqueenel càlculd’aquestestaulesvaassolirunagranprecisió.

Enlesmatemàtiquesdel’Almagest nohitrobemnomésunamatemàticaabstracta,pura:elcòmput matemàticescomençaaobrircamí,sensecomplexos.

Abansd’acabarelcapítol I estudiatambémoltsaspectesdelatrigonometriaesfèrica;defet,l’Almagest vainfluirenlatrigonometriadetotal’antiguitat,itoteslestaulesastronòmiquesaparegudesfinsal segle XII hitenenlabasefonamental.

Escoltem,peracabar,elmateixPtolemeu.Seguramenteraconscientqueeldeixantdelasevaobra creariasolcsinesborrables:

Sémoltbéquesócmortal,criaturad’unsoldia.

Peròsilamevamentsegueixelssinuosospassosdelesestrelles aleshoreselsmeuspeusnoesquedendurantgairetempsalaterra, isostingutpelmateixZeusimmortal m’alimentofinsalasacietatd’ambrosia,elmenjardiví.

4.3. El triangle auri major o triangle de Price

Peracabar,proposoalgunproblemacomplementariperalsquetinguincuriositatiganesdepensar. Ésfàcildemostrarquel’únictrianglerectanglequetéelscostatsenprogressióaritmèticahadeserel quetélesmidesdelaconegudaternapitagòrica3,4i5(operextensió,qualsevoltrianglerectangle semblant,comaraeldemides6,8i10).Totsaquestsespodenconsiderardelamateixaforma(isomorfs),iéselquealgunsanomenentrianglesagrategipci:espottrobarcomaformageneradorade lapiràmidedeKefren,enlasevasemisecciómeridiana(Ghyka,1953).

Tambéespotdemostrarquel’únictrianglerectanglequetéelscostatsformantunaprogressiógeomètricatélesmides1, √Φ i Φ (oqualsevolaltrecongruent).Aquestésl’anomenattriangleaurimajor otriangledePrice(deuelnomalmatemàticanglèsW.A.Price,queopinavaqueéspresentenlagran piràmidedeKheops).Tambéaltrescientíficsihistoriadorsdelaciènciaconsiderenquelasemisecció meridianad’aquestapiràmideésuntriangleauriambcostatsproporcionalsa1, √Φ i Φ,respectivament.Espotdibuixarfàcilmentapartirdelesconstruccionsanteriorsqueheexplicat(enlafigura8 éseltriangle CDG).

Figura 8. El triangle auri major.

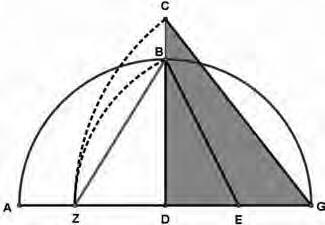
Aquestdibuixl’heobtingutapartirdeldelafigura5.Recordemque DG = 1.Elpunt E éselpuntmitjà delsegment DG,i D determinaunaseccióàuriasobre GZ.Desprésnoméscalprendreladistància GC = GZ = Φ iconsiderarlapropietat:

1 + Φ = Φ2 perdemostrarque DC = √Φ

Passatsmésdequatremilanysdesquevaserconstruïda,nopodemprecisarexactamentlesmides delagranpiràmide,jaquehapatitmodificacionspercausesdiverses.Espotcomprovar,però,que encaraactualments’adiuenforçaalesdeltriangleauri.Totiaixò,nodeixadeserunaopiniódiscutible. Iencaraquefosencertada,aquestfetaïllatnoimplicariaelconeixementconscientdelaproporció àuriaenl’àmbitdelaculturaegípcia.

Unavisióplatònicadelconeixementensfaconsiderarquelesmatemàtiquesjaexisteixenenelseu reialme,mésenllàdelesquepodemarribaraconèixer,iquedefetelllibredelanaturaestàescrit enllenguatgematemàtic,comdeiaGalileu.Peròquinessónlesquevanarribaraconèixerelsconstructorsdelespiràmides?Sónpoqueslesestructuresarquitectòniquesquehangenerattantsmites icontrovèrsiescomlagranpiràmide.

Explico,noméscomamostra,unad’aquesteshistòriesinsòlites.L’historiadorgrecHeròdot,considerat elparedelahistoriografia,vavisitarEgipteelsegle V aC.Segonsdiversosautorsvadeixarescrit:«El quadratdel’alturadelapiràmideésigualalasuperfícied’unadelessevescares».Silapropietat enunciadaéscerta,espotdemostrarambunscàlculssenzillsqueeltrianglequeformaelsemiperfil delagranpiràmideésuntriangleaurimajorexacte.Hodeixocomunrepte,totiquese’npottrobar lasolucióconsultantlesfontsadequades(Livio,2009).

Elmésinsòlitd’aquestahistòriarauenelfetquedurantmésd’unsegles’haanatcitantenàmbits «científics»unaafirmacióqueHeròdotnovafermai.Noméscaldriaconsultarlafontoriginal,elllibre II, anomenat«Euterpe»,delsnoullibresd’Històries,enelparàgraf124.Jasesapquenormalmentl’aigua ésméspuracommésproperessiguinlesdeus.

5. Conclusions. Implicacions didàctiques

Enunarevistacomaquesta,interessadaperladidàcticadelesmatemàtiques,nopodemdeixarde fer-nosunapregunta:Quinsdelsaspectescontemplatsenaquestarticlesónaplicablesal’aula?

Ésclarquenototselsalumnessolenassolirels5nivellsdeVanHiele.Ladeduccióformalielrigor difícilmentsónassoliblespelsestudiantsnouniversitaris.Síquepodranassolirfàcilmentelmètode deconstrucció,visualitzar,experimentar...

Totiaixò,abordarunproblemacomeldelaconstrucciódelpentàgonregular(ialtresderelacionats) potarribarasermoltenriquidoriengrescador,comhohaestatperami.Tambépotsuggerirreflexionsdetotamenasobreladimensióculturaldelesmatemàtiquesielseunotableimpacteenel desenvolupamentdelahumanitat,osobrelespeculiaritatsqueladistingeixendelesaltresformes deconeixementicomsen’hadeplantejardemaneraadientl’ensenyament.

Elstempscanvienitambéhofalasocietatd’unaformaaccelerada,irreversible.Novesideessobre l’ensenyamentdelesmatemàtiquesneixenambforçaarreudelmón.Diversesideesquesónconvergentsenelsseuseixosprincipalsensconvidenaprestarunaatencióespecialaldesenvolupamentde

competènciesohabilitatscomarapensarmatemàticament,saberargumentar,representaricomunicar,resoldre,modelitzar...itotaixòencontextosreals,nogairellunyansdel’experiènciaquotidiana. Elmónrealsignifical’entornsocial,personal,laboral,científic...enelqualvivim.

Desdelesmatemàtiqueshemd’educarlespersonesperquèespuguinbeneficiardelaculturamatemàticaipuguinactuar,delamillormanerapossible,enelmónrealenquèhandeviure.Icalfer-hodes delafacetapersonal,socialiprofessional,tantenelpresentcomenelfuturmésomenysprevisible.

Ladidàcticadelageometriaésunadelespartsdels curricula quehaestatsotmesaamésvicissituds enelsdarreresanys.L’agostdel1976,durantlacelebraciódel’ICME(InternationalCongressonMathematicalEducation)aKarlsruhe,elgrangeòmetraanglèsMichaelAtiyahvadir,enunaconferència plenària:

HeudestronataEuclides,hiesticd’acord.Peròdequinamaneraheusubstituïtl’ensenyament delageometria?Lamatemàticaques’ensenyaavuienlamajoriadelspaïsosestàencaramés allunyadadelarealitat,perquènotécapsuportgeomètric.S’hadetenirencomptequelaintuïció geomètricaésiseràsemprelafontméspoderosaperalacomprensiódemoltstemes.Pertant,el pensamentgeomètrichadeserestimulatalmàximpossibleientotselsnivells.

Desprésdelapreponderànciadelageometriad’Euclidesdurantmoltssegles,idel’abandóinjustificat delageometriaintuïtivaosintèticaacausadelaimplantaciódelamatemàticamoderna,itambéper unúsexclusivistadelageometriaanalítica,11 avuiesconsideraunanecessitatineludiblerecuperarel contingutespacialiintuïtiudelageometria.

SegonsMigueldeGuzmán(2007):

Quanparlodepensamentgeomètricnoemrefereixoal’ensenyamentdelageometriaméso menysfonamentadaenels Elements d’Euclides,sinóaalgunacosamésbàsicaiprofundaqueésel conreud’aquellesporcionsdelamatemàticaqueprovenendelacapacitatdel’homeperexplorar racionalmentl’espaifísicenquèviu,lafigura,laformafísica,iintentenestimular-la.

Quanesdiuqueésnecessariquelesmatemàtiquesincideixinenel mónreal,podemcaureenun paranyioblidar-nosdelmónmental,indissolubled’aixòde«fermatemàtiques».Aquestmónmental éstanrealcomelmónfísic.Moltsproblemesreals,ambsolucionsreals,nos’haurienresoltsenseun saltalmónabstracte,laboratorifecunddemoltinventsmatemàtics.

Estractad’explorarracionalmentelmónfísic,ésadir,ambmodelsmentals.Aixòéslaveritableessènciadelamatemàticaquenopodemoblidaral’horaensenyar-la.Determinarl’alturadelsalt,com fer-loitrobar-hielmomentadequatsóntasquesquecaltenirencompteenelprocés.

L’any1995esvacelebraraCatàniaelcongrésICMI«StudyonGeometry».Desprésd’undebatmolt enriquidoresvaarribarainteressantsconclusions,recollidesenunapublicació(Mammana,1998).12 Enrecomanolalecturaatotselsinteressatsenqualsevolaspectedeladidàcticadelageometria,ja queseguramenthitrobaranmésd’unarespostasimésnomeditada,jaqueaquestcongrésesva prepararambanysd’antelacióifòrumsdedebatprevis.

11.Totielsseusèxitsindiscutibles,l’úsdel’àlgebrageomètricadevegadesfaelsproblemesirresolublesosimplement implantejables.Vegeu,sino,certsproblemesgeomètricsdelesOlimpíadesmatemàtiques.

12.Algunsdelsarticlesd’aquestapublicacióespodentrobartraduïtsal’adreçahttp://www.euclides.org(vegeumapa delweb).Tambéhipodemtrobarunresumdels Elements d’Euclides.

Quèhandeconteniroquècontenenelsnous curricula delageometriaendiversospaïsosdelmón? Quinaéslatendènciageneral?Comn’hadeserl’ensenyamententoteslesdiferentsetapesdel’escola?Quinpaperhihandetenirlavisualització,l’exploracióintuïtiva,elraonamentilademostració? Compodenincidirlesnovestecnologiesenelsprocessosd’aprenentatge?Aquestsaspectesimolts d’altressóndesenvolupatsenlesactescorresponents.Amés,eldebatésbenviuinohaperdut actualitatenaquestsdarrersanys.

Enúltimlloc,vullexpressarelmeuagraïmentalsprofessorsicompanysdelcursdepostgraude DidàcticadelesMatemàtiquesdelaUPF(curs2008-2009),degratsrecords.Senseelseuestímuli comprensióaquestarticlenohauriasortitalallumnihauriaquedatal’ombra,perinexistent.

6. Referències

Boyer,CarlB.(1999). Historiadelamatemática.Madrid:Alianza.

Buhigas,Jaime.(2008). Ladivinageometría.Madrid:LaEsferadelosLibros. Cockcroft,W.H.(1985). Lasmatemáticassícuentan.InformeCockcroft.Madrid:ServiciodePublicacionesdelMinisteriodeEducaciónyCiencia.

DeGuzmán,Miguel.(2007).EnseñanzadelaCienciasylaMatemática. RevistaIberoamericanadeEducación,43,19-58.Madrid:OrganizacióndeEstadosIberoamericanosparalaEducación,laCienciayla Cultura.

Euclides.(1991). Elementos.Madrid:Gredos.[Obracompletaentresvolums.1rvolum:llibres I-IV.2n volum:llibres V-IX.3rvolum:llibres X-XIII].

Fritz,Kurt.(1945).ThediscoveryofincommensurabilitybyHipassusofMetapontum. AnnalsofMathematics,46,242-264.Princeton.

Ghyka,Matila.(1953).Estéticadelasproporcionesenlanaturalezayenlasartes.BuenosAires:Poseidón.

GonzálezUrbaneja,PedroMiguel.(2004).Lahistòriadelamatemàticacomarecursdidàcticiinstrumentd’integracióculturaldelamatemàtica.Reconstruccióinformàticadelsproblemeshistòrics ambfortaincidènciaalaclassedematemàtiques.Annex:Elsincommensurables[enlínia].Barcelona:Memòriadeltreballrealitzatdurantlallicènciad’estudisaprovadapelDepartamentd’Educació. http://www.xtec.cat/sgfp/llicencies/200304/memories/801a.htm[Consulta:25-VII-2011].

Livio,Mario.(2009). Thegoldenratio. NovaYork.BroadwayBooks. MacTutorHistoryofMathematicsClaudiusPtolemybiography[enlínia].http://www.gap-system.org/ ~history/Biographies/Ptolemy.html[Consulta:25-VII-2011].

Mammana,C.iVillani,V.(ed.).(1998). PerspectivesontheTeachingofGeometryforthe21stCentury.An ICMIStudySeries:NewICMIStudy,vol.5.

NCTM.(2003). PrincipiosyestàndaresparalaEducaciónMatemática.Sevilla:SociedadAndaluzadeEducaciónMatemáticaThales.

OCDE.ThePISA2003:AssesmentFramework.Mathematics,Reading,ScienceandProblemSolving KnowledgeandSkills.París.

Pedersen,Olaf(1974). AsurveyoftheAlmagest.Odense:OdenseUniversityPress.

PlaiCarrera,Josep(2009). LiuHui.Nuevecapítulosdelamatemáticachina.Madrid:Nivola.

Plató.(2003). LaRepública.Llibre VII.València:UniversitatdeValència.ServeidePublicacions.

Pólya,G.(1982). Cómoplanteariresolverproblemas.[10areimpressió].Mèxic:Trillas.

Ptolemeu,Claudi(1984). Ptolemy’sAlmagest.[TraduccióianotacionsdeG.J.Toomer].Londres:Duckworth.

PuigAdam,Pedro(1960) Lamatemáticaysuenseñanzaactual.Madrid:MinisteriodeEducaciónNacional.

RomeroVallhonesta,Fàtima;MassaEsteve,M.Rosa.(2003).ElteoremadePtolemeu. Biaix,21,31-36. Girona.

Santaló,LluísA.(1993). Lamatemàtica:unafilosofiaiunatècnica.ViciGirona:EumoiUniversitatde Girona.

Vernet,Joan;Parés,Ramon(2004). LaCiènciaenlahistòriadelsPaïsosCatalans.[VolumI].Institutd’EstudisCatalansiUniversitatdeValència.

Intuïcionsdelsalumnes desecundàriasobre laprobabilitat. Unarecercasobrelainfluència deltreballempíricenelcasd’un

esdevenimentcompost

FermíRojoCort

INSMiquelBoschiJover,Artés(Barcelona),frojo@xtec.cat

JordiDeulofeuPiquet

DepartamentdeDidàcticadelesMatemàtiquesilesCiències UniversitatAutònomadeBarcelona,jordi.deulofeu@uab.cat

Resum Abstract

Enaquestarticleespresentaunainvestigació relacionadaambdosconceptesprobabilístics,l’espai mostralilaprobabilitatd’unesdevenimentcompost, realitzadaambalumnesde2nd’ESO.Enelcampdela probabilitatéssabutqueunensenyamentefectius’ha defomentarenelconeixementpreviperpartdels professorsdelesintuïcionsquepresentenels alumnes.Enaquestsentit,undelsobjectiusd’aquest treballésdeterminariclassificarlesintuïcionsdels alumnesenrelacióambelsdosconceptesesmentats. Aquestatascas’harealitzatseguintelsparàmetres següents:elconjuntd’estratègiesdesenvolupades,la comprensiódelessituacionspresentadesila naturalesadelesargumentacionsenrelacióambels diferentssignificatsquepotprendrelaprobabilitat. Peral’obtenciódelesdadess’hautilitzatunadeles provesd’avaluaciódelescompetènciesbàsiques aplicadespelDepartamentd’Educacióenelsanys 2006-2007.Paral·lelament,s’haanalitzatlainfluència deltreballempíricenlaformacióilamodificacióde lesintuïcionsdelsalumnes.Enaquestsentit,els resultatsdelainvestigacióassenyalenuncamía seguirperajudarelsestudiantsacrearintuïcions correctes,ialavegadamostrenquecertesintuïcions quepodeninterferirenaquestcamísovintsón evitablesambl’ajutdel’experimentació.

Thispaperpresentsaninvestigationwithtwo probabilisticconcepts,thesamplespaceandthe probabilityofacompoundevent,madewith 13-14yearsstudents.Inthefieldofprobabilityitis knownthateffectiveteachingshouldbepreceded byresearchintotheprimaryintuitivesubstrateof therelevantsubject.Inthissense,oneofthe objectivesofthisstudyistodeterminateand classifythestudents’intuitionsaboutthetwo conceptsmentionedabove.Thistaskwascarried outaccordingtothefollowingparameters:theset ofstrategiesdeveloped,theunderstandingofthe situationspresentedandthenatureofthe students’argumentsinrelationtothedifferent meaningsoftheconceptofprobability.Toobtain thedata,weusedoneofthebasicskillstest implementedbytheEducationDepartmentin 2006-2007.Simultaneously,weanalyzedthe influenceofempiricalworkintheformationand modificationofthestudents’intuitions.Inthis sense,theresultsoftheinvestigationindicatea wayforwardtohelpstudentscreatecorrect intuitionsshowing,atthesametime,thatthe existenceofcertainintuitionsthatcaninterferein theirwayareoftenavoidablewiththehelpof experimentation.

1. Introducció: intuïció, matemàtiques i probabilitat

Enmatemàtiques,laintuïciótéunpaperquepodríemqualificard’ambigu.Enefecte,avegadesuna qüestiónonecessàriamentgairecomplexaesrespondemanera intuïtiva,que,desprésd’unareflexió mésaprofundida,esdemostraqueésfalsa.Oal’inrevés:unaafirmacióque intuïtivament esdonaria perfalsaalcapd’unquanttempsesdemostraqueéscerta.Una intuïció,doncs,permésbrillantque sigui,noéssuficient;potcaldremoltdetreballperpoderarribaraunademostracióquelalegitimio, contràriament,unademostracióquelainvalidi.

Enprobabilitatesdonenmoltesfalsesintuïcions,jaque,alesimprecisionsdellenguatge(confusió entreelllenguatgehabitualielmatemàtic,quesovintfaservirlesmateixesparaulesambunsentit mésrestrictiu,peròmésprecís)calafegir-hilesconclusionsimpròpiesqueestreuend’unaexperiència concreta,sensetenirencomptequeleslleisdelaprobabilitatesrefereixensempreaprediccions globalsinopasaexperiènciesparticulars.

Enelcampdeladidàcticadelaprobabilitat,s’hademostratqueunensenyamentefectius’hadefonamentarenelconeixementprevirespecteaaquestesintuïcionsquepresentenelsestudiants,jaque, quans’ensenyaalgunacosanova,elsalumnesconstrueixenaquestnouconeixementconnectantla novainformacióamblaqueellsjahavienassumitprèviamentcomacorrecta.

Elcursescolar2006-2007,elfetquel’institutontreballàvemfosresponsabledel’aplicaciódeles provesdelescompetènciesbàsiquesproposadespelDepartamentd’Educacióensvabrindaruna oportunitatexcel·lentperduratermeunainvestigacióeneltema.Unadelesprovestractavaels conceptesd’espaimostralideprobabilitatd’unesdevenimentdesd’unavessanttotalmentintuïtiva ipresentavaactivitatsaalumnesquenohavienrebutinstruccióprèviasobreeltema.Totselsalumnesquecursaven2nd’ESOd’arreudeCatalunyahavienderealitzarlesprovesi,pertant,disposàvem delesrespostesdelsalumnesdelcentreontreballàvem.Comresponienelsalumnessenseinstrucciódavantd’aquestestasques?Icomaquestsresultatspodienajudaraprendredecisionspertalde millorarl’ensenyamentefectiuenaquestcamp?

SegonselsestudisdeFischbein(1991),lespersonesfanservirintuïcionserròniesenelraonament probabilístic.Sen’hanestudiatcertsaspectes,comaralesintuïcionsdirigidesperunasèriedemecanismesinvestigatsperpsicòlegsididactesdelamatèriaanomenadesheurístiques(Tversky&Kahneman,1982).Altresinvestigacionshanintentatdeterminarquinpapertélainstruccióeneldesenvolupamentdelraonamentprobabilístic(Fischbein,1984).Noobstantaixò,hihadeterminatsaspectes quenohanestatgaireinvestigats.Enparticular,noconeixemcapestudiqueesrefereixidemanera explícitaalpaperquetél’experimentació,entesacomlageneracióil’anàlisidedadesperpartdels alumnes,enlacreacióomodificaciódelesintuïcionsdelsindividus,concretamentdelesintuïcions ques’utilitzenperferelpasdel’empirismeal’anticipaciódavantdesituacionsaleatòries.

Aquestarticlepresentaunapartdelarecercamotivadaperlesqüestionsanteriors(Rojo,2009).Els objectiusfonamentalsdelarecercasónelssegüents:

1.Determinarlesintuïcionsdelsalumnessobre espaimostral i probabilitatd’unesdevenimentcompost enlessituacionsproposadesperlescompetènciesbàsiques.

2.Classificarlesintuïcionsiinterpretar-lesd’acordambelmodeldescritenelmarcteòricescollit.

3.Analitzarlainfluènciadeltreballempíricenlacreacióilamodificaciódelesintuïcionsdels alumnes.

Enconcret,enaquestarticleveuremelsresultatsobtingutsenrelacióambelstresobjectiuscentrantnosenuncasconcretirepresentatiudelsdiferentsqueesvanestudiarenlarecerca.

2. Referents teòrics: intuïcions i nivells de raonament

PeralnostreestudisónespecialmentinteressantselstreballsdeFischbein(1975,1984,1991,1997) enelcampdelesintuïcionsitambélesinvestigacionsdePolaki(2000,2005)enrelacióambels raonamentsensituacionsaleatòries.

Fischbein(1975)esvainteressarperl’exploraciódelsfonamentsintuïtiusiprecursorsdelconeixementprobabilísticpertaldemostrarqueelsnenstenenideescorrectesparcialmentformades,iva analitzarl’efectedelainstruccióenlamillorad’aquestesintuïcions.Vaatorgar,també,unagranimportànciaalpaperdelaintuïciócomacomponentdelaintel·ligència.Enaquestaobra,Fischbein consideraquel’ensenyamentd’unanovamatèria,pertalquesiguiefectiu,had’anarpreceditd’una detalladainvestigaciósobreelsubstratintuïtiuqueentenenelsalumnes,delamateixamaneraque ésnecessarianalitzarelterrenysobreelqualesvolconstruirunnouedifici.L’estudidelesintuïcions potmaterialitzar-seenelcampdelaprobabilitat,jaquelacomplexitatdelessituacionsquotidianes ensindueixaadoptarcontínuamentuncomportamentprobabilístic.Lanecessitatdeprendredecisionsensobligaaferestimacionsintuïtivesdepossibilitats(lamajoriadevegades,detipussubjectiu). Elsinfantss’enfrontendesdemoltpetitsaunarealitatregida,enmoltscasos,perleslleisdel’atzar.

Lesintuïcions,segonsFischbein,sónprocessoscognitiusqueintervenendirectamentenlesaccions pràctiquesomentalsdelsindividus,iquetenenlescaracterístiquessegüents:immediatesa,globalitat, capacitatd’extrapolar,estructurabilitat,iautoevidència.Enpoquesparaules:laimmediatesasignifica quesorgeixenambfreqüènciadeformaespontàniatotiserelresultatdelamaduraciódemoltes experiènciesanteriors;elcaràcterglobals’oposaaladescomposicióenparts;lesintuïcionsvanmés enllàd’uncasparticulari,encertsentit,tenenuncaràcterteòriciperaixòserveixenperextrapolarofer prediccions;diversesintuïcionsesrelacionenentresiformantestructuresderaonament,ifinalment acostumenaserautoevidentsperal’individu,demaneraqueperaellnonecessitendemostració.

Hihatressituacionsqueespodenpreveureenrelacióambelsubstratintuïtiu:

1.Lainformaciótransmesadurantelprocésd’aprenentatgeestrobaambunaintuïcióprèviacompatible,iaquestacompatibilitatespotutilitzardirectamentenl’ensenyament(perexemple,«la distanciaméscurtaentredospuntséslalíniarecta»).

2.Laintuïcióprèviaésoposadainoéscompatible,demaneraques’arribaaunacontradiccióentre laintuïcióprimàriaielfetobjectiuodemostrable(perexemple,«elconjuntdelsnombresracionals ésequipotentambelconjuntdelsnombresenters»).

3.L’absènciadecapintuïcióprèviapertinentalainformacióproporcionada(perexemple,«lesmedianesd’untriangleestallenenunpunt»).

Fischbeinanomena intuïcióprimària aquellesqueexisteixenabansiindependentmentdequalsevolensenyamentsistemàticintencionat,i intuïcionssecundàries aquellesquesónsistemàticament construïdesdurantelprocésd’ensenyament.

Unaconclusióglobaldelsseusestudis(Fischbein,1984i1991)ésquel’irregular,iavegadessorprenent,substratintuïtiuhadesersistemàticamentexploratabansdel’inicidelaconstrucciód’un sistemaconceptualenelcampdelaprobabilitat.Així,siunvolintentardesenvolupar,apartirde

l’ensenyament,unsubstratintuïtiufort,correcte,coherentiformalperalraonamentprobabilístic, s’hauràd’enfrontarambunaàmpliavarietatd’intuïcionserrònies,biaixos,tendènciesemocionalsi malentesos.

D’altrabanda,Polaki(2005)analitzaleshabilitatsdelsestudiantsfinsa14anysenelmomentde generarunconjuntderesultatsassociatsaunesdevenimentcompostenrelacióambesdeveniments simplesicompostos,i,enparticular,alllançamentdedosdaus.

Polakiconsideraque,pertalqueelsalumnespuguincomprendreexperimentscompostos,hande sercapaçosde:

• generarelsconjuntscompletsderesultatspercadaexperiment,i

• analitzariutilitzarlacomposició,lasimetriaol’experimentaciósobrel’espaimostralcomabase perferbonesprediccionsprobabilístiques.

D’acordambaixò,conclouqueelsconceptesd’espaimostraliprobabilitatd’unesdevenimentconstitueixenunboncontextperexplorarleshabilitatsdelsestudiantsenelmomentd’enfrontar-sea esdevenimentscompostos.

Apartird’aquestesconsideracions,calferreferènciaal’estructuradelpensamentprobabilísticque presentaPolaki(2000),laqualdescriuelpensamentprobabilísticdelsestudiantsapartirdecincpilars: espaimostral,probabilitatd’unesdeveniment,comparaciódeprobabilitats,probabilitatcondicional iindependència.Lavalidaciódel’estructuraproposadaperPolakielvaportarasuggerirl’existència dequatrenivells,quevaanomenar:subjectiu(nivell1),detransició(nivell2),quantitatiuinformal (nivell3)inumèric(nivell4).

TalcomdescriuPolaki(2000),elsestudiantsqueraonenanivell1generalmentdonenrespostesde tipussubjectiu,incloent,finsitot,raonamentsdetipusdeterministes.Perexemple,argumentaran queunnombredeterminatésmésprobablequesurtiquenopasunaltreenelllançamentd’undau «perquèéselseufavorit»obé«perquèsolsortiraixí».

Contràriament,elsestudiantsdenivell2tenenmésèxital’horadeferprediccionsenesdeveniments simplesicomencenautilitzarraonamentsquantitatiusvàlids,totiqueinformalsideformainconsistent,perpredirquinéselresultatmésomenysprobable.Perexemple,aquestsestudiantsfaranservir l’expressió«3de6»sise’lsdemanalaprobabilitatd’obtenirunnombreparellenelllançamentd’un dau.Noobstantaixò,aquestllenguatgeinformalquantitatius’utilitzadeformaforçainconsistentia vegadeselsalumnesesremetenaraonamentssubjectius.Aquestfetsel’haanomenat reconeixement delaincertesasensesaberquantificar-la.

Enunnivell3,elsestudiantssóncapaços,perexemple,degenerarconjuntscompletsderesultats peresdevenimentscompostosfentservirunaestratègiaparcialmentgenerativa.Ienelnivell4,els estudiantsjasóncapaçosd’utilitzarunaestratègiacompleta.Perexemple,unadelestasquesquees vaproposarésllistartoteslespossiblescombinacionsdedinarenunrestaurantlacartadelqualconté 7platsi3begudes.Elsestudiantsagafavencadascundelsplatsielcombinavenamblesdiferents begudesdemaneraqueobtenienelconjuntde21resultats.English(citatenPolaki,2005)anomena aquestaestratègia comptaquilòmetres.

3. Disseny de la recerca

3.1. Objecte de l’anàlisi: una prova de les competències bàsiques

Apartirdelesprovesielsresultatsdelescompetènciesbàsiquesqueesvanrealitzaralscentresde secundàriadeCatalunyaaalumnesde2nd’ESO,13-14anys,elscursos2005-06i2006-07,enquè s’avaluava,entremoltesaltrescoses,elpasdel’empirismeal’anticipaciódavantdesituacionsd’atzar idesdelasevavessantmésintuïtiva,vamrealitzarunestudisobrelesintuïcionsquepresentenels alumnesenelmomentderesoldresituacionscontextualitzadesd’aquestamenaambesdeveniments compostos.Caltenirencomptequeaquestsalumnesnohavienrebutinstruccióprèviaespecíficadel tema,peròdisposaven,d’acordambl’activitatd’avaluacióproposadaenlaprovadelescompetències bàsiques,d’unasèriededadesqueellsmateixoshavienobtingutexperimentalment.

Pertald’avaluarlescompetènciesbàsiquesentrel’alumnatde13-14anys,elDepartamentd’Educació vaproposarunconjuntd’activitatsestructuradesenquatreprovesd’avaluació:lesproves1i2es realitzavenperescritindividualment,laprova3esrealitzavaindividualmentensuportTICi,finalment, laprova4esrealitzavaperescritenpetitgrup(3o4alumnes),ambobservacióendirectedeltreball delsgrups.

Laprova4,anomenada«Unparelldedaus»,vaserl’escollidacomadocumentd’estudiperalanostra recerca.Aquestaprovas’encarregavad’avaluarlescompetènciesbàsiquessegüents:

• M5-Planificariseguirestratègiesderesoluciódeproblemes,imodificar-lessinoesmostrenprou eficaces.

• M9-Compararlafactibilitatdefetsaleatorisensituacionssimples.

Enaquestaactivitat,queesrealitzavaengrupsdequatre,elsalumneshaviendetirardosdaus50 vegadespertald’operarelsnúmerosquesortienenlestiradesiestudiarlesfreqüènciesambquèes repetienelsresultats.Abans,però,derealitzarlestirades,elsalumness’havienderepartirlestasques següents:

1.Unmembredelgruphaviad’efectuarlasumadelsdosnúmerosqueanavenapareixentalsdaus encadatirada.

2.Unaltrehaviad’efectuar-nelaresta(elmésgranmenyselméspetit)

3.Unaltrehaviad’efectuar-nelamultiplicació.

4.Elquartmembredelgrupsimplements’haviadefixarenquineraelnúmeromésgrandelsdos. Enelcasquealgungrupfosformatúnicamentpertresmembres,aquestadarreratascanoes realitzava.

Aixídoncs,lafeinaquese’lsdemanavaeralad’anotarelsresultatsdelesoperacionsmentreesfeien lestiradesi,enacabat,respondreunseguitdepreguntesenrelacióambelsresultatsobtingutsila freqüènciaamblaquals’havienobtingut.Lespreguntesestavenestructuradesenlesactivitats19i 20delesproves.

L’activitat19tractadelconcepted’esdevenimentelemental,lasevaidentificacióigeneració.Elsalumnesuncopidentificatsielsesdevenimentsllistatserenpossiblesono,haviendegenerarelsdiferents casosfavorablesqueportenacadascundelsesdeveniments.

Així,amblafinalitatdeprovocarunareflexióquepermetilaimmersió,demaneraindividualitzada, enlaqüestiócentraldelaprova(l’estudidefenòmensaleatoris),espretenia,d’unabanda,ajudar

aferelpasdel’empirisme(dadesobtingudes)al’anticipació(dadespossibles),pasindispensable peral’èxitgeneraldelaprova.D’altrabanda,tambéespreteniafacilitarlareflexióquepermetés enelseumomentmesurarla«magnituddepossibilitat»queteniacadaresultat,demanantquees fesunaanàlisidecasos,pasquehauriadepermetrefinalmentefectuarunaestimacióqualitativa delaprobabilitatdecadaesdeveniment,obé,finsitot(malgratquenoeral’objectiudelaprova), quantificar-neaquestaprobabilitat.Ésenaquestpasdel’anticipacióenquèelsalumneshaviende recórreralessevesintuïcionspertaldedonarunaresposta,correctaono,al’activitat,isónaquestes intuïcionslesqueintentaremextreuredelesdiferentsrespostesdonadespelsalumnes.

D’altrabanda,l’activitat20tractadelconcepted’espaimostral,totiquedemaneraindirecta,idelconcepted’esdevenimentmésprobable.Encadascundelsapartats,elsalumneshaviendeferunestudi del’espaimostralidelasevaestructura.Enprimerlloc,pertalded’escriuretotselsesdeveniments quenoenformavenpart,elsestudiantshaviendegenerarelconjuntcompletd’esdevenimentselementalsperalesquatreoperacionsproposades(tascarecomanadaperPolaki[2005]pertald’arribar acomprendreelconcepted’experimentcompost)i,ensegonlloc,caliaferl’anàlisidel’estructurade l’espaimostralidelsdiferentscasosfavorablesdecadaesdeveniment,pertaldepoderarribaraveure quinssónelsesdevenimentsmésprobables.

Laguiad’aplicaciódelaprovadecompetènciesbàsiquesemmarcavaaquestaactivitateneltipusde treballques’hidemanaiquehemdescritanteriorment:discussióenpetitsgrupspertald’aconseguir ferelpasdel’empirismeal’anticipació.Aquestpaséselqueespreteniaavaluarambaquestaactivitat, iencapcaselsconceptesnielsprocedimentsespecíficsdelateoriadelaprobabilitat,mésenllàde lasevavessantintuïtiva.Aquestavessantintuïtivaqueespreteniaposarenmarxaambladiscussió éselquevolíemexplorariestudiar.

Elsegonapartatdel’activitat20eraunacontinuaciónaturaldel’anterior,talcomindicaPolakide comcaltractarlaintroducciód’experimentscompostos.Aquíl’anàlisimésprecisadelespossibilitats preniamésvalor:janoestractavaqueconcloguessinqueunresultaterapossibleonoentantque hihaviapossibilitatsdelsdausqueelfeienpossible,sinóqueestractavadequantificariraonarquins erenméspossiblesqued’altres.

Eltercerapartatera,encertamanera,laculminaciódelpasdel’empirismeal’anticipacióques’havia provocatenelsanteriors,totiquerealmenterapossibleabordaraquestaactivitatambunprocedimentempíriccentratacomptar«quantsparellshaviensortitencadaoperació»(defettambéés ensimateixunamanerad’efectuarunaanticipacióbasadaenrecomptes«delquehaviapassat»).

Laresolucióòptimad’aquestaactivitat,il’argumentaciócorresponent,caliaesperar-laenl’anàliside possibilitatsenglobadesenladicotomiaparell/imparell.

3.2. Procediments d’obtenció de dades i població d’estudi

Larecollidadedadesesvaduratermeapartirdeduesfasesbendiferenciades:

• Unaprimera,queinicialmenthaviadeserl’única,onesvanrecollirlesrespostesdel73alumnesde l’IESGorgs(CerdanyoladelVallès)alaprova4delescompetènciesbàsiques.Estavendistribuïtsen tresgrupsclasse(de24,24i25alumnes,respectivament)ilesdadesesvanrecollirentressessions mésomenysseguides.D’araenendavant,ensreferiremaaquestgrupcomelGrupA.

• Lasegonafasevatenirunescaracterístiquesdiferentsdelesdescritesanteriorment,jaqueun coprecollideslesprimeresdades,idesprésdefer-neunaprimeralectura,esvanconsiderarinsufi-

cientsatenentalsnostresobjectius.Peraixò,esvadecidirtornararecollirdadesambunapoblació diferentapartirdelsalumnesd’unaltrecentre,enaquestcas,de47alumnesdesegond’ESOde l’IESMiquelBoschiJover(Artés).

Aquestasegonafaseesvadividirenduesparts,totesduesde60minutscadascuna.Enlaprimeraels 47alumneshaviendedebatreirespondrelesmateixespreguntesdelaprova4delescompetències peròsensellançamentdedaus.Lafinalitatd’aquestaprimerafaseeraladerecollirdadesqueserien comparadesamblesdelsmateixosestudiantsuncophavienfetelllançamentdelsdaus,iaixípoder estudiarlainfluènciadel’empirismeenl’anàlisidelesdiferentssituacionsplantejades.Ensreferirem alesdadesd’aquestgrupcomelGrupB1.

Lasegonapartvaserl’aplicaciódelaprovaals47alumnestalcomindicavenlesinstruccionsd’aplicacióis’haviafetalprimercentre.Peralarestadeltreball,ensreferiremalesdadesd’aquestgrup comelGrupB2.

Entotal,vanrespondrealsdosqüestionarisels47alumnesdistribuïtsendosgrupsclasseamb5i 6grupsrespectivament.Esvanpassarelsdiferentsqüestionarisenquatresessionsdiferents,dues perdia.

GRUPA

73 alumnes 3 classes(24,24i25)

Agrupacions aleatòriesde3o4 alumnes

GRUPB 47alumnes 2classes(23i24)

Agrupacions aleatòriesde 3o4alumnes

Realitzaciódela prova4delesCB (inclou experimentació)

B1:realitzaciódel qüestionari(sense experimentació)

B2:realitzacióde laprova4delesCB (inclou experimentació)

3.3.Trets metodològics i instrument per a la recollida de dades

Tenintencomptequelesfinalitatsdeltreballteniencomaobjectius«identificar»i«explicar»intuïcions delsnostresalumnes,vamabordarladisjuntivaenfocamentquantitatiu/qualitatiu.

Així,l’anàlisiqueesvaduratermesecentràenduesfases:unestudiquantitatiudelesrespostes correctesdelsalumnesqueparticiparenenlarecerca,iunestudiqualitatiudelesrespostesverbals alesproves,classificant-lesapartirdelmarcteòricconstruït.

Peracadascunadelesoperacionsesvanclassificarelsmotiusexposatspelsalumnesenelsdiferents grups(A,B1iB2)is’analitzarenseguintunasèriedeparàmetresrelacionatsambelsdiferentsaspectes

descritsenelmarcteòric,intentantcercar-hiunapossibleinterpretació.Aquestsparàmetresvanser: elconjuntd’estratègiesdesenvolupades(nivellderaonamentenquèelsalumnestreballensegons elsdescritsperPolaki,2000),lacomprensiódelasituacióidelspropòsitsplantejats(explícitiimplícit), ilanaturalesadelesargumentacionsdonadesenrelacióambelsdiferentssignificatsqueelconcepte deprobabilitatpotprendre.

Lesrespostesesvanclassificarentresgransblocs:equiprobabilitat,anàlisisubjectivaianàlisicombinatòria.

Equiprobabilitat: Esconsiderenelsresultatsqueespodenobtenirenl’experimentcompostigual deprobables.Consegüentment,perunalumnequepensiaixítantpotsortirunnombrecomunaltre inohihajustificacióperpensarqueuncertvalortéunafreqüènciaabsolutamajor.

Anàlisisubjectiva: Elsalumnesatribueixenunacreençapersonalalfetquehagisortitmésvegadesuncertvalor.Aquestsraonamentssubjectiusprovenen,encasosméselaborats,deraonaments quantitatius(sovintinvàlids).

Anàlisicombinatòria: Aquesttipusderaonaments,mésomenyssofisticats,estanrelacionatsamb unestudidelacomposiciódel’espaimostral,ieltipusderespostesfanreferència,d’unamanerao altra,alnombredecasosfavorablesperobteniruncertesdeveniment.Caltenirpresentquemolts individuspresentenanàlisiscombinatòriesquepodensererrònies.

4. Resultats, discussió i conclusions

Pertaldemostrarelsresultatsdelainvestigació,analitzaremambdetalll’estudidel’esdeveniment mésprobableenelcasdelasuma(casrepresentatiudelarecerca)enrelacióambelsobjectiusdela investigació.Delsaltrescasosnoenpresentemelsresultats,queespodentrobaraRojo(2009),però síqueelsesmentem,demanerageneral,enlapartdeconclusions,encomparacióambelsobtinguts enelcasdelasuma,jaqueenalgunsaspectesdifereixenclarament.

4.1. En relació amb les intuïcions que presenten els alumnes

Enlataula1esreflecteixenelsresultats,enpercentatges,obtingutspelsdiferentsgrupsenelmomentderaonarquineral’esdevenimentmésprobableenelcasdelasuma. N representaelnombre d’agrupacionsdecadascundelsgrups.

Categoria

Anàlisisubjectiva

Anàlisicomb.correcta

Anàlisicomb.errònia

Senseresposta

Taula 1. Esdeveniment més probable (cas de la suma).

Talcomespotobservaralataula1,laintuïcióerròniaméspresentésl’equiprobabilitat:afectagairebé lameitatdelesrespostesdelgrupA,disminueixaunaquartapartenelgrupB1(totirepresentarel 60%delesrespostesincorrectes)iacabadesapareixentenlesrespostesdelgrupB2.Aquestaintuïció estavajustificada,principalment,perdostipusderaonaments:d’unabanda,aquellsqueprovenien d’unaconcepciólligadaalafreqüènciadelconceptedeprobabilitat,ipertanterenrespostesamb unaanàlisitotalmentempíricaapartirdelquehaviasucceït,i,del’altra,elsqueproveniend’una concepcióintuïtivadelconcepte,justificantlaigualtatdeprobabilitatscomunefectepuramentde l’atzar,senseesperarunresultatmésqueunaltre.L’heurísticadel’enfocamentdelresultataïllat podria influirenaquesttipusderaonaments.Enqualsevold’aquestesduesopcions,elsalumnesnoassoliren l’objectiudelatasca:l’anàlisiapartird’unrecomptedecasos.

Enelcasderespostesenquèesconsideravendiferentsprobabilitats,lesjustificacionsvarenserde dostipus.D’unabanda,lesdetipussubjectiuambelementssobrecreencesipreferènciespersonals, derivadesd’unaconcepciósubjectivadelconceptedeprobabilitat,i,del’altra,lesquepresentaven unaanàlisidelescombinacionsdelsdiferentsesdevenimentsi,pertant,unestudidelacomposició del’espaimostral.

Calanotarquelaproporciód’alumnesqueutilitzarenunraonamentdetipuscombinatorinovavariar gaireentreelsestudiantsdelsgrupsB1iA,i,encanvi,vaaugmentarfinsalatotalitatenelsestudiants delgrupB2.

EnrelacióambelsresultatsobtingutsperFischbein,vàremcorroborarelfetqueelsalumnesd’aquestaedattenenlacapacitatintuïtivad’avaluarl’estructuradel’espaimostral,ipodenbasarels seusraonamentsapartird’aquestaestructura.Arabé,alapràcticavàremveurequeelsnostresestudiantsconstruïenobél’espaimostral Ω1 ,amb36esdeveniments,obéunespaimostralméspetit, queanomenarem Ω2 ,amb21esdeveniments.Pertaldeserprecisos,l’espai Ω1 espotconstruircom elproductedelconjunt {1,2,3, ... ,6} perellmateix.Demanerasimilar,podemdefinirelsegonespai mostral Ω2 comelquocientd’Ω1 mòdullasimetriaquerelacionaelspunts(x,y )i(y,x )d’Ω1 .Enel model Ω1 ,elsdosdaus,totinopoder-losdistingiralapràctica,esmantenen individuals,mentreque enelcasde Ω2 ,s’identifiquenresultatsindistingibles(perexemple,[2,1]i[1,2]).

4.2. En relació amb la influència del treball empíric

Lametodologiaemprada,realitzantlaprovaaunprimergruptalcomlapresentavaelDepartament d’Educacióiaunsegongrup,primersensellançamentdedausiseguidamentambllançament,ens vapermetrecompararresultatsiconcloureelquepresentemacontinuació.

Pelquefaalainfluènciadeltreballempíric,enprimerllocvampoderobservarqueelsefectesila influènciadel’empirismevanvariarenrelacióambelsconceptesinvolucratsiamblesoperacions presentadesenlaprovadelescompetènciesbàsiques.

Pelquefaalaidentificacióialadeterminaciódel’espaimostral,l’empirismehitinguéunpaper gairebéneutre.Elfetdeposseirunasèriededadesexperimentalsnomésvainfluir,demanerapositiva, enladeterminaciódel’espaimostralcorresponentalproductedelsvalorsdelsdosdaus.Elfetde poderobservarquinsvalorss’obtenienafavorílaidentificaciódelscasosimpossibles.

Pelquefaalasumaialaresta,l’empirismevaserunfactorquenodistorsionàeltractamentconjunt delainformaciórecollidad’ambduesoperacions.Contràriamentalquenosaltrespodríemesperar,

elgrupquenorealitzàlapartempíricaéselquevaobtenirunpercentatgemésaltderespostes ambanàlisicombinatòriacorrectes.Elfetdenoposseirdadesempíriquesinopoderbasar-hiles respostesvaferqueelsalumneshaguessindecercarunmotiuquejustifiquéslasevaeleccióiestudiar lacomposiciódel’espaimostral.Aixímateix,elsresultatsd’aquestgrupmillorarendemaneranotable gràciesal’empirisme.

Ensíntesi,comparantdemaneraglobalelsresultatsobtingutssegonslescaracterístiquesenquè vanrealitzarlesproveselstresgrups,podemconclourequeelfetdeproposaralsalumneslarealitzaciódelesprovessensefaseexperimentaliseguidamentambllançamentdedauspotenciàl’èxiten laresoluciódelatasca,afavorintl’anàlisiapartirderaonamentscombinatorisirecomptedecasos. Milloraconsiderablementelsnivellsderaonamentdelsestudiantsenaquestesanàlisis,ampliantel totaldecasosquecadaestudiantanalitza,iprovocaunaclaradisminució(finsitotdesaparició)de lesintuïcionserròniesqueinflueixenenaquestsraonaments.

Enelgràfic1mostremelpercentatgederespostesambanàlisicombinatòriaperacadascunadeles operacionstractadesigrups.Podemobservarqueelscasosenquèlamillorafoumésconsiderable vanserlasumailaresta,seguitdelproducteidelcasmésprobable.

5. Implicacions didàctiques

Enlainvestigació,iambl’objectiud’analitzarelprocésd’ensenyament/aprenentatgedelsconceptes d’atzariprobabilitat,vamescollirunadelesprovesdelescompetènciesbàsiquesutilitzadespelDepartamentd’Educacióamblafinalitatdefacilitarelementsquepermetessinlareflexióiladiscussió enlapresadedecisionssobreaspectesdegestiódelcurrículum.Ambaquestafinalitatensproposem,acontinuació,analitzarlespossiblesaportacionsdelanostrarecercaalprocésd’ensenyament iaprenentatgedelesmatemàtiquesi,enparticular,alsconceptesprobabilísticsinvolucrats.

Alavistadelsresultatsobtinguts,podemconclourequeuncamíaseguirperajudarelsestudiantsa construirintuïcionscorrectessobreelsconceptesd’espaimostral,probabilitatilasevarelacióambla corresponentestructuradel’espaimostral,ésutilitzaractivitatsd’ensenyamentenquè,primerament, l’estudiantcerquil’espaimostralifaciprediccionssobrelespossibilitatsd’obtenirdiferentsesdevenimentsenexperimentsaleatorissenzills(simplesicompostos),comperexempleelllançamentd’un

Suma

Resta

Producte

Nombre major Cas més probable

Grup A

Grup B1

Grup B2

Figura 1. Resultats per a les diferents operacions de cada grup (%).

dauodos,seguidamentobtinguidadesempíriquesd’aquestsexperimentsifinalmentanalitzidenou lessituacionspresentades.Lestasquesambaquestaestructuraculminarienamblacomparacióentrelespossibilitatsexperimentalsgeneradesilessevesprediccionsoriginals.

Arabé,totiqueaquestcamíanteriorhemvistquefuncionaproubé(d’acordambelsresultatsdel gràfic1)enelscasosdelasumaidelaresta,estemd’acordambelsuggerimentdeKonold(1995) segonselquallasimplerealitzaciódeprediccionsilasevacomparacióamblesdadesobtingudes experimentalmentnosónsempresuficientspertalqueelsestudiantscanviïnlessevesintuïcions,ja que,comenelcasdelproducteidelnombremésalt,lesdadesnorevelenambprouclaredattotsels resultatsquevolíemqueelsnostresestudiantsveiessinilavariabilitatdelesdadespotjugaralguna malapassada.

Aixídoncs,uncamíquecomplementalamancançaenaquestscasos,d’acordamblesideesdePolaki (2005),seriaampliarlestasquesanteriorsamblasimulaciódelsexperiments,ambl’ajudadel’ordinador,mostrantlesdadesalsalumnesidemanant-losquereexamininlessevesrespostesilesdiscuteixin enpetitsgrups.

D’altrabanda,id’acordambBatanero(2002),hemvistcomelsdiferentssignificatsdelconceptede probabilitatsónpresentsdeformaintuïtivaenelsraonamentsdelsestudiantsicompodenvariar segonseltipusdetascarealitzada.Calen,enl’ensenyamentdelaprobabilitat,activitatsdetipusexperimentalidetipusformalperajudarelsestudiantsaconèixerelsdiferentstipusdesignificatsia superarlespossiblesdificultatsquepodenpresentar.

Unaaltradelesrecomanacionsdidàctiquesqueesdesprèndel’estuditérelacióambl’estructuraque presentalaprovadelsdausdelescompetènciesbàsiques,enquèesconsideraadientlajerarquia presentada:identificaciódecasospossiblesiimpossiblesapartirdecasosparticulars;generalització, cercantidescrivintl’espaimostralpertinent,ipredicciódeprobabilitatsd’esdevenimentsapartirde l’anàlisidel’estructuradel’espaimostral.Tenintencomptequeelsalumnesnomésinicienaquesta anàlisiquanse’lsfacalcularipredirprobabilitatsd’esdeveniments,calpresentarsituacionsquepromoguinaquesttipusdetasques.Calemfatitzaritreballarlarelacióentrel’estructuradel’espaimostral ielcàlculdeprobabilitatsd’esdevenimentscompostosapartird’aquestaestructura.

TalcomindicaPolaki(2005)pertalqueelsalumnespuguincomprendreelsexperimentscompostos handesercapaçosdegenerarlatotalitatdelsesdevenimentselementalsd’uncertexperimentianalitzariutilitzarl’estructuradel’espaimostralcomabaseperferprediccionsprobabilístiques.D’acord ambaixòiambl’anàlisirealitzada,laprova4,quetractaelsconceptesd’espaimostralideprobabilitatd’unesdeveniment,constitueixunboncontextperexplorarlesintuïcionsdelsestudiantsenel momentd’enfrontar-seadiferentstipusd’esdevenimentsenexperiènciescompostes.

L’estudidelsubstratintuïtiuenrelacióambelconcepted’espaimostralharevelatl’existènciad’un substratcompatible.Aquestacompatibilitatespotutilitzarperal’ensenyamentefectiudelconcepte. Noobstantaixò,caltenirencompteque,enelcasdelsdosdaus,quanesvolestudiarl’estructurade l’espaimostraltrobemunaintuïcióerròniaquenopermetdistingir-nel’ordre.

Enrelacióambelsconceptesdeprobabilitatd’unesdevenimentirelacióamblacomposiciódelpertinentespaimostral,larecercahamostratquehihaunseguitd’intuïcionsoposadesquecalteniren compteenelmomentdel’ensenyamentil’aprenentatged’aquestsconceptes.Aquestesintuïcions són,principalmentipergraudepresència,l’equiprobabilitatilasubjectivitat,lesqualsespodenevitar odisminuir,talcomhemvistenlanostrarecerca,ambl’ajutdel’experimentació.

6. Bibliografia

Batanero,C.(2005).Significadosdelaprobabilidadenlaeducaciónsecundaria. RevistaLatinoamericanadeInvestigaciónenMatemáticaEducativa,8(3),247-263.

BataneroC.,HenryM.iParzyszB.(2005).Thenatureofchanceandprobability.A:G.A.Jones(ed.). Exploringprobabilityinschool:Challengesforteachingandlearning,15-37.NovaYork:SpringerScience +BusinessMedia.

Fischbein,E.(1975). Theintuitivesourcesofprobabilisticthinkinginchildren.Dordrecht:Reidel.

Fischbein,E.,Barbat,I.iMinzat,I.(1975).Primaryandsecondaryintuitionsintheintroductionofprobability.A:E.Fischbein(ed.), Theintuitivesourcesofprobabilisticthinkinginchildren.[Apèndix1,139-155]. Reidel:Dordrecht.

Fischbein,E.iGazit,A.(1984).Doestheteachingofprobabilityimproveprobabilisticintuitions? EducationalStudiesinMathematics, 15,1-24.

Fischbein,E.,Nello,M.S.iMarino,M.S.(1991).Factorsaffectingprobabilisticjudgementsinchildren andadolescents. EducationalStudiesinMathematics,22,523-549.

Fischbein,E.iSchnarch,D.(1997).Theevolutionwithageofprobabilistic,intuitivelybasedmisconceptions. JournalforResearchinMathematicsEducation,28,96-105.

Garfield,J.(1995).Howstudentslearnstatistics. InternationalStatisticalReview,63,25-34.

Godino,J.D.,Batanero,C.iCañizares,M.J.(1987). Azaryprobabilidad.Fundamentosdidácticosypropuestascurriculares. Madrid:Síntesis.

HuguesGalindo,E.(2001).Estudiosobreheurísticasempleadasporestudiantesensusrazonamientos probabilísticos. MemoriasdelaXISemanaRegionaldeInvestigaciónydocenciaenMatemáticas,82-88. Hermosillo:UniversidaddeSonora.

Kahneman,D.,Slovic,P.iTversky,A.(1982). Judgementunderuncertainty:heuristicsandbiases.Cambridge:CambridgeUniversityPress.

Konold,C.(1995). Confessionsofacoinflipperandwould-beinstructor.TheAmericanStatistician,49(2), 203-209.

Lecoutre,M.iDurand,J.(1988).Jugementsprobabilistesetmodèlescognitifs:Etuded’unesituation aleatoire. EducationalStudiesinMathematics,19(3),357-368.

Muñoz,A.(1998).Algunasideaspreconcebidassobreprobabilidad. Suma,29,29-34.

Polaki,M.V.,Lefoka,P.J.iJones,G.A.(2000).Developingacognitiveframeworkfordescribingand predictingBasothostudents’probabilisticthinkin. BoleswaEducationalResearchJournal,17,1-21.

Polaki,M.V.(2005).Dealingwithcompoundevents.A:G.A.Jones(ed.), Exploringprobabilityinschool: Challengesforteachingandlearning,191-214.NovaYork:SpringerScience+BusinessMedia.

Rojo,F.(2009). Probabilitaticompetènciesbàsiques:unestudidelesintuïcionsdelsalumnesde2n d’ESO. [TreballdeRecerca.ProgramadedoctoratdeDidàcticadelesCiènciesidelesMatemàtiques]. Bellaterra:UniversitatAutònomadeBarcelona.Documentnopublicat.

Serrano,L.,Batanero,C.,Ortiz,J.J.iCañizares,M.J.(1998).Heurísticasysesgosenelrazonamiento probabilísticodelosestudiantesdesecundaria. Educaciónmatemática,10(1),7-25.

—(2001).Concepcionesdelosalumnosdesecundariasobremodelosprobabilísticosenlassecuenciasderesultadosaleatorios. Suma, 36,23-32.

Speiser,R.,Walter,C.(1998).Twodice,twosamplesspaces.A:L.Pereira-Mendoza,L.SeuKea,T.Wee Kee,&W.K.Wong(ed.), ProceedingsoftheFifthInternationalConferenceontheTeachingofStatistics [Vol.1,1041-1047].Holanda:InternationalStatisticalInstitute.

Jocsdecartes imatemàtiques

LluísSabaterAnticó ProfessordeMatemàtiquesal’IESLlançà lsabate1@xtec.cat

Resum Abstract

Quanrelacionemlesmatemàtiquesambelsjocs decartes,normalmentlesimaginematravésde laprobabilitat.Peròtambél’aritmèticahi contribueix,sobretotenel dissenydetrucs com veuremenaquestarticle(idepassada,hi veuremcomtambéajudenafomentarles relacionssocials: quinamillormanerad’atreure l’atencióquejugantaserunendevinador?)

WhenwerelateMathstocardgames,weusually imagineitintermsofProbability.However, Arithmeticalsocontributestoit,especiallyinthe designoftricks,aswewillseeinthisarticle(and, moreover,wewillseehowtheyalsohelpto promotesocialrelations: couldwefindabetter waytoattractpeople’sattentionthatplayingto beafortune-teller?)

Lesmatemàtiquessónpresentsenlamajoriadejocsdecartes,encaraqueenalgunscasosaquesta presènciasiguimínima,comaraenelrecomptedepuntsdesprésd’unapartida.Enelcasdelpòquer, l’escaladevaloraciódelesdiferentscombinacionsvaenfunciódeladificultatd’assolir-les,ésadir,es basaenlacombinatòriaielcàlculdeprobabilitats:untrioésmésfàcild’aconseguirqueunpòquer peròmésdifícilqueunadobleparella.

Inonoméssónpresentsenelsjocs,sinóqueenmoltscasostambéestrobenenelstrucsd’endevinar cartes.Algunssóndemurris(perexemple,eld’endevinarunacartatriadaal’atzaridespréscol locada entrelesaltres:l’endevinadormiradissimuladamentlacartaanterioroposterior),peròd’altrespermetenunaanàlisimatemàticai,apartird’aquestaanàlisi,espodendissenyaraltrestrucssemblants.

Aixòéselquepreténmostraraquestarticle:com,apartirdel’anàlisimatemàticad’untrucinicial, dissenyar-ned’altres.

1.Comendevinarlasumade3cartesapartirdelescartesquesobren després d’un senzill procés de fer-ne 3 piles

Estractaqueunapersona(A)endevinilasumade3cartesqueunaaltrapersona(B)hatriat,sabent noméselnombredecartesquesobrendesprésdefer3trespiles(unperacadacarta)delamanera

següent:silacartatéelnúmero x ,lapilaesfaposantcartes(qualssevol)finsa arribara12 (perexemple, si x = 4,posem9cartes,corresponentsalsnúmeros4,5,6,7,8,9,10,11i12quehihaentreel4iel 12,ambdósinclosos).

Aleshoreslapersona A comptaelnombredecartessobrantsdesprésdeferles3pilesisapelresultat delasumadeles3cartesinicialsdecadapila.

L’exempleesrefereixaunjocdecartesespanyoles—oros,copes,espasesibastos,del’1al12cada coll;pertant,48cartes—,peròespotadaptaralescartesfranceses.

1.1. Mètode

Suposemqueelsnúmerosdelescartestriadesper B són a, b i c,idiem K alasuma(K = a + b + c).

Lapiladelacarta a tindrà13 a cartes,ladela b entindrà13 b,iladela c entindrà13 c.Per tant,alespileshihauràentotal(13 a) + (13 b) + (13 c)cartes,ésadir,39 (a + b + c):haurem apilat39 K cartesiensobraran48 (39 K ),ésadir,9 + K cartes.

Pertant,siperexemplehansobrat16cartes,tindremque9 + K = 16,ipertant K = 7.Lasumade les3cartestriadesper B és7.

Fixem-nosquelaquantitatdecartessobrantsvade12a45(si B tria3asos,cadapilatindrà12cartes ipertantensobraran12,mentrequesi B escull3reis,cadapilatindrà1cartaipertantensobraran 45),perquè K ésunvalorentre3i36.

1.2. Altres variants d’aquest truc

1.2.1. Canviant el nombre de cartes de cada pila

Silespileslesfem arribarfinsa20 (perexemple)encomptesdefinsa12,aleshorespotpassarqueno sobrincartessinóqueenfaltin(sitriem3asos,perexemple),peròlaresoluciódeljocéslamateixa:

Diemigualmentque K = a + b + c.Lapiladelacarta a té21 a cartes,ladela b enté21 b,ila dela c enté21 c.Pertant,tenimposades63 K cartesiensobren48 (63 K ),ésadir, K 15. Evidentment,enelcasquefaltincartespercompletarles3piless’hauràdediralapersona A quantes n’hanfaltat.

Així,siperexemplesobren16cartes,tindremque K 15 = 16,ipertant K = 31;lasumadeles3 cartesés31(perexemple,duessotesiuncavall).Obésihanfaltat4cartes,tindremque K 15 = 4, ipertant K = 11;lasumadeles3cartesés11(perexemple,doscincsiunas).

Fixem-nosquelaquantitatdecartesquesobrenofaltenvade 12a21(si B hatriat3asos,cadapila tindrà20cartesipertantenfaltaran12,mentrequesi B tria3reis,cadapilatindrà9cartesipertant sobraran21cartes)perquè K téunvalorentre3i36.

Generalitzant,sipartimdelabasequeambpilesdefinsa12carteselnombredesobrantsés9 + K , on K éslasumaques’had’endevinar, silespilestenenxcartes (normalment x hadesermajoroigual que12imenoroigualque24,pelfetquelescartesvandel’1al12iquehiha48cartes),aleshores el nombredecartessobrantsserà 9 + K 3 · (x 12),ésadir, K 3x + 45,quetambépotescriure’s K + 3 (15 x ).

DEMOSTRACIÓ:Sifempilesd’x cartes,partintdelfetqueperapilesdefinsa12elresultatdelessobrants és9 + K ,comquearahemposat x 12cartesmésacadapilaensobraran3 (x 12)menys,iper tants’handerestaraltotaldecartessobrants:9 + K 3 · (x 12),laqualcosadóna K 3x + 45.

Així,perexemple,silescartesinicialsdelespilessónun1,un4iun8,iarribemfinsa17,cadapila tindrà17,14i10cartesrespectivamentipertantensobraran48 (17 + 14 + 10),ésadir,7cartes,i pertantlasumadelescartesinicialss’obtéde K 3 · 17 + 45 = 7,queés K = 13,efectivament.

Itambéarribantfinsa17,sisurtendosasosiun2,posaremalespiles17,17i16cartes,respectivament, perlaqualcosafaltaran2cartes,cosaquecomhemditabanss’hadecomunicaral’endevinador(A), ialeshoreslasumas’obtindràresolent K 3 · 17 + 45 = 2,quedóna K = 4,efectivament.

Enel casx = 15(amb3pilesdefinsa15cartes),resultaque lasumaKdelescartescoincideixambel nombredecartessobrants, jaque3 15 = 45.

OBSERVACIÓIMPORTANT:Així,doncs,aquestseriaelcasméssenzillperaplicareltruc.

1.2.2. Canviant el nombre de piles de

cartes

Variantelnombredepilesdecartes,ésadir,nonecessàriament3pilessinó N,iarribantfinsa x cartes acadapila,lafórmulaquedónaelnombredecartessobrantsés K N · x + (48 N),quetambé potescriure’s K N (x + 1) + 48.

Vegem-nedosexemples:

• Amb4piles(N = 4)iarribantfinsa12acadaun(x = 12),silescartessónperexempleduessotes, un5iun6,alespileshihauràrespectivament3,3,8i7cartes,ésadir,21cartesposadesentotal, ipertantensobren27.Elvalorde K espotobteniraixí: K 4 (12 + 1) + 48 = 27,quedónacom aresultat K = 31,efectivament.

• Finsitotarribantfinsa15(perexemple)iqueensfaltincartes,s’aplicalamateixafórmula:suposem quetenimsdosasos,un2iun3,ialespileshauremdetenir-hi15,15,14i13cartes,respectivament; ésadir,57cartesposadesi,pertant,enfaltaran9,cosaquecomunicaremal’endevinador A. Aleshores,lasumadeles4cartess’obtédelamanerasegüent: K 4 · (15 + 1) + 48 = 9,que dóna K = 7,efectivament.

seccions seccions rcions

pensar per pensar un minut

JordiDeulofeu

DepartamentdeDidàcticadelaMatemàticailesCiències

UniversitatAutònomadeBarcelona jordi.deulofeu@uab.cat

Unasecciócomaquesta,dedicadaaproposaricomentarproblemes,recreacionsijocsmatemàtics, nopodiapassarperaltquefaunamicamésd’unanyensvadeixarMartinGardner(1914-2010), filòsofiperiodistadeformació,matemàticdevocacióidetreball,sensdubteelmillorimésprolífic divulgadori,m’atreviriaadir, agitador delesmatemàtiquesdelsegle XX.Dedicar-liunpetitarticle comaquest,però,ésunafeinacompromesa,jaquel’obradeGardneréstanvoluminosa,interessant idiversa,tantpelquefaalcontingutcomalnivelldedificultat,queesfadifícilfer-neunatriacoherent. Peraixòavui,idemaneraexcepcional,lesreferènciesalpersonatgeialasevaobraocuparanmés quelapropostadeproblemes,quetanmateixnofaltarà.

Lasevadilatadaobraescritadurantmésdecinquantaanys—encarael2008vapublicarunarevisió d’undelsseustreballsmésantics, Origami,Eleusis,andtheSomaCube—comprènmésd’uncentenar dellibres,unaquinzenadelsqualscorresponenalarecopilaciódelsseusarticlesalarevista Scientific American,enlacèlebresecciótitulada«MathematicalGames».

Almargedelespropostesdeproblemes,recreacionsijocsod’exposicionsdetotamenadeteoriesmatemàtiques,lesintroduccionsdelsseusllibressón,almeuentendre,unapetitajoiaenelseu conjunt,iensmostrenelseupensament,avegadespolèmic,peròsempred’unagranlucidesa.Me n’agradaespecialmentunaforisme,queheutilitzatmésd’unavegadaenelsmeusarticlessobrejocs: «Encaraquehihapoquescosesmésentretingudesqueelspassatemps,pelquerepresentenderepteal’enginyialacapacitatderaonar,lafunciód’aquestsjocsnoésúnicamentrecreativa;comva assenyalarJ.E.Littlewood.Unbonpassatempsmatemàticpotaportarmésalamatemàticaqueuna dotzenad’articlesmediocres».

SifaigunamiradaenrereitractoderecordarquinéselGardnerquem’hainteressatmés,hede començarsensdubtepeldivulgadordejocs;perexempledel’eleusis,elgranjocdeRobertAbbott queGardnervadonaraconèixerenunarticledel1959,ivatornar-hienunaltredel1977,totsdosenla jamíticasecció«MathematicalGames»,quevaescriuredel1956al1981.Desdefamoltsanyspractico aquestjocambunacollad’amicsunavegadaalmesacasadel’OriolComas,iuspucassegurarque ésdelsmésgenialsques’haninventatmai:nos’assemblaacapaltreperquèl’objectiuésendevinar laregla,proposadaencadarondaperundelsjugadors,laqualcosaalteral’essènciadequalsevol

joc,enquèobjectiusireglessempreestandonatsapriori.Avui,afortunadament,podemconèixerde primeramàl’obrad’aquestgrancreadordejocs,itambédelaberints,recollitsenelllibre Diezjuegos quenoseparecenanada (R.Abbott,2008).

Gardnernoésundidactaperòalgunsdelsseustreballspodenserútilsperal’ensenyamentdeles matemàtiques.Enrecordounmagníficarticlesobreelsnombresnegatiusqueemvacanviarlesidees queteniasobreelseuensenyament(«Lanocióndenúmeronegativoyloarduoqueresultaentenderla»,1977),i,persobredetot,consideroqueelseullibre Aha!Insight (Freeman&Company,1978) ésunmagníficexempledecomapartird’unproblemarecreatiu,avegadesd’unasimplebroma,és possiblearribaraungranteoremaounapropietatmatemàticarellevant.

Gardnerhaestattambéundivulgadord’obresrelacionadesamblaciència.Desdefaanyscol lecciono versionsdelscontesdeLewisCarrollsobreAlícia.Elprimerqueenvaigtenirillegirfou Alíciaenterrademeravelles,versiódelpoetaJosepCarneril lustratperLolaAnglada(1927),i,juntamentamb aquest,elquemésaprecioés Aliciaanotada,l’ediciódeMartinGardnerdel1960(encastellà,1984) ilarevisióqueelmateixGardnerenvaferel1998(encastellà,Akal,2010).Lesàmpliesipertinents notesdeGardnerensmostrenlaquantitatdedetallsmatemàtics,lògicsilingüísticsques’amaguen darrereelcontedeCarroll.

Haigdedirperacabarelscomentarissobrel’obradeGardner,iabansdeproposarelsproblemes d’avui,quesihetrigatmésdelquehauriavolgutaescriureaquestarticlehaestatpelfetquela relecturadelsseustreballs,quedarreramentteniaunamicaoblidats,m’hatornataengrescarcom enelsvellstempsfinsalpuntd’obligar-menovamentaagafarpaperillapisiapassarbonesestones pensantenelsreptessempreestimulantsdel’autor.

ComençarélapropostadeproblemesambunaparadoxaquedónanomaundelsllibresdeGardner: Elahorcamientoinesperadoyotrosentretenimientosmatemáticos (1991).

1.Laparadoxadelpenjat. Unjutgecondemnaunpresoneralaforcaiemetlasentènciaun dissabte:«Seràspenjatalmigdiaundelsproperssetdies,perònosabràsquindiaseràfinsqueno t’avisinelmatídeldiaescollit».L’advocatdelpresonerlidiu:«noetpreocupis,noespodràexecutar lasentència,jaque,evidentment,eldarrerdia,dissabte,noetpodenpenjar,jaquelatardaabansho sabries.Sidescartemeldissabte,eldivendrestampocpotser,jaquedijousalatardahosabries.Hi aixísuccessivament,finsaarribaralprimerdia».Davantd’aquestraonament,lògicamentimpecable, elpresoneresquedatranquil,peròresultaquedijousalmatílicomuniquenqueelpenjaranaquell diai,efectivament,ellnos’hoesperava,perlaqualcosalasentènciadeljutgesembla,ara,perfectamentcorrecta.Larealitat,doncs,refutaunargumentlògicaparentmentimpecable,iaixòéselque faatractivalaparadoxa.

Gardner,enelllibreesmentat,comentadiferentsexplicacionssobrelaparadoxa,d’origenincert,i sobrelaqualesvanescriurediversosarticleselsanyscinquantaiseixanta.

Eneltercercapítoldelllibre MathematicalPuzzlesandDiversions (1959),primerrecopilatoridelsarticlesdelarevista ScientificAmerican,Gardnerproposaunapetitacol·lecciódeproblemesinteressants:

2.Tallantuncub. Tenimuncubdefustaidisposemd’unaserraperdividir-loencubsméspetitstots iguals,fenttallsrectes.Sielvolemdividiren8cubsnecessitarem3tallsisienvolem27,podemfer-ho amb6talls.Éspossiblereduirelnombredetallssidesprésdecadatallpodemrecol·locarlesparts obtingudesenelstallsanteriors?Passaelmateixsielnombredecubsésmésgran,perexemple,64?

Enelllibre Nuevospasatiemposmatemáticos (1972),elprimerquevaigconèixerdelnostreautor,hi trobemeljocdeHip,creatpelmateixGardner:

3.EljocdelHip. Enuntaulerquadratde36caselles(6x6)dosjugadorsvanposantpeons(un blancsil’altrenegres)alescasellesbuides.Perdlapartidaeljugadorqueencol locarunpeóforma unquadrat(ésadir,faquequatrepeonsdelseucolorsiguinelsvèrtexd’unquadrat).

Gardnerexplicaquedesprésdecreareljocestavasegurqueunapartidanopodiaacabarentaules, peròpoctempsdesprésdeproposar-lounestudiantdematemàtiqueslivamostrarquesíqueera possible.Usproposoprimerquecalculeuelnombredequadratsqueespodenformarenuntaulerde 6x6i,siusharesultatsenzill,quetracteudegeneralitzar-hoperaqualsevoltaulerquadrat.Després, tornantaltaulerde6x6,trobeuunaconfiguraciófinal(amb18peonsnegresi18deblancs)onno s’hagiformatcapquadrat.

Acabarél’articled’avuiambunparelldejocsd’estratègiaquenohetrobatencapllibredeMartin Gardner,sinoenuninteressantdossierdeproblemessobrejocsdenimescritperMichelCritoni publicatalarevista Tangente («Hors-sérien.20:jeuxmathématiques»,2004).Elprimernouscostarà gensderesoldre:n’hihaprouambpoquesproves.Elsegon,encanvi,ésforçaméscomplicat:

4.Escriureunnombre. EnPauienRogerjuguenaunjocqueconsisteixaescriureunúnicnombre dediversesxifres.EnPauescriulaprimeraxifra(diferentde0),queseràladel’esquerradelnombrequeaniranconstruint.AcontinuacióenRogerescriuunaxifra,queseràladeladretadel’anterior, respectantlesreglessegüents:

a)Desprésd’un9espotescriurequalsevolxifra.

b)Desprésd’unaxifrainferiora9calescriureunaxiframésgran.

c)Cadascunadelesxifrespotaparèixerenelnombrecomamàxim3vegades.

Elsjugadors,pertorns,vanescrivintunaxifraquesituensemprealadretadeladarreraxifraescrita, respectantlesreglesanteriors.Eljugadorquenopotescriurecapxifrarespectantlesreglesanteriors perdlapartida.Quindelsdosjugadors,enPauoenRoger,téunaestratègiaguanyadora?Quinaés l’estratègiaquepermetguanyarsempreenaquestjoc?

5.Etdeixocomençar. EnRogerienPautenendavantseuunapilaamb1.993fitxes.Enelseutorn cadascúpotagafarentreunai n fitxes,on n ésunnombreenterentre25i250.Eljugadorqueagafa ladarrerafitxaperdlapartida.EnRogerlidiuaenPau:«Etdeixocomençar,jaquehaintuïtquehiha unaestratègiaquepermetqueelsegonjugadorguanyi».Quinéselvalorde n?

Comsempre,esperoquepasseuunaestonaentretingudaiquel’articleushagianimatarecuperar algunadelesobresdeMartinGardner.Sinoenteniucapamà,usrecomanolarecopilaciódelsseus articlesal ScientificAmerican,editadael2005perlaMathematicalAssociationofAmerica,ambun CD-ROMdemésdequatremilpàginesquecontéelsquinzellibreseditatsanteriormentsobreel tema.

Bibliografia

Abbott,R.(2008). Diezjuegosquenoseparecenanada.Barcelona:RBA.

Carroll,L.(1998). Aliciaanotada.Aliciaenelpaísdelasmaravillas/Atravésdelespejo. EdiciódeMartin Gardner.Madrid:Akal.

Criton,M.(2004).ProblèmesdejeuxdeNim.JeuxMathématiques. Tangente.Hors-série,20,90-93.

Gardner,M.(1959). MathematicalPuzzlesandDiversions.[cap. III:«Nineproblems»,30-42].NovaYork: Simon&Schuster.

—(1972). Nuevospasatiemposmatemáticos.Madrid:Alianza.

—(1977).Lanocióndenúmeronegativoyloarduoqueresultaentenderla. ScientificAmerican,11, 102-106.

—(1991). Elahorcamientoinesperadoyotrosentretenimientosmatemáticos.Madrid:Alianza.

—(2005). MartinGardner’sMathematicalGames. Washington,D.C.:MathematicalAssociationofAmerica.

LestorresdeHanoi sónfranceses?

ClaudiAlsina

claudio.alsina@upc.edu

Faanys,quanaCatalunyaencaranoteníemcaprestaurantxinèsifaltavendècadesperal’arribada delsbasarsidelstallersclandestinstèxtils,lescoses«orientals»tenienuncertmisteriatractiu.Molts magslocalsesdisfressavendexinesositriavenunsobrenomfalsamentxinèsperaportarmésmisteri alessevesactuacions.TotsmenjàvemFlanChinoElMandarín,colàvemlescosespel xino delacuina, l’actualplaçadelaViladelbarrideGràciadeBarcelonaesdeiaplaçad’Orient,hihaviaelsBanysdels OrientalsalaBarcelonetaitriomfavalamarcacosmèticaMaderasdeOriente.Comveuremimmediatament,totaixòtémoltaveureamblestorresdeHanoi.

ÉdouardLucas(Amiens,1842-París,1891)fouunmatemàticfrancès,oficiald’artilleria,professordesecundàriaalliceudeSaintLouisialdeCarlemagne,col·laboradordel’ObservatorideParís,investigador iaficionatalaqueavuiendiríemmatemàticarecreativa.Certament,unapersonalitatpolièdrica.

Enl’àmbitmatemàtic,Lucashatranscenditpelsseusestudissobrel’anomenadasuccessiódeLucas: 1,3,4,7,11,18...Defet,LucasvapartirdelasuccessiódeFibonacciiencomptesdecomençaramb elsprimerstermes1,1...vainvestigarquèpassavaeniniciarlaseqüènciaambdosnombresenters positius a, b...ianar-nesumantdosdeseguitsperobtenirelsegüent.Combésabemara,almarge delsdostermesinicialslasuccessiódelesraonsdecadatermepelseuanteriortendeixenalaraó àuriaonombred’or.SónmolteslescuriositatsdescobertesperLucasjugantambla seva successiói laclàssicadeFibonacci,aixícomamblesrelacionsambelsnombresprimersdeMersenne.

Peròelquevolemremarcaraquíésl’aficiódeLucasperlamatemàticarecreativa,ipodemconsiderar queenfouundelspioners.Vaanarpublicantunpopularrecull Récréationsmathématiques entre 1882i1894,ivaserl’inventordelespopularstorresdeHanoi.Aquestjoc,del1883,vaserpatentat aFrançaambaquestnomoriental,iLucassignavacom«Prof.N.ClausdeSiam,mandarídelCol·legi deLi-Sou-Stian»

Lucasvacreurequeuncertmisteriorientalajudariaenormementafereljocméspopular.Iperacabar decompletaraquestprocésd’orientalització,ellmateixvaescriurela llegenda quehihadarrere.

Aquestpopularjocconstadetresbarretesverticals.Alaprimera hihancol·locatsdiversosdiscsforadatsiordenatsdeformaque cadascunésméspetitqueeldesota,iestractadefericomptar elspassosnecessarisperresoldreelproblemadetraslladaruna unels n-discs,delaprimerabarretaalatercera,demaneraque undiscnoentinguimaiundemésgranasobre.

Segonsunadeles llegendes delProf.N.ClausdeSiam,l’origen deljocestrobaenunsmonjosasiàticsdeltempledeBenarés, quehavienderesoldreelproblemadelestorresamb64discs... totsabentqueenacabareljocserialafidelmón.Siper n discs calfer2n 1moviments,per n = 64resultaque,nomésqueels monjostardessin1segonamourecadadisc,necessitarienmés de500.000milionsd’anysperacabar.Semblavaclar,doncs,que lafidelmónquedavabenllunyana.

Aquestjocésuncasinteressantdecreixementexponencial,incloulaideaderecursivitatiportamolt béalaidead’algorisme.Pertant,ésunjocinteressantperalaclassedematemàtiquesiactualment se’ntrobentotdeversionsvirtuals.Peròelqueensdiuaquestahistòriatambéésunaaltracosa:la possibilitatdepresentarlesmatemàtiquesd’unamanerarecreativa,envoltadesdellegendesque motivinaresoldreelsreptesplantejats.MoltscopselprofessorManolo Coque PazosdelaCorunya hafettallersdetangramsvestitdexinèsperanimarelsalumnesdelasevaclasseodetallersaentrar eneltema.Elfijustificaelsmitjans.

Édouard Lucas

La FEEMCAT(Federaciód’Entitats per al’Ensenyament de les Matemàtiques a Catalunya),laSCM(Societat Catalanade Matemàtiques),la RealAcademiadeCiencias i la anuncienla FundaciónVodafoneEspaña convocatòria peral’admissióenelseu

projecteESTALMATaCatalunya (Deteccióiestímuldeltalentprecoçenmatemàtiques)

Objectiudelprojecte :fomentarl’aficióihabilitatespecialenmatemàtiquesdenoisinoiesque viuenaCatalunyaiamb datadenaixementdel’any1998,1999i2000.

Activitats:Totselsdissabtesdelperíodelectiudelscursos2011-2012i2012-2013,de10ha13ha laFacultatdeMatemàtiquesiEstadística(FME)delaUPC,aBarcelona.

Aquestesactivitatsserangratuïtes peralsnoisinoiesseleccionats,elsparesotutorsdelsquals s’haurandecomprometreaportar-losirecollir-losaleshoresesmentades.

Procésdeselecció:

La selecciódel grupde 24nois i noies queparticiparanenelprojectetéduesfases:

1. Testd’aptitud: eldissabte2dejunyde2012ales10halesciutatsdeBarcelona,Girona, LleidaiReus.

2. Entrevistapersonal ambelsparesotutorsielsnois/espreseleccionats/des.

Inscripció:

formulari

Lamare,elpareotutorlegalhaurand’omplirunquetrobaranalapàginawebdel’organització,www.estalmat.org.Veuranquehihaunenllaçespecialperalsdetallsd’aquestaconvocatòria,iunaltreenllaçonpodranllegirinformaciódelprojecteaCatalunya.

Termini: finsal31demaigde2012.

Dadesqueesdemanen: nomidatadenaixementdel’alumne/ainteressat/daaparticiparenel projecteESTALMAT,adreça,correuelectrònic,númerodetelèfondecontacteicentreescolaron estudiadurantelcurs2011-2012.

aquinapoblaciódesitjarienferlaprova (Barcelona,Reus,Gironao Caldràqueindiquin Lleida).

Lallistad’inscritsielsdetallsdelarealitzaciódelaprovadeseleccióespodranconsultaralweb www.estalmat.org,promoció2011-2013.Tambéespotdemanarinformaciósobreelprocés d’inscripcióaNúriaFuster,SocietatCatalanadeMatemàtiques(telèfon:933248583;correu electrònic:nfuster@iecat.net).

Sistemes dereferència

MartaBerini

Equador: llatí aequator,-oris,‘queiguala’.

Paral· · ·lel: delgrec παρ ´ α ‘alcostatde’id’´ αλληλους ‘unesialtres’:‘línieslesunesalcostatdelesaltres’.

Meridià: delllatí meridianus,-a,-um (de medius,-a,-um ‘mig’i dies,-ei ‘dia’)‘migdia’.

Eclipsi: delgrec ἔκλειψις ‘desaparició’.

Longitud: delllatí longitudo,-inis ‘longitud,llargària’.

Latitud: delllatí latitudo,-inis ‘amplada,latitud,extensió’.

Mapa d’Herodot, s.aC, quan encara es creia que laTerra tenia forma de cilindre. V

Demòcrit,mortc.370aC,consideràqueelmónhabitato oikoumenen (d’onprovélaparaula‘ecumènic’)teniaformaderectangleambdimensionsunavegadaimitjamésdellargada(longitud)que d’amplada(latitud).

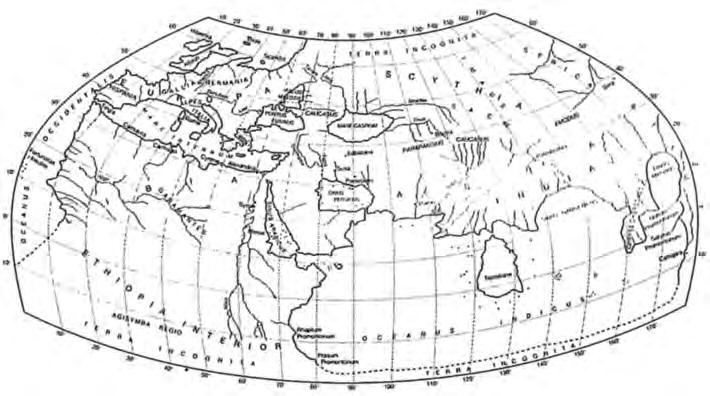
Mapa de Ptolemeu, s.dC, quan ja es va acceptar que laTerra tenia forma rodona. II

Eixosdecoordenadescartesians.Eixos: delllatí axis,-is ‘eix’; coordenades: delllatí cum + ordinatus,-a,-um ‘ordenadaenfileraconjuntament’; cartesians: deCartesius,nomllatinitzatdeDescartes.

Abscissa: delllatí abscissus,-a,-um ‘tallada’.

Ordenada: delllatí ordinatus,-a,-um ‘ordenadaenfilera’.

Unadelesprimeresrepresentacionsgràfiquesconegudes.Gràficdelsegleoseglequemostrala inclinaciódelesòrbitesdelsdeuplanetesdelSistemaSolarqueesconeixienenaquellaèpoca.JohnD. Barrow,,Paidós,2008.

ImágenesdelCosmos

cròniques cròniques riques s

PremiMariaAntòniaCanals

LaFederaciód’Entitatsperal’EnsenyamentdelesMatemàtiquesaCatalunya(FEEMCAT),laSocietat BaleardeMatemàtiquesSBM-XEIXilaSocietatd’EducacióMatemàticadelaComunitatValenciana Al-Kwhrizm āī sónentitatsqueaglutinenprofessorsdematemàtiquesdetotselsnivellseducatiusal territoridel’àmbitlingüísticcatalà.

TotestressónmembresdelaFederacióEspanyoladeProfessorsdeMatemàtiques(FESPM)ihiparticipenactivamentassumintdiferentsresponsabilitats,comaralasecretariad’alumnat,ladireccióde larevista Suma ol’organitzaciód’unesJornadesperal’Aprenentatgeil’EnsenyamentdelesMatemàtiques(JAEM)ambressòatotl’Estat.

Arrandelaconfluènciad’interessosil’existènciadelligamsculturals,laSocietatBalearvaconvocar unaprimerareunióelgenerdel2010aMallorcacomaITrobadadeSocietatsdeMatemàtiquesde ParlaCatalana,quevatenircontinuïtatelmarçdel2011aBenicàssim.

Aaquestestrobadesescomparteixenexperiènciesise’nplanifiquendenoves.Enaquestcontext esplantejadonarunnouimpulsalPremiMariaAntòniaCanals,peraprojectespràcticsd’innovació educativadirigitsal’ensenyamentdelamatemàtica,adreçatsalssegüentsnivellseducatius:educació infantil(0-6),educacióprimària(6-12),educaciósecundària(12-18)iuniversitària.

ElPremiMariaAntòniaCanals,decaràcterbiennal,vaserinstauratl’any2000perlaFEEMCATipresentatpúblicamentenelmarcdelacelebraciódelCEM2000alaciutatdeMataró.Erenmomentsde creixementdel’associacionismeentorndel’educaciómatemàticaiderefermamentenl’úsdelallenguacatalana,dospilarsquelaMariaAntònianos’hacansatmaidedefensar.Amés,eraelmoment oportúpermirard’engrescarelsprofessionalsdel’educaciódetotselsnivellseducatiusaposar-se encontacte,comunicar-seiposarencomútotallòquetreballaveniaprenienamblasevafeinaales aules.Ésenaquestmarcqueelpremipreténserunimpulsperal’educaciómatemàtica.Mésdedeu anysdesprés,lestresassociacionsenllenguacatalanavolencontinuarhomenatjantaqui,comvadir elllavorspresidentdeFEEMCATXavierVilella,continuasent«MariaAntònia,mestrademestres,una personadeprofundesconviccionsquetéfeenelsseusalumnes[...].Hoesperatotdetotsitotes, decadascúsobrequihatingutl’oportunitatd’influir.Inosaltresliagraïmqueenstrametiaquestes actituds,quesiguiunmodelaseguir».

Eljuratestaràintegratperunmembredecadascunadelessocietatsqueconvoquenelpremi,un membredelaredacciódelarevista NouBiaix,unespecialistaendidàcticadelesmatemàtiquesiel secretarigenerald’unadelessocietatsconvocants.

S’atorgaràunsolpremipernivell,queeljuratpodràdeclarardesert.

Elstreballspremiatspodranserdifososperlesentitatsconvocantsperqualsevolmitjàisiescauala revista NouBiaix

Esperemqueaquestarevisiódelpremihidoniunnouimpuls,iengresquiacompartirexperiènciesi adifondrelesbonesideeseneducaciómatemàtica.

creamat el racó del creamat

El racó del(i també del MMACA) creamat

Agraïmalscompanysdel NouBiaix quehagindeciditendegaraquestaseccióialsdel creamat que vulguincompartirambelMMACAelseuracó.Compartirésviure,diuen,i creamat iMMACAcompartimmoltmésqueunespaifísic:tambécompartimunespaicultural,finsitotemocional.Aixídoncs, augurem-nosunallargaifeliçvida,tantanosaltrescomalarevista,enaquestanovaetapa.

Pensantqueelslectorsdel NouBiaix jaensconeixen,itenintencomptequeelprojectedel’associacióvacomençarcomungrupdinsdelaFEEMCATivarecórrertoteslesjornadesdelesdiferents associacionsfederades,recordaremenpoquesparauleselsorígens,elsuportquedesdelcomençamentvamrebredel’ICEdelaUPC,delaSocietatCatalanadeMatemàtiquesidelDepartament d’Ensenyament.

Estemclaramentlligatsaaquestsinicis,alanostravocaciódidàcticad’estimularl’aprenentatgedeles matemàtiques(tantcognitivamentcomemocionalment)ialavocaciódesuportexternalesactivitats queesfanalscentresescolars.

VaferfaltaunanyimigpermuntarlaprimeraexposicióaAlella(novembre2008)idesprésnohem parat:Figueres,Girona(XIVJAEM),Centelles,Castelldefels,altrecopGirona,Saragossa,Barcelona(UB, UPCiUAB)iBerga.Exposicionsdedimensionsgransipetites,queensanavenobligantapensarnoves propostes,elaborarnousmaterialsiafercréixerelnostre patrimoni (japodemomplirunsbons400m2 d’exposició!)Tenintencomptequeensfaltavaexperiènciaenl’aspectemuseístic,entemesd’espais idepatrocinadors...detot,tretdel’entusiasme,noestàgensmalament.Pencaires!(Gràcies).

Mentrestantse’nspresentavennovesoportunitats:intervencionsbreus,queenscomportenunesforçpersonalieconòmicnotable,peròqueensdemanavencompanysquehanestatalnostrecostat desdelcomençament:jornadesdelaFEEMCAT,Matefest,FemMates,provesCangur...Otambéens cridavenenmanifestacionsdecaraalgranpúblic:FestadelaCiència,Planta’t,CiènciaalCarrer.Això demanavaencaraméscompromís,peròensvadonaraconèixerforadel’estrictegremidelprofessoratdematemàtiques,ienshapermèsprogramarfuturescol laboracionsambentitatstaninteressants comRecercaenAcció,elMuseudelaMàgiadeBarcelona,elMuseudelJoguetdeFigueres,l’ONCE, elMuseudeCiènciesNaturalsdeBarcelona,elmNacTecdeTerrassa,elCentredeDissenyd’Equips IndustrialsdelaUPCilesuniversitatsdeCatalunya.Hemcomençattambéamoure’nsenelpanorama internacional,ambmoltaprudènciaibenconscientsqueencarasompeixetsmassapetitspernedar marendins.

Totaixòenshaobligatapensarnovesformesd’intervencióidivulgació:miniimicroxerrades,tallers ràpids,concursosdeproblemes,intervencionsradiofòniques...Enshemtrobatexposantenllocsque

noestanpensatsperaaquestafunció(biblioteques,centresperagentgran...)iencaramenyspera unapropostacomlanostra,quenecessitatemps,espais,taules,monitors,etc.

Elprofessorattambéensdemanavapoderportarl’exposicióalesescolesiadaptarlesactivitatsales aules,aixíqueensvamposaratreballarendosprojectes:unsmaterialsdeformatméspetit(DIN A3oDINA2)illeuger,queespoguéstransportarfàcilmentiarribaraixíalesescolesialsaltresllocs quedèiem;iunesfitxesdidàctiquesqueconnectessinlesexposicionsalscurrículums,mostressin elscontingutsmatemàticsquehihadarreredelsmòdulsiqueelstempsbreusd’unaexposicióno permetentractar,peròqueespodenportaraclasse(oacasa)perfer-neobjected’untreball,tant personalcomcol lectiu,mésaprofunditicomplet.Eraunamaneraderespondrealessol licituds queensarribend’unprofessoratqueelaborafitxespròpiesquanportaelseualumnatavisitarles nostresexposicions.Unaprimeraversiódela Guiadidàctica iunsprototipsdelsmòdulsdeformat reduïtsónobjected’unacomunicacióiuntallerqueelMMACAhapreparatperalesXVJAEMde Gijón.Decaraalnoucurstenimprevistcontinuarcompletantaquestestasques.

Darreramenttambéhemmantingutcontactesambl’ONCE.Elsnostresmaterialssónbàsicament manipulables,iaquestfetconnectaalaperfeccióambaquestaorganització.Alamajoriademòduls noelscalenmodificacions,ocap,perserunboninstrumentperalagentinvident.Arrand’això,i haventconstatatl’entusiasmeilabonapredisposiciódel’ONCE,volemapostarperaconseguirunes exposicionsobertesatotselspúblics,senseexcepcions.

Tambéestemampliantl’ofertadelesxerrades(d’unahoradedurada:desdelageometriadeles bombollesdesabófinsalsrellotgessolarsilesinfinitesmaneresderodar,rodolarogirar),idelesmini (1/2h)imicro(15minuts),sobretemestandiferentscomelcàlcul,elsjocsgeomètricsod’estratègia, lescorbes,elsmiralls,l’optimització,etc.

Continuaremmuntantexposicions,quedemicaenmicatenenmésdurada,queensdónalapossibilitatd’atendreméscentresescolarsidediferentsetapeseducatives,comperexempleLleida,Sabadell, BanyolesiManresa,queensvolenacollirproperamentambunsespaisdedimensionsnotablesiper untempsmésllarg,queensdonaràl’oportunitatdecomprovarsilanostrapropostapotaguantar encartellera duranttotunanyescolarienllaçardiversesmodalitatscoml’exposició,lesxerradesiels tallers.

Comptemambunnuclisòlidd’associatsiambunaxarxa(queesperemqueescontinuïampliant) decol laboradorspuntualsmoltgenerososicompetents,ientreells,unes panteresgrises quetenen moltavitalitaticompetència(quinaenvejadejubilats!).Icomptemtambéambelfenomenpotser mésinteressant:lacol laboraciód’ungrupd’estudiantsqueensajudafentdemonitors.

Ensagradasubratllaraquestafunciódeformacióque,apartirdel’exposiciódeCentelles,realitzem ambestudiantsdelaFacultatd’EducaciódelaUVIC.DespréshanarribatestudiantsdeMatemàtiques, deCiències,deDidàcticadelesMatemàtiques,delsmàstersd’Educació,imoltad’aquestagentjove harepetitmésd’unavegada,fetquedemostra,amésd’entusiasmeidisponibilitat,queaquestaexperiènciaésútilperentrarencontacteamblaprofessiódocent,encaraquemitjançantunamodalitat unamicainusual,peròquetémésfuturdelquepotsemblar.Aixíhotestimonial’intensdebatinternacionalsobrelesprofessionsnecessàriesdecaraalafruïciód’unaofertamuseísticaque,almenysa Europa,s’hamultiplicatperunfactor100apartirdelfinaldelaSegonaGuerraMundial.Actualment, aEuropahihaunsquarantamilmuseus!,ambuncreixementimportantdel’ofertatecnològica(per recuperarlesplantesquelapostindustrialitzaciódeixabuides)icientíficaamblaintencióexplícitade fomentarvocacions.

Estàclarqueelsmuseustenenunpaperfonamentalentotselsprojectesdelacomunitateducativa, d’educaciópermanentid’educaciónoformal.Nosaltresmateixos,enlanostraexperiènciadirecta, tancurtairecentitanarreladaal’ofertaescolar,hempogutcomprovarl’extraordinàriaacollidade lanostrapropostaentreelpúblicadult.TantalaCasadeCulturadeGironacomalaUBvamtenir unnombresemblantdepúblicescolaridevisitantslliures(estemparlantdetresmilcinc-centesa quatremilvisitesentressetmanes,enhorarivespertíoelsdissabtes).AlCasaldelaGentGrande Berga,elsalumnesdelesescolesesqueixavenperquèelsavissempreestavenfentlesactivitatsino deixavenprouespaialsestudiants!

Ensagradacompartiraquestsresultatsambtotelprofessoratperquèaquestésunèxitcol lectiu,de totselsdocentsdematemàtiquesque,durantanysimoltsovintenperfectasolitud,hananatexperimentantmetodologiesactives,produintmaterialsiportant-losal’aula,mantenintlesassociacions, elsCRPielsgrupsdetreball.Nosaltresvenimd’allà,iaixícontinuemtreballant,recollintireelaborant aquestavaluosaobraquecontinuaviva.

TenimmoltclarqueelMMACAnoenglobatotaaquestaextraordinàriavitalitatdelarealitatque esmoual’entorndel’ensenyamentideladivulgaciódelesmatemàtiques.Novolemenglobaro projectarlanostraombrasobrelesrealitatslocalsqueelaborenmaterialsiestratègies.Volemser unllocdetrobada,dediscussióid’amplificaciód’aquestesiniciatives.Somunaassociacióobertaa novesincorporacionsiacol laboracionspuntuals,tantara,quejase’nsacumulenfeines,comenun futur,quantindremunaseuipodremrealitzarunsmòdulsque,perdimensions,costosoeltipus d’instal·lacióquenecessiten,finsaranohempogutferihemhagutdeposposar.

I,finalment,estempotenciantlanostrapàginaweb:www.mmaca.cat,ianiremdesenvolupantel museuvirtual,adaptantisimulantlespropostesquefemal’exposició.Esteutotsconvidatsadonar-hiuna bonaullada,afercrítiques,aproposaralternativesoademanarexplicacions:ésunamaneradecomençaraparticiparenelnostreprojectei,després,sidonemcrèdital’antigasaviesaxinesaquandiu «Nofacispreguntes,fesexperiències»,nofaltaràresmésqueentraraserpartdelMMACA,elMuseu deMatemàtiquesdeCatalunya.

L’equipdel creamat

Màster Oficial de Recerca en Didàctica deles Matemàtiques i de les Ciències

DepartamentdeDidàctica delaMatemàticailes CiènciesExperimentals–UAB

Lafinalitatdel

éscapacitarl’estudiantperidentificarunproblemaderecercaenl’àmbitdel’educació matemàticaocientífica,tantformalcomnoformal,persituar-loenelseucontextsocialiteòric, donant-hirespostaatravésdelesmetodologiesadientsicomunicar-neelsresultatsiles conclusionsalacomunitatcientíficaieducativaialesadministracionscorresponents.

MàsterOficialdeRecercaenDidàcticadelesMatemàtiquesidelesCiències Elsestudiantsaquivadirigitaquestmàstersónaquellsllicenciats,diplomatsograduatsque,a mésdecomplirelsrequisitsilescondicionsestablertesperlanormativaoficial,teneninterèsen:

Aprofundiricontribuiralscampsdeconeixementpropisdelesàreesdedidàcticadeles matemàtiquesidelesciènciesid’àreesafins,atravésdeprocessosderecercadecaràcterfonamental.

Incidirenlainnovacióeducativa,atravésdeprocessosderecercadecaràcteraplicaten elsdiferentscontextosdaprenentatgematemàticicientífic.

Conèixerelsmecanismesperalamilloradelaformaciódelsagentsresponsables d’educarenmatemàtiquesienciènciesalapoblació,tantenàmbitsformalmentinstitucionalitzatscomforad’ells.

Analitzarelsaspectessocials,culturalsipolíticsimplicatsenl’educaciódelapoblacióen matemàtiquesienciències,ambl’objectiudefer-hiincidència,tantanivelld’institucions comdepolítiqueseducatives.

Avaluar,entenentl’avaluaciócomaprocésderegulaciótantinterncomextern,lapràctica docent,lainnovacióilaformacióqueespromouen.

Haversuperatambèxitaquestmàsterpermet,entrealtrescoses,al’estudiantiniciareldoctorat enl’àmbitdeladidàcticadelesmatemàtiquesidelesciències.

Pla d’estudis:60 crèditsECTS.

Enfunciódelaformacióprèviadel’estudiant,lacoordinaciódelmàsterpodràdemanarquees cursincomplementsdeformació.

Preu:elcurs2012-2013,elpreudelsmàstersoficialsdelaUABsesituacapals40percrèdit peralsestudiantsdepaïsoscomunitarisiperalsestrangersambresidència.

Informaciói inscripció:

http://www.uab.cat/servlet/Satellite/estudiar/masters-oficials/informacio-general/recerca-en-didacticade-les-matematiques-i-de-les-ciencies-1096480139517.html?param1=1096482842172

Peramésinformació: conxita.marquez@uab.cat

Normes per a la presentació de contribucions

1.Larevista NouBiaix acceptaperalasevapublicaciócontribucionsoriginalsrelacionadesambexperiènciesdidàctiques,activitatsd’ensenyamentiaprenentatge,escritsd’opinió,dedivulgacióid’investigacióenelcampdelamatemàticaielseuensenyamentenqualsevolnivelleducatiu.

2.Lescontribucionsrebudesseransotmesesaunaavaluacióprèviaacàrrecdedosespecialistesreconeguts.L’acceptaciódelapublicacióserànotificadadirectamental’autorambunaindicaciódela dataaproximadadepublicació.Encasqueunacomunicaciónofosacceptada,tambésen’enviarà notificació.

3.Peralapresentaciódetreballsoriginals,l’autortrametràal’adreçanoubiaix@gmail.comunarxiu, preferiblementenWord,ambundocumentadobleespaiiambmargesamplis(65caràctersperlínia). Elsgràfics,diagramesifigureshaurandeseroriginals(nofotocopiats).Elsarxiusgràficsespresentaran enformatepsotif.

4.Lacontribucióhauràd’incloureeltítol,elnomdel’autoroautors,lasevaadreçaprofessionalcompletailasevaadreçaelectrònica.S’adjuntaràunresumnomésllargde300paraulesencatalàianglès.Al finaldeldocuments’inclouràobligatòriamentlabibliografiaperordrealfabèticdecognoms,d’acord amblanormativaAPA;exemples:

Articles

Albertí,M.(2002).LesMatemàtiquesdesd’unaperspectivacultural:Etnomatemàtiques. Biaix,20,6-25. Llibres

Godino,J.,Font,V.(2003). Razonamientoalgebraicoparamaestros.Granada:UniversidaddeGranada.

Capítolsdellibres

Edo,M.,Revelles,S.(2004).Situacionesmatemáticaspotencialmentesignificativas.DinsM.Antóni B.Moll(ed.), EducaciónInfantil.OrientacionesyRecursos(0-6años) (p.410/103-410/179).Barcelona:Praxis.

Actesdecongressos

Morales,M.,Font,V.,Planas,N.(2004).Estudiomicroetnográficoentornoaunconocimientomatemáticosituado.DinsA.Franzéialtres(ed.), ActasdelaIReuniónCientíficaInternacionalsobreEtnografíayEducación (CD-ROM).València:Germanía,PolisPaideia.

Pàginesweb

Ibanyez,A.,Paolu,N.,Pedreira,J.(2007).RelojBinariodesobremesa,aMicrosiervos. http://www.microsiervos.com/archivo/gadgets/reloj-binario-sobremesa.html

5.Lescontribucionsacceptadesquedaranenpropietatde Noubiaix ipodranserimpresessenseautoritzacióexpressadel’autor.Peralasevareproducciótotaloparcial,sen’hauràdesol·licitarl’autoritzacióa NouBiaix.Encasdetreballspresentatsperdiferentsautors,s’enténqueelprimerautortéla conformitatdelsaltres.

6.Elsarticlesespublicaranenllenguacatalana.NomésestraduiranalcatalàlescontribucionsacceptadesrealitzadesperautorsnoresidentsalsPaïsosCatalans.

7.Elsautorsesresponsabilitzarandelcomplimentdelesnormesestablertesperal’autoritzaciódela reproducciódematerialprocedentd’altresfontsbibliogràfiques.

8.Elsarticlestindranunaextensiód’entre6i12pàginesdetext—ésadir,untotalmàximde12.000 caràcters—,incloseslesnotesapeudepàgina.Podrananaracompanyatsd’il·lustracions,sempre quenosuperinl’extensiódeduespàgines.Endefinitiva,totcomplet—quaneltextcontinguiquadres,figures,fotografies,gràfics,mapes,etc.—nopodràsuperar,encapcas,les15pàgines.