Nou Biaix, 30

Setembre 2011 Revista de la FEEMCAT i la SCM

Noubiaix, un espai de col·laboració

L’any1992—anyolímpicaCatalunya—naixiaunarevistadedidàcticadelamatemàtica d’àmbitnacionalcatalàques’hamantingutfidelalsseuspropòsitsfundacionalsdurant gairebévintanys.

Al’editorialdelnúmero1llegim:

Biaix volserunespaidecomunicacióentretotselsquiexerciml’ensenyamentdeles matemàtiques.

Acceptem,comapremisainqüestionable,quel’‘‘acteformatiu’’ésunprocésquevamésenllàdel’actuaciópuntuald’unaclasse,d’uncurs,queduraanysis’aconsegueixambl’esforçdemoltsprotagonistes—l’alumne,elsmestres,elsprofessors,elsdocentsuniversitaris—iqueresultad’unaformació iestudi,d’unsialtres,‘‘sordaiconstant’’.

És,defet,lapremissaqueenl’esmentatnúmerode Biaix s’expressavaambelstermessegüents:

Veiemclarqueeltractamentdel’educaciómatemàticanoespotrestringiracapnivelld’edatconcret,sinóquehadeserconsideradaglobalment;elcaràcterprogressiud’aquestadisciplinailaseva relacióamblescapacitatsintel lectualsfanqueelseuplantejamentaunacertaedatinvolucriles edatsprecedents.Ésenaquestsentit,doncs,quea Biaix hitécabudatothom

És,doncs,moltcoherentqueduesentitatsrepresentatives,enconjunt,dela‘‘totalitat’’deprofessionalsdeladocènciadelamatemàticacatalanacomsónlaFEEMCAT—queaplegaprincipalment mestresiprofessorsd’ensenyamentsecundari—ilaSCM—queaplegaprofessorsd’ensenyament secundariiprofessorsdenivellsuperior—uneixinl’esforçilavoluntatd’intervenirenelmapaformatiu‘‘global’’catalàdelamatemàticaatravésdelarevista Biaix,totaportantlesiniciatives,elsconeixements,elsinteressos,lesexperiències,lacultura,laformaciódelsmembresd’ambduesassociacions.

Fruitd’aquestacoherènciaid’unavoluntatdecol laboraciólleial—ques’had’anarconsolidantamb elsresultatsdelspropersvolums—s’hadeciditdeduratermeunanovaetapade Biaix —queprenel nomde Noubiaix—ambunConsellderedacciócodirigiticoparticipatiambelpropòsitquecada volumconstidedosnúmeros.

Esperemidesitgemqueaquestainiciativa—quenovoltrencarresdelquejas’haassolit,ansal contrari,preténpotenciaralmàximl’antigainiciativade Biaix,tanfructífera—siguicompartidapels membresdelaSCMidelaFEEMCATtotdonant-lisuportamblasevaparticipacióactiva—através delacol laboraciódirecta—ipassiva—atravésdelapropagandail’entusiasme.

LaMequèienJosep—comadirectorsdelConselleditor—itotelConselleditorensesforçaremtant comcalguipertalqueelprojecteesdevinguiunarealitatmésforta,méscoparticipada,mésplural, mésricaencaraque Biaix

VolemagrairalsequipsdirectiusdelaFEEMCATidelaSCMelsesforçosquehanfetperllimarles dificultatsinicials—quetotanovaaventuracomporta—ihaginaconseguittrobarlamaneradefer possibleaquestprojectetanengrescador.

Màster OficialdeRecercaen Didàctica deles Matemàtiques i deles Ciències

DepartamentdeDidàctica delaMatemàticailes CiènciesExperimentals–UAB

Lafinalitatdel

éscapacitarl’estudiantperidentificarunproblemaderecercaenl’àmbitdel’educació matemàticaocientífica,tantformalcomnoformal,persituar-loenelseucontextsocialiteòric, donant-hirespostaatravésdelesmetodologiesadientsicomunicar-neelsresultatsiles conclusionsalacomunitatcientíficaieducativaialesadministracionscorresponents.

MàsterOficialdeRecercaenDidàcticadelesMatemàtiquesidelesCiències Elsestudiantsaquivadirigitaquestmàstersónaquellsllicenciats,diplomatsograduatsque,a mésdecomplirelsrequisitsilescondicionsestablertsperlanormativaoficial,teneninterèsen:

AprofundiricontribuiralscampsdeconeixementpropisdelesàreesdeDidàcticadeles MatemàtiquesidelesCiènciesid’àreesafins,atravésdeprocessosderecercadecaràcterfonamental.

Incidirenlainnovacióeducativa,atravésdeprocessosderecercadecaràcteraplicaten elsdiferentscontextosd'aprenentatgematemàticicientífic.

Conèixerelsmecanismesperalamilloradelaformaciódelsagentsresponsables d’educarenmatemàtiquesienciènciesalapoblació,tantenàmbitsformalmentinstitucionalitzatscomforad’ells.

Analitzarelsaspectessocials,culturalsipolíticsimplicatsenl’educaciódelapoblacióen matemàtiquesienciències,ambl’objectiudefer-hiincidència,tantanivelld’institucions comdepolítiqueseducatives.

Avaluar,entenentl’avaluaciócomaprocésderegulaciótantinterncomextern,lapràctica docent,lainnovacióilaformacióqueespromouen.

Haversuperatambèxitaquestmàsterpermet,entrealtrescoses,al’estudiantiniciareldoctorat enl’àmbitdeladidàcticadelesMatemàtiquesidelesCiències.

Pla d’estudis:60 crèditsECTS.

Enfunciódelaformacióprèviadel’estudiant,lacoordinaciódelmàsterpodràdemanarquees cursincomplementsdeformació.

Preu:Elcurs2011-2012elpreudelsmàstersoficialsdelaUABésde32,60*percrèditperals estudiantsdepaïsoscomunitarisiperalsestrangersambresidència.

* Pendentde l’aprovació del Decretde preus de laGeneralitatde Catalunya.

Informaciói inscripció:

http://www.uab.cat/servlet/Satellite/postgrau/masters-i-postgraus-1096480137925.html

Per amésinformació: conxita.marquez@uab.cat

Elperíode de preinscripciófinalitza el 17 dejunyde 2011

articl artices les rticles

Influènciadelcontext delsenunciatsdedosproblemes PISA2003enelspercentatgesde resolucionscorrectesdel’alumnat dequartd’ESO.Estudipergènere

AntonioJoséGarcíaBernabéu

IESMontserratMiróiVilà agarc222@xtec.cat

Resum Abstract

Elsmitjansdecomunicaciósovintutilitzenels resultatsdelesprovesPISAperanalitzarel nostresistemaeducatiu.Habitualment,es treuenconclusionsglobalsdel’ensenyamenta Catalunya(oqualsevolpaísquehihagi participat)sensetenirencomptetotselsfactors quehanestatanalitzatsenl’estudiPISA. Elsproblemesdematemàtiquesdelesproves PISAesfonamentenenvuitcompetències bàsiquesisónelsmateixosperatotl’alumnat detotselspaïsosquehiparticipen.Semblaque seriadesitjablequeelcontextdelsenunciats d’aquestsproblemesnoinfluïssinenels percentatgesderesolucionscorrectes(jaque, d’aquests,estreuenconclusionsqueinflueixen enlespolítiqueseducatives).

Enaquestarticles’intentaanalitzarsiels percentatgesderesolucionscorrectesdedos problemesPISA2003,canviasise’nmodificael contextdelsenunciats.

Comespotveureenelcapítol8deresultats, s’hacomprovatque,amblamostrade371 alumnesutilitzadaenaquestestudi,elcontext delsenunciatsd’aquestsproblemessíque influeixenelspercentatgesderesolucions correctes.

Unaltreresultatqueenshemtrobatique considereminteressantdedestacar,haestat queelcontextdelsenunciatsd’aquests problemesinflueixmésenlesnoies queenelsnois.

ThemediaoftenusetheresultsofthePISAteststo analyseoureducationsystem.Globalconclusions areoftenjumpedtoaboutteachinginCatalonia (oranyothercountryinvolved)without consideringallthefactorswhichhavebeen analysedatthePISAreport.

TheMathsproblemsatthePISAtestsarebasedon eightbasicskillsandtheyarethesameforall studentsinallthecountriestakingpart.Afitting targetmightbeforthewordingsofsuchproblems nottoinfluencethepercentagesofcorrectanswers (sincethosepercentageshaveanimpacton educationpolicies).

Thispaperaimsatanalysingwhetherthe percentagesofcorrectanswerstotwoPISA2003 problemschangewhenthecontextoftheir wordingismodified.

Asonemayreadintheresultschapter,ithasbeen provedthat,withthe371-studentsampleusedfor ourreport,thecontextofthewordingsofthese problemsdoeshaveaninfluenceonthe percentagesofcorrectanswers.

Anotherresultwhichhasbeenreached,whichwe considerinterestingenoughtopointout,isthefact thatthecontextsofthewordingsofthe aforementionedproblemshaveadeeperimpact ongirlsthanonboys.

1.Introducció

Enaquestarticleexposaremelsprincipalsresultatsd’unarecercaquantitativafetadinsdelMàsterde RecercaenDidàcticadelesMatemàtiquesidelesCiènciesdelaUABdurantelcurs2008-2009,sota ladirecciód’enLluísBibiloni.

L’objectiuprincipald’aquestarecercavaserestudiarsielpercentatged’alumnesqueresolenbédos problemesproposatsalesprovesPISA2003canviasiesmodificaelcontextdelsenunciatsd’aquests problemes.

Enaquestarecercavanparticipar126alumnesdetercerd’ESOdedosinstitutsperferunaprovapilot i371alumnesdequartd’ESOpertanyentsasisinstitutspúblics,uncol·legiconcertatiuncol·legi privatdediferentsindretsdeCatalunya(Banyoles,Barcelona,LaRocadelVallès,Mataró,Montcadai Reixac,iReus).

Analitzantelspercentatgesderesolucionscorrectesdelsproblemesenestudi,vamtrobardiferències, estadísticamentsignificatives,entrediferentsgrupsd’alumnes;perexemple,entrel’alumnatPISA iel NOPISA;peròunresultatqueensvasorprendre—perquènoestavabuscat—vaserladiferència entreelspercentatgesdelsproblemesbenresoltspelsnoisiperlesnoiesquevanparticiparenaquest estudii,enconcret,vamcomprovarqueelcontextdelsenunciatsd’aquestsproblemesinflueixmolt mésenlesnoiesqueenelsnois.

2.ElsproblemesPISA2003estudiatsilessevesmodificacions

DelsproblemesalliberatsPISA2003,vamseleccionar-nedosperferaquestestudii,decadaun d’aquests,envamferduesnovesredaccions.Elsenunciatsdelsnousproblemesesvanredactaramb laintencióqueelcontextfosméspròximalavidaquotidianadel’alumnati,d’aquestamanera,poder comprovarqueelspercentatgesderespostescorrectesaugmentenrespectedelsproblemesoriginals.AquestesnovesredaccionsvanservalidadesperdiferentsprofessorsiprofessoresdelaUABi del’ensenyamentsecundari.

Acontinuaciópresentemelsproblemesestudiats;elprimerproblemadecadagrupésl’originalPISA 2003ielsaltresdossónlesmodificacionsquen’hemredactat.

• Problema ROBATORIS (originalPISA2003)

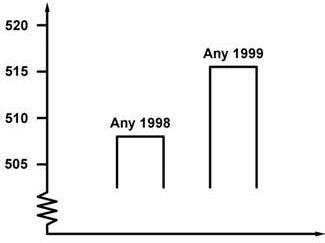
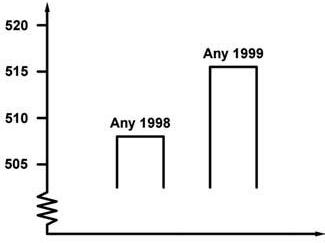
UnpresentadordeTVvamostraraquestgràficivadir:

Elgràficmostraquehihaungranaugmentdelnombrederobatoriscomparant1998amb1999

Consideresquel’afirmaciódelpresentadorésunainterpretacióraonabledelgràfic?

Dónaunaexplicacióquefonamentilatevaresposta.

• Problema VIATGEDEFIDECURS (primerproblemamodificatdelproblema ROBATORIS)

Unparelivamostraralseufillaquestgràficivadir:

Elgràficmostraquehihahagutungranaugmentenelnombred’eurosquevalelviatgedefidecurs comparantelquevacostarel2007ambelquecostaaquestany2008i,pertant,nopodràsparticipar enaquestviatge.

Consideresquel’afirmaciódelpareésunainterpretacióraonabledelgràfic?

Dónaunaexplicacióquefonamentilatevaresposta.

• Problema DESPESESANUALS (segonproblemamodificatdelproblema ROBATORIS)

Unparevamostraralseufillaquestgràficilivadir:

Elgràficmostraquehihahagutungranaugmentenelnombred’eurosquet’hedonatperalesteves despesesenunanycomparantl’any2007ambel2008

Consideresquel’afirmaciódelpareésunainterpretacióraonabledelgràfic?

Dónaunaexplicacióquefonamentilatevaresposta.

• Problema TERRATRÈMOL (originalPISA2003)

Esvaemetreundocumentalsobreterratrèmolsilafreqüènciaambquèaquestsocorren.Eldocumentalincloïaundebatsobrelapossibilitatdepredirelsterratrèmols.

Ungeòlegvadir:‘‘Enelspropersvintanys,lapossibilitatqueocorriunterratrèmolalaciutatde Zedésdosdetres’’.

Quinadelessegüentsopcionsreflecteixmillorelsignificatdel’afirmaciódelgeòleg?

a) 2 3 × 20 = 13,3;pertant,entre13i14anysapartird’arahihauràunterratrèmolalaciutatdeZed.

b) 2 3 ésmésque 1 3 ,pertant,espotestarsegurquehihauràunterratrèmolalaciutatdeZeden algunmomentenelspropers20anys.

c)LaprobabilitatquehihagiunterratrèmolalaciutatdeZedenalgunmomentenelspropers 20anysésmésgranquelaprobabilitatquenohihagicapterratrèmol.

d )Noespotdirelquepassarà,perquèningúpotestarsegurdequantindràllocunterratrèmol.

• Problema ACCIDENTSDETRÀNSIT (primerproblemamodificatdelproblema TERRATRÈMOL)

EsvaemetreundocumentalsobreelsaccidentsdetrànsitalaciutatdeZedilafreqüènciaamb quèaquestsocorren.Eldocumentalincloïaundebatsobrelapredicciódelapossibilitatdepatir unaccident.

Eldirectorgeneraldetrànsitvadir:‘‘Enelspropersvintanys,lapossibilitatqueunjovequeacaba detreure’selcarnetdeconduirtinguiunaccidentdetrànsitésdosdetres’’.

Quinadelessegüentsopcionsreflecteixmillorelsignificatdel’afirmaciódeldirectorgeneralde trànsit?

a) 2 3 × 20 = 13,3;pertant,entre13i14anysapartird’araaquestjovetindràunaccidentdetrànsit.

b) 2 3 ésmésque 1 3 ,pertant,espotestarsegurqueenalgunmomentenelspropers20anysaquest jovetindràunaccidentdetrànsit.

c)Laprobabilitatqueaquestjovetinguiunaccidentdetrànsitenalgunmomentenelspropers 20anysésmésgranquelaprobabilitatquenotinguicapaccident.

d )Noespotdirelquepassarà,perquèningúpotestarsegurdequanunjovepottenirunaccident detrànsit.

• Problema LAMORT (segonproblemamodificatdelproblema TERRATRÈMOL)

Esvaemetreundocumentalsobrelapreparaciópsicològicadavantlamortd’unapersonaestimadailafreqüènciaambquèunjovepotpatirlamortd’unbonamicounabonaamiga.El documentalincloïaundebatsobrelapossibilitatdepredirquanunapersonapatiràlamortd’un amicoamiga.

Unpsicòlegvadir,dirigint-seaunjovede15anysqueparticipavaeneldebat:‘‘Enelspropersvint anys,lapossibilitatquetupateixislamortd’unbonamicounabonaamigaésdosdetres’’.

Quinadelessegüentsopcionsreflecteixmillorelsignificatdel’afirmaciódelpsicòleg?

a) 2 3 × 20 = 13,3;pertant,entre13i14anysapartird’araesmoriràunbonamicounabonaamiga d’aquestjove.

b) 2 3 ésmésque 1 3 ,pertant,espotestarsegurqueesmoriràunbonamicounabonaamiga d’aquestjoveenalgunmomentenelspropers20anys.

c)Laprobabilitatqueesmoriunbonamicounabonaamigad’aquestjoveenalgunmomenten elspropers20anysésmésgranquelaprobabilitatquenose’nmoricap.

d )Noespotdirelquepassarà,perquèningúpotestarsegurdequanesmoriràunbonamico unabonaamigad’aquestjove.

3.Testsestadísticsidefinicions

Perferaquestarecerca,enprimerllocesvaescollirunamostrad’alumnesdequartd’ESOiesvan estudiarelspercentatgesderespostescorrectesd’aquestsproblemesendiferentsgrupsd’alumnes ambalgunacaracterísticaencomú,perexemple:alumnatdequartd’ESOengeneral,elsilesalumnesquenohanrepetitcapcurs,elsilesalumnesquehanrepetitalguncurs,elsnois,lesnoies,etc. Desprésesvanestudiaraquestspercentatgesaplicantel testestadísticdecontrastdelvalord’unaproporció oel testestadísticdecontrastd’igualtatdeproporcions.

Enelnostrecas,elprimertestensdónalaprobabilitat, α,queelpercentatgederespostescorrectes d’unproblemaquehaobtingutungrupd’alumnessiguiigualaundeterminatvalor,perexemple, lamitjanaderespostescorrectesquevateniraquestproblemaaCatalunya.Elsegontestensdónalaprobabilitat, α,quesiguinigualselsdospercentatgesderespostescorrectesobtingutsendues mostresd’alumnesdiferents.Percalcularaquestesprobabilitats,aqueststeststenenencompteel valordelspercentatgesielnombred’individusdelamostra.

Enlestaulessegüentsespotveurecomcanvialaprobabilitat, α,d’acceptarqueelsdospercentatges donatssiguiniguals;enlaprimera,hemmantingutfixoselspercentatgesihemmodificatelnombre d’individusdelamostra,mentreque,enlasegona,hemfixatelnombred’individusihemcanviatels percentatges.

Perentendremillorelsignificatdelsvalorsd’α comentareml’últimafiladelataula1.Ambaquests nombresd’individusdelesduesmostres(200alumnesi150alumnes,respectivament),espotpensar queladiferènciadepercentatges(50%i40%,respectivament)ésnomésacausadel’atzarique,en realitat,aquestspercentatgeshauriendeserelmateix;aquestpensamentté‘‘només’’unaprobabilitat desercertd’un3,16%.

Taula 2. Test de contrast de proporcions amb fixació del nombre d’individus i canvi dels percentatges.

Enaquestarticle,lesafirmacionsfetessobreelsproblemesenestudiesfaranambdiferentsgrausde seguretatsegonselsvalorsd’α trobats.S’escriurà:

a) Nos’hatrobatcapdiferènciasignificativa,obé,noesfaràcapafirmació,sielvalord’α ésmajorque 0,1.

b) Hihaindicis,si α estàal’interval[0,05,0,1].

c)Esfaràl’afirmaciósensecapcomentari,si α estàal’interval[0,02,0,05].

d ) Ladiferènciatrobadaésmoltsignificativa,si α ésmenorque0,02.

4.Provapilot

Esvarealitzarunaprovapilot,amblaintenciódeseleccionarla‘‘millor’’versiódecadaundelsdos problemesPISA2003,ésadir,aquellaque,enelseupercentatgederespostescorrectes,seseparés mésdelseuproblemaoriginalPISA2003.Enpensarqueelscontextosdelsnousproblemeserenmés pròximsalavidaquotidianadel’alumnat,s’estavamoltsegurquelesnovesredaccionstindrienun majorpercentatged’encertsi,pertant,esvadecidirferlaprovapilotambalumnesdetercerd’ESO dedosinstituts.

Esvadecidirposaracadaprovaunmateix problemacontrol,diferentdelsqueaquíestanredactats, anomenat Escombraria, escollitentreelsproblemesPISA2003,pertaldecomprovarquel’alumnat quefeiacadaprovaeraequivalent,respectedelasevacapacitatderesoldreproblemesPISA2003. EntretotselsproblemesPISA2003,vamescollirelproblema Escombraria perquèelseupercentatge derespostescorrectesaCatalunya(45,5%)ésmoltsemblantalpercentatgedelproblema Robatoris (43,3%)ialproblema Terratrèmol (47,7%).

Encadagrupd’alumnes,esvanrepartiraquestestresproves(vegeulataula3),seguintl’ordrealfabètic delscognoms,perintentarquelestresprovesestiguessindistribuïdesal’atzar.

Taula3.Resultatsdelaprovapilotamb126alumnes.

Ambels126alumnesquevanparticiparenlaprovapilot,esvanobtenirelspercentatgesderespostes correctesqueestrobenalataula3.

Analitzantlesdadesambeltestestadísticdecontrastd’igualtatdeproporcions,esvaobservarque:

a) Hihaindicis queelproblema DESPESESANUALS ésmésdifícilqueelproblema ROBATORIS.

b)Elproblema VIATGEDEFIDECURS ésmésfàcilqueelproblema ROBATORIS

c)Elsproblemes ACCIDENTSDETRÀNSIT i LAMORT tenenpercentatgesderespostescorrectesmolt semblantsalproblema TERRATRÈMOL.

Semblavaquelasuposicióinicial—elpercentatgederespostescorrectesdelsproblemesmodificats augmenta—noméseracertaenunadelesquatreversionsdelsproblemes;amés,unaversióva tenirunpercentatgederespostescorrectesmenorqueelproblemaoriginali,finalment,l’alumnat quevaferaquestaprovapilot—alumnesdetercerd’ESO—engeneraltenienunanymenysque l’alumnatquehaviadeparticiparenl’estudidefinitiu.Tenintencomptetotaixò,esvadecidirno rebutjarcapversiódelsproblemesoriginalsi,pertant,esvanestudiarlesduesversionsdecadaun delsdosproblemesPISA2003.

5. Disseny de les proves per fer l’

estudi definitiu

Decadaundelsdosproblemesaestudiar,hihaviadosproblemesmodificatsques’haviendecompararambelseucorresponentproblemaoriginal.Pertalquecadaundelsquatreproblemespogués serresoltenlesmateixescircumstànciesiquealgunesvariablesdel’alumnatquepodieninfluirenels resultatsfinals(comelcansamentolamotivacióperferlaprova),fossin—enpromig—equivalents enelsquatreproblemes,esvandissenyarquatreprovesdiferentsperferl’estudidefinitiu(vegeula taula4),deformaque:

a)Totl’alumnatvaferunmateixproblemacontrolinicial, SELECCIÓ, iunaltreproblemacontrol, TIPUS DECANVI,alfinaldelaprova.

Vamvolerposarunmateixproblemacontrolinicialperintentarquetotl’alumnats’enfrontés alsproblemesenestudiambungraudeconcentraciósemblant.Ivamposarunproblemacontrolfinal,ambtrespreguntes,perquèvolíemtenirpercentatgesderesolucionscorrectesd’altres problemesPISA2003queensajudessinaferlescomparacionsdepercentatgesdelsproblemes enestudi.Elspercentatgesderesolucionscorrectesd’aquestsproblemesenspodienservirper tenirindicisqueduesmostresd’alumneserenequivalentsrespectealasevacapacitatdere-

Taula4.Estructuradelesprovesdefinitives.

soldreproblemesPISA2003,obéqueungrupd’alumneseramillorqueunaltrequanresolia aquestsproblemesPISA2003.

b)Cadaproblemaoriginalilessevesversionsocupavenelmateixllocdintredelesproves.

c)Cadaalumne/ahaviaderesoldreunproblemaoriginaliunproblemamodificatdel’altreproblema original.

6. Equivalènciaperresoldreels problemescontrol dels diferents grups d’alumnes que han fet cada prova

Encompararelpercentatgetotalderespostescorrectesdels problemescontrol, noesvatrobarcap diferènciasignificativaentreelsquatregrupsd’alumnes.Pertant,aquestfetenspermetiacontinuar amblarecercaiconsiderarcomavàlidselsresultatsestadísticsquevamtrobar.Detotesmaneres, vamferdosestudis:(1)estudiantladiferènciadepercentatgessensetenirencompteels problemes control i(2)tenintencompteelspercentatgesdels problemescontrol,talcoms’explicaacontinuació.

7. Càlculsperconsiderar lapossibleinfluènciadel nivell decapacitat de l’alumnat per resoldre els problemes control en els percentatges dels problemes en estudi

Amésdel’estudidelspercentatgesderesolucionscorrectesdecadatriodeproblemes,comparant elspercentatgesmitjançantel testdecontrastd’igualtatdeduesproporcions,vamferunestudiparal lel quevaconsistiratenirencomptelespetitesdiferènciesdepercentatgesderesolucionscorrectes delsdos problemescontrol entreelsdiferentsgrupsd’alumnesestudiats.

Comqueels problemescontrol vanserplantejatsatotl’alumnatquevaferaquestesproves,vamfer lasuposicióquelespetitesdiferènciesdepercentatgesderespostescorrectesd’aquestsproblemes indicavenlespetitesdiferènciesde‘‘capacitatmatemàtica’’entreelsdiferentsgrupsd’alumnesi,per tant,vamtraslladaraquestesdiferènciesalsproblemesenestudi;unavegadacorregitselspercentatgesderespostescorrectesdelsproblemesenestudi,vamaplicarel testdecontrastdelvalord’una proporció.

Perentendremilloraquestprocediment,posareml’exemplesegüent:

Taula 5. Percentatges de respostes correctes de l’alumnat que va fer els problemes i , i percentatges de respostes correctes dels. (Tot l’alumnat).

ROBATORIS DESPESES ANUALS problemes control

Elpercentatgederespostescorrectesdelsdos problemescontrol del’alumnataquiesvaplantejar elproblema ROBATORIS,vaserun4,5%superioralquevaobtenirl’alumnatqueselivaplantejarel problema DESPESESANUALS;pertant,perferaquestestudiesvaconsiderarquel’alumnatqueva ferelprimerproblemateniaunpercentatgederesolucionscorrectesun4,5%superior,enqualsevol problema,quel’alumnatquevafer-neelsegon.

Siessuposaqueelproblema ROBATORIS téexactamentlamateixadificultatqueelproblema DESPESESANUALS,sabentqueelsegonvaobtenirun52,6%derespostescorrectes,elprimerhauriade tenirun4,5%mésderespostescorrectes,ésadir,un55,0%.

Ara,sicompararemelpercentatgeteòric(55,0%)delproblema ROBATORIS ambelreal(60,7%),utilitzantel testdecontrastdelvalord’unaproporció,observemque hihaindicis queelprimerproblemaés mésdifícilqueelsegon.

Taula 6. Càlcul del percentatge teòric del problema respecte del problema i la seva significació estadística. (Tot l’alumnat).

60,7% 183 55%

Tambéespotferelmateixestudi,peròal’inrevés;l’alumnataquiesvaplantejarelproblema DESPESES ANUALS vaferun4,3%menysde problemescontrol quel’alumnatqueselivaplantejarelproblema ROBATORIS,pertant,perferaquestestudiesvaconsiderarquel’alumnatquevaferelprimerproblemavatenirunpercentatgederesolucionscorrectesun4,3%inferior,enqualsevolproblema,que l’alumnatqueenvaferelsegon.

Siessuposaqueelproblema DESPESESANUALS téexactamentlamateixadificultatqueelproblema ROBATORIS;sabentqueelsegonvaobtenirun60,7%derespostescorrectes,elprimerhauriadetenir un4,3%menysderespostescorrectes,ésadir,un58,1%.

Sicompararemelpercentatgeteòric(58,1%)delproblema DESPESESANUALS ambelreal(52,6%), utilitzantel testdelvalord’unaproporció,observemque nohihaindicis perdirqueunproblemaés mésfàcilquel’altre.

DESPESES ANUALS

Taula 7. Càlcul del percentatge teòric del problema respecte del problema i la seva significació estadística. (Tot l’alumnat).

Elprimervalord’α trobatindicaque hihaindicis queladiferènciadepercentatgesentreaquests problemeséssignificativa,peròelsegonvalord’α voldirque nohihaindicis queladiferènciade percentatgestrobadasiguisignificativa,pertant,siesconsideral’opciómésconservadora,lamenys arriscada,esconclouràque nohihaindicis queladiferènciadepercentatgesderesolucionscorrectes siguisignificativa.Enaquestarticle,perinterpretarunresultat,s’escolliràelmajordelsdosvalorsd’α ques’hantrobat.

8.Principalsresultatsidiscussiódel’estudi

8.1. A lumnatPISA

L’alumnatquevaserestudiatenaquestarecercafeiaquartd’ESOenelcurs2008-09:d’aquests,els quetenienlamateixaedatquel’alumnatquevaparticiparenlesprovesPISA2003erenelsnascuts l’any1993.

L’alumnatquevanéixeral’any1993ihaviaviscutalmenysdosanysaCatalunyaéselqueanomenarem alumnatPISA, ivanser288alumnes.

Encadagrup-classe,esvanrepartirlesquatreprovesperordrealfabètic,esperantque,d’aquestaforma,l’alumnatquefeiacadaprovafosprouequivalent,quantalasevacapacitatperresoldreaquests problemes.Aquestasuposiciólavamcomprovar,jaqueelmínimvalord’α trobatvaser0,1452iper tant,aquestarecercapodiacontinuar.

Alestaules8i9,espodenveureelspercentatgesderesolucionscorrectesdecadaproblemaen estudi.

Taula 8. Nombre d’alumnes i percentatges dels problemes i , i percentatges dels (Alumnat PISA).

ROBATORIS, DESPESES ANUALS ACCIDENTS DE TRÀNSIT problemes control.

Taula 9. Nombre d’alumnes i percentatges dels problemes ii percentatges dels. (Alumnat PISA).

TERRATRÈMOL, ACCIDENTS DE TRÀNSIT LA MORT, problemes control

Ambaquestesdades,vampodercomprovarque:

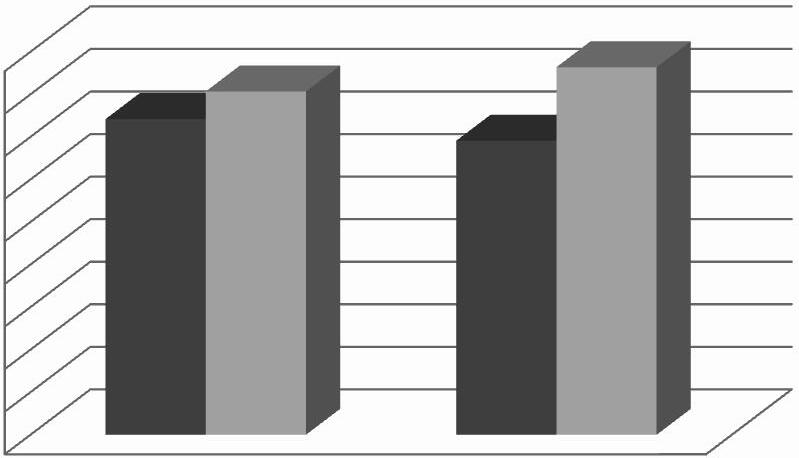
A)Sensetenirencompteels problemescontrol :

a) Hihaindicis queelproblema DESPESESANUALS és mésdifícil queelproblema VIATGEDEFIDE CURS.

b) Hihaindicis queelproblema TERRATRÈMOLésmésdifícil queelproblema ACCIDENTSDE TRÀNSIT.

c)Elproblema ACCIDENTSDETRÀNSIT és mésfàcil queelproblema LAMORT

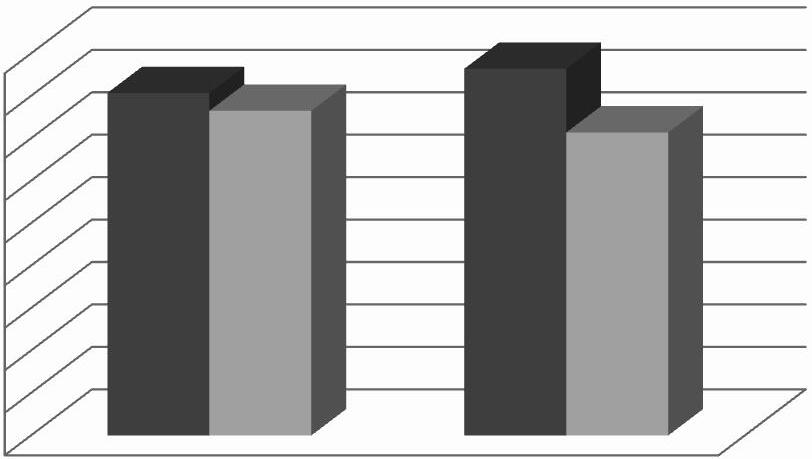
B)Tenintencompteels problemescontrol :

a)Elproblema DESPESESANUALSésmésdifícil queelproblema VIATGEDEFIDECURS i,amés, la diferènciatrobadaenelspercentatgesésmoltsignificativa

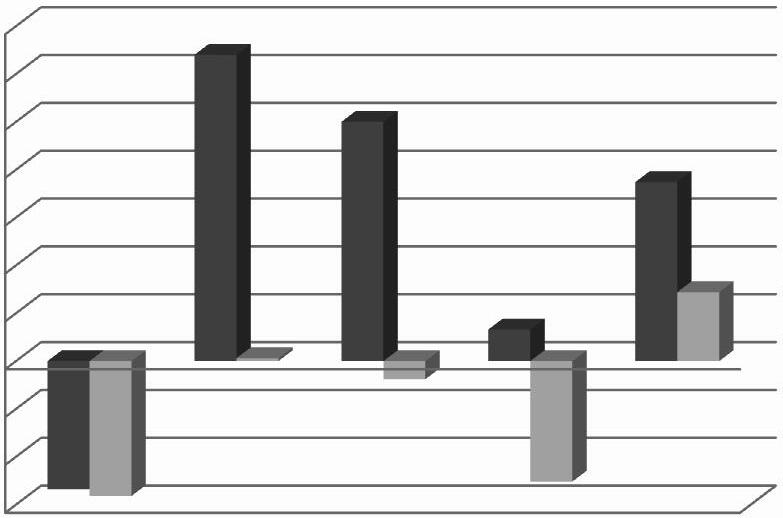
Figura1. Comparaciódelspercentatgesderespostescorrectesdelsproblemescontrolidels problemes (C) i (D). (AlumnatPISA). DESPE

b) Hihaindicis queelproblema TERRATRÈMOLésmésdifícil queelproblema ACCIDENTSDE TRÀNSIT

Figura 2. Comparació dels percentatges de respostes correctes dels problemes control i dels problemes (CD) i (A). (Alumnat PISA).

TERRATRÈMOLACCIDENTS DE TRÀNSIT

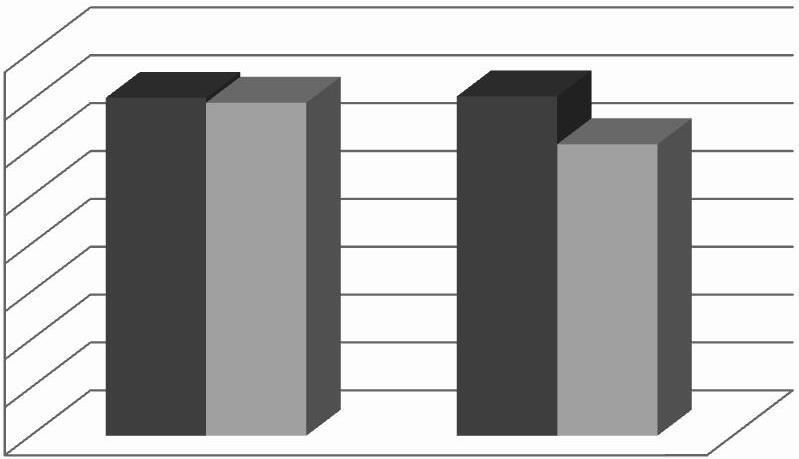
c) Hihaindicis queelproblema TERRATRÈMOLésmésfàcil queelproblema LAMORT.

Figura 3. Comparació dels percentatges de respostes correctes dels problemes control i els problemes (CD) i (B). (Alumnat PISA).

TERRATRÈMOLLA MORT

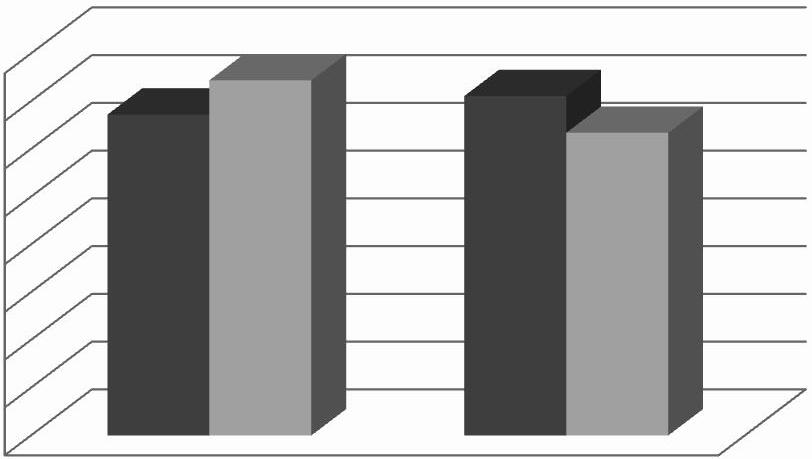
PR

d )ElproblemaACCIDENTSDETRÀNSITésmésfàcilqueelproblemaLAMORT,amés,ladiferència depercentatgesderesolucionscorrectesésmoltsignificativa.

Figura4. Comparaciódelspercentatgesderespostescorrectesdelsproblemescontrolidels problemes (A) i (B). (AlumnatPISA).

8.2. Estudi per gènere

Acontinuaciófaremunestudipergèneredelesdiferènciesdepercentatgesderespostescorrectes trobadesambtotl’alumnatparticipantinonomésamb l’alumnatPISA

Enlesquatretaulessegüents,espresententoteslesdadesperpoderferl’estudiestadístic.

Taula 10. Nombre d’alumnes i percentatges dels problemes i i percentatges dels. (Totes les noies).

ROBATORIS, DESPESES ANUALS ACCIDENTS DE TRÀNSIT, problemes control

Taula 11. Nombre d’alumnes i percentatges dels problemes i , i percentatges dels. (Totes les noies).

TERRATRÈMOL, ACCIDENTS DE TRÀNSIT LA MORT problemes control

ROBATORIS, DESPESES ANUALS

Taula 12. Nombre d’alumnes i percentatges dels problemes i , i percentatges dels. (Tots els nois).

ACCIDENTS DE TRÀNSIT problemes control

Taula 13. Nombre d’alumnes i percentatges dels problemes i , i percentatges dels. (Tots els nois).

A)Sensetenirencompteels problemescontrol :

Toteslesnoies

a)Elproblema ROBATORISésmésdifícil queelproblema VIATGEDEFIDECURS

b)Elproblema DESPESESANUALSésmésdifícil queelproblema VIATGEDEFIDECURS i ladiferència depercentatgesésmoltsignificativa.

c)Elproblema TERRATRÈMOLésmésdifícil queelproblema ACCIDENTSDETRÀNSIT i ladiferència depercentatgesderespostescorrectesésmoltsignificativa.

d )Elproblema ACCIDENTSDETRÀNSITésmésfàcil queelproblema LAMORT

Totselsnois

Novamtrobarcapdiferènciadepercentatgessuficientmentsignificativaentreelsproblemesen estudi,jaqueelvalorméspetitd’α vaser0,1214.

B)Tenintencompteels problemescontrol :

Toteslesnoies

a)Elproblema ROBATORISésmésdifícil queelproblema VIATGEDEFIDECURS i ladiferènciade percentatgesderespostescorrectesésmoltsignificativa

problemescontrol

Figura5. Comparaciódelspercentatgesderespostescorrectesdels idels problemes (AB) i (D). ( Toteslesnoies).

ROBATORIS VIATGE DEFI DE CURS

b)Elproblema DESPESESANUALSésmésdifícil queelproblema VIATGEDEFIDECURS i ladiferència depercentatgesderespostescorrectesésmoltsignificativa

Figura6. Comparaciódelspercentatgesderespostescorrectesdels idels problemes (C) i (D). ( Toteslesnoies).

c)Elproblema TERRATRÈMOLésmésdifícil queelproblema ACCIDENTSDETRÀNSIT

problemescontrol

Figura7. Comparaciódelspercentatgesderespostescorrectesdels idels problemes (CD) i (A). ( Toteslesnoies).

d )Elproblema ACCIDENTSDETRÀNSITésmésfàcil queelproblema LAMORT

problemescontrol

Figura8. Comparaciódelspercentatgesderespostescorrectesdels idels problemes (A) i (B). ( Toteslesnoies).

Totselsnois

a) Hihaindicis queelproblema ROBATORISésmésfàcil queelproblema DESPESESANUALS.

Figura9. Comparaciódelspercentatgesderespostescorrectesdels i delsproblemes (AB) i (C). ( Totselsnois).

problemescontrol ROBATORISDESPESESANUALS

b)Elproblema TERRATRÈMOLésmésfàcil queelproblema LAMORT.

Figura10. Comparaciódelspercentatgesderespostescorrectesdels i delsproblemes (CD) i (B). ( Totselsnois).

problemescontrol TERRATRÈMOLL AMORT

c)Elproblema ACCIDENTSDETRÀNSITésmésfàcil queelproblema LAMORT.

problemescontrol

Figura11. Comparaciódelspercentatgesderespostescorrectesdels i delsproblemes (A) i (B). ( Totselsnois).

8.3.Comparació deresultatsdetotes lesnoiesidetotselsnois

Siconsideremelconjuntdetotselsproblemes, nohihacapindici quelesdiferènciesdepercentatges deresolucionscorrectesentrelesnoiesielsnoissiguinsignificatives,ésadir,ambaquestapoblació d’alumnes;novampoderafirmarqueungènerevafermilloraquestsproblemesquel’altre.

Vamanalitzarcadaundelsproblemesenestudiisíquevamtrobardiferències,estadísticamentsignificatives,enelspercentatgesderesolucionscorrectesi,pertant,espodiaafirmarque:

a)Lesnoiesvantenirunpercentatgede respostescorrectesméselevat queelsnoisenelproblema SELECCIÓ i ladiferènciadepercentatgesésmoltsignificativa

b)Lesnoiesvan ferpitjor elproblema ROBATORIS i ladiferènciadepercentatgesésmoltsignificativa.

c)Lesnoiesvan fermillor elproblema ACCIDENTSDETRÀNSIT.

d ) Hihaindicis quelesnoiesvan ferpitjor elproblema DESPESESANUALS

Enelsdosgràficssegüents(figures12i13),espotveurequeelcontextd’aquestsproblemesvan influirmésenlesnoiesqueenelsnois:aixòespotinterpretarveientquelainclinaciódelssegments —queuneixenelspuntsiqueindiquenelspercentatgesderespostescorrectesdecadaproblema ambelsaltresdos—ésmajorenlesnoiesqueenelsnois.

Figura12. Comparació, per gènere, delavariaciódelspercentatgesderespostescorrectesdels problemes:i ROBATORIS,DESPESESANUALS VIATGE DEFI DE CURS.

Figura13. Comparació, per gènere, delavariaciódelspercentatgesderespostescorrectesdels problemesi. TERRATRÈMOL,ACCIDENTSDETRÀNSITL AMORT

Espotvisualitzarlainfluènciadelcontextdelsenunciatsenlesnoiesienelsnoisamblafigura14 següent:

Figura14. Comparació, per gènere, delsincrementsodisminucionsdelspercentatgesderespostes correctesdelsproblemesmodificats, respectedelpercentatgedelsoriginals.

Cadagrupdeduesbarrescorresponalavariaciódepercentatges—respectedelsproblemesoriginals—delsproblemes: DESPESESANUALS,VIATGEDEFIDECURS,ACCIDENTSDETRÀNSIT i LAMORT,i l’últimgrupcorresponalamitjanadetoteslesvariacions(sensetenirencompteelsignedelavariació).Enaquestúltimgrupespotveurecomlavariaciódepercentatgesdelsproblemesmodificats, respectealsoriginalsPISA2003,ésmésdeldobledegranenelgrupdenoies(18,7%)queenelgrup denois(7,2%).

9. Conclusió

Inicialment,l’objectiuprincipald’aquestarecercavaserintentarcomprovar,estadísticament,queen ferelcontextdelsenunciatsd’algunsproblemesPISA2003méspròximalavidaquotidianadel’alumnat,elpercentatgederespostescorrectesaugmentaria.Aquestarecercanoconsistiaacomprovar que,enferelsproblemes‘‘mésrealistes’’1 ,l’alumnatelsresoliamésfàcilment,sinóque,amés,introduïaladificultatqueelsenunciatsdelsproblemes,quantalformat,laredaccióileseinesmatemàtiquesperresoldre’ls,haviendeserelmésidènticamentpossiblealsoriginals.Quanesvanseleccionar lesredaccionsdefinitives,s’estavamoltsegurquetotselspercentatgesdelsnousproblemesserien superiorsalsdelsoriginals.

Enferlaprovapilotamb126alumnesdetercerd’ESOhivahaverunagransorpresa,enprincipinegativa:elproblemaoriginal ROBATORIS vatenirun43%derespostescorrectes,mentrequeelnou problema DESPESESANUALS vatenir-neun28%.Unasegonasorpresavaserqueelproblemaoriginal TERRATRÈMOL ilesduesversionsd’aquest—problemes ACCIDENTSDETRÀNSIT i LAMORT vantenirpercentatgesmoltiguals.Només,elnouproblema VIATGEDEFIDECURS (63%)vatenirun percentatgesuperioralseuoriginal ROBATORIS (43%).Aquestfetdemostraquelaintuïcióinicialpodia nosercerta.

Probablement,ladiferènciad’edat,deconeixements,d’experiènciadelavidaquotidianaid’altres factorsentreelprofessoratil’alumnat,faque—algunesvegades—estinguiunavisiódiferentsobre ladificultatd’unproblema.

1.PalmT.(2007).

Enferl’estudidefinitiu,vamcomprovarque hihadiferènciessignificatives i,finsitot, moltsignificatives enelspercentatgesderespostescorrectesd’algunsproblemes;aixòvoldirque,abandadeqüestionsd’atzar,hihaalumnesqueferbé(omalament)unproblemadepèndelcontextdelseuenunciat, ésadir,hihaalumnesquefanbé(omalament)unproblemaisiselicanviaelcontextdel’enunciatpassenafer-lomalament,(obé).Aixòdemostraque,perresoldrecorrectamentunproblema,no nomésfafaltatenirelsconeixementsmatemàticsadients,sinóque,probablement,esconfirmaque: ‘‘elfracàsd’unindividuenlaresoluciód’unproblema,quanencanvitéelsconeixementsnecessaris,esderivadelapresènciadefactorsmetacognitiusinocognitiusqueinhibeixenl’apropiadautilitzaciód’aquest coneixement;aquestsaspectessónelssegüents:afectesiactituds,creences,controlifactorscontextuals2 ’’.

Tambés’havistenaquestarticlequeelcontextdelsenunciatsd’aquestsproblemesinflueixende formadiferentenlesnoiesqueenelsnoisquevanparticiparenaquestestudi.Siescomparentotes lesnoiesambtotselsnois,esveuqueelcontextd’aquestsproblemesinflueixenmésenlesnoies queenelsnois,jaque hihaunadiferènciadepercentatgesmoltsignificativa enelsproblemes SELECCIÓ i ROBATORIS, hihadiferènciasignificativa enelproblema ACCIDENTSDETRÀNSIT i hihaindicisde diferència enelproblema DESPESESANUALS. HemcomparatlesmitjanesdelspercentatgesdevariacionsdelsproblemesenestudirespectedelsoriginalsPISA2003ihemvistqueaquestavariacióen lesnoies(18,7%)ésmésdeldoblequeenelsnois(7,2%).

10. Bibliografia

España,MinisteriodeEducaciónyCiencia,DirecciónGeneraldeEducaciónyCultura.(2003). EURYDICE Competenciasclave. Madrid:Autores.

España,MinisteriodeEducaciónyCiencia,InstitutoNacionaldeEvaluaciónyCalidaddelSistema Educativo.(2005). PISA2003.PruebasdeMatemáticasydeSolucióndeProblemas. Madrid:Autores.

Palm,T.(2007).Impactofauthenticityonsensemakinginwordproblemsolving. Educationalstudis inmathematics,67,37-58.

Puig,L.(2008).Sentidoyelaboracióndelcomponentedecompetenciadelosmodelosteóricoslocalesenlainvestigacióndelaenseñanzayaprendizajedecontenidosmatemáticosespecíficos. PNA, 2(3),87-107.

Pujol,R.(2006). Diagnosisobreladisposiciódel’alumnataaprendreatravésdelaResoluciódeProblemes. Recercaeducativaempíricaemprantunproblemaproposatal’informePISA.TreballdeMàster.Barcelona: UAB.

Rico,L.(2006).MarcoteóricodeevaluaciónenPISAsobrematemáticasyresolucióndeproblemas. RevistadeEducación,númeroextraordinario,275-294.

Vila,A.(2001). ResoluciódeProblemesdematemàtiques:identificació,origeniformaciódelssistemesde creencesenl’alumnat.Algunsefectessobrel’abordatgedelsproblemes.Tesidoctoral.Barcelona:UAB.

2.Lester,GarolafoiKroll(1989),citatsperVila(2001,p.45).

Quantaaiguamésqueterra hihaalnostreplaneta?

AdelaTerraza

CEIPFructuósGelabert,Barcelona adelaterraza@gmail.com

LourdesFigueiras

DepartamentdeDidàcticadelaMatemàticailesCiènciesExperimentals UniversitatAutònomadeBarcelona lourdes.figueiras@uab.cat

Resum Abstract

Hihaviaunavegadaunaescola.Ial’escola,hi haviaunaclassed’educacióinfantilqueesdeia falcons.Ialaclassedelsfalcons,hihavia vint-i-cincnensinenesquevoliensaber-hotot sobreelmarsielsoceans.Aixídoncs,van començarafer-sepreguntes,aconsensuar-les,a valorarlespossibilitatsqueteniendetrobar-hi resposta,agaudirestudiantiparlantdeciències amblessevesfamílies.Undiavasorgirla pregunta‘‘Quantaaiguamésqueterrahihaal nostreplaneta?’’ienelprocésdetrobar-hila resposta,elsnensilesnenesvantrobar-seamb fraccions,percentatges,metresquadrats, vèrtexs,arestes,cares,metrescúbicsinombres moltimoltgrans.

Onceuponatime,therewasaschool.Andinthis school,therewasaclassroomnamedhawks.And thetwentyfivechildrenfromtheclassroomnamed hawkswantedtoknoweverythingtherewasto knowaboutoceansandseas.Thereforethey begantoasksomequestions,tomakesome agreements,toevaluatetheirpossibilitiestoobtain answers.Andtheyhadagoodtimestudyingand talkingaboutscienceathome.Oneday,the questionwas:‘‘Howmuchmorewaterthanlandis thereonEarth?’’,andintheprocessoffindingthe answer,theyencounteredfractions,percentages, squaremeters,vertices,edges,facets,cubicmeters andsomeverybignumbers.

Elperquèdetotplegat:enrealitatamiemrondavapelcaplaidead’introduirelsnúmerosfinsala centena.Estàvemduentatermeelprojecte marsioceans,ibuscavalamaneraqueaquestaintencióquedésemmarcadadinselsinteressosqueelprojectegenerava.Lacosaestavadifíciljaqueels nensinenesdelaclassedeP5Falconsmanifestaveninquietuds,interrogantsicuriositatsmoltimolt concretesdelafaunamarinaprincipalment.Estantjocapficadaenaquestaideaicomqueresnoés casual,unmatívaarribaral’escolalaClàudiaiemvadir:‘‘Mira,Adela,m’hanregalataquestllibreque explicacosesdelsmarsielsoceans!’’.Obroelllibreienlaprimerapàginahihaviaaquestainformació:

El97%del’aiguadelplanetaprovédemars,oceansirius.

Perfecte!,javeiajoresoltalasituació.Haviatrobatlajustificacióquebuscava.Aratotseriabufarifer ampolles.

Desprésd’unaconversad’allòmésinteressant,elsmeusalumnesvanconsensuarquevolientrobar respostaalapreguntasegüent:Quinapartdelplanetaésterraiquinapartn’ésaigua?Aixídoncs, aquestavaserlapreguntaqueesvanendurescritaenunpaperpertald’investigar-laamblesrespectivesfamílies.Calexplicarqueal’escola(actualmentsomunaescoladeP3atercericreixemun nivellcadacurs),anemconstruintdesdelsinteressosdelsnensinenesidesdelesintencionsdels professionalsqueelsacompanyem.Aixídoncs,senseunllibredetextounaltretipusdeproposta pautadaapriori,lacol laboracióiparticipaciódelesfamíliesésfonamental.

Jotenialesmevesexpectativesianavafentlesmevescabòries...Elsmeusconeixementsprevisem deienquelacosaestavaaixí:d’unabanda,el30%,idel’altra,el70%aproximadament.Pensavaen materialsperportaralaclasse,enladesena...

Elretorn

Elretorndelesinvestigacionsfamiliarsvaserforçaheterogeni.Amesuraqueanavenarribantles respostesjoanavaprenentconsciènciaquesí,queefectivamentintroduirialacentenaitambéaltres conceptesmatemàticsenelsqualsnohaviapensatenunprincipi.Ésadir,quelespreguntesneixen, creixenifinsitotesreprodueixen.Persortnomoren,estransformenienstransformen.Usposoalcas:

—Cincnensinenesvanportarunainformacióquedeiaquedecada10partsdelplaneta,7eren aiguai3erenterra.

—Sisnensineneshavienesbrinatquetresquartespartsdelplanetaerenaiguaiunaquartapart eraterra.

—Nounensinenesaportavenunadocumentacióquedeiaqueel30%eraterraiel70%eraaigua. (Perfitrobavael100explícitament).

—Iunanena,laMaria...txa,txa,txa,txannnn...vaportarescritqueelplanetaté1386000000km3 d’aigua!,(delvolumdeterra,però,noendeiares...).

L’organització

Elprimerquevamfervaserferpilesambelspapersqueensproporcionavenunamateixainformació.Uncopfetalaclassificació,necessitàvemexposar-laafideveure-labé,familiaritzar-nosambla diversitatderespostesifermésfàcilqueelsnensinenesqueproposavencadatipusdiferentens expliquessincoml’entenien.

Toteslesrespostesqueexplicavenqueelplanetateniasetdesenespartsd’aiguaitresdesenesparts deterra,venienacompanyadesd’ungràficotaula.

Elmateixvapassaramblainformacióquedeiaquehihaviatresquartespartsd’aiguaiunaquarta partdeterra.Pertant,elsuportvisualvasermoltútil.

Pelquefaalesinformacionsqueparlavend’un30%deterraid’un70%d’aiguad’unabandaide 1.386.000.000km3 d’aigua,novenienacompanyadesdecapsuportvisualqueajudésafer-seuna ideadelamagnitudquerepresentaven.

Larepresentació

Organització de les aportacions, agrupades segons el tipus de resposta.

Perrepresentar3desenespartsi7desenesparts,vammanipularrectanglesdefustanaturalqueels nensinenestenienal’abastal’aulaperferconstruccionsentred’altrescoses.Enposavenunsobre l’altreounalcostatdel’altresobrelataulafinsarribaradeu,iseparavendespréselstrescorresponents alaterradelssetcorresponentsal’aigua.

Després,sobrepaper,vamutilitzarelrecursproporcionatperunafamíliaquehaviaretallatunmapamundifísic:posantensetpartselsmarsioceansretallats,ienlestrespartsrestants,elsretalls corresponentsalscontinents.

Enelcasdelestresquartespartsiunaquartapart,vamferserviruncercledividitenquadrants,ja queaquestarepresentacióeralaquetotsellshavienproporcionatenlasevadocumentació.Enuna safatahihaviamoltsquartsdecercledecolorverdienunaaltra,moltsquartsdecercledecolorblau. Lapropostaconsistiaaagafarelsquadrantsdecerclenecessarispermuntaruncerclecomplet.Els agafavend’unenun,tresblausiunverddirectament.Totsverbalitzavenelqueanaventrianti,en tenir-los,totsdeien:jatincelsquatrequarts!

Enunprincipi,laintencióeraconstruirambellsunagraelladedeuperdeuisituarenlescaselles elsnúmeroscorresponentsfinsarribaraunacentena,peròdepaciènciaiatenciócontinuadanon’hi haviamassaifinalmentlavaigconstruirjoilavamomplirentretots.Escansavenivamferservirtres sessionsperomplirlescentcaselles.Vamposarenelsprimerstrentanúmerospaperdecel lofana verdrepresentantlaterra,idesprésd’assegurar-nosquelarestaerensetanta,vamposarpaperde cel·lofanablauperrepresentarelmar.Vandescobrirqueelsnúmerosmésgransdedeupermeten agruparen‘‘bossesdedeucoses’’totique,devegades,tambéquedaven‘‘cosessoltes’’.Peril·lustrarho,entranscricunareflexió:

Ésclar,alaclassesom25.Aixòvoldirquehihadosgrupsde10i5nensmés,perquèsihihaguessin 10nensmés,jaenseriaunaltrede10ienseríem30.

Mentretotaixòpassava,jonoparavadepensarcomintegrarialainformaciósobreelvolumd’aigua: quinoquinsrecursosserienelsquemillorservirienperrepresentarelmetrecúbic,jaqueeraevident queelquilòmetrecúbicresultavainabastable.Larepresentaciódelmetrecúbictambéaportariala grandiositat,laimmensitatdelaquantitatd’aigua,demaneraqueafegiriaalaxifraelsnouzerosque hifaltaven.

Cercantelsraconsdelamemòria,pelquefaalespossibilitatsirecursosquepodemtrobaral’escola, vaigrecordarquefadoscursosvamcomprarunmaterialperal’aulade psico queconsistiaenunes varesdemetreambunscubsblancsquefand’encaixos.Vaigpujarambelmaterialalaclasseiemvaig sentirsalvada.Al’escolaconsideremmoltimportantquepersonesespecialitzadesenelsinteressos queensocupenforminpartdelanostraquotidianitat.Aixídoncs,emvaigreuniramblaLourdesili vaigproposarquefosellalaqueexpliquésalsnensineneslaqüestiódelmetrecúbic.Vaquedarforça sorpresa.Segonslessevesparaules,nohaviaimaginatunapropostasimilar,iesvaoferirràpidament acol laborar.Elmateriallavaestimularforçaiesvamostrarmoltengrescada.

Lasortdecompartirunprojecte

Efectivament,lapropostaemvaestimular.L’Adelaemvadonardotzevaresflexiblesdecolorvermell, vuitpetitespecesdecolorblanc,iemvaproposarladifíciltascad’explicaranensinenesdecincosis anysquèésunmetrecúbic.Quanestàsacostumadaapensarenmatemàtiques,vastraduintsense dificultatalseuargot,demaneraquevaigmarxardel’escolapensantqueportavaalesmanslesdotze arestesd’uncubielsseusvuitvèrtex.Lesarestesfeienexactamentunmetre,demaneraqueamb allòn’hihaviaprouperconstruiral’aulaelmetrecúbic.Després,proposariaalsnensqueentressina dintreambl’objectiudegenerarexperiènciesamblamidadelseucosquepoguessinrecuperaren altressituacionsperportaratermeestimacionsraonables.

Peròl’activitatalmeucapnoparava.Pensarenpoliedresetportaquasibéimmediatamentalafascinantfórmulad’Euler.Inoésquetinguéslapretensiódeconduirelsinfantscapaquí,peròaixòemva ajudaraposarnomaunacosaquetrobavaafaltarenelmaterialqueduiaalesmans:lessiscaresdel cub.Idecopivoltavaigimaginarcomunadelesarestesqueportavaalamàcomençavaaestirar-se ocupantunespaideduesdimensionsis’aturavaenformaralterraunmetrequadrat.Necessitavasis metresquadratsdepaperd’embalar!

Eldiaabansd’anaral’escola,vaigenganxarunmetrequadratdepaperaunadelesarestesivaig retallarunesaltrescincpecesigualsperportar-lesal’escola.

L’emociódecompartirl’aprenentatge

L’AdelahaviarecordatalmatílainformacióquelaMariahaviaportatsobrelaquantitatd’aiguaque hihaviaalaTerra,ihaviaanunciatalsnensilesnenesquejohianiriaalatarda.Peròningúd’ellssabia benbéaquè.Quanvaigarribar-hiidesprésdelespresentacionsoportunes,enunarotllanaesvafer públicelmisteri:aquelldiaconeixeríem,nimésnimenysque...elmetrecúbic!Quinasorpresa,Déu n’hido!Aixòsíqueseriamoltemocionant...

Elmaterialvaanartrobantapocapocelseullocalcub:Primervamagafarunavaraiunreglaquetenienalaclasseitotsconeixien.Elreglefeiaunmetreivamcomprovarquelavaratenialamateixalongitud.‘‘Quinescosespodemmesurarambaquestavara?’’.Aleshoresvammesurarl’alçadadel’Ariadna,quefaunamicamésd’unmetre,elbraçd’enMiguel,queenfalameitataproximadament... ‘‘Iladistànciafinsalaporta?,lapodemmesurarambaquestavara?’’.‘‘Ennecessitemmés’’.‘‘Quantesmés?’’.‘‘Nohosé...tresoquatre’’.

Acontinuació,esvaanunciarunagransorpresa...Lanostraarestavacomençaraestirar-se,iaestirarse,comsivolguésconvertir-seenunacatifa.Iesvaestirarfinsaconvertir-seenunquadrat.EnMaxva comprovarqueacadaundelscostatsdelquadratpodiacol locarunaarestai,desprésd’unir-lespels extrems,se’nsvapresentar...lasenyora Metrequadrat !Nopodíemdeixar-lasensecara,demaneraque laLaiaesvadecidiraagafarelscolorsivapintarunacaramacadedebò.Ambarracadesitot.Vam consensuarquepodíemdescriurelasenyoraMetrequadratdientqueteniaformadequadratique elsseusquatrecostatsfeienexactamentunmetredellarg.Lavamferservirpermesurarlapissarra, elterra,ilasuperfíciedelaporta.

Finalment,aquellmetrequehaviacrescutfinsaconvertir-seenunquadrattambévacréixerd’alçada iesvaanarelevant,arribantaocuparunespaidetresdimensionsperalqualhavíemnecessitatdotze arestesd’unmetre.Acabàvemdeconstruirunmetrecúbic.Elsnensilesnenesvandistribuirpelterra elscincretallsd’unmetrequadrat,vandibuixarunacaragegantacadaunilesvananarenganxant

alcub.Ialeshores,esvapresentar,totbufó,...elsenyor Metrecúbic. Eracuriósdeveritat,perquèno teniapasunaniduescares,sinóqueentenia...Vaigpreguntaralsnensquantescaresteniaelcub. ‘‘Quatre’’.‘‘Una’’.‘‘Sis’’,vadirlaNina.‘‘Ésveritatqueentésis.Comésqueleshascomptadestan ràpid?’’‘‘Doncsperquèésigualqueundaucomdel’Ocaperòmésgran,ieneldauentensfinsalsis’’.

L’Arnauvasortiracomptartoteslescaresfinsquetothomestavaconvençutqueelnúmerodecares erensisivamdeixarquejuguessinperveurequantsnenshicabiencòmodament.

Laclasseestavaapuntd’acabar,il’Adelavacompartirambtotsquantsmetrescúbicscomaquest —perònoplensdenens,sinóplensd’aigua—,téelnostreplaneta,ivaescriurealapissarraun nombrebengran:

Elplaerdedescobrirlesmatemàtiquesdelprojectemarsioceans

Finsaquí,lanarraciódel’experiènciaqueensvaferarribaradescobrirambelsnenselmetrecúbic. Vaigapropar-memoltalprojectequehavienportatatermeivaigobservartotalamatemàticaquehi haviadarreradetotelquel’Adela,elsnensilesneneshavienconstruïtarrandelapregunta:‘‘Quina partdelplanetaésterraiquinapartn’ésaigua?’’.

Vaigcomprovarquelamajoriadelesfamílieshavieninterpretatlapreguntaentermesdelaraóentre lasuperfíciedelplanetacobertadeterrailasuperfíciecobertad’aigua.Estracta,sensedubte,d’una interpretaciómoltraonable,atèsqueaproximarelvolumd’aigua,tenintencomptel’orografiadel fonsmarínohadeserunatascagensfàcil.Iniparlar-ned’aproximarelvolumdeterradelplaneta, suposantfinsitotqueparlemnomésdel’escorça...Elcasésquefinalmentlapreguntaensvaportar aparlard’àreaidevolum,peròvanhaver-himoltesméscosesinteressants.

Quanelsnensjuguenambdeupecesdefustaienseparentresiset,estan manipulant unconceptede fracciómoltrudimentariperòabsolutamentbàsicperaunasòlidaaproximacióaaquestconcepte, queformalitzaranmoltmésendavant.Nonomésaixò.Tambéhanpintatdeverdtresfilesd’una graellaquetédeufilesideucolumnes.Hanobservatqueéselmateixexplicarquehanpintattres delesdeufiles,quetrentanúmerosdelscentqueambtantesforçhanaconseguit.Elsnensiles nenesnecessitenrecuperarexperiènciesd’aquesttipusperaproximar-secòmodamental’estudide fraccionsequivalentsipercentatges.

Tambéhanmanipulatsectorscircularsperrepresentarlespartsd’untot,simulantelsdiagramesde sectorsambelsqualsestrobarand’aquíaunsanys.Iunapetitaobservació:éscertquetresquarts isetdesensnosónfraccionsequivalents,peròtotesduesaproximen,mésomenysacuradament, laquantitatd’aiguadelplaneta,queeral’objectiu.D’altrabanda,sielsnensilesneneshanaprèsa representarunafracciómitjançantpecesdefusta,podranintentarferservirmésendavantaquest recurspercomprovarque,efectivament,nosónfraccionsequivalentsibenprobablementtrobaran enelcamíqueunquarticincvintenssíquehosón.

Nomésemquedaunacosa...Unafamíliahaviaretallatunmapamundifísic.Havienseparatelscontinents ilesillesdelespartscobertesd’aiguaileshavienanat enganxantsobreunfulldelesmateixesdimensions delmapa,cuidadosamentdividitendeufranges.Tres partsapareixiencobertesdeterraiset,d’aigua.Elmapanoeraunaprojeccióqualsevol.

EralaprojecciódePeters:unadelesmoltesqueconservenlesàreestotiladistorsiódelaforma.Abans, l’alumnahaviacompartitamblarestadelaclasseque, demapes,n’hihamolts,iquenototsserveixenpera lesmateixescoses.Efectivament,elretallablenohauriafuncionatambqualsevolmapainomésaquesta observacióenspodriaportaraunaltreprojecteplede sorpreses,dematemàtiques,d’històriesillegendes:la cartografia.

L’AdelaitotselsnenesilesnenesdelaclassedeFalconsamblessevesfamíliessónelsgransprotagonistesd’aquestahistòriaplenadematemàtiquesidecavalletsdemar,estrellesdemar,dofins, sardines,balenes,escates,aletescaudals,aletespectorals,aletesdorsals,calamars,pops,ventoses, tentacles,taurons,crancs,plàncton,petxines,nautilus,amonites,carolines...Moltesgràciesatots!

Finsaquí,elsnostresrelatsenprimerapersona.Noestandesconnectatsnialmarge,l’undel’altre. Defet,hanestatcompartitsdesdelseuiniciihemsentitlanecessitatdefer-vos-elsarribaraixí,amb laintensitatambquèhohemviscut,amblail lusió,l’emocióielrepteprofessionalproporcionats perl’experiència.

Hemaprèsmolt.Cadascundelsnensinenes,peròtambéelsadultsquehemtingutl’ocasiódeparticiparenaquestaaventura.Ensensentimsatisfetsiintuïmquemésenllàdel’horitzó,hihamolts marsioceansperdescobrir.Cadapasquefemenspreparaperseguirnavegant,confiatsenles pròpiespossibilitatsirecursos.

Hemconstatatuncopmésquel’aprenentatgeéspersonal,perònoaprenemcosessols,aprenem cosesambelsaltres.Aquestaconstatacióésclauenlanostraescola.Iaratambéhohemcompartit ambtotsvosaltres.Haestatunplaer!

Bibliografia

Domenech,J.(2009). Elogidel’educaciólenta.Barcelona:Graó.

InfantsdelesescolesdeReggioEmilia.(2005). Sabataimetre Elsinfantsilamida.Barcelona:Associació demestresRosaSensat.

Alsina,À.(2004). Comdesenvoluparelpensamentmatemàticdels0als6anys. Barcelona:Eumo.

Turismematemàtic: experiènciapersonal

EduardRecasens

Dept.MatemàticaAplicadaIII,UPC.Barcelona eduardo.recasens@upc.edu

Desdetempsanticsl’ésserhumàcultivathadesitjatviatjarperconèixermón,i,sibéenunpassatno gairellunyà,lesdificultatsperviatjarerennotables,elprogressiudesenvolupamentdelstransports hohafetcadavegadaméspossiblefinsque,finalment,apartirdelsanys60,lapossessiópersonal d’automòbililaconstruccióarreud’autopisteshadonatllocaungrancanvi:eldesigdeviatjarper poderveurellocspintorescositottipusd’atraccionsturístiquesjaestàal’abastd’unagranmajoria. Ambtot,faltavaquelcomquehaviad’atiaralmàximaquestafanyviatgerdel’ésserhumà,emrefereixo al’apariciódel’Internet;l’accésfàciliràpidalainformacióhaposataldescoberttotunmuntde paratgesillocsquejuntambl’abaratimentdelsvolsinternacionalshaesperonataquestafanyd’anar avisitartotelquefacifaltaimés,i,comnopodiaserd’altramanera,tambéaquestafanyhaarribatal mónmatemàtic.Perdetectar-honoméscalqueescriviuparaulesdel’estil‘‘turisme’’i‘‘matemàtiques’’ (endiferentsidiomes)alGoogleijaveureuquèpassa.Ferdeturistesmatemàtics(enunsentitampli) segurquehohemfettotsnosaltresalgunavegada:desd’anaravisitarlaPedreraperveure’nels arcscatenaris,finsallòd’anaraunallibreriaounabibliotecaperveurellibresdematemàtiques—ara aquest,aral’altre—,segonsenscridinl’atenció.

Lamevaaficióaferturismevedesqueerapetit;defet,allòquemésm’agradavadel’escolaera quananàvemd’excursió.Lamevaaficióaferturismematemàticvacomençareldiaque,fentturisme debiblioteca,vaigtoparamblarevista MathematicalIntelligencer.Enaquestarevistaquadrimestral hihaunaseccióanomenada‘‘TheMathematicalTourist’’,onesparladellocsenquèhihacoses relacionadesambelmóndelesmatemàtiquesquemereixenservisitades;aquestsarticlesacostumen aanaracompanyatsd’explicacionsmatemàtiquesihistòriques,amésdeportarmapesifotografies. Sónmoltcomplets.Llavorsse’mvaacudirque,alaFacultat(FME),podríemincloureunasecciósobre turismematemàticenlapublicaciómensualqueanomenem‘‘ElFulldelaFME’’.Haviadeseruna cosamoltcurtajaque,comn’indicaelnom,lapublicaciótotalconsisteixenunfull.Lapropostava seracceptadaidesdel’octubredel2002haaparegutunasecciódeturismematemàticanomenada ‘‘ElsrodamónsdelaFME’’,enquèhihanparticipatdiferentsmembresdelaFME.Aquestapublicació téedicióelectrònica.

Recentment,JosepPlam’hainvitatacol laboraral Noubiaix explicantalgunesdelesmevesexperiènciescomaturistamatemàticialavegadam’hainvitataobrirunanovaseccióqueestiguidedicada alturismematemàtic,enlaqualpuguinparticiparelslectorsde Noubiaix.Pensoqueésunabona idea.Totselsquellegimaquestarevistadebensegurquehemdedicatiseguiremdedicantunapart importantdelanostravidaalesmatemàtiques:estudiant-les,explicant-les,resolent-neproblemes,

fent-nerecerca,anantacongressos,etc.Lesintangiblesidealitatsmatemàtiquesquetractemdiàriament —nombres,polinomis,figuresgeomètriques,funcions, matrius,vectors,gràfiques,corbes,superfícies,derivades,etc.—,detantqueenparlemquejasónunapart mésdelanostrarealitat.És,pertant,unplaerreconèixeraquestesidealitatsmatemàtiquesenlesmés diversesobjectivacionsdelmónmaterial:construccionsarquitectòniques,obresd’enginyeria,traçatsurbanístics,enrajolats,mosaics,rellotgesdesol,instrumentsdedibuiximesura,escultures,pintures,relleus, dissenysdejardins,restesarqueològiques...Itambéés unplaerlavisitaalsllocsonhanviscut(oviuen)els creadorsdetotaaquestaidealitat-realitatmatemàtica:pobles,cases,col·legis,universitats,acadèmies,biblioteques,cafès,llacs,illes,observatorisastronòmics, piràmides,etc.Veurei,siéspossible,llegirelsdocumentsquehanescrit,elstextosquehanestudiat,els instrumentsmatemàticsquehanemprat;veurecom hanestatrepresentatsatravésdeltempsenpinturesi escultures,veurecomsónrecordatsenplaquescommemoratives,entombes,etc.

L’objectiud’obrirunasecciósobreturismematemàtic a Noubiaix ésbenclar:estractadetenirunespaion elslectorsd’aquestarevistapuguinexposarlesseves experiènciespersonalscomaturistesmatemàtics.Es tractaqueenviïnalarevistaunescritambfotografies d’algunavisitaturisticomatemàticai—espotdonar també—,unaexplicaciómatemàticaihistòricad’allò ques’havisitat.Aixídoncs,desd’aramateixquedeu invitatsaparticipar-hi.

Elquearaveacontinuacióésunpetitresumdelamevaexperiènciacomaturistamatemàtic.

Undelsprimersviatgesdevacancesquevaigferen quèvaigincloureunasubrutamatemàticavaserel del’estiudel2003;aquellestiuemvaigproposarfer unavisitaturísticaalnorddeFrançaipassarunsdiesa Bruges.Vaigrecordarllavorsquehaviallegital MathematicalIntelligencer quelacasaonhavianascutKepler eraaWeilderStadtiqueaquestpobletestrobavaa uns140Kmal’estd’Estrasburg.Esdeiaal’articleque lacasaeraaraunpetitmuseuquereuniadiferentsobjectesienparticular,elseumodelcosmològic. Llavors,pertald’anar-hi,vaigdissenyarunarutaqueincloguésWeilderStadtideretrucvaquedar inclosalaSelvaNegra(aixòsolpassar,d’afegirllocsforaderuta,amballòque‘‘jaquehemarribatfins aquí...’’.ElpobletdeKeplerésmoltbonic...hihaunagranplaçacentralambunaestàtuadeKepler acompanyadad’altresmotiusastronòmics;lacasadeKeplerestrobaenundelsextremsdelaplaçai

Foto1

Foto2

ésdel’estildelescasesquetotshavíemdibuixatdepetits(foto1).Elmuseuésinteressant,peròallò quemésemvainteressarvaserlamaterialitzaciódelmodelcosmològic(foto2)queKeplerhavia dibuixatalseullibredejoventut MysteriumCosmographicum (1596).KeplervoliatrobarunaexplicacióracionalalfetquenoméshihaguessinsisplanetesalvoltantdelSol(elsplanetesconegutsal segle XVII erenMercuri,Venus,laTerra,Mart,JúpiteriSaturn),illavors,elfetgeomètricquenoméshi haguéscincpoliedresregularsli’nvadonarlaclauexplicativa.Vaintercalarambenginylessisesferes orbitalsambelscincsòlidsplatònics.Ambelpasdelsanysvacomprovarquelesdadesd’observació noescorresponienambelseuteòricmodelcosmològicitotplegatvaacabaramblaformulacióde lestreslleisqueavuiportenelseunom,uneslleisquealavegadadestruïenelseuplatònicsomni cosmològicdejoventut.

Enaquestmateixviatgedel’estiudel2003vaigpassarperNancyperveurelacasanataldePoincaré. DesprésvaigvisitarNeuf-Brisach,unapetitavil ladeperímetreoctogonal,ambcarrerscartesianamentdistribuïtsalvoltantd’unagranplaçaquadrada(foto3).Lahistòriad’aquestacuriosavilad’Alsàcia—situadaauns70Kmalsudd’Estrasburg—,esremuntaaltempsdeLluísXIV,quanpeltractat deRyswick(1697)esvahaverdecedirlaplaçafortaanomenadaBrisacalsaustríacs(avuipertanya Alemanya),llavors,elreimanàal’arquitectemilitarVaubanqueconstruísunanovaplaçafortificada al’esquerradelRiniencaradacapalaperdudaBrisac:aquestvaserl’origendeNeuf-Brisach.

DecamícapaBrugesemvaigaturaraBrussel lesperveure‘‘l’osd’Ishango’’(foto4).Aquestostéuns 20.000anysiportamarcatsunssenyalsqueelsarqueòlegsinterpretencomasenyalsnumèrics:a Internetpodeutrobarmoltainformaciód’aquestosqueestàbenguardatenunavitrinadel’Institut ReialdeCiènciesNaturalsdelacapitalbelga;l’osfoudescobertcapelsanyscinquantadelsegle XX perl’arqueòlegbelgaHeinzelindeBraucourt,propdelllacEdward(Àfricacentral).Eldiaquevaiganar

Foto3

Foto4

almuseufeiamoltacalor—eraunatardadelmesd’agostilessalesestavenpràcticamentbuides—, peròvaigtenirunagratasorpresaquanvaigarribaralasalaonesguardal’os:justaquelldiahihaviala visitad’unaescolacentreafricana,demaneraque,desobte,emvaigtrobarenvoltatdenensinenes africans,algunsd’ellsencuriositsdavantd’aquellosmatemàticmentred’altresestavenresolentexercicisnumèricspreparatspelmuseuperaunamillorcomprensiódel’osquevisitaven.Veritablement, nopodiahavertrobatunmillorambientpervisitarl’osd’Ishango(foto5).IjaqueemtrobavaaBrusselles,vaiganaravisitarl’Atomium (foto6),unaespectacularestructuracúbicad’aluminide103metres d’alçada,ambnouesferesd’acerde18metresdediàmetrecadascuna.Aquestaconstruccióquerepresentauncristalldeferroaugmentatcentseixantacincmilmilionsdevegades,fouconstruïdal’any 1958ambmotiudelaFiraUniversal;jolateniaposadaalcapdesdelsonzeanys,formavapartdeles il lustracionsdelllibredegeografiauniversaldesegondebatxillerat,iara,desprésdequarantaanys, perfilapodiaveurealseulloc.FinalmentvaigarribaraBruges.Brugesmereixestadajaqueallòqueés mésbonicéspassejardenitpelsseusacanalatscarrersisoparmusclosalaplaçacentralambunabonagerradecervesa.ABrugesésonvanéixerSimonStevin(vegeufoto14),unenginyerque,el1585, vapublicarenflamenc DeThiende,unllibretdetrenta-sispàginesenquès’explicavaalseuropeus

Foto5

Foto6

lamanerad’escriureicalcularambdecimals.Aquest llibretesvatraduirelmateixanyalfrancèssotaelnom LaDisme itinguéungranèxit,peròcaldirqueStevin nofouelprimerautilitzardecimals:moltabansjase’n trobenalamatemàticaxinesaialamatemàticaàrab,i F.Vietan’aconsellaval’úsel1579,peròfoujustatravés delllibredeStevinquelarepresentaciódecimaldela partfraccionàriaespopularitzàentreastrònoms,banquers,comerciantsialtresusuarisdelcàlcularitmètic. LaciutatdeBrugeslihadedicatunaplaçaqueenportaelnom,ambestàtuainclosa.

DetornadacapaBarcelonavaigpassarperDunkerque perveuresihihaviaalgunacosaquerecordésDelambremesurantelmeridiàquevaservirdebasepera l’establimentdelmetre,perònovaigsabertrobar-hi res...quisapsihihaalgunacosa...Tampocvaigtenir sortaSaint-Omer,moltapropdeDunkerque:havia llegitqueenaquestaciutatdel’extremnorddeFrança hihavianascutLiouvilleivaiganaral’oficinadeturismeapreguntarsihihaviaalgunacosaqueelrecordés, perònosabienpasdequielsparlava.Davantlameva insistènciavananarabuscarungruixutllibreonhihaviaregistratselsnaixementsdelsegle XIX illavorsvan trobarJosephLiouville,nascutel1809...VanestarmoltcontentsdesaberqueaSaint-Omerhihavia nascutunmatemàticimportant.DesdellavorsnohepassatmésperSaint-Omer:hauranfetalguna cosaperrecordaraLiouville?

SortintdeParísvaiganaraBourg-la-Reineperveurelacasanatald’ÉvaristeGalois:noespotvisitar,peròhihaunaplacacommemorativaqueelrecorda.Mésavall,enelmateixcarrer,vaigtenirla sorpresadeveurelacasaonvamorirCondorcet.

TambévaigpassarperlaciutatdeChartresi,envisitarlaCatedral,vaigobservarquealafaçana principalhihaviaunesesculturesquerepresentavenlesdisciplinesdeltríviumielquadríviumitambé PitàgoresiEuclidesentred’altres(foto7).Dinslacatedral,justquans’entraperlaportaprincipal,hi haungranlaberintalterra,queelspelegrinsrecorrencerimoniosament.

SortintdeChartresemvaigdirigircapaPoitiers—queestroba300Kmalsud—:hovaigferper podervisitarelpobleonhavianascutRenéDescartes.Aquestpoblequearas’anomenaDescartes, s’anomenavaantigamentLaHayeperòel1802livanposarelnomdeLaHaye-Descartesiel1967li vantreureLaHaye.LacasanataldeDescartesestrobaalbellmigdelcarrerprincipal—quetambé lihanposatelnomde‘‘Descartes’’—;bé,defet,eralacasadel’àviamaterna.Descarteshivaviure finsalsdeuanys:desprésvaentrarcomainternalcol·legidelsjesuïtesdeLaFlèche.Avuilacasaes potvisitariésunpetitmuseuquerecullalgunescosesdeDescartes,tampocnogaires.Alaplaçadel poblehihaunaestàtuaquerepresentaDescartes.EnunviatgeposteriorvaiganaralaciutatdeLa FlèchepervisitarelCollègeRoyalHenrileGrand—aquestedificiqueavuiésunaescoladeformació militaranomenada‘‘Prytanéenationalmilitaire’’fouenelsegle XVII uncol legiregentatpelsjesuïtesi ésonDescartesvaserinternat—;enaquestllocésonvaaprendreels Elements d’Euclidesatravésdel tractatdeClavius.Segonsemvanexplicar,l’edificinohaviacanviatgairedesdelstempsdeDescartes

Foto7

ilacapellanohaviacanviatgens;aixídoncs,vaigseuredurantunaestonaenundelsbancsdefusta delacapellaiemvaigimaginaraljoveDescartesalmeucostat.

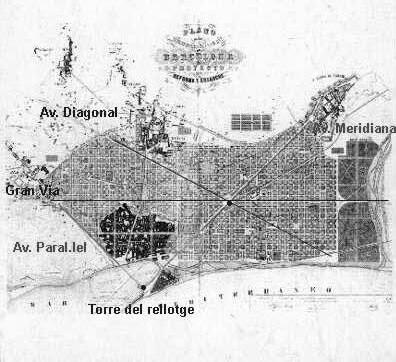
Aquestviatgedel’estiudel2003vaserundelsprimersenquèvaigpracticarelturismematemàtic;desprésn’hefetd’altres...peròaravoldriaparlardelturismematemàticacasanostra.Jovisca Barcelonaihefetunesquantessortidesmatemàtiquesperlaciutat.AlPortVell,hevistlaTorredel Rellotge(molldePescadors;foto8).Aquestatorreésunamaterialitzaciódelpuntenquèestallen perpendicularmentl’AvingudadelParal lel(41◦ 22 33 nord)ambl’AvingudaMeridiana(2◦ 13 45 est;foto9).ApropdelaTorredelRellotge,alterra,hihaunafileraderajolesenumeradesseguintla successiódeFibonacci,unarepresentacióartísticadeltorinèsMarioMerz.AlgunscarrersdeBarcelonatenennomsmatemàtics:laDiagonal,elParal·lel,laMeridiana,carrerdelTriangle(CiutatVella), carrerdeDescartes(SantGervasi),carrerdeCopèrnic(SantGervasi),carrerd’Euclides(Horta),carrerde Pitàgores,carrerd’Arquímedes(SantAndreu),EsteveTerradas(Vallcarca),i,propdelaplaçadeCerdà, hihalaplaçadelesMatemàtiques.AlaplaçadeMariaCristina,queestrobaalaDiagonal,alabanda dretadireccióTarragona,hihadibuixadaalterralacorbaanalemàtica,unacorbaenformadevuit allargatrelacionadaamballòqueenastronomias’anomenal’equaciódeltemps,queésladiferència entreelmigdiasolarielmigdiasolarmitjà.

Alaplatjad’Ocata-Masnou,hihaunmonòlitambunaplacaquediu‘‘EnaquestpuntdeCatalunya s’acabaelmeridiàverd,elsenderdellargrecorregutqueressegueixelmeridiàdeParís.Ladistància entreDunquerkeilaplatjad’Ocatamesuradaalsegle XVIII s’utilitzàperdefinirlaunitatdelongitud: elmetre’’.Aquestmeridià—queestrobaa2◦ 20 14 al’estdelmeridiàdeGreenwich—,sorgeixdel marperalgunaplatjadeDunquerke,faunavisitaal’ObservatorideParís,travessatotFrança,arriba alPirineuCatalàpelcolldePal(sobreSetcases)is’endinsadenoualmarperlaplatjad’Ocata.

ATerrassa,hihalaMasiaFreixa,unnotableedificimodernistaqueutilitzal’arcparabòlicpertotarreu.

Porrera(Priorat)éselpobledeCatalunyaambmésrellotgesdesol. Etcètera.

Ésinteressantbuscar,enunentornaccessibled’onvivim,cosesd’interèsturisticomatemàtic:segur quen’hiha.D’altrabanda,desderecentmenthihaunsquantsllibresqueproposenrutesturistico-

F

matemàtiquesperCatalunya.L’AjuntamentdeBarcelonavapublicarunaguia,jafaunsquantsanys, titulada PassejadesperlaBarcelonacientífica,deXavierDuraniMercèPiqueras.TeresaTicóhaescrit PasseigMatemàticperCatalunya:aquestllibre,amésdeproposardiferentsitineraris,portaexplicacionsmatemàtiquesencaminadesatreballarambalumnesdesecundària.Recentment,unllibrede ClaudiAlsina—GeometriaparaTuristas—,descriumésde125llocspervisitararreudelmón,alguns d’aquestssónaCatalunya.

Ferturismematemàtictéelseupuntd’aventurajaquelamajoriadellocsquehomesproposavisitar estrobenforadelesrutesusualsdelturismemassificati,pertant,solencostardetrobar.Recordo lavegadaqueemvaigproposarveureelmetrepatró.Elsnascutsabansdel1970—perfixaruna data—,recordareuque,enaquelltemps,elsllibresdefinienelmetrecomladeumilionèsimapartde lalongituddelquadrantdelmeridiàterrestre,iafegienqueaquestaunitats’haviamaterialitzatenuna barradeplatíiridiatqueesconservavaal’OficinaInternacionaldePesosiMesuresdeSèvres(París). Estractava,doncs,d’anaraSèvres,unaciutatenganxadaaParís.ArribaraSèvresvaserfàcil;elque novasergensfàcilvasertrobarelBIPM(BureauInternational...):vaighaverdedonarunesquantes voltesabansnodescobrísqueelBIPMestrobaallotjatenuncomplexcientíficdenom‘‘Pavillon deBreteuil’’,elqual,alhora,estrobasituatenmigd’unturó(comaraMontjuïc)anomenat‘‘Parcde St-Cloud’’.ElfetésqueaquestparcfafronteraambSèvresperòpertanyaSt-Cloudiaquestésel motiupelqualnofiguraalmapalocaldeSèvres;tampoclagentaquipreguntavasabiaresdelBIPM (peròencanvisabienqueaSèvreshihaviaunimportantmuseudeporcellanes).Quan,finalment, vaigtrobarelBIPM,vaigsaberque,perraonsdeseguretaticonservació,noespodiavisitar,iens vandirquealConservatoireNationaldesArtsetMétiersaParíshihaviaunarèplicadelmetrepatró endemésd’altrespatronsd’altresmesures.Aixídoncs,jaqueeraallà,aquellmatívaigvisitarelmuseu deporcellanes—queésforçainteressant—,ialatardavaiganaraParísaveurelarèplicadelmetre patróilesdelesaltresmesures.

Tambérecordolavegadaque,arreld’unaconferència sobreGiuseppePeanoal’Institutd’EstudisCatalans, vaigsaberque,feiapoc,laciutatdeCuneohaviadedicatalmatemàticitaliàunaesculturaqueconsistiaen unagranpedraonesrepresentavalafamosaisorprenentcorbacontínuaqueompleunquadrat.Naturalment,deseguidavaigpensarquehaviad’anaraCuneo.Peanovanéixerel1858aSpinetta,unllogaretveí deCuneoqueestrobaaunscentquilòmetresalsudde Torí.ATorívaexercirdeprofessoralaUniversitatiel 1888vapublicarel Calcologeometrico,queésonapareixperprimeravegadal’axiomàticad’EspaiVectorial talcomavuilatrobemalsllibresd’àlgebralineal.Una vegadaaCuneo,vaigpreguntaradiferentspersones perl’escultura,peròningúsabiadequèelsparlava... cansat,isentjatard,vaigentrarasoparalRistorante ZuavodiSpadaiallàvaresultarquenotansolssabien oneral’esculturasinóqueenconeixienl’escultor,de nomDarioGhibaudo.Llavors,l’endemàalmatívaig anaraveurel’escultura(foto10)itotseguitvaiganar aSpinettaaveurelacasanataldePeano,quetampocerafàcildetrobar.L’encertvaserpreguntar-hoa uncapellàambunallargasotanaquesemblavasorgit

d’unapel lículaitaliananeorealista.L’home—queestavaparlantalcarrerambgentdelpoble—,es vaquedarmoltsorprèsialhoracontentquealgús’interessésperlacasadePeano(ellielsaltresamb quiparlavas’hireferiencom‘‘ilnostromatematico’’).Elcapellàambllargasotanaesvaoferirmolt amablementaacompanyar-nos-hijaquelacasaestrobavaalmigdelcampalcostatd’unagranja anomenada‘‘TettoGalant’’;pelcamíensvaexplicarqueelleraamicdelafamíliaiquehaviaparlat algunesvegadesamblagermanadePeano.

AquestsúltimsanysGoogle,ViquipèdiaiGoogleMaps m’hanajudatd’allòmésal’horadeprepararunviatge.Unexemplerecent:josabiaqueB.Riemann,per problemesdesalut,haviadeciditpassartemporades aItàliaacausadelseuclimamésbenignequenopas eldeGöttigen,onellexerciadeprofessoruniversitari, itambésabiaque,japroperalsquarantaanys,mentre passavaunsdiesderepòsalcostatdelllacMaggiore,vapatirunatuberculosiquelivaprovocarlamort. ElquenosabiaeraelllocexacteonRiemannhavia fetestada.PerlaViquipèdiavaigsaberqueellloces diuSelascaiqueconsisteixenunapetitaagrupació decasesescampadesperlesfaldesdelsturonsque donenalllacMaggiore,propdelaciutatdeVerbania: pertant,necessitavaunmapalocalbendetallat.LlavorsvaigutilitzarGoogleMapsperlocalitzarSelascai elcamíperarribar-hi,ivaigferbéjaque insitu lesindicacionsnoerenpasgairebones...eracombuscaruna casaenunad’aquestesurbanitzacionsresidencialsactuals.Vaserbonicarribar-hiipassejarperaquellsmeravellososindretsitaliansques’hanconservatforçabé desdeltempsenquèRiemannhipassejava.

Ibé,araquejaheexplicatalgunadelesmevesexperiènciescomaturistamatemàtic,voldriaacabar ambalgunespropostesdeviatge,perbéquealgunesd’aquestesencaranolesheportataterme.

UnllocrelativamentproperaBarcelonaésTolosa.Enaquestaciutatfrancesapodreuveurelamusa queinspiravaFermat(foto11);ésunaobradel’escultorfrancèsdelsegle XIX ThéophileEugèneVictor BarrauilatrobareualasaladelsIl·lustresdel’Ajuntament,alaplaçadelCapitol.Fentunsquaranta

Foto11

quilòmetrescapalnord-oests’arribaaBeaumont-de-Lomagne,lavilaonvanéixerFermat;enpodeu visitarlacasanatal,avuirestauradaiconvertidaenmuseu.SipasseuperCarcassona,moltaprop d’aquestaciutatpodeuferunrecorregutperles‘‘Villagescirculaires’’:totaunasèriedepobletsfrancesosambestructuraurbanísticacircular:Bram,Cambieure,Alaigne,Fenouille,etc.(foto12).

SianeuaLondres,heud’anaral’històricObservatorideGreenwich,onpodreutrepitjarl’arrencada delmeridiàzero,amésdevisitarl’observatori(quebés’homereix).JaaLondres,podeuarribarfinsa laciutatuniversitàriadeCambridgei,uns70quilòmetresmésamunt,alacasaonNewtonvanéixer el1642;s’anomenaWoolsthorpeManoriestrobaalcostatdelpobletdeColsterworth.Ésaquíon Newtonesvainstal larelsanys1665-1666,quanesvatancarlaUniversitatdeCambridgeacausade lapesta.Newtonteniallavors23anysiésonesdiuquevacaurelapomaquelivainspirarlateoria delagravitacióuniversal,peròenaquestmateixllociperlamateixaèpoca,comNewtonexplica, ‘‘...vaigdescobrirelmètodedelessèriesaproximativesilareglaperreduirqualsevolpotènciad’un binomiaaquestessèries,[...]vaigdescobrirelmètodedetangentsdeGregoryiSlusius,[...]vaigdescobrirelmètodedefluxions,[...]vaigdesenvoluparlateoriadelscolors[...]ivaigcomençaratreballar elmètodeinversdelesfluxions’’.

AneupujantiarribareuaEdimburg:podreuveurelacasaonvanéixerJohnNapier,l’inventordels logaritmesneperians;lacasaestrobasituadaenelpatidelauniversitatqueenportaelnom.

Arahauríeud’agafarunferri(ounavió)ianaraDublínperveureelBroughamBridge(foto13).Passejantperlaribadelcanalquehipassapersota,el16d’octubredel1843,aWilliamHamilton,‘‘comun llampec’’livavenirlaideadecomhaviademultiplicarelsquaternions,unesnovesentitatscreades perell,iques’escriuen a + bi + cj + ck,pertrobaruntractamentalgèbricdelesrotacionsal’espai detresdimensions.Hamiltonvagravarenelpontlesfórmulesbàsiquespermultiplicaraquestsnous nombres,essencialmenti2 =j2 =k2 = 1,ij=k,jk=i,ki=j,peròelpasdeltempshaesborrataquesta inscripcióqueavuiésrecordadaenunaplacacommemorativa.

SianeuaCuneoaveurelacorbadePeanopodeuarribarfinsaTorí,queésunaciutatitalianadellargs carrersemporxatsambanticscafèsiexcel lentspastisseries;inooblideuqueaquestaéslaciutat deLagrange...Elcarreronhihalacasanatalenportaelnom—‘‘viaLagrange’’—i,seguintaquest carrer,s’inicialavia‘‘Accademiadellescienze’’,onhihal’AcadèmiadeCiènciesdeTorídelaqualen foumembrefundador:vallapenavisitar-nel’edifici;al’entradadel’Acadèmiahihaunaestàtuade

Lagrange.PodeullavorsbaixarfinsaRomaianaralVaticàperadmirar‘‘L’Escolad’Atenes’’:elfrescqueRafaelvapintarenunadelesparetsde‘‘lesEstances’’. Enaquestaimaginativarepresentaciópictòrica,Rafael hireuneixdiferentsfilòsofsgrecsquecobreixenprop d’unmil·lenni.Hiha,entred’altres,Pitàgores,Parmènides,Heràclit,Plató,Aristòtil,EuclidesiPtolemeu.La perspectivadelquadreésimpressionant.

Abansd’arribaraRoma,pareuaPisa,onhihaunaestàtuadeFibonaccia‘‘IlCamposanto’’situatala‘‘Piazza deiMiracoli’’,onhiha‘‘IlCampanile’’o‘‘torreinclinada’’,ianeutambéaCintoia,propdeFlorència,avisitar‘‘IlGiardinodiAchimede’’,uninteressantmuseude lesmatemàtiques,iuns200Kmmésavalltrobareuel pobletdeValentano,on—aViaCarloAlberto,9—, el22desetembrede1765vanéixerelmatemàticmés citat,desprésdePitàgores,pelsestudiantsdesecundària:PaoloRuffini.

AvuiquetothomvaaPraga,ésbosaberque,enaquestaciutat,TychoBrahehivatreballarelsúltims quatreanysdelasevavidaiquelessevesobservacionsastronòmiquesforenbàsiquesperal’obra deKepler.AlaplaçacentraldePraga,hihal’esglésiadeNostraSenyoradeTýn,queésonBraheestà enterrat.L’observatoriestrobaalcimd’unturó,albarridelcastell.

TambépodeuanaraEstocolmaveureunaplaçasuperel líptica,la‘‘SergelsTorg’’ensuec(vegeuelRodamonsdelaFMEdefebrerde2007).PodeuanarASaintLouis(Missouri,EUA)aveureunespectacular arccatenarivisitableperdins—el‘‘GatewayArch’’—,obradel’arquitected’origenfinlandèsEeroSaarinen(Rodamons,marçde2003).PodeuanaralaUniversitatdeColúmbiaaNovaYorkperveurela famosarajolababilònica‘‘Plimpton322’’(foto15).PodeuanaraAbashiri,alJapó,pervisitarel‘‘Centre delesMeravellesMatemàtiques’’d’Okhotsk,queésuncentred’animaciócientificoculturalsobreles matemàtiques(Rodamons,marçde2005).Podeuanaralazonaarqueològicad’Uxmal,alapenínsula

Foto 14

delYucatán—aMèxic—,perveurelapiràmideonvacauremortalmentWitoldHurewicz,l’autordel llibre Sobreecuacionesdiferencialesordinarias que,elsd’unacertaedat,recordareudequanestudiàveu alaFacultatdelaUB(Rodamons,octubrede2005).PodeuanaraSantPetersburgaveurequèqueda d’EuleriarribarfinsaKönigsbergperpassejarpelsponts,siésqueenquedaalgundesprésdela desfetadelasegonaguerra.PodeuanaraKhiva,al’Uzbequistan,perveureunamonumentalestàtua deal-Khwarizmi.Podeuanar...

Podemanaramoltsllocs—n’hihamolts—,noméscalqueensfixembéenlesmatemàtiquesque llegim,sobretotenlasevahistòria,i,comjahecomentatabans,Internetenfaràlaresta.Animeu-vosa formarpartdelclubdelsviatgersmatemàticsquecadavegadaésmésnombrós.Animeu-vosienvieu lacrònicad’allòquevisiteua Noubiaix

Unacudit

ManuelUdina

Sangakus. Contemplacióiraó RamonNolla

DepartamentdeMatemàtiques

InstitutPonsd’Icart

1.Introducció

Vaigsaberdel’existènciadels sangakus l’any2005,atravésd’unsuplementdelarevista Tangente dedicatalaculturajaponesa.1 Entrediversesqüestions,parlavabreumentdelamatemàticajaponesa, wasan—,delperíodeEdo(1603-1867)id’unadelessevesmanifestacions,els sangakus 2

Figura 1. Fragment dea la prefectura de Nagasak i ia la prefectura d’Ehime. sangaku sangaku

Aquestsconsistienentauletesdefustaques’oferienenelstemplesbudistesisantuarissintoistes japonesosentreelsegle XVII iladècadadels70enelsegle XIX.SegonsFukagawa-Rothman(2008),la mésantigaconservadaésdel’any1683,iestrobaalaprefecturadeTochigi.Tanmateix,enundiaridel viatgedeYamaguchiKanzan(1781-1850)pelJapó,esregistrenproblemesdevuitanta-set sangakus quetrobaenelseurecorregut,und’aquestsdatatl’any1668.Actualment,esconservenalvoltantde nou-centestauletesienelstextoshiharegistresdemésdemilset-centesquehandesaparegut.

1.VegeuBoursin etal.(2005).

2. Wasan éstraduïtcoma san ‘‘matemàtica’’i wa ‘‘japonesa’’.Murata(2001)matisaitradueix san coma‘‘càlcul’’o ‘‘aritmètica’’ielcomparaambelterme‘‘matemàtica’’deconnotacionsdiferents,perquèesderivadeltermegrec mathema o mathemata (μαθ ηματα)ques’atribuïaatotallòqueeratemad’estudienlaculturaoccidental.Delamateixamanera tradueix gaku ‘‘aprenentatge’’o‘‘ciència’’.Així sangaku,queéstraduïthabitualmentcoma‘‘tauletamatemàtica’’—vegeu Fukagawa-Rothman(1998)iHoriuchi(2005)—,significarialiteralment‘‘aprenentageociènciadelcàlcul’’.

Espenjavendelesparetsiràfecsdelesteulades,icontenienproblemesmatemàtics,majoritàriament geomètrics,enquèespresentavencomposicionsatractives,perlasevabellesaformaliplàstica,de cercles,polígons,el·lipsesi,tambéenalgunscasos,figurestridimensionalsjuntamentambelsenunciats.Algunescontenienlessolucionsimoltpoques,elprocedimentperarribar-hi.Tambéhiconstava elnomielpobledel’autoridelmestreambquihavienestudiat.

Quantalasevapresentació,imatgescomlesdelafigura1,provoquend’antuviunapreciableisuggestiuimpactevisualambindependènciadelcontingutdel’enunciatquel’acompanya,laqualcosa elshadonatelrangd’objectesartístics.Laracionalitzaciód’aquestimpacteemconfirma,talcomresumeixoenl’esquemadelafigura2,quelacontemplaciódelesimatgesdels sangakus produeixuna percepcióqueenmoltscasosestradueixenunsentimentdeprofundnivellestètic.3 Aquestsentimentportaalaintuïciód’unaharmoniaentrelespartsdelaimatge,d’unarealitatques’escapa,de vegadesaparentmentclara,devegadesocultaenunacol·lecciódesordenadad’objectes.Aquesta intuïciópotserreconduïdaperactivarunmovimentdelaraódirigitaexplicar-la,elqualpotutilitzar diversosllenguatgesperfer-sepresentiassolirpodercomunicatiu.Entreelsmatemàticsjaponesos creadorsd’aquestesimatges,elllenguatgepreferitfoueldel’àlgebraambafirmacionsconstruïdesa partird’algunespropietatsgeomètriqueseuclidianesdelesfiguresimplicades.

contemplació percepció estètica intuïció d’harmonia moviment de la raó explicació de l’harmonia

Figura 2. Etapes experimentades en l’observació dels sangakus.

2.Elcaràcterjaponèsielcostumdepenjar sangakus

Ésunlloccomúentrelamajoriad’historiadorsque,perendinsar-seenlacomprensiódelesdiferents metodologiesempradeseneldesenvolupamentdelesmatemàtiquesperdiferentscivilitzacionso endiferentsperíodes,cal,amésdeconèixerelsdesenvolupamentspropisdelamatèria,estudiarla culturacorresponentenlessevesvessantsdiverses.4 D’aquestamaneraelscostums,lescondicions socialsimaterials,ilainfluènciadelpensamentfilosòficpodenguiarlacomprensiósobrel’elecció delsproblemes,lesidees,elseutractamentilestècniquesemprades.

Enaquestmarcenspreguntemsobrelescausesdelcostumdepenjar sangakus.D’unabanda,des demoltsseglesenrere,elsfidelssintoistesfeienofrenesalsdéus(kami)enelssantuaris.Creienque als kami elsagradavenelscavallsiaquellsquenon’oferienundeviupresentavenundibuixsobre unatauletad’uncavallpintat.Aixínoésestranyqueesfessinaltresofrenespintadessobretauletesi entreaquestesels sangakus podienserofrenesdefidelsdevots.

Peròerasimpleiúnicamentdevocióohiintervenienaltresinteressos?Crecquelaqüestióésde naturalesasimilaralaqueenspodemplantejarrespectedelsexvotsquetrobemenalgunescapelles iesglésiesdelesnostrescontrades(figura4).

3.Unaaproximacióalconceptedecontemplacióenelcampdel’artdesdelanostracultura,elpodemtrobara Mundó(2004),p.12.

Contemplacióvoldiraturar-seaconsiderarunaobrad’art,mirar-la,escoltar-laambcalmaidurantl’estonaque calgui,afidedescobrir-nelabellesaformalipenetrarenelseucontingutprofund.

Enquèafegiriaqueaquestamiradahauriadeserd’unaqualitatqueportésl’ànimaaunestatsilenciósibuitperquèlacosa observadaen‘‘serescoltada’’poguésactuarsensepassarpercapfiltreinstal latenella.

4.VegeuPla(2009),p.53,ielprefacideRobson(2008).

Hihahagutpersonesmoltdevotesquehanpenjatunvaixelloalgunaltreobjecteambagraïment perunabonatemporadadepesca,lasuperaciód’unatempestaolacuraciód’unamalaltia.Alhora,hi hal’orgull,quenotéresaveureambladevoció,queoriginaelreconeixementpúblicdelafabricació d’unexvotdegranqualitatartística.També—perquèno?—,hihalaintencióperpartdel’artesàde donar-seaconèixerambfinalitatsmercantils.AlgunacosasemblantpothaverpassatalJapó.

Ésrellevant,ambvistaaunainterpretaciód’aquestcostum,elcomentaridel Sanpobuttankai (‘‘No temeuderectificar’’;1673),moltvaloratpelshistoriadors,quetrobemaHoriuchi(1998),p.136,

Deuserunamoda?Éscadacopmésfreqüentques’inscriguinproblemesdematemàtiques (sobretauletes)perexposar-losaquíoallàenelssantuaris.Tractant-sedetauletesvotives, homesperatrobar-hifórmulesd’invocació.Quannon’hiha,enspreguntemquèéselque pretenenrealmentsinócantarlloancesalpropigeni.

Enelmateixarticle,Horiuchifareferènciaalacompetènciaentreescoles.Desprésd’unaanàliside lescondicionshistòriquesenquèesprodueixenels sangakus,conclou,respectedelaconcepció d’activitatd’entretenimentques’atribueixalasevacreació,que5

Lamodadelestauletes,enlaquals’havistdurantmoltdetempslaprovaqueaquestaciència( wasan)eradesenvolupadacomunpurentreteniment,s’inscriviaenuncontexthistòric 5.VegeuHoriuchi(1998),p.145.Tambécital’articleFukagawa-Rothman(1998),comun‘‘exempleperfecte’’dela maneraqueelsobservadorsnaïfsinterpretenlestauletes.

Figura 3. Tauletes a les prefectures de Kyoto i Fukuok a, amb dos s al centre de la fotografia de l’esquerra.

angakus

Figura 4. Ex vots d’embarcacions a l’església de Sant Magí al Portal del Carro de Tarragona.

precísmarcatperlacreixentdifusiódeladisciplinaenelmónrural,laprofessionalitzaciódels mestresdelacapitali,finalment,lafortacompetènciaentrelesescoles.Enaquestcontext,les tauletesjuguenelpaperd’instrumentsdecomunicacióidepublicitatcòmodesd’ús,econòmics,eficaçosimésespectacularsqueelstractats.

Finalment,comunelementmésd’aquestaanàlisi,apuntoqueenelmeucasparticularunaporta d’entradaaltipusdesensibilitatjaponesamelavaproporcionarlaimatgeinicialdel’articledela revistadelmeuprimercontacteambels sangakus.Allí esreproduïal’estampapictòricadelafigura5,quedespréstornariaatrobarmoltesvegadesquancercava informaciósobrelaculturailahistòriadelJapóenel períodeEdo.Enaquestapintura,estrobentracesper al’estudideltipusdesensibilitatdelcaràcterjaponès, delamateixamaneraquelestrobemenlarestadeles artstradicionalscomlacal ligrafia,lacerimòniadelte, l’elaboraciódehaikus,elteatre,l’arranjamentfloralide jardins,iquetambéesmanifestaenlavessantartística delespresentacionsdels sangakus

Davantl’obra,tenimunapercepciódedesenllaçobert quehemdecompletarapartirdelacontemplació,la qualgeneraunmovimentinternambconsciènciade nopermanènciaifugacitatdelescosesielsfenòmens.Elquadrenoparladeldestídelspescadors sotalatempesta,nidelsimbolismedelmontFujialfons,sielposaalmateixnivellquelesonades—color,llum,traçada,perilld’explosióiarrabassament—,osirepresentaelpoloposatd’aquestes—estabilitat,seguretat,solidesa.Tampocs’entreveul’estatd’ànimdelspescadors,noméshihala presènciaordenadaenfrontantelmaradvers.SesentenprotegitspelmontFuji?Sesentenamenaçatsperl’onada?Sesentenformantpartdetotal’accióforadeltempsiimmersosenaquestasense capmésplantejament?Eldetalldel’escumadelagranonadaésnomésunrecursplàsticdelpintor oinfonalgunacaracterísticaal’acció?L’observadoresconverteixenprotagonistais’obreunaporta alameditació.

Referint-seaaquestasensibilitat,escriuOctavioPaz,6

NiantesniahoraelJapónhasidoparanosotrosunaescueladedoctrinas,sistemasofilosofíassinounasensibilidad.LocontrariodelaIndia:nonoshaenseñadoapensarsinoasentir. Cierto,enestecasonodebemosreducirlapalabra sentir alsentimientooalasensación;tampocolasegundaacepcióndelvocablo( dictamen,parecer)convieneenteramentealoque quieroexpresar.Esalgoqueestáentreelsentimientoylaidea.Losjaponesesusanlapalabra kokoro: corazón.PeroyaensutiempoJoséJuanTabladaadvertíaqueeraunatradiciónengañosa:‘‘ kokoro esmás,eselcorazónylamente,lasensaciónyelpensamientoylasmismas entrañas,comosialosjaponesesnolesbastarasentirsóloconelcorazón’’.Lasvacilaciones queexperimentamosalintentarreducirestetérmino,laformaenquelosdossentidos,elafectivoyelintelectual,sefundenenélsinfundirsecompletamente,comosiestuvieseenperpetuo vaivénentreunoyotro,constituyeprecisamenteelsentido(lossentidos)de sentir.

D’altrabanda,aquestasensibilitatésdeltotcoherentambelssistemesfilosòficsireligiososadoptats pelsjaponesos:elbudismeenlasevavessantzenquebuscaeldespertaralarealitatúltimapar6.Vegeulaintroducciód’OctavioPaza Matsuo (1694),p.10.

Figura5.

tintdelaconsciènciadenopermanènciaicaducitat,utilitzantelbinomimeditació-acciópereducarl’atenció,ielsintoismeo‘‘viadelsdéus’’constituïtsperelementsnaturals,nocionsabstractesi lesànimesdelsmorts,demaneraquetoteslesparcel·lesdelavidaesdevindriensagrades.Aquests sistemes,ambindependènciadelesdisposicionsgovernamentalsdecadaperíodehistòricimalgrat algunsenfrontaments,llunydeserantagònicsforensovintviscutspelsjaponesosenqualitatdedues caresd’unamateixareligióenquèelsbudesielsbodhisattvasilesdivinitatsdelsintoismeerenemanacionsd’unamateixarealitatiesconstituïenenguiesprotectorscapaldespertar.7

Aquestasensibilitatnoésladelatradicióoccidental,peròespotexperimentaraïllantalgunselements.Enaquestaspecte,al’èpocaenquèvaigdescobrirels sangakus emtrobavatreballantsobre dissenysd’arcs,rosassesiornamentacionsd’edificismedievals8 (figura6).

Unacosaésveureunaobraacabada,compactaitancadacompotserunacatedralounademostració rigorosaisensefissuresd’unteoremamatemàtic,iunaaltra,aïllariobservarunelementcomelsdela figura6ounaimatged’un sangaku quenoformapartd’unentramatmésgranqueeltancaifinsitot l’ofega.Enelprimercas,eltancamentilaperfecciódel’obraensmantéadistància;enelsegoncas, se’nsinvitaaparticipar,apassardelacontemplacióal’acció.Així,laprimeraimpressióqueprodueixen aquestselementsoriginaalgunacosasimilaralmovimentcomentatentresensacióipensament,que almeuentendreguardaparal·lelismesambl’esquemadelafigura2iensapropaalcaràcterjaponès.

3.Introduccióalamatemàticajaponesa wasan9

Eldesenvolupamentdel wasan coincidíambl’èpocadegoverndelsTokugawa,conegudacoma períodeEdo(1603-1868),enquèelJapórestàunificatienpau,ielpoderrealestavaenmansdel governadorqueinstal làelseugovernaEdo(Tòquio).Elsnoblesguerrers(samurais)haguerende buscarnovesformesdesubsistir.Algunsesconvertirenenmestresitinerantsod’escolesrurals( juku). Aquestaèpocacoincidíambunperíodedetancamentiaïllamentdelpaís(sakoku).Enladècadadel 1630,elcristianismequedàeradicatiel1639elsúltimsportuguesosforenexpulsats.L’úniccontacte ambOccidentfou,sotagransrestriccions,ambelscomerciantsholandesos.Aquestsfeienelsseus intercanvisconfinatsenl’illaartificialdeDeshima,de200per70metres,alportdeNagasaki.

7.VegeuRobson(2007).Peraunavisiódelafilosofiaireligióorientalenlasevavessantmísticaésinteressant,desdel nostrepuntdevistadepensamentoccidentalhereudelatradiciógrega,l’aportaciódeCapra(1975).

8.AqueststreballsesfeienenunestilsimilarenalgunsaspectesalsdeTicó(2004)iSykes(1912),apoderserdirectamentsobreelterrenyobédesdel’observaciódefotografies.

9.Peraunaintroducció,vegeuelscapítols1-3deFukagawa-Rothman(2008).TrobemunaaportacióclàssicaaSmithMikami(1914)iunestudiaprofunditicríticambl’anterioraHoriuchi(1994).

Figura 6. Catedral de Santa Maria,Tarragona. Església d’Orsanmichelle, Florència. Seminari,Tarragona.

Figura 7. Fragment de paravent () que presenta l’illa de Deshima al port de Nagasak i. byobu

Aquestestatdecoses,juntamblasensibilitatjaponesa,influídemaneradecisivaenl’apariciógraduald’unamaneradefermatemàtiquespròpia(wasan).Aquestapresentaduesvessantsnoantagòniques10 :

• Artística.Esmanifestaenl’elaboracióde sangakus depresentaciómoltacuradaienquèelcomponentestèticresideixtantenlaplàsticacomenelprocediment(jutsu)deresolució—quanhiés—, moltconcísidegranclaredatperòquepotamagarunaanàlisidelproblemaiunseguitdecàlculs peraconseguir-lodegrancomplexitat.N’hihaviaquepresentavenforçacomplexitatiespodien resoldregràciesalagranactivitatdesenvolupadaenlavessantcientífica.L’adjectiu artístic liescau notansolspermotiusestèticssinópeltipusd’organitzaciódelesescoles,similaralmodel iemoto queseguienlesescolesd’artstradicionalsjaponeses.11

• Científicaoderecerca.Latrobemenelcontingutdelstractatsescritsperl’elitdelacapitalEdo, enquèesdesenvolupenrecerquesdelmésaltnivell12 .Aquestesadopteniassimilen,durantbona partdelsegle XVII,latradicióxinesaperdespréstrencar-hiidesenvoluparformespròpiesderecerca, principalmentdelamàdeSekiTakakazu(1640?-1708)ielseudeixebleTakebeKatahiro(16641739).

Enelcampdel’àlgebra,latradicióxinesaésmésunaeinaperresoldreproblemesquenounamatèria ques’estudiïperellamateixa.Finsitotquans’estudiaambindependènciadelsproblemes,esfasota laperspectivademillorarlestècniquesambvistaalasevaresolució.Encanvi,enlatradiciójaponesahihaunesforçdegeneralització,defer-neunapresentacióabstractaidecrearunaestructura delsprocessosderesolució.Unexempledelesconseqüènciesd’aquestaorientaciómésabstracta éslaintroducciód’unaàlgebra escrita.Aquestaestàinspiradaenlarepresentacióxinesaqueutilitza

10.VegeuHoriuchi(1998),p.135.

11.Enla Guiad’escolesiemoto (XVIII-XIX)seciten,entred’altres,duesescolesdecerimòniadelte,tresescolesdeflauta, duesescolesd’arranjamentdeflorsisetescolesdematemàtiques.El iemoto éselcapdel’escola,exerceixunaautoritatabsoluta sobreelsmembresdel’escola,fixaelscontingutsdelseuartiatorgalesllicènciesalsaprenentsperpoderimpartirelsseus ensenyamentsquesovintnoméscomparteixenambelsmembresdel’escola.Generalmenteltítoléshereditariseguintlalínia filial,encaraquetambéesdónaelprocedimentd’adopcióperpoderatorgareltítolaunapersonadeforadel’àmbitfamiliar. Untretquediferencialesescolesdematemàtiquesdelarestaéselfetdenoserhereditària.VegeuOgawa(2001),p.145,i Bodiford(2002),núm.5del’edicióde2007.

12.Amésdelesreferènciesdelprincipidelasecció,vegeuHoriuchi(1989).

lamanipulacióderegletssobreunataula,perrepresentarnombres,operacionsiequacions,però incorporennovetatscomladequelesdadespodensernumèriquesoliterals.Així,enpoderser literalselscoeficientsdelesequacions,podenampliarlessevesrecerquesiestudiar,perexemple,les condicionsd’existènciadesolucionsd’unaequacióolacompatibilitatdelesdadesd’unproblema.

Engeometria,gràciesalesrecerqueseneldominidel’àlgebra,aconsegueixenalgunsresultatsque avancenelsdescobrimentsoccidentals,llunydel’úsdeleseinesdelageometriaanalíticaiprojectiva introduïdesperDescartes-FermatiDesargues,idelesdelcàlculdiferencialiintegralenlesrecerques d’àrees,volums,màximsimínimsdeterminatsperexpressionspolinòmiquescomlaqueespotobtenirenelproblema9delasecció7.Perestablirlesequacionsalgèbriquesquedeterminaranles solucionsdelsproblemesgeomètrics,utilitzenprincipalmentlesreglesdela‘‘base-perpendicularhipotenusa’’(teoremadePitàgores),‘‘doblehipotenusa-perpendicular’’(càlculdel’alturad’untriangleenfunciódelscostats,apartirdelsdostrianglesrectanglesquedetermina),ilasemblançade trianglesrectangles.Tambésóndegranenginyioriginalitatlessevesrecerquessobreelcercle.

Quelamatemàticajaponesanoésherevadelatradicióoccidentalesjustificaenunapartperla políticad’aïllamentdelpaís,peròtambépelcaràcterjaponèsquenomostrainterèsamuntarun granedificiteòricqueexpliquielsresultatsobtingutsenlessevesrecerquesal’estildelatradició iniciadaenelsegle VI aCaGrècia.SegonsTakebe,13

Lesmatemàtiquesconsisteixenenl’establimentderegles,l’aclarimentdelprincipidelsprocedimentsielcàlculdelsnombres.Quantaaquestatasca,esdiràqueés‘‘conforme’’sielprincipi ésaclarit,sielprocedimentésexplicatisielsnombressóncalculatsambl’ajutd’aquestprocediment.Esdiràqueés‘‘contrària’’sielprocedimentésavaluatpermitjàdelsnombresisiel principiéscercatambl’ajutdelprocediment. (Tetsujutsusankei14 ,1722).

Larecerca‘‘permitjàdelprincipi’’resideixenelgeniilaintuïciónascudesdel’atenció,laqualportaa unavisiódirectadelafontdecomprensiódelproblemaoprocedimentestudiat.SegonsTakebe,un representantprivilegiatéselmètodedel tianyuan que,apartirdelprincipidelaintroducciódel’elementdesconegutidel’establimentd’unaequacióapartirdelescondicionsdelproblema,permet, ambunprocedimentquenomésimplicamultiplicacionsisumesaplicadesd’unamanerarecurrent, obtenirlasoluciód’unaclassemoltgrandeproblemes15

Larecerca‘‘permitjàdelsnombres’’consisteixenl’elaboraciódetemptejosdecàlculsobrevalors numèricsconcretspertald’orientarelsmatemàticssobreelresultatquanel‘‘principi’’ésdedifícil accés.Nohihaunavisiódirectadelafontdelproblemaoprocediment,sinóques’hiarribaperuna marxainversaal’anterior.Unexempleelproporcionenelsprocedimentsperalcàlculdelalongitud del’arcidelcercle16

Encapmomentesparladededucciólògicaapartird’unsprimersprincipisodedemostraciótalcom l’entenemenlanostratradició.Mésaviatesparladedescobrimentperviaintuïtivaparal lelaal’ús delpensamentque,moltesvegades,raonainductivament.Aquítornemaaquellmovimententre pensamentisensaciódequèparlàvemalprincipi,propidelcaràcterjaponèsiqueassimilapartde l’activitatmatemàticaaunart.

13.VegeuHoriuchi(1994)p.305iseg.

14.SegonsesdiscuteixaHoriuchi(1994),p.273i303,estraduiria:‘‘Elclàssicdelprocedimentperacumulacióo connexió’’(d’exemplesocasosparticularsestudiats).

15.Vegeumésendavantlasecció5.2,p.8.

16.Peraaquestúltim,vegeuOgawa(2001),p.141-143,iHoriuchi(1994),p.279-302.

4.Elsre

gletsdecàlcul

Sabem—pelstextosescritsmésqueperlestauletes—que,perresoldreelsproblemesdels sangakus, esrecorriaal’aplicaciódelteoremadePitàgoresidelasemblançadetrianglesambllenguatgealgèbric,ialaposteriorresoluciódelesequacionsresultants.Esrepresentavenelsnombresilesequacions ambreglets.Enelcasjaponès,espresentavensobreuntaulerquadriculatitenienunaversióescrita quepermetiaintroduircoeficientsliterals.Elsnombresespresentavencomesmostraalafigura8. Lesunitatsd’ordreimparell,talcomesveu,alcostatsuperioresquerre;ilesd’ordreparell,alcostat inferioresquerre.Elsnombresnegatiusipositiusespresentavenambregletsdecolorsnegreivermell respectivament,ienlarepresentacióescritaespodiatrobarunregletinclinatsobrelarepresentació delesunitatssielnombreeranegatiu.Pelzeroesdeixavaunespaibuiti,enlarepresentacióescrita, espodiatrobarrepresentatperunpetitcercle.Lesoperacionsaritmètiquesesfeienmanipulantels reglets17 . 1 23 45 6 7

Figura 8. Al costat superior esquerre, les unitats, centenes, desenes de miler, etc. Al costat inferior esquerre, les desenes, milers, centenes de miler, etc. A la dreta, una diferència.

Peraltractamentd’equacions,estriaunalíniahoritzontaldereferènciaquerepresental’element desconegut(yuan)olalíniaquerepresental’elementconstant(tai).Llavorsleslíniesimmediatament inferiorsrepresentenlessegones,terceres,quartespotències,etc.,comesmostraenl’esquemaadjunt,

tai

yuan x 0 x 1 x 2 x 3

equivala21x 3 5x 2 + 7 = 0,otambéalpolinomi21

Presentemunproblemadedificultatbaixa18 ,desdepuntsdevistadiversosqueposendemanifestla diferènciadelsestilsiinteressosentreel wasan,elmodeleuclidiàielmodelderesolucióperradicals.

Enunciat. Doscerclesderadirsóntangentsalalínial.Talcomesmostraalafigura,unquadratdecostat ttocaambdóscercles.Trobeutenfuncióder .

17.VegeuMartzloff(1987),p.185-210,Pla(2009),p.99-103,iSmith-Mikami(1914),p.18-29de2004.

18.VegeuFukagawa-Rothman(2008),p.95.Agafaremelsenunciatstalcomallíespresenten.Aquestsnorecullen totalainformaciódelesfiguresimplicadessinóquefanreferènciaalaimatgequepresenten.

sangaku

r t l

Localització:Santuari Katayamahikode Murahisagun Ok ayama (1873).

5.1. Resolució 1. Anàlisi i resolució algèbrica per radicals a l’estil de sec undària

Sitracemleslíniesauxiliarsdelafigura9,podemaplicarelteoremadePitàgores,is’obté19 , 2x r l r 2x r x x

Figura9.Líniesauxiliarsperal’anàlisi.

Finalment,en2x < r ,elcostatdelquadratés2x = 2r 5

5.2. Resolució 2. Anàlisi i resolució algèbrica a l’estil wasan

L’àlgebra wasan peral’extracciód’arrelsutilitzaelmètodexinèsdel tianyuan20 amblesincorporacions delesrecerquespròpiesdel wasan.Peralaresoluciódelnostreproblema—enquè,perpresentar algunesdelespartsdelcàlculdemaneramésentenedora,estudiaremelcasparticularderadiigual a160unitats—,unesbósdelprocedimentaniriamésomenysaixí21

19.AquestéselcamíqueesproposaallectoraFukagawa-Rothman(2008),p.123,senseexplicaciódelsmètodesde resoluciód’equacionsenlatradició wasan

20. Tian ‘‘cel’’, yuan ‘‘origen’’.Enjaponès tengenjutsu omètodedel’elementcelestial.

21.Noesperdgeneralitatperquèlaproporcionalitatentreelcostatielradiesmantenen.Peraunapresentaciódel tianyuan,vegeuHoriuchi(1994),p.91-116.

1)Elecciódel’elementdesconegutoincògnitaipresentaciódelselementsresultantsdel’anàlisi delproblemamitjançantelsregletsdecàlcul.Enelnostreproblema,siconsideremeltriangle rectangledelafigura9,elselementsdel’anàlisisón,

(1) (2) (3)

(1)Meitatdelcostatdelquadrat: x

2)Manipulacióalgèbricadelselementspresentatsambvistaaserrelacionatsenunaequaciómitjançantl’aplicaciód’algunsdelsteoremescitatsanteriorment,peralaqualcosadisposendeles reglesdesuma,multiplicacióipotènciesdelesconfiguracionsalgèbriquesdereglets(polinomis)queenresulten.L’equacióquedarepresentadaperladiferènciadeduesexpressionsalgèbriquesquehandeseriguals.Així,lesoperacionsperobtenirl’equaciómitjançantelteoremade Pitàgoresserien:

Llavors,pelteoremadePitàgoresidividintper5,obtenim x 2 192x + 5120 = 0.Efectivament:

3)Resoluciódel’equacióperunmètodesimilaraldeRuffini-Hornerd’aproximacionssuccessives.Si x0 i x0 + x1 sónlesduesprimeresaproximacionsal’arrelde ax 2 + bx + c,espotdeduird’unaanàlisi delesduesidentitatssegüentsunamanerad’actuarque,entred’altrescoses,evitaelcàlculde potències:

(1) ax 2 0 + bx0 + c = (ax0 + b)x0 + c (2) a(x0 + x1 )2 + b(x0

Així,per(1)i(2)sabemque x0 + x1 seràunabonaaproximaciósiapliquemd’unamaneraadequada laregladeRuffinitalcomlaconeixem—sensepensarendivisiódepolinomisnidescomposicions factorials—,ambvistaaaconseguirquelasuccessió c,(1)i(2)tendeixiazero.Aixòéselquefeien desde,comamínim,elsegle XIII elsmatemàticsxinesos.22 Concretament,

22.VegeuMartzloff(1987),p.231-247de1997,Pla(2009),p.187-196,iSmith-Mikami(1914),p.50-56de2004.

1 [a] 192 b

30 [x0 ] 30 [ax0 ]

1 [a] 162 ax0 + b

30 [x0 ] 30 [ax0 ]

1 [a] 132 2ax0 + b

[c]

(ax0 + b)x0 + c

2 [x1 ]

Consegüentment,l’arrelés x = x0 + x1 = 32ielcostatval2x = 64,ésadir, 2 5 delradi.

5.3. Resolució3. Anàlisiiresolució geomètricaa l’estildela tradició euclidiana gregaclàssica en el marc del teorema de Pitàgores

Unadelespossibilitatsdeplantejamentdelaqüestióperpartdelsgeòmetresgrecshaguéssigut sotalaformad’unproblemadeconstrucciód’abastmésgeneral,delqualobtindríemlaconstrucció concretaifinsitotlarelaciódelcostatenfunciódelradicomunsubproducte.Primerament,se’ns demanariaconstruirelquadratinscritentreelsdoscerclestangentsdelaconfiguraciódonadailaseva rectatangentexterna.Ambl’úsdelmètodedel’anàlisi23 ,—enelmarcdelsteoremesI.47(teoremade Pitàgores)iII.7(quadratd’unadiferència)dels Elements d’Euclides—,podrientransformarelproblema enund’enunciatgeomètricmésgeneral.Aquestaanàlisi,queesfonamentaràenelsteoremesI.47, II.1,II.4iII.7dels Elements ialgunsdeparal lelismeicongruènciadelprimerllibre,podriaanarméso menysaixísiensimplifiquemelllenguatge24 :

Suposemelproblemaresolt,ésadir,quehemconstruïtelquadratdecostat YL i Z éselpuntmitjàdel costatadjacent.Totseguitcaldriadescriuretotesleslíniestraçadesalafigura10.Llavors,siobservem lesrelacionsdelesfiguresimplicades,tenim,

O R S X TL Y Z Figura10.Líniesdel’anàlisi.

23.Vegeuelllibre7dePapos(III)ielcapítol3deNolla(2006).

24.Quanescrivim AB2 i AB · CD s’hauriadellegir‘‘elquadratconstruïtsobre AB’’i‘‘elrectangledecostats AB i CD’’. Quanescrivimquedossegmentsodospolígonssónigualsvoldirquetenenrespectivamentiguallongitudoàrea.Finalment, siescrivim n s,enquè s ésunsegmentounasuperfíciei n ∈ Q,ensreferimaunsegmentosuperfíciequeguardaamb s una relació n delongitudoàrea.

a) OX 2 + XY 2 = OY 2 [I.47]

b) OX 2 + 2 OT XT = OT 2 + XT 2 [II.7]

c) XY 2 + 2 XZ YZ = XZ 2 + YZ 2 [II.7]

d ) XZ = OS = OT = OY,RS = YZ [PerconstruccióielllibreI]

e) XT = YL = 2 YZ ⇒ XT 2 =

f )2 OT XT = 2 OY 2

g)2 XZ YZ = 2 OY YZ [(d)]

h)Sisumemlesàreesimplicadesen(b)i(c)tenim

i)Llavors OY 2 +

j )Llavors6 · OY · YZ =

D’aquestamanera,sianomenem

elproblemas’hauriareduïtenelseullenguatgealsegüent:

• Donatsunsegment AB iunquadrat PG decostat PQ,apliqueusobre AB,ambdefected’unquadrat AD,unrectangle BD d’àreaigualaladelquadrat PG.

Figura11.Enunciaticonstrucció.

Aquestenunciat,enelnostrellenguatgeisi r éselradidelacircumferència,ésequivalentalaresolució del’equacióambincògnita x , x (a x ) = b2 , enquè a = 6r 5 ,b2 = r 2 5

= semicostatdelquadrataconstruir.

Enaquestpunt,l’anàlisiseguiriai,uncopacabada,lapresentacióclàssicaquefariendelasoluciódel problemaserialad’ocultaraquestaanàlisi,donarlaconstruccióilademostraciódelasevavalidesa25 Sisimplifiquemelllenguatge,laconstruccióilasoluciópodrienanaraixí26 :

25.Noespresentalacontinuaciódel’anàlisiperòpodeuconsultar-la,juntamblad’altresconstruccionssimilars,a Nolla(2006),cap.2,p.88-102.

26.Peralademostració,transformemelllenguatged’EuclidesenelllenguatgequePla(2009;p.258-281),anomena geometriadeltangram.Enaquestaestractadedemostrarqueduesfiguresdiferents,enelnostrecasunrectangleiungnòmon (diferènciadequadratsambunanglesuperposat),tenenlamateixasuperfícieapartirdelasevacomposicióambunesfigures

Construcció: Considerem[figura12dreta],

• Elpuntmitjà M d’AB ielpunt K sobrelamediatriud’AB amb MK = PQ

• Undelspunts X d’intersecciódelacircumferència(K,AM)amb AB

Llavorselrectanglebuscattécostats BX i XD = XA

Demostració: Enlafigura12podemveurequel’àreadelrectangle BD construïtésigualaladel quadratsobre PQ donat. MK = PQ KX = AM

= PQ (I.47)

Figura12. Àreadelrectangle= àreadel quadratsobre. BD PQ

Elspassosdelademostraciósónlestransformacionsambconservaciód’àreesde:

• Elrectangleenungnòmon.

• Elgnòmonenladiferènciadedosquadrats.

• Ladiferènciadedosquadratsenunquadratsobre KM = PQ,pelteoremaI.47dels Elements

Finalment,elsubproducteenformad’expressiódelcostatdelquadrat2x = 2 AX enfunciódelradi r , queéselqueinteressavaalsmatemàticsjaponesos,l’obtindrienimmediatamentdeconsiderarpeces q quadradesbàsiquesdecostat u = r / 5.Aixís’obté(recordemque AB = a = 6r / 5,PG = b2 = r 2 / 5): AB = 6u ⇒ MB = 3u ⇒ LB = 9q i,enser PG = 5q, esconclouque LS = 9q 5q = 4q ⇒ MX = 2u ⇒ AX = MB

5.4. Resolució 4. Anàlisiiresolució geomètricaa l’estildela tradició euclidiana gregaclàssica en el marc de la teoria de la semblanç a

Totiquelaresolucióanteriorserveixpercompararlesformesdetractamentalgèbricielsinteressos delesduestradicions,ésinteressantpresentarunaanàlisienelmarcdelateoriadelasemblançaque emsemblaméselegant.

• Suposemelproblemaresoltisiguin A elpuntmitjàdelabasedelquadrat, BC eldiàmetreperpendicularalarectai T elvèrtexdelquadratquetocaalacircumferència.

• Elstriangles Δ APT i Δ ABC sónrectangles PT / PA = 2 = BC / BA

bàsiques.Enprincipi,lesfiguresbàsiquessónlesmateixesenlesduescomposicions,peròespotgeneralitzareltractament ambfiguresbàsiquesdiferents.ElsteoremesdelfinaldelllibreIielsdelllibreIIdels Elements sónsusceptiblesdeserpresentats enaquestllenguatge.

Figura13.Anàlisiambsemblança.

• Pertant,elstriangles Δ APT i Δ ABC sónsemblants(criteri C A C desemblança),itenenl’angle PAT = BAC

• Consegüentment,elspunts A, T i C estanalineatsil’anàlisis’haacabatperquèsabemconstruirel segment AC ielpunt T quedeterminaelquadrat.

Obtindremlarelacióentreelradiielcostatdelquadratapartirdelasemblançadelstrianglesde l’anàlisianterioriobservantlapartdretadelafigura13.

6.comarecursosd’aula Sangakus

Alasecció5hemmostrattractamentsenelsaspectesalgèbricigeomètricdelsproblemescontingutsenels sangakus.Aixòestradueixenelfetqueespodenutilitzarenlesactivitatsambalumnes demaneraqueesreflecteixilacomplementarietatdelsllenguatgesdel’àlgebrailageometria,ien diferentsetapesdedesenvolupamentdelpensamenticoneixement.Siagafemcomareferènciael modeldeVanHiele27 ,espodencrearrecursosipresentacionsperal’alumnatqueestrobimajoritàriamentimplicatenelsseustresprimersnivells:visualitzacióoreconeixement,anàlisi,ordenació oclassificació28 .Laideainicialésdereproduirambl’alumnatlesdiferentsetapespresentadesen l’esquemadelafigura2ambvistaapercebrelamatemàticacomunfenomencultural,unaviad’enriquimentpersonali,finalment,constatarlavalidesadelsseusllenguatgesenelplaracionaliassolir-ne elsrudiments.Lesetapesespodencobrirdelamanerasegüent:

• Davantdelaimpossibilitatderealitzareltreballsobreelterrenyesfaunaintroducciódel’entorn onestrobaelproblemaambvistaacrearunestatperceptiufavorable.Acontinuació,espresentalaimatgedel sangaku queesvolestudiarsensecaptipusmésd’informació.(Contemplaciópercepcióestètica-intuïciód’harmonia).

• Desprésd’unsminuts,esconvidaelsalumnesafer-neunarepresentacióacuradaamàalçadaies debatsobrelesdificultatsquesorgeixenambvistaaunarepresentaciósatisfactòriailespropietats geomètriquesobservades.(Intuïciód’harmonia-movimentdelaraó).

27.Peraunapresentaciódelmodel,vegeuFouz-Donosti(2005).

28.Ambalumnesmoltexperimentatsenspodríemimplicarenlaintroduccióenelnivelldededuccióformal.

• Esplantejaelproblemaperresoldrequepotserelmateixqueproposal’enunciatdel sangaku o qualsevolaltrequehagisorgitcomeldefer-neunarepresentacióambregleicompàs.Aquíes potoptarperelaborarundocumentperal’alumnequeelguiïenl’anàlisidelproblema.Finalment esfaunreculldelsmètodesilespropietatsutilitzadesenl’estudi.També,enfunciódelsobjectius perseguitsideltipusd’alumnat,espotaprofundirenelseuestudiabstracte.(Movimentdelaraóexplicaciódel’harmonia).

Quantaldocument-guia,se’npodentrobartresaNolla-Masip(2009),delsqualsunaversiódelprimer vaserexperimentadaambalumnesdetercerd’ESOambresultatsencoratjadors.Cadascundelstres documentsespresentaambl’estructurasegüent:

a)Activitatguiadaperal’alumnat.

b)Fulldelprofessorperal’activitatqueincloueltipusd’alumnataquivadirigida,lesqüestions curricularsimplicadesiunapropostad’activitatscomplementàries.Algunsd’aquestsaspecteses desenvolupenenunannexd’einescomplementàriesperalprofessorat.

c)Propostaderesoluciódelsdiferentsapartatsdel’activitat.

D’aquestsdocuments-guia,elsdosprimersestandedicatsal’estudidelproblemapresentatenla secció5ieltercer,al’estudidelproblema2delasecció7.

7.

G

aleriadeperalasecund

àriaielprofessorat sangakus

Espresentendotzeenunciatsadaptatsde sangakus denivelldedificultatdivers.Amésderesoldrela qüestióproposada,espreténfer-nelaconstrucció.Elssisprimerssónadequatsperelaborarrecursos apartirdelsegoncicled’ESO,ielssisúltims,peral’alumnatdeBATitreballsderecerca.

Enunciat1. Trobeularelacióentreelsradis, r i R,delcercleméspetit ielcerclequeincloutoteldisseny,sielsaltresdoscerclesinscritssón igualsielsseuscentresestansobreeldiàmetredelcerclegran.

Solució: r = R 3

Referència: Ito etal. (2003,p.231)

Enunciat2. Silesfiguresinscriteseneltrianglerectangle sónuntriangleequilàter,unquadratiuncercletangent entotselsseuscontactes,trobeularelacióentreelcostat l deltriangleequilàterielcatetvertical c

Solució: l = √3 1 c

Referència: Fukagawa-Rothman(2008;p.99)iNollaMasip(2009;p.29-59).

Enunciat3. Elsarcsdelesfiguressónquartsdecercleambelcentre sobreelsdosvèrtexsdelabasedelquadratdecostat a.Trobeula relacióentreelradi R delcerclegrani a,iladelradi r delcerclepetit i a

Solució: R = 3 8 a,r = 1 6 a

Referència: Fukagawa-Pedoe(1989;p.41)iHuvent(2008;p.77-80).

Enunciat4. Entreelscinccerclesderadi a inscritsenelcerclegran deradi2a hihadostipusdecerclesméspetitsinscritstangencialmentderadis R > r .Trobeularelacióentre R i r .

Solució: R = 2 2 √2 r

Referència: Ito etal. (2003;291).

Enunciat5. Trobeularelacióentreelstresradis,—R, r1 i r2 —,dels cerclesinscritsrespectivamententrehipotenusa-catet,vertical-catet, horitzontalilacircumferència.

Solució: R = r1 + r2 + √2r1 r2

Referència: http://www.sangaku.info/images/Sangaku_Nagasaki

Enunciat6. Elscerclesinscritsentreeltriangleequilàterdecostat a i elsdossegmentstenenelmateixradi r .Trobeularelacióentre r i a

Solució: r = √3 √2 a 2

Referència: Fukagawa-Rothman(2008;p.152).

Enunciat7. Elsdoscerclespetitstenenelmateixradi r .Sianomenem a elradidelcerclecircumscriti R elradidel’altrecercleinscrit, trobeu r enfuncióde R ide a.

Solució: r = 2√R √a √R

Referència: http://www.sangaku.info/images/Sangaku_Nagasaki

Enunciat8. Elscerclesinscritsentrelesparal·lelessóntangents.Trobeularelacióentreelsradis r1 delgran,i r2 , r3 delspetits.

Solució: r 2 1 = 4r2 r3

Referència: Fukagawa-Pedoe(1989;p.4)iHuvent(2003;p.62-64).

Enunciat9. Enuntrianglerectangledecatethoritzontal a fixicatet vertical x variabletracemunsectorambcentrealvèrtexsuperiori radi x ,talcomindicalafigura.Siinscrivimunquadratdecostat y —quedepènde x —,entreelsectorieltriangle,trobeuelmàxim valorde y

Solució: y = √2 1 a 2

Referència: Fukagawa-Rothman(2008;p.120).

Enunciat10. Entredossectorsdecercleconcèntricstalsqueelradi delgranéseldobledelpetithihainscritselscerclesdelafigura. Aquestaéssimètricarespected’uneixverticalquepassapelcentre delssectors.Trobeularelacióentreelsradis, r < R,delsdoscercles méspetits.

Solució: R r = 31 2 8√3

Referència: http://pagesperso-orange.fr/gery.huvent/

Enunciat11. Tenimcinccerclesinscritsenunacircumferènciade radi a,amblestangènciesqueesmostrenalafigura.Elstresméspetitstenenelmateixradi r ,elsdosmésgrans,elmateixradi R.Trobeu larelacióentre a i r

Solució: a = 1 + 2 4√2 + 5 7 r

Referència: http://isaniwa.ddo.jp/homotsu/city/sangaku/html/ sangaku07.htm

Enunciat12. Aquestésunproblemainspiratenl’observaciód’alguns sangakus ambconfiguracionsdecerclestangentscoml’anterior.Tenimlaconfiguraciódelaimatgeadjuntaenquètrescercles inscritstenenelscentressobreundiàmetredelcercleexterior.Esdemanadeconstruirlafigurafixantelmésgrandelstrescerclescitats.

Referències

Bodiford,W.M.(2002).Soke:HistoricalIncarnationsofaTitleanditsEntitlements. KeikoShokon:ClassicalWarriorTraditionsofJapan,vol3,BerkeleyHeights:KoryuBooks.[Reeditatahttp://www.koryu.com/ library/wbodiford1.html,2007.]

Boursin,D.etal.(2005).SpécialJapon. Tangente,107.

Fouz,F.(2003).Sangaku:Geometríaenlostemplosjaponeses. SIGMA,22,173-190.

Capra,F.(2007). TheTaoofPhysics.1975.Traduccióespanyolaacàrrecd’AlmaA.Martell, ElTaodela Física.Málaga:Sirio.

Eecke,P.(1933). Pappusd’Alexandrie.LaCollectionMathématique.Bruges.[ReeditatperLibrairieScientifiqueetTechniqueAlbertBlanchard,París,1982].

Euclides(c.300aC). Elements.[TraduccióespanyolaacàrrecdeMaríaLuisaPuertasambintroducció deLuísVega(1994), Elementos,entresvolums.Madrid:Gredos].

Fouz,F.iDonosti,B.(2004/2005).ModelodeVanHieleparaladidàcticadelageometría. Unpaseopor lageometría,67-81.

Fukagawa,H.iPedoe,D.(1989). JapaneseTempleGeometry.Problems.Canadà:TheCharlesBabage ResearchCentre.

Fukagawa,H.iRothman,T.(1998).JapaneseTempleGeometry. ScientificAmerican.[Traducciófrancesa:GéométrieetreligionauJapon. PourlaScience,249].

—(2008). SacredMathematics.JapaneseTempleGeometry.NewJersey:PrincetonUniversityPress.

Heath,SirTh.(1908). TheThirteenBooksofEuclid’sElements.Cambridge:CambridgeUniversityPress. [ReeditatperDover,NovaYork,1956].

Horiuchi,A.(1989).Surunpointderuptureentrelestraditionschinoiseetjaponaisedesmathématiques. Revued’histoiredessciences,vol.42,4,375-390.

—(1994). Lesmathématiquesjaponaisesal’époqued’Edo.París:LibrairiephilosophiqueJ.Vrin.

—(1998).Lesmathématiquespeuvent-ellesn’êtrequepurdivertissement?Uneanalysedestablettes votivesdemathématiquesàl’époqued’Edo. Extrême-Orient,Extrême-Occident,20,135-156.

—(2005).Lagéométrieàl’usagedesDieuxauJapon?Dossier:Mathématiquesexotiques. Pourla science ÉditionfrançaisedeScientificAmerican,abril/juny,32-37.

Huvent,G.(2008). Sangaku.Lemystèredesénigmesgéométriquesjaponaises.París:Dunod. Ito,E.etal.(2003). JapanesetemplemathematicalproblemsinNaganoPref.Japan.Nagano:Kyoikushokan.

Martzloff,J.(1987). Histoiredesmathématiqueschinoises.París:Masson.[Traduccióanglesaacàrrecde StephenS.Wilson, AHistoryofChineseMathematics.Berlín:Springer,1997].

Matsuo,B.(1981). Okunohosomichi.1694.[Traduccióespanyolaacàrrecd’OctavioPaziEikichiHayashiyaambintroducciód’OctavioPaz, SendasdeOku.Barcelona:SeixBarral].

Mundó,A.M.(2004). Lacontemplaciódelabellesaenl’art.Barcelona:Amicsdel’artromànic-IEC.

Murata,T.(2001).IndigenousJapaneseMathematicsWasan. JournalofJapaneseTradeandIndustry, vol.20,2,50-55.

Nolla,R.(2006). EstudisiactivitatssobreproblemesclaudelaHistòriadelaMatemàtica.Barcelona:SCMIEC.

Nolla,R.iMasip,R.(2009). Sangakus.Recursosdegeometria.http://www.xtec.cat/∼rnolla/Sangaku/ SangWEB/PDF/Sangak_4.pdf

Ogawa,T.A(2001).ReviewoftheHistoryofJapaneseMathematics. Revued’histoiredesmathématiques,7,137-155.

Pla,J.(2009). LiuHui.Nuevecapítulosdelamatemáticachina.Madrid:Nivolalibrosyediciones.

Robert,J.(2007).Quandlesdieuxdescendentdesbouddhas:l’osmoseentreshintôetbouddhisme auJapon. Religions&Histoire,13,74-81.

Robson,E.(2008). MathematicsinAncientIraq.PrincetonandOxford:PrincetonUniversityPress.

Smith,D.iMikami,Y.(1914). AHistoryofJapaneseMathematics.Chicago:OpenCourtPub.Co.[Reeditat perDover,NovaYork,2004].

Sykes,M.(1912). SourceBookofProblemsforGeometry.Norwood:NorwoodPress.[ReeditatperDale SeymourPublications,PaloAlto,1997].

Ticó,T.(2004). PasseigmatemàticperCatalunya.Lleida:Pagèseditors.

Vera,F.(1970). Científicosgriegos,2volums.Madrid:Aguilar.

Presentaciódediapositivesassociadaal’article:

http://www.xtec.net/∼rnolla/Sangaku/Sangakus3b.pdf

Algunespàgineswebd’interèspelsseusregistres,fotografiesivisualitzacions: http://www.cut-the-knot.org/pythagoras/Sangaku.shtml

http://isaniwa.ddo.jp/homotsu/city/sangaku/sangaku\_e.html http://www.sangaku.info/ http://www.wasan.jp/index.html

Incertesaiprobabilitat.Un passeigperalgunesparadoxes iproblemesclàssicsdela teoriadelaprobabilitat

JosepLluísSolé

DepartamentdeMatemàtiques,UAB

Resum Abstract

Elshumanssemprehantemutlaincertesaque governalessevesvides.Enaquesttreball,femla descripciód’unpasseigamableperlesnostres reaccionsdavantdel’aleatorietat,desdelsvells tempspassats—quanvaserdivinitzada—,fins alamatematitzacióquerepresentalateoriade laprobabilitat,que,segonsLaplace,noésmés queelbonsentitreduïtalcàlcul.Considerarem algunespreguntesquejaapareixenala correspondènciaentrePascaliFermat,enel naixementdelateoria,aixícomalgunsdels problemesclàssics,comelfamósproblemade lestresportes,l’apostaalamartingalaoel passeigaleatoriambbarreres,seleccionatsentre l’immensnúmerodesorprenentsresultatsi paradoxesd’aquestateoria.

1.Introducció

Thehumansalwayshavefearedtheuncertainty thatdirectstheirlives.Inthispaper,wedescribea kindwalkalongourbehaviorinfrontof randomness,fromtheoldtimes,whenitwas divinized,untilthepresentmathematical treatmentwiththeTheoryofProbability,that,as Laplacewrote,isonlythecommonsensereduced tocalculus.Wewillconsiderthefirstquestionsthat appearinthecorrespondenceamongPascaland Fermat,atthedawnoftheTheory,andalsosome ofthemostclassicalproblems,asforinstancethe martingalebetting,andtherandomwalkbetween barriers,selectedinthesorichandenormoussetof surprisingresultsandparadoxesofthisTheory.

Elshomessemprehantemutlaincertesais‘hanpreocupatperl’atzarqueelsgovernalesvides.Així com,quasifinsalsegle XIX,lesciutatsaixecavenaltsmursdepedraperprotegir-sedelsenemicsexteriors(quesempreacabavensentinútilsilesvileserenconquerides),tambéelshomess‘hanrodejat d’altesmurallesfísiquesimentalsperprotegir-sedelaincertesa,senseserconscientsqueaquesta s‘emportaràlavictòriafinal.

Podemtrobarmoltescitesd’autorsclàssicsquefanreferènciaaldominiquel’atzarilaincertesatenen sobrenosaltres.Enrecordaremtansolstres.Hipodríeuafegirlesvostrespreferides.

Nohemd’estranyar-nosquel’atzarpuguitantsobrenosaltres,siconsideremelfetquevivim isomperatzar (Sèneca).

Quèésl’home?UnvaixellexposatatotselsultratgesdelaFortuna. Totésatzar.Comaljocdedaus,veighomesambfortunaid’altressensesort (Electra, Eurípides).

Elsnostresavantpassatsgrecsiromansconvertirenl’atzarenmiteivandivinitzar-lo.Eldestídels homeseraunaresponsabilitatdelsdéus.Crearen,dintredelseuesquemamitològic,representacions divinesqueerenlesencarregadesderegirlesvidesdelshomes.Alafigura1,esmostrenl’estàtua querepresentaladeessaTyche(quesignificafortunaengrec),trobadaaAntioquia,iunfrisenquè apareixenZeusiNèmesi,laqualmarcavaeldestídelséssersmoridors.Alsseuspeus,veieularodade laFortuna,metàforadelavariabilitatdelasort,del’alternançadetempsd’alegriaidedissortassociada alcamídetothome.

Alafigura2,veieulaimatged’unpergamímedieval,onesrepresentatambélarodadelaFortuna, queensenlairaiensfacaureenelcursdelanostravida,enelseugirconstant.Aquestametàforaera moltdelgustdelsteòlegsmedievals.

2. Unamicadefilosofia

Ésnormalpreguntar-nosquèésl’atzariperquèhihaincertesa.Podríemdistingirduesposicionsben clares.

Laprimeralíniaconsideraquelaincertesaésunproblemamotivatperlalimitaciódelnostreconeixement.HopodemresumirenlafamosafrasedePierreSimon,marquèsdeLaplace,enelseucèlebre Assaigfilosòficsobrelesprobabilitats [9]:

Unaintel ligènciaqueenunmomentdeterminatconeguéstoteslesforcesqueregeixenala natura,ilasituaciórespectivadetotselséssersquelacomponen,sifossuficientmentgran peranalitzartotesaquestesdades,podriaenglobarenunasolafórmulaelsmovimentsdels cossosmésgransdel’Universielsdel’àtomméslleuger.Resliseriaincert,itantelfuturcom elpassatestarienpresentsdavantdelsseusulls.

Lasegonaposicióconsideralaincertesacomunaqualitatintrínsecadelanatura.Lamodernafísica quàntica,lafísicadelqueésmoltpetit,ésadir,delmóndel’àtomidelespartículeselementals,

Figura 1. Tyche d’Antioquia. Nèmesi.

Figura 2. Roda de la Fortuna.

ensdiuquel’atzaréspropidelanatura,inotansolsunaconseqüènciadelanostraintel ligència imperfecta.

Deixeu-mecitardosfamososfísicsdelseglepassatqueil·lustrenaquestaidea.

Jocrecquel’indeterminisme,queéslanovalidesadelacausalitatrigorosa,ésnecessariino tansolspossible (Heisenberg).

Elquenoestàrodejatd’incertesaésimpossiblequesiguicert (Feynman).

Podríemresumirlesduesposicionsdientqueperalaprimera,enelcasqueDéuexistís,comque seliatribueixunaintel·ligènciainfinita,peraellnohihauriaatzar.Laincertesaésunproblemaepistemològic,delconeixementforçosamentlimitatdelshomes.Encanvi,peralasegonaposició,la incertesaésintrínsecaalanatura,pertant,peraDéutambéhihauriaatzar.Laincertesaseriauna qüestióontològica,unapropietatdel’ésser.

Aquestacontrovèrsiaenllaçaambladisputaeternaentreeldeterminismeilacausalitatabsolutaper unabanda,ilapresènciad’incertesaidellliurealbirperaltra.JaSantAgustí,enelllunyàsegle IV, espreocupàperlaqüestió,doncslieradifícild’acceptarunDéuinfinitamentbondadósiquefes viurehomescondemnatsforçosamentaunespeneseternesinevitables.Aquestadualitatfouobjecte d’apassionatsdebats,tantfilosòficscomteològics.

Poincarétambécontribuíalapolèmicaamblasevadefiniciód’unproblemamalposat,quedonàlloc alnaixementdelquearas‘anomenacaosdeterminístic.Elleraundeterministaconvençuti,pertant, creiaquesisabéssimlesequacionsdiferencialsquemodelenl’evoluciód’unsistemaipoguéssim precisar-nelescondicionsinicials,ensseriaconegudal’evoluciófutura.Perònielnostremodelés perfecte,nilescondicionsinicialsespodendeterminarexactament,icomque,encertsmodels,les solucionsquesurtendecondicionsinicialsmoltproperes,iqueamblanostraprecisiónopodem distingir,s‘allunyenmoltenpassareltemps,nohiseriapossibleeldeterminisme.Aixòelportàala necessitatd’introduirl’atzarsegonslaprimeralíniafilosòficaquehempresentat,ladeveure‘lcomun problemaepistemològic.Usrecomanollegirlabrillantintroduccióalseucurs CalculdesProbabilités [12],quetambéésuncapítoldelseuassaig Ciènciaimètode [13].

3.Jociatzar. Unamicad’història

Demoltantic,elshomeshanpracticatelsjocsd’atzar.EnelcantIIIdela Ilíada,elpoetaensexplica demaneraadmirablecomeldeíficAlexandre(Hèctor)il’aqueuMenelau,elmaritburlatd’Helena, esjuguenalasortquiseràelprimeratirarlallançadebronzeenelseucombatsingular.Posenles penyoresenuncascqueHèctorsacsejamirantenrereielpoetaensexplica:‘‘Comunllamplasort deParisvasortir’’.

Comentaremaradosdelsprimersaleatoritzadors,elstaliielsdaus.

• Elstali

Elprimeraleatoritzadorsemblaquevaserunosdeltalóanomenat astragalus.Entrelesrestesde lesexcavacionsarqueològiquessen‘hantrobatambunafreqüènciamoltsuperioralsaltresossos. Aquestfethaportat,potserdeformaagosarada,elsexpertsadirqueenlesllarguesnitsdelsnostres avantpassats,elsjocsd’atzarhierenbenpresents.

Astràgal

Articulació anterior talocalcània

Si del tars

Articulació posterior talocalcània

Alafigura3,veieuuns talus (astràgals).Fixeu-vosquetenen quatrecaresnoiguals,alesqualsse‘lsdonavapuntuacions1, 3,4,6.Lajugadamésvaloradaeratreure,entirar-loquatrevegades,aquestasèriedepuntuacions(s‘anomenava‘‘Venus’’ enlaRomaclàssica),ilamésdesfavorable,obtenirquatreuns (‘‘gos’’).

Delagranaficiódelsromansajugar-hi,n‘ésunamostralasegüentfrasedePropertius(50aC).‘‘Joesperavaqueemsortís unVenusambelstalifavorables,peròl’odiatgossortiasempre’’.

Enunatombaegípcia,datadacapa3500anysabansdeCrist, hihapintatsunhomeiunadonajugant-hi.Alafigura4teniu unaestàtuaromanamoltbella,quepodeuveureenelMuseu Vaticà,iquerepresentaunnenllançantels tali

• Elsdaus

Elsdausmésanticsqueesconeixen(3000aC)hanestattrobatsaShahr-i-Sokhta,alsud-estdel’Iran.Sónelsqueesmostrenalafigura5.

Altresdausremarcablesperlasevaantiguitatiperfecciósón elstrobatsaMesopotàmia(2700aC),iaEgipte(1370aC).

Elsromansn’erenmoltaficionats.L’emperadorAugustvaprohibirjugar-hi,excepteeneltempsdelesSaturnàlies.Horaci, perlasevabanda,criticaelsjovesquejuguenadausenlloc dededicar-sealescosesdeprofit.

Comveieu,elsvellssemprehancriticatelsjovesambargumentssemblants.

Al’èpocamedievaltambés‘hijugavamolt.Aixòprovocà,perexemple,queSantLluís,reideFrança, elsprohibís.

Calcani

Fi

Valadirtambéqueéscuriosal’arrelfilològicadela paraulaatzar.Ésunmotd’origenàrab,quepodeu veureescritenlafigura6,iquesignificaflor.

L’explicació,segonsdiuJoanCorominesenelseu diccionarietimològic,ésqueelsàrabsjugavenamb unsdausqueteniendibuixosalessevescares,com passaambelsactualsdepòquer.Lacaramésvaluosateniadibuixadaunaflor,l’asdelpòqueri,perextensió,elnomàrabdeflorvaesdevenirelquetantesllengüesoccidentalsutilitzenperdesignarl’atzar.

Eltermellatíquedesignaeldaués alea (recordemlafamosafrasedeJuliCesarenl’inicidelaguerra civil‘‘Aleaiactaest’’),iésl’arreldelnostremotaleatori.

Eljocdedausmoltaviatinteressàalsestudiosos.Destaquemlesobres:

DeVetula,escritperRicharddeFournival(1200-1250),queéselprimerestudisobredaus. LiberdeLudoAlae,deCardano(1501-1576).

TambéGalileu(1613-1624)escrivísobreeltemaal’obra SopraleScopertedeiDadi.

• Origendelateoriadelaprobabilitat

Lacreençaqueeldestíilaincertesaerencosadelsdéusésseguramentlaraóqueexplicaperquè elnaixementdelateoriadelaprobabilitatvasertantardà.D’altrabanda,semblacontradictorique sobrel’atzarilaincertesaenpuguemdiralgunacosa.RecordemlafrasedelprofessorBertrand, citadaalpròlegdel CalculdesProbabilités dePoincaré:‘‘Comensatrevimadircosessobrel’atzar? Noésl’atzarl’antítesidetotallei?’’[12].

Peròelsmatemàticssónvalentsitemeraris.S’hihanatrevitis’hiatreveixenencara!!

Elnaixementdelateoriadelaprobabilitatesprodueixalsegle XVII,amblabreucorrespondència entreFermatiPascal,queduradeljuny/juliolfinsalsetembre/octubrede1654,motivadaperles preguntesqueunjugadoraristòcrata,elChevalierdelaMéré,faaPascal.Alafigura7teniuelsretrats

Figura6

d’enFermatienPascal.Usrecomanoelmagníficestudisobreaquestacorrespondènciaquetrobareu alcapítol6delllibre Obramatemàticavària [6]dedicatal’obradeFermat.

Éscuriósderecordarl’opinióqueelsdoscientíficstenensobreelChevalierdelaMéré,quenoés matemàtic(al’època,anomenatsgeòmetres).

Jen‘aipasletempsd’envoyerlademostrationd’unedifficultéquietonnaitfortMonsieurde Méré,carilatrésbonesprit,maisiln‘estpasgéomètre,etça,commevoussavez,estungran default.

ElmarquèsdeLaplace(tambéalafigura7)comentaqueésremarcablequeunaciència,quecomençà ambl’estudidelsjocsd’atzar,hagiesdevingutundelsmésimportantsobjectesdelconeixement humà.

Ellmateixafirmacomaconclusiódelseu Assaigfilosòficsobrelesprobabilitats [9],queaquestanoés resmésqueelbonsentitaplicatalcàlcul.

4. Laprobabilitatvistapelsmatemàtics. Com modelen la incertesa els matemàtics?

Explicaremsensegairesdetallsquinaésl’axiomàticaintroduïdal’any1933perKolmogorov[8].Davant d’unexperimentaleatori,consideremelconjuntdetotselsresultats,queanomenem Ω.Perexemple, enelcasdelllançamentd’unamoneda, Ω serà

Ω = {cara,creu}

Sitiremconsecutivamentduesvegadesunamoneda,

Ω = {(cara,cara), (cara,creu), (creu,cara), (creu,creu)} (1)

Enelcasd’undau

= {1, 2, 3, 4, 5, 6}

Unesdevenimentésunaafirmacióquefemsobreelresultatdelnostreexperimenttalque,unavegadarealitzataquest,podemdirsis‘hacomplertono.Perexemple,enelcasd’undau,obtenirun númeroparellésunesdeveniment.

Sienelllançamentdeldautansolspodemveuresisurtunapuntuacióparellaosenar,l’afirmació ‘‘obtenirundosounquatre’’noésunesdeveniment,jaquenopodremassegurarsempresis‘ha produïtono(perexemple,siobtenimunacaraparellanosabremsihaestatundosounquatre,o haestatunsis).

Aunesdevenimentlipodemassociarelsubconjuntd’Ω formatpelsresultatsquesatisfanl’afirmació lligadaal’esdeveniment.Perexemple,aobtenirunacaraparellaentirarundauliassociemelconjunt {2, 4, 6}

Elqueensdescriul’experimentéselconjuntdetotselsesdeveniments,jaqueelconjuntassociat noestàdeterminatdemaneraúnica.Perexemple,sitiremconsecutivamentduesmonedes,podem triarcoma Ω elconjuntdescriten(1)oelconjuntdelessuccessionsdezerosiuns.

Aquestconjuntdetotselesdevenimentso,sivoleu,elconjuntdelssubconjuntsassociatsalsesdeveniments,had’incloure Ω,isertancatdavantdelcomplementari,lesunionsfinitesilesinterseccions finites(sivolguéssimserprecisos,hauríemdedirnumerableenllocdefinit,peròaixòhodeixemper aunaaltraocasió).

Elcomplementaricorresponanegarl’esdeveniment,launiódedosatenirllocl’unol’altre,ilaintersecciódedosaesdevenir,demanerasimultània,l’unil’altre.

Elterceringredientéslaprobabilitat,ésadir,unnúmeroentre0i1queassignemalsesdeveniments, iqueensindicalafacilitatambquèaquestesprodueix.

Aquestaassignaciónolapodemferdequalsevolmanera,sivolemtenireldretdedir-liprobabilitat. Perquèpuguemparlardeprobabilitats‘hadecomplirque

• P(surtiqualsevolresultat) = 1.

• P(nopassil’esdeveniment) = 1 P(passi)

• Si A i B nopodenpassaralavegada,aleshores P(passil’esdeveniment A oel B) = P(passi A) + P(passi B).(Aquínoentremeneltemade σ -additivitat.)

Aixòdarrerhoescriuremtenintencomptequeelsubconjuntassociatal’esdevenimentquepassi A o B corresponalauniódelsdossubconjuntsassociatsrespectivamental’esdeveniment A ial B, delamanerasegüent:

P(A ∪ B) = P(passi A) + P(passi B), si A ∩ B = ∅

Podemfer-nosaralasegüentpregunta:Quinaéslaprobabilitatqueassignemaunesdeveniment?

Enladefinicióclàssica,l’assignacióesfapermitjàdel’expressió

P(A) = casosfavorables casospossibles

Pertant,laprobabilitatesredueixaunproblemadecomptar.Perexemple,enelcasd’unamoneda perfecta,laprobabilitatquesurticaraserà 1 2

Enundauperfecte,laprobabilitatquesurtiun5oun6serà 2 6 .

Sitiremdosdaus,l’espai Ω deresultatsserà

Comptant,podemtrobarfàcilmentlesprobabilitatsdelssegüentsesdeveniments: P(sumasigui7) = 6 36 = 1 6 , jaqueelscasosfavorablessónlesparellesquehihaaladiagonalquevadel(6,1)al(1,6).

P(sumasigui2o3) = 3 36 = 1 12 ,

perquèelscasosfavorablessónlesparelles(1,1),(2,1)i(1,2).

• Elproblemadel’aniversari

Pregunta: Quinaéslaprobabilitatque,enungrupde k personesquecoincideixenenunareunió,n‘hi hagialmenysduesquefacinelsanyselmateixdia?

Percontestaraquestapreguntatansolshemdecomptar.Suposemunanyde365dies(notenim encomptequehihaanysdetraspàs),itambéquehihacomamàxim365persones,jaquesin‘hi haméséssegurquehihaalgunacoincidència.Les k personespodencelebrarelsseusaniversaris de365k maneresdistintes.

Aleshores, P(almenysunacoincidència) = 1 P(capcoincidència).

Percalcularlaprobabilitatquenohihagicapcoincidència,ordenemels k assistentsipensem així:elprimerpotferl’aniversariqualsevoldiadel’any,elsegonpotfer-lototselsdiesexcepteel queelsfaelprimer...ieldarrerpodràtenirl’aniversarienels365 k + 1diesnoocupatsperles altrespersones.Pertant,

P(almenysunacoincidència) = 1

365 × 364 × 363 ×···× (365 k + 1)

365k

Sicalculemaquestaprobabilitatperadiferentsvalorsde k ,veiemenlataulasegüentque,sihiha 23persones,laprobabilitatdetrobaralgunacoincidènciaésjamésgranque 1 2

5. DosproblemesclàssicsresoltsenlacorrespondènciaentrePascaliFermat

Comaltresexemplesd’aplicaciódeladefinicióclàssica,presentaremduesdelesqüestionsresoltes enlacorrespondènciaentrePascaliFermat.UnesbonesreferènciessónelllibresobreFermat[6]ja citat,ieldeSzekely[14],enelqualtrobareuunbonreculldeparadoxesdelateoriadelaprobabilitat.

• Laparadoxadeladivisió

Aquestproblemajaesdescriuenunmanuscritdel1380.LucaPaccioli(1494)eltornàaplantejar enlasevaobra SummadeArithmetica,Geometria,ProportionietProporcionalita

Pregunta: Dosjugadorsjuguenaunjocenquètenenlamateixaprobabilitatdeguanyarodeperdre, perexempleacaraicreuambunamonedajusta.Posensobrelataulalamateixaquantitatdediners

idecideixenques‘hoemportaràtotquiarribiprimerasisvictòries.Eljocs‘interrompquanvan5a3.Com s‘handedividirlesapostes?

Tartàgliaproposàdividir-lesenunaproporcióde2a1,Pacciolide5a3,iPeveronide6a1.

PascaliFermat,encanvi,proposaren7a1,ielseuraonamenteraelsegüent:

Enelmomentenquèelsdosjugadorsdeixendejugarambunapuntuacióde5a3,necessiten comamàximtrespartidesmésperestarsegursquealgúarribaasisvictòries.

Aqueststresjocsaddicionalspodenanardevuitmaneresdiferents.Lesdescrivimdientquiguanya cadascunadelestrespartides,utilitzantlalletra A o B segonssiéselprimeroelsegonjugadorel queguanyaeljoc.

Pertant,elscasosfavorablesalprimerjugador,enelsentitquearribaasisjocsguanyatsabansque l’altre,són:

AAA,AAB,ABB,ABA,BAB,BAA,BBA, inomésn’hihaundefavorablealsegonjugador,el BBB

Aixòimplicaquelaproporcióenlaquals‘handerepartirlesaposteshadeser7a1.

• Laparadoxadelaproporció

ElChevalierdelaMéréjasabiaquelaprobabilitatdetreureun6entirarundauera 1 6 ,iladetenirun doble6entirardosdaus 1 36 .Nosaltreshopodemdeduirtansolscomptant,iutilitzantladefinició clàssica.

Sitiremundauquatrecops,laprobabilitatdeteniralmenysun6és

Pertant,ésfavorableapostaraaquestesdeveniment;encanvi,nohoésapostaratreurealmenys un6sitiremeldauuna,duesotresvegades,jaquelessevesprobabilitatsrespectivessón1 5 6 , 1 5 6 2 ,1 5 6 3 ,totesinferiorsa0,5.Aaquestvalor4,l’anomenemelvalorcrític,ésadir,elvalor méspetitde n peralqual1 5 6 n supera 1 2

Aratiremalmateixtempsdosdausimiremelmínimnúmerodetiradesdelsdosdausperalqualla probabilitatdetreurealmenysundoble6superi0,5.Enaquestasituació,laprobabilitatdetreure undoble6és 1 36 ,ésadir,unsisèdelaprobabilitatdetreureun6enllançarundau.

Hihavia,entreelsjugadorsdel’època,unareglaquedeiaquesilaprobabilitatdelquebusquem esdivideixper k ,elvalorcríticcorresponentquedamultiplicatper k .Enelnostrecas, k = 6i,per tant,esperaríemqueelnouvalorcríticfos6 × 4 = 24.

Peròsicalculemlaprobabilitatdetreurealmenysundoble6en24tiradesdedosdaus,obtenim 1 35 36 24 = 0,49140 ... inferiora0,5,iaixòimplicaque24noéselvalorcríticd’aquestexperiment.

Pregunta: Perquènoésvàlidalaregladelaproporciódelsvalorscríticsqueafirmaria,enaquesta situació,quesilaprobabilitatbaixaalasisenapart,elvalorcríticquedamultiplicatper6?

Aquestproblemajal’haviaestudiatCardanoabansquePascaliFermat.

Plantegem-loengeneral.Consideremunjocontenimunaprobabilitat p deguanyar.Definim l’esdeveniment A comqueen k repeticionsindependentsalmenysguanyemunavegada(més endavantexaminaremelconcepted’independència.Quedem-nosaraamblaideaquesónesdevenimentsquenos‘influeixenentreellsitalsquelaprobabilitatquepassinalmateixtempsésel productedelessevesprobabilitats).Laprobabilitatd’A,utilitzantelsegonaxioma,és

1 (1 p)k

Aquestaexpressióéscreixentamb k ,ivolemtrobarperaquina k superaoarribaa0,5,ésadir,el valorcrític.Pertant,hemderesoldrel’equació

(1 p)x = 1 2 , iobtenim x = ln2 ln(1 p)

DesenvolupantperTaylortenimqueln(1

,iposant-hoal’expressióde x dóna

= ln2 p + p2 2 + demaneraque,tansolssi p ésmoltpetit,podempensar x ≈ ln2 p ,ésadir,espotparlard’uncomportamentdeproporcionalitatinversa,queéselquecreienelsjugadorsquesemprehaviadepassar.

6.Interpretaciófreqüencialisubjectivadelaprobabilitat

Ladefiniciódeprobabilitatquehemutilitzattéelproblemaquenoprioritzacappossibleresultat. Perexemple,noensserviriaenelssegüentscasos:

• Unamonedacarregadademaneraquelacarasiguimésprobablequelacreu.

• Pertrobarlaprobabilitatqueunaembarassadatinguibessonada.

Perevitaraquestproblema,s‘utilitzalainterpretaciófreqüencialdelaprobabilitat.Aquestaensdiu quesirepetiml’experimentmoltesvegadesdemanera independent,laquantitat

fn (A) = nombredevegadesquepassa A en n experiments n

tendeix,quan n vaa ∞,capauncertnúmeroqueanomenaremlaprobabilitatdel’esdeveniment A Aixòésunaversiónaïfdelalleidelsgransnombres.Comamatemàticshauríemdedirquèentenem araperconvergència,perònoentraremenaquestsmomentsenaquesttema.

Alafigura8,perexemple,veiemquelafreqüènciadelescaresentirarrepetidamentunamoneda justavacapa 1 2 .

Sitiremsimultàniament50monedesjustesimiremelnúmerodecares,aquestpotserqualsevol enterentre0i50.Repetimelllançamentdeles50monedes1.000vegades,ifemlagràficadeles freqüènciescorresponentsacadascundelsvalorspossibles.Obtenimlacampanadelafigura9,la quals‘apropaaladistribuciódeprobabilitatsteòricadels51possiblesvalorsdelanostravariable (del0al50),ques‘anomenaunabinomial 50, 1 2 .Elgràficestàfetambels applets d’unapàginaweb absolutamentrecomanable[16].

Avegadesnotésentitlarepeticiódelmateixexperimenti,pertant,nopodemusarlainterpretació freqüencial.Enaquestcasunaalternativaéslainterpretaciósubjectiva,enquèlaprobabilitatdepèn del’opinióquetenimdelafacilitatqueesprodueixil’esdevenimentconsiderat.

Ésimportantremarcarque,siguiquinasiguilainterpretacióquefem,eltractamentmatemàticésel mateix.

Figura8

Figura9

Sisabemquehapassatl’esdeveniment B,aleshorespodemparlardelaprobabilitatcondicionadade l’esdeveniment A respectedel’esdeveniment B,queanomenarem P(A|B).

Intuïtivamentcorresponareescriurel’espaimostraltenintencompteque B hapassat,inormalitzar lesprobabilitatsdividintperlaprobabilitatdel’esdeveniment B respecteelqualcondicionemperquè sumin1.Perexemple,enelcasdetirarsimultàniamentdosdaus,sisabemquelasumaés7, B és

iaquestconstitueixelnouespai Ω condicional.

Ara,laprobabilitatdecadaelementseràlaqueteniaabansdecondicionar,querecordemera 1 36 , divididaperladel’esdeveniment B respectealqualcondicionem,queés 6 36 ,pertant 1 6 .Comqueen l’espaioriginalladistribuciódeprobabilitatserauniforme,tambéhoseràenelnou,queté6elements i,pertant,enaquestcas,hauríempogutarribaralresultattansolscomptantenl’espaicondicional. Aixòensportaalaconegudadefinició

(A|B) = P(A ∩ B) P(B) , si P(B

Elconcepted’independència,queabanshemesmentat,ésfonamentalenlateoriadelesprobabilitats.Ensdiuquesiconeixemque B hapassat,aixònoensmodificalaprobabilitatd’A,ésadir,si P(B) > 0,aleshores P(A|B) = P(A).Deladefiniciódeprobabilitatcondicionadaendeduïmqueésequivalenta P(A ∩ B) = P(A) · P(B),ésadir,laprobabilitatquepassinalhoraelsesdeveniments A i B ésigual alproductedelesprobabilitatsrespectives.

Vegem-nedosexemplessorprenents,quemotivaranelsegüentcomentaridelprobabilistaHoffmanJorguensen[7]:

Detotaixò,elquen‘hemdetreurecomaconseqüènciaésquemaihemdebasar-nosmassa enlanostraintuïcióquancalculemprobabilitatscondicionades,sinóenelsnostrescàlculs.

• Elproblemadelaparelladefills

Pregunta1: Sisabemqueunaparellatédosfills,iund’ellsésunanena,quinaéslaprobabilitatque l’altresiguitambéunanena?

L’espai Ω originalés,abansdecondicionar,

{(nen,nen), (nen,nena), (nena,nen), (nena,nena)}, enquèelprimerelementdecadaparellacorresponalfillgran.Laprobabilitatdecadaelement és 1 4

Elconjunt B respectealqualcondicionem,ipertantelnouespai Ω condicionalés

{(nen,nena), (nena,nen), (nena,nena)},

jaqueencadaparellahihad’haveralmenysunanena.Laprobabilitatdecadaelementés,en aquestescenaricondicionat,laqueteniaabans, 1 4 ,divididaperladel’esdevenimentrespecteal qualcondicionem P(hihaalmenysunanena) = P(B) = 3 4 ,pertant, 1 3 .Fixem-nosquehauríem pogutarribaraaquestmateixresultatobservantdirectamentl’espai Ω condicional.

Aleshores,enaquestasituació,laprobabilitatqueelsdosfillssiguinneneséslaprobabilitatcondicionadade(nena,nena),ésadir, 1 3

Pregunta2: Sisabemqueunaparellatédosfills,ielgranésunanena,quinaseràlaprobabilitatque l’altresiguitambéunanena?

L’esdeveniment B respectealqualaracondicionemés

{(nena,nen), (nena,nena)}

i,pertant,aquestéselnouespaicondicional.Laprobabilitatdecadaundelsdoselementsés 1 2 , valorqueobtenimtambéendividirlaprobabilitatsensecondicionar, 1 4 ,perladel’esdeveniment B = {elmésgranésunanena},queval 1 2 .

Larespostaésaralaprobabilitatde(nena,nena)enaquestnouescenaricondicional,queés 1 2 Observemqueésdistintadel’obtingudaenlaqüestióanterior.

Pregunta3: (Potseréslaméssorprenentdelestres).Sabemquelaparellatédosfills,iqueund’ells ésunanena.Undiatrobemelparepassejantambunanena.Quinaseràlaprobabilitatquel’altrefill tambésiguiunanena?

Encaraquesemblaquelasituacióéslamateixaqueladelaprimeraqüestió,sisuposem(queés moltsuposar)queelfillquel’acompanyahaestattriatal’atzar(ésadir,elgranielpetittenenla mateixaprobabilitatd’acompanyarelpareaquelldia),l’espai Ω originalésara (nenA,nen), (nen,nenA), (nenA,nena), (nen,nenaA), (nenaA,nen), (nena,nenA), (nenaA,nena), (nena,nenaA), enquè A majúsculaensindicaquindelsdosfillsacompanyaelpare.Cadaelementtéaraprobabilitat 1 8

Pertant,elconjunt B respectealqualcondicionem,quecomsabemseràelnouespai Ω és (nen,nenaA), (nenaA,nen), (nenaA,nena), (nena,nenaA)}, jaqueésunanenalaqueacompanyaelpare.Cadaelementtéprobabilitat 1 4 .Enaquestescenari, l’esdevenimentqueensinteressa,elsdosfillssónnenes,serà

{(nenaA,nena), (nena,nenaA)} quetéprobabilitat 1 4 + 1 4 = 1 2 ,igualqueenlaqüestiósegona.

Intuïtivamentsemblavaquelainformaciódequèdisposemaraéslamateixaqueenlaprimera qüestió,peròacabemdeveurequelesprobabilitatssóndiferentsi,pertant,lanostraintuïcióno eracorrectaenaquestcas.

• ElproblemadevonSavant

Aquestésunproblemaquevaprovocarmoltapolèmicaenelseumoment.Unaexcel·lentreferènciaésl’articlepublicata TheAmericanStatistician [10].

Pregunta: Enunconcursdetelevisióhemdetriarentretresportes tancades.Darrerad’unadelesporteshihaunautoialesaltresnohi hacappremi.

Triemlaporta1,ielpresentadorensobrela3,enquènohihaelpremi.

Enspreguntensivolemcanviarlaportaescollida,queésla1,perla2, queencaraestàtancada.

Hofaríeu?

L’espai Ω inicialsemblaformatpelselements(AGG),(GAG)i(GGA),enquècadascunadelestres lletrescorresponrespectivamentalaporta1,2i3.La G ensindicaquenohihaelpremidarrerala porta,ila A quehihal’auto.

Quanelpresentadorenshaobertlaporta3iveiemquenohihapremi,l’espaicondicionales redueixalsdosprimerselements,cadascunambunaprobabilitat 1 2 .Guanyarcanviantvoldirdeixar laporta1perla2,iqueenla2hihagil’auto.Aixòcorresponal’element(GAG),quetéprobabilitat 1 2 .Sembla,doncs,indiferentcanviar.

Enaquestraonamentnotenimencomptequinaestratègiasegueixelpresentadorperobriruna delesportes.Suposemaraqueaquestnoobriràmailaportaquetéelpremi,ienelcasquepugui triarentreduesportesperobrir,quevoldirqueelcotxeestàdarreralaporta1,queéslaquetenim, escullla2ola3amblamateixaprobabilitat.

Comquehemtriatlaporta1,l’espai Ω seriaara

{(AGG2), (AGG3), (GAG3), (GGA2)} , enelqualelnúmerofinalensindicalaportaobertapelpresentador.Recordemqueaquestnopot maiobrirlaporta1,jaqueéslaquenosaltreshemtriat,niunaportaonhihagil’auto.

Ladistribuciódeprobabilitatsésladelataulasegüent,

(AGG2) (AGG3) (GAG3) (GAG2) 1

Formulemaltravegadalapregunta:Quinaserialaprobabilitatdeguanyarencanviar(esdevenimentquedenotemper Ws ),sielpresentadorhaobertlaporta3,enquènohihal’auto(esdeveniment D3)?

Aquestaprobabilitatlacalculemmitjançantl’expressióhabitual, P(Ws |D3) = P(Ws ∩ D3) P(D3) = P(GAG3) P (AGG3), (GAG3) =

Pertant,aracanviarésaconsellable!!

Hemsuposat,doncs,unaestratègiadelpresentador.Peròpodríempensarqueentéunaaltra.Com amatemàtics,ensinteressageneralitzarlasituació.

Anomenem pij laprobabilitatqueelpresentadorobrilaporta j ,sil’autoestrobarerelaporta i

Evidentment, pi2 + pi3 = 1jaqueelpresentadornopotobrirmailaporta1,queéslaquehemtriat.

L’espaideprobabilitatinicialestaràaraformatpelselements

{(AGG2), (AGG3), (GAG2), (GAG3), (GGA2), (GGA3)} amblasegüentdistribuciódeprobabilitat,onhemdividitper3pernormalitzarlamesurademaneraquelasumasigui1.

(AGG2) (AGG3) (GAG2) (GAG3) (GGA2) (GGA3) p12 3 p13 3 p22 3 p23 3 p32 3 p33 3

Laprobabilitatbuscadalatrobaremaplicantunaaltravegadalafórmuladelaprobabilitatcondicionada,

P(Ws |D3) = P(Ws ∩ D3) P(D3) = P(GAG3) P (AGG3), (GAG3) = p23 p13 + p23

Perexemple,consideremaralasegüentestratègiadelpresentador, p12 = p,p13 = 1 p = q,p22 = p33 = 0,p23 = p32 =

enlaqualnoobremaiunaportaambpremi,isipottriarentreobrirlaporta2ola3,perquènohi hal’autoencapdelesdues,hofaambprobabilitatsrespectives p i q = 1 p

Enaquestcas, P(Ws |D3) = p23 p13 + p23 = 1 1 + q ,quesempreéssuperioroiguala 1 2

Si q = 1,quesignificaqueelpresentadorobrelaporta3semprequeelcotxenohisigui,laprobabilitatcondicionadaserà 1 2 i,pertant,seràindiferentcanviar.

Sitriem p23 , p13 i p23 demaneraqueescompleixilacondició 1 p23 p13 + p23 > 1 2 , queésequivalenta p23 < p13 ,aleshorescanviarseràdesfavorable.Observemquelacondicióens implicaque p23 nopotser1,icomque p22 + p23 = 1,deduïmque p22 > 0,ésadir,elpresentador téunaestratègiaenquèpodriahaverobertlaporta2encaraquedarrerehihaguéselcotxei,per tant,elconcurspodriahaveracabatsensequeelconcursant,quehatriatlaporta1,tinguéscap opció.

Conclusió:Percontestarlapreguntainicialhemdetenirencomptel’estratègiadelpresentador.

Sil’experimentconsisteixamirarelvalord’unacertavariable(perexemple,elresultatdetirarun dau),aleshoresenrepetir-lodemaneraindependent(recordemquelaindependènciaésequivalent aquelaprobabilitatquepassinalavegadaqualsevolnúmerofinitd’esdevenimentsindependents

éselproductedelesprobabilitatsdecadascund’ells),lamitjanadelsresultatsqueanemobtenint s‘acosta,quanelnúmerod’experimentsvaainfinit,aunvalorqueanomenem esperança.Altrecop aquí,comabans,hauríemdeprecisarelsentitdelaconvergència,peròtampochientremara.

Elquediemenelparàgrafanteriorésunaversiónaïfdelalleidelsgransnombres.Enelcasd’undau just,l’esperançaserà3,5.Enlafigura10s‘il·lustraaquestaaproximació.

Sihiha n possiblesresultatsdelnostreexperiment,elsqualsdenotemper x1 , ..., xn ,itenenprobabilitatsrespectives p1 , , pn ,,l’esperançaescalculaamblasegüentexpressió:

E (X ) = n i=1 pi xi

Noteu,pertant,quel’esperançaésunamitjanaponderadaiquefísicamentcorrespondriaalcentre degravetatdelsvalorsdelavariableambpesosdonatsperlesprobabilitats.

Perexemple,enelcasd’undau, E (X ) = 1 6 × 1 + 1 6 ×

Imaginemquejuguemaunjocenelqualtenimunaprobabilitat p deguanyar.Siguanyemens donenunaquantitat a,isiperdemhemdepagar-la.L’esperançadelsguanysserà

E (guanys) = pa (1 p)a = a(2p 1)

Podemclassificarelsjocssegonselsignedel’esperançaanterior:

• Si p = 1 2 ,aleshores E (guanysnets) = 0idiremqueeljocésjust.

• Si p < 1 2 ,aleshores E (guanysnets) < 0il’anomenaremjocdesfavorable.

• Si p > 1 2 ,aleshores E (guanysnets) > 0il’anomenaremjocfavorable.

Unjocqualsevol(ambesperançafinita)tambéelclassificaremdelamateixamanerasegonselsigne del’esperançadelsguanysnets.

Elnomestàmotivatperlalleidelsgransnombresdescritaabans.Sieljocésfavorable,l’esperança deguanyséspositivaiaixòimplicaquesijuguemmoltesvegadeslamitjanadelsguanysobtinguts s‘acostaràal’esperança,ipertantaunnúmeropositiu.Peraixòsemblaqueensconvéjugar-hi.

Comabans,hauríemd’explicarquèvoldirenelnostrecontext‘‘acostar-se’’,peròtampocnohientrarem.Elslectorsinteressatspodenconsultarqualsevoltextdeprobabilitats.

Arajapodemrespondrealasegüentqüestió:Quantenshandepagarsiapostemperquèsurtiun tresentirarundau,sivolemqueeljocsigui JUST,iacceptemqueperdemuneurosinoguanyem?

Recordemque P(3) = 1 6 i P(nosurt3) = 1 1 6 = 5 6 .Aleshores

Fixeu-vosquelaproporcióentreelqueguanyemielqueperdemenjugaraaquestjoc,enelcasque siguiunjocjust,éselquociententrelaprobabilitatdeperdreilaprobabilitatdeguanyar,is‘expressa enaquestcascom5a1.Silaproporcióentreelqueguanyemielqueperdemfosméspetita,per exemple3a1,eljocseriadesfavorableperanosaltres.Lesapostesvénenusualmentdescrites peraquesttipusdeproporcionsievidentmentsempreestanorganitzadesdemaneraqueesdevinguinjocsdesfavorablesperaljugadorifavorablesal’empresa.

Remarca:Jugaraunjocjustnoimplicaqueelsguanysnetsesmantinguinpropdelzero.Podem construirjocsambesperançazero,quehemanomenatjustos,talsquelesnostrespèrduesacumuladessuperinambprobabilitat1qualsevolnúmerotriatprèviamentquan n →∞.Evidentment,ningú noparlariadejustíciaenaquestescenari.EnelmagníficllibredeFeller[5],podreutrobarunexemple d’aquestasituaciótanparadoxal.

9.Distribuciógeomètrica

Apostem1euroenunjoc,demaneraquesiguanyemrebem1euroextraienstornenelquehem apostat,iencascontrarielperdem.Sianemrepetintlajuguescasuposantindependència,ifemel gràficdelsguanysacumulats(positiusonegatius),tenimunatrajectòriatípicad’un passeigaleatori, comlamostradaenlafigura11,fetatambéambels applets de[16].ElcapítolIIIdelllibredeFeller[5] ésunamagníficareferènciasobreelparadoxalcomportamentdelesmarxesaleatòries.

Qüestió1: Suposemquejuguemrepetidamentaunjocenelqualtenimunaprobabilitat p deguanyar. Quinaseràlaprobabilitatdeguanyarperprimeravegadaalatirada n?

Sisuposemquelestiradesnotenenresaveure(independència),laprobabilitatdelaseqüènciade longitud n,queexpressemper

P,P, ... ,P,G n

onla P ila G signifiquenrespectivamentjocperdutiguanyat,ienlaqueguanyemperprimeravegada eneljoc n,seràelproductedelesprobabilitatsrespectives,ésadir,

D’altrabanda,laprobabilitatdenoguanyarmaiés1 P(guanyaralgunavegada),iaquestadarrera serà,sianomenem X latiradaenlaqualguanyemperprimercop,lasèriesegüent:

gura11

Comque P(X = n) = (1 p)n 1 p,aixòés,lasumad’unaprogressiógeomètricadeprimerterme p i deraó r = 1 p.Pertant,tenim p + p(1 p) + p(1 p)2 + = p 1 (1 p) = p p = 1

Comaconseqüència,laprobabilitatdeguanyarenunmomentoaltreés1.

Calculemaral’esperançadelavariable X (lespartidesquehemdejugarfinsaguanyar),laqualés E (X ) = 1p + 2(1 p)p + ··· + n(1 p)n 1 p + ··· = p ∞ n=1 n(1

Utilitzemaltravegadal’expressiódelasumadelsinfinitstermesd’unaprogressiógeomètricaper escriure ∞ n=1 (1 p)n = 1 p 1 (1 p) = 1 p p

Enderivarelsdoscostatsdelaigualtat(enaquestcontextpodemfer-ho),tenim

i,pertant,multiplicantper p ensqueda

)

Aixòensdiu,perexemple,quesiguanyarvoldirqueentirar20monedesjustesalmateixtemps surtin20cares,queésunesdevenimentquetéunaprobabilitat 1 220 ,elnúmeromitjàdevegadesque hauremdetirarles20monedesserà220

Aquestresultatenssuggereixque,sirepetimsuficientscopsl’experiment,lescosesambprobabilitat petitaacabenpassant,encaraquepotserhauremd’esperarmolt.

Fi

10.Problemadelamartingala

Suposemquejuguemaunjoconguanyemambprobabilitat p.Apostem x eurosisiguanyemens entornen2x ,iencascontrariperdeml’aposta x L’esperançadelsguanysnetsserà,doncs,

(guanysnets)

iaquestaquantitatésnegativasi p < 1 2

Existeixunaestratègiad’apostesanomenada martingala (elnomespensaquevedeMartingues, unaciutatdelaProvença),quesemblaconvertiraquestjocdesfavorableenundefavorable.Jugar alamartingalavoldirdoblarl’apostaquanperdem,ianar-hofentfinsqueguanyem,momenten quèdeixemdejugar.Comhemvistque,ambprobabilitat1,enunatiradaoaltraguanyem,tenimla il lusióqueobtindremunbeneficiassegurat.

Estudiemaraaquestasituacióambmésdetall.

Siapostem n vegadesseguides,començantper1euro,aplicantl’estratègiademartingala,ésadir, doblantl’apostaquanperdemfinsqueguanyemperprimercopenlatiradaenèsima,laquantitat totalapostadaserà

Comqueenlajugada n hemapostat2n 1 ,silasortensésfavorable,rebremeldoble,ésadir,2n euros.Elsguanysnetsserandoncs2n (2n 1),ésadir,d’1euro.

Enlataulasegüentdonemlaprobabilitatdeguanyarperprimeravegadaenelsjocs1,2 ,talcom hemtrobatenlasecciódedicadaaladistribuciógeomètrica,ihirecalquemquesempreelbenefici netobtingutés1.

jocsjugats probabilitat apostaacumulada guany

Elscasinos,però,limitenl’apostamàximai,d’altrabanda,lanostrafortunaéslimitada.Pertant,no podemdoblarindefinidament.

Perestudiaraquestasituacióreal,suposemquedisposemd’uncapital1

2n 1 , quecomsabemsuma2n 1.Aixòimplicaperanosaltresquepodremjugar,aplicantlatècnicade martingala,comamàxim n vegadesabansdequedar-nossenseres.Aleshores,sicalculeml’esperança delsguanysnets,tenim

E (guanysnets) = 1P(guanyarenalgunadeles n possiblestirades) (2n 1)P(perdreles n tirades)

Substituintlesprobabilitatscalculadesabans,tenimquel’esperançaés

Observeuquelaprobabilitatdeguanyarenalgunadelesprimeres n tiradeséslasumade n termes d’unageomètrica,

Pertant,

Si p = 1 2 ,l’esperançaés0.

Si p < 1 2 ,l’esperançaserànegativa,idecreixcapamenysinfinitquan n →∞

Aquestresultatensdiuquel’estratègiademartingalanoconverteixeljocdesfavorableenfavorable. Pertant,podríemrecordarlafrasequehihaescritaal’entradadel’infernenla DivinaComèdia de Dant,

ELSQUEENTREUAQUÍABANDONEUQUALSEVOLESPERANÇA.

Lateoriadelesmartingalesésunelementmoltimportantenl’estudidel’evoluciódelaincertesaamb eltemps.Concretament,lesmartingalessónuntipusdeprocessosestocàsticsquemodelen,curiosament(contraelqueelnomd’entradafasuposar),elsjocsjustos.Perconèixerméssobremartingales podeuconsultarlesreferències[11]i[15].

11.Problemadelaruïna

Peracabaraquestpasseigperlateoriadelaprobabilitat,tractaremelproblemadelaruïnad’un jugador.Unareferènciaexcel lenttornaaserelllibredeFeller[5].

Imagineuquejuguemaunjoconlaprobabilitatdeguanyarés p i,pertant,ladeperdreés q = 1 p Siguanyem,incrementemlanostrafortunaen1euro,isiperdem,disminuïmelnostrecapitalenla mateixaquantitat.

Comencemajugaramb i euros,0 ≤ i ≤ a,on i ésunnúmeronaturali a ésunnúmeronaturalfixat. Anemjugantfinsquetenimunaquantitat a d’eurosoensarruïnem.Arruïnar-sevoldirarribara0 abansquealabarreradenivell a.Aquestasituacióseriaunnouexempledepasseigaleatori,elqual evolucionaentreduesbarreres,unaalnivellzeroil’altraalnivell a

Denotemper qi laprobabilitatd’arruïnar-nossicomencemjugantamb i euros.Arruïnar-nos,comhem dit,significaarribarabansalabarrerainferiorquealasuperior.Si0 < i < a,desprésdelaprimera partidatindrem i + 1euros,siguanyem,i i 1,siperdem;pertant,pelteoremadelesprobabilitats totals

qi = P(arruïnar-nos,sortintde i) = P(arruïnar-nos,sortintde i,guanyantenlaprimeratirada)+ + P(arruïnar-nos,sortintde i,perdentenlaprimeratirada) = P(arruïnar-nos,sortintde i + 1)P(guanyarlaprimeratirada)+ + P(arruïnar-nos,sortintde i 1)P(perdrelaprimeratirada), ésadir,amblanotacióintroduïda,

Comque p + q = 1,tenintencomptelaigualtatanteriorpodemescriure

Arreglant-hoarribema

Dividintper p ensqueda

D’altrabanda, q0 = 1jaquesisortimde0jaestemarruïnats,i qa = 0perquèsijasomalnostre objectiunojugueminoenspodemarruïnar.

Aquestesseranlescondicionsdecontorndelproblema,ipertant

Si p i q sóndiferents,sumemlesequacionsanteriorsifixant-nosenlescancel·lacionstenim

Utilitzaremaralescondicionsinicials.Siposem i = a,comque qa = 0,ensqueda,

ésadir,unaequaciódelaforma

Resolent-la,tenim q1 = K K + 1 ,ipertant

Aïllant qi a(3),tenim

Substituintenaquestaigualtatl’expressió(4)pera q1 iambunamicad’àlgebraobtenim

Pertrobarlaprobabilitatd’arribaralabarrerasuperiorabansd’arruïnar-nos,sortintd’unafortuna i, tansolshemd’intercanviarelpaperde q i p,ielsdelesduesbarreres,pertant

Podemcomprovarque1 = pi + qi .Aixòensindicaquesempre(unprobabilistaprecísdiriaamb probabilitat1)arribemaunabarreraoaltra,ésadir,eljocs‘acabaràinoestaremperunaeternitat vivintentrelesduesbarreres.

Elraonamentanteriornovalper p = q = 1 2 .Enaquestcashemd’argumentardemaneradiferent.

Recordemque

Comque q p = 1, lasumaquehihaenelprimerparèntesideltermedretdelaigualtatés1 + + 1 = i 1.

Tenim,doncs,

Si i = a laigualtatanteriors‘escriu

Comque qa = 1,veiemque q1 = a 1

Percalcularenaquestescenarilaprobabilitatd’arribarprimeralabarrerasuperiorquealainferior raonemcomabans,intercanviant i per a i,ipertant

pi = 1 a i a

Fixeu-vosquearatambélasuma pi + qi és1.Aixòensindicaqueenaquestcas,comabans,també semprearribaremaalgunadelesduesbarreresambprobabilitat1.

Miremaraunexempleconcret.Imaginemquecomencemamb100eurosivolemjugarfinsque arribema110eurosoensarruïnem,ique q = p

Lafórmula(5)pera i = 100i a = 110serà

Sijuguemaunjocamb p = 0,493i q = 1 p = 0,507,posantaquestsvalorsa(7)obtenim q100 = 0,253.

Enelcasque p = q = 1 2 ,hemdeduïtque qi = 1 i a .Ambelsmateixosvalorsdeldarrerexempleara q100 = 0,091,ésadir,lescosescanvienmoltsieljocésjustjaquelaprobabilitatd’arruïnar-sebaixa significativament!!

Enlataulasegüentpresentemelscàlculsperadiferentsvalorsdelafortunainicial i,delaprobabilitat deguanyar p,idelaquantitatobjectiu a.Enlesduesdarrerescolumneshihalesesperancesdels guanysidelnúmerodejocsnecessarisperarribaraalgunadelesduesbarreres.

Enl’últimalíniaveiemperexemplequesieljocensésdesfavorable,encaraquesortimapropdela barrerasuperior(tansolsensfalta1europerarribar-hi),laprobabilitatd’arruïnar-nosésimportant, 0,333.

Qüestió: Quinaéslaquantitatqueseriaconvenientd’apostarcadavegadapermillorarlaprobabilitat d’arribaralabarrerasuperiorabansquealzero(ruïna)?

Sienelprimercasestudiatapostem2eurosenllocd’1,podemadaptarlesfórmulescanviant100per 50i110per55.Aleshores

isubstituintelsvalors p = 0,493i q = 1 p = 0,507,ensdónaunaprobabilitatd’arruïnar-nosde 0,165,quanabanserade0,253.

Siapostem5euroscadacop,hauremdecanviarel100iel110per20i22,iensquedaràunaprobabilitatderuïnade0,118.Pertant,millorencara.

Del’expressióperalaprobabilitatderuïnadeduïmquelamillorestratègiaenunjocdesfavorable ésjugarsempreal’apostamàxima,demaneraqueenunasolatiradapuguemarribaralabarrera superior,inodeixaractuarlatendènciaaanarcapalaruïna.

Bé.Hemarribatalfinaldelnostrepasseig.L’aplicabilitatdetotesaquestesideesalamodelització delaincertesaésenorme.Lesmartingales,lesmarxesaleatòries...sónmoltpresentsenelsestudis financersienmoltsaltrescamps.Això,però,ensportariaaunaltrearticle...

Alsquevulgueucontinuaraquestamablepasseigusrecomanarial’articled’enCorberanienMontes [3],aixícomelsquetrobareualapàginawebdelarevistaelectrònica Mat 2 [17],entreelsqualsassenyaleml’estudidelasorprenentparadoxadelsdossobres,escritperlaMercèFarré[4],juntament ambelsdeBardinasobrerècordsipassejosaleatoris([1]i[2]).

Referències

Bardina,X.(2007).Quantsrècordsveuremalllargdelanostravida? Mat 2 .DepartamentdeMatemàtiquesdelaUAB.(http://mat.uab.cat/matmat/).

—(2008).Caminantal’atzartotselscaminsportenaRoma. Mat 2 .DepartamentdeMatemàtiquesde laUAB.(http://mat.uab.cat/matmat/).

Corberan,A.iMontes,F.(2000).Perversionesytrampas. LaGaceta,vol.3,2(RMSE).

Farré,M.(2008).Laparadoxadelsdossobres:modelsdeljocisimulacions. Mat 2 .Departamentde MatemàtiquesdelaUAB.(http://mat.uab.cat/matmat/).

Feller,W.(1988). Introducciónalateoriadeprobabilidadesysusaplicaciones.Limusa(vol.I).

Fermat,P.de(2008). Obramatemàticavària.[TraducciócomentadaianotadaperJ.Pla,P.ViaderiJ. Paradís.Publicacionsdel’IEC].

Hoffman-Jorgensen,J.(1994). ProbabilitywithaviewtowardApplications,vol.I.Chapman&Hall(ProbabilitySeries).

Kolmogorov,A.N.(1933).GrunbegriffederWahrscheinlichkeitrechnung.[Traduccióanglesa: FoundationoftheTheoryofProbability.ChelseaPublishingCompany,1950].

Laplace,P.S.de(1985). Ensayofilosóficosobrelasprobabilidades.Ellibrodebolsillo,1147.Madrid: AlianzaEditorial.

Morgan,J.P.,Chaganty,N.R.,Dahiya,R.C.iDoviak,M.J.(1991).Let‘smakeadeal:ThePlayerDilemma. TheAmericanStatistician,vol.45,4,284-289.

Nualart,D.(1989).Lesmartingalesilessevesaplicacionsdesd’unaperspectivahistòrica. Butlletídela SocietatCatalanadeMatemàtiques,4.

Poincaré,H.(1980). CalculdesProbabilités.LesgrandesclassiquesGauthier-Villars.(1912).ÉditionsJacquesGabay.

CienciayMétodo.Austral,409.Espasa-Calpe.

Székely,G.J.(1986). ParadoxesinProbabilityTheoryandMathematicalStatistics.Mathematicsandits appication.DordrechtEditors. Williams,D.(1991). ProbabilitywithMartingales.CambridgeUniversityPress. UniversityofAlabamainHuntsville.http://www.math.uah.edu/stat/applets/ Materialsmatemàtics. Mat 2 .http://mat.uab.cat/matmat/

Unaaproximació etimològica1: etimologiadeltriangle

ideltrianglerectangle

MartaBerini

Triangle: delllatí triangulus-i (de trestria: tres,i angulus-i:angle,quesignifica‘‘racó’’,‘‘cantonada’’, ‘‘angostura’’).Engrecclàssic: τρ ´ ιγων oν (trígonon),de τρ ˜ ις (treîs):tres,i γων ´ ια (gonía):angle:tres angles.

Triangle equilàter:delllatí aequilaterusaum( d’aequusaum: igual; latuseris:costat);engrec: ισ ´ oπλ υρ oν

Triangle isòsceles:delllatí isosceles-is, iaquest,delgrec. ´ ισ oσκ λ ´ ης (isoskelés),quesignificacames iguals(de ¨ ισ oς [ísos]:iguali σκ ´ λoς [skélos]:cama).

Triangle escalè:delllatí scalenusaum iaquest,delgrec. σκαλην ´ oς (skalenós):desigual.

Trianglerectangle constadedosmots: triangle i rectangle

Triangle rectangle: delllatí rectangulus-i (rectusaum: recte, angulus-i:angle).Engrecclàssic, ´ oρθ oγ ´ ωνι oς (orthogónios),d’ ´ oρθ ´ oς (orthós):recte,i γων ´ ια (gonia):angle.

Unaaproximació etimològica2: etimologiadelselements deltrianglerectangle

MartaBerini

Hipotenusa: delgrec ´ υπoτ ´ ιν oυσα (hypoteinousa),iaquesta,d’ ´ υπ ´ o (hypo),‘‘asota’’i τ ´ ιν ιν (teinein),‘‘tensar’’,ésadir,‘‘tensarpersota’’,enal lusióalaformaprimitivadelsconstructorsd’angles rectes.

Catet: delgrec κατ ´ α (kata),‘‘capavall’’,i ιημι (iemi),‘‘anar’’:‘‘elquecaucapavall’’,‘‘elquecauperpendicularment’’.

Totaixòquedareflectitenlafigurasegüent:

Unaaproximació etimològica3: equinoccisisolsticis

MartaBerini

Dia: delllatí dies,ambelmateixsignificat.

Nit: delllatí nox,ambelmateixsignificat.

Sol: delllatí sol,ambelmateixsignificat.

Equinocci: delllatí aequus (‘‘igual’’)i nox (‘‘nit’’),quevoldirnitigualquedia.

Solstici: delllati solstitium:sol (‘‘sol’’)i status (‘‘estàtic’’),quevoldir‘‘quanelsolestàparat’’.

ÉseldiaenelqualelSolpassad’anaraugmentant/disminuintl’angledel’alturamàximaalmigdia solaracomençaradisminuir-la/augmentar-la(solsticid’estiu/solsticid’hivern).

Equinocci de primavera

Solstici d’estiu

Equinocci de tardor

Solstici d’hivern

Tròpic de Càncer

Latitud 42º

Cercle polar àrtic

Equinocci de primavera

Gràfic comparatiu de la variació de l’angle de l’altura màxima del Sol al migdia solar en les latituds 62º, 42º i 23º37’al llarg d’un any. El dia del solstici d’estiu el Sol al migdia té l’altura màxima i el dia del solstici d’hivern el Sol al migdia té l’altura mínima.

Autor dels gràfics: Antoni Gomà.

Solstici d’estiu

Equinocci de tardor

Equinocci de primavera

Solstici d’hivern

Solstici d’estiu

Solstici d’hivern

rajos del sol rajos del sol

La FEEMCAT (Federaciód’Entitats per al’Ensenyament de les Matemàtiques a Catalunya ),laSCM(Societat Catalanade Matemàtiques),la RealAcademiadeCiencias i la anuncienla FundaciónVodafoneEspaña convocatòria peral’admissióenelseu

projecteESTALMATaCatalunya

(Deteccióiestímuldeltalentprecoçenmatemàtiques )

Objectiudelprojecte :fomentarl’aficióihabilitatespecialenmatemàtiquesdenoisinoiesque viuenaCatalunyaiamb datadenaixementdel’any1998ol’any1999

Activitats :Totselsdissabtesdelperíodelectiudelscursos2011-2012i2012-2013,de10ha13ha laFacultatdeMatemàtiquesiEstadística(FME)delaUPC,aBarcelona.

Aquestesactivitatsserangratuïtes peralsnoisinoiesseleccionats,elsparesotutorsdelsquals s’haurandecomprometreaportar-losirecollir-losaleshoresesmentades.

Procésdeselecció:

La selecciódel grupde 24nois i noies queparticiparanenelprojectetéduesfases:

1. Testd’aptitud: eldissabte4dejunyde2011ales10halesciutatsdeBarcelona,Girona, LleidaiReus.

2. Entrevistapersonal ambelsparesotutorsielsnois/espreseleccionats/des.

Inscripció:

Lamare,elpareotutorlegalhaurand’omplirun formulari quetrobaranalapàginawebde l’organització,www.estalmat.org.Veuranquehihaunenllaçespecialperalsdetallsd’aquesta convocatòria,iunaltreenllaçonpodranllegirinformaciódetalladadelprojecteaCatalunya.

Termini :del’1demaigfinsal28demaigde2011.

Dadesqueesdemanen:nomidatadenaixementdel’alumne/ainteressat/daenlaparticipació enelprojecteESTALMAT,adreça,correuelectrònic,númerodetelèfondecontacteicentre escolaronestudiadurantelcurs2010-2011.

Caldràqueindiquin aquinapoblaciódesitjarienferlaprova (Barcelona,Reus,Gironao Lleida).

Lallistad’inscritsielsdetallsdelarealitzaciódelaprovadeseleccióespodranconsultaralweb www.estalmat.org,promoció2011-2013.Tambéespotdemanarinformaciósobreelprocés d’inscripcióaNúriaFuster,SocietatCatalanadeMatemàtiques(telèfon:933248583;correu electrònic:nfuster@iecat.net).

seccions seccions rcions

JordiDeulofeu

DepartamentdeDidàcticadelaMatemàticailesCiències

UniversitatAutònomadeBarcelona jordi.deulofeu@uab.cat

Vullcomençarelmeuarticled’avuidonantlabenvingudaal Noubiaix idesitjantquelanovaetapa delarevistasiguifructíferaiduradoraisignifiquiunpasendavantquegaranteixilaconsolidacióde l’únicarevistaencatalàdedicadaíntegramental’educaciómatemàtica.Aixímateix,agraeixoalnou equipdedirecciódelarevistalaconfiançaquem’handemostratpermetentquelamevajaantiga secció,iniciadaenel Biaix 18(2001),segueixiformantpartd’aquestanovaetapa.Pensoque,permolt quecanviïnlescoses,enunarevistad’aquestescaracterístiques,hadecontinuarhavent-hiarticles relacionatsamblaresoluciódeproblemes,elsjocsilesrecreacionsmatemàtiques,quetenencom aprimeraintencióladeferpassarunabonaestonaallectoratravésdelreptequesuposalapropostad’unproblemaod’unaendevinallai,comasegona,ladeproporcionarideesirecursospera l’ensenyamentdelesmatemàtiquesadiferentsnivells.

Seguintlaideadelsmeusarticlesanteriors,iniciadaenelnúmero24,itenintencomptequeel Noubiaix mantélanumeracióis’iniciaambelnúmero30—unnombreprourodó—,abansdeproposar elsproblemesd’avui,començaréfentunapetitareferènciaaaquestnombre.D’entradahaigdedir queel30noésunnombredelsquepodríemanomenar‘‘espectaculars’’enelsentitderemetre’nsa unaideaopropietatmatemàticaespecialmentimportant,nitampocaunagranquantitatdepetites propietats.

Tanmateix,podemcitaralgunescuriositatsenquèapareixaquestnombre:30éselnombred’arestes tantdeldodecàedrecomdel’icosàedreque,comadualsquesón,tenenelmateixnombred’arestes,mentres’intercanvienelsaltreselements:12(caresdeldodecàedreivèrtexdel’icosàedre)i20 (vèrtexdeldodecàedreicaresdel’icosàedre).Seguintamblageometria,vallapenarecordarque hihanomésdostrianglespitagòricstalsqueelseuperímetreésigualalasevaàrea:elsdecostats 5-12-13i6-8-10,ielnombrequeexpressaaquestesmesuresésenelprimercas30ienelsegon,24.

Enelcampdelateoriadenombres,30éselnombremésgrantalquetotsaquellsnombresmenors queelliquesónprimersambellsóntambéprimers;elsaltressón:2,3,4,6,8,12,18,24.D’altrabanda, sidefinimcoma primordial de p,on p ésunnombreprimer,comelnombreques’obtéenmultiplicar totselsprimersmenorsoigualsa p,resultaque30éselprimordialde5,ésadir,eltercerprimordial: p(2) = 2, p(3) = 2 · 3 = 6, p(5) = 2 · 3 · 5 = 30, p(7) = 210, p(11) = 2310,etc.Noteuqueaquesta definicióéslarestriccióalsnombresprimersdelconceptedefactoriald’unnombrenatural.

Finalment,deixantdebandaque30éselnombredediesd’unmes(enrealitatnomésquatredels mesosdelnostrecalendaritenen30dies,peròenl’anticcalendariegipcitotselsmesostenien30 dies),peralsaficionatsalsjocsialsproblemescombinatoris,diremque30ésl’àreadelmenortauler rectangularenelqualuncavalld’escacspotferunrecorregutquepassipertoteslescasellesiacabi onhacomençat(s’enténquelaunitatdesuperfícieéslacasella).

Deixantjalespresentacions,començarélapropostadeproblemesd’avuiambduessituacionsrelacionadesambelsnombresnaturals.Totesduessemblend’entradaprousenzilles,idefethosón, peròsilesanalitzemunamicaafonsveuremqueaquestasimplicitatnoestàrenyidaambl’interès matemàticdelesmateixesielfetquetotesduespermeteninteressantsgeneralitzacionsquejano sóntansenzilles.

Problema1. Ensdonensisdígits—perexemple:4,5,6,7,8,9—,iambaquestsformemparelles denombresdetresxifres,utilitzant-lostotsunasolavegada.Comformaremelsdosnombrespertal quelasevadiferènciasiguimàxima?Isivolemqueladiferènciasiguimínima?

Formulataixí,elproblemaéssenzillielsdosapartatstenensolucióúnica.Defet,lamevacompanya deldepartament,LourdesFigueiras,queésquime’lvaproposar,l’haviatrobatenunllibredetext deprimària(Ed.VicensVives,6ècurs)ivaobservarlesresolucionsdelsalumnesdelciclesuperiorde primària.Laprimerapart(diferènciamàxima)nosemblatenirgairessecrets,peròlasegona(diferència mínima)ésforçamésinteressant:lageneralitzacióasisdígitsqualssevolésjad’unacertacomplexitati mostraque,encertscasos,lasoluciópotnoserúnica.Sabríeutrobar-nequins?Tambélaintroducció del0enspotportaradiscutirlavalidesadecertessolucionsencasosparticulars.Quines?Apartir d’aquí,podemplantejaraltresqüestions,comperexemple:Peraquinesxifres,ladiferènciaseràla menorpossible?Quèpassasicanviemdesistemadenumeració?

Nocaldirquelasituacióqueplantejaelproblemaemsemblaunaexcel·lentactivitatpertreballara classe,ambalumnesdelciclesuperiordeprimàriaidelprimercicled’ESO,jaqueportaaunainteressantreflexiósobreelsistemadenumeraciódecimalipotsertreballadaanivellsdecomplexitatmolt diferents,segonsquinessiguinlesqüestionsqueformulemisegonsquinsiguielnivelldegeneralització.

Problema2. Considereuelsdígitsdel’1al9,iambaquestsformeuelsnombresquevulgueu(emprantcadadígitunavegadainomésuna);sumeuelsnombresobtinguts.Perexemple:217 + 34 + 56 + 8 + 9 = 324.Quinsnombresheudeformarpertalqueelresultatdelasumasigui100?

Potseralgúdevosaltresjaconeixiaelproblema:elproposaPólyaenelseucèlebre Howtosolveit,però jo,totihaverrellegitaquestllibremésd’unavegada,nol’haviafetmai.Potserl’haviavistim’havia semblatpocinteressant:evidentment,unerror(iméstractant-sedePólya).EnLluísBibilonime’l vaproposarmentrecercàvemproblemesdenombresidereflexiósobreelsistemadenumeració decimal,quefessin‘‘pensar’’alsnostresestudiantsdelmàsterdesecundària.

Comtotselsbonsproblemes,admetdiversespreguntes,entreaquestes:Elproblematésolucióúnica, témésd’unasolucióonoentécap?Quèpassasiensuprimiuunadelesxifres?,isienrepetiuuna? Quinaéslasumamínimaqueenpodeuobtenir?,ilamàxima?

Seguirél’articled’avuiambunparelldeproblemesdegeometriaquem’hasuggeritenXavierValls; totsdosespodenresoldrepermètodeselementals.

Problema3. Demostreuquel’àread’undodecàgonregularésigualatresvegadesl’àread’unquadratquetépercostatelradidelacircumferènciacircumscritaaldodecàgon.

Sitreballeuenaquestproblema,veureuquenotémassadificultat,peròelresultatésbonicicoma conseqüènciasen’obtéque π hadesermésgranque3.

Problema4. Donatstrespuntsenelpla,trobeu-neunquarttalquelasumadedistànciesd’aquest alstresprimerssiguimínima.

Bensegurquemoltsdevosaltresconeixeuaquestproblema,jaqueelpuntquecerquemésl’anomenat puntdeFermat.Peròsempreésborevisitarelsclàssicsitractardetrobarunanovamanerade resoldreelproblema.

Acabarélasecciód’avuiaprofitantquedarreramentheestattreballantenunllibresobrejocs(Deulofeu,2010),amblapropostad’unpetitjocd’estratègiaperadosjugadors.Seguiréanomenant-lo problemajaquel’objectiudelseuestudinoéselpropid’unjoc(guanyaraunadversari),sinódeterminarperaquindelsdosjugadorshihaunaestratègiaquelipermetiguanyarsempre,facielque facil’altrejugador.Enaquestsentit,quanhemtrobatl’estratègia,eljocdeixadeserrealmentunjoc perpassaraserunproblemaresolt.

Problema5. Jocd’estratègiaperadosjugadors.Poseu15fitxesalineadessobrelataula.Alseutorn, cadajugadorretiraunaoduesfitxes,peròsienvoltreureduesnoméspotfer-hosilesfitxessónveïnes (noespodenagafarduesfitxessientreaquestesn’hihaalgunaaltraobésihihaunomésespais buitsdeixatsperfitxesprèviamentretirades).Eljugadorquetreuladarrerafitxaéselguanyador.Pera quinjugador(elprimeroelsegon)hihaunaestratègiaguanyadora?L’estratègiaespotgeneralitzar aunnombrequalsevoldefitxes?Quèpassasiespodentreuremésdeduesfitxesenunajugada semprequesiguinveïnes?

Atotsaquellsqueusagradenaquestsjocsienconeixeuelsméshabituals,nouscostaràgensveurela relacióentreaquestjocil’anomenat Margarida;aquestdarrerésigualalproposat—mateixesregles imateixobjectiu—,peròinicialmentlesfitxesestandisposadesenunacircumferència(sivoleu,en elspètalsd’unamargarida,id’aquíveelnomdeljoc).Podríeuraonarperquèelcanvienladisposició inicialfaqueenllocdeguanyarunjugadorhofacil’altre?

Comsempre,desitjoquepasseuunabonaestonapensantenelsproblemesielsjocsproposatsavui, ifinslapropera.

Referències

Deulofeu,J.(2010). Prisioneroscondilemasyestrategiasdominantes.Col·leccióElmundoesmatemático.Barcelona:RBA.

Pólya,G.(1957). Howtosolveit.NovaJersey:PrincetonUniversityPress.

Encarahihamisterisambelspentàgons?

Aquestaéslabonicahistòriadelesrajolespentagonals,enlaqualintervenendiversosmatemàtics, ungrandivulgadoriunamestressadecasa.

Benaviattrianglesequilàters,quadratsihexàgonsregularsvanmostrarlasingularitatd’ésserelsúnics polígonsregularsquedeterminavenmosaicsperiòdicsenelpla.Sorprenentment,elspentàgonsregulars(ambtoteslessevesproporcionsàuriesielseumagníficacoblamentespacialtancanteldodecàedreregular)nopodienenrajolarelpla.Comsemprepassaenmatemàtiques,aquestessituacions obrenmultituddepreguntes.

Vaserimmediatadonar-sequetottrianglepodiaenrajolarelplai,pertant,quetotquadrilàtertambé serviaderajola.Ielshexàgons?El1918,K.Reinhardtvaaconseguirdescriurelestresclassesd’hexàgonsconvexosqueenrajolen(Gardner,1988).

S’hapogutdemostrar(Kerschner,1969;Niven,1978)quecappolígonconvexambsetoméscostats potenrajolar.

Ielspentàgonsconvexos?Exclososelsregularsdelpanorama,aviatvancomençaraaparèixeralguns pentàgonsnoregularsqueerenbonesrajoles,perexemple,pentàgonsprovinentsdedividirunhexàgonregularenduesotrespecespentagonals(Klarner,1981).Concretament,K.Reinhardtenva descriurecinctipusel1918iR.B.Kerselmer,tresmés...cinquantaanysdesprés,el1968.

El1975,R.Jamesvadescobrirunnovètipusivetaquíqueunamestressadecasaamericana,Marjorie Rice,fascinadapelproblemavaanar-nedescobrintquatremés,entre1976i1977.El1985,R.Steinva descobrirelcatorzètipus...ienelsdarrersvint-i-cincanys,nosen’hantrobatmés.Aixídoncs,tenim unrepertoridecatorzetipusderajolespentagonalsperònos’hapogutdemostrarsienfalten...un interessantproblemaobertquetancaria,comacabemdeveure,elproblemadelsenrajolamentsper polígonsconvexos.

Darrered’aquestrelat,hivanjugarunpaperclauelsarticlesdeMartinGardnerqueparlavendel problema,explicant-nelesnovetatsiincentivantlasevarecerca.MarjorieRiceamblasevaimplicació

(apartirdelalecturadeGardner),fentdibuixosambunretoladoralesrajolesblanquesdelaseva cuinafinsaaconseguirafegirquatrejoiesalacol·lecció,resultatambéunaescenamemorable.

Aixídoncs,delahistòria(inacabada)delesrajolespentagonalsenpodemextreureunaconseqüència positiva:hihaproblemesricsquepodenincentivarl’esperitderecerca,enquèmoltagenthipot treballar,totdescobrintdepaselplaerdefer-ho.Lesnostresclasseshisónconvidades.

Referències

Alsina,C.iNelsen,R.(2010). CharmingProofs.AJourneyintoElegantMathematics,Washington:MathematicsAssociationofAmerica.

Gardner,M.(1988). TimeTravelandOtherMathematicalBewilderments.NovaYork:Freeman.

Kerschner,R.B.(1969).Pavingtheplane.APL TechnicalDigest, 8,4-10.

Klarner,D.A.(1981). TheMathematicalGardner. Boston:Prindle,WeberandSchmidt.

Niven,I.(1978).Convexpolygonsthatcannottiletheplane. AmericanMathematicalMonthly,85,785792.

File Pentagon Tilings - Marjorie Rice.

cròniques cròniques riques s

XIConcursdefotografiamatemàtica del’ABEAM

DavidAlonso · CarlesdeCubas · AnnaDarnaculleta · PilarFigueras · FranciscoMoreno SantiagoVilches

L’AssociaciódeBarcelonaperal’Estudiil’AprenentatgedelesMatemàtiques(ABEAM)téperobjectiufomentarl’estudidelsdiferentsproblemesrelacionatsambl’aprenentatgedelesmatemàtiquesi afavorirtantlaformaciódelprofessoratcomlasevaimplicacióenlainvestigaciódeproblemesdidàctics.Unadelesactivitatsqueorganitzal’ABEAMéselConcursdeFotografiaMatemàtica,l’objectiu delqualésferveureal’alumnatquelesmatemàtiquesestanimmersesenlarealitatqueelsenvolta. Elpassat20demaig,alasalad’actesdel’Institutd’Educaciódel’AjuntamentdeBarcelona,vatenir llocl’actedelliuramentdelspremisdel’onzenaedició.

Elconcursfotogràficestàdividitencinccategories:

1)5èi6èdeprimària, 2)1rcicled’ESO, 3)2ncicled’ESO, 4)batxillerat,ciclesformatiusiformaciód’adults, 5)professorat.

Lesfotografieshandeduruntítolquefacireferència,d’algunamanera,alcontingutmatemàticde l’obra,ambgràciaioriginalitat.

Laprimerafasedelconcursesfalocalmentalscentresparticipants.Aquestsorganitzenelseuconcurs itrienunguanyadorpercategoria.Posteriorment,lesfotografiesguanyadoress’envienal’ABEAM, d’onsurtelguanyadordecadanivell.Elterminidelliuramentdelesfotografiesal’ABEAMésposterior alafestivitatdeSantJordi;esmirad’afavorirlacoincidènciadelconcurslocaldefotografiaambaltres premisliterarisqueesfanalscentresperaquestafestivitat.

Lesfotografiespremiadesenl’ediciód’enguanyhanestat:

1rnivell. Desdebenpetitsamblesmatemàtiques,del’AnnaGarciaMartí, alumnadel’EscolaJoanRoca.Aquestafotografiaensmostraunelement tanhabitualperalsnadonscomésunbiberó,peròinsinuantque,per pocqueparemesment,jadesdebenpetitsestemenvoltatsdematemàtiques.Podríemdirque,finsitot,lesmamem.

2nnivell. Setrillscònicsproporcionals,del’ÒscarVilches Baldonado,alumnedel’INSElSui.Unaltravegadaesmostrendoselementsbenquotidians:dossetrillsdediferents midesquel’autorrelacionaamballòqueaprènalaclasse degeometria.Elcromatismedelapostadesolafegeixa lafotografiaunacalidesaextraordinària.

3rnivell. Gràficdebarreslíquid,delaCarlaColl,alumna del’INSPereBarnils.L’autoraéscapaçdeferunametàforaentregotsemplenatsfinsadiferentsalçadesiundiagramadebarres.Mésenllàdelcontingutmatemàticde lafotografia,eljocdellumsdotalafotografiad’unagran bellesa.

4tnivell. Decreixementexponencialdelatemperatura,de l’AlbertVegaValeri,alumnedel’INSMiquelBoschiJover. Enaquestnivelljaescomencenanotarelscontingutscurricularsméselevats.D’aquestamanera,lafotografiapremiadaésunaperfectaformad’introduirlaideaclaudel càlculdiferencialque,anivelllocal,lescorbesespoden aproximarperd’altresméssenzilles.Amés,elfactorneu permetcrearunjocdeparaulesamblestemperatures.

5ènivell. Compàsdelvent,delMartíCasadevall,professordel’INSArquitecteManelRaspall.L’autordetectaordregeomètricenl’acciódelventsobreunaplantaenmig d’unentornaparentmenthostil.Unafotografiamoltsuggerent.

Elsmembresdel’organitzaciócadavegadaenssentimmésgratamentsorpresosambl’inventivadels participantsilasevacapacitatdeveurematemàtiquespertotarreu.Evidentment,elproblemasorgeix quans’hadetriarnomésunafotografiaguanyadorapernivell.Ésperaixòque,desdefatresedicions, hemvolgutcompartiraquestadificultatambelsparticipantsdelconcurs:hemofertalsassistentsa l’actedelliuramentdepremislapossibilitatdetriar,d’entretoteslesfotografiesambaccèssitopremi (exceptelesdelnivellprofessorat),aquellaquemereixl’importantpremideguanyadoradelpúblic.

Guanyadoradelpúblic. 90+90=180,del’AnnaBodiValera,alumna deprimercicled’ESOdel’INSMontserrat.Laimaginacióilacreativitat, quesóndueseinesessencialsperalesmatemàtiques,esdonenlamà perpodersumarmagnitudsdiferents,iensdeixenambelregustd’un somriureentranyable.Aquestafotografiahaviaobtingutunaccèssitde lasevacategoria.

Totselsfinalistesiguanyadorssónobsequiatsambunlotdellibresdel’editorialBarcanovaiundiploma.Amés,elsguanyadorstenenelpremiaddicionald’unacàmeradigitalcedidaperl’empresaCasio.

L’organitzaciódelconcurs,enpartgràciesal’aportaciódel’ICEdelaUPC,regalavalsdecompraals tresprimersclassificatsdelesdiferentscategoriesaixícomalguanyadordelpremidelpúblic.Tots elscentresparticipantsrebenundiplomaacreditatiu.

Mirantcapenrere,semblamoltllunyanalaprimeraediciód’aquestconcurs,queesvaferal2000,coincidintambl’anyinternacionaldelesmatemàtiques.Aquellanylaparticipacióvaserde20centresi,a pocapoc,haanatcreixentfinsales150inscripcions,ipropde450fotografies,del’ediciód’enguany.

Enaquestsentit,lasocialitzaciódel’úsdelescàmeresdigitalsilamateixaconsolidaciódelconcurs, hafetque,enlesdarreresedicions,elcreixementennombredeparticipantss’hagiestabilitzaten20 centresperany.

L’equiporganitzadordelconcursdefotografiamatemàticadel’ABEAMvolagrairalsparticipantsi patrocinadorslasevacol laboració.Tanmateix,animemalscentresdeprimària,secundària,cicles iformaciód’adultsaparticiparenladotzenaedició.

Referències

Lesbasesdeparticipacióilesfotografiesfinalistesdelesdiferentsedicionsdelconcursespoden trobaralapàginawebdel’ABEAM:http://www.abeam.info

creamat el racó del creamat

Enprimerlloc,volemdonarlabenvingudaal Noubiaix totdesitjant-lillargavidaalserveidel’educació matemàtica.Tambéagraïmalsresponsablesdel Noubiaix quehaginvolgutdedicarunaseccióal creamat.Procuraremestaral’alçadad’aquestaconfiança.

Voldríemdedicaraquestprimerescritaexposarundelsprojectesquemésill·lusióensfa,l’Aplicació deRecobrimentCurricular(ARC),quearas’estàposantal’abastdelprofessorat.

El creamat,comacentreespecíficdesuportalainnovacióilarecercaeducativaenmatemàtiques, hanascutenunmomentenquèconvergiendosaspectes:

—Elcol·lectiudedocentsdematemàtiqueshaviagenerat,alllargd’anys,moltsimoltbonsmaterialsdidàctics,fruitd’unavitalitatcol·lectivaexcepcional.Tanmateix,però,aquestsrecursos, abundantsidiversos,estavendispersosisovinterenpocaccessibles.

—S’estavaestrenantunanovaorganitzaciócurricularqueresponiaaunnouenfocamentbasat enlaideadecompetènciaideprocés.

Enaquestmarc,ensplantejàvemdiversespreguntes:Composaral’abastdetotelprofessoratrecursosiexperiènciesquelipuguinserútilsenlasevaclasse?I,alainversa:comdonardifusióapropostes concretesaportadesperdocentsapartirdelasevaexperiència?Comdonarsuportamestresiprofessoratenlaimplementaciódelnoucurrículum?

Perrespondreaaquestesqüestionsvasorgirlaideadeconstruirunaaplicacióinformàtica,consultableatravésd’Internet,quepermetésposaradisposiciódelprofessoratunaseleccióderecursos vinculatsalcurrículum.Aixívanéixerl’ARC.Laimatgesegüentdescriulaideaques’acabad’expressar, ambl’entesaquecadapeçarectangularésunapropostadidàcticaquel’enllaçaadiferentscontinguts curriculars:

Elgràficanteriorjustificaunamicalaideade‘‘recobriment’’quehemvolgutrecollirenelnomde l’aplicació.

Calassenyalarque,inicialment,l’ARCportavaelnomd’ARC-CercaMatitansolsatenial’àreadematemàtiques.Després,elsaltresCESIREesvanuniralprojecteiactualmentl’ARC(jasensel’afegitde

CercaMat)esproposadonarsuporttambéaaltresmatèries:ciènciesexperimentals,llengües,ciències socials,tecnologia...

Quanenl’ARCesfaciunacercaapartird’uncontingutcurricularconcret,esproposarantotsaquells recursosquehiestiguinenllaçats.Cadascunad’aquestespropostescontéundocumentadreçatal professorat(queanomenemnucli)onhihaunadescripciódelrecursiorientacionsdidàctiquesque podenserútilsal’horadeportar-loal’aula.Aixímateix,moltsovint,hihafitxersannexosentreels qualshihamaterialperal’alumnat.Lacercaespotfer,demaneraàgil,apartirdelsítemsdelcurrículumitambéapartird’altresetiquetesoparaulesclauque,totinoaparèixerpotserexplícitamenten elcurrículum,sónd’úshabitualentrelespersonesqueensdediquemal’educaciómatemàtica.Els resultatspodenvisualitzar-seenformadetaulaodemaneradetallada.Lapresentacióenformade taulatél’aspectequeesmostraenlacapturadepantallasegüent:

Peracadapropostahihaunaimatgerelacionada,unhipervinclealcontingutcomplet,unadescripciómoltbreuilaindicaciódeltipusderecursdequèestracta.Enlavisualitzaciómésdetalladaes potaccedirtantal’explicaciócompletadelapropostaadreçadaaldocentcomalsmaterialspera l’alumnat.Aixímateix,hihaobservacionsreferentsalescompetènciesiprocessosques’hitreballen ialesconnexionsambaltresmatèries.

Imaginem-nos,perexemple,unaprofessoraounprofessorque,durantelpropermes,esproposa treballarlesfiguresplanesaprimercursd’ESO.Apartdelmaterialdequèpuguidisposar(propio deldepartament),pottenirinterèsaconèixeraltrespropostesd’activitatsperalaclasse.L’ARClipre-

sentaràunventalldepossibilitatsdetipusdiversentrelesqualstriaràaquellesqueliresultinmés adequades,siguipercomplementarelsseusmaterials,siguiperatendresegmentsespecíficsd’alumnat,siguiperincorporaraunmoodle...

Desdeldissenyinicial,enelqualvampodercomptaramblaparticipaciód’unequipdemestresi professorat,s’haprocuratquel’ARCtinguiquatrecaracterístiques:

—Permanència.Semblaadequatassegurarelmantenimentalllargdeltempsdelsrecursostot evitant,enlamesuradelpossible,enllaçosinsegursquepuguinquedarobsoletsenpocsmesos.Peraquestaraóesvaoptarperemmagatzemarelsnuclisdelespropostesielsdocuments adjunts.

—Completesa.Elpropòsitconsisteixarecobrirtotelcurrículumdematemàtiques,desdel’educacióinfantilfinsalbatxillerat.Inicialment,s’hanaportatmoltespropostesdeprimercursd’ESO perdonarsuportalprofessoratqueaquestcursparticipaenelprojecteeduCAT1x1.Tanmateix, però,laideaésatendretoteslesetapes.

—Diversitat.L’ARCneixamblafinalitatdeserviralamajoriadelprofessorat.Peruncostat,elscontingutssónpensatsperpoder-neferunatriaques’adaptiadiferentssensibilitatsiestilsdocents i,perl’altre,lamajoriadematerialsadreçatsal’alumnatsóneditablesperquèeldocentpugui ferladarreraadaptacióperalseualumnat.Així,s’hipodentrobarelementsdediferentstipus: recursosTAC,contextosgeneralsdelavidaquotidiana,imatgesirepresentacions,materials manipulables,enllaços,jocsorecreacionsmatemàtiques,referèncieshistòriques,treballsfora del’aula,vídeos...

—Aplicabilitat.L’ARChauriadesertambéunaeinad’intercanvid’activitatsdeclasseentredocents.Convindràprocurarqueelsrecursosquecontinguipuguinresultartaninteressantscom siguipossibleenlapràcticad’aula.

Lautilitatdel’ARCdependràsobretotdelaqualitatdelespropostesdidàctiquesquecontingui.En aquestsentit,el creamat hacomptat(idesitjacontinuarcomptant!)amblacol laboraciód’unbon grupdemestresiprofessoratquehihanfetaportacions,siguidemaneravoluntària,siguienelmarc d’unallicènciad’estudis,siguiformantpartd’ungrupdetreball,siguiperencàrrecconcret...Novolem deixard’aprofitaraquestaoportunitatperposardemanifestelnostreagraïmentperaquestatasca!

Enelmomentenquès’elaboraaquestescrit(estiudel2010),s’estàacabantd’implementarl’aplicació is’estaniniciantlestasquesdetesteig,alhoraques’hivanincorporantcontinguts.Finsarahihaintroduïdes365propostesperatotselsnivells,desdel’educacióinfantilalbatxillerat,encaraque,majoritàriament,coms’hacomentat,estanadreçadesaprimercursd’ESO.Uncopesfacipúblicl’ARCdonaremdifusiódel’adreçad’accésatravésdelawebdel creamat id’altresmitjansquetinguemal’abast.

Potserenpublicar-seaquestprimernúmerodel Noubiax,l’ARCjaestaràenfuncionamenttotique, bensegur,quedaràmoltdecamíperanarresolentlesdificultatsnaturalsdeposadaenmarxaid’anarloenriquintenelscontinguts.Enaquestsentit,desitgemquel’ARCacabid’implementar-sedemaneracorrecta,quepuguicontinuarcomptantamblacol·laboraciódemestresiprofessoratperanar-li aportantpropostesconcretesi,sobretot,quesiguibenútilperdonarsuportal’ensenyamentdeles matemàtiques.

L’equipdel creamat