BSCM, 29-2

BUTLLETÍ

DE LA SOCIETAT LA SOCIETAT CATALANA

DE DEDE DE MATEMÀTIQUES MATEMÀTIQUES

Institut d’Estudis Catalans Institut d’Estudis Catalans

Volum 29 ● Número 2 ● Desembre 2014

©delsautorsdelsarticles

EditatperlaSocietatCatalanadeMatemàtiques filialdel’Institutd’EstudisCatalans CarrerdelCarme,47 08001Barcelona

Textrevisatlingüísticament perlaUnitatdeCorrecciódelServeiEditorialdel’IEC.

ImprèsaLimpergraf,SL PolígonindustrialCanSalvatella CarrerdeMogoda,29-31 08210BarberàdelVallès

ISSN:0214-316-X DipòsitLegal:B.19272-1987

Sónrigorosamentprohibides,sensel’autoritzacióescritadelstitularsdel copyright,lareproducciótotaloparciald’aquestaobraperqualsevolprocedimentisuport,incloent-hilareprografia ieltractamentinformàtic,ladistribuciód’exemplarsmitjançantllogueroprésteccomercial,la inclusiótotaloparcialenbasesdedadesilaconsultaatravésdexarxatelemàticaod’Internet. Lesinfraccionsd’aquestsdretsestansotmesesalessancionsestablertesperleslleis.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.2,2014

Índex

TimG.Myers,FrancescFont,VincentCreganiMichelleM.MacDevette Nanomatemàtiques:modelitzaciómatemàticaalananoescala..................115

JosepPlaiCarrera Joseph-LouisLagrange: inmemoriam .............................................135

ArturoValdivia Matemàticafinanceraentempsdecrisi...........................................167

Englishsummaries.....................................................................199

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.2,2014.Pàg.115–134. DOI:10.2436/20.2002.01.55

Nanomatemàtiques: modelitzaciómatemàticaalananoescala

TimG.Myers,FrancescFont,VincentCreganiMichelleM.MacDevette

Resum: Enaquestarticleexposemtresproblemesestudiatsrecentmentalgrupde MatemàticaIndustrialdelCentredeRecercaMatemàtica,enelsqualsl’aproximaciódel continuresultavàlidaperadescriurefenòmensalananoescala:

1. Transferènciadecalorennanofluids:elsresultatsexperimentalsqueconfirmenl’incrementdelacapacitatdetransferircalordelsnanofluidsrespectedels fluidsestàndardsónsovintcontradictoris.Mitjançantunaanàlisidecapalímit mostraremcomelmodelmatemàticutilitzatennombrosesocasionsperjustificarl’incrementenlatransferènciadecalordelsnanofluidspreveu,defet,una disminuciód’aquestapropietat.

2. Fusiódenanopartícules:lesnanopartículesmostrenunincrementabruptedela velocitatdetransiciódefaseamesuraqueelseuradidecreix.Presentaremun modelmatemàticquedescriuaquestfenomen.Elmodelpreveutempstotalsde transiciósòlid-líquidqueconcordenamblesobservacionsexperimentals.

3. Incrementdelfluxd’unfluidennanotubsdecarboni(CNT):mostraremqueels resultatsexperimentalssobrel’incrementdefluxennanotubsdecarbonies podenexplicarmitjançantlesequacionsestàndarddeladinàmicadefluidsamb laincorporaciód’unacapad’extinció(depletionlayer )alainterfícieentreelfluid ielsòlid.

Paraulesclau: nanotubs,nanofluids,nanopartícules,transferènciadecalor,conductivitattèrmica,canvidefase.

ClassificacióMSC2010: 80A20,76T99,80A22.

1Introducció

Lananotecnologiatractaambmaterialsenquè,comamínim,lalongitud d’unadelestresdimensionsespacialsésinferiora100 nm.Enelsúltimsanys lananotecnologiahatingutunimpacteextraordinariendiversoscampscomla medicina,labiotecnologia,lainformàtica,laproducciód’energia,laconstrucció,

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

elscosmèticsol’enginyeriadematerials.Larecercananotecnològicahaestat conduïdaprincipalmentperlaquímica,lafísica,labiologiail’enginyeriai, encanvi,lamatemàticaaplicadahihatingutunrolmenysimportant.Tot iaixí,comenmoltsaltrescampsdelaciència,lamodelitzaciómatemàtica podriaexercir-hiunpapersignificatiu.Enaquestarticledescriuremtrescasos relacionatsamblananotecnologiaonlamodelitzaciómatemàticailautilització detècniquesestàndarddelamatemàticaaplicadahanestatclauihanpermès obtenirresultatsmoltrellevants.

Elsproblemesestudiatsenlesseccionsquevénenacontinuaciósónla transferènciadecalorennanofluids,latransiciódefaseennanopartícules il’incrementdelfluxd’unfluidatravésdenanotubsdecarboni.Encadascun delsproblemestractatselsmodelsmatemàticsdesenvolupatsfanservirla teoriadelcontinu,fetqueenscondueixalapreguntasegüent:finsaquina longitudd’escalaésaplicablelateoriadelcontinu?Larespostasenzillaésquela teoriadelcontinuespotaplicarsemprequelesvariacionsestadístiquesdeles propietatsmaterials,comaraladensitat,siguinpetites.Peralsfluidsaquesta variaciósovints’estimaenl’1%[1].Basant-seenaquestvalorNguyen etal. [35] estimenunamidacríticade10i90 nm peralíquidsigasos,respectivament. Però,comparantsimulacionsdedinàmicamolecularambcàlculsbasatsen lesequacionsdeNavier-Stokes,Travis etal. [44]mostrenquelateoriadel continuespotaplicaraladinàmicadel’aiguafinsa3 nm.Thomas etal. [43] suggereixenunvalorinferiord’1.66 nm.Siestractadetransferènciadecalor,la midamínimasuggeridaésde2 nm [20],encaraqueaquestlímitpotdependre deltipusdematerial,ialtresautorsestableixenvalorsentre2i5nm[26,27].

Unnanofluidésunfluidqueconténanopartícules.Observacionsexperimentalshanmostratqueafegirnanopartículesaunfluidbasepotproduiruna milloraenlasevaconductivitattèrmicaicapacitatdetransferircalor.Undels reptesimportantsdelasocietatmodernaconsisteixamantenirelsaparells electrònicsaunatemperaturaòptimaperalseufuncionament.Enelsúltims anys,lagrandàriadelsaparellss’haanatreduintdemaneraprogressivafins alpuntqueelsmecanismesactualsderefredamentresulteninsuficients.Els nanofluidshanestatproposatscomacandidatsprincipalsperaproporcionar mecanismesderefredamenteficientsperalesnovestecnologies.Alasecció2 investiguemunmodelestàndardquedescriuladinàmicad’unnanofluidique mostraque,contràriamental’opinióestesa,lasevacapacitatdetransferircalor ésinferioraladelcorresponentfluidbase.

Amésdeservircomaadditiusperamillorarlespropietatdefluidsrefrigerants,lesnanopartículestenenunagranvarietatd’aplicacionsalamedicina, elmediambient,lafabricaciódenousmaterialsil’emmagatzematged’energia[3].Enmedicina,espodenferservirperamillorarladiagnosiiterapia d’enfermetats,comaagentsportadorsdefàrmacsocomaprincipisactius.A causadel’estabilitatquímicaipropietatsòptiquesdel’or,lesnanopartícules d’aquestmaterialsónlesmésutilitzades.Elseuúsmésestèsésenlateràpia d’hipertèrmiadetumorsocomaagentsdecontrastperal’obtenciód’imatges mèdiques[10].Encertescircumstàncies,ésimportantquelesnanopartícules,

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 117

desprésdecompletarlasevafuncióprincipal,esdesintegrinenpetitsclústers omolèculesquepuguinserfàcilmentexpulsatsdelcos.Alasecció3modelitzaremelcanvidefasesòlid-líquidennanopartícules.Hofaremintroduint modificacionspertinentsalproblemaclàssicdeStefan,quemodelitzaprocessos decanvidefasemitjançantlateoriadelcontinu.

Elsnanotubsdecarboni(CNT)sónnanoestructurescilíndriquesformades apartirdegrafèiquetenenpropietatsinsòlites:sónmoltbonsconductors tanttèrmicscomelèctrics,imostrenunaduresaiforçamecànicainusuals. Comaconseqüència,larecercadelspossiblesusosiaplicacionsdelsCNTs’ha intensificatdemaneranotableenelsúltimsanys.Unadelesaplicacionsés alaindústriatèxtiliesbasaenlesobservacionsqueindiquenqueelsCNT transportenl’aiguamoltmésdepressadelqueprediulateoriaestàndarddela dinàmicadefluids.Articlesalesrevistes Science i Nature [22, 30]varenindicar inicialmentunincrementdelavelocitatdetresordresdemagnitud.Estudis mésactuals[47]estimenunfactormultiplicatiude45comaincrementmàxim. Enlasecció4,femservirunconceptedeladinàmicadefluidsnonewtonians peraexplicarperquèl’incrementdelavelocitatdel’aiguaatravésdelsCNTés moltméselevatqueelqueprediulateoriaclàssica.Elmodelquepresentem tambésuggereixunainterpretaciófísicadelacondiciódelliscamentdeNavier (Navierslipcondition).

2Transferènciadecalorennanofluids

Hihaunagranquantitatd’articlesexperimentalsqueposendemanifestl’eficiènciail’augmentdelacapacitatdetransferènciadecalordelsnanofluids: vegeu,perexemple,elrecullfeta[25].Noobstantaixò,hihaunaquantitat creixentd’estudisqueevidencienelcontrari,enparticularl’articledereferència deBuongiorno etal. [9],elqualconclouquenohihacapaugmentanòmal enlaconductivitattèrmicadelsnanofluidsestudiats.Defet,Buongiorno[8] prèviamentvadesenvoluparundelsmodelsméspopularsenelcampdela dinàmicadenanofluids,elqualvautilitzarperconclourequeelcoeficientde transferènciadecalor(HTC)augmentaquanlaconcentraciódenanopartículesdelfluidaugmenta.RecentmentMacDevette etal. [29]varenpresentarun modelquasiidèntici,mitjançantlateoriaestàndarddelacapalímit,varen arribaralaconclusiócontrària.Tambéexpliquenperquèelresultatobtingut perBuongiorno etal. ésdiferentiperquèalgunsdelsarticlesméscitatsque vanferservirelmateixmodeltambéarribenaconclusionserrònies.

Enl’estatestacionariladinàmicad’unnanofluidesdescriumitjançantles equacionssegüents:

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

on u = (u,v) éslavelocitat, p lapressió, ˜ τ eltensordetensions, T latemperaturai φ lafraccióvolumètricadenanopartícules.Elsparàmetresquedepenen de φ són ρnf , χnf , knf irepresentenladensitat,elproductedelacalorespecíficailaconductivitattèrmicadelnanofluid.Elssubíndexs bf , np i nf indicaran fluidbase,nanopartículesinanofluid,respectivament.Elstermesdifusiusamb elsparàmetres CB i CT representenelmovimentbrowniàilatermoforesi,respectivament.Elmovimentbrowniàs’inclouperquèlesnanopartículessóncossos tanpetitsquelavibraciódelesmolèculesdelfluidn’afectaelmoviment.La termoforesiindicaquelespartículesesmouenmitjançantelsgradientsde temperatura,unfetquesucceeixperquèlesmolèculescalentesvibrenmés ràpidamentquelesmolèculesfredes.Pertant,enpresènciad’ungradientde temperaturalesnanopartículessónempesescapalabandamésfreda.Les condicionsdecontorndelsistemasón,pera y = 0,

(5) querepresentaunfluxconstantisenselliscament.Al’entrada, x = 0,és

(6) condicionsqueindiquenqueinicialmentelfluidestàbenmesclat.

Perestudiarlacapacitatdelfluidd’extreurecalordelsistemafemúsdeles variablesescaladesdelacapalímit

(7)

on A corresponaunaescaladetemperaturaencaraperdeterminar, U ésla velocitatdelfluidal’infinit(farfieldvelocity ), Re = ρbf UL/µbf éselnúmero deReynoldsi µbf éslaviscositatdinàmicadelfluidbase.Elsparàmetresfísics quevarienelsescalemambelsvalorsdelfluidbase ˆ

. (9)

Eliminantelsbarretsdelanotació,l’equacióreescaladapera φ esdevé

(φu) = γ

+

, (10)

on γ = CB Aρbf /µnf i λ = CT /(CB A).L’escaladetemperaturaquedadeterminadaapartirdelacalorproporcionadaalsistema.Pertant,lacondicióde contorn (5) laredimensionalitzemdemaneraque kbf A√ReL 1Ty = Q,iescollim A = QL/(kbf √Re).Típicament,perananofluids γ ∼O(10 5),demanera queeltermedominantde(10)és

(φu) = φ∇· (u) + u ·∇

≈ 0. (11)

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 119

Fentservirl’expressiódeladensitatdelnanofluid, ρnf = φρnp + (1 φ)ρbf , l’equaciódecontinuïtatenestatestacionari(1)esdevé

(12)

Partintdel’expressió (11) isubstituint u ·∇φ =−φ∇·u al’equació (12) s’obté lacondiciód’incompressibilitatdelfluid ∇· u = 0.Llavors,l’expressió (11) es potescriurecom

·∇φ = 0, (13)

queindicaque φ ésconstantalllargdeleslíniesdecorrent.Físicamentaixò significaquel’efectedelmovimentbrowniàidelatermoforesialadifusióés tanpetitquelespartículessimplementesmouenambelfluidinoelsarriba l’inputdecalordelcontorn.Elfetque γ tinguiunvalortanpetitindicaqueel transportperdifusiócausatpelmovimentbrowniàiperlatermoforesimai notéunrolimportantenelfluxenlacapalímit.Aixímateix,que φ sigui constantimplicaqueparàmetrescom ρnf , µnf i knf sóntambéconstants. Comaconseqüència,elmodelespotsimplificardemaneraconsiderable,ies potaplicarunaanàlisiestàndarddelacapalímita u i T .Enaquestcas,les equacionsenl’estatestacionarisón

(14)

(17)

onelsubíndex i denotaelvaloral’entradai Pr = µbf χbf /(ρbf kbf ) éselnúmero dePrandtl.L’equació (16) implicaque p = p(x) icomque,enacostar-nosa l’infinit, y →∞, u → 1, v → 0,l’equació (15) ensindicaque px = 0.Llavors,el problemaesredueixa

+ v

=

2 , (18)

on νi = µi/ρi.Peracompletarelmodelimposemlescondicionsdecontorn redimensionalitzadessegüents:

u = v = 0,kiTy =−1quan y = 0, (19) u = 1,v = 0,T = 0quan y → 0. (20)

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

Elmètodedelaintegraldebalançdelacalor(HBIM),descrita[33],espotutilitzar pertrobarsolucionsaproximadesperalavelocitatdelfluidilatemperaturadela capalímit.L’HBIMconsisteixatriarunpolinomiperaaproximartantlavelocitat comlatemperaturadinsd’unacapalímitfinita, δ peralavelocitati δT pera latemperatura.L’aproximacióperalavelocitatapropdelcontornconcorda satisfactòriamentamblasolucióexactacorresponentobtingudamitjançant l’anomenat mètodedeBlasius ].Malauradament,elproblematèrmicnoté solucióexactaiensforçaautilitzarunmètodeaproximat.

Figura1: Perfilsdelescapeslímitperalatemperaturailavelocitat peravalorsdelafraccióvolumètrica φin = 1, 5, 10 %,representades perleslíniesdepunts,discontínuesicontínues,respectivament,peral nanofluidAl2 O3-aigua.

Lafigura1mostralacapalímitperalavelocitatilatemperaturaenfunció delaposicióperadiferentsvalorsdelafraccióvolumètrica φin = 1, 5, 10 %, utilitzantvalorsdelsparàmetrescorresponentsaaiguaambnanopartículesd’alúmina(Al2 O3).L’ampladadelacapalímitaugmentaamblafraccióvolumètrica, iaixòindicaqueelnanofluidpotextreureméscalorambunnombreméselevat denanopartícules.D’altrabanda,lavelocitatdecreixquanlafraccióvolumètrica creix,comesmostraenlafigura2peralsmateixosvalorsde φ,ésadir,la transferènciademassaésméslenta,fetqueimplicaunefecteadversperala transferènciadecalor.Aixídoncs,elsgràficsmostrenque,pertalqueelnanofluidtinguipropietatsfísiquesòptimes,s’hadetrobarunaconcentracióòptima denanopartículesqueaugmentisuficientmentelfluxdecalor(incrementant k) sensedisminuïrelfluxdemassademanerasignificativa(incrementant µ).

Elparàmetreclaud’aquestestudiéselcoeficientdetransferènciadecalor(HTC).Diversosautorsreivindiquenqueaquestparàmetreaugmentasignificativamentamblaconcentraciódenanopartícules.Unadefiniciódel’HTCque reflecteixcorrectamentl’inputd’energiadelsistemaés

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 121

Figura2: Predicciódelavelocitatmitjançantl’HBIMperalesfraccions volumètriques φin = 1, 5, 10 %,quecorresponenalalíniadepunts, discontínuaicontínua,respectivament,peralnanofluidAl2 O3-aigua.

Lafigura3mostral’HTCenfunciódeladistància,fentservirparàmetrescorresponentsananofluidsd’aiguaoetilenglicolcomafluidbaseinanopartícules d’alúmina.Clarament,l’HTCdecreixquanaugmentalafraccióvolumètrica.Ésa dir,elmodelmostraquel’HTCdelsnanofluidsnoaugmentasinóquedecreix,a pesardelamultitudd’estudisexistents,basatsenelmateixmodel,queafirmen totalmentelcontrari(peraunavaloraciómésdetalladad’algunsd’aquestsestudisvegeu[29]).Perexemple,l’anàlisidecapalímitfetaaBuongiorno etal. [9] ésnomésvàlidaenunaregiótresordresdemagnitudméspetitaquel’amplada delasubcapalaminari,pertant,associadaincorrectamentalaregióexterior delfluxdelfluid.Altrespossiblesfontsdediscrepànciaentrel’estudipresenti treballsanteriorssón:interpretacionsdiferentsdel’HTC,hipòtesiserròniesper taldereduirelgraudedificultatdelmodelivalorsincorrectesdelsparàmetres utilitzats.

Figura3: Variaciódel’HTCenfunciódeladistànciaperalfluidbase (cercles),etilenglicoloaigua,i φin = 1, 5, 10 %,corresponentsaleslínies depunts,discontínuaicontínua,respectivament.

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

Elnostretreballnoprovademaneraconcloentqueelsnanofluidsnopuguin millorarlacapacitatd’extreurecalord’unsistema;éspossiblequel’observació d’aquestincrementenalgunsdelsexperimentssiguidegudaamecanismes físicsnoinclososenelmodelpresent.Amésamés,enshemlimitatainvestigarnanofluidsd’aiguaietilenglicolambnanopartículesde Al2 O3;altres combinacionsfluid-sòlidpodriencomportarunaugmentdelatransferènciade calor.

Larecercaennanofluidsésuncampextremamentactiu.Unaàreaonels nanofluidshandemostratserprometedorsésenl’avençdelatecnologiasolar.Enparticular,enelscaptadorssolarsd’absorciódirecta(DASC).ElsDASC sónfluidsqueabsorbeixenitransfereixenenergiasolar.Noobstantaixò,a causadelasevabaixacapacitatd’absorció,elsfluidsestàndardsónineficientsperaabsorbirradiaciósolar.Perexemple,l’aiguanomésabsorbeix un13%del’energiasolardisponible[36].S’hamostrat,però,quenanopartículesdispersesenelfluiddelcaptadorsolarenmillorenlespropietatsòptiquesitermofísiques[15].DASCbasatsennanofluids(oNDASC)fanservirlespropietatsòptiquesitermofísiquesdelsnanofluidsperaabsorbiri dispersarlaradiaciósolar.Estudisexperimentalsrecentsdemostrenqueels NDASCtenenmoltpotencialperaaprofitardemaneraméseficientl’energiasolarqueelscaptadorssolarsconvencionals.Perexemple,s’hantrobat incrementsenl’eficiènciadel10–30%[37,41,45,50].

Actualment,elsNDASCnosóneconòmicamentviables[41].Undelsreptes tecnològicsmésimportantsdelsegle xxi éseldedesenvoluparunsistema, globalmentieconòmicamentviable,capaçdeconvertirenergiasolarenenergia tèrmicademaneraeficientiquepuguicompetirambelssistemesactualsde generaciód’energiapermitjàdecombustiblesfòssils.Pertald’aconseguir-hoés imprescindiblefomentarlarecerca,tantteòricacomexperimental,ennanofluids. Actualment,unadeleslíniesdetreballdelnostregrupés,precisament,la recercademètodesméseficientsperaconvertirenergiasolarenenergia tèrmicamitjançantelsnanofluids.

3Fusiódenanopartícules

Actualment,lesnanopartículessónuntemamoltactiud’investigaciógràcies alessevespropietatsúniquesilagranquantitatdenovesaplicacionsque ofereixenencampscoml’òptica,l’electrònica,labiomedicina,lananolitografia, etc.[3, 24, 40].Unadelesraonsdelseucomportamentinusualésl’altvalordel quociententrelaproporciód’àtomsalvolumialasuperfíciedelananopartícula,quen’afectademaneramoltsignificativalespropietatsmaterials[20].Un exempleconcretés,combésesap,ladavalladadelatemperaturadefusióa mesuraquelagrandàriadelananopartículaesredueix[40].Elsexperiments deBuffatiBorel[7]mostrenunadisminuciódelatemperaturadefusiód’uns 500 K enpartículesd’orderadilleugeramentsuperiorsa1 nm.Lessimulacions dedinàmicamoleculardeShim etal. [40]mostrendisminucionsdemésde 800 K persotadelatemperaturadefusióestàndard(disminuciód’un40%)

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 123

perananopartículesd’orderadid’uns0.8 nm.Elsmedicamentsambbaixa solubilitatenaiguapodenseradministratsenformadenanopartículesper millorar-nel’absorció.Bergese etal. [6]iLiu etal. [28]estudienantibiòticsi medicamentsantianginosos,quemostrenunadisminuciódelatemperatura defusiód’uns30 K (disminuciód’un10%).Acausadelabaixatoxicitatdel’or, lesnanopartículesd’aquestmaterialtambépodenserbonesportadoresde medicamentsodegensperateràpiesgèniques[39].Moltesaplicacionsrequereixenquelesnanopartículesesdissolguindesprésdecomplirlasevafunció principalipassinatravésdelsistemacomamolèculesoclústersdispersos. Pertant,ésimportantentendrelasevarespostaaestímulstèrmics,aixícomel seucomportamentencanviardefase.

Siladensitatilacalorespecíficaromanenaproximadamentconstants,la temperaturadefusióespotestimarmitjançantl’expressiósegüentdeGibbsThomsongeneralitzada

on Lm éslacalorlatent, Tm latemperaturadefusió, T ∗ m latemperaturadefusió estàndard, ∆c = cl cs lavariaciódelacalorespecíficaentreelsòlidiellíquid, σ latensiósuperficiali κ lacurvaturamitjana.Femnotarqueconsideremels canvisdepressiómenyspreables.Pertant,enl’obtencióde (22),s’haprescindit d’untermeaddicionalquetéencompteelscanvisdepressiódelsistema[4]. Enlafigura4escomparal’expressiódeGibbs-Thomsongeneralitzadaamb dadesexperimentalsdenanopartículesd’ord’entre2i12 nm [18].Lafigura interiormostraquel’expressió(22)ésmultievaluadairesultainadequadaper adeterminarlatemperaturadefusióperaradispropersalaunitat.Lalínia contínuacorresponal’expressiódeGibbs-Thomsongeneralitzadailalínia discontínuarepresentalatemperaturadefusiómitjançantl’expressióclàssica deGibbs-Thomson(i.e.,substituint ∆c = 0a (22)).Finalment,lalíniaderatlles ipuntscorresponalaconegudafórmuladePawlow[18].

Elmodelmatemàticquepresentemacontinuacióespotsituardinsdelgrup conegutcoma problemesdefronteramòbil o problemesdeStefan [13, 21]. Aquestmodelesdiferenciadelsmodelsclàssicsenelfetqueelvalordela temperaturaalafronteramòbilnoésconstantsinóquedepèndeltemps,com succeeixenelprocésdesolidificaciódelíquidssubrefredats[14, 17].Lacondició deStefan,quedescriudemaneraapropiadalafusiód’unananopartículaesfèrica, éslasegüent:

(23)

(24) on T(r,t) representalatemperaturadelafaselíquida, θ(r,t) latemperaturadelafasesòlidai R = R(t) laposiciódelafronteraentrelesduesfases.

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

Figura4: Variaciódelatemperaturadefusiódel’orenfunciódelradi delananopartícula.Lalíniacontínuarepresental’expressiódeGibbsThomsongeneralitzada,ladiscontínualaformareduïda(cl = cs ),lade puntsiratlleséslafórmuladePawlowielsdiamantsrepresentenlesdadesexperimentals.Elgràficinteriormostraquelafórmulageneralitzada deGibbs-Thomsondeixadeservàlidaperavalorspropersa1nm.

Lescondicionsdecontornsón T(1,t) = 1, T(R,t) = θ(R,t) = Tm i θr (0,t) = 0. Finalment,lacondiciódeStefanproporcionaunaequacióperalaposiciódela fronteraentreelsòlidiellíquid

Latemperaturadefusióredimensionalitzada, Tm,esdeterminavia

Elsparàmetresresultantsdelaredimensionalitzaciósón

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 125

amb ∆T = TH T ∗ m,on TH éslatemperaturaaplicadaalasuperfíciedela nanopartícula.

Ambunincrementdelatemperaturade ∆T = 10 K s’obté β ≈ 8,40,12 peral’aigua,l’orielplom,respectivament.Òbviament,comméspetités l’increment ∆T ,mésgranéselvalorde β.Acausadelvolumreduïtdeles nanopartícules,l’energiarequeridaperfondre-lesésmoltpetita:unincrement lleugerdelatemperatura, ∆T ,alasuperfíciedelananopartículaéssuficient perafondre-lademanerapràcticamentinstantània.Pertant,treballaramb valorsaltsdelnúmerodeStefan,on β 1,ésunasuposicióraonableenaquest context.Caldestacarqueunvalorpetitde β indicaunprocésdefusióràpid,ja quelatemperatura TH ésmoltmésgranquelatemperaturadefusió, T ∗ m,mentre queunvalorde β elevatimplicaunprocéslent,jaque TH ésproperaa T ∗ m (tot iaixò,elstermes ràpid i lent sónrelatiusjaquelesescalesdetempssónde l’ordredelpicosegon).Aixòindicaunarelacióentrel’escaladetempsi β;per tant,fentúsd’aquestarelacióreescalemeltempsmitjançant t = βτ ibusquem solucionsdeltipus T = T0 + T1/β +··· .Peralafaselíquidatindrem

amblessolucionsrespectives

Seguintelmateixprocedimentperalatemperaturadelafasesòlida, θ,obtenim

Substituint

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

queespotacoblaralaformadiferencialdel’equaciódeGibbs-Thomson

Aquestesequacionsestansubjectesalescondicionsinicials R(0) = 1i Tm(0), on Tm(0) esdeterminaresolentl’equació (26) amb R = 1.Pertant,elsistema original,consistentenduesequacionsenderivadesparcialssubjectesaun dominiespecificatperlacondiciódeStefaniacoblataunaequacióquedescriula temperaturadefusió,s’hapogutreduiraduesequacionsdiferencialsordinàries deprimerordre.

Figura5: Evoluciódelfrontdecanvidefase R(t) envariablesredimensionalitzades(multiplicant R pelradioriginal, R0 = 10 nm,i t pera l’escalatemporal,2.7ps,espodenobtenirelsvalorsaescalareal).

Alafigura5esmostralaposiciódelafronteraentreelsòlidiellíquid, R(t), enfunciódeltemps.Leslíniesdiscontínuescorresponenalasolucióaproximada ileslíniescontínuesalasoluciónumèricaperdiferènciesfinitesdelsistema complet, (23)–(26).Elstresgrupsdecorbesdiferentscorresponena:(i)solució delmodelutilitzantlaformageneralitzadadel’equaciódeGibbs-Thomson, (ii)soluciósuposant cs = cl al’equaciódeGibbs-Thomsonperònoalacondició deStefan(aquestaésl’aproximacióadoptadaa[32])i(iii)lasoluciódelmodel mésestàndardon cs = cl i Tm = T ∗ m (problemaclàssicdeStefan).Ésevidentque lasoluciódelmodelestàndardsobreestimademanerasignificativaeltemps

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 127

totaldetransiciódefase(enunordredemagnitud).Elsgrups(i)i(ii)mostren que,amesuraqueelradidelafasesòlidadecreix,laderivadadelacorba augmentaitendeixainfinit.Enl’últimestadidelatransicióespreveuquela partículadesapareixisobtadament.Aquestfenomende«fusióabrupta»vaser observatenelsexperimentsdescritsa[26].Alafigura6esmostraelperfildela temperaturadelesfasessòlidailíquidaamesuraquelapartículavacanviant defase.Lalíniadepuntsindicaquelatemperaturadefusiódecreixambel temps;lalíniadiscontínuaéslatemperaturadelafasesòlida,ilacontínua,la delafaselíquida.

Unaobservacióinteressantenlafigura6éselfetquelatemperaturadel sòlidéssuperioralatemperaturadefusió.Aquestfenomennosucceeixenels problemesestàndarddecanvisdefasei,suposadament,ésdegutalfetquela temperaturadefusiódecreixmésràpidamentquelatemperaturaenelsòlid. Llavors,encontradelquepassaalamacroescala,alananoescalaelsòlidajuda queelprocésdefusiósiguimésràpid.

Figura6: Perfilsdelatemperaturaal’interiord’unananopartículaen diferentsinstantsdelprocésdecanvidefase.Leslíniescontínuesrepresentenlatemperaturadelafaselíquida,lesdiscontínueslatemperatura delafasesòlidailalíniadepuntsrepresentalatemperaturadecanvide fase.

A[19]espottrobarunaextensiód’aquestmodelons’inclouelcanvide densitatentrelesduesfases.Actualment,elnostregruptreballaperaincor-

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

poraraaquestsmodelsaltrestipusdemecanismesdetransferènciadecalor importantsalananoescala,com,perexemple,eltransportbalísticcausatper lainteraccióentrefonons.

4Incrementdelfluxd’unfluidennanotubsdecarboni(CNT)

Elmodelclàssicquedescriuelfluxd’unfluidatravésd’unconductecilíndrices descriumitjançantl’equaciódeHagen-Poiseuille,quedónal’expressiósegüent peralflux:

QHP =−πR4pz/(8µ), (36)

on pz éselgradientdepressióatravésdelconducte, R éselradii µ laviscositatdelfluid.Ésunfetbenconegutqueelfluxd’unfluidenunCNTés significativamentsuperioralvalorquepreveu(36).

Unamanerafreqüentd’explicaraquestaugmentésintroduintunalongitud delliscament(slip-length)enelmodel.Aixòsignificaquelacondiciódeno lliscament u(R) = 0esreemplaçaper u(R) =−Ls ∂u(R) ∂r , (37)

on Ls éslalongituddelliscamenti u lavelocitatiaixís’obtélamodificació següentdel’expressiódelflux:

Típicament,alabibliografia,l’incrementdelfluxesdefineixcomlaproporció entreelfluxobservatielfluxpredit, slip = Qslip/QHP .Clarament,qualsevol magnitudd’aquestincrementpotserajustadamitjançantunvalorapropiat de Ls .Siescomparalateoriaambelsexperimentsalamicroescala,s’arribaa valorsraonablesdelalongituddelliscament,elsqualssónmoltinferiorsales dimensionsdelconducte.Quanestractadenanoconductes,però,leslongituds delliscamentsóndel’ordredemicres.Actualment,nohihacapteoriapera poderpredirlalongituddelliscamentd’unfluidqueflueixencontacteamb unsòlid,peròsíquen’hihaunaperalsgasos.Enaquestcas,lalongitudde lliscamentésdel’ordredelatrajectòrialliuremitjana(meanfreepath)deles molèculesdelgas[48](peral’aigualatrajectòrialliuremitjanaésde0.3 nm).Per taldesercoherentsamblessevesobservacionsexperimentals,Holt etal. [22]i Majumder etal. [30]estimenlongitudsdelliscamentdel’ordredemicres.Com ésesperable,valorstanelevatsdelalongituddelliscamentenestudissobre CNThanportatmoltsautorsaqüestionarlavalidesadelmodelmodificatde Hagen-Poiseuille[42, 46].Cottin-Bizonne etal. [12]afirmenquelalongitudde lliscamenthauriadetenirunúnicvalorindependentdelradidelconducteimolt inferioralsqueesdonenenestudisprevis.Aquestsvalorsexperimentalstan elevatss’atribueixenalapresènciadepartículeshidrofòbiquescontaminants.

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 129

Unaexplicacióalternativaalcomportamentdelalongituddelliscament esbasaenelfetqueelsCNTsónhidrofòbics.Laforçad’atraccióentreles molèculesd’aiguaésmésgranquel’atraccióentreelsòlidhidrofòbicil’aigua[16].Haestatpostulatquelahidrofobicitatespotpresentarenllacunesde gas,enunacapad’extincióoenlaformaciódevapor:toteslesdescripcions coincideixenenl’existènciad’unaregiódebaixaviscositatproperaalaparet, queexperimentalmentespotinterpretarcomunlliscament«aparent»[16, 34].

Poynor etal. [38]indiquenquelessevesdadesderadiaciódesincrotródemostrensenseambigüitatsquelacapad’extincióesformaquanl’aiguaes trobaamblasuperfíciehidrofòbica.Amésamés,lescapesd’extincióhanestat pronosticadesmitjançantsimulacionsdedinàmicamolecular[31]iobservadesexperimentalment.Joseph etal. [23]varenobservarunacapad’extinció delligamsd’hidrogen.Barrat etal. [5]varenmostrarquelaprimeracapade molèculesd’aiguaesredueixenpresènciad’unaparethidrofòbica.

Suposantquehihaunacapad’extinció,lesequacionsestàndarddela dinàmicadefluidsespodenferservirutilitzantunmodeldebiviscositat,amb unfluxdelfluidprincipalqueocupaelcentredelconducteiunaregiód’extinció properaalaparetambunaviscositatinferior.Aplicantlacondiciódecontinuïtat alavelocitatialatensiótallant(shearstress)enlainterfícieentrelesdues regions,definidaper r = α,elfluxespotexpressarcom

on µ1, µ2 representenlaviscositatestàndardilaviscositatdelacapad’extinció, respectivament,essent µ1 µ2,i α éselradidelaregióprincipal(elsexperimentsambCNTindiquenungruixdelacapad’extincióde δ = 0.7 nm,ipertant α = R 0.7 nm).L’incrementdelfluxesdefineixcomelquocient µ = Qµ /QHP . Utilitzantdadesde[47]s’obtéque µ2 ≈ 0.018µ1,queconcordaambelfetquela viscositatdel’aireidel’oxigensónaproximadament0 02vegadesladel’aigua. Caldestacarqueaquestssóngasosinmediatamentdisponiblesenexperiments fetsambaigua:l’airepotserarrossegatoestardissoltenl’aigua,mentreque l’oxigenn’ésundelscomponents.

Peralfluxd’ungashihaunateoriaqueexplicaelseulliscamentsobreuna superfíciesòlida;tanmateix,nohihacapteoriaqueexpliquielmateixfenomen peraunfluid.Encompararlesexpressionsanteriorsperalfluxd’unfluid amblliscamenticapad’extinciós’arribaal’expressiósegüentdelalongitudde lliscamentd’unfluid:

Aquestaexpressióésunafunciómonòtonamentdecreixentde R (Thomas et al. [42]jahavienpronosticataquesttipusdecomportament).Amés,teninten compteque µ1/µ2 1,espodenidentificartresrègimsdiferents:

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

1. Peraconductessuficientmentamples,talsque δ/R µ2/µ1,llavors µ ≈ 1.Nohihacapaugmentdelfluxapreciableilacondiciódecontornde nolliscamentéssuficient, Ls ≈ 0.Aquestrègimésvàlidaproximadament pera R> 3 µm.Ésadir,enconductesamplesambsuperfíciesllisesno s’observacaplliscament.

2. Peraconductesd’ampladamoderada,talsque (δ/R)(µ1/µ2) ésd’ordre1 però δ/R 1;llavorsnoméseltermeprincipalde Ls téunefecterellevant i

(41)

Aquestrègimésvàlidpera R ∈ [21 nm, 3µ m] icorresponaunalongitud delliscamentconstant, Ls = δµ1/µ2.Nombrososarticlesconstatenlongitudsdelliscamentde20a40 nm peraradisdesd’unsquantsnanòmetres finsaunscentenarsdenanòmetres[11,12].

3. Peraconductesmoltestrets,on δ/R ésdel’ordredelaunitat,s’hadefer servirl’expressiócompletade µ ilalongituddelliscamentvariaambel radidelconducte.Thomas etal. [43]apuntenque Ls variaamb R pera R ∈ [1 6, 5] nm imostrenque ≈ 32quan R = 3 5 nm.Elnostremodel prediu ≈ 33.2peraaquestvalorde R.Tambéprediuunincrement màxim(obtingutsubstituint R = δ)d’aproximadament50,queconcorda amb45delesobservacionsdeWhitby etal. [47].

Sidefinimunaviscositatmitjana,igualantelsfluxosdelsmodelsambbiviscositativiscositatúnica,llavorsclaramentlaviscositatmitjanadecreixambel radidelconducte(jaquelaregiód’extincióocuparàunaporciómésgrandel conductequan R decreixi).Aquestresultatconcordaambsimulacionsfetes recentment[43,49].

5Conclusió

Enaquestarticlehemdescritdemanerabreutresproblemesd’interèsgeneral peralananociència.Totitreballarallímitdelateoriadelcontinu,elsmodels presentatsmostrenconcordànciaamblesobservacionsexperimentals,amés deproporcionarinformacióvaluosasobrediversosfenòmenscaracterísticsde lananoescala.Defet,elmodeldecapalímitperalsnanofluidscontradiula granmajoriad’estudisexperimentals,peròestàenlalíniadenouscorrentsde recercai,enparticular,delsresultatsd’unestudidereferènciaqueimplicaque moltsdelsexperimentsanteriorshanarribataconclusionserrònies.

Lamodelitzaciómatemàticaalananoescalatambépotproporcionarinformacióvaluosasobreproblemesmacroscòpics.Perexemple,l’absènciad’una teoriaperacalcularlalongituddelliscamentquanunfluidesmouencontacte ambunasuperfíciesòlida.L’estudidelfluxd’unfluidennanotubsdecarboni haportataunaexpressióperalalongituddelliscamentenfunciódel’amplada delacapad’extincióilaviscositatdelgasdisponible.Elnostreestudimés

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 131

recentsobrecanvisdefaseennanopartícules[19]inclouelcanvidedensitat entrelesfasessòlidailíquida.Elsresultatsmostrenque,amesuraqueelradi tendeixainfinit,ladiferènciaentreelsdosmodels(tantsis’hiincloucomsino elcanvidedensitat)esmantéfixaal15%.Elcanvienladensitatésgeneralment omèsenelproblemadeStefan,mentrequeelnostreestudimostraqueaquest canvitéunpapermoltimportant.

Agraïments

LarecercadeTimG.MyershaestatfinançadaperlabecaMarieCurieInternationalReintegrationGrantIndustrialApplicationsofMovingBoundaryProblems, Grantno.FP7-256417,ilabecadelMinisterideCiènciaiInnovacióMTM201123789.FrancescFontiMichelleM.MacDevetteagraeixenelsuportd’unabeca doctoraldelCentredeRecercaMatemàtica.VincentCreganhaestatfinançat mitjançantlabecaMarieCurieInternationalReintegration.

Referències

[1] Abragall,P.;Nguyen,N.-T. Nanofluidics.Norwood:ArtechHouse,2009.

[2] Acheson,D.J. Elementaryfluiddynamics.NovaYork:TheClarendon Press:OxfordUniversityPress,1990.(OxfordAppliedMathematicsand ComputingScienceSeries)

[3] Ahmad,F.;Pandey,A.K.;Herzog,A.B.;Rose,J.B.;Gerba,C.P.;Hashsham, S.A. «Environmentalapplicationsandpotentialhealthimplicationsof quantumdots». J.Nanopart.Res.,14(8)(2012),1038.

[4] Alexiades,V.;Solomon,A.D. Mathematicalmodelingofmeltingand freezingprocesses.1aed.Washington,D.C.:HemispherePublishingCorporation,1993.

[5] Barrat,J.-L.;Bocquet,L. «Influenceofwettingpropertiesonhydrodynamicboundaryconditionsatafluid-solidinterface». FaradayDiscuss., 112(1999),119–128.

[6] Bergese,P.;Colombo,I.;Gervasoni,D.;Depero,L.E. «Meltingofnanostructureddrugsembeddedintoapolymericmatrix». J.Phys.Chem.B, 108(40)(2004),15488–15493.

[7] Buffat,Ph.;Borel,J.-P. «Sizeeffectonthemeltingtemperatureofgold particles». Phys.Rev.A,13(6)(1976),2287–2298.

[8] Buongiorno,J. «Convectivetransportinnanofluids». J.HeatTransfer., 128(3)(2005),240–250.

[9] Buongiorno,J.[etal.]. «Abenchmarkstudyonthethermalconductivity ofnanofluids». J.Appl.Phys.,106(2009),094312.

[10] Cherukuri,P.;Glazer,E.S.;Curley,S.A. «Targetedhyperthermiausing metalnanoparticles». Adv.DrugDeliv.Rev.,62(3)(2010),339–345.

[11] Choi,C.-H.;Westin,J.A.;Breuer,K.S. «Apparentslipflowsinhydrophilic andhydrophobicmicrochannels». Phys.Fluids,15(10)(2003),2897–2902.

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

[12] Cottin-Bizonne,C.;Cross,B.;Steinberger,A;Charlaix,E. «Boundary sliponsmoothhydrophobicsurfaces:Intrinsiceffectsandpossibleartifacts». Phys.Rev.Lett.,94(5)(2005),056102.

[13] Crank,J. Freeandmovingboundaryproblems.Oxford:ClarendonPress: OxfordUniversityPress,1984.(OxfordSciencePublications)

[14] Davis,S.H. Theoryofsolidification. Cambridge:CambridgeUniversity Press,2001.(CambridgeMonographsonMechanics)

[15] Eastman,J.A.;Choi,S.U.S.;Li,S.;Yu,W.;Thompson,L.J. «Anomalously increasedeffectivethermalconductivitiesofethyleneglycol-basednanofluidscontainingcoppernanoparticles». Appl.Phys.Lett.,78(6)(2001), 718–720.

[16] Eijkel,J.C.T.;vandenBerg,A. «Nanofluidics:Whatisitandwhatcan weexpectfromit?». Microfluid.Nanofluid.,1(3)(2005),249–267.

[17] Font,F.;Mitchell,S.;Myers,T.G. «One-dimensionalsolidificationof supercooledmelts». Int.J.HeatMassTrans.,62(2013),411–421.

[18] Font,F.;Myers,T.G. «Sphericallysymmetricnanoparticlemeltingwitha variablephasechangetemperature». J.Nanopart.Res.,15(2013),2086.

[19] Font,F.;Myers,T.G.;Mitchell,S.L. «Amathematicalmodelfornanoparticlemeltingwithdensitychange». Microfluid.Nanofluid. (2014).DOI: 10.1007/s10404-014-1423-x.

[20] Guisbiers,G.;Kazan,M.;VanOverschelde,O.;Wautelet,M.;Pereira,S. «Mechanicalandthermalpropertiesofmetallicandsemiconductive nanostructures». J.Phys.Chem.C,112(11)(2008),4097–4103.

[21] Hill,J.M. One-dimensionalStefanproblems:anintroduction.Harlow:LongmanScientific&Technical;NovaYork:JohnWiley&Sons,Inc.,1987. (PitmanMonographsandSurveysinPureandAppliedMathematics;31)

[22] Holt,J.K.;Park,H.G.;Wang,Y.;Stadermann,M.;Artyukhin,A.B.;Grigoropoulos,C.P.;Noy,A.;Bakajin,O. «Fastmasstransportthroughsub2-nanometercarbonnanotubes». Science,312(5776)(2006),1034–1037.

[23] Joseph,S.;Aluru,N.R. «Whyarecarbonnanotubesfasttransportersof water?». NanoLett.,8(2)(2008),452–458.

[24] Karmakar,S.;Kumar,S.;Rinaldi,R.;Maruccio,G. «Nano-electronicsand spintronicswithnanoparticles». J.Phys.:Conf.Ser.,292(2011),012002.

[25] Kleinstreuer,C.;Feng,Y. «Experimentalandtheoreticalstudiesofnanofluidthermalconductivityenhancement:Areview». NanoscaleRes.Lett., 6:229(2011).

[26] Kofman,R.;Cheyssac,P.;Lereah,Y.;Stella,A. «Meltingofclusters approaching0D». Eur.Phys.J.D,9(1)(1999),441–444.

[27] Kuo,C.-L.;Clancy,P. «Meltingandfreezingcharacteristicsandstructural propertiesofsupportedandunsupportedgoldnanoclusters». J.Phys. Chem.B,109(28)(2005),13743–13754.

Nanomatemàtiques:modelitzaciómatemàticaalananoescala 133

[28] Liu,X.;Yang,P.;Jiang,Q. «Sizeeffectonmeltingtemperatureofnanostructureddrugs». Mater.Chem.Phys.,103(1)(2007),1–4.

[29] MacDevette,M.M.;Myers,T.G.;Wetton,B. «Boundarylayeranalysis andheattransferofananofluid». Microfluid.Nanofluid.,17(2)(2014), 401–412.

[30] Majumder,M.;Chopra,N.;Andrews,R.;HindsB.J. «Nanoscalehydrodynamics:Enhancedflowincarbonnanotubes». Nature,438(44)(2005), p.44.

[31] Matthews,M.T.;Hill,J.M. «NanofluidicsandtheNavierboundarycondition». Int.J.Nanotechnol.,5(2/3)(2008),218–242.

[32] McCue,S.W.;Wu,B.;Hill,J.M. «Classicaltwo-phaseStefanproblemfor spheres». Proc.R.Soc.Lond.Ser.AMath.Phys.Eng.Sci.,464(2096)(2008), 2055–2076.

[33] Myers,T.G. «Optimalexponentheatbalanceandrefinedintegralmethods appliedtoStefanproblems». Int.J.HeatMassTrans.,53(5–6)(2010), 1119–1127.

[34] Neto,C.;Evans,D.R.;Bonaccurso,E.;Butt,H.-J.;Craig,V.S.J. «Boundary slipinNewtonianliquids:areviewofexperimentalstudies». Rep.Prog. Phys.,68(12)(2005),2859–2897.

[35] Nguyen,N-T.;Werely,S.T. FundamentalsandApplicationsofMicrofluidics 2aed.Norwood:ArtechHouse,2006.

[36] Otanicar,T.P.;Phelan,P.E.;Golden,J.S. «Opticalpropertiesofliquids fordirectabsorptionsolarthermalenergysystems». Sol.Energy,83(7) (2009),969–977.

[37] Otanicar,T.P.;Phelan,P.E.;Prasher,R.S.;Rosengarten,G.;Taylor, R.A. «Nanofluid-baseddirectabsorptionsolarcollector». J.Renewable SustainableEnergy,2(2010),033102.

[38] Poynor,A.;Hong,L.;Robinson,I.K.;Granick,S.;Zhang,Z.;Fenter, P.A. «Howwatermeetsahydrophobicsurface». Phys.Rev.Lett.,97(26) (2006),266101.

[39] Rana,S.;Bajaj,A.;Mout,R.;Rotello,V.M. «Monolayercoatedgold nanoparticlesfordeliveryapplications». Adv.DrugDeliv.Rev.,64(2) (2012),200–216.

[40] Shim,J.-H.;Lee,B.-J.;Cho,Y.W. «Thermalstabilityofunsupportedgoldnanoparticle:Amoleculardynamicsstudy». Surf.Sci.,512(3)(2002),262–268.

[41] Taylor,R.A.;Phelan,P.E.;Otanicar,T.P.;Walker,C.A.;Nguyen,M.; Trimble,S.;Prasher,R. «Applicabilityofnanofluidsinhighfluxsolar collectors». J.RenewableSustainableEnergy,3(2011),023104.

[42] Thomas,J.A.;McGaughey,A.J.H. «Reassessingfastwatertransport throughcarbonnanotubes». NanoLett.,8(9)(2008),2788–2793.

T.G.Myers,F.Font,V.CreganiM.M.MacDevette

[43] Thomas,J.A.;McGaughey,A.J.H.;Kuter-Arnebeck,O. «Pressure-driven waterflowthroughcarbonnanotubes:Insightsfrommoleculardynamics simulation». Int.J.Therm.Sci.,49(2)(2010),281–289.

[44] Travis,K.P.;Todd,B.D.;Evans,D.J. «DeparturefromNavier-Stokes hydrodynamicsinconfinedliquids». Phys.Rev.E,55(4)(1997),4288–4295.

[45] Tyagi,H.;Phelan,P.;Prasher,R. «Predictedefficiencyofananofluidbaseddirectabsorptionsolarreceiver». ASME,131(4)(2007),729–736.

[46] Verweij,H.;Schillo,M.C.;Li,J. «Fastmasstransportthroughcarbon nanotubemembranes». Small,3(12)(2007),1996–2004.

[47] Whitby,M.;Cagnon,L.;Thanou,M.;Quirke,N. «Enhancedfluidflow throughnanoscalecarbonpipes». NanoLett.,8(9)(2008),2632–2637.

[48] White,F.M. ViscousFluidFlow.2aed.NovaYork:McGraw-Hill,1991.

[49] Ye,H.;Zhang,H.;Zhang,Z.;Zheng,Y. «Sizeandtemperatureeffectson theviscosityofwaterinsidecarbonnanotubes». NanoscaleRes.Lett.,6 (2011),87.

[50] Yousefi,T.;Veysia,F.;Shojaeizadeh,E.;Zinadini,S. «Anexperimental investigationontheeffectof Al2 O3-H2Onanofluidontheefficiencyof flat-platesolarcollectors». Renew.Energy,39(1)(2012),293–298.

TimG.Myers,VincentCregan CentredeRecercaMatemàtica CampusdeBellaterra,EdificiC 08193Bellaterra,Barcelona,Spain i

DepartamentdeMatemàticaAplicadaI UniversitatPolitècnicadeCatalunya Barcelona,Spain {tmyers,vcregan}@crm.cat

FrancescFont MACSI DepartmentofMathematicsandStatistics UniversityofLimerick Limerick,Ireland francesc.font@ul.ie

MichelleM.MacDevette CentreforResearchinComputationalandAppliedMechanics UniversityofCapeTown CapeTown,SouthAfrica michelle.macdevette@uct.ac.za

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.2,2014.Pàg.135–165. DOI:10.2436/20.2002.01.56

Joseph-LouisLagrange: inmemoriam

JosepPlaiCarrera

Ilneleurafalluqu’unmomentpourfaire tombercettetête,etcentannéespeut-être nesuffirontpaspourenreproduireunesemblable.1

Resum: AquestarticleésunhomenatgeaJoseph-LouisLagrangeenocasiódeldoscentsaniversaridelasevamort.Tétresparts:unaprimerapartdecairebiogràfic;la segonareculllasevaproducciócientíficademaneramoltsuccinta,ilatercera,lamés matemàticaiextensa,explicitaalgunsdelsresultatsassolitsperl’insignematemàtic.

Paraulesclau: Joseph-LouisLagrange,biografiad’unmatemàtic,històriadelesmatemàtiques.

ClassificacióMSC2010: 01A50,01A70.

1Introducció

Joseph-LouisLagrangeésundelsgransmatemàticsdel’èpocadelaRevolucióidel’Imperifrancesos—enparaulesdeNapoleóBonaparte(1769–1821), «laimmensapiràmidedelaciènciamatemàtica»(vegeu[6,ediciócastellanade2010,p.178]).Talcomjavaigdefensarenunaltreindret(vegeu[89, p.33–34]),elsinsignesmatemàticsd’aquestperíode—recordem-loscronològicament:Joseph-LouisLagrange(1736–1813),MarieJeanAntoinedeCaritat Condorcet(1743–1794),GaspardMonge(1746–1818),PierreSimonLaplace (1749–1827),AdrienMarieLegendre(1752–1833),LazareNicolasMarguerite Carnot(1753–1823)—sónelsartífexsdeldesenvolupamentdelanovamatemàticadelsegle xviii (geometriaanalítica,càlculdiferencialiintegral,càlcul devariacions,càlculdeprobabilitats,aritmètica,aplicaciódelamatemàticaa

1 SónlesparaulesqueLagrangelidiguéaJean-BaptisteJosephDelambre(1749–1822)en conèixerlamort,alaguillotina,delseuamicAntoineLaurentLavoisier(1743–1794),que,pels seusestudis,ésconsideratelparedelaquímica.Vegeu[16,p.46].

JosepPlaiCarrera

lafísicaial’astronomia,equacionsdiferencials,sèriesinfinites,etc.)ilavan aconduiral’extremdelessevespossibilitats,comreconeixLagrange(vegeula terceracitaciódelap.138).Aquestaaportacióféuindispensableuna«revolució científica»(vegeu[14,ediciócastellana,p.22–29])enelmóndelamatemàtica: uncanvideparadigmaepistemològicimetodològic.

2Gotesbiogràfiques

PodemdividirlavidadeLagrangeentresperíodesbendiferenciats,quecorresponenalescircumstànciesielsindretsonvadesenvoluparlatascainvestigadora idocent.2 Aquestsperíodessón(vegeu[44,ediciófrancesade1984,p.309]):

• ElquepassaalavilanataldeTorí,onneixeldia25degenerdel’any1736 ionviufinsal’any1766.Dura,doncs,unatrentenad’anys.

• Elques’esténdel1766al1787iquecomprènlasevaactivitatal’Acadèmia deBerlín3 icobreixvint-i-unanysdelasevavida.

• ElquepassaaParís:s’inicial’any1787is’extingeixamblasevamort,que s’esdevéel10d’abrilde1813alssetanta-sisanyscomplerts.

Joseph-LouisLagrangeneixalaciutatitaliana deToríambelnomdeGiuseppeLodovicoLagrangia,peròdesdejovesignacomaLodovico La-GrangeoLuigiLagrange,adoptantlagrafia francesaenelcognom.Pernaixença,doncs,és italià,però,peradopció,francès.

Elseuprimertreballimprès,datatel27de juliolde1754,estitula LetteradiLuigiDela GrangeTournier 4

Éselfillil legítim—l’únicdelsonzegermans queaconsegueixarribaral’edatadulta—deGiuseppeFrancescoLodovico—tresorerdel’Office desTravauxPublicsetFortificationsdeSardenya,establertaTorí—ideTeresaGrosso—filla d’unmetgedeCambiano,unaciutatproperaa Torí.

Joseph-LouisLagrange Torí,25degenerde1736París,10d’abrilde1813

Lafamíliaerabenestant—tantelparecomlamareproveniendefamíliesben assentadeseconòmicament—,peròl’ànsiaespeculativadelpareféuque,quan arribàelmoment,noquedésresdigned’heretar.AquestfetobligàJoseph-Louis ahaverdetreballar,unfetqueconsiderava«laprimeracausadetotelquede feliçliesdevindria».Enunaocasió,digué:

2 Pertaldeconfegiraquestabiografiam’hebasaten[16],[77],[44]i[6,ediciócastellanade 2010,p.178–198],moltmésnovel.ladaquelesanteriors.Hompotrecórrertambéa[45,p.14–20], a«Joseph-LouisLagrange(1736–1813)»dinsdelaweb TheMacTutorHistoryofMathematics archive,ifinalmenta[3,p.330–339].

3 L’AcadèmiaReialdeCiènciesdePrússiafoufundadaaBerlínel18demarçde1701,quatre anysdesprésdel’AcadèmiadelesArtsdeBerlín,alaqualhomesrefereixtambéambelnom AcadèmiadelesArtsdeBerlín,breumentAcadèmiadeBerlín.Vegeu[5,tom1,capítol2].

4 Peraprofundirenlesvariacionsdelnomalllargdelavida,vegeu[44,ediciófrancesa,p.309].

Joseph-LouisLagrange: inmemoriam137

Sihaguéstingutfortunafamiliar,probablementnohauriafetdelamatemàtica elmeuafer.Ialeshores,quinsbeneficishauriaaconseguitenunaaltracarrera del’èpocacomparablesalsdelavidatranquil lapròpiadel’estudiós,amb aquestaseqüelaradiantd’èxitsindiscutiblesenungènereeminentmentdifícil iambaquestaconsideracióenverslamevapersonaquehaanatcreixentdia rerediafinsara?5

Elseuparedesitjavaqueesdediquésal’advocaciai,alcomençament,JosephLouisnohitinguéinconvenient.Fouprecisamentquanaprofundiaenl’estudi delgrecidelllatíqueconeguél’obrad’Euclides(iii aC)id’Arquimedes(287 aC–212aC),peròsemblaquenol’impressionarengaire.Alsdissetanys,ambla lecturad’unamonografiad’EdmondHalley(1656–1742)—elprestigiósastrònom anglèsamicd’IsaacNewton(1642julià,1643gregorià–1727)—,s’adonàdela superioritatdelcàlculrespectedelageometria.Entotal’obramantéaquesta tendènciaquesintetitzalafrasedelaintroducciódela Méchaniqueanalytique (vegeu[76,tom11,p. xii]):

Homnotrobaràcapfiguraenaquesttext.Elsmètodesques’hiexposenno precisennideconstruccionsnideraonamentsgeomètricsomecànics;només calenoperacionsalgèbriquessotmesesauneslleisregularsiuniformes.Els quiestimenl’anàlisiveurancomcreixelseudominiimen’estaranagraïts.

ElDecretreialdel28desetembrede1755nomenaLagrangeprofessorde lesÉcolesRoyalesd’Artillerieambunsouanualde250escuts,untracteque, enelsonzeanysqueLagrangevaviureaTorí,nofoumillorat.

Lasevatascacreativa—delaqualfaréunaressenyabreualasecció3— portaLeonhardEuler(1707–1783)aelogiar-lodavantdelseusuperiorjeràrquic PierreLouisMoreaudeMaupertuis(1698–1759),presidentdel’Acadèmiade Berlín.Enelstreballsestrobaunadefensainspiradadel principidelamínima acció,unfetqueportaMaupertuisaindicar-lique,tanaviatcomespresenti l’ocasió,lioferiràunacàtedraaPrússiamoltmésavantatjosaqueladeTorí. Lagrange,però,refusal’oferiment.Encontrapartida,el2desetembrede1756 —quanteniavintanys—ésnomenatmembrecorresponentdel’Acadèmiade Berlínenlacategoriad’associatestranger.

PlacadedicadaaLagrange

5Vegeu[16,p.16].

L’any1757,GiuseppeAngeloSaluzzodiMenusiglio(1734–1810),elmetgeGiovanniFrancesco Cigna(1734–1790)iLagrangevancrearunasocietat científicaquefoulallavordel’AcadèmiadeCiènciesdeTorí.6 Unadelestasquesprincipalsdela Societateralapublicaciódeles Miscellaneaphilosophico-mathematicaSocietatisprivatæTaurinensia,en laquallaparticipaciódeLagrangefoumoltimportant.7

6 L’anomenarenSocietàPrivataTorineseieraelprimernuclidelafuturaAccademiadelle ScienzediTorino(1783),delaqualSaluzzofouelpresidentfinsal1788.

7 Elstresprimersvolumsapareguerenelsestiusde1759,1762i1766,quanLagrangeencara viviaaTorí.Elquartvolum,corresponentalsanys1766–1769iqueapareguél’any1773,contenia

JosepPlaiCarrera

L’any1763,Lagrange—quenohaviasortitmaideTorí—marxacapaParís, onésmoltbenacollitgràciesalamemòriasobrelalibraciódelaLluna.En elviatgedetornadaaTorísojornaaGinebraon,aconsellatperJeanBaptiste leRondD’Alembert(1717–1783),coneixl’il.lustrefilòsofiescriptorfrancès François-MarieArouet,dit Voltaire (1694–1778).

Alatardorde1765,D’Alembert—amblaintenciódemillorar-lilasituació professionalquetéaTorí—liofereixunllocaBerlínqueLagrangerefusaamb lesparaules(vegeu[44,ediciófrancesa,p.315]):

Mentrehihagi monsieur Eulernoemsemblaqueemconvingui.

Aixònoobstant,D’AlembertlicomunicaqueEulerabandonaBerlínper tornaraSantPetersburgilidemanaqueacceptielrelleu,unapossibilitatque ellmateixjahaviasuggeritaFrederic ii elGran.

Lagrangeprenpossessiódelcàrrecdedirectordelaclassedematemàtiquesdel’AcadèmiadeBerlíneldia6denovembrede1766.Enaquestaciutat faamistatambJean-HenriLambert(1728–1777)iambJohann iii Bernoulli (1744–1807).

Lesobligacionsqueadquireixambl’Acadèmiesónlalecturad’unamemòria mensualque,enalgunesocasions,seràpublicadaal Recueildel’Académie —en total,enpublicaseixanta-tres—iladirecciódetreballsdematemàtiques.Noté, encanvi,capresponsabilitatdocent,unaactivitatquerecuperarà,peròd’una maneramoltesporàdica,al’èpocaparisenca.

Onzemesosdesprésd’haver-seinstal.lataBerlínescasaamblasevacosina VittoriaConti,ques’hiacabadetraslladar.EnunacartaadreçadaaD’Alembert eljuliolde1769,diu(vegeu[44,ediciófrancesa,p.315]):

Lamevadona—unacosinaquehaviscutacasadelamevafamíliadurant moltdetemps—ésbonamestressadecasai,amés,notépretensions.

Elmatrimoninotinguéfills.Vittoriaemmalalteixi,desprésdesuportaruna malaltiallarga—durantlaqualLagrangese’ncuidaambmoltadedicació—,mor l’any1783.ÉsenaquestperíodequanLagrangeexpressalasevapreocupació pelfuturdelamatemàtica(vegeu[69]):

[…]Començoasentirquelainèrciacreixapocapociaramateixnopucrespondredelquefaréelspropersdeuanys.Emsemblaquearalaminaés massaprofundaique,sinohihaalgúquedescobreixifilonsnous,tardo d’horacaldràabandonar-la.

I,tanmateix,aquestsanysberlinesossónanysd’unagranproductivitaten elsqualsconsolidaelcàlculilesaplicacionsdelesmatemàtiquesalafísica del’èpocatorinesaihiaprofundeixalhoraqueendegarecerquesenl’àlgebra depolinomisienaritmètica,unaciènciaqueconsideraheretadadeClaude GaspardBachetdeMéziriac(1581–1638),malgratlesenormesaportacions degudesaEuler.L’activitatl’ajudaasuperarlamalaltiailamortdeVittoria. quatrememòriesdeLagrangeconfegidesaBerlínel1767,1768i1770.Vegeu[44,ediciófrancesa, p.311–312].

Joseph-LouisLagrange: inmemoriam139

AquestafeinaladescriuenlacartaaD’Alembertdel’1d’abrilde1781(vegeu [68]):

[…]Lesmevesocupacionsesredueixenacultivarambtranquil litatien silencilamatemàtica.Nohiharesquem’apressiitreballomésperplaer quepeldeure.Sóccomelsgransmestresqueconstrueixen:faig,desfaig, refaig,finsqueemtrobocòmodeambeltreballqueheelaborat,quelcom ques’esdevémoltrarament.

UnadelestasquesqueportaatermedesprésdelamortdeVittoriaésel tancamentdela Méchaniqueanalytique —unaobraquehaviaprojectatals dinouanysdurantl’èpocatorinesa—,compodemllegiralacartaadreçadaa Laplace(vegeu[71]):

Hecompletatgairebédeltotuntractatsobremecànicaanalíticaquees fonamentasolamentenelprincipiofórmuladelaprimerasecciódela memòriaqueusadjunto;nosé,però,niquanniaonelpodréimprimiri,per això,nom’apressoaferelsdarrersretocs.

Laqüestiódel’ediciólaresoll’abatMarie,unanticamicdeLegendre,que vaconvènceruneditorparisenc.Elllibreapareixfinalmentl’any1788,quan Lagrangepateixunadepressióprofunda.

Aquestadepressiól’haprovocada,d’unabanda,lamortdeVittoriai,de l’altra,ladelreiFrederic ii elGran(1712–1786),esdevingudael17d’agost, ambelqueaixòcomportadepèrduadesuportenl’àmbitcientíficberlinès. ÉsaleshoresquanHonoréGabrielRiqueti,comtedeMirabeau(1749–1791), promouquesiguireclamatperaanaraParís.Elcontracteques’estableix perduràmalgratelscanvisderègimques’esdevinguerenaFrança.Alhora Prússialiconcedeixunapensióqueesvamantenirfinsal’any1792.

LagrangeabandonaBerlínel18demaigde1787iel29dejuliolesdevé pensionistaveteràdel’AcadémiedeSciencesdeParis,8 delaqualeramembre associatestrangerdesdel22demaigde1772.

Ésbenacollitpelseruditsparisencsperl’ampliventalldeconeixementsque té—metafísica,història,religió,lingüística,medicina,botànica,etc.—quelcom queresponaunaregladeconductaquehaviaadoptatfeiatemps(vegeu[44, ediciófrancesa,p.325]):

Crecque,engeneral,undelsprincipisdelssavisésmantenirunacord estricteamblesnormesdelpaísentotallòqueexperimenta,finsitotquan nosónraonables[…].

Aixònoobstant,quanparlahofausantuntodedubte,iacostumaa començarl’explicacióamb«nosé»(vegeu[16,p.54].

I,malgratquemainoprenpartitenelsesdevenimentspolíticsdel’època —reialisme,Revolució,Imperi—,semblatalmentque,enesperit,mostrauna certasimpatiaperlaRevolució.

L’any1792demanalamàdeRenée-François-AdélaideLeMonnier(1767–1833),filladel’astrònomPierre-CharlesLeMonnier(1715–1799),uncol lega 8Sel’anomenaAcadèmiadeParís.

del’Académie.Escasenel31demaig.Ladiferènciad’edatésdevint-i-cinc anys.Elmatrimonitampocnovatenirfillsperò,comelprimer,éstranquil. Sónanyspolíticamentconvulsosperalamonarquia,quesignaelcontracte dematrimoniel3dejunyperindicar«comelsn’és,deplaent,launió».El13 d’agostlafamíliareialeraempresonadaalaTourduTemple.

Tambésónanysdifícilsperalscientífics:el28demarçde1794,Condorcet sesuicidaiel8demaigLavoisierésdecapitatsotal’imperide laTerreur (vegeu lanota1).

Unsanysabans—el8demaigde1790—9 l’AssembléeNationalehavia decretatlaunificaciódelesmesures,quelcomqueconfiàal’Académiede Sciences.Malgratlasupressiódel’Académie,esdevingudael8d’agostde1793, laComissióesmanté.Lagrangeenformapart,comapresident,desdel’inici finsalfinal.

El30d’octubrede1794,perdecret,s’institueixl’ÉcoleNormale,quetécom aobjectiuformardocentsiuniformitzarl’ensenyament.Solamentduratres mesosionzedies;enaquestperíodeLagrange—quetéLaplacecomaajudant— hiensenyamatemàticaelemental.

GràciesalsesforçosdeGaspardMonge,l’11demarçde1794escreal’École CentraledesTravauxPublicsque,seguidament,esdevél’ÉcolePolytechnique —queencaraavuiperdura.Lagrangehiensenyaanàlisimatemàticafinsa l’any1799,enquèelsucceeixSylvestre-FrançoisLacroix(1765–1843).

Apartirdel1799Lagrangeformapart—ambLaplace,Monge,ClaudeLouis Berthollet(1748–1822)iCarnot,entred’altres—d’unsenatconservadorcreat perBonaparteiquesubsisteixdurantl’Imperi.Repaleshoresmoltesdistincions, comaral’OrdredelaLégiond’Honneur,eltítoldeComted’Empire(1808), ielnomenamentdeGrandCroixdel’OrdreImperialdelaRéunion(1813),creat perl’emperadorel1811.

PeròLagrangejaestàmoltmalaltiespera,ambresignació,elmomentdelamort,que s’esdevéel10d’abril.Tresdiesméstardés enterratalPanthéon,unmonumentdedicatals «GrandesHommes»per«laPatriereconnaissante».ElselogisfúnebressónllegitsperLaplace, ennomdelSenat,iperBernardGermainÉtiennedeLaville-sur-Illon,comtedeLacépède (1756–1825),ennomdel’Académie.Tambéa Itàliaseliretenhomenatgespúblics,peròno pasaixíaBerlínque,enaquellsmoments,es trobaenplenainsurrecciócontraelsfrancesos.

TombadeLagrange

CriptadelPanthéon París

L’emperadorfacomprarelstreballsimanuscritsdel’insignematemàtic —italiàdenaixençaperòfrancèsd’adopció,quiendubta?—ielsconfia,perala sevasalvaguarda,al’InstitutdeFrance.

9 Vegeu http://smdsi.quartier-rural.org/histoire/8mai70.htm.Aixònoobstant,no s’instauraràaFrançafinsal7d’abrilde1795.Vegeu[98].

3Notessobrelaproducciócientífica

L’obradeJoseph-LouisLagrangeésmoltdiversaiextensa.10 Elsàmbitsd’estudi mésimportantselsheconcretatenordrealfabètic,enlallistasegüent,ielshe acompanyatd’unabibliografia adhoc:

1.Àlgebra:[101],[80],[93].

2.Astronomia:[32],[81],[100].

3.Aritmèticaoteoriadenúmeros:[95],[104],[36].

4.Càlculdevariacions:[97],[37].

5.Equacionsdiferencials:[2],[41].

6.Filosofiadel’anàlisimatemàtica:[20].

7.Mecànica:[72],[12],[13],[9].

8.Sèries:[91,capítol ii,p.140–159],[27].11

L’articledeJeanItard[44]faunapresentació—forçarecomanableperla capacitatdesíntesid’aquesthistoriadorfrancèsdelamatemàtica—desetantadostreballsdeLagrange,ambunadescripcióbreudelscontingutsielssituaen elseullocenlavidadel’insignetorinès.12 Enfaréunaselecciómoltsuccinta: n’explicitaréeltítol,elperíodeenquèelvarealitzar([T]pertorinès,[B]per berlinèsi[P]perparisenc)ilacitacióbibliogràficacorresponent.

3.1Lagrangecomamatemàticaplicat

EnlafaseinicialdelasevaproduccióLagrangese’nsmostracomun matemàtic aplicat —resoluciódeproblemessuggeritsperlamecànica,l’astronomia,la gravitació,etc.Tanmateix,nooblidamaielaborarlateoriamatemàticaqueli calperassolirl’objectiuques’haplantejat.

Primertreball. L’any1754faimprimirunamemòriaenformadecarta,enitalià, adreçadaaGiulioCarlodiFagnano(1682–1766)(vegeu[47]),ondesenvolupauncàlculformalqueesfonamentaenl’analogiaquehihaentre elbinomideNewtonilesdiferènciessuccessivesdelproductededues funcions,delaqualhaviaenviatunanotíciaaEulerabansdelapublicació delamemòria.13 [T] Lacorbatautòcrona. El30desetembreescriuunaaltracartaaFagnano—que s’haperdut—,enquèestudiala corbatautòcrona. RecordemqueGalileoGalilei(1564–1642),enlacartaadreçadaaGuidobaldodelMonte(1545–1607)de29denovembrede1602[28]afirmaque

10Latrobemrecollidaenelscatorzevolumsressenyatsa[76].Espotconsultartambé[96].

11 Moltsd’aquestsítems—ambmésomenysdetalliextensió—espodentrobarenllibres d’històriadecairemésgeneralcomara[84,vol. iii i iv],[11,vol.4],[82,vol. ix],[46],[39]i[40]. Vegeutambé[89].

12Unadescripcióméshumanitzadaéslaques’ofereixa[16].

13 Uncopsortípublicats’assabentàqueelresultatestrobavajaenlacorrespondènciaentre GottfriedWilhelmLeibniz(1646–1716)iJohannBernoulli(1667–1748).

JosepPlaiCarrera

elperíoded’oscil.laciódelpèndoldepèn només delalongituddelpèndol, però,encanvi, nodepèn nidelamassanidel’amplada.AquestaafirmacióseràanalitzadaperChristiaanHuygens(1629–1695)al’Horologium oscillatorium (1673)[42],ondemostraquecalquelacorbaquedescrigui elpèndolsiguiuna cicloide —queéslacorbadedescensmínimocorba tautòcronaoisòcrona.Aquestresultat—mínimtempsdecaiguda—ésel queagafaJakobBernoulli(1654–1705)enlasevasoluciódelproblema delabranquistòcrona,delqualparlaremmésendavantalapàgina151 (vegeu[88,p.66–68]).

Lagrangededicàdostreballsmésal’estudidelacorbatautòcrona:el primerfouunacomunicacióal’AcadèmiadeBerlínel4demarçde1767 (vegeu[55])enlaqualfeiaservirideesincipientsdelcàlculdevariacions. Foucriticatperl’acadèmicAlexisFontainedesBertins(1707–1771).Lagrangelivarespondreambl’article Nouvellesréflexionssurlestautochrones, publicatel1770(vegeu[60]). [B]

Elcàlculdevariacions. És,però,apartirdel’any1755—teniadinouanys— quanLagrangeespreocupadelque,enuntreballde1766,Euleranomena càlculdevariacions (vegeueltítolde[25]).Diu:«Éselprimerfruitdels meusestudis».14

Lestècniquesquevadesenvoluparperalcàlculdevariacionsseranla basedela Méchaniqueanalytique. Lessèriesrecurrentsilaprobabilitat. L’any1776enunacartaaLaplace—on indicaquehacomençatlatraducciófrancesade Thedoctrineofchances d’AbrahamDeMoivre(1667–1754)(vegeu[18])quenopensacontinuar iqueescongratulaqueLaplacehoestiguifent—liesmentaquelamemòria[50]eraunaintroduccióalateoriadelaprobabilitatque,permanca detemps,nodesenvoluparà.Lagrangerecuperaràenelstreballs[66], [49]i[65]lasevaideadel’úsdesèriesrecurrentsperalaresolucióde problemesplantejatsperDeMoivre. [T,B] Sobreelso. TambéésenaquestsanysquanLagrangeespreocupadelateoria delso.15 Enlaprimeradelesobresquededicaaaquestaqüestiófauna declaraciódeprincipisqueemsemblaquevallapenaderetenir(vegeu[50, p.40]):

Ilaconcordànciadelsmeusresultatsambl’experiènciaservirà,potser,perdestruir elsprejudicisd’aquellsaquielsdesesperaquelamatemàticanopuguiaportar mailallumvertaderaalafísica.Ésundelsprincipalsobjectiusquem’heplantejat aracomara. [T]

LalibraciódelaLluna. L’any1763s’interessaperlalibraciódelaLlunaarran delapropostadelconcursperal’any1764del’AcadémiedesSciences:

14 Vegeu[57,p.154].LesaportacionsdeLagrangeestrobenrecollidesa«Recherchessurla méthodedemaximisetminimis»[48]ia«Surlaméthodedesvariations»[53].Lestècniques empradeslessintetitzaa[51].

15Sónelstreballsqueesrecullena[76,tom i,p.39–148;151–316;319–332].

Joseph-LouisLagrange: inmemoriam143

CompodemexplicarlaraóperlaquallaLlunapresentasemprelamateixacaraa laTerra;idequinamanerapodemdeterminarpermitjàdelesobservacionside lateoria,sil’eixd’aquestPlanetaestrobasubjecteaalgunamenademoviment propiques’assemblialqueconeixemdelaTerraiqueprodueixlaprecessióila nutació.

Peraestudiaraquestproblemafaservirel segonprincipidelesvelocitats virtuals quepresentaunlligamíntiminecessariamblestècniquesdel càlculdevariacions.16 [T,B]

Elproblemadelstrescossos. Tambéespresentaalconcursde1768ambuna memòriamoltnotablesobrelateoriadelstrescossos—Sol,TerraiLluna. Ésunaqüestiód’unagranprofunditatiqueobretotuncampderecerca novell.17 Despréshogeneralitzaal’estudidelssiscossos:Sol,Júpiteriles sevesquatrellunes.Aquestsestudisserienrepresos,vint-i-quatreanys méstard,perLaplace.

Tambéenaquestaocasióesbasaenleslleisdeladinàmica:eslimitaa considerar,enl’aire,lespartículesqueestrobenalineadesialeshores recorrealproblemadelescordesquevibren,ambelqualelsgeòmetres noestavenpasd’acord;elsmostraqueelsseuscàlculssóndeficients, ielaboraunasoluciógeneral.18 [B]

Estudissobreladinàmicadelsfluids. Eneldecennisegüentespreocupapel comportamentdelmovimentdelsfluids;elprimertreball,llegital’Académieel22denovembrede1781,espublical’any1783(vegeu[70]).[B]

3.2Lagrangecomamatemàticpur

Ara,encanvi,enstrobemambunLagrangeentèscomamatemàticpur—és adir,plantejairesolproblemespropisdelamatemàticaensimateixaque aprofundeixenenlanaturalesaielcomportamentdelsseusobjectesmés preuatscomaraelsnúmerosenters,elspolinomis,etc.

L’equaciódePell. Dedicadiversostreballsademostrarl’existènciadesolució del’equaciódePell,d’acordambelnomqueliatribuíEuler,19 y 2 Ax2 = 1, on x i y = 0sónenterspositiusi A noésunquadratperfecte.20 [B]

16 Vegeu[52].Aquesttreballseràmilloratdemanerasensibleenuntreballulteriorde1780: [67].

17 Vegeu[62].Aqueststreballselporten,d’unamaneranatural,al’estudidelespertorbacionsi alateoriadelpotencialquedesenvolupàdurantelsanyssetantadelsegle xviii.Tambévalla penaindicarquetractademaneraexplícitaelconceptede determinant ;vegeu[46,vol. ii,p.800] o[40,p.320–322].

18 Calremarcarlaideaquetinguéd’invertirelsumatoriilaintegraliqueelportarendemanera inconscientals coeficientsdeFourier.Vegeu[46,vol. ii,p.510–511].

19 El1738—vegeu[22]—Eulerparlad’unproblemaaritmètic,però,encanvi,el1759parlaja delproblemadePell—vegeu[24].Peramésinformació,vegeulanota31.

20 Vegeu[55],publicatel1769.Alesnotesqueacompanyenel VollständigeAnleitungzur Algebra d’Euler—vegeu[63]—ofereixunademostraciómoltméssimplificada.

JosepPlaiCarrera

Unproblemaaritmètic. Ofereixlaprimerademostraciócompletadelteorema deBachet: Totnúmeronaturaléslasumadequatrequadratsenters.Es basaenlesdemostracionsinacabadesd’Euler.21 [B]

ElteoremadeWilson. El13dejunyde1771llegeixal’AcadèmiadeBerlín unademostraciómoltoriginaldelteoremadeWilson: Si p ésunnúmero primer, (p 1)! + 1 ésmúltiplede p (vegeu[61]).[B]

Laresoluciódelesequacionsalgèbriques. Unadelesqüestionsdelamatemàticaquepreocupavadesdefeiatempseraelcomportamentdeles equacionspolinòmiques.L’any1770,Lagrangefaunaaportaciónotable enlamemòriaextensa«Réflexionssurlarésolutionalgébriquedeséquations»onanalitzaenprofunditatelsalgorismesderesoluciód’equacions polinòmiquessubministratspelsmatemàticsquel’hanpreceditenla qüestió(vegeu[59]).

Aquestamemòrianotablelacompletaunaaltramemòria[75]queproporcionamètodesperadeterminararrelsaproximadesdelesequacions polinòmiques,ienlaqualanalitzaeltreballdeD’Alembertrelatiual teoremafonamentaldel’àlgebra ionreconeixlavalidesadelademostració deD’Alembertamblesparaulessegüents:«Aquestademostracióésmolt enginyosai,almeuparer,nodeixaresadesitjarpelquefaal’exactitud» (vegeu[15]i[64,p.479]);iquecontétambélalleid’interpolació—avui conegudaambelnomde lleid’interpolaciódeLagrange—quetrobemales lliçonsquedonàal’ÉcoleNormalel’any1795,sibéjahaviaestatindicada perEdwardWaring(1734–1798)l’any1779iEuler,el1783(vegeu[73] i[103].I,peramésinformació,[83]). [B,P]

Clocaquestasíntesibreuambdostractatsalhorametodològicsiepistemològics:

Lamecànicaanalítica. Lagrangelapresentacom unamaneranovaderesoldreproblemesdela mecànicadelscossos,tantsisónsòlidscomsi sónfluids,basant-seperatotsellsenelsmateixosprincipis.Així,alsvint-i-tresanyshaviacopsatjaelsfonamentsdelessevesgransobres, obresqueserienadmiradespertotselseruditsdel’època(vegeu[16,p.20]).Elsprincipis enquèesbasasón principisdeminimalització. [T,B,P]

Méchanique analytique (1788) Pàginamanuscrita

Lateoriadelesfuncionsanalítiques. Ésuntractatd’índoleepistemològicaon Lagrangefaunapresentacióclarairigorosa—ialhoraparcial—delcàlcul diferencial(vegeu[74]). [P] 21Vegeu[58],aparegutl’any1772.

Joseph-LouisLagrange: inmemoriam145

4Algunsresultatsmatemàticsexplicitats

Emsemblaqueaquest inmemoriam aLagrangeseriacoixsinodiguésquelcom d’algunesdelessevesaportacionsmatemàtiques;dedico,doncs,aquestasecció aferunrepàsbreud’algunesd’aquestesaportacions.Enaquestrepàs,tanmateix, noaprofundeixoenlesqüestionsdequètracto—suposoqueellectorentéja uncertconeixement—;solamentemfixoenalgunsdetallshistòricsiend’altres derelatiusal’originalitatdel’obradeLagrange.

4.1Àlgebra

L’objectiudeltreballdeLagrangede1770, Réflexionssurlarésolutionalgébrique deséquations [59],éstrobar,apartirdel’anàlisi—lareflexió—delsmètodesde resoluciódelacúbicailaquàrticageneralsassolitspelsmatemàticsquel’han preceditenl’estudidelproblema,uncamíperapoderresoldrela quíntica general quesiguidelanaturalesafinsaleshoresassolida,ésadir, perradicals. Recordemque,elmateixany,Alexandre-ThéophileVandermonde(1735–1796)establia: Totaequació X p 1 = 0,amb p primer,ésresolubleperradicals. Hoestablia,però,solamentperalscasos p = 2, 3, 5, 7i11.Lademostració generalladonariaCarlFriedrichGauss(1777–1855),ales Disquisitionesarithmeticæ (1801)[31](vegeu-nelatraducciócatalanadeGriseldaPascual,[86]). Entenemper equaciópolinòmicageneral unaequacióenlaqualelscoeficients són«paràmetres»—ésadir,totalmentgenerals.Enconcret,sónequacionsde laforma

(1)

Elslligamsestructuralsdelesarrelsde (1) sónsemprefuncionssimètriques i,deretruc,sónexpressablescomafuncionsracionalsdelscoeficientsde l’equacióinicialque,enprincipi,sónelementsgenèricsde Q (respectivament, de K),viales fórmulesdeCardano-Viète idel teoremafonamentaldelesfuncions simètriques. 23 Aquestaanàlisielportaaestablirunadefinicióidosteoremes bàsicsqueconstitueixenl’inicid’uncanvideparadigmarespectedelsalgebristes quel’havienprecedit,compalesenelsexemplesquesegueixenelsenunciats següents(vegeu[59,§100,p.374–379]):

Definició. Diemquelafuncióracional ϕ(x1,...,xn),funciódelesarrels x1,...,xn de (1),admettoteslespermutacionsdelafuncióracional ψ(x1,...,xn) si,inoméssi, ϕ(x1,...,xn) ésinvariantpertotapermutacióquedeixainvariant ψ(x1,...,xn). 24

22Elcospodriasermésgeneral;entotcas,elscoeficientssóngenèricsenelcosenqüestió.

23 AquestteoremafouintuïtperAlbertGirard(1595–1632)[35],aprofunditperIsaacNewton [85,p.102]idemostratperEdwardWaring[102,p.76].Lagrangeelconsidera«autoevident»[59, p.372].

24 Lagrangelesanomena funcionssemblants isuposaquesónfuncionsracionals.Vegeu[59, §88,p.350–351].

JosepPlaiCarrera

TeoremaI. Siunafuncióracionaldelesarrelsde (1), ϕ(x1,...,xn),admettotes lespermutacionsd’unaaltrafunció ψ(x1,...,xn) (i,potser,d’altres),aleshores lafunció ϕ espotexpressarcomunafuncióracionalde ψ elscoeficientsdela qualsónfuncionsracionalsdelsdel’equaciógeneral.

Unexemplesenzillajudaràacopsarelsignificatdelteorema.Considerem l’equacióquadràticageneral aX2 + bX + c = 0delaqualsuposemquelesarrels són x1, x2.Lafunció projeccióprimera π 1 2 (x1,x2) := x1 admetlesmateixes permutacionsdelesvariables x1, x2 quelafunció t(x1,x2) := x1 x2:solament laidentitat.Pertant, x1 = 1 2 b a + t(x1,x2) . Recordem,depassada,queel discriminant del’equaciódesegongrauanteriorés ∆ := a2 (x1 x2)2 = a2 x2 1 + x2 2 2 x1 x2 = (x1 + x2)2 4 x1 x2 = a2 b a 2 4 c a = b2 4 ac.Pertant, t(x1,x2) := √∆ = √b2 4 ac,irecupereml’expressióbenconegudaderesoluciódel’equaciódesegongraugeneral x1 =− b 2 a + 1 2 a √∆ =− b 2 a + 1 2 a √b2 4 ac.Elcàlculde x2 ésaraelemental,ja que x1 + x2 =− b a ,idóna x2

TeoremaII. Siunafuncióracionaldelesarrelsde (1), ϕ(x1,...,xn),noadmet toteslespermutacionsd’unaaltrafuncióracional ψ(x1,...,xn),sinóquepren r valorsdiferents,aleshoreslafunció ϕ ésarreld’unaequaciódegrau r els coeficientsdelaqualsónfuncionsracionalsde ψ idelscoeficientsdel’equació general [59,§103,p.382–387].

Comaexempled’aplicaciódelteoremaanterior,considereml’equaciógeneraldetercergrau X3 + a2X2 + a1X + a0 ilesfuncionsdelessevesarrels ϕ = x1 i ψ = x1x2.Lespermutacionsquedeixenfixa ψ sónlaidentitatilaqueintercanvia x1 i x2.Peraquestespermutacions ϕ prendosvalors: x1 i x2.Aleshores ϕ és arreldel’equaciódesegongrau (Y x1)(Y x2) = Y 2 (x1 + x2)Y + x1x2 = 0. Eltermeindependentdelpolinomiés ψ ielcoeficientdegrau1és

(x1 + x2) =−(x1 + x2 + x3 x3) =− a2 x1x2x3 x1x2 =−a2 + a0 ψ .

Entrelesfuncionsdelesarrels,Lagrangeintrodueixlesanomenades resolventsprimeres,definidescom:

ρ = x1 + ξx2 + ξ2 x3 +···+ ξn 1 xn, on1,ξ,ξ2,...,ξn 1 sónles n arrelsenèsimesdelaunitat,ques’utilitzen,per exemple,enlaresoluciódelacúbicacomveuremacontinuació.

ProcedimentdeLagrange. Volemresoldrel’equaciógeneral(1).Comencem ambunafunciósimètricadelesarrelscomara ϕ0 := x1 +···+ xn.Ésinvariant perales n!permutacionsdelesarrels x1,...,xn.

Siguiara ϕ1(x1,...,xn) unafuncióquepren r valorsquansotmetemles variables x1,...,xn alespermutacions σ ∈ Sn.Aleshores,pelteoremaII, ϕ1 seràarreld’unaequaciódegrau r , g1(Y) = 0,elscoeficientsdelaqual seranfuncionsracionalsde ϕ0 idelscoeficientsdel’equaciógeneral.

Joseph-LouisLagrange: inmemoriam147

Siguiara ϕ2(x1,...,xn) unafuncióquepren s valorsquansotmetemlesvariables x1,...,xn alespermutacions σ ∈ Sn quedeixeninvariant ϕ1(x1,...,xn) Seràl’arreld’unaequaciódegrau s, g2(Y) = 0,ambcoeficientsenelcosde funcionsracionalsde ϕ1 ielscoeficientsdel’equaciógeneral.

Obtenimunasuccessió ϕ0,ϕ1,ϕ2,..., finsquearribema x1 (quenomés admetlaidentitat).Sónarrelsd’equacions g1(Y) = 0, g2(Y) = 0, g3(Y) = 0,..., degraus r,s,t,... Aquestesequacionssónles resolventsdeLagrange de l’equació(1).

Sicadaunadelesequacions g1(Y) = 0, g2(Y) = 0, g3(Y) = 0,..., és resolubleperradicals,l’equaciógeneral(1)seràresolubleperradicals.

Vegemaraelmètodeanterioraplicatalacúbica.Consideremlafunció—el cubdelaresolventprimera— ϕ(x1,x2,x3) := x1 + ξx2 + ξ2 x3 3 ,on ξ3 = 1, associadaalacúbicageneral X3 + pX + q = 0.Prendosvalors A i B quan sotmetemlesarrels x1, x2, x3 alessusbtitucionspossiblesde S3 quedeixen fix s(x1,x2,x3) := x1 + x2 + x3.Pertantsónlesarrelsd’unaequaciódesegon grau—enconcretdel’equació Z 2 + 27 qZ 27 p3 = 0—i,pertant,resoluble perradicals.25 Améstenim

Sumemiobtenim x1 = 3 √A + 3 √B.Lesaltresarrelss’obtenenanàlogament. L’hemresoltperradicals—quelcomquejahaviaaconseguitel1535Niccolò Fontana,(1499–1557),dit Tartaglia (elQuec).Laresoluciódelaquàrticala tractademaneraanàloga.

Aleshores,pled’esperança,aplicaelmètodealaquínticaiestrobaquela resolventésunasèxtica—pertantméscomplexaderesoldrequelaquees proposavainicialment.26

Serà,doncs,impossibleresoldrelaquínticaperradicals?Gaussaixího afirmataxativamentel1801.Aquestaanàlisi—quehompodriapensarqueés fallida—obrelaportaalesrecerquesdePaoloRuffini(1765–1822)[94],Niels HerikAbel(1802–1829)[1]iÉvaristeGalois(1811–1832)[30].Enparticular, Ruffiniestableixque quan n> 4,nohihacapfunciódelesarrelsqueprengui 3 o 4 valors [94,vol.2,p.162–170]id’aquíendedueixla impossibilitat de resoldrelaquínticageneral.Però,perajustificar-ho,recorrealfetsegüent (supòsitdeRuffini): Siunaequacióésresolubleperradicals,lesexpressionsde 25Ésunexerciciveureque A + B =−27 q i A · B =−27p3 26 Vegeu[59,§74,p342].Diu:«Maisnoun’entreronspointicidanscedétailqui,outrequ’il exigeraitdescalculstrès-longs,nesauraitd’ailleursjeteraucunelimièresurlarésolutiondes équationsdecinquièmedegré;carcommelaréduiteen z estdesixièmedegré,elleneserapas résolubleamoinsqu’ellenepuisses’assabaiseraundegréinférieuraucinquième»:[«Noens estendremenelsdetallsque,abandad’exigircàlculsmassallargs,tampocnoensaportarien llumalaresoluciódelaquíntica;atèsquelareduïdaen z ésdegrausisè,noseràpasresoluble, llevatquepuguemabaixar-liperdessotadelgraucinquè»].

JosepPlaiCarrera

lesarrelsespodenexpressarpermitjàderadicalsquesónfuncionsracionals delesarrelsambcoeficientsenelcosdelscoeficientsdel’equacióinicialquecal resoldreidelesarrelscomplexesdelaunitatcorresponents [94,p.11].Aquest resultatl’establiria,però,Abelenlasevademostraciódelaimpossibilitatde resoluciódelaquínticageneral.PeraconsultareltreballdeRuffini,vegeu[93, capítol viii];perald’Abel,[87],iperaldeGalois,[90].

4.1.1ElteoremadeLagrangedelateoriadegrups. Valadirque,enaquest context,licalqueelconjuntdelespermutacionsdelesarrelsestrenquide maneraadequada(vegeu[92,cinquenaedició,p.207–209]).

AquestresultatelvaestablirLagrangequanencaranos’haviaintroduïtel conceptede grup,originarideGalois.Utilitzantaraaquestanocióelresultatde Lagrangeéselsegüent:

TeoremadeLagrangedelateoriadegrups. Si H ésunsubgrupd’un grup G —totssóngrupsdepermutacionsd’arrels—,aleshoresl’ordredelsubgrup H —elnombred’elements—divideixl’ordredelgrup G

4.2Aritmèticaoteoriadenúmeros

EnaquestàmbitLagrangefatresaportacionsqueesrecullenalsllibresd’història delamatemàtica:lademostraciódelafórmuladeWilson,lasoluciódelproblema deBachetilaresoluciódel’equaciódePell.Comentaremaquílaprimera il’última.

4.2.1LafórmuladeWilson. AquestafórmulajaeraconegudapelsmatemàticsindisientrobemlaprimerapetjadaenBh¯askara i (∼600–∼680);la retrobemenIbnal-Haytham(∼1000).AOccident,27 l’enunciaEdwardWaring l’any1770,quel’atribueixalseudeixeble,JohnWilson(1741–1793);capdels dos,emperò,nolademostra.28

TeoremadeWilson. Si p ésunnúmeroprimer, (p 1)! + 1 ésmúltiplede p L’any1771,Lagrangen’ofereixunademostraciórealmentsimple(vegeu[61]). Totconsisteixaconsiderarelpolinomi

(x + 1)(x + 2) (x + p 1) = xp 1 + A1 xp 2 +···+ Ap 1,

27 Hihaconstànciaque,unsegleabans,jal’haviaintuïtLeibniz[99,p.114]peròmainolava publicar.Diu:«Productuscontinuorumusqueadnumerumquiantepraeceditdatumdivisusper datumrelinquit1(velcomplementumadunum?)sidatussitprimitivus.Sidatussitderivativus relinquetnumerumquicumdatohabeatcommunemmensuramunitatemajorem»(Elproducte detotselsentersqueprecedeixenunenterdonat,quanesdivideixperaquestenter,dóna1siel númeroenterésprimer.Siéscompost,dónaunnúmeroquetéunfactorcomúmajorque1amb l’enterdonat).

28 Vegeu[102,p.218,icomaproblema5,enl’edicióde1782,p.380]d’EdwardWaring.En l’esmentadapàginadelaterceralliçó,hillegim:«Hancmaximeelegantemprimorumnumerorum proprietateminvenitvirclarissimus,rerumquemathematicarumperitissimusJoannesWilson Armiger»(Unpersonatgeil lustreimoltexpertenmatemàtiques,JohnWilson,trobàaquesta propietatelegantdelsnúmerosprimers).

Joseph-LouisLagrange: inmemoriam149

asubstituir x per x +1iamultiplicar-hototper x +1.Comparantelscoeficients enresultaque kAk,amb1 ≤ k ≤ p 2,i,pertant,cada Ak,amb1 ≤ k ≤ p 2 ésmúltiplede p i,amés, (p 1)Ap 1 = 1 + A1 +···+ Ap 2.D’ontrivialment

Ap 1 + 1ésmúltiplede p;però Ap 1 = (p 1)!

D’aquestresultatendedueixel teoremapetitdeFermat ifinalmentdemostraelrecíprocdelteoremadeWilson(breumenticlaraexposata[19,vol. i, p.62–63]).

Tanmateix,Lagrangeofereixunteoremamésgeneral—queéselquevalla penad’indicar—,avuiconegut,comtantsd’altres,ambelnomde teoremade Lagrange. 29 Diu:

TeoremadeLagrange. Sigui p unnúmeroprimeri

f(X) = an X n + an 1 X n 1 +···+ a1 X + a0,

amb ak ∈ Z (k = 0, 1,...,n), n> 1 i an ≡ 0(mod p).Llavorslacongruència

f(X) ≡ 0(mod p)

té,comamàxim, n arrelsdiferentsmòdul p. 30

I,sibéLagrangenoendedueixelteoremadeWilson,éspossiblefer-ho (vegeu[10,p.102–104]).

4.2.2Laresoluciódel’equaciódePell. Estractad’estudiarl’equaciódiofàntica,conegudaambelnomd’equaciódePell:31

x2 Ay 2 = 1,x,y ∈ Z, i A ∈ N, noquadratperfecte. (2)

Eulers’haviaadonatdelfetsegüent:

Lemad’Euler. Si p, q ésunasoluciópositivade x2 Ay 2 = 1,aleshores p q és unaconvergentdeldesenvolupamentde √A enfracciócontínua [24,p.32].

S’adonàtambédellema:

29Vegeu[56,p.667–669].Falademostració—queésvàlidaengeneral—enuncasconcret.

30 EstàenunciatenelllenguatgedeGauss,quel’estableixa[31,§43,ediciócatalana,p.40–41].

31 Comjaheditalanota19,elnomfouerròniamentatribuïtaJohnPellperEuler,quepotserel vaconfondreambelmatemàticanglèsLordBrouncker(1620–1684),quefouelprimermatemàtic europeuqueintentàdetrobarunasoluciógeneral.Totcomençaambunproblemaquel’any1657 PierredeFermatplantejaaJohnWallis(1616–1703),elmatemàticanglèsmésnotabledel’època. Jahaviaestatestudiatprofusamentpelsmatemàticsindis,peròOccidentnoentindriaconeixementfinspassatsunscent-cinquantaanysquanLagrangeentrobàlasoluciógeneral.L’any 628,Brahmagupta(598–668)en BrahmaSphutaSiddhanta desenvolupàel mètodechakravala Aquesttextfoutraduïtpelsàrabsl’any773itraduïtalllatíacomençamentsdelsegle xii.Aquest mateixsegleBh¯askara ii (1114–1185)iNarayanaPandit(∼1340–∼1400)enel xiv assolirenla determinaciódelasoluciógeneral.Recordem,depassada,queelproblemafamósdelsbous d’Arquimedesportaalaresoluciód’unaequaciódePell,lasoluciódelaqualvahaverd’esperar adisposard’ordinadors.

Unahistòriaexcel.lentdel’equaciódePellés[105]iuntextteòricplantejatenformade problemesés[4].

JosepPlaiCarrera

Lema. Si p q ésunaconvergentdeldesenvolupamentde √A enfracciócontínua, existeixunenter k amb |k| < 1 + 2√A talque p2 Aq2 = k

Tanmateix,nofoucapaçdeveurequeaquestmètodesempredónasolucions ique totes lessolucionssónconvergentsde √A.ÉsLagrangequiestableixel resultatsegüent(vegeu[54,p.672,678i686]):

TeoremadeLagrange. L’equació (2) sempreadmetsolucionsenteres.32

Ianalitzantelcomportamentdeldesenvolupamentenfracciócontínua de √A,tambéproporcionauna infinitat deparelles (p,q) peralesquals f(x,y) = x2 Ay 2 prenunmateixvalor R (vegeu[54,§28,p.727]).

Amés,estableixunalgorismeforçasimpleperadeterminar totes lessolucionsdel’equació(2).

AlgorismedeLagrange. Si p1, q1 éslasoluciópositivamínimade (2),aleshoresqualsevolaltrasolució p, q de (2) ésunaparelladeterminada pn, qn obtingudadelaidentitat:33

4.3Elcàlculdevariacions

Alahistòriadelamatemàtica,abansdel’apariciódelcàlculdiferencial,la preocupacióperlesqüestionsrelativesalamaximitzacióilaminimitzacióde magnitudshaestatmoltesparsa.Noésestrany,enmancaval’eina.Aixòno obstant,erapossible,comféuZenodor(∼200aC–∼140aC),plantejardesdela geometria problemesisoperimètrics.

Portadade Méchanique analytique (1788)

MoltsdelsenunciatsdeZenodorelsconeixemgràciesauncomentariqueTeód’Alexandria(∼335–∼405)féual’Al’magest dePtolemeu (∼90–∼168).Euclidesusaria—modegeomètric—el camímínim perdonarlalleidela reflexiódelallum

Unaltreàmbit—quetrigariaseglesaplantejarse—enelqualapareixenproblemesd’optimització éselqueproporcionalafísica.Perexemple,Pierrede Fermatrecorreriaal tempsmínim ialseumètode demàximsimínimsperaestablirlalleidela refracciódelallum (vegeu[26,p.183–199]).Leibniz s’adonariaqueelllenguatgedel càlculdiferencial que acabavad’introduirenl’articlede1684[17,traducció castellanadeJavierdeLorenzo,p.271–281]eraelllenguatgeidoniperatractaraquestamenadeproblemes.

32 Vegeu[54,§15,p.693].Tanmateix,aconsello,perlasimplificacióassolidaqueesbasaen laperiodicitatdeldesenvolupamentenfracciócontínuade √A,[63,§37,capítol iv,p.743i següents].

33Vegeu[54,§15,p.695i§17,p.698–703].

Joseph-LouisLagrange: inmemoriam151

TambéIsaacNewton,al’escolidelaproposició34delllibre ii delatercera ediciódel Philosophiænaturalisprincipiamathematica (1687),plantejariauna qüestiód’índolefísica—laformaquehaviadetenirunsòlidderevoluciópera presentarmínimaresistènciaaunfluidenelqualesdesplaçava—quecomporta determinarunafuncióqueminimitziunaintegral.

Laconsciènciadelaimportànciad’aquestamenade problemes—problemesdemaximització/minimització d’integrals—tél’origenl’any1696quaneljovedels germansBernoulli,Johann,plantejàelqueavuiesconeixcomel problemadelabraquistòcrona (vegeu[7, vol. i,p.161]):Quinaéslacorbaquehadeseguirun puntquecaulliurementd’unpuntaunaltresivolem queeltempssiguimínim.

Quatredelsmatemàticsmésrellevantsdelmoment —Newton,Leibniz,elgermàgrandeJohannBernoulli, Jakob(vegeu[17,p.391]),ielmarquèsdeL’Hôpital (1661–1704)—n’oferirenlasolucióalcostatdelade Johann.Lescincsolucionsesvanpublicaral’Acta Eruditorum del’any1697.

EstàtuadeLagrange ViaLagrange Torí

LasoluciódeJakobBernoullisuggeríaLeonhard Eulerunmètodegeneral:elqueavuiconeixemcom el càlculdevariacions.Defet,Euler alterava unaordenada—l’afectavad’una variació.Ambaquestmètodeiunagranimaginaciód’índolegeomètrica,veu dequinamaneraaquestavariacióafectalesderivades y ,y ,... ilaintegral J definidaalafórmula (4).Euler,a[23](vegeutambé[17,p.399–406]),sintetitza treballsanteriorsiestableix,enllenguatgeactual,elresultatsegüent(vegeu [21,p.178]):

Teoremad’Euler. Consideremunaintegraldelaforma

Llavors,lafunció y = y(x) queminimitzaomaximitzaelvalorde J hade satisferl’equaciódiferencial

34 L’integrand f(x,y,y ) depènfuncionalmentde x, y, y ,itambéendepenen fy i fy . D’aquestamaneracalentendre(5).Recordemque f

JosepPlaiCarrera

Ésfàcildeconstatarquel’equaciódiferencial(5)ésequivalenta

fy fy x fy y y fy y y = 0 35 (6)

Atèsquelafunció f ésconegudaenstrobemdavantd’unaequaciódiferencial ordinàriadesegonordre,en y(x),nolineal.

Precisamentl’anyenquèapareixel Methodusinveniendi,Pierre-LouisMoreau deMaupertuis,arrandelessevesrecerquessobrelateoriadelallum,publicavael principidemínimaacció;podemreformular-lodientque leslleisdelanaturalesa s’atenenalprincipid’economia.Euler,quemanteniacorrespondènciaamb Maupertuis,reformulariaaquestprincipi,enunapèndixdeltextesmentat,com unteoremadinàmicil’inclouriadinselcàlculvariacional.

Lagrange,sempreamatental’obrad’Euler,començariaapreocupar-sepel càlculdevariacionsel1750.Teniadinouanys.Lasevaaportaciófoulade descartarlatècnicabasadaenlageometria,introduïdaperBernoulliiEuler, isotmetrelateoriaamètodesanalítics.Enlasecciósegüentveuremcom preocupavaaLagrangeaconseguirunmètodeanalíticquegarantíselrigorde l’anàlisi.

LaideadeLagrange,adiferènciadelad’Euler,eracercardirectamentuna funció y(x) dinsunafamíliadefuncionsquepassenpelsdospunts (x1,y1), (x2,y2);36 enconcret,consideralesfuncionsdelaforma y(x) + δy(x),on δ —unsímbolintroduïtperLagrange—indicavalavariacióenterade y(x). Enintroduiraquestanovafunciódinsdel’integrandde J, J = x2 x1 f(x,y,y )dx,

laintegralesveiaalteradaiespodiadeterminarl’increment ∆J: ∆J = x2 x1 f(x,y + δy,y + δy ) f(x,y,y ) dx.

Malgratquelafunció f(x,y,y ) depèndetresvariables—queLagrangemira comaindependents—,atèsquela x novaria,potdesenvoluparl’integrandde ∆J ensèriedeTaylordeduesvariables.S’obtenen,d’antuvi,termesen δy i δy ,despréstermesdesegongrauenaquestsincrements,etc.,demaneraque:

35Recordemque fy

36 Elseutreballmésnotableenaquesttemafou[51].Recordemque,cincanysabans,enuna cartaaEuler,haviabatejataquestmètodeambelnomde mètodedevariacions peròEuler l’any1756elrebatejariaambelnomactual: càlculdevariacions.

Joseph-LouisLagrange: inmemoriam153

on

δJ = x2 x1 fy δy + fy δy dx (7)

δ2 J = x2 x1 fyy (δy)2 + fyy (δy)(δy ) + fy y (δy )2 dx, .

Aixíobtélesvariacionssuccessivesde J: δJ, δ2 J,etc. AleshoresLagrangeafirmaque,si y(x) proporcionaunextrem,llavors

δJ = 0iafegeix,senseexplicitar-nelaraó,que d i δ commuten:37

δy = d(δy) dx

Isubstituint-hoa(7)obté:

δJ = x2 x1 fy δy + fy d dx (δy) dx

que,integrantperpartsiusantelfetque δy s’anul laentre x1 i x2,dóna:

δJ = x2 x1 fy δy d dx fy δy dx.

I,atèsque δJ = 0peracadavariació δy,Lagrangeconclouqueelcoeficient de δy hadeser0ique,pertant,s’obtél’equaciód’Euler: fy d dx fy = 0.

HeusacíundiàlegfructíferentreLagrangeiEulerquepermetuncanvi deperspectivaenlesaportacionsdeljovematemàticitalofrancès.

4.4Lamínimaaccióenlamecànica

Laquantitat A,conegudacoml’acció,esdefineixper

A = Ldt, on L s’anomenaactualmentel lagrangià 38 Ellagrangiàméssimpled’unsistema ésl’energiacinètica T menysl’energiapotencial V :

L(x,t) = T(x,t) V(x,t).

37AixòhoaclaririaEulermésendavant.

38Lesideesd’aquestaobramagnasónlesquejahaviaaplicatabansel1764;vegeu[52,p.9].

JosepPlaiCarrera

Sifemquel’acciósiguimínima,obtindreml’equaciód’Euler-Lagrange. 39 Enefecte,consideremuncamíextremal x(t) entreelspuntsfixos x(t0) i x(t1),iunmovimentalllargdelcamí.Latrajectòriaésexpressadaperla funció a(t),ilavelocitat v(t) canviad’acordamb:

x(t) → x(t) + a(t),v(t) → v(t) + a(t).

Siprenem a(t) moltpetitperòdemaneraque x(t) + a(t) passipelspunts

fixos x(t0) i x(t1),podemafirmarque a(t0) = a(t1) = 0. Totaixòafectaellagrangià.Peraaproximacionsdeprimerordredel’element petit a(t),ellagrangiàestransformadelamanerasegüent:

L(x,v) → L(x + a,v + a) = L(x,v) + a(t) ∂L ∂x + a(t) ∂L ∂v .

Pertant,l’accióestransformad’acordamb A → A + δA,on: δA =

.

Elsegontermequehihadinselparèntesiespotintegrarperparts:

1 t0 dt da dt ∂L ∂v = a(t) ∂L ∂v

1 t0 t1 t0 dta(t) d dt ∂L ∂v .

Atèsque a(t0) = a(t1) = 0,lapartjaintegrada(entreclaudàtors)s’anul.la. Enresultaque δA val:

δA = dta(t) ∂L ∂x d dt ∂L ∂v .

Pera a(t) arbitrari,peraminimitzarl’acció(ésadir,sifem δA = 0), l’expressióquehihadinsdelsparèntesishadeserzero.Sihoreescrivimen coordenadesgeneralitzades q,enllocde x,i ˙ q,enllocde v,obtenim: ∂L ∂q d dt ∂L ∂q = 0, queésl’equaciód’Euler-Lagrange(vegeu[72,p.332,340]).

4.5ElsmultiplicadorsdeLagrange

Alapàgina77delvolum11deles Ouevres deLagrange—elvolumqueconté eltomprimerdela Méchaniqueanalytique—hillegim(vegeu[72,p.77–78]):

39 Aquestaideas’usaprofusamentenmecànicaquànticaienfísicadelespartícules,enparticular quanestractaamb teoriesgauge.

Joseph-LouisLagrange: inmemoriam155

§1. Mètodedelsmultiplicadors.

2.Siguin

L = 0, M = 0, N = 0,...

lesdiferentsequacionsdelescondicionsqueimposalanaturalesadelsistema, onlesquantitats L, M, N,..., sónfuncionsfinitesdelesvariables x, y, z, s , y , z ,... ;silesdiferenciem,obtenim

d L = 0,d M = 0,d N = 0,...,

queproporcionenlarelacióquehihad’haverentrelesdiferencialsd’aquestes variables.Engeneral,lesusaremcomaequacionsdecondicióentreaquestes diferencials[ ].

Ara,atèsqueaquestesequacionsnoméslesnecessitemperaeliminarun nombresemblantdediferencialsenlafórmulageneraldel’equilibri,segonsla qualcadaundelscoeficientsdelesdiferencialsrestantshadesernul,noés difícilprovar,permitjàdel’eliminaciódelesequacionslineals,ques’obtindran elsmateixosresultatssis’afegeixenal’equacióques’estudialesdiferents equacionsdecondició d L = 0, d M = 0, d N = 0,..., cadaunamultiplicada peruncoeficientindeterminat;seguidament,s’igualaazerolasumadetots elstermesqueestrobenmultiplicatsperunamateixadiferencial.Aixòdonarà tantesequacionsparticularscomdiferencials;aleshoreshomeliminad’aquestes darreresequacionselscoeficientsindeterminatsambelsqualshemmultiplicat lesequacionsdecondició.

3.Enresultaaquestareglaextremamentsimpleperatrobarlescondicions d’equilibridelsistemaarbitrariquese’nsproposi[... ]

Comveiem,Lagrangedónael mètodedelsmultiplicadors comunaeinaen untextquetécomaobjected’estudideterminatsresultatsdelafísica.

Enllenguatgeactual,estractadetrobarunmàxim(omínim)localdela funció f(x,y) quanestàsotmesaalacondició g(x,y) = 0.Sidesignemel conjuntdenivellde g per A = (x,y) : g(x,y) = 0 ,estractadetrobarun punt (x0,y0) peralqual f(x,y) ≤ f x0,y0 peratot (x,y) ∈ A

Lagrangeobservaqueelgradientde f x0,y0 grad f x0,y0 40 ésortogonalalvectortangent x (t0),y (t0) delacorbadenivell A (vegeu[72, p.78]i[41,p.325–326]).Pertant,enl’extremlocal,elsvectors grad f x,y i grad g(x,y) tenenlamateixadirecció,iaixòportaalacondiciónecessària

grad f x,y = λ grad g(x,y),g(x,y) = 0 (si grad f x0,y0 = 0).Elparàmetre λ éselqueanomenem multiplicadorde Lagrange.Lesequacionsanteriorsrepresententrescondicionsperalsparàmetres x, y, λ.Siintroduïmlafunció L(x,y,λ) := f(x,y) λg(x,y),lestres condicionsanteriorsespodensubstituirpergrad L(x,y,λ) = 0.

40 Recordemque grad f éselvector grad f = ( ∂f ∂x1 , ∂f ∂x2 ,..., ∂f ∂xn ) = ( ∂ ∂x1 , ∂ ∂x2 ,..., ∂ ∂xn )f =∇f , on ∇ s’anomena nabla iprovéd’unaarpaassíria.Vegeu[33,p.138].

JosepPlaiCarrera

4.6Lateoriadelesfuncionsanalítiques

Portada41de Théoriedes fonctionsanalitiques

Elcàlculdiferencialplantejavaunamuniódeproblemesdecaireepistemològicitambémetodològic, comvanposardemanifestabastamentelsseusdetractors,elmésparadigmàticdelsqualsfouGeorge Berkeley(1685–1753),quea TheAnalyst,oraDiscourseAddressedtoanInfidelMathematician —l’astrònom EdmondHalley—feiaveurel’anomaliaquesuposa treureconclusionsquevolenserrigorosesapartir d’inconsistèncieslògiquesiconceptesambigus.

D’altrabanda,laresoluciódelproblemadelacordavibrant—queportavaalaresoluciód’unaequació diferencialenderivadesparcialsdesegonordre— obriaunaescletxa,genstrivial,alsconceptesde funció ide continuïtat

Calia,doncs,d’algunamaneraestablirunateoriadefuncionsproucoherent isòlidapertaldepoder,simésno,pal liaraquestsproblemesque,encaraque ningúnon’eraconscient,portarienmoltsmaldecapsicontribuirienalacrisi defonamentsdefinalsdelsegle xix (vegeu,perexemple,[8]).

AixòéselqueintentàferLagrangeenlaseva ThéoriedesFonctionsAnalytiques (1797).42 Voliaferunapresentaciócompletadelcàlculqueevitéstota referènciaalsinfinitesimals,alsdiferencialsialslímits.

L’aproximaciólagrangianaesbasavaaconsiderareldesenvolupamenten sèriedepotènciesd’unafunció f(x).D’aquestamaneracreiaquepodriaoferir unamenadecàlculdetipusalgebraicdelateoriadefuncions,atèsque,si substituïa x per x + i,obtenial’expressió—decairepolinòmicinfinit—

f(x + i) = f(x) + pi + qi2 + ri3 +··· , (8) enlaqual p,q,r,..., erenfuncionsde x qued’algunamaneradepeniende f(x) Perl’obradeNewton—i,sobretot,d’Euler—sabiaquelamajoriadelesfuncions particularsqueelserenfamiliarserend’aquestamena.Però,hoerentotes, d’aquestamena?Lagranges’esforçaaprovar-ho.Avuisabemquesolament sónd’aquesttipusles funcionsanalítiques en x —unnomqueéshereude l’obradeLagrange.Aviat,Augustin-LouisCauchy(1789–1857)provariaquela funció f(x) = e 1 x2 non’és,d’analítica.

Lagranges’adonatambéque p éslaprimeraderivadade f(x) iintrodueix tantlanotació f (x) comelnomde derivada.Perveurequisónelsaltres coeficientsprocedeixdelamanerasegüent:a (8),substitueix i per i + o i

41 Contélainscripció«AuCm.Maffredelapart/duConseildel’EcolePolytechnique/L.»Jean-FrançoisMaffrefouprofessordel’Écolesobrelaconstrucciódeponts.Vegeu http://www.vialibri. net/552display/year 1797 1.html

42 Peraunapetitamostrad’aquesttext,vegeu[17,p.388–391]queacompanyaaltresintents defonamentarelcàlculenbasessòlides.

Joseph-LouisLagrange: inmemoriam157

desenvolupa;d’altrabanda,també,a (8),substitueix x per x + o idesenvolupa. Comparaelscoeficientsdelesduesexpressionsiobté:

q(x) = 1 2 p (x) = 1 2 f (x), r(x) = 1 3! q (x) = 1 3! f (x), s(x) = 1 4! r (x) = 1 4! f (x), etc.

Aixíobservaque,defet, (8) éseldesenvolupamenten sèriedeTaylor de f(x):

f(x + i) = f(x) + f (x)i + 1 2 f (x)i2 + 1 3! f (x)i3 +··· , (9)

iafirmaqueésfàcilveurequeelscoeficients f (x),f (x),... coincideixen amblesderivadessuccessivesdelafunció f(x).Tanmateix,aixòdepèndelfet que(8)siguiderivabletermeatermerespectede i. Eneltext—concretamentalcapítol vii—hiapareixel residudeLagrange delasèriedeTaylor.

A(9)substitueix x per x i:

f(x) = f(x i) + f (x i)i + 1 2 f (x i)i2 + 1 3! f (x i)i3 +··· (10)

Ara,a(10),substitueix i per xz iintrodueixelresidu:

f(x) = f(x xz) + f (x xz)xz + 1 2 f (x xz)(xz)2 +··· ···+ 1 n! f (n)(x xz)(xz)n + xn+1R(x,z), (11) queéstambél’expressióutilitzadaperTaylorperdefinirelresidu.Derivant termeatermerespectede z,elstermess’eliminendedosendosis’obté: R (x,z) = zn n! f (n+1)(x xz). (12)

Si M i N sónelmàximielmínimde f (n+1)(x xz) pera z ∈ [0, 1],s’obté: Mzn n! ≤ R (x,z) ≤ Nzn n! (13)

Integrantentre0i1,resulta: Mzn+1 (n + 1)! ≤ R(x,z) ≤ Nzn+1 (n + 1)! pera z ∈ [0, 1]. (14)

Si,finalment,fem z = 1,obtenim M (n + 1)! ≤ R(x, 1) ≤ N (n + 1)! . (15)

JosepPlaiCarrera

AraLagrangeusaelteoremadelvalorintermediperalafunció f (n+1) (x xz) (n+1)! iobtél’expressió R(x, 1) = f (n+1)(x xz) (n + 1)! pera z ∈ [0, 1]. (16)

Perfi,substitueixaquestaexpressióa(11)amb z = 1iobté: f(x) = f(0) + f (0)x + f (0) 2 x2 +···+ f (n)(0) n! xn + f (n+1)(u) (n + 1)! xn+1 , amb u = x xz ∈ [0,x].

L’èxitd’aquestapresentacióidelsseusresultatsnofaria,però,quepassés desapercebudalanecessitatd’aprofundirenlanocióde continuïtat deles funcionsilesqüestionsrelacionadesambl’existènciademàximsimínimsidel teoremadelvalormitjà,peròaixòhofarienmatemàticsdelsegle xix comara, perexemple,Cauchy.43

Referències

[1] Abel,N.H. «Mémoiresuruneclasseparticulièred’équationsrésolubles algébriquement». JournaldeCrelle,26(1829),131–156.

[2] Archibald,T.;Fraser,C.;Grattan-Guinnes,I. (organitzadors).«The HistoryofDifferentialEquations,1670–1950».JornadesaOberwolfach, del31d’octubreal6denovembrede2004, MathematischesForschungsinstitutOberwolfach,reportn.51/2004.

[3] Ball,W.W.R. Ashortaccountofthehistoryofmathematics.3aed. Londres:Macmillan,1901.

[4] Barbeau,E.J. Pell’sequation.NovaYork:Springer-Verlag,2003.(Problem BooksinMathematics)

[5] Bartholmèss,C. Histoirephilosophiquedel’AcadémiedePrussedepuis Leibnizjusqu’àSchelling.París:LibrairieduMarcDucloux,1850.

[6] Bell,E.T. Menofmathematics.NovaYork:SimonandSchuster,1937. [Traduccióalfrancèsd’AmiGandillon: Lesgrandsmathématiciens.París: Payot,1939.Reeditatl’any1959.TraduccióalcastellàdeFelipeJiménez deAsúa: Losgrandesmatemáticos.BuenosAires,Argentina:Editorial Losada,1948.Reeditatl’any2010.]

[7] Bernoulli,J. Opera.4v.Ginebra:1742.Reeditat,ambunaintroducció deJ.E.Hofmann,perGeorgOlmsVerlag,Hildesheim,1968.

[8] Bos,H.J.M.;Bunn,R.;Dauben,J.W.;Grattan-Guinness,I.;Hawkins, T.W.;Pedersen,K.M. Fromthecalculustosettheory,1630–1910.Anintroductoryhistory Grattan-Guinness,I. (ed.).Londres:GeraldDuckworth

43 Peramésinformacióvegeu,perexemple,latesidoctoraldeJudithGrabiner,llegidaaHarvard l’any1966irecollidaa[38].

Joseph-LouisLagrange: inmemoriam159

&Co.Ltd.,1980.[TraduccióalcastellàdeMarianoMartínezPérez: Del cálculoalateoríadeconjuntos,1630–1910.Unaintroducciónhistórica Madrid:AlianzaEditorial,1984.]

[9] Brizard,A.J. AnintroductiontoLagrangianmechanics.Hackensack, N.J.:WorldScientificPublishing,2008.

[10] Burton,D.M. Elementarynumbertheory.Boston,Mass.;Londres:Allyn andBacon,1976.ReeditatperW.C.BrownPublishers,Dubuque,IA,1989.

[11] Cantor,M. VorlesungenüberGeschichtederMathematik.4v.Berlín: Teubner,1880–1907.

[12] Capecchi,D. Lagrangeelastoriadellameccanica.Bari:Progedit,2005.

[13] Capecchi,D.;DeAngelis,M.;Sepe,V. Cinematicapianadeicorpirigidi. Milà: cisu,2005.

[14] Cohen,I.B. RevolutioninScience.Cambridge,Mass.:BelknapPress,1985. [TraduccióalcastellàdeDanielZadunaisky: RevoluciónenCiencia.Barcelona:EditorialGedisa,1988.]

[15] D’Alembert,J.L.R. «Recherchessurlecalculintégral». Actesdel’AcadémiedesSciencesdeParis (1746),182–224.

[16] Delambre,J.-B.J. «NoticesurlavieetlesouvragesdeM.leComteJ.L.Lagrange».A:[76,p. ix–li].

[17] deLorenzo,J. AnálisisInfinitesimal.Madrid:Tecnos,1987,17–29.[Traduccióal’anglèsdeltextdeLeibniza: ASourceBookinMathematics, 1200–1800.Cambridge,Mass.:HarvardUniversityPress,1969.]

[18] DeMoivre,A. Thedoctrineofchances:Amethodofcalculatingthe probabilitiesofeventsinplay.Londres:W.Pearson,1718.Reeditatper ChelseaPublishingCo.,NovaYork,1967.

[19] Dickson,L.E. Historyofthetheoryofnumbers.3v.Washington:Carnegie InstituteofWashington,1919.Reeditat,entresvolums,perChelsea PublishingCo.,NovaYork,1971,iperDoverPublications,Inc.,NovaYork, 2005.

[20] Edwards,C.H.,Jr. Thehistoricaldevelopmentofthecalculus.NovaYork; Heidelberg:Springer-Verlag,1979.

[21] Euler,L. «Curvarummaximiminimiveproprietategaudentiuminventio novaetfacilis». MemorieacademiaescientiarumPetropolitanæ,8(1736), 159–190.

[22] Euler,L. «Desolvtioneproblematvmdiophanteorvmpernvmerosintegros». CommentariiacademiaescientiarumPetropolitanæ,6(1738), 175–188.

[23] Euler,L. Methodusinveniendilineascurvasmaximiminimiveproprietate gaudentes,sivesolutioproblematisisoperimetricilattissimosensuaccepti. Lausane;Ginebra:MarcumMicaelemBousquet,1774.[Traduccióalcastellàd’AlbertoDou: Euler,L. Métododemáximosymínimos.Barcelona:

JosepPlaiCarrera

PublicacionsdelaUniversitatAutònomadeBarcelonailaUniversitat PolitècnicadeCatalunya,1993.]

[24] Euler,L. «DeusunovialgorithmiinproblematePellianosolvendo». Novi CommentariiacademiaescientiarumPetropolitanæ,11(1767),28–66. [D’acordamblesanotacionsfoupresentatal’AcadèmiadeSantPetersburg el15d’octubrede1759,iunaaltravegadael23demaigde1763.]

[25] Euler,L. «Elementacalculivariationum». NoviCommentariiacademiaescientiarumPetropolitanæ,10(1766),51–93.SantPetersburg:Saint PetersburgKaiserlicheAcademiederWissenschaften,1770.

[26] Fermat,P.de Fermat.OperaVaria.Barcelona: iec,2008.[Traduccióal catalàambcomentarisinotesdePlaiCarreraJ,ParadísJ.iViader,P.]

[27] Ferraro,G. Theriseanddevelopmentofthetheoryofseriesuptotheearly 1820s.NovaYork:Springer,2008.(SourcesandStudiesintheHistoryof MathematicsandPhysicalSciences)

[28] Galilei,G. «CartaaGuidobaldodelMontede29denovembrede1602». A:[29,vol. x,p.97–100].

[29] Galilei,G. LeOperediGalileoGalilei.21v.Florència:G.Barbera,1968.

[30] Galois,E. «Mémoiresurlesconditionsderésolubilitédeséquationspar radicaux». JournaldeMathématiquesPuresetAppliées (1831),417–433. Vegeu[79,p.21–38].

[31] Gauss,C.F. Disquisitionesarithmeticæ.Leipzig:GerhardFleischer,1801. [TraduccióalcatalàdeGriseldaPascualXufré,[86].]

[32] Gauthier,A. Essaihistoriquesurleproblèmedestroiscorps.París:Mlle V.Courcier,1817.

[33] Gibbs,J.W. Vectoranalysis.Yale:YaleUniversity,1907.Elaboratapartir deleslliçonsdeJ.WillardGibbsiEdwindBidwellWilson.Reimprèsper DoverPublications,NovaYork,1960.

[34] Gillispie,C.C. BiographicalDictionaryofMathematicians:reference biographiesfromtheDictionaryofScientificBiography.4v.NovaYork: CharlesScribner’sSons,1970.

[35] Girard,A. Inventionnouvelleenl’Algèbre.Amsterdam:Blauew,1629. ReeditatperD.BierensDeHaan,MuréFrères,Leiden,1884.

[36] Goldman,J.R. Thequeenofmathematics.Ahistoricallymotivatedguide tonumbertheory.Wellesley,Mass.:AKPeters,1998.

[37] Goldstine,H.H. Ahistoryofthecalculusofvariationsfromthe17th throughthe19thcentury.NovaYork;Berlín:Springer-Verlag,1980.(StudiesintheHistoryofMathematicsandPhysicalSciences;5)

[38] Grabiner,J.V. Thecalculusasalgebra.J.-L.Lagrange,1736–1813.Nova York:GarlandPublishing,1990.

[39] Grattan-Guinness,I. (ed.). CompanionEncyclopediaoftheHistoryand PhilosophyoftheMathematicalSciences.2v.Londres:Rouledge,1994.

Joseph-LouisLagrange: inmemoriam161

[40] Grattan-Guinness,I. TheFontanaHistoryoftheMathematicalSciences: theRainbowofMathematics.Hammersmith:FontanaPress,1997.

[41] Hairer,E.;Wanner,G. Analysisbyitshistory.NovaYork:Springer,2008. (UndergraduateTextsinMathematics.ReadingsinMathematics)

[42] Huygens,C. Horologiumoscillatorium.París:F.Muguet,1673.

[43] Itard,J. Essaisd’histoiredesmathématiques.París:LibrairieScientifique etTechniqueAlbertBlanchard,1984.

[44] Itard,J. «Lagrange(Joseph-Louis)».A:[34,vol. iii,p.1301–1315],enanglès,obéa http://www.encyclopedia.com/topic/Joseph-Louis Louis Lagrange.aspx,ia[43,p.309–334],enfrancès.

[45] James,I. Remarkablemathematicians.FromEulertovonNeumann.Washington,D.C.:MathematicalAssociationofAmerica;Cambridge:CambridgeUniversityPress,2002.(MAASpectrum)

[46] Kline,M. Mathematicalthoughtfromancienttomoderntimes.NovaYork: OxfordUniversityPress,1972.[TraduccióalcastellàdeCarlosFernándeziAlejandroGarciadiego,sotalacoordinaciódeJesúsHernández: El pensamientomatemáticodelaantigüedadanuestrosdías.3v.Madrid: AlianzaEditorial,1992.]

[47] Lagrange,J.-L. «CartaaGiulioCarlodiFagnanode27dejuliolde1754». A:[76,tom7,1877,p583–588].

[48] Lagrange,J.-L. «Recherchessurlaméthodedemaximisetminimis». MiscellaneaTaurinensia,vol. i,3–20.A:[76,tom1,1867,p.3–20].

[49] Lagrange,J.-L. «Surl’intégrationd’uneéquationdifférentielleàdifférencesfinies,quicontientlathéoriedessuitesrécurrentes». Miscellanea Taurinensia,vol. i,23–36.A:[76,tom1,1867,p.23–36].

[50] Lagrange,J.-L. «Recherchessurlanatureetlapropagationduson». MiscellaneaTaurinensia,vol. i,39–148.A:[76,tom1,1867,p.39–148].

[51] Lagrange,J.-L. «Essaid’unenouvelleméthodepourdétérminerlesmaximaetlesminimadesformulesintégralesindéfinies». MiscellaneaTaurinensia,vol, i,173–195.A:[76,tom1,1867,p.335–362].[Traducció parcialal’anglèsa[17,p.407–413].]

[52] Lagrange,J.-L. «RecherchessurlalibrationdelaLune,danslesquelles ontâchederésoudrelaquestionproposéeeparl’Académieroyaledes sciencespourlePrixdel’année1764». Prixdel’AcadémieRoyaledes SciencesdeParis,vol. ix (1764).A:[76,tom6,1870,p.5–61].

[53] Lagrange,J.-L. «Surlaméthodedesvariations». MiscellaneaTaurinensia, vol. iv,p.37–63.A:[76,tom2,1868,p.37–63].

[54] Lagrange,J.-L. «Solutiond’unproblèmearithmétique». MiscellaneaTaurinensia,vol. iv,p.671–731.A:[76,tom1,1867,p.671–731].

[55] Lagrange,J.-L. «Surlasolutiondesproblèmesindéterminésdusecond degré». Mémoiresdel’AcadémieroyaledesSciencesetBelles-Lettresde Berlin,vol. xxiii (1769).A:[76,tom2,1868,p.377–535].

JosepPlaiCarrera

[56] Lagrange,J.-L. «Nouvelleméthodepourrésoudrelesproblèmesindéterminésennombresentiers». Mémoiresdel’AcadémieroyaledesScienceset Belles-LettresdeBerlin,vol. xxiv (1770).A:[76,tom2,1868,p.655–726].

[57] Lagrange,J.-L. «CartaaD’Alembertde20denovembrede1769».A:[76, tom14,1892,p.153–156].

[58] Lagrange,J.-L. «Démonstrationd’unthéorèmed’arithmétique». Mémoiresdel’AcadémieroyaledesSciencesetBelles-LettresdeBerlin,(1770). A:[76,tom3,1892,p.189–201].

[59] Lagrange,J.-L. «Réflexionssurlarésolutionalgébriquedeséquations». Mémoiresdel’AcadémieroyaledesSciencesetBelles-LettresdeBerlin, (1770)i(1771).A:[76,tom3,1892,p.205–421].

[60] Lagrange,J.-L. «Nouvellesréflexionssurlestautochrones». Nouveaux Mémoiresdel’AcadèmieroyaledesSciencesetLettresdeBerlin,vol. i (1770),97–122.A:[76,tom3,1869,p.157–186].

[61] Lagrange,J.-L. «Démonstrationd’unthéorèmenouveauconcernantles nombrespremiers». NouveauxMémoiresdel’AcadèmieroyaledesSciences etBelles-LettresdeBerlin,(1771).A:[76,tom3,1892,p.425–438].

[62] Lagrange,J.-L. «Essaisurleproblèmedestroiscorps». Prixdel’Académie RoyaledesSciencesdeParis,vol. ix (1772).A:[76,tom6,1869,p.229–331].

[63] Lagrange,J.-L. Additionsauxélémentsd’algèbred’Euler.Lió:Bruyset, 1774.A:[76,tom7,1877,p.5–180].

[64] Lagrange,J.-L. «Surlaformedesracinesimaginairesdeséquations». NouveauxMémoiresdel’AcadèmieroyaledesSciencesetBelles-Lettresde Berlin (1772).A:[76,tom3,1877,p.479–516].

[65] Lagrange,J.-L. «Recherchessurlessuitesrécurrentesdontlestermes varientdeplusieursmanièresdifférentes,ousurl’intégrationdeséquationslinéairesauxdifférencesfiniesetpartielles;etsurl’usagedeces équationsdanslathéoriedeshasards». NouveauxMémoiresdel’AcadèmieroyaledesSciencesetBelles-LettresdeBerlin (1775).A:[76,tom4, 1869,p.151–251].

[66] Lagrange,J.-L. «CartaaLaplacede30dedecembrede1776».A:[76, tom14,1892,p.66–68].

[67] Lagrange,J.-L. «ThéoriedelalibrationdelaLuneetdesautresphénomènesquidépendentdelafigurenonsphériquedecetteplanète». NouveauxMémoiresdel’AcadèmieroyaledesSciencesetBelles-Lettresde Berlin (1780).A:[76,tom5,1870,p.5–122].

[68] Lagrange,J.-L. «CartaaD’Alembertd’1d’abrilde1781».A:[76,tom14, 1892,p.360,carta164].

[69] Lagrange,J.-L. «CartaaD’Alembertde21desetembrede1781».A:[76, tom14,1892,p.368,carta167].

Joseph-LouisLagrange: inmemoriam163

[70] Lagrange,J.-L. «Mémoiresurlathéoriedumouvementdesfluides».A: [76,tom4,1869,p.695–748].

[71] Lagrange,J.-L. «CartaaLaplacedel15desetembrede1782».A:[76, tom14,1882,p.116,carta20].

[72] Lagrange,J.-L. Méchaniqueanalytique.París:ChezlaVeuveDesainte, 1888.A:[76,tom11,1788].

[73] Lagrange,J.-L. «Leçonsélémentairessurlesmathématiquesdonnéesà l’ÉcoleNormaleen1795». Journaldel’ÉcolePolytechnique, viieet viiie cahiers,tom ii,1812.A:[76,tom7,1877,p.183–288].

[74] Lagrange,J.-L. Théoriedesfonctionsanalytiquescontenantlesprincipesducalculdifférentieldégagésdetouteconsidérationd’infiniment petits,d’évanouissans,delimitesetdefluxions,etréduitsàl’analysealgébriquedesquantitésfinies.París:MlleCourcier,1797.A:[76,tom9,1881, p.13–413].

[75] Lagrange,J.-L. Traitédelarésolutiondeséquationsnumériquesdetous lesdegrés.París:Courcier,1808.

[76] Lagrange,J.-L. ŒuvresdeLagrange.PublicadesperJ.-A.Serretencatorze volums:1867,1868,1869,1869,1870,1873,1877,1879,1881,1884, 1888,1889,1882,1892.

[77] Loria,G. «G.L.Lagrangenellavitaenelleopere». Ann.Mat.,20(1913), 9–52.Reimprèsa[78,p.293–333].

[78] Loria,G. Scritti,conferenze,discorsi.Pàdua:CasaEditriceDott.,1937.

[79] Malet,A. (ed.). Obrad’ÉvaristeGalois.Barcelona: iec,1984.(Monografies delaSecciódeCiències;1)

[80] Marachia,S. Storiadell’algebra.Nàpols:LiguoriEditore,2002.

[81] Marchal,C. Thethree-bodyproblem.Amsterdam:ElsevierScience Publishers,B.V.,1990.(StudiesinAstronautics;4)

[82] Marie,M.M. Histoiredessciencesmathématiquesetphysiques.París: Gauthier-Villars,1883–1888.12t.en4v.

[83] Meijering,E. «Achronologyofinterpolationfromancientastronomy tomodernsignalandimageprocessing». ProceedingsoftheIEEE,90(3) (2002),319–342.

[84] Montucla,J.E. Histoiredesmathématiques.4v.París:Jombert,1754. ReeditatperLibrairieScientifiqueetTechniqueAlbertBlanchard,París, 1968.

[85] Montucla,J.E. ArithmeticaUniversalis.Cambridge:1707.[Traduccióa l’anglèsdeD.T.Whiteside(ed.): MathematicalWorksofIsaacNewton, ii. Londres:JohnsonReprintCo.,1964.]

[86] PascualiXufré,G. Disquisicionsaritmètiques.Barcelona: iec,1996.

JosepPlaiCarrera

[87] Pesic,P. Abel’sproof.Anessayonthesourcesandmeaningofmathematicalunsolvability.Cambridge,Mass.:MITPress,2003.

[88] PlaiCarrera,J. «Lahelenadelasmatemáticas». Quaderns,Fundació CaixadePensions,43(1989),61–71.

[89] PlaiCarrera,J. «LesmatemàtiquesielsmatemàticsdelaRevolució Francesa». ButlletídelaSocietatCatalanadeMatemàtiques,11(2)(1996), 31–78.

[90] PlaiCarrera,J. «La Mémoire d’ÉvaristeGalois,anotadaicomentada». Pendentdepublicació.

[91] Reiff,R.A. GeschichtederunendlichenReihen.Tübingen:H.Laupp’sche Buchhandlung,1889.ReimprèsperMartinSändig,Wiesbaden,1969,i novamentperBiblioBazaar.

[92] ReyPastor,J. ResumendelasLeccionesdeAnálisisMatemático.Madrid: 1915.Reeditatambeltítol: LeccionesdeÁlgebra.Toledo:A.Medina,1924 i1931;Madrid:C.Bermejo,1947;Madrid:NuevasGráficas,1954i1960.

[93] Rosso,R. CorsodiStoriadellaalgebra,2012.

[94] Ruffini,P. Riflessioniintornoallasoluzionedelleequazionialgebraiche generali;opuscolodelcav.dott.PaoloRuffini.Mòdena:Societàtipografica, 1813.Esreculla: OpereMatematiche Bertolotti,E. (ed.).3v.Roma: CremonesedellaCasaEditricePerrella,1953–1954.

[95] Scharlau,W.;Opolka,H. VonFermatbisMinkowski.EineVorlesung überZahlentheorieundihreEntwicklung.Berlín;NovaYork:SpringerVerlag,1980.[Traduccióal’anglèsdeW.K.BühleriG.Cornell: From FermattoMinkowski:lecturesonthetheoryofnumbersanditshistorical development.NovaYork:Springer,1985.]

[96] Taton,R. «Inventairechronologiquedel’oeuvredeLagrange». Rev.Hist. Sci.,27(1974),3–36.

[97] Todhunter,I. Ahistoryofthecalculusofvariationsduringthenineteenthcentury.Londres:MacMillan,1873.ReproduïtaNovaYork:Dover Publications,1949.

[98] Thomasset,T. HistoireduSystèmemétrique.

[99] Vacca,G. «SuimanoscrittiineditidiLeibniz». BollettinodiBibliografiae diStoriadelleScienzeMatematicheeFisiche,2(1899),113–166.

[100] Valtonen,M.;Karttunen,H. Thethree-bodyproblem.Cambridge:CambridgeUniversityPress,2006.

[101] vanderWaerden,B.L. Ahistoryofalgebra.Fromal-Khw¯arizm¯ıtoEmmy Noether.Berlín:Springer-Verlag,1985.

[102] Waring,E. Meditationesalgebraicæ.Cambridge:Archdeacon,1770.

[103] Waring,E. «ProblemsconcerningInterpolations». Proceedingsofthe RoyalSocietyofLondon.PhilosophicalTransactionsoftheRoyalSociety, 69,59–67.

Joseph-LouisLagrange: inmemoriam165

[104] Weil,A. Numbertheory.Anapproachthroughhistory.FromHammurapi toLegendre.Boston,Mass.:BirkhäuserBoston,1984.

[105] Whitford,E.E. ThePellequation.NovaYork:CollegeoftheCityofNew York,1912.

DepartamentdeProbabilitat,LògicaiEstadística FacultatdeMatemàtiques UniversitatdeBarcelona GranViadelesCortsCatalanes,585 jpla@ub.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.2,2014.Pàg.167–197. DOI:10.2436/20.2002.01.57

Matemàticafinanceraentempsdecrisi

ArturoValdivia

Sovintespreguntaquèfaqueuntemamatemàticsigui interessant.Algunesdelesqualitatsquevénenalament sónlautilitat,labellesa,laprofunditatilafertilitat.La utilitatsolmesurar-seperl’aplicaciódeltemaforadeles matemàtiques.Labellesaésunaqualitatatractivaquetenen moltesmatemàtiques,totiquesovintnomésunullentrenat lapotveure.Laprofunditatveatravésdelavinculacióamb múltiplesideesitemesquesovintsemblenforadelcontext original.Ilafertilitatsignificaque,ambunesforçraonable, s’aconsegueixenresultatsnous,algunsd’útils,algunsde bonics,ipotserd’altresmésprofunds,queesperenser descoberts.

PeterForrester

Elpreuqueelshomesbonspaguenperlasevaindiferència verselsassumptespúblicséseldesergovernatsperhomes malvats.

Resum: Enaquesttreballespresentenalgunsdelsprocessosicàlculsestocàstics importantsperalateoriaquantitativadelrisccreditici.Aquestabrancadelamatemàtica financeratécomaobjected’estudielscontractesambriscdefallida,ésadir,contractes enelsqualsexisteixelriscdepatirunapèrduaeconòmicaacausadel’incompliment —intencionatono—delesobligacionsadquiridesperalgunadelespartsquesignenel contracte.Aquesttipusdecontractesésomnipresentenlacrisieconòmicaactual;per això,enaqueststempsdecrisimundial,ensinteressadiscutir-losdesdelamatemàtica financera.

Paraulesclau: càlculestocàstic,matemàtiquesfinanceres,modelitzacióestocàstica, processosestocàstics,risccreditici.

ClassificacióMSC2010: 60-01,60H30,60G05.

AquesttreballfouelguanyadordelPremiAlbertDoudel’any2012.

Plató

ArturoValdivia

1Introducció

Bella, fèrtil, profunda i útil sónpotseralgunsdelsadjectiususualsquefaria servirunmatemàtical’horadereferir-seaunafórmula,obéaqualsevol altreobjectematemàtic.Noobstantaixò,foradelgremicientífic,la—mala— experiènciaensdiuqueelsadjectiusmésfreqüentssobreunaequaciósolen sersenzillament complicada i incomprensible.Elquesemblaincreïble,almenys finsacertpunt,ésqueunafórmulapuguiser culpable dedestruirl’economia mundial,talcomanunciavaeltitulard’unarticlepublicatrecentmentperlaBBC (vegeu[25]).L’equacióacusadaésla fórmuladeBlack-Merton-Scholes perquè estimaelpreudelcontractefinancerconegutper opcióeuropeadevenda. 1 Senseentrararacomaraendetalls,heusaquílafórmulasentenciada:

Aquestafórmula,quevamerèixerelPremiNobeld’Economiael1997,vaser obtingudaal’inicidelsanyssetantaperFischerBlack(1938–1995),RobertC. MertoniMyronS.Scholes(vegeu[8]i[43]).

D’esquerra adreta,Black,MertoniScholes.

EnelmodeldemercatconsideratperaobtenirlafórmulasesegueixlapropostadePaulSamuelson(1915–2009)—guanyadordelPremiNobeld’Economia de1970—demodelarl’evoluciódelpreudelsactiusentermesdel’exponenciald’un movimentbrownià. 2 Aquestapropostaprovédel’evidènciaempírica segonslaqualelsincrementsdellogaritmedelpreusónindependents;una característicaqueposademanifestjustamentelmovimentbrownià.Defet,la ideaoriginald’usarunmodelprobabilísticpermodelarelmercatdevalorsés habitualmentatribuïdaaLuisBachelier(1870–1946),elqual,el1900,icom

1 Aquestcontracteesformalitzaentreduesparts,el compradordel’opció iel venedordel’opció Ensignarelcontracte,elcompradordel’opcióadquireixeldret—perònol’obligació—devendre uncertproductealvenedordel’opció,perunpreupredeterminatal’horadesignarelcontracte. Enelcontracteesdeterminatambéladataenlaqualseràpossibleexercireldretdevenda.

2 Elprocésconegutcoma movimentbrownià ésanomenataixíenhonoralbotànicRobert Brown(1773–1858),elqualvaobservarelmovimentmoltirregulardepartículesdepol.lendins del’aigua.

apartdelseutreballdoctoral[1],vaferundelsprimersestudismatemàtics sobreelmovimentbrownià.3 ÉsperaquestesrelacionsqueRobertA.Jarrow, unalumnedeMertondequiparlaremtambémésendavant,anomena pare, avi i besavi delamatemàticafinanceraentempscontinuMerton,Samuelsoni Bachelier,respectivament(vegeu[29]).

D’altrabanda,enelscàlculsqueportenfinalmental’obtenciódelafórmula (1) esfaúsdellemad’Itô,resultatclau4 delcàlculestocàsticdesenvolupat perKiyoshiItô(1915–2008),guanyadordelspremisGauss2006iWolf1987. D’acordambJarrow,abansdeltreballdeMertonningúenlaprofessiófinancera teniaconeixementdellemad’Itô;avui,encanvi,ésunaeinafonamental.

D’esquerraadreta,Bachelier,ItôiSamuelson.

LafórmuladeBlack-Merton-Scholesés,pertant,unexemplequeelsresultats dematemàtiquesfinanceresesbasenfortamentenelsprocessosielscàlculs estocàsticsusatspermodelarelfenomenobjected’estudi.

EltreballdeBlack,MertoniScholesvaposarordreaunasituaciómésaviat caòtica,onlavaloraciód’opcions—lesqualserenproducteshabitualsdes d’almenyselsegle xvii—esbasavaenlasimpleintuïciórespecteaunmercatla dinàmicadelqualnoestavabendefinida(vegeu[52]).Calpreguntar-se,doncs, sihauríempogutevitarladestrucciódel’economiamundialprenentdecisions apartirdelaintuïció,enllocd’emprarlafórmuladeBlack-Merton-Scholes.

Independentmentdesiunmodelmatemàticés bo o dolent,laresponsabilitat delseuús,ilainterpretacióposteriordelsseusresultats,recauenlespersones. Pertant,culpardelacrisiunaequaciósemblaiguald’absurdqueculparl’aritmèticadetotselsfrausfiscals.Enqualsevolcas,talacusacióensrecordaque l’objectiudeladivulgaciódelaciènciarauainformarelpúblicicapacitar-lo perquèaprofitielconeixementcientíficquanjutgi,perexemple,lalegitimitat

3 Després,el1905—o AnnusMirabilis—AlbertEinstein(1879–1955)vatreballartambéen eltema.Noobstantaixò,vaserNorbertWiener(1894–1964)elprimeraprecisarlaformulació matemàticadelmovimentbrownià—queenconseqüènciaéstambéconegutcoma procésde Wiener

4 Uncomentarisobreaquesttemaperpartdel’AcadèmiaNacionaldeCiènciesdelsEstats Units: SensetenirencompteelteoremadePitàgoresenlacontesa,ésdifícilpensarenunresultat matemàticqueavuidiasiguimésbenentèsimésàmpliamentaplicatalmónqueel lemad’Itô Aquestresultattéelmateixpaperenelcàlculestocàsticqueelteoremafonamentaldelcàlculen elcàlculclàssic.Ésadir,ésel sinequanon deltema.

ArturoValdivia

d’undeuteolesveritablesimplicacionsderivadesd’emprar,correctamento incorrectament,unafórmulamatemàticaounaaltraenqualsevolàmbit,no nomésenelfinancer.Senseaquestconeixement,osenselacapacitatd’usar-lo, noéspossiblediferenciarentrelafórmulaqueapareixa (1) ilaqueapareixa lafigura1.Laprimeraésproducted’untreballseriós,productedel’evolució d’unmodelcientíficquecombinal’esforçielconeixementd’especialistesde diversesdisciplinesdelamatemàticaialtresciències.Lasegonafórmulaés simplementundisbarat.

Figura1: Coméspossibledecidirsenseconeixement?I,senseladivulgacióadequada,coméspossibleusarelconeixementgeneratperla comunitatcientífica?

Usemelterme risccreditici quanensreferimalriscdepatirunapèrdua econòmicaacausadel’incompliment—intencionalono—delesobligacions contretesperalgunadelespartsquesignenuncontracte.Comqueaquest tipusdecontractesésomnipresentenlacrisieconòmicaactual,s’estudiendes dediferentsàreesdelconeixement.Aquestarticletécomaobjectiupresentar algunesdelesideesbàsiquesrelacionadesambl’estudidelrisccrediticides dela teoriaquantitativadelrisccreditici,queésunabrancadelamatemàtica financera.Mostraremalgunsdelsconceptesitècniquesméssignificatiusdeles tendènciesactualsd’aquestateoria.

Enlaprimerapartpresentaremelsprocessos(vegeulasecció2)ielscàlculs estocàstics(vegeulasecció3)necessarisperalamodelitzaciódelrisccreditici. Estudiaremalgunsdelsprocessosestocàsticsclàssics(cadenesdeMarkov, processosdeLévy,dePoissonideWiener),d’altresd’interèsrecent(processos dememòriallargaiprocessosd’àmbit)imotivaremlaintegracióestocàstica respecteaalgunsd’aquestsprocessos.Enlasegonapartexplicaremalgunes ideesbàsiquesdelamatemàticafinanceraipresentaremelsdospuntsdevista tradicionalsdelateoriaquantitativadelrisccreditici,quesónel puntdevista estructural iel puntdevistadeformareduïda.Finalment,discutiremalguns aspectesdelpaperqueexerceixlamatemàticafinanceraactualment;ambaixò destacaremlanecessitatquelacomunitatmatemàtica,engeneral,s’interessi peltemaireinterpretiambnousullsl’epígrafdePlatóqueobreaquestarticle.

2Processosestocàsticsenlamodelitzaciódelrisc

Donatunespaideprobabilitat (Ω, F , P),anomenarem procésestocàstic (Xt )t∈I unafamíliadevariablesaleatòries Xt : Ω →S,on I ésun conjuntd’índexs i S l’anomenat espaid’estats o espaidevalors.Enelscasosméshabituals I espren coma N0, Z, [0,T ],obé R,demaneraquel’índex t sesolinterpretarcomel temps.Exemplesde S,comveuremacontinuació,sónconjuntsfinits, Zn,o bé Rn .

Intuïtivament,unprocésestocàsticespotpensarcomunamaneraderepresentarl’evoluciód’unfenomenelcomportamentdelqualsiguitanirregular queconvinguiconsiderar-loaleatori.Aquestsprocessossónundelsobjectes centralsdelaprobabilitatmoderna,ielsescenarisenelsqualspodenseraplicatsinclouendiversesàreesdelesciènciesexperimentalsilesciènciessocials. Defet,unmateixprocésestocàsticpotservirperamodelarfenòmensdiferents que,almenysaprimeravista,semblariendesconnectats.Aquestfetesténla nociód’universalitat quedónaelteoremacentraldellímitiensfaevocarla frased’EliakimH.Moore,amblaqualSamuelsonobreelseullibre[57]:

L’existènciad’analogiesentreelscomponentscentralsdediversesteories implical’existènciad’unateoriageneralsubjacent,laqualunificales teoriesparticularspelquefaaaquestscomponentscentrals.

Algunsdelsexemplesclàssicsd’aplicacióprovenendel’estudidelcanvi climàtic,creixementdetumors,epidèmies,expansióderumorsenunaxarxa social,evoluciódelpreudelsactiusenlaborsa,detecciód’emissiódepartícules, dinàmicadepoblacions,filtratgedesenyals,hidrologia,lingüística,optimització, recurrènciadeterratrèmols,teoriadelcontrol,teoriadecuesiturbulènciade fluids(vegeu[3, 56, 61]).Noobstantaixò,lametodologiadefonspermetabordar tambéproblemesdelamatemàticabàsica.Undelsexemplesfavoritsrelacionats ambaixòésl’estudidels grafsaleatoris,concepteintroduïtperPaulErd˝osi AlfrédRényialfinaldelsanyscinquanta(vegeu[23]).Enaquestescenari,es podenferservirtècniquesprobabilístiquesperadonarexemplesdel’existència degrafsambcaracterístiquesespecífiques.

Acontinuació,presentemalgunsprocessosestocàsticsrelacionatsamb lamodelitzacióenmatemàtiquesfinanceres,d’algunsdelsqualssen’haconsolidatlapràctica.AquestéselcasdelescadenesdeMarkov,elprocésde Poisson,elprocésdeWienerialtresprocessosdeLévy.Altresprocessosque presentemtenenuninterèsmésrecentielsmodelscorresponentsencaraestan endiscussió.Ensreferimalsprocessosd’àmbitialsprocessosfraccionaris.Ens centraremenelsprocessosambconjuntsd’índexscontinus,iensreferima [51,63,62]peraladiscussiódelamatemàticafinanceraatempsdiscret.

2.1ProcessosdeLévyil’evoluciódelspreus

Coms’haesmentatjaenlaintroducció,elmodeldeSamuelsonproposamodelar l’evoluciódelpreudelsactiusutilitzantl’exponenciald’unmovimentbrownià.

ArturoValdivia

L’evidènciaempíricarelacionadaambaquestapropostaésqueellogaritmedels preustéincrementsindependents.

Unaltrefetempíricqueespotconsideraréslapossibilitatqueelpreu tinguiunacaigudaopujadasobtades.Enaltresparaules,quel’evoluciódel preusiguidiscontínua.Aquestesdiscontinuïtatsespodendonardesprésde l’aparicióinesperadad’unesdevenimentsignificatiu,compotserunfenomen climàtic,uncanvilegislatiu,unademanda,undescobrimentcientífic,etc.

ElprocésdeWiener,omovimentbrownià,tétrajectòriescontínues,de maneraquenopotposardemanifestladiscontinuïtatenl’evoluciódelpreu suggeridaperl’evidènciaempírica.Unamaneraderesoldreaixòésagregantun procésdePoisson,elqualmodelitzaels salts idónallocadiscontinuïtats.Més generalment,laideaésmodelarl’evoluciódelspreusutilitzantunprocésde Lévy.Precisemladefiniciód’aquestsprocessos.

Definició1. Unprocésestocàstic (Lt )t∈[0,T] s’anomena procésdeLévy sisatisfà lescondicionssegüents:5

1. L0 = 0.

2. Té incrementsestacionaris,ésadir,ladistribuciódelsincrements Lt+s Lt depènnomésde t s,inode t.

3. Té incrementsindependents,ésadir,si r<s ≤ t<u llavors Lu Lt i Ls Lr sónvariablesaleatòriesindependents.

UnacaracterísticaimportantdelsprocessosdeLévyésqueperatot t ∈ [0,T], Lt téunadistribucióinfinitamentdivisible.Recordemqueunadistribució F es diu infinitamentdivisible siperatotenter n> 1existeixenvariablesaleatòries ξ1,...,ξn independentsiidènticamentdistribuïdestalsque ξ1 +···+ ξn té distribució F .AquestéselcasdelesdistribucionsnormalidePoisson.Pera veureque Lt téefectivamentunadistribucióinfinitamentdivisiblen’hihaprou

5 Perexcloureprocessosqueinclouensaltsenmomentspredeterminats(noaleatoris)s’ha d’imposartambélacondició limh→0 P(|Lt+h Lt |≥ ε) = 0peratot ε> 0.Referènciesclàssiques sobreprocessosdeLévyilessevesaplicacionsenfinancesespodentrobara[58,12,59,60].

D’esquerraadreta,Lévy,PoissoniWiener.

ambconsiderarlasumatelescòpica

Lt = n 1 k=0 L(k+1)∆ Lk∆ ,n> 1, ∆ := t/n. (2)

Aquestasumamostraque Lt espotescriurecomlasumaarbitràriadevariables independents L(k+1)∆ Lk∆,ambdistribucióigualalade L∆.Elresultatrecíproc tambééscert:totadistribucióinfinitamentdivisibledefineixunprocésdeLévy.6

Definició2. El movimentbrownià,o procésdeWiener,ésunprocésdeLévy (Wt )t∈[0,T] enelqual,peratots s, t:0 ≤ s<t ≤ T ,elsincrements Wt Ws tenenunadistribuciónormal N(0,t s).

Definició3. El procésdePoisson ésunprocésdeLévy (Nt )t∈[0,T] enelqual, peratots s, t:0 ≤ s<t ≤ T ,elsincrements Nt Ns tenenunadistribucióde Poissonambparàmetre λ(t s)

2.1.1Saltsiteoriadelaruïna. ElprocésdePoisson (Nt )t≥0 potutilitzar-se permodelarelstempsenquèocorrendeterminatsesdeveniments.Perexemple, comveuremenlasecció4,lafallidaenunaempresaespotmodelarcomel primermomentenquèundeterminatparàmetreeconòmicexperimentaun salt i.e.,incrementodecrement.Perexemple,sidefinimqueunesdeveniment tindràllocenelprimermomentenquè (Nt )t≥0 tinguiunsalt, i.e., τ := inf{t ∈ [0,T] : Nt = 1}= inf{t ∈ [0,T] : Nt > 0}, (3)

llavorspodemdemostrarque τ tédistribucióexponencial, i.e., P(τ>t) = exp( λt).Enefecte, P(τ>t + s) = P(Nt+s = 0) = P(Ns = 0,Nt+s Ns = 0) = = P(Ns = 0)P(Nt+s Ns = 0) = P(Ns = 0)P(Nt = 0).

Lesprimeresidentitatssesegueixendequeelsincrementsde (Nt )t≥0 són independentsiestacionaris.

ObserveuqueenunprocésdePoissontotselsincrementssóndegrandària1. Aixòespotgeneralitzardemaneraquelagrandàriadelssaltstinguiuna distribuciódonada.

Definició4. Sigui (Nt )t≥0 unprocésdePoissonambintensitat λ,isigui (ξk)k∈N unasuccessiódevariablesindependentsiidènticamentdistribuïdes ambllei F .Suposemque (Nt )t≥0 i (ξk)k∈N sónindependents.Un procésde Poissoncompost amb intensitat λ> 0i distribuciódelagrandàriadelssalts F ésunprocésestocàstic (Jt )t≥0 definitper

Jt := Nt k=1 ξk,t ≥ 0.

6Vegeu,perexemple,elcorol lari11.6a[58].

ArturoValdivia

ElprocésdePoissoncompostespotutilitzarperdonarunmodelclàssic enlateoriadelaruïna(vegeu[17]).Enefecte,podemmodelarelcapitald’una asseguradoradelamanerasegüent:

on C0 ésunaconstantquerepresentaelcapitalinicialdel’asseguradorai ct representaelcapitalquepaguenenconjunttotselsassegurats.Finalment, ξk representaelsimportsqueperdoqueguanyal’asseguradoraquanundels clientstéunaccident.Aquestmodelcorresponalaintuïcióqueelsaccidents vanocorrentenmomentsaleatoris(modelatspelssaltsde (Nt )t∈[0,T]),ique l’importdecadascund’aquellsascendeixa ξk, k ∈ N

2.1.2Trajectòriesisimulaciód’unprocésestocàstic. Sifixemunescenari ω ∈ Ω,podemconsiderarl’aplicació α X(ω,α).Anomenarem trajectòria de ω aquestaaplicacióiladenotaremper X(ω).Lasimulaciódeprocessos estocàsticss’enténcomlasimulaciódetrajectòries.Enlafigura2esmostrala simulaciódeduestrajectòries.Comhemesmentatabans,lestrajectòriesdel procésdeWiener (Wt )t∈[0,T] sóncontínues.7

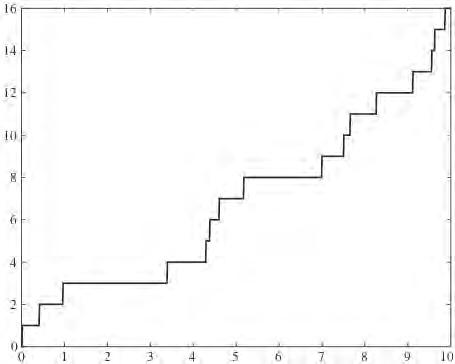
Figura2: EsmostraunatrajectòriadelprocésdeWiener(esquerra)i unadelprocésdePoisson(dreta).

Lasumatelescòpicade (2),ilapropietatqueelsincrements Wt+∆ Wt són independentsitenendistribució N(0, ∆),enssuggereixenl’algoritmesegüent perasimularunatrajectòriad’unprocésdeWienerenunaparticióde [0,T] amb N puntsequidistants {tk := kT/N, 0 ≤ k ≤ N} detemps:

7Unapresentaciódelsnousdesenvolupamentsenl’àreadesimulacióespottrobara[54].

Algoritme1:Simulaciód’unatrajectòriad’unprocésdeWienerenunapartició de [0,T] amb N puntsequidistants {tk := kT/N, 0 ≤ k ≤ N} detemps.

1. Definir W0 := 0.

2. Desde k = 1 finsa N

a) Generarlavariablealeatòria X ambdistribució N(0, T N ).

b) Definir Wtk := Wtk 1 + X

DemanerasimilartenimunalgoritmeperasimularunprocésdePoisson. Comqueaquestprocésésesglaonat,noméshemdesimularelsmomentsen quèesprodueixenelssalts.Recordemquesi U ésunavariablealeatòriaamb unadistribucióuniformeen (0, 1),llavors X :=− ln(U)/λ téunadistribució exponencialambparàmetre λ.

Algoritme2:Simulaciódelssaltsd’unprocésdePoisson.

1. Definir t := 0, idefinirunvector S.

2. Generar U ambdistribucióuniformea (0, 1)

3. Actualitzarelvalorde t amb t ln(U)/λ.

4. Mentre t<T

a) Agregar t alvector S

b) Generar U ambdistribucióuniformeen (0, 1).

c) Actualitzarelvalorde t amb t ln(U)/λ

2.2CadenesdeMarkovilesagènciesdequalificació

Una agènciadequalificacióderisc ésunaempresadedicadaaavaluarelrisc crediticialqualestanexposatsdeterminatsproductesfinancersofertsperempreses,pergovernsregionalsoperestats.Laqualificació—o rating—assignada descriufinsaquinpunttériscelproducted’acordambelscriterisdecada agència.Elsinversorsutilitzenaquestesqualificacionsperaobtenirinformació sobreelsproductesfinancersenelsqualsdesitgeninvertir.

Algunsexemples8 d’agènciesdequalificacióquepodemtrobarúltimament enelsmitjanssónDun&Bradstreet,Fitch,Moody’siStandard&Poor’s.Arran delescrítiquesisospitessobreelfuncionamentd’aquestesagències,han aparegutalgunesiniciativespertald’estructurarcomunitats—noempreses!— dequalificació.9

8 Espottrobarunallistaextensad’agènciesdequalificacióa http://www.defaultrisk.com. 9Unaideainteressantsobreaquesttemaespottrobara http://www.wikirating.org.

ArturoValdivia

Elsproductesfinancerssónmonitoritzatsirequalificatsconstantment.En conseqüència,unacadenadeMarkovdónaunmodelperalscanvisdequalificació—o migraciócreditícia—queexperimentaunproducteatravésdeltemps (vegeu[30]).Precisemaquestconcepte.

Definició5. Sigui S={s0,s1,...,sn} unespaidevalorsambunaquantitat finitad’elements,elsqualsanomenarem estats.Una cadenadeMarkov ésun procésestocàstic C : Ω × N0 →S amblapropietatque

Unestat si esdiu absorbent si P(C

Figura3: AndrejMarkov(1856–1922)iunexempled’unacadenade Markov.

.

LesqualificacionsqueaplicaStandard&Poor’ssón,demillorapitjor, AAA, AA+, AA, AA , A+, A, A , BBB+, BBB, BBB , BB+, BB, BB , B+, B, B , CCC+, CCC, CCC , CC, C,i D.DemaneraqueelsestatsdelacadenadeMarkov associadaserien S={AAA,AA+,AA,AA ,...,CCC ,CC,C,D}.

L’estat D s’enténcoml’estatdefallida—o default,enanglès.Suposaremque unavegadaques’arribaal’estatdefallidajanoéspossiblesortir-ne,ésadir, quel’estatdefallidaésunestatabsorbentdelacadenadeMarkov.

Undelsproblemesmésimportantsenaquestmodeléscalcularlaprobabilitat d’arribaral’estatdefallidaabansd’untemps T ∈ N o,equivalentment,calcular ladistribuciódeltempsaleatori(cf.(3)) τ := inf {k ∈{0, 1, 2,...,T } : Ck = D} . (5)

Vegemcomespotcalcularaquestadistribució.Consideremlamatriudefinida per

P := pij = P(C1 = sj | C0 = si) n i,j=1

L’entrada pij ésigualalaprobabilitatdepassaral’estat sj ,atèsquel’estat actualés si.Aquestamatriuesdenomina matriudetransició.Lessevespotències descriuenelscanvisd’estat—o transicions—delacadena.Mésespecíficament, si p(k) ij éslaprobabilitatque,partintdel’estat si,s’arribial’estat sj després d’exactament k passos,llavorsesdemostraque

Pertant,laprobabilitatquepartintdel’estat s0 = AAA noarribemal’estatde fallida sn = D abansde T passosésiguala

(τ>T) = j≠n p(T) 1j = 1 p(T) in .

2.3EspiraldeWiener,movimentbrowniàfraccionari

ElprocésdePoissonieldeWienersatisfanunacondicióanàlogaal’expressada a (4),ésadir,donatelvaloractual,l’evoluciófuturadelprocésésindependent delseupassat.Diremqueunprocésés markovià sicompleixaquestacondició. Veuremacontinuacióunageneralitzaciódelmovimentbrownià—el moviment browniàfraccionari—quepotdeixardesermarkoviàiexhibir,encanvi,una memòriallarga,ésadir,quevalorsfutursdelprocésestiguincorrelacionats ambelsseusvalorspassats.

ElmovimentbrowniàfraccionarivaserintroduïtperAndrejKolmogorov (1903–1987)quanestudiavalesanomenades espiralsdeWiener,mentreque BenoîtMandelbrot(1924–2010)iJohnVanNessvandesenvolupardiverses propietatsd’aquestprocés(vegeu[42,18]).

Definició6. Sigui A unconjuntd’índexsiguala [0,T] oa R.Diremqueel procésestocàstic (BH t )t∈A ésun movimentbrowniàfraccionarideparàmetre H ∈ (0, 1) sisatisfàlescondicionssegüents:

1. BH 0 = 0.

2. Ésun procésgaussià, i.e.,peratotconjuntfinitd’índexs t1,...,tk es compleixque (BH t1 ,...,BH tk ) téunadistribuciónormalmultivariada.

3. Bt téunaesperançaiguala0,peratot t ∈ A.

4.Peracada s,t ∈ A escompleixque

E[BH s BH t ] = 1 2 (s2H + t2H −|t s|2H ). (6)

ArturoValdivia

Mandelbrotvadenominarelparàmetre H paràmetredeHurst,enhonora HaroldHurst(1880–1978),elqualambelsseusestudisestadísticssobreels desbordamentsdelriuNilvatrobarquedadesmoltllunyaneseneltemps estavencorrelacionades.Aquestacaracterísticadememòriallargaesmodela béambelmovimentbrowniàfraccionari.

Actualment,l’aplicaciód’aquestprocésenmatemàtiquesfinanceress’estudia endiversesdireccions.Perexemple,comunageneralitzaciódelamodelització del’evoluciódelspreusdelsactius,reemplaçantelmovimentbrowniàper unmovimentbrowniàfraccionari(vegeu[47]).També,comunmodelpera l’evoluciódevariablesmacroeconòmiques,comelstipusd’interès,elsquals, segonsl’evidènciaempírica,nosónmarkovians(vegeu[5]).

Lesestructuresfractals10 tenenunacaracterísticaimportantconegudacoma autosimilitud,queintuïtivamentpodempensarcomlainvariànciaenl’estructura en ferzoom enunadelesparts.Elmovimentbrowniàfraccionariéstambé autosimilarenelsentitestadísticprecisatperlaproposiciósegüent.11

Proposició7. Si (BH t )t∈I ésunmovimientbrowniàfraccionarideparàmetre H ∈ (0, 1),aleshores12

(s H BH st )t∈I d = (BH t )t∈I ,s> 0.

Sifixem H = 1 2 i A = [0,T ] llavorsobtenimelmovimentbrowniàestàndard quehemvistabans.Demaneraqueelmovimentbrowniàtambéésautosimilar. Caldestacarque H = 1/2ésl’únicvalorperalqual (BH t )t∈I téincrements independents.

10 BenoîtMandelbrotésbenconegutpelseullibretitulat Lageometriafractaldelanatura (vegeu[39]).En[40]i[41]espodentrobaralgunesideesdecaracterístiquesfractalsassociades amblamatemàticafinancera.

11 Lademostraciód’aquestresultatésunaconseqüènciaimmediatadelfetquelafuncióde covariànciade(6)éshomogèniad’ordre2H

12Elsímbol d = denotaigualtatendistribució.

D’esquerraadreta,KolmogoroviMandelbrot.

Figura4: Al’esquerraapareixelfractalconegutcoma flocdeneude Koch,ialadretaunatrajectòriad’unmovimentbrowniàfraccionariamb unaseccióampliadaperamostrarautosimilitud.

2.4Campsestocàsticsiprocessosd’àmbit

Enladefinicióde procésestocàstic quehemestablertal’inicidelasecció2 esmentemqueelconjuntd’índexs I solserunsubconjuntde R.Unaextensió naturalconsisteixaprendreunconjuntd’índexsentempsiespai,ésadir, delaforma J := R ×X,onlanovacomponent espacial potser,perexemple, X= Rn.Anomenarem campestocàstic aquestaextensióiladenotaremper (I(t,x))(t,x)∈J . Un campd’àmbit ésuncampestocàstic (I(t,x))(t,x)∈J talque,peracada (t,x) ∈ R ×X,elvalorde I(t,x) depènd’uncertconjunt A(t,x) ⊂ (−∞,t] ×X, elqualdenominem àmbitassociata (t,x).Unàmbit A(t,x) potserbastant general,peròésusualtriar-lodemaneraquesiguihomogenienespaiien temps,ésadir,fixat A(0, 0) ⊂ (−∞, 0) ×X,esdefineixperacada (t,x) ∈J l’àmbit A(t,x) :={(s,i) ∈J : (s t,i x) ∈ A(0, 0)}.Elrold’unàmbit A(t,x) ésestabliruncondecausalitat,definintquinsesdevenimentspassatstenen efecteenelvalorpresentdelcampestocàstic.Pensarem,doncs,que I(t,x) és donatper

I(t,x) = A(t,x) g(t,x)(s,ξ)σ(s,ξ)L(ds, dξ), (7) on g ésunafunciódeterminista,la volatilitat σ ésunaltrecampestocàsticila integrals’had’entendrecomunaintegralestocàstica(tipusWalsh[66])respecte delamesuraaleatòria L.Peramésdetallssobreladefinicióprecisade camp d’àmbit ensreferima[3, 2, 14].Noobstantaixò,esmentemqueunamanera demotivar (7) ésconsiderarequacionsenderivadesparcialsperturbadesper un sorollblancenespaiitemps (cf.[46]).Usaremunaheurísticasimilarenla secció3.3permotivarlesequacionsdiferencialsestocàstiquesenelsentitd’Itô.

Un procésd’àmbit (Xθ )θ∈I éslarestricciód’uncampd’àmbit (I(t,x))(t,x)∈J alllargd’unacorba α,ésadir,donatunsubconjuntde R, I,iunacorba α : I→J, (Xθ )θ∈I ésdonatper Xθ := I(α(θ)).Aquestsprocessosvanser

introduïtsamitjandeladècadapassadaperBarndorff-Nielsen,Schmiegeli col laboradors(vegeu[3]),ambl’objectiudemodelarlaturbulènciaenfluidsi elcreixementdetumors.Actualments’estudienlespropietatsteòriquesiles possiblesaplicacionsd’aquestsprocessos.Enparticular,quantal’estuditeòric, unalíniaderecercatractadeldesenvolupamentd’uncàlculestocàsticassociat. Pelquefaalesaplicacionsfinanceres,s’estudia,perexemple,laviabilitatde modelarvariablesmacroeconòmiquesipreusdederivatsfentservirprocessos d’àmbit(vegeu[14]),aixícomlasevaaplicacióenproblemesderisccreditici (vegeulasecció4).Mésencara,s’estudialapossibilitatdemodelardirectament elvalordederivatsfinancerssensenecessitatd’imposarunadinàmicaespecífica peralspreusdelsactius,contrastantaixòambelsenfocamentsclàssicsque obtenenelvalordelsderivatsapartirdelsupòsitd’unadinàmicaespecíficaper al’evoluciódelspreusdelsactius.

3Càlculestocàstic

Comencemperfixarunespaideprobabilitat (Ω, F , P) iconsideremunprocésde Wiener (Wt )t∈[0,T].Anomenarem filtració totasuccessiócreixentde σ -àlgebres (Ft )t∈[0,T].Donatunprocésestocàstic (Xt )t∈[0,T],anomenarem filtraciónatural generadaper X lafiltraciódefinidaper FX := (F X t := σ(Xs ,s ≤ t))t∈[0,T ].

Enlesaplicacions,lesfiltracionsrepresentenlainformaciódisponiblesobreel fenomenestudiat.Mésespecíficament, F X t0 representalainformaciódisponible queprovéd’observarelfenomen—modelatper (Xt )t∈[0,T]—finsauntemps t0

3.1Laintegralestocàstica

Laintegralestocàsticaesdefineixendospassos.Primer,esconstrueixlaintegral comunaisometria I0 : ET → L2([0,T ] × Ω),sent ET unaclassede processos esglaonats,ésadir,processosdelaforma ut := n j=1 uj 1[tj 1,tj )(t),t ∈ [0,T], (8)

on0 =: t0 ≤···≤ tn := T i,peracada j = 1,...,n, uj pertanya L2(Ω) iés Ftj 1 -mesurable.Sigui ΛT l’adherènciade ET a L2([0,T ] × Ω).Elsegonpasde laconstruccióésestendre I0 aunaisometria I : ΛT → L2(Ω).Demaneraquesi un → u a L2([0,T ] × Ω),aleshores I(u) := lim I0(un),enelsentitde L2(Ω), ET

T I L2(Ω).

Peralprimerpasdelaconstrucciódefinimlaintegralde u = (ut )t∈[0,T] ∈ET coma ET I0 → L2(Ω) n j=1

Vegem-neunexemple.Siconsideremelprocésesglaonatsegüent:

1 1(tj 1,tj ](t),n ≥ 1,t ≥ 0,

espotveureque un → W iqueescompleixlaigualtatsegüent:

Aixòcontradiulaintuïcióquetindríemenelcàlculdeterminista:si x : [0,T ] → R ésunafunciódeterministadiferenciabletalque x0 = 0(escrivint xt enllocdel clàssic x(t)),llavors

(9)

Fixeu-vosquelaintegralestocàsticanoescomportacomlaintegraldeRiemannStieltjesenelsentitsegüent.Consideremunasuccessiódeparticions Πn := (tn 0 := 0 ≤ tn 1 ≤···≤ tn rn := T) talqueelpasdelaparticiótendeixia0.Sigui λ ∈ [0, 1] idefinim τ n k := (1 λ)tn k + λtn k+1.Espotdemostrarque

onellímitésenelsentitde L2(Ω).Ésadir,peracada λ tenimunaintegral diferent.Siprenem λ = 0recuperemladefiniciódelaintegrald’Itô.Mentreque siprenem λ = 1 2 teniml’anomenada integralestocàsticadeFisk-Stratonovich. Elsegonpasdelaconstruccióésméstècnicil’ometempersimplicitaten l’exposició.Peraunaexposiciómésdetalladasobreaquestesideesensreferim a[36,53,65].

3.2Processosilemad’Itô

Un procésd’Itô ésunprocésestocàsticdelaforma

ArturoValdivia

onelsprocessos (us )s∈[0,T] i (vs )s∈[0,T] satisfandeterminadescondicions.Per conveni,unaformaalternativad’escriureelprocésésenlaseva formadiferencial dXt = ut dWt + vt dt.

Laintegralestocàsticarespectede (Wt )t∈[0,T ] quehemdefinitespotestendre aunaintegralestocàsticarespectedelprocésd’Itô (Xt )t∈[0,T ] coma T 0 fs dXs = T 0 fs us dWs + T 0 fs vs ds.

Consideremara n processosdeWienerindependents (W (k) t )t∈[0,T], k = 1,...,n Definimun procésd’Itô n-dimensional comunprocés X = (Xt := (X(1) t ,...,X(n) t ))t∈[0,T] enquècadacomponentésunprocésd’Itô dX(k) t = n j=1 u(k,j) t dW (j) t + v (k,j) t dt,k = 1,...,n,t ∈ [0,T].

Ellemad’Itôensdiusi f ésunafunció f : [0,T] × Rn → R declasse C1,2,llavors escompleixque

f(t,X(1) t ,...,X(n) t ) = f(0,X0) + t 0 ∂ ∂t f(s,Xs ) ds + t 0 ∂ ∂x f(s,Xs ) dXs + + 1 2 n k,j=1 ∂2 ∂xk∂xj f(t,Xt )(dX(k) t )(dX(j) t ),

on (dXt )2 escalculad’acordamblesreglessegüents:dW (k) t × dW (j) t = δkj dt, dW (k) t × dt = dt × dW (k) t = dt × dt = 0.

Enparticular,siprenemlafunció (t,(x(1),x(2))) x(1)x(2),obtenimla fórmulasegüentd’integracióperparts: X(2) t X(1) t = X(2) 0 X(1) 0 t 0 X(2) s dX(1) s t 0 X(1) s dX(2) s +

3.3Equacionsdiferencialsestocàstiques

Elmovimentbrowniàéstanirregularquenoéspossibledefinir-ne,enelsentit ordinari,laderivadarespectedeltemps.Enefecte,unatrajectòriatípicadel movimentbrownià,encaraquecontínua,noésdiferenciableencappunt.No obstantaixò,síqueéspossibledonarunsentitaladerivada(vegeu[26, 27])i aixòdónallocal’anomenat sorollblanc W(t) := dWt dt (vegeu[46,definició1]o[35, exemple3.13]).Senseentrarenmésdetalls,pensemaraformalmenten ˙ W per taldedesenvoluparl’heurísticasegüent:sil’equaciódiferencialdeterminista13 dxt dt = f(t,xt ) (11)

13Comen(9)aquíhemescrit xt encomptesde x(t)

éspertorbadaadditivamentmitjançantelsorollblanc,obtenimunaequació novadelaforma

dxt dt = f(t,xt ) + ˙ W(t). (12)

Arabé,d’unabanda,enelcàlculdeterministal’equaciódiferencial (11) espot plantejarcoml’equacióintegral xt = x0 + t 0 f(s,xs ) ds.

Mentreque,d’altrabanda,enelcàlculd’Itô ˙ W(t) idt escombinenperformar eldiferencialbrowniàdWt ,demaneraquel’equaciópertorbada (12) pren l’expressióformal

dxt = f(t,xt ) dt + dWt , laqualhad’entendre’sestrictamentcomelprocésd’Itô

xt = x0 + t 0 f(s,xs ) ds + Wt (13)

Mésgeneralment,per equaciódiferencialestocàstica (EDE )

dXt = f(t,Xt ) dt + σ(t,Xt )dWt ,

X0 = x0,

entendremunamanerad’escriureformalmentelprocésd’Itô:

Xt = x0 + t 0 f(s,Xs ) ds + t 0 σ(s,Xs ) dWs .

Ambdeterminadeshipòtesissobreelscoeficients f i σ éspossibleestablir l’existènciaiunicitatdelasoluciód’unaEDE(vegeu[53,capítol9.2]i[48, capítol5.2]).Noobstantaixò,ellemad’ItôpotservirperaresoldreunaEDE quanesconjecturacompodriaser-nelasolució.Perexemple,l’estructurade l’EDEsegüent

dYt = Yt (µ dt + σ dWt ), Y0 = 1, enssuggereixconsiderarunasoluciódeformaexponenciali,enefecte,si apliquemellemad’Itôalafunció F(t,x) := exp (µ 1 2 σ 2)t + σx podem comprovarquelasoluciód’aquestaEDEés (It := F(t,Wt ))t≥0

LesEDEvanserinicialmentestudiadesperItô,amblafinalitatdeconstruir determinatsprocessosmarkoviansapartirdelsseusgeneradorsinfinitesimals (cf.[36]).Desdellavors,lesEDEhanestataplicadesextensivamentadiverses àrees;ellectorinteressatenpodràtrobaruntractatcompleta[48].Calesmentar quetambééspossibledefinirEDEenlesqualselpaperdelmovimentbrowniàés reemplaçatperunprocésdeLévygeneral.AquestesEDEdirigidesperprocessos

ArturoValdivia

deLévytenenaplicacionsalamatemàticafinancera,perexemplepermodelar intensitatsdefallida (vegeulasecció4.1.2i[60,capítol5]).Sobreaplicacions enaltresdisciplines,esmentemqueunaequaciócomara (13),peròenlaqual canviemelmovimentbrowniàperunaltreprocésdeLévy,potservirpera modelarl’evoluciódelestemperaturesdelaTerraenelsúltims250000anys (vegeu[64,secció12.4]).

3.4Integracióestocàsticarespected’unmovimentbrowniàfraccionari

El1969MolchaniGolosov[44]vanrepresentarelmovimentbrowniàfraccionari (BH t )t∈[0,T] ambparàmetredeHurst H ∈ ( 1 2 , 1) coma

on K ésunnuclideterministadequadratintegrablequeactuaa L2[0,T] per14 K[f](s) :=

on Γ éslafunciógammad’Euler.

Enelcasd’integrandsdeterministesespotconstruirunaintegralestocàsticarespectede (BH t )t∈[0,T] seguintlesideesdelaconstrucciódelaintegral d’Itô(vegeu[47]).Primeresdefineixlaintegralperalaclasse E defuncions esglaonades,ésadir,funcions u : [0,T ] → R delaforma u(t) := n j=1 uj 1[tj 1,tj )(t),t ∈ [0,T],

on0 =: t0 ≤···≤ tn := T i u1,...,un ∈ R.Comasegonpas,considerem inicialmentl’espaideHilbert H definitcomlacompletacióde E respectedela normadonadaper(cf.(6)) 1[0,t], 1[0,s] H := 1 2 (s2H + t2H −|t s|2H ).

Espotdemostrar(vegeu[50, 49])que H és massagran,enelsentitquenoés necessàriamentunespaidefuncions,sinódedistribucionsd’ordrenegatiu.De maneraquehemderestringir-nosaunsubespai H ,elqualidentificaremamb

|H| := f : [0,T] → R H(2H 1) T 0 T 0 |f(u)||f(v)||u v|2H 2 du dv< ∞

14 Fixeu-vosqueaquestnucliespotexpressarentermesdelcàlculfraccionarideRiemannLiouville(vegeu[55]).

D’aquestamaneratenimlainclusió L2[0,T] ⊂|H|⊂H ,ilaintegralobtinguda satisfà t 0 f(s) dBH s = t 0 K[f](s) dWs .

Encaraqueenaquestaseccióhempartitdelacaracteritzacióde (14) per ferfrontalaintegraciórespectedelmovimentfraccionari,tambééspossible considerarunacaracteritzaciódiferent,habitualmentanomenada representació demitjanesmòbils deMandelbrotiVanNess[42];vegeu,perexemple[16].No obstantaixò,ésimportantdestacarqueambambduescaracteritzacionsespot construirunaintegralestocàstica(pelquefaalmovimentbrowniàfraccionari) seguintlesmateixesidees.Algunesrelacionsentreambduescaracteritzacions espodentrobara[34].

4Teoriaquantitativadelrisccreditici

Podríemdir, grossomodo,queun contractefinancer ésunacordperaintercanviardinerssegonsunesreglesdeterminades.Generalment,l’acordsesigna entreduesparts(personesoinstitucions)quepodemanomenar comprador i venedor.L’opcióeuropeadevendaquehemesmentatenlaintroduccióésun exempledecontractefinancer.Anomenarem benefici —o payoff,enanglès—el pagamentqueelvenedorprometalcomprador,iel preudelcontracte seràla quantitatdedinersqueelcompradorhadedonaralvenedoracanviderebre elbeneficipromès.

Coms’haesmentatjaenlaintroducció,elrisccrediticiesrefereixalriscde patirunapèrduaeconòmicaacausadel’incompliment—intencionatono—15 delesobligacionsd’algunadelespartsquesignenelcontracte.Quanesdóna aquestincomplimentesdiuquehasucceïtl’esdevenimentdefallida.Eltemps enquèaquestesdevenimentsucceeixesdiu tempsdefallida 16 L’estudide contractesambfallidaespotferdesdediferentspuntsdevista.Nosaltres consideremelproblemadesdelabrancadelamatemàticafinanceradenominada teoriaquantitativadelrisccreditici

Subjacentalnostremercatconsideraremunespaideprobabilitat (Ω, F , P) iunafiltració F = (Ft )t≥0 ques’interpretaràcomlainformaciódisponibleal mercat.Suposaremquetoteslesvariablesaleatòriesielsprocessosestocàstics consideratsestandefinitsa (Ω, F , P).

Consideraremcontractesfinancersambriscdefallidaquetinguinunbenefici delaforma17

X1{τ>T } + X1{τ≤T },

15 Unexempled’incomplimentintencionatésquanl’obligacióconstitueixun deuteillegítim (vegeu[19]).D’altrabanda,l’incomplimentpotsernointencionat,perexemple,quanunadeles partsnotéelsrecursoseconòmicsnecessarisperamantenirlessevesobligacions.

16 Enanglès,elstermes esdevenimentdefallida i tempsdefallida estradueixencom default event i defaulttime,respectivament.

17 Aquestbeneficiespotferméscomplex,perexemple,agregantunsumand Zτ 1{τ≤T } enelqual (Zt )t∈[0,T] representael procésderecuperació,elqualdeterminaunpagamentderecuperació querepelcompradorjustenelmomentenquèesprodueixlafallida.Vegeu,perexemple,la secció2de[6].

ArturoValdivia

on τ éslavariablealeatòriaquemodelaeltempsdefallida, X ∈ L2(Ω, FT ) ésel pagamentpromèsencasquenohihagifallidai ˜ X ∈ L2(Ω, FT ) éselpagament promèsencasdefallida.Undelsproblemesprincipalsdelamatemàticafinanceraconsisteixadefiniricalcularel preuadequat 18 d’underivat.Engeneral,el preuadequatésdelaforma19

t (X) := E∗ X exp

ds Ft ,t ∈ [0,T], (15)

onelbenefici X pertanya L2(Ω, FT ),elprocésestocàstic (rt )t∈[0,T] modelael tipusd’interèsalnostremercat, P∗ ésunaprobabilitatequivalent20 a P —de vegadesdenominada probabilitatneutral—i E∗ ésl’esperançarespectede P∗ . Enconseqüència,undelsproblemesprincipalsenelrisccrediticiéscalcular expressionsdeltipus

Lamajorpartdelsestudisdedicatsalrisccrediticitéaveureamblamodelització deltempsdefallida.Laliteraturasobreaquesttemasesoldividirsegonsdos tipusd’enfocamentsconegutscoml’enfocamentestructural il’enfocament deformareduïda.Elsorígensdelprimerespodenbasarenelstreballsde Black,MertoniScholes,mentrequeelsdelsegonesbaseneneltreballde Jarrow21 iTurnbull[32]ilesextensionsfetesa[33, 21](vegeu[10, 31]).Aquests dosenfocamentssesolenconsiderarcompetitiusiaïllatsl’undel’altre,ila informaciódisponibleésunadelesprincipalsdiferènciesentretotsdospunts devista(vegeu[31]).Noobstantaixò,diversosestudishanmostratescenaris enelsqualsespotpassardel’unal’altre(e.g.,[20, 24, 11])obéenelsquals totsdosenfocamentshijuguenunpaper(e.g.,[10]).Finsitots’hanproposat puntsdevistaunificats(e.g.,[4, 67])enelsqualseltempsdefallidaésmodelat comelprimermomentenquèuncertprocésestocàsticcreuaunabarrera.

4.1Elpreud’unboambfallida

Elsbonssónunobjected’estudicentralenmatemàticafinancerajaqueatravés d’ellséspossibleestructurarcontractesméscomplexos.

18 Per preuadequat s’had’entendreunpreuquenodonilloca oportunitatsd’arbitratge Intuïtivament,espotpensarque,quanelmercatéslliured’oportunitatsd’arbitratge,perguanyar dinersnecessàriamenthomhad’exposar-sealrisc.Peraunestudidetallatsobrel’arbitratge referimellectorinteressata[7].

19 Peral’obtenciódel’equació (15) ellectorinteressatpotconsultar[6, 22, 37, 52, 65].Pera unapresentaciódetalladasobrel’operador E∗[·|Ft ],vegeu[28].

20 Duesmesuresdeprobabilitatdefinidessobreelmateixespaidemesura (Ω, F ), ν1 i ν2,són equivalentssiperacada A ∈F ,escompleixque ν1(A) = 0 ⇐⇒ ν2(A) = 0. 21Coms’haesmentatenlaintroducció,JarrowésundelsestudiantsdeMerton.

Definició8. Un bo amb estructuradecupons (ci,ti)i=1,...,n, valornominal N> 0 i maduresa T> 0ésuncontractefinancerambbenefici

enquè c1,...,cn ≥ 0i0 ≤ t1,...,tn ≤ T sónunesquantitatsidates,respectivament,fixadesenelcontracte.Quan c1 =···= cn = 0,esdiuqueelboésun bosensecupons

Estudiaremacontinuacióelproblemadevalorarbonsambfallida,desdels dosenfocamentsdelateoriaquantitativadelrisccreditici.Enelcasdelmodel estructural,seguimelmodeldeMerton,jaque,sibéésunmodelsimplista, permetpresentarlescomplicacionsitècniquesdecàlculqueapareixentípicamentdinsdelmodelestructural.Obtindrem,enparticular,lafórmulade Black-Merton-Scholes.

4.1.1Enfocamentestructural. Aquestésl’escenari:

1. Unaempresavenunbosensecupons,ambvalornominal N imaduresa T .

2. Lespolítiquesdereestructuraciódel’empresaestableixenqueesdeclararà lafallidasielcapitalcaupersotad’unnivellcrític.

3. Encasdefallidaespagarà,comarecuperació,unafracció α ∈ [0, 1] del capitaldel’empresaaltempsdelamaduresa.

Suposemqueelcapitald’unaempresaielnivellcríticestanmodelatspels processosestocàstics (St )t∈[0,T] i ( t )t∈[0,T]

Llavorsaquestbotériscdefallidaieltempsdefallidaestàmodelatper

:= inf t ≥ 0: St ≤ t , (17)

ambelconveniqueinf ∅=∞.Pertant,aquestboambfallidatéunbenefici

Envirtutdelafórmula (16) ilalinealitatdel’esperança,elpreud’aquest contracteés

(18)

ElmodeldeMerton. Sigui (W ∗ t )t∈[0,T] un P∗-movimentbrowniàestàndard. EnelmodeldeMertoneltipusd’interèsesconsideraconstant,diguem-n’hi r . Elcapitaldel’empresaesmodelacomelmovimentbrowniàgeomètric, i.e., comlasolució22 del’equaciódiferencialestocàstica(EDE) dSt = St ((r κ) dt + σ dW ∗ t ), (19) 22Vegeulasecció3.3.

ArturoValdivia

onelsparàmetres κ i σ> 0sóninterpretatscomelsdividendsilavolatilitatdel capital,respectivament.Finalment,labarreraquedisparalafallidaesdefineix, nomésenlamaduresadelbo,coma T = N,detalmaneraque τ = 1{ST <N}. Aixípodemreescriureelpreua(18)coma

Elprimersumandescalculadirectamentenresoldrel’EDEde (19) iusarles propietatsbàsiquesdelmovimentbrownià.Enefecte,

on Φ representalafunciódedistribuciógaussianaestàndard.L’equació (20) se segueixdelfetque,comhemvistenlasecció3.3,lasolucióal’EDEde(19)és

Aixímateix, (21) esdedueixdelfetque,condicionata Ft , σ(W ∗ T W ∗ t ) ésuna variablealeatòriaambdistribució N(0,σ 2(T t))

Elcàlculdelsegonsumandespotferdemaneraanàlogasifemprimerun canvideprobabilitat.Sigui P(S) laprobabilitatdefinidaentermesdelaseva derivadadeRadon-Nikodým d

, P∗-quasisegurament.

Denotemper E(S) l’esperançarespectedelaprobabilitat P(S).Pelteoremade Girsanov23 sabemque P(S) ésequivalenta P∗,aixíquepodemaplicarlaregla deBayes24 perobtenirlarelaciósegüent:

dP(S) dP∗ 1{ST <N} Ft = = e(r

Ambargumentssimilarsalsutilitzatsenl’obtencióde (21) espotmostrarque E∗ dP(S) dP∗ Ft =

23Vegeu,perexemple,laseccióA.15de[45].

24Engeneral,pera Y ∈F ,obtenim

E∗ Y dP(S) dP∗ Ft = E∗ dP(S) dP∗ Ft E(S) [Y |Ft ] .

Vegeu,perexemple,ellemaA.1.4de[45].

jaque,condicionata Ft , σ(W ∗ T W ∗ t ) ésunavariablealeatòriaambdistribució log-normal,ambmitjana σWt 1 2 σ 2T ivariància σ 2(T t) D’altrabanda,elteoremadeGirsanovtambéensasseguraque (W (S) := W ∗ t σt)t∈[0,T] segueixun P(S)-movimentbrowniàestàndard,demaneraque, talcomhemfetambelprimersumand,podemcalcularque

(S) (ST <N |Ft ) = Φ

Comaconclusióobtenim

Lafórmulaacusadadedestruirl’economiamundial. Delafórmula (22), prenent α = 1i κ = 0,podemobtenirlafórmuladeBlack-Merton-Scholes (1). Peraveure-ho,recordemqueuna opcióeuropeadevenda ambmaduresa altemps T ipreud’exercici N ésuncontractefinancermitjançantelqual elcompradordel’opcióadquireixeldret—perònol’obligació—devendre determinatproductealvenedordel’opció,i T éselmomentenelqualespot ferlavenda,i N elpreuquecalpagarperaquestproducte.Si ST éselpreual mercatdelproducteeneltemps T ,llavorselbeneficidel’opciódevendaés (N ST )+ := max{N ST , 0}

Aleshoresn’hihaprouambveureque N 1{τ>T } + ST 1{τ≤T } = N 1{ST ≥N} + ST 1{ST <N} = N (N ST )+.

Pertant,éssuficientcombinarlesexpressions(16)i(22)peraobtenir

∗ e r(T t)(N ST )+ |Ft = Ne r(T t) D(t,T) = = Ne r(t T)

St N + (r σ 2 2 )(T t)

St N + (r + σ 2 2 )(T t)

.

ExtensionsdelmodeldeMerton. Elmodelconsideratabansespotestendre considerant:

ArturoValdivia

• Barreresestocàstiquesperadefinirlafallida.

• Tipusd’interèsestocàstics.

• Altresdinàmiquesperalcapitaldel’empresaieltipusd’interès(e.g., modelarusantl’exponenciald’unprocésdeLévyod’unmovimentbrownià fraccionari).

Cadascunad’aquestesextensionsresponaldesigdemodelarcaracterístiquesespecífiquesdelfenomenques’observenenlapràctica.Òbviament, cadascunadónallocaproblemesnousi,pertant,aldesenvolupamentd’eines matemàtiquesnoves.Perexemple,elfetdeconsiderarbarreresestocàstiques portaal’estudideltempsdexocd’unbrowniàpelquefaaunabarreraestocàstica.Aquestésunproblemadelqualnomésestenensolucionsparcials,inoés fàciltrobarfórmulesexplícitesquanlabarreradeixadeserunarecta.25 Modelar elstipusd’interèsdemaneraestocàsticacomplicaclaramentelscàlculsdela fórmula (16).D’altrabanda,modelarl’evoluciódelcapitalmitjançantprocessos diferentscomportalanecessitatdedesenvoluparelcàlculestocàsticielcàlcul numèriccorresponents.Lacomplexitatd’estendreelmodelsimultàniamenten aquestestresdireccionsésevident.

4.1.2L’enfocamentdeformareduïdaperalrisccreditici. Comhemvist, enl’enfocamentestructural,l’esdevenimentdefallidaésendogenilamodelitzaciórecausobreladinàmicaassumidaperalsprocessosquedescriuen l’evoluciódelcapitaldel’empresailabarreracrítica.Encontrast,enl’enfocamentdeformareduïda,esconsideraquel’esdevenimentdefallidaésexogeni lamodelitzaciórecausobreladinàmicaassumidaperala intensitatdefallida (γt )t∈[0,T] iel procésderisc

Enl’enfocamentdeformareduïdasesuposaquelaprobabilitatdefallidaestà descritaper (γt )t∈[0,T] segonslarelaciósegüent:

∗(τ>t |Ft ) = e Γt = exp t 0 γ

A[60,capítol5]espottrobarunadescripciód’algunsmodelsusualspera processosderiscidetècniquesperacalibrarlaintensitatdefallidaapartir d’altrescontractesambelriscdefallidacomlesdenominades permutesd’incomplimentcreditici —obé, creditdefaultswaps.Calesmentarque,donatun modelperalprocésderisc,sempreéspossibleconstruiruntempsd’aturada quesatisfaci (23),perexemple,prenent τ comelprimersaltd’unprocésde Poisson(cf. (3))alqualhemcanviateltempsfentservir (Γt )t≥0;vegeu-neels detallsa[38].

25Ellectorinteressatpottrobarunrecullderesultatsrelacionatsa[9].

Unaaltradiferènciasubstancialentreambdósenfocamentsésqueenl’enfocamentestructurallainformaciódereferència(F)éssuficientmentricapera sabersil’esdevenimentdefallidahaocorregut26 ono.Mentrequeaixònopassa enl’enfocamentd’intensitat,acausadelanaturalesaexògenadel’esdeveniment defallida.Encanvi,lainformaciódisponiblealmercatquedamodeladaperla filtracióengrandida27 G := (Gt )t∈[0,T] definidacoma

Gt := (Ft ∨ σ(τ ∧ s),s ≤ t).

Perconstrucció,amblainformaciódonadaper G síquepodemsabersil’esdevenimentdefallidahaocorregutono.Denotaremper H := (Ht )t∈[0,T] la filtraciónaturalgeneradapelprocés (Ht := 1{τ≤t})t∈[0,T].Ambaquestanotació escriurem G = F ∨ H.

Elcàlculdelspreusdederivatsesbasaenelresultatsegüent,habitualment denominat ellemaclaudel’enfocamentdeformareduïda. 28

Lema9. Siguin 0 ≤ t<s ≤ T .Si X és GT -mesurablealeshorestenimque

Laimportànciad’aquestresultatésdegudaalfetsegüent.Peracalcular eltermedel’esquerrade (24),enprincipi,hauríemdecomptarlainformació contingudaa Gt ;noobstantaixò,lanostrafiltraciódereferènciaésméspetita, i.e., Ft ⊂Gt .Malgrataixò,aquestlemaclauenspermetexpressaraquest càlculentermesd’esperancescondicionadesalainformacióde Ft ,quesíque coneixem.

Usantellemaclaupodemdonarl’expressiógeneraldelpreud’unbosense cupons,ambvalornominal N imaduresa T .Enefecte,fentservir (15) i (24),el preud’aquestboés D(t,T) = NE∗ 1{τ>T } exp

Comhemesmentatabans,unapartdelaimportànciaquetél’estudidels bonsrauenelfetquecontractesméscomplexosespodenexpressarentermes debons.Enconseqüència,elcàlculdelpreud’aquestscontractesestàrelacionat ambelcàlculd’expressionscomlaqueapareixa (25).Elcàlculexplícitd’aquesta 26Ésadir, {τ>t}∈Ft peratot t,osigui, τ ésun tempsd’aturada respectedelafiltració F 27A[15]espottrobarunaexposiciósobreeltemadel’engrandimentdelesfiltracions. 28Vegeulasecció5de[6]ilasecció8de[37].

ArturoValdivia

expressiódepèndelmodelquesuposemperaltipusd’interèsiperalaintensitat defallida.Observem,noobstantaixò,queelpreudelboambfallidaequival alpreud’unbosensefallidaenelqualeltipusd’interèsnoés (rt )t≥0 sinó (rt + λt )t≥0

Unexemplerecentéselques’ocupademodelareltipusd’interèsielprocés deriscpermitjàdeprocessosfraccionarisoprocessosd’àmbit.Totiqueles tècniques,lacomplexitatdecàlculilesimplicacionsdecadascunad’aquestes opcionssónsignificativamentdiferents,entotsdoscasosespotobteniruna expressiótancadapera (25).Enelcasd’unmodelquefaservirprocessos fraccionaris(vegeu[5]),aquestaexpressióésdelaforma

D(t,T) = eA(t,T) exp f(s,t,T) dBH s ,

on A i f sónfuncionsdeterministesquedepenennomésdelsparàmetresdel model,ilaintegralésrespected’unbrowniàfraccionariambparàmetrede Hurst H> 1 2 .Enelcasdelmodelquefaservirunprocésd’àmbit,espotobtenir unaexpressióamblamateixaestructuraperòenlaqual,comesmentemen lasecció2.4,laintegralestocàsticas’hadeprendreenelsentitdeWalsh[66] irespecteauna mesuraaleatòriadeWiener (vegeu[13]).

5Conclusions

Enaquestarticlehempresentatalgunesdelesidees,delsmodelsideles tècniquesbàsicsdelateoriaquantitativadelrisccreditici.Lallistadereferències bibliogràfiques—clàssiquesirecents—quehemcitatalllargdeltextpermetrà allectoraprofundirenlamatèriaitrobartotununiversdetemesquenohan estattractatsaquí.

Hemintentatmostrarexemplesclàssicsjuntamentambpropostesdediscussióirecercaactuals,amblafinalitatdeposardemanifestquel’estudidela matemàticafinanceraésuncampactiuiendesenvolupamentconstant.Més encara,hemprocurattambéferveurequeelsproblemestractatsenaquesta brancadelesmatemàtiquestenenunagrancomplexitatteòricaiquelesseves aplicacionscomprenenescenarisendiversesbranquesdelaciència.

Quintipusdematemàtiquesesfanenlabrancadematemàtiquesfinanceres?

Ésunapreguntarecurrentavuiendia,perpartdelsmatemàticsitambédels científicsidelpúblicengeneral.Esperemqueaquestarticlehagiservitpera donarunarespostaparcialaaquestapreguntai,ambsort,haverconvençutel lectordelanecessitatdeparticiparenaquestabrancabella,fèrtil,profundai útildelesmatemàtiques.

Agraïments

L’autoragraeixaladoctoraMartaSanz-Soléquel’hagiencoratjataferaquest treballenelmarcdelPremiAlbertDou.Agraeixtambéalrevisoranònimla sevalecturadetalladaielssuggerimentspertinentsquevanpermetremillorar laversiópreliminard’aquestarticle.

Referències

[1] Bachelier,L. «Théoriedelaspéculation». Ann.Sci.ÉcoleNorm.Sup.(3), 17(1900),21–86.

[2] Barndorff-Nielsen,O.E.;Benth,F.E.;Veraart,A.E.D. «Ambitprocesses andstochasticpartialdifferentialequations».A: Advancedmathematical methodsforfinance.Heidelberg:Springer,2011,35–74.

[3] Barndorff-Nielsen,O.E.;Schmiegel,J. «Ambitprocesses:withapplicationstoturbulenceandtumourgrowth».A: Stochasticanalysisand applications.Berlín:Springer,2007,93–124.(AbelSymp.;2)

[4] Bélanger,A.;Shreve,S.E.;Wong,D. «Ageneralframeworkforpricing creditrisk». Math.Finance,14(3)(2004),317–350.

[5] Biagini,F.;Fink,H.;Klüppelberg,C. «Afractionalcreditmodelwithlong rangedependentdefaultrate». StochasticProcess.Appl.,123(4)(2013), 1319–1347.

[6] Bielecki,T.R.;Rutkowski,M. Creditrisk:modelling,valuationandhedging. Berlín:Springer-Verlag,2002.(SpringerFinance)

[7] Björk,T. Arbitragetheoryincontinuoustime.Oxford:OxfordUniversity Press,1998.

[8] Black,F.;Scholes,M. «Thepricingofoptionsandcorporateliabilities». J.Polit.Econ.,81(1973),637–654.

[9] Borodin,A.N.;Salminen,P. HandbookofBrownianmotion-factsand formulae.2aed.Basilea:BirkhäuserVerlag,2002.(Probabilityandits Applications)

[10] Campi,L.;Çetin,U. «Insidertradinginanequilibriummodelwithdefault: apassagefromreduced-formtostructuralmodelling». FinanceStoch., 11(4)(2007),591–602.

[11] Çetin,U.;Jarrow,R.;Protter,P.;Yildirim,Y. «Modelingcreditriskwith partialinformation». Ann.Appl.Probab.,14(3)(2004),1167–1178.

[12] Cont,R.;Tankov,P. Financialmodellingwithjumpprocesses.BocaRaton,Fla.:Chapman&Hall/CRC,2004.(Chapman&Hall/CRCFinancial MathematicsSeries)

[13] Corcuera,J.M.;Farkas,G.;Schoutens,W.;Valkeila,E. «Ashortrate modelusingambitprocesses».A: Malliavincalculusandstochasticanalysis. NovaYork:Springer,2013,525–553.(SpringerProc.Math.Stat.;34)

[14] Corcuera,J.M.;Farkas,G.;Valdivia,A. «Ambitprocesses,theirvolatilitydeterminationandtheirapplications».A: Korolyuk,V.;Limnios,N.; Mishura,Y.;Sakhno,L.;Shevchenko,G. (ed.). Modernstochasticsand applications.Springer,2014.

[15] Corcuera,J.M.;Valdivia,A. «Enlargementsoffiltrationsandapplications»(Preprint2011),disponiblea http://arxiv.org/abs/1201.5870.

ArturoValdivia

[16] Delgado,R.;Jolis,M.;Utzet,F. «Mandelbrotil’atzar». Butlletídela SocietatCatalanadeMatemàtiques,27(2)(2012),121–160.

[17] Dickson,D.C.M.;Waters,H.R. «Thedistributionofthetimetoruinin theclassicalriskmodel». AstinBull.,32(2)(2002),299–313.

[18] Doukhan,P.;Oppenheim,G.;Taqqu,M.S. Theoryandapplicationsof long-rangedependence.Boston:Birkhäuser,2003.

[19] DuchGuillot,G.[etal.]. Vivirendeudocracia.Icariaeditorial,2011.

[20] Duffie,D.;Lando,D. «Termstructureofcreditspreadswithincomplete accountinginformation». Econometrica,69(2001),633–664.

[21] Duffie,D.;Singleton,K.J. «Modelingtermstructuresofdefaultable bonds». Rev.Financ.Stud.,12(4)(1999),197–226.

[22] Elliot,R.J.;Kopp,P.E. Mathematicsoffinancialmarkets.2aed.Nova York:Springer,2005.(SpringerFinance/SpringerFinanceTextbooks)

[23] Erd˝os,P.;Rényi,A. «Onrandomgraphs.I». Publ.Math.Debrecen,6(1959), 290–297.

[24] Guo,X.;Jarrow,R.A.;Zeng,Y. «Creditriskmodelswithincomplete information». Math.Oper.Res.,34(2)(2009),320–332.

[25] Harford,T. «Black-Scholes:Themathsformulalinkedtothefinancial crash».BBCNewsMagazine,27abril2012,disponiblea http://www. bbc.com/news/magazine-17866646.

[26] Hida,T. Brownianmotion.NovaYork;Berlín:Springer-Verlag,1980[Traduït deljaponèsperl’autoriT.P.Speed.](ApplicationsofMathematics;11)

[27] Hida,T.;Kuo,H.-H.;Potthoff,J.;Streit,L. Whitenoise.Aninfinitedimensionalcalculus.Dordrecht:KluwerAcademicPublishersGroup,1993. (MathematicsanditsApplications;253)

[28] Jacod,J.;Protter,P. Probabilityessentials.Berlín:Springer-Verlag,2000. (Universitext)

[29] Jarrow,R.A. «SpeechinhonorofRobertC.Merton».MathematicalFinance DayLifetimeAchievementAward,1999.

[30] Jarrow,R.A.;Lando,D.;Turnbull,S.M. «AMarkovmodelfortheterm structureofcreditriskspreads». Rev.Financ.Stud.,10(2)(1997),481–523.

[31] Jarrow,R.A.;Protter,P. «Structuralversusreducedformmodels:anew informationbasedperspective». JournalofInvestmentManagement,2(2) (2004),1–10.

[32] Jarrow,R.A.;Turnbull,S.M. «Creditrisk:drawingtheanalogy». Risk Magazine,5(9)(1992).

[33] Jarrow,R.A.;Turnbull,S.M. «Pricingderivativesonfinancialsecurities subjecttocreditrisk». J.Finance,50(1995),53–85.

[34] Jost,C. «TransformationformulasforfractionalBrownianmotion». StochasticProcess.Appl.,116(10)(2006),1341–1357.

[35] Khoshnevisan,D. «Aprimeronstochasticpartialdifferentialequations». A: Aminicourseonstochasticpartialdifferentialequations.Berlín:Springer, 2009,1–38.(LectureNotesinMath.;1962)

[36] Kuo,H.-H. Introductiontostochasticintegration.NovaYork:Springer,2006. (Universitext)

[37] Lamberton,D.;Lapeyre,B. Introductiontostochasticcalculusappliedto finance.2aed.BocaRaton,Fla.:Chapman&Hall/CRC,2008.(Chapman& Hall/CRCFinancialMathematicsSeries)

[38] Lando,D. «OnCoxprocessesandcreditriskysecurities». Rev.Derivatives Res.,2(1998),99–120.

[39] Mandelbrot,B.B. Thefractalgeometryofnature.SanFrancisco,Calif.: W.H.FreemanandCo.,1982.

[40] Mandelbrot,B.B. «Howfractalscanexplainwhat’swrongwith WallStreet». Sci.Am.,15setembre2008,disponiblea http://www. scientificamerican.com/article/multifractals-explain-wallstreet/.

[41] Mandelbrot,B.B.;Hudson,R.L. The(mis)behaviorofmarkets.Afractal viewofrisk,ruin,andreward.NovaYork:BasicBooks,2004.

[42] Mandelbrot,B.B.;VanNess,J.W. «FractionalBrownianmotions,fractionalnoisesandapplications». SIAMRev.,10(4)(1968),422–437.

[43] Merton,R. «Theoryofrationaloptionpricing». TheBellJournalofEconomicsandManagementScience,4(1973),141–183.

[44] Molchan,G.M.;Golosov,J. «Gaussianstationaryprocesseswithasymptoticallyapowerspectrum». Soviet.Math.Dokl.,10(1969),134–137.

[45] Musiela,M.;Rutkowski,M. Martingalemethodsinfinancialmodelling. 2aed.Berlín:Springer-Verlag,2005.(StochasticModellingandApplied Probability;36)

[46] Nualart,D. «Equacionsenderivadesparcialsestocàstiquespertorbades perunsorollblanc». ButlletídelaSocietatCatalanadeMatemàtiques,14(1) (1999),85–98.

[47] Nualart,D. «StochasticintegrationwithrespecttofractionalBrownian motionandapplications».A: Stochasticmodels.Providence,R.I.:Amer. Math.Soc.,2003,3–39.(Contemp.Math.;336)

[48] Øksendal,B.K. Stochasticdifferentialequations;anintroductionwith applications.6aed.Heidelberg:Springer,2013.(Universitext)

[49] Pipiras,V.;Taqqu,M.S. «IntegrationquestionsrelatedtofractionalBrownianmotion». Probab.TheoryRelatedFields,118(2)(2000),251–291.

ArturoValdivia

[50] Pipiras,V.;Taqqu,M.S. «Areclassesofdeterministicintegrandsfor fractionalBrownianmotiononanintervalcomplete?» Bernoulli,7(6) (2001),873–897.

[51] Pliska,S. Introductiontomathematicalfinance:discretetimemodels.Malden:BlackwellPublishers,1997.

[52] Protter,P. «Apartialintroductiontofinancialassetpricingtheory». StochasticProcess.Appl.,91(2)(2001),169–203.

[53] Revuz,D.;Yor,M. ContinuousmartingalesandBrownianmotion.3aed. Berlín:Springer-Verlag,1999.(GrundlehrenderMathematischenWissenschaften;293)

[54] Rubinstein,R.Y.;Kroese,D.P. SimulationandtheMonteCarlomethod. 2aed.Hoboken,N.J.:Wiley-Interscience[JohnWiley&Sons],2008.(Wiley SeriesinProbabilityandStatistics)

[55] Samko,S.G.;Kilbas,A.A.;Marichev,O.I. Fractionalintegralsandderivatives.Theoryandapplications.Yverdon:GordonandBreachScience Publishers,1993.

[56] Samorodnitsky,G. «Longrangedependence». Found.TrendsStoch.Syst., 1(3)(2006),163–257.

[57] Samuelson,P.A. FoundationsofEconomicAnalysis.Cambridge,Mass.: HarvardUniversityPress,1947.

[58] Sato,K. Lévyprocessesandinfinitelydivisibledistributions.Cambridge: CambridgeUniversityPress,1999.(CambridgeStudiesinAdvancedMathematics;68)

[59] Schoutens,W. Lévyprocessesinfinance:pricingfinancialderivatives.Nova York:JohnWiley&Sons,2003.

[60] Schoutens,W.;Cariboni,J. Lévyprocessesincreditrisk.Chichester:John Wiley&Sons,2009.

[61] Schuss,Z. Theoryandapplicationsofstochasticprocesses.Ananalytical approach.NovaYork:Springer,2010.(AppliedMathematicalSciences;170)

[62] Shiryaev,A.N. Essentialsofstochasticfinance.Facts,models,theory.River Edge,N.J.:WorldScientificPublishingCo.,1999.(AdvancedSerieson StatisticalScience&AppliedProbability;3)

[63] Shreve,S.E. Stochasticcalculusforfinance.I.Thebinomialassetpricing model.NovaYork:Springer-Verlag,2004.(SpringerFinance)

[64] Solé,J.Ll. «Elmóndelesvariablessensemomentsfinitsdetotselsordres: delaparadoxadeSantPetersburgalsprocessosdeLévy». Butlletídela SocietatCatalanadeMatemàtiques,27(1)(2012),63–113.

[65] Steele,J.M. Stochasticcalculusandfinancialapplications.NovaYork: Springer-Verlag,2001.(ApplicationsofMathematics(NewYork);45)

[66] Walsh,J.B. «Anintroductiontostochasticpartialdifferentialequations». A: Écoled’ÉtédeProbabilitésdeSaint-Flour,XIV-1984.Berlín:Springer,1986, 265–439.(LectureNotesinMath.;1180)

[67] Wong,D. «Aunifyingcreditmodel». CapitalMarkesGroupTechnical Report (1998).

UniversitatdeBarcelona GranViadelesCortsCatalanes,585 08007Barcelona,Espanya arturo.valdivia@ub.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.2,2014.Pàg.199–200

Englishsummaries

TimG.Myers,FrancescFont,VincentCregan,andMichelleM.MacDevette Nanomaths:mathematicalmodellingatthenanoscale

InthispaperwediscussthreeproblemsrecentlystudiedwithintheIndustrial MathsResearchGroupattheCentredeRecercaMatemàtica,wherecontinuum theorymaybeappliedtodescribenanoscalephenomena:

1. Heattransferwithnanofluids:Experimentalresultsconcerningtheremarkableheattransfercharacteristicsofnanofluidsareattimescontradictory.Weapplyaboundarylayeranalysistoshowthatastandard modelwhichhasbeenusedbymanyauthorstopredictanimprovement inheattransferwithincreasingnanoparticleconcentrationinfactshows adecrease.

2. Nanoparticlemelting:Nanoparticlesoftenexhibitasharpincreasein meltingrateasthesizedecreases.Amathematicalmodelwillbepresented whichpredictsthisphenomenaandexplainstheexperimentallyobserved abruptmeltingofthesmallestnanoparticles.

3. Enhancedflowincarbonnanotubes(CNTs):Thismodelshowsthatthe experimentallyobservedenhancementcanbeexplainedusingstandard flowequationsbutwithadepletionlayerbetweentheliquidandsolid interfaces.TheresultsalsoprovideonephysicalexplanationfortheNavierslipcondition.

Keywords: nanotubes,nanofluids,nanoparticles,heattransfer,thermalconductivity,phasechange.

MSC2010SubjectClassification:80A20,76T99,80A22.

JosepPlaiCarrera

Joseph-LouisLagrange:inmemoriam

ThisarticleisatributetoJoseph-LouisLagrangeintheoccasionofthetwo hundredthanniversaryofhisdeath.Ithasthreeparts:thefirstpartisbiographical;thesecondincludessuccintlyyourscientificproduction;andthethird, mostextensiveandmathematics,explainssomeoftheresultsachievedbythe famousmathematician.

Keywords: Josep-LouisLagrange,biographyofamathematician,historyof mathematics.

MSC2010SubjectClassification: 01A50,01A70.

ArturoValdivia

Financialmathematicsintimesofcrisis

Inthispaperwepresentsomeoftheimportantstochasticprocesses,andtheir correspondingstochasticcalculus,forquantitativecreditrisktheory.This branchofmathematicalfinancefocusesonthestudyofdefaultableclaims,that istosay,financialcontractspronetoeconomiclossesproducedwhenoneofthe partiessigningthecontractfails—whetherintentionallyorunintentionally—to fulfilitscontractualobligations.Thesekindsofcontractsareubiquitousinthe currenteconomiccrisis;thusweareinterestedindiscussingthesecontracts fromamathematicalfinancepointofviewinthesetimesofglobalcrisis.

Keywords: stochasticcalculus,mathematicalfinance,stochasticmodelling, stochasticprocesses,creditrisk.

MSC2010SubjectClassification: 60-01,60H30,60G05.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorial,percorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassificació permatèriesMSC2010.

Lesversionsdefinitivesdelsarticlesacceptatss’handepresentarencodiTEX, preferentmentenl’estilLATEXpropidel Butlletí.Aquestestilespotobtenira lespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Femnotarque enaquestapublicaciós’utilitzapreferentmentelpuntperaseparardecimals, enllocdelacomarecomanadaperl’IEC,pertaldefacilitarlacomprensióde lesexpressionsmatemàtiques.Pertald’accelerarelprocésdeproducció,es pregaalsautorsquesegueixinlesindicacionscontingudeseneldocument d’exemple.

Laversióenpaperdel Butlletí s’imprimeixenblancinegre.Quanun articlecontinguifiguresencoloriesconsidericonvenient,l’autorproporcionarà unaversiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateixmodificaràelscomentarisquefacinreferènciaalcolorde lesfigures.Enqualsevolcasel Butlletí publicaràl’originalencolorenelseu formatelectrònic.

Elsautorsdelsarticlespublicatsal Butlletí enreteneneldretdecòpia (copyright)iautoritzenl’IECadifondre’ls,tantatravésdelapublicacióimpresa commitjançantelsportalsdigitalspropisod’altresambquès’estableixinels convenisoportunsaaquestefecte.Ésresponsabilitatdelsautorsassegurar queesdisposadelsdretsdereproducciódelsgràficsidelesfiguresquehi apareguin.CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigital delseuarticleiunexemplarimprèsdelnúmerodel Butlletí enelquales publiqui.

Lacorrespondènciaadministrativarelacionadaambel Butlletí s’had’adreçaralaSCM.

Comitèeditorial

JuliàCufí(editorencap) DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona jcufi@mat.uab.cat

BartomeuColl

Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella

Dep.deMatemàticaAplicadaiAnàlisi UniversitatdeBarcelona fagella@maia.ub.es

JosepMariaFont

Dep.deProbabilitats,LògicaiEstadística UniversitatdeBarcelona jmfont@ub.edu

ArmengolGasull

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gasull@mat.uab.cat

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta) DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rcamps@mat.uab.cat

JorgeMateu

DepartamentdeMatemàtiques UniversitatJaumeI mateu@mat.uji.es

MarcNoy DepartamentdeMatemàticaAplicadaII UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas

DepartamentdeMatemàticaAplicadaI UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

AgustíReventós DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona agusti@mat.uab.cat

MartaSanz-Solé Dep.deProbabilitats,LògicaiEstadística UniversitatdeBarcelona marta.sanz@ub.edu

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatfilialdel’Institutd’EstudisCatalans,quecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesfinalitatsdela SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.La SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadela SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

La SCM editalespublicacionsperiòdiques SCM/Notícies i Butlletídela SocietatCatalanadeMatemàtiques.Elssocisdela SCM reben,gratuïtament, aquestesduespublicacions.

La SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiques d’arreudelmón,mitjançantelsqualselssocisdela SCM obtenenunareduccióenlaquotadesocid’aquestessocietats.Aixímateix,elssocisdela SCM podenfer-sesocisdelaSocietatMatemàticaEuropeapagantunaquota complementària.

LaJuntaDirectivadela SCM estàconstituïdaperlespersonessegüents:

President:XavierJarqueiRibera

Vicepresident:EnricVenturaiCapell

Adjuntaavicepresidència:IolandaGuevaraiCasanova

Secretari:AlbertRuiziCirera

Tresorera:NatàliaCastellanaiVila

Vocals:NúriaFagellaiRabionet,JosepGranéiManlleu,Agustí ReventósiTarrida,CarlesRomeroiChesa,OriolSerraiAlbó,Esther Silberstein,ManelUdinaiAbelló

Delegatdel’IEC:JoanGirbauiBadó

L’adreçadela SCM éscarrerdelCarme,47,08001Barcelona.Telèfon: 933248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: http://scm.iec.cat.

El Butlletí de la Societat Catalana de Matemàtiques publica, en llengua catalana, exposicions matemàtiques de qualitat, que puguin interessar a un nombre elevat de lectors. Es donarà prioritat a aquells treballs en què destaquin la claredat d’exposició i l’interès general del tema. El Butlletí està obert a tots els camps de la matemàtica i també als aspectes matemàtics de les ciències experimentals, la tecnologia, l’economia, etc., així com a altres àrees, com la història, la didàctica i la filosofia, sempre que els treballs tinguin un component matemàtic important. També tenen cabuda al Butlletí aquells articles que desenvolupin un aspecte significatiu de la problemàtica de la professió matemàtica al nostre país.

El Butlletí publica un volum a l’any, dividit en dos números, que es trameten gratuïtament a tots els socis. El Butlletí es publica també en format electrònic. L’edició electrònica del Butlletí pot obtenir-se des del portal de revistes científiques en línia de l’IEC o al servidor http://scm.iec.cat.

La correspondència administrativa s’ha d’adreçar a la Societat Catalana de Matemàtiques.

Editor en cap

Julià Cufí

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Comitè editorial

Bartomeu Coll

Dep. de Matemàtiques i Informàtica

Universitat de les Illes Balears

Núria Fagella

Dep. de Matemàtica Aplicada i Anàlisi

Universitat de Barcelona

Josep Maria Font

Dep. de Probabilitats, Lògica i Estadística

Universitat de Barcelona

Armengol Gasull

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Gábor Lugosi

ICREA i Departament d’Economia

Universitat Pompeu Fabra

Societat Catalana de Matemàtiques

Carrer del Carme, 47 - 08001 Barcelona tel. 933 248 583 - fax 932 701 180

scm@iec.cat - http://scm.iec.cat

Editora adjunta

Rosa Camps

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Jorge Mateu

Departament de Matemàtiques

Universitat Jaume I

Marc Noy

Departament de Matemàtica Aplicada II

Universitat Politècnica de Catalunya

Francesc Planas

Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya

Agustí Reventós

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Marta Sanz-Solé

Dep. de Probabilitats, Lògica i Estadística Universitat de Barcelona