IL Foundation Grade 6 - Math by infinity-learn

IL FOUNDATION SERIES

MATHEMATICS

IL Foundation Series - Mathematics Class 6

Legal Disclaimer

This book is intended for educational purposes only. The information contained herein is provided on an “as-is” and “as-available” basis without any representations or warranties, express or implied. The authors (including any affiliated organizations) and publishers make no representations or warranties in relation to the accuracy, completeness, or suitability of the information contained in this book for any purpose.

The authors (including any affiliated organizations) and publishers of the book have made reasonable efforts to ensure the accuracy and completeness of the content and information contained in this book. However, the authors (including any affiliated organizations) and publishers make no warranties or representations regarding the accuracy, completeness, or suitability for any purpose of the information contained in this book, including without limitation, any implied warranties of merchantability and fitness for a particular purpose, and non-infringement. The authors (including any affiliated organizations) and publishers disclaim any liability or responsibility for any errors, omissions, or inaccuracies in the content or information provided in this book.

This book does not constitute legal, professional, or academic advice, and readers are encouraged to seek appropriate professional and academic advice before making any decisions based on the information contained in this book. The authors (including any affiliated organizations) and publishers disclaim any liability or responsibility for any decisions made based on the information provided in this book.

The authors (including any affiliated organizations) and publishers disclaim any and all liability, loss, or risk incurred as a consequence, directly or indirectly, of the use and/or application of any of the contents or information contained in this book. The inclusion of any references or links to external sources does not imply endorsement or validation by the authors (including any affiliated organizations) and publishers of the same.

All trademarks, service marks, trade names, and product names mentioned in this book are the property of their respective owners and are used for identification purposes only.

No part of this publication may be reproduced, stored, or transmitted in any form or by any means, including without limitation, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the authors (including any affiliated organizations) and publishers.

The authors (including any affiliated organizations) and publishers shall make commercially reasonable efforts to rectify any errors or omissions in the future editions of the book that may be brought to their notice from time to time.

Subject to Hyderabad jurisdiction only.

ISBN 978-81-985304-8-6

Second Edition

KNOWING OUR NUMBERS 1

1.1 INTRODUCTION TO NUMBER SYSTEMS

In this chapter, we expand our understanding of numbers, reflecting on how humanity evolved to handle large quantities through collective effort. Numbers help us count objects, compare quantities, and organise information. We encounter numbers in various contexts, from counting tangible objects to mathematical operations like addition, subtraction, multiplication, and division. Building on previous knowledge, we dive deeper into number patterns, sequences, and mathematical operations, fostering curiosity and exploration in mathematics.

1.2 PLACE VALUE AND FACE VALUE

1.2.1 Place value

Place value refers to the value of a digit based on its position or place in a number.

Example: In the number 529, the place value of the digit 5 is 500, the place value of the digit 2 is 20 and the place value of the digit 9 is 9.

That is, 529 = 500 + 20 + 9

1.2.2 Face value

Face value is the actual value of the digit itself, irrespective of its position in the number.

Example: In the number 3201, the face value of the digit 3 is 3, the face value of the digit 2 is 2, the face value of the digit 0 is 0, and the face value of the digit 1 is 1.

1.3 COMPARING AND ORDERING NUMBERS

1.3.1 Comparing numbers

Comparing numbers involves determining if the number is smaller, greater, or equal to another number based on their values. We follow certain rules for comparing numbers, as given below:

• If the two numbers have different number of digits, then the number with more number of digits is greater.

• If the two numbers have equal number of digits, then we compare the digits from the leftmost places in both numbers.

Example: The number 43394 is greater than 9221, i.e. 43394 > 9221. The number 24356 is smaller than 24389. (The digits in tens place of both numbers 5 < 8)

1.3.2 Ordering numbers

Ordering numbers refers to arranging a set of numbers in a specific sequence based on their numerical values.

Ascending order

Ascending order refers to arranging a set of numbers from the smallest value to the largest value.

Example: In ascending order, the numbers 112, 5031, 19112, 312, and 5742 can be written as: 112 < 312 < 5031 < 5742 < 19112.

Descending order

Descending order refers to arranging a set of numbers from the largest value to the smallest value.

Example: In descending order, the numbers 13921, 2100, 704, 4668, and 9081 can be written as: 13921 > 9081 > 4668 > 2100 > 704.

1.4 FORMATION OF NUMBERS

The formation of numbers is the process of creating numerical values by combining digits according to specific rules or patterns.

1.4.1 Formation of 4-digit number

To form a 4-digit number, we need to understand the place value system. Each digit in a number occupies a specific place value position, such as ones, tens, hundreds, and thousands.

Example: To make different 4-digit numbers in such a way that no digit is repeated by using the digits 3, 8, 1, 9 is given by:

1389, 1398, 1839, 1893, 1938, 1983, 3189, 3198, 3819, 3891, 3918, 3981, 8139, 8193, 8319, 8391, 8913, 8931, 9138, 9183, 9318, 9381, 9813, 9831

Here, the smallest 4-digit number formed by the digits 3, 8, 1, 9 is 1389. The greatest 4-digit number formed by the digits 3, 8, 1, 9 is 9831.

1.4.2 Shifting digits

Shifting digits involves changing the position of digits within a number.

Example: If the digit at the thousands place of the 4-digit number 7021 is exchanged with the digit in the tens place, the new number formed is 2071.

The number 7021 is greater than the number 2071.

1.5 PLACE VALUE CHARTS

Place value charts assist in properly aligning digits, showing where they belong in a number. Using these charts, we can understand the value of digits in different positions more easily.

There are two main types of place value charts:

The Indian System of Numeration and,

The International System of Numeration

The difference between the two charts is the placement of commas and the nomenclature of different place values.

1.5.1 Indian system of numeration

The Indian place value chart is used in determining digit values based on their position in numbers, following the Indian numeral system. It organises 10-digit numbers into periods like ones, thousands, lakhs, and crores, separated by commas using the 3 : 2 : 2 rule. According to this rule, commas are placed after every 3, 2, and 2 digits from the right, respectively.

In words, the number can be written as:

5,26,49,325 = Five crores twenty six lakhs forty nine thousand three hundred twenty five.

Note: In the Indian system of numeration, following the crore period, the subsequent periods are referred to as Arab, Kharab, Neel, Padma, and Shankha.

1.5.2 International system of numeration

The International numeral system, used globally, follows the order of ones, tens, hundreds, thousands, and beyond. In its place value chart, numbers are grouped into periods like ones, thousands, millions, separated by commas every 3 digits from the right.

Expanded form of the number:

42,025,232 = 4 × 10,000,000 + 2 × 1,000,000 + 0 × 100,000 + 2 × 10,000 + 5 × 1,000 + 2 × 100 + 3 × 10 + 2 × 1

Number name of the number:

42,025,232 = Forty two million twenty five thousand two hundred thirty two.

Note:

In the International system of numeration, following the million period, the subsequent periods are referred to as Billion, Trillion, Quadrillion, and Quintillion.

Example 1: Write the place values of the two 3s in 39531 and find the difference between these two place values.

Solution:

In 39531, the first 3 occurs in ten thousands place.

So, its place value = 3 × 10,000 = 30,000

The second 3 occurs in the tens place.

So, its place value = 3 × 10 = 30

The difference between the two place values of 3 = 30,000 - 30 = 29,970

Hence, the difference between the two place values of 3 in the number 39531 is 29,970.

SOLVED EXAMPLES

Example 2: Compare the numbers 95320 and 193912.

Solution:

The number 95320 is a 5-digit number, and the number 193912 is a 6-digit number.

We know that a 6-digit number is greater than a 5-digit number.

Hence, 193912 is greater than 95320.

Example 3: Arrange the following numbers in descending order: 3941, 9352, 8291, 8820.

Solution:

All the given numbers have an equal number of digits, so let’s compare the following numbers from the leftmost digit.

Among the given numbers, 9352 is the greatest, while 3941 is the smallest.

The leftmost digit of the numbers 8291 and 8820 is the same.

Now, let’s compare the second digit from the left.

Since 2 < 8. So, 8291 < 8820.

Hence, the numbers in descending order are 9352 > 8820 > 8291 > 3941.

Example 4: Form the smallest and the greatest 5-digit numbers using 1, 0, 3, 7, and 5 without repetition.

Solution:

To form the smallest 5-digit number using the digits 1, 0, 3, 7, and 5 without repetition, arrange them in ascending order. The smallest number would start with the smallest non-zero digit, which is 1.

So, the smallest 5-digit number is 10357.

To form the greatest 5-digit number using the same digits without repetition, arrange them in descending order. The greatest number would start with the largest digit, which is 7.

So, the greatest 5-digit number is 75310.

Example 5: Express the number 29502401 with commas according to both the Indian and International systems. And write the number name in both systems.

Solution:

Indian system: 2,95,02,401 = Two crores ninety five lakhs two thousand four hundred one.

International system: 29,502,401 = Twenty nine million five hundred two thousand four hundred one.

1.6 CONVERSION OF UNITS

A unit is a standard quantity used to express and compare the magnitude of a physical quantity. Units provide a reference point against which other measurements can be made. They help in quantifying various physical properties such as length, weight, capacity (volume), time, temperature, etc. Given are several units of length, mass, and capacity and their conversions required to measure smaller or bigger quantities.

1.6.1 Units of length

The standard unit of length is 'metre' and is denoted as 'm'.

Example: 5 km = 5 × 1000 m = 5000 m

1.6.2 Units of mass

The standard unit of mass is 'gram' and is denoted as 'g'. × 10 × 10 × 10 ×

Example: 8 hg = 8 × 100 g = 800 g

1.6.3 Units of capacity

The standard unit of capacity (volume) is 'litre' and is denoted as 'L'. × 10 × 10 × 10 × 10 × 10 × 10

Example: 3 dL = (3 ÷ 10) L = 0.3 L

1.7 LARGER NUMBERS

1.7.1 Large numbers in practice

Operations (addition, subtraction, multiplication, and division) on large numbers are solved using place value systems where each digit's position determines its value relative to others.

Addition of large numbers

Example: Add 5,39,951 and 5,50,360.

Solution: 5,39,951 + 5,50,360 10,90,311

Subtraction of large numbers

Example: Subtract 2,25,525 from 7,03,142.

Solution:

7,03,142 - 2,25,525 4,77,617

Multiplication of large numbers

Example: Multiply 73,451 with 326.

Solution: × 73,451 326 + + 4,40,706 14,69,020

2,20,35,300

2,39,45,026

Division of large numbers

Example: Divide 43,056 by 48.

Solution:

1.7.2 Word problems on large numbers

Example: In an examination, a student multiplied 15,472 by 35 instead of 53. By how much was his answer greater than or less than the correct answer?

Solution:

The student’s answer = 15,472 × 35 × 15,472 35 + 77,360 4,64,160 5,41,520

Correct answer = 15,472 × 53 × 15,472 53 + 46,416 7,73,600 8,20,016

Thus, the incorrect answer is less than the correct answer by 8,20,016 - 5,41,520 =8,20,016 5,41,520 2,78,496

SOLVED EXAMPLES

Example 1: If a mass weighs 350 grams, what is its weight in kilograms?

Solution:

Given, the weight of the mass = 350 g

= 1 350kg 1000 × = 0.35 kg

Hence, the weight of the mass in kilograms is 0.35 kg.

Example 2: If a liquid container holds 2.5 litres of water, how many millilitres does it hold?

Solution:

Capacity of a liquid container = 2.5 L = 2.5 × 1000 mL = 2500 mL

Hence, the liquid container can hold 2500 mL of water.

Example 3: The population of City A is 56,78,901, and the population of City B is 34,56,789. What is the total population of both cities?

Solution:

Given, the population of City A = 56,78,901

The population of City B = 34,56,789

The total population of both cities = 56,78,901 + 34,56,789 + 56,78,901

34,56,789

91,35,690

Hence, the total population of both cities is 91,35,690.

Example 4: A company produced 16,329 units of product A and 24,501 units of product B. If the production cost per unit of product A is 13, and the production cost per unit of product B is 11, then what is the total production cost for both products?

Solution:

For product A:

Production cost per unit = 13

Number of units produced = 16,329

Total cost for product A = 13 × 16,329 = 2,12,277

For product B:

Production cost per unit = 11

Number of units produced = 24,501

Total cost for product B = 11 × 24,501 = 2,69,511

Now, let's calculate the total production cost:

Total production cost = Total cost for product A + Total cost for product B

Total production cost = 2,12,277 + 2,69,511

Total production cost = 4,81,788

So, the total production cost for both products is 4,81,788.

1.8 ESTIMATION AND APPROXIMATION

Estimation is making a close guess about a value based on available information.

Example: The population of a city in the year 2030 is estimated to be around 5.1 lakhs.

Approximation is finding a value that is near the exact value, often using mathematical methods.

Example: The total cost of groceries is 3020, which can be approximated to 3000.

Similarly, we come across many situations where getting exact values is difficult. In these cases, we rely on approximate values instead.

1.8.1 Rounding off numbers

Rounding off numbers involves simplifying the value of a number to a more convenient form by replacing it with a nearby value that is easier to work with. This is typically done by adjusting the digits of the number according to specific rounding rules.

Rounding off a number to the nearest 10

• Look at the digit in the ones place of the given number.

• If the digit in the ones place is less than 5, change the ones digit to 0, and leave the other digits unchanged.

• If the digit in the ones place is 5 or greater, increase the tens digit by 1 and change the ones digit to 0.

Example: 834 to the nearest ten is 830, and 978 to the nearest ten is 980.

Rounding off a number to the nearest hundred

• Look at the digit in the tens place of the given number.

• If the digit in the tens place is less than 5, change the tens and ones digit to 0, and leave the other digits unchanged.

• If the digit in the tens place is 5 or greater, increase the hundreds digit by 1 and change the tens and ones digit to 0.

Example: 539 to the nearest hundred is 500, and 1053 to the nearest hundred is 1100.

Rounding off a number to the nearest thousand

• Look at the digit in the hundreds place of the given number.

• If the digit in the hundreds place is less than 5, change the hundreds, tens, and ones digit to 0, and leave the other digits unchanged.

• If the digit in the hundreds place is 5 or greater, increase the thousands digit by 1 and change the hundreds, tens, and ones digit to 0.

Example: 2395 to the nearest thousand is 2000, and 38821 to the nearest thousand is 39000.

1.8.2 More about estimation

To estimate the sum

When adding numbers, round each number to the nearest whole number or a convenient place value and then perform the operation.

Example: Estimate the sum of 429 and 239 correct to nearest ten.

Solution:

Round off each given number to the nearest ten.

429 to nearest ten = 430

239 to nearest ten = 240

So, the required sum = 430 + 240 = 670

Hence, the sum of 429 and 239 to the nearest ten is 670.

To estimate the difference

When subtracting numbers, round each number to the nearest whole number or a convenient place value and then perform the operation.

Example: Estimate the difference between 35821 and 22929 correct to the nearest thousand.

Solution:

Round off each given number to the nearest thousand.

35821 to nearest thousand = 36000

22929 to nearest thousand = 23000

So, the required difference = 36000 - 23000 = 13000

Hence, the difference of 35821 and 22929 to the nearest thousand is 13000.

To estimate the product

For multiplication, round each number to a reasonable approximation and then calculate the result.

Example: Estimate the product of 24 and 57 correct to the nearest ten.

Solution:

Round off each given number to the nearest ten.

24 to nearest ten = 20

57 to nearest ten = 60

So, the required product = 20 × 60 = 1200

Hence, the product of 24 and 57 corrected to the nearest ten is 1200.

To estimate the quotient

For division, round each number to a reasonable approximation and then calculate the result.

Example: Find the estimated quotient for 792 ÷ 369, taking each number correct to the nearest hundred.

Solution:

Round off each given number to the nearest hundred.

792 to nearest hundred = 800

369 to nearest hundred = 400

So, the required quotient = 800 ÷ 400 = 800 400 = 2

Hence, the quotient for 792 ÷ 369, by taking each number corrected to the nearest hundred is 2.

1.9 ROMAN NUMBERS

Roman numerals are one of the early systems of writing numerals. Although they have largely been replaced by Arabic numerals in modern times for everyday arithmetic and mathematical purposes. However, they are still occasionally used today in certain contexts, such as numbering chapters, outlines, or indicating the year on buildings or monuments.

The Roman numerals:

I, II, III, IV, V, VI, VII, VIII, IX, X

denote 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 respectively. This is followed by XI for 11, XII for 12,... till XX for 20.

Some more Roman numerals are:

The rules for the system are:

• If a symbol is repeated, its value is added as many times as it occurs: i.e., II is equal to 2, XX is 20 and XXX is 30.

• A symbol is not repeated more than three times. But the symbols V, L and D are never repeated.

• If a symbol of smaller value is written to the right of a symbol of greater value, its value gets added to the value of the greater symbol.

VI = 5 + 1 = 6, XII = 10 + 2 = 12, and LXV = 50 + 10 + 5 = 65

• If a symbol of smaller value is written to the left of a symbol of greater value, its value is subtracted from the value of the greater symbol.

IV = 5 - 1 = 4, IX = 10 - 1 = 9, XL = 50 - 10 = 40, and XC = 100 - 10 = 90

• The symbols V, L, and D are never written to the left of a symbol of greater value, i.e., V, L, and D are never subtracted.

The symbol I can be subtracted from V and X only.

The symbol X can be subtracted from L, M and C only.

Example: What is the Roman numeral representation for the number 79?

Solution:

79 = 70 + 9

= (50 + 10 + 10) + 9

= LXX + IX

= LXXIX

Note:

Furthermore, the representation of Roman numerals greater than 5000 is given as: ,,,,,,,,,,,,, V5000X10000L50000C100000D500000M1000000

SOLVED EXAMPLES

Example 1: Estimate the sum of the numbers 611 and 236 to:

i. the nearest tens ii. the nearest hundreds

Solution:

i. Round off each given number to the nearest ten.

611 to nearest ten = 610

236 to nearest ten = 240

So, the required sum = 610 + 240 = 850

Hence, the estimated sum of 611 and 236 to the nearest ten is 850.

ii. Round off each given number to the nearest hundred.

611 to nearest hundred = 600

236 to nearest hundred = 200

So, the required sum = 600 + 200 = 800

Hence, the estimated sum of 611 and 236 to the nearest hundred is 800.

Example 2: Estimate the product of 73 and 464 by rounding off the first number to the nearest ten and the other number to the nearest hundred.

Solution:

Let’s round off the given numbers to the nearest ten and hundred.

73 to the nearest ten = 70

464 to the nearest hundred = 500

So, the required product = 70 × 500 = 35,000

Hence, the estimated product of 73 and 464 by rounding off the first number to the nearest ten, and the other number to the nearest hundred is 35,000.

Example 3: Convert the following Roman numeral to a Hindu-Arabic numeral. i. XCIX ii. CXCII

Solution: i. XCIX = XC + IX = 90 + 9 = 99 ii. CXCII = C + XC + II = 100 + 90 + 2 = 192

QUICK REVIEW

• Place value refers to the value of a digit based on its position or place in a number.

• Face value is the actual value of the digit itself, irrespective of its position in the number.

• Comparing numbers involves determining if the number is smaller, greater, or equal to another number based on their values.

• Ordering numbers refers to arranging a set of numbers in a specific sequence based on their numerical values.

• The formation of numbers is the process of creating numerical values by combining digits according to specific rules or patterns.

• Place value charts help align digits correctly, showing where they belong in a number. There are mainly two types: Indian system of numeration and International system of numeration.

• A unit is a standard quantity used to express and compare the magnitude of a physical quantity.

• The standard unit of length is metre and is denoted as m.

• The standard unit of mass is gram and is denoted as g.

• The standard unit of capacity (volume) is litre and is denoted as L

• Estimation is making a close guess about a value based on available information.

• Approximation is finding a value that is near the exact value, often using mathematical methods.

• Roman numerals are one of the early systems of writing numerals. The Roman numerals I, II, III, IV, V, VI, VII, VIII, IX, and X denote 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 respectively.

WORKSHEET - 1

I. PLACE VALUE AND FACE VALUE, COMPARING AND ORDERING NUMBERS, FORMATION OF NUMBERS, PLACE VALUE CHARTS

1. Find the sum of the place values of 2 and 8 in number 32708.

2. Find the difference between the place values of 5 and 9 in the number 5914.

3. In the number 8725, what is the quotient when dividing the place value of 8 by the face value of 2?

4. Which is greater?

i. 3842 or 3482

ii. 259010 or 25910

5. Which is smaller?

i. 380308 or 308380

ii. 43520 or 43250

6. Write the following numbers in ascending order: 10101, 11010, 10010, 11001.

7. Write the following numbers in descending order: 417, 471, 477, 411.

8. Form the greatest and the smallest 4-digit numbers using the digits: 2, 4, 6, 7 without repetition.

9. Write all possible three-digit numbers using the digits 3, 2, and 7, if repetition of any digit is not allowed.

10. Form the smallest 5-digit numbers using the digits 9, 2, 0, 1, and 5 (without repeating the digits) and with the condition that 5 is at the tens place.

11. Write the following numerals using the International System of Numeration in words.

i. 13001040

ii. 7323578

12. Write the following number names in numeral form.

i. Thirty two million sixty hundred fifteen thousand four ii. Two crore five lakhs eighty one thousand five hundred ninety one

II. CONVERSION OF UNITS, LARGER NUMBERS

1. Shyam went to the grocery store to buy apples. He bought 2.4 kg of apples. When he got home, he realised he needed to share them equally with his two friends, Javed and Amy. If Javed and Amy each get an equal share, how many grams of apples will each of them receive?

2. During Diwali celebrations, Rohan's family decorates their house with fairy lights. Rohan's father bought 15 m of fairy lights to decorate their balcony. If Rohan wants to know how many centimetres of fairy lights they have in total, how many centimetres of fairy lights did his father buy?

3. A number exceeds 6,45,789 by 2,34,567. What is the number?

4. Ramesh has 25 m of ribbon and wants to use it to make bows for gift packages. If each bow requires 1 m 20 cm of ribbon, how many bows can he make, and how much ribbon will be left?

5. The population of a suburb was 2,45,310 in the year 2022. In the year 2023, it increased by 14,720. What was the population of the suburb at the end of the year 2023?

6. A car manufacturing plant assembles 4,000 cars every day. How many cars will the plant assemble in the month of July?

7. A bakery bakes 3,500 loaves of bread every day. How many loaves of bread will the bakery bake in the month of June?

8. The cost of one television set is 36,800. What will be the total cost of 20 such television sets?

9. A student has 50,000 sheets of paper. If each sheet makes 6 pages of a notebook, how many notebooks of 150 pages can be made using the above sheets?

10. A juice pitcher contains 5 L and 750 mL of juice. How many identical cups can this juice fill if the capacity of each cup is 150 mL?

11. The distance between two landmarks, P and Q, is 2 km and 800 m. A runner runs from P to Q and back to P every day. How much distance did he cover in 7 days?

12. Three different buckets contain 7,650 mL, 6,200 mL, and 5,400 mL of paint. What is the total quantity of paint in the three buckets?

III. ESTIMATION AND APPROXIMATION, ROMAN NUMBERS

1. Estimate the sum of each pair of numbers to the nearest tens. i. 3942 and 235 ii. 506 and 794

2. Estimate each difference to the nearest hundred. i. 41744 - 41356 ii. 7830 - 7183

3. Estimate each of the following products by rounding off each number to the nearest tens. i. 601 × 67 ii. 135 × 53

4. Estimate each of the following quotients by rounding off each number to the nearest thousand. i. 5847 ÷ 2199 ii. 24343 ÷ 47901

5. There are 897 cherry trees on the plantation. The farmer plans to plant 312 more cherry trees. Estimate how many cherry trees will be there on the plantation, correct to the nearest hundred.

6. Convert the given Roman numeral to Hindu-Arabic numerals. i. XLV ii. DCCCXC

7. Convert the given Hindu-Arabic numeral to Roman numerals. i. 679 ii. 3706

8. Subtract the Roman numeral CCX from MDCLXVIII. Write the result in Roman numerals.

WORKSHEET - 2

I. MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER

1. Find the difference between the face values of 7 and 6 in number 75601. a. 69,400 b. 70600 c. 13

2. What is the sum of the face value of 3 and the place value of 5 in number 9350? a. 53

350

3. Which one of the following is incorrect?

a. 565 > 556 b. 909 < 990

c. 232 > 232

4. Which of the following numbers are in ascending order?

a. 30303, 30033, 33300, 33003

c. 33003, 33300, 30033, 30303

d. 665 > 656

b. 33300, 33003, 30303, 30033

d. 30033, 30303, 33003, 33300

5. How many 3-digit numbers are there between 599 and 2000?

a. 400

b. 399

c. 401

d. 501

6. Find the smallest 5-digit number using the digits 0, 1, 2, 3, and 4 without repeating the digits.

a. 10234 b. 12340

c. 12304 d. 10024

7. How many 4-digit numbers are formed using the digits 2, 0, 1, and 6, if repetition of any digit is not allowed?

a. 24

b. 18

c. 21

d. 12

8. According to the Indian System of Numeration, which of the following placements of commas is correct for the number 904324201?

a. 904,324,201 b. 90,43,24,201

c. 9,04,32,42,01 d. 904,32,42,01

9. Find the numeral form for the number name, 'Two million twenty thousand two’.

a. 2,20,002

b. 2,020,020

c. 2,020,002

10. How many decimetres are there in 1.5 kilometres?

a. 1500

b. 15000

c. 150

11. A number exceeds 9,75,623 by 4,56,321. What is the number?

a. 14,13,944

b. 14,31,944

c. 14,31,844

d. 2,02,002

d. 150000

d. 14,13,844

12. A factory produces 7,250 widgets every day. How many widgets will the factory produce in the month of May?

a. 2,24,750

b. 2,04,750

c. 2,17,500

d. 2,07,500

13. A person has 45,000 sheets of paper. If each sheet makes 10 pages of a workbook, how many workbooks of 300 pages can be made using the above sheets?

a. 300

b. 150

c. 3000

d. 1500

14. A paint can contain 12 L of paint. How many identical paint bottles can this paint fill if the capacity of each bottle is 500 mL?

a. 24 b. 18

c. 12

d. 6

15. The distance between two villages, M and N, is 4 km 250 m. A walker walks from M to N and back to M every day. How much distance did he cover in 12 days?

a. 120 km

b. 102 km

c. 96 km

d. 90 km

16. What is the estimated difference of 13531-10293 to the nearest thousand?

a. 3000

b. 2000

c. 4000

d. 1000

17. Estimate the product of 57 and 826 by rounding off the first number to the nearest ten and the other number to the nearest hundred.

a. 40,000

b. 45,000

c. 48,000

18. Write the Roman numeral for the Hindu-Arabic number 379.

a. CCCLXXIX

b. CCLXXIX

c. CCCLXIX

19. What is the value of the Roman numeral MMXXII?

a. 2204

b. 2024

c. 2022

20. Which one of the following is equal to the product of XXV and XII?

a. CCL

II. FILL IN THE BLANKS

b. CCC

c. CCXX

d. 54,000

d. CCLXIX

d. 2202

d. XXXVII

1. The difference between the greatest and the smallest 5-digit number is _________.

2. The smallest 4-digit number using the digits 1, 0, and 2 with a repetition of one digit is __________.

3. 100 million = _____ lakhs.

4. The numeral form of the number name, 'Seventy crore seven lakhs seventy thousand seven’ is __________.

5. If a number exceeds 5,23,409 by 1,20,678. Then the number is __________.

6. The sum of the numbers 666777, 667766, and 676767 is __________.

7. The price of one laptop is `42,500. The cost of 15 such laptops will be __________.

8. The estimated sum of 61 + 35 to the nearest ten is _____.

9. The value of the Roman numeral MCMLXIV is __________.

10. The sum of the Roman numerals CCXXII and MCDXLV is __________

III. SUBJECTIVE QUESTIONS

1. What is the product of the face values of 4 and 7 in the number 4792?

2. Form the greatest and the smallest 5-digit numbers using the digits: 1, 0, 2, 9, 7 without repetition.

3. How many four-digit numbers are possible using the digits 5, 0, 8, and 6, if repetition of any digit is not allowed?

4. Form the greatest 4-digit numbers using the digits 1, 9, 6, and 4 (without repeating the digits) and with the condition that 4 is at the thousands place.

5. Write the following numerals using the Indian System of Numeration in words. i. 40440044 ii. 2910291

6. If a book weighs 800 grams, what is its weight in kilograms?

7. Kiran has 15 m of fabric and plans to sew curtains for her living room. If each curtain requires 2 m 80 cm of fabric, how many curtains can she make, and how much fabric will be left?

8. The population of the town was 1,25,840 in the year 2022. In the year 2023, it increased by 9,560. What was the population of the town at the end of the year 2023?

9. Estimate the product of 89 and 573 by rounding off the first number to the nearest ten and the other number to the nearest hundred.

10. Convert the Roman numeral CDXCII to Hindu-Arabic numerals.

WHOLE NUMBERS 2

2.1 INTRODUCTION TO WHOLE NUMBERS

We have learned that the counting numbers 1, 2, 3, ... are referred to as natural numbers like the number of months in a year or the number of candies in a box. In this chapter, we will explore whole numbers.

When we include zero (0) in the set of natural numbers, we obtain a new set of numbers known as whole numbers.

Note: All natural numbers are whole numbers, but all whole numbers are not natural numbers.

2.2 PREDECESSORS AND SUCCESSORS

The number that comes immediately after any given number, or the number obtained by adding 1 to any given number, is known as its successor

Example: 5 is the successor of 4.

The number that comes immediately before any given number, or the number obtained by subtracting 1 from any given number, is known as its predecessor.

Example: 19 is the predecessor of 20.

2.3 THE NUMBER LINE

2.3.1 Whole numbers on a number line

To represent whole numbers on a number line, follow these steps:

• Begin by drawing a line.

• Mark a point 0 on the line.

• Then, mark another point to the right of 0 and label it as 1. The distance between these two points is referred to as the unit distance.

• Continue marking points as 2, 3, 4, ... on the line, with each consecutive point being at a unit distance from the previous one. The following line represents whole numbers on a number line.

0 1 2 3 4 5 6 7 8

2.3.2 Addition on the number line

We can add two or more whole numbers on a number line. While adding two numbers, we should move towards the right of any one of the given numbers.

Example: We can represent 5 + 6 = 11 on the number line as follows.

2.3.3 Subtraction on the number line

We can also subtract whole numbers on a number line. While subtracting two numbers, we should move towards the left on the number line.

Example: We can represent 13 – 5 = 8 on the number line as follows.

2.3.4 Multiplication on the number line

We can also multiply two whole numbers using a number line.

Example: We can represent 5 × 2 = 10 on the number line as follows.

Starting from 0, we move 2 units five times to the right until we reach 10.

SOLVED EXAMPLES

Example 1: Write the predecessor of each of the following:

i. 483692

Solution:

ii. 5983210

i. Predecessor of 483692 = 483692 – 1 = 483691

ii. Predecessor of 5983210 = 5983210 – 1 = 5983209

iii. Predecessor of 600000 = 600000 – 1 = 599999

iii. 600000

Example 2: Write the successor of each of the following:

i. 986959

ii. 3840517

iii. 9989899

Solution:

i. Successor of 986959 = 986959 + 1 = 986960

ii. Successor of 3840517 = 3840517 + 1 = 3840518

iii. Successor of 9989899 = 9989899 + 1 = 9989900

Example 3: Write the successor and predecessor of 2006389. Also, find their difference.

Solution:

The successor of 2006389 is 2006390 and the predecessor of 2006389 is 2006388.

The difference: 2006390 - 2006388 = 2.

Example 4: Represent 4 × 4 on a number line.

Solution:

Start from 0, move 4 steps at a time to the right of zero. Make such four moves so that we can reach the result.

1 2

3 4 5 6 7 8 9 10 11 12 13 14 15 16

Hence, 4 × 4 = 16.

Example 5: What is the product of successor and predecessor of 999?

Solution:

The successor of 999 = 999 + 1 = 1000

The predecessor of 999 = 999 - 1 = 998

∴ Their product = 998 × 1000 = 998000

Example 6: Represent 1 + 6 using the number line.

Solution:

Start from 1, since we add 6 to this number, we make 6 moves to the right, i.e., 1 to 2, 2 to 3, 3 to 4, 4 to 5, 5 to 6, 6 to 7 as shown.

0 1 2 3 4 5 6 7 8 9

The last tip of the arrow represents 7, which is the sum of 1 and 6.

∴ 1 + 6 = 7

2.4 PROPERTIES OF WHOLE NUMBERS

2.4.1 Addition

Closure: The sum of two whole numbers is always a whole number.

Example: 3 + 5 = 8

Commutative: Changing the order of addends does not change the sum.

Example: 3 + 5 = 5 + 3

Associative: The grouping of addends does not change the sum.

Example: (3 + 5) + 7 = 3 + (5 + 7)

2.4.2 Subtraction

Closure: The difference between two whole numbers may not always be a whole number.

Example: 7 5 = 2 (whole number) and 5 7 = 2 (not a whole number).

Commutative: Subtraction is not commutative; changing the order changes the result.

Example: 8 - 5 ≠ 5 - 8 ⇒ (3 ≠ -3).

Associative: Subtraction is not associative; changing the grouping changes the result.

Example: (10 - 5) - 3 ≠ 10 - (5 - 3) ⇒ 5 - 3 ≠ 10 - 2 ⇒ (2 ≠ 8).

2.4.3 Multiplication

Closure: The product of two whole numbers is always a whole number.

Example: 3 × 4 = 12

Commutative: Changing the order of numbers does not change the product.

Example: 3 × 4 = 4 × 3

Associative: The grouping of numbers does not change the product.

Example: (3 × 4) × 2 = 3 × (4 × 2)

2.4.4 Division

Closure: Division of whole numbers may not always result in a whole number.

Example: 10 ÷ 3 = 3.333...

Commutative: Division is not commutative; changing the order changes the result.

Example: 10 ÷ 5 ≠ 5 ÷ 10 10 ÷ 5 = 2, but 5 ÷ 10 = 0.5

Associative: Division is not associative; changing the grouping changes the result.

Example: (20 ÷ 4) ÷ 2 ≠ 20 ÷ (4 ÷ 2)

(20 ÷ 4) ÷ 2 = 5 ÷ 2 = 2.5, but 20 ÷ (4 ÷ 2) = 20 ÷ 2 = 10

2.4.5 Distributive property

Distributive property of multiplication over addition

If a, b, and c are three whole numbers, then a × (b + c) = (a × b) + (a × c).

Distributive property of multiplication over subtraction

If a, b, and c are three whole numbers, then a × (b – c) = (a × b) – (a × c).

2.4.6 Additive identity

The additive identity property states that when zero is added to any whole number, the result is the same whole number.

In other words, for any whole number a, a + 0 = a

2.4.7 Multiplicative identity

Multiplicative identity is a number which, when multiplied by any whole number, then the value remains the same.

Let a be any whole number, then 1 × a = a × 1 = a.

So, 1 is the multiplicative identity of whole numbers.

SOLVED EXAMPLES

Example 1: Find out whether 2455 + 2223 = 2223 + 2455.

Solution:

LHS (Left hand side) = 2455 + 2223 = 4678.

RHS (Right hand side) = 2223 + 2455 = 4678.

∴ Both sides are equal. Hence verified.

Example 2: Find the sum using suitable rearrangement.

i. 1436 + 586 + 564

ii. 364 + 517 + 636 + 983

Solution:

We can solve this using commutative and associative properties.

i. 1436 + 586 + 564 = 1436 + 564 + 586 = (1436 + 564) + 586 = 2000 + 586 = 2586

ii. 364 + 517 + 636 + 983 = 364 + 636 + 517 + 983 = (364 + 636) + (517 + 983) = 1000 + 1500 = 2500

Example 3: In a school canteen, Seeta spends ₹35 on noodles and ₹20 on cold drinks every day. How much money does Seeta spend in 1 week?

Solution:

We know that 1 week = 7 days

Seeta spends on noodles in 7 days = ₹35 × 7 = ₹245

Seeta spends on cold drinks in 7 days = ₹20 × 7 = ₹140

Thus, the total money spent by Seeta in 1 week

= ₹(245 + 140) = ₹385

Hence, Seeta spends ₹385 in 1 week.

Example 4: An officer bought 30 tables and 30 chairs. If the cost of a table is ₹500 and that of a chair is ₹250, how much did the officer spend?

Solution:

Cost of 1 table = ₹500

Cost of 1 chair = ₹250

The total money spent by the officer on 30 tables and 30 chairs is

= (₹500 × 30) + (₹250 × 30) = (₹500 + ₹250) × 30

= ₹750 × 30 = ₹22500

Hence, the officer spent ₹22500.

Example 5: What is the value of 500 × 681 × 0 × 501?

Solution:

We have, 500 × 681 × 0 × 501

We will group the number as follows.

(500 × 681) × (0 × 501) = 3,40,500 × 0 = 0

When we multiply the number by 0, we get 0 as a result.

Hence, the value of 500 × 681 × 0 × 501 is 0.

2.5 PATTERNS IN MATHEMATICS

A pattern in mathematics is a sequence of numbers, shapes, or objects that follows a specific rule. Patterns help us identify trends and predict what comes next.

Example 1: (Increasing by 3):

Sequence: 2, 5, 8, 11, 14, 17, ...

Common difference: +3

To find the next term, add 3 to the last number: 17 + 3 = 20.

Example 2:

1 2 4 8 16

This is the pictorial way to visualise the sequence of powers of 2, i.e. 20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16 and so on.

2.5.1 Patterns in numbers

Number patterns follow specific rules or orders, commonly observed in mathematics, especially with whole numbers.

0, 1, 2, 3, 4, 5,.....

The branch of mathematics which studies the pattern in whole numbers is called number theory.

Arithmetic patterns (Arithmetic Sequences):

An arithmetic pattern adds a constant value, as represented by the sequence 2, 4, 6, 8, 10, where 2 is added each time.

In an arithmetic pattern, each term is created by adding or subtracting the same number, called the common difference.

Example: (Decreasing by 4):

Sequence: 20, 16, 12, 8, 4, 0, ...

Common difference: -4

To find the next term, subtract 4 from the last number: 0 - 4 = -4.

Geometric patterns (Geometric sequences):

A geometric pattern involves multiplying by the same value, like in the sequence 2, 4, 8, 16, 32, where each term is multiplied by 2.

In a geometric pattern, each term is obtained by multiplying the previous term by the same number, called the common ratio.

Example: (Multiplying by 2)

Sequence: 1, 2, 4, 8, 16, 32, ...

Common ratio: ×2

To find the next term, multiply the last term by 2: 32 × 2 = 64.

Skip counting patterns:

Skip counting involves counting by a specific number, such as 2s, 5s, or 10s.

Example: (Skip counting by 5s)

Sequence: 5, 10, 15, 20, 25, 30, ...

To find the next term add 5 the last number: 30 + 5 = 35.

Square number patterns:

A square number is the result of multiplying a number by itself.

Example: (Square numbers)

Sequence: 1, 4, 9, 16, 25, 36, ...

These are 12, 22, 32, 42, 52, 62, ...

To find the next term, square the next number: 72 = 49.

Odd and even number patterns:

Odd and even numbers follow their own patterns.

Even Number Pattern:

Sequence: 2, 4, 6, 8, 10, 12, ...

Even numbers are divisible by 2.

To find the next term, add 2: 12 + 2 = 14.

Odd Number Pattern:

Sequence: 1, 3, 5, 7, 9, 11, ...

Odd numbers are not divisible by 2.

To find the next term, add 2: 11 + 2 = 13

Prime number patterns:

Prime numbers are numbers greater than 1 that can only be divided by 1 and themselves.

Example: (Prime numbers)

Sequence: 2, 3, 5, 7, 11, 13, 17, 19, ...

Virahānka numbers (Fibonacci sequence):

The Virahānka numbers (Fibonacci Sequence) is a special number pattern where each number is the sum of the two previous numbers in the sequence.

Example: (Virahānka numbers):

Sequence: 1, 2, 3, 5, 8, 13, 21, 34, ...

Rule: Start with 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, ...

To find the next term, add the two previous numbers: 21 + 34 = 55.

Triangular numbers:

The triangular number sequence is the representation of the numbers in the form of an equilateral triangle arranged in a series or sequence. It can be represented using dots arranged in equilateral triangle or triangular shape.

Example: (Trianglar numbers):

Sequence: 1, 3, 6, 10, 15, 21, ...

These numbers can be calculated by adding the next whole number to the previous sum.

Multiples of a number:

Multiples of a number are the results of multiplying that number by integers.

Example: (Multiples of 4):

Sequence: 4, 8, 12, 16, 20, 24, ...

To find the next term, multiply the last term by 4: 4 × 7 = 28.

2.5.2 Visualising number sequence

Visualising number sequences helps us understand patterns, allowing us to identify rules and predict the next numbers more easily.

Here are some examples that include visual or pictorial representations using dots for better understanding:

2.5.3 Relation among number sequences

Number sequences can be related to each other in surprising ways, enhancing our understanding.

Example: What happens when we start adding up odd numbers?

1 = 1

1 + 3 = 4

1 + 3 + 5 = 9

1 + 3 + 5 + 7 = 16

1 + 3 + 5 + 7 + 9 = 25

1 + 3 + 5 + 7 + 9 + 11 = 36

This can be visualised in two ways:

Another example of such a relation between sequences: Adding up and down

Let us look at the following pattern:

1 = 1

1 + 2 + 1 = 4

1 + 2 + 3 + 2 + 1 = 9

1 + 2 + 3 + 4 + 3 + 2 + 1 = 16

1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25

1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36

This seems to provide yet another way of calculating the square numbers by adding the counting numbers up and down!

2.5.4 Patterns in shapes

Shape sequences are a crucial type of shape pattern that mathematicians study. These shapes may be in one, two, or three dimensions (1D, 2D, or 3D) or even more dimensions.

Examples:

Regular polygons:

Complete graphs:

Stacked squares:

Stacked triangles:

Koch snowflake:

QUICK REVIEW

• The numbers 1, 2, 3, ..., which are used for counting, are known as natural numbers.

• If 1 is added to a natural number, its successor is obtained. If 1 is subtracted from a natural number, its predecessor is obtained.

• Every natural number has a successor. Every natural number except 1 has a predecessor.

• If the number zero is added to the collection of natural numbers, the collection of whole numbers is obtained.

• Every whole number has a successor. Every whole number except zero has a predecessor.

• All natural numbers are whole numbers, but not all whole numbers are natural numbers.

• To represent whole numbers on a line, a point is marked on it and labelled 0. Then, points to the right of 0 are marked out at equal intervals and labelled as 1, 2, 3, .... Thus, a number line with the whole numbers represented on it is obtained. Number operations such as addition, subtraction, and multiplication can be easily performed on the number line.

• Addition corresponds to moving to the right on the number line, whereas subtraction corresponds to moving to the left. Multiplication corresponds to making jumps of equal distance starting from zero.

• Whole numbers follow closure, commutative and associative properties for addition and multiplication.

• A mathematical pattern is a sequence of numbers, shapes, or objects that follows a specific rule. Number patterns follow specific rules or sequences, often seen in mathematics, particularly with whole numbers.

• The branch of mathematics which studies the pattern in whole numbers is called number theory.

• By visualising number sequences, we can better recognise patterns, which helps us identify underlying rules and make predictions about the next numbers more easily.

WORKSHEET - 1

I. INTRODUCTION TO WHOLE NUMBERS

1. Write the next three natural numbers after 999.

2. Write the three whole numbers occurring just before 90009.

3. Which is the smallest natural number?

4. How many whole numbers are there between 112 and 160?

5. Give 5 whole numbers smaller than 5 and four natural numbers smaller than 5.

6. When we subtract a natural number from itself, we get a _______ number.

7. We can represent a number of fruits in a basket using natural numbers, but we represent the number of fruits in an empty basket with _____, which is a whole number.

II. PREDECESSOR AND SUCCESSOR

1. Write the successor of:

i. 6540701

ii. 980199

v. 4244569 vi. 1221344

2. Write the predecessor of:

i. 2 ii. 20000

v. 3245543 vi. 6553455

III. THE NUMBER LINE

iii. 9999999

iv. 3445670

iii. 298090 iv. 7854321

vii. 223443 viii. 9778647

1. In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line. Also, write them with the appropriate sign(>, <) between them.

i. 830 ___ 803

iii. 78065 ___ 78605

2. Add the following using a number line. i. 3 + 9

12 + 5

3. Subtract the following using a number line. i. 5 – 4

6 – 1

4. Multiply the following using a number line.

i. 2 × 3 ii. 7 × 2

ii. 170 ___ 107

iv. 999999 ____ 1000000

3 × 3 × 3

4 × 2 × 2

IV. PROPERTIES OF ADDITION AND SUBTRACTION OF WHOLE NUMBERS

1. Simplify the following using suitable property.

i. 496 × 450 - 496 × 380 ii. 836 × 105

iii. 166 × 180 × 0

2. Use the suitable property to simplify each of the following and also name them.

i. 148 × 16 × 125 ii. 348 × 505

iii. 198 × 994 iv. 586 × 4 + 586 × 6

3. Using distributive property, 258 × 1008 =

a. 258 + 1000 + 8

c. 258 × 1000 + 8

4. Which of the following does not represent zero?

b. 258 × 1000 + 258 × 8

d. 1000 + 8 × 258

a. 1 0 b. 09 × c. 0 2 d. 33 2

5. 22 × (22 + 22) is equal to a. 968 b. 986 c. 988 d. 966

6. Find the sum by suitable rearrangement: 1 + 2 + 3 + 4 + 196 + 197 + 198 + 199.

a. 700 b. 900 c. 800 d. 1000

7. Using suitable property, find the value of 1265 × 1265 – 1265 × 265.

a. 1265000

b. 126500 c. 12650

PATTERNS IN MATHEMATICS

d. 1265

1. 36 is both a triangular number and a square number! That is, 36 dots can be arranged perfectly both in a triangle and in a square. Make pictures to illustrate this!

2. How would you describe the following sequence of numbers?

Find the next number in the sequence.

WORKSHEET - 2

I. MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER

1. Which of the following whole numbers does not have a predecessor?

a. 2 b. 0 c. 1

2. What is the value of n if (9 × 4) + (n × 5) = 9 × (4 + 5)?

1000

a. 9 b. 4 c. 5 d. 0

3. The additive identity for the set of whole numbers is a. 1 b. 0 c. 2 d. Does not exist

4. What is the successor of 871929?

a. 872030 b. 871930 c. 872930 d. 971929

5. What is the identity element with respect to multiplication?

a. 0 b. 2 c. 1

6. The value of 2575 ÷ 25 + 2575 ÷ 2575 is

-1

a. 1 b. 103 c. 104 d. 102

7. If a is any whole number, then 0 + a is

a. a

b. 1

c. 0

8. The value of c in (18 + 9) + 45 = 18 + (9 + c) is a. 9 b. 54 c. 45

9. The value of 258 × 96 + 258 × 4 is

d. Not defined

a. 2580 b. 258 c. 25800 d. 100

10. What is the successor of the predecessor of 1 lakh?

a. 1,00,001

11. Solve: 1446 × 0 × 8432

b. 1,00,000

a. 12192672

b. 1446

c. 99,999

d. 99,998

c. 8432 d. 0

12. The population of a town is 20,000. If 7000 are men and 9200 are women, find the number of children.

a. 13,000

b. 3,880

c. 13,800

d. 3,800

13. Identify the pattern for the following sequence and find the next number. 2, 3, 5, 8, 12, 17, 23, ____.

a. 28

b. 29

c. 30

d. 31

14. Identify the pattern for the following sequence and find the next number. 1, 8, 27, 64, 125, ___.

a. 205 b. 216 c. 225 d. 230

15. Identify the pattern for the following sequence and find the next number. 100, 98, 95, 90, 83, ____.

a. 87 b. 72

16. Which of the following is not a triangular number?

a. 15

II. FILL IN THE BLANKS

1. One is the __________ natural number.

2. 400 is the __________ of 399.

3. Zero is the __________ whole number.

4. 600 is the __________ of 599.

5. All natural numbers are __________ numbers.

6. The predecessor of a two-digit number is never a _____ digit number.

7. The natural number 1 has _____ predecessor.

8. _____ whole number lies between 11 and 12.

9. The whole number _____ has no predecessor.

III. ASSERTION AND REASON

1. Assertion: 1000 is the successor of 999.

Reason: We get the successor of a whole number, if we subtract 1 from it.

a. Both assertion and reason are true and reason is the correct explanation of assertion.

b. Both assertion and reason are true but reason is not the correct explanation of assertion.

c. Assertion is true but reason is false.

d. Assertion is false but reason is true.

2. Assertion: 8932 is greater than 8392.

Reason: A greater number lies on the right side of one of the two whole numbers on the number line.

a. Both assertion and reason are true and reason is the correct explanation of assertion.

b. Both assertion and reason are true but reason is not the correct explanation of assertion.

c. Assertion is true but reason is false.

d. Assertion is false but reason is true.

3. Assertion: If a is a whole number, then a + 0 = 0 + a = a.

Reason: If a and b are whole numbers, then a + b is also a whole number.

a. Both assertion and reason are true and reason is the correct explanation of assertion.

b. Both assertion and reason are true but reason is not the correct explanation of assertion.

c. Assertion is true but reason is false.

d. Assertion is false but reason is true.

4. Assertion: If a = 16, b = 12, then a × b = 192 is a whole number.

Reason: Multiplying two whole numbers always results in a whole number.

a. Both assertion and reason are true and reason is the correct explanation of assertion.

b. Both assertion and reason are true but reason is not the correct explanation of assertion.

c. Assertion is true but reason is false.

d. Assertion is false but reason is true.

5. Assertion: The sum of 278 + 691 + 221 is 1901.

Reason: If a, b, and c are three whole numbers, then (a + b) + c = a + (b + c).

a. Both assertion and reason are true and reason is the correct explanation of assertion.

b. Both assertion and reason are true but reason is not the correct explanation of assertion.

c. Assertion is true but reason is false.

d. Assertion is false but reason is true.

IV. SUBJECTIVE QUESTIONS

1. What is the difference between the successor and predecessor of the place value of 2 in 2,35,716?

2. Find the value of (565 + 565) + (278 + 278).

3. What number should be replaced by x?

(6 × 2)+(x × 3) = 6 × (2 + 3)

4. Calculate: 21 × 95 × 0.

5. Find the sum of 437 + 200 + 633 using the properties of addition.

6. Find the value of 5 – 4 by using a number line.

7. 90 oranges can be packed in one box. How many boxes will be required to pack 7200 oranges?

8. Using distributive law, find 937 × 1007.

9. Find the sum: 1 + 2 + 3 + 4 + 96 + 97 + 98 + 99.

10. Write down the successor and predecessor of 2009009.

11. In a shop, one notebook costs ₹15, a pencil costs ₹10 and a pen costs ₹20. How much money does Meena spend on 3 notebooks, 5 pencils and 2 pens?

12. Find the predecessor of the difference between the smallest 7-digit number and the largest 4-digit number.

13. Can you find a similar pictorial explanation for how adding counting numbers in an upward and downward sequence, such as 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, and so on, results in square numbers?

14. What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Explain it with a picture?

15. What happens when you start to add up hexagonal numbers, i.e., take 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37, ? Which sequence do you get? Explain it using a picture of a cube.

16. Study the pattern:

1 × 8 + 1 = 9

12 × 8 + 2 = 98

123 × 8 + 3 = 987

1234 × 8 + 4 = 9876

12345 × 8 + 5 = 98765

Write the next two steps.

17. Observe the following pattern and find the missing digits.

112 = 121

1012 = 10201

10012 = 1002001

1000012 = 1____2____1

100000012 = ________

PLAYING WITH NUMBERS 3

3.1 NUMBERS ARRANGEMENT

Rani has 6 marbles and wants to arrange them into rows with an equal number of marbles in each row. She tries various arrangements:

i. 1 marble in each row:

Number of rows = 6

Total number of marbles = 1 × 6 = 6

ii. 2 marbles in each row:

Number of rows = 3

Total number of marbles = 2 × 3 = 6

iii. 3 marbles in each row:

Number of rows = 2

Total number of marbles = 3 × 2 = 6

Unable to find arrangements for 4 or 5 marbles per row, she concludes with all 6 marbles in one row.

iv. 6 marbles in a row:

Number of rows = 1

Total number of marbles = 6 × 1 = 6

From these calculations, Rani observes that 6 can be written as a product of two numbers in different ways as:

616

623

632

661 =× =× =× =×

From 6 = 2 × 3, it can be said that 2 and 3 exactly divide 6. Thus, 1, 2, 3, and 6 are exact divisors of 6. Hence, 1, 2, 3, and 6 are factors of 6, being exact divisors.

3.2 FACTORS AND MULTIPLES

When two or more natural numbers are multiplied, then the product obtained is called the multiple of each of the numbers involved. Each of those numbers is referred to as a factor of the product.

Example: Consider 2 multiplied by 3, resulting in 6.

236 ×=

Here, 6 is a multiple of both 2 and 3. Also, 2 and 3 are two factors of 6.

Factors, which are exact divisors of a number, have the following properties:

• 1 is a factor of every number.

• Every number is a factor of itself.

• Every factor of a number is less than or equal to the number.

• The number of factors of a given number is finite.

Example: List all the factors of:

i. 128 ii. 54

Solution:

i. 128 = 1 × 128; 128 = 2 × 64; 128 = 4 × 32; 128 = 8 × 16

Thus, the factors of 128 are 1, 2, 4, 8, 16, 32, 64, and 128.

ii. 54 = 1 × 54; 54 = 2 × 27; 54 = 3 × 18; 54 = 6 × 9

Hence, all the factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54.

Multiples, on the other hand, are products of a given number and any non-zero whole number. They have the following properties:

• A number is a multiple of each of its factors.

• Every number is a multiple of itself.

• Every multiple of a number is greater than or equal to the number.

• The number of multiples of a given number is infinite.

Example: Find the first five multiples of:

i. 32 ii. 23

Solution:

i. The first five multiples of 32 are:

32 × 1 = 32; 32 × 2 = 64; 32 × 3 = 96; 32 × 4 = 128; 32 × 5 = 160.

ii. The first five multiples of 23 are:

23 × 1 = 23; 23 × 2 = 46; 23 × 3 = 69; 23 × 4 = 92; 23 × 5 = 115.

3.3 PRIME AND COMPOSITE NUMBERS

The numbers having only two factors, i.e., 1 and the number itself, are called prime numbers.

Example: 2, 3, 4, and 5 are some prime numbers.

The numbers having more than 2 factors are called composite numbers.

Example: 4, 6, 8, 9, and 10 are some composite numbers.

3.4 EVEN AND ODD NUMBERS

The numbers which are multiples of 2 i.e., ,,,,,, 24681012 … or the numbers having 0, 2, 4, 6 , or 8 at ones place are called even numbers.

Example: 0, 2, 4, 6, 8, 10, 12, 14, ... are some examples of even numbers.

The numbers which are not multiples of 2 i.e., ,,,,,, 1357911 … or the numbers having 1, 3, 5, 7, or 9 at ones place are called odd numbers.

Example: 1, 3, 5, 7, 9, 11, 13, 15, ... are some examples of odd numbers.

SOLVED EXAMPLES

Example 1: Find the factors of 12 and 14.

Solution:

121122634 =×=×=×

∴ The factors of 12 are 1, 2, 3, 4, 6, and 12.

1411427 =×=×

∴ The factors of 14 are 1, 2, 7, and 14.

Example 2: Find the first five multiples of 15.

Solution: ;;;; 511515230153451546015575 ×=×=×=×=×=

∴ 15, 30, 45, 60, and 75 are the first five multiples of 5.

Example 3: Which of the following are prime numbers? 96, 23, 41, 65, 91, 10, 31, 71, 43

Solution:

Among the numbers given, 23, 41, 31, 71, and 43 are prime numbers because they only have two factors.

Example 4: Determine if the number 53 is a prime number or a composite number.

Solution:

The factors of 53 are 1 and 53. Since 53 is only divisible by two numbers, 1 and itself, it is considered a prime number.

Example 5: Determine if 6 is a prime number or a composite number.

Solution:

The factors of 6 are 1, 2, 3, and 6. Since 6 can be divided evenly by more than two numbers (1, 2, 3, and itself), it is considered a composite number.

Example 6: Select the odd and even numbers from the following: 96342, 186481, 639123, 257770, 46819, 315768

Solution:

Odd numbers are 186481, 639123, 46819. Even numbers are 96342, 257770, 315768.

3.5 TESTS FOR DIVISIBILITY OF NUMBERS

3.5.1 Divisibility by 2

A natural number is divisible by 2, if its unit digit is divisible by 2, meaning it ends with 0, 2, 4, 6, or 8.

Example: Numbers like 4096, 23548, and 34052 are divisible by 2 since they end with 6, 8, and 2, respectively.

3.5.2 Divisibility by 3

A natural number is divisible by 3, if the sum of its digits is divisible by 3.

Example: Let's take the number 2143251. The sum of its digits (2 + 1 + 4 + 3 + 2 + 5 + 1) equals 18, which is divisible by 3. Thus, 2143251 is divisible by 3.

3.5.3 Divisibility by 4

A natural number is divisible by 4, if the last two digits (tens digit and ones digit) of the number are divisible by 4.

Example: Numbers like 4096, 53216, 548, and 4000 are all divisible by 4 as the numbers formed by their last two digits are divisible by 4.

3.5.4 Divisibility by 5

A natural number is divisible by 5, if its unit digit is either 0 or 5.

Example: Numbers like 4095 and 235060 are divisible by 5 as their unit places have 5 and 0, respectively.

3.5.5 Divisibility by 6

A number is divisible by 6, if it is divisible by both 2 and 3.

Example: Consider the number 753618. Since its unit digit is 8, it is divisible by 2. Additionally, the sum of its digits (7 + 5 + 3 + 6 + 1 + 8 = 30) is divisible by 3. Therefore, 753618 is divisible by 6.

3.5.6 Divisibility by 8

A number is divisible by 8, if the number formed by its last three digits (hundreds, tens, and units digits) is divisible by 8.

Example: Numbers like 15840, 5432, and 7096 are divisible by 8 as the numbers formed by their last three digits are divisible by 8.

3.5.7 Divisibility by 9

A natural number is divisible by 9, if the sum of its digits is divisible by 9.

Example: Consider the number 125847. The sum of digits = 1 + 2 + 5 + 8 + 4 + 7 = 27.

As 27 is divisible by 9, the number 125847 is divisible by 9.

3.5.8 Divisibility by 10

A number is divisible by 10, if its ones digit is 0.

Example: 20, 150, 650, and 500 are the numbers divisible by 10 as its ones digit is 0.

3.5.9 Divisibility by 11

A number is divisible by 11, if the difference between the sum of the digits in odd places and the sum of the digits in even places of the number is either 0 or a multiple of 11.

Example: Let's take the number 9582540. Now, the sum of digits in odd places minus the sum of digits in even places from the right equals (0 + 5 + 8 + 9) - (4 + 2 + 5) = 11, which is divisible by 11. Hence, 9582540 is divisible by 11.

SOLVED EXAMPLES

Example 1: Which of the following numbers are divisible by 6?

i. 936452 ii. 3640152 iii. 482649

iv. 93428910 v. 4286160

Solution:

i. For 936452, it's divisible by 2 since 2 is at its ones place. However, when we add its digits: 9 + 3 + 6 + 4 + 5 + 2 = 29, which is not divisible by 3. Hence, 936452 is not divisible by 6.

ii. 3640152 is divisible by 2 as 2 is at its ones place. Additionally, the sum of its digits: 3 + 6 + 4 + 0 + 1 + 5 + 2 = 21, which is divisible by 3. Therefore, 3640152 is divisible by 6.

iii. 482649 is not divisible by 2. Therefore, 482649 is not divisible by 6.

iv. For 93428910, it's divisible by 2 since 0 is at its ones place. Moreover, the sum of its digits: 9 + 3 + 4 + 2 + 8 + 9 + 1 + 0 = 36, which is divisible by 3. Therefore, 93428910 is divisible by 6.

v. 4286160 is divisible by 2 as 0 is at its ones place. Similarly, the sum of its digits: 4 + 2 + 8 + 6 + 1 + 6 + 0 = 27, which is divisible by 3. Thus, 4286160 is divisible by 6.

Example 2: Which of the following numbers are divisible by 11?

i. 9050602 ii. 1052524 iii. 1105645

iv. 7680794 v. 23505

Solution:

i. Sum of digits at odd places = 2 + 6 + 5 + 9 = 22

Sum of digits at even places = 0 + 0 + 0 = 0

Their difference = 22 - 0 = 22, which is divisible by 11.

∴ 9050602 is divisible by 11.

ii. Sum of digits at odd places = 4 + 5 + 5 + 1 = 15

Sum of digits at even places = 2 + 2 + 0 = 4

Their difference = 15 - 4 = 11, which is divisible by 11.

∴ 1052524 is divisible by 11.

iii. Sum of digits at odd places = 5 + 6 + 0 + 1 = 12

Sum of digits at even places = 4 + 5 + 1 = 10

Their difference = 12 - 10 = 2, which is not divisible by 11.

∴ 1105645 is not divisible by 11.

iv. Sum of digits at odd places = 4 + 7 + 8 + 7 = 26

Sum of digits at even places = 9 + 0 + 6 = 15

Their difference = 26 - 15 = 11, which is divisible by 11.

∴ 7680794 is divisible by 11.

v. Sum of digits at odd places = 5 + 5 + 2 = 12

Sum of digits at even places = 0 + 3 = 3

Their difference = 12 - 3 = 9, which is not divisible by 11.

∴ 23505 is not divisible by 11.

Example 3: Which of the following numbers are divisible by 5 and by 10?

i. 198645 ii. 384050 iii. 196450

iv. 1386425 v. 432190

Solution:

Numbers which are divisible by 5 are 198645, 384050, 196450, 1386425, and 432190.

Numbers which are divisible by 10 are 384050, 196450, and 432190.

Example 4: Which of the following numbers are divisible by 4 and by 8?

i. 78636 ii. 7721848 iii. 370264

iv. 1463356 v. 444184

Solution:

i. Number formed by last two digits of 78636 is 36, which is divisible by 4.

∴ 78636 is divisible by 4.

Also, the number formed by the last three digits of 78636 is 636, which is not divisible by 8.

∴ 78636 is not divisible by 8.

ii. Number formed by last two digits of 7721848 is 48, which is divisible by 4.

∴ 7721848 is divisible by 4.

Also, the number formed by the last three digits of 7721848 is 848, which is divisible by 8.

∴ 7721848 is divisible by 8.

iii. Number formed by last two digits of 370264 is 64, which is divisible by 4.

∴ 370264 is divisible by 4.

Also, the number formed by the last three digits of 370264 is 264, which is divisible by 8.

∴ 370264 is divisible by 8.

iv. Number formed by last two digits of 1463356 is 56, which is divisible by 4.

∴ 1463356 is divisible by 4.

Also, the number formed by the last three digits of 1463356 is 356, which is not divisible by 8.

∴ 1463356 is not divisible by 8.

v. Number formed by last two digits of 444184 is 84, which is divisible by 4.

∴ 444184 is divisible by 4.

Also, the number formed by the last three digits of 444184 is 184, which is divisible by 8.

∴ 444184 is divisible by 8.

3.6 COMMON FACTORS AND COMMON MULTIPLES

3.6.1 Common factors

To find the factors, we can use the multiplication as well as the division method. To check if two or more numbers have common factors between them, we follow the below steps:

Step 1: Write the given numbers.

Step 2: Write all the possible factors of the given numbers.

Step 3: Find the factors which are the same in both the numbers.

Step 4: Encircle the common factors.

This way, we can easily find common factors between two or more numbers.

Example:

Factors of 30 are: 1 , 2 , 3 , 5, 6 , 10, 15, 30

Factors of 42 are: 1 , 2 , 3 , 6 , 7, 14, 21, 42

Therefore, the common factors of 30 and 42 are 1, 2, 3, and 6.

3.6.2

Common multiples

To find common multiples, we list the multiples of each number and then we find their common multiples.

Example:

To find the common multiples of 2 and 4, we list their multiples and then find their common multiples.

Multiples of 2: 2, 4 , 6, 8 , 10, 12, 14, 16, 18, 20, 22, 24, etc.

Multiples of 4: 4 , 8 , 12, 16 , 20, 24, 28, 32, 36, 40, etc.

Therefore, common multiples of 2 and 4: 4, 8, 12, 16, 20, 24, etc.

3.7 PRIME FACTORISATION

The process in which a given number is factorised into prime factors is called prime factorisation. There are two methods to find the prime factors of a number.

i. By short division method

ii. By factor tree

Example: Using the short division method, let's prime factorise the following: i. 198 ii. 264

Solution: i. 2 198 3 99 3 33 11 11 1

Thus, the prime factorisation of 198 is 2 × 3 × 3 × 11. ii. 2 264 2 132 2 66 3 33 11 11 1

Thus, the prime factorisation of 264 is 2 × 2 × 2 × 3 × 11.

Example: Using the factor tree, let's prime factorise the following: i. 92 ii. 36

Solution:

i. Factor tree of 92 is,

∴ Prime factorisation of 92 = 2 × 2 × 23

ii. Factor tree of 36 is,

∴ Prime factorisation of 36 = 2 × 2 × 3 × 3

3.8 CO-PRIME NUMBER

Co-prime numbers are pairs of numbers that do not have any common factor other than 1. There should be a minimum of two numbers to form a set of co-prime numbers. Such numbers have only 1 as their highest common factor.

Example: Check whether 3 and 16 are co-prime or not.

Solution:

Factors of 3: 1, 3

Factors of 16: 1, 2, 4, 8, 16

Here, the only common factor between 3 and 16 is 1.

Thus, HCF (3, 16) = 1

Thus, 3 and 16 are both coprime numbers.

3.9 HIGHEST COMMON FACTOR

The highest factor among all the common factors of two or more numbers is called the Highest Common Factor (HCF) or Greatest Common Divisor (GCD).

Let us learn to find the HCF by different methods:

1. Prime factorisation method

2. Long division method

3. Common division method

3.9.1 Prime factorisation method

In this method, first we find the prime factors of each number and then find the product of factors which are common in all the numbers.

Example: Find the HCF of 120, 180, and 250 by the prime factorisation method.

Prime factorisation of 120 = 2 × 2 × 2 × 3 × 5

Prime factorisation of 180 = 2 × 2 × 3 × 3 × 5

Prime factorisation of 250 = 2 × 5 × 5 × 5

So, HCF of 120, 180 and 250 = 2 × 5 = 10.

3.9.2 Long division method

In this method, first we divide the greater number by the smaller number. If there is any remainder, then divide the divisor by remainder and repeat the process until we get the remainder as 0. The last divisor is the HCF of the numbers.

Example: Find the HCF of 144 and 196 by using long division method.

Solution:

∴ HCF of 144 and 196 is 4.

Note: To find the HCF of three numbers by the long division method, find the HCF of any two numbers as defined, and then divide the third number by the HCF of the first two numbers until we get 0 as the remainder.

Example: Find the HCF of 224, 252, and 84 by long division method.

Solution:

∴ HCF of 224 and 84 is 28. 28 252 9 -252 0

∴ HCF of 224, 252, and 84 is 28.

3.9.3

Common division method

In this method, first, we find the smallest common prime factor of the given numbers, then divide all the numbers by the common prime factor and write the quotients just below the corresponding numbers. Divide the quotients by the smallest common prime factor till there is no common prime factor left by which all quotients can be divided. The product of the common prime factors so obtained is the HCF of the numbers.

Example: Find the HCF of 42, 84, and 24 by common division method.

Solution:

2 42, 84, 24

3 21, 42, 12 7, 14, 4

∴ HCF of 42, 84, and 24 = 2 × 3 = 6.

3.10 LOWEST COMMON MULTIPLE

In this method, first we divide the given numbers by the smallest prime number which exactly divides them and write the quotients below the corresponding numbers. Divide the quotients by their smallest common prime numbers till we get 1 as the quotient of each of number. Product of all the divisors so obtained is the LCM of the given numbers.

Example: Find the LCM of 125, 350, and 245 by common division method.

Solution:

2 125, 350, 245

5 125, 175, 245

5 25, 35, 49

5 5, 7, 49

7 1, 7, 49

7 1, 1, 7 1, 1, 1

∴ LCM of 125, 350, and 245 = 2 × 5 × 5 × 5 × 7 × 7 = 12250

3.11 RELATIONSHIP BETWEEN HCF AND LCM

The LCM and HCF of two given numbers are related to the given numbers by the following relationship.

or, HCF × LCM = Product of two given numbers

or, HCF × LCM = First number × Second number

or, LCM = FirstNumber×SecondNumber HCF

or, HCF = FirstNumber×SecondNumber LCM

Example: The LCM of two numbers is 378, and their HCF is 9. If one of the numbers is 63, then find the other number.

Solution:

We know that, LCM × HCF = The product of two numbers

Let the other number be x.

∴ The other number is 54.

SOLVED EXAMPLES

Example 1: Find the common factors of:

i. 30, 60, 80 ii. 24, 36, 48

Solution:

i. Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30

Factors of 60 = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Factors of 80 = 1, 2, 4, 5, 8, 10, 16, 20, 40, 80

∴ Common factors of 30, 60, 80 = 1, 2, 5, 10.

ii. Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24

Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36

Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48

∴ Common factors of 24, 36, 48 = 1, 2, 3, 4, 6, 12.

Example 2: Three brands, A, B, and C, of biscuits are available in packets of 12, 15, and 21 biscuits, respectively. If a shopkeeper wants to buy an equal number of biscuits of each brand, what is the minimum number of packets of each brand he should buy?

Solution:

Three brands, A, B, and C, of biscuits are available in packets of 12, 15, and 21 biscuits, respectively. Also, a shopkeeper wants to buy an equal number of biscuits of each brand for that we need to find the LCM of 12, 15, and 21.

2 12, 15, 21

2 6, 15, 21

3 3, 15, 21

5 1, 5, 7

7 1, 1, 7 1, 1, 1

∴ The LCM of 12, 15, and 2122357420 =××××=

Thus, the required number of packets of brand 420 A = = 35, 12

The required number of packets of brand 420 B = = 28 15

And the required number of packets of brand 420 C = = 20 21 .

Example 3: In a seminar, the number of participants in Hindi, English, and Mathematics are 60, 84, and 108, respectively. Find the minimum number of rooms required if in each room the same number of participants are to be seated and all of them being in the same subject.

Solution:

The number of participants in each room must be the HCF of 60, 84, and 108. In order to find the HCF of 60, 84, and 108, we first find the HCF of 60 and 84.

Therefore, HCF of 60 and 84 is 12.

Now, we find the HCF of 12 and 108.

Clearly, HCF of 12 and 108 is 12.

Hence, the HCF of 60, 84, and 108 is 12.

Therefore, in each room maximum 12 participants of same subject can be seated.

We have,

The total number of participants = 60 + 84 + 108 = 252. 252

Number of rooms required = = 21. 12 ∴

Example 4: The HCF of two numbers is 6. If the numbers are 24 and 42, find their LCM.

Solution:

Product of two numbers HCFLCM=× 24 × 42

24 × 42 = 6 × LCMLCM = = 168 6 ⇒

Hence, the LCM of 24 and 42 is 168.

QUICK REVIEW

• The factor of a number is an exact divisor of that number.

• Multiple of any number is the product of the number and any natural number.

• The number which ends with 0, 2, 4, 6 or 8 is an even number

• The number which ends with 1, 3, 5, 7 or 9 is an odd number.

• Prime numbers are those numbers that have only two factors: 1 and the number itself. 2 is the only prime number that is even.

• Composite numbers are numbers which have more than 2 factors.

• The two numbers having only 1 as a common factor are called co-prime numbers.

• Any number is divisible by: 2, if its unit place digit is 0, 2, 4, 6 or 8.

3, if the sum of their digits is divisible by 3.

4, if the number formed by last two digits is divisible by 4.

5, if its unitsplace digit is either 0 or 5.

6, if the number is divisible by both 2 and 3.

8, if the number formed by the last three digits is divisible by 8.

9, if the sum of digits is divisible by 9.

10, if its unit place digit is 0.

11, if the difference of sum of even place digits and that of odd place digits from the right is divisible by 11.

12, if the number is divisible by both 3 and 4.

• If two numbers are divisible by a number, then their sum and difference are also divisible by that number.

• The highest common factor (HCF) of two or more numbers is the greatest among all their common factor.

• The least common multiple (LCM) of two or more number is the lowest among all their common.

WORKSHEET - 1

I. NUMBERS ARRANGEMENT, FACTORS AND MULTIPLES

1. Write all the factors of the following numbers:

2. Write the first five multiples of:

3. Match the items in column 1 with the items in column 2.

Column 1

i. 35

ii. 15

Column 2

a. Multiple of 8

b. Multiple of 7

iii. 16

iv. 20

v. 25

c. Factor of 30

d. Factor of 50

e. Factor of 20

II. PRIME AND COMPOSITE NUMBERS, EVEN AND ODD NUMBERS

1. What is the sum of any two

i. Odd numbers? ii. Even numbers?

2. State whether the following statements are true or false:

i. The sum of three odd numbers is even.

ii. The sum of two odd numbers and one even number is even.

iii. The product of three odd numbers is odd.

iv. If an even number is divided by 2, the quotient is always odd.

v. All prime numbers are odd.

vi. Prime numbers do not have any factors.

vii. The sum of two prime numbers is always even.

viii. 2 is the only even prime number.

ix. All even numbers are composite numbers.

x. The product of two even numbers is always even.

3. The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers upto 100.

4. Separately write down the prime and composite numbers less than 20.

5. What is the greatest prime number between 1 and 10?

6. Express the following as the sum of two odd primes.

i. 44 ii. 36 iii. 24 iv. 18

7. Give three pairs of prime numbers whose difference is 2.

8. Which of the following numbers are prime?

i. 23 ii. 51 iii. 37 iv. 26

9. Write seven consecutive composite numbers less than 100, so that there is no prime number between them.

10. Express each of the following numbers as the sum of three odd primes:

i. 21 ii. 31 iii. 53 iv. 61

11. Write five pairs of prime numbers less than 20, whose sum is divisible by 5.

12. Fill in the blanks:

i. A number which has only two factors is called a ___________.

ii. A number which has more than two factors is called a ____________.

iii. 1 is neither ___________ nor ____________.

iv. The smallest prime number is _____________.

v. The smallest composite number is ______________.

vi. The smallest even number is _____________.

III. TESTS FOR DIVISIBILITY OF NUMBERS

1. Using divisibility tests, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10; by 11 (say, yes or no):

2. Using divisibility tests, determine which of the following numbers are divisible by 4 and by 8: i. 572 ii. 726352 iii. 5500 iv. 6000 v. 12159 vi. 14560 vii. 21084 viii. 31795072 ix. 1700 x. 2150

3. Using divisibility tests, determine which of following numbers are divisible by 6:

i. 297144 ii. 1258 iii. 4335 iv. 61233

v. 901352 vi. 438750 vii. 1790184 viii. 12583

ix. 639210 x. 17852

4. Using divisibility tests, determine which of the following numbers are divisible by 11: i. 5445 ii. 10824 iii. 7138965 iv. 70169308

v. 10000001 vi. 901153

5. Write the smallest digit and the greatest digit in the blank space of each of the following numbers so that the number formed is divisible by 3:

i. __6724 ii. 4765__2

IV. COMMON FACTORS AND MULTIPLES

1. Find the common factors of:

i. 20 and 28 ii. 15 and 25 iii. 35 and 50 iv. 56 and 120

2. Find the common factors of:

i. 4, 8, and 12 ii. 5, 15, and 25

3. Find first three common multiples of:

i. 6 and 8 ii. 12 and 18

4. Write all the numbers less than 100 which are common multiples of 3 and 4.

5. Which of the following numbers are co-prime?

i. 18 and 35 ii. 15 and 37 iii. 30 and 415 iv. 17 and 68 v. 81 and 16 vi. 216 and 215

6. If a number is divisible by both 5 and 12, then which other number will that number always be divisible by?

V. PRIME FACTORISATION AND CO-PRIME NUMBERS

1. Here are two different factor trees for 60. Write the missing numbers. i.

2. Write the greatest 4-digit number and express it in terms of its prime factors.

3. The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.

4. The sum of two consecutive odd numbers is divisible by 4. Verify this statement with the help of some examples.

5. In which of the following expressions, prime factorisation has been done?

i. 24234 =××

ii. 567222 =×××

iii. 70257 =××

iv. 54239 =××

6. Check co-prime numbers from the given set of numbers 21 and 24; 13 and 15; 17 and 18.

VI. HCF, LCM, RELATIONSHIP BETWEEN HCF AND LCM

1. Find the HCF of the following numbers:

i. 18, 48 ii. 30, 42 iii. 18, 60 iv. 70, 105, 175 v. 91,112,49 vi. 18,54,81

2. What is the HCF of two consecutive

i. numbers ii. even numbers iii. odd numbers

3. HCF of co-prime numbers 4 and 15 was found as follows by factorisation: 422and 1535=×=× ; since there is no common prime factor, the HCF of 4 and 15 is 0. Is the answer correct? If not, what is the correct HCF?

4. Find the LCM of the following numbers: i. 9 and 4 ii. 12 and 5 iii. 6 and 5 iv. 15 and 4

Observe a common property in the obtained LCMs. Is LCM the product of two numbers in each case?

5. Find the LCM of the following numbers in which one number is the factor of the other. i. 5, 20 ii. 6, 18 iii. 12, 48 iv. 9, 45

What do you observe in the results obtained?

6. The length, breadth, and height of a room are 825 cm, 675 cm, and 450 cm respectively. Find the longest tape which can measure the three dimensions of the room exactly.

WORKSHEET - 2

I. MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER

1. 55 is not a multiple of:

a. 1 b. 5 c. 22

2. The sum of the factors of 35 is:

a. 84 b. 13

3. Which of the following numbers has a LCM 60?

a. (12, 5, 7)

4. 532460 is not divisible by:

a. 10

5. The number 53 is a:

a. Odd number

c. Composite number

6. HCF of 70, 105, and 175 is:

b. (12, 5, 60)

b. 5

a. 35 b. 135

c. 40 d. 48

c. (2, 6, 10)

d. (3, 6, 10)

c. 3 d. 4

b. Prime number

d. Both odd and prime number

c. 1050 d. 7

7. I am the fifth multiple of the LCM of 2 and 7. What number am I?

a. 80 b. 70

c. 75

d. 65

8. Determine the number nearest to 100000 but greater than 100000, which is exactly divisible by each of 8, 15 and 21.

a. 100800

9. 96 is not a multiple of:

a. (5, 15)

b. 100900

b. (3, 8)

c. 100700

d. 100600

c. (8, 12)

d. (4, 24)

10. The HCF of two numbers is 23 and their LCM is 1449. If one of the numbers is 161, then find the other.

a. 207 b. 23 c. 211 d. 209

II. SUBJECTIVE QUESTIONS

1. Write the first five multiples of 13.

2. Check if, 401 is a prime number or not.

3. Determine the prime factorisation of 840.

4. Find the LCM of 40, 144, and 180.

5. What is the least number divisible by 16, 20, and 24?

6. Find the HCF of 36, 56, and 86.

7. Find the largest number which divides 245 and 1029 leaving remainder 5 in each case.

8. Three city tour buses leave the bus stop at 9:00 am. Bus A returns every 30 minutes, Bus B returns every 20 minutes, and Bus C returns every 45 minutes. What is the next time, all buses will return to the bus stop at the same time?

9. Find the greatest number of 5-digits which when divided by 3, 5, 8, and 12 will have 2 as remainder.

10. State, whether the numbers 27 and 29 are twin primes or co-primes.

11. Check the divisibility of 226180 by 2, 3, and 5.

12. A rectangular room is 20 m 16 cm long and 15 m 60 cm wide. It is paved with square tiles of the same size. Find the greatest size of each tile.

13. Find the LCM and HCF of 54, 108, and 288 by prime factorisation method.

14. The floor of a room 9 m × 6.75 m is to be paved by square marble slabs. Find the maximum size of each slab. How many slabs will be required in all?

15. Using divisibility tests, determine whether 438340 is divisible by 3, 4, 8, 10 or not?

16. Replace the star ( ∗ ) by the smallest number, so that:

i. 78 ∗ 964 may be divisible by 9.

ii. 75 ∗ may be divisible by 4.

iii. 2 ∗ 345 may be divisible by 3.

III. CASE STUDIES

Anjali has a habit of listing all the definitions, formulae, and properties of every chapter in her notes as a chart for quick revision. After learning the concept of 'Prime and Composite Numbers’, she lists down the following points in her chart.

Prime and Composite Numbers:

• The numbers having only two factors, i.e., 1 and itself, are called prime numbers.

For example: 2, 3, 5, 7, 11, 13, 17, 19, etc.

• The numbers having more than two factors are called composite numbers.

For example: 4, 6, 8, 9, 10, etc.

• There is no largest prime number.

• If the difference between two prime numbers is 2, then they are called twin primes.

For example: (3, 5),(5, 7),(11, 13),(17, 19), etc.

On seeing this chart her mother asked her following questions, try to answer them.

1. The total number of even prime numbers in the set of natural numbers is

a. 1

b. 2

2. Which of the following is composite?

a. 31

b. 51

c. 3 d. Can't be determined

c. 61 d. 91

3. Which of the following cannot be expressed as sum of two odd primes?

a. 26 b. 34

c. 37 d. 70

4. Which of the following statements is correct?

a. Every odd number is prime.

c. Every prime is odd.

b. Every even number is composite.

d. Every composite is not even.

5. Which of the following pairs of numbers are not twin primes?

a. (11, 13)

b. (71, 73)

c. (81, 83) d. (59, 61)

BASIC GEOMETRICAL IDEAS 4

4.1 POINT

A point is a mark of position. It has no length, breadth, or thickness. It is often represented by a dot and is denoted by a single capital letter.

Example:

A B P

The tip of a compass, the sharpened end of a pencil, and the pointed end of a needle are real-life examples of a point.

4.2 LINE SEGMENT

Fold a piece of paper and unfold it; you see a fold. This gives an idea about the line segment. It has two endpoints, A and B.

Let A and B be two points in a plane. Connect A to B by all possible routes. Then, the shortest path from A to B is called the line segment AB. Line segment AB is the same as line segment BA. It is denoted by AB or BA

Note: A line segment contains an infinite number of points.

Example: Consider the edge of a box or the edge of a postcard. These are real-world examples of line segments.

Measuring a line segment: The measurement of a line segment involves determining its definite length. We measure the length of a line segment by using a graduated ruler, and to avoid positioning error (Parallax error), we use a divider.

Note: The units of length are related as follows: 1 km = 1000 m, 1 m = 100 cm, and 1 cm = 10 mm.

4.3 RAY

A line segment extended endlessly in one direction is called a ray.

Example: The line segment AB, extended endlessly in the direction from A to B, is a ray denoted by AB

, called ray AB.

A B

Here, the arrow indicates the direction.

Properties:

1. The ray AB has one endpoint, namely A, called its initial point.

2. Aray has no definite length and extends indefinitely in only one direction.

3. Usually, AB

is not the same as BA

4. BA

is a ray with initial point B and extends endlessly in the direction from B to A.

A B

So AB

and BA

are two different rays.

Can a ray have more than one name?

A ray can have more than one name. For example, observe ray AB, its initial point is A, and its direction is from A to B. It can also be named as ray AD, ray AC but not as ray DC.

A D B C

Note: A ray contains an infinite number of points.

Co-initial rays: Co-initial rays are an unlimited number of rays that can be drawn in different directions with a given point, say O, as the initial point.

F O D E

Here OA,OB, OC, OD, OE, OF

are called co-initial rays as all these rays have the same initial point 'O'.

Here, AP

and AQ

are co-initial rays.

Note: We cannot draw the complete picture of a ray on paper. Only we can represent it on paper. Whereas we can draw the line segment completely on the paper.

Rays of light from a candle, beam of light from a light house are real life examples of rays.

4.4 LINE

A line segment extended endlessly in both directions is called a line. For example, if we extend a line segment AB on both sides and mark it with arrows at two ends, we get a line, denoted by AB

or BA

and called line AB or line BA.

A B

Sometimes, we represent the lines with small letters: l, m, n, etc.

1. The two arrows of a line drawn in opposite directions indicate that the line has unlimited length, i.e. it can be extended up to any distance on either side.

2. A line may be straight or curved, but when we say "a line," we mean a straight line. The basic idea of a line is its straightness and its infinite extension in both directions.

Curved L ines

3. An unlimited number of lines can be drawn through a given fixed point. The adjoining figure shows a fixed point A. It is clear from the figure that an unlimited number of lines can be drawn through A.

4. One and only one line can be drawn through any two fixed points. In the adjoining figure, A and B are two fixed points. It is clear from the figure that only one line can be drawn through the fixed points A and B.

5. Every line has an infinite (uncountable) number of points in it.

4.4.1 Naming a line

A B

The first line can be called AB

or BA

The second line can be called AB

, AC

, AD

, BC

, BD

, CD

, BA

, CA

A B C D

, DA

, CB

, DB

, DC

Properties:

1. A line has no endpoints. It contains an infinite number of points.

2. It has infinite length but no thickness.

3. The line segment is a part of the line.

4. The number of line segments possible from n given points such that no three points are collinear is (1)

4.5 PLANE

A flat surface which extends endlessly in all directions is called a plane.

A plane has infinite length and breadth but has no thickness.

Part of a plane: A part of a plane has a boundary.

Example: The surface of the top of a table is a part of a plane, which has a boundary.

Plane figures: Triangle, Rectangle, Circle, etc. are plane figures. We draw them in a plane and call them plane figures. A cube is not a plane figure.

Space: A ball that encloses a volumetric portion is called a part of a space. The portion enclosed by an infinitely large ball is called space. A space has infinite length, breadth, and thickness.

4.6 PARALLEL LINES

Two straight lines are said to be parallel to each other if they lie in the same plane and do not meet even when extended indefinitely in both directions.

The given figure shows two lines, AB and CD, that are parallel to each other.

The line AB is parallel to the line CD and is symbolised by writing AB||CD. It is read as line AB is parallel to line CD.

A B C D

4.7 INTERSECTING LINES

If two lines lie in the same plane and are not parallel to each other, they are called intersecting lines.

The figure given above shows two lines, AB and CD, that are not parallel. Such lines either intersect at point O or will intersect at point O if extended.

1. The distance between two parallel lines is always the same, whereas the distance between two non-parallel lines (lines that are not parallel) keeps changing.

2. Two different lines in a plane are either parallel or they intersect at only one point.

3. The definitions of parallel lines and intersecting lines are applicable only when the lines are in the same plane, i.e. when the lines are co-planar.

4.8 CONCURRENT LINES

If three or more straight lines in the same plane pass through the same point, the lines are called concurrent lines, and the point is called the point of concurrence.

The given figure shows the concurrent lines AB, CD, EF and GH; all these lines are in the same plane and pass through the same point P. Clearly, point P is the point of concurrence.

4.9 CURVES

A plane figure formed by a continuous and smooth-flowing line without retracing any portion of the line other than single points is called a curve. In everyday language, a curve means not straight, but in mathematics, a curve can be a straight line as well.

Shown below are some examples of curves.

Position of a point with respect to a curve: In the curve below, A, B, and C are the three points.

1. The region consisting of all points lying outside a curve is called the exterior of the curve. Point A is an exterior point.

2. The region consisting of all points lying inside a curve is called the interior of the curve. Point B is an interior point.

3. The region consisting of all points on the curve is called the boundary of the curve. Point C is on the boundary of the curve.

4.10 POLYGONS

A polygon is a closed curve bounded by several straight lines.

Regular polygon: A polygon is equilateral if all its sides are the same length. A polygon is equiangular if all its angles are the same measure. A polygon is regular if it is both equilateral and equiangular.

4.10.1 Types of polygons

A polygon is usually classified by its number of sides, as shown below.

Triangle: A triangle is a plane closed figure bounded by three-line segments.

The adjoining figure shows a triangle ABC bounded by the three-line segments AB, BC and CA.

A

B

C

The line segments AB, BC and CA that form triangle ABC are called the sides of triangle ABC.

Rectangle: A rectangle is a plane-closed figure bounded by four-line segments such that:

i. The opposite line segments (sides) are equal.

ii. Each angle of the figure is 90° .

The adjoining figure shows a rectangle ABCD bounded by the line segments AB, BC, CD, and DA such that:

D

A

i. The opposite line segments (sides) are equal.

i.e. AB = CD and AD = BC

C

B

ii. Each angle of it is 90°, i.e. angle A = angle B = angle C = angle D = 90°

Square: A square is a plane-closedfigure bounded by four line segments (sides) such that:

i. The four line segments are equal to each other.

ii. Each angle of the figure is 90°

The adjoining figure shows a square ABCD bounded by the line segments AB, BC, CD and DA such that:

i. The four-line segments (sides) are equal, i.e. AB = BC = CD = DA

ii. Each angle in it is 90°

i.e. angle A = angle B = angle C = angle D = 90° .

4.11 ANGLES

An angle is formed when two straight lines or rays meet at a common endpoint. The common point of contact is called the vertex of an angle. The word "angle" comes from a Latin word named "angulus," meaning "corner."

The symbol ' ∠ ' represents an angle. Angles are measured in degrees (°) using a protractor.

For example, 45 degrees is represented as 45° .

4.11.1 Parts of angles

Vertex: A vertex is a corner of an angle, a point where two lines or sides meet. O is the vertex in the given figure.

Arms: The two sides of the angle, joined at a common endpoint, are called arms. OA and OB are arms of an angle.

Initial side: Also known as the reference line, it is a straight line from where an angle is drawn. OB is the reference line.

Terminal side: It is the side up to which the angle measurement is done. In the given diagram below, OA is the terminal side.

Interior of an angle: The interior of an angle is the region that lies within an angle. In other words, it is the region bounded by the arms of an angle.

The shaded portion of the given figure shows the interior of the AOB.

Exterior of an angle: The exterior of an angle is the region that lies outside the angle. The shaded portion of the adjoining figure shows the exterior of the AOB.

SOLVED EXAMPLES

Example 1: Define what a polygon is and provide two examples.

Solution:

A polygon is a closed figure formed by joining three or more line segments. Each line segment is called a side of the polygon, and the point where two sides meet is called a vertex. Examples of polygons include triangles and rectangles.

Example 2: Draw a rough sketch of:

a. open curve

b. closed curve

Solution: is an open curve (a) (b) is a closed curve

Example 3: Draw a rough sketch of a closed curve made up of line segments.

Solution:

The required curve is ABCD closed with the line segments AB, BC, CD and DA.

Example 4: Identify the points which are:

i. In the interior

ii. In the exterior

iii. On the closed curve in the given figure

Solution:

i. Points P, Q and R are in the interior of the closed curve.

ii. Points S and T are in the exterior of the closed curve.

iii. Points U and V are on the closed curve.

Example 5: Name all the angles in the given figure. A B C D

Solution:

In the given figure, the names of all the angles are:

i. ∠ ABC

ii. ∠ BCD

iii. ∠ CDA

iv. ∠ DAB

Example 6: In the given figure, name all the line segments:

A B C D E

Solution:

In the given figure, the names of the line segments are AB, BC, CD, DE, EA, DA, DBandEC.

QUICK REVIEW

• A point determines a location. It is usually denoted by a capital letter.

• A line segment corresponds to the shortest distance between two points. The line segment joining points A and B is denoted by AB .

• A ray is a portion of the line starting at a point and going in one direction endlessly.

• A line is obtained when a line segment like AB is extended on both sides indefinitely; it is denoted by AB

or sometimes by a single small letter like l.

• Two lines in a plane are said to be parallel if they do not meet.

• Two distinct lines meeting at a point are called intersecting lines.

• If three or more straight lines in the same plane pass through the same point, the lines are called concurrent lines, and the point is called the point of concurrence.

• Any drawing (straight or non-straight) done without lifting the pencil may be called a curve. In this sense, a line is also a curve.

• A simple curve is one that does not cross itself.

• A curve is said to be closed if its ends are joined; otherwise, it is said to be open

• A polygon is a simple closed curve made up of line segments. Here,

i. The line segments are the sides of the polygon.

ii. Any two sides with a common endpoint are adjacent sides.

iii. The meeting point of a pair of sides is called a vertex.

iv. The endpoints of the same side are adjacent vertices.

v. The join of any two non-adjacent vertices is diagonal

• An angle is made up of two rays starting from a common starting or initial point. Two rays OA

and OB

make AOB∠ (also called BOA∠ ).

• An angle leads to three divisions of a region: on the angle, the interior of the angle, and the exterior of the angle.

WORKSHEET - 1

I. BASIC CONCEPTS OF GEOMETRY

1. State which of the following is a plane closed figure:

2. Give two examples from your surroundings for each of the following:

i. Points ii. Plane surfaces

iii. Line segments

iv. Curved surfaces

3. Under what condition will two straight lines in the same plane have:

i. Only one point in common. ii. No point in common.

iii. An infinite number of points in common.

4. If possible, draw diagrams in support of your answer. Mark two points, A and B, on a page of your exercise book. Mark a third point P such that:

i. P lies between A and B, and the three points A, P, and B are collinear.

ii. P does not lie between A and B, yet the three points are collinear.

iii. The three points do not lie in a line.

5. State whether the following pairs of lines or rays appear to be parallel or intersecting.

6. Correct the statement if it is wrong:

i. A ray can be extended infinitely on either side. ii. A ray has a definite length.

iii. A line segment has a definite length. iv. A line has two endpoints.

v. A ray has only one endpoint.

7. Discuss the number of lines that can be drawn through:

i. Two fixed points. ii. One given point.

iii. Three non-collinear points. iv. Three collinear points.

8. The shaded region of the given figure shows a plane:

a. Name:

i. Three collinear points.

ii. Three non-collinear points.

iii. A pair of intersecting lines.

b. State whether the below statements are true or false:

i. Line DE is contained in the given plane P.

ii. Lines BA and DE intersect at point C.

iii. Points B, D, and C are collinear.

iv. Points D, E, and B are collinear.

9. Mark two points, P and Q, on a piece of paper. How many lines can you draw:

i. Passing through both the points P and Q?

ii. Passing through the point Q?

iii. Passing through the point P?

10. What is a line segment? Provide an example.

11. Position a scale (ruler) on a sheet of paper and secure it with one hand. Next, draw two line segments, AB and CD, along the longer edges of the scale. Determine whether segment AB is parallel to or perpendicular to segment CD.

12. Refer to your textbook:

i. Determine the number of pairs of edges that are parallel to each other.

ii. Determine the number of pairs of edges that are perpendicular to each other.

13. Give an example from your surroundings for each of the following:

i. Parallel lines.

ii. Perpendicular lines

iii. Intersecting lines

14. State whether the below statements are true/false.

i. The maximum number of lines through three collinear points is three.

ii. The maximum number of lines through three non-collinear points is three.

iii. Two parallel lines always lie in the same plane.

iv. Concurrent lines always meet at the same point.

v. A surface can be plane or curved.

vi. There are an infinite number of points in a line segment of length 9 cm.

vii.There are an infinite number of points in a line.

viii. A plane has an infinite number of lines.

ix. A plane has an infinite number of points.

x. Two non-parallel line segments will always intersect.

xi. All equilateral triangles are isosceles also.

WORKSHEET - 2

I. MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER

1. Which of the following shapes has four equal sides and four right angles?

a. Triangle

2. What is a polygon?

b. Rectangle

a. A straight path between two points

c. Circle

b. A closed figure formed by joining three or more line segments

c. A figure with no straight lines

d. A figure with four sides of equal length.

3. Which of the following shapes exhibits symmetry?

a. Circle b. Rectangle

d. Pentagon

c. Triangle d. Square.

4. What is the name of the point where two rays or line segments meet to form an angle?

a. Endpoint

b. Vertex

5. Which of the following is NOT a polygon?

a. Triangle

b. Square

6. The number of diagonals of a pentagon is:

7. The number of diagonals of a triangle is:

c. Midpoint

d. Intersection

c. Circle d. Pentagon.

8. The number of lines passing through five points such that no three of them are collinear is:

9. The number of line segments in the given figure is:

A B C D E

10. The number of triangles in the given figure is:

11. The number of angles in the given figure is:

12. If the sum of two angles is greater than 180°, then which of the following is not possible for the two angles?

a. Two obtuse angles

c. One obtuse angle and one acute angle

b. One reflex angle and one acute angle

d. Two right angles.

13. If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?

a. One right angle and one acute angle

c. One obtuse angle and one acute angle

b. Two acute angles

d. Two right angles

a. 14

12 c. 13

c. 4 d. 3

II. FILL IN THE BLANKS

1. ______ is a three-sided plane closed figure.

2. A square is a plane-closed figure which is not bounded by _______.

3. A rectangle is a ______ sided plane _______.

4. A rectangle has opposite sides ________ and adjacent sides ________ to each other.

5. The sides of a square are ________ to each other, and each angle is __________.

6. A polygon of six sides is called a _______.

7. A triangle with each of its sides having different lengths is called a ______ triangle.

III. SUBJECTIVE QUESTIONS

1. Mark a point O on a piece of paper. Using a pencil and a ruler, draw a line passing through point O. Then, draw one more line through point O. How many lines can you draw through O? Record your observations in a statement.

2. Mark two points, A and B, on a plain sheet of paper. Using a pencil and a ruler, draw a line through points A and B. Draw another line through points A and B. What do you notice? Write down your observations.

3. Draw two straight lines on a sheet of paper so that the lines drawn:

i. Do not intersect

ii. Appear to intersect when extended

iii. Intersect each other

4. Draw a figure to show that:

i. Points A, B, and C are collinear.

ii. Lines AB, CD and EF are concurrent.

5. In your notebook, sketch two rays emanating from the same initial point O, each going in opposite directions. Provide a specific name for the resulting figure.

6. In each figure given below, write the number of line segments used.

7. The number of common points in the two angles marked in the given figure is:

8. The number of common points in the two angles marked in the given figure is:

9. The common part between the two angles, BAC and DAB, in the given figure is:

IV. STATE TRUE OR FALSE

1. An angle of 0° is an acute angle.

2. A horizontal line and a vertical line always intersect at acute angles.

3. If the arms of an angle on the paper are decreased, the angle decreases.

4. If line PQ || line m, then line segment PQ || m.

5. Two parallel lines meet each other at some point.

6. If the arms of an angle on the paper are decreased, the angle increases.

7. Two line segments may intersect at two points.

8. Many lines can pass through two given points.

9. Only one line can pass through a given point.

10. Two angles can have exactly three points in common.

UNDERSTANDING ELEMENTARY SHAPES 5

5.1 INTRODUCTION

We see various types of 3D shapes in our surroundings. These 3D shapes are formed from line segments, angles, triangles, polygons and circles. Let us learn how we can compare the sizes of 2D shapes in different ways.

5.2 MEASURING LINE SEGMENTS

We have drawn and seen so many line segments. A triangle consists of three segments, while a quadrilateral comprises four. A line segment is a fixed portion of a line, which is why we can measure a line segment. This measure of each line segment is a unique number called its length. To compare any two-line segments, we find a relation between their lengths. This can be done in several ways.

5.2.1 Comparison by observation

Can you determine which one is longer just by looking at them? You will notice that line segment AB is longer.

However, your usual judgment may not always be reliable. Consider the below line segments, for instance:

The difference in lengths between these two may not be obvious. This is why we need other ways of comparison.

5.2.2 Comparison by tracing

To see if AB or CD is longer, we use tracing paper. We will trace segment CD and put the traced part on AB. Now, we can tell which one is longer. But this method needs accurate tracing.

Additionally, if you want to compare the given segments with another length, you must trace them again. This can be hard because you can't trace every time you want to compare.

5.2.3 Comparison using a ruler and a divider

Have you looked at all the tools in your toolbox? You have a ruler and a divider, among other things.

Divider

Look at the ruler with marks on one side. It's divided into 15 parts, each 1 centimetre long. Each centimetre is further divided into 10 smaller parts, each 1 millimetre long.

A

B

Place the zero mark of the ruler at A. Read the mark against B, which gives us the length of AB. Suppose the length is 5.8 cm, we may write it as Length AB = 5.8 cm or more simply as AB = 5.8 cm.

Note: 1 mm is 0.1 cm, 2 mm is 0.2 cm, and so on. So, 2.3 cm will mean 2 cm and 3 mm.

5.2.4 Positioning error

There is room for errors even in the above procedure. The thickness of the ruler may cause difficulties in reading the marks on it.

The eye should be correctly positioned just vertically above the mark to get an accurate measure. Otherwise, errors can happen due to the angular viewing.

Wrong eye position

Correct eye position

Wrong eye position

1 2 3 4

Object to be measured

Ruler

5.3 ANGLES, TYPES OF ANGLES, AND THEIR ROTATIONS

5.3.1 Right, straight, and complete angle

Right angle: The right angle is exactly equal to 90° .

Straight angle: A straight angle is equal to 180°

Revolution: Turning by two straight angles (or four right angles) in the same direction makes a full turn. This one complete turn is called one revolution.

Complete angle: The angle for one revolution is a complete angle. A complete angle is one complete revolution or equal to 360°

5.3.2 Right, straight, and complete angle by direction and clock

Let us understand the concept of right and straight angles by directions.

NORTH

EAST

WEST

SOUTH

When we move from North to East, we form an angle of 90°, which is called a right angle.

You stand facing north.

By ’right-angled-turn’ clockwise, you now face east.

By another ’right-angled-turn’ you finally face south.

UNDERSTANDING

When we move from North to South, we form an angle of 180°, which is called a straight angle.

When we turn four right angles in the same direction, we return to the initial position. For example, making a clockwise turn from North to North again forms an angle of 360°, which is called a complete angle. This is called one revolution.

5.3.3

Acute angle

An angle smaller than a right angle is called an acute angle. These are acute angles.

5.3.4 Obtuse angle

If an angle is larger than a right angle but smaller than a straight angle, it is called an obtuse angle. These are obtuse angles.

House

5.3.5 Reflex angle

Book reading desk

A reflex angle is an angle that measures greater than 180 degrees but less than 360 degrees. Example: Think of a clock showing 7 o'clock, where the minute and hour hands create an angle that is larger than a straight line (180 degrees) but less than going all the way around the clock (360 degrees). This angle is a reflex angle.

5.4 MEASURING ANGLES

We use a 'Right-angle tester' to determine the angles as acute, obtuse, or reflex. However, it can't precisely compare two obtuse angles for size. To measure angles precisely, we need to use a 'protractor'.

We call this a 'degree measure’. One complete revolution is divided into 360 equal parts. Each part is a degree. We write 360° to say 'three hundred sixty degrees’.

5.4.1 The protractor

You can use a protractor from your instrument box. It has a curved edge divided into 180 equal parts, each called a 'degree'. The markings start from 0° on the right side and end at 180° on the left side, and vice versa.

Suppose you want to measure an angle ABC.

1. Place the protractor so that the midpoint (M in the figure) of its straight edge lies on the vertex B of the angle.

2. Align the protractor such that BC matches the straight edge of the protractor.

3. The protractor has two scales: use the scale where the 0° mark lines up with the straight edge (i.e. with ray BC

4. The degree measurement of the angle is indicated by the mark where BA meets the curved edge.

We write m ∠ ABC = 40°, or simply ∠ ABC = 40° .

5.5 PERPENDICULAR LINES

When two lines intersect, and the angle between them is a right angle, then the lines are said to be perpendicular. If a line AB is perpendicular to CD, we write AB ⊥ CD.

5.6 CLASSIFICATION OF TRIANGLES

Do you remember a polygon with the least number of sides? That is a triangle.

Let us read more about the different types of triangles.

5.6.1 Naming triangles based on sides

A triangle with all unequal sides is called a scalene triangle.

A triangle having two equal sides is called an isosceles triangle.

UNDERSTANDING ELEMENTARY SHAPES

A triangle having all equal sides is called an equilateral triangle.

5.6.2 Naming triangles based on angles

An acute-angled triangle has all angles less than 90°, a right-angled triangle has one 90° angle, and an obtuse-angled triangle has one angle greater than 90° .

Acute-angled Triangle Right-angled Triangle Triangle

Obtuse-angled

Example: Determine the types of the following triangles:

(a) A triangle with side lengths 6 cm, 7 cm, and 8 cm.

(b) ∆ PQR such that PQ = QR = PR = 4 cm.

Solution:

(a) A triangle with lengths of sides 6 cm, 7 cm, and 8 cm has all sides of unequal lengths. Hence, it is a scalene triangle.

(b) ∆ PQR such that PQ = QR = PR = 4 cm has all its sides of equal lengths. Hence, it is an equilateral triangle.

5.7 CLASSIFICATION OF QUADRILATERALS

We know that a quadrilateral is a polygon with four sides. Now, we will discuss special types of quadrilaterals such as square, rectangle, parallelogram, rhombus, trapezium, and kite.

5.7.1 Square

A square is a quadrilateral with four equal sides and four right angles (90-degree angles).

In the figure, PQRS is a square with PQ = QR = RS = SP; ∠P = ∠Q = ∠R = ∠S = 90°

Example: If a square has a side of length 5 cm, what is its perimeter?

Solution:

The perimeter of a square is the sum of all its side lengths. Since all sides of a square are equal, the perimeter is 4 × side length = 4 × 5 cm = 20 cm.

5.7.2 Rectangle

A rectangle is a quadrilateral with four right angles (90-degree angles). Its opposite sides are equal in length.

In the figure, ABCD is a rectangle with ∠A = ∠B = ∠C = ∠D = 90°; AB = DC and AD = BC.

5.7.3 Parallelogram

A quadrilateral in which both pairs of opposite sides are parallel is a parallelogram.

• The opposite sides of a parallelogram are equal.

• The opposite angles of a parallelogram are equal.

• The diagonals of a parallelogram are unequal in length.

In the given figure, ABCD is a parallelogram with AB  DC and AD  BC; ∠A = ∠C and ∠ B = ∠ D; AD = BC and AB = DC.

Example: In the given figure, ABCD is a parallelogram. Find x.

3x +20 5x -12

Solution:

We know that if ABCD is a parallelogram, then the opposite sides are equal. Therefore,

AD = BC

⇒ 5x – 12 = 3x + 20

⇒ 5x – 3x = 20 + 12

⇒ 2x = 32

⇒ x = 16 cm

5.7.4 Rhombus

A rhombus is a quadrilateral with four equal sides. Its opposite angles are equal, but they are not necessarily right angles.

In the given figure, PQRS is a rhombus with PQ || SR, PS || QR; PQ = QR = RS = SP ; ∠P = ∠R and ∠S = ∠Q

5.7.5 Trapezoid

A trapezoid is a quadrilateral with one pair of opposite sides that are parallel.

In the given figure, PQRS is a trapezium with PQ || SR.

5.7.6 Kite

A kite is a quadrilateral with two pairs of adjacent sides that are equal in length, and its diagonals intersect at right angles.

In the given figure, PQRS is a kite with PQ = PS and RQ = RS.

5.8 POLYGONS

You have learned about triangles (3 sides) and quadrilaterals (4 sides) until now. Now, let's expand our understanding of polygons to include shapes with more sides. We may classify polygons according to the number of their sides.

5.9 LINES AND ANGLES

5.9.1 Collinear and non-collinear points

Collinear points are a set of three or more points that exist on the same straight line.

P, Q, and R are collinear points as they lie on the same straight line.

Non-collinear points are a set of points that do not lie on a single line. We cannot draw a single straight line through these points. An example of non-collinear points is provided below:

In the figure, points M, N, O, P, and Q are non-collinear points since they do not lie on the same straight line.

5.9.2 Complementary angles

When the sum of two angles is 90°, then the angles are known as complementary angles.

For example, if angle A is 30°, then its complement angle B would be 60° because 30° + 60° = 90° .

5.9.3 Supplementary angles

When the sum of two angles is 180°, then the angles are known as supplementary angles.

Look at the below diagram with two angles: 130° and 50°. Since they add up to 180°, they are called supplementary angles.

5.9.4 Adjacent angles

Adjacent angles are two angles that are side by side and share a common vertex and side.

Here, ∠ AOC and ∠ BOC are adjacent angles as they share a common vertex (O) and a common side (OC).

5.9.5 Linear pair of angles

When two lines intersect each other at a single point, linear pairs of angles are formed.

If two angles form a linear pair, the angles are supplementary, whose measures add up to 180° . Therefore, linear pairs of angles always sum up to 180° .

Linear pair of angles: ( ∠ 1 and ∠ 4); ( ∠ 2 and ∠ 4); ( ∠ 2 and ∠ 3); ( ∠ 1 and ∠ 3)

5.9.6 Vertically opposite angles

Linear Pair of Angles and and and and

When two lines cross each other, the angles on opposite sides of the intersection are called vertical angles or vertically opposite angles. A pair of vertically opposite angles is always equal.

In the example below, ( ∠ 1, ∠ 3) and ( ∠ 2, ∠ 4) are vertical angles.

SOLVED EXAMPLES

Example 1: Find the complement of 30°

Solution:

We know that the sum of complementary angles = 90° .

As the given angle is 30°, then,

The complement of 30° is 90° - 30° = 60°

Example 2: Find the supplement of the angle 1 4 of 240° .

Solution:

Step 1: Convert 1 4 of 240°

That is, 1 4 × 240° = 60°

Step 2: Supplement of 60° = 180° - 60° = 120°

Therefore, the supplement of the angle 1 4 of 240° is 120° .

Example 3: Are the following angles adjacent? Explain.

Solution:

i. ∠ 1 and ∠ 2 are not adjacent because they don't share a side.

ii. ∠ 1 and ∠ 2 are not adjacent because their interiors overlap.

iii. ∠ 1 and ∠ 2 are adjacent because they have a common arm and a common vertex, and the interiors do not overlap.

Example 4: In the given figure, AOC is a straight line. Find x.

A C O

Solution:

We know that ∠ AOB and ∠ COB are linear pairs. It can be written as ∠ AOB + ∠ COB = 180°

Substituting the values, we get:

⇒ x + 25° + 3x + 15° = 180°

⇒ 4x + 40° = 180°

⇒ 4x = 180° – 40° = 140°

⇒ x = 140 4 = 35°

i. ii. iii.

Example 5: Find ∠ x in the given figure.

x-10)

Solution:

Given: ∠ APC = 120° , ∠ BPD = (2x - 10)°

In the given figure,

⇒ ∠ APC = ∠ BPD (Vertically opposite angles)

⇒ 120° = (2x - 10)°

⇒ 120° + 10° = 2x°

⇒ 130° = 2x

⇒ x = 65°

QUICK REVIEW

• A protractor helps us measure angles in degrees.

• A right angle measures 90°, while a straight angle measures 180°

• An angle is acute if it is smaller than a right angle and obtuse if it is larger than a right angle but less than a straight angle.

• A reflex angle is larger than a straight angle.

• Triangles can be classified as following based on their angles:

Nature of angle in the triangle Name

• All angles are less than 90°

• One angle is a right angle

• One angle is greater than 90° but less than 180° .

• One angle is greater than 180° .

• Acute-angled triangle

• Right-angled triangle

• Obtuse-angle triangle

• Reflex-angled triangle

• Triangles can be classified as the following based on the lengths of their sides:

• All three sides are of unequal length

• Any two sides are of equal length

• All three sides are of equal length

• Scalene triangle

• Isosceles triangle

• Equilateral triangle

• Two angles are called complementary when their measures add up to 90°

• Two angles are called supplementary when their measures add up to 180° .

WORKSHEET - 1

I. MEASURING LINE SEGMENTS, ANGLES, AND THEIR ROTATIONS

1. A, B and C are three points such that AB = 4 cm, BC = 3 cm, and AC = 7 cm. Which one of them lies between the other two?

2. If point D is the midpoint of line segment AB, and AD measures 13 cm, what is the length of line segment AB?

3. The length of line segment PQ is 42 cm. Points R and S trisect the line segment PQ. What is the length of RS and SQ?

4. Which of these two angles is larger? Make an estimate first and then verify by measuring them.

5. Answer the following questions according to the given figure.

UNDERSTANDING ELEMENTARY SHAPES

i. Which angle is formed if you are facing North and turn clockwise to face South?

ii. Which angle is formed if you are facing East and cover 1 4 of revolution anti-clockwise? In which direction are you facing now?

6. How many right angles make a complete revolution?

7. What is the measure of 1 2 of a right angle?

8. What will be the angle made by the minute and hour hand of a clock when the time is 6 o'clock?

9. Find the angle measure between the hands of the clock in each figure. Also, write it in terms of a revolution.

10. If a clock's minute hand is at 12, and the hour hand is at 3, what angle do they form?

II. CLASSIFICATION OF TRIANGLES AND QUADRILATERALS

1. Name the types of triangles formed in each of the following in two different ways:

2. Match the following:

i. 3 sides of equal lengths

ii. 2 sides of equal lengths

iii. All sides are of different lengths

iv. 3 acute angles

v. 1 right angle

vi. 1 obtuse angle

a. Scalene

b. Isosceles

c. Obtuse-angled

d. Right-angled

e. Equilateral

f. Acute-angled

3. The angles of a triangle are 40°, 40° and 100°, respectively. Which type of triangle is it?

4. If a square has a side length of 6.5 cm, what is its perimeter?

5. The consecutive sides of a parallelogram are in the ratio of 3:4, and the perimeter is 70 cm. Determine the lengths of the sides of the parallelogram.

III. LINES AND ANGLES

1. If x and (x + 30°) are complements of each other, then find the value of x.

2. If z and (z + 50°) are supplements of each other, then find the value of z.

3. An angle is double its complement. Find the angle.

4. The measure of an angle is 30° less than its supplement. Find the measure of the angles.

5. Find an angle which is two fifth of its supplement.

6. If ∠ AOC and ∠ BOC are supplemetary angles and are in ratio 5:7, then find:

i. ∠ AOC

ii. ∠ BOC

7. Identify two pairs of adjacent angles, vertically opposite angles and linear pairs in the given figure.

8. In the given figure, find the value of z.

9. In the given figure, if AOC is a straight line, then find the value of x.

10. Find the values of the angles x, y, and z in the given figure:

WORKSHEET - 2

I. MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER

1. Which of the following is the possible measure of the ∠ AOB in the figure given below?

2. What is the estimated measure of the angle shown in the figure below?

3. How many lines are perpendicular to line p?

a. 1 b. 3 c. 4 d. 2

4. Based on the figure provided, which of the following statements is incorrect?

12 11 10 9 8 7 6 4 3 2 1 0 5

a. PS = VY

c. Y is the midpoint of WZ

b. QT = RU = WZ

d. T is the midpoint of RV

5. In the given figure, AB = 4 cm, AD = 18 cm, BC = 6 cm, and AE = 20 cm. What is the measure of CD and DE, respectively?

A B C D E

a. 2 cm and 8 cm b. 8 cm and 2 cm

c. 4 cm and 4 cm d. 3 cm and 5 cm

6. If three points, A, B, and C, are on a line such that AC + CB = AB, then which of the following must be true?

a. A lies between points B and C.

c. C lies between points A and B.

b. B lies between points A and C.

d. A is equidistant from C and B.

7. The number of sides of a polygon is four more than the number of sides of a pentagon. What is the name of the polygon?

a. Hexagon b. Heptagon c. Octagon d. Nonagon

8. A triangle has sides of lengths 8 cm, 9 cm, and 11 cm, respectively. Which type of triangle is it?

a. Isosceles b. Equilateral c. Scalene

d. Isosceles right-angled

9. The angles of a triangle are 40°, 40° and 100°, respectively. Which type of triangle is it?

a. Isosceles b. Acute-angled c. Scalene d. Right-angled

10. Which of the following quadrilaterals has all sides of equal length?

a. Rectangle b. Parallelogram c. Square d. Trapezium

11. Which of the following pairs of angles are complementary?

a. 0°, 60°

b. 20°, 60°

c. 20°, 70°

d. 30°, 90°

12. In the given figure, AOB is a straight line, and the ray OC stands on it. Find the value of x. (3x +5)° ° (2x -25)

a. 46°

II. FILL IN THE BLANKS

b. 40° c. 30° d. 16°

1. Two intersecting lines are said to be perpendicular if the angle between them is __________.

2. An acute angle is more than __________ and less than __________.

3. If the sum of two angles equals a straight angle, and one angle is acute, then the other angle must be __________.

4. The measure of a reflex angle is more than __________ and less than __________.

5. A heptagon has __________ sides.

6. Tulsi constructed a triangle with sides of 5 cm each. She can call it a/an ________triangle.

7. If angle P and angle Q are supplementary, and the measure of angle P is 60°, then the measure of angle Q is __________.

III. SUBJECTIVE QUESTIONS

1. Verify whether D is the mid-point of AG .

2. Find the complementary angle of 80°

3. Find the supplementary angle of 90° .

4. The consecutive sides of a parallelogram are in the ratio of 3 : 4, and the perimeter is 70 cm. Determine the lengths of the sides of the parallelogram.

5. In the given figure, two straight lines, PQ and RS, intersect each other at O. If ∠ POT = 75° , find the values of a+b+c.

ANSWER KEY

1. KNOWING OUR NUMBERS

Worksheet 1

I. Place value and face value, comparing and ordering numbers, formation of numbers, place value charts

1. 2008

2. 4100

3. 4000

4. i. 3842 ii. 259010

5. i. 308380 ii. 43250

6. 10010, 10101, 11001, 11010

7. 477, 471, 417, 411

8. Greatest 4-digit number: 7642

Smallest 4-digit number: 2467

9. 237, 273, 327, 372, 723, 732

10. 10259

11. i. 13,001,040 = Thirteen million one thousand forty ii. 7,323,578 = Seven million three hundred twenty three thousand five hundred seventy eight

12. i. 32,615,004 ii. 2,05,81,591

II. Conversion of units, larger numbers

1. Each will receive 1200 grams.

2. 1500 cm

3. 8,80,356

4. 20 bows and 100 cm of ribbon is remaining.

5. 2,60,030

6. 1,24,000

7. 1,05,000

8. 7,36,000

9. 2,000 notebooks

10. 39 cups

11. 39200 m or 39 km 200 m

12. 19,250 mL of paint

III. Estimation and approximation, roman numbers

1. i. 4180 ii. 1300

2. i. 300 ii. 600

3. i. 42000 ii. 7000

4. i. 3 ii. 0.5

5. 1200

6. i. 45 ii. 890

7. i. DCLXXIX ii. MMMDCCVI

8. 1458

Worksheet 2

I. Multiple choice questions with single correct answer

1. d 2. a 3. c 4. d 5. a

6. a 7. b 8. b 9. c 10. b

11. b 12. a 13. d 14. a 15. b

16. c 17. c 18. a 19. c 20. b

II. Fill in the blanks

1. 89,999

2. 1002

3. 1000

4. 70,07,70,007

5. 6,44,087

6. 20,11,310

7. ₹6,37,500

8. 100

9. 1964

10. 1667

III. Subjective questions

1. 28

2. Greatest 5-digit number: 97210

Smallest 5-digit number: 10279

3. 18

4. 4961

5. i. 4,04,40,044 = Four crores four lakhs forty thousand forty four ii. 29,10,291 = Twenty nine lakhs ten thousand two hundred ninety one

6. 0.8 kg

7. 5 curtains, 100 cm will be left

8. 1,35,400

9. 54,000

10. 492

2. WHOLE NUMBERS

Worksheet 1

I. Introduction to whole numbers

1. 1000, 1001, 1002

2. 90008, 90007, 90006

3. 1

4. 47

5. 0, 1, 2, 3, 4 and 1, 2, 3, 4

6. Whole

7. Zero

II. Predecessor and successor

1. i. 6540702 ii. 980200 iii. 10000000 iv. 3445671

v. 4244570 vi. 1221345

2. i. 1 ii. 19999 iii. 298089 iv. 7854320 v. 3245542 vi. 6553454 vii. 223442 viii. 9778646

III. The number line

1. i. 830 > 803 ii. 170 >107 iii. 78065 < 78605 iv. 999999 < 1000000

ANSWER KEY

2. NA

3. NA

4. NA

IV. Properties of addition and subtraction of whole numbers

1. i. 34720 ii. 87780 iii. 0

2. i. 292000 ii. 175740 iii. 196812 iv. 5860

3. b

4. a

5. a

6. c

7. a

V. Patterns in Mathematics

1. NA

2. Hexagonal pattern, 61 Worksheet 2

I. Multiple choice questions with single correct answer

1. b 2. a 3. b 4. b 5. c

6. c 7. c 8. c 9. c 10. b

11. d 12. d 13. c 14. b 15. b

16. c

II. Fill in the blanks

1. Smallest

2. Predecessor

3. Smallest

4. Successor

5. Whole

6. Single

7. No

8. 13

9. 0

III. Assertion and reason

1. c 2. a 3. b 4. a 5. d

IV. Subjective questions

1. 2

2. 2

3. 6

4. 0

5. 1270

6. NA

7. 80 boxes

8. 943559

9. 400

10. Successor =2009010 and Predecessor =2009008

11. ₹135

12. 990000

13. NA

14. Sequence: 7, 19, 37, 61

15. Cube of natural numbers: 1, 8, 27, 64, 125

16. 123456 × 8 + 6 = 987654

1234567 × 8 + 7 = 9876543

17. 2 10000110000200001 = 2 10000001100000020000001 =

3. PLAYING WITH NUMBERS

Worksheet 1

I. Numbers arrangement, factors and multiples

1. i. Factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.

ii. Factors of 15 are 1, 3, 5, and 15.

iii. Factors of 21 are 1, 3, 7, and 21.

iv. Factors of 27 are 1, 3, 9, and 27.

v. Factors of 12 are 1, 2, 3, 4, 6, and 12.

vi. Factors of 20 are 1, 2, 4, 5, 10, and 20.

vii. Factors of 18 are 1, 2, 3, 6, 9, and 18.

viii. Factors of 23 are 1 and 23.

ix. Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.

2. i. First five multiples of 5 are 5, 10, 15, 20, 25.

ii. First five multiples of 8 are 8, 16, 24, 32, 40.

iii. First five multiples of 9 are 9, 18, 27, 36, 45.

3. (i) → (b); (ii) → (d); (iii) → (a); (iv) → (f); (v) → (e)

II. Prime and composite numbers, even and odd numbers

1. i. Even number

ii. Even number

2. i. False ii. True

iii. True iv. False

v. False vi. False

vii. False viii. True

ix. False x. True

3. (17 and 71); (37 and 73); (79 and 97).

4. Prime numbers: 2, 3, 5, 7,11,13, 17,19

Composite numbers: 4, 6, 8, 9, 10, 12, 14,15, 16, 18.

5. 7

6. i. 44 = 3 + 41 ii. 36 = 5 + 31

iii. 24 = 7 + 17 iv. 18 = 7 + 11

7. Three pairs of prime numbers whose difference is 2 are 3 and 5; 5 and 7; 11 and 13.

8. 23 and 37 are prime numbers. Thus, numbers in option (a) and (c) are prime.

ANSWER KEY

9. 90, 91, 92, 93, 94, 95, 96

10. i. 21 = 3 + 7 + 11

ii. 31 = 3 + 11 + 17

iii. 53 = 13 + 17 + 23

iv. 61 = 13 + 19 + 29

11. (2, 3); (2, 13); (3, 17); (7, 13); (5, 5)

12. i. Prime number

ii. Composite number

iii. Prime, composite

iv. 2

v. 4

vi. 2

III. Tests for divisibility of numbers

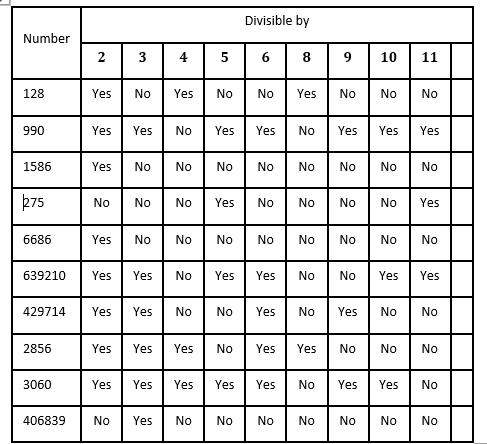
2. i. 572 is divisible by 4 and is not divisible by 8.

ii. 726352 is divisible by 4 and also by 8.

iii. 5500 is divisible by 4 and not divisible by 8.

iv. 6000 is divisible by 4 and divisible by 8.

v. 12159 is not divisible by 4 and 8.

vi. 14560 is divisible by 4 and 8.

vii. 21084 is divisible by 4 and not di visible by 8.

viii. 31795072 is divisible by 4 and 8.

ix. 1700 is divisible by 4 and not divisible by 8.

x. 2150 is not divisible by 4 and 8.

3. i. 297144 is divisible by 6.

ii. 1258 is not divisible by 6.

iii. 4335 is not divisible by 6.

iv. 61233 is not divisible by 6.

v. 901352 is not divisible by 6.

vi. 438750 is divisible by 6.

vii. 1790184 is divisible by 6.

viii. 12583 is not divisible by 6.

ix. 639210 is divisible by 6.

x. 17852 is not divisible by 6.

4. i. In 5445, is divisible by 11.

ii. In 10824, is divisible by 11.

iii. In 7138965, is not divisible by 11.

iv. In 70169308, is divisible by 11.

v. In 10000001, is divisible by 11.

vi. In 901153, is divisible by 11.

5. i. The smallest digit will be 2 and the greatest digit will be 8.

ii. The smallest digit will be 0 and the greatest digit will be 9.

IV. Common factors and multiples

1. i. 1, 2 and 4 ii. 1 and 5

iii. 1 and 5 iv. 1, 2, 4 and 8

2. i. 1, 2 and 4 ii. 1 and 5

3. i. 24, 48 and 72 ii. 36, 72 and 108

4. 12, 24, 36, 48, 60, 72, 84, and 96

5. i. 18 and 35 are co-prime numbers.

ii. 15 and 37 are co-prime numbers.

iii. 30 and 415 are not co-prime numbers. iv. 17 and 68 are not co-prime numbers. v. 81 and 16 are co-prime numbers.

vi. 216 and 215 are co-prime numbers.

6. 60

V. Prime factorisation and co-prime numbers

1. i. The missing numbers are 3 and 2.

ii. Since, 60302,30103 =×=× and 1052 =×

2. The greatest four-digit number is 9999. 99993311101∴=×××

3. NA

4. NA

5. In expressions, ii. and iii. prime factorisation has been done.

6. 13 and 15 are coprime, 17 and 18 are coprime

VI. HCF, LCM, relationship between HCF and LCM

1. i. 6 ii. 6 iii. 6 iv. 35 v. 7 vi. 9

2. i. 1 ii. 2 iii. 1

3. No, HCF = 1

4. i. 36 ii. 60 iii. 30 iv. 60

5. i. 20 ii. 18 iii. 48 iv. 45

6. 75

ANSWER KEY

Worksheet 2

I. Multiple choice questions with single correct answer

1. c 2. d 3. b 4. c 5. d

6. a 7. b 8. a 9. a 10. a

II. Subjective questions

1. 13, 26, 39, 52, 65

2. 401 is a prime number

3. 840 = 2 × 2 × 2 × 3 × 5 × 7

4. 720

5. 240

6. 2

7. 16

8. 180

9. 99962

10. NA

11. 226180

12. 24 cm

13. HCF = 18, LCM = 864

14. 12

15. 438340 is divisible by 4, 10 and not divisible by 3 and 8.

16. i. 2 ii. 2 iii. 1

III. Case studies

1. a 2. b 3. c 4. d 5. c

4: BASIC GEOMETRICAL IDEAS

Worksheet 1

I. Basic concepts of geometry

1. i, iii, iv, vi, and viii.

2. NA

3. i. Intersecting lines

ii. Parallel lines

iii. Coincident or identical lines

4. NA

5. Parallel lines = ii and iii

Intersecting lines = i and iv

6. i. A ray can be extended infinitely on either side.

ii. A ray does not have a definite length; it extends infinitely in one direction.

iii. A line segment has a definite length.

iv. A line has infinitely many points and does not have end points.

v. A ray has one end point (the initial point) and extends infinitely in one direction.

7. i. One line

ii. Infinitely many lines

iii. One line for any two points

iv. One line

8. NA

9. NA

10. NA

11. NA

12. NA

13. NA

14. i. T ii. F iii. T

iv. F v. T vi. F

vii. T viii. T ix. T

x. T xi. T

Worksheet 2

I. Multiple choice questions with single correct answer

1. b 2. b 3. d 4. b 5. c 6. a 7. c 8. c 9. d 10. c 11. c 12. d 13. a

II. Fill in the blanks

1. Triangle

2. Equal

3. Four, Figure

4. Equal, Perpendicular

5. Equal, 90°

6. Hexagon

7. Scalene

III. Subjective questions

1. NA 2. NA 3. NA

4. NA 5. NA 6. i. 10 ii. 12 iii. 13

7. 2

8. 3

9. Vertex A and Ray AB

IV. State True or False 1. F 2. F 3. T 4. F 5. F 6. F 7. T 8. T 9. F 10. T

5: UNDERSTANDING ELEMENTARY SHAPES

Worksheet 1

I. Measuring line segments, angles, and their rotations

1. Point B

2. 26 cm

3. RS = 14 cm and SQ = 14 cm

4. ∠B

5. i. 180o ii. 90o, North 6. 4

7. 45o

8. 180o

9. i. 90o or 1 4 of a revolution

ii. 180o or 1 2 of a revolution

10. Right angle

II. Classification of triangles and quadrilaterals

1. i. Isosceles triangle and acute angled triangle

ii. Scalene triangle and right-angled triangle

iii. Scalene triangle and obtuse angled triangle

ANSWER

3. Obtuse

4. 180o and 360o

5. 7

6. Equilateral

7. 120o

III. Subjective questions

1. Yes, D is the mid-point of AG.

2. 10o

3. 90o

4. 15 cm and 20 cm

5. 153o

iv. Equilateral triangle and acute angle triangle

2. i-e, ii-b, iii-a, iv-f, v-d, vi-c

3. Isosceles triangle

4. 26 cm

5. 15 cm and 20 cm

III. Lines and angles

1. 30o

2. 65o

3. 60o

4. 105o and 75o

5. 360 7 °

6. i. 75o ii. 105o

7. Adjacent angles:

( ) ( ) POY,YOQ;YOQ,QOX ∠∠∠∠

Vertically opposite angles: POY∠ and QOX;POX∠∠ and QOY∠

Linear pair:

( ) ( ) QOX,XOP;XOP,POY ∠∠∠∠

8. 167°

9. 12°

10. 55, 125, 125 xyz ∠=°∠=°∠=°

Worksheet 2

I. Multiple choice questions with single correct answer

1. d 2. c 3. d 4. c 5. b

6. c 7. d 8. c 9. a 10. c 11. c 12. b

II. Fill in the blanks

1. 90o

2. 0o and 90o