PHYSICS
IL Foundation Series - Physics Class 10
Legal Disclaimer
This book is intended for educational purposes only. The information contained herein is provided on an “as-is” and “as-available” basis without any representations or warranties, express or implied. The authors (including any affiliated organizations) and publishers make no representations or warranties in relation to the accuracy, completeness, or suitability of the information contained in this book for any purpose.
The authors (including any affiliated organizations) and publishers of the book have made reasonable efforts to ensure the accuracy and completeness of the content and information contained in this book. However, the authors (including any affiliated organizations) and publishers make no warranties or representations regarding the accuracy, completeness, or suitability for any purpose of the information contained in this book, including without limitation, any implied warranties of merchantability and fitness for a particular purpose, and non-infringement. The authors (including any affiliated organizations) and publishers disclaim any liability or responsibility for any errors, omissions, or inaccuracies in the content or information provided in this book.
This book does not constitute legal, professional, or academic advice, and readers are encouraged to seek appropriate professional and academic advice before making any decisions based on the information contained in this book. The authors (including any affiliated organizations) and publishers disclaim any liability or responsibility for any decisions made based on the information provided in this book.
The authors (including any affiliated organizations) and publishers disclaim any and all liability, loss, or risk incurred as a consequence, directly or indirectly, of the use and/or application of any of the contents or information contained in this book. The inclusion of any references or links to external sources does not imply endorsement or validation by the authors (including any affiliated organizations) and publishers of the same.
All trademarks, service marks, trade names, and product names mentioned in this book are the property of their respective owners and are used for identification purposes only.
No part of this publication may be reproduced, stored, or transmitted in any form or by any means, including without limitation, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the authors (including any affiliated organizations) and publishers.
The authors (including any affiliated organizations) and publishers shall make commercially reasonable efforts to rectify any errors or omissions in the future editions of the book that may be brought to their notice from time to time.
Subject to Hyderabad jurisdiction only.
Copyright © 2025 Rankguru Technology Solutions Private Limited. All rights reserved.
ISBN 978-81-985539-6-6
Second Edition
LIGHT - REFLECTION AND REFRACTION 1
1.1 INTRODUCTION TO LIGHT
Light is a form of energy that causes vision sensations. Light makes things around us visible. The light may have been emitted by the object or may have been reflected by it. Objects that give out light of their own are called luminous objects.
Examples: The Sun, the stars, and glow worms are natural sources of light.
Objects that do not give out light of their own but reflect other's light are called non-luminous objects.
Examples: Planets, the Moon, the Earth, books, etc.
Objects are classified into three types based on how they transmit, absorb or scatter light.
i) Transparent objects allow light to pass through them, and we can see objects clearly through them.
Examples: Air, thin glass, clear water of shallow depth, etc.
ii) Opaque objects do not allow light to pass through them.
Examples: Stone, wood, rubber, etc.
iii) Translucent objects allow light to pass through them partially. But things can not be clearly seen. Here, the light is absorbed to a great extent.
Examples: Ground glass, oiled paper, tracing paper, etc.
1.2 REFLECTION OF LIGHT
Reflection is a phenomenon where waves, such as light or sound, encounter a surface and rebound. When an incident wave reaches a boundary, it returns to the medium it originated from, following the laws of reflection.
1.2.1 Laws of reflection
i) The angle of incidence is equal to the angle of reflection, and ii) The incident ray, the normal at the point of incidence, and the reflected ray all lie in the same plane.
These laws of reflection apply to all types of reflecting surfaces.
Incident Ray
Angle of Incident Angle of Reflection
Reflected Ray
Plane Mirror
Fig. 1.1 (a) Reflection on plane mirror
1.2.2 Plane mirror
A plane mirror is a flat, smooth reflecting surface that reflects light in a predictable manner, obeying the law of reflection. It produces virtual images that are upright and laterally inverted compared to the objects they reflect.
Characteristics of the image of a real object formed due to reflection at a plane mirror
The image formed by a plane mirror is virtual, erect, of the same size, and at the same distance from the mirror.
Incident ray
Object
Reflected ray Reflectedray Incidentray
Image
Fig. 1.1 (b) Image formed by plane mirror
Field of view of an object for a given plane mirror
The field of view is the region between the extreme reflected rays and depends on the location of the object in front of the mirror. If our eye lies in the field of view, then only we can see the image of the object; otherwise, we cannot.
Rotating plane mirror
• If the plane mirror is rotated by an angle 'θ' in an anti-clockwise direction but the source is fixed, then the reflected ray is turned by an angle '2θ' in the anti-clockwise direction.
Fig. 1.1 (c) Rotating plane mirror in anti-clockwise direction
• If the plane mirror is fixed, and the incident ray is turned by an angle 'θ' in a clockwise direction, then the reflected ray is turned by the angle 'θ' in an anti-clockwise direction.
Fig. 1.1 (d) When plane mirror is fixed and incident ray is turned by an angle 'θ'
1.3 SPHERICAL MIRRORS
The reflecting surface of a spherical mirror may be curved inwards or outwards. Spherical mirrors are mainly classified as:
Concave mirror: If the convex surface is silvered, then the concave surface acts as a reflecting surface, and such a mirror is called a concave mirror.
Convex mirror: If the concave surface is silvered, then the convex surface acts as a reflecting surface and such a mirror is called a convex mirror.

1.3.1 Terms related to spherical mirrors
i. Pole: The centre of the reflecting surface of a spherical mirror is a point called the pole. It lies on the surface of the mirror. The pole is usually represented by the letter P.
ii. Centre of curvature (C): The reflective surface of a spherical mirror constitutes a section of a sphere, and the centre of this sphere is called the centre of curvature (C). This point, denoted as C, is located outside the reflective surface of the mirror. For concave mirrors, C is positioned in front of the mirror, while for convex mirrors, C is situated behind the mirror. You may note this in Fig. 1.3 (a) and (b).
iii. Radius of curvature: The radius of the sphere, of which the mirror forms a part, is called the radius of curvature of the mirror. It is represented by the letter R. You may note that the distance PC is equal to the radius of curvature in Fig. 1.3.
iv. Principal axis: The line joining the pole and centre of curvature is called the principal axis.
v. Principal focus (F): It is a point on the principal axis of the mirror where a beam of light parallel to the principal axis, after reflection, either actually meets or appears to meet. The principal focus is represented by the letter F.
vi. Focal length (f): The distance between the pole and the principal focus of the mirror is called the focal length. It is represented by the letter f.
Fig. 1.3 (a) Concave mirror & (b) Convex mirror
vii. Aperture: The diameter of the enclosed circular portion of the spherical mirror is called its aperture. In the case of small-aperture spherical mirrors, the radius of curvature is determined to be twice the focal length, expressed as R = 2f. Consequently, this indicates that the principal focus of a spherical mirror is positioned at the midpoint between the pole and the centre of curvature.
1.3.2 Sign convention for spherical mirrors
While dealing with the reflection of light by spherical mirrors, we shall follow a system of signs called the New Cartesian Sign Convention, which are as follows:
i) The pole is taken to be the origin, and the principal axis is the x - axis.
ii) All the distances are measured from the pole.
iii) Positive distances are recorded along the path of incident rays.
iv) Negative distances are assigned to measurements opposite to the direction of the incident rays.
v) Heights above the principal axis are considered positive.
vi) Depths below the principal axis are considered negative.
vii) Positive angles are measured counterclockwise from the normal, while negative angles are measured in a clockwise direction from the normal.
Object on the left
1.3.3 Image formation by spherical mirrors
The position, size, and nature of the image formed by a concave mirror for different positions of the object are as follows:
Table 1.1 (a) Image formation by a concave mirror for different positions of the object
The position, size and nature of the image formed by a convex mirror for different positions of the object are as follows:
Position of the object
At infinity
Between infinity and the pole P
image
At focus F behind the mirror
Between P and F, behind the convex mirror
diminished Virtual and erect
Virtual and erect
Table 1.1 (b) Image formation by a convex mirror for different positions of the object
1.4 REPRESENTATION OF IMAGES FORMED BY SPHERICAL MIRRORS USING RAY DIAGRAMS
1.4.1 Image formation due to spherical mirrors
The position of the image and its nature, formed due to spherical mirrors, depends on the distance of the object from the mirror.
To locate the position of the image, we draw two rays from the object, make them incident on the mirror and trace the reflected rays. The point of intersection of the reflected rays gives the image of the object.
The frequently used rays to draw a ray diagram are:
Ray 1: A ray through the centre of curvature that strikes the mirror normally is reflected back along the same path.
Concave mirror
Concave mirror
Convex mirror
Convex mirror
Fig. 1.5 (i) Ray diagram 1 of concave mirror and convex mirror
Ray 2: A ray parallel to the principal axis after reflection either actually passes through the principal focus F (or) appears to diverge from it.
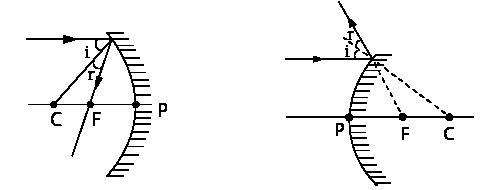
Fig. 1.5 (ii) Ray diagram 2 of concave mirror and convex mirror
Ray 3: A ray passing through the principal focus F (or) a ray which appears to converge at F is reflected parallel to the principal axis.
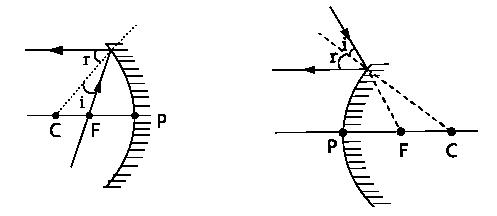
Fig. 1.5 (iii) Ray diagram 3 of concave mirror and convex mirror
Ray 4: A ray striking at the pole 'P' is reflected symmetrically back in the opposite direction.
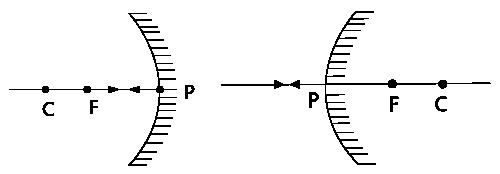
1.5 (iv) Ray diagram 4 of concave mirror and convex mirror
Note: Although countless rays start from a given point of an illuminated object, it is possible to locate the position of an image formed in a spherical mirror by taking any of the two rays discussed above.
1.4.2 Image formation by a concave mirror
Case (i): When the object is at infinity
Characteristics of the image:
i) The image is real.
ii) The image is inverted.
iii) The image is highly diminished.
iv) The image is formed at the principal focus.
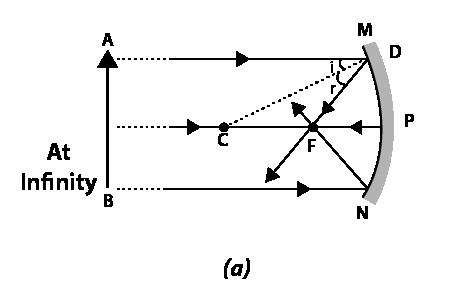
Fig. 1.6 (a) When the object is at infinity
Case (ii): When the object is beyond the centre of curvature
Characteristics of the image:
i) The image is real.
ii) The image is inverted.
iii) The image is diminished.
iv) The image is formed between C and F.
Fig. 1.6 (b) When the object is beyond C
Case (iii): When the object is at the centre of curvature
Characteristics of the image:
i) The image is real.
ii) The image is inverted.
iii) The image is of the same size as the object.
iv) The image is formed at the centre of curvature.
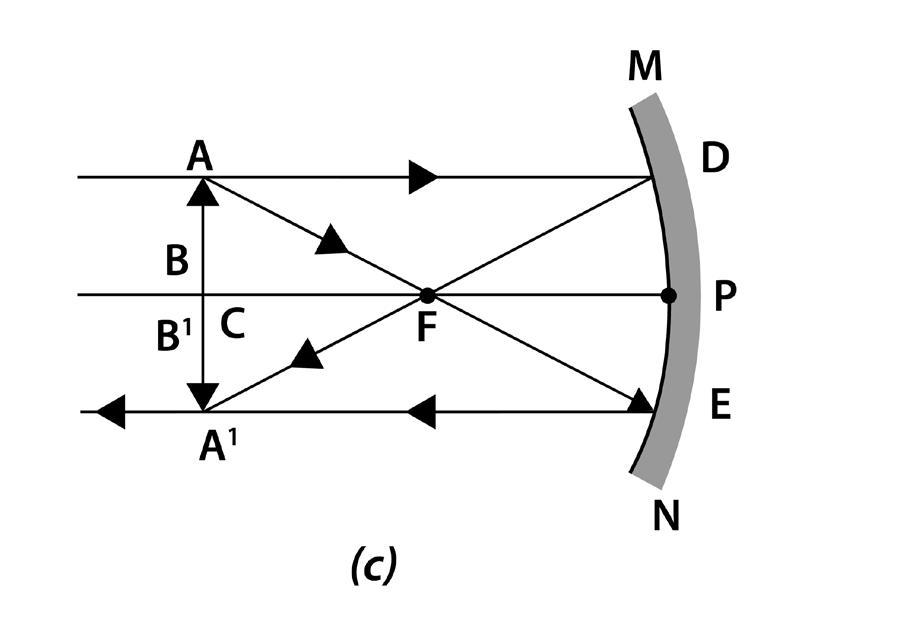
Fig. 1.6 (c) When the object is at C
Case (iv): When the object is in between the centre of curvature and the principal focus
Characteristics of the image:
i) The image is real.
ii) The image is inverted.
iii) The image is enlarged.
iv) The image is formed beyond the centre of curvature.
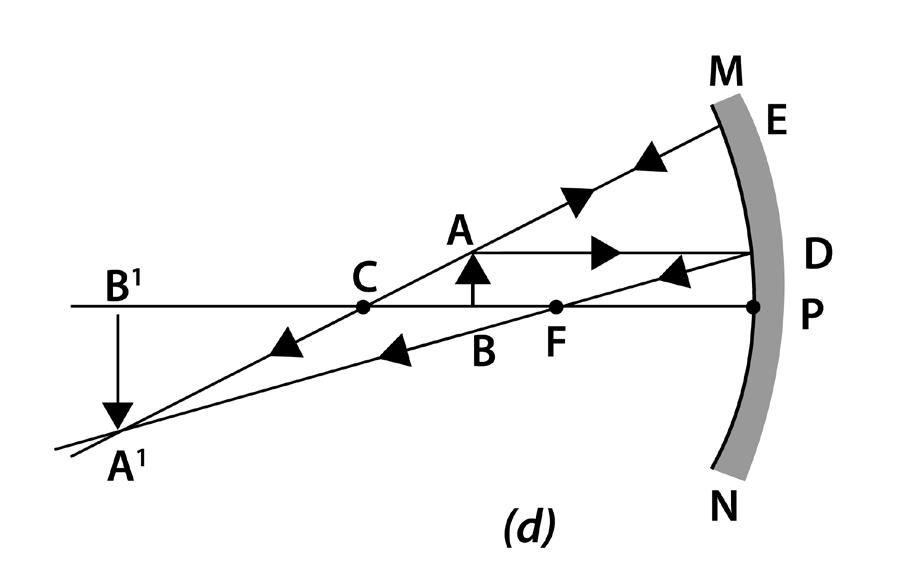
1.6 (d) When the object is between C and F
Case (v): When the object is at the principal focus
Characteristics of the image:
i) The image is real.
ii) The image is inverted.
iii) The image is highly enlarged.
iv) The image is formed at infinity.
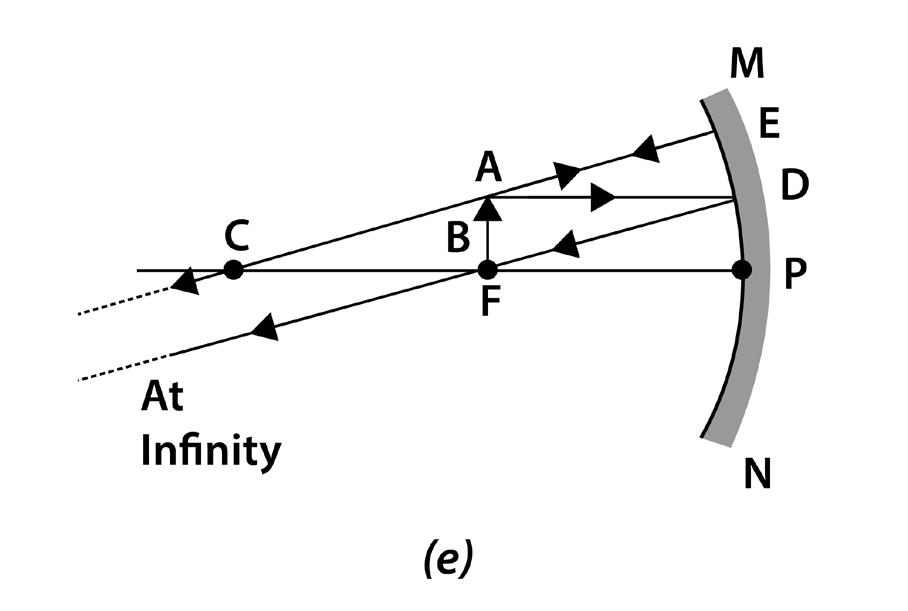
1.6 (e) When the object is at principal focus
Case (vi): When the object is in between the principal focus and the pole
Characteristics of the image:
i) The image is virtual.
ii) The image is erect (or) upright.
iii) The image is magnified.
iv) The image is formed behind the concave mirror.
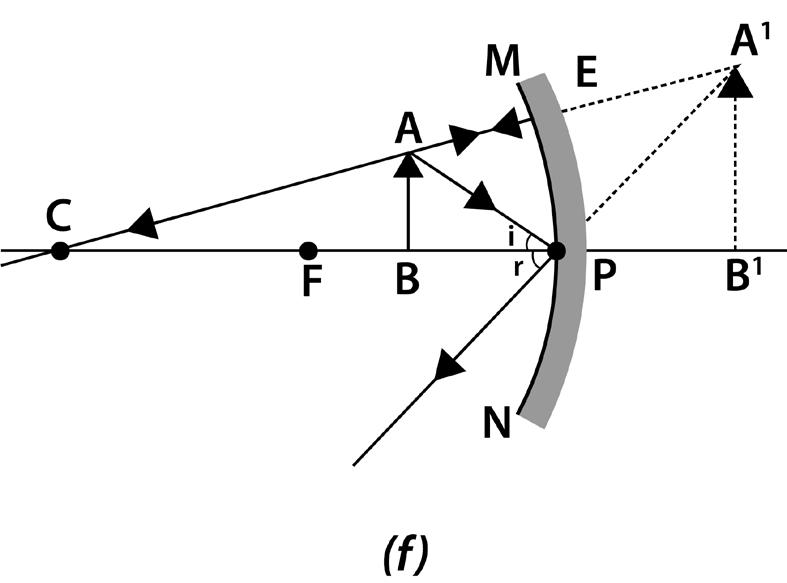
Fig. 1.6 (f) When the object is in between the principal focus and the pole
Note: From the above ray diagrams, we can observe that as the object moves towards the mirror, the image moves away from the mirror. This is true till the object reaches focus from infinity.
Uses of concave mirrors
Concave mirrors find widespread applications in various devices and settings. They are employed in torches, searchlights, and vehicle headlights to generate intense parallel beams of light. Shaving mirrors often utilize concave mirrors to provide an enlarged view of the face. Dentists use these mirrors to observe magnified images of patients' teeth. Additionally, large concave mirrors play a role in concentrating sunlight to generate heat in solar furnaces.
1.4.3 Image formation by a convex mirror
Case (i): When the object is at infinity
Characteristics of the image:
i) The image is virtual.
ii) The image is erect.
iii) The image is highly diminished.
iv) The image is formed at the principal focus.
1.7 (i) When object is at infinity
Case (ii): When the object is anywhere between the pole and infinity
Characteristics of the image:
i) The image is virtual.
ii) The image is erect.
iii) The image is diminished.
iv) The image is formed between the pole and the principal focus.
Uses of convex mirrors
Convex mirrors serve various practical purposes due to their unique properties. One common application is safety mirrors in parking lots, driveways, and tight corners. The outward curvature of convex mirrors provides a wide field of view, allowing users to see a larger area and detect potential obstacles or oncoming traffic. Additionally, convex mirrors are widely used as side mirrors
on vehicles to eliminate blind spots and enhance road safety. Their ability to produce smaller but upright images is beneficial for observing a broader perspective.
Note :
1. A concave mirror is also known as a converging mirror (for a real object).
2. A convex mirror is also known as a diverging mirror (for a real object).
1.5 MIRROR FORMULA AND MAGNIFICATION
The mirror formula and magnification are important concepts in optics, particularly when dealing with mirrors. They help in understanding and predicting the characteristics of images formed by mirrors.
1.5.1 Mirror formula
In the context of a spherical mirror, several key distances are defined.
(i) The object distance (denoted as u) is the distance between the object and the pole of the mirror.
(ii) The image distance (denoted as v) represents the distance between the image and the pole of the mirror.
(iii) The focal length (denoted as f) is the distance from the pole to the principal focus.
The relationship among these quantities is given by the mirror formula, expressed as
This formula is valid in all situations for all spherical mirrors for all positions of the object.
1.5.2 Magnification
The magnification generated by a spherical mirror is expressed as the ratio of the height of the image to the height of the object. It is usually represented by the letter m. If h is the height of the object and h′ is the height of the image, then the magnification m produced by a spherical mirror is given by:
Height of the image h
Height of the object(h)
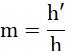
The magnification m is also related to the object distance (u) and image distance (v). It can be expressed as:
Magnification (m) = =
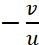
Note :
1. The height of the object is taken to be positive as the object is usually placed above the principal axis.
2. The height of the image should be taken as positive for virtual images. It should be taken as negative for real images.
3. If ' m ' is positive, then the image is virtual and erect.
4. If ' m ' is negative, then the image is real and inverted.
5. If m > 1, then the image is bigger than the object.
6. If m < 1, then the image is smaller than the object.
7. If m = 1, then the image size is equal to the object size.
SOLVED EXAMPLES
Example 1: Find the focal length of a convex mirror whose radius of curvature is 32 cm.
Solution:
Given R = 32 cm
We know that f = R/2
⇒f = 32/2 = 16 cm
Example 2: A concave mirror produces three times magnified (enlarged) real image of an object at 10 cm in front of it; where is the image located?
Solution:
Magnification m = -3
Object distance (u) = -10 cm
Image distance (v) = ?
we know that m = (-v)/u
⇒-3 = (-v)/(-10)⇒ v = -30 cm
Thus, the image is located at a distance of 30 cm in front of the mirror.
Example 3: An object, 4 cm in size, is placed at 25 cm in front of a concave mirror of focal length 15 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Find the nature and the size of the image.
Solution:
Given,
Size of object, h4.0 cm =+ ;
Object distance, u = -25.0 cm ;
Focal length, f15.0 cm =− ; Image distance, v = ?
Size of image, h ′ = ?
Using the mirror formula, 111 vuf += we get,
15.03.02.0
v75.075.0 −+− ==
v37.5 cm =− . So, the screen should be placed at 37.5 cm from the mirror, and the image is real. Now, magnification, hv m hu ′ ==− () () () 37.5 cm4.0 cm vh h u 25.0 cm −+ =−=− ′
Height of the image, h6.0 cm =− ′ hh⇒′>
Thus, the image is inverted and enlarged.
1.6 REFRACTION
1.6.1 Refraction of light
Refraction of light is a phenomenon that occurs when light waves pass from one transparent medium to another, causing a change in the path of the light ray. This change in path is due to the difference in the optical density of the two media.
During refraction
• The phase of vibration of particles remains constant.
• Frequency remains constant.
• Speed or velocity changes.
• Wavelength changes.
BOUNDARY
Apparent shift of objects
Refraction can also cause the apparent shift of objects when viewed through different media. This phenomenon is known as apparent displacement or apparent shift.
Here are two examples illustrating the refraction of light:
Pencil in a glass of water
When you place a pencil in a glass of water, it may appear bent at the point where it enters the water. This effect is due to the refraction of light as it passes from the air (lower optical density) into the water (higher optical density). The light changes direction at the air-water interface, causing the apparent bending of the pencil.
Fish in a pond
If you observe fish swimming in a pond from above the water's surface, you may notice that the position of the fish seems slightly raised compared to its actual location. This displacement is caused by the refraction of light as it travels from water (higher optical density) to air (lower optical density). The change in the direction of light makes the fish appear to be higher in the water than it actually is.
Apparent position of fish Real position of fish
Refraction through a rectangular glass slab
When light passes through the glass slab, it gets refracted at the two parallel, equal, and opposite surfaces of the glass slab.
Let’s do an activity to understand the refraction of light through a glass slab. Fix a sheet of white paper on a drawing board using drawing pins.
i) Place a rectangular glass slab over the sheet in the middle.
ii) Draw the outline of the slab with a pencil and name it ABCD.
iii) Take four identical pins.
iv) Fix two pins, say E and F, vertically such that the line joining the pins is inclined to the edge AB.
v) Look for the images of the pins E and F through the opposite edge.
vi) Fix two other pins, say G and H, such that these pins and the images of E and F lie on a straight line.
vii) Remove the pins and the slab.
viii) Join the positions of the tip of the pins E and F and produce the line up to AB. Let EF meet AB at O. Similarly, join the positions of the tip of the pins G and H and produce it up to the edge CD. Let HG meet CD at O'.
ix) Join O and O'. Also, produce EF up to P, as shown by a dotted line in Fig 1.8(d).
Fig. 1.8(d) Refraction of light through a rectangular glass slab
Here, we can note that the light ray has changed its direction at points O and O'. Both points O and O' lie on surfaces separating two transparent media. Draw a perpendicular NN’ to AB at O and another perpendicular MM' to CD at O'. The light ray at point O has entered from a rarer medium to a denser medium, that is, from air to glass. Note that the light ray has bent towards the normal. At O', the light ray has entered from glass to air, that is, from a denser medium to a rarer medium. The light here has bent away from the normal. Compare the angle of incidence with the angle of refraction at both refracting surfaces AB and CD.
In Fig. 1.8 (d), a ray EO is incident at an angle on surface AB, called the incident ray. OO' is the refracted ray, and O'H is the emergent ray.
Here, the emergent ray is parallel to the direction of the incident ray. The perpendicular distance between the original path of the incident ray and the emergent ray coming out of the glass slab is called lateral displacement of the emergent ray of light.
1.6.2 Laws of refraction
The following are the laws of refraction of light:
First law
The incident ray, the refracted ray and the normal at the point of incidence lie in the same plane.
Second law
Snell's law: It states that the ratio between the sine of the angle of incidence and the sine of the angle of refraction for two given optical media is a constant.
sini constant sinr =
This constant is called the refractive index of the second medium with respect to the first.
1.6.3 The refractive index
When light goes from one medium to another, it changes its path. This change in direction is expressed by the refractive index of the respective mediums, and it is denoted as µ.
Absolute refractive index
It is defined as the ratio of the speed of light in air (c) to that of the speed of light in a given medium (v).
∴μ=c/v
• It has no units and no dimensional formula.
• For a given light, the denser the medium, the lesser the speed of light, the greater the refractive index.
• Eg: VGlass < VWater, μG > μW
• For a given light and a medium, the refractive index is equal to the ratio of the wavelength of light in air to that in a medium.
λ µ=λ λ0= wavelength in air ; λ = wavelength in medium
Relative refractive index
When light passes from one medium to the other, the refractive index of medium 2 relative to 1 is written as 1μ2 and is defined as
[Principle of Reversibility of light]
Conditions for no refraction
i) When the angle of incidence is 0, it suffers no refraction.
ii) If the refractive indices of both optical media are equal, then it suffers no refraction.
SOLVED EXAMPLES
Example 1: Light enters from air into glass, having a refractive index of 1.50. What is the speed of light in glass? The speed of light in air is 3 × 108 ms-1.
Solution:
We know that, 8 Speed of light in air
Refractive index of glass Speed of light in glass 310 1.50 Speed of light in glass = × ⇒=
Speed of light in the glass 8 81 310 210ms 1.5 × ==×
Thus, the speed of light in glass is 2 × 108ms-1
Example 2: You are given kerosene, turpentine and water. In which of these does the light travel fastest? [μk = 1.4, μw = 1.33, μt = 1.47 ]
Solution:
We know that, speed of light in air
Refractive index speed of light in medium = speed of light in air so, speed of light in medium refractive index =
From the above relation, the speed of light is maximum in the medium, which has the lowest refractive index. Out of kerosene, turpentine and water, water has the lowest refractive index of 1.33. So, the light will travel fastest in water.
1.7 LENSES
A lens is a transparent refracting medium bounded between two spherical (or) one spherical and the other plane surface.
Basically, lenses are two types:
i) convex lens
ii) concave lens
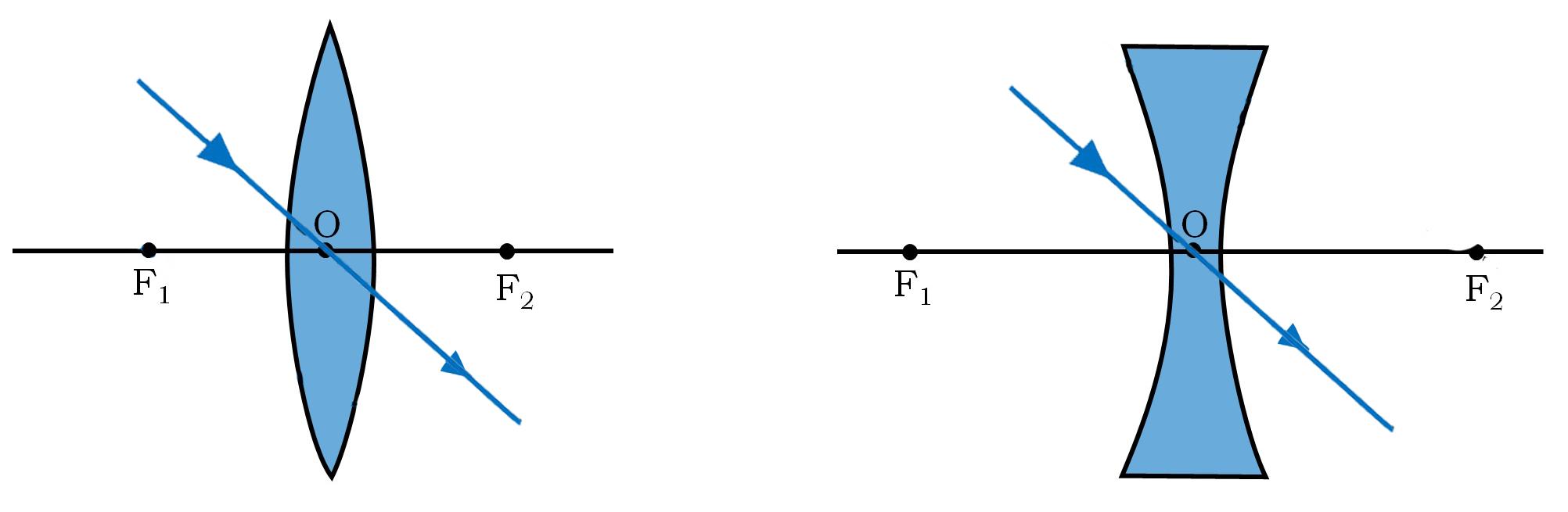
Fig. 1.9 (i) Lenses
Convex lens: A convex lens is thicker in the middle than at the edges.
Concave lens: A concave lens is thinner at the centre than the edges.
1.7.1 Terms related to lenses
• Centre of curvature: The centre of an imaginary sphere of which the given curved surface is a part is called the centre of curvature.
• Radius of curvature: Radius of the imaginary sphere in which the given curved surface is a part.
• Principal axis: It is a straight line passing through the centres of curvature of two surfaces of the lens.
• Optical centre: The geometrical centre of the lens is called the optical centre.
• Principal focus: The principal focus of a convex lens is a point on its principal axis through which light rays parallel to the principal axis converge after passing through the lens. The principal focus of a concave lens is a point on its principal axis from which light rays, originally parallel to the axis, appear to diverge after passing through the concave lens.
• Focal length: The focal length of a lens is the distance between the optical centre and the principal focus of the lens.
• Aperture: The effective diameter of the circular outline of a spherical lens is called its aperture.

1.7.2 Refraction by spherical lenses
Rules for obtaining images formed by lenses:
The image is formed at that point where at least two refracted light rays meet (or appear to meet).
Rule 1: A ray passing through the optical centre proceeds undeviated through the lens.
1.10 (i) Rule 1
Rule 2: A ray passing through the first focus or directed towards it, after refraction from the lens, becomes parallel to the principal axis.
1.10 (ii) Rule 2
Rule 3: A ray passing parallel to the principal axis, after refraction through the lens, passes or appears to pass through focus.
F1 O O
1.7.3 Image formation by lenses
1.10 (iii) Rule 3
The position, the relative size, and the nature of the image formed for convex and concave lenses are as follows:
For convex lens
S. No Position of the object Position of the image
i) At infinity At focus F2
ii) Between ∞ and 2F1 Between F2 and 2F2
and inverted
and inverted
iii) At 2 F1 At 2F2 Same size Real and inverted
iv) Between 2F1 and F1 Beyond 2F2 Enlarged Real and inverted
v) At F1 At infinity Enlarged Real and inverted
vi) Between O and F1 On the same side of the lens as the object Enlarged Virtual and erect
Table 1.2 (a)Nature, position, and relative size of the image formed by a convex lens
For concave lens
S. No. Position of the object
Position of the image Relative size of the image Nature of the image i) At infinity At focus F1 Highly diminished, point-sized Virtual and erect
ii) Between infinity and optical centre O of the lens
Between focus F1 and optical centre O
Diminished Virtual and erect
Table 1.2 (b) Nature, position, and relative size of the image formed by a concave lens
A concave lens will always give a virtual, erect, and diminished image, irrespective of the position of the object.
1.7.4 Image formation in lenses using ray diagrams
The ray diagrams for the image formation in a convex lens for a few positions of the object are shown in Fig. 1.11 (i).
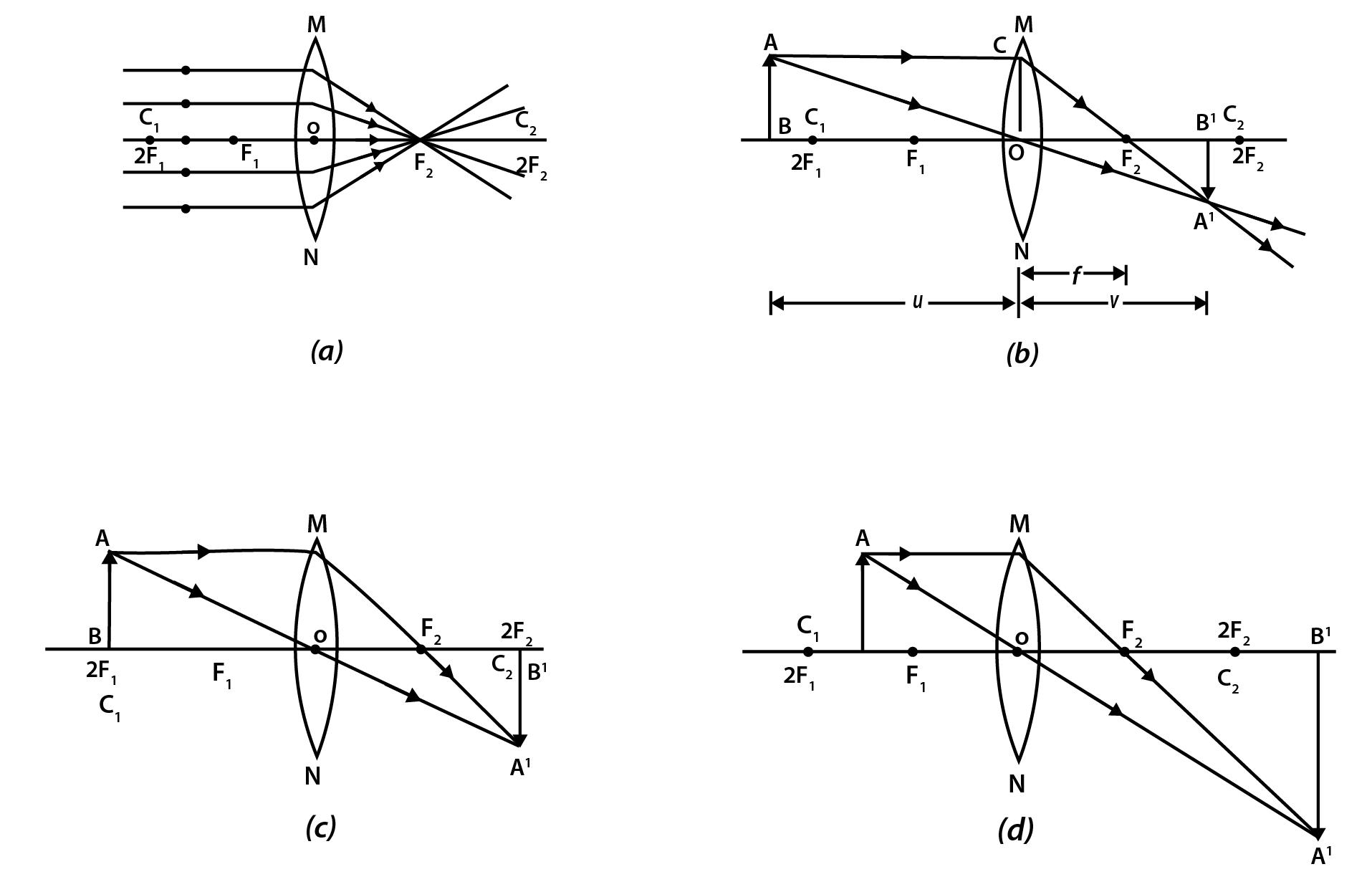
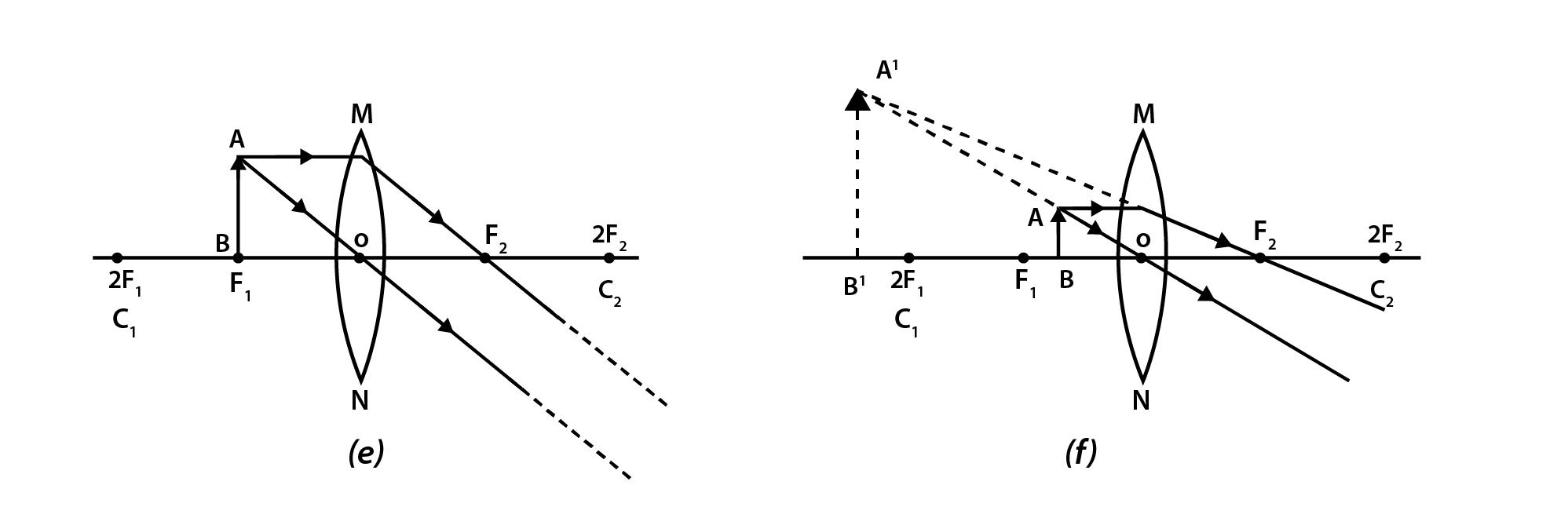
The ray diagrams for the image formation in a concave lens for a few positions of the object are shown in Fig. 1.11 (ii).
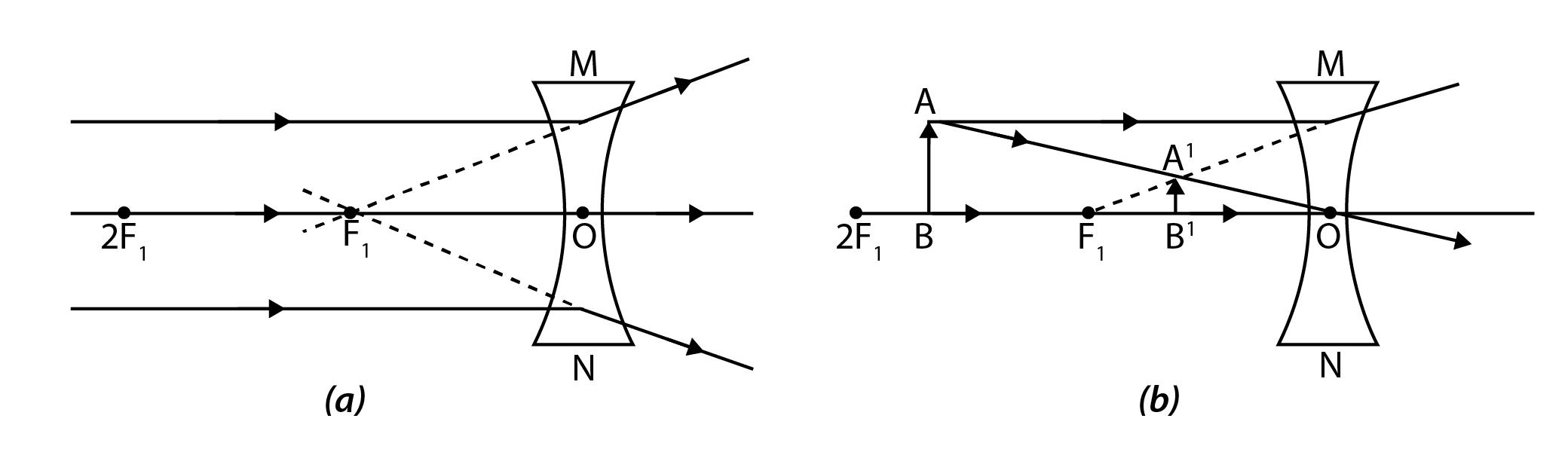
Fig. 1.11 (ii) Image formed by a concave lens
1.7.5 Sign convention for spherical lenses
The coordinate sign convention for spherical lenses is as follows:
• The optic centre is taken to be the origin, and the principal axis is the X-axis.
• All the distances are measured from the optic centre.
• Distances measured in the direction of incident rays are taken as positive.
• Distances measured in the direction opposite to that of the incident rays are taken as negative.
• Distances above the principal axis are taken as positive.
• Distances below the principal axis are taken as negative.
1.8 LENS FORMULA AND MAGNIFICATION
Before deriving the lens formula, it is essential to understand how light bends at a single spherical surface. When light passes from one medium (refractive index
fR R ) to another (refractive index
through a curved surface of radius R, the relation between object distance (u), image distance(v), and refractive indices is given by:
µµ µµ 21 21 vu R
Medium (1) Rarer
Medium (2) Denser
Fig. Refraction through spherical surface Fig. 1.12 Refraction through spherical surface
fR R
1.8.1 Lens formula
An object AB is placed in front of a convex lens with focal length f at a distance u from the optic centre C. Then image A'B' is formed at a distance v from the optic centre C.
From the triangle: A' B' C and ABC,
AB AB CB CB (1)
From triangles A' B' F and CDF but CD = AB
′′′
AB
AB = FB CF -(2)
From (1) and (2)
CB
CB = FB' CF = CB'-CF CF '
According to the sign convention,
CB uCBv CF f
v u vf f
vf vu uf
uv uf vf ,,
Dividing both sides by uv,v
f 1 11 1
Fig. 1.13 Lens Formula
Example 1: An object 5 cm in length is held 25 cm away from a converging lens of focal length 10 cm. Draw the ray diagram and find the position, size, and nature of the image formed.
Solution:
Here h0 = 5 cm, hi = ?, u = -25 cm, v = ?, f = +10 cm [convex lens]
Using the mirror formula,
11
Negative sign shows that the image is inverted and real. A diminished (3.3 cm) image is formed at 16.7 cm on the right side of the lens.
Example 2: A concave lens of focal length 15 cm forms an image 10 cm from the lens. How far is the object placed from the lens? Draw a ray diagram.
Solution: u vcm(virtual image) fcm(concave lens) ?; 10 15 11 1
Lens maker’s formula
An equation which relates the focal length (f) of a lens to the radii of curvature of the lens and the relative refractive index of the lens material with the surroundings is called the lens maker's formula.
When the lens is placed in a medium,
Where μ2 is the refractive index of the lens medium, μ1 is the refractive index of the surrounding medium, and R1 and R2 are the radii of curvature of the surfaces.
When the lens is used in air μ1=1, μ2 =μ
Silvering of lens
Silvering of a lens involves coating one of its surfaces with a thin layer of reflective material, typically silver or aluminium, to create a mirror. This process is used to make mirrors and enhance optical properties. Here are examples of different types of lenses:
i. Plano-convex lens Case: If the flat side (plano side) of a plano-convex lens is silvered, it forms a concave mirror on that side. Turning a plano-convex lens with its flat side towards the incident light creates a concave mirror, which is useful in applications like projectors.
ii. Plano-concave lens Case: If the flat side (plano side) of a plano-concave lens is silvered, it forms a convex mirror on that side.
Example: A plano-concave lens with its flat side silvered can be used as a security or surveillance mirror, creating a convex mirror effect.
iii. Bi-convex lens Case: If one of the convex surfaces of a bi-convex lens is silvered, it forms a concave mirror on that side.
Example: Using a bi-convex lens with one convex side silvered can create a concave mirror for applications like focusing light.
iv. Bi-concave lens Case: If one of the concave surfaces of a bi-concave lens is silvered, it forms a convex mirror on that side.
Example: A bi-concave lens with one concave side silvered can be employed as a convex mirror, perhaps in artistic or decorative applications.
Combination of Lens and Mirror
To find the effective focal length for the combination of lens and mirror:
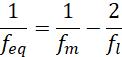
1.8.2 Magnification
It is the ratio of the size of the image to the size of the object.
Magnificatio n= size of the image size of the object = immage distan ce object distance = v u
1.9 POWER OF A LENS
The reciprocal of the focal length (expressed in metres) of a lens is called its power.
Power, P = 1/f( in metres) (or) P = 100/f(in cm)
i) Unit of power is dioptre (D).
ii) The power of a converging lens is positive.
iii) The power of a diverging lens is negative.
1.10 COMBINATION OF LENSES
1.10.1 Combination of thin lenses in contact
i) When two lenses of focal lengths f1 and f2 are kept in contact, then a) the focal length of the combination is 1/f = 1/f1 +1/f2 b) the power of the combination is P = P1+P2
ii) When two lenses of focal lengths fI and f2 are separated by a distance ' d ', then a) the focal length of the combination is 1/f = 1/f1 + 1/f2 - d/(f1 f2 ) b) the power of the combination is P = P1 + P2 - dP1 P2
iii) When a converging lens and a diverging lens of equal focal length are combined, then the focal length of the combination is infinite, and the power is zero. Thus, the combination acts like a glass slab.
SOLVED EXAMPLES
Example 1: A person needs a lens of power -4.5 D for the correction of her vision.
What is the focal length of the corrective lens?
Solution:
Focal length of the lens f = 1/P = 1/(-4.5) = -0.22 m or -22 cm.
Example 2: An equiconvex lens of radii of curvature 10 cm and refractive index 3/2 is silvered at one face, as shown in the figure. Find the type and focal length of the resultant mirror. µ = ³ 2
Solution:
f10
For mirror
2 m R 10 f 5cm 22 ===−
Combination of lens and mirror.
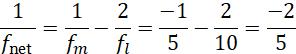
It will behave as a concave mirror with a focal length of 2.5 cm.
QUICK REVIEW
• Reflection of light: Light comes back into the same medium from a boundary separating two media, which is called reflection.
• Concave mirror: If the convex surface is silvered, then the concave surface acts as a reflecting surface, and such a mirror is called a concave mirror.
• Convex mirror: If the concave surface is silvered, then the convex surface acts as a reflecting surface, and such a mirror is called a convex mirror
• Principal focus (F): It is a point on the principal axis where a beam of light parallel to the principal axis, after reflection, either actually meets or appears to meet. It is denoted by ' F '.
• Focal length (f): The distance of the focus from the pole of the mirror is called the focal length of the mirror.
• Relation between focal length (f) and radius of curvature ( R ) of a spherical mirror:
⇒ f = R/2
• Magnification: It is the ratio of the height of the image to the height of the object i e h v m hu ==
• 111 Mirror formula: uvf +=
• Refraction: The phenomenon due to which a ray of light deviates from its original path while travelling from one optical medium to another optical medium is called refraction.
• Laws of Refraction
First law: The incident ray, the refracted ray, and the normal at the point of incidence lie in the same plane.
Second law/Snell's law: It states that the ratio between the sine of the angle of incidence and the sine of the angle of refraction for two given optical media is a constant.
• Absolute refractive index: It is defined as the ratio of the speed of light in free space (c) to that of the speed of light in a given medium (v).
• Relative refractive index: When light passes from one medium to the other, the refractive index of medium 2 relative to 1 is written as 1μ2 and is defined as
• Lens: A lens is a transparent refracting medium bounded between two spherical (or) one spherical and the other plane surface.
• Convex lens: A convex lens is thicker in the middle than at the edges.
• Concave lens: A concave lens is thinner at the centre than the edges. There are three types of concave lenses.
• Lens makers formula:
•

•
• Power of a lens: The reciprocal of focal length is called the power of a lens. P=1/f
• Lenses in contact: When two or more thin lenses are kept in contact with each other such that they have the same principal axis then the effective focal length of a resultant lens is
I. Reflection of
1. What is the angle of incidence of a ray if the reflected ray is at an angle of 90° to the incident ray?
a. 30° b. 45°
2. The mirrors used near the sharp turnings are
a. Convex mirrors
c. Plane mirrors
3. The mirror used in ATM centres is
a. Concave
c. Plane
c. 90°
b. Concave mirrors
d. Both b and c

b. Convex
d. Either plane or concave
4. Statement (A): Convex mirrors are used in street lights.
Statement (B): Concave mirrors are used as reflectors in headlights.
a. Both A and B are true
c. A is true, and B is false
b. Both A and B are false
d. A is false, and B is true
5. Assertion (A): Convex mirror is used as a rearview mirror in automobiles.
Reason (R): The field view of the convex mirror is more.
a. Both A and R are true; R is the correct explanation of A
b. Both A and R are true; R is not the correct explanation of A
c. A is true, R is false
d. A is false, R is true
6. Assertion (A): A concave mirror is used as a shaving mirror.
Reason (R): When an object is placed between the pole and the focus of a concave mirror, a virtual, erect, and magnified image is formed.
a. Both A and R are true; R is the correct explanation of A
b. Both A and R are true; R is not the correct explanation of A
c. A is true, R is false
d. A is false, R is true
II. Representation of images, mirror formula, and magnification
1. For a concave mirror with a focal length of 20 cm, match the following.
Object distance Nature of image
a) 10 cm
b) 30 cm
c) 40 cm
d) 50 cm
a. a-S, b-P, c-Q, d-R
c. a-Q, b-R, c-S, d-P
P) Magnified, inverted and real
Q) Equal size, inverted and real
R) Diminished, inverted and real
S) Magnified, erect and virtual
b. a-P, b-Q, c-R, d-S
d. a-R, b-S, c-P, d-Q
2. The distance at which a boy should stand in front of a convex mirror of focal length 2.5 cm so that his image has a height equal to half of the original height is
a. 5 m b. 2.5 m c. 7.5 m d. 1 m
3. The distance of the object from a concave mirror of focal length 10 cm so that the image size is four times the size of the object will be a. 12.5 cm b. 10 cm c. 8.5 cm d. 15 cm
4. An object is placed on the principal axis of a concave mirror of a focal length of 10 cm at a distance of 8.0 cm from the pole. Then, the position and nature of the image is
a. 40 cm, real
c. 20 cm, real
5. If m > 1, then the image will be
a. Smaller than the object
c. Equal to the size of the object
b. 40 cm, virtual
d. 20 cm, virtual
b. Bigger than the object
d. None
6. A 3 cm tall object is placed at a distance of 7.5 cm from a convex mirror of a focal length of 6 cm. Then, the image will form at
a. 30/35 cm
b. 3/35 cm c. 30/9 cm d. 4/3 cm
7. An object is placed at a distance of 30 cm in front of a convex mirror. It forms an image at 10 cm, the magnification will be
a. 1/3 b. 1/5 c. 3 d. 5
8. A concave mirror forms a real image of a 20 cm high object on a screen placed 5.0 m away from the mirror. The height of the image is 50 cm. Then, the focal length is
a. 143 m b. 1.43 m
c. 14.3 cm d. none
9. A point object 'O' is placed midway between two concave mirrors placed apart at a distance 'd'. Then the value of 'd' for which object and image coincide is [Each mirror has focal length f.]
a. f, 2f
b. 2f,3f
c. f, 4f
d. 2f,4f
10. In a concave mirror experiment, an object is placed at a distance x1 from the focus, and its image is formed at a distance x2 from the focus. The focal length of the mirror is
a. x1 x2
b. X X 12
c. X/X12 d. (x1+ x2)/2
11. A car is fitted with a convex side-view mirror of a focal length of 20 cm. A second car, 2.8 m behind the first car, is overtaking the first car at a relative speed of 15 m/s. The speed of the image of the second car, as seen in the mirror of the first one, is
a. 1/10 m/s
b. 1/15 m/s
c. 10 m/s d. 15 m/s
12. A 4 cm tall object is placed at a distance of 10 cm from a convex mirror of focal length 8 cm. Where will the image form?
a. 40/3 cm
b. 4/30 cm
c. 40/9 cm d. 8/20 cm
13. A 1 cm object is placed perpendicular to the principal axis of a convex mirror of a focal length of 7.5 cm. Find the object's distance from the mirror if the size of the image is 0.6 cm.
a. 3 cm
b. 5 cm
c. 7.5 cm d. 10 cm
14. A 2 cm high object is placed on the principal axis of a concave mirror at a distance of 12 cm from the pole. If the image is inverted, real and 5.0 cm high, then the location of the image and the focal length of the mirror are
a. 40 cm, 8.6 cm
c. 30 cm, 6.6 cm
b. 30 cm, 8.6 cm
d. 10 cm, 6.6 cm
15. A convex mirror forms an image which is (1/n) times the size of the object. If the focal length of the mirror is 'f', then the distance of the object is
a. f/n
b. (n-1)f
c. nf
d. (n+1)f
16. An object of length 2.5 cm is placed at a distance of 15f from a concave mirror, where ‘f’ is the magnitude of the focal length of the mirror and the length of the object is perpendicular to the principal axis. The length of the image and the nature of the image are
a. 2.5/14 cm, diminished, real, inverted
b. 2.5/41 cm, diminished, virtual, inverted
c. 5.2/14 cm, diminished, real, inverted
d. 2.5/14 cm, diminished, virtual, inverted
III. Refraction
1. The refractive index of water is 4/3, and glass is 3/2 with respect to air. The refractive index of glass with respect to water is
a. 1/2
b. 4/3
c. 7/8
d. 9/8
2. The relative refractive index of two media is 0.80 . In one of them, light has wavelength 6000Å and travels at 2.4×(108 m)/s. This light is refracted into the second medium. Its frequency in the second medium is
a. 4×1014 Hz
3. Match the following:
Column-I
b. 6×1014 Hz
c. 2×1014 Hz d. 3.2×1014 Hz
Column-II
i) μ1 = μ2 p) Snell's law
ii) μ1 sinθ1 = μ2 sinθ_2
iii) μ1 > μ2
iv) μ1 < μ2
a. i-s, ii-p, iii-q, iv-r
c. i-s, ii-q, iii-p, iv-r
q) light ray bends away from normal
r) light ray bends towards normal
s) light ray goes undeviated
b. i-q, ii-s, iii-r, iv-p
d. i-r, ii-q, iii-p, iv-s
4. A ray of light is incident at the glass-water interface at an angle i. If it emerges finally parallel to the surface of water, then the value of μg would be
a. 4/3 sini
c. 4/3
IV. Lenses, lens formula, and magnification
b. 1/sini
d. 1
1. When a convex lens of focal length f is cut into two equal halves perpendicular to the principal axis, then each part of the lens has a focal length of
a. f
b. 2f
c. f/2
d. f/4
2. If the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm, then the refractive index of the material of a plano-convex lens is
a. 3/4
b. 5/4
c. 1/2
d. 4/3
3. A convex lens produces a real image m times the size of the object. The distance of the object from the lens is
a. 1 + m f m b. 1 m f m c. (m-1)f
(m+1)f
4. A concave lens of focal length f produces an image (1/n) times the size of the object. The distance of the object from the lens is
a. (n-1)f
c.
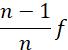
b. (n+1)f
d.
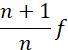
5. The nature of the graph between 1/u and 1/v for a convex lens, where u is the distance of the object and v is that of the image is
a. Straight line
c. Ellipse
b. Parabola
d. Hyperbola
6. A convex lens of focal length ' f ' produces a real image 3 times the size of an object; the distance of the object from the lens is
a. 2f/3 b. 3f/2 c. 3f/4
4f/3
7. A concave lens of focal length f produces an image 1/3 of the size of the object; the distance of the object from the lens is
a. 2f b. 3f/2 c. 4f
2f/3
8. A convex lens is placed somewhere in between an object and a screen. The distance between the object and the screen is 48 cm. If the numerical value of the magnification produced by the lens is 3, then the focal length of the lens is a. 16 cm
12 cm
9 cm
4.5 cm
9. A convex lens has a focal length of 10 cm; the location and nature of the image, if a point object is placed on the principal axis at a distance of 9.8 cm, is
a. 490 cm on the side of the object, real
b. 510 cm on the side of the object, virtual
c. 490 cm on the side of the object, virtual
d. 510 cm on the side of the object, real
10. A convex lens produces a double-size real image when an object is placed at a distance of 18 cm from it. The position of the object to produce a triple-size real image is a. 10 cm
18 cm
16 cm
32 cm
11. A convex lens is in contact with a concave lens. The magnitude of the ratio of their focal length is 2/3. Their equivalent focal length is 30 cm. What are their individual focal lengths?
a. -15 cm, 10 cm
c. 75 cm, 50 cm
b. -10 cm,15 cm
d. -75 cm, 50 cm
12. A biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is
a. virtual and at a distance of 16 cm from the mirror
b. real and at a distance of 16 cm from the mirror
c. virtual and at a distance of 20 cm from the mirror
d. real and at a distance of 20 cm from the mirror
13. The focal lengths of the objective and the eyepiece of a compound microscope are 2.0 cm and 3.0 cm, respectively. The distance between the objective and the eyepiece is 15.0 cm. The final image formed by the eyepiece is at infinity. The two lenses are thin. The distance in cm of the object and the image produced by the objective, measured from the objective lens, respectively, are
a. 2.4 and 12.0
c. 2.0 and 12.0
b. 2.4 and 15.0
d. 2.0 and 3.0
14. The size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30 cm is 2 cm. If a concave lens of focal length 20 cm is placed between the convex lens and the image is at a distance of 26 cm from the convex lens, then calculate the new size of the image.
1.25 cm
2.5 cm
V. Power and combination of lenses
1. On reducing the focal length of a lens, its power
a. increases
c. does not change
1.05 cm
b. decreases
2 cm
d. first increases then decreases
2. A plano-convex lens, when silvered on the plane side, behaves like a concave mirror of a focal length of 60cm. However, when silvered on the convex side, it behaves like a concave mirror with a focal length of 20cm. The refractive index of the lens is: a. 3.0
1.5
1.0
2.0
WORKSHEET - 2
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
1. The focal length of a convex mirror is 20 cm. What will its radius of curvature be a. 10 cm b. 20 cm
30 cm
2. The ratio of focal length to that of the radius of curvature of a spherical mirror is a. 1:2
2:1
1:4
3. A convex mirror has a focal length of 0.5 m. Its radius of curvature is
10 cm
100 cm
25 cm
40 cm
4:1
2.5 cm
4. For a mirror linear magnification, 'm' comes out to be +2. The conclusion that can be drawn from this is
a. mirror is concave
c. object lies between pole and infinity
b. mirror can be convex (or) concave
d. object lies beyond focus
5. Assertion (A): The radius of curvature of a concave mirror is 20 cm. If a real object is placed at 10 cm from the pole of the mirror, the image is formed at infinity.
Reason (R): When an object is placed at the focus, its image is formed at infinity.
a. Both A and R are true, and R is the correct explanation of A
b. Both A and R are true, and R is not the correct explanation of A
c. A is true, R is false
d. A is false, R is true
6. Among the following, a virtual image can be formed by
a. Plane mirror
c. Concave mirror
b. Convex mirror
d. All of the given options
7. Match the following:
Column - I Column - II
A) Concave mirror, u < f
B) Concave mirror, u > f
C) Concave mirror, f < u < 2f
D) Convex mirror, u< f
E) Concave mirror, u > 2f
a. A-R, B-Q and S, C-S, D-P, E-Q
c. A-R, B-R and S, C-S, D-P, E–Q
8. Match the following:
P) Virtual, diminished image
Q) Real, diminished image
R) Virtual, enlarged image
S) Real, enlarged image
b. A-Q, B-Q and S, C-S, D-P, E-R
d. A-P, B-Q, S, C-S, D-P, E-Q
Column - I Column - II
1) An object is placed at the focus before a convex mirror
2) An object is placed at the centre of curvature before a concave mirror
3) An object is placed at the focus before a concave mirror
4) An object is placed at the centre of curvature before a convex mirror
a. 1 - B, 2 - D, 3 - A, 4 – E
c. 1 - C, 2 - B, 3 - A, 4 – E
A) Magnification is -∞
B) Magnification is 0.5
C) Magnification is +1
D) Magnification is -1
E) Magnification is 0.33
b. 1 - A, 2 - D, 3 - C, 4 - B
d. 1 - B, 2 - A, 3 - D, 4 - C
9. An object is 30 cm from a spherical mirror along the central axis. The abSolutionute value of lateral magnification is 1/2. The image produced is inverted. The focal length of the mirror is
a. f = 15 cm
b. f = -10 cm
c. f = -20 cm
d. f = -25 cm
10. A concave mirror has a focal length of 20 cm. If an object is placed at a distance of 30 cm from the pole of the mirror, then the image distance and transverse magnification, respectively, are
a. 60 cm, -2
b. 60 cm, 3
c. 50 cm, 2
d. 50 cm, 3
11. The image formed by a convex mirror of focal length 30 cm is a quarter of the size of the object. Then, the distance of the object from the mirror is
a. 90 cm
b. 120 cm
c. 60 cm
d. 30 cm
12. A car has a driving mirror with a focal length of 40 cm. Another car of the same dimensions is 12 m away from the mirror of the first car. The position of the second car, as seen in the mirror of the first car is
a. 36 cm
b. 49 cm c. 39 cm d. 44 cm
13. The magnification 'm', the image distance 'v', and the focal length 'f' of a spherical mirror are related as
14. A concave mirror has a radius of curvature of 24 cm. The distance of an object from the mirror if an image is formed which is virtual and 3 times the size of the object is
a. 4 cm
b. 6 cm
c. 8 cm d. 10 cm
15. A convex mirror and a concave mirror with a radius of 10 cm each face each other and are 15 cm apart. A point object is placed midway between them. The position of the final image, if the reflection takes place at the concave mirror and then at the convex mirror, is
a. at the pole of the concave mirror
b. at the pole of the convex mirror
c. coincident with the object itself d. 5 cm behind the convex mirror
16. 1μ2 = 1/2μ1 is an account of
a. Principle of reversibility of light
c. Principle of reversibility of medium
b. Principle of reversibility of sound
d. Principle of reversibility of heat
17. A bird is flying down vertically towards the surface of water in a pond with constant speed. There is a fish inside the water. If that fish is exactly vertically below the bird, then the bird will appear to the fish to be at the height of:
a. farther away than its actual distance.
b. closer than its actual distance.
c. moving faster than its actual speed.
d. moving slower than its actual speed.
18. A small air bubble is at a distance of 3 cm from the centre of a glass sphere of radius 9 cm. When viewed from the nearest side, the bubble appears to be at a distance of 5 cm from the surface. It's apparent distance when viewed from the farthest side.
a. 5 cm
b. 10 cm
c. 15 cm
d. 20 cm
19. If the refractive index of a diamond is 2.4, then the velocity of light in a diamond is
a. 3 × 108 m/s
c. 1.25 × 108 m/s
b. 2 × 108 m/s
d. 1 × 108 m/s
20. The radius of curvature of one surface of a double convex lens is three times the other. If the focal length of the lens is 30 cm and the refractive index of the lens is 3/2, then the radius of curvature of that surface is
a. 20 cm
b. 40 cm
c. 60 cm d. 80 cm
21. A lens made from a material of absolute refractive index n1 is placed in a medium of absolute refractive index n2. The focal length of the lens is related to n1 and n2 as
a. f ∝ (n1- n2 )
c. f ∝ n1+ n2
b. f ∝ 1/(n1+ n2 )
d. f ∝ 1/(n1- n2 )
22. A convex lens of focal length 15 cm is made of a material with a refractive index of 1.2. When placed in water (n = 1.3), it will behave as a
a. Converging lens of focal length 15 cm
b. Converging lens of focal length different than 15 cm
c. Diverging lens of focal length 15 cm
d. Diverging lens of focal length different than 15 cm
23. In the below figure, points C1 and C2 denote the centres of curvature, then the focal length of the thin lens is
20 cm
24. A double convex lens has two surfaces of equal radii R and refractive index, μ=1.5 we have,
a. f = b. f = R
c. f = -R
d. f = 2R
25. A thin lens of focal length +12 cm is immersed in water (μ = 1.33). Its new focal length is [μg= 1.5]
a. 24 cm
36 cm
48 cm
12 cm
26. Let 'm' represent the magnification of a lens. Assume the object to be real, then among the following the incorrect option is
a. m is positive when the image formed by the convex lens is virtual
b. m is positive when the image formed by the concave lens is virtual
c. m is positive when the image formed by the concave lens is real
d. 'm' may be positive when the image formed by the convex lens is virtual
27. A convex lens of focal length 16 cm forms a virtual image of double the size of the object. The distance of the object from the lens is
28. When a lens of focal length f is cut into two equal halves parallel to the principal axis, then each part of the lens has the focal length
a. f b. 2f
c. d.
29. A lens is made by two watch glasses attached together with their concave faces towards each other. The radius of curvature of each surface is 20 cm. If the lens prepared contains air and is immersed in water, then it behaves as
a. Converging lens of focal length 20 cm
b. Converging lens of focal length 30 cm
c. Diverging lens of focal length 40 cm
d. Diverging lens of focal length 30 cm
30. A cylindrical vessel of diameter 12 cm contains 800 πcm3 of water. A cylindrical glass piece of diameter 8.0 cm and height 8.0 cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays, locate its image. The index of refraction of glass is 1.50, and that of water is 1.33
a. 7.1 cm above the bottom
c. 10.1 cm above the bottom
b. 9.1 cm above the bottom
d. 12.1 cm above the bottom
31. A biconvex thick lens is constructed with glass (μ = 1.50). Each of the surfaces has a radius of 10 cm, and the thickness at the middle is 5 cm. Locate the image of an object placed far away from the lens.
a. 2.5 cm from the other side of the lens
c. 10 cm from the other side of the lens
b. 9.1 cm from the other side of the lens
d. 1.5 cm from the other side of the lens
32. A converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with a common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. The locations of the two images that are formed are
a. One at 15 cm and the other at 24 cm from the lens away from the mirror
b. One at 20 cm and the other at 24 cm from the lens away from the mirror
c. One at 15 cm and the other at 20 cm from the lens away from the mirror
d. One at 40 cm and the other at 20 cm from the lens away from the mirror
THE HUMAN EYE AND THE COLOURFUL WORLD 2
2.1 THE HUMAN EYE
2.1.1
Structure of the human eye
The human eye is one of our body's most valuable and sensitive sense organs. Unlike other senses, the eye provides us with the unique ability to discern and appreciate colours. Often compared to a camera, the lens system of our eyes forms images on the retina. Light enters through the cornea, a transparent bulge on the front surface of the eyeball. Most refractions happen at the outer surface of the cornea. The eyeball, roughly spherical, has a diameter of about 2.3 cm.





Ciliarybody and muscle



body


Situated behind the cornea is the iris, a dark muscular diaphragm that regulates the size of the pupil. The pupil is the opening in the centre of the iris that regulates the amount of light entering the eye. The eye lens, working in tandem with the cornea, adjusts focal length for focusing objects at varying distances on the retina. The retina, a delicate membrane containing numerous lightsensitive cells, forms an inverted real image of the observed object. Upon illumination, these cells activate and generate electrical signals transmitted to the brain via the optic nerves.
The brain performs the intricate task of interpreting signals, allowing us to perceive objects as they truly appear. Thus, the human eye stands out as a sophisticated sensory instrument, contributing significantly to our understanding and appreciation of the beautiful and colourful world surrounding us.
2.1.2
Power of accommodation
The eye lens is made up of a flexible, jelly-like material, which undergoes modifications in the curvature. The distance between the lens and the retina is fixed in the human eye. Therefore, the eye alters the power of the lens to focus on different objects, which is facilitated by the ciliary muscles. This adjustment influences the lens' focal length, with relaxation causing thinning and an increase in focal length for clear, distant vision. Conversely, contraction thickens the lens, reducing focal length for clear vision of nearby objects. This ability to alter focal length is termed accommodation. However, there exists a minimum limit of decreasing the focal length, which is evident when attempting to read a page held too closely, leading to blurred vision and eye strain.
Near point (least distance of distinct vision): Approximately 25 cm for a young adult with normal vision.
Far point of the eye: Represents the farthest distance for clear vision.
Far point extends to infinity: For a normal eye, the far point reaches infinity.
Normal vision range: Encompasses clear visibility between 25 cm and infinity. With age, our eye lens may develop cataracts, characterised by cloudiness and milky appearance, resulting in partial or complete vision loss. Vision restoration is achievable through cataract surgery.
2.2 DEFECTS OF VISION AND THEIR CORRECTION
When the eye cannot focus the image on the retina, the eye is said to have a defect of vision.
2.2.1
Myopia
Definition: Myopia, commonly known as near-sightedness, is a vision condition where an individual can see nearby objects clearly but struggles to see distant objects.
Characteristics: Individuals with myopia have a near point closer than infinity, allowing clear vision only up to a few metres. In a myopic eye, the image of a distant object is formed in front of the retina instead of directly on it.

Causes: Myopia occurs when the eyeball is too long or the lens is too curved, causing the image to form in front of the retina.
Correction: Myopia can be corrected by using a concave lens with a suitable power. This concave lens helps bring the image back onto the retina, effectively correcting the visual defect.
(a) Far point of a myopic eye
(b) Myopic Eye
(c) Correction for myopia
Fig. 2.2 Myopia
2.2.2 Hypermetropia
Definition: Hypermetropia, also referred to as far-sightedness, is a vision condition where an individual can see distant objects clearly but struggles to see nearby objects distinctly.
Characteristics: Individuals with hypermetropia experience a near point that is farther away than the normal near point of 25 cm. Reading materials need to be held beyond 25 cm for comfortable reading. This occurs because the light rays from the nearby objects are focused behind the retina.
Causes: Hypermetropia occurs when the eyeball is too short or the lens is too flat, causing the image to form behind the retina.
Correction: Hypermetropia can be corrected by using a convex lens with an appropriate power. Convex lenses, typically incorporated into eyeglasses, provide the additional focusing power required to form the image on the retina, correcting the visual defect.
(a) Near point of a Hypermetropic eye
(b) Hypermetropic eye
(c) Correction for Hypermetropic eye
Fig. 2.3 Hypermetropia
2.2.3 Presbyopia
Definition: Presbyopia is a visual defect associated with ageing, where individuals experience difficulty seeing nearby objects comfortably and distinctly without corrective eyeglasses.
Characteristics: The near point gradually recedes as the power of accommodation decreases with age. This results in challenges for individuals to see nearby objects clearly.
Causes: Presbyopia arises due to the gradual weakening of the ciliary muscles and reduced flexibility of the eye lens, both of which are natural age-related changes.
Correction: Corrective measures for presbyopia often involve the use of bifocal lenses. Bifocals, which may include both concave and convex lenses, have an upper portion with a concave lens for distant vision and a lower part with a convex lens for near vision. Here, the eye cannot focus clearly on horizontal and vertical planes simultaneously.
Modern correction methods: In contemporary times, refractive defects like presbyopia can be addressed not only through traditional eyeglasses but also with contact lenses or surgical interventions, providing individuals with various options for vision correction.
2.2.4 Astigmatism
Definition: Astigmatism is a refractive error characterized by an irregular corneal shape, leading to distorted or blurred vision. Here, the eye cannot focus clearly on horizontal and vertical planes simultaneously.
Characteristics: Blurred vision, eyestrain, and headaches are common symptoms of astigmatism.
Causes: Irregular corneal shape or curvature deviations in the lens cause light to focus unevenly on the retina.
Modern correction methods: Corrective lenses (glasses or contact lenses), toric contact lenses, and surgical options like toric intraocular lenses (IOLs) provide effective correction.
2.2.5 Cataract
Definition: Cataract is the clouding of the eye's natural lens, resulting in gradual vision deterioration.
Characteristics: Symptoms include blurry vision, sensitivity to light, and difficulty with night vision.
Causes: Ageing, prolonged sun exposure, diabetes, and certain medications contribute to cataracts development.
Modern correction methods: Phacoemulsification surgery, intraocular lens (IOL) implantation, and laser-assisted techniques offer successful cataract removal and vision restoration.
2.3 PRISM
2.3.1
What is a prism?
A prism is a transparent optical element with flat, polished surfaces that refract light. It typically has two triangular bases and three rectangular sides. When light enters a prism, it undergoes multiple refractions, causing the different colours within the light spectrum to spread out or disperse, creating a spectrum of colours. Prisms are commonly used in optics for tasks such as splitting light into its constituent colours (dispersion) or bending light at specific angles. They play a crucial role in various optical instruments, including cameras and various scientific experiments.
2.3.2
Refraction of light through a prism
Consider a prism with cross-section ABC, where AB and AC are refracting surfaces, and ∠BAC is the prism's angle. Placed in air, a ray PQ incident on the surface AB refracts along QR, with an incident angle, i, and a refracted angle, r. As the ray QR strikes the surface AC, transitioning from a denser to a rarer medium, if the angle of incidence, r', is within the critical angle, the ray refracts in the air along RS, forming the angle, i'. The angle, i, is also termed the angle of emergence. Without the prism, the incident ray would follow an undeviated path PQTU, but due to the prism, the final ray now travels along RS. The angle ∠UTS = δ is known as the angle of deviation.
From ∆TQR,
∠UTS = ∠TQR + ∠TRQ
δ=(∠TQV ∠RQV) + (∠TRV ∠QRV)
=(i - r)+(i' - r')
=(i + i') -(r + r')............................(1)
Fig. 2.4 Refraction of light through prism
From the quadrilateral AQVR,
∠A + ∠QVR = 1800
Also, from ∆QRV,
r + r' + ∠QVR = 1800
So, r + r' = ∠A
Substituting in (1),
δ = i + i ∠A
Minimum deviation
It is found that the angle of deviation δ varies with the angle of incidence, i, of the ray incident on the prism. The variation is shown in the figure, and for one angle of incidence, the deviation is minimum δm, i.e., at minimum deviation, the angle of emergence of the ray equals the angle of incidence, i.
i = i'
Relation between refractive index and the angle of minimum deviation
Let the angle of minimum deviation be δm. For minimum deviation, i = i' and r = r'. We have:
δm= i + i - ∠A= 2i - ∠A
or, i = ∠A + δm 2 Also, r + r' = ∠A, or, r = ∠A 2 The refractive
SOLVED EXAMPLES
Example 1: A prism is kept in the air such that for a 600 angle of incidence, the angle of refraction A, angle of deviation δ, and angle of emergence e become equal. What will be the minimum angle of incidence of a ray that is transmitted through the prism?
Solution: Given, i = 60°, A = δ= e ie A eA andi e A m A 1 2 2 sin/ sin/
Here, the angle of deviation is minimum (∴i = e)
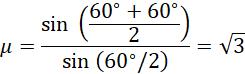
= 1.73
Example 2: For a prism of refractive index 1.732, the angle of minimum deviation is equal to the angle of the prism. What will be the angle of the prism?
Solution:
When A= δm , we can have:
Here, we are also given, m = 1.732= √3
2.4.1 Total internal reflection in nature and its technological applications
Total internal reflection (TIR): The phenomenon due to which a ray of light, while travelling from an optically denser medium to an optically rarer medium, gets reflected into the optically denser medium at the surface of separation is called total internal reflection
Denser medium
Rarer medium i=θC i r r=90° No refracted ray III II I
C
Fig. 2.5 Total internal reflection
Critical angle (θc ): The angle of incidence in a denser medium, for which the angle of refraction in the rarer medium is 90∘, which is called the critical angle.
Conditions for total internal reflection:
1. Rays of light must travel from an optically denser medium to an optically rarer medium.
2. The angle of incidence in the optically denser medium must be greater than the critical angle.
Relation between refractive index and critical angle: Consider a ray of light AB, travelling in an optically denser medium, such that the angle of refraction in the optically rarer medium is 90∘. In such a case, ∠ABM is the critical angle.
As the ray of light is travelling from medium 2 to medium 1,
∴ 2m1 = sin i sin r or 2m1 = sin c sin 90° ∴ 1 2m1 = sin 90° sin c
1m2 = sin 90° sin c ⇒ 1m2 = 1 sin c
Consequences of total internal reflection
Due to total internal reflection:
• An air bubble in water appears shining.
• A diamond glitters.
• Mirages are formed in deserts.
Optically denser medium (2)
Fig. 2.6 Light travelling at the critical angle
• The images are formed in cold countries due to looming.
• The upper surface of the water in a glass beaker held above the eye level appears silvery. Optically rarer medium (1)
Optical fibre: Total internal reflection is the basic principle of a branch of physics known as fibre optics. An optical fibre is a very thin fibre made of glass or plastic with a radius of the order of a micrometre (10-6 m). A bundle of such thin fibres forms a light pipe.
Uses of optical fibres:
• Optical fibres are used in the communication field since they are thin, lightweight, flexible and interference-free.
• Optical fibres are also used to transmit different telephone signals simultaneously without any interference by superposing the signals on an optical beam. The response time reduces since the velocity of transmission is high.
• Optical fibres are used in laparoscopes and endoscopes to visually examine inaccessible regions in the human body.
• Optical fibres, in the form of photometric sensors, are used to measure the blood flow in the heart.
• Optical fibre sensors are also used to measure temperature and pressure.
• Optical fibres in the form of refractometers are used to determine the refractive indices of liquids.
Conditions for total internal reflection
• The light ray should travel from a denser medium to a rarer medium.
• Angle of incidence in the denser medium should be greater than the critical angle.
SOLVED EXAMPLES
Example 1: If the refractive index of a glass is 1.5, then find its critical angle. {Given sin-1 (1/2) = 300 sin-1 (2/3) = 41.80 sin-1 (3/4) = 48.60 sin-1 (4/5) = 53.130 }
Solution:
From the relation between the critical angle and refractive index, we know:
The critical angle of glass is 42 degrees.
Example 2: A ray of monochromatic light is incident on one refracting face of a prism at an angle of 750. It passes through the prism, and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2, then what is the angle of incidence of the first face of the prism?
Solution:
From the figure,
From Snell's law, at B,
2.5 DISPERSION
2.5.1 Dispersion of white light by a glass prism
When a white light passes through a prism, it splits into its constituent colours. This phenomenon is called dispersion, and it arises because the refractive index of a prism is different for different wavelengths. So, different wavelengths passing through a prism are deviated at different angles, violet is deviated the most while red the least, giving rise to a display of colours known as the spectrum
Example: Rainbow, the most colourful phenomenon in nature, is primarily due to the dispersion of sunlight by raindrops suspended in the air.
Angular dispersion: It is the difference in deviation between any two colours. ( ) vrvr Angular dispersion A ddmm=-=-
where δv and δr are the deviations for violet and red light, respectively, and A is the angle of the prism.
Dispersive power: It is the ratio of angular dispersion to the mean deviation. ( ) vr 1 mm w m= -
where mv and mr are the refractive indices for violet and red light, and m is the refractive index for the mean wavelength (typically yellow light).
2.5.2 Rainbow formation
A rainbow is always formed in a direction opposite to that of the Sun. Rainbow is caused by the dispersion of white sunlight by tiny water droplets in the atmosphere. Water droplets act as tiny prisms. They refract and disperse the incident sunlight, then reflect it internally and finally refract it again when it comes out of a raindrop.
Sunlight
42o
Primary rainbow
Formation: Primary rainbows occur when sunlight is both refracted and internally reflected within raindrops, creating a single arc of colours.
Characteristics: A primary rainbow has red on the outer edge and violet on the inner edge. The order of colours is reversed compared to a spectrum.
Explanation: Sunlight enters a raindrop, undergoes refraction, reflects off the inner surface, and exits the drop. The process disperses light into its spectrum.
Fig. 2.8 (b) Primary and secondary rainbow formation
Secondary rainbow
Formation: Secondary rainbows are a result of double internal reflection of sunlight inside raindrops, creating a fainter and broader outer arc.
Characteristics: A secondary rainbow has its colours reversed compared to the primary, with red on the inner edge and violet on the outer edge.
Explanation: Sunlight undergoes two internal reflections inside raindrops before exiting. This produces a secondary spectrum with a broader separation of colours.
2.6 ATMOSPHERIC REFRACTION
Atmospheric refraction is the bending of light rays as they pass through the Earth's atmosphere, primarily caused by variations in the air density due to temperature gradients. This phenomenon affects the apparent position of celestial objects, making them appear slightly displaced from their actual positions. It is responsible for phenomena such as the twinkling of stars, the apparent flattening of the Sun's disc during sunrise and sunset, and the mirages observed in certain atmospheric conditions. Atmospheric refraction occurs because the refractive index of air changes with temperature, leading to the bending of light rays as they travel through different layers of the atmosphere.
2.6.1 Twinkling of stars
The twinkling of stars is a result of atmospheric refraction as starlight traverses the Earth's atmosphere. The continuous refraction in the atmosphere, which has a gradually changing refractive index, causes the starlight to bend towards the normal. Consequently, the apparent position of a star slightly differs from its actual position, especially when observed near the horizon. This atmospheric condition is dynamic, leading to a fluctuating apparent position of the star. Since
stars are distant and point-sized light sources, the varying path of the light rays entering the eye results in a flickering effect, causing stars to appear intermittently brighter or fainter.
Star Apparent star postition
Ray path
Refractive index increasing
Fig. 2.9 Apparent position of a star
Why do planets not twinkle?
Unlike stars, planets appear closer to the Earth and are seen as collections of many small sources of light. Because of this, the overall variation in light from planets evens out, reducing the twinkling effect that stars have. As a result, planets appear more steady and constant in their brightness.
2.6.2 Advance sunrise and delayed sunset
Visibility before and after sunrise/sunset: The Sun becomes visible to us approximately 2 minutes before the actual sunrise and remains visible for about 2 minutes after the actual sunset. This phenomenon is attributed to atmospheric refraction.
Actual sunrise and sunset: The term 'actual sunrise' refers to the precise moment when the Sun crosses the horizon. The same applies to 'actual sunset'.
Time difference: The time difference between the actual sunset and the apparent sunset is roughly 2 minutes. This discrepancy is a result of atmospheric refraction, causing a delay in the Sun's disappearance below the horizon.
Apparent flattening of the Sun's disc: Another consequence of atmospheric refraction is the apparent flattening of the Sun's disc during sunrise and sunset. This optical effect contributes to the Sun's altered appearance as it nears the horizon.
Fig. 2.10 Atmospheric refraction at sunrise and sunset
2.7 SCATTERING OF LIGHT
Scattering of light refers to the phenomenon where light waves deviate from their original path due to interaction with various particles or irregularities in a medium. This deviation occurs when light encounters small particles, such as dust, water droplets, or molecules, causing the light to change direction.
2.7.1 Mie scattering
Mie scattering, a form of elastic scattering, occurs when the size of particles (e.g., water droplets in clouds) is larger than the wavelength of light, leading to non-uniform light scattering.
Wavelength independence: Mie scattering is less dependent on the wavelength. The size of the scattering particles plays a crucial role, making clouds with water droplets appear white.
Cloud appearance: Clouds filled with water droplets scatter light across all wavelengths, resulting in a white appearance. Full clouds, lacking available light for scattering, appear darker.
2.7.2 Rayleigh scattering
Rayleigh scattering is another form of elastic scattering where the scattering efficiency depends on the wavelength of light and the size of scattering particles.
Particle size effect: Small particles, such as oxygen and nitrogen molecules, are more effective at scattering shorter wavelengths (blue or violet). This phenomenon is responsible for the blue colour of the sky on clear days.
Wavelength impact: Blue light with a shorter wavelength is scattered about ten times more than red light with a longer wavelength in the upper atmosphere. This leads to the perception of a blue sky as the scattered blue light reaches the eyes.
Optical fibre scattering: Rayleigh scattering is also observed in the scattering of optical signals through optical fibres, demonstrating its broader relevance in different contexts.
2.7.3 Tyndall effect
The Tyndall effect is a phenomenon observed in a heterogeneous mixture of minute particles, including smoke, tiny water droplets, suspended dust particles, and air molecules, present in the atmosphere. When a beam of light encounters these fine particles, the path of the beam becomes visible as the light is diffusely reflected by the particles. The Tyndall effect is prominently seen when a fine beam of sunlight enters a smoke-filled room through a small hole, making the scattering of light by colloidal particles visible. Additionally, this effect can be witnessed when sunlight passes through a dense forest canopy, where tiny water droplets in the mist contribute to the scattering of light.
The colour of the scattered light is contingent on the size of the scattering particles. Very fine particles primarily scatter blue light, while larger particles scatter light of longer wavelengths. In cases where the size of the scattering particles is sufficiently large, the scattered light may even appear white.
2.7.4 Why is the colour of the clear sky blue?
The molecules and fine particles in the Earth's atmosphere are smaller than the wavelength of visible light, leading to more effective scattering of shorter wavelengths, particularly blue light, compared to the longer wavelengths like red light. As a result, when sunlight traverses the atmosphere, the fine particles scatter blue light more strongly, making the scattered blue light visible to our eyes. Without the atmosphere, the sky would appear dark, as there would be no scattering. At very high altitudes, where scattering is not prominent, the sky looks dark.
Why are danger signal lights red?
Danger signal lights are often red because red is least scattered by fog or smoke, making it visible at a distance.
2.7.5 Colour of the Sun at sunrise and sunset
During sunrise, the light rays coming from the sun have to travel a greater distance in the earth's atmosphere before reaching our eyes. In this journey, the shorter wavelengths of light are scattered out, and only longer wavelengths are able to reach our eyes. Since the blue colour has a shorter wavelength and the red colour has a longer wavelength, the red colour is able to reach our eyes after the atmospheric scattering of light. Therefore, the sun appears reddish early in the morning.
Sun near horizon
Blue scattered away Sun appears reddish
Sun nearly overhead
Less blue scattered
Colour of sun early in the morning
QUICK REVIEW
• The main parts of an eye are the cornea, iris, pupil, lens, retina and optic nerves
• The ciliary muscles attached to the eye lens can change their thickness to enable us to see near and distant objects. This feature of the eye is called accommodation
• Myopia (near-sightedness): A vision condition where an individual can see nearby objects clearly but struggles to see distant objects distinctly.
• Hypermetropia (far-sightedness): A vision condition where an individual can see distant objects clearly but struggles to see nearby objects distinctly.
• Presbyopia: A visual defect associated with ageing, where individuals experience difficulty in seeing nearby objects comfortably and distinctly without corrective eyeglasses.
• The angle of deviation of the prism is: δ = i + i' - A
• The phenomenon due to which a ray of light, while travelling from an optically denser medium to an optically rarer medium gets reflected into the optically denser medium at the surface of separation is called total internal reflection.
• The relation between the refractive index and the angle of minimum deviation μ = sin i sin r
• The angle of incidence in a denser medium, for which the angle of refraction in the rarer medium is 900, which is called the critical angle
• The relation between the refractive index and critical angle 1μ2 = 1 sin c
• The phenomenon in which a beam of white light separates into its component colours when it passes through a prism or another optical medium is called dispersion.
• ( ) vrvr Angular dispersion A ddmm=-=-
• Atmospheric refraction is the bending of light rays as they pass through the Earth's atmosphere, primarily caused by variations in air density due to temperature gradients.
WORKSHEET - 1
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
I. The human eye, defects of vision, and their corrections
1. A person cannot see objects kept beyond 2 m distinctly. This defect can be corrected by using a lens of power:
a. +0.5D b. -0.5D c. +0.2D
-0.2D
2. The near point of a hypermetropic eye is 1 m. What is the power of the lens required to correct this defect? Assume that the near point of the normal eye is 25 cm.
+3D
-2D
+2D
-3D
3. The impact of an image on the retina persists for: a. 1/10 s b. 1/16 s c. 10 s d. 20 s
4. The far point of a short-sighted eye is 100 cm. Which of the following lenses should we use to see distant objects clearly?
a. A convex lens of focal length 50 cm
b. A concave lens of focal length 100 cm
c. A concave lens of focal length 50 cm
d. A convex lens of focal length 100 cm
5. Which of the following statements is correct?
a. A person with myopia can see distant objects clearly.
b. A person with hypermetropia can see nearby objects clearly.

c. A person with myopia can see nearby objects clearly.
d. A person with hypermetropia cannot see distant objects clearly.
6. Assertion (A): In bright light, the size of the pupil is small.
Reason (R): The pupil controls the amount of light entering the eye.
a. Both A and R are correct, and R is the correct explanation of A.
b. Both A and R are correct, but R is not the correct explanation of A.
c. A is correct, but R is incorrect.
d. R is correct, but A is incorrect.
II. Prism
1. Consider the following traces of the path of a ray of light passing through a glass prism. Identify the diagram which shows the correct path of a ray of light.
2. The path of a ray of light passing through a glass prism is shown below.
In the diagram, the angle of incidence, the angle of emergence, and the angle of deviation, respectively, are:
X, R and T
X, Q and P
Y, Q and T
Y, Q and P
3. The path of a ray of light passing through a glass prism is shown below.
In this diagram, the angle of prism, angle of incidence, angle of emergence, and angle of deviation, respectively, have been represented by:
a. O, Y, Z and N
c. O, X, M and Z
b. P, Y, M and Z
d. P, X, Z and N
4. Assertion (A): The refractive index of the prism depends on the material of the prism.
Reason (R): The dispersive power of the prism is independent of the material of the prism.
a. Both A and R are true, and R is the correct explanation of A.
b. Both A and R are true, but R is not the correct explanation of A.
c. A is true, but R is false.
d. A is false, but R is true.
5. Deviation δ produced by a prism of refractive index μ and small angle A is given by:
a. δ = (μ–1)A
b. δ = (μ–1)A
c. δ = (A–1)μ
d. δ = (A+1)μ
6. If the refracting angle of a prism is 600 and the minimum deviation is 300, then the angle of incidence will be:
a. 300 b. 450 c. 600 d. 900
7. A ray of light passes through an equilateral glass prism in such a manner that the angle of incidence is equal to the angle of emergence, and each of these angles is equal to (3/4) of the angle of the prism. The angle of deviation is:
a. 450 b. 700 c. 390 d. 300
8. For a prism having an angle of prism 600 and μ=√2, the angle of minimum deviation is:
a. 300 b. 450 c. 600 d. 900
9. A glass prism has μ=1.5 and the refracting angle is 90°. If a ray falls on it with an angle of incidence of 300, then the angle of emergence is:
a. 600 b. 300
c. 450
d. The ray will not emerge out of this prism
10. A light ray, going through a prism of angle 60°, is found deviating by 30°. The refractive index of the prism is: a. μ ≥ √2
μ ≤ √2
μ = √2
11. The angle of minimum deviation for an equilateral prism made of a material of refractive index 1.732 and the angle of incidence for the said deviation are:
a. 600, 300 b. 600, 600 c. 300, 600 d. 300, 300
12. A prism ABC (with BC as the base) is placed in different orientations. A narrow beam of white light is incident on the prism, as shown below. In which of the following cases, after dispersion, the third colour from the top corresponds to the colour of the sky?
13. Which of the following diagram represents the refraction of light through a prism correctly?
14. What will happen to the components of white light that emerge after passing through a prism, if a second identical prism is placed in an inverted position with respect to the first prism?
a. We get VIBGYOR.
b. We get ROYGBIV.
c. We get white light.
d. None of these
15. When light falls on a prism, the result can be:
a. Inversion
b. Magnification c. Elongation d. Deviation
16. A monochromatic ray of light after passing through the prism produces:
a. Seven colours only
III. Total internal reflection
b. Five colours only c. Two colours only d. One colour only
1. Assertion (A): When a white light passes through a glass slab, it does not produce any spectrum.
Reason (R): In a glass slab, both the refracting faces are parallel.
a. Both A and R are correct, but R is the correct explanation of A.
b. Both A and R are correct, and R is not the correct explanation of A.
c. A is correct, but R is incorrect.
d. R is correct, but A is incorrect.
2. The angle of the prism is 60o and its refractive index is √2. At minimum deviation condition, what is the possible value of the angle of incidence? a. 45° b. 30°
3. The critical angle between an equilateral prism and air is 45°. If the incident ray is perpendicular to the refracting surface, then
a. Light goes from an optically rarer medium to an optically denser medium.
b. It is totally reflected from the second surface and emerges out perpendicularly from the third face into the air.
c. It is totally reflected from the second and third refracting surfaces and finally emerges out from the first surface.
d. It is totally reflected from all the sides of the prism and never emerges out.
4. When a light ray suffers reflection, at the interface between air and glass, the change of phase in the reflected wave is equal to:
a. Zero b. π/4 c. π/2 d. π
5. Total internal reflection takes place only if:
a. Light goes from an optically rarer medium to an optically denser medium.
b. Light goes from an optically denser medium to an optically rarer medium.
c. The refractive indices of the two media are close to each other.
d. The refractive indices of the two media are widely different.
6. Mirage and looming occur due to:
a. Reflection
c. Diffraction
7. Optical fibres are based on:
a. Total internal reflection
c. Refraction
b. Refraction
d. Total internal reflection
b. Less scattering
d. Less absorption coefficient
8. Among the following, the consequence of total internal reflection is:
a. A diamond glittering
c. Shallow depth of swimming pool
b. An air bubble in water
d. Twinkling of stars
SURFACE
9. In optical fibres,
a. The refractive index of the inner region is equal to the outer region.
b. The refractive index of the inner region is less than the outer region.
c. The refractive index of the inner region is greater than the outer region.
d. There is no relation between the refractive index of the inner region and the outer region.
10. Assertion (A): The images formed by total internal reflection are much brighter than those formed by mirrors or lenses.
Reason (R): There is no loss of intensity in total internal reflection.
a. Both A and R are true, and R is the correct explanation of A.
b. Both A and R are true, but R is not the correct explanation of A.
c. A is true, but R is false.
d. A is false, but R is true.
11. Optical fibres are used in:
a. Laparoscope b. Endoscope
c. Sensors used to measure temperature d. All the above
12. Assertion (A): Optical fibres are widely used in communication networks.
Reason (R): Optical fibres are small in size, lightweight, and flexible, and there is no scope for interference in them.
a. Both A and R are true, and R is the correct explanation of A.
b. Both A and R are true, but R is not the correct explanation of A.
c. A is true, but R is false.
d. A is false, but R is true
13. Assertion (A): Endoscopy involves the use of optical fibres to study internal organs. Reason (R): Optical fibres are based on phenomena of total internal reflection.
a. Both A and R are true, and R is the correct explanation of A.
b. Both A and R are true, but R is not the correct explanation of A.
c. A is true, but R is false.
d. A is false, but R is true.
14. If the critical angle for total internal reflection from a medium to vacuum is 300, then the velocity of light in the medium is:
a. 3×108 m/s b. 1.5×108 m/s c. 6×108 m/s d. √3×108 m/s
15. When the surface of the lake is calm, a fish submerged in water will see the entire outside world within an inverted cone whose apex is situated at the eye of the fish and the cone subtends an angle of:
a. 100 b. 600 c. 980 d. 300
IV. Dispersion, atmospheric refraction and scattering of light
1. Twinkling of stars is due to the atmospheric:
a. Dispersion of light by water droplets.
b. Refraction of light by different layers of varying refractive indices.
c. Scattering of light by dust particles.
d. Internal reflection of light by clouds.
2. Which of the following statements is correct regarding the propagation of different colours of white light in the air?
a. Red light moves the fastest.
b. Blue light moves the fastest.
c. All the colours of the white light move with the same speed.
d. Yellow light moves with the same mean speed as that of the red and violet light.
3. Which of the following phenomena contributes significantly to the reddish appearance of the Sun at sunrise or sunset?
a. Dispersion of light
c. Total internal reflection of light
b. Scattering of light
d. The reflection of light from the earth
4. The bluish colour of the water in deep seas is due to:
a. The presence of algae and other plants found in water
c. The scattering of light
WORKSHEET - 2
b. The reflection of the sky in water
d. Absorption of light by the sea
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
1. The focal length of the eye lens increases when eye muscles:
a. Are relaxed and lens becomes thinner
c. Are relaxed and lens becomes thicker
b. Contract and lens becomes thicker
d. Contract and lens becomes thinner
2. A boy has myopia, and he uses spectacles of focal length -80 cm. What is the power of the lens?
a. -1.25D
b. -2D
c. -1D
3. Which of the following is a possible reason for myopia?
a. Excessive curvature of the eye
c. Decrease in the size of the eye lens
d. None of these
b. The focal length of the eye lens is too long
d. Minimal curvature of the eye
4. Your grandfather uses spectacles for his presbyopia defect. Through which part of the spectacles, does he see the letters in the newspaper while reading?
a. Upper
b. Lower
c. Middle d. Any part
5. In the study of the spectrum, the prism is placed in the minimum deviation position to make the spectrum:
a. Visible
b. Magnified
c. Line spectrum d. Well-defined
6. A prism is placed in water. The angle of minimum deviation will:
a. Increase
b. Decrease c. Remain same d. None of the above
7. A beam of white light is incident on a hollow glass prism. Then, the light emerging from the prism gives:
a. A spectrum with all the colours bent away from the base.
b. A spectrum with all the colours bent towards the base such that violet is bent the most and red the least
c. A spectrum with all colours bent towards the base such that violet is bent the least and red the most
d. No spectrum.
8. For a given prism, the angle of incidence is changed from 0° to 90°; the angle of deviation will will also:
a. Increase
c. First decrease and then increase
b. Decrease
d. First increase and then decrease
9. For a ray of light incident on a prism of angle A, the wrong statement is:
a. The angle of deviation will increase as A increases.
b. The angle of deviation will increase as the refractive index of the prism increases.
c. The angle of deviation for the violet colour is more than the angle of deviation for the red colour
d. All colours into which the ray is dispersed emerge as a parallel beam.
10. Which of the following phenomena of light are involved in the formation of a rainbow?
a. Reflection, refraction, and dispersion
b. Refraction, dispersion, and internal refraction
c. Refraction, dispersion, and internal reflection
d. Dispersion, scattering of light, and total internal reflection
11. The colour for which the critical angle is maximum in the water-air system is:
a. Red
c. Yellow
b. Violet
d. It is the same for all colours.
12. If the critical angle for water is (48.2)0, then its refractive index is:
a. 13.4
b. 1.34
c. 0.134
d. 0.0134
13. A rainbow is seen due to:
a. Interference by thin films
c. Dispersion of sunlight
14. Dispersion is the term used to describe:
a. The propagation of light in straight lines
b. Scattering of sunlight
d. Diffraction of sunlight
b. The splitting of a beam of light into its component colours
c. The bending of a beam of light when it strikes a mirror
d. The change that takes place in white light after passing through glass
15. The danger signals are red in colour. These can be easily seen from a distance because among all the other colours, the red light:
a. Is scattered the most by smoke or fog
c. Is absorbed the most by smoke or fog
b. Is scattered the least by smoke or fog
d. Moves fastest in the air
16. In total internal reflection, when the angle of incidence is equal to the critical angle for the pair of media in contact, what will the angle of refraction be?
a. 180°
c. 00
b. 900
d. Equal to the angle of incidence
17. Assertion (A): The twinkling of stars is due to the reflection of light.
Reason (R): The velocity of light changes while travelling from one medium to the other.
a. Both A and R are correct, but R is the correct explanation of A.
b. Both A and R are correct, and R is not the correct explanation of A.
c. A is correct, but R is incorrect.
d. R is correct, but A is incorrect.
18. Assertion (A): Danger signals are of red colour.
Reason (R): The velocity of red light is maximum and thus, has more visibility in the dark.
a. Both A and R are correct, but R is the correct explanation of A.
b. Both A and R are correct but R is not the correct explanation of A.
c. A is correct, but R is incorrect.
d. R is correct, but A is incorrect.
19. Assertion (A) : The space appears dark to an astronaut.
Reason (R) : There is no atmosphere in space.
a. Both A and R are correct, but R is the correct explanation of A.
b. Both A and R are correct, and R is not the correct explanation of A.
c. A is correct, but R is incorrect.
d. R is correct, but A is incorrect.
20. Assertion (A): The formation of mirages in hot deserts is a phenomenon of total internal reflection.
Reason (R): The air close to the land is hotter than the air far from the land in a hot desert. So, total internal reflection takes place.
a. A is correct, but R is wrong.
b. A is wrong, but R is correct.
c. Both A and R are correct, but R does not explains A.
d. Both A and R are correct, and R explains A.
21. Assertion (A): A secondary rainbow has all the colours of the primary rainbow but is inverted. Reason (R): The secondary rainbow is formed by a single total internal reflection.
a. Both A and R are true, and R is the correct explanation of A.
b. Both A and R are true, and R is not the correct explanation of A.
c. A is true, but R is false.
d. A is false, but R is rue.
22. Statement(A): A person may have a normal ability of accommodation of the eye lens, and yet may be myopic or hypermetropic.
Statement(B): When the eyeball is of normal length, but the eye lens partially loses its ability of accommodation (as happens with increasing age for any normal eye), the 'defect' is called presbyopia.
a. A is false, but B is true.
c. Both A and B are true.
b. A is true, but B is false.
d. Both A and B are false.
23. If refractive indices for water and glass are 4/3 and 5/3, respectively, and the light ray tends to go from glass to water, then the critical angle is:
a. sin-1(4/3) b. sin-1(5/3) c. sin-1(4/5) d. sin-1(5/4)
24. The critical angle for a light wave going from a medium in which wavelength is 4000A0 to a medium in which its wavelength is 6000A0, is: a. 300 b. 450
600
sin-1(2/3)
25. A bulb is placed at a depth of 2√7 m in water, and the floating opaque disc is placed over the bulb so that the bulb is not visible from the surface. The minimum diameter of the disc is: a. 42 m b. 6 m c. 2√7 m d. 12 m
26. An optical fibre (μ = 1.72) is surrounded by a glass coating (μ = 1.50). The critical angle for the total internal reflection at the fibre-glass interface is:
a. sin-1(85/75) b. sin-1(75/86) c. sin-1(2/15) d. sin-1(2/17)

3.1 INTRODUCTION TO ELECTRICITY
Electricity- The word comes from 'elektron', which means amber in Greek. It is a kind of fossiled gum with a straw-yellow colour. Ancient Greek philosopher Thales found out that when amber is rubbed with wool, it develops a strange property of attracting tiny bits of dry paper, dry straw, dry pieces of leaves, etc., towards itself.
Sometime later, in the seventeenth century, Dr. William Gilbert reconstructed Thales' experiment. He showed that not only amber and wool combinations but many other combinations such as an ebonite rod and cat's skin, glass rod and silk, sealing wax and wool, etc., also develop similar properties when rubbed with each other.
The substances that acquire this strange property of attraction were said to be charged with electricity or electrified (from the Greek word 'elektron').
The phenomenon due to which a suitable combination of bodies on rubbing, gets electrified is called electricity.
3.2 ELECTRIC CHARGE
Atom: An atom is the smallest particle of matter. If you could keep dividing an object, say a gold ring, into smaller and smaller pieces, you would finally get the smallest possible particle of gold. This is an atom.
Fig. 3.1 Structure of an atom
In the centre of each atom is a nucleus. This can remind you of the sun in the centre of the solar system. The nucleus contains two kinds of tiny particles: protons and neutrons. Orbiting around the nucleus are even smaller particles called electrons like the planets around the sun. Electrons play an essential role in many physical phenomena. Electricity is one such phenomenon.
Electric charge: Protons have what we call a positive (+) charge. Electrons have a negative (-) charge and neutrons have no charge; they are neutral. Usually, atoms have the same number of electrons and protons. Hence an atom has no charge; it is neutral.
Like charge repel, and unlike charges attract each other
Fig. 3.2 Like and unlike charges
• The SI unit of charge is coulomb(C).
• Charge of electron = -1.6 × 10-19 C
• Charge of proton = +1.6 × 10-19 C
• Mass of electron = 9.1 × 10-31 kg
• Study of charges at rest is called static electricity.
• Study of charges in motion is called current electricity.
Making Observation: Comb your hair briskly 20 - 30 times. After combing, bring your comb near your hair (but do not allow the contact). Observe. You will see that your hair starts flying or moving towards the comb with a very low chit-chit sound. Why does it happen so?
This happens, because due to combing, your hair and comb both get charged. When you comb your hair, it runs against the comb and makes the atoms of the comb and your hair lose and gain electrons. This loss and gain of electrons leads to the development of charge on the atoms of the comb and those of your hair. The charge developed is strong enough to move light-weight things like hair.
This atom losses an electron and gains positive charge
3.2.1 Conductors and insulators
This atom gains an electron and becomes negatively charged
There are substances which have free electrons in them. These substances allow electrons to flow through them. Electrons move and make the electricity flow. Such substances, which carry electricity, are known as conductors. They are mostly metals like copper, silver and aluminium. Other substances, mostly nonmetals like plastic, paper and cloth, do not have free electrons. Therefore, electrons that do not allow the electricity to pass through them are called insulators
A conductor allows the electric current to flow through it. That is why the electric wiring of our houses is made of conductors like copper. They carry the current from the source and light a bulb, thus enabling us to even at night or in the dark. However, the wires are never bare and are covered by insulators. This prevents electric shocks.
3.2.2 Properties of electric charge
The electric charge has the following three basic properties:
1. The additive nature of electric charges: The additivity of electric charge means that the total charge of a system is the algebraic sum of all the individual charges located at different points inside the system.
If a system contains charges q1, q2, ..., qn, then its total charge is q = q1 + q2 +....+qn
The total charge of a system containing four charges, 3μC, -4μC, 2μC, and -3μC, is q = 3μC - 4μC + 2μC - 3μC = -2μC.
2. The quantisation of electric charge: It is observed that the electric charge of any body, large or small, is always an integral multiple of a certain minimum amount of charge. This basic charge is the charge on an electron, which is denoted by 'e' and has a magnitude 1.6 × 10-19 coulomb. Thus, the charge of an electron is negative, and that of a proton is positive.
The experimental fact that electric charges occur in discrete amounts instead of continuous amounts is called the quantisation of electric charge. The quantisation of electric charge means that the total charge (q) of a body is always an integral multiple of a basic quantum of charge (e), i.e.,
ELECTRICITY
q = ne, where n = 0, ±1, ±2, ±3, ...
Cause of quantisation: The basic cause of quantisation of electric charge is that during rubbing only an integral number of electrons can be transferred from one body to another.
The quantization of electric charge is an experimentally verified law:
• The experimental laws of electrolysis discovered by Faraday first suggested the quantisation of electric charge.
• Millikan's oil drop experiment in 1912 on the measurement of electric charge further established the quantisation of electric charge.
3. Conservation of charge: According to the law of conservation of charge, if some amount of matter is isolated in a certain region of space and no matter either enters or leaves this region by moving across its boundary, then whatever other changes may occur in the matter inside, its total charge will not change with time. This is the law of conservation of charge which states:
• The total charge of an isolated system remains constant.
• The electric charges can neither be created nor destroyed; they can only be transferred from one body to another.
The charge conservation is a global phenomenon, i.e., the total charge of the entire universe remains constant.
Let’s take an example to understand this: when a glass rod is rubbed with a silk cloth, it develops a positive charge. But at the same time, the silk cloth develops an equal negative charge. Thus, the net charge of the glass rod and the silk cloth is zero, as it was before rubbing.
Take another example, the rock salt ionizes in an aqueous solution as follows:
NaCl ⇌ Na+ + Cl-
As the total charge is zero before and after the ionization, the charge is conserved.
SOLVED EXAMPLES
Example 1: Calculate the number of electrons constituting one coulomb of charge.
Solution:
We know that the charge of an electron is 1.6 × 10-19 coulomb.
Now, if the charge is 1.6 × 10-19 C, No. of electrons = 1
So,
If the charge is 1C, then the no. of electrons
Thus, 1 coulomb of charge has 6.25 × 1018 electrons.
Thus, coulomb is a very big unit of electric charge.
Example 2: When a comb is drawn through a person's hair on a dry day, it causes 1022 electrons to leave the person's hair and stick to the comb. Calculate the charge carried by the comb.
Solution:
Here n = 1022, e = 1.6 × 10-19 C
∴q = ne = 1022 × 1.6 × 10-19 = 1.6 × 103C
As the comb has an excess of electrons,
∴ Charge on comb = -1.6 × 103 C.
Example 3: If a body gives out 109 electrons every second, how much time will be required to get a total charge of 1C from it?
Solution: Number of electrons given out by the body in one second = 109
Charge given out by the body in one second = ne
= 109 × 1.6 × 10-19 C
= 1.6 × 10-10 C
Time required to get a charge of 1.6 × 10-10 C = 1 s
Time required to get a charge of 1 C
Thus, for a body emitting 109 electrons per second, it will take nearly 200 years to get a charge of 1 C.
3.3 ELECTRIC CURRENT
3.3.1 Electric current
The electric current is defined as the rate of flow of charge through any cross-section of a conductor.
If a net charge 'Q' passes through any cross-section of the conductor in time 't', then the average current 'I' is given by
Average current, I = Q t
Current is a scalar quantity. It is a macroscopic quantity, like the mass of a body or the volume of a container. In SI units, current is one of the fundamental physical quantities. It is dimensionally denoted by [I] or [A]. The direction of current is the direction of flow of positive charge (or) opposite to the direction of flow of negative charge.
Ampere: If one coulomb of charge passes through a cross-section of the conductor per second, then the current is one ampere.
3.3.2 Constituents of current in differernt cases
1. Current in solid conductors: In solid conductors like metals, the valence electrons of the atoms do not remain attached to individual atoms but are free to move throughout the volume of the conductor. Under the effect of an external electric field, these free electrons move in a definite direction, causing electric current in the conductors. Thus, free electrons are the current constituents in solid conductors.
2. Current in electrolytes: In an electrolyte like NaCl solution, there are positively and negatively charged ions (Na+, Cl-). These are forced to move in definite directions under the effect of an external electric field, causing an electric current. Thus in electrolytes, the current is due to positively and negatively charged ions.
3. Current in gases: Generally, gases are insulators of electricity. But they can be ionized by applying a high potential difference at low pressures, or by their exposure to the x-rays etc. The ionized gas contains positive ions and electrons. Thus, positive ions and electrons constitute current in gases.
4. Current in semi-conductors: In semi-conductors the flow of current is due to holes and free electrons.
Example 1: If a total of 6.0 × 1016 electrons pass through any cross-section of a conducting wire per second, find the current.
Solution: The total charge crossing the cross section in one second is,
Q = ne
= 6.0 × 1016 × 1.6 × 10-19 C = 9.6 × 10-3 C
The value of current, I = Q t = 9.6×10-3 C 1s = 9.6 × 10-3 A
Example 2: If 1020 electrons, each having a charge of 1.6 × 10-19 C, pass from a point A towards another point B in 0.1s, what will be the current in ampere?, and what will be its direction?
Solution:
Here, n = 1020, e = 1.6 × 10-19 C, t = 0.1 s
The value of current, I = Q t = ne t = 1020×1.6×10-19 C 0.1s = 160 A
The direction of the current is from B to A.
Example 3: How many electrons pass through a lamp in one minute if the current is 300 mA?
Solution:
3.4 ELECTRIC POTENTIAL AND POTENTIAL DIFFERENCE
3.4.1 Electric field
• The region around the charge where another charge experiences the force is called an electric field.
• A charge at rest always produces an electric field only.
• A charge in motion produces both electric and magnetic fields.
• The electric field is a vector field.
3.4.2 Electric lines of force
The path of a unit positive charge in the electrical field is called the electric line of force.
• Electric lines of force usually start from a positive charge and end at a negative charge.
3.4 Electric field lines
• Electric lines of force never cross each other, as this would result in a point having two directions of intensity, which is absurd.
3.4.3 Electric potential
When two different charged bodies are kept in contact, charge flows from the body with a higher charge density to the one with a lower density until both bodies acquire a common electric property called electric potential.
Definition: The work done to bring a unit positive charge from an infinite distance to a point in the electric field is defined as the electrical potential at that point.
(or)
The potential energy per unit charge at a point in an electric field is called the electric potential at that point.
Electric potential, V= U q ⇒V= W app q (U= Wapp)
W app is the work done by the applied force to move the unit charge from infinity to the particular point.
A potential ' V ' can be positive, negative, or zero, depending on signs and magnitudes of q and Wapp
• It is a scalar quantity.
• Its SI unit is J/C (or) volt.
• Its dimensional formula is [M1L2 T-3I-1 ].
The potential of the earth is considered to be zero, because on adding and removing charge, there is no change in the state of charge of the earth due to its large size.
3.4.4 Electric potential difference between two points
The negative of work done by the electrostatic force (due to an external electric field) to move a unit charge from one point to another.
(or)
The work done to bring a unit positive charge from one point to another point in the electric field is defined as the electric potential difference
ΔV = Vf - Vi = W q = W app q
A potential difference can be positive, negative, or zero, depending on the signs and magnitudes of q and W.
• It is a scalar quantity.
• Its SI unit is J/C (or) volt.
• Its dimensional formula is [M1L2 T-3I-1 ].
One Volt: If a work of 1 joule is done to bring a unit positive charge from infinite to a point in the electrical field, then the potential at that point is said to be one volt.
SOLVED EXAMPLES
Example 1: If 5 joules of work is done in moving 12.5 × 1018 electrons from one end to the other end of a conductor, what is the potential difference between the two ends of the conductor?
Solution: The charge on 6.25 × 1018 electrons is 1C.
∴ the charge on 12.5 × 1018 electrons is 2C.
∴Q = 2C.
Work done (W) in moving 2C charge = 5 J.
The potential difference (V) between the ends of the conductor is
V Work done ch e J C JC
Vvolts arg . .. 5 2 25 25 1
Example 2: If 100 J of work has to be done in moving an electric charge of 4C from a place, where the potential is -10 V to another place, where the potential is V volt, find the value of V.
Solution: Here, WAB = 100 J, q0 = 4C, VA = -10 V, VB = V,
3.5 CIRCUIT DIAGRAM
3.5.1 Source of electric current
A power station is the main source of electricity that lights our houses and runs our electrical appliances. These power stations are mostly situated away from the city. The electricity generated in these power stations is brought to our houses through thick wires. There are a variety of ways in which electricity is produced in these power stations. The following are the ways by which electricity is generated in various power stations: by burning coal, from natural gas, from water, from wind power, from solar energy or by building power stations in rivers.
3.5.2 Dry cell
At times, there are power failures; you must have lighted a torch often in such a situation. Have you wondered where this electricity comes from? The source of electric current in a torch is the dry cell.
Dry cells are available in the market. They have different sizes and different capacities. Each cell has two terminals: positive (marked +) and negative (marked - ). You must have seen the marks. In dry cells, chemicals are stored, which react and produce electricity. This runs the electrical devices. Once these chemicals are used up or exhausted, we must throw away the cell.
Positive terminal
Muslin bag with chemicals(carbon and manganese dioxide)
Negative terminal
A touch lights up using electricity from a dry cell
3.6 Dry Cell
Note: Two or more cells connected together are called a battery.
3.5.3 Bulb
Now, let us see a conventional bulb from the inside. A bulb has a glass case mounted on a metallic base as shown in the figure. Glass
3.7 Light Bulb
Inside the glass case, you see a thin wire coil called the filament. As electric current passes through the filament of the bulb, the filament's temperature rises to about 2500° C. The filament is made from a metal called tungsten. Tungsten is the most temperature-resistant material known. When this filament becomes very hot, it emits light. However, tungsten is highly reactive when hot. Therefore, light bulbs are filled with an inert gas such as nitrogen or argon to prevent the filament from reacting with air.
Remember, never touch the bulb after it lights because it is hot enough to burn your fingers. A bulb has to be connected to two terminals.
3.5.4
Simple electric circuit
A circuit is the closed path through which an electric current flows. The different parts of a circuit are called components of the circuit.
The current will flow when the circuit is continuous and unbroken. The driving force that pushes charge (electrons) around the circuit is produced by the potential difference between two points and is produced by the cell or a battery, and is called the electromotive force (e.m.f)
A source of electricity, i.e., the cell or battery or the mains, is a device through which current can flow (like a bulb); a switch to open or close the circuit, and connecting wires made of a metal (usually copper) are the components of a circuit.
Fig. 3.8 Simple electric circuit
The figure shows a simple circuit. When the switch is on, the circuit is closed, and the bulb glows. When off, the circuit is open, and the bulb does not glow.
Current flows from the positive terminal of the cell through the circuit to the negative terminal of the cell. You know that the direction of the flow of current is opposite the direction of the flow of electrons.
3.5.5 Symbols for various parts of a circuit
Fig. 3.9 Symbols of electric components
When we want to depict electrical gadgets and circuits diagrammatically, then they have to be represented through certain symbols. Drawing the diagram of a complete gadget is time consuming and complicated. Thus, to simplify the diagram of a circuit, the parts of the circuit are shown with the help of symbols. The symbols or diagrammatic representations in the figure are used while drawing a circuit diagram.
3.5.6 Circuit diagram
It is the diagrammatic representation of an electric circuit by how and which the electric components present in the circuit by using their symbols.
BULB
Fig. 3.10 Circuit diagram
3.6 OHM’S LAW
3.6.1 Ohm's law
Statement: At constant temperature, current flowing through a conductor is directly proportional to the potential difference applied across it.
V ∝ I [At constant temperature]
V = (constant)I
R is a constant called the resistance of the conductor
V = RI
• The devices that obey Ohm's law are called ohmic conductors
• Metal alloys obey Ohm's law.
• For ohmic conductors, the graph between I-V is a straight line.
Fig. 3.11 I-V graph for ohmic conductors
• The slope of the graph gives conductance.
• The devices that do not obey Ohm's law are called non-ohmic conductors
Vacuum tubes, transistors, discharge tubes, and thermistors are non-ohmic conductors. The graph drawn between I and V is a curve, as shown in the figures.
tube)
Fig. 3.12 I-V graph for non-ohmic conductors
3.6.2 Resistance (R)
The opposition offered to the flow of electric charge in a conductor is called resistance
From Ohm's law, R = V I
The ratio of the potential difference across the conductor to the current passing through the conductor is called the resistance of the conductor.
If V = 1 volt, and I = 1 ampere, then R = 1 Volt 1 Ampere = 1ohm
• Its SI unit is ohm (Ω).
• Its dimensional formula is [ML2T-3I-2].
• A conductor having some resistance is called a resistor
One Ohm: If a unit amount of current passes through a conductor whose ends are maintained at a unit potential difference, then the resistance of the conductor is said to be one ohm.
3.6.3 Factors affecting the resistance
The resistance of a the conductor depends upon the length, area of cross-section, nature of conductor, and the temperature of the conductor.
The resistance of a conductor is directly proportional to the length of the conductor (l), and inversely proportional to the area of its cross-section (A)
R ∝ l, R ∝ 1 A ,
⇒R ∝ l A ,
R = (constant) l A , where ' ρ ' is the constant known as the specific resistance or the resistivity of conductor.
R = ρ.l A
⇒ρ = RA l
SOLVED EXAMPLES
Example 1: When a 12 V battery is connected across an unknown resistor, a current of 2.5 mA flows through the circuit. Find the value of the resistance of the resistor.
Solution:
V = 12 V,
I = 2.5 mA = 2.5 × 10-3 A
∴ R = V I , = 12 2.5×10-3 = 4800Ω
Example 2: An electric bulb whose resistance is 60Ω is connected to a source of potential difference of 230 V. Find the current flowing through it.
Solution: The potential difference (V) applied to the bulb = 230 V
The resistance (R) of the bulb = 60Ω
The current (I) flowing through the bulb = ?
According to Ohm's law:
= IR
= V R = 230 60
I = 3.83 A.
3.6.4 Validity (or) limitations of Ohm's law
a) Ohm's law is valid only for linear or ohmic conductors such as metals. For linear or ohmic conductors, I versus V graphs are straight lines passing through the origin, as shown in A and B.
Fig. 3.13
b) Ohm's law is not universal as it does not hold well in the case of gases, crystal-rectifiers, thermionic valves, transistors, carbon, mica, vacuum tubes, thermistors, and most electrolytes. The devices or substances that do not obey Ohm's law are called non-ohmic or nonlinear conductors.
For these, the I versus V graph is not a straight line, but they are in the form of curves for different materials.
Note: The equation V= IR is applicable for all linear and nonlinear conductors, while Ohm's law (V∝I) is not applicable for nonlinear conductors.
By drawing a graph between voltage and current across conductors, we observe that many conductors obey Ohm's law. Their resistance is called Ohmic resistance or linear resistance. But Ohm's law does not always hold true. If we replace the resistance wire with a torch bulb in an electrical circuit and note down the values of current (I) for different voltages (V), we can see that the entire V-I graph drawn is not a straight line (Fig. 3.14). For low values of V, it remains a straight line and then becomes curved. At a high voltage, the current through the filament of the bulb increases leading to a rise in the temperature of the filament which becomes higher and higher as the current increases in the filament. The ratio, V I , for the low value of I, provides the resistance of the filament. Ohm's law holds in metallic wires for low values of current only.
3.14 V-I graph for conductors
In the above figure, the dashed line represents the linear Ohm's law. The solid line is the voltage V versus current I for a good conductor.
Note the different scales for negative and positive values of the voltage and current. Other examples of non-ohmic resistances are vacuum diodes, semiconductor diodes, transistor liquid electrolytes, etc. In the Vacuum diode, Ohm's law does not hold even for low values of current.
Fig. 3.16 Graph showing the variation of I versus V for gas
The relation between V and I is not unique, i.e., there is more than one value of V for the same current I. A material exhibiting such behaviour is gas.
Note: In general, electrolytes do not obey Ohm's law. But copper sulphate solution with copper electrodes obeys Ohm's law even though it is an electrolyte.
3.7
ELECTRICAL RESISTIVITY, CONDUCTIVITY, AND TEMPERATURE D DEPENDENCE OF RESISTIVITY
3.7.1 Resistivity
As we know, the resistance of the conductor is directly proportional to its length, and inversely proportional to its area of cross-section, we can write:
R ∝ l A ,
⇒R = ρl A , where ρ is the specific resistance or resistivity of the material of the conductor.
Now, let us define the specific resistance of the conductor. If l = 1 m, A = 1 m2, then ρ = R.
Resistivity: The resistance of a conductor of unit length and unit area of the cross-section is called specific resistance or resistivity of the material of the conductor.
• The SI unit of specific resistance is ohm-meter (Ω-m).
• The dimensional formula of specific resistance is [ML3 T-3I-2]
A perfect conductor would have zero resistivity, and a perfect insulator would have infinite resistivity. Metals and alloys have the smallest resistivities and are the best conductors. The
resistivities of insulators are greater than those of the metals by an enormous factor, of the order of 1022.
3.7.2 Conductivity
Conductivity is the measure of the ability of a material to conduct electric current through it. It is the reciprocal of resistivity. σ = 1 ρ = l RA
• S.I. unit: siemen / m ; (Sm-1)
• For insulators σ = 0.
• For perfect conductors, σ is infinity.
SOLVED EXAMPLES
Example 1: An aluminium wire has a radius of 0.25 mm and a length of 75 m. If the resistance of the wire is 10Ω, calculate the resistivity of aluminium.
Solution:
Here, r = 0.25 mm = 0.25 × 10-3 m, L = 75 m, R = 10Ω
Resistivity,
Example 2: A cylinder of a material is 10 cm long and has a cross-section of 2 cm2. If its resistance along the length is 20 Ω, what will its resistivity value be, in number and units?
Solution:
Resistivity ρ = RA/l = (20Ω × 2 cm2)/(10 cm) = 4Ωcm.
Example 3: A copper wire has a diameter of 0.5 mm and a resistivity of 1.6 × 10-8 ohm - m. What will the length of this wire be to make its resistance of 10 ohms? How much does its resistance change if the diameter is doubled?
Solution: i) Given d = 0.5 mm

We know that R= ρl/A l RA R r
ii)Since the diameter is doubled d2= 2 d.(and d1=d)
∴ the decrease in resistance = 10 - 2.5 = 7.5Ω.
3.7.3 Dependence of resistivity on temperature
The resistivity of a material is found to be dependent on the temperature. Different materials do not exhibit the same dependence on temperatures. Over a limited range of temperatures that are not too large, the resistivity of a metallic conductor is approximately given by:
ρT= ρo [1+α(T-To )] ........(1)
Where ρ T is the resistivity at a temperature T and ρ o is the same at a reference temperature T0 α is called the temperature coefficient of resistivity , and from Eq.(1), the dimension of α is (Temp)-1.
The relation of Eq.(1) implies that a graph of ρT plotted against T would be a straight line. At temperatures much lower than 0∘ C, however, the graph, deviates considerably from a straight line. Thus, the equation can be used approximately over a limited range of T around any reference temperature T0, where the graph can be approximated as a straight line.
(10-8Ωm)
Resistivity T of copper as a function of temperature T
T(K) Resistivity (10-8Ωm)
200 400 600800
Resistivity T of nichrome as a function of absolute temperature T
Temperature dependence of resistivity for a typical semiconductor
3.17 Graph of ρ versus T
Some materials, such as Nichrome (an alloy of nickel, iron, and chromium), exhibit a very weak dependence of resistivity with temperature. Manganin and constantan have similar properties. These materials are thus widely used in wire-bound standard resistors since their resistance values would change very little with temperature.
Unlike metals, the resistivity of semiconductors decreases with increasing temperatures. A typical dependence is shown in the above figure.
We can qualitatively understand the temperature dependence of resistivity,
ρ = 1 σ = m ne2 τ
ρ thus depends inversely both on the number n of free electrons per unit volume and on the average time τ between collisions. As we increase temperature, the average speed of the electrons, which act as the carrier's time of collisions τ, thus decreases with temperature.
In a metal, n is not dependent on temperature to any appreciable extent, and thus, the decrease in the value of τ with the rise in temperature causes ρ to increase, as we have observed. For insulators and semiconductors, however, n increases with temperature. This increase more than compensates for any decrease in τ in the equation, so that for such materials, ρ decreases with temperature.
3.8 SYSTEM OF RESISTORS
3.8.1 Flow of electricity through a circuit
Electricity cannot flow through the circuit unless the circuit is complete.
Fig. 3.18 Circuit
3.8.2 Series and Parallel circuits
Series circuit: When several resistances or bulbs are connected end-to-end in a circuit, the current from the cell flows through them in only one path. Such a circuit is called a series circuit. The second end of one resistance is connected to the first end of another.
The more number of bulbs put in the circuit, the less their brightness, as more bulbs offer more resistance to the flow of electrons. If one bulb stops working, then all the other bulbs that are connected will also stop glowing.
SERIES CIRCUIT
Fig. 3.19 Series circuit
Parallel circuit: When each resistance or bulb is connected separately with the cell, then a parallel circuit is formed. In such a connection, one end of all the resistances is connected to the positive terminal of the cell, while the other end of the resistances is connected to the negative terminal. The current from the cell breaks up into different paths of branches, and flows through different bulbs. The number of paths or branches depends on the number of bulbs.
All bulbs, in this case, glow with equal brightness. Adding one more bulb to the circuit will not reduce the brightness of the other bulbs.
PARALLEL CIRCUIT
Fig. 3.20 Parallel circuit
3.8.3 Series combination
Consider a number of resistors connected in series by joining them end to end so that the same current passes through all the resistors. In the following figure, three resistors of resistances R1, R2, and R3 are shown connected in series. The combination is connected to a battery at ends A and D. Let a current I flow through the series combination when it is connected to a battery of voltage V. Potential differences V1, V2 and V3 are developed across R1, R2 and R3, respectively due to this current I, then V1= IR1, V2= IR2 and V3 = IR3. But the sum of V1, V2 and V3 is equal to V, i.e.,
V = V1 + V2 + V3
⇒V = IR1 + IR2 + IR3
3.21 Series combination of resistance
If the equivalent resistance of this series combination is R, then
V = IR= I(R1+R2+R3 ) or R= R1+R2+R3
This arrangement may be extended for any number of resistors.
R = R1+R2+R3+R4+ .
Thus, the equivalent resistance of a series combination of resistors is equal to the sum of the resistances of all the resistors.
Hence, the equivalent resistance of the series combination is greater than the greatest resistance in the combination.
In the series combination of resistors,
• Since the same current flows in all resistors Itotal = I1= I2= I3=
• The total pd is Vtotal = V1+V2+V3+⋯
• From ohms law V= IR and V∝R V1: V2: V3:………...= R1:R2:R3:………..
• When two resistors, R1 and R2, are connected in series, then
3.8.4 Parallel combination
Connect the resistors in parallel by joining one end at one point and the other end at another point. In parallel combination same potential difference exists across all resistors.
Fig. shows the parallel combination of three resistors of resistances R1,R2 and R3. Let the combination be connected to a battery of voltage V and draw a current I from the source.
Fig. 3.23 Parallel combination of resistance
The main current divides into three parts. Let I1, I2, and I3 be the currents flowing through the resistors R1, R2, R3, respectively, then I1= V/R1, I2= V/R2 and I3= V/R3.
The main current is the sum of I1, I2, and I3.
i.e., I = I1+I2+I3 or l V R V R V R 12 3
If the equivalent resistance of the combination is R, then V= IR or I= V/R. V R V R
The process may be extended for any number of resistors so that, 11 11 1 12 34 RR RR R
ELECTRICITY
From this, we infer that the reciprocal of the equivalent of resistance of a parallel combination is equal to the sum of the reciprocals of individual resistances.
For two resistors in parallel,
Hence, the equivalent resistance of parallel combination will be less than the least resistance value in the combination.
In the parallel combination of resistors,
• Vtotal = V1= V2= V3=
• Itotal = I1+I2+I3+⋯ •
SOLVED EXAMPLES
Example 1: Find the effective resistance when 1Ω, 10Ω, and 4Ω resistances are connected in series.
Solution:
When resistors are connected in series, the effective resistance is given by,
Reff= R1+R2+R3
Reff = 1+10+4= 15Ω
Example 2: Find the equivalent resistance when 3Ω and 6Ω resistances are connected in parallel.
Solution:
When resistances are connected in parallel, the equivalent resistance is given by,
Reff= 2Ω
Example 3: A battery of 9V is connected in series with resistors of 0.2Ω, 0.3Ω, 0.4Ω, 0.5Ω, and 12Ω, respectively. How much current would flow through the 12Ω resistor?
Solution:
Since all the resistors are connected in series, the effective resistance of the combination is:
RR RRR R s 12 34 5 02 03 04 05 12 13 4 ... .
Since all the resistances are connected in series, I remain constant.
The current through the resistor of 12Ω is:
R V R A s = == 9 13 4 067 .
Example 4: How many 176Ω resistors (in parallel) are required to carry 5A on a 220V line?
Solution:
I = 5 A
V = 220 V R = 176Ω
The resistance of the combination,
R V l 220 5 44
The number of resistors connected in parallel to get 44Ω of resistance is: 44 176 176 44 4 n n
Example 5: In the figure given below, put in an ammeter to measure the current through the resistor, and a voltmeter to measure the voltage across the 12Ω resistor. What would be the reading in the ammeter and the voltmeter?
ELECTRICITY
Solution:
Since all three resistors are in series
R eq = R1+R2+R3 = 5+8+12 = 25Ω
∴, the current in the circuit is
I = V R = 6 25 = 0.24 A
∴ the reading of the ammeter is 0.24 A
The potential difference across the 12Ω resistor is:
V = IR = (0.24)(12) = 2.88 V
∴ The voltmeter reading is 2.88 V.
Example 6: An electric lamp of resistance 100Ω, a toaster of resistance 50Ω, and a water filter of resistance 500Ω are connected in parallel to a 220V source. What is the resistance of an electric iron connected to the same source taken with as much current as all three appliances, and what is the current through it?
Solution:
Given that the resistance of the lamp, R1= 100Ω
The resistance of the toaster, R2= 50Ω
The resistance of the water filter, R3= 500Ω
Since these three appliances are connected in parallel, the effective resistance of the combination is:
∴ the current through the three appliances is I= V/Rp = (220×4)/125= 7.04 A.
Since the electric iron connected to the same source takes as much current as all three appliances
∴ the resistance of the electric iron is 31.25Ω, The current passing through the iron is 7.04A.
3.9 CELL
3.9.1
Electric cell
An electric cell is a device in which a constant potential difference is maintained between the two conductors (or terminals) either by chemical reaction or by mechanical action. Inside an electric cell, either chemical energy or mechanical energy is converted into electrical energy, which is used to maintain constant potential differences between the terminals. When connected to the circuit, an electric cell drives charges in the external circuit, constituting the electric current. Hence, the electric cell is the source of electric current in the circuit. It is also called a battery.
A cell essentially consists of two terminals. The terminal at a higher potential is called a positive terminal, while the other terminal at a lower potential is called the negative terminal. The ability of an electric cell to drive charges in a circuit is called the EMF of a cell.
Electric cells are of two kinds: Primary cells and secondary cells.
• Primary cells: These are the cells that provide current as a result of a chemical reaction but cannot be recharged, i.e., the chemical reaction is irreversible. Simple voltaic cells, Leclanche cells, Daniel cells, dry cells, etc., are examples of primary cells.
• Secondary cells: These are the cells that can be recharged after use. Thus, as a result of a reversible reaction, the electrical energy can be stored in them. Lead accumulator, Ni-Fe, or alkali accumulatosr are the secondary cells.
ELECTRICITY
3.9.2 EMF of a cell
Basically, a cell has two electrodes, called the positive (P) and the negative (N), which are immersed in an electrolytic solution. Dipped in the solution, the electrodes exchange charges with the electrolyte. The positive electrode has a potential difference V+ (V+>0) between itself and the electrolyte solution immediately adjacent to it. Similarly, the negative electrode develops a negative potential -(V)(V-≥0) relative to the electrolyte adjacent to it. When there is no current, the electrolyte has the same potential throughout, so that the potential difference between P and N is V+-(-V- )= V++V-. This difference is called the electromotive force (EMF) of the cell and is denoted by ε. Thus, ε= V++V->0.
To maintain a continuous flow of current through a conductor AB of resistance ' R ', we should always keep A at a positive (higher) potential, and B at a negative (lower) potential. For this purpose, we connect a cell with its positive terminal to A, and its negative terminal to B, as shown in the figure. Through the chemical action, the cell always maintains P at a constant positive potential, and Q at a constant negative potential.
Fig. 3.25
In the external circuit, the current (+ve charge) flows from P to Q via the conductor AB. But inside the cell, the same positive charge must move from a lower potential to a higher potential.
EMF of a cell: It is defined as the work done in carrying a unit positive charge through the complete circuit, including the flow of charge inside the cell.
The EMF is measured in the units of joule/coulomb (JC-1 ), which is 'volt'. Thus, emf has the same units as that of voltage or potential difference.
The EMF depends on the nature of the electrolyte, the metal of the electrodes, and the temperature of the electrolyte. The EMF of a cell does not depend on the size of the cell i.e., on the area of plates and distance between them.
The EMF is not a force, but it is the work done to drive the charge in the circuit. Hence, the EMF is a scalar quantity.
3.9.3 Internal resistance of a cell
The internal resistance of a cell is the resistance of the electrolyte between the anode and the cathode.
The magnitude of the internal resistance of a cell depends upon:
1. The distance between the plates (r ∝ d)
2. The area and size of the plates (r ∝ 1/A)
3. The nature of the electrolyte.
4. The strength of the electrolyte or the concentration (r ∝ e).
5. The area of the cross-section of the electrolyte through which the current flows.
6. The internal resistance depends on temperature. It decreases with the increase in temperature.
7. The internal resistance of a cell can be accurately measured using a potentiometer.
Note:
• An ideal cell is one that has no internal resistance, i.e., internal resistance r = 0 for an ideal cell.
• The difference between a new torch light cell and an old one is not in the EMF. The decrease in EMF will be very small. But, the difference is due to an increase in internal resistance. After prolonged use, the internal resistance increases by a factor of 103.
3.9.4 Relation between emf and potential difference
A resistance ' R ' is connected across a cell of an EMF' E ' having an internal resistance ' r ' as shown. Let V and V1 be the P.Ds across the external resistance 'R', and the internal resistance ' r ' of the cell, respectively.
Then, E = V+V1 ……..(1)
The resistance of the circuit = (R+r)
V= IR, and V1 = Ir (from Ohm's law)
Now, E = IR + Ir ⇒ E= I(R+r)
⇒ I = E/(R+r)
⇒ V = E-Ir
Important points:
• When a cell is charging, its potential difference is V= E + Ir ⇒ V > E, ie., the potential difference is greater than EMF.
• When a cell is discharging, its potential difference is V= E - Ir ⇒ V < E, i.e., potential difference is less than EMF.
• If the internal resistance of a cell ( r ) is zero, then the potential difference across the cell is equal to its EMF V= E. (open circuit)
• The potential difference V ≤ E. (closed circuit)
• The internal resistance of the ideal cell is zero.
3.9.5 Distinction between e.m.f. of a cell and potential difference
EMF of a cell
1. The EMF is the maximum potential difference between the electrodes of a cell, when the cell is in its open circuit
2. The EMF is independent of the resistance of the circuit. It depends on the nature of the electrodes and the nature of the electrolyte of the cell.
3. It is used as a source of energy.
4. The EMF is a cause.
3.9.6 Grouping of cells
Potential difference
1. It is the difference of potentials between two points in a closed circuit.
2. The potential difference depends upon the resistance between the two points of the circuit and the current flowing through the circuit.
3. It is measured between any two points of the electric circuit.
4. Potential difference is an effect.
Only a limited amount of current can be drawn from a single cell. In many experiments, the current required may be much more than that can be supplied by a single cell. To have a large value of current, the cells are usually connected in series or in parallel, or the cells are mixed groups.
There are three types of grouping of identical cells:
1. Cells in series 2. Cells in parallel 3. Cells in Mixed grouping
3.9.7 Cells in series
Consider ' n ' identical cells each of EMF E, and internal resistance r are connected to the external resistor of resistance R, as shown in Fig. 3.29(a).
For series combination, the negative terminal of the first cell is connected to the positive terminal of the second, the negative terminal of the second cell to the positive terminal of the third, and so on.
When the cells are connected in series, the total EMFof the series combination is equal to the sum of the EMFs of the individual cells. Thus,
The equivalent EMF of n cells in series,
E eq = E+E+ upto n terms = nE
The equivalent internal resistance of n cells in series, r eq = r+r+⋯ upto n terms = nr
The total resistance of the circuit = nr+R
Fig. (b) shows the effective EMF and the internal resistance in the circuit when the cells are connected in series. If I is current in the circuit, then I totalresis ce nE nr R total e m f tan 1
Special cases:
Case (i): If R≪nr, R can be neglected in comparison to nr. Then I = nE nR = E R Thus, the current in the external resistor is the same as the maximum current due to a single cell.
Case (ii): If R≫nr, then nr can be neglected as compared to R, then I = nE R Thus, the current in the external resistor is n times the current due to a single cell.
ELECTRICITY
From this, we can conclude that the maximum current can be drawn from the series combination of cells, if the value of the external resistance is very high, as compared to the internal resistance of the cells.
Note: The series combination is advantageous:
• When large EMF is required.
• When the internal resistance is negligible compared to the external resistance Wrongly connected cells in series
If ' n ' cells, each of EMF 'E', and internal resistance ' r ' are connected in series, and by mistake 'm' cell are wrongly connected to an external resistance ' R ', then,
Fig. 3.28
i) The effective EMF of the combination. E' = (n-2m)E [n>2 m]
ii) The total internal resistance = nr
iii) The total resistance of the circuit = R + nr
iv) The current through the external resistor, i = ((n-2m)E)/(R+nr)
() () () ( 11 22 12 12 2 )( )
lr r
Cells in series opposition: Consider, in the series combination of two cells, if the negative terminal of the first cell is connected to the negative terminal of the second cell between points A and C, as shown in Fig.
Let E1 and E2 be the EMF of the two cells. Let r1, r2 be their internal resistances, respectively. Let the cells be delivering the current in a circuit.
Let VA,VB and VC be the potential at points A, B, and C, and I be the current flowing through them. The potential difference between the positive and negative terminals of the first cell,
3.29
The two cells in series opposing
VAB= VA-VB = E1 - Ir1
The potential difference between the positive and negative terminals of the second cell.
VBC= VC-VB = E2+Ir2
The P.D. between A and C of the two cells,
VAC = VA-VC = (VA-VB )+(VB-VC ) = E1-Ir1-E2-Ir2 = (E1-E2 )-I(r1+r2 ) (i)
Let the series combination of the two cells be replaced by a single cell between A and C of EMF Eeq, and the internal resistance req, then,
VAC= E eq -Ir eq …(ii)
Comparing (i) and (ii), we get Eeq= E1-E2 and r eq = r1+r2
Then, the equivalent EMF of the two cells is Eeq= E1-E2, but the equivalent internal resistance is r eq = r1+r2.
SOLVED EXAMPLES
Example 1: Two cells A and B with the same EMF of 2 V each, and with internal resistances rA= 3.5Ω, and rB= 0.5Ω are connected in series with an external resistance R= 3Ω. Find the terminal voltages across the two cells.
Solution:
The current through the circuit i = ε/(R+r) = (2+2)/(3+3.5+0.5) = 4/7
i) R = 3Ω, rA= 3.5Ω, E = 2 V
The terminal voltages at A, VA = E-ir = 2 - (4/7 × 3.5) = 0 volt
ii) rB= 0.5Ω, R = 3Ω, E = 2 V
The terminal voltage at B, VB= E-ir = 2 - (4/7 × 0.5) = 1.714 volts.
Example 2: Two cells, A and B, each of 2V, are connected in series to an external resistance R= 1 ohm. The internal resistance of A is rA= 1.9 ohm, and B is rB= 0.9 ohm. Find the potential difference between the terminals of A.
Solution:
The total current through the circuit, i= voltage/total resistance = 4/(1+1.9+0.9) = 4/3.8 A.
The potential difference at A,VA = ε-ir = 2-(4/3.8×1.9) = 2-2 = 0.
3.9.8 Cells in parallel
The cells are connected in parallel by connecting their positive terminals to one end of the external resistance, and their negative terminals to the other end of the external resistance. When the cells are connected in parallel, the total EMF of the parallel combination remains equal to the EMF of a single cell.Therefore, the total EMF of the cells = E …..(1)
When 'n' identical cells, each of EMF E, and internal resistance r are connected to the external resistor of resistance R as shown in the figure.
3.30 Cells in parallel
The internal resistance of the cells also comes in parallel. The equivalent internal resistance req is given by 1/rp = 1/r+1/r+⋯ upto n terms = n/r
or req= r/n. …..(2)
As R and r eq are in series, the total resistance in the circuit = R+r/n.
The current flowing through the circuit is given by I= E/(R+r/n)= nE/(nR+r) .....(3)
Special cases:
Case (i): If R ≪ r, then R can be neglected compared to r.
∴I = nE/r
Thus, the current in the external resistance is n times the current due to a single cell.
Case (ii): If r ≪ R, then r can be neglected as compared to nR.
∴I= nE/nR = E/R
The current in the external resistance is the same as that due to a single cell.
Thus, the maximum current can be drawn from the parallel combination of cells if the external resistance is very low compared to the internal resistance of the cells.
Note: The parallel combination is preferred:
• When a large current is required.
• When the external resistance is negligible compared to the internal resistance.
3.9.9 Mixed grouping of cells
If the cells are connected as shown in the figure, they are said to be connected in mixed grouping. Let there be n cells in series in one row and m rows of cells in parallel. Suppose all the cells are identical. Let each cell be of EMF E and internal resistance r.
3.31
The total number of cells = mn
In each row, there are n cells in a series. Therefore, their total internal resistance = nr. Their effective EMF = nE
Since there are m rows of cells in parallel, the total internal resistance (rp ) of all the cells given by 11 1
rnrnr up to mtimes m nr p …
Or, r p = nr/m.
The total resistance in the circuit = R+nr/m
The effective EMF of the cells = nE
The current in the external resistance R is given by,
l nE Rnrm mnE mR nr
l nE R nr m mnE mR nr / () 1
For maximum current, the denominator (mR+nr) must be minimum.
Minimum occurs when: mR+nr=2mRnr (mR+nr)=4mRnr 2 . .
On rearranging:
(mR-nr)=0 mR=nr R= nr m 2
i.e.,
External resistance = Total internal resistance of all the cells.
We get the maximum current in the mixed grouping of cells if the value of external resistance is equal to the total internal resistance of all the cells.
Note: Mixed grouping is used to draw maximum power.
3.9.10 Kirchhoff's laws
Ohm's law gives the current-voltage relation in simple electrical circuits. But when the circuit is complicated, it will be difficult to find current distribution by Ohm's law. Kirchhoff, in 1842, formulated the following two laws that enabled us to find the distribution of current in complicated electrical circuits or electrical networks.
1. Kirchhoff's First Law (Junction Law or Current law)
Junction rule: At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.
The distribution of current at a junction in the circuit:
ELECTRICITY
I1 + I2 = I3 + I4 or I1 + I2 - I3 - I4 = 0
If we take currents approaching point A in the figure as positive, and those leaving the point as negative, then the above relation may be written as:
I1 + I2 + (-I3) + (-I4 ) = 0
Hence, the first law may be stated in other words: 'the algebraic sum of currents at a junction is zero.' Kirchhoff's first law tells us that there is no accumulation of charge at any point if a steady current flows in it. The net charge coming towards the point should be equal to that going away from it at the same time.
ΣI = 0 ....(1)
Note: Thus, Kirchhoff's first law is in accordance with the law of conservation of charge since no charge can accumulate at a junction.
2. Kirchhoff's Second Law (Loop Law or Potential law)
Loop rule: The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero. In mathematical form, the loop theorem (Kirchhoff's second law) can be expressed as ΣV= 0.
In terms of potential drops and EMFs, the law is expressed as Σ(iR)+ΣE= 0
Sign conventions
a) The change in potential in traversing a resistance in the direction of current is -IR, while in the opposite direction +IR, as shown in the figure.
b) The change in potential in traversing an EMF source from negative to positive is +E while in the opposite direction, it is -E, irrespective of the direction of current in the circuit, as shown in the figure.
Fig. 3.34
Example:
Apply Kirchhoff's second law to the loop ABCDA, then,
-iR1-iR2-iR3+E= 0
∴i= E R1 +R2+R3
Example:
Apply Kirchhoff's second law to the loop ADCBA, then,
Example:
Apply Kirchhoff's second law to the loop ABFGA, then +E1-I3 R3-I1 R1= 0
Apply Kirchhoff's second law to the loop BCDFB, then -E2 +I2 R2+I3 R3= 0
Apply Kirchhoff's second law to the loop ABCDFGA, then +E1-E2+I2 R2-I1 R1= 0
Note
1.The second law implies that electric energy given to the charge by a source of EMF is lost in passing through the resistance.
2.This law represents 'conservation of energy' as if the sum of potential changes around a closed loop is not zero; unlimited energy could be gained by repeatedly carrying a charge around a loop.
SOLVED EXAMPLES
Example 1: Find the EMF(V) and the internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of EMFs V1 and V2 and internal resistances r1 and r2, respectively, with polarities, as shown in the figure.
Solution:
The EMF of the battery is equal to the potential difference across the terminals when no current is drawn from the battery (for the external circuit). Here, all the elements in the circuit are in series.
The current in the internal circuit = i
∴ i = Net emf
Total resistance or i = V1+V2 r1+r2
∴VA-VB = V1-ir1 [∵V1 cell is discharging ]
or VA-VB= V1- V1+V2 r1+r2 r1
or, VA-VB = V1 r2 +V2 r1 r1+r2
∴, the equivalent EMF of the battery = V
∴V= V1 r2 -V2 r1 r1+r2
(ii) The internal resistance of the equivalent battery. r1 and r2 are in parallel.
ELECTRICITY
Example 2: Consider the network as shown in the figure. Current is supplied to the network by two batteries, as shown. Find the values of currents I1, I2, and I3. The direction of the currents is indicated by the arrows.
Solution:
By applying Kirchhoff's first law to junction C, we get,
I1+I2-I3= 0 …..(1)
By applying Kirchhoff's second law to the closed meshes ACDA and BCDB, we get,
51 21 12 0
51 21 12 2
31 21 60
31 21 63 13 13 13 23 () ()
On solving, I1= 1.548 A.
I2= 0.58 A and I3= I1+I2= 2.3128 A
Example 3: In the given circuit, values are as follows: ε1= 2V, ε2= 4V, R1= 1Ω, and R2= R3= 1Ω. Calculate the currents through R1, R2, and R3
Solution:
Let i1, i2 be the currents across R1 and R3, and (i1+i2 ) be the current across R2. Their direction is taken as:
By using Kirchoff's second law for the AGFBA loop:
-i1 R1-(i1+i2 ) R2+E1 = 0
i1+i1+i2 = 2
⇒2i1+i2 = 2 (1)
From Kirchoff's second law for BCDEB loop
-i2 R3-(i1+i2 ) R2+E2 = 0
i2+i1+i2 = 4
⇒i2+2i2 = 4 (2)
Solving equation (1) and (2), we get i1 = 0A, i2 = 2A
Thus, the current across R1 is 0, while that across R3 and R2 are 2A each.
3.10 HEATING EFFECT OF ELECTRIC CURRENT
The phenomenon of the production of heat in a resistor by the flow of an electric current through it is called the heating effect of current or Joule heating.
3.10.1
Joule's law
Whenever an electric current is passed through a conductor, it becomes hot after some time. This indicates that the electrical energy is being converted into heat energy. This effect is known as the heating effect of current or the Joule heating effect.
If we reverse the direction of the flow of current, heat is still produced in the conductor. Joule heating is an irreversible phenomenon, and it cannot be used to convert heat into electrical energy.
According to Joule's law, the current passing through a conductor produces heat.
The quantity of heat produced ' Q ' is equal to the work done by the electric field on the free electrons. If constant current ' i ' passes through a conductor for time ' t ' under a potential difference ' V ', then work done (W) in the time ' t ' is:
W= Vit
This work is converted into energy in the conductor. It means the electric current through a conductor produces thermal energy in the conductor, and the conductor gets heated.
∴, the thermal energy produced, Q= i2Rt.
From the above equation, we can say that:
• The heat produced in a given conductor in a given time is proportional to the square of the current passing through it. i.e., Q∝i2
• The heat produced in a given conductor and current is proportional to the time for which the current passes through it. i.e., Q∝t
• The heat produced in a given conductor by the current in a given time is proportional to the resistance of the conductor. i.e., Q∝R
These laws are known as Joule's laws.
Electric heaters, electric irons, electric bulbs, electric stoves, etc., are some of the instruments which work on Joule's law and convert electrical energy into heat energy.
3.10.2
Practical Applications of Heating Effect of Electric Current
1. Household heating appliances: Household heating appliances utilize the heating effect of current and include various electrical devices, such as room heaters, electric toasters, electric irons, electric ovens, electric kettles, geysers, etc. The design of these appliances necessitates the careful selection of an appropriate resistor with high resistance, ensuring efficient conversion of electric power into heat. The preferred choice for the heating element in many household appliances is nichrome due to several advantageous properties:
• High melting point
• Large resistivity
• Tensile strength, allowing easy formation into wires
• Resistance to oxidation when heated in the presence of oxygen
2. Electric fuse: Electric fuses serve as safety devices to safeguard electrical appliances from excessive currents and play a crucial role. Fuse wires, placed in series with the live wire of the circuit, are designed with high resistivity and a low melting point. Typically composed of a tin (63%) and lead (37%) alloy, the fuse wire melts and interrupts the circuit when the current surpasses the safety threshold. This proactive measure prevents potential damage to the electrical installations.
To ensure effective protection, the choice of a fuse wire with a suitable current rating (e.g., 1A, 2A, 3A, 5A, 10A) depends on the specific load within the circuit. For instance, when using an electric iron with a power rating of 1 kW connected to an electric main of 220 V, a current of (1000/220) A, i.e., 4.54 A, flows in the circuit. Accordingly, a fuse with a 5 A rating is required for optimal safety.
SOLVED EXAMPLES
Example 1: Compute the heat generated while transferring 96,000 C of charge in one hour through a potential difference of 50 V.
Solution:
Q = 96,000C
t = 1hr= 3600 s
V = 50 V
∴ the heat produced H = VQ = 96,000×50 = 48×105 J
= 4.8×106 J

Example 2: An electric iron of resistance 20Ω takes a current of 5 A. Calculate the heat developed in 30 s.
Solution:
Given that, R= 20Ω
i= 5 A
t= 30 s
∴Heat developed, H = i2Rt = 52×20×30 = 15000 J = 15 kJ
3.11 ELECTRIC POWER
3.11.1 Electric power
The rate at which electrical work is done by the source of EMF in maintaining the current in an electric circuit is called the electric power of the circuit.
If a current of ' i ' ampere flows through a conductor for a time of ' t ' second under a potential difference of ' V ' volt, then electric work done to maintain the current is given by W = Vit joule.
∴, the electric power, P = W/t = Vit/t = Vi ……(1)
SI unit - Watt or Js-1
If V= 1 volt and i= 1 ampere then P= 1 watt
Thus, the power of an electric current is said to be one watt if one ampere current flows in it against a potential difference of 1 volt.
The biggest units of electric power are kilowatt (kW) and megawatt (MW)
1 kW= 1000 W and 1MW = 106 W
The commercial unit of power is horsepower (H.P), where 1H.P= 746 watt
Expression for electric power in terms of i and R
According to Ohm's law, V = iR
Now equation (1) becomes P = i2 R…. (2)
Expression for electric power in terms of V and R
We know that V = iR ⇒ i = V/R
Now equation (1) becomes, P = V2/R
SOLVED EXAMPLES
Example 1: An electric bulb is rated 220 V and 100 W. When it is operated on 110 V, the power consumed will be ___________.
Solution:
R = V2/P = ((220)2)/100 = 484Ω.
∴Power consumed when the bulb is operated at 110 V is P = V2/R = ((110)2)/484 = 25 W
Example 2: An electric motor takes 5 A from a 220 V line. Determine the power of the motor and the energy consumed in 2h.
Solution:
i = 5A, V = 220V, t = 2h = 2×60×60 = 7200s.
Power(P) = Vi = (220)(5) = 1100W
∴ the energy consumed W = Vit = 220 × 5 × 7200 = 7.92×106 J.
Example 3: Several electric bulbs designed to be used on a 220 V electric supply line are rated 10 W. How many lamps can be connected in parallel with each other across the two wires of the 220 V line if the maximum allowable current is 5 A?
Solution:
V = 220 V, P = 10 W, i = 5 A
The total resistance of the fuse circuit R = V/i = 220/5 = 44Ω
The resistance of each bulb = V2/P = ((220)2)/10 = 4840Ω
The number of bulbs of resistance 4840Ω each are connected in parallel to get 44Ω resistance is 44 = 4840/n ⇒ n= 4840/44 = 110
3.11.2 Commercial unit of energy
Our household consumption of electrical energy is measured in kilowatt-hours. One kilowatt-hour is defined as the electrical energy consumed at the rate of one kilowatt (one thousand watts) for one hour.
1 kilowatt-hour = (1000 watts )(1 hour) = (1000 watts)(3600 seconds) = 36×105 joules
1 kilowatt-hour = 36×105 joules
Usually, we call this 1kWh as one 'unit', and our household electrical consumption is charged accordingly. The number of units mentioned in our monthly electrical bill refers to the number of kilowatt-hours of energy consumed over the month.
If the number of appliances of wattage W1, W2, etc., are operating for hours h1, h2, etc., respectively at the specified voltage 'electrical energy consumed' in their operation
E = [W1 h1+W2 h2+⋯] = ∑Wh [as P = (E/t)])
However, the practical unit of electrical energy is kWh,
So, E = (ΣW1 h1)/1000 kWh = (ΣW1 h1)/1000 units
And if each unit costs C Rs, the cost of consumed electric energy (i.e., electric bill) will be Rs(C×E).
For example, suppose the cost of 1kWh is Rs 5. Then, if the household uses 9kWh of energy, the total cost of the electricity consumed will be 9 × Rs 5 = 45 Rs.
SOLVED EXAMPLES
Example 1: A household uses the following electric appliances:
• A refrigerator rated 400 W for 2 hours each day.
• Two electric fans rated 80 W each for 12 hours each day.
• Six electric tubes rated 18 W each for 6 hours each day.
Calculate the electricity bill of the household for the month of June if the cost per unit of electric energy is ₹3.00.
Solution:
Energy consumed by refrigerator of rating 400 W for two hours each day
= P × t = 400 W × 2 h = 400/1000 kW × 2 h = 0.8kWh
Energy consumed by two electric fans of rating 80 W each for twelve hours each day
= 2 × P × t = 2 × 80 W × 12 h = 160/1000 kW × 12 h = 1.92 kWh
Energy consumed by six electric tubes of rating 18 W each for 6 hours each day
= 6 × P × t = 6 × 18W × 6h = 108/1000 W × 6h = 0.648 kWh
Total energy consumed in the month of June (30 days)
= (0.8 + 1.92 + 0.648) × 30 kWh
= 3.368×30 = 101.04 kWh
Electricity bill for the month of June = ₹101.04 × 3 = ₹303.12.
Example 2: Calculate the monthly bill if the following appliances are used as indicated below at the rate of ₹5 per unit.
• A heater of 1000 watts for 2 hours daily.
• Ten 60-watt bulbs for 5 hours daily.
Solution:
Energy consumed by the 1000 watt heater for 2 hours = 1000 × 2 = 2000 watt hour
Energy consumed by ten 60 watt lamps for 5 hours = 10×60×5 = 3000 watt hour
Total energy consumed per day = 2000+3000 = 5000 watt hour = 5 kWh
Total energy consumed for the month = 5 × 30 = 150 kWh
Cost per kWh = Rs. 5
Cost for 150kWh = 150×5 = Rs. 750.
QUICK REVIEW
• There are two types of charges: Protons, which have a positive (+) charge, and electrons which have a negative (-) charge.
• Substances that carry electricity are known as conductors. They are mostly metals like copper, silver and aluminium. Other substances, mostly non-metals, like plastic, paper, and cloth, do not have free electrons. Therefore, electrons that do not allow the electricity to pass through them are called insulators.
• The electric charge has the following three basic properties: 1. Additivity 2. Quantisation 3. Conservation
• The electric current is defined as the rate of flow of charge through any cross-section of a conductor.
• The region around the charge where another charge experiences the force is called an electric field
• The path of unit positive charge in the electrical field is called the electric lines of force
• Work done to bring unit positive charge from an infinite distance to a point in the electric field, is defined as electrical potential at that point.
• The work done to bring a unit positive charge from one point to another point in the electric field is defined as the electric potential difference,
• ΔV= Vf - Vi= W/q = Wapp/q
• A circuit diagram is the diagrammatic representation of an electric circuit based on how and which electric components are present in the circuit by using their symbols.
ELECTRICITY
• Ohm’s Law: At constant temperature, the current flowing through a conductor is directly proportional to the potential difference applied across the conductor.
• Property of opposition offered to the flow of charge by conduction is called Resistance.
• The resistance of a conductor depends upon the length, the area of the cross-section, the nature and temperature of the conductor.
• The resistance of a conductor of a unit length and a unit area of the cross-section is called the specific resistance or resistivity of the material of the conductor.
• Conductivity is the measure of the ability of a material to conduct electric current through it. It is the reciprocal of resistivity.
• The resistivity of a metallic conductor is approximately given by, ρT= ρo [1+α(T-To)]
• If the equivalent resistance of the series combination is R, then R= R1+R2+R3…..
• If the equivalent resistance of the parallel combination is R, then,
1 R = 1 R1 + 1 R2 + 1 R3 …..
• An electric cell is a device in which a constant potential difference is maintained between the two conductors (or terminals) either by chemical reaction or by mechanical action
• The ability of an electric cell to drive charges in a circuit is called the EMF of a cell.
• Electric cells are of two kinds: Primary cells and secondary cells
• The internal resistance of a cell is the resistance of the electrolyte between the anode and the cathode.
• The relation between EMF and potential difference is, V = E-Ir.
• There are three types of grouping of identical cells.
1. Cells in series 2. Cells in parallel 3. Cells in mixed grouping
• Kirchhoff's first law (Junction law or Current law): At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.
• Kirchhoff's second law (Loop law or Potential law): The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero. In mathematical form, the loop theorem (Kirchhoff's second law) can be expressed as ΣV= 0.
• In terms of potential drops and EMFs, the law is expressed as Σ(iR)+ΣE= 0
• The phenomenon of the production of heat in a resistor by the flow of an electric current through it is called the heating effect of current or Joule heating
• According to Joule's law, the current passing through a conductor produces heat.
• Thermal energy produced, Q= i2 Rt.
• The rate at which electrical work is done by the source of EMF in maintaining the current in an electric circuit is called the electric power of the circuit.
• Electric power, P= Vi= i2 R= V2/R
• Our household consumption of electrical energy is measured in kilowatt-hours
• 1 kilowatt-hour = 36×105 joules
WORKSHEET - 1
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
I. Introduction to electricity
1. The charge of an electron is
a. +1.6 × 10-19 C
b. -1.6 × 10-19 C
c. 3.2 × 10-19 C d. -3.2 × 10-19 C
2. The charge of a neutron is
a. +1.6 × 10-19 C
c. 3.2 × 10-19 C
3. S. I. unit of charge is
a. Coulomb
b. Ampere
4. Which among the following is an insulator?
a. Copper
c. Plastic
5. Which among the following is a conductor?
a. Plastic
b. Paper

b. -1.6 × 10-19 C
d. Zero
c. Volt
b. Aluminium
d. Silver
c. Cloth
6. The form of electricity where charges are at rest is called
a. Static electricity
c. Current electricity
d. Joule
d. Silver
b. Dynamic electricity
d. All the above
7. The form of electricity where charges are in motion is called
a. Static electricity
c. Current electricity
8. The mass of the electron is
a. 1.6 × 10-27 kg
c. 9.1 × 10-28 kg
b. None
d. Both a and b
b. 9.1 × 10-31 kg
d. 9.1 × 1031 kg
9. Which among the following is a conductor of electricity?
a. Copper
c. Air
b. Pure water
d. Eraser
ELECTRICITY
10. The one that is different from the others is
a. Distilled water
c. Lemon water
b. Rainwater
d. Sea water
II. Electric current, electric potential and potential difference
1. A current of 1 A flows through a copper wire. The number of electrons that will pass a given point in each second is
a. 6.25 × 1019
6.25 × 1018
6.25 × 1017
2. Electric current arises from the flow of charged particles, now
a. In metals, it is mainly due to the flow of electrons
b. In a semiconductor, it is mainly due to the flow of holes
c. In electrolytes, it is mainly due to the flow of negative ions
d. In discharge tubes at low pressure, it is due to the flow of positive ions
3. In an electric circuit containing a battery, the charge inside the battery
a. Always goes from the positive terminal to the negative terminal
b. May go from the positive terminal to the negative terminal
c. Always goes from the negative terminal to the positive terminal
d. Does not move
4. The area of the current-time graph gives
a. Current
c. Potential
6.25 × 1016
b. Charge
d. Resistance
5. A metallic resistor is connected across a battery. If the number of collisions of the free electrons with the lattice is decreased in the resistor, then the current will
a. Increase
c. Remain the same
b. Decrease
d. Become zero
6. What is the total charge that passes through a circuit when an electric current of 1 ampere flows through it for a duration of 40 seconds?
a.
7. The charge on an electron is 1.6 × 10-19 coulombs. What is the number of electrons passing through the wire per second when 1 ampere of current flows through the wire?
a. 625 × 1019
c. 6.25 × 1019
b. 0.0625 × 1019
d. 0.625 × 1019
8. On moving a charge of 40 coulombs by 2 cm, 20 J of work is done. Then, the potential difference between the points is:
a. 0.4 V
b. 5 V
c. 2.5 V
d. 0.5 V
9. The electric potentials at the two ends of a conductor are 10 V and 5 V, respectively. 5 J of work needs to be done to move a certain amount of charge from the end at a higher potential to the end at a lower potential. Find the amount of charge moved.
a. 0.1 coulomb
c. 1.2 coulomb
10. Assertion (A): Electric current is a vector quantity.
b. 1.0 coulomb
d. 1.5 coulomb
Reason (R): It has both magnitude and specific direction.
a. Both A and R are true, and R is the correct explanation of A
b. Both A and R are true, and R is the incorrect explanation of A
c. A is true, R is false
d. A is false, R is true
III. Circuit diagram
1. When the switch is in the OFF state, the circuit is
a. Open, and the current does not flow in the circuit
b. Closed, and the current flows in the circuit
c. Incomplete, and the current flows through any part of the circuit
d. Complete, and the current does not flow through the bulb only
2. A switch can be connected
a. To the positive terminal of the battery only
b. Anywhere in the circuit
c. To the negative terminal of the battery
d. Do any terminal of the battery
3. Which of the following statements regarding a compass needle is false?
a. It is a tiny magnet that rests in the North-South direction.
b. It gets deflected when a magnet is brought close to it.
c. It gets deflected when the current flows in a nearby wire.
d. It gets deflected when heated.
4. In a battery,
a. Two or more cells are connected to each other in any manner
b. The positive terminal of one cell is connected to the positive terminal of the next cell
c. Two or more cells are connected in such a way that the positive terminal of one cell is connected to the negative terminal of the next cell
d. There is only one cell
5. In a symbol of a battery, the positive end is represented by
a. A long line
c. A curve
b. A short line
d. A plus sign
6. When two or more bulbs are connected in the same electrical circuit is called
a. Parallel circuit
c. Multiple circuit
b. Series circuit
d. Complex circuit
7. A circuit in which there is more than one path through which electric current is flowing is called
a. parallel circuit
c. multiple circuit
8. Tungsten is used inside a bulb because it
a. Is easily available
c. Is an insulator
b. series circuit
d. complex circuit
b. Is a good conductor of electricity
d. Gets heated easily
9. The main source of electricity that lights our houses and runs our electrical appliances is
a. A dry cell
c. A battery
b. A power station
d. All the above
10. __________ is a device which can break the circuit or make the circuit.
a. A touch
c. A conductor
b. A switch
d. An insulator
IV. Ohm’s law, electrical resistivity, conductivity, and temperature dependence of resistivity
1. The relation ΔV= ΔI × R is valid for
a. Ohmic devices
c. Ohmic as well as Non-Ohmic devices
2. The current in a wire depends
a. Only on the potential difference applied
b. Only on the resistance of wire
c. Both a and b
d. Volume of conductor
b. Non-Ohmic devices
d. Insulators
3. A curve in figures is the graph between ' V ' and ' I '. Among them, the one that follows Ohm's law is
4. As temperature increases, the ratio of resistivity to conductivity
a. Increases
c. Remains constant
b. Decreases
d. May increase or decrease depending on the temperature
5. If the length of the wire is increased, then its resistivity
a. Increases
c. Remains the same
b. Decreases
d. may increase (or) may decrease
6. The resistivity of the metal increases with an increase in temperature because
a. The concentration of electrons in the conductor decreases
b. The concentration of electrons in the conductor increases
c. The average distance between the metal ions increases
d. The speed of the electrons in the metal decreases
7. If the resistance of a resistor is 100Ω, the conductance is a. 10-2 Ω
8. In the case of a semiconductor, the temperature coefficient of resistance is
a. Positive
c. Zero
b. Negative
d. Either positive or negative
9. The current-voltage graph for a given metallic conductor at two different temperatures, T1 and T2, are as shown in the figure. Then
a. Nothing can be said about T1 and T2
b. T1 < T2
c. T1 > T2
d. T1 = T2
ELECTRICITY
10. A metallic resistor is connected across a battery. If the number of collisions of the free electrons with the lattice somehow decreases in the resistor, then the current will
a. Increase b. Decrease
c. Remain constant
d. Become zero
11. A 10 Ω thick wire is stretched so that its length becomes three times, and then the new resistance of the wire is
10 Ω
30 Ω
90 Ω
10/9 Ω
12. A uniform wire of resistance R is uniformly compressed along its length until its radius becomes n times the original radius. Now, the resistance of the wire becomes a. R/n4
R/n2
R/n
nr
13. The mass of three copper wires is in the ratio 1:3:5, and their lengths are in the ratio 5:3:1. The ratio of their electrical resistances is
14. The resistance of a wire of cross-section area 20 cm2 is 10 Ω. The resistance of the same wire when its area of cross-section becomes 10 cm2 is
10 Ω
15. Assertion (A): When the radius of a copper wire is doubled, the specific resistance increases. Reason (R): The specific resistance is independent of the cross-section of the material used.
a. Both A and R are true, and R is the correct explanation of A
b. Both A and R are true, and R is the incorrect explanation of A
c. A is true, R is false
d. A is false, R is true
16. Statement A: The potential difference across the ends of a conductor is doubled, and the current through it also gets doubled.
Statement B: A long wire has more resistance, and a short wire of the same material has less resistance.
a. Both A and B are true
c. A is true and B is false
V.
System of resistors
b. Both A and B are false
d. A is false and B is true
1. When a number of cells are connected such that the positive terminal of one cell is connected to the negative terminal of the next cell, then the combination of cells is in:
a. Series
b. Parallel
c. Mixed circuit
d. None of the above
2. When the cells are connected in series, the current output of the combination:
a. Increases
c. Remains the same
b. Decreases
d. None of the above
3. When a number of cells are connected in such a way that they have a common positive terminal and a common negative terminal, then the cells are connected in:
a. Series
c. Mixed circuit
b. Parallel
d. None of the above
4. When the identical cells are connected in parallel, the electromotive force of cells is :
a. more than one cell
c. same as one cell
5. The effective resistance between points A and B is
b. less than one cell
d. none of the above
4 Ω
6. The effective resistance between points A and B is
a. 13/12 Ω b. 12/13 Ω c. 9 Ω
7. Which of the following connections is used in household circuits?
a. Series b. Parallel
Cell
5 Ω
c. Both a and b d. None of these
1. The relation between EMF(E) and potential difference (V) of an ideal cell is
a. V= E
b. V>E
c. V<E
d. V≤E
2. If the current in a source of EMF is in the direction of EMF, then the energy of the source
a. Increases
c. Remains the same
b. Decreases
d. Zero
ELECTRICITY
3. The internal resistance of a cell depends on the
a. Nature of the electrolyte
c. Size of the electrodes
4. The EMF of a cell depends on the
a. Nature of the electrolyte
c. Both A and B
b. Concentration of the electrolyte
d. All of the above
b. Metal of the electrodes used in the cell
d. None
5. A cell of internal resistance of 0.5Ω and emf 2 V is connected to a resistance of 9.5Ω. The p.d across the terminals of the cell is
a. 2 V
1.9 V
1.8 V
1.5 V
6. Four cells each of emf 2 V and resistance 0.4Ω are joined in parallel, then the EMFof the parallel combination is a. 4 V
2 V
8 V
1 V
7. ' n ' identical cells are connected across an external resistance R; if the current across R is the same when the cells are either connected in series or connected in parallel, the internal resistance of each cell is
a. R/2
2R
R/4
R
8. Two cells of emf E1 and E2 are connected in series in a circuit. Let r1 and r2 be the internal resistance of the cells. The current through the circuit is
a. I= (E1+E2)/(r1+r2 )
c. I= (E1+E2)/(r1-r2 )
b. I= (E1- E2)/(r1+r2 )
d. I= (E1-E2)/(r1-r2 )
9. A uniform wire of resistance 36Ω is bent in the form of a circle. The effective resistance across the points ' A ' and ' B ' is
10. A 25 W, 220 V bulb, and another 100 W,220 V bulb are connected in series. This arrangement is then connected to the main switch. The bulb that will glow brighter is the
a. 25 W bulb
c. First 25 W and then 100 W
11. Using Kirchhoff's law, find VAB
b. 100 W bulb
d. Both with the same brightness
12. The effective resistance of the given figure is (between x and y )
VII. Heating effect of electric current and electric power
1. If a current ' i ' is passed through a wire of resistance ' R ' for time ' t ', then the heat generated in the wire is
a. i2Rt b. i2R/t c. i3Rt d. i2/Rt
2. The thermal energy of the resistor is directly proportional to
a. i2 b. R c. t d. All the above
3. If the resistance of a wire is made four times, keeping the potential difference across it constant, then the number of times heat is produced in it varies by a. 4
1/4
2
4. The heat produced by a 200 W electric heater in one hour is a. 7.2 × 105 J
72 × 105 J
62 × 105 J
1/2
6.2 × 105 J
5. An electric bulb marked 15 V is connected to a battery of 15 V, which has a negligible resistance. If the resistance offered by the bulb is 5Ω, the power of the bulb is ________W. a. 225 b. 75
30
45
6. A 100 watt, 220 V bulb is connected across a 110 V supply. The actual power consumed by the bulb will be
25 watt
50 watt
100 watt
200 watt
7. An electric bulb marked as 40 W and 220 V is used in a circuit of supply voltage 100 V. Now, its power is
Passage: Q.8-Q.10: A household circuit consists of 5 bulbs with a wattage of 40 watts each, and 4 fans with a wattage of 100 watts each. It blinks 10 hours per/day.
8. How much energy is consumed by the bulbs for 30 days? a. 40 units b. 60 units c. 80 units
100 units
9. How much energy is consumed by the fans for 30 days? a. 80 units b. 100 units c. 120 units d. 150 units
10. What is the electricity bill at the end of the month if the cost of each unit is ₹4?
a. ₹ 620 b. ₹ 650 c. ₹ 720
₹ 750
WORKSHEET - 2
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
1. If a negatively charged body attracts another body, the other body
a. Must be negatively charged
c. Must be neutral
2. What constitutes current in a metal wire?
a. Electrons
c. Atoms
b. Must be positively charged
d. May be positively charged or neutral
b. Protons
d. Molecules
3. Materials that allow larger currents to flow through them are called
a. Insulators
c. Conductors
4. Good conductors have many loosely bound
a. Atoms
b. Protons
b. Semiconductors
d. Alloys
c. Molecules d. Electrons
5. Conventionally, the directions of the current is taken as
a. The direction of flow of negative charge
b. The direction of flow of atoms
c. The directions of flow of molecules
d. The direction of flow of positive charge
6. Choose a substance that is different from others with regard to the conduction of electricity.
a. Copper
b. Aluminium c. Silver d. Rubber
7. If I is the current through a wire and e is the charge of the electron, then the number of electrons in t seconds will be given by
a. Ie/t
b. Ite
c. e/It
8. How many electrons constitute a current of one microampere?
a. 6.25 × 106
9. One ampere is equal to
b. 6.25 × 1012
c. 6.25 × 109
d. It/e
d. 6.25 × 1015
a. 106 μA b. 10-6 μA c. 10-3 μA d. 10 μA
10. The work done in moving a unit positive charge across two points in an electric circuit is a measure of
a. Current
c. Power
b. Resistance
d. Potential difference
ELECTRICITY
11. Electric potential is
a. A scalar quantity
c. Neither scalar nor vector
12. 1 volt is equal to
a. 1 J
b. 1C/J
b. A vector quantity
d. Sometimes scalar and sometimes vector
c. 1 J/C
d. None of these
13. How much work is done in moving a charge of two coulombs from a point at 118 volts to a point at 128 volts?
a. 10 J
b. 20 J
c. 1/10 J d. None of these
14. A graph is plotted between the potential difference (applied across the ends of a conductor) and the current (following through the conductor). The the graph is a straight line
a. Intersecting both the axes
c. Having an intercept on the Y–axis
15. Ohmic conductors
a. Obey Ohm's law
c. Obey Ohm's law sometimes
16. The fixed resistance is called
a. Rheostat
b. Resistor
17. The variable resistance is called
a. Resistor
18. One ohm is equal to
a. 106 MΩ
c. 10-6 MΩ
b. Rheostat
b. Having an intercept on the X-axis
d. None of the above
b. Do not obey Ohm's law
d. None of these is true
c. Key
c. Open switch
b. 109 MΩ
d. None of the above
d. Switch
d. None of these
19. The reciprocal of resistance is conductance. If the unit of resistance is ohm, the unit of conductance will be
a. Ohm
b. Volt
20. The unit of conductivity can be expressed in
a. Mho
b. Ohm-1
21. The SI unit of specific resistance is
a. Ohm m
c. Mho
c. Siemen
b. Ohm m-1
22. The reciprocal of resistivity of a conductor is
a. Conductance
c. Conductivity
d. Ohm metre-1
d. Ohm-1 m-1
c. Ohm m2 d. Ohm-1
b. Capacitance
d. None of these
23. The slope of current (I) versus voltage (V) graph gives I O
a. Resistance
c. Conductivity
24. What is the current (I) in the circuit?
1/2 A
2 A
25. What is the current in the circuit shown below?
b. Resistivity
d. Conductance
3/2 A
none of these
26. If the resistance of a manganin wire of 1 mm2 cross-sectional area is 15Ω, the resistance of a manganin wire of the same length, but of a cross-section of 3mm2 is
10Ω
15Ω
ELECTRICITY
27. If the potential differences across three resistances connected in parallel are V1, V2, and V3, the potential difference across the total resistance V=
a. V1 + V2 + V3
c. V1 - V2 - V3
b. V1 = V2 = V3
d. 1/V1 + 1/V2 + 1/V3
28. If the area of a cross-section of a wire is increased, its resistance
a. Increases
c. Remains the same
b. Decreases
d. May increase (or) may decrease
29. The area covered under the electric current-time graph gives the
a. Electric potential
c. Electric resistance
b. Electric charge
d. Electric field strength
30. If two resistances, R1 and R2 (R1 < R2), are connected in parallel, the equivalent resistance of the system (R) is such that a. R<R1 b. R1<R<R2
31. The symbol for variable resistance is
32. The law of resistances in series is
a. I= 1/I1 +1/I2 +1/I3
c. R= R1 + R2 + R3
33. The S.I unit of resistance is
b. I= I1 + I2 + I3
d. 1/R= R1 + R2 + R3
a. ohm b. volt/ampere c. both ohm and volt/ampere d. none of these
34. The laws of resistance in parallel is
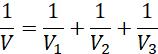
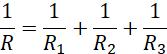
35. If a copper wire is stretched to make it 0.1% longer, find the percentage change in its resistance.
a. 0.1% b. 0.2% c. 0.3% d. 0.4%
36. If 100 J of heat is produced each second in a 2Ω resistor, the potential difference across the resistor will be
a. 30 V b. 25 V c. 20 V d. 10√2 V
37. The number of electrons present in 1 coulomb is equal to
38. A voltmeter is always
a. Connected in series to the circuit
c. Both a & b
b. Connected in parallel to the circuit
d. None of these
39. If a number of resistors are connected in parallel, then
a.
c.
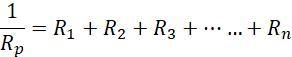
40. As temperature increases
a. resistance of conductor decreases
c. resistance of conductor increases
b.
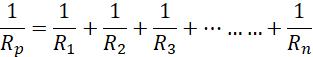
d. both a & c
b. resistance of conductors does not change
d. all the above
41. Ohm's law will hold well under which of the following conditions?
a. The temperature should be maintained as a constant
b. The material should not be a gaseous conductor
c. The material should not be a semiconductor
d. All the above
42. If a wire of resistance 1Ω is stretched to double its length, then resistance will be
a. 1/2Ω b. 2Ω c. 1/ 4Ω
4Ω
43. When 1 J of work is done to move a charge of 1 C from a point to another point, then the potential difference between the two points in a given circuit will be
1 V
4 V
8 V
zero
44. A certain household has consumed 200 units of energy during a month. Its value in joules will be
a. 3.6 × 1010 b. 7.2 × 1010
c. 3.6 × 108 d. 7.2 × 108
45. The value of equivalent resistance between points A and B in the given circuit will be
ELECTRICITY
46. While doing their experiment on finding the equivalent resistance of two resistors connected in series, students A, B and C set up their circuits as shown. The correct setup is that of
a. Students A and B
c. Students C and A
47. A fuse wire eventually has a
a. High resistance and high melting point
b. Low resistance and high melting point
c. High resistance and low melting point
d. None of these
b. Students B and C
d. All the three students
48. An electric iron draws a current of 15 A from a 220 V supply. What is the cost of using iron for 30 minutes every day for 15 days if the cost of a unit (unit = 1 kWhr ) is 2 rupees?
a. Rs. 49.5 b. Rs. 60 c. Rs. 40
Rs. 10
49. A technician has 10 resistors, each of resistance 0.1Ω. The largest and smallest resistance that he can obtain by combining these resistors are
a. 10Ω and 1Ω resp.
c. 1Ω and 0.01Ω resp.
b. 1Ω and 0.1Ω resp.
d. 0.1Ω and 0.01Ω resp.
50. An electric iron is connected to a 200 V mains supply and draws a current of 4.0 A. What is the power rating of the iron?
a. 800 W
50 W
106 W
112 W
51. In the circuit shown, the heat produced per second in 5 ohms resistance due to the current through it is 50 J/s. Then, the heat generated per second in 2 ohms resistance is
a. 5 J/s b. 4 J/s
9 J/s
10 J/s
52. Five resistances are connected, as shown in the figure. If the total current flowing is 0.5 A, then the potential difference VA-VB is
6 (ohms)
6 (ohms) 6 (ohms) 6 (ohms) 6 (ohms) B 0.5 A
12 (ohms) a. 4 V b. 8 V c. 6 V
2 V
53. Three bulbs with individual power ratings of 12 W, 2 W, and 6 W, respectively are connected as per the circuit diagram below. Find the amount of heat dissipated by each bulb in 10 seconds.
ELECTRICITY
a. 8 J, 1.33 J, 4 J
b. 120 J, 20 J, 60 J
c. 10 J, 0.277 J, 2.5 J d. 12 J,1.66 J, 5 J
54. Two resistors, R and 2R, are connected in series in an electric circuit. The thermal energy developed in R and 2R is in the ratio of _________.
a. 2:1 b. 1:1
55. What is the resistance between P and Q?
1:4
1:2
3/4 Ω
4/3 Ω
16/3 Ω
56. In the circuit shown below, the reading of the voltmeter V will be
Infinity
57. Which of the following networks yields the maximum effective resistance between A and B?
58. What is the resistance between A and B in the given network?
59. What is the resistance across A and B in the following circuit?
60. The equivalent resistance between P and Q in the given circuit will be
1Ω
61. How will the reading in ammeter A be affected if another identical bulb Q is connected in parallel to P in the given figure? The voltage is maintained at a constant value.
Mains
a. The reading will be reduced to one-half
b. The reading will not be affected
c. The reading will be double the previous value
d. The reading will be increased four-fold
62. In the given circuit shown, the ammeter A reads 5 A, and the voltmeter V reads 20 V. The correct value of resistance R is
a. Exactly 4Ω
c. Slightly less than 4Ω
b. Slightly greater than 4Ω
d. Zero
63. Refer to the circuit given below. What would be the readings in the ammeter and the voltmeter?
a. 0.58 A, 8 V
8 A, 0.67 V
0.67 A, 8 V
0.67 A, 4 V
64. Assertion (A): The ammeter is always connected in series with the circuit in which the current is to be measured.
Reason (R): An ammeter should have very low resistance.
a. Both A and R are correct, but R is the correct explanation of A
b. Both A and R are correct. and R is not the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect
65. The resistance of a wire of 0.02 cm radius is 8Ω. If the resistivity of the material of the wire is 40 × 10-8 ohm-meter, find the length of the wire. a. 2.512 m b. 2.332 m
66. Assertion (A): Ohm's law is not a law of nature (i.e., not a universal law).
Reason (R): Ohm's law is not applicable for vacuum tubes, transistors, thermistors and when temperature is variable.
a. Both A and R are correct, but R is the correct explanation of A
b. Both A and R are correct, and R is not the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect
67. Assertion (A): Nichrome is used in making the heating elements of electrical appliances.
Reason (R): The resistivity of alloys are much higher than those of pure metals.
a. Both A and R are correct, but R is the correct explanation of A
b. Both A and R are correct, and R is not the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect
68. Assertion (A): Resistivity of a conductor is independent on dimensions of conductor.
Reason (R): Resistance of a unit length and unit area of cross-section of conductor is resistivity.
a. Both A and R are correct, but R is the correct explanation of A
b. Both A and R are correct, and R is not the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect

MAGNETIC EFFECTS OF ELECTRIC CURRENT
4.1 INTRODUCTION TO MAGNETISM
The magnetic effects of electric current were first discovered by Hans Christian Oersted. An electric charge in motion sets up a magnetic field around it. An electric charge moving in an external magnetic field experiences a force. A stationary electric charge produces only an electric field. But a moving electric charge produces both an electric field and a magnetic field.
4.1.1 Oersted's observation
One day, Oersted noticed that when an electric current flowed through a wire, it caused a nearby compass needle to deflect from its usual north-south orientation.
This observation led Oersted to conclude that there must be a relationship between electricity and magnetism. Prior to this discovery, it was widely believed that electricity and magnetism were unrelated phenomena. Oersted's experiment demonstrated that an electric current produces a magnetic field, and this laid the groundwork for the development of electromagnetism
Magnetic effect of electric current
4.1 Magnetic effect of electric current
4.2 MAGNETIC FIELD AND FIELD LINES
4.2.1 Magnetic field
An electric field surrounds any electric charge. In addition to containing an electric field, the region of space surrounding any moving electric charge also contains a magnetic field.
Or
"The space around a magnet in which its influences can be felt is known as magnetic field".
The direction of the magnetic field B at any location is the direction in which the north pole of a compass needle points at that location, i.e., N → S.
4.2.2 Magnetic field lines
We can represent the magnetic field by drawing magnetic field lines. The given figure shows how the magnetic field lines of a bar magnet can be traced with the aid of a compass.
A bar magnet has a magnetic field around it. This field is 3D in nature and often represented by lines leaving north and entering south.
One can display magnetic field patterns of a bar magnet using small iron filings, as shown in Figure 4.3.

Properties of magnetic field lines
1. The direction of the magnetic field is tangent to the field line at any point in space. A small compass will point in the direction of the field line.
2. The strength of the field is proportional to the closeness of the lines. It is exactly proportional to the number of lines per unit area perpendicular to the lines (called the areal density).
3. Magnetic field lines can never cross each other.
4. Magnetic field lines are continuous. They go from the north pole to the south pole with respect to the magnet, but with respect to the compass, they go from the south pole to the north pole.
4.3 BAR MAGNET
4.3.1 Geomagnetism
A bar magnet aligns itself in a specific direction with respect to Earth's magnetic field. This alignment occurs because Earth itself acts like a giant magnet, with magnetic north and south poles. The north-seeking pole of a bar magnet points towards Earth's magnetic north pole, and the southseeking pole points towards Earth's magnetic south pole.
This phenomenon is a manifestation of the interaction between the magnetic field produced by the bar magnet and Earth's magnetic field. Earth's magnetic field is thought to be generated by the movement of molten iron and nickel in its outer core, creating a complex magnetic structure. When a bar magnet is freely suspended, it tends to align itself along the magnetic field lines of Earth.
It's important to note that the geographic North Pole, where Earth's rotational axis intersects its surface, is not precisely aligned with the magnetic north pole. The angle between these two points is called magnetic declination, and it varies depending on the geographic location. Consequently, the alignment of a bar magnet with the Earth's magnetic field considers both the magnetic poles and the specific magnetic characteristics of the Earth's surface in a given location.
4.3.2 Magnetic properties of materials
Diamagnetism
Diamagnetic substances exhibit a tendency to move from stronger to weaker parts of an external magnetic field, contrary to the attraction observed in materials like iron.
Some examples are bismuth, copper, lead, carbon, water, and zinc which experience repulsion when subjected to a magnetic field.
Paramagnetism
Paramagnetic substances weakly magnetise when exposed to an external magnetic field, moving from regions of weak magnetic fields to strong magnetic fields, displaying a weak attraction to magnets.
Some examples include materials like aluminium, sodium, calcium, and lithium. These are paramagnetic substances, and their magnetic behaviour is characterised by a mild response to external magnetic influences.
Ferromagnetism
Ferromagnetic substances become strongly magnetised in an external magnetic field, demonstrating a robust tendency to move from weak to strong magnetic fields, exhibiting strong attraction to magnets.
Types of ferromagnets:
1. Hard ferromagnets: Materials like Alnico and naturally occurring lodestone retain magnetisation even after the removal of the external field, forming permanent magnets, such as compass needles.
2. Soft ferromagnets: Materials like soft iron lose magnetisation when the external field is removed. These materials are used in various applications.
Examples of ferromagnetic elements: Iron, cobalt, nickel, and gadolinium are examples of elements exhibiting ferromagnetic properties. Each of these elements demonstrates unique magnetic behaviour.
4.4 BASIC MATHEMATICS
4.4.1
Scalars and vectors
A scalar is a physical quantity that has magnitude only. A vector is a physical quantity that possesses magnitude and direction and obeys the vector law of addition.
Because scalars possess only magnitudes, they are real numbers that can be positive, negative, or zero. Physical quantities that are scalars include temperature, time, and speed. The force, velocity, and displacement are examples of physical quantities that are vectors. The magnitude of a vector is always taken to be a non-negative number. When a vector represents a physical quantity, the units of the vector are taken to be the same as the units of its magnitude (Newton, meter per second, meter, etc.).
4.4.2 Geometrical representation of vectors
Any vector A can be represented geometrically as a directed line segment (an arrow), as shown in Fig. 4.4. The magnitude of A is denoted by A, and the direction of A is specified by the sense of the
arrow and the angle θ that it makes with a fixed reference line. While using graphical methods, the length of the arrow is drawn proportional to the magnitude of the vector. Observe that the representation shown in Fig. 4.4 is complete because both the magnitude and direction of the vector are indicated.
Fixed reference line
Fig. 4.4 Vector representation
We see that a vector does not possess a unique line of action because moving a vector to a parallel line of action changes neither its magnitude nor its direction.
4.4.3
Vector addition
A) Parallelogram law of vector addition
If two vectors acting on a point at the same time are represented in magnitude and direction by the two adjacent sides of a parallelogram drawn from a point, their resultant vector is represented in magnitude and direction by the diagonal of the parallelogram drawn from the same point.
Let the two vectors ,
A and
Fig. 4.5 Parallelogram law of vector addition
B , inclined at angle θ, be acting on a particle at the same time. Let them be represented in magnitude and direction by two adjacent sides
OP and
OS of parallelogram OPQS, drawn from a point O.
According to the parallelogram law of vectors, their resultant vector R will be represented by the diagonal
OQ of the parallelogram.
Magnitude of R → 22 RAB2ABcos =++θ .......(1)
Direction of R → Bsin tan ABcosβ=θ+θ .......(2)
Special Cases
i) When two vectors are acting in the same direction, then ,cos ° θ=θ=01 , and θ= 0 sin .
Fig. 4.6 Vectors acting in the same direction
22 2 from(1),RAB2AB(1)(AB)(AB) b0 from(2),tan 0(or)0. AB(1) =++=+=+ × β==β=° +
For two vectors acting in the same direction, the magnitude of the resultant vector is equal to the sum of the magnitudes of two vectors and acts along the direction of A and B .
ii) When two vectors are acting in opposite directions. then ° θ=θ=− 1801 ,cos and θ= 0 sin .
22 2 from(1),RAB2AB(1)(AB)(AB)or(BA) B0 from(2),tan 0(or)0or180. AB(1) =++−=−=−− × β==β=°° +−
For two vectors acting in opposite directions, the magnitude of the resultant vector is equal to the difference of the magnitudes of the two vectors and acts in the direction of the bigger vector.
iii) When two vectors act at right angles to each other.
B R A β
Fig. 4.7 Vectors acting at right angle ° θ=θ=θ= 9010 ,sinandcos
=++=+ 22 22 20 RABAB()AB
β= + 1 0 B() tan AB()
Example: Two forces, 10 N and 15 N, are acting on a body. What can be the maximum and minimum resultant force on the body?
Solution:
Here, 1015222 AN;BN;RABABcos ===++θ
a) R will be maximum if θ= 1 cos
Then, =+=+=101525 RAB N in the direction of A and B .
b) R will be minimum if cos θ=−1
Then, R = A - B or B - A
RN∴=−=15105 in the direction of B
Vector addition obeys
1. Commutative law, ABBA +=+
2. Distributive law, m(A + B) = mA + mB
3. Associative law, ()() ABCABC ++=++
B) Triangle law of vector addition
"If two vectors acting on a particle at the same time are represented in magnitude and direction by the two sides of a triangle taken in one order, their resultant vector is represented in magnitude and direction by the third side of the triangle taken in the opposite order".
Let the two vectors, A
and B
Fig. 4.8 Triangle law of vectors addition
, inclined at an angle θ , be acting on a particle at the same time. Let them be represented in magnitude and direction by two sides OP
and PQ
of triangle OPQ , taken in the same order.
Then, according to the triangle law of vector addition, the resultant R is represented by the third side OQ of the triangle, taken in the opposite order.
Magnitude of R →
Using cosine law, RABABcos()ABABcos =+−π−θ=++θ222 22 22
Direction of R →
Using sine rule, we get
4.4.4 Subtraction of vectors
Subtraction of a vector B from a vector A is defined as the addition of vector B (negative of vector B ) to vector A . Thus, ABA(B) −=+−
The laws of vector addition, such as the triangle law of vectors and the parallelogram law of vectors, are equally applicable to the process of subtraction of vectors.
ifistheanglebetweenAandB,thenanglebetweenAandBis(180) Bsin(180) Therefore,RAB2ABcos(180)andtan ABcos(180)
It is important to note that i) vector subtraction does not follow the commutative law, i.e., ABBA −≠−
ii) vector subtraction does not follow the associative law, i.e., A-(B - C)(A - B) - C ≠
4.4.5 Scalar product of two vectors
The scalar product of two vectors, P and Q , is defined as the product of the magnitudes of P and Q and of the cosine of the angle θ formed by P and Q . The scalar product of P and Q is denoted by P . Q such that P.Q|P||Q|cos=θ
Note that the expression just defined is not a vector but a scalar, which explains the name scalar product; because of the notation used, P . Q is also referred to as the dot product of the vectors P and Q
The scalar product of two vectors, P and Q , can be expressed in terms of their rectangular components. Resolving P and Q into components, we first write
()() xyzxyz P.QPiPjPkQiQjQk =++⋅++
i.ijjkk =⋅=⋅= 111
i.jjkki =⋅=⋅= 000
Thus, the expression obtained for P.Q reduces to z xxyy z P.QPQPQPQ =++
In the particular case when P and Q are equal, we note that 2222 xyz PPPPPP ⋅=++=
Properties
a) It is always a scalar and is positive if the angle between the vectors is acute (i.e., ° < 90 ) and negative if the angle between them is obtuse (i.e., °° <θ≤ 90180 )(Fig. 4.10)
b) It is commutative, i.e., ABBA ⋅=⋅
c) It is distributive, i.e., A(BC)ABAC ⋅+=⋅+⋅
d) As by definition, A.BABcos=θ The angle between the vectors
Fig. 4.10
e) ABA(Bcos)B(Acos) ⋅=θ=θ
Geometrically, Bcosθ is the projection of B onto A and Acosθ is the projection of A onto B , as shown. So, A.B is the product of the magnitude of A and the component of B along A and vice versa.
Component of B along
Component of A along AB BAcosAB B ⋅ =θ==⋅
f) For two perpendicular vectors 90 θ=° . So, 0 AB⋅=
g) Scalar product of two vectors will be maximum when cosmaxθ== 1 , i.e., 0 θ=° , i.e., vectors are parallel max (AB)AB⇒⋅=
h) If the scalar product of two non-zero vectors vanishes, then the vectors will be orthogonal.
i) The scalar product of a vector by itself is termed as a self dot product and is given by (A)AAAAcosAAAA =⋅=⋅θ=⇒=⋅ 22
j) In case of unit vector,
nniijjkk1 ⇒⋅=⋅=⋅=⋅= ,
nniijjkk1 ⇒⋅=⋅=⋅=⋅=
nniijjkk1 ⇒⋅=⋅=⋅=⋅= n,n,n11cos01 =××°=
nniijjkk1 ⇒⋅=⋅=⋅=⋅=
k) In case of orthogonal unit vectors, ˆˆ i,j and ˆˆˆˆˆˆˆ k;ijjkki0 ⋅=⋅=⋅= xyzxyzxxyyzz
AB(iAjAkA).(iBjBkB(ABABAB) ) ⋅=++++=++
Example: If the Vectors ˆˆˆ Paiaj3k =++
and ˆˆˆ Qai2jk =−− are perpendicular to each other, find the value of a?
Solution: If vectors P and Q are perpendicular, ˆˆˆˆˆˆ
P.Q0(aiaj3k).(ai2jk)0 ⇒=⇒++−−=
22 a2a30a3aa30 ⇒−−=⇒−+−= a(a3)1(a3)0a1,3 ⇒−+−=⇒=−
4.4.6 Cross product of two vectors
Let us determine the vector product of any two of the unit vectors ˆˆ i,j , and ˆ k . Consider first the product ˆˆ ij × Fig. 4.11 (a). Since both vectors have a magnitude equal to 1 and since they are at a right angle to each other, their vector product will also be a unit vector. This unit vector must be ˆ k since the vectors ˆˆ i,j , and ˆ k are mutually perpendicular and form a right handed triad. On the other hand, it follows from the right hand rule that the product ˆˆ ji × will be equal toˆ k (Fig. 4.11 (b)).
Fig. 4.11 (a) Cross product of ˆˆ ij × and (b) Cross product of ˆˆ ji ×
Finally, it should be observed that the vector product of a unit vector with itself, such as ˆˆ ii × , is equal to zero since both vectors have the same direction. The products of the various possible pairs of unit vectors are ˆˆˆˆˆˆˆˆ
We can now easily express the vector product V of two given vectors, P and Q , in terms of the rectangular components of these vectors. Resolving P and Q into components, we first write
VPQ(PiPjPk)(QiQjQk) =×=++×++
Making use of the distributive property, we express V as the sum of vector products, such as xy
PiQj. × Observing that each of the expressions obtained is equal to the vector product of two unit vectors, such as ˆ i and ˆ j multiplied by the product of two scalars, such as PxQy, and recalling the identities (4), we obtain, after factoring out
i,j, and
k
The rectangular components of the vector product V are thus found to be
We observe that its right hand member represents the expansion of a determinant. The vector product V can, thus, be expressed in the following form, which is more easily memorised
Properties
i. The vector product of two vectors is always a vector perpendicular to the plane containing the two vectors, i.e., orthogonal to both the vectors, A and B , though the vectors A and B may or may not be orthogonal.
ii. The vector product is distributive when the order of the vectors is strictly maintained, i.e., A(BC)ABAC. ×+=×+×
iii. The self cross product, i.e., product of a vector by itself vanishes, i.e., is a null vector.
AAAAsin0n0.
iv. In case of unit vector
v. In the case of orthogonal unit vectors, ˆˆ i,j , and ˆ k , in accordance with the right hand thumb rule,
vi. In terms of components,
SOLVED EXAMPLES
Example 1: Find AB ×
Soluton:
if
Ai2j4k =−+
and
B3ij2k.
Example 2: Let a force F be acting on a body free to rotate about a point O and let r be the position vector of any point P on the line of action of the force. Then, torque () τ of this force about point O is defined as, rFτ=×
Soluton: rFτ=×
= 2
11
3
. Given,
F(2i3jk)N =+−
and
F(ij6k)m =−+
. Find the torque on this force.
6 1
i(118)j(112)k(32) −−−−++
(17i13j5k)Nmτ=−++ .
4.5 BIOT-SAVART'S LAW
The magnetic induction dB at a point P due to an infinitesimally small element of current (length dl and current I ) at a distance r is given by
0 µ is called the permeability of free space.
In SI unit, 7 0410µ=π× henry/metre(H/m)
4.6 MAGNETIC FIELD DUE TO A CURRENT-CARRYING CONDUCTOR
4.6.1 Magnetic field due to current through a straight conductor
A current-carrying conductor behaves like a magnet. The current passing through the conductor causes the magnetic field around it.
The magnetic field produced by a straight conductor is circular.
The magnetic lines of force are concentric circles with their centres lying on the axis of the conductor. The plane of the circle is perpendicular to the direction of the current. The magnitude of the magnetic field produced increases as the current through the wire increases. As the distance from the wire increases, the magnitude of the magnetic field produced at a given point decreases. If the current flows through the conductor in an upward direction, then the magnetic lines of force are formed in an anticlockwise direction and vice versa. The direction of the magnetic field associated with a current-carrying conductor is given by the right hand thumb rule.
The magnetic induction B due to a straight wire of finite length carrying current I at a distance d is given by
where 1φ and 2φ are the angles made by upper and lower ends of the wire with the perpendicular distance d at the point of observation.
If the wire is infinitely long, then 1290 φ=φ=°
Hence, 002II B 4d2d µµ=×= ππ .
4.6.2 Right hand thumb rule

A practical method for determining the direction of the magnetic field linked to a current-carrying conductor is as follows:
Imagine holding a straight current-carrying conductor in your right hand, aligning your thumb in the direction of the current flow. The fingers of your hand will naturally curl around the conductor, indicating the direction of the magnetic field lines. This method is commonly referred to as the right hand thumb rule.
4.6.3 Magnetic field due to a current through a circular loop
At each point along a current-carrying circular loop, the magnetic field representation in the form of concentric circles expands progressively as we move away from the wire. As we approach the centre of the circular loop, these larger circles begin to manifest as straight lines. The application of the right hand rule ensures that each section of the current-carrying wire contributes to the magnetic field lines consistently, all pointing in the same direction within the loop. This phenomenon results in the appearance of straight magnetic field lines at the centre of the loop, forming a distinct pattern due to the collective influence of every point on the wire.
At the centre of the circular loop, all the magnetic field lines are in the same direction, which increases the strength of the magnetic field.
The magnitude of the magnetic field produced by a circular loop at its centre is directly proportional to the current passing through the circular loop but inversely proportional to the radius of the circular loop.
4.15 (a) Magnetic field lines produced by a current-carrying circular loop
Magnetic induction on the axis of a circular current-carrying coil is given by
where R is the radius of the coil, x is the distance of any point on the axis from the centre of the coil, and I is the current in the coil.
4.15 (b) Magnetic induction due to a circular coil
i. The direction of B is as shown in the figure. For current in an anticlockwise direction, B is out of the page, along the axis of the coil.
ii. If the fingers of the right hand are curled along the direction of the flow of current, then the thumb points in the direction of B
iii. Magnetic field at the centre of the coil
iv. Magnetic field at a point on the axis of the coil, when xR , is
where NIAc =M = magnetic dipole moment of the currentcarrying coil. Thus, a current-carrying coil of the area of cross section A and the number of turns N, carrying a current I, can be regarded as the magnetic dipole of the magnetic moment NIA.
4.6.4 Magnetic field due to a current in a solenoid
A coil of many circular turns of insulated copper wire wrapped closely in the shape of a cylinder is called a solenoid
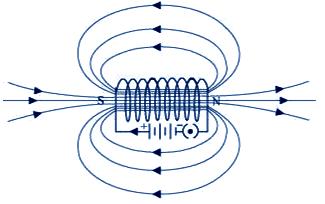
Fig. 4.16 (a) Magnetic induction due to a solenoid
When an electric current is passed through the solenoid, it produces a magnetic field around it. The magnetic field produced by a current-carrying solenoid is similar to the magnetic field produced by a bar magnet. The magnetic field lines inside the solenoid are in the form of parallel straight lines. That means the strength of the magnetic field is the same at all the points inside the solenoid. If a current-carrying solenoid is suspended freely, it will come to rest, pointing in the north and south directions.
The strong magnetic field produced inside a current-carrying solenoid can be used to magnetise a piece of magnetic material, like soft iron, when placed inside the solenoid.
The strength of the magnetic field produced by a current-carrying solenoid depends on:
i. The number of turns in the solenoid.
ii. The strength of the current in the solenoid.
iii. The nature of the 'core material' used in making the solenoid.
Fig. 4.16 (b) Magnetic field induction due to a solenoid
At a point outside the solenoid, the magnetic field induction due to current becomes weak. When the solenoid is more and more tightly packed, the field due to the current through the solenoid becomes zero.
The magnetic field induction B at a point well inside the solenoid of infinite length, having n turns per unit length carrying current I is given by
0 BnI =µ , in any medium BnI,where0r =µµ=µµ .
Magnetic field induction B due to a solenoid of finite length (l) at a point on the axis, having N turns and n turns per unit length, i.e., N n l = carrying current I is given by
0 Bni(sinsin), 2 µ =α+β
where , αβand, αβ are the angles made by the lines joining the point and edges of the solenoid with the axis.
Bar magnet as an equivalent solenoid
The magnetic field produced by a current-carrying solenoid is similar to the magnetic field produced by a bar magnet. The magnetic field lines inside the solenoid are in the form of parallel straight lines similar to the bar magnet. That means the strength of the magnetic field is the same at all the points inside the solenoid. When a current-carrying solenoid is suspended freely, it will come to rest, pointing in the geographical north and south directions similar to that of the bar magnet.
SOLVED EXAMPLES
Example 1: Two concentric circular coils, A and B, have radii of 25cm and 15cm and carry currents 10A and 15A, respectively. A has 24 turns, and B has 18 turns. The direction of currents is in the opposite order. The magnetic induction at the common centre of the coils is
Solution:
For coil A, N24,I10A,andR25cm ===
For coil B,
N = 18, I = 15A, and R = 15cm
The magnetic induction at the common centre of the concentric circular coils, A and B, can be calculated using the formula for the magnetic field at the centre of a circular coil:
The magnetic fields due to the two coils add up vectorially at the centre since they are in opposite directions. Therefore, the total magnetic field at the centre is given by:
Hence the correct answer is µ 0 420T
Example 2: In a wire of circular form, 4A current is flowing to have a magnetic induction as 1T µ at its centre. The radius of the circle should be approximately
Solution:
The radius of the circular wire can be calculated using the formula for the magnetic field at the centre of a circular loop of the wire:
Hence, the correct answer is 2.5m
Example 3: A solenoid of diameter 100cm has a magnetic field of 2.9 × 105 N/Ampsm . If it has 100 turns, determine the current flowing through it.
Solution:
Given:
Number of turns N=100
Length 1 = Lm
Magnetic field 29105=× B.N/Ampsm
The magnetic field formula is given by
The current flowing through the coil is expressed by,
4.7 MOTION IN A MAGNETIC FIELD
When a charged particle moves within a magnetic field, the magnetic force exerted on it is perpendicular to its velocity. As a result, no work is performed, and there is no alteration in the magnitude of the particle’s velocity, although the direction of momentum may undergo changes. This is in contrast to the force generated by an electric field, qE, which can possess a component parallel (or antiparallel) to the motion, allowing for the transfer of both energy and momentum.
In examining the motion of a charged particle within a uniform magnetic field, let’s explore the scenario where the velocity (v) is perpendicular to the magnetic field (B).
Fig. 4.17 Motion in a magnetic field
The force acting perpendicularly, denoted as q(v × B), functions as a centripetal force, inducing circular motion that is perpendicular to the magnetic field. If the velocity (v) and magnetic field (B) are mutually perpendicular, the particle will trace a circular path.
FORCE ON A CURRENT-CARRYING CONDUCTOR IN A MAGNETIC FIELD
When a current-carrying conductor is placed in an external magnetic field, then it experiences magnetic force.
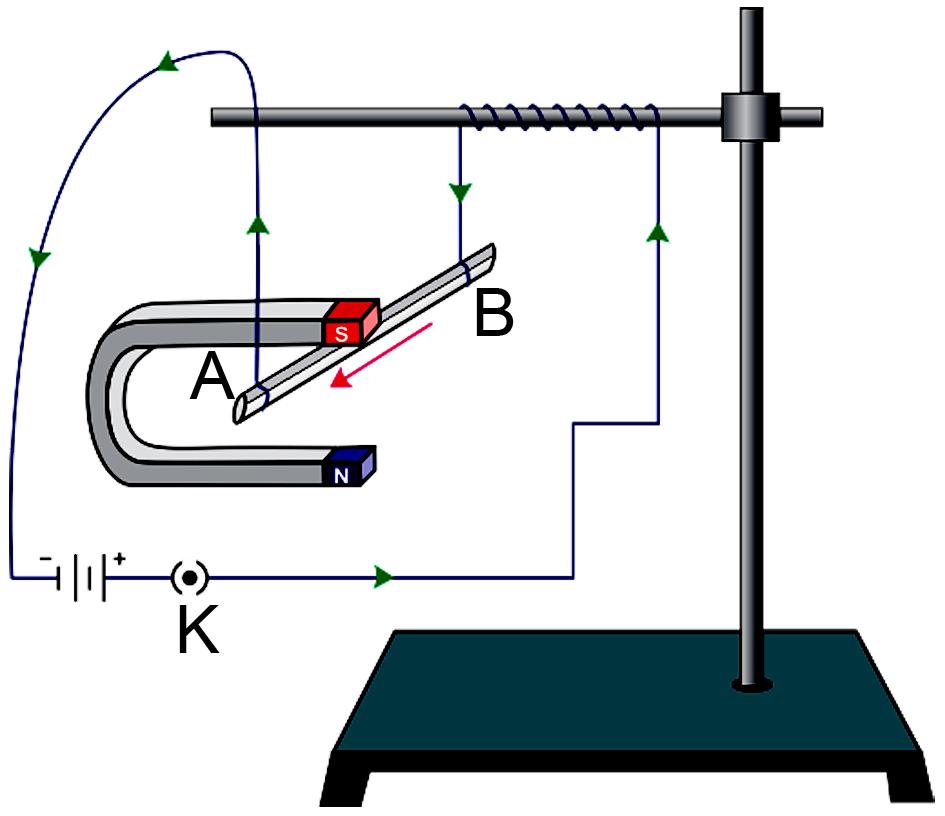
Fig. 4.18 (a) Current carrying conductor placed in magnetic field
The direction of force is also reversed when the direction of current through the conductor is changed. The direction of force acting on a current-carrying conductor placed in a magnetic field is perpendicular to the direction of the current and the magnetic field.
If a current-carrying conductor of length l is placed, making an angle θ with the direction of the magnetic field of induction B, then the force exerted by the magnetic field on the conductor is F = BIl sin θ where I is the current.

Fig. 4.18 (b) A current-carrying conductor
Note: i) If θ = 0o, then F = 0 = minimum ii) If θ = 90o, then F = Bil = maximum
If the direction of the current in a conductor and the direction of the magnetic field are known, then the direction of force acting on the current carrying conductor can be found by Fleming's left hand rule.
4.8.1 Fleming's left hand rule
According to Fleming’s left hand rule, stretch the thumb, forefinger, and middle finger of your left hand so that they are mutually perpendicular to each other. If the forefinger points in the direction of the magnetic field and the middle finger in the direction of the current, then the thumb will indicate the direction of motion or the force acting on the conductor.
4.8.2
The electric motor
A motor is a device which converts electrical energy into mechanical energy.
Principle: Electric motor works on the principle of magnetic effects of electric current, i.e., when a rectangular coil is placed in a magnetic field and current is passed through it, a force acts on the coil which rotates it continuously.
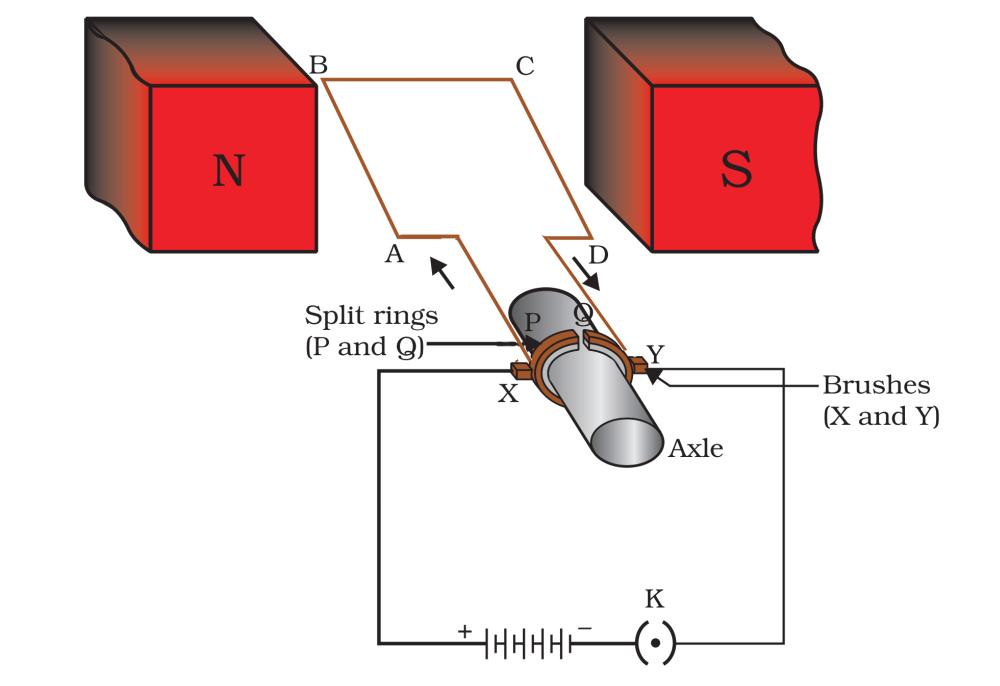
• A device which reverses the direction of current through a circuit is called a commutator. The function of commutator rings is to reverse the direction of current flowing through the coil for every half revolution.
• In electric motors, the split ring acts as a commutator
• The function of carbon brushes is to make contact with the rotating rings of the commutator and, through them, to supply current to the coil.
In commercial motors
• An electromagnet in place of the permanent magnet is used.
• Large number of turns of the conducting wire in the current carrying coil.
• A soft iron core on which the coil is wounded.
• The soft iron core, on which the coil is wound, plus the coils, is called an armature.
• Electric motor is used in electric fans, washing machines, refrigerators, mixer-grinders, etc.
• A common electric motor works on direct current. So, it is called the D.C. motor or the direct current motor.
Working: When a current is allowed to flow through the coil ABCD by closing the switch, the coil starts rotating anticlockwise. This happens because a downward force acts on the length AB, and at the same time, an upward force acts on the length CD. As a result, the coil rotates anticlock wise.
Current in the length AB flows from A to B ,and the magnetic field acts from left to right, which is normal for the length AB. Therefore, according to Fleming’s left hand rule, a downward force acts on the length AB. Similarly, the current in the length CD flows from C to D and the magnetic field acts from left to right, which is normal for the flow of current. Therefore, an upward force acts on the length CD. These two forces cause the coil to rotate anticlockwise.
After half a rotation, the position of AB and CD interchange. The half-ring Q comes in contact with brush X, and the half-ring P comes in contact with brush Y. Hence, the direction of current in the coil ABCD gets reversed.
The current flows through the coil in the direction DCBA. The reversal of current through the coil ABCD repeats after each half-rotation. As a result, the coil rotates unidirectionally. The split rings help to reverse the direction of current in the circuit.
4.8.3 Electromagnetic induction
The process in which a change in the magnetic field around a conductor produces induced EMF across its ends is called electromagnetic induction.
Faraday’s magnetic flux experiment: Faraday conducted an experiment to explore the relationship between magnetic flux and induced current.
Magnetic flux: Magnetic flux in electromagnetism is defined as the surface integral of the normal component of the magnetic field B over a given surface. Typically represented by ϕ (phi), it quantifies the magnetic field passing through a surface. The SI unit for magnetic flux is the Weber (Wb), with derived units expressed in volt-seconds. In the CGS system, the unit of magnetic flux is the Maxwell.
We can change the magnetic field around the conductor by two methods:
i) Using coil and bar magnet
In this setup, he took a circular coil connected to a galvanometer. Using a strong bar magnet, Faraday observed the galvanometer’s deflection when the north pole of the magnet was moved towards and away from the coil. Similar observations were made with the south pole of the magnet. The key conclusions were:
• When the magnet approached the coil, the galvanometer showed deflection in one direction.
• When the magnet moved away from the coil, the galvanometer showed deflection in the opposite direction.
• Stationary positioning of the magnet near the coil resulted in no deflection.
Conclusion: The change in magnetic flux, caused by the movement of the magnet, induced a current in the coil. The direction of the induced current depended on the direction of the change in magnetic flux.
ii) Using two coils
Faraday extended his investigations to demonstrate electromagnetic induction using two coils - a primary coil (p) and a secondary coil (s). The primary coil was connected to a key, a rheostat, and a battery, while the secondary coil was connected to a galvanometer. The key observations were:
• Pressing the key in the primary coil caused the galvanometer to deflect in one direction.
• Releasing the key resulted in a deflection in the opposite direction.
• Holding the key pressed, maintaining a steady current in the primary coil, caused no deflection in the galvanometer.
• Increasing the current in the primary coil, using the rheostat, induced a current in the secondary coil in the same direction as the primary coil.
Conclusion: Faraday demonstrated that a changing current in the primary coil could induce a current in the secondary coil, and the direction of the induced current could be controlled by varying the primary current.
Fleming’s right hand rule: Stretch the thumb, the forefinger and the central finger of right hand in mutually perpendicular directions. The forefinger represents the direction of the magnetic field, the thumb represents the direction of motion of the conductor, and the central finger represents the direction of the induced current in the conductor.
4.8.4 Electric generator
The electric generator converts mechanical energy into electrical energy.
Principle: An electric generator works on the principle of electromagnetic induction, i.e., when the magnetic field continuously changes around the coil, then induced EMF is produced in it. The current produced in an AC generator is alternating current. A current that changes direction after equal intervals of time is called an alternating current.
To get a direct current, a split ring type commutator must be used. Thus, a unidirectional current is produced. The generator is called a DC generator.
Construction: The generator consists of a rotating rectangular coil ABCD placed between the two poles of a permanent magnet. The two ends of this coil are connected to the two rings, R1 and R2
The two conducting stationary brushes, B1 and B2, are kept pressed separately on the rings, R1 and R2, which are internally attached to an axle.
The axle may be mechanically rotated from outside to rotate the coil inside the magnetic field. The outer ends of the two brushes are connected to the galvanometer.
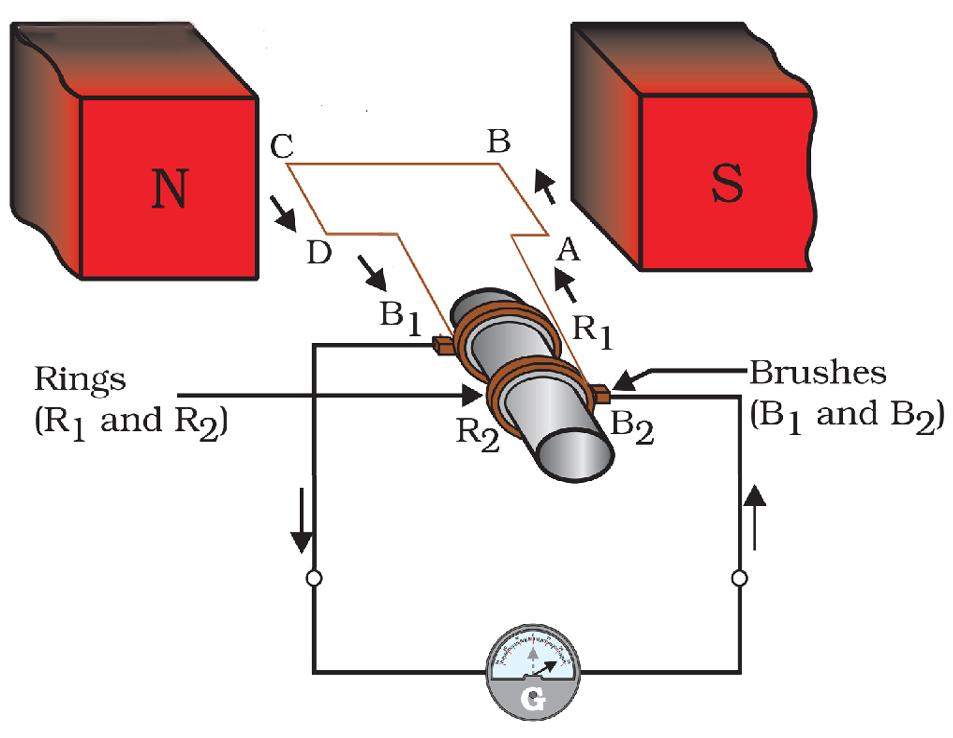
Working: When the axle attached to the two rings is rotated such that the arm moves up in the magnetic field produced by the permanent magnet.
When the coil ABCD is rotated anticlockwise, induced currents are set up in the arms along AB and CD. Hence, an induced current flows in the direction ABCD. If there are large numbers of turns in the coil, the current generated in each turn adds up to give a large current through the coil. That means the current in the external circuit flows from B1 to B2
Differences between alternating current and direct current
Direct Current
• If the current flows in one direction only, it is called a direct current.
• The positive and negative polarity of a direct current is fixed.
• Some sources of direct current are dry cell batteries, car batteries, and D.C. generators.
Alternating Current
• If the current reverses direction after equal intervals of time, it is called alternating current.
• Most of the power stations in India generate alternating current.
• The alternating current produced in India reverses its direction every 1 100 s second.
• The positive and negative polarity of an alternating current is not fixed.
• Some of the sources which produce a.c are powerhouse generators, car alternators, and bicycle dynamos.
Advantages of AC over DC
• AC can be transmitted over long distances without much loss of electrical energy.
• AC generators are used in power stations to generate electricity.
SOLVED EXAMPLES
Example 1: A current-carrying wire is immersed in a magnetic field that is perpendicular to the plane of the conductor. What happens to the force on the conductor if the current in the wire is doubled?
Solution:
The force on the conductor gets doubled if the current in the wire is doubled.
Magnetic field is represented as B.
When a current-carrying wire is put in a magnetic field, it is subjected to a magnetic force.
The magnetic force on a current-carrying wire may be calculated as:
F = ILB Sin θ, where I is the current in the wire, L is the length of the wire, B is the magnetic field, and θ is the angle between the current and magnetic field.
Since magnetic force F = ILB Sin θ is the force on the current wire in a magnetic field, in this case, the force is proportional to the current flowing through the circuit. Hence, if the current in the wire is doubled, the force on the conductor is also doubled.
Example 2: A semicircular current loop is placed in a uniform magnetic field of 1 tesla, as shown. If the radius of the loop is 1 m, the magnetic force on the loop is:
4.9 TORQUE
Torque on a rectangular current loop in a uniform magnetic field is the rotational force experienced by the loop due to the interaction between the magnetic field and the current flowing through the loop.
4.9.1 Torque on a current loop
A rectangular coil of area A, containing n turns and carrying a current i, is placed in a uniform magnetic field of induction B.
Fig. 4.25 Torque on a current loop
If θ is the angle between normal to the plane of the coil and the magnetic field, then the torque on the coil is
BiAnsinMBsin(or)MB(MagneticmomentMniA) τ=θ=θτ=×=
If 01800 θ=°°τ= (or),then (minimum)
If 90 θ=° , then BiAn τ= (maximum)
The work done to turn the coil from angle θ1 to θ2 is () 12 =θ−θ WMBcoscos
If 12 0 ° θ=θ=θ and , then () 1 =−θWMBcos
The change in P.E of the coil when the coil is rotated from 0 to 180 ° = 2MB
If α is the angle between the plane of the coil and the magnetic field, then the torque on the coil, τ=α BiAncos.
4.10
DOMESTIC ELECTRIC CIRCUITS
Electric power supply: Homes receive electric power through a main supply, either overhead electric poles or underground cables. The main supply consists of live wire (positive, usually red insulation) and neutral wire (negative, usually black insulation). The potential difference between live and neutral wires is typically 220 V.
Mains connection at meter-board: The wires pass into an electricity meter through a main fuse at the meter-board in the house. A main switch connects them to the line wires in the house. Electricity is supplied to separate circuits within the house.
Circuit separation: Two separate circuits are often used: one with a 15A current rating for highpower appliances, and the other with a 5A current rating for lights and fans.
Earth wire for safety: The earth wire (green insulation) is connected to a metal plate deep in the earth near the house. It serves as a safety measure, especially for appliances with metallic bodies. The earth wire provides a low-resistance conducting path for any leakage of current, preventing severe electric shocks.
Schematic diagram of domestic circuits
Figure 4.26 provides a schematic diagram of a common domestic circuit. Different appliances can be connected across live and neutral wires. Each appliance has a separate switch for turning the current on/off.
Over-loading: If too many electrical appliances with high power ratings are switched on at the same time, they draw an extremely large current from the circuit. This is known as overloading.
• Overloading can also occur if too many appliances are connected to a single socket. Due to an extremely large current flowing through them, the copper wires of household wiring get heated to a very high temperature, and a fire may start.
Short-circuiting: The direct contact of a live wire and a neutral wire is called a short circuit.
• The current flowing through the wires becomes very large and heats the wires to a dangerously high temperature,
• To save the circuit from damage due to over-loading or short-circuiting, a fuse of proper rating is put in each circuit.
Electric fuse: An electric fuse is a device which is used to limit the current in an electric circuit. The fuse safeguards the circuit and the electrical appliances from being damaged.
• The fuse wire is generally an alloy of lead and tin. It has a low melting point and breaks the circuit if the current exceeds a safe value.
• Electric fuses are always connected in series in an electric circuit because when the circuit current exceeds a specified value due to voltage fluctuations, the fuse wire gets heated and melts. Thus, it breaks the connections, and no current flows.
QUICK REVIEW
• Magnetic field: The space around a magnet in which its influences can be felt is known as magnetic field.
• Like poles of a magnet repel each other and unlike poles of a magnet attract each other.
• Magnetic field line: It is the path along which a hypothetical free north pole would tend to move.
• Magnetic field lines emerge from the north pole and merge at the south pole.
• Inside the magnet, the magnetic field lines are from the south pole to the north pole.
• A scalar is a quantity that has magnitude only.
• A vector is a quantity that possesses magnitude and direction.
• Vector addition methods: (i) Parallelogram law of vector addition and (ii) Triangle law of vector addition
• Subtraction of a vector B from a vector A is defined as the addition of vector B (negative of vector B) to vector A . Thus A B = A + (-B)
• The dot product of two vectors P and Q can be expressed in terms of their rectangular components. =++ xxyyzz P.QPQPQPQ
• The cross product V of two given vectors P and Q can be expressed in terms of the rectangular components of these vectors.
• The current passing through the conductor causes the magnetic field around it. If the direction of the current changes, the direction of the magnetic field produced by the electric current is also changed.
CURRENT
• The direction of the magnetic field associated with a current-carrying conductor is given by the right hand thumb rule.
• Right hand thumb rule: Imagine that you are holding the current-carrying wire in your right hand so that your thumb points in the direction of the current, then the curling of fingers represent the direction of the magnetic field lines around the wire.
• Magnetic field due to a current through a circular loop: The magnetic field lines are circular near the current-carrying loop. At the centre of the circular loop, the magnetic field lines are straight.
• The magnitude of the magnetic field produced by a circular loop at its centre is
o directly proportional to the current passing through the circular loop.
o inversely proportional to the radius of the circular loop.
• Solenoid: A coil of many circular turns of insulated copper wire wrapped closely in the shape of a cylinder is called a solenoid.
• The strength of the magnetic field produced by a current-carrying solenoid depends on
o The number of turns in the solenoid, the strength of the current in the solenoid and the nature of the 'core material' used in making the solenoid.
• Electromagnet: An electromagnet works on the magnetic effect of current. The combination of solenoid and a soft iron core is called an electromagnet.
• Force on a current carrying conductor in a magnetic field: When a current-carrying conductor is placed in an external magnetic field, then it experiences a magnetic force.
• The direction of the force is also reversed when the direction of current through the conductor is changed.
• Force acting on a current-carrying conductor depends on the magnitude of the magnetic field and the angle made by the conductor with the direction of the magnetic field and the current. F = BIl sin θ
• Fleming’s left hand rule: Stretch the thumb, the forefinger, and the middle finger of the left hand into mutually perpendicular directions. Then, the central finger represents the direction of the current, the forefinger represents the direction of the magnetic field, and the thumb represents the direction of motion of the conductor.
• The maximum force is exerted on a current-carrying conductor only when it is perpendicular to the direction of the magnetic field.
• No force acts on a current-carrying conductor when it is parallel to the magnetic field.
• The electric motor: A motor is a device which converts electrical energy into mechanical energy.
• Electromagnetic induction: The process by which a change in the magnetic field around a conductor produces induced EMF across its ends is called electromagnetic induction.
• The electric generator converts mechanical energy into electrical energy.
WORKSHEET - 1
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
I. Magnetic field, field lines and bar magnet
1. Lines of the magnetic field around a current carrying a straight conductor will be
a. Straight lines parallel to the conductor
b. Circular in a plane parallel to the conductor
c. Circular in a plane perpendicular to the conductor
d. Straight, perpendicular to the conductor
2. Inside the magnet, the field lines move ____________.
a. From the south pole to the north pole
c. Normal to the north pole
3. Magnetic field is not associated with
a. A charge in uniform motion
c. A decelerated charge
b. From the north pole to the south pole
d. In random direction
b. An accelerated charge
d. A stationary charge
4. A live wire is hidden in a wall. Its position can be located with the help of
a. Watt-meter
b. Moving coil galvanometer
c. Magnetic needle
d. The position of the live wire cannot be located without breaking the wall.
5. If a copper wire carries a direct current, then the magnetic field associated with the current will be
a. Only inside the wire
c. Both inside and outside the wire
6. Magnetic field lines ____________.
a. Can intersect at neutral points
c. Can not intersect more than one point
b. Only outside the wire
d. Neither inside nor outside the wire
b. Can intersect within the magnet
d. Never intersect with each other
7. Which of the following is false about magnetic field lines?
a. The magnetic field lines emerge from the north pole and merge at the south pole, outside the magnet.
b. The field is stronger near the poles.
c. Magnetic field lines are continuous in nature.
d. Magnetic field lines are open curves
8. Assertion (A): Magnetic field interacts with a moving charge and not with a stationary charge
Reason (R): A moving charge produces a magnetic field
a. Both A and R are correct, and R is the correct explanation of A
b. Both A and R are correct, but R is not the correct explanation of A
c. A is correct, R is incorrect
d. A is incorrect, R is correct
II. Basic mathematics
1. Two vectors are given by 23532.=−+−=+− aijkandbijk If 320 +−= abc . Then, the third vector c is
a. ˆˆˆ 4913 +− ijk
c. ˆˆˆ 4913ijk
2. Choose the correct statements
a. () += ScalarVectorscalarorvector
c. Scalar Vector = scalar (or) vector
4913−−+ijk
2313 −+ ijk
b.) = Vector b scalar Vector
d. Vector - Vector = vector
3. A carrom board [ 44 × ftft square] has the queen at the centre. The queen hit by the striker moves to the front edge, rebounds, and goes into the hole behind the striking line. Then, find the magnitude of displacement of the queen
a. From the centre of the front edge is 4 10 3 ft
b. From the centre to the front edge is 2 10 3 ft
c. From the front edge to the hole is 4 10 3 ft
d. From the centre to the hole is 22 ft

4. A force ˆˆˆ (22) ++ ijkN is acting on a body shifted it from (1, 2, 0) to (2, 3, 4) in the same frame of reference. The vector component of the force along the displacement of the body
a. 5ˆˆˆ 23 6 ++ ijk
c. 11ˆˆˆ 18(4) ++ ijk
b. 5ˆˆˆ 2 6 ++ ijk
d. 11ˆˆˆ 8(4) −+ ijk
5. Area of the triangle whose base is given by ˆˆˆ =++ Aijk and one of the two sides by ˆˆ 43=+ Bjk is
a. 26 b. 26 2
6. A particle is acted upon by a force
c. 5 2 d. 5
ˆˆˆ (2)=−+
FijkN. If the particle is at P(-1m, 2m, 3m), the torque of the force about Q(2m, 3m, 1m) is:
a. Zero b. ˆˆˆ (3) −+ ijk Nm
c. ˆˆˆ (357) ++ ijk Nm
7. The value of p so that vectors
d. ˆˆˆ (23) +− ijk Nm
(2),(23) −++− ijkijk , and ˆˆˆ (35) ++ ipjk are coplanar should be:
a. 16 b. -4 c. 4 d. -8
8. If ||3..|| ABABthenthevalueofB , A ×=+
is :
a. ()1/2 223 ++ ABAB
b. ()221/2 ++ ABAB
c. 1 2 22 3 ++ AB AB d. A+B
9. The diagonals of a parallelogram are represented by vectors ˆˆˆ 543=−+ Aijk and
ˆˆˆ 32 =+− Bijk. The area of the parallelogram is :
a. 171 unit
b. 72 unit
c. 171 unit
10. AandB are two vectors. ()() +×− ABAB can be expressed as:
a. × BA b. () 2 × BA
d. 72 unit
c. () 2 × AB d. zero
11. The vertices of a triangle are A(3, 2, 1), B(1, -1, 2), and C(2, 1, 1). The area of the triangle will be:
a. 2 unit
b. 2 2 unit
c. (3)/2 unit
d. 2 3 unit
III. Biot-savart law and motion in a magnetic field
1. The value of the intensity of the magnetic field at a point due to a current-carrying conductor depends on the?
a. Current
b. Distance from the conductor
c. Both the distance from the conductor and the current
d. Neither the distance from the conductor nor the current
2. The value of the magnetic field due to a small element of current - carrying conductor at a distance r and lying on the plane perpendicular to the element of the conductor is:
a. Minimum
c. Zero
b. Maximum
d. Inversely proportional to the current
3. A wire carrying 100 A is bent into a circular loop of 5 cm radius. The magnetic field at its centre in Tesla is
a. 22.56 × 10-4
c. 12.56 × 10-4
b. 23.08 × 10-4
d. 40.06 × 10-4
4. A vertical straight conductor carries a current vertically upwards. A point P lies to the east of it at a small distance and another point Q lies to the west at the same distance. The magnetic field at P is :
a. Greater than at Q
b. Same as at Q
c. Less than at Q
d. Greater or less than at Q depending upon the strength of the current
IV. Magnetic field due to a current - carrying conductor
1. A circular coil carrying current behaves as a
a. Bar magnet b. Horseshoe magnet c. Magnetic shell d. Solenoid
2. A long, straight wire carries a current along the z-axis. One can have two points in the x-y plane such that
i. The magnitude of magnetic field inductions are equal
ii. The directions of magnetic field inductions are same
iii. The magnitude of magnetic field inductions are unequal
iv. The direction of magnetic field induction at one point is opposite to that at other point.
a. i and iii are correct
c. i, ii, and iv are correct
b. ii and iv are correct
d. All are correct
3. Magnetic induction field due to a short bar magnet on its equatorial line at a certain distance is B. Its value at the same distance on the axial line is
a. 2B b. 2 B c. 3B d. 3 B
4. Magnetic field inside the solenoid is
a. Radial
b. Uniform c. Both a and b d. Circular
5. The right hand thumb rule is used to determine the direction of which of the following?
a. The electric field around a charged object
b. The magnetic field around a current-carrying straight wire
c. The force experienced by a charged particle in a magnetic field
d. The direction of electron flow in a conductor
6. In a wire of circular form, 4A current is flowing to have a magnetic induction as 1μT at its centre. The radius of the circle should be approximately
a. 2.5 m
b. 2.8 m c. 2.25 m d. 2.1 m
7. The magnetic field in the solenoid ___________________ when the number of turns increases?
a. Increases
c. Remains constant
b. Decreases
d. Becomes zero
8. The magnetic field strength of a solenoid can be increased by inserting which of the following materials as the core?
a. Copper
b. Silver c. Iron d. Aluminum
9. The right hand thumb rule is used to find
a. Force on a charged particle passing through the magnetic field.
b. Force on a current carrying conductor placed in a magnetic field.
c. Direction of induced current.
d. Direction of B around a current carrying straight conductor.
10. Assertion (A): When theccurrent is represented by a straight line, the magnetic field will be circular.
Reason (R): According to right hand rule, the direction of force is parallel to the magnetic field.
a. Both A and R are correct, and R is the correct explanation of A
b. Both A and R are correct, but R is not the correct explanation of A
c. A is correct, and R is incorrect
d. A is incorrect, and R is correct
V. Force on a current - carrying conductor in a magnetic field
1. A horizontal overhead power line is at a height of 4m from the ground and carries a current of 100A from east to west. The magnetic field directly below it on the ground is () 71 0410µ=π× TmA
a. 2.5107 × T southward
c. 5106 × T southward
b. 5106 × T northward
d. 2.5107 × T northward
2. A wire in the form of a square of side ’a’ carries a current ‘i‘. Then, the magnetic induction at the centre of the square is (magnetic permeability of free space 0 =µ )
3. A circular coil, A, has a radius of R, and the current flowing through it is T. Another circular coil, B, has a radius of 2R. If 2I is the current flowing through it, then, the magnetic field at the centre of the circular coils is in the ratio of
4:1
4. Two long conductors, separated by a distance ’d’, carry currents l1 and l2 in the same direction. They exert a force ’F’ on each other. Now, the current in one of them is increased two times, and its direction is reversed. The distance is also increased to 3d. The value of the force between them is
5. An infinitely long conductor PQR is bent to form a right angle, as shown. Current ‘I‘ flows through PQR. The magnetic field due to this current at the point M is B1. Now, another infinitely long straight conductor QS is connected to Q so that the current is 1 2 in QR as well as in QS, the current in PQ remains unchanged. The magnetic field at M is now B2. The ratio 1 2 B B is given by
1 2
1
VI. Torque and domestic electric circuits
2 3
2
1. There is no force on a moving charge in a magnetic field when its direction of motion is
a. Parallel to the direction of the magnetic field
b. At an angle of 45 ° to the magnetic field
c. At an angle of 30 ° to the magnetic field
d. Perpendicular to the magnetic field
2. A circular loop of area 0.01m2 carrying current 10A is placed parallel to a magnetic field of intensity of 0.1 T. The torque (in Nm) acting on the loop is
a. 1.1
b. 0.8
c. 0.001
d. 0.01
3. A wire of length 'L' metre carrying a current 'i' ampere is bent in the form of a circle. The magnitude of its magnetic moment is
4. At the time of the short circuit, the current in the circuit
a. Reduces substantially
c. Increases heavily
WORKSHEET - 2
b. Does not change
d. Vary continuously
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
1. Among the following, a diamagnetic substance is
a. Gold
b. Iron
c. Aluminium
2. Copper is a diamagnetic material, but copper chloride is
a. Dia magnetic
b. Para magnetic
c. Ferro magnetic
3. The magnetic materials are strongly attracted by the magnets
a. Dia
b. Para
c. Anti ferro
d. Cobalt
d. Ferri magnetic
d. Ferro
4. The substance that aligns perpendicularly to the magnetic field when suspended
a. Ferri
5. Alnico is an alloy of
b. Dia
a. Aluminium, cobalt, nickel
c. Aluminium, iron, cobalt
c. Para
b. Cobalt, nickel, iron
d. Steel, cobalt, nickel
d. Ferro
6. Which of the following types of materials is not very important for engineering applications
a. Ferro magnetic
c. Dia magnetic
b. Para magnetic
d. None
7. The attraction of a magnetic substance by the poles of a magnet is
a. Minimum
b. Zero
c. Maximum
8. Earth’s magnet has its south pole situated near the
a. Geographic north
b. Geographic south
c. Geographic west
d. None of these
d. Geographic east
9. The property that differentiates a magnet from other substances is its :
a. Attractive property
c. Both a and b
b. Directive property
d. None of the above
10. A rectangular coil of copper wires is rotated in a magnetic field. The direction of the induced current changes once in each
a. Two revolutions
c. Half revolution
11. Choose the wrong statement.
b. One revolution
d. One-fourth revolution
a. Magnetic poles always exist in pairs b. Magnetic poles are always of equal strengths
c. Like poles repel each other
d. Unlike poles repel each other
12. If a bar magnet is cut lengthwise into 3 parts, the total number of poles will be
a. 2
b. 3
c. 4
13. The magnetic effect of electric current was discovered by
a. Maxwell
b. Oersted
c. Ampere
d. 6
d. Faraday
14. A compass needle just above a wire in which electrons are moving towards east will point
a. East
b. West
c. North
15. It is a common notion that the Earth’s magnetism is due to the
a. Presence of a huge permanent magnet in the interior of the earth
b. Presence of electric currents circulating in the interior of the earth
c. Influence of the Sun’s magnetic field
d. Influence of a nuclear explosion
16. Magnetite is a/an
a. Natural magnet
c. U - shaped magnet
17. Magnetic lines of force
a. Are mere directions
b. Have no physical reality
b. Electromagnet
d. None of these
d. South
c. Can be used to indicate the direction of the magnetic field at a point.
d. All the above
18. Choose the correct statement.
a. Lines of force are not imaginary lines
c. Lines of force do not intersect each other
b. Lines of force cannot be mapped on paper
d. Lines of force always intersect each other
19. Magnetic lines of force
a. Form closed loops
c. Are crowded to gather near the poles
20. A coil carrying current behaves as a/an
a. Magnet
b. Motor
b. Cannot intersect
d. All the above
c. Dynamo
d. Electric dipole
21. By inserting a soft iron piece into a solenoid, the strength of the magnetic field
a. Increases
c. First decreases then increases
b. Decreases
d. Remains unchanged
22. By increasing the number of turns in the coil, the strength of the magnetic field
a. Decreases
c. First decreases then increases
b. Increases
d. Remains unchanged
23. If the current in the coil decreases, the strength of the magnetic field.
a. Decreases
b. Increases
c. Sometimes decreases and sometimes increases d. Remains unchanged
24. The best material to be used for making an electromagnet is
a. Stainless steel
b. Silver
25. A magnetic field cannot exert any force on a
a. Moving magnet
c. Moving Charge
26. A magnetic field can exert force on a
a. Stationary magnet
c. Soft iron
b. Stationary magnet
d. Stationary charge
b. Moving charge c. Moving magnet
d. Nickel
d. All of these
27. A wire carrying a current of 5A is placed perpendicular to the magnetic induction of 2T. The force on each centimetre of the wire is
a. 0.1 N
b. 100 N
c. 10 N
28. The touching of the live wire and neutral wire directly is known as
a. Power rating
d. 1 N
b. Short circuiting c. Overloading d. Any of these
29. The potential difference between the live wire and the neutral wire in India is
a. 110 V
b. 50 V
c. 220 V
30. An electric fuse works on the __________ effect of current.
a. Heating
b. Magnetic
c. Chemical
d. none of these
d. None of these
31. The commonly used safety fuse wire is made of
a. Copper
b. Lead
c. Nickel d. An alloy of tin and lead
32. In a safety fuse, the temperature to which the wire gets heated is inversely proportional to the
a. Radius of the wire
c. Square of the radius of the wire
b. Cube of the radius of the wire
d. Fourth power of the radius of the wire.
33. The alloy which is mainly used for making permanent magnets
a. Iron
b. Alnico
34. A fuse in an electric circuit acts as a
a. Current multiplies
c. Power multiplier
c. Wood d. Copper
b. Voltage multiplies
d. Safety device
35. The magnetic field due to a circular wire at its centre, is
a. In the plane of wire
c. Perpendicular to the plane of wire
b. 30o to the plane of wire
d. None of the above.
36. A commutator changes the direction of the current in the coil of
a. A DC motor
c. A DC motor and a DC generator
37. Which of the following statements is correct?
a. AC generator generates a lower voltage.
b. DC generator generates a higher voltage.
b. A DC motor and an AC generator
d. An AC generator
c. AC generator has a permanent magnet, whereas a DC generator has an electromagnet.
d. There is a split-ring commutator in a DC generator but not in an AC generator.
38. An electric motor works based on
a. Magnetic effects of electric current b. Electromagnetic induction
c. Heating effects of electric current
d. None of these
39. In an experiment, a horseshoe magnet is placed around a current-carrying wire such that the magnetic field is perpendicular to the wire. What will be observed regarding the direction of the force on the wire?
a. The wire deflects according to Fleming’s Left-Hand Rule.
b. The wire deflects towards the north pole of the magnet.
c. The wire does not experience any deflection.
d. The wire deflects towards the south pole of the magnet.
40. In electric generators, mechanical energy is converted into
a. Magnetic energy
c. Electrical energy
b. Sound energy
d. Chemical energy
41. Two identical circular loops of metal wire are lying on a table without touching each other. Loop 'A’ carries a current which increases with time. In response, loop 'B’
a. Remains stationary
c. Is repelled by the loop 'A’
b. Is attracted by the loop 'A'
d. Rotates about its CM with CM fixed
42. Assertion (A): When a magnet is immersed in iron filings, more iron filings are attracted at the centre of a bar magnet
Reason (R): Magnet has maximum pole strength at its poles.
a. Both A and R are correct, but R is not the correct explanation of A
b. Both A and R are correct, and R is the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect
43. Assertion (A): A freely suspended current-carrying solenoid comes to rest in East-West directions.
Reason (R): A current - carrying solenoid behaves like a bar magnet.
a. Both A and R are correct, but R is not the correct explanation of A
b. Both A and R are correct, and R is the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect
44. Assertion (A): A current-carrying conductor produces the magnetic field.
Reason (R): Moving charges produce both the magnetic field as well as the electric field.
a. Both A and R are correct, but R is not the correct explanation of A
b. Both A and R are correct, and R is the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect
45. Assertion (A): Safety fuses are made of materials having low melting points.
Reason (R): Safety fuses should resist the electric current that exceeds the limit.
a. Both A and R are correct, but R is not the correct explanation of A
b. Both A and R are correct, and R is the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect
46. Assertion (A): In electric motors, the split ring acts as a commutator.
Reason (R): A device which reverses the direction of current through a circuit is called a commutator.
a. Both A and R are correct, but R is not the correct explanation of A
b. Both A and R are correct, and R is the correct explanation of A
c. A is correct, but R is incorrect
d. R is correct, but A is incorrect

FORCE AND MOTION
5.1 TYPES OF MOTION
5.1.1 Linear motion
Translatory or linear motion refers to the linear movement of a rigid body when subjected to an external force. When an applied force acts on a stationary rigid body that is free to move, the body undergoes translational motion, moving along a straight path in the direction of the force.
An example of translational motion is observed when pushing a ball lying on a floor, causing it to move in a straight line.
5.1.2 Rotational motion
Rotational motion is characterized by the rotation of a rigid body around an axis when a force is applied at a suitable point while the body is pivoted. This type of motion results from the turning effect of the force and is known as rotational motion.
For instance, when a wheel is pivoted at its centre, and a force is applied tangentially to its rim, the wheel rotates about its centre. Another example is the rotational motion of a door's handle when a force is applied normally to it.
Kinematics of rotatory motion
Consider a rigid body rotating about a given fixed line. Consider a particle P of the body. At t = 0, the particle position is P0.
At time t, the particle moves to P and Ð POP o = θ
Fig. 5.3 Kinematics of rotatory motion
Angular displacement (θ)
When a particle is moving on the circumference of a circle, the line joining the position of the particle at any instant of time and the centre of the circle is called a radius vector. As the particle moves on the circle, the radius vector rotates.
The angle turned by a body rotating about a given axis or particle moving on a circle from some reference line is called angular displacement.
• It is dimensionless (as θ = s /r) but has an SI unit: radian. Some other units are degree or revolution.
2 360 1 p rad rev ==
• If a body makes 'n’ revolutions, then its angular displacement, θ = 2πn
Angular velocity (ω)
As the position of the particle moving on the circle changes with time, the particle possesses angular velocity. The rate of change of angular displacement of a particle is called angular velocity.
If the change of angular displacement of a particle rotating is Δθ in a time interval Δt, then average angular velocity, ω is given by
θ1 - angular position of the particle at t1
θ2 - angular position of the particle at t2
If a body makes n rotations in t seconds, then
ω=
avg (2n) [] rad/s t π
If T is the time period of revolution and f is the frequency, then ω = 2π/T = 2πf
Angular acceleration (α)
When the angular velocity of a particle changes with time, the particle will have angular acceleration. The rate of change of angular velocity of a particle is called angular acceleration. Let
ω1 and ω2 be the instantaneous angular speed at time t1 and t2, then average angular acceleration
Relation Among angular variables: If the angular acceleration is constant
Relation among linear and angular variables
1. Angular displacement and linear displacement
∆=∆θ⋅
sr
Where s is the linear displacement
r is the radius of rotation
q is the angular displacement
2. Angular velocity and linear velocity
vr=×ω
Where v is the linear velocity
r is the radius
ω is the angular velocity.
3. Angular acceleration and linear acceleration
T ar=a
Where T a is the tangential acceleration r is the radius a is the angular acceleration.
Also, 2 2 r v ar r ==ω , which is along the radius towards the centre.
For a rigid body as angular variables (, and )θωα are the same for all points, the corresponding linear variables Tr (i.e., s, v, a and a ) will depend on r. The greater the distance of points from the axis of rotation, the greater the linear variables.
In a circle, as tangent and radius are always normal to each other, so will T a and r a . The acceleration, 22 aaaTr =+ .
SOLVED EXAMPLES
Example 1: A flywheel increases its angular velocity from 120 rad/s to 180 rad/s in 5 seconds. Calculate its angular acceleration during this time.
Solution:
To calculate angular acceleration (α), we can use the formula:
where:
•Δω is the change in angular velocity,
•Δt is the change in time.
In this case, the initial angular velocity (ω0 ) is 120 rad/s, the final angular velocity (ω) is 180rad/s, and the time interval (Δt) is 5 seconds.
180 rad/s120 rad/s60 rad/s 60 rad/s 12 rad/s t5 s
Therefore, the angular acceleration during this time is 12 rad/s2.
Example 2: Calculate the linear acceleration of a particle moving in a circle of radius 0.4 m at the instant when its angular velocity is 2 rads-1 and its angular acceleration is 5 rads-2
Solution:
Here, r = 0.4 m, ω = 2 rads-1, α = 5 rads-2
Tangential acceleration,
aT = rα = 0.4×5 = 2ms-2
Centripetal acceleration, 222 c 0.421.6ms=ω=×=ar
Total linear acceleration,
Example 3: The angular velocity of a particle moving along a circle of radius 50 cm is increased in 5 minutes from 100 revolutions per minute to 400 revolutions per minute. Find angular acceleration.
Solution:
Given: Initial angular velocity, 1 1 200 rads 60 π
Final angular velocity,
Time, t = 5 min = 300sec
Angular acceleration,
MOMENT OF FORCE (TORQUE)
Consider the door of your classroom and try to turn or rotate it by applying force at various points on the door. We find it difficult if the point of application of force is nearer to the axis of rotation or hinges. And if the force applied is exactly on the hinges, the door cannot move. Have you observed that a tight wheel nut cannot be unscrewed with bare hands, but the same can be done quite easily
using a jockey rod or a spanner? These examples suggest that the rotating effect is decided not only by the magnitude of applied force but also by the way it is applied.
Consider the following Fig. 5.4, when the lever arm length is doubled, it is seen that the effect of force required to turn the nut is halved.
Fig. 5.4 Effect of force when the lever arm length is doubled
If F is applied parallel to the lever arm of the spanner, it is observed that there is no 'turning effect'. And if F is applied at an angle ' θ ' to the lever arm, as shown in figure Fig. 5.5, the component Fsinθ alone participates in rotating the system.
Fig. 5.5 When F is applied parallel to the lever arm and when F is applied at an angle θ
Hence, the rotational analogue of force is moment of force. It is also referred to as torque.
5.2.1 Torque
Torque (τ): It is defined as the turning effect of force about a fixed point and is measured as the product of the magnitude of force and the perpendicular distance of the line of action of the force from the fixed point.
5.2.2 Factors affecting the turning of a body
1. Magnitude of applied force: The turning effect on a body is influenced by the magnitude of the force applied. A greater force applied at a specific point on the body results in a more significant turning effect. This factor highlights the role of force in inducing rotational motion.
2. Distance from the axis of rotation: The distance of the line of action of the force from the axis of rotation (or pivoted point) is a crucial factor in determining the turning effect on a body. This distance, known as the lever arm or moment arm, affects how effectively the force produces rotation. A longer lever arm enhances the turning effect.
5.2.3 Unit of moment of force
• Unit of moment of force = unit of force × unit of distance
• The S.I. unit of force is newton and that of distance is metre, so the S.I. unit of moment of force is newton × metre. This is abbreviated as Nm.
• The C.G.S. unit of moment of force = dyne cm.
• If force is expressed in gravitational units, the moment of force in the SI system is kilogramforce times meter (kgf×m), whereas in the CGS system, the unit is gram-force times centimetre (gf×cm).
These units are related as follows:
1Nm10 dyne 10cm
10 dyne cm
1kgfm9.8 Nm
1gfcm980 dyne cm
5.2.4 Measurement of moment of force (or torque)
The magnitude of moment of the force or torque of force F about the point O is given by
From figure = r sin θ
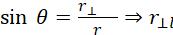
∴τ = rFsinθ, where' θ ' is the angle between and
Torque of a force about a point 'O' in vector form is given by
• The direction of torque is perpendicular to the plane containing both r and F. Its direction can be determined by using the right-hand thumb rule.
• Moment of a force has dimensions [ML2T-2 ]. Its dimensions are the same as those of work and energy.
• SI unit of moment of force is Newton meter (Nm)
• Torque produced by a force about an axis can be zero in the following cases:
i. If the force vector passes through the axis of rotation.
ii. If the force vector is parallel to the axis of rotation.
E.g., Pushing at a door edgewise (i.e. in its plane).
5.2.5 Clockwise and anticlockwise moments
Moment of force which tends to produce rotation anticlockwise is taken as positive, and clockwise direction is taken as negative.
Direction of anticlockwise moment: The direction of the anticlockwise moment is oriented along the axis of rotation, pointing outward from the centre.
Direction of clockwise moment: Conversely, the direction of the clockwise moment is along the axis of rotation, but it points inward.
Factors influencing rotation: The direction of rotation induced by applying a force to a pivoted body is determined by two key factors:
1. Point of application: The specific point on the body where the force is applied influences the direction of rotation. Changing the point of application alters the resulting moment of force.
2. Direction of force: The direction in which the force is applied also plays a crucial role. Fig. 5.7 illustrates how changing the point of application from A to B produces different anticlockwise and clockwise moments in a pivoted disc.
Pivot
Anticlockwise (Positive)
Clockwise (Negative)
(a) By changing the point of application of force
Axle
Anticlockwise (Positive)
Axle
Clockwise (Negative)
(b) By changing the direction of force
5.7 Anticlockwise and clockwise moments
5.2.6 Common examples of moment
of force
1. Advantage in door operation: When opening or shutting a door, a force (F) is applied normal to the door at its handle (P), located at the maximum distance from the hinges. This arrangement ensures that a smaller force at a larger perpendicular distance generates the necessary moment of force to facilitate door movement.
5.8(a) Opening of a door
2. Efficient design of hand flour grinder: The upper circular stone of a hand flour grinder is equipped with a handle positioned near its rim. This strategic placement, at the maximum distance from the centre, allows for easy rotation with minimal force applied at the handle, rotating about the iron pivot at its centre.
3. Steering wheel rotation technique: In turning a steering wheel, a tangential force is applied to the rim of the wheel. By changing the point of application of force without altering the force's direction, the sense of rotation of the wheel is changed. For instance, applying force F at point A results in anticlockwise rotation, while applying the same force at point B leads to clockwise rotation.
(a) Anticlockwise Rotation
(b) Clockwise Rotation
4. Bicycle steering mechanism: In a bicycle, turning the wheel anticlockwise involves applying a small force on the foot pedal of a toothed wheel, which is larger than the rear wheel. This design, with a substantial perpendicular distance between the point of force application and the axle, enhances the efficiency of turning. The interconnected wheels are linked by a chain running through their teeth.
SOLVED EXAMPLES
Example 1: Find out the torque on the door if a force of 10 N is applied at 0.4 m from the hinge.
Solution:
The torque (τ) exerted on the door can be calculated using the formula:
τ = F r
where:
F is the force applied, and r is the distance from the hinge (axis of rotation) where the force is applied.
Given:
Force (F) = 10 N
Distance from the hinge (r) = 0.4 m
Substitute these values into the formula:
τ = 10N × 0.4m
Now, calculate the result:
τ = 4 Nm
Therefore, the torque on the door is 4 Nm when a force of 10 N is applied 0.4 meters from the hinge.
Example 2: The handle of the door is at a distance of 40 cm from the axis of rotation. If a force of 5 N is applied on the handle in a direction 30o with the plane of the door, then the torque is
Solution:
We have,
Hence, the torque acting on the body is 1Nm.
5.3 COUPLE
5.3.1 What is a couple?
Two equal, unlike parallel forces whose lines of action are not the same constitute a couple. The moment (or) torque of a couple is the product of either force and the perpendicular distance between them. (or)
The moment of a couple is the vector sum of torque produced by the two forces individually about a fixed point.
5.3.2 Examples of couple
1. Opening a nut with a wrench: To loosen the nut of a car wheel, equal forces (denoted as F) are applied at opposite ends of the wrench's arm in opposite directions. This creates a turning effect, allowing the nut to be opened.
Wrench
Fig 5.9(a) Opening the nut of a car wheel with a wrench
2. Turning a water tap: When turning a water tap, a similar principle is applied. Equal and opposite forces are exerted to rotate the tap, regulating the flow of water.
Fig 5.9(b) Turning a water tap
3. Tightening the cap of an inkpot: The action of tightening the cap of an inkpot involves applying a pair of forces in opposite directions, leading to the rotational motion necessary for securing the cap.
4. Turning the key in a lock: Similar to the other examples, turning the key in a lock requires the application of two equal and opposite forces to achieve the rotational motion needed to unlock or lock the mechanism.
5. Winding a clock (or watch) with a key: Winding a clock or watch involves the application of a pair of forces, or a couple, to rotate the key. This winding action stores potential energy in the clock's mechanism.
6. Turning the steering of a motor car: When steering a motor car, a couple of forces are applied to turn the steering wheel. This action results in the rotational motion required to navigate the vehicle.
7. Driving the pedal of a bicycle: The act of driving the pedal of a bicycle involves applying forces in pairs, contributing to the rotational motion of the pedal. This motion is crucial for propelling the bicycle forward.
5.3.3 Moment of couple
The moment of a couple is the vector sum of torque produced by the two forces individually about a fixed point.
12 + τ=ττ
The magnitude of torque is τ = Fdperpendicular
The moment of a couple is constant at any point.
QUICK REVIEW

• A rigid body, when acted upon by a force, can have two kinds of motion: linear or translational motion and rotational motion.
• Translational motion refers to the linear movement of a rigid body when subjected to an external force.
• Rotational motion is characterised by the rotation of a rigid body around an axis when a force is applied at a suitable point while the body is pivoted.
• Angular displacement, θ = s /r
• Angular velocity, ω = Δθ/Δt
• Angular acceleration, α = Δω/Δt
• Torque (τ): It is defined as the turning effect of force about a fixed point.
• Torque is measured as the product of the magnitude of the force and the perpendicular distance of the line of action of the force from the fixed point.
•τ = r⊥ar F
• Moment of force, which tends to produce rotation in the anticlockwise direction, is taken as positive, and in the clockwise direction, it is taken as negative
• Two equal, unlike parallel forces whose lines of action are not the same constitute a couple.
• The moment of a couple is the vector sum of torque produced by the two forces individually about a fixed point. 12 + τ=ττ
WORKSHEET - 1
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
I. Rotational motion
1. How is angular velocity () ω related to linear velocity (v) in a rotating object?

2. If a rotating disc changes its angular speed at the rate of 70rad/s for 10 seconds. Calculate its angular acceleration during this time.
a. 2 0.7rad/s
7rad/s
c. 2 700rad/s d. 2 70rad/s.
3. If an object undergoes uniform circular motion, what can be said about its angular acceleration?
a. It is constant
c. It is increasing
b. It is zero
d. It is decreasing
4. A particle is in circular motion. The direction of the angular velocity is along
a. The tangent to the circular path
c. The outward radius
b. The inward radius
d. The axis of rotation
5. Calculate the angular acceleration of an object if its angular velocity changes at the rate of 50 rad/s for 5 seconds.
6. Calculate the time taken by an object if its angular velocity is 46 rad/s and acceleration is 23 rad/s2. a. 2s
7s
7. Calculate the angular acceleration of an object if its angular displacement is 45 radians and its time is 3 seconds.
8. Calculate the angular acceleration of an object if its angular velocity changes at the rate of 90 rad/s for 4 seconds.
9. A wheel is rotating at 2 radians per second. What is the linear velocity of a point on its rim if the radius is 0.5 meters?
a. 1 m/s
b. 2 m/s
c. 3 m/s
d. 4 m/s
10. If an object is rotating with a constant angular velocity, how does its linear velocity change as you move farther from the axis of rotation?
a. Linear velocity increases
c. Linear velocity remains constant
b. Linear velocity decreases
d. It depends on the mass of the object
11. If an object is not rotating, what can be said about its angular velocity?
a. It is zero
c. It is constant
b. It is infinite
d. It cannot be determined
12. A particle is rotating with constant angular velocity ) (2 ω=++
aijk rad/sec such that the axis of rotation is passing through the origin. When the particle passes the point (1 m, 2 m,3 m), its velocity is found to be v =(42) ij m/s. Then the value of 'a' is
a. 3
b. 2/3
c. 2 d. 1
13. A particle is rotating with a constant velocity of 10 rad/sec about the Z axis. The magnitude of its velocity when it is passing through the point (1 m, 1 m, 1 m) is
a. 103m/s
b. 20m/s
c. 102m/s
d. 52m/s
14. A wheel has an angular acceleration of 3.0 rad/s2 and an initial angular speed of 2.00 rad/s. In a time of 2s, it has rotated through an angle (in radians) of
a. 6
b. 10
c. 12 d. 4
15. If a bicycle wheel is rotating at 120 rpm and has a radius of 0.3 m, what is its angular velocity in rad/s?
a. 2rad/s p
b. 4rad/s p
c. 6rad/s p d. 8rad/s p
16. A wheel starts from rest and experiences an angular acceleration of 6 rad/s2 for 3 seconds. Determine its final angular velocity.
a. 9 rad/s
b. 12 rad/s
c. 15 rad/s d. 18 rad/s
17. When a ceiling fan is switched on, it makes 10 revolutions in the first 3 seconds. Assuming a uniform angular acceleration, how many revolutions will it make in the next 3 seconds?
a. 10
b. 20
c. 30 d. 40
18. A planet is moving around its sun in a circular manner. The angular velocity of the planet is 0.5 rad/s. The distance of the planet from its sun is estimated at 1,00,000 km. Find out the linear velocity of the planet.
a. 5×105 m/s
b. 5×107 m/s c. 50×107 rad/s d. 500×107 m/s
19. A particle moves in a circular path with an angular velocity of 3rad/s and an angular acceleration of 4 rad/s2. If the radius of the circular path is 0.5m, what is the total linear acceleration of the particle at that instant?
a. 5.0 ms-2
b. 3.5 ms-2
c. 5.5 ms-2 d. 4.5 ms-2
20. A body of mass 10 kg revolves in a circle with a diameter 0.4 m, making 1000 revolutions per minute. Calculate its centripetal acceleration.
II. Torque and couple
1. The magnitude of torque is maximum when
a. The radius vector is perpendicular to the force vector
c. The angle between the radius vector and the force vector is 45°
b. The radius vector is parallel to the force vector
d. The angle between the radius vector and the force vector is 60°
2. A circular disc is rotated along clockwise direction in horizontal plane. The direction of torque is
a. Horizontally right side
c. Vertically upwards
b. Horizontally left side
d. Vertically downwards
3. Let be the force acting on a particle, having position vector, r , and be the torque of this force about the origin, then
a. 0andF0 r ⋅τ=⋅τ≠
c. 0andF0 r ⋅τ≠⋅τ≠
0andF0 r ⋅τ≠⋅τ=
4. During the rotation of a body, the position vector is along the x-axis, and the force vector is along the y-axis, then the direction of the torque is
a. Along x–y plane
c. Along +ve z–axis
b. Along –ve z–axis
d. Along x–z plane
5. The direction of position vector r is towards the south, and the direction of force F is towards the east, then, the direction of torque is
a. Towards the north
c. Vertically upward
6. Which of the following is wrong?
b. Towards the west
d. Vertically downward
a. The direction of the torque is parallel to the axis of rotation
b. The direction of the moment of couple is perpendicular to the plane of rotation of a body
c. The torque vector is perpendicular to both the position vector and the force vector
d. The direction of the force vector is always perpendicular to both the directions of position and torque vector
7. The handle of a door is at a distance of 40 cm from the axis of rotation. If a force of 5 N is applied on the handle in the direction of 30° with the plane of the door, then the torque is
a. 0.8 Nm b. 1 Nm c. 1.6 Nm d. 2 Nm
8. A torque of 0.5 Nm is required to drive a screw into a wooden frame with the help of a screwdriver. If one of the two forces of couple produced by the screwdriver is 50 N, the width of the screwdriver is a. 0.5 cm b. 0.75 cm c. 1 cm
1.5 cm
9. Assertion (A): Torque is due to the transverse component of force only. The radial component has no role to play.
Reason (R): This is because the transverse component produces rotation and the radial component opposes the rotation.
a. Both A and R are correct and R is the correct explanation of A.
b. Both A and R are correct and R is not the correct explanation of A.
c. A is correct, R is incorrect.
d. A is incorrect, R is correct.
10. The mathematical expression of torque is
11. Torque produced by a force about an axis can be zero if
a. The force vector passes through the axis of rotation
b. The force vector is parallel to the axis of rotation
c. The force vector is perpendicular to the axis of rotation
d. Both a and b
Both a & b
12. If F(2i3j)N =− and r(3i2j)m =+ , then torque is
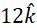
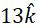
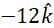
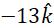
13. Find the torque of a force ˆˆ ij ˆ 7+3-5k about the origin. The force action of a particle whose position vector is ˆ i ˆˆ jk-+ a. ˆˆ 2 ˆ i12j10k ++
ˆ i ˆˆ jk-+
ˆ i ˆˆ jk++
ˆˆ ijk ˆ 10 ++
14. What constant torque should be applied to a disc of mass 10 kg and diameter 50 cm so that it acquires an angular velocity of 2π rad s-1 in 4s? The disc is initially at rest and rotates about an axis through the centre of the disc and in a plane perpendicular to the disc
a. 0.49 Nm b. 0.049 Nm c. 4.9 Nm
15. In which of the following cases can we produce a couple?
a. When we turn a doorknob
c. While spinning a ball
WORKSHEET - 2
490 Nm
b. When we use a screwdriver
d. All the above
MULTIPLE CHOICE QUESTIONS WITH SINGLE CORRECT ANSWER
1. The physical quantities that are variable in uniform circular motion are
a. Speed
c. Centripetal acceleration
b. Magnitude of acceleration
d. Angular velocity
2. The direction of angular acceleration of a body moving in a circle in the plane of the paper is
a. Along the tangent
c. Along the radius outward
b. Along the radius inward
d. Along perpendicular to the plane of the paper
3. A particle is acted upon by a force of constant magnitude, which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
a. Its velocity is constant
c. Its KE is constant
b. Its acceleration is constant
d. It moves in a circular path
4. In case of uniform circular motion, choose the correct statement.
a. The direction of centripetal force depends upon the direction of rotation
b. The direction of centripetal force does not depend upon the direction of rotation
c. The direction of centripetal force is towards the centre of the circular path
d. Both b and c
5. A body is in pure rotation and ω=ν/r
a. The particle at a larger distance from the axis has a smaller angular velocity
b.ω is ∞ for the particles that are closer to the axis of rotation
c ω is independent of r
d.ω is 0 for all particles
6. The magnitude of .v ω
a. zero b. 1 c ∞ d. vω
7. According to Bohr's theory, an electron revolves around the nucleus in a circular orbit in an atom with constant angular velocity. The necessary centripetal force is provided by
a. Electrostatic force between the nucleus and electron
b. Gravitational force between the nucleus and electron
c. Nuclear force between the nucleus and electron d. Tension force between the nucleus and electron
8. Many great rivers flow towards the equator; what effect does the sediment they carry to sea have on the rotation of the earth?
a. The rotation of the earth slows down
c. No effect on the rotation of the earth
b. The rotation of the earth speeds up
d. None
9. Statement (A): A rigid body executes both translatory and rotatory motion
Statement (B): A rigid body executes pure rotational motion when it is acted upon by an unbalanced torque
a. A is false, B is true
c. A is true, B is false
b. Both A and B are true
d. Both A and B are false
10. If the second hand of a watch completes one revolution in 1 minute, then the average angular velocity is
a π/10 rads-1 b π/20 rads-1 c. π/30 rads-1 d π/15 rads-1
11. The average angular velocity of the spinning of the earth is
c. 3π 43,200 rads-1
7π 21,600 rads-1
12. When a motorcyclist takes a U-turn in 4 seconds, the average angular velocity of the motor cyclist is
π rad s-1
π/2 rad s-1
π/3 rad s-1
π/4 rad s-1
13. A ball of mass 200g is on one end of a string of length 20 cm. If it is revolved in a horizontal circle at an angular frequency of 6 rpm, then the angular velocity is a π/5 rad s-1
2π/3 rad s-1
7π/5 rad s-1
3π/5 rad s-1
14. A wheel is making revolutions about its axis with uniform acceleration. Starting from rest, it reaches 100rev/s in 4 seconds. The angular acceleration is
a. 5 rev/s2
c. 100 rev/s2
b. 25 rev/s2
d. 500π radians/s2
15. A wheel is making revolutions about its axis with uniform acceleration. Starting from the rest, it reaches 100 rev/s in 4 seconds. What is the angle rotated during these 4 seconds?
a. 400π rad
200π rad
50π rad
75π rad
16. A wheel is rotating with uniform angular acceleration, and it covers 50 revolutions in the first five seconds after the start. The angular acceleration of the wheel is
a. 2rev/s2
b. 3 rev/s2
c. 4 rev/s2
d. 7 rev/s2
17. A circular disc is rotating about its own axis. An external opposing torque of 0.02Nm is applied on the disc by which it comes to rest in 5 seconds. The initial angular momentum of the disc is
a. 0.1 kg2s-1
b. 0.04 kg2s-1
c. 0.025 kg2s-1
d. 0.01 kg2s-1
18. The acceleration of a train travelling at 40 m/s as it goes around a curve of 160 m in radius is
a. 10 ms2
b. 20 ms2
c. 30 ms2
d. 40 ms2
19. A particle moves in a circle of radius 20 cm. Its linear speed is given by v=2t where ' t ' is in second and ' v ' in metre/ second. Find the radial and tangential acceleration at t=3 s
a. 6 ms-2, 4 ms-2
c. 120 ms-2, 160 ms-2
b. 60 ms-2, 40 ms-2
d. 180 ms-2, 2 ms-2
20. A particle moves in a circular path with decreasing speed. Choose the correct statement.
a. Angular momentum remains constant. b. Acceleration (a ) is towards the centre.
c. Particle moves in a spiral path with decreasing radius d. The direction of angular momentum remains constant
21. A point mass is rotating in a horizontal circle with constant angular acceleration. Initial angular velocity is 20π radian/second, which changes to 40π radian/second in a time span of 10 seconds. Calculate the total number of revolutions in this time interval.
a. 150 b. 1500 c. 1.5
22. The axis of rotation of a purely rotating body
15
a. May pass through a particle of the body b. Must pass through a particle of the body
c. May pass through the centre of mass d. Must pass through the centre of mass
23. A metallic circular wheel is rotating about its own axis without friction. If the radius of the wheel expands by 0.2%, the percentage change in its angular velocity
a. Increases by 0.1%
c. Increases by 0.2%
b. Decreases by 0.2%
d. Decreases by 0.4%
24. The shaft of a motor rotates at a constant angular velocity of 12000 r.p.m. The radians it has turned in 1 second are
a. 4000
25. A force of F23ijk=+ acts at a point (2, -3, 1). Then, the magnitude of torque about the point (0, 0, 2) will be :
a. 6 units b. 35 units c. 65 units d. 85 units
26. Find the torque about the origin when a force of 3j N acts on a particle whose position vector is 2km
27. The moment of the force,
ˆˆ 87
4 ijk
74
8 ijk
F456kat(2
,0,3) ij =+--
, about the point (2,-2,-2), is given by:
28. What is the torque exerted by a force of 10 N applied at a distance of 2 meters from the axis of rotation at an angle of 60o?
a. 102Nm b. 10Nm c. 103Nm d. 1003Nm
29. The angular velocity of a minute's hand in a wall clock is: (in rad-1)
30. The moment of force applied on a door is 18 Nm, and a force of 4.5 N is applied by a boy; the distance of the handle from the pivot is
a. 0.25 m
0.75 m
2.25 m
4.0 m
31. According to Kepler's laws, a planet moves in an elliptic orbit with the sun at a focus of the ellipse. Taking the planet and the sun to be point masses, the torque on the planet with respect to the sun [Hint: As force is central τ=0 ]
a. Is zero at all times
c. Can be non-zero but constant in time
b. Varies with time
d. Cannot be defined for an elliptical orbit
32. The diameter of a solid disc is 0.5 m, and its mass is 1.6 kg. What torque is required to increase its angular velocity about an axis perpendicular to its plane from zero to 120 rotations/minute in 8 seconds?
a. 10N/m p b. 20N/m p c. /20 N/m p
33. If r(2ij)m;F(i2j) =+=+
N, then the magnitude and direction of torque is
a. 4 Nm along 45° with x–axis (or) y–axis
/40 N/m p
b. 3 Nm along 45° with x–axis (or) y–axis
c. 4 Nm along z-axis d. 3 Nm along z-axis
34. Given, ˆˆ F(2i3)N ˆ jk=+ and ˆˆ r(ij6m ˆ k) =-+
. Find the torque of this force.
a. ˆˆ (17i13jm ˆ 5k)N -++ b. ˆˆ (17i13j5k)Nm ˆ ++
c. ˆˆ (17i13jm ˆ 5k)N --+ d. ˆˆ (17i13j10k)Nm ˆ -++
35. Among the following, the incorrect statement for moment of force is
a. Moment of force has dimensions [ML2 T-2]
b. S.I unit of moment of force N-m
c. Moment of force which tends to produce rotation anticlockwise is taken as positive.
d. Moment of force which tends to produce rotation anticlockwise is taken as negative.
2: THE HUMAN EYE AND THE COLOURFUL WORLD Worksheet 1
I.The human eye, defects of vision, and their corrections
Ohm’s law, electrical resistivity,
