Headstart - Math Coursebook 5

Aligned with NEP 2020

COURSEBOOK

With HEADSTART APP

MATHS COURSEBOOK

Aligned with NEP 2020

Headstart Maths Coursebook - Class 5

Legal Disclaimer

This book is intended for educational purposes only. The information contained herein is provided on an “as-is” and “as-available” basis without any representations or warranties, express or implied. The authors (including any affiliated organizations) and publishers make no representations or warranties in relation to the accuracy, completeness, or suitability of the information contained in this book for any purpose.

The authors (including any affiliated organizations) and publishers of the book have made reasonable efforts to ensure the accuracy and completeness of the content and information contained in this book. However, the authors (including any affiliated organizations) and publishers make no warranties or representations regarding the accuracy, completeness, or suitability for any purpose of the information contained in this book, including without limitation, any implied warranties of merchantability and fitness for a particular purpose, and non-infringement. The authors (including any affiliated organizations) and publishers disclaim any liability or responsibility for any errors, omissions, or inaccuracies in the content or information provided in this book.

This book does not constitute legal, professional, or academic advice, and readers are encouraged to seek appropriate professional and academic advice before making any decisions based on the information contained in this book. The authors (including any affiliated organizations) and publishers disclaim any liability or responsibility for any decisions made based on the information provided in this book.

The authors (including any affiliated organizations) and publishers disclaim any and all liability, loss, or risk incurred as a consequence, directly or indirectly, of the use and/or application of any of the contents or information contained in this book. The inclusion of any references or links to external sources does not imply endorsement or validation by the authors (including any affiliated organizations) and publishers of the same.

All trademarks, service marks, trade names, and product names mentioned in this book are the property of their respective owners and are used for identification purposes only.

No part of this publication may be reproduced, stored, or transmitted in any form or by any means, including without limitation, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the authors (including any affiliated organizations) and publishers.

The authors (including any affiliated organizations) and publishers shall make commercially reasonable efforts to rectify any errors or omissions in the future editions of the book that may be brought to their notice from time to time.

Subject to Hyderabad jurisdiction only.

Copyright © 2024 Rankguru Technology Solutions Private Limited. All rights reserved.

ISBN 978-81-967554-1-6

First Edition

Preface

Dear Parents, Educators, and Guardians,

In the ever-evolving landscape of education, the National Education Policy (NEP) 2020 is a pivotal milestone, emphasizing the critical role of ages 3 to 6 in shaping a child’s mental faculties. Moving away from the traditional method of memorization, it highlights the significance of key learning goals, places a greater emphasis on multidisciplinary education, and aims to nurture the creative talents of every learner.

Aligned with the visionary NEP 2020, we proudly introduce the “HeadStart Programme” by Infinity Learn— an innovative educational initiative meticulously designed to fortify your child’s foundation during their most formative years. Tailored for Grades 1 to 5, this program aims to instil a passion for learning and establishes a formidable academic base.

The HeadStart Program unfolds a tailored educational experience, commencing with Grades 1 and 2, where the focus lies on making numbers (Math) comprehensible and fostering exploratory learning in Environmental Studies (EVS). Progressing into Grades 3, 4, and 5, the program expands to encompass critical mathematical thinking, exploration of Science, and a nuanced understanding of society, environment, and global citizenship in Social Studies.

Equipped with thoughtfully crafted course books, home reinforcement workbooks, and a cutting-edge learning app, the HeadStart Program leverages both traditional and digital tools to ensure a comprehensive educational experience.

What is the HeadStart Advantage?

We firmly believe that enhancing creativity, logical and critical thinking in the early years will pave the way for a robust foundation in Mathematics and Science during the middle years. This, in turn, positions learners for success in senior-grade challenges, differentiating them in high-stakes exams such as JEE, NEET, and CUET.

For educators, we provide meticulously designed lesson plans and in-class videos, ensuring uniform and effective teaching methodologies. Our mission encapsulates the question ‘Baccha Seekha ki Nahi’—did the child learn?—as we are dedicated to ensuring that each child’s learning journey is not merely a progression but a meaningful and enriching experience.

We invite you to join us in this exciting new chapter of your child’s education. The “HeadStart Programme” is more than a curriculum; it’s a pathway to nurturing a lifelong passion for learning. Let’s provide our children with the optimal start in their educational journey.

Warm regards,

The Infinity Learn Team

Large Numbers

My Study Plan

Large numbers

Indian place value system

Comparing and ordering numbers

Forming numbers

Predecessor and successor

International place value system

Rounding off the numbers

Roman numerals

Let’s Recall

Write the smallest and the greatest 6-digit numbers using the digits 1, 6, 3, 5, 4 and 7 only once.

Smallest number = __________________.

Greatest number = __________________.

Thinking Zone

How many different 4-digit numbers can be formed using the digits 1 and 5?

Let’s Learn

Large Numbers

Look at the given abacus. It represents the greatest 6-digit number, i.e., 9,99,999.

We read it as nine lakh ninety-nine thousand nine hundred ninety-nine.

On adding 1 to 9,99,999 (9,99,999 + 1), we get 10,00,000.

10,00,000 is the smallest 7-digit number. We read it as ‘ten lakhs’.

Similarly, the below abacus represents the greatest 7-digit number i.e., 99,99,999.

We read it as ninety-nine lakh ninety-nine thousand nine hundred ninety-nine.

TTh L Th H T O

On adding 1 to 99,99,999 (99,99,999 + 1),we get 1,00,00,000.

1,00,00,000 is the smallest 8-digit number. We read it as ‘one crore’.

Similarly the below abacus represents the greatest 8-digit number i.e., 9,99,99,999.

We read it as nine crore ninety-nine lakh ninety-nine thousand nine hundred ninety-nine.

On adding 1 to 9,99,99,999 i.e., (9,99,99,999 + 1),we get 10,00,00,000.

10,00,00,000 is the smallest 9-digit number. We read it as ‘ten crores’.

TTh

Indian Place Value System

In India, we use the Indian place value system, which has main four periodsones, thousands, lakhs and crores

The ones period has three places for ones, tens, and hundreds, while the other periods have two places each.

INDIAN PLACE VALUE CHART

PERIODS CRORES

(TL)

(L)

DIGITS

To write a 7-digit, 8-digit or a 9-digit number, we group the digits according to these periods and use commas to separate them.

Starting from the right, the first comma is placed after 3 digits; then the next commas are placed after every 2 digits.

For example: 39742011 can be re-written as 3,97,42,011.

When reading or writing the numbers in words, we start with the crores’ period, then move to the number in the lakhs’ period, then move on to the thousands’ period and finally, the number in the ones’ period.

The digits in the same period are read or written in words together along with the name of the period in singular form, except for the ones period; we do not write its period name.

Example:

20,97,194 can be read or written in words as twenty lakh ninety-seven thousand one hundred ninety-four.

Example 1: Your family has `103459871 in the bank. Insert commas suitably and write 103459871 according to the Indian place value system.

Solution:

So, 103459871 = 10,34,59,871 and can be read or written in words as ten crore thirty-four lakh fifty-nine thousand eight hundred seventy-one.

Let’s Learn

Face Value and Place Value

The face value of a digit in a number remains the same. It doesn’t depend on the position of the digit.

For example, in the number 85,03,941:

• The face value of 8 is 8.

• The face value of 5 is 5.

• The face value of 0 is 0.

• The face value of 3 is 3.

• The face value of 9 is 9.

• The face value of 4 is 4.

• The face value of 1 is 1.

The place value of a digit is determined by its position in a number.

The place value of a digit is equal to the product of the digit and the value of the place it occupies.

To find the place value of a digit, we can use the formula:

Place Value = Face Value × Position of the Digit in the Number

For example, the place values of all the digits in 34,19,75,052 are as follows:

5,000 70,000 9,00,000 10,00,000 4,00,00000 30,00,00,000 Place Value

1. Identify and write the number represented on each abacus according to the Indian place value system.

a. The number shown on this abacus is __________.

b. The number shown on this abacus is __________.

2. Insert commas suitably and write the number names of the following, according to Indian place value system.

a. 2153475 = ______________________________________________

b. 17894673 = ______________________________________________

3. Write the numerals and place the commas correctly.

a. Three crore fifty-one lakh twenty-one thousands three hundred seven = __________.

b. Seventy one lakh two thousand two hundred ten = __________.

4. The place value of 5 in 75,43,218 is _________________ .

5. The face value of 8 in 89,765,431 is ___________________.

Let’s Learn

Comparing and Ordering Numbers

Comparing numbers

Comparing numbers helps us find which one is greater or smaller.

We have already learnt that:

• The > sign stands for ‘greater than’

• The < sign stands for ‘less than’

• The = sign stands for ‘equal to’

We also know how to compare small numbers. The same rules apply to large numbers as well.

1. Start by comparing the number of digits in the two numbers. The one with more digits is greater.

For example: 1097432 and 209812

1097432 has seven digits.

209812 has only six digits.

So, 10,97,432 > 20,98,12.

2. If both numbers have the same number of digits, compare them digit by digit from left to right. Stop at the first place where you find different digits. The number with the larger digit at that place is greater.

For example: 220822 and 224091

Here, 220822 and 224091 both have the same number of digits, i.e., 6

To compare them, we need to follow the given steps:

Step 1: Write the digits of the two numbers in a place value chart as shown below.

Step 2: Look at the digits in the lakhs and ten thousands place of the two numbers. They are the same.

Step 3: Look at the digits in the thousands place of the two numbers. They are different.

Here, 4 > 0.

So, 2,24,091 > 2,20, 822.

Example: The population of Pihu’s city is 548197389 people, while the population of a nearby city is 543297388 people. Which city has a higher population?

Solution:

To find the answer, we compare the two numbers: 548197389 and 543297388. Here, both the numbers have 9 digits.

Step 1: Write the digits of the two numbers in a place value chart as shown below.

Step 2: Look at the digits in the ten crores and crores places of both the numbers. They are the same.

Step 3: Look at the digits in the ten lakhs place of the two numbers. They are different.

Here, 8 > 3.

So, 54,81,97,389 > 54,32,97,388.

So, Pihu’s city has a higher population.

Ordering numbers

Ordering numbers means arranging numbers in a specific order. Numbers can be ordered in two ways: ascending order and descending order.

Ascending order

Ascending order is arranging the numbers from the smallest to the greatest.

For example: 1 < 2 < 3 < 4 < 5.

Descending order

Descending order is arranging the numbers from the greatest to the smallest.

For example: 5 > 4 > 3 > 2 > 1.

Example 1:

Write the following numbers in ascending and descending order.

6,67,049

14,65,824

7,987

9,95,313

Solution:

First compare the numbers.

Here,

6,67,049 has six digits.

14,65,824 has seven digits.

7,987 has four digits.

9,95,313 has six digits.

So, 14,65,824 has maximum number of digits and 7,987 has least number of digits. Whereas 6,67,049 and 9,95,313 have equal number of digits.

We know the number with more digits is greater and the one with fewer digits is smaller.

So, 14,65,824 is the greatest and 7,987 is the smallest.

Now comparing the numbers with same number of digits i.e., 6,67,049 and 9,95,313.

Step 1: Write the digits of the two numbers in a place value chart as shown below.

Step 2: Look at the digits in the lakhs place of both numbers. They are different.

Here, 9 > 6.

So, 9,95,313 > 6,67,049.

And we have 14,65,824 as the greatest and 7,987 as the smallest numbers. Therefore, the ordering is as follows:

Ascending order: 7,987 < 6,67,049 < 9,95,313 < 14,65,824 (smallest to greatest)

Descending order: 14,65,824 > 9,95,313 > 6,67,049 > 7,987 (greatest to smallest)

Let’s Practise - 2

1. Compare the following using <, > or =.

a. 55432562 ______ 65264652

b. 234581822 ______ 256482288

c. 983098 ______ 983483

d. 7041581 _____ 0704581

2. Write the following sets of numbers in ascending and descending order.

a. 19,23,54,208

53,64,802

94,64,008

3,12,24,802

Ascending order:

Descending order:

b. 1,41,29,412

1,14,29,214

1,18,39,412

1,08,90,900

Ascending order:

Descending order:

Let’s Learn

Forming the Greatest and the Smallest Numbers

We can arrange numbers in ascending or descending order to form the greatest and the smallest numbers using a given set of digits.

To form the greatest number from a given set of digits, arrange them in descending order.

For example, with the digits 6, 5, 1, 3, and 4

Descending order is 6 > 5 > 4 > 3 > 1.

So, the greatest number is 65,431.

To form the smallest number, arrange the digits in ascending order. If one of the given digits is 0, always write 0 at the second place from the left instead of the extreme left to get the smallest number.

For example, with the digits 7, 2, 0, 4, and 1.

Ascending order is 0 < 1 < 2 < 4 < 7.

So, the smallest number is 01247, but since it is not a 5-digit number, we cannot place 0 in the 1st place from the left. Instead, we shift 0 to the 2nd place from the left.

Therefore, the smallest number is 10247.

Example 1: Form the greatest and smallest 7-digit numbers using the digits 7, 4, 8, 6, 5, 2, 1. Use each digit only once.

Solution: To form the greatest 7-digit number, arrange the digits in descending order

8 > 7 > 6 > 5 > 4 > 2 > 1

Hence, the greatest 7-digit number is 87,65,421.

To form the smallest 7-digit number, arrange the digits in ascending order

1 < 2 < 4 < 5 < 6 < 7 < 8

Hence, the smallest 7-digit number is 12,45,678.

Example 2: Form the greatest and smallest 8-digit numbers with the digits 5, 4, 7, 8, 6, 1, 0, 2 used only once.

Solution: To form the greatest 8-digit number, arrange the digits in descending order

8 > 7 > 6 > 5 > 4 > 2 > 1 > 0

Hence, the greatest 8-digit number is 8,76,54,210.

To form the smallest 8-digit number, arrange the digits in ascending order

0 < 1 < 2 < 4 < 5 < 6 < 7 < 8

To make it the smallest 8-digit number, place the digit 0 at second place from the left.

Hence, the smallest 8-digit number is 1,02,45,678.

‘FORTY’ is the only number that has its letters in alphabetical order, and ‘ONE’ is the only number that has its letters in the reverse alphabetical order.

Let’s Practise - 3

1. Form the smallest and the greatest numbers using the given digits only once.

a. 9, 4, 5, 0, 8, 7, 3, 2

Smallest number =

Greatest number =

b. 4, 0, 8, 2, 3, 6, 1

Smallest number =

Greatest number =

c. 8, 0, 9, 5, 1, 2, 7, 3

Smallest number =

Greatest number =

Successor and Predecessor

The successor of any number is the number that comes just after it.

The successor of any number can be found by adding 1 to it.

For example, the successor of 1244 = 1244 + 1 = 1245.

The predecessor of any number is the number that comes just before it.

The predecessor of any number can be found by subtracting 1 from it

For example, the predecessor of 1244 = 1244 – 1 = 1243.

Example 1: Find the predecessor and successor of 2,34,54,879.

Solution:

Predecessor of 2,34,54,879 = 2,34,54,879 – 1

Hence, the predecessor of 2,34,54,879 is 2,34,54,878.

Successor of 2,34,54,879 = 2,34,54,879 + 1

Hence, the successor of 2,34,54,879 is 2,34,54,880.

1. Write the predecessor of the followings number.

a. _________________, 23355641 b. _________________, 20309754

c. _________________,18093331

d. _________________, 9873003

2. Write the successor of the following numbers.

Let’s Practise - 4 Let’s Learn

a. 42089832, _________________

c. 90814114 , _________________

b. 87549791 , _________________

d. 30938343 , _________________

International Place Value System

The International place value system is used in many countries around the world.

In this system, the periods are ones, thousands, and millions. Each period consists of three places.

Like the Indian place value system, the international place value system also uses commas to separate periods. Starting from the right, every comma is placed after 3 digits.

For example, 285259113 can be written as 285,259,113.

When reading or writing the numbers in words, we start with the millions’ period, then move to the number in the thousands’ period, and finally, the number in the ones’ period.

The digits in the same period are read or written in words together along with the name of the period in singular form, except for the ones period we do not write its period name.

Example:

285,259,113 is read or written in words as “Two hundred eighty-five million two hundred fifty-nine thousand one hundred thirteen.”

1. Insert commas suitably and write the number names of the following, according to the international place value system.

a. 76168729 = ______________________________________________ ______________________________________________

b. 48845367 = ______________________________________________ ______________________________________________.

c. 8359498 = ______________________________________________ ______________________________________________.

d. 4805029 = ______________________________________________ ______________________________________________.

2. Place the commas correctly and write the numerals.

a. Seventy-five million eight hundred twenty-six thousand four hundred forty-two _______________________.

b. Fifty-seven million ninety-six thousand four hundred twenty-nine _______________________.

c. Nine million three hundred eighty-seven thousand two hundred forty-six _______________________.

d. Sixty million two hundred thirty-four thousand one hundred eleven _______________________. Let’s Practise - 5

Let’s Learn

Rounding Off

Rounding off is a method of estimating or making a guess. We use estimation when we need to calculate quickly and when the exact answer is not important. Rounding off involves finding a number that is close to the original number and easy to recall.

For example, expressing the population of a town as 7,54,000 is easier than using the exact figure of 7,54,369.

When we round a number to a lower value, it is called rounding down and when we round it to a higher value, it is called as rounding up.

Rounding off to the nearest tens

To round off a number to the nearest tens, check the ones digit.

If the digit at ones place is 5 or greater than 5, then change the tens digit into its successor and place 0 at ones place.

For example:

If we round off 23,357 to the nearest tens place, the answer will be 23,360.

As the ones place is more than 5, the tens place digit will change to its successor.

If the digit at ones place is less than 5, then keep the tens place digit the same and put 0 at ones place.

For example:

If we round off 13,472 to the nearest tens place, then the answer will be 13,470.

As the digit at ones place is less than 5, the tens place digit will not change.

Rounding off to the nearest hundreds

To round off a number to the nearest hundreds, check the tens digit.

If the digit at tens place is 5 or more than 5, then change the hundreds digit into its successor and put 0 at tens place and ones place.

For example:

If we round off 23,367 to its nearest hundreds place, the answer will be 23,400.

As the tens place is more than 5, the hundreds place digit will change to its successor.

If the digit at tens place is less than 5, then keep the hundreds place digit the same and put 0 at tens place and ones place.

For example:

If we round off 13,422 to the nearest hundreds place then the answer will be 13,400.

As the digit at tens pace is less than 5, the hundreds place digit will not change.

Rounding off to the nearest thousands

To round off a number to nearest thousands, check the hundreds place digit.

If the digit at hundreds place is 5 or more than 5 then change the thousands place digit into its successor and put 0 at hundreds, tens, and ones place.

For example:

If we round off 11,649 to its nearest thousands place digit then the answer will be 12,000.

As the hundreds place digit is more than 5, the thousands place digit will change to its successor.

If the digit in the hundreds place is less than 5 then keep the thousands place digit the same and put 0 at hundreds, tens, and ones place.

For example:

If we round off 12,443 to the nearest thousands place digit then the answer will be 12,000. As the hundreds place digit is less than 5, the thousands place digit will not change.

Let’s Practise - 6

1. Round off the following numbers to the nearest tens.

a. 34115 = _______

b. 33723 = ________

2. Round off the following numbers to the nearest hundreds.

a. 38918 = ________

b. 231026 =________

3. Round off the following numbers to the nearest thousands.

a. 972021 = ________

b. 750912 =________

Let’s Learn

Roman Numerals

The Roman numeral system is an ancient numeral system used by Romans. They used combinations of symbols to represent numbers.

Ancient Romans used the 7 symbols: I, V, X, L, C, D, and M to represent numbers.

Roman numerals in Hindu-Arabic system

I represents 1

V represents 5

X represents 10

L represents 50

C represents 100

D represents 500

M represents 1000

Rules for writing Roman numerals

Rule 1

When a symbol is repeated, its value is added as many times as it occurs.

For example, III = 1 + 1 + 1 = 3, or XX = 10 + 10 = 20.

Rule 2

The symbol can be repeated up to three times only. But the symbols V, L and D are never repeated.

For example, we cannot write IIII or VV.

Rule 3

When a symbol of smaller value is written to the right of a symbol of greater value, the result is the sum of the values.

For example, VIII = 5 + 1 + 1 + 1 = 8, or, XV = 10 + 5 = 15.

Rule 4

When a symbol of a smaller value is written to the left of a symbol of greater value, the result is the difference of the values.

For example, IV = 5 – 1 = 4, or XL = 50 – 10 = 40.

Rule 5

We can write a symbol of a smaller value to the left only once to subtract it from symbol of a greater value.

For example, we cannot write IIV.

Rule 6

The symbols V, L and D are never written to the left of a symbol of a greater value, i.e., V, L and D are never subtracted.

For example, we cannot write VX.

Rule 7

I can be subtracted only from V and X

X can be subtracted only from L, M, and C.

Rule 8

When a symbol of a smaller value is between two symbols of greater value, it is subtracted from the symbol on its right.

For example, XIV = 10 + (5 - 1) = 14

Rule 9

Roman numerals do not follow the place value system.

Rule 10

There is no symbol for zero (0) in Roman numerals.

Following these rules, we can write:

Roman Numerals for 1 to 20

Example 1: Write 37 using Roman Numerals.

Solution:

Step 1: Break the given number into simpler numbers.

37 = 30 + 7 = (10 + 10 + 10) + (5 + 2)

Step 2: Replace the numbers with Roman symbols.

= X + X + X + V + II

Step 3: Combine all the symbols together to get the final answer. = XXXVII

Therefore, 37 can be written as XXXVII.

Example 2: Write 61 using Roman Numerals.

Solution:

Step 1: Break the given number into simpler numbers.

61 = 50 + 10 + 1

Step 2: Replace the numbers with Roman symbols.

= L + X + I

Step 3: Combine all the symbols together to get the final answer. = LXI

Therefore, 61 can be written as LXI.

Let’s Practise - 7

1. Write the Roman numerals for the following numbers.

a. 44 = ____.

c. 59 = ____.

b. 48 = ____.

d. 79 = ____.

2. Write the Hindu-Arabic number for the following Roman numerals.

a. LXXXIV = _________.

c. XLVIII = _________.

Let’s Sum Up

b. XCII = _________.

d. LXVIII = _________.

10,00,000 is the smallest 7-digit number, and 99,99,999 is the greatest 7-digit number.

1,00,00,000 is the smallest 8-digit number, and 9,99,99,999 is the greatest 8-digit number.

10,00,00,000 is the smallest 9-digit number.

The Indian place value system has four periods: ones, thousands, lakhs, and crores.

The ones period has three places while the other periods have two places each.

The International place value system has three periods: ones, thousands, and millions. In this system, each periods consists of three places.

Rounding off is a way of estimating. We use estimation when we want to calculate quickly and when the exact answer is not important.

Life Skills

You are an artist planning to sell your artwork. Two buyers have expressed interest. The first person is ready to pay ₹97,40,971 and the second person is ready to pay ₹97,44,910. To determine whose offer is better, which amount should you choose, and why?

Cross-Curricular Connections

Science:

You are studying about the distance from the Sun to the Earth, which is roughly 149600000 kilometres. Write this distance in words using both the Indian and the International place value systems.

21st Century Skills

Make a chart explaining the Roman numeral system. Use the internet to learn more about when this system was invented or first used. Decorate your chart with pictures.

Extend Your Knowledge

In Roman numerals we only have 7 symbols.

To represent large numbers in Roman numeral, we put a bar (a line) over symbol which mean it is multiplied by 1000.

For example:

V represents 5,000 (V multiplied by 1,000)

X represents 10,000 (X multiplied by 1,000)

Tip for the Parent

Encourage your child to compare the distances and identify which places are closer and which are away to develop the understanding of large numbers.

For example: You could look up the distances between your home city and various places you have travelled to.

Operations with Large Numbers 2

My Study Plan

• Addition of large numbers

• Subtraction of large numbers

• Multiplication of large numbers

• Division of large numbers

• Estimation in operations

Let’s Recall

1. Write the face value and place value of the coloured digit in each number given below.

2. Form the greatest and smallest 6-digit numbers using the digits 8, 5, 0, 2, 3 with repetition.

a. Greatest number: _______________________________________________

b. Smallest number: _______________________________________________

3. Form the greatest and smallest 5-digit numbers using the digits 7, 8, 9, 0, 1 without repetition.

a. Greatest number: ________________________________________________

b. Smallest number: ________________________________________________

4. Write the predecessor and successor of each of the following numbers. a.

Thinking Zone

Which of the following is correct and why?

13 + 2 × 3 – 1 = 18

13 + 2 × 3 – 1 = 44

Discuss with your teacher.

Let’s Learn

Addition of Large Numbers

We know the four basic operations: addition, subtraction, multiplication, and division. These are called fundamental operations. These operations are performed with large numbers exactly in the same way as with smaller numbers. Let’s learn about the first fundamental operation, that is addition.

Here are the steps to follow:

Step 1: Write the numbers one below the other, ensuring that the ones are under ones, tens are under tens, and so on.

Step 2: Start adding from the rightmost column (ones) and move to the left, adding one column at a time.

Step 3: If the sum in a column is more than 9, you may need to carry over the extra to the next greater place value column.

Let us understand this better with some examples.

Example 1: Add 76,81,364 to 15,71,531.

Solution: To add 76,81,364 and 15,71,531, we simply add the corresponding digits in each place value.

So, when we add 76,81,364 and 15,71,531, the sum we get is 92,52,895.

Example 2: Add 1,83,94,568 to 1,57,45,531.

Solution: To add 1,83,94,568 and 1,57,45,531, we add the corresponding digits in each place value.

So, when we add 1,83,94,568 and 1,57,45,531, the sum we get is 3,41,40,099.

Properties of addition

The properties of addition are the rules we can follow when adding numbers. Using these properties makes calculations easier and helps solve tricky problems in math.

Let’s learn the main properties of addition.

Identity Property: The identity property of addition states that when a number is added to 0, the sum is always the number itself.

For example:

• 7521 + 0 = 7521

• 3095 + 0 = 3095

Commutative Property: The commutative property of addition states that we can add two numbers in any order, and the sum will remain the same.

For example:

• 21 + 25 = 25 + 21 = 46

• 250 + 300 = 300 + 250 = 550

Associative Property: According to the associative property of addition, changing the grouping of numbers does not affect the sum of numbers.

For example:

• (8 + 4) + 6 = 8 + (4 + 6) = 18

• (2 + 9) + 1 = 2 + (9 + 1) = 12

Let’s Practise - 1

1. Add the following numbers.

2. Add the numbers 97, 134, and 203 using the associative property of addition.

3. Find the missing number using the property of addition.

360 + (495 + 810) = (360 + 495) + _______

4. Fill in the blanks:

a. 12453648 + 0 = _____

b. 3773939 + 1 = ______

c. 2312334 + 1211484 = 1211484 + _________

d. 54 + (83 + 66) = (54 + 66) + ____

Let’s Learn

Subtraction of Large Numbers

When we subtract, we take away one number from another to find the difference.

Here are the steps to follow:

Step 1: Write the larger number on top and the smaller number below it.

Step 2: Start subtracting from the rightmost column (ones) and move to the left, subtracting in one column at a time.

Step 3: If a digit in the above number is smaller than the one below it, you might need to borrow or regroup from the next greater place value column.

Let’s understand this with an example.

Example: Find the difference of 34,148 and 21,389.

Solution:

Starting from the rightmost column (ones), 8 minus 9 is not possible, so we borrow 1 from the tens column.

Now, 18 minus 9 equals 9.

Similarly, we subtract the digits in other columns.

So, 34,148 minus 21,389 equals 12,759.

Properties of Subtraction:

Now let us learn the properties of subtraction.

1. When a number is subtracted from itself, the result is always 0.

For example:

• 7521 – 7521 = 0

• 3095 – 3095 = 0

2. When 0 is subtracted from a number, the difference is the number itself.

For example: • 1628 − 0 = 1628

Let’s Practise - 2

1. Solve the following:

a. 52675 – 51238

b. 434720 – 342541

c. 76528354 – 56416214

2. Fill in the blanks:

a. 8745164 – 1 = ________

b. 8322498 – 0 = ________

c. 23456253 – 23456253 = ________

Let’s Learn

Multiplication of Large Numbers

When we multiply two numbers, the first number is called the multiplicand, and the second number that multiplies it, is called the multiplier. The result obtained after multiplying them is called the product.

Example:

Multiplicand Multiplier Product

Let us say that we have a 5-digit number such as 54,218, and we want to multiply it by a 3-digit number such as 413. Here is how you can do it step by step:

Step 1: Arrange the digits in the multiplicand and multiplier correctly.

Step 2: Multiply the multiplicand by the digit in the ones place of the multiplier.

Multiply 54218 by 3.

Step 3: Multiply the multiplicand by the digit in the tens place of the multiplier.

Multiply 54218 by 1.

Step 4: Multiply the multiplicand by the digit in the hundreds place of the multiplier.

Multiply 54218 by 4.

Step 5: Combine the products by adding 162654, 542180, and 21687200.

Thus, the product of 54218 and 413 is 2,23,92,034.

Let’s Practise - 3

1. What is the product of 456 and 789?

2. If there are 234 students in each of the 58 classrooms in a school, what is the total number of students in the school?

3. A garden has 324 rows of flowers, and each row has 785 flowers. What is the total number of flowers in the garden?

Let’s Learn

Properties of Multiplication:

Properties of multiplication are special rules that make it easier to simplify math problems that involve multiplication. Let us learn the properties of multiplication.

Identity Property: The identity property of multiplication states that when a number is multiplied by 1, the product is always the number itself.

For example:

• 6528 × 1 = 6528

• 9079 × 1 = 9079

Zero Property: The zero property of multiplication states that when we multiply any number by 0, the result is always 0.

For example:

• 1827 × 0 = 0

• 5434 × 0 = 0

Commutative Property: The commutative property of multiplication states that we can multiply two numbers in any order, and the product will remain the same.

For example:

• 2 × 5 = 5 × 2 = 10

• 7 × 9 = 9 × 7 = 63

Associative Property: According to the associative property of multiplication, changing the grouping of numbers does not affect the product of numbers.

For example:

• (4 × 6) × 3 = 4 × (6 × 3) = 72

• (5 × 7) × 8 = 5 × (7 × 8) = 280

Distributive Property: The distributive property of multiplication states that multiplication can be distributed over addition as well as subtraction. This property helps us solve the expressions with brackets.

For example:

• 2 × (3 + 4) = (2 × 3) + (2 × 4) = 6 + 8 = 14

• 5 × (3 - 2) = (5 × 3) - (5 × 2) = 15 - 10 = 5

Multiplication by 10, 100, 1000:

Multiplying a number by 10, 100, or 1000 is a way to make it bigger by adding zeros at the end of it.

Multiplying by 10:

When we multiply a number by 10, we make it ten times bigger. To do so, we add a zero at the end of the number.

Example:

• 5 × 10 = 50 (5 becomes 50 by adding a zero)

• 7 × 10 = 70 (7 becomes 70 by adding a zero)

Multiplying by 100:

When we multiply a number by 100, we make it a hundred times bigger. To do so, we add two zeroes at the end of the number.

Example:

• 4 × 100 = 400 (4 becomes 400 by adding two zeroes)

• 9 × 100 = 900 (9 becomes 900 by adding two zeroes)

Multiplying by 1000:

When we multiply a number by 1000, we make it a thousand times bigger. In this case, we add three zeroes at the end of the number.

Example:

• 3 × 1000 = 3000 (3 becomes 3000 by adding three zeroes)

• 7 × 1000 = 7000 (7 becomes 7000 by adding three zeroes)

Let’s Practise - 4

1. Fill in the blanks to solve the following:

a. 219 × 1 = _____

b. 754 × 0 = _____

c. 513 × 43 = _____ × 513 = 22,059

d. 1243 × _____ = 0

e. 5324 × _____ = 5324

f. 914 × 10 = _____

g. 74 × _____ = 7400

h. 562 × 1000 = _____

Let’s Learn

Division of Large Numbers

Now, let us learn about the last fundamental operation, division.

Division is a mathematical operation used to split a quantity or number into equal parts or groups.

In a division problem:

• The number to be divided is known as the dividend.

• The number by which the dividend is divided is known as the divisor.

• The outcome of division is called the quotient.

• The number that remains after division is called the remainder.

Let us understand the division process with the help of an example.

Example: Divide 856 by 4.

Step 1: Set it up

Write the division problem like this:

4 8 5 6

Step 2: Divide the first digit

Divide the first digit of the dividend (856) by the divisor (4).

Here, 8 ÷ 4 = 2. Write 2 above the division bar.

2 4 8 5 6 – 8 0

Step 3: Bring down the next digit

Bring down the next digit (5) next to 0 under the division bar.

Step 4: Divide the new number

Now, divide the new number (5) by the divisor (4). 5 ÷ 4 = 1. Write 1 above the division bar.

2 1 4 8 5 6 – 8 0 5 – 4 1

Step 5: Bring down the next digit

Bring down the next digit (6) next to 1 under the division bar.

2 1 4 8 5 6 – 8 0 5 – 4 1 6

Step 6: Divide the new number

Now, divide the new number (16) by the divisor (4). 16 ÷ 4 = 4. Write 4 above the division bar. 2 1 4 4 8

Step 7: Check the remainder

Since there is no remainder (the last subtraction gives 0), you have your answer.

Final Answer: 856 ÷ 4 = 214

So, 856 divided by 4 equals 214.

Properties of Division:

Now, let us learn the properties of division.

1. When a number is divided by 1, the quotient is the number itself.

For example:

• 1242285 ÷ 1 = 1242285

• 3439965 ÷ 1 = 3439965

2. When a number is divided by itself, the quotient is 1.

For example:

• 3211943 ÷ 3211943 = 1

• 802370 ÷ 802370 = 1

3. When 0 is divided by any number, the quotient is 0.

For example:

• 0 ÷ 2341070 = 0

• 0 ÷ 2145378 = 0

4. Division by 0 is undefined.

For example:

• 231776 ÷ 0 = undefined

• 3222812 ÷ 0 = undefined

Let’s Practise - 5

1. Solve the following division problems and determine the quotient and remainder in each case:

a. 233684 ÷ 7

b. 124532 ÷ 6

c. 2324076 ÷ 12

d. 2343468 ÷ 8

2. Fill in the blanks.

a. 231542 ÷ 231542 = ______

b. 0 ÷ 120898 = ________

c. 242368 ÷ _____ = 242368

d. 124514 ÷ ______ = 1

Let’s Learn

Estimation in Operations

Estimation is a useful mathematical skill that helps us get a rough idea or approximate value of a number or result without having to calculate it precisely. Let’s break down estimation in addition, subtraction, multiplication, and division.

Estimation in Addition:

Estimation in addition involves finding an approximate sum of two or more numbers without calculating the exact result.

Example: If we want to add 48 and 73, we can round these numbers to the nearest tens (50 and 70) and then add them mentally. So, 50 + 70 = 120. This is an estimate of the sum.

Estimation

in Subtraction:

Estimation in subtraction involves finding an approximate difference between two numbers without calculating the exact result.

Example: For 96 – 57, we can round these numbers to the nearest tens (100 and 60) and then subtract them mentally. So, 100 – 60 = 40. This is an estimate of the difference.

Estimation in Multiplication:

Estimation in multiplication involves finding an approximate product of two numbers without calculating the exact result.

Example: If we need to multiply 37 by 24, we can round these numbers to the nearest tens (40 and 20) and then multiply them mentally. So, 40 × 20 = 800. This is an estimate of the product.

Estimation

in Division:

Estimation in division involves finding an approximate quotient of two numbers without calculating the exact result.

Example: For 187 ÷ 8, we can round these numbers to the nearest tens (190 and 10) and then divide them mentally. So, 190 ÷ 10 = 19. This is an estimate of the quotient.

1. Estimate the sum of 628 + 247 by rounding each number to the nearest tens.

2. Round off 145 and 87 to the nearest tens and estimate their difference.

3. Estimate the product of 236 and 18 by rounding off each number to the nearest tens.

4. Estimate the quotient of 256 ÷ 8 by rounding off each number to the nearest tens.

Let’s Sum Up

1. Addition:

• When adding large numbers, line up the digits correctly.

• Start adding from the rightmost digit (ones place) and carry over if the sum is greater than 9.

• Continue this process from right to left until all digits are added.

2. Subtraction:

• Line up the digits correctly when subtracting large numbers.

• Start subtracting from the rightmost digit (ones place) and borrow if necessary.

• Continue this process from right to left until all digits are subtracted.

3. Multiplication:

• To multiply large numbers, use the long multiplication method.

• Multiply each digit of one number by each digit of the other number starting from the ones place or the rightmost column.

• Add up all the products to get the final result.

4. Division:

• Use long division when dividing large numbers.

• Divide the leftmost digits of the dividend by the divisor to get the quotient.

• Multiply the divisor by the quotient and subtract the product from the dividend to get the remainder.

• Bring down the next digit of the dividend and continue the process until you have the complete quotient.

5. Estimation:

• Estimating can help you quickly check if your answer is reasonable.

• Round off large numbers to the nearest tens and then perform calculations with the rounded numbers.

Life Skills

Imagine you are planning a dream vacation to a destination of your choice. Research the costs of travel, accommodation, activities, and meals. Then, create a budget and calculate how much money you would need to save.

Cross-Curricular Connections

Social Studies:

Pihu is on a road trip with her family from Kashmir to Kanyakumari a distance of 3,676 km. On the first day, they drive 287 km; on the second day, they drive 319 km. How many more kilometres do they need to travel?

21st Century Skills

Form the largest 5-digit number and the smallest 2-digit number by using the digits 8, 5, 2, 3, 1 without repetition, and then find the product.

An integer is a whole number without a decimal or fractional part. Integers include both negative and positive numbers and also zero. Examples of integers include 3, 0, 1, 7, 23, 96, 1,141 and so on.

The set of integers, denoted as Z comprises:

Positive numbers: The numbers that are greater than zero

Negative numbers: The numbers that are less than zero

And zero itself, which is neither a negative nor a positive number.

Extend Your Knowledge

Tip for the parent

• Relate mathematical operations on large numbers to real-life situations. Discuss scenarios where large numbers are encountered, such as measuring distances, handling money, or understanding population figures.

• Teach your child the importance of estimation. Before diving into calculations, encourage them to round off numbers to the nearest tens.

Fractions

My Study Plan

Proper, improper, and mixed fractions

Like, unlike, and equivalent fractions

Comparing and ordering of fractions

Addition and subtraction of fractions

Multiplication and division of fractions

Fractions in real life

Let’s Recall

Fractions represent the parts of a whole or collection of objects. It consists of two numbers separated by a horizontal line. The number on the top of the line is called the numerator. The number below the line is called the denominator.

1. Write the fraction representing the shaded portion in the boxes below.

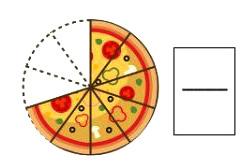
2. Sonu brought a pizza. He cut it into 10 equal pieces and ate 3 of them. What fraction of the pizza did he eat?

Thinking Zone

Imagine you have a daily schedule with different activities. If you dedicate 1 6 th of your day to homework and 2 6 th to other activities, what fraction of the day is left for relaxation and free time?

Let’s Learn

Based on the numbers present in the numerator and denominator, there are different types of fractions.

Proper, Improper, and Mixed fractions

Proper fractions

A proper fraction is a fraction where the numerator is smaller than the denominator.

Example: 3 4 is a proper fraction because numerator (3) is smaller than the denominator (4).

Proper fractions are always less than 1.

Improper fractions

An improper fraction is a fraction where the numerator is equal to or greater than the denominator.

Example: 7 6 is an improper fraction because the numerator (7) is greater than the denominator (6).

Improper fractions are equal to or greater than 1.

Mixed fractions

A mixed fraction is a combination of a whole number and a proper fraction. It represents a quantity more than one whole, along with some smaller parts.

Example: 5 2 6 is a mixed fraction. Here, 5 is the whole number, and 2 3 is the proper fraction part. Improper fractions can be converted to mixed fractions and vice versa.

Converting improper fractions into mixed fraction

To convert an improper fraction to a mixed fraction, we follow these steps:

Step 1: We divide the numerator by the denominator.

Step 2: The number we get from the division as quotient becomes the whole number part of the mixed number.

Step 3: The remainder becomes the numerator of the proper fraction and denominator remains the same.

Step 4: Combine the whole number and the proper fraction to create the mixed number.

Let us take an example:

Example 1: Convert 17 6 into a mixed number.

Solution:

Here, numerator = 17 and denominator = 6

Step 1: Divide numerator by denominator. 17 ÷ 6 2 6 17 - 12 5

Here, Quotient = 2, and Remainder = 5

Step 2: Write whole part and proper fraciton.

Whole part = 2, Proper fraction = 5 6 .

Step 3: Combine whole part and proper fraction.

Hence, 17 6 = 2 5 6

Converting mixed fractions into improper fraction

To convert a mixed fraction to an improper fraction, we follow these steps:

Step 1: We multiply the whole number part by the denominator.

Step 2: The number we get from the multiplication is added with the numerator of the fraction. This becomes the numerator of the fraction.

Step 3: The denominator stays the same as before.

Let us take an example:

Example: Convert 3 4 7 into improper fraction.

Solution: 3 4 7

Here, whole part = 3, numerator = 4, and denominator = 7

Step 1: Multiplying whole part and denominator.

3 × 7 = 21

Step 2: Adding numerator and number we get as result in step 1.

21 + 4= 25

Step 3: Writing improper fraction.

Number we get in step 2 becomes the numerator and denominator remains the same.

Hence, 3 4 7 = 25 7

Let’s Practise - 1

1. Convert the following into mixed fraction.

2. Convert the following into improper fraction.

Let’s Learn

Like Fractions

Like fractions have the same denominator, which is the number at the bottom of the fraction. For example, 3 4 and 2 4 are like fractions because they have the same denominator, 4.

Similarly, 1 5 , 2 5 , 3 5 , 4 5 , are all like fractions, since they have the same denominator, 5.

Unlike Fractions

Unlike fractions have different denominators. For example, 1 3 and 5 6 are unlike fractions because their denominators (3 and 6) are different. Similarly, 2 3 , 4 5 , 7 9 are unlike fractions as their denominators are different.

Equivalent Fractions

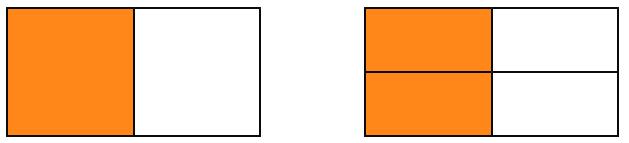
Equivalent fractions are different fractions that actually represent the same amount or the same part of a whole, even though they look different. They have different numerators and denominators but represent the same portion or value. For example:

1 2 and 2 4 are equivalent fractions because when you shade these fractions on a shape, they show the same amount or part of the whole.

Equivalent fractions also represent the same point on the number line.

To find equivalent fractions, of a given fraction we multiply or divide the numerator and denominator by the same number. For instance:

To find equivalent fractions of 1 2 , multiply the numerator and denominator by 2, 3, 4, and 5 one by one.

1 × 2

2 × 2 = 2 4

1 × 3

2 × 3 = 3 6

1 × 4

2 × 4 = 4 8

1 × 5

2 × 5 = 5 10

Reducing fractions to their lowest terms

Reducing fractions to their lowest terms means simplifying them so that the numerator (top number) and denominator (bottom number) have no common factors other than 1.

Example 1:

Let us take the fraction 4 8 .

Step 1: Find a number that both the numerator and denominator can be divided by. In this case, both 4 and 8 can be divided by 4.

4 ÷ 4 = 1

8 ÷ 4 = 2

Step 2: Rewrite the fraction using the numbers from step 1.

So, 4 8 = 1 2

Example 2:

Consider the fraction 6 9 .

Step 1: Find a number that divides evenly into both the numerator and denominator. Both 6 and 9 can be divided by 3.

6 ÷ 3 = 2

9 ÷ 3 = 3

Step 2: Rewrite the fraction using the numbers from step 1.

Therefore, 6 9 = 2 3

Comparing and Ordering Fraction

Fractions can be compared in the following ways:

Comparing fractions with the same denominator

• When fractions have the same denominator, we compare them by looking at their numerators. The fraction with the greater numerator is larger.

• For example, comparing 3 5 and 2 5 , since the denominators are the same (both 5), we compare the numerators: 3 is greater than 2, so 3 5 is larger than 2 5 .

Comparing fractions with the same numerator

• When fractions have the same numerator, compare them by looking at their denominators. The fraction with the smaller denominator is larger.

• For example, comparing 2 3 and 2 5 , since the numerators are the same (both are 2), we compare the denominators: 3 is less than 5, so 2 3 is larger than 2 5 .

Comparing fractions with different numerators and denominators

• For fractions with different numerators and denominators, convert them to like fractions before comparing them.

• We use the concept of equivalent fractions to make like fractions.

Let us understand it through an example:

Example: Compare the fractions 3 8 and 2 5 .

Solution:

Let us solve the problem step by step:

Step 1: Find the common denominator

• Let us convert the given fractions into like fractions. We can do this using the LCM of 8 and 5. the LCM of 8 and 5, is 40.

Step 2: Obtain equivalent fractions

• Let us convert the given fractions to their equivalent fractions to obtain the required like fractions.

• 3 8 × 5 5 = 15 40

• 2 5 × 8 8 = 16 40

Step 3: Compare the numerators:

Now that both fractions have the same denominator (40), compare the numerators directly.

15 40 and 16 40

Since 16 is greater than 15, 16 40 > 15 40

Therefore, 2 5 is greater than 3 8

Thinking Zone

You and your friend decide to share a bag of popcorn. You take one-fourth of the bag, and your friend takes one-fifth of the same size of the bag. Who ends up with more popcorn?

Ordering fractions

Ordering fractions involves comparing fractions and arranging them either in ascending (from smallest to largest) or descending (from largest to smallest) order.

Let us understand it with an example:

Example: Arrange the fraction 2 3 , 1 3 , and 3 4 in descending order.

Solution:

Here is a step-by-step solution for arranging the fractions 2 3 , 1 3 , and 3 4 in descending order:

Step 1: Write down the fractions: 2 3 , 1 3 , 3 4

Step 2: Find a common denominator for all the fractions.

The LCM of 2, 3, and 4 is 12. So, the common denominator is 12.

Step 3: Convert the fractions to equivalent fractions with the common denominator.

• 2 3 × 4 4 = 8 12 • 1 2 × 6 6 = 6 12 • 3 4 × 3 3 = 9 12

Step 4: Arrange the fractions based on their numerators in descending order

In the fractions 8 12 , 6 12 and 9 12 , the numerators are 8, 6, and 9 respectively.

We know that when fractions have the same denominator, the fraction with the greater numerator is larger.

Since, 9 > 8 > 6, therefore, the correct order is 9 12 > 8 12 > 6 12 .

So, the fractions in descending order are

1. Compare the fractions and write “>, <, or =” in the box.

2. Arrange the fractions in ascending order.

1 9 , 5 9 , 4 9

3. Arrange the fractions in descending order.

2 5 , 6 7 , 5 8

Let’s Learn

Addition and Subtraction of Fractions

Addition of fractions

In the previous grade you have learned how to do addition of like fractions. Now, let us quickly recap it, and understand how to do it for unlike and mixed fractions.

Addition of like fractions

To add like fractions,

Step 1: Add their numerators and keep the denominator the same.

Step 2: Reduce the number to its simplest form.

Step 3: If the answer is an improper fraction, convert it into a mixed number.

Example: Add 5 9 and 8 9

Solution:

Step 1: Adding numerators and keeping the denominator same.

5 + 8 9 = 13 9

Step 2: Fraction is already in simplest form.

Step 3: Converting it into mixed fracion.

Divide numerator by denominator.

1

9 13 - 9 4

We get, 13 9 = 1 4 9

Hence, 5 9 + 8 9 = 1 4 9 .

Addition of unlike fractions

To add unlike fractions,

Step 1: Convert all the fractions into like fractions.

Step 2: Add the numerators.

Step 3: Simplify the fraction (if needed).

Example: Add 1 3 and 5 5 .

Solution:

Step 1: Since the fractions have different denominators (3 and 5), we must find the Least Common Multiple (LCM), which is 15 in this case.

Create equivalent fractions with the LCM as the denominator.

• 1 3 × 5 5 = 5 15

• 3 5 × 3 3 = 9 15

Step 2: Add the like fractions.

5 15 + 9 15 = 5 + 9 15 = 14 15

Since, 14 15 cannot be further simplified.

Hence, 1 3 + 3 5 = 14 15

Addition of mixed fraction

To add,

Step 1: Change mixed fractions to improper fractions.

Step 2: Add them using the method for adding unlike fractions.

Step 3: Convert the result back into mixed fractions.

Example 3: Add 2 3 4 and 3 1 4 .

Solution:

Step 1: Convert these fractions into improper fractions.

2 3 4 = 2 × 4 + 3 4 = 11 4

3 1 4 = 3 × 4 + 1 4 = 13 4

Step 2: Add both fractions.

In 11 4 and 13 4 , the denominator is same (4).

Therefore, 11 4 + 13 4 = 11 + 13 4 = 24 4

Step 3: Simplify or reduce to lowest terms.

24 4 = 6

Hence, 2 3 4 + 3 1 4 = 6

Let’s Learn

Subtraction of Fractions

Now, let us understand how to perform subtraction.

Subtraction of like fractions

To subtract like fractions,

Step 1: Subtract their numerators and keep the denominator the same.

Step 2: Reduce the number to its simplest form.

Step 3: If the answer is an improper fraction, convert it into a mixed number.

Example: Subtract 15 23 from 17 23 .

Solution:

We need to find 17 23 –15 23

Step 1: Subtracting numerators and keeping denominator same.

17 – 15 23 = 2 23 .

Step 2: Fraction is already in simplest and proper form.

Hence, 17 23 –15 23 = 2 23

Subtraction of unlike fractions

To subtract unlike fractions,

Step 1: Convert the fractions into like fractions.

Step 2: Subtract the numerators while keeping the common denominator the same.

Step 3: Simplify the result to its lowest terms.

Step 4: If the answer is an improper fraction, convert it into a mixed number.

Example: Subtract 7 11 –5 9

Solution:

Step 1: Since the denominators are different, let us convert them to like fractions.

LCM of 11 and 9 is 99.

So, the common denominator is 99.

Find the equivalent fraction with denominator 19.

• 7 11 = 7 11 × 9 9 = 63 99

• 5 9 = 5 9 × 11 11 = 55 99

Step 2: Subtract the numerators while keeping the common denominator the same.

63 99 –55 99 = 63 – 55 99 = 8 99

Step 3: Fraction is already in simplest and proper form.

Hence, 7 11 –5 9 = 8 99

Subtraction of mixed fractions

Step 1: Change mixed fractions to improper fractions.

Step 2: Convert unlike fractions into like fractions using the Least Common Multiple (LCM) of the denominators.

Step 3: Subtract the like fractions and express the result as a mixed fraction if required.

Example: Subtract 6 1 4 from 9 3 4

Solution:

Step 1: Change mixed fractions to improper fractions.

• 6 1 4 = 6 × 4 + 1 4 = 25 4

• 9 3 4 = 9 × 4 + 3 4 = 39 4

Step 2: Since the given fractions are like fractions, subtract them.

39 4 –25 4 = 39 – 25 4 = 14 4

Step 3: Reduce the fraction to its simplest form and write it in mixed fraction. 14 4 = 7 2

7 2 = 3 1 2 Hence, 9 3 4 – 6 1 4 = 3 1 2 .

Let’s Practise - 3

1. Solve the following:

2. Calculate the following:

Let’s Learn

Multiplication of Fractions

Multiplication of fractions can be done in many ways.

Multiplication of a fraction by a whole numbers

To multiply a fraction by a whole number, follow these three simple steps:

Step 1: Multiply the numerator by the whole number.

Step 2: Keep the denominator the same as the original fraction.

Step 3: Simplify the fraction, if needed, and if it is an improper fraction, convert it into a mixed fraction.

Let us understand it with some examples:

Example 1: Find 2 7 × 3.

Solution: 2 7 × 3 = 2 × 3 7 = 6 7

Hence, 2 7 × 3 = 6 7

Example 2: Find 5 × 4 7

Solution: 5 × 4 7 = 5 × 4 7 = 20 7 = 2 6 7

Hence, = 5 × 4 7 = 2 6 7

Multiplication of a fraction by another fraction

To multiply a fraction by a fraction, follow the below steps:

Step 1: Multiply the numerators.

Step 2: Multiply the denominators.

Step 3: Simplify the fraction, if needed.

Product of their numerators

Thus, Product of two fractions =

Product of their denumerators

Let us take an example:

Example: Find the product:

Solution:

1 2 × 1 7 = 1 × 1 2 × 7 = 1 14

Hence, 1 2 × 1 7 = 1 14

While multiplying mixed fractions first convert them to improper fractions and then calculate the product.

1. Find:

a. 6 7 × 2 =

c. 1 5 × 1 7 =

Let’s Learn

Division of Fractions

b. 11 4 7 × 2 =

d. 2 5 × 1 6 =

Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.

Understanding division with fractions requires knowing the concept of the reciprocal of a fraction.

The reciprocal called the multiplicative inverse, is obtained by flipping the fraction or interchanging the numerator and denominator. The reciprocal of any natural number is 1 upon the given number.

For example, the reciprocal of 7 is 1 7 the reciprocal of 5 is 1 5 and so on.

Let us take an example:

Example: Find the reciprocal of 3 2 .

Solution:

Given fraction: 3 2

To find the reciprocal, swap the numerator and denominator.

Therefore, the reciprocal of 3 2 is 2 3

Division of a whole number by a fraction

To divide a whole number by a fraction, follow these steps:

Step 1: Invert the fraction to find its reciprocal and replace the division symbol with a multiplication symbol.

Step 2: Multiply the whole number by the reciprocal.

Step 3: Simplify the resulting fraction (If needed).

Let’s understand these steps with the help of an example:

Example: Find 3 ÷ 1 2

Solution:

Given: 3 ÷ 1 2

Step 1: First, find the reciprocal of 1 2 .

The reciprocal of 1 2 is 2 1

Step 2: Multiply the whole number by the reciprocal.

3 × 2 1 = 3 ×2 1 = 6 1 = 6

Hence, 3 ÷ 1 2 = 6

Division of a fraction by a whole number

To divide a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number.

Let us take an example:

Example: Find 3 4 ÷ 3

Solution:

Given: 3 4 ÷ 3

Step 1: First, find the reciprocal of 3.

The reciprocal of 3 is 1 3

Step 2: Multiply the fraction by the reciprocal.

3 4 × 1 3 = 3 ×1 4 ×3 = 3 12 = 1 4

Hence, 3 4 ÷ 3 = 1 4

Division of a fraction by another fraction

When dividing one fraction by another, we multiply the first fraction (dividend) by the reciprocal of the second fraction (divisor).

Let’s understand this with an example:

Example: Find 3 5 ÷ 1 2 ,

Solution:

Given: 3 5 ÷ 1 2

Step 1: First, find the reciprocal of the divisor i.e., 1 2 .

The reciprocal of 1 2 is 2 1

Step 2: Multiply the first fraction by reciprocal.

3 5 × 2 1 = 3 ×2 5 ×1 = 6 5

Step 3: Convert the improper fraction into a mixed fraction. So, 6 5 = 1

Let’s Practise - 5

1. Find:

Let’s Learn

Fractions in Real Life

We find fractions in our everyday life.

Example 1: Seema dyes dresses. She had to dye 50 dresses. She has so far finished 30 dresses. What fraction of dresses has she finished?

Solution:

Total number of dresses = 50

Dresses that are completely dyed = 30

Fraction of dresses finished = Dresses that are complete dyed

Fraction of dresses finished = 30 50

Fraction of dresses finished = 3 5

Total number of dresses

Therefore, fraction of dresses finished by Seema is 3 5

Word Zone

Dye: To change the colour of something using a special liquid.

Example 2: Rishu read 25 pages of a book containing 100 pages. Rajat read 3 4 of the same book. Who read less?

Solution:

Rishu reads 25 pages out of 100 pages.

Fraction of 25 pages out of 100 pages = 25 100 = 1 4

Rajat reads 3 4 of the same book.

Now, let us compare the fractions 1 4 and 3 4

We know that when fractions have the same denominator, the fraction with the greater numerator is larger.

Since, 3 > 1, therefore, 1 4 > 3 4 .

Hence Rishu reads less pages.

Example 3: Deepa had 5 6 of a cake. She gave 2 6 out of that to her younger brother. How much cake is left with her?

Solution:

Deepa originally had 5 6 of a cake, and she gave 2 6 to her younger brother.

To find out how much is left, we subtract the amount given away from the original amount:

5 6 − 2 6

To subtract these fractions, we need a common denominator, which is already 6 in this case. Subtract the numerators while keeping the denominator the same:

5 6 − 2 6 = 5 − 2 6 = 3 6

Now, 3 6 is equivalent to 1 2 when simplified.

So, Deepa has 1 2 of the cake left.

Let’s Practise - 6

1. Solve the following problems:

a. Danish is reading a book that has 120 pages. After a few hours, he has read 72 pages. What fraction of the book has he read?

b. Ankit covered 45 pages of a comic book with 150 pages. Aditi read 1 2 of the same comic. Who read less?

c. Sarah had 4 7 of a pizza. She shared 2 5 of it with her friend. How much pizza does Sarah have left?

d. A car runs 16 km using 1 litre of petrol. How much distance will it cover using 5 4 litres of petrol.

The grip-sizes of tennis racquets are often in mixed numbers. For example, one size is ‘3 7 8 inches’ and ‘4 3 8 inches’ is another.

Zone

Let’s Sum Up

Fractions with the same denominator are called like fractions..

Fractions with different denominators are called unlike fractions.

Fractions that represent the same value are called equivalent fractions.

A fraction is said to be in the simplest (or lowest) form if its numerator and the denominator have no common factor except 1.

Fractions with the same denominator are added by combining their numerators.

Fractions with the same denominator are subtracted by taking the difference of their numerators.

Fractions with the same denominator are called like fractions..

Fractions with different denominators are called unlike fractions.

Fractions that represent the same value are called equivalent fractions.

A fraction is said to be in the simplest (or lowest) form if its numerator and the denominator have no common factor except 1.

Fractions with the same denominator are added by combining their numerators.

Life Skills

During a school event, you and your friend decided to combine your snacks to share with everyone. You brought 2 5 of a bag of popcorn, and your friend brought 3 8 of a bag of chips by weight.

What fraction of the combined snacks do you have in total?

Cross-Curricular Connections

Physical Education:

During physical education class, you run for 15 minutes out of a 1-hour session. What fraction of the class time is spent running?

21st Century Skills

Imagine you are following a recipe that calls for 3 4 cup of flour, but you only have a 1 2 cup measuring cup and a 1 4 cup measuring cup. How can you accurately measure 3 4 cup of flour using these two measuring cups?

Extend Your Knowledge

Fractions can be converted into decimals, and vice versa. For instance, 1 2 is equivalent to 0.5 in decimal form.

Tip for the Parent

• Relate fractions to everyday situations. For example, cutting a pizza into slices, sharing candies, or dividing a cake can be great examples.

• Involve your child in the kitchen to introduce fractions through measuring ingredients. For example, ask them to measure 1 2 cup of flour or 1 4 teaspoon of salt.

• Encourage your child to draw fractions. This can help them visualize the concept and gain a deeper understanding.

Fractions

My Study Plan

Proper, improper, and mixed fractions

Like, unlike, and equivalent fractions

Comparing and ordering of fractions

Addition and subtraction of fractions

Multiplication and division of fractions

Fractions in real life

Let’s Recall

Fractions represent the parts of a whole or collection of objects. It consists of two numbers separated by a horizontal line. The number on the top of the line is called the numerator. The number below the line is called the denominator.

1. Write the fraction representing the shaded portion in the boxes below.

2. Sonu brought a pizza. He cut it into 10 equal pieces and ate 3 of them. What fraction of the pizza did he eat?

Thinking Zone

Imagine you have a daily schedule with different activities. If you dedicate 1 6 th of your day to homework and 2 6 th to other activities, what fraction of the day is left for relaxation and free time?

Let’s Learn

Based on the numbers present in the numerator and denominator, there are different types of fractions.

Proper, Improper, and Mixed fractions

Proper fractions

A proper fraction is a fraction where the numerator is smaller than the denominator.

Example: 3 4 is a proper fraction because numerator (3) is smaller than the denominator (4).

Proper fractions are always less than 1.

Improper fractions

An improper fraction is a fraction where the numerator is equal to or greater than the denominator.

Example: 7 6 is an improper fraction because the numerator (7) is greater than the denominator (6).

Improper fractions are equal to or greater than 1.

Mixed fractions

A mixed fraction is a combination of a whole number and a proper fraction. It represents a quantity more than one whole, along with some smaller parts.

Example: 5 2 6 is a mixed fraction. Here, 5 is the whole number, and 2 3 is the proper fraction part. Improper fractions can be converted to mixed fractions and vice versa.

Converting improper fractions into mixed fraction

To convert an improper fraction to a mixed fraction, we follow these steps:

Step 1: We divide the numerator by the denominator.

Step 2: The number we get from the division as quotient becomes the whole number part of the mixed number.

Step 3: The remainder becomes the numerator of the proper fraction and denominator remains the same.

Step 4: Combine the whole number and the proper fraction to create the mixed number.

Let us take an example:

Example 1: Convert 17 6 into a mixed number.

Solution:

Here, numerator = 17 and denominator = 6

Step 1: Divide numerator by denominator.

17 ÷ 6 2 6 17 - 12 5

Here, Quotient = 2, and Remainder = 5

Step 2: Write whole part and proper fraciton.

Whole part = 2, Proper fraction = 5 6 .

Step 3: Combine whole part and proper fraction.

Hence, 17 6 = 2 5 6

Converting mixed fractions into improper fraction

To convert a mixed fraction to an improper fraction, we follow these steps:

Step 1: We multiply the whole number part by the denominator.

Step 2: The number we get from the multiplication is added with the numerator of the fraction. This becomes the numerator of the fraction.

Step 3: The denominator stays the same as before.

Let us take an example:

Example: Convert 3 4 7 into improper fraction.

Solution: 3 4 7

Here, whole part = 3, numerator = 4, and denominator = 7

Step 1: Multiplying whole part and denominator.

3 × 7 = 21

Step 2: Adding numerator and number we get as result in step 1.

21 + 4= 25

Step 3: Writing improper fraction.

Number we get in step 2 becomes the numerator and denominator remains the same.

Hence, 3 4 7 = 25 7

Let’s Practise - 1

1. Convert the following into mixed fraction.

2. Convert the following into improper fraction.

Let’s Learn

Like Fractions

Like fractions have the same denominator, which is the number at the bottom of the fraction. For example, 3 4 and 2 4 are like fractions because they have the same denominator, 4.

Similarly, 1 5 , 2 5 , 3 5 , 4 5 , are all like fractions, since they have the same denominator, 5.

Unlike Fractions

Unlike fractions have different denominators. For example, 1 3 and 5 6 are unlike fractions because their denominators (3 and 6) are different. Similarly, 2 3 , 4 5 , 7 9 are unlike fractions as their denominators are different.

Equivalent Fractions

Equivalent fractions are different fractions that actually represent the same amount or the same part of a whole, even though they look different. They have different numerators and denominators but represent the same portion or value. For example:

1 2 and 2 4 are equivalent fractions because when you shade these fractions on a shape, they show the same amount or part of the whole.

Equivalent fractions also represent the same point on the number line.

To find equivalent fractions, of a given fraction we multiply or divide the numerator and denominator by the same number. For instance:

To find equivalent fractions of 1 2 , multiply the numerator and denominator by 2, 3, 4, and 5 one by one.

1 × 2

2 × 2 = 2 4

1 × 3

2 × 3 = 3 6

1 × 4

2 × 4 = 4 8

1 × 5

2 × 5 = 5 10

Reducing fractions to their lowest terms

Reducing fractions to their lowest terms means simplifying them so that the numerator (top number) and denominator (bottom number) have no common factors other than 1.

Example 1:

Let us take the fraction 4 8 .

Step 1: Find a number that both the numerator and denominator can be divided by. In this case, both 4 and 8 can be divided by 4.

4 ÷ 4 = 1

8 ÷ 4 = 2

Step 2: Rewrite the fraction using the numbers from step 1.

So, 4 8 = 1 2

Example 2:

Consider the fraction 6 9 .

Step 1: Find a number that divides evenly into both the numerator and denominator. Both 6 and 9 can be divided by 3.

6 ÷ 3 = 2

9 ÷ 3 = 3

Step 2: Rewrite the fraction using the numbers from step 1.

Therefore, 6 9 = 2 3

Comparing and Ordering Fraction

Fractions can be compared in the following ways:

Comparing fractions with same denominator

• When fractions have the same denominator, we compare them by looking at their numerators. The fraction with the greater numerator is larger.

• For example, comparing 3 5 and 2 5 , since the denominators are the same (both 5), we compare the numerators: 3 is greater than 2, so 3 5 is larger than 2 5 .

Comparing fractions with the same numerator

• When fractions have the same numerator, compare them by looking at their denominators. The fraction with the smaller denominator is larger.

• For example, comparing 2 3 and 2 5 , since the numerators are the same (both are 2), we compare the denominators: 3 is less than 5, so 2 3 is larger than 2 5 .

Comparing fractions with different numerators and denominators

• For fractions with different numerators and denominators, convert them to like fractions before comparing them.

• We use the concept of equivalent fractions to make like fractions.

Let us understand it through an example:

Example: Compare the fractions 3 8 and 2 5 .

Solution:

Let us solve the problem step by step:

Step 1: Find the common denominator

• Let us convert the given fractions into like fractions. We can do this using the LCM of 8 and 5. the LCM of 8 and 5, is 40.

Step 2: Obtain equivalent fractions

• Let us convert the given fractions to their equivalent fractions to obtain the required like fractions.

• 3 8 × 5 5 = 15 40

• 2 5 × 8 8 = 16 40

Step 3: Compare the numerators:

Now that both fractions have the same denominator (40), compare the numerators directly.

15 40 and 16 40

Since 16 is greater than 15, 16 40 > 15 40

Therefore, 2 5 is greater than 3 8

Thinking Zone

You and your friend decide to share a bag of popcorn. You take one-fourth of the bag, and your friend takes one-fifth of the same size of the bag. Who ends up with more popcorn?

Ordering fractions

Ordering fractions involves comparing fractions and arranging them either in ascending (from smallest to largest) or descending (from largest to smallest) order.

Let us understand it with an example:

Example: Arrange the fraction 2 3 , 1 3 , and 3 4 in descending order.

Solution:

Here is a step-by-step solution for arranging the fractions 2 3 , 1 3 , and 3 4 in descending order:

Step 1: Write down the fractions: 2 3 , 1 3 , 3 4

Step 2: Find a common denominator for all the fractions.

The LCM of 2, 3, and 4 is 12. So, the common denominator is 12.

Step 3: Convert the fractions to equivalent fractions with the common denominator.

• 2 3 × 4 4 = 8 12 • 1 2 × 6 6 = 6 12 • 3 4 × 3 3 = 9 12

Step 4: Arrange the fractions based on their numerators in descending order

In the fractions 8 12 , 6 12 and 9 12 , the numerators are 8, 6, and 9 respectively.

We know that when fractions have the same denominator, the fraction with the greater numerator is larger.

Since, 9 > 8 > 6, therefore, the correct order is 9 12 > 8 12 > 6 12 .

So, the fractions in descending order are

1. Compare the fractions and write “>, <, or =” in the box.

2. Arrange the fractions in ascending order.

1 9 , 5 9 , 4 9

3. Arrange the fractions in descending order.

2 5 , 6 7 , 5 8

Let’s Learn

Addition and Subtraction of Fractions

Addition of fractions

In the previous grade you have learned how to do addition of like fractions. Now, let us quickly recap it, and understand how to do it for unlike and mixed fractions.

Addition of like fractions

To add like fractions,

Step 1: Add their numerators and keep the denominator the same.

Step 2: Reduce the number to its simplest form.

Step 3: If the answer is an improper fraction, convert it into a mixed number.

Example: Add 5 9 and 8 9

Solution:

Step 1: Adding numerators and keeping the denominator same.

5 + 8 9 = 13 9

Step 2: Fraction is already in simplest form.

Step 3: Converting it into mixed fracion.

Divide numerator by denominator.

1

9 13 - 9 4

We get, 13 9 = 1 4 9

Hence, 5 9 + 8 9 = 1 4 9 .

Addition of unlike fractions

To add unlike fractions,

Step 1: Convert all the fractions into like fractions.

Step 2: Add the numerators.

Step 3: Simplify the fraction (if needed).

Example: Add 1 3 and 5 5 .

Solution:

Step 1: Since the fractions have different denominators (3 and 5), we must find the Least Common Multiple (LCM), which is 15 in this case.

Create equivalent fractions with the LCM as the denominator.

• 1 3 × 5 5 = 5 15

• 3 5 × 3 3 = 9 15

Step 2: Add the like fractions.

5 15 + 9 15 = 5 + 9 15 = 14 15

Since, 14 15 cannot be further simplified.

Hence, 1 3 + 3 5 = 14 15

Addition of mixed fraction

To add,

Step 1: Change mixed fractions to improper fractions.

Step 2: Add them using the method for adding unlike fractions.

Step 3: Convert the result back into mixed fractions.

Example 3: Add 2 3 4 and 3 1 4 .

Solution:

Step 1: Convert these fractions into improper fractions.

2 3 4 = 2 × 4 + 3 4 = 11 4

3 1 4 = 3 × 4 + 1 4 = 13 4

Step 2: Add both fractions.

In 11 4 and 13 4 , the denominator is same (4).

Therefore, 11 4 + 13 4 = 11 + 13 4 = 24 4

Step 3: Simplify or reduce to lowest terms.

24 4 = 6

Hence, 2 3 4 + 3 1 4 = 6

Let’s Learn

Subtraction of Fractions

Now, let us understand how to perform subtraction.

Subtraction of like fractions

To subtract like fractions,

Step 1: Subtract their numerators and keep the denominator the same.

Step 2: Reduce the number to its simplest form.

Step 3: If the answer is an improper fraction, convert it into a mixed number.

Example: Subtract 15 23 from 17 23 .

Solution:

We need to find 17 23 –15 23

Step 1: Subtracting numerators and keeping denominator same.

17 – 15 23 = 2 23 .

Step 2: Fraction is already in simplest and proper form.

Hence, 17 23 –15 23 = 2 23

Subtraction of unlike fractions

To subtract unlike fractions,

Step 1: Convert the fractions into like fractions.

Step 2: Subtract the numerators while keeping the common denominator the same.

Step 3: Simplify the result to its lowest terms.

Step 4: If the answer is an improper fraction, convert it into a mixed number.

Example: Subtract 7 11 –5 9

Solution:

Step 1: Since the denominators are different, let us convert them to like fractions.

LCM of 11 and 9 is 99.

So, the common denominator is 99.

Find the equivalent fraction with denominator 19.

• 7 11 = 7 11 × 9 9 = 63 99

• 5 9 = 5 9 × 11 11 = 55 99

Step 2: Subtract the numerators while keeping the common denominator the same.

63 99 –55 99 = 63 – 55 99 = 8 99

Step 3: Fraction is already in simplest and proper form.

Hence, 7 11 –5 9 = 8 99

Subtraction of mixed fractions

Step 1: Change mixed fractions to improper fractions.

Step 2: Convert unlike fractions into like fractions using the Least Common Multiple (LCM) of the denominators.

Step 3: Subtract the like fractions and express the result as a mixed fraction if required.

Example: Subtract 6 1 4 from 9 3 4

Solution:

Step 1: Change mixed fractions to improper fractions.

• 6 1 4 = 6 × 4 + 1 4 = 25 4

• 9 3 4 = 9 × 4 + 3 4 = 39 4

Step 2: Since the given fractions are like fractions, subtract them.

39 4 –25 4 = 39 – 25 4 = 14 4

Step 3: Reduce the fraction to its simplest form and write it in mixed fraction. 14 4 = 7 2

7 2 = 3 1 2 Hence, 9 3 4 – 6 1 4 = 3 1 2 .

Let’s Practise - 3

1. Solve the following:

2. Calculate the following:

Let’s Learn

Multiplication of Fractions

Multiplication of fractions can be done in many ways.

Multiplication of a fraction by a whole number

To multiply a fraction by a whole number, follow these three simple steps:

Step 1: Multiply the numerator by the whole number.

Step 2: Keep the denominator the same as the original fraction.

Step 3: Simplify the fraction, if needed, and if it is an improper fraction, convert it into a mixed fraction.

Let us understand it with some examples:

Example 1: Find 2 7 × 3.

Solution: 2 7 × 3 = 2 × 3 7 = 6 7

Hence, 2 7 × 3 = 6 7

Example 2: Find 5 × 4 7

Solution: 5 × 4 7 = 5 × 4 7 = 20 7 = 2 6 7

Hence, = 5 × 4 7 = 2 6 7

Multiplication of a fraction by another fraction

To multiply a fraction by a fraction, follow the below steps:

Step 1: Multiply the numerators.

Step 2: Multiply the denominators.

Step 3: Simplify the fraction, if needed.

Product of their numerators

Thus, Product of two fractions =

Product of their denominators

Let us take an example:

Example: Find the product:

Solution: 1 2 × 1 7 = 1 × 1 2 × 7 = 1 14

Hence, 1 2 × 1 7 = 1 14

While multiplying mixed fractions first convert them to improper fractions and then calculate the product.

1. Find:

a. 6 7 × 2 =

c. 1 5 × 1 7 =

Let’s Learn

Division of Fractions

b. 11 4 7 × 2 =

d. 2 5 × 1 6 =

Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.

Understanding division with fractions requires knowing the concept of the reciprocal of a fraction.

The reciprocal called the multiplicative inverse, is obtained by flipping the fraction or interchanging the numerator and denominator. The reciprocal of any natural number is 1 upon the given number.

For example, the reciprocal of 7 is 1 7 the reciprocal of 5 is 1 5 and so on.

Let us take an example:

Example: Find the reciprocal of 3 2 .

Solution:

Given fraction: 3 2

To find the reciprocal, swap the numerator and denominator.

Therefore, the reciprocal of 3 2 is 2 3

Division of a whole number by a fraction

To divide a whole number by a fraction, follow these steps:

Step 1: Invert the fraction to find its reciprocal and replace the division symbol with a multiplication symbol.

Step 2: Multiply the whole number by the reciprocal.

Step 3: Simplify the resulting fraction (If needed).

Let’s understand these steps with the help of an example:

Example: Find 3 ÷ 1 2

Solution:

Given: 3 ÷ 1 2

Step 1: First, find the reciprocal of 1 2 .

The reciprocal of 1 2 is 2 1

Step 2: Multiply the whole number by the reciprocal.

3 × 2 1 = 3 ×2 1 = 6 1 = 6

Hence, 3 ÷ 1 2 = 6

Division of a fraction by a whole number

To divide a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number.

Let us take an example:

Example: Find 3 4 ÷ 3

Solution:

Given: 3 4 ÷ 3

Step 1: First, find the reciprocal of 3.

The reciprocal of 3 is 1 3

Step 2: Multiply the fraction by the reciprocal.

3 4 × 1 3 = 3 ×1 4 ×3 = 3 12 = 1 4

Hence, 3 4 ÷ 3 = 1 4

Division of a fraction by another fraction

When dividing one fraction by another, we multiply the first fraction (dividend) by the reciprocal of the second fraction (divisor).

Let’s understand this with an example:

Example: Find 3 5 ÷ 1 2 ,

Solution:

Given: 3 5 ÷ 1 2

Step 1: First, find the reciprocal of the divisor i.e., 1 2 .

The reciprocal of 1 2 is 2 1

Step 2: Multiply the first fraction by reciprocal.

3 5 × 2 1 = 3 ×2 5 ×1 = 6 5

Step 3: Convert the improper fraction into a mixed fraction. So, 6 5 = 1

Let’s Practise - 5

1. Find:

Let’s Learn

Fractions in Real Life

We find fractions in our everyday life.

Example 1: Seema dyes dresses. She had to dye 50 dresses. She has so far finished 30 dresses. What fraction of dresses has she finished?

Solution:

Total number of dresses = 50

Dresses that are completely dyed = 30

Fraction of dresses finished = Dresses that are completely dyed

Total number of dresses

Fraction of dresses finished = 30 50

Fraction of dresses finished = 3 5

Therefore, fraction of dresses finished by Seema is 3 5

Word Zone

Dye: To change the colour of something using a special liquid.

Example 2: Rishu read 25 pages of a book containing 100 pages. Rajat read 3 4 of the same book. Who read less?

Solution:

Rishu reads 25 pages out of 100 pages.

Fraction of 25 pages out of 100 pages = 25 100 = 1 4

Rajat reads 3 4 of the same book.

Now, let us compare the fractions 1 4 and 3 4

We know that when fractions have the same denominator, the fraction with the greater numerator is larger.

Since, 3 > 1, therefore, 1 4 > 3 4 .

Hence Rishu reads less pages.

Example 3: Deepa had 5 6 of a cake. She gave 2 6 out of that to her younger brother. How much cake is left with her?

Solution:

Deepa originally had 5 6 of a cake, and she gave 2 6 to her younger brother.

To find out how much is left, we subtract the amount given away from the original amount:

5 6 − 2 6

To subtract these fractions, we need a common denominator, which is already 6 in this case. Subtract the numerators while keeping the denominator the same:

5 6 − 2 6 = 5 − 2 6 = 3 6

Now, 3 6 is equivalent to 1 2 when simplified.

So, Deepa has 1 2 of the cake left.

Let’s Practise - 6

1. Solve the following problems:

a. Danish is reading a book that has 120 pages. After a few hours, he has read 72 pages. What fraction of the book has he read?

b. Ankit covered 45 pages of a comic book with 150 pages. Aditi read 1 2 of the same comic. Who read less?

c. Sarah had 4 7 of a pizza. She shared 2 5 of it with her friend. How much pizza does Sarah have left?

d. A car runs 16 km using 1 litre of petrol. How much distance will it cover using 5 4 litres of petrol?

The grip-sizes of tennis racquets are often in mixed numbers. For example, one size is ‘3 7 8 inches’ and ‘4 3 8 inches’ is another.

Fact Zone

Let’s Sum Up

Fractions with the same denominator are called like fractions..

Fractions with different denominators are called unlike fractions.

Fractions that represent the same value are called equivalent fractions.

A fraction is said to be in the simplest (or lowest) form if its numerator and the denominator have no common factor except 1.

Fractions with the same denominator are added by combining their numerators.

Fractions with the same denominator are subtracted by taking the difference of their numerators.

Fractions with the same denominator are called like fractions..

Fractions with different denominators are called unlike fractions.

Fractions that represent the same value are called equivalent fractions.

A fraction is said to be in the simplest (or lowest) form if its numerator and the denominator have no common factor except 1.

Fractions with the same denominator are added by combining their numerators.

Life Skills

During a school event, you and your friend decided to combine your snacks to share with everyone. You brought 2 5 of a bag of popcorn, and your friend brought 3 8 of a bag of chips by weight.

What fraction of the combined snacks do you have in total?

Cross-Curricular Connections

Physical Education:

During physical education class, you run for 15 minutes out of a 1-hour session. What fraction of the class time is spent running?

21st Century Skills

Imagine you are following a recipe that calls for 3 4 cup of flour, but you only have a 1 2 cup measuring cup and a 1 4 cup measuring cup. How can you accurately measure 3 4 cup of flour using these two measuring cups?

Extend Your Knowledge

Fractions can be converted into decimals, and vice versa. For instance, 1 2 is equivalent to 0.5 in decimal form.

Tip for the Parent

• Relate fractions to everyday situations. For example, cutting a pizza into slices, sharing candies, or dividing a cake can be great examples.

• Involve your child in the kitchen to introduce fractions through measuring ingredients. For example, ask them to measure 1 2 cup of flour or 1 4 teaspoon of salt.

• Encourage your child to draw fractions. This can help them visualize the concept and gain a deeper understanding.

Decimals

My Study Plan

Decimals

Decimal place value chart

Expanded form of decimals

Like and unlike decimals

Comparing and ordering decimals

Converting fractions into decimals

Converting decimals into fractions

Addition and subtraction of decimals

Multiplication of decimals

Division of decimals

Recall

fraction of an hour is 45 minutes.

2. Look at the images below and identify if they are like fractions or unlike fractions.

Thinking Zone

Imagine you are dividing a pizza into 8 equal slices, and each friend takes one slice.

a. What fraction of the pizza did each person get?

b. Now, think about expressing this fraction differently, using a dot (.) instead of a slash (/). How would you represent it? Have a discussion with your teacher about it.

Let’s Learn

Decimals

Look at the fractions1 10 , 3 100 , 23 1000

These fractions have denominators 10, 100, and 1000. They are called decimal fractions. Decimal fraction can be written in either fractional form or decimal form. The numbers written with a dot in decimal form are called decimal numbers.

A decimal number has two parts: the whole number part and the decimal part. These parts are separated by a decimal point (.).

1 . 4

Whole number part

Decimal part

Decimal point

Tenth

If we divide one whole into ten parts, each part is called ‘one-tenth’.

In the picture below, the shaded part represents 1 10 or one-tenth of the whole strip.

In decimal notation, 1/10 is written as 0.1 and read as ‘zero point one’.

Similarly, the fraction representing the shaded part is 3 10 and the fraction for the unshaded part is 7 10 .

In decimal form, 3 10 equals 0.3, and 7 10 equals 0.7. 0.3 is pronounced as ‘zero point three’, and 0.7 is pronounced as ‘zero point seven’.

Hundredth

If we divide one whole into hundred parts, each part is called ‘one-hundredth’.

Look at the picture below.

1 100

Here, the grid is divided into 100 equal sections. The shaded area within this grid represents 1 100 , referred to as ‘one-hundredth’.

In decimal form, 1 100 is written as 0.01, and it is read as ‘zero point zero one’.

Thousandth

If we divide one whole into thousand parts, each part is called ‘one-thousandth’.

Look at the below picture.

Here, the grid is divided into 1000 equal sections. The shaded area within this grid represents 1 1000 , referred to as ‘one-thousandth’.

In decimal form, 1 1000 is written as 0.001, and it is read as ‘zero point zero zero one’.

Let’s Learn

Decimal Place Value Chart

Like ordinal numbers, decimals are also represented in the place value chart.

In the above place value chart,

1. Moving left increases the place value by 10.

2. Moving right decreases the place value by 10.

3. The decimal point acts as the separator between the whole number and the decimal parts.

Example 1: Write the place value of each digit in 248.154

Solution: We can represent this number in the place value chart, as below.

Here, the place value of each digit is, as below.

248.154 2 hundreds = 200 4 tens = 40 8 ones = 8

Reading decimal numbers

thousandths = 4 1000 = 0.004

hundredths = 5 100 = 0.05

tenths = 1 10 = 0.1

We read whole numbers as usual, and introduce the decimal part digit by digit.

For example:

Decimal number Read as

3.7 three and seven tenths three point seven

208.19 two hundred eight and nineteen hundredths two hundred eight point one nine

47.186 forty-seven and one hundred eighty-six thousandths forty-seven point one eight six

Expanded Form of Decimals

Decimal numbers can be expanded in the following three forms: place value form, decimal form, and fractional form.

Example: Expand 342.516

Solution:

Let us write the number in the place value form.

From above, we can say that

342.516 = 3 hundreds + 4 tens + 2 ones + 5 tenths + 1 hundredths + 6 thousandths

Decimal form

342.516 = 300 + 40 + 2 + 0.5 + 0.01 + 0.006

Fractional form

Let’s Practise - 1

1. Write the following decimals in the decimal place value chart.

2. Write the following decimals in their expanded form.

Let’s Learn

Like and Unlike Decimals

You may have already learned about like and unlike fractions. Similarly, we also have like and unlike decimals.

Like decimals

Decimals with the same number of decimal places to the right of the decimal point are called ‘like decimals’.

Example: 4.54, 27.09, and 172.69 are like decimals because they all have two decimal places.

Unlike decimals

Decimals with different numbers of decimal places to the right of the decimal point are called ‘unlike decimals’.

Example: 4.4, 13.45, and 14.056 are unlike decimals as they have one, two, and three decimal places, respectively.

Converting unlike decimals into like decimals

To make unlike decimals into like decimals, follow these steps:

1. Find the decimal number with the highest number of decimal places.

2. Add one or more zeroes to the right of other decimal numbers so that they all have the same number of decimal digits.

Let’s understand this better using an example.

Example: Convert 0.126, 35.45, 3.45, and 6.142 into like decimals.

Solution:

Among these decimals, 0.126 and 6.142 have the most decimal places (3).

To make them all similar, adjust the others to have three decimal places. Therefore, 35.45 becomes 35.450 and 3.45 becomes 3.450.

Comparing and Ordering Decimals

You are familiar with comparing and arranging numbers in ascending and descending order. We can do the same with decimals as well. To compare two or more decimal numbers, follow these steps:

Step 1: Convert unlike decimals to like decimals.

Step 2: Compare the whole number part of the decimals. The decimal with the larger whole number part is greater.

Step 3: If the whole number parts are equal, compare the tenths place. The decimal with the larger digit in the tenths place is considered greater.

Step 4: If the tenths place digits are equal, proceed to compare the hundredths place, and so on.

Example 1: Compare 43.4 and 18.67.

Solution:

Step 1: Convert the given decimals to like decimals. We get 43.40 and 18.67

Step 2: Compare the whole number part of the decimals.

In 43.40, the whole number part is 43, and in 18.67, the whole number part is 18.

Since 43 is greater than 18, we conclude that 43.40 > 18.67.

Let’s Practise - 2

1. Convert the given unlike decimals into like decimals.

a. 4.201, 23.88, 142.011, 20.3, 154.77 _____________________________________________________

b. 1.3, 2.02, 4.0, 12.2 _____________________________________________________

2. Compare the following decimals using <, >, or =.

a. 24.56 _____ 43.5

c. 936.23 _______925.323

Let’s Learn

Converting Fractions into Decimals

493.57 ______ 472.76

We know that decimals are fractions with denominators 10, 100, 1000, etc.

Conversion when denominator is 10, 100, 1000, etc.

Step 1: Count the number of zeros in the denominator after 1.

Step 2: Count an equal number of places in the numerator, starting from the ones place, and place the decimal point.

Step 3: Add leading zeros if there are not enough digits in the numerator.

Example 1: Convert 17 10 into a decimal.

Solution:

The number of zeros in the denominator = 1

Therefore, the decimal point moves 1 place to the left.

So, 17 10 = 1.7

Example 2: Convert 431 1000 into a decimal.

Solution:

The number of zeros in the denominator = 3

Therefore, the decimal point moves 3 places to the left.

So, 431 1000 = 0.431

Conversion when denominator is converted to 10, 100, 1000, etc.

Step 1: Multiply the fraction with a common number to get 10, 100, 1000, etc., as the denominator.

Step 2: Count the number of zeros in the denominator after 1.

Step 3: Count an equal number of places in the numerator, starting from the ones place and place the decimal point.

Step 4: Add leading zeros if there are not enough digits in the numerator.

Example 1: 13 20

Solution: 13 20 5 5 65 100 065 ×= = .

Conversion when denominator can not be converted to 10, 100, 1000, etc.

Step 1: Divide the numerator by the denominator.

Step 2: Complete the division until a non-zero remainder is left.

Step 3: Place a decimal point in the dividend and the quotient.

Step 4: Put a zero to the right of the dividend and remainder, and divide again.

Step 5: Repeat step 4 until either the remainder is zero or the required number of decimal places has been obtained.

Converting Decimals into Fractions

To convert decimals into fractions, we follow the steps given below.

Step 1: Remove the decimal point from the decimal number to get the numerator of the fraction.

Step 2: To get the denominator, write ‘1’ followed by as many zeros as there were decimal places in the original decimal number.

Let us take a few examples to understand it.

a. 0.4 becomes 4 10 .

c. 11.467 becomes 11467 1000 .

Fact Zone

b. 0.55 becomes 55 100 .

Decimals with same value are called equivalent decimals.

For example

9/10 = 9.0/10 = 0.9, 90/100 = 90.0/100 = 0.90, 900/1000 = 900.0/1000 = 0.900

0.9 = 0.90 = 0.900 as the value of a decimal number does not change when zeros are added at the right of the decimal number.

Let’s Learn

Addition and Subtraction of Decimals

Step 1: Write the numbers one below the other, such that the decimal points of all numbers are in the same column.

The digits having the same place value should be in the same column.

Note: In subtraction, write the smaller number below the larger number.

Step 2: Convert into like decimals if necessary.

Step 3: Add/Subtract as you would with whole numbers

Step 4: In the result (sum or difference), place the decimal exactly below the decimal point in the numbers.

Example 1: Add 2.84, 31.205, 346.7, and 0.6.

Solution:

Step 1: Convert to like decimals.

2.84 = 2.840, 31.205 = 31.205, 346.7 = 346.700, 0.6 = 0.600

Step 2: Arrange the numbers in columns and perform the addition as if they were whole numbers.

Thus, the answer is 381.345.

Example 2: Subtract 23.45 from 38.2.

Solution:

Step 1: Convert to like decimals.

38.2 = 38.20, 23.45 = 23.45

Step 2: Arrange them in columns and subtract as if they were whole numbers.

Write the larger number first.

Thus, the answer is 14.75.

Let’s Practise - 3

1. Arrange the given decimals in columns and then add.

a. 152.93, 100.195, 21.209, 1.112 b. 134.42, 12.612, 3.341, 0.624

T O t h

2. Arrange the given decimals in columns and then subtract.

a. 72.55 – 29.34

b. 431.7 – 49.237

Multiplication of Decimals

Besides adding and subtracting, we can also multiply the decimal numbers by whole numbers or by another decimal number.

Multiplying a decimal by a whole number

To multiply a decimal number by a whole number,

Step 1: Write the decimal number as a whole number.

Step 2: Multiply this number by the given whole number as you would multiply two whole numbers.

Step 3: In the result (product), place the decimal point in such a way that the product and decimal number have same number of decimal places.

Example 1: Multiply 1.45 by 12.

Since 1.45 has decimal before two digits, we put the decimal before the last two digits in the product.

Hence, 1.45 x 12 = 17.40.

Multiplying a decimal by another decimal

To multiply one decimal number by another decimal number, follow these steps:

Step 1: Write the decimal numbers as whole numbers.

Step 2: Multiply the given decimals as we would multiply any two whole numbers.

Step 3: Count the number of decimal places.

Step 4: In the result (product), place the decimal point so that it is equal to the sum of the decimal places of both the multiplicands and the multipliers.

Example 1: Multiply 13.07 by 1.05.

Now, since 13.07 and 1.05 together have four digits after decimal, we put the decimal point before the last four digits in the product.

Hence, 13.07 × 1.05 = 13.7235.

Multiplying a decimal by 10, 100, 1000….

When we multiply a decimal number by 10, 100, 1000, and so on, the decimal point in the product moves to the right by the same number of positions as there are zeros in the multiplier.

For example:

3.234 × 10 = 3.234 = 32.34

3.234 × 100 = 3.234 = 323.4

3.234 × 1000 = 3.234 = 3234.0

Let’s Practise - 4

1. Solve the following.

a. 3.4 × 5 = ___________ b. 10.45 × 15 = ___________

2. Multiply the given decimals.

a. 0.064 × 0.07 = ___________ b. 14.145 × 0.30 = ___________

3. Solve the following.

a. 45.678 × 10 = b. 9.7890 × 1000 =

Let’s Learn

Division of Decimals

Besides multiplying, we can also divide the decimal numbers by whole numbers or by another decimal number.

Division of a decimal by a whole number

To divide a decimal by a whole number, we follow these steps.

Step 1: Divide the decimal by the whole number as we would with whole numbers.

Step 2: After completing the division, place the decimal point in the quotient in the same position as in the dividend.

Example: Divide 88.25 by 5.

Solution:

Step 1: Divide 88.25 by 5

Step 2: Since the dividend has decimal point after two digits, the quotient will also have decimal point after two digits.

Therefore, 88.25 ÷ 5 = 17.65.

Division of a decimal by another decimal

To divide a decimal by another decimal, we follow the below steps.

Step 1: Make the divisor a whole number by moving the decimal point.

Step 2: Multiply the dividend by 10, 100, or 1000 depending on the number of decimal places in the divisor.

Step 3: Divide the new dividend by the whole number divisor.

Step 4: Place the decimal point in the quotient as in the same position of the dividend.

Example: Divide 4.446 by 0.19.

Solution:

∴ 4.446 ÷ 0.19 = 23.4.

Division of a decimal by 10, 100, 1000

When we divide a decimal number by 10, 100, 1000, and so on, the decimal point in the product moves to the left by the same number of positions as there are zeros in the divisor.

Example:

652.1 ÷ 10 = 65.21

652.1 ÷ 100 = 6.521

652.1 ÷ 1000 = 0.6521

Let’s Practise - 5

1. Solve the following.

a. 0.245 ÷ 3 b. 5.421 ÷ 0.5 c. 3.345 ÷ 0.6

d. 6.875 ÷ 100 e. 9.7650 ÷ 1000

Let’s Sum Up

A fraction where the denominator is a power of 10, such as 10, 100, 1000, and so on, is called a decimal fraction.

A decimal number comprises two parts: the whole number part and the decimal part. These parts are separated by a decimal point (.).

We can use three forms to write decimals in the expanded form: the place value form, the decimal form, and the fractional form.

We can convert decimals to fractions and fractions to decimals.

Decimals with the same number of decimal places to the right of the decimal point are called ‘like decimals’.

Decimals with different numbers of decimal places to the right of the decimal point are called ‘unlike decimals’.

We can compare, order, add, subtract, multiply, and divide decimal numbers.

Life Skills

Aayu is excited to support an animal shelter by contributing bags of pet food. Each bag costs ₹19.75 and provides food for one animal for a week. Aayu aims to purchase sufficient bags to feed 42 animals for a week. Upon checking his piggy bank, he discovers he has saved ₹375.50. How much additional money does he require to acquire all the bags of pet food for the shelter?

Science:

A beaker contains 1.75 litres of water. If 0.45 litres of water evaporates while boiling the water, how much water is left in the beaker in litres?

21st Century Skills

Examine the decimal numbers in the grid. What is special about these numbers and the grid?

(Hint: Try adding the decimal numbers horizontally, vertically, and diagonally. What do you observe?)

These numbers are known as __________ numbers.

Extend Your Knowledge

Decimal numbers are of two types: terminating decimal numbers and non-terminating decimal numbers.

Terminating decimal numbers have a fixed number of digits after the decimal point.

For example, when we convert the fraction ¼ to a decimal number, we get 0.25. There are only 2 digits after the decimal place.

Non-terminating decimal numbers have endless digits after the decimal place.

For example, when we convert the fraction 1/3 to a decimal number, we get 0.3333333….

Write your own examples of both types of decimal numbers.

Tip for the Parent

Encourage your child to practise decimals in daily activities like shopping. Discuss prices and quantities to improve their understanding of decimals.

Percentage

My Study Plan

Percent

Converting a percentage into a fraction and vice versa

Converting a percentage to a decimal and vice versa

Finding the value of the percentage of a given quantity

Calculating a quantity as a percentage of the total quantity

Application of percentage in real life

Let’s Recall

You have learnt fractions and decimals. Let’s do a quick review of these concepts.

1. Pihu’s mother made pizza. She cut the pizza into 8 slices. Pihu ate 3 slices of the pizza. What fraction of pizza did Pihu eat?

2. Aayu has 25 sweets. He gives 5 sweets to his sister.

a. Write the fraction of sweets Aayu gave his sister.

b. When we convert this fraction to a decimal number, we get _____.

Thinking Zone

When you visit a store during a sale, you will often see signboards saying things like '50% off' or '25% off'. Let’s say you have been wanting to buy a new storybook for a while now, but it costs Rs. 500, and you have only managed to save Rs. 280 in your piggy bank till now. Now you see that the book is being sold at 50% off. If you know how to calculate percentages, you will find that you have saved enough to buy the book.

Think of other places where you have seen % (the percent sign).

Let’s Learn

Percent

Now that you know why it is useful to learn about percentages, let’s dive into the topic!

'Percent' comes from the Latin word 'per centum', meaning 'per hundred'. It is used to express something as a part of a hundred.

The symbol for 'percent' is '%.'

Let’s take an example.

A new housing complex is being built in your neighbourhood. The advertisement in the newspaper says that in the complex, 20% of the buildings are bungalows, 30% are row houses, and 50% are multi-storey apartments. What does this mean?

• '20% bungalows' means 20 out of every 100 buildings in the housing complex are bungalows.

• '30% row houses' means 30 out of every 100 buildings in the complex are row houses.

• '50% multi-storey apartment buildings' means 50 out of every 100 buildings are apartment blocks.

Converting a Percentage into a Fraction

To convert a percentage into a fraction,

• Remove the '%' symbol.

• Write the percentage as a fraction with a denominator of 100.

• Simplify the fraction to its lowest terms.

Let’s understand this better with an example.

Example 1: Convert the following percentages into fractions:

a. 45%

Converting a Fraction into a Percentage

Fractions with denominator 100

To convert fractions with a denominator of 100 into percentages, we simply replace the denominator with the '%' symbol.

For example,

becomes 45%, 52

becomes 52%, and,

becomes 76%.

Fractions with denominator other than 100

If the fraction's denominator is not 100, we can follow one of two methods:

Method 1: Convert the fraction into an equivalent fraction with a denominator of 100 and replace the denominator with '%.'

Method 2: Multiply the fraction by 100 and add the '%' symbol to the result. Let’s look at an example to understand this more clearly.

Example 1: Convert the following fractions into percentages using both the methods.

a.

Solution:

Let’s Practise - 1

1. Express the following fractions as percentages.

a. 25 100 = ________

b. 3 5 = ________

2. Express the following percentages as fractions in their simplest form.

a. 30% = ________

Let’s Learn

b. 120% = ________

Converting a Percentage to a Decimal

We know that a fraction can be converted into a decimal number and vice versa. Similarly, a percentage can also be converted into a decimal number.

Methods to convert a percentage into a decimal,

Method 1: Remove the '%' symbol and divide the number by 100 to express it in decimal form.

For example:

a. 44% = 44 100 = 0.44

b. 3.8% = 38 100 . = 0.038

Method 2: Remove the '%' symbol and move the decimal point two places to the left. If needed, add extra zeroes at the beginning before converting it into a decimal.

a. 45% = 45.0% = 0.45 b. 75% = 75.0% = 0.75

Converting a Decimal to a Percentage

We can also convert a decimal number to a percentage.

To convert a decimal into a percentage, we can use either of these two methods:

Method 1: Multiply the decimal by 100 and add the '%' symbol to the result.

For example:

a. 0.6 becomes (0.6 × 100)% = 60%. b. 0.4 becomes (0.4 × 100)% = 40%.

Method 2: Express the number as a fraction, then multiply it by 100 and add the '%' symbol to the result.

For example,

a. 0.7 becomes ( 7 10 × 100)% = 70%. b. 0.12 becomes ( 12 100 × 100)% = 12%.

Let’s Practise-2

1. Convert the following decimals to percentages.

2. Convert these percentages into decimals.

Let’s Learn

Finding the Value of the Percentage of a Given Quantity

Remember the example of the book sale? Without knowing how to find the value of 50% of the original price of the book, you will not know if you have saved enough to buy it. So, let’s see how to find the value of the percentage.

To find a percentage of a given quantity, follow these steps:

Step 1: Convert the percentage to a fraction.

So, in our example, we write 50% as a fraction.

We get: 50% = 50 100

Step 2: Multiply the fraction by the given quantity.

In our example, the quantity is the original price of the book, i.e., 500.

Thus, 50% of 500 is: 50 100 500 250 ×=

So, the new price of the book is 250.

Let’s look at another example.

Example: What is 30% of 150 km?

Solution:

Step 1: Convert the percentage to a fraction: 30% = 30 100

Step 2: Multiply the fraction by the given quantity: 30 100 150 × km = 45 km.

Therefore, 30% of 150 km is 45 km.

Let’s Learn

Calculating a Quantity as a Percentage of the Total Quantity

To find a quantity as a percentage of the total amount, follow these steps:

Step 1: Use the given quantity as the numerator and the total quantity as the denominator.

Numerator (Given Quantity)

Denominator (Total Quantity)

Step 2: Multiply the resulting fraction by 100 to find the percentage.

Let us solve an example:

Example 1: What percent of 30 is 3?

Solution:

Step 1: We divide 3 by 30, i.e, 3 30 .

Step 2: 3 30 100 10 ×= %

So, 3 is 10% of 30.

Here’s another example.

Example 2: A farmer is selling oranges in the market. But 1000 grams out of the 50 kilograms of oranges in his basket are spoilt. What percent of oranges are spoilt?

Solution:

We need to find what percentage of 50 kg is 1000 g.

Use the given quantity (1000 g) as the numerator and the total quantity (50 kg) as the denominator.

Remember, when we are comparing any two quantities, their units must be the same.

For example, in this case, we will convert 1000 g to kg. Therefore, 1000 g = 1 kg.

Now, let us substitute the value of the numerator and the denominator.

Numerator (Given Quantity)

Denominator (Total Quantity) = 1 50 100 2 ×= %

Multiply the fraction by 100 to determine the percentage.

1 50 100 2 ×= %

Therefore, 2% of the total oranges are spoilt.

Let’s Practise - 3

1. Find the value of given percentages.

a. 25% of 400 houses b. 30% of 1500 apples

c. 45% of 1000 km

2. Find the percentage of the given quantity from the total quantity.

a. 800 paise of `40 b. 4 hours of a day

c. 100 mL of 2 L

Let’s Learn

Application of Percentage in Real-Life

We know that percentages are useful in real life. Let’s look at some examples to understand this better.

Example 1: Pihu and Aayu are solving math puzzles. Pihu completed 48 out of 60 puzzles correctly, and Aayu solved 80 out of 100 correctly. Who has a higher success rate of solving math puzzles?

Solution:

To determine who has a higher success rate in solving math puzzles, let's calculate the percentage of puzzles each has solved correctly.

First, let's calculate Pihu's success rate:

Step 1: Use the number of puzzles Pihu solved as the numerator and the total number of puzzles as the denominator.

Pihu's success rate: 48 60

Step 2: Multiply the fraction by 100 to get the percentage.

Pihu's Percentage: 48 60 100 80 ×= %

Next, let's calculate Aayu's success rate:

Step 1: Use the number of puzzles Aayu solved as the numerator and the total number of puzzles as the denominator.

Aayu's success rate: 80 100

Step 2: Multiply the fraction by 100 to get the percentage.

Aayu's Percentage: 80 100 100 80 ×= %

Both Pihu and Aayu had an 80% success rate in solving math puzzles, so they performed equally well.

Example 2: In a jar, there were 80 marbles. If 15% of the marbles were taken out, how many marbles remained in the jar?

Solution:

To find the number of marbles left in the jar, follow these steps:

Step 1: Convert the given percentage into a fraction.

15% = 15

100

Step 2: Multiply the fraction by the total number of marbles in the jar.

15% of 80 = 15 100 80 × = 12 marbles

So, the number of marbles remaining in the jar is = 80 – 12 = 68 marbles.

Let’s Practise - 4

1. Ritu, a florist, has 800 flowers in her shop. Find the percentage of each type of flower based on the quantities provided below:

Roses: 200 Tulips: 150 Daisies: 100 Lilies: 150 Orchids: 200

2. Deepak reads for 3 hours every day. What percentage of his day does he spend reading?

3. Ali owns a car showroom. Out of 350 cars in his showroom, 210 cars are white coloured. Find out the percentage of cars in Ali’s showroom that are not white in colour.

4. Liza works in a bakery. Out of the 42 cakes she decorated in a day 21 were chocolate-falvoured and 6 were strawberry-flavoured. Find the percentage of chocolate and strawberry cakes out of 42 total cakes.

Fact Zone

Approximately 70% of the Earth's surface is covered by water.

Let’s Sum Up

'Percent' comes from the Latin word 'per centum', meaning 'per hundred'. It's used to express something as a part of a hundred.

Fractions can be converted to percentages by multiplying 100% and vice versa. Decimals also can be converted to percentages by multiplying 100% and vice versa.

Percentages are widely used in our daily life.

Life Skills

It is your birthday party, and you are treating 10 of your friends with ice creams. 30% of your friends want to order chocolate ice cream, 30% want to order strawberry ice cream and 40% want sundaes. How many of each type of ice-cream should you order?

Cross-Curricular Connections

Social Studies:

A village has total population of 2500 and out of total only 45% can cast their vote. Find out how many percent of people can vote.

21st Century Skills

Aruna received a 20% increase in her weekly allowance. If her original allowance was ₹5000, how much is her new weekly allowance after the increase? Explain the steps you would take to find the answer.

Extend Your Knowledge

The Amazon rainforest is the largest tropical rainforest in the world. It is located in South America. It produces 20% of Earth’s oxygen!

Tip for the Parent

Explain to your child how we use percentages in daily life and ask them to practise by calculating real numbers. For example, the next time you visit a restaurant and receive the bill, ask your child to calculate 10% of the total to tip the waiter.

My Study Plan

Geometry

Angles and its measurement

Types of Angles

Types of Lines

Polygons and their types

Triangles and its types

Elements of a Circle

Construction of a Circle

Let’s Recall

You have learnt about lines, line segments and rays in the previous class. Let’s do a quick warm-up of these concepts.

1. Which geometrical term best describes the figure? Tick the correct option.

Curve

b. Line Segment c. Line

a. Ray

b. Point c. Line

a. Ray

b. Line c. Point

•

a. Ray

b. Point

c. Ray

Let’s Learn

In earlier classes, you learnt about line segments and rays. Now we learn about some figures that are formed by joining them.

Angles

An angle is a geometric figure formed by two rays sharing a common endpoint, known as the vertex.

The two rays that make up the angle are called its arms. Angles are measured in degrees or radians to describe the extent of separation between these rays.

For example, ray OA and ray OB forms an angle with point O as the vertex.

The two rays that make up the angle are called its arms, and the shared starting point is known as the vertex of the angle.

Angles are typically measured in degrees or radians to describe the extent of separation between these rays.

Naming an Angle

An angle can be named in different ways:

• With three capital letters, e.g., ∠AOB or ∠BOA, with the vertex in the middle.

• Using a single capital letter for the vertex, like ∠O.

Parts of an angle

An angle has two parts: the inside (interior) and the outside (exterior). The interior of an angle is the space between its arms, and the exterior is the space outside the arms.

In the diagram, points X, Y, and Z are inside angle ∠PQR, while points A, B, and C are outside it.

Points in the interior and exterior of an angle

Measuring Angles

Angles are measured in degrees using a protractor, which has a baseline at its bottom edge with 0 at the centre. The protractor's curved edge has two scales, the inner and outer scales, both ranging from 0° to 180°. Each scale is divided into 180 equal parts, with each division representing one degree (°). baseline

Example 1: Measure ∠XYZ using a protractor.

Measuring an angle

Solution: To measure ∠XYZ,

Step 1: Place the protractor so its centre aligns with vertex Y, and its baseline matches line YZ.

Step 2: Start from mark Z on the curved edge and note where line YX intersects the inner scale, which in this instance is at 55°.

Thus, ∠XYZ = 55°

Measurement using a protractor

Classification of Angles

Angles are categorized based on their measurements. Here are the different types of angles:

Acute Angle

An angle with a measurement less than 90° is called an acute angle.

For example, in the figure, ∠XYZ measures 55°, making it an acute angle.

Obtuse Angle

An angle with a measurement greater than 90° but less than 180° is called an obtuse angle.

For instance, in the figure, ∠LMN measures 130°, classifying it as an obtuse angle.

Obtuse angle

Right

Angle

An angle with a measurement of 90° is called a right angle.

In the given figure, ∠ABC measures 90°, making it a right angle.

Right angle

Complementary Angles

Two angles are complementary if their measures sum up to 90°.

In the adjacent figure, ∠ABC and ∠DEF are complementary angles because their measures, 55° and 35°, add up to 90°.

Complementary angles

Supplementary Angles

Two angles are supplementary if their measures add up to 180°. Each angle is considered the supplement of the other.

In the figure, ∠ABC and ∠DEF are supplementary because their measures add up to 180° (60° + 120° = 180°).

1. Measure the angle and write it's type.

2. Determine whether the given pairs of angles are complementary or supplementary.

a. ∠A = 60° and ∠B = 30° b. ∠P = 40° and ∠Q = 140° c. ∠A = 55° and ∠B = 125° d. ∠A = 40° and ∠B = 50°

Let’s Learn

You already know that a line is an infinitely long, straight path with no width, and which is made up of an infinite number of points extending in both directions. Now we will learn about types of lines.

Types of Lines

Lines can be categorized as follows:

Coplanar Lines:

These lines lie on the same plane. In the figure, line PQ and line RS are coplanar lines.

Coplanar lines

Parallel Lines:

These lines never intersect or cross each other, and the distance between them remains constant.

Thinking Zone

Mark a point on the paper. Draw lines passing through this point. How many lines can you draw?

In the figure, line AB and line CD are parallel to each other. They are denoted by the symbol ||, so we write AB || CD.

Parallel lines

Intersecting Lines:

When two or more lines in a plane cross each other, they are called intersecting lines. In the diagram, lines AB and CD intersect at point O, making them intersecting lines.

Intersecting lines

Perpendicular Lines:

These lines intersect at right angles. In the figure, lines PQ and RS intersect at a right angle, represented by the symbol ⊥, so we write RS ⊥ PQ.

Perpendicular lines

It's worth noting that in the given diagram, angles ∠RXQ, ∠RXP, ∠SXQ, and ∠SXP are all right angles.

1. Classify the following lines and state the identified feature.

Let’s Learn

Now that we know about lines and angles, let us learn about polygons.

Polygon

A polygon is a closed shape formed by connecting three or more-line segments. Polygons can be categorized based on the number of sides they have:

Types of polygons

Name of the polygon

Quadrilateral

Number of sides and angles

A triangle has three sides and three angles.

A quadrilateral has four sides and four angles.

Square and Rectangle are examples of quadrilaterals.

Pentagon A pentagon has five sides and five angles.

Square Rectangle

Hexagon A hexagon has six sides and six angles.

Heptagon A heptagon has seven sides and seven angles.

Octagon An octagon has eight sides and eight angles.

The headquarters of the United States’ Department of Defense is called the Pentagon, because the building is 5-sided. The Pentagon is the largest office building in the world and about 25,000 people work in the building!

Let’s

Learn

Now let us look at triangles in more detail.

Triangles

A triangle is formed by 3 line segments. It is symbolized by ∆.

In the figure, ∆ABC has 3 sides, 3 vertices and 3 angles.

Sides: AB, BC, and CA.

Vertices: A, B, and C.

Angles: ∠ABC, ∠BCA, and ∠CAB.

Triangle

Fact Zone

Interior and Exterior of a Triangle

When a triangle is drawn on a plane, it creates three distinct regions:

Points in the interior, exterior and on the boundary of a triangle

a. Interior of the triangle: This includes all points within the triangle. In ∆PQR, points A, C, and X are inside the triangle.

b. Exterior of the triangle: This includes all points outside the triangle. For ∆PQR, points Y and B are outside the triangle.

c. Boundary of the triangle: This consists of all points lying directly on the triangle itself. Points Z and E are on the boundary of the triangle.

Let us look at an example now.

Example:

Name the triangle shown in the following figure and write the:

a. sides of this triangle.

b. angles of this triangle.

c. point lying in the interior of the triangle.

d. points lying in the exterior of the triangle.

Solution:

Triangle Name: ∆PQR

a. Sides of ∆PQR: PQ, QR, and RP

b. Angles of ∆PQR: ∠PQR, ∠QRP, and ∠RPQ

c. Point inside the triangle: A

d. Points outside the triangle: G and X

Classification of triangles based on their side lengths

Triangles can be categorized as scalene, isosceles, or equilateral depending on the lengths of their sides.

Triangle Description Example

Scalene Triangle

Isosceles Triangle

In a scalene triangle, all three sides have different lengths.

In ∆PQR, the sides PQ, QR, and RP have distinct lengths.

Equilateral Triangle

An isosceles triangle has two sides of equal length.

In ∆ABC, AB and AC are of the same length.

An equilateral triangle has all three sides of equal length.

In ∆PQR, all sides PQ, QR and PR are of same length.

Classification of triangles based on their angles

Triangles can be grouped into three categories based on the measurements of their angles.

Triangle Description Example

Acute-Angled Triangle

In an acute-angled triangle, all three angles are acute, meaning they are less than 90°.

∆XYZ is an acute-angled triangle because ∠X = 70°, ∠Y = 30°, and ∠Z = 80°.

Y

Right-Angled Triangle

ObtuseAngled Triangle

A right-angled triangle has one angle that measures 90°. ∆ABC is a right-angled triangle because ∠B = 90°.

An obtuse-angled triangle has at least one obtuse angle, meaning it is greater than 90°. ∆PQR is an obtuse-angled triangle since ∠Q = 130°. P

90°B C

2. A ladder is placed against a wall.

What type of triangle is formed in this case?

Ladder against a wall

1. Match the following.

Now we move away from polygons to a unique geometrical shape - the circle.

Circle

A circle is a closed curve formed by an infinite number of equidistant points, all surrounding a fixed point known as the centre.

Circle

Elements of a circle

Circumference: The length of the curved boundary of a circle is referred to as its circumference.

Radius: All points on the circle's boundary are equidistant from its centre. This distance from the centre to the circumference is called the radius of the circle.

In the figure, O is the centre, and OQ represents the radius of the circle.

Radius and circumference

Diameter: A line that passes through the centre of the circle and has its endpoints on the circle's circumference is termed the diameter of the circle.

Centre

In the figure, line PR is the diameter.

A diameter divides the circle into two equal halves, each known as a semicircle. The length of the diameter is twice the length of the radius.

Diameter = 2 × radius

Chord: A chord is any line segment connecting two distinct points on the circle's circumference. A chord may or may not pass through the centre of the circle. In the figure, PR is a chord. The longest chord of a circle is its diameter.

Arc: A segment of the circle's circumference is called an arc of the circle. In the figure, PR is an example of such an arc.

Construction of a Circle

We use a compass to draw a circle. One arm of the compass has a metal point while the other arm has a place to fix a pencil.

Let us now learn to draw a circle.

Example 1: Draw a circle of radius 4 cm using a compass.

Solution:

Step 1: Attach a pencil to the compass.

Step 2: Adjust the compass arms to a 4 cm width using a ruler.

Step 3: Place the compass's pointed end on your paper.

Step 4: Gently hold the needle arm and rotate the pencil arm to draw a smooth circle.

This process will give a circle with a 4 cm radius.

Let’s Practise-4

1. Draw a circle of radius:

a. 3 cm

b. 4.5 cm

2. Draw a circle of radius 6 cm and mark the following elements on it.

a. Radius OA

b. Chord PQ c. Arc MN

3. If the diameter of the circle is 14 cm, then find the radius of the circle.

4. If the radius of the circle is 5 cm, then find the length of the longest chord of that circle.

Let’s Sum Up

An angle is created when two rays share a starting point.

The two rays that make up the angle are called its arms, and the shared starting point is known as the vertex of the angle.

Angles are measured in degrees.

Based on their measurement, angles can be classified as acute angles, right angles and obtuse angles.

When the sum of two angles adds up to 90°, they are called complimentary angles.

When the sum of two angles adds up to 180°, they are called supplementary angles.

A circle has infinite number of radii (plural of radius). Fact Zone

Lines can be coplanar, intersecting, parallel or perpendicular.

A polygon is a closed shape formed by connecting three or more, line segments. Based on the number of sides, they are classified as triangle, quadrilateral, pentagon, hexagon, heptagon, octagon etc.

Triangles can be classified as equilateral, scalene or isosceles based on the lengths of their sides.

Triangles are classified as acute-angled, right-angled or obtuse-angled based on the measures of their angles.

A circle is a closed curve formed by an infinite number of equidistant points, all surrounding a fixed point known as the centre.

The parts of a circle include its circumference, centre, radius, diameter, chord and arc.

Life Skills

Your school has a round playground and the teacher tells your class that the school wants to build a wall around the playground. What part of the playground must be measured to find the length of the wall?

If the playground is to be divided into two equal halves, along which line of the circular playground should the division be made? Draw the playground and show how it can be divided into two equal halves.

Physical Education

Draw stick figures of yourself doing exercises and identify the different types of angles that are made by your limbs.

Cross-Curricular Connections

21st Century Skills

Divide the students in pairs. They have to draw three different clocks with hands of the clocks forming different angles. Then they also have to write the time that each clock is showing.

a. Hands of the clock to make right angle between them.

b. Hands of the clock to make an angle less than a right angle between them.

c. Hands of the clock to make an angle greater than a right angle between them.

Extend Your Knowledge

Tangrams are a fascinating and ancient Chinese puzzle game that consists of seven flat pieces called "tans." These pieces are traditionally cut from a square and can be rearranged to form a variety of shapes and figures.

Tips for the Parent

• Encourage your child to explore objects around the house and identify the Polygons. For example, doors and windows are quadrilaterals, as are kites. A Diwali lantern can be in a hexagon shape.

• Provide your child with opportunities to draw and construct geometric shapes. Encourage them to sketch different types of triangles, draw circles, or create their own polygons.

House

Boat

Tower Pyramid

Perimeter, Area, and Volume

My Study Plan

• Perimeter of 2D shapes, including squares, rectangles, triangles, and polygons with given side lengths

• Area of 2D shapes, such as squares, triangles, and rectangles, using appropriate formulas and units

• Volume of 3D shapes, like cubes and cuboids, using appropriate formulas and units

Let’s Recall

1. Find the sum of the lengths for each of the following figures:

2. Aayu takes a walk around the park, following the path shown below. What is the total distance he covers in one complete round of the park?

Let’s Learn

Perimeter

The distance around a closed figure is called its perimeter. It is the sum of the length of all the sides of the figure. For example, to find the perimeter of the figure ABCD shown, find the sum of the lengths of its four sides.

The word “perimeter” comes from the Greek word “peri,” meaning “around,” and “metron,” meaning “measure.” So, quite literally, “perimeter” means “measure around.”

Perimeter of the figure ABCD = AB + BC + CD + DA

Polygons

A polygon is a two-dimensional geometric figure that has a finite number of sides. The sides of a polygon are made of straight-line segments connected to each other end to end.

Fact Zone

The line segments of a polygon are called sides or edges. The point where two line segments meet is called a vertex or corner.

A triangle is an example of a polygon made with three sides. Let us learn how to find the perimeter of the following polygons.

Perimeter of a Triangle

Look at the triangle with sides ‘a’, ‘b’, and ‘c’.

Since triangles are three-sided polygons, the perimeter of a triangle is the sum of its sides, that is, a + b + c.

Let us find the perimeter of a triangle with sides 4 cm, 5 cm and 6 cm.

The perimeter of the triangle would be the sum of its sides, that is, 4 cm + 5 cm + 6 cm = 15 cm.

Perimeter of a Rectangle

Look at the rectangle with its length and breadth represented as ‘l‘ and ‘b’, respectively.

The perimeter of the rectangle = l + b + l + b = 2 (l + b)

Hence, the perimeter of a rectangle = 2 (length + breadth).

Let us find the perimeter of a rectangle with l = 7 cm and b = 3 cm. The perimeter of the given rectangle would be 7 cm + 3 cm + 7 cm + 3 cm = 20 cm.

Or, 2 (7 cm + 3 cm) = 20 cm.

Perimeter of a Square

Look at the square with sides represented by ‘s’.

The perimeter of the square = s + s + s + s = 4 × s.

Hence, the perimeter of a square = 4 × side.

Let us calculate the perimeter of a square with s = 2 cm . The perimeter of the given square would be 2 cm + 2 cm + 2 cm + 2 cm = 8 cm. Or, 4 × 2 = 8 cm.

Let’s Practise-1

1. Find the perimeter of a:

a. triangle with sides 3 cm, 4 cm, and 5 cm.

b. rectangle with length = 8 cm and breadth = 6 cm

c. square with side 7 cm.

2. Find the perimeter of an equilateral triangle with each side 8.7 cm.

3. Chandan wants to fence a community garden which measures 114.6 m by 278.96 m. Find the perimeter of the garden.

Regular and Irregular Polygons

Regular Polygons

A polygon is called regular when all its sides have the same length.

Look at the regular pentagon with sides represented as ‘s’ units.

Since pentagons are five-sided polygons, the perimeter of a pentagon is the sum of its five sides, that is, s + s + s + s + s = 5s.

Hence, the perimeter of a regular pentagon = 5 × side.

For example, the perimeter of a regular pentagon with s = 6 cm would be 6 + 6 + 6 + 6 + 6 = 30 cm.

Or, 5 × 6 = 30 cm.

Similarly, the perimeter of a regular hexagon with s = 5 cm would be 5 + 5 + 5

+ 5 + 5 + 5 = 30 cm.

Or, 6 × 5 = 30 cm.

Irregular Polygons

An irregular polygon is a polygon with sides of different lengths. To find the perimeter of an irregular polygon, we add up the lengths of all its sides.

For example, the perimeter of the given irregular polygon = 4 m + 5 m + 7 m + 3 m = 19 m.

Let’s have a look at the following example to understand this concept better.

In the given figure, two dimensions, AB and AF, are missing. However, we can calculate them from the given data. Since the opposite sides of a figure are parallel, we extend the side AF and CD until they meet at point G.

As AB and CG are parallel, their measures are equal.

So, AB = CD + EF = 4 + 3 cm = 7 cm. Also, AF = BC - DE = 6 – 2 = 4 cm.

The perimeter of the figure = 7 cm + 6 cm + 4 cm + 2 cm + 3 cm + 4 cm = 26 cm.

In this way, we can find the missing lengths of the sides and hence, the perimeter.

Let’s Practise-2

1. Find the perimeter of the following figures:

Area

Area represents the space covered by a shape and is expressed in square units. The unit of area depends on the unit of length used to measure the sides of a shape. If the lengths are measured in centimetres (cm), the area will be in square centimetres (cm²). If the lengths are in millimetres (mm), the area will be in square millimetres (mm²). Similarly, if the lengths are measured in metres (m), the area will be in square metres (m²).

Measuring Area Using a Squared Paper

We can find the area of regular and irregular figures by counting the squares enclosed on a squared paper.

Step 1: Count those squares which are completely enclosed by the figure as 1.

Step 2: Count those squares which are half enclosed by the figures as 1 2 .

Step 3: Count those squares which are enclosed more than half by the figure as 1.

Step 4: Ignore those squares which are enclosed less than half by the figure. The sum of all the squares obtained is the area of the figure.

Example: Find the area of the following figures if the area of each square is 1 sq. cm.

a. Number of squares enclosed by the figure

Complete squares = 16

Half squares = 8

Area of the figure = (16 + 1 2 × 8) sq. cm.

= (16 + 4) sq. cm. = 20 sq. cm.

b. Number of squares enclosed by the figure

Complete squares = 4

Half squares = 2

More than half squares = 5

Less than half squares = 7 (ignore it)

Area of the figure = (4 + 1 2 × 2 + 5) sq. cm. = (4 + 1 + 5) sq. cm. = 10 sq. cm.

Area of a figure covering half a rectangle

A triangle is drawn in the rectangle with squares of 1 sq. cm.

The triangle is exactly half of the rectangle. The rectangle is filled with 32 squares.

Area of the rectangle = 32 sq. cm.

Thus, the area of the triangle = 1 2 × 32 = 16 sq. cm.

Example: Find the area of the triangle if area of each square is 1 sq. cm.

Solution:

Divide the rectangle into two smaller rectangles so that the triangle contains the half of each smaller rectangle.

Area of coloured rectangle = 24 sq. cm.

Area of white rectangle = 18 sq. cm.

Area of triangle = 1 2 × 24 + 1 2 × 18 = 12 + 9 = 21 sq. cm.

1. Find the area of the following figures if each square is of 1 sq cm.

(i) Which figure has the greatest area?

(ii) Which figure has the smallest area?

2. Find the area of the following figures if the area of each square is 1 sq cm.

(i) Which figure has the greatest area?

(ii) Which figure has the smallest area?

3. Find the area of the following figures if the area of each square is 1 sq cm.

Thinking Zone

Draw three different closed figures, each composed of 5 squares and having different perimeters.

Measuring Area using Formulas

Area of a Rectangle

Look at the rectangle with sides ‘l’and ‘b’.

Since the space occupied by a rectangle is l × b, its area would be length × breadth.

[Note: If the sides are not in the same units, convert the sides to the same units before finding the area of a shape.]

For example, the area of the rectangle with sides 4 cm and 6 cm would be product of its sides = 4 cm × 6 cm = 24 cm2.

Example: Find the area of a rectangle whose length is 8 m and breadth is 10 cm.

Solution: Length = 8 m, breadth = 10 cm = 10 100 = 1 10 m

Area of a rectangle = l × b = 8 × 1 10 = 0.8 sq m.

Thus, the area of the rectangle is 0.8 sq m.

Area of a Square

A square is a polygon with 4 equal sides.

To find its area, multiply the length of one side by itself.

The area of a square with side s units would be A = s × s

For example, the area of the square with sides 4 cm, would be the multiplication of its sides = 4 × 4 = 16 sq cm.

Example: Find the area of a square garden, whose each side is 20 m.

Solution: Area of the square = s × s = 20 × 20 = 400 sq m.

Farmers use area calculations to optimize crop yields and plan irrigation.

Area of a Triangle

The area of a triangle is the space inside the shape.

To find the area of a triangle, we use the formula:

Area of a triangle = 1 2 × base × height

For example, the area of the triangle with base 4 cm and height 8 cm would be 1 2 × 4 × 8 = 16 cm².

Let’s Practise - 4

1. Find the area of a rectangle with length 6 cm and width 4 cm.

2. Calculate the area of a square with sides of length 5 cm.

3. A triangle has base 10 m and height 8 m. What is its area?

4. Which carpet is bigger: a rectangular carpet measuring 14 m in length and 11.6 m in breadth or a square carpet of side 15 m?

Volume

The volume of a solid, liquid, or gas is the amount of the space it occupies. It represents the measurement of the space taken up by any object.

Look at this activity involving water and marbles to understand this concept.

The rise in the water level after placing marbles in a glass represents the volume of the marbles.

Volume is measured in standard units such as litres, cubic centimetres (cm³), and cubic metres (m³). It is denoted as L, cm³, and m³, respectively.

Measurement of volume helps us understand how much space an object or container can hold.

Remember: Always work with the same units, convert them, if needed.

1 sq m = 10,000 sq cm

1 sq m = 100 sq dm

1 sq dm = 100 sq cm

Volume by Counting Cubes

The number of unit cubes that completely fill the object is its volume. Depending on the size of the object, millimetre, centimetre, or metre cubes can be used to fill the solids.

Example: Find the volume of the box by filling it with 1 cm cubes.

Solution: Fill the box with one layer of unit cubes and count them. There are 10 cubes in a layer and 3 such layers fill the box completely.

Layer

We can see that 30 cubes of 1 cm fill the entire box. So, the volume of the box is 30 cm3.

Example: Let us find the volume of the given object.

Solution: Each cube is of side 1 cm. Add the number of cubes in each layer.

The volume of the object is 15 cm3.

Volume by using Formula

Volume of Cuboid

A cuboid is a three-dimensional (3D) shape with six rectangular faces, where each face has four right angles. It is also known as a rectangular prism. The volume of a cuboid represents the amount of space it occupies.

We can find its volume using unit cubes.

Imagine filling the cuboid with identical unit cubes, then count the total number of cubes used. Multiply the length, width and height of the cuboid to find its volume.

Let’s understand this through an example.

To find the volume of a big box filled with unit cubes, follow these steps:

• Note the dimensions of the box: length = 20 cm, width = 10 cm, and height = 6 cm.

• In one layer, arrange 20 unit cubes along the length and 10 unit cubes along the width, giving 200 unit cubes in the first layer.

• Since the height is 6 cm, 6 layers of 200 unit cubes can be arranged along the height.

• The total number of unit cubes in the box is 20 × 10 × 6 = 1200 unit cubes.

• As each unit cube has a volume of 1 cm³, the volume of 1200 unit cubes is 1200 cm³.

• Thus, the volume of the box can be found by multiplying its three dimensions (20 cm × 10 cm × 6 cm) to get 1200 cm³.

Let’s use a few examples to understand this concept better:

Example 1: The given model of a cuboid is prepared using unit cubes. Find the volume of the model.

Solution: The number of cubes in the bottom layer is 4 × 3 = 12.

Three such layers are there in the model, so the total number of cubes is 4 × 3 × 3 = 36.

Ice cream is measured and sold in litres and millilitres, not in grams or kilograms.

Since each cube has a volume of 1 cubic cm, the volume of the model is 36 cm3.

Example 2: Find the volume of the given cuboid.

Solution: The volume of a cuboid is calculated by multiplying its length (l), width (w), and height (h).

Given, l = 8 m, w = 3 m and h = 4 m, the volume is 8 × 3 × 4 = 96 m³.

Let’s Practise - 5

1. Find the volume of each of the following solids, if each cube has a side measuring 1 cm.

2. What is the volume of a cube with each side measuring 3 centimetres?

3. Calculate the volume of a cuboid with dimensions 5 cm (length), 4 cm (width), and 6 cm (height).

Thinking Zone

If we double the length of a cube’s side, how much will its volume increase?

Let’s Sum Up

• Perimeter is the sum of the lengths of all the sides in a polygon. For example, perimeter of a rectangle is determined by 2 (length + breadth) and perimeter of a square is 4 × side.

• Area is the space covered by a shape and is expressed in square units. Area of a rectangle = length × breadth, Area of a square = side × side, and Area of a triangle = 1/2 × base × height

• Volume is the space occupied by any object, be it solid, liquid or gas. Volume of a cuboid = length × width × height.

Cross-curricular Connections

Imagine you have a rectangular garden with a length of 6 metres and a width of 4 metres. You want to plant different types of flowers like rose, jasmine, and sunflower in this garden. Each flower needs 0.25 square metres of space to grow properly. Calculate the total area of the garden and then determine how many flowers you can plant in it. Additionally, if each flower requires 0.5 litres of water every day, estimate how many litres of water you would need to water all the flowers in your garden for a week.

Life Skills

A community centre is organizing a food drive for a local shelter. The centre received various food items, including bags of rice, each covering an area of 1.5 square metres. The storage room available for the donations is in the shape of a rectangle, measuring 8 metres in length and 6 metres in width. How many bags of rice can the storage room accommodate?

Extend Your Knowledge

Area of Pathways

To find the area of the pathways shown below, split the paths into rectangles and squares without any overlaps

For example, a garden of length 150 m and width 60 m has a 10 m wide pathway running lengthwise through the middle. Find the area of the pathway. As the pathway ABCD is running lengthwise, length (AD) of the pathway = 150 m and breadth (AB) of the pathway = 10 m

Area of the pathway = length × breadth = 150 m × 10 m = 1500 sq m

Thus, the area of the pathway is 1500 sq m.

21st Century Skills

Trace your hand on a piece of squared paper and determine the area of your handprint.

Tip for the Parent

• Engage your child with calculations related to real-life examples like finding the volume of a swimming pool, perimeter of a carrom board, area of the play room, etc.

Measurement

My Study Plan

Metric system

Conversion of metric units

Operations on metric units

Calculate averages

Let’s Recall

In earlier classes, you learned about the units of measurement for quantities such as length, weight, and capacity. Let's have a quick recap of these concepts.

1. Aayu and his mother are buying apples. Which of the following measurements will the shopkeeper use to sell the apples?

a. Metre

b. Kilogram

c. Kilometre

d. Litre

2. Which of the following is an example of a non-standard unit of measurement?

a. Kilogram

b. Metre

c. Handspan

d. Litre

Let’s Recall

3. Aayu fills a water bottle with 1000 cm of water. Is the unit of measurement, correct? If not, what is the correct unit of measurement for the amount of liquid in a bottle or container?

Thinking Zone

Imagine you’re cooking a recipe that needs 300 grams of flour, but your kitchen scale only measures in kilograms. How would you convert grams to kilograms to measure the correct amount of flour? Discuss with your teacher.

Let’s Learn

Metric System

The metric system is an international system of measurement that uses basic units like metre (for length), gram (for weight), and litre (for capacity). It includes both larger and smaller metric units. Larger units are created by multiplying the basic units by multiples of 10, and smaller units are formed by dividing the basic units by multiples of 10.

Here are some common units in the metric system:

Bigger units

Units of Mass

Base unit

Units of Capacity

Base unit

From the table above, we can draw the following conclusions:

• Each unit is 10 times the unit to its immediate right. For example, 1 decagram (dag) equals 10 grams (g), and 1 hectolitre (hL) equals 10 decalitres (daL).

• Each unit is 1 10 of the unit to its immediate left. For example, 1 decilitre (dL) is

of 1 litre (L).

Let’s Practise - 1

1. Fill in the blanks.

a. 1 hL = _______ daL

c. 6 dam = _______ m

e. 1 mg = _______g

1 dag = _______ g

8 kg = _______ dag

Conversion of Metric Units

'Conversion of Metric Units' is a way of changing one unit of measurement to another within the metric system.

Conversion of Metric Units

Larger to Smaller Unit

Smaller to Larger Unit

Look at the flowchart below, which shows how we convert between larger and smaller units.

Larger to smaller unit

To convert from a larger unit to a smaller unit, we multiply.

Smaller to larger unit

To convert from a smaller unit to a larger unit, we divide.

Thus, we can create the table for length, weight, and capacity as follows:

Let’s understand these concepts through some examples.

Example 1: Convert 25 kilometres into metres.

Solution:

Since, 1 km = 1,000 m

Hence, 25 km = 25 × 1,000 m = 25,000 m.

Example 2: Convert 55 kilolitres and 5 litres into litres.

Solution:

We know that 1 kL = 1,000 L

Therefore, 55 kL = 55 × 1,000 = 55,000 L

Now, add the two values:

55,000 L + 5 L = 55,005 L

So, 55 kL and 5 L is equal to 55,005 L.

Example 3: Convert 125 grams to kilograms.

Solution:

To convert from g to kg, we move towards the left thrice.

So, we divide by 1000.

125 125 1000 0 125 g= kg = .

Therefore, 125 grams is equal to 0.125 kilograms.

Example 4: Convert 3 centimetres to decimetres (dm) and metres (m).

Solution:

We know that:

1 cm = 1 10 dm

So, 3 cm = 3 1 10 × = 3 10 = 0.3 dm

Also, 1 cm = 1

So, 3 cm = 3 1

So, the conversion is:

• 3 cm = 0.3 dm

• 3 cm = 0.03 m

1. Convert the following quantities as indicated:

a. 350 g = _____ kg

b. 15 mg = _____ kg

c. 2500 mL = _____ L

d. 6 dam = _____ m

Let’s Learn

Operation on Metric Units

'Operation on Metric Units' involves performing mathematical operations, such as addition, subtraction, multiplication, and division, using metric units of measurement.

Let's look at how to perform basic operations on metric units:

Addition and subtraction

When adding or subtracting quantities with the same unit, simply perform the operation.

For example,

1. 5 m + 20 m = 25 m

2. 12 kg – 7 kg = 5 kg

When adding or subtracting quantities with different units, convert them to the same unit before performing the operation.

For example, if we have 2 km and 1,500 m, convert either one to the other unit before adding. For instance, convert 2 km to m (2,000 m) and then add 2,000 m + 1,500 m = 3,500 m.

Multiplication and division

When multiplying or dividing quantities with the same unit, simply perform the operation.

For example, if you have a rectangular field with a length of 10 m and a width of 5 m, the area is the product of length and width:

Area = 10 m × 5 m = 50 m2

When multiplying or dividing quantities with different units, convert them to the same unit before performing the operation.

For example, to divide 2500 grams by 0.5 kilograms, convert 0.5 kilograms to grams (500 grams) and then perform the division.

So, 2500 500 grams grams = 5

Let’s Practise - 3

1. Solve the following.

a. 4 km + 3 km 700 m

b. 60 kg 8 g + 44 kg 82 g

c. 25 m 15 cm + 80 m 30 cm

2. Raju has 63 m of ribbon. If he cuts 56 m and 21 cm of ribbon from it, what length of ribbon will be left?

3. A small pack contains 250 mL of juice. How many such packs are needed to fill a jug with a capacity of 2L?

4. How many packets of 900 mg snacks can be made from 45 kg of snacks?

Let’s Learn

Average

You must have heard the term ‘average’ many times. Do you know what it means and how to calculate it?

Average is a way of expressing the middle value of a set of numbers. It is also known as the mean.

For example, Aayu wants to distribute 15 chocolates among his 3 friends equally. So, he divides 15 by 3. 15 3 = 5

Thus, we observe that, on average, each friend gets 5 chocolates.

To find the average, we first add all the numbers in a set and then divide the sum by the total number of values.

The formula is

Average= Sumofvalues

Number of valu es

If we have n values, represented as x1, x2, x3, …, xn, the average is:

Average n = ++ ++ xx xx n 12 3 ...

Remember, average can only be calculated if all the given values are of the same unit.

Let us understand this with an example:

Example: Imagine you have the heights of five students in your class, and you want to find the average height. The heights, measured in centimetres, are :

Student 1: 120 cm

Student 2: 130 cm

Student 3: 110 cm

Student 4: 140 cm

Student 5: 125 cm

Solution:

To find the average height, we first add all the heights and then divide the sum by the number of students.

Average height = 120 130 110 140 125 5 ++++

Add the heights: 120 + 130 + 110 + 140 + 125 = 625

Now, divide by the number of students (which is 5):

Average height = 625 5 =125

So, the average height of the students in your class is 125 cm.

Let’s Practise - 4

1. Find the average of 30, 31, 33, 32, 34, 20, 23.

2. Find the average daily pocket money of a group of 5 friends who receive ₹60, ₹90, ₹105, ₹ 85, and ₹100, respectively.

3. Four friends ran a race, and their times (in seconds) were 150, 130, 160, and 140. What is the average time they took to finish the race?

4. Rahul scored 45 marks in Math, 65 in English, 45 in Hindi, 85 in Science, and 65 in Social Studies. What is his average score?

The average of identical numbers is equal to the number itself. For example, to find the average of 6, 6, 6, 6, 6:

Average = 66666 5 30 5 6 ++++ ==

Let’s Sum Up

• The metric system is a system of measurement that uses basic units like metre (for length), gram (for weight), and litre (for capacity).

• Larger units are created by multiplying the basic units by multiples of 10, and smaller units are formed by dividing the basic units by multiples of 10.

• We can add, subtract, multiply, and divide metric measurements of the same type.

• Average is a measure that represents the value within a set of numbers.

• The formula for calculating the average is:

Sum of values

Average = Number of values

Life Skills

A chocolate maker produces various flavours of chocolate. If 5 mint chocolates weigh 250 g, 7 orange chocolates weigh 420 g, and 10 milk chocolates weigh 650 g, find the average weight of each type of chocolate. Also, determine which kind of chocolate is the lightest.

Cross-Curricular Connections

Science:

The average temperature in a city in the past week was 22°C. If the temperatures for six days were 20°C, 24°C, 22°C, 21°C, 23°C, and 25°C, what was the temperature on the seventh day?

Social Studies:

The distance between two cities on a map is 5 cm. If the scale of the map is 1 cm = 50 km, what is the actual distance between these two cities in kilometres?

21st Century Skills

Aayu's father works in a hospital as a doctor. He prescribes a patient to take cough syrup twice daily. In what quantity should the medicine be taken? Should it be in millilitres (mL) or litres (L)?

Extend Your Knowledge

In the world of measurement, we use different units to measure things like length, weight, and capacity.

When you go from one country to another, they might use different units, which can be interesting!

For instance, in India, we measure weight in grams and kilograms, but in the US, they use ounces and pounds. So, if you want to buy something and it is measured in a different unit, you might need to convert it.

For example, 1 pound is about 453 grams.

Tips for the Parent

• Teach your child about comparing different units of measurement. Help them understand the relationships between units, such as how many centimetres are in a metre or how many grams are in a kilogram.

• Engage in group activities where your child has to work with friends or siblings to find the average of a set of numbers.

Time

My Study Plan

Time

Conversion of time

24 Hour clock

Addition and subtraction of time

Calendar

Let’s Recall

A clock has 12 numbers. It has two hands, a short one for the hours and a long one for the minutes. Some clocks also have a very thin hand for the seconds.

Let’s recall the relationships between these time units:

• 1 year = _____ days

• 1 week = _____ days

• 1 day = _____ hours

• 1 hour = _____ minutes

Thinking Zone

If your favourite cartoon show starts at 6:00 pm and ends at 6:45 pm, how long does the show last?

Let’s Learn

Time is a measurement that helps us understand when events happen. It is divided into smaller units like seconds, minutes, and hours. We use clocks to keep track of time.

Conversion of Units of Time

Time can be converted from one unit to the other. The conversions of time from unit to unit are:

Seconds to minutes or minutes to seconds

• 1 minute = 60 seconds

• To convert seconds to minutes, divide the number of seconds by 60.

Example: Convert 120 seconds into minutes.

120 seconds ÷ 60 = 2 minutes

• To convert minutes to seconds, multiply the number of minutes by 60.

Example: Convert 3 minutes into seconds.

3 minutes × 60 = 180 seconds

Minutes to hours or hours to minutes

• 1 hour = 60 minutes

• To convert minutes to hours, divide the number of minutes by 60.

Example: Convert 120 minutes to hours.

120 minutes ÷ 60 = 2 hours

• To convert hours to minutes, multiply the number of hours by 60.

Example: Convert 4 hours to minutes.

4 hours × 60 = 240 minutes

Word Zone

Events: Happenings

Hours to days or days to hours

• 1 day = 24 hours

• To convert hours to days, divide the number of hours by 24.

Example: Convert 48 hours to days.

48 hours ÷ 24 = 2 days

• To convert days to hours, multiply the number of days by 24.

Example: Convert 3 days to hours.

3 days × 24 = 72 hours

Days to weeks or weeks to days

• 1 week = 7 days

• To convert days to weeks, divide the number of days by 7.

Example: Convert 14 days to weeks.

14 days ÷ 7 = 2 weeks

• To convert weeks to days, multiply the number of weeks by 7.

Example: Convert 3 weeks into days.

3 weeks × 7 = 21 days

Let us look at some examples based on the conversion of units of time.

Example 1: If a school bus takes 2 hours and 10 minutes to travel from home to school, how many minutes does the journey take?

Solution: We know that 1 hour is the same as 60 minutes. So, let’s start with the 1 hour: 1 hour = 60 minutes

So, 2 hours = 2 × 60 = 120 minutes

Now, we also have 10 more minutes. Add that to the 120 minutes: 120 minutes + 10 minutes = 130 minutes

So, the journey from home to school takes 130 minutes in total.

Example 2: If you read a book for 2 hours and 15 minutes each day, how many minutes do you spend reading in a week?

Solution: Let us solve the given problem step by step.

Convert Hours to Minutes:

• In 1 hour, there are 60 minutes.

• So, in 2 hours, there are 2 × 60 = 120 minutes.

Add Minutes:

• You read for 2 hours and 15 minutes each day.

• Add the 120 minutes (2 hours) to the 15 minutes, giving you 135 minutes each day.

Calculate Weekly Reading Time:

• If you read 135 minutes each day, multiply this by the number of days you read in a week.

• Assuming you read every day, there are 7 days in a week.

• The total minutes spent reading in a week = 135 × 7 = 945 minutes.

So, if you read a book for 2 hours and 15 minutes each day, you spend 945 minutes reading in a week.

Let’s Practise - 1

1. Fill in the blanks.

a. 4 hours = _____ minutes = _____ seconds.

b. 3 weeks = _____ days = ____ hours.

c. 2 days =___ hours = ____ minutes.

2. Emma ran a race and finished in 15 minutes and 30 seconds. How many seconds did it take her to complete the race?

3. If one movie is 2 hours and 20 minutes long, how many minutes will 3 movies of the same length last altogether?

4. If a school day is 6 hours long and each class is 45 minutes long, how many classes can you have in one school day?

Let’s Learn

24 Hour Clock

A clock has twelve numbers on it, from 1 to 12. These numbers represent the hours in a day. The hour hand on the clock goes around in a circle two times to show all the hours in a full day.

But in places like trains, planes, and the army, a clock with 24 hours is used.

On the 24-hour clock, there are no “a.m.” or “p.m.” Instead, it has a four-digit number, whose first two numbers tell us the hours and the last two tell us the minutes.

It is a way of telling time that uses the numbers 00:00 to 23:59 to represent the hours and minutes in a day.

On the 24-hour clock, the day starts at midnight (00:00) and goes through the hours of the day until it reaches midnight again. This is different from the 12-hour clock, which repeats the same 12 hours twice a day.

For example:

5:00 a.m. on the 12-hour clock is 05:00 on the 24-hour clock.

4:30 p.m. on the 12-hour clock is 16:30 on the 24hour clock.

Conversion of the 12-hour clock into a 24hour clock

To convert a time from a 12-hour clock to a 24-hour clock, we follow these steps:

Morning (a.m.)

If it is a time in the morning (a.m.), keep the same hours.

For example, 7:30 a.m. on a 24-hour clock is 07:30.

Afternoon/Evening (p.m.)

If it is a time in the afternoon or evening (p.m.), add 12 to the hours.

For example, 4:45 p.m. on a 24-hour clock is 16:45 (4 + 12 = 16).

Conversion of the 24-hour clock into 12-hour clock

To convert a time from a 24-hour clock to a 12-hour clock, we follow these steps:

Morning (00:00 to 11:59)

If the time is between 00:00 and 11:59, use the same hours and add a.m.

For example, 09:30 on a 12-hour clock is also 09:30 a.m.

Afternoon/Evening (12:00 to 23:59)

If the time is between 12:00 and 23:59, subtract 12 from the hours.

For example, 17:45 on a 12-hour clock is 5:45 p.m. (17 – 12 = 5).

1. Convert the following into 24-hours format.

a. 9:15 a.m. _________________________

b. 9:30 p.m. _________________________

2. Convert the following into 12-hours format:

a. 02:30 hours _________________________

b. 13:15 hours _________________________

Addition of Time

To add the units of time together, we can follow the steps below:

Step 1: Align Units

When adding time, align the units. For example, add minutes to minutes, and hours to hours.

Step 2: Carry Over

If the sum of minutes is 60 or more, convert minutes into hours and carry over the extra hours to the hours.

Example:

Let’s say we want to add 2 hours and 30 minutes to 3 hours and 45 minutes.

Start with minutes:

30 + 45 = 75 minutes.

Since 75 minutes is more than 60, carry over 1 hour to the hour place, and we have 15 minutes left.

So,

Now add the hours: 2 hours + 3 hours + 1 hour (from the carry-over) = 6 hours.

So,

Hence, 2 hours 30 minutes + 3 hours 45 minutes = 6 hours 15 minutes.

Let’s Learn

Subtraction of Time

To subtract units of time, we can follow the steps below:

Step

1: Align Units

When subtracting time, align the units. For example, subtract minutes from minutes and hours from hours.

Step 2: Borrowing

If any digit of the top number (minuend) is smaller than the digit of the bottom number (subtrahend), we will need to borrow from the next higher unit.

For example, if we subtract minutes and the top digit is smaller, borrow 1 hour and add 60 minutes to the top digit.

Example:

Let’s say we want to subtract 4 hours and 30 minutes from 7 hours and 15 minutes.

Solution:

Start with minutes:

Since 15 is smaller than 30, borrow 1 hour (60 minutes) from the hours place, making it 6 hours.

Subtract the minutes: (60 + 15) – 30 = 75 – 30 = 45 minutes.

Now subtract the hours:

6 hours – 4 hours (subtrahend) = 2 hours.

So,

Hence, 7 hours 15 minutes – 4 hours 30 minutes = 2 hours 45 minutes

Let’s Practise - 3

1. What is the result of adding 2 hours and 45 minutes to 1 hour and 30 minutes?

2. If Sarah started reading a book at 7:20 PM and finished at 9:45 PM, how long did she spend reading?

3. What is the difference between 4 hours 15 minutes and 2 hours 30 minutes?

4. If a movie starts at 8:40 PM and ends at 11:15 PM, how long is the movie?

Let’s Learn

Calendar

A calendar is a series of pages that show the days, weeks, and months of a particular year. It helps us keep track of time.

• It has twelve months, and each month has a different number of days.

• January is the first month of the year.

• December is the last month of the year.

• After December, it’s January again and a new year begins.

• All months other than February have 30 or 31 days.

• February has 28 days in most of the years.

• But every fourth year, there are 29 days in February.

• The year February has 29 days is called a leap year.

• A leap year has 366 days instead of 365 days.

Fact Zone

The number of days in a month can be found be remembered using knuckles and the gaps in-between.

Months on the knuckles have 31 days.

Days in a week

A week has 7 days.

A week starts on a Sunday and ends on a Saturday. These are the days of the week in the correct order.

Months in a year

There are 12 months in a year, and each month has a name.

Reading a calendar

A calendar is used to keep a record of important events such as festivals, anniversaries, etc. , in the form of dates. The format of a date is:

DD denotes the days of the month.

It can be 01-31 in two digits.

MM denotes the months of the year.

It can be 01-12 in two digits.

YY denotes the last two digits of a year.

For 2024, we will write 24 only.

For example, in the format DD/MM/YY, ‘12/05/24’ represents the 12th day of May in the year 2024.

We can see that 12/05/24 is a Sunday.

Example 1: You are curious about the day Christmas will fall on in the year 2024.

Solution:

We know that Christmas falls on the 25th of December every year.

Open the calendar for the year 2024.

Go to the December page.

Mark the 25th day.

This way we can see that Christmas will fall on a Wednesday.

1. Fill in the blanks.

a. A week has ______ days.

b. A _______ can be used to track the important events.

c. A leap year has ________ days.

d. 10th month of the year is ______________.

2. Use the below calendar and answer the following.

a. The electricity bill is due on the first Saturday of August. What is the due date of the bill? ____________________

b. What is the date of the last Sunday of August? ____________________

c. Which day of the week is August 29th? ____________________

d. Which day of the week is August 8th? ____________________

e. How many Wednesdays are there in August? ____________________

f. How many days are there in August? ____________________

Let’s Sum Up

Time is a way we measure and understand the duration of events and activities.

Time can be grouped into various units. The unit conversion chart is given below as follows:

A clock has twelve numbers on it, from 1 to 12. These numbers represent the hours in a day.

On the 24-hour clock, there are no “a.m.” or “p.m.” Instead, it has a four-digit number, whose first two numbers tell us the hours and the last two tell us the minutes.

We use 00:00 to 23:59 to represent the hours and minutes in a day in a 24 hour clock.

A calendar is a series of pages that shows the days, weeks, and months of a particular year. It helps us keep track of time.

Life Skills

We have different units of time, like seconds, minutes, hours, and days, to help us understand time better. Can you name some things you do in a minute? How about in an hour?

Cross-Curricular Connections

Social Studies:

Understanding the calendar is crucial for planning in agriculture, particularly harvesting. It allows us to schedule and prioritise which crops to harvest based on their growth cycles and maturity.

21st Century Skills

Imagine you have a time machine that can take you to any period in the past or future. If you could visit any time in history or see what the future holds, where would you go and why?

Extend Your Knowledge

Did you know that the time on your clock is different for everyone around the world?

That’s because the Earth is huge, like a giant ball, and it takes 24 hours to spin around completely. Because of this, different parts of the world have different times.

For example, let’s say it’s 5:00 pm on your clock, but it would be 6:30 am in the USA because they are in a different time zone.

Time zones help us understand what time it is in different places. Can you explore more about time zones and write what you learn in your notebook?

Tips for the Parent

• Help your child allocate specific time slots for homework. This teaches them to manage their time efficiently.

• Encourage the use of timers for various activities. Set a timer for completing homework, chores, or playtime. This helps develop a sense of urgency and teaches them to allocate time appropriately.

Money

My Study Plan

Unitary methods in money

Cost price (CP) and selling price (SP)

Profit and loss

Profit percentage and loss percentage

Profit and loss in real life situations

Let’s Recall

In the previous class we have learnt about the units of money used in India and their conversions. We also explored how to do calculations with money and practised using a method called the unitary method.

Let us do a quick warm-up of these concepts.

Solve the following.

1. If the cost of 8 dolls is `128, then what will be the cost of 6 dolls?

2. Convert the following from rupees to paise.

a. `247.50 = _______ paise

b. `28.2 = _______ paise

Thinking Zone

You have `100 saved in your piggy bank. If you buy a notebook for `30, then how much money do you have left? What percentage of your money did you save?

Let’s Learn

Unitary Method

The unitary method is a helpful tool for solving word problems related to money. In this method, we start by calculating the cost of one item and then use this value to determine the cost of as many items as needed.

Example 1: If the cost of 10 notebooks is `150, then what will be the cost of 15 notebooks?

Solution:

Cost of 10 notebooks = `150

Cost of 1 notebook = 150 ÷ 10 = `15

Cost of 15 notebooks = 15 × 15 = `225

Therefore, the cost of 15 notebooks is `225.

Example 2: If the cost of 1 dozen bananas is `120, find the cost of 6 bananas.

Solution:

1 dozen = 12

Hence, cost of 12 bananas = `120

Cost of 1 banana = 120 ÷ 12 = `10 1 dozen = 12

Cost of 6 bananas = 10 × 6 = `60

Therefore, the cost of 6 bananas is `60.

Example 3: `3,720, find the cost of 5 packets of almonds.

Solution:

Cost of 12 packets = `3,720

Cost of 1 packet = 3720 ÷ 12 = ` 310

Cost of 5 packets = 310 × 5 = `1,550

Therefore, the cost of 5 packets of almonds is `1,550.

Example 4: If the cost of 15 toys is `6,000, then how many toys can you get for `16,000?

Solution:

Cost of 15 toys = `6,000

Cost of 1 toy = 6000 ÷ 15 = `400

Now we need to find how many toys we can get for `16,000.

To find this we will divide `16,000 by the cost of 1 toy. = 16000 ÷ 400 = 40

Therefore, we can buy 40 toys with `16,000.

Let’s Practise - 1

1. Solve the following:

a. If the cost of 25 packets of crayons is `1,250, then what’s the cost of 3 packets of crayons?

b. If five dozen mangoes cost `7,200 then how much would 24 such mangoes cost?

c. If you can buy 8 shirts for `2,400, then how many shirts can you buy for ` 4,500.

Let’s Learn

Profit and Loss

Profit is when you make more money than you spend, and loss is when you spend more money than you make. Understanding these concepts is important for managing our money wisely in day to day lives. Let us begin with learning some important terms related to it.

Cost price and selling price

Raju is a fruit seller. He buys fruits from the wholesale market and sells them to his customers.

The price at which Raju buys the fruits is known as its cost price. It is denoted as CP.

Word Zone

Wholesale: Bulk selling at lower prices

Price: Cost

Raju hires a truck and few labourers to bring these fruits to his shop. His shop is well maintained and also has electricity connection. Do you think Raju will have to spend money for all this as well? Yes! he has to pay for these additional expenses which are known as overhead expenses or overheads. This is always added to the cost price.

Thus, the total cost price is calculated as:

Total CP = CP + Overhead Expenses.

The price at which Raju sells his fruits to the customers is known its selling price. It is denoted as SP.

This entire process of buying and selling results in shopkeepers getting a profit or a loss.

Selling Price (SP) = Cost Price (CP) + Profit (P)

Profit and loss

When an item is sold for a higher price than it was bought, the seller makes a profit.

Here, selling price > cost price.

So the formula for profit is,

Profit (P) = Selling Price (SP) – Cost Price (CP)

On the other hand, if the selling price is lower than the cost price, the seller makes a loss.

Here, selling price < cost price.

So the formula for loss is,

Loss (L) = Cost Price (CP) – Selling Price (SP)

When the cost price (CP) and selling price (SP) are the same, there is neither profit nor loss.

Word Zone

Additional expenses: Extra costs

Here, selling price = cost price.

Example 1: Leena purchased a video game for `620 and later sold it for `700. Did Leena make a profit or loss and by how much?

Solution:

Given, CP = `620 and SP= `700

Since, SP > CP, there is a profit.

We know that,

Profit = SP – CP = `700 – `620 = `80

Thus, Leena made a profit of `80.

Example 2: Sameer bought a used bicycle for `5,500. He spent `900 on repairs and `400 on a new seat. He sold the bicycle for `6,800. Determine his profit or loss.

Solution:

Given, CP of bicycle = `5,500

Overhead expenses = `900 + `400 = `1300

Total CP = CP of bicycle + Overhead expenses = 5500 + 1300 = `6,800

SP of bicycle = `6,800

Since, CP = SP = `6,800.

There is neither profit nor loss.

Example 3: A grocery store owner bought 100 cans of cold drinks at `20 each and sold all of them for a total of `2,500. Calculate the owner’s profit or loss.

Solution: Given,

CP of 100 cans of cold drinks = `20 × 100 = `2000

SP = `2500

Since, SP > CP, there is a profit.

Profit = SP – CP = `2500 – `2000 = `500

Thus, there is a profit of `500.

1. Solve the following:

a. Imagine you started a small business of selling handmade crafts. You spent ₹500 on materials and had additional expenses of ₹100 for renting a booth to showcase your crafts. You earned ₹800 from selling your crafts. Calculate whether you made profit or loss and by how much?

b. A vegetable vendor bought 4 baskets of vegetables at ₹200 each. If he sold all the baskets at ₹700, then find the profit or loss that occurred in this transaction.

c. Arun bought a company for ₹1,55,55,786 and a few years later he sold it for ₹3,45,78,900. Find the profit or loss incurred by Arun.

Let’s Learn

Profit and Loss Percent

To compare and evaluate these transactions in terms of profit or loss, we express them as percentages.

Profit percent and loss percent

The profit or loss can be converted to a percentage. It is always calculated on the cost price.

Formulas for Profit and Loss Percent:

Let us look at some examples.

Example 1: Pihu bought a pen for `100 and sold it for `150, making a profit of `50. Aayu purchased a shirt for `600 and sold it for `750, resulting in a profit of `150. Which transaction is more beneficial?

Solution:

To find out who made more profit, we must find out the profit percentage in both the cases.

Pihu’s profit percentage is:

Profit% = Profit Cost Price × 100 = 50 100 × 100

= 50%

Aayu’s profit percentage is:

Profit% = Profit Cost Price × 100 = 150 600 × 100 = 25%

Since, the profit % of Pihu is greater than Aayu, therefore we can say that her transaction is more profitable.

Example 2: Find the profit % if the CP of an article is `500 and the profit on its sale is `75.

Solution:

Given, CP of the article = `500, Profit = `75

Profit% = Profit Cost Price × 100 = 75 500 × 100 = 15%

Thus, the profit % on the sale of the article is 15%.

Example 3: Aayu bought a smartphone for `4,200 and made a loss of `300. Calculate the loss percentage in this case.

Solution:

Given, CP = `4,200, Loss = `300

Loss% = Loss Cost Price × 100 = 300 4200 × 100 = 7.14%

Thus, the loss % on the sale of the smartphone is 7.14%.

Example 4: Remi purchased a used laptop for `15,000 and incurred an additional expense of `1,200 for upgrades. She subsequently sold the laptop for `16,500. Calculate her profit or loss percentage.

Solution:

Given, cost price (CP) of the laptop = `15000 Additional expenses = `1200

Total CP = 15000 + 1200 = `16,200

Selling price (SP) of the laptop = `16,500

In this case, CP < SP, so she made a profit.

Profit = Selling Price – Cost Price = 16500 – 16200 = `300

Now, to find the profit percentage:

Profit% = Profit Cost Price × 100 = 300 16200 × 100 = 1.85%

Therefore, Remi’s profit percentage is 1.85%.

To find selling price when cost price and profit% or loss% are given

Example 5: Calculate the selling price (SP) of a bicycle when its cost price (CP) is `2,500, and the profit percentage is 8%.

Solution:

Given, CP of the bicycle = `2,500, Profit% = 8%

Profit% = Profit Cost Price × 100

8 = Profit 2500 × 100

8 × 2500 100 = Profit

Profit = `200

Profit = Selling Price – Cost Price

SP of the bicycle = Profit + Cost Price = 200 + 2500 = `2,700

Therefore, the selling price of the bicycle is `2,700.

To find cost price when selling price and profit or loss % are given

Example 6: Find the cost price (CP) of a television when its selling price (SP) is `24,000, and it is sold at a loss of 10%.

Solution:

Given:

SP = `24,000

Loss% = 10%

We need to find the CP.

Let us try to solve this using unitary method.

Suppose the CP is `1, then 10% of `1 is the loss.

Loss = 10 100 × 1 = 1 10

Now, loss = CP – SP

So, 1 10 = 1 – SP SP = 1 –1 10 SP = 9 10

This means that for CP of `1 the SP is ` 9 10 .

Now our SP = `24,000

So, our CP would be 24000 ÷ 9 10 = 24000 × 10 9

= `26,666.66 or `26,667 (rounded up)

Therefore, the cost price of the laptop is approximately `26,667.

Fact Zone

Did you know that collecting rare items, sports memorabilia, or vintage toys is not just fun, but it can also turn into a treasure hunt for profit? Some people have made money by finding and selling these special things, turning their hobbies into exciting and profitable adventures!

1. Ravi bought a saree for `2,000 and sold it at a 10% profit. What is the selling price?

2. Aarti purchased a mobile phone for `12,000 and spent `1,500 on repairs. To make a 20% profit, what should be the selling price?

3. If Sarah bought a bicycle for `200 and sold it for `250, then what is the percentage profit she made?

4. Priya bought a gold necklace for `25,000 and sold it at an 8% profit. What is the selling price?

5. Deepak bought a `15,000 refrigerator and spent `2,500 on installation. To earn a 12% profit, find the selling price.

6. Jack sold his old video game console for `80, but he originally bought it for `100. What is the percentage loss he incurred?

Let’s Sum Up

In the unitary method, the cost of one item is calculated and used to find the cost of any desired quantity.

Cost price (CP) is the price at which an item is bought. Selling price (SP) is the price at which an item is sold.

If SP > CP, there is a profit. Profit (P) = SP – CP

If SP < CP, there is a loss. Loss (L) = CP – SP

If SP = CP, there is neither profit nor loss.

Profit % = Profit Cost Price × 100

Loss % = Loss Cost Price × 100.

Life Skills

Raj, who operates a computer store, bought five laptops for `30,000 each. He sold three of them for `35,000 each, while he gave away the other two for free as donation to a local school. Did Raj make a profit or suffer a loss, and by how much?

Cross-Curricular Connections

21st Century Skills Science:

The government has contracted ABC Aerospace to build a satellite for its space program. Imagine, ABC Aerospace bought satellite components from different suppliers, and the total cost price is `9,50,00,000. ABC Aerospace aims for a 25% profit. What should the satellite’s selling price be?

Imagine you want to sell homemade cookies, and it costs you `150 to make 12 cookies. You plan to sell each cookie for `20. How much profit will you make if you sell all the cookies in one batch? What should you think about when setting the selling price to ensure a profit?

Extend Your Knowledge

In different countries, people use different kinds of currencies. Currency is the type of money used in a country to buy things and trade goods and services. Like, in one place, they might use Rupees, and in another place, they use Dollars or Yen. So, when people travel from one country to another or do business with someone from a different country, they might need to change their money to the local currency. Let us understand this with the help of an example.

Imagine you are planning a trip to Europe and have 10,000 Indian Rupees. The exchange rate is 1 Indian Rupee = 11 1000 Euros.

To find out how many Euros you will get:

10,000 INR × 11 1000 (exchange rate) =110 Euros

WORLD CURRENCIES

So, you will receive 110 Euros in exchange for your 10,000 Indian Rupees.

Tips for the Parent

• Let your child participate in activities like grocery shopping. Give them a budget and ask them to help you choose items without exceeding the budget. Also encourage them to save a portion of their pocket money or any money they receive.

• Introduce simple financial activities like setting up a small “store” at home, where your child can “buy” and “sell” items using play money. This handson approach helps reinforce the concepts of profit and loss in a fun and practical way.

Symmetry, Patterns, and Nets

My Study Plan

Symmetry

Rotational symmetry

Tessellation

Patterns

Nets

Views

Let’s Recall

If the red line is a line of symmetry, then complete the given figures.

Thinking Zone

Have you wondered why aeroplanes are symmetrical?

Try to compare aeroplanes to birds. Do you think aeroplanes can fly if they are not symmetrical?

Let’s Learn

Symmetry

An object is said to have symmetry if it can be divided into two identical halves.

The line that divides the object into its identical halves is called the line of symmetry. Let us look at some examples of symmetrical figures.

Some figures have multiple lines of symmetry.

Line of Symmentry

For example, a rectangle has two lines of symmetry, while a square has four lines of symmetry.

The line of symmetry can be replaced with a mirror, and it would also complete the image with the reflection. This can be seen in the image given below.

There are also some figures that are not symmetrical. This means that there is no line of symmetry that can make these images mirror halves of each other.

Bees make honeycomb cells in the shape of a hexagon. A regular hexagon is a symmetrical figure and it has six lines of symmetry.

2. Match the following images with their mirror halves. Let’s Practise - 1

1. Tick the figures that are symmetrical. Also draw a line of symmetry for those symmetrical figures.

Let’s Learn

Rotational Symmetry

Rotational symmetry occurs when we can turn or rotate a shape around a centre point, and it looks the same after a certain amount of turning. For example, if a square is rotated by a right angle, then the square still looks the same.

Let us do an activity to understand this.

Draw a square and mark one corner as O.

Now, rotate the page by 90 degrees or by one-fourth rotation.

Now, rotate the page by 180 degrees or by a half rotation.

So, from this activity we can say that a square is a rotational symmetry.

Position After 3600 turn

Let’s Practise - 2

1. List down the letters in the English alphabet that look the same after half a turn.

2. Give half a turn to the numbers from 0 to 9. List down which of them still look the same.

3. Find out 4-digit numbers which look the same on half a turn and list them here. For example, 8008.

4. Circle the pictures which will look the same on half a turn? (Hint: Try rotating your book and check.)

Tessellation

Tessellations are patterns made by fitting together shapes without any gaps or overlaps.

For example, think of a honeycomb made by bees. The hexagonal cells fit together without leaving any gaps, creating a pattern that covers the entire honeycomb.

Shapes used in tessellations can be triangles, squares, hexagons, or other shapes that fit together neatly. Artists, designers, and even architects use tessellations to create beautiful and repeating patterns in art, buildings, or even sidewalks. Here are some examples of tessellations.

Honeycomb

Let’s Practise - 3

1. Identify and tick ( ) the shapes that tessellate.

Let’s Learn

Patterns

A pattern consists of a design or sequence that repeats. This repetition can involve numbers or shapes in the sequence.

Patterns by rotation

When we rotate a shape by a definite turn, we get a pattern. Here are some examples:

N N N N

Patterns of numbers

Magic triangles

Magic triangles are a type of mathematical puzzle where numbers are arranged in a triangle shape with a unique pattern. Each arm of the triangle has three numbers and the sum of all these numbers is the same for all three sides.

Let us understand this using an example:

Here the three sides have the following addition:

6 + 3 + 2 = 11

2 + 5 + 4 = 11

6 + 1 + 4 = 11

As we can see, the sum is 11 in all the cases.

Magic Squares

Magic squares are mathematical puzzles made up of a grid of numbers where the sum of each row, each column, and both main diagonals all add up to the same number. Each number appears only once in the square.

Try completing this Magic square.

Fill this square using all the numbers from 21 to 29.

Rule: The sum equals to 75, and no number is used more than once.

Here is the correct solution for this magic square: 22 21 23 28 24 25 26 27 29

We notice that the sum of each row, each column, and both main diagonals have a sum of 75.

1. Fill this square using all the numbers from 46 to 54. Rule: The total of each line is 150.

2. Look at this pattern of numbers and fill in the blank.

3. What will come next? Draw and fill in the empty boxes.

4. Fill in the blanks for a magic triangle.

Let’s Learn

Nets

Shapes that have two dimensions, like length and breadth, are called two dimensional shapes. For example, rectangle, square, and triangle.

Shapes with three dimensions, which include length, breadth, and height, are known as three dimensional shapes.

For example, cube, cuboid, and cone.

A net is a flat 2-D shape that, when folded, forms a 3-D shape. It is created by unfolding the surface of a 3-D shape to display each of its faces.

For example, look at the net of a matchbox.

Let us observe the following 3D shapes and their nets. Net of a Cube

Let’s Practise - 5

1. Match the following net structures with their 3-D shapes.

Let’s Learn

Views

An object appears to be different if we look at it from different viewpoints.

Understanding the different views of objects involves imagining how an object looks from various perspectives: front, side, and top. Let us see all these views one by one by taking the example of a car.

Front View

The front view of an object is what you see when you look at it from the front. It shows the part that faces you directly.

Here is the front view of a car.

Side View

The side view is what you see when you look at the object from one of its sides, showing how wide or narrow it is.

Here is the side view of a car.

Perspective: A particular way of seeing or understanding something Word Zone

Top View

The top view shows what the object looks like when viewed from directly above. It helps understand the shape and size of the object from a bird’s-eye view.

Here is the top view of a car.

Understanding these different views helps in creating a complete picture of an object.

Let us take an example of almirah:

Let’s Practise - 6

1. Observe the images in column A and fill in the blanks in column B with front, side, and top views. The first one is done for you.

Column A Column B

Front view

Let’s Sum Up

An object is said to have symmetry if it can be divided into two identical halves from the middle.

The line that divides the object into its identical halves is called the line of symmetry.

Rotational symmetry happens when we can turn or rotate a shape around a centre point, and it looks the same after a certain amount of turning.

Tessellations are patterns made by fitting together shapes without any gaps or overlaps.

A pattern consists of a design or sequence that repeats. This repetition can involve numbers or shapes in the sequence.

A net is a flat 2-D shape that, when folded, forms a 3-D shape. It’s created by unfolding the surface of a 3-D shape to display each of its faces.

An object appears to be different if we look at it from different viewpoints.

Life Skills

Observe the brick patterns on a wall which is being constructed. Does it remind you of a tessellation? Why is it important for a wall to not have any gaps in between?

Cross-Curricular Connections

English:

There are 5 vowels in the English Alphabet, a, e, i, o, and u. Write these letters on a page and check which of them have rotational symmetry.

21st Century Skills

Why is symmetry important in art and design? Create a design using various shapes that have symmetry.

Extend Your Knowledge

A kaleidoscope is a fun toy that shows many colorful patterns when you look through it. It uses mirrors to produce images that have several lines of symmetry.

Tip for the Parent

• Talk to your child about symmetrical patterns seen in architecture, designs, or natural objects like leaves, flowers, and insects. Discuss the symmetrical views of buildings or everyday objects.

My Study Plan

• Data

• Tally marks

• Pictograph

• Bar graph

• Pie charts

Data Handling

Let’s Recall

Below is a bar graph representing the favourite colours of Class V students.

Observe the graph and answer the following questions.

1. Which is the most liked colour? __________

2. How many students chose blue as their favourite colour? __________

3. Which colour is the least preferred? __________

4. How many more students preferred red over pink? __________

5. Find out the total number of students who participated in the survey regarding their favourite colour. __________

Thinking Zone

If you have surveyed your classmates to pick their favourite sport from options like cricket, baseball, football, volleyball, and basketball, and no one has chosen baseball, how would you represent it in both the pictograph and the bar graph?

Let’s Learn

Data

Data is a collection of information. Data consists of numerical or non-numerical figures representing various types of information.

Types of data

The types of data are categorised into two ways: one is by data type, and the other is by the collection method.

Based on data type

Qualitative data: It does not have a numerical value but contains various characteristics about objects, such as colour, shape, etc.

For example:

The colour of fish in an aquarium –pink, green, blue, yellow, red.

Quantitative data: This is numerical data. It includes information like age, height, weight, etc.

For example:

Weight of students in a class (in kg) – 48, 32, 41, 37, 28.

Based on the collection method

Depending on the source, it can be classified as primary or secondary data.

Primary data: It is the original information that has been collected for a specific purpose. It is a pure and raw form of data.

Secondary data: It is sourced from an existing data source. It is the data that has already been collected and is available to use.

Data organisation

It is a simple practise of classifying and categorising data to make it easy to understand. We can use tables, graphs, and pie charts to organise data.

The following are the simple ways to represent the data:

1. Tally chart

3. Bar graphs

2. Pictograph

4. Pie chart

Let’s Practise - 1

1. Observe the statement and write whether it is true (T) or false (F) in the provided space.

a. Quantitative data has numerical data. [ ]

b. Secondary data is information that has already been gathered and is ready for use.

c. Data only consists of numerical data.

2. Write down two situations where you can observe qualitative and quantitative data.

a. Qualitative data:

b. Quantitative data:

Let’s Learn

Tally Chart

A tally chart uses vertical lines or tally marks to represent data, typically grouping them in sets of five. After four marks, a diagonal line is drawn to indicate the fifth.

Tally charts are a simple and effective way to organise and count data.

For example: The blood groups of 20 students are recorded as given below:

Arrange the information in a table using tally marks.

Solution:

Statistics is a branch of mathematics that deals with the collection, representation, analysis, and interpretation of numerical data.

Let’s Learn

Pictograph

A pictograph is the pictorial representation of any data.

Example:

In a reading competition, four students participated – Tanya, Rahil, Ankush, and Saumya. They were supposed to read as many pages as they could in an hour.

Name of the Students

Ankush

Saumya

Number of pages read

Key: ♠ = 20 pages

Answer the following questions based on the above pictograph.

a. Who read the highest number of pages?

b. What is the total number of pages read by Saumya?

c. How many more pages did Saumya read compared to Ankush?

Solution:

a. From the given pictograph, Tanya read the highest number of pages.

b. The total number of pages read by Saumya = 5 × 20 = 100

c. The total number of pages read by Saumya = 100

The total number of pages read by Ankush = 3 × 20 = 60

Difference = 100 – 60 = 40

So, Saumya read 40 more pages than Ankush.

Let’s Practise - 2

a. Complete the table using tally marks.

1. The data of two-wheelers owned by 30 families is listed below.

b. Find the number of families having two or more two-wheelers.

2. Following is the data showing the quantity of fruits in a store.

Fruits

Apples

Number of fruits

Strawberries

Key: ♠ = 10 fruits

Observe the pictograph above and answer the following questions.

a. How many bananas are present in the store? __________

b. Identify two fruits which are present in the same quantity. __________

c. Which fruit is of the least quantity in the store? __________

d. Which fruit is the most abundant in the store? __________

Let’s Learn

Bar Graphs

A bar graph is a pictorial representation of the data with rectangular bars. It usually compares different categories. There are various types of bar graphs.

Vertical bar graph

A vertical bar graph displays data with bars going up and down along the y-axis. Each bar represents a category, and its length corresponds to the quantity or value given to that category. It helps compare values of different categories by looking at the heights of the bars.

Horizontal bar graph

This graph displays data with bars extending horizontally along the x-axis. Each bar represents a category, and its length indicates the quantity or value given to

that category. It is effective for comparing values across different categories by looking at the lengths of the bars.

For example, Raj’s results in five subjects in an examination are given in the following table:

The vertical and horizontal bar graphs for the above data are given below:

Double bar graph

Double-bar graphs are used to represent two sets of data on a single graph. In this type of graph, the two sets are positioned next to each other at varying heights based on their values.

For example, the table shows the number of boys and girls for classes 1, 2, 3, 4, and 5.

The double bar graph for the above data is given as:

Number of boys and girls

Let’s Practise - 3

1. The following table gives information about the circulation of newspapers (dailies) in a town in five languages.

Language English Kannada Hindi Punjabi Gujarati Number of newspapers 6000 3000 7500 1500 2000

a. Create a bar graph for the provided data, using a scale of 1000 newspapers.

b. How many language newspapers have a circulation below 5000?

2. During a week-long survey from Monday to Sunday, temperatures in Hyderabad and Delhi were measured and represented in a bar graph.

in two cities

a. What was the highest temperature recorded in Hyderabad during the week?

b. On which day did Delhi have the lowest temperature?

c. How many degrees higher was the temperature in Hyderabad on Tuesday compared to Delhi?

d. If the temperatures in Hyderabad and Delhi were added together on Wednesday, what would be the total?

Let’s Learn

Pie Chart

A circle graph, also known as a pie chart, visually represents data. It is a simple way to compare and analyse individual data points. The data categories are shown within a circle, divided into sectors. Each sector’s size represents the quantity of its category.

Construction of a pie chart

A pie chart is based on a 360° circle. It divides this circle into sectors to represent different components. To find the size of each sector, you can use the formula:

Central angle = Value of the component Sum of all values × 360°

Here are the steps to create a pie chart:

Step 1: Calculate the central angle for each component.

Step 2: Draw a circle and divide it into sectors based on these angles, starting from the horizontal or vertical and moving clockwise.

Step 3: Label each sector with its activity and provide a title for the chart. For example, in the school’s survey, the total number of students who participated in the Olympiad exams is 90, and the central angle for each component is calculated below:

The pie chart for the data is shown below:

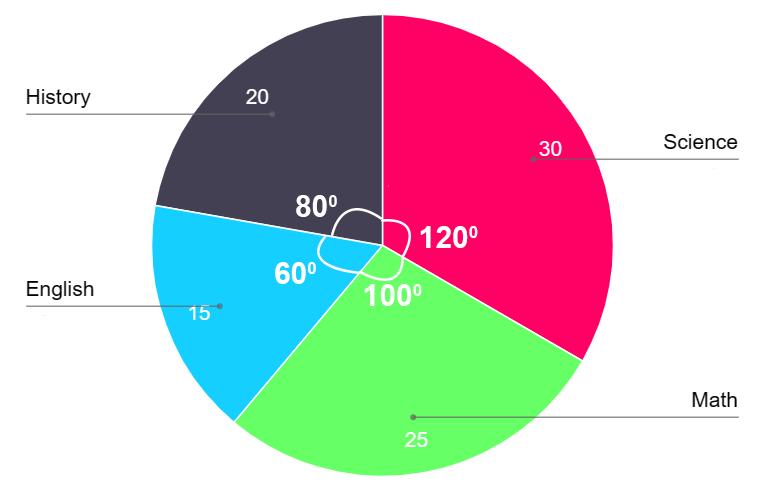
Let’s Practise - 4

1. Create a pie chart to show the favourite fruits of grade 5 students. The data is as follows: 30 like apples, 25 like watermelons, 20 like bananas, and 25 like oranges.

2. Given below is the information of viewers watching different types of channels on TV.

Create a pie chart and colour(in red) the portion that shows the least viewers.

Let’s Sum Up

• Data represent various kinds of information and can be categorized based on the type of data collected (qualitative and quantitative) or the method of collection(primary and secondary).

• Tally chart uses tally marks to represent data.

• A pictograph is a pictorial representation of data.

• A bar graph(vertical or horizontal) is a representation of data using rectangular bars. A double bar graph is used to compare two datasets.

• In a pie chart, the data categories are shown in a circle using sectors of different sizes and with different angles.

Study the double bar graph given below and answer the questions that follow:

a. What information is compared in the given double bar graph?

b. For which months of 2008 was the minimum temperature greater than the months of 2009?

c. For which month do you see the maximum variation in the two temperatures?

Cross-Curricular Connections

English:

Read the paragraph below and complete the given table.

In a Kerala village, Arun, a curious boy, found joy in monsoons. One stormy day, he discovered a colourful parrot, Neela, near a puddle. They danced in the rain, sparking a village-wide celebration. Neela’s squawks became the anthem for rainy days, turning a gloomy day into a cherished memory for everyone in Kerala.

From the above paragraph, prepare the tally chart for the words with two or more letters and answer the following questions.

Number of words with Tally marks Total number of words

2 letters

3 letters

4 letters

5 letters

6 letters

More than 6 letters

a. How many two-letter words are used in the paragraph? __________

b. How many words have five letters or more? __________

Science:

In a botanical garden, the number of different types of plants are as follows:

Draw a bar graph to represent the above information and answer the following questions.

a. Which type of plant has the maximum number in the garden?

b. Which type of plant has the minimum number in the garden?

21st Century Skills

Conduct a survey of 30 individuals about their preferred ice cream flavour: Vanilla, Chocolate, Butterscotch, Kesar Pista, and Pista Badam.

Complete the tally chart given below:

Ice cream flavours Tally marks Number of people

Vanilla

Chocolate

Butterscotch

Kesar Pista

Pista Badam

Create a pie chart based on the data.

Extend Your Knowledge

Histogram:

A histogram is an alternative way to represent given data. It is also called a frequency histogram. It shows numerical information using rectangular bars. Similar to a bar graph, the height of each bar shows how often a particular piece of data occurs. A histogram differs from a bar graph because the vertical columns are drawn right next to each other without any spaces in between.

For example, a table displaying the estimated lengths, in millimetres (mm), of 40 leaves collected from various parts of a specific plant species.

The histogram for the above data is given as:

Number of leaves

Length(mm)

Tip for the Parent

Encourage your child to collect data on the total number of members in 20 families within the neighbourhood. Use bar graphs and pie charts to visually represent and discuss the data, improving their understanding of organising and interpreting information.

ANSWER KEY

CH-01: Large Numbers

Let’s Practise – 1

1. (a) 4231252 (b) 536562841

2. (a) 21,53,475

Twenty-One Lakh Fifty-Three Thousand Four Hundred Seventy-Five

2. (b) 1,78,94,673

One Crore Seventy-Eight Lakh Ninety-Four Thousand Six Hundred Seventy-Three

3. (a) 3,51,21,307 (b) 71,02,210

4. 5,00,000 5. 8

Let’s Practise – 2

1. a. 55432562 < 65264652

b. 234581822 < 256482288

c. 983098 < 983483

d.7041581 > 0704581

2. (a) Ascending order:

53,64,802 < 94,64,008 < 3,12,24,802 < 19,23,54,208

Descending order:

19,23,54,208 > 3,12,24,802 > 94,64,008 > 53,64,802

(b) Ascending order:

1,08,90,900 < 1,14,29,214 < 1,18,39,412 < 1,41,29,412

Descending order:

1,41,29,412 > 1,18,39,412 > 1,14,29,214 > 1,08,90,900

Let’s Practise – 3

1. a. Smallest number = 2345789

Greatest number = 98754320

b. Smallest number = 123468 ; Greatest number = 8643210

c. Smallest number = 1235789 ; Greatest number = 98753210

Let’s Practise – 4

1. (a) 23355640 (b) 20309753 (c) 18093330 (d) 9873002

2. (a) 42089833 (b) 87549792 (c) 90814115 (d) 30938344

Let’s Practise – 5

1. a. 76,168,729 = Seventy-six million, one hundred sixty-eight thousand, seven hundred twenty-nine

b. 48,845,367 = Forty-eight million, eight hundred forty-five thousand, three hundred sixty-seven

c. 8,359,498 = Eight million, three hundred fiftynine thousand, four hundred ninety-eight

d. 4,805,029 = Four million, eight hundred five thousand, twenty-nine

2. a. 75,826,442 b. 57,096,429

c. 9,387,246 d. 60,234,111

Let’s Practise – 6

1. (a) 34120 (b) 33720

2. (a) 38900 (b) 231000

3. (a) 972000 (b) 751000

Let’s Practise – 7

1. a. 44 = XLIV b. 48 = XLVIII

c. 59 = LIX d. 79 = LXXIX

2. a. LXXXIV = 84 b. XCII = 92

c. XLVIII = 48 d. LXVIII = 68

ANSWER KEY

CH-02: Operations with Large Numbers

Let’s Practise – 1

1. (a) 399070 (b) 63756232

2. (97 + 134) + 203 = (97 + 203) + 134 = 434

3. 810

4. (a) 12453648 (b) 3773940 (c) 2312334 (d) 83

Let’s Practise – 2

1. (a) 1437 (b) 92179 (c) 20112140

2. (a) 8745163 (b) 8322498 (c) 0

Let’s Practise – 3

1. 359784 2. 13572 3. 254340

Let’s Practise – 4

1. (a) 219 (b) 0 (c) 43 (d) 0 (e) 1 (f) 9140 (g) 100

(h) 562000

Let’s Practise – 5

1.(a) Quotient = 33383 Remainder = 3

(b) Quotient = 20755 Remainder = 2

(c) Quotient = 193673 Remainder = 0

(d) Quotient = 292933 Remainder = 4

2. (a) 1 (b) 0 (c) 1 (d) 124514

Let’s Practise – 6

1. 880 2. 60 3. 4800 4. 26

CH-03: Factors and Multiples

Let’s Practise – 1

1. 5 2. 24 3 28

4. (a) 3 (b) prime and composite (c) 4 (d) 11

Let’s Practise – 2

1. (d) 5551 2. (b) 2569 3. (a) T (b) T (c) T (d) F

Let’s Practise – 3

1. (a) 2×3×13 (b) 2×2×3×11 (c) 2×3×3×17

Let’s Practise – 4

1. (c) 84 2. 13, 26, 39, 52, 65

3. (a) 28, 35, 42, 49 (b) 72, 90, 108, 126

Let’s Practise – 5

1. (a) 1, 2, 4 (b) 1, 3 2. (a) 15 (b) 3

3. (a) 9 (b) 12 4. (a) 4 (b) 12 5. 12

Let’s Practise – 6

1. Multiples of 6: 6, 12, 18, 24, 30, 36

Multiples of 9: 9, 18, 27, 36, 45, 54

Common multiples are 18 and 36

2. (a) 60 (b) 42 3. (a) 18 (b) 192

4. (a) 12 (b) 5 5. 30

Let’s Practise – 7 1. 15 2. 36 3. 48

CH-04: Fractions

Let’s Practise – 1

1. (a) 5 0 5 (b) 2 23 30 (c) 4 8 25 (d) 10 29 30

2. (a) 53 8 (b) 190 9 (c) 255 10 (d) 230 7

Let’s Practise – 2

1. (a) 3 5 < 4 5 (b) 5 8 > 4 9 (c) 2 7 < 5 9 (d) 2 7 < 5 9 2. 1 9 < 4 9 < 5 9

Let’s Practise – 3

1. (a) 10 7 (b) 101 72 (c) 95 12

2. (a) 4 13 (b) 35 48 (c) 2 1 5

Let’s Practise – 4

1. (a) 12 7 (b) 162 7 (c) 1 35 (d) 1 15

ANSWER KEY

Let’s Practise – 5

1. (a) 7 2 (b) 4 35 (c) 1 6 (d) 5 6

Let’s Practise – 6

1. 72 120 2. Ankit 3. 6 35 4. 20 km

CH-05: Decimals

Let’s Practise – 1

2. (a) 20 +3+ 3 1000

(b) 300 + 10 +5+ 9 10 + 5 100 + 9 1000

(c) 50 +1+ 4 10 + 5 100 + 4 1000

(d) 40 +7+ 5 10 + 1 100 + 4 1000

Let’s Practise – 2

1. (a) 4.201, 23.880, 142.011, 20.300, 154.770

(b) 1.30, 2.02, 4.00, 12.20

2. (a) 24.56 < 43.5 (b) 493.57 > 472.76

(c) 936.23 > 925.323

Let’s Practise – 3

1. (a) 275.446 (b) 150.997

2. (a) 43.21 (b) 382.463

Let’s Practise – 4

1. (a) 17.0 (b) 156.75 2. (a) 0.00448 (b) 4.2435

3. (a) 456.78 (b) 9789.0

Let’s Practise – 5

1. (a) 0.0816… (b) 10.842 (c) 5.575 (d) 0.06875 (e) 0.0097650

CH-06: Percentage

Let’s Practise – 1

1. (a) 25% (b) 60% 2. (a) 3 10 (b) 6 5

Let’s Practise – 2

1 (a) 5% (b) 64% (c) 100% (d) 20% (e) 33%

2. (a) 0.45 (b) 1.09 (c) 0.66 (d) 0.72 (e) 0.30

Let’s Practise – 3

1. (a) 100 houses (b) 450 apples (c) 450 km

2. (a) 20% (b) 16.67% (c) 5%

Let’s Practise – 4

1. Roses: 25% Tulips: 18.75% Daisies: 12.5%

Lilies: 18.75% Orchids: 25%

2. 12.5% 3. 40%

4. 50% of Chocolate cakes and 14.28% of Strawberry cakes.

CH-07: Geometry

Let’s Practise – 1

1. (a) Acute (b) Obtuse (c) Right

2. (a) Complementary (b) Supplementary

(c) Supplementary (d) Complementary

Let’s Practise – 2

1. (a) Parallel Lines (b) Perpendicular Lines

(c) Intersecting Lines (d) Coplanar Lines

Let’s Practise – 3

2. Right angled triangle

Let’s Practise – 4

3. 7 cm 4. 10 cm

CH-08: Perimeter, Area, and Volume

Let’s Practise – 1

1. (a)12cm (b)28cm (c)28cm

2. 26.1cm

3. 787.12m

ANSWER KEY

Let’s Practise – 2

1. (a) 58 cm (b) 40 cm

Let’s Practise – 3

1. (a)7 sq cm (b)12 sq cm (c)8 sq cm (d)10 sq cm

(i) (b) (ii) (a)

2. (a) 13 sq cm (b) 20 sq cm (c) 14 sq cm

(i) (b) (ii) (a)

3. (a) 15 sq cm (b) 24 sq cm

Let’s Practise – 4

1. 24 sq cm 2. 25 sq cm 3. 40 sq m

4. Square carpet

Let’s Practise – 5

1. (a) 5 cm3 (b) 10 cm3 (c) 10 cm3 (d) 12 cm3

2. 27 cm3 3. 120 cm3

CH-09: Measurement

Let’s Practise – 1

1. (a) 10 (b) 10 (c) 60 (d) 800 (e) 1 1000

Let’s Practise – 2

1. (a) 0.35 kg (b) 0.000015 (c) 2.5 L (d) 60 m

Let’s Practise – 3

1. (a) 7km 700m (b) 104kg 90g (c) 105m 45cm

2. 6 m 79 cm 3. 8 4. 50,000

Let’s Practise – 4

1. 29 2. 88 rupees 3. 145 sec 4. 61

CH-10: Time

Let’s Practise – 1

1. (a) 240 minutes = 14400 seconds

(b) 21 days = 504 hours (c) 48 hours = 2880 minutes 2. 930 seconds 3. 420 minutes 4. 8

Let’s Practise – 2

1. (a) 09:15 (b) 21:30 2. (a) 2:30 am (b) 1:15 pm

Let’s Practise – 3

1. 4 hours 15 minutes 2. 2 hours 25 minutes

3. 1 hour 45 minutes 4. 2 hours 35 minutes

Let’s Practise – 4

1. (a) 7 (b) calendar (c) 366 (d) October

2. (a) 3 August (b) 25 August (c) Thursday (d) Thursday (e) 4 (f) 31

CH-11: Money

Let’s Practise – 1

1. (a) ₹150 (b) ₹2880 (c) 15 shirts

Let’s Practise – 2

1. (a) Profit ₹200 (b) Loss ₹100 (c) Profit = ₹1,90,23,114

Let’s Practise – 3

1. ₹2200 2. ₹16200 3. 25%

4. ₹27,000 5. ₹19,600 6. 20%

CH-12: Symmetry, Patterns, and Nets

Let’s Practise – 2

1. H, I, N, O, S, X and Z 2. 0, 1 and 8

3. 1001, 1111, 1881, 8008, 8118, 8888

CH-13: Data Handling

Let’s Practise – 1

1. (a) T (b) T (c) F

Let’s Practise - 2

2. (a) 50 bananas (b) Apples and Oranges (c) Strawberries (d) Apples and Oranges

Let’s Practise - 3

Join the World of Infinite Learning

Infinity Learn by Sri Chaitanya is India’s fastest-growing edtech company dedicated to powering learners’ progress. Backed by Sri Chaitanya’s legacy of over 39 years, we are committed to delivering high–quality education to learners using cutting-edge technology.

We equip learners with essential cognitive skills like inquiry and logical thinking, during their early developmental years by introducing programs on Higher Order Thinking Skills, Product Design & Robotics. These skills form a strong foundation for developing higher aptitude in Mathematics and Science.

As these learners progress through their academic journey, we provide personalised learning in Mathematics and Science for a strong foundation. And, for higher grades the programs are designed to deliver exceptional results in competitive exams.

5 Lakh+ Learners across India

COURSEBOOK

The IL HEADSTART Series 1–5 is a comprehensive series that follows the latest guidelines established by NCERT and CBSE. It seamlessly aligns with the National Education Policy (NEP) of 2020, which strongly emphasises promoting various effective learning approaches such as hands-on, discovery-based, experiential, inquiry-based, and competency-based learning. These approaches are all geared towards enabling students to grasp concepts and acquire the essential skills necessary for effective learning in the 21st century.

This series is thoughtfully structured around thematic concepts, with a primary focus on fostering the holistic development of each learner. The exercises integrated within the series have been meticulously designed to cater to varying levels of difficulty to assess learners across a wide spectrum of skills, ranging from Lower Order Thinking Skills to Higher Order Thinking Skills.

Key Features

Learning Outcomes aligned with NCERT's recommendations

A diverse array of pedagogical elements in line with NEP 2020

Tailored pedagogical approaches specific to each subject

Chapters designed to harmonise with a thematic educational approach

Colourful and lively visuals that enhance conceptual clarity

Practice exercises stratified by difficulty levels

Address