MOTION IN A STRAIGHT LINE CHAPTER 3
Chapter Outline
3.1 Position, Distance, and Displacement
3.2 Speed
3.3 Velocity
3.4 Acceleration
3.5 Equations of Kinematics
3.6 Graphical Representation of Motion
3.7 Relative Velocity in One Dimension
■ Kinematics: The study of motion without considering its cause.
■ Motion and rest are relative terms.
■ The chapter starts with motion in one dimension (straight line motion), then extends to two-dimensional motion.
■ In straight line motion, the line joining successive positions is straight.
■ The origin is the reference point for locating the particle's position.
■ Frame of Reference: A coordinate system (x, y, z axes) with an origin (O) used to describe the position of an object, along with a clock to measure time.
■ If the position of an object changes over time, it is in motion; if not, it is at rest.
■ Rest and Motion:
An object is at rest if its position does not change with time or relative to a fixed point.
An object is in motion if its position continuously changes with respect to a fixed point and time.
3.1 POSITION, DISTANCE, AND DISPLACEMENT
3.1.1 Position and Path Length
■ “Length of actual path between initial and final positions is called distance or path length.”
3.1.2 Displacement
■ Displacement is the shortest straightline distance from the initial to the final position, regardless of the path.
■ Let x1 and x2 be the positions of an object at the instants t1 and t2, respectively. Then, displacement is 21∆=−xxx in the time interval 21∆=−ttt .
■ Distance is a scalar with only magnitude, while displacement is a vector with both magnitude and direction. -160-120240360400m -+x x ROQP 0
■ For example, displacement of the car in moving from O to P is 21(360m)0m360mxxx ∆=−=+−=+
■ The displacement has a magnitude of 360 m and is directed in the positive x direction, as indicated by the + sign.
■ Similarly, the displacement of the car from P to Q is 240 m – 360 m = –120 m. The
negative sign indicates that the direction of displacement is in negative x direction.
■ We should remember that the magnitude of displacement may or may not be equal to the path length traversed by an object.
Application
■ Consider a particle moving from A to B along a curve, as shown. AB
The distance travelled is equal to the length of the curve AB, whereas the magnitude of the displacement is equal to the length of the straight line AB.
■ If a person walks from A to B and then from B to C, as shown, then path length travelled = AB + BC = 7 m displacement = AC = 5 m.
AB C 3m 5m 4m
■ A particle moves over an arc PQ of a circle of radius R, subtending an angle θ at the centre.
PQ RR O θ
Distance travelled = arc PQ = R θ
Displacement = straight line PQ = 2Rsin 2 θ
Key Insights:
■ If a particle starts and ends at the same point, displacement is zero.
CHAPTER 3: Motion in a Straight Line
■ However, the distance covered is not zero.
■ Therefore, a particle can travel a certain distance without having any displacement
■ Distance > Displacement.
TEST YOURSELF
1. A particle covers half of the circle of radius r. Then, the displacement and distance of the particle are, respectively,
(1) 2πr, 0 (2) 2r, πr
(3) ,2r 2 πr (4) πr, r
2. A body moves from x = –1 to x = 4 and then to x = –4. Which of the following is correct?
(1) Its displacement is zero.
(2) The distance covered by it is 5 units.
(3) Its displacement is –3.
(4) Distance covered by it is 9 units.
Answer Key
(1) 2 (2) 3
3.2 SPEED
■ The distance travelled by a body in unit time is called its speed. It is a scalar quantity. CGS unit of speed is cms–1 and its SI unit is ms–1
3.2.1 Uniform Motion
■ If an object covers equal displacement in equal time intervals, it is said to be in uniform motion along a straight line.
■ The position-time graph of such motion is a straight line.
x(m)
Ot(s)
Uniform Speed
■ If a particle moving along a straight line (say x -axis) travels equal distances in equal intervals of time, however small the intervals may be, then the particle is moving with uniform speed .
3.2.2 Non-uniform Speed or V ariable Speed
■ If a particle travels unequal distances in equal time intervals or equal distances in unequal time intervals, it is said to be moving with non-uniform speed.
■ Examples:
Motion of a freely falling body.
Motion of a body thrown vertically upwards.
3.2.3 Average Speed
■ For a particle in motion (uniform or non-uniform), the ratio of total distance travelled to the total time of motion is called average speed.
Average speed
Totaldistancetravelled Totaltime =
■ If s1, s2, s3......s n are the distances travelled by a particle in the time intervals t1, t2, t3 tn, respectively, then,
speed
3.2.4 Instantaneous Speed
■ Instantaneous speed is the speed of a particle at a specific moment in time, or the limit of average speed as the time interval (∆t) approaches zero.
■ If ∆ x is the distance travelled by a particle in a time interval ∆ t, then
Speed = ∆ ∆ x t
■ If the time interval ∆ t is chosen to be very small, i.e., ∆t → 0, then the corresponding speed is called instantaneous speed.
0 Instantaneousspeed t xdx Lt tdt ∆→ ∆ ∴== ∆
Applications
■ A body travelling between two positions travels first half of the distance with speed v1 and the next half of the distance with speed v2. The average speed of total motion is 12 12 2 + vv vv
Let x be the total distance be tween two positions.
Let t 1 be the time for first half and t 2 be the time for the next half of the distan ce.
■ A body is travelling between two positions A and B. It travels from A to B with speed v1 and then from B to A in the same path with speed v2. The average speed of tot al motion is 12 12 2 + vv vv
■ A body is travelling between two positions. The total distance is divided into n equal parts. These parts are travelled with speed v 1 , v 2 , v 3 ..... v n , respectively. The average speed of total motion is such t hat 123 1111 Averagespeed =+++ n n vvvv
■ A body travelling between two positions travels with speed v1 for time t1 and then with speed v 2 for time t 2 . For the total
CHAPTER 3: Motion in a Straight Line
motion,
Averagespeed
■ A body travelling between two positions travels first half of the time with speed v1 and the next half of the time with speed v2. The average speed of total motion is 12 2 + vv
■ A body travelling between two positions travels for the time intervals t1, t2, t3..........t n with speeds v1, v2, v3,...........v n, respectively
AverageTotaldistance speedTotaltime
Solved example
1. A particle traversed half of the distance with a velocity of V0. The remaining parts of the distance was covered with velocity V 1 for half of the time and with V 2 for the other half of the time. Find the mean velocity of the particle averaged and the whole time of motion.
Try yourself:
1. A particle moves from point A to point B along a straight line. C is the midpoint of AB. e particle moves from A to C with velocity V and from C to B with velocity 2V. Find the average velocity of the particle. Ans: 4V/3
TEST YOURSELF
1. A car travels a distance of ‘x’ with speed v1 and then x distance further with velocity v2 in the same direction. e average speed of the car is
Average velocity for the first half of distance =
( It is constant.) Average velocity for total path
2. During the first 18 min of a 60 min trip, a car has an average speed of 11 ms–1. What should be the average speed for remaining 42 min so that car is having an average speed of 21 ms–1 for the entire trip? (1) 25.3 ms–1 (2) 29.2 ms–1 (3) 31 ms–1 (4) 35.6 ms–1
Answer Key (1) 3 (2) 1
3.3 VELOCITY
■ The displacement of a body in unit time is called its velocity. It is a vector quantity. CGS unit of velocity is cms–1 and SI unit is ms–1 .
■ Dimensional formula is [L 1T–1]
3.3.1 Uniform Velocity
■ Uniform velocity: When a body covers equal displacements in equal time intervals
■ This motion is expressed by an equation of the form
x = vt + b
■ where x is the position coordinate of the particle, t is the time, v and b are certain constants. In this equation, position is a linear function of time. Hence, the position–time graph is a straight line, the slope of which is a constant (v) and is equal to uniform velocity of particle. t x b o
■ Position–time graph of an object in uniform motion
When t = 0, x0 = b the above equation can be written as x = vt + x 0 . where x 0 indicates the initial position of the particle from the origin.
3.3.2 Non-uniform Velocity
■ Non-uniform velocity occurs when a body has unequal displacements in equal time intervals or equal displacements in unequal time intervals.
Key Insights:
■ The displacement variation may be due to change in magnitude or change in direction of motion or both.
3.3.3 Average Velocity
■ For a particle in motion (uniform or nonuniform), the ratio of total displacement to the total time interval is called average velocity.
AverageTotaldisplacement velocityTotaltime =
Average21 velocity == ∆ xx v t
■ Consider the motion of the car in the figure given below.
■ As seen from the plot, the average velocity of the car between time t = 5 s and t = 7 s is
211 21 (27.410.0)m8.7ms (75)s == = xx v tt
■ Geometrically, this is the slope of the straight line P 1 P 2 connecting the initial position P1 to the final position P2, as shown in fig.
3.3.4 Instantaneous Velocity
■ Instantaneous velocity is the velocity at a specific moment, or the limit of average velocity as the time interval (∆t) approaches zero
■ If ∆ S is the displacement by a particle in a time interval ∆ t then
■ If the time interval ∆ t is chosen to be very small, i.e., ∆ t → 0, the corresponding velocity is called instantaneous velocity. 0 Instantaneousvelocity t SdS Lt tdt ∆→ ∆ == ∆
■ The instantaneous velocity is the rate of change of position with time.
■ The velocity at a particular instant is equal to the slope of the tangent drawn on the position–time graph at that instant.
Key Insights:
■ 22 11 ; ==∫∫ st st ds vdsvdt dt
■ Average speed is always greater than or equal to average velocity.
■ For motion from A to B and back with velocities v1 and v2, the average velocity is zero due to zero displacement.
■ In variable motion, average velocity depends on the time interval.
■ In uniform motion, average velocity is constant for all time intervals.
■ The magnitude of average velocity equals average speed for straight-line motion and is a scalar.
■ In uniform motion, instantaneous velocity equals average velocity.
Solved example
2. A particle is at x = +5 m at t = 0, x = –7 m at t = 6 s, and x = +2 m at t = 10 s. Find the average velocity of the particle during the intervals
(a) t = 0 to t = 6 s
(b) t = 6 s to t = 10 s, (c) t = 0 to t = 10 s.
Sol. From the definition of average velocity, 21 21
(a) The average velocity between the times t = 0 to t = 6 s: 11225m,0,7m,6s=+==−= xtxt Hence, 211 1 21 75 2ms 60 xx v tt ===−
(b) The average velocity between the times t2 = 6 s to t3 = 10 s is ( ) 321 2 32 279 2.25ms 1064 xx v tt ====
CHAPTER 3: Motion in a Straight Line
(c) The average velocity between times t1= 0 to t3=10 s is
Try yourself:
2. A particle is at x = 0 at t = 0, x = –2 m at t = 2 s and at x = 4 m at t = 5 s. Find the average velocity of the particle.
Ans: 0.8 m/s
TEST YOURSELF
1. The displacement of a particle starting from rest at t = 0 is given by s = 9t2 – 2t3 e time in seconds at which the particle will attain zero velocity is (1) 8 s (2) 6 s (3) 4 s (4) 3 s
2. The distance travelled by a particle is related to time t as x = 4t2 . e velocity of the particle at t = 5 s is (1) 40 ms–1 (2) 25 ms–1 (3) 8 ms–1 (4) 20 ms–1
Answer Key
(1) 4 (2) 1
3.4 ACCELERATION
■ Acceleration is the rate at which a particle's velocity changes as it moves.
■ Acceleration is defined as the rate of change of velocity.
■ The average acceleration: ratio of change in velocity over a time interval to the time interval.
■ Let V1 and V2 be the velocities of a particle at instants t1 and t2 respectively. Now, AverageChangeinvelocity accelerationTime =
■ It is a vector. It is in the direction of change in velocity.
■ SI unit of acceleration is ms –2 , and its dimensional formula is [L1T–2].
Key Insights:
■ Velocity variation can be due to a change in magnitude (speed) or direction of velocity, resulting in acceleration.
■ Examples:
A car increasing speed on a straight road has acceleration due to a change in speed.
A stone whirled in a horizontal circle with constant speed has acceleration due to a change in direction.
A stone whirled in a vertical circle with changing speed has acceleration due to both magnitude and direction changes.
■ Acceleration can be positive (speed increasing) or negative (speed decreasing)
■ For positive acceleration, the velocity vector and acceleration vector are in the same direction, but for negative acceleration, the velocity and acceleration vectors are opposite.
3.4.1 Instantaneous Acceleration
■ The acceleration of a particle at a particular instant of time is called its instantaneous acceleration.
3.4.2 Deceleration or Retardation
■ If the speed is decreasing with time, then acceleration is negative and is called deceleration or retardation.
3.4.3 Uniform Acceleration
■ Uniform acceleration: When the average acceleration equals the instantaneous acceleration at any instant, it is constant and does not vary with time.
■ Alternatively, if a body has equal changes in velocity in equal time intervals, it is said to be moving with uniform acceleration.
Solved example
3. Instantaneous velocity of a particle moving along a straight line is given by v = (2t + 3) m/s. Find its instantaneous acceleration at t = 2 s.
Sol. ( ) 2322m/s. dvd at dtdt ==+=
Try yourself:
3. A particle is moving along a straight line and at time = t, its position is given by s = (2t + 5t2)m. Find its acceleration.
Ans: 10 2m/s
TEST YOURSELF
1. A vehicle moving in a straight road has its speed changed from 5 m/s to 8 m/s in 2 s. What is its average acceleration? (1) 1 m/s2 (2) 1.5 m/s2 (3) 2 m/s2 (4) Zero
2. e velocity of a particle is zero at t = 0.
Key Insights:
■ Instantaneous acceleration
a) The acceleration at t = 0 must be zero.
b) The acceleration at t = 0 may be zero.
c) If the acceleration is zero from t = 0 to t = 10 s, the speed is also zero in this interval.
d) If the speed is zero from t = 0 to t = 10 s the acceleration is also zero in this interval.
(1) a, b, and d are correct.
(2) b, c, and d are correct.
(3) a, c, and d are correct.
(4) a, b, and c are correct.
Answer Key (1) 2 (2) 2
3.5 EQUATIONS OF KINEMATICS
■ Kinematical equations are useful to solve problems in one dimensional motion of a particle with constant acceleration.
3.5.1 Kinematical Equations of Motion of a Particle Moving along a Straight Line with Uniform Acceleration
■ The equations of motion are as follows:
Velocity as a function of time, v = u + at
Displacement as a function of time, 12 2 =−=+ fi Sxxutat
Position as a function of time, 12 2 =++fi xxutat
Velocity as a function of displacement, v2 – u2 = 2as
Displacement in nth second of motion, 1 2
n Suan
Displacement = (Average velocity) × time 2 +
uv St θ y x
CHAPTER 3: Motion in a Straight Line
■ In the first method, the straight line, whose slope has to be determined, is extended. In the second method, from any two points on the line, perpendiculars are drawn onto both x and y-axes.
■ The respective coordinates (foots of perpendiculars) are noted. The ratio of difference of y-coordinates to x-coordinates gives the slope of this straight line.
21 = yy m xx
3.5.2 Acceleration due to Gravity (g)
■ Acceleration due to gravity: The uniform acceleration of a freely falling body towards the Earth's center due to gravity.
Denoted by ‘g’.
Its value is constant for all bodies at a given location, regardless of size, shape, or material.
If air resistance is ignored, all bodies, regardless of mass, fall at the same rate.
The value of g changes from place to place on Earth's surface.
■ It has maximum (greatest) value at the poles of the earth. The value is nearly 9.83 m/s2. It has minimum (least) value at the equator of the earth. The value is nearly 9.78 m/s2
■ The average value of g on earth’s surface is 9.8 m/s2
■ On the surface of moon, 1.672 m/s 6 gearth g ==
On the surface of sun, g = 274 m/s2
■ The acceleration due to gravity of a body is always directed downwards towards the centre of the earth, whether a body is projected upwards or downwards.
■ When a body is falling towards the earth, its velocity increases; g is positive.
■ When a body is projected upwards, its velocity decreases; g is negative.
■ The acceleration due to gravity at the centre of the earth is zero.
3.5.3 Equations of Motion for Freely Falling Body
■ Motion of all the dropped bodies falling towards the earth, when air resistance is ignored, is known as free fall.
For a freely falling body, u = 0, a = + g
∴ (i) v = u + at ⇒ v = gt
(ii) S = ut + 1 2 at2 ⇒ S = 1 2 gt2
(iii) v2 – u2 = 2aS ⇒ v2 = 2gS (iv)
Key Insights:
■ For a freely falling body, the ratio of distances travelled in 1 second, 2 seconds, 3 seconds, .... = 1 : 4 : 9 : 16... so on
■ For a freely falling body, the ratio of distances travelled in successive seconds = 1 : 3 : 5 : 9 ..... so on.
■ The fraction of distance fallen in nth second is ( ) 2 21 = n Sn Sn
■ ( ) ( )21,21 22 =+−=+− nm aa SunSum ( ) −=− nm SSanm ∴= nm SS a nm
■ Let n = m + 1. Then, ( ) 11+ −=+−= mm SSamma
(or) 1+ =+ mm SSa
■ In uniformly accelerated motion, the distance travelled in every second increases by an amount equal to the magnitude of acceleration.
Application
■ A body dropped freely from a multistorey building can reach the ground in t1 seconds. It is stopped in its path after t 2 seconds and again dropped freely from the point. Find the further time taken by it to reach the ground.
1H2 t2 t3=? H3 t1
We know that, H1 = H2 + H 3 222222 123123 111 222 ⇒=+⇒=+ gtgtgtttt
22 312∴=− ttt
Solved examples
4. Two bodies begin to fall freely from the same height. The second body begins to fall ‘ τ ’ s after the first. After what time from the beginning of first body does the distance between the bodies become equal to ?
Sol. Let the time of fall of the 1st body be t seconds. Time of fall of second body = t – τ
Distances of free fall of the bodies in the above time intervals, respectively, are ( ) 22 12 ; 22 gtgtHH −τ == Therefore, 2 12 1 2 =−=τ−τ HHgtg
2 τ ∴=+ τ t g
5. If a freely falling body covers half of its total distance in the last second of its journey, find its time of fall.
Sol. Suppose, t is the time of free fall.
12 2 = hgt ....... (1) ( ) 12 1 22 =− h gt ....... (2)
Solving (1) and (2), ( ) 22s,=+ t since 22 is not acceptable.
Try yourself:
4. Two balls are dropped to the ground from different heights. One ball is dropped 2 s after the other, but both strike the ground at the same time, 5 s after the first is dropped.
a) What is the difference in the heights from which they were dropped?
b) From what height was the first ball dropped?
Ans: (a) 78.4 m, (b) 122.5 m.
3.5.4 Equations of Motion for Vertically Projected Body
■ For a body projected vertically upwards, a = – g (since velocity and acceleration vectors are opposite).
∴ (i) =+⇒=− vuatvugt
(ii) 2211 22 =+⇒=− SutatSutgt
(iii) ( ) 222222 −=⇒−=− vuaSvugS
(iv) 11 22
3.5.5 Motion Parameters of a Body Projected Vertically Upwards
Maximum Height (Hmax)
■ “For a body projected vertically upwards, the maximum vertical displacement from
CHAPTER 3: Motion in a Straight Line
ground about which its velocity is zero is called its maximum height.”
■ Expression: Let a body be projected vertically upwards with initial velocity u.
2 max2
∴= u H g
Time of Ascent (t a)
■ “For a body projected upwards, the time to reach the maximum height is called time of ascent.”
■ Expression: Let a body be projected vertically upwards with initial velocity u.
∴= a u t g
Time of Descent (td)
■ “For a body projected upwards, the time to travel from maximum height to the point of projection on ground is called time of descent.”
■ Expression: Let a body be projected vertically upwards with velocity u
Step 1: For upward motion, ( ) 2 max 2 max 02 2 −=−
∴= ugH u H g Initial µ S - H max velocity = 0
Step 2: For downward motion, S = ut + 1 2 gt2 Here, initial velocity = 0,
a = +g, t = td, S = H max
Key Insights:
■ For a body projected vertically upwards, time of ascent ( ta) = Time of descent ( td) = u g
Time of Flight (tf)
■ “For a body projected vertically upwards, the sum of time of ascent and time of descent is called time of flight ( t f).” It is the total time for which the body remains in air.
■ Time of flight = Time of ascent + Time of descent
f = t a + td
Velocity of the Body on Reaching the Point of Projection (Vstriking)
■ Let a body be projected vertically upwards with initial velocity u.
■ The body reaches the point of projection once again after the time of flight ( tf)
We know that, V = u + at Here,
■ The body reaches the point of projection with the same speed of projection but in opposite direction.
Key Insights:
■ For a body projected vertically upwards, s–t, v–t, and a–t graphs are as follows: 2 2 u g u g 2u g t
rs v -v t -g t a
■ For a freely falling body, s–t, v–
, a–t graphs are as follows:
■ In a vertically projected body, velocity is maximum at projection, decreases, and becomes zero at the highest point.
■ A body can have zero velocity and non-zero acceleration (e.g., at the highest point).
■ Velocity during the upward journey equals velocity during the downward journey (numerically).
■ Thus, projection velocity = striking velocity (numerically)
■ Change in velocity in the entire journey = 2u {( ∆ v = vf – vi = u – (–u) = 2u}
■ Velocity at half maximum height = 2 u : Using the equation, v2 – u2 = 2as, we have, a = –g, 112 222 == u sH g , we get ( ) 22 2222 2 42 −=−×⇒−= uu vugvu g 2 2 22 ⇒=⇒= uu vv
■ Velocity at 3th 4 of maximum height = 2 u :
Using the equation, v2 – u2 = 2as,
we have, a = –g, 332 442 == u sH g , we get, ( ) −=−×⇒−= 22 222233 2 84 uu vugvu g
⇒=⇒= 2 2 42 uu vv
■ Distance covered by a body projected vertically up in the 1st second of its upward journey = distance covered by it in the last second of its entire journey = 2 ug :
We know that, for a body projected vertically up, 1 2 =−−
n sugn
Substituting n = 1 gives 12 =− sug (clearly, the distance travelled in last second is same as that of 1st second).
■ Distance covered by a body projected vertically up in the last one second of its upward journey = distance covered by it in the 1st second of its downward journey
= 2 g :
For a body falling downwards, we know that 12 2 = sgt
Substituting t = 1 gives us 2 = sg (clearly, the distance travelled in 1 st second in the downward journey is same as that of last second of upward journey).
■ Time taken by body projected vertically up body to reach 3th 4 of maximum height = 2 a t :
We know that, for a body projected vertically up, v = u – gt 2 ⇒=− u ugt
CHAPTER 3: Motion in a Straight Line
(since, at 3th 4 of maximum height, velocity = 2 u ) 1 222 ⇒=⇒=⇒=× a uu gtttt g
■ A body projected vertically up takes a time 1 1 2 =− a tt to reach half of maximum
height. We know that, for a body projected vertically up, v = u – gt. 2 ⇒=− u ugt (since, at half of maximum height, velocity = 2 u ) 1 1 22 1 1 2
⇒=− a uu ugtt g tt
■ For a body thrown vertically up, maximum height H = 12 8 gT , where ‘T’ is the time of flight:
We know that time of flight 2 2 =⇒=ugTTu g
∴ Maximum height 2 2 212 228 === gT u HgT gg
■ When air resistance is taken into account:
Time of ascent is less than that in vacuum.
Time of ascent is less than time of descent.
The speed of the body when it reaches the point of projection is less than the speed of projection.
O R u mg R v u mg
F = mg + R F = mg – R =+ R ag m 1 =− agRm
0 = u – at a v = 0 + a1td
u t
■ For dropped bodies:
Same resistance force R ⇒ a = g – R/m
If m is more, a is more ⇒ heavier body falls first.
If R is proportional to m , then acceleration is same for both ⇒ both the balls fall simultaneously at the same time.
If m is same, R is less for smaller body; a = g – (R/m) is more for smaller body ⇒ Smaller body falls first.
Solved example
6. Body 1 is released from the top of a tower. At the same instant, body 2 is projected vertically up, as shown. Then: h
a) Height at which they meet is
Sol. Let the two meet after a time ‘t’ seconds. Then, sum of the distances covered by both must be equal to height of the tower.
i.e., S1+S2= h
b) The time after which their velocities are equal is .
Sol. Let the velocities be equal after a time ‘ t’.
c) Ratio of distances covered when the magnitudes of their velocities are equal is S1 : S2 =
Sol. From above, velocities are equal after a time 2 = u t g In this time,
Try yourself:
5. A body falls freely from a height ‘ H’. After t seconds of fall, gravity ceases to act. Find the time of flight. Ans: 2 tH T gt
3.5.6 Vertical Projection of an Object from a Tower
■ Expression for height of tower: Suppose, a body is projected upwards vertically with initial velocity u from the top of tower.
Initial velocity of the body = u
■ Net displacement of body = S = +x – x – H = –H
■ Time of travel = t
■ We know that, 12 2 =+ Sutat
■ Here, 2 2 ,,, 1 2 1 2
Key Insights:
■ This is a quadratic equation in time.
■ Comparing with the standard quadratic equation,
ax2 + bx + c = 0, we get 22±+ = tuugH g
Application
CHAPTER 3: Motion in a Straight Line
■ A balloon is rising up vertically. A stone is dropped from the balloo n, when the velocity of balloon is ‘ u ’. At the instant, the stone's velocity is also ‘ u ’ vertically upwards. So, the stone moves upwards until its velocity becomes zero and again falls down to ground in ‘t’ seconds, just like a body projected from the top of a t ower. u
The height of the balloon from the ground when the stone is dropped is 12 2 =−+ hutgt
The stone is a fr eely falling body with respect to balloon.
The height of balloon from the ground when the stone reaches the ground is 12 1 2 = hgt
Key Insights:
■ If the balloon is rising with upward acceleration ‘a’, the distance between the balloon and the stone after ‘t’ seconds is ( ) 12 2 =+ sgat
Application
■ Three bodies are pr ojected from towers of same height, as shown. First one is projected vertically up with a velocity ‘ u’. The second one is thrown down vertically with the same velocity and the third one is dropped as a freely falling body. If t1, t2, and t3 are the times taken by them to reach the ground, then:
a) Velocity of projection is ( ) 12 1 2 =− ugtt
12 u=u 3 u=0
Clearly, the extra time taken by the first body (t1 – t2) is equal to the time of flight of first body above the tower. ( ) 1212 21 i.e., 2 −=⇒=− u ttugtt g
Height of the tower is 12 1 2 = hgtt
We know that, for a body projected vertically up, 12 2 =− sutgt ( ) 22 111211 111 222 ⇒=−=−− hutgtgtttgt 12 1 2 = hgtt
The time taken for free fall in the third case is given by 12. = ttt
For a falling body, 2 = h t g but, 2 1212 12 2 =⇒== h hgttttt g 12 2 == free h ttt g
■ A body projected vertically upwards from ground is at the same height h from the ground at two instants of time t 1 and t 2 (both being measured from the instant of projection) Now,
( ) 12 1 2 = hgtt
velocity of projection = ( ) 12 1 2 =+ ugtt
H max ( )2 12 1 8 =+gtt
a body dropped from height h takes time 12tt to reach the ground
Solved examples
7. A body is projected vertically up with velocity u from a tower. It reaches the ground with velocity nu. The height of the tower is
Sol. v2 – u2 = 2as; Here, u = u, v = nu, a = –g, s = –H 22 22 ()2 (1)2 −= −= nuugH nugH 2 2 (1) 2 ∴=− u Hn g
8. A balloon starts from rest and moves vertically upwards with an acceleration g /8 ms –2. A stone falls from the balloon after 8 s from the start. Find the time taken by the stone to reach the ground. (g = 9.8 ms–2)
Sol. Step-1: To find the distance of the stone above the ground, fromwhich it begins to fall from the balloon: 12 2 =+ Sutat ; here, s = h, u = 0, a = g/8 1284 28
g hg
g Vg
=+=
Step-2: The velocity of the balloon at this height can be obtained from v = u + at 08 8
This becomes the initial velocity (u|) of the stone as the stone falls from the balloon at the height h ∴ u| = g
Step-3: For the total motion of the stone, 12| 2 =− hgtut
Here, h = 4g, u| = g, t = time of travel of stone.
4122280 2 ∴−=−∴−−= ggtgttt
Solving for ‘t’, we get t = 4 and –2 s.
Ignoring negative value of time, t = 4 s.
Try yourself:
6. A stone is dropped into water from a bridge 44.1 m above the water. Another stone is thrown vertically downward 1 s later. Both strike the water simultaneously. What was the initial speed of the second st one?
Ans: 12.25 ms–1
3.5.7 Derivation of equations of motion using calculus method
■ Let us suppose, that an object moves in a straight line with uniform acceleration a. The initial velocity of the object is u ( t = 0) and v is its velocity after time interval t(t = t).
Velocity–Time Relation
Changeinvelocity = Time ∴= ∴ dv aa dt where dv is change in velocity in time dt.
∴ dv=adt
■ Integrating both sides within the condition, we get
Invectorform,thisequationcanbewrittenas
Distance-Time Relation
■ The instantaneous velocity of the object is given by , = ds v dt
or, ds=vdt= (u+at)dt or,ds=udt+atdt
CHAPTER 3: Motion in a Straight Line
■ Integrating both sides within the conditions, we get, 000 =+ ∫∫∫ stt dsudtatdt 2 2 0 1 22
■ In vector form, this equation can be written as 12 2 =+ sutat
Velocity–Displacement Relation
Rateofchangeofdisplacement dvdvdsdv av dtdsdtds ds v dt adsvdv ==×=×
■ Integrating both sides within the conditions, we get, ( ) 2 0 2222 ; 2 2orv2
Invectorformthisequationcanbewrittenas .2
TEST YOURSELF
1. A particle starts with an initial velocity of 10.0 ms–1 along x-direction and accelerates uniformly at the rate of 2.0 ms–2. The time taken by the particle to reach the velocity of 60.0 ms–1 is (1) 25 s (2) 3 s (3) 6 s (4) 30 s
2. A car accelerates from rest with 2 ms –2 on a straight line path and then comes to rest after applying brakes. Total distance travelled by the car is 100 m in 20 s. Then, the maximum velocity attained by the car is
(1) 5 ms–1 (2) 10 ms–1 (3) 15 ms–1 (4) 20 ms–1
3. A truck starts from rest with an acceleration of 1.5 m/s2 while a car 150 m behind starts from rest with an acceleration of 2 m/s2. How long will it take for both the truck and the car to be side by side?
(1) 2.45 s (2) 5 s (3) 24.5 s (4) 5.3 s Answer Key
(1) 1 (2) 2 (3) 3
1) Particle at rest
2) Particle with uniform velocity x = 0 at t = 0
The equation of motion is x = ut But s = x2 – x1 = x– 0 = x x
3) Particle with uniform acceleration, x0 = 0 at t = 0
The equation of motion is x – x0 = s
4) Particle with uniform acceleration, x = x0 att = 0
The equation of motion is x – x0 = s
= ut + 1 2 at2 ⇒ x = x0 + ut + 1 2 at2
3.6 GRAPHICAL REPRESENTATION OF MOTION
3.6.1 Position – Time Graphs ( x - t graphs )
■ Graphs are drawn with time along x-axis and position (displacement with respect to origin) along y–axis
Significance
i) The slope of the tangent at any point gives the instantaneous velocity.
ii) The slope of the chord between two points gives average velocity.
i) A straight line parallel to x-axis
ii) x0 indicates initial position with respect to origin
straight line with positive slope
A parabola with increasing slope
i) A parabola with increasing slope
ii) Intercept on y-axis is initial position x0
Context
Shape of graph
Comment on shape of graph
5) Particle with uniform retardation x0 = 0 at t = 0
The equation of motion is x = s = ut + 1 2 at2 ( x0 = 0)
Where ‘a’ is negative
6) Particle projected vertically upwards
The equation of motion is s = x = ut
3.6.2 Velocity–Time Graphs (v–t Graphs)
■ Graphs are drawn with time along x-axis and velocity along y-axis.
Significance
■ The slope of the tangent at any point gives the instantaneous acceleration.
CHAPTER 3: Motion in a Straight Line
A parabola with decreasing slope
i) A parabola
ii) Its slope decrease from +K to zero and there after from zero to –K where K is instantaneous slope
■ The slope of the chord between two positions gives average acceleration.
■ The area under the graph of velocity versus time, between the time axis and the ordinates at the initial and final times, gives the displacement in that time interval.
2) Particle with uniform velocity (u)
The equation of motion is v = constant = u
3) Particle with uniform acceleration, with velocity = 0 at t = 0
The equation of motion is v = at
i) A straight line parallel to x-axis ii) slope = 0, acceleration = 0 iii) y intercept = initial velocity = u
i) A straight line with positive slope
Slope = acceleration = constant
4) Particle with uniform acceleration, with velocity = u at t = 0
The equation of v = u + at
5) Particle with uniform retardation with velocity = u at t = 0
The equation of motion is v = u + at where a is negative
6) Particle projected vertically upwards
The equation of motion is, v = u – gt
3.6.3 Graphical Treatment: Kinematical Equations of Motion of a Body with Uniform Acceleration
■ The velocity time graph is a straight line with positive slope. The graph i s given by the line AB.
i) A straight line with positive slope
ii) Intercept on y – axis = u
iii) Slope = acceleration = constant
i) A straight line with negative slope
ii) Slope = retardation = constant
i) A straight line with negative slope
ii) The net area bounded by the curve is zero
iii) Net displacement in the time of flight = 0
iv) OA = time of ascent = u/g AB = time of descent = u/g OB = time of flight = 2 u/g
Solved example
9. The displacement - time graphs of two particles P and Q are as shown in the figure. The ratio of their velocities VP and VQ will be
■ To show that v = u + at
The slope of velocity time graph gives the acceleation of the particle.
Sol. The velocity of a particle is equal to the slope of time - displacement straight line.
CHAPTER 3: Motion in a Straight Line
Try yourself:
7. The a - t graph is shown in the figure. The maximum velocity attained by the body from rest will be
Ans: 55 m/s
■ To show that 12 2 Sutat =+
The area under the velocity–time graph with x–axis (time axis) gives the displacement in the bounded time interval. Here, the area bounded by the line AB with x-axis gives the displacement.
∴ S = Area of rectangle OACD + Area of triangle ABC
■ To show that v2 = u2 + 2as: Again, s = Area of trapezium OABD
Solved example
10. Velocity–time graph for the motion of a certain body is shown in Fig. Explain the nature of this motion. Find the initial velocity and acceleration and write the equation for the variation of displacement with time. What happens to the moving body at point B? How does the body move after this moment?
A Bts Vm/s C 0 5 51015
The velocity – time graph is a straight line with –ve slope. The motion is uniformly retarding up to point B and there after uniformly accelerated up to C.
At point B the body stops and then its direction of velocity reversed.
The initial velocity at point A is v 0 = 7 ms–1. 1 07ms7-22 ==ms=0.64ms 11s11 fovv a t = ∆
The equation of motion for this body which gives variation of displacement with time is 122 70.6470.32 2 Stttt =−=−
Try yourself:
8. F igure given here shows the variation of velocity of a particle with time. Find the following :
i) Displacement during the time intervals.
(a) 0 to 2 seconds
(b) 2 to 4 seconds
(c) 4 to 7 seconds
ii) Accelerations at (a) t = 1 seconds
(b) t = 3 seconds
(c) t = 6 seconds
iii) Average acceleration
(a) between t = 0 to t = 4 seconds
(b) between t = 0 to t = 7 seconds
iv) Average velocity during the motion.
TEST YOURSELF
1. Which of the following position-time graphs shows motion with zero acceleration?
2. A body starts from rest at time t = 0, the acceleration time graph is shown in the figure. The maximum velocity attained by the body will be Acceleration (m/s2) Time (seconds) 10 11 (1) 110 m/s (2) 55 m/s (3) 650 m/s (4) 550 m/s
3. An elevator is going up. The variation in the velocity of the elevator is as given in the graph. What is the height to which the elevator takes the passengers (in m)?
Answer Key (1) 3 (2) 2 (3) 36
3.7 RELATIVE VELOCITY IN ONE DIMENSION
■ Let x A (0) and x B (0) be positions of objects A and B, respectively, at time t = 0. Their positions xA(t) and xB(t) at time t are given by: ()(0)()(0) =+=+ AAABBB xtxvtxtxvt
■ Then, the displacement from object A to object B is given by ()()() =− BABA xtxtxt = [xB(0) – xA(0)] + (vB – vA)t = xBA(0) + (vB – vA)t
■ It tells us that as seen from object A, object B has a velocity vB – vA because the
displacement from A to B changes steadily by the amount vB – vA in each unit of time. We say that the velocity of object B relative to object A is =− BABA vvv
■ Similarly, velocity of object A relative to object B is: =− ABAB vvv
Special Cases:
■ If vB = vA then vB – vA = 0. Now, the equation ()()(0)(0). −=− BABA xtxtxx Therefore, the two objects stay at a constant distance ( ) (0)(0)BAxx apart, and their position–time graphs are straight lines parallel to each other, as shown in fig. The relative velocity vAB or vBA is zero in this case.
-0123456-1 2 20 40 x(m) t(s) A B
■ If two objects are moving in same direction and vA > vB, then vB – vA is negative. One graph is steeper than the other and they meet at a common point.
-0123456-1 2 20 40 x(m)
(s)
For example, suppose v A = 20 ms –1 and xA(0) = 10 m; and vB = 10 ms–1, xB(0) = 40 m; vBA = vB – vA = 10 – 20 = –10 m/s
CHAPTER 3: Motion in a Straight Line
−=−+− ()()(0)(0)() BABABA xtxtxxvvt
0 = (40 – 10) + (–10) t ⇒ t = 3 s
∴ They meet after t = 3 s
At this instant, they are both at a position ()()70m == AB xtxt Thus , object A overtakes object B at this time.
■ Suppose vA and vB are moving in opposite directions, then they have opposite signs. Now, velocity of B with respect A is vA+vB
-0123456-1 2 20 40 60 x(m) t(s)
For example, if in the above example, object A is moving with 20 ms –1 starting at x A(0) = 10 m and object B is moving with –10 ms–1 starting at xB(0) = 40 m,
xB(t) – xA(t) = xB (0) – xA (0) + (vB – vA)t 0 = (40 – 10) + (–10 – 20) t
30 – 30t = 0
t = 1 s
The two objects meet at t = 1 s.
The velocity of B relative to A, vBA = [–10 – (20)] ms–1 = –30 ms–1 = –vAB.
In this case, the magnitude of vBA or vAB (= 30 ms–1) is greater than the magnitude of velocity of A or that of B. If the objects under consideration are two trains, then for a person sitting on either of the two, the other train seems to go very fast.
Note that the equations are valid even if vA and vB represent instantaneous velocities.
# Exercises
JEE MAIN
Level-I
Position, Distance, and Displacement
Single Option Correct MCQs
1. A particle moves from A to B in a circular path of radius R, covering an angle θ, as shown in the figure. Find the ratio of distance and magnitude of displacement of the particle.
CHAPTER 3: Motion in a Straight Line
2. A person moves 30 m north, then 20 m east, and then 302 south-west. Find his displacement from the original position.
(1) 14 m south-west
(2) 28 m south
(3) 10 m west
(4) 15 m east
Speed
Single Option Correct MCQs
3. A vehicle moves for 10 minutes at 20 ms –1 due north and stops for five minutes. Then, it continues due north at 40 ms –1 for 20 minutes. Average speed of the vehicle in the entire journey is.
(1) 2.857 ms–1
(2) 285.7 ms–1
(3) 28.57 ms–1
(4) 2857 ms–1
Acceleration
Single Option Correct MCQs
4. An object may have
a) varying speed without having varying velocity
b) varying velocity without having varying speed
c) non-zero acceleration without having varying velocity
d) non-zero acceleration without having varying speed.
(1) a, b, and c are correct.
(2) b and d are correct.
(3) a, b, and d are correct.
(4) a and d are correct.
5. A point moves in a straight line so that its displacement x (in m) at time t (in s) is given by x2 = 1 + t2. Its acceleration in m/s2 at time t is
(1) 3 t x (2) 3 t x
(3) 2 3 1 t xx
(4) 2 11 xx
Numerical Value Questions
6. A car moving on a straight road accelerates from a speed of 4.1 m/s to a speed of 6.9 m/s in 5.0 s. What was its average acceleration? (in m/s2)
Equations of Kinematics
Single Option Correct MCQs
7 A body is released from the top of a tower of height h and takes ‘T’ seconds to reach the ground. The position of the body at T/2 seconds is
(1) 4 h from ground (2) 3 4 h from ground (3) 8 h from ground (4) 5 4 h from ground
8. A ball is thrown upwards from the ground with an initial speed of u . The ball is at a height of 80 m at two times, the time interval being 6 s. Find u. Take g = 10 m/s2 (1) 50 m/s (2) 20 m/s (3) 25 m/s (4) 75 m/s
9. An object reaches a maximum vertical height of 23.0 m when thrown vertically upward on the earth. How high would it travel on the moon where the acceleration due to gravity is about one sixth that on the earth? Assume that initial velocity is the same. (1) 138 m (2) 100 m (3) 10 m (4) 69 m
10. A freely falling body covers_____ of total distance in 3rd second.
(1) 8% (2) 35.5% (3) 55.55% (4) 45.5%
11. An object, moving with a speed of 6.25 m/s, is decelerated at a rate given by 2.5,=− dv v dt where v is the instantaneous speed. The time taken by the object to come to rest would be (1) 2 s (2) 4 s (3) 8 s (4) 1 s
12 The acceleration a of a particle moving with an initial velocity u varies with distance x , = akx where k is a constant. The distance covered by the particle when its velocity becomes 3u is given by (1) 2 323 u k
(2) (3ku2)4/3
(3) 2 623 u k
(4) 2 23 3 u k
13. A bullet moving at 20 m/s strikes a wooden plank and penetrates 4 cm before coming to a stop. The time taken for it to stop is (1) 0.08 s (2) 0.16 s
(3) 0.04 s (4) 0.004 s
14. Two stones are falling at a place from heights in the ratio 2 : 3. Their velocities, on reaching the ground, are in the ratio
(1) 3:2 (2) 2:3 (3) 2 : 3 (4) 3 : 2
15. How long does it take a brick to reach the ground, if dropped from a height of 65 m? What will be its velocity just before it reaches the ground? (g = 9.8 m/s2)
(1) 2 s, 10 m/s
(2) 3.64 s, 35.67 m/s
(3) 12 s, 120 m/s
(4) 5 s, 20 m/s
Numerical Value Questions
16. A particle starting from rest moves along x axis with acceleration of 4 m/s 2 . After 2 seconds, the acceleration is reversed in direction, keeping the magnitude constant. If the total distance travelled in metres before coming to rest is 4n, Find n.
17. With what speed (in m/s) should a body be thrown upwards so that the· distances traversed in the 5 th second and 6 th second are equal?
18. The initial velocity of a particle is u and the acceleration at the time t is at, where a is a constant. Then, the velocity v at the time t is given by 22 at vu n =+ . find the value of n.
19. If a stone is thrown upwards with a velocity of 9.8 m/s, then how much time (in seconds) will it take to come back?
Level-II
Speed
Numerical Value Questions
1. A car covers AB distance with first one-third at velocity v 1 ms –1, second one -third at 2 ms–1, and last one-third at v3 ms–1. If v3 = 3 v1, v2 = 2 v1 and v1 = 11 ms–1, then the average velocity of the car is ms–1 (2022)
Equations of Kinematics
Single Option Correct MCQs
5. A car accelerates from rest at a constant rate α for some time, after which it decelerates at constant rate b and comes to rest. If the total time elapsed is t, then the maximum velocity acquired by the car is
(1)
Velocity
Single Option Correct MCQs
2. The displacement x of a particle moving in one direction is given by 3 tx=+ , where x is in metre and t in seconds. What is its displacement when its velocity is zero?
(1) 3 m/s
(2) 2 m/s
(3) 1 m/s
(4) zero
Acceleration
Numerical Value Questions
3. The displacement of a particle starting from rest at t = 0 is given by S = 9t2 – 2t3. The time in seconds at which the particle will attain zero acceleration is 3 sec. x Then, x = .
4. A particle is moving in a straight line such that its velocity is increasing at 5 ms–1 per metre. The acceleration of the particle is ms–2 at a point where its velocity is 20 ms–1 .
6. A goods train, accelerating uniformly on a straight railway track, approaches an electric pole standing on the side of the track. Its engine passes the pole with velocity u and the guard’s room passes with velocity v. The middle wagon of the train passes the pole with a velocity
7. Two cars 1 and 2 starting from rest, are moving with speeds V1 and V2 m/s (V1 > V2). Car 2 is ahead of car 1 by ‘S’ metres when the driver of car 1 sees car 2. What minimum retardation should be given to car 1 to avoid collision?
8. When a ball is dropped into a lake from a height of 4.9 m above the water level, it hits the water with a velocity v and then sinks to the bottom with the constant velocity v. It reaches the bottom of the lake 5.0 s after it is dropped. The approximate depth of the lake is
(1) 19 .6 m
(2) 29.4 m
(3) 39.2 m
(4) 73.5 m
9. A balloon is rising vertically upwards with a constant velocity of 15 ms–1. When it is at a height of 50 m above the ground, a stone is dropped from it. Find the time taken by the stone to hit the ground.
(1) 5 s
(2) 7 s
(3) 10 s
(4) 12 s
10. A ball is released from a height h. t1 and t2 are the time required to complete the first half and second half of the distance, respectively. Then, choose the correct relation between t1 and t2.
(1) ( ) 12 2 tt =
(2) ( ) 12 21 tt =−
(3) ( ) 21 21 tt =+
(4) ( ) 21 21 tt =−
11. A ball is thrown upwards vertically with a certain velocity so that it reaches a maximum height h. Find the ratio of the time in which it is at height 3 h while going up and coming down, respectively.
(1) 21 21 + (2) 32 32 +
(3) 31 31 + (4) 1 3
12. The displacement of a particle varies with time t as s = at 2 – bt 3. The acceleration of the particle will be zero at time t equal to
(1) a/b
(2) a/3b
(3) 3b/a
(4) 2a/3b
13. The velocity of the bullet becomes one–third after it penetrates 4 cm in a wooden block. Assume that bullet is facing a constant resistance during its motion in the block. The bullet stops completely after travelling (4 + x) cm inside the block. The value of x is
(1) 2.0
(2) 1.0
(3) 0.5
(4) 1.5
14. The velocity of a particle is v = v 0 + gt + ft2. If its position is x = 0 at t = 0, then its displacement after unit time ( t = 1) is
(1) v0 + 2g + 3f
(2) v0 + g/2 + f/3
(3) v0 + g + f
(4) v0 + g/2 + f
15. A parachutist, after bailing out, falls 50 m without friction. When parachute opens, it decelerates at 2 ms–2. He reaches the ground with a speed of 3 m/s. At what height did he bail out?
(1) 293 m
(2) 111 m
(3) 91 m
(4) 182 m
Numerical Value Questions
16. A body covers 200 cm in the first 2 s and 220 cm in the next 4 s, under constant acceleration. Velocity of the body (in cm/s) after 7 s is:
17. The ratio of the distance travelled by a falling body in the last second of its motion to that in the last but one second is 7 : 5. The velocity (in m/s) with which body strikes the ground is (g = 10 m/s2).
18. If a particle is moving along a straight line given by the relation s = 2 – 3t + 4t3 where s is in cm., and t is in seconds. its average velocity during the third second (in cm/s) is .
19. A car is moving with a speed of 150 kmph and after applying the brake, it will move 27 m before it stops. If the same car is moving with a speed of one–third of the reported speed, then it will stop after travelling m distance.
20. From the top of a tower, a ball is thrown vertically upward, which reaches the ground in 6 s. A second ball thrown vertically downward from the same position with the same speed reaches the ground in 1.5 s. A third ball, released from rest from the same location, will reach the ground in ______ s.
21. A ball is thrown vertically u pwards with a velocity of 19.6 ms–1 from the top of a tower. The ball strikes the ground after 6 s. The height from the ground up to which the ball can rise will be m.
k The value of k is (use g = 9.8 m/s2)
22. If the velocity of a body related to displacement x is given by 500024m/s,=+ vx then the acceleration of the body is m/s2.
CHAPTER 3: Motion in a Straight Line
Graphical Representation of Motion
Single Option Correct MCQs
23. A body is thrown vertically upwards. Which one of the following graphs correctly represents the velocity vs time graph?
24. The acceleration versus time graph of a particle moving in a straight line is shown in fig. The velocity–time graph of the particle would be
2 0 t(s) a (ms–2)
(1) a straight line (2) a parabola (3) a circle (4) an ellipse
25. The velocity–displacement graph describing the motion of a bicycle is shown in the figure
The acceleration–displacement graph of the motion of a bicycle is best described by
Numerical Value Questions
26. The speed versus time graph for a particle is shown in the figure. The distance travelled (in m) by the particle during the time interval t = 0 to t = 5 s will be .
27. The acceleration–time graph of a particle moving along a straight line is shown. After what time in seconds, does the particle attains its initial velocity?
Relative
Velocity
in One Dimension
Single Option Correct MCQs
28. Pavankumar reached the metro station and found that the escalator was not working. He walked up the stationary escalator in time 2 minutes. On other days, if he remains
stationary on the moving escalator, then the escalator takes him up in time 1 minute. The time taken by him to walk up on the moving escalator will be
(1) 1 min (2) 3 min
(3) 4/3 min (4) 2/3 min
29. When two bodies approach each other with different speeds, the distance between them decreases by 120 m for every one minute. If they are moving in the same direction, the distance between them increases by 90 m for every one minute. The speeds of the bodies are
(1) 2 ms–1 and 0.5 ms–1
(2) 3 ms–1 and 2 ms–1
(3) 1.75 ms–1 and 0.25 ms–1
(4) 2.5 ms–1 and 0.5 ms–1
30. Train A and train B are running on parallel tracks in the opposite directions with speeds of 36 km/hour and 72 km/hour, respectively. A person is walking in train A in the direction opposite to its motion with a speed of 1.8 km/hour. Speed (in ms –1) of this person, as observed from train B, will be close to (take the distance between the tracks as negligible)
(1) 29.5 ms–1
(2) 28.5 ms–1
(3) 31.5 ms–1
(4) 30.5 ms–1
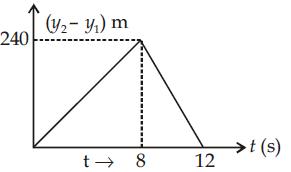
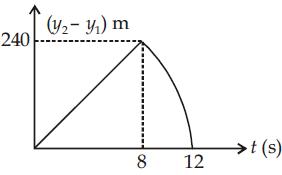
31. Two stones are thrown up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s, respectively. Which of the following graphs best represents the time variation of the relative position of the second stone with respect to the first?
(Assume that stones do not rebound after hitting the ground and neglect air resistance,
CHAPTER 3: Motion in a Straight Line
take g = 10 m/s2) (The figures are schematic and not drawn to scale)
Numerical Value Questions
32. A police van moving on a highway with a speed of 30 km/h fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km/h. If the muzzle speed of the bullet is 150 m/s, with what speed (in m/s) does the bullet hit the thief’s car?
33. A person in lift, which ascends up with acceleration 10 ms –2, drops a stone from a height of 10 m. The time of descent is (in s) [g = 10 ms–2].
Level-III
1. Velocity of an object (in SI units) depends on displacement as ( ) 33 24 8 VKy = , where K is const ant. Then, the acceleration (in m/s2), when y = 16 m, is
(1) 8K2/3 (2) 8 (3) 8K4/3 (4) 32K4/3
2. A car starts from rest with an acceleration 6 m/s2, which decreases to zero linearly with time, in 10 s, after which the car continues to travel with constant speed. The time required for the car to travel 400 m from the start is 16.67t s. The value of ‘t’ is .
3. Two trains A and B are moving on the same track in opposite directions with velocity 25 m/s and 15 m/s, respectively. When the separation between them becomes 225 m, drivers of both the trains apply brakes, producing uniform retardation in train A, while retardation of train B increases linearly with time at the rate of 0.3 m/s3. The minimum retardation of train A to avoid collision will be
(1) 2 m/s2 (2) 2.5 m/s2
(3) 2.25 m/s2 (4) 2.75 m/s2
4. The ratio of the numerical values of the average velocity and average speed of a body is always (1) unity (2) unity or less than 1 (3) unity or more (4) less than unity
5. A body moves in a straight line along y-axis. Its distance y (in metres) from the origin is given by y = 8t – 3t2. The average speed in the time interval from t = 0 seconds to t = 1 second is
(1) –4 ms–1 (2) zero (3) 5 ms–1 (4) 6 ms–1
6. The acceleration (a) of a particle travelling along a straight line varies with distance x as a = (8 – 2 x ) ms –2. Assuming that the particle starts from rest from the origin of the coordinate system, the maximum velocity of the particle is
(1) 43m (2) 42m
(3) 52m (4) 62m
7. A car starting from rest accelerates at the rate f through a distance S, and then continues at constant speed for time t, and then decelerates at the rate f/2 to come to rest. If the total distance traversed is 15 S, then
(1) S = ft
(2) S = 1/6 ft2
(3) S = 1/72 ft2
(4) S = 1/4 ft2
8. On a foggy day, two drivers spot each other when 80 m apart. They were travelling at 70 kmph and 80 kmph. Both apply brakes simultaneously, which retards the cars at the rate of 5 m/s2. Which of the following statements is correct?
(1) The collision will be averted.
(2) The collision will takes place.
(3) They will cross each other.
(4) None of the above.
9. An NCC parade is going at a uniform speed of 6 km/h under a mango tree, on which a monkey is sitting at a height of 19.6 m. At any particular instant, the monkey drops a mango. A cadet will receive the mango, whose distance from the tree at the time of drop, is (Given: g = 9.8 m/s 2)
(1) 5 m (2) 3.33 m
(3) 19.8 m (4) 24.5 m
10. A body is projected vertically upward with a velocity v and, after some time, it returns to the point from which it was projected. The average velocity and average speed of the body for the total time of flight are
(1) /2and/2 vv (2) 0 and v/2
(3) 0 and 0 (4) /2and0 v
11. The relation 336 tx=+ describes the displacement of a particle in one direction where x is in metres and t is in seconds. The displacement, when the velocity is zero, is
(1) 24 m (2) 12 m
(3) 5 m (4) zero
12. A body falls from height h. The v–s graph is (1) s v (2) s v (3) v s (4) v s
(1) 3 5 (2) 1
(3) 5 3 (4) 1 2
14. A ball is dropped from a building of height 45 m. Simultaneously, another ball is thrown up with a speed of 40 m/s. The relative speed of the balls varies with time as (1) t0 (2) t1
(3) t2 (4) 1 t
15. Two particles A and B start from the same point ( x = 0 and t = 0) and move in the positive x -direction. In a time interval of 2.00 s after they start, their velocity u varies with time t, as shown in the following figures. What is the maximum separation between the particles during this time interval?
u(m/s) u(m/s) 0 0
(1) 1.00 m (2) 1.25 m (3) 1.50 m (4) 2.00 m
13. From v–t graph shown, the ratio of distance to displacement in 25 s of motion is 0 20 5 15 t(s) m/s 10 10 20 25 -20
16. A stone is thrown vertically upward with a speed v0 from a cliff of height H. Find the average speed of stone till the moment it reaches the ground. Given: H = 100 m, v0 = 10 m/s, g = 10 m/s2 .
(1) 64 m/s 1+21
(2) 110 m/s 1+21
(3) 55 m/s
(4) ( ) 1101+21m/s
Numerical Value Questions
17. A particle is moving along the x -axis. At instant t0, instantaneous velocity is equal to average velocity between t = 0 to t = t0. The value of t0 is 16 s. n
5 8 s(m)
The value of n is _________.
18. A ball is thrown vertically upwards from the roof of a building with a certain velocity. It reaches the ground in 9 s. When it is thrown downward from the roof with the same initial speed, it takes 4 s to come to the ground. How much time (in second) will it take to reach the ground if it is just released from rest from the roof?
19. The x–t plot of a car is shown in the figure. If the average velocity is zero in the time interval between 0 and t, then t = s.
minimum time in which the train may reach from one station to the other, separated by a distance d = 500 m, is t0 = 5 n s. The value of n is
21. A man swims to and fro along the bank of a river with a velocity v relative to water. If the velocity of flow is u, the average speed of the man is ( ) 22 , vu Nv . where ‘N’ is (for to and fro motion)
22. A stone is dropped from a height h . Simultaneously, another stone is thrown up from the ground with such a velocity that it can reach a height of 4 h. The time when two stones cross each other is ,
kg where k is
23. In quick succession, a large number of balls are thrown up vertically in such a way that the next ball is thrown up when the previous ball is at the maximum height. If the maximum height is 5m, then find the number of balls thrown up per second (g = 10ms–2).
24. A point initially at rest, moves along x-axis. Its acceleration varies with time as a = (6 t + 5) m/s 2. If it starts from origin, the distance covered in 2 s is m.
20. The maximum acceleration or deceleration that a train may have is a = 5 ms –2 . The
25. The acceleration of a marble in a certain fluid is proportional to the speed of the marble squared and is given (in SI units) by 2 3 v a =− for v > 0. If the marble enters this fluid with a speed of 1.50 m/s, how long (in seconds) will it take before the marble’s speed is reduced to half of its initial value?
26. A particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position (in m) of the particle at time t = 5 s?
(m/s)
27. Two trains of length 180 m are moving on parallel tracks. If they move in the same direction, then they cross each other in 15 s, and if they move in opposite directions, then they cross in 1 7s. 2 Then, find the sum of their speeds (in m/s).
THEORY-BASED QUESTIONS
Single Option Correct MCQs
1. Which of following statements is incorrect?
(1) Path length is a scalar quantity whereas displacement is a vector quantity.
(2) The magnitude of displacement is always equal to the path length traversed by an object over a given time interval.
(3) The displacement depends only on the end points whereas path length depends on the actual path followed.
(4) The path length is always positive whereas displacement can be positive, negative and zero.
2. In one dimensional motion, instantaneous speed V satisfies 0 ≤ V < V0.
(1) The displacement in time T must always take non-negative values.
(2) The displacement x in time T satisfies –v0T < x < v0 T
(3) The acceleration is always a non–negative number.
(4) The motion has no turning point.
3. When a particle moves in a straight line with increasing speed, the correct sign of acceleration ‘a’ and velocity ‘v’ can be
(1) v = +ve, a = –ve
(2) v = +ve, a = +ve
(3) v = – ve, a = –ve
(4) Both 2 and 3
4. What determines the nature of the path followed by a particle?
(1) Speed
(2) Velocity
(3) Acceleration
(4) None of these
5. Mark the correct option.
(1) For uniform velocity motion, average acceleration of a particle is non-zero.
(2) For accelerated motion, .0, > av where a and v are acceleration and velocity of the particle.
(3) For decelerated motion, .0, > av where a and v are acceleration and velocity of the particle.
(4) In a constant acceleration motion along a straight line, the distance covered must be equal to displacement.
6. For a moving body at any instant of time,
(1) if the body is not moving, the acceleration is necessarily zero
(2) if the body is slowing down, the retardation is negative
(3) if the body is slowing down, the distance is negative
(4) if displacement, velocity, and acceleration at that instant are known, we can find the displacement at any given time in future
7. For a freely falling body, at the point of dropping,
(1) acceleration is not zero but velocity is zero
(2) velocity is not zero but acceleration is zero
(3) both velocity and acceleration are not zero
(4) both velocity and acceleration are zero
8. A ball is projected upwards. Its acceleration at the highest point is (1) zero (2) directed upwards (3) directed downwards (4) such as cannot be predicted
9. If two balls of the same density but different masses are dropped from a height of 100 m, then
(1) both will reach the ground together (2) both will not be able to reach the ground (3) the first one will reach the ground first and second one after that (4) thensecond one will come first and the first one after that
10. A stone is released from an elevator going up with an acceleration ‘a’. The acceleration of the stone after the release is
(1) a upward (2) (g – a) upward (3) (g – a) downward (4) g downward
11. A body is thrown upward with a velocity of 29.23 ms–1. Distance travelled in first second of upward motion is
(1) 2.3 m (2) 6 m (3) 9.8 m (4) 4.9 m
12. The x–t graph shown in figure represents.
Displacement Time
(1) constant velocity
(2) velocity of the body is continuously changing
(3) instantaneous velocity
(4) The body travels with constant speed up to time t1 and then stops
13. Which of the following velocity–time graphs shows a realistic situation for a body in motion?
(1)
14. A lift is moving downwards with acceleration
a. A man in the lift drops a ball inside the lift. The acceleration of the ball, as observed by the man in the lift and a man standing stationary on the ground, are, respectively?
(1) g, g
(2) g – a, g – a
(3) g – a, g
(4) a, g
CHAPTER 3: Motion in a Straight Line
Statement Type
Each question has two statements, statement I and statement II. In light of the given statements, mark the correct answer as
(1) if both statement I and statement II are correct,
(2) If both statement I and statement II are incorrect,
(3) If statement I correct but statement II is incorrect,
(4) If statement I incorrect but statement II is correct.
15. S-I : If speed is zero at an instant, acceleration at that instant, may be non-zero.
S-II : The instantaneous speed is always equal to the magnitude of instantaneous velocity.
Assertion and Reason Questions
Directions for following questions (Q.No 16-23)
In each of the following questions, a statement of Assertion (A) is given, followed by a corresponding statement of Reason (R). Mark the correct answer as
(1) If both (A) and (R) are true and (R) is the correct explanation of (A)
(2) If both (A) and (R) are true and (R) is not the correct explanation of (A)
(3) If (A) is true and (R) is false
(4) If (A) is false and (R) is true
16. (A) : A negative acceleration of a body can be associated with a ‘speeding up’ of the body.
(R) : Increase in speed of a moving body is independent of the direction of motion.
17. (A) : The time taken by a particle to slide down along different smooth chords of a sphere, starting from highest point of the sphere, is same.
(R) : Length of such a chord is proportional to acceleration of the particle along it.
18. (A) : If air resistance is considered, then time of ascent and time of descent will be different.
(R) : Magnitudes of acceleration will be different in upward and downward motions.
19. (A) : Area under velocity–time graph gives displacement.
(R) : Area under acceleration–time graph gives velocity.
20. (A) : A lift is ascending with decreasing speed, which means that acceleration of lift is downwards.
(R) : A body always moves in the direction of its acceleration.
21. (A) : The zero velocity of a particle at any instant always implies zero acceleration at that instant.
(R) : A body is momentarily at rest when it reverses its direction of motion.
22. (A) : Acceleration is the rate of change of velocity.
(R) : A body having non-zero acceleration can have a constant velocity.
23. (A) : The position–time graph of a body moving uniformly is a straight line parallel to position axis.
(R) : The slope of position–time graph in a uniform motion gives the velocity of an object.
JEE ADVANCED LEVEL
Multiple Option Correct MCQs
1. If a body is accelerating, (1) it may speed up
(2) it may speed down
(3) it may move with same speed
(4) it may move with same velocity
2. An object moves with constant acceleration a. Which of the following is also constant?
(1) dv
3. A car accelerates from rest at a constant rate of 2 m/s2 for some time. Then, it retards at a constant rate of 4 m/s2 and comes to rest. It remains in motion for 6 s. Then,
(1) its maximum speed is 8 m/s
(2) its maximum speed is 6 m/s
(3) it travelled a total distance of 24 m
(4) it travelled a total distance of 18 m
4. A particle is moving in a straight line with initial velocity u and retardation av, where v is the velocity at any time. Then,
(1) the particle will cover a total distance of u a
(2) the particle will come to rest after time 1 a
(3) the particle will continue to move for a very long time
(4) The velocity of the particle will become u/2 after time 1 a
5. A particle is thrown vertically in upward direction and passes three equally spaced windows of equal height. Then,
(1) the average speed of the particle while passing the windows satisfies the relation
(2) the time taken by the particle to cross the windows satisfies the relation t1 < t2 <
(3) the magnitude of the acceleration of the particle, while crossing the windows, satisfies the relation a1 = a2 ≠ a3
(4) the change in the speed of the particle, while crossing the windows, would satisfies the relation ∆ v1 < ∆ v2 <
6. A particle is projected vertically upwards in vacuum with a speed u. Then,
(1) when it rises to half of its maximum height, its speed becomes u/2
(2) when it rises to half of its maxim um height, its speed becomes 2 u
(3) the time taken to rise to half of its maximum height is half the time taken to reach its maximum height
(4) the time taken to rise to three-fourth of its maximum height is half the time taken to reach its maximum height
7. A boy sees a ball go up and then down through a window 2.45 m high. If the total time that ball is in sight in 1 s, the height above the window that the ball rises to is approximately
(1) 2.45 m (2) 4.9 m
(3) 0.3 m (4) 0.49 m
8. A ball, projected from the bottom of a tower, is found to go above the tower and is caught by the thrower at the bottom of the tower after a time interval t1. An observer at the top of the tower sees the same ball go up above him and then come back at his level in a time interval t2. The height of the tower is
( ) 22 812 gtt (4) ( ) 22 212 gtt
9. The motion of a body is given by the equation ( ) ( ) 84 dvt vt dt =− , where v(t) is speed in m/s and t is in seconds. If the body was at rest at t = 0, then
(1) the terminal speed is 2 m/s
(2) the speed varies with the time as v(t) = 2(1 – e–4t) m/s
(3) the speed is 0.1 m/s when acceleration is half of the initial value .
(4) the magnitude of the initial acceleration is 8 m/s2
10. Equation of a particle moving along the x axis is x = u(t – 2) + a(t – 2)2. Then, (1) the initial velocity of the particle is u
(2) the acceleration of the particle is a
(3) the acceleration of the particle is 2 a
(4) a t = 2, the particle is at origin
11. A jet plane starts from rest at S = 0 and it is subjected to acceleration, as shown. Then, which of the following is true?
(1) Velocity at S = 60 m is 46.47 m/s.
(2) Velocity at S = 150 m is 58.1 m/s.
(3) Acceleration at S = 60 is 13.5 m/s2
(4) Velocity will be maximum at S = 75.
12. Graph represents motion of an object along x–axis for 80 s. Then, x(m)
(1) the magnitude of displacement of the object for the entire journey is 5 m
(2) the distance travelled by the object is 9 m
(3) speed of object at t = 20 s is 0.1 m/s
(4) average speed for entire journey is 0.05 m/s
13. A particle has initial velocity 10 m/s. It moves due to constant retarding force along the line of velocity which produces a retardation of 5 m/s2. Then,
(1) The maximum displacement in the direction of initial velocity is 10 m
(2) The distance travelled in first 3 seconds is 7.5 m
(3) The distance travelled in first 3 seconds is 12.5 m
(4) The distance travelled in first 3 seconds is 17.5 m
Numerical Type Questions
14. If the body covers equal displacements in successive intervals of time t1, t2, and t3 in a straight path, then, if the intervals can be shown as 123123 111 , −+= ++ k tttttt find k.
15. The engine of a motorcycle can produce a maximum acceleration of 5 ms–2. Its brakes can produce a maximum retardation of 10 ms–2. The minimum time (in s) in which it can cover a distance of 1.5 km is .
16. A train starts from station A with uniform acceleration a1 for some distance and then goes with uniform retardation a2 for some more distance to come to rest at station B. The distance between the stations is 4 km and the train takes 1/15 h to complete this journey. If acceleration is in km per minute unit, then show that 12 11 x aa += . Find the value of x.
17. A ball of mass 0.5 kg is dropped from a height of 10 m. The height, at which the magnitude of velocity becomes equal to the magnitude of acceleration due to gravity, is m. (Use g = 10 m/s2).
18. A ball is dropped from height h = 100 m, from the surface of a planet. If, in the last 1/2 s of its journey, it covers a distance of 19 m, then the acceleration due to gravity (in ms–2) on that planet is
19. A train starting from rest is accelerated and the instantaneous acceleration is given by 2 , 10 m/s 1 + v where v is the velocity in m/s.
Find the distance (in m) in which the train attains a velocity of 54 km/ph.
20. A car moves rectilinearly from station A to the next station B (rest to rest) with an acceleration varying according to the law f = (a −bx), where a and b are constants and x is the distance from the station A. If th e
maximum velocity is k a b , then the value of k is
21. On a two lane road, car A is travelling with a speed of 36 km/h. Two cars B and C approach car A in opposite directions with a speed of 54 km/h each. At a certain instant, when the distance AB is equal to AC, both 1 km, B decided to overtake A before C does. What minimum acceleration (in m/s 2) of car B is required so that B can overtake A before C does?
Integer Type Questions
22. A train stops at two stations s distance apart and takes time t on the journey from one station to the other. Its motion is first of uniform acceleration a and then immediately of uniform retardation b. Then, the relation between a, b, s, and t is 112 . 2 kt abs += The value of ‘k’ is
23. If a body is projected vertically up, its velocity decreases to half of its initial velocity at a height ‘h’ above the ground. Then, maximum height reached by it is . 3 ph Find the value of p.
24. A bullet fired vertically up from the ground reaches a height of 40 m in its path from the ground and it takes further time 2 s to reach the same point during descent. The total time of flight is s. (g = 10 ms–2)
25. A body projected up reaches a point A in its path at the end of 4th second and reaches the ground after 5 s from the start. The height of A above the ground is [ g = 10 m/s 2 ] (in m) .
26. A body falls for 5 s from rest. If the acceleration due to gravity of the earth ceases to act, the distance it travels in the next 3 s is (in m) . [g = 9.8 m/s2]
27. A stone is thrown vertically up from a bridge with velocity 3 ms–1. If it strikes the water under the bridge after 2 s, the bridge is at a height of . [g = 10 ms–2] (in m)
28. A particle moves along a straight line in such a way that its acceleration is increasing at the rate of 2 m/s3. Its initial acceleration and velocity were 0. The distance covered by it in t = 3 seconds is
29. The acceleration of a particle staring from rest and travelling along a straight line is shown in figure. The maximum speed of the particle is 3 × 10n m/s. Then, n = .
30. A motorboat going downstream overcomes a raft at point A. One hour later it turns back and meets the raft again at a distance 6 km from point A. Find the river velocity in (kmph).
Passage-based Questions
Passage-I:
A car starts moving rectilinearly (initial velocity zero), first with an acceleration of 5 m/s2, then uniformly, and finally, decelerating at the same rate till it stops. Total time of journey is 25 s and average velocity during the journey is 72 km/h.
31. Maximum speed attained during the journey is m/s.
32. Car travels with uniform speed for time s.
Passage-II:
A balloon is rising vertically upwards at a velocity of 10 m/s. When it is at a height of 45 m from the ground, a parachutist bails out from it. After 3 s, he opens his parachute and decelerates at a constant rate of 5 m/s2. (Take g = 10 m/s2)
33. The height of the parachute above the ground when he opens his parachute, is m.
CHAPTER 3: Motion in a Straight Line
34. The distance of the parachutist from the balloon at t = 3 s is m.
Passage-III:
A particle starts with initial velocity 4 m/s and moves such that the acceleration is given by
35. Its velocity after a displacement of 38 m 3 is (1) 9 m/s (2) 62/3 m/s (3) 3 m/s (4) 6 m/s
36. Its velocity after a time interval of 4 s is (1) 16 m/s (2) 112 m/s (3) 112 m/s 5 (4) 81 m/s
Passage-IV:
The figure shows position–time graph of two riders C and D. Based on the information represented by the graph, answer the following questions.
37. At t = 0 s, (1) C is moving and D is at rest (2) D is moving and C is at rest (3) C and D are both moving (4) C and D are both at rest
38. At t = 0 s,
(1) C has a greater velocity than D (2) D has a greater velocity than C (3) C and D have the same velocity (4) C is accelerating
Passage-V:
The velocity–time graph of a particle moving along a straight line is as shown in fig. The rate of acceleration and deceleration is constant and it is equal to 5 ms–2. If the average velocity during the motion is 20 ms–1, then t ms–1 V 20 time(s)
39. The maximum velocity of the particle is
(1) 20 m/s
(2) 25 m/s
(3) 30 m/s
(4) 40 m/s
40. The value of t is
(1) 5 s (2) 10 s
(3) 20 s (4) 52s
Passage-VI:
A person walks up a stationary escalator in t1 seconds. If he remains stationary on the escalator, then it can take him up in t2 seconds. The length of the escalator is L .(Take t 1 = 2 s, t 2 = 3 s, L = 10 m)
41. Determine the speed of the man with respect to the escalator.
42. How much time would it take him to walk up the moving escalator?
Matrix Matching
43. The equation of motion of particle is described in column-I. At t = 0, particle is at origin and at rest.
Column I Column II
A. x = 3t2 + 2t I) Velocity of particle in t = 1 s is 8 m/s.
B. V = 8t II) Particle moves with uniform acceleration.
C. a = 16t III) Particle moves with variable acceleration.
D. V = 6t – 3t2 IV) Acceleration of the particle at t = 1 s is 2 m/s2
(V) Particle will change its direction of motion.
(A) (B) (C) (D)
(1) I, II I, III I, III III, V
(2) I, II I, II I, III III, V
(3) III, V I, II I, III III, V (4) I, III III, V I, III I, II
44. Match the following regarding translational motion of a particle.
Column I Column II
A. Rate of change of displacement I) Magnitude of average velocity
B. Average speed is always greater than or equal to II) Initial to final position
C. e direction of displacement is III) Velocity
D. Motion under gravity is considered as the case of IV) Uniform acceleration
Pick the correct option.
(A) (B) (C) (D)
(1) III I II IV
(2) I II III IV
(3) III I IV II
(4) I III II IV
The displacement versus time curve is given.
Column I Column II
A. OA I) Velocity increases with time linearly.
B. AB II) Velocity decreases with time.
C. BC III) Velocity is independent of time.
D. CD IV) Velocity is zero.
(A) (B) (C) (D)
(1) IV III II I
(2) II I IV III
(3) I III II IV
(4) IV II IV I
46. Figure shows displacement– time graph of particles moving along a straight line. Column I gives information of different particles A, B, C, D and Column II gives information related to its motion. Match the columns. A x t B C D
Column I Column II
A. e particle A is I) Uniform acceleration
B. e particle B is II) Uniform retardation
C. e particle C is III) Uniform velocity
CHAPTER 3: Motion in a Straight Line
D. e particle D is IV) Projected vertically upwards V) At rest
Which of the following option is correct
(A) (B) (C) (D)
(1) V I III II
(2) V III I II
(3) I II III IV
(4) II I IV III
47. Match Column-I with Column-II.
Column-I (x–t graph) Column-I (v–t graph)
Choose the correct answer from the options given below.
(A) (B) (C) (D)
(1) I IV III II
(2) I II III IV
(3) II III IV I
(4) I III IV II
FLASHBACK (Previous JEE Questions)
JEE Main
1. A cyclist starts from the point P of a circular ground of radius 2 km and travels along its circumference to the point S . The displacement of cyclist is : (2024) P 0 R S Q
(1) 6 km (2) 4 km
(3) 8 km (4) 8 km
2. A particle is moving in a straight line. The variation of position ‘x’ as a function of time ‘ t ’ is given as x = ( t 3 −6 t 2 +20 t +15)m The velocity of the body when its acceleration becomes zero is: (2024)
(1) 4 m/s (2) 8 m/s
(3) 10 m/s (4) 6 m/s
3. A particle initially at rest starts moving from reference point. x = 0 along x-axis, with velocity v that varies as 4xm/s v = . The acceleration of the particle is ____ms −2 (2024)
4. A bullet is fired into a fixed target looses one third of its velocity after travelling 4 cm. It penetrates further D × 10−3 m before coming to rest. The value of D is: (2024)
(1) 32 (2) 5
(3) 3 (4) 4
5. A body falling under gravity covers two points A and B separated by 80 m in 2s. The distance of upper point A from the starting point is ________ m (use g = 10 ms−2) (2024)
6. A body starts moving from rest with constant acceleration covers displacement S1 in first (p – 1) seconds and S2 in first p seconds. The displacement S1+S2 will be made in time: (2024)
(1) (2p+1)s
(2) ( ) 2 221pps −+
(3) (2p–1)s
(4) (2p2−2p+1)s
7. A ball rolls off the t op of a stairway with horizontal velocity u . The steps are 0.1 m high and 0.1 m wide. The minimum velocity u with which that ball just hits the step 5 of the stairway will be 1 x ms where x = ___________ [use g = 10m/s2]. (2024)
8. The displacement and the increase in the velocity of a moving particle in the time interval of t to (t+1)s are 125 m and 50 m/s, respectively. The distance travelled by the particle in (t+2)th s is _________ m. (2024)
9. Train A is moving along two parallel rail tracks towards north with speed 72 km/h and train B is moving towards south with speed 108 km/h. Velocity of train B with respect to A and velocity of ground with respect to B are (in ms−1): (2024)
(1) –30 and 50
(2) –50 and –30
(3) –50 and 30
(4) 50 and –30
10. A body is moving with constant speed, in a circle of radius 10 m. The body completes one revolutions in 4 s. At the end of the third second, the displacement of body (in m) from its starting point is (2023)
(1) 15 π (2) 102
(3) 30 (4) 5 π
11. A disc is rolling without slipping on a surface. The radius of the disc is R . At t = 0, the topmost point on the disc is A, as shown in figure. When the disc completes half of its rotation, the displacement of point A from its initial position is (2023) R (1) 2R (2) ( ) 2142 R +π (3) ( ) 142 R +π (4) ( )21 R π+
12. A horse rider covers half the distance with 5 m/s speed. The remaining part of the distance was travelled with speed 10 m/s for half the time and with speed 15 m/s for other of the time. The mean speed of the rider, averaged over the whole-time motion, is m/s. 7 x The value of x is (2023)
13. A particle is moving with constant speed in a circular path. When the particle turns by an angle of 90°, the ratio of instantaneous velocity to its average velocity is :2 x π . The value of x will be (2023) (1) 5 (2) 2 (3) 1 (4) 7
14. The position–time graphs for two students A and B returning from the school to their homes are shown in figure. (2023)
(A) A lives closer to the school.
(B) B lives closer to the school.
(C) A takes lesser time to reach home .
(D) A travels faster than B.
3: Motion in a Straight Line
(E) B travels faster than A.
Choose the correct answer from the options given below.
(1) (A) and (E) only (2) (A), (C), and (E) only (3) (A), (C), and (D) only (4) (B) and (E) only
15. A passenger sitting in a train A moving at 90 km/h observes another train B moving in the opposite direction for 8 s. If the velocity of the train B is 54 km/h, then length of train B is (2023)
(1) 120 m (2) 200 m
(3) 320 m (4) 80 m
CHAPTER TEST-JEE MAIN
Single Option Correct MCQs
1. Four initial and final positions of a man on the x-axis are given as i) (–3, 7 m) ii) (–7, –3 m) iii) (–7 m, 3 m) iv) (3, –7 m)
Which pair gives the negative displacement? (1) (–3 m, 7 m) (2) (–7 m, –3 m) (3) (–7 m, 3 m) (4) (3 m, –7 m)
2. An object moves with speed v 1 , v 2 , and v 3 along a line segment AB, BC, and CD, respectively, as shown in figure. If AB = BC and AD = 3AB, then the average speed of the object will be A B C D
(1) ( ) 123 3 vvv ++
(2) ( ) 123 122331 3vvv vvvvvv ++
(3) ( ) 123 3123 vvv vvv ++
(4) ( ) 123 3122331 vvv vvvvvv ++
3. A boy walks to his school at a distance of 6 km with a constant speed of 2.5 kmph and walks back with a constant speed of 4 kmph. His average speed for the round trip expressed in kmph, is (1) 24/13 (2) 40/13 (3) 3 (4) 1/2
4. A particle is moving with constant speed in a circular path. When the paricle turns by an angle of 90°, the ratio of instantaneous velocity to its average velocity is 2. π= x The value of x is (1) 5 (2) 2 (3) 1 (4) 7
5. The relation between time t and distance x is t = αx2 + bx, where α and b are constants. The retardation is
(1) 2 α v3 (2) 2 b v3 (3) 2 α b v3 (4) 2 b 3v3
6. A scooter accelerates from rest for time t1 at constant rate a1, then retards at a constant rate a 2 for time t 2, and comes to rest. The correct value of 1 2 t t will be (1) 1 2
(2)
(4)
7. A bullet fired into a fixed target looses half of its velocity after penetrating 3 cm. How much further will it penetrate before coming to rest, assuming that it faces constant resistance to motion?
(1) 3.0 cm (2) 2.0 cm (3) 1.5 cm (4) 1.0 cm
8. A particle moving with unifrom retardation covers distances 18 m, 14 m, and 10 m in successive seconds. It comes to rest after travelling a further distance of (1) 50 m (2) 8 m (3) 12 m (4) 42 m
9. For an object moving with uniform acceleration, travelling 50 m in 5th s, and 70 m in 7th s,
a) its initial velocity is 5 m/s
b) its acceleration is 20 m/s 2
c) its travels 100 m in 9th s
d) its average velocity during 9th s is 90 m/s (1) a is true. (2) a and d are true. (3) a and b are true. (4) a and c are true.
10. A particle starts moving from rest with uniform acceleration. It travels a distance x in the first 2 s and a distance y in the next 2 s. Then,
(1) y = x (2) y = 2x (3) y = 3x (4) y = 4x
11. From a tower of height H, a particle is thrown vertically upwards with speed u. The time taken by the particle to hit the ground is ‘n’ times that taken by it to reach the highest point of its path. The relation between H, u, and n is
(1) 2gH = n2u2 (2) gH = (n–2)2u2
(3) 2gH = nu2(n – 2) (4) gH = (n – 2)u2
12. When a ball is thrown up vertically with velocity υ 0, it reaches a maximum height of h. If one wishes to triple the maximum height, then the ball should be thrown with velocity
(1) 30 υ (2) 3 n 0
(3) 9 n 0 (4) 0 3 2 υ
13. A balloon starts from rest and moves vertically upwards with a uniform acceleration -2 ms. 8 g A stone falls from the balloon after 8 s from the start. Find the time taken by the stone to reach the ground.
(g = 9.8 ms–2)
(1) 4 s (2) 3 s
(3) 2 s (4) 6 s
14. A particle is dropped to fall freely under gravity. In the first ‘t’ seconds, it covers s1 and in the next ‘t’ seconds, it covers s2.Then, t is given by
(1) 21ss g (2)
(4)
15. A particle is released from rest from a tower of height 3h. The ratio of times to fall equal heights h from the top is (i.e., t1 : t2 : t3)
(1) 3 : 2 : 1
(2) 3:2:1
(3) ( ) ( ) 1:21:32
(4) 9 : 4 : 1
16. A stone projected vertically up with velocity v from the top of a tower reaches the ground with velocity 2v. The height of the tower is (1) 2 2 v g (2)
(4)
17. Two cars P an d Q start from a point at t he same time in a straight line and their positions are represented by X P(t ) = ( at + bt2) and XQ(t) = (ft – t2). At what time does the car A have double the velocity of B?
(1) 1 af b + (2) ( )21 af b + (3) 2 24 fa b + (4) ( ) 21 fa b +
18. The variation of quantity A with quantity B, plotted in figure, describes the motion of a particle in a straight line.
A
B
(a) Quantity B may represent time.
(b) Quantity A is velocity, if motion is uniformly accelerated.
(c) Quantity A is velocity, if motion is uniform.
(d) Quantity A is acceleration, if motion is uniform.
(1) a and c are correct.
(2) b and d are correct.
(3) a and b are correct.
(4) a, b, and d are correct.
19. The acceleration of a moving body can be found from
(1) area under velocity–time graph
(2) area under distance–time graph
(3) slope of velocity–time graph
(4) slope of distance–time graph
20. A bus is moving with a speed of 10 ms–1 on a straight road. A scooterist wishes to overtake the bus in 100 s. If the bus is at a distance of 1 km from the scooterist, with what speed should the scooterist chase the bus?
(1) 40 ms–1 (2) 25 ms–1
(3) 10 ms–1 (4) 20 ms–1
Numerical Value Questions
21. An athelete takes 2.0 s to reach his maximum speed of 18.0 km/h. What is the magnitude of his average acceleration?
22. For a body travelling with uniform acceleration, its final velocity is 1807,=− vx where x is the distance travelled by the body. Then, the acceleration (in m/s2) is –0.5n. Find n.
23. The displacement of a particle moving with a constant acceleration in the nth second is given by S n = 2 + 0.4n. Then, initial velocity is units.
24. A stone is dropped into a well, which is 20 m deep. Another stone is thrown downward with velocity v, one second later. If both the stones reach the water surface in the well simultaneously, then, v is equal to ms–1 (g = 10 ms–2).
25. A freely falling body, starting from rest, travels % of total distance in 5 th second (which is last second) [g = 10 ms–2].
CHAPTER TEST-JEE ADVANCED
JEE Advanced Pattern
1. A person measures the depth of a well by measuring the time interval between drooping a stone and receiving the sound of impact with the bottom of the well. The error in his measurement of time is δ T = 0.01 seconds, and he measures the depth of the well to be L = 20 m. The acceleration due to gravity g = 10 m/s2 and the velocity of sound is 300 m/s. Then, the fractional error in the measurement, δ L/L, is closest to (1) 0.2% (2) 1% (3) 3% (4) 5%
2. A splash is heard 3.12 s after a stone is dropped into a 45 m deep well. The speed of sound in air, in ms−1, is [g = 10 ms–2]
3. A lead ball, dropped into a lake from a diving board 5 m above the water, hits the water with a certain velocity and then sinks to the bottom with the same constant velocity. If it reaches the bottom in 3 s after it is dropped, then the depth of the lake (in m) is [ g = 10 ms–2] .
4. A stone is dropped into a well 20 m deep. Another stone is thrown downward with velocity v, one second later. If both stones reach the water surface in the well simultaneously, v is equal to ms–1 (g = 10 ms–2)
5. An object moving with a speed of 6.25 m/s, is decelerated at a rate given by 2.5,=− dv v dt where v is instantaneous speed. The time taken by the object to come to rest would be
6. A rocket is moving in a gravity–free space with a constant acceleration of 2 ms–2 along + x direction (see figure). The length of a chamber inside the rocket is 4 m. A ball is thrown from the left end of the chamber in + x direction with a speed of 0.3 ms–1, relative to the rocket. At the same time, another ball is thrown in – x direction with a speed of 0.2 ms–1 from its right end, relative to the rocket. The time, in seconds, when the two balls hit each other is . 4 m a=2 ms 0.3 ms 0.2 ms –1 –1 –2
7. A 200 m long train is moving with a velocity of 72 kmh–1. The time taken by the train cross a 1 km long bridge (in s) is (56 + x). Then, find the value of x.
8. An express train moving at 30 m/s reduces its speed to 10 m/s at a distance of 240 m. If the breaking force is increased by 12.5% in the beginning, find the distance (in m) that it travels before coming to rest.
9. A train travelling along a straight track with a speed of 2 ms–1 begins to accelerate with 2 , 2 m/s a v = where v is in ms –1 . Find its velocity after 3 seconds, in m/s.
10. A particle is moving in one-dimensional motion on the x-axis. (1) If it slows down while moving from x = 4 m to x = 3 m, then its velocity is negative and acceleration is positive.
(2) If its acceleration is negative, it must be slowing down.
(3) If it approaches the origin from negative x-axis, then its velocity is negative.
(4) It slows down from x = −3 m to x = −2 m and speeds up from x = −2m to x = −1 m. Sign of acceleration changes from negative to positive.
11. At t = 0, an arrow is fired vertically upwards with a speed of 100 m/s. A second arrow is fired vertically upwards with the same speed at t = 5 s. Then, (g = 10 m/s2)
(1) the two arrows will be at the same height above the ground at t = 12.5 s
(2) the two arrows will reach their starting points at t = 20 s and at t = 25 s
(3) the ratio of the speeds of the first and second arrows at t = 20 s will be 2 : 1
(4) the maximum height attained by either arrow will be 1000 m
12. A stone is projected vertically upwards at t = 0. The net displacement of stone is zero in time interval between t = 0 to t = T s.
Choose the correct statement(s). (Neglect air friction)
(1) From time 4 T t = s to 3 4 T t = s, the average velocity is zero.
(2) The change in velocity from time t = 0 to 4 T t = s is the same as change in velocity from 8 T t = s to 3 s. 8 = T t
(3) The distance travelled from t = 0 to 4 = T t s is larger than distance travelled from s 4 = T t s to 3 s. 4 = T t
CHAPTER 3: Motion in a Straight Line
(4) The distance travelled from s 2 = T t to 3 s 4 = T t is half the distance travelled from s 2 = T t to t = T s.
13. The motion of a body falling from rest in a resisting medium is described by the equation , =− dv ABv dt where A and B are constants. Then,
(1) initial acceleration of the body is A
(2) the velocity at which acceleration becomes zero is A/B
(3) the velocity at any time is ( ) 1 ABt e B
(4) all the above are incorrect.
14. A particle starts from rest and travels with constant acceleration a. After a time of ‘t0’ its acceleration direction gets reversed. Identify the correct options.
(1) Its velocity when it returns back to initial point is 20. at
(2) Its velocity when it returns back to initial point is 2at0
(3) Total distance travelled by particle when it reaches back to initial point is 2 at0 2
(4) Time taken to come back to initial point ( ) 220. + t
15. Velocity–time graph of a particle moving along a straight line is shown in figure. Choose the correct option(s). v (m/s) 20 40 –10 0 10 6 t (s)
(1) Average velocity of the particle through complete motion is zero.
(2) Average speed of the particle is 5 m/s.
(3) Distance travelled by the particle in 40 s is 200 m.
(4) Displacement of the particle during first 20 s is 100 m.
16. Two cars start in a race with velocities u 1 and u 2 and travel in a straight line with acceleration α and b. If both reach the finish line at the same time, the range of the race is
(1) ( ) ( ) ( ) 12 212 2 uu uuβ−α β−α
(2) ( ) ( ) ( ) 12 212 2 uu uuα−β β+α
(3) ( ) ( ) 2 12 2 2 uu β−α
(4) 212 uu βα
17. A car is moving on a horizontal road, whose acceleration versus position graph is drawn below. At the initial moment of time, when the particle was at x = 0, its speed was 10m/s . Find the speed of the particle when it reaches x = 8 m.
ANSWER KEY
JEE Main-Topic wise
(1) 84m/s (2) 10 m/s
(3) 110m/s (4) 11 m/s
18. Initially, car A is 10.5 m ahead of car B. Both start moving at time t = 0 in the same direction along a straight line. The velocity –time graph of two cars is shown in figure. The time when the car B will catch the car A will be
Questions (1) 2 (2) 2 (3) 4 (4) 3 (5) 2 (6) 4 (7)
4 (22) 3 (23) 4
JEE Advanced Exercise (1) 1,2,3 (2) 2 (3) 1,3 (4) 1,3 (5) 1,2,4 (6) 2,4 (7) 3 (8) 3 (9) 1,2,4 (10) 3,4 (11) 1,2,3 (12) 1,2,3 (13) 1,2,3 (14) 3 (15) 30 (16) 2 (17) 5 (18) 8 (19) 123.75 (20) 2 (21) 1 (22) 1 (23) 4 (24) 6 (25) 20 (26) 147 (27) 14 (28) 9 (29) 1 (30) 3 (31) 25 (32) 15 (33) 30 (34) 45 (35) 1 (36) 1 (37) 3 (38) 1 (39) 2 (40) 1 (41) 5 (42) 1.2 (43) 2 (44) 1 (45) 3 (46) 2 (47) 1
Flashback (JEE Main) (1) 3 (2) 2 (3) 8 (4) 1 (5) 45 (6) 2 (7) 2 (8) 175 (9) 3 (10) 2 (11) 3 (12) 50 (13) 2 (14) 1 (15) 3
Chapter Test
JEE Main (1) 4 (2) 2 (3) 2 (4) 2 (5) 1 (6) 2 (7) 4 (8) 2 (9) 2 (10) 3 (11) 3 (12) 1 (13) 1 (14) 1 (15) 3 (16) 2 (17) 3 (18) 3 (19) 3 (20) 4 (21) 2.5 (22) 7 (23) 2.2 (24) 15 (25) 36
JEE Advanced (1) 2 (2) 375 (3) 20 (4) 15 (5) 2 (6) 2 (7) 4 (8) 240 (9) 4 (10) 1,4 (11) 1,2,3 (12) 1,2,3 (13) 1,3 (14) 1,3,4 (15) 1,2,3,4 (16) 1 (17) 2 (18) 1