1 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 1
90 MINUTTER 1 Hva heter planfigurene? A B C D E F G H 2 Hva
A B C D E F 3 Hva er omkretsen til figuren? 6 4,5 5
KAPITTELPRØVE 6 − NIVÅ 1
heter romfigurene?
4 Hva er omkretsen til sirkelen når diameteren er 1? 1
5 Hva er arealet av figuren? 6
3 7
5
6 Målene inne i fryseboksen er 1 m lang, 0,5 m bred og 0,8 m høy. Hva er volumet av fryseboksen? Regn bare med tall og ikke med benevning. 0,8
0,5 1
7 Esken har fire sider og en bunn. Hva er overflaten til esken på utsiden?

2 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 1
60
22 20
8 Regn ut hypotenusen c når a = 3 og b = 4.
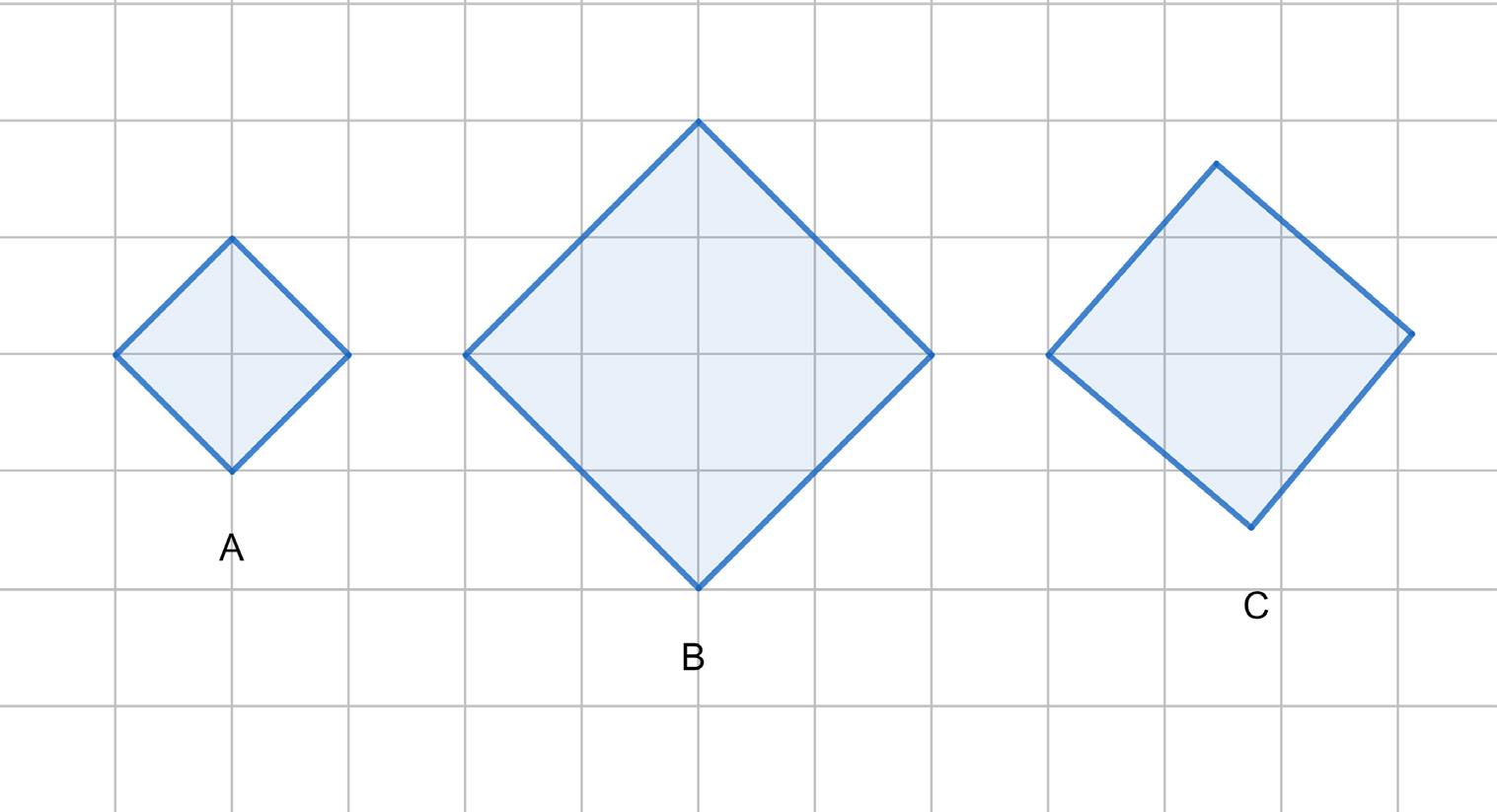
9 Hvilke av figurene er formlike?

3 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 1
10 Hvilke setninger er riktige?
A Siden AB er dobbelt så lang som siden DE.
B Siden DE er dobbelt så lang som AB.
C Siden DF er dobbelt så lang som AC.
D Siden BC er det halve av siden EF.
E De to trekantene er formlike.
11 Tegn et forsvinningspunkt fra kuben til horisontallinjen.

4 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 1
horisontallinje
12 Speil figuren ABC om y-aksen.

5 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 1
KAPITTELPRØVE 6 − NIVÅ 2
90 MINUTTER
1 A Hva er vinkelsummen i en trekant? B Hva er vinkelsummen i en sirkel? C Hva er vinkelsummen i en firkant? 2 Hva er omkretsen til figuren? 2
5 5
5
4 3 Hva er omkretsen til sirkelen når radius er 0,5? 0,5 4 Sidene i kvadratet er 8. Den hvite fargen er en halv sirkel. Hva er arealet av den blå fargen? 8
1 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 2
5 Katrine har et armbånd med 19 perler. Perlene er like store og har en radius på 2. Hvor langt er armbåndet uten lås?
6 Christian kjøper to pizzaer, en liten og en stor.
Den minste pizzaen har en diameter på 27 og koster 98 kroner.
Den største har en diameter på 40 og koster 188 kroner. Hvilken pizza gir mest for pengene?


5 En kaffekopp som er ¾ full med kaffe, har en form som en halv kule.
3/4Innvendig diameter til koppen er 5. Hva er volumet til en ¾ full kaffekopp?
2 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 2
6 Klasse 4A har naturfag og dyrker bakterier i en petriskål.

Skålen har en diameter på 9 og en høyde på 2.
Hvor mye kan en petriskål inneholde (romme)?

7 Hypotenusen er 3, og den ene kateten er 1.
Hvor langt er det ned fra midten av taket til gulvet i andre etasje? 8
ABC ~ ∆ DEF
Hvor stor blir hypotenusen i den store trekanten?
Hvor store blir de to katetene i den lille trekanten?
3 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 2
8 5 6 C E B AD
∆
A
B
F
9 Tegn et forsvinningspunkt fra kuben til horisontallinjen.
horisontallinje
10 Speil figuren A, B, C om y-aksen.

4 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 2
KAPITTELPRØVE 6 − NIVÅ 3
90 MINUTTER
1 A Bruk rutenettet til å finne verdien av a.
B Hva er omkretsen til figuren? 2a
a
2 A Hva er diameteren til sirkelen når omkretsen er 3,14?
B Hva er omkretsen av sirkelen når en side til kvadratet er 6? 6
1 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 3
3 Hvilken setning er riktig?
A I en trekant hvor vinklene er 30°, 60° og 90°, vil den lengste kateten alltid være det halve av hypotenusen.
B I en trekant hvor vinklene er 30°, 60° og 90°, vil den korteste kateten alltid være det halve av hypotenusen.
C I en trekant hvor vinklene er 30°, 60° og 90°, vil den korteste kateten og den lengste kateten alltid være like lang som hypotenusen.
4 Hva er arealet av figuren? b
5 En sjokoladeeske har form som et trekantet prisme.
























Bruk målene på tegningen og regn ut volumet av esken.
SJOKOLADE









6 En kake har en diameter på 24 og en høyde på 8. Kaken er dekket med marsipan.

Hvor stor overflate dekker marsipanen?
7







Fatima skal kjøpe en stige for å male en husvegg.
Husveggen er 7 meter høy, og hun trenger en lang stige. Hun setter stigen 3,5 meter fra husveggen.
Hvor lang stige må hun minst kjøpe?
Rund av svaret til et helt tall.
2 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 3
a a a c
17 2 2
3,5
7 x
8 Ole skal lage et båthus. Han lager en formlik modell av huset i tre.


A Hvor høy er x?
B Vis hvordan du kommer fram til svaret.
3 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 3
D C A B
H G 1 2
x 200 300
9 Tegn et forsvinningspunkt fra kuben til horisontallinjen.
horisontallinje
10 Speil figuren A, B, C om y-aksen.

4 GRIP 3 MATEMATIKK KAPITTEL 6 · GEOMETRI − UTEN BENEVNING KAPITTELPRØVE 6 − NIVÅ 3



































