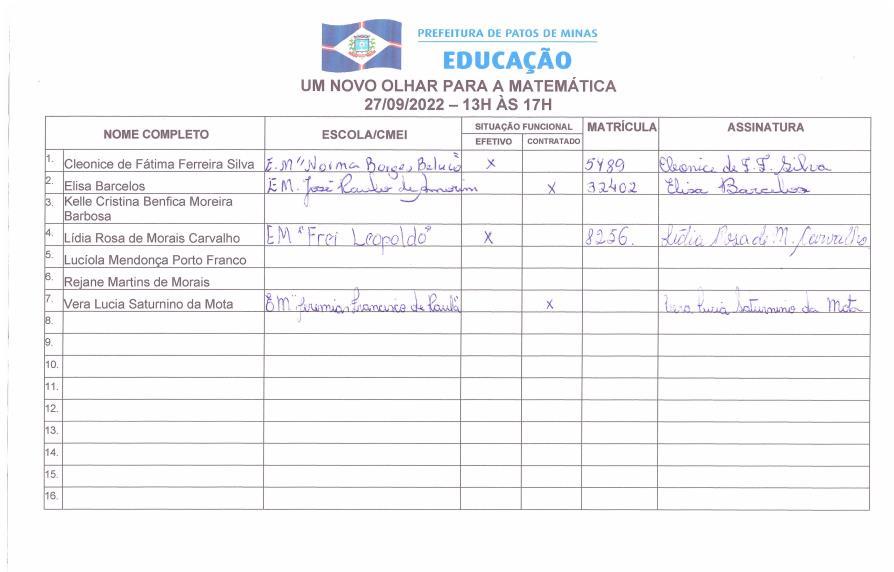
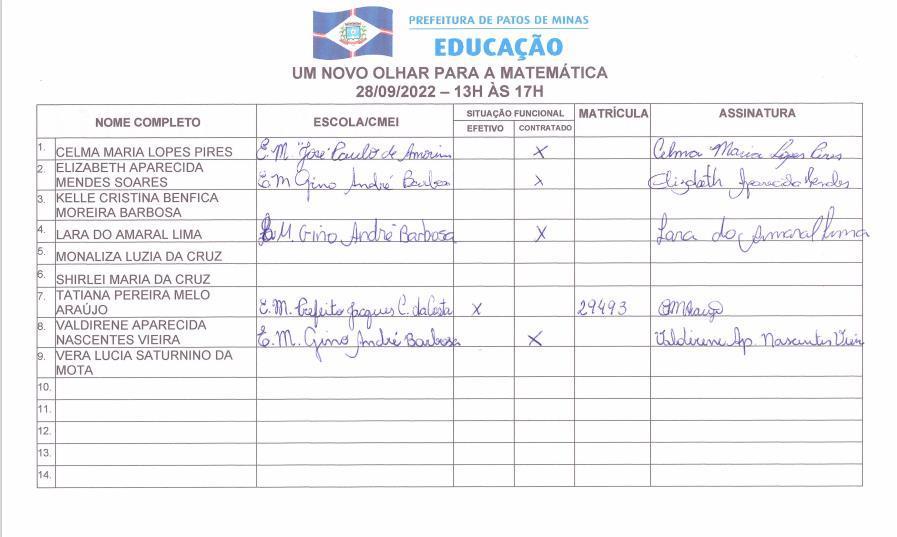
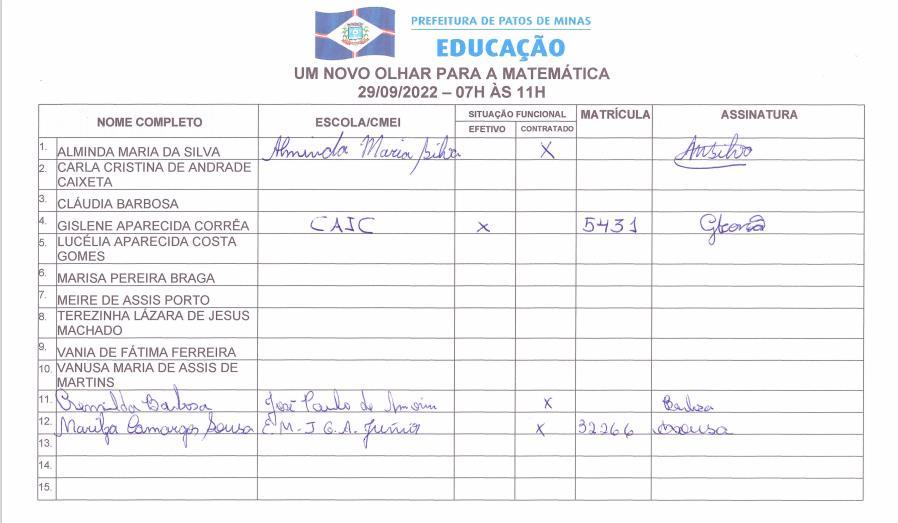
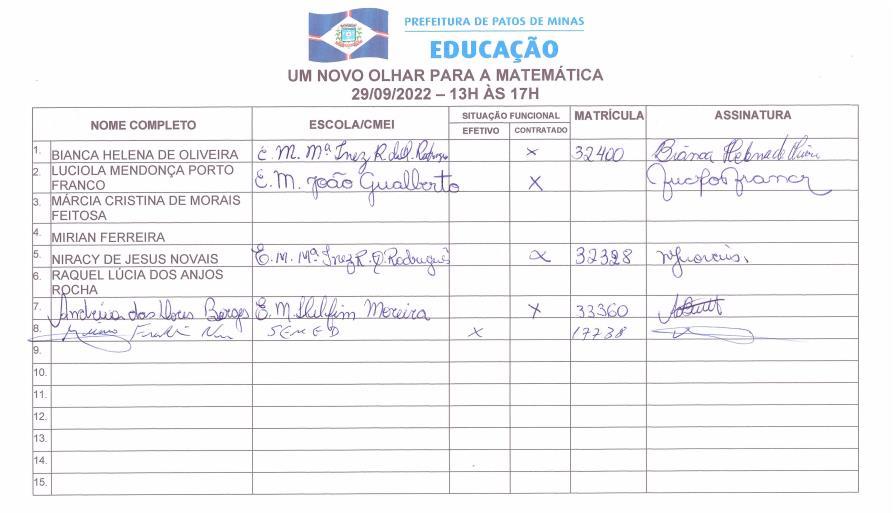
Portifóliodaoficina













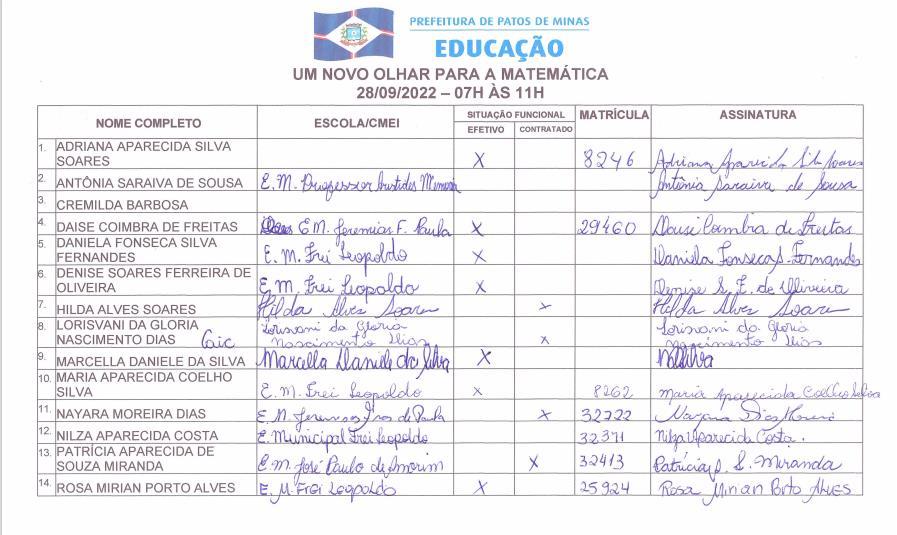
























No momento em que você traduz a naturalidade da matemática como uma condição de estar no mundo... ...Você democratiza a possibilidade da naturalidade da matemática, e isso é cidadania.
 Paulo Freire
Paulo Freire
Considerações iniciais Ensinar matemática pela resolução de problemas é uma forma eficaz de aprendizagem. No entanto, é preciso romper com o tradicional esquema de apresentação do conteúdo pelo professor, com apresentação de modelos e regras. seguido de uma série de exercícios repetitivos e pouco desafiadores. Novas estratégias de ensino podem ser pensadas. É importante, considerar o contexto em que estamos inseridos. Quais são os interesses dos estudantes? Que linguagem é mais atrativa para eles? Certamente, as crianças e o adolescentes de hoje, conhecem a linguagem da gamificação. Pensando nisso propomos uma atividade diferente para sua prática.

Desenvolvimento
Partindo do pressuposto de que a prática pedagógica, muitas vezes se fundamenta da prática pessoal de aprendizagem, entendemos que é importante nos ouvir. Propor uma reflexão sobre as experiências pessoais de ensino e de aprendizagem da Matemática. Apreciaremos a imagem da obra "O Porto" de Tarsila do Amaral. E depois, discutiremos sobre onde está a matemática.

Logo em seguida nos propomos a assistir ao vídeo "Matemática é..." (Matemática humanista).
Conversaremos sobre o papel do educador na visão de José Moran. E para finalizar, apresentaremos uma proposta de gamificação para a sala de aula.
A gamificação na sala de aula, se inicia com a escolha dos avatares de cada cursista. Em seguida, todos se posicionam na malha ou na plataforma de jogo. (Impressão em banner)

A partir desse momento, serão apresentados diferentes desafios aos cursistas. Após a finalização de cada um, aqueles que finalizarem com êxito o que foi solicitado no desafio, marcam pontuação no banner. Ao final do encontro, é possível, ver a pontuação dos participantes e premia-los conforme critérios estabelecidos.
Após a premiação dos vencedores, os cursistas deverão confeccionar as suas caixas de jogos. E serão premiados com os arquivos de jogos preparados para a formação.
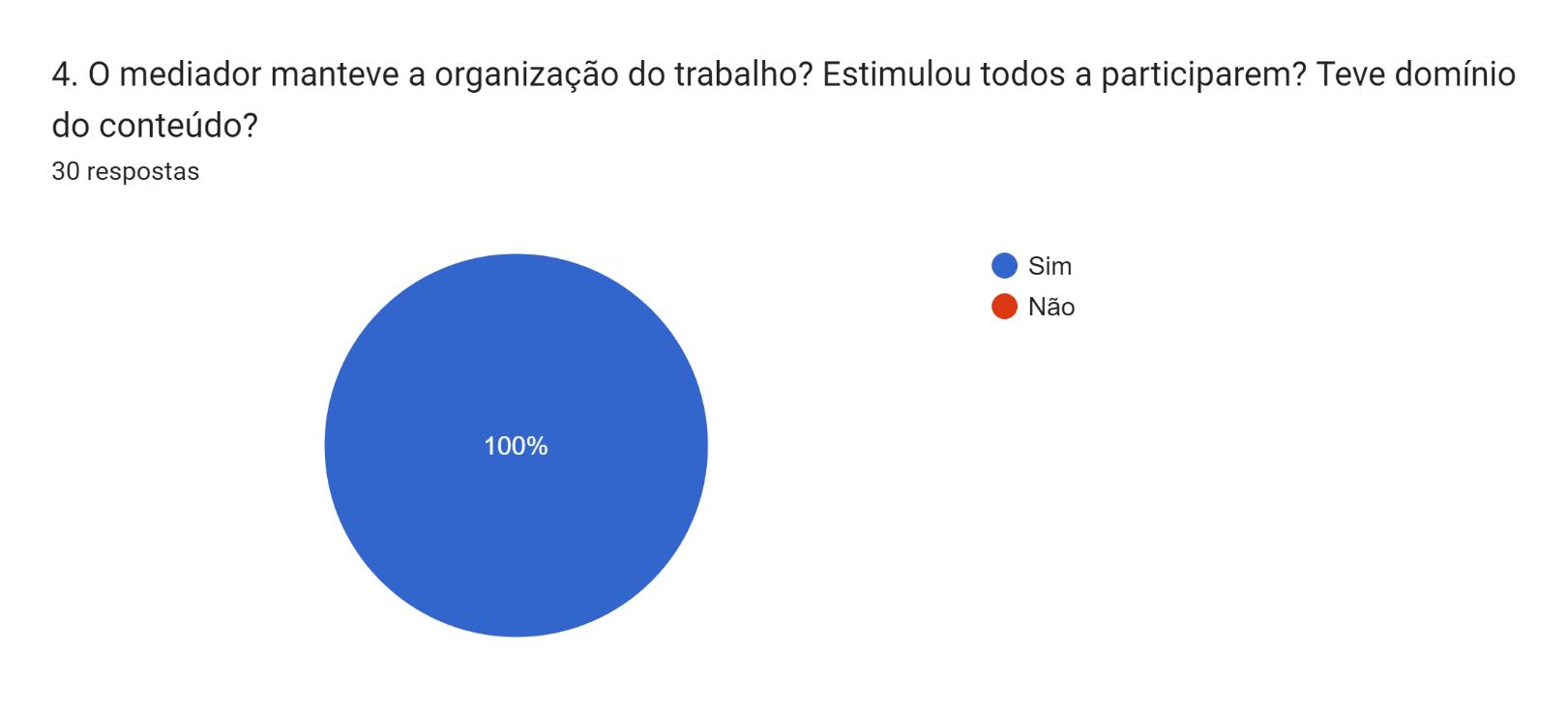
Ao final do encontro os cursistas deverão avalia-lo por meio de formulário on-line. (Q.R)
Ao final do encontro, espera se que os cursistas, tenham refletido sobre a importância de naturalizar a matemática. O objetivo principal é torná-la acessível a todos os estudantes.
Acreditamos que com a mudança de postura do professor, possamos incentivá-los a produzir aulas cada vez mais criativas e dinâmicas e assim contribuir para a melhorar os índices de proficiência em Matemática na rede.

Moran, J. M. (2012). Contribuições para uma pedagogia da educação online. In: M. Silva, Educação online: teorias, práticas, legislação, formação corporativa (pp. 40-52). São Paulo, Brasil: Paulinas. Schlemmer, Eliane. "Games e Gamificação: uma alternativa aos modelos de EaD." RIED. Revista Iberoamericana de Educación a Distancia (2016).





Criação de jogos Mais jogos
Práticas e materiais pedagógicos
Medidas
As 4 operações
Matemática educação infantil
Como criar jogos
Matemática lúdica na educação infantil Mais oficinas como essa
Como construir jogos matemáticos
Criação de jogos on line e concreto
Construção de jogos
Construção de jogos e trabalhar com o canva
Repetir oficinas de matemática
O uso de aplicativos com tutorial. Jogos online e jogos concretos jogos
Mais práticas!!!
Jogos concretos
Aplicativos para criar jogos.
Tidos possíveis
Como criar jogos online
Criar jogos no tablet. Aprender a manusear
Oficinas de matemática do 6° ano ao 9°
Continuação da oficina




No momento em que você traduz a naturalidade da matemática como uma condição de estar no mundo... ...Você democratiza a possibilidade da naturalidade da matemática, e isso é cidadania.
 Paulo Freire
Paulo Freire
Considerações iniciais Ensinar matemática pela resolução de problemas é uma forma eficaz de aprendizagem. No entanto, é preciso romper com o tradicional esquema de apresentação do conteúdo pelo professor, com apresentação de modelos e regras. seguido de uma série de exercícios repetitivos e pouco desafiadores. Novas estratégias de ensino podem ser pensadas. É importante, considerar o contexto em que estamos inseridos. Quais são os interesses dos estudantes? Que linguagem é mais atrativa para eles? Certamente, as crianças e o adolescentes de hoje, conhecem a linguagem da gamificação. Pensando nisso propomos uma atividade diferente para sua prática.

Desenvolvimento
Partindo do pressuposto de que a prática pedagógica, muitas vezes se fundamenta da prática pessoal de aprendizagem, entendemos que é importante nos ouvir. Propor uma reflexão sobre as experiências pessoais de ensino e de aprendizagem da Matemática. Apreciaremos a imagem da obra "O Porto" de Tarsila do Amaral. E depois, discutiremos sobre onde está a matemática.

Logo em seguida nos propomos a assistir ao vídeo "Matemática é..." (Matemática humanista).
Conversaremos sobre o papel do educador na visão de José Moran. E para finalizar, apresentaremos uma proposta de gamificação para a sala de aula.
A gamificação na sala de aula, se inicia com a escolha dos avatares de cada cursista. Em seguida, todos se posicionam na malha ou na plataforma de jogo. (Impressão em banner)

A partir desse momento, serão apresentados diferentes desafios aos cursistas. Após a finalização de cada um, aqueles que finalizarem com êxito o que foi solicitado no desafio, marcam pontuação no banner. Ao final do encontro, é possível, ver a pontuação dos participantes e premia-los conforme critérios estabelecidos.
Após a premiação dos vencedores, os cursistas deverão confeccionar as suas caixas de jogos. E serão premiados com os arquivos de jogos preparados para a formação.
Ao final do encontro os cursistas deverão avalia-lo por meio de formulário on-line. (Q.R)
Ao final do encontro, espera se que os cursistas, tenham refletido sobre a importância de naturalizar a matemática. O objetivo principal é torná-la acessível a todos os estudantes.
Acreditamos que com a mudança de postura do professor, possamos incentivá-los a produzir aulas cada vez mais criativas e dinâmicas e assim contribuir para a melhorar os índices de proficiência em Matemática na rede.

Moran, J. M. (2012). Contribuições para uma pedagogia da educação online. In: M. Silva, Educação online: teorias, práticas, legislação, formação corporativa (pp. 40-52). São Paulo, Brasil: Paulinas. Schlemmer, Eliane. "Games e Gamificação: uma alternativa aos modelos de EaD." RIED. Revista Iberoamericana de Educación a Distancia (2016).













Obra da fase chamada Neo Pau


O Porto
de paisagens interioranas de fazenda e natureza, características da fase de 1924-1928.
Informações sobre a obra: Nome: O Porto Técnica: óleo sobre tela Tamanho original: 70cm x 100cm Localização: Localização: Banco Central do Brasil, Brasília, DF Ano: 1953 Artista: Tarsila do Amaral






“O papel do educador é mobilizar o desejo de aprender, para que o aluno se sinta sempre com vontade de conhecer mais” (MORAN, 2012, p. 33).







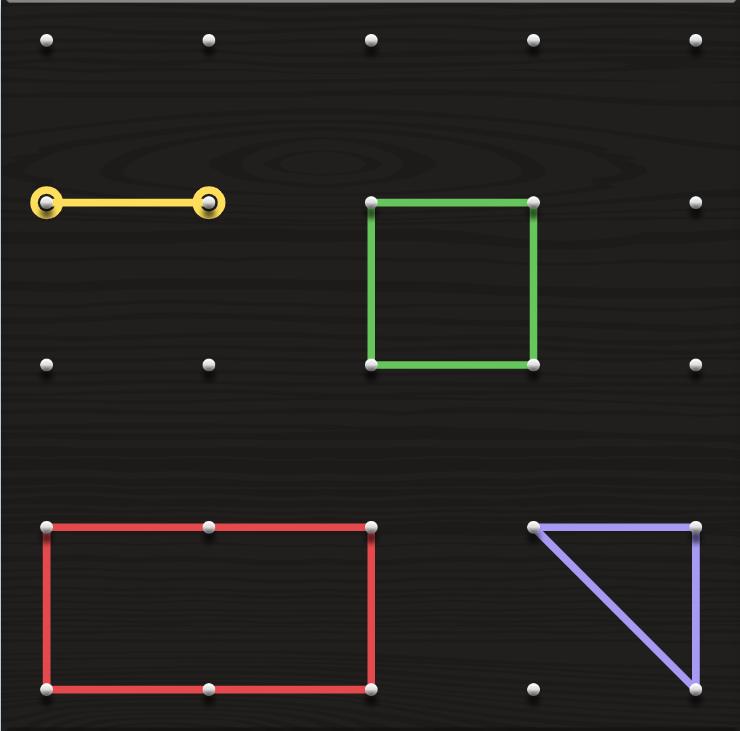















Submeter-se a um processo de gamificação não significa necessariamente participar de um jogo, mas sim apropriar-se de seus aspectos mais eficientes (estética, mecânicas e dinâmicas) para desfrutar dos benefícios que costumam ser obtidos com eles (SCHLEMMER, 2016)


O planejamento fechado e engessado e o uso da criatividade desorganizada podem implicar em improvisação, que pode fazer com que o docente perca o foco e deixe de potencializar sua prática. MORAN, 2012.



















































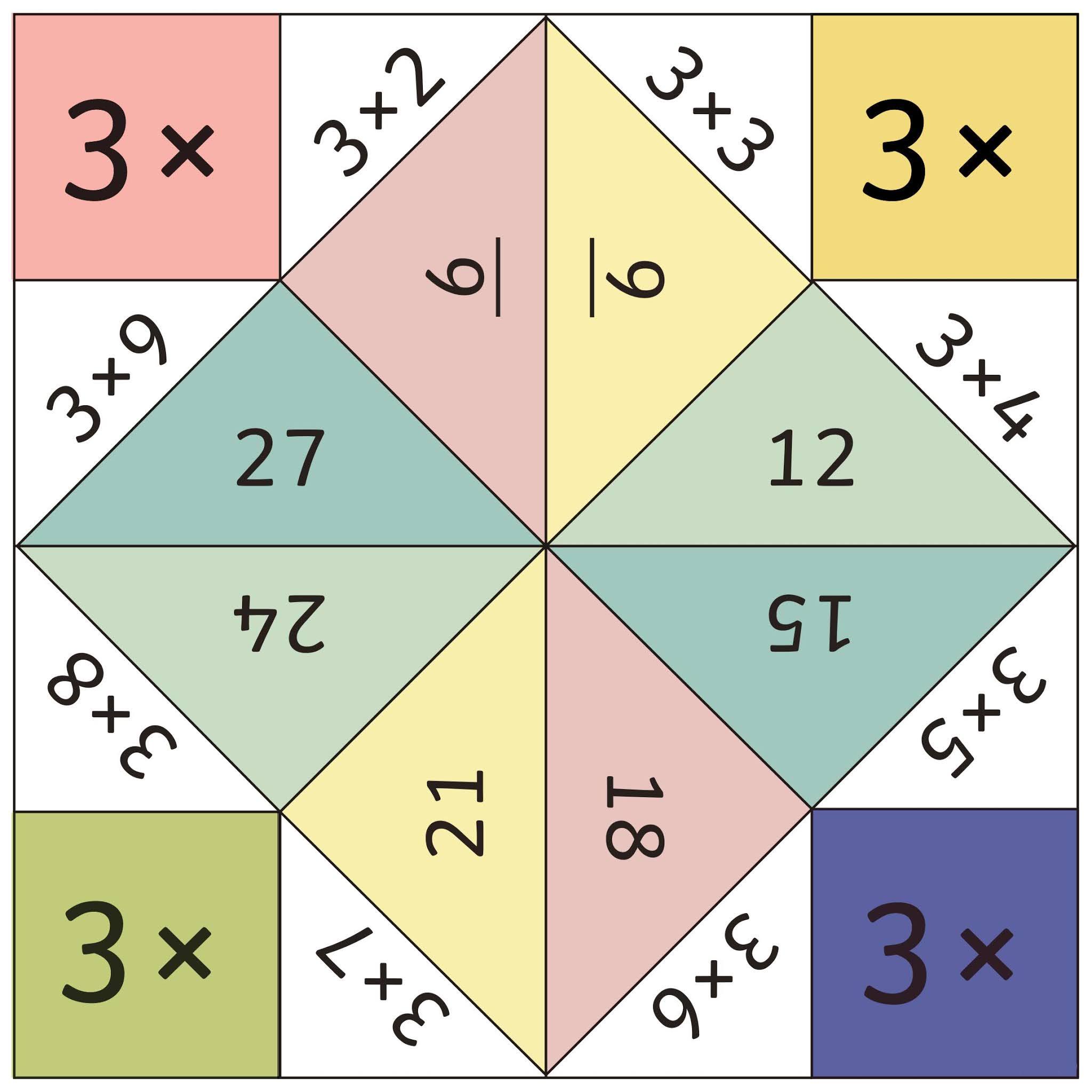

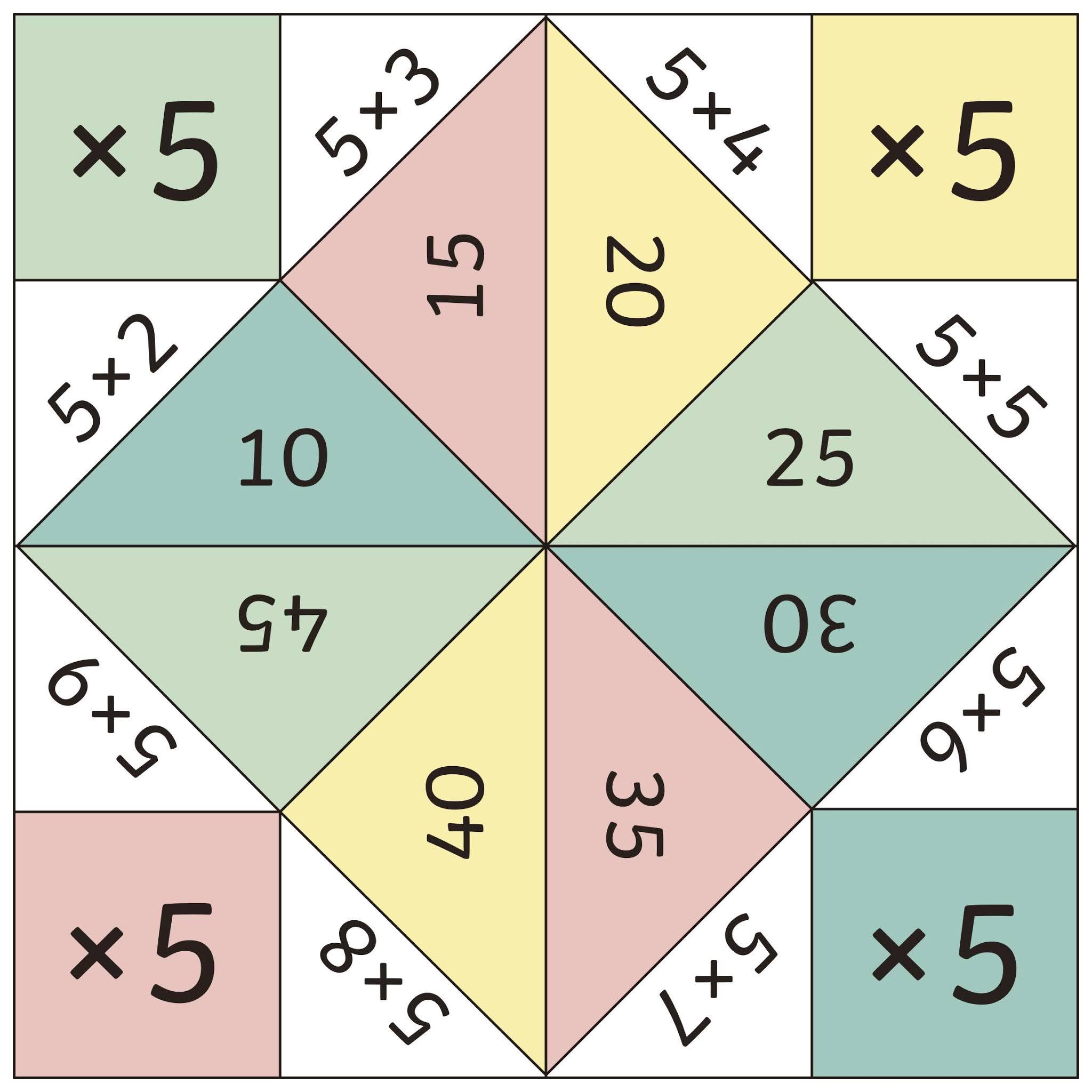


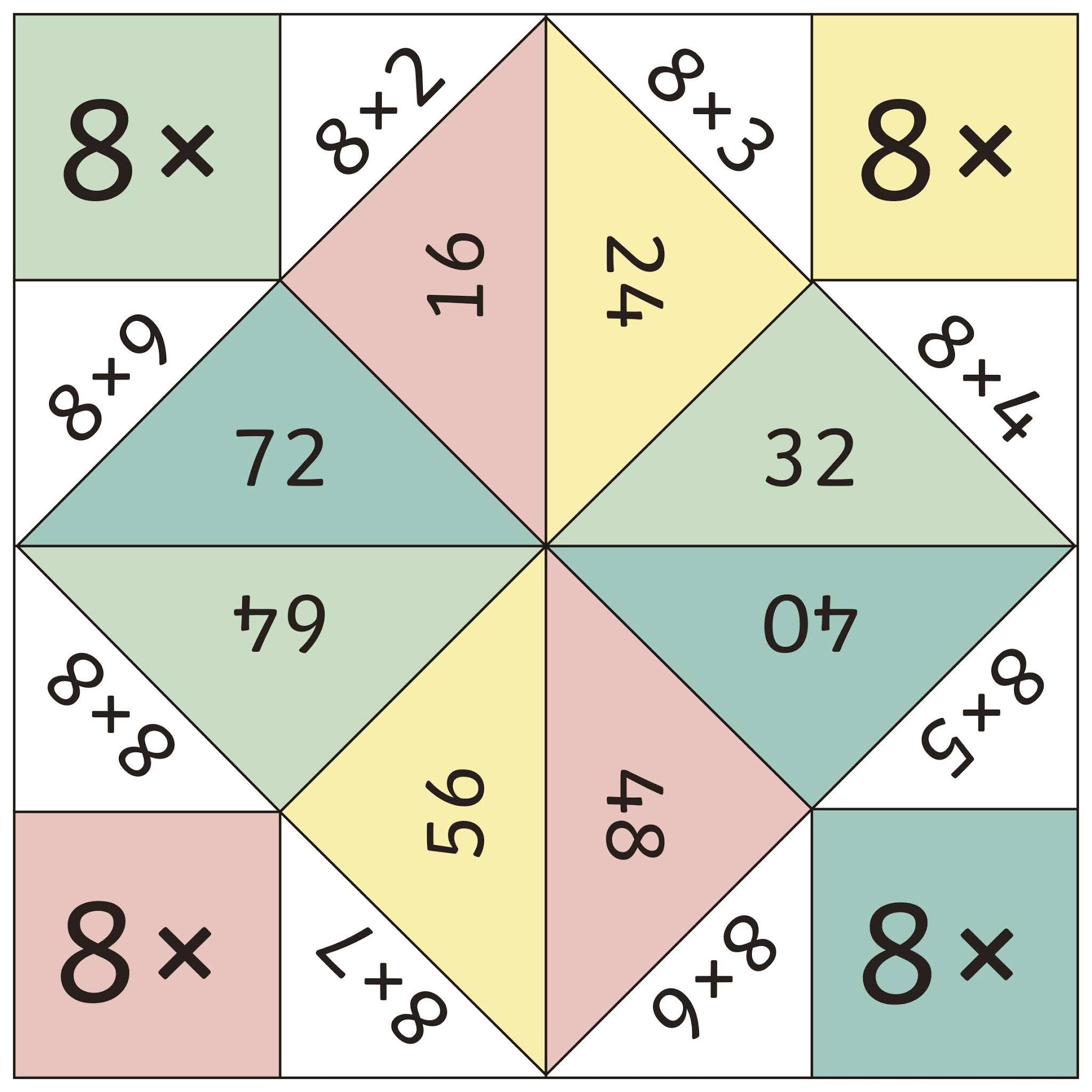

Habilidades: Ler e interpretar situações-problema que envolvam as operações fundamentais.
Construir gradativamente as representações de um número fracionário e decimal. (moedas)
Especificação: 06 cartelas/ 01 dado/20 marcadores dinheirinho (cédulas e moedas).
Número de jogadores: 07
Procedimento: Distribuir uma cartela para cada jogador e escolher uma criança para ser o banqueiro. Os jogadores, cada um na sua vez, deverão jogar o dado e receber do banqueiro a quantia sorteada. Caso esta quantia seja suficiente para comprar um ou mais produtos(s) e os valor(es) do(s) mesmo(s). O banqueiro, fazendo uso da calculadora, deverá marcar (os) produto(s) de sua cartela, o jogador deverá comunicar a todos os participantes qual é o(s) produtos e o(s) valores d(os) mesmo(s). O banqueiro, fazendo uso da calculadora, deverá marcar o(s) produto(s) comprado(s). Caso a quantia sorteada não seja suficiente para a compra, o jogador guarda o dinheiro e espera a próxima rodada para efetuar esse procedimento. Ganhará o jogo aquele que conseguir comprar todos os produtos de sua cartela primeiro.

























































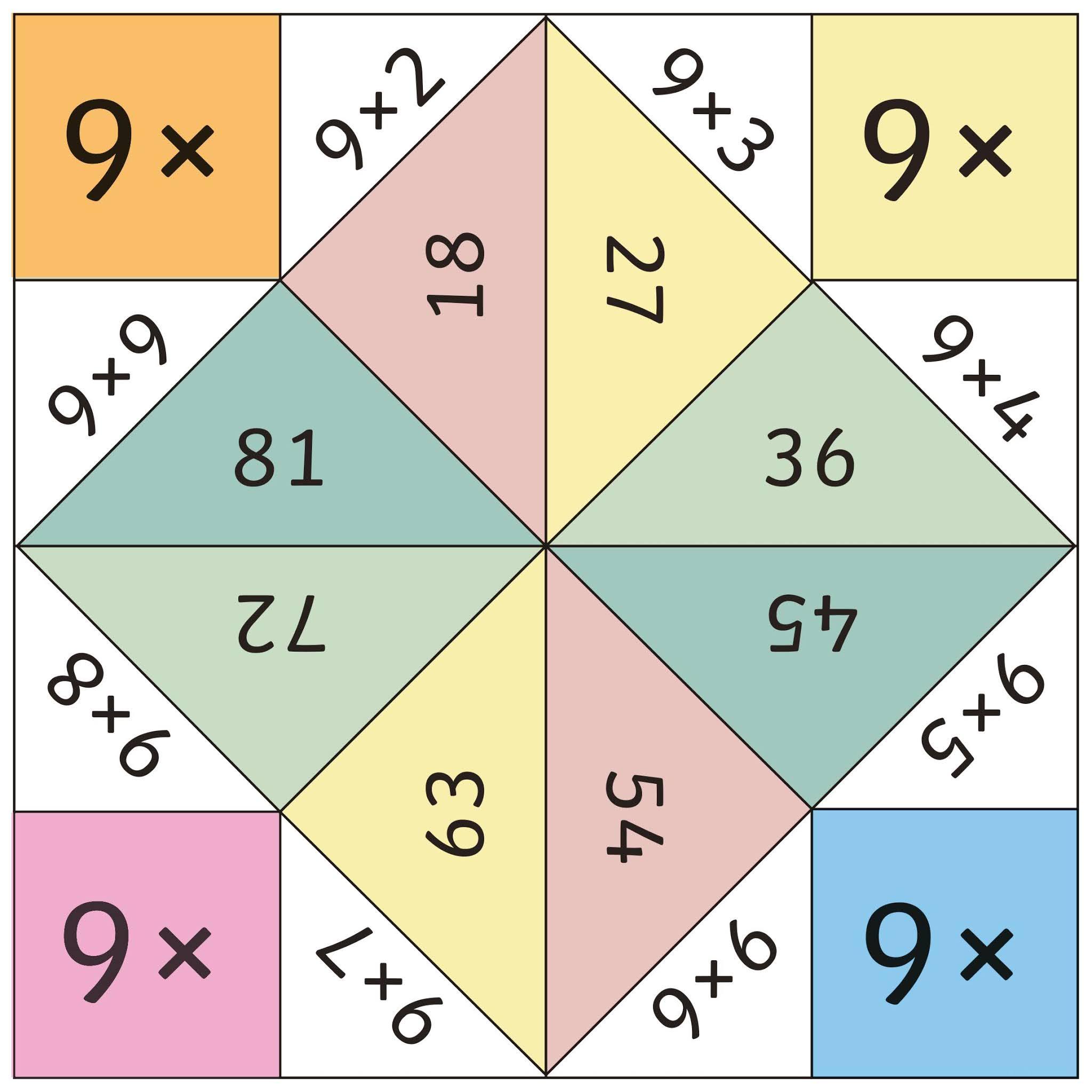
Tamanho: 18x8 cm
90 peças (com as operações)
Tamanho 3x3 cm.
Utilização:

Nº de jogadores: 2 a 4
Procedimento: Coloca se o tabuleiro sobre a mesa para que todos os jogadores tenham uma visão global dos resultados. As demais peças deverão ficar com um jogador que não esteja participando do jogo, para que o mesmo diga em voz alta cada uma das operações. À medida que cada peça é "cantada", os jogadores deverão encontrar no tabuleiro o resultado correspondente, colocando o dedo sobre o mesmo.
O primeiro a fazer isto recebe a peça "cantada", se o resultado estiver errado, o jogador deverá devolver uma peça, caso ainda não tenha nenhuma fica devendo. Vence quem conseguir o maior número de peças.
Possibilita:
Desenvolvimento da percepção, atenção e memória. fixar os fatos fundamentais da multiplicação.
OBS.: Origem do nome deste jogo "LINCE", mamífero carnívoro, ao qual os antigos atribuíam o poder de ver através das paredes. Portanto diz-se que uma pessoa que possui visão aguçadíssima, tem olhos de "lince"


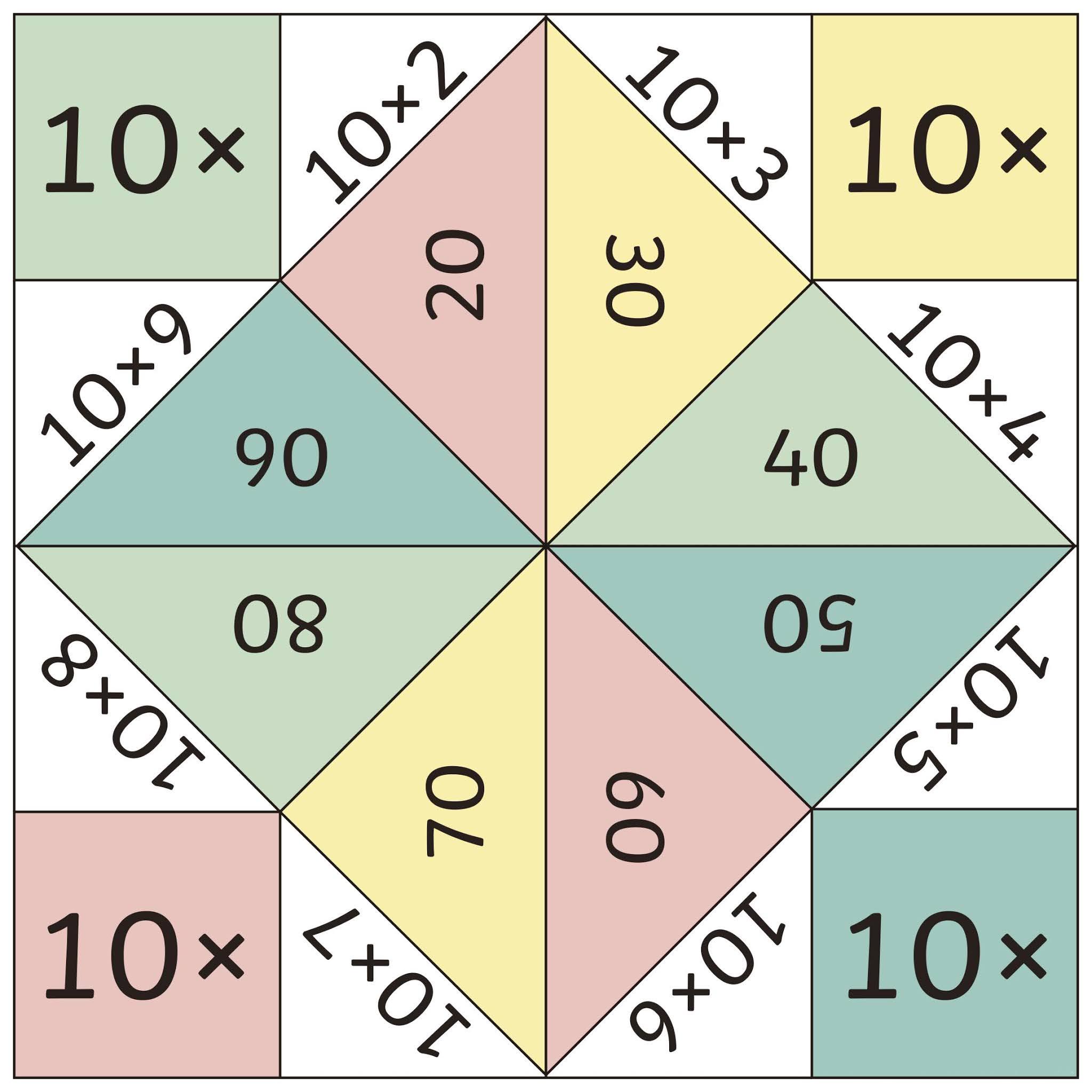
Tamanho: 18x8 cm
90 peças (com as operações)
Tamanho 3x3 cm.
Utilização:

Nº de jogadores: 2 a 4
Procedimento: Coloca se o tabuleiro sobre a mesa para que todos os jogadores tenham uma visão global dos resultados. As demais peças deverão ficar com um jogador que não esteja participando do jogo, para que o mesmo diga em voz alta cada uma das operações. À medida que cada peça é "cantada", os jogadores deverão encontrar no tabuleiro o resultado correspondente, colocando o dedo sobre o mesmo.
O primeiro a fazer isto recebe a peça "cantada", se o resultado estiver errado, o jogador deverá devolver uma peça, caso ainda não tenha nenhuma fica devendo. Vence quem conseguir o maior número de peças.
Possibilita:
Desenvolvimento da percepção, atenção e memória. fixar os fatos fundamentais da multiplicação.
OBS.: Origem do nome deste jogo "LINCE", mamífero carnívoro, ao qual os antigos atribuíam o poder de ver através das paredes. Portanto diz-se que uma pessoa que possui visão aguçadíssima, tem olhos de "lince"




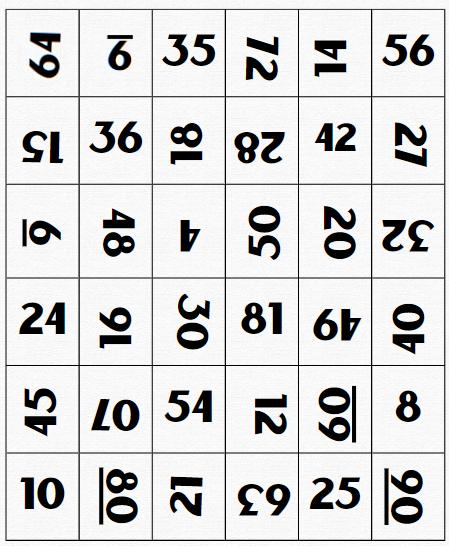
Tabuleiro quadriculado e numerado de 1 a 100. (100 quadrados), Fichas ou sementes de cores diferentes. 3 ou 4 dados Conteúdo:
Cáculo mental, soma de dados, contagem, comparação de quantidades.


No mesmo tabuleiro, um de cada vez joga os dados. O jogador poderá realizar qualquer uma das quatro operações, calculando as quantidades e marcando no tabuleiro com sua ficha ou semente. Cada jogador poderá colocar quantas fichas conseguir calcular usando os números dos tirados no dado. Exemplo: O jogador tirou nos dados os números 2, 5 e 6.
por diante...
O vencedor é o que primeiro preencher as 51 casas.
Para crianças menores pode ser jogado apenas usando as operações de adição e subtração e dimunuindo quantidades.
É importante que o jogo seja desenvolvido gradativamente.
Número de participantes: Individual. Como jogar: As peças devem ser distribuídas nos espaços vazios do tabuleiro, de forma que nenhum número antecessor e/ou sucessor fique vizinho na lateral ou na diagonal.

Construir o significado do número natural, utilizando diferentes estratégias para qualificar elementos. Analisar e interpretar situações problema compreendendo alguns significados das operações, em especial, da adição e subtração; Desenvolver a atenção e a concentração.
1 régua com 14 marcações redondas para encaixar a bolinha, em duas cores diferentes e uma divisão no centro; 2 marcadores; 1 dado.

Cada participante ficará de um lado do tabuleiro do vai-vem.
Um único marcador será colocado no centro. Sorteia-se no par ou ímpar quem dará início ao jogo.
Cada um, na sua vez lançará o dado e caminhará com o marcador para o seu lado do vai-vem, contando o número de casas que o dado indicar. A contagem sempre deverá ser feita a partir da casa que está à frente daquela que o marcador parou.
Vencerá o jogo aquele que conseguir chegar à última casa do seu lado do vai e vem, o que deverá acontecer somente se o participante tirar o dado o número exato de casas que faltam para tal. Caso falte apenas para chegar ao final e o participante tirar o número 5 no dado, por exemplo, este deverá fazer a contagem das 2 casas, passando a vez ao próximo participante.




